三角函数的定义与三角变换典型例题分析及针对训练

合集下载

三角函数和解三角形典型题及常见题汇总

三角函数和解三角形典型题及常见题汇总三角函数是数学中重要的分支之一，它与解三角形问题密切相关。

本文将对三角函数的基本概念进行介绍，并通过解典型题和常见题的方式，帮助读者更好地理解和应用三角函数。

一、三角函数的基本概念1. 正弦函数（sine function）：对于一个角α，它的正弦值（sinα）等于其对边与斜边的比值，可以表示为sinα = 对边/斜边。

2. 余弦函数（cosine function）：对于一个角α，它的余弦值（cosα）等于其邻边与斜边的比值，可以表示为cosα = 邻边/斜边。

3. 正切函数（tangent function）：对于一个角α，它的正切值（tanα）等于其对边与邻边的比值，可以表示为tanα = 对边/邻边。

二、解三角形典型题1. 已知两边及夹角（SSA）：当已知一个三角形的两边和夹角时，可以利用正弦定理求解第三边的长度。

具体步骤是：a) 使用正弦定理：sinA/a = sinB/b = sinC/c，其中A、B、C分别表示三个角的度数，a、b、c分别表示这些角所对应的边长。

b) 带入已知数据，求解未知边的长度。

2. 已知两个边及对应角（SSS）：当已知一个三角形的两个边及其夹角时，可以利用余弦定理求解第三边的长度。

具体步骤是：a) 使用余弦定理：c^2 = a^2 + b^2 - 2ab*cosC，其中a、b、c分别表示三角形的边长，C表示对应的角度。

b) 带入已知数据，求解未知边的长度。

三、常见题汇总1. 解三角形：已知三个角或两个角及一边的情况下，求解三角形的边长和角度。

2. 三角函数的图像与性质：通过画图并观察三角函数的周期、对称轴、最大最小值等性质。

3. 三角方程的求解：根据给定的三角方程，使用三角函数的性质和恒等式进行推导和求解。

4. 三角函数的应用：在物理、工程等领域中，通过三角函数可以描述和求解各种周期性现象，如电流的变化、振动的周期等。

结束语通过学习三角函数和解三角形的典型题目，我们能够更好地理解和运用三角函数的概念和公式。

三角函数与解三角形题型归纳及习题含详解

2 简而言之即“奇变偶不变，符号看象限”. 题型归纳及思路提示
题型 53 终边相同的角的集合的表示与区别思路提示
（1）终边相同的角的集合的表示与识别可用列举归纳法和双向等差数列的方法解决.
（2）注意正角、第一象限角和锐角的联系与区别，正角可以是任一象限角，也可以是坐标轴角；锐角是正角，也是第一象限角，第一象限角不包含坐标
4. 熟练运用同角三角函数函数关系式和诱导公式进行三角函数式的化简、求值
和简单恒等式的证明.
命题趋势探究
1.一般以选择题或填空题的形式进行考查.
2.角的概念考查多结合函数的基础知识.
3.利用同角三角函数关系式和诱导公式进行三角函数式的化简、求值是重要考点. 知识点精讲一、基本概念
正角---逆时针旋转而成的角；（1）任意角负角---顺时针旋转而成的角；
二、任意角的三角函数 1.定义已知角终边上的任一点 P(x, y) （非原点 O ），则 P 到原点 O 的距离
r OP x2 y2 0 . sin y , cos x , tan y .
r
r
x
此定义是解直三角形内锐角三角函数的推广.类比，对 y ，邻 x ，斜 r ，如图 4-2 所示.
的终边逆时针旋转整数圈，终边位置不变.
注：弧度或 rad 可省略（5）两制互化：一周角= 3600 2 r 2 （弧度），即 1800 .
r
1（弧度）
180
0
57.30
57018
故在进行两制互化时，只需记忆 1800 ，10 两个换算单位即可：如： 180
5 5 1800 1500 ； 360 36 .
C. 0, ，是第一、二象限角

三角函数典型例题及分析

第12讲三角函数高考试题中的三角函数题相对比较传统，难度较低，位置靠前，重点突出。

因此，在复习过程中既要注重三角知识的基础性，突出三角函数的图象、周期性、单调性、奇偶性、对称性等性质。

以及化简、求值和最值等重点内容的复习，又要注重三角知识的工具性，突出三角与代数、几何、向量的综合联系，以及三角知识的应用意识。

一、知识整合1．熟练掌握三角变换的所有公式，理解每个公式的意义，应用特点，常规使用方法等；熟悉三角变换常用的方法——化弦法，降幂法，角的变换法等；并能应用这些方法进行三角函数式的求值、化简、证明；掌握三角变换公式在三角形中应用的特点，并能结合三角形的公式解决一些实际问题．2．熟练掌握正弦函数、余弦函数、正切函数、余切函数的性质，并能用它研究复合函数的性质；熟练掌握正弦函数、余弦函数、正切函数、余切函数图象的形状、特点，并会用五点画出函数sin()y A x ωϕ=+的图象；理解图象平移变换、伸缩变换的意义，并会用这两种变换研究函数图象的变化．二、高考考点分析2004年各地高考中本部分所占分值在17～22分，主要以选择题和解答题的形式出现。

主要考察内容按综合难度分，我认为有以下几个层次：第一层次：通过诱导公式和倍角公式的简单运用，解决有关三角函数基本性质的问题。

如判断符号、求值、求周期、判断奇偶性等。

第二层次：三角函数公式变形中的某些常用技巧的运用。

如辅助角公式、平方公式逆用、切弦互化等。

第三层次：充分利用三角函数作为一种特殊函数的图象及周期性、奇偶性、单调性、有界性等特殊性质，解决较复杂的函数问题。

如分段函数值，求复合函数值域等。

三、方法技巧1.三角函数恒等变形的基本策略。

（1）常值代换：特别是用“1”的代换，如1=cos 2θ+sin 2θ=tanx ·cotx=tan45°等。

（2）项的分拆与角的配凑。

如分拆项：sin 2x+2cos 2x=(sin 2x+cos 2x)+cos 2x=1+cos 2x ；配凑角：α=（α+β）－β，β=2βα+－2βα-等。

专题三：三角函数与三角变换(附参考答案)

专题三：三角函数与三角变换（附参考答案）1.高考要求解读1.1考纲要求：1.1.1三角函数 1.任意角、弧度制（1）了解任意角的概念和弧度制的概念（2）能进行弧度与角度的互化。

2.三角函数（1）理解任意角三角函数（正弦、余弦、正切）的定义。

（2）能利用单位圆中的三角函数线推导出απαπ±±,2的正弦、余弦、正切的诱导公式，能画出x y x y x y tan ,cos ,sin ===的图像，了解三角函数的周期性。

（3）正确理解正弦函数、余弦函数在[]π2,0上的性质（如单调性、最大值和最小值、图像与x 轴的交点等），理解正切函数在⎪⎭⎫⎝⎛-2,2ππ内的单调性。

（4）理解同角三角函数的基本关系式：.tan cos sin ,1cos sin 22x xxx x ==+ （5）了解函数)sin(ϕω+=x A y 的物理意义；能画出函数)sin(ϕω+=x A y 的图像，了解参数ϕω,,A 对函数图像变化的影响。

（6）会用三角函数解决一些简单实际问题，体会三角函数是描述周期变化现象的重要函数模型。

1.1.2三角恒等变换1.两角和与差的三角函数公式（1）会用向量的数量出两角差的余弦公式。

（2）会用两角差的余弦公式推导出两角差的正弦、正切公式。

（3）会用两角差的余弦公式推导出两角和的正弦、余弦、正切公式和二倍角的正弦、余弦、正切公式，了解他们的内在联系。

2.简单的三角恒等变换能运用上述公式进惊醒简单的恒等变换（包括导出积化和差、和差化积、半角公式，但不要求记忆）。

1.2考点解读1.2.1考情分析三角函数是高考的考查热点，命题的一般模式为一个选择题（或填空题）和一个解答题，其中选择题（填空题）一般多为基础题，解答题为中档题。

解答题多为三角函数与三角变换的综合问题或三角函数与其他知识的教会问题。

近年宁夏高考题，命题从三角函数与解三角形结合的问题出发命题的趋势明显。

高考中三角函数所占分值大约在10~14分之间。

2020年高考数学(文)二轮专项复习专题03 三角函数与解三角形含答案

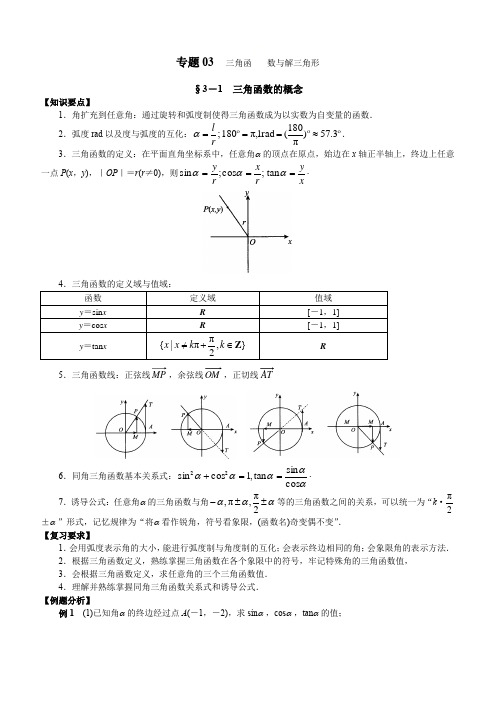
专题03 三角函数与解三角形§3－1 三角函数的概念【知识要点】1．角扩充到任意角：通过旋转和弧度制使得三角函数成为以实数为自变量的函数．2．弧度rad 以及度与弧度的互化：οοο3.57)π180(rad 1,π180;≈===r l α． 3．三角函数的定义：在平面直角坐标系中，任意角α 的顶点在原点，始边在x 轴正半轴上，终边上任意一点P (x ，y )，｜OP ｜＝r (r ≠0)，则;cos ;sin r x r y ==αα⋅=xy αtan5．三角函数线：正弦线，余弦线OM ，正切线6．同角三角函数基本关系式：⋅==+αααααcos sin tan ,1cos sin 22 7．诱导公式：任意角α 的三角函数与角ααα±±-2π,π,等的三角函数之间的关系，可以统一为“k ·2π±α ”形式，记忆规律为“将α 看作锐角，符号看象限，(函数名)奇变偶不变”．【复习要求】1．会用弧度表示角的大小，能进行弧度制与角度制的互化；会表示终边相同的角；会象限角的表示方法． 2．根据三角函数定义，熟练掌握三角函数在各个象限中的符号，牢记特殊角的三角函数值， 3．会根据三角函数定义，求任意角的三个三角函数值． 4．理解并熟练掌握同角三角函数关系式和诱导公式．【例题分析】例1 (1)已知角α 的终边经过点A (－1，－2)，求sin α ，cos α ，tan α 的值；(2)设角α 的终边上一点),3(y P -，且1312sin =α，求y 的值和tan α ．解：(1)5||==OA r ，所以.2tan ,55cos ,55252sin ==-==-=-==x y r x r y ααα(2),13123sin ,3||22=+=+==y y y OP r α 得⎪⎩⎪⎨⎧=+>13123022y y y ，解得.3236tan ,6-=-===x y y α 【评析】利用三角函数的定义求某一角三角函数值应熟练掌握，同时应关注其中变量的符号．例2 (1)判断下列各式的符号：①sin330°cos(－260°)tan225° ②sin(－3)cos4 (2)已知cos θ ＜0且tan θ ＜0，那么角θ 是( ) A ．第一象限角 B ．第二象限角 C ．第三象限角 D ．第四象限角 (3)已知α 是第二象限角，求角αα2,2的终边所处的位置．解：如图3－1－1，图3－1－2(1)①330°是第四象限角，sin330°＜0；－260°是第二象限角，cos(－260°)＜0；225°是第三象限角，tan225°＞0；所以sin330°cos(－260°)tan225°＞0.②－3是第三象限角，sin(－3)＜0；5是第四象限角，cos5＞0，所以sin(－3)cos5＜0或：－3≈－3×57.3°＝－171.9°，为第三象限角；5≈5×57.3°＝286.5°，是第四象限角【评析】角的终边所处的象限可以通过在坐标系中逆时针、顺时针两个方向旋转进行判断，图3－1－1，图3－1－2两个坐标系应予以重视．(2)cos θ ＜0，所以角θ 终边在第二或第三象限或在x 轴负半轴上tan θ ＜0，所以角θ 终边在第二或第四象限中，所以角θ 终边在第二象限中，选B.【评析】角的终边在各个象限中时角的函数值的符号应熟练掌握，(3)分析：容易误认为2α是第一象限角，其错误原因为认为第二象限角的范围是),π,2π(α 是第二象限角，所以2k π＋2π＜α ＜2k π＋π，(k ∈Z )，所以,2ππ2π4ππ+<<+k k )(Z ∈k 如下图3－1－3，可得2α是第一象限或第三象限角，又4k π＋π＜2α ＜4k π＋2π，2α 是第三象限或第四象限角或终边落在y 轴负半轴的角．【评析】处理角的象限问题常用方法(1)利用旋转成角，结合图3－1－1，图3－1－2，从角度制和弧度制两个角度处理； (2)遇到弧度制问题也可以由)π180(rad 1=°≈57.3°化为角度处理； (3)在考虑角的终边位置时，应注意考虑终边在坐标轴上的情况． (4)对于象限角和轴上角的表示方法应很熟练．如第一象限角：)(,2ππ2π2Z ∈+<<k k k α，注意防止2π0<<α的错误写法．例3 (1)已知tan α ＝3，且α 为第三象限角，求sin α ，cos α 的值； (2)已知31cos -=α，求sin α ＋tan α 的值；(3)已知tan α ＝－2，求值：①ααααcos sin cos sin 2-+；②sin 2α ＋sin α cos α ．解：(1)因为α 为第三象限角，所以sin α ＜0，cos α ＜0⎪⎩⎪⎨⎧=+=1cos sin 3cos sin 22αααα，得到.1010cos 10103sin ⎪⎪⎩⎪⎪⎨⎧-=-=αα (2)因为031cos <-=α，且不等于－1，所以α 为第二或第三象限角，当α 为第二象限角时，sin α ＞0，,22cos sin tan ,322cos 1sin 2-===-=ααααα 所以⋅-=+324tan sin αα 当α 为第三象限角时，sin α ＜0，,22cos sin tan ,322cos 1sin 2==-=--=ααααα 所以⋅=+324tan sin αα综上所述：当α 为第二象限角时，324tan sin -=+αα，当α 为第三象限角时，⋅=+324tan sin αα 【评析】已知一个角的某一个三角函数值，求其余的三角函数值的步骤：(1)先定所给角的范围：根据所给角的函数值的符号进行判断(2)利用同角三角函数的基本关系式，求其余的三角函数值(注意所求函数值的符号) (3)当角的范围不确定时，应对角的范围进行分类讨论(3)(法一)：因为tan α ＝－2，所以.cos 2sin ,2cos sin αααα-=-= ①原式1cos 3cos 3cos cos 2cos cos 4=--=--+-=αααααα，②原式＝(－2cos α )2＋(－2cos α )cos α ＝2cos 2α ，因为⎩⎨⎧=+-=1cos sin cos 2sin 22αααα，得到51cos 2=α，所以⋅=+52cos sin sin 2ααα (法二)：①原式,112141tan 1tan 21cos sin 1cos sin 2=--+-=-+=-+=αααααα②原式⋅=+-=++=++=5214241tan tan tan cos sin cos sin sin 22222αααααααα 【评析】已知一个角的正切值，求含正弦、余弦的齐次式的值：(1)可以利用αααcos sin tan =将切化弦，使得问题得以解决； (2)1的灵活运用，也可以利用sin 2α ＋cos 2α ＝1，αααcos sin tan =，将弦化为切．例4 求值：(1)tan2010°＝______； (2))6π19sin(-＝______； (3)⋅+---+-)2πcos()π3sin()2π3sin()πcos()π2sin(ααααα解：(1)tan2010°＝tan(1800°＋210°)＝tan210°＝tan(180°＋30°)＝3330tan =ο (2)216πsin )6ππsin()6ππ3sin(619πsin )6π19sin(==+-=+-=-=-或:216πsin )6ππsin()6ππ3sin()6π19sin(==--=--=-【评析】“将α 看做锐角，符号看象限，(函数名)奇变偶不变”，6π2π26ππ-⨯-=--，可以看出是2π的－2倍(偶数倍)，借助图3－1－2看出6ππ--为第二象限角，正弦值为正．(3)原式)2πcos()πsin()]2π(πsin[)cos (sin ααααα---+--=⋅⋅⋅⋅-=-=--=αααααααααsin 1sin cos cos sin sin )2πsin(cos ·sin【分析】αα-⨯=-2π32π3，将α 看做锐角，借助图3－1－2看出α-2π3为第三象限角，正弦值为负，2π的3倍(奇数倍)，改变函数名，变为余弦，所以可得ααcos )2π3sin(-=-，同理可得ααsin )2πcos(=+-，所以原式αααααααcsc sin 1sin sin cos )cos (sin -=-=---=⋅⋅⋅.【评析】诱导公式重在理解它的本质规律，对于“将α 看做锐角，符号看象限，(函数名)奇变偶不变”要灵活运用，否则容易陷入公式的包围，给诱导公式的应用带来麻烦．例5 已知角α 的终边经过点)5πsin ,5πcos (-，则α 的值为( ) A ．5π- B ．5π4 C )(,π5πZ ∈+-k k D ．)(,π25π4Z ∈+k k解：因为05πsin ,05πcos >>，所以点)5πsin ,5πcos (-在第二象限中，由三角函数定义得，5πtan 5πcos 5πsin tan -=-==x y α，因为角α 的终边在第二象限，所以)π25π4tan(5π4tan )5ππtan(tan k +==-=α，所以，)(,π25π4Z ∈+=k k α，选D ．例6 化简下列各式：(1)若θ 为第四象限角，化简θθ2sin 1tan - (2)化简θθ2tan 1cos +(3)化简)4πcos(4sin 21--解：(1)原式＝|cos |cos sin |cos |tan cos tan 2θθθθθθθ===，因为θ 为第四象限角，所以cos θ ＞0，原式＝θθθθsin cos cos sin ==⋅，(2)原式＝⋅==+=+=|cos |cos cos 1cos cos sin cos cos cos sin 1cos 222222θθθθθθθθθθθ当θ 为第二、三象限角或终边在x 轴负半轴上时，cos θ ＜0，所以原式1cos cos -=-=θθ，当θ 为第一、四象限角或终边在x 轴正半轴上时，cos θ ＞0，所以原式1cos cos ==θθ.(3)原式|4cos 4sin |)4cos 4(sin 4cos 4sin 212+=+=+=.4弧度属于第三象限角，所以sin4＜0，cos4＜0，所以原式＝－(sin4＋cos4)＝－sin4－cos4．【评析】利用同角三角函数关系式化简的基本原则和方法：(1)函数名称有弦有切：切化弦；(2)分式化简：分式化整式；(3)根式化简：无理化有理(被开方式凑平方)，运用||2x x =，注意对符号的分析讨论；(4)注意公式(sin α ±cos α )2＝1±2sin α cos α ＝1±sin2α 的应用．例7 扇形的周长为定值L ，问它的圆心角θ (0＜θ ＜π)取何值时，扇形的面积S 最大?并求出最大值．解：设扇形的半径为)20(Lr r <<，则周长L ＝r ·θ ＋2r (0＜θ ＜π) 所以44214421)2(2121ππ2,22222222++=++=+==⋅=+=θθθθθθθθθθL L L r r S L r ．因为844244=+⨯≥++θθθθ，当且仅当θθ4=，即θ ＝2∈(0，π)时等号成立．此时16812122L L S =⨯≤，所以，当θ ＝2时，S 的最大值为162L .练习3－1一、选择题1．已知32cos -=α，角α 终边上一点P (－2，t )，则t 的值为( ) A ．5 B ．5± C ．55 D ．55±2．“tan α ＝1”是“Z ∈+=k k ,4ππ2α”的( )A ．充分而不必要条件B ．必要不而充分条件C ．充要条件D ．既不充分也不必要条件3．已知点P (sin α －cos α ，tan α )在第一象限，则在[0，2π]上角α 的取值范围是( )A ．)4π5,π()4π3,2π(Y B ．)4π5,π()2π,4π(YC ．)2π3,4π5()4π3,2π(YD ．)π,4π3()2π,4π(Y4．化简=+οο170cos 10sin 21( ) A ．sin10°＋cos10° B ．sin10°－cos10° C ．cos10°－sin10°D ．－sin10°－cos10°二、填空题5．已知角α ，β 满足关系2π0;<<<βα，则α －β 的取值范围是______． 6．扇形的周长为16，圆心角为2弧度，则扇形的面积为______．7．若2π3π,sin <<=ααm ，则tan(π－α )＝______． 8．已知：2π4π,81cos sin <<=ααα，则cos α －sin α ＝______．三、解答题9．已知tan α ＝－2，且cos(π＋α )＜0，求(1)sin α ＋cos α 的值 (2)θθ2cos sin 22-－的值10．已知21tan =α，求值： (1)ααααcos sin cos 2sin -+； (2)cos 2α －2sin α cos α ．11．化简ααααααααtan 1tan cos sin ]π)1cos[(]π)1sin[()πcos()πsin(2+++++++-⋅k k k k§3－2 三角变换【知识要点】1．两角和与差的正弦、余弦、正切公式sin(α ＋β )＝sin α cos β ＋cos α sin β ；sin(α －β )＝sin α cos β －cos α sin β ； cos(α ＋β )＝cos α cos β －sin α sin β ；cos(α －β )＝cos α cos β ＋sin α sin β ；⋅+-=--+=+βαβαβαβαβαβαtan tan 1tan tan )tan(;tan tan 1tan tan )tan(2．正弦、余弦、正切的二倍角公式sin2α ＝2sin α cos α ：cos2α ＝cos 2α －sin 2α ＝1－2sin 2α ＝2cos 2α －1；⋅-=ααα2tan 1tan 22tan 【复习要求】1．牢记两角和、差、倍的正弦、余弦、正切公式，并熟练应用； 2．掌握三角变换的通法和一般规律； 3．熟练掌握三角函数求值问题．【例题分析】例1 (1)求值sin75°＝______；(2)设54sin ),π,2π(=∈αα，则=+)4πcos(α______； (3)已知角2α的终边经过点(－1，－2)，则)4πtan(+α的值为______；(4)求值=+-οο15tan 115tan 1______．解：(1)=︒︒+︒︒=︒+︒=︒30sin 45cos 30cos 45sin )3045sin(75sin 222322+⨯21⨯426+=． (2)因为53cos ,54sin ),π,2π(-==∈ααα所以， 1027)5453(22sin 22cos 22)4πcos(-=--=-=+ααα(3)由三角函数定义得，342tan 12tan2tan ,22tan2-=-==αααα，所以71tan 1tan 1tan 4πtan 14πtantan )4πtan(-=-+=-+=+ααααα. (4)3330tan )1545tan(15tan 45tan 115tan 45tan 15tan 115tan 1=︒=︒-︒=︒︒+︒-︒=︒+︒-⋅==-=+-=+-3330tan )1545tan(15tan 45tan 115tan 45tan 15tan 115tan 1οοοοοοοοo【评析】两角的和、差、二倍等基本三角公式应该熟练掌握，灵活运用，这是处理三角问题尤其是三角变换的基础和核心．注意αααtan 1tan 1)4πtan(-+=+和αααtan 1tan 1)4πtan(+-=-运用．例2 求值： (1)=-12πsin 12πcos3______； (2)cos43°cos77°＋sin43°cos167°＝______； (3)=++οοο37tan 23tan 337tan 23tan o______．解：(1)原式)12πsin 3πcos 12πcos 3π(sin 2)12πsin 2112πcos 23(2-=-= 24πsin 2)12π3πsin(2==-=.【评析】辅助角公式：,cos ),sin(cos sin 2222ba a xb a x b x a +=++=+ϕϕ⋅+=22sin b a b ϕ应熟练掌握，另外本题还可变形为=-)12πsin 2112πcos 23(2 -12πcos 6π(cos 2.24πcos 2)12π6πcos(2)12πsin 6πsin ==+=(2)分析所给的角有如下关系：77°＋43°＝120°，167°＝90°＋77°，原式＝cos43°cos77°＋sin43°cos(90°＋77°)＝cos43°cos77°－sin43°sin77°＝cos(43°＋77°)＝cos120°＝⋅-21 (3)分析所给的角有如下关系：37°＋23°＝60°，函数名均为正切，而且出现两角正切的和tan a ＋tan β 与两角正切的积tan α tan β ，所有均指向公式⋅-+=+βαβαβαtan tan 1tan tan )tan(∵,337tan 23tan 137tan 23tan )3723tan(60tan =︒︒-︒+︒=+=οοο∴,37tan 23tan 3337tan 23tan οοοο-=+∴337tan 23tan 337tan 23tan =++οοοo ．【评析】三角变换的一般规律：看角的关系、看函数名称、看运算结构．以上题目是给角求值问题，应首看角的关系：先从所给角的关系入手，观察所给角的和、差、倍是否为特殊角，然后看包含的函数名称，以及所给三角式的结构，结合三角公式，找到题目的突破口．公式βαβαβαtan tan 1tan tan )tan(-+=+的变形tan α＋tan β ＝tan(α ＋β )(1－tan α tan β )应予以灵活运用．例3 41)tan(,52)tan(=-=+βαβα，则tan2α ＝______； (2)已知1312)4πsin(,53)sin(),π,4π3(,=--=+∈ββαβα，求)4πcos(+α的值．解：(1)分析所给的两个已知角α ＋β ，α －β 和所求的角2α 之间有关系(α ＋β )＋(α －β )＝2α ，=-++=)]()tan[(2tan ββa a a 1813415214152)tan()tan(1)tan()tan(=⨯-+=-+--++βαβαβαβα，(2)∵)π,4π3(,∈βα，∴)43,2π(4π),π2,23π(π∈-∈+ββα，又∵53)sin(-=+βα，∴54)cos(=+βα；∵1312)4πsin(=-β，∴135)4πcos(-=-β．)4πsin()sin()4πcos()cos()]4π()cos[()4πcos(-++-+=--+=+ββαββαββαα65561312)53()135(54-=⨯-+-⨯=. 【评析】此类题目重在考察所给已知角与所求角之间的运算关系，主要是指看两角之间的和、差、倍的关系，如αββαααββα2)(,4π)4π()(，+-=+=--+++=)(βα)(βα-等，找到它们的关系可以简化运算，同时在求三角函数值时应关注函数值的符号．例4 如图，在平面直角坐标系xOy 中，以Ox 轴为始边做两个锐角α ，β ，它们的终边分别与单位圆相交于A ，B 两点，已知A ，B 的横坐标分别为552,102.(Ⅰ)求tan(α ＋β )的值； (Ⅱ)求α ＋2β 的值．解：由三角函数定义可得552cos ,102cos ==βα，又因为α ，β 为锐角，所以55sin ,1027sin ==βα，因此tan α ＝7，21tan =β (Ⅰ)3tan tan 1tan tan )tan(-=-+=+βαβαβα；(Ⅱ) 34tan 1tan 22tan 2=-=βββ，所以12tan tan 12tan tan )2tan(-=-+=+βαβαβα， ∵α ，β 为锐角，∴4π32,2π320=+∴<+<βαβα 【评析】将三角函数的定义、两角和的正切、二倍角的正切公式结合在一起进行考查，要求基础知识掌握牢固，灵活运用；根据三角函数值求角，注意所求角的取值范围．例5 化简(1)12cos2sin22sin 22cos 2-+αααα；(2).2sin 3)4πcos()4πcos(2x x x +-+解：(1)原式⋅+-=--=--=-=)4πsin(2sin cos cos sin sin cos cos sin 2cos 22αααααααααα (2)法一：原式x x x x x 2sin 3)sin 22cos 22)(sin 22cos 22(2++-= x x x 2sin 3sin cos 22+-=⋅+=+=+=)6π2sin(2)2sin 232cos 21(22sin 32cos x x x x x法二：,2π)4π()4π(=--+x x 原式x x x 2sin 3)4πcos()]4π(2πcos[2+--+=x x x x x 2sin 3)2π2sin(2sin 3)4πcos()4πsin(2+--=+---=⋅+=+=)6π2sin(22sin 32cos x x x【评析】在进行三角变换时，应从三个角度：角的关系、函数的名称、所给运算式的结构全面入手，注意二倍角的变式(降幂升角)和辅助角公式的应用，此类变换是处理三角问题的基础．例6 (1)已知α 为第二象限角，且415sin =α，求12cos 2sin )4πsin(+++ααα的值． (2)已知323cos sin 32cos 62-=-x x x ，求sin2x 的值．解：(1)因为α 为第二象限角，且415sin =α，所以41cos -=α，原式.2cos 42)cos (sin cos 2)cos (sin 221)1cos 2(cos sin 2)cos (sin 222-==++=+-++=ααααααααααα 【评析】此类题目为给值求值问题，从分析已知和所求的三角式关系入手，如角的关系，另一个特征是往往先对所求的三角式进行整理化简，可降低运算量．(2)因为32sin 32cos 32sin 322cos 16+-=-+⋅x x x x3233)6π2cos(323)2sin 212cos 23(32-=++=+-=x x x 所以0)6π2sin(,1)6π2cos(=+-=+x x 216πsin )6π2cos(6πcos )6π2sin(]6π)6π2sin[(2sin =+-+=-+=x x x x【评析】在进行三角变换时，应从三个角度：角的关系、函数的名称、所给运算式的结构全面入手，注意二倍角的变式(降幂升角)22cos 1sin ,22cos 1cos 22αααα-=+=和辅助角公式的应用，此类变换是处理三角问题的基础，因为处理三角函数图象性质问题时往往先进行三角变换．练习3－2一、选择题1．已知53sin ),π,2π(=∈αα，则)4πtan(+α等于( ) A ．71 B ．7 C ．71-D ．－72．cos24°cos54°－sin24°cos144°＝( ) A ．23-B ．21 C ．23 D ．21-3．=-o30sin 1( ) A ．sin15°－cos15° B ．sin15°＋cos15° C ．－sin15°－cos15° D ．cos15°－sin15°4．若22)4πsin(2cos -=-αα，则cos α ＋sin α 的值为( )A ．27-B ．21-C ．21 D ．27 二、填空题 5．若53)2πsin(=+θ，则cos2θ ＝______． 6．=-οο10cos 310sin 1______．7．若53)cos(,51)cos(=-=+βαβα，则tan α tan β ＝______． 8．已知31tan -=α，则=+-ααα2cos 1cos 2sin 2______．三、解答题 9．证明⋅=++2tan cos 1cos .2cos 12sin ααααα10．已知α 为第四象限角，且54sin -=α，求ααcos )4π2sin(21--的值．11．已知α 为第三象限角，且33cos sin =-αα. (1)求sin α ＋cos α 的值；(2)求αααααcos 82cos 112cos2sin82sin 522-++的值．§3－3 三角函数【知识要点】12．三角函数图象是研究三角函数的有效工具，应熟练掌握三角函数的基本作图方法．会用“五点法”画正弦函数、余弦函数和函数y ＝A sin(ω x ＋ϕ)(A ＞0，ω ＞0)的简图．3．三角函数是描述周期函数的重要函数模型，通过三角函数体会函数的周期性．函数y ＝A sin(ω x ＋ϕ)(ω ≠0)的最小正周期：||π2ω=T ；y ＝A tan(ω x ＋ϕ)(ω ≠0)的最小正周期：||πω=T ．同时应明确三角函数与周期函数是两个不同的概念，带三角函数符号的函数不一定是周期函数，周期函数不一定带三角函数符号．【复习要求】1．掌握三角函数y ＝sin x ，y ＝cos x ，y ＝tan x 的图象性质：定义域、值域(最值)、单调性、周期性、奇偶性、对称性等．2．会用五点法画出函数y ＝sin x ，y ＝cos x ，y ＝A sin(ω x ＋ϕ)(A ＞0，ω ＞0)的简图，掌握图象的变换方法，并能解决相关图象性质的问题．3．本节内容应与三角恒等变换相结合，通过变换，整理出三角函数的解析式，注意使用换元法，转化为最基本的三个三角函数y ＝sin x ，y ＝cos x ，y ＝tan x ，结合三角函数图象，综合考察三角函数性质【例题分析】例1 求下列函数的定义域(1)xxy cos 2cos 1+=；(2)x y 2sin =.解：(1)cos x ≠0，定义域为},2ππ|{Z ∈+≠k k x x (2)sin2x ≥0，由正弦函数y ＝sin x 图象(或利用在各象限中和轴上角的正弦函数值的符号可得终边在第一二象限，x 轴，y 轴正半轴上) 可得2k π≤2x ≤2k π＋π，定义域为},2πππ|{Z ∈+≤≤k k x k x例2 求下列函数的最小正周期 (1))23πsin(x y -=；(2))4π2πtan(+=x y ；x y 2cos )3(2=； (4)y ＝2sin 2x ＋2sin x cos x ；(5)y ＝｜sin x ｜．解：(1)π|2|π2=-=T ．(2)22ππ==T ．(3)214cos 2124cos 1+=+=x x y ，所以2π=T .(4)1)4π2sin(212cos 2sin 2sin 22cos 12+-=+-=+-⨯=x x x x x y ，所以T ＝π．(5)y ＝｜sin x ｜的图象为下图，可得，T ＝π．【评析】(1)求三角函数的周期时，通常利用二倍角公式(降幂升角)和辅助角公式先将函数解析式进行化简，然后用||π2ω=T (正余弦)或||πω=T (正切)求最小正周期． (2)对于含绝对值的三角函数周期问题，可通过函数图象来解决周期问题．例3 (1)已知函数f (x )＝(1＋cos2x )sin 2x ，x ∈R ，则f (x )是( ) A ．最小正周期为π的奇函数 B ．最小正周期为π的偶函数 C ．最小正周期为2π的奇函数 D ．最小正周期为2π的偶函数 (2)若函数f (x )＝2sin(2x ＋ϕ)为R 上的奇函数，则ϕ＝______． (3)函数)2π2π(lncos <<-=x x y 的图象( )解：(1),,44cos 12sin 21)cos sin 2(21sin cos 2)(2222R ∈-====x xx x x x x x f 周期为2π，偶函数，选D (2)f (x )为奇函数，f (－x )＝－f (x )，所以2sin(－2x ＋ϕ)＝－2sin(2x ＋ϕ)对x ∈R 恒成立，即sin ϕcos2x －cos ϕsin2x ＝－sin2x cos ϕ－cos2x sin ϕ，所以2sin ϕcos2x ＝0对x ∈R 恒成立，即sin ϕ＝0，所以ϕ＝k π，k ∈Z ．【评析】三角函数的奇偶性问题可以通过奇偶性定义以及与诱导公式结合加以解决．如在本题(2)中除了使用奇偶性的定义之外，还可以从公式sin(x ＋π)＝－sin x ，sin(x ＋2π)＝sin x 得到当ϕ＝2k π＋π或ϕ＝2k π＋π，k ∈Z ，即ϕ＝k π，k ∈Z 时，f (x )＝2sin(2x ＋ϕ)可以化为f (x )＝sin x 或f (x )＝－sin x ，f (x )为奇函数．(3)分析：首先考虑奇偶性，f (－x )＝lncos(－x )＝lncos x ＝f (x )，为偶函数，排除掉B ，D 选项考虑(0，2π)上的函数值，因为0＜cos x ＜1，所以lncos x ＜0，应选A 【评析】处理函数图象，多从函数的定义域，值域，奇偶性，单调性等方面综合考虑．例4 求下列函数的单调增区间(1))3π21cos(-=x y ;(2) ]0,π[),6π2sin(2-∈+=x x y ； (3) x x y 2sin 32cos -=；(4))23πsin(2x y -=解：(1)y ＝cos x 的增区间为[2k π＋π，2k π＋2π]，k ∈Z ，由π2π23π21ππ2+≤-≤+k x k 可得3π14π43π8π4+≤≤+k x k )3π21cos(-=x y 的增区间为Z ∈++k k k ],3π14π4,3π8π4[，(2)先求出函数)6π2sin(2+=x y 的增区间Z ∈+-k k k ],6ππ,3ππ[然后与区间[－π，0]取交集得到该函数的增区间为]6π5,π[--和]0,3π[-，(3))3π2cos(2)2sin 232cos 21(2+=-=x x x y ，转化为问题(1)，增区间为 Z ∈++k k k ],6π5π,3ππ[(4)原函数变为)3π2sin(2--=x y ，需求函数)3π2sin(-=x y 的减区间， 2π3π23π22ππ2+≤-≤+k x k ，得12π11π12π5π+≤≤+k x k ， )23πsin(2x y -=的增区间为.],12π11π,12π5π[Z ∈++k k k【评析】处理形如y ＝A sin(ω x ＋ϕ)＋k ，(ω ＜0)的函数单调性时，可以利用诱导公式将x 的分数化正，然后再求相应的单调区间．求三角函数单调区间的一般方法：(1)利用三角变换将解析式化为只含有一个函数的解析式，利用换元法转化到基本三角函数的单调性问题． (2)对于给定区间上的单调性问题，可采用问题(2)中的方法，求出所有的单调增区间，然后与给定的区间取交集即可．例5 求下列函数的值域(1)函数1)6π21cos(2++-=x y 的最大值以及此时x 的取值集合(2))3π2,6π(,sin 2-∈=x x y (3) )3π,2π(),3π2cos(2-∈+=x x y (4)y ＝cos2x －2sin x解：(1)当Z ∈+=+k k x ,ππ26π21时，1)6π21cos(-=+x ，函数的最大值为3，此时x 的取值集合为},3π5π4|{Z ∈+=k k x x(2)结合正弦函数图象得：当)3π2,6π(-∈x 时，1sin 21≤<-x该函数的值域为(－1，2](3)分析：利用换元法，转化为题(2)的形式．)6π,3π(),3π2cos(2-∈+=x x y ，,3π23π23π),6π,3π(<+<-∴-∈x x Θ设3π2+=x t ，则原函数变为3π23π,cos 2<<-=t t y ，结合余弦函数图象得：1cos 21≤<-t ，所以函数的值域为(－1，2]．(4)y ＝－2sin 2x －2sin x ＋1，设t ＝sin x ，则函数变为y ＝－2t 2－2t ＋1，t ∈[－1，1]，因为⋅++-=23)21(22t y 结合二次函数图象得，当t ＝1时，函数最小值为－3，当21-=t 时，函数最大值为23，所以函数的值域为].23,3[-【评析】处理三角函数值域(最值)的常用方法： (1)转化为只含有一个三角函数名的形式，如y ＝A sin(ω x ＋ϕ)＋k ，y ＝A cos(ω x ＋ϕ)＋k ，y ＝A tan(ω x ＋ϕ)＋k 等，利用换元法，结合三角函数图象进行处理． (2)转化为二次型：如A sin 2x ＋B sin x ＋C ，A cos 2x ＋B cos x ＋C 形式，结合一元二次函数的图象性质求值域．例6 函数y ＝sin(ω x ＋ϕ)的图象(部分)如图所示，则ω 和ϕ的取值是( )A ．3π,1==ϕω B ．3π,1-==ϕω C ．6π,21==ϕω D ．6π,21-==ϕω解：π)3π(3π24=--=T ，即ωπ2π4==T ，所以21=ω，当3π-=x 时，0])3π(21sin[=+-⨯ω，所以Z ∈+=k k ,6ππω，选C例7 (1)将函数x y 21sin =的图象如何变换可得到函数)6π21sin(+=x y 的图象(2)已知函数y ＝sin x 的图象，将它怎样变换，可得到函数)3π2sin(2-=x y 的图象解：(1)x y 21sin =−−−−−−−−→−个单位图象向左平移3π)6π21sin()3π(21sin +=+=x x y (2)法一：y ＝sin x −−−−−−−−→−个单位图象向右平移3π)3πsin(-=x y −−−−−−−−−−−−−−−→−倍横坐标变为原来图象上点的纵坐标不变21,)3π2sin(-=x y−−−−−−−−−−−−−−−→−倍纵坐标变为原来图象上点的横坐标不变2,)3π2sin(2-=x y法二：y ＝sin x −−−−−−−−−−−−−−→−倍横坐标变为原来图象上点的纵坐标不变21,x y 2sin = −−−−−−−−→−个单位图象向右平移6π)6π(2sin -=x y−−−−−−−−−−−−−−−→−倍纵坐标变为原来图象上点的横坐标不变2,)3π2sin(2-=x y【评析】由y ＝sin x 的图象变换为y ＝A cos(ω x ＋ϕ)(ω ＞0)的图象时，特别要注意伸缩变换和横向平移的先后顺序不同，其横向平移过程中左右平移的距离不同．例8 (1)函数)3π21sin(2-=x y 的一条对称轴方程为( ) A ．3π4-=x B ．6π5-=x C ．3π-=x D ．3π2=x (2)函数)3π2cos(-=x y 的对称轴方程和对称中心的坐标解：(1)法一：)3π21sin(2-=x y 的对称轴为Z ∈+=-k k x ,2ππ3π21，即Z ∈+=k k x ,3π5π2，当k ＝－1时，3π-=x ，选C法二：将四个选项依次代入)3π21sin(2-=x y 中，寻找使得函数取得最小值或最大值的选项当3π-=x 时，22πsin 2)3π6πsin(2-=-=--=y ，选C (2) )3π2cos(-=x y 的对称轴为Z ∈=-k k x ,π3π2，即Z ∈+=k k x ,6π2π对称中心：,,2ππ3π2Z ∈+=-k k x 此时Z ∈+=k k x ,12π52π所以对称中心的坐标为Z ∈+k k ),0,12π52π(【评析】正余弦函数的对称轴经过它的函数图象的最高点或最低点，对称中心是正余弦函数图象与x 轴的交点，处理选择题时可以灵活运用．例9 已知函数)0(),2πsin(sin 3,sin )(2>++=ωωωωx x x x f 的最小正周期为π． (1)求ω 的值． (2)求f (x )在区间]3π2,0[上的值域． (3)画出函数y ＝2f (x )－1在一个周期[0，π]上的简图．(4)若直线y ＝a 与(3)中图象有2个不同的交点，求实数a 的取值范围．解：(1)x x xx f ωωωcos sin 322cos 1)(+-=21)6π2sin(212cos 21sin 23+-=+-=x x x ωωω 因为函数f (x )的最小正周期为π，且ω ＞0，所以π2π2=ω，解得ω ＝1 (2)由(1)得21)6π2sin()(+-=x x f ，因为3π20≤≤x ，所以6π76π26π≤-≤-x ，结合正弦函数图象，得1)6π2sin(21≤-≤-x因此2321)6π2sin(0≤+-≤x ，即f (x )的取值范围为]23,0[(3)由(1)得)6π2sin(21)(2-=-=x x f y(4)由图象可得，－2＜a ＜2且a ≠－1．【评析】本节内容应与三角恒等变换相结合，利用降幂升角公式和辅助角公式等三角公式化简三角函数解析式，整理、变形为只含有一个函数名的解析式，如y ＝A sin(ω x ＋ϕ)(ω ＞0)或y ＝A cos(ω x ＋ϕ)(ω ＞0)的形式，利用换元法，结合y ＝sin x 、y ＝cos x 的图象，再研究它的各种性质，如求函数的周期，单调性，值域等问题，这是处理三角函数问题的基本方法．练习3－3一、选择题1．设函数),2π2sin()(-=x x f x ∈R ，则f (x )是( ） A ．最小正周期为π的奇函数 B ．最小正周期为π的偶函数 C ．最小正周期为2π的奇函数 D ．最小正周期为2π的偶函数 2．把函数y ＝sin x (x ∈R )的图象上所有的点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的21倍(纵坐标不变)，得到的图象所表示的函数是( ) A ．R ∈-=x x y ),3π2sin( B ．R ∈+=x x y ),6π2sin(C ．R ∈+=x x y ),3π2sin(D ．R ∈+=x x y ),32π2sin(3．函数)3π2sin(+=x y 的图象( )A ．关于点(3π，0)对称B ．关于直线4π=x 对称C ．关于点(4π，0)对称D ．关于直线3π=x 对称4．函数y ＝tan x ＋sin x －｜tan x －sin x ｜在区间)2π3,2π(内的图象大致是( ）二、填空题5．函数)2πsin(sin 3)(x x x f ++=的最大值是______． 6．函数)]1(2πcos[)2πcos(-=x x y 的最小正周期为______．7．函数)2π0,0)(sin(<<>+=ϕωϕωx y 的图象的一部分如图所示，则该函数的解析式为y ＝______．8．函数y ＝cos2x ＋cos x 的值域为______．三、解答题9．已知函数f (x )＝2cos x (sin x －cos x )＋1，x ∈R ． (Ⅰ)求函数f (x )的对称轴的方程； (Ⅱ)求函数f (x )的单调减区间． 10．已知函数.34sin 324cos 4sin2)(2+-=xx x x f (Ⅰ)求函数f (x )的最小正周期及最值； (Ⅱ)令)3π()(+=x f x g ，判断函数g (x )的奇偶性，并说明理由．11．已知R ∈>++=a a x x x x f ,0(,cos sin 32cos 2)(2ωωωω，a 为常数)，且满足条件f (x 1)＝f (x 2)＝0的｜x 1－x 2｜的最小值为2π． (Ⅰ)求ω 的值； (Ⅱ)若f (x )在]3π,6π[-上的最大值与最小值之和为3，求a 的值．§3－4 解三角形【知识要点】1．三角形内角和为A ＋B ＋C ＝πA CB -=+π,2π222=++C B A ，注意与诱导公式相结合的问题． 2．正弦定理和余弦定理正弦定理：r CcB b A a 2sin sin sin ===，(r 为△ABC 外接圆的半径)．余弦定理：abc b a C ac b c a B bc a c b A 2cos ;2cos ;2cos 222222222-+=-+=-+=&. a 2＝b 2＋c 2－2bc cos A ；b 2＝a 2＋c 2－2ac cos B ；c 2＝a 2＋b 2－2ab cos C ．3．在解三角形中注意三角形面积公式的运用：21=∆ABC S ×底×高.21=∆ABC S ab sin .sin 21sin 21B ac A bc C == 4．解三角形中注意进行“边角转化”，往往结合三角变换处理问题．【复习要求】1．会正确运用正余弦定理进行边角的相互转化；2．会熟练运用正弦定理和余弦定理解决三角形中的求角，求边，求面积问题．【例题分析】例1 (1)在△ABC 中，3=a ，b ＝1，B ＝30°，则角A 等于( )A ．60°B ．30°C ．120°D ．60°或120° (2)△ABC 中，内角A ，B ，C 所对的边分别为a 、b 、c ，满足等式(a ＋b )2＝ab ＋c 2，则角C 的大小为______. (3)在△ABC 中，若sin A ∶sin B ∶sin C ＝5∶7∶8，则∠B 的大小是______． (4)在△ABC 中，若31tan =A ，C ＝150°，BC ＝1，则AB ＝______．解：(1)∵,23sin ,30sin 1sin 3,sin sin =∴=∴=A A B b A a ο又∵a ＞b ，∴A ＞B ＝30°，∴A ＝60°或120°，(2)∵(a ＋b )2＝ab ＋c 2，∴a 2＋b 2－c 2＝－ab ，∴,120,2122cos 222ο=∴-=-=-+=C ab ab ab c b a C (3)∵CcB b A a sin sin sin ==，sin A ∶sin B ∶sin C ＝5∶7∶8. ∴a ∶b ∶c ＝5∶7∶8，∴21852*******cos 222=⨯⨯-+=-+=ac b c a B ，∴B ＝60°． (4)分析：已知条件为两角和一条对边，求另一条对边，考虑使用正弦定理，借助于31tan =A 求sin A 210,150sin 10101,sin sin ,1010sin ,31tan =∴=∴==∴=AB AB B AC A BC A A οΘΘ. 【评析】对于正弦定理和余弦定理应熟练掌握，应清楚它们各自的使用条件，做到合理地选择定理解决问题．例2 (1)在△ABC 中，a cos A ＝b cos B ，则△ABC 一定是( ) A ．直角三角形 B ．等边三角形 C ．等腰三角形 D ．等腰三角形或直角三角形 (2)在△ABC 中，2sin B ·sin C ＝1＋cos A ，则△ABC 的形状为( ) A ．直角三角形 B ．等边三角形 C ．等腰三角形 D ．等腰直角三角形解：(1)法一：BbA a sin sin =Θ，a cos A ＝b cos B ， ∴sin A cos A ＝sin B cos B ，∴sin2A ＝sin2B ，∵2A ，2B ∈(0，2π)，∴2A ＝2B 或2A ＋2B ＝π，∴A ＝B 或2π=+B A ，选D ．法二：∵a cos A ＝b cos B ，∴acb c a b bc a c b a 2)(2)(222222-+=-+，整理得(a 2－b 2)(a 2＋b 2－c 2)＝0．所以：a ＝b 或a 2＋b 2＝c 2，选D ．(2)∵2sin B ·sin C ＝1＋cos A ，cos(B ＋C )＝cos(π－A )＝－cos A ， ∴2sin B ·sin C ＝1－(cos B cos C －sin B sin C )， ∴cos B cos C ＋sin B ·sin C ＝1， ∴cos(B －C )＝1，∵B ，C ∈(0，π)，∴B －C ∈(－π，π)， ∴B －C ＝0，∴B ＝C ，选C ．【评析】判断三角形形状，可以从两个角度考虑(1)多通过正弦定理将边的关系转化为角的关系，进而判断三角形形状，(2)多通过余弦定理将角的关系转化为边的关系，进而判断三角形形状，通常情况下，以将边的关系转化为角的关系为主要方向，特别需要关注三角形内角和结合诱导公式带给我们的角的之间的转化．例3 已知△ABC 的周长为12+，且sin A ＋sin B ＝2sin C (1)求边AB 的长；(2)若△ABC 的面积为C sin 61，求角C 的度数．解：(1)由题意及正弦定理，得⎪⎩⎪⎨⎧=++=++ABAC BC AC BC AB 212，解得AB ＝1． (2)由△ABC 的面积C C AC BC S sin 61sin 21=⋅=，得31=⋅AC BC ，因为2=+AC BC ，所以(BC ＋AC )2＝BC 2＋AC 2＋2AC ·BC ＝2，可得3422=+AC BC ，由余弦定理，得212cos 222=-+=⋅BC AC AB BC AC C ，所以C ＝60°．例4 在△ABC 中，∠A 、∠B 、∠C 所对的边长分别为a 、b 、c ，设a 、b 、c 满足条件b 2＋c 2－bc ＝a 2和b c ＝321+，求∠A 和tan B 的值．解(1)由已知和余弦定理得212cos 222=-+=bc a c b A ，所以∠A ＝60°． (2)分析：所给的条件是边的关系，所求的问题为角，可考虑将利用正弦定理将边的关系转化为角的关系．在△ABC 中，sin C ＝sin(A ＋B )＝sin(60°＋B )，因为BBB B B BC b c sin sin 60cos cos 60sin sin )60sin(sin sin οοο+⋅=+==.32121tan 123+=+=B所以⋅=21tan B 【评析】体现了将已知条件(边321+==b c )向所求问题(角tan B →sin a ，cos α )转化，充分利用了正弦定理和三角形内角关系实现转化过程．例5 在△ABC 中，内角A ，B ，C 对边的边长分别是a ，b ，c ，已知c ＝2，3π=C ． (Ⅰ)若△ABC 的面积等于3，求a ，b ；(Ⅱ)若sin C ＋sin(B －A )＝2sin2A ，求△ABC 的面积．解：(Ⅰ)由余弦定理abc b a C 2cos 222-+=及已知条件得，a 2＋b 2－ab ＝4，又因为△ABC 的面积等于3，所以3sin 21=C ab ，得ab ＝4．联立方程组⎩⎨⎧==-+,4,422ab ab b a 解得a ＝2，b ＝2．(Ⅱ)由题意得sin(B ＋A )＋sin(B －A )＝4sin A cos A ，(sin B cos A ＋cos B sin A )＋(sin B cos A －cos B sin A )＝4sin A cos A ，即sin B cos A ＝2sin A cos A ，当cos A ＝0时，332,334,6π,2π====b a B A ，当cos A ≠0时，得sin B ＝2sin A ，由正弦定理得b ＝2a ，联立方程组⎩⎨⎧==-+,2,422a b ab b a 解得334,332==b a . 所以△ABC 的面积332sin 21==C ab S .【评析】以上两例题主要考查利用正弦定理、余弦定理来确定三角形边、角关系等基础知识和基本运算能力．以及三角形面积公式B ac A bc C ab S ABC sin 21sin 21sin 21===∆的运用．同时应注意从题目中提炼未知与已知的关系，合理选择定理公式，综合运用正弦定理和余弦定理实现边角之间的转化．例6 如图，测量河对岸的塔高AB 时，可以选与塔底B 在同一水平面内的两个测点C 与D ，现测得∠BCD ＝α ，∠BDC ＝β ，CD ＝s ，并在点C 测得塔顶A 的仰角为θ ，求塔高AB ．解：在△BCD 中，∠CBD ＝π－α －β ．由正弦定理得．sin sin CBDCDBDC BC ∠=∠所以)sin(sin sin sin βαβ+=∠∠=⋅s CBD BDC CD BC ．在Rt △ABC 中，⋅+=∠=⋅)sin(sin tan tan βαβθs ACB BC AB例7 已知在△ABC 中，sin A (sin B ＋cos B )－sin C ＝0，sin B ＋cos2C ＝0，求角A ，B ，C 的大小．解：sin A sin B ＋sin A cos B －sin(A ＋B )＝0，sin A sin B ＋sin A cos B －(sin A cos B ＋cos A sin B )＝0， sin A sin B －cos A sin B ＝sin B (sin A －cos A )＝0，因为sin B ≠0，所以sin A －cos A ＝0，所以tan A ＝1，4π=A ，可得BC +=4π3，所以02sin sin )22π3cos(sin )4π3(2cos sin =+=++=++B B B B B B ，sin B ＋2sin B cos B ＝0，因为sin B ≠0，所以12π,3π2,21cos ==-=C B B .【评析】考查了三角形中角的相互转化关系，同时兼顾了两角和、二倍角、诱导公式等综合应用．练习3－4一、选择题1．在△ABC 中，若A ∶B ∶C ＝1∶2∶3，则a ∶b ∶c ＝( ) A ．1∶2∶3B ．2:3:1C ．1∶4∶9D ．3:2:12．在△ABC 中，角A 、B 、C 的对边分别为a ，b ，c ，3,3π==a A ，b ＝1，则c ＝( ) A ．1B ．2C ．13-D ．33．△ABC 中，若a ＝2b cos C ，则△ABC 的形状一定为( ) A ．等边三角形 B ．直角三角形 C ．等腰三角形 D ．等腰直角三角形4．△ABC 的三内角A ，B ，C 的对边边长分别为a ，b ，c ，若b a 25=，A ＝2B ，则cos B ＝( ) A ．35B ．45 C ．55 D ．65二、填空题5．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a ＝1，3π,3==C c ，则A ＝______． 6．在△ABC 中，角ABC 的对边分别为a 、b 、c ，若ac B b c a 3tan )(222=-+，则角B 的值为______．7．设△ABC 的内角6π=A ，则2sinB cosC －sin(B －C )的值为______． 8．在三角形ABC 中，∠A 、∠B 、∠C 的对边分别为a 、b 、c ，若b cos C ＝(2a －c )cos B ，则∠B 的大小为______. 三、解答题9．在△ABC 中，53tan ,41tan ==B A . (Ⅰ)求角C 的大小；(Ⅱ)若AB 的边长为17，求边BC 的边长．10．如图，某住宅小区的平面图呈扇形AOC ．小区的两个出入口设置在点A 及点C 处，小区里有两条笔直的小路AD ，DC ，且拐弯处的转角为120°．已知某人从C 沿CD 走到D 用了10分钟，从D 沿DA 走到A 用了6分钟．若此人步行的速度为每分钟50米．求该扇形的半径OA 的长(精确到1米)．11．在三角形ABC 中，5522cos ,4π,2===B C a ，求三角形ABC 的面积S ．专题03 三角函数与解三角形参考答案练习3－1一、选择题：1．B 2．B 3．B 4．C 二、填空题 5．)0,2π(-6．16 7．21mm - 8．23- 三、解答题9．解：(1)⋅-=+=-=>55cos sin ,55cos ,552sin ,0cos ααααα (2)原式＝222)sin 1(sin sin 21cos 1sin 21θθθθθ-=+-=-+-=⋅+=-=-=5521sin 1|sin 1|θθ 10．解：(1)原式51tan 2tan -=-+=αα(2)原式.0tan 1tan 212=+-=αα11．解：当k 为偶数时，原式.0cos sin cos sin 1cos sin 1cos sin .cos sin )cos (sin cos sin 22=+-=++---=αααααααααααααα 当k 为奇数时，原式01cos sin )cos (sin =+-=αααα，综上所述，原式＝0．练习3－2一、选择题1．A 2．C 3．D 4．C 二、填空题 5257-6．4 7．21 8．65- 三、解答题 9．解：左边=====2tan 2cos 22cos2sin22cos2sin 2cos 2cos cos 2cos sin 22222.ααααααααααα右边.10．解：原式)sin (cos 2cos 1cos 2cos sin 21cos )2cos 2(sin 12ααααααααα-=-+-=--=，因为α 为第四象限角，且54sin -=α，所以53cos =α，所以原式514=. 11．解：(1)由a a a a cos sin 21)cos (sin 2-=-＝31可得32cos sin 2=αα，所以a a a a cos sin 21)cos (sin 2+=+＝35，因为α 为第三象限角，所以sin α ＜0，cos α ＜0，sin α ＋cos α ＜0，所以315cos sin -=+αα. (2)原式αααααααααcos cos 3sin 4cos )12cos 2(3sin 4cos 82cos 6sin 4522+=-+=-++=3tan 4+=α，因为51tan 1tan cos sin cos sin -=-+=-+αααααα，所以2531515tan -=+-=α，所以原式.52932534-=+-⨯= 练习3－3一、选择题1．B 2．C 3．A 4．D 二、填空题5．2 6．2 7．)3π2sin(+=x y 8．]2,89[- 三、解答题9．解：x x x x x x f 2cos 2sin 1cos 2cos sin 2)(2-=+-=＝)4π2sin(2-x . (1)Z ∈+=-k k x ,2ππ4π2，对称轴方程为Z ∈+=k k x ,8π32π， (2)Z ∈+≤-≤+k k x k ,2π3π24π22ππ2，即Z ∈+≤≤+k k x k ,8π7π8π3π，f (x )的单调减区间为Z ∈++k k k ],8π7π,8π3π[．10．解：(I)∵⋅+=+=-+=)3π2sin(22cos 32sin )4sin 21(32sin )(2x x x x x x f∴f (x )的最小正周期.π421π2==T当1)3π2sin(-=+x 时，f (x )取得最小值－2；当1)3π2sin(=+x 时，f (x )取得最大值2．(Ⅱ)由(I)知⋅+=+=)3π()().3π2sin(2)(x f x g x x f 又⋅=+=++=∴2cos 2)2π2sin(2]3π)3π(21sin[2)(xx x x g).(2cos 2)2cos(2)(x g xx x g ==-=-Θ∴函数g (x )是偶函数．11．解：(1)12cos 2sin 32sin 322cos 12)(+++=+++⨯=a x x a x xx f ωωωω,1)6π2sin(2+++=a x ω由满足条件f (x 1)＝f (x 2)＝0的｜x 1－x 2｜的最小值为2π，可得的最小正周期为π，所以ω ＝1．。

三角函数定义知识点及例题[练习与答案]超强推荐

三角函数的定义专题关键词：三角函数的定义终边弧长公式扇形面积同角的基本关系学习目标：理解角的概念，掌握同角三角函数基本关系☆ 对角的概念的理解：（1）无界性 R ∈α 或 ),(+∞-∞ （2）周期性（3）终边相同的角的表示：（1）α终边与θ终边相同(α的终边在θ终边所在射线上)⇔2()k k αθπ=+∈Z ，注意：相等的角的终边一定相同，终边相同的角不一定相等.如与角1825-的终边相同，且绝对值最小的角的度数是＿＿＿，合＿＿＿弧度。

（答：25-；536π-）（2）α终边与θ终边共线(α的终边在θ终边所在直线上) ⇔()k k αθπ=+∈Z . （3）α终边与θ终边关于x 轴对称⇔2()k k αθπ=-+∈Z . （4）α终边与θ终边关于y 轴对称⇔2()k k απθπ=-+∈Z . （5）α终边与θ终边关于原点对称⇔2()k k απθπ=++∈Z .（6）α终边在x 轴上的角可表示为：,k k Z απ=∈；α终边在y 轴上的角可表示为：,2k k Zπαπ=+∈；α终边在坐标轴上的角可表示为：,2k k Zπα=∈.如α的终边与6π的终边关于直线x y =对称，则α＝____________。

（答：Zk k ∈+,32ππ）☆ 角与角的位置关系的判断（1）终边相同的角（2）对称关系的角（3）满足一些常见关系式的两角例如：若α是第二象限角，则2α是第_____象限角：一、三）☆ 弧长公式：||l R α=，扇形面积公式：211||22S lR R α==，1弧度(1rad)57.3≈.例如：已知扇形AOB 的周长是6cm ，该扇形的中心角是1弧度，求该扇形的面积。

（答：22cm ）☆ 三角函数的定义：高中阶段对三角函数的定义与初中的定义从本质上讲不同。

但既有联系，又有区别。

定义：设α是任意一个角，P (,)x y 是α的终边上的任意一点（异于原点），它与原点的距离是220r x y =+>，那么sin ,cos y x r r αα==，()tan ,0y x x α=≠，cot x y α=(0)y ≠，sec r x α=()0x ≠，()csc 0r y y α=≠。

专题11 三角函数定义与三角函数恒等变换——2021年高考数学专项复习含真题及解析

专题11 三角函数定义与三角函数恒等变换考点36 三角函数定义1．（2018•新课标Ⅰ，文11）已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点(1,)A a ，(2,)B b ，且2cos23α=，则||(a b -= ) A ．15BCD ．1【答案】B【解析】角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点(1,)A a ，(2,)B b ，且2cos23α=，22cos22cos 13αα∴=-=，解得25cos 6α=，|cos |α∴=，|sin |α∴=，|sin ||tan |||||21|cos |b a a b ααα-==-===-，故选B ．2．（2014新课标I ，文2）若tan 0α>，则A. sin 20α> B ． cos 0α> C ． sin 0α> D ． cos20α> 【答案】A【解析】由tan 0α>知，α在第一、第三象限，即2k k ππαπ<<+（k Z ∈），∴222k k παππ<<+，即2α在第一、第二象限，故只有sin 20α>，故选A ．3．（2011全国课标理5文7）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ= （A ）45-(B)35- (C) 35 (D) 45【答案】B【解析】在直线2y x =取一点P （1，2），则rsin θ=y r∴cos2θ=212sin θ-=35-，故选B ．4．（2018浙江）已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边过点34(,)55P --．(1)求sin()απ+的值；(2)若角β满足5sin()13αβ+=，求cos β的值．【解析】(1)由角α的终边过点34(,)55P --得4sin 5α=-，所以4sin()sin 5απα+=-=． (2)由角α的终边过点34(,)55P --得3cos 5α=-，由5sin()13αβ+=得12cos()13αβ+=±．由()βαβα=+-得cos cos()cos sin()sin βαβααβα=+++，所以56cos 65β=-或16cos 65β=-．考点37同角三角函数基本关系与诱导公式1．（2019•新课标Ⅱ，文11）已知(0,)2πα∈，2sin2cos21αα=+，则sin (α= )A ．15B C D 【答案】B 【解析】2sin2cos21αα=+，∴可得：24sin cos 2cos ααα=，(0,)2πα∈，sin 0α>，cos 0α>，cos 2sin αα∴=，22222sin cos sin (2sin )5sin 1ααααα+=+==，∴解得：sin α，故选B ． 2．（2016新课标卷3，理5）若，则 (A)(B) (C) 1 (D) 【答案】A 【解析】由，得或，所以，故选A ． 3．（2016全国课标卷3，文6）若，则（）（A ）（B ）（C ）（D ）3tan 4α=2cos 2sin 2αα+=6425482516253tan 4α=34sin ,cos 55αα==34sin ,cos 55αα=-=-2161264cos 2sin 24252525αα+=+⨯=tan 13θ=cos2θ=45-15-1545【答案】D4．（2013浙江）已知，则（） A ．B ．C ．D ．【答案】C【解析】由2210(sin 2cos )()2αα+=可得2222sin 4cos 4sin cos 10sin cos 4αααααα++=+，进一步整理可得23tan 8tan 30αα--=，解得tan 3α=或1tan 3α=-，于是22tan 3tan 21tan 4ααα==--，故选C ． 5．(2012江西)若，则tan2α=（）A ．−B ．C ．−D ．【答案】B【解析】分子分母同除cos α得：sin cos tan 11,sin cos tan 12αααααα++==--∴tan 3α=-，∴22tan 3tan 21tan 4ααα==- 6．（2013广东）已知，那么 A ． B ． C ． D ．【答案】C 【解析】，选C ． 7．（2016•新课标Ⅰ，文14）已知θ是第四象限角，且3sin()45πθ+=，则tan()4πθ-= ．【答案】43-210cos 2sin ,=+∈αααR =α2tan 344343-34-sin cos 1sin cos 2αααα+=-3434434351sin()25πα+=cos α=25-15-152551sin()sin(2+)sin cos 2225πππαπααα⎛⎫+=+=+== ⎪⎝⎭【解析】θ是第四象限角，∴222k k ππθπ-+<<，则22,444k k k Z ππππθπ-+<+<+∈，又3sin()45πθ+=，4cos()45πθ∴+=，∴)4cos(θπ-=)4sin(θπ+ =53，4sin()cos()445ππθθ-=+=，则)4tan(πθ-=)4tan(θπ-- =)4cos()4sin(θπθπ---=5354- =34-． 8．（2013新课标Ⅱ，理15）若θ为第二象限角，1tan()42πθ+=，则sin cos θθ+= ．【答案】【解析】（法1）由1tan()42πθ+=得，tan θ=13-，即cos 3sin θθ=-，∵22sin cos 1θθ+=， θ为第二象限角，∴sin θ=10，cos θ=10-，∴sin cos θθ+=5-． 9．(2014江苏)已知，．(1)求的值；(2)求的值．【解析】（1）∵()sin 2ααπ∈π，，，∴cos α== ()sin sin cos cos sin sin )444αααααπππ+=+=+=；（2）∵2243sin 22sin cos cos 2cos sin 55αααααα==-=-=，∴()()314cos 2cos cos2sin sin 2666525ααα5π5π5π-=+=+⨯-=考点38三角恒等变换1．（2020全国Ⅰ理9）已知() 0,πα∈，且3cos28cos 5αα-=，则sin α= （）AB ．23C ．13 D【答案】A【思路导引】用二倍角的余弦公式，将已知方程转化为关于cos α的一元二次方程，求解得出cos α，再用同角间的三角函数关系，即可得出结论．),2(ππα∈55sin =α)4sin(απ+)265cos(απ-【解析】3cos28cos 5αα-=，得26cos 8cos 80αα--=，即23cos 4cos 40αα--=，解得2cos 3α=-或cos 2α=（舍去），又()0,,sin απα∈∴==，故选A ．2．（2020全国Ⅱ理2）若α为第四象限角，则（）A ．02cos >αB ．02cos <αC ．02sin >αD ．02sin <α 【答案】D【思路导引】由题意结合二倍角公式确定所给的选项是否正确即可．【解析】当6πα=-时，cos 2cos 03πα⎛⎫=-> ⎪⎝⎭，选项B 错误；当3πα=-时，2cos 2cos 03πα⎛⎫=-< ⎪⎝⎭，选项A 错误；由α在第四象限可得：sin 0,cos 0αα<>，则sin 22sin cos 0ααα=<，选项C 错误，选项D 正确，故选D ．3．（2020全国Ⅲ文5）已知sin sin 13θθπ⎛⎫++= ⎪⎝⎭，则sin 6θπ⎛⎫+= ⎪⎝⎭ （）A ．12 B C ．23D 【答案】B【思路导引】将所给的三角函数式展开变形，然后再逆用两角和的正弦公式即可求得三角函数式的值．【解析】由题意可得：1sin sin 12θθθ++=，则：3sin 12θθ+=1cos 2θθ+=从而有：sin coscos sin 66ππθθ+=，即sin 6πθ⎛⎫+= ⎪⎝⎭B ． 4．（2020全国Ⅲ理9）已知2tan tan 74θθπ⎛⎫-+= ⎪⎝⎭，则tan θ= （）A ．2-B ．1-C ．1D ．2 【答案】D【思路导引】利用两角和的正切公式，结合换元法，解一元二次方程，即可得出答案．【解析】2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭，tan 12tan 71tan θθθ+∴-=-，令tan ,1t t θ=≠，则1271t t t +-=-，整理得2440t t -+=，解得2t =，即tan 2θ=．故选D ．5．（2019•新课标Ⅱ，理10）已知(0,)2πα∈，2sin2cos21αα=+，则sin(α=)A．15B C D【答案】B【解析】2sin2cos21αα=+，∴24sin cos2cosααα=，(0,)2πα∈，sin0α>，cos0α>，cos2sinαα∴=，22222sin cos sin(2sin)5sin1ααααα+=+==，∴sinα，故选B．6．（2019•新课标Ⅲ，文5）函数()2sin sin2f x x x=-在[0，2]π的零点个数为() A．2B．3C．4D．5【答案】B【解析】函数()2sin sin2f x x x=-在[0，2]π的零点个数，即：2sin sin20x x-=在区间[0，2]π的根个数，即2sin sin2x x=，即0)cos1(sin=-xx，即0sin=x或1cos=x，∵∈x[0，2]π，∴ππ2,,0=x，故选B．7．（2019•新课标Ⅰ，文7）tan255(︒=)A．2-B．2-+C．2D．2【答案】D【解析】∵tan255tan(18075)tan75tan(4530)︒=︒+︒=︒=︒+︒1tan45tan3021tan45tan30+︒+︒======+-︒︒故选D．8．（2018•新课标Ⅲ，理4文4）若1sin3α=，则cos2(α=)A．89B．79C．79-D．89-【答案】B【解析】1sin3α=，217cos212sin1299αα∴=-=-⨯=，故选B．9．（2017新课标卷3，文4）已知4sin cos3αα-=，则sin2α=A．79-B．29-C．29D．79【答案】A【解析】因为()2sin cos 17sin 22sin cos 19ααααα--===-- ，故选A ．10．（2016•新课标Ⅱ，理9）若3cos()45πα-=，则sin 2(α= )A ．725B ．15C ．15-D ．725-【答案】D【解析】法31:cos()45πα︒-=，297sin 2cos(2)cos2()2cos ()1212442525πππαααα∴=-=-=--=⨯-=-，法32:cos()cos )45πααα︒-=+=，∴19(1sin 2)225α+=，97sin 2212525α∴=⨯-=-，故选D ．11．（2015新课标Ⅰ，理2）sin20°cos10°-con160°sin10°=A ．2-B ．2C ．12-D ．12【答案】D【解析】原式=sin20°cos10°+cos20°sin10°=sin30°=12，故选D ． 12．（2014新课标Ⅰ，理8）设(0,)2πα∈，(0,)2πβ∈，且1sin tan cos βαβ+=，则 A ．32παβ-=B ．22παβ-=C ．32παβ+=D ．22παβ+=【答案】B【解析】∵sin 1sin tan cos cos αβααβ+==，∴sin cos cos cos sin αβααβ=+ ()sin cos sin 2παβαα⎛⎫-==- ⎪⎝⎭，,02222ππππαβα-<-<<-<∴2παβα-=-，即22παβ-=，选B13．（2013新课标Ⅰ，文6 ）（A （B （C （D 【答案】A【解析】因为2sin 23α=，所以21cos ()[1cos 2()]424ππαα+=++=1(1sin 2)2α-=16，故选A ．， 14．（2015重庆）若tan 2tan5πα=，则3cos()10sin()5παπα--＝（）A ．1B ．2C ．3D ．4 【答案】C【解析】3cos()10sin()5παπα-=-33cos cos sin sin 1010sin cos cos sin 55ππααππαα+-33cos tan sin 1010tan cos sin55ππαππα+=- 33cos2tan sin 105102tan cos sin 555ππππππ+=-33cos cos 2sin sin 510510sin cos55ππππππ+= ＝155(cos cos )(cos cos )21010101012sin 25πππππ++-3cos103cos 10ππ==，选C ． 15．（2012山东）若，，则（） A ．B ．C ．D ．【答案】D【解析】由可得，，，故选D ． 16．（2011浙江）若02πα＜＜，02πβ-＜＜，1cos()43πα+=，cos()42πβ-=cos()2βα+= A ．33 B ．33- C ．539 D ．69- 【答案】C 【解析】cos()cos[()()]2442βππβαα+=+--cos()cos()442ππβα=+-⎥⎦⎤⎢⎣⎡∈2,4ππθ8732sin =θ=θsin 5354474342ππθ⎡⎤∈⎢⎥⎣⎦，],2[2ππθ∈812sin 12cos 2-=--=θθ4322cos 1sin =-=θθsin()sin()442ππβα++-，而3(,)444πππα+∈，(,)4242πβππ-∈，因此sin()4πα+=，sin()42πβ-=则1cos()233339βα+=⨯+=． 17．（2020全国Ⅱ文13）设32sin -=x ，则=x 2cos ．【答案】19【思路导引】直接利用余弦的二倍角公式进行运算求解即可．【解析】22281cos 212sin 12()1399x x =-=-⨯-=-=．故答案为：19．18．（2020江苏8）已知22sin ()43πα+=，则sin2α的值是________．【答案】13【解析】∵22sin ()43πα+=，由2112sin ()(1cos(2))(1sin 2)42223ππααα+=-+=+=，解得1sin 23α=．19．（2020浙江13）已知tan 2θ=，则cos2θ= ；πtan 4θ⎛⎫-= ⎪⎝⎭ ．【答案】35-；13【思路导引】利用二倍角余弦公式以及弦化切得cos2θ，根据两角差正切公式得tan()4πθ-【解析】22222222cos sin 1tan 3cos 2cos sin cos sin 1tan 5θθθθθθθθθ--=-===-++，tan 11tan 41tan 3πθθθ-⎛⎫-== ⎪+⎝⎭，故答案为：35-；13． 20．（2020北京14）若函数()sin()cos f x x x ϕ=++的最大值为2，则常数ϕ的一个取值为．【答案】2π【解析】∵()sin()cos f x x x ϕ=++sin cos cos sin cos x x x ϕϕ=++sin cos cos (sin 1)x x ϕϕ=++)x θ=+，则22cos(sin 1)4ϕϕ++=，22cos sin 2sin 1ϕϕϕ+++12sin 14ϕ=++=，∴sin 1ϕ=，∴2πϕ=．21．（2018•新课标Ⅱ，理15）已知sin cos 1αβ+=，cos sin 0αβ+=，则sin()αβ+= ．【答案】12-【解析】sin cos 1αβ+=，两边平方可得：22sin 2sin cos cos 1ααββ++=，①，cos sin 0αβ+=，两边平方可得：22cos 2cos sin sin 0ααββ++=，②，由①+②得：22(sin cos cos sin )1αβαβ++=，即22sin()1αβ++=，2sin()1αβ∴+=-，1sin()2αβ∴+=-． 22．（2018•新课标Ⅱ，文15）已知51tan()45πα-=，则tan α= ．【答案】32【解析】51tan()45πα-=，1tan()45πα∴-=，则11tan()tan1563544tan tan()14451421tan()tan 11445ππαππααππα+-++=-+=====----⨯．23．（2017新课标卷，文14）已知π(0)2a ∈，，tan α=2，则πcos ()4α-=__________．【解析】由tan 2α=得sin 2cos αα=，又22sincos 1αα+=，所以21cos 5α=，因为(0,)2πα∈，所以cos αα==，因为cos()cos cos sin sin444πππααα-=+，所以cos()4525210πα-=+=．24．（2019北京9）函数f (x )=sin 22x 的最小正周期是 ________．【解析】因为21cos 411sin 2cos 4222x f x x x -===-（）（），所以f x （）的最小正周期2π4T ==25．（2019江苏13）已知tan 2π3tan 4αα=-⎛⎫+ ⎪⎝⎭，则πsin 24α⎛⎫+ ⎪⎝⎭的值是_________．【答案】10【解析】由tan 23tan()4αα=-π+，得tan 23tan tan 41tan tan 4ααα=-π+π-，所以tan (1tan )21tan 3ααα-=-+，解得tan 2α=或1tan 3α=-．当tan 2α=时，22tan 4sin21tan 5ααα==+，221tan 3cos21tan 5ααα-==-+，43sin(2)sin2cos cos2sin 444525210αααπππ+=+=⨯-⨯=．当1tan 3α=-时，22tan 3sin21tan 5ααα==-+，221tan 4cos21tan 5ααα-==+，所以34sin(2)sin2cos cos2sin 444525210αααπππ+=+=-⨯+⨯=．综上，sin(2)4απ+． 26．（2017北京）在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称．若1sin 3α=，则cos()αβ-=___________．【答案】79- 【解析】∵角α与角β的终边关于y 轴对称，所以2k αβππ+=+，所以1sin sin(2)sin 3k βππαα=+-==，cos cos βα=-； 222cos()cos cos sin sin cos sin 2sin 1αβαβαβααα-=+=-+=-2172()139=⨯-=-． 27．（2017江苏）若1tan()46πα-=，则tan α= ．【答案】75【解析】tan()tan 744tan tan[()]4451tan()tan 44ππαππααππα-+=-+==--⨯． 28．（2015四川）=+ 75sin 15sin ．【答案】2【解析】．29．（2015江苏）已知tan2α=-，()1tan7αβ+=，则tanβ的值为_______．【答案】3【解析】12tan()tan7tan tan()321tan()tan17αβαβαβααβα++-=+-===++-．30．（2013四川）设sin2sinαα=-，(,)2παπ∈，则tan2α的值是_____．【解析】sin22sin cos sinαααα==-，则1cos2α=-，又(,)2παπ∈，则tanα=22tantan21tanααα===-31．（2012江苏）设α为锐角，若4cos65απ⎛⎫+=⎪⎝⎭，则sin212απ⎛⎫+⎪⎝⎭的值为．【答案】50217【解析】因为α为锐角，cos()6πα+=45，∴sin()6πα+=35，∴sin2(,2524)6=+παcos2(7)625πα+=，所以sin(50217251722]4)6(2sin[)122=⨯=-+=+ππαπα．32．（2018江苏）已知,αβ为锐角，4tan3α=，cos()αβ+=．(1)求cos2α的值；(2)求tan()αβ-的值．【解析】(1)因为，，所以．因为，所以，因此，．6sin15sin75sin15cos152sin(1545)2+=+=+=4tan3α=sintancosααα=4sin cos3αα=22sin cos1αα+=29cos25α=27cos22cos125αα=-=-(2)因为为锐角，所以．又因为，所以，因此．因为，所以，因此，． 33．（2014江西）已知函数()()()θ++=x x a x f 2cos cos 22为奇函数，且04=⎪⎭⎫⎝⎛πf ，其中()πθ，，0∈∈R a ．（1）求θ，a 的值；（2）若⎪⎭⎫ ⎝⎛∈-=⎪⎭⎫ ⎝⎛ππαα，，2524f ，求⎪⎭⎫ ⎝⎛+3sin πα的值．【解析】（1）因为()()()22cos cos 2f x a x x θ=++是奇函数，而212cos y a x =+为偶函数，所以2cos(2)y x θ=+为奇函数，又()0,θπ∈，得2πθ=．所以()f x =2sin 22cos x a x -⋅+（）由04=⎪⎭⎫ ⎝⎛πf ，得(1)0a -+=，即 1.a =- （2）由（1）得：()1sin 4,2f x x =-因为12sin 425f αα⎛⎫=-=- ⎪⎝⎭，得4sin ,5α= 又2παπ⎛⎫∈ ⎪⎝⎭，，所以3cos ,5α=- 因此sin sin cos sin cos 333πππααα⎛⎫+=+= ⎪⎝⎭ 34．（2013广东）已知函数． (1) 求的值； (2) 若，求．【解析】（1）() 1.3124f πππ-== （2）33cos ,52πθ=由于<θ<2π，所以4sin 5θ===-， ,αβ(0,π)αβ+∈cos()αβ+=sin()αβ+=tan()2αβ+=-4tan 3α=22tan 24tan 21tan 7ααα==--tan 2tan()2tan()tan[2()]1+tan 2tan()11ααβαβααβααβ-+-=-+==-+(),12f x x x R π⎛⎫=-∈ ⎪⎝⎭3f π⎛⎫⎪⎝⎭33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭6f πθ⎛⎫- ⎪⎝⎭因此6612f θθπππ⎛⎫⎛⎫-=-- ⎪ ⎪⎝⎭⎝⎭341cos sin .44452525θθθπππ⎛⎫⎛⎫=-==⨯-⨯=- ⎪ ⎪⎝⎭⎝⎭。

高三数学三角函数三角恒等变换解三角形试题答案及解析

高三数学三角函数三角恒等变换解三角形试题答案及解析1.已知函数的图象上关于轴对称的点至少有3对，则实数的取值范围是（）A．B．C．D．【答案】A【解析】原函数在轴左侧是一段正弦型函数图象，在轴右侧是一条对数函数的图象，要使得图象上关于轴对称的点至少有对，可将左侧的图象对称到轴右侧，即，应该与原来轴右侧的图象至少有个公共点如图，不能满足条件，只有此时，只需在时，的纵坐标大于，即，得．【考点】分段函数，函数图象，正弦型函数，对数函数2.若，则函数的最大值是___________．【答案】【解析】由题意因为，所以，所以函数的最大值是．【考点】求最大值．3.已知，，则下列不等式一定成立的是A．B．C．D．【答案】D【解析】,【考点】三角函数的性质4.若，且为第二象限角，则（）A．B．C．D．【答案】B【解析】由得又为第二象限角，所以，选B．【考点】两角差余弦公式5.设函数对任意的，都有，若函数，则的值是（）A．1B．-5或3C．-2D．【答案】C【解析】根据题意有是函数图像的对称轴，从而有，所以有，故选C．【考点】三角函数的性质．6.设的最小值为，则．【答案】【解析】，根据题意，结合二次函数在某个区间上的最值问题，对参数进行讨论，当时，其最小值为，所以不合题意，当时，其最小值为，解得，当时，其最小值为，无解，所以．【考点】倍角公式，二次函数在给定区间上的最值问题．7.设函数对任意的，都有，若函数，则的值是（）A．1B．-5或3C．D．-2【答案】D【解析】根据题意有是函数图像的对称轴，从而有，所以有，故选D．【考点】三角函数的性质．8.下列函数中，以为最小正周期的偶函数是（）A．y=sin2x+cos2xB．y=sin2xcos2xC．y=cos（4x+）D．y=sin22x﹣cos22x【答案】D【解析】因为A项为非奇非偶函数，B项是奇函数，C项是奇函数，只有D项是符合题意的，故选D．【考点】诱导公式，倍角公式，三角函数的奇偶性和周期．9.函数的最大值为．【答案】【解析】解析式表示过的直线的斜率，由几何意义，即过定点（4，3）与单位圆相切时的切线斜率为最值．所以设切线得斜率为k，则直线方程为，即 ,【考点】三角函数最值【方法点睛】本题主要考查三角函数最值问题及转化的思想，解决问题的根据是根据所给函数式子转化为直线与圆的位置关系问题，即将所给式子看做定点与单位圆上点的连线的斜率的范围问题，通过模型转化使问题定点巧妙解决，属于经典试题．10.（本题满分12分）如图，在中，边上的中线长为3，且，．（1）求的值；（2）求边的长．【答案】（1）（2）4【解析】（1）利用角的关系，再结合两角差正弦公式展开就可求解（2）先在三角形ABD中，由正弦定理解出BD长，即CD长：由正弦定理，得，即，解得…故；再在三角形ADC中由余弦定理解出AC：；AC= 4试题解析：（1）（2）在中，由正弦定理，得，即，解得…故，从而在中，由余弦定理，得；AC= 4 ；【考点】正余弦定理11.中，，则的最大值为．【答案】【解析】设，由余弦定理的推论，所以，设，代入上式得，，故，当时，此时，符合题意，因此最大值为，故答案为：．【考点】解三角形．【思路点睛】首先假设，然后再根据余弦定理的推论，可得，找到与的关系，再设，代入上式得，利用根的判别式，进而求出结果．本题的关键是利用余弦定理的推论．12.已知函数的部分图象如图所示．（1）求函数的解析式；（2）若，求函数在区间上的单调减区间．【答案】（1）；（2），．【解析】（1）由图象中的最高点和最低点的纵坐标得到关于的方程组求得，再利用图象得到函数的周期，进而得到值，最后代入最低点坐标或最高点坐标结合的范围求出，即得到函数的解析式；（2）先求出，利用两角和差的正弦公式将其化为的形式，再利用整体思想求其单调递减区间．试题解析：（1）由图知，解得，又，所以，所以，将点代入，得，再由，得，所以；（2）因为由，解得；又，故所求的单调减区间为，．【考点】1.三角函数的图象与性质；2.三角恒等变形．13.已知角的终边经过点（-4，3），则= ，= ；【答案】;【解析】由题意可得.【考点】任意角三角函数的定义.14.在△ABC中，a、b、c分别是角A、B、C的对边，且．（Ⅰ）求角B的大小；（Ⅱ）若，求△ABC的面积．【答案】（Ⅰ）；（Ⅱ）．【解析】（Ⅰ）在解三角形的背景下，考查正弦定理，余弦定理，知值求值．（Ⅱ）综合余弦定理，求三角形的面积公式，需要把作为整体求之．试题解析：（Ⅰ）由正弦定理得将上式代入已知即，即．∵∵∵B为三角形的内角，∴．（Ⅱ）由余弦定理得，结合，可得，所以△ABC的面积．【考点】正弦定理，余弦定理，三角形的面积公式．15.在△中，角，，所对的边分别为，，，表示△的面积，若，，则．【答案】【解析】∵，∴，∴，∴，．∵，∴，∴，∴，∴．【考点】解三角形．【思路点睛】先利用余弦定理和三角形的面积公式可得，可得，再用正弦定理把中的边换成角的正弦，利用两角和公式化简整理可求得，最后根据三角形内角和，进而求得．16.中，角A，B，C的对边分别为a，b，c，若的面积，则 .【答案】【解析】由余弦定理，，又，，，即，，．【考点】1、余弦定理；2、同角三角函数的基本关系；3、三角形面积公式.【思路点睛】本题主要考查的是余弦定理、同角三角函数基本关系、三角形的面积公式，属于容易题.因为题目求，且的面积，边的平方的形式一般想到余弦定理，面积展开后利用余弦定理即可求得与的关系，从而利用同角三角函数的基本关系求得.17.（2012•安徽）设△ABC的内角A、B、C所对边的长分别为a、b、c，且有2sinBcosA=sinAcosC+cosAsinC．（Ⅰ）求角A的大小；（Ⅱ）若b=2，c=1，D为BC的中点，求AD的长．【答案】（Ⅰ）；（Ⅱ）【解析】（Ⅰ）根据2sinBcosA=sinAcosC+cosAsinC，可得2sinBcosA=sin（A+C），从而可得2sinBcosA=sinB，由此可求求角A的大小；（Ⅱ）利用b=2，c=1，A=，可求a的值，进而可求B=，利用D为BC的中点，可求AD的长．解：（Ⅰ）∵2sinBcosA=sinAcosC+cosAsinC∴2sinBcosA=sin（A+C）∵A+C=π﹣B∴sin（A+C）=sinB＞0∴2sinBcosA=sinB∴cosA=∵A∈（0，π）∴A=；（Ⅱ）∵b=2，c=1，A=∴a2=b2+c2﹣2bccosA=3∴b2=a2+c2∴B=∵D为BC的中点，∴AD=．【考点】余弦定理；三角函数的恒等变换及化简求值．18.在中，已知．（Ⅰ）求sinA与角B的值；（Ⅱ）若角A,B,C的对边分别为的值．【答案】（Ⅰ）；（Ⅱ），．【解析】（I）给出了关于角的两个三角函数值，利用诱导公式和同角三角函数的基本关系式可求得其正弦、余弦，再根据三角形的性质可求得的值；（II）在第一问的基础上，利用正弦定理可求得边，再由余弦定理求边，注意利用三角形基本性质舍解．试题解析：（Ⅰ）∵，，又∵，．∵，且，．（Ⅱ）由正弦定理得，，另由得，解得或（舍去），，．【考点】三角函数的诱导公式，同角三角函数的基本关系式及利用正、余弦定理在解三角形．19.已知，则的值为．【答案】．【解析】，故填：．【考点】三角恒等变形．20.在中，角A，B，C的对边分别为，，，若，则角的值为（）A．或B．或C．D．【答案】A．【解析】，，∴或，故选A．【考点】余弦定理．【思路点睛】由已知条件，可先将切化弦，再结合正弦定理，将该恒等式的边都化为角，然后进行三角函数式的恒等变形，找出角之间的关系；或将角都化成边，然后进行代数恒等变形，可一题多解，多角度思考问题，从而达到对知识的熟练掌握．21.为了得到函数的图象，只需把函数图象上的所有点（）A．横坐标缩短到原来的倍，纵坐标不变B．横坐标伸长到原来的2倍，纵坐标不变C．纵坐标缩短到原来的倍，横坐标不变D．纵坐标缩短到原来的2倍，横坐标不变【答案】A【解析】这是一个三角函数的图象变换问题，一般的为了得到函数的图象，只需把函数的图象上所有点的横坐标伸长（）或缩短（）到原来的倍（纵坐标不变）即可，因此为了得到函数的图象，只需把函数图象上的所有点横坐标缩短到原来的倍，纵坐标不变，故选A.【考点】三角函数的图象变换．【方法点睛】本题是一个三角函数的图象变换问题，属于容易题.一般的要得到函数（其中）的图像可按以下步骤进行：先把的图象向左（）或向右（）平移个单位，再将所得函数的图象上各点的横坐标扩大（）或缩小（）为原来的（纵坐标不变），再把所得函数图象上各点的纵坐标扩大（）或缩小（）为原来的倍（横坐标不变），最后再将所得图像向上（）或向下（）平移个单位，即可得到函数的图象.22.如图，在中，，，点在边上，且，.（I）求；（II）求的长.【答案】（Ⅰ）；（Ⅱ），.【解析】（Ⅰ）由图可知，所以，又，所以，再由两角差的正弦公式可求得；（Ⅱ）由题意可用正弦定理、余弦定理即可求出、的长，在中，有，又从而可求得；在中，由余弦定理得，，从而可求出.试题解析：（Ⅰ）在中，因为，所以，所以（Ⅱ）在中，由正弦定理得，在中，由余弦定理得，所以【考点】1.解三角形；2.两角差的正弦公式.23.设的内角对边分别为，已知，且.（1）求角的大小；（2）若向量与共线，求的值.【答案】(1);(2)。

高中数学三角函数及三角恒等变换精选题目(附解析)

高中数学三角函数及三角恒等变换精选题目（附解析）一、三角函数的定义若角α的终边上任意一点P (x ，y )(原点除外)，r ＝|OP |＝x 2＋y 2，则sin α＝y r ，cos α＝x r ，tan α＝y x (x ≠0)．1.已知角α的终边过点P (－3cos θ，4cos θ)，其中θ∈⎝ ⎛⎭⎪⎫π2，π，则sin α＝________，tan α＝________.[解析] ∵θ∈⎝ ⎛⎭⎪⎫π2，π，∴cos θ＜0，∴r ＝x 2＋y 2＝9cos 2θ＋16cos 2θ＝－5cosθ，故sin α＝y r ＝－45，tan α＝y x ＝－43.[答案] －45 －43 注：利用三角函数定义求函数值的方法当已知角的终边所经过的点或角的终边所在的直线时，一般先根据三角函数的定义求这个角的三角函数值，再求其他．但当角经过的点不固定时，需要进行分类讨论．求与正切函数有关问题时，不要忽略正切函数自身的定义域．2．已知点M ⎝ ⎛⎭⎪⎫13，a 在函数y ＝log 3x 的图象上，且角θ的终边所在的直线过点M ，则tan θ＝( )A ．－13 B ．±13 C ．－3D ．±3解析：选C 因为点M ⎝ ⎛⎭⎪⎫13，a 在函数y ＝log 3x 的图象上，所以a ＝log 313＝－1，即M ⎝ ⎛⎭⎪⎫13，－1，所以tan θ＝－113＝－3，故选C.3．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos 2θ＝( )A ．－45B ．－35 C.35D.45解析：选B 在角θ的终边上任取一点P (a,2a )(a ≠0)．则r 2＝|OP |2＝a 2＋(2a )2＝5a 2. 所以cos 2θ＝a 25a 2＝15，cos 2θ＝2cos 2 θ－1＝25－1＝－35.4．若θ是第四象限角，则点P (sin θ，tan θ)在第________象限．解析：∵θ是第四象限角，则sin θ＜0，tan θ＜0， ∴点P (sin θ，tan θ )在第三象限．答案：三二、同角三角函数的基本关系及诱导公式①牢记两个基本关系式sin 2α＋cos 2α＝1及sin αcos α＝tan α，并能应用两个关系式进行三角函数的求值、化简、证明．②诱导公式可概括为k ·π2±α(k ∈Z)的各三角函数值的化简公式．记忆规律是：奇变偶不变，符号看象限．其中的奇、偶是指π2的奇数倍或偶数倍，变与不变是指函数名称的变化．5.已知2＋tan (θ－π)1＋tan (2π－θ)＝－4，求(sin θ－3cos θ)(cos θ－sin θ)的值．[解] 法一：由已知得2＋tan θ1－tan θ＝－4，∴2＋tan θ＝－4(1－tan θ)，解得tan θ＝2.∴(sin θ－3cos θ)(cos θ－sin θ ) ＝4sin θcos θ－sin 2θ－3cos 2θ ＝4sin θcos θ－sin 2θ－3cos 2θsin 2θ＋cos 2θ＝4tan θ－tan2θ－3tan2θ＋1＝8－4－34＋1＝15.法二：由已知得2＋tan θ1－tan θ＝－4，解得tan θ＝2.即sin θcos θ＝2，∴sin θ＝2cos θ.∴(sin θ－3cos θ)(cos θ－sin θ)＝(2cos θ－3cos θ)(cos θ－2cos θ)＝cos2θ＝cos2θsin2θ＋cos2θ＝1tan2θ＋1＝15.注：三角函数式的求值、化简、证明的常用技巧(1)化弦：当三角函数式中三角函数名称较多时，往往把三角函数化为弦，再化简变形．(2)化切：当三角函数式中含有正切及其他三角函数时，有时可将三角函数名称都化为正切，再变形化简．(3)“1”的代换：在三角函数式中，有些会含有常数1，常数1虽然非常简单，但有些三角函数式的化简却需要利用三角函数公式将“1”代换为三角函数式．6．若sin(π＋α)＝35，且α是第三象限角，则sin⎝⎛⎭⎪⎫π2＋α－cos⎝⎛⎭⎪⎫π2＋αsin⎝⎛⎭⎪⎫π2－α－cos⎝⎛⎭⎪⎫π2－α＝()A．1B．7 C．－7 D．－1解析：选B由sin(π＋α)＝35，得sin α＝－35.又α是第三象限角，所以cos α＝－4 5，所以sin⎝⎛⎭⎪⎫π2＋α－cos⎝⎛⎭⎪⎫π2＋αsin⎝⎛⎭⎪⎫π2－α－cos⎝⎛⎭⎪⎫π2－α＝cos α＋sin αcos α－sin α＝－45＋⎝ ⎛⎭⎪⎫－35－45－⎝ ⎛⎭⎪⎫－35＝7.7．已知sin θ＋cos θ＝43，且0＜θ＜π4，则sin θ－cos θ的值为( )A.23 B ．－23 C.13D ．－13解析：选B ∵sin θ＋cos θ＝43，∴1＋2sin θcos θ＝169，则2sin θcos θ＝79.又0＜θ＜π4，所以sin θ－cos θ＜0，故sin θ－cos θ＝－(sin θ－cos θ)2＝－1－2sin θcos θ＝－23，故选B.8．已知α为第三象限角，且sin α＋cos α＝2m,2sin αcos α＝m 2，则m 的值为________．解析：由(sin α＋cos α)2＝1＋2sin αcos α，得4m 2＝1＋m 2，即m 2＝13.又α为第三象限角，所以sin α<0，cos α<0，则m <0，所以m ＝－33.答案：－339．已知sin(3π－α)＝2cos ⎝ ⎛⎭⎪⎫3π2＋β，cos(π－α)＝63cos(π＋β)，且0＜α＜π，0＜β＜π，求sin α和cos β的值．解：由已知，得sin α＝2sin β，① 3cos α＝2cos β，②由①2＋②2，得sin 2α＋3cos 2α＝2，即sin 2α＋3(1－sin 2α)＝2，所以sin 2α＝12. 又0＜α＜π，则sin α＝22. 将sin α＝22代入①，得sin β＝12.又0＜β＜π，故cos β＝±32.三、简单的三角恒等变换两角和与差的正弦、余弦、正切公式 ①sin(α±β)＝sin αcos β±cos αsin β； ②cos(α±β)＝cos αcos β∓sin αsin β； ③tan(α±β)＝tan α±tan β1∓tan αtan β.二倍角的正弦、余弦、正切公式 ①sin 2α＝2sin αcos α；②cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α； ③tan 2α＝2tan α1－tan 2α.10.已知tan α＝2. (1)求tan ⎝ ⎛⎭⎪⎫α＋π4的值；(2)求sin 2αsin 2α＋sin αcos α－cos 2α－1的值．[解] (1)tan ⎝ ⎛⎭⎪⎫α＋π4＝tan α＋tan π41－tan αtan π4＝2＋11－2×1＝－3.(2)sin 2αsin 2α＋sin αcos α－cos 2α－1＝2sin αcos αsin 2α＋sin αcos α－2cos 2α＝2tan αtan 2α＋tan α－2＝2×24＋2－2＝1.注：条件求值的解题策略(1)分析已知角和未知角之间的关系，正确地用已知角来表示未知角． (2)正确地运用有关公式将所求角的三角函数值用已知角的三角函数值来表示．(3)求解三角函数中给值求角的问题时，要根据已知求这个角的某种三角函数值，然后结合角的取值范围，求出角的大小．11．若θ∈⎣⎢⎡⎦⎥⎤π4，π2，sin 2θ＝378，则sin θ＝( )A.35 B.45 C.74D.34解析：选D 因为θ∈⎣⎢⎡⎦⎥⎤π4，π2，所以2θ∈⎣⎢⎡⎦⎥⎤π2，π，所以cos 2θ<0，所以cos 2θ＝－1－sin 22θ＝－18.又cos 2θ＝1－2sin 2θ＝－18，所以sin 2θ＝916，所以sin θ＝34.12．已知sin ⎝ ⎛⎭⎪⎫α＋π3＋sin α＝－435，－π2＜α＜0，则cos ⎝ ⎛⎭⎪⎫α＋8π3等于( )A ．－45 B ．－35 C.35D.45解析：选D 因为sin ⎝ ⎛⎭⎪⎫α＋π3＋sin α＝－435，所以sin ⎝ ⎛⎭⎪⎫α＋π3＋sin ⎝ ⎛⎭⎪⎫α＋π3－π3＝－435，所以sin ⎝ ⎛⎭⎪⎫α＋π3＋sin ⎝ ⎛⎭⎪⎫α＋π3cos π3－cos ⎝ ⎛⎭⎪⎫α＋π3sin π3＝－435，所以32sin ⎝ ⎛⎭⎪⎫α＋π3－32cos ⎝ ⎛⎭⎪⎫α＋π3＝－435，所以－3⎣⎢⎡⎦⎥⎤12cos ⎝ ⎛⎭⎪⎫α＋π3－32sin ⎝ ⎛⎭⎪⎫α＋π3＝－435，即－3cos ⎝ ⎛⎭⎪⎫α＋π3＋π3＝－435，cos ⎝ ⎛⎭⎪⎫α＋2π3＝45，所以cos ⎝ ⎛⎭⎪⎫α＋8π3＝cos ⎝ ⎛⎭⎪⎫α＋2π3＝45，故选D.13．(2017·全国卷Ⅲ)已知sin α－cos α＝43，则sin 2α＝( )A ．－79B ．－29 C.29D.79解析：选A 将sin α－cos α＝43的两边进行平方，得sin 2 α－2sin αcos α＋cos 2α＝169，即sin 2α＝－79.14．已知向量a ＝(1，－3)，b ＝⎝ ⎛⎭⎪⎫sin x ，2cos 2x 2－1，函数f (x )＝a ·b .(1)若f (θ)＝0，求2cos 2θ2－sin θ－12sin ⎝ ⎛⎭⎪⎫θ＋π4的值；(2)当x ∈[0，π]时，求函数f (x )的值域．解：(1)∵a ＝(1，－3)，b ＝⎝ ⎛⎭⎪⎫sin x ，2cos 2x 2－1，∴f (x )＝a ·b ＝sin x －3⎝ ⎛⎭⎪⎫2cos 2x 2－1＝sin x －3cos x .∵f (θ)＝0，即sin θ－3cos θ＝0，∴tan θ＝3，∴2cos 2θ2－sin θ－12sin ⎝ ⎛⎭⎪⎫θ＋π4＝cos θ－sin θsin θ＋cos θ＝1－tan θtan θ＋1＝1－33＋1＝－2＋ 3.(2)由(1)知f (x )＝sin x －3cos x ＝2sin ⎝ ⎛⎭⎪⎫x －π3，∵x ∈[0，π]，∴x －π3∈⎣⎢⎡⎦⎥⎤－π3，2π3，当x －π3＝－π3，即x ＝0时，f (x )min ＝－3；当x －π3＝π2，即x ＝5π6时，f (x )max ＝2，∴当x ∈[0，π]时，函数f (x )的值域为[－3，2]．。

三角函数与三角恒等变换例题与习题

三角函数与三角恒等变换专题复习高考动态 (3)复习建议 (3)专题一：任意角及其三角函数 (4)考点一：终边相同的角的集合 (4)考点二：弧长及面积公式 (6)考点三：任意角的三角函数的定义 (8)考点四：三角函数值的符号及其取值范围 (9)考点五：同角三角函数的基本关系 (11)考点六：诱导公式及其应用 (13)专题二：三角函数的图象与性质 (14)考点一：三角函数的定义域、值域 (14)考点二：三角函数的单调性、周期性 (17)考点三：三角函数的奇偶性、对称性 (20)考点四：三角函数的最值 (22)考点五：三角函数的图象和性质的综合 (24)附1：高考真题回放与示例 (27)附2：高考经典题组训练 (28)专题三：函数y＝A sin(ωx＋φ)的图象与性质 (29)考点一：y＝A sin(ωx＋φ)的图象及平移伸缩变换 (30)考点二：求函数y＝A sin(ωx＋φ)的解析式 (32)考点三：函数y＝A sin(ωx＋φ)的图象与性质的综合应用 (35)考点四：三角函数模型的应用 (38)考点五：三角函数的综合 (40)附1：高考真题回放与示例 (42)附2：高考经典题组训练 (44)专题四：和差角和二倍角的三角函数 (46)概述： (46)公式汇总 (46)考点一：给角求值 (48)考点二：给值求值 (52)考点三：给值求角 (55)考点四：型 (57)考点五：型 (59)熟悉考查内容与形式，从而有效地复习。

①小题，重在基础：三角函数小题考查的重点在于基础知识：解析式、图象及图象变换、两域(定义域、值域)、四性(单调性、奇偶性、对称性、周期性)以及简单的三角变换(求值、化简及比较大小)．②大题，重在本质：有关三角函数的解答题，考查基础知识、基本技能和基本方法．③应用，融入三角形之中：这种考点既能考查解三角形的知识与方法，又能考查运用三角公式进行恒等变换的技能．主要解法是充分利用三角形的内角和定理、正(余)弦定理、面积公式等，并结合三角公式进行三角变换．专题一：任意角及其三角函数任意角的三角函数主要包括，任意角的概念、角度值和弧度制的转换、弧长面积公式、任意角的三角函数的概念、单位圆及其三角函数线、同角三角函数的关系、诱导公式。

高二数学三角函数三角恒等变换解三角形试题答案及解析

高二数学三角函数三角恒等变换解三角形试题答案及解析1.．【答案】【解析】故答案为：．【考点】两角和与差的三角公式．2.若函数在区间上单调递增，则的最小值是（）A．B．C．D．【答案】D【解析】依题意，，令，在区间上，，单调递增，，所以；【考点】1．导数与单调性；2．化归的思想；3.函数在内是（）A．增函数B．减函数C．有增有减D．不能确定【答案】A【解析】函数，可得，所以函数在内是增函数．故选：A．【考点】利用导数研究函数的单调性．4.（12分）．已知在△ABC中，内角A，B，C所对的边长分别为a，b，c，且tan A＋tan B＝．（1）求角B的大小；（2）若，求sinA·sinC的值．【答案】（1）；（2）【解析】（Ⅰ）已知等式左边利用同角三角函数间的基本关系化简，整理后根据sinC不为0求出cosB的值，即可确定出B的度数；（Ⅱ）已知等式去分母整理后得到关系式，利用余弦定理列出关系式，把得出关系式及cosB的值代入，并利用正弦定理化简，即可求出sinAsinC的值试题解析：（Ⅰ）已知等式变形得：sinAcosA+sinBcosB=2sinCcosA，去分母得：sinAcosB+sinBcosA=2sinCcosB，即sin（A+B）=2sinCcosB=sinC，∵sinC≠0，∴cosB=12，则B=60°；（Ⅱ）由，整理得：，∵cosB=12，∴，由正弦定理得：sin2B=2sinA·sinC=，则sinA·sinC=【考点】1．同角间三角函数关系；2．正弦定理5.将函数的图象上所有点的横坐标伸长到原来的倍（纵坐标不变），再将所得图象向左平移个单位，则所得函数图象对应的解析式为（）A．B．C．D．【答案】D【解析】将函数的图象上所有点的横坐标伸长到原来的倍（纵坐标不变），得到函数的图像，再将所得图象向左平移个单位，则所得函数图象对应的解析式为．故选D．【考点】三角函数图像变换：周期变换、左右平移．6.已知在△ABC中,三个内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且,则tanC等于（）A．B．C．D．【答案】C【解析】【考点】1．余弦定理解三角形；2．同角间三角函数关系7.已知在△ABC中，内角A，B，C所对的边长分别为a，b，c，且tan A＋tan B＝．（1）求角B的大小；（2）若＋＝3，求sin Asin C的值．【答案】（1）；（2）【解析】（1）由题意切化弦，同分可得，整理可得，即可求得；（2）根据已知式子同分可得，由余弦定理得到，再结合正弦定理即可得到试题解析：（1）由题意可得：因为，所以，又因为，所以（2）有题意可得：即由余弦定理可得：，得到有正弦定理：【考点】1．正余弦定理；2．化简求值8.（本题满分11分）若的内角所对的边分别为，且满足（1）求；（2）当时，求的面积．【答案】（1）；（2）．【解析】（1）因为正弦定理，所以化为，因为三角形内角有，所以即，所以；（2）由余弦定理，得，而，，得，即，因为三角形的边，所以，则．试题解析：（1）因为由正弦定理，得，又，从而，由于所以（2）解法一：由余弦定理，得，而，，得，即因为，所以，故面积为．解法二：由正弦定理，得从而又由知，所以故，所以面积为．【考点】1．正弦定理与余弦定理；2．三角形的面积公式．9.在中，已知，,则的长为____________________．【答案】【解析】由正弦定理可得【考点】正弦定理解三角形10.（本小题满分10分）在△ABC中，是方程的一个根，（1）求；（2）当时，求△ABC周长的最小值．【答案】（1）（2）【解析】（1）解一元二次方程得到方程的根，结合三角函数有界性得到的值，从而求得大小；（2）由三角形余弦定理结合，可将转化为的表达式，从而求得其最小值，得到周长的最小值试题解析：（1）又是方程的一个根（2）由余弦定理可得：则：当时，c最小且，此时△ABC周长的最小值为．【考点】1．余弦定理解三角形；2．一元二次方程的根11.在△ABC中，角A，B，C所对的边分别为a，b，c，若（b－c）cosA＝acosC，则cosA＝_____【答案】【解析】由正弦定理可将已知条件转化为【考点】正弦定理与三角函数基本公式12.在△ABC中，cosA＝，sinB＝，则cosC的值为．【答案】【解析】由cosA＝，sinB＝得【考点】三角函数基本公式13.在△ABC中，如果，且为锐角，试判断此三角形的形状．【答案】等腰直角三角形．【解析】判定三角形的形状由三角形的三边长或三个角来确定．由可确定．根据正弦定理，可确定角，从而确定三角形的形状．试题解析：因为，所以,又为锐角，所以．，．由正弦定理得：，即展开得：，即，则，所以△ABC是等腰直角三角形．【考点】1．三角形形状；2．正弦定理；14.在△中，分别为角所对的边，若，则此三角形一定是（）A．正三角形B．直角三角形C．等腰三角形D．等腰或直角三角形【答案】C【解析】,三角形为等腰三角形【考点】1．正弦定理解三角形；2．三角函数基本公式15.在中，、、分别是三内角A、B、C的对应的三边，已知（1）求角C的大小；（2）满足的是否存在？若存在，求角A的大小．【答案】（1）；（2）不存在【解析】（1）由正弦定理将变形可得到关于角C的关系式，进而求得角C的大小；（2）结合角C的大小将变形求解A角，若A角存在则三角形存在试题解析：（1）由正弦定理，得因为由则（2）由（1）知，于是=这样的三角形不存在。

三角函数性质与应用例题和知识点总结

三角函数性质与应用例题和知识点总结一、三角函数的基本定义在直角三角形中，正弦（sin）、余弦（cos）和正切（tan）分别定义为：正弦：对边与斜边的比值，即sinθ ＝对边／斜边。

余弦：邻边与斜边的比值，即cosθ ＝邻边／斜边。

正切：对边与邻边的比值，即tanθ ＝对边／邻边。

二、三角函数的性质1、周期性正弦函数和余弦函数的周期都是2π，即 sin(x ＋2π) ＝ sin(x)，cos(x ＋2π) ＝ cos(x)；正切函数的周期是π，即 tan(x ＋π) ＝ tan(x)。

2、奇偶性正弦函数是奇函数，即 sin(x) ＝ sin(x)；余弦函数是偶函数，即cos(x) ＝ cos(x)。

3、值域正弦函数和余弦函数的值域都是－1, 1，正切函数的值域是 R（全体实数）。

4、单调性正弦函数在π/2 ＋2kπ, π/2 ＋2kπ 上单调递增，在π/2 ＋2kπ, 3π/2 ＋2kπ 上单调递减（k∈Z）。

余弦函数在2kπ, π ＋2kπ 上单调递减，在π ＋2kπ, 2π ＋2kπ 上单调递增（k∈Z）。

正切函数在（π/2 ＋kπ, π/2 ＋kπ) 上单调递增（k∈Z）。

三、三角函数的应用例题例 1：已知一个直角三角形的一个锐角为 30°，斜边为 2，求这个直角三角形的两条直角边的长度。

解：因为一个锐角为 30°，所以 sin30°＝ 1/2，cos30°＝√3/2。

设 30°角所对的直角边为 a，邻边为 b，则：a ＝ 2×sin30°＝ 2×（1/2) ＝ 1b ＝ 2×cos30°＝ 2×（√3/2) ＝√3例 2：求函数 y ＝ 2sin(2x ＋π/3) 的最大值和最小值，并求出取得最值时 x 的值。

解：因为正弦函数的值域为－1, 1，所以 2sin(2x ＋π/3) 的值域为－2, 2。

高中数学三角函数经典例题及详解

高中数学三角函数经典例题及详解高中数学三角函数专题复考试要求：三角函数是一类最典型的周期函数。

本单元的研究可以帮助学生在用锐角三角函数刻画直角三角形中边角关系的基础上，借助单位圆建立一般三角函数的概念，体会引入弧度制的必要性。

同时，我们可以利用几何直观和代数运算的方法研究三角函数的周期性、奇偶性（对称性）、单调性和最大（小）值等性质；探索和研究三角函数之间的一些恒等关系；并且利用三角函数构建数学模型，解决实际问题。

内容包括：角与弧度、三角函数概念和性质、同角三角函数的基本关系式、三角恒等变换、三角函数应用。

1）角与弧度了解任意角的概念和弧度制，能进行弧度与角度的互化，体会引入弧度制的必要性。

2）三角函数概念和性质①借助单位圆理解任意角三角函数（正弦、余弦、正切）的定义，能画出这些三角函数的图象，了解三角函数的周期性、奇偶性、最大（小）值。

借助单位圆的对称性，利用定义推导出诱导公式（α±π，α±π的正弦、余弦、正切）。

②借助图象理解正弦函数在[0,2π]上、余弦函数在[0,2π]上、正切函数在(-π/2,π/2)上的性质。

③结合具体实例，了解y=Asin(ωx+φ)的实际意义；能借助图象理解参数ω，φ，A的意义，了解参数的变化对函数图象的影响。

3）同角三角函数的基本关系式理解同角三角函数的基本关系式sinx+cosx=4）三角恒等变换①经历推导两角差余弦公式的过程，知道两角差余弦公式的意义。

②能从两角差的余弦公式推导出两角和与差的正弦、余弦、正切公式，二倍角的正弦、余弦、正切公式，了解它们的内在联系。

③能运用上述公式进行简单的恒等变换（包括推导出积化和差、和差化积、半角公式，这三组公式不要求记忆）。

5）三角函数应用会用三角函数解决简单的实际问题，体会可以利用三角函数构建刻画事物周期变化的数学模型。

经典题型：一、求值化简型这类问题常常用到的公式包括三角函数定义、同角三角函数关系式、诱导公式、和差倍公式、降幂公式、辅助角公式。

(完整版)三角函数知识点及练习题含答案,推荐文档

y
++
o -
-x
y
-+
o -
+
x
y
-+
o +
-
x
、、、、、
、、、、、
、、、、、
6、三角函数线正弦线：MP; 余弦线：OM;
正切线： AT.
a的的的 P、 x,y) r
x
y T
P O M Ax
7. 三角函数的定义域：三角函数 f (x) sinx f (x) cosx f (x) tanx
8．如果 π ＜θ＜ π ，那么下列各式中正确的是( )
4
2
A．cosθ＜tanθ＜sinθ
B．sinθ＜cosθ＜tanθ
C．tanθ＜sinθ＜cosθ
D．cosθ＜sinθ＜tanθ
9．若 A、B 是锐角△ABC 的两个内角，则 P（cosB－sinA，sinB－cosA）在( )
A．第一象限
任意角
1．D 2．Ｃ 3．Ａ 4．Ｄ
三角函数
1．B 2．A 3． C 4．D 5． A 6． C 7．B
11．A
12．±4
4 ±
5
13．［ π ， 3π ］ 14． 0 22
15．二
16．［0， π ］∪（ π ， π ］∪（ 3π ，2π） 17．（ π ， 3π
4
24
2
44
8．D
9． D
10． D
③终边不相同，它们的同名三角函数值一定不相同；
④不相等的角，同名三角函数值也不相同．
其中正确的个数是( )
A．0
B．1
C．2
D．3
2．若角 α、β 的终边关于 y 轴对称，则下列等式成立的是( )

2023年高考数学二轮复习热点重点难点专练——三角函数定义与三角函数恒等变换(含答案解析)

重难点10三角函数定义与三角函数恒等变换1.三角函数的定义中常见的三种题型及解决方法(1)已知角α的终边上的一点P的坐标，求角α的三角函数值．方法：先求出点P到原点的距离，再利用三角函数的定义求解．(2)已知角α的一个三角函数值和终边上一点P的横坐标或纵坐标，求与角α有关的三角函数值．方法：先求出点P到原点的距离(带参数)，根据已知三角函数值及三角函数的定义建立方程，求出未知数，从而求解问题．(3)已知角α的终边所在的直线方程(y＝kx，k≠0)，求角α的三角函数值．方法：先设出终边上一点P(a，ka)，a≠0，求出点P到原点的距离(注意a的符号，对a 分类讨论)，再利用三角函数的定义求解．2.对sinα，cosα，tanα的知一求二问题(1)利用sin2α＋cos2α＝1可实现α的正弦、余弦的互化，利用sinαcosα＝tanα可以实现角α的弦切互化．(2)由一个角的任意一个三角函数值可求出这个角的另外两个三角函数值，因为利用“平方关系”公式求平方根，会出现两解，需根据角所在的象限判断符号，当角所在的象限不明确时，要进行分类讨论．3.利用诱导公式把任意角的三角函数转化为锐角三角函数的步骤任意负角的三角函数――――――→利用诱导公式三或一任意正角的三角函数――――――――→利用诱导公式一0～2π的角的三角函数――――――――→利用诱导公式二或四或五锐角三角函数也就是：“负化正，大化小，化到锐角就好了”．4．三角函数式化简的原则和方向(1)切化弦，统一名．(2)用诱导公式，统一角．(3)用因式分解将式子变形，化为最简．也就是：“统一名，统一角，同角名少为终了”．5.三角函数式求值的三种题型(1)给角求值：该类问题中给出的角一般都不是特殊角，需要通过三角恒等变换将其变为特殊角，或者能够正负相消，或者能够约分相消，最后得到具体的值．(2)给值求值：一般是给出某些角的三角函数值，求另外一些角的三角函数值，解题的关键在于“变角”，使相关角相同或具有某种关系．(3)给值求角：实质上可转化为“给值求值”，即通过求角的某一个三角函数值来求角．在选取函数时，遵循以下原则：①已知正切函数值，选正切函数．②已知正弦、余弦函数值，若角的范围是0，π2，选正弦、余弦函数皆可，若角的范围是(0，π)，选余弦函数，若角的范围是－π2，π2，选正弦函数．2023年高考仍将重点考查同角三角函数基本关系及三角恒等变换，同时要注意三角函数定义的复习，题型仍为选择题或填空题，难度为基础题或中档题.（建议用时：40分钟）一、单选题1．sin 20cos 70sin10sin 50︒︒+︒︒的值是（）A ．14B ．32C ．12D ．342．设θ是第二象限的角，则必有（）A ．tancot 22θθ>B ．tancot22θθ<C ．sincos22θθ>D ．sincos22θθ<3．已知2sin 23α=，(0,)απ∈，则sin cos αα+=（）A ．153B ．153-C ．53D ．53-4．已知2sin 23α=，则2cos 4πα⎛⎫+ ⎪⎝⎭=（）A ．16B ．15C ．14D ．135．函数2cos 3cos 2y x x =-+的最小值为（）A ．2B ．0C ．14-D ．66．已知πsin sin =31θθ⎛⎫++ ⎪⎝⎭，则πsin =6θ⎛⎫+ ⎪⎝⎭（）A ．12B ．33C ．23D ．227．已知2tan θ–tan(θ+π4)=7，则tan θ=（）A ．–2B ．–1C ．1D ．28．已知α为第二象限角，3sin 5α=，则sin 2α=.A ．2425-B ．1225-C ．1225D ．24259．已知4sin cos 3αα-=，则sin 2α=．A ．79-B ．29-C ．29D ．7910．已知θ是第三象限的角，且445sin cos 9+=θθ，那么sin 2θ的值为A ．223B ．223-C ．23D ．23-11．4cos50°﹣tan40°=（）A ．2B ．232+C ．3D ．221-12．已知角θ的顶点与原点重合，始边与横轴的正半轴重合，终边在直线y=2x 上，则cos 2θ=（）A ．35-B ．45-C ．23D ．34二、填空题13．如果12cos 13θ=-，3π,π2θ⎛⎫∈ ⎪⎝⎭，那么πcos 4θ⎛⎫+ ⎪⎝⎭=_______．14．已知2sin ()4πα+=23，则sin 2α的值是____.15．在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称.若1sin 3α=，则cos()αβ-=___________.16．若3sin sin 10,2παβαβ-=+=，则sin α=__________，cos 2β=_________．三、解答题17．已知A 、B 、C 是ABC 三内角，向量(1,3),(cos ,sin )m n A A =-= ，且1m n ⋅=．(1)求角A ；(2)若221sin 23cos sin BB B+=--，求tan C ．18．已知函数()2sin cos cos 2f x x x x =+．(1)求π4f ⎛⎫⎪⎝⎭的值；(2)设2(0,π),22f αα⎛⎫∈= ⎪⎝⎭，求sin α的值．重难点10三角函数定义与三角函数恒等变换1.三角函数的定义中常见的三种题型及解决方法(1)已知角α的终边上的一点P 的坐标，求角α的三角函数值．方法：先求出点P 到原点的距离，再利用三角函数的定义求解．(2)已知角α的一个三角函数值和终边上一点P 的横坐标或纵坐标，求与角α有关的三角函数值．方法：先求出点P到原点的距离(带参数)，根据已知三角函数值及三角函数的定义建立方程，求出未知数，从而求解问题．(3)已知角α的终边所在的直线方程(y＝kx，k≠0)，求角α的三角函数值．方法：先设出终边上一点P(a，ka)，a≠0，求出点P到原点的距离(注意a的符号，对a 分类讨论)，再利用三角函数的定义求解．2.对sinα，cosα，tanα的知一求二问题(1)利用sin2α＋cos2α＝1可实现α的正弦、余弦的互化，利用sinαcosα＝tanα可以实现角α的弦切互化．(2)由一个角的任意一个三角函数值可求出这个角的另外两个三角函数值，因为利用“平方关系”公式求平方根，会出现两解，需根据角所在的象限判断符号，当角所在的象限不明确时，要进行分类讨论．3.利用诱导公式把任意角的三角函数转化为锐角三角函数的步骤任意负角的三角函数――――――→利用诱导公式三或一任意正角的三角函数――――――――→利用诱导公式一0～2π的角的三角函数――――――――→利用诱导公式二或四或五锐角三角函数也就是：“负化正，大化小，化到锐角就好了”．4．三角函数式化简的原则和方向(1)切化弦，统一名．(2)用诱导公式，统一角．(3)用因式分解将式子变形，化为最简．也就是：“统一名，统一角，同角名少为终了”．5.三角函数式求值的三种题型(1)给角求值：该类问题中给出的角一般都不是特殊角，需要通过三角恒等变换将其变为特殊角，或者能够正负相消，或者能够约分相消，最后得到具体的值．(2)给值求值：一般是给出某些角的三角函数值，求另外一些角的三角函数值，解题的关键在于“变角”，使相关角相同或具有某种关系．(3)给值求角：实质上可转化为“给值求值”，即通过求角的某一个三角函数值来求角．在选取函数时，遵循以下原则：①已知正切函数值，选正切函数．②已知正弦、余弦函数值，若角的范围是0，π2，选正弦、余弦函数皆可，若角的范围是(0，π)，选余弦函数，若角的范围是－π2，π2，选正弦函数．2023年高考仍将重点考查同角三角函数基本关系及三角恒等变换，同时要注意三角函数定义的复习，题型仍为选择题或填空题，难度为基础题或中档题.（建议用时：40分钟）一、单选题1．sin 20cos 70sin10sin 50︒︒+︒︒的值是（）A ．14B ．32C ．12D ．34【答案】A【解析】()()11sin 20cos70sin10sin 50sin 90sin 50cos60cos 4022︒︒+︒︒=︒+-︒-︒+-︒⎡⎤⎡⎤⎣⎦⎣⎦1111sin 50cos 402242=-︒-+︒111cos 40cos 40422=-︒+︒14=.故选：A.2．设θ是第二象限的角，则必有（）A ．tancot 22θθ>B ．tancot22θθ<C ．sincos22θθ>D ．sincos22θθ<【答案】A【解析】22sin cos sin cos cos 22222tancot122tan cossincos sin sin 22222θθθθθθθθθθθθθ---=-===- θ是第二象限的角，tan 0,sin 0,cos 0θθθ∴<><，即2tancot 022tan θθθ-=->，tancot 22θθ∴>，A 正确，B 错误;θ是第二象限的角，即(2,2)(),2k k k Z πθπππ∈++∈(,)()242k k k Z θππππ∴∈++∈当(2,2)()242k k k Z θππππ∈++∈时，22sin cos cos 022θθθ-=->，可得sin cos 022θθ>>，D 错误；当53(2,2)()242k k k Z θππππ∈++∈时，22sin cos cos 022θθθ-=->，可得sincos 022θθ<<，C 错误；故选：A.3．已知2sin 23α=，(0,)απ∈，则sin cos αα+=（）A ．153B ．153-C ．53D ．53-【答案】A【解析】由2sin 22sin cos 03ααα==>，又(0,)απ∈，所以π(0,)2α∈，所以sin cos 0αα+>，又()25sin cos 12sin cos 3αααα+=+=，所以3sin co 5s 1αα+=或3sin cos 15αα+=-（舍去），所以3sin co 5s 1αα+=.故选：A ．4．已知2sin 23α=，则2cos 4πα⎛⎫+ ⎪⎝⎭=（）A ．16B ．15C ．14D ．13【答案】A 【解析】21cos(2)2cos ()42παπα+++==1sin 22α-=2132-=16,故选A.5．函数2cos 3cos 2y x x =-+的最小值为（）A ．2B ．0C ．14-D ．6【答案】B【解析】因为2cos 3cos 2y x x =-+，设cos t x =，则()223132()1124y t t t t =-+=---≤≤，由二次函数性质可得当[]1,1t ∈-上单调递减，所以当1t =，()23211y t t t =-+-≤≤取最小值，最小值为0，故当2,Zx k k π=∈时，函数2cos 3cos 2y x x =-+取最小值，最小值为0，故选：B.6．已知πsin sin =31θθ⎛⎫++ ⎪⎝⎭，则πsin =6θ⎛⎫+ ⎪⎝⎭（）A ．12B ．33C ．23D ．22【答案】B【解析】由题意可得：13sin sin cos 122θθθ++=，则：33sin cos 122θθ+=，313sin cos 223θθ+=，从而有：3sin coscos sin663ππθθ+=，即3sin 63πθ⎛⎫+= ⎪⎝⎭.故选：B.7．已知2tan θ–tan(θ+π4)=7，则tan θ=（）A ．–2B ．–1C ．1D ．2【答案】D【解析】2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭ ，tan 12tan 71tan θθθ+∴-=-，令tan ,1t t θ=≠，则1271tt t+-=-，整理得2440t t -+=，解得2t =，即tan 2θ=.故选：D.8．已知α为第二象限角，3sin 5α=，则sin 2α=.A ．2425-B ．1225-C ．1225D ．2425【答案】A【解析】因为α为第二象限，所以cos 0α<，即24cos 1sin 5αα=--=-，所以4324sin 22sin cos 25525ααα==-⨯⨯=-，选A.9．已知4sin cos 3αα-=，则sin 2α=．A ．79-B ．29-C ．29D ．79【答案】A【解析】()2sin cos 17sin 22sin cos 19ααααα--===--.所以选A.10．已知θ是第三象限的角，且445sin cos 9+=θθ，那么sin 2θ的值为A ．223B ．223-C ．23D ．23-【答案】A【解析】∵22sin cos 1θθ+=，∴4422sin cos 2sin cos 1θθθθ++=，∵445sin cos 9+=θθ，∴2242sin cos 9θθ=，∵角是第三象限角即322,2k k k Z ππθππ+<<+∈，∴24234,k k k Z ππθππ+<<+∈，∴22sin 23θ=，故选A ．11．4cos50°﹣tan40°=（）A ．2B ．232+C ．3D ．221-【答案】C【解析】4cos50°﹣tan40°=4sin40°﹣tan40°======．故选C12．已知角θ的顶点与原点重合，始边与横轴的正半轴重合，终边在直线y=2x 上，则cos 2θ=（）A ．35-B ．45-C ．23D ．34【答案】A【解析】找θ角终边上一点(1,2)，则25sin 5θ=，5cos 5θ=，所以223cos 2cos sin 5θθθ=-=-故选A.二、填空题(共0分)13．如果12cos 13θ=-，3π,π2θ⎛⎫∈ ⎪⎝⎭，那么πcos 4θ⎛⎫+ ⎪⎝⎭=_______．【答案】7226-【解析】因12cos 13θ=-，3π,π2θ⎛⎫∈ ⎪⎝⎭，则25sin 1cos 13θθ=--=-，所以πππ122527cos cos cos sin sin 244413213226θθθ⎛⎫⎛⎫+=-=-⨯--⨯=- ⎪ ⎪⎝⎭⎝⎭.故答案为：7226-14．已知2sin ()4πα+=23，则sin 2α的值是____.【答案】13【解析】22221sin ()(cos sin )(1sin 2)4222παααα+=+=+Q 121(1sin 2)sin 2233αα∴+=∴=故答案为：1315．在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称.若1sin 3α=，则cos()αβ-=___________.【答案】79-【解析】试题分析：因为α和β关于y 轴对称，所以π2π,k k αβ+=+∈Z ，那么1sin sin 3βα==，22cos cos 3αβ=-=（或22cos cos 3βα=-=），所以()2227cos cos cos sin sin cos sin 2sin 19αβαβαβααα-=+=-+=-=-.16．若3sin sin 10,2παβαβ-=+=，则sin α=__________，cos 2β=_________．【答案】3101045【解析】[方法一]：利用辅助角公式处理∵2παβ+=，∴sin cos βα=，即3sin cos 10αα-=，即3101010sin cos 101010αα⎛⎫-= ⎪ ⎪⎝⎭，令10sin 10θ=，310cos 10θ=，则()10sin 10αθ-=，∴22k k Z παθπ-=+∈，，即22k παθπ=++，∴310sin sin 2cos 210k παθπθ⎛⎫=++== ⎪⎝⎭，则224cos 22cos 12sin 15ββα=-=-=.故答案为：31010；45.[方法二]：直接用同角三角函数关系式解方程∵2παβ+=，∴sin cos βα=，即3sin cos 10αα-=，又22sin cos 1αα+=，将cos 3sin 10αα=-代入得210sin 610sin 90αα-+=，解得310sin 10α=，则224cos 22cos 12sin 15ββα=-=-=.故答案为：31010；45.三、解答题17．已知A 、B 、C 是ABC 三内角，向量(1,3),(cos ,sin )m n A A =-= ，且1m n ⋅= ．(1)求角A ；(2)若221sin 23cos sin B B B+=--，求tan C ．【答案】(1)π3A =；(2)853tan 11C +=.【解析】（1）∵1m n ⋅= ，∴(1,3)(cos ,sin )1A A -⋅=，即cos 3sin 1A A -+=，312(sin cos )122A A -=，1sin()62A π-=，∵0πx <<，ππ5π666A -<-<，∴ππ66A -=，∴π3A =；（2）由题知：2212sin cos 3cos sinB B B B +=--，所以()2222sin cos 2sin cos 3cos sin B B B B B B ++=--整理得22sin sin cos 2cos 0B B B B --=，∴cos 0B ≠，∴2tan tan 20B B --=，∴tan 2B =或tan 1B =-，而tan 1B =-时，22cos sin 0B B -=，与已知矛盾，舍去，∴tan 2B =，∴tan tan 23853tan tan[()]tan()1tan tan 11123A B C A B A B A B π+++=-+=-+=-=-=--．18．已知函数()2sin cos cos 2f x x x x =+．(1)求π4f ⎛⎫ ⎪⎝⎭的值；(2)设2(0,π),22f αα⎛⎫∈= ⎪⎝⎭，求sin α的值．【答案】(1)1(2)264+【解析】（1）由已知，函数()2sin cos cos 2sin 2cos 2f x x x x x x =+=+，所以πππsin cos 101422f ⎛⎫=+=+= ⎪⎝⎭.（2）π()sin 2cos 22sin 24f x x x x ⎛⎫=+=+ ⎪⎝⎭，所以π2π12sin sin 24242f ααα⎛⎫⎛⎫⎛⎫=+=⇒+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，因为()0,πα∈，所以ππ5π,444α⎛⎫+∈ ⎪⎝⎭，所以2ππ3cos 1sin 442αα⎛⎫⎛⎫+=±-+=± ⎪ ⎪⎝⎭⎝⎭，①当π3cos 42α⎛⎫+= ⎪⎝⎭时，ππππππ26sin sin sin cos cos sin 4444444αααα⎡⎤-⎛⎫⎛⎫⎛⎫=+-=+-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦而当()0,πα∈时，sin 0α>，所以此种情况不成立；②当π3cos 42α⎛⎫+=- ⎪⎝⎭时，ππππππ26sin sin sin cos cos sin 4444444αααα⎡⎤+⎛⎫⎛⎫⎛⎫=+-=+-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.所以sin α的值为264+.。

专题练第12练三角函数的概念与三角恒等变换

第12练三角函数的概念与三角恒等变换1．(2021·北京)函数f (x )＝cos x －cos 2x ，试判断函数的奇偶性及最大值( ) A ．奇函数，最大值为2 B ．偶函数，最大值为2 C ．奇函数，最大值为98D ．偶函数，最大值为98答案 D解析由题意，f (－x )＝cos(－x )－cos(－2x ) ＝cos x －cos 2x ＝f (x )，所以该函数为偶函数，又f (x )＝cos x －cos 2x ＝－2cos 2x ＋cos x ＋1 ＝－2⎝⎛⎭⎫cos x －142＋98，所以当cos x ＝14时，f (x )取最大值98.2．(2021·全国甲卷)若α∈⎝⎛⎭⎫0，π2，tan 2α＝cos α2－sin α，则tan α等于( ) A.1515 B.55 C.53 D.153答案 A解析方法一因为tan 2α＝sin 2αcos 2α＝2sin αcos α1－2sin 2α，且tan 2α＝cos α2－sin α，所以2sin αcos α1－2sin 2α＝cos α2－sin α，解得sin α＝14.因为α∈⎝⎛⎭⎫0，π2，所以cos α＝154，tan α＝sin αcos α＝1515. 方法二因为tan 2α＝2tan α1－tan 2α＝2sin αcos α1－sin 2αcos 2α＝2sin αcos αcos 2α－sin 2α＝2sin αcos α1－2sin 2α，且tan 2α＝cos α2－sin α，所以2sin αcos α1－2sin 2α＝cos α2－sin α，解得sin α＝14.因为α∈⎝⎛⎭⎫0，π2，所以cos α＝154，tan α＝sin αcos α＝1515. 3．(2020·全国Ⅰ)已知α∈(0，π)，且3cos 2α－8cos α＝5，则sin α等于( ) A.53 B.23 C.13 D.59答案 A解析由3cos 2α－8cos α＝5，得3(2cos 2α－1)－8cos α＝5，即3cos 2α－4cos α－4＝0，解得cos α＝－23或cos α＝2(舍去)．又因为α∈(0，π)，所以sin α>0，所以sin α＝1－cos 2α＝1－⎝⎛⎭⎫－232＝53. 4．(2018·全国Ⅰ)已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点A (1，a )，B (2，b )，且cos 2α＝23，则|a －b |等于( )A.15B.55C.255 D ．1 答案 B解析由cos 2α＝23，得cos 2α－sin 2α＝23，∴cos 2α－sin 2αcos 2α＋sin 2α＝23，又cos α≠0，∴1－tan 2α1＋tan 2α＝23，∴tan α＝±55，即b －a 2－1＝±55，∴|a －b |＝55. 5．(2022·新高考全国Ⅱ)若sin(α＋β)＋cos(α＋β)＝22cos ⎝⎛⎭⎫α＋π4sin β，则( ) A ．tan(α－β)＝1 B ．tan(α＋β)＝1 C ．tan(α－β)＝－1 D ．tan(α＋β)＝－1 答案 C解析由题意得sin αcos β＋cos αsin β＋cos αcos β－sin αsin β＝22×22(cos α－sin α)·sin β，整理得sin αcos β－cos αsin β＋cos αcos β＋sin αsin β＝0，即sin(α－β)＋cos(α－β)＝0，所以tan(α－β)＝－1，故选C.6．(多选)(2021·新高考全国Ⅰ)已知O 为坐标原点，点P 1(cos α，sin α)，P 2(cos β，－sin β)，P 3(cos(α＋β)，sin(α＋β))，A (1,0)，则( ) A ．|OP 1―→|＝|OP 2―→| B ．|AP 1―→|＝|AP 2―→| C.OA →·OP 3―→＝OP 1―→·OP 2―→ D.OA →·OP 1―→＝OP 2―→·OP 3―→ 答案 AC解析由题意可知， |OP 1―→|＝cos 2α＋sin 2α＝1， |OP 2―→|＝cos 2β＋(－sin β)2＝1，所以|OP 1―→|＝|OP 2―→|，故A 正确；取α＝π4，则P 1⎝⎛⎭⎫22，22，取β＝5π4，则P 2⎝⎛⎭⎫－22，22，则|AP 1―→|≠|AP 2―→|，故B 错误；因为OA →·OP 3―→＝cos(α＋β)，OP 1―→·OP 2―→＝cos αcos β－sin αsin β＝cos(α＋β)，所以OA →·OP 3―→＝OP 1―→·OP 2―→，故C 正确；因为OA →·OP 1―→＝cos α，OP 2―→·OP 3―→＝cos βcos(α＋β)－sin βsin(α＋β) ＝cos(α＋2β)，取α＝π4，β＝π4，则OA →·OP 1―→＝22，OP 2―→·OP 3―→＝cos 3π4＝－22，所以OA →·OP 1―→≠OP 2―→·OP 3―→，故D 错误．7．(2022·北京)若函数f (x )＝A sin x －3cos x 的一个零点为π3，则A ＝________；f ⎝⎛⎭⎫π12＝________. 答案 1 － 2解析依题意得f ⎝⎛⎭⎫π3＝A ×32－3×12＝0，解得A ＝1，所以f (x )＝sin x －3cos x ＝2sin ⎝⎛⎭⎫x －π3，所以f ⎝⎛⎭⎫π12＝2sin ⎝⎛⎭⎫π12－π3＝2sin ⎝⎛⎭⎫－π4＝－ 2. 8．(2020·江苏)已知sin 2⎝⎛⎭⎫π4＋α＝23，则sin 2α的值是________．答案 13解析因为sin 2⎝⎛⎭⎫π4＋α＝23，所以1－cos ⎝⎛⎭⎫π2＋2α2＝23，即1＋sin 2α2＝23，所以sin 2α＝13.9．(2022·枣庄模拟)已知sin ⎝⎛⎭⎫π6－α＝23，则cos ⎝⎛⎭⎫2α－4π3等于( ) A ．－59 B.59 C ．－13 D.13答案 A解析 cos ⎝⎛⎭⎫2α－4π3＝cos ⎝⎛⎭⎫－π＋2α－π3 ＝－cos ⎝⎛⎭⎫2α－π3＝－cos ⎝⎛⎭⎫π3－2α ＝－⎣⎡⎦⎤1－2sin 2⎝⎛⎭⎫π6－α ＝－⎝⎛⎭⎫1－2·29＝－59. 10．(2022·南京师大附中模拟)已知sin x ＋cos x ＝－15，则cos 2x 等于( )A ．－2425B.725 C ．－725D ．±725答案 D解析因为sin x ＋cos x ＝－15，故(sin x ＋cos x )2＝125，所以2sin x cos x ＝－2425，故x 为第二或第四象限角，则(sin x －cos x )2＝4925，故sin x －cos x ＝±75，即cos x －sin x ＝±75，所以cos 2x ＝cos 2x －sin 2x＝(cos x ＋sin x )(cos x －sin x )＝±725.11．(2022·淄博模拟)cos 10°2sin 10°－2cos 10°等于( )A.32B. 2C. 3 D ．2 答案 A 解析cos 10°2sin 10°－2cos 10°＝cos 10°－4sin 10°cos 10°2sin 10°＝cos 10°－2sin 20°2sin 10°＝cos 10°－2sin (30°－10°)2sin 10°＝cos 10°－(cos 10°－3sin 10°)2sin 10°＝32.12．(2022·潍坊模拟)在平面直角坐标系Oxy 中，若角α的顶点在坐标原点，始边在x 轴的正半轴上，且终边经过点P (－1,2)，则sin α(1＋sin 2α)sin α＋cos α等于( )A ．－65B ．－25 C.25 D.65答案 C解析因为角α的终边经过点P (－1,2)，所以x ＝－1，y ＝2，r ＝|OP |＝5，所以sin α＝y r ＝255，cos α＝x r ＝－55，则sin 2α＝2sin αcos α＝－45，故sin α(1＋sin 2α)sin α＋cos α＝25×⎝⎛⎭⎫1－45555＝25. 13．(多选)(2022·重庆巴蜀中学模拟)已知f (x )＝5sin x ＋12cos x (x ∈R )在x ＝x 0处取得最大值a ，则( ) A ．a ＝13B ．f ⎝⎛⎭⎫x 0＋π2＝－13C ．sin x 0＝513D ．cos ⎝⎛⎭⎫2x 0＋π4＝－2338 答案 ACD解析由题设知f (x )＝13sin(x ＋φ)且sin φ＝1213，cos φ＝513，则f (x 0)＝13sin(x 0＋φ)＝a ＝13，A正确；所以sin(x 0＋φ)＝1，而f ⎝⎛⎭⎫x 0＋π2＝13sin ⎝⎛⎭⎫x 0＋π2＋φ ＝13cos(x 0＋φ)＝0，B 错误；由上知x 0＝2k π＋π2－φ且k ∈Z ，则sin x 0＝sin ⎝⎛⎭⎫π2－φ＝cos φ＝513，C 正确；同理cos x 0＝1213，则cos ⎝⎛⎭⎫2x 0＋π4＝22(cos 2x 0－sin 2x 0)＝22(2cos 2x 0－1－2sin x 0cos x 0) ＝－2338，D 正确．14．(2022·潮汕模拟)小说《三体》中的“水滴”是三体文明派往太阳系的探测器，由强相互作用力材料制成，被形容为“像一滴圣母的眼泪”．小刘是《三体》的忠实读者，他利用几何作图软件画出了他心目中的水滴(如图)，由线段AB ，AC 和优弧BC 围成，其中BC 连线竖直，AB ，AC 与圆弧相切，已知“水滴”的水平宽度与竖直高度之比为74，则cos ∠BAC 等于( )A.1725B.437C.45D.57 答案 A解析设优弧BC 的圆心为O ，半径为R ，连接OA ，OB ，OC ，如图所示，易知“水滴”的水平宽度为|OA |＋R ，竖直高度为2R ，则由题意知|OA |＋R 2R ＝74，解得|OA |＝52R ，AB 与圆弧相切于点B ，则OB ⊥AB ，在Rt △ABO 中，sin ∠BAO ＝|OB ||OA |＝R 52R ＝25，由对称性可知∠BAO ＝∠CAO ，则∠BAC ＝2∠BAO ， ∴cos ∠BAC ＝1－2sin 2∠BAO ＝1－2×⎝⎛⎭⎫252＝1725.15．(2022·宜宾模拟)已知tan α＋tan β＝3，cos αcos β＝14，则sin(α＋β)＝________.答案 34解析 tan α＋tan β＝sin αcos β＋cos αsin βcos αcos β＝3，因为cos αcos β＝14，所以sin αcos β＋cos αsin β＝sin(α＋β) ＝3cos αcos β＝34.16．(2022·陕西宝鸡中学模拟)sin(θ＋75°)＋cos(θ＋45°)－3cos(θ＋15°)＝________. 答案 0解析 sin(θ＋75°)＋cos(θ＋45°)－3cos(θ＋15°) ＝sin(θ＋15°＋60°)＋cos(θ＋45°)－3cos(θ＋15°)＝sin(θ＋15°)cos 60°＋cos(θ＋15°)sin 60°＋cos(θ＋45°)－3cos(θ＋15°) ＝12sin(θ＋15°)＋32cos(θ＋15°)＋cos(θ＋45°)－3cos(θ＋15°)＝12sin(θ＋15°)－32cos(θ＋15°)＋cos(θ＋45°) ＝sin 30°sin(θ＋15°)－cos 30°cos(θ＋15°)＋cos(θ＋45°) ＝－cos(θ＋45°)＋cos(θ＋45°)＝0.[考情分析] 三角函数的概念与三角恒等变换是高考常考内容，主要考查三角函数的概念、同角三角函数关系式、诱导公式，以及三角恒等变换的综合应用，给值求值问题．试题难度中等，常以选择题、填空题的形式出现．一、三角函数的定义、诱导公式及基本关系式核心提炼1．同角三角函数基本关系式：sin 2α＋cos 2α＝1，sin αcos α＝tan α⎝⎛⎭⎫α≠k π＋π2，k ∈Z . 2．(sin α±cos α)2＝1±2sin αcos α.3．诱导公式：在k π2＋α，k ∈Z 的诱导公式中“奇变偶不变，符号看象限”．练后反馈题目 4 8 9 10 13 正误错题整理：二、两角和与差的三角函数核心提炼两角和与差的正弦、余弦、正切公式： sin(α±β)＝sin αcos β±cos αsin β； cos(α±β)＝cos αcos β∓sin αsin β； tan(α±β)＝tan α±tan β1∓tan αtan β.练后反馈题目 5 6 7 11 15 16 正误错题整理：三、三角恒等变换核心提炼1．二倍角公式：sin 2α＝2sin αcos α，cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α，tan 2α＝2tan α1－tan 2α.2．半角公式：sin α2＝±1－cos α2，cos α2＝±1＋cos α2，tan α2＝±1－cos α1＋cos α＝sin α1＋cos α＝1－cos αsin α. 3．辅助角公式：a sin x ＋b cos x ＝a 2＋b 2sin(x ＋φ)，其中tan φ＝ba .练后反馈题目 1 2 3 12 14 正误错题整理：1．[T3补偿](2022·西安模拟)已知θ∈⎝⎛⎭⎫3π2，2π，且cos 2θ＋cos θ＝0，则sin 2θ＋sin θ等于( ) A ．0 B. 3 C ．－ 3 D ．2 答案 C解析由cos 2θ＋cos θ＝0，得2cos 2θ＋cos θ－1＝0，即(cos θ＋1)(2cos θ－1)＝0，因为θ∈⎝⎛⎭⎫3π2，2π，所以cos θ>0，进而得cos θ＝12，故θ＝5π3，所以sin 2θ＋sin θ＝sin 10π3＋sin 5π3＝sin 4π3＋sin ⎝⎛⎭⎫－π3＝－2sin π3＝－ 3.2．[T4补偿](2022·郑州模拟)已知α∈⎝⎛⎭⎫0，π2，且sin 2α＋sin 2α＝710，则cos 2α等于( ) A.35 B.45 C ．－35 D ．－45答案 B解析依题意知，2sin αcos α＋sin 2αsin 2α＋cos 2α＝710，即2tan α＋tan 2αtan 2α＋1＝710，整理得3tan 2α＋20tan α－7＝0，因为α∈⎝⎛⎭⎫0，π2，即tan α>0，解得tan α＝13，所以cos 2α＝cos 2α－sin 2αcos 2α＋sin 2α＝1－tan 2α1＋tan 2α＝45. 3．[T12补偿](2022·长春模拟)已知角α的终边与单位圆交于点P ⎝⎛⎭⎫63，－33，则sin ⎝⎛⎭⎫π2－α＋cos(π－2α)等于( )A ．－33 B.6＋13 C.33 D.6－13 答案 D解析由已知sin ⎝⎛⎭⎫π2－α＋cos(π－2α) ＝cos α－cos 2α，因为角α的终边与单位圆交于点P ⎝⎛⎭⎫63，－33，所以cos α＝63⎝⎛⎭⎫632＋⎝⎛⎭⎫－332＝63， cos 2α＝2cos 2α－1＝13，所以cos α－cos 2α＝63－13＝6－13. 4．[T10补偿](2022·毕节模拟)函数f (x )＝sin x ＋cos x ＋sin 2x 的最大值为( )A ．1B ．1－ 2C ．1＋ 2D ．3答案 C解析 f (x )＝sin x ＋cos x ＋sin 2x＝sin x ＋cos x ＋2sin x cos x ，令t ＝sin x ＋cos x ＝2sin ⎝⎛⎭⎫x ＋π4，所以t ∈[－2，2]，则t 2＝(sin x ＋cos x )2＝1＋2sin x cos x ，所以2sin x cos x ＝t 2－1，所以原函数可化为y ＝t 2＋t －1，t ∈[－2，2]，对称轴为t ＝－12，所以当t ＝2时，y ＝t 2＋t －1取得最大值，所以函数f (x )的最大值为(2)2＋2－1＝1＋2，即f (x )＝sin x ＋cos x ＋sin 2x 的最大值为1＋ 2.5．[T9补偿](2022·衡水模拟)已知sin ⎝⎛⎭⎫α＋π6＝－13，则cos ⎝⎛⎭⎫4π3－α＝________. 答案 13解析 cos ⎝⎛⎭⎫4π3－α＝－cos ⎝⎛⎭⎫π3－α ＝－cos ⎝⎛⎭⎫π2－α－π6 ＝－sin ⎝⎛⎭⎫α＋π6＝13. 6．[T11补偿](2022·淄博模拟)sin 12°(2cos 212°－1)3－tan 12°＝________. 答案 18解析因为sin 12°(2cos 212°－1)3－tan 12° ＝sin 12°cos 12°cos 24°3cos 12°－sin 12°＝14sin 48°2sin 48°＝18.。

三角函数典型例题分析

三角函数典型例题分析目录0°～360°间的三角函数.典型例题分析 (3)弧度制.典型例题分析 (3)任意角的三角函数.典型例题分析一 (5)任意角的三角函数.典型例题精析二 (7)同角三角函数的基本关系式.典型例题分析 ............................. 诱导公式.典型例题分析............................................. 用单位圆中的线段表示三角函数值.典型例题分析 ....................... 三角公式总表....................................................... 正弦函数、余弦函数的图象和性质.典型例题分析 (28)函数y=Asin(wx+j)的图象·典型例题分析............................... 正切函数、余切函数的图象和性质·典型例题分析 ....................... 已知三角函数值求角·典型例题分析 ................................... 全章小结........................................................... 高考真题选讲.......................................................0°～360°间的三角函数·典型例题分析例1已知角α的终边经过点P(3a，-4a)(a＜0，0°≤α≤360°)，求解α的四个三角函数．解如图2-2：∵x=3a，y=-4a，a＜0例2求315°的四个三角函数．解如图2-3，在315°角的终边上取一点P(x，y)设OP=r，作PM垂直于x轴，垂足是M，可见∠POM=45°注：对于确定的角α，三角函数值的大小与P点在角α的终边上的位置无关，如在315°的角的终边上取点Q(1，-1)，计算出的结果是一样的．弧度制·典型例题分析角度与弧度的换算要熟练掌握，见下表．例2将下列各角化成2kπ+α(k∈Z，0≤α＜2π)的形式，并确定其所在的象限。

高考数学中的三角函数变换题目讲解

高考数学中的三角函数变换题目讲解数学是高考中最重要的科目之一，其中数学中的三角函数变换题目是学生们经常会遇到的难点。

本文将从三角函数基本概念讲解、基本变换公式以及高考题目解析等几个方面，详细讲解高考数学中的三角函数变换题目。

一、三角函数基本概念讲解1.1 正弦函数正弦函数是三角函数中非常重要的一种函数，它是指以圆的弦长与半径之比为变数的函数。

在平面直角坐标系中，设角α的终边与x轴正向夹角为α，则点P(x,y)在单位圆上的坐标为（cosα,sinα），其中y=sinα。

1.2 余弦函数余弦函数也是三角函数中非常重要的一种函数，它是指以圆的余弦与半径之比为变数的函数。

同样，在平面直角坐标系中，设角α的终边与x轴正向夹角为α，则点P(x,y)在单位圆上的坐标为（cosα,sinα），其中x=cosα。

1.3 正切函数正切函数也是三角函数中非常重要的一种函数，它是指以圆上某一点的纵坐标与横坐标之比为变数的函数。

在平面直角坐标系中，设角α的终边与x轴正向夹角为α，则点P(x,y)在单位圆上的坐标为（cosα,sinα），其中tanα=y/x。

二、基本变换公式2.1 周期性变换对于三角函数来说，它具有很强的周期性特征。

而这个周期性变换的公式为f(x)=f(x±2kπ)，其中k为任意整数。

例如，对于正弦函数来说，它的周期为2π，那么当α为0时，sinα=sin(α±2kπ)。

同理，对于余弦函数和正切函数来说，它们的周期也为2π。

2.2 对称性变换对于三角函数来说，它们具有很强的对称性特征。

具体来说，它包括偶函数和奇函数两种类型。

偶函数指在坐标系中关于y轴对称的函数，如余弦函数；奇函数指在坐标系中关于原点对称的函数，如正弦函数。

三、高考题目解析3.1 知识点：正弦函数的基本变换及简单应用例题：已知函数y=sin(x)的周期为2π，对函数进行一次平移变换y=sin(x-π/2)，求平移前的函数周期。

新高考数学复习知识点讲解与练习75---三角函数的概念、诱导公式及三角恒等变换

新高考数学复习知识点讲解与练习三角函数的概念、诱导公式及三角恒等变换一、选择题(本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知角α的终边经过点(m ，3m )，若α＝7π3，则m 的值为() A ．27 B.127 C ．9 D.19 答案B解析由正切函数的定义可得tan 7π3＝3m m＝m 13－12＝3，则m －16＝3，所以m ＝(312)－6＝3－3＝127，故选B.2．已知α是第四象限角，sin α＝－1213，则tan α＝()A ．－513 B.513 C ．－125 D.125 答案C解析因为α是第四象限角，sin α＝－1213，所以cos α＝1－sin 2α＝513，故tan α＝sin αcos α＝－125.3．已知角α的终边与单位圆x 2＋y 2＝1交于点P ⎝ ⎛⎭⎪⎫12，y 0，则cos 2α＝()A ．－12 B.12 C ．－32 D ．1 答案A解析由三角函数的定义知，cos α＝12，∴cos 2α＝2cos 2α－1＝2×⎝ ⎛⎭⎪⎫122－1＝－12.4．(2020·全国Ⅲ卷)已知2tan θ－tan ⎝ ⎛⎭⎪⎫θ＋π4＝7，则tan θ＝()A ．－2B ．－1C ．1D ．2 答案D解析 2tan θ－tan ⎝ ⎛⎭⎪⎫θ＋π4＝2tan θ－1＋tan θ1－tan θ＝7，解得tan θ＝2.故选D.5．(2020·全国Ⅰ卷)已知α∈(0，π)，且3cos 2α－8cos α＝5，则sin α＝() A.53 B.23 C.13 D.59答案A解析由3cos 2α－8cos α＝5，得3(2cos 2α－1)－8cos α＝5，即3cos 2α－4cos α－4＝0，解得cos α＝－23或cos α＝2(舍去)．又因为α∈(0，π)，所以sin α>0，所以sin α＝1－cos 2α＝1－⎝ ⎛⎭⎪⎫－232＝53.故选A. 6．已知sin α＋cos α＝13，则sin 2⎝ ⎛⎭⎪⎫π4－α＝()A.118B.1718C.89D.29 答案B解析对sin α＋cos α＝13平方得1＋sin 2α＝19，∴sin 2α＝－89，∴sin 2⎝ ⎛⎭⎪⎫π4－α＝1－cos ⎝ ⎛⎭⎪⎫π2－2α2＝1－sin 2α2＝1718. 7．已知点A 的坐标为(43，1)，将OA 绕坐标原点O 逆时针旋转π3至OB ，则点B 的纵坐标为()A.332B.532C.112D.132 答案D解析设∠AOx ＝θ，则|OA |＝|OB |＝7，sin θ＝17，cos θ＝437，∴sin ⎝ ⎛⎭⎪⎫θ＋π3＝12sin θ＋32cos θ＝1314，∴点B 的纵坐标为|OB |sin ⎝ ⎛⎭⎪⎫θ＋π3＝132.8．设sin α＋sin β＝13，则sin α－cos 2β的最大值为()A ．－35B ．－23C ．－1112 D.49 答案D解析因为sin α＋sin β＝13，所以sin α＝13－sin β.因为－1≤sin α≤1，所以－23≤sin β≤1.所以sin α－cos 2β＝13－sin β－1＋sin 2β＝⎝ ⎛⎭⎪⎫sin β－122－1112，当sin β＝－23时，sin α－cos 2β有最大值49.9．(2020·北京卷)2020年3月14日是全球首个国际圆周率日(π Day)．历史上，求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似，数学家阿尔·卡西的方法是：当正整数n 充分大时，计算单位圆的内接正6n 边形的周长和外切正6n 边形(各边均与圆相切的正6n 边形)的周长，将它们的算术平均数作为2π的近似值．按照阿尔·卡西的方法，π的近似值的表达式是()A ．3n ⎝ ⎛⎭⎪⎫sin 30°n ＋tan 30°nB ．6n ⎝ ⎛⎭⎪⎫sin 30°n ＋tan 30°nC ．3n ⎝ ⎛⎭⎪⎫sin 60°n ＋tan 60°nD ．6n ⎝ ⎛⎭⎪⎫sin 60°n ＋tan 60°n答案A解析设单位圆的内接正6n 边形的周长为C 1，外切正6n 边形的周长为C 2，如图(1)所示，sin 360°12n ＝BC 1，∴BC ＝sin 30°n ，∴AB ＝2sin 30°n ，C 1＝12n sin 30°n .如图(2)所示，tan 360°12n ＝B ′C ′1，∴B ′C ′＝tan 30°n ，∴A ′B ′＝2tan 30°n ，C 2＝12n tan 30°n .∴2π＝C 1＋C 22＝6n ⎝ ⎛⎭⎪⎫sin 30°n ＋tan 30°n ，∴π＝3n ⎝ ⎛⎭⎪⎫sin 30°n ＋tan 30°n .故选A.10．(2021·北京东城区统检)设α，β是三角形的两个内角，下列结论中正确的是() A ．若α＋β<π2，则sin α＋sin β< 2 B ．若α＋β<π2，则cos α＋cos β< 2 C ．若α＋β>π2，则sin α＋sin β>1 D ．若α＋β>π2，则cos α＋cos β>1 答案A解析因为α∈⎝ ⎛⎭⎪⎫0，π2，所以π2－α∈⎝ ⎛⎭⎪⎫0，π2，又因为sin α在⎝ ⎛⎭⎪⎫0，π2上单调递增，cos α在⎝ ⎛⎭⎪⎫0，π2单调递减，若α＋β<π2，则β<π2－α，则sin α＋sin β<sin α＋sin ⎝ ⎛⎭⎪⎫π2－α＝sin α＋cos α＝2sin ⎝ ⎛⎭⎪⎫α＋π4∈(0，2]，则A 正确；cos α＋cos β>cos α＋cos ⎝ ⎛⎭⎪⎫π2－α＝cos α＋sin α＝2sin ⎝ ⎛⎭⎪⎫α＋π4∈(0，2]，则B 错；若α＋β>π2，则β>π2－α，则sin α＋sin β>sin α＋sin ⎝ ⎛⎭⎪⎫π2－α＝sin α＋cos α＝2sin ⎝ ⎛⎭⎪⎫α＋π4∈(0，2]，则C 错；cos α＋cos β<cos α＋cos ⎝ ⎛⎭⎪⎫π2－α＝cos α＋sin α＝2sin ⎝ ⎛⎭⎪⎫α＋π4∈(0，2]，则D 错．二、填空题(本大题共7小题，多空题每题6分，单空题每题4分，共36分)11．若tan ⎝ ⎛⎭⎪⎫α－π4＝16，则tan α＝________．答案75解析tan α＝tan ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫α－π4＋π4 ＝tan ⎝ ⎛⎭⎪⎫α－π4＋tan π41－tan ⎝ ⎛⎭⎪⎫α－π4tan π4＝16＋11－16＝75. 12．(2021·稽阳联考)已知角α的终边过点(－1，2)，则tan α＝________，sin 2α＝________．答案－2 －45解析由三角函数的定义可知sin α＝25，cos α＝－15，则tan α＝－2，sin 2α＝2sin αcos α＝－45.13．(2020·浙江卷)已知tan θ＝2，则cos 2θ＝________，tan ⎝ ⎛⎭⎪⎫θ－π4＝__________．答案－3513解析由题意，cos 2θ＝cos 2θ－sin 2θ ＝cos 2θ－sin 2θcos 2θ＋sin 2θ＝1－tan 2θ1＋tan 2θ＝1－41＋4＝－35. tan ⎝ ⎛⎭⎪⎫θ－π4＝tan θ－tan π41＋tan θ·tan π4＝tan θ－11＋tan θ＝2－11＋2＝13.14．已知α∈R ，sin α＋2cos α＝102，则tan α＝________；tan 2α＝________．答案3或－13 －34解析由sin α＋2cos α＝102两边平方可得sin 2α＋4sin α·cos α＋4cos 2α＝52，故sin 2α＋4sin αcos α＋4cos 2αsin 2α＋cos 2α＝52，即tan 2α＋4tan α＋4tan 2α＋1＝52，解得tan α＝3或tan α＝－13.当tan α＝3时，tan 2α＝2tan α1－tan 2α＝－34；当tan α＝－13时，tan 2α＝2tan α1－tan 2α＝－34. 15．已知3sin 2x ＋2sin 2y ＝2sin x ，则sin 2x ＋sin 2y 的最大值为________，最小值为________．答案490解析3sin 2x ＋2sin 2y ＝2sin x ⇒sin 2y ＝sin x －32sin 2x ⇒sin 2x ＋sin 2y ＝sin x －12sin 2x ＝12－12(sin x －1)2，由于sin 2y ＝sin x －32sin 2x ≥0，由已知条件知sin x ≥0，∴32sin x －1≤0⇒sin x ∈⎣⎢⎡⎦⎥⎤0，23，故sin 2x ＋sin 2y ＝12－12(sin x －1)2∈⎣⎢⎡⎦⎥⎤0，49.16．(2021·苏州一调)已知sin 2α－2＝2cos 2α，则sin 2α＋sin 2α＝________．答案1或85解析由sin 2α－2＝2cos 2α得sin 2α－2(1＋cos 2α)＝0，即2sin αcos α－4cos 2α＝0，所以cos α＝0或tan α＝2，当cos α＝0时，sin 2α＋sin 2α＝1－cos 2α＋2sin αcos α＝1，当tan α＝2时，sin 2α＋sin 2α＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝tan 2α＋2tan αtan 2α＋1＝22＋2×222＋1＝85.17．(2020·新高考山东卷)某中学开展劳动实习，学生加工制作零件，零件的截面如图所示．O 为圆孔及轮廓圆弧AB 所在圆的圆心，A 是圆弧AB 与直线AG 的切点，B 是圆弧AB 与直线BC 的切点，四边形DEFG 为矩形，BC ⊥DG ，垂足为C ，tan ∠ODC ＝35，BH ∥DG ，EF ＝12 cm ，DE ＝2 cm ，A 到直线DE 和EF 的距离均为7 cm ，圆孔半径为1 cm ，则图中阴影部分的面积为______ cm 2.答案5π2＋4解析如图，连接OA ，过A 作AP ⊥EF ，分别交EF ，DG ，OH 于点P ，Q ，R .由题意知AP ＝EP ＝7 cm ，又DE ＝2 cm ，EF ＝12 cm ，所以AQ ＝QG ＝5 cm ，所以∠AHO ＝∠AGQ ＝π4. 因为OA ⊥AH ，所以∠AOH ＝π4，所以∠AOB ＝3π4. 设AR ＝x cm ，则OR ＝x cm ，RQ ＝(5－x ) cm. 因为tan ∠ODC ＝35，所以tan ∠ODC ＝5－x 7－x ＝35，解得x ＝2，则OA ＝2 2 cm.所以S ＝S 扇形AOB ＋S △AOH －S 小半圆＝12×3π4·(22)2＋12×4×2－12π·12＝5π2＋4 (cm 2)．三、解答题(本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤) 18．(本小题满分14分)已知f (x )＝ cos 2（n π＋x ）·sin 2（n π－x ）cos 2[（2n ＋1）π－x ](n ∈Z )．(1)化简f (x )的表达式； (2)求f ⎝ ⎛⎭⎪⎫π2 018＋f ⎝ ⎛⎭⎪⎫504π1 009的值．解(1)当n 为偶数，即n ＝2k (k ∈Z )时， f (x )＝cos 2（2k π＋x ）·sin 2（2k π－x ）cos 2[（2×2k ＋1）π－x ]＝cos 2x ·sin 2（－x ）cos 2（π－x ）＝cos 2x ·（－sin x ）2（－cos x ）2＝sin 2x ；当n 为奇数，即n ＝2k ＋1(k ∈Z )时，f (x )＝cos 2[（2k ＋1）π＋x ]·sin 2[（2k ＋1）π－x ]cos 2{[2×（2k ＋1）＋1]π－x }＝cos 2[2k π＋（π＋x ）]·sin 2[2k π＋（π－x ）]cos 2[2×（2k ＋1）π＋（π－x ）]＝cos 2（π＋x ）·sin 2（π－x ）cos 2（π－x ）＝（－cos x ）2sin 2x （－cos x ）2＝sin 2x .综上得f (x )＝sin 2x .(2)由(1)得f ⎝ ⎛⎭⎪⎫π2 018＋f ⎝ ⎛⎭⎪⎫504π1 009＝sin 2π2 018＋sin 21 008π2 018＝sin 2π2 018＋sin 2⎝ ⎛⎭⎪⎫π2－π2 018＝sin 2π2 018＋cos 2π20 18＝1.19．(本小题满分15分)已知cos ⎝ ⎛⎭⎪⎫x －π4＝210，x ∈⎝ ⎛⎭⎪⎫π2，3π4.(1)求sin x 的值；(2)求cos ⎝ ⎛⎭⎪⎫2x ＋π3的值．解(1)因为x ∈⎝ ⎛⎭⎪⎫π2，3π4，所以x －π4∈⎝ ⎛⎭⎪⎫π4，π2，sin ⎝ ⎛⎭⎪⎫x －π4＝1－cos 2⎝ ⎛⎭⎪⎫x －π4＝7210.所以sin x ＝sin ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫x －π4＋π4＝sin ⎝ ⎛⎭⎪⎫x －π4cos π4＋ cos ⎝ ⎛⎭⎪⎫x －π4sin π4＝7210×22＋210×22＝45. (2)因为x ∈⎝ ⎛⎭⎪⎫π2，3π4，故cos x ＝－1－sin 2x ＝－1－⎝ ⎛⎭⎪⎫452＝－35，sin 2x ＝2sin x cos x ＝－2425，cos 2x ＝2cos 2x －1＝－725.所以cos ⎝ ⎛⎭⎪⎫2x ＋π3＝cos 2x cos π3－sin 2x sin π3＝－725×12＋2425×32＝243－750.20．(本小题满分15分)已知α，β∈(0，π)，且tan α＝2，cos β＝－7210. (1)求cos 2α的值； (2)求2α－β的值．解(1)因为tan α＝2，所以cos 2α＝cos 2α－sin 2α＝cos 2α－sin 2αcos 2α＋sin 2α＝1－tan 2α1＋tan 2α＝1－41＋4＝－35. (2)因为α∈(0，π)，tan α＝2，所以α∈⎝ ⎛⎭⎪⎫0，π2.因为cos 2α＝－35，所以2α∈⎝ ⎛⎭⎪⎫π2，π，sin 2α＝45.因为β∈(0，π)，cos β＝－7210，所以sin β＝210且β∈⎝ ⎛⎭⎪⎫π2，π.所以sin(2α－β)＝sin 2αcos β－cos 2αsin β＝45×⎝ ⎛⎭⎪⎫－7210－⎝ ⎛⎭⎪⎫－35×210＝－22. 又2α－β∈⎝ ⎛⎭⎪⎫－π2，π2，所以2α－β＝－π4. 21．(本小题满分15分)(2021·温州适应性考试)如图，在单位圆上，∠AOB ＝α⎝ ⎛⎭⎪⎫π6＜α＜π2，∠BOC ＝π3，且△AOC 的面积为237.(1)求sin α的值；(2)求2cos ⎝ ⎛⎭⎪⎫α2－π3sin ⎝ ⎛⎭⎪⎫α2＋π6的值．解(1)S △AOC ＝12sin ⎝ ⎛⎭⎪⎫α＋π3＝237，∴sin ⎝ ⎛⎭⎪⎫α＋π3＝437，∵π6＜α＜π2， ∴π2＜α＋π3＜5π6，∴cos ⎝ ⎛⎭⎪⎫α＋π3＝－17，sin α＝sin ⎝ ⎛⎭⎪⎫α＋π3－π3＝sin ⎝ ⎛⎭⎪⎫α＋π3cos π3－cos ⎝ ⎛⎭⎪⎫α＋π3sin π3＝437×12＋17×32＝5314.(2)2cos ⎝ ⎛⎭⎪⎫α2－π3sin ⎝ ⎛⎭⎪⎫α2＋π6＝2sin ⎝ ⎛⎭⎪⎫α2－π3＋π2sin ⎝ ⎛⎭⎪⎫α2＋π6＝2sin 2⎝ ⎛⎭⎪⎫α2＋π6＝1－cos ⎝ ⎛⎭⎪⎫α＋π3＝87.22．(本小题满分15分)已知向量a ＝(sin ωx ，cos ωx )，b ＝(cos φ，sin φ)⎝ ⎛⎭⎪⎫ω>0，π3<φ<π，函数f (x )＝a ·b 的最小正周期为2π，其图象经过点M ⎝ ⎛⎭⎪⎫π6，32.(1)求函数f (x )的解析式；(2)已知α，β∈⎝ ⎛⎭⎪⎫0，π2，且f (α)＝35，f (β)＝1213，求f (2α－β)的值．解(1)依题意有f (x )＝a ·b ＝sin ωx cos φ＋ cos ωx sin φ＝sin(ωx ＋φ)．∵函数f (x )的最小正周期为2π，∴T ＝2πω，解得ω＝1. 将点M ⎝ ⎛⎭⎪⎫π6，32代入函数f (x )的解析式，得sin ⎝ ⎛⎭⎪⎫π6＋φ＝32，∴π6＋φ＝π3＋2k π，k ∈Z 或π6＋φ＝2π3＋2k π，k ∈Z . ∵π3<φ<π，∴π6＋φ＝2π3，∴φ＝π2.故f (x )＝sin ⎝ ⎛⎭⎪⎫x ＋π2＝cos x .(2)依题意有cos α＝35，cos β＝1213，而α，β∈⎝ ⎛⎭⎪⎫0，π2，∴sin α＝1－⎝ ⎛⎭⎪⎫352＝45，sin β＝1－⎝ ⎛⎭⎪⎫12132＝513，∴sin 2α＝2425，cos 2α＝cos2α－sin2α＝925－1625＝－725，∴f(2α－β)＝cos(2α－β)＝cos 2αcosβ＋sin 2αsin β＝－725×1213＋2425×513＝36325.11 / 11。