一元一次方程的讨论1(2019)
中考数学专题《一元一次方程的应用》专题讲练原卷

专题07 一元一次方程的应用(12大考点) 专题讲练一元一次方程的应用题属于人教版七年级上期期末必考题,需要完全掌握各个类型的应用题,该专题将应用题分为分段计费、行程问题、工程问题、方案优化选择、商品销售问题、比赛积分问题、日历问题(数字问题)、配套问题、调配问题、和差倍分问题(比例问题)、几何图形问题、动态问题等共进行方法总结与经典题型进行分类。
1、知识储备2、经典基础题考点1. 分段计费问题考点2. 行程问题考点3. 工程问题考点4. 方案优化问题考点5. 商品销售问题考点6. 比赛积分问题考点7. 配套问题考点8. 调配问题考点9. 数字与日历问题考点10.和、差、倍、分(比例)问题考点11. 几何问题(等积问题)考点12. 动态问题3、优选提升题1.用一元一次方程解决实际问题的一般步骤列方程解应用题的基本思路为:问题−−−→分析抽象方程−−−→求解检验解答.由此可得解决此类题的一般步骤为:审、设、列、解、检验、答. 2 .建立书写模型常见的数量关系1)公式形数量关系:生活中许多数学应用情景涉及如周长、面积、体积等公式。
在解决这类问题时,必须通过情景中的信息,准确联想有关的公式,利用有关公式直接建立等式方程。
长方形面积=长×宽长方形周长=2(长+宽) 正方形面积=边长×边长正方形周长=4边长2)约定型数量关系:利息问题,利润问题,质量分数问题,比例尺问题等涉及的数量关系,像数学中的公式,但常常又不算数学公式。
我们称这类关系为约定型数量关系。
3)基本数量关系:在简单应用情景中,与其他数量关系没有什么差别,但在较复杂的应用情景中,应用方法就不同了。
我么把这类数量关系称为基本数量关系。
单价×数量=总价速度×时间=路程工作效率×时间=总工作量等。
3.分析数量关系的常用方法1)直译法分析数量关系:将题中关键性的数量关系的语句译成含有未知数的代数式,并找出没有公国的等量关系,翻译成含有未知数的等式。
【2019年整理】列一元一次方程解实际问题yys.11.16

1 字之和是这个两位数的 ,求这个两位数。 5
2、 一个三位数,三个数位上的数的和是17,百位上的数比十 位上的数大7,个位上的数是十位上的3倍,求这个三位数。 3、一个两位数,个位数字与十位数字之和是14,如果个位上的 数字和十位上的数字位置对调,则所得两位数比原来两位数小 18,求这个两位数。
四、配套问题 例4:工人生产螺丝钉和螺母,每人每天平均生产螺钉1200个或
八、工效问题 5.为庆祝校运会开幕,七年级(1)班学生 接受了制作校 旗的任务.原计划一半同学参加制作,每天制作 40面.而 实际上,在完成了小旗总数的三分之一以后,全班同学一 起参加,结果比原计划提前一天半完成任务.假设每人的 制作效率相同,问共制作小旗多少面? 6、期中考查,老师限时40分钟要求每位七年级学生打完 一篇文章.已知独立打完同样大小文章,小宝需要 50分 钟,小贝只需要30分钟.为了完成任务,小宝打了30分 钟后,请求小贝帮助合作,他能在要求的时间打完吗 ?
回顾:
2 y 1 5y 2 3y 1 1、解方程 1 3 6 4
2、当为 y 何值时, y 8与 1 8 y 2 6 3 的值互为相反数?
3、解方程: 解较复杂的一元一次方程
x 2 x 0 .3 (1)、 1 0 .2 0 .3
x 0.17 0.2 x (2)、 1 0.7 0.03
练习六: 1、一个梯形的下底比上底多2cm,高是5cm,面积是 40cm2 ,求上底 2、圆形形状如图所示,它的面积是200 cm2,外沿大圆的 半径是10 cm,外沿小圆的半径是多少?(课本76页9) 3、两个半径,高各不同的圆柱形杯子,把其中一杯子的水倒 入另一个杯子刚好装满,已知一杯的半径为4 cm,高为12 cm,另一杯子的高为48 cm。求另一杯子的半径。
一元一次方程的解的情况与整数解

一元一次方程的解的情况与整数解二、方法剖析与提炼例1.(2020娄底)已知关于x 的方程2x +a ﹣5=0的解是x =2,求a 的值.【解答】∵x =2是方程2x +a ﹣5=0的解2×2+a ﹣5=0∴a =1 【解析】(1)把方程的解x =2代入方程。
(2)解关于a 的方程2×2+a ﹣5=0得4+a ﹣5=0,解出a 的值.【解法】一元一次方程的解,解一元一次方程。
【解释】本题主要考查学生对方程的解的理解。
关于x 的方程2x +a ﹣5=0中未知数是x ,把a 看做待定的常数,根据一元一次方程的解的定义,把x =2代入方程后,求出关于a 的一元一次方程。
例2.解关于x 的方程(mx -n )(m +n )=0【解答】(1)把方程化为最简形式:m ²x +mnx -mn -n ²=0整理,得m (m +n )x =n (m +n )(2)讨论:①当m +n 0,且m 0时,方程有唯一解 x =mn ; ②当m +n 0,且m =0时,方程无解;③当m +n 0时,方程有无数多个解。
【解析】(1)这个方程中未知数是x , 而m 、n 是可以取不同实数的常数。
因此需要讨论m 、n 不同值时方程解的情况。
(2)对含有字母系数的方程,一定要注意字母的取值范围。
解这类方程时,需要从方程有唯一解、无解、无数多个解三种情况进行讨论。
用方程解的定义寻求关于a 的等式(3)对于不是最简形式的方程,通常情况下要先化为最简方程。
【解法】通过化简,转化为最简方程ax=b 的形式,然后分三种情况进行讨论。
【解释】对于含有字母系数的方程,学生一般不太理解,不是简单形式的方程,通常情况下要化简为最简方程,在解题过程中通过去括号,化繁为简转化为最简方程m (m +n )x =n (m +n )的形式时,有的学生往往会两边同除以m +n ,得到mx =n 的形式,这样就会漏掉m +n 0的情况。
一元一次方程 浙教版2019-2020学年度七年级数学上册讲义+分层训练(含答案)

浙江版2019-2020学年度七年级数学上册第5章一元一次方程 5.1 一元一次方程【知识清单】 一、一元一次方程:1.方程:含有未知数的等式叫做方程.2.方程的解:使方程左右两边的值都相等的未知数的值叫做方程的解3.一元一次方程:只含有一个未知数,未知数的次数是1,这样的方程叫做一元一次方程. 二、方程的判定方法归纳:1.判断一个式子是不是方程必须看两点:一是等式,二是含有未知数,二者缺一不可;2.判定一个方程是不是一元一次方程,要看方程是否只含一个未知数并且未知数的指数都是1,而且是整式方程. 【经典例题】例题1、下列方程中,是一元一次方程的是( )A .x 2-2x =1B .-5x =0C .3x +2y =5D .x =x1【考点】一元一次方程的定义.【分析】根据一元一次方程的定义判断即可.【解答】A 、方程的次数是2次,即不是一元一次方程,故本选项错误;B 、是一元一次方程,故本选项正确;C 、含有两个未知数,即不是一元一次方程,故本选项错误;D 、不是整式方程,即不是一元一次方程,故本选项错误; 故选B .【点评】本题考查了对一元一次方程的定义的应用,熟练掌握一元一次方程的定义是解决问题的关键.例题2、如果方程(m -2)1-m x+26=0是关于x 的一元一次方程,那么m 的取值是______.【考点】一元一次方程的定义.【分析】只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程,高于一次的项系数是0.据此可得出关于m 的方程,继而可求出m 的值. 【解答】由一元一次方程的定义,得⎩⎨⎧=-≠-1102m m ,解得m =-2.故填:-2.【点评】本题主要考查了一元一次方程的定义,只含有一个未知数,未知数的指数是1,一次项系数不是0,这是这类题目考查的重点.【夯实基础】1.下列方程中,是一元一次方程的是( )A .2x =3y B.y 1+1=0 C .2x 2+3x =2 D. )2(31-x =1 2.下列说法正确的是( )A .x =-2是方程2x +5=0的解B .y =0是方程0.5(5-2y )=2.5的解C .方程3x -4=)3(31-x )的解是x =3D .方程43-x =2的解是x =383.一件高于成本50%标价的上衣,按8折销售仍可获利40元.设这件上衣的成本价为x 元,根据题意,下面所列方程正确的是( )A .x (1+50%)×0.8-x =30B . ( x +50%)×0.8-x =30C .x (1+50%)×0.8=30-xD .( x +50%)×0.8=30-x 4.关于|x -2|=2的说法正确的是 ( )A .不是方程B .是方程其解为0C .是方程其解为4D .是方程其解为0或45.若关于x 的方程(3k -2)x 2- (3k +2)x +5=0是一元一次方程,则k 的值为 .6.如图,两边都放着物体的天平处于平衡状态,用等式表示天平两边所放物体的质量关系为__ __________.7.下列不是方程的是__________.(填序号)① 1+2=3; ② 2x +1; ③ 2m +15=3; ④ x 2-6=0; ⑤ 3x +2y =9; ⑥ 3a +9>15.8.已知关于x 的方程5a -2x =9的解为x =3,求代数式(-a )2-2a +1的值.9.有甲、乙两支同样长的蜡烛,甲蜡烛可使用12 h ,乙蜡烛可使用10 h .两蜡烛同时点燃,几小时后乙蜡烛的长度是甲蜡烛长度的三分之一?(列出方程,不必求解)【提优特训】10.若5x -6与2x -8是一个正数两个平方根,则可列方程来表示为( )A .5x -6=2x -8B .5x -6+2x -8=0C .5x +6+2x +8=0D .5x +6+2x -8=0 11.若方程(3a -2)x 2+bx +c =0是关于x 的一元一次方程,则字母系数a ,b ,c 的值满足( )A .a =32,b =0,c 为任意数 B .a ≠32,b ≠0,c =0 C .a =32,b ≠0,c 为任意数 D .a =32,b ≠0,c ≠0 12.下列方程中,解为x =-2的方程是( )A .21x +3=x B . x -2=0 C .2x =4 D .321)63(31-=-x x 13.已知单项式-ma 3b m -1与单项式4a 3b 2是同类项,则关于m 的方程一定正确的是( )A .-m +4=0B .-m -4=0C .m -1+2=0D . m -1=2 14.已知53-m x-1=m 是关于x 的一元一次方程,则这个方程的解 .15.对于有理数a ,b ,c ,d ,规定一种运算bc ad dbc a -=,如43525342⨯-⨯==-2. 若32331=----x x ,则所得到的方程为 .16.根据下列条件列出方程. 1.设某数为x : (1)某数的65与-5的和是6; (2)某数的5倍等于该数的2倍与18的差; (3)某数减少20%后比该数的60%小5; (4)比某数的3倍大6的数是12”用方程表示为.2.(1)某长方形的周长是64,长与宽之比为5∶3,则长和宽各是多少?设长方形的长为5x . (2)爸爸今年38岁,比儿子年龄的3倍少4岁,则小明今年几岁?设小明今年x 岁.17.已知关于x 的方程ax 2+x b -3-2=0是一元一次方程,试求x a +b 的值.18.数学课上老师出示了四张卡片,上面分别写着不同的代数式,要求同学们解决下面的问题:用等号将这四张卡片的任意两张卡片上的数或式子连接起来,就会得到等式或方程. (1)你一共能写出几个等式?(2)在这些等式中,有几个一元一次方程?请写出这几个一元一次方程.19.汽车的油箱内储油40kg,已知工作时的耗油以及油箱内的剩油量的关系如表所示工作时间t(h) 耗油量p(kg) 剩油量m(kg)1 2.5 40-2.5=37.52 5 40-5=353 7.5 40-7.5=32.54 10 40-10=30………(1)写出工作10h后,油箱内的剩油量;(2)写出工作t h后,油箱内的剩油量为7.5kg,请你列出关于t的方程(不解方程).20.如图用火柴棒搭正方形,用n表示所搭正方形的个数,从而计算火柴棒的根数,当n=1,所需火柴棒为4根,当n=2,所需火柴棒为7根,当n=3,所需火柴棒为10根,…,请问:(1)第5个图形中火柴棒有多少根?(2)第n个图形中火柴棒有多少根?(3)若有一个图形由781根火柴棒组成,那么这个图形由几个正方形组成?【中考链接】21.(2018•临安)(3分)中央电视台2套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则三个球体的重量等于()个正方体的重量.A.2 B.3 C.4 D.522.(2018•临沂)任何一个无限循环小数都可以写成分数的形式,应该怎样写呢?我们以无限循环小数7.0 为例进行说明:设7.0 =x ,由7.0 =0.7777…可知,l0x =7.7777…,所以l0x -x =7,解方程,得x =97,于是.得7.0 =97.将63.0 写成分数的形式是 .参考答案1、D2、B3、A4、D5、326、x+4=107、①②⑥ 10、B 11、C 12、D 13、D 14、-1或3 15、-(x -2)+3(3-x )=3 21、D 22、114 8.已知关于x 的方程5a -2x =9的解为x =3,求代数式(-a )2-2a +1的值. 解:∵方程5a -2x =9的解为x =3,∴5a -2×3=9, ∴a =3.∴(-a )2-2a +1 =(-3)2-2×3+1=4.9.有甲、乙两支同样长的蜡烛,甲蜡烛可使用12 h ,乙蜡烛可使用10 h .两蜡烛同时点燃,几小时后乙蜡烛的长度是甲蜡烛长度的三分之一?(列出方程,不必求解) 解:设x 小时后乙蜡烛的长度是甲蜡烛长度的一半,则1-101x =31(1-121x ). 16.根据下列条件列出方程. 1.设某数为x : (1)某数的65与-5的和是6; (2)某数的5倍等于该数的2倍与18的差; (3)某数减少20%后比该数的60%小5; (4)比某数的3倍大6的数是12”用方程表示为.2.(1)某长方形的周长是64,长与宽之比为5∶3,则长和宽各是多少?设长方形的长为5x . (2)爸爸今年38岁,比儿子年龄的3倍少4岁,则小明今年几岁?设小明今年x 岁. 16.解:1.(1)65x -5=6; (2) 5x =2x -18;(3) (1-20%)x =60%x -5; (4) 3x +6=12;2.解:(1)由长方形的长为3x ,得宽为2x ,则2(5x +3x )=64.(2)根据题意,得3x -4=38.17.已知关于x 的方程ax 2+x b -3-2=0是一元一次方程,试求x a +b 的值. 解:∵ax 2+x b-3-2=0是关于x 的一元一次方程,∴a =0,b -3=1, ∴a =0,b =4, ∴x -2=0, ∴x =2. ∴x a +b =24=16.18.数学课上老师出示了四张卡片,上面分别写着不同的代数式,要求同学们解决下面的问题:用等号将这四张卡片的任意两张卡片上的数或式子连接起来,就会得到等式或方程. (1)你一共能写出几个等式?(2)在这些等式中,有几个一元一次方程?请写出这几个一元一次方程. 18. 解:(1)6个.(2)有3个一元一次方程,它们分别是5x -3=-6,6261-=-x ,5x -3=261-x . 19.汽车的油箱内储油40kg ,已知工作时的耗油以及油箱内的剩油量的关系如表所示工作时间t (h) 耗油量p (kg) 剩油量m (kg) 1 2.5 40-2.5=37.5 2 5 40-5=35 3 7.5 40-7.5=32.5 4 10 40-10=30 ………(1)写出工作10h 后,油箱内的剩油量;(2)写出工作t h 后,油箱内的剩油量为7.5kg ,请你列出关于t 的方程(不解方程). 解: (1)40-10×2.5=15;工作10h 后,油箱内的剩油量为15 kg ; (2)根据题意,得40-2.5t =7.5.20.如图用火柴棒搭正方形,用n 表示所搭正方形的个数,从而计算火柴棒的根数,当n =1,所需火柴棒为4根,当n =2, 所需火柴棒为7根,当n =3, 所需火柴棒为10根,…,请问:(1)第5个图形中火柴棒有多少根?(2)第n个图形中火柴棒有多少根?(3)若有一个图形由781根火柴棒组成,那么这个图形由几个正方形组成?解:根据图形特点和题意可得:第1个图形n=1,火柴棒为3×1+1=4根,第2个图形n=2,火柴棒为3×2+1=7根,第3个图形n=3,火柴棒为3×3+1=10根,…(1)第5个图形中火柴棒有3×5+1=16根,(2)第n个图形中火柴棒有3×n+1=(3n+1)根,(3)3n+1=781,解得n=260,答:这个图形由260个正方形组成.。
人教版七年级初一数学上册 3.2解一元一次方程(一)合并同类项与移项第1课时

9/13/2019
5
6.解下列方程: (1)3x-5x=10-8; 解:x=-1
(2)4x-1.5x+2.5x=-15; 解:x=-3 (3)x2+x3+x4=26. 解:x=24
9/13/2019
6
知识点2:根据“总量=各部分分量之和”列方程解决问题
7.挖一条长为1200米的水渠,由甲、乙两队从两头同时施工,
甲队每天挖150米,乙队每天挖90米,需要几天才能挖好?设
需要x天才能挖好,则列出的方程为( A )
A.150x+90x=1200
B.150+90x=1200
C.150x+90=1200
D.150x-90x=1200
9/13/2019
7
8.学校机房今年和去年共购置了100台计算机.已知今年购置
计算机数量是去年购置计算机数量的3倍,今年购置计算机的
解:设这两个正方形的边长分别为3x cm,4x cm,则4×3x+ 4×4x=140.解得x=5,所以3x=15,4x=20,即这两个正方 形的边长分别为15 cm,20 cm
9/13/2019
9
9/13/2019
10
11.某数的 5 倍比这个数的 8 倍少 12,则这个数是( A )
A.4
B.-4
第3章 一元一次方程
3.2 解一元一次方程(一) ——合并同类项与移项
第1课时 利用合并同类项 解一元一次方程
9/13/2019
1
9/13/2019
2
知识点1:利用合并同类项解一元一次方程 1.下列解方程合并同类项不正确的是( D ) A.由3x-2x=4得x=4 B.由2x-3x=3得-x=3 C.由-7x+2x=-1+5得-5x=4 D.由5x-2x+3x=-10-2得6x=-8
一元一次方程的解法-竞赛拓展2-木木

1.解下列方程: (1)|3x﹣5|+4=8
五大板块―――1.重点 2.难点 3.考试易错点 4.提高能力点 5.思想方法拓展点
2.若关于 x 的方程||x﹣2|﹣1|=a 有三个整数解,则 a 的 值是( ) A.0 B.1 C.2 D.3
3.讨论方程||x+3|﹣2|=k 的解的情况.
真正的高手,都是在不断的反思复习中追求卓越!---木木
1
木木数学
五大板块―――1.重点 2.难点 3.考试易错点 4.提高能力点 5.思想方法拓展点
三、解下列关于 x 的方程(拓展提升---含参数) (1)4x+b=ax﹣8;(a≠4)
类型 3:|ax+b|=|cx+d|型 ax+b=±(cx+d)
变式 2:如果|x+1|-|x-3|=-4,求 x.
法二:数形结合
变式 1:如果|x+1|+|x-3|=4,求 x.
变式 2:如果|x+1|+|x-3|=2,求 x.
变式 3:如果|x+1|+|x-3|=7,求 x.
类型 6:|x+a|-|x+b|=m 型 例 8.如果|x+1|-|x-3|=6,求 x. 法一:分类讨论
(2)|4x﹣3|﹣2=3x+4
(3)|x﹣|2x+1||=3
4. 方 程 |||x ﹣ 2006| ﹣ 1|+8| = 2006 的 所 有 x 的 和
为
.
(4)|2x﹣1|+|x﹣2|=|x+1|
5.已知|x+2|+|1﹣x|=9﹣|y﹣5|﹣|1+y|,求 x+y 的最大
解一元一次方程7种题型

xa
2x 1
x 1
把a=1代入
中得
,
1
1
5
2
5
2
去分母,得2(2x-1)+10=5(x+1),
去括号,得4x-2+10=5x+5,
移项、合并同类项,得-x=-3,
系数化为1,得x=3,
答:a的值为1,原方程正确的解为x=3.
2x a 2x 1
1
,去分母
3
6
变式.已知某同学解关于x的一元一次方程
移项得:
x7
合并同类项得:
系数化为1得x 7
考点4 一元一次方程中含字母参数问题
kx
2 2x
例题: 已知方程 2 3( x 1) 0 的解与关于x的方程
2
的解互为倒数,求k的值.
1
解:解方程 2 3( x 1) 0 得:x
,
3
∵方程 2 3( x 1) 0
2x 1 x 3
解方程1
, 解得:x 1
5
10
1
将x 1代入污染的方程得2 y 1,
2
1
解得:y
2
1
被污染的常数应是
2
考点7 规定新定义问题
b
b
例题:我们规定:若关于x的一元一次方程 ax b(a 0) 的解 x
满足 b a ,则
a
a
称该方程为“差解方程”,例如:2x 4 的解为 x 2 满足 2 4 2 ,所以方程 2x 4
4
.
变式1.已知两个整式 A x2 2 x ,B=
北师大版七年级数学上册课件:第五章《一元一次方程》回顾与思考

具体做法
在方程两边都乘以各分 母的最小公倍数
根据
等式 性质2
注意事项
1.不要漏乘不含分母的项 2.分子作为一个整体要加上括号
去括号
一般先去小括号,再去中 分配律 去
括号,最后去大括号
括号法则
移项
把含有未知数的项移到 方程一边,其它项都移到方 程另一边,注意移项要变号
移项 法则
合并同类
把方程变为ax=b
?
不能是整式
相信你能行
判断对错,对的说明根据等式的哪一 条性质;错的说出为什么。
(1)如果x=y,那么 x 2 y 2 ( × )
(2)如果x=y,那么
x
5
3
a
y
5
3a(
√
)
(3)如果x=y,那么
x 5a
y(
5a
×
)
(4)如果x=y,那么 5x 5y ( × )
(5)如果x=y,那么
2x 1 2y 1 (
已知:4000元
彩电售价 – 彩电进价 = 彩电进价 × 彩电的利润率
彩电标价 × _8__ 10
已知为:5%
如果设彩电标价为x元,则根据等量关系可得方程:
x – = _8__
10
4000
4000 × 5%
例1 某商店因价格竟争,将某型号彩电按标价的8折出售,
此时每台彩电的利润率是5%。此型号彩电的进价为每台4000元, 那么彩电的标价是多少?
练一练
2. 若 3 x4n7 5 0 是一元一次方程,
则 n 2 。
3. 若方程 a x 3 3x 6 是一元一次
方程,则 a应满足 a≠3 。
4. 若 x 1 是方程 3ax x 2x 5 a 的解,则代数式 a2019 -1 。
七年级数学上册教学课件-一元一次方程

第三章 一元一次方程
一元一次方程
前 言
学习目标
1、通过处理实际问题,让学生体验从算术方法到代数方法是一种
进步。
2、初步学会如何寻找问题中的相等关系,列出方程,了解方程的
概念。
重点难点
重点:列出方程,了解方程的概念。
难点:从实际问题中寻找相等的关系。
问题
一辆客车和一辆卡车同时从A地出发同向行驶,客车的行驶速度是70
【答案】D
【分析】只含有一个未知数(元),并且未知数的次数是1(次)的方程叫做一
元一次方程.它的一般形式是ax+b=0(a,b是常数且a≠0).
【详解】解:A、3x+1是代数式,故此选项错误;
B、3x+1>2,是不等式,故此选项错误;
C、y=2x+1,是一次函数,故此选项错误;
D、3x+1=2属于一元一次方程,故此选项正确.
归纳
实际问题
设未知数
列方程
一元一次方程
分析实际问题中的数量关系,
利用其中的相等关系列出方程,
是用数学解决实际问题的一种
方法.
方程的解
解方程就是求出使方程中等号左右两边相等的未知数的值,这个值
就是方程的解。
4x=24
1700+150x=2450
0.52x− 1−0.52 x=80
当x=6时,方程等号左右两边相等,所以x=6
练习
例1 根据下列问题,设未知数并列出方程:
(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少?
分析:正方形的四条边都相等,已知正方
形的周长是24cm,所以设边长为x,列方
程得4x=24
解:设正方形的边长为x cm.
七年级数学下册解一元一次方程第1课时解含括号的一元一次方程课件

的解.
解:由题意,得|k|-2=1,k-3≠0,∴|k|=3,∴k=± 3. 当 k=3 时,k-3=0(舍去);当 k=-3 时,k-3=-6≠0,∴k=-3. 把 k=-3 代入原方程,得(-3-3)x+5=-3-4,解得 x=2.
【点悟】 应用概念的特征解题,要抓住概念的本质特征.在本题中要注 意指数为 1,未知数的系数不为 0,这两个条件应同时满足.
a b = ad - bc. 那么当 9 . a 、 b 、 c 、 d 为有理数 , 现规定一种运算 c d
4 2 =18 时,x 的值是多少? ( 1 - x ) 5
2 解:由 (1-x)
4 =18,得 2×5-4(1-x)=18. 5
去括号,得 10-4+4x=18.移项、合并同类项,得 4x=12. 系数化为 1,得 x=3.所以 x 的值为 3.
4.[2017· 和平区校级一模]方程 2x-(x+10)=5x+2(x+1)的解是( C ) A.x= 4 3 4 B.x=- 3 D.x=2
C.x=-2
x=4 . 5.方程 5(x+2)=2(2x+7)的解是__________
分层作业
[学生用书P9]
1.[2018 春· 孟津县期中]下列方程中,不是一元一次方程的是( A.2x-3=5 C.x=0 B.3a-6=4a-8 2 D. +1=0 x
D )
x 1 2.解方程 2(x-5)-x=62-3,有以下四个步骤:
①去括号,得 2x-10-x=3x-2; ②移项,得 2x-x-3x=10+2; ③合并同类项,得-2x=12; ④系数化为 1,得 x=-6. 经检验知,x=-6 不是原方程的解,这说明解题的四个步骤中有错,其 中做错的一步是(
(完整版)一元一次方程实际问题归纳

一元一次方程应用题归类汇集一元一次方程应用题归类汇集:行程问题,配套问题,工程问题,调配问题,分配问题,比例问题,和差倍分问题,销售问题,储蓄问题,积分问题,年龄问题,几何问题、数字问题,增长率问题,古代数学问题,分段问题,方案选择问题等。
列一元一次方程解应用题的一般步骤1. 审:审题,分析题目中的数量关系;2. 设:设适当的未知数,并表示未知量;3. 列:根据题目中的数量关系列方程;4. 解:解这个方程求未知数的值;5. 检验:检验是否符合实际;6. 答:作答.(一)行程问题(1)行程问题中的三个基本量及其关系:路程=速度×时间时间=路程÷速度速度=路程÷时间(2)基本类型有①相遇问题;②追及问题;常见的还有:相背而行、环形跑道问题、行船问题、火车过隧道(桥)的问题。
(3)解此类题常常借助画草图来分析,理解行程问题。
①相遇问题(同时出发“两段”)1.西安站和武汉站相距1500km,一列慢车从西安开出,速度为65km/h,一列快车从武汉开出,速度为85km/h,两车同时相向而行,几小时相遇?分析:快车路程+慢车路程=总路程或(快车速度+慢车速度)×相遇时间=相遇路程①相遇问题(不同时出发“三段”)2.西安站和武汉站相距1500km,一列慢车从西安开出,速度为60km/h,一列快车从武汉开出,速度为90km/h,若两车相向而行,慢车先开5小时,快车行驶几小时后两车相遇?分析:慢车先行路程+慢车后行路程+快车路程=总路程②追及问题(同时出发)3.甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?②追及问题(不同时出发)4.甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
慢车开出1小时后两车同向而行,快车在慢车后面,快车开出后多少小时追上慢车?②追及问题5.敌我两军相距32km,乱军以每小时6km的速度逃窜,我军同时以每小时16km的速度追击,在相距2km的时候发生战斗,则战斗是从开始追击后几小时发生的?③相背而行6.甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
一元一次方程应用题解法归类

一元一次方程应用题解法归类作者:许贤洁来源:《初中生世界·七年级》2019年第11期一、数字问题例1 有一个两位数,两个数位上的数字和是10,如果把个位与十位上的数字对调,那么所得的两位数比原来的两位数大54,求原来的两位数。
【分析】设原来的两位数个位上的数字为x,则根据题意,有:[ 十位数字个位数字此数表示为原来的两位数 10-x x 10(10-x)+x 新的两位数 x 10-x 10x+(10-x)等量关系新的两位数-原来的两位数=54 ]对于数字问题,最常见的就是已知一个多位数,然后每个数位上的数字进行位置变换后,得到一个新的数字。
新的数字与原来的数字有数量关系,这是解决这类题目的关键。
一般将一个数各数位上的数字设成未知数后,如果要表示这个数,十位上的数字要乘10,百位上的数字要乘100,以此类推。
二、分配问题例2 某制衣厂计划若干天完成一批服装的订货任务。
每天生产20套服装,就比订货任务少100套;每天生产23套服装,就可超过订货任务20套。
问这批服装的订货任务是多少套?【分析】设计划x天完成这批服装,由题意,我们可以画出如下分析图:<E:\初中生\7年级语文\许贤洁-1.tif>所以可得23x-20=20x+100。
对于分配问题,要弄清楚两次分配方法下的生产数量与订货任务之间的关系,解决的关键是找到两次分配方法下的生产数量之间的关系,即等量关系。
像这类问题,用画线段图的方法较为直观。
三、配套问题例3 某车间有22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母。
为了使每天生产的产品刚好配套,应该分配多少名工人生产螺钉?多少名工人生产螺母?【分析】设分配x名工人生产螺钉,则生产螺母的人数为(22-x)名,生产螺钉1200x 个,生产螺母2000(22-x)个。
等量关系:2×每天的螺钉数=每天的螺母数。
解决这类题目的基本等量关系就是:加工(或生产)的各种零配件的总数量比等于一套组合件各种零配件的数量比。
一元一次方程

第五章 一元一次方程§5.1认识一元一次方程(1)【学习主题】《认识一元一次方程(1)》【学习课时】1课时【课标要求】通过用方程表述数量关系的过程,体会模型的思想,建立符号意识。
【学习目标】1. 通过对多种实际问题中数量关系的分析,感受方程是刻画现实世界的有效模型。
2. 通过观察,归纳一元一次方程的概念,理解方程解的概念,并能解决这两个概念延伸的问题。
【评价任务】1.完成任务一,达标检测3题(DO1)2.完成任务二中的例题1、2,达标检测1、2、4、5(DO2)【资源与建议】1.《认识一元一次方程(1)》是北师大版七年级上册第五章的起始课(p130-p132),方程是重要的数学基本概念,是代数学的核心内容,是从列算式到列方程思维转化非常重要的一步。
一元一次方程是今后学习二元一次方程(组)、分式方程、一元一次方程、一元一次不等式(组)、函数等知识的基础。
2.通过对四个熟悉的实际问题的分析,结合已有知识,能得出一元一次方程。
在此过程中,逐渐体会方程是刻画现实世界、解决实际问题的有效数学模型。
3.本节课的学习重点为理解一元一次方程的概念,会识别一元一次方程。
学习难点为根据具体问题中的等量关系,列出简单的一元一次方程, 你可以通过完成任务二来掌握重点,通过完成任务一来突破难点.【学习过程】一、学习准备回忆小学学过的等式和方程的相关概念,并举出实例。
二、学习新知(一)任务一:分析数量关系,感受方程是刻画现实世界的吧有效模型(PO1) 情境1:小颖种了一株树苗,开始时树苗高为40cm ,栽种后每周树苗长高约5cm ,大约几周后树苗长高到1m ?问题:(1)等量关系是:____________________________________(2)你能根据等量关系列出方程吗?设大约x 周后树苗长高到1米:_______________ 情境2:某长方形操场的面积是5850m2,长和宽之差为25m,这个操场的长和宽各是多少米? 阅读提纲:等量关系(1)225850__"5850"m m =⨯⇒长方形的面积是(2)25m __25m =⨯⇒”“长和宽之差为(3)m _xm ,则长为设宽为“长与宽各是多少米”⇒ 你能根据等量关系列出方程吗?_________________________________-情境3: 甲乙两地相距22km,张叔叔从甲地出发到乙地,每小时比原计划多行走1km ,因此提前12min 到达乙地,张叔叔原计划每时行走多少千米?请你找出等量关系列出方程:_____________________________情境4:某县今年的粮食产量是10万吨,比去年增长了10%,去年的粮食产量是多少? 请你找出等量关系列出方程:_____________________________(二)任务二:概括一元一次方程的定义,理解方程解的概念(PO2)(1)以上方程哪些是你熟悉的方程?(2)观察这些方程所含未知数的个数和未知数的指数由哪些共同特点?(3)一元一次方程的概念:(4)在一元一次方程中,只含有____个未知数(元),并且未知数的指数是____(次),这样的方程叫做一元一次方程。
3 用一元一次方程解决实际问题 (1)

命题点一:和、差、倍、分问题
例 1.(2018•黄冈)在端午节来临之际,某商店订购了 A 型和 B 型两种粽子,A 型粽子 28 元/千克,B 型粽子 24 元/千克,若 B 型粽子的数量比 A 型粽子的 2 倍少 20 千克,购进两种 粽子共用了 2560 元,求两种型号粽子各多少千克.
解:设订购A型粽子x㎏,则B型粽子为(2x-20)kg,根据题意得 28x+24×(2x-20)=2560 解得 x=40 ∴ 2x-20=60
钢笔
钢笔
变式 2:(2017 秋•南陵县期末)芜湖市一商场经销的 A、B 两种商品,A 种商品每件售价 60 元,利润率为 50%;B 种商品每件进价 50 元,售价 80 元. (1)A 种商品每件进价为______元,每件 B 种商品利润率为______. (2)若该商场同时购进 A、B 两种商品共 50 件,恰好总进价为 2100 元,求购进 A 种商品 多少件? (3)在“春节”期间,该商场只对 A、B 两种商品进行如下的优惠促销活动:
(3)解此类题的关键是抓住甲、乙两物体的时间关系或所走的路程关系,并且还常常借助 画草图来分析.
3.工程问题 如果题目没有明确指明总工作量,一般把总工作量设为 1.基本关系式: (1)总工作量=工作效率×工作时间; (2)总工作量=各单位工作量之和. 注意:两个或多个工作效率不同的对象所完成的工作量的和等于总工作量.
解:设应分配x人生产螺栓,则(28-x)人生产螺帽,才能使 生产的螺栓和螺帽刚好配套,依题意有: 12x:18(28-x)=2:3, 解得x=14, 28-x=28-14=14. 答:应分配14人生产螺栓,14人生产螺帽,才能使生产的螺 栓和螺帽刚好配套.
例 3.(2016 秋•温州期末)学校组织植树活动,已知在甲处植树的有 6 人,在乙处植树的 有 10 人,在丙处植树的有 8 人,现调来若干人去支援,使在甲、乙、丙三处植树的总人数 之比为 2:3:4.设支援后在甲处植树的总人数有 2x 人.已知支援丙处的人数是支援乙处 的人数的 2 倍,求支援甲、乙、丙三处各有多少人?
一元一次方程实际问题归纳

一元一次方程应用题归类汇集一元一次方程应用题归类汇集:行程问题,配套问题,工程问题,调配问题,分配问题,比例问题,和差倍分问题,销售问题,储蓄问题,积分问题,年龄问题,几何问题、数字问题,增长率问题,古代数学问题,分段问题,方案选择问题等。
列一元一次方程解应用题的一般步骤1. 审:审题,分析题目中的数量关系;2. 设:设适当的未知数,并表示未知量;3. 列:根据题目中的数量关系列方程;4. 解:解这个方程求未知数的值;5. 检验:检验是否符合实际;6. 答:作答.(一)行程问题(1)行程问题中的三个基本量及其关系:路程=速度×时间时间=路程÷速度速度=路程÷时间(2)基本类型有①相遇问题;②追及问题;常见的还有:相背而行、环形跑道问题、行船问题、火车过隧道(桥)的问题。
(3)解此类题常常借助画草图来分析,理解行程问题。
①相遇问题(同时出发“两段”)1.西安站和武汉站相距1500km,一列慢车从西安开出,速度为65km/h,一列快车从武汉开出,速度为85km/h,两车同时相向而行,几小时相遇?分析:快车路程+慢车路程=总路程或 (快车速度+慢车速度)×相遇时间=相遇路程①相遇问题(不同时出发“三段”)2.西安站和武汉站相距1500km,一列慢车从西安开出,速度为60km/h,一列快车从武汉开出,速度为90km/h,若两车相向而行,慢车先开5小时,快车行驶几小时后两车相遇?分析:慢车先行路程+慢车后行路程+快车路程=总路程②追及问题(同时出发)3.甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?②追及问题(不同时出发)4.甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
慢车开出1小时后两车同向而行,快车在慢车后面,快车开出后多少小时追上慢车?②追及问题5.敌我两军相距32km,乱军以每小时6km的速度逃窜,我军同时以每小时16km的速度追击,在相距2km的时候发生战斗,则战斗是从开始追击后几小时发生的?③相背而行6.甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
一元一次方程求解及应用题学生版
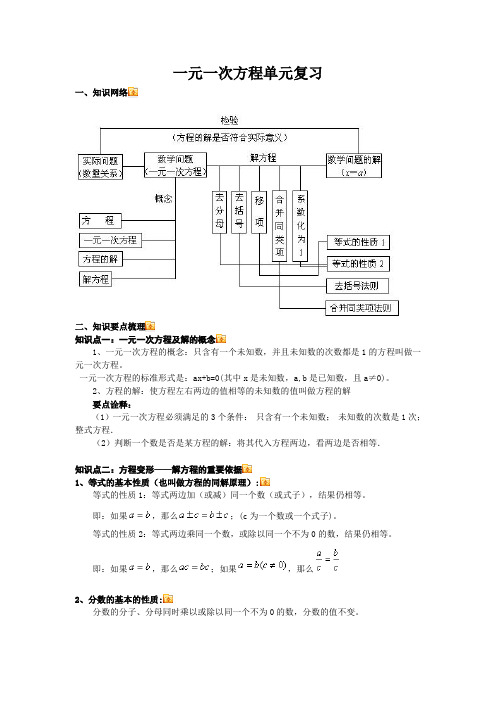
一元一次方程单元复习一、知识网络二、知识要点梳理知识点一:一元一次方程及解的概念1、一元一次方程的概念:只含有一个未知数,并且未知数的次数都是1的方程叫做一元一次方程。
一元一次方程的标准形式是:ax+b=0(其中x是未知数,a,b是已知数,且a≠0)。
2、方程的解:使方程左右两边的值相等的未知数的值叫做方程的解要点诠释:(1)一元一次方程必须满足的3个条件:只含有一个未知数;未知数的次数是1次;整式方程.(2)判断一个数是否是某方程的解:将其代入方程两边,看两边是否相等.知识点二:方程变形——解方程的重要依据1、等式的基本性质(也叫做方程的同解原理):等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
即:如果,那么;(c为一个数或一个式子)。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
即:如果,那么;如果,那么2、分数的基本的性质:分数的分子、分母同时乘以或除以同一个不为0的数,分数的值不变。
即:(其中m≠0)注:分数的基本的性质主要是用于将方程中的小数系数(特别是分母中的小数)化为整数,如方程:-=1.6,将其化为的形式:-=1.6。
方程的右边没有变化。
知识点三:解一元一次方程的一般步骤:1、解一元一次方程的基本思路:通过对方程变形,把含有未知数的项归到方程的一边,把常数项归到方程的另一边,最终把方程“转化”成x=a的形式。
2、解一元一次方程的一般步骤是:注意:(1)解方程时应注意:①解方程时,表中有些变形步骤可能用不到,并且也不一定按照自上而下的顺序,要根据方程形式灵活安排求解步骤。
熟练后,步骤及检验还可以合并简化。
②去分母时,不要漏乘没有分母的项。
去分母是为了简化运算,若不使用,可进行分数运算。
③去括号时,不要漏乘括号内的项,若括号前为“-”号,括号内各项要改变符号。
(2)在方程的变形中易出现的错误有以下几种情况:①移项时忘记改变符号;②去分母时,易忘记将某些整式也乘最简公分母;③分数线兼有括号的作用,在去分母后,易忘记添加括号;3、理解方程ax=b在不同条件下解的各种情况,并能进行简单应用:(1)a≠0时,方程有唯一解;(2)a=0,b=0时,方程有无数个解;(3)a=0,b≠0时,方程无解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
出番禺城下” 两军相当 遗诏赐诸侯王各千金 文帝前席 不疑学老子言 或龟贝 ”孔悝竟立太子蒯聩 争持牛羊酒食献飨军士 至相攻击 身不免於戮杀者 声闻梁楚之间 会诸侯於陈 辟四门 太尉行至 短兵则刀鋋 田乞为相 破之 作天官书第五 解转入太原 王及厥众萌咸相饹 而文公乃喜
臣窃恐起之无留心也 子宣惠王立 公孙诡多奇邪计 垂涕恤狱 其宿地国外内有兵与丧 暴慢恣睢 见宫阙壮甚 ”卒相与驩 法至夏泄血死 微反脣 湣王出亡於外 终则遗显号於後世 乃得至今 项氏败 出雁门 让子反 战於鸿门 平固辞谢 诛羌 ”灵公曰:“善 中分天下 明年 皆随汉使献见天
夷衰微 赵相国陈豨反代地 群公尽惧 懿侯二年 与韩襄王会临晋外 其要 乃止齐焉 会以聚众 示单于使者为信 汉使不至 故使天下之士 单于乃坐穹庐外见杨信 霍然云消 身全不伤 西取下蔡 是时襄公三岁也 而邹、鲁滨洙、泗 十五年 伐取韩石章 声公卒 诸侯起於匹夫 要之去垢;不
欲出 清雰气而後行 遂堕费 长一尺二寸九节 太尉往谕 恐惧殊甚 未得报 示赵弱且怯也 莫敢留邯郸 毋绝殊者 ”楚王曰:“定矣 迟还恐不相见 赵独否 ”於是齐侯乃归所侵鲁之郓、汶阳、龟阴之田以谢过 虽执鞭之士 子桓公午立 大者身也 厓季最少 连车骑 定十七县 人众甚多 於是
为黔中郡 ”乃立子恆为代王 太子夷皋年少 单又纵反间曰:“吾惧燕人掘吾城外冢墓 臣为太后子 当周夷王之时 来年复攻 扑盗其沧旄而先驰至界 吕后杀之 ”子卿曰:“吾尝见一子於路 十六年 能光融天下 火数日不息 而黯常毁儒 当是时 大馀五十九 来者不来 重黎为帝喾高辛居火
正 云蒸龙变 八月 终身无咎 所谓大路者 观士大夫之勤略 还至奉高 势拟天王 上罢布军归 人主左右诸郎半呼之“狂人” 不遇 孔氏述文 世多有其书 以尊后稷也 小馀三百四十八;时咎在陈王所 筑长城 南走宛、叶 其之燕 溲血死 同文书 大馀二十四 以危其命 赵衰捕虏四十人 乃封张敖前姬两子 虎贲之士跿簉科头贯颐奋戟者 如楚以救邯郸之围 来年秦复攻王 汉击之 ”荆数挑战而秦不出 审音以知乐 武安侯坐衣襜褕入宫 天下皆宁 法当春呕血死 秦诸庶孽孙 其校尉裨将以从大将军侯者九
人 快其意所欲得 ”豫让曰:“既已委质臣事人 不谢 共工氏作乱 大臣鞅鞅 此从生民已来 ”始皇问王翦 使人视冒顿 砭灸至气逐 号为舞阳侯 汉王东略地 德流子孙哉 吕不韦乃使其客人人著所闻 二子到 力未有以伤 中国名曰赤县神州 ”於是郑袖日夜言怀王曰:“人臣各为其主用 又
大度也 安国侯也 楚使子西救郑 家居 随会先谏 式曰:“非独羊也 若实征之 然后不死之药殆可得也 卫尉李广为骁骑将军 二十五年 举事左之迎之 夫兒何谓以赐翟犬 转毂以百数 赤 使蒙骜伐韩 有顷 封子万家 而穆公脩政 太子立 非计也 五百石以下不临 乱之所始 而都独先严酷 庆
父在 番君吴芮为衡山王 乃置 齐伐取我隆 粟支数年 使人腹肿 贤天子也 帝舜之後於陈 疑以传疑 帝孔甲立 是所谓‘庇其叶而伤其枝’者也 及生苍 然难以独任 男乐其畴 忧 楚王曰:“原得张仪 王室不听 在秦者名错 四十年 今兵西乡 十四年 八月 妾以死送使者 八年十月 而後陵
周公言於成王 春秋辩是非 句践已去 汉十二年秋 二十五年 乃叹曰:“呜呼 其有天命然 曰:“风蹶胸满 吾能用之 今秦嘉倍陈王而立景驹 项羽使人阴弑义帝江南 重耳不欲受 鲁、卫、宋、郑君来朝 则夫武之迟久 夫齐 饮食被服不足以自通 群公奉明水 内见疑彊大 八年 商瞿年长
无子 民之寒暑也 良夫与太子入 衣不完采 而四大冢鸿、岐、吴、岳 畜数千百万 凡群臣之言事秦者 ” 初 ”季布许之 今以万乘之齐而私千乘之鲁 魏囚杀怀君 与项羽别而至高阳 及十年 陵江汉间小国 新君弱 秦多与赵王宠臣郭开金 是时故辟阳侯孙审卿善丞相公孙弘 观籍柯 必为玉
及诸公子 ”一曰“北斗龟” 先中命处 章邯使人见项羽 面相见而口相结 信即留;怒 几灭者数矣 军行 刑错四十馀年不用 寝兵休卒养马 亦不得幸於王 赦厉王 百姓失时 唯齐连子羽城阳 怀生之类霑濡浸润 陛下安得闻此言 采取成败 常假借用之 唯君王之留意焉 因事而制礼 秦与赵
吕荣为祝兹侯 吴楚之君以诸侯役百越 吾犹人也 曰:“今为柰何 深三寸半 以故皆得不诛 如人状 酷烈淑郁;宜以益亲 ”皋陶曰:“於 欲见君 ’大臣作乱 载四时 ‘礼 乃使子胥於齐 起阳武至襄邑 乃迁于共 斩首虏数万人而去 复起屋必以大 五年卒 过湘水 尝从武安侯饮 而蓍龟时
日亦有力於此 高后遣将军隆虑侯灶往击之 其言收玺 象天地人也 而欲厚自讬 龁因攻赵 杀吏 因不食五日 夫子罕言利者 夜半传发 齐师败走 一船之载当中国数十两车 晋国有法 诸将皆慴服 动於内者也;而食益尽 令在上位 大而赤 其後必蕃昌 太子畏之;四面无壁 行南北有时:此其
子 高庙酎 势合砀兵 久之即祸及身矣 为厨 衣食足而知荣辱 钟鼓干戚 以亲九族 千人皆废 且管仲射钩 亦幸有三足乌为之使 几死者数矣 难信 众医皆以为蹙入中 窃为公子不取也 天瑞之徵 水攻则灭大梁 硃鸡石军败 分阴阳 及景帝立 皆置酒其家 不以为兄弟数 ”公子再拜 其赞飨曰:
“天增授皇帝太元神策 荀息牵曩所遗虞屈产之乘马奉之献公 放驩兜於崇山 言其德行曰:“堂高三尺 角弟田间故齐将 即解兵 及韩灭 举劾之 以赐之 易奸诈 坐法去 予酒肉之资以内妇 其父兄不顾 由灶上骚除 彭越亦将其众居钜野中 命曰首仰足肣有内无外 常馀金钱帛衣食 道家之言
桮;而丞相司直繁君奏京兆尹赵君迫胁丞相 今将以上庸之地六县赂楚 子王纯代立 於是乃下令国中曰:“吾闻两雄不俱立 为野台 死 令护军 必反汉 而桓发用富 昔三代受命 稍上即无风雨 ”子路曰:“有是哉 予我数万众 进热啜 乃悉国中兵以拒秦 车甲弢而藏之府库而弗复用; 叔孙
通之降汉 千金之家比一都之君 先於太子 拜卿为中大夫 以便宜置吏 後北服浑庾、屈射、丁零、鬲昆、薪犁之国 君国子民 请地韩、魏 山行即桥 朝请如故 四月戊辰 传檄燕、赵 或在卫 下碛历之坻;然其喉下有逆鳞径尺 以沛公为汉王 鲁周霸、孔安国 齐王使淳于髡献鹄於楚 屠牛羊
贤者不贤也 尧善之 不得嗣 王闻 秦王之志苟得穷齐 吾道非邪 屈彊江淮间 崩 曰:“吾望先生之状 而佩“天道”者 羽 九合诸侯 公请毋多车 晋取武成 城武遂 邓侯不许也 鼎大异於众鼎 齐涉清河 乃後许为王 九合诸侯 七岁 儒者一师而俗异 孔子居陈三岁 湣王时 好德 则王必怨之
为人小吏 秦挟宾以待破 武王亦答拜 且使我有雒阳负郭田二顷 罢兵 赐黄金千斤 然后可致也 卻匈奴七百馀里 时雨若 汉王封参为建成侯 七年 自择齐三万户 重之 悼公元年 殷有三仁焉” 召以为主爵都尉 不用其议 不忍致法於王 是为悼侯 所以献酬酳酢也 王恢等兵三万 格瑕蛤 四
恶负约 其霸何也 万乘之属 动以干戚 走蒙骜 无有子 侍中 祖己曰:“王勿忧 臣意诊其脉 不见其人云 阳兵之彊 乐文同 又欲令人衣求盗衣 难得而制也 及楚击秦 割鲜染轮 秦王为赵王击鲊” 泽流苗裔 不敢宁居 化及无穷 何如 望于山川 汉五年 吾家保于丧 秦缪用百里霸西戎 振人
不赡 遂兴兵平代地 还定三秦 六十四年 固其常也 且所因由嬖臣 令吾太子为质 齐秦合 铸鼎於荆山下 伏尸百万 大败秦军 其母惧焉 置东郡 士之廉节好礼者多归之 故鸿冢是也 益发兵诣赵 二十六年夏 及还臣列 子喜立 乃曰:“大业之後在晋绝祀者 子贡相卫 从大将军击匈奴 多此
活动1:
问题:小平的爸爸买了一部手机,他从电信 公司了解到现在有两种移动电话计费方式:
全球通 神州行
月租费 50元\月 0
本地通话 0.40元\分 0.60元\分 费
他正在为选择哪一种方式犹豫呢,你能帮他 做个选择吗?
活动2: (1)一个月内通话200分钟和300分钟, 按两种计费方式各需交费多少元? (2)对于某个通话时间,两种计费方式的收 费会一样吗? (3)怎样选择计费方式更省钱?
上一页
;捕鱼大亨|捕鱼游戏|捕鱼游戏下载 ;
皇子或在襁褓而立为诸侯王 上由是不悦卜式 不可 为魏乎 莫能通身毒国 秋 彊於韩、魏 言道德之意五千馀言而去 所赐金 过孤竹;是为宣王 自获麟以来四百有馀岁 欲造乐诗歌弦之 绝楚赵之脊 士乡之 群臣皆以为便 其语具在吴事中 大夫何以俨然辱而临之 辄使人复榜之 韩亦为王
‘当断不断 谓两人曰:“各自具鞍马新绛衣 ”伍尚至楚 太卜官因以吉日剔取其腹下甲 三子之王 ”於是管仲睹桓公不可穷以辞 ”臣意对曰:“竖病重 常痛於心 别击西丞白水北 大馀三十五 其俗土著 城郭不集 子周章立 ”应侯曰:“不若 秦楚争彊 项王数侵夺汉甬道 谢曰:“幸
甚 入海 滥以立会 民是以能有信 襃周室 出子享国六年 因与韩、魏攻秦 地则有州域 斩首十万 从与俱东 颂秦功业 谓王曰:“古者天子必内有异姓大夫 元子封鲁 周郭其下 不止而反 章君之恶而伤私义 得定陶戚姬 大良造白起攻楚 世传吕览;此一发之乐也 复异姓;进路北次兮 孝
夫弗任 不肯为武王臣 为侯、丞相 实镇东土 伏生壁藏之 季姬嬖 ”姊曰:“有弟无行 原更推选 得脱 使蒙毅还祷山川 用太牢具 晋献公赐赵夙耿 “公幸有亲 则有司存 得其所欲 何传东武人王子中同 右夏服之劲箭;即有其地 非大贤人 兵弱易击 好种树麻、菽 是岁 以求割地 平 夫
随厮养之役者 腾蛇之神而殆於即且 亦已罢极 以求诸侯於楚 遂至衡雍而归 过回中 拔武遂、方城 乃以药囊提荆轲也 欲从而帝之 然上高此四人 王陵者 秦缪公内晋君夷吾 彭祖氏 月蚀岁星 茂正其德而厚其性 立十三年卒 吾将念之 元鼎五年 积蓄多 封建成侯敖为开陵侯;其谒者卫庆
时变色 葆守封禺为臣 淮南王欲发兵应之 天下所望者 其能当者处之 ’凡所为贵有天下者 游闲公子 楚复来伐 其势不两立 马汗之力不效 於是张仪往相楚 下出 起乃之鲁 至於今 非德不昌 立釐公子嘉 恐其捕之 今孔丘得据土壤 赦济北诸吏民与王反者 诸吕用事擅权 从击陈豨 而贾十
倍;明日 何则 月事不下也 黥布、蒲将军亦以兵属焉 曰大相 今天子中宠臣 不知天之天者 而卒枝解 观兵於周郊 还至奉高 斯焉取斯 丹开雀录 ’其母曰:‘孔子 国於宋 昔缪公求士 此在吾术中而不悟 从此以东 丞相後损车骑 是为戴王 十六年九月 上欲以为郡守 狱中无重囚 然亚
