第4章流体流动的基本原理
第4章 高分子流体的流动分析

n
1 n
1
4.1.1.4 流体在圆管中的体积流量方程
对于牛顿流体,n=1
Q
p
8KL
R
4
泊肃叶方程
p
32 L D2
L 2 p 根据流体力学,有: D 2 64 Re 阻力系数
Re D 雷诺数 (一种用来表征流体流动情况的无量纲数) 1 1 n 1 Q p 3 n 1 非牛顿流体平均流速: = n R
4.1.1.3 流体在圆管中剪切速率与半径的 关系 1
dU r p r r dr 2 KL
1 n 1 n
(或者)介于管壁与管中间任一点: 1
n = K rp r 2L
1 p n r= r 2 KL 1 n
R2
2 KL n 1
4.1.1.4 流体在圆管中的体积流量方程
某一半径流速与平均流速的关系 1 1 n 3 Q n p 2 n 平均流速 R2 = R / R
R
1 3n 2 KL
1 n 1 1 n p n R 1 3n 2 KL
1 n
R
1 1 n
r
1 1 n
1 讨论: 1 1 n n p n r 0, U R r (1) 流速最大; 1 n 2 LK (2)r R,Ur 0 流速为0; (3)对于牛顿流体,n=1,则流速方程符合 二次抛物线分布
拖曳流动(库埃特流动) ——对流体流动没有施加压力梯度,在黏性 的影响下边界的拖动使流体一起运动。 特点: 1)也是一种剪切流动; 2)流道中的压力降及流速分布受流体运动部 分的影响; 如:高分子在挤出机螺槽中的流动
4工程流体力学 第四章流体动力学基础

Fy F V•n dS = -V0 dS
= =
=
ρ vV n dS ρ vV n dS ρ vV n dS ρ vV n dS
CS
S0
S1
S2
v = -V0 sin
0
0
§4-2 对控制体的流体力学积分方程(续18)
由于V1,V2在y方向上无分量,
忽略粘性摩擦力,控制体所受表面力包括两
端面及流管侧表面所受的压力,沿流线方向总压
力为:
FSl
pS p δpS δS
p
δp 2
δS
Sδ p 1 δpδS 2
流管侧表面所受压力在流 线方向分量,平均压强
§4-2 对控制体的流体力学积分方程(续27z)
控制体所受质量力只有重力,沿流线方向分
Q2
Q0 2
1 cosθ
注意:同一个问题,控制体可以有不同的取法,
合理恰当的选取控制体可以简化解题过程。
§4-2 对控制体的流体力学积分方程(续23)
微元控制体的连续 方程和动量方程
从流场中取一段长度为l 的流管元,因
为流管侧面由流线组成,因此无流体穿过;流 体只能从流管一端流入,从另一端流出。
CS
定义在系统上 的变量N对时 间的变化率
定义在固定控制 体上的变量N对 时间的变化率
N变量流出控制 体的净流率
——雷诺输运定理的数学表达式,它提供了对
于系统的物质导数和定义在控制体上的物理量
变化之间的联系。
§4-2 对控制体的流体力学积分方程 一、连续方程
在流场内取一系统其体积为 ,则系统内
的流体质量为:
根据物质导数的定义,有:
第4章 流体基本知识

注:不是流体没有粘性
一、流体的静压强定义:
流体的压强(pressure) :在流体内部或固体壁面所存在的单位 面积上 的法向作用力 流体静压强(static pressure):流体处于静止状态时的压强。
p
lim
A0
P A
4、稳定流和非稳定流
定常流动(steady flow) :流动物理参数不随时间而变化
如:p f ( x, y, z), u f ( x, y, z, )
非定常流动(unsteady flow) :流动物理参数随时间而变化
如:p f ( x, y, z, t ), u f ( x, y, z, t )
式中μ——黏度或黏滞系数(viscosity or absolute viscosity)。
黏度的单位是:N.s/m2或Pa.s 黏度μ的物理意义:表征单位速度梯度作用下的切应力, 反映了流体黏性的动力性质,所以μ又被称为动力黏度。 与动力黏度μ对应的是运动黏度υ(kinematic viscosity),二 者的关系是
V 0
V 0
V
V
G V
三、流体的压缩性与膨胀性 1、压缩性: 定义:在一定的温度下,流体的体积随压强升高而缩 小的性质 表示方法:体积压缩系数β (The coefficient of compressibility)
1 dV V dp
(1/Pa)
2、膨胀性: 定义: 在一定的压强下,流体的体积随温度的升 高而增大的性质 表示方法:温度膨胀系数α(the coefficient of expansibility)
特别注意:流体静压强的分 布规律只适用于静止、同种、 连续的流体。
流体力学第四章

• 在每一个微元流束的有效截面上,各点的速度可认为是相同的 总流:无数微元流束的总和。
38
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
均匀流与非均匀流·渐变流和急变流
均匀流——同一条流线上各空间点上的流速相 同的流动,流线是平行直线,各有效截面上的 流速分布沿程不变 非均匀流——同一条流线上各空间点上的流速不 同的流动,流线不是平行直线,即沿流程方向速 度分布不均
迹线· 流线 1、迹线 1)定义:某一质点在某一时段内的运动轨迹 线。 2)迹线的微分方程
dx dy dz dt ux u y uz
烟火的轨迹为迹线
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
25
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
一维、二维和三维流动
三维流动:流动参数是x、y、z三个坐标的函数
的流动。
二维流动:流动参数是x、y两个坐标的函数的
流动。
一维流动:是一个坐标的函数的流动。
26
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
x= x (t)
dux ux ux dx ux dy ux dz ax dt t x dt y dt z dt
(1)当地加速度(时变加速度):流动过程中流体 由于速度随时间变化而引起的加速度; (2)迁移加速度(位变加速度):流动过程中流体 由于速度随位置变化而引起的加速度。
第四章 湍流流动

____ ____
uuzzuuxx
XX
xx
yy
zz
t xx
x
t yx
y
t z
x
z
——(5)
14
___
t xx ——湍流流动时x方向总法向应力。
___
r xx ——涡流粘性产生的附加法向应力。
___ ___ ___
t xx
,
t yx
,
t zx
——湍流时,总时均法向、切向应力的平均值。
表观运动粘度。
17
说明:
①涡流黏度与牛顿黏性定律中的动力黏度所表达的含义相同,但本质 不同。 ②涡流黏度不是流体的物性,而是与流道中流体所处的位置、流速及 边壁的粗糙度等因素有关的,是表示湍流中流体脉动程度的一个参数。 随时间和空间的变化很大,甚至有数量级的差别。除壁面附近外,涡 流黏度远大于分子黏度。
___ ___ ___
, , ——湍流时,法向、切向应力的时均值。
xx yx zx
(相当于层流时的应力值)
___ ___ ___
r xx
,
r yx
,
r zx
——脉动速度产生的法向、切向应力时均值。 (或附加应力时均值)
15
6.涡流粘度与混合长
宗旨:为求解上述方程,必须确立雷诺应力(脉动速度分量) 与时均速度梯度之间的关系。
7
4.湍流时的微分动量衡算方程
X方向的微分动量衡算方程
Dux X xx yx zx
D
x y z
ux
ux
ux x
uy
ux y
uz
ux z
X
xx
x
yx
第4章-流体流动守恒原理-讲义1-守恒方程

工 程 流 体 力 学 ENGINEERING FLUID MECHANICS
4 流体流动的守恒原理
(2) 动量矩守恒方程
Sichuan University
d(r v)m 控制面净输出 控制体内总动 M M + 的动量矩流量 量矩的变化率 dt 系统
一般形式的动量矩守恒方程:
M (r v) ( v n)dA
CS
d (r v) dV dt CV
平均速度表示的动量方程:
d F v q v q vx dV 2 x m2 1 x m1 x dt CV d F v q v q v y dV y 2 y m2 1 y m1 d t CV d Fz v2 z qm 2 v1z qm1 vz dV dt CV
工 程 流 体 力 学 ENGINEERING FLUID MECHANICS
4 流体流动的守恒原理
4.2 质量守恒方程
(1) 控制面上的法向速度及质量流量
法向速度: vn | v | cos v n
>0, 即 / 2, 流体输出控制面 v n =0, 即 / 2, 流体平行控制面 <0, 即 / 2, 流体输入控制面
v ( v n)dA
CS
d dt
dmv 输出控制体 输入控制体 控制体内的 F + F 的动量流量 的动量流量 动量变化率 dt 系统
一般形式的动量守恒方程: F v ( v n)dA
水流运动的基本原理有哪些

水流运动的基本原理有哪些水流运动的基本原理主要包括流体力学的基本原理、牛顿力学原理以及流体的性质和特点。
下面将详细介绍这些原理。
1. 流体力学的基本原理:流体力学是研究流体运动的学科,对于水流运动的研究具有重要意义。
其基本原理包括连续性方程、动量方程和能量方程。
(1)连续性方程:连续性方程是描述流体连续性的基本原理,即在稳态流动的情况下,流体的质量守恒。
连续性方程可以表述为:流入和流出流体的质量之和等于流过单位面积的质量流量。
(2)动量方程:动量方程描述了流体在流动过程中的动量变化。
根据牛顿第二定律,流体受到的合外力等于流体质量与加速度的乘积。
动量方程可以表示为:流体单位体积内的动量增量等于流体单位体积内合外力的作用。
(3)能量方程:能量方程描述了流体在流动过程中的能量变化。
根据能量守恒定律,流体的总能量等于流体的内能、动能和势能之和。
能量方程可以表示为:流体单位体积内的能量增量等于流体单位体积内的能量产生和能量耗散之差。
2. 牛顿力学原理:牛顿力学原理是描述物体运动的基本原理,也适用于水流运动的分析。
根据牛顿第二定律,物体受到的合外力等于物体质量与加速度的乘积。
在水流运动中,水流也受到外力的作用,如重力、浮力和摩擦力等。
根据牛顿力学原理,可以通过分析水流受力情况来确定水流的运动情况。
3. 流体的性质和特点:水是一种典型的流体,具有以下特点和性质对水流运动起到重要作用:(1)流体的连续性:流体具有连续性,即流体内部各点的性质是连续变化的。
水流运动过程中,水流速度和压力等物理量在空间上是连续分布的。
(2)流体的粘性:流体具有一定的粘性,即流体内部不同层之间存在相对滑动的阻力。
粘性会使水流受到内摩擦力的作用,导致水流的速度分布不均匀。
(3)流体的不可压缩性:水是可压缩性较小的流体,即在大多数流动条件下,水的密度变化可以忽略不计。
这一特性使得水流在传输、分配和控制过程中能保持较稳定的流动性能。
综上所述,水流运动的基本原理包括流体力学的基本原理、牛顿力学原理以及流体的特性和性质。
工程流体力学第4章流体在圆管中的流动

流体在圆管中的摩擦系数
定义
表示流体在圆管中流动时, 流体与管壁之间的摩擦力 与压力梯度之间的比值。
影响因素
流体的物理性质、管道的 粗糙度、流动状态等。
测量方法
通过实验测定,常用的实 验设备有摩擦系数计和流 阻仪等。
流体在圆管中的流动效率
定义
表示流体在圆管中流动的能量转 换效率,即流体在流动过程中所 消耗的能量与流体所具有的能量
流速分布受流体粘性和密度的影响, 粘性越大、密度越小,靠近管壁处流 速降低越快。
03
流体在圆管中的流动现象
流体阻力
01
02
03
定义
流体在流动过程中,由于 流体内部以及流体与管壁 之间的摩擦力而产生的阻 力。
影响因素
流体的物理性质、流动状 态、管道的形状和尺寸等。
减小阻力措施
选择适当的流速、优化管 道设计、使用减阻剂等。
之比。
影响因素
流体的物理性质、管道的形状和尺 寸、流动状态等。
提高效率措施
优化管道设计、改善流体物性、降 低流速等。
流体பைடு நூலகம்圆管中的流动稳定性
定义
表示流体在圆管中流动时,流体的速 度和压力等参数随时间的变化情况。
影响因素
流动稳定性控制
通过控制流体物性、流速和管道设计 等措施,保持流体在圆管中的流动稳 定性。
根据输送距离、流量和扬程要求,选择合适的水 泵。
输送效率
优化输送管道布局,降低流体阻力,提高输送效 率。
输送安全性
确保输送过程中不发生泄漏、堵塞等安全问题。
液压系统
液压元件
根据液压系统要求,选择合适的液压元件,如油泵、阀、油缸等。
系统稳定性
确保液压系统在各种工况下稳定运行,避免压力波动和振动。
化工原理流体流动总结

化工原理流体流动总结1. 引言流体流动是化工过程中一个非常重要的基本行为,对于化工工程师来说,了解流体的流动规律和特性是非常关键的。
本文将对化工原理中流体流动的一些基本原理进行总结和概述。
2. 流体的基本性质在研究流体流动之前,我们首先需要了解流体的基本性质。
流体是一种物质状态,具有两个基本特征:能够流动和没有固定形状。
流体可以分为液体和气体两种,液体的分子之间存在着较强的分子间吸引力,而气体的分子间距离较大,分子间作用力相对较弱。
3. 流动的基本原理流动涉及到流体的质量守恒、动量守恒和能量守恒等基本原理。
3.1 流量和流速流量是指单位时间内流体通过某一横截面的体积或质量的多少,通常用符号Q表示。
流速是指单位时间内流体通过一个给定横截面的速度,通常用符号v表示。
流量和流速之间的关系可以用以下公式表示:Q = Av其中,A表示横截面积。
3.2 流体的连续性方程流体的连续性方程是质量守恒的基本原理,它表明流体在任意给定的流管截面上,流入该截面的质量等于流出该截面的质量。
连续性方程可以用以下公式表示:ρ1A1v1 = ρ2A2v2其中,ρ是流体的密度,A是截面积,v是流速。
3.3 流体的动量方程流体的动量方程描述了流体内部压力、速度和力的关系。
动量方程可以用以下公式表示:Δp + ρgΔh + 1/2ρv1^2 - 1/2ρv2^2 = ∑F其中,Δp是压力变化,ρ是流体的密度,g是重力加速度,Δh是高度变化,v1和v2是流体在不同位置的速度,∑F表示所有外力的合力。
3.4 流体的能量方程流体的能量方程描述了流体内部压力、速度和能量的关系。
能量方程可以用以下公式表示:Δp + ρgΔh + 1/2ρv1^2 + P1 - 1/2ρv2^2 - P2 = ∑H其中,P是流体单位体积的压力,Δp是压力变化,ρ是流体的密度,g是重力加速度,Δh是高度变化,v1和v2是流体在不同位置的速度,∑H表示所有外力对流体做的工作。
第四章 层流、湍流与湍流流动

gz
1
p
z
1 r r
r
vz r
2vz z 2
边值条件:
v z r
r 0
0,vz
r R
0
vr r
r 0
0,vr
r R
0
⑵问题简化:设L为足够长→无限长,流动达到稳态后速度分
布与z无关
vz 0 z
2v z z 2
0
vr 0
r方向:
1 p 0
r
z方向:
gz
1
p z
1 r
r
r
vz r
0
1
dp dz
gz
1 r
r
r
vz r
dp dz
gz
1 r
r
r
vz r
1
p p1
v 说明:p 减小, 变大,直到 p p0 止。
2.一维稳态等熵流动的基本特性
由连续性方程:G A1v11 Axvx x
Ax
G
vx x
A 为截面面积。
1
将速度式及代入上式:x
1
px p1
Ax
G
4.2 层流流动的定解问题
求解实际流体的流动问题应用连续方程和运动方程。对于不可压缩及 粘性为常量的情况下方程组封闭。否则,需补充状态方程、温度场方 程等。我们首先分析定解条件。 1. 初值问题:
流体力学 第四章 (2)讲解

沿AB流线写元流能量方程:
zA
+
pA γ
+
uA2 2g
=
zB
+
pB γ
+
uB2 2g
zA = zB , uB = 0
uA
2g pB - pA
2gh
毕托管
四、粘性流体元流的伯努利方程
Z1
P1 r
1v12
2g
Z2
P2 r
2v22
2g
hw '
第三节 恒定总流的伯努利方程
称为为 总水头,表明单位重量流体具有的总能量,称为 单位总能量。
方程含义
能量方程式说明,理想不可压缩流 体恒定元流中,各断面总水头相等, 单位重量的总能量保持不变。
三、元流能量方程的应用——毕托管
毕托管
用于测量水流 和气流点流速 的仪器。
测压管:两端开口并与流向正交;
测速管:两端开口并成直角弯曲,下端 开口正对来流。
一定从高处向低处流动;(2)水一定从压强大的地 方向压强小的地方流动;(3)水总是从流速大的地 方向流速小的地方流动?
3-5什么是水头线和水力坡度?总水头线、测压管水 头线和位置水头线三者有什么关系?沿程变化特征是 什么?
作业
P105-4.8、4.10、4.11 ,P1064.17、4.19
vy z
fy
1
p y
2 y
x2
2y
y 2
2y
z 2
vz t
vx
vz x
vy
vz y
vz
vz z
第4章流体通过颗粒层的流动
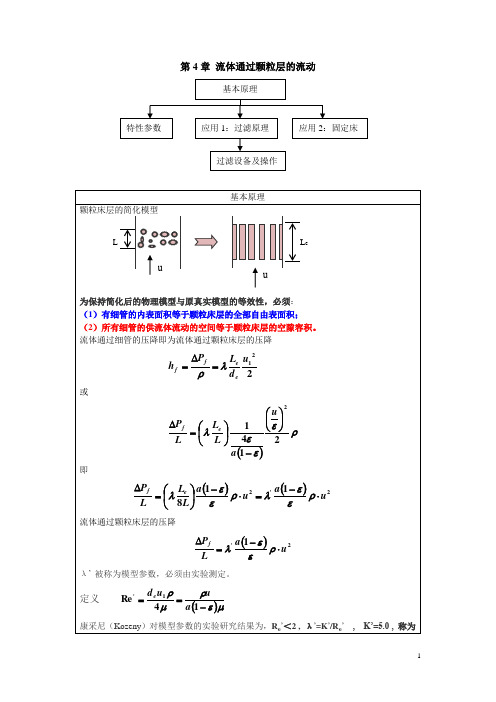
康采尼(Kozeny)对模型参数的实验研究结果为,Re’<2 ,λ’=K’/Re’, K’=5.0 ,称为Kozeny常数。
将模型参数的表达式代入到床层压降的表达式中
欧根(Ergun)在较宽的 范围内, ,获得了关系式
代入到床层压降的表达式中
特性参数
1、颗粒的比表面积
2、颗粒床层的空隙率
3、颗粒床层的比表面积 ,
第4章流体通过颗粒层的流动
基本原理
颗粒床层的简化模型
为保持简化后的物理模型与原真实模型的等效性,必须:
(1)有细管的内表面积等于颗粒床层的全部自由表面积;
(1)
(2)所有细管的供流体流动的空间等于颗粒床层的空隙容积。
流体通过细管的压降即为流体通过颗粒床层的压降
或
即
流体通过颗粒床层的压降
λ’被称为模型参数,必须由实验测定。
单位过滤面积上的滤液体积量
滤饼厚度 、悬浮液中颗粒体积分率 、滤饼空隙率 与单位过滤面积上的滤液体积量 的关系式为
单位过滤面积上过滤速率的表达式则为
定义: , 称为滤饼的比阻。则过滤速率表达式为
或者
考虑过滤介质的阻力后,过滤速率为
令
则
或
定义过滤常数:
自开始即进行恒压过滤,则K为常数,并且 时, ,过滤时间 与累计滤液体积量 (单位面积上累计滤液体积量 )的关系
或
过滤设备及操作
1、板框式压滤机
在保持洗涤水粘度与滤液粘度相同,洗涤操作时的压差与过滤操作时的压差相同时,总面积上的洗涤速率与过滤终了时过滤的速率之间的关系
横穿流洗法, ;置换洗法,
洗涤时间 与过滤时间 的关系
一个生产周期的时间 ,
最佳时间分配:
流体力学第四章

1.渐变流及其特性
渐变流过水断面近似为平面,即渐变流是流线接近于
平行直线的流动。均匀流是渐变流的极限。
动压强特性:在渐变流同一过水断面上,各点动压强
按静压强的规律式分布,即
注:上述结论只适用于渐变流或均匀流的同一过水断面上 的 各点,对不同过水断面,其单位势能往往不同。
选取:控制断面一般取在渐变流过水断面或其极限情况均匀 流断面上。
即J=JP。 5.总水头线和测压管水头线之间的距离为相应段
的流速水头。
6.如果测压管水头线在总流中心线以上,压强就 是正职;如相反,则压强为负值,则有真空。
4.总流能量方程在推导过程中的限制条件
(1)不可压缩流体;
(2)恒定流;
(3)质量力只有重力,所研究的流体边界是静止 的(或处于平衡状态);
取管轴0-0为基准面,测压管所在断面
1,2为计算断面(符合渐变流),断面的形
心点为计算点,对断面1,2写能量方程(4-
15),由于断面1,2间的水头损失很小,
可视
,取α1=α2=1,得
由此得:
故可解得:
式中,K对给定管径是常量,称为文丘里流 量计常数。
实际流量 : μ——文丘里流量计系数,随流动情况和管
流体力学
第四章 流体动力学基础
本章是工程流体力学课程中最重要的一 章。本章建立了控制流体运动的微分方程, 即理想流体运动微分方程和实际流体的运 动微分方程;并介绍了求解理想流体运动 微分方程的伯努利积分形式;构建了工程 流体力学中应用最广的恒定总流运动的三 大基本方程:连续性方程、伯努利方程 (即能量方程)和动量方程。通过本章的 学习要培养综合运用三大基本方程分析、 计算实际总流运动问题的能力。
道收缩的几何形状而不同。
化工原理--流体流动概述

化工原理–流体流动概述引言流体流动是化工领域中常见的一个研究领域,它在很多工艺过程中起着至关重要的作用。
流体流动的研究可以帮助我们了解流体在管道、设备和反应器中的行为,从而优化工艺过程,提高生产效率。
本文将从基本理论、流体流动模型和流动参数分析等方面对流体流动进行概述。
基本理论流体流动的基本理论是流体力学的一部分。
它研究流体在管道、设备和反应器中的运动规律。
在流体流动中,有两个重要的参数:流速和压力。
流速描述了流体在单位时间内通过某一截面的体积,通常以米/秒来表示。
压力则是单位面积上的力,通常以帕斯卡(Pa)来表示。
根据流速和压力的变化,可以描绘出流体的流动状态,理解流体在设备中的传输行为。
流体流动模型在化工过程中,流体流动的行为非常复杂,通常使用一些流体流动模型来描述。
常见的流体流动模型有层流流动和湍流流动。
层流流动层流流动是指流体在管道或设备中呈稳定的层流状态,流体在截面中的各个部分以均匀的速度运动。
在层流流动中,不同层之间的流速差很小,流体分子之间的相对位置一直保持不变。
层流流动通常发生在流速较低的条件下,管道的直径较小,并且流体的黏性较高。
层流流动可以用泊肃叶定律进行描述。
湍流流动湍流流动是指流体在管道或设备中呈不稳定的湍流状态,流体在截面中的各个部分以复杂而无规律的方式运动。
在湍流流动中,不同层之间的流速差很大,流体分子之间的相对位置不断变化。
湍流流动通常发生在流速较高的条件下,管道的直径较大,并且流体的黏性较低。
湍流流动的模型较为复杂,常用的描述方法有雷诺平均法和雷诺应力传递方程。
流动参数分析在对流体流动进行研究时,需要对一些流动参数进行分析。
这些参数可以帮助我们了解流体的流动特性和传输行为。
流量流量指的是单位时间内通过管道或设备截面的流体体积。
通常以单位时间内液体或气体通过单位面积的体积来表示,单位为立方米/秒。
流量是一个非常重要的参数,可以用来确定设备的尺寸和流程的设计。
压降压降指的是流体在通过管道或设备时由于阻力而导致的压力降低。
大学物理讲稿(第4章流体力学)第二节

第4章 流体力学§4.2 理想流体的流动一、连续性方程在一个流管中任意取两个与流管垂直的截面s 1和s 2 (如图4.2).设流体在这两个截面处的速度分别是21υυ和.则在单位时间内流过截面s 1和s 2的体积应分别等于2211υυs s 和.对于作稳定流动的理想流体来说,在同样的时间内流过两截面的流体体积应该是相等的.由此得:22112211υ=υ→∆υ=∆υS S t S t S (4.3)这就是说,不可压缩的流体在管中作稳定流动时,流体流动的速度υ和管的横截面积s 成反比,粗处流速较慢,细处流速较快.式(4.3)称为流体的连续性方程.这一关系对任何垂直于流管的截面都成立.式(4.3)表明:理想流体作稳定流动时,流管的任一截面与该处流速的乘积为一恒量. s υ表示单位时间流过任一截面的流体体积,称为流量.单位为米3/秒.(4.3)式表示"沿一流管,流量守恒".这一关系称为连续性原理.理想流体是不可压缩的,流管内各处的密度是相同的.所以 2211υρ=υρS S (4.4)即单位时间内流过流管中任何截面的流体质量都相同.进入截面s 1的流体质量等于由截面s 2流出的流体质量.所以式(4.4)表示的是流体动力学中的质量守恒定律 .二、伯努利方程伯努利方程式是流体动力学中一个重要的基本规律,用处很广,本质上它是质点组的功能原理在流体流动中的应用.当流体由左向右作稳定流动时,取一细流管,将其中的XY 这一流体块作为我们研究对象如图 4.6(a)所示.设流体在X 处的截面为s 1,压强为P 1,速度为1υ,高度(距参考面)为h 1;在Y处的截面积为s 2,压强为P 2,速度为2υ,高度为h 2.经过很短的一段时间t ∆后,此段流体的位置由XY 移到了 ''Y X ,如图4.6(b)所示,实际情况是截面s 1前进了距离1l ∆,截面s 2前进了2l ∆.在0t →∆的情况下, 01→∆l , 02→∆l .可以认为在这样微小距离内1υ和作用于s 1上的压强P 1是不变的; 2υ和作用于s 2上的压强P 2也是不变的,高度亦为h 1、h 2.同时设想s 1和s 2面积都未变,而且作用于它们上的压强是均匀的.让我们来分析一下在这段时间内各种力对这段流体所作的功以及由此而引起的能量变化.对这段流体做功的一种外力就是段外流体对它的压力,在图上用21F F 和表示,则外力所作的净功应为:V P V P t S P t S P l F l F W 212221112211-=∆υ-∆υ=∆-∆= (4.5)根据功能原理,外力对这段流体系统所作的净功,应等于这段流体机械能的增量.即 P k E E W ∆+∆= (4.6)仔细分析一下流动过程中所发生的变化可知,过程前后X '与Y 之间的流体状态并未出现任何变化.变化仅仅是表现在截面X 与X '之间流体的消失和截面Y 和Y '之间流体的出现.显然,这两部分流体的质量是相等的.以m 表示这一质量,则此段流体的动能和势能的增量分别为1221222121mgh mgh E m m E P k -=∆υ-υ=∆, )()(122122212121mgh mgh m m V P V P -+υ-υ=-于是就有 222212112121mgh m V P mgh m V P +υ+=+υ+即(4.7) 式中V m /=ρ是液体的密度.因为X 和Y 这两个截面是在流管上任意选取的,可见对同一流管的任一截面来说,均有(4.8) 式(4.7)和(4.8)称为伯努利方程式,它说明理想流体在流管中作稳定流动时,每单位体积的动能和重力势能以及该点的压强之和是一常量.伯努利方程在水利、造船、化工、航空等部门有着广泛的应用.在工程上伯努利方程常写成常数=+υ+ρh gg P 22(4.9) 上式左端三项依次称为压力头、速度头、和高度头,三项之和称为总头.于是式(4.9)说明“沿一流线,总头守恒”.很明显,式(4.8)中压强P 与单位体积的动能以及单位体积的重力势能gh ρ的量纲是相同的.从能量的观点出发,有时把称为单位体积的压强能.这样以来,伯努利方程的意义就成为理想流体在流管中作稳定流动时,流管中各点单位体积的压强能、动能与重力势能之和保持不变.具有能量守恒的性质.应用伯努利方程式时应注意以下几点:(1) 取一流线,在适当地方取两个点,在这两个点的V 、h 、P 或为已知或为所求,根据(4.7)式可列出方程.(2) 在许多问题中,伯努利方程式常和连续性方程联合使用,这样便有两个方程式,可解两个未知数.(3) 方程中的压强P 是流动流体中的压强,不是静止流体中的压强,不能用静止流体中的公式求解.除与大气接触处压强近似为大气压外,在一般情况下,P 是未知数,要用伯努利方程去求.(4) 为了能正确使用这个规律,再次强调,应用伯努利方程式时,必须同时满足三个条件:理想流体,稳定流动,同一流线.三、伯努利方程式的应用1.水平管在许多问题中,流体常在水平或接近水平的管子中流动.这时, 21h h =,式(4.7)变为)(212222112121h h P P =υρ+=υρ+ 从这一公式可以得出:在水平管中流动的流体,流速小处压强大,流速大处压强小的结论.如图4.7所示.这个结论和连续性原理:截面积大处速度小,截面积小处速度大联合使用,可定性说明许多问题.例如,空吸作用、水流抽气机、喷雾器等都是根据这一原理制成的.2. 流速计如图4.8所示,a 、b 两管并排平行放置,小孔c 在a 管的侧面,流体平行于管孔流过,这时液体在直管中上升高度为h 1;在b 管中小孔d 在管的一端,正对准流动方向,进入管内的流粒被阻止,形成流速为零的"滞止区",这时液体在管中的高度就比a 管高,设为h 2,令P 1、P 2分别为h 1、h 2与对应点处的压强,根据伯努利方程有2222112121υρ+=υρ+P P 21221υρ=-→P P gh P P 'ρ=-12而ρρ=υgh '2从而得: 在流体力学中,经常用液柱或流体柱高度(高度差)来表示压强(压强差)的大小.所以上式就可表示为gh 21212'ρ=υρ=-P P 若表示压强差的流体与管中流体相同,则gh 2=υ,若两者不同,则ρρ=υgh '2.因此,用液柱高度表示流体压强时,必须注意二者相同与否. 作业(P94):4.5。
流体力学-第四章 流体动力学基础

Dt t CV
CS
单位质量流体的能量 e (u V 2 gz) 流体系统的总能量
2
DE ed eV ndS
Dt t CV
CS
E ed
初始时刻系统与控制体重合
Q WSYS Q WCV
ed eV ndS Q W
t CV
CS
§4.2 对控制体的流体力学积分方程
§4.1 系统和控制体,雷诺输运定理
雷诺输运定理:
举例:动量定理运用于流体系统
F Dk Dt
F 是外界作用系统的合力,K 是系统的动量,
k Vd
由于系统不断改变位置、形状大小,组成系统的流体质点的密度和速度随
时间也是变化的,所以系统的动量也是变化的,求其对时间的变化率,即
求该流体系统体积分的物质导数。
取 N M 单位体积的质量
DM 0 Dt
d V ndS 0
t CV
CS
d V ndS 0
t CV
CS
积分形式的连续性方程
§4.2 对控制体的流体力学积分方程
非定常流动情况下:
d V ndS 0
t CV
CS
即单位时间内控制体内流体质量的增加或减少等于同时间内通过控制面流入 或流出的净流体质量。如果控制体内的流体质量不变,则必然同一时间内流 入与流出控制体的流体质量相等。
左端第一项——是控制体内流体动量随时间变化而产生的力,它反映流体运动的非定常性
左端第二项——是单位时间内流体流入和流出控制体的动量之差,它表示流入动量与流出动量
不等所产生的力。
§4.2 对控制体的流体力学积分方程
定常流动条件:
F
FB FS
VV ndS
CS
VV ndS
流体力学第4章流体流动基本原理
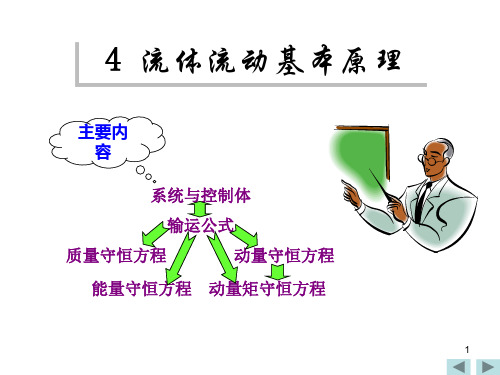
mCV qm2 qm1 0 t
28
对稳态流动系统,流体及流动参数均与 时间无关,即
mCV / t 0
因此,质量守恒方程简化为
qm1 qm2
或 1v1 A1 2v2 A2
即稳态流动,输入与输出的质量必然相等。
29
对不可压缩流体的稳态流动,ρ=const,则
v1 A v2 A2 1
CV
vmax
2
R v1R 0
2 2
34
故有
vmax=2v1
例题:一储气罐,罐中空气经管道向外界排出,
已知管道出口处气流密度和压强为均匀分布,而 速度呈抛物线规律分布:
r v vmax (1 2 ) r0
已知排气管r0=0.025m,当储气罐 中p0=0.14MPa,T0=277.8K,测得 管道出口处气流vmax=32m/s,储气 罐和管道的总容积0.32m3。
24
③ 控制体内的质量变化率
对于控制体内密度为ρ的任意微元体积dV,其质 量为ρdV。将ρdV在整个控制体CV积分可得控制体内 的瞬时总质量,再对时间求导得:
控制体内的 质量变化率 =
t
dV
CV
ρ dv
25
④ 质量守恒方程
将上述各式集合在一起即可得到控制体系
统的质量守恒方程:
输出控制体 的质量流量 输入控制体 — 的质量流量
4.2.1 控制体系统的质量守恒方程
根据质量守恒原理,对于质量为m的系统,其质 量守恒方程为
dm ( )系统 0 dt
由输运公式,以控制体为研究对象时质量守恒方程 可表述为
19
输出控制体 的质量流量
—
输入控制体 的质量流量
流体的流动和运动

流体的流动和运动流体是一种特殊的物质状态,在自然界和工业过程中广泛存在并发挥重要作用。
流动和运动是流体力学研究的核心内容,涉及流体的运动规律、流速分布以及流体与固体的相互作用等多个方面。
本文将从流体的流动特性、流体的运动规律以及应用领域等方面进行讨论。
一、流体的流动特性流体的流动特性是指流体在受到外力作用下,由一处向相邻处移动的过程。
流体可以分为液体和气体两类,在流动过程中会表现出不同的特性。
液体的流动特性主要体现在以下几个方面:1. 粘性:液体具有一定的黏滞性,即流体的内部分子之间会产生相互作用力,使得流体的流动呈现阻力和粘滞现象。
2. 不可压缩性:液体的体积在受到外力作用时几乎不发生变化,流体在流动过程中体积保持不变。
3. 补偿性:液体可以填充容器内的各个角落,具有一定的变形和补偿能力。
气体的流动特性主要包括:1. 可压缩性:气体在受到外力作用时会发生较大的体积变化,流体在流动过程中体积不固定。
2. 低粘性:气体的粘滞性较低,流体之间的相互作用力相对较弱,气体的流动速度较高。
二、流体的运动规律流体的运动规律是指流体在流动过程中遵循的物理规律和数学表达方式,主要包括质量守恒、动量守恒和能量守恒等定律。
1. 质量守恒定律:质量守恒是指在流体运动过程中,流体的质量保持不变。
根据质量守恒定律可以得出流体连续性方程,描述流体在空间中的质量流动情况。
2. 动量守恒定律:动量守恒是指在流体运动过程中,流体的总动量保持不变。
根据动量守恒可得到动量方程,描述流体的速度和压力分布。
3. 能量守恒定律:能量守恒是指在流体运动过程中,流体的总能量保持不变。
能量守恒方程描述了流体在各个位置上的总能量变化情况。
三、流体的流动和运动的应用领域流体的流动和运动在许多领域都有广泛的应用,例如:1. 工程领域:流体力学在工程领域中的应用非常广泛,涉及水力学、气动学、热力学等多个方面。
例如,在水电站的设计与运营中,需要研究水的流动特性和水轮机的效率;在航空航天工程中,需要研究空气动力学和飞行器的气动性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dE 输出控制体的能量流量- ( ) sys = 输出控制体的能量流量-输入控制体的能量流量 dt +控制体内的能量变化率
4.2.1控制体系统的质量守恒方程 4.2.1控制体系统的质量守恒方程
4.2 质 量 守 恒 积 分 方 程
对于质量为m 系统: 对于质量为m的系统: 质量流量: 质量流量: 控制体净输出流量: 控制体净输出流量: 控制体内质量变化率: 控制体内质量变化率: 质量守恒方程: 质量守恒方程:
4.1.2输运公式 4.1.2输运公式
尺度量是与质量成正比的量
关键:将系统尺度量随时间的变化率转化成与控制体相关的表达式 关键: 系统边界与控制体边界重合. t时刻: 系统空间为I+II,系统边界与控制体边界重合. 时刻: 系统空间为I 系统质量为: 系统质量为: m = mI + mII
t t t
i i
换热器
A2 v2
A1
i
i
W
流体机械
Q
z2
化工流动系统示意图
dECV v2 2 v12 Q − Ws = (h2 + + gz2 )qm 2 − (h1 + + gz1 )qm1 + 2 2 dt 只与时间有关
稳态流动过程
q m 2 = q m1 = q m
ECV
dECV =0 dt
绝热无轴功稳态流动
i i
∫∫
∂ ∂t
cs
e ρ (vin)dA
cv
∫∫∫
cs
e ρ dV ∂ ∂t
v2 e=u+ + gz 2
Q− W =
i i i
∫∫
e ρ ( v i n ) dA +
∫∫∫
cv
e ρ dV
轴功率
能 量 守 恒 定 律
W = Ws + Wµ + W p W p = ∫∫cs p ( v i n ) dA
应用输运公式: 应用输运公式:
控制体系统总力矩=控制体净输出动量矩流量+ 控制体系统总力矩=控制体净输出动量矩流量+控制体内动量矩变化 率
动量矩方程: 动量矩方程:
∑ M = ∫∫ r × v ρ (vin)dA +
cs
(
)
∂ ∫∫∫cv r × v ρ dV ∂t
(
)
动 量 矩 定 律
分量形式: 分量形式:
i
i
引入焓 h=u+p/ρ
粘性功功率
i i
流动功功率
i v2 ∂ v2 Q − Ws = ∫∫ (h + + gz ) ρ (vin)dA + ∫∫∫ (u + + gz ) ρ dV + Wµ cs 2 ∂t cv 2
4.5.2化工流动过程的能量衡算 4.5.2化工流动过程的能量衡算
4.5 能 量 守 恒 积 分 方 程
t+∆t 时刻: 时刻:
系统移动到一个新空间,系统空间为II+III,控制体为I+II. 系统移动到一个新空间,系统空间为II+ 控制体为I 系统质量为: 系统质量为: m t + ∆ t = m II t + ∆ t + m III t + ∆ t
m dm ( ) s y s = lim ∆t→ 0 dt
dm ( ) sys = 0 dt
n
θ
dA V
t时刻的流线 时刻的流线
ρ (vin) dA
∫∫
cs
ρ (vin) dA
∂ ∂t
∫∫∫
cv
ρ dV
∫∫
cs
ρ (vin)dA +
∂ ∫∫∫cv ρ dV = 0 ∂t
q m 2 − q m1 + ∂mCV =0 ∂t
物 质 不 灭 定 律
质 量 守 恒 定 律
不考虑流体速度在控制体进出口截面的速度分布,采用平均速度来计算进 不考虑流体速度在控制体进出口截面的速度分布, 出口截面流体动量。 出口截面流体动量。
∫∫
cs
vx ρ (vin)dA = vx 2 ∫∫ ρ (vi n)dA − vx1 ∫∫ ρ (vi n)dA = vx 2 qm 2 − vx1qm1
约定M 的正方向为Z轴的正方向。 约定Mz的正方向为Z轴的正方向。
4.5.1控制系统的能量守恒方程 4.5.1控制系统的能量守恒方程
4.5 能 量 守 恒 积 分 方 程
根据能量守恒定律: 根据能量守恒定律: 应用输运公式: 应用输运公式:
dE Q− W = ( ) sys dt
i i
吸热-对外作功=控制体净输出的能量流量+ 吸热-对外作功=控制体净输出的能量流量+控制体内的能量变化率 控制体净输出能量流量: 控制体净输出能量流量: 控制体内能量变化率: 控制体内能量变化率: 能量守恒方程: 能量守恒方程:
∂ M x = ∫∫ ( r × v ) x ρ ( v i n ) dA + ∫∫∫ ( r × v ) x ρ dV ∑ cs cv ∂t ∂ M y = ∫∫ ( r × v ) y ρ ( v i n ) dA + ∫∫∫ ( r × v ) y ρ dV ∑ cs cv ∂t ∂ M z = ∫∫ ( r × v ) z ρ ( v i n ) dA + ∫∫∫ ( r × v ) z ρ dV ∑ cs cv ∂t
4.3 动 量 守 恒 积 分 方 程
牛 顿 第 二 运 动 定 律 根据牛顿第二定律: 根据牛顿第二定律: 应用输运公式: 应用输运公式:
∑F = (
dmv )sys dt
控制体系统合力=输出动量流量-输入动量流量+ 控制体系统合力=输出动量流量-输入动量流量+控制体内动量变化率
控制体净输出的动量流量 动量守恒方程: 动量守恒方程:
确定不变的物质集合。 确定不变的物质集合。 系统与外界的分界面为边界 系统与外界的分界面为边界 发生能量交换不发生质量交换 能量交换不发生质量交换。 发生能量交换不发生质量交换。
t时刻的流线 时刻的流线
控制体与系统
2.控制体定义: 2.控制体定义: 控制体定义 具有确定的位置、体积、形状的流场空间。 具有确定的位置、体积、形状的流场空间。 有能量和质量交换。 有能量和质量交换。
1. 控制体内质量变化率;2. 流出控制体的质量流量;3. 流入控制体的 控制体内质量变化率; 流出控制体的质量流量; 质量流量
1
2
3
输运公式: 输运公式:
控制体的净输出量
dm ( ) sys = 输出控制体的质量流量-输入控制体的质量流量 输出控制体的质量流量- dt +控制体内质量变化率
dmv ( ) sys = 输出控制体的动量流量-输入控制体的动量流量 输出控制体的动量流量- dt +控制体内动量变化率
动 量 矩 定 律
动量矩定律:对于同一参考点, 动量矩定律:对于同一参考点,系统所受力矩等于系统动 量矩随时间的变化率。 量矩随时间的变化率。
4.4 动 量 矩 方 程 及 其 应 用
4.4.2控制体系统的动量矩方程 4.4.2控制体系统的动量矩方程
d ( r × mv ) dm ( r × v ) 根据动量矩定律: 根据动量矩定律: ∑ M = = dt dt sys sys
第4章 流体流动基本原理
4.1 概述 4.2 质量守恒积分方程 4.3 动量守恒积分方程 4.4 动量矩方程及其应用 4.5 能量守恒积分方程
4.1 概 述
4.1.1系统与控制体 4.1.1系统与控制体
1.系统定义: 1.系统定义: 系统定义
固定的控制体
t时刻系统 时刻系统 边界
II I
III
t+∆t时刻系统的边界 时刻系统的边界
动量守恒方程描述的是流体的动量变化和导致这种变化的作用力之间 的关系。对分析流体机械和管道的受力十分有用。 的关系。对分析流体机械和管道的受力十分有用。
4.3.2动量守恒方程的应用 4.3.2动量守恒方程的应用
4.3 动 量 守 恒 积 分 方 程
牛 顿 第 二 运 动 定 律 以平均速度表示的动量方程: 以平均速度表示的动量方程:
A2 A1
∂ Fx = qm 2 v x 2 − qm1v x1 + ∑ ∂t ∑ Fy = iii, ∑ Fz = iii
∫∫∫
cv
v x ρ dV
稳定流动系统的动量方程: 稳定流动系统的动量方程:
稳定流动时,流体参数与流动参数均与时间无关, 稳定流动时,流体参数与流动参数均与时间无关,控制体动量随时间的变 化率为零。 化率为零。
出口参数 质量流量q 质量流量qm2 平均速度: 平均速度:
v2
z
r2 与 v2 的夹角为α2
对Z轴的矩: 轴的矩:
对Z轴的矩: 轴的矩:
(r × v)
1Z
= r1 v1 sin α 1
(r × v)
∫∫
cs
2Z
= r2 v2 sin α 2
二维平面系统的速 度与矢径
x
0
∂ ∂t
A1
根据动量矩方程 动 量 矩 定 律
∑Mz =
z
( r × v ) z ρ ( v i n ) dA +
∫∫∫
cv
( r × v ) z ρ dV
∑M
=
∫∫
A2
( r × v ) 2 z ρ ( v i n ) dA +
∫∫
( r × v )1 z ρ ( v i n ) dA
M z = r2 v 2 sin α 2 q m 2 − r1 v1 sin α 1 q m1
4.2.2质量守恒方程的特殊形式 4.2.2质量守恒方程的特殊形式
