山东省诸城市桃林镇2017届中考数学压轴题专项汇编专题25全等三角形的存在性
山东省诸城市桃林镇2017届中考数学压轴题专项汇编专题15角含半角模型

专题 15角含半角模型破题策略1.等腰直角三角形角含半角如图,在△ ABC中, AB= AC,∠ BAC=90°,点 D, E在 BC上且∠ DAE=45°(1)△BAE∽△ADE∽△CDA22 2(2)BD+CE=DE.A45°CBD E证明( 1)易得∠ADC=∠B+∠BAD=∠EAB,因此△ BAE∽△ ADE∽△ CD A.(2)方法一(旋转法):如图1,将△ABD绕点A逆时针旋转90°获得△ACF,连接EF.A45° FCBD E则∠ EAF=∠ EAD=45°, AF=AD,因此△ ADE∽△ FAE (SAS ).因此 DE=EF.而 CF= BD,∠ FCE=∠ FCA+∠ ACE=90°,因此 BD+CE= CF+ CE=EF= DE.方法二(翻折法):如图2,作点B对于AD 的对称点F,连接AF, DF,EF.A45°CBD EF由于∠ BAD+∠ EAC=∠ DAF+∠ EAF,又由于∠ BAD=∠ DAF,则∠ FAE=∠ CAE, AF= AB= AC,因此△ FAE∽△ CAE(SAS).因此 EF=E C.而 DF = BD ,∠ DFE =∠ AFD +∠ AFE =90°,22222因此 BD + EC = FD + EF = DE .【拓展】 ①如图, 在△ ABC 中,AB = AC ,∠ BAC =90°, 点 222延伸线上,且∠ DAE =45°,则 BD + CE = DE .D 在 BC 上,点 E在 BC的 ABD CE能够经过旋转、翻折的方法来证明,如图:FAAFBDCEBDCE②将等腰直角三角形变为随意的等腰三角形:如图,在△ABC 中, AB = AC ,点D ,E 在BC 上,且∠ DAE=1∠ BAC ,则以BD ,DE ,EC 为三边长的三角形有一个内角度数为180°2-∠ BA C .ABD EC能够经过旋转、翻折的方法将BD , DE , EC 转移到一个三角形中,如图:AAFBDECBDECF2.正方形角含半角如图 1,在正方形ABCD中,点E,F 分别在边BC, CD上,∠ EAF=45°,连接 EF,则:B A B ABH A45°45°E EEGC FD C F D CFD图1 图 2 图 3(1)EF=BE+DF;(2)如图 2,过点A作AG⊥EF于点G,则AG=AD;(3)如图 3,连接BD交AE于点H,连接FH.则FH⊥AE.(1)如图 4,将△ABE绕点A逆时针旋转 90°获得△ADI证明.B AEC FD I图 4则∠ IAF=∠ EAF=45°, AI = AE,因此△ AEF∽△ AIF( SAS),因此 EF= IF = DI+ DF= BE+ DF.(2)由于△AEF∽△AIF,AG⊥EF,AD⊥IF,因此 AG= A D.(3)由∠HAF=∠HDF=45°可得A,D,F,H四点共圆,进而∠ AHF=180°-∠ ADF=90°,即 FH⊥ AE.【拓展】①如图,在正方形 ABCD中,点 E,F 分别在边 CB, DC 的延伸线上,∠ EAF=45°,连接EF,则 EF= DF- BE.EABF C D能够经过旋转的方法来证明. 如图:EABFC G D②如图,在一组邻边相等、对角互补的四边形ABCD 中, AB =AD ,∠ BAD +∠ C =180 °,点 E ,F 分别在 BC 、 CD 上,∠ EAF = 1∠ BAD ,连接 EF ,则 EF=BE+DF.2BAECFD能够经过旋转的方法来证明. 如图:BAECFDG例题解说例1 如图 1,点 E 、F 分别在正方形 ABCD 的边 BC 、 CD 上,∠ EAF = 45° .( 1) 试判断 、 FD 之间的数目关系 .BE 、EF( 2) 如图 2,在四边形 ABCD 中,∠ BAD ≠ 90°, AB = AD .∠ B +∠ D = 180°,点 E 、F 分别在、 上,则当∠EAF 与∠BAD 知足关系时,仍BC CD有 EF = BE + FD .( 3)如图 3.在某公园的同一水平面上,四条通道围成四边形ABCD .已知 AB = AD= 80m ,∠ B = 60°,∠ ADC = 120°,∠ BAD = 150°,道路 BC ,CD 上分别有景点E , F ,且 AE ⊥ AD . DF = 40( 3 -1) m .现要在 E 、F 之间修一条笔挺的道路,求这条道路 EF 的长.( 结果取整数,参照数据: 2 = 1.41 , 3 = 1.73 )A DFADDAFFB EC B ECBEC图 1图 2图3解: ( 1)由“正方形内含半角 模型”可得 EF = BE + FD . (2)∠ BAD = 2∠ EAF ,原因以下:如图 4,延伸 CD 至点 G ,使得 DG = BE .连接 AG. 易证△ ABE ≌△ ADG (SAS ) . 因此 AE = AG ,即 EF = BE + DF = DG + DF =GF .进而证得△ AEF ≌△ AGF ( SSS ).因此∠ EAF = ∠ GAF = 1 ∠ EAG = 1∠ BAD .22AGHGDFDFABEC图 4BCE图 5( 3)如图 5,将△ ABE 绕点 A 逆时针旋转 1 50 °至△ ADG .连接AF .由题意可得∠ BAE = 60°因此△ ABE 和△ ADG 均为等腰直角三角形 .过点 A 作 AH ⊥ DG 于点 H .则DH = 1AD = 40m , AH =3AD = 403 m.2 2而 DF = 40( 3 - 1) m.因此∠ EAF =∠ GAF =45° . 可得△ EAF ≌△ GAF (SAS ).因此 EF = GF =80m+40( 3 - l ) m ≈109. 2m.例 2 如图,正方形ABCD 的边长为 a ,BM 、 DN 分别均分正方形的两个外角,且知足∠ MAN= 45°.连接 MC 、 NC 、 MN .( 1)与△ ABM 相像的三角形是, BM DN =(用含有 a 的代数式表示) ;( 2)求∠ MCN 的度数;( 3)请你猜想线段BM、DN和 MN之间的等量关系,并证明你的结论. ADB NCM解:( 1)△NDA,a2 .( 2)由( 1)可得BM AB,AD ND因此BM DC.BC DN易证∠ CBM=∠ NDC=45°,因此△ BCM∽△ DNC.则∠ BCM=∠ DNC,因此∠MCN =360°一∠BCD一∠BCM一∠DCN=270°-(∠DNC+∠DCN)=270°-( 180°-∠DNC)=135°.(3)BM2DN 2MN 2,证明以下:如图,将△ ADN绕点 A顺时针旋转90°,获得△ABE,连接EM.易得 AE=AN.∠ MAE=∠ MAN=45°,∠ EBM=90°,因此△ A ME≌△ AMN.(SAS).则 ME= MN.在 Rt △BME中,BM2 BE2 EM 2因此BM2 DN 2 EM 2 .ADBCNEM倒 3 如图,在四边形ABCD中, AD∥ BC,∠ BCD=90°, AB=BC+ AD,∠ DAC=45°, E 为上一点,且∠= 45°. 若=4,求△的面积 .CD BAE CD ABEB CEA D图1解:如图1.过点A作CB的垂线,交CB的延伸线于点F.由∠ DAC=45°,∠ ADC=90°,可得 AD= CD.因此四边形ADCF为正方形.进而 AF= FC=4.令 BC= m,则 AB=4+ m, BF=4- m.2 2在 Rt △AFB中,有 16+( 4 -m)一( 4+m)如图 2.将△ADE绕点A逆时针旋转90°至△AFG.易证△ AGH≌△ AEB.令 DE= n,则 CE=4- n, BE= BG=3+n在 Rt △BCE中,有1+( 4-n)2=( 3+n)2,解得n=4 .因此 BG=25.7 7 1AF BG 50进而SABE SABG .2 7G F B CEA D图 2进阶训练1.如图,等边△ ABC的边长为1,D是△ ABC外一点且∠ BDC=120°,BD= CD,∠ MDN=60°,求△AMN的周长.ANM BCD△ AMN 的周长是 2【提示】如图,延伸AC 至点 ,使得CE = ,连接DE. 先证△≌△ ,再证△MDNEBMBMDCED≌△ EDN 即可 .ANMBCDE2.如图, 在正方形 ABCD 中,连接 BD ,E 、F 是边 BC ,CD 上的点, △CEF 的周长是正方形 ABCD 周长的一半, AE 、 AF 分别与 BD 交于 M 、 N ,试判断线段 BM 、 DN 和 MN 之间的数目关系,并 证明.ADNFMBEC解: 2+2=2.BM DN MN【提示 】由△ CEF 周长是正方形 ABCD 周长的一半,想到“正方形角含半角”,进而旋转构造协助线解决问题(如图1),证△ AEF ≌△ AGF ,得∠ MAN = 1∠ BAD = 4,而后,再由“等腰2直角三角形含半角”(如图2)即可证得.GH GADADNNFFMMBE CBEC图1图23.如图,在△ ABC 中,∠ ACB =90°,点 D 在边 AB 上, DE ⊥ BC 于点 E ,且 DE = BC ,点 F 在边 AC 上,连接 BF 交 DE 于点 G ,若∠ DBF =45°, DG =27,BE = 3,求 CF 的长.5ADGBE解: CF =12.5【提示 】如图,将 DE 向左平移至 BH ,连接 HD 并延伸交 AC 于点 I ,则四边形 HBCI 为正方形. 将△ BHD 绕点 B 顺时针旋转 90°至△ BCJ ,则点 J 在 AC 的延伸线上. 连结 DF ,由“正方形角含半角模型”可得 DF = DH + CF ,∠ DFB =∠ JFB =∠ DGF ,所以 DF = DG ,进而求得CF 的长.F CAHDIGFCBEJ。
山东省潍坊市诸城市2017届九年级上学期期中考试数学(解析版)
一、选择题(共12小题,每小题3分,满分36分)1.如图,在△ABC 中,DE ∥BC ,且AE=CE ,则△ADE 与四边形DBCE 的面积之比等于( ).A .1B .12 C .13 D .14【答案】C .考点:相似三角形的判定与性质.2.如图,某水库堤坝横断面迎水坡AB 的坡比是BC=50m ,则迎水坡面AB 的长度是( ).A .100mB .mC .150mD .【答案】A . 【解析】试题分析:根据题意可得BC AC =,把BC=50m ,代入即可算出AC 的长,再利用勾股定理算出AB 的长即可.∵堤坝横断面迎水坡AB 的坡比是1:,∴BC AC =BC=50m ,∴m ,∴,故选:A .考点:解直角三角形的应用-坡度坡角问题.3.若一元二次方程x2+bx+5=0配方后为(x﹣3)2=k,则b,k的值分别为().A.0,4 B.0,5 C.﹣6,5 D.﹣6,4【答案】D.【解析】试题分析:先把(x﹣3)2=k化成x2﹣6x+9﹣k=0,再根据一元二次方程x2+bx+5=0得出b=﹣6,9﹣k=5,然后求解即可.∵(x﹣3)2=k,∴x2﹣6x+9﹣k=0,∵一元二次方程x2+bx+5=0配方后为(x﹣3)2=k,∴b=﹣6,9﹣k=5,∴k=4,∴b,k的值分别为﹣6、4;故选D.考点:解一元二次方程-配方法.4.如图,要使△ABC∽△CBD,则下列选项中不能作为条件添加的是().A.BC2=BD∙BA B.∠A=∠BCD C.AC2=AD∙AB D.∠BDC=∠ACB【答案】C.【解析】试题分析:图中已知条件是∠ABC=∠CBD,所以根据“两角法”、“两边及其夹角法”进行添加条件即可.如图,∠ABC=∠CBD.A、若添加BC2=BD∙BA即BC BABD CB=时,可以判定△ABC∽△CBD,故本选项错误;B、若添加∠A=∠BCD时,可以判定△ABC∽△CBD,故本选项错误;C、若添加AC2=AD∙AB即AC ABAD AC=时,可以判定△ABC∽△ACD,故本选项正确;D、若添加∠BDC=∠ACB时,可以判定△ABC∽△CBD,故本选项错误;故选:C.考点:相似三角形的判定.5.如图,在Rt△ABC中,∠C=90°,AB=6,cosB=23,则BC的长为().A.4 B.C D 【答案】A.【解析】试题分析:根据cosB=23,可得CBAB=23,再把AB的长代入可以计算出CB的长.∵cosB=23,∴CBAB=23,∵AB=6,∴CB=23×6=4,故选:A.考点:锐角三角函数的定义.6.关于x的一元二次方程x2﹣5x+p2﹣2p+5=0的一个根为1,则实数p的值是().A.4 B.0或2 C.1 D.﹣1【答案】C.【解析】试题分析:本题根据一元二次方程的根的定义、一元二次方程的定义求解.∵x=1是方程的根,由一元二次方程的根的定义,可得p2﹣2p+1=0,解此方程得到p=1.故本题选C.考点:一元二次方程的解.7.轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是()海里.A.B.C.50 D.25【答案】D.【解析】试题分析:根据题中所给信息,求出∠BCA=90°,再求出∠CBA=45°,从而得到△ABC为等腰直角三角形,然后根据解直角三角形的知识解答.如图:根据题意,∠1=∠2=30°,∵∠ACD=60°,∴∠ACB=30°+60°=90°,∴∠CBA=75°﹣30°=45°,∴△ABC为等腰直角三角形,∵BC=50×0.5=25,∴AC=BC=25(海里).故选D.考点:1.等腰直角三角形;2.方向角.8.如果关于x的一元二次方程kx2x+1=0有两个不相等的实数根,那么k的取值范围是().A.k<12B.k<12且k≠0 C.﹣12≤k<12D.﹣12≤k<12且k≠0【答案】D.【解析】试题分析:根据方程有两个不相等的实数根,则△>0,由此建立关于k的不等式,然后就可以求出k的取值范围.由题意知:2k+1≥0,k≠0,△=2k+1﹣4k>0,综合k的取值范围是-12≤k<12,且k≠0.故选:D.考点:根的判别式.9.为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF 交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有().A.1组 B.2组 C.3组 D.4组【答案】C.考点:1.相似三角形的应用;2.解直角三角形的应用.10.如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是().A.16B.13C.12D.23【答案】B.【解析】试题分析:延长A′B′交BC于点E,根据大正方形的对角线长求得其边长,然后求得小正方形的边长后即可求两个正方形的相似比.∵在正方形ABCD中,BC=AB=3,延长A′B′交BC于点E,∵点A′的坐标为(1,2),∴OE=1,EC=A′E=3﹣1=2,∴OE:BC=1:3,∴AA′:AC=1:3,∵AA′=CC′,∴AA′=CC′=A′C′,∴A′C′:AC=1:3,∴正方形A′B′C′D′与正方形ABCD的相似比是13.故选B.考点:1.位似变换;2.坐标与图形性质.11.如图,边长为1的正方形ABCD 绕点A 逆时针旋转30°到正方形AB ′C ′D ′,图中阴影部分的面积为( ).A .12 B .1 D .1 【答案】C . 【解析】试题分析:设B ′C ′与CD 的交点为E ,连接AE ,利用“HL ”证明Rt △AB ′E 和Rt △ADE 全等,根据全等三角形对应角相等∠DAE=∠B ′AE ,再根据旋转角求出∠DAB ′=60°,然后求出∠DAE=30°,再解直角三角形求出DE ,然后根据阴影部分的面积=正方形ABCD 的面积﹣四边形ADEB ′的面积,列式计算即可得解.如图,设B ′C ′与CD 的交点为E ,连接AE ,在Rt △AB ′E 和Rt △ADE 中,'AE AE AB AD⎧=⎨=⎩,∴Rt △AB ′E ≌Rt △ADE(HL ),∴∠DAE=∠B ′AE ,∵旋转角为30°,∴∠DAB ′=60°,∴∠DAE=12×60°=30°,∴DE=1,∴阴影部分的面积=1×1﹣2×(12×1)=1.故选:C .考点:1.旋转的性质;2.正方形的性质.12.如图,Rt △ABC 中,AB ⊥AC ,AB=3,AC=4,P 是BC 边上一点,作PE ⊥AB 于E ,PD ⊥AC 于D ,设BP=x ,则PD+PE=( ).A .5x +3B .4-5xC .72D .21212525x x -【答案】A . 【解析】试题分析:先根据勾股定理求得BC 的长,再根据相似三角形的判定得到△CDP ∽△CAB ,△BPE ∽△BCA ,利用相似三角形的边对应成比例就不难求得PD+PE 了.∵在Rt △ABC 中,AB ⊥AC ,AB=3,AC=4,∴由勾股定理得BC=5,∵AB ⊥AC ,PE ⊥AB ,PD ⊥AC ,∴PE ∥AC ,PD ∥AB ,∴△CDP ∽△CAB ,△BPE ∽△BCA ,∴PD PC AB BC =,PE BP AC BC =,∴PD=3(5)5x -,PE=45x ,∴PD+PE=3(5)5x -+45x =5x+3.故选A . 考点:1.相似三角形的判定与性质;2.勾股定理.二、填空题(共6小题,每小题3分,满分18分)13.观察下列等式 ①sin30°=12 cos60°=12②sin45° cos45°③sin60° cos30° …根据上述规律,计算sin2a+sin2(90°﹣a)= .【答案】1.【解析】试题分析:根据①②③可得出规律,即sin2a+sin2(90°﹣a)=1,继而可得出答案.由题意得,sin230°+sin2(90°﹣30°)=1;sin245°+sin2(90°﹣45°)=1;sin260°+sin2(90°﹣60°)=1;故可得sin2a+sin2(90°﹣a)=1.故答案为:1.考点:互余两角三角函数的关系.14.如图,在一块长为22米、宽为17米的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米.若设道路宽为x米,则根据题意可列出方程为.【答案】(22﹣x)(17﹣x)=300.【解析】试题分析:把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程.设道路的宽应为x米,由题意有(22﹣x)(17﹣x)=300,故答案为:(22﹣x)(17﹣x)=300.考点:由实际问题抽象出一元二次方程.15.如图,△ABC中,DE∥FG∥BC,且S△ADE=S梯形DFGE=S梯形FBCG,DE:FG:BC= .【答案】1.【解析】试题分析:由平行线可得△ADE ∽△AFG ∽△ABC ,进而利用相似三角形面积比等于对应边的平方比,即可得出结论.∵S △ADE =S 梯形DFGE =S 梯形FBCG ,∵DE ∥FG ∥BC ,∴△ADE ∽△AFG ∽△ABC ,∴ADE AFGS S∆∆=12,ADE ABCS S∆∆ =13,由于相似三角形的面积比等于对应边长的平方比,∴DE :FG :BC=11. 考点:相似三角形的判定与性质.16.已知线段AB 的长为2,以AB 为边在AB 的下方作正方形ACDB .取AB 边上一点E ,以AE 为边在AB 的上方作正方形AENM .过E 作EF ⊥CD ,垂足为F 点,如图.若正方形AENM 与四边形EFDB 的面积相等,则AE 的长为 .1. 【解析】试题分析:设AE=x ,则BE=2﹣x ,就有EFDB 的面积为2(2﹣x ),正方形AENM 的面积=x 2,根据正方形AENM 与四边形EFDB 的面积相等建立方程求出其解即可.设AE=x ,则BE=2﹣x ,由图形得x 2=2(2﹣x ),解得:x 11,x 2=1(舍去)﹣1. 考点:一元二次方程的应用.17.如图,将45°的∠AOB 按下面的方式放置在一把刻度尺上:顶点O 与尺下沿的端点重合,OA 与尺下沿重合,OB 与尺上沿的交点B 在尺上的读数恰为2cm .若按相同的方式将37°的∠AOC 放置在该刻度尺上,则OC 与尺上沿的交点C 在尺上的读数约为 cm .(结果精确到0.1cm ,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)【答案】2.7. 【解析】试题分析:过点B 作BD ⊥OA 于D ,过点C 作CE ⊥OA 于E .首先在等腰直角△BOD 中,得到BD=OD=2cm ,则CE=2cm ,然后在直角△COE 中,根据正切函数的定义即可求出OE 的长度.过点B 作BD ⊥OA 于D ,过点C 作CE ⊥OA 于E .在△BOD 中,∠BDO=90°,∠DOB=45°,∴BD=OD=2cm ,∴CE=BD=2cm .在△COE 中,∠CEO=90°,∠COE=37°,∵tan37°=CEOE≈0.75,∴OE ≈2.7cm .∴OC 与尺上沿的交点C 在尺上的读数约为2.7cm .故答案为2.7.考点:解直角三角形的应用.18.已知a ≠b ,且a 、b 满足a 2﹣3a ﹣4=0,b 2﹣3b ﹣4=0,那么a b +ba的值等于 . 【答案】﹣174. 【解析】试题分析:由a 、b 满足a 2﹣3a ﹣4=0、b 2﹣3b ﹣4=0,可得出a 、b 是方程x 2﹣3x ﹣4=0的两个根,利用根与系数的关系即可得出a+b=3、ab=﹣4,将a b +b a 变形成22()ababa b -+,代入数据即可得出结论.∵a 、b满足a 2﹣3a ﹣4=0,b 2﹣3b ﹣4=0,∴a 、b 是方程x 2﹣3x ﹣4=0的两个根,∴a+b=3,ab=﹣4,∴a b +b a =22ab a b +=22()ab aba b -+=22(4)43-⨯--=﹣174.故答案为:﹣174. 考点:1.根与系数的关系;2.分式的值.三、解答题(共6小题,满分66分)19.解关于x 的方程: (1)(2x ﹣5)2=(x ﹣2)2 (2)(1+x )2+(1+x )=12(3)x2+ax+b=0(配方法)【答案】(1)x1=3,x2=73.(2)x1=2,x2=﹣5.(3)当a2﹣4b<0时,方程无解.当a2﹣4b≥0时,x=﹣2a±.【解析】试题分析:(1)利用直接开方法解即可.(2)移项,利用因式分解法解即可.(3)根据配方法的步骤解即可.试题解析:(1)∵(2x﹣5)2=(x﹣2)2,∴2x﹣5=±(x﹣2),∴x1=3,x2=73.(2)∵(1+x)2+(1+x)=12,∴(1+x)2+(1+x)﹣12=0∴(1+x+4)(1+x﹣3)=0,∴1+x+4=0或1+x﹣3=0,∴x1=2,x2=﹣5.(3)∵x2+ax+b=0,∴x2+ax=﹣b,∴x2+ax+(2a)2=(2a)2﹣b,∴(x+2a)2=244ba-,当a2﹣4b<0时,方程无解.当a2﹣4b≥0时,x=﹣2a.考点:1. 直接开方法解一元二次方程;2.解一元二次方程-配方法;3.解一元二次方程-因式分解法.20.如图,在正方形ABCD中,E、F分别是边BC、CD上的点,CEBE=13,CF=DF,连接AE、AF、EF,并延长FE交AB的延长线于点G.(1)若正方形的边长为4,则EG等于;(2)求证:△ECF∽△FDA;(3)比较∠EAB与∠EAF的大小.【答案】(1);(2)证明参见解析;(3)∠EAF<∠EAB.【解析】试题分析:(1)先根据正方形边长得CF=2,由平行相似得:△FCE ∽△GBE ,则FC CE BG BE=,代入求得BG=6,根据勾股定理得:;(2)根据已知边的长度分别求EC FD =12,CF AD =24=12,则EC FD =CF AD,再由正方形性质得:∠C=∠D=90°,则△ECF ∽△FDA ;(3)先根据(2)中的△ECF ∽△FDA ,得∠CFE=∠DAF ,EF FA =CE DF =12,证明∠EFA=90°,分别计算∠EAB 与∠EAF 的正切值,根据两锐角正切大的角大,得出结论.试题解析:(1)∵四边形ABCD 是正方形,∴AB=CD=BC=4,∠ABC=90°,DC ∥AB ,∵CF=DF ,∴CF=12CD=2, ∵DC ∥AG ,∴△FCE ∽△GBE ,∴FC CE BG BE =,∵CE BE =13,∴FC BG =13,BE=34BC=34×4=3,∴2BG =13,∴BG=6,在Rt △BEG 中,=;故答案为:;(2)∵四边形ABCD 是正方形,∴BC=AD=DC=4,∠C=∠D=90°,∵DF=FC=2,CE=1,∴EC FD =12,CF AD =24=12,∴EC FD =CF AD,∴△ECF ∽△FDA ;(3)∵△ECF ∽△FDA ,∴∠CFE=∠DAF ,EF FA =CE DF =12,∵∠DFA+∠DAF=90°,∴∠CFE+∠DFA=90°,∴∠EFA=90°,∴tan ∠EAF=EF FA =12,∵CE BC =14,∴tan ∠EAB=EB AB =34,∵12<34,∴∠EAF <∠EAB .考点:相似形综合题.21.已知一元二次方程x 2﹣2x+m ﹣1=0. (1)当m 取何值时,方程有两个不相等的实数根?(2)设x 1,x 2是方程的两个实数根,且满足x 12+x 1x 2=1,求m 的值.【答案】(1)m <2;(2)m=74. 【解析】试题分析:(1)若一元二次方程有两不等实数根,则根的判别式△=b 2﹣4ac >0,建立关于m 的不等式,即可求出m 的取值范围.(2)x 1是方程的实数根,就适合原方程,可得到关于x 1与m 的等式.再根据根与系数的关系知,x 1x 2=m ﹣1,故可求得x 1和m 的值.试题解析:(1)根据题意得△=b2﹣4ac=4﹣4×(m﹣1)>0,解得m<2;(2)∵x1是方程的实数根,∴x12﹣2x1+m﹣1=0 ①,∵x1,x2是方程的两个实数根,∴x1•x2=m﹣1,∵x12+x1x2=1,∴x12+m﹣1=1 ②,由①②得x1=0.5,把x=0.5代入原方程得,m=74.考点:1.根与系数的关系;2.一元二次方程的解;3.根的判别式.22.今年“五一“假期.某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°.已知A点海拔121米.C点海拔721米.(1)求B点的海拔;(2)求斜坡AB的坡度.【答案】(1)521米.(2)1:2.4.【解析】试题分析:(1)过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足,构造直角三角形ABE 和直角三角形CBD,然后解直角三角形.(2)求出BE的长,根据坡度的概念解答.试题解析:如图,过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足.在C点测得B点的俯角为30°,∴∠CBD=30°,又BC=400米,∴CD=400×sin30°=400×12=200(米).∴B点的海拔为721﹣200=521(米).(2)∵BE=DF=521﹣121=400米,又∵AB=1040米,米,∴AB的坡度i AB=BEAE=400960=512.故斜坡AB的坡度为1:2.4.考点:1.解直角三角形的应用-坡度坡角问题;2.解直角三角形的应用-仰角俯角问题.23.某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产76件,每件利润10元.每提高一个档次,每件利润增加2元.(1)每件利润为14元时,此产品质量在第几档次?(2)由于生产工序不同,产品每提高1个档次,一天产量减少4件.若生产第x档的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;若生产某档次产品一天的总利润为1080元,该工程生产的是第几档次的产品?【答案】(1)第3档次;(2)y=﹣8x2+128x+640;第5档次.【解析】试题分析:(1)由每提高一个档次,每件利润增加2元,14﹣10=4,需要提高2个档次,由此即可解决问题.(2)根据一天的利润=生产的件数×每件的利润,即可求出y与x的关系,再列出方程即可解决问题.试题解析:(1)由每提高一个档次,每件利润增加2元,每件利润为14元时,14﹣10=4,4÷2=2,需要提高2个档次,所以此产品质量在第3档次.(2)由题意y=[10+2(x﹣1)][76﹣4(x﹣1)]=﹣8x2+128x+640.(1≤x≤10).当y=1080时,﹣8x2+128x+640=1080,解得x=5或11(舍弃).所以工程生产的是第5档次的产品时,一天的总利润为1080元.考点:1.二次函数的应用;2.一元二次方程的应用.24.如图1,小红家阳台上放置了一个晒衣架.如图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点立于地面,经测量:AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条直线,且EF=32cm.(1)求证:AC∥BD;(2)求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°);(3)小红的连衣裙穿在衣架后的总长度达到122cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.(参考数据:sin61.9°≈0.882,cos61.9°≈0.471,tan61.9°≈0.553;可使用科学计算器)【答案】(1)证明参见解析;(2) 61.9°;(3) 小红的连衣裙会拖落到地面.理由参见解析.【解析】试题分析:(1)根据等角对等边和对顶角相等得出∠OAC=∠OCA=12(180º-∠AOC )和∠OBD=∠ODB=12(180º-∠BOD ),∠AOC=∠BOD 进而利用平行线的判定得出即可;或利用三角形相似和平行线判定可得出结论;(2)首先过点O 作OM ⊥EF 于点M ,则EM=16cm ,利用cos ∠OEF=1683417EM OE ==≈0.471,即可得出∠OEF 的度数;(3)首先证明Rt △OEM ∽Rt △ABH ,进而得出AH 的长即可.试题解析:(1)方法一:∵AB 、CD 相交于点O ,∴∠AOC=∠BOD ,∵OA=OC ,∴∠OAC=∠OCA=12(180º-∠AOC ),同理可证:∠OBD=∠ODB=12(180º-∠BOD ),∴∠OAC=∠OBD ,∴AC ∥BD ;方法二:AB=CD=136cm ,OA=OC=51cm ,∴OB=OD=85cm ,∴35OA OC OB OD ==,又∵∠AOC=∠BOD ,∴△AOC ∽△BOD , ∴∠OAC=∠OBD ;∴AC ∥BD ;(2)在△OEF 中,OE=OF=34cm ,EF=32cm ;过点O 作OM ⊥EF 于点M ,则EM=16cm ;∴cos ∠OEF=1683417EM OE ==≈0.471,用科学计算器求得∠OEF=61.9°;(3)方法一:小红的连衣裙会拖落到地面;在Rt △OEM 中, =30cm ,过点A 作AH ⊥BD 于点H ,同(1)可证:EF ∥BD ,∴∠ABH=∠OEM ,则Rt △OEM ∽Rt △ABH ,∴OE OM AB AH =,AH=3013612034OM AB OE ⨯== cm ,因为小红的连衣裙垂挂在衣架后的总长度122cm >晒衣架的高度AH=120cm .所以小红的连衣裙会拖落到地面.方法二:小红的连衣裙会拖落到地面;同(1)可证:EF ∥BD ,∴∠ABD=∠OEF=61.9°;过点A 作AH ⊥BD 于点H,在Rt△ABH中sin∠ABD=AHAB,AH=AB×sin∠ABD=136×sin61.9°=136×0.882≈120.0cm,因为小红的连衣裙垂挂在衣架后的总长度122cm>晒衣架的高度AH=120cm.所以小红的连衣裙会拖落到地面.考点:1.相似三角形的应用;2.解直角三角形的应用.。
山东省诸城市桃林镇2017届中考数学压轴题专项汇编专题21等腰三角形的存在性

专题21 等腰三角形的存在性破解策略以线段AB 为边的等腰三角形构造方法如图1所示:等腰三角形的另一个顶点在线段AB 的垂直平分线上,或以A ,B 为圆心、AB 长为半径的圆上(不与线段AB 共线).解等腰三角形的存在性问题时,若没有明确指出等腰三角形的底或腰,就需要进行分类讨论.通常这类问题的解题策略有:(1)几何法:先分类讨论,再画出等腰三角形,后计算.如图2,若AB =AC ,过点A 作AD ⊥BC ,垂足为D ,则BD =CD ,∠BAD =∠CAD ,从而利用锐角三角函数、相似三角形等知识解决问题.(2)代数法:先罗列三边长,再分类讨论列方程,然后解方程并检验. 有时候将几何法和代数法相结合,可以使得解题又快又好. 例题讲解例1 如图,正方形ABCD 的边长是16,点E 在AB 边上,AE =3,F 是BC 边上不与B ,C 重合的一个动点,把△EBF 沿EF 折叠,点B 落在B ′处.若△CDB ′恰为等腰三角形,则DB ′=.解 16或①如图1,当CB ′=CD 时,点F 与点C 重合,不符合题意,舍去; ②如图2,当DB ′=CD 时,DB ′=16;③如图3,当DB ′=B ′C 时,过点B 作GH ∥AD ,交AB 于点G ,交CD 于点H . 显然G ,H 分别为AB ,CD 的中点.由题意可得B ′E =13,DH =BG =8,所以EG =5, 从而B ′G12,B ′H =4, 所以DB.A BCDEFB ′图1ABCD 图2DB例2如图,在△ABC 中,∠ACB =90°,AC =4cm ,BC =3cm .如果点P 由点B 出发沿BA 方向向点A 匀速运动,同时点Q 由点A 出发沿AC 方向向点C 匀速运动,它们的速度均为1cm/s .连图1A BC DEB ′(F )接PQ ,设运动时间为t (s )(0<t <4),∴QH =945t -,PQ=(1)求直线AC 的解析式; (2)在y 轴上是否存在点P ,直线PD 与矩形对角线AC 交于点M ,使得△DMC 为等腰三角形?若存在,直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.-5=4,且与解:(1)∵抛物线的对称轴为x =-2, ∴m =-4.∵抛物线与x 轴只有一个交点, ∴m 2-4n =0. 从而n =4.(2)原抛物线的表达式为y =-x 2-4x -4=-(x +2)2.所以抛物线C 的表达式为y =x 2-1.(3)假设点D 存在,设点D 的坐标为(d ,d 2-1). 如图,作DH ⊥y 轴于点H ,则DH 2= d 2,BH 2=(d 2-2)2. 若△BPD 是等边三角形,则有DH BHd 2=3(d 2-2)2, 解得d =或d =. 所以满足条件的点D 存在,分别为D 12),D 22),D 313), D 413). 例5 如图,在平面直角坐标系中,抛物线y =12x 2-3x -8与x 轴交于A ,B 两点,与y 轴交于点C ,直线l 经过原点O ,与抛物线的一个交点为D ,与抛物线的对称轴交于点E (3,-4),连结CE ,若P 是y 轴负半轴上的一个动点,设其坐标为(0,m ),直线PB 与直线l 交于点Q .试探究:当m 为何值时,△OPQ 是等腰三角形.解由抛物线y=12x2-3x-8=12(x-8)(x+2),可得点A,B,C的坐标分别为(-2,0),(8,0)(0,-8).所以CE5=OE,所以△OEC是顶角为钝角的等腰三角形,即∠OEC>90°,△OPQ曲等腰三角形有三种可能:①当PO=PQ时,即∠OPQ为顶角,显然∠POQ=∠COE,所以∠OPQ=∠OEC>90°,由题意可知这种可能性不存在;②当OP=OQ时,则∠OPQ=∠OQP.如图1,过点E作PQ的平行线,分别交x轴,y轴于点F,G,则∠OGE=∠OPQ=∠OQP=∠OEG,所以OG=OE=5,即点G的坐标为(0,-5),所以直线GE的表达式为y=13x-5,所以点F的坐标为(5,0).而OP OB OG OF=,所以8515m=-,即83m=-;③当QO =QP 时,则∠QPO =∠QOP =∠OCE ,所以CE ∥PQ , 如图2,设直线CE 与x 轴交于点H .由C ,E 两点的坐标可得直线CE 的表达式为,y =43x -8. 所以点H 的坐标为(6,0).OC OHOP OB =, 所以868m =-,即323m =-. 综上可得,当m 的值为83-或323-时,△OPQ 是等腰三角形.进阶训练1.如图,在Rt △ABC 中,∠ACB = 90°,AC =6,BC =8,点D 以每秒1个单位长度的速度由点A 向点B 匀速运动,到达B 点即停止运动,M ,N 分别是AD ,CD 的中点,连结MN ,设点D 运动的时间为t ,若△DMN 是等腰三角形,求t 的值.A BCDM N【答案】t =5,6或365时,△DMN 是等腰三角形. 2.设二次函数y =x 2+2ax +22a (a <0)的图象顶点为A ,与x 轴的交点为B ,C .(1)当△ABC 为等边三角形时,求a 的值, (2)当△ABC 为等腰直角三角形时,求a 的值. 【答案】(1)a;(2)a3.如图,在平面直角坐标系中,点A 的坐标为(-2,0),点B 的坐标为(0,2),E 为线段AB 上的一个动点(不与点A ,B 重合),以E 为顶点作∠OFT =45°,射线ET 交线段OB 于点F ,C 为y 轴正半轴上一点,且OC =A B .抛物线y=x 2+mx +n 经过A ,C 两点.(1)求此抛物线的函数表达式;(2)求证:∠BEF=∠AOE;(3)当△EOF为等腰三角形时,求此时点E的坐标.【答案】(1)y2+(2)略;(3)点E的坐标为(-1,1),,2).【提示】(2)由∠BAO=∠FEO=∠ABO=45°即可证;(3)分类讨论:①当OE=OF时,点E与点A重合,不符合题意;②点EO=EF时(如图1),易证△AFO≌△BFE,从而BE=AC=2,再过点E作EH⊥y轴,即可求得点E2;③当FE=FD时(如图2),此时△BFE和△OFE均为等腰直角三角形,求得点E(-1,1).4.如图,抛物线y=ax2-6x+c与x轴交于点A(-5,0),B(-1,0),与y轴交于点C,P是抛物线上的一个动点,连结PA,过点P作y轴的平行线交直线AC于点D,请问:△APD 能否为等腰三角形?若能,求出此时点P的坐标;若不能,请说明理由.【答案】△APD能为等腰三角形,点P的坐标为(-2,3),(-1,0),7),,--7).【提示】由点A,B的坐标可得抛物线的表达式为y=ax2-6x-5.从而得到C(0,-5).所以直线AC:y=-x-5.可设点P(m,-m2-6m-5),则D(m,-m-5).△APD为等腰三角形有三种情况,由∠ADP=45°或135°.用代几结合解决问题.①当AP =AD 时,∠FAD =90°,得P (一2,3); ②当AP =PD 时,∠APD =90°,得P (1,0); ③当AD =PD时,可列方程255m m ++,从而m=P,-7)7).5.如图,抛物线y =ax 2+2x -3与x 轴交于A ,B 两点,且点B 的坐标为(1,0).直线y =23x -49分别与x 轴,y 轴交于C ,F 两点.Q 是直线CF 下方的抛物线上的一个动点,过点Q 作y 轴的平行线,交直线CF 干点D .点E 在线段CD 的延长线上,连结QE ,问:以QD 为腰的等腰△QDE 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.【答案】存在,以QD 为腰的等腰△QDE 的面积最大值为5413【提示】有题意可得抛物线的解析式为y =x 2+2x -3,点C (23,0),F (0,-49),从而tan ∠EDQ =tan ∠OFC =32,如图,作QG ⊥CE 于点G ,设DQ =t ,则QGt ,DG t ,若DQ =DE ,则DE =2DG ,从而△QDE 的面积为S =12DE ·QG =613t 2显然613t 2t2所以当DQ =EQ 时,S 取最大值.设点Q (x ,x 2+2x -3),则t =QD =-x 2-43x +239,可得t =3时,S max =5413。
山东省诸城市桃林镇桃林初中2017届中考数学压轴题专项汇编:专题6轴对称之最短路径(附答案)

专题6 轴对称之最短路径破解策略用轴对称思想解决线段最值问题是常用的方法,本质是利用三角形三边关系解决问 题.常见的题型有:1.已知:在直线l 同恻有A .l 上找一点P ,使得AP +PB 最小.作法:如图.作点A 关于直线l 的对称点A ’,连结A 'B ,与直线,的交点就是点P2.已知:在直线l 同侧有A ,B 两点,在l 上找一点P ,使得|AP -PB |最小作法:如图,连结AB ,作线段AB 的垂甫平分线.与直线l 的交点就是点P3.已知:在直线l 同侧有A ,B 两点,在l 上找一点P .使得|AP -PB |最大A ll作法:如图,连结BA 并延长,与直线,的交点就是点P4.已知:在直线l 同侧有A ,B 两点.在l 上找两点C ,D (其中CD 的长度固定,等于 所给线段d ),使得AC +CD +DB 最小,作法:如图,先将点A 向右平移口个单位长度到点A ',作A '关于直线l 的对称点A ", 连结A "B ,与直线l 的交点就是点D .连结A 'D ,过点A 作AC ∥A 'D ,交直线l 于点C .则 此时AC '+CD +DB 最小.5.已知:在 MON 内有一点P ,在边ON ,OM 上分别找点Q ,R ,使得PQ +QR +RP 最AlAlalN作法:如图,分别作点P关于射线OM的对称点P',P",连结P'P",与射线ON,OM的交点就是点Q,R.6.已知:在∠MON内有一点P,在边OM,ON上分别找点R,Q.使得PR+QR最小N作法:如图,作点P关于射线OM的对称点P',作P'Q⊥ON,垂足为Q,P'Q与射线ON 的交点就是R.7.已知:在 MON 内有两点P ,Q ,在边OM ,ON 上分别找点R ,S .使得PR +RS +SQ 最小.作法:如图,作点P 关于射线OM 的对称点P ',作点Q 关于射线ON 的对称点Q ',连 纳P 'Q '.与射线OM ,ON 的交点就是R ,S . 例题讲解例1 (1)如图1,等边△ABC 中,AB =2,E 是AB 的中点,AD 是高,在AD 上作出点P ,使BP +EP 的值最小,并求BP +PE 的最小值.QNN(2)如图2,已知⊙O的直径CD为2,»AC的度数为60°,点B是»AC的中点,在直径CD上作出点P,使BP+AP的值最小,并求BP+AP的最小值.(3)如图3,点P是四边形ABCD内一点,BP=m,∠ABC=α,分别在边AB,BC上作出点M,N,使△PMN的周长最小,并求出这个最小值(用含m,α的代数式表示).CDCCB图1 图2 图3解HNMFEPACDBP CDAB CDE(1B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,这点就是所求的点P);(2B关于CD的对称点E,连接AE交CD于一点,这点就是所求的点P);(3)分别作点P关于边AB,BC的对称点E,F,连结EF,分别与边AB,BC交于点M,N,线段EF的长度即为△PMN的周长的最小值.如图,连结BE,BF,∠EBF=2∠ABC=2α,BE=BF=BP=m.过点B作BH⊥EF于点H,所以∠EBH=12∠EBF=α,EH=FH.在Rt△BEH中,sinα=EHBE,所以EH =BE ·sin α=m ·sin α, 所以EF =2m ·sin α,即PM +PN +MN =EF =2m ·sin α.例2 如图,在平面直角坐标系xOy 中,分别以点A (2,3),B (3,4)为圆心,以1,3为半径作⊙A ,⊙B ,M ,N 分别是⊙A ,⊙B 上的动点,点P 为x 轴上的动点,求PM +PN 的最小值.解 如图,作⊙A 关于x 轴的对称图形⊙A ´,连结A ´B ,与x 轴交于点P ,与⊙A ´交点为M ´,与⊙B 交点为N ,连结P A ,P A 与⊙A 交点为M ,则此时P A +PB 值最小,从而PM +PN 值也最小,最小值为线段M ´N 的长.如图,易得A ´(2,-3),由两电间距离公式得A ´B =.故M ´N =4,即PM +PN =-4.例3 如图1,等边△ABC 的边长为6,AD ,BE 是两条边上的高,点O 为其交点. P ,N 分别是BE ,BC 上的动点.Q O N EPBDCAACDBPENO图1 图2(1)当PN +PD 的长度取得最小值时,求BP 的长度;(2)如图2,若点Q 在线段BO 上,BQ =1,求QN +NP +PD 的最小值.Q 'D 'ACDBPENO Q D 'O NEPBDCA图3 图4解 (1)由等边三角形轴对称的性质可得,点D 关于BE 的对称点D ´在AB 上,且为AB 的中点.如图3,过点D ´作BC 的垂线,垂足为N ´,D ´N 交BE 于点P ,连结PD ´,则PD ´= P D . 此时D ´N 的长度即为PN +PD 长度的最小值. 显然D ´N ∥AD ,即点N 为BD 的中点. 所以BN =14BC =32, 从而BP =cos BNPBN∠(2)如图4,作点Q 关于BC 的对称点Q ´,则BQ ´=1,∠CBQ ´=30°. 点D ´是点D 关于BE 的对称点,连接D ´Q ´,交BE 于点P ,交BC 于点N . 此时D ´Q ´即为QN +NP +PD 的最小值. 显然∠D ´BQ ´=90°,所以D ´Q= 即QN +NP +PD进阶训练1.两平面镜OM , ON 相交于点O ,且OM ⊥ON ,一束光线从点A 出发,经过平面镜反射后,恰好经过点B ,光线可以只经过平面镜OM 反射后过点B ,也可以只经过平面镜ON 反射后过点B .除了这两种作法外,还有其他方法吗?如果有,请在图中画出光线的行进路线,保留作图痕迹,并简要说明理由.'B''答案:作点A关于OM的对称点A´,作点B关于ON的对称点B´,连接A´B´,与OM,ON分别交于点D,C.光线行进路线如图.2.(1)在A和B两地之间有一条河,现要在这条河上建一座桥CD,桥建在何处才能使从A到B的路径最短?(假定河的两岸是平行的直线,桥要与河岸垂直)(2)如图2,在A和B两地之间有两条河,现要在这两条河上各建一座桥,分别是MN和PQ,桥分别建在何处才能使从A到B的路径最短?(假定河的两岸是平行的直线,桥要与河岸垂直)解:(1)如图,过点B作BB’垂直于河岸,且使BB’长度等于这条河宽,连接AB’交河的一岸于点C,过点C作CD垂直于河岸,与另一岸交点为D,则CD即为架桥最合适的位置.(2)如图,过点A作AA’垂直于距点A较近的河岸,且使AA’长等于该河宽,同样,过点B作BB’垂直于距点B较近的河岸,且使BB’长等于河宽,连接A’B’分别交两条河相邻的河岸于点N,P,过点N作NM垂直于该河河岸,与另一岸交点为M,过P作PQ垂直于该河河岸,与另一岸交点为Q,则MN,PQ即为架桥最合适的位置.ABB A图1 图23.如图,直线334y x=+分别与x轴,y轴交于点A,B,抛物线y=-x2+2x+1与y轴交于点C.若点E在抛物线y=-x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值.提示:作点C关于对称轴x=1的对称点C’,则C’(2,1).过点C’作C’F⊥AB于点F,且于对称轴交于点E,此时FC’的长为CE+EF的最小值.连接C’B,C’A,作C’K⊥x轴于点K,则S△ABC=S△ABD+S△梯形C’KOB-S△C’KA=AB⋅FC’,解得FC’=145,则CE+EF的最小值是145.。
中考数学几何模型22个精选——存在性问题

中考数学几何模型22个精选——存在性问题
1.三角形存在性问题
2.平行四边形存在性问题
目录1
一、直角三角形的存在性
1.几何法平面直角坐标系中已知条线段,构造直角三角形,用的是“两线圆':分别过已知线段的两个端点作已知线段的垂线,再以已知线段为直径作圆。
2.两点间距离公式代数法,代数法解题步:
•(1)表示出A、B、C的坐标
•(2)表示出线段AB、AC、BC的长(两点间距离公式)
•(3)分类列方程
•3)解方程
•(4)检验。
二、等腰三角形的存在
1.“两圆一线”几何法,又叫两圆一中垂。
2.两点间距离公式代数法,代数法解题步骤:
•(1)列出三边长的平方
•(2)分类列方程;
•(3)解方程;
•(4)检验。
注:若△ABC是等腰三角形,那么可以分为①AB=AC;②AB=BC;③AC=BC三种情况
练习
三、平行四边形的存在性
分析:平移法的原理是平行四边形的对应边平行且相等;对点法的原理平行四边形对角线互相平分.
常考类型:1.三定一动2.二定二动。
山东省诸城市桃林镇桃林初中2017届中考数学压轴题专项汇编:专题30函数与面积(附答案)

专题30 函数与面积破解策略解决函数与面积问题的常用方法有 1.割补法当所求图形的面积没有办法直接求出时,我们采取分割或补全图形再分割的方法来表示所求图形的面积,如图:EDC BADCBADCBAS △ABC =S △ABD +S △BCD S 四边形ABCD =S △ABC +S △ACD S 四边形ABCD =S 四边形ADCE +S △BCEN FMDBAECBAS △ABC =S 梯形AEFC -S △AEB -S △CBF S 四边形ABCD =S △ABD +S 梯形BDNM -S △BCM -S △DCN 一般步骤为:(1)设出要求的点的坐标;(2)通过割补将要求的图形转化成通过条件可以表示的图形面积相加减; (3)列出关于所设参数的方程求解; (4)检验是否每个坐标都符合题意. 2.等积变换法利用平行线间的距离处处相等,根据同底等高,将所求图形的面积转移到另一个图形中,如图所示:nmD C EBA直线m ∥直线n S △ABC =S △ABD =S △ABE例如,在平面直角坐标系中经常作已知三角形一边的平行线去进行等积变换,xS △ABC =S △ABD =S △ABE一般步骤: (1) 设出直线表达式,两条平行的直线k 值相等; (2) 通过已知点的坐标,求出直线表达式; (3) 求出题中要求的点;(4)检验是否每个坐标都符合题意.3、铅锤法三角形的铅垂高指无论三角形怎么放,上方顶点到下方顶点的纵向距离(不是两点之间的距离,而是指两点之间上下距离,左右横向不用考虑).在平面直角坐标系中经常向x 轴y 轴作垂线,然后利用铅锤法,如图一般步骤:(1)设出点的坐标;(2)向x 轴y 轴作垂线对图形进行分割,利用铅锤法表示图形面积; (3)根据题意列方程求解; (4)检验是否符合题意. 4.等比转换法若已知条件中的图形是相似的,可以将面积比转化为图形的线段比;若已知条件中的图形是同底或等底 的,可以将面积比转化为图形的对应高的比;若已知条件中的图形是同高或等高 的,可以将面积比转化为图形的对应底的比 一般步骤:(1)设出点的坐标;(2)将图形的面积比转化为图形的线段比; (3)列方程,求出参数; (4)检验是否符合题意. 例1如图,直线x y 21=与双曲线)0(>=k x ky 交A 、B 两点,且点A 的横坐标为4, (1) 求k 的值 (2) 若双曲线)0(>=k xky (3)过原点O 的另一条直线l 交双曲线)0(>=k xky )于P ,Q 两点(P 点在第一象限),若由点A ,B ,P ,Q 为顶点组成的四边形面积为24,求点P 的坐标.解(1)∵点A 横坐标为4, 把x =4代入x y 21=中 得y =2, ∴A (4,2), ∵点A 是直线x y 21=与双曲线)0(>=k xky )的交点, ∴k =4×2=8;(2)解法一:如图,∵点C 在双曲线上, 当y =8时,x =1, ∴点C 的坐标为(1,8).过点A . C 分别做x 轴、y 轴的垂线,垂足为M 、N ,得矩形DMON . ∵S 矩形ONDM =32,S △ONC =4,S △CDA =9,S △OAM =4. ∴S △AOC =S 矩形ONDM −S △ONC −S △CDA −S △OAM =32−4−9−4=15;解法二:如图,过点C.A分别做x轴的垂线,垂足为E.F,∵点C在双曲线y=8x上,当y=8时,x=1,∴点C的坐标为(1,8).∵点C.A都在双曲线y=8x上,∴S△COE=S△AOF=4,∴S△COE+S梯形CEFA=S△COA+S△AOF.∴S△COA=S梯形CEF A.∵S梯形CEFA=12×(2+8)×3=15,∴S△COA=15;(3)∵反比例函数图象是关于原点O的中心对称图形,∴OP=OQ,OA=OB,∴四边形APBQ是平行四边形,∴S△POA=S平行四边形APBQ×14=14×24=6,设点P 的横坐标为m (m >0且m ≠4), 得P (m ,8m ),过点P 、A 分别做x 轴的垂线,垂足为E . F , ∵点P 、A 在双曲线上, ∴S △POE =S △AOF =4, 若0<m <4,如图,∵S △POE +S 梯形PEFA =S △POA +S △AOF , ∴S 梯形PEFA =S △POA =6. ∴21 (2+m8)⋅(4−m )=6 ∴m 1=2,m 2=−8(舍去), ∴P (2,4);若m >4,如图,∵S △AOF +S 梯形AFEP =S △AOP +S △POE , ∴S 梯形PEFA =S △POA =6. ∴21 (2+m8)⋅(m −4)=6, 解得m 1=8,m 2=−2(舍去), ∴P (8,1).∴点P 的坐标是P (2,4)或P (8,1).例2如图,抛物线c bx ax y ++=2的对称轴为直线x =2,且与x 轴交于A 、B 两点,且与x 轴交于A 、B 两点.与y 轴交于点C .其中AI (1,0),C (0,-3). (1)求抛物线的解析式;(2)若点P 在抛物线上运动(点P 异于点A ).当△PBC 面积与△ABC 面积相等时.求点P的坐标;解:(1)由题意,得,解得∴抛物线的解析式为.(2)①令,解得∴B(3,0)当点P在x轴上方时,如图1,过点A作直线BC的平行线交抛物线于点P,易求直线BC的解析式为,∴设直线AP的解析式为,∵直线AP过点A(1,0),代入求得.∴直线AP的解析式为解方程组,得∴点当点P在x轴下方时,如图1设直线交y轴于点,把直线BC向下平移2个单位,交抛物线于点,得直线的解析式为,解方程组,得∴综上所述,点P的坐标为:,例3 如图,在平面直角坐标系xOy中,抛物线23y ax bx=+-(a≠0)与x轴交于A(-2,0),B(4.0)两点,与y轴交于点C.(1)求抛物线的表达式;(2)点P从点A出发,在线段AB上以每秒3个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒1个电位长度的速度向点C运动,其中一个点到达终点时.另一个点也停止运动,当△PBQ存在时,问:运动多少秒时,△PBQ的面积最大,晟大面积是多少?(3)当△PBQ的面积最大时,在BC下方的抛物线上是否存在点K.使S△CBK∶S△PBQ=5∶2?若存在,求点K的坐标;若不存在,请说明理由.x解(1)因为抛物线与x轴交于A(-2,0),B(4,0)两点,所以y=a(x+2)(x-4)=ax2-2ax-8a.所以-8a=-3,解得38a=.b=-2a=-34.所以抛物线的表达式为233384y x x=--.(2)如图1.过点Q作QH⊥x轴于点H.x图1在Rt△BCO中,OB=4,OC=3,所以BC=5.sin B=35.在Rt△BQH中,BQ=t.所以QH=BQ·sin B=35t.所以S△PBQ=12BP·QH=12(6-3t)×35t=()29911010t--+.因为0≤t≤2,所以当t=1时,△PBQ的面积最大,最大面积是910.(3)方法一:等比转化法当△PBQ的面积最大时,t=1,此时P是AB的中点,点P的坐标为(1,0),BQ=1.如图2,因为△PBC与△PBQ是等高三角形,所以S△PBC∶S△PBQ=BC∶BQ=5∶1.x图2当S △CBK ∶S △PBQ =5∶2时,S △PBC ∶S △CBK =2∶1.因为△PBC 与△CBK 是同底三角形,所以对应高的比是2∶1.如图3,在x 轴上点B 的右侧取一点D .使得BD =12BP ,则点D 的坐标为11,02⎛⎫⎪⎝⎭,x图3过点D 作BC 的平行线交抛物线于点K ,过点K 作KF ⊥x 轴于点E . 设点K 的坐标为()()3,248x x x ⎛⎫+- ⎪⎝⎭.由KE CD DE BO =,得()()324381142x x x -+-=-. 整理得2430x x -+=.解得11x =,23x =. 所以点K 的坐标为(1,278-)或(3,158-). 方法二:铅垂法由S △CBK ∶S △PBQ =5∶2,S △PBQ =910,得S △CBK =94.如图4.过点K 作x 轴的垂线交BC 于点F ,设点K 的坐标为233,384x x x ⎛⎫-- ⎪⎝⎭.x图4由于点F 在直线BC 上,所以点F 的坐标为3,34x x ⎛⎫- ⎪⎝⎭.所以KF =22333333348482x x x x x ⎛⎫⎛⎫----=-+ ⎪ ⎪⎝⎭⎝⎭.△CBK 被KF 分割为△CKF 和△BKF .它们以FK 为底的高的和为OB =4. 所以S △CBK =2133942824x x ⎛⎫⨯⨯-+= ⎪⎝⎭,解得11x =,23x =.所以点K 的坐标为(1,278-)或(3,158-). 进阶训练1.如图,抛物线y =-x 2+bx +c 与x 轴交于A (-1,0),B (3,0)两点,与y 轴交于点C ,抛物线的对称轴与抛物线变于点P .与直线BC 相交干点M ,连结P B .(1)位于第一象限内的抛物线上是否存在点D .使得△BCD 的面积最大?若存在,求出点D 的坐标及△BCD 面积的最大值;若不存在,请说明理由.(2)抛物线上是否存在点Q ,使得△QMB 与△PMB 的面积相等?著存在.求出点Q 的坐标;若不存在,请说明理由.x【答案】(1)存在,点D的坐标为315,24⎛⎫⎪⎝⎭,S△BCD取最大值278;(2)存在,点Q的坐标为(2,3),⎝⎭或⎝⎭.【提示】(1)由题意可得y=-x2+2x+3.设D(t,-t2+2t+3).作DH⊥x轴于点H,则S△BCD=S梯形DCOH+S△BDH-S△BOC=-32t2+92t=-23327228t⎛⎫-+⎪⎝⎭.从而当t=32时,S△BCD取得最大值等,此时点D315,24⎛⎫⎪⎝⎭.(2)易得直线BC的表达式为y=-x+3.点P,M的坐标分别为(1,4),(1,2).直线PM与x轴交于点E(1,0).所以PM=EM过点产且与直线BC平行的直线为y-x+5.过点E且与BC平行的直线为y=-x+1.两直线与抛物线的交点即为满足条件的点Q,所以点Q为Q1(2,3),Q2⎝⎭,Q3⎝⎭x2.如图,抛物线y =213222x x --与T 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴的负半轴交于点C ,P 是x 轴下方抛物线上的一个动点(不与点C 重合).连结P B .P C .设△PBC 的面积为S , (1)求S 的取值范围;(2)若△PBC 的面积S 为正整数,则这样的△PBC 共有个.x【答案】(1)0<S <5;(2)11个,【提示】(1)设点P 的坐标为213,222m m m ⎛⎫-- ⎪⎝⎭,如图,过点P 作一轴的平行线,交BC于点F ,则可得点F 的坐标为1,22m m ⎛⎫- ⎪⎝⎭.①当点P 在BC 下方的抛物线上时.可得FP =-2122m m +,从而S =12PF ·OB =-(m -2)2+4,此时0<S ≤4;②当点P 在BC 上方、x 轴下方的抛物线上时.S 最大=S △ABC =5.此时0<S <5,即得解. (2)点P 在x 轴下方、BC 上方时,面积为1,2,3,4的三角形各一个;点P 在BC 下方时,面积为1,2,3的三角形各2个,面积为4的三角形为1个,共11个满足条件的△PB C .x3.如围,抛物线E :y =x 2经过点A (1,m ),以原点为顶点的抛物线E 2经过点B (2,2),点A ,B 关于y 轴的对称点分别为点A ′,B ′.P 为第一象限内的抛物线E 1上与点A 不重台的一点,连结OP 并延长与抛物线E 2相交于点P ′,求△P AA ′与△P ′BB ′的面积之比.x2【答案】14PAA P BB S S '''=△△. 【挺示】易得点A (1,1).抛物线E 2表达式为y =212x .如图,过点P 作PC ⊥x 轴,垂足为C ,PC 交直线AA '于点E ;过点P ′作P ′D ⊥x 轴,垂足为D .P 'D 交直线BB ′于点F .依题意可设P (c ,c 2),P ′(d ,212d ).其中c >0,c ≠1.因为tan ∠POC =tan ∠P 'O D .则2212d c c d =.可得d =2c .222211211122111422242222PAA P BB AA PE c c S S c BB P F d ''''⋅⨯⨯--====⨯-''⋅⨯⨯-△△. x2。
山东省诸城市桃林镇2017届中考数学压轴题专项汇编专题2函数与方程

专题2 函数与方程、不等式的关系破解策略1.函数与方程的关系(1)关于x 的一元二次方程ax 2+bx +c =0(a ≠0)的解⇔抛物线y =ax 2+bx +c (a ≠0)与x 轴交点的横坐标的值;(2)关于x 的一元二次方程ax 2+bx +c =mx +n (am ≠0)的解⇔抛物线y =ax 2+bx +c(a ≠0)与直线y =mx +n (m ≠0)交点的横坐标的值.2.函数与不等式的关系(1)关于x 的不等式ax 2+bx +c >0(a ≠0)的解集⇔抛物线y =ax 2+bx +c (a ≠0)位于x 轴上方的所有点的横坐标的值;(2)关于x 的不等式ax 2+bx +c <0(a ≠0)的解集⇔抛物线y =ax 2+bx +c (a ≠0)位于x 轴下方的所有点的横坐标的值;(3)关于x 的不等式ax 2+bx +c >mx +n (ma ≠0)的解集⇔抛物线y =ax 2+bx +c (a ≠0)位于直线y =mx +n (m ≠0)上方的所有点的横坐标的值;(4)关于x 的不等式ax 2+bx +c <mx +n (ma ≠0)的解集⇔抛物线y =ax 2+bx +c (a ≠0)位于直线y =mx +n (m ≠0)下方的所有点的横坐标的值.例题讲解例1 在平面直角坐标系xOy 中,抛物线y =mx 2-2mx -2(m ≠0)与y 轴交于点A ,其对称轴与x 轴交于点B .若该抛物线在-2<x <-1这一段位于直线l :y =-2x +2的上方,并且在2<x <3这一段位于直线AB 的下方,求该抛物线的表达式.解:如图,因为抛物线的对称轴是x =1,且直线l 与直线AB 关于对称轴对称. 所以抛物线在-1<x <0这一段位于直线l 的下方.又因为抛物线在-2<x <-1这一段位于直线l 的上方,所以抛物线与直线l 的一个交点的横坐标为-1.当x =-1时,y =-2×(-1)+2=4,则抛物线过点(-1,4),将(-1,4)代入y =mx 2-2mx -2,得m +2m -2=4,则m =2.所以抛物线的表达式为y =2x 2-4x -2.例2 已知y =ax ²+bx +c (a ≠0)的自变量x 与函数值y 满足:当-1≤x ≤1时,-1≤y ≤1,且抛物线经过点A (1,-1)和点B (-1,1).求a 的取值范围.解:因为抛物线y =ax ²+bx +c 经过A (1,-1)和点B (-1,1),代入得a +b +c =-1,a -b +c =1,所以a +c =0,b =-1,则抛物线y =ax ²-x -a ,对称轴为x =12a.①当a <0时,抛物线开口向下,且x =12a<0,如图可知,当12a≤-1时符合题意,所以-12≤a<0.当-1<12a<0时,图像不符合-1≤y≤1的要求,舍去.②当a>0时,抛物线开口向上,且x=12a>0.如图可知,当12a≥1时符合题意,所以0<a≤12.当0<12a<1时,图像不符合-1≤y≤1的要求,舍去.综上所述,a的取值范围是-12≤a<0或0<a≤12.例3在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,'b)给出如下定义:1 '1b abb a ≥⎧=⎨-<⎩,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(﹣2,5)的限变点的坐标是(﹣2,﹣5).(1)若点P在函数y=﹣x+3(﹣2≤x≤k,k>﹣2)的图象上,其限变点Q的纵坐标b′的取值范围是﹣5≤b′≤2,求k的取值范围;(2)若点P在关于x的二次函数y=x2﹣2tx+t2+t的图象上,其限变点Q的纵坐标b′的取值范围是b′≥m或b′<n,其中m>n.令s=m﹣n,求s关于t的函数解析式及s的取值范围.解:(1)依题意,y=﹣x+3(x≥﹣2)图象上的点P的限变点必在函数y=313-21x xx x-+≥⎧⎨-≤<⎩的图象上.∴b′≤2,即当x=1时,b′取最大值2.当b′=﹣2时,﹣2=﹣x+3.∴x=5.当b′=﹣5时,﹣5=x﹣3或﹣5=﹣x+3.∴x=﹣2或x=8.∵﹣5≤b′≤2,由图象可知,k的取值范围是5≤k≤8.(2)∵y=x2﹣2tx+t2+t=(x﹣t)2+t,∴顶点坐标为(t,t).若t<1,b′的取值范围是b′≥m或b′<n,与题意不符.若t≥1,当x≥1时,y的最小值为t,即m=t;当x<1时,y的值小于﹣[(1﹣t)2+t],即n=﹣[(1﹣t)2+t].∴s=m﹣n=t+(1﹣t)2+t=t2+1.∴s关于t的函数解析式为s=t2+1(t≥1),当t=1时,s取最小值2,∴s的取值范围是s≥2.1);点B;5≤k≤8;s≥2.进阶训练1.若关于x的一元二次方程x2+ax+b=0有两个不同的实数根m,n(m<n),方程x2+ax +b=1有两个不同的实数根p,q(p<q),则m,n,p,q的大小关系为()A.m<p<q<n B.p<m<n<q C.m<p<n<q D.p<m<q<nB【提示】函数y=x2+ax+b和函数y=x2+ax+b-1的图像如图所示,从而得到p<m<n <q解:函数y=x2+ax+b如图所示:2.在平面直角坐标系xOy中,p(n,0)是x轴上一个动点,过点P作垂直于x轴的直线,交一次函数y=kx+b的图像于点M,交二次函数y=x²-2x-3的图像于点N,若只有当-2<n<2时,点M位于点N的上方,求这个一次函数的表达式.y=-2x+1【提示】依据题意并结合图像可知,一次函数的图像与二次函数的图像的交点的横坐标分别为-2和2,由此可得交点坐标分别为-2和2,由此可得交点坐标为(-2,5)和(2,-3)将交点坐标分别代入一次函数表达式即可3.在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-5的图像与x轴有两个公共点,若m取满足条件的最小整数,当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n,求n的值n的值为-2【提示】根据已知可得m=1.图像的对称轴为直线x=32.当n≤x≤1<32时,函数值y随自变量x的增大而减小,所以当x=1时,函数的值为-6,当x=n时,函数值为4-n.所以n2-3n-4=4-n,解得n=-2或n=4(不符合题意,舍去),则n的值为-2。
全等三角形的存在性

全等三角形的存在性(讲义)一、知识点睛全等三角形存在性的处理思路1.分析特征:分析背景图形中的定点、定线及不变特征,结合图形间的对应关系及不变特征考虑分类.2.画图求解:①目标三角形确定时,根据对应关系分类,借助边相等、角相等列方程求解;②目标三角形不确定时,先从对应关系入手,再结合背景中的不变特征分析,综合考虑边、角的对应相等和不变特征后列方程求解.3.结果验证:回归点的运动范围,画图或推理,验证结果.二、精讲精练1.如图,抛物线C1经过A,B,C三点,顶点为D,且与x轴的另一个交点为E.(1)求抛物线C1的解析式.(2)设抛物线C1的对称轴与x轴交于点F,另一条抛物线C2经过点E(抛物线C2与抛物线C1不重合),且顶点为M(a,b),对称轴与x轴交于点G,且以M,G,E为顶点的三角形与以D,E,F为顶点的三角形全等,求a,b的值.(只需写出结果,不必写出解答过程)2. 如图,在平面直角坐标系中,抛物线24y ax bx =++与x 轴的一个交点为A (-2,0),与y 轴的交点为C ,对称轴是直线x =3,对称轴与x 轴交于点B . (1)求抛物线的函数表达式.(2)若点D 在x 轴上,在抛物线上是否存在点P ,使得 △PBD ≌△PBC ?若存在,直接写出点P 的坐标;若不存在,请说明理由.3. 如图,在平面直角坐标系xOy 中,抛物线2y ax bx c =++与y 轴交于点C (0,4),对称轴直线2x =与x 轴交于点D ,顶点为M且DM =OC +OD .(1)求该抛物线的解析式.(2)设点P (x ,y )是第一象限内该抛物线上的一动点,△PCD 的面积为S ,求S与x 之间的函数关系式,并写出自变量x 的取值范围.(3)设点Q 是y 轴右侧该抛物线上的一动点,若经过点Q 的直线QE 与y 轴交于点E ,是否存在以O ,Q ,E 为顶点的三角形与△OQD 全等?若存在,求出直线QE 的解析式;请说明理由.4. 如图,在平面直角坐标系中,直线1l 过点A (1,0)且与y 轴平行,直线2l 过点B (0,2)且与x 轴平行,直线1l 与2l 相交于点P .点E 为直线2l 上一点,反比例函数k y x=(0k >)的图象过点E 且与直线1l 相交于点F .(1)若点E 与点P 重合,求k 的值.(2)连接OE ,OF ,EF .若2k >,且△OEF 的面积为△PEF 面积的2倍,求点E 的坐标.(3)是否存在点E 及y 轴上的点M ,使得以M ,E ,F 为顶点的三角形与△PEF 全等?若存在,求出点E 的坐标;若不存在,请说明理由.【参考答案】 1. (1)223y x x =-++(2)a =7,b =2或a =7,b =-2或a =-1,b =2或a =-1,b =-2或a =1,b =-4或a =5,b =-4或a =5,b =42. (1)213442y x x =-++(2)(18(18--+---,,(4(4+, 3.(1)21242y x x =-++(2)214(022S x x x =-+<<+(3)122y x =+,y =6或724y x =- 4.(1)2 (2)(3,2)(3)3(2)8,,8(2)3,学生做题前请先回答以下问题问题1:全等三角形的判定有哪些?问题2:全等三角形存在性问题中如何确定分类标准,分类标准确定的依据是什么?问题3:全等三角形存在性问题的处理思路是什么?问题4:全等三角形存在性问题与相似三角形存在性问题处理时的异同有哪些?全等三角形的存在性(一)1.如图1,直线y=-2x+4与x轴、y轴分别交于点A,B,点P(x,y)在直线y=-2x+4上,过点P作AB的垂线,与x轴、y轴分别交于点E,F.若△EOF与△AOB全等,则点P的坐标为( )A. B.C.D.2.如图2,已知点A,B 在抛物线上,且点A在第四象限,点B在第一象限,A,B 两点的横坐标满足方程.连接OB,OA,AB,将线段OB绕点O顺时针旋转90°得到线段OC.若D是坐标平面内一点,且△OAB和△OCD全等,则符合题意的点D的坐标为( )图1 图2A.B.C.D.3.如图3,抛物线经过三点,线段BC与抛物线的对称轴相交于点D.P为该抛物线的顶点,连接PA,AD,DP,线段AD与y轴相交于点E.若Q为平面直角坐标系中的一点,且以Q,C,D为顶点的三角形与△ADP全等,则图3 点Q的坐标为( )A. B.C.D.学生做题前请先回答以下问题问题1:全等三角形的判定有哪些?问题2:全等三角形存在性问题的处理思路是什么?全等三角形的存在性(二)1.如图1已知抛物线与x轴交于A,B两点(点A 在点B的左侧),与y轴交于点C,直线与x轴交于点D.在第一象限内,若直线上存在点P,使得以P,B,D为顶点的三角形与△OBC全等,则点P的坐标为( )A.(4,1),(0,3)B.(4,1),(3,2)或(1,2)C.(4,1),(0,3)或(3,2)D.(4,1),(4,-1),(3,2)或(3,-2)2.如图2,直线与x轴、y轴分别交于A,B两点,C是直线上不与A,B重合的动点.过点C的另一直线CD与y轴相交于点D,若以B,C,D为顶点的三角形与△AOB全等,则点C的坐标为( )A. B.C.D.图1 图23.如图3所示,抛物线的顶点为A,直线与y轴的交点为B ,其中.若Q为抛物线的对称轴直线l上一个动点,在对称轴左侧的抛物线上存在点P,使以P,Q,A为顶点的三角形与△OAB全等,则点P的坐标为( )A.图3 B.C.D.学生做题后建议通过以下问题总结反思问题1:结合试题1分析,如何确定分类标准?问题2:画图求解时需要根据分析得到的不变特征,结合两个三角形全等的判定进行分析,试题1中利用的是哪一个全等三角形的判定?问题3:全等三角形存在性问题与相似三角形存在性问题处理时的异同有哪些?学生做题前请先回答以下问题问题1:在处理全等三角形的存在性问题时首先要分析不变特征,那么如何分析不变特征?问题2:在全等三角形存在性问题处理时,依据不变特征处理的核心依据是什么?问题3:课堂所讲解示范的,一般会用哪个判定?问题4:全等三角形存在性处理时都需要考虑哪些方面?问题5:已经学习了平行四边形,菱形,矩形,正方形,相似三角形以及全等三角形等各种存在性,存在性问题处理的框架是什么?全等三角形的存在性(三)1.如图1,已知抛物线与x轴的交点为A,D (A在D的右侧),与y轴的交点为C,点B与点C关于对称轴对称.点M是抛物线上的一点,使得△CMD≌△CMB,则点M的坐标为( )A. B. C. D.2.如图2,已知抛物线与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C,对称轴与x轴交于点D.M 为抛物线上一点,E是x轴上的一点,使得△DMC≌△DME,则点M 的坐标为( ) 图1图2A.B.C.D.3.如图3,已知抛物线与x轴交于A,B两点,与y轴交于C点.若点E在x轴上,点P是抛物线在第一象限上的图3 点,△APC≌△APE,则点P的坐标为( )A. B. C. D.学生做题后建议通过以下问题总结反思问题1:结合第2题考虑全等三角形存在性问题的处理框架是什么?学生做题前请先回答以下问题问题1:全等三角形的判定有哪些?问题2:全等三角形存在性问题的处理思路是什么?问题3:试题1中如何分析不变特征?问题4:试题1中分析不变特征,确定△OPC≌△POQ利用的是全等三角形的哪一个判定?全等三角形的存在性(四)1.如图1,抛物线与y轴交于点C,P是x轴上一个动点,Q是抛物线上异于点C的一个动点.若△OPC≌△POQ,则点Q 的坐标为( )A. B.C.D.2.如图2,抛物线与y轴交于点A,对称轴与x轴交于点B.D是x轴上的一个动点,P是抛物线上的一个动点,使得△DPB≌△ABP,求点P的坐标.(1)要求点P的坐标有如下考虑:分析可知,需要结合A,D和图2 公共边BP的相对位置进行分类讨论.当A,D在BP的同侧时,以A,D,B,P组成的四边形为_________(填“平行四边形”或“等腰梯形”或“梯形”);当A,D在BP的异侧时,此时以A,D,B,P组成的四边形为_________(填“平行四边形”或“等腰梯形”或“梯形”).A.平行四边形,梯形B.梯形,平行四边形C.平行四边形,等腰梯形D.等腰梯形,平行四边形( )(2)(上接第2题)当A,D在BP的异侧时,点P的坐标为A.(6,4)B.C.D.4.如图4,抛物线与x轴交于A(-2,0),B(1,0)两点,与y轴交于点C(0,2),P为抛物线x轴上方的一个动点,Q为y轴负半轴上的一个动点.若△ABP≌△BAQ,则点P的坐标为( )A. B.(-1,2) C. D.条件不足,无法求解图4学生做题前请先回答以下问题问题1:全等三角形存在性问题的处理思路是什么?问题2:已经学习了平行四边形,菱形,矩形,正方形,相似三角形以及全等三角形等各种存在性,存在性问题处理的框架是什么?全等三角形的存在性(五)1.如图1,二次函数的顶点为A,与y轴的交点为B.若⊙M 的圆心为,半径为r,过点A向该圆作切线,切点为N,若△AMN与△ABO全等,则满足题意的m,r的值分别为( )A. B.C.D.2.如图2,已知直线与抛物线相交于A,B两点,且点为抛物线的顶点,点B在x轴上.若P是抛物线的第二象限的图象上的一点,使得△POB与△POC全等,则点P 的坐标为( )A. B.C.D.图1 图23.直角坐标系中,O是坐标原点,D 是过三点的抛物线上的一点(不与点A重合).若以D,O,C为顶点的三角形与△AOC全等,则点D的坐标为( )A. B. C.D.4.如图4,在平面直角坐标系中,直线l 经过.M为x 轴上的一点且,点P,Q在线段AB上.若以O,P,图4 Q为顶点的三角形与△OMP全等,则点P的坐标为( )A. B. C.D.问题1:结合第2题考虑不变特征是什么?分类标准是什么?问题2:结合第4题考虑不变特征是什么?如何确定分类标准?依据是什么?学生做题前请先回答以下问题问题1:动点问题的处理思路是什么?问题2:动点问题分析运动过程,需要关注四要素是什么?、问题3:全等三角形的判定有哪些?问题4:全等三角形存在性问题的处理思路是什么?全等三角形的存在性(六)1.如图1,在△ABC中,AB=AC=10cm,BC=8cm,D为AB的中点.点P在BC边上以3cm/s的速度由点B向点C运动;同时点Q在AC边上以相同的速度由点C向点A运动,其中一个点到达终点时另一个点也随之停止运动.当△BPD与△CQP全等时,点P运动的时间为( )图1 A. B. C. D.2.如图2,抛物线与x轴交于A,B两点,与y轴交于点C.点P是x轴上一动点,点Q是x轴上方抛物线上的一( )个动点.若△AQC与△AQP全等,则点Q的坐标为3.如图3,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x轴于点H.在抛物线上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标为( )图3 A. B.C.D.学生做题后建议通过以下问题总结反思问题1:结合试题1考虑,不变特征是什么?△BPD与△CQP利用的是三角形全等的哪一个判定?问题2:试题2中,如何确定分类标准?。
2017年中考数学专题复习资料--全等三角形含答案(共11页)

A 12
F
C D E B
4 已知: AD 平分∠ BAC , AC=AB+BD ,求证:: AC 平分∠ BAD , CE⊥ AB ,∠ B+ ∠ D=180°,求证: AE=AD+BE
6 如图,四边形 ABCD 中,AB ∥ DC ,BE 、CE 分别平分∠ ABC 、∠ BCD ,且点 E 在 AD 上。求证:BC=AB+DC 。
P D A
C E
B
11 如图,△ ABC 中, AD 是∠ CAB 的平分线,且 AB=AC+CD ,求证:∠ C=2∠B A
C
D
B
12 如图: AE、 BC交于点 M, F 点在 AM上, BE∥ CF,BE=CF。 求证: AM是△ ABC的中线。
A
F
B
M
C
E
13 已知:如图, AB=AC,BD AC, CE AB,垂足分别为 D、 E,BD、 CE 相交于点 F 。 求证: BE=CD. C D
7 已知: AB=CD ,∠ A= ∠D ,求证:∠ B= ∠ C
A
D
B
C
8.P 是∠ BAC 平分线 AD 上一点, AC>AB ,求证: PC-PB<AC-AB C
A
P
D
B
9 已知, E 是 AB 中点, AF=BD , BD=5 ,AC=7 ,求 DC D
F
C
A
E
B
10.如图,已知 AD∥ BC,∠ PAB 的平分线与∠ CBA 的平分线相交于 E,CE 的连线交 AP 于 D .求证: AD +BC = AB.
17.如图 9 所示,△ ABC 是等腰直角三角形,∠ ACB = 90°, AD 是 BC 边上的中线,过 C 作 AD 的垂 线,交 AB 于点 E,交 AD 于点 F,求证:∠ ADC =∠ BDE .
2022年山东省诸城市桃林镇桃林初中2017届中考数学压轴题专项汇编:专题

原创不容易,【关注】店铺,不迷路!专题18弦图模型破解策略1.内弦图如图,在正方形ABCD中,BF⊥CG,CG⊥D,N,P,Q在正方形ABCD边上,且四边形MUPQ为正方形,则△QBM≌△MCN≌△NDP≌△PAQ.证明因为∠B=∠QMN =∠C=90°,所以∠BQM+∠QMB=∠QMB+∠NMC=90°,所以∠BQM=∠NMC.又因为QM=MN,所以△QBM≌△MCN.同理可得△Q≌△MCN≌△NDP≌△PAQ.AQNBMCPD3.括展(1)如图,在Rt△AB和Rt△BLK中,QB=BL,QM⊥BK,所以△QBM≌△BLK.AEB⊥BK,所以∠KBL+∠QMB=∠KBI十∠K=90°所以∠QMB=∠K,又因为QB=BL.所以△QBM≌△BLK.QKEBML例题讲解例1四边形ABCD是边长为4的正方形,点E在边AD所在的直线上,连结CE,以CE为边,作正方形CEFG(点D,F在直线CE的同侧),连结BF.当点E 在线段AD上时,AE=1,求BF的长.FEDGABC解如图,过点F作F⊥BN,点M,N分别在边BC,CD上,若=11BN,则=.15AMDN的值.AMDCGD(3)如图3,在四边形ABCD中,∠ABC =90°,AB=AD=10,BC=CD-5,AM⊥DN,点M,N分别在边BC,AB上,求DFG解(1))如图4.过点A作AP∥EF.交CD于点P,过点B作BQ∥G⊥BN.所以由(1)中的结论可得所以BNEF11==.AMGABAB(3)如图5.过点D作平行于AB的直线,交过点A 且平行于BC的直线于点P,交BC的延长线于点S.则四边形ABSR是平行四边形.因为∠ABC=90°,所以四边形ABSR是矩形.所以∠R=∠S=90°,RS=AB=10,AR=BS.因为AM⊥DN.所以由(1)中的结论可得DNAR=.AMAB设SC=x,DS=y,则AR=BS=5+x.RD=10-y,所以在Rt △CSD中,x2+y2=25.在Rt△ARD中.(5+x)2+(10-y)2=100.x2y225联立方程组?,222?(5?x)?(10?y)?10?x??5?x?3得?(舍),或?.y?0y?4??所以AR=5+x=8,所以DNAR84===.AMAB105DCMRANB进阶训练1.如图,在平面直角坐标系中,经过点A的双曲线,y=k(k>0)同时经过点B.且x点A在点B的左侧,点A的横坐标为2.∠AOB =∠OBA=45°,则k=____.yABOx2.如图,巳知∠ABC=90°,D是直线AB上的点,AD=BC.E是直线BC上的一点,且CE=BD.直线AE,DC相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.【素材积累】司马迁写《史记》汉朝司马迁继承父业,立志著述史书。
中考数学压轴题专题全等三角形的存在性

专题25 全等三角形的存在性破解策略全等三角形的存在性问题的解题策略有:(1)当有一个三角形固定时(三角形中所有边角为定值),另一个三角形会与这个固定的三角形有一个元素相等;再根据全等三角形的判定,利用三角函数的知识(画图)或。
列方程来求解.(2)当两个三角形都不固定时(三角形中有角或边为变量),若条件中有一条边对应相等时,就要使夹这条边的两个角对应相等,或其余两条边对应相等;若条件中有一个角对应相等时,就要使夹这个角的两边对应相等,或再找一个角和一条边对应相等.例题讲解%例1 如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(-2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.(1)求抛物线的表达式;(2)若点D在x轴上,在抛物线上是否存在点P,使得△PBD≌△PBC若存在,求点P 的坐标;若不存在,请说明理由.(3)若点M在y轴的正半轴上,连结MA,过点M作MA的垂线,交抛物线的对称轴于点N.问:是否存在点M,使以点M、A、N为顶点的三角形与△BAN全等若存在,求出点M的坐标;若不存在,请说明理由.—解:(1)由题意可列方程组 424032a b b a -+=⎧⎪⎨-=⎪⎩ , 解得1432a b ⎧=-⎪⎪⎨⎪=⎪⎩,所以抛物线的表达式为213442y x x =-++.(2)显然OA =2, OB =3, OC =4. 所以225BC OB OC BA =+==. 若△P BD ≌△PBC ,则BD = BC =5,PD =PC所以D 为抛物线与x 轴的左交点或右交点,点B ,P 在CD 的垂直平分线上, (①若点D 为抛物线与 x 轴的左交点,即与点A 重合.如图1,取AC 的中点E ,作直线BE 交抛物线于P 1(x 1,y 1),P 2(x 2.y 2)两点. 此时△P 1BC ≌△P 1BD ,△P 2BC ≌△P 2 B D .由A 、C 两点的坐标可得点E 的坐标为(-1,2). 所以直线BE 的表达式为1322y x =-+.$联立方程组2132213442y x y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩,解得114261262x y ⎧=-⎪⎨-+=⎪⎩,224261262x y ⎧=+⎪⎨--=⎪⎩ .所以点P 1,P 2的坐标分别为(4一26,1262-+).(4+26,1262--).②若D 为抛物线与x 轴的右交点,则点D 的坐标为(8,0). 如图2,取CD 的中点F .作直线BF 交抛物线于P 3(x 3,y 3),P 4(x 4,,y 4)两点. 此时△P 3BC ≌△P 3BD ,△P 4BC ≌△P 4 B D . :由C 、D 两点的坐标可得点F 的坐标为(4,2), 所以直线BF 的表达式为y =2x -6.联立方程组22613442y x y x x =-⎧⎪⎨=-++⎪⎩,解得331418241x y ⎧=-+⎪⎨=-+⎪⎩,441418241x y ⎧=--⎪⎨=--⎪⎩ 所以点P 3,P 4的坐标分别为(-1+41,-8+241),( -1-41,-8-241), 综上可得,满足题意的点P 的坐标为(426126-+),(426126--,。
山东省诸城市桃林镇2017届中考数学压轴题专项汇编 专题4 图形的分割与拼接

专题4 图形的分割与拼接破解策略把一个几何图形按某种要求分成几个图形,就叫做图形的分割;反过来,按一定的要求也可以把几个图形拼接成一个完美的图形,就叫做图形的拼接.通常,我们会将一个或多个图形先分割,再拼接成一种指定的图形. 常见的图形的分割与拼接有: 1.三角形分割成两个等腰三角形 (1)已知:Rt△ABC ,∠BAC =90°. 作法:取斜边BC 的中点D ,连结A D . 结论:△DAB 和△DAC 是等腰三角形.D AB C(2)已知:△ABC ,∠BAC ≥∠B ,∠C =2∠B .作法:在边BC 上作一点D ,使得点D 在AB 的垂直平分线上,连结A D . 结论:△DAB 和△DAC 是等腰三角形.DCB A(3)已知:△ABC ,∠ACB =3∠B.作法:在边AB 上作一点D ,使得点D 在BC 的垂直平分线上,连结C D . 结论:△DBC 和△CAD 是等腰三角形.ABDC2.三角形分割成多个等腰三角形(1)已知:任意等腰△ABC ,AB =A C . ①作法:一条垂线+两条斜边中线.结论:△EAD ,△FAD ,△EBD ,△FCD 均为等腰三角形.ABFCED②作法:一条角平分线+两条平行线.结论:△AFD ,△FBD ,△EBD ,△DEC 均为等腰三角形.DECF BA③作法:两条角平分线+一条平行线.结论:△AEF ,△EBD ,△FCD ,△DBC 均为等腰三角形.ABF CE D(2)已知:等腰△ABC ,∠B =∠C =36°.作法:在BC 上取两点D ,E ,使得其分别在AB ,AC 的垂直平分线上,连结AD ,AE .结论:△DAB ,△ADE ,△EAC 均为含36°内角的等腰三角形,所以可以无限分等腰三角形.36°36°ABCDE(3)已知:等腰△ABC ,AB =AC ,∠A =36°. 作法:作∠ABC 的平分线BD ,交AC 于点D .结论:△DAB ,△BCD 均为含36°内角的等腰三角形,所以可以无限分等腰三角形.AB 36°DC(4)已知:任意△AB C .作法:一条垂线+两条斜边中线.结论:△EAD ,△FAD ,△EBD ,△FCD 均为等腰三角形.AB CDEF3.三角形的剪拼(1)剪拼成直角三角形.作法:取AB ,AC 的中点D ,E ;过D 作BC 的垂线,垂足为点F ;过点A 作BC 的平行线,分别交直线DF ,EF 于点G ,H . 结论:△FGH 为直角三角形.D HG EFCB A(2)剪拼成等腰三角形. 作法:取AB 、AC 的中点D 、E ,连结DE 的垂直平分线FG 交BC 于点G ;过点A 作BC 的平分线,分别交直线GD 、GE 于点H 、I 结论:△GHI 为等腰三角形F GIHD EC BA(3)剪拼成平行四边形.作法:取BC 、AC 的中点D 、E ,分别过点A 作BC 的平行线,交直线DE 于点F . 结论:四边形ABDF 为平行四边形.EFDCBA(4) 剪拼成矩形.①作法:取AB 、AC 的中点D 、E ,分别过点D 、E 作BC 的垂线,垂足为F 、G .过点A 作BC 的平行线,分别交直线FD 、GE 于点H 、I . 结论:四边形HFGI 为矩形.I H ED GAB C②作法:取AB 、AC 的中点D 、E ,分别过点B 、C 作直线DE 的垂线,垂足为F 、G . 结论:四边形FBCG 为矩形.F G ED CBA③作法:取BC 、AC 的中点D 、E ,过点A 作BC 的平行线,交直线DE 于点F ;分别过点A 、F 作BC 的垂线,垂足为G 、H结论:四边形AGHF 为矩形(先将△ABC 剪拼成平行四边形ABDF ,再将平行四边形剪拼成矩形AGHF )EFH D G CB A(5)剪拼成正方形(三角形一边上的高是该边长的一半).①作法:取BC 、AC 的中点D 、E ,过点A 作BC 的平行线,交直线DE 于点F ,分别过A 、F 作BC 的垂线,垂足为G 、H . 结论:四边形AGHF 为正方形.ABC GDHFE②作法:取AB 、AC 的中点D 、E ,分别过点D 、E 作BC 的垂线,垂足为F 、G ;过点A 作BC 的平行线,分别交直线FD 、GE 于点H 、I 结论:四边形HFGI 为正方形CB AFGD EH I(6)剪拼成等腰梯形.作法:作AD =AB 交BC 于点D ,取AC 的中点E ,过点E 作AD 的平行线,交BC 于点F ,过点A 作BC 的平行线,交直线FE 于点G . 结论:四边形AGFB 为等腰梯形.GFDECBA4.矩形的剪拼(1)剪拼成直角三角形作法:取AD 中点E ,连结CE 并延长,交直线AB 于点F . 结论:△FBC 是直角三角形.FEDCB A(2)剪拼成等腰三角形①作法:延长CD 至点E ,使得DE =CD ,连结AC 、AE . 结论:△ACE 为等腰三角形,其中AC =AEA CDE②作法:取AB 、CD 、AD 的中点E 、F 、G ,连结GE 、GF 并延长,分别交直线BC 于点H 、I 结论:△GHI 为等腰三角形,其中GH =GIIHGA BCD E F③作法:取AD 的中点E ,向矩形外作AD 的垂线EF ,使得EF =AB ,连结FB 、FC 结论:△FBC 为等腰三角形,其中FB =FCAB CDEF④作法:取BC 、CD 、AD 的中点E 、F 、G ,连结FE 、FG 并延长,分别交直线AB 于H 、L 结论:△FHI 为等腰三角形,其中FH =FI(3)剪拼成菱形.作法:取BC 的中点E ,向矩形外作BC 的垂线EG ,使得EG =AB ,取AD 的中点F ,连结BG 、GC 、CF 、F B .结论:四边形BGCF 为菱形GABCDEF(4)剪拼成正方形作法:延长CB 至点E ,使得BE =AB ,以EC 为直径作圆,交BA 的延长线于点F;在BC 上取一点G ,使得BG =BF ,过点F 作BF 的垂线,过点G 作BG 的垂线,两线交于点H 结论:四边形BGHF 为正方形5.正方形的剪拼(1)两个正方形剪拼成一个正方形作法:连结AE ,过点A 作AI 丄AE 交CB 的延长线于点I ;分别以E ,I;为圆心AE 长为半径画弧,交于点H ,连结HI 、HE . 结论:四边形AEHI 为正方形NHLGFEDC BA(2)一个正方形剪拼成两个正方形作法:以B 为端点在正方形ABCD 内部作射线,分别过A 、C 、D 作射线的垂线,垂足分别为E 、F 、G ,再分别过点A 、C 作DG 的垂线,垂足分别为H 、I 结论:四边形AEGH 和四边形CFGI 为正方形.进阶训练1. 在△ABC 中,∠ABC =∠ACB =63°,如图1,取三边中点,可以把△ABC 分割成四个等腰三角形,请你在图2中,用另外四种不同的方法把△ABC 分割成四个等腰三角形,并标明分割后的四个等腰三角形的底角的度数(如果经过变换后两个图形重合,则视为同一种方法)图2图1C BACB AABCABC C BA答案:2. 小明在研究四边形的相关性质时发现,在不改变面积的条件下,一般梯形很难转化为菱形,但有些特殊的梯形通过分割可以转化为菱形,如图1,已知在等腰梯形ABCD 中,AD ∥BC ,CD =2AD ,∠C =60°.图2图1CBADDABC(1)果将该梯形分割成几块,然后可以重新拼成菱形,试在图1中画出变化后的图形; (2)在完成上述任务后,他又试着在直角梯形(如图2,AD ∥BC ,CD =2AD ,∠C =60°)中,将梯形分成几块,拼成新的图形;①它能拼成一个菱形吗?如果能,请画出相应的图形; ②它能拼成一个正方形吗?如果能,请画出相应的图形. 答案:(1)能拼成菱形:CB AD(2)能拼成菱形:DA B C能拼成正五边形DAB C3.下列网格中的六边形ABCDEF是由一个边长为6的正方形剪去左上角一个边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.(1)根据剪拼前后图形的面积关系求出拼成的正方形的边长;(2)如图甲,把六边形ABCDEF沿EH,BG剪成①,②,③三个部分,请在图甲中画出将②,③与①拼成的正方形,然后标出②,③变动后的位置;(3)在图乙中画出一种与图甲不同位置的两条剪裁线,并画出将此六边形剪拼成的正方形.图甲图乙答:(1)(2)如图;(3)如图:。
山东省诸城市桃林镇2017届中考数学压轴题专项汇编专题25全等三角形的存在性

专题25 全等三角形的存在性破解策略全等三角形的存在性问题的解题策略有:(1 )当有一个三角形固定时(三角形中所有边角为定值) ,另一个三角形会与这个固定的三角形有一个元素相等;再根据全等三角形的判定,禾U用三角函数的知识(画图) 或列方程来求解.(2)当两个三角形都不固定时(三角形中有角或边为变量),若条件中有一条边对应相等时,就要使夹这条边的两个角对应相等,或其余两条边对应相等;若条件中有一个角对应相等时,就要使夹这个角的两边对应相等,或再找一个角和一条边对应相等.例题讲解例1如图,在平面直角坐标系中,抛物线y= ax2+ bx+ 4与x轴的一个交点为A(- 2, 0),与y 轴的交点为C,对称轴是x= 3,对称轴与x轴交于点B.(1)求抛物线的表达式;(2)若点D在x轴上,在抛物线上是否存在点P,使得△PBC若存在,求点P的坐标;若不存在,请说明理由.(3)若点M在y轴的正半轴上,连结MA过点M作MA的垂线,交抛物线的对称轴于点N.问:是否存在点M使以点M A N为顶点的三角形与△ BAN全等?若存在,求出点M424a -2b 4=0解:(1)由题意可列方程组解得2a427②当AM= NB MN= BA 时,可列方程组:4 m 2 = n 29 (m -n)2 =25(2)显然 OA= 2, OB= 3, OC= 4.所以 BC OB 2 OC 2 =5 = BA . 若^ P BD^ PBC 贝U BD= BC= 5, PD= PC所以D 为抛物线与x 轴的左交点或右交点,点 B P 在CD 的垂直平分线上,①若点D 为抛物线与x 轴的左交点,即与点 A 重合.如图1,取AC 的中点E ,作直线BE 交抛物线于P i (x i , y i ), F 2 (X 2. y 2)两点. 此时△ RBC^AP i BD △ RBC ^A R BD.由A 、C 两点的坐标可得点 E 的坐标为(一1, 2). 所以直线BE 的表达式为y = _〔x -.2 22②若D 为抛物线与x 轴的右交点,则点 D 的坐标为(8, 0).如图2,取CD 的中点F .作直线BF 交抛物线于P 3 (X 3, y s ), P 4 (X 4, , y 4)两点. 此时△ P s BC^AP s BD △ RBC^A P 4 BD.由C D 两点的坐标可得点 F 的坐标为(4, 2), 所以直线BF 的表达式为y = 2x — 6.联立方程组厂罕6 3 ,解得卜一仆化,广“一色 y--[X -x 4ys--8 2.4i y4--8-2.4i 所以点.P J , R 的坐标分别为(一i + - 4i , — 8 + 2』4i ), ( — i — ■ 4i , — 8— 2 ■- 4i ),综上可得,满足题意的点 P 的坐标为(4 一 26, 「26), (4+ 26 , 土丄6 ),2 2(—i + ■■■'4i , — 8 + 2」4i )或(一i — ■- 4i , — 8 — 2>..;4i ).(3) 由题意可设点 M(0 , m ), N(3 , n ),且m >0 ,则 AM= 4+ m i , MN= 9 +( m — n ) 2 , B N = n 2. 而/ AM =Z ABN= 90° , 所以△ AMNf A ABN 全等有两种可能:①当 AM= AB, M = BN 时,所以此时点M 的坐标为(0 ,.2i ).所以抛物线的表达式为^-1x 22x 4 • 4 21丄-i y 「x +- 联立方程组 2i 2 -y =—— x +—x +4 / 42,解得 y i - 26 ^ 26 ,X2 =4 26-^26 .y 2 二所以点P i , P 2的坐标分别为( 4 一炉,土亚6 ). (4 +V26 ,-1 - 26 )2可列方程组4 m 2 =25 9 (m —n)2 二n 2m 2 n 2 =-2i_ _5 N (舍),3m^2解得 2 ,5所以此时点M 的坐标为(0, 2).2点E 在OA 上.如图1. 此时DF 丄OA 所以OF=晅。
山东省诸城市桃林镇2017届中考数学压轴题专项汇编 专题13“Y”形模型

专题13“Y ”形模型破解策略当图形具有邻边相等的这一特征时,可以把图形的某部分绕其邻边的公共端点旋转到另一位置,将分散的条件相对集中起来,从而解决问题.因为正方形、正三角形的边长相等,所以在这两种图形中常常应用旋转变换.(1)如图,等边△ABC 内有一点P ,连结AP ,BP ,CP ,将△BPC 绕点B 逆时针旋转60°得到△BP 'A ,则△BPP '是等边三角形;△APP '的形状由AP ,BP ,CP 的长度决定.AC(2)如图,正方形ABCD 内有一点P ,连结AP ,BP ,CP ,将△BPC 绕点B 逆时针旋转90°得到△BP 'A ,则△BPP '是等腰直角三角形;△APP '的形状由AP ,BP ,CP 的长度决定.P'B这类题目中不提旋转,而是通过旋转添加辅助线,从而解决问题. 例题讲解例1已知:在△ABC 中,∠BAC =60°.(1)如图1,若AB =AC ,点P 在△ABC 内,且PA =3,PC =4,∠APC =150°,求PB 的长;图1ACB【答案】解:(1)如图4,将△APC 绕点A 顺时针旋转60°,得到△AQB ,连结PQ . 易证△PAQ 是等边三角形.从而在△PQB 中,有∠PQB =90°,PQ =3,BQ =4, 所以PB =5图4ABC【答案】解:(1)如图4,将△APC 绕点A 顺时针旋转60°,得到△AQB ,连结PQ . 易证△PAQ 是等边三角形.从而在△PQB 中,有∠PQB =90°,PQ =3,BQ =4, 所以PB =5图4ABC(2)如图2,若AB =AC ,点P 在△ABC 外,且PA =3,PB =5,PC =4,求∠APC 的度数;图2PB【答案】(2)如图5,将△APC 绕点A 顺时针旋转60°,得到△AQB ,连结PQ . 易证△PAQ 是等边三角形.从而在△PQB 中,有PQ =3,BQ =4,PB =5, 所以∠PQB =90°,从而∠APC =∠AQB =30°.图5PBQ(3)如图3,若AB =2AC ,点P 在△ABC 内,且PAPB =5,∠APC =120°,求PC 的长;图3BA C【答案】(3)如图6,作△AQC ,使得AQ =12AP ,CQ =12BP ,连结PQ . 易证△ACB ∽△AQP .从而在△QPC 中,有∠QPC =90°,PQ =32,QC =52, ∴PC =2图6QBA例2如图,正方形ABCD 外有一点E ,满足ED =EC ,且∠DEA =15°,求证:△DEC 为等边三角形.EAB C证明如图,过点D 作DF ⊥DE ,且DF =DE ,连结CF 交AE 于点G ,连结EF . 易证△ADE ≌△CDF ,所以∠DFC =∠DEA =15°,从而∠FGE =∠FDE =90°,∠GFE =30°. 所以GE =12EFDFCE ,所以∠GEC =45°,∠DEC =60°, 即△DEC 为等边三角形.FEA BC进阶训练1.(1)如图1,在正方形ABCD 内有一点P ,PA,PB,PC =1,则∠BPC 的度数为________;图1DABC【答案】1.(1)135°;【提示】如图,将△BPC 旋转至△BP 'A ,连结PP ',证△AP 'P 是直角三角形即可.P'DC(2)如图2,在正六边形ABCDEF 内有一点P ,PA =,PB =4,PC =2,则∠BPC 的度数为________,正六边形ABCDEF 的边长为________.图2D AB【答案】(2)120°;GD 2.(1)如图1,在等边△ABC 中,AC =7,点P 在△ABC 内,且∠APC =90°,∠BPC =120°,求△APC 的面积;(2)如图2,在四边形ABCD 中,AE ⊥BC ,垂足为点E ,∠BAE =∠ADC ,BE =CE =2,CD =5,AD =k ·AB (k 为常数),求BD 的长(用含k 的式子表示)图2EDC BA图1PCBA(1)△APC 的面积为(2)BD【提示】(1)如图,将△ABP 绕点B 顺时针旋转60°至△CBQ ,连结PQ .易证△PQC 为含30°的直角三角形.令BP =m ,则PQ =m ,从而AP =CQ,PC =2m ,然后解Rt △APC 即可. (2)如图,连结AC ,显然AC =AB ,将△ABD 绕点A 逆时针旋转∠BAC 的度数至△ACQ ,连接DQ ,则△ABC ∽△ADQ ,从而DQ =k ·BC =4k .作AF ⊥DQ 于点F ,则∠DAF =∠BAE =∠ADC ,所以AF ∥CD ,即∠CDQ =90°.在Rt △CDQ 中,由勾股定理可得BD =CQQPCBAQFECB A。
山东省诸城市桃林镇2017届中考数学压轴题专项汇编专题14共顶点模型

专题 14共极点模型破解策略1.等边三角形共极点等边△ ABC与等边△ DCE, B、C、 E 三点共线.AFDG HB C E连结 BD、 AE交于点 F, BD交 AC于点 G, AE交 DC于点 H,连结 CF、GH,则:(1)△BCD≌△ACE;(2)AE=BD;(3)∠AFB=∠DFE= 60°;(4)FC均分∠BFE;(5)BF=AF+FC,EF=DF+FC;(6)△CGH为等边三角形.CA CB证明(1)由已知条件可得∠ ACE∠ BCD,则△BCD≌△ACE.EC DC(2)由( 1)得AE=BD;(3)由( 1)得∠GAF=∠GBC,而∠AGF=∠BGC,因此∠DFE=∠AFB=∠ACB= 60°.(4)方法一如图 1,过点C分别作BD、AE的垂线,垂足分别为M、N.由( 1)知S△ACE=S△BCD,即1BD·CM=1AE·CN,因此CM=CN,故FC均分∠BFE.2 2AFDMNB C E图1方法二由∠ CAF=∠ CBF,可得 A、 B、 C、 F 四点共圆,因此∠BFC=∠ BAC=60°.同理可得∠ CFE=∠ CDE=60°.因此 FC均分∠ BFE.(5)如图 2,作∠FCI= 60°,交BD于点I,则△CFI为等边三角形.易证△ BCI≌△ ACF,因此 BI= AF, IF = CI = F C.进而 BF= BI+ IF = AF+ CF.同理可得 EF= DF+F C.AMFDNBCE图1( 6)易证△ ACH ≌△ BCG ( ASA ) 可得 CG = CH ,而∠ GCH = 60°,因此△ CGH 为等边三角形.2.等腰直角三角形共极点等腰 Rt △ ABC 与等腰 Rt △ DCE 中,∠ ACB =∠ DCE = 90°.AAIF DDHCCBE BG JE图1图 2如图 1,连结 BD 、 AE 交于点 F ,连结 FC 、 AD 、 BE ,则:( 1)△ BCD ≌△ ACE ; ( 2) AE = BD ; ( 3) AE ⊥ BD ;( 4) FC 均分∠ BFE ;2222( 5) AB + DE =AD + BE( 6) BF = AF + 2 FC , EF = DF + 2 FC ;( 7)如图 2,若 G 、I 分别为 BE 、 AD 的中点,则 GC ⊥ AD 、 IC ⊥ BE (反之亦然);( 8) S △ ACD =S △ BCE证明( 1)(2)( 3)(4)证明见“等边三角形共极点” ;( 5)由于 AE ⊥ BD ,由勾股定理可得 222222AB + DE =( AF +BF )+( DF + EF ),2+ 2=( 2+ 2)+( 2+ 2 )ADBEAF DFBF EF2 222因此 AB + DE =AD + BE( 6)如图 3,过点 C 作 ⊥ ,交于点,则△为等腰直角三角形.CK FCBD K CFK易证△ BCK ≌△ ACF ,因此 BK = AF .进而 BF = BK + KF = AF + 2 FC ,同理可得 EF = DF + 2 F C .ADFKCBE 图 3(7)①如图 4,延伸GC,交AD延伸线于点H,延伸CG至点K,使得GK=GC,连结BK.易证∠ KBG=∠ CEG,BK= EC= C D.由题意可得∠ ACD+∠ BCE=∠ CBE+∠ CEB+∠ BCE=180°,因此∠ ACD=∠ CBE+∠ CEB=∠ CBG+∠ GBK=∠ CBK.可得△ ACD≌△ CBK(SAS)则∠ CAD=∠ BCK,因此∠ ACH+∠ CAH=∠ ACH+∠ BCK=90°,故 GC⊥ A D.ADHCB G EK图 4②如图 5,CJ⊥BE,延伸JC交AD于点T,分别过点A,D作IJ的垂线,垂足分别为M、 N.由已知可得△AMC≌△ CJB;△ DNC≌△ CJE,因此 AM= DN= CJ,故有△ AMI≌△ DNI,因此 AI= DI,即可证.A MINDCB JE图 5(8)在( 7)中的证明过程中可获得S△ACD=S△BCE;也能够用下边的方法来证明如图6,过点D作DP⊥AC于点P,过点E作EQ⊥BC,交BC延伸线于点Q.易证△ DPC≌△ EQC( AAS).因此 DP= EQ,故1DP· AC=1EQ· BC,即 S△ACD= S△BCE 2 2ADPQCB E图 63.等腰三角形共极点等腰△ ACB与等腰△ DCE中, AC= BC, DC= CE,且∠ ACB=∠ DCE.A DFEB C连结 BD, AE交于点 F,则:(1)△BCD≌△ACE;(2)AE=BD;(3)∠AFB=∠ACB;(4)FC均分∠BFE.4.相像三角形共极点△ ACB与△ ECD中,AC BC,∠ACB=∠EC D.EC DCDA FG EB C连结 BD, AE交于点 F,则:(1)△BCD∽△ACE;(2)∠AFB=∠AC B.证明( 1)由已知可得BC ACDC EC∠ BCD∠ ACE因此△ ACE∽△ BC D.( 2)由( 1)可得∠CAF=∠CBF.设 AC与 BD的交点为 G,则∠ AGF=∠BGC,因此∠ AFB=∠ AC B.例题解说例 1 如图 1,在△ABC中,BC=4,以线段AB为边作△ABD,使得AD=BD,连结DC,再以DC为边作△CDE,使得 DC= DE,∠ CDE=∠ ADB=.( 1)如图 2,当∠CDE=45°且=90°时,用等式表示线段AD, DE之间的数目关系;(2)将线段CB沿着射线CE的方向平移,获得线段EF,连结BF,AF.①若= 90°,依题意补全图 3,求线段AF的长;②请直接写出线段 AF的长(用含的式子表示)解( 1)AD+DE= 4.(2)①如图 4,连结AE交BC于点G,设DE与BC的交点为H.由“等腰直角三角形共极点”可得△ADE≌△ BDC( SAS)因此 AE= BC,∠ EGC=∠ EDC=90°由于线段CB沿着射线CE的方向平移,获得线段 EF.因此AE= BC=FE=4,AE⊥ EF.因此AF=2EF=4 2.② AF=8sin .2如图 5,连结AE交BC于点G.由“等腰直角三角形共极点”可得∠ AEF=∠ EGC=∠ EDC=FE= BC= AE 过点 E 作 EH⊥AF于点 H则∠ AEH=1∠ AEF=12 2因此 AF=2AH=2AE sin=8sin.2 2例 2 如图 1,在△中, 、 E 分别是、 上的点,且∥ ,将△绕A 点顺ABCDAB ACDE BCADE时旋转必定角度,连结 BD ,CE ,获得图 2,而后将 BD , CE 分别延伸至 M 、N ,使 DM = 1BD ,EN = 1CE ,连结 AM , AN , MN ,获得图 3. 22( 1)若= ,请研究以下数目关系;ABAC①在图 2 中, BD 与 CE 的数目关系是; ②在图 3 中,猜想 AM 与 AN 的数目关系,∠ MAN 与∠ BAC 的数目关系,丙证明你的猜 想:( 2)若 AB = k · AC ( K > 1),按上述操作方法,获得图 4,请持续研究: AM 与 AN 的数量关系;∠ 与∠ 的数目 关系.MANBAC解 ( 1)① BD = CE .②AM = AN ,∠ MAN =∠ BA C . 证明以下:由“等腰三角形共极点”可得△ CAE ≌△ BAD ( SAS )因此 CE = BD ,∠ ACN =∠ ABM因此 BM = CN进而△ ABM ≌△ ACN (SAS ) 因此 AM = AN ,∠ BAM =∠ CAN 即∠ MAN =∠ BA C .( 2) AM = kAN ,∠ MAN =∠ BA C . 证明以下:由“相像三角形共极点”可得△ CAE ∽△ BAD ,因此因此BD ABk ,∠ ACN =∠ ABM CE AC BM AB kCNAC进而△ ABM ∽△ ACN因此 AM = kAN ,∠ BAM =∠ CAN即∠ MAN =∠ BA C .进阶训练1.在平行四边形ABCD中,∠A=∠ DBC,过点 D作 DE= DF,且∠ EDF=∠ ABD,连结 EF,EC,N、 P 分别为 EC, BC的中点,连结诶NP.(1)如图 1,若点E在DP上,EF与DC交于点M,尝试究线段NP与MN的数目关系及∠ABD与∠ MNP知足的等量关系;(2)如图 2,若点M在线段EF上,当点M在何地点时,你在( 1)中获得的结论仍旧建立?写出你确立的点M的地点,并证明(1)中的结论.解( 1)NP=NM,∠ABD+∠MNP= 180°(2)M是线段EF的中点.【提示】( 1)证DP⊥BC,DC⊥EF,依据直角三角形斜边中线定理可得NP= NM=1CE,∠ ABD 2+∠ MNP=2∠ PDC+2∠ DCP=180°;或许连结 BE,CF(如图),由“等腰三角形共极点”可证得结论.(2)如图,连结BE,CF,取EF中点G.连结NG,由“等腰三角形共极点”和中位线定理,即可获得点 M与点 G重合时(1)中结论仍建立.2.如图 1,在△ABC中,∠ACB= 90°,AC=BC,∠EAC= 90°,点M为射线AE上随意一点(不与点 A 重合),连结 CM,将线段 CM绕点 C按顺时针方向旋转90°获得线段 CN,直线 NB分别交直线 CM、射线 AE于点 F、D.2.如图 1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线 AE上随意一点(不与 A 重合),连结 CM,将线段CM绕点 C 按顺时针方向旋转90°获得线段CN,直线 NB 分别交直线CM、射线 AE于点 F、D.(1)直接写出∠NDE的度数;(2)如图 2、图 3,当∠EAC为锐角或钝角时,其余条件不变,( 1)中的结论能否发生变化?假如不变,选用此中一种状况加以证明;假如变化,请说明原因;(3)如图 4,若∠EAC=15°,∠ACM=60°,直线CM与 AB交于 G, BD=62,其余2条件不变,求线段AM的长.解:( 1)∠NDE=90°;(2)( 1)中结论不变,证明略;(3) 6.【提示】( 2 )由“共极点模型”可得△ACM≌△ BCN,因此∠ BNC=∠ AMC,进而获得∠ MDN =∠ MCN=90°.(3)由题意可得,∠B AE=30°,∠ AMG=∠AGM=75°,而又(1)可得∠ NDE=90°,所以 AB=2BD=6 2 .如图,过点G作 GH⊥ BC于点 H,则 CH= 3 GH= 3 BH,进而AG= 3 BG,因此AG+3AG=6 2 ,解得AM=AG=6 .3BGHDENMACF3. 如图, △与△DEF 都是等腰三角形,, 的中点均为,且顶角∠=∠ABCAB EFOACBEDF= α ,直线 BF , CD 交于点 G ,连结 AG .现将图中△ DEF 绕点 O 旋转,请你确立 AG 取最小值和最大值时点G 的地点.BEOFD GCA答案:以BC 为直径作⊙,直线交于点1, 2, 则1为AG 取最小值时点G 的地点,2HG GGG为 AG 取最大值时点G 的地点 .BG 2E OHFG1DCGA【提示】 如图, 连结 CO ,DO ,建立两个相像的“直角三角形共极点”,=∠ BOC =90°,进而点 G 在以 BC 为直 径的圆上.进而获得∠BGCBEOFDCGA。
山东省诸城市桃林镇2017届中考数学压轴题专项汇编 专题1 一元二次方程的特殊根

专题1 一元二次方程的特殊根破解策略1.一元二次方程的有理根关于x 的一元二次方程ax 2+bx +c =0(a ≠0,a ,b ,c 为有理数)存在有理根的条件为:b 2-4ac 是一个有理数的平方.解决一元二次方程ax 2+bx +c =0(a ≠0,a ,b ,c 为有理数)的有理根问题时,一般的解题策略有:(1)利用“判别式的取值范围”解题①讨论二次项系数的情况,当a ≠0时,求出判别式;②根据已知条件得待定系数的取值范围,再求出判别式的取值范围,筛选出其中为有理数的平方的数; ③求出待定系数的可能取值,并检验.(2)利用“判别式是一个有理数的平方”解题①讨论二次项系数的情况,当a ≠0时,将方程的系数整数化,求出判别式;②将判别式写成△=M 2-t 的形式(M 为关于待定系数的整式,t 为整数),设M 2-t =m 2(m 为非负有理数)③可得(M+m )(M-m)=t ,解此不定方程;④求出待定系数的可能取值,并检验.2.一元二次方程的整数根对于一元二次方程ax 2+bx +c =0(a ≠0,a ,b ,c 为有理数)而言,方程的根为整数且必为有理数,所以有理根存在的条件是整数根存在的必要条件.解决方程ax 2+bx +c =0的整数根问题,除了利用“判别式的取值范围”和“判别式是一个有理数的平方”来解题外,还可以利用“根与系数的关系”和“因式分解”来解决问题.(1)利用“根与系数的关系”解题①讨论二次项系数的情况,当a ≠0时,利用根与系数的关系求出两根的和与积;②将两根的和与积的代数式写成一个整式与一个分式的和的形式(类似于分离常量); ③由分式的结果一定为整数,根据整除的性质得到分式的分母一定是分子的约数,从而求出待定系数的可能取值;(2)利用“因式分解”解题①讨论二次项系数的情况,当a ≠0时,将方程化为(m 1x +n 1)(m 2x +n 2)=0的形式;②求出方程的两根,x 1=11m n -和x 2=22m n -; ③利用分离常量的方法,将11m n -,22m n -变成一个常数与一个分式的和; ④根据整除的性质,得到分式的分母一定是分子的约数,从而求出待定系数的可能取值; ⑤将待定系数的可能取值代入原方程检验并确定结果.需要注意的是,要看清楚题中说的是方程有整数根还是方程的根为整数.3.分离常量在利用“根与系数的关系”解题和利用“因式分解”解题的过程中都提到了分离常量,所谓分离常量就是从分式中化出一个常数,例如: ①131131113112+-=+-++=+-+=+-m m m m m m m m ; ②111111)1(11112+--=+-++-=+---=+--m m m m m m m m ; ③112111)1(21122132++=++++=+++=++m m m m m m m m ;④123121)1(31233113++-=++++-=++--=+--m m m m m m m m . 例题讲解:例1 已知整数m 满足6<m <20,如果关于x 的一元二次方程mx 2—(2m -1)x +m -2=0有有理根,求m 的值及方程的根.解: 若原方程的根为有理数,则△=(2m -1)2—4m (m -2)=4m +1应为某个有理数的平方.已知6<m <20,所以25<4m +1<81,而4m +1是奇数,从而4m +1=49,得m =12,所以原方程变为12x 2—23x +10=0, 解得x 1=32,x 2=45. 故m =12时,方程有有理根,此时方程的根为x 1=32,x 2=45. 例2 设m 是不为零的整数,关于x 的一元二次方程mx 2-(m -1)x +1=0有有理根,求m 的值.解 若原方程的根为有理数,则△=(m -1)2—4m =(m -3)2—8应为某个有理数的平方.令(m -3)2—8=n 2 (n >0),显然n 也为整数,所以(m -3+n )(m -3-n )=8.由于m -3+n >m -3-n ,并且(m -3+n )+(m -3-n )=2(m -3)是偶数,所以m -3+n 和m -3-n 同奇偶, 所以⎩⎨⎧=-=+2n 3-m 4n 3-m 或⎩⎨⎧-=---=+-4323n m n m ;解得⎩⎨⎧==1611n m ,⎩⎨⎧==1022n m (舍). 所以当m =6时,方程有两个有理根,分别为x 1=21,x 2=31.例3 关于x 的一元二次方程rx 2+(r +2)x +r -1=0有且只整数根,求整数r 的值.解: 当r =0时,原方程无整数根;当r ≠ 0时,由根与系数的关系可得x 1+x 2=r r 2+-=-1-r 2,x 1•x 2=r r 1-=1-r1. 因为x 1,x 2都是整数, 所以x 1+x 2和x 1•x 2均为整数,从而r 2,r1均为整数. 而r 为整数,所以r =±1.当r =-1时,原方程的解不为整数,不符合条件;当r =1时,原方程的解为x 1=0,x 2=-3.综上可得,整数r =1.例4 在平面直角坐标系中,我们不妨将横坐标、纵坐标均为整数的点称之为“中国结”,若二次函数y =(k 2-3k +2)x 2+(2k 2-4k +1)x +k 2-k (k 为常数)的图象与x 轴相交得到两个不同的“中国结”,试问:该函数的图象与x 轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?解:令y =0,即(k 2-3k +2)x 2+(2k 2-4k +1)x +k 2-k =0,因式分解,得[(k -1)x +k ][(k -2)x +k -1]=0解得x 1=1111---=--k k k ,x 2=21121---=---k k k , 由题意可得x 1,x 2均为整数,所以11-k ,21-k 也均为整数, 设11-k =m (m ≠0,m 为整数),则k =m1+1, 所以mm m m m m k -+-=-+--=-=-+=-11111)1(1211121, 所以1-m =±1,即m 1=0(舍),m 2=2,从而得到k =23. 所以二次函数表达式为y =41-x 2-21x +43=41-(x +1)2+1 二次函数图象如下图所示,则该函数的图象与x 轴所围成的平面图形中(含边界),一共包含6个“中国结”,分别为:(-3,0),(-2,0),(-1,0),(-1,1),(0,0),(1,0).进阶训练1.已知m 为有理数,问:k 为何值时,关于x 的方程x 2-4mx +4x +3m 2-2m +4k =0的根为有理数?解:k =-45 【提示】若原方程的根为有理数,则△=4[m 2—6m +4(1-k )]应为某个有理数的平方. 所以4(1-k )=9,即k =-45. 2.已知关于x 的方程x 2-2(2m -3)x +4m 2-14m +8=0(m >0)有两个不相等的实数根,若12<m<40,且方程的两个根均为整数,求整数m 的值.解:m =24.【提示】若原方程的根为有理数,则△=4(2m +1)应为某个有理数的平方,由12<m <40,所以25<2m +1<81,而2m +1为奇数,则2m +1=49,即m =24.3.已知方程(k 2-1)x 2-3(3k -1)x +18=0有正整数根,求整数k 的值.解:k =0,1,2,4,5.【提示】先讨论二次项系数是否为0,当k =1时,方程有正整数根,当k 2-1=0时,原方程可整理为[(k +1)x -6][(k -1)x -3]=0,解得x 1=16+k ,x 2=13-k ,而方程有正整数根,所以k =0,1,2,4,5,综上,k =0,1,2,4,5.4.求使关于x 的方程(a +1)x 2-(a 2+1)x +2a 2-6=0的根均为整数的所有整数a .解:a =-3,-2,0,1.【提示】①当a =-1时,方程变为-2x -4=0,解得x =-2,符合要求;②当a ≠-1时,设方程的两个整数根为x 1,x 2,则由根与系数的关系可得x 1+x 2=112++a a =a -1+12+a ,x 1•x 2=1622+-a a =2(a-1)-14+a . 因为x 1,x 2都是整数,所以x 1+x 2和x 1•x 2均为整数,即12+a 为整数,所以a =-3,-2,0,1. 经检验,得到当a =-3,-2,0,1时,方程的根均为整数.本文档仅供文库使用。
山东省诸城市桃林镇中考数学压轴题专项汇编 专题17 一线三等角模型-人教版初中九年级全册数学试题

专题17 一线三等角模型破解策略在直线AB 上有一点P ,以A ,B ,P 为顶点的∠1,∠2,∠3相等,∠1,∠2的一条边在直线AB 上,另一条边在AB 同侧,∠3两边所在的直线分别交∠1,∠2非公共边所在的直线于点C ,D .1.当点P 在线段AB 上,且∠3两边在AB 同侧时. (1)如图,若∠1为直角,则有△ACP ∽△BP D .321DBPAC(2)如图,若∠1为锐角,则有△ACP ∽△BP D .3CDBPA证明:∵∠DPB =180°-∠3-∠CPA ,∠C =180°-∠1-∠CPA ,而∠1=∠3 ∴∠C =∠DPB ,∵∠1=∠2,∴△ACP ∽△BPD(3)如图,若∠1为钝角,则有△ACP ∽△BP D .231DBPAC2.当点P 在AB 或BA 的延长线上,且∠3两边在AB 同侧时. 如图,则有△ACP ∽△BP D .321CPDBA证明:∵∠DPB =180°-∠3-∠CPA ,∠C =180°-∠1-∠CPA ,而∠1=∠3 ∴∠C =∠DPB ,∵∠1=∠2=∠PBD ,∴△ACP ∽△BPD3.当点P 在AB 或BA 的延长线上,且∠3两边在AB 异侧时. 如图,则有△ACP ∽△BP D .321CDBAP证明:∵∠C =∠1-∠CPB ,∠BPD =∠3-∠CPB ,而∠1=∠3 ∴∠C =∠BP D .∵∠1=∠2,∴∠PAC =∠DBP .∴△ACP ∽△BP D . 例题讲解例1:已知:∠EDF 的顶点D 在△ABC 的边AB 所在直线上(不与点A ,B 重合).DE 交AC 所在直线于点M ,DF 交BC 所在直线于点N .记△ADM 的面积为S 1,△BND 的面积为S 2. (1)如图1,当△ABC 是等边三角形,∠EDF =∠A 时,若AB =6,AD =4,求S 1S 2的值;(2)当△ABC 是等腰三角形时,设∠B =∠A =∠EDF =α. ①如图2,当点D 在线段AB 上运动时,设AD =a ,BD =b ,求S 1S 2的表达式(结果用a ,b和a 的三角函数表示).②如图3,当点D 在BA 的延长线上运动时,设AD =a ,BD =b ,直接写出S 1S 2的表达式.NFC ME BDAF NME BD ACFN DABEM C图1 图2 图3解:(1)如图4,分别过点M ,N 作AB 的垂线,垂足分别为G ,H .则S 1S 2=12MG AD 12NH BD =14AD AM sin A BD BN sinB .由题意可知∠A =∠B =60º,所以sin A =sin B =32. 由“一线三等角模型”可知△AMD ∽△BDN . ∴AM ADBD BN=,从而AM BN =AD BD =8,∴S 1S 2=12.(2)①如图5,分别过点M ,N 作AB 的垂线,垂足分别为G ,H .则S 1S 2=12MG AD12NH BD =14AD AM sin A BD BN sinB .由“一线三等角模型”可得△AMD ∽△BDN , 所以AM ADBD BN=,从而AM BN =AD BD =ab , 所以S 1S 2=14a ²b ²sin²a ; ②如图6,分别过点M ,N 作AB 的垂线,垂足分别为G ,H .HGCM EBA DN F则S 1S 2=12MG AD12NH BD =14AD AM sin A BD BN sinB .由“一线三等角模型”可得△AMD ∽△BDN ,所以AM ADBD BN=,从而AM BN =AD BD =ab , 所以S 1S 2=14a ²b ²sin²a ; 例2:如图,在等腰三角形ABC 中,∠BAC =120°,AB =AC =2,点D 是BC 边上的一个动点(不与B 、C 重合),在AC 上取一点E ,使∠ADE =30°.(1)设BD =x ,AE =y ,求y 关于x 的函数关系式并写出自变量x 的取值X 围; (2)当△ADE 是等腰三角形时,求AE 的长.ECD B A解(1)∵△ABC 是等腰三角形,且∠BAC =120°, ∴∠ABD =∠ACB =30°, ∴∠ABD =∠ADE =30°,∵∠ADC =∠ADE +∠EDC =∠ABD +∠DAB , ∴∠EDC =∠DAB , ∴△ABD ∽△DCE ;∵AB =AC =2,∠BAC =120°, 过A 作AF ⊥BC 于F , ∴∠AFB =90°, ∵AB =2,∠ABF =30°, ∴AF =12AB =1, ∴BF 3 ∴BC =2BF =23 则DC =23x ,EC =2-y ∵△ABD ∽△DCE , ∴AB DCBD CE=,∴2232xx y-=-, 化简得:21322y x x =-+()023x <<. ECDBA(2)①当AD =DE 时,如图2, △ABD ≌△DCE ,则AB =CD ,即2=23x -,x =232-,代入21322y x x =-+解得:y =423-,即AE =423-, ②当AE =ED 时,如图,∠EAD =∠EDA =30°,∠AED =120°, 所以∠DEC =60°,∠EDC =90°则ED =12EC ,即y =12 (2-y ) 解得y =23,即AE =23;③当AD =AE 时,有∠AED -∠EDA =30°,∠EAD =120° 此时点D 和点B 重合,与题目不符,此情况不存在. 所以当△是ADE 等腰三角形时,AE =4-3AE =23ABCE进阶训练1.如图,在△ABC 中,AB =AC ,点E 在BC 边上移动(不与点B ,C 重台).满足∠DEF =∠B ,且点D ,F .分别在边AB ,AC 上.当点E 移动到BC 的中点时,求证:FE 平 分∠DF C .DFECBA1.略【提示】由题意可得∠B =∠DEF =∠C.由“一线三等 角模型”可得△BDE ∽△CEF ,可得BE CF =DEEF.而BE =CE · 所以CE CF =DEEF,从而△DEF ∽ECF .所以∠DEF =∠EFC ,即FE 平分∠DF C .2. 如图,在等边△ABC 中,点D ,E 分别在AB ,BC 边上,AD =2BE =6.将DE 绕点E 顺时针旋转60°,得到EF .取EF 的中点G ,连结AG .延长CF 交AG 于点H .若2AH=5HG ,求BD 的长.GH FEDCBA2.BD =9.【提示】如图,过点F 作FI ∥AC 交BC 于点I .则∠FIE =∠ACB =∠AB C .易证△DBE ≌△EIF ,则IF =BE ,IE =BD ,所以BC +BE =AD ,即IC =BE =IF ,则∠ACH = ∠BCH =30°.延长CH 变AB 于点J ,则CJ ⊥AB ,.A = BJ 分别过点G ,E 作AB 的垂线段,垂足为K ,L ,·则KL =KJ ·AJJK=AH HG =52,所以AJ :JK :KL :BL =5:2:2:l .因为BE =3,∠LEB = 30°,所以BL =1.5.AB =15.所以BD=9.BI。
山东省诸城市桃林镇中考数学压轴题专项汇编 专题26 相似三角形的存在性
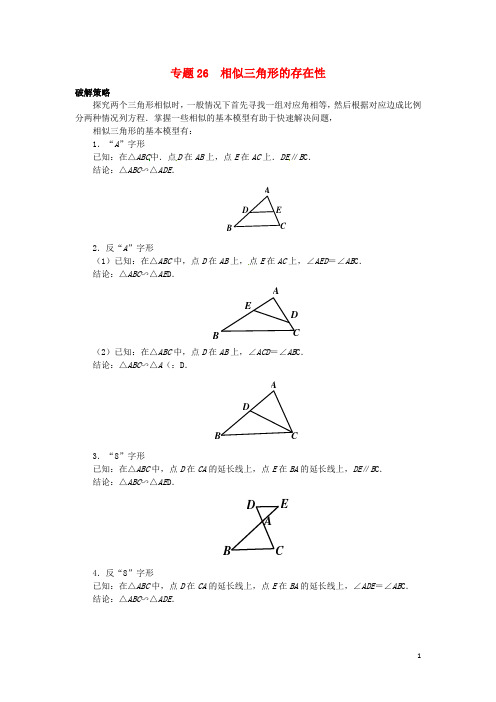
专题26 相似三角形的存在性破解策略探究两个三角形相似时,一般情况下首先寻找一组对应角相等,然后根据对应边成比例分两种情况列方程.掌握一些相似的基本模型有助于快速解决问题, 相似三角形的基本模型有: 1.“A ”字形已知:在△ABC 中.点D 在AB 上,点E 在AC 上.DE ∥B C . 结论:△ABC ∽△ADE .D E CBA2.反“A ”字形(1)已知:在△ABC 中,点D 在AB 上,点E 在AC 上,∠AED =∠AB C . 结论:△ABC ∽△AE D .A BCD E(2)已知:在△ABC 中,点D 在AB 上,∠ACD =∠AB C . 结论:△ABC ∽△A (:D .A BCD3.“8”字形已知:在△ABC 中,点D 在CA 的延长线上,点E 在BA 的延长线上,DE ∥B C . 结论:△ABC ∽△AE D .ABCD E4.反“8”字形已知:在△ABC 中,点D 在CA 的延长线上,点E 在BA 的延长线上,∠ADE =∠AB C . 结论:△ABC ∽△ADE .ABCDE5.双垂直已知:△ABC 中,∠BAC =90o ,AD 为斜边BC 上的高. 结论:△ABC ∽△DBA ,△ABC ∽△DAC ,△ABD ∽△CA D .DBCA6.一线三等角(1)已知Rt △ABC 和Rt △CED ,B ,C ,E 三点共线,90B E ACD ∠=∠=∠=o . 结论:△ABC ∽△CE D .DBC(2)已知△ABC 和△CDE ,B ,C ,E 三点共线,90B E ACD ∠=∠=∠<o . 结论:△ABC ∽△CE D .DBEA(3)已知△ABC 和△CED ,B ,C ,E 三点共线,90B E ACD ∠=∠=∠>o . 结论:△ABC ∽△CE D .D例题讲解例1如图,已知A (-1,0),B (4,0),C (2,6)三点,G 是线段AC 上的动点(不与点A ,C 重合).若△ABG 与△ABC 相似,求点G 的坐标.xyCBAOG解:设直线AC 的表达式为y sx t =+,把A ,C 两点坐标代入可得062s t s t =+⎧⎨-=+⎩,解得22s t =-⎧⎨=-⎩.所以直线AC 的表达式为22y x =--.设点G 的坐标为(k ,-2k -2),因为点G 与点C 不重合, 所以△ABG 与△ABC 相似只有△AGB ∽△ABC 一种情况. 所以AG ABAB AC=. 而AB =5, 22(21)(6)35AC =++-=, 22(1)(22)51AG k k k =++--=+,所以5135k +=, 即513k +=, 解得123k =, 283k =-(舍).所以点G 的坐标210(,)33-.例2 如图,抛物线2(2)(4)y x x =+-与x 轴交于点A ,B (点A 在B 的左侧),与y 轴交于点C ,CD ∥x 轴交抛物线于点D . P 是抛物线上一点,问:是否存在点P , 使以P ,A ,B 为顶点的三角形与△ABD 相似(△PAB 与△ABD 不重合)?若存在,求出点P 的坐标;若不存在,说明理由.xyDCBAO解:存在.因为点A (-2,0),B (4,0),C (0,2-,过点D (2,2-DE ⊥AB 于点E ,由勾股定理得32,6AD BD ==.①如图,当△1P AB ∽△ABD 时,1PB AB AB BD=, 所以166PB =. 过点1P 作11PM ⊥AB 于点1M ,所以111PM DE PB BD =, 解得1162PM =.∵11BM BEPB BD =,∴112BM =,∴点1P 的坐标为(-8,62), 因为此时点1P 不在抛物线上,所以此种情况不存在.②当△2P AB ∽△BDA 时,2P B ABAB AD=,所以262P B =.过点2P 作22P M ⊥AB 于点2M , 所以222P M DE P B AD =,解得2222P M =.因为22BM AE P B AD=,所以28BM =, 所以点2P 的坐标为(-4,22),将x =-4代入抛物线的表达式得22y =, 所以点2P 在抛物线上.③由抛物线的对称性可知:点2P 与点3P 关于直线x =1对称, 所以3P 的坐标为(6,22).④当点4P 位于点C 处时,两个三角形全等,所以点4P 的坐标为(0,2-).综上所得,点P 的坐标为(-4,22),(6,22)或(0,2-)时,以P ,A ,B 为顶点的三角形与△ABD 相似.xyM 2P 2M 3P 3P 1M 1DC (P 4)BA O例3 如图,已知直线3y x =-+与x 轴、y 轴分别交于A ,B 两点,抛物线2y x bx c =-++经过A ,B 两点,点P 在线段OA 上,从点O 出发,向点A 以1个单位/秒的速度匀速运动;同时,点Q 在线段AB 上,从点A 出发,向点B 以2个单位/秒的速度匀速运动,连接PQ ,设运动时间为t 秒.设抛物线顶点为M ,连接BP ,BM ,MQ ,问:是否存在t 的值,使以B ,Q ,M 为顶点的三角形与以O ,B ,P 为顶点的三角形相似?若存在,请求出t 的值;若不存在,请说明理由.xyQMBAOP解: ∵3y x =-+与x 轴交于点A ,与y 轴交于点B , ∴ A 点坐标为(3,0),B 点坐标为(0,3),将A (3,0),B (0,3)代入2y x bx c =-++, 得9303b c c -++=⎧⎨=⎩,解得23b c =⎧⎨=⎩,所以抛物线的解析式为2223(1)4y x x x =-++=--+. ∴点M 的坐标为(1,4),22112MB =+=. 所以222BM AB AM +=, 90MBA ∠=o .如图, 设运动时间为t 秒, 则OP =t , (3)2BQ t =-.①当△BOP ∽△QBM 时,MB BQOP OB=, 即2(3)23t t -=,整理得: 2330t t -+=, 而234130∆=-⨯⨯<,所以此种情况不存在;②当△BOP ∽△MBQ 时, MB BQ OB OP=, 即 2(3)23t t -=,解得94t =. 所以当94t =时,以B ,Q ,M 为顶点的三角形与以O ,B ,P 为顶点的三角形相似. xyQMBAOP进阶训练1.如图,在平面直角坐标系xOy 中,抛物线234y x bx c =-++的图象交x 轴于()4,0A ,()1,0B -两点,交y 轴于点C .(1)求抛物线的表达式和对称轴;(2)若P 是线段OA 上的一点(不与点O ,A 重合),Q 是AC 上一点,且PQ =PA ,在x 轴上是否存在点D ,使得△ACD 与△APQ 相似?如果存在,请求出点D 的坐标;如不存在,请说明理由.xyBACOQP解:(1)抛物线的表达式为239344y x x =-++,对称轴为32x =(2)存在.点D 的坐标为()4,0-,7,08⎛⎫⎪⎝⎭.[提示](2)由题意知△APQ 为等腰三角形,如果△ACD 与△APQ 相似,那么△ACD 也是等腰三角形.①如图1,当AD 为底边时,D ,A 关于y 轴对称,此时点D 的坐标为()4,0-; ②如图2.当AC 为底边时,58DA AC =,所以58DA =,此时点D 的坐标为7,08⎛⎫⎪⎝⎭. xy 图1ODCAxy图2OCDA2.如图,设抛物线22y ax bx =+-与x 轴交于不同的点()1,0A -,(),0B m ,与y 轴交于点C ,已知ACB =90°.(1)求m 的值和抛物线的表达式;(2)已知点()1,D n 在抛物线上,过点A 的直线1y x =+交抛物线与另一点E .若点P 在x 轴上,是否存在这样的点P ,使得以点P ,B ,D 为顶点的三角形与△AEB 相似?xyEACB OD解:2.(1)4m =,抛物线的表达式为213222y x x =--; (2)存在.点P 的坐标为13,07⎛⎫ ⎪⎝⎭或22,05⎛⎫- ⎪⎝⎭【提示】(1)由已知条件可得OA =1,OC =2,易证△AOC ∽△COB ,从而m =OB =4,再将A ,B 两点的坐标代入表达式即可求得.(2) 易求得点()1,3D -,()6,7E ,分别过点D ,E 作x 轴的垂线,垂足分别为H ,G .易证EAG =DBH .所以△PBD 和△AEB 相似存在两种情况:①如图1,当△ABE ∽△BPD 时,有AB BPAE BD=,得点P 的坐标为13,07⎛⎫⎪⎝⎭②如图2,当△ABE ∽△BDP 时,有AB BD AE BP =,得点P 的坐标为22,05⎛⎫- ⎪⎝⎭. xy图1EACBODH GP xy图2EACB ODP3.如图,抛物线223y x x =--与x 轴交于A ,B 两点(点B 在点A 的右侧),与y 轴交于点C ,直线l 经过A ,C 两点,点Q 在抛物线位于y 轴左侧部分上运动,直线m 经过B ,Q 两点,与y 轴交于点N ,与直线l 交于点G .问:是否存在直线m ,使得直线l ,m 与x 轴围成的三角形和直线l ,m 与y 轴围成的三角形相似(不包括全等)?若存在,求出直线m 的表达式,若不存在,请说明理由.xymlG BN CA O Q解.存在,直线m 的表达式为113y x =-.【提示】根据AGB =GNC +GCN .所以当△AGB ∽△NGC 时,只能AGB =CGB =90°,所以△AOC ≌△NOB ,所以直线m 的表达式为113y x =-.。
【配套K12】山东省诸城市桃林镇2017届中考数学压轴题专项汇编 专题21 等腰三角形的存在性

专题21 等腰三角形的存在性破解策略以线段AB 为边的等腰三角形构造方法如图1所示:等腰三角形的另一个顶点在线段AB 的垂直平分线上,或以A ,B 为圆心、AB 长为半径的圆上(不与线段AB 共线).解等腰三角形的存在性问题时,若没有明确指出等腰三角形的底或腰,就需要进行分类讨论.通常这类问题的解题策略有:(1)几何法:先分类讨论,再画出等腰三角形,后计算.如图2,若AB =AC ,过点A 作AD ⊥BC ,垂足为D ,则BD =CD ,∠BAD =∠CAD ,从而利用锐角三角函数、相似三角形等知识解决问题.(2)代数法:先罗列三边长,再分类讨论列方程,然后解方程并检验. 有时候将几何法和代数法相结合,可以使得解题又快又好. 例题讲解例1 如图,正方形ABCD 的边长是16,点E 在AB 边上,AE =3,F 是BC 边上不与B ,C 重合的一个动点,把△EBF 沿EF 折叠,点B 落在B ′处.若△CDB ′恰为等腰三角形,则DB ′= .解 16或①如图1,当CB ′=C D 时,点F 与点C 重合,不符合题意,舍去; ②如图2,当DB ′=CD 时,DB ′=16;③如图3,当DB ′=B ′C 时,过点B 作GH ∥AD ,交AB 于点G ,交CD 于点H . 显然G ,H 分别为AB ,CD 的中点.由题意可得B ′E =13,DH =BG =8,所以EG =5, 从而B ′G12,B ′H =4, 所以DB.图1ABCD 图2A BCDEFB ′DB例2 如图,在△ABC 中,∠ACB =90°,AC =4cm ,BC =3cm .如果点P 由点B 出发沿BA 方向向点A 匀速运动,同时点Q 由点A 出发沿AC 方向向点C 匀速运动,它们的速度均为1cm/s .连图1A BC DEB ′(F )接PQ ,设运动时间为t (s )(0<t <4),∴QH =945t -,PQ =;(1)求直线AC 的解析式; (2)在y 轴上是否存在点P ,直线PD 与矩形对角线AC 交于点M ,使得△DMC 为等腰三角形?若存在,直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.-54),=3 4,且与解:(1)∵抛物线的对称轴为x =-2, ∴m =-4.∵抛物线与x 轴只有一个交点, ∴m 2-4n =0. 从而n =4.(2)原抛物线的表达式为y =-x 2-4x -4=-(x +2)2.所以抛物线C 的表达式为y =x 2-1.(3)假设点D 存在,设点D 的坐标为(d ,d 2-1). 如图,作DH ⊥y 轴于点H ,则DH 2= d 2,BH 2=(d 2-2)2. 若△BPD是等边三角形,则有DH BHd 2=3(d 2-2)2, 解得d =或d =. 所以满足条件的点D 存在,分别为D 12),D 22),D 313), D 413). 例5 如图,在平面直角坐标系中,抛物线y =12x 2-3x -8与x 轴交于A ,B 两点,与y 轴交于点C ,直线l 经过原点O ,与抛物线的一个交点为D ,与抛物线的对称轴交于点E (3,-4),连结CE ,若P 是y 轴负半轴上的一个动点,设其坐标为(0,m ),直线PB 与直线l 交于点Q .试探究:当m 为何值时,△OPQ 是等腰三角形.解由抛物线y=12x2-3x-8=12(x-8)(x+2),可得点A,B,C的坐标分别为(-2,0),(8,0)(0,-8).所以CE5=OE,所以△OEC是顶角为钝角的等腰三角形,即∠OEC>90°,△OPQ曲等腰三角形有三种可能:①当PO=PQ时,即∠OPQ为顶角,显然∠POQ=∠COE,所以∠OPQ=∠OEC>90°,由题意可知这种可能性不存在;②当OP=OQ时,则∠OPQ=∠OQP.如图1,过点E作PQ的平行线,分别交x轴,y轴于点F,G,则∠OGE=∠OPQ=∠OQP=∠OEG,所以OG=OE=5,即点G的坐标为(0,-5),所以直线GE的表达式为y=13x-5,所以点F的坐标为(5,0).而OP OB OG OF=,所以8515m=-,即83m=-;③当QO =QP 时,则∠QPO =∠QOP =∠OCE ,所以CE ∥PQ , 如图2,设直线CE 与x 轴交于点H .由C ,E 两点的坐标可得直线CE 的表达式为,y =43x -8. 所以点H 的坐标为(6,0). OC OHOP OB=, 所以868m =-,即323m =-. 综上可得,当m 的值为83-或323-时,△OPQ 是等腰三角形.进阶训练1.如图,在Rt △ABC 中,∠ACB = 90°,AC =6,BC =8,点D 以每秒1个单位长度的速度由点A 向点B 匀速运动,到达B 点即停止运动,M ,N 分别是AD ,CD 的中点,连结MN ,设点D 运动的时间为t ,若△DMN 是等腰三角形,求t 的值.A BCDM N【答案】t =5,6或365时,△DMN 是等腰三角形. 2.设二次函数y =x 2+2ax +22a (a <0)的图象顶点为A ,与x 轴的交点为B ,C .(1)当△ABC 为等边三角形时,求a 的值, (2)当△ABC 为等腰直角三角形时,求a 的值. 【答案】(1)a;(2)a3.如图,在平面直角坐标系中,点A 的坐标为(-2,0),点B 的坐标为(0,2),E 为线段AB 上的一个动点(不与点A ,B 重合),以E 为顶点作∠OFT =45°,射线ET 交线段OB 于点F ,C 为y 轴正半轴上一点,且OC =A B .抛物线y=x 2+mx +n 经过A ,C 两点.(1)求此抛物线的函数表达式;(2)求证:∠BEF=∠AOE;(3)当△EOF为等腰三角形时,求此时点E的坐标.【答案】(1)y2+(2)略;(3)点E的坐标为(-1,1),,2).【提示】(2)由∠BAO=∠FEO=∠ABO=45°即可证;(3)分类讨论:①当OE=OF时,点E与点A重合,不符合题意;②点EO=EF时(如图1),易证△AFO≌△BFE,从而BE=AC=2,再过点E作EH⊥y轴,即可求得点E,2);③当FE=FD时(如图2),此时△BFE和△OFE均为等腰直角三角形,求得点E(-1,1).4.如图,抛物线y=ax2-6x+c与x轴交于点A(-5,0),B(-1,0),与y轴交于点C,P是抛物线上的一个动点,连结PA,过点P作y轴的平行线交直线AC于点D,请问:△APD 能否为等腰三角形?若能,求出此时点P的坐标;若不能,请说明理由.【答案】△APD能为等腰三角形,点P的坐标为(-2,3),(-1,0),7),,--7).【提示】由点A,B的坐标可得抛物线的表达式为y=ax2-6x-5.从而得到C(0,-5).所以直线AC:y=-x-5.可设点P(m,-m2-6m-5),则D(m,-m-5).△APD为等腰三角形有三种情况,由∠ADP=45°或135°.用代几结合解决问题.①当AP =AD 时,∠FAD =90°,得P (一2,3); ②当AP =PD 时,∠APD =90°,得P (1,0); ③当AD =PD时,可列方程255m m +=+,从而m=P,-7)7).5.如图,抛物线y =ax 2+2x -3与x 轴交于A ,B 两点,且点B 的坐标为(1,0).直线y =23x -49分别与x 轴,y 轴交于C ,F 两点.Q 是直线CF 下方的抛物线上的一个动点,过点Q 作y 轴的平行线,交直线CF 干点D .点E 在线段CD 的延长线上,连结QE ,问:以QD 为腰的等腰△QDE 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.【答案】存在,以QD 为腰的等腰△QDE 的面积最大值为5413【提示】有题意可得抛物线的解析式为y =x 2+2x -3,点C (23,0),F (0,-49),从而tan ∠EDQ =tan ∠OFC =32,如图,作QG ⊥CE 于点G ,设DQ =t ,则QGt ,DG t ,若DQ =DE ,则DE =2DG ,从而△QDE 的面积为S =12DE ·QG =613t 2显然613t 2t2所以当DQ =EQ 时,S 取最大值.设点Q (x ,x 2+2x -3),则t =QD =-x 2-43x +239,可得t =3时,S max =5413。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题25 全等三角形的存在性
破解策略
全等三角形的存在性问题的解题策略有:
(1)当有一个三角形固定时(三角形中所有边角为定值),另一个三角形会与这个固
定的三角形有一个元素相等;再根据全等三角形的判定,利用三角函数的知识(画图)或列方程来求解.
(2)当两个三角形都不固定时(三角形中有角或边为变量),若条件中有一条边对应
相等时,就要使夹这条边的两个角对应相等,或其余两条边对应相等;若条件中有一个角对应相等时,就要使夹这个角的两边对应相等,或再找一个角和一条边对应相等.
例题讲解
例1 如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(-2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.
(1)求抛物线的表达式;
(2)若点D在x轴上,在抛物线上是否存在点P,使得△PBD≌△PBC?若存在,求点P 的坐标;若不存在,请说明理由.
(3)若点M在y轴的正半轴上,连结MA,过点M作MA的垂线,交抛物线的对称轴于点N.问:是否存在点M,使以点M、A、N为顶点的三角形与△BAN全等?若存在,求出点M 的坐标;若不存在,请说明理由.
解:(1)由题意可列方程组
4240
3
2
a b
b
a
-+=
⎧
⎪
⎨
-=
⎪⎩
,解得
1
4
3
2
a
b
⎧
=-
⎪⎪
⎨
⎪=
⎪⎩
,
所以抛物线的表达式为213
442
y x x =-++.
(2)显然OA =2, OB =3, OC =4.
所以5BC BA =. 若△P BD ≌△PBC ,则BD = BC =5,PD =PC
所以D 为抛物线与x 轴的左交点或右交点,点B ,P 在CD 的垂直平分线上, ①若点D 为抛物线与 x 轴的左交点,即与点A 重合.
如图1,取AC 的中点E ,作直线BE 交抛物线于P 1(x 1,y 1),P 2(x 2.y 2)两点. 此时△P 1BC ≌△P 1BD ,△P 2BC ≌△P 2 B D .
由A 、C 两点的坐标可得点E 的坐标为(-1,2). 所以直线BE 的表达式为1322
y x =-+.
联立方程组2132213442y x y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩
,解得114x y ⎧=⎪⎨=⎪⎩
224x y ⎧=+⎪⎨=
⎪⎩ . 所以点P 1,P 2的坐标分别为(4
).(4
.
②若D 为抛物线与x 轴的右交点,则点D 的坐标为(8,0).
如图2,取CD 的中点F .作直线BF 交抛物线于P 3(x 3,y 3),P 4(x 4,,y 4)两点. 此时△P 3BC ≌△P 3BD ,△P 4BC ≌△P 4 B D .
由C 、D 两点的坐标可得点F 的坐标为(4,2), 所以直线BF 的表达式为y =2x -6.
联立方程组22613
442y x y x x =-⎧⎪
⎨=-++⎪⎩
,解得3318x y ⎧=-+⎪⎨=-+⎪⎩
,4418x y ⎧=-⎪⎨=--⎪⎩所以点P 3,P 4的坐标分别为(-1
,-8+
),( -1
,-8-
), 综上可得,满足题意的点P 的坐标为(4
),(4
,
(-1
,-8+
)或(-1
,-8-
).
(3)由题意可设点M (0,m ),N (3,n ),且m >0,
则AM 2=4+m 2,MN 2=9+(m -n )2,BN 2=n 2. 而∠AMN =∠ABN =900
, 所以△AMN 与△ABN 全等有两种可能: ①当AM =AB ,MN =BN 时,
可列方程组222
4259()m m n n
⎧+=⎪
⎨+-=⎪⎩
,解得11m n ⎧=⎪⎨=⎪⎩
22m n ⎧=⎪⎨=⎪⎩
(舍), 所以此时点M 的坐标为(0
).
②当AM =NB ,MN =BA 时,可列方程组:222
49()25
m n
m n ⎧+=⎪⎨+-=⎪⎩·
解得11
325
2m n ⎧=⎪⎪⎨⎪=-⎪⎩
,223252m n ⎧=-⎪⎪⎨
⎪=⎪⎩(舍) 所以此时点M 的坐标为(0,
3
2
). 综上可得,满足题意的点M 的坐标为(0
)或(0,
32
). 例2 如图,在平面直角坐标系xoy 中,△ABO 为等腰直角三角形,∠ABO = 900
,点A 的坐标为(4.0),点B 在第一象限.若点D 在线段BO 上,OD = 2DB ,点E ,F 在△OAB 的边上,且满足△DOF 与△DEF 全等,求点E 的坐标.
图1 图2 解: 由题意可得OA =4,从而OB =AB
=.所以OD =23OB
,BD =13
OB
=.
①当点F 在OA 上时,
(ⅰ)若△DFO ≌△DFE ,点E 在OA 上.如图1.
此时DF ⊥OA ,所以OF
=43,所以OE =2OF =83,即点E 的坐标为(8
3
,0). (ⅱ)若△DFO ≌△DFE ,点F 在AB 上,如图2.
此时ED =OD =2BD ,所以sin ∠BED =BD ED =12
;所以∠BED =300
, 从而BE
AE
过点E 作EG ⊥OA 于点G .则EG =AG
=2, 所以OG
=2,即点E
的坐标为(2
,2).
图3 图4
(ⅲ)若△DFO ≌△FDE ,点E 在AB 上,如图3.
此时DE ∥OA ,所以BD =BE . 从而AE =OD
, 过点E 作EG ⊥OA 于点G , 则EG =AG
=43
, 所以OG =83,即点E 的坐标为(83
,4
3).
②当点F 在AB 上时,只能有△ODF ≌△AFD ,如图4. 此时DF ∥0A .且点E 与点A 重合, 即点E 的坐标为(4,0). 综上可得,端足条件的点E 的坐标为(8
3
,0),
(2+
,2),(83
,4
3)或(4,0).
迸阶训练
1.如图,在平面直角坐标系xOy 中,已知抛物线2
1382
y x x =--与y 轴变于点C . 直线l ;4
3
y x =-
与抛物线的对称轴交于点E .连结CE ,探究;抛物线上是否存在一点F , 使得△FOE ≌△FCE ..若存在,请写出点F 坐标;若不存在,请说明理由.
答案:
存在.点F
的坐标为(3-
,-4
)或(34)
2. 如图,在平面直角坐标系xOy 中,直线l 1过点A (1,0)且与y 轴平行.直线l 2
过点B (0,2)且与x 轴平行,直线l 1与l 2相交于点P .E 为直线l 2上一点,反比例函数k
y x
=(k >0)的图象过点E 且与直线l 1相交干点F .
(1)若点E与点P重合,求k的值;
(2)是否存在点E及y轴上的点M,使得以点M,E,F为顶点的三角形与△PEF全等?若存在,求点E的坐标:若不存在,请说明理由.
备用图
答案:
(1)k=2
(2)存在.点E的坐标为(
3
8
,2)或(
8
3
,2)
【提示】(2)易得点E(
3
k
,2),F(1,k).①如图1,当k<2时,只能有△MEF≌△PEF.过点F作FH⊥y轴于点H,易证△BME∽△HFM,用k表示相关线段的长度,从而得到BM=
1
2
,再解Rt△BME,得k=
3
4
,所以点E的坐标为(
3
8
,2);②如图2,当k>2时,只能有△MEF≌△PFE.过点F作FQ⊥y轴于点Q,同①可得点E的坐标为(
8
3
,2)
图1
图2
3.如图,抛物线2
y ax bx c
=++经过A
(-,0),B
(0),C(0,3)三点,线段BC与抛物线的对称轴交干D,该抛物线的顶点为P,连结PA,A D.线段AD与y轴相交于点E.
(1)求该抛物线的表达式;
(2)在平面直角坐标系中是否存在一点Q .使以Q ,C ,D 为顶点的三角形与△ADP 全等?若存在,求出点Q 的坐标;若不存在,请说明理由.
答案:
(1
)抛物线的表达式为2133y x x =-
+ (2)存在.点Q
的坐标为(4),
2),
(-1)或(0,7).
【提示】(2)方法一:易求直线BC
:3y x =-
+,从而点D
2),可得CD =PD ,所以△QCD 与△ADP 全等有两种情况.设点Q 坐标,通过两点间距离公式列出QC ,QD ,AP ,AD 的长.再分类讨论列方程组,从而求得点Q 点坐标.
方法二:连接CP ,易证△CDP 为等边三角形,∠ADC =60°,所以∠PDA =120°.
△QCD 与△ADP 全等有两种情况,①如图1,∠DCQ =120°,CQ =DA =4,此时点Q 1的坐标为
(0,7),点Q 2
的坐标为(-1);
②如图2,∠CDQ =120°,DQ =DA =4,此时点Q 3的坐标为
-2),点Q 4的坐标为
(4)。
