线段的垂直平分线的性质—展示课件
合集下载
线段垂直平分线的性质课件

线段垂直平分线的性质课件
目录
• 线段垂直平分线的定义 • 线段垂直平分线的性质 • 线段垂直平分线的应用 • 线段垂直平分线的证明
01
线段垂直平分线的定义
定义
垂直平分 线
过线段中点且垂直于线段所在直线的 直线。
线段垂直平分线定理
线段垂直平分线上的任意一点到线段 两端点的距离相等。
垂直平分 设线段AB的中点为M,线段AB的垂直平分线与线段AB的交点为N。
2. 过M作直线ME⊥AB交AB于E点。
证明性质三
01
02
03
04
3. 在直角三角形AEN和BMN 中,由于∠AEN=∠BMN=90°
和MN是垂直平分线,所以 ∠AMN=∠BME。
4. 由于AM=BM,根据ASA 全等条件,得到 △AEN≌△BMN。
01
02
03
确定线段的中点
使用测量工具或计算中点 坐标的方法确定线段的中 点。
画垂直线
在确定的中点处,作垂直 于线段所在直线的垂线。
连接端点
使用测量工具或计算坐标 的方法,连接线段的两个 端点到垂足。
垂直平分线的性质
距离性质
角平分线性质
垂直性质
垂直平分线上的任意一 点到线段两端点的距离
相等。
垂直平分线将角平分, 即角平分线上的任意一 点到角的两边距离相等。
垂直平分线是垂直于线 段所在直线的直线。
轴对称性质
垂直平分线是轴对称图 形,关于垂直平分线对 称的两点连线与垂直平
分线垂直。
02
线段垂直平分线的性质
性质一
总结词
线段垂直平分线上的任意一点到线段两端点的距离相等。
详细描述
这是线段垂直平分线最基本和重要的性质。如果一个点位于 线段的垂直平分线上,那么这个点到线段两个端点的距离必 定相等。这一性质在几何学中有着广泛的应用,例如在解决 与中点、距离和对称性相关的问题时。
目录
• 线段垂直平分线的定义 • 线段垂直平分线的性质 • 线段垂直平分线的应用 • 线段垂直平分线的证明
01
线段垂直平分线的定义
定义
垂直平分 线
过线段中点且垂直于线段所在直线的 直线。
线段垂直平分线定理
线段垂直平分线上的任意一点到线段 两端点的距离相等。
垂直平分 设线段AB的中点为M,线段AB的垂直平分线与线段AB的交点为N。
2. 过M作直线ME⊥AB交AB于E点。
证明性质三
01
02
03
04
3. 在直角三角形AEN和BMN 中,由于∠AEN=∠BMN=90°
和MN是垂直平分线,所以 ∠AMN=∠BME。
4. 由于AM=BM,根据ASA 全等条件,得到 △AEN≌△BMN。
01
02
03
确定线段的中点
使用测量工具或计算中点 坐标的方法确定线段的中 点。
画垂直线
在确定的中点处,作垂直 于线段所在直线的垂线。
连接端点
使用测量工具或计算坐标 的方法,连接线段的两个 端点到垂足。
垂直平分线的性质
距离性质
角平分线性质
垂直性质
垂直平分线上的任意一 点到线段两端点的距离
相等。
垂直平分线将角平分, 即角平分线上的任意一 点到角的两边距离相等。
垂直平分线是垂直于线 段所在直线的直线。
轴对称性质
垂直平分线是轴对称图 形,关于垂直平分线对 称的两点连线与垂直平
分线垂直。
02
线段垂直平分线的性质
性质一
总结词
线段垂直平分线上的任意一点到线段两端点的距离相等。
详细描述
这是线段垂直平分线最基本和重要的性质。如果一个点位于 线段的垂直平分线上,那么这个点到线段两个端点的距离必 定相等。这一性质在几何学中有着广泛的应用,例如在解决 与中点、距离和对称性相关的问题时。
线段的垂直平分线的性质课件共17张PPT

A
P
O
B
课堂小结
(1)本节课学习了哪些内容? (2)线段垂直平分线的性质和判定是如何得到的?
两者之间有什么关系? (3)如何判断一条直线是否是线段的垂直平分线?
P
∴ 点P 在AB 的垂直平分线上.
与一条线段两个端点距离相
等的点,在这条线段的垂直平分
线上.
A C
B
探索并证明线段垂直平分线的判定
你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点?
这些点能组成什么几何图形?
P
在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
l
P 用符号语言表示为:
∵ CA =CB,l⊥AB,
∴ PA =PB.
A
C
B
探索并证明线段垂直平分线的性质
线段垂直平分线的性质: 线段垂直平分线上的点与这条线段两个端点的距离
相等.
课堂练习
线段垂直平分线上的点与这条 线段两个端点的距离相等.
A
P3 P2
P1 B
l
探索并证明线段垂直平分线的性质
证明:“线段垂直平分线上的点到线段两端点的距
离相等.”
已知:如图,直线l⊥AB,垂足为C,AC =CB,点
P 在l 上.
求证:PA =PB.
l
P
A
C
B
探索并证明线段垂直平分线的性质
证明:∵ l⊥AB,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、 A
P
O
B
课堂小结
(1)本节课学习了哪些内容? (2)线段垂直平分线的性质和判定是如何得到的?
两者之间有什么关系? (3)如何判断一条直线是否是线段的垂直平分线?
P
∴ 点P 在AB 的垂直平分线上.
与一条线段两个端点距离相
等的点,在这条线段的垂直平分
线上.
A C
B
探索并证明线段垂直平分线的判定
你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点?
这些点能组成什么几何图形?
P
在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
l
P 用符号语言表示为:
∵ CA =CB,l⊥AB,
∴ PA =PB.
A
C
B
探索并证明线段垂直平分线的性质
线段垂直平分线的性质: 线段垂直平分线上的点与这条线段两个端点的距离
相等.
课堂练习
线段垂直平分线上的点与这条 线段两个端点的距离相等.
A
P3 P2
P1 B
l
探索并证明线段垂直平分线的性质
证明:“线段垂直平分线上的点到线段两端点的距
离相等.”
已知:如图,直线l⊥AB,垂足为C,AC =CB,点
P 在l 上.
求证:PA =PB.
l
P
A
C
B
探索并证明线段垂直平分线的性质
证明:∵ l⊥AB,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、 A
13.1.2线段的垂直平分线的性质课件ppt17197
y
B (-4, 2)
·
5 4 3 2
1 1 2
· C’(-3, -4)
-4 -3 -2 -1 0 -1 -2 -3 -4
思考: 关于y轴 B’ (4, 2) 对称的 点的坐 标具有 x 3 4 5 怎样的 关系?
·
· C(3, -4)
归纳:关于y轴对称的点的坐标的特 点是:
练习:
横坐标互为相反数,纵坐标相等. (简称:纵轴纵相等)
过这个点分别做x轴和y轴的垂线段,垂足分别ห้องสมุดไป่ตู้ 是这个点的横坐标和纵坐标,记做(x,y)。 4、怎样做一个点关于一条直线的对称点?
探究1: 请同学们在直角坐标系中标出下列各点 并画出下列各点关于x轴对称的对称点. A (2,3) B (-4, 2) C(3, - 4)
思考:关于x轴对称的点的坐标具有 怎样的关系?
A
2 3 4 5
B
-4
-3
-2
-1
x
轴对称关系(关于y轴对称)
活动二:
2、已知右边圆脸中眼睛A的坐标 (4,3)嘴角 ) 为( C的 (2,3)B的坐标为( 坐标为( ( 4,1)D的坐标为( (2,1)。 )
5
y
你能根据 轴对称的 性质写出 左边圆脸 的眼睛和 嘴角的坐 标吗?
· · C D · ·
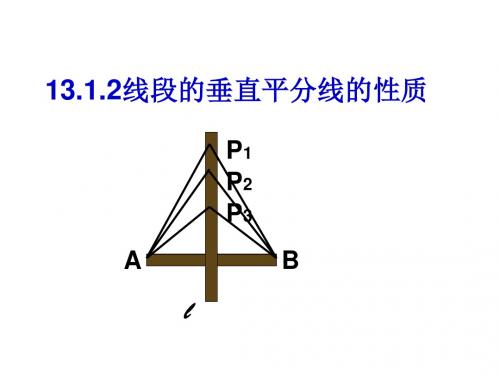
13.1.2线段的垂直平分线的性质
P1 P2 P3 A B
l
线段垂直平分线:
经过线段的中点并且垂直于这条 线段的直线,叫做这条线段的垂 直平分线。
∵直线l是线段AB的垂直平分线
A
o
B
∴AO=BO l⊥AB
l
探索并证明线段垂直平分线的性质
如图,直线l 垂直平分线段AB,P1,P2,P3,…是 l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距 离之间的数量关系. P3 相等. P2 性质1:线段垂直平分线上的点与这条 P1 线段两个端点的距离相等. A B l
B (-4, 2)
·
5 4 3 2
1 1 2
· C’(-3, -4)
-4 -3 -2 -1 0 -1 -2 -3 -4
思考: 关于y轴 B’ (4, 2) 对称的 点的坐 标具有 x 3 4 5 怎样的 关系?
·
· C(3, -4)
归纳:关于y轴对称的点的坐标的特 点是:
练习:
横坐标互为相反数,纵坐标相等. (简称:纵轴纵相等)
过这个点分别做x轴和y轴的垂线段,垂足分别ห้องสมุดไป่ตู้ 是这个点的横坐标和纵坐标,记做(x,y)。 4、怎样做一个点关于一条直线的对称点?
探究1: 请同学们在直角坐标系中标出下列各点 并画出下列各点关于x轴对称的对称点. A (2,3) B (-4, 2) C(3, - 4)
思考:关于x轴对称的点的坐标具有 怎样的关系?
A
2 3 4 5
B
-4
-3
-2
-1
x
轴对称关系(关于y轴对称)
活动二:
2、已知右边圆脸中眼睛A的坐标 (4,3)嘴角 ) 为( C的 (2,3)B的坐标为( 坐标为( ( 4,1)D的坐标为( (2,1)。 )
5
y
你能根据 轴对称的 性质写出 左边圆脸 的眼睛和 嘴角的坐 标吗?
· · C D · ·
13.1.2线段的垂直平分线的性质
P1 P2 P3 A B
l
线段垂直平分线:
经过线段的中点并且垂直于这条 线段的直线,叫做这条线段的垂 直平分线。
∵直线l是线段AB的垂直平分线
A
o
B
∴AO=BO l⊥AB
l
探索并证明线段垂直平分线的性质
如图,直线l 垂直平分线段AB,P1,P2,P3,…是 l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距 离之间的数量关系. P3 相等. P2 性质1:线段垂直平分线上的点与这条 P1 线段两个端点的距离相等. A B l
线段的垂直平分线的性质时(共8张PPT)

AB1的长为半径作弧,两弧相交于C、
2
D两点;
折叠、用刻度尺等
A
B ⑵作直线还C可D 以. 折叠、
CD即为用所刻求度的直尺线等.
D
你还有其他的方法作一条线段的垂直平分线吗?
第3页,共8页。
Байду номын сангаас
三、解决问题
练习:见教材第63页例2.
例2 如图,△ABC和△AˊBˊCˊ是两个成轴对称的图形
,请作出它的对称轴.
线段的垂直平分线的性质时
第1页,共8页。
一、提出问题
1.如果我们感觉两个平面图形是成轴对称的,
你准备用什么方法去验证?
2.两个成轴对称的图形,不经过折叠,
你用什么方法作出它的对称轴?
第2页,共8页。
二、学习新知
例1 如图,已知线段AB,用直尺和圆规作 AB 的垂直平分线.
C
⑴分别以点A、B为圆心,以大于
A
B
C 第7页,共8页。
D
五、课堂小结
本节课你学到了什么? 1.线段垂直平分线的作法.
2.作成轴对称的图形的对称轴的几种常见方法:
(1)将图形对折;
(2)用尺规作图; (3)用刻度尺先取一对对称点连线的中点,
然后作垂线.
3.有许多图形的对称轴不止一条.
第8页,共8页。
第5页,共8页。
四、实践和应用
1.作出下列图形的一条对称轴,和同学比较 一下,你们作的对称轴一样吗?
无数条
第6页,共8页。
2.如图,角是轴对称图形吗?如果是,
画出它的对称轴.
如图,角是轴对称图形吗?如果是, 你还有其他的方法作一条线段的垂直平分线吗? 作出下列图形的一条对称轴,和同学比较一下,你们作的对称轴一样吗? 1.线段垂直平分线的作法. 如图,角是轴对称图形吗?如果是, 如图,角是轴对称图形吗?如果是, 如果是一个轴对称图形,你怎样作出它的 如果是一个轴对称图形,你怎样作出它的
16.2 线段的垂直平分线(课件)冀教版数学八年级上册

解
读 点 P 在
径画弧,交 l 于 A,B 两点;
直线 l
②作线段 AB 的垂直平分线 CD,
上
CD 即为直线 l 的垂线
图示
返回目录
第二课时 线段垂直平分线的判定和画法
考
点
清
单
解
读
返回目录
续表
①以点 P 为圆心,适当长为半径
点 P
画弧,交 l 于 A,B 两点;②分
在直
别以点 A,B 为圆心,适当长为
16.2 线段的垂直平分线
第一课时 线段垂直平分线的性质
● 考点清单解读
● 重难题型突破
● 易错易混分析
第一课时 线段垂直平分线的性质
■考点
返回目录
线段垂直平分线的性质定理
考
点
内容
清
单
线段垂直平分线上的点到线段两端的距
解
读 性质
离相等条件:点在线段的垂直平分线上
定理
结论:这个点到线段两端的距离相等
考
点
清
单
解
读
[解题思路]
[答案]9
返回目录
第一课时 线段垂直平分线的性质
返回目录
重 ■题型 线段垂直平分线的性质定理的应用
难
例
如图,在△ABC 中,∠A=60°,∠B=45°.若边
题
型 AC 的垂直平分线 DE 交边 AB 于点 D,交边 AC 于点 E,
突
破 连接 CD,则∠DCB 的度数为 (
返回目录
解题通法
涉及尺规作图的题目,首先要根据作图方
重
难
题 法或作图痕迹判断出所作图形,再结合题目所给条件解决
型 问题.
读 点 P 在
径画弧,交 l 于 A,B 两点;
直线 l
②作线段 AB 的垂直平分线 CD,
上
CD 即为直线 l 的垂线
图示
返回目录
第二课时 线段垂直平分线的判定和画法
考
点
清
单
解
读
返回目录
续表
①以点 P 为圆心,适当长为半径
点 P
画弧,交 l 于 A,B 两点;②分
在直
别以点 A,B 为圆心,适当长为
16.2 线段的垂直平分线
第一课时 线段垂直平分线的性质
● 考点清单解读
● 重难题型突破
● 易错易混分析
第一课时 线段垂直平分线的性质
■考点
返回目录
线段垂直平分线的性质定理
考
点
内容
清
单
线段垂直平分线上的点到线段两端的距
解
读 性质
离相等条件:点在线段的垂直平分线上
定理
结论:这个点到线段两端的距离相等
考
点
清
单
解
读
[解题思路]
[答案]9
返回目录
第一课时 线段垂直平分线的性质
返回目录
重 ■题型 线段垂直平分线的性质定理的应用
难
例
如图,在△ABC 中,∠A=60°,∠B=45°.若边
题
型 AC 的垂直平分线 DE 交边 AB 于点 D,交边 AC 于点 E,
突
破 连接 CD,则∠DCB 的度数为 (
返回目录
解题通法
涉及尺规作图的题目,首先要根据作图方
重
难
题 法或作图痕迹判断出所作图形,再结合题目所给条件解决
型 问题.
线段的垂直平分线的性质PPT课件

A
• 如图所示,在△ABC中,
AB=AC=32,MN是AB
的垂直平分线,且有
M
BC=21,求△BCN的周长。
N
B
C
第20页/共26页
如图,七(1)班与七(2)班两个班的学生 分别在M、N两处参加植树劳动,现要在道路AB、AC 的交叉区域内设一个茶水供应点P,使P到两条道路的 距离相等,且PM=PN,请你用折纸的方法找出P点并 说明理由。
P
∴ ∠PCA =∠PCB=900. 又 AC =CB,PC =PC, ∴ △PCA ≌△PCB(SAS) ∴ PA =PB.
线段垂直平分线的性质:
线段垂直平分线上的点与这条
线段两个端点的距离相等.
A
C
B
用几何语言表示为: ∵ CA =CB,l⊥AB, ∴ PA =PB.
第3页/共26页
课堂练习
练习1 如图,在△ABC 中,BC =8,AB 的中垂线 交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等 于__8____.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上
M
∴ 直线AM 是线段BC 的垂直
平分线.
B
D
C
第9页/共26页
尺规作图
经过已知直线外一点作这条直线的垂线。
已知:直线AB和AB外一点C 使它经过点C.
做法:
(1)任意取一点K ,使点K与点
C 在直线AB两旁.
(2)以点C为圆心,CK为半径作弧 ,交AB于点D和点E.
B
第7页/共26页
课堂练习P62
2 如图,AD⊥BC,BD =DC,点C 在AE 的垂直平
分 线 上 , AB , AC , CE 的 长 度 有 什 么 关 系 ?
• 如图所示,在△ABC中,
AB=AC=32,MN是AB
的垂直平分线,且有
M
BC=21,求△BCN的周长。
N
B
C
第20页/共26页
如图,七(1)班与七(2)班两个班的学生 分别在M、N两处参加植树劳动,现要在道路AB、AC 的交叉区域内设一个茶水供应点P,使P到两条道路的 距离相等,且PM=PN,请你用折纸的方法找出P点并 说明理由。
P
∴ ∠PCA =∠PCB=900. 又 AC =CB,PC =PC, ∴ △PCA ≌△PCB(SAS) ∴ PA =PB.
线段垂直平分线的性质:
线段垂直平分线上的点与这条
线段两个端点的距离相等.
A
C
B
用几何语言表示为: ∵ CA =CB,l⊥AB, ∴ PA =PB.
第3页/共26页
课堂练习
练习1 如图,在△ABC 中,BC =8,AB 的中垂线 交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等 于__8____.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上
M
∴ 直线AM 是线段BC 的垂直
平分线.
B
D
C
第9页/共26页
尺规作图
经过已知直线外一点作这条直线的垂线。
已知:直线AB和AB外一点C 使它经过点C.
做法:
(1)任意取一点K ,使点K与点
C 在直线AB两旁.
(2)以点C为圆心,CK为半径作弧 ,交AB于点D和点E.
B
第7页/共26页
课堂练习P62
2 如图,AD⊥BC,BD =DC,点C 在AE 的垂直平
分 线 上 , AB , AC , CE 的 长 度 有 什 么 关 系 ?
第2课时 线段的垂直平分线的性质(一)ppt课件

三边垂直平分线的交点 B. 三条角平分线的交点 C. 三条高的交点 D. 三边中线的交点
5. 在联欢晚会上,有A,B,C三名同窗站在一个三角形的 三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放 一个木凳,谁先抢到凳子谁获胜,为使游戏公平,那么凳子
应放的最适当的位置在△ABCD的( )
A. 三边中线的交点 B. 三条角平分线的交点 C. 三边上高的交点 D. 三边中垂线的交点
8. 如图13-1-25,有A,B,C三个居民小区,其位置成三 角形,现决议在三个小区之间建筑一个休闲广场,使广场到 三个小区的间隔相等,那么广场应建在 _三__边__垂_直__平__分__线__的_交__点__处____.
分层练习·B组
9. 知:如图13-1-26,直线AB与直线BC相交于点B,点D是 直线BC上一点. 求作一点E,使直线DE∥AB,且点E到B,D 两点的间隔相等.
解:如答图13-1-4. 作法如下. ①作BD的垂直平分线MN; ②经点D作DE∥AB,交MN于点E. ∴点E即为所求.
10. 如图13-1-27,AO,OB是相互垂直的墙壁,墙角O处是 一鼠洞,一只猫在A处发现了B处的一只老鼠正向洞口逃窜, 假设猫以与老鼠同样的速度去追捕老鼠,请在图中作出最快 能截住老鼠的位置C.
①AO=BO;②PO⊥AB; ③∠APO=∠BPO;④点P在线段AB的垂直平分线上.
A. 1个
B. 2个
C. 3个
D. 4个
典型例题
新知2:线段的垂直平分线的画法以及运用 【例3】某公园有海盗船、摩天轮、碰碰车三个文娱工程, 现要在公园内建一个售票中心,使得三个文娱工程所处位置 到售票中心的间隔相等,请在图13-1-19中确定售票中心的 位置.
的度数是( )
5. 在联欢晚会上,有A,B,C三名同窗站在一个三角形的 三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放 一个木凳,谁先抢到凳子谁获胜,为使游戏公平,那么凳子
应放的最适当的位置在△ABCD的( )
A. 三边中线的交点 B. 三条角平分线的交点 C. 三边上高的交点 D. 三边中垂线的交点
8. 如图13-1-25,有A,B,C三个居民小区,其位置成三 角形,现决议在三个小区之间建筑一个休闲广场,使广场到 三个小区的间隔相等,那么广场应建在 _三__边__垂_直__平__分__线__的_交__点__处____.
分层练习·B组
9. 知:如图13-1-26,直线AB与直线BC相交于点B,点D是 直线BC上一点. 求作一点E,使直线DE∥AB,且点E到B,D 两点的间隔相等.
解:如答图13-1-4. 作法如下. ①作BD的垂直平分线MN; ②经点D作DE∥AB,交MN于点E. ∴点E即为所求.
10. 如图13-1-27,AO,OB是相互垂直的墙壁,墙角O处是 一鼠洞,一只猫在A处发现了B处的一只老鼠正向洞口逃窜, 假设猫以与老鼠同样的速度去追捕老鼠,请在图中作出最快 能截住老鼠的位置C.
①AO=BO;②PO⊥AB; ③∠APO=∠BPO;④点P在线段AB的垂直平分线上.
A. 1个
B. 2个
C. 3个
D. 4个
典型例题
新知2:线段的垂直平分线的画法以及运用 【例3】某公园有海盗船、摩天轮、碰碰车三个文娱工程, 现要在公园内建一个售票中心,使得三个文娱工程所处位置 到售票中心的间隔相等,请在图13-1-19中确定售票中心的 位置.
的度数是( )
13.1.2.1 线段的垂直平分线的性质 课件(共22张PPT)人教版数学八年级上册

例5:如图,在Rt△ABC中,∠ACB=90°,D是AB上一点, BD=BC,过点D作AB的垂线交AC于点E,连接BE.求证: BE垂直平分CD.
证明:∵∠ACB=90°,DE⊥AB, ∴∠EDB=∠ACB=90°.∵BD=BC,BE=BE, ∴Rt△BED≌Rt△BEC,点B在CD的垂直平分线上, ∴DE=CE,∴点E在CD的垂直平分线上, ∴BE垂直平分CD.
13.1 轴对称
13.1.2线段的垂直平分线的性质
13.1.2.1 线段的垂直平分线的性质
学习目标
1.通过学生自主探究,理解并掌握线段垂直平分线的性质和判定,会用 线段的垂直平分线的性质和判定解决简单的数学问题,培养学生解决问 题的能力.
2.学生经历动手实践、合作交流、演绎推理的过程,培养学生的动手操 作能力和逻辑推理能力.
4.如果将已知、求证换一下位置,还能成立吗?试着探究一下.
如图,已知 PA=PB,
求证:点 P 在 AB 的垂直平分线上.
证明:如图,过点 P 作 AB 的垂线 l 交 AB 于点 C,
在
R
t△PAC
和
Rt△PB
C
中,
PA=PB, CP=CP,
∴R t △PAC≌R t △PB C(H L ).
∴AC=BC.∴直线 l 垂直平分 AB,
∴点 P 在 AB 的垂直平分线上.
小组讨论
1.如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平 分线ON交于点O,分别交BC于点D,E,△ADE的周长为5 cm. (1)求BC的长;(2)求证:点O在线段BC的垂直平分线上.
(1)解:∵OM,ON分别是线段AB,AC的垂直平分线, ∴AD=BD,AE=CE.∵△ADE的周长=AD+AE+DE=5 cm, ∴BC=BD+DE+EC=5 cm.
线段的垂直平分线的性质课件ppt

平移等距性
在平移变换中,垂直平分线上的 点到线段两个端点的距离相等, 且等于平移的距离。
旋转变换中应用
旋转不变性
垂直平分线在旋转变换下保持不变, 即旋转后的图形仍然保持垂直平分线 的性质。
旋转等角性
以垂直平分线上一点为旋转中心,旋 转任意角度后,所得图形与原图形关 于该点对称。
对称变换中应用
对称中心
思路拓展与延伸
拓展1
探究线段垂直平分线与三角形的关系。例如,已知三角形ABC 中,D是AB的中点,DE垂直于AC于点E,求证:DE是AB的垂 直平分线。
拓展2
将线段垂直平分线的性质应用于实际问题中。例如,在建筑 设计或工程测量中,如何利用线段的垂直平分线性质来确定 某点的位置或某线段的长度。
易错点提示与防范策略
THANKS
感谢观看
线段的垂直平分线是对称中心,即关于垂直平分线的对称点连线的中点就是垂 直平分线与线段的交点。
对称轴
线段的垂直平分线也是对称轴,即关于垂直平分线对称的两个图形是全等的。
05
典型例题解析与思路拓展
典型例题解析
例题1
已知线段AB和点C,D分别是AB,BC的中点,求证:CD是AB的垂直平分线。
解析
根据中点的定义,可知AC=CB,BD=DA。因为CD是AB的中线,所以CD垂直于AB。 又因为AC=CB,所以角ACD=角BCD,从而角ADC=角BDC。根据角平分线的性质, 可知CD平分角ADB,所以CD是AB的垂直平分线。
性质1
垂直平分线上的任意一点 到线段两端的距离相等。
性质2
线段的垂直平分线是其对 称轴,即线段关于垂直平 分线对称。
判定方法
判定定理
一条直线是某线段的垂直 平分线当且仅当该直线过 线段的中点且与该线段垂 直。
在平移变换中,垂直平分线上的 点到线段两个端点的距离相等, 且等于平移的距离。
旋转变换中应用
旋转不变性
垂直平分线在旋转变换下保持不变, 即旋转后的图形仍然保持垂直平分线 的性质。
旋转等角性
以垂直平分线上一点为旋转中心,旋 转任意角度后,所得图形与原图形关 于该点对称。
对称变换中应用
对称中心
思路拓展与延伸
拓展1
探究线段垂直平分线与三角形的关系。例如,已知三角形ABC 中,D是AB的中点,DE垂直于AC于点E,求证:DE是AB的垂 直平分线。
拓展2
将线段垂直平分线的性质应用于实际问题中。例如,在建筑 设计或工程测量中,如何利用线段的垂直平分线性质来确定 某点的位置或某线段的长度。
易错点提示与防范策略
THANKS
感谢观看
线段的垂直平分线是对称中心,即关于垂直平分线的对称点连线的中点就是垂 直平分线与线段的交点。
对称轴
线段的垂直平分线也是对称轴,即关于垂直平分线对称的两个图形是全等的。
05
典型例题解析与思路拓展
典型例题解析
例题1
已知线段AB和点C,D分别是AB,BC的中点,求证:CD是AB的垂直平分线。
解析
根据中点的定义,可知AC=CB,BD=DA。因为CD是AB的中线,所以CD垂直于AB。 又因为AC=CB,所以角ACD=角BCD,从而角ADC=角BDC。根据角平分线的性质, 可知CD平分角ADB,所以CD是AB的垂直平分线。
性质1
垂直平分线上的任意一点 到线段两端的距离相等。
性质2
线段的垂直平分线是其对 称轴,即线段关于垂直平 分线对称。
判定方法
判定定理
一条直线是某线段的垂直 平分线当且仅当该直线过 线段的中点且与该线段垂 直。
《线段的垂直平分线》PPT课件

练习
1. 如图,在△ABC中,AB的垂直平分线分别交 AB,BC于点D,E,∠B=30°,∠BAC= 80°, 求∠CAE的度数.
答:∠CAE=50°.
2.已知:如图,点C,D是线段AB外的两点,且 AC =BC,AD=BD,AB与CD相交于点O.
求证:AO=BO.
证明: ∵ AC =BC,AD=BD, ∴ 点C和点D在线段AB的垂直平分线上, ∴ CD为线段AB的垂直平分线.
练习
用尺规完成下列作图(只保留作图痕迹,不要 求写出作法).
1. 如图,在直线l上求作一点P,使PA= PB.
已知:如图,在△ABC中,AB,BC的垂直平分线相交于点P,
求证:点P也在AC的垂直平分线上
证明:连接AP,BP,CP.
∵点P在线段AB的垂直平分线上, A
∴PA=PB
同理,PB=PC.
中考 试题
例
如图,在△ABC中,BC=8cm,AB的垂直
平分线交AB于点D,交边AC于点E,△BCE 的周长等于18cm,则AC的长等于( C ).
A.6cm B.8cm C.10cm D.12cm
解析 ∵DE是AB的垂直平分线, ∴AE=BE(线段垂直平分线上的点到线段两端点的距离相等).
又∵在△BCE中,
∴EB=EA ∴△AEC的周长
=AC+CE+EA
C E
=AC+CE+EB
=AC+BC
B
=4+5 =9
D A
做一做
已知:如图,P为∠MON内一点,OM⊥PA 于E,ON⊥PB于F,EA=EP,FB=FP,若AB 长为15cm,求△PCD的周长。
M A
E C
线段的垂直平分线PPT课件

4
14.1 线段的垂直平分线
命题:线段垂直平分线上的点和这条线段两个
端点的距离相等。
M
已知:如图,直线MN⊥AB,垂足为C, 且AC=CB. 点P在MN上.
求证:PA=PB
证明:∵MN⊥AB
∴ ∠ PCA= ∠ PCB=90º
在 ΔPAC和Δ PBC中,
AC=BC
∠ PCA= ∠ PCB
A
PC=PC
结你论能:依据三例角1形得三到边什垂么直结平论分?线交于一点,
这一点到三角形三个顶点的距离相等。
.
10
实际问题1
某区政府为了方便居民的生活,计划在三个住宅 小区A、B、C之间修建一个购物中心,试问,该购物 中心应建于何处,才能使得它到三个小区的距离相等。
A
B
?
.
C
11
14.1 线段的垂直平分线
实际问题
A
B
L
京 津 高速公路
.
3
14.1 线段的垂直平分线
动手操作:作线段AB的中垂线MN,垂足 为C;在MN上任取一点P,连结PA、PB;量 一量:PA、PB的长,你能发现什么?
M P
PA=PB
P1A=P1B ……
由此你能得到什么规律?
命题:线段垂直平分线上的点和
这条线段两个端点的距离相等。
A
C
B
.
P1 N
逆定理 到一个角的两边 逆定理 和一条线段两个
的距离相等的点,在这 端点距离相等的点,在这
个角的平分线上。
条线段的垂直平分线上。
.
18
作 业:
1. P123. 1. 2 2、在V型公路(∠AOB) 内部,有两个村庄C、D。 你能选择一个纺织厂的厂 址P,使P到V型公路的距 离相等,且使C、D两村 O 的工人上下班的路程一样 吗?
线段的垂直平分线的性质PPT优秀版

∴ △PCA ≌△PCB(SAS) A
C
B
∴ PA =PB.
探索并证明线段垂直平分线的性质
线段垂直平分线的性质:
线段垂直平分线上的点与这条
l
线段两个端点的距离相等.
P
A
C
B
用几何语言表示为:
∵ CA =CB,l⊥AB 或 ∵点P在线段AB的垂直平分线上
∴ PA =PB.
∴PA =PB.
例题讲解
例1 如图,AD⊥BC,BD =DC,点C 在AE 的垂直平
周长等于50,求△BAC的周长.
A
D E
B
C
例题讲解
变式3 如图,在△ABC中,AB的垂直平分线交
AB于点D,交AC于点E,△BCE的周长等于50,
△BAC的周长等于80,求AD的长.
A
D E
B
C
探索并证明线段垂直平分线的判定
反过来,如果PA =PB,那么点P 是否在线段AB 的 垂直平分线上呢?
能找到多少个到线段AB 两端点距离相等的点? ∴ △PCA ≌△PCB(SAS) ∴ PA =PB. ∴ △PCA ≌△PCB(SAS) 练习1 因为AD为BC的中垂线,所以 。
A
D E
B
C
例题讲解
变式2 如图,在△ABC中,AB的垂直平分线交
AB于点D,交AC于点E,已知AD=15, △BCE的
点P 在线段AB 的垂直平分线上.
已知:如图,PA =PB. 求证:点P 在线段AB 的垂直平 分线上.
探索并证明线段垂直平分线的判定
已知:如图,PA =PB.求证:点P 在线段AB 的垂直平分线上.
证明:如图,作PC⊥AB 则∠PCA =∠PCB =90°. 在Rt△PCA 和Rt△PCB 中, ∵ PA =PB,PC =PC, ∴ Rt△PCA ≌Rt△PCB(HL). ∴ AC =BC. 又 PC⊥AB, ∴ 点P 在线段AB 的垂直平分线上
