弧度制导学案
高中数学第一章三角函数1.3弧度制导学案北师大版必修4

1.3 弧度制问题导学1.角度制与弧度制的互化活动与探究1(1)把112°30′化成弧度;(2)把-5π12化成度.迁移与应用把下列各角从度化成弧度或从弧度化成度.(1)67°30′;(2)810°;(3)108°;(4)135°;(5)7π;(6)-5π2;(7)23π4;(8)-4π5.1.角度与弧度的互化.(1)原则:牢记180°=π rad,充分利用1°=π180rad ,1 rad =⎝ ⎛⎭⎪⎫180π°进行换算. (2)方法:设一个角的弧度数为α,角度数为n ,则α rad =⎝⎛⎭⎪⎫α·180π°;n °=n ·π180 rad . 2.将角度制化为弧度制,当角度制中含有“分”“秒”单位时,应先将它们统一转化为“度”,再利用1°=π180rad 化为弧度即可.以弧度为单位表示角时,常把弧度写成多少π的形式.如无特殊要求,不必把π写成小数.2.用弧度表示终边相同的角及区域角活动与探究2已知角α=2 005°,(1)将α改写成β+2k π(k ∈Z,0≤β<2π)的形式,并指出α是第几象限的角; (2)在区间[-5π,0)上找出与α终边相同的角.迁移与应用已知角α的终边与π3的终边相同,求角α3在[0,2π)内的值.(1)用弧度表示终边相同的角所有与角α终边相同的角,连同角α在内,构成的集合用弧度可表示为{β|β=2k π+α,k ∈Z },这里α应为弧度数.(2)在某个区间内寻找与α终边相同的角β ①首先表示β的一般形式.②然后根据区间范围讨论k 的值.③最后把k 的值代入β的一般形式求出.活动与探究3用弧度表示顶点在原点,始边重合于x 轴的非负半轴,终边落在图中的阴影部分内的角的集合(不包括边界).迁移与应用用弧度表示顶点在原点,始边与x轴的非负半轴重合,终边落在阴影部分内的角的集合,如图所示,包括边界.区域角的表示方法(1)要用终边相同的角的表示形式表示出以阴影部分的边界为终边的角,并注意旋转的方向及两边界角的大小顺序;(2)表达式中角度制与弧度制不能混用;(3)要分清阴影部分是否包括边界,以确定表达式中是否带“等号”.3.弧长公式及扇形面积公式的应用活动与探究4扇形AOB的周长为8 cm,圆心角为α(0<α<2π).(1)若这个扇形的面积为3 cm2,求圆心角α的大小;(2)求这个扇形的面积取得最大值时圆心角α的大小.迁移与应用如图所示,已知扇形AOB的圆心角为120°,半径长为6,求:(1)AB的长;(2)弓形ACB的面积.(1)在弧度制下的弧长公式及扇形面积公式中,由α,r,l,S中的两个量可以求出另外的两个量,即用方程的思想“知二求二”.(2)求扇形的面积关键是求得扇形的圆心角、半径、弧长三个量中的任意两个量.相反,也可由扇形的面积结合其他条件,求扇形的圆心角、半径、弧长.解题时要注意公式的灵活变形及方程思想的运用.当堂检测1.下列说法中,错误的是( ).A.用角度制和弧度制度量任一角,单位不同,量数也不同B.1°的角是周角的1360,1 rad的角是周角的12πC .1 rad 的角比1°的角要大D .用角度制和弧度制度量角,都与圆的半径无关2.已知扇形的圆心角为2π3弧度,半径为2,则扇形的面积为( ).A .83π B.43C .2π D.4π33.把-1 485°写成2k π+α(0≤α<2π,k ∈Z )的形式是( ).A .-8π+π4B .-8π-7π4C .-10π-π4D .-10π+7π44.(1)300°化为弧度是________;(2)-5π6化为度是________;(3)终边落在如图的阴影部分(包括边界)的角的集合是________.5.已知扇形的周长为6 cm ,面积为2 cm 2,求扇形圆心角α(0<α<2π).课前预习导学 【预习导引】1.(1)1360(2)1弧度的角 rad 弧度 弧度预习交流1 略预习交流2 30° 45° 120°0 π12 π3 5π12 3π4 5π6 5π4 3π2 3.正数 负数 0预习交流3 (1)32 (2)π34.|α|πr 180 |α|r |α|πr 2360 12lr 12|α|r 2预习交流4 (1)提示:此公式可类比三角形的面积公式来记忆.(2)π2 3π2课堂合作探究 【问题导学】活动与探究1 解:(1)112°30′=112.5°=112.5×π180=2252×π180=5π8;(2)-5π12=-⎝ ⎛⎭⎪⎫5π12×180π°=-75°. 迁移与应用 (1)3π8rad(2)9π2rad (3)3π5rad (4)3π4rad(5)1 260° (6)-450° (7)1 035° (8)-144°活动与探究2 解:(1)2 005°=2 005×π180=401π36=5×2π+4136π.又π<41π36<3π2,所以α与41π36终边相同,是第三象限角.(2)与α角终边相同的角为2k π+41π36,k ∈Z .由-5π≤2k π+41π36<0,可得-52-4172≤k <-4172.∵k ∈Z ,∴k =-3,-2,-1.∴在区间[-5π,0)上,与角α终边相同的角是-31π36,-103π36,-175π36.迁移与应用 π9,7π9,13π9活动与探究3 解:(1)图①中以OB 为终边的角为330°,可看成是-30°,化为弧度,即-π6,而75°=75×π180=5π12,∴⎩⎨⎧⎭⎬⎫θ|2k π-π6<θ<2k π +5π12,k ∈Z .(2)图②中以OB 为终边的角为225°,可看成是-135°,化为弧度,即-3π4,而135°=135×π180=3π4,∴⎩⎨⎧⎭⎬⎫θ|2k π-3π4<θ<2k π+3π4,k ∈Z .迁移与应用 解:(1) ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪2k π+π6≤α≤2k π+5π4,k ∈Z .(2)⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪2k π-π3≤α≤2k π+π6,k ∈Z . (3)⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪k π+π4≤α≤k π+2π3,k ∈Z. 活动与探究4 解:设扇形AOB 的半径为r ,弧长为l ,(1)由题意可得⎩⎪⎨⎪⎧2r +l =8,12lr =3,解得⎩⎪⎨⎪⎧r =3,l =2,或⎩⎪⎨⎪⎧r =1,l =6,∴α=l r =23或α=lr =6.(2)∵2r +l =8,∴S 扇=12lr =12(8-2r )·r =-r 2+4r =-(r -2)2+4,∴当r =2时,S 扇形最大取4,此时l =4,α=lr=2. 迁移与应用 (1)4π(2)12π-9 3 【当堂检测】 1.A 2.D 3.D4.(1)5π3(2)-150°(3)⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪3π4+2k π≤α≤5π4+2k π,k ∈Z5.1弧度或4弧度。
§5.2弧度制导学案

§5.2 弧度制 导学案目标要求:通过探究使学生认识到角度值和弧度制都是度量角的制度,通过总结引入弧度制的好处,学会归纳整理并认识到任何新知识的学习,都会为解决实际问题带来方便,从而激发学生的学习兴趣;培养学生学好数学的信心,学会运用联系的观点认识事物。
重点:理解弧度制的意义,并能进行角度和弧度的换算。
难点:弧度的概念及其与角度的关系。
学习过程一、自主学习:预习教材完成下列问题:1.在初中几何里,我们学习过角的度量, 1度的角是怎样定义的呢?2. 除了用角度度量外,还有没有其它度量角的办法呢?3.什么是1弧度的角?其单位是什么?4.角度与弧度的转化:360=rad 180= rad90= rad60= rad1= rad ≈ rad 1rad= ≈ =3.什么叫弧度制?4.弧长公式: l= =二、合作探究:1.把下列各角从度化成弧度.(1)135; (2)90; (3)60; (4)45;2.把下列各角从弧度化成度.(1)2π ; (2) ; (3); (4)。
3.时间经过4h,时针、分针各转了多少度?各等于多少弧度?三、精讲点拨3602π= rad 180π=r a d 1801π=︒rad 0.01745≈rad 1rad =︒)180(π5718'≈例1、把下列各角从度化为弧度: (1)0252 (2)0/1115变式练习 把下列各角从度化为弧度:(1)22 º30′ (2)—210º (3)1200º (4) 030 (5)'3067︒ 例2、把下列各角从弧度化为度: (1)35π (2) 3.5变式练习:把下列各角从弧度化为度: (1)12π(2)—34π (3)103π(4)4π(5) 2归纳:把角从弧度化为度的方法是:把角从度化为弧度的方法是:四、当堂检测:1、把下列各角化为0-2π间的角加上2k π( k 是整数)的形式,并指出它们是哪个象限的角。
弧度制_导学案 2

AA弧度制一、学习目标:1、 了解弧度制的概念,并会用之解决简单问题2、 通过角度与弧度表示圆的弧长及面积,使学生认识到角度制和弧度制都是度量角的制度,并能相互转换重点:理解弧度制的意义,并能进行角度和弧度的换算 难点:弧度的概念及其角度的关系。
二、预习案角度制:用角度作为度量角的单位;弧度制:用弧度作为度量角的单位。
(一)、阅读课本,回答下列问题: 1、(请用自己的语言表述)在初中几何里,我们学习过角的度量,1°的角是怎样定义的呢?2、作半径不等的甲、乙两个圆,在每个圆上做出等于半径的弧长,连接圆心与弧的两个端点,得到两个角,将乙图移到甲图上,两个角有什么样的关系?3、(请同学们用自己的语言表述)1弧度的规定:________________________________。
4、如图:圆O 的半径为1(单位圆),∠AOB 所对的弧长为1,则∠AOB =________rad ; ∠AOC 所对的弧长为1,则∠AOC =_________rad ;周角所对的弧长是圆的周长,为_____,则周角=______°=________rad 。
所以180°=_______rad ; 1°=________rad ≈0.01745 rad ;1rad=_______°≈57.3°=57°18’ 5、弧长公式与扇形面积公式: 在半径为R 的圆中,1、360°角所对的弧长l =_____,面积S=_____;1°角所对的弧长l =_______ ,面积S=________在角度制中,弧长l =___________,面积S=__________ (设所对圆心角为n °)2、2πrad 角所对的弧长l =_____,面积S=______;1rad 角所对的弧长l =______,面积S=________; 在弧度制中,弧长l =_______,面积S= _________ (设所对圆心角为αrad )=__________(已知所对弧长为l )(二)预习检测:1、下列四个说法中,不正确的是( ) A 、半圆所对的圆心角是πrad B 、周角的大小等于2πC 、1弧度的圆心角所对的弧长等于该圆的半径D 、大圆中1弧度的角比小圆中1弧度角大 2、6π=_____°,4π=_____°,3π= _____°,2π= _____°120°=________,135°=_______,150°=_______,180°=_________3、把—1480°化为弧度,并写成2k π+α(k ∈Z )的形式,其中0<α<2π)4、已知扇形AOB 的周长是6cm,该扇形的圆心角是1弧度,求该扇形的面积三、温馨提示:(1) 正角的弧度数是正数,负角的弧度数是负数,零角的弧度数是0; (2) 角α的弧度数的绝对值|α|=l r(l 为弧长,r 为半径);(3) 用角度制和弧度制来度量零角,单位不同,但数量相同(都是0); (4) 用角度制和弧度制来度量任意非零角,单位不同,数量也不同;(5) 角度制和弧度制不能混用,如k •360°+3π这种写法是不妥当的。
高中数学 112 弧度制导学案 新人教版必修4 学案

弧度制导学案1、弧度的定义:_______________________________________________,记作_________.2、特殊角的弧度数与角度制(1)_____360=︒ (2)rad rad ________1≈=︒ (3)︒≈=30.57____1度rad3、弧长公式: 扇形的面积公式:例1、把下列各角从弧度化为度,把下列各角从度化为弧度。
(1)53π(2)5.3 (3)︒252(4)'1511︒例2、已知扇形的周长为cm 8,圆心角为45,求该扇形的面积。
一、练习检测与拓展延伸 1.写出写列各角的弧度数: 角度 0153045607590120135150弧度角度 180210225240270300315330360弧度2.12π的角化成角度制是( ) A 、︒15 B 、︒30 C 、︒60 D 、︒753、下列各角中与︒-120角终边相同的角为( ) A 、π34 B 、π65-C 、π34-D 、π677.已知扇形的周长为20 cm,当它的半径和圆心角各取什么值时, 才能使扇形的面积最大?最大面积是多少?章节与课题1课时 总课时 062课时本课时学习目标或学习任务1.理解弧度制的意义,能正确进行弧度与角度的换算,熟记特殊角的弧度数.2.了解角的集合与实数集R 之间的一一对应关系.3.掌握弧度制下的弧长公式,会利用弧度制解决某些简单的实际问题.本课时重点难点 弧度的意义,弧度与角度的换算每日一言如果命运是块顽石,我就化为大锤,将它砸得粉碎!——欧拉。
高中数学《弧度制》导学案
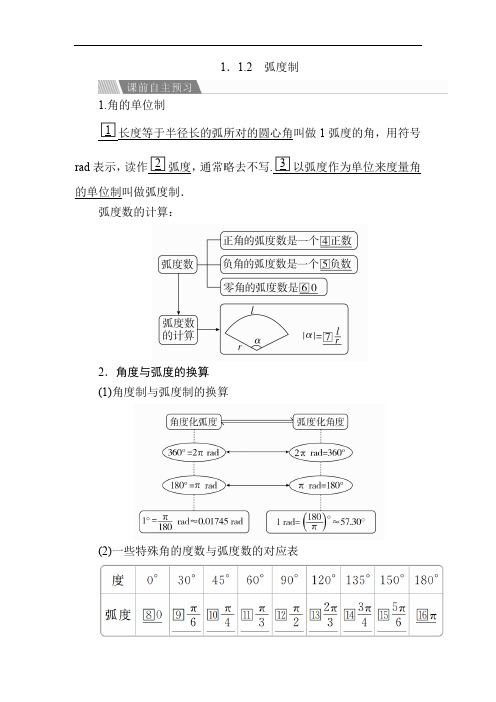
1.1.2弧度制1.角的单位制□1长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号rad表示,读作□2弧度,通常略去不写.□3以弧度作为单位来度量角的单位制叫做弧度制.弧度数的计算:2.角度与弧度的换算(1)角度制与弧度制的换算(2)一些特殊角的度数与弧度数的对应表3.扇形的弧长及面积公式 设扇形的半径为r ,弧长为l ,α(0<α<2π)为其圆心角的弧度数,n 为圆心角的角度数,则扇形的弧长:l =□17n πr 180=□18αr ,扇形的面积:S =□19n πr 2360=□2012lr =□2112α·r 2.1.判一判(正确的打“√”,错误的打“×”)(1)大圆中1弧度角比小圆中1弧度角大.( )(2)圆心角为1弧度的扇形的弧长都相等.( )(3)用弧度表示的角都是正角.( )(4)“度”和“弧度”是度量角的两种不同的度量单位.( ) 答案 (1)× (2)× (3)× (4)√2.做一做(1)(教材改编P 9T 5)在半径为5 cm 的圆中,圆心角为周角的23的角所对的圆弧长为( )A.4π3 cmB.20π3 cmC.10π3 cmD.50π3 cm答案 B解析 记r =5,圆心角α=23×2π=4π3,∴l =|α|r =20π3.(2)-135°化为弧度为________,11π3化为角度为________.答案 -3π4 660°解析 -135°=-135×π180=-3π4,11π3=113×180°=660°.探究1弧度制的概念例1下列命题中,假命题是()A.“度”与“弧度”是度量角的两种不同的度量单位B.一度的角是周角的1360,一弧度的角是周角的12πC.弧度制下,角与实数之间建立了一一对应关系D.不论是用角度制还是用弧度制度量角,它们均与圆的半径长短有关解析根据角度和弧度的定义,可知无论是角度制还是弧度制,角的大小与圆的半径长短无关,而是与弧长与半径的比值有关,所以D是假命题.选项A,B,C均为真命题.答案D拓展提升角度制和弧度制的比较(1)弧度制是以“弧度”为单位来度量角的单位制,而角度制是以“度”为单位来度量角的单位制.(2)1弧度的角是指等于半径长的弧所对的圆心角,而1度的角是指圆周角的1360的角,大小显然不同.(3)无论是以“弧度”还是以“度”为单位来度量角,角的大小都是一个与“半径”大小无关的值.(4)用“度”作为单位度量角时,“度”(即“°”)不能省略,而用“弧度”作为单位度量角时,“弧度”二字或“rad”通常省略不写.但两者不能混用,即在同一表达式中不能出现两种度量方法.【跟踪训练1】下列叙述中正确的是()A.1弧度是1度的圆心角所对的弧B.1弧度是长度为半径的弧C .1弧度是1度的弧与1度的角之和D .1弧度是长度等于半径长的弧所对的圆心角的大小,它是角的一种度量单位答案 D解析 弧度是度量角的大小的一种单位,1弧度是长度等于半径的圆弧所对圆心角的大小.故选D.探究2 角度和弧度的换算例2 把下列各角用另一种度量制表示出来:112°30′;36°;-5π12;3.5.解 112°30′=2252×π180=5π8.36°=36×π180=π5.-5π12=-5π12×⎝ ⎛⎭⎪⎫180π°=-75°. 3.5=3.5×⎝ ⎛⎭⎪⎫180π°≈3.5×57.3°=200.55°(或200°33′). 拓展提升用弧度制表示角时“弧度”二字可以省略不写,而用角度制表示角时要特别注意单位“°”不能丢,因为1°与1是完全不同的两个角.【跟踪训练2】 (1)-300°化为弧度是( )A .-4π3B .-5π3C .-7π4D .-7π6(2)8π5化为度数是( )A .278°B .280°C .288°D .318°答案 (1)B (2)C解析 (1)-300°=-300×π180=-5π3.(2)8π5=85×180°=288°.探究3 用弧度制表示角的集合例3 已知角α=2005°.(1)将α改写成β+2k π(k ∈Z,0≤β<2π)的形式,并指出α是第几象限的角;(2)在[-5π,0)内找出与α终边相同的角.解 (1)2005°=2005×π180rad =401π36rad =⎝ ⎛⎭⎪⎫5×2π+41π36 rad , 又π<41π36<3π2,∴角α与41π36终边相同,是第三象限的角.(2)与α终边相同的角为2k π+41π36(k ∈Z ),由-5π≤2k π+41π36<0,k ∈Z 知k =-1,-2,-3.∴在[-5π,0)内与α终边相同的角是-31π36,-103π36,-175π36.拓展提升用弧度制表示终边相同的角2k π+α(k ∈Z )时,其中2k π是π的偶数倍,而不是整数倍,还要注意角度制与弧度制不能混用.【跟踪训练3】 (1)将-1125°表示成2k π+α,0≤α<2π,k ∈Z 的形式为________;(2)用弧度表示终边落在阴影部分内(不包括边界)的角的集合.答案 (1)-8π+7π4 (2)见解析解析 (1)∵-1125°=-⎝⎛⎭⎪⎫1125×π180=-25π4, 而-25π4=-8π+7π4,∴-1125°=-8π+7π4.(2)因为终边落在OA 处的角θ=2k π+5π12,k ∈Z ,终边落在OB 处的角θ=2k π-π6,k ∈Z ,所以终边落在阴影部分的角的集合为⎩⎨⎧⎭⎬⎫θ⎪⎪⎪2k π-π6<θ<2k π+5π12,k ∈Z . 探究4 扇形的弧长及面积公式的应用例4 (1)已知扇形的周长为8 cm ,圆心角为2,则扇形的面积为________cm 2;(2)已知一半径为R 的扇形,它的周长等于所在圆的周长,那么扇形的圆心角是多少弧度?面积是多少?解析 (1)设扇形的半径为r cm ,弧长为l cm ,由圆心角为2 rad ,依据弧长公式可得l =2r ,从而扇形的周长为l +2r =4r =8,解得r =2,则l =4.故扇形的面积S =12lr =12×4×2=4 cm 2.(2)设扇形的弧长为l ,由题意得2πR =2R +l ,所以l =2(π-1)R ,所以扇形的圆心角是l R =2(π-1),扇形的面积是12lR =(π-1)R 2.答案 (1)4 (2)见解析拓展提升弧度制下涉及扇形问题的解题策略(1)明确弧度制下扇形的面积公式是S =12lr =12|α|r 2(其中l 是扇形的弧长,r 是扇形的半径,α(0<α<2π)是扇形的圆心角).(2)涉及扇形的周长、弧长、圆心角、面积等的计算,关键是先分析题目已知哪些量求哪些量,然后灵活运用弧长公式、扇形面积公式直接求解或列方程(组)求解.【跟踪训练4】 已知扇形AOB 的圆心角为120°,半径为6,求:(1)AB ︵的长; (2)扇形所含弓形的面积(即阴影面积).解 (1)∵120°=2π3,∴AB ︵的长l =2π3×6=4π.(2)S 扇形AOB =12lr =12×4π×6=12π.如图所示,过点O 作OD ⊥AB ,交AB 于D 点,于是有S △OAB =12×AB ×OD =12×2×33×3=93,∴弓形的面积为S 扇形AOB -S △AOB =12π-9 3.1.弧度制与角度制的区别与联系(1)区别①单位不同.弧度制以“弧度”为度量单位,角度制以“度”为度量单位; ②定义不同.(2)联系不管以“弧度”还是以“度”为单位的角的大小都是一个与圆的半径大小无关的定值.2.角度制与弧度制换算时应注意的问题(1)弧度制与角度制的互化是一种比例关系的变形,具体变化时,可牢记以下公式:π180=弧度角度,只要将已知数值填入相应的位置,解出未知的数值,再添上相应的单位即可.(2)用弧度为单位表示角的大小时,“弧度”两字可以省略不写,这时弧度数在形式上虽是一个不名数,但我们应该把它理解为名数,如sin2是指sin(2弧度),π=180°是指π弧度=180°;但如果以度为单位表示角时,度就不能省去.(3) 用弧度为单位表示角时,常常把弧度数写成多少π的形式,如无特殊要求,不必把π写成小数,如45°=π4弧度,不必写成45°≈0.785弧度.(4)度化为弧度时,应先将分、秒化为度,再化为弧度.(5)角度制和弧度制表示的角不能混用.如α=2k π+30°,k ∈Z ;β=k ·90°+π4,k ∈Z ,都不正确.1.2145°转化为弧度数为( )A.163B.322C.16π3D.143π12答案 D解析 2145°=2015×π180 rad =143π12 rad.2.α=-2 rad ,则α的终边在( )A .第一象限B .第二象限C .第三象限D .第四象限答案 C解析 ∵1 rad ≈57.30°,∴-2 rad ≈-114.60°.故α的终边在第三象限.3.在△ABC 中,若A ∶B ∶C =3∶5∶7,则角A ,B ,C 的弧度数分别为________.答案 π5,π3,7π15解析 A ∶B ∶C =3∶5∶7,则A 占总度数的33+5+7=15; B 占总度数的53+5+7=13; C 占总度数的73+5+7=715. 三角形的内角和为π,则A 为π5,B 为π3,C 为7π15.4.用弧度制表示终边落在第二象限的角的集合为________.答案 ⎩⎨⎧α⎪⎪⎪⎭⎬⎫2k π+π2<α<2k π+π,k ∈Z 解析 若角α的终边落在第二象限,则2k π+π2<α<2k π+π,k ∈Z . 5.(1)把310°化成弧度;(2)把5π12 rad 化成角度;(3)已知α=15°,β=π10,γ=1,θ=105°,φ=7π12,试比较α,β,γ,θ,φ的大小.解 (1)310°=π180 rad ×310=31π18 rad.(2)5π12 rad =⎝ ⎛⎭⎪⎫180π×5π12°=75°. (3)解法一(化为弧度):α=15°=15×π180=π12.θ=105°=105×π180=7π12.显然π12<π10<1<7π12,故α<β<γ<θ=φ.解法二(化为角度):β=π10=π10×⎝ ⎛⎭⎪⎫180π°=18°,γ=1≈57.30°,φ=7π12×⎝ ⎛⎭⎪⎫180π°=105°.显然,15°<18°<57.30°<105°,故α<β<γ<θ=φ.A 级:基础巩固练一、选择题1.下列各式中正确的是( )A .π=180B .π=3.14C .90°=π2 radD .1 rad =π 答案 C解析 A 选项,π rad =180°,故错误;B 选项,π≈3.14,故错误;C 选项,90°=π2rad ,故正确;D 选项,1 rad =⎝ ⎛⎭⎪⎫180π°,故错误.故选C.2.扇形的半径变为原来的2倍,而弧长也增加为原来的两倍,则( )A .扇形的面积不变B .扇形圆心角不变C .扇形面积增大到原来的2倍D .扇形圆心角增大到原来的2倍答案 B解析 由弧度制定义,等于半径长的圆弧所对的圆心角叫做1弧度的角,所以一扇形所在圆的半径增加为原来的2倍,弧长也增加到原来的2倍,弧长与半径之比不变,所以,扇形圆心角不变,故选B.3.把-11π4表示成θ+2k π(k ∈Z )的形式,使|θ|最小的θ为( )A .-3π4 B.π4 C.3π4 D .-π4答案 A解析 ∵-11π4=-2π-3π4,∴θ=-3π4.又-11π4=-4π+5π4,∴θ=5π4.∴使|θ|最小的θ=-3π4.4.若α=2k π-354,k ∈Z ,则角α所在象限是( )A .第一象限B .第二象限C .第三象限D .第四象限答案 C解析 ∵-9<-354<-8,∴-3π<-354<-3π+π2.∴-354在第三象限,故α也在第三象限.5.若一圆弧长等于其所在圆的内接正三角形的边长,则其圆心角的弧度数的绝对值为( )A.π3B.2π3C. 3D .2答案 C解析 设所在圆的半径为r ,圆内接正三角形的边长为2r sin60°=3r ,所以弧长3r 的圆心角的弧度数为3r r = 3.二、填空题6.将-1485°化成2k π+α(0≤α<2π,k ∈Z )的形式为________.答案 -10π+7π4解析 -1485°=-1485×π180=-33π4=-10π+7π4.7.扇形AOB ,半径为2 cm ,|AB |=2 2 cm ,则AB ︵所对的圆心角弧度数为________. 答案 π2解析 ∵|AO |=|OB |=2,|AB |=22,∴∠AOB =90°=π2.8.若角α的终边与8π5角的终边相同,则在[0,2π]上,终边与α4角的终边相同的角是________________. 答案 2π5,9π10,7π5,19π10解析 由题意,得α=8π5+2k π,∴α4=2π5+k π2(k ∈Z ).令k =0,1,2,3,得α4=2π5,9π10,7π5,19π10.三、解答题9.用弧度制表示终边在图中阴影区域内角的集合(包括边界),并判断2019°是不是这个集合的元素.解 ∵150°=5π6,∴终边在阴影区域内角的集合为S ={β⎪⎪⎪⎭⎬⎫5π6+2k π≤β≤3π2+2k π,k ∈Z .∵2019°=219°+5×360°=⎝ ⎛⎭⎪⎫219π180+10π rad ,又 5π6<219π180<3π2,∴2019°∈S .10.扇形AOB 的周长为8 cm.(1)若这个扇形的面积为3 cm 2,求圆心角的大小;(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB . 解 (1)设扇形的圆心角为θ,扇形所在圆的半径为R .依题意有⎩⎪⎨⎪⎧ 2R +Rθ=8,12θ·R 2=3,解得θ=23或6.即圆心角的大小为23弧度或6弧度.(2)设扇形所在圆的半径为 x cm ,则扇形的圆心角θ=8-2xx .于是扇形的面积是S =12x 2·8-2xx =4x -x 2=-(x -2)2+4.故当x =2 cm 时,S 取到最大值.此时圆心角θ=8-42=2弧度,弦长AB =2·2sin1=4sin1(cm).故扇形的面积取得最大值时圆心角等于2弧度,弦长AB 等于4sin1 cm.B 级:能力提升练1.已知一扇形的中心角是α,所在圆的半径是R ,若扇形的周长是一定值C (C >0),该扇形的最大面积为( )A.C 4B.C 24C.C 216D.C 22答案 C解析 设扇形的半径为R ,则扇形的弧长为C -2R ,则S =12(C -2R )R =-R 2+C 2R =-⎝ ⎛⎭⎪⎫R -C 42+⎝ ⎛⎭⎪⎫C 42,当R =C 4,即α=C -2R R =2时,扇形的面积最大,最大面积为C 216.故选C.2.如图所示,动点P ,Q 从点A (4,0)出发沿圆周运动,点P 按逆时针方向每秒钟转π3弧度,点Q 按顺时针方向每秒钟转π6弧度,求P ,Q 第一次相遇所用的时间及P ,Q 各自走过的弧长.解 设P ,Q 第一次相遇时所用的时间为t 秒,则t ·π3+t ·⎪⎪⎪⎪⎪⎪-π6=2π,解得t =4. 即第一次相遇时所用的时间为4秒.P 点走过的弧长为:4π3×4=16π3,Q 点走过的弧长为:8π-16π3=8π3.。
弧度制导学案优选版

§1.1.2弧度制和弧度制与角度制的换算导学案【学习目标】了解弧度制,并能进行弧度与角度的换算。
【学习过程】 一、自主学习 (一)知识链接:复习1。
写出终边在下列位置的角的集合。
(1)x 轴: ; (2)y 轴: 。
2.角度制规定,将一个圆周分成 份,每一份叫做 度, 故一周等于 度,平角等于 度,直角等于 度。
0n 的圆弧长为l ,圆的半径为r ,则l = ;rl= 。
(二)自主研讨:(预习教材P6-P9) 探究一:弧度制定义:长度等于半径长的圆弧所对的圆心角叫做1弧度角,记作1rad ,这种度量角的单位制称为 。
新知: ① 正角的弧度数是 数,负角的弧度数是 数,零角的弧度数是 。
② 角α的弧度数的绝对值 lrα=(l 为弧长,r 为半径)反思:360°= rad ;1800 = rad; 1°= rad ≈ rad ;1 rad =≈=;αrad =;n °= rad试试:完成特殊角的度数与弧度数的对应表:3。
角的集合与实数集R 之间是 对应关系。
4. 设扇形的圆心角是αrad ,弧长为l ,半径为r , 则扇形面积公式S ==二、合作探究例1:按要求解答下列各题: (1)把3730'︒化成弧度,(2)把35rad π化成度。
例2:用弧度制表示:(1)终边在x 轴上的角的集合,(2)终边在y 轴上的角的集合。
例3:利用弧度制证明扇形面积公式:(1)12S lR =, (2)212S R α=。
三、交流展示1、使用换算公式,把下列各角的度数化为弧度数:(1)︒-240; (2)︒-225; (3)︒12;(4)︒1080; (5)'3022︒; (6)︒5.157;2.把下列各角的弧度数化为度数: (1)12π; (2)35π; (3)103π; (4)8π; (5)23π-; (6)65π-;3.下午正2点时,时针和分针的夹角为( ) A.6π B. 4π C. 3π D. 2π4.α=2rad ,则α终边在( )5.半径为2的圆的圆心角所对弧长为6,则其圆心角为 rad 。
1.1《弧度制》导学案

1.1.2 弧度制一、学习目标1.理解弧度制的意义;2.能正确的应用弧度与角度之间的换算;3.记住公式||lα=(l为以.α作为圆心角时所对圆弧的长,r为圆半径);r4.熟练掌握弧度制下的弧长公式、扇形面积公式及其应用。
二、重点、难点弧度与角度之间的换算;弧长公式、扇形面积公式的应用。
三、学习过程(一)复习:初中时所学的角度制,是怎么规定1角的?角度制的单位有哪些,是多少进制的?(二)为了使用方便,我们经常会用到一种十进制的度量角的单位制——弧度制。
<我们规定> 叫做1弧度的角,用符号表示,读作。
r的弧所对的圆心角分别为多少?练习:圆的半径为r,圆弧长为2r、3r、2<思考>:圆心角的弧度数与半径的大小有关吗?由上可知:如果半径为r的园的圆心角α所对的弧长为l,那么,角α的弧度数的绝对值是:,α的正负由决定。
正角的弧度数是一个,负角的弧度数是一个,零角的弧度数是。
<说明>:我们用弧度制表示角的时候,“弧度”或rad 经常省略,即只写一实数表示角的度量。
例如:当弧长4l r π=且所对的圆心角表示负角时,这个圆心角的弧度数是4||4l rr r παπ-=-=-=-.(三) 角度与弧度的换算3602π=rad 180π=rad1801π=︒rad 0.01745≈rad 1rad =︒)180(π5718'≈例1、把下列各角从度化为弧度:(1)0252 (2)0/1115变式练习:把下列各角从度化为弧度:(1)22 º30′ (2)-210º (3)1200º (4) 030 (5)'3067︒例2、把下列各角从弧度化为度:(1)35π (2) 3.5变式练习:把下列各角从弧度化为度:(1)12π (2)-34π (3)103π (4)4π (5) 2归纳:把角从弧度化为度的方法是:把角从度化为弧度的方法是:<试一试>:一些特殊角的度数与弧度数的互相转化,请补充完整(四)在弧度制下分别表示轴线角、象限角的集合(1)终边落在x轴的非负半轴的角的集合为;x轴的非正半轴的角的集合为;终边落在y轴的非负半轴的角的集合为;y轴的非正半轴的角的集合为;所以,终边落在x轴上的角的集合为;落在y轴上的角的集合为。
弧度制导学案

弧度制一、学习目标1.理解并掌握弧度制的定义,领会弧度制定义的合理性;2.掌握并运用弧度制表示的弧长公式、扇形面积公式;3.熟练地进行角度制与弧度制的换算;4.理解角的集合与实数集R 之间建立的一一对应关系5.通过弧度制的学习,理解并认识到角度制与弧度制都是对角度量的方法,二者是辨证统一的,而不是孤立、割裂的关系.二、重点难点重点是理解弧度制的概念以及角度制与弧度制之间的换算;难点是弧度制概念的理解。
三、自学指导自学课本P6到P8内容,完成下列问题.四、新课学习:1、复习回顾1)、角度制规定:将一个圆周分成360份,每一份叫做1度,故一周等于360度,平角等于180度,直角等于90度等等. 2)、在角度制下 360n 1802r l r n S ππ==扇扇2、新课学习:弧度制的定义:等于半径长的圆弧所对的圆心角叫做1弧度的角,用符号rad 表示,读作弧度。
用弧度作单位来度量角的制度叫做弧度制。
在这种规定下,圆周长所对的圆心角为π2rad,半圆所对的圆心角为π rad ,︒90=2πrad,你能继续往下推吗?请你填写书上第6页的表格。
注:1、一般地,正角的弧度数是一个正数(正实数),负角的弧度数是一个负数(负实数),零角的弧度数是零。
这里,α的正负由角α的终边的旋转方向决定。
2、用角度制和弧度制度量零角,单位不同,数量相同;用角度制和弧度制度量任一非零角,单位不同,数量也不同。
练习:请你填下列表格。
角度0°15°45°弧度角度 90° 270°弧度更进一步,我们可以得到:︒=180rad π'185730.57)180(101745.01801︒=︒≈︒=≈=︒ππrad radrad利用上面的方法,我们可以把任意一个角度转换成弧度,或将任意一个弧度转化成角度。
例:按照下列要求,把67°30′化成弧度。
1)精确值; 2)精确到0.001的近似值。
弧度制汇报课导学案.doc

§1.1.2弧度制【教学内容分析】(1)弧度制的定义,角度制与弧度制的转换。
(2)弧度制表示的弧长公式,扇形面积公式的应用。
【学习目标】1、知识与技能(1)理解并掌握弧度制的定义;(2)掌握并运用弧度制表示的弧长公式、扇形面积公式;(3)熟练地进行角度制与弧度制的换算;(4)角的集合与实数集7?之间建立的一一对应关系.(5)使学生通过弧度制的学习,理解并认识到角度制与弧度制都是对角度量的方法,二者是辨证统一的,而不是孤立、割裂的关系.2、过程与方法创设情境,引入弧度制度量角的大小,通过探究理解并掌握弧度制的定义,领会定义的合理性•根据弧度制的定义推导并运用弧长公式和扇形面积公式.以具体的实例学习角度制与弧度制的互化.3、情态与价值通过本节的学习,使同学们掌握另一种度量角的单位制-一弧度制,理解并认识到角度制与弧度制都是对角度量的方法,二者是辨证统一的,而不是孤立、割裂的关系.为下一节学习三角函数做好准备.【学习重点】重点:品解并掌握弧度制定义;熟练地进行角度制与弧度制地互化换算;弧度制的运用.【学习难点】难点:理解弧度制定义,弧度制的运用.【使用说明和学法指导】在我们所掌握的知识中,知道角的度量是用角度制,但是为了以后的学习,我们引入了弧度制的概念,我们一定要准确理解弧度制的定义,在理解定义的基础上熟练掌握角度制与弧度制的互化.(一)课前准备复习1:写出终边在下列位置的角的集合.(1) x轴:_________________ . (2) y轴:_______________ .(3) _________________________ 第三象限:__________________________ . (4)第一、三象限: .复习2:角可以用度为单位进行度量,1度的角等于周角的________ 。
这种用度为单位度量角的单位制叫做角度制。
故一周等于 ____ 度,平角等于_____ 度,直角等于 _____ 度.角度制中1° = ' ,1' =60"。
弧度制导学案

弧度制导学案一、导学目标1.了解弧度制的定义和计算方法。
2.掌握角度与弧度之间的转换关系。
3.能够在实际问题中应用弧度制进行计算。
二、知识导入在几何学和三角学中,我们通常使用度数来度量角的大小。
例如,一个圆的周长是360度。
然而,当我们涉及到复杂的几何和三角函数计算时,度数制并不是最方便的。
为了解决这个问题,数学家们引入了弧度制。
三、弧度制的定义和计算方法1. 弧度的定义:弧度是角度的一种度量方式,它是指在半径为1的圆中所对应的圆弧长度。
我们用符号“rad”表示弧度。
例如,一个完整的圆周对应的弧长是2π,所以一个完整的圆周对应的角度是360度或2π弧度。
2. 弧度的计算方法:对于任意一个角度θ,我们可以通过以下公式将其转换为弧度:弧度 = (θ×π) / 1803. 例题:将60度转换为弧度。
解答:弧度 = (60 ×π) / 180= π / 3四、角度与弧度的转换关系1. 角度转换为弧度的公式:弧度 = (θ×π) / 1802. 弧度转换为角度的公式:角度 = (弧度× 180) / π3. 例题:将π/4弧度转换为角度。
解答:角度 = (π/4 × 180) / π= 45度五、实际问题中的弧度计算除了转换角度与弧度之外,我们还可以应用弧度制进行实际问题的计算。
1. 弧长公式:在一个圆形的轨道上,当我们沿着圆的边界行进一段距离时,我们所走过的弧长即为弧度所对应的圆弧的长度。
弧长公式如下:弧长 = 弧度×半径2. 弧度与度数的比较:使用弧度制进行计算时,有时候可以更方便地进行数值比较。
例如,当我们在解决三角函数运算时,很多函数表格都是基于弧度制给出的。
六、总结通过本次学习,我们了解了弧度制的定义和计算方法,掌握了角度与弧度之间的转换关系,并学会了在实际问题中应用弧度制进行计算。
弧度制在几何学和三角学中有着广泛的应用,能够更方便地进行各种数学计算。
§1.1.2《弧度制》导学案

高一数学 编号:SX--01--002§1.1.2《弧度制》导学案撰稿:梁倩 审核:尹德荣 时间:2009.11.10 姓名: 班级: 组别: 组名: 【学习目标】 1﹑能说出弧度、弧度制的定义. 2﹑学会弧度与角度的互化. 3﹑知道弧度公式与扇形面积公式之间的区别和联系. 【重点难点】 ▲重点:弧度的意义,角度与弧度的计算. ▲难点:弧度的概念及其与角度的关系. 【知识链接】 1﹑我们已经学习了任意角的概念,所谓的角实质上是 , 按照旋转方向不同,角可以分为 . 2﹑初中我们已经学过角度制,在角度制中,︒1角的规定为 .【学习过程】 阅读课本2页到3页的内容,尝试回答以下问题: 知识点1:弧度制的概念 问题1﹑怎样把角度表示的角转化为实数?把角度的有关运算转化为我们较为常用的实数运算呢? 问题2﹑弧度的定义是什么?弧度制如何表示? 问题3﹑rad 2可以写为2吗?︒2可以写为2吗?问题4﹑弧度的大小与所作圆的半径大小有关系吗?问题5﹑完成课本第6页表格的内容.问题6﹑角α的弧度数是如何定义的?问题7﹑α的正负如何决定?知识点2:弧度与角度的换算关系问题1﹑在半径为r的圆中,当圆心角为周角时,怎样用两种不同制进行换算呢?问题2﹑角度与弧度应如何进行转化?问题3﹑填写下列特殊角的度数与弧度的对问题4﹑与︒30终边相同的角该如何表示?分别用角度制与弧度值表示.阅读课本第8页例3的内容,尝试回答以下问题:知识点3:弧长公式与扇形面积问题1﹑若已知扇形半径、圆心角,能否求出该圆心角所对弧长和扇形面积?问题2﹑根据弧度的定义能否求出弧长和扇形面积?问题3﹑扇形面积与弧长有什么关系?问题4﹑已知扇形OAB 的圆心角为︒120,半径为6,求扇形弧长及面积.【基础达标】A1﹑⑴将下列角度转化为弧度.①︒36 ②︒-150 ③︒1095 ④︒1440⑵将下列弧度转化为角度. ①6π- ②π310-③32B2﹑已知弧长为cm 50的弧所对的圆心角为︒300,求这条弧所在的圆的半径.B3﹑①已知α为锐角,那么α2是( ). A 第一象限角 B 第二象限角 C 小于︒180的正角 D 第一或第二象限角 ②已知α是第一象限的角,那么2α是( ). A 第一象限角 B 第二象限角C 第一或第二象限角D 第一或第三象限角【小结】【当堂检测】 将rad π125-化为角度.【课后反思】本节课我最大的收获是 我还存在的疑惑是 我对导学案的建议是。
弧度制 导学案
1.1.2 弧度制 导学案学习目标:1.理解弧度制的意义;2.能正确的应用弧度与角度之间的换算;3.记住公式||lrα=(l 为以.α作为圆心角时所对圆弧的长,r 为圆半径); 4.熟练掌握弧度制下的弧长公式、扇形面积公式及其应用。
学习重点:弧度与角度之间的换算;学习难点:弧长公式、扇形面积公式的应用。
导入新知1.度量角的单位制2.弧度数:一般地,正角的弧度数是一个________,负角的弧度数是一个________,零角的弧度数是________.如果半径为r 的圆的圆心角α所对的弧长为l ,那么,角α的弧度数的绝对值是|α|=________.这里,α的正负由角α的终边的旋转方向决定.3.弧度制与角度制的换算公式4.扇形的弧长及面积公式设扇形的半径为R ,弧长为l ,α(0<α<2π),n °(0<n <360)为其圆心角,则【探究1】 (1)下列命题中,正确的命题是________.①1°的角是周角的1360,1 rad 的角是周角的12π;②1 rad 的角等于1度的角;③180°的角一定等于π rad 的角;④“度”和“弧度”是度量角的两种单位.(2)①把-157°30′化成弧度;②把25π化成度.【探究2】(1)与角2π3终边相同的角是( )A.11π3 B .2k π-2π3(k ∈Z )C .2k π-10π3(k ∈Z )D .(2k +1)π+2π3(k ∈Z )(2)用弧度表示顶点在原点,始边重合于x 轴的非负半轴,终边落在阴影部分内的角的集合.(不包括边界,如图)【探究3】已知扇形的圆心角为2π3弧度,半径为2,则扇形的面积是( )A.8π3B.43 C .2π D.4π3。
弧度制(导学案)

《5.1.2弧度制》一:学习目标1.了解弧度制下,角的集合与实数集之间的一一对应关系.2.理解“1弧度的角”的定义,掌握弧度与角度的换算、弧长公式和扇形面积公式,熟悉特殊角的弧度数二、导学指导与检测导学指导导学检测及课堂展示阅读相关材料,完成相应练习知识点一度量角的两种单位制1.角度制:(1)定义:用作为单位来度量角的单位制.(2)1度的角:周角的,记作1°2.弧度制:(1)定义:以作为单位来度量角的单位制.1弧度记作1 rad(rad可省略不写)(2)1弧度的角:长度等于长的圆弧所对的圆心角.知识点二弧度数的计算在弧度制下,角的集合与实数集R之间建立起一一对应的关系,每一个角都有唯一的一个实数(等于这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应。
思考比值lr与所取的圆的半径大小是否有关?答案一定大小的圆心角α所对应的弧长与半径的比值是唯一确定的,与半径大小无关.知识点三角度与弧度的互化角度化弧度弧度化角度360°=2π rad2π rad=360°180°=π radπ rad=180°1°=π180rad≈0.017 45 rad 1 rad=⎝⎛⎭⎫180π°≈57.30°度数×π180=弧度数弧度数×⎝⎛⎭⎫180π°=度数知识点四弧度制下的弧长与扇形面积公式设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则(1)弧长公式:l=αR.(2)扇形面积公式:S=12lR=12αR2三、巩固诊断:1.下列说法中,错误的是( )A .半圆所对的圆心角是π radB .周角的大小等于2πC .1弧度的圆心角所对的弧长等于该圆的半径D .长度等于半径的弦所对的圆心角的大小是1弧度2.若α=-2 rad ,则α的终边在( )A .第一象限B .第二象限C .第三象限D .第四象限3.时钟的分针在1点到3点20分这段时间里转过的弧度为( )A.143π B .-143π C.718 π D .-718π 4.在半径为10的圆中,4π3的圆心角所对弧长为( ) A.40π3 B.20π3 C.200π3 D.400π35.周长为9,圆心角为1 rad 的扇形面积为________.6已知一扇形的周长为40 cm ,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?四、堂清、日清记录。
秋人教A版数学必修四1.1.2《弧度制》word导学案

秋人教A版数学必修四1.1.2《弧度制》word导学案1.1.2 弧度制【学习目标】1.理解弧度制的意义,能正确地进行弧度与角度的换算,熟记特殊角的弧度数2.掌握弧度制下的弧长公式和扇形的面积公式,会利用弧度制解决某些简单的实际问题 3.了解角的集合与实数集之间可以建立起一一对应的关系【学习重点、难点】弧度的概念,弧度与角度换算【自主学习】一、复习引入请同学们回忆一下初中所学的1的角是如何定义的?二、建构数学 1.弧度制角还可以用__________为单位进行度量,___________________________________叫做1弧度的角,用符号_____表示,读作________。
2.弧度数:正角的弧度数为_________,负角的弧度数为_________,零角的弧度数为_____如果半径为r的圆心角所对的弧的长为1,那么,角α的弧度数的绝对值是_________。
这里,α的正负由____________________________________决定。
3.角度制与弧度制相互换算360°=_________rad 180°=_________rad1°=_________rad 1 rad=_________°≈ _________°4.角的概念推广后,在弧度制下, ________________与______________之间建立起一一对应的关系:每个角都有唯一的一个实数(即_______________)与它对应;反过来,每一个实数也都有________________(即_______________)与它对应。
5.弧度制下的弧长公式和扇形面积公式:角?的弧度数的绝对值|?|?______________ (l为弧长,r为半径)弧长公式:____________________________扇形面积公式:____________________________【典型例题】例1.把下列各角从弧度化为度。
弧度制导学案

4-02 §1.1.2 弧度制1. 掌握弧度制的定义;2. 学会弧度制与角度制互化;R 一一对应关系.一学案(一) 课前准备(预习教材P 6~ P 8,找出疑惑之处) 复习1:任意角:定义:角能够看成是 所形成的图形。
正角: 负角: 零角: 这样通过定义就把角从0~360推广到了任意角。
复习2:角度制:(1)定义:以 作为单位来度量角的单位制。
符号: (2)规定:将一个圆周分成 份,每一份叫做 度,故一周等 于 度。
复习3:在角度制下,扇形弧长公式为 ;扇形面积公式为 。
(二)新课导学 弧度制(1)定义:以 作为单位来度量角的单位制。
符号: (2)规定:1弧度的角:长度等于 所对的圆心角。
即若=AB r ,则AOB=1rad ∠,弧度(rad ) 类比:若1=1.5AB r ,则1AOB =∠ rad2=2AB r ,则2AOB =∠ rad 3=2AB r ,则3AOB =∠ rad 归纳:若=AB r α,则AOB=∠ rad推广探究:如图,半径为r 的圆的圆心与原点重合,角α的始边与x 轴的非负半轴重合,交圆于点A ,终边与圆交于点B . 请完成表格。
① 正角的弧度数是 数,负角的弧度数是 数,零角的弧度数是 . ② 角α的弧度数的绝对值 α=,α的正负由 决定.③角度制与弧度制的转换公式o r Crl =2roAAB y xAαOB根据180=rad π,得1=rad 1801801rad=ππ⎧⎪⎪⎨⎛⎫⎪ ⎪⎪⎝⎭⎩例题例1:把6730'化成弧度.例2:把35rad π化成度.※小结:在具体运算时,“弧度”二字和单位符号“rad ”可省略,如:3表示3rad练习:1.将以下弧度与角度实行互化. -43π= ;310π= ;-210°= ; 75°= . 2. 若α=-3,则角α的终边在( ).A. 第一象限B. 第二象限C. 第三象限D. 第四象限 3.半径为2的圆的圆心角所对弧长为6,则其圆心角为 rad . 4.课本P9习题1.1第7题 5.课本P9习题1.1第8题例3利用弧度制证明以下关于扇形的公式(R 是圆的半径).:1l R 2122l R 132S lR。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《§3弧度制》导学案 班级: 姓名: 组名:
一、学习目标:
1、知识与技能:
1)了解弧度制的概念,体会弧度是一种度量角的单位。
2)能进行弧度与角度的互化。
3)能初步运用弧度制表示的弧长公式、扇形面积公式,解决相关问题。
2、过程与方法:
通过单位圆中的圆心角引入弧度的概念的学习过程,对比两种度量角的方法,探究角度制与弧度制之间的互化,理解弧度的作用和适用性。
3、情感态度与价值观:
通过弧度制的学习,使学生体会不同表象下面相同事物的本质。
二、学习重、难点
重点: 弧度制概念的理解,弧度与角度的互化。
难点: 弧度制的建立与应用。
三、学法:
通过角度制与弧度制的对比学习,理解、掌握弧度制下的有关公式。
学 习 过 程
例1解:
例2解:
一、复习巩固(我明白这些知识) 1、什么叫正角?什么叫负角?什么叫零角? 2、写出与α角终边相同的角的集合。
3、用度作为单位来度量角的单位制叫做角度制,规定1 度的角等于 。
二 、新知探究(试一试,你一定会有收获的!)
我们介绍角的另一种表示方法:弧度制
1、弧度制的定义;在以单位长为半径的圆中, 的弧所对的圆心角为1弧度的角,它的单位符号是 ,读
作 ,以 作为单位度量角的单位制,叫做弧度制。
2、角度与弧度的互化
因为周角的弧度数是2π,而在角度制下它是︒360,
所以 =︒360 rad
=︒180 rad
=︒1 ≈rad rad
=rad 1()︒≈ = 例1、把45︒化成弧度。
例2、把rad 5
3π化成角。
3 、任意角的弧度数与实数的对应关系;
正角的弧度数是一个 ;负角的弧度数是一个 ;零角的弧度 数是 。
4、角的弧度数的计算 如果半径为r 的圆心角α所对弧的长为l ,那么角α的弧度数的绝对值是: α= 。
5、扇形弧长的计算: 弧度制:l = ;
角度制:l = 。
(n 表示角度数)
例3、已知扇形OAB 的圆心角α为120︒,半径为6 cm, 求扇形弧长及所含弓形面积。
例4、将下列各角化为2(02,)k k Z πααπ+≤<∈的形式,并判断其所在象限。
(1)193
π; (2) 315-︒; (3) 1485-︒。
例3解:
例4解:
1、解:
2、解:
3、解: 三、自我评价与课堂练习(相信自我,收获成功)
1、把下列度化成弧度:
15︒; 75︒; 6730'︒; 135-︒。
2、把下列弧度化成度:
73π-; 35π; 256
π; 5。
3、将下列各角化成2(02,)k k Z πααπ+≤<∈的形式,并判断其所在象限。
(1)163
π; (2)256π-; (3)173π-。
四、归纳整理,整体认识
(1)请学生回顾本节课所学过的知识内容有哪些?所涉及到的
主要数学思想方法有那些?
(2)在本节课的学习过程中,还有那些不太明白的地方,请向
老师提出。
(3)你在这节课中的表现怎样?你的体会是什么?。
