成都理工大学 高数下 重修 PPT D11_1对弧长曲线积分
合集下载
高等数学课件D111对弧长和曲线积分知识分享

证: 根据定义
n
L
f
(x,
y)ds
lim f
0k1
(k,k)sk
2020/8/3
高等数学课件
机动 目录 上页 下页 返回 结束
设各分点对应参数为 tk(k 0 ,1 , ,n ),
点 (k,k)对应参数为 k [tk 1,tk],
skttkk 1 2(t)2(t)dt
2 (k )2 (k ) tk, k [tk 1,tk]
例3. 计算 I x ds, 其中L为双纽线 L ( x 2 y 2 ) 2 a 2 ( x 2 y 2 )( a 0 )
解: 在极坐标系下 L:r2a2co2s,
y
它在第一象限部分为
ds
L 1 :r a c2 o( 0 s 4 )
o
x
利用对称性 , 得
I
4 L1
xds
404r()co sr2()r2()d
二、对弧长的曲线积分的计算法
基本思路: 求曲线积分 转 化 计算定积分
定理: 设f(x,y)是定义在光滑曲线弧
L:x(t),y (t)( t )
上的 L 连f 续( x 函,y 数) d ,s 则 曲 线f 积[ 分( t ) L,f(( xt) ,y)d] s2 存 ( t) 在 ,且2 ( t) d t
2020/8/3
高等数学课件
机动 目录 上页 下页 返回 结束
一、对弧长的曲线积分的概念与性质
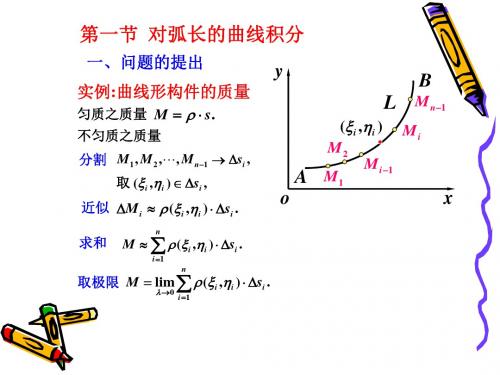
1.引例: 曲线形构件的质量
B
假设曲线形细长构件在空间所占
弧段为AB , 其线密度为 (x,y,z),
为计算此构件的质量, 采用
(k,k,k)
Mk Mskk1
“大化小, 常代变, 近似和, 求极限”
11-1对弧长的曲线积分22259
n
并作和式 f (i ,i ) si ,如果当各小弧段的 长度的最大值 0时, i 1
这和式的极限存在, 则称此极限为函数 f ( x, y)在曲线弧L上对弧长的
曲线积分或 第一类曲线积分, 记作L f ( x, y)ds,
被积函数
n
即:
L
f ( x, y)ds
lim
0
i 1
f (i ,i ) si
积分弧段
积分和式
对弧长
2、存在条件:
当 f ( x, y)在光滑曲线弧 L上连续时,
对弧长的曲线积分 L f ( x, y)ds 存在.
注意:1、若 L是分段光滑的 (L L1 L2 )
f ( x, y)ds f ( x, y)ds f ( x, y)ds.
L1 L2
L1
L2
2、函数f ( x, y)在闭曲线 L上对弧长的
曲线积分记为 L f ( x, y)ds.
3、推广
函数 f ( x, y, z)在空间曲线弧 上对弧长的曲线积分为
n
f ( x, y, z)ds
lim 0
i 1
f (i ,i , i ) si .
解 由对称性, 知 x2ds y2ds z2ds.
故 I 1 ( x2 y2 z2 )ds
3
a2 ds 3
2a3 . 3
( ds 2 a)
四、几何与物理意义
(1) 当( x, y)表示 L的线密度时, M L ( x, y)ds ;
解
I
2
y
2
1 ( y)2dy 2
并作和式 f (i ,i ) si ,如果当各小弧段的 长度的最大值 0时, i 1
这和式的极限存在, 则称此极限为函数 f ( x, y)在曲线弧L上对弧长的
曲线积分或 第一类曲线积分, 记作L f ( x, y)ds,
被积函数
n
即:
L
f ( x, y)ds
lim
0
i 1
f (i ,i ) si
积分弧段
积分和式
对弧长
2、存在条件:
当 f ( x, y)在光滑曲线弧 L上连续时,
对弧长的曲线积分 L f ( x, y)ds 存在.
注意:1、若 L是分段光滑的 (L L1 L2 )
f ( x, y)ds f ( x, y)ds f ( x, y)ds.
L1 L2
L1
L2
2、函数f ( x, y)在闭曲线 L上对弧长的
曲线积分记为 L f ( x, y)ds.
3、推广
函数 f ( x, y, z)在空间曲线弧 上对弧长的曲线积分为
n
f ( x, y, z)ds
lim 0
i 1
f (i ,i , i ) si .
解 由对称性, 知 x2ds y2ds z2ds.
故 I 1 ( x2 y2 z2 )ds
3
a2 ds 3
2a3 . 3
( ds 2 a)
四、几何与物理意义
(1) 当( x, y)表示 L的线密度时, M L ( x, y)ds ;
解
I
2
y
2
1 ( y)2dy 2
成都理工大学-高数下-重修-PPT-D11-2对坐标曲线积分市公开课一等奖省赛课获奖PPT课件

第二节
一、对坐标曲线积分概念 与性质
二、 对坐标曲线积分计算法
三、两类曲线积分之间联络
对坐标曲线积分
第1页
一、 对坐标曲线积分概念与性质
1. 引例: 变力沿曲线所作功.
设一质点受以下变力作用
在 xOy 平面内从点 A 沿光滑曲线弧 L 移动到点 B,
求移
“大化小”
沿 移动到
解: (1)
(2) 参数方程为
试求力场对质点所作功.
其中 为
第13页
例5. 求
其中
从 z 轴正向看为顺时针方向.
解: 取 参数方程
第14页
三、两类曲线积分之间联络
设有向光滑弧 L 以弧长为参数 参数方程为
已知L切向量方向余弦为
则两类曲线积分有以下联络
第15页
类似地, 在空间曲线 上两类曲线积分联络是
设 L 为xOy 平面内从 A 到B 一条有向光滑
弧,
若对 L 任意分割和在局部弧段上任意取点,
都存在,
在有向曲线弧 L 上
对坐标曲线积分,
则称此极限为函数
或第二类曲线积分.
其中,
L 称为积分弧段 或 积分曲线 .
称为被积函数 ,
在L 上定义了一个向量函数
极限
第5页
若 为空间曲线弧 , 记
称为对 x 曲线积分;
L 参数方程为
则曲线积分
连续,
存在, 且有
第8页
尤其是, 假如 L 方程为
则
对空间光滑曲线弧 :
类有
第9页
例1. 计算
其中L 为沿抛物线
解法1 取 x 为参数, 则
解法2 取 y 为参数, 则
高等数学课件--D11_1对弧长曲线积分

0
k 1
2 2
n
注意 (t ) (t ) 连续
lim f [ ( k ) lim( k ) f ( k , k ) sk , ] 0
0
k 1 k 1
2012-10-12 同济版高等数学课件
目录 上页 下页 返回 结束
n
n
因此
2012-10-12
2 cos ( 2 sin )
2
( 2 sin )
I 9
2
d 2d
2 0
2π
2 d 18 π
同济版高等数学课件
目录 上页 下页 返回 结束
例7. 有一半圆弧 其线密度 求它对原点处单位质量质点的引力.
解: d Fx k
d Fy k
目录
如果曲线 L 的方程为
则有
a
b
f ( x, ( x) ) 1 2 ( x) d x
如果方程为极坐标形式: L : r r ( ) ( ), 则
f ( r ( ) cos , r ( ) sin ) r 2 ( ) r 2 ( ) d
y O
L
y ds
( )
2
L R x
x R cos L: y R sin
3
R sin
2
2
2
( R sin ) ( R cos ) d
3
2
2
sin 2 R sin d 2 R 2 4
z ds
2
x ds
k 1
2 2
n
注意 (t ) (t ) 连续
lim f [ ( k ) lim( k ) f ( k , k ) sk , ] 0
0
k 1 k 1
2012-10-12 同济版高等数学课件
目录 上页 下页 返回 结束
n
n
因此
2012-10-12
2 cos ( 2 sin )
2
( 2 sin )
I 9
2
d 2d
2 0
2π
2 d 18 π
同济版高等数学课件
目录 上页 下页 返回 结束
例7. 有一半圆弧 其线密度 求它对原点处单位质量质点的引力.
解: d Fx k
d Fy k
目录
如果曲线 L 的方程为
则有
a
b
f ( x, ( x) ) 1 2 ( x) d x
如果方程为极坐标形式: L : r r ( ) ( ), 则
f ( r ( ) cos , r ( ) sin ) r 2 ( ) r 2 ( ) d
y O
L
y ds
( )
2
L R x
x R cos L: y R sin
3
R sin
2
2
2
( R sin ) ( R cos ) d
3
2
2
sin 2 R sin d 2 R 2 4
z ds
2
x ds
高等数学-第七版-课件-11-1 对弧长的曲线积分

四 、对弧长的曲线积分的应用
对弧长的曲线积分
一、对弧长的曲线积分的概念 二 、对弧长的曲线积分的性质
三 、对弧长的曲线积分的计算
四 、对弧长的曲线积分的应用
曲线弧的质心
x
L
x ( x , y )ds
L
(x ,y )ds
y
L
y ( x , y )ds
L
(x ,y )ds
(3) 在上述公式中,下限α一定小于上限β. (4) 口诀:变量参数化、一小二起下.
L
f ( x, y )ds f (t ), (t ) 2 ( t ) 2 ( t )dt ( )
特例 (1)
y ( x ) ( x0 x X ) L:
对弧长的曲线积分
一、 对弧长的曲线积分的概念
二 、对弧长的曲线积分的性质
三 、对弧长的曲线积分的计算 四 、对弧长的曲线积分的应用
线性性质
f( x, y) g( x, y) ds f ( x, y)ds g( x, y)ds. L L L
可加性
则曲线积分 L f ( x , y )ds存在, 且
L
f ( x, y )ds f (t ), (t ) 2 ( t ) 2 ( t )dt ( )
注
(1) 对弧长的曲线积分的计算归结为计算一个定积分!
(2) 化为定积分中的三个变化 L f(x,y) ds [α,β] f (t ), (t ) 2 ( t ) 2 ( t )dt
三 变 、 一 注 意
[α,β] 积分弧段 L 被积函数 f ( x , y ) f ( ( t ), ( t )) 弧长元素 ds 2 ( t ) 2 ( t )dt 一点注意 下限一定小于上限
对弧长的曲线积分
一、对弧长的曲线积分的概念 二 、对弧长的曲线积分的性质
三 、对弧长的曲线积分的计算
四 、对弧长的曲线积分的应用
曲线弧的质心
x
L
x ( x , y )ds
L
(x ,y )ds
y
L
y ( x , y )ds
L
(x ,y )ds
(3) 在上述公式中,下限α一定小于上限β. (4) 口诀:变量参数化、一小二起下.
L
f ( x, y )ds f (t ), (t ) 2 ( t ) 2 ( t )dt ( )
特例 (1)
y ( x ) ( x0 x X ) L:
对弧长的曲线积分
一、 对弧长的曲线积分的概念
二 、对弧长的曲线积分的性质
三 、对弧长的曲线积分的计算 四 、对弧长的曲线积分的应用
线性性质
f( x, y) g( x, y) ds f ( x, y)ds g( x, y)ds. L L L
可加性
则曲线积分 L f ( x , y )ds存在, 且
L
f ( x, y )ds f (t ), (t ) 2 ( t ) 2 ( t )dt ( )
注
(1) 对弧长的曲线积分的计算归结为计算一个定积分!
(2) 化为定积分中的三个变化 L f(x,y) ds [α,β] f (t ), (t ) 2 ( t ) 2 ( t )dt
三 变 、 一 注 意
[α,β] 积分弧段 L 被积函数 f ( x , y ) f ( ( t ), ( t )) 弧长元素 ds 2 ( t ) 2 ( t )dt 一点注意 下限一定小于上限
对弧长曲线积分课件

对弧长的曲线积分的结果是一个标量, 与积分路径无关,只与起点和终点有 关。
02 对弧长的曲线积分性质
线性性质
总结词
线性性质是指对弧长的曲线积分满足线性运算规则,即对弧长的曲线积分可以按照线性组合进行计算 。
详细描述
对于两个或多个函数的线性组合,其对应的对弧长的曲线积分等于各函数对弧长的曲线积分的线性组 合。即,如果 $f(x) 和 g(x)$ 是定义在同一直线上的函数,那么 $(f(x) + g(x))$ 的对弧长的曲线积分 等于 $f(x)$ 的对弧长的曲线积分加上 $g(x)$ 的对弧长的曲线积分。
要点二
平面曲线的面积
通过计算平面曲线围成的区域的面积,可以利用曲线积分 的方法。这种方法在几何学、物理学等领域有广泛应用。
平面曲线的曲率和挠率
平面曲线的曲率
曲率描述了曲线在某一点的弯曲程度。通过计算弧长曲 线积分,可以得到曲线的曲率。这对于分析曲线的形状 和性质具有重要意义。
平面曲线的挠率
挠率是描述曲线在垂直方向上的变化率,即曲线在某一 点的倾斜程度。通过计算弧长曲线积分,可以得到曲线 的挠率。这对于研究曲线的全局几何特征具有重要意义 。
积分区间的可加性
总结词
积分区间的可加性是指对弧长的曲线积分可以在不同的区间上分别计算,然后再 相加。
详细描述
如果函数 $f(x)$ 在两个不重叠的区间 $[a, b]$ 和 $[c, d]$ 上有定义,那么 $f(x)$ 在整个区间 $[a, b] cup [c, d]$ 上的对弧长的曲线积分等于在 $[a, b]$ 和 $[c, d]$ 上的对弧长的曲线积分之和。
03 对弧长的曲线积分的应用
平面曲线的长度
总结词
对弧长的曲线积分可以用来计算平面曲线的长度。
02 对弧长的曲线积分性质
线性性质
总结词
线性性质是指对弧长的曲线积分满足线性运算规则,即对弧长的曲线积分可以按照线性组合进行计算 。
详细描述
对于两个或多个函数的线性组合,其对应的对弧长的曲线积分等于各函数对弧长的曲线积分的线性组 合。即,如果 $f(x) 和 g(x)$ 是定义在同一直线上的函数,那么 $(f(x) + g(x))$ 的对弧长的曲线积分 等于 $f(x)$ 的对弧长的曲线积分加上 $g(x)$ 的对弧长的曲线积分。
要点二
平面曲线的面积
通过计算平面曲线围成的区域的面积,可以利用曲线积分 的方法。这种方法在几何学、物理学等领域有广泛应用。
平面曲线的曲率和挠率
平面曲线的曲率
曲率描述了曲线在某一点的弯曲程度。通过计算弧长曲 线积分,可以得到曲线的曲率。这对于分析曲线的形状 和性质具有重要意义。
平面曲线的挠率
挠率是描述曲线在垂直方向上的变化率,即曲线在某一 点的倾斜程度。通过计算弧长曲线积分,可以得到曲线 的挠率。这对于研究曲线的全局几何特征具有重要意义 。
积分区间的可加性
总结词
积分区间的可加性是指对弧长的曲线积分可以在不同的区间上分别计算,然后再 相加。
详细描述
如果函数 $f(x)$ 在两个不重叠的区间 $[a, b]$ 和 $[c, d]$ 上有定义,那么 $f(x)$ 在整个区间 $[a, b] cup [c, d]$ 上的对弧长的曲线积分等于在 $[a, b]$ 和 $[c, d]$ 上的对弧长的曲线积分之和。
03 对弧长的曲线积分的应用
平面曲线的长度
总结词
对弧长的曲线积分可以用来计算平面曲线的长度。
高等数学11.1对弧长的曲线积分

一、问题的提出
B L M n 1
( i , i ) M i M2 M i 1 M1
物质曲线L的质量M
A
o 分割 M 1 , M 2 , , M n1 其中一段弧为 si , 近似 取 ( i ,i ) si , M i ( i , i ) si .
x
近似值
(2)
f ( x , y ) 1,
L 弧长 ds ; L
z f ( x, y)
(3) 当 f ( x , y )表示立于L上的柱面
在 ( x , y ) 处的高时
S
柱面面积
s
L
L
f ( x , y )ds .
三、第一类曲线积分的计算
定理
设 f ( x , y )在曲线弧 L上有定义且连续 , x ( t ), ( t ) L的参数方程为 : y ( t ), 其中 ( t ), ( t )在[ , ]上具有一阶连续导数 , 且
( )
ds
r ( ) r ( )d ,
2 2
s
r 2 ( ) r 2 ( )d .
第十一章 曲线积分与曲面积分
定积分的积分区域: OX轴上的[a,b] 二重积分: 平面区域D 三重积分:空间区域Ω
§1.
一、问题的提出
对弧长的曲线积分
y
两个端点为A,B, 设有物质曲线L, 线密度为 在L上任意一点 M ( x , y ) 处,
纯粹物理的目的是揭示我们这个可 以认识的世界的规律,纯粹数学的目的 则是揭示人类认识能力的规律。 西尔维斯特(英国数学家) 数学是打开科学大门的 钥匙……轻视数学将造成对 一切知识的危害。 F.培根(英国思想家)
《对弧长的曲线积分》课件
其他实际问题中的应用
曲线积分可用于电路和工程学中描述电流和磁场的 路径积分。
四、总结
曲线积分和弧长的关系
曲线积分可以使用弧长来表示。曲线积分的计算 基于弧长。
总结和拓展
通过本课程,您已经了解了对弧长的曲线积分的 基本概念,计算方法和应用。您还可以拓展研究 其他应用,如计算弯曲量和曲率。
五、参考文献
曲线积分的计算可以分为第一型和第二
股定理计算弧长。
型的积分。第一型积分是对曲线在各点
的函数值进行积分,第二型积分是对曲
线的切线和每点法向量的积进行积分。
3
面积的计算
利用二重积分的方法,可以计算由曲线 围成的面积。这种计算有时是研究曲线 性质的关键。
三、应用
物理学中的应用
曲线积分可用于描述物理学上的某些概念,如力和 能量的路径的课程。本次课程将介绍如何计算弧长和曲 线积分,以及其应用于物理学和其他实际问题中。我们将深入研究这一主题, 让您从中受益。让我们开始吧!
一、基本概念
曲线积分的定义
曲线积分是指在弧线上的积分。它可以用来计算弧线上某些量的累积变化,如速度、位移和 质量分布。
弧长的概念
弧长是曲线从起点到终点的长度。它是计算曲线积分的基本量。
曲线的参数方程与弧长公式
曲线的参数方程可以用来方便地计算弧长。通常采用勾股定理和导数的知识来推导弧长公式。
二、计算方法
1
利用参数方程计算弧长
通过曲线的参数方程,我们可以得到它
曲线积分的计算方法
2
在每个点的切线,从而确定其弧长。通 过把切线摆放为三角形,我们可以用勾
• 高等数学教材 • 学术论文及期刊
11-1对弧长的曲线积分 (2)

ea 1.
于是, e x2 y2 ds L
e x2 y2 ds
e x2 y2 ds e x2 y2 ds
oA
AB
oB
(ea
1)
a
4
ea
(ea
1)
(2 a )ea 2.
4
返回
【例7】计算
其中为球面 x2 y2
z2
9 2
与平面x
z
1 的交线.
【解】
:
1 2
(
x
1 2
L
:
x y
(
y.
y),
c y d.
ds 1 2( y) dy.
L f ( x, y)ds cd f [ ( y), y] 1 2( y)dy. (c d ) 返回
例6 求I L yds,
其中L : y2 4x,从(1,2)到(1,2)一段.
解 L : x ( y) y2 , 2 y 2.
4
( y)
y 2
.
I L yds
22 y
1 ( y )2 dy 2
y y2 4x
2
o1 x
2
2
2
y
1
y2 4
dy
0.
返回
Ex 计算 e x2 y2 ds. 其中L是由曲线 x 2 y 2 a 2 , 直 L 线 x 0, 和y x 在第一象限中所围的图形边界。
解
e x2 y2 ds
L
e x2 y2 ds
e x2 y2 ds e x2 y2 ds
oA
AB
oB
oA : x 0, 0 y a. ds dy.
y
e x2 y2 ds
11-1对弧长的曲线积分-PPT精品文档31页

f(x ,y ) d s b f[x ,(x )1 ]2 (x ) d.x(ab)
L
a
西南科技大学理学院
( 2 ) L : x ( y ) c y d .
f(x ,y ) d s df[(y )y ] ,1 2 (y ) d .y
L
c
(cd)
西南科技大学理学院
2 、 x 2 yzds , 其 中 L 为 折 线 ABCD , 这 里 A , B , C , D 依 次 为 点 (0,0,0),(0,0,2),(1,0,2),(1,3,2);
3 、 ( x 2 y 2 )ds , 其 中 L 为 曲 线 L
x a (cos t t sin t )
西南科技大学理学院
4.性质
( 1 ) L [ f ( x , y ) g ( x , y ) d ] L f s ( x , y ) d L g s ( x , y ) d . s
(2 )L k(x f,y )d s k L f(x ,y )ds (k 为)常 . 数
积分弧段
曲线形构件的质量 ML(x,y)d.s
西南科技大学理学院
2.存在条件:
当f(x, y)在光滑曲 L上线 连弧 ,续 对时 弧长的曲线
Lf(x,y)ds存.在
3.推广:
函数 f(x,y,z)在空间 曲 上线 对弧 弧长的曲线积
n
f(x ,y,z)d sl i0im 1f(i,i,i) si.
y
a (sin
t t cos
t)
(0 t 2 ) ;
4、 计 算 L y ds ,其 中 L 为 双 纽 线
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
转化
计算定积分
是定义在光滑曲线弧 且
上的连续函数, 则曲线积分
L
f ( x, y ) d s
f [ (t ) , (t )] 2 (t ) 2 (t ) d t
n
证: 根据定义
lim f ( k , k )sk
0 k 1
目录 上页 下页 返回 结束
3
2
1
0
O
1x
目录
上页
下页
返回
结束
例3. 计算
其中L为双纽线
(x2 y2 ) 2 a2 (x2 y2 ) ( a 0 )
解: 在极坐标系下
它在第一象限部分为
y
(0 π ) 4
π 4 r cos
L1 : r a cos 2
利用对称性 , 得
O
x
4 4
目录 上页 下页 返回 结束
例6. 计算
其中 为球面
x 2 y 2 z 2 9 与平面 x z 1的交线 . 2
1 ( x 1 )2 1 y 2 1 2 4 , 化为参数方程 解: : 2 x z 1 x 2 cos 1 2 0 2π : y 2 sin z 1 2 cos 2 则
ds
( 2 sin )
2
( 2 sin ) d 2d
2
9 2π I 2 d 18 π 2 0
目录 上页 下页 返回 结束
思考与练习
y x2 y2 1周长为a , 求 1. 已知椭圆 L : 3 4 3 (2 xy 3x 2 4 y 2 ) ds 2 O 2x L
在曲线
都存在, 则称此极限为函数
上对弧长的曲线积分, 或第一类曲线积分. 称为被积函数, 称为积分弧段 .
曲线形构件的质量 M ( x, y, z ) ds
目录 上页 下页
Mk sk M k 1
返回
结束
如果 L 是 xOy 面上的曲线弧, 则定义对第一类曲线积 分为 n
lim( ] lim f [ ( k ) 0 k ) f ( k , k )sk ,
0 k 1
k 1
目录 上页 下页 返回 结束
n
因此
说明:
(1) sk 0, t k 0, 因此积分限必须满足 !
(2) 注意到
ds (d x) 2 (d y ) 2 (t ) (t ) d t
L f ( x, y) ds lim0 f ( k ,k )sk k 1
如果 L 是闭曲线 , 则记为 f ( x, y ) ds . L 思考: 若在 L 上 f (x, y)≡1, 问 d s 表示什么?
L
目录
上页
下页
返回
结束
二、对弧长的曲线积分的计算法
基本思路: 求曲线积分 定理:
因此上述计算公式相当于“换元法”.
y
ds d y dx x x
上页 下页 返回 结束
2
2
O
目录
如果曲线 L 的方程为
b
则有
f ( x, ( x) ) 1 2 ( x) d x a
如果方程为极坐标形式: L : r r ( ) ( ), 则
f (r ( ) cos , r ( ) sin ) r 2 ( ) r 2 ( ) d
推广: 设空间曲线弧的参数方程为
: x (t ), y (t ) , z (t ) ( t )
则
f ( x, y , z ) d s
f ( (t ) , (t ), (t ) ) 2 (t ) 2 (t ) 2 (t ) d t
设各分点对应参数为
点 ( k ,k ) 对应参数为
s k
则
tk
t k 1
2 (t ) 2 (t ) d t
2 ( k ) 2 ( k ) t k ,
lim f [ ( k ) , ( k ) ]
0 k 1
n
n
注意 2 (t ) 2 (t ) 连续
π 0 4 a 2 cos
0
r 2 ( ) r 2 ( ) d
d
目录 上页 下页 返回 结束
例4. 计算曲线积分 线
其中 为螺旋
的一段弧.
2
解:
( x
2
y z ) ds
2
a k
2
2
0
2π
[a 2 k 2 t 2 ] d t
2π 2 a k 2 (3a 2 4 π 2 k 2 ) 3
第一类曲线积分
目录
上页
下页
返回
结束
一、第一类曲线积分的概念与性质
1.引例: 曲线形构件的质量 假设曲线形细长构件在空间所占 弧段为AB , 其线密度为
B
Mk ( k ,k , k ) s k M k 1
为计算此构件的质量, 采用
n
“大化小, 常代变, 近似和, 求极限”
可得
M
A
k 1
目录
上页
下页
返回
结束
2.定义
设 是空间中一条有限长的光滑曲线,
义在 上的一个有界函数, 若通过对 的任意分割 和对
局部的任意取点, 下列“乘积和式极限”
( k ,k , k )
f ( k ,k , k )sk 0
lim
记作
k 1
n
f ( x, y , z ) d s
目录 上页 下页 返回 结束
例1. 计算
其中 L 是抛物线
上点 O (0,0)
与点 B (1,1) 之间的一段弧 . 解: L : y x 2 ( 0 x 1)
x x 1 4 x 2 dx
0 0 1
1
y
B(1,1)
y x2 L
1 (1 4x 2 ) 12 1 ( 5 5 1) 12
提示: 利用对称性
L 2 xy ds 0
x2 y2 原式 = 12 ( )ds 12 ds 12a L 4 L 3
分析:
L
2 xy ds
L上
2 xy ds
L下
2 xyds
2x
2 x( )
目录 上页 下页 返回 结束
计算定积分
是定义在光滑曲线弧 且
上的连续函数, 则曲线积分
L
f ( x, y ) d s
f [ (t ) , (t )] 2 (t ) 2 (t ) d t
n
证: 根据定义
lim f ( k , k )sk
0 k 1
目录 上页 下页 返回 结束
3
2
1
0
O
1x
目录
上页
下页
返回
结束
例3. 计算
其中L为双纽线
(x2 y2 ) 2 a2 (x2 y2 ) ( a 0 )
解: 在极坐标系下
它在第一象限部分为
y
(0 π ) 4
π 4 r cos
L1 : r a cos 2
利用对称性 , 得
O
x
4 4
目录 上页 下页 返回 结束
例6. 计算
其中 为球面
x 2 y 2 z 2 9 与平面 x z 1的交线 . 2
1 ( x 1 )2 1 y 2 1 2 4 , 化为参数方程 解: : 2 x z 1 x 2 cos 1 2 0 2π : y 2 sin z 1 2 cos 2 则
ds
( 2 sin )
2
( 2 sin ) d 2d
2
9 2π I 2 d 18 π 2 0
目录 上页 下页 返回 结束
思考与练习
y x2 y2 1周长为a , 求 1. 已知椭圆 L : 3 4 3 (2 xy 3x 2 4 y 2 ) ds 2 O 2x L
在曲线
都存在, 则称此极限为函数
上对弧长的曲线积分, 或第一类曲线积分. 称为被积函数, 称为积分弧段 .
曲线形构件的质量 M ( x, y, z ) ds
目录 上页 下页
Mk sk M k 1
返回
结束
如果 L 是 xOy 面上的曲线弧, 则定义对第一类曲线积 分为 n
lim( ] lim f [ ( k ) 0 k ) f ( k , k )sk ,
0 k 1
k 1
目录 上页 下页 返回 结束
n
因此
说明:
(1) sk 0, t k 0, 因此积分限必须满足 !
(2) 注意到
ds (d x) 2 (d y ) 2 (t ) (t ) d t
L f ( x, y) ds lim0 f ( k ,k )sk k 1
如果 L 是闭曲线 , 则记为 f ( x, y ) ds . L 思考: 若在 L 上 f (x, y)≡1, 问 d s 表示什么?
L
目录
上页
下页
返回
结束
二、对弧长的曲线积分的计算法
基本思路: 求曲线积分 定理:
因此上述计算公式相当于“换元法”.
y
ds d y dx x x
上页 下页 返回 结束
2
2
O
目录
如果曲线 L 的方程为
b
则有
f ( x, ( x) ) 1 2 ( x) d x a
如果方程为极坐标形式: L : r r ( ) ( ), 则
f (r ( ) cos , r ( ) sin ) r 2 ( ) r 2 ( ) d
推广: 设空间曲线弧的参数方程为
: x (t ), y (t ) , z (t ) ( t )
则
f ( x, y , z ) d s
f ( (t ) , (t ), (t ) ) 2 (t ) 2 (t ) 2 (t ) d t
设各分点对应参数为
点 ( k ,k ) 对应参数为
s k
则
tk
t k 1
2 (t ) 2 (t ) d t
2 ( k ) 2 ( k ) t k ,
lim f [ ( k ) , ( k ) ]
0 k 1
n
n
注意 2 (t ) 2 (t ) 连续
π 0 4 a 2 cos
0
r 2 ( ) r 2 ( ) d
d
目录 上页 下页 返回 结束
例4. 计算曲线积分 线
其中 为螺旋
的一段弧.
2
解:
( x
2
y z ) ds
2
a k
2
2
0
2π
[a 2 k 2 t 2 ] d t
2π 2 a k 2 (3a 2 4 π 2 k 2 ) 3
第一类曲线积分
目录
上页
下页
返回
结束
一、第一类曲线积分的概念与性质
1.引例: 曲线形构件的质量 假设曲线形细长构件在空间所占 弧段为AB , 其线密度为
B
Mk ( k ,k , k ) s k M k 1
为计算此构件的质量, 采用
n
“大化小, 常代变, 近似和, 求极限”
可得
M
A
k 1
目录
上页
下页
返回
结束
2.定义
设 是空间中一条有限长的光滑曲线,
义在 上的一个有界函数, 若通过对 的任意分割 和对
局部的任意取点, 下列“乘积和式极限”
( k ,k , k )
f ( k ,k , k )sk 0
lim
记作
k 1
n
f ( x, y , z ) d s
目录 上页 下页 返回 结束
例1. 计算
其中 L 是抛物线
上点 O (0,0)
与点 B (1,1) 之间的一段弧 . 解: L : y x 2 ( 0 x 1)
x x 1 4 x 2 dx
0 0 1
1
y
B(1,1)
y x2 L
1 (1 4x 2 ) 12 1 ( 5 5 1) 12
提示: 利用对称性
L 2 xy ds 0
x2 y2 原式 = 12 ( )ds 12 ds 12a L 4 L 3
分析:
L
2 xy ds
L上
2 xy ds
L下
2 xyds
2x
2 x( )
目录 上页 下页 返回 结束
