5.21三垂线定理练习题
三垂直模型经典例题

三垂直模型经典例题
下面是一个经典的三垂直模型例题:
已知直角三角形ABC中,角A = 90°,垂足为D。
边长AC = 8cm,边长AB = 6cm。
求垂直AD的长度。
解法:
首先用勾股定理计算出BC的长度:BC = √(AC^2 - AB^2) = √(8^2
- 6^2) = √(64 - 36) = √28 = 2√7 cm。
根据垂直模型中的定理,垂直AD和BD的长度应满足:AD/BD = AC/BC。
代入已知条件进行计算:AD/BD = 8/2√7,将BD移到分母上:AD = 8BD/2√7,简化得到:AD = 4BD/√7 cm。
计算BD的长度可以利用勾股定理:BD = √(AB^2 - AD^2) =
√(6^2 - (4BD/√7)^2) = √(36 - (16BD^2/7))。
将这个方程两边平方,整理得到:49BD^2 = 7(36 - 16BD^2/7),继续整理得到:49BD^2 = 252 - 16BD^2,合并同类项得到:65BD^2 = 252,解得:BD^2 = 252/65。
求开平方根得到:BD = √(252/65) cm。
将BD的值代入前面的表达式中,计算出AD的长度:AD =
4(√(252/65))/√7 = 4√(252/7)/√65 cm。
垂直AD的长度为4√(252/7)/√65 cm,约等于2.78 cm。
三垂线定理

1.直接利用三垂线定理证明下列各题:
(1) PA⊥正方形ABCD所在平面,O为对角线BD的中点 求证:PO⊥BD,PC⊥BD (2) 已知:PA⊥平面PBC,PB=PC,M是BC的中点, 求证:BC⊥AM
(3) 在正方体AC1中,求证:A1C⊥B1D1,A1C⊥BC1
P
P
D1
C1
A
D
O
A
B
C
(1)
∴ ∠AFC= ∠MDF , ∴ ∠DMF+∠AFC=∠DMF+∠MDF= 90°,
∴ DM ⊥AF,又ABC-DEF为直三棱柱,∴ CF⊥EF,又EF⊥DF,∴ EF⊥平面AF,由三 垂线定理知AE⊥DM
能力拓展:
2、过Rt ∆BPC的直角顶点P作线段PA ⊥平面BPC,求证: ∆ABC的垂心H是P点在平面ABC内的射影。
3. 如果一个角所在平面外一点到角的两边距离相等 那么这一点在平面上的射影在这个角的平分线上。
已知:∠BAC在平面内,点P,PE⊥AB,PF⊥AC,
PO⊥ ,垂足分别是E、F、O,PE=PF
求证:∠BAO=∠CAO
P
分析: 要证 ∠BAO=∠CAO
只须证OE=OF, OE⊥AB,OF⊥AC
?
?
?
A
高三数学三垂线定理

[单选,A1型题]女婴,11个月,其营养需要与成人最主要的不同之处是()A.基础代谢所需的营养素和能量B.生长发育所需的营养素和热量C.食物特殊动力作用所需的热量D.活动所需的营养素与热量E.排泄物中热量的损失 [多选]以下计量单位的符号,其表达错误的是()。A.msB.KmC.nmD.mμmE.1/m3 [问答题,简答题]发电机强励值是多少? [填空题]1780年,女服中出现一种机能性的夹克叫() [多选]MEN2的筛查项目包括()。A.RET基因突变筛查B.基础和刺激后的血清降钙素C.尿儿茶酚胺和甲氧基肾上腺素D.血清钙E.空腹血糖 [单选]下面可以作为知识产权投资入股的是()A、专利许可使用权B、专利权C、著作改编权D、连锁经营权 [单选]产褥期保健重点不包括以下哪几项()。A.注意产妇情绪变化B.采用孕产妇营养膳食C.注射乙肝疫苗D.指导母乳喂养E.注意卫生 [单选]从()入手,立足当前,着眼长远,整体推进,突出重点,综合施策,标本兼治,全面提高质量管理水平,推动建设质量强国,促进经济社会又好又快发展。A.强化法治、落实责任、加强惩处、增强全社会质量意识;B.强化法制、落实责任、加强监督、增强全社会质量意识;C.强化法治、 [单选]队列研究()A.只能计算比值比来估计相对危险度B.不能计算相对危险度C.不能计算特异危险度D.既可计算相对危险度,又可计算特异危险度E.既不能计算特异危险度,也不能计算相对危险度 [单选]下列各项中,属于企业现金流量表“经营活动产生的现金流量”的是()。A.收到的现金股利B.支付的银行借款利息C.收到的处置价款D.支付的经营租赁租金 [判断题]检验检疫机构对获得《出口玩具质量许可证》企业出口的玩具实行抽查检验。()A.正确B.错误 [单选]有关肠源性感染的描述,哪一项不正确()A.与肠道菌群失调有关B.与肠粘膜屏障功能损害有关C.肠源性感染主要引起肠道功能失调D.与免疫功能下降有关E.肠道细菌和毒素可经肠道侵入播散全身 [单选]下列有关脊柱的描述哪项错误()A.由椎骨以及椎间盘、椎间关节、韧带等连接装置组成B.有四个生理弯曲C.仰卧位时T最高D.仰卧位时T最低E.椎管内有三个潜在的腔隙 [填空题]流挂的主要原因有:()、()等。 [单选]下列哪一项不构成商业秘密侵权()A.以盗窃、利诱、胁迫或者其他不正当手段获取权利人的商业秘密B.违反约定或者违反权利人保守秘密的要求、披露、使用或者允许他人使用所掌握的商业秘密的行为C.披露、使用或者许可他人使用以上述手段获取的商业秘密的行为D.第三人不知或不应 [问答题,简答题]提升机电气设备火灾的防范措施有哪些? [单选]能够用于激光光动力疗法的药物是()A.吲哚青绿B.荧光素钠C.丙酮D.血卟啉衍生物E.甲醇 [单选]作出具体行政行为的公务员,因其是以所在国家行政机关的名义进行,()。A.故成为行政诉讼的共同被告B.故成为行政诉讼的被告C.故不能成为行政诉讼的第三人D.故不能成为行政诉讼的被告 [填空题]地秤推拉支点和重点时,若在承载器上加砝码后计量杠杆达到平衡,其示值误差是()。 [单选]以下属于工人培训的有()。A.岗位培训B.继续教育C.学历教育D.班组长培训 [问答题,论述题]激励问题成员的方法有哪些? [单选]行政不当是指行政主体所为的同行政违法相并列的一种有()的行为。A.瑕疵B.错误C.不当D.责任 [单选]()既标识了一个网络,又标识了该网络上的一台特定主机。A.主机名B.MAC地址C.IP地址D.物理地址 [填空题]所有电气设备的()均应有良好的接地装置。使用中不准将接地装置()或对其进行()。 [填空题]R717的标准沸点是(),凝固温度是()。 [填空题]消费心理学的发展史可分为萌芽草创阶段、()阶段和确立地位阶段。 [单选]脑栓塞的临床表现不正确的是()。A.患者较年轻B.多有风湿性心瓣膜病史C.起病急骤D.多有脑膜刺激征E.可有偏瘫失语 [填空题]真正的客户服务是根据客户()使他获得满足,而最终使客户感觉到他受到重视,把这种好感铭刻在他的心里,成为企业的忠实的客户。 [单选,A型题]以下哪项不属于食管的生理性狭窄()A.与咽连接处B.主动脉弓压迹C.左主支气管压迹D.食管下段鸟嘴样狭窄E.与胃连接部位 [单选,A2型题,A1/A2型题]关于有机氯农药叙述不正确的是()。A.有致畸性和致癌性B.急性中毒可出现肝肾损伤C.我国现已停止生产使用D.慢性中毒损害肝脏、血液E.蓄积性强但易降解 [问答题,案例分析题]男性,66岁。主诉:反复咳嗽、咳痰9年,加重1周就诊。请针对该案例,说明问诊内容与技巧。 [单选,A2型题,A1/A2型题]对自杀及其预防的认识正确的是()A.自杀的人是真的想死B.谈论自杀的人不会真的去死C.不能与有自杀念头的人谈自杀D.有自杀行为者需要精神医学干预E.危机过去也就是意味着自杀危险性结束 [单选]船舶对水航程SL,对地航程SG,船速VE,航时t,若SL<VEt,且SG>SL,则船舶航行在()情况下。A.顺风顺流B.顶风顶流C.顺风顶流D.顶风顺流 [问答题,简答题]消毒 [问答题,简答题]写出机械效率的定义式,并分析影响机械效率的因素。 [单选,A4型题,A3/A4型题]男,30岁,反复阵发性心动过速史10余年,每次心动过速突然发作,持续数十分钟至数小时,此次心动过速发作1小时而来医院就诊。体格检查:BP100/70mmHg,心脏无扩大,心率200次/分,节律规则。最可能的临床诊断为()A.阵发性室性心动过速B.阵发性室上性心动 [单选,A1型题]有尿意即迫不及待地要排尿且难以自控,是()A.尿失禁B.尿潴留C.尿频D.尿急E.尿痛 [单选,A2型题,A1/A2型题]半抗原通常须与下列何种物质结合才具免疫原性()。A.羊毛脂B.免疫佐剂C.免疫增强剂D.液状石蜡E.载体 [单选]紫花地丁来源于()A.菊科B.豆科C.毛茛科D.堇菜科E.唇形科 [单选,A1型题]关于免疫耐受,错误的是()A.多次注射耐受原可延长免疫耐受状态B.静脉注射抗原易诱导免疫耐受C.聚合的蛋白抗原易诱导免疫耐受D.遗传背景与免疫耐受相关E.克隆清除是形成免疫耐受的机制之一
三垂线定理和其典型例题
解: 作PH⊥平面ABC, P
连AH交BC于E,连PE
∵PA、PB、PC两两垂直
∴PA⊥平面PBC ∴PA⊥BC
AH为PA在平面ABC内旳射影 A H
C E
∴BC⊥AH
B
在Rt△PBC中,PE= -4--×-6-- = -1-2--
42+62
13
在Rt△APE中,AE= PA2+PE2= 9+ -11-43-4 = -2-1-32--9
.P α
思索:
1。两条异面直线在同一平面 内旳射影旳位置关系怎样?
2。一种三角形在另一平面 中旳射影可能是什么图形?
二、平面旳斜线、垂线、射影
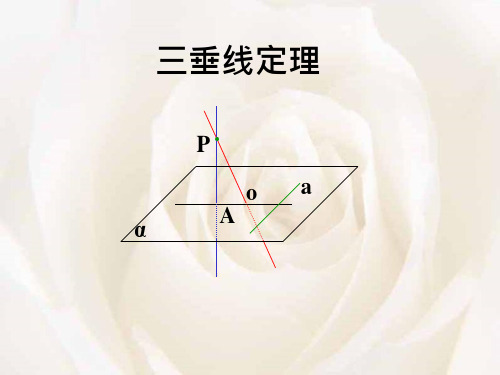
三垂线定理
PO是平面α旳斜线, O为斜足; PA是平面α旳垂线, A为垂足; AO是PO在平面α内旳射影.
P
oa
假如a α, a⊥AO,
α
A
思索a与PO旳位置关
系怎样?
结论:a⊥PO 为何呢?
二、三垂线定理:
三垂线定理
在平面内旳一条直线,假如和这个平面旳一条
斜线旳射影垂直,那么它也和这条斜线垂直。
PA⊥α aα
① PA⊥a AO⊥a
② a⊥平面PAO PO 平面PAO
③
a⊥PO
P
a
Ao α
① 线面垂直
②
③
线线垂直
线面垂直
线线垂直
性质定理
鉴定定理
性质定理
对三垂线定理旳阐明:
A
B
90°
C
45°
D
小结
三垂线定理
三垂线定理:在平面内旳一条直线,假如 和这个平面旳一条斜线旳射影垂直,那么它也 和这条斜线垂直。
高三数学三垂线定理

[单选]某公司目标资本结构为权益资本与债务资本各占50%,明年将继续保持。已知今年实现税后利润600万元,预计明年需要增加投资资本800万元,假设流通在外普通股为200万股,如果采取剩余股利政策,明年股东可获每股股利为()。A、1元B、2元C、3元D、5元 [多选]根据我国《民法通则》以及相关的法律规范的规定,能够引起债的发生的法律事实,即债的发生根据,主要有()。A.不当得利B.无因管理C.合同D.侵权行为E.不可抗力 [单选]下列基质中,不适于栽培根系纤细的花卉植物的是()。A、珍珠岩B、陶粒C、水D、岩棉 [单选]修船质量的好坏,关系着船舶的使用寿命和经济性,因此必须抓好修理前的准备、修理时的监修和修理后的()三个主要工作环节,以确保短修期、低修费、高质量的船舶修理。A.试验B.调校C.检查D.验收 [单选,A2型题,A1/A2型题]Hayem液中NaCl的主要作用是()A.调节细胞渗透压B.防腐作用C.防止细胞黏附D.固定细胞形态E.提高稀释液比密 [单选]甲公司持有一张商业汇票,到期委托开户银行向承兑人收取票款。甲公司行使的票据权利是()。A.付款请求权B.利益返还请求权C.票据追索权D.票据返还请求权 [名词解释]人员配备 [单选]对多发性骨髓瘤诊断具有决定性意义的检查是()A.骨髓穿刺涂片形态学检查B.外周血涂片检查C.血沉测定D.血清钙、磷和碱性磷酸酶测定E.血清免疫电泳 [问答题]一架装载如下的飞机的地板的最小承载限制是多少?货盘尺寸-长37.5宽35货盘重量-34磅系留装置-23磅货物重量-1,255.4磅 [单选]26岁,女,婚后2年未孕,月经规律,现停经41天,近1周觉乳房胀痛,尿妊娠试验阳性,基础体温曲线示高温相已达28天,最可能的诊断为().A.卵巢早衰B.早期妊娠C.月经前期D.子宫性闭经E.垂体性闭经 [单选]卧式锅壳式蒸汽锅炉,锅壳内上部为蒸汽,下部为水,()必须浸没于水中。A、锅壳B、烟管C、喉管D、集箱 [单选]石油凝固点高低与其()量有关。A.蜡B.胶质C.硫D.碳 [单选]何谓"六气"()A.风、湿B.寒、火C.暑D.燥E.以上都是 [判断题]各种定期储蓄存款的到期日,以对年、对月、对日为准。如遇到期日为该月没有的日期,以月底为到期日。A.正确B.错误 [单选,A2型题,A1/A2型题]乌梅丸证的治法是()。A.寒温并用,健脾除湿B.清上温下,安蛔止痛C.寒温并用,和胃消痞D.寒温并用,健脾止利E.清上温下,安蛔止呕 [多选]建设工程债产生的根据有()。A.合同B.侵权C.公正D.不当得利E.无因管理 [单选]乳腺癌CDFI特点是()。A.无血流信号B.彩色血流不丰富,血管数目少C.彩色血流丰富,呈高速低阻血流D.彩色血流丰富,呈高速高阻血流E.彩色血流不丰富,呈高速低阻血流 [单选]描述尾状叶位置错误的是A.位于门脉横部的后方B.位于肝圆韧带的下方C.位于静脉韧带的右后方D.位于下腔静脉的左前方E.位于静脉韧带后、下腔静脉前方 [多选]高压断路器按用划分,除有发电机保护用断路器外,还应有()。A.电动机用断路器B.线路用断路器C.供电用断路器D.变压器用断路器 [单选]该病房楼内设有上下层相连通的走廊、敞开楼梯、自动扶梯、传送带等开口部位时,应按上下连通层作为一个防火分区,其允许最大建筑面积之和不应超过《高层民用建筑设计防火规范(2005年版)》(GB50045--1995)的规定。当上下开口部位设有()等分隔设施时,其面积可不叠加计算。 [单选]为了保护未成年人的身心健康及其合法权益,促进未成年人健康成长,根据宪法,我国制定了《中华人民共和国未成年人保护法》,下列描述与《未成年人保护法》不一致的是:()A.保护未成年人,主要是学校老师和家长共同的责任。B.教育与保护相结合是保护未成年人工作应遵循的 [单选]关于骨肿瘤手术后的护理措施,下面描述不正确的是()A.术后抬高患肢,预防肿胀B.髋部手术,髋关节外展中立或内旋C.术后48小时开始作肌肉的等长收缩D.良性肿瘤术后3周开始功能锻炼E.人工关节置换术者,手术2~3周后功能锻炼 [单选,A1型题]下列哪项不符合一侧动眼神经麻痹()。A.上睑下垂,眼球不能向上、下和内侧转动B.眼球向对侧、向上、向下注视时出现复视C.眼球向外或外下方斜视D.瞳孔散大,光反射消失,调节反射存在E.瞳孔散大,光反射及调节反射均消失 [单选]关于现代出版业行业用语“页”“面”“页码”的说法,错误的是()。A."页码"用于标注书页的张数B."1页"就是"1张"C.任何一种书刊的面数都是偶数D.出版业务中应尽量用"面"表示书页数量 [单选]事业单位在财产清查中发现事业用材料盘亏,其中属于正常损耗的应()。A.计入当期经营支出B.计入当期事业支出C.直接抵减一般基金D.冲减事业用材料盘盈价值 [单选]“医院”的正确读音是()。A、yiyuànB、yīyuànC、yīyuàngD、yīyuè [单选]()通过手指上的弯曲传感器、扭曲传感器和手掌上的弯度传感器、弧度传感器,来确定手及关节的位置和方向,从而实现环境中的虚拟手及其对虚拟物体的操纵。A.跟踪球B.数据手套C.头盔显示器D.立体眼镜 [单选]金属与电解质溶液接触,经过一定的时间之后,可以获得一个稳定的电位值,这个电位值通常称之为()。A.保护电位B.腐蚀电位C.开路电位D.闭路电位 [单选]对于大型人员密集场所或特殊工程外的一般建设工程,其消防验收方式为()。A.施工单位应当向公安机关消防机构申请消防验收B.建设单位应当先行备案后进行消防验收C.可以不经消防验收,由公安机关消防机构进行抽查D.在验收后应当报公安机关消防机构备案 [单选]砂、石筛应采用()孔筛。A.方B.圆C.三角 [名词解释]欲望 [单选]职业道德不仅有(),也有一定的历史继承性。A、价值观念B、技术延续C、法律色彩D、创造性 [单选]调查单位和调查对象是个体和总体关系。如调查对象是全部工业企业,则调查单位是()。A.每一工业企业中的每个职工B.每一工业企业中的厂长C.每一工业企业由的每个车间D.每一工业企业 [单选,A2型题,A1/A2型题]关于会阴的描述,正确的是()A.广义的会阴前方为耻骨联合上缘B.狭义的会阴是指尿道口与肛门之间的软组织C.会阴包括皮肤、肌肉、筋膜及骨骼D.会阴体厚3~4cm,呈楔状E.会阴组织妊娠时的延展性差,分娩时容易裂伤 [填空题]媒介组合可有多种方式,最主要的方式有三种:()组合、()组合、自用媒介与租用媒介组合。 [单选]规定采矿许可证制度的法律是()。A.煤炭法B.矿产资源法C.矿山安全法D.安全生产法 [判断题]浮选精矿灰分高时,应减少捕收剂用量;尾矿灰分高时,想提高尾煤泥发热量,应减少捕收剂用量。A.正确B.错误 [填空题]洗液用到出现()时就失去了去污能力,不能继续使用. [单选,A1型题]长期全胃肠外营养(TPN)病人,出现高渗性非酮性昏迷的主要原因是()A.微量元素缺乏B.深静脉插管感染致败血症C.渗透性利尿,水、电解质失衡D.病人胰岛素方面不足E.内毒素中毒 [单选]根据企业所得税法律制度的规定,下列各项中,在计算企业所得税时适用25%税率的是()。A.在中国境内设立机构、场所且取得的所得与其所设机构、场所有实际联系的非居民企业B.符合条件的小型微利企业C.国家需要重点扶持的高新技术企业D.在中国境内未设立机构、场所的非居民企
三垂线定理及其逆定理测试题(含答案)

三垂线定理及其逆定理测试题(含答案)
三垂线定理是平面几何中的基本定理之一,它指出:在一个三角形中,三条垂线的交点是三角形的垂心。
同时,如果在一个三角形中,垂心落在三角形内部,那么这个三角形是锐角三角形;如果垂心落在三角形外部,那么这个三角形是钝角三角形。
在解题时,需要掌握三垂线定理的基本概念和性质。
例如,在一个直角三角形中,垂线的长度恰好等于斜边的一半;在一个等边三角形中,垂线的长度恰好等于高的三分之一。
此外,还需要掌握一些相关的定理和公式,例如勾股定理、正弦定理、余弦定理等。
通过掌握三垂线定理及其相关知识,可以解决各种三角形的问题,例如求三角形的周长、面积、角度等。
同时,三垂线定理也是其他几何定理的基础,例如欧拉线定理、费马点定理等。
总之,掌握三垂线定理及其相关知识,对于解决平面几何问题具有重要的意义。
三垂线定理练习课一

三垂线定理练习课一教学目标1.进一步理解、记忆并应用三垂线定理及其逆定理;2.理解公式cosθ1·cosθ2=cosθ的证明及其初步应用;3.理解正方体的体对角线与其异面的面对角线互相垂直及其应用;教学重点和难点教学的重点是进一步掌握三垂线定理及其逆定理并应用它们来解有关的题.教学的难点是在讲公式cosθ1·cosθ2=cosθ应用时比较θ2与θ的大小.教学设计过程例1如图1,AB和平面α所成的角是θ1;AC在平面α内,BB′⊥平面α于B′,AC和AB的射影AB′成角θ2,设∠BAC=θ.求证:cosθ1·cosθ2=cosθ.(1)θ2=90°,因为θ2=90°,所以cosθ2=0,因此cosθ=cosθ1·cosθ2=0,故θ=90°.当θ=90°时,我们也可以证明θ2=90°.一条直线如果和斜线的射影垂直,那么它就和斜线垂直.这就是三垂线定理.一条直线如果和斜线垂直,那么它就和斜线的射影垂直.这就是三垂线定理的逆定理.所以,我们可以这样说,这个公式是三垂线定理及其逆定理的一般情况,而三垂线定理及其逆定理是这公式的特殊情况.现在我们来研究在θ2是锐角时,θ2与θ的大小.(2)0°<θ2<90°.师:在这个条件下,我们怎样来比较θ2与θ的大小?生:因为0°<θ1<90°,所以0<cosθ1<1,又因为0°<θ2<90°,所以0<cosθ2<1.又因为cosθ=cosθ1·cosθ2,所以0<cosθ1<1,而且cosθ=cosθ1·cosθ2<cos θ2,在锐角条件下,余弦函数值大的它所对应的角小.所以θ2<θ.师:现在我们来讨论当θ2是钝角时,θ2与θ的大小.(3)90°<θ2<180°.在这个条件下,我们不再用公式cosθ1·cosθ2=cosθ做理论上的证明来比较θ2与θ的大小,而是一起来看模型(或图形).我们假设θ2的邻补角为θ′2,θ的邻补角为θ′,即θ2+θ′2=180°,θ+θ′=180°.在模型(或图形)中我们可以看出当θ2是钝角时,θ也是钝角,所以它们的两个邻补角θ′2和θ′都是锐角,由对第二种情况的讨论我们知道θ′2<θ′.由等量减不等量减去小的大于减去大的,所以由θ2=180°-θ′2,θ=180°-θ′,可得θ2>θ.根据以上讨论现在小结如下:当θ2=90°时,θ=θ2=90°,它们都是直角.当0°<θ2<90°时,θ2<θ,它们都是锐角;当90°<θ2<180°时,θ2>θ,它们都是钝角.关于公式cosθ1·cosθ2=cosθ的应用,今后还要随着课程的进展而反复提到.现在我们来看例2.例2如图2,在正方体ABCD-A1B1C1D1中,求证:(1)A1C⊥平面C1DB于G;(2)垂足G为正△C1DB的中心;(3)A1G=2GC.师:我们先来证明第(1)问.要证直线与平面垂直即要证什么?生:要证A1C与平面C1DB内两条相交的直线垂直.师:我们先证A1C为什么与DB垂直?生:连AC,对平面ABCD来说,A1A是垂线,A1C是斜线,AC是A1C在平面ABCD上的射影,因为AC⊥DB(正方形的性质),所以 A1C⊥DB.(三垂线定理)同理可证A1C⊥BC1.因为A1C⊥平面C1DB(直线与平面垂直的判定理)(在证A1C⊥BC1时,根据情况可详、可略,如果学生对应用三垂线定理还不太熟悉,则可让学生把这证明过程再叙述一遍,因为这时是对平面B1BCC1来说,A1B1是垂线,A1C是斜线,B1C是A1C在平面B1BCC1上的射影,由B1C⊥BC1,得A1C⊥BC1)师:现在来证第(2)问,垂足G为什么是正△C1DB的中心?生:因为A1B=A1C1=A1D,所以BG=GC1=DG,故G是正△C1DB的外心,正三角形四心合一,所以G是正△C1DB的中心.师:现在来证第(3)问,我们注意看正方体的对角面A1ACC1,在这对角面内有没有相似三角形?生:在正方体的对角面A1ACC1内,由平面几何可知△A1GC1∽△OGC,且A1C1∶OC=A1G∶GC,所以A1G∶GC=2∶1,因此A1G=2GC.师:例2是在正方体的体对角线与其异面的面对角线互相垂直引申而来,而例2也是一个基本的题型,对于以后证有关综合题型时很有用.所以对例2的证明思路和有关结论,尽可能的理解、记住.现在我们来看例3.例3如图3,已知:Rt△ABC在平面α内,PC⊥平面α于C,D为斜边AB的中点,CA=6,CB=8,PC=12.求:(1)P,D两点间的距离;(2)P点到斜边AB的距离.师:现在先来解第(1)问,求P,D两点间的距离.师:现在我们来解第(2)问,求P点到AB边的距离.生:作PE⊥AB于E,连CE则CE⊥AB.(三垂线定理的逆定理)PE就是P点到AB边的距离.师:要求PE就要先求CE,CE是直角三角形ABC斜边上的高,已知直角三角形的三边如何求它斜边上的高呢?生:可用等积式CE·AB=AC·CB,即斜边上的高与斜边的乘积等于两直角边的乘积.师:这个等积式是怎样证明的?生:有两种证法.因CE·AB是Rt△ABC面积的二倍,而AC·CB也是Rt△ABC面积的二倍,所以它们相等;也可用△BCE∽△ABC,对应边成比例推出这个等积式.师:这个等积式很有用,根据这个等积式,我们可以由直角三角形的三边求出斜边上的高,这个等积式以后在求有关距离问题时会常常用到,所以要理解、记住、会用.现在就利用这等积式先求CE,再求PE.师:通过这一题我们要区分两种不同的距离概念及求法;在求点到直线距离时,经常要用到三垂线定理或其道定理;在求直角三角形斜边上的高时会利用上述的等积式来求斜边上的高.现在我们来看例4.例4如图4,已知:∠BAC在平面α内,POα,PO⊥平面α于O.如果∠PAB=∠PAC.求证:∠BAO=∠CAO.师:当我们观察了模型后,很容易就猜想到了结论.即斜线PA在平面α上的射线是∠BAC 的角平分线所在的直线,现在想一想可以有几种证法?生:作OD⊥AB于D,作OE⊥AC于E,连PD,PE,则PD⊥AB,PE⊥AC.所以Rt△PAD≌Rt△PAE,因此PD=PE,故OD=OE,所以∠BAO=∠CAO.师:今天我们讲了公式cosθ1·cosθ2=cosθ.能否用这公式来证明这题.(利用这公式来证明这个题,完全是由学生想到的,当然如果有的班学生成绩较差,思路不活,也可做些必要的提示)生:因为∠PAO是斜线与平面α所成的角,所以可以考虑用公式cosθ1·cosθ2=cosθ.∠PAO相当于θ1;∠PAB=∠PAC它们都相当于θ,由公式可得θ2=θ′2,即∠BAO=∠CAO.师:今天我们是应用三垂线定理及其逆定理来解这四个例题.例1、例2、例4是三个基本题.对这三个题一定要会证、记住、会用.关于这三个题的应用,以后还会在讲课过程中反复出现.在高考题中也曾用到.作业课本第33页第13题.。
三垂线定理及其逆定理测试题(含答案).docx

三垂线定理及其逆定理一、单选题(共8道,每道12分)1.如图,BC 是Rt8sc 的斜边,过点A 作AABC 所在平面a 的垂线AP,连接PB, PC,过 点A 作AD 丄BC 于点D,连接PD,那么图中的直角三角形共有()A.4个B.6个C.7个D.8个答案:D 解题思路:丄平面a,・•・"在平面a 內的射影为血,W4D1BC,由三垂线定理可得,PD 丄BC,:.AABC, A ABD, AACD, APBD, APCD, \PAB 、'PAD 、△刃C 均为直角三角形,共8个,故选D.2.如图,在正方体中,已为时G 的中点,则下列与直线CE 垂直的是()难度:三颗星知识点:三垂线定理A.直线ACB.直线直°】c.直线AD ID.直线A"答案:B解题思路:如图,连接B\D\,则点E在久耳上,•・•点C在平面内的射影是C】,・•・CE在平面箱8匸4]内的射影是C、E ,•・• C0丄胪],由三垂线定理可得,CE1B.D,;在四边形4%C]C中,qcjuc, 易得」£C不可能和CE垂直;■/ .\DjlBC, ^All QC,而BC, C]C明显与CE不垂直,・•・4刀],A.A不可能和C£垂直.综上,选B.试题难度:三颗星知识点:三垂线定理3.如图,在AABC屮,ZACB=90°,直线I过点A且垂直于平面ABC,动点尸厂,当点P逐渐远离点A 时,ZPCB 的度数()A.逐渐变大B.逐渐变小C.不变D.先变大再变小答案:C解题思路:由题意可得,AC1BC,丁刃丄平面ABC,由三垂线定理的逆定理可得,5C1PC,/.ZPC5=90°,即乙PCB 的度数保持不变,故选C.试题难度:三颗星知识点:三垂线定理4.己知三棱锥P-ABC 的高为PH,若P 到厶ABC 的三边的距离相等,且点H 在厶ABC 内,则点 H 为厶ABC 的( )A.垂心B.重心C.外心D.内心答案:D解题思路:由题意,作岀符合题意的图形,过点P 分别作PE 丄曲于点E PF 丄彳C 于点F,连接PE PF, HE, HF,B•・• PH丄平面ABC,・•・PE在平面ABC內的射影为HE,\'PElAB f由三垂线定理的逆定理可得,HE1AB,同理可得:HFlAC f':PE=PF,:.HE=HF,即点H到AB, AC的距离相等,同理可证,点H到三边的距离都相等, ・•・点刃是△ ABC的内心,故选D.试题难度:三颗星知识点:三垂线定理5.四面体ABCD中,棱AB, AC, AD两两垂直,则顶点A在底血BCD上的正投影H为△ BCD 的()A.重心B.垂心C.外心D.内心答案:B解题思路:由题意,作岀符合题意的图形,连接 阳,DH 、W451JC, AS1AD,•「IB 丄平面ACD,:.AB1CD,•・•刃是"在底面BCD 的正投影,・•・BH 是AB 在平面BCD 內的射影,由三垂线定理的逆定理可得,BH1CD, 同理可得,DH1BC, ・•・点刃是的垂心,故选B.6.已知二面角a-AB-P 的平面角是锐角,C 是平面a 内一点(点C 不在棱AB 上),D 是点C 在平面卩上的射影,E 是棱AB 上满足ZCEB 为锐角的任一点,那么()答案:A 解题思路:难度:三颗星知识点:三垂线定理A. ZCEB>ZDEBB. ZCEB 二 ZDEBC.ZCEBvZDEBD.ZCEB 和ZDEB 的大小关系不能确定如图,过点C作CF丄■毎于点F,连接DF,9:CD1AB9 CF1AB,丄平面CDF,.\DF1AB,在RxACDF中,CF>DF,CF DFJ tanZC£5 = — , tanZDEB =—,EF EF由CFADF可知,/CEE>/DEB, 故选A.试题难度:三颗星知识点:三垂线定理7.如图,A0丄平而a,垂足为点0,方Cu平面G, BC丄0B,若ZABO=45°,ZCOB=30°,则ZBAC的余弦值为()苗屁A~ B.〒答案:B 解题思路:':AO 丄平面 a, PCu 平面a, BC\_OB, 由三垂线定理可得,ABLBC f 设 03=2,TZ 总BO=45。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、正三棱柱111ABC A B C 的所有棱长都为2,D 为1CC 中点.求证:1AB ⊥1A BD .
2、已知两个正四棱锥P -ABCD 与Q -ABCD 的高分别为1和2,AB =4.证明PQ ⊥平面ABCD .
3、已知:M ∩N =AB ,PQ ⊥M 于Q ,PO ⊥N 于O ,OR ⊥M 于R ,求证:QR ⊥AB .
4、已知如图(1)所示,矩形纸片AA ′A ′1A 1,B 、C 、B 1、C 1 分别为AA ′,A 1A ′的三等分点,将矩形纸片沿BB 1,CC 1折成如图(2)形状(正三棱柱),若面对角线AB 1⊥BC 1,求证:A 1C ⊥AB 1.
5、如图,在四棱锥P-ABCD 中,PD ⊥平面ABCD ,PD=DC=BC=1,AB=2,AB ∥DC ,∠BCD=900。
求证:PC ⊥BC ;
例1题图
Q
B
C
P
A
D O
M
A
B
C D
1
A
1
C
1
B
6、如图所示,PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.
(1)求证:MN∥平面PAD. (2)求证:MN⊥CD.
(3)若∠PDA=45°,求证:MN⊥平面PCD.
7、在空间四边形ABCD中,AB⊥CD,AH⊥平面BCD,求证:
BH⊥CD
8、如图,正方形ABCD和四边形ACEF所在的平面互相垂直.EF∥
AC,AB=2,CE=EF=1.
(1)求证:AF∥平面BDE;(2)求证:CF⊥平面BDE.
9、如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点求证:(1)直线EF∥平面PCD;(2)平面BEF⊥平面
PAD.。
