专题5 热点专题专训
热点专题5细胞自噬与细胞凋亡-2025年生物学高考总复习课件

高考总复习·生物学
A.细胞自噬会导致肝癌细胞中的原癌基因和p53基因发生突变 B.自吞小泡是由内质网或高尔基体的双层膜脱落后形成的 C.丙过程中待清除的蛋白质需要经过受体蛋白LAMP2a介导才能进入溶 酶体内 D.细胞自噬与细胞坏死不存在本质区别
返回导航
高考总复习·生物学
【解析】根据题干信息可知,细胞自噬能通过激活原癌基因过度表达和 抑制p53基因表达来促发肝癌,基因没有发生突变,A错误。自吞小泡是 由内质网或高尔基体的单层膜脱落后形成的,B错误。根据题干信息 “丙过程的活性与溶酶体膜上可利用的受体蛋白LAMP2a的数量呈正相 关”可知,丙过程中待清除的蛋白质需要经过受体蛋白LAMP2a介导才 能进入溶酶体,C正确。细胞坏死是被动的病理性死亡,对机体是有害 的;细胞自噬是指细胞将自身受损衰老的细胞器及蛋白质等通过溶酶体 降解的过程,对机体是有利的,二者有着本质的区别,D错误。
返回导航
高考总复习·生物学
2.基因Bax和Bcl-2分别促进和抑制细胞凋亡。研究人员利用siRNA干扰技 术降低TRPM7基因表达,研究其对细胞凋亡的影响,结果如图所示。下 列叙述错误的是( D )
A.细胞衰老和细胞凋亡都受遗传信息的调控 B.TRPM7基因可能通过抑制Bax基因的表达来抑制细胞凋亡 C.TRPM7基因可能通过促进Bcl-2基因的表达来抑制细胞凋亡 D.可通过特异性促进癌细胞中TRPM7基因的表达来治疗相关癌症
返回导航
返回导航
高考总复习·生物学ห้องสมุดไป่ตู้
【解析】结合图示可以看出,自噬前体来自内质网,溶酶体来自高尔基 体,A正确;水解酶存在于溶酶体中,其化学本质是蛋白质,蛋白质的 合成场所是核糖体,B错误;自噬体的形成涉及膜融合过程,因此需要 借助于膜的流动性完成,且该过程中需要消耗能量,C正确;当细胞养 分不足时,细胞可通过自噬作用为生命活动提供原料和能量,因此在能 量供应不足时细胞自噬作用增强,D正确。
湘教版高中地理选择性必修1 热点专题5 第五章 自然环境的整体性与差异性

热点·微专题
地理 选择性必修1 自然地理基础 配湘教版 第五章 自然环境的整体性与差异性
热点 海南热带云雾林 [背景材料] 热带云雾林指的是潮湿地区经常被云雾掩盖的森林,多分布在热带 山地的山顶或山脊。因为受到风力大、气温偏低、空气湿度较大、土壤 等因素影响,云雾林的森林群落高度、外貌、生物多样性和群落结构外 貌等与低海拔热带森林都有着明显的区别。
地理 选择性必修1 自然地理基础 配湘教版 第五章 自然环境的整体性与差异性
第2题,热带云雾林位于海拔较高的山地,土层不会太厚;寄生、附生 植物不直接与土壤接触,因此要从寄生的生物中吸取充足的养分才能生 存;人类活动影响小和气温较低不是影响寄生、附生植物生长的主要因 素。第3题,从图中可知,云雾林水汽充足,气候湿润,海拔高,位置 偏远,成为很多动植物的避难所;由材料可知云雾林是热带雨林的一 种,泛指海拔较高的山地生长的原始热带雨林,原始热带雨林地区一般 人烟稀少,而且从材料和图中看不出有人为开发和保护;地处山顶,风 力较强;热带雨林中自然环境较复杂,动植物种类也较丰富。
地理 选择性必修1 自然地理基础 配湘教版 第五章 自然环境的整体性与差异性
微专题 维护生物多样性,探究物种丰富的原因
[知识归纳] 1.生物多样性(物种)丰富的原因
分析角度 水热条件
答题思路 地处低纬度(热带),热量丰富,物种丰富,繁衍生长速 度快
地理 选择性必修1 自然地理基础 配湘教版 第五章 自然环境的整体性与差异性
地理 选择性必修1 自然地理基础 配湘教版 第五章 自然环境的整体性与差异性
海南岛的热带云雾林主要分为热带山地常绿林和热带山顶矮林两大 类,主要分布在霸王岭、尖峰岭、黎母山、五指山、吊罗山和鹦哥岭等 林区海拔1 200米以上的山顶或山脊,分布环境平均气温在19 ℃左右, 日平均空气相对湿度能达到88%以上,云雾出现频率高,风力强劲,土 壤含水量常处于饱和状态。一般植物靠根得到水分,而热带云雾林多利 用树叶吸食雾水以此获取水分,植株相对矮小,树干弯曲。近年来受全 球气候变化的影响,与其他森林相比,热带云雾林的生存环境变得更加 脆弱。
专题五 世界地理的人文要素

专题五世界地理的人文要素【考点归纳】【亚洲】一、基本概况1.人口:亚洲是世界人口最多的大洲,人口超过1亿的国家(中国、日本、印尼、印度、巴基斯坦、孟加拉国)主要位于亚洲,主要所在的地区为南亚。
2.人口的分布:亚洲的东部和南部人口稠密(地形平坦、气候温暖湿润、交通便利),西部和北部人口稀疏(西部干旱,北部气候寒冷)。
3.人种:东亚和东南亚主要是黄色人种,南亚和西亚主要是白色人种,南亚也有黑色人种。
4.宗教:发源于南亚的宗教:佛教和印度教,发源于西亚的宗教:基督教、伊斯兰教和犹太教。
5.经济发展状况:日本是发达国家,其余都是发展中国家,其中中国和印度属于金砖国家,中国有“世界工厂”之称,印度被称为“世界办公室”。
二、东南亚1.人口的分布:东南亚人口集中分布在大河的冲积平原、河口三角洲和沿海地带。
2.农业:东南亚是热带经济作物的重要产地[天然橡胶\棕油、椰子、椰油、蕉麻],粮食作物为水稻。
原因:热带季风气候和热带雨林气候,水热条件充足。
3.国家:与中国(云南省)接壤:缅甸、老挝、越南;唯一的内陆国是老挝;花园城市:新加坡,三大稻米出口国:泰国、越南、缅甸,马六甲海峡沿岸的国家:马来西亚、新加坡、印度尼西亚。
三、南亚1.南亚作物的分布2.印度的三大城市:印度棉纺织中心孟买;麻纺织中心加尔各答;印度的硅谷班加罗尔。
孟买、加尔各答发展纺织工业的有利条件:靠近原料产地,临海交通便利。
3.印度的信息技术产业在世界上占有重要地位的,发展信息技术产业的优势条件①人力资源丰富,劳动力成本低②语普及,信息技术发展较早4.印度是佛教的发源地,现在主要信仰印度教,泰姬陵是伊斯兰教的建筑风格。
四、西亚1.西亚成为热点地区原因:(1)地理位置重要地处五海三洲之地(2)石油资源丰富(3)水资源缺乏(4)文化差异2.农业:西亚属于热带沙漠气候终年炎热干燥,在干旱的自然环境下,西亚的畜牧业和灌溉农业别具特色。
畜牧业:土耳其的安卡拉羊毛、阿富汗的紫羊羔皮,农业:两河平原是重要的灌溉农业区。
2023年中考道德与法治热点专题复习专题5 推进乡村振兴 全面深化改革

党( )
• A.立党为公、执政为民的执政理念
A
• B.认真践诺,承担责任的大国风范
• C.全心全意为人民服务的根本宗旨
• D.同步富裕,全面小康的奋斗目标
• 3.中央农村工作会议强调,牢牢守住保障国家粮食安全和不发 生规模性返贫两条底线。会议指出,要全力抓好粮食生产和重要 农产品供给,稳定粮食面积,大力扩大大豆和油料生产,确保 2022年粮食产量稳定在1.3万亿斤以上。C 守住这两条底线( )
• 4.2021年7月22日,《中共中央国务院关于新时代推动中部地区 高质量发展的意见》印发。这是党中央统筹两个大局,顺应新时 代新要求作出的重大决策部署。其主要目标是:到2025年,中部 地区质量变革、效率变革、动力变革取得突破性进展,投入产出 效益大幅提高,综合实力、内生动力和竞争力进一步增强。到 2035年,中部地区现代化经济体系基本建成,产业整体迈向中高 端,城乡区域协调发展达到较高水平,绿色低碳生产生活方式基 本形成,开放型经济体制机制更加完善,人民生活更加幸福安康 ,基本实现社会主义现代化,共同富裕取得更为明显的实质性进 展。
• 13.实现中华民族伟大复兴,是中华民族近代以来最伟大的梦想 。实现中国梦,就是要实现国家富强、民族振兴、人民幸福。
• 14.坚持中国特色社会主义道路,坚持中国特色社会主义理论, 坚持中国特色社会主义制度,发展中国特色社会主义文化。
• 15.到本世纪中叶,把我国建成富强民主文明和谐美丽的社会主 义现代化强国。
• 材料二:2022年2月22日,《中共中央 国务院关于做好2022年全 面推进乡村振兴重点工作的意见》发布。文件指出,牢牢守住保 障国家粮食安全和不发生规模性返贫两条底线,突出年度性任务 、针对性举措、实效性导向,充分发挥农村基层党组织领导作用 ,扎实有序做好乡村发展、乡村建设、乡村治理重点工作,推动 乡村振兴取得新进展、农业农村现代化迈出新步伐。
热点专题系列(5) 动力学、动量和能量观点在力学中的应用

热点专题系列(五)动力学、动量和能量观点在力学中的应用热点概述:处理力学问题的三个基本观点:①动力学观点(牛顿运动定律、运动学基本规律);②能量观点(动能定理、机械能守恒定律、功能关系与能量守恒定律);③动量观点(动量定理、动量守恒定律)。
熟练应用三大观点分析和解决综合问题是本专题要达到的目的。
[热点透析]动量与动力学观点的综合应用1.解动力学问题的三个基本观点(1)力的观点:用牛顿运动定律结合运动学知识解题,可处理匀变速运动问题。
(2)能量观点:用动能定理和能量守恒观点解题,可处理非匀变速运动问题。
(3)动量观点:用动量定理和动量守恒观点解题,可处理非匀变速运动问题。
2.力学规律的选用原则(1)如果要列出各物理量在某一时刻的动力学关系式,可用牛顿第二定律。
(2)研究某一物体受到力的持续作用发生运动状态改变时,一般用动量定理(涉及时间的问题)或动能定理(涉及位移的问题)去解决问题。
(3)若研究的对象为一物体系统,且它们之间有相互作用,一般用动量守恒定律和能量守恒定律(机械能守恒定律)去解决问题,但需注意所研究的问题是否满足守恒的条件。
(4)在涉及相对位移问题时则优先考虑能量守恒定律,系统克服摩擦力所做的总功等于系统机械能的减少量,即转变为系统内能的量。
(5)在涉及碰撞、爆炸、打击、绳绷紧等物理现象时,需注意到这些过程一般均隐含有系统机械能与其他形式能量之间的转换,这种问题由于作用时间都极短,因此用动量守恒定律去解决。
(2020·湖北省七市州教科研协作体高三下学期5月联考)如图甲所示,在光滑水平面上有一小车,其质量M=2 kg,车上放置有质量m A=2 kg的木板A,木板上有可视为质点的物体B,其质量m B=4 kg。
已知木板A与小车间的动摩擦因数μ0=0.3。
A 、B 紧靠车厢前壁,A 的左端与小车后壁间的距离为x =2 m 。
现对小车施加水平向右的恒力F ,使小车从静止开始做匀加速直线运动,经过1 s 木板A 与车厢后壁发生碰撞,该过程中A 的速度—时间图象如图乙所示,已知重力加速度大小g =10 m/s 2,最大静摩擦力等于滑动摩擦力。
中考总复习道德与法治5-热点专题五 道德建设润人心

标杆和身边榜样。他们舍小我、顾大家,以初心坚守岗位,用担当奉献 情怀。他们用平常心做不平常事,用小爱凝聚人间大爱,是社会文明风 尚的领跑者。
1.“中国好人”获得国家和人民的高度认可和评价说明了什么? (1)承担责任,既有代价也有回报,包括物质方面和精神方面。 (2)不言代价与回报的奉献精神,是社会责任感的集中体现。 (3)生命的意义不在于长短,而在于对社会的贡献。
1.谈谈中共中央宣传部等部门表彰与宣传全国道德模范对实现强国梦的 意义。 (1)有利于传递社会正能量,培养公民的社会责任感。 (2)有利于培育社会主义核心价值观,在全社会树立正确的价值导向。 (3)有利于弘扬民族精神,传承中华传统美德。 (4)有利于人们形成正确的世界观、人生观和价值观;有利于营造良好的 社会氛围;等等。 2.开展全国道德模范评选活动对青少年有哪些影响? (1)有利于增强青少年的社会责任感。
1.在竞赛场馆里,引导观众、维持秩序;在主媒体中心,为来宾答疑解
惑、提供帮助;在闭环驻地,悉心接待、事无巨细……志愿者用专业的
服务和饱满的热情迎接四海宾朋,为保障简约、安全、精彩的奥运盛
会贡献着自己的力量。这说明志愿者们( B )
①倾力奉献社会 ②勇于承担责任 ③获得精神滋养 ④实现生命价
值
A.①②③
(3)有利于维护社会公平正义,传递社会正能量。 (4)有利于提高人们的思想道德水平,有利于践行社会主义核心价值观。 (5)有利于构建社会主义和谐社会。 (6)有利于凝聚强大的精神力量,为实现中华民族的伟大复兴提供强大精 神支撑。 4.青少年学生应如何向“中国好人”学习? (1)树立远大理想,努力学习科学文化知识,立志成才,报效祖国。 (2)积极承担历史使命,为民族复兴贡献力量,积极承担社会责任,参加社 会实践活动,不断提升人生价值。
备战2023年高考地理时事热点专题训练5 台湾问题含详解
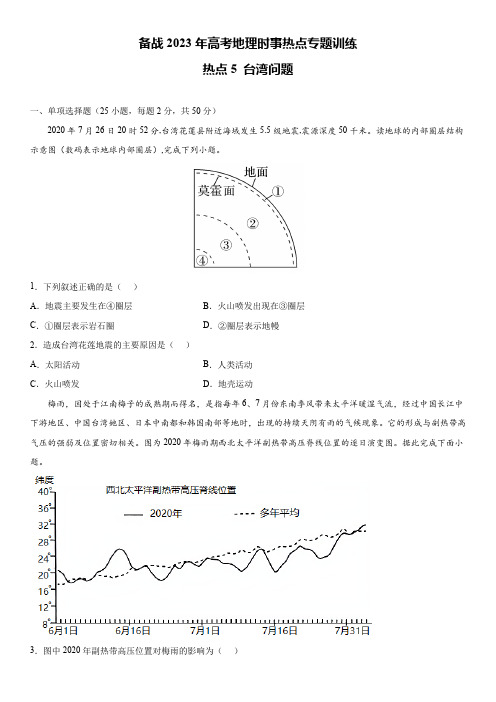
备战2023年高考地理时事热点专题训练热点5 台湾问题一、单项选择题(25小题,每题2分,共50分)2020年7月26日20时52分,台湾花莲县附近海域发生5.5级地震,震源深度50千米。
读地球的内部圈层结构示意图(数码表示地球内部圈层),完成下列小题。
1.下列叙述正确的是()A.地震主要发生在④圈层B.火山喷发出现在③圈层C.①圈层表示岩石圈D.②圈层表示地幔2.造成台湾花莲地震的主要原因是()A.太阳活动B.人类活动C.火山喷发D.地壳运动梅雨,因处于江南梅子的成熟期而得名,是指每年6、7月份东南季风带来太平洋暖湿气流,经过中国长江中下游地区、中国台湾她区、日本中南都和韩国南部等地时,出现的持续天阴有雨的气候现象。
它的形成与副热带高气压的强弱及位置密切相关。
图为2020年梅雨期西北太平洋副热带高压脊线位置的逐日演变图。
据此完成下面小题。
3.图中2020年副热带高压位置对梅雨的影响为()A.减弱B.空梅C.增强D.先强后弱4.2020年7月中下旬,我国江淮地区的天气多为()A.连晴高温B.台风频繁C.连绵阴雨D.风和日丽读我国台湾省铁路分布图,完成下面小题。
5.台湾岛修建的铁路是环岛铁路,没有直接联系东西部的横向铁路。
据图思考,这样选择线路主要是考虑了哪种因素对铁路建设的影响()A.地形因素B.河流因素C.气候因素D.矿产因素6.台湾岛铁路呈环状分布于山间盆地和河谷地带的主要原因()①客货运量大②地势相对和缓,工程造价低,难度小③水源充足④地势低、热量条件好A.①②B.③④C.①③D.②④福建省是古代海上丝绸之路的起点,作为“21世纪海上丝绸之路”的核心区,目前已经开始行动,正在构建“一带一路”重要的互联互通枢纽。
近些年来,继福建、台湾之间产业的“一次转移”之后,福建内部工业的“二次转移”势头良好,尤其是劳动密集型工业纷纷向省内中西部转移。
下图为福建省示意图。
据此完成下面小题。
7.泉州、漳州和厦门被称为“闽南金三角”,该地区成为福建乃至中国东部地区最具活力经济区域之一的主要原因有()①农业基础好,发展历史悠久②强化基础设施建设,三市间公共交通智能管理系统先进③三市工业产业集群聚集,集约发展优势凸显④临近台湾,闽台经济合作活力强A.①②③B.①②④C.①③④D.②③④8.近年来福建内部工业的“二次转移”,其主要原因是()A.高素质人才流失B.资源枯竭,产业转型的需要C.劳动力、土地价格上涨D.迁往内地,保障生产的安全读台湾海峡及附近周边海域不同时间海水温度等值线分布图,完成下面小题。
高中物理解题高手:专题5 抛体运动

专题五 抛体运动[重点难点提示]物体只在重力作用下的运动统称为抛体运动.常见的抛体运动有自由落体、竖直上抛、平抛及斜抛等运动形式.抛体运动是典型的匀变速运动,尽管其运动轨迹可能是直线,也可能是曲线,但抛体运动的加速度都为重力加速度,因此,对抛体运动进行分析和研究,抓住其运动特征及初始条件,并灵活运用匀变速运动的相关规律,对求解有关运动学问题具有典型意义和重要作用.此类问题往往成为历年高考命题的热点.一、平抛运动问题1、对于“平抛运动”,你可以相对于地面,把它看作是水平方向上的匀速运动与竖直方向上的自由落体运动的合运动;你也可以相对斜面,把它看作是平行于斜面的,初速度为v 0cosθ、加速度为gcosθ的匀加速运动,与垂直于斜面,初速度为v 0sinθ、加速度为-gsinθ的匀减速运动的合运动;以后如有必要,你还可以有其它的分析方法。
这就是物理思想,是物理学研究方法的基础和出发点。
深刻理解物理思想,是掌握研究方法的关键。
2.对平抛运动之所以有各种不同的分析方法,是由力与运动的矢量特性决定的,在研究具体的实际例题中,应注意研究矢量变化规律的特殊性。
3.如果物体的合理不是重力,但是也是恒力,那么它将做类平抛运动,在与初速度垂直方向上的分运动是初速度为零的匀加速度直线运动。
带电粒子在电场中运动、在符合场中的运动,有很多属于这种运动。
二、竖直上抛问题竖直上抛运动是匀变速直线运动,其上升阶段为匀减速运动,下落阶段为自由落体运动。
它有如下特点:1.上升和下降(至落回原处)的两个过程互为逆运动,具有对称性。
有下列结论: (1)速度对称:上升和下降过程中质点经过同一位置的速度大小相等、方向相反。
(2)时间对称:上升和下降经历的时间相等。
2.竖直上抛运动的特征量:(1)上升最大高度:S m =gV 220.(2)上升最大高度和从最大高度点下落到抛出点两过程所经历的时间:gV t t 0==下上.]自由落体一个物体从塔顶上下落,在到达地面前最后1s 内通过的位移是整个位移的9/25,求塔高。
专题五促进民族团结共建和谐中国【最新】

专题五促进民族团结共建和谐中国【热点聚焦】l、十八大规划各民族和谐发展十八大报告指出,要全面正确贯彻落实党的民族政策,坚持和完善民族区域自治制度,牢牢把握各民族共同团结奋斗、共同繁荣发展的主题,深入开展民族团结进步教育,加快民族地区发展,保障少数民族合法权益,巩固和发展平等团结互助和谐的社会主义民族关系,促进各民族和睦相处、和衷共济、和谐发展。
2、少数民族事业“十二五”规划2012年7月12日,国务院颁布《少数民族事业“十二五”规划》。
在《规划》中指出少数民族事业建设的主要任务:①着力推动民族地区加快发展,不断改善各族人民生产、生活条件。
②大力发展教育、科技、卫生、就业和社会保障事业,不断提高民族地区基础公共服务水平。
③着力发展少数民族文化事业和文化产业,不断满足各族人民精神文化需求。
④不断巩固和发展民族团结进步事业,营造各民族和谐发展的社会环境。
⑤加强少数民族各类人才队伍建设,提升民族地区发展的智力支撑能力。
⑥加强民族理论政策体系和民族法律法规体系建设,提高民族工作的决策和管理水平。
⑦继续加大民族工作交流合作力度,不断提升对外和对港澳台的交流与合作水平。
⑧努力构建民族事务服务体系,不断提高民族事务管理和服务水平。
3、全国扶持人口较少民族发展经验交流会2012年8月21奎23日,全国扶持人口较少民族发展经验交流会在黑龙江省佳木斯市召开。
扶持人口较少民族发展,是党中央、国务院作出的一项童t决策.是新世纪、新阶段民族工作的一项重要任务,是深入贯彻落实科学发展观的迫切需要,是实现全面建设小康社会的重要举措.是发展民族团结进步事业的必然要求。
4、保护少数民族特色文化2012年12月5日国家民委印发《少数民族特色村寨保护与发展规划纲要(2011—2015年)》。
少数民族特色村寨在产业结构、民居式样、村寨风貌以及风俗习惯等方面都集中体现了少数民族经济社会发展特点和文化特色,集中反映了少数民族聚落在不同时期、不同地域、不同文化类型中形成和演变的历史过程。
2019年贵阳中考道德与法治时政热点专题训练-专题5 讲好中国故事 弘扬民族精神

专题五讲好中国故事弘扬民族精神热点聚焦1.全国宣传思想工作会议8月19日至20日在北京召开。
中共中央总书记、国家主席、中央军委主席习近平出席会议并发表重要讲话。
习近平总书记围绕讲什么中国故事、如何讲好中国故事、怎样展现好中国形象作出深刻论述,提出明确要求。
随着中国日益走近世界舞台中央,中国与世界深度融合、相互激荡,讲好中国故事,传播好中国声音,向世界展现真实、立体、全面的中国,是宣传思想战线的重要使命任务。
2.党的十九大报告指出,要坚定文化自信,推动社会主义文化繁荣兴盛。
文化是一个国家、一个民族的灵魂。
文化兴国运兴,文化强民族强。
没有高度的文化自信,没有文化的繁荣兴盛,就没有中华民族的伟大复兴。
要坚持中国特色社会主义文化发展道路,激发全民族文化创新创造活力,建设社会主义文化强国。
中国特色社会主义文化,源自于中华民族五千多年文明历史所孕育的中华优秀传统文化,熔铸于党领导人民在革命、建设、改革中创造的革命文化和社会主义先进文化,植根于中国特色社会主义伟大实践。
3.2017年12月15日晚,北京2022年冬奥会会徽“冬梦”和冬残奥会会徽“飞跃”正式亮相。
北京2022年冬奥会会徽“冬梦”,以中国书法“冬”字为主体,将抽象的滑道、冰雪运动形态与书法巧妙结合。
运用中国书法的艺术形态,将厚重的东方文化底蕴与国际化的现代风格融为一体。
在“BEIJING 2022”字体的形态上汲取了中国书法与剪纸的特点,增强了字体的文化内涵和表现力,也体现了与会徽图形的整体感和统一性。
4.塞罕坝——地球上一抹夺目的“中国绿”。
2017年12月4日至6日,第三届联合国环境大会在肯尼亚内罗毕如期召开,在众多与会嘉宾中,河北塞罕坝机械林场的代表陈彦娴、刘海莹、于士涛颇受追捧——以三人为代表的三代塞罕坝人55年创造的荒原变林海的人间奇迹令世界惊叹,塞罕坝那一抹位于世界东方的“中国绿”也惊艳了世界。
55年,塞罕坝从人迹罕至的荒原变成了112万亩世界上面积最大的人工林;55年,一代又一代塞罕坝人不忘初心、牢记使命、不懈努力、接续奋斗,创造出了举世瞩目的绿色奇迹;55年,从“沙地变林海,让荒原成绿洲”,塞罕坝人用信念和意志,铸就了“牢记使命、艰苦创业、绿色发展”的塞罕坝精神。
专题5 近代资本主义制度的确立

专题精练
一、选择题
1 . (2018· 新疆乌鲁木齐 )《大国崛起的文化准备》中提到:“一个民族要崛
起,要有三个方面的改变:第一是人心的改变;第二是政治制度的改变;第三是器 物和经济的改变。”以英国为例,与其政治制度改变相关的事件是( A ) A.资产阶级革命 C.宪章运动 B.工业革命 D.殖民扩张
第 11 页
第二篇 攻专题 ·能力提升
中考复习与训练历史 ·配川教版
6.某班级举办“资产阶级革命”图文展,拟分“英国”“美国”“法国”三个
篇章。应入选“法国”篇的是( D ) A.①② C.②③ B.①④ D.③④
第 12 页
第二篇 攻专题 ·能力提升
中考复习与训练历史 ·配川教版
7.(2017·山东泰安)一位意大利爱国者在1814年写道:“没有人比我更意识到 我们应该向拿破仑表示感激,没有人比我更懂得湿润意大利土壤并使之恢复生气的 每一滴慷慨的法国人鲜血的价值。”这是指法国大革命( C )
英国资产阶 事件 级革命
日本明治维 新
1868年 幕府统治严 重阻碍了资 本主义的发 展
起止 1640~1688年 1775~1783年 1789~1794年 时间 封建专制统 根本 治严重阻碍 原因 了资本主义 的发展 英国的殖民统 治严重阻碍了 北美资本主义 经济的发展 腐朽的封建专 制制度严重阻 碍了资本主义 的发展
事件
性质
英国资产阶级革命 美国独立战争 法国大革命 资产阶级革命
作用 都促进了资本主义发展
第 17 页
第二篇 攻专题 ·能力提升
中考复习与训练历史 ·配川教版
二、材料解析题
12.阅读下列材料,回答问题。 材料一 英国资产阶级革命经过近50年的革命的动荡和反复,终于推翻了封建
专题五 厚植文化自信 传承中国精神--中考道德与法治二轮时政热点复习

热点专题五:厚植文化自信、传承中国精神一、背景材料:1.70多个国家将中文纳入国民教育体系7月7日,外交部发言人在回答记者提问时指出,截止2020年底,全球共有180多个国家和地区开展中文教育,70多个国家将中文纳入国民教育体系,外国正在学习中文的人数超过了2000万,累计学习和使用中文的人数接近2亿。
2.中国共产党人精神谱系第一批伟大精神2021年9月29日,党中央批准了中央宣传部梳理的第一批纳入中国共产党人精神谱系的伟大精神,这些精神是:建党精神;井冈山精神、苏区精神、长征精神、遵义会议精神、延安精神、抗战精神、红岩精神、西柏坡精神、照金精神、东北抗联精神、南泥湾精神、太行精神(吕梁精神)、大别山精神、沂蒙精神、老区精神、张思德精神;抗美援朝精神、“两弹一星”精神、雷锋精神、焦裕禄精神、大庆精神(铁人精神)、红旗渠精神、北大荒精神、塞罕坝精神、“两路”精神、老西藏精神(孔繁森精神)、西迁精神、王杰精神;改革开放精神、特区精神、抗洪精神、抗击“非典”精神、抗震救灾精神、载人航天精神、劳模精神(劳动精神、工匠精神)、青藏铁路精神、女排精神;脱贫攻坚精神、抗疫精神、“三牛”精神、科学家精神、企业家精神、探月精神、新时代北斗精神、丝路精神(民族精神具有与时俱进的品格)伟大的建党精神内涵:形成了坚持真理、坚守理想,践行初心、担当使命,不怕牺牲、英勇斗争,对党忠诚、不负人民的伟大建党精神。
3.3.2021年7月25日17点38分,我国世界遗产提名项目“泉州:宋元中国的世界海洋商贸中心”顺利通过联合国教科文组织第44届世界遗产委员会会议审议,成功列入《世界遗产名录》,我国世界遗产总数升至56项。
二、知识链接:1.中华文化的特点---------------文化的价值----------- (理解)2.中华文化的传承与发展。
----------3.坚定文化自信。
------------ (探究)4.中华传统美德的内涵及其价值。
【核心考点总动员】专题5:离子方程式和氧化还原反应方程式的书写

考点五离子方程式和氧化还原方程式的书写【母题再现】题型介绍:离子方程式和氧化还原方程式的书写为高考的必考题型,考查方式为填空题。
一些省市在工艺流程题或探究性实验题中考查,还有有些省的命题中考查基本概念和基本理论的答题中涉及方程式的书写。
这类题型涉及离子反应的基本原理,氧化还原反应的规律及产物的判断,氧化还原反应方程式配平的基本方法等相关知识。
高考选题:【2022年高考上海卷】(本题共12分)NaCN超标的电镀废水可用两段氧化法处理:(1)NaCN与NaClO反应,生成NaOCN和NaCl(2)NaOCN与NaClO反应,生成Na2CO3、CO2、NaCl和N2已知HCN(K i=×10-10)有剧毒;HCN、HOCN中N元素的化合价相同。
完成下列填空:(1)第一次氧化时,溶液的3含L的废水,实际至少需NaClO___g(实际用量应为理论值的4倍),才能使NaCN含量低于L,达到排放标准。
(4)(CN)2与Cl2的化学性质相似。
(CN)2与NaOH溶液反应生成_________、__________和H2O。
【答案】(1)碱性;防止生成HCN,造成人员中毒或污染空气。
(2)2OCN-3ClO-=CO32-CO2↑3Cl-N2↑(3)14900(4)NaOCN、NaCN【解析】【考点定位】考查氧化还原反应方程式书写、计算、元素周期律等有关判断【名师点睛】对于HA HA-,K i=,一定温度下电离平衡常数的大小通常是用来衡量酸性强弱的主要依据,K i值越大说明酸性越强。
HCN的K i=×10-10,说明HCN是极弱的酸,NaCN属于强碱弱酸盐,极易水解使水溶液表现碱性,即NaCN只能存在于碱性环境中。
若调整NaCN溶液2C2Col物质获得电子的多少,获得电子越多,其氧化能力就越强。
2.【2022浙江理综化学】Ⅰ.6分请回答:(1)H2O2的电子式___________。
(2)镁燃烧不能用CO2灭火,用化学方程式表示其理由________________。
2020版高考历史(通史版)大二轮专题复习新方略讲义:热点主题五 Word版含解析

热点主题五谁主沉浮——构筑人类命运共同体,追踪世界大国崛起世界不同国家有不同的崛起之路,或以贸易取胜,或以军事取胜;世界大国崛起具有不同的条件,其兴衰实质反映了世界经济、政治格局的演变。
自新航路开辟的五百年来,各国人民为实现强国之梦而孜孜追求,其中也留下了深刻的经验教训。
可以肯定的是建立永久和平、共同繁荣的和谐世界,构筑人类命运共同体将是人类共同努力的方向。
今天的中国,正走在中华民族伟大复兴的道路上,一定会和平崛起!一、“日不落帝国”的兴衰1.英国的崛起:十七、十八世纪成为世界最大的殖民国家。
(1)地理优势:新航路的开辟,大西洋沿岸取代地中海区域成为欧洲商贸枢纽,伦敦成为国际贸易中心之一。
(2)经济优势:在重商主义政策、圈地运动影响下,英国资本主义迅速发展。
工业革命使得英国实力大增。
(3)政治优势:1688年“光荣革命”后逐步建立起君主立宪制。
(4)殖民优势:英国先后打败西班牙、荷兰、法国,成为当时世界上最大殖民国家。
(5)“世界工厂”:18世纪中后期至19世纪中后期,英国最早进行工业革命,确立世界经济霸权。
2.英国的衰落:19世纪中后期至二战后,英国国际地位开始下降,“世界工厂”地位丧失,经济地位动摇,殖民体系崩溃;追随美国。
(1)经济:①20世纪30年代出现了凯恩斯主义,核心主张是政府应该加强对经济的干预。
②对中国:参与瓜分中国狂潮和八国联军侵华战争。
③20世纪70年代加入欧洲共同体,融入经济区域化和全球化的浪潮。
(2)政治:地位衰落,追随美国,参加了北大西洋公约组织。
(3)进入20世纪90年代以来,所在欧盟成为国际舞台上不可轻视的力量。
二、美国的强国之路1.美国的建立(1)美国的独立:1776年美国宣布脱离英国,建立美利坚合众国。
1783年英国承认美国独立。
(2)1787年宪法:取得民族独立后,美国制定了1787年宪法,规定了联邦制、三权分立和人民主权的政治原则,为国家的长期稳定发展打下了基础。
2020年中考数学热点冲刺5 操作探究问题(含答案解析)

热点专题5 操作探究问题实践操作性问题以趣味性强、思维含量高为特点,在具体的实践操作中主要有以下类型:(1)裁剪、折叠、拼图等问题,往往与面积与对称性相联系;(2)画图、测量、猜想、证明等探究性问题,往往要求答题者在给定的操作规则下,进行探索研究、大胆猜想、发现结论,进而提高个人的创新能力与实践能力.在2019年的中考中,操作性行问题主要包含几何体的展开与折叠,图案设计、程序框输入,尺规作图、几何图形的探究等题型,分值不一,难度不等.考向1几何体的展开与折叠1.(2019·济宁)如图,一个几何体上半部为正四校锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是()A B C D【答案】B【解析】选项A和C带图案的一个面是底面,不能折叠成原几何体的形式;选项B能折叠成原几何体的形式;选项D折叠后下面带三角形的面与原几何体中的位置不同.2.(2019·山西)某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与"点"字所在面相对的面上的汉字是( )A.青B.春C.梦D.想【答案】B【解析】根据正方体的展开与折叠中面的关系,可知与"点"字所在面相对的面上的汉字是春,故选B . 考向2 图案设计与几何变换1.(2019·烟台)小明将一张正方形纸片按如图所示的顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙),AOB ∠的度数是 .【答案】22.5︒【解析】在解本题的过程中,可以找一张正方形的纸片进行如题操作,通过测量,来得到答案,也可以利用图形的轴对称的性质,直接得到AOB ∠的度数是22.5︒.2.(2019·南充)如图,正方形MNCB 在宽为2的矩形纸片一端,对折正方形MNCB 得到折痕AE ,再翻折纸片,使AB 与AD 重合,以下结论错误的是( )A .210AB =+B .CD BC C .2BC CD EH =g D .sin AHD ∠【答案】A【解析】在Rt AEB ∆中,AB == //AB DH Q ,//BH AD ,∴四边形ABHD 是平行四边形,AB AD =Q ,∴四边形ABHD 是菱形,AD AB ∴=1CD AD AD ∴===,∴CD BC =,故选项B 正确,24BC =Q ,1)4CD EH ==g ,2BC CD EH ∴=g ,故选项C 正确, Q 四边形ABHD 是菱形,AHD AHB ∴∠=∠,sin sin AE AHD AHB AH ∴∠=∠==D 正确,故选:A . 3.(2019 · 北京)已知30AOB ∠=︒,H 为射线OA 上一定点,1OH =,P 为射线OB 上一点,M 为线段OH 上一动点,连接PM ,满足OMP ∠为钝角,以点P 为中心,将线段PM 顺时针旋转150︒,得到线段PN ,连接ON .(1)依题意补全图1;(2)求证:OMP OPN ∠=∠;(3)点M 关于点H 的对称点为Q ,连接QP .写出一个OP 的值,使得对于任意的点M 总有ON=QP ,并证明.解:(1)见下图(2)证明:∵30AOB ∠=︒,∴在△OPM 中,=180150OMP POM OPM OPM ︒-∠-∠=︒-∠∠, 又∵150MPN ∠=︒,∴150OPN MPN OPM OPM ∠=∠-∠=︒-∠,∴OMP OPN ∠=∠. (3)如下图,过点P 作PK ⊥OA 于K ,过点N 作NF ⊥OB 于F∵∠OMP=∠OPN ,∴∠PMK=∠NPF , 在△NPF 和△PMK 中,90NPF PMKNFO PKM PN PM ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△NPF ≌△PMK (AAS ),∴PF=MK ,∠PNF=∠MPK ,NF=PK , 又∵ON=PQ ,在Rt △NOF 和Rt △PKQ 中,ON PQ NF PK =⎧⎨=⎩,∴Rt △NOF ≌Rt △PKQ (HL ),∴KQ=OF ,备用图图1A设,MK y PK x ==,∵∠POA=30°,PK ⊥OQ ,∴2OP x =,∴,OK OM y ==-,∴2OF OP PF x y =+=+,)1MH OH OM y =-=--,1KH OH OK =-.∵M 与Q 关于H 对称,∴MH=HQ ,∴11y -++=2y -+,又∵KQ=OF ,∴22y x y -+=+,∴(22x =+,∴1x =,即PK=1, 又∵30POA ∠=︒,∴OP=2. 考向3 程序输入与规律探究1.(2019·重庆A 卷)按如图所示的运算程序,能使输出y 值为1的是 ( ) A .m=1,n=1 B .m=1,n=0 C .m=1,n=2D .m=2,n=1【答案】D .【解析】∵m=1,n=1,∴y=2m +1=3;∵m=1,n=0,∴y=2n -1=-1;∵m=1,n=2,∴y=2m +1=3;∵m=2,n=1,∴y=2n -1=1.故选D .18.(2019·东营)如图,在平面直角坐标系中,函数x y 33=和x y 3-=的图象分别为直线1l ,2l ,过1l 上的点A 1(1,33)作x 轴的垂线交2l 于点A 2,过点A 2作y 轴的垂线交1l 于点A 3,过点A 3作x 轴的垂线交2l 于点A 4…,一次进行下去,则点2019A 的横坐标为 .【答案】:-31009【解析】:本题考查坐标里的点规律探究题,观察发现规律:A 1(1,33),A 2(1,3-),A 3(-3,3-),A 4(-3,33),A 5(9,33),A 6(9,39-),A 7(-27,39-),……A 2n+1[(-3)n ,3×(-3)n ](n 为自然数),2019=1009×2+1,所以A 2019的横坐标为:(-3)1009=-31009. 考向4 尺规作图1.(2019·长沙)如图,Rt △ABC 中,∠C=90°,∠B=30°,分别以点A 和点B 为圆心,大于12AB 的长为半径作弧,两弧相交于M 、N 两点,作直线MN ,交BC 于点D ,连接AD ,则∠CAD 的度数是( )A .20°B .30°C .45°D .60°【答案】B【解析】在△ABC 中,∵∠B=30°,∠C=90°,∴∠BAC=180°-∠B -∠C=60°,由作图可知MN 为AB 的中垂线,∴DA=DB ,∴∠DAB=∠B=30°,∴∠CAD=∠BAC -∠DAB=30°,故本题选:B .2.(2019·兰州)如图,矩形ABCD ,∠BAC=60°,以点A 为圆心,以任意长为半径作弧分别交AB ,AC 于点M ,N 两点,再分别以点M ,N 为圆心,以大于21MN 的长作半径作弧交于点P ,作射线AP 交BC 于点E ,若BE=1,则矩形ABCD 的面积等于 .【答案】【解析】在矩形ABCD 中,∠BAC=60°,∴∠B=90°,∠BCA=30°,∵AE 平分∠BAC ,∴∠BAE=∠EAC=30°∵在Rt △ABE 中,BE=1,∴AE=1sin30︒=2,AB=1tan30=︒EAC=∠ECA=30°,∴EC=AE=2,∴S矩形ABCD=AB ⋅BC=3.(2019·济宁)如图,点M 和点N 在∠AOB 内部.(1)请你作出点P ,使点P 到点M 和点N 的距离相等,且到∠AOB 两边的距离也相等(保留作图痕迹,不写作法);(2)请说明作图理由.解:(1)画出∠AOB 的角平分线,画出线段MN 的垂直平分线,两者的交点就得到P 点.(2)作图的理由:点P 在∠AOB 的角平分线上,又在线段MN 的垂直平分线上,∠AOB 的角平分线和线段MN 的垂直平分线的交点即为所求.4. (2019·长春)图①、图②、图③处均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C、D、E、F均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.(1)在图①中以线段AB为边画一个△ABM,使其面积为6.(2)在图②中以线段CD为边画一个△CDN,使其面积为6.(3)在图③中以线段EF为边画一个四边形EFGH,使其面积为9,且∠EFG=90°.解:(1)如图所示;(2)如图所示;(3)如图所示.考向5 几何探究1.(2019·武汉)问题背景:如图1,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P,可推出结论:PA+PC=PE.问题解决:如图2,在△MNG中,MN=6,∠M=75°,MG=24.点O是△MNG内一点,则点O到△MNG 三个顶点的距离和的最小值是___________.【答案】【解析】由题构造等边△MFN,△MHO,图中2个彩色三角形全等(△MFH≌△MNO(SAS))∴OM+ON+OG=HO+HF+OG,∴距离和最小值为(Rt△FQG勾股定理)2.(2019·山西)综合与实践动手操作:第一步:如图1,正方形纸片ABCD沿对角线AC所在的直线折叠,展开铺平,再沿过点C的直线折叠,使点B,点D都落在对角线AC上.此时,点B与点D重合,记为点N,且点E,点N,点F三点在同一条直线上,折痕分别为CE,CF.如图2.第二步:再沿AC所在的直线折叠,△ACE与△ACF重合,得到图3.第三步:在图3的基础上继续折叠,使点C与点F重合,得到图4,展开铺平,连接EF,FG,GM,ME,如图5.图中的虚线为折痕.问题解决:(1)在图5中,∠BEC的度数是_____,AEBE的值是_____;(2)在图5中,请判断四边形EMGF的形状,并说明理由;(3)在不增加字母的条件下,请你以图5中的字母表示的点为顶点,动手画出....一个菱形(正方形除外),并写出这个菱形:_______.【解题过程】(1)∵正方形ABCD,∴∠ACB=45°,由折叠知:∠1=∠2=22.5°,∠BEC=∠CEN,BE=EN,∴∠BEC=90°-∠1=67.5°,∴∠AEN=180°-∠BEC-∠CEN=45°,∴cos45°=ENAE=,AEEN=,AE AEBE EN=(2)四边形EMGF是矩形.理由如下:∵四边形ABCD是正方形,∴∠B=∠BCD=∠D=90°,由折叠可知:∠1=∠2=∠3=∠4,CM=CG,∠BEC=∠NEC=∠NFC=∠DFC,∴∠1=∠2=∠3=∠4=°904=22.5°,∴∠BEC=∠NEC=∠NFC=∠DFC=67.5°,由折叠知:MH,GH分别垂直平分EC,FC,∴MC=ME,GC=GF.∴∠5=∠1=22.5°,∠6=∠4=22.5°,∴∠MEF=∠GFE=90°.∵∠MCG=90°,CM=CG,∴∠CMG=45°,又∵∠BME=4图2F∠1+∠5=45°,∴∠EMG=180°-∠CMG -∠BME=90°,∴四边形EMGF 是矩形; (3)答案不唯一,画出正确的图形(一个即可).菱形FGCH (或菱形EMCH )3.(2019·淮安)如图①,在△ABC 中,AB=AC=3,∠BAC=100°,D 是BC 的中点.小明对图①进行了如下探究:在线段AD 上任取一点P ,连接PB .将线段PB 绕点P 按逆时针方向旋转80°,点B 的对应点是点E ,连接BE ,得到△BPE.小明发现,随着点P 在线段AD 上位置的变化,点E 的位置也在变化,点E 可能在直线AD 的左侧,也可能在直线AD 上,还可能在直线AD 的右侧. 请你帮助小明继续探究,并解答下列问题:(1)当点E 在直线AD 上时,如图②所示.①∠BEP= °; ②连接CE ,直线CE 与直线AB 的位置关系是 .(2)请在图③中画出△BPE ,使点E 在直线AD 的右侧,连接CE.试判断直线CE 与直线AB 的位置关系,并说明理由.(3)当点P 在线段AD 上运动时,求AE 的最小值.【解题过程】(1)①由题意得,PE=PB ,∠BPE=80°,∴∠BEP=︒=︒-︒50280180; ②如图所示,∵AB=AC ,D 是BC 的中点,∠BAC=100°,∴∠ABC=︒=︒-︒402100180,∵∠BEP=50°,∴∠BCE=∠CBE=40°,∴∠ABC=∠BCE ,∴CE ∥AB .答案:①50°;②平行 (2)在DA 延长线上取点F ,使∠BFA=∠CFA=40°,总有△BPE ∽△BFC . 又∵△BPF ∽△BEC ,∴∠BCE=∠BFP=40°,∴∠BCE=∠ABC=40°,∴CE ∥AB .(3)当点P 在线段AD 上运动时,由题意得PB=PE=PC , ∴点B 、E 、C 在以P 为圆心、PB 为半径的圆上,如图所示:∴AE 的最小值为AC=3.。
中考数学一轮复习第二部分热点专题突破专题5化“斜”为“直”课件4.ppt

A.43
B.54
C.65
D.76
1 2 3 4 5 6 7 8 9 10 11
【解析】如图,作FN∥AD,交AB于点N,交B∥CD,
∵FN∥AD,∴四边形ANFD是平行四边形,
∵∠D=90°,∴四边形ANFD是矩形,
∵AE=3DE,设DE=a,
则AE=3a,AD=AB=CD=FN=4a,AN=DF=2a,
【解析】我们可以认为这里的正方形ABCD是“斜放”在一组平行线中,正因为“斜放”才
给我们带来难度,我们通过“过点A作AF⊥l3分别交l2,l3于点E,F,过点C作CH⊥l2分别交 l2,l3于点H,G”即可实现“化直”的目的.
类型1
类型2
类型3
【答案】 过点A作AF⊥l3分别交l2,l3于点E,F,过点C作CH⊥l2分别交l2,l3于点H,G.
( 1 )求b,c的值; ( 2 )点P为二次函数y=-x2+bx+c的图象在第一象限部分上的一动点,其横坐标为 x( 0<x<3 ),写出四边形OAPB的面积S关于点P的横坐标x的函数关系式,并求S的最大 值. 【解析】( 1 )用待定系数法求解;( 2 )过点P作PC⊥x轴于点C,过点P作PD⊥y轴于点 D,四边形AOBP转化为矩形CPDO和Rt△BDP,Rt△APC.用关于x的式子表示出这三个 图形的面积,即可求出四边形OAPB的面积S关于x的函数关系式,从而求出S的最大值.
类型3
【名师点拨】 解答本题的关键是过点A作AF⊥BC于点F,从而把关于斜△ABE的问题 转化为两个直角三角形( Rt△ABF和Rt△AEF )的问题.其实这种通过作垂线或平行线 把斜三角形化成直角三角形的方法在解直角三角形问题中极为常见,注意学习体会.
备战2023年高考地理时事热点专题训练5 台湾问题含详解

备战2023年高考地理时事热点专题训练5台湾问题含详解(一)台湾问题一直是中国的核心利益和重大问题,也是国际关注的焦点之一。
自1949年中华人民共和国成立后,台湾地区与祖国大陆之间的关系一直存在着分裂与对立。
台湾问题的核心是两岸关系的和平发展和统一问题。
近年来,伴随着台湾的政治和经济变化,台湾问题的热度不断上升,成为地理时事热点之一。
台湾地区的政治形势一直备受关注。
台湾自20世纪80年代以来逐渐实现了从威权主义到民主主义的转变,这一过程中涌现了许多重要的政治事件。
例如,1996年的“两岸危机”及其后果、2000年的首次台湾地区领导人选举、2008年的“九二共识”、2016年的“9合一选举”等都对台湾政治产生了重大影响。
这些政治事件不仅反映了台湾地区内部政党的权力竞争,也影响到两岸关系的发展。
各个政党和政治派别之间的角力,为台湾问题的解决和两岸关系的和平发展带来了新的变数。
与此同时,台湾地区的经济发展也备受关注。
台湾地区经济发达,是世界上重要的制造业和电子信息产业基地之一。
它以高科技产业和创新能力著称,对全球电子信息产业有着重要的影响力。
然而,由于台湾地区经济高度依赖大陆市场,近年来两岸关系的不稳定和政治争议对台湾经济产生了一定的压力。
此外,全球经济的变化也对台湾地区的经济发展带来了挑战。
因此,台湾地区经济的稳定和发展仍然是其中一个地理时事的焦点。
除了政治和经济问题,台湾地区的社会变革也备受关注。
台湾地区的社会发展和价值观念正在经历着深刻的变化。
例如,同性婚姻合法化、妇女权益的保护、青年就业等问题在台湾社会引起了广泛的讨论和争议。
这些社会变革不仅反映了台湾地区社会的进步和多元化,也对传统的社会结构和价值观念带来了挑战。
这些社会问题与台湾问题密切相关,将对两岸关系的发展产生重要的影响。
综上所述,台湾问题是一个热点、复杂且长期存在的问题。
它不仅涉及到两岸关系的发展和和平统一的目标,也关乎中国的核心利益和国家的统一。
