第5章 频率响应
合集下载
第5章频率响应法
第 5 章频率响应法频率响应法是控制理论的重要组成部分，是分析和综合控制系统的一种工程实用方法。
它不仅适用于单变量系统，而且也可以推广至多变量系统。
它的特点是：不必求解系统的高阶微分方程，可直接根据频率特性曲线的形状及其特征量来研究系统的性能。
其突出的优点是：物理意义明确，可用实验的方法求出系统的频率特性和传递函数；而且计算量小，方法形象和直观，因而广为工程界所采用。
根据它在系统分析和综合中的应用，将频率响应法分为两部分：频率响应分析法和频率响应综合法，并分别在第 5 章和第6 章讨论。
在这一章里主要介绍：频率响应法的基本概念和控制系统频率特性曲线的绘制方法，以及它在系统分析与综合中的应用，重点在于其基本概念和应用。
5.1 频率特性频率响应法起源于通讯学科。
它的基本思想是：将控制系统的变量也看作是信号；这些信号通过傅里叶(Fourier) 分析，对于周期信号可展开为傅氏级数，对于非周期信号可进行傅氏变换，它们均可视为由不同频率成分的正弦信号所合成的；线性定常系统各个变量的运动，就是系统对各个不同频率信号响应叠加的结果。
频率响应法的优点：第一，这种方法具有鲜明的物理意义。
第二，可以用实验方法测出系统的频率特性，并获得其传递函数以及其它形式的数学模型。
第三，它是一种图解法，形象直观、计算量小。
频率响应法也存在一定的局限性：首先它只适用于线性定常系统。
其次，频率响应法的筒便和实用性是以它的工程近似性为代价的。
5.1.1 频率特性的基本概念首先考察图 5.1 一阶RC 电路图图 5.1 所示的简单系统。
该系统为一阶RC 电路。
该电路的微分方程为：（5.1）系统的传递函数为：（5.2）图 5.1 一阶 RC 电路图若外施正弦输入电压，则可得系统的输出响应为：式中等号右边的第一项为输出响应的暂态分量，第二项为输出响应的稳态分量。
当t趋于无穷大时第一项的暂态分量将趋于零，故系统的稳态输出响应为：可以看到：在正弦输入电压作用下系统的稳态输出，是与输入同频率的正弦电压，其幅值为输入幅值的倍，相角比输入的迟后arctgωT。
自控 邹伯敏第05章1
0 ≤ ξ ≤ 0.707
图5-16 Mr与ζ 的关系曲线
2010-12-27 第五章 频率响应 14
自动控制理论 5. 滞后因子
e −τjω
G ( jω ) = e −τjω = 1
ϕ (ω ) = −τω
图5-17 滞后因子的相频特性
2010-12-27 第五章 频率响应 15
自动控制理论
二、开环系统的伯德图
例5-2 G ( s ) H ( s ) =
10 (1 + 0.1s ) 绘制Bode图。 s (1 + 0.5 s )
解： （1）幅频特性
G ( jω ) =
10 (1 + j
ω
10 2
) )
16
jω (1 + j
ω
2010-12-27
第五章 频率响应
自动控制理论
L (ω ) = 20 lg 10 − 20 lg ω − 20 lg 1 − ( ) 2 + 20 lg 1 + ( ) 2 2 10
图5-9
2010-12-27
1 (1 + jωT ) −的对数幅频曲线、渐近线和相角曲线
第五章 频率响应
9
自动控制理论
由于(1 + jωT )与(1 + jωT ) −1 互为倒数,则有
20 lg 1 + jωT = −20 lg arg(1 + jωT ) = − arg( 1 1 + jω T
试绘制系统的幅频和相频特性曲线。 解：令
S ， jq =
10( j 2 + 1) ( j 2 + 2 + j 3)( j 2 + 2 − j 3)
第5章-2010频率响应
duo duo 则： = t =0 = ±ω Uom dt max dt t =π S π 须使： 须使： R > 2π f Uom 否则将引起输出波形失真 µA741，Uom= 10 V 最高不失真频率为 8 kHz ， 2. 全功率带宽 BWP 输出为最大峰值电压时不产生明显失真的最高工作频率 三、高速宽带集成运放 ， 当 BWG > 2 MHz， BWP > 20 kHz， ，
ZR = R
ZC =
1 jω C
=
R 1 R+ jω C
=
1 1 1+ jω RC
令
1 1 , fL = RC = τ , ω L = 2π R C RC
则：
& Au =
其中： 其中：
ωL 1+ jω
& Au =
1
=
1 fL 1+ jf
f fL
=
f j fL 1+ j
& = Au ∠ϕ f
fL
幅频特性
令： RC = τ , ω H = 1 , f H =
RC
1 2π RC
得：
& Au =
1 f 1+ j fH
& Au =
1 f 2 1+ （ ） fH
幅频特性
其中： 其中：
f ϕ = − arg tg fH
（1）若 f
相频特性
= fH ：
o
& Au ≈ 0.707
ϕ = −45
（2）若 f << fH： ） & A ≈1
用渐进线取代曲线
-40
幅频特性波特图
高通
模电第5章
低通电路： 二. 低通电路：频率响应
f<<fH时放大 倍数约为1 倍数约为
fH
1 Uo 1 jω C = Au = = 1 1 + jωRC Ui R+ jω C
1 1 = 令f H = ，则Au 2 πRC 1+ j f fH
1 Au = 1 + ( f fH )2 = arctan( f f ) H
fL
= 1 ， = 45 0； f = f L : Au 2 f f
f << f L : A << 1， u ≈
fL fL Au 也下降10倍；当 f 趋于0时， u 趋于0，趋于90 0 。 A
，表明 f 每下降10倍,
画出特性曲线如图， 称为下限截止频率。 画出特性曲线如图， fL称为下限截止频率。
' 高频段： 的影响， 开路。 高频段：考虑 Cπ 的影响，C 开路。 '
'
一. 中频电压放大倍数
Uo Ausm = Us U i U b'e U o = U U Us i b'e
带负载时： 带负载时： Ausm = 空载时： 空载时：
rb'e Ri [ g m ( Rc ∥ RL )] Rs + Ri rbe
5.2 晶体管的高频等效电路
5.2.1 混合π模型：形状像Π，参数量纲各不相同 混合π模型：形状像Π
完整的混合π模型 一. 完整的混合 模型 结构：由体电阻、结电阻、结电容组成。 结构：由体电阻、结电阻、结电容组成。
因面积大 而阻值小
因多子浓 度高而阻 值小
rbb’：基区体电阻 rb’e’：发射结电阻 Cπ：发射结电容 re：发射区体电阻 rb’c’：集电结电阻 C：集电结电容 rc：集电区体电阻
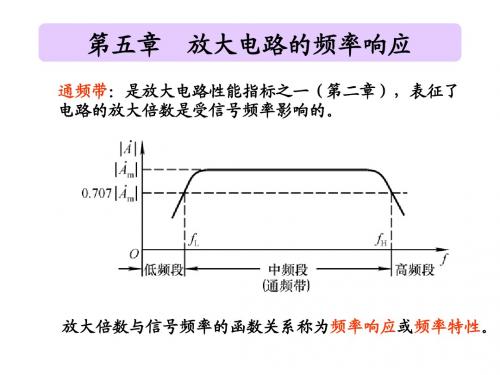
第五章 放大电路的频率响应
1 fH 2 RC
1 fL 2 RC
当信号频率等于上（下）限频率时，放大电路的 增益下降3dB，且产生±45°相移
近似分析时，可用折线化的波特图表示电路的频 率特性
一个电容对应的渐进线斜率为20dB/十倍频
简单 RC 电路的频率特性
Ui
•
R C
Uo
•
Ui
•
C R
Uo
•
RC 低通电路
RC 高通电路
Au
• |Au |
1 0.707
1 f 1 j fH
1 0.707
Au
1 fL 1 j f
|Au |
fL
f
•
O
fH f
f
O
O –45° –90°
90° 45° O
f
研究频率响应的方法 (1) 三个频段的划分 1) 中频区(段) 特点:Aus与f无关
与f无关
5.4 单管放大电路的频率响应
本节以单管共射电路为例，介绍频率响应的一般 分析方法。
5.4.1 单管共射放大电路的频率响应
1、画出全频段的微变等效电路
+VCC RB C1 + . Ui VT RL . Uo RC C2 + + . Ui _ RB rb′e
C1
rbb′ . gmUb'e Cπ′
C2 + RC . RL U o _
R
fL
L 1 1 下限截止频率 2 2 2 RC
Au பைடு நூலகம்
1
L 1 j
1 fL 1 jf
f j fL f 1 j fL
1、RC高通电路的频率响应
第5章 放大电路的频率响应
4. 晶体管的频率参数 1) 共射极截止频率fβ
由微变等效分析可知:
根据式(5.2.4), 将混合 П 型等效电路中c、e输出端短路, 则得图5.2.4。
第5章 放大电路的频率响应 图5.2.4 计算̇β=̇Ic/̇Ib 的等效电路
第5章 放大电路的频率响应
其幅频特性和相频特性的表达式为
式中 可见β为具有一个转折频率fβ的频率特性曲线, 如图5.2.5所示。fβ称为共射极 截止频率, 其值主要决定于管子的结构。
式中，ω 为输入信号的角频率, R1C1为回路的时间常数τ，
第5章 放大电路的频率响应 图5.1.2 用来模拟放大电路高频 特性的RC低通电路
第5章 放大电路的频率响应
令 则式(5.1.2)变为
AuH为高频电压增益, 其幅值|̇AuH|和相角φH分别为
第5章 放大电路的频率响应
1) 幅频特性 幅频响应波特图可按式(5.1.5)由下列步骤画出: 当f≪fH时,
第5章 放大电路的频率响应 图5.2.3 低频等效电路
第5章 放大电路的频率响应
晶体管放大电路的高频特性决定于混合 Π 型等效电路的参数gm、rbb'、 rb'e、 Cb'e及Cb'c。这些参数可用β、rbe、fT及Cob来表示。因此, 可用β、rbe、fT 及Cob来衡量晶体管的高频性能。
第5章 放大电路的频率响应
可求得̇A'u的表达式如下:
第5章 放大电路的频率响应
因为Cb‘c很小,β)re=(1+β)UT/IE。Cb'e为发射结电容。
3) 集电结参数rb'c和Cb'c
rb'c表示集电结的结电阻, 由于集电结工作时处于反向偏置。Cb'c为集电结电
由微变等效分析可知:
根据式(5.2.4), 将混合 П 型等效电路中c、e输出端短路, 则得图5.2.4。
第5章 放大电路的频率响应 图5.2.4 计算̇β=̇Ic/̇Ib 的等效电路
第5章 放大电路的频率响应
其幅频特性和相频特性的表达式为
式中 可见β为具有一个转折频率fβ的频率特性曲线, 如图5.2.5所示。fβ称为共射极 截止频率, 其值主要决定于管子的结构。
式中，ω 为输入信号的角频率, R1C1为回路的时间常数τ，
第5章 放大电路的频率响应 图5.1.2 用来模拟放大电路高频 特性的RC低通电路
第5章 放大电路的频率响应
令 则式(5.1.2)变为
AuH为高频电压增益, 其幅值|̇AuH|和相角φH分别为
第5章 放大电路的频率响应
1) 幅频特性 幅频响应波特图可按式(5.1.5)由下列步骤画出: 当f≪fH时,
第5章 放大电路的频率响应 图5.2.3 低频等效电路
第5章 放大电路的频率响应
晶体管放大电路的高频特性决定于混合 Π 型等效电路的参数gm、rbb'、 rb'e、 Cb'e及Cb'c。这些参数可用β、rbe、fT及Cob来表示。因此, 可用β、rbe、fT 及Cob来衡量晶体管的高频性能。
第5章 放大电路的频率响应
可求得̇A'u的表达式如下:
第5章 放大电路的频率响应
因为Cb‘c很小,β)re=(1+β)UT/IE。Cb'e为发射结电容。
3) 集电结参数rb'c和Cb'c
rb'c表示集电结的结电阻, 由于集电结工作时处于反向偏置。Cb'c为集电结电
第五章 放大电路频率响应
ωH 2π
1 2 ππ o C o
fH为RoC’o低通电路的上限频率。 那么
Au
1 j 1 （ f
f fH ）
2
1 1 j ω ωH
1 1 j f fH
（2）频率特性
fH
①幅频特性分析
Au
1 1 ( f fH )
2
当f<<fH时（即中频及以下）： A u 1； 当f=fH时：
R rbe //rbb ( Rs // Rb )
Ausm Uo rbe Ri gm Rc Rs Ri rbe Us
二、单管共源放大电路及其等效电路
单管共源放大电路及其等效电路
在中频段 C 开路，C短路，中频电压放大倍数为
gs
A um
Uo
gm U
gs
( R d // R L )
gs
g m RL
Ui
U
在高频段，C短路，考虑 C gs 的影响，Rg和 C 组成 低通电路，上限频率为：
其近似波特图自行画出。
四、高频段的频率特性
1.高频段交流通路
2.电路的输出电阻Ro与管子的结电容Ccb、Cbe以及输出电 路元件分布电容Co组成低通电路
C o 为Ccb、Cbe以及Co的等效电容。考虑
它们的影响后，uce中不同频率成分在 等效电容上的分压不同。利用相量分压 法讨论分压，进而得频率特性。
和低频段下降的主要原因分别是什么。
本章讨论的问题：
1.为什么要讨论频率响应？如何讨论一个RC网络的频 率响应？如何画出频率响应曲线？
2.晶体管与场效应管的h参数等效模型在高频下还适应吗？ 为什么？ 3.什么是放大电路的通频带？哪些因素影响通频带？如何 确定放大电路的通频带？ 4.如果放大电路的频率响应窄，应该怎么办？ 5.对于放大电路，通频带愈宽愈好吗？ 6.为什么集成运放的通频带很窄？有办法展宽吗？
第五章 频率响应法1
本章用到的基础知识
欧拉公式：cosθ sinθ
1 2 1
e jθ e jθ e jθ e jθ
2j
log
a
b1
b2
bn
log
a
b1
log
a
b2
log
a
bn
对数运算：log
a
b1 b2
log
a b1
log
a
b2
log abx xlog ab
复数运算：a
c
jb jd
a c
jbc jd c
1 Tl2 2
j2 lTl
1.采用对数坐标，可将幅值的乘除运算化为加减运算；
2.传函中典型环节的乘积关系变为对数坐标图上的加减运
算后能够明显反映出各典型环节对总的对数坐标图的影
响，为分析每个环节的影响提供了方便。
23
5-2 典型环节频率特性的绘制
自动控制系统通常由若干环节构成，根据它们的基本特
性，可划分成几种典型环节。本节将介绍典型环节频率特性
输入信号为 r(t) X sint
R(s)
C(s)
G(s)
图5-1 系统方框图
8
则输入信号的拉氏变换是：
X
X
R(s) s2 2 (s j)(s j)
系统的传递函数通常可以写成：
N(s)
N(s)
G(s) D(s) (s p1 )(s p2 )(s pn )
由此得到输出信号的拉氏变换：
表示，易于绘制，且具有一定的精确度。通常可用这种
近似的对数坐标图对系统进行分析。如果需要精确的对
数坐标图，可对这种近似的坐标图进行适当的修正即可。
21
3.简化计算
欧拉公式：cosθ sinθ
1 2 1
e jθ e jθ e jθ e jθ
2j
log
a
b1
b2
bn
log
a
b1
log
a
b2
log
a
bn
对数运算：log
a
b1 b2
log
a b1
log
a
b2
log abx xlog ab
复数运算：a
c
jb jd
a c
jbc jd c
1 Tl2 2
j2 lTl
1.采用对数坐标，可将幅值的乘除运算化为加减运算；
2.传函中典型环节的乘积关系变为对数坐标图上的加减运
算后能够明显反映出各典型环节对总的对数坐标图的影
响，为分析每个环节的影响提供了方便。
23
5-2 典型环节频率特性的绘制
自动控制系统通常由若干环节构成，根据它们的基本特
性，可划分成几种典型环节。本节将介绍典型环节频率特性
输入信号为 r(t) X sint
R(s)
C(s)
G(s)
图5-1 系统方框图
8
则输入信号的拉氏变换是：
X
X
R(s) s2 2 (s j)(s j)
系统的传递函数通常可以写成：
N(s)
N(s)
G(s) D(s) (s p1 )(s p2 )(s pn )
由此得到输出信号的拉氏变换：
表示，易于绘制，且具有一定的精确度。通常可用这种
近似的对数坐标图对系统进行分析。如果需要精确的对
数坐标图，可对这种近似的坐标图进行适当的修正即可。
21
3.简化计算
南京理工大学考研-自动控制原理第五章 频域响应法
j
0
ω (0 )
积分环节的幅相曲线
3. 微分环节:G(s)=s
G(jω)= jω= ω∠π/2
G ( j ) , G ( j ) 90
j
ω (0 ) 0
微分环节幅相曲线
4. 惯性环节:G(s)=1/(Ts+1)
1 1 jarctg T 频率特性 G ( j ) e 22 1 j T 1 T
j
0 ω=∞
1/2 -45o
1 ω=0
ω=1/T
惯性环节
5. 一阶微分环节:G(s)=Ts+1
2 2ja rctg T 频率特性 G ( j ) 1 j T 1 T e
j
ω (0 ) 0
1
一阶微分环节
6. 振荡环节
1 G ( s ) 2 ( s / ) 2 ( s / ) 1 n n
j t
2 j
2 j
G ( jw ) A sin( t ( )) A sin( t ( )) c
A() G( j) () G( j)
幅频特性 相频特性
线性系统的稳态输出是和输入具有相同频率的正弦信号， 其输出与输入的幅值比为 输出与输入的相位差
A s in t
系统
稳态输出
m m 1 b s b s b s b 0 1 m 1 m A C ( s ) G ( s ) R ( s ) n n 1 2 2 s a s a s a s 1 n 1 n
即： C ( s ) i
- s 8. 延迟环节 G(s) e
-j G(j ) e
0
ω (0 )
积分环节的幅相曲线
3. 微分环节:G(s)=s
G(jω)= jω= ω∠π/2
G ( j ) , G ( j ) 90
j
ω (0 ) 0
微分环节幅相曲线
4. 惯性环节:G(s)=1/(Ts+1)
1 1 jarctg T 频率特性 G ( j ) e 22 1 j T 1 T
j
0 ω=∞
1/2 -45o
1 ω=0
ω=1/T
惯性环节
5. 一阶微分环节:G(s)=Ts+1
2 2ja rctg T 频率特性 G ( j ) 1 j T 1 T e
j
ω (0 ) 0
1
一阶微分环节
6. 振荡环节
1 G ( s ) 2 ( s / ) 2 ( s / ) 1 n n
j t
2 j
2 j
G ( jw ) A sin( t ( )) A sin( t ( )) c
A() G( j) () G( j)
幅频特性 相频特性
线性系统的稳态输出是和输入具有相同频率的正弦信号， 其输出与输入的幅值比为 输出与输入的相位差
A s in t
系统
稳态输出
m m 1 b s b s b s b 0 1 m 1 m A C ( s ) G ( s ) R ( s ) n n 1 2 2 s a s a s a s 1 n 1 n
即： C ( s ) i
- s 8. 延迟环节 G(s) e
-j G(j ) e
第5章放大电路的频率响应
＋ Ui C ＋ Uo
－
－
(b) 高频段极间电容的影响
结束
第 5章
放大电路的频率响应
一、高通电路
图5.1.1 高通电路及频率响应
结束
第 5章
放大电路的频率响应
RC高通电路的电压增益： ( s) U R 1 o Au ( s ) 1 1 U i ( s) R 1 j C jRC 1 1 1 fL L 令 2RC RC
A ush
R rbe //(rbb Rs // Rb ) U U U U 0 s be 0 U U U U
s s s be
1 Ri rbe jRC ( g m R L) 1 Rs Ri rbe 1 jRC
f fL f 2 1 ( ) fL
f 180 （90 arctg ) fL f 90 arctg fL
结束
第 5章
放大电路的频率响应
三、高频电压放大倍数
图5.4.4 单管共射放大电路的高频等效电路
结束
第 5章
放大电路的频率响应
rbe rbe Ri Us Ui U s rbe rbe Rs Ri
'
U b'e (1
U ce U b 'e
(c)
)
1 j C m
令
U ce U b'e
K ,则
U b'e (1 K ) U b 'e I 1 1 j C m j (1 K )C m
'
结束
第 5章
放大电路的频率响应
－
－
(b) 高频段极间电容的影响
结束
第 5章
放大电路的频率响应
一、高通电路
图5.1.1 高通电路及频率响应
结束
第 5章
放大电路的频率响应
RC高通电路的电压增益： ( s) U R 1 o Au ( s ) 1 1 U i ( s) R 1 j C jRC 1 1 1 fL L 令 2RC RC
A ush
R rbe //(rbb Rs // Rb ) U U U U 0 s be 0 U U U U
s s s be
1 Ri rbe jRC ( g m R L) 1 Rs Ri rbe 1 jRC
f fL f 2 1 ( ) fL
f 180 （90 arctg ) fL f 90 arctg fL
结束
第 5章
放大电路的频率响应
三、高频电压放大倍数
图5.4.4 单管共射放大电路的高频等效电路
结束
第 5章
放大电路的频率响应
rbe rbe Ri Us Ui U s rbe rbe Rs Ri
'
U b'e (1
U ce U b 'e
(c)
)
1 j C m
令
U ce U b'e
K ,则
U b'e (1 K ) U b 'e I 1 1 j C m j (1 K )C m
'
结束
第 5章
放大电路的频率响应
第5章放大电路的频率响应
f L(H)
1 = 2 πτ
4、频率响应有幅频特性和相频特性两条曲线。 、频率响应有幅频特性和相频特性两条曲线。
5.2、ቤተ መጻሕፍቲ ባይዱ大电路的频率参数 5.2、放大电路的频率参数
高通 电路 低通 电路 下限频率
f bw = f H f L
上限频率
在低频段，随着信号频率逐渐降低，耦合电容、 在低频段，随着信号频率逐渐降低，耦合电容、旁路电 容等的容抗增大，使动态信号损失，放大能力下降。 容等的容抗增大，使动态信号损失，放大能力下降。 在高频段，随着信号频率逐渐升高， 在高频段，随着信号频率逐渐升高，晶体管极间电容和 分布电容、寄生电容等杂散电容的容抗减小， 分布电容、寄生电容等杂散电容的容抗减小，使动态信号 损失，放大能力下降。 损失，放大能力下降。
f << fβ 时，& ≈ β0； β
& β βo
β f = fβ 时 β = 0 ≈ 0.707β0 ， = -45°； ，& 2 & ≈ fβ β ；f →∞时 β →0， →-90° f >> fβ 时 β ， ，& 0 f
电流放大倍数的波特图: 电流放大倍数的波特图: 采用对数坐标系
折线化近似画法
晶体管的高频等效电路
1、混合π模型：形状像Π，参数量纲各不相同 混合π模型：形状像Π
结构：由体电阻、结电阻、结电容组成。 结构：由体电阻、结电阻、结电容组成。 因面积大而 阻值小
因多子浓度 高而阻值小
rbb’：基区体电阻 rb’e’：发射结电阻 Cπ：发射结电容 re：发射区体电阻 rb’c’：集电结电阻 C：集电结电容 rc：集电区体电阻
C连接了输入回路 和输出回路， 和输出回路，引入 了反馈， 了反馈，信号传递 有两个方向， 有两个方向，使电 路的分析复杂化。 路的分析复杂化。
第五章 频率响应法3
2.关于P的说明 P表示F(s)=1+G(s)H(s)在s右半平面上的极点数。由
F(s)的表达式可知1+G(s)H(s)的极点就是G(s)H(s)的极点。 换言之，P表示开环传函G(s)H(s)在s右半平面上的极点数。
当开环传函G(s)H(s)在s右半平面上没有极点时P=0,由
N=Z-P可知闭环系统稳定的充要条件是N=0.也即对于开环
1
在s平面的右半部有无零点的问题，
也就是闭环传函在s平面的右半面 0
有无极点的问题。
s
R
2
如果在s平面上选择一条能够整 3
个包围s右半平面的封闭曲线，则幅 角原理就可用来分析系统的稳定性。
1.正虚轴：s j, 频率由0变化到
2.半径为无穷大的右半圆：s Re j , R ,由
进行，为应用幅角原理，选择
F(s) 1 G(s)H(s) 1 A(s) C(s) B(s)D(s) A(s)C(s)
B(s) D(s)
B(s)D(s)
A(s)
(s)
1
G(s) G(s)H(s)
1
B(s)
A(s) Cs
B(s) Ds
A(s)D(s) B(s)D(s) A(s)C(s)
1.F(s)的零点为闭环传函的极点,F(s)的极点为开环传函的极点
(s) G(s) 1 A(s) C(s)
A(s)D(s)
1 G(s)H(s) B(s) D(s) B(s)D(s) A(s)C(s)
F(s) 1 G(s)H(s) 1 A(s) C(s) B(s)D(s) A(s)C(s)
B(s) D(s)
B(s)D(s)
由F(s)的特点可以看出F(s)取上述特定形式具有两个优点：
第五章频率响应
分析滤波电路，就是求解电路的频率特性，即求解Au (Aup （通带放大倍数） ) 、 fp和过渡带的斜率 。
滤波电路的分类：
无源滤波电路：仅有无源元件（R、C、L） 组成
有源滤波电路：有无源元件和有源元件（双 击型晶体管、单级型管、集成运放）共同组 成
1.无源低通滤波器：
信号频率趋于零时，电容容抗 趋于无穷大（开路），通带放 大倍数:
切比雪夫(Chebyshev) 贝塞尔（Bessel）
图7.4.15三种类型二阶LPF幅频特性
7.4.3 其它滤波电路
一、高通滤波电路
高通滤波电路与低通滤波电路具有对称性
1.压控电压源二阶 高通滤波电路
2.无限增益多路反馈 二阶高通滤波电路
图7.4.16二阶高通滤波电路
二阶有源高通滤波器
A u
时域(t)变量t是实数， 复频域F(s)变量s是复数。变 量s又称“复频率”。
拉氏变换建立了时域与复频域(s域）之间的联系。 s=jw，当中的j是复数单位，所以使用的是复频域。
通俗的解释方法是，因为系统中有电感X=jwL、电 容X=1/jwC，物理意义是，系统H(s)对不同的频率分 量有不同的衰减，即这种衰减是发生在频域的，所 以为了与时域区别，引入复数的运算。 在复频域计算的形式仍然满足欧姆定理、KCL、 KVL、叠加法。
A
R 1
u 1 ( f )2 j3 f
f
f
0
0
图7.4.8简单二阶低通电路的幅频特性
二、反相输入低通滤波器
1.一阶电路
令信号频率＝0，求出 通带放大倍数
A
R 2
up
R
1
电路的传递函数
图7.4.11反相输入一阶
第5章 放大电路的频率响应(1)
5 - 1 - 25
例1： 已知某电路的波特图如图所示。 （1）电路的中频电压增益 ＝ -32 。 ＝ 30 dB， A um
（2）电路的下限频率fL≈ 10 Hz，上限频率fH≈ 100 kHz。
（3）电路的电压放大倍数 ＝ 的表达式 A u
A u 32 (1 10 f )( 1 j 5 ) jf 10 或A u 3.2 jf f f ( 1 j )( 1 j 5 ) 10 10
5 - 1 - 34
例3（p243 自测题一）选择正确答案填入空内。
（ 3）当信号频率等于放大电路的fL 或 fH时，放大倍数 的值约下降到中频时的 B 。 A.0.5倍 B.0.7倍 C.0.9倍 即增益下降 A 。 A.3dB B.4dB C.5dB （4）对于单管共射放大电路，当f ＝ fL时，输出与输 入相位关系是 C 。 A.＋45˚ B.－90˚ C.－135˚ 当f ＝ fH时，输出与输入的相位关系是 C 。 A.－45˚ B.－135˚ C.－225˚
模拟电子技术基础
第十七次课
河北科技大学信息学院
基础电子教研室
5-1-1
第五章 放大电路的频率响应
. 频率响应概述
. 晶体管的高频等效模型 . 放大电路的频率响应
5-1-2
5.1 频率响应概述
一、 频率响应的概念： 在放大电路中，放大倍数与信号频率的函数关系， 称为频率响应或频率特性。
放大电路中由于C，L及晶体管极间电容的存在，电路对不 同频率的信号具有不同的放大能力。 在第二章中2.1介绍电路性能时，简单说明了通频带的概念。 指出放大电路对某一频率范围的信号能正常放大，这个频率范围 称为通频带。 了解电路对不同频率信号的放大能力，在使用电路前应查阅 资料，了解通频带，确定电路的适用范围。
例1： 已知某电路的波特图如图所示。 （1）电路的中频电压增益 ＝ -32 。 ＝ 30 dB， A um
（2）电路的下限频率fL≈ 10 Hz，上限频率fH≈ 100 kHz。
（3）电路的电压放大倍数 ＝ 的表达式 A u
A u 32 (1 10 f )( 1 j 5 ) jf 10 或A u 3.2 jf f f ( 1 j )( 1 j 5 ) 10 10
5 - 1 - 34
例3（p243 自测题一）选择正确答案填入空内。
（ 3）当信号频率等于放大电路的fL 或 fH时，放大倍数 的值约下降到中频时的 B 。 A.0.5倍 B.0.7倍 C.0.9倍 即增益下降 A 。 A.3dB B.4dB C.5dB （4）对于单管共射放大电路，当f ＝ fL时，输出与输 入相位关系是 C 。 A.＋45˚ B.－90˚ C.－135˚ 当f ＝ fH时，输出与输入的相位关系是 C 。 A.－45˚ B.－135˚ C.－225˚
模拟电子技术基础
第十七次课
河北科技大学信息学院
基础电子教研室
5-1-1
第五章 放大电路的频率响应
. 频率响应概述
. 晶体管的高频等效模型 . 放大电路的频率响应
5-1-2
5.1 频率响应概述
一、 频率响应的概念： 在放大电路中，放大倍数与信号频率的函数关系， 称为频率响应或频率特性。
放大电路中由于C，L及晶体管极间电容的存在，电路对不 同频率的信号具有不同的放大能力。 在第二章中2.1介绍电路性能时，简单说明了通频带的概念。 指出放大电路对某一频率范围的信号能正常放大，这个频率范围 称为通频带。 了解电路对不同频率信号的放大能力，在使用电路前应查阅 资料，了解通频带，确定电路的适用范围。
《模拟电子技术基础》第三版习题解答第5章放大电路的频率响应题解
第五章 放大电路的频率响应自 测 题一、选择正确答案填入空。
（1）测试放大电路输出电压幅值与相位的变化，可以得到它的频率响应，条件是 。
A.输入电压幅值不变，改变频率B.输入电压频率不变，改变幅值C.输入电压的幅值与频率同时变化（2）放大电路在高频信号作用时放大倍数数值下降的原因是，而低频信号作用时放大倍数数值下降的原因是 。
A.耦合电容和旁路电容的存在B.半导体管极间电容和分布电容的存在。
C.半导体管的非线性特性D.放大电路的静态工作点不合适（3）当信号频率等于放大电路的f L 或f H 时，放大倍数的值约下降到中频时的。
A.0.5倍B.0.7倍C.0.9倍 即增益下降。
A.3dBB.4dBC.5dB（4）对于单管共射放大电路，当f ＝ f L 时，o U 与iU 相位关系是。
A.＋45˚B.－90˚ C.－135˚当f ＝ f H 时，o U 与iU 的相位关系是。
A.－45˚ B.－135˚ C.－225˚ 解：（1）A （2）B ，A （3）B A （4）C C二、电路如图T5.2所示。
已知：V C C ＝12V ；晶体管的C μ＝4pF ，f T =50MHz ，'bb r ＝100Ω, β0＝80。
试求解：（1）中频电压放大倍数smu A ； （2）'πC ；（3）f H 和f L ； （4）画出波特图。
图T5.2解：（1）静态与动态的分析估算：∥178)(mA/V2.69k 27.1k 27.1k 17.1mV26)1(V 3mA 8.1)1(Aμ 6.22c m bee b'i s ismTEQ m b be i e b'bb'be EQe b'c CQ CC CEQ BQ EQ bBEQCC BQ -≈-⋅+=≈=Ω≈=Ω≈+=Ω≈+=≈-=≈+=≈-=R g r r R R R A U I g R r R r r r I r R I V U I I R U V I u ββ（2）估算'πC ：pF1602)1(pF214π2)(π2μc m 'μTe b'0μπe b'0T ≈++=≈-≈+≈C R g C C C f r C C C r f πππββ（3）求解上限、下限截止频率：Hz14)π(21kHz 175π21567)()(i s L 'πH s b b'e b'b s b b'e b'≈+=≈=Ω≈+≈+=CR R f RC f R r r R R r r R ∥∥∥（4）在中频段的增益为dB 45lg 20sm ≈u A频率特性曲线如解图T5.2所示。
模电基础第5章 频率响应
第5章 频率响应
第5章 频率响应
5–1 频率响应的概念 5–2 单级共射放大器的高频响应 5–3 共集电路的高频响应 5–4 共基电路的高频响应 5–5 差分放大器的频率响应 5–6 场效应管放大器的高频响应 5–7 放大器的低频响应 5–8 多级放大器的频率响应 5–9 建立时间tr与上限频率fH的关系 5–10 举例及计算机仿真
b rbb′
b′
Cb′e
Rs
Cb′e
rb′e
.
Us
. gmUb′e
第5章 频率响应
R′L c ＋
rce
RC
RL
. Uo
－
e
(b)
图5–6 (a)电路；(b)等效电路(设RB1‖RB2>>Rs)
AuI
0.707 AuI
(5–4)
BW fH fL fH
(5–5)
GH 20lg Au ( jfH ) 20lg AuI 3dB
(5–6)
GL 20lg Au ( jfL ) 20lg AuI 3dB
G BW AuI BW AuI fH
(5–7)
第5章 频率响应
5–2单级共射放大器的高频响应
第5章 频率响应
三、不失真条件––理想频率响应 综上所述，若放大器对所有不同频率分量信号的 放大倍数相同，延迟时间也相同，那么就不可能产生 频率失真，故不产生频率失真的条件为
Au ( j ) Au ( j ) /_ ( j ) _ Au ( j ) K (常数） ( j ) td (td也为常数）
第5章 频率响应
|Au(jω)| 0.7 07A| uI|
|AuI|
L 半功率点
半功率点 H
理想幅频特性 实际幅频特性
第5章 频率响应
5–1 频率响应的概念 5–2 单级共射放大器的高频响应 5–3 共集电路的高频响应 5–4 共基电路的高频响应 5–5 差分放大器的频率响应 5–6 场效应管放大器的高频响应 5–7 放大器的低频响应 5–8 多级放大器的频率响应 5–9 建立时间tr与上限频率fH的关系 5–10 举例及计算机仿真
b rbb′
b′
Cb′e
Rs
Cb′e
rb′e
.
Us
. gmUb′e
第5章 频率响应
R′L c ＋
rce
RC
RL
. Uo
－
e
(b)
图5–6 (a)电路；(b)等效电路(设RB1‖RB2>>Rs)
AuI
0.707 AuI
(5–4)
BW fH fL fH
(5–5)
GH 20lg Au ( jfH ) 20lg AuI 3dB
(5–6)
GL 20lg Au ( jfL ) 20lg AuI 3dB
G BW AuI BW AuI fH
(5–7)
第5章 频率响应
5–2单级共射放大器的高频响应
第5章 频率响应
三、不失真条件––理想频率响应 综上所述，若放大器对所有不同频率分量信号的 放大倍数相同，延迟时间也相同，那么就不可能产生 频率失真，故不产生频率失真的条件为
Au ( j ) Au ( j ) /_ ( j ) _ Au ( j ) K (常数） ( j ) td (td也为常数）
第5章 频率响应
|Au(jω)| 0.7 07A| uI|
|AuI|
L 半功率点
半功率点 H
理想幅频特性 实际幅频特性
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
e
图5―4 晶体管的高频小信号混合π等效电路
10
第5章 频率响应 章
二、共射短路电流放大系数β(jω)及其上限频率fβ 根据β的定义 其中： = gm 而
g mU b′e Ic β ( j ) = = I b c, e短路 Ib
β0 β0 = (1 + β 0 )re rb′e
β 0 = h fe 零频共射短路电流放大系数
23
第5章 频率响应 章
四、频率特性的波特图近似表示法 将式(5―24)用对数频率响应来表示，即
20 lg Aus ( jω ) (dB ) = 20 lg AuIs
ω 1+ j ωH
AuIs
( dB )
AuIs Au ( jω ) = === H ( s ) = s ω 1+ j 1+
ωH
ωH
可得如图5-9（c）所示的波特图，在处有一拐点，此处有-3dB 的误差。高频区以-20dB/Dec斜率下降。
I1 Z N A(jω) ＝ U2 U1 Z2 (a) I2
＋
U1
＋
U2
－
Z1
－
I1
I2 N Z1 A(jω) ＝ U2 U1 Z2 U2
＋
U1
＋ －
－
(b)
图5―7密勒定理及等效阻抗 (a)原电路； (b)等效后的电路
17
第5章 频率响应 章
图5-6(b)中Cb’C的阻抗为：Z =
1 j C b ' c
＋ －
＋ －
. Us′
. Us
－
(b)
－
图5―8密勒等效后的单向化等效电路 (a)单向化模型； (b)进一步的简化等效电路
19
第5章 频率响应 章
′ 图中 : Ci = Cb′e + CM = Cb′e + (1 + g m RL )Cb′c ′ Rs = rb′e ( RS + rb′b )
rb′e rb′e U s′ = Us = Us Rs + rb′b + rb′e Rs + rbe
13
1 fT ≈ β o f β = >> f β 2πreCb′e
第5章 频率响应 章
即在f>>fβ时，任意频率与该频率时的的乘积等于特征频 率。
四、共基短路电流放大系数α(jω)及fα 因为
β ( jω ) α0 α ( jω ) = = 1 + ( jω ) 1 + j ω ωα β0 ωα = (1 + β 0 )ω β ,α = 1 + β0
2
第5章 频率响应 章
振幅频率失真和相位频率失真都是由电路的线性电 抗元件引起的，故又称为线性失真。
3
第5章 频率响应 章
二、线性失真和非线性失真 线性失真和非线性失真同样会使输出信号产生畸 变，但两者有许多不同点： 1.起因不同 起因不同 线性失真由电路中的线性电抗元件引起； 非线性失真由电路中的非线性元件引起。 2.结果不同 结果不同 线性失真只会使各频率分量信号的比例关系和时 间关系发生变化，或滤掉某些频率分量的信号，但决 不产生输入信号中所没有的新的频率分量信号。
统称为理想频率响应。如图5-2所示。
5
第5章 频率响应 章
|A u(jω)| K 0 0
(jω)
ω
ω ∞ω
(a)
图5―2理想频率响应
(b)
(a)理想振幅频率响应；(b)理想相位频率响应
6
第5章 频率响应 章
5―1―2实际的频率特性及通频带定义 实际的振幅频率特性一般如图5―3所示。振幅频 率响应划分为三个区域，即中频区、低频区和高频区。 并定义上限频率fH、下限频率fL以及通频带BW。 上限频率fH：为高频区放大倍数下降为中频区的0.707 时所对应的频率，即 下限频率fL：
1 0
fβ
fT
f
图5―5 |β(jω)|与频率f的关系曲线
12
第5章 频率响应 章
三、 特征频率fT 定义：|β(jω)|=1时所对应的频率，如图5―5所示。 当f= fT时（fT>>fβ):
β ( jf T ) =
β0
fT 2 1+ ( ) fβ
≈
β0 fβ
fT
=1
当f>>fβ时： β0 fβ β ( j ) ≈ f β ( j ) = β 0 f β f 由上两式可得： f β ( j ) = f T
fα ≈ fT >> f β
14
第5章 频率响应 章
5―2―2共射放大器的高频响应分析 一、共射放大器的高频小信号等效电路 电路及高频等效电路分别如图5-6(a)(b)所示。Cb’C跨 接在输入回路与输出回路之间，所以首先应用密勒定理 将其作单向化近似。
15
第5章 频率响应 章
二、密勒定理以及高频等效电路的单向化模型 密勒定理可以将跨接在网络输入端与输出端之间 的阻抗分别等效为并接在输入端与输出端的阻抗。 如图5―7(a)所示的网络等效为图5-7(b)的网络后：
等效到输入端的阻抗Z1为： Z1 = U 1 =
I1
U1 U 1U 2 ZFra bibliotek=Z
=
1
U2
Z ′ 1 Au
U1
等效到输入端的阻抗Z2为： Z 2 =
U2
I2
U2 式中， A = U1
' u
′ Au = = Z ′ U 2 U 1 Au 1 Z U2
16
为N网络的电压增益。
第5章 频率响应 章
图5―3实际的放大器幅频响应
8
第5章 频率响应 章
若用分贝表示增益G，则
G H = 20 lg Au ( jf H ) = 20 lg AuI 3dB G L = 20 lg Au ( jf L ) = 20 lg AuI 3dB
故又称H和L点为-3dB频率点，BW为-3dB带宽，表示为 BW-3dB 中频区增益AuI与通频带BW是放大器的两个重要指标， 但两者是一对矛盾的指标，所以利用增益频带积来表征放大 器的性能。增益频带积尽可能大。
Au ( jf H ) = 0.707 AuI
Au ( jf L ) = 0.707 AuI
通频带BW： BW=fH-fL≈fH 上、下限频率所对应的H和L点又称为半功率点。
7
第5章 频率响应 章
|A u(jω)| 理想幅频特性 |A uI| 0.707|A uI| L 半功率点 低频区 0 fL BW －3dB fH 中频区 半功率点 H 实际幅频特性 高频区 f
|A u(jω)| 40 20 0 ω (d) 0
(ωH) ＝45°
－2
0d B/
10倍 频 程
ωH ωH
0.01ωH 0.1ωH ωH
10ωH
ω
ω
(b)
－45° －90°
－45° －90°
图5―9考虑管子极间电容影响的共射放大器频率响应 (a)幅频特性；(b)相频特性；(c)幅频特性波特图； (d)相频特性波特图
利用图5―8(b)的单向化简化模型，我们很快可以 估算出电路的频率响应和上限频率fH。
20
第5章 频率响应 章
三、高频增益表达式及上限频率 由图5―8(b)可见
ωH ′ rb′c β o RL ′ 式中 : 中频区放大倍数AuIs = g m RL = Rs + rbe Rs + rbe 1 上限角频率ω H = 2πf H = ′ Rs Ci
根据式(5―26)、(5―27)画出单级共射放大器的幅 频特性和相频特性分别如图5―9(a),(b)所示。在半功率 点处对应的附加相移为-45°，而当频率f≥10fH 以后， 附加相移趋向于最大值(-90°)。
22
第5章 频率响应 章
|A u(j )| ω (a) 0 (j ) ω 0
|AuIs| 0.707|A uIs| ω (c)
第5章 频率响应 章
第5章 频率响应 章
5―1 频率响应的概念 5―2 单级共射放大器的高频响应 5―3 共集电路的高频响应 5―4 共基电路的高频响应 5―5 差分放大器的频率响应 5―6 场效应管放大器的高频响应 5―7 放大器的低频响应 5―8 多级放大器的频率响应 5―9 建立时间 r与上限频率 H的关系 建立时间t 与上限频率f 5―10 举例及计算机仿真
24
第5章 频率响应 章
五、负载电容和分布电容对高频响应的影响 负载电容和分布电容的存在，将使高频响应变差，fH变低。 令CL为负载电容和电路分布电容对高频响应的影响总和，运 用戴维南定理将图5-10(a)等效为5-10(b)。
UCC RB1 C1 ＋ Rs . Us RL CL RC
＋ C2
Ro ≈ RL ′ ′ uo
1
第5章 频率响应 章
5―1 频率响应的概念
5―1―1频率失真及不失真条件 频率失真及不失真条件 一、频率失真 由于电抗元件的存在，使得放大器对不同频率信号 分量的放大倍数和延迟时间不同，而产生的信号失真称为 频率失真。 振幅频率失真：由于放大倍数随频率变化而引起的失真。 （对不同谐波的放大能力不同） 相位频率失真：放大器对不同频率分量信号的延迟不同所 引起的失真。
4
第5章 频率响应 章
三、不失真条件——理想频率响应 不失真条件 理想频率响应 不失真条件：放大器对所有不同频率分量信号的放 大倍数相同，延迟时间也相同，即：
Au ( jω ) = Au ( jω ) ∠ ′ ( jω ) Au ( jω ) = K (常数）
振幅频率响应 相位频率响应
( jω ) = ωt d (t d 也为常数）
1 1 Z = = ′ ′ 1 Au jωCb′c (1 Au ) jωCM ′ Au 1 1 Z2 = Z= = ′ Au 1 ′ ′ Au 1 jωCb′c ( ) jωC M ′ Au Z1 =