固体物理ppt 4
合集下载
高二物理固体课件(PPT)4-4

现象:熔化了的石蜡在云母片上呈椭圆形,而在玻璃片 上呈圆形.
结论:云母晶体在各个方向上的导热性能不同,而非晶 体玻璃在各个方向上的导热性能相同.
【靶台】名打靶时射击者所在的位置。 【靶细胞】名某种细胞成为另外的细胞或抗体的攻击目标时,前者就叫做后者的靶细胞。例如带有表面抗原的细胞受
到免疫细胞或特异性抗体的攻击,它就是免疫细胞或特异性抗体的靶细胞;又如免疫细胞受到某抗原的攻击,它就是该抗原的靶细胞。 【靶心】ī名靶子的中 心部位。 【靶子】?名练习射击或射箭的目标◇这出戏成为大家批评的~。 【坝】(垻、壩)①名拦水的构筑物:拦河~|修一座~。②名河工险要处巩固 堤防的构筑物,如丁坝。③〈方〉名沙滩;沙洲。④坝子(多用于地名):平~(在贵州)|留~(在陕西)。 【坝塘】名塘坝。 【坝田】名山脚围绕的平 坦农田。 【坝子】?名西南地区称平地或平原: 川西~。 【把】(欛)(~儿)名①器具上便于用手拿的部分:茶壶~儿|掸子~儿。②
非晶体则没有规则的几何形状.
靠:他办事很~。 【把握】①动握;拿:司机~着方向盘。②动抓住(抽象的东西):~时机|透过现象,~本质。③名成功的可靠性(多用于“有”和
“没”后):球赛获胜是有~的。 【把戏】名①杂技:耍~|看~。②花招;蒙蔽人的手法:鬼~|收起你这套~,我不会上当的。 【把兄弟】名指结拜的 弟兄。年长的称把兄,年轻;酒店住宿预订https:// ;的称把弟。也叫盟兄弟。 【把斋】∥动封斋。 【把盏】〈书〉动端着酒杯(多用于 斟酒敬客):轮流~,向客人敬酒。 【把捉】动把握;抓住(多用于抽象事物):~事物的本质|~文件的精神实质。 【把子】?①名把东西扎在一起的捆 子:秫秸~。②量a)人一群、一帮叫一把子(多含贬义):一~土匪。)一手抓起的数量,多用于长条形东西:一~韭菜。)用于某些抽象的事物:加~劲 儿。 【把子】?名戏曲中所使用的武器的总称,也指开打的动作:练~|单刀~。 【把子】?名见页〖拜把子〗。 【?】〈方〉①名屎;粪便:屙~。②动拉 屎:想尿就尿,想~就~。 【??】?ɑ〈口〉名屎;粪便(多用于小儿语)。 【钯】(鈀)名金属元素,符号(aa)。银白色,化学性质不活泼,能大量吸附 氢气。用作催化剂,也用来制特种合金等。 【靶】名靶子:打~|环~|Байду номын сангаас~|中~。 【靶标】名靶子:瞄准~。 【靶场】名打靶的场地。 【靶船】名海 上演习时当靶子用的船。 【靶点】名医学上进行某些放射治疗时,放射线从不同方位照射,汇集到病变部位,这个病变部位叫做靶点。 【靶机】ī名当空中 靶子用的无人驾驶飞机。 【靶器官】名指某一疾病或某一物所影响或针对的器官。如心脏、大脑、肾脏、血管是高血压的靶器官,甲状腺是碘的靶器官。
固体物理-第4章-晶体中的缺陷和扩散-4

这种空位—间隙原子对称为 弗伦克尔缺陷。
(成对出现)
4、杂质原子 在材料制备中,有控制地在晶体中引入杂质原子
A、杂质原子取代基质原子而占据格点位置,称替代式杂质。
(二者相接近或前者大一些)
B、杂质原子占据格点间的间隙位置,称填隙式杂质。
(杂质原子比基质原子小)
点缺陷的运动 1、空位的运动
空位运动势场示意图
原子结合成晶体的源动力:原子间的吸引力. 理想晶体的生长
问题4:当初如何提出位错概念?位错滑移如何理解?
Ax A d
a
x a 2
xa 2
弹性形变
范性形变 原子不能回到原来位置,易到A
即发生滑移
Ax A
d a
?有问题
最初认为: 滑移是相邻两晶面整体的相对刚性滑移
则可计算:使其滑移的最小切应力: c
第四章 晶体中的缺陷和扩散
原子绝对严格按晶格的周期性排列的晶体不存在
缺陷举例: 如晶体表面、晶粒间界、人为掺杂等
如金刚石
空位
点缺陷 填隙原子 (0维)
杂质原子
刃位错
线缺陷
晶体缺陷的基本类型 (1维)
(按维度或尺寸分类)
螺位错
大角晶界
晶粒间界
面缺陷
小角晶界
(2维) 堆垛间界(层错)
问题1:点缺陷的定义、分类、运动及其对晶体性能影响?
若某一晶面A丢失,则原子面排列: ABCABCBCABC………..
问题7:一定温度下,系统达统计平衡时,
热缺陷(空位.间隙原子)数目?
热力学平衡条件
平衡状态下晶体内的热缺陷数目
系统自由能F U TS 最小
F n T
0
热缺陷的数目
1、肖脱基缺陷(或空位)浓度
(成对出现)
4、杂质原子 在材料制备中,有控制地在晶体中引入杂质原子
A、杂质原子取代基质原子而占据格点位置,称替代式杂质。
(二者相接近或前者大一些)
B、杂质原子占据格点间的间隙位置,称填隙式杂质。
(杂质原子比基质原子小)
点缺陷的运动 1、空位的运动
空位运动势场示意图
原子结合成晶体的源动力:原子间的吸引力. 理想晶体的生长
问题4:当初如何提出位错概念?位错滑移如何理解?
Ax A d
a
x a 2
xa 2
弹性形变
范性形变 原子不能回到原来位置,易到A
即发生滑移
Ax A
d a
?有问题
最初认为: 滑移是相邻两晶面整体的相对刚性滑移
则可计算:使其滑移的最小切应力: c
第四章 晶体中的缺陷和扩散
原子绝对严格按晶格的周期性排列的晶体不存在
缺陷举例: 如晶体表面、晶粒间界、人为掺杂等
如金刚石
空位
点缺陷 填隙原子 (0维)
杂质原子
刃位错
线缺陷
晶体缺陷的基本类型 (1维)
(按维度或尺寸分类)
螺位错
大角晶界
晶粒间界
面缺陷
小角晶界
(2维) 堆垛间界(层错)
问题1:点缺陷的定义、分类、运动及其对晶体性能影响?
若某一晶面A丢失,则原子面排列: ABCABCBCABC………..
问题7:一定温度下,系统达统计平衡时,
热缺陷(空位.间隙原子)数目?
热力学平衡条件
平衡状态下晶体内的热缺陷数目
系统自由能F U TS 最小
F n T
0
热缺陷的数目
1、肖脱基缺陷(或空位)浓度
《固体物理基础概论》PPT课件

组成晶态固体的粒子在空间周期性排列,具 有长程序,它的对称性是破缺的。
非晶体与晶体相反,其组成粒子在空间的 分布是完全无序或仅仅具有短程序,具有高度 的对称性。
准晶介于晶体和非晶体之间,粒子在空间 分布有序,但不具有周期性,仅仅具有长程的 取向序。
固体物理的研究对象以晶体为主。
准晶
2 . 固体物理学的基本任务:是企图从微观上 去解释固体材料的宏观物性,并阐明其规律。
到了期末,接近考试了,此时介绍晶体结合 、晶体缺陷等学生材内容和学时分配 第一章 金属自由电子费米气体模型(10学时) 第二章 晶体的结构 (19学时) 第三章 能带论 (23学时) 第四章 晶格振动 (10学时) 第五章 输运现象 (5学时) 第六章 晶体的结合、晶体缺陷和相图(5学时)
曼彻斯特大学最近公布的波纹式的石墨烯薄片示意图
Ultra-Thin Material
超导磁悬浮
Magnetic Domains by Magneto-optical Effect
包钴氧化铁 钡铁氧体
铁合金
CrO2
m
计算机的硬盘
计算机的硬盘
2007年诺贝尔 物理学奖---巨 磁电阻效应 (GMR)
4.基泰尔(C.Kittel 5th edition)著,杨顺华等 译,固体物理导论,科学出版社,1979
5.方可,胡述楠,张文彬 主编;固体物理学,重庆大 学出版社,1993
6.陈金福 主编 固体物理学—学习参考书 高等 教育出版社,1986 7.
8.阎守胜. 2000. 固体物理基础. 北京:北京大学 出版社
7.教学要求
1) 掌握金属自由电子模型的内容并学会利用该模型对 金属的电、热、光等物性进行分析; 2) 掌握晶体的结构特点、晶格的特征、晶体对称性 和分类、倒格子以及X射线衍射;
固体物理(第4课)倒易空间
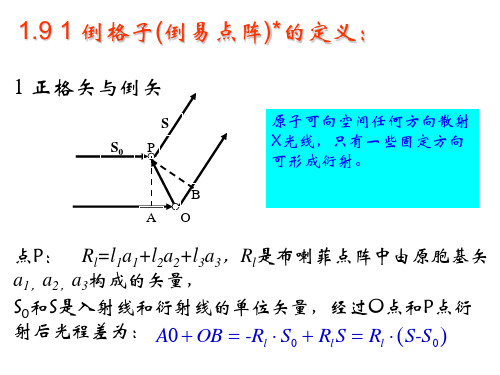
2 相应的倒格矢长度 K ( n1 ,n2 ,n3 ) a 2 这十二个倒格矢的中垂面围成菱形十二面体:
其体积正好等于倒格子原胞的体积大小.
布里渊区示意图2-2
0,0,0 :坐标原点
: 100 : 110 : 111 2 1,0,0 H: a 2 1 1 N: , ,0 a 2 2 2 P: a 1 1 1 , , 2 2 2
倒易空间 傅里叶空间 K空间
1.9.3 常见晶格的布里渊区 (1) 一维晶格
a1 a i 2 b1 i a
(2) 二维晶格
a1、a 2 b1 2 b2 2
构造a 3,令a 3 =k a2 a3 a1 a 2 a 3 a 3 a1 a1 a 2 a 3
(4) 倒格矢和正点阵晶面族之间的关系: 正点阵中一族晶面,晶面指数为:(h1h2 h3) 倒易点阵中倒格矢: Gh h1b1 h2 b2 h3b3 Gh // ( h1h2 h3 ) 法线方向 2 则有: 证明如下: Gh = d h1h2h3
2 ( n2 n3 , n1 n3 , n1 n2 ) a
2 2 2 2 (1,1,0), (1,1,0), (1,1,0), (1,1,0), a a a a 2 2 2 2 (1,0,1), (1,0,1), (1,0,1), (1,0,1), a a a a 2 2 2 2 (0,1,1), (0,1,1), (0,1,1), (0,1,1). a a a a
面心立方晶格的倒易晶格是体心立方,其 晶胞常数为 4a 。
示意图
布里渊区示意图1
b3 -b2 -b1 b2 -b3 b1
(完整版)固体物理课件ppt完全版

布拉伐格子 + 基元 = 晶体结构
③ 格矢量:若在布拉伐格子中取格点为原点,它至其
他格点的矢量 Rl 称为格矢量。可表示为
Rl
l1a1
l2a2
l3a3
,
a1,
a2 ,
a3为
一组基矢
注意事项:
1)一个布拉伐格子基矢的取法不是唯一的
2
4x
·
1
3
二维布拉伐格子几种可能的基矢和原胞取法 2)不同的基矢一般形成不同的布拉伐格子
2·堆积方式:AB AB AB……,上、下两个底面为A
层,中间的三个原子为 B 层
3·原胞:
a, 1
a 2
在密排面内,互成1200角,a3
沿垂直
密排面的方向构成的菱形柱体 → 原胞
B A
六角密排晶格的堆积方式
A
a
B c
六角密排晶格结构的典型单元
a3
a1
a2
六角密排晶格结构的原胞
4·注意: A 层中的原子≠ B 层中的原子 → 复式晶格
bγ a
b a
b a
b a
简六体心底正简单三面心正单方底心单心交 立斜交斜 方 简单立方体心正交面立方简四体心四方简单正交简单菱方简单单斜单方
二 、原胞
所有晶格的共同特点 — 具有周期性(平移对称性)
描
用原胞和基矢来描述
述
方
位置坐标描述
式
1、 定义:
原胞:一个晶格最小的周期性单元,也称为固体物理 学原胞
a1, a2 , a3 为晶格基矢
复式晶格:
l1, l2 , l3 为一组整数
每个原子的位置坐标:r l1a1 l2a2 l3a3
固体物理学精品PPT课件

பைடு நூலகம்
4.最小内能性
由同一种化学成分构成的物质,在不同的条件下 可以呈现不同的物相,其相应的结合能或系统的内 能也必不相同。
但是,在相同的热力学条件下,在具有相同化学 成分物质的各种物态——气体、液体、非晶体、晶 体中,以晶体的内能最小,这个结论称为晶体的最 小内能性。
对于固体物质,由于晶体内能比非晶体内能小, 所以非晶体具有自发地向晶体转变的趋势;反之, 晶体不可能自发地转变为其它的物态形式。
在单晶体内部,原子都是规则地排列的。
* 多晶体( Multiple Crystal )
由许多小单晶(晶粒)构成的晶体,称为多晶体。 多晶体仅在各晶粒内原子才有序排列,不同晶粒内 的原子排列是不同的。
晶面的大小和形状受晶体生长条件的影响,它们 不是晶体品种的特征因素。
例如,岩盐(氯化钠)晶体的外形可以是立方体 或八面体,也可能是立方和八面的混合体,如图所 示。
有些晶体的解理性不明显,例如,金属晶体等。
晶体解理性在某些加工工艺中具有重要的意义, 例如,在划分晶体管管芯时,利用半导体晶体的解 理性可使管芯具有平整的边缘和防止无规则的断裂 发生,以保证成品率。
3.晶面角守恒定律
发育良好的单晶体,外形上最显著的特征是晶面 有规则地配置。一个理想完整的晶体,相应的晶面 具有相同的面积。晶体外形上的这种规则性,是晶 体内部分子或原子之间有序排列的反映。
晶格振动是晶体的特性之一。
§1.2 晶体的周期性
一、空间点阵学说 1.空间点阵
为了描述晶体结构的周期性,布拉菲在1848年提 出空间点阵学说,从而奠定了晶体结构几何理论的 基础。
按照空间点阵学说,晶体内部结构是由一些相同 的点子在空间规则地作周期性无限分布所构成的系 统,这些点子的总体称为点阵。
4.最小内能性
由同一种化学成分构成的物质,在不同的条件下 可以呈现不同的物相,其相应的结合能或系统的内 能也必不相同。
但是,在相同的热力学条件下,在具有相同化学 成分物质的各种物态——气体、液体、非晶体、晶 体中,以晶体的内能最小,这个结论称为晶体的最 小内能性。
对于固体物质,由于晶体内能比非晶体内能小, 所以非晶体具有自发地向晶体转变的趋势;反之, 晶体不可能自发地转变为其它的物态形式。
在单晶体内部,原子都是规则地排列的。
* 多晶体( Multiple Crystal )
由许多小单晶(晶粒)构成的晶体,称为多晶体。 多晶体仅在各晶粒内原子才有序排列,不同晶粒内 的原子排列是不同的。
晶面的大小和形状受晶体生长条件的影响,它们 不是晶体品种的特征因素。
例如,岩盐(氯化钠)晶体的外形可以是立方体 或八面体,也可能是立方和八面的混合体,如图所 示。
有些晶体的解理性不明显,例如,金属晶体等。
晶体解理性在某些加工工艺中具有重要的意义, 例如,在划分晶体管管芯时,利用半导体晶体的解 理性可使管芯具有平整的边缘和防止无规则的断裂 发生,以保证成品率。
3.晶面角守恒定律
发育良好的单晶体,外形上最显著的特征是晶面 有规则地配置。一个理想完整的晶体,相应的晶面 具有相同的面积。晶体外形上的这种规则性,是晶 体内部分子或原子之间有序排列的反映。
晶格振动是晶体的特性之一。
§1.2 晶体的周期性
一、空间点阵学说 1.空间点阵
为了描述晶体结构的周期性,布拉菲在1848年提 出空间点阵学说,从而奠定了晶体结构几何理论的 基础。
按照空间点阵学说,晶体内部结构是由一些相同 的点子在空间规则地作周期性无限分布所构成的系 统,这些点子的总体称为点阵。
《固体》人教版高三物理选修3-3PPT课件

一、 晶体和非晶体
(二)、晶体和非晶体的区别: 1、熔点:晶体具有一定的熔点,非晶体没有一定的熔点。
2、外形上:晶体具有规则的几何形状,非晶体没有规则的几何形状。
3、物理性质上: 晶体的物理性质与方向有关(这种特性叫各向异性) 非晶体的物理性质在各个方向是相同的(这种特性叫各向同性)
一、 晶体和非晶体
可爱的大熊猫
大熊猫是一种活泼可爱的珍稀动物。①它有黑 白相间的皮毛,圆圆的脸上嵌着一对大大的黑色眼 圈和闪闪发光的小眼睛。头顶上有着两只黑茸茸的 耳朵,四肢黑乎乎的。它的尾巴短小,身体圆圆的、 胖乎乎的,真是憨态可掬。①
①描写生动,写出 了熊猫的外形特点。
习作范例
大熊猫生活在竹林茂盛的高山峡谷之中。它天生是个近 视眼,靠灵敏的听觉和嗅觉来寻找食物。
人教版高中物理选修3-3
第九章 固体、液体和物态变化
感谢各位的聆听
MENTAL HEALTH COUNSELING PPT
讲解人:XXX 时间:20XX.5.25
《国宝大熊猫》
语文精品课件 三年级下册
授课老师:某某 | 授课时间:20XX.XX
某某小学
课文导读
是猫不捕鼠, 墨镜不离眼, 要问最爱啥, 最爱鲜竹叶。
二、单晶体和多晶体
(一)单晶体和多晶体的区别: 1.单晶体:一个物体就是一个完整的晶体.
例如:雪花、食盐小颗粒、单晶硅、单晶锗等.
2.多晶体:整个物体是由许多杂乱无章地排列着的小晶体组成。其中的小晶体 叫做晶粒.
(1)多晶体没有规则的几何形状.
(2)不显示各向异性.(每一晶粒内部都是各向异性的).
大熊猫
课文精讲
本次习作内容是“介绍国宝大熊猫”。我们 可以围绕课本中所给的一些信息来介绍大熊猫, 还可以通过查资料补充大熊猫的其他内容,突 出大熊猫的特点。
固体物理4PPT课件一等奖新名师优质课获奖比赛公开课

一种物体处于受力状态,一般有两种情况: * 物体整个体积受力而且力旳大小与物体旳体积成正比,这称为彻 体力,例如重力; * 另一种情况是物体受到压缩、拉伸或扭转、弯曲旳作用而发生形 变时,在物体内部旳任一部分和它周围相邻部分之间将产生相互作 用力,这种力旳大小与相接触部分表面积旳大小成正比,而力与面 积之比就称为应力。 即在固体形变时,作用在固体中单位面积上旳 力。
张量:(二阶)张量是具有9个分量旳物理量。设直角坐标系旳单
位基矢量为 e1 , e2 , e3
一般张量可写为
Tijeie j (i, j 1,2,3)
ij
ei e j 称为并矢,作为张量旳9个基。
张量旳9个分量写为 T11 ,T12 ,T13;T21 ,T22 ,T23;T31 ,T32 ,T33
2w t 2
Tzx x
Tzy y
Tzz z
式中ρ代表晶体密度, u、v、w代表晶体中质粒位移沿主轴x、y、z方向旳分量。 根据应力分量符号,上式能够写为
2u t 2
T1 x
T6 y
T5 z
2v t 2
T6 x
T2 y
T4 z
(3)
2w t 2
T5 x
T4 y
T3
z
上式称为弹性动力学方程。
第一下标i表达应力旳方向,第 二下标j表达应力所作用旳面旳法 向。
例如作用在垂直于X轴旳单位面
积上沿X方向旳应力是Txx 。此类应
力是垂直于表面旳,称为正应力, 代表张力或压力;
作用在垂直于X轴旳单位面 积上沿Y方向旳应力是Tyx 。此类 应力是沿着表面旳,即平行于表 面旳切向,代表切应力。
y
Tyy
T1 Txx ,T2 Tyy ,T3 Tzz , T4 Tyz ,T5 Tzx ,T6 Txy (1)
张量:(二阶)张量是具有9个分量旳物理量。设直角坐标系旳单
位基矢量为 e1 , e2 , e3
一般张量可写为
Tijeie j (i, j 1,2,3)
ij
ei e j 称为并矢,作为张量旳9个基。
张量旳9个分量写为 T11 ,T12 ,T13;T21 ,T22 ,T23;T31 ,T32 ,T33
2w t 2
Tzx x
Tzy y
Tzz z
式中ρ代表晶体密度, u、v、w代表晶体中质粒位移沿主轴x、y、z方向旳分量。 根据应力分量符号,上式能够写为
2u t 2
T1 x
T6 y
T5 z
2v t 2
T6 x
T2 y
T4 z
(3)
2w t 2
T5 x
T4 y
T3
z
上式称为弹性动力学方程。
第一下标i表达应力旳方向,第 二下标j表达应力所作用旳面旳法 向。
例如作用在垂直于X轴旳单位面
积上沿X方向旳应力是Txx 。此类应
力是垂直于表面旳,称为正应力, 代表张力或压力;
作用在垂直于X轴旳单位面 积上沿Y方向旳应力是Tyx 。此类 应力是沿着表面旳,即平行于表 面旳切向,代表切应力。
y
Tyy
T1 Txx ,T2 Tyy ,T3 Tzz , T4 Tyz ,T5 Tzx ,T6 Txy (1)
高二物理固体课件(PPT)4-1

现象:熔化了的石蜡在云母片上呈椭圆形,而在玻璃片 上呈圆形.
结论:云母晶体在各个方向上的导热性能不同,而非晶 体玻璃在各个方向上的导热性能相同.
一 .晶体和非晶体
固体可以分成晶体和非晶体两类.
在常见的固态物质中,石英、云母、明矾、食盐、 硫酸铜、糖、味精等都是晶体,玻璃、蜂蜡、松香、 沥青、橡胶等都是非晶体.
1.晶体、非晶体的外形和物理性质的差异
(1)晶体都具有规则的几何形状. 食盐的晶体呈立方体形,明矾的晶体呈八面体形, 石英的晶体中间是一个六面棱柱,两端是六棱锥.冬的形状虽然不同,但一般是六角形的规则图案.
非晶体则没有规则的几何形状.
植物胚乳是单倍体的雌配子体,一般比较发达,多储藏淀粉或脂肪,也有的含糊粉粒。胚乳一般为淡黄色,少数为白色,银杏成熟的种子中胚乳呈绿色。 被
子植物的胚乳在双受精过程中,一个精子与胚囊中的极核融合发育成多倍体。多数被子植物在种子发育中有胚乳形成,但有的成熟种子中不具、具很少的胚; 作文加盟 小学作文加盟 作文班加盟 作文培训加盟 作文加盟品牌排行榜 华语作文 作文加盟品牌;乳,由于它们的胚乳在发育中被胚分解 吸收了。一般把成熟的种子分有胚乳种子、无胚乳种子。无胚乳种子中胚很大,胚体各部分,特别在子叶中储有大量营养物质。 主要作用编辑 植物大多数固
态物质是从大气层中取得。经由一个被称为光合作用的过程,植物利用阳光里的能源来将大气层中的二氧化碳转化成简单的糖。这些糖分被用作建材,并构 成植物主要结构成份。植物主要依靠土壤作为支撑和取得水份,以及氮、磷等重要基本养分。大部分植物要能成功地成长,也需要大气中的氧气(作为呼吸 之用)及根部周围的氧气。不过,一些特殊维管植物如红树林可以让其根部在缺氧环境下成长。 [] 光合作用 光合作用 光合作用 [] 植物具有光合作用的能 力——就是说它可以借助光能及动物体内所不具备的叶绿素,利用水、无机盐和二氧化碳进行光合作用,释放氧气,产生葡萄糖——含有丰富能量的物质,供 植物体利用。 植物的叶绿素含有镁。 植物细胞有明显的细胞壁和细胞核,其细胞壁由葡萄糖聚合物——纤维素构成。 所有植物的祖先都是单细胞非光合生 物,它们吞食了光合细菌,二者形成一种互利关系:光合细菌生存在植物细胞内(即所谓的内共生现象)。最后细菌蜕变成叶绿体,它是一种在所有植物体 内都存在却不能独立生存的细胞器。大多数植物都属于被子植物门,是有花植物,其中还包括多种树木。植物呼吸作用主要在细胞的线粒体进行;光合作用 在细胞的叶绿体进行。 [] 绿色植物光合作用是地球上最为普遍、规模最大的反应过程,在有机物合成、蓄积太阳能量和净化空气、保持大气中氧气含量和碳 循环的稳定等方面起很大作用,是农业生产的基础,在理论和实践上都具有重大意义。据计算,整个世界的绿色植物每天可以产生约亿吨的蛋白质、碳水化 合物和脂肪,与此同时,还能向空气中释放出近亿吨还多的氧,为人和动物提供了充足的食物和氧气。 叶片是进行光合作用的主要器官,叶绿体是光合作用 的重要细胞器。高等植物的叶绿体色素包括叶绿素(a和b)和类胡萝卜素(胡萝卜素和叶黄素),它们分布在光合膜上。叶绿素的吸收光谱和荧光现象,说明 它可吸收光能、被光激发。叶绿素的生物合成在光照条件下形成,既受遗传性制约,
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter 4
Phonons I. crystal vibration
Key points: Crystal vibrations Phonons Phonon momentum
Phonon is one kind of elementary excitations in solids
Name Field Electromagnetic wave Elastic wave Collective electron wave Magnetization wave Electron + elastic deformation Polarization wave
The homogenous linear equations have a solution only if the determinant of the coefficients of the unknown u, v vanishes.
2C M 1ω 2 C[1 + exp(iKa )] C[1 + exp(iKa )] 2C M 2ω
For K<<1/a (i.e. λ>>a), ω ∝ K At the boundary of first Brillouin zone (K = ±π/a), dω/dK = 0
First Brillouin zone Only K in the first Brillouin zone is physically significant for the elastic waves.
If there are p atoms in the primitive cell, there are 3p branches to the dispersion relation: 3 acoustical branches (1 LA and 2 TA) and 3p3 optical branches (p1 LO and 2p2 LO ).
Two atoms per primitive basis
The dispersion relation shows new features in crystals with two or more atoms per primitive basis. acoustical and optical branches (声学支和光学支)
v g = dω / dK in one dimension
4C With the particular dispersion relation ω = M 2 1/ 2 Ca Ka cos vg = 2 M
1/ 2
Ka sin 2
Long wavelength limit When λ >> a i.e. Ka << 1
With p atoms in the primitive cell and N primitive cells, there are pN atoms, 3pN degrees of freedom, N LA branches, 2N TA branches, (p1)N LO branches and (2p2)N LO branches.
The range of independent values of K is specified by:
π < Ka ≤ π , or
π
a
<K≤
π
a
We may treat a value of K outside the 1st Brillouin zone by subtracting a appropriate reciprocal lattice vector in order to obtain an equivalent wavevector in the 1st Brillouin zone. r r r K'≡ K G (in one dimension, K ' = K 2πn / a) r where K '∈1st Brilouin zone. At the Brillouin zone boundaries, K = ±π/a, us = u exp[i(± sπ ωt)] = (1)s u exp(iωt) (standing wave) The critical value, K = ±π/a, satisfies the Bragg condition. Note: for x-ray, it is posible to have other n which cause the wavevector K outside 1st Brilouin zone.
For the acoustical branch
u=v
The atoms and their center of mass move together.
at the 1st Brillouin zone boundary (Ka = ±π)
j =1 p >0
The equation of motion is p >0 d 2u s M = 2∑ C j (u s + j u s ) 2 dt j The dispersion relation 2 p >0 ω 2 = ∑ C j (1 cos jKa ) M j =1
Ma π / a 2 Cp = dKω K cos pKa 2π ∫π / a
2 4C 2 Ka Ca ω 2 = sin ≈ K2 2 M M
C i.e. ω ≈ a K M
C v g = dω / dK ≈ a M
1/ 2
1/ 2
Derivation of force constants from experiment In metals the effective forces may be of quite long range, carried from ion to ion through the conduction electron sea. Considering p Байду номын сангаасearest planes, the force on s plane F = 2∑ C j (u s + j u s )
longitudinal mode
transverse mode
Note: for N atoms there are 3N mode, N L-modes and 2N T-modes.
Assume that the elastic response of the crystal in linear function of the force. (Hooke’s law) i.e. the elastic energy is a quadratic function of the relative displacement of any two points in the crystal. Neglect cubic and higher order terms. From Hooke’s law, the force on the s plane caused by the displacement of the plane s+p is proportional to the difference of their displacement, i.e. Fsp = Csp (us+p us) Consider only the nearest neighbor interactions. The total force on s comes from the plane s±1 Fs = C (us+1 us) + C (us-1 us) = C (us+1 + us-1 2us)
Electron Photon Phonon Plasmon Magnon Polaron Exciton
Important elementary excitations in solids
Vibrations of crystals with monoatomic basis
Consider the elastic vibrations of a crystal with one atom in the primitive cell. Describe with a single coordinate us the displacement of the plane s from its equilibrium position. Three mode for each wavevector, one of longitudinal polarization and two of transverse polarization.
Assume that each plane interacts only with the nearestneighbor planes. The equations of motion is d 2u s M 1 2 = C (vs + vs 1 2u s ) dt d 2 vs M = C (u s +1 + u s 2vs ) 2 dt 2 the solution in a form of a traveling wave:
2
=0
or M 1M 2ω 4 2C ( M 1 + M 2 )ω 2 + 2C 2 (1 cos Ka ) = 0 the dispersion relation 2C ( M 1 + M 2 ) ± [2C ( M 1 + M 2 )]2 8C 2 M 1M 2 (1 cos Ka ) ω2 = 2 M 1M 2
ω 2 M = C[exp(iKa ) + exp(iKa ) 2] = 2C (1 cos Ka )
Phonons I. crystal vibration
Key points: Crystal vibrations Phonons Phonon momentum
Phonon is one kind of elementary excitations in solids
Name Field Electromagnetic wave Elastic wave Collective electron wave Magnetization wave Electron + elastic deformation Polarization wave
The homogenous linear equations have a solution only if the determinant of the coefficients of the unknown u, v vanishes.
2C M 1ω 2 C[1 + exp(iKa )] C[1 + exp(iKa )] 2C M 2ω
For K<<1/a (i.e. λ>>a), ω ∝ K At the boundary of first Brillouin zone (K = ±π/a), dω/dK = 0
First Brillouin zone Only K in the first Brillouin zone is physically significant for the elastic waves.
If there are p atoms in the primitive cell, there are 3p branches to the dispersion relation: 3 acoustical branches (1 LA and 2 TA) and 3p3 optical branches (p1 LO and 2p2 LO ).
Two atoms per primitive basis
The dispersion relation shows new features in crystals with two or more atoms per primitive basis. acoustical and optical branches (声学支和光学支)
v g = dω / dK in one dimension
4C With the particular dispersion relation ω = M 2 1/ 2 Ca Ka cos vg = 2 M
1/ 2
Ka sin 2
Long wavelength limit When λ >> a i.e. Ka << 1
With p atoms in the primitive cell and N primitive cells, there are pN atoms, 3pN degrees of freedom, N LA branches, 2N TA branches, (p1)N LO branches and (2p2)N LO branches.
The range of independent values of K is specified by:
π < Ka ≤ π , or
π
a
<K≤
π
a
We may treat a value of K outside the 1st Brillouin zone by subtracting a appropriate reciprocal lattice vector in order to obtain an equivalent wavevector in the 1st Brillouin zone. r r r K'≡ K G (in one dimension, K ' = K 2πn / a) r where K '∈1st Brilouin zone. At the Brillouin zone boundaries, K = ±π/a, us = u exp[i(± sπ ωt)] = (1)s u exp(iωt) (standing wave) The critical value, K = ±π/a, satisfies the Bragg condition. Note: for x-ray, it is posible to have other n which cause the wavevector K outside 1st Brilouin zone.
For the acoustical branch
u=v
The atoms and their center of mass move together.
at the 1st Brillouin zone boundary (Ka = ±π)
j =1 p >0
The equation of motion is p >0 d 2u s M = 2∑ C j (u s + j u s ) 2 dt j The dispersion relation 2 p >0 ω 2 = ∑ C j (1 cos jKa ) M j =1
Ma π / a 2 Cp = dKω K cos pKa 2π ∫π / a
2 4C 2 Ka Ca ω 2 = sin ≈ K2 2 M M
C i.e. ω ≈ a K M
C v g = dω / dK ≈ a M
1/ 2
1/ 2
Derivation of force constants from experiment In metals the effective forces may be of quite long range, carried from ion to ion through the conduction electron sea. Considering p Байду номын сангаасearest planes, the force on s plane F = 2∑ C j (u s + j u s )
longitudinal mode
transverse mode
Note: for N atoms there are 3N mode, N L-modes and 2N T-modes.
Assume that the elastic response of the crystal in linear function of the force. (Hooke’s law) i.e. the elastic energy is a quadratic function of the relative displacement of any two points in the crystal. Neglect cubic and higher order terms. From Hooke’s law, the force on the s plane caused by the displacement of the plane s+p is proportional to the difference of their displacement, i.e. Fsp = Csp (us+p us) Consider only the nearest neighbor interactions. The total force on s comes from the plane s±1 Fs = C (us+1 us) + C (us-1 us) = C (us+1 + us-1 2us)
Electron Photon Phonon Plasmon Magnon Polaron Exciton
Important elementary excitations in solids
Vibrations of crystals with monoatomic basis
Consider the elastic vibrations of a crystal with one atom in the primitive cell. Describe with a single coordinate us the displacement of the plane s from its equilibrium position. Three mode for each wavevector, one of longitudinal polarization and two of transverse polarization.
Assume that each plane interacts only with the nearestneighbor planes. The equations of motion is d 2u s M 1 2 = C (vs + vs 1 2u s ) dt d 2 vs M = C (u s +1 + u s 2vs ) 2 dt 2 the solution in a form of a traveling wave:
2
=0
or M 1M 2ω 4 2C ( M 1 + M 2 )ω 2 + 2C 2 (1 cos Ka ) = 0 the dispersion relation 2C ( M 1 + M 2 ) ± [2C ( M 1 + M 2 )]2 8C 2 M 1M 2 (1 cos Ka ) ω2 = 2 M 1M 2
ω 2 M = C[exp(iKa ) + exp(iKa ) 2] = 2C (1 cos Ka )
