四川省资阳市雁江区初中2015届中考数学适应性检测试题
2015年四川资阳中考数学试卷

资阳市2015年高中阶段教育学校招生统一考试数 学全卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
全卷满分120分。
考试时间共120分钟。
注意事项:1.答题前,请考生务必在答题卡上正确填写自己的姓名、准考证号和座位号。
考试结束,将试卷和答题卡一并交回。
2.选择题每小题选出的答案须用2B 铅笔在答题卡上把对应题目....的答案标号涂黑。
如需改动,用橡皮擦擦净后,再选涂其它答案。
非选择题须用黑色墨水的钢笔或签字笔在答题卡上对应题号位置作答,在试卷上作答,答案无效。
第Ⅰ卷(选择题 共30分)一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个选项符合题意。
1.6-的绝对值是 A .6B .6-C .16D .16-2.如图1是一个圆台,它的主视图是3.下列运算结果为a 6的是 A .a 2+a 3 B .a 2·a 3 C .(-a 2)3 D .a 8÷a 2 4.一组数据3、5、8、3、4的众数与中位数分别是 A .3,8B .3,3C .3,4D .4,35.如图2,已知AB ∥CD ,∠C =70°,∠F =30°,则∠A 的度数为A .30°B .35°C .40°D .45°3-6.如图3,已知数轴上的点A 、B 、C 、D 分别表示数-2、1、2、3,则表示数的点P 应落在线段A .AO 上B .OB 上C .BC 上D .CD 上7.若顺次连接四边形ABCD 四边的中点,得到的图形是一个矩形,则四边形ABCD 一定是 A .矩形 B .菱形 C .对角线相等的四边形 D .对角线互相垂直的四边形 8.如图4,AD 、BC 是⊙O 的两条互相垂直的直径,点P 从点O出发,沿O →C →D →O 的路线匀速运动,设∠APB =y (单位:度),那么y 与点P 运动的时间x (单位:秒)的关系图是9.如图5,透明的圆柱形容器(容器厚度忽略不计)的高为12cm ,底面周长为10cm ,在容器内壁离容器底部3 cm 的点B 处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm 的点A 处,则蚂蚁吃到饭粒需爬行的最短路径是A .13cmB.CD.10.如图6,在△ABC 中,∠ACB =90º,AC =BC =1,E 、F 为线段AB 上两动点,且∠ECF =45°,过点E 、F 分别作BC 、AC 的垂线相交于点M ,垂足分别为H 、G .现有以下结论:①AB②当点E 与点B 重合时,MH =12;③AF+BE=EF ;④MG •MH =12,其中正确结论为A .①②③B .①③④C .①②④D .①②③④第Ⅱ卷(非选择题 共90分)二、填空题:(本大题共6个小题,每小题3分,共18分)11.太阳的半径约为696000千米,用科学记数法表示为_______千米.12.一个多边形的内角和是外角和的3倍,则这个多边形的边数是_______. 13.某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成右图统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有_________人.14.已知:()260a +,则224b b a --的值为_________. 15.如图7,在平面直角坐标系中,点M 为x 轴正半轴上一点,过点M 的直线l ∥y 轴,且直线l 分别与反比例函数8y x =(x >0)和ky x=(x >0)的图象交于P 、Q 两点,若S △POQ =14,则k 的值为__________.16.已知抛物线p :y =ax 2+bx +c 的顶点为C ,与x 轴相交于A 、B 两点(点A在点B 左侧),点C 关于x 轴的对称点为C ′,我们称以A 为顶点且过点C ′,对称轴与y 轴平行的抛物线为抛物线p 的“梦之星”抛物线,直线AC ′为抛物线p 的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y =x 2+2x +1和y =2x +2,则这条抛物线的解析式为_____________________.三、解答题:(本大题共8个小题,共72分)解答应写出必要的文字说明、证明过程或演算步骤。
四川省资阳市雁江区初中2015届中考适应性检测题试卷分析

四川省资阳市雁江区初中2015届中考适应性检测题试卷分析一、选择题:考查知识点:相反数的定义、科学计数法表示较大的数、众数和中位数、指数幂的性质和二次根式有意义的条件及其勾股定理和平行线的知识,分式有意义的条件相结合、锐角三角形的定义和勾股定理相结合、直线圆的位置关系、平行四边形的判定、反比例函数与一次函数的交点个数问题、二次函数图像与函数关系、轴对称最短路线问题和圆周角定理相结合。
选择题难度:1-9题:难度较低,适合中等学生做。
考查题型不多,但是每一个知识点都有考到的,每一个知识点都濒及到,让学生必须掌握每一个知识点。
10题:考点:轴对称最短路线问题和圆周角定理相结合。
试题分析:作点B关于MN的对称点B’,连接OA、OB’、AB’,根据轴对称确定最短线问题,AB’与M的交点个数即为所求的使PA+PB的值最小的点,根据在同圆或等圆中,同狐所对的圆周角等于圆心角的一半求出角AON=2角AMN,在求出角NOB’,然后求出角AOB’=90°,从而判断出三角形AOB’是等腰山角形,根据等腰三角形的性质求解即可得出答案。
难度分析:该题难度偏难,是综合性题型。
二、填空题:考查知识点:二次根式有意义的条件,分式有意义的条件、平行线的性质、概率公式、一次函数图像上点的坐标特征和等边三角形的性质以及坐标与图形变化--平移的结合考查、动点问题的函数图像。
填空题难度:11-12题:难度很低,属于得分题。
(必须得分)13-15题:难度中等,属于易错题。
(仔细看题)16题:难度偏难,属于不一的分题。
(学生综合知识要强)题型不多,考察的知识点都是常考点,涉及到重要的考题部分。
考查学生对知识的掌握程度。
16题:考点:一次函数图像上点的坐标特征和等边三角形的性质以及坐标与图形变化--平移的结合考查、动点问题的函数图像。
试题分析:根据从图2可以看出当Q点到B点时的面积为9,求正方形的边长,再利用三角形的面积公式得出EF所在的直线对应的函数关系。
四川省资阳市2015年中考数学试卷(含答案解析)

资阳市2015年中考数学试卷全卷分为第I卷(选择题)和第H卷(非选择题)两部分,共4页。
全卷满分120分。
考试时间共120分钟。
注意事项:1.答题前,请考生务必在答题卡上正确填写自己的姓名、准考证号和座位号。
考试结束,将试卷和答题卡一并交回。
2 •选择题每小题选出的答案须用2B铅笔在答题卡上把对应题目.的答案标号涂黑。
如需改动,用橡皮擦擦净后,再选涂其它答案。
非选择题须用黑色墨水的钢笔或签字笔在答题卡上对应题号位置作答,在试卷上作答,答案无效。
第I卷(选择题共30分)一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个选项符合题意。
1. -6的绝对值是A. 6B. -6C.-61 D. ——6考点:绝对值.•分析:根据负数的绝对值是它的相反数,可得负数的绝对值. 解答:解:6|=6,故选:A.点评:本题考查了绝对值,负数的绝对值是它的相反数. 2•如图1是一个圆台,它的主视图是考点:简单几何体的三视图.分析:主视图是从物体正面看,所得到的图形.解答:解:从几何体的正面看可得等腰梯形,故选:B.点评:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.3.下列运算结果为a6的是2 3 2 3 2 3 8 2A . a + a B. a a C. (—a )D. a考点:同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.. 分析:根据合并同类项、同底数幂的乘除法以及积的乘方和幂的乘方进行计算即可.解答:解:A、a3%2不能合并,故A错误;B、a2?a3=a5,故 B 错误;C、(- a2?)3= - a6,故 C 错误;D、a8%2=a6,故 D 正确;故选 D .点评:本题考查了同底数幂的乘除法、合并同类项以及积的乘方和幂的乘方,是基础知识要熟练掌握.4.一组数据3、5、8、3、4的众数与中位数分别是A .3 , 8B .3 , 3C .3, 4D .4 , 3考点:众数;中位数.. 分析:根据中位数和众数的定义求解:众数是一组数据中出现次数最多的数据,注意众数可以不止一个;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.解答:解:把这组数据从小到大排列:3、3、4、5、8,3 出现了2 次,出现的次数最多,则众数是3 .处于中间位置的那个数是4,由中位数的定义可知,这组数据的中位数是4;点评:本题为统计题,考查中位数与众数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.众数是一组数据中出现次数最多的数据,注意众数可以不止一个.5.如图2,已知AB // CD, / C=70 ° / F=30 °则/ A的度数为A. 30 °B. 35 °C. 40 °D. 45 °考点:平行线的性质.• 专题:计算题.分析:先根据平行线的性质得/ BEF = / C=70°,然后根据三角形外角性质计算/ A的度数. 解答:解:AB// CD ,•••/ BEF = / C=70° ,•// BEF = / A+/ F,•••/ A=70°- 30° =40°.故选C.点评:本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.6.如图3,已知数轴上的点A、B、C、D分别表示数—2、1、2、3,则表示数3—- 5的点P应落在线段 A O B C DA. AO 上r “」-3 41 0 1 2 3 4 B . OB 上图孑C. BC 上 D . CD 上考点:估算无理数的大小;实数与数轴.分析:根据估计无理数的方法得出0V 3- _< 1,进而得出答案.解答:解:T 2< "< 3,• 0< 3 - ";f h< 1 ,B故表示数3- ":' 2■的点P应落在线段OB上.故选:B .点评:此题主要考查了估算无理数的大小,得出匸的取值范围是解题关键.7.若顺次连接四边形 ABCD 四边的中点,得到的图形是一个矩形,则四边形 ABCD —定是A .矩形C .对角线相等的四边形D .对角线互相垂直的四边形考点:中点四边形.•分析:首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行 四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由 此得解. 解答:已知:如右图,四边形EFGH 是矩形,且 E 、F 、G 、H 分别是AB 、BC 、CD 、AD的中点,求证:四边形 ABCD 是对角线垂直的四边形. 证明:由于 E 、F 、G 、H 分别是AB 、BC 、CD 、AD 的中点, 根据三角形中位线定理得: EH // FG // BD , EF // AC // HG ; •••四边形EFGH 是矩形,即EF 丄FG , ••• AC 丄 BD ,故选:D .点评:本题主要考查了矩形的性质和三角形中位线定理,解题的关键是构造三角形利用三 角形的中位线定理解答.&如图4, AD 、BC 是O O 的两条互相垂直的直径,点P 从点0出发,沿C T DO的路线匀速运动,设/ APB=y (单位:度),那么y 与点P 运动的时间x (单位:秒)的关B .菱形考点:动点问题的函数图象. •分析:根据图示,分三种情况:(1)当点P 沿O f C 运动时;(2)当点P 沿C T D 运动时;(3)当点P 沿D T O 运动时;分别判断出 y 的取值情况,进而判断出 y 与点P 运动的时 间x (单位:秒)的关系图是哪个即可.解答:解:(1)当点P 沿O T C 运动时, 当点P 在点0的位置时,y=90° , 当点P 在点C 的位置时, •/ OA=OC , ••• y=45° ,••• y 由90°逐渐减小到45° (2) 当点P 沿C T D 运动时, 根据圆周角定理,可得 y 三90°+ 2=45° (3) 当点P 沿D T O 运动时, 当点P 在点D 的位置时,y=45° , 当点P 在点0的位置时,y=90°, • y 由45°逐渐增加到90° 故选:B .点评:(1)此题主要考查了动点问题的函数图象,解答此类问题的关键是通过看图获取信 息,并能解决生活中的实际问题,用图象解决问题时,要理清图象的含义即学会识图.系图是(2)此题还考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.考点:平面展开-最短路径问题.分析:将容器侧面展开,建立 A 关于EF 的对称点A',根据两点之间线段最短可知 A B 的 长度即为所求. 解答:解:如图:•••高为12cm ,底面周长为10cm ,在容器内壁离容器底部 3cm 的点B 处有一饭粒, 此时蚂蚁正好在容器外壁,离容器上沿 3cm 与饭粒相对的点 A 处,/• AD=5cm , BD=12 - 3+AE=12cm ,•••将容器侧面展开,作 A 关于EF 的对称点A', 连接A B ,贝U AB 即为最短距离, A B=二’|「屮 |i :-=13( Cm)•故选:A .点评:本题考查了平面展开——最短路径问题,将图形展开,利用轴对称的性质和勾股 定理进行计算是解题的关键•同时也考查了同学们的创造性思维能力.10 .如图 6,在△ ABC 中,/ ACB=90o, AC=BC=1 , E 、F 为线段 AB 上两动点,且/ ECF=45 °过点E 、F 分别作BC 、AC 的垂线相交于点 M ,垂足分别为H 、G.现有以下结论:①AB= 2 ;-6 -9•如图5,透明的圆柱形容器(容器厚度忽略不计)的高为 12cm ,底面周长为10cm ,在容器内壁离容器底部 蚂蚁正好在容器外壁,且离容器上沿 行的最短路径是A • 13cmB • 2 61 cm 3 cm 的点B 处有一饭粒,此时一只3 cm 的点A 处,则蚂蚁吃到饭粒需爬 C • . 61 cm D •2 34 cm图5②当点E与点B重合时,MH =〔:③AF+BE=EF :④MG?MH=],其中正确结论为2 2A .①②③B .①③④C.①②④ D .①②③④考点:相似形综合题.•分析:①由题意知,△ ABC是等腰直角三角形,根据等腰直角三角形即可作出判断;②如图1,当点E与点B重合时,点H与点B重合,可得MG // BC,四边形MGCB是矩形,进一步得到FG是厶ACB的中位线,从而作出判断;③如图2所示,SAS可证△ ECF◎△ ECD,根据全等三角形的性质和勾股定理即可作出判断;④根据AA可证△ ACE BFC,根据相似三角形的性质可得AF?BF=AC?BC=1,由题意知四边形CHMG 是矩形,再根据平行线的性质和等量代换得到MG?MH=—AE X 二BF=_AE?3F=—AC?3C=,依此即可作出判断.2 2 2 2 2解答:解:①由题意知,△ ABC是等腰直角三角形,二ABi -二廿工:,故①正确;②如图1,当点E与点B重合时,点H与点B重合,••• MB 丄BC,Z MBC=90°,•/ MG 丄AC,•••/ MGC=90°=Z C= / MBC ,••• MG // BC,四边形MGCB是矩形,••• MH=MB = CG,•••/ FCE =45° = / ABC ,Z A= / ACF =45°,• CE=AF=BF,• FG是厶ACB的中位线,•• GC= AC=MH,故②正确;2③如图2所示,•/ AC=BC,Z ACB=90°,•••/ A=Z 5=45°.将厶ACF顺时针旋转90°至厶BCD ,贝U CF=CD,/ 仁/4,/ A= / 6=45°; BD=AF ;•••/ 2=45°,•••/ 1+ / 3= / 3+ / 4=45°,•••/ DCE= / 2.在厶ECF和厶ECD中,r CF=CD•Z2=ZDCE,CE=CEL•△ ECF 也厶ECD ( SAS),• EF=DE.•••/ 5=45° , •••/ BDE=90° ,••• DE 2=BD 2+BE 2,即即 E 2=AF 2+BE 2,故③错误;④ •••/ 7= / 1+ / A=Z 1+45°= / 1 + Z 2= / ACE ,•••/ A=Z 5=45° , • △ ACEBFC , • v ' ..,BC BF• AF?BF=AC?BC=1 ,由题意知四边形 CHMG 是矩形, • MG // BC , MH=CG , MG // BC , MH // AC ,CH^E . CG =世「=「;—=、,U . VIL I =:;=-故④正确. 故选:C .点评:考查了相似形综合题,涉及的知识点有:等腰直角三角形的判定和性质,平行线的 判定和性质,矩形的判定和性质,三角形中位线的性质,全等三角形的判定和性质,勾股 定理,相似三角形的判定和性质,综合性较强,有一定的难度.第口卷(非选择题 共90 分)、填空题: (本大题共6个小题,每小题 3分,共18分) 11•太阳的半径约为 696000千米,用科学记数法表示为 __________ 千米. 考点:科学记数法一表示较大的数.心A E;MH= BF ,2MG?MHBF= A E ?B F = ,AC ?B C=,分析:科学记数法的表示形式为axio n的形式,其中1<ai< 10, n为整数•确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同•当原数绝对值〉10时,n是正数;当原数的绝对值< 1时,n是负数.解答:解:将696 000千米用科学记数法表示为 6.96 >105千米.点评:此题考查科学记数法的表示方法. 科学记数法的表示形式为 a xi0n的形式,其中1<ai< 10, n为整数,表示时关键要正确确定a的值以及n的值.12. 一个多边形的内角和是外角和的3倍,则这个多边形的边数是__________ .考点:多边形内角与外角.•分析:任何多边形的外角和是360°即这个多边形的内角和是3X360°. n边形的内角和是(n-2)?180°如果已知多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.解答:解:设多边形的边数为n,根据题意,得(n-2)?180=3X 36Q解得n=8.则这个多边形的边数是 &点评:已知多边形的内角和求边数,可以转化为方程的问题来解决. 考查了相似形综合题,涉及的知识点有:等腰直角三角形的判定和性质,平行线的判定和性质,矩形的判定和性质,三角形中位线的性质,全等三角形的判定和性质,勾股定理,相似三角形的判定和性质,综合性较强,有一定的难度.13. 某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1〜2 (不含1)小时的学生有______ 人.考点:用样本估计总体.•分析:先求出每周课外阅读时间在1〜2 (不含1)小时的学生所占的百分比,再乘以全校的人数,即可得出答案.解答:解:根据题意得:1200 X =240 (人),7+10+14+19答:估计每周课外阅读时间在1〜2 (不含1)小时的学生有240人;故答案为:240.点评:本题考查从统计表中获取信息的能力,及统计中用样本估计总体的思想.14. 已知:(a +6 $ + J b2 -2b -3 =0,则2b2—4b —a 的值为___________ .考点:非负数的性质:算术平方根;非负数的性质:偶次方.分析:首先根据非负数的性质可求出a的值,和2b2- 2b=6,进而可求出2b2- 4b- a的值.解答:解:•••(a+6)2+ —三—=0,2••• a+6=0 , b2- 2b- 3=0 ,解得,a=- 6, b2- 2b=3,可得2b2- 2b=6,贝U 2b2- 4b - a=6 -( - 6)=12 ,故答案为12.点评:本题主要考查了非负数的性质,初中阶段有三种类型的非负数:绝对值、偶次方、二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.15. 如图7,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线I // y轴,且直线I分别与反比例函数y =8(x> 0)和y』(x> 0)的图象交于P、Q两点,若S MOQ=14 ,x x则k的值为___________ .k的几何意义.考点:反比例函数与一次函数的交点问题;反比例函数系数分析:由于S M°Q=S A OMQ+S S MP,根据反比例函数比例系数k的几何意义得到|k|+ :为8|=14,2 2然后结合函数y=的图象所在的象限解方程得到满足条件的k的值.x解答:解:T S A PO Q=S^OMQ+S^ OMP ,•••|k|+ X|8|=14,2 2•••|k|=20,而k v 0,• k= - 20.故答案为-20.点评:本题考查了反比例函数比例系数k的几何意义:在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.也2考查了反比例函数与一次函数的交点问题.216. 已知抛物线p:y=ax+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C',我们称以A为顶点且过点C',对称轴与y轴平行的抛物线为抛物线p的梦之星”抛物线,直线AC'为抛物线p的梦之星”直线•若一条抛物线的梦之星”抛物线和梦之星”直线分别是y= x2+ 2x+ 1和y= 2x+ 2,则这条抛物线的解析式为考点:抛物线与x轴的交点;二次函数的性质.专题:新定义.分析:先求出y=x2+2x+1和y=2x+2的交点C的坐标为(1, 4),再求出梦之星"抛物线y=x2+2x+1的顶点A坐标(-1, 0),接着利用点C和点C关于x轴对称得到C (1,- 4),则可设顶点式y=a (x- 1)2- 4,然后把A点坐标代入求出a的值即可得到原抛物线解析式.解答:解:••• y=x 2+2x+ 仁(x+1) 2, A 点坐标为(-1, 0), 解方程组”占加+1得$"1或产\L y=2x+2[v=0 〔尸4•••点C 的坐标为(1 , 4), •••点C 和点C 关于x 轴对称, 二 C ( 1,- 4),设原抛物线解析式为 y=a (x - 1) 2-4, 把A (- 1, 0)代入得4a - 4=0,解得a=1, •原抛物线解析式为 y= (x - 1) 2- 4=x - 2x - 3. 故答案为y=x - 2x - 3.点评:本题考查了二次函数与 x 轴的交点:求二次函数y=ax 2+bx+c (a , b , c 是常数,a ^0 与x 轴的交点坐标,令 y=0,即ax 2+bx+c=0,解关于x 的一元二次方程即可求得交点横坐 标.△ =b 2- 4ac 决定抛物线与x 轴的交点个数,△ =b 2- 4ac > 0时,抛物线与x 轴有2个 交点;△ =b 2 - 4ac=0时,抛物线与x 轴有1个交点;△ =b 2- 4ac v 0时,抛物线与x 轴没 有交点.三、解答题: (本大题共8个小题,共72分)解答应写出必要的文字说明、证明过程或演 算步骤。
2015年四川省资阳市中考数学试卷及解析

2015年四川省资阳市中考数学试卷一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个选项符合题意.21•世纪*教育网A . 6 B. ﹣6 C . D . 2.(3分)(2015•资阳)如图是一个圆台,它的主视图是( )A .B.C.D.6A . a 2+a 3B . a 2•a 3C . (﹣a 2)3D . a 8÷a 2 A .3,8 B . 3,3 C . 3,4 D . 4,3 5.(3分)(2015•资阳)如图,已知AB ∥CD ,∠C=70°,∠F=30°,则∠A 的度数为( )A . 30°B .35° C . 40° D . 45° 6.(3分)(2015•资阳)如图,已知数轴上的点A 、B 、C 、D 分别表示数﹣2、1、2、3,则表示数3﹣的点P 应落在线段( )A . AO 上B . OB 上C . BC 上D . CD 上 7.(3分)(2015•资阳)若顺次连接四边形ABCD 四边的中点,得到的图形是一个矩形,则四边形ABCD A . 矩形 B . 菱形 C . 对角线相等的四边形 D . 对角线互相垂直的四边形 8.(3分)(2015•资阳)如图,AD 、BC 是⊙O 的两条互相垂直的直径,点P 从点O 出发,沿O →C →D →O的路线匀速运动.设∠APB=y (单位:度),那么y 与点P 运动的时间x (单位:秒)的关系图是( )9.(3分)(2015•资阳)如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm ,底面周长为10cm ,在容器内壁离容器底部3cm 的点B 处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm 的点A 处,则蚂蚁吃到饭粒需爬行的最短路径是( )2cm 210.(3分)(2015•资阳)如图,在△ABC 中,∠ACB=90°,AC=BC=1,E 、F 为线段AB 上两动点,且∠ECF=45°,过点E 、F 分别作BC 、AC 的垂线相交于点M ,垂足分别为H 、G .现有以下结论:①AB=;②当点E 与点B 重合时,MH=;③AF+BE=EF ;④MG •MH=,其中正确结论为( )二、填空题:(本大题共6个小题,每小题3分,共18分) 11.(3分)(2015•资阳)太阳的半径约为696 000千米,用科学记数法表示为 千米. 12.(3分)(2015•资阳)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是. 13.(3分)(2015•资阳)某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读14.(3分)(2015•资阳)已知:(a+6)2+=0,则2b2﹣4b﹣a的值为.15.(3分)(2015•资阳)如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y 轴,且直线l分别与反比例函数y=(x>0)和y=(x>0)的图象交于P、Q两点,若S△POQ=14,则k 的值为.16.(3分)(2015•资阳)已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B 左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为.三、解答题:(本大题共8个小题,共72分)解答应写出必要的文字说明、证明过程或演算步骤.17.(7分)(2015•资阳)先化简,再求值:(﹣)÷,其中x满足2x﹣6=0.18.(8分)(2015•资阳)学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:(1)本次调查中,王老师一共调查了名学生;(2)将条形统计图补充完整;(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.19.(8分)(2015•资阳)学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.(1)求篮球和足球的单价;(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.20.(8分)(2015•资阳)北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,≈1.7)21.(9分)(2015•资阳)如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).(1)求双曲线的解析式;(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.22.(9分)(2015•资阳)如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连接DE.(1)求证:DE是⊙O的切线;(2)连接AE,若∠C=45°,求sin∠CAE的值.23.(11分)(2015•资阳)如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.(1)求证:△ADE≌△DCF;(2)若E是CD的中点,求证:Q为CF的中点;(3)连接AQ,设S△CEQ=S1,S△AED=S2,S△EAQ=S3,在(2)的条件下,判断S1+S2=S3是否成立?并说明理由.24.(12分)(2015•资阳)已知直线y=kx+b(k≠0)过点F(0,1),与抛物线y=x2相交于B、C两点.(1)如图1,当点C的横坐标为1时,求直线BC的解析式;(2)在(1)的条件下,点M是直线BC上一动点,过点M作y轴的平行线,与抛物线交于点D,是否存在这样的点M,使得以M、D、O、F为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由;(3)如图2,设B(m.n)(m<0),过点E(0.﹣1)的直线l∥x轴,BR⊥l于R,CS⊥l于S,连接FR、FS.试判断△RFS的形状,并说明理由.2015年四川省资阳市中考数学试卷参考答案与试题解析一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个选项符合题意.21•世纪*教育网2.(3分)(2015•资阳)如图是一个圆台,它的主视图是()65.(3分)(2015•资阳)如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为()6.(3分)(2015•资阳)如图,已知数轴上的点A、B、C、D分别表示数﹣2、1、2、3,则表示数3﹣的点P应落在线段()﹣的点的取值范围是解题关键.7.(3分)(2015•资阳)若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD8.(3分)(2015•资阳)如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O 的路线匀速运动.设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是()9.(3分)(2015•资阳)如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是()2cm 210.(3分)(2015•资阳)如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=;②当点E与点B重合时,MH=;③AF+BE=EF;④MG•MH=,其中正确结论为()MH=×AE BF=,依此即可作出判断.=,故∴GC=AC=MH,故②正确;=,=;==;,AE MH=MH=×BF=AC BC=二、填空题:(本大题共6个小题,每小题3分,共18分)11.(3分)(2015•资阳)太阳的半径约为696 000千米,用科学记数法表示为 6.96×105千米.12.(3分)(2015•资阳)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是8 .13.(3分)(2015•资阳)某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有240 人.析:的人数,即可得出答案.1200×=240(人),14.(3分)(2015•资阳)已知:(a+6)2+=0,则2b2﹣4b﹣a的值为12 .15.(3分)(2015•资阳)如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y 轴,且直线l分别与反比例函数y=(x>0)和y=(x>0)的图象交于P、Q两点,若S△POQ=14,则k 的值为﹣20 .|k|+×|8|=14,然后结合函数y=的图象所在的象限解方程得到满足条件的k的△|k|+×故答案为﹣20.坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持16.(3分)(2015•资阳)已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B 左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为y=x2﹣2x﹣3 .解方程组得或三、解答题:(本大题共8个小题,共72分)解答应写出必要的文字说明、证明过程或演算步骤.17.(7分)(2015•资阳)先化简,再求值:(﹣)÷,其中x满足2x﹣6=0.÷•.当x=3时,原式=.18.(8分)(2015•资阳)学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:(1)本次调查中,王老师一共调查了20 名学生;(2)将条形统计图补充完整;(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.男生和一位女生的概率为:=19.(8分)(2015•资阳)学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.(1)求篮球和足球的单价;(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.,学校可用于购买这批篮球和足球的资金最多为由题意可得:,解得:40≤x≤50,∵x为正整数,∴x=40,41,42,43,44,45,46,47,48,49,50,∴共有11种购买方案.(3)由题意可得y=120x+90(100﹣x)=30x+9000(40≤x≤50)∵k=30>0,∴y随x的增大而增大,∴当x=40时,y有最小值,y最小=30×40+9000=10200(元),所以当x=40时,y最小值为10200元.点评:本题考查了一次函数的应用,解决本题的关键是根据已知条件,列出一元一次方程和一元一次不等式组,应用一次函数的性质解决问题.20.(8分)(2015•资阳)北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,≈1.7)考点:解直角三角形的应用.分析:过C点作AB的垂线交AB的延长线于点D,通过解Rt△ADC得到AD=2CD=2x,在Rt△BDC中利用锐角三角函数的定义即可求出CD的值.解答:解:作CD⊥AB交AB延长线于D,设CD=x 米.Rt△ADC中,∠DAC=25°,所以tan25°==0.5,所以AD==2x.Rt△BDC中,∠DBC=60°,由tan 60°==,解得:x≈3米.所以生命迹象所在位置C的深度约为3米.点评:本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.21.(9分)(2015•资阳)如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).(1)求双曲线的解析式;(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.b=Q坐标.,∴y=x+1,x+1得:;∵Q(a,b)在y=上,,时,可得=,即,∴a﹣2=2b,即a﹣2=,时,可得=,即,4=或﹣1+21+222.(9分)(2015•资阳)如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连接DE.(1)求证:DE是⊙O的切线;(2)连接AE,若∠C=45°,求sin∠CAE的值.BE=CE=AB=BC=2xBE=CE=AB=BC=2==23.(11分)(2015•资阳)如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.(1)求证:△ADE≌△DCF;(2)若E是CD的中点,求证:Q为CF的中点;(3)连接AQ,设S△CEQ=S1,S△AED=S2,S△EAQ=S3,在(2)的条件下,判断S1+S2=S3是否成立?并说明理由.得出比例式CQ=DE,CE=DE=DC=AD=DECF∴,,,(),24.(12分)(2015•资阳)已知直线y=kx+b(k≠0)过点F(0,1),与抛物线y=x2相交于B、C两点.(1)如图1,当点C的横坐标为1时,求直线BC的解析式;(2)在(1)的条件下,点M是直线BC上一动点,过点M作y轴的平行线,与抛物线交于点D,是否存在这样的点M,使得以M、D、O、F为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由;(3)如图2,设B(m.n)(m<0),过点E(0.﹣1)的直线l∥x轴,BR⊥l于R,CS⊥l于S,连接FR、FS.试判断△RFS的形状,并说明理由.x+1,RFS=,解之,得所以直线BC的解析式为:y=﹣x+1;x+1,∴MD=﹣x+1﹣x2,x+1x当﹣﹣)当﹣﹣(,,),,==,RFS=∠。
2015年中考真题精品解析 数学(资阳卷)精编word版(解析版)

全卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
全卷满分120分。
考试时间共120分钟。
注意事项:1.答题前,请考生务必在答题卡上正确填写自己的姓名、准考证号和座位号。
考试结束,将试卷和答题卡一并交回。
2.选择题每小题选出的答案须用2B铅笔在答题卡上把对应题目....的答案标号涂黑。
如需改动,用橡皮擦擦净后,再选涂其它答案。
非选择题须用黑色墨水的钢笔或签字笔在答题卡上对应题号位置作答,在试卷上作答,答案无效。
第Ⅰ卷(选择题共30分)一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个选项符合题意。
1.6-的绝对值是()A.6 B.6-C.16D.16-【答案】A.考点:绝对值的意义.2.如图1是一个圆台,它的主视图是()【答案】B.【解析】试题分析:圆台从正面看是一个梯形,因此圆台的主视图是梯形,故答案选B.考点:简单几何体的主视图.3.下列运算结果为a6的是()A.a2+a3B.a2·a3C.(-a2)3D.a8÷a2【答案】D.【解析】试题分析:选项A不能够计算;选项B a2·a3= a5;选项C(-a2)3=- a6;选项D a8÷a2= a6.故答案选D.考点:幂的有关运算.4.一组数据3、5、8、3、4的众数与中位数分别是()A.3,8 B.3,3 C.3,4 D.4,3【答案】C.考点:众数;中位数.5.如图2,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为()A.30°B.35°C.40°D.45°【答案】C.【解析】试题分析:由两直线平行,同位角相等可得∠C=∠FEB=70°,再根据三角形的一个外角等于与它不相邻的两个内角的和即可得∠A=∠FEB—∠F=40°.故答案选C.考点:平行线的性质;三角形的一个外角等于与它不相邻的两个内角的和.6.如图3,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示数3P应落在线段()A.AO上B.OB上C.BC上D.CD上【答案】B.【解析】2和3之间可得30和1之间,符合条件的只有选项B.故答案选B.考点:二次根式的估算;数轴.7.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是()A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形【答案】D.考点:三角形中位线定理;矩形的性质;平行线的性质.8.如图4,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是()【答案】B.考点:圆周角定理;动点函数图象.9.如图5,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3 cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是()A.1mB.261C61D.34【答案】A.【解析】试题分析:蚂蚁怎么爬最短问题,处理思路是“展开”“找点”“连线”.沿蚂蚁所在直线展开得到长方形,确定蚂蚁和饭粒的位置,本题中蚂蚁在玻璃杯外壁,要到达饭粒位置需先到达杯口,再到饭粒位置,可借助对称找对蚂蚁位置对称点,借助“两点之间,线段最短”找出蚂蚁所爬路径,再由勾股定理计算最短距离.具体过程如下,图5圆柱侧面展开如图,作点A 关于杯口的对称点A′,则AE =A′E=3,连接A′C,A′C 的长度即为蚂蚁吃到饭粒需爬行的最短路径.过点C 作CB ⊥AA′于点B ,则BE =9,BC =5 ∴A′B=12,在Rt △A′BC中,由勾股定理得:'13AC = ,故蚂蚁到达蜂蜜的最短距离为1m,故答案选A.考点:轴对称作图;平面展开最短路径问题;勾股定理.10.如图6,在△ABC 中,∠ACB =90º,AC =BC =1,E 、F 为线段AB 上两动点,且∠ECF =45°,过点E 、F 分别作BC 、AC 的垂线相交于点M ,垂足分别为H 、G .现有以下结论:①AB②当点E 与点B 重合时,MH =12;③AF+BE=EF ;④MG •MH =12,其中正确结论为( )A .①②③B .①③④C .①②④D .①②③④【答案】C. 【解析】试题分析:在Rt △ABC 中,由勾股定理可得E 与点B 重合时(图1),点H 也与B 重合,∠ECF=45°可得F 为AB 的中点,又因GM ∥BC ,可得G 为AC 的中点,所以MH=12AC=12,故②正确;由∠AEC=∠B+∠ECB=∠FCE+∠ECB=45°+∠ECB=∠FCB ,又因∠A=∠B=45°,所以△AEC ∽△BCF ,根据相似三角形对应边的比相等可得AE ACBC BF=,所以AE BF BC AC =.又因222AB BC AC =+,AB=AC ,所以212AE BF AB =,设AF=a ,BE=b,EF=c ,代入可得(a+c )(b+c )=21()2a b c ++,化简得222a b c +=,即222AF BE EF +=,故③不正确;易证△AGF ∽△EMF, △EHB ∽△EMF,根据相似三角形面积的比等于相似比可得22AGF EHB 22EMF EMF ,S S S S AF BE EF EF ∆∆∆∆==,这两个式子相加可得22AGF EHB 2EMF S S S AF BE EF∆∆∆++=,又因222AF BE EF +=(③中已证),所以可得AGF EHB EMF S S S ∆∆∆+=.因此,△ABC 的面积就等于矩形GCHM 的面积,所以MG•MH=12AC •BC=12,故④正确,所以正确的结论有①②④三个,故答案选C.图1考点:相似三角形的判定及性质;勾股定理;矩形的性质.第Ⅱ卷(非选择题共90分)二、填空题:(本大题共6个小题,每小题3分,共18分)11.太阳的半径约为696000千米,用科学记数法表示为_______千米.【答案】6.96×105.考点:科学记数法.12.一个多边形的内角和是外角和的3倍,则这个多边形的边数是_______.【答案】8.【解析】试题分析:根据n边形的外角和是360°可得这个多边形的内角和为1080°,由多边形的内角和公式可得(n-2)×180=1080,解得n=8.考点:多边形的内角和公式;多边形的外角和是360°.13.某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成右图统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有_________人.【答案】240.【解析】试题分析:根据表格中的数据可计算出抽查了50名学生,每周课外阅读时间在1~2(不含1)小时的学生有10人,占20%,所以该校每周课外阅读时间在1~2(不含1)小时的学生大约有1200×20%=240人.考点:用样本估计总体.14.已知:()260a+,则224b b a--的值为_________.【答案】12.【解析】试题分析:由()260a +可得a —6=0,2230b b --=,所以a=—6,223b b -=,代入224b b a--可得22242(2)23612b b a b b a --=--=⨯+=.考点:2a .15.如图7,在平面直角坐标系中,点M 为x 轴正半轴上一点,过点M 的直线l ∥y 轴,且直线l 分别与反比例函数8y x =(x >0)和ky x=(x >0)的图象交于P 、Q 两点,若S △POQ =14,则k 的值为__________.【答案】—20. 【解析】试题分析:由l ∥y 并且与反比例函数8y x =(x >0)的图象交于点P ,可得S △POM =4.根据S △POQ =14可得S △QOM =S △POQ—S △POM =10.又因ky x=(x >0)的图象交直线l 于点Q ,且图象在第四象限,所以k=—20. 考点:反比例函数k 的几何意义.16.已知抛物线p :y =ax 2+bx +c 的顶点为C ,与x 轴相交于A 、B 两点(点A 在点B 左侧),点C 关于x 轴的对称点为C′,我们称以A 为顶点且过点C ′,对称轴与y 轴平行的抛物线为抛物线p 的“梦之星”抛物线,直线AC′为抛物线p 的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y =x 2+2x +1和y =2x +2,则这条抛物线的解析式为_____________________. 【答案】223y x x =--.考点:阅读理解题;求函数的交点坐标;求函数的解析式.三、解答题:(本大题共8个小题,共72分)解答应写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分7分)先化简,再求值:2112()111x x x x +-÷-+-,其中x 满足260x -= 【答案】原式2=2x +,当3x =时,原式2=5.【解析】试题分析:先根据分式的运算法则进行化简,然后再解方程后代入求值. 试题解析:解:原式2112(1)(1)(1)(1)1x x x x x x x x ⎡⎤+-+=-÷⎢⎥-++--⎣⎦22(1)(1)(1)(1)x x x x x +=÷-++-(1)(1)2(1)(1)2x x x x x +-=⨯-++2=2x + 2603x x -=∴=当3x =时,原式2=5考点:分式的混合运算;分式的化简求值.18.(本小题满分8分)学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A :特别好,B :好,C :一般,D :较差)后,再将调查结果绘制成两幅不完整的统计图(如图8).请根据统计图解答下列问题:(1)本次调查中,王老师一共调查了_______名学生; (2)将条形统计图补充完整;(3)为了共同进步,王老师从被调查的A 类和D 类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.【答案】(1)20;(2)详见解析;(3)12.试题解析:(1)20.(2)如图(3)列表如下:A 类中的两名男生分别记为A 1和A 2共有6种等可能的结果,其中,一男一女的有3种,所以所选两位同学恰好是一位男生和一位女生的概率为:2163 考点:条形统计图;扇形统计图;用列表法求概率.19.(本小题满分8分)学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元. (1)求篮球和足球的单价;(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的23,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?(3)若购买篮球x 个,学校购买这批篮球和足球的总费用为y (元),在(2)的条件下,求哪种方案能使y 最小,并求出y 的最小值.【答案】(1)一个篮球120元,一个足球90元;(2)11种购买方案;(3)当x=40时,y 的最小值是10200元. 【解析】试题分析:(1)设一个篮球x 元,则一个足球(30)x -元,根据等量关系“2个篮球的钱+3个足球的钱=510”列出方程23(30)510x x +-=,解得x 即可求得一个篮球的价格,再表示出一个足球的价格即可;(2)设购买篮球x 个,足球(100)x -个,根据题目中的不等关系“篮球的数量≥足球的数量×23,买篮球的总钱数+买足球的总钱数≤10500”列出不等式组2(100)312090(100)10500x x x x ⎧≥-⎪⎨⎪+-≤⎩,解得4050x ≤≤,根据x 取整数即可确定购买方案;(3)根据题意求出y 与x 的函数关系式,再根据x 的的取值范围和一次函数的性质即可得出答案.试题解析:(1)设一个篮球x 元,则一个足球(30)x -元,由题意得: 23(30)510x x +-=解得:120x =所以一个篮球120元,一个足球90元.(2)设购买篮球x 个,足球(100)x -个,由题意可得:2(100)312090(100)10500x x x x ⎧≥-⎪⎨⎪+-≤⎩ 解得:4050x ≤≤因为x 为正整数,所以共有11种购买方案。
[中考真题]2015年数学中考试卷 四川资阳
![[中考真题]2015年数学中考试卷 四川资阳](https://img.taocdn.com/s3/m/8f20ae0bc5da50e2524d7f89.png)
2015年四川省资阳市中考数学试卷一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个选项符合题意.21•世纪*教育网1.﹣6的绝对值是( )A.6B.-6C.61D. -61 2.如图是一个圆台,它的主视图是( )A .B .C .D . 下列运算结果为6a 的是( )A .32a a +B .32a a ÷C .32)(a -D . 28a a ÷ 4.一组数据3、5、8、3、4的众数与中位数分别是( )A . 3,8B . 3,3C . 3,4D .4,35.如图,已知AB ∥CD ,∠C=70°,∠F=30°,则∠A 的度数为( )A . 30°B . 35°C . 40°D .45°6.如图,已知数轴上的点A 、B 、C 、D 分别表示数﹣2、1、2、3,则表示数3﹣的点P 应落在线段( )A .AO 上B . OB 上C . BC 上D . CD 上若顺次连接四边形ABCD 四边的中点,得到的图形是一个矩形,则四边形ABCD 一定是A . 矩形B . 菱形C . 对角线相等的四边形D . 对角线互相垂直的四边形( )8.如图,AD 、BC 是⊙O 的两条互相垂直的直径,点P 从点O 出发,沿O→C→D→O 的路线匀速运动.设∠APB=y (单位:度),那么y 与点P 运动的时间x (单位:秒)的关系图是( )A .B .C .D .9.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm ,底面周长为10cm ,在容器内壁离容器底部3cm 的点B 处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm 的点A 处,则蚂蚁吃到饭粒需爬行的最短路径是( )A . 13cmB . 261cmC . 61cmD .234cm10.如图,在△ABC 中,∠ACB=90°,AC=BC=1,E 、F 为线段AB 上两动点,且∠ECF=45°,过点E 、F 分别作BC 、AC 的垂线相交于点M ,垂足分别为H 、G .现有以下结论:①AB=2;②当点E 与点B 重合时,MH=21;③AF+BE=EF ;④MG•MH=21,其中正确结论为( )A ①②③B ①③④C ①②④D ①②③④. . . .二、填空题:(本大题共6个小题,每小题3分,共18分)11.太阳的半径约为696 000千米,用科学记数法表示为 千米.12.若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .13.某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有 人.每周课外阅读时间(小时) 0~1 1~2 (不含1) 2~3 (不含2)超过3人 数7 10 14 1914.已知:(a+6)2+322--b b =0,则2b 2﹣4b ﹣a 的值为 .15.如图,在平面直角坐标系中,点M 为x 轴正半轴上一点,过点M 的直线l ∥y 轴,且直线l 分别与反比例函数y=x 8(x >0)和y=xk (x >0)的图象交于P 、Q 两点,若S △POQ =14,则k 的值为 .16.已知抛物线p :y=ax 2+bx+c 的顶点为C ,与x 轴相交于A 、B 两点(点A 在点B 左侧),点C 关于x 轴的对称点为C′,我们称以A 为顶点且过点C′,对称轴与y 轴平行的抛物线为抛物线p 的“梦之星”抛物线,直线AC′为抛物线p 的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x 2+2x+1和y=2x+2,则这条抛物线的解析式为 .三、解答题:(本大题共8个小题,共72分)解答应写出必要的文字说明、证明过程或演算步骤.17.先化简,再求值: 12)1111(2-+÷+--x x x x ,其中x 满足2x ﹣6=0.18.学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A :特别好,B :好,C :一般,D :较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:(1)本次调查中,王老师一共调查了 名学生;(2)将条形统计图补充完整;(3)为了共同进步,王老师从被调查的A 类和D 类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.19.学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.(1)求篮球和足球的单价;(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的32,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案? (3)若购买篮球x 个,学校购买这批篮球和足球的总费用为y (元),在(2)的条件下,求哪种方案能使y 最小,并求出y 的最小值.20.北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A 、B 两处均探测出建筑物下方C 处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C 的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,3≈1.7)21.如图,直线y=ax+1与x 轴、y 轴分别相交于A 、B 两点,与双曲线y=xk (x >0)相交于点P ,PC ⊥x 轴于点C ,且PC=2,点A 的坐标为(﹣2,0).(1)求双曲线的解析式;(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.22.如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E 为BC的中点,连接DE.(1)求证:DE是⊙O的切线;(2)连接AE,若∠C=45°,求sin∠CAE的值.23.如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.(1)求证:△ADE≌△DCF;(2)若E是CD的中点,求证:Q为CF的中点;(3)连接AQ,设S△CEQ=S1,S△AED=S2,S△EAQ=S3,在(2)的条件下,判断S1+S2=S3是否成立?并说明理由.24.已知直线y=kx+b (k≠0)过点F (0,1),与抛物线y=41x 2相交于B 、C 两点.(1)如图1,当点C 的横坐标为1时,求直线BC 的解析式;(2)在(1)的条件下,点M 是直线BC 上一动点,过点M 作y 轴的平行线,与抛物线交于点D ,是否存在这样的点M ,使得以M 、D 、O 、F 为顶点的四边形为平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由;(3)如图2,设B (m .n )(m <0),过点E (0.﹣1)的直线l ∥x 轴,BR ⊥l 于R ,CS ⊥l 于S ,连接FR 、FS .试判断△RFS 的形状,并说明理由.1. A 解析:|﹣6|=6,故选:A .点评:本题考查了绝对值,负数的绝对值是它的相反数.2.B 解析:从几何体的正面看可得等腰梯形,故选:B .点评:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.3. D 解析:A 、23a a ÷不能合并,故A 错误;B 、523a a a =∙,故B 错误;C 、632)(a a -=-,故C 错误;D 、628a a a =÷,故D 正确;故选D .点评:本题考查了同底数幂的乘除法、合并同类项以及积的乘方和幂的乘方,是基础知识要熟练掌握.C 解析:把这组数据从小到大排列:3、3、4、5、8,3出现了2次,出现的次数最多,则众数是3.处于中间位置的那个数是4,由中位数的定义可知,这组数据的中位数是4;4. 故选C .点评:本题为统计题,考查中位数与众数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.众数是一组数据中出现次数最多的数据,注意众数可以不止一个.5. C 解析:∵AB∥CD,∴∠BEF=∠C=70°,∵∠BEF=∠A+∠F,∴∠A=70°﹣30°=40°.故选C.点评:本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.6. B 解析:∵2<5<3,∴0<3﹣5<1,故表示数3﹣5的点P应落在线段OB上.故选:B.点评:此题主要考查了估算无理数的大小,得出5的取值范围是解题关键.7. D 解析:已知:如右图,四边形EFGH是矩形,且E、F、G、H分别是AB、BC、CD、AD的中点,求证:四边形ABCD是对角线垂直的四边形.证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;∵四边形EFGH是矩形,即EF⊥FG,∴AC⊥BD,故选:D.点评:本题主要考查了矩形的性质和三角形中位线定理,解题的关键是构造三角形利用三角形的中位线定理解答.8.B 解析:(1)当点P沿O→C运动时,当点P在点O的位置时,y=90°,当点P在点C的位置时,∵OA=OC,∴y=45°,∴y由90°逐渐减小到45°;(2)当点P沿C→D运动时,根据圆周角定理,可得y≡90°÷2=45°;(3)当点P 沿D→O 运动时,当点P 在点D 的位置时,y=45°,当点P 在点0的位置时,y=90°,∴y 由45°逐渐增加到90°.故选:B .点评:(1)此题主要考查了动点问题的函数图象,解答此类问题的关键是通过看图获取信息,并能解决生活中的实际问题,用图象解决问题时,要理清图象的含义即学会识图.(2)此题还考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.9. A 解析:解:如图:∵高为12cm ,底面周长为10cm ,在容器内壁离容器底部3cm 的点B 处有一饭粒, 此时蚂蚁正好在容器外壁,离容器上沿3cm 与饭粒相对的点A 处,∴A ′D=5cm ,BD=12﹣3+AE=12cm ,∴将容器侧面展开,作A 关于EF 的对称点A ′,连接A ′B ,则A ′B 即为最短距离,A ′B=2222125+=+'BD D A=13(Cm ).故选:A .点评:本题考查了平面展开﹣﹣﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.10. C 解析:①由题意知,△ABC 是等腰直角三角形,∴AB=222=+BC AC ,故①正确;②如图1,当点E 与点B 重合时,点H 与点B 重合,∴MB ⊥BC ,∠MBC=90°,∵MG ⊥AC ,∴∠MGC=90°=∠C=∠MBC ,∴MG ∥BC ,四边形MGCB 是矩形,∴MH=MB=CG ,∵∠FCE=45°=∠ABC ,∠A=∠ACF=45°,∴CE=AF=BF ,∴FG 是△ACB 的中位线,∴GC=21AC=MH ,故②正确; ③如图2所示,∵AC=BC ,∠ACB=90°,∴∠A=∠5=45°.将△ACF 顺时针旋转90°至△BCD ,则CF=CD ,∠1=∠4,∠A=∠6=45°;BD=AF ;∵∠2=45°,∴∠1+∠3=∠3+∠4=45°,∴∠DCE=∠2.在△ECF 和△ECD 中,,∴△ECF ≌△ECD (SAS ),∴EF=DE .∵∠5=45°,∴∠BDE=90°,∴222222BE +AF =E ,即BE +BD =DE ,故③错误;④∵∠7=∠1+∠A=∠1+45°=∠1+∠2=∠ACE ,∵∠A=∠5=45°,∴△ACE ∽△BFC , ∴BFAC =BC AF , ∴AF•BF=AC•BC=1,由题意知四边形CHMG 是矩形,∴MG ∥BC ,MH=CG ,MG ∥BC ,MH ∥AC , ∴ABBF AC CG AB AE BC CH ==;, 即21;21BF MH AE MG ==, ∴MG=22AE ;MH=22BF , ∴MG•MH=22AE×22BF=21AE•BF=21AC•BC=21, 故④正确.故选:C .点评:考查了相似形综合题,涉及的知识点有:等腰直角三角形的判定和性质,平行线的判定和性质,矩形的判定和性质,三角形中位线的性质,全等三角形的判定和性质,勾股定理,相似三角形的判定和性质,综合性较强,有一定的难度.11. 6.96×510 解析:将696 000千米用科学记数法表示为6.96×510千米点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.12. 8 解析:设多边形的边数为n ,根据题意,得(n ﹣2)•180=3×360,解得n=8.则这个多边形的边数是8.点评:已知多边形的内角和求边数,可以转化为方程的问题来解决13. 240 解析:根据题意得:1200×191410710+++=240(人), 答:估计每周课外阅读时间在1~2(不含1)小时的学生有240人;故答案为:240.点评: 本题考查从统计表中获取信息的能力,及统计中用样本估计总体的思想.14. 12 解析:∵(a+6)2+322--b b =0,∴a+6=0,b 2﹣2b ﹣3=0,解得,a=﹣6,b 2﹣2b=3,可得2b 2﹣2b=6,则2b 2﹣4b ﹣a=6﹣(﹣6)=12,故答案为12点评: 本题主要考查了非负数的性质,初中阶段有三种类型的非负数:绝对值、偶次方、二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.15. -20 解析:∵O M P △O M Q △PO Q △S +S =S ,∴|k|+×|8|=14,∴|k|=20,而k <0,∴k=﹣20.故答案为﹣20.点评: 本题考查了反比例函数比例系数k 的几何意义:在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.也考查了反比例函数与一次函数的交点问题.16.y=2x ﹣2x ﹣3 解析:∵y=2x +2x+1=2)1(+x ,∴A 点坐标为(﹣1,0), 解方程组得或, ∴点C ′的坐标为(1,4),∵点C 和点C ′关于x 轴对称,∴C (1,﹣4),设原抛物线解析式为y=a 2)1(-x ﹣4,把A (﹣1,0)代入得4a ﹣4=0,解得a=1,∴原抛物线解析式为y=2)1(-x ﹣4=2x ﹣2x ﹣3.故答案为y=2x ﹣2x ﹣3.点评: 本题考查了二次函数与x 轴的交点:求二次函数y=a 2x +bx+c (a ,b ,c 是常数,a ≠0)与x 轴的交点坐标,令y=0,即a 2x +bx+c=0,解关于x 的一元二次方程即可求得交点横坐标.△=2b ﹣4ac 决定抛物线与x 轴的交点个数,△=2b ﹣4ac >0时,抛物线与x 轴有2个交点;△=2b ﹣4ac=0时,抛物线与x 轴有1个交点;△=2b ﹣4ac <0时,抛物线与x 轴没有交点.17.解析:根据分式混合运算的法则把原式进行化简,再求出x 的值代入进行计算即可 解:原式=222)1)(1()1)(1(212)1)(1(112+=+-+∙+-=-+÷+-+-+x x x x x x x x x x x x ∵2x ﹣6=0,∴x=3,当x=3时,原式=52. 点评: 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.18. 解析:(1)由题意可得:王老师一共调查学生:(2+1)÷15%=20(名);(2)由题意可得:C 类女生:20×25%﹣2=3(名);D 类男生:20×(1﹣15%﹣50%﹣25%)﹣1=1(名);继而可补全条形统计图;(3)首先根据题意列出表格,再利用表格求得所有等可能的结果与恰好选中一名男生和一名女生的情况,继而求得答案.解:(1)根据题意得:王老师一共调查学生:(2+1)÷15%=20(名);故答案为:20;(2)∵C 类女生:20×25%﹣2=3(名);D 类男生:20×(1﹣15%﹣50%﹣25%)﹣1=1(名);如图:(3)列表如下:A 类中的两名男生分别记为A1和A2,男A1 男A2 …(7分) 女A男D 男A1男D 男A2男D 女A 男D女D 男A1女D 男A2女D 女A 女D共有6种等可能的结果,其中,一男一女的有3种,所以所选两位同学恰好是一位男生和一位女生的概率为:2163 . 点评: 此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图.用到的知识点为:概率=所求情况数与总情况数之比.19. 解析:(1)设一个篮球x 元,则一个足球(x ﹣30)元,根据“买两个篮球和三个足球一共需要510元”列出方程,即可解答;(2)设购买篮球x 个,足球(100﹣x )个,根据“篮球购买的数量不少于足球数量的32,学校可用于购买这批篮球和足球的资金最多为10500元”,列出不等式组,求出x 的取值范围,由x 为正整数,即可解答;(3)表示出总费用y ,利用一次函数的性质,即可确定x 的取值,即可确定最小值. 解答: 解:(1)设一个篮球x 元,则一个足球(x ﹣30)元,由题意得:2x+3(x ﹣30)=510,解得:x=120,∴一个篮球120元,一个足球90元.(2)设购买篮球x 个,足球(100﹣x )个, 由题意可得:⎪⎩⎪⎨⎧≤-+-≥10500)100(90120)100(32x x x x , 解得:40≤x ≤50,∵x 为正整数,∴x=40,41,42,43,44,45,46,47,48,49,50,∴共有11种购买方案.(3)由题意可得y=120x+90(100﹣x )=30x+9000(40≤x ≤50)∵k=30>0,∴y 随x 的增大而增大,∴当x=40时,y 有最小值,y 最小=30×40+9000=10200(元),所以当x=40时,y 最小值为10200元.点评: 本题考查了一次函数的应用,解决本题的关键是根据已知条件,列出一元一次方程和一元一次不等式组,应用一次函数的性质解决问题.20. 解析:过C 点作AB 的垂线交AB 的延长线于点D ,通过解Rt △ADC 得到AD=2CD=2x ,在Rt △BDC 中利用锐角三角函数的定义即可求出CD 的值.解答: 解:作CD ⊥AB 交AB 延长线于D ,设CD=x 米.Rt △ADC 中,∠DAC=25°,所以tan25°=AD CD =0.5, 所以AD=5.0CD =2x . Rt △BDC 中,∠DBC=60°,由tan 60°=342=-x x , 解得:x ≈3米.所以生命迹象所在位置C 的深度约为3米.点评: 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.21. 解析:(1)把A 坐标代入直线解析式求出a 的值,确定出直线解析式,把y=2代入直线解析式求出x 的值,确定出P 坐标,代入反比例解析式求出k 的值,即可确定出双曲线解析式;(2)设Q (a ,b ),代入反比例解析式得到b=a4,分两种情况考虑:当△QCH ∽△BAO 时;当△QCH ∽△ABO 时,由相似得比例求出a 的值,进而确定出b 的值,即可得出Q 坐标. 解:(1)把A (﹣2,0)代入y=ax+1中,求得a=21,∴y=21x+1, 由PC=2,把y=2代入y=21x+1中,得x=2,即P (2,2), 把P 代入y=xk 得:k=4, 则双曲线解析式为y=x4; (2)设Q (a ,b ),∵Q (a ,b )在y=x 4上, ∴b=a4, 当△QCH ∽△BAO 时,可得BO QH AO CH =,即122b a =-, ∴a ﹣2=2b ,即a ﹣2=a8, 解得:a=4或a=﹣2(舍去),∴Q (4,1);当△QCH ∽△ABO 时,可得AO QH BO CH =,即212b a =-, 整理得:2a ﹣4=a4, 解得:a=1+3或a=1﹣3(舍),∴Q (1+3,23﹣2).综上,Q (4,1)或Q (1+3,23﹣2).点评: 此题属于反比例函数综合题,涉及的知识有:相似三角形的性质,待定系数法确定直线解析22. 解析:(1)连接DO ,DB ,由圆周角定理就可以得出∠ADB=90°,可以得出∠CDB=90°,根据E 为BC 的中点可以得出DE=BE ,就有∠EDB=∠EBD ,OD=OB 可以得出∠ODB=∠OBD ,由的等式的性质就可以得出∠ODE=90°就可以得出结论.(2)作EF ⊥CD 于F ,设EF=x ,由∠C=45°,得出△CEF 、△ABC 都是等腰直角三角形,根据等腰直角三角形的性质和勾股定理求得BE=CE=2x ,AB=BC=22x ,AE=10x ,进而就可求得sin ∠CAE 的值.解:(1)连接OD ,BD ,∴OD=OB∴∠ODB=∠OBD .∵AB 是直径,∴∠ADB=90°,∴∠CDB=90°.∵E 为BC 的中点,∴DE=BE ,∴∠EDB=∠EBD ,∴∠ODB+∠EDB=∠OBD+∠EBD ,即∠EDO=∠EBO .∵BC 是以AB 为直径的⊙O 的切线,∴AB ⊥BC ,∴∠EBO=90°,∴∠ODE=90°,∴DE 是⊙O 的切线;(2)作EF ⊥CD 于F ,设EF=x∵∠C=45°,∴△CEF 、△ABC 都是等腰直角三角形,∴CF=EF=x ,∴BE=CE=2x ,∴AB=BC=22x ,在RT △ABE 中,AE=x BE AB 1022=+,∴sin ∠CAE=1010=AE EF .点评: 本题考查了圆周角定理的运用,直角三角形的性质的运用,等腰三角形的性质的运用,切线的判定定理的运用,勾股定理的运用,解答时正确添加辅助线是关键.式,待定系数法确定反比例函数解23. 解析:(1)由正方形的性质得出AD=DC ,∠ADE=∠DCF=90°,再由SAS 即可证出△ADE ≌△DCF ;(2)先证出∠DAE=∠CEQ ,再证明△ADE ∽△ECQ ,得出比例式AD CE DE CQ =,证出CQ=21DE ,即可得出结论; (3)先证明△AEQ ∽△ECQ ,得出△AEQ ∽△ECQ ∽△ADE ,得出面积比等于相似比的平方,再由勾股定理即可得出结论.解(1)证明:∵四边形ABCD 是正方形,∴AD=DC ,∠ADE=∠DCF=90°,在△ADE 和△DCF 中,,∴△ADE ≌△DCF (SAS );(2)证明:∵E 是CD 的中点,∴CE=DE=21DC=21AD , ∵四边形AEHG 是正方形,∴∠AEH=90°,∴∠AED+∠CEQ=90°,∵∠AED+∠DAE=90°,∴∠DAE=∠CEQ ,∵∠ADE=∠DCF ,∴△ADE ∽△ECQ , ∴AD CE DE CQ ==21, ∴CQ=21DE , ∵DE=CF ,∴CQ=21CF , 即Q 为CF 的中点;(3)解:321S =S +S 成立;理由如下:如图所示:∵△ADE ∽△ECQ , ∴AEQE DE CQ =, ∵DE=CE , ∴AE QE CE CQ =, ∵∠C=∠AEQ=90°,∴△AEQ ∽△ECQ ,∴△AEQ ∽△ECQ ∽△ADE ,∴232221)(,)(AQAE S S AQ EQ S S ==, ∴222223221)()(AQAE EQ AQ AE AQ EQ S S S S +=+=+ ∵222AQ =AE +EQ , ∴3221S S S S +=1, ∴321S =S +S .点评: 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识;本题综合性强,难度较大,需要多次证明三角形相似才能得出结论.析式,熟练掌握待定系数法是解本题的关键.24. 解析:(1)首先求出C 的坐标,然后由C 、F 两点用待定系数法求解析式即可;(2)因为DM ∥OF ,要使以M 、D 、O 、F 为顶点的四边形为平行四边形,则DM=OF ,设M (x ,﹣43x+1),则D (x ,241x ),表示出DM ,分类讨论列方程求解; (3)根据勾股定理求出BR=BF ,再由BR ∥EF 得到∠RFE=21∠BFR ,同理可得∠EFS=∠CFS ,所以∠RFS=∠BFC=90°,所以△RFS 是直角三角形.解答: 解:(1)因为点C 在抛物线上,所以C (1,41), 又∵直线BC 过C 、F 两点,故得方程组: ⎪⎩⎪⎨⎧=+=411b k b 解之,得⎪⎩⎪⎨⎧=-=143b k ,所以直线BC 的解析式为:y=﹣43x+1; (2)要使以M 、D 、O 、F 为顶点的四边形为平行四边形,则MD=OF ,如图1所示, 设M (x ,﹣43x+1),则D (x ,241x ), ∵MD ∥y 轴,∴MD=﹣43x+1﹣241x , 由MD=OF ,可得|﹣43x+1﹣241x |=1, ①当﹣43x+1﹣241x =1时, 解得x=0(舍)或x=﹣3,所以M (﹣3,413), ②当﹣43x+1﹣241x =﹣1时, 解得,x=2413±-, 所以M (2413--,841317+)或M (2413+-,841317-), 综上所述,存在这样的点M ,使以M 、D 、O 、F 为顶点的四边形为平行四边形,M 点坐标为M (﹣3,413)或M (2413--,841317+)或M (2413+-,841317-); (3)过点F 作FT ⊥BR 于点T ,如图2所示,∵点B (m ,n )在抛物线上,∴2m =4n ,在Rt △BTF 中, BF=222222)1(4)1()1(+=+-=+-=+n n n m n TF BT ,∵n >0,∴BF=n+1,又∵BR=n+1,∴BF=BR .∴∠BRF=∠BFR ,又∵BR ⊥l ,EF ⊥l ,∴BR ∥EF ,∴∠BRF=∠RFE ,∴∠RFE=∠BFR ,同理可得∠EFS=∠CFS ,∴∠RFS=21∠BFC=90°, ∴△RFS 是直角三角形.点评: 本题主要考查了待定系数法求解析式,平行四边形的判定,平行线的性质,勾股定理以及分类讨论和数形结合等数学思想.。
2015年四川资阳中考数学试题1

资阳市2015年高中阶段教育学校招生统一考试数学全卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
全卷满分120分。
考试时间共120分钟。
注意事项:1.答题前,请考生务必在答题卡上正确填写自己的姓名、准考证号和座位号。
考试结束,将试卷和答题卡一并交回。
2.选择题每小题选出的答案须用2B铅笔在答题卡上把对应题目....的答案标号涂黑。
如需改动,用橡皮擦擦净后,再选涂其它答案。
非选择题须用黑色墨水的钢笔或签字笔在答题卡上对应题号位置作答,在试卷上作答,答案无效。
第Ⅰ卷(选择题共30分)一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个选项符合题意。
1.6-的绝对值是A.6 B.6-C.16D.16-2.如图1是一个圆台,它的主视图是3.下列运算结果为a6的是A.a2+a3B.a2·a3C.(-a2)3D.a8÷a24.一组数据3、5、8、3、4的众数与中位数分别是A.3,8 B.3,3 C.3,4 D.4,35.如图2,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为A.30°B.35°C.40°D.45°6.如图3,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示数3-5的点P应落在线段A .AO 上B .OB 上C .BC 上D .CD 上7.若顺次连接四边形ABCD 四边的中点,得到的图形是一个矩形,则四边形ABCD 一定是A .矩形B .菱形C .对角线相等的四边形D .对角线互相垂直的四边形8.如图4,AD 、BC 是⊙O 的两条互相垂直的直径,点P 从点O 出发,沿O →C →D →O 的路线匀速运动,设∠APB =y (单位:度),那么y 与点P 运动的时间x (单位:秒)的关系图是9.如图5,透明的圆柱形容器(容器厚度忽略不计)的高为12cm ,底面周长为10cm ,在容器内壁离容器底部3 cm 的点B 处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm 的点A 处,则蚂蚁吃到饭粒需爬行的最短路径是A .13cmB .261cmC .61cmD .234cm10.如图6,在△ABC 中,∠ACB =90º,AC =BC =1,E 、F 为线段AB 上两动点,且∠ECF =45°,过点E 、F 分别作BC 、AC 的垂线相交于点M ,垂足分别为H 、G .现有以下结论:①AB =2;②当点E 与点B 重合时,MH =12;③AF+BE=EF ;④MG•MH =12,其中正确结论为A .①②③B .①③④C .①②④D .①②③④第Ⅱ卷(非选择题 共90分)二、填空题:(本大题共6个小题,每小题3分,共18分)11.太阳的半径约为696000千米,用科学记数法表示为_______千米.图512.一个多边形的内角和是外角和的3倍,则这个多边形的边数是_______. 13.某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成右图统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有_________人.14.已知:()226230a b b ++--=,则224b b a --的值为_________.15.如图7,在平面直角坐标系中,点M 为x 轴正半轴上一点,过点M 的直线l ∥y 轴,且直线l 分别与反比例函数8y x =(x >0)和ky x=(x >0)的图象交于P 、Q 两点,若S △POQ =14,则k 的值为__________.16.已知抛物线p :y =ax 2+bx +c 的顶点为C ,与x 轴相交于A 、B 两点(点A 在点B 左侧),点C 关于x 轴的对称点为C′,我们称以A 为顶点且过点C ′,对称轴与y 轴平行的抛物线为抛物线p 的“梦之星”抛物线,直线AC′为抛物线p 的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y =x 2+2x +1和y =2x +2,则这条抛物线的解析式为_____________________.三、解答题:(本大题共8个小题,共72分)解答应写出必要的文字说明、证明过程或演算步骤。
2015年资阳市中考数学试题解析

资阳市2015年中考数学试卷全卷分为第I卷(选择题)和第H卷(非选择题)两部分,共4页。
全卷满分120分。
考试时间共120分钟。
注意事项:1.答题前,请考生务必在答题卡上正确填写自己的姓名、准考证号和座位号。
考试结束,将试卷和答题卡一并交回。
2 •选择题每小题选出的答案须用2B铅笔在答题卡上把对应题目.的答案标号涂黑。
如需改动,用橡皮擦擦净后,再选涂其它答案。
非选择题须用黑色墨水的钢笔或签字笔在答题卡上对应题号位置作答,在试卷上作答,答案无效。
第I卷(选择题共30分)一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个选项符合题意。
1. -6的绝对值是1 1A. 6B. -6C. —D.—6 6考点:绝对值.分析:根据负数的绝对值是它的相反数,可得负数的绝对值.解答:解:| - 6|=6 , 故选:A.点评:本题考查了绝对值,负数的绝对值是它的相反数.2 •如图1是一个圆台,它的主视图是单几何体的三视图. 分析:主视图是从物体正面看,所得到的图形. 解答:解:从几何体的正面看可得等腰梯形,故选:B. 点评:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.3 .下列运算结果为a6的是A. a2+ a3B. a2• a3C. (—a2)3D. a8-a2考点:同底数幕的除法;合并同类项;同底数幕的乘法;幕的乘方与积的乘方.分析:根据合并同类项、同底数幕的乘除法以及积的乘方和幕的乘方进行计算即可. 解答:解:A、a3-a2不能合并,故A错误;B a2?a3=a5,故B错误;C (- a2?)3=- a6,故C错误;8 2 6 丄/ 十”D、a +a =a,故D 正确;故选D.点评:本题考查了同底数幕的乘除法、合并同类项以及积的乘方和幕的乘方,是基础知识要熟练掌握.4 .一组数据3、5、8、3、4的众数与中位数分别是A. 3, 8B. 3, 3C. 3, 4D. 4, 3考点:众数;中位数.分析:根据中位数和众数的定义求解:众数是一组数据中出现次数最多的数据,注意众数可以不止一个;找中位数要把数据考点:简图1 A. B.按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.解答:解:把这组数据从小到大排列:3、3、4、5、8,3出现了2次,出现的次数最多,则众数是3.处于中间位置的那个数是4,由中位数的定义可知,这组数据的中位数是4;故选C.点评:本题为统计题,考查中位数与众数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.众数是一组数据中出现次数最多的数据,注意众数可以不止一个.5.如图2,已知AB// CD Z C=70°,Z:F=30°,则Z A的度数为——BA. 30°B.35°C. 40°D. 45°厶—D考点平行线的性质.图2专题计算题.分析先根据平行线的性质得Z BEF=/ C=70,然后根据二角形外角性质计算ZA的度数.解答解:••• AB//CD•••/ BEFK C=70 ,•••/ BEF=/ A+Z F,•••/ A=70°- 30° =40°.故选C.点评:本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.6.如图3,已知数轴上的点A、B C D分别表示数-2、1、2、3,则表示数3- 5的点P应落在线段B.OB上A O B C DA. AO上-3 -2 -1 0 1 2 3 4C. BC上D.CD上图孑考点: 估算无理数的大小;实数与数轴分析: 根据估计无理数的方法得出0 v 3-血v 1,进而得出答案.解答: 解:••• 2V 3,O v 3 - y .:v 1,故表示数3-匸的点P应落在线段OB上.故选:B.点评:此题主要考查了估算无理数的大小,得出匸的取值范围是解题关键.7 •若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一r曰疋是A.矩形B.菱形 C •对角线相等的四边形D.对角线互相垂直的四边形考点:中点四边形.分析:首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.解答:已知:如右图,四边形EFGH是矩形,且E F、G H分别是AB BC CD AD的中点,求证:四边形ABCD是对角线垂直的四边形.证明:由于E、F、G H分别是AB、BC CD AD的中点,根据三角形中位线定理得:EH// FG// BD EF// AC// HG•••四边形EFGH是矩形,即EF丄FG.ACLBD故选:D.H//\O1F点评:本题主要考查了矩形的性质和三角形中位线定理,解题的关键是构造三角形利用三角形的中位线定理解答.8.如图4, AD BC是O O的两条互相垂直的直径,点P从点O出发,沿O-D^O 的路线匀速运动,设/ APB=y (单位:度),那么y与点P运动的时间x (单位:秒)的关系图是考点:动点问题的函数图象.分析:根据图示,分三种情况:(1)当点P沿C IC运动时;(2)当点P沿C TD运动时;(3)当点x (单位:秒解答:解:P沿D-O运动时;分别判断出y的取值情况,进而判断出y与点P运动的时间卜)的关系图是哪个即可.(1)当点P沿O^C运动时,当点P在点0的位置时,y=90°,当点P在点C的位置时,•/ OA=O Q••• y=45°,•••y由90°逐渐减小到45°;(2)当点P沿C^D运动时, 根据圆周角定理,可得y=90°+ 2=45°;(3)当点P沿D2O运动时,当点P在点D的位置时,y=45°, 当点P在点0的位置时,y=90°,• y由45°逐渐增加到90°.故选:B.点评:(1)此题主要考查了动点问题的函数图象,解答此类问题的关键是通过看图获取信息,并能解决生活中的实际问题,用图象解决问题时,要理清图象的含义即学会识图.(2)此题还考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.9.如图5,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部 3 cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是A. 13cmB. 2 61 cmC. 、. 61 cmD. 2 34 cm考点:平面展开-最短路径问题.分析:将容器侧面展开,建立A关于EF的对称点A',根据两点之间线段最短可知A'B的长度即为所求.解答:解:如图:•••高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,• A D=5cm BD=1A 3+AE=12cm•••将容器侧面展开,作A关于EF的对称点A',连接A B,贝U A'B即为最短距离,A B=图5=13(cm . 故选:A .点评:本题考查了平面展开——最短路径问题,将图形展开,利用轴对称的性质和勾股 定理进行计算是解题的关键•同时也考查了同学们的创造性思维能力.10.如图 6,在厶 ABC 中, / ACB 90o, AC=BG1 , E 、F 为线段 AB 上两动点,且/ ECF=45° 过点E 、F 分别作BC AC 的垂线相交于点 M 垂足分别为 HG 现有以下结论:AMH 丄:③AF+BE=EF ④MGMH 丄,其中正2 2B .①③④D.①②③④考点:相似形综合题.…分析:①由题意知,△ ABC 是等腰直角三角形,根据等腰直角三角形即可作出判断;② 如图1,当点E 与点B 重合时,点H 与点B 重合,可得 MG BC 四边形 MGCB 是矩形, 进一步得到 卩6是厶ACB 的中位线,从而作出判断;③ 如图2所示,SAS 可证△ ECF^A ECD 根据全等三角形的性质和勾股定理即可作出判断;④ 根据AA 可证△ AC 0A BFC 根据相似三角形的性质可得 AF?BF=AC?BC=1由题意知四边 形 CHMG 是矩形,再根据平行线的性质和等量代换得到MG?MH=^AEX 丄BF= AE?BF= AC?BC=,依此即可作出判断.2 2 2 2 2解答:解:①由题意知,△ ABC 是等腰直角三角形,••• AB=「 _.|;「'=吋:■■,故①正确; ②如图1,当点E 与点B 重合时,点 H 与点B 重合,A .①②③ C.①②④确结论为•/ AC=BC Z ACB=90 ,• / A=Z 5=45°.将A ACF 顺时针旋转90°至厶BCD 则 CF=CD / 仁/4,/ A=Z 6=45°;•••/ 2=45°,• / 1+/ 3=/3+/4=45°, • / DCE / 2.在厶ECF 和厶ECD 中,••• MBL BC / MBC=90 , •/ MG_ AC•••/ MGC=90 =Z C=Z MBC• M G BC 四边形MGC 是矩形, • M H=MB=CG•••/ FCE=45 =Z ABC / A=Z ACF=45• C E=AF=BF• F G 是厶ACB 的中位线, BD=AF• G C= AC=MH 故②正确;2③如图2所示,rCF=CD • Z 2=ZDCE ,L CE=CE•••△ ECF^A ECD( SAS ,••• EF=DE•••/ 5=45°, •••/ BDE=90 ,• D E 2=BD 2+B E 2,!即 E^A F+B E ,故③错误;④•••/ 7=/ 1+Z A=Z 1+45° =/ 1+Z 2=Z ACE •••/ A=/ 5=45°,• △ AC 0A BFCBC BF• AF?BF=AC?BC=1 由题意知四边形 CHM (是矩形, • MG/ BC MH=C(MG/ BC MH/ AC ,•也型.色_BF厂],即”社二’;THJI,• MG?MH= AEX —BF= AE?BF= AC?BC=,2 2 2 2 2故④正确. 故选:C.点评:考查了相似形综合题,涉及的知识点有:等腰直角三角形的判定和性质,平行线的 判定和性质,矩形的判定和性质,三角形中位线的性质,全等三角形的判定和性质,勾股 定理,相似三角形的判定和性质,综合性较强,有一定的难度.第口卷(非选择题 共90 分)二、填空题:(本大题共6个小题,每小题3分,共18分)11•太阳的半径约为 696000千米,用科学记数法表示为 ___________________ 千米.考点:科学记数法一表示较大的数.分析:科学记数法的表示形式为 a x 10n 的形式,其中1W |a| v 10, n 为整数•确定n 的值 时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同. 当 原数绝对值〉10时,n 是正数;当原数的绝对值v 1时,n 是负数.解答:解:将696 000千米用科学记数法表示为 6.96 x 105千米.〔;-]1G= A E ; MH=点评:此题考查科学记数法的表示方法•科学记数法的表示形式为a x I0n的形式,其中1w|a| v 10, n为整数,表示时关键要正确确定a的值以及n的值.12 •一个多边形的内角和是外角和的3倍,则这个多边形的边数是_______________ .考点:多边形内角与外角.分析:任何多边形的外角和是360°,即这个多边形的内角和是3X 360°. n边形的内角和是(n - 2)?180°,如果已知多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.解答:解:设多边形的边数为n,根据题意,得(n- 2)?180=3X 360,解得n=8.则这个多边形的边数是 &点评:已知多边形的内角和求边数,可以转化为方程的问题来解决. 考查了相似形综合题,涉及的知识点有:等腰直角三角形的判定和性质,平行线的判定和性质,矩形的判定和性质,三角形中位线的性质,全等三角形的判定和性质,勾股定理,相似三角形的判定和性质,综合性较强,有一定的难度.13. 某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1〜2 (不含1)小时的学生有人.考点:用样本估计总体.分析:先求出每周课外阅读时间在1〜2 (不含1)小时的学生所占的百分比,再乘以全校的人数,即可得出答案.解答:解:根据题意得:1200X =240 (人),7+1014+19答:估计每周课外阅读时间在1〜2 (不含1)小时的学生有240人;故答案为:240.点评:本题考查从统计表中获取信息的能力,及统计中用样本估计总体的思想.14. _________________________________________________________ 已知:(a +6 j+J b2_2b_3 =0,则2b2—4b—a 的值为____________________________________________ .考点:非负数的性质:算术平方根;非负数的性质:偶次方.分析:首先根据非负数的性质可求出a的值,和2b2- 2b=6,进而可求出2b2- 4b- a的值.解答:解:T(a+6)2+「- =0,2••• a+6=0, b - 2b- 3=0,2解得,a= - 6, b - 2b=3,2可得2b - 2b=6,则2b2- 4b- a=6-( - 6) =12,故答案为12.点评:本题主要考查了非负数的性质,初中阶段有三种类型的非负数:绝对值、偶次方、二次根式(算术平方根)•当它们相加和为0时,必须满足其中的每一项都等于0.15. 如图7,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线I // y轴, 且直线I分别与反比例函数y=8( x > 0)和y=^( X> 0)的图象交于P、Q两点,若&POE4,X X则k的值为_______________ .考点:反比例函数与一次函数的交点问题;反比例函数系数k的几何意义.分析:由于S^PO=S^OM+S^OMP根据反比例函数比例系数k的几何意义得到'|k|+ ' x |8|=14 ,2 2然后结合函数y=,的图象所在的象限解方程得到满足条件的k的值.x解答:解:VS △PO Q=S\OM+S\OMP丄x |8|=14 ,2 2•••|k|=20 ,而k v 0,• k=- 20.故答案为-20.点评:本题考查了反比例函数比例系数k的几何意义:在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是-|k|,且保持不变.也2考查了反比例函数与一次函数的交点问题.16. 已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A B两点(点A在点B左侧),点C关于x轴的对称点为C,我们称以A为顶点且过点C,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC为抛物线p的“梦之星”直线. 若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y = x2+ 2x+ 1和y = 2x + 2,则这条抛物线的解析式为_______________________________ .考点:抛物线与x轴的交点;二次函数的性质.专题:新定义.分析:先求出y=x2+2x+1和y=2x+2的交点C'的坐标为(1,4),再求出“梦之星”抛物线y=x2+2x+1 的顶点A坐标(-1, 0),接着利用点C和点C关于x轴对称得到C (1 , - 4),则可设2顶点式y=a (x - 1) - 4 ,然后把A点坐标代入求出a的值即可得到原抛物线解析式. 解答:解:V y=x +2x+ 仁(x+1),■'■A 点坐标为(-1, 0),解方程组(尸'十2齢1得严T 或产1,,y=2x+2[y=0 I 尸4•••点C'的坐标为(1, 4),•••点C 和点C'关于x 轴对称, 二 C ( 1,- 4),设原抛物线解析式为 y=a (x - 1) 2 - 4, 把A (- 1, 0)代入得4a - 4=0,解得a=1,2 2•原抛物线解析式为 y= (x - 1) - 4=x - 2x - 3.故答案为y=x 2 - 2x - 3.2点评:本题考查了二次函数与 x 轴的交点:求二次函数y=ax +bx+c (a , b , c 是常数,a 和) 与x 轴的交点坐标,令 y=0,即ax +bx+c=0 ,解关于x 的一元二次方程即可求得交点横坐 标.△ =b 2- 4ac 决定抛物线与x 轴的交点个数, △ =b 2- 4ac > 0时,抛物线与x 轴有2个2 2交点;△ =b - 4ac=0时,抛物线与x 轴有1个交点;△ =b - 4ac v 0时,抛物线与x 轴没 有交点.三、解答题:(本大题共8个小题,共72分)解答应写出必要的文字说明、证明过程或演算步骤。
四川省资阳市雁江区初中2015届中考适应性检测理综试题

四川省资阳市雁江区初中2015届中考适应性检测理科综合全卷分为物理、化学两部分,共8页。
全卷满分130分。
考试时间共120分钟。
注意事项:1.答题前,请考生务必在答题卡上正确填写自己的姓名、准考证号和座位号。
考试结束,将试题卷和答题卡一并交回。
2.各学科的选择题,每小题选出的答案须用2B 铅笔在答题卡上把对应题目的答案标号涂黑,如需改动,用橡皮擦擦净后,再选涂其它答案。
3.各学科的非选择题须用0.5 mm 黑色墨水签字笔在答题卡上对应题号答题位置作答;在试卷上作答,答案无效。
物理部分(满分70分)一、单项选择题(本题包括7小题.在每小题给出的四个选项中,选出一个符合题意的最佳选项,多选、不选或错选均不得分,每小题3分,共21分)1.对下列各图所示光现象的解释中正确的是( )A .潜水艇内人员通过潜望镜看到的物体的像同实际物体上下、左右都是一致的B .平静的水面上倒映着岸边的景物,这是光的折射形成的C .手的影子是光沿直线传播形成的正立的虚像D .通过放大镜看图片的细微之处,看到的是放大的实像2.《舌尖上的中国2》聚焦于普通人的家常菜,让海内外观众领略了中华饮食之美,如图所示,通过煎、炒、蒸、拌烹调的四种美食中所包含的物理知识,认识正确的是()A .煎:煎锅一般用铁制造,主要是利用了铁的比热容大B .炒:主要是通过做功的方式使藜蒿和腊肉的内能增加C .蒸:是通过热传递和高温水蒸气液化放热,将榆钱饭蒸熟D.拌:香葱和豆腐拌着才能入味,说明分子没有做无规则运动A B CD3.下列关于声的说法正确的是( )A .用大小不同的力敲击同一音叉是为了探究音调与频率的关系B .人们可以用声学仪器接收到超声波判断地震的方位和强度C .倒车雷达是利用回声定位探测车后的障碍物D .给摩托车安装消声器是阻断噪声的传播4.下列各图关于力现象的情景解释正确的是( )A .“蛟龙号”潜水器在下潜过程中受到海水的压强变大,受到的浮力不变B .盲人行走过程不会偏离“盲道”是因为盲道路面凹凸不平,对盲人的脚底产生的压强比其它道产生的压强大C .飞机是依靠空气的浮力而升空的D .箱子没有被推动时箱子所受的摩擦力大于推力5.下列说法中正确的是( )A .用镍铬合金做保险丝主要是因为它的电阻率大、熔点低B .光是一种电磁波,由c =λf 可知波长越长的光波,传播速度越快C .带电体能吸引轻小的物体是因为两者之间一个带正电,另一个带负电D .家庭电路中当用电器功率增大时,通过保险丝的电流就增大6.如图所示是课本中的四个实验,关于其对应的实验结论,下列说法中正确的是( )①甲图说明大气压强的存在;②乙图说明重力势能可以转化为机械能;③丙图说明通电导体在磁场中受到力的作用;④丁图说明超声波的存在。
(完整版)四川省资阳市2015年中考数学试卷及答案(word版),推荐文档

资阳市2015年中考数学试卷一、选择题:(本大题共10个小题,每小题3分,共30分)1.的绝对值是6-A .6B .C . D . 6-1616-2.如图1是一个圆台,它的主视图是3.下列运算结果为a 6的是A .a 2+a 3B .a 2·a 3C .(-a 2)3D .a 8÷a 24.一组数据3、5、8、3、4的众数与中位数分别是A .3,8B .3,3C .3,4D .4,35.如图2,已知AB ∥CD ,∠C =70°,∠F =30°,则∠A 的度数为A .30°B .35°C .40°D .45°6.如图3,已知数轴上的点A 、B 、C 、D 分别表示数-2、1、2、3,则表示数3P 应落在线段A .AO 上B .OB 上C .BC 上D .CD 上7.若顺次连接四边形ABCD 四边的中点,得到的图形是一个矩形,则四边形ABCD 一定是A .矩形B .菱形C .对角线相等的四边形D .对角线互相垂直的四边形8.如图4,AD 、BC 是⊙O 的两条互相垂直的直径,点P 从点O 出发,沿O →C →D →O 的路线匀速运动,设∠APB =y (单位:度),那么y 与点P 运动的时间x (单位:秒)的关系图是9.如图5,透明的圆柱形容器(容器厚度忽略不计)的高为12cm ,底面周长为10cm ,在容器内壁离容器底部3 cm 的点B 处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm 的点A 处,则蚂蚁吃到饭粒需爬行的最短路径是A .13cmB .cm CD .10.如图6,在△ABC 中,∠ACB =90º,AC =BC =1,E 、F 为线段AB 上两动点,且∠ECF =45°,过点E 、F 分别作BC 、AC 的垂线相交于点M ,垂足分别为H 、G .现有以下结论:①AB ;②当点E 与点B 重合时,MH =;③AF+BE=EF ;④MG•MH=,其中正确结论为1212A .①②③B .①③④C .①②④D .①②③④图5二、填空题:(本大题共6个小题,每小题3分,共18分)11.太阳的半径约为696000千米,用科学记数法表示为_______千米.12.一个多边形的内角和是外角和的3倍,则这个多边形的边数是_______.13.某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有 人. 每周课外阅读时间(小时)0~11~2(不含1)2~3(不含2)超过3人 数710141914.已知:,则的值为_________.()260a +=224b b a --15.如图7,在平面直角坐标系中,点M 为x 轴正半轴上一点,过点M 的直线l ∥y 轴,且直线l 分别与反比例函数(x >0)和(x >0)的图象交于P 、Q 两点,若S △POQ =14,则k 的值为8y x =k y x=__________.16.已知抛物线p :y =ax 2+bx +c 的顶点为C ,与x 轴相交于A 、B 两点(点A 在点B 左侧),点C 关于x 轴的对称点为C′,我们称以A 为顶点且过点C ′,对称轴与y 轴平行的抛物线为抛物线p 的“梦之星”抛物线,直线AC′为抛物线p 的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y =x 2+2x +1和y =2x +2,则这条抛物线的解析式为_____________________.三、解答题:(本大题共8个小题,共72分)17.(本小题满分7分)先化简,再求值:,其中满足2112()111x x x x +-÷-+-x 260x -=18.(本小题满分8分)学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A :特别好,B :好,C :一般,D :较差)后,再将调查结果绘制成两幅不完整的统计图(如图8).请根据统计图解答下列问题:(1)本次调查中,王老师一共调查了_______名学生;(2)将条形统计图补充完整;(3)为了共同进步,王老师从被调查的A 类和D 类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.19.(本小题满分8分)学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.(1)求篮球和足球的单价;(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的,23学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?(3)若购买篮球x 个,学校购买这批篮球和足球的总费用为y (元),在(2)的条件下,求哪种方案能使y 最小,并求出y 的最小值.20.(本小题满分8分)北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图9,某探测队在地面A 、B 两处均探测出建筑物下方C 处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB =4米,求该生命迹象所在位置C 的深度.(结果精确到121.(本小题满分9分)如图10,直线y =ax +1与x 轴、y 轴分别相交于A 、B 两点,与双曲线y =(x >0)相交于点P ,PC ⊥x 轴于点C ,且PC =2,点A 的坐标为.kx 2,0 ()(1)求双曲线的解析式;(2)若点Q 为双曲线上点P 右侧的一点,且QH ⊥x 轴于H ,当以点Q 、C 、H 为顶点的三角形与△AOB 相似时,求点Q 的坐标.22.(本小题满分9分)如图11,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E 为BC的中点,连接DE.(1)求证:DE是⊙O的切线;(2)连接AE,若∠C=45°,求sin∠CAE的值.23.(本小题满分11分)如图12,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.(1)求证:△ADE≌△DCF;(2)若E是CD的中点,求证:Q为CF的中点;(3)连接AQ,设S△CEQ=S1,S△AED=S2,S△EAQ=S3,在(2)的条件下,判断S1+S2=S3是否成立?并说明理由.24.(本小题满分12分)已知直线y=kx+b (k ≠0)过点F (0,1),与抛物线y =x 2相交于B 、C 两14点.(1)如图13-1,当点C 的横坐标为1时,求直线BC 的解析式;(2)在(1)的条件下,点M 是直线BC 上一动点,过点M 作y 轴的平行线,与抛物线交于点D ,是否存在这样的点M ,使得以M 、D 、O 、F 为顶点的四边形为平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由;(3)如图13-2,设(m <0),过点的直线l ∥x 轴,BR ⊥l 于R ,CS ⊥l 于S ,连接,B m n ()01E (,)FR 、FS .试判断△RFS 的形状,并说明理由.1、A.2、B.3、D.4、C.5、C.6、B.7、D.8、B.9、A.10、C①由题意知,△ABC是等腰直角三角形,根据等腰直角三角形即可作出判断;②如图1,当点E与点B重合时,点H与点B重合,可得MG∥BC,四边形MGCB是矩形,进一步得到FG是△ACB的中位线,从而作出判断;③如图2所示,SAS可证△ECF≌△ECD,根据全等三角形的性质和勾股定理即可作出判断;④根据AA可证△ACE∽△BFC,根据相似三角形的性质可得AF•BF=AC•BC=1,由题意知四边形CHMG是矩形,再根据平行线的性质和等量代换得到MG•MH=AE×BF=AE•BF=AC•BC=,依此即可作出判断.解答:解:①由题意知,△ABC是等腰直角三角形,∴AB==,故①正确;②如图1,当点E与点B重合时,点H与点B重合,∴MB⊥BC,∠MBC=90°,∵MG⊥AC,∴∠MGC=90°=∠C=∠MBC,∴MG∥BC,四边形MGCB是矩形,∴MH=MB=CG,∵∠FCE=45°=∠ABC,∠A=∠ACF=45°,∴CE=AF=BF,∴FG是△ACB的中位线,∴GC=AC=MH,故②正确;③如图2所示,∵AC=BC,∠ACB=90°,∴∠A=∠5=45°.将△ACF顺时针旋转90°至△BCD,则CF=CD,∠1=∠4,∠A=∠6=45°;BD=AF;∵∠2=45°,∴∠1+∠3=∠3+∠4=45°,∴∠DCE=∠2.在△ECF和△ECD中,,∴△ECF≌△ECD(SAS),∴EF=DE.∵∠5=45°,∴∠BDE=90°,∴DE2=BD2+BE2,即E2=AF2+BE2,故③错误;④∵∠7=∠1+∠A=∠1+45°=∠1+∠2=∠ACE,∵∠A=∠5=45°,∴△ACE∽△BFC,∴=,∴AF•BF=AC•BC=1,由题意知四边形CHMG是矩形,∴MG∥BC,MH=CG,MG∥BC,MH∥AC,∴=;=,即=;=,∴MG=AE;MH=BF,∴MG•MH=AE×BF=AE•BF=AC•BC=,故④正确.故选:C.11、6.96×105千米. 12、8.13、240. 14、12. 15、﹣20. 16、y=x2﹣2x﹣3.解答:解:∵y=x2+2x+1=(x+1)2,∴A点坐标为(﹣1,0),解方程组得或,∴点C′的坐标为(1,4),∵点C和点C′关于x轴对称,∴C(1,﹣4),设原抛物线解析式为y=a(x﹣1)2﹣4,把A(﹣1,0)代入得4a﹣4=0,解得a=1,∴原抛物线解析式为y=(x﹣1)2﹣4=x2﹣2x﹣3.17、解:原式=÷=•=.∵2x﹣6=0,∴x=3,当x=3时,原式=.18、解:(1)根据题意得:王老师一共调查学生:(2+1)÷15%=20(名);故答案为:20;(2)∵C类女生:20×25%﹣2=3(名);D类男生:20×(1﹣15%﹣50%﹣25%)﹣1=1(名);如图:(3)列表如下:A类中的两名男生分别记为A1和A2,男A1男A2…(7分)女A男D男A1男D男A2男D女A男D女D男A1女D男A2女D女A女D共有6种等可能的结果,其中,一男一女的有3种,所以所选两位同学恰好是一位男生和一位女生的概率为:=.1、解:(1)设一个篮球x元,则一个足球(x﹣30)元,由题意得:2x+3(x﹣30)=510,解得:x=120,∴一个篮球120元,一个足球90元.(2)设购买篮球x个,足球(100﹣x)个,由题意可得:,解得:40≤x≤50,∵x为正整数,∴x=40,41,42,43,44,45,46,47,48,49,50,∴共有11种购买方案.(3)由题意可得y=120x+90(100﹣x)=30x+9000(40≤x≤50)∵k=30>0,∴y随x的增大而增大,∴当x=40时,y有最小值,y最小=30×40+9000=10200(元),所以当x=40时,y最小值为10200元.20、解:作CD⊥AB交AB延长线于D,设CD=x 米.Rt△ADC中,∠DAC=25°,所以tan25°==0.5,所以AD==2x.Rt△BDC中,∠DBC=60°,由tan 60°==,解得:x≈3米.所以生命迹象所在位置C的深度约为3米.21、解:(1)把A(﹣2,0)代入y=ax+1中,求得a=,∴y=x+1,由PC=2,把y=2代入y=x+1中,得x=2,即P(2,2),把P代入y=得:k=4,则双曲线解析式为y=;(2)设Q(a,b),∵Q(a,b)在y=上,∴b=,当△QCH∽△BAO时,可得=,即=,∴a﹣2=2b,即a﹣2=,解得:a=4或a=﹣2(舍去),∴Q(4,1);当△QCH∽△ABO时,可得=,即=,整理得:2a﹣4=,解得:a=1+或a=1﹣(舍),∴Q(1+,2﹣2).综上,Q(4,1)或Q(1+,2﹣2).22、解:(1)连接OD,BD,∴OD=OB∴∠ODB=∠OBD.∵AB是直径,∴∠ADB=90°,∴∠CDB=90°.∵E为BC的中点,∴DE=BE,∴∠EDB=∠EBD,∴∠ODB+∠EDB=∠OBD+∠EBD,即∠EDO=∠EBO.∵BC是以AB为直径的⊙O的切线,∴AB⊥BC,∴∠EBO=90°,∴∠ODE=90°,∴DE是⊙O的切线;(2)作EF⊥CD于F,设EF=x∵∠C=45°,∴△CEF、△ABC都是等腰直角三角形,∴CF=EF=x,∴BE=CE=x,∴AB=BC=2x,在RT△ABE中,AE==x,∴sin∠CAE==.23、1)证明:∵四边形ABCD是正方形,∴AD=DC,∠ADE=∠DCF=90°,在△ADE和△DCF中,,∴△ADE≌△DCF(SAS);(2)证明:∵E是CD的中点,∴CE=DE=DC=AD,∵四边形AEHG是正方形,∴∠AEH=90°,∴∠AED+∠CEQ=90°,∵∠AED+∠DAE=90°,∴∠DAE=∠CEQ,∵∠ADE=∠DCF,∴△ADE∽△ECQ,∴=,∴CQ=DE,∵DE=CF,∴CQ=CF,即Q为CF的中点;(3)解:S1+S2=S3成立;理由如下:如图所示:∵△ADE∽△ECQ,∴,∵DE=CE,∴,∵∠C=∠AEQ=90°,∴△AEQ∽△ECQ,∴△AEQ∽△ECQ∽△ADE,∴,,∴=()2+()2=,∵EQ2+AE2=AQ2,∴=1,∴S1+S2=S3.24、解:(1)因为点C在抛物线上,所以C(1,),又∵直线BC过C、F两点,故得方程组:解之,得,所以直线BC的解析式为:y=﹣x+1;(2)要使以M、D、O、F为顶点的四边形为平行四边形,则MD=OF,如图1所示,设M(x,﹣x+1),则D(x,x2),∵MD∥y轴,∴MD=﹣x+1﹣x2,由MD=OF,可得|﹣x+1﹣x2|=1,①当﹣x+1﹣x2=1时,解得x1=0(舍)或x1=﹣3,所以M(﹣3,),②当﹣x+1﹣x2,=﹣1时,解得,x=,所以M(,)或M(,),综上所述,存在这样的点M,使以M、D、O、F为顶点的四边形为平行四边形,M点坐标为(﹣3,)或(,)或(,);(3)过点F作FT⊥BR于点T,如图2所示,∵点B(m,n)在抛物线上,∴m2=4n,在Rt△BTF中,BF====,∵n>0,∴BF=n+1,又∵BR=n+1,∴BF=BR.∴∠BRF=∠BFR,又∵BR⊥l,EF⊥l,∴BR∥EF,∴∠BRF=∠RFE,∴∠RFE=∠BFR,同理可得∠EFS=∠CFS,∴∠RFS=∠BFC=90°,∴△RFS是直角三角形.。
2015年资阳市中考数学试题及答案

数卑"共"。
全H20分十片 全*分为第I 卷(选择❻)和和1矗(“逸啊)两部' 苇何* 120分忡。
注意幕项: ―号和座位号•考必结束・持钺 I. $❻林・请考生务必虚答將卡上正瑣填頁自己妁社名'' :'卷和怎題卡一并交凹。
卜卜“应助目的冬案标号涂黑2如需改动.2通择砧H 皿出X"用2B 哒在糾上工展“字笔在答題卡上对期强 用橡皮瞭擦净后.弄逸涂其它签赛.非选择题须用黑色*水的I丑作耶.庄试昙上作菩.签赛无效。
、、第I 卷(选择题共3°勺)-、选择和本大题“鷺寫、爲.共3。
分)在毎小题给出的四个选项职只有A."上B. OB 上C. BC 上D. CD 上7.若顺次连接四边形肋CQ 四边的中点,得到的图形是〜删,则四边形肋CD -定是 A.矩形 B.菱形 C.对角线相等的四边形D •对角线互相垂直的四边形资吋昭吐和页(矣4页)L Y 的对值足 ci4. 一组数据3、5、8、3. 4的众数与中位数分别是 A 3, 8B, 3, 3 C. 3, 4 5. 如图2,已知AB//CD, ZO70°, ZF=30°.则乙4的度数为 A 30°B ・ 35。
C ・ 40°D. 4, 3D. 6. 如图3.已知数轴上的点久B 、C. D 分別农示数_2、1、2、3.则表示 3 -厉的点P 应落在线段•3 ・2 ・1 0 i 2 3 4图3D.A. 62.如图1是一个圆台.它的主觇图是B 45°D厶—M 座丄工筈2 ][( * 4頁)8如图 4. 初・8C •是©o 的 两条互相垂血的4 直矗•点尸从点O 出发.沿U DP 的路线匀速 运幼.设厶人PAy (单位•陆)9•如国5.透明的圆露囂律警沪运动的时间讥啊秒)的关系图是10cm.在桶内壁离容器底J (宿警度忽如计)的舟为12cm.底喇周长为 曦•叫器阳山的点‘处.则蚂蚁吃到饭粒需爬行的最短般好在各器外A ,3cmB 2辰 5 C. Veicm D. 2屈 cm 过牡 煤噪飲丫: J ;:""%'心心' • E 、尸删液肋上卿动点,nZ£CF-45°. EE' "分别作眈、力的垂线相交于点%垂足分别为航G .现育以F 结论:②当点£与点8匝合时,倔弓;③AF +BE=EF ;④MGM7";.英中正确结论为A. (D®(3) C第II 卷(非选择题共90分)二.填空鬆:(本大題共6个小題•每小題3分.共】8分) II.太阳的半空约为696000千米.用科学记数法表示为 ____ 千米. 12 •个多边形的内角和展外角和的3假则这个多边形的边数足— 13. 某学校为了解本校学生课 外阅读的情况•从全体学生中随机 抽取了部分学生进行调資,并将调 翻陳绘制成右图统计及已如该校全体学生人数为1200人,由此可以估计毎周课外阅读时间在卜2(不含I )柯的学生有 _________ 人14. 已知:(“6)%■肪不°・则26'-的值为 ------------------ • 15.如图7.在平面直角坐标系中•点“为x 轴正半轴上一鳳过点 “的直线力轴,且瞬/分别与反比例函数(“°)和V “每周课外阅读 时间(扌) (K11~2 (不含】) 2-3 (不含2)葩3 人数 7 1014 19B.cm图S 图4EBW7]A"的用簟欢于帆Q 快仏 若品“=|4.则•帕值为 _____ _____IE L 和撤™<frr.(的風戟为「七"抽川愛 m H 阻|点t 卓丿件电月左別h 点 匚关于対称点为c\^fuffu 4为頂盘HJ1点L •对IW 写* 的勵勒缆为(ft 勧罐卫的“莎N 城“拋如.n 纯机为拋拘纯卩的帶十這 若-睾鼬物疑的“娜上却伽物地和“擁之城“直 址分却是y^x z+2x+ I fUy=2n-2. 1«这条抛脚蜒的解折式为 ____________________三*解苓販Y 本大麗其S 牛小K*共72 5> |梨普庭歸出必至的文字说聯、证耶过理或演算步17 f 杪範淸甘7井[希化尚*评来fft:f-一- - £~P * $节» 其申 * 満足 2i - 6 =; 0rfl 案小恥漓分8介I 学校宣施斬M 樫改眾门来.讐生的学习能力有了说K 琨胡,丘屋闻为进 一步了解审班学生“主学习、合作交流的现弑,対该班部分乍性进行阔僅,把调能曽果分底四类{八 符别好「Bi 好+ G -股* 6 4JLS) J6・再将调 连结果绘剖成两幅不完眾的统ii 图{却图町 谪權? 据竦计團解讐下列问题; 2(1) 亭次调直屮”王髭师一共凋豐了:名学生7(2) 将拯形统计图补充完整;: (?)为了共同进步.壬老师从被调谨的疋宾和 _ D 类学生中分别选城一名学生进行“兵教兵”互助学 厂 习,清用列表或関鞫状图的方法求出恰奸选屮一名 鸦生和一名女生的槪議「19. (本小轉满分9分】学檯需盟购买一批篮球和界球.记知…个篮球比 个足昧的进价嬴30 无*买两个篮球和三个足球一扶需要510元.(1) ^篮球和曲的单价:(2 :楹鞘实际缶卷.学枝雌购买篮球枕足球共100个*捷中篮球购莫的数域不少于妃球製惟 的? +学校可用于购买这批槪珠拥足球的资金融铁为10500元站间河几种购浜方士? 3(3) 若购买盤球h 个*学狡购买这批篮球相足球的总铁用为丁〔元)■在心)的条件厂 求哪种方案能小,并求出F 的最小值.20, (本小軀満分«分)北哀时间20H 年04月25 U 14 Ll 5>t 尼泊 系发生BA 级强烈地餐・我国积极组抢险从赴地展灾区参与抢险工作.如 图9,某探测队在地面八R 两处均探溜出建筑物下方C 处有生冊迹叙 已 金, 知探阚线仃地面的夹角分别是瓷咗*0人“沖恥4米・求该住命迹象所住位 ■ <7的深度(貉果将确到丨米参苇数妣H 価5 4 3煜普巾讥1曲5宜05 73=1.7)5i ly ..........4 I 父 .... H ...... .2 . ■ ■……… nc°賞别 图a-】ISS-2—J "本小尊满分9分)如图I 。
2015年资阳市中考数学适应性考试题(附答案)

2015年资阳市中考数学适应性考试题(附答案)安岳县初中2015届学业水平暨高中阶段招生适应性考试参考答案及评分意见一、选择题1―5 CBBCB 6―10 DCCBC 二、填空题11.1.05×105 12.4 13.1.6 14.20° 15.3 16.210 三、解答题 17.解:原式 =x-2x-1•(x+1)(x-1)(x-2)2 2分 =x+1x-2 3分方程x2-6=5x的解为:x1=6 x2=-1 5分∵x=-1时分式无意义,∴当x=6时,原式=6+16-2=74 7分(1)30. 2分(2)在Rt△BHP中,∠PBH=600,∵PHPB=sin∠PBH,18.解:∴PB=PH sin∠PBH=30sin60°=203 4分在△ABP中,∠APB=60°-15°=45°,∠ABP=180°-∠PBH-∠ABC=180°-60°-30°=90° 5分∴△ABP是等腰直角三角形, 6分∴AB=PB=203≈34.6(米) 7分答:A、B两点间的距离约为34.6米. 8分19.解:(1)画树状图得: 4分∵共有16种等可能的结果,小明和母亲随机各摸球一次,均摸出白球的只有1种情况,∴小明和母亲随机各摸球一次,均摸出白球的概率是:116; 6分(2)由(1)得:共有16种等可能的结果,小明和母亲随机各摸球一次,至少有一人摸出黄球的有7种情况,∴小明和母亲随机各摸球一次,至少有一人摸出黄球的概率是:716. 8分20.解:(1)在Rt△OAC中,设OC=m,∵tan∠AOC=ACOC=2,∴AC=2×OC=2m,∵S△OAC=12×OC×AC=12×m×2m=1,∴m2=1,∴m=±1(负值舍去),∴A点的坐标为(1,2), 2分把A点的坐标代入y1=k1x中,得k1=2,∴反比例函数的表达式为y1=2x, 3分把A点的坐标代入y2=k2x+1中,得k2+1=2,∴k2=1,∴一次函数的表达式y2=x+1; 4分( 2)B点的坐标为(-2,-1), 6分当0<x<1和x<-2时,y1>y2. 8分21.解:(1)BM+DN=MN成立. 1分如下图1,在MB的延长线上,截得BE=DN,连接AE,易证:△ABE≌△AND,∴AE=AN. 2分∴∠EAB=∠NMD.∴∠BAD=90°,∠NAM=45°∴∠BAM+∠NMD=45°.∴∠E AB+∠BAM=45°.∴∠EAM=∠NAM 又AM 为公共边,∴△AEM≌△ANM ,∴ME=MN,∴ME=BE+BM=DN+BM.∴DN+BM=MN. 4分 (2)DN-BM=MN. 5分理由如下:如图2,在DC 上截取DF=BM,连接AF.∵AB=AD,∠ABM=∠ADF=90°,∴△ABM≌△ADF (SAS )∴AM=AF,∠MAB=∠FAD. 7分∴∠MAB+∠BAF=∠FAD+∠BAF=90°,即∠MAF=∠BAD=90°.又∠MAN=45°,∴∠NAF=∠MAN=45°.∵AN=AN,∴△MAN≌△FAN.∴MN=FN,即 MN=DN-DF=DN-BM; 9分22.解:(1)未租出的设备为x-27010套,所有未出租设备支出的费用为(2x-540)元; 2分(2)∵y=(40-x-27010)x-(2x-540)=-110x2+65x+540; 4分∴当月租金为300元时,租赁公司的月收益为11040元,此时租出设备37套;当月租金为350元时,租赁公司的月收益为11040元,此时租出设备32套. 5分因为出租37套和32套设备获得同样的收益,如果考虑减少设备的磨损,应该选择出租32套;如果考虑市场占有率,应该选择37套; 6分(3)由(2)知y=-110x2+65x+540=- 110(x-325)2+11102.5 7分∴当x=325时,y有最大值11102.5.但是当月租金为325元时,出租设备的套数为34.5套,而34.5不是整数 8分故出租设备应为34(套)或35(套).即当月租金为330元(租出34套)或月租金为320元(租出35套)时,租赁公司的月收益最大,最大月收益均为11100元.…………………………10分23.解:如图3(1)∵OA=OC,∴∠A=∠ACO,又∵∠COB=2∠A,∠COB=2∠PCB,∴∠A=∠ACO=∠PCB,又∵AB是⊙O的直径,∴∠ACO+∠OCB=90°,∴∠PCB+∠OCB=90°,∴∠PCO=90°,即OC⊥CP,而OC是⊙O的半径,∴PC是⊙O的切线;................... ..........(3分)(2)∵AC=PC,∴∠A=∠P,∴∠A=∠ACO=∠PCB=∠P,又∵∠COB=∠A+∠ACO,∠ CBO=∠P+∠PCB,∴∠COB=∠CBO,∴BC=OC,∴BC=12AB; 6分(3)连接MA,MB,∵点M是弧AB的中点,∴ ,∴∠ACM=∠BCM,∵∠ACM=∠ABM,∴∠BCM=∠ABM,又∵∠BMN=∠BMC,∴△MBN∽△MCB,∴BMMC=MNBM,8分∴BM2=MN•MC,又∵AB是⊙O的直径,,∴∠AMB=90°,AM=BM,∴AB=4,∴BM=22,∴MN•MC=BM2=(22)2=8 10分24.解:(1)由题意,得,解得,∴所求抛物线的解析式为y=-12x2+x+4 (2)如图4,设点Q的坐标为(m,0),过点E作EG⊥x 轴于点G,由-12x2+x+4=0,得x1=-2,x2=4, ∴点B的坐标为(-2,0),∴AB=6,BQ= m +2 ∵QE∥AC,∴△BQE∽△BAC ,∴EGCO=BQBA 即EG4= m+26,∴EG=2m+43………… .5分∴ S△CQE=S△CBQ-S△EBQ=12BQ•CO-12BQ•EG =12(m+2)(4-2m+43) =-13m2+23m+83=3, ∴ m2-2m-8=-9, ∴m=1 ∴Q(1,0) 7分(3)存在 8分在△ODF 中,①若DO=DF,∵A(4,0),D(2,0),∴AD =OD=DF=2, 又在Rt△AOC 中,OA=OC=4,∴∠OAC= 45° ∴∠DFA=∠OAC= 45°∴∠ADF=90° 此时,点F的坐标为(2,2)由,得x1=1+5,x2=1-5 此时,点P 的坐标为:P(1+5,2 )或P(1-5,2 ) 9分②如图5,若FO=FD,过点F作FM⊥ 轴于点M,由等腰三角形的性质得:OM=12OD=1,∴AM=3 ∴在等腰直角三角形△AMF中,MF=AM=3 ∴F(1,3) 由-12x2+x+4=3,得x1=1+3,x2=1-3 此时,点P的坐标为:P(1+3,3)或P(1-3,3) ………………………………10分③若OD=OF,∵OA=OC=4,且∠AOC=90°,∴AC= 42 ∴点O到AC的距离为22,而OF=OD=2<22 此时,不存在这样的直线l,使得△ODF是等腰三角形. 11分综上所述,存在这样的直线l,使得△ODF是等腰三角形.所求点P的坐标为: P(1+5,2 )或P(1-5,2 )或P(1+3,3)或P(1-3,3)……… …………………12分。
(完整版)四川省资阳市年中考数学试卷及答案(版),推荐文档

果绘制成统计表.已知该校全体学生人数为 1200 人,由此可以估计每周课外阅读时间在 1~2(不含 1)
小时的学生有 人.
每周课外阅读时 0~1 1~2
2~3
超过 3
间(小时)
(不含 1) (不含 2)
人数
7 10
14
19
14.已知: a 62 b2 2b 3 0 ,则 2b2 4b a 的值为
17.(本小题满分 7 分)先化简,再求值:
( 1 1 ) x 2 ,其中 x 满足2x 6 0 x 1 x 1 x2 1
18.(本小题满分 8 分)学校实施新课程改革以来,学生的 学习能力有了很大提高.王老师为进一步了解本班学生自主 学习、合作交流的现状,对该班部分学生进行调查,把调 查结果分成四类(A:特别好,B:好,C:一般,D:较差)
21.(本小题满分 9 分)如图 10,直线 y=ax+1 与 x 轴、y 轴分别相交于 A、B两点,与双曲线 k y=x(x>0)相交于点 P,PC⊥x 轴于点 C,且 PC=2,点 A的坐标为()2, 0 . 1 求双曲线的解析式; 2 若点 Q 为双曲线上点 P 右侧的一点,且 QH⊥x 轴于 H, 当以点 Q、C、H 为顶点的三角形与△AOB 相似时,求点 Q 的坐标.
资阳市 2015 年中考数学试卷
一、选择题:(本大题共 10 个小题,每小题 3 分,共 30 分)
1. 6 的绝对值是
A.6
B. 6
C. 1 6
2. 如图 1 是一个圆台,它的主视图是
D. 1 6
3.
下列运算结果为 a6 的是
A.a2+a3
B.a2·a3
C.(-a2)3
D.a8÷a2
4.
一组数据 3、5、8、3、4 的众数与中位数分别是
四川省资阳市中考数学试卷及答案doc
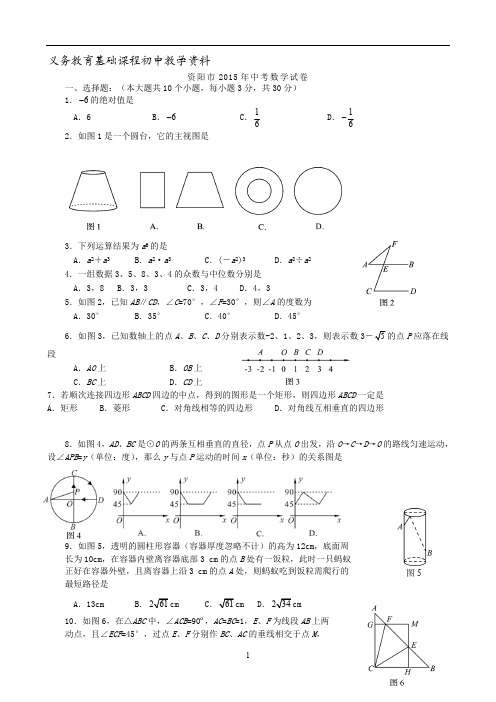
图5
10.如图 6,在△ABC 中,∠ACB=90º,AC=BC=1,E、F 为线段 AB 上两 动点,且∠ECF=45°,过点 E、F 分别作 BC、AC 的垂线相交于点 M,
1
垂足分别为 H、G.现有以下结论:①AB= 2 ;②当点 E 与点 B 重合时,
MH= ;③AF+BE=EF;④MG•MH= ,其中正确结论为
9.如图 5,透明的圆柱形容器(容器厚度忽略不计)的高为 12cm,底面周 长为 10cm,在容器内壁离容器底部 3 cm 的点 B 处有一饭粒,此时一只蚂蚁 正好在容器外壁,且离容器上沿 3 cm 的点 A 处,则蚂蚁吃到饭粒需爬行的 最短路径是 A.13cm B. 2 61 cm C. 61 cm D. 2 34 cm
2
1 2
1 2
15.如图 7,在平面直角坐标系中,点 M 为 x 轴正半轴上一点,过点 M 的直线 l∥y 轴,且直线 l 分别 8 k 与反比例函数 y (x>0) 和 y (x>0) 的图象交于 P、 Q 两点, 若 S△POQ=14, 则 k 的值为__________. x x 16.已知抛物线 p: y=ax2+bx+c 的顶点为 C,与 x 轴相交于 A、B 两点(点 A 在点 B 左侧) ,点 C 关于 x 轴的对称点为 C′,我们称以 A 为顶点且过点 C′,对称轴与 y 轴平行的抛物线为抛物线 p 的“梦之星” 抛物线,直线 AC′为抛物线 p 的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分 别是 y=x2+2x+1 和 y=2x+2,则这条抛物线的解析式为_____________________. 三、解答题:(本大题共 8 个小题,共 72 分) 17. (本小题满分 7 分)先化简,再求值:
资阳市2015年九年级下学期第一次月考数学试题及答案

AB C O D一、选择题(本大题共10个小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一个选项是符合题目的要求的)1.2-的相反数是( )A. 2B.-2C. 12D. -122.如图,⊙O 的弦CD 与直径AB 相交,若∠ACD =35°, 则∠BAD =( ) A .55° B .40° C .35° D .30° 3.已知二次函数y =x 2+x +2 与一次函数y =2x -1在同一坐标系 中的交点个数是( )A .0个B . 1个C .2 个D .无法确定4.将抛物线222y x =+向右平移1个单位后所得抛物线的解析式是( )A .223y x =+;B .221y x =+;C .22(1)2y x =++;D .22(1)2y x =-+.5.2014年第九届原创新春祝福短信微博大赛作品充满了对马年浓浓的祝福,主办方共收到原创祝福短信作品41430条,将41430用科学记数法表示应为( )A .341.4310⨯B .44.14310⨯C .500414310⨯D .54.14310⨯6.经过某十字路口的汽车,它可能继续直行,也可能向左或向右转。
若这三种可能性大小相同,则两辆汽车经过该十字路口全部继续直行的概率为( )A .13B .23C .19D .12 7.已知圆O 的直径是方程25240x x --=,且点A 到圆心O 的距离为6,则点A 在( )A .圆O 上B .圆O 内C . 圆O 外D .无法确定8.函数1y ax =+与21y ax bx =++(0a ≠)的图象可能为( )9.下列四个命题中,正确的有( )①圆的对称轴是直径;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.A.4个B.3个C.2个D.1个10.已知二次函数2y ax bx c =++的图象如图,其对称轴1-=x ,给出下列结果①24b ac >;②0abc >;③20a b +=;④0a b c ++>;⑤0a b c -+<,则正确的结论是( )A .①②③④B .②④⑤C .②③④D .①④⑤二、填空题(本大题6个小题,每小题3分,共18分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1四川省资阳市雁江区初中2015届中考数学适应性检测试题本试题分第I 卷(选择题)和第II 卷(非选择题)两部分.第I 卷1至2页,第II 卷2至4页,共4页.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效,满分120分,考试时间120分钟.考试结束后,将本试题卷和答题卡一并交回.第I 卷(选择题 共30分)注意事项:每小题选出的答案不能答在试卷上,须用2B 铅笔在答题卡上把对应题目的答案标号涂黑。
如需改动,用橡皮擦擦净后,再选涂其它答案.一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个选项符合题意.1.6的相反数是( )A.6B.-6C.-16 D.162.据报道,某小区改进用水设备,在十年内帮助该住小区的居民累计节水1800000吨.将1800000用科学记数法表示应为( )A.0.18×107B.1.8×106C.1.8×107D.18×1053.小敏同学跳绳7次测试成绩如下(单位:分):8.5,7,9,8,9,8.5,9.这组数据的中位数和众数分别为( )A.8,9B.9,8.5C.8.5,9D.8,8.5 4.下列说法正确的是( ) A.若21--x x 有意义,则有x ≥1且x ≠2 B .勾股定理是a 2+b 2=c 2C.夹在两条平行线间的线段相等D.a 0=15.如图,在Rt △ABC 中,∠C =90°,BC =6,AC =8,那么sinA 的值等于( ) A.43 B.34 C.53 D.546.已知⊙O 的直径是16cm ,点O 到同一平面内直线l 的距离为9cm ,则直线l 与⊙O 的位置关系是( )A.相交B.相切C.相离D.无法判断7.点P 、Q 、R 是平面内不在同一条直线上的三个定点,点M 是平面内任意一点,若P 、Q 、R 、M 四点恰能构成一个平行四边形,则在平面内符合这样条件的点M 有( )A.1个B.2个C.3个D.4个8.正比例函数y =x 与反比例函数y =x4的图象交于A (2,2)、B (﹣2,﹣2)两点,当x >x4时,x 的取值范围是( ) A .﹣2<x <0或x >2 B .﹣2<x <0或0<x <2 C .x >2 D .x <﹣2 9.已知抛物线y =ax 2+bx +c (a ≠0)经过点(1,1)和(﹣1,0).下列结论:①b 2>4ac ;②抛物线的对称轴为x =-a41; ③a ﹣b +c =0;④当a <0时,抛物线与x 轴必有一个交点在点(1,0)的右侧.其中结论正确的个数有( )(第5题图)(第8题图)2(第16题图)A.4个B.1个C.2个D.3个10.如图,MN 是半径为2的⊙O 的直径,点A 在⊙O 上,∠AMN =30°,点B 为劣弧AN 的中点.点P 是直径MN 上一动点,则PA +PB 的最小值为( )A .42B .2C .4D .22第II 卷(非选择题 共90分)注意事项:必须使用0.5毫米黑色签字笔在答题卡上题目指示的答题区域内作答.作图时可先用铅笔绘出,确认后再用0.5毫米黑色签字笔描清楚. 答在试题卷上无效.二、填空题 :(本大题共6个小题,每小题3分,共18分).11.要使式子121-x 在实数范围内有意义,则x 的取值范围是 . 12.如图,已知AB ∥CD ,∠1=150°,则∠2= .13.100件外观相同的产品中有6件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是 .14.如图,直线y =2x +8与x ,y 轴分别交于A ,B 两点,以OB 为底边在y 轴右侧作等腰三角形OBC ,将点C 向左平移,使其对应点C ′恰好落在直线AB 上,则点C ′的坐标为 .15.在平面直角坐标系xOy 中,一次函数8y x =-的图像与函数xy 8=(x >0)的图像相交于点A ,B ,设点A 的坐标为(1x ,1y ),那么长为1x ,宽为1y 的矩形的面积为 ,周长为 16. 如图①,在正方形ABCD 中,点P 沿边DA 从点D 开始向点A 以2cm/s 的速度移动;同时,点Q 沿边AB 、BC 从点A 开始向点C 以3cm/s 的速度移动.当点P 移动到点A 时,P 、Q 同时停止移动.设点P出发x s 时,△PAQ 的面积为y cm 2,y 与x 的函数图像如图2 所示, 则线段EF 所在的直线对应的函数关系式为 .三、解答题(本大题共8个小题,共72分,解答题应写出必要的文字说明,证明过程或演算步骤). 17.(本小题满分7分) ( 1)计算:(6.28-2π)0+(-16)-2-2cos60°; (2)解方程:37x -=28x -18.(本小题满分8分)某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题: 某校初中生阅读教科书情况统计图表 (第10题图)(第12题图) (第14题图)(第15题图)图① 图②3(1)求样本容量及表格中a ,b ,c 的值,并补全统计图; (2)若该校共有初中生2500名,请估计该校“重视阅读教科书”的初中人数;(3)①根据上面的统计结果,谈谈你对该校初中生阅读教科书的现状的看法及建议; ②如果要了解全省初中生阅读教科书的情况,你认为应该如何进行抽样? 19.(本小题满分8分)某海域有A 、B 、C 三艘船正在捕鱼作业,C 船突然出现故障,向A 、B 两船发出紧急求救信号,此时B 船位于A 船的北偏西47°方向,距A 船26海里的海域,C 船位于A 船的北偏东58°方向,同时又位于B 船的北偏东88°方向. (1)求∠ABC 的度数;(2)A 船以每小时40海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时). (参考数据:2≈1.414,3≈1.732)20.(本小题满分8分)如图,在平面直角坐标系中,Rt △PBD 的斜边PB 落在y 轴上,tan ∠BPD =21.延长BD 交x 轴于点C ,过点D 作DA ⊥x 轴,垂足为A ,PD 与x 轴交于点E ,OA =8,OB =6. (1)求点C 的坐标; (2)若点D 在反比例函数y =xk(k >0)的图象上,求反比例函数的解析式. 21.(本小题满分9分)受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,某服装厂每件衣服原材料的成本1y (元)与月份x (8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本2(元)与月份x 的函数关系式为2y =x +74(8≤x ≤12,且x 为整数).(1) 请观察表格中的数据,用学过的函数相关知识求1y 与x 的函数关系式.(2) 若去年该衣服每件的出厂价为105元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量1p (万件)与月份x 满足关系式1p =0.1x +1.1(1≤x ≤7,且x 为整数); 8至12月的销售量2p (万件)与月份x 满足关系式2p =-0.1x +3(8≤x ≤12,且x 为整数),该厂去年哪个月利润最大?并求出最大利润. 22.(本小题满分9分)如图,已知等边△ABC ,AB =16,以AB 为直径的半圆与BC 边交于点D ,过点D 作DF ⊥AC ,垂足为F ,过点F 作FG ⊥AB ,垂足为G ,连结GD . (1)求证:DF 是⊙O 的切线; (2)求FG 的长;(3)求tan ∠FGD 的值.(第18题图) (第20题图)(第19题图)423.(本小题满分11分)如图1,已知在平行四边形ABCD 中,AB =10,BC =16,sinB =35,点P 是边BC 上的动点,以CP 为半径的圆C 与边AD 交于点E 、F (点F 在点E 的右侧),射线CE 与射线BA 交于点G .(1)当圆C 经过点A 时,求CP 的长;(2)联结AP ,当AP ∥CG 时,求弦EF 的长; (3)当△AGE 是等腰三角形时,求CG 的长.24.(本小题满分12分)如图,在平面直角坐标系中,A 是抛物线y =x 2上的一个动点,且点A 在第一象限内.AE ⊥y 轴于点E ,点B 坐标为(0,6),直线AB 交x 轴于点C ,点D 与点C 关于y 轴对称,直线DE 与AB 相交于点F ,连结BD .设线段AE 的长为a ,△BED 的面积为S . (1)当a =3时,求S 的值.(2)求S 关于a (a)的函数解析式. (3)①若S =32时,求BFAF的值; ②当aBFAF=k ,猜想k 与a 的数量关系并证明.雁江区初中2015届适应性检测数学参考答案一、选择题(每小题3分,共30分)1—5:BBCAC 6—10:CCADD二、填空题(每小题3分,共18分) 11、x>; 12、30°; 13.350; 14、(﹣2,4); 15、8,16;16、y =-6x +18三、解答题(共8个小题,满分72分): 17、(本小题满分7分) 解:(1)原式=1+36﹣1……………2分=36; ………………3分(2)去分母得:3x -24=2x ﹣14解得:x =10………….6分经检验x =10是分式方程的解………7分 18.(本小题满分8分)(第22题图) (第24题图)P·5解:(1)由题意可得出:样本容量为:57÷0.285=200(人), ∴c =200×0.36=72, a =200﹣57﹣72-9=62,b =62÷200=0.31, ……3分 补全的统计图如图所示:(2)若该校共有初中生2500名,该校“重视阅读数学教科书”的初中人数约为:2500×0.31=775(人); ……6分(3)①根据以上所求可得出:只有31%的学生重视阅读教科书,有40.5%的学生不重视阅读教科书或说不清楚,可以看出大部分学生忽略了阅读教科书,同学们应重视阅读教科书,从而获取更多的学科课外知识和对相关习题、定理的深层次理解与认识. …7分②如果要了解全省初中生阅读教科书的情况,应随机抽取不同的学校以及不同的年级进行抽样,进而分析.……8分 19.(满分8分)解:解:(1)∵BD ∥AE , ∴∠DBA +∠BAE =180°,∴∠DBA =180°-47°=133°,∴∠ABC =133°-88°=45°;……3分 (2)作AH ⊥BC 于点H , ……4分∴∠C =180°﹣45°﹣47°-58°=30°, ∵∠ABC =45°,∴AH =ABsin 45°=13,∴A C =2AH =26. ……6分 则A 到出事地点的时间是:40≈13 1.41420 ≈0.92(小时). ……7分答:约0.92小时能到达出事地点. ……8分……5分620.(满分8分)解:Rt △PBD 的斜边PB 落在y 轴上, ∴BD ⊥PD ,又DA ⊥x 轴,OC ⊥OB∴∠BDP=∠CDP=∠BOC=∠COP=∠DAO=∠DAC=90° 于是∠BPD+∠OEP=∠DCE+∠DEC=90°, 又∠OEP =∠DEC∴∠BPD =∠DCE ……2分 ∴tan ∠DCE=tan ∠BPD ==BOOC∴CO=2BO=12C 点坐标是(12,0); ……4分 (2)∵tan ∠DCE=tan ∠BPD = =DAAC∴DA=AC= (OC-OA)=(12-8)=2∴D (8,2). ……6分 点D 在反比例函数y =(k >0)的图象上, ∴k =8×2=16 ……7分∴反比例函数的解析式为 y =16x. ……8分 21.(满分9分) (1) 由表格中数据可猜测,1y 是x 的一次函数.设1y =k x +b 则69271k b k b +=⎧⎨+=⎩解得:267k b =⎧⎨=⎩∴1y =2x +67,经检验其它各点都符合该解析式,∴1y =2x +67(1≤x ≤7,且x 为整数). ……3分 (2)设去年第x 月的利润为w 万元.当1≤x ≤7,且x 为整数时,w =1p (105-8-1y )=(0.1x +1.1)(97-2x -67)= -0.2(2x -4x -165)=-0.2()22x -+1695, ∴当x =2时,w 最大=1695万元; ……5分当8≤x ≤12,且x 为整数时, w =2p (105-8-2y )=(-0.1x +3)(97-x -774)=0.1()690532+-x x =0.12532x ⎛⎫- ⎪⎝⎭+0.1×(690-2534 )随x 的增大而减小∴当x =8时,w 最大=33万元. ……8分∴该厂去年2月利润最大,最大利润为1695万元. ……9分 22.(满分9分)解:(1)证明:连结OD ,如图, ∵△ABC 为等边三角形, ∴∠C =∠A =∠B =60°, 而OD =OB ,∴△ODB 是等边三角形, ……1分 ∴∠ODB =60°, ∴∠ODB =∠C ,∴OD ∥AC , ……2分 ∵DF ⊥AC , ∴OD ⊥DF ,∴DF 是⊙O 的切线; ……3分 (2)∵OD ∥AC ,点O 为AB 的中点, ∴OD 为△ABC 的中位线,∴BD =CD =8. ……4分 在Rt △CDF 中,∠C =60°, ∴∠CDF =30°, ∴CF =CD =4,∴AF =AC ﹣CF =16﹣4=12, ……5分在Rt △AFG 中, ∵∠A =60°,∴FG=AF×sinA =12×……6分(3)过D作DH⊥AB于H.∵FG⊥AB,DH⊥AB,∴FG∥DH,∴∠FGD=∠GDH.……7分在Rt△BDH中,∠B=60°,∴∠BDH=30°,∴BH =BD=4,DH =BH =4.在Rt△AFG中,∵∠AFG=30°,∴AG =AF=6,∵GH=AB﹣AG﹣BH=16﹣6﹣4=6,∴tan∠GDH ==,∴tan∠FGD=tan∠GDH =.……9分23.(满分11分)解:(1)如图1,设⊙O的半径为r,当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,∵sinB=3 5∴cosB =∴BH=AB•cosB=8,∴AH=AB•sinB=6,CH=BC-BH=8 ……2分89∴AC ==10,∴此时CP =CA=r =10; ……3分(2)如图2,若AP ∥CE ,APCE 为平行四边形, ∵CE =CP ,∴四边形APCE 是菱形, 连接AC 、EP ,则AC ⊥EP , ∴AM =CM =21CA =5, ……5分 由⑴知,AB =AC , 则∠ACB =∠B ,∴CP =CE ==254, 过C 作CN ⊥EF 于N则EF =2EN =222CN CE -72; ……7分(3)如图3,∵cosB =,∴∠B <45°, ∵∠BCG <90°, ∴∠BGC >45°,∵∠AEG =∠BCG ≥∠G AE =∠B ,∴当∠AEG =∠GAE 时,∠BCG =∠B ,A 、E 、G 重合, ∴只能∠AGE =∠AEG , ……8分 ∵AD ∥BC ,∴△GAE ∽△GBC , ∴=,∴1CB AEBG AG==,N Q10即BC =BG =AB +AG 16=10+AG∴AG =6=AE ……9分 过G 作GQ⊥AE 于Q ,则GQ=AGsin∠GAE=6×35=185, AQ=AGcos ∠G AE=6×=245,EQ=AE-AQ=6-245=6,……10分 又由△GAE ∽△GBC ,得GC BC GE AE=,即166CG =,∴CG ……11分 24.(满分12分)解:(1)∵点A 在二次函数y =x 2的图象上,AE ⊥y 轴于点E 且AE =a ,∴点A 的坐标为(a , a 2),当a =时,点A 的坐标为(,3),……1分 ∵点B 的坐标为(0,6), ∴BE =OE =3.∵AE ⊥y 轴, ∴AE ∥x 轴,∴△ABE ∽△CBO , ∴==,∴CO =2,∵点D 和点C 关于y 轴对称, ∴DO =CO =2, ∴S =BE •DO =×3×2=3; ……3分(2)(I )当0<a (如图1), ∵点D 和点C 关于y 轴对称, ∴△BOD ≌△BOC , ∵△BEA ∽△BOC ,∴△BEA ∽△BOD , ……4分 ∴=,即BE •DO =AE •BO =6 a .11 ∴S =BE •DO =×6 a =3 a ; ……5分 (II )当a>6时(如图2),同(I )解法得:S =BE •DO =AE •OB =3a ,由(I )(II )得,S 关于m 的函数解析式为 S =3a (a >0且a ≠6). ……7分(3)①如图3,连接AD ,∵△BED 的面积为2,∴S =3a =2,∴点A 的坐标为(23,43), ……8分∵==k ,∴S △ADF =k •S △BDF ,S △AEF =k •S △BEF ,∴===k ,设。
