经济数学复习第二章导数与微分

合集下载

(整理)经济数学基础讲义第2章导数与微分

第2章导数与微分2.1 极限概念研究函数是利用极限的方法来进行；极限是一个变量在变化过程中的变化趋势. 例1 圆的周长的求法.早在公元263年，古代数学家刘徽用圆内接正四边形、正五边形、正八边形、正十六边形……等的边长近似圆的周长，显然随着边数的增加，正多边形的边长将无限趋近圆的周长.例2 讨论当+∞→x 时，x1的变化趋势.例3 讨论一个定长的棒，每天截去一半，随着天数的增加，棒长的变化趋势。

“一尺之棰，日截其半，万世不竭”——庄子•天下定义2.3 设函数)(x f 在点0x 的邻域（点0x 可以除外）内有定义，如果当x 无限趋于0x （但0x x ≠）时，)(x f 无限趋近于某个常数A ，则称x 趋于0x 时，)(x f 以A 为极限，记为A x f x x =→)(lim 0或A x f →)( )(0x x →若自变量x 趋于0x 时，函数)(x f 没有一个固定的变化趋势，则称函数)(x f 在0x 处没有极限.在理解极限定义时要注意两个细节：1.0x x →时，（0x x ≠）2.⎩⎨⎧→<→>→00000)()(x x x x x x x x （包括这两种情况）例1 讨论2x y =时, 22lim x x →=？解：求极限时，可以利用极限的概念和直观的了解，我们可以借助几何图形来求函数的极限.由几何图形可以看出，当2→x 时，42→=x y ，即22lim x x →=4 例2 讨论函数112--=x x y ,当1→x 时的极限11lim 21--→x x x解：此函数在1=x 处没有定义，可以借助图形求极限.由图形得到211lim 21=--→x x x2.1.3 左极限和右极限考虑函数x y =，依照极限的定义，不能考虑0→x 的极限. 因为x y =在0<x 处无定义.又如函数⎩⎨⎧>≤=010)(x x x x f ，如果讨论0→x 是的极限，则函数分别在0<x 和0>x 时不是同一个表达式，必须分别考虑.由此引出左右极限的概念. 定义2.4 设函数f x ()在点x 0的邻域（x 0点可以除外）内有定义，如果当x x <0且x 无限于x 0（即x 从x 0的左侧趋于x 0，记为x x →-0）时，函数f x ()无限地趋近于常数L ，则称当x 趋于x 0时，f x ()以L 为左极限，记作= L ；如果当x x >0且x 无限趋于x 0（即x 从x 0的右侧趋于x 0，记为x x →+0）时，函数f x ()无限地趋近于常数R ，则称当x 趋于x 0时，f x ()以R 为右极限，记作= R .极限存在的充分必要条件：极限)(lim 0x f xx →存在的充分必要条件是：函数f x ()在0x 处的左，右极限都存在且相等.即例3 ⎩⎨⎧>≤=010)(x x x x f , 求)(lim 0x f x → 解：注意到此函数当x =0的两侧表达式是不同，在0点处分别求左、右极限.11lim )(lim 00==++→→x x x f ，0lim )(lim 0==--→→x x f x x可见左右极限都存在但不相等；由几何图形易见,由极限的定义知，函数在某点处有极限存在需在该点处的左右端同趋于某个常数，因此此函数在0点处极限不存在. 2.1.4 无穷小量0)(lim 0=→x f x x 称当0x x →时，)(x f 为无穷小量，简称无穷小.补充内容：无穷小量是一个特殊的变量，它与有极限变量的关系是：变量y 以为A 极限的充分必要条件是：y 可以表示成A 与一个无穷小量的和，即)0(lim lim =+=⇔=ααA y A y无穷小量的有以下性质：性质1 有限个无穷小量的和是无穷小量；性质2 有限个无穷小量的乘积是无穷小量；性质3 有界函数与无穷小量的乘积是无穷小量. 无穷大量：在某个变化过程中，绝对值无限增大且可以大于任意给定的正实数的变量称为无穷大量.例如因为+∞=+∞→xx 2lim ，所以，当+∞→x 时，x 2是无穷大量.无穷小量与无穷大量有如下“倒数关系”：定理：当0x x →（或∞→x ）时，若)(x f 是无穷小（而0)(≠x f ），则)(1x f 是无穷大；反之，若)(x f 是无穷大，则是无穷小.例4 2x y =，当0→x 时，?2→x解：由图形可知，当0→x 时，02→x ，当0→x 时，2x 是无穷小量. 2.2 极限的运算2.2.1 极限的四则运算法则在某个变化过程中，变量v u ,分别以B A ,为极限，则B A v u v u ±=±=±lim lim )lim(，B A v u v u ⋅=⋅=⋅lim lim )lim(例1 求22lim x x → 解：422)lim )(lim ()(lim lim 22222=⨯==⋅=→→→→x x x x x x x x x 例2 求11lim 21--→x x x解：21)1(lim 1)1)(1(lim 11lim 1121=+=-+-=--→→→x x x x x x x x x例3 求xx x x +-∞→2231lim解：31)13()11(lim 31lim22222=+-=+-∞→∞→xx x x x x x x x 例4 求xx x 11lim 0-+→解：)11()11)(11(lim 11lim00++++-+=-+→→x x x x x x x x )11(lim++=→x x xx 21111lim=++=→x x 2.2.2 两个重要极限 1.1sin lim0=→xxx几何说明：如图，设x 为单位圆的圆心角，则x 对应的小三角形的面积为2sin x，x 对应的扇形的面积为2x ，x 对应的大三角形的面积为2tan x 当0→x 时，它们的面积都是趋于0的，即之比的极限是趋于1的.例1 xxx 3sin lim0→解：x x x 3sin lim 0→=333sin 3lim0=→x x x 333sin lim 0=→xxx 2.e )11(lim =+∞→xx x e )1(lim 10=+→x x x 例2 求极限xx x)311(lim +∞→ 解: 31313313e ])311(lim [)311(lim )311(lim =+=+=+∞→⋅∞→∞→x x x x x x xx x例3 求极限xx x 10)21(lim -→解 2221)2(211e ]))2(1(lim [))2(1(lim )21(lim ---→--→→=-+=-+=-x x xx xx x x x2.3 函数的连续性定义设函数)(x f 在点0x 的邻域内有定义，若满足)()(lim 00x f x f xx =→，则称函数)(x f 在点0x 处连续.点0x 是)(x f 的连续点. 函数间断、间断点的概念如果函数f x ()在点x 0处不连续，则称f x ()在点x 0处发生间断.使f x ()发生间断的点x 0，称为f x ()的间断点例如函数32,x y x y ==，x y x y cos ,sin ==，xy x y e ,ln ==在定义域内都是连续的.例1 ⎩⎨⎧>-≤+=13211)(x x x x x f ,问)(x f 在1=x 处是否连续？注意：此函数是分段函数，1=x 是函数的分段点.解: 1)32(lim )(lim 11-=-=++→→x x f x x ，2)1(lim )(lim 11=+=--→→x x f x x )(lim 1x f x →不存在，)(x f 在1=x 处是间断的. 例2 ⎪⎩⎪⎨⎧=≠=001sinx x xx y ,问)(x f 在0=x 处是否连续？解: )0(01sinlim )(lim 0f xx x f x x ===→→ （无穷小量×有界变量=无穷小量）∴)(x f 在0=x 处是连续的. 结论:（1）基本初等函数在其定义域内是连续的；（2）连续函数的四则运算、复合运算在其有定义处连续；（3）初等函数在其定义区间内是连续的.例3xx x x 220cos 1e lim ++→解: 21110cos 01e cos 1e lim 220220=+=++=++→x x x x 注意： xx x 22cos 1e ++是初等函数，在0=x 处有定义，利用结论有极限值等于函数值. 2.4 导数与微分的概念本节的主要内容是导数与微分的概念. 三个引例边际成本问题瞬时速率问题曲线切线问题引例1：边际成本问题 C —总成本，q —总产量已知时当q q q q C C ∆+→=00),(（当自变量产生改变量，相应的函数也产生改变量）)()(0q q C q C ∆+→），qq C q q C ∆-∆+)()(00（成本平均变化率），qq C q q C q ∆-∆+→∆)()(lim 000（边际成本）引例2: 瞬时速率问题路程S 是时间t 的函数)(t S ，当t 从t t t ∆+→00时，)(t S 从)()(00t t S t S ∆+→tt S t t S ∆-∆+)()(00 （平均速率）t t S t t S t ∆-∆+→∆)()(lim000 （在0t 时刻的瞬时速率）引例3：曲线切线问题考虑曲线)(x f y =在0x x =处的切线斜率.当x x x ∆+→00时，对应的y y y ∆+→00，曲线上))(,(00x f x 和))(,(00x x f x x ∆+∆+两点间割线的斜率为xx f x x f ∆-∆+=)()(tan 00φ（当0→∆x 时），xx f x x f x x ∆-∆+==→∆→∆)()(limtan lim tan 000φα 称为切线的斜率.qq C q q C q C q ∆-∆+=→∆)()(lim)(000tt S t t S t S t ∆-∆+=→∆)()(lim)(000xx f x x f x f x ∆-∆+=→∆)()(lim)(000关于函数)(x f y =x x x ∆+→00，)()(00x x f x f ∆+→，考虑极限xx f x x f x ∆-∆+→∆)()(lim000定义设函数)(x f y =在点0x 的邻域内有定义，当自变量x 在点0x 处取得改变量)0(≠∆x 时，函数y 取得相应的改变量.)()(00x f x x f y -∆+=∆ 若当0→∆x 时，两个改变量之比xy∆∆的极限 x x f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000存在，则称函数)(x f y =在点0x 处可导，并称此极限值为 )(x f y =在点0x 处的导数，记为)(0x f '或0x x y ='或d d x x xf =或d d x x x y =即 )(0x f '=xx f x x f x ∆-∆+→∆)()(lim000若极限不存在，则称函数)(x f y =在点0x 处不可导. 在理解导数定义时要注意：导数也是逐点讨论的. 导数定义的意义· 数量意义变化率 · 经济意义边际成本 · 几何意义切线的斜率例1 2)(x x f y ==，求.)2(,)3(,)1(-'''f f f思路：先求)(x f '，再求)(0x f '.解：因为22)()(,)(x x x x f x x f ∆+=∆+=x x x x x xx x x xx f x x f x x x 2)(2lim )(lim )()(lim202200=∆∆+∆=∆-∆+=∆-∆+→∆→∆→∆ 所以x x x f 2)()(2='='，426321-=-'='='）（，）（，）（f f f 例2 x xg ln )(=，求).5.0(),10(g g ''解: 因为)ln()(,ln )(x x x x g x x g ∆+=∆+=xx x x x xx x xx x x xx x x xx g x x g ∆→∆→∆→∆→∆∆+=∆+∆=∆-∆+=∆-∆+10000)(ln lim ln 1lim ln )ln(lim )()(limx x xx x x xx x 1e ln ]lim ln[1110==∆+=⋅∆→∆）（所以2)5.0(,101)10(='='g g 导数公式 xx 1)(ln ='求导步骤1、求)(x f '；2、求0)(x x x f ='.注意：)(x f '是)(x f 的导函数，函数在0x 处的导数值0)()(0x x x f x f ='=' 微分的概念设)(x f y =，导数)(d )(d d d x f y xx f x y '='==，两边同乘x d ，得到函数的微分. 微分 x x f x y x f y d )(d )(d d '='== 导数公式xx x x c 1)(ln )(0)(1='='='-αααxx x xa a a x x x x e )e (ln )(sin )(cos cos )(sin ='='-='='微分公式由导数公式可以得到微分公式x x x x x d )(d )(11--=='αααααα x xx xx d 1)(ln d 1)(ln ==' x x x x x d cos )(sin d cos )(sin ==' x x x x x d sin )(cos d sin )(cos -=-='x a a a a a a x x x x d ln )(d ln )(=='2.5 导数的计算导数的加法法则设)(),(x v x u 在点x 处可导，则)()(x v x u ±在点x 处可导亦可导，且)()())()((x v x u x v x u '±'='± )())((x v c x cv '='（c 为常数）加法公式证明)()())()((x v x u x v x u '+'='+证：设)()()(x v x u x f +=，则)()()(x x v x x u x x f ∆++∆+=∆+，)()()(x v x u x f +=xx f x x f x v x u x f x ∆-∆+='±='→∆)()(lim))()(()(0xx v x u x x v x x u x ∆+-∆++∆+=→∆))()(())()((lim0])()()()([lim 0xx v x x v x x u x x u x ∆-∆++∆-∆+=→∆x x v x x v x x u x x u x x ∆-∆++∆-∆+=→∆→∆)()(lim)()(lim 00)()(x v x u '+'= 由已知条件，)(),(x v x u 均可导. 导数的乘法法则设)(),(x v x u 在点x 处可导，则)()(x v x u ⋅在点x 处可导亦可导，且)()()()())()((x v x u x v x u x v x u '+'=' )()()())((x v c x v c x v c x cv '='+'='导数除法法则设)(),(x v x u 在点x 处可导，则)()(x v x u 在点x 处可导亦可导，且 )()()()()())()((2x v x v x u x v x u x v x u '-'='（0)(≠x v ）例1 设函数1453+-=x x y ，求?='y析：现在分别知道幂函数和常数函数的导数公式，利用上述法则可求它们组合后函数的导数. 解： )1()4()5(3'+'-'='x x y （利用加法法则）1)(4)(53'+'-'=x x )())((x v c x cv '='=4152-x （利用导数公式0)(,)(1='='-c x x ααα）例2 设x x x y ln 243+-=，求y '.解：)ln 2()()4(3'+'-'='x x x y)(ln 2)()(43'+'-'=x x x （提示 xx xx 1)(ln 21)(='=' ）212x =xx221+-例3 设4cos 3xy x+=，求y '. 解：)4cos ()3('+'='x y x（提示x x a a a x x sin )(cos ln )(-='='）)sin (413ln 3x x -+=4sin 3ln 3xx -=例4 x x y ln 213+-=，?='y解：因为x x y ln 212123+-=（由对数的性质：x x x ln 21ln ln 21==）所以 xx y 21232+='（其中常数的导数为0）例5 设xx y e 2=，求y '.解：利用导数的乘法法则，)(e e )(22'+'='xxx x y （利用导数公式xx e )e (='）)2(e e e 22x x x x x x x +=+=例6 4x y =，求y '.解：<方法1> 由导数基本公式344)(x x =' <方法2> 利用导数的乘法法则224x x x y ⋅==3222222224422)()()()(x x x x x x x x x x x x y =⋅+⋅='⋅+⋅'='⋅='='说明无论用哪种方法其结果是唯一的. 例7 xxy sin =，求y '. 解：<方法1> 将函数看成x xy sin 1=，利用乘法法则求导. 22cos sin cos 1sin 1)(sin 1sin )1(x x x x x x x x x x x x y +-=+-='+'='<方法2> 利用导数的除法法则求导2sin cos )sin (xxx x x x y -='=' 其中x x v x x u ==)(,sin )(.两个结果是完全一样的. 例8 求)(tan 'x解：xx x x x x x x x 22cos 1cos )sin (sin cos cos )cos sin ()(tan =--⋅='=' （利用三角公式1cos sin 22=+x x ）同理可求x x 2sin 1)(cot -='. 2.5.2 复合函数求导法则问题：2)32(+=x y ，求?='y 100)32(+=x y ，则?='y解：第一个问题2)32(+=x y ，求导数没有直接公式可用.方法1：将函数展开9124)32(22++=+=x x x y利用加法法则有128+='x y方法2：将函数写成两个因式乘积的形式 )32)(32()32(2++=+=x x x y ，利用四则运算法则求导数.)32(4)32(2)32(2+=+++='x x x y第二个问题100)32(+=x y ，展开？共101项，求导很麻烦.写成因式乘积的形式，求导也将很麻烦.在这节课我们将介绍复合函数求导法则.讨论100)32(+=x y ，引进中间变量32+=x u9999)32(2002100d d d d d d +=⋅==='x u xu u y x y y 2.5.2 复合函数求导法则定理设y=f (u ),u=(x ),且u (x )在点x 处可导，y=f (u )在点u=x )处可导，则复合函数y=f ((x ))在点x 处可导，且)()(x u f y x φ''='或x u x u y y '⋅'='复合函数求导步骤·分清函数的复合层次，找出所有的中间变量；·依照法则，由外向内一层层的直至对自变量求导.多层复合的函数求导数对于多层复合的函数，即若)(),(),(x v v u u f y φϕ===，则)()()(x v u f y φϕ'''=' 或x v u x v u y y '⋅'⋅'='注意：多层复合的函数求导数仍是经过一切中间变量直至对自变量求导.问题: 求由方程122=+y x 所确定的隐函数)(x y y =的导数y '？解：先将y 从方程中解出来，得到21x y -=和21x y --=分别求导21x xy --='和21x xy -=' 将21x y -=和21x y --=分别代入，得 yx y -=' 01232=+--y x x （1）由（1）解得:)13(212+-=x x y 0e e =-+x xy y （2）在（2）中0),(=y x F 隐含)(x y y =隐函数求导方法步骤·方程两边求导，)(x y y =；·整理方程，求出y '.例1 求下列函数的导数或微分（1）xy 2e =，求.y ' 解：方法一: 由x x x x y e e e e )11(2⋅===+x x x y 222e 2e e =+='.这是用导数的乘法法则.方法二: 利用复合函数求导法则，设x u y u2,e ==x x u u u y 2e 2)e (='⋅'='（其结果是完全一样的) （2）x y e =，求.y ' 解：利用复合函数求导法则，设x u y u ==,e x u x u u x x u y e 2121e )e (⋅=⋅='⋅'='.（3）x y cos ln =，求y d .解：利用复合函数求导法则，设x u u y cos ,ln ==x x xx u u u y x u tan )sin (cos 1)(cos 1)(ln -=-='='⋅'=',x x y d tan d -= 例2 设21x y -= ，求).0(y '解：先求一般点上函数的导数，再将0=x 代入求得结果. 设21,x u u y -==，利用复合函数求导法则，221)2(21)1()(x x x ux u y x u --=-='-⋅'=',.0)0(='y 例3 设函数)2(sin 32x y +=，求y '. 解：（首先对函数进行分解，找出所有中间变量）322,sin ,x v v u u y +===,23cos 2x v u y ⋅⋅='2333)2cos()2sin(2x x x ⋅+⋅+=)2cos()2sin(6332x x x +⋅+= 例4 求函数321x y -=，求y '. 解：2311,x u u y -==)1()1(3121312'-⋅-='-x x y 322)1(32---=x x 例5 设函数x y 1cos 3=，求y '. 解: xv v u y u 1,cos ,3=== x v u u x v y )1()(cos )3(''⋅'=' [21)()1(---='='x x x ] )1)(sin )(3ln 3(2xv u --=)1)(1sin )(3ln 3(21cos x x x --=x x x 1cos 231sin 3ln ⋅⋅= 例6 求由方程122=+y x 所确定的隐函数)(x y y =的导数y '.解：方程两边对自变量x 求导数，此时y 是中间变量.022='+y y x ,解出yx y -='（与前面的结果相同）. 例7 求由方程0e e =++x y xy 所确定的隐函数)(x y y =的导数y '？解：方程两边对自变量x 求导数，此时y 是中间变量.0e e =+'++'x y y x y y ,解得注意：在隐函数的导数结果中常常含有y .例8 求双曲线1=xy 在点（1，1）处的切线斜率. 分析：此题是求隐函数在某点处的导数.解：因为0='+y x y ,所以xy y -=',且在点（1，1）处的切线斜率1)1,1(-='y2.6 高阶导数 )(x f 的高阶导数例1：4)(x x f = 34)(d )(d x x f xx f ='=22212)(d )(d d )d )(d d(x x f x x f x x x f =''==x x f xx f 24)(d )(d 33='''= 一般地，)(x f y =，函数的n 阶导数记为)(d d )()(x f y xy n n n n == 例1 求函数522-+=x x y 的二、三阶导数. 解： 14+='x y ，4=''y ，0='''y例2 求)1ln(x y +=的二阶导数至n 导数. 解： xy +='11，2)1(1)11()(x x y y +-='+=''=''， 32)1(1)!2()1(x y +-=''' … n n n x n y )1(1)!1()1(1)(+--=-。

导数微分知识点总结

导数微分知识点总结一、微分的定义微分是微积分中的基本概念之一。

在微积分中，微分是用来描述函数在某一点上的变化率的概念。

设函数y=f(x)，若x在x_0处有一个增量Δx，对应的函数值的增量Δy=f(x_0+Δx)-f(x_0)，那么函数f(x)在点x_0处的微分dy=f'(x_0)dx，其中f'(x_0)是函数f(x)在点x_0处的导数。

二、导数的定义导数是微分的数学概念，是用来描述函数在某一点上的变化率的概念。

设函数y=f(x)，在x_0处导数f'(x_0)的定义为：若极限lim_(Δx→0)(f(x_0+Δx)-f(x_0))/Δx存在，那么称该极限为函数f(x)在x_0处的导数，记作f'(x_0)。

导数描述了函数在某一点上的瞬时变化率，也可以用偏导数来描述多元函数的变化率。

三、微分和导数的关系微分和导数是密切相关的概念，它们之间存在着密切的联系。

微分dy=f'(x_0)dx，其中f'(x_0)是函数f(x)在点x_0处的导数，可见微分和导数之间有直接的联系。

微分是导数的一种应用，而导数也可以通过微分来求得。

四、微分和导数的性质1.导数的性质：（1）常数的导数为0: (c)'=0（2）幂函数的导数: (x^n)'=nx^(n-1)（3）和差函数的导数: (f(x)+g(x))'=f'(x)+g'(x)，(f(x)-g(x))'=f'(x)-g'(x)（4）积函数的导数: (f(x)g(x))'=f'(x)g(x)+f(x)g'(x)（5）商函数的导数: (f(x)/g(x))'=[f'(x)g(x)-f(x)g'(x)]/g^2(x)（6）复合函数的导数: 若y=f[g(x)]，则y'=(f[g(x)])'=f'(g(x))g'(x)2.微分的性质：（1）微分的线性性质：若函数y=f(x)和y=g(x)的微分分别为dy=f'(x)dx和dy=g'(x)dx，那么有：d(af(x)+bg(x))=adf(x)+bdg(x)（2）微分的乘法法则：若函数y=f(x)和y=g(x)的微分分别为dy=f'(x)dx和dy=g'(x)dx，那么有：d(f(x)g(x))=f(x)dg(x)+g(x)df(x)五、导数的计算方法1.通过定义求导：根据导数的定义，可以直接求出给定函数的导数。

《经济数学》-第二章导数与微分

所以 y | x | 在x =0连
而
续
f(0)
lim
x0
y x
lim
x0
x x
1
f(0)
lim
x0
y x
lim

x x
1
即函数 y | x | 在x=0处左右导数不相等,从而在 x=0不可导. 由此可见，函数在某点连续是函数在该点可导的必要条件，但不是充分条件
即可导定连续,连续不一定可导.
前页后页结束
f
( x0 )
lim
x0
y x
lim tan
tan
k
所以，导数 f (x0 ) 的几何意义是曲线y = f (x) 在点M0(x0,f(x0)) 处的切线斜率.
M
P
M0
x0
x0 x
前页后页结束
设函数y=f(x)在点处可导，则曲线y=f(x)在点处的切线方程为： y f ( x0 ) f ( x0 )( x x0 ). 而当 f (x0 ) 时,曲线 f ( x) 在 M0 的切线方程为
此时x为割线两端点M0，M 的横坐标之差，而 y
则为M0，M 的纵坐标之差，所以 y 即为过M0，M两点的
x
割线的斜率.
M
M0
x0
x0 x
前页后页结束
曲线y = f (x)在点M0处的切线即为割线M0M当M沿曲
线y=f(x)无限接近 M0时的极限位置M0P，因而当 x 0
时，割线斜率的极限值就是切线的斜率.即：
2.2 导数的运算
2.2.1 函数的和、差、积、商的求导法则
定理一设函数u(x)与v(x) 在点x处均可导，则:
(1)[u( x) v( x)]' u' ( x) v' ( x); (2)[u( x)v( x)]' u' ( x)v( x) u( x)v' ( x),

导数与微分章节总结

导数与微分章节总结导数与微分是微积分学中的重要概念，在现代科学和技术中有着广泛的应用。

导数是微积分中研究函数变化率的基本工具，微分则是导数的一种表达形式和应用。

一、导数的定义导数是函数在某一点处的变化率，是函数图像在该点的切线斜率。

对于可导函数y=f(x)，其在点x处的导数定义为：$$\lim_{h\to0}\frac{f(x+h)-f(x)}{h}$$也可以表示为：$$f'(x)=\lim_{\Delta x\to0}\frac{\Delta y}{\Delta x}$$其中，$\Delta y=f(x+\Delta x)-f(x)$，$\Delta x$为自变量的增量。

二、导数的性质1.导数可加性和可乘性：若$f(x)$和$g(x)$在某一点$x_0$可导，则$(f+g)'(x_0)=f'(x_0)+g'(x_0)$，$(f\cdotg)'(x_0)=f'(x_0)g(x_0)+f(x_0)g'(x_0)$。

2.导数的链式法则：若$y=f(u)$与$u=g(x)$都可导，则复合函数$y=f(g(x))$在$x=a$处可导，且有$y'=f'(g(x))\cdot g'(x)$。

3.导数的反函数法则：若$f(x)$在点$x_0$处可导且$f'(x_0)\ne0$，则$f(x)$在该点的反函数$f^{-1}(y)$在点$y_0=f(x_0)$处可导，且有$(f^{-1})'(y_0)=\frac{1}{f'(x_0)}$。

三、微分的定义微分是反映函数在某一点处变化的一个量。

对于可导函数$y=f(x)$，在点$x_0$处的微分定义为：$$\mathrm{d}y=f'(x_0)\cdot\mathrm{d}x$$其中，$\mathrm{d}y$和$\mathrm{d}x$分别为函数$y=f(x)$在$x_0$处的微小增量和自变量$x$在$x_0$处的微小增量。

大一上学期《高等数学》知识整理-第二章导数与微分

大一上学期《高等数学》知识整理-第二章导数与微分第二章导数与微分1.导数的定义。

对于一个在x0的某个邻域内有定义的函数，当自变量x在x0处取得增量Δx时，相应地函数y取得增量Δy=f(x0+Δx)-f(x0)，如果当Δx→x0时Δy/Δx的极限存在，则称函数y=f(x)在x0点可导，并称这个极限为函数y=f(x)在x0处的导数。

通俗地讲，就是描述某个函数在某点增长或下降的瞬时速度，这个“速度”的单位为y每x，即每变化一个单位的x，y变化多少。

与物理学中定义米/秒是一个性质的。

把函数f(x)的导数看做是关于x的函数，即得到函数f(x)的导函数f'(x)，简称导数。

（以上的“x0”中的“0”都是x 的下标，下同。

）导数也可以用微分的形式记作dy/dx，这个后面会提及。

2.在导数的定义中，如果Δx从左边趋向x0或从右边趋向x0，那么对应的导数被称为左导数和右导数。

只有f(x)在x0处的左导数和右导数相等，才能称f(x)在x0处可导。

举个例子，绝对值函数y=|x|，其在x=0处的左导数是-1（即x每增大1，y减小1），右导数是1，两者不相等，所以该函数在x=0处不可导。

如图所示。

绝对值函数y=|x|的导数是符号函数y=sgn(x)，但是不包含x=0（单独的符号函数y=sgn(x)，当x=0时，y=0）。

3.用定义法可以求初等函数的导数，本质上就是求极限。

比如说求y=x²在x=a处的导数，即就是求Δx→0时((a+Δx)²-a²)/Δx的极限。

求得结果为2a了解即可，还不如求导公式来得快。

下图为求该极限的过程，也就是用定义求y=x²的导数的过程。

4.函数的可导性与连续性的关系。

我们有定理：如果函数y=f(x)在点x0处可导，则f(x)在x0处必连续。

但反过来就不一定了。

归纳为一句话：连续不一定可导，可导一定连续。

y=|x|就是一个例子。

该函数在定义域内处处连续但是在x=0时不可导（因为左右极限不一样）。

专升本第二讲导数与微分

第二讲导数与微分考点：1、理解导数的概念，掌握导数的定义。

2、能利用导数定义判断函数的可导性，会判断分段函数分段点处的可导性。

3、掌握导数的几何意义，会表示切线方程与法线方程。

4、了解可导性与连续性之间的关系。

5、熟练掌握导数计算的基本公式，四则运算法则，复合函数求导链式法则，隐函数求导法，参数方程求导法，对数求导法以及高阶导数的计算。

6、理解函数微分的基本概念，会求函数的微分，了解可导与可微之间的关系。

典型题目：1、求)1ln(2x x y ++=的导数2、求函数x ey 1sin 2=的导数 3、已知0=-+e xy e y ,求dy dx 4、22ln arctan y x xy += 5、求曲线03275=--+x x y y 上在0=x 的点处的切线方程6、 sin (tan )x y x =，求y '. 7、求函数)4)(3()2)(1(----=x x x x y ()4>x 的导数 8、设()0f x m '=,求下列极限:(1) ()()x x f x x f x ∆-∆-→∆0003lim ; (2) ()()xx x f x x f x ∆∆--∆+→∆23lim 000 9、设)(x f 在]1,1[-上有界,2sin )()(x x f x g =,求)0(g '.10、设()⎪⎩⎪⎨⎧=≠=.0,0;0,1sin )(x x x x g x f 且)0()0(g g '==0,证明:0)0(='f . 11、设()x x x y sin +=,求dxdy . （导数()x f '为()x f 的边际函数）12、某企业每月生产x 吨产品的总成本C (单位:千元)是产量x 的函数()20102+-=x x x C .如果每吨产品的销售价格为2万元,试求每月生产8吨时的边际利润.13、设市场对某商品的需求量Q 是价格p 的函数275p Q -=,求4=p 时的边际需求,并说明其经济意义.（对于一般的x ,如果()x f y =是可导函数,且()0f x ≠,则：()().y x f x f x η'= 是x 的函数,称为()x f 的弹性函数(简称为弹性)）14、设某种商品的需求函数为p Q -=50,p 为价格()500<<p ,试求:当30p =的需求弹性，并解释其经济意义。

经济数学基础(上)导数与微分笔记整理

经济数学基础（上）数学笔记整理第二章导数与微分（P49）目录一、导数的符号要清楚1二、导数的几何意义1三、可导与连续的关系1四、导数的基本公式与练习题1五、切线方程问题4六、复合函数的求导5七、隐函数的导数9八、高阶导数10九、微分11十、可微、可导和连续、极限的关系12一、导数的符号要清楚（P51，52都有），最简单的就是二、导数的几何意义（P55）函数y=f（x）在点处的导数就是曲线y=f（x）在点（）处切线的斜率，k=，∴切线的方程为y三、可导与连续的关系（P56，2.1.5）定理2.1和注意可导连续（充分条件）y=f（x）的图像在点处出尖，则f（x）在处不可导。

例：y=，图像如下,此时，当x=0时，图像出尖，不可导。

四、导数的基本公式与练习题（P65~66，2.2.6的 1.，2.，3.，）就记书上的前8个就行了，其他的不用记再多记2个：①②【练习1：求导】①解：有分式，商的导数不好算，可以先化简。

∴∴【注意ln7为常数，常数的导数为0哦！】=②解决此题有2种方法，方法一是直接求。

方法二是先打开，再求。

你觉得怎么简单就怎么来。

一般情况是先打开再做比较容易，有时是怎么做都一样的。

方法一：直接求。

要用到乘积的导数。

（先打开再做就用不着乘积的导数，看过程就知道哪个方法简单了。

）=2（）+=10=30方法二：先打开，再求导。

=5=10∴【练习2：求导】①解：【注意：ln6为常数，导数也为0哦！】②解：③解：④解：⑤很容易能看出来，此题必须要化简了。

你要是想用商的导数来求的话，是够麻烦的了。

解：∵=（）·=∴⑥这题就不能化简了，怎么着都是麻烦。

商的导数会背吗？要用了。

注意所有公式都必须要会背哦！==【书上的题P75，3，4】P75,3.求导（2）这题就是怎么做都行，你想用乘积的方法做就直接挑战吧。

但是为了简单，我们的习惯就是先打开，再求导。

∵=2∴（4）此题也可以直接，前提是你必须会背两个公式。

导数与微分重点知识点总结

导数与微分重点知识点总结导数和微分是微积分中的重要概念，对于理解函数的性质和解决实际问题起着至关重要的作用。

本文将对导数与微分的重点知识点进行总结。

一、导数的定义与性质1. 导数的定义：如果函数f(x)在点x处的导数存在，那么导数可以定义为f'(x) = lim(h→0) [f(x+h)-f(x)]/h。

导数表示函数在某一点的瞬时变化率。

2. 导数的几何意义：导数等于函数图像在某点的切线斜率，也可以表示函数图像在该点的切线与x轴正方向夹角的正切值。

3. 导数的性质：导数存在的函数在该点必然连续，导数具有可加性和数乘性，即对于函数f(x)和g(x)，有[f(x)±g(x)]' = f'(x)±g'(x)和[cf(x)]'= cf'(x)。

二、常见函数的导数公式1. 幂函数：对于f(x) = x^n，其中n为实数，导数为f'(x) = nx^(n-1)。

2. 指数函数：对于f(x) = a^x，其中a为正实数且a≠1，导数为f'(x)= a^x·ln a。

3. 对数函数：对于f(x) = logₐx，其中a为正实数且a≠1，导数为f'(x) = 1/(x·ln a)。

4. 三角函数：对于f(x) = sin x，导数为f'(x) = cos x；对于f(x) = cos x，导数为f'(x) = -sin x；对于f(x) = tan x，导数为f'(x) = sec² x。

5. 反三角函数：例如arcsin x的导数为1/√(1-x²)，arccos x的导数为-1/√(1-x²)，arctan x的导数为1/(1+x²)。

三、微分的定义与应用1. 微分的定义：对于函数y = f(x)，若f(x)在某一点x处有定义且可导，那么对应的微分dy为dy = f'(x)dx。

《经济数学》第2章

当
时,曲线
在
的法线方程为
而当
时,曲线
在
的法线方程为
(即法线平行y轴).
例3
求函数
的导数
解: (1)求增量:
(2)算比值:
(3)取极限:
同理可得: 特别地, .
例4
求曲线
在点
处的切线与法线方程.
解:因为在点
,由导数几何意义,曲线的切线与法线的斜率分别为:
于是所求的切线方程为:
即法线方程为: 即
相应的增量为
从上式可以看出，
的线性函数
这表明
这部分就是面积
的增量的主要部分（线性主部）
所以上式可写成
定义设函数如果函数
所以
即为过M0，M两点
M0
的割线的斜率.
曲线y = f (x)在点M0处的切线即为割线M0M当M沿曲
线y=f(x)无限接近时的极限位置M0P，因而当
时，割线斜率的极限值就是切线的斜率.即：
所以，导数
的几何意义
M
是曲线y = f (x) 在点M0(x0,f(x0)) 处的切线斜率.
M0
设函数y=f(x)在点处可导，则曲线y=f(x)在点处的切线方程为：当时,曲线在的切线方程为而
例：设u=u(x),v=v(x),w=w(x)在点x处均
可导，则
例1 解：
例2 设解：
例3 求y = tanx 的导数
解：
即类似可得
例4 求 y = secx 的导数解：
即类似可得
2.2.2 基本初等函数的导数
基本导数公式表
例5
解：
2.2.3 复合函数的导数
定理二如果函数在x处可导，而函数在x处可导，且有或注：对于多次复合的函数，其求导公式类似，此法则也称链导法

经济数学2.1导数的概念

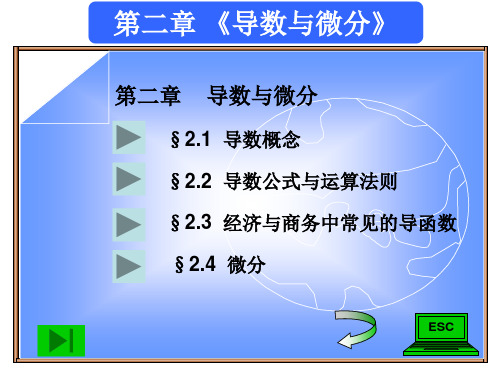
y ( x x )3 x 3
导函数
3 x 2 x 3 x ( x ) 2 ( x ) 3,
( x x )3 x 3 y lim x x 0
lim [ 3 x 2 3 x x ( x ) 2 ] 3 x 2.
M M M MM y 0
T
x
ESC

o
3
x 0 x0 x
x
一、变化率问题举例
案例
1
何谓曲线的切线？
y f (x)
当点 M 沿着曲线 y f ( x )趋于 y 点 M 0 时, 割线 M 0 M 便绕着点 M 0 转动；当点 M 无限趋于点 M 0 时割线的极限位置是 M 0T , 割线则称直线 M 0T 为曲线 y f ( x ) f ( x0 x ) 过点 M 0 处的切线. f ( x0) 切线
便绕着点 M 0 转动；当点 M f ( x0 x ) 无限趋于点 M 0 时，割线的极限位置是 M 0T , 切线 f ( x ) y 则称直线 M 0T 为曲线 f ( x ) 过点 M 0 处的切线.
0
M0
x

1
o
ESC
x 0 x0 x
x
一、变化率问题举例
案例
1
何谓曲线的切线？
ESC
二. 导数定义
函数在区间上的导数定义
定义2.2 若函数 y f ( x ) 在区间 ( a , b ) 内任意一点处都可导，则称函数 f ( x )在区间 (a , b) 内可导．
记作 f ( x ) 或即
y 或
dy 或 dx
df . dx

经济微积分学-导数与微分

第一节导数的概念
三、导数的几何意义
由切线斜率问题的讨论及导数定义可知：函数y=f（x）在点x0处的导数f′（x0）的几何意义是曲线y=f（x）在点M（x0，y0）处的切线斜率，即
f′（x0）=tanα. 其中，α是切线的倾斜角.根据导数的几何意义及直线的点斜式方程可得，曲线y=f（x）在给定点M（x0，y0）处的切线方程是 y-y0=f′（x0）（x-x0）. 过切点M（x0，y0）且与切线垂直的直线叫作曲线y=f（x）在点M（ x0，y0）的法线.若f′（x0）≠0，则法线方程为 y-y0=-1f′（x0）（x-x0）.
（1）将方程F（x，y）=0的两端对x求导，在求导过程中把y看成x的函数，y的函数看成是x的复合函数；
（2）求导后，解出y′即可（式子中允许有y出现）.
第二节函数的求导法则
四、反函数的求导法则
法则5:设函数x=φ（y）在区间D内单调，在y处可导，且φ′（y）≠0，则其反函数y=f（x）在x=φ（y）处也可导，且
Dy/dx=1/dx/dy或f′（x）=1/φ′（y）.
第二节函数的求导法则
五、参数方程所确定的函数的导数
在实际应用中，函数y与自变量x的关系常常通过某一参数变量t表示出来，即
x=φ（t） y=ψ（t），t为参数称为函数的参数方程. 由于y是参数t的函数，由x=φ（t）知t是x的函数，所以，y通过t确定为 x的复合函数.于是，由复合函数的求导法则及反函数的导数公式有 dydx=dydt·dtdx=dydtdxdt=ψ′（t）φ′（t）
第一节导数的概念
二、导数的概念
定义1:设函数y=f（x）在点x0某邻域内有定义，当自变量x在x0处有增量 Δx时，相应地函数y有增量

第二章导数和微分共31页word资料

第二章导数和微分微分学是微积分的重要组成部分.微分学的基本概念是导数和微分，导数反映函数相对于自变量的变化快慢的程度，而微分则是描述当自变量有微小改变时，函数改变量的近似值.本章我们将详细讨论导数、微分的概念，建立导数与微分的基本公式和运算法则，解决初等函数的求导与微分问题.第一节导数的概念一、引例1.变速直线运动的速度设某质点沿直线运动,在时刻t 时,质点所在位置()s s t =,当时间从时刻0t 变化到0t t +∆时,质点经过的路程为00()()s s t t s t ∆=+∆-,则质点在0t 到0t t +∆时间段内的平均速度为00()()s t t s t s v t t+∆-∆==∆∆. 当t ∆很小时,可用v 近似表示物体在0t 时刻的速度.当0t ∆→时,如果极限0lim t st∆→∆∆存在,则称此极限为质点在时刻0t 的瞬时速度,即000()()limlim t t s t t s t sv t t∆→∆→+∆-∆==∆∆. 2.切线问题设曲线()y f x =的图形为图2-1, 点00(,)M x y 为曲线上一定点,在曲线上另取一点00(,)N x x y y +∆+∆,作割线MN ,当点N 沿曲线趋于M 时,如果割线MN 绕点M 旋转而趋于极限位置MT ,直线MT 就称为曲线()y f x =在点M 处的切线.当MN 趋向MT 时,其倾角ϕ也趋向切线倾角α,因此切线MT 的斜率为00000()()tan lim tan limlimx x x f x x f x yK x xαϕ∆→∆→∆→+∆-∆====∆∆.二、导数的定义上面的两个问题,虽然实际意义各不相同,但讨论方法是一致的,所求量都归结为0x ∆→时yx∆∆的极限.一般地,我们有如下导数的概念. 定义设函数()y f x =在点0x 的某邻域内有定义,若极限0000()()limlimx x f x x f x yx x ∆→∆→+∆-∆=∆∆ 存在,则称函数()f x 在点0x 处可导,并称这个极限值为函数()y f x =在点0x 处的导数,记为'0()f x ,0'x x y =,d d =x x yx或d d x x f x=.即'00000()()()limlimx x f x x f x yf x x x∆→∆→+∆-∆==∆∆. 令0x x x =+∆,则0x ∆→时有0x x →,因此'000()()()limx x f x f x f x x x →-=-.如果000()()limx f x x f x x ∆→+∆-∆不存在,则称函数()y f x =在0x 处不可导.如果000()()lim x f x x f x x ∆→+∆-=∞∆,此时()y f x =在0x 处不可导,但通常也说函数()y f x =在0x 处导数为无穷大.下面利用导数的定义计算：例1 已知0()1,f x '=求()()0002lim x f x x f x .x→--V V V解：()()()()()00000002lim22lim 222x x f x x f x xf x x f x x f x .→→----=--'=-=-V V V V V V如果函数()y f x =在开区间I 内每一点处都可导,就称函数()f x 在I 内可导,这时对于任意x I ∈,都对应着()f x 的一个确定的导数值,这样的对应关系就构成了一个新的函数,这个函数称为原来函数()f x 的导函数,简称为导数,记作'()f x ,'y ,d d y x 或d d f x. 导函数定义为'0()()()limx f x x f x f x x∆→+∆-=∆.函数()f x 在0x 处的导数'0()f x 就是导函数'()f x 在0x 处的函数值,即''0()()x x f x f x ==.下面根据导数的定义求一些简单函数的导数. 例2 求函数()f x C =(C 为常数)的导数.解 ()()0y f x x f x C C ∆=+∆-=-=, '000limlim 0,x x y y x x∆→∆→∆===∆∆即 '()0C =.例3 求函数()nf x x =(n 为正整数)的导数.解 ()()()n ny f x x f x x x x ∆=+∆-=+∆-122[()]n n n n x nx C x x x --=∆⋅+∆++∆L ,'12200limlim[()]n n n n x x y y nx C x x x x --∆→∆→∆==+∆++∆∆L1n nx -=.即 '1()n n x nx-=.后边我们将证明对一般幂函数y x α=(α为任意实数)也有'1()x xααα-=.例如,当0x ≠时,'1'2211()()x x x x --==-=-,1''2()x ==例4 求函数()sin f x x =的导数.解 sin()sin 2cos()sin 22x xy x x x x ∆∆∆=+∆-=+, '00sin2lim lim 2cos()cos 2x x x y x y x x x x∆→∆→∆∆∆==+=∆∆,即 '(sin )cos x x =. 同理可得 '(cos )sin x x =-.例5 求函数xy a =(0,1a a >≠)的导数. 解 (1)x xx x x y aa a a +∆∆∆=-=-,ln '000011lim lim limln lim ln .∆∆∆→∆→∆→∆→∆--===∆∆∆∆==∆x x a x xx x x x x x y a e y a a x x x x aa a a x即 '()ln x xa a a =.特别地,当a e =时有'()x x e e =.极限000()()lim x f x x f x x ∆→+∆-∆存在的充分必要条件是000()()lim x f x x f x x -∆→+∆-∆及000()()lim x f x x f x x+∆→+∆-∆都存在且相等,这两个极限分别称为函数()f x 在点0x 处的左导数和右导数，记作'0000()()()lim x f x x f x f x x--∆→+∆-=∆,'0000()()()lim x f x x f x f x x ++∆→+∆-=∆. 左导数和右导数统称为单侧导数.由函数极限与其左、右极限之间的关系可知，定理函数()f x 在点0x 处可导的充分必要条件是左导数'0()f x -和右导数'0()f x +都存在且相等.如果函数()f x 在开区间(,)a b 内可导,且'()f a +及'()f b -都存在,则称()f x 在闭区间[,]a b 上可导.三、导数的几何意义函数()y f x =在点0x 处的导数'0()f x 在几何上表示曲线()y f x =在点00(,())M x f x 处切线的斜率.即'0()tan f x α=.其中α是切线的倾角,参见图2-1.如果()y f x =在点0x 处可导,则曲线在点00(,())M x f x 处切线方程为'000()()()y f x f x x x -=-.过切点00(,())M x f x 且与切线垂直的直线叫做曲线()y f x =在点M 处的法线,如果'0()0f x ≠,则法线方程为00'01()()()y f x x x f x -=--. 特别地,若'0()0=f x ,则曲线在点00(,())M x f x 处的切线方程为0()=y f x ,法线方程为0=x x ;若()y f x =在0x 处的导数为∞,则切线方程为0=x x ,法线方程为0()=y f x .例6求曲线y =(1,1)处的切线方程和法线方程.解'y =,则在点(1,1)处切线斜率'112x k y===,所以切线方程为 11(1)2y x -=-,即210x y -+=.法线方程为12(1)y x -=--,即230x y +-=.四、函数的可导性与连续性的关系定理如果函数()y f x =在点0x 处可导,则它在点0x 处一定连续. 证因为()f x 在点0x 处可导,即'00lim()x yf x x ∆→∆=∆,所以'0000lim lim()lim lim ()00x x x x y y y x x f x xx ∆→∆→∆→∆→∆∆∆=∆=⋅∆=⋅=∆∆,故()y f x =在点0x 处一定连续. 定理证毕.注意这个定理的逆命题不成立,即函数()f x 在某一点处连续,则在该点处()f x 未必可导.请看下面的例子.例7 设函数()f x x =,讨论()f x 在0x =处连续性及可导性.解因为0lim ()lim 0x x x f x x →→→===且(0)0f =，所以()f x x =在0x =处连续.由于(0)(0)xy f x f x x x∆∆+∆-==∆∆∆,所以 '000(0)lim lim lim 1x x x x y xf x x x----∆→∆→∆→∆∆-∆====-∆∆∆,'000(0)lim lim lim 1x x x x y xf x x x++++∆→∆→∆→∆∆∆====∆∆∆, 显然''(0)(0)f f -+≠,因此()f x x =在0x =处不可导.由以上讨论可知,函数在某点连续是函数在该点可导的必要条件,但不是充分条件.习题2-11. 设2()4f x x =,按定义求'(1)f -.2. 一物体的运动方程为3S t =,求该物体在3t =时的瞬时速度. 3. 求下列函数的导数:(1) y =(2) y =;(3) y =(4) y x =4.求曲线sin y x =在点1(,)62π处的切线方程和法线方程. 5.讨论下列函数在指定点处的连续性与可导性.(1) 2,0,(),0x x f x x x ⎧≥=⎨<⎩在0x =处;(2) 1arctan ,0,()0,0x x f x xx ⎧≠⎪=⎨⎪=⎩在0x =处; (3) 21sin ,0,()0,0x x f x xx ⎧≠⎪=⎨⎪=⎩在0x =处. 6.设函数2,1,(),0,x x f x ax b x ⎧≤=⎨+>⎩若函数()f x 在点1x =处连续且可导,则a 和b 应取何值?7.已知函数sin ,0,(),0,x x f x x x <⎧=⎨≥⎩求'()f x .8.单项选择题.(1)设()f x 在点0x x =处可导,则'0()f x = [ ].(A) 000()()limx f x x f x x ∆→-∆-∆; （B ）000()()lim 2h f x h f x h h→+--;（C ）000()(2)lim 2x f x f x x x →-+; （D ）0()(0)lim x f x f x→-;(2)函数()f x 在点0x x =处连续是()f x 在点0x x =处可导的 [ ]. (A) 必要条件; (B) 充分条件;(C) 充分必要条件; (D) 既非充分又非必要条件.第二节函数的求导法则用导数的定义求函数的导数是复杂的和困难的,从本节开始将介绍函数的求导法则,利用这些求导法则和基本初等函数的导数公式,可以比较方便地求出常见初等函数的导数.一、导数四则运算法则定理1 设函数()u u x =及()v v x =都在点x 处可导,那么它们的和、差、积、商（分母不等于0）也均在x 点可导，且'''[()()]()()u x v x u x v x ±=±. （2.1） '''[()()]()()()()u x v x u x v x u x v x ⋅=+ （2.2）'''2()()()()()[]()()u x u x v x u x v x v x v x -= （2.3）证只证明（2.1）式，（2.2）和（2.3）可同样证明. 令()()y u x v x =±,则[()()][()()]y u x x v x x u x v x x x∆+∆±+∆-±=∆∆ ()()()()u x x u x v x x v x x x+∆-+∆-=±∆∆, 所以'0limx y y x∆→∆=∆00()()()()lim limx x u x x u x v x x v x x x∆→∆→+∆-+∆-=±∆∆ ''()()u x v x =±.定理证毕.公式（2.1），（2.2）可推广到有限多个函数的情况，如推论1 设有限多个()i u x (1,2,,i n =L )在x 处均可导,则''''1212(()()())()()()n n u x u x u x u x u x u x +++=+++L L .推论2 设()u u x =,()v v x =,()w w x =在点x 处均可导,则''''()uvw u vw uv w uvw =++.推论3 设()u x 在点x 处可导,C 为常数,则''[()]()Cu x Cu x =.例1 设23cos ln 2y x x =+-,求'y .解 2'''(3)(cos )(ln 2)y x x =+-6sin x x =-.例2 设sin xy e x =,求'y .解 '''()sin (sin )x x y e x e x =+sin cos (sin cos ).x x xe x e x e x x =+=+例3 设tan y x =,求'y .解 '''sin (tan )()cos x y x x==''2(sin )cos sin (cos )cos x x x x x-=22222cos sin 1sec cos cos x x x x x+===. 即'2(tan )sec x x =.类似可求得'2(cot )csc x x =-.例4 设sec y x =,求'y .解 ''''221(cos )sin (sec)()cos cos cos x xy x x x-==== sec tan x x =,即'(sec )sec tan x x x =.类似可得'(csc )csc cot x x x =-.二、反函数的求导公式定理4 设函数()y f x =在区间x I 上单调、可导且'()0f x ≠,则它的反函数1()x f y -=在对应区间y I 上也单调、可导,且1''1[()]()f y f x -=或d 1d d d x yy x=. 证任取y y I ∈,给y 以增量0y ∆≠,由()y f x =的单调性知1()x f y -=在y I 上也单调,从而11()()0x f y y f y --∆=+∆-≠,于是1x y yx∆=∆∆∆.因为()y f x =连续,所以1()x fy -=也连续,故lim 0y x ∆→∆=.从而1''0011[()]lim()lim y x x f y y y f x x-∆→∆→∆===∆∆∆. 定理证毕.例5 arcsin y x =,(1,1)x ∈-,求'y .解 arcsin y x =,(1,1)x ∈-是sin x y =,(,)22y ππ∈-的反函数,故''11(sin )cos y y y ====即'(arcsin )x =类似可得下列导数公式:'(arccos )x ='21(arctan )1x x =+, '21(arccot )1x x =-+. 例6 求函数log a y x =(0,1)a a >≠的导数.解函数log a y x =是函数yx a =的反函数,因为'()ln y ya a a =,故'11(log )ln ln a y x a a x a==, 即'1(log )ln a x x a=. 特别地,当a e =时,'1(ln )x x=. 三、复合函数的求导法则定理 5 设函数()u g x =在点x 处可导,函数()y f u =在对应点()u g x =处可导,则复合函数(())y f g x =在点x 处可导，且其导数为''d ()()d y f u g x x =或d d d d d d y y ux u x=⋅. 证设x 取得增量x ∆,则u 取得相应的增量u ∆,从而y 取得相应的增量y ∆,即()()u g x x g x ∆=+∆-, ()()y f u u f u ∆=+∆-,当0u ∆≠时,有y y ux u x∆∆∆=⋅∆∆∆. 因为()u g x =可导,则必连续,所以0x ∆→时,0u ∆→,因此000limlim limx u x y y ux u x ∆→∆→∆→∆∆∆=⋅∆∆∆, 即''d ()()d yf ug x x=. 当0u ∆=时,可以证明上述公式仍然成立. 定理证毕.例7 设函数2x y e =,求'y .解 2x y e =是由u y e =,2u x =复合而成的,因为d d u ye u =,d 2d u x x=, 所以2d d d 22d d d u x y y u e x xe x u x=⋅==. 例8 设函数2ln(2)y x =+，求'y .解 2ln(2)y x =+是由ln y u =,22u x =+复合而成的,故2d d d 122d d d 2y y u x x x u x u x =⋅=⋅=+. 当复合函数求导法则应用比较熟练后,可以不写出复合过程.例9 设函数y =求'y .解 23''1(12)(12)3y x x -=--231(12)(2)3x -=--=例10 设函数1sinxy e=,求'y .解 1sin '211(cos )()xy ex x=-1sin 211cos x e x x=-.例11 设函数ln cos()xy e =,求'y .解 '1(sin())cos()x x xy e e e =-⋅ tan()x x e e =-.例12 设0x >,证明:'1()x x μμμ-=(其中μ为任意实数).证由于ln xx eμμ=,所以'ln 'ln '11()()(ln )x x x e e x x x x μμμμμμμμ--====.例13 设函数ln(y x =,求'y . 解 'y ===.四、基本导数公式与求导法则1. 基本导数公式(1) '()0C =;(2) '1()x xμμμ-=,特别地'211()xx =-,'=; (3) '(sin )cos x x =; (4) '(cos )sin x x =-;(5) '2(tan )sec x x =; (6) '2(cot )csc x x =-; (7) '(sec )sec tan x x x =; (8) '2(csc )csc cot x x x =-;(9) '()x xe e =; (10) '()ln x xa a a =;(11) '1(ln )x x =; (12) '1(log )ln a x x a=; (13) '(arcsin )x =(14) '(arccos )x =(15) '21(arctan )1x x =+; (16) '21(cot )1arc x x=-+. 2.函数的和、差、积、商的求导法则设()u u x =，()v v x =均可导，则(1) '''()u v u v ±=±; (2) '''()uv u v uv =+;(3) ''()Cu Cu =; (4) '''2()u u v uv v v-=. 3.复合函数的求导法则设()y f u =,()u g x =,且()f u ,()g x 均可导,则d d d d d d y y u x u x=⋅或'''()()()y x f u g x =.例14 设函数y =求'y .解 '2)y x =-=22=例15 设函数2sin1x y x=+,求'y . 解 '''222(sin)(cos )()111x x x y x x x ==+++ 222212(cos )1(1)x x x x x x +-⋅=++22221cos (1)1x x x x -=++. 习题2-21.求下列函数的导数:(1) 235y x x =-+; (2) 212y x x =+; (3) 3y=; (4) ln y x x =;(5) 3cos y x x =; (6) 2ln 3xe y x=+;(7) 11x y x -=+; (8) 251xy x =+; (9) sin sin x x y x x=+; (10) 2ln cos y x x x =. 2.求下列函数在给定点的导数: (1)sin cos y x x =-，求'6x yπ=和'4x yπ=；（2）23()55x f x x =+-，求'(0)f 和'(2)f . 3.求曲线22y x x =+-的切线方程,使该切线平行于直线30x y +-=. 4.求下列函数的导数:(1)7(35)y x =+; (2)sin(24)y x =-; (3)32x y e -=; (4)22ln()y a x =-;(5)2cos y x =; (6) y =(7)arctan xy e =; (8)2(arcsin )y x =. 5.求下列函数的导数:(1)2(arccos )2x y =; (2)ln cot 2x y =;(3)y =; (4)y e =(5)y = (6)23(ln )y x =;(7)ln ln ln y x =; (8)ln tan2x y =; (9)1ln sin y x=; (10)1tan x y e =.6.求下列函数的导数: (1)21arctan ln(1)2y x x x =-+; (2)x xx xe e y e e ---=+.7.设()f x 可导,求d d y x . (1)1(arcsin )y f x=; (2)()()x f x y f e e =;(3)22(sin )(cos )y f x f x =+.第三节高阶导数设一物体作直线运动,其速度()v t 是位移()s t 对时间t 的导数,而加速度()a t 又是速度()v t 的变化率,即d d d ()()d d d v s a t t t t==. 我们把导数的导数称为二阶导数.一般地,函数()y f x =的导数''()y f x =仍是x 的函数,因此,如果'()f x 在点x 处仍然可导,则'()f x 在点x 处的导数称为()f x 在点x 处的二阶导数,记为"y 或22d d yx,即''''()y y =或22d d d ()d d d y yx x x=.类似地,二阶导数"y 的导数称作()f x 的三阶导数,三阶导数的导数称为四阶导数,分别记为"'y ,(4)y.(1)n y -的导数称作()f x 的n 阶导数,记作()n y ,()()n fx ,d d n n yx或d ()d n n f x x .二阶及二阶以上的导数统称为高阶导数, 相应地'()f x 称为一阶导数.例1 求函数2325y x x =++的各阶导数.解 '2'(325)62y x x x =++=+,'''()(62)6,0(3).n y x y n =+==≥一般地，若10110() (0),n n n n n y P x a x a x a x a a --==++++≠L 则()()0!,0 (1).n k y n a y k n ==≥+例2 求函数(0,1)xy a a a =>≠的n 阶导数.解 'ln xy a a =,''2ln xy a a =,'''3ln xy a a =,(4)4ln x y a a =,L ,()ln .n x n y a a =特别地，()().n x x e e =例3 求sin y x =的n 阶导数.解 ''(sin )cos sin()2y x x x π===+,'''2[sin()]cos()sin()222y x x x πππ=+=+=+,''''223[sin()]cos()sin()222y x x x πππ=+=+=+,(4)'334[sin()]cos()sin()222y x x x πππ=+=+=+,L ,()sin()2n n y x π=+.类似可得, ()(cos )cos()2n n x x π=+.例4 求ln(1)y x =+的n 阶导数.解 ''1[ln(1)]1y x x=+=+, ''2(1)y x -=-+, '''312(1)y x -=⋅⋅+,(4)4(1)23(1)yx -=-⋅⋅+,L ,1()(1)(1)!(1)n n nn yx ---=+. 如果函数()u u x =及()v v x =都在点x 处具有n 阶导数，那么显然()()u x v x +及()()u x v x -也在点x 处具有n 阶导数，且()()()()nn n u v u v .±=±但乘积()()u x v x ⋅的n 阶导数并不如此简单.由()uv u v uv '''=+首先得出()2uv u v u v uv ,''''''''=++ ()33uv u v u v u v uv .'''''''''''''''=+++用数学归纳法可以证明()()()()()()()()()()()()()12012!11!n n n n n k k n nn k k k n k n n u v u v nuv u v n n n k u v uv k C u v ----=-'''⋅=+++--++++=∑L L L上式称为莱布尼兹（Leibniz ）公式.例5 22xy x e ,=求()20y.解设22xu e ,v x ,==则()()221220kk xu e k ,,,,==L()()2203420kv x,v ,v k ,,,,'''====L代入莱布尼兹公式，得()()()()20202220221921822022201922022222!22095.x x x xx y x e e x e x e e x x =⋅=⋅+⋅⋅+⋅=++习题2-31.求下列函数的二阶导数:(1)22ln y x x =+; (2)sin xy e x -=;(3)tan y x =; (4)ln(y x =;(5)21x y x=-; (6)2(1)arccot y x x =+;(7)23xy x e =; (8)2cos ln y x x =.2.求下列函数的导数值:(1)34()(10)f x x =+,求'''(0)f ;(2)2()x f x xe =,求''(1)f ;(3)()x e f x x=,求''(2)f .3.设()f u 二阶可导,求22d d yx.(1)2()y f x =; (2)1()y f x=; (3)ln[()]y f x =; (4)()f x y e -=.4.验证函数cos xy e x =满足关系式:'''220y y y -+=.第四节隐函数和参数方程所确定的函数的导数一、隐函数的导数函数()y f x =表示两个变量y 与x 之间的对应关系,这种对应关系可以用各种不同方式表达,如sin y x =,y =这样的函数称为显函数.有些函数的表达式却不是这样的,例如方程2310x y +-=表示一个函数y =但这个函数关系是隐含在这一方程中的,这样的函数称为隐函数.一般地,如果变量x 和y 满足一个方程(,)0F x y =,在一定条件下,能确定y 是x 的函数,那么称方程(,)0F x y =确定了一个隐函数.与此相对应,具有()y f x =形式的函数称为显函数.把一个隐函数化为显函数,称为隐函数显化.但有些隐函数显化是相当困难的,如2sin()ln()0xy x y -+=.下面通过具体例子说明不进行显化的隐函数求导方法. 例1 求由方程0xyxy e e -+=确定的隐函数()y y x =的导数. 解方程两边对x 求导并注意()y y x =,则得''0x y xy y e e y +-+=,解得'x y e y y e x-=+ (0)ye x +≠.例2 求由方程57230y xy x x +--=所确定的隐函数在0x =处的导数0d d x y x=.解方程两边对x 求导,有46d d 5221210d d y yy y x x x x++--=, 由此得644d 1212 (520)d 52y x y y x y +-=+≠+. 因为当0x =时,由原方程得0y =,所以60040d 12121d 522x x y y x y xy ===+-==+. 例3 求曲线224x xy y ++=在点(2,2)-处的切线方程. 解方程两边对x 求导,有''220x xy y yy +++=,则'(2)2x y y x y-+=+,'(2,2)1y-=.于是曲线在点(2,2)-处的切线方程为(2)1(2)y x --=⋅-,即40x y --=.例4 求由方程1sin 02x y y -+=所确定的隐函数的二阶导数22d d y x .解由原方程得d 1d 1cos 0d 2d y yy x x--=. 于是d 2d 2cos y x y=-. 上式两边对x 再求导,仍注意()y y x =,得2223d 2sin d 4sin d (2cos 0)d (2cos )(2cos )yy y y x y x y y -⋅-==-≠--. 例5 设函数sin (0)xy x x =>,求'y .解在sin xy x=两边取对数,得ln sin ln y x x =.将上式两边对x 求导,有'11cos ln (sin )y x x x y x=+. 于是'sin (cos ln )xy y x x x =+sin sin (cos ln )xx x x x x=+.例6设y =,求'y .解两边取对数,得1ln [ln(1)ln(2)ln(3)]3y x x x =+++-+,两边对x 求导,得'1111[]3123y y x x x =+-+++. 即'111)123y x x x =+-+++.这种先取对数再求导的方法称为对数求导法.一般地,对幂指函数,以及经多次乘、除、乘方和开方运算构成的函数，用对数求导法比较简便.二、由参数方程所确定的函数的导数.若y 与x 的函数关系是由参数方程(),()x t y t ϕψ=⎧⎨=⎩确定的,则称此函数为由参数方程所确定的函数.在实际问题中,需要计算由参数方程所确定的函数的导数,但从参数方程中消去参数t ,有时会很困难.下面给出直接由参数方程求出它所确定的函数导数的方法.设()t ϕ，()t ψ均可导，且()t ϕ有反函数1()t x ϕ-=，则由参数方程所确定的函数就是复合函数1[()]y x ψϕ-=，利用复合函数及反函数的求导法则,得''d d d d 1()d d d d d ()d y y t y t x x t x t t tψϕ===，即''d ()d ()y t x t ψϕ=. 如果()x t ϕ=,()y t ψ=是二阶可导的,则由新的参数方程''(),d ()d ()x t y t x t ϕψϕ=⎧⎪⎨=⎪⎩可得'2'''''''2'3()d ()'d()d ()()()()()d d d '()[()]t yy t t t t t x x x t t ψψϕϕψϕϕϕ-===. 例7 设1,1,x t t y t ⎧=+⎪⎨⎪=+⎩求d d yx .解2d 11d x t t =-,d 1d yt=,于是222d d 1d d 1d 11d y y t t x x t t t===-- (1t ≠±). 例8 已知椭圆的参数方程cos ,sin ,x a t y b t =⎧⎨=⎩求椭圆在4t π=处的切线方程.解当4t π=时,得点)M ，在M 点处切线斜率为 ''444d (sin )cos d (cos )sin t t t y b t b t b K x a t a taπππ=======--.于是,椭圆在M 点处的切线方程为()22b y x a -=--或0bx ay +=. 例9 设21,cos ,x t y t ⎧=+⎨=⎩求222d d t yxπ=.解 d d sin d d d 2d y y tt x x t t==-, 2223sin ()'d sin cos 2d (1)'4ty t t t t x t t--==+, 于是223322d sin cos 2d 4t t yt t tx t πππ==-==.习题2-41.求下列方程所确定的隐函数的导数d d y x. (1) 2290y xy -+=; (2) 1cos sin 2y x y =+; (3) 22sin xx y ey -=; (4) x y xy e +=;(5) 1yy xe =+; (6) y xx y =.2.求由方程sin()ln()xy y x x +-=所确定的隐函数()y x 在0x =处的导数d d x y x=.3.求椭圆221169x y +=在点处的切线方程和法线方程. 4.用对数求导法求下列函数的导数.(1) 2(sin )x y x =;(2) y =(3) 23(1)(1)x x y x -=+; (4) 1(1cos )x y x =+. 5.求下列参数方程所确定函数的导数d d y x. (1) 232,3;x t t y t t ⎧=-⎪⎨=-⎪⎩ (2) (1sin ),cos ;x t t y t t =-⎧⎨=⎩ (3) cos ,sin ;x a t y at t =⎧⎨=⎩(4)sin ,cos .ttx e t y e t ⎧=⎪⎨=⎪⎩ 6.求下列参数方程所确定的函数的二阶导数22d d y x.(1) 23,;x at y bt ⎧=⎪⎨=⎪⎩ (2) 2ln(1),arctan .x t y t t ⎧=+⎨=-⎩ 7.求曲线2,ttx e y e-⎧=⎪⎨=⎪⎩在0t =处的切线方程及法线方程. 第五节函数的微分一、微分的定义引例如图2-2所示,设有半径为0x 的圆形金属薄片,受温度影响,半径改变了x ∆,这时面积的增量为222000()2()S x x x x x x ππππ∆=+∆-=∆+∆,其中02x x π∆是x ∆的线性函数,2()x π∆是x ∆的高阶无穷小,因此,当x ∆很小时,金属薄片的面积改变量02S x x π∆≈∆.图 2-2定义设函数()y f x =在某区间内有定义,如果在点0x 处给自变量一增量x ∆,函数的增量00()()y f x x f x ∆=+∆-可表示为()y A x o x ∆=∆+∆,其中A 是不依赖于x ∆的常数,则称函数()f x 在0x 处是可微的,而A x ∆叫做函数()f x 在点0x 处相应于自变量增量x ∆的微分,记作d y ,即d y A x =∆.定理函数()y f x =在点0x 处可微的充分必要条件是函数()y f x =在点0x 处可导,且'0()A f x =.证必要性设函数()y f x =在点0x 处可微,即00()()()y f x x f x A x o x ∆=+∆-=∆+∆.上式两边同除以x ∆,得()y o x A x x∆∆=+∆∆, 所以0limx yA x ∆→∆=∆,即函数()f x 在点0x 处可导,且'0()f x A =.充分性设函数()y f x =在点0x 处可导,即'00lim()x yf x x ∆→∆=∆.由极限与无穷小的关系,有'0()yf x xα∆=+∆, 其中0lim 0x α∆→=,故'0()y f x x x α∆=∆+∆.因为'0()f x 与x ∆无关,且0lim0x xxα∆→∆=∆,所以函数()y f x =在点0x 处可微,且'0d ()y f x x =∆.定理证毕.通常把自变量的增量x ∆称为自变量的微分,记作d x ,则函数()y f x =在x 处的微分'd ()d y f x x =,从而有'd ()d yf x x=. 因此,导数也叫做微商.微分的几何意义曲线()y f x =在点00(,())M x f x 处的切线MT 的方程为'000()()()y f x f x x x -=-,由于'00()()d f x x x y -=,所以0d ()y y f x =-,即d y 就是曲线的切线上点的纵坐标的相应增量,见图2-3.当'0()0f x ≠，且x ∆很小时,有d y y ∆≈.例1 求函数2()y f x x ==当x 由1改变到1.01时的微分.解函数的微分为d '()2y f x x x x =∆=∆.由已知条件1x =,0.01x ∆=,故10.01d 210.010.02x x y =∆==⨯⨯=.二、基本初等函数的微分公式与微分运算法则由'd ()d y f x x =可知,求微分d y ,只要求出导数'()f x ,再乘以d x 即可. 1.基本初等函数的微分公式(1)d()0 ()C C =为常数; (2)1d()d x xx μμμ-=;(3)d(sin )cos d x x x =; (4)d(cos )sin d x x x =-; (5)2d(tan )sec d x x x =; (6)2d(cot )csc d x x x =-; (7)d(sec )sec tan d x x x x =; (8)d(csc )csc cot d x x x x =-;图2-3(9)d()d x x e e x =; (10)d()ln d x xa a a x =; (11)1d(ln )d x x x =; (12)1d(log )d ln a x x x a=; (13)d(arcsin )x x =; (14)d(arccos )x x =;(15)21d(arctan )d 1x x x =+; (16)21d(arccot )d 1x x x =-+.2.函数和、差、积、商的微分法则(1)d()d d u v u v ±=±; (2)d()d Cu C u =; (3)d()d d uv v u u v =+; (4)2d d d()uv u u vv v -=. 三、微分的形式不变性设()y f u =可导，这里u 是自变量，则微分'd ()d ;y f u u =另一方面，若()y f u =及()u g x =均可导,这里u 是中间变量，则复合函数[()]y f g x =的微分为''d ()()d ,y f u g x x =由于'()d d g x x u =,所以'd ()d y f u u =.由此可见,无论u 是自变量还是中间变量,微分形式'd ()d y f u u =保持不变.这一性质称为微分的形式不变性.例2 设ax by e+=,求d y .解因为''()ax bax b y eax b e a ++=+=,所以d d ax b y ae x +=.或者由微分的形式不变性，有d d()d .ax b ax b ye ax b ae x ++=+=例3 求2sin 3xy e x =的微分.解 2d d(sin 3)xy e x =22sin 3d()d(sin 3)x x x e e x =+22sin32d 3cos3d x xx e x e x x =⋅+⋅ 2(2sin 33cos3)d xe x x x =+.四、微分在近似计算中的应用如果()y f x =在点0x 处可导,且'0()0f x ≠,则当x ∆很小时,有'000()()()y f x x f x f x x ∆=+∆-≈∆,即'000()()()f x x f x f x x +∆≈+∆.例4 利用微分求0sin 29的近似值. 解令()sin f x x =,取06x π=,180x π∆=-,由'()cos f x x =得0'00sin 29()()f x f x x ≈+∆sin(cos )()66180πππ=+-10.4842=≈. 例5 证明当x 较小时，sin x x ≈.证取()sin f x x =，(0)0f =，'(0)cos1x f ===，则'sin (0)(0)x f f x ≈+，即sin x x ≈.当x 很小时，类似有下列近似公式（1）ln(1)x x +≈ （2）1xe x ≈+（3）tan x x ≈ （4）(1)1x x αα+≈+习题2-51.求下列函数的微分：（1）21xy x=-；（2）sin 2y x x =；（3）ln y x=（4）y =；（5）22tan (12)y x =+；（6）2sin x y e =. 2.设2290y xy -+=，求d y . 3.计算下列函数值的近似值：（1 （2）0'sin 3030. 4.证明当x 很小时下列近似公式成立：（1）ln(1)x x +≈；（21x n≈+. 总习题二（A 类）1.设函数,0,(),0x e x f x ax b x ⎧≥=⎨+<⎩在点0x =处可导,求a 和b .2.讨论下列函数在指定点处的连续性及可导性: (1) ln(1),0,(),0x x f x x x +≥⎧=⎨<⎩ 在0x =处;(2) ()sin f x x = 在0x =处.3.在抛物线2y x =上过横坐标为11x =及23x =的两点作割线,问该抛物线上哪一点的切线平行于这条割线?4.证明：双曲线2xy a =上任一点处的切线与两坐标轴围成的三角形的面积等于22a . 5.求下列函数的导数:(1) 2tan y x =; (2) arcsin(2)y x =+; (3) sin 2x x y a+=; (4) 1ln 1ln xy x-=+;(5) 22(arcsin )y x =; (6) 21ln tan(2)y x x=+;(7) 1arctan()1x y x +=-; (8) 2y =;(9) arcsin y x =; (10) 11()1x x y x +=-. 6.求下列函数的导数:(1) 21sin ,0,()0,0;x x f x xx ⎧≠⎪=⎨⎪=⎩(2) 21,0,()21,01,2, 1.x f x x x x x ⎧≤⎪=+<≤⎨⎪+>⎩7.设()3sin 2xf x x =,求'''(0)f .8.求下列方程所确定的隐函数的导数d d y x: (1) 2230xy y ++=; (2) cos cos 10x y =; (3) 222xyx y++=;(4) arctanyx=. 9.求下列方程所确定的隐函数的二阶导数22d d yx.(1)1yy xe =+; (2)arctan y x y =+.10.求下列参数方程所确定的函数的二阶导数22d d yx:(1) 2,21;t x y t ⎧=⎪⎨⎪=-⎩(2)cos ,sin ;x a t y b t =⎧⎨=⎩ (3) ''(),()(),x f t y tf t t t ⎧=⎪⎨=-⎪⎩设''()f t 存在且不为零. 11.求下列函数的微分:(1) 2ln y x x =;(2) y x =;(3) cos(3)xy e x -=-; (4) 221arctan 1x y x-=+. 12.求下列方程确定的隐函数的微分: (1) ln 1yxxe ye y -+=;(2) sin()y xy =.（B 类）一.填空题.1.已知2x =是()f x 的连续点,且2()lim32x f x x →=-,则'(2)_________f =.2.已知'(3)2f =,则0(3)(3)lim ___________2h f h f h→--=.3.设21,cos ,x t y t ⎧=+⎨=⎩则22d ___________d yx=.4.设函数()y y x =由方程cos()0x yexy ++=确定,则d _____________d yx=. 5.曲线ln y x =上与直线1x y +=垂直的切线方程为______________.6.函数()f x 在0x 可导是()f x 在点0x 连续的___________条件, ()f x 在点0x 连续是()f x 在点0x 可导的__________条件.二.选择题.1.设20,()(),0,x f x x g x x >=≤⎩其中()g x 是有界函数,则()f x 在0x =处 [ ].(A) 极限不存在; (B) 极限存在但不连续; (C) 连续但不可导; (D) 可导.2.已知函数()f x 有任意阶导数，且'2()[()]f x f x =，则当n 为大于2的正整数时，()f x 的n 阶导数()()n fx 是 [ ].(A) 1![()]n n f x +; (B) 1[()]n n f x +;(C) 2[()]nf x ; (D) 2![()]nn f x .3.设22()3f x x x x =+,则使()(0)n f存在的最高阶数n 为 [ ].(A) 0; (B) 1; (C) 2; (D) 3.4.若函数()f x 可导，且'2()sin [sin(1)]f x x =+，(0)4f =，则()f x 的反函数()x y ϕ=当自变量y 取值为4时导数值为 [ ].(A)21sin (sin 4); (B) 21sin (sin 5);第 94 页 (C) 0; (D)21sin (sin1). 三．解答题1.设函数()y y x =由方程()f x y xe e =确定，其中''()f x 存在，且'()1f x ≠，求''y .2.设()()()f x a bx a bx ϕϕ=+--，其中()x ϕ在区间(,)-∞+∞内有定义且在a 处可导，求'(0)f .3.设32()3(1)(1)1f x x x x =-+--，求'(1)f 及''(1)f .4.设函数1sin ,0,()0,0,x x f x x x α⎧≠⎪=⎨⎪=⎩问α满足什么条件时，()f x 在0x =处（1）连续;（2）可导;（3）导数连续. 5.若()f x 可导，求lim [()()]n ab n f x f x n n→∞+-- (,0)a b ≠. 6.设一多项式()f x 满足'''()(1)()3()0xf x x f x f x +-+=，且(0)1f =，求该多项式.7.设()f x 满足113()()2f x f x x+=，求'()f x .。

《经济数学基础》重难点解析一元函数微分学(下)——导数与微分

《经济数学基础》重难点解析第2章一元函数微分学(下)——导数与微分1. 理解导数定义。

理解导数定义时，要解决下面几个问题：（1）牢记导数定义的极限表达式；（2）会求曲线的切线方程；（3）知道可导与连续的关系(可导的函数一定连续，连续的函数不一定可导)。

例1 填空、选择题（1）设f x x x ()=++11，则=')0(f （）。

A ．不存在 B .1 C . 0 D . -1解因为1->x 时111)(=++=x x x f ，是常数函数，而点0=x 在),1(+∞-范围内，故 =')0(f 0。

正确的选项是C 。

（2）设f x x ()ln =，则=-→1)(lim x x f x 1（）。

A ．1 B . e -12 C . 0 D . 不存在解如果单看求极限=-→1)(lim x x f x 11ln lim 1-→x x x ，很难求出结果。

但是若联想到01ln =以及导数的定义，即有=-→1)(lim x x f x 11ln lim 1-→x x x 11ln ln lim 1--=→x x x =1)(ln ='x x =0 故正确的选项是C 。

（3）极限)(sin )sin(lim000=∆-∆+→∆x x x x x A. 1 B. cos x 0 C. sin x 0 D.不存在解这个极限的表达式正是函数sin x 在点x 0处导数的定义，即有=∆-∆+→∆x x x x x 000sin )sin(limcos x 0 故正确的选项是B 。

（4）设)(x f 在0=x 处可导，且0)0(=f ，则=→xx f x )(lim 0( )。

A.不存在 B. )0(f ' C. 0 D. 任意解因已知)(x f 在0=x 处可导，且0)0(=f ，将)(x f 看成)0()(f x f -,x 看成0-x ，则=→x x f x )(lim 00)0()(lim 0--→x f x f x 就是)(x f 在0=x 处的导数，故 =→xx f x )(lim 0)0(f ' 正确选项是B 。

《经济数学基础》微积分部分复习Word版

《经济数学基础》微积分部分复习第一篇微分学第一章函数一、本章考核点1、掌握函数奇偶性的判定，掌握总成本、平均成本、收入、利润函数的概念及表达式，掌握五个基本初等函数的概念及表达式。

2、熟练掌握函数定义域、求函数值、复合函数的复合与分解的计算。

二、基本概念基本初等函数、函数的奇偶性、总成本、平均成本、收入、利润函数奇偶性：若f(-x)=f(x)，则函数f(x)为偶函数若f(-x)=－f(x)，则函数f(x)为奇函数若f(x)不满足上述两式，则函数f(x)为非奇非偶函数总成本函数：10C C C += 隐含条件： 0)0(C C =平均成本：q CC =总收入函数：pq R = 隐含条件：0)0(=R总利润函数：C R L -=基本初等函数：常数：y=C幂函数：αx y =指数函数：xa y =对数函数：x y log = 自然对数：x y ln = 三角函数：正弦函数 y=sinx 余弦函数 y=cosx 正切函数 y=tanx 余切函数 y=cotx 三、计算1、求函数的定义域重点是已知函数的解析式求函数的定义域——四个限制已知函数的解析式求定义域，有以下几个限制：①分式的分母不为零； ②对数的真数大于零；③开偶次方的被开方数非负；④2tan ππ+≠=k x x y 中πk x x y ≠=中cot 其中k=0, ±1,2,3,…… 2、求函数值3、复合函数的分解第二章极限、导数与微分一、本章考核点1、熟练掌握极限的计算、导数微分的计算。

2、掌握函数间断点的求法，判断分段函数分段点是否有极限、是否连续。

二、计算1、极限——数列的极限、函数的极限方法：利用四则运算性质、利用两个重要极限公式 2、导数和微分方法：利用导数的四则运算法则和导数基本公式；复合函数的导数；隐函数的导数；高阶导数 3、求函数的间断点——两种类型初等函数：初等函数在其定义域内连续 ——函数无定义的点即为初等函数的间断点；分段函数：分段函数的间断点存在于分段点中。

第二章导数与微分知识点

第二章导数与微分一、导数1．导数的定义: 由“变速直线运动的瞬时速度”、“平面曲线的切线斜率”引出设函数()x f y =在点0x 的某领域内有定义，自变量x 在0x 处有增量x ∆，相应地函数增量()()00x f x x f y -∆+=∆。

如果极限 ()()xx f x x f x yx x ∆-∆+=∆∆→∆→∆0000lim lim存在，则称此极限值为函数()x f 在0x 处的导数（也称微商），记作()0x f '，或0x x y ='，0x x dx dy =，()0x x dx x df =等，并称函数()x f y =在点0x 处可导。

如果上面的极限不存在，则称函数()x f y =在点0x 处不可导。

注：函数()x f 在0x 处的导数，就是导函数f ’(x)在点在0x 处的函数值，即()0x f '=f ’(x)|x=x0。

多数情况下用求导法则，有时用定义求导更方便。

如题中函有f(x)，而不是具体的方程时。

2、单侧导数右导数：()()()()()x x f x x f x x x f x f x f x x x ∆-∆+=--='++→∆→+000000lim lim 0左导数：()()()()()xx f x x f x x x f x f x f x x x ∆-∆+=--='--→∆→-000000lim lim 0则有()x f 在点0x 处可导()x f ⇔在点0x 处左、右导数皆存在且相等。

3、导数的几何意义如果函数()x f y =在点0x 处导数()0x f '存在，则在几何上()0x f '表示曲线()x f y =在点()()00,x f x 处的切线的斜率，即：()0x f '=K=tan a 。

切线方程：()()()000x x x f x f y -'=-法线方程：()()()()()010000≠'-'-=-x f x x x f x f y 注：切线与法线垂直，切线的斜率与法线的斜率乘积为负1，即：K 切 * K 法 = -1。

第2章导数与微分总结

1、极限的实质是：动而不达导数的实质是：一个有规律商的极限。

规律就是:2、导数的多种变式定义：lim 丄一x)f°)是描述趋近任意 x 时的斜率。

而x 03、I若x 没趋近到x0，那么除法得到的值是这段的平均斜率，如果趋近到了 x0,得到的就是这点的斜率一一导数。

4、可导与连续的关系:1基础总结lim -= limx 0 x x 0 f(x X)f(x)xlim x x o f(x )f (x o )X o叫号严可以刻画趋近具体x0时的斜率。

lim o要注意细心观察发现,导数的实质是定义在某点的左右极限。

既然定义在了某点上，该点自然存在，而且还得等于左右极限。

因此，可导一定是连续的。

反之，如果连续，不一定可导。

不多说。

同理，如果不连续，肯定某点要么无定义，要么定义点跳跃跑了，肯定极限有可能存在，但是导数绝不会存在。

同理要注意左右导数的问题。

如果存在左或者右导数，那么在左侧该点一定是存在的。

如：f(x) x,x 0这个函数，在0点就不存在左导数，只存在右导数。

为什么嫩？看定义:万不要以为导数是一种简单的极限，极限是可以在某点无定义的，而导数却是该点必须存在! 由此引发了一些容易误判的血案: 例如:A 旦主^謎IC m F 左电鼓 pg 总生戟乞f ( x) f (x)-中的f(x))至u 底是神马。

比如求上图limf(x x) f(x)x 0xlimf(X X)f(0)。

x 0定义里面需要用到f(0)啊！因此，千中 iimf (x)论) x 1x x 0,这个f(x0)千万要等于2/3，而不是1 ！定义解决时候一定要注意问。

X X o由此也可以知道，f (x)2x 3, x 1这个函数是不存在导数的，也不存在左导数,3只存在右导数。

5、反函数的导数与原函数的关系:注意，求反函数时候不要换元。

因为换了元虽然对自身来讲函数形式不变, 与原函数融合运算时候就算是换了一个不是自己反函数的一个函数进行运算果显然是错误的。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

f (x)在点 x可导,自变量
在点的改变量为 x ,乘积 f ( x) x 称为函数在点
x
这时,也称函数 f (x) 在点
通常把自变量的改变量 x称为自变量的微分,记作 dx,即于是函数 f (x) 的微分,一般记作
x 可微.函数的微分记作dy ,即 dy f (x) x.
1 1 x2 1 (16) (arc cot x) ESC 2 1 x
(15) (arctan x)
二、导数公式与运算法则
设函数
(1)代数和 [u ( x) v( x)]可)都是可导函数,则
(u v) u v
(2)乘积
第二章导数与微分
第二章导数与微分
导数概念
导数公式与运算法则
复合函数的导数
高阶导数
微分
ESC
一、导数的概念
定义2.1设函数 y f (x) 在点右邻近有定义,若极限
x0
及其左
f (x0 x) f (x0) y lim lim x x0 x x0
存在, 则称函数 f (x) 在点 x0 可导,并称此极限值为函数 f (x) 在点 x0 的导数, 记作
例4 求下列函数的导数
y sin3 x, （1）
（2） y 2ln5x
（3）y e5x ln x
（4） y=sinex22x+3 （5） y cos23x
tan1 （6） y 2 x （7） y sin2(23x)
ESC
四. 高阶导数
（8）
y lncos x
x （10）y 43x2
练习
若
y tan x 则 dy ? 2
ESC
六. 基本初等函数的微分公式
(1) d(C) 0
一定要熟记!!!
(10) d(cot x) csc2 xdx (2) d(x) x 1dx (11) d(sec x) sec x tan xdx (3) d(ax) ax ln adx (12) d(csc x) csc x cot xdx (13) d(arcsin x) 1 2 dx (4) d(ex) exdx 1 x (5) d(log a x) 1 dx (14) d(arccos x) 1 2 dx x ln a 1 x (15) d(arctan x) 1 2 dx (6) d(ln x) 1 dx 1 x x (7) d(sin x) cos xdx (16)d(arc cot x) 1 2 dx 1 x (8) d(cos x) sin xdx
(9) d(tan x) sec xdx
2
ESC
六. 基本初等函数的微分公式
微分的四则运算法则设函数 u u x ，可微 v v x ，则
d uv vdu udv
d u v du dv
d cu cdu，（c为常数）
u vdu udv d( ) ， (v 0) 2 v v
二、导数公式与运算法则
设函数
u u (x), v v(x)都是可导函数,则
可导,且
u (x ) (3)若v(x) 0,商 v (x )
(u ) u v u v 2 v v
C ) C v esp : ( v v2
ESC
二、导数公式与运算法则
例3 求下列函数的导数
x 的微分.
x
dy f (x) dx.
即函数的微分等于函数的导数与自变量的微分的乘积.
ESC
五. 微分定义
例7 求下列函数的微分： y x3e2 x ； (2) y arctan 1 ．（3） y f (e2x) (1) x 2 2x 3 2x 3x e 2 x e x2e2 x (3 2 x) 解 (1) y 所以 dy ydx x 2e2 x (3 2 x)dx ． 1 2 dx ． x 1 y d (2) 2， y 2 1 1 x 1 x 1 2 x （3） y 2 f (e2x)e2x dy 2 f (e2x)e2xdx
（1） y （2） y
x 3 log 3 x 3 sin
3 x 3

4
,
x3 ln x 2 cos x,
x log x2xln xex 3 x
（3）y=
（4）
y e 2, 1 x
(5) y xtan xcot x
ESC
三. 复合函数的导数法则八、洛必达法则
f (x0),
y x x0, dy dx
x x0
,
或
df dx
x x0
.
ESC
一、导数的概念
即或
f (x0 x) f (x0) f (x0) lim . x x0
f (x) f (x0) f (x0) lim . x x0 x x0
定义2.2 若函数 y f (x) 在区间 ( a, b) 内任意一点处都可导，则称函数 f ( x )在区间 (a , b) 内可导．
（3）设 f (x) ln x ，求 lim f (x 3x) f (x) x x0
ESC
一、导数的概念
（4）设 f (x) ln2 ，求
lim f (x x) f (x) x x0
例2 求曲线 y ex 1 在 x 0 处的切线方程。练习：求曲线
ESC
ESC
y x 在 x1 处的切线方程。
ESC
二、导数公式与运算法则
(1) (C) 0
一定要熟记!!!
(2) (x) x 1 x a x ln a (3) (a ) x ex (4) (e ) (5) (log a x) 1 x ln a
(6) (ln x) 1 x (7) (sin x) cos x (8) (cos x) sin x
ESC
六. 基本初等函数的微分公式
例7求
例8
d(cos2x)
求函数
y excos4x 的微分解：dy cos4xd (ex)exd (cos4x) cos4xexd (x)ex(sin4x)d (4x)
ex cos4xdx4exsin4xdx ex(cos4x 4sin4x)dx
(u v) u v u v
u( x) v( x) 可导, 且
ESC
esp : (C v) C v
(u v w) u v w u v w u v w
乘积法则可推广到有限个函数的情形.例如,对三个函数的乘积,有
记作即
f (x ) 或
y 或
dy 或 dx
df . dx
ESC
f (x Δx) f (x) Δy f (x) lim lim . Δx Δ x0 Δx Δ x0
一、导数的概念
例1设函数 y f ( x)在点 x0 处可导，按导数的定义，确定出 A 的值。
f (x 2x) f (x ) 0 0 A (1) lim x x0 f (x x) f (x ) 0 0 A (2) lim x x0
(10) (cot x) csc 2 x (11) (sec x) sec x tan x (12) (csc x) csc x cot x
(13) (arcsin x)
(14) (arccos x)
1 1 x2
1 1 x2
sec 2 x (9) (tan x)
例5 求下列函数的二阶导数. (1) y 2x33x2 5 ；
（9） y cos2
y xcos x ． y x2ex (３)
(2)
ESC
四. 高阶导数
例6
求下列函数的 n 阶导数. (1) y 5x ； (2) y e2 x．
ESC
五. 微分定义
定义2.6 设函数 y