数值分析简明教程(第二版)课后习题答案
《数值分析简明教程》第二版(王能超 编著)课后习题答案 高等教育出版社

-------------------------------------------------------------------------------0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分-------------------------------------------------------------------------------0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
数值分析简明教程第二版课后习题答案(供参考)

0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
《数值分析简明教程》(第二版)王能超课后习题答案

532 a= = 0.9726 547 b = 285 = 0.05 2 ( f , ϕ1 ) = 369321.5 ,解之得 5696 ,∴ y = 0.9726 + 0.05 x .
yn = yn −1 + hf ( xn −1 , yn −1 ) = yn −1 + h ⋅ ( axn −1 + b)
故 yn −1 = yn −2 + h ⋅ ( axn − 2 + b)
LL y1 = y0 + h ⋅ ( ax0 + b)
将上组式子左右累加,得
yn = y0 + ah( x0 + L + xn −2 + xn −1 ) + nhb = ah(0 + h + 2h L + ( n − 2) h + (n − 1) h) + nhb
第一章 题 12 给定节点 x0 = −1 , x1 = 1 , x2 = 3 , x3 = 4 ,试分别对下列函数导出拉格朗日插 值余项: (1) (1) (2) (2) 解 (1) f
(4)
f ( x) = 4 x3 − 3 x + 2 f ( x) = x 4 − 2 x3 ( x) = 0 ,
1.5
5 ≈ × 9
8 8 5 8 + × + × 2 2 3 9 4 + ( 0 + 1) 9 3 4+− + 1 4+ + 1 5 5 = 3.141068 .
数值分析简明教程第二版课后习题答案(供参考)
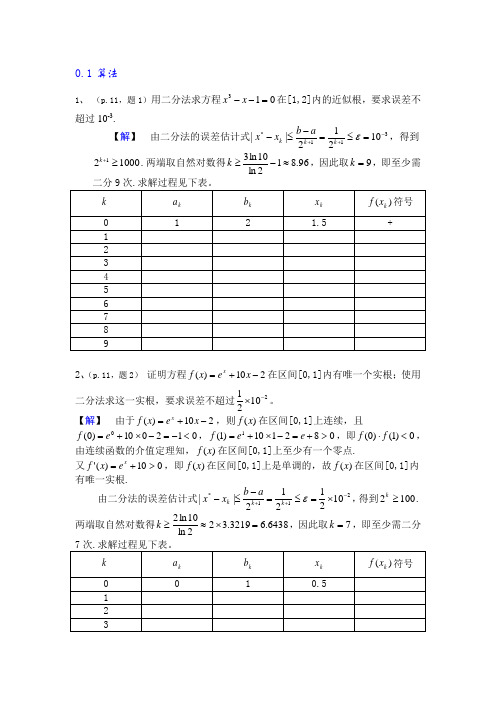
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数值分析简明教程第二版课后习题答案高等教育出版社
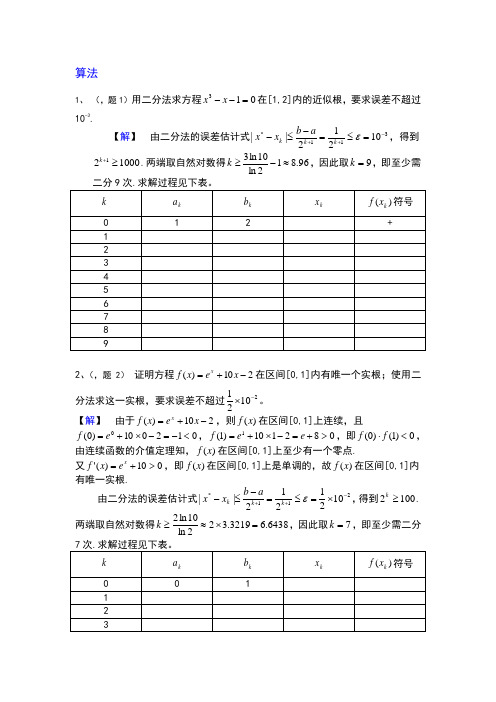
算法1、 (,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分误差1.(,题8)已知e=…,试问其近似值7.21=x ,71.22=x ,x 2=,718.23=x 各有几位有效数字并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数值分析简明教程(第二版)课后习题答案(习题3)

数值分析P97页 习题三 2 解:()()2112230.2()10.210.80.80.20.80.20.80.61440.4613n n n n n y y y x y y y y +=+--=+⨯-==+⨯--⨯==同理,7. 解:()()()22212111,0.1(2)11,0.1(2)112p n n n n n n c n n n n p n n p c y y hf x y y y x y y hf x y y y x y y y +++⎧=+=+⨯-⎪+⎪⎪=+=+⨯-⎨+⎪⎪=+⎪⎩111230.1,0.097,0.09850.1913,0.2737p c y y y y y =====同理,11. 解:()112341213243123412340.2226833830.223830.228330.21, 1.4, 1.58, 1.05,(0.2) 2.30041.0986,0.7692,0.8681,0.5780,(0.4)2.4654n n nn n n y y k k k k k y k y k k y k k y k k k k k y k k k k y +⎧=+⨯+++⎪⎪=-⎪⎪⎪=--⨯⨯⎨⎪⎪=--⨯⨯⎪⎪=--⨯⨯⎪⎩==========同理,13. 解:()()[]()[]()110.220.22321,00,(0.2)0.181(0.4)(0.2)3(0.2)10.1810.1310.18110.3267(0.6)(0.4)3(0.4)(0.2)0.32670.1310.3267(10.181)0.4468n n nn hy y y y y y y y y y y y y y y +-''=+-'=-=='=+-=+⨯⨯--=⎡⎤⎣⎦''=+-=+⨯⨯---=⎡⎤⎣⎦(0.8)0.5454,(1)0.6265y y ==同理,习题四),(,121)('sin 21)('cos 21)(.2∞-∞∈<≤-==x x xx x x ϕϕϕ证明:迭代函数 所以在均收敛。
数值分析简明教程课后习题答案(第二版)
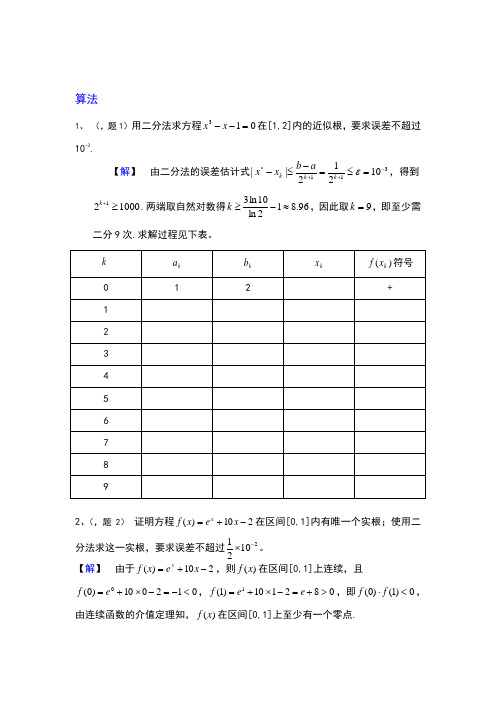
算法1、 (,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需二分9次.求解过程见下表。
2、(,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分7次.求解过程见下表。
误差1.(,题8)已知e=…,试问其近似值7.21=x ,71.22=x ,x 2=,718.23=x 各有几位有效数字并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε;%85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数值分析简明教程第二版(王超能)习题答案24页全解word版[1]
![数值分析简明教程第二版(王超能)习题答案24页全解word版[1]](https://img.taocdn.com/s3/m/b6157a37168884868762d65e.png)
数值分析简明教程第二版(王超能)习题答案24页全解0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
《数值分析简明教程》第二版(王能超 编著)课后习题答案 高等教育出版社

0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数值分析简明教程第二版课后习题答案 高等教育出版社

算法1、 (,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分误差1.(,题8)已知e=…,试问其近似值7.21=x ,71.22=x ,x 2=,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数值分析简明教程(第二版)课后习题答案
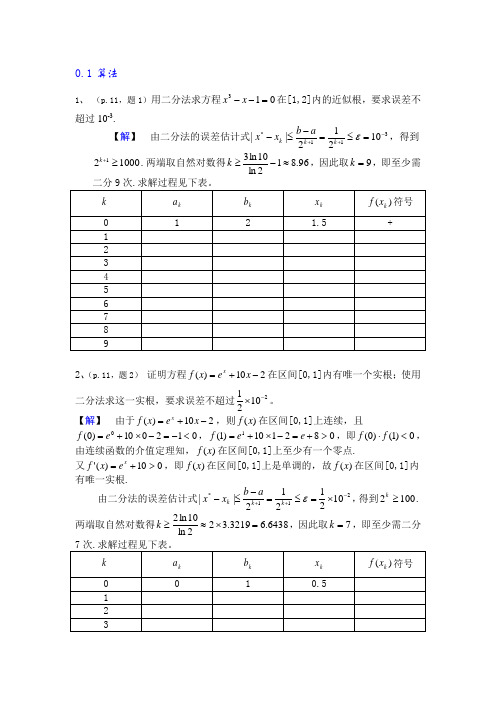
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
《数值分析简明教程》第二版[王能超编著]课后习题答案解析高等教育出版社
![《数值分析简明教程》第二版[王能超编著]课后习题答案解析高等教育出版社](https://img.taocdn.com/s3/m/5c81dc54168884868762d6c3.png)
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε;%0184.0718.20005.0||333=<-=x x e r ε。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需二分9次.求解过程见下表。
2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分7次.求解过程见下表。
0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
评 (1)经四舍五入得到的近似数,其所有数字均为有效数字;(2)近似数的所有数字并非都是有效数字.2.(p.12,题9)设72.21=x ,71828.22=x ,0718.03=x 均为经过四舍五入得出的近似值,试指明它们的绝对误差(限)与相对误差(限)。
【解】 005.01=ε,31111084.172.2005.0-⨯≈<=x r εε; 000005.02=ε,62221084.171828.2000005.0-⨯≈<=x r εε;00005.03=ε,43331096.60718.000005.0-⨯≈<=x r εε;评 经四舍五入得到的近似数,其绝对误差限为其末位数字所在位的半个单位.3.(p.12,题10)已知42.11=x ,0184.02-=x ,4310184-⨯=x 的绝对误差限均为2105.0-⨯,问它们各有几位有效数字?【解】 由绝对误差限均为2105.0-⨯知有效数字应从小数点后两位算起,故42.11=x ,有三位;0184.02-=x 有一位;而0184.01018443=⨯=-x ,也是有一位。
1.1泰勒插值和拉格朗日插值1、(p.54,习题1)求作x x f sin )(=在节点00=x 的5次泰勒插值多项式)(5x p ,并计算)3367.0(5p 和估计插值误差,最后将)5.0(5p 有效数值与精确解进行比较。
【解】由x x f sin )(=,求得x x fcos )()1(=;x x f sin )()2(-=;x x fcos )()3(-=;x x f sin )()4(=;x x fcos )()5(=;x x f sin )()6(-=,所以)(5x p 500)5(200)2(00)1(0)(!5)()(!2)())(()(x x x f x x x f x x x f x f -++-+-+=5)5(2)2()1(!5)0(!2)0()0()0(x f x f x f f ++++= 53!51!31x x x +-=插值误差:)(5x R 66060)6(!61)(!6|)sin(|)(!6|)(|x x x x x f ≤-=-=ξξ,若5.0=x ,则 )3367.0(5p 3303742887.0!53367.0!33367.03367.053≈+-=,而5665105.01002.2!63367.0)3367.0(--⨯<⨯≈≈R ,精度到小数点后5位,故取33037.0)3367.0(5=p ,与精确值 330374191.0)3367.0sin()3367.0(==f 相比较,在插值误差的精度内完全吻合!2、(p.55,题12)给定节点4,3,1,13210===-=x x x x ,试分别对下列函数导出拉格朗日余项:(1)234)(3+-=x x x f ;(2)342)(x x x f -=【解】依题意,3=n ,拉格朗日余项公式为 ∏=-=3)4(3)(!4)()(i i x x fx R ξ(1)0)()4(=x f→ 0)(3=x R ;(2)因为!4)()4(=x f,所以)4)(3)(1)(1()4)(3)(1)(1(!4)()()4(3---+=---+=x x x x x x x x f x R ξ3、(p.55,题13)依据下列数据表,试用线性插值和抛物线插值分别计算)3367.0sin(的近【解】依题意,3=n ,拉格朗日余项公式为 ∏=-=3)4(3)(!4)()(i i x x fx R ξ (1) 线性插值因为3367.0=x 在节点0x 和1x 之间,先估计误差2))(max())((2)sin())((!2)('')(1010101x x x x x x x x x x x x f x R --≤--=--=ξξ 421021201.0⨯=≤;须保留到小数点后4为,计算过程多余两位。
010)(x-x 1)x)(1x P [])sin()()sin()(1)sin()sin(01100110100101x x x x x x x x x x x x x x x x x x -+--=--+--= )(1x P [])32.0sin()3367.034.0()34.0sin()32.03367.0(02.01-+-=[])32.0sin(0033.0)34.0sin(0167.002.01⨯+⨯=3304.0≈(2) 抛物线插值 插值误差:)(2x R ))()((6)cos())()((!3)('''210210x x x x x x x x x x x x f ----=---=ξξ 632101021601.036))()(m ax (-⨯=⨯≈---≤x x x x x x01y=(x-x 0)(x-x 1)(x-x 2)xy 2抛物线插值公式为:)(2x P )sin())(())(()sin())(())(()sin())(())((202120112101200201021x x x x x x x x x x x x x x x x x x x x x x x x x x x ----+----+----=⎥⎦⎤⎢⎣⎡-----+--=)sin(2))(()sin())(()sin(2))((02.012011200212x x x x x x x x x x x x x x x )3367.0(2P[])36.0sin(7555.2)34.0sin(911.38)32.0sin(8445.302.01025⨯-⨯+⨯=- [])36.0sin(7555.2)34.0sin(911.38)32.0sin(8445.302.01025⨯-⨯+⨯=- 33037439.0= 经四舍五入后得:330374.0)3367.0(2=P ,与 330374191.0)3367.0sin(=精确值相比较,在插值误差范围内完全吻合!1.3分段插值与样条函数1、(p.56,习题33)设分段多项式 ⎩⎨⎧≤≤-++≤≤+=211210)(2323x cx bx x x x x x S是以0,1,2为节点的三次样条函数,试确定系数b ,c 的值. 【解】依题意,要求S(x)在x=1节点函数值连续:)1(1111211)1(2323+-=-⨯+⨯+⨯=+=S c b S ,即:)1(1=+c b一阶导数连续: )1(12161213)1('22'+-=+⨯⨯+⨯=⨯+⨯=S c b S ,即:)2(12-=+c b解方程组(1)和(2),得3,2=-=c b ,即⎩⎨⎧≤≤-+-≤≤+=21132210)(2323x x x x x x x x S由于)1(221262123)1(''''+-=⨯-⨯⨯=+⨯⨯=S S ,所以S(x) 在x=1节点的二阶导数亦连续。
2、 已知函数211xy +=的一组数据,2,1,0210===x x x 和2.0,5.0,1210===y y y ,(1)求其分段线性插值函数;(2)计算)5.1(f 的近似值,并根据余项表达式估计误差。
【解】(1)依题意,将x 分为[0,1]和[1,2]两段,对应的插值函数为)()(21x S x S 和,利用拉格朗日线性插值公式,求得15.05.00101101)(101001011+-=⨯--+⨯--=--+--=x x x y x x x x y x x x x x S ;8.03.02.01215.0212)(212112122+-=⨯--+⨯--=--+--=x x x y x x x x y x x x x x S(2) 93076923076.05.111)5.1(2≈+=f ,而 35.08.05.13.0)5.1(2=+⨯-=S ,实际误差为:05.00423.0|)5.1()5.1(|2≤=- S f 。
由422)3(322)2(22)1()1()1(24)(,)1()31(2)(,)1(2)(x x x x fx x x fx xx f+-=+--=+-=,可知5.0)1()2(2==f M ,则余项表达式5.00625.05.05.0!2|)2)(1(|!2|)(|)(422)2(≤==⨯≤--=M x x f x R ξ1.4 曲线拟合1、(p.57,习题35)用最小二乘法解下列超定方程组:⎪⎪⎩⎪⎪⎨⎧=+=+=-=+72623531142y x y x y x y x 【解】 构造残差平方和函数如下: 2222)72()62()353()1142(),(-++-++--+-+=y x y x y x y x y x Q ,分别就Q 对x 和y 求偏导数,并令其为零:0),(=∂∂x y x Q : )1(176=-y x ,0),(=∂∂yy x Q : )2(48463=+-y x ,解方程组(1)和(2),得24176.1273173486,04029.3273481746≈⨯+⨯=≈+⨯=y x2、(p.57,习题37)用最小二乘法求形如2bx a y += 的多项式,使之与下列数据相拟合。
