一种简化动态矩阵控制的仿真研究
控制系统仿真(sumulink)

第六章控制系统仿真控制系统仿真一般采用如下两种形式进行仿真分析:针对单输入—单输出系统的信号流图形式面向多输入—多输出系统的状态空间形式控制系统仿真的主要研究内容是通过系统的数学模型和计算方法,编写程序运算语句,使之能自动求解各环节变量的动态变化情况,从而得到关于系统输出和所需要的中间各变量的有关数据、曲线等,以实现对控制系统性能指标的分析与设计。
一般地来说,实现控制系统的仿真有以下几个步骤:1、根据建立的数字模型以及计算机精度和时间等要求,确定采用的数值计算方法;2、将数学模型按算法要求通过分解、综合、等效变换等方法转换成适于在计算机上运行的公式、方程等;3、用合适的开发语言进行算法编程和实现;4、通过上机运行调试,不断加以改进,使之正确反映系统各项动态性能指标,并得到理想的仿真结果。
围绕以上步骤,控制系统仿真近年来不断发展,不断更新,基于MATLAB语言开发的专门应用于控制系统分析与设计的工具箱,对控制系统仿真技术的发展及应用起到巨大的推动作用。
本章主要是围绕着控制系统仿真实现的问题,研究仿真的几种常用方法,主要包括:基于状态空间法的系统仿真、非线性系统的仿真以及离散系统的仿真,并重点阐述了Simulink动态仿真软件的操作与应用。
希望通过本章的学习使大家能够较系统地了解目前控制系统仿真领域的研究方法和实现手段,并从中掌握基本的系统仿真实现的技巧和能力。
6.1 状态空间法系统仿真控制系统的动态模型经常是转化成以状态方程的形式给出的,一般采用四阶龙格-库塔数值积分方程算法进行求解与分析仿真,这就是状态空间法仿真的基本方法。
一、四阶龙格-库塔(Runge-Kutta)法闭环控制系统最常见的两种描述方式为:传递函数法和状态空间法,而且这128两种方法之间可以相互转换。
如果系统是由传递函数来描述的,则应用??的转换方法,可以方便地将传递函数表达式转换成状态空间表达式。
已知系统的状态方程为:=+=Cxy Bu Ax x(6-1)其中A 、B 、C 为系统的系数矩阵,由式(6-1)可知系统为一阶微分方程组的矩阵表达式,因此采用四阶龙格-库塔法进行求解和仿真,其求解步骤和方法如下:1、由Bu Ax x+= ,可知Bu Ax x t f +=),(; 2、根据四阶龙格-库塔法的递推公式:++++=++=++=++==+)22(6),()2,2()2,2(),(43211n 3423121k k k k h x x hk x h t f k k h x h t f k k h x h t f k x t f k n n n n n n k n n (6-2)其中,k ,k ,k 为对应n 维状态空间变量的四组导数,每组为n 维列向量。
预测控制MATLAB仿真与设计

动态矩阵控制算法实验报告院系:电子信学院姓名:***学号:*********专业:控制理论与控制工程导师:***MATLAB环境下动态矩阵控制实验一、实验目的:对于带有纯滞后、大惯性的研究对象,通过动态控制矩阵的MATLAB的直接处理与仿真实验,具有较强的鲁棒性和良好的跟踪性。
输入已知的控制模型,通过对参数的选择,来取的良好的控制效果。
二、实验原理:动态矩阵控制算法是一种基于被控对象非参数数学模型的控制算法,它是一种基于被控对象阶跃响应的预测控制算法,以对象的阶跃响应离散系统为模型,避免了系统的辨识,采用多步预估技术,解决时延问题,并按照预估输出与给定值偏差最小的二次性能指标实施控制,它适用于渐进稳定的线性对象,系统动态特性中存在非最小相位特性或纯滞后都不影响算法的直接使用。
三、实验环境:计算机 MATLAB2016b四、实验步骤:影响控制效果的主要参数有:1)采样周期T与模型长度N在DMC中采样周期T与模型长度N的选择需要满足香农定理和被控对象的类型及其动态特性的要求,通常需要NT后的阶跃响应输出值接近稳定值。
2)预测时域长度PP对系统的快速性和稳定性具有重要影响。
为使滚动优化有意义,应使P 包含对象的主要动态部分,P越小,快速性提高,稳定性变差;反之,P越大,系统实时性降低,系统响应过于缓慢。
3)控制时域长度MM控制未来控制量的改变数目,及优化变量的个数,在P确定的情况下,M越小,越难保证输出在各采样点紧密跟踪期望输出值,系统响应速度缓慢,可获得较好的鲁棒性,M越大,控制机动性越强,改善系统的动态性能,但是稳定性会变差。
五、实例仿真(一)算法实现设GP(s)=e-80s/(60s+1),采用DMC后的动态特性如图1所示,采样周期T=20s,优化时域P=10,M=2,建模时域N=20。
MATLAB程序1:g=poly2tfd(1,[60 1],0,80);%通用传函转换为MPC模型delt=20; %采样周期nt=1; %输出稳定性向量tfinal=1000; %截断时间model=tfd2step(tfinal,delt,nt,g);%传函转换为阶跃响应模型plant=model;%进行模型预测控制器设计p=10;m=2;ywt=[];uwt=1;%设置输入约束和参考轨迹等控制器参数kmpc=mpccon(plant,ywt,uwt,m,p);%模型预测控制器增益矩阵计算tend=1000;r=1;%仿真时间[y,u,yrn]=mpcsim(plant,model,kmpc,tend,r);%模型预测控制仿真t=0:20:1000;%定义自变量t的取值数组plot(t,y)xlabel(‘图一DMC控制动态响应曲线(time/s)’);ylabel(‘响应曲线’);结果如下:Percent error in the last step response coefficientof output yi for input uj is :2.2e-05%Time remaining 1000/1000Time remaining 800/1000Time remaining 600/1000Time remaining 400/1000Time remaining 200/1000Time remaining 0/1000Simulation time is 0.003 seconds.结论:采用DMC后系统调整时间减小,响应的快速性好,无超调。
第4章 动态矩阵控制_2010

∑ a Δu (k + j − i)
i
+ aN Δu (k + j − N ), ( j = 1, 2,
y0 (k + j k ) =
, n)
(4-4)
上式右端的后二项即为过去输入对输出n步预测值,记为
i = j +1
∑ a Δu (k + j − i) + a
i
N −1
N
2010-2-17
第4章 动态矩阵控制
10
南京信息工程大学信息与控制学院 南京信息工程大学信息与控制学院
2010-2-17
第4章 动态矩阵控制
11
南京信息工程大学信息与控制学院 南京信息工程大学信息与控制学院
2010-2-17
第4章 动态矩阵控制
12
南京信息工程大学信息与控制学院 南京信息工程大学信息与控制学院
14
南京信息工程大学信息与控制学院 南京信息工程大学信息与控制学院
2010-2-17
第4章 动态矩阵控制
四、DMC的主要特征和优点
(一)DMC的主要特征
(1)预测模型采用阶跃响应特性建模; (2)设计过程中固定格式是:用二次型目标函数决定最优 值增量序列,考虑到各种约束条件时,求最优解相当费时; (3)参数调整:用改变二次型目标函数中的权系数阵Q, R来实现。
2
南京信息工程大学信息与控制学院 南京信息工程大学信息与控制学院
2010-2-17
第4章 动态矩阵控制 一、 预测模型
从被控对象的阶跃响应出发,对象动态特性用一 系列动态系数 a1 , a2 , , aN 即单位阶跃响应在采样时刻的 值来描述,p称为模型时域长度,aN是足够接近稳态 值的系数。
机器人控制系统的建模与仿真方法研究

机器人控制系统的建模与仿真方法研究随着科技的不断进步,机器人技术的发展迅猛,机器人在各个领域的应用越来越广泛。
为了实现高效、稳定的机器人行为控制,建立准确的控制系统模型和进行仿真研究是至关重要的。
本文旨在探讨机器人控制系统的建模与仿真方法,介绍常用的建模方法,并分析仿真模型的建立及其应用。
一、机器人控制系统的建模方法1. 几何模型法几何模型法是一种常用的机器人控制系统建模方法。
该方法通过描述机器人的几何形状、关节结构和运动轨迹,建立机器人系统的几何模型。
常用的几何模型包括DH法、SDH法和Bishop法等。
其中,DH法是最经典的一种方法,通过参数化建立机器人的运动学模型,用于描述关节变量和坐标系之间的关系,从而实现机器人的运动规划和控制。
2. 动力学模型法动力学模型法是一种更加复杂而全面的机器人建模方法。
该方法基于牛顿运动定律和动力学原理,综合考虑机器人的质量、惯性、关节力矩和外力等因素,建立机器人系统的动力学模型。
动力学模型法可以更准确地描述机器人的运动和力学特性,对于复杂的机器人控制任务具有重要意义。
3. 状态空间模型法状态空间模型法是一种抽象程度较高、数学表达简洁的机器人控制系统建模方法。
该方法通过描述机器人系统的状态以及状态之间的转移规律,以矩阵的形式进行表示。
状态空间模型法适用于系统动态特性较强、多输入多输出的机器人系统,能够方便地进行控制器设计和系统分析。
二、机器人控制系统的仿真方法1. MATLAB/Simulink仿真MATLAB/Simulink是一种广泛应用于机器人控制系统仿真的工具。
Simulink提供了丰富的模块库和仿真环境,可以方便地构建机器人系统的仿真模型,并进行系统的可视化、实时仿真和参数调整。
通过Simulink,我们可以对机器人的运动学和动力学模型进行建模,并通过调整控制参数来优化机器人的控制性能。
2. 三维虚拟仿真三维虚拟仿真是一种直观、真实的机器人控制系统仿真方法。
纸机定量水分动态矩阵控制参数设计的仿真研究

№. 5 Vo. 4 12
陕 西科 技 大学 学 报
J OURNAL OF S HAANXIUNI RSI VE TY CI OF S ENC 8 E LTECHNOLOGY
0c .2 06 t 0
・
6 ・ 3
文 章 编 号 :O O 8 1 2 0 )5 0 6 - 0 1O 一5 1 {0 6 O — 0 3 5
量:
2 D MC算 法的 S MUL NK 实 现 I I
按D MC算 法 , MAT AB语 言 的 S MUL NK仿 真 工具箱 中建 立 了纸机 D 在 L I I MC控 制 的仿 真结 构 图 , 并 在 MATL AB的 D b re中按 该 DMC算 法计 算 出各模 块 的参 数 值 , stp rm 命令 向仿 真结 构 图 中 e ug 由 e— aa
收 稿 日期 :0 6 0 — 1 20 — 5 4
作者简介 : 朝霞(92 )女, 陈 1 7 一 , 贵州 省 锦屏 县 人 , 师 , 士 , 究 方 向 : 纸 过程 自动 化 讲 硕 研 造
维普资讯
・ 4 6 ・
陕 西 科 技 大 学 学 报
可知 : N<4 当 0时 , 值 的增 大对 系统 性能 的影 响非 常 明显 , N> 4 N 当 O以后 , 值 的增大对 超调 量 几乎 无 N
影 响 , 调整 时 间的影 响也 趋 于平缓 , 对 因而决定 模 型长度 N 取 4 。 0
控制( DMC 算 法 , ) 分析 了 DMC算 法 中各 参数 对纸机 控 制性 能的影 响 。结果 显示 , 3参数 选取 " - 合理 时控 制 系统具有 良好 的稳 定性 、 鲁棒 性和 抗干扰 性 能 。
利用半实物仿真技术的动态矩阵控制研究与实现

( T i a n j i n Ke y L a b o r a t o r y f o r C o n t r o l T h e o r y a n d A p p l i c a t i o n s i n C o mp l i c a t e d S y s t e ms , S c h o o l o f E l e c t r i c a l E n g i n e e r i n g ,
T i a n j i n Un i v e r s i t y o f T e c h n o l o g y , Ti a n j i n 3 0 0 3 8 4 , C h i n a )
Ab s t r a c t : To s o l v e t h e p r o b l e m t h a t t h e d y n a mi c ma t r i x c o n t r o l a l g o r i t h m i s l i mi t e d b y t h e h a r d wa r e e q u i p me n t a n d c o n t r o l l e d p r o c e s s ,t h e r e s e a r c h t e c h n i q u e a n d i mp l e me n t i n g p r o c e s s o f h a r d wa r e - i n - l o o p s i mu l a t i o n i s p u t f o r wa r d .Ta k i n g u s e o f t h e d i s — t r i b u t e d c o n t r o l s y s t e m ( DC S)wh i c h i s b u i l t b y h a r d wa r e - i n - l o o p s i mu l a t i o n t e c h n o l o g y ,t h e r e s e a r c h a n d i mp l e me n t a t i o n o f t h e d y n a mi c ma t r i x c o n t r o l a l g o r i t h m b a s e d o n t h e me t h a n o l p r o d u c t i o n s i mu l a t i o n mo d e l t h r o u g h a d v a n c e d c o n t r o l s t a t i o n,e n g i n e e r
基于MATLAB多变量DMC算法的仿真技术研究

基于MATLAB多变量DMC算法的仿真技术研究摘要:利用MATLAB开发系统的仿真程序,以试验室的CSTR模型为研究对象,用动态矩阵控制算法建立仿真模型,实现多输入多输出系统的控制,绘制出调节曲线,分析各个参数对系统性能的影响。
结果表明,该控制算法得到较好的控制效果。
关键词:机理建模动态矩阵控制(DMC) CSTR系统过程控制在工业生产中广泛应用着各种反应器,连续搅拌反应是非常重要的反应过程,能代表许多反应系统的特性。
同时,连续搅拌反应器(CSTR)模型比其他连续反应器类型简单。
控制系统大多为多变量控制,各被控量与输出量之间有紧密的联系,而且被动对象有较大的时间滞后,PID算法不能达到控制要求。
1 连续搅拌反应器及其数学模型1.1 CSTR过程分析用连续搅拌反应器实现冷热水混合,Q1、Q2、T1、T2分别为热水和冷水的流量及温度。
温度、液位具有较强的耦合性,冷水、热水分别流入冷热水的水槽,进入混和器进行混合。
控制进水电磁阀的开度,调节温度和液位。
1.2 机理建模建模是基于以下假设:(1)1号容器和2号容器中的液体为同种液体;(2)3号容器中的冷热液体混合均匀。
根据物料守恒定律(见式1):根据能量守衡定律:3号容器中液体单位时间内热量的变化率应等于1号容器和2号容器单位时间内带入的热量,减去3号容器流出液体带走的热量,见式(5):2 动态矩阵控制动态矩阵控制(DMC)是预测控制的一种。
DMC算法以系统的的阶跃响应模型作为内部模型,适用于渐进稳定的线性对象。
对于非线性对象,可以在工作点处线性化,包括模型预测控制、滚动优化和反馈校正等技术方法。
2.1 控制器设计温度和液位具有较强的耦合性,而且有较长的时间滞后。
因此,对温度和液位的控制通常采用DMC预测控制算法,得到的控制量不直接加到控制对象上,而是把由液位偏差经DMC算法得到的控制量作为控制注入水的流量,把由温度偏差经DMC算法得到的控制量作为控制注入水量的参考值。
针对不稳定对象的改进动态矩阵控制

针对不稳定对象的改进动态矩阵控制张诚;佃松宜【摘要】针对一般动态矩阵控制算法不能直接用于不稳定对象这一问题,提出一种改进的动态矩阵控制设计方法。
该方法先设计由内环控制器构成的反馈环节来稳定对象,再对稳定后的对象进行动态矩阵控制设计。
采用现代频域法中的传递函数互质分解法设计内环控制器,并对设计的内环控制器进行抗扰性能和鲁棒性能的H2优化,优化后的内环控制器可独立地调节系统的抗扰性,也能有效地改善系统的鲁棒性。
通过 Matlab仿真实验与现有方法进行比较,结果表明:本文方法能明显改善系统的鲁棒性和抗扰性。
%Considering the fact that dynamic matrix control algorithm fails to be directly used for unstable ob-jects,an improved dynamic matrix control was proposed,of which,the inner-loop controller constitutes a feed-back loop to stabilize the objects and then designs a dynamic matrix control for it.Making use of coprime fac-torization method,the inner-loop controller was designed and optimized in H2 for a disturbance rejection and robustness.The results of Matlab simulation show that the optimized inner-loop controller can independently adjust disturbance rejection performance and obviously improve system’s robustness.【期刊名称】《化工自动化及仪表》【年(卷),期】2014(000)011【总页数】3页(P1229-1231)【关键词】动态矩阵控制;不稳定对象;互质分解法【作者】张诚;佃松宜【作者单位】四川建筑职业技术学院,四川德阳 618000;四川大学,成都610065【正文语种】中文【中图分类】TH70120世纪70年代中期,动态矩阵控制(Dynamic Matrix Control,DMC)就应用在美国壳牌石油公司的生产装置上[1,2]。
基于动态矩阵预测控制的油田污水处理系统的仿真研究

Gu a n Fe n g,Li Z h e n l i n
( Ma c h i n e r y& S t o r a g e& Tr a n s p o r t a t i o n E n g i n e e r i n g I n s t i t u t e 。 C h i n a Un i v e r s i t y o f P e t r o l e u m, B e i j i n g ,1 0 2 2 0 0 , C h i n a )
研究 。结果表明 : 基于该方法的控制系统 具有强抗 干扰性 , 快 速响应性 , 良 好 的鲁棒性 , 稳态误差小等特点 , 对油 田污水处理系 统智能控制技术的发展具 有促进作用 。
关键 词 : 动态矩阵
预测控制
油田
污水处理系统
仿真
中图分类号 : T P 2 7 3
文献标志码 : A
Ab s t r a c t :Co n t r a p o s e t o t h e d i s a d v a n t a g e o f l o w a u t o ma t i o n l e v e l o f o i l f i e l d s e wa g e t r e a t me n t s y s t e m a n d c o mp l e x s y s t e m a n d d i f f i c u l t y t o e s t a b l i s h a c c u r a t e ma t h e ma t i c a l mo d e 1 ,a me t h o d b a s e d o n d y n a mi c m a t r i x p r e d i c t i v e c o n t r o l i s p u t f o r wa r d, a n d s i mu l a t i o n a n a l y s i s i s p r o c e s s e d . Th e b a s i c p r i n c i p l e o f d y n a mi c ma t r i x p r e d i c t i v e c o n t r o l a n d s i mu l a t i o n r e s e a r c h b a s e d o n o i l f i e l d s e wa g e t r e a t me n t s y s t e m ma t h e ma t i c a l mo d e l a r e ma i n l y e x p o u n d e d . Th e r e s u l t s s h o w t h a t t h e c o n t r o l s y s t e m b a s e d o n t h i s me t h o d h a s c h a r a c t e r i s t i c s o f s t r o n g a n t i — i n t e r f e r e n c e ,f a s t r e s p o n s e ,g o o d r o b u s t n e s s a n d s ma l l s t e a d y - s t a t e e r r o r . I t wi l l l a r g e l y
动态矩阵算法控制的仿真研究

a近 似 、
化 I、 力 冶金 机械 等 l .电 k 部门得到 了成 功的应
用
等 口 阶跃 响应的稳态 缸 . 1t 成的数批I 象 rI 1 构 f J j
a …a1 称 为模型 墩 、。
1预测控制的基本原 理
预洲控 制硅 ・ 新 n l 种 " 算机 制 算法, R 使
航 空控 制q 取得
邦 恃 制
r 大的成功 . 很 但 在 1I 制中f t N 性 ¨益 叫妊 、 、控 l4 :  ̄
现 以动态矩 阵控制 ( M D C)为例 .说 J 项删控 制
的 丛奉原 .如I 所, 萼l I
(】 I 按现代控制 论}汁控制 系统 时.要求 建 讧 殳
实现有效控 制
J 考 迹l 参轨
l
对象
L一预 模 — 渊
吲 l I 柚 患 咋 … 职
7 0年代以来 , 一种新 蜊的控制方法——预 测控制
的问 l 在T业 J r -受到 广泛 欢迎 ,j 已往打油 、 ・ H1 ・ t
存 D C・. ‘ M { 先需‘ I 婴测定 对象 l位阶跃 响啦的 采样值 H() Il .一.N N 建模时域 ._= , f 2
维普资讯
奠木蕾曩
c. 一o‘ . o● rIolua r  ̄ 4
酗 缒阵 濯控制的仿 真酬究
S n lt n a d Re e r h Ba e n Dy a c Marx Co to g rl m im a i n s a c s d o n mi ti n r lAI o ih o
近 儿十年来.以状 态 f 法 为核心 内容的现代控 i t J 制删论收 得 / 凡的 啦展 .在航 很
动态矩阵控制MATLAB代码

动态矩阵控制MATLAB代码1 %预测控制书上的P79例5-1得到的输出曲线趋近于⽆穷不对不知错误在哪⾥ pid控制器也是趋近于⽆穷⼤2 %不明⽩采样周期Ts怎么⽤,什么意思3 %将阶跃响应离散状态空间模型的采样周期都设为Ts=5预测步长P=50 M=1都有了很好的效果4 %所以有两个重要的参数:采样周期Ts 预测步长P 还有M参数的作⽤,要弄清楚5 clear all6 %传递函数模型7 %{8 num=[8611.77];9 p1=[1,1.1,36.3025];10 p2=[1,0.5,237.2225];11 den=conv(p1,p2);12 sys=tf(num,den);13 %}14 sys=tf(0.6,[2400851]);1516 Ts=5;%Ts为采样周期17 delay=0;%延迟时间即纯滞后模块18 startvalue=0;%系统初始输出值19 x1=startvalue;20 x2=0;21 c=3;%阶跃值22 pipestartvalue=0;%管温初始值23 step1=101;%仿真长度注意变量名字不能与MATLAB中的函数名相同否则函数不能再调⽤24 %P=50;%效果最好之前⼀直不稳定可能是因为P取得太⼩或者是采样周期T保持了⼀致25 %M=1;26 P=50;27 M=1;28 Q=eye(P);%构造预测输出误差加权矩阵29for i=1:1:delay30 Q(i,i)=0;31 end %预测输出误差加权阵,对应纯滞后长度的权值为032 S=zeros(P);%构造移位矩阵33for i=1:1:P34if i<P35 S(i,i+1)=1;36 end37if i==P38 S(P,P)=1;39 end40 end41 R1=eye(M);%构造控制增量加权矩阵R42 %R=0.1*R1;43 R=0.0*R1;44 HT=linspace(1,1,P);45 H=HT';%构造误差校正向量46for i=2:1:P47 H(i)=0.9;48 end49 d1=linspace(0,0,M);%构造向量d50 d1(1)=1;51 d=d1;5253 %给单位阶跃响应序列a1赋值54 %{55for i=1:1:step156 a11(i)=1*(1-exp(-i*T/60));%采样周期T57 end58 figure59 plot(a11);title('阶跃响应1');60 %}61 t=0:5:500;62 %t=0:0.5:100;63 [a11,t0]=step(sys,t);%横轴时间与书上的数量级相差太⼤,不知原因64 figure65 plot(a11);title('阶跃响应step');66 %{67for i=1:1:4068 a11(i)=a1(10*i);%为了与书上的数量级保持⼀致乘以系数求预测模型参数书上的例5-169 end70 %}71 %{72 a1=1-1.1835*exp(-0.55*t).*sin(6*t+1.4973)-0.18038*exp(-0.25*t).*sin(15.4*t-1.541);73 figure74 plot(a1);title('表达式求得的阶跃响应');75 %}7677 %计算AT A为动态矩阵,AT为其转置78for i=1:1:P79for j=1:1:M80if j<=i81 A(i,j)=a11(i-j+1);82 end83if j>i&j<M84 A(i,j)=0;85 end86if i>M87 A(i,j)=a11(i-j+1);88 end89 end90 end91 AT=A';92 %计算DT93 DT=d*inv(AT*Q*A+R)*AT*Q;%计算得到控制向量DT94 a=a11(1:P);%计算a列向量95 %a=a';% %96 qu1=linspace(0,0,P);97 qu1(1)=1;%构建取1向量98for i=1:1:step199 Uk(i)=0;%初始化UK,⽤来记录控制量100 Yk1(i)=0;%初始化Yk1,⽤来记录实际仿真输出值101 end102 Uk=Uk';103 Yk1=Yk1';104for i=1:1:P105 Y0(i)=startvalue;%初始化106 Yp0k1(i)=0;107 Ycork1(i)=0;108 end109 Y0=Y0';110 Yp0k1=Yp0k1';111 Ycork1=Ycork1';112 y1k1=0;113 daltauk=0;%初始化控制增量114 uk1=pipestartvalue;% 0115 uk2=0;116 yk1=0;117 yk2=0;118for n=1:1:step1+90119 %x2=(0.98^(n*1))*1+(1-0.98^(n*1))*c;%参考轨迹参数a=0.992120 %x1=x2;121 Yrk1(n)=3;%计算参考轨迹yrk1,记录到Yrk1(i)122 %参考轨迹设为定值3 可以看出PID控制器输出有超调,⽽DMC可以快速稳定的达到设定值⽆超调123 end124 Yrk1=Yrk1';125 %仿真第⼀步126 Yp0k1=Y0;127 TempYrk1=Yrk1(1:P);128 daltauk=DT*(TempYrk1-Yp0k1);129 uk2=uk1+daltauk;%计算当前控制量uk130 uk1=uk2;131 Uk(1)=uk1;132 Yk1(1)=Y0(1);%第⼀步采样值保存到Yk1133 yk1=Y0(1);%第⼀步不⽤移位操作,直接取实际系统的输出值作为预测值134 Y1k1=Yp0k1+a*daltauk;%⼀步预测135 %{136 %Ts=5;137 As=[ -1.6,-17.13,-2.18,-8.41;16,0,0, 0; 0,8,0,0;0,0,8,0];%状态空间⽅程系数138 As=eye(4)+As*Ts;139 Bs=[4;0;0;0];140 Bs=Bs*Ts;141 Cs=[0,0,0,2.102];142 xs0=[0;0;0;0];143 xs1=[0;0;0;0];144 %}145146 %Ts=5;147 As=[-0.03542,-0.02667;0.01563,0];148 As=eye(2)+As*Ts;149 Bs=[0.125;0];150 Bs=Bs*Ts;151 Cs=[0,0.128];152 xs0=[0;0];153 xs1=[0;0];154155 %第⼆步及其以后的仿真156for i=2:1:step1157 %前15步,由于纯滞后,所以输出为0158 %if i<=delay159 %采样 yk1160 %yk2=-0.01667*yk1+0.125*0.1333*0;%对象离散模型161 %yk2=-0.2315*yk1+0.6991*0;162 %end163 %if i>delay164 %yk2=-0.01667*yk1+0.125*0.1333*Uk(i-delay);%离散模型的参数165 %yk2=-0.2315*yk1+0.6991*Uk(i-delay);166 %end167 xs1=As*xs0+Bs*uk1;168 yk2=Cs*xs1;169 xs0=xs1;170171 %if yk2<=startvalue172 % yk2=startvalue;173 %end174 yk1=yk2;175 Yk1(i)=yk1;%采样结束,并保存到Yk1中176 Y0k1=Y1k1;177 y1k1=qu1*Y0k1;%计算y1k1,即Y0k1的第⼀个元素178 Ycork1=Y0k1+H*(yk2-y1k1);%计算校正预测值179 Yp0k1=S*Ycork1;%移位,计算初始预测值180 TempYrk2=Yrk1(i:i+P-1);181 daltauk=DT*(TempYrk2-Yp0k1);182 uk2=uk1+daltauk;183 %{184if uk2>4;185 uk2=4;186 end187 %}188if uk2<0189 uk2=0;190 end191192 uk1=uk2;193 Uk(i)=uk1;194 Y1k1=Yp0k1+a*daltauk;%⼀步预测195 end196 Yrklend=Yrk1(1:step1);%整理计时器值,做曲线时使⽤197 figure198 x=Ts*(1:step1);199 plot(t,Yrklend,t,Yk1);%将实际输出与期望输出两条曲线画在⼀张图中,要保证⼆者⽮量长度相同200 title(['预测时域P=',num2str(P)]);201202 %以下为增量式PID控制算法203 y(1)=0;204 kp=0.35; % 0.4效果会好⼀些曲线形式相同205 ki=0.1; % 0.54206 kd=0.62; % 0.2207 actual=0;208 e=0;209 e1=0;210 e2=0;211 uk0_pid=0;212 x0=[0;0];213 x1=[0;0];214215for i=1:1:step1-1216 e=Yrk1(i)-actual;217 %e=set-actual;218 increase=kp*(e-e1)+ki*(e)+kd*(e-2*e1+e2);219 uk_pid=uk0_pid+increase;220 %y(i+1)=-0.2315*y(i)+0.6991*uk_pid;%离散模型参数离散模型参数可由传递函数得到ss(system) 221222 x1=As*x0+Bs*uk_pid;223 y(i+1)=Cs*x1;224 x0=x1;225226 e1=e;227 e2=e1;228 actual=y(i+1);229 uk0_pid=uk_pid;230 nums(i)=e;231 end232 Yrklend=Yrk1(1:step1);233 x=1.*(1:step1);234 figure235 plot(x,Yk1,'b',x,y,'r');%将DMC控制与PID控制的输出值,画在⼀张表上进⾏⽐较236 title(['预测时域P=',num2str(P)]);237 figure238 plot(x,y,'r');title(['采样周期Ts=',num2str(Ts)]);%PID控制器输出曲线注意参数的选择,尤其是采样周期Ts,控制时域P,⼀般都是先选定M,再调整P。
动态矩阵控制算法的仿真研究及PLC应用

动态矩阵控制算法的仿真研究及PLC应用吴海中;田沛【摘要】针对具有大迟延、大惯性、时变和非线性等特性的主汽温系统,传统PID 已无法满足工业生产的需要.采用动态矩阵控制(DMC)算法,对主蒸汽温度系统进行控制仿真,并利用西门子S7-300 PLC的S7-SCL语言,将DMC算法封装成可供用户调用的功能块,完成了DMC算法的PLC实现.为了增强主蒸汽温度控制系统的抗干扰性,将DMC算法与PID控制策略相结合,设计了DMC-PID串级控制结构,以充分发挥DMC对大延迟对象适应能力强和PID抗干扰能力强的优点.针对主汽温系统时变和非线性的特性,在DMC算法中添加了模型切换策略,完成了对主汽温系统多模型控制的仿真,实现了不同模型之间平滑切换.引入性能指标,通过粒子群算法对DMC控制参数进行优化,结合国电智深EDPF-NT DCS系统,对荥阳电厂主汽温系统进行控制试验.试验结果表明,DMC算法在主汽温控制系统中具有着良好的控制效果,提高了系统动静态性能指标.【期刊名称】《自动化仪表》【年(卷),期】2018(039)003【总页数】5页(P31-34,38)【关键词】主汽温系统;DCS;DMC算法模块;优化控制站;PLC;串级控制;多模型控制;动态矩阵控制【作者】吴海中;田沛【作者单位】华北电力大学控制与计算机工程学院,河北保定071003;华北电力大学控制与计算机工程学院,河北保定071003【正文语种】中文【中图分类】TH861;TP2730 引言工业生产中,一些惯性较大的系统具有非线性、时变等[1]特点,容易被各种因素干扰。
尤其是近年来电厂向大容量发电机组发展[2],对控制系统的要求越来越高,传统PID算法已难以满足工业生产的需要[3]。
而基于传统方法的系统模型最优控制方案,在工业现场往往无法实现最优控制[4]。
由于预测控制对被控对象模型要求不高,现代控制理论很难在过程工业中得到广泛应用[5],其主要原因就是需要高精度的对象模型。
基于Matlab的Simulink结构动力仿真方法探究

闰欣 宇 , 杨睿珊 2
( 1 . 西南 科 技大 学 土木 工程 与建 筑学 院 , 四川绵 阳 6 2 1 0 1 0; 2 . 西 南科 技大 学 外 国语 学 院 , 四川 绵 阳 6 2 1 0 1 0 )
变化 的位移 函数 。用振 型分解 法求解该 运动方程 , 对 于多 自 由度体 系 , ( f )= x q ( t )
在上式 中 :
l
k :[ 1 , 1 , 1 , 1 , 1 , 1 , 1 ] 4 . 2 e 7 ; %层 间刚 度根 据 D值法 可
计算 出各层 刚度
( t )= 抽( t ) 可 以这样理解 上式体 系 的位移 可 以看作 是 由各个振 型
1 结构 动力 学方 程
Ma t l a b是 M a t r i x L a b o r a t o r y的简称 , 意为 是矩 阵实 验室 。 顾名思 义 Ma t l a b 是 以计算 矩阵和数组为核心软件 , 对矩 阵迭
代 编程 计算 的功 能相 当强 大。S i m u l i n k是 Ma t l a b中一 个用 来对 动态系统进行建模 、 仿 真和分析 的软 件包 , 它具有 直观 、
简便 、 易于理解 的特点 。本 文 采用 振型 分解法 计算 其振 型 ,
分别乘 以相 应组 合 系数 q ( t ) , g ( t ) 后 叠加 而成 。换 句 话
【 摘 要】 M a t l a b 是 当今科 学应用 中最优秀 的软件之 一 , 它具 有强大的科学计算和 可视化功 能 , 简单且
易于操作 , 特 别是 其拥 有 3 0多种 不 同领域 的 工具箱 。S i m u l i n k是 Ma t l a b的重要 组件 之一 , 它提 供 的动 态 系 统建模 , 仿真 对于求解结构动力反应在结构振动控 制 方面尤为 简便 。通过 M a t l a b使 用振型 分解 法对结构 进 行 S i m u l i n k 仿真, 再与 S a p 2 0 0 0建立 的框 架平 面模 型进行 时程 分析 , 再 与模型进 行 比较 , 说 明 了该 方法 的实
简化DMC解耦控制及其仿真研究

简化DMC解耦控制及其仿真研究
李玉红;刘红军;王东风;韩璞
【期刊名称】《华北电力大学学报(自然科学版)》
【年(卷),期】2004(031)004
【摘要】基于文献[6]提出的简化算法的思想,根据控制增量的变化趋势提出了动态矩阵解耦控制的简化算法,给出两种设计方案,该方案使多变量动态矩阵控制算法中的矩阵求逆运算简化为数的求逆(倒数)运算,运算量大大减少,运算速度大大提高,并针对单元机组负荷控制系统进行仿真研究,结果证实了该算法的有效性.
【总页数】4页(P48-51)
【作者】李玉红;刘红军;王东风;韩璞
【作者单位】华北电力大学,控制科学与工程学院,河北,保定,071003;华北电力大学,控制科学与工程学院,河北,保定,071003;华北电力大学,控制科学与工程学院,河北,保定,071003;华北电力大学,控制科学与工程学院,河北,保定,071003
【正文语种】中文
【中图分类】TP273
【相关文献】
1.多变量PID型神经元网络控制系统及在除氧器水位解耦控制中的仿真研究 [J], 程启明;郑勇
2.轴带双馈发电机的空载并网控制和功率解耦控制仿真研究 [J], 冯玉龙;艾钢
3.基于DMC-PID串级控制的再热汽温控制系统的仿真研究 [J], 郭若飞;张欣宇;张旭;王文兰
4.基于解耦控制的飞机飞行控制方法仿真研究 [J], 艾剑良;朱书峰;高明
5.基于解耦控制的飞机飞行的控制方法仿真研究 [J], 朱书峰;艾剑良
因版权原因,仅展示原文概要,查看原文内容请购买。
单值动态矩阵控制的应用研究

() 3
提 出来 的 , 它是基 于非 参 数 模 型 的一 种 有代 表 性 的预 测控 制算法 , 在工 业 中得到 了成功 的应用 , 并
引 起 研 究 者 的 广 泛 兴 趣 一 。 但 传 统 的 D MC算
… :0, 口 求 出初值 Y ( k+L) k 则 r ( / )为 :
Y ( + ) k 0 ( / )= l , N ’ “ — , ’a  ̄, 。 a , 一. , l’ , L2 ’
— — — —— ・ ・ — — — — - —
n I十
Ⅱ “ 一 N + 1 ( )+{ k)= n( ) ( Z △ ( k一 】 () )+ k () 】
看 出 , 控 制 效 果相 当 好 。 其 2 单 值 动 态 矩 阵 控 制 算 法
一
通 常 . 型存 在误 差 , 系统 的 预 测输 出值 , 模 故 需 用实 际输 出误 差校正 . : 即 ( k+ / ) = Y ( k + L / )+ ( k o( )k uk ( )+
i +] [ k— N) △ k一 L1 x △ ( , (
Ⅳ + , , “ 一1 : )… ( ) () 5
式 中 : Z1 “【I ): 口 + Ⅱ Z + … + a, l ~ a z
0
在 递推 一步 后 , k+1 时刻 的预测模 型输 出初 值 Y ( k+L+1/ +1 ) 以采 用近 似 的求 取 。( )( )可
法 , 算时 间 较长 、 采 用较 长 的采样 周 期 , 能 计 需 不 直接 应用 于动 态过程 较快 的快速 被控 对象 中 。为
动态矩阵控制在网络时延补偿中的应用研究

进行 了研究 , 并结合动态时延预估补偿 的方法 , 减小 了
网络延迟抖动 , 提高 了系统准确精度 , 有效地克服了随
机 时延对控制品质 的不利影响。
( + ] ; ( ) 控 制 增 量 向量 , △ , k k P) △ k 为 且 c( )=
第一 作者邓 睿 , ,9 7年 生, 为华 东理 工大 学控 制理论 与 控制 工 女 17 现
程 专业在 读硕 士研 究生 ; 主要从 事 网络控制 系统 等方 面的研 究。
1 0
P ROC S AUTOM AT ON NS ES I TRUM ENT ATI ON L3 . a 0 0 Vo 1 No 5 M y2 1
式 ( ) 是 在 k时 刻 解 得 的 最 优 控 制 增 量 5 就
[ uk A ( + ) A ( + 1 ]; A () uk 1 … uk M一 )TP为优化时域
长度 , 为控制时域长度 , Ⅳ为模型时域长度 , 通常满足
≤P ≤Ⅳ; A为动态矩阵, 是描述 系统动态特性 的阶跃
呼 应系 数 。
修改 稿收到 日期 : 0 O 1 。 2 9一 8— 8 0
0 引言
网络控 制 系统 N S ntokdcnr yt s 具 C ( e re ot l s m ) w os e 有资源共享 、 连接线数少 、 易于扩展 和维护等 优点 ; 但 其存在的 回路 时间延迟 降低 了系统 的控制性 能 , 严重
时还 会 导致 系统 破 坏 。
1 动态 矩阵控 制算法
摘
要 :在 网络 控制 系统 中 , 随机传输 时延 大大 降低 了系统的控 制性 能 , 导 致 系统 的不 稳 定。针 对 以太 网 在 网络 控制 系统 中的随 并
动态矩阵预测控制算法在过程控制中的应用研究

测值需在预测模型输出的基础上用实际输出误差修 正 ,即
有简单动态响应的对象 , M = 1~2 ; 对于包括有振 荡等复杂动态响应的对象 , M = 4~8 。必须注意 M ≤P 。
控制权矩阵 R 的选取 : R 的主要作用是对ΔU 的变化剧烈程度进行约束 , 从而限制过大的控制量 变化引起对执行器的冲击 。由于控制阀输入信号有
二 、动态矩阵预测控制 ( DM C) 算法 动态矩阵预测控制算法是预测控制的一种重要 典型代表算法 ,由 Culter (1980 年) 提出的 。他具有 预测模型 、在线滚动优化和误差反馈校正等基本特
收稿日期 :2004 - 08 - 29 作者简介 :作者简介 :周福恩 (1972 - ) ,吉林长春人 ,在读硕士研究生 ,主要研究方向为预测控制 ;
动态矩阵预测控制算法在过程控制中的应用研究逐步加入反映对象受干扰或模型失配时针对于被控对象gp采用动态矩阵预测控制算法对其进行仿真结论本文对于复杂的过程控制系统采用了动态矩阵预测控制算法并针对具体的被控对象采用matlabimul调整参数少且调整规则简单等优点它优于传统的pid算法但是只适用于自衡渐稳系统
毕效辉 (1954 - ) ,陕西扶风人 ,副教授 ,硕士导师 ,主要研究方向为自适应与灰色预测控制 。
·43 ·
长沙航空职业技术学院学报 第 4 卷
点 。其独特特点是采用易于测取的对象阶跃响应做 模型 ,算法简单 ,计算量较少 、鲁棒性强 ,适用于有纯 时延 、开环渐进稳定的非最小相位系统 。
= diag (0. 004 ,0. 004) , H = (1 ,1 ,1 ,1 ,1 ,1 , 1 , 1 , …,
1) ;设定值 y r = 1 仿真结果如下 :
DMC算法MATLAB编程及仿真
一、前言工业生产的过程是复杂的,建立起来的模型也是不完善的。
即使是理论非常复杂的现代控制理论,其效果也往往不尽人意,甚至在一些方面还不及传统的PID控制。
20世纪70年代,人们除了加强对生产过程的建模、系统辨识、自适应控制等方面的研究外,开始打破传统的控制思想,试图面向工业开发出一种对各种模型要求低、在线计算方便、控制综合效果好的新型算法。
在这样的背景下, 预测控制的一种,也就是动态矩阵控制(DMC )首先在法国的工业控制中得到应用。
因此预测控制不是某种统一理论的产物,而是在工业实践中逐渐发展起来的。
预测控制中比较常见的三种算法是模型算法控制(MAC),动态矩阵控制(DMC )以及广义预测控制。
本篇所采用的是动态矩阵控制,其采用增量算法,因此在消除稳态余差方面非常有效。
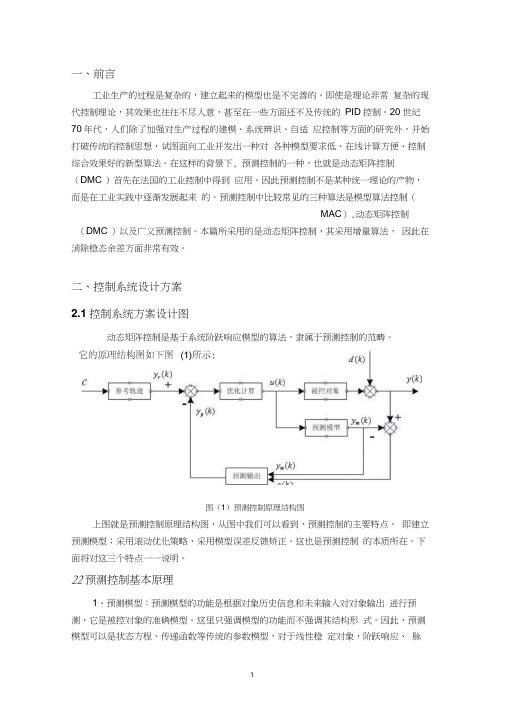
二、控制系统设计方案2.1控制系统方案设计图动态矩阵控制是基于系统阶跃响应模型的算法,隶属于预测控制的范畴。
图(1)预测控制原理结构图上图就是预测控制原理结构图,从图中我们可以看到,预测控制的主要特点。
即建立预测模型;采用滚动优化策略,采用模型误差反馈矫正。
这也是预测控制的本质所在。
下面将对这三个特点一一说明。
22预测控制基本原理1、预测模型:预测模型的功能是根据对象历史信息和未来输入对对象输出进行预测,它是被控对象的准确模型。
这里只强调模型的功能而不强调其结构形式。
因此,预测模型可以是状态方程、传递函数等传统的参数模型,对于线性稳定对象,阶跃响应、脉冲响应这类非参数模型也可以作为预测模型使用。
预测模型具有展示系统未来动态行为的功能,这样,就可以利用预测模型来预测未来时刻被控对象的输出变化及被控变量与其给定值的偏差,作为控制作用的依据,使之适应动态系统所具有的因果性的特点,得到比常规控制更好的控制效果。
2、滚动优化:预测控制是一种优化控制算法,它是通过某一性能指标的最优来确定未来的控制作用。
这一性能指标涉及到系统未来的行为。
如,通常可取被控对象输出在未来的采样点上跟踪某一期望轨迹的方差最小,性能指标中涉及到的系统未来的行为,是根据预测模型由未来的控制策略决定的。
Matlab环境下基于OPC技术实现动态矩阵控制 (1)

G( s) =
Kp T Ps +
1 e- Ss ,
式中
K p 、T p 、S 为 过程 的增
益、时间常数和时滞。由上位机的 OPC 服务器实
时获取 FF 现场总线采集现场设备数据并动态显
示, 实现设备的实时数据和历史数据共享以及报
警等功能。动态矩阵控制算法在监控端实现, 通
过 Matlab 的 m 语言, 利用其强大的计算与动态 显示能力对水箱系统进行控制。并将 OPC 服务
法, 得到数字控制信号, 将其写入 OP C 服务器的
控制变量( 标签) 经 NCS- F I105 变送器则将现场
总线数字量控制信号转换为 0- 10V 的电压信号, 送到电动调节阀, 通过调节阀的开度达到控制液
位的目的。
图 1 控制系统结构 Fig. 1 Th e st ruct u re of t he cont rol sys tem
2 客户端与 OPC 服务器通讯
首先, M at lab 客户端 应先生成 OP C 服务器 支持的 OP C 对象, OPC 数据访问对象由分层结 构构成。即一个 OPC 服务器对象具有一个作为 子对象的 OP C 组集合对象。在这个 OPC 组集合 对象里可以添加多个的 OPC 组对象。各个 OPC 组对象都具有一个作为子对象 OPC 标签集合对
程序和解释如下: ho st Inf o = opcserv er inf o ( c远程/ 本地 服务 器名c) ; % 连接远程/ 本地服务器
allServ ers = host Inf o. Ser verIDc; da = o pcda (c 服 务 器 名c, c OPC 服 务 器 名c) ;
域, 对于渐近稳定的对象, 阶跃响应在某一时刻
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一种简化动态矩阵控制的仿真研究王娜王东风张德利褚明铢(华北电力大学控制科学与工程学院,河北保定,071003)摘要:针对动态矩阵控制中涉及到矩阵的求逆,计算量大的缺点提出一种简化的算法,该算法引入控制增量的期望衰减因子,使控制增量在控制时域内逐步接近于零,这样算法中的矩阵求逆简化为纯数值求逆(即取倒数),使运算量大大减少提高计算效率的同时也减少了控制参数的调节,因此算法的实时性较强,便于微机编程实现。
文章最后,将上述算法对两个典型被控对象进行了仿真,分析了仿真的结果,说明改进的DMC算法在保证实时性以及被控对象的动态性能方面均有益处。
关键词:动态矩阵控制;预测控制;仿真中图分类号: TP 273 文献标识码:ASimulation Research of Simplified Dynamic Matrix ControlWang Na Wang Dong-feng Zhang De-li Chu Ming-zhu(Control of control science and engineering, North China Electric Power University, Baoding, 071003) Abstract: The calculation of inverse matrix control is involved in dynamic matrix control, so the computation quantity is very large. Aiming at this shortage, a decay factor is introduced to make the control increment come to zero in the control horizon. In this way, calculation of inverse matrix control is reduced to numerical inversion, the computation quantity and the control parameters are greatly reduced. The algorithm has strong real-time quality and it is convenience for programming in computer. Applying this algorithm in two representative controlled objects, simulation results show that simplified algorithm is helpful for real-time and dynamic quality.Keywords: Predictive control;Dynamic matrix control;Simulation引言动态矩阵控制(DMC)算法[1]是一种基于对象阶跃响应预测模型、滚动实施并结合反馈校正的优化控制算法,是预测控制算法之一。
DMC算法适用于渐近稳定的线性对象。
由于该算法比较简单,鲁棒性强,近年来已在冶金、石油、化工等工业过程中得到十分成功的应用。
经过多年的发展,动态矩阵控制的理论研究有了很大的进展,而且,在许多领域成功的报道也是层出不穷。
但随着工业的发展,动态矩阵控制的常规算法不能满足实际的需要,于是在算法上有了很大的发展[2][3]。
本文对动态矩阵控制(DMC)算法提出了一种简化的设计,引入控制增量的期望衰减因子,使控制增量在控制时域内逐步接近于零,这样动态矩阵控制的顺序开环控制增量的计算由M×M 维矩阵求逆简化为纯数值求逆(即取倒数),使运算量大大减少,提高了计算效率,而且也减少了参数的调节,使得微机编程实现方便。
1.动态矩阵控制(DMC)算法动态矩阵控制利用被控对象的单位阶跃响应采样数据作为预测模型。
设被控对象的单位阶跃采样数据为{a1,a2,…},对于渐近稳定的系统,其阶跃响应在若干个采样周期后就趋于稳态值,即a N≈a(∞),因此可以用单位阶跃响应采样数据的前有限项描述系统的动态特性:{a1,a2,…a N};由线性系统的叠加原理,可以得到系统输出的预测模型为:Y m(k+1)=AΔU(k)+A0U(k-1) ,(1)其中:Y m(k+1)=[y m(k+1/k),y m(k+2/k),…,y m(k+P/k)]T,ΔU(k)=[Δu(k),Δu(k+1),…,Δu(k+M-1)]T,U(k-1)=[u(k-N+1),u(k-N+2),…u(k-1)]T,A—动态矩阵;MPMPPPaaaaaaA⨯+--⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=11121ˆˆˆˆˆˆ)1(1312211ˆˆˆˆˆˆˆˆˆ-⨯+----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=NPPNNNNNNaaaaaaaaaA。
则(1)式是用过去施加于系统的控制量表示初值的预测模型输出。
由于模型误差和干扰等的影响,系统的输出预测值需要在预测模型输出的基础上用实际输出误差修正,即Y P(k+1)=Y m(k+1)+h[y(k)-y m(k)]=AΔU(k)+A0U(k-1)+h e(k) ,(2)式中:Y P(k+1)=[y P(k+1),y P(k+2),…,y P(k+P)]T,Y P(k+1)—系统输出预测矢量;e(k)=y(k)-y m(k);h=[h1,h2,…,h p]T,h—误差修正系数。
优化下列性能指标:J P=[y P(k+1)-y r(k+1)]T Q[y P(k+1)-y r(k+1)]+ΔU T(k)λΔU(k) ,(3)其中:Y r(k+1)=[ y r(k+1), y r(k+2), …, y r(k+P)]T是参考轨迹;Q=diag(q1,q2,…,q P), P是预测时域;λ=diag(λ1,λ2,…,λM), M是控制时域;得到:ΔU(k)=(A T QA+λ)-1A T Q[Y r(k+1)-A0U(k-1)-h e(k)],(4)即时控制增量取为:Δu(k)=d T[Y r(k+1)-A0U(k-1)-h e(k)] ,其中:d T=(1,0,…,0) (A T QA+λ)-1A T Q 为取首行运算。
2.动态矩阵控制(DMC)的改进算法M对应于矩阵(A T QA+λ)的维数,在计算动态控制系数d i时,必须对该矩阵求逆,因此,减小M有利于控制系数的计算。
特别当M=1时,矩阵求逆退化为求倒数,计算量将显著减小。
然而如对象的动态较为复杂,则取M=1不能得到好的动态响应[4]。
在这种情况下,必须在兼顾计算量的同时适当加大M。
为使系统具有满意的动态特性的同时计算量减少引入期望衰减因子使矩阵求逆转化为数值求逆,减少计算量及调节参数。
DMC算法的“滚动优化”策略是:在每一个时刻k,要确定从该时刻起的M个控制增量Δu(k),Δu(k+1),…,Δu(k+M-1)使被控对象在其作用下未来P个时刻的输出预测值尽可能接近给定的期望值,(4)式给出了这M个控制增量的最优值,但并不把它们都当作应实现的解,而是取其中的即时控制增量Δu(k)构成实际控制u(k)=u(k-1)+Δu(k)作用于对象。
到下一个时刻又提出类似的优化问题求出Δu(k+1)。
因此我们希望控制增量Δu(k+i), (i=0,1,2,…,M-1)在M步以内逐步趋于0,即M步之后不再调节,基于这一思想,引入控制增量的期望衰减因子,提出了简化算法设计方案[5][6]。
为了使Δu(k+i)以指数形式趋于0,可取控制增量Δu(k+i)=αiΔu(k),其中i=0,1,2,…,M-1,期望衰减因子α∈(0,1)为常数,则k,k+1,…,k+M-1时刻的控制增量变为:ΔU(k)=[1,α,α2,…αM-1]TΔu(k)=AαΔu(k),(5)其中:Aα=[1,α,α2,…αM-1]T由此可得实际输出误差修正后的预测模型输出为:Y P(k+1)= AΔU(k)+A0U(k-1)+h e(k)= A uΔu(k)+A0U(k-1)+h e(k) ,(6)其中:A u=A﹒Aα将新的预测输出(6)式代替(2)式重新代入性能指标(3)式可得Δu(k)= (A u T QA u+AαTλAαT)-1A u T Q[Y r(k+1)-A0U(k-1)-h e(k)],(7)u(k)=u(k-1)+Δu(k),(8)比较式(7)与式(4),在式(4)中有M*M 维的求逆运算(A T QA+λ)-1,在式(7)中,由于A u=A﹒Aα是一列向量,所以(A u T QA u+AαTλAαT)-1只是纯数值求逆,即倒数,其计算量大为减少,运算速度大大提高。
3.仿真研究3.1 二阶系统仿真取被控对象为大惯性环节,设被控对象传递函数为:2)182(994.2)(+=ssG分别采用简化动态矩阵控制(SDMC)算法与一般动态矩阵控制(CDMC)算法进行仿真研究,图中虚线为简化算法,实线为一般算法,并给出了调节参数q,λ,P,M, α相应的取值。
02004006008001000t/soutput图1 一般算法:q=0.1,λ=100, P=100,M=5简化算法:q =0.1,λ=100,P=100, M=5,α=0.1 Fig.1 common algorithm : q=0.1,λ=100, P=100,M=5 Simple algorithm : q =0.1,λ=100,P=100, M=5,α=0.10.511.522.5t/soutput图2 一般算法:q =1, λ=1, P =100, M =5 简化算法:q =1, λ=1 ,P =100, M =5, α=0.1 Fig.2 common algorithm : q =1, λ=1, P =100, M =5 Simple algorithm : q =1, λ=1 ,P =100, M =5, α=0.10200400600800100000.511.5t/so u t p u t02004006008001000-50513t/so u t p u t图3 一般算法:q =50, λ=0.1, P =100, M=5 简化算法:q =50, λ=0.1, P =100,M =5, α=0.1 Fig.3 common algorithm : q =50, λ=0.1, P =100, M=5 Simple algorithm : q =50, λ=0.1, P =100,M =5, α=0.13.2 高阶系统仿真取被控对象为高阶次环节, 设被控对象传递函数为:1s.421119.145.215062545.20)(2+⋅++=s ss G分别采用简化动态矩阵控制(SDMC )算法与一般动态矩阵控制(CDMC )算法进行仿真研究 ,图中虚线为简化算法,实线为一般算法,并给出了调节参数q ,λ,P ,M , α 相应的取值。
