20第15章时间序列-R
时间序列自相关方程

时间序列自相关方程时间序列自相关方程是一种用于描述时间序列数据内部关联性的方法。
它可以帮助我们理解数据的趋势和周期性,并预测未来的变化。
本文将介绍时间序列自相关方程的基本概念、应用和局限性。
一、什么是时间序列自相关方程时间序列是按照时间顺序排列的一系列数据点的集合。
自相关方程是通过计算时间序列数据点与其自身滞后一定时间的数据点之间的相关性来描述数据的内在关联性。
时间序列自相关方程可以表达为:R(t) = Cov(X(t), X(t-h)) / (Var(X(t)) * Var(X(t-h))),其中R(t)表示时间t和时间t-h之间的自相关系数,Cov表示协方差,Var表示方差。
1. 趋势分析:通过计算时间序列数据点与其滞后数据点之间的自相关系数,可以得到数据的趋势信息。
如果自相关系数接近于1,则表示数据存在较强的正向趋势;如果自相关系数接近于-1,则表示数据存在较强的负向趋势。
2. 周期性分析:时间序列数据通常会呈现出一定的周期性。
通过计算时间序列数据点与其滞后数据点之间的自相关系数,可以判断数据的周期性。
如果自相关系数在某个滞后期内达到峰值,则表示数据存在该滞后期的周期性。
3. 预测分析:时间序列自相关方程可以用于预测未来的数据变化。
通过计算时间序列数据点与其滞后数据点之间的自相关系数,可以确定未来数据与过去数据的关系,从而进行预测。
三、时间序列自相关方程的局限性时间序列自相关方程在一些情况下可能会存在局限性。
1. 数据的非平稳性:如果时间序列数据存在趋势或季节性等非平稳性,那么自相关方程可能无法很好地描述数据的关联性。
2. 数据的非线性关系:自相关方程假设时间序列数据的关联性是线性的,但实际上数据的关联性可能是非线性的。
在这种情况下,自相关方程可能无法准确描述数据的关联性。
3. 数据的噪声干扰:时间序列数据往往会受到各种噪声的干扰,这些噪声可能会对自相关方程的计算结果产生影响。
时间序列自相关方程是一种用于描述时间序列数据内部关联性的方法。
商务与经济统计学习笔记整理安德森第13版

商务与经济统计学习笔记整理安德森第13版2018/12/11开始阅读,2019/1⽉14⽇完成
正常页3min/per_page,有难度页5min/per_page
正常每天1-1.5⼩时阅读。
共计耗时36⼩时。
同期开始学习Python(⽬前⾄递归函数)
学习笔记⼤纲:
第20章指数
第19章质量管理的统计⽅法
第18章⾮参数⽅法
第17章时间序列分析及预测
第16章回归分析:建⽴模型
第15章多元回归
第14章简单线性回归
第13章实验设计与⽅差分析
第12章多个⽐率的⽐较、独⽴性及拟合优度检验
第11章总体⽅差的统计推断
第10章两总体均值和⽐例的推断
第9章假设检验
第8章区间估计
第7章抽样和抽样分布
第6章连续型概率分布
第5章离散型概率分布。
时间序列数据分析R语言案例

时间序列数据分析R语言案例时间序列数据分析是一种专门用于分析和预测时间序列数据的统计方法。
时间序列数据是按照时间顺序排列的观测数据,在金融、经济、气象等领域都有广泛的应用。
在本文中,将介绍一个使用R语言进行时间序列数据分析的案例。
假设我们有一个销售数据集,包含了过去几年每月的销售额数据。
我们的目标是分析销售趋势,并且预测未来的销售额。
下面是具体的步骤。
第一步是导入数据。
我们可以使用R语言中的`read.csv(`函数来导入包含销售数据的CSV文件,并将数据存储在一个数据框中。
```Rsales_data <- read.csv("sales_data.csv")```第二步是查看数据的结构和摘要统计信息,以便了解数据集的特征。
```Rstr(sales_data)summary(sales_data)```第三步是将时间列转换为时间序列对象。
在R中,可以使用`as.Date(`函数将日期列转换为`Date`对象,并使用`ts(`函数将数据转换为时间序列对象。
sales_data$date <- as.Date(sales_data$date, format = "%Y-%m-%d")sales_ts <- ts(sales_data$sales, start = 2024, frequency = 12)```第四步是对时间序列数据进行可视化。
可以使用`plot(`函数将销售时间序列数据绘制成折线图,以便观察数据的趋势和季节性。
```Rplot(sales_ts, main = "Monthly Sales", xlab = "Year", ylab = "Sales")``````R```第六步是检验时间序列数据的平稳性。
可以使用`adf.test(`函数或`kpss.test(`函数对时间序列数据进行单位根检验或Kwiatkowski–Phillips–Schmidt–Shin(test for the Null hypothesis of stationarity)检验。
(完整word版)时间序列分析基于R__习题答案及解析
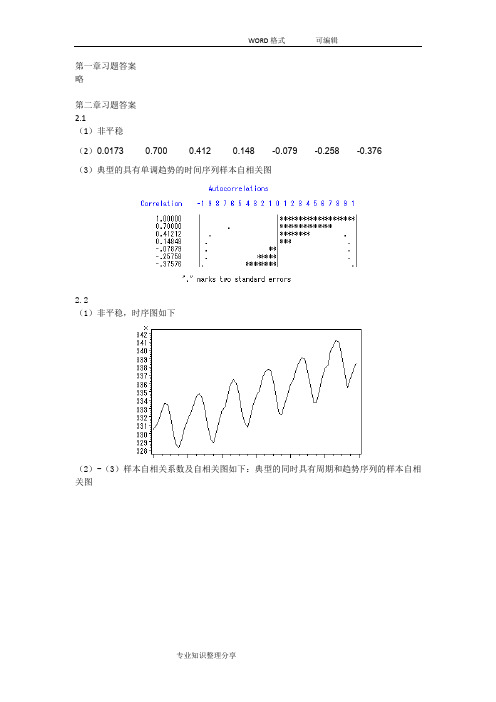
第一章习题答案略第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2c λ=3c λ=-无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
课后习题答案-时间序列分析及应用(R语言原书第2版)

stationary.
(b) Find the autocovariance function for {Yt}. Cov(Yt,Yt − k) = Cov(X,X) = σ2 for all t and k, free of t (and k). (c) Sketch a “typical” time plot of Yt. The plot will be a horizontal “line” (really a discrete-time horizontal line)
relation functions are the same for θ = 3 and θ = 1/3. For simplicity, suppose that the process mean is known
to be zero and the variance of Yt is known to be 1. You observe the series {Yt} for t = 1, 2,..., n and suppose that you can produce good estimates of the autocorrelations ρk. Do you think that you could determine which value of θ is correct (3 or 1/3) based on the estimate of ρk? Why or why not?
时间序列分析基于R——习题答案

第一章习题答案略第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2λ=3λ=无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
时间序列建模的完整教程用R语言
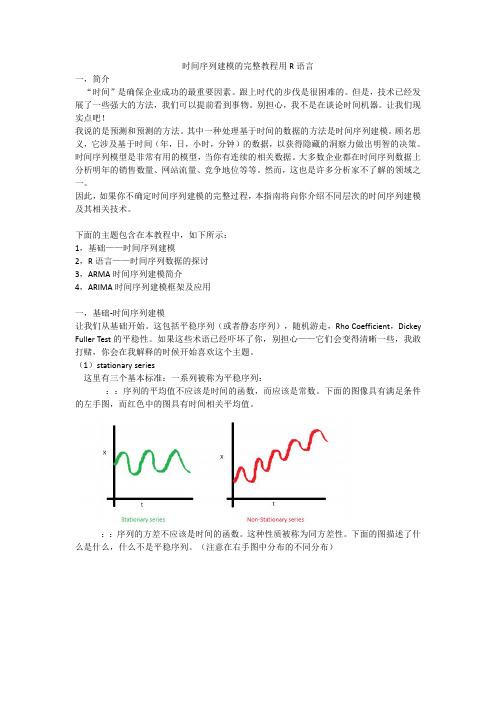
如果我们尝试绘制这个图表,它会看起来像这样:
你注意到 MA 和 AR 模型的区别了吗?在 MA 模型中,噪声/冲击随时间迅速消失。AR 模型对冲击具有持久的影响。 AR 模型与 MA 模型的区别 AR 和 MA 模型之间的主要区别是基于~时间序列对象在不同时间点之间的相关性。 X (T) 和 X( T-N)之间的相关性,对于 n 阶的 MA 总是为零。这直接源于 MA 模型中 x( t)和 x
/WOP/RandomWalk.html
想象一下,你坐在另一个房间里,看不到那个女孩。你想预测女孩的位置随着时间的推移。 你会有多精确?当然,随着女孩的位置变化,你会变得越来越不准确。在 T=0,你完全知 道那个女孩在哪里。下一次,她只能移动到 8 个方格,因此你的概率下降到 1/8,而不是 1, 而且它一直在下降。现在让我们来尝试一下这个时间序列。
时间序列建模的完整教程用 R 语言 一,简介 “时间”是确保企业成功的最重要因素。跟上时代的步伐是很困难的。但是,技术已经发 展了一些强大的方法,我们可以提前看到事物。别担心,我不是在谈论时间机器。让我们现 实点吧! 我说的是预测和预测的方法。 其中一种处理基于时间的数据的方法是时间序列建模。 顾名思 义,它涉及基于时间(年,日,小时,分钟)的数据,以获得隐藏的洞察力做出明智的决策。 时间序列模型是非常有用的模型, 当你有连续的相关数据。 大多数企业都在时间序列数据上 分析明年的销售数量、网站流量、竞争地位等等。然而,这也是许多分析家不了解的领域之 一。 因此, 如果你不确定时间序列建模的完整过程, 本指南将向你介绍不同层次的时间序列建模 及其相关技术。 下面的主题包含在本教程中,如下所示: 1,基础——时间序列建模 2,R 语言——时间序列数据的探讨 3,ARMA 时间序列建模简介 4,ARIMA 时间序列建模框架及应用 一,基础-时间序列建模 让我们从基础开始。这包括平稳序列(或者静态序列),随机游走,Rho Coefficient,Dickey Fuller Test 的平稳性。如果这些术语已经吓坏了你,别担心——它们会变得清晰一些,我敢 打赌,你会在我解释的时候开始喜欢这个主题。 (1)stationary series 这里有三个基本标准:一系列被称为平稳序列: ::序列的平均值不应该是时间的函数,而应该是常数。下面的图像具有满足条件 的左手图,而红色中的图具有时间相关平均值。
r语言读取时间序列

r语言读取时间序列1.引言1.1 概述概述时间序列分析是一种重要的数据分析方法,它在许多领域中都具有广泛的应用,例如经济学、金融学、气象学等。
时间序列数据是按照时间顺序排列的观测值序列,它们展现了随时间推移而变化的趋势和规律。
要进行时间序列分析,首先需要将时间序列数据导入分析工具中。
R语言是一种功能强大的统计分析工具,它提供了丰富的函数和包用于时间序列分析。
在R语言中,读取时间序列数据是进行分析的第一步。
本文将介绍R语言中读取时间序列的几种常用方法和技巧。
首先,我们可以使用R中的read.csv或read.table函数来读取以逗号或制表符分隔的时间序列数据。
这些函数可以将数据读入到一个数据框中,每一列对应一个时间点,每一行对应一个变量。
另一种常用的读取时间序列数据的方法是使用R中的read.zoo函数。
read.zoo函数可以直接读取以时间作为索引的数据文件,无需进行额外的处理。
它支持多种时间格式,如年-月、年-月-日、年-月-日时:分:秒等。
另外,R语言中还有许多专门用于读取特定类型时间序列数据的包,如xts和zoo包。
这些包提供了更加灵活和高效的方法来读取和处理时间序列数据。
例如,xts包提供了一个xts类,它可以存储和操作时间序列数据,包括快速的日期和时间索引,以及对时间序列数据的各种运算和统计分析。
总结起来,本文将介绍R语言中读取时间序列数据的几种常见方法,包括使用基本的读取函数如read.csv和read.table,以及使用专门的时间序列包如xts和zoo。
通过学习和掌握这些方法,读者将能够更加灵活和高效地读取和处理时间序列数据,并开展相关的时间序列分析。
接下来,在第2节中,我们将介绍R语言的基本概念,以及时间序列分析的重要性。
1.2 文章结构文章结构部分的内容应该包括一些介绍和解释,以说明整篇文章的组织方式和目的。
下面是一种可能的写法:在本篇文章中,我们将探讨如何使用R语言来读取时间序列数据。
时间序列分析基于r第2版

时间序列分析基于r第2版《时间序列分析基于R第2版》(Time Series Analysis and Its Applications: With R Examples, 2nd Edition)是由Shumway和Stoffer合著的一本经典时间序列分析教材。
该书详细介绍了时间序列分析的理论和实践应用,并使用R语言进行实例演示和编程实现。
以下是《时间序列分析基于R第2版》的主要内容概述:第1章:时间序列分析简介介绍时间序列分析的基本概念和应用领域,并概述本书的内容和使用R语言进行时间序列分析的优势。
第2章:时间序列的基本特性介绍时间序列的基本特性,包括平稳性、自相关性和白噪声等概念,并通过实例演示如何使用R进行时间序列数据的可视化和描述性统计分析。
第3章:时间序列的线性模型介绍时间序列的线性模型,包括自回归模型(AR)、滑动平均模型(MA)和自回归滑动平均模型(ARMA)等,并通过R语言实现模型的参数估计和预测。
第4章:时间序列的谱分析介绍时间序列的谱分析方法,包括周期图和功率谱密度估计等,并通过R语言实现谱分析方法的应用和结果可视化。
第5章:时间序列的非线性模型介绍时间序列的非线性模型,包括ARCH、GARCH和非线性AR模型等,并通过R语言实现模型的参数估计和预测。
第6章:时间序列的状态空间模型介绍时间序列的状态空间模型,包括线性状态空间模型和非线性状态空间模型,并通过R语言实现模型的参数估计和预测。
第7章:多变量时间序列分析介绍多变量时间序列分析的方法,包括向量自回归模型(VAR)、向量误差修正模型(VEC)和协整模型等,并通过R语言实现模型的参数估计和预测。
第8章:季节性和周期性时间序列介绍季节性和周期性时间序列的分析方法,包括季节性自回归移动平均模型(SARMA)和周期性自回归移动平均模型(PARMA)等,并通过R语言实现模型的参数估计和预测。
第9章:时间序列的预测介绍时间序列的预测方法,包括简单指数平滑、Holt线性趋势模型和ARIMA模型等,并通过R语言实现模型的参数估计和预测。
r语言:时间序列ARMA基础学习

r 语言:时间序列ARMA 基础学习01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 ######################################### 术语 ##################################白噪音:其均值=0,并且独立分布的(同时间无关)#稳定时间序列:任意j--i 时间段的序列:其均值相等#自相关系数acf 图:研究y[t]同y[t-l]序列之间的相关性# 在纯的ma(q)序列下,acf 图形表现为q+1以后的自相关系数约为0(虚线内) #偏相关系数pacf 图:在y[t]同y[t-l]之间的序列固定的情况下,研究研究y[t]同y[t-l]序列之间的相关性# 在纯的ar(p)序列下,pacf 图形表现为p+1以后的偏相关系数约为0(虚线内)#扩展相关系数图eacf :如果y[t]不是纯的ar 或ma ,而是arma (混合体),无法通过acf 确定q ,也不能通过pacf 确认p ,需要通过eacf 确认p 和q################################################################################################################################### 模拟产生ma ar arma 序列 ######################################################## MA 时间序列的模拟试验:产生一个ma 时间序列y.ma<-function(a1,a2,a3=0,a4=0,num=200,pic=TRUE){#MA 滑动平均时间序列的模拟(也可以使用filter 函数) e<-rnorm(num,0,1)#模拟白噪声,均值=0result<-0result[1]<-e[1]result[2]<-e[2]-a1*e[1]222324252627282930313233343536 result[3]<-e[3]-a1*e[2]-a2*e[1]result[4]<-e[4]-a1*e[3]-a2*e[2]-a3*e[1]for(t in 5:num){ result[t]<-e[t]-a1*e[t-1]-a2*e[t-2]-a3*e[t-3]-a4*e[t-4] }#构造一个ma型时间序列if(pic==TRUE){#画图形dev.new()ts.plot(result,main=paste("y.ma[t]=e[t]-",a1,"*e[t-1]-",a2,"*e[t-2]-",a3,"*e[t-3]-",a4,"*e[t-4]的时间序列散点图"))dev.new()lag.plot(result, 9, do.lines=FALSE)dev.new()par(mfrow=c(2,1))acf(result, 30,main=paste("y.ma自相关图,y.ma[t]=e[t]-",a1,"*e[t-1]-",a2,"*e[t-2]-",a3,"*e[t-3]-",a4,"*e[t-4]")) pacf(result, 30,main=paste("y.ma偏自相关图,y.ma[t]=e[t]-",a1,"*e[t-1]-",a2,"*e[t-2]-",a3,"*e[t-3]-",a4,"*e[t-4]")) }result}y.ma<-y.ma(0.92,0.65)结果一:绘制散点图结果二:绘制出y[t]同y[t-1](延迟1)、y[t-2](延迟2)……..y[t-9](延迟9)的2维散点图,用以观察y[t]同y[t-i]的相关性(i=1–9)结果三:绘制自相关和偏自相关图(在虚线外的表示有相关性)可以看到:1)在纯的ma(q)序列下,acf 图形表现为q+1以后的自相关系数约为0(虚线内)2)在纯的ma(q)序列下,pacf 则不规则的会大于1/-1可以通过acf 图确定q 的数值01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 ##### AR 时间序列的模拟试验:产生一个ar 时间序列y.ar<-function(b1,b2,b3=0,b4=0,num=200,pic=TRUE){#AR 自回归型时间序列的模拟(也可以使用filter 函数)e<-rnorm(num,0,1)#模拟白噪声,均值=0result<-0result[1]<-e[1]result[2]<-e[2]+b1*result[1]result[3]<-e[3]+b1*result[2]+b2*result[1]result[4]<-e[4]+b1*result[3]+b2*result[2]+b3*result[1]for(t in 5:num){ result[t]<-e[t]+b1*result[t-1]+b2*result[t-2]+b3*result[t-3]+b4*result[t-4] }#构造一个ar 型时间序列 if(pic==TRUE){#画图形dev.new()ts.plot(result,main=paste("y.ar[t]=e[t]+",b1,"*y.ar[t-1]+",b2,"*y.ar[t-2]+",b3,"*y.ar[t-3]+",b4,"*y.ar[t-4]的时间序列散点图"))dev.new()lag.plot(result, 9, do.lines=FALSE)dev.new()par(mfrow=c(2,1))acf(result, 30,main=paste("y.ar 自相关图,y.ar[t]=e[t]+",b1,"*y.ar[t-1]+",b2,"*y.ar[t-2]+",b3,"*y.ar[t-3]+",b4,"*y.ar[t-4]"))pacf(result, 30,main=paste("y.ar 偏自相关图,y.ar[t]=e[t]+",b1,"*y.ar[t-1]+",b2,"*y.ar[t-2]+",b3,"*y.ar[t-3]+",b4,"*y.ar[t-4]"))}result}y.ar<-y.ar(0.92,-0.65)结果一:绘制散点图结果二:绘制出y[t]同y[t-1](延迟1)、y[t-2](延迟2)……..y[t-9](延迟9)的2维散点图,用以观察y[t]同y[t-i]的相关性(i=1–9)结果三:绘制自相关和偏自相关图(在虚线外的表示有相关性)1)在纯的ar(q)序列下,pacf 图形表现为q+1以后的自相关系数约为0(虚线内) 2)在纯的ar(q)序列下,acf 则不规则的会大于1/-1 可以通过pacf 图确定p 的数值01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 ##### ARMA 时间序列的模拟试验:产生一个arma 时间序列 library(TSA) y.arma<-function(a1,a2,a3=0,a4=0,b1,b2,b3=0,b4=0,num=200,pic=TRUE){ result<-y.ma(a1=a1,a2=a2,a3=a3,a4=a4,pic=F,num=num)+y.ar(b1=b1,b2=b2,b3=b3,b4=b4,pic=F,num=num)#产生自回归滑动平均时间序 exp.str<-paste("y.arma[t]=e[t]-",a1,"*e[t-1]-",a2,"*e[t-2]-",a3,"*e[t-3]-",a4,"*e[t-4]+",b1,"*y.arma[t-1]+",b2,"*y.arma if(pic==TRUE) {#画图形 dev.new() ts.plot(result,main=paste(exp.str,"的时间序列散点图")) dev.new() lag.plot(result, 9, do.lines=FALSE) dev.new() par(mfrow=c(2,1)) acf(result, 30,main=paste(exp.str,"的自相关图")) pacf(result, 30,main=paste(exp.str,"的偏自相关图")) } print(paste(exp.str,"的扩展相关图。
时间序列分析——基于R答案

时间序列分析——基于R 王燕答案第一章时间序列分析简介略第二章时间序列的预处理#========================================## 2.5习题-1##========================================library(tseries)par(mfrow=c(1,2))x=rep(1:20)temp=ts(x)plot(temp)#不是平稳序列as.vector(acf(temp)$acf[1:6])#序列的自相关系数递减到零的速度相当缓慢,#在很长的延迟时期里,自相关系数一直为正,#而后又一直为负,在自相关图上显示出明显的#三角对称性,这是具有单调趋势的非平稳序列#的一种典型的自相关图形式。
这和该序列时序#图显示的显著的单调递增性是一致的。
#======================================== ## 2.5习题-2##======================================== library(tseries)par(mfrow=c(1,2))volcano.co2=read.table('习题2.2数据.txt',sep='\t',header=F) data=ts(as.vector(t(as.matrix(volcano.co2))),start=c(1975,1)) plot(data)#不是平稳序列as.vector(acf(data,lag.max=23)$acf)#序列自相关系数长期位于零轴的一边。
这是#具有单调趋势序列的典型特征,同时自相关#图呈现出明显的正弦波动规律,这是具有周#期变化规律的非平稳序列的典型特征。
自相#关图显示出来的这两个性质和该序列时序图#显示出的带长期递增趋势的周期性质是非常#吻合的。
#========================================## 2.5习题-3##======================================== library(tseries)par(mfrow=c(1,2))rain=read.table('习题2.3数据.txt',sep='\t',header=F) data=ts(as.vector(t(as.matrix(rain))),start=c(1945,1)) plot(data)#该序列为平稳序列as.vector(acf(data,lag.max = 23)$acf)#该序列的自相关系数一直都比较小,#基本控制在2倍的标准差范闹以内,#可以认为该序列自始至终都在零轴附#近波动,这是随机性非常强的平稳时#间序列通常具有的自相关图特征。
R语言时间序列中文教程

R语言时间序列中文教程2012特别声明:R语言是免费语言,其代码不带任何质量保证,使用R语言所产生的后果由使用者负全责。
前言R语言是一种数据分析语言,它是科学的免费的数据分析语言,是凝聚了众多研究人员心血的成熟的使用范围广泛全面的语言,也是学习者能较快受益的语言。
在R语言出现之前,数据分析的编程语言是SAS。
当时SAS的功能比较有限。
在贝尔实验室里,有一群科学家讨论提到,他们研究过程中需要用到数据分析软件。
SAS的局限也限制了他们的研究。
于是他们想,我们贝尔实验室的研究历史要比SAS长好几倍,技术力量也比SAS强好几倍,且贝尔实验室里并不缺乏训练有素的专业编程人员,那么,我们贝尔实验室为什么不自己编写数据分析语言,来满足我们应用中所需要的特殊要求呢?于是,贝尔实验室研究出了S-PLUS语言。
后来,新西兰奥克兰大学的两位教授非常青睐S-PLUS的广泛性能。
他们决定重新编写与S-PLUS相似的语言,并且使之免费,提供给全世界所有相关研究人员使用。
于是,在这两位教授努力下,一种叫做R的语言在奥克兰大学诞生了。
R基本上是S-PLUS的翻版,但R是免费的语言,所有编程研究人员都可以对R语言做出贡献,且他们已经将大量研究成果写成了R命令或脚本,因而R语言的功能比较强大,比较全面。
研究人员可免费使用R语言,可通过阅读R语言脚本源代码,学习其他人的研究成果。
笔者曾有幸在奥克兰大学受过几年熏陶,曾经向一位统计系的老师提请教过一个数据模拟方面的问题。
那位老师只用一行R语句就解答了。
R语言的强大功能非常令人惊讶。
为了进一步推广R语言,为了方便更多研究人员学习使用R语言,我们收集了R语言时间序列分析实例,以供大家了解和学习使用。
当然,这是非常简单的模仿练习,具体操作是,用复制粘贴把本材料中R代码放入R的编程环境;材料中蓝色背景的内容是相关代码和相应输出结果。
经过反复模仿,学习者便能熟悉和学会。
需要提醒学习者的是:建议学习者安装了R语言编程,再继续阅读本材料;执行R 命令时,请删除命令的中文注解,没使用过在命令中加入中文;如果学习者是初次接触R或者Splus,建议先阅读<<R语言样品比较应用举例>>,如果学习者比较熟悉R语言,还可以阅读优秀时间序列读物Ecomometrics in R,也可以上QuickR 网站。
时间序列预测 r平方的方法

时间序列预测r平方的方法
在时间序列预测中,R平方是一种常用的拟合优度度量,用来衡量模型对历史数据的拟合程度。
R平方的值越高,说明模型对历史数据的拟合越好。
R平方的计算公式如下:
●R^2=1-\frac{\sum\limits_{i=1}^n(y_i-\hat{y}_i)^2}{\sum\limits_{i=1}^n(y_i-\bar{y
})^2}
其中:
1.yi是第i个观测值
2.y^i是模型对第i个观测值的预测值
3.yˉ所有观测值的平均值
R平方值的取值范围为0到1。
当R平方值为0时,说明模型对历史数据的拟合程度为零,模型完全无法解释历史数据的变化。
当R平方值为1时,说明模型对历史数据的拟合程度为完美,模型可以完全解释历史数据的变化。
在时间序列预测中,R平方值的意义是:
●R平方值越高,说明模型对历史数据的拟合越好,模型的预测能力也越强。
●R平方值越低,说明模型对历史数据的拟合越差,模型的预测能力也越弱。
时间序列-AR模型

xt 3 t 2 t 1 t
3 2
xt n t n1 t n2 t 1 t
p
称为AR(p)模型的自回归系数多项式。 若α(u)=0的根都在单位圆外时,称此为 平稳的AR(p)模型,否则为非平稳的AR(p)模 型,或广义的AR(p)模型。 注: 条件α(u)=0的根都在单位圆外,称为平 稳性条件。
7
例1.2 如果时间序列xt 满足
2 xt xt 1 t 3
t 0, 1,
bp (Cx (1), Cx (2), , Cx ( p))
(1 , 2 , , p )
R p p / Cx (0) d p bp / Cx (0)
19
例如一阶自回归模型AR(1):
xt xt 1 t
因为系数多项式 1 u 0的解为u 1 /
(B) 1 1 B 2 B p B
2
p
16
差分方程式可用框图表示: 设想有一个 滤波器,输入的是某种平稳序列,而输出的 则是白噪声序列,即
xt
自回归滤波器
ε
t
易见,滤波器成为一个对时间序列进行 变换的实体,变换前的序列称为输入,经滤波 器变换的得到的序列称为输出。
Cx (2)1 Cx (1) 2 Cx ( p 3) p Cx (3)
24
Cx ( p 1)1 Cx ( p 2) 2 Cx (0) p Cx ( p)
C x (0) C x (1) C x (1) C x (2) C ( p 1) C ( p 2) x x C x ( p 2) 1 C x (2) C x ( p 3) 2 C x (3) C x (0) p C x ( p)
时间序列预测

对St(1)计算结果影响较大,应取前几项的平均值。
A的确定
1:当时间序列呈现较稳定的水平趋势时,应选较小的α 值, 一般可在0.05~0.20之间取值; 2:当时间序列有波动,但长期趋势变化不大时,可选稍大 的α 值,常在0.1~0.4之间取值; 3:当时间序列波动很大,长期趋势变化幅度较大,呈现明 显且迅速的上升或下降趋势时,宜选择较大的α 值,如可在 0.6~0.8间选值,以使预测模型灵敏度高些,能迅速跟上数 据的变化;
将上表数据分为等距的三段,每段两个数据。分别计算三点坐标得到:
1200 +1400
1+ 2
x1 =
2
= 1300 t1 = 2 = 1.5
1620 +1862
3+4
x2 =
2
= 1741 t2 = 2 = 3.5
2127 + 2413
5+6
x3 =
2
= 2270 t3 = 2 = 5.5
抛物线趋势的分割平均法
M
(1) t-2
n
...
M
(1) t -( n-1)
xt T at btT
其中
at
2M
(1) t
-
M
(2) t
bt
2 n-
1
(
M
(1) t
-
M
( t
2
)
)
二次移动平均法
例
观察年份 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002
二次指数平滑法
二次指数平滑的计算公式
S (2) t
St(1)
时间序列课程设计时序图

时间序列课程设计时序图一、教学目标本章节的教学目标是使学生掌握时间序列的基本概念、方法和应用,能够运用时间序列分析解决实际问题。
具体目标如下:1.知识目标:(1)理解时间序列的定义、特点和分类;(2)掌握时间序列的常用预处理方法;(3)熟悉时间序列的平稳性检验、自相关函数和偏自相关函数的计算;(4)掌握时间序列的常见模型及其应用。
2.技能目标:(1)能够运用时间序列分析方法对实际数据进行分析和预测;(2)能够运用编程语言(如Python、R等)实现时间序列分析的相关算法;(3)能够撰写时间序列分析的报告,清晰地表达分析结果和结论。
3.情感态度价值观目标:(1)培养学生的数据分析能力和科学思维;(2)培养学生对时间序列分析方法和技术的兴趣;(3)培养学生运用时间序列分析解决实际问题的意识和责任感。
二、教学内容本章节的教学内容主要包括时间序列的基本概念、预处理方法、平稳性检验、自相关函数和偏自相关函数的计算、常见模型及其应用。
具体安排如下:1.时间序列的定义、特点和分类;2.时间序列的预处理方法(如差分、季节性调整等);3.时间序列的平稳性检验(如ADF检验、KPSS检验等);4.时间序列的自相关函数和偏自相关函数的计算;5.时间序列的常见模型(如ARIMA模型、AR模型、MA模型等)及其应用;6.实际案例分析:运用时间序列分析方法解决实际问题。
三、教学方法本章节的教学方法采用讲授法、案例分析法和实验法相结合的方式。
具体方法如下:1.讲授法:通过讲解时间序列的基本概念、方法和应用,使学生掌握相关理论知识;2.案例分析法:分析实际案例,让学生了解时间序列分析在实际问题中的应用;3.实验法:引导学生运用编程语言进行时间序列分析的实践操作,巩固所学知识。
四、教学资源本章节的教学资源包括教材、参考书、多媒体资料和实验设备。
具体资源如下:1.教材:《时间序列分析与应用》;2.参考书:《时间序列分析的理论与实践》、《时间序列分析的R语言应用》;3.多媒体资料:时间序列分析的PPT课件、视频讲座等;4.实验设备:计算机、统计软件(如Python、R等)。
R语言时间序列中的时间设置

R语⾔时间序列中的时间设置
时间序列的不同时间分段设置
1. 普通的时间序列:年、⽉、季
1 myserises<-ts(data,start=,end=,frequency=)#其中frequency=1代表年;frequency=12代表⽉;frequency=4代表季度数据
2. 如果以天为单位的时间序列
1 t<-ts(1:365,frequency=1,start=as.Date("2017-05-01"))
2 s<-as.Date("2017-05-01")
3 date<-seq(from=s,by=1,length.out=365)
4 t<-data.frame(date,t)
或者可以利⽤zoo包进⾏⼀次排序
1 t<-seq(as.Date("2017-05-01"),length=365,by="day")
2 library(zoo)
3 mydata<-zoo(1:365,t)
3. 如果是以⼩时或者分钟为单位的话
1 #使⽤strptime函数
2 x<-strptime("2017-05-01 00:00:00","%Y-%m-%d %H:%M:%S")+900*1:10#这句代码的意思是设置成以15分钟为间隔的10个时间序列
3 library(zoo)
4 data<-zoo(1:10,x)
5 plot(data)#画出⼀个时序图
其实strptime()函数可以将时间序列分割成想要的频率模式,在这⾥是以秒为单位,15分钟的间隔就是15*60=900s。
r语言 时间序列相关系数

r语言时间序列相关系数时间序列相关系数是用来衡量两个时间序列之间相关性的统计量。
在R语言中,我们可以使用corr.test()函数来计算相关系数。
相关系数可以帮助我们了解两个变量之间的线性关系的强度和方向。
在R语言中,我们可以使用ts()函数将数据转换为时间序列对象。
然后,我们可以使用corr.test()函数来计算两个时间序列之间的相关系数。
该函数会返回一个结果对象,其中包含了相关系数的值、p 值以及置信区间等信息。
我们需要加载所需的包。
在R中,我们可以使用library()函数来加载包。
在这篇文章中,我们将使用"ts"包和"stats"包。
```Rlibrary(ts)library(stats)```接下来,我们需要准备一些时间序列数据进行演示。
我们可以使用自带的AirPassengers数据集作为示例。
这个数据集包含了1949年到1960年间每月的国际航空客运量数据。
我们可以使用该数据集创建两个时间序列对象。
```Rdata(AirPassengers)ts1 <- AirPassengers[1:120] # 取前120个观测值作为时间序列1ts2 <- AirPassengers[13:132] # 取第13到132个观测值作为时间序列2```现在,我们可以使用corr.test()函数来计算两个时间序列之间的相关系数。
该函数的第一个参数是要计算相关系数的时间序列对象。
第二个参数是另一个时间序列对象。
我们可以将结果保存在一个变量中。
```Rresult <- corr.test(ts1, ts2)```通过打印结果,我们可以查看相关系数的值、p值以及置信区间等信息。
```Rprint(result)```在结果中,我们可以看到相关系数的值为0.893,p值为0.0001712。
这表明两个时间序列之间存在着强烈的正相关关系。
也就是说,当一个时间序列增加时,另一个时间序列也会增加。
季节分解模型实例分析_SPSS 统计分析从入门到精通_[共3页]
![季节分解模型实例分析_SPSS 统计分析从入门到精通_[共3页]](https://img.taocdn.com/s3/m/38d4efb5caaedd3382c4d32f.png)
时间序列分析 第 15 章分析,再将分析结果综合起来组成一个对原始时间序列的总模型。
1.时间序列的4种成分(1)长期趋势(Long term trend),记为T。
表示序列取值随时间逐渐增加、减少或不变的长期发展趋势。
例如:全球人口总数随着时间推移,正在逐步增长;人口死亡率,由于医疗技术的进步及生活水平的提高,出现了长期向下的趋势。
另外,同一序列在不同时期可能表现出不同的长期趋势,例如:某商品的销量,在产品初期具有向上趋势;在产品成长期有加速向上的趋势;在产品成熟期表现出缓慢增长的趋势;在产品末期呈向下的趋势。
(2)季节趋势(Seasonal component),记为S。
表示由于受到季节因素或某些习俗的影响,而出现的有规则的变化规律。
例如:电风扇和空调的销售量,在夏季多而冬季少;每一天的交通流量,在上下班时间出现高峰,其余时间则较为稳定;圣诞节之前,玩具的销售量总会增加等。
(3)循环趋势(Cyclical component),记为C。
表示序列取值沿着趋势线有如钟摆般循环变动的规律。
循环趋势的周期长短和波动幅度是主要的研究对象。
有时一个时间序列的循环是由多个小循环组合而成的,例如:总体经济指标的循环,就是由各个产业的循环组合而成。
(4)不规则趋势(Irregular component),记为I。
表示把时间序列中的长期趋势、季节趋势和循环趋势都去除后余下的部分。
一般而言,长期趋势、季节趋势和循环趋势都受到规则性因素的影响,只有不规则趋势是随机性的,它发生的原因有自然灾害、天气突变、人为的意外因素等。
2.季节分解模型的种类对于时间序列中各变动因素之间的关系,通常有两种不同的假设:加法关系假设和乘法关系假设,相应地就有了时间序列季节分解的加法模型和乘法模型。
(1)加法模型。
加法模型假设:时间序列是由4种成分相加而成的;各成分之间彼此独立,没有交互影响。
如果以Y表示某个时间序列,它的加法模型就为:Y=T+C+S+R。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/3/26
《统计学实验》第15章时间序列分析
15-9
【统计理论】
由于篇幅有限,本章案例中仅对HoltWinter加法模型和Holt-Winter乘法模型的 理论模型进行简单介绍。
2020/3/26
《统计学实验》第15章时间序列分析
15-10
【统计理论】
Holt-Winter加法模型,该方法适用于具有 线性趋势和加法季节变化的序列。平滑后 的序列由下式(15.1)给出: yˆtk at btk Stk , t s 1, s 2,L ,T (15.1)
15-4
三、实验内容
运用R软件对数据进行指数平滑和季节分解。
2020/3/26
《统计学实验》第15章时间序列分析
15-5
第15章时间序列分析
15.1 指数平滑法 15.2 时间序列的季节分解
2020/3/26
《统计学实验》第15章时间序列分析
15-6
15.1 指数平滑法
【例15.1】 (数据文件为li15.1.csv) 选取 2000年至2015年我国月度社会消费品零售 总额数据(亿元),利用指数平滑方法试对该 数据进行分析。
2020/3/26
《统计学实验》第15章时间序列分析
15-7
【统计理论】
指数平滑法是在加权移动平均法基础上改 进而来的一种广泛使用的统计分析方法。 它通过计算一系列指数平滑值来消除不规 则变动,以反映时间序列的长期趋势。指 数平滑法既是对时间序列进行修匀的一种 方法,也可以直接用于预测,还可以用于 估计预测模型的参数。
2020/3/26
《统计学实验》第15章时间序列分析
15-11
【统计理论】
需要用简单的方法给出季节因子的第一年 的初值,以及截距初值和斜率初值。三个 系数可由下面的递推式(15.2)得到:
at ( yt Sts ) (1 )(at1 bt1) bt (at at1) (1 )bt1 St ( yt at ) (1 )Sts
15-17
【软件操作】
setwd("D:/R-Statistics/data/chap-15") #设定工作路径
x=read.csv("li15.1.csv",header=T) #从li15.1.csv中读入样本数据x
tx=ts(x$RetailSales,start=c(2000,1),freq=12)
yˆtk (at btk)Stk , t s 1, s 2,L ,T(15.4)
2020/3/26
《统计学实验》第15章时方法给出季节因子的第一年 的初值,以及截距初值和斜率初值。三个 系数可由下面的递推式(15.5)得到:
at
yt St s
(1 )(at1
统计学实验 —SPSS和R软件应用与实例
(第二版)
主编:费宇
2020/3/26
《统计学实验》第15章时间序列分 析
15-1
第15章 时间序列分析
2020/3/26
《统计学实验》第15章时间序列分析
15-2
一、实验目的
1. 运用R软件分析时间序列数据,掌握R软 件 中 的 HoltWinters() 滤 波 函 数 作 时 间 序 列的指数平滑和decompose()函数作季节 分解。
图15.1给出了通过指数平滑后观测值和拟合值的时间序列图,可以看出,指数平 滑方法可以很好的估计出我国月度社会消费品零售总额数据的变化趋势和周 期波动。
(15.2)
2020/3/26
《统计学实验》第15章时间序列分析
15-12
【统计理论】
预测值由式(15.3)计算得到:
yˆT k aT bT k ST k s
(15.3)
2020/3/26
《统计学实验》第15章时间序列分析
15-13
【统计理论】
Holt-Winter乘法模型,该方法适用于具有 线性趋势和乘法季节变化的序列。平滑后 的序列由下式(15.4)给出:
2. 掌握运用R软件中的函数对时间序列数据 进行分析的基本操作过程,并能读懂R软 件输出的结果。
2020/3/26
《统计学实验》第15章时间序列分析
15-3
二、实验环境
1. 系统软件Windows2007或更高版本; 2. 统计软件R.3.3.1或更高版本。
2020/3/26
《统计学实验》第15章时间序列分析
bt1)
bt (at at1) (1 )bt1
St
yt at
(1 )Sts
(15.5)
2020/3/26
《统计学实验》第15章时间序列分析
15-15
【统计理论】
预测值由式(15.6)计算得到:
yˆT k (aT bT k )ST ks
(15.6)
2020/3/26
《统计学实验》第15章时间序列分析
2020/3/26
《统计学实验》第15章时间序列分析
15-18
【软件操作】
#定义RetailSales为时间序列类型数据
(m=HoltWinters(tx,seasonal="mult")) #显示HoltWinter指数平滑法的参数估计结果,其 中参数seasonal为滤波 #函数中的季节趋势,seasonal="mult"表示季节效 应为乘法效应
2020/3/26
《统计学实验》第15章时间序列分析
15-8
【统计理论】
指数平滑模型 (Gardner, 1985) 分为季节 性模型和非季节性模型。季节性模型只有 在为活动数据集定义了周期时才可用。常 见的指数平滑模型有一次指数平滑模型、 二次指数平滑模型、Holt-Winter无季节性 模型、Holt-Winter加法模型和Holt-Winter 乘法模型。
15-16
【软件操作】
R软件的HoltWinter()滤波函数可以完成时 间序列数据的指数平滑,如果已经有文本 格式的样本数据文件li15.1.csv储存在"D:/RStatistics/data/chap-15"中,可以采用以下 程序读入样本数据x,具体程序如下:
2020/3/26
《统计学实验》第15章时间序列分析
plot(m) #HoltWinter指数平滑法拟合效果图 运行后可得指数平滑后的拟合效果图如图15.1所示。
2020/3/26
《统计学实验》第15章时间序列分析
15-19
图15.1 通过指数平滑后观测值和拟合值的时间序列图
2020/3/26
《统计学实验》第15章时间序列分析
15-20
【结果分析】
