西安铁一中分校数学旋转几何综合中考真题汇编[解析版]
西安市铁一中学中考数学几何综合压轴题易错专题

西安市铁一中学中考数学几何综合压轴题易错专题一、中考数学几何综合压轴题1.(1)方法选择如图①,四边形ABCD是O的内接四边形,连接AC,BD,AB BC AC==.求证:BD AD CD=+.小颖认为可用截长法证明:在DB上截取DM AD=,连接AM…小军认为可用补短法证明:延长CD至点N,使得DN AD=…请你选择一种方法证明.(2)类比探究(探究1)如图②,四边形ABCD是O的内接四边形,连接AC,BD,BC是O的直径,AB AC=.试用等式表示线段AD,BD,CD之间的数量关系,并证明你的结论.(探究2)如图③,四边形ABCD是O的内接四边形,连接AC,BD.若BC是O的直径,30ABC∠=︒,则线段AD,BD,CD之间的等量关系式是______.(3)拓展猜想如图④,四边形ABCD是O的内接四边形,连接AC,BD.若BC是O的直径,::::BC AC AB a b c=,则线段AD,BD,CD之间的等量关系式是______.解析:(1)方法选择:证明见解析;(2)【探究1】:2BD CD=;【探究2】32BD CD AD=+;(3)拓展猜想:c aBD CD ADb b=+.【分析】(1)方法选择:根据等边三角形的性质得到∠ACB=∠ABC=60°,如图①,在BD上截取DM=AD,连接AM,由圆周角定理得到∠ADB=∠ACB=60°,得到AM=AD,根据全等三角形的性质得到BM=CD,于是得到结论;(2)类比探究:如图②,由BC是⊙O的直径,得到∠BAC=90°,根据等腰直角三角形的性质得到∠ABC=∠ACB=45°,过A作AM⊥AD交BD于M,推出△ADM是等腰直角三角形,求得2根据全等三角形的性质得到结论;【探究2】如图③,根据圆周角定理和三角形的内角和得到∠BAC=90°,∠ACB=60°,过A作AM⊥AD 交BD于M,求得∠AMD=30°,根据直角三角形的性质得到MD=2AD,根据相似三角形的性质得到3,于是得到结论;(3)如图④,由BC是⊙O的直径,得到∠BAC=90°,过A作AM⊥AD交BD于M,求得∠MAD=90°,根据相似三角形的性质得到BM=c b CD ,DM=a bAD ,于是得到结论. 【详解】(1)方法选择:∵AB BC AC ==,∴60ACB ABC ∠=∠=︒,如图①,在BD 上截取=DM AD ,连接AM ,∵60ADB ACB ∠=∠=︒,∴ADM ∆是等边三角形,∴AM AD =,∵ABM ACD ∠=∠,∵120AMB ADC ∠=∠=︒,∴()ABM ACD AAS ∆≅∆,∴BM CD =,∴BD BM DM CD AD =+=+;(2)类比探究:如图②,∵BC 是O 的直径,∴90BAC ∠=︒,∵AB AC =,∴45ABC ACB ∠=∠=︒,过A 作AM AD ⊥交BD 于M ,∵45ADB ACB ∠=∠=︒,∴ADM ∆是等腰直角三角形,∴AM AD =,45AMD ∠=︒, ∴DM =,∴135AMB ADC ∠=∠=︒,∵ABM ACD ∠=∠,∴()ABM ACD AAS ∆≅∆,∴BM CD =, ∴BD BM DM CD =+=;[探究2]如图③,∵若BC 是O 的直径,30ABC ∠=︒,∴90BAC ∠=︒,60ACB ∠=︒,过A 作AM AD ⊥交BD 于M ,∵60ADB ACB ∠=∠=︒,∴30AMD ∠=︒,∴2MD AD =,∵ABD ACD ∠=∠,150AMB ADC ∠=∠=︒,∴ABMACD ∆∆,∴BM AB CD AC==∴3BM CD =, ∴32BD BM DM CD AD =+=+;故答案为32BD CD AD =+;(3)拓展猜想:c a BD BM DM CD AD b b=+=+; 理由:如图④,∵若BC 是O 的直径,∴90BAC ∠=︒,过A 作AM AD ⊥交BD 于M ,∴90MAD ∠=︒,∴BAM DAC ∠=∠,∴ABMACD ∆∆, ∴BM AB c CD AC b==, ∴c BM CD b=, ∵ADB ACB ∠=∠,90BAC NAD ∠=∠=︒,∴ADMACB ∆∆, ∴AD AC b DM BC a==, ∴a DM AD b =, ∴c a BD BM DM CD AD b b=+=+. 故答案为c a BD CD AD b b=+. 【点睛】本题考查了圆周角定理,圆内接四边形的性质,相似三角形的判定和性质,等腰直角三角形的性质,等边三角形的性质,正确的作出辅助线是解题的关键.2.情境观察:将矩形ABCD 纸片沿对角线AC 剪开,得到△ABC 和△A′C′D ,如图1所示.将△A′C′D 的顶点A′与点A 重合,并绕点A 按逆时针方向旋转,使点D 、A (A′)、B 在同一条直线上,如图2所示.观察图2可知:与BC 相等的线段是 ▲ ,∠CAC′= ▲ °.问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB=k AE,AC=k AF,试探究HE与HF之间的数量关系,并说明理由.解析:情境观察:AD(或A′D),90问题探究:EP=FQ. 证明见解析结论: HE=HF. 证明见解析【详解】情境观察AD(或A′D),90问题探究结论:EP=FQ.证明:∵△ABE是等腰三角形,∴AB=AE,∠BAE=90°.∴∠BAG+∠EAP=90°.∵AG⊥BC,∴∠BAG+∠ABG=90°,∴∠ABG=∠EAP.∵EP⊥AG,∴∠AGB=∠EPA=90°,∴Rt△ABG≌Rt△EAP. ∴AG=EP.同理AG=FQ. ∴EP=FQ拓展延伸结论: HE=HF.理由:过点E 作EP ⊥GA ,FQ ⊥GA ,垂足分别为P 、Q.∵四边形ABME 是矩形,∴∠BAE=90°,∴∠BAG+∠EAP=90°.AG ⊥BC ,∴∠BAG+∠ABG=90°,∴∠ABG=∠EAP .∵∠AGB=∠EPA=90°,∴△ABG ∽△EAP ,同理△ACG ∽△FAQ ,∵AB= k AE ,AC= kAF ,∴EP=FQ.∵∠EHP=∠FHQ ,∴Rt △EPH ≌Rt △FQH. ∴HE=HF3.如图①,在Rt OAB ∆中,90,,AOB OA OB D ∠=︒=为OB 边上一点,过D 点作DC AB ⊥交AB 于点C ,连接AD ,E 为AD 的中点,连接,OE CE .(观察猜想)(1)①,OE CE 的数量关系是___________②,OEC OAB ∠∠的数量关系是______________(类比探究)(2)将图①中BCD ∆绕点B 逆时针旋转45︒,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;(拓展迁移)(3)将BCD ∆绕点B 旋转任意角度,若2,3BD OB ==,请直接写出点,,O C B 在同一直线上时OE 的长.解析:(1)①OE CE =;②2OEC OAB ∠=∠;(2)成立,证明见解析;(3)OE 的长为2或22【分析】(1)①根据直角三角形斜边上的中线等于斜边的一半,即可得到答案;②由①知OE CE AE ==,利用等边对等角和三角形的外角性质,得到2OED OAE ∠=∠,2DEC EAC ∠=∠,然后即可得到答案;(2)①过点E 作EF AB ⊥交BO 的延长线于点F ,EF 与AO 交于点G ,利用等腰直角三角形的性质,证明EFO EBC ∆≅∆,即可得到结论成立;②由全等三角形的性质,求出∠OEC=90°,即可得到结论成立;(3)根据旋转的性质,点,,O C B 在同一直线上可分为两种情况:①点C 在线段OB 上;②点C 在OB 的延长线上;利用等腰直角三角形的性质,分别求出OE 的长度,即可得到答案.【详解】解:(1)如图,在△AOD 和△ACD 中,∵90AOB ∠=︒,E 为AD 中点,12OE AD ∴=, 90ACD ∠=︒,E 为AD 中点, 12CE AD ∴=, OE CE ∴=;②90AOB ∠=︒,E 为AD 中点,,OE AE ∴=OAE AOE ∴∠=∠,∴2OED OAE ∠=∠;同理可得:2DEC EAC ∠=∠,2()OED DEC OAE EAC ∴∠+∠=∠+∠,2OEC OAB ∴∠=∠.(2)成立.证明:①如图,过点E 作EF AB ⊥交BO 的延长线于点,F EF 与AO 交于点G ,∵OAB ∆是等腰三角形,∴45ABO ∠=︒∵EF BE ⊥,∴45F ∠=︒,∴EF BE =,∴,,AEG OFG BCD ∆∆∆均为等腰直角三角形,∴,,AE DE GE FG BD OF BC ====,又∵∠=∠F CBD ,∴EFO EBC ∆≅∆,∴OE CE =;②EFO EBC ∆≅∆,∴OEF CEB ∠=∠,90OEC OEB CEB OEB OEF ∴∠=∠+∠=∠+∠=︒,45OAB ∠=︒,2OEC OAB ∴∠=∠;(3)OE 的长为2或22;∵在等腰直角BCD ∆中,2BD =, 1BC ∴=,由(2)可知,OE CE =,90OEC ∠=︒,∴OEC ∆是等腰直角三角形,∴22OE OC =; 当点,,O C B 在同一直线上时,有①点C 在线段OB 上;如图:∴2OC OB BC =-=,∴22OE == ②点C 在OB 的延长线上;如图:∴314OC OB BC =+=+=, ∴2222OE OC ==; 综上所述,OE 的长为2或22;【点睛】本题考查了旋转的性质,等腰直角三角形的判定和性质,解直角三角形,全等三角形的判定和性质,直角三角形斜边上的中线等于斜边的一半,以及三角形的外角性质等,综合能力强,知识的运用广泛.解题的关键是熟练掌握所学的性质进行解题,注意运用数形结合的思想和分类讨论的思想进行分析.4.如图,已知ABC ∆和ADE ∆均为等腰三角形,AC BC =,DE AE =,将这两个三角形放置在一起.(1)问题发现如图①,当60ACB AED ∠=∠=︒时,点B 、D 、E 在同一直线上,连接CE ,则CEB ∠的度数为__________,线段AE 、BE 、CE 之间的数量关系是__________;(2)拓展探究如图②,当90ACB AED ∠=∠=︒时,点B 、D 、E 在同一直线上,连接CE .请判断CEB ∠的度数及线段AE 、BE 、CE 之间的数量关系,并说明理由;(3)解决问题如图③,90ACB AED ∠=∠=︒,25AC =2AE =,连接CE 、BD ,在AED ∆绕点A 旋转的过程中,当DE BD ⊥时,请直接写出EC 的长解析:(1)60,BE AE CE ︒=+;(2)45,2CEB BE AE CE ∠=︒=+;(3)2242【分析】(1)证明△ACE ≌△ABD ,得出CE=AD ,∠AEC=∠ADB ,即可得出结论;(2)证明△ACE ∽△ABD ,得出∠AEC=∠ADB ,2BD CE =,即可得出结论;(3)先判断出2BD CE =,再求出210AB =,①当点E 在点D 上方时,先判断出四边形APDE 是矩形,求出AP=DP=AE=2,再根据勾股定理求出,BP=6,得出BD=4;②当点E 在点D 下方时,同①的方法得,AP=DP=AE=1,BP=4,进而得出BD=BP+DP=8,即可得出结论.【详解】(1)在△ABC 为等腰三角形,AC=BC ,∠ACB=60°,∴△ABC 是等边三角形,∴AC=AB ,∠CAB=60°,同理:AE=AD ,∠ADE=∠EAD=60°,∴∠EAD=∠CAB ,∴∠EAC=∠DAB ,∴△ACE ≌△ABD (SAS ),∴CE=AD ,∠AEC=∠ADB ,∵点B 、D 、E 在同一直线上,∴∠ADB=180°-∠ADE=120°,∴∠AEC=120°,∴60CEB ∠=︒∵DE=AE ,∴BE=DE+BD=AE+CE ,故答案为60°,BE=AE+CE ;(2)45,CEB BE AE ∠=︒=.理由如下:ABC ∆和ADE ∆均为等腰三角形, 90ACB AED ∠=∠=︒,,,45AD AB EAD CAB EDA ∴===∠=∠=∠=︒,EAC DAB ∠=∠∴,AEC ADB ∴∆∆∽,AB AD BD AC AE CE∴===,BD AEC ADB ∴=∠=∠,点B 、D 、E 在同一直线上,180135,135ADB EDA AEC ∴∠=︒-∠=︒∴∠=︒,1359045,CEB AEC AED EB ED BD AE ∴∠=∠-∠=︒-︒=︒=+=+.45,CEB BE AE ∴∠=︒=;(3)由(2)知,△ACE ∽△ABD , ∴BD =,在Rt △ABC 中,AC = ∴AB ==①当点E 在点D 上方时,如图③,过点A 作AP ⊥BD 交BD 的延长线于P ,∵DE ⊥BD ,∴∠PDE=∠AED=∠APD ,∴四边形APDE 是矩形,∵AE=DE ,∴矩形APDE 是正方形,∴AP=DP=AE=2,在Rt △APB 中,根据勾股定理得, 226BP AB AP =-=∴BD=BP-AP=4, ∴1222CE BD ==; ②当点E 在点D 下方时,如图④,同①的方法得,AP=DP=AE=2,BP=4,∴BD=BP+DP=8,∴22CE == 即:CE 的长为2242【点睛】此题是几何变换综合题,主要考查了旋转的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,等边三角形的性质,判断出△ACE ∽△ABD 是解本题的关键. 5.在Rt ABC ∆中,90,7,2ACB AB AC ︒∠===,过点B 作直线//m AC ,将ABC ∆绕点C 顺时针旋转得到A B C ''∆(点,A B 的对应点分别是,A B ''),射线,CA CB ''分别交直线m 于点,P Q .(1)问题发现:如图1所示,若P 与A '重合,则ACA '∠的度数为_________________ (2)类比探究:如图2,所示,设A B ''与BC 的交点为M ,当M 为A B ''中点时,求线段PQ 的长;(3)拓展延伸:在旋转过程中,当点,P Q 分别在,CA CB ''的延长线上时,试探究四边形PA B Q ''的面积是否存在最小值,若存在,直接写出四边形PA B Q ''的最小面积;若不存在,请说明理由解析:(1)60°;(2)72;(3)存在,33【分析】(1)由旋转可得:AC=A'C=2,进而得到3∠A'BC=90°,可得cos ∠A'CB=3BC A C '=,即可得到∠A'CB=30°,∠ACA'=60°; (2)根据M 为A'B'的中点,即可得出∠A=∠A'CM ,进而得到PB=3BC A C '=tan ∠BQC=tan ∠33,进而得出PQ=PB+BQ=72; (3)依据S 四边形PA'B′Q =S △PCQ -S △A'CB '=S △PCQ 3S 四边形PA'B′Q 最小,即S △PCQ 最小,而S △PCQ =123,利用几何法或代数法即可得到S △PCQ 的最小值=3,S 四边形PA'B′Q =3-3 【详解】解(1)由旋转得:2AC A C '==,90,7,2,3ACB AB AC BC ︒∠===∴=90,//ACB m AC ︒∠=, 90A BC ︒'∴∠=,3cos BC A CB A C '∴∠==' 30A CB ︒'∴∠=,60A CA ︒'∴∠=;(2)因为M 是AA '中点,所以A CM MA C ''∠=∠,A MA C '∠=∠,A A CM '∴∠=∠,3tan tan PCB A ∠=∠=∴, 332PB ∴==. ∵∠PCQ=∠PBC=90°,∴∠BQC+∠BPC=∠BCP+∠BPC=90°,∴∠BQC=∠BCP=∠A ,3tan tan BQC A ∴∠=∠=223BQ BC ∴=⨯=, 72PQ PB BQ ∴=+=; (3) 3PA B Q PCQ A CB PCQ S S S S ''''∆=-=-,PA B Q S ''∴最小,即PCQ S 最小,1322PCQ S PQ BC PQ ∴=⨯=, 取PQ 的中点G ,190,2PCQ CG PQ ︒∠=∴=,即PQ=2CG , 当CG 最小时, PQ 最小,CG PQ ∴⊥, CG 与CB 重合,CG 最小,∵CG 的最小值为3,PA B Q S ''∴33=-.【点睛】本题属于四边形综合题,主要考查了旋转的性质,解直角三角形以及直角三角形的性质的综合运用,解题时注意:旋转变换中,对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.6.在Rt ABC 中,9072ACB AB AC ∠=︒==,,,过点B 作直线m AC ∥,将ABC 绕点C 顺时针旋转得到A B C '''(点A B ,的对应点分别为A B '',).(1)问题发现如图1,若P 与A 重合时,则ACA '∠的度数为____________;(2)类比探究:如图2,设AB 与BC 的交点为M ,当M 为A B ''的中点时,求线段PQ 的长;(3)拓展延伸在旋转过程中,当点P Q ,分别在CA CB '',的延长线上时,试探究四边形PA B O ''的面积是否存在最小值.若存在,直接写出四边形PA B O ''的最小面积;若不存在,请说明理由.解析:(1)60︒;(2)72;(3)33 【分析】(1)由旋转可得:AC=A'C=2,进而得到3∠A'BC=90°,可得cos BC A CB A C ''∠==,即可得到∠A'CB=30°,∠ACA'=60°;(2)根据M 为A'B'的中点,即可得出∠A=∠A'CM ,进而得到32PB ==,依据tan ∠Q=tan ∠,进而得出PQ=PB+BQ=72;(3)依据S 四边形PA'B′Q =S △PCQ -S △A'CB '=S △PCQ S 四边形PA'B′Q 最小,即S △PCQ 最小,而S △PCQ =12,利用几何法或代数法即可得到S △PCQ 的最小值=3,S 四边形PA'B′Q =3-【详解】解:(1)由旋转可得:2AC A C ''==,90,2ACB AB AC ∠=︒==,BC ∴90ACB ∠=︒,m AC ∥,90A BC '∴∠=︒,cos BC A CB A C '∴∠==' 30A CB '∴∠=︒,60ACA ∴'∠=︒.(2)M 为A B ''的中点,A CM MA C ''∴∠=∠,山旋转可得,MA C A '∠=∠,A A CM '∴∠=∠,tan tan PCB A ∴∠-∠32PB ∴==,tan tan BQC PCB ∠=∠=2BQ BC ∴===, 72PQ PB BQ ∴=+=;(3)S 四边形PA B Q PCQ A CB PCQ S S S ''''==-△△△S ∴四边形PA B Q ''最小即PCQ S 最小,12PCQ S PQ BC ∴=⨯⨯=△, 取PQ 的中点C ,90PQC ∠=︒,12CC PQ '∴=,即2PQ CC '=,当CG 最小时,PQ 最小,CG PQ ∴⊥,即CG 与CB 正合时,CG 最小,min 3CG ∴=,min 23PQ =,PCQ S ∴△的最小值3=, S 四边形PA B Q ''=33-.【点睛】此题考查四边形综合题,旋转的性质,解直角三角形以及直角三角形的性质的综合运用,解题关键在于掌握旋转变换中,对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.7.(1)问题发现如图1,在OAB 和OCD 中,OA OB =,OC OD =,40AOB COD ∠=∠=︒,连接,AC BD 交于点M .填空:①AC BD 的值为______;②AMB ∠的度数为______.(2)类比探究如图2,在OAB 和OCD 中,90AOB COD ∠=∠=︒,30OAB OCD ∠=∠=︒,连接AC 交BD 的延长线于点M .请判断AC BD的值及AMB ∠的度数,并说明理由; (3)拓展延伸在(2)的条件下,将OCD 绕点O 在平面内旋转,,AC BD 所在直线交于点M ,若1OD =,3OB =,请直接写出当点A 与点O D 、在同一条直线上时AD 的长.解析:(1)①1;②40︒;(2)3AC BD =90AMB ∠=︒.理由见解析;(3)2或4.【分析】(1)①证明△COA ≌△DOB (SAS ),得AC=BD ,比值为1;②由△COA ≌△DOB ,得∠CAO=∠DBO ,然后根据三角形的内角和定理先求∠OAB+∠OBA 的值,再求∠AMB 的值即可;(2)根据锐角三角比可得OD OB OC OA =,根据两边的比相等且夹角相等可得△AOC ∽△BOD ,根据相似撒尿性的性质求解即可;(3)当点A 与点O D 、在同一条直线上,有两种情况:如图3和图4,然后根据旋转的性质和勾股定理,可得AD 的长.【详解】(1)①∵40AOB COD ∠=∠=︒,∴∠BOD=∠AOC ,又∵OA OB =,OC OD =,∴△BOD ≌△AOC ,∴BD=AC , ∴AC BD =1; ②∵40AOB ∠=︒,∴∠OAB+∠OBA=140°,∵△BOD ≌△AOC ,∴∠CAO=∠DBO ,∴∠CAO+∠OAB+∠ABM=∠DBO+∠OAB+∠ABM=∠OAB+∠OBA=140°,∴∠AMB=40︒;(2)如图2,3AC BD =90AMB ∠=︒.理由如下:Rt COD 中,30DCO ∠=︒,90DOC ∠=︒,3tan 30OD OC ∴=︒= 同理得:3tan 30OB OA =︒= OD OB OC OA∴=, 90AOB COD ∠=∠=︒,AOC BOD ∴∠=∠,AOC BOD ∴△∽△,3AC OC BD OD∴==∠CAO=∠DBO , ∵∠BEO+∠DBO=90°,∴∠CAE+∠AEM=90°,∴∠AMB=90°;(3) ∵∠A=30°,3OB =∴OA=tan 30OB =3.如图3,当点D 和点A 在点O 的同侧时,∵1OD =,∴AD=3-2=2;如图4,当点D 和点A 在点O 的两侧时,∵1OD =,,OA=3∴AD=3+1=4.综上可知,AD 的长是2或4.【点睛】本题是三角形的综合题,主要考查了三角形全等和相似的性质和判定,相似三角形的判定与性质,解直角三角形,旋转的性质,以及分类讨论的数学思想,解题的关键是能得出:△AOC ∽△BOD ,根据相似三角形的性质,并运用类比的思想解决问题,本题是一道比较好的题目.8.如图1,在ABC 中,2AB AC ==,120BAC ∠=︒,点,D E 分别是,AC BC 的中点,连接DE .(1)探索发现:图1 图2图3图1中,AB BC 的值为_____________;AD BE 的值为_________; (2)拓展探究 若将CDE △绕点C 逆时针方向旋转一周,在旋转过程中AD BE 的大小有无变化,请仅就图2的情形给出证明;(3)问题解决当CDE △旋转至,,A D E 三点在同一直线时,直接写出线段BE 的长.解析:(1)33;33 (2)见解析 (3)3932+或3932- 【分析】(1)先判断出∠AEB=90°,再判断出∠B=30°,进而的粗AE ,再用勾股定理求出BE ,即可得出结论;(2)先判断出,进而得出△ACD ∽△BCE ,即可得出结论;(3)分点D 在线段AE 上和AE 的延长线上,利用含30度角的直角三角形的性质和勾股定理,最后用线段的和差求出AD ,即可得出结论.【详解】解:解: (1)如图1,连接AE,∵AB=AC=2,点E 分别是BC 的中点,∴AE ⊥ BC,∴∠AEC=90° ,∵AB=AC=2,∠BAC=120° ,∴∠B=∠C=30°,在Rt △ABE 中,AE=12AB=1,根据勾股定理得,BE 3∵点E 是BC 的中点,∴BC=2BE =23∴323AB BC ∵点D 是AC 的中点, ∴AD=CD=12AC=1,∴AD 3BE 3故答案为:33,33; (2)无变化,理由:由(1)知,CD=1,3CE BE == ∴3CD CE =3AC BC =∴3CD AC CE BC == 由(1)知,∠ACB=∠DCE=30°,∴∠ACD=∠BCE,∴△ACD ∽△BCE,∴3AD AC BE BC == (3)线段BE 393+393- 当点D 在线段AE 上时,如图2,过点C 作CF ⊥AE 于F,∠CDF=180°﹣∠CDE=60°,∴∠DCF=30°,∴1122DF CD ==, ∴33CF DF == 在Rt △AFC 中,AC=2,根据勾股定理得,2213AF AC CF =- ∴131+ 由(2)知,3AD BE = ∴3933BE +==当点D 在线段AE 的延长线上时,如图3,过点C 作CG ⊥AD 交AD 的延长线于G,∵∠CDG=60°,∴∠DCG=30°, ∴1122DG CD ==, ∴332CG DG ==, 在Rt △ACG 中,根据勾股定理得,132AG =, ∴1312AD AG DG -=-=, 由(2)知,33AD BE =, ∴39332BE AD -==即:线段BE 的长为3932+或3932-.【点睛】此题是相似形综合题,主要考查了等腰三角形的性质,含30度角的直角三角形的性质,勾股定理,相似三角形的判定和性质,构造出直角三角形是解本题的关键.9.综合与实践数学问题:(1)如图1,ABC 是等腰直角三角形,过斜边的中点D 作正方形DECF ,分别交BC ,AC 于点E ,F ,则AB ,BE ,AF 之间的数量关系为______.问题解决:(2)如图2,在任意Rt ABC 内,找一点D ,过点D 作正方形DECF ,分别交BC ,AC 于点E ,F ,若AB BE AF =+,求ADB ∠的度数;图2拓展提升:(3)如图3,在(2)的条件下,分别延长ED ,FD ,交AB 于点M ,N ,则MN ,AM ,BN 的数量关系为______.图3(4)在(3)的条件下,若3AC =,4BC =,则MN =______.解析:(1))2AB AF BE +;(2)135°;(3)222MN AM BN =+;(4)2512【分析】(1)根据等腰直角三角形的斜边与直角边的关系及正方形的性质即可得出数量关系; (2) 延长AC 至点P ,使FP BE =,连接DP ,根据正方形的性质易证DFP DEB △△≌,从而可得DP =DB ,进而可证ADP ADB △△≌,从而可得12DAC DAB CAB ∠=∠=∠,12ABD CBD ABC ∠=∠=∠,由三角形内角和定理即可求得∠ADB 的度数; (3)由正方形的对边平行的性质易得AM =DM ,BN =DN ,从而在Rt △MDN 中,由勾股定理即可得MN 、AM 、BN 的数量关系;(4)由(2)知FP =BE ,即可求得DE =DF =1,根据相似三角形的性质可分别求得EM 、FN 的长,从而可得DM 、DN 的长,在Rt △MDN 中,由勾股定理即可求得MN 的长.【详解】(1)∵ABC 是等腰直角三角形,且AB =AC , ∴2AB AC =,∠A =∠B =45°,∵四边形DECF 是正方形,且D 是AB 的中点,∴DF =FC =CE =DE ,∠DFA =∠DEB =90°,DF ∥BC ,DE ∥AC ,∴∠ADF =∠B =45°,∠BDE =∠A =45°,∴AF =DF ,BE =DE ,∴F 、E 分别是AC 、BC 的中点,∴CF =BE ,∴AC =AF +CF =AF +BE , ∴()2AB AF BE =+;(2)延长AC 至点P ,使FP BE =,连接DP .∵四边形DECF 是正方形,∴DF DE =,90DFC DEC ∠=∠=︒.∵FP BE =,90DFC DEB ∠=∠=︒,DF DE =,∴()SAS DFP DEB ≌△△.∴DP DB =.∵AB AF BE =+,AP AF FP =+,FP BE =,∴AP AB =.又∵DP DB =,AD AD =,∴()SSS ADP ADB ≌△△.∴12DAC DAB CAB ∠=∠=∠. 同理可得:12ABD CBD ABC ∠=∠=∠.∵90ACB ∠=︒,∴90CAB CBA ∠+∠=︒. ∴()1452DAB ABD CAB CBA ∠+∠=∠+∠=︒. ∴()180135ADB DAB ABD ∠=︒-∠+∠=︒.(3)∵DF ∥BC ,DE ∥AC ,∴∠CBD =∠NDB , ∠DAC =∠ADM ,∵ABD CBD ∠=∠,DAC DAB ∠=∠,∴∠ABD =∠NDB ,∠ADM =∠DAB ,∴BN =DN ,AM =DM .在Rt △MDN 中,由勾股定理得:22222MD DN MN AM BN ==++故答案为:222MN AM BN =+,(4)∵△ABC 是直角三角形,AC =3,BC =4,∴由勾股定理得:AB =5,设正方形DECF 的边长为x ,由(2)知,AP =AB =5,BE =FP ,CP =AP -AC =2,∵FP =CP +CF ,BE =BC -CE ,即4-x =2+x ,解得x =1,∴BE =BC -CE =3,AF =AC -CF =2,∵EM ∥AC ,FN ∥BC ,∴△BME ∽△BAC ,△AFN ∽△ACB ∴34ME BE AC BC ==,23FN AF BC AC ==, ∴94ME =,83FN =. ∵DM =ME -DE =54,DN =FN -DF =53,2512MN ==. 故答案为:2512MN =. 【点睛】 本题考查了正方形的性质,等腰三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理等知识,截长补短法作辅助线是本题的关键.10.如图(1),已知点G 在正方形ABCD 的对角线AC 上,GE ⊥BC ,垂足为点E ,GF ⊥CD ,垂足为点F .(1)证明与推断:①求证:四边形CEGF 是正方形;②推断:AG BE的值为 :(2)探究与证明:将正方形CEGF 绕点C 顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG 与BE 之间的数量关系,并说明理由:(3)拓展与运用:正方形CEGF 在旋转过程中,当B ,E ,F 三点在一条直线上时,如图(3)所示,延长CG 交AD 于点H .若AG=6,GH=22,则BC= .解析:(1)①四边形CEGF 是正方形;22)线段AG 与BE 之间的数量关系为2;(3)5【分析】(1)①由GE BC ⊥、GF CD ⊥结合BCD 90∠=可得四边形CEGF 是矩形,再由ECG 45∠=即可得证;②由正方形性质知CEG B 90∠∠==、ECG 45∠=,据此可得CG 2CE=、GE //AB ,利用平行线分线段成比例定理可得;(2)连接CG ,只需证ACG ∽BCE 即可得; (3)证AHG ∽CHA 得AG GH AH AC AH CH ==,设BC CD AD a ===,知AC 2a =,由AG GH AC AH =得2AH a 3=、1DH a 3=、10CH =,由AG AH AC CH =可得a 的值. 【详解】(1)①∵四边形ABCD 是正方形,∴∠BCD=90°,∠BCA=45°,∵GE ⊥BC 、GF ⊥CD ,∴∠CEG=∠CFG=∠ECF=90°,∴四边形CEGF 是矩形,∠CGE=∠ECG=45°,∴EG=EC ,∴四边形CEGF 是正方形;②由①知四边形CEGF 是正方形,∴∠CEG=∠B=90°,∠ECG=45°,∴2CG CE =,GE ∥AB , ∴2AG CG BE CE==故答案为2;(2)连接CG ,由旋转性质知∠BCE=∠ACG=α, 在Rt △CEG 和Rt △CBA 中,CE CG =22、CB CA =22, ∴CG CE =2CA CB= ∴△ACG ∽△BCE , ∴2AG CA BE CB == ∴线段AG 与BE 之间的数量关系为2;(3)∵∠CEF=45°,点B 、E 、F 三点共线,∴∠BEC=135°,∵△ACG ∽△BCE ,∴∠AGC=∠BEC=135°,∴∠AGH=∠CAH=45°,∵∠CHA=∠AHG , ∴△AHG ∽△CHA ,∴AG GH AH AC AH CH==, 设BC=CD=AD=a ,则2a ,则由AG GH AC AH =222AH a=, ∴AH=23a , 则DH=AD ﹣AH=13a ,22CD DH +10, ∴由AG AH AC CH =23210a a a = 解得:55故答案为5【点睛】本题考查了正方形的性质与判定,相似三角形的判定与性质等,综合性较强,有一定的难度,正确添加辅助线,熟练掌握正方形的判定与性质、相似三角形的判定与性质是解题的关键.11.问题背景:如图1,在矩形ABCD 中,23AB =,30ABD ∠=︒,点E 是边AB 的中点,过点E 作EF AB ⊥交BD 于点F .实验探究:(1)在一次数学活动中,小王同学将图1中的BEF 绕点B 按逆时针方向旋转90︒,如图2所示,得到结论:①AE DF=_____;②直线AE 与DF 所夹锐角的度数为______. (2)小王同学继续将BEF 绕点B 按逆时针方向旋转,旋转至如图3所示位置.请问探究(1)中的结论是否仍然成立?并说明理由.拓展延伸:在以上探究中,当BEF 旋转至D 、E 、F 三点共线时,则ADE 的面积为______. 解析:(1)32,30°;(2)成立,理由见解析;拓展延伸:133398+或133398- 【分析】(1)通过证明FBD EBA ∆∆∽,可得32AE BE DF BF ==,BDF BAE ∠=∠,即可求解; (2)通过证明ABE DBF ∆∆∽,可得32AE BE DF BF ==,BDF BAE ∠=∠,即可求解; 拓展延伸:分两种情况讨论,先求出AE ,DG 的长,即可求解.【详解】解:(1)如图1,30ABD ∠=︒,90DAB ∠=︒,EF BA ⊥,3cos 2BE AB ABD BF DB ∴∠===, 如图2,设AB 与DF 交于点O ,AE 与DF 交于点H ,BEF ∆绕点B 按逆时针方向旋转90︒,90DBF ABE ∴∠=∠=︒,FBD EBA ∴∆∆∽, ∴32AE BE DF BF ==,BDF BAE ∠=∠, 又DOB AOF ∠=∠,30DBA AHD ∴∠=∠=︒,∴直线AE 与DF 所夹锐角的度数为30,故答案为:32,30; (2)结论仍然成立, 理由如下:如图3,设AE 与BD 交于点O ,AE 与DF 交于点H ,将BEF ∆绕点B 按逆时针方向旋转,ABE DBF ∴∠=∠, 又32BE AB BF DB ==, ABE DBF ∴∆∆∽,∴32AE BE DF BF ==,BDF BAE ∠=∠, 又DOH AOB ∠=∠,30ABD AHD ∴∠=∠=︒,∴直线AE 与DF 所夹锐角的度数为30.拓展延伸:如图4,当点E 在AB 的上方时,过点D 作DG AE ⊥于G ,23AB =30ABD ∠=︒,点E 是边AB 的中点,90DAB ∠=︒,3BE ∴=2AD =,4DB =,30EBF ∠=︒,EF BE ⊥,1EF ∴=,D 、E 、F 三点共线,90DEB BEF ∴∠=∠=︒,2216313DE BD BE ∴-=-30DEA ∠=︒, 11322DG DE ∴==, 由(2)可得:32AE BE DF BF ==, ∴32131AE=+, 3932AE +∴=, ADE ∴∆的面积11393131333922228AE DG ++=⨯⨯=⨯⨯=; 如图5,当点E 在AB 的下方时,过点D 作DG AE ⊥,交EA 的延长线于G ,同理可求:ADE ∆的面积11393131333922228AE DG --=⨯⨯=⨯⨯=; 故答案为:133398+或133398-. 【点睛】 本题是几何变换综合题,考查了矩形的性质,相似三角形的判定和性质,直角三角形的性质,旋转的性质等知识,利用分类讨论思想解决问题是解题的关键.12.如图1,△ABC 和△DCE 都是等边三角形.探究发现(1)△BCD 与△ACE 是否全等?若全等,加以证明;若不全等,请说明理由.拓展运用(2)若B 、C 、E 三点不在一条直线上,∠ADC =30°,AD =3,CD =2,求BD 的长.(3)若B 、C 、E 三点在一条直线上(如图2),且△ABC 和△DCE 的边长分别为1和2,求△ACD 的面积及AD 的长.解析:(1)全等,理由见解析;(2)BD 133)△ACD 3AD 3 【分析】(1)依据等式的性质可证明∠BCD =∠ACE ,然后依据SAS 可证明△ACE ≌△BCD ; (2)由(1)知:BD =AE ,利用勾股定理计算AE 的长,可得BD 的长;(3)过点A 作AF ⊥CD 于F ,先根据平角的定义得∠ACD =60°,利用特殊角的三角函数可得AF 的长,由三角形面积公式可得△ACD 的面积,最后根据勾股定理可得AD 的长.【详解】解:(1)全等,理由是:∵△ABC 和△DCE 都是等边三角形,∴AC =BC ,DC =EC ,∠ACB =∠DCE =60°,∴∠ACB +∠ACD =∠DCE +∠ACD ,即∠BCD =∠ACE ,在△BCD 和△ACE 中,CD CE BCD ACE BC AC =⎧⎪∠=∠⎨⎪=⎩, ∴△ACE ≌△BCD (SAS );(2)如图3,由(1)得:△BCD ≌△ACE ,∴BD =AE ,∵△DCE 都是等边三角形,∴∠CDE =60°,CD =DE =2,∵∠ADC =30°,∴∠ADE =∠ADC +∠CDE =30°+60°=90°,在Rt △ADE 中,AD =3,DE =2, ∴229413AE AD DE =+=+=,∴BD =13;(3)如图2,过点A 作AF ⊥CD 于F ,∵B 、C 、E 三点在一条直线上,∴∠BCA +∠ACD +∠DCE =180°,∵△ABC 和△DCE 都是等边三角形, ∴∠BCA =∠DCE =60°,∴∠ACD =60°,在Rt △ACF 中,sin ∠ACF =AF AC,∴AF =AC ×sin ∠ACF =33122⨯=, ∴S △ACD =113322222CD AF ⨯⨯=⨯⨯=, ∴CF =AC ×cos ∠ACF =1×1122=,FD =CD ﹣CF =13222-=, 在Rt △AFD 中,AD 2=AF 2+FD 2=2233322⎛⎫⎛⎫+= ⎪ ⎪ ⎪⎝⎭⎝⎭, ∴AD =3.【点睛】本题考查等边三角形的性质,全等三角形的判定与性质,解直角三角形,勾股定理等,第(3)小题巧作辅助线构造直角三角形是解题的关键.13.(性质探究)如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,AE 平分∠BAC ,交BC 于点E .作DF ⊥AE 于点H ,分别交AB ,AC 于点F ,G .(1)判断△AFG 的形状并说明理由.(2)求证:BF =2OG .(迁移应用)(3)记△DGO 的面积为S 1,△DBF 的面积为S 2,当1213S S =时,求AD AB的值. (拓展延伸)(4)若DF 交射线AB 于点F ,(性质探究)中的其余条件不变,连结EF ,当△BEF 的面积为矩形ABCD 面积的110时,请直接写出tan ∠BAE 的值.解析:(1)等腰三角形,理由见解析;(2)见解析;(3545105【分析】 (1)如图1中,△AFG 是等腰三角形,利用全等三角形的性质证明即可.(2)如图2中,过点O作OL∥AB交DF于L,则∠AFG=∠OLG.首先证明OG=OL,再证明BF=2OL即可解决问题.(3)如图3中,过点D作DK⊥AC于K,则∠DKA=∠CDA=90°,利用相似三角形的性质解决问题即可.(4)设OG=a,AG=k.分两种情形:①如图4中,连接EF,当点F在线段AB上时,点G 在OA上.②如图5中,当点F在AB的延长线上时,点G在线段OC上,连接EF.分别求解即可解决问题.【详解】(1)解:如图1中,△AFG是等腰三角形.理由:∵AE平分∠BAC,∴∠1=∠2,∵DF⊥AE,∴∠AHF=∠AHG=90°,∵AH=AH,∴△AHF≌△AHG(ASA),∴AF=AG,∴△AFG是等腰三角形.(2)证明:如图2中,过点O作OL∥AB交DF于L,则∠AFG=∠OLG.∵AF=AG,∴∠AFG=∠AGF,∵∠AGF=∠OGL,∴∠OGL=∠OLG,∴OG=OL,∵OL ∥AB ,∴△DLO ∽△DFB , ∴=OL DO BF BD , ∵四边形ABCD 是矩形, ∴BD =2OD ,∴BF =2OL ,∴BF =2OG .(3)解:如图3中,过点D 作DK ⊥AC 于K ,则∠DKA =∠CDA =90°,∵∠DAK =∠CAD ,∴△ADK ∽△ACD ,∴=DK CD AD AC, ∵S 1=12•OG •DK ,S 2=12•BF •AD ,又∵BF =2OG ,121=3S S , ∴2==3DK CD AD AC ,设CD =2x ,AC =3x ,则AD = 25x , ∴5==2AD AD AB CD . (4)解:设OG =a ,AG =k .①如图4中,连接EF ,当点F 在线段AB 上时,点G 在OA 上.∵AF =AG ,BF =2OG ,∴AF =AG =k ,BF =2a ,∴AB =k +2a ,AC =2(k +a ),∴AD 2=AC 2﹣CD 2=[2(k +a )]2﹣(k +2a )2=3k 2+4ka ,∵∠ABE =∠DAF =90°,∠BAE =∠ADF ,∴△ABE ∽△DAF , ∴=BE AE AB AD , ∴=2BE k k a AD+, ∴()2=k k a BE AD+, 由题意:()211022k k a a AD+⨯⨯⨯=AD •(k +2a ), ∴AD 2=10ka ,即10ka =3k 2+4ka ,∴k =2a ,∴AD = 25a ,∴BE = ()2k k a AD+= 455a ,AB =4a , ∴tan ∠BAE =55BE AB =. ②如图5中,当点F 在AB 的延长线上时,点G 在线段OC 上,连接EF .∵AF =AG ,BF =2OG ,∴AF =AG =k ,BF =2a ,∴AB =k ﹣2a ,AC =2(k ﹣a ),∴AD 2=AC 2﹣CD 2=[2(k ﹣a )]2﹣(k ﹣2a )2=3k 2﹣4ka ,∵∠ABE =∠DAF =90°,∠BAE =∠ADF ,∴△ABE ∽△DAF ,∴BE AE AB AD =, ∴2BE k k a AD=-, ∴ ()2k k a BE AD -=,由题意:()211022k k a a AD-⨯⨯⨯=AD •(k ﹣2a ), ∴AD 2=10ka ,即10ka =3k 2﹣4ka ,∴k = 143a , ∴AD = 21053a , ∴()2810545k k a BE a AD -==,AB = 83a , ∴tan ∠BAE = 10515BE AB =, 综上所述,tan ∠BAE 的值为55或10515. 【点睛】本题是一道综合题,主要涉及到等腰三角形的判定及其性质、全等三角形的判定和性质、三角形中位线定理、相似三角形的判定及其性质、勾股定理的应用等知识点,解题的关键是综合运用所学到的相关知识.14.如图,四边形ABCD 是正方形,点O 为对角线AC 的中点.(1)问题解决:如图①,连接BO ,分别取CB ,BO 的中点P ,Q ,连接PQ ,则PQ 与BO 的数量关系是_____,位置关系是____;(2)问题探究:如图②,AO E ∆'是将图①中的AOB ∆绕点A 按顺时针方向旋转45︒得到的三角形,连接CE ,点P ,Q 分别为CE ,BO '的中点,连接PQ ,PB .判断PQB ∆的形状,并证明你的结论;(3)拓展延伸:如图③,AO E ∆'是将图①中的AOB ∆绕点A 按逆时针方向旋转45︒得到的三角形,连接BO ',点P ,Q 分别为CE ,BO '的中点,连接PQ ,PB .若正方形ABCD 的边长为1,求PQB ∆的面积.解析:(1)12PQ BO =,PQ BO ⊥;(2)PQB ∆的形状是等腰直角三角形,理由见解析;(3)316 【分析】 (1)根据题意可得PQ 为△BOC 的中位线,再根据中位线的性质即可求解;(2)连接O P '并延长交BC 于点F ,根据题意证出 O PE FPC ∆'∆≌,'O BF ∆为等腰直角三角形,BPO ∆'也为等腰直角三角形,由'PQ O B ⊥且PQ BQ =可得PQB ∆是等腰直角三角形;(3)延长O E '交BC 边于点G ,连接PG ,'O P .证出四边形O ABG '是矩形,EGC ∆为等腰直角三角形,' O GP BCP ∆∆≌,再证出O PB ∆'为等腰直角三角形,根据图形的性质和勾股定理求出O′A ,O′B 和BQ 的长度,即可计算出PQB ∆的面积.【详解】解:(1)∵点P 和点Q 分别为CB ,BO 的中点,∴PQ 为△BOC 的中位线,∵四边形ABCD 是正方形,∴AC ⊥BO ,∴12PQ BO =,PQ BO ⊥; 故答案为:12PQ BO =,PQ BO ⊥; (2)PQB ∆的形状是等腰直角三角形.理由如下:连接O P '并延长交BC 于点F ,由正方形的性质及旋转可得AB BC =,∠90ABC =°,AO E ∆'是等腰直角三角形,//O E BC ',O E O A '='.∴O EP FCP ∠'=∠,'PO E PFC ∠=∠.又∵点P 是CE 的中点,∴CP EP =.∴ ()O PE FPC AAS ∆'∆≌.∴''O E FC O A ==,'O P FP =.∴AB O A CB FC -'=-,∴BO BF '=.∴'O BF ∆为等腰直角三角形.∴'BP O F ⊥,'O P BP =.∴BPO ∆'也为等腰直角三角形.又∵点Q 为'O B 的中点,∴'PQ O B ⊥,且PQ BQ =.∴PQB ∆的形状是等腰直角三角形.(3)延长O E '交BC 边于点G ,连接PG ,'O P .∵四边形ABCD 是正方形,AC 是对角线,∴45ECG ∠=︒.由旋转得,四边形O ABG '是矩形,∴O G AB BC '==,90EGC ∠=︒.∴EGC ∆为等腰直角三角形.∵点P 是CE 的中点,∴PC PG PE ==,90CPG ∠=︒,45EGP ∠=︒.∴' ()O GP BCP SAS ∆∆≌.∴O PG BPC ∠'=∠,O P BP '=.∴90O PG GPB BPC GPB ∠'-∠=∠-∠=︒.∴'90O PB ∠=︒.∴O PB ∆'为等腰直角三角形.∵Q 是O B '的中点, ∴12PQ O B BQ ='=,PQ O B ⊥'. ∵1AB =, ∴2O A '=2226()12O B '=+, ∴6BQ ∴116632216PQB S BQ PQ ∆=⋅==. 【点睛】本题考查正方形的性质、等腰直角三角形的判定与性质、旋转图形的性质、三角形中位线定理、全等三角形的判定与性质和勾股定理,根据题意作出辅助线构造全等三角形是解题的关键.15.(证明体验)(1)如图1,AD 为ABC 的角平分线,60ADC ∠=︒,点E 在AB 上,AE AC =.求证:DE 平分ADB ∠.(思考探究)(2)如图2,在(1)的条件下,F 为AB 上一点,连结FC 交AD 于点G .若FB FC =,2DG =,3CD =,求BD 的长.(拓展延伸)(3)如图3,在四边形ABCD 中,对角线AC 平分,2BAD BCA DCA ∠∠=∠,点E 在AC 上,EDC ABC ∠=∠.若5,25,2BC CD AD AE ===,求AC 的长.解析:(1)见解析;(2)92;(3)163【分析】(1)根据SAS 证明EAD CAD ≌△△,进而即可得到结论; (2)先证明EBD GCD ∽,得BD DE CD DG=,进而即可求解; (3)在AB 上取一点F ,使得AF AD =,连结CF ,可得AFC ADC ≌,从而得DCE BCF ∽,可得,CD CE CED BFC BC CF=∠=∠,4CE =,最后证明EAD DAC ∽,即可求解.【详解】解:(1)∵AD 平分BAC ∠,∴EAD CAD ∠=∠,∵,==AE AC AD AD ,∴()EAD CAD SAS ≌,∴60ADE ADC ∠=∠=︒,∴18060EDB ADE ADC ∠=︒-∠-∠=︒,∴BDE ADE =∠∠,即DE 平分ADB ∠;(2)∵FB FC =,∴EBD GCD ∠=∠,。
西安铁一中分校数学全等三角形中考真题汇编[解析版]
![西安铁一中分校数学全等三角形中考真题汇编[解析版]](https://img.taocdn.com/s3/m/f95059d6783e0912a3162a29.png)
西安铁一中分校数学全等三角形中考真题汇编[解析版] 一、八年级数学轴对称三角形填空题(难)1.在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=12BC,则△ABC的顶角的度数为_____.【答案】30°或150°或90°【解析】试题分析:分两种情况;①BC为腰,②BC为底,根据直角三角形30°角所对的直角边等于斜边的一半判断出∠ACD=30°,然后分AD在△ABC内部和外部两种情况求解即可.解:①BC为腰,∵AD⊥BC于点D,AD=12 BC,∴∠ACD=30°,如图1,AD在△ABC内部时,顶角∠C=30°,如图2,AD在△ABC外部时,顶角∠ACB=180°﹣30°=150°,②BC为底,如图3,∵AD⊥BC于点D,AD=12 BC,∴AD =BD =CD ,∴∠B =∠BAD ,∠C =∠CAD ,∴∠BAD +∠CAD =12×180°=90°, ∴顶角∠BAC =90°, 综上所述,等腰三角形ABC 的顶角度数为30°或150°或90°.故答案为30°或150°或90°.点睛:本题考查了含30°交点直角三角形的性质,等腰三角形的性质,分类讨论是解题的关键.2.如图,在ABC 中,点A 的坐标为()0,1,点B 的坐标为()0,4,点C 的坐标为()4,3,点D 在第二象限,且ABD 与ABC 全等,点D 的坐标是______.【答案】(-4,2)或(-4,3)【解析】【分析】【详解】把点C 向下平移1个单位得到点D (4,2),这时△ABD 与△ABC 全等,分别作点C ,D 关于y 轴的对称点(-4,3)和(-4,2),所得到的△ABD 与△ABC 全等.故答案为(-4,2)或(-4,3).3.在平面直角坐标系xOy 中,已知点A (2,3),在x 轴上找一点P ,使得△AOP 是等腰三角形,则这样的点P 共有_____个.【答案】4【解析】【分析】以O 为圆心,OA 为半径画弧交x 轴于点P 1、P 3,以A 为圆心,AO 为半径画弧交x 轴于点P 4,作OA 的垂直平分线交x 轴于P 2.【详解】解:如图,使△AOP 是等腰三角形的点P 有4个.故答案为4.【点睛】本题考查了在平面直角坐标系中寻找等腰三角形,掌握两圆一线找等腰三角形是解题的关键.4.在锐角三角形ABC中.BC=32,∠ABC=45°,BD平分∠ABC.若M,N分别是边BD,BC上的动点,则CM+MN的最小值是____.【答案】4【解析】【分析】过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC于N′,则CE即为CM+MN 的最小值,再根据32ABC=45°,BD平分∠ABC可知△BCE是等腰直角三角形,由锐角三角函数的定义即可求出CE的长.【详解】解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC于N′,则CE即为CM+MN的最小值,∵32ABC=45°,BD平分∠ABC,∴△BCE 是等腰直角三角形,∴CE=BC•cos45°=32×2=4. ∴CM+MN 的最小值为4.【点睛】本题考查了轴对称最短路线问题,难度较大,根据题意作出辅助线,构造出等腰直角三角形,利用锐角三角函数的定义求解是解答此题的关键.5.如图,线段AB ,DE 的垂直平分线交于点C ,且72ABC EDC ∠=∠=︒,92AEB ∠=︒,则EBD ∠的度数为 ________ .【答案】128︒【解析】【分析】连接CE ,由线段AB ,DE 的垂直平分线交于点C ,得CA=CB ,CE=CD ,ACB=∠ECD=36°,进而得∠ACE=∠BCD ,易证∆ACE ≅∆BCD ,设∠AEC=∠BDC=x ,得则∠BDE=72°-x ,∠CEB=92°-x ,BDE 中,∠EBD=128°,根据三角形内角和定理,即可得到答案.【详解】连接CE ,∵线段AB ,DE 的垂直平分线交于点C ,∴CA=CB ,CE=CD ,∵72ABC EDC ∠=∠=︒=∠DEC ,∴∠ACB=∠ECD=36°,∴∠ACE=∠BCD ,在∆ACE 与∆BCD 中,∵CA CBACE BCDCE CD=⎧⎪∠=∠⎨⎪=⎩,∴∆ACE≅∆BCD(SAS),∴∠AEC=∠BDC,设∠AEC=∠BDC=x,则∠BDE=72°-x,∠CEB=92°-x,∴∠BED=∠DEC-∠CEB=72°-(92°-x)=x-20°,∴在∆BDE中,∠EBD=180°-(72°-x )-(x-20°)=128°.故答案是:128︒.【点睛】本题主要考查中垂线的性质,三角形全等的判定和性质定理以及三角形内角和定理,添加辅助线,构造全等三角形,是解题的关键.6.如图,在Rt ABC△中,AC BC=,D是线段AB上一个动点,把ACD沿直线CD折叠,点A落在同一平面内的A'处,当A D'平行于Rt ABC△的直角边时,ADC∠的大小为________.【答案】112.5︒或67.5︒【解析】【分析】当A D'平行于Rt ABC△的直角边时,有两种情况,一是当A D BC'时,二是当A D AC'时,两种情况根据折叠的性质及等腰三角形的性质进行角度的计算即可.【详解】如图1,当点D 在线段AB 上,且A D BC '时,45A DB B '∠=∠=︒,45180ADC A DC '∴∠+∠-=︒︒,解得112.5A DC ADC '∠=∠=︒.图1如图2,当A D AC '时,45A DB A '∠=∠=︒,45180ADC A DC '∴∠+∠+=︒︒,解得67.5A DC ADC '∠=∠=︒.图2【点睛】本题考查了翻折变换的性质,等腰直角三角形的性质,掌握折叠的性质是解题关键.7.如图,在△ABC 中,AB =AC ,点D 、E 在BC 的延长线上,G 是AC 上一点,且CG =CD ,F 是GD 上一点,且DF =DE .若∠A =100°,则∠E 的大小为_____度.【答案】10【解析】【分析】由DF=DE ,CG=CD 可得∠E=∠DFE ,∠CDG=∠CGD ,再由三角形的外角的意义可得∠GDC=∠E+∠DFE=2∠E ,∠ACB=∠CDG+∠CGD=2∠CD G ,进而可得∠ACB=4∠E ,最后代入数据即可解答.【详解】解:∵DF =DE ,CG =CD ,∴∠E=∠DFE,∠CDG=∠CGD,∵GDC=∠E+∠DFE,∠ACB=∠CDG+∠CGD,∴GDC=2∠E,∠ACB=2∠CDG,∴∠ACB=4∠E,∵△ABC中,AB=AC,∠A=100°,∴∠ACB=40°,∴∠E=40°÷4=10°.故答案为10.【点睛】本题考查等腰三角形的性质以及三角形外角的定义,解题的关键是灵活运用等腰三角形的性质和三角形的外角的定义确定各角之间的关系.8.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC为格点三角形,在图中最多能画出_____个格点三角形与△ABC成轴对称.【答案】6【解析】【分析】根据网格结构分别确定出不同的对称轴,然后作出轴对称三角形即可得解.【详解】如图,最多能画出6个格点三角形与△ABC成轴对称.故答案为:6.【点睛】本题考查了利用轴对称变换作图,熟练掌握网格结构并准确找出对应点的位置是解题的关键,本题难点在于确定出不同的对称轴.9.如图,△ABC中,AC=DC=3,BD垂直∠BAC的角平分线于D,E为AC的中点,则图中两个阴影部分面积之差的最大值为________.【答案】9 2【解析】【分析】首先证明两个阴影部分面积之差=S△ADC,当CD⊥AC时,△ACD的面积最大.【详解】延长BD交AC于点H.设AD交BE于点O.∵AD⊥BH,∴∠ADB=∠ADH=90°,∴∠ABD+∠BAD=90°,∠H+∠HAD=90°,∵∠BAD=∠HAD,∴∠ABD=∠H,∴AB=AH,∵AD⊥BH,∴BD=DH,∵DC=CA,∴∠CDA=∠CAD,∵∠CAD+∠H=90°,∠CDA+∠CDH=90°,∴∠CDH=∠H,∴CD=CH=AC,∵AE=EC,∴S△ABE=14S△ABH,S△CDH=14S△ABH,∵S△OBD−S△AOE=S△ADB−S△ABE=S△ADH−S△CDH=S△ACD,∵AC=CD=3,∴当DC⊥AC时,△ACD的面积最大,最大面积为12×3×3=92.故填:92.【点睛】本题考查等腰三角形的判定和性质,三角形中线的性质等知识,解题的关键是学会用转化的思想思考问题.10.如图,在△ABC中,AB=AC,AB边的垂直平分线DE交AC于点D.已知△BDC的周长为14,BC=6,则AB=___.【答案】8【解析】试题分析:根据线段垂直平分线的性质,可知AD=BD,然后根据△BDC的周长为BC+CD+BD=14,可得AC+BC=14,再由BC=6可得AC=8,即AB=8.故答案为8.点睛:此题主要考查了线段的垂直平分线的性质,解题时,先利用线段的垂直平分线求出BD=AD,然后根据三角形的周长互相代换,即可其解.二、八年级数学轴对称三角形选择题(难)11.在平面直角坐标系中,等腰△ABC的顶点A、B的坐标分别为(0,0)、(2,2),若顶点C落在坐标轴上,则符合条件的点C有()个.A.5 B.6 C.7 D.8【答案】D【解析】【分析】要使△ABC是等腰三角形,可分三种情况(①若AC=AB,②若BC=BA,③若CA=CB)讨论,通过画图就可解决问题.【详解】①若AC =AB ,则以点A 为圆心,AB 为半径画圆,与坐标轴有4个交点;②若BC =BA ,则以点B 为圆心,BA 为半径画圆,与坐标轴有2个交点(A 点除外); ③若CA =CB ,则点C 在AB 的垂直平分线上.∵A (0,0),B (2,2),∴AB 的垂直平分线与坐标轴有2个交点.综上所述:符合条件的点C 的个数有8个.故选D .【点睛】本题考查了等腰三角形的判定、垂直平分线的性质的逆定理等知识,还考查了动手操作的能力,运用分类讨论的思想是解决本题的关键.12.已知∠AOB =30°,点P 在∠AOB 内部,P 1与P 关于OB 对称,P 2与P 关于OA 对称,则P 1,O ,P 2三点构成的三角形是 ( )A .直角三角形B .钝角三角形C .等边三角形D .等腰三角形 【答案】C【解析】【分析】根据题意,作出相应的图形,然后对相应的角进行标记;本题先证明P 1,O ,P 2三点构成的三角形中1260POP ∠=︒,然后证边12OP OP OP ==,得到P 1,O ,P 2三点构成的三角形为等腰三角形,又因为该等腰三角形有一个角为60︒,故得证P 1,O ,P 2三点构成的三角形是等边三角形。
西安铁一中分校数学有理数中考真题汇编[解析版]
![西安铁一中分校数学有理数中考真题汇编[解析版]](https://img.taocdn.com/s3/m/cbe6a84cc8d376eeafaa3181.png)
一、初一数学有理数解答题压轴题精选(难)1.同学们都知道表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离,试探索:(1)求 ________.(2)找出所有符合条件的整数,使得.满足条件的所有整数值有________(3)由以上探索,猜想对于任何有理数x,是否有最大值或最小值?如果有最大值或最小值是多少?有最________(填“最大”或“最小”)值是________.【答案】(1)7(2)-3,-2,-1,0,1,2;(3)最小;3【解析】【解答】(1)原式=|5+2|=7.故答案为: 7;(2)令x+3=0或x-2=0时,则x=-3或x=2.当x<-3时,- (x+3) - (x-2) =5 ,-x-3-x+2=5,解得x=-3(范围内不成立)当-3≤x≤2时,(x+3) - (x-2) = 5,x+3-x+1=4,0x=0,x为任意数,则整数x=-3,-2,-1, 0,1,当x>2时,(x+3) + (x-2) = 5,x=2(范围内不成立) .综上所述,符合条件的整数x有: -3, -2, -1, 0,1,2.故答案为:-3,-2,-1,0,1,2;(3) 由(2) 的探索猜想,对于任何有理数x,有最小值为3,令x-3=0或x-6=0时,则x=3,x=6当x<3时,-(x-3)-(x-6)=-2x+3﹥3当3≤x≤6时,x-3-(x-6)=3,当x>6时,x-3+x-6=2x-9>3∴对于任何有理数x,有最小值为3【分析】(1)直接去括号,再按照去绝对值的方法去掉绝对值就可以了;(2)要求x的整数值可以进行分段计算,令x+3=0或x-2=0时,分为3段进行计算,最后确定x的值.(3)根据(2)方法去绝对值,分为3种情况去绝对值符号,计算三种不同情况的值,最后讨论得出最小值.2.阅读下面的材料:如图1,在数轴上A点衰示的数为a,B点表示的数为b,则点A到点B的距离记为AB.线段AB的长可以用右边的数减去左边的数表示,即AB﹣b﹣a.请用上面的知识解答下面的问题:如图2,一个点从数轴上的原点开始,先向左移动1cm到达A点,再向左移动2cm到达B 点,然后向右移动7cm到达C点,用1个单位长度表示1cm.(1)请你在数轴上表示出A.B.C三点的位置:(2)点C到点人的距离CA=________cm;若数轴上有一点D,且AD=4,则点D表示的数为________;(3)若将点A向右移动xcm,则移动后的点表示的数为________;(用代数式表示)(4)若点B以每秒2cm的速度向左移动,同时A.C点分别以每秒1cm、4cm的速度向右移动.设移动时间为t秒,试探索:CA﹣AB的值是否会随着t的变化而改变?请说明理由.【答案】(1)解:如图所示:(2)5;﹣5或3(3)﹣1+x(4)解:CA﹣AB的值不会随着t的变化而变化,理由如下:根据题意得:CA=(4+4t)﹣(﹣1+t)=5+3t,AB=(﹣1+t)﹣(﹣3﹣2t)=2+3t,∴CA﹣AB=(5+3t)﹣(2+3t)=3,∴CA﹣AB的值不会随着t的变化而变化【解析】【解答】(2)CA=4﹣(﹣1)=4+1=5(cm);设D表示的数为a,∵AD=4,∴|﹣1﹣a|=4,解得:a=﹣5或3,∴点D表示的数为﹣5或3;故答案为5,﹣5或3;( 3 )将点A向右移动xcm,则移动后的点表示的数为﹣1+x;故答案为﹣1+x;【分析】(1)根据题意容易画出图形;(2)由题意容易得出CA的长度;设D表示的数为a,由绝对值的意义容易得出结果;(3)将点A向右移动xcm,则移动后的点表示的数为-1+x;(4)表示出CA和AB,再相减即可得出结论.3.阅读材料,并回答问题如图,有一根木棒MN放置在数轴上,它的两端M、N分别落在点A、B.将木棒在数轴上水平移动,当点M移动到点B时,点N所对应的数为20,当点N移动到点A时,点M所对应的数为5.(单位:cm)由此可得,木棒长为__________cm.借助上述方法解决问题:一天,美羊羊去问村长爷爷的年龄,村长爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,116岁了,哈哈!”美羊羊纳闷,村长爷爷到底是多少岁?(1)请你画出示意图,求出村长爷爷和美羊羊现在的年龄.(2)若羊村中的小羊均与美羊羊同岁,老羊均与村长爷爷同岁。
西安市铁一中学中考数学几何综合压轴题模拟专题
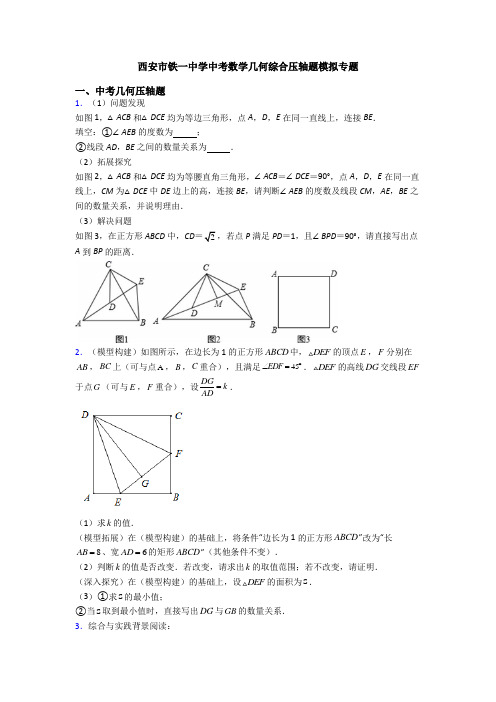
西安市铁一中学中考数学几何综合压轴题模拟专题一、中考几何压轴题1.(1)问题发现如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:①∠AEB的度数为;②线段AD,BE之间的数量关系为.(2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.(3)解决问题如图3,在正方形ABCD中,CD=2,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.2.(模型构建)如图所示,在边长为1的正方形ABCD中,DEF的顶点E,F分别在AB,BC上(可与点A,B,C重合),且满足45EDF∠=︒.DEF的高线DG交线段EF于点G(可与E,F重合),设DGk AD=.(1)求k的值.(模型拓展)在(模型构建)的基础上,将条件“边长为1的正方形ABCD”改为“长8AB=、宽6AD=的矩形ABCD”(其他条件不变).(2)判断k的值是否改变.若改变,请求出k的取值范围;若不改变,请证明.(深入探究)在(模型构建)的基础上,设DEF的面积为S.(3)①求S的最小值;②当S取到最小值时,直接写出DG与GB的数量关系.3.综合与实践背景阅读:“旋转”即物体绕一个点或一个轴做圆周运动.在中国古典专著《百喻经·口诵乘船法而不解用喻》中记载:“船盘回旋转,不能前进.”而图形旋转即:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转,这个定点叫做旋转中心,转动的角叫做旋转角.综合实践课上,“睿智”小组专门探究了正方形的旋转,情况如下:在正方形ABCD 中,点O 是线段BC 上的一个动点,将正方形ABCD 绕点O 顺时针旋转得到正方形A B C D ''''(点A ',B ',C ',D 分别是点A ,B ,C ,D 的对应点).设旋转角为α(0180α<<︒).操作猜想:(1)如图1,若点O 是BC 中点,在正方形ABCD 绕点旋转过程中,连接AA ',BB ',DD ',则线段AA '与DD '的数量关系是_______;线段AA '与BB '的数量关系是________.探究验证:(2)如图2,在(1)的条件下,在正方形ABCD 绕点O 旋转过程中,顺次连接点B ,B ',C ,C ',B .判断四边形''BB CC 的形状,并说明理由.拓展延伸:(3)如图3,若2BO CO =,在正方形ABCD 绕点O 顺时针旋转的过程中,设直线BB '交线段AA '于点P .连接OP ,并过点O 作OQ BB '⊥于点Q .请你补全图形,并直接写出OPOQ的值. 4.随着教育教学改革的不断深入,数学教学如何改革和发展,如何从“重教轻学”向自主学习探索为主的方向发展,是一个值得思考的问题.从数学的产生和发展历程来看分析,不外乎就是三个环节:(观察猜想)-(探究证明)-(拓展延伸).下面同学们从这三个方面试看解决下列问题:已知:如图1所示将一块等腰三角板BMN 放置与正方形ABCD 的B 重含,连接 AN 、CM ,E 是AN 的中点,连接BE .(观察猜想)(1)CM 与 BE 的数量关系是________,CM 与BE 的位置关系是___________;(探究证明)(2)如图2所示,把三角板 BMN 绕点B 逆时针旋转(090)αα<<,其他条件不变,线段CM 与BE 的关系是否仍然成立,并说明理由;(拓展延伸)(3)若旋转角45α=︒,且2NBE ABE ∠=∠,求BCBN的值. 5.在矩形ABCD 中,ADk AB=(k 为常数),点P 是对角线BD 上一动点(不与B ,D 重合),将射线PA 绕点P 逆时针旋转90°与射线CB 交于点E ,连接AE .(1)特例发现:如图1,当k =1时,将点P 移动到对角线交点处,可发现点E 与点B 重合,则PAPE= ,∠AEP = ;当点P 移动到其它位置时,∠AEP 的大小 (填“改变”或“不变”);(2)类比探究:如图2,若k ≠1时,当k 的值确定时,请探究∠AEP 的大小是否会随着点P 的移动而发生变化,并说明理由;(3)拓展应用:当k ≠1时,如图2,连接PC ,若PC ⊥BD ,//AE PC ,PC =2,求AP 的长.6.在ABC 与CDE △中,90ACB DCE ∠=∠=︒且CAB CDE θ∠=∠=︒,点D 始终在线段AB 上(不与A 、B 重合).(1)问题发现:如图1,若45θ=度,DBE ∠的度数______,BEAD=______; (2)类比探究:如图2,若30θ=度,试求DBE ∠的度数和BEAD的值; (3)拓展应用:在(2)的条件下,M 为DE 的中点,当3AC =BM 的最小值为多少?直接写出答案.7.(1)问题提出:如图①,在矩形ABCD 中,3AB AD ,点E 为边BC 上一点,连接AE ,过点E 作对角线AC 的垂线,垂足为F ,点M 为AE 的中点,连接MB ,MF ,BF .可知MBF 的形状为______;(2)深人探究:如图②,将CEF △在平面内绕点C 顺时针旋转,请判断MBF 的形状是否变化,并说明理由;(提示:延长EF 到E ',使E F EF '=;延长AB 到A ',使A B AB '=,连接CE ',AE ',A E ',构造全等三角形进行证明)(3)拓展延伸:如果3AD =,2CE =,在CEF △旋转过程中,当点A ,E ,F 在同一条直线上时,请直接写出MF 的长. 8.综合与实践数学活动课上,老师让同学们结合下述情境,提出一个数学问题:如图1,四边形ABCD 是正方形,四边形BEDF 是矩形.探究展示:“兴趣小组”提出的问题是:“如图2,连接CE .求证:AE ⊥CE .”并展示了如下的证明方法:证明:如图3,分别连接AC ,BD ,EF ,AF .设AC 与BD 相交于点O . ∵四边形ABCD 是正方形,∴OA =OC =12AC ,OB =OD =12BD ,且AC =BD . 又∵四边形BEDF 是矩形, ∴EF 经过点O ,∴OE =OF =12EF ,且EF =BD . ∴OE =OF ,OA =OC .∴四边形AECF 是平行四边形.(依据1) ∵AC =BD ,EF =BD , ∴AC =EF .∴四边形AECF 是矩形.(依据2) ∴∠CEA =90°, 即AE ⊥CE . 反思交流:(1)上述证明过程中“依据1”“依据2”分别是什么? 拓展再探:(2)“创新小组”受到“兴趣小组”的启发,提出的问题是:“如图4,分别延长AE ,FB 交于点P ,求证:EB =PB .”请你帮助他们写出该问题的证明过程.(3)“智慧小组”提出的问题是:若∠BAP =30°,AE =31-,求正方形ABCD 的面积.请你解决“智慧小组”提出的问题. 9.综合与实践(1)问题发现:正方形ABCD 和等腰直角△BEF 按如图①所示的方式放置,点F 在AB 上,连接AE 、CF ,则AE 、CF 的数量关系为 ,位置关系为 .(2)类比探究:正方形ABCD 保持固定,等腰直角△BEF 绕点B 顺时针旋转,旋转角为α(0°<α ≤360°),请问(1)中的结论还成立吗?请就图②说明你的理由:(3)拓展延伸:在(2)的条件下,若AB = 2 BF = 4,在等腰直角△BEF 旋转的过程中,当CF 为最大值时,请直接写出DE 的长.10.如图1,已知ABC 和ADE 均为等腰直角三角形,点D 、E 分别在线段AB 、AC 上,90C AED ∠=∠=︒.(1)观察猜想:如图2,将ADE 绕点A 逆时针旋转,连接BD 、CE ,BD 的延长线交CE 于点F .当BD 的延长线恰好经过点E 时,点E 与点F 重合,此时,①BDCE的值为______; ②∠BEC 的度数为______度;(2)类比探究:如图3,继续旋转ADE ,点F 与点E 不重合时,上述结论是否仍然成立,请说明理由;(3)拓展延伸:若2AE DE ==.10AC BC ==,当CE 所在的直线垂直于AD 时,请你直接写出线段BD 的长.11.将两个完全相同的三角形纸片ABC 和DEC 重合放置,其中90,30C B E ∠=︒∠=∠=︒.(1)操作发现:如图2,固定,ABC 使DEC 绕点C 旋转,设BDC 的面积为1,S AEC 的面积为2,S 当点D 恰好落在AB 边上时,则1S 与2S 的数量关系是 ;(2)猜想论证:当DEC 绕点C 旋转到如图3所示的位置时,小明猜想()1中1S 与2S 的数量关系为相等,并尝试分别作出了BDC 和AEC 中BC CE 、边上的高,DM AN 、请你证明小明的猜想,即证明:12S S .(3)拓展探究:已知60ABC ∠=︒,点D 是角平分线上的一点,,4,//BD CD BE DE AB ==交BC 于点E (如图4).若射线BA 上存在点F ,使DCF BDE S S =△△,请直接写出相应的BF 的长.12.如图(1),在矩形ABCD 中,AD =nAB ,点M ,P 分别在边AB ,AD 上(均不与端点重合),且AP =nAM ,以AP 和AM 为邻边作矩形AMNP ,连接AN ,CN. (问题发现)(1)如图(2),当n =1时,BM 与PD 的数量关系为 ,CN 与PD 的数量关系为 . (类比探究)(2)如图(3),当n =2时,矩形AMNP 绕点A 顺时针旋转,连接PD ,则CN 与PD 之间的数量关系是否发生变化?若不变,请就图(3)给出证明;若变化,请写出数量关系,并就图(3)说明理由. (拓展延伸)(3)在(2)的条件下,已知AD =4,AP =2,当矩形AMVP 旋转至C ,N ,M 三点共线时,请直接写出线段CN 的长13.探究:如图1和图2,四边形ABCD 中,已知AB =AD ,∠BAD =90°,点E 、F 分别在BC 、CD 上,∠EAF =45°.(1)①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系;②如图2,若∠B、∠D都不是直角,但满足∠B+∠D=180°,线段BE、DF和EF之间的结论是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=22.点D、E均在边BC边上,且∠DAE=45°,若BD=1,求DE的长.14.(探究证明)(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:如图①,在矩形ABCD中,EF⊥GH,EF分别交AD、BC于点E、F,GH分别交AB、DC于点G、H,求证:EF AB GH AD;(结论应用)(2)如图②,将矩形ABCD沿EF折叠,使得点B和点D重合,若AB=2,BC=3.求折痕EF的长;(拓展运用)(3)如图③,将矩形ABCD沿EF折叠.使得点D落在AB边上的点G处,点C落在点P处,得到四边形EFPG,若AB=2,BC=3,EF=2103,请求BP的长.15.在△ABC中,AC=BC,∠ACB=α,点D为直线BC上一动点,过点D作DF∥AC交直线AB于点F,将AD绕点D顺时针旋转α得到ED,ED交直线AB于点O,连接BE.(1)问题发现:如图1,α=90°,点D在边BC上,猜想:①AF与BE的数量关系是;②∠ABE=度.(2)拓展探究:如图2,0°<α<90°,点D 在边BC 上,请判断AF 与BE 的数量关系及∠ABE 的度数,并给予证明. (3)解决问题如图3,90°<α<180°,点D 在射线BC 上,且BD =3CD ,若AB =8,请直接写出BE 的长.16.(性质探究)如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,AE 平分∠BAC ,交BC 于点E .作DF ⊥AE 于点H ,分别交AB ,AC 于点F ,G . (1)判断△AFG 的形状并说明理由. (2)求证:BF =2OG . (迁移应用)(3)记△DGO 的面积为S 1,△DBF 的面积为S 2,当1213S S =时,求ADAB的值. (拓展延伸)(4)若DF 交射线AB 于点F ,(性质探究)中的其余条件不变,连结EF ,当△BEF 的面积为矩形ABCD 面积的110时,请直接写出tan ∠BAE 的值.17.如图1,在菱形ABCD 中,4,120AD B ︒=∠=,点E ,F 分别是AC ,AB 上的点,且1,232AE AD AF ==,猜想:①DECF的值是_______; ②直线DE 与直线CF 所成的角中较小的角的度数是_______.(2)类比探究:如图2,将绕AEF ∆点A 逆时针旋转,在旋转的过程中,(1)中结论是否成立,就图2的情形说明理由.(3)拓展延伸:在AEF ∆绕点A 旋转的过程中,当,,D E F 三点共线时,请直接写出CF 的长.18.(1)问题情境:如图1,已知等腰直角ABC ∆中,90ABC ∠=︒,6AB =,E 是AC 上的一点,且2CE =,过E 作ED BC ⊥于D ,取AE 中点F ,连接BF ,则BF 的长为_______(请直接写出答案) 小明采用如下的做法:延长AB 到H ,使AB BH =,连接EH ,B 为AH 中点,F 为AE 的中点,BF ∴是AEH ∆的中位线……请你根据小明的思路完成上面填空;(2)迁移应用:将图1中的CDE ∆绕点C 作顺时针旋转,当CE AC ⊥时,试探究BF 、AC 、CE 的数量关系,并证明你的结论.(3)拓展延伸:在旋转的过程中,当A 、C 、D 三点共线时,直接写出线段BF 的长. 19.综合与实践:问题情境:在数学课上,以“等腰直角三角形为主体,以点的对称为基础,探究线段间的变化关系”.如图1,在ABC 中,90ACB ∠=︒,AC BC =,点E 为ACB ∠的角平分线CD 上一动点但不与点C 重合,作点E 关于直线BC 的对称点为F ,连接AE 并延长交CB 延长线于点H ,连接FB 并延长交直线AH 于点G . 探究实践:(1)勤奋小组的同学发现AE BF =,请写出证明; 探究发现:(2)智慧小组在勤奋小组的基础上继续探究,发现线段FG ,EG 与CE 存在数量关系,请写出他们的发现并证明; 探究拓展:(3)如图2,奇异小组的同学在前两个小组探究的基础上,连接GC ,得到三条线段GE ,GC 与GF 存在一定的数量关系,请直接写出.20.综合与实践动手实践:一次数学兴趣活动,张老师将等腰Rt AEF 的直角顶点A 与正方形ABCD 的顶点A 重合(AE AD >),按如图(1)所示重叠在一起,使点E 在CD 边上,连接BF .则可证:ADE ≌△△______,______三点共线;发现问题:(1)如图(2),已知正方形ABCD ,E 为DC 边上一动点,DC nDE =,AF AE ⊥交CB 的延长线于F ,连结EF 交AB 于点G .若2n =,则AG BG =______,AGE BGFS S =△△______; 尝试探究:(2)如图(3),在(1)的条件下若3n =,求证:5AG GB =;拓展延伸:(3)如图(4),在(1)的条件下,当n =______时,AG 为GB 的6倍(直接写结果,不要求证明).【参考答案】***试卷处理标记,请不要删除一、中考几何压轴题1.(1)①60°;②相等;(2)∠AEB=90°,AE=2CM+BE ,证明见解析;(3),【分析】(1)由条件易证△ACD ≌△BCE ,从而得到:AD=BE ,∠ADC=∠BEC .由点A ,D ,E 在同一 解析:(1)①60°;②相等;(2)∠AEB =90°,AE =2CM +BE ,证明见解析;(3)31-31+ 【分析】(1)由条件易证△ACD ≌△BCE ,从而得到:AD =BE ,∠ADC =∠BEC .由点A ,D ,E 在同一直线上可求出∠ADC ,从而可以求出∠AEB 的度数.(2)仿照(1)中的解法可求出∠AEB 的度数,证出AD =BE ;由△DCE 为等腰直角三角形及CM 为△DCE 中DE 边上的高可得CM =DM =ME ,从而证到AE =2CH +BE .(3)由PD =1可得:点P 在以点D 为圆心,1为半径的圆上;由∠BPD =90°可得:点P 在以BD 为直径的圆上.显然,点P 是这两个圆的交点,由于两圆有两个交点,接下来需对两个位置分别进行讨论.然后,添加适当的辅助线,借助于(2)中的结论即可解决问题.【详解】解:(1)①如图1.∵△ACB 和△DCE 均为等边三角形,∴CA =CB ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACD =∠BCE .在△ACD 和△BCE 中,∵AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ∴△ACD ≌△BCE (SAS ),∴∠ADC =∠BEC .∵△DCE 为等边三角形,∴∠CDE =∠CED =60°.∵点A ,D ,E 在同一直线上,∴∠ADC =120°,∴∠BEC =120°,∴∠AEB =∠BEC ﹣∠CED =60°.故答案为:60°.②∵△ACD ≌△BCE ,∴AD =BE .故答案为:AD =BE .(2)∠AEB =90°,AE =BE +2CM .理由:如图2.∵△ACB 和△DCE 均为等腰直角三角形,∴CA =CB ,CD =CE ,∠ACB =∠DCE =90°,∴∠ACD =∠BCE .在△ACD 和△BCE 中,CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ∴△ACD ≌△BCE (SAS ),∴AD=BE,∠ADC=∠BEC.∵△DCE为等腰直角三角形,∴∠CDE=∠CED=45°.∵点A,D,E在同一直线上,∴∠ADC=135°,∴∠BEC=135°,∴∠AEB=∠BEC﹣∠CED=90°.∵CD=CE,CM⊥DE,∴DM=ME.∵∠DCE=90°,∴DM=ME=CM,∴AE=AD+DE=BE+2CM.(3)点A到BP 31-31+.理由如下:∵PD=1,∴点P在以点D为圆心,1为半径的圆上.∵∠BPD=90°,∴点P在以BD为直径的圆上,∴点P是这两圆的交点.①当点P在如图3①所示位置时,连接PD、PB、PA,作AH⊥BP,垂足为H,过点A作AE⊥AP,交BP于点E,如图3①.∵四边形ABCD是正方形,∴∠ADB=45°.AB=AD=DC=BC2,∠BAD=90°,∴BD=2.∵DP=1,∴BP3∵∠BPD=∠BAD=90°,∴A、P、D、B在以BD为直径的圆上,∴∠APB=∠ADB=45°,∴△PAE是等腰直角三角形.又∵△BAD是等腰直角三角形,点B、E、P共线,AH⊥BP,∴由(2)中的结论可得:BP=2AH+PD,∴3=2AH +1,∴AH =312-.②当点P 在如图3②所示位置时,连接PD 、PB 、PA ,作AH ⊥BP ,垂足为H ,过点A 作AE ⊥AP ,交PB 的延长线于点E ,如图3②.同理可得:BP =2AH ﹣PD ,∴3=2AH ﹣1,∴AH =312+. 综上所述:点A 到BP 的距离为312-或312+. 【点睛】本题考查了等边三角形的性质、正方形的性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、圆周角定理、三角形全等的判定与性质等知识,考查了运用已有的知识和经验解决问题的能力,是体现新课程理念的一道好题.而通过添加适当的辅助线从而能用(2)中的结论解决问题是解决第(3)的关键.2.(1)=1;(2)改变, ;(3)①= ;②GB=()DG .【分析】(1)利用三点共线,可以求出k=1;(2)当点G 与点E 重合时,DG 取最小值,当点F 与点C 重合时,DG 取最大值,进而求出k 的取解析:(1)k =1;(2≤≤10210k ;(3)①S =38 ;②GB=21)DG.【分析】(1)利用三点共线,可以求出k=1;(2)当点G与点E重合时,DG取最小值,当点F与点C重合时,DG取最大值,进而求出k的取值范围;(3)①设BE=m,BF=n,利用一元二次方程的根与系数的关系进行和不等式进行求解;②根据①求出的EF=222-,由于ΔDEF为等腰三角形,EF为底,所以G为EF中点,易得GB=21-)DG.-,进而可以求出GB=(21【详解】如图1所示,把ΔDAE,ΔDCF分别沿着DE、DF翻折,在正方形ABCD中,∠ADC=∠DAB=∠DCB=90°’,AD=CD,∴∠ADE+∠CDF=∠ADC-∠EDF=90°-45°=45°,∴翻折后,AD,CD重合.设重合线为AG',则∠DG'E=∠DG'F=90°,∴DG'⊥EF,且E、G'、F三点共线,则G'在EF上。
陕西省西安铁一中2017-2018学年八年级下学期期中考试数学试题(解析版)

2017-2018西安铁一中初二下期中数学
一、精心选一选,相信自己的能力!(每题3分,共30分)
1.下列汽车标志中既是轴对称图形又是中心对称图形的是(
).A .
B .
C .
D .
【答案】C 【解析】一个图形绕着中心点旋转
180后能与自身重合,我们把这种图形叫做中心对称图形.如果一个图形沿某条直线折叠后,直线两旁的部分能够互相重合,
那么这个图形关于这条直线对称(轴对称).A .是轴对称图形,不是中心对称图形;
B .不是轴对称图形,也不是中心对称图形;
C .是轴对称图形,也是中心对称图形;
D .是轴对称图形,不是中心对称图形.
故选C .
2.下列命题:①对顶角相等;②同位角相等,两直线平行;③若a b ,则a b ;④若0x ,则220x x ;其中逆命题一定成立的有(
).A .②
B .①④
C .②④
D .①②③④【答案】A
【解析】各项的逆命题为:
①相等的角是对顶角.(错)eg :如图,
12,但1和2不是对顶角;②两直线平行,同位角相等.
(对);③若a
b ,则a b .(错)a b ;④若220x x ,则0x .(错)0x
或2.故选A .
2
1
3.在ABC △内部取一点P ,使得点P 到ABC △的的三边距离相等,则点
P 是ABC △的().A .三条高的交点
B .三条角平分线的交点
C .三条中线的交点
D .三边的垂直平凡线的交点【答案】B。
陕西省西安市西安铁一中学2024届中考押题数学预测卷含解析

陕西省西安市西安铁一中学2024届中考押题数学预测卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若CD=2,AB=8,则△ABD的面积是()A.6 B.8 C.10 D.122.据相关报道,开展精准扶贫工作五年以来,我国约有55000000人摆脱贫困,将55000000用科学记数法表示是()A.55×106B.0.55×108C.5.5×106D.5.5×1073.一个几何体的三视图如图所示,该几何体是()A.直三棱柱B.长方体C.圆锥D.立方体4.将不等式组2(23)3532x xx x-≤-⎧⎨+⎩>的解集在数轴上表示,下列表示中正确的是( )A.B.C.D.5.下列说法中,正确的是()A.不可能事件发生的概率为0B.随机事件发生的概率为1 2C.概率很小的事件不可能发生D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次6.(2016四川省甘孜州)如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径'AA的长为()A.πB.2πC.4πD.8π7.化简16的结果是()A.±4 B.4 C.2 D.±28.比较4,17,363的大小,正确的是()A.4<17<363B.4<363<17C.363<4<17D.17<363<49.如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是()A.613B.513C.413D.31310.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC、∠BCD,则∠P的度数是( )A.60°B.65°C.55°D.50°二、填空题(共7小题,每小题3分,满分21分)11.二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(12,﹣2);⑤当x<12时,y随x的增大而减小;⑥a+b+c>0中,正确的有______.(只填序号)12.分解因式:2x3﹣4x2+2x=_____.13.一个布袋中装有1个蓝色球和2个红色球,这些球除颜色外其余都相同,随机摸出一个球后放回摇匀,再随机摸出一个球,则两次摸出的球都是红球的概率是_____.14.下面是“作已知圆的内接正方形”的尺规作图过程.已知:⊙O.求作:⊙O的内接正方形.作法:如图,(1)作⊙O的直径AB;(2)分别以点A,点B为圆心,大于AB的长为半径作弧,两弧分别相交于M、N两点;(3)作直线MN与⊙O交于C、D两点,顺次连接A、C、B、D.即四边形ACBD为所求作的圆内接正方形.请回答:该尺规作图的依据是_____.15.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P与点B,C都不重合),现将△PCD沿直线PD折叠,使点C落到点F处;过点P作∠BPF的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是()16.圆锥的底面半径是4cm,母线长是5cm,则圆锥的侧面积等于_____cm1.17.因式分解:a2﹣a=_____.三、解答题(共7小题,满分69分)18.(10分)如图,一盏路灯沿灯罩边缘射出的光线与地面BC交于点B、C,测得∠ABC=45°,∠ACB=30°,且BC =20米.(1)请用圆规和直尺画出路灯A到地面BC的距离AD;(不要求写出画法,但要保留作图痕迹)(2)求出路灯A离地面的高度AD.(精确到0.1米)(参考数据:2≈1.414,3≈1.732).19.(5分)为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+1.设这种产品每天的销售利润为w元.求w与x之间的函数关系式.该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?20.(8分)某市飞翔航模小队,计划购进一批无人机.已知3台A型无人机和4台B型无人机共需6400元,4台A 型无人机和3台B型无人机共需6200元.(1)求一台A型无人机和一台B型无人机的售价各是多少元?(2)该航模小队一次购进两种型号的无人机共50台,并且B型无人机的数量不少于A型无人机的数量的2倍.设购进A型无人机x台,总费用为y元.①求y与x的关系式;②购进A型、B型无人机各多少台,才能使总费用最少?21.(10分)在汕头市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,电子白板的价格是电脑的3倍,购买5台电脑和10台电子白板需要17.5万元,求每台电脑、每台电子白板各多少万元?22.(10分)某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:(1)本次调查的学生总数为_____人,被调查学生的课外阅读时间的中位数是_____小时,众数是_____小时;并补全条形统计图;(2)在扇形统计图中,课外阅读时间为5小时的扇形的圆心角度数是_____;(3)若全校九年级共有学生800人,估计九年级一周课外阅读时间为6小时的学生有多少人?23.(12分)在锐角△ABC 中,边BC 长为18,高AD 长为12如图,矩形EFCH 的边GH 在BC 边上,其余两个顶点E 、F 分别在AB 、AC 边上,EF 交AD 于点K ,求EF AK的值;设EH =x ,矩形EFGH 的面积为S ,求S 与x 的函数关系式,并求S 的最大值.24.(14分)解方程(1)2430x x --=;(2)()22(1)210x x ---=参考答案一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1、B【解题分析】分析:过点D 作DE ⊥AB 于E ,先求出CD 的长,再根据角平分线上的点到角的两边的距离相等可得DE =CD =2,然后根据三角形的面积公式列式计算即可得解.详解:如图,过点D 作DE ⊥AB 于E ,∵AB =8,CD =2,∵AD 是∠BAC 的角平分线,90C ,∠=︒∴DE =CD =2,∴△ABD 的面积11828.22AB DE =⋅=⨯⨯= 故选B.点睛:考查角平分线的性质,角平分线上的点到角两边的距离相等.2、D【解题分析】试题解析:55000000=5.5×107, 故选D .考点:科学记数法—表示较大的数3、A【解题分析】根据三视图的形状可判断几何体的形状.【题目详解】观察三视图可知,该几何体是直三棱柱.故选A .本题考查了几何体的三视图和结构特征,根据三视图的形状可判断几何体的形状是关键.4、B【解题分析】先解不等式组中的每一个不等式,再把不等式的解集表示在数轴上即可. 解:不等式可化为:11x x ≤⎧⎨>-⎩,即11x -<≤. ∴在数轴上可表示为.故选B .“点睛”不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.5、A【解题分析】试题分析:不可能事件发生的概率为0,故A正确;随机事件发生的概率为在0到1之间,故B错误;概率很小的事件也可能发生,故C错误;投掷一枚质地均匀的硬币100次,正面向上的次数为50次是随机事件,D错误;故选A.考点:随机事件.6、B【解题分析】试题分析:∵每个小正方形的边长都为1,∴OA=4,∵将△AOB绕点O顺时针旋转90°得到△A′OB′,∴∠AOA′=90°,∴A点运动的路径'AA的长为:904180π⨯=2π.故选B.考点:弧长的计算;旋转的性质.7、B【解题分析】根据算术平方根的意义求解即可.【题目详解】=4,故选:B.【题目点拨】本题考查了算术平方根的意义,一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根,正数a有一个正的算术平方根,0的算术平方根是0,负数没有算术平方根.8、C【解题分析】根据【题目详解】解:易得:且所以363<4<17,故选C.【题目点拨】本题主要考查开平方开立方运算。
西安铁一中分校小升初数学期末试卷真题汇编[解析版]
![西安铁一中分校小升初数学期末试卷真题汇编[解析版]](https://img.taocdn.com/s3/m/29d7367526284b73f242336c1eb91a37f0113257.png)
西安铁一中分校小升初数学期末试卷真题汇编[解析版]一、选择题1.军军参加团体操表演,他的位置用数对表示是(3,7),如果这时的方队是一个正方形,参加团体操表演的至少有()人。
A.9 B.21 C.49 D.1002.一堆煤的34是120吨,求这堆煤有多重.不正确的算式是()A.120×34B.120÷3×4 C.120÷343.一个三角形三个内角度数的比是2∶3∶5,这个三角形是()三角形。
A.锐角B.直角C.钝角D.无法确定4.甲乙两筐苹果,甲筐32千克,乙筐x千克.从甲筐拿4千克放入乙筐,两筐苹果就一样重.下列方程正确的是().A.32-X=4 B.X+4=32 C.X-8=32 D.X+4=32-4 5.观察下面的立体图形,下列说法正确的是( ).A.从正面和左面观察到的形状相同B.从上面和左面观察到的形状相同C.从正面和上面观察到的形状相同D.从左面和右面观察到的形状相同6.将一个圆柱体木头削成一个最大的圆锥,下列说法错误的是()。
A.削去部分的体积占圆柱的13B.圆锥的体积占圆柱的13C.削去部分的体积是圆锥的2倍D.圆锥的体积占削去部分的127.与奇数a相邻的两个奇数是()。
A.a-1和a+1 B.a-3和a+3 C.a-2和a+2 D.a-1和a+38.一种电视机提价110后,又降价110,现价()原价.A.高于B.等于C.低于9.将正方形纸片对折三次(如图所示),再沿AB剪去一个等腰直角三角形,展开铺平得到的图形是()。
A .B .C .二、填空题10.0.05升=(________)立方厘米 35小时=(________)分 1.2公顷=(________)公顷(________)平方米11.( )∶20=()8 =0.8=4÷( )=( )%。
12.已知a =2×3×m ,b =2×2×5×m ,如果ab 的最小公倍数是420,则a 和b 的最大公因数是(________)。
西安铁一中分校七年级下册数学期末试卷真题汇编[解析版]
![西安铁一中分校七年级下册数学期末试卷真题汇编[解析版]](https://img.taocdn.com/s3/m/1f5c3b60001ca300a6c30c22590102020740f227.png)
西安铁一中分校七年级下册数学期末试卷真题汇编[解析版]一、解答题1.如图1,AB //CD ,点E 、F 分别在AB 、CD 上,点O 在直线AB 、CD 之间,且100EOF ∠=︒.(1)求BEO OFD ∠+∠的值;(2)如图2,直线MN 分别交BEO ∠、OFC ∠的角平分线于点M 、N ,直接写出EMN FNM ∠-∠的值;(3)如图3,EG 在AEO ∠内,AEG m OEG ∠=∠;FH 在DFO ∠内,DFH m OFH ∠=∠,直线MN 分别交EG 、FH 分别于点M 、N ,且50FMN ENM ∠-∠=︒,直接写出m 的值.2.已知,AB ∥CD ,点E 在CD 上,点G ,F 在AB 上,点H 在AB ,CD 之间,连接FE ,EH ,HG ,∠AGH =∠FED ,FE ⊥HE ,垂足为E . (1)如图1,求证:HG ⊥HE ;(2)如图2,GM 平分∠HGB ,EM 平分∠HED ,GM ,EM 交于点M ,求证:∠GHE =2∠GME ;(3)如图3,在(2)的条件下,FK 平分∠AFE 交CD 于点K ,若∠KFE :∠MGH =13:5,求∠HED 的度数.3.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.小明的思路是:过P作PE∥AB,通过平行线性质,可得∠APC=∠APE+∠CPE=50°+60°=110°.问题解决:(1)如图2,AB∥CD,直线l分别与AB、CD交于点M、N,点P在直线I上运动,当点P 在线段MN上运动时(不与点M、N重合),∠PAB=α,∠PCD=β,判断∠APC、α、β之间的数量关系并说明理由;(2)在(1)的条件下,如果点P在线段MN或NM的延长线上运动时.请直接写出∠APC、α、B之间的数量关系;(3)如图3,AB∥CD,点P是AB、CD之间的一点(点P在点A、C右侧),连接PA、PC,∠BAP和∠DCP的平分线交于点Q.若∠APC=116°,请结合(2)中的规律,求∠AQC 的度数.4.阅读下面材料:小亮同学遇到这样一个问题:已知:如图甲,AB//CD,E为AB,CD之间一点,连接BE,DE,得到∠BED.求证:∠BED=∠B+∠D.(1)小亮写出了该问题的证明,请你帮他把证明过程补充完整.证明:过点E作EF//AB,则有∠BEF=.∵AB//CD,∴//,∴∠FED=.∴∠BED=∠BEF+∠FED=∠B+∠D.(2)请你参考小亮思考问题的方法,解决问题:如图乙,已知:直线a//b,点A,B在直线a上,点C,D在直线b上,连接AD,BC,BE平分∠ABC,DE平分∠ADC,且BE,DE所在的直线交于点E.①如图1,当点B在点A的左侧时,若∠ABC=60°,∠ADC=70°,求∠BED的度数;②如图2,当点B在点A的右侧时,设∠ABC=α,∠ADC=β,请你求出∠BED的度数(用含有α,β的式子表示).5.已知//AM CN ,点B 为平面内一点,AB BC ⊥于B .(1)如图1,求证:90A C ∠+∠=︒;(2)如图2,过点B 作BD MA ⊥的延长线于点D ,求证:ABD C ∠=∠;(3)如图3,在(2)问的条件下,点E 、F 在DM 上,连接BE 、BF 、CF ,且BF 平分DBC ∠,BE 平分ABD ∠,若AFC BCF ∠=∠,3BFC DBE ∠=∠,求EBC ∠的度数.二、解答题6.问题情境:如图1,AB ∥CD ,∠PAB =130°,∠PCD =120°,求∠APC 的度数. 小明的思路是:如图2,过P 作PE ∥AB ,通过平行线性质来求∠APC . (1)按小明的思路,易求得∠APC 的度数为 度;(2)如图3,AD ∥BC ,点P 在射线OM 上运动,当点P 在A 、B 两点之间运动时,∠ADP =∠α,∠BCP =∠β.试判断∠CPD 、∠α、∠β之间有何数量关系?请说明理由; (3)在(2)的条件下,如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合),请你直接写出∠CPD 、∠α、∠β间的数量关系.7.如图所示,已知//AM BN ,点P 是射线AM 上一动点(与点A 不重合),BC 、BD 分别平分ABP ∠和PBN ∠,分别交射线AM 于点C 、D ,且60CBD ∠=︒ (1)求A ∠的度数.(2)当点P 运动时,APB ∠与ADB ∠之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律. (3)当点P 运动到使ACB ABD =∠∠时,求ABC ∠的度数.8.已知:ABC 和同一平面内的点D .(1)如图1,点D 在BC 边上,过D 作//DE BA 交AC 于E ,//DF CA 交AB 于F .根据题意,在图1中补全图形,请写出EDF ∠与BAC ∠的数量关系,并说明理由;(2)如图2,点D 在BC 的延长线上,//DF CA ,EDF BAC ∠=∠.请判断DE 与BA 的位置关系,并说明理由.(3)如图3,点D 是ABC 外部的一个动点.过D 作//DE BA 交直线AC 于E ,//DF CA 交直线AB 于F ,直接写出EDF ∠与BAC ∠的数量关系,并在图3中补全图形.9.已知//a b ,直角ABC 的边与直线a 分别相交于O 、G 两点,与直线b 分别交于E 、F 点,90ACB ∠=.(1)将直角ABC 如图1位置摆放,如果46AOG ∠=,则CEF ∠=______; (2)将直角ABC 如图2位置摆放,N 为AC 上一点,180NEF CEF ︒∠+∠=,请写出NEF ∠与AOG ∠之间的等量关系,并说明理由.(3)将直角ABC 如图3位置摆放,若140GOC ∠=,延长AC 交直线b 于点Q ,点P 是射线GF 上一动点,探究POQ ∠,OPQ ∠与PQF ∠的数量关系,请直接写出结论.10.如图1,在平面直角坐标系中,()()02A a C b ,,,,且满足()240a b a b ++-+=,过C 作CB x ⊥轴于B(1)求三角形ABC 的面积.(2)发过B 作//BD AC 交y 轴于D ,且,AE DE 分别平分,CAB ODB ∠∠,如图2,若,90()CAB ACB a αββ∠=∠=+=︒,求AED ∠的度数.(3)在y 轴上是否存在点P ,使得三角形ABC 和三角形ACP 的面积相等?若存在,求出P 点坐标;若不存在;请说明理由.三、解答题11.(1)如图1所示,△ABC 中,∠ACB 的角平分线CF 与∠EAC 的角平分线AD 的反向延长线交于点F ;①若∠B =90°则∠F = ;②若∠B =a ,求∠F 的度数(用a 表示);(2)如图2所示,若点G 是CB 延长线上任意一动点,连接AG ,∠AGB 与∠GAB 的角平分线交于点H ,随着点G 的运动,∠F +∠H 的值是否变化?若变化,请说明理由;若不变,请求出其值.12.如图,在ABC 中,ABC ∠与ACB ∠的角平分线交于O 点.(1)若40A ∠=︒,则BOC ∠= ︒; (2)若A n ∠=︒,则BOC ∠= ︒;(3)若A n ∠=︒,ABC ∠与ACB ∠的角平分线交于O 点,ABO ∠的平分线与ACO ∠的平分线交于点1O ,,2016O BD ∠的平分线与2016O CE ∠的平分线交于点2017O ,则2017O ∠=︒.13.如图1,已知线段AB 、CD 相交于点O ,连接AC 、BD ,我们把形如图1的图形称之为“8字形”.如图2,∠CAB 和∠BDC 的平分线AP 和DP 相交于点P ,并且与CD 、AB 分别相交于M 、N .试解答下列问题:(1)仔细观察,在图2中有 个以线段AC 为边的“8字形”; (2)在图2中,若∠B=96°,∠C=100°,求∠P 的度数;(3)在图2中,若设∠C=α,∠B=β,∠CAP=13∠CAB ,∠CDP=13∠CDB ,试问∠P 与∠C 、∠B 之间存在着怎样的数量关系(用α、β表示∠P ),并说明理由; (4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F 的度数为 .14.如图,直线//PQ MN ,一副直角三角板,ABC DEF ∆∆中,90,45,30,60ACB EDF ABC BAC DFE DEF ︒︒︒︒∠=∠=∠=∠=∠=∠=.(1)若DEF ∆如图1摆放,当ED 平分PEF ∠时,证明:FD 平分EFM ∠.(2)若,ABC DEF ∆∆如图2摆放时,则PDE ∠=(3)若图2中ABC ∆固定,将DEF ∆沿着AC 方向平移,边DF 与直线PQ 相交于点G ,作FGQ ∠和GFA ∠的角平分线GH FH 、相交于点H (如图3),求GHF ∠的度数.(4)若图2中DEF ∆的周长35,5cm AF cm =,现将ABC ∆固定,将DEF ∆沿着CA 方向平移至点F 与A 重合,平移后的得到''D E A ∆,点D E 、的对应点分别是''D E 、,请直接写出四边形'DEAD 的周长.(5)若图2中DEF ∆固定,(如图4)将ABC ∆绕点A 顺时针旋转,1分钟转半圈,旋转至AC 与直线AN 首次重合的过程中,当线段BC 与DEF ∆的一条边平行时,请直接写出旋转的时间.15.已知,//AB CD ,点E 为射线FG 上一点.(1)如图1,写出EAF ∠、AED ∠、EDG ∠之间的数量关系并证明; (2)如图2,当点E 在FG 延长线上时,求证:EAF AED EDG ∠=∠+∠;(3)如图3,AI 平分BAE ∠,DI 交AI 于点I ,交AE 于点K ,且EDI ∠:2:1CDI ∠=,20AED ∠=︒,30I ∠=︒,求EKD ∠的度数.【参考答案】一、解答题1.(1) ;(2)的值为40°;(3). 【分析】(1)过点O 作OG ∥AB ,可得AB ∥OG ∥CD ,利用平行线的性质可求解; (2)过点M 作MK ∥AB ,过点N 作NH ∥CD ,由角平分线的定义可设∠BEM 解析:(1)260BEO DFO ∠+∠=︒ ;(2)EMN FNM ∠-∠的值为40°;(3)53.【分析】(1)过点O 作OG ∥AB ,可得AB ∥OG ∥CD ,利用平行线的性质可求解;(2)过点M 作MK ∥A B ,过点N 作NH ∥CD ,由角平分线的定义可设∠BEM =∠OEM =x ,∠CFN =∠OFN =y ,由∠BEO +∠DFO =260°可求x -y =40°,进而求解;(3)设直线FK 与EG 交于点H ,FK 与AB 交于点K ,根据平行线的性质即三角形外角的性质及50FMN ENM ∠-∠=︒,可得50KFD AEG ∠-∠=︒,结合260AEG n OEG DFK n OFK BEO DFO ∠=∠=∠∠+∠=︒,,,可得11180100AEG AEG KFD KFD n n ∠+∠+︒-∠-∠=︒,即可得关于n 的方程,计算可求解n 值. 【详解】证明:过点O 作OG ∥AB ,∵AB ∥CD , ∴AB ∥OG ∥CD ,∴180180BEO EOG DFO FOG ∠+∠=︒∠+∠=︒,,∴360BEO EOG DFO FOG ∠+∠+∠+∠=︒, 即360BEO EOF DFO ∠+∠+∠=︒, ∵∠EOF =100°,∴∠260BEO DFO +∠=︒;(2)解:过点M 作MK ∥AB ,过点N 作NH ∥CD ,∵EM 平分∠BEO ,FN 平分∠CFO , 设BEM OEM x CFN OFN y ∠=∠=∠=∠=,, ∵260BEO DFO ∠+∠=︒∴21802260BEO DFO x y ∠+∠=+︒-=︒, ∴x -y =40°,∵MK ∥AB ,NH ∥CD ,AB ∥CD , ∴AB ∥MK ∥NH ∥CD ,∴EMK BEM x HNF CFN y KMN HNM ∠=∠=∠=∠=∠=∠,,, ∴EMN FNM EMK KMN HNM HNF ∠+∠=∠+∠-∠+∠() x KMN HNM y =+∠-∠-=x -y =40°,故EMN FNM ∠-∠的值为40°;(3)如图,设直线FK 与EG 交于点H ,FK 与AB 交于点K ,∵AB ∥CD ,∴AKF KFD ∠=∠,∵AKF EHK HEK EHK AEG ∠=∠+∠=∠+∠, ∴KFD EHK AEG ∠=∠+∠, ∵50EHK NMF ENM ∠=∠-∠=︒, ∴50KFD AEG ∠=︒+∠, 即50KFD AEG ∠-∠=︒,∵AEG n OEG ∠=∠,FK 在∠DFO 内,DFK n OFK ∠=∠.∴1180180CFO DFK OFK KFD KFD n∠=︒-∠-∠=︒-∠-∠ ,1AEO AEG OEG AEG AEG n ∠=∠+∠=∠+∠,∵260BEO DFO ∠+∠=︒, ∴100AEO CFO ∠+∠=︒,∴11180100AEG AEG KFD KFD n n ∠+∠+︒-∠-∠=︒,即(180)1KFD AEG n ⎛⎫⎪⎝∠⎭+-∠︒=, ∴115080n ⎛⎫⎪⨯⎭︒︒⎝+=, 解得53n = . 经检验,符合题意, 故答案为:53.【点睛】本题主要考查平行线的性质,角平分线的定义,灵活运用平行线的性质是解题的关键.2.(1)见解析;(2)见解析;(3)40° 【分析】(1)根据平行线的性质和判定解答即可;(2)过点H 作HP ∥AB ,根据平行线的性质解答即可; (3)过点H 作HP ∥AB ,根据平行线的性质解答即可.解析:(1)见解析;(2)见解析;(3)40° 【分析】(1)根据平行线的性质和判定解答即可;(2)过点H 作HP ∥AB ,根据平行线的性质解答即可; (3)过点H 作HP ∥AB ,根据平行线的性质解答即可. 【详解】证明:(1)∵AB ∥CD , ∴∠AFE =∠FED , ∵∠AGH =∠FED ,∴∠AFE=∠AGH,∴EF∥GH,∴∠FEH+∠H=180°,∵FE⊥HE,∴∠FEH=90°,∴∠H=180°﹣∠FEH=90°,∴HG⊥HE;(2)过点M作MQ∥AB,∵AB∥CD,∴MQ∥CD,过点H作HP∥AB,∵AB∥CD,∴HP∥CD,∵GM平分∠HGB,∠BGH,∴∠BGM=∠HGM=12∵EM平分∠HED,∠HED,∴∠HEM=∠DEM=12∵MQ∥AB,∴∠BGM=∠GMQ,∵MQ∥CD,∴∠QME=∠MED,∴∠GME=∠GMQ+∠QME=∠BGM+∠MED,∵HP∥AB,∴∠BGH=∠GHP=2∠BGM,∵HP∥CD,∴∠PHE=∠HED=2∠MED,∴∠GHE=∠GHP+∠PHE=2∠BGM+2∠MED=2(∠BGM+∠MED),∴∠GHE=∠2GME;(3)过点M作MQ∥AB,过点H作HP∥AB,由∠KFE:∠MGH=13:5,设∠KFE=13x,∠MGH=5x,由(2)可知:∠BGH=2∠MGH=10x,∵∠AFE+∠BFE=180°,∴∠AFE=180°﹣10x,∵FK平分∠AFE,∴∠AFK=∠KFE=12∠AFE,即1(18010)132x x︒-=,解得:x=5°,∴∠BGH=10x=50°,∵HP∥AB,HP∥CD,∴∠BGH=∠GHP=50°,∠PHE=∠HED,∵∠GHE=90°,∴∠PHE=∠GHE﹣∠GHP=90°﹣50°=40°,∴∠HED=40°.【点睛】本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质定理以及灵活构造平行线是解题的关键.3.(1)∠APC=α+β,理由见解析;(2)∠APC=α-β或∠APC=β-α;(3)58°【分析】(1)过点P作PE∥AB,根据平行线的判定与性质即可求解;(2)分点P在线段MN或NM的延长线解析:(1)∠APC=α+β,理由见解析;(2)∠APC=α-β或∠APC=β-α;(3)58°【分析】(1)过点P作PE∥AB,根据平行线的判定与性质即可求解;(2)分点P在线段MN或NM的延长线上运动两种情况,根据平行线的判定与性质及角的和差即可求解;(3)过点P,Q分别作PE∥AB,QF∥AB,根据平行线的判定与性质及角的和差即可求解.【详解】解:(1)如图2,过点P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,∴∠APE=α,∠CPE=β,∴∠APC=∠APE+∠CPE=α+β.(2)如图,在(1)的条件下,如果点P在线段MN的延长线上运动时,∵AB∥CD,∠PAB=α,∴∠1=∠PAB=α,∵∠1=∠APC+∠PCD,∠PCD=β,∴α=∠APC+β,∴∠APC=α-β;如图,在(1)的条件下,如果点P在线段NM的延长线上运动时,∵AB∥CD,∠PCD=β,∴∠2=∠PCD=β,∵∠2=∠PAB+∠APC,∠PAB=α,∴β=α+∠APC,∴∠APC=β-α;(3)如图3,过点P,Q分别作PE∥AB,QF∥AB,∵AB∥CD,∴AB∥QF∥PE∥CD,∴∠BAP=∠APE,∠PCD=∠EPC,∵∠APC=116°,∴∠BAP+∠PCD=116°,∵AQ平分∠BAP,CQ平分∠PCD,∴∠BAQ=12∠BAP,∠DCQ=12∠PCD,∴∠BAQ+∠DCQ=12(∠BAP+∠PCD)=58°,∵AB∥QF∥CD,∴∠BAQ=∠AQF,∠DCQ=∠CQF,∴∠AQF+∠CQF=∠BAQ+∠DCQ=58°,∴∠AQC=58°.【点睛】此题考查了平行线的判定与性质,添加辅助线将两条平行线相关的角联系到一起是解题的关键.4.(1)∠B,EF,CD,∠D;(2)①65°;②180°﹣【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图1,过点E作EF∥AB,当点B在点A的左侧时,根据∠ABC=60°,解析:(1)∠B,EF,CD,∠D;(2)①65°;②180°﹣11 22 aβ+【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图1,过点E作EF∥AB,当点B在点A的左侧时,根据∠ABC=60°,∠ADC=70°,参考小亮思考问题的方法即可求∠BED的度数;②如图2,过点E作EF∥AB,当点B在点A的右侧时,∠ABC=α,∠ADC=β,参考小亮思考问题的方法即可求出∠BED的度数.【详解】解:(1)过点E作EF∥AB,则有∠BEF=∠B,∵AB∥CD,∴EF ∥CD ,∴∠FED =∠D ,∴∠BED =∠BEF +∠FED =∠B +∠D ;故答案为:∠B ;EF ;CD ;∠D ;(2)①如图1,过点E 作EF ∥AB ,有∠BEF =∠EBA .∵AB ∥CD ,∴EF ∥CD .∴∠FED =∠EDC .∴∠BEF +∠FED =∠EBA +∠EDC .即∠BED =∠EBA +∠EDC ,∵BE 平分∠ABC ,DE 平分∠ADC ,∴∠EBA =12∠ABC =30°,∠EDC =12∠ADC =35°,∴∠BED =∠EBA +∠EDC =65°.答:∠BED 的度数为65°;②如图2,过点E 作EF ∥AB ,有∠BEF +∠EBA =180°.∴∠BEF =180°﹣∠EBA ,∵AB ∥CD , ∴EF ∥CD . ∴∠FED =∠EDC . ∴∠BEF +∠FED =180°﹣∠EBA +∠EDC .即∠BED =180°﹣∠EBA +∠EDC ,∵BE 平分∠ABC ,DE 平分∠ADC ,∴∠EBA =12∠ABC =12α,∠EDC =12∠ADC =12β, ∴∠BED =180°﹣∠EBA +∠EDC =180°﹣1122a β+. 答:∠BED 的度数为180°﹣1122a β+. 【点睛】本题考查了平行线的判定与性质,解决本题的关键是熟练掌握平行线的判定与性质. 5.(1)见解析;(2)见解析;(3).【分析】(1)先根据平行线的性质得到,然后结合即可证明;(2)过作,先说明,然后再说明得到,最后运用等量代换解答即可; (3)设∠DBE=a ,则∠BFC=3解析:(1)见解析;(2)见解析;(3)︒=∠105EBC .【分析】(1)先根据平行线的性质得到C BDA ∠=∠,然后结合AB BC ⊥即可证明;(2)过B 作//BH DM ,先说明ABD CBH ∠=∠,然后再说明//BH NC 得到CBH C ∠=∠,最后运用等量代换解答即可;(3)设∠DBE =a ,则∠BFC =3a ,根据角平分线的定义可得∠ABD =∠C =2a ,∠FBC =12∠DBC =a +45°,根据三角形内角和可得∠BFC +∠FBC +∠BCF =180°,可得∠AFC =∠BCF 的度数表达式,再根据平行的性质可得∠AFC +∠NCF =180°,代入即可算出a 的度数,进而完成解答.【详解】(1)证明:∵//AM CN ,∴C BDA ∠=∠,∵AB BC ⊥于B ,∴90B ∠=︒,∴90A BDA ∠+∠=︒,∴90A C ∠+∠=︒;(2)证明:过B 作//BH DM ,∵BD MA ⊥,∴90ABD ABH ∠+∠=︒,又∵AB BC ⊥,∴90ABH CBH ∠+∠=︒,∴ABD CBH ∠=∠,∵//BH DM ,//AM CN∴//BH NC ,∴CBH C ∠=∠,∴ABD C ∠=∠;(3)设∠DBE=a,则∠BFC=3a,∵BE平分∠ABD,∴∠ABD=∠C=2a,又∵AB⊥BC,BF平分∠DBC,∠DBC=a+45°∴∠DBC=∠ABD+∠ABC=2a+90,即:∠FBC=12又∵∠BFC+∠FBC+∠BCF=180°,即:3a+a+45°+∠BCF=180°∴∠BCF=135°-4a,∴∠AFC=∠BCF=135°-4a,又∵AM//CN,∴∠AFC+∠NCF=180°,即:∠AFC+∠BCN+∠BCF=180°,∴135°-4a+135°-4a+2a=180,解得a=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.【点睛】本题主要考查了平行线的性质、角平分线的性质及角的计算,熟练应用平行线的性质、角平分线的性质是解答本题的关键.二、解答题6.(1)110°;(2)∠CPD=∠α+∠β,见解析;(3)当P在BA延长线时,∠CPD=∠β-∠α;当P在AB延长线上时,∠CPD=∠α-∠β【分析】(1)过P作PE∥AB,通过平行线性质求∠A解析:(1)110°;(2)∠CPD=∠α+∠β,见解析;(3)当P在BA延长线时,∠CPD=∠β-∠α;当P在AB延长线上时,∠CPD=∠α-∠β【分析】(1)过P作PE∥AB,通过平行线性质求∠APC即可;(2)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;(3)画出图形,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.【详解】解:(1)过点P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,∴∠A+∠APE=180°,∠C+∠CPE=180°,∵∠PAB=130°,∠PCD=120°,∴∠APE=50°,∠CPE=60°,∴∠APC=∠APE+∠CPE=110°.故答案为110°;(2)∠CPD=∠α+∠β,理由是:如图3,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β;(3)当P在BA延长线时,∠CPD=∠β-∠α,理由是:如图4,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠CPE-∠DPE =∠β-∠α;当P在AB延长线时,∠CPD=∠α-∠β,理由是:如图5,过P作PE∥AD交CD于E,∵AD ∥BC ,∴AD ∥PE ∥BC ,∴∠α=∠DPE ,∠β=∠CPE ,∴∠CPD =∠DPE -∠CPE =∠α-∠β.【点睛】本题考查了平行线的性质和判定的应用,主要考查学生的推理能力,题目是一道比较典型的题目,分类讨论是解题的关键.7.(1);(2)不变化,,理由见解析;(3)【分析】(1)结合题意,根据角平分线的性质,得;再根据平行线的性质计算,即可得到答案;(2)根据平行线的性质,得,;结合角平分线性质,得,即可完成求解 解析:(1)60A ∠=;(2)不变化,2APB ADB ∠=∠,理由见解析;(3)30ABC ∠=【分析】(1)结合题意,根据角平分线的性质,得ABN ∠;再根据平行线的性质计算,即可得到答案;(2)根据平行线的性质,得APB PBN ∠=∠,ADB DBN ∠=∠;结合角平分线性质,得2APB ADB ∠=∠,即可完成求解;(3)根据平行线的性质,得ACB CBN ∠=∠;结合ACB ABD =∠∠,推导得ABC DBN ∠=∠;再结合(1)的结论计算,即可得到答案.【详解】(1)∵BC ,BD 分别评分ABP ∠和PBN ∠, ∴1122CBP ABP DBP PBN ∠=∠∠=∠,, ∴2ABN CBD ∠=∠又∵60CBD ∠=,∴120ABN ∠=∵//AM BN ,∴180A ABN ∠+∠=∴60A ∠=;(2)∵//AM BN ,∴APB PBN ∠=∠,ADB DBN ∠=∠又∵BD 平分PBN ∠∴2PBN DBN ∠=∠,∴2APB ADB ∠=∠;∴APB ∠与ADB ∠之间的数量关系保持不变;(3)∵//AD BN ,∴ACB CBN ∠=∠又∵ACB ABD =∠∠,∴CBN ABD ∠=∠,∵ABC CBN ABD DBN ∠+∠=∠+∠∴ABC DBN ∠=∠由(1)可得60CBD ∠=,120ABN ∠= ∴()112060302ABC ∠=⨯-=. 【点睛】本题考查了角平分线、平行线的知识;解题的关键是熟练掌握角平分线、平行线的性质,从而完成求解.8.(1)图见解析,,理由见解析;(2),理由见解析;(3)图见解析,或.【分析】(1)根据平行线的画法补全图形即可得,根据平行线的性质可得,由此即可得;(2)如图(见解析),先根据平行线的性质可解析:(1)图见解析,EDF BAC ∠=∠,理由见解析;(2)//DE BA ,理由见解析;(3)图见解析,EDF BAC ∠=∠或180EDF BAC ∠+∠=︒.【分析】(1)根据平行线的画法补全图形即可得,根据平行线的性质可得,EDF BFD B B D AC F ∠=∠∠∠=,由此即可得;(2)如图(见解析),先根据平行线的性质可得BAC BOD ∠=∠,再根据等量代换可得EDF BOD ∠=∠,然后根据平行线的判定即可得;(3)先根据点D 的位置画出如图(见解析)的两种情况,再分别利用平行线的性质、对顶角相等即可得.【详解】(1)由题意,补全图形如下:EDF BAC∠=∠,理由如下:DE BA,//∴∠=∠,EDF BFDDF CA,//∴∠=∠,BABFD C∴∠=∠;EDF BACDE BA,理由如下:(2)//如图,延长BA交DF于点O,DF CA,//∴∠=∠,BAC BOD∠=∠,EDF BAC∴∠=∠,EDF BOD//∴;DE BA(3)由题意,有以下两种情况:∠=∠,理由如下:①如图3-1,EDF BAC//DE BA,E EAF∴∠+∠=︒,180DF CA,//E EDF∴∠+∠=︒,180∴∠=∠,EAF EDF由对顶角相等得:BAC EAF∠=∠,∴∠=∠;EDF BAC②如图3-2,180EDF BAC ∠+∠=︒,理由如下://DE BA ,180EDF F ∴∠+∠=︒,//DF CA ,BAC F ∴∠=∠,180EDF BAC ∴∠+∠=︒.【点睛】本题考查了平行线的判定与性质等知识点,较难的是题(3),正确分两种情况讨论是解题关键.9.(1)136°;(2)∠AOG+∠NEF =90°,理由见解析;(3)当点P 在GF 上时,∠OPQ =140°﹣∠POQ+∠PQF ;当点P 在线段GF 的延长线上时,140°﹣∠POQ =∠OPQ+∠PQF .解析:(1)136°;(2)∠AOG +∠NEF =90°,理由见解析;(3)当点P 在GF 上时,∠OPQ =140°﹣∠POQ +∠PQF ;当点P 在线段GF 的延长线上时,140°﹣∠POQ =∠OPQ +∠PQF .【分析】(1)如图1,作CP ∥a ,则CP ∥a ∥b ,根据平行线的性质可得∠AOG =∠ACP ,∠BCP +∠CEF =180°,然后利用∠ACP +∠BCP =90°即可求得答案;(2)如图2,作CP ∥a ,则CP ∥a ∥b ,根据平行线的性质可得∠AOG =∠ACP ,∠BCP +∠CEF =180°,然后结合已知条件可得∠BCP =∠NEF ,然后利用∠ACP +∠BCP =90°即可得到结论;(3)分两种情况,如图3,当点P 在GF 上时,过点P 作PN ∥OG ,则NP ∥OG ∥EF ,根据平行线的性质可推出∠OPQ =∠GOP +∠PQF ,进一步可得结论;如图4,当点P 在线段GF 的延长线上时,同上面方法利用平行线的性质解答即可.【详解】解:(1)如图1,作CP∥a,a b,∵//∴CP∥a∥b,∴∠AOG=∠ACP,∠BCP+∠CEF=180°,∴∠BCP=180°﹣∠CEF,∵∠ACP+∠BCP=90°,∴∠AOG+180°﹣∠CEF=90°,∵∠AOG=46°,∴∠CEF=136°,故答案为136°;(2)∠AOG+∠NEF=90°.理由如下:如图2,作CP∥a,则CP∥a∥b,∴∠AOG=∠ACP,∠BCP+∠CEF=180°,而∠NEF+∠CEF=180°,∴∠BCP=∠NEF,∵∠ACP+∠BCP=90°,∴∠AOG+∠NEF=90°;(3)如图3,当点P在GF上时,过点P作PN∥OG,∴NP∥OG∥EF,∴∠GOP=∠OPN,∠PQF=∠NPQ,∴∠OPQ=∠GOP+∠PQF,∴∠OPQ=140°﹣∠POQ+∠PQF;如图4,当点P在线段GF的延长线上时,过点P作PN∥OG,∴NP∥OG∥EF,∴∠GOP=∠OPN,∠PQF=∠NPQ,∵∠OPN=∠OPQ+∠QPN,∴∠GOP=∠OPQ+∠PQF,∴140°﹣∠POQ=∠OPQ+∠PQF.【点睛】本题考查了平行线的性质以及平行公理的推论等知识,属于常考题型,正确添加辅助线、灵活应用平行线的判定和性质是解题的关键.10.(1)4;(2)45°;(3)P(0,-1)或(0,3)【分析】(1)根据非负数的性质得到a=−b,a−b+4=0,解得a=−2,b=2,则A (−2,0),B(2,0),C(2,2),即可计算出解析:(1)4;(2)45°;(3)P(0,-1)或(0,3)【分析】(1)根据非负数的性质得到a=−b,a−b+4=0,解得a=−2,b=2,则A(−2,0),B (2,0),C(2,2),即可计算出三角形ABC的面积=4;(2)由于CB ∥y 轴,BD ∥AC ,则∠CAB =∠ABD ,即∠3+∠4+∠5+∠6=90°,过E 作EF ∥AC ,则BD ∥AC ∥EF ,然后利用角平分线的定义可得到∠3=∠4=∠1,∠5=∠6=∠2,所以∠AED =∠1+∠2=12×90°=45°;(3)先根据待定系数法确定直线AC 的解析式为y =12x +1,则G 点坐标为(0,1),然后利用S △PAC =S △APG +S △CPG 进行计算.【详解】解:(1)由题意知:a =−b ,a−b +4=0,解得:a =−2,b =2,∴ A (−2,0),B (2,0),C (2,2),∴S △ABC =1AB BC=42⋅; (2)∵CB ∥y 轴,BD ∥AC ,∴∠CAB =∠ABD ,∴∠3+∠4+∠5+∠6=90°,过E 作EF ∥AC ,∵BD ∥AC ,∴BD ∥AC ∥EF ,∵AE ,DE 分别平分∠CAB ,∠ODB ,∴∠3=∠4=∠1,∠5=∠6=∠2,∴∠AED =∠1+∠2=12×90°=45°;(3)存在.理由如下:设P 点坐标为(0,t ),直线AC 的解析式为y =kx +b ,把A (−2,0)、C (2,2)代入得: -2k+b=02k+b=2⎧⎨⎩,解得1k=2b=1⎧⎪⎨⎪⎩, ∴直线AC 的解析式为y =12x +1,∴G 点坐标为(0,1),∴S △PAC =S △APG +S △CPG =12|t−1|•2+12|t−1|•2=4,解得t =3或−1,∴P 点坐标为(0,3)或(0,−1).【点睛】本题考查了绝对值、平方的非负性,平行线的判定与性质:内错角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,内错角相等.三、解答题11.(1)①45°;②∠F=a;(2)∠F+∠H的值不变,是定值180°.【分析】(1)①②依据AD平分∠CAE,CF平分∠ACB,可得∠CAD=∠CAE,∠ACF=∠ACB,依据∠CAE是△ABC解析:(1)①45°;②∠F=12a;(2)∠F+∠H的值不变,是定值180°.【分析】(1)①②依据AD平分∠CAE,CF平分∠ACB,可得∠CAD=12∠CAE,∠ACF=12∠ACB,依据∠CAE是△ABC的外角,可得∠B=∠CAE-∠ACB,再根据∠CAD是△ACF的外角,即可得到∠F=∠CAD-∠ACF=12∠CAE-12∠ACB=12(∠CAE-∠ACB)=12∠B;(2)由(1)可得,∠F=12∠ABC,根据角平分线的定义以及三角形内角和定理,即可得到∠H=90°+12∠ABG,进而得到∠F+∠H=90°+12∠CBG=180°.【详解】解:(1)①∵AD平分∠CAE,CF平分∠ACB,∴∠CAD=12∠CAE,∠ACF=12∠ACB,∵∠CAE是△ABC的外角,∴∠B=∠CAE﹣∠ACB,∵∠CAD是△ACF的外角,∴∠F=∠CAD﹣∠ACF=12∠CAE﹣12∠ACB=12(∠CAE﹣∠ACB)=12∠B=45°,故答案为45°;②∵AD平分∠CAE,CF平分∠ACB,∴∠CAD=12∠CAE,∠ACF=12∠ACB,∵∠CAE是△ABC的外角,∴∠B=∠CAE﹣∠ACB,∵∠CAD是△ACF的外角,∴∠F=∠CAD﹣∠ACF=12∠CAE﹣12∠ACB=12(∠CAE﹣∠ACB)=12∠B=12a;(2)由(1)可得,∠F=12∠ABC,∵∠AGB与∠GAB的角平分线交于点H,∴∠AGH=12∠AGB,∠GAH=12∠GAB,∴∠H=180°﹣(∠AGH+∠GAH)=180°﹣12(∠AGB+∠GAB)=180°﹣12(180°﹣∠ABG)=90°+12∠ABG,∴∠F+∠H=12∠ABC+90°+12∠ABG=90°+12∠CBG=180°,∴∠F+∠H的值不变,是定值180°.【点睛】本题主要考查了三角形内角和定理、三角形外角性质的综合运用,熟练运用定理是解题的关键.12.(1)110(2)(90 +n)(3)×90°+n°【分析】(1)根据角平分线的性质,结合三角形的内角和定理可得到角之间的关系,然后求解即可;(2)根据BO、CO分别是∠ABC与∠ACB的角平解析:(1)110(2)(90 +12n)(3)201712×90°+20182018212n°【分析】(1)根据角平分线的性质,结合三角形的内角和定理可得到角之间的关系,然后求解即可;(2)根据BO、CO分别是∠ABC与∠ACB的角平分线,用n°的代数式表示出∠OBC与∠OCB的和,再根据三角形的内角和定理求出∠BOC的度数;(3)根据规律直接计算即可.【详解】解:(1)∵∠A=40°,∴∠ABC+∠ACB=140°,∵点O是∠AB故答案为:110°;C与∠ACB的角平分线的交点,∴∠OBC+∠OCB=70°,∴∠BOC=110°.(2)∵∠A=n°,∴∠ABC+∠ACB=180°-n°,∵BO、CO分别是∠ABC与∠ACB的角平分线,∴∠OBC +∠OCB =12∠ABC +12∠ACB =12(∠ABC +∠ACB )=12(180°﹣n °)=90°﹣12n °,∴∠BOC =180°﹣(∠OBC +∠OCB )=90°+12n °.故答案为:(90+12n );(3)由(2)得∠O =90°+12n °,∵∠ABO 的平分线与∠ACO 的平分线交于点O 1, ∴∠O 1BC =34∠ABC ,∠O 1CB =34∠ACB , ∴∠O 1=180°﹣34(∠ABC +∠ACB )=180°﹣34(180°﹣∠A )=14×180°+34n °, 同理,∠O 2=18×180°+78n °, ∴∠O n =112n +×180°+11212n n ++- n °, ∴∠O 2017=201812×180°+20182018212-n °, 故答案为:201712×90°+20182018212-n °. 【点睛】 本题考查了三角形内角和定理,角平分线定义的应用,注意:三角形的内角和等于180°. 13.(1)3;(2)98°;(3)∠P=(β+2α),理由见解析;(4)360°.【分析】(1)以M 为交点的“8字形”有1个,以O 为交点的“8字形”有2个; (2)根据角平分线的定义得到∠CAP=∠解析:(1)3;(2)98°;(3)∠P=(β+2α),理由见解析;(4)360°.【分析】(1)以M 为交点的“8字形”有1个,以O 为交点的“8字形”有2个;(2)根据角平分线的定义得到∠CAP=∠BAP ,∠BDP=∠CDP ,再根据三角形内角和定理得到∠CAP+∠C=∠CDP+∠P ,∠BAP+∠P=∠BDP+∠B ,两等式相减得到∠C ﹣∠P=∠P ﹣∠B ,即∠P=(∠C+∠B ),然后把∠C=100°,∠B=96°代入计算即可;(3)与(2)的证明方法一样得到∠P=(2∠C+∠B ).(4)根据三角形内角与外角的关系可得∠B+∠A=∠1,∠C+∠D=∠2,再根据四边形内角和为360°可得答案.【详解】解:(1)在图2中有3个以线段AC为边的“8字形”,故答案为3;(2)∵∠CAB和∠BDC的平分线AP和DP相交于点P,∴∠CAP=∠BAP,∠BDP=∠CDP,∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,∴∠C﹣∠P=∠P﹣∠B,即∠P=(∠C+∠B),∵∠C=100°,∠B=96°∴∠P=(100°+96°)=98°;(3)∠P=(β+2α);理由:∵∠CAP=∠CAB,∠CDP=∠CDB,∴∠BAP=∠BAC,∠BDP=∠BDC,∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,∴∠C﹣∠P=∠BDC﹣∠BAC,∠P﹣∠B=∠BDC﹣∠BAC,∴2(∠C﹣∠P)=∠P﹣∠B,∴∠P=(∠B+2∠C),∵∠C=α,∠B=β,∴∠P=(β+2α);(4)∵∠B+∠A=∠1,∠C+∠D=∠2,∴∠A+∠B+∠C+∠D=∠1+∠2,∵∠1+∠2+∠F+∠E=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.故答案为360°.14.(1)见详解;(2)15°;(3)67.5°;(4)45cm;(5)10s或30s或40s 【分析】(1)运用角平分线定义及平行线性质即可证得结论;(2)如图2,过点E作EK∥MN,利用平行线性解析:(1)见详解;(2)15°;(3)67.5°;(4)45cm;(5)10s或30s或40s【分析】(1)运用角平分线定义及平行线性质即可证得结论;(2)如图2,过点E作EK∥MN,利用平行线性质即可求得答案;(3)如图3,分别过点F、H作FL∥MN,HR∥PQ,运用平行线性质和角平分线定义即可得出答案;(4)根据平移性质可得D′A=DF,DD′=EE′=AF=5cm,再结合DE+EF+DF=35cm,可得出答案;(5)设旋转时间为t秒,由题意旋转速度为1分钟转半圈,即每秒转3°,分三种情况:①当BC∥DE时,②当BC∥EF时,③当BC∥DF时,分别求出旋转角度后,列方程求解即可.【详解】(1)如图1,在△DEF中,∠EDF=90°,∠DFE=30°,∠DEF=60°,∵ED平分∠PEF,∴∠PEF=2∠PED=2∠DEF=2×60°=120°,∵PQ∥MN,∴∠MFE=180°−∠PEF=180°−120°=60°,∴∠MFD=∠MFE−∠DFE=60°−30°=30°,∴∠MFD=∠DFE,∴FD平分∠EFM;(2)如图2,过点E作EK∥MN,∵∠BAC=45°,∴∠KEA=∠BAC=45°,∵PQ∥MN,EK∥MN,∴PQ∥EK,∴∠PDE=∠DEK=∠DEF−∠KEA,又∵∠DEF=60°.∴∠PDE=60°−45°=15°,故答案为:15°;(3)如图3,分别过点F、H作FL∥MN,HR∥PQ,∴∠LFA=∠BAC=45°,∠RHG=∠QGH,∵FL∥MN,HR∥PQ,PQ∥MN,∴FL∥PQ∥HR,∴∠QGF+∠GFL=180°,∠RHF=∠HFL=∠HFA−∠LFA,∵∠FGQ和∠GFA的角平分线GH、FH相交于点H,∴∠QGH=12∠FGQ,∠HFA=12∠GFA,∵∠DFE=30°,∴∠GFA=180°−∠DFE=150°,∴∠HFA=12∠GFA=75°,∴∠RHF=∠HFL=∠HFA−∠LFA=75°−45°=30°,∴∠GFL=∠GFA−∠LFA=150°−45°=105°,∴∠RHG=∠QGH=12∠FGQ=12(180°−105°)=37.5°,∴∠GHF=∠RHG+∠RHF=37.5°+30°=67.5°;(4)如图4,∵将△DEF沿着CA方向平移至点F与A重合,平移后的得到△D′E′A,∴D′A=DF,DD′=EE′=AF=5cm,∵DE+EF+DF=35cm,∴DE+EF+D′A+AF+DD′=35+10=45(cm),即四边形DEAD′的周长为45cm;(5)设旋转时间为t秒,由题意旋转速度为1分钟转半圈,即每秒转3°,分三种情况:BC∥DE时,如图5,此时AC∥DF,∴∠CAE=∠DFE=30°,∴3t=30,解得:t=10;BC∥EF时,如图6,∵BC∥EF,∴∠BAE=∠B=45°,∴∠BAM=∠BAE+∠EAM=45°+45°=90°,∴3t=90,解得:t=30;BC∥DF时,如图7,延长BC交MN于K,延长DF交MN于R,∵∠DRM=∠EAM+∠DFE=45°+30°=75°,∴∠BKA=∠DRM=75°,∵∠ACK=180°−∠ACB=90°,∴∠CAK=90°−∠BKA=15°,∴∠CAE=180°−∠EAM−∠CAK=180°−45°−15°=120°,∴3t=120,解得:t=40,综上所述,△ABC绕点A顺时针旋转的时间为10s或30s或40s时,线段BC与△DEF的一条边平行.【点睛】本题主要考查了平行线性质及判定,角平分线定义,平移的性质等,添加辅助线,利用平行线性质是解题关键.15.(1),证明见解析;(2)证明见解析;(3).【分析】(1)过E作EH∥AB,根据两直线平行,内错角相等,即可得出∠AED=∠AEH+∠DEH=∠EAF+∠EDG;(2)设CD与AE交于点H∠+∠=∠,证明见解析;(2)证明见解析;(3)解析:(1)EAF EDG AED∠=︒.EKD80【分析】(1)过E作EH∥AB,根据两直线平行,内错角相等,即可得出∠AED=∠AEH+∠DEH=∠EAF+∠EDG;(2)设CD与AE交于点H,根据∠EHG是△DEH的外角,即可得出∠EHG=∠AED+∠EDG,进而得到∠EAF=∠AED+∠EDG;α+5°,再根(3)设∠EAI=∠BAI=α,则∠CHE=∠BAE=2α,进而得出∠EDI=α+10°,∠CDI=12α+5°+α+10°+20°,求得据∠CHE是△DEH的外角,可得∠CHE=∠EDH+∠DEK,即2α=12α=70°,即可根据三角形内角和定理,得到∠EKD的度数.【详解】解:(1)∠AED=∠EAF+∠EDG.理由:如图1,过E作EH∥AB,∵AB∥CD,∴AB∥CD∥EH,∴∠EAF=∠AEH,∠EDG=∠DEH,∴∠AED=∠AEH+∠DEH=∠EAF+∠EDG;(2)证明:如图2,设CD与AE交于点H,∵AB∥CD,∴∠EAF=∠EHG,∵∠EHG是△DEH的外角,∴∠EHG=∠AED+∠EDG,∴∠EAF=∠AED+∠EDG;(3)∵AI平分∠BAE,∴可设∠EAI=∠BAI=α,则∠BAE=2α,如图3,∵AB∥CD,∴∠CHE=∠BAE=2α,∵∠AED=20°,∠I=30°,∠DKE=∠AKI,∴∠EDI=α+30°-20°=α+10°,又∵∠EDI:∠CDI=2:1,∴∠CDI=12∠EDK=12α+5°,∵∠CHE是△DEH的外角,∴∠CHE=∠EDH+∠DEK,即2α=12α+5°+α+10°+20°,解得α=70°,∴∠EDK=70°+10°=80°,∴△DEK中,∠EKD=180°-80°-20°=80°.【点睛】本题主要考查了平行线的性质,三角形外角性质以及三角形内角和定理的综合应用,解决问题的关键是作辅助线构造内错角,运用三角形外角性质进行计算求解.解题时注意:三角形的一个外角等于和它不相邻的两个内角的和.。
西安铁一中分校数学轴对称填空选择中考真题汇编[解析版]
![西安铁一中分校数学轴对称填空选择中考真题汇编[解析版]](https://img.taocdn.com/s3/m/6254e449770bf78a64295426.png)
西安铁一中分校数学轴对称填空选择中考真题汇编[解析版]一、八年级数学全等三角形填空题(难)1.如图,△ABC 的三边AB 、BC 、CA 的长分别为30、40、15,点P 是三条角平分线的交点,将△ABC 分成三个三角形,则APB S ∆︰BPC S ∆︰CPA S ∆等于____.【答案】6:8:3【解析】【分析】由角平分线性质可知,点P 到三角形三边的距离相等,即三个三角形的AB 、BC 、CA 边上的高相等,利用面积公式即可求解.【详解】解:过点P 作PD ⊥BC 于D ,PE ⊥CA 于E ,PF ⊥AB 于F∵P 是三条角平分线的交点∴PD=PE=PF∵AB=30,BC=40,CA=15∴APB S ∆︰BPC S ∆︰CPA S ∆=30∶40∶15=6∶8∶3故答案为6∶8∶3.【点睛】 本题主要考查了角平分线的性质和三角形面积的求法. 角平分线上的点到两边的距离相等. 难度不大,作辅助线是关键.2.如图,在ABC 中,点A 的坐标为()0,1,点B 的坐标为()0,4,点C 的坐标为()4,3,点D 在第二象限,且ABD 与ABC 全等,点D 的坐标是______.【答案】(-4,2)或(-4,3)【解析】【分析】【详解】把点C向下平移1个单位得到点D(4,2),这时△ABD与△ABC全等,分别作点C,D关于y轴的对称点(-4,3)和(-4,2),所得到的△ABD与△ABC全等.故答案为(-4,2)或(-4,3).3.如图,ABE△,BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,连接OB,下列结论正确的有_________.①AD EC=;②BM BN=;③MN AC;④EM MB=;⑤OB平分AOC∠【答案】①②③⑤.【解析】【分析】由题意根据全等三角形的判定和性质以及等边三角形的性质和角平分线的性质,对题干结论依次进行分析即可.【详解】解:∵△ABE,△BCD均为等边三角形,∴AB=BE,BC=BD,∠ABE=∠CBD=60°,∴∠ABD=∠EBC,在△ABD和△EBC中,AB BEABD EBCBD BC⎧⎪∠∠⎨⎪⎩===∴△ABD≌△EBC(SAS),∴AD=EC,故①正确;∴∠DAB=∠BEC,又由上可知∠ABE=∠CBD=60°,∴∠EBD=60°,在△ABM 和△EBN 中,MAB NEB AB BEABE EBN ∠∠⎧⎪⎨⎪∠∠⎩=== ∴△ABM ≌△EBN (ASA ),∴BM=BN ,故②正确;∴△BMN 为等边三角形,∴∠NMB=∠ABM=60°,∴MN ∥AC ,故③正确;若EM=MB ,则AM 平分∠EAB ,则∠DAB=30°,而由条件无法得出这一条件,故④不正确;如图作,,BG AD BH EC ⊥⊥∵由上可知△ABD ≌△EBC ,∴两个三角形对应边的高相等即BG BH =,∴OB 是AOC ∠的角平分线,即有OB 平分AOC ∠,故⑤正确.综上可知:①②③⑤正确.故答案为:①②③⑤.【点睛】本题考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质以及等边三角形的性质和角平分线的性质与平行线的判定是解题的关键.4.如图,AD 是△ABC 的角平分线,DF⊥AB,垂足为F ,DE=DG ,△ADG 和△AED 的面积分别为48和36,求△EDF 的面积________.【答案】6【解析】【分析】作DM=DE交AC于M,作DN⊥AC,利用角平分线的性质得到DN=DF,将三角形EDF的面积转化为三角形DNM的面积来求.【详解】作DM=DE交AC于M,作DN⊥AC,∵AD是△ABC的角平分线,DF⊥AB,∴DF=DN,∵DE=DG,∴DG=DM,∴Rt△DEF≌Rt△DMN(HL),∵DG=DM, DN⊥AC,∴MN=NG,∴△DMN≌△DNG,∵△ADG和△AED的面积分别为48和36,∴S△MDG=S△ADG-S△ADM=48-36=12,∴S△DEF=12S△MDG=1212=6,故答案为:6【点睛】本题考查了角平分线的性质及全等三角形的判定及性质,正确地作出辅助线,将所求的三角形的面积转化为另外的三角形的面积来求是解题关键.5.在△ABC中,∠ABC=60°,∠ACB=70°,若点O到三边的距离相等,则∠BOC=_____°.【答案】115或65或22.5【解析】【分析】先画出符合的图形,再根据角平分线的性质和三角形的内角和定理逐个求出即可.【详解】解:①如图,∵点O到三边的距离相等,∴点O是△ABC的三角的平分线的交点,∵∠ABC=60°,∠ACB=70°,∴∠OBC=12∠ABC=30°,1OCB2∠=∠ACB=35°,∴∠BOC=180°﹣∠OBC﹣∠OCB=115°;②如图,∵∠ABC=60°,∠ACB=70°,∴∠EBC=180°﹣∠ABC=120°,∠FCB=180°﹣∠ACB=110°,∵点O到三边的距离相等,∴O是∠EBC和∠FCB的角平分线的交点,∴∠OBC=12∠EBC=60°,1OCB2∠=∠FCB=55°,∴∠BOC=180°﹣∠OBC﹣∠OCB=65°;③如图,∵∠ABC=60°,∠ACB=75°,∴∠A=180°﹣∠ABC﹣∠ACB=45°,∵点O到三边的距离相等,∴O是∠EBA和∠ACB的角平分线的交点,∴∠OBA=12∠EBA=12×(180°﹣60°)=60°,1OCB2∠=∠ACB=37.5°,∴∠BOC=180°﹣(∠OBA+∠ABC+∠OCB)=180°﹣(60°﹣60°﹣37.5°)=22.5°;如图,此时∠BOC =22.5°,故答案为:115或65或22.5.【点睛】此题主要考查三角形的内角和,解题的关键是根据题意分情况讨论.6.如图,在△ABC 中,AC=BC ,∠ACB=90°,M 是AB 边上的中点,点D 、E 分别是AC 、BC 边上的动点,连接DM 、ME 、CM 、DE, DE 与CM 相交于点F 且∠DME=90°.则下列5个结论: (1)图中共有两对全等三角形;(2)△DEM 是等腰三角形; (3)∠CDM=∠CFE ;(4)AD 2+BE 2=DE 2;(5)四边形CDME 的面积发生改变.其中正确的结论有( )个.A .2B .3C .4D .5【答案】B【解析】【分析】 根据等腰三角形的性质,三角形内角和定理,得出:△AMC ≌△BMC 、△AMD ≌△CME 、△CMD ≌△BME,根据全等三角形的性质得出DM=ME 得出△DEM 是等腰三角形,及∠CDM=∠CFE ,再逐个判断222AD +BE =DE CEM CDM ADM CDM ACM ABC CDME 1S =S +S =S +S =S =S 2△△△△△△四边形 即可得出结论.【详解】解:如图在Rt △ABC 中,∠ACB=90°,M 为AB 中点,AB=BC∴AM=CM=BM ,∠A=∠B=∠ACM=∠BCM=45°,∠AMC=∠BMC=90°∵∠DME=90°.∴∠1+∠2=∠2+∠3=∠3+∠4=90°∴∠1=∠3,∠2=∠4在△AMC 和△BMC 中AM=BM MC MC AC BC ⎧⎪=⎨⎪=⎩∴△AMC ≌△BMC在△AMD 和△CME 中A=MCE AM=CM 1=3∠∠⎧⎪⎨⎪∠∠⎩∴△AMD ≌△CME在△CDM 和△BEMDCM=B CM=BM2=4∠∠⎧⎪⎨⎪∠∠⎩∴△CMD ≌△CME共有3对全等三角形,故(1)错误∵△AMD ≌△BME∴DM=ME∴△DEM 是等腰三角形,(2)正确∵∠DME=90°.∴∠EDM=∠DEM=45°,∴∠CDM=∠1+∠A=∠1+45°,∴∠EDM=∠3+∠DEM=∠3+45°,∴∠CDM=∠CFE,故(3)正确在Rt △CED 中,222CE CD DE +=∵CE=AD ,BE=CD∴222AD +BE =DE 故(4)正确(5)∵△ADM ≌△CEM∴ADM CEM S =S △△ ∴CEM CDM ADM CDM ACM ABC CDME 1S =S +S =S +S =S =S 2△△△△△△四边形 不变,故(5)错误 故正确的有3个故选:B【点睛】本题主要考查了等腰直角三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识,通过推理论证每个命题的正误是解决此类题目的关键.7.如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC边上的中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②EF=AP;③2S四边形AEPF=S△ABC;④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)有BE+CF=EF;上述结论中始终正确的序号有__________.【答案】①③【解析】【分析】根据题意,容易证明△AEP≌△CFP,然后能推理得到①③都是正确.【详解】∵AB=AC,∠BAC=90°,点P是BC的中点,∴∠EAP=12∠BAC=45°,AP=12BC=CP.①在△AEP与△CFP中,∵∠EAP=∠C=45°,AP=CP,∠APE=∠CPF=90°-∠APF,∴△AEP≌△CFP,∴AE=CF.正确;②只有当F在AC中点时EF=AP,故不能得出EF=AP,错误;③∵△AEP≌△CFP,同理可证△APF≌△BPE.∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△BPE=12S△ABC,即2S四边形AEPF=S△ABC;正确;④根据等腰直角三角形的性质,2PE,所以,EF随着点E的变化而变化,只有当点E为AB的中点时,2PE=AP,在其它位置时EF≠AP,故④错误;故答案为:①③.【点睛】本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,证得△AEP和△CFP 全等是解题的关键,也是本题的突破点.8.如图,已知AB∥CD,O为∠CAB、∠ACD的角平分线的交点,OE⊥AC于E,且OE=2,CO=3,则两平行线间AB、CD的距离等于________.【答案】4【解析】试题解析:如图,过点O 作MN ,MN ⊥AB 于M ,交CD 于N ,∵AB ∥CD ,∴MN ⊥CD ,∵AO 是∠BAC 的平分线,OM ⊥AB ,OE ⊥AC ,OE=2,∴OM=OE=2,∵CO 是∠ACD 的平分线,OE ⊥AC ,ON ⊥CD ,∴ON=OE=2,∴MN=OM+ON=4,即AB 与CD 之间的距离是4.点睛:要明确:①角的平分线上的点到角的两边的距离相等,②从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,③平行线间的距离处处相等.9.把两个三角板如图甲放置,其中90ACB DEC ∠=∠=︒,45A ∠=︒,30D ∠=︒,斜边12AB =,14CD =,把三角板DCE 绕着点C 顺时针旋转15︒得到△11D CE (如图乙),此时AB 与1CD 交于点O ,则线段1AD 的长度为_________.【答案】10【解析】试题分析:如图所示,∠3=15°,∠1E =90°, ∴∠1=∠2=75°, 又∵∠B=45°,∴∠OF 1E =∠B+∠1=45°+75°=120° ∴∠1D FO=60° ∵∠C 11D E =30°,∴∠5=∠4=90°, 又∵AC=BC ,AB=12, ∴OA=OB=6 ∵∠ACB=90°,∴CO=12AB=6, 又∵C 1D =CD=14, ∴O 1D =C 1D -OC=14-6=8, 在Rt △A 1D O 中,222211A 6810D OA OD =+=+=点睛:本题主要考查的就是旋转的性质、三角形的外角性质、直角三角形的性质及判定以及勾股定理的应用.解决这个问题的关键就是首先根据三角形外角的性质以及旋转图形的性质得出△AO 1D 为直角三角形,然后根据直角三角形的性质得出AO 和O 1D 的长度,最后根据直角三角形的勾股定理得出答案.10.如图:△ABC 中,∠ACB=90°,∠CAD=30°,AC=BC=AD ,CE ⊥CD ,且CE=CD ,连接BD ,DE ,BE ,则下列结论:①∠ECA=165°,②BE=BC ;③AD ⊥BE ;其中正确的是_________【答案】①②③【解析】如图,(1)∵AC=AD ,∠CAD=30°,∴∠ACD=∠ADC=18030752-=, ∵CE ⊥DC ,∴∠DCE=90°,∴∠ACE=∠ACD+∠DCE=165°.故①正确;(2)由(1)可知:∠ACB=∠DCE=90°,∴∠ACE-∠DCB=∠DCE-∠DCB ,即∠ACD=∠BCE ,在△ACD 和△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ∴△ACD ≌△BCE ,∴BE=AD=BC.故②正确;(3)延长AD 交BE 于点F ,∵△ACD ≌△BCE ,∴∠2=∠CAD=30°,∵AC=BC ,∠ACB=90°,∴∠CAB=∠3=45°,∴∠1=∠CAB-∠CAD=15°,∴∠AFB=180°-∠1-∠2-∠3=90°,∴AD ⊥BE.故③正确;综上所述:正确的结论是①②③.二、八年级数学全等三角形选择题(难)11.如图,在△ABC中,∠ABC=45°, BC=4,以AC为直角边,点A为直角顶点向△ABC的外侧作等腰直角三角形ACD,连接BD,则△DBC的面积为( ) .A.8 B.10 C.42D.82【答案】A【解析】【分析】将△ABD绕着点A顺时针旋转90°得到△AEC,BD与EC交于点O,连接BE,根据旋转的性质得到AE=AB,∠BAE=∠DOC=90°,过D点作DF⊥BC,证△EBC≌BFD,可得DF=BC=4,再用三角形面积公式即可得出答案.【详解】解:如下图所示,将△ABD绕着点A顺时针旋转90°得到△AEC,BD与EC交于点O,连接BE,根据旋转的性质可知EC=BD,AE=AB,∠BAE=∠DOC=90°,∴△ABE是等腰直角三角形,∴∠ABE=45°,又∵∠ABC=45°,∴∠EBC=90°,∵∠BDF+∠DBF=90°,∠ECB+∠DBF=90°,∴∠BDF=∠ECB在△EBC和△BFD中EBC=BFD=90ECB=BDFEC=BD⎧∠∠⎪∠∠⎨⎪⎩∴△EBC≌△BFD(AAS)∴DF=BC=4∴△DBC的面积=11BC DF=44=822⋅⨯⨯故选A.【点睛】本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定,是一道综合性较强的题,难度较大,关键是正确的作出辅助线构造全等三角形.12.如图,在△ABC和△DCB中,AB=DC,AC与BD相交于点E,若不再添加任何字母与辅助线,要使△ABC≌△DCB,则还需增加的一个条件是()A.AC=BD B.AC=BC C.BE=CE D.AE=DE【答案】A【解析】由AB=DC,BC是公共边,即可得要证△ABC≌△DCB,可利用SSS,即再增加AC=DB即可.故选A.点睛:此题主要考查了全等三角形的判定,解题时利用全等三角形的判定:SSS,SAS,ASA,AAS,HL,确定条件即可,此题为开放题,只要答案符合判定定理即可. 13.如图,已知等腰Rt△ABC和等腰Rt△ADE,AB=AC=4,∠BAC=∠EAD=90°,D是射线BC 上任意一点,连接EC.下列结论:①△AEC△ADB;②EC⊥BC ;③以A、C、D、E为顶点的四边形面积为8;④当BD=时,四边形AECB的周长为10524;⑤当BD=32B时5;其中正确的有()A .5个B .4个C .3 个D .2个 【答案】B【解析】解:∵∠BAC =∠EAD =90°,∴∠BAD =∠CAE ,∵AB =AC ,AD =AE ,∴△AEC ≌△ADB ,故①正确; ∵△AEC ≌△ADB ,∴∠ACE =∠ABD =45°,∵∠ACB =45°,∴J IAO ECB =90°,∴EC ⊥BC ,故②正确;∵四边形ADCE 的面积=△ADC 的面积+△ACE 的面积=△ADC 的面积+△ABD 的面积=△ABC 的面积=4×4÷2=8.故③正确;∵BD =2,∴EC =2,DC =BC -BD =422-=32,∴DE 2=DC 2+EC 2,=()()22322+=20,∴DE =25,∴AD =AE =252=10.∴AECB 的周长=AB +DC +CE +AE =442210+++=45210++,故④正确;当BD =32BC 时,CD =12BC ,∴DE =221322BC BC ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭=10BC =5AB .故⑤错误. 故选B .点睛:此题是全等三角形的判定与性质的综合运用,熟练掌握等腰直角三角形的性质是解答此题的关键.14.如图,BD 是∠ABC 的角平分线,AD ⊥AB ,AD=3,BC=5,则△BCD 的面积为( )A .7.5B .8C .10D .15【答案】A【解析】 作DE⊥BC 于E ,根据角平分线的性质,由BD 是∠ABC 的角平分线,AD⊥AB,DE⊥BC,求出DE=DA=3,根据三角形面积公式计算S △BCD =12×BC×DE=7.5, 故选:A .15.如图,点 D 是等腰直角△ABC 腰 BC 上的中点,点B 、B′ 关于 AD 对称,且BB′ 交AD 于 F,交 AC 于 E,连接 FC 、 AB′,下列说法:① ∠BAD=30°; ② ∠BFC=135°;③ AF=2B′ C;正确的个数是()A.1 B.2 C.3 D.4【答案】B【解析】【分析】依据点D是等腰直角△ABC腰BC上的中点,可得tan∠BAD=12,即可得到∠BAD≠30°;连接B'D,即可得到∠BB'C=∠BB'D+∠DB'C=90°,进而得出△ABF≌△BCB',判定△FCB'是等腰直角三角形,即可得到∠CFB'=45°,即∠BFC=135°;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C;依据△AEF与△CEB'不全等,即可得到S△AFE≠S△FCE.【详解】∵点D是等腰直角△ABC腰BC上的中点,∴BD=12BC=12AB,∴tan∠BAD=12,∴∠BAD≠30°,故①错误;如图,连接B'D,∵B、B′关于AD对称,∴AD垂直平分BB',∴∠AFB=90°,BD=B'D=CD,∴∠DBB'=∠BB'D,∠DCB'=∠DB'C,∴∠BB'C=∠BB'D+∠DB'C=90°,∴∠AFB=∠BB'C,又∵∠BAF+∠ABF=90°=∠CBB'+∠ABF,∴∠BAF=∠CBB',∴△ABF≌△BCB',∴BF=CB'=B'F,∴△FCB'是等腰直角三角形,∴∠CFB'=45°,即∠BFC=135°,故②正确;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C,故③正确;∵AF>BF=B'C,∴△AEF与△CEB'不全等,∴AE≠CE,∴S△AFE≠S△FCE,故④错误;故选B.【点睛】本题主要考查了轴对称的性质以及全等三角形的判定与性质的运用,如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.16.如图,,,,点D、E为BC边上的两点,且,连接EF、BF则下列结论:≌;≌;;,其中正确的有( )个.A.1B.2C.3D.4【答案】D【解析】【分析】根据∠DAF=90°,∠DAE=45°,得出∠FAE=45°,利用SAS证明△AED≌△AEF,判定①正确;由△AED≌△AEF得AF=AD,由,得∠FAB=∠CAD,又AB=AC, 利用SAS证明≌,判定②正确;先由∠BAC=∠DAF=90°,得出∠CAD=∠BAF,再利用SAS证明△ACD≌△ABF,得出CD=BF,又①知DE=EF,那么在△BEF中根据三角形两边之和大于第三边可得BE+BF>EF,等量代换后判定③正确;先由△ACD≌△ABF,得出∠C=∠ABF=45°,进而得出∠EBF=90°,判定④正确.【详解】‚解:①∵∠DAF=90°,∠DAE=45°,∴∠FAE=∠DAF-∠DAE=45°.在△AED与△AEF中,,∴△AED≌△AEF(SAS),①正确;②∵△AED≌△AEF,∴AF=AD,∵,∴∠FAB=∠CAD,∵AB=AC,∴≌,②正确;③∵∠BAC=∠DAF=90°,∴∠BAC-∠BAD=∠DAF-∠BAD,即∠CAD=∠BAF.在△ACD与△ABF中,,∴△ACD≌△ABF(SAS),∴CD=BF,由①知△AED≌△AEF,∴DE=EF.在△BEF中,∵BE+BF>EF,∴BE+DC>DE,③正确;④由③知△ACD≌△ABF,∴∠C=∠ABF=45°,∵∠ABE=45°,∴∠EBF=∠ABE+∠ABF=90°.④正确.故答案为D.【点睛】本题考查了勾股定理,全等三角形的判定与性质,等腰直角直角三角形的性质,三角形三边关系定理,相似三角形的判定,此题涉及的知识面比较广,解题时要注意仔细分析,有一定难度.17.如图,在▱ABCD 中,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,连接EF 、CF ,则下列结论中①∠DCF =123,1x x ==-∠BCD ;②EF =CF ;③S △BEC =2S △CEF ;④∠DFE =3∠AEF .一定成立的是( )A .①②B .①③④C .①②③D .①②④【答案】D【解析】①∵F 是AD 的中点,∴AF=FD ,∵在?ABCD 中,AD=2AB ,∴AF=FD=CD ,∴∠DFC=∠DCF ,∵AD ∥BC ,∴∠DFC=∠FCB ,∴∠DCF=∠BCF ,∴∠DCF=12∠BCD ,故此选项正确;延长EF ,交CD 延长线于M ,∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠A=∠MDF ,∵F 为AD 中点,∴AF=FD ,在△AEF 和△DFM 中,∠A =∠FDMAF =DF ∠AFE =∠DFM ,∴△AEF ≌△DMF (ASA ),∴FE=MF ,∠AEF=∠M ,∵CE⊥AB,∴∠AEC=90°,∴∠AEC=∠ECD=90°,∵FM=EF,∴FC=FM,故②正确;③∵EF=FM,∴S△EFC=S△CFM,∵MC>BE,∴S△BEC<2S△EFC故S△BEC=2S△CEF错误;④设∠FEC=x,则∠FCE=x,∴∠DCF=∠DFC=90°-x,∴∠EFC=180°-2x,∴∠EFD=90°-x+180°-2x=270°-3x,∵∠AEF=90°-x,∴∠DFE=3∠AEF,故此选项正确.故正确的有:①②④.故选D.18.如图,把ΔABC剪成三部分,边AB,BC,AC放在同一直线上,点O都落在直线MN 上,直线MN∥AB.在ΔABC中,若∠AOB=125°,则∠ACB的度数为()A.70°B.65°C.60°D.85°【答案】A【解析】【分析】利用平行线间的距离处处相等,可知点O到BC、AC、AB的距离相等,得出O为三条角平分线的交点,根据三角形内角和定理和角平分线的定义即可得出结论.【详解】如图1,过点O作OD⊥BC于D,OE⊥AC于E,OF⊥AB于F.∵MN∥AB,∴OD=OE=OF(平行线间的距离处处相等).如图2:过点O作OD'⊥BC于D',作OE'⊥AC于E',作OF'⊥AB于F'.由题意可知:OD =OD ',OE =OE ',OF =OF ',∴OD '=OE '=OF ',∴图2中的点O 是三角形三个内角的平分线的交点.∵∠AOB =125°,∴∠OAB +∠OBA =180°-125°=55°,∴∠CAB +∠CBA =2×55°=110°,∴∠ACB =180°-110°=70°.故选A .【点睛】本题考查了三角形的内心,平行线间的距离处处相等,角平分线定义,解答本题的关键是判断出OD =OE =OF .19.在ABC 中,2,72A B ACB ∠=∠∠≠︒,CD 平分ACB ∠,P 为AB 的中点,则下列各式中正确的是( )A .AD BC CD =-B .AD BC AC =- C .AD BC AP =-D .AD BC BD =-【答案】B【解析】【分析】 可在BC 上截取CE=CA ,连接DE ,可得△ACD ≌△ECD ,得DE=AD ,进而再通过线段之间的转化得出线段之间的关系.【详解】解:∵∠A=2∠B,∴∠A﹥∠B∴BC﹥AC∴可在BC上截取CE=CA,连接DE(如图),,∴∠ACD=∠BCD∵CD平分ACB又∵CD=CD,CE=CA∴△ACD≌△ECD,∴AD=ED,∠CED=∠A=2∠B又∠CED=∠B+∠BDE∴∠B=∠BDE∴AD=DE=BE,∴BC=BE+EC=AD+AC所以AD=BC-AC故选:B若A选项成立,则CD=AC,∴∠A=∠CDA=∠CDE=∠CED=2∠B=2∠EDB∴∠CDA+∠CDE+∠EDB=180°即5∠EDB=180°∴∠EDB=36°∴∠A=72°,∠B=36°∴∠ACB=72°与已知∠ACB≠72°矛盾,故选项A不正确;假设C选项成立,则有AP=AC,作∠BAC的平分线,连接FP,∴△CAF≌△PAF≌△PBF,∴∠CFA=∠AFP=∠PFB=60°∠B=30°,∠ACB=90°当∠ACB=90°时,选项C才成立,∴当∠ACB≠72°时,选项C不一定成立;假设D选项成立,则AD=BC-BD由图可知AD=BA-BD∴AB=BC∴∠A=∠ACB=2∠B∴∠A+∠ACB+∠B=180°∴∠B=36°,∠ACB=72这与已知∠ACB≠72°矛盾,故选项D不成立.故选:B【点睛】本题考查的是考查的是利用角的平分线的性质说明线段之间的关系.,,20.如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是().A.①②B.①②③C.①②④D.①②③④【答案】C【解析】【分析】如图,连接AP,根据HL判定△APR和△APS全等,即可说明①正确;由△APR和△APS 全等可得∠RAP=∠PAC,再根据等腰三角形性质推出∠QAP=∠QPA,得到∠QPA=∠BAP,根据平行线判定推出OP//AB,即②正确;在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等;连接RS,与AP交于点D,先证△ARD≌△ASD,即RD=SD;运用等腰三角形的性质即可判定.【详解】解:如图,连接AP∵PR⊥AB,PS⊥AC,PR=PS∴△APR≌△APS∴AS=AR,∠RAP=∠PAC即①正确;又∵AQ=PQ∴∠QAP=∠QPA∴∠QPA=∠BAP∴OP//AB,即②正确.在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等,故③错误.如图,连接PS∵△APR≌△APS∴AR=AS,∠RAP=∠PAC∴AP垂直平分RS,即④正确;故答案为C.【点睛】本题主要考查了全等三角形的性质和判定,角平分线性质的应用,熟练掌握全等三角形的判定和性质是解答本题的关键21.如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=12BF;④AE=BG.其中正确的是A.①②B.①③C.①②③D.①②③④【答案】C【解析】【分析】根据∠ABC=45°,CD⊥AB可得出BD=CD,利用AAS判定Rt△DFB≌Rt△DAC,从而得出DF=AD,BF=AC.则CD=CF+AD,即AD+CF=BD;再利用AAS判定Rt△BEA≌Rt△BEC,得出CE=AE=12AC,又因为BF=AC所以CE=12AC=12BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.【详解】解:∵CD⊥AB,∠ABC=45°,∴△BCD是等腰直角三角形.∴BD=CD.故①正确;在Rt△DFB和Rt△DAC中,∵∠DBF=90°−∠BFD,∠DCA=90°−∠EFC,且∠BFD=∠EFC,∴∠DBF=∠DCA.又∵∠BDF=∠CDA=90°,BD=CD,∴△DFB≌△DAC.∴BF=AC;DF=AD.∵CD=CF+DF,∴AD+CF=BD;故②正确;在Rt△BEA和Rt△BEC中.∵BE平分∠ABC,∴∠ABE=∠CBE.又∵BE=BE,∠BEA=∠BEC=90°,∴Rt△BEA≌Rt△BEC.∴CE=AE=12 AC.又由(1),知BF=AC,∴CE=12AC=12BF;故③正确;连接CG.∵△BCD是等腰直角三角形,∴BD=CD.又DH⊥BC,∴DH垂直平分BC.∴BG=CG.在Rt△CEG中,∵CG是斜边,CE是直角边,∴CE<CG.∵CE=AE,∴AE<BG.故④错误.故选C.【点睛】本题考查了等腰直角三角形、等腰三角形的判定与性质、全等三角形的判定与性质.此类问题涉及知识点较多,需要对相关知识点有很高的熟悉度.22.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是()A.①②③B.①②④C.①③④D.①②③④【答案】D【解析】分析:根据三角形内角和定理以及角平分线定义判断①;根据全等三角形的判定和性质判断②③;根据角平分线的判定与性质判断④.详解:在△ABC中,∵∠ACB=90°,∴∠BAC+∠ABC=90°,又∵AD、BE分别平分∠BAC、∠ABC,∴∠BAD+∠ABE=(∠BAC+∠ABC)=45°,∴∠APB=135°,故①正确.∴∠BPD=45°,又∵PF⊥AD,∴∠FPB=90°+45°=135°,∴∠APB=∠FPB,又∵∠ABP=∠FBP,BP=BP,∴△ABP≌△FBP,∴∠BAP=∠BFP,AB=FB,PA=PF,故②正确.在△APH和△FPD中,∵∠APH=∠FPD=90°,∠PAH=∠BAP=∠BFP,PA=PF,∴△APH≌△FPD,∴PH=PD,故③正确.∵△ABC的角平分线AD、BE相交于点P,∴点P到AB、AC的距离相等,点P到AB、BC的距离相等,∴点P到BC、AC的距离相等,∴点P在∠ACB的平分线上,∴CP平分∠ACB,故④正确.故选D.点睛:本题考查了角平分线的判定与性质,三角形全等的判定方法,三角形内角和定理.掌握相关性质是解题的关键.23.下列两个三角形中,一定全等的是( )A.两个等边三角形B.有一个角是40︒,腰相等的两个等腰三角形C.有一条边相等,有一个内角相等的两个等腰三角形D.有一个角是100︒,底相等的两个等腰三角形【答案】D【解析】【分析】根据全等三角形的判定方法及等腰三角形的性质对各个选项进行分析,从而得到答案.【详解】解:A、当两个等边三角形的对应边不相等时,这两个等边三角形也不会全等,故本选项错误;B、当该角不是对应角时,这两个等腰三角形也不会全等,故本选项错误;C、当两个等腰三角形的对应边与对应角不相等时,这两个等腰三角形也不会全等,故本选项错误;D、等腰三角形的100°角只能是顶角,则两个底角是40°,它们对应相等,所以由全等三角形的判定定理ASA或AAS证得它们全等,故本选项正确;故选D.【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.24.具备下列条件的两个三角形,可以证明它们全等的是( ).A.一边和这一边上的高对应相等B.两边和第三边上的中线对应相等C.两边和其中一边的对角对应相等D.直角三角形的斜边对应相等【答案】B【解析】【分析】根据判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL分别进行分析.【详解】解:A、一边和这边上的高对应相等,无法得出它们全等,故此选项错误;B、两边和第三边上的中线对应相等,通过如图所示方式(倍长中线法)可以证明它们全等(△ABC≌△A′B′C′),故此选项正确..C、两边和其中一边的对角对应相等,无法利用ASS得出它们全等,故此选项错误;D、直角三角形的斜边对应相等,无法得出它们全等,故此选项错误.故选:B.【点睛】本题考查三角形全等的判定方法,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.25.如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有()A.2种B.3种C.4种D.6种【答案】C【解析】【分析】①②:求出OBC=∠OCB,推出∠ACB=∠ABC即可的等腰三角形;①③:证△EBO≌△DCO,得出∠EBO=∠DCO,求出∠ACB=∠ABC即可;②④:证△EBO≌△DCO,推出OB=OC,求出∠ABC=∠ACB即可;③④:证△EBO≌△DCO,推出∠EBO=∠DCO,OB=OC,求出∠OBC=∠OCB,推出∠ACB=∠ABC即可.【详解】解:有①②,①③,②④,③④,共4种,①②,理由是:∵OB=OC,∴∠OBC=∠OCB,∵∠EBO=∠DCO,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,∴AB=AC,即△ABC是等腰三角形;①③,理由是:∵在△EBO和△DCO中BEO CDOEOB DOC OB OC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EBO≌△DCO,∴∠EBO=∠DCO,∵∠OBC=∠OCB(已证),∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,即AB=AC,∴△ABC是等腰三角形;②④,理由是:∵在△EBO和△DCO中BEO CDOEOB DOC BE CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EBO≌△DCO,∴OB=OC,∴∠OBC=∠OCB,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,即AB=AC,∴△ABC是等腰三角形;③④,理由是:∵在△EBO和△DCO中BEO CDOEOB DOC BE CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EBO≌△DCO,∴∠EBO=∠DCO,OB=OC,∴∠OBC=∠OCB,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,即AB=AC,∴△ABC是等腰三角形;故选C.26.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.A.1 B.1或3 C.1或7 D.3或7【答案】C【解析】【分析】分两种情况进行讨论,根据题意得出BP=2t=2和AP=16-2t=2即可求得.【详解】解:因为AB=CD,若∠ABP=∠DCE=90°,BP=CE=2,根据SAS证得△ABP≌△DCE,由题意得:BP=2t=2,所以t=1,因为AB=CD,若∠BAP=∠DCE=90°,AP=CE=2,根据SAS证得△BAP≌△DCE,由题意得:AP=16-2t=2,解得t=7.所以,当t的值为1或7秒时.△ABP和△DCE全等.故选C.【点睛】本题考查全等三角形的判定,判定方法有:ASA,SAS,AAS,SSS,HL.27.如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则下列结论,其中正确的是()①△AFB≌△AEC;②BF=CE;③∠BFC=∠EAF;④AB=BC.A.①②③B.①②④C.①②D.①②③④【答案】A【解析】【分析】根据题意结合图形证明△AFB≌△AEC;利用四点共圆及全等三角形的性质问题即可解决.【详解】如图,∵∠EAF=∠BAC ,∴∠BAF=∠CAE ;在△AFB 与△AEC 中,AF AE BAF CAE AB AC ⎧⎪∠∠⎨⎪⎩===, ∴△AFB ≌△AEC (SAS ),∴BF=CE ;∠ABF=∠ACE ,∴A 、F 、B 、C 四点共圆,∴∠BFC=∠BAC=∠EAF ;故①、②、③正确,④错误.故选A..【点睛】本题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是准确找出图形中隐含的全等三角形,灵活运用四点共圆等几何知识来分析、判断、推理或证明.28.如图所示,设甲、乙、丙、丁分别表示△ABC ,△ACD ,△EFG ,△EGH .已知∠ACB =∠CAD =∠EFG =∠EGH =70°,∠BAC =∠ACD =∠EGF =∠EHG =50°,则叙述正确的是( )A .甲、乙全等,丙、丁全等B .甲、乙全等,丙、丁不全等C .甲、乙不全等,丙、丁全等D .甲、乙不全等,丙、丁不全等【答案】B【解析】【分析】 根据题意即是判断甲、乙是否全等,丙丁是否全等.运用判定定理解答.【详解】解:∵∠ACB=CAD=70°,∠BAC=∠ACD=50°,AC 为公共边,∴△ABC ≌△ACD ,即甲、乙全等;△EHG 中,∠EGH=70°≠∠EHG=50°,即EH≠EG ,虽∠EFG=∠EGH=70°,∠EGF=∠EHG=50°,∴△EFG 不全等于△EGH ,即丙、丁不全等.综上所述甲、乙全等,丙、丁不全等,B 正确,故选:B .【点睛】本题考查的是全等三角形的判定,但考生需要有空间想象能力.判定两个三角形全等的一般方法有:SSS 、SAS 、AAS 、HL .找着∠EGH=70°≠∠EHG=50°,即EH≠EG 是正确解决本题的关键.29.如图,已知在正方形ABCD 中,点E F 、分别在BC CD 、上,△AEF 是等边三角形,连接AC 交EF 于G ,给出下列结论:①BE DF =; ② 15DAF ∠=;③AC 垂直平分EF ; ④BE DF EF +=.其中结论正确的共有( ).A .1个B .2个C .3个D .4个 【答案】C【解析】试题分析:四边形ABCD 是正方形,∴AB=BC=CD=AD ,∠B=∠BCD=∠D=∠BAD=90°.∵△AEF 等边三角形,∴AE=EF=AF ,∠EAF=60°.∴∠BAE+∠DAF=30°.∴Rt △ABE ≌Rt △ADF (HL ),∴BE=DF (故①正确).∠BAE=∠DAF ,∴∠DAF+∠DAF=30°,即∠DAF=15°(故②正确),∵BC=CD ,∴BC ﹣BE=CD ﹣DF ,即CE=CF ,∵AE=AF ,∴AC 垂直平分EF .(故③正确). 设EC=x ,由勾股定理,得EF=x ,CG=x ,AG=AEsin60°=EFsin60°=2×CGsin60°=x , ∴AC=, ∴AB=, ∴BE=﹣x=, ∴BE+DF=x ﹣x≠x .(故④错误).∴综上所述,正确的有3个.考点:正方形的性质;全等三角形的判定与性质;线段垂直平分线的性质;等边三角形的性质.30.如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边三角形ABC 和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②AP=BQ;③PQ∥AE;④DE=DP;⑤∠AOE=120°;其中正确结论的个数为()A.2个B.3个C.4个D.5个【答案】C【解析】【分析】①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE,故①正确;②由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△ACP≌△BCQ (ASA),所以AP=BQ;故②正确;③根据②△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知③正确;④根据∠QCP=60°,∠DPC=∠BCA+∠PAC>60°,可知PD≠CD,可知④错误;⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,由平角的性质可得∠AOE=120°,可知⑤正确;【详解】①∵△ABC和△CDE为等边三角形∴AC=BC,CD=CE,∠BCA=∠DCB=60°∴∠ACD=∠BCE∴△ACD≌△BCE(SAS)∴AD=BE,故①正确;由(1)中的全等得∠CBE=∠DAC,且BC=AC,∠ACB=∠BCQ=60°∴△CQB≌△CPA(ASA),∴AP=BQ,故②正确;∵△CQB≌△CPA,∴PC=PQ,且∠PCQ=60°∴△PCQ为等边三角形,∴∠PQC=∠DCE=60°,∴PQ∥AE,故③正确,∵∠QCP=60°,∠DPC=∠BCA+∠PAC>60°,∴PD≠CD,∴DE≠DP,故④DE=DP错误;∵BC∥DE,∴∠CBE=∠BED,∵∠CBE=∠DAE,∴∠AOB=∠OAE+∠AEO=60°,∴∠AOE=120°,故⑤正确,故选C.【点睛】本题考查了全等三角形的判定与性质,利用了等边三角形的判定与性质,全等三角形的判定与性质,平行线的判定与性质,综合性较强,题目难度较大.。
西安铁一中分校数学轴对称解答题中考真题汇编[解析版]
![西安铁一中分校数学轴对称解答题中考真题汇编[解析版]](https://img.taocdn.com/s3/m/acfd0a9eed630b1c59eeb5cc.png)
西安铁一中分校数学轴对称解答题中考真题汇编[解析版]一、八年级数学轴对称解答题压轴题(难)1.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?画出图形,写出结论不证明.【答案】(1)见解析;(2)见解析【解析】【分析】(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;(2)根据题意画出图形,连接AD,构造△DAF≌△DBE.得出FD=ED ,∠FDA=∠EDB,再算出∠EDF=90°,即可得出△DEF是等腰直角三角形.【详解】解:(1)连结AD ,∵AB=AC ,∠BAC=90° ,D为BC中点 ,∴AD⊥BC ,BD=AD ,∴∠B=∠BAD=∠DAC=45°,又∵BE=AF ,∴△BDE≌△ADF(SAS),∴ED=FD ,∠BDE=∠ADF,∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,∴△DEF为等腰直角三角形.(2)连结AD∵AB=AC ,∠BAC=90° ,D为BC中点 ,∴AD=BD ,AD⊥BC ,∴∠DAC=∠ABD=45° ,∴∠DAF=∠DBE=135°,又∵AF=BE ,∴△DAF≌△DBE(SAS),∴FD=ED ,∠FDA=∠EDB,∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.∴△DEF为等腰直角三角形.【点睛】本题利用了等腰直角三角形底边上的中线平分顶角,并且等于底边的一半,还利用了全等三角形的判定和性质,及等腰直角三角形的判定.2.再读教材:宽与长的比是5-12(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,问题解决:(1)图③中AB=________(保留根号);(2)如图③,判断四边形 BADQ的形状,并说明理由;(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.【答案】(1)5;(2)见解析;(3)见解析; (4) 见解析.【解析】分析:(1)由勾股定理计算即可;(2)根据菱形的判定方法即可判断;(3)根据黄金矩形的定义即可判断;(4)如图④﹣1中,在矩形BCDE上添加线段GH,使得四边形GCDH为正方形,此时四边形BGHE为所求是黄金矩形.详解:(1)如图3中.在Rt△ABC中,AB=22AC BC+=2212+=5.故答案为5.(2)结论:四边形BADQ是菱形.理由如下:如图③中,∵四边形ACBF是矩形,∴BQ∥AD.∵AB∥DQ,∴四边形ABQD是平行四边形,由翻折可知:AB=AD,∴四边形ABQD是菱形.(3)如图④中,黄金矩形有矩形BCDE,矩形MNDE.∵AD5AN=AC=1,CD=AD﹣AC51.∵BC=2,∴CDBC51-,∴矩形BCDE是黄金矩形.∵MNDN15+=512,∴矩形MNDE是黄金矩形.(4)如图④﹣1中,在矩形BCDE上添加线段GH,使得四边形GCDH为正方形,此时四边形BGHE为所求是黄金矩形.长GH=5﹣1,宽HE=3﹣5.点睛:本题考查了几何变换综合题、黄金矩形的定义、勾股定理、翻折变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考创新题目.3.已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求ABFACFSS的值.【答案】(1)①见解析;②见解析;(2)2【解析】【分析】(1)①只要证明∠2+∠BAF=∠1+∠BAF=60°即可解决问题;②只要证明△BFC≌△ADB,即可推出∠BFC=∠ADB=90°;(2)在BF上截取BK=AF,连接AK.只要证明△ABK≌CAF,可得S△ABK=S△AFC,再证明AF=FK=BK,可得S△ABK=S△AFK,即可解决问题;【详解】(1)①证明:如图1中,∵AB=AC,∠ABC=60°∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BN,∴∠ADB=90°,∵∠MBN=30°,∠BFD=60°=∠1+∠BAF=∠2+∠BAF,∴∠1=∠2②证明:如图2中,在Rt△BFD中,∵∠FBD=30°,∴BF=2DF,∵BF=2AF,∴BF=AD,∵∠BAE=∠FBC,AB=BC,∴△BFC≌△ADB,∴∠BFC=∠ADB=90°,∴BF⊥CF(2)在BF上截取BK=AF,连接AK.∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,∴∠CFB=∠2+∠4+∠BAC,∵∠BFE=∠BAC=2∠EFC,∴∠1+∠4=∠2+∠4∴∠1=∠2,∵AB=AC,∴△ABK≌CAF,∴∠3=∠4,S△ABK=S△AFC,∵∠1+∠3=∠2+∠3=∠CFE=∠AKB,∠BAC=2∠CEF,∴∠KAF=∠1+∠3=∠AKF,∴AF=FK=BK,∴S△ABK=S△AFK,∴ABFAFCS2S∆∆=.【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质、直角三角形30度角性质等知识,解题的关键是能够正确添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.4.已知如图1,在ABC∆中,AC BC=,90ACB∠=,点D是AB的中点,点E是AB边上一点,直线BF垂直于直线CE于点F,交CD于点G.(1)求证:AE CG=.(2)如图2,直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M,求证:BE CM=.【答案】(1)证明见解析;(2)证明见解析.【解析】【分析】(1)首先根据点D是AB中点,∠ACB=90°,可得出∠ACD=∠BCD=45°,判断出△AEC≌△CGB,即可得出AE=CG;(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC,∠ACM=∠CBE=45°,得出△BCE≌△CAM,进而证明出BE=CM.【详解】(1)∵点D是AB中点,AC=BC,∠ACB=90°,∴CD⊥AB,∠ACD=∠BCD=45°,∴∠CAD=∠CBD=45°,∴∠CAE=∠BCG.又∵BF⊥CE,∴∠CBG+∠BCF=90°.又∵∠ACE+∠BCF=90°,∴∠ACE=∠CBG.在△AEC和△CGB中,∵CAE BCGAC BCACE CBG∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AEC≌△CGB(ASA),∴AE=CG;(2)∵CH⊥HM,CD⊥ED,∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,∴∠CMA=∠BEC.在△BCE和△CAM中,BEC CMAACM CBEBC AC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE≌△CAM(AAS),∴BE=CM.【点睛】本题考查了全等三角形的判定与性质,等腰直角三角形的性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.5.知识背景:我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定,在第十三章《轴对称》中学习了等腰三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题.问题:如图1,ABC是等腰三角形,90BAC∠=︒,D是BC的中点,以AD为腰作等腰ADE,且满足90DAE∠=︒,连接CE并延长交BA的延长线于点F,试探究BC与CF之间的数量关系.图1发现:(1)BC与CF之间的数量关系为 .探究:(2)如图2,当点D是线段BC上任意一点(除B、C外)时,其他条件不变,试猜想BC与CF之间的数量关系,并证明你的结论.图2拓展:(3)当点D在线段BC的延长线上时,在备用图中补全图形,并直接写出BCF 的形状.备用图【答案】(1)BC CF =;(2)BC CF =,证明见解析;(3)画图见解析,等腰直角三角形.【解析】【分析】(1)根据等腰三角形的性质即可得BC CF =;(2)由等腰直角三角形的性质可得()ABD ACE SAS ∴≌,再根据全等三角形的性质及等角对等边即可证明;(3)作出图形,根据等腰三角形性质易证()ABD ACE SAS ∴≌,进而根据角度的代换,得出结论.【详解】解:(1)BC CF =.∵△ABC 是等腰三角形,且90BAC ∠=︒,AB AC ∴=,45B ACB ∠=∠=︒.90DAE ∠=︒,DAE BAC ∴=∠∠,DAE DAC BAC DAC ∴∠-∠=∠-∠,BAD CAE ∴∠=∠.ADE 是以AD 为腰的等腰三角形,AD AE ∴=.在ABD △与ACE △中,AB AC =,BAD CAE ∠=∠,AD AE =,()ABD ACE SAS ∴≌,45ACE B ∴∠=∠=︒.45ACB =︒∠,90BCF ACB ACE ∴∠=∠+∠=︒,90B F ∴∠+∠=︒,45F ∴∠=︒,B F ∴∠=∠,BC CF ∴=.(2)BC CF =. 证明:ABC 是等腰三角形,且90BAC ∠=︒,AB AC ∴=,45B ACB ∠=∠=︒.90DAE ∠=︒,DAE BAC ∴=∠∠,DAE DAC BAC DAC ∴∠-∠=∠-∠,BAD CAE ∴∠=∠.ADE 是以AD 为腰的等腰三角形,AD AE ∴=.在ABD △与ACE △中,AB AC =,BAD CAE ∠=∠,AD AE =,()ABD ACE SAS ∴≌,45ACE B ∴∠=∠=︒.45ACB =︒∠,90BCF ACB ACE ∴∠=∠+∠=︒, 90B F ∴∠+∠=︒,45F ∴∠=︒,B F ∴∠=∠,BC CF ∴=.(3)BCF 是等腰直角三角形.提示:如图,ABC 是等腰三角形,90BAC ∠=︒,AB AC ∴=,45B ACB ∠=∠=︒.90DAE ∠=︒,DAE BAC ∴=∠∠,DAE DAC BAC DAC ∴∠+∠=∠+∠,BAD CAE ∴∠=∠.ADE 是以AD 为腰的等腰三角形,AD AE ∴=.在ABD △与ACE △中,AB AC =,BAD CAE ∠=∠,AD AE =,()ABD ACE SAS ∴≌,45ACE B ∴∠=∠=︒.45ACB =︒∠,90BCF ACB ACE ∴∠=∠+∠=︒,90B BFC ∴∠+∠=︒,45BFC ∴∠=︒,B BFC ∴∠=∠,BCF ∴是等腰三角形,90BCF ∠=︒,BCF ∴是等腰直角三角形.【点睛】本题考查等腰三角形及全等三角形的性质,熟练运用角度等量代换及等腰三角形的性质是解题的关键.6.如图所示,已知ABC ∆中,10AB AC BC ===厘米,M 、N 分别从点A 、点B 同时出发,沿三角形的边运动,已知点M 的速度是1厘米/秒的速度,点N 的速度是2厘米/秒,当点N 第一次到达B 点时,M 、N 同时停止运动.(1)M 、N 同时运动几秒后,M 、N 两点重合?(2)M 、N 同时运动几秒后,可得等边三角形AMN ∆?(3)M 、N 在BC 边上运动时,能否得到以MN 为底边的等腰AMN ∆,如果存在,请求出此时M 、N 运动的时间?【答案】(1)10;(2)点M 、N 运动103秒后,可得到等边三角形AMN ∆;(3)当点M 、N 在BC 边上运动时,能得到以MN 为底边的等腰AMN ∆,此时M 、N 运动的时间为403秒. 【解析】【分析】(1)设点M 、N 运动x 秒后,M 、N 两点重合,1102x x ⨯+=;(2)设点M 、N 运动t 秒后,可得到等边三角形AMN ∆,如图①,1AM t t =⨯=,102AN AB BN t =-=-根据等边三角形性质得102t t =-;(3)如图②,假设AMN ∆是等腰三角形,根据等腰三角形性质证ACB ∆是等边三角形,再证ACM ∆≌ABN ∆(AAS ),得CM BN =,设当点M 、N 在BC 边上运动时,M 、N 运动的时间y 秒时,AMN ∆是等腰三角形,故10CM y =-,302NB y =-,由CM NB =,得10302y y -=-;【详解】解:(1)设点M 、N 运动x 秒后,M 、N 两点重合,1102x x ⨯+=解得:10x =(2)设点M 、N 运动t 秒后,可得到等边三角形AMN ∆,如图①1AM t t =⨯=,102AN AB BN t =-=-∵三角形AMN ∆是等边三角形∴102t t =- 解得103t = ∴点M 、N 运动103秒后,可得到等边三角形AMN ∆. (3)当点M 、N 在BC 边上运动时,可以得到以MN 为底边的等腰三角形,由(1)知10秒时M 、N 两点重合,恰好在C 处,如图②,假设AMN ∆是等腰三角形,∴AN AM =,∴AMN ANM ∠=∠,∴AMC ANB ∠=∠,∵AB BC AC ==,∴ACB ∆是等边三角形,∴C B ∠=∠,在ACM ∆和ABN ∆中,∵AC AB C B AMC ANB =⎧⎪∠=∠⎨⎪∠=∠⎩,∴ACM ∆≌ABN ∆(AAS ),∴CM BN =,设当点M 、N 在BC 边上运动时,M 、N 运动的时间y 秒时,AMN ∆是等腰三角形, ∴10CM y =-,302NB y =-,CM NB =,10302y y -=- 解得:403y =,故假设成立. ∴当点M 、N 在BC 边上运动时,能得到以MN 为底边的等腰AMN ∆,此时M 、N 运动的时间为403秒.【点睛】考核知识点:等边三角形判定和性质,全等三角形判定和性质.理解等腰三角形的判定和性质,把问题转化为方程问题是关键.7.八年级的小明同学通到这样一道数学题目:△ABC为边长为4的等边三角形,E是边AB 边上任意一动点,点D在CB的延长线上,且满足AE=BD.(1)如图①,当点E为AB的中点时,DE=;(2)如图②,点E在运动过程中,DE与EC满足什么数量关系?请说明理由;(3)如图③,F是AC的中点,连接EF.在AB边上是否存在点E,使得DE+EF值最小?若存在,求出这个最小值;若不存在,请说明理由.(直角三角形中,30°所对的边是斜边的一半)【答案】(1)32)DE=CE,理由见解析;(3)这个最小值为7;【解析】【分析】(1)如图①,过点E作EH⊥BC于H,由等边三角形的性质可得BE=DB=AE=2,由直角三角形的性质可求BH=1,EH3(2)如图②,过E作EF∥BC交AC于F,可证△AEF是等边三角形,AE=EF=AF=BD,由“SAS”可证△DBE≌△EFC,可得DE=CE;(3)如图③,将△ABC沿AB翻折得到△ABC',连接C'F交AB于点E',连接CE',DE',过点F作FH⊥AC'于点H,由“SAS”可证△ACE'≌△AC'E',可得C'E'=CE',可得当点C',点E',点F三点共线时,DE+EF的值最小,由勾股定理可求最小值.【详解】(1)如图①,过点E作EH⊥BC于H,∵△ABC 为边长为4的等边三角形,点E 是AB 的中点,∴AE =BE =2=DB ,∠ABC =60°,且EH ⊥BC ,∴∠BEH =30°,∴BH =1,EH 3=BH 3=,∴DH =DB +BH =2+1=3,∴DE 2293DH EH =+=+=23.故答案为:23;(2)DE =CE.理由如下:如图②,过E 作EF ∥BC 交AC 于F .∵△ABC 是等边三角形,∴∠ABC =∠ACB =∠A =60°,AB =AC =BC.∵EF ∥BC ,∴∠AEF =∠ABC =60°,∠AFE =∠ACB =60°,∴∠AEF =∠AFE =∠A =60°,∴△AEF 是等边三角形,∴AE =EF =AF ,∴AB ﹣AE =AC ﹣AF ,∴BE =CF.∵∠ABC =∠ACB =∠AFE =60°,∴∠DBE =∠EFC =120°,且AE =EF =DB ,BE =CF ,∴△DBE ≌△EFC (SAS),∴DE =CE ,(3)如图③,将△ABC 沿AB 翻折得到△ABC ',连接C 'F 交AB 于点E ',连接CE ',DE ',过点F 作FH ⊥AC '于点H.∵将△ABC 沿AB 翻折得到△ABC ',∴AC =AC '=BC =BC '=4,∠BAC =∠BAC '=60°,且AE '=AE ',∴△ACE '≌△AC 'E '(SAS),∴C 'E '=CE ',由(2)可知:DE '=CE ',∴C 'E '=CE '=DE '.∵DE +EF =C 'E +EF =C 'E '+EF ,∴当点C ',点E ',点F 三点共线时,DE +EF 的值最小.∵F 是AC 的中点,∴AF =CF =2,且HF ⊥AC ',∠FAH =180°﹣∠CAB ﹣∠C 'AB =60°,∴AH =1,HF 3=AH 3=,∴C 'H =4+1=5,∴C 'F 22'253C H HF =+=+=27,∴DE +EF 的最小值为27.【点睛】本题是三角形综合题,考查了等边三角形的判定和性质,直角三角形的性质,全等三角形的判定和性质,折叠的性质,添加恰当辅助线是解答本题的关键.8.在等边ABC ∆中,点O 在BC 边上,点D 在AC 的延长线上且OA OD =.(1)如图1,若点O 为BC 中点,求COD ∠的度数;(2)如图2,若点O 为BC 上任意一点,求证AD AB BO =+.(3)如图3,若点O 为BC 上任意一点,点D 关于直线BC 的对称点为点P ,连接,AP OP ,请判断AOP ∆的形状,并说明理由.【答案】(1)30;(2)见解析;(3)AOP ∆是等边三角形,理由见解析.【解析】【分析】(1)根据三角形的等边三角形的性质可求1302CAO BAC ∠=∠=︒且,90AO BC AOC ⊥∠=︒,根据OA OD =,等腰三角形的性质得到D ∠的度数,再通过内角和定理求AOD ∠,即可求出COD ∠的度数.(2)过O 作//OE AB ,OE 交AD 于E 先证明COE ∆为等边三角形,再根据等边三角形的性质求120AEO ∠=︒,120DCO ∠=︒,再证明()AOE DOC AAS ∆≅∆,得到CD EA =,再通过证明得到EA BO =、AB AC =通过,又因为AD AC CD =+,通过等量代换即可得到答案.(3)通过作辅助线先证明()ODF OPF SAS ∆≅∆,得到OP OD =,又因为OA OD =,得到AO=OP ,证得AOP ∆为等腰三角形,如解析辅助线,由(2)可知得AOE DOC ∆≅∆得到AOE DOC ∠=∠,通过角的关系得到60AOP COE ∠=∠=°,即可证得AOP ∆是等边三角形.【详解】(1)∵ABC ∆为等边三角形∴60BAC ∠=︒∵O 为BC 中点∴1302CAO BAC ∠=∠=︒ 且,90AO BC AOC ⊥∠=︒∵OA OD =∴AOD ∆中,30D CAO ∠=∠=︒∴180120AOD D CAO ∠=︒-∠-∠=︒∴30COD AOD AOC ∠=∠-∠=︒(2)过O 作//OE AB ,OE 交AD 于E∵//OE AB∴60EOC ABC ∠=∠=︒60CEO CAB ∠=∠=︒∴COE ∆为等边三角形∴OE OC CE ==180120AEO CEO ∠=︒-∠=︒180120DCO ACB ∠=︒-∠=︒又∵OA OD =∴EAO CDO ∠=∠在AOE ∆和COD ∆中AOE DOC EAO CDO OA OD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AOE DOC AAS ∆≅∆∴CD EA =∵EA AC CE =-BO BC CO =-∴EA BO =∴BO CD =,∵AB AC =,AD AC CD =+∴AD AB BO =+(3)AOP ∆为等边三角形证明过程如下:连接,PC PD ,延长OC 交PD 于F∵P D 、关于OC 对称∴,90PF DF PFO DFO =∠=∠=︒在ODF ∆与OPF ∆中,PF DF PFO DFO OF OF =⎧⎪∠=∠⎨⎪=⎩∴()ODF OPF SAS ∆≅∆∴OP OD =,POC DOC ∠=∠∵OA OD =∴AO=OP∴AOP ∆为等腰三角形过O 作//OE AB ,OE 交AD 于E由(2)得AOE DOC ∆≅∆∴AOE DOC ∠=∠又∵POC DOC ∠=∠∴AOE POF ∠=∠∴AOE POE POF POE ∠+∠=∠+∠即AOP COE ∠=∠∵AB ∥OE ,∠B=60°∴60COE B ∠=∠=︒∴60AOP COE ∠=∠=°∴AOP ∆是等边三角形.【点睛】本题是考查了全等三角形和等边三角形的综合性问题,灵活应用全等三角形的性质得到边与角的关系,以及等边三角形的性质是解答此题的关键.9.小明在学习了“等边三角形”后,激发了他的学习和探究的兴趣,就想考考他的朋友小崔,小明作了一个等边ABC ∆,如图1,并在边AC 上任意取了一点F (点F 不与点A 、点C 重合),过点F 作FH AB ⊥交AB 于点H ,延长CB 到G ,使得BG AF =,连接FG 交AB 于点l .(1)若10AC =,求HI 的长度;(2)如图2,延长BC 到D ,再延长BA 到E ,使得AE BD =,连接ED ,EC ,求证:ECD EDC ∠=∠.【答案】(1)HI =5;(2)见解析.【解析】【分析】(1)作FP∥BC交AB于点P,证明APF∆是等边三角形得到AH=PH,再证明PFI BGI∆≅∆得到PI=BI,于是可得HI =12AB,即可求解;(2)延长BD至Q,使DQ=AB,连结EQ,就可以得出BE=BQ,得出△BEQ是等边三角形,就可以得出BE=QE,得出△BCE≌△QDE就可以得出结论.【详解】解:如图1,作FP∥BC交AB于点P,∵ABC∆是等边三角形,∴∠ABC=∠A=60°,∵FP∥BC,∴∠APF=∠ABC=60°, ∠PFI=∠BGI,∴∠APF=∠A=60°,∴APF∆是等边三角形,∴PF=AF,∵FH AB⊥,∴AH=PH,∵AF=BG,∴PF=BG,∴在PFI∆和BGI∆中,PIF BIGPFI BGIPF BG∠=∠⎧⎪∠=∠⎨⎪=⎩,∴PFI BGI∆≅∆,∴PI=BI,∴PI+PH=BI+AH=12AB,∴HI=PI+PH =12AB=1102⨯=5;(2)如图2,延长BD至Q,使DQ=AB,连结EQ,∵△ABC 是等边三角形,∴AB=BC=AC ,∠B=60°.∵AE=BD ,DQ=AB ,∴AE+AB=BD+DQ ,∴BE=BQ .∵∠B=60°,∴△BEQ 为等边三角形,∴∠B=∠Q=60°,BE=QE .∵DQ=AB ,∴BC=DQ .∴在△BCE 和△QDE 中,BC DQ B Q BE QE =⎧⎪∠=∠⎨⎪=⎩,∴△BCE ≌△QDE (SAS ),∴EC=ED .∴∠ECD=∠EDC.【点睛】本题考查了等边三角形的判定及性质的运用,全等三角形的判定及性质的运用,解答时作出相应辅助线构造全等三角形是关键.本题难度较大,需要有较强的综合能力.10.数学课上,张老师举了下面的例题:例1 等腰三角形ABC 中,110A ∠=,求B 的度数.(答案:35)例2 等腰三角形ABC 中,40A ∠=,求B 的度数.(答案:40或70或100) 张老师启发同学们进行变式,小敏编了如下两题:变式1: 等腰三角形ABC 中,∠A=100°,求B 的度数.变式2: 等腰三角形ABC 中,∠A= 45° ,求B 的度数.(1)请你解答以上两道变式题.(2)解(1)后,小敏发现,A ∠的度数不同,得到B 的度数的个数也可能不同.如果在等腰三角形ABC中,设A x∠=,当B只有一个度数时,请你探索x的取值范围.【答案】(1)变式1: 40°;变式2: 90°或67.5°或45°;(2)90°≤<180°或x=60°【解析】【分析】(1)根据等腰三角形的性质和三角形内角和定理,分类讨论,即可得到答案;(2)在等腰三角形ABC中,当B只有一个度数时,A∠只能作为顶角时,或∠A=60°,进而可得到答案.【详解】变式1:∵等腰三角形ABC中,∠A=100°,∴∠A为顶角,∠B为底角,∴∠B=1801002-=40°;变式2: ∵等腰三角形ABC中,∠A= 45°,∴当AB=BC 时,∠B =90°,当AB=AC 时,∠B =67.5°,当BC=AC时∠B =45°;(2)等腰三角形ABC中,设A x∠=,当90°≤x<180°,∠A为顶角,此时,B只有一个度数,当x=60°时,三角形ABC是等边三角形,此时,B只有一个度数,综上所述:90°≤x<180°或x=60°【点睛】本题主要考查等腰三角形的性质,分类讨论思想的应用,是解题的关键.。
西安市铁一中学九年级数学上册第三单元《旋转》检测卷(含答案解析)

1.下列图形中,不是中心对称图形的是( )
A. B. C. D.
2.如图,将△ABC绕点A旋转,得到△AEF,下列结论正确的个数是()
①△ABC ≌△AEF;②AC=AE;③∠FAB=∠EAB;④∠EAB=∠FAC.
A.1B.2C.3D.4
3.如图,在 中, , , , 由 绕点 顺时针旋转得到,其中点 与点 、点 与点 是对应点,连接 ,且点 、 、 在同一条直线上,则 的长为()
24.如图,已知△ABC的三个顶点的坐标分别为A(﹣6,0)、B(﹣2,3)、C(﹣1,0).
(1)请直接写出与点B关于坐标原点O的对称点B1的坐标;
(2)将△ABC绕坐标原点O顺时针旋转90°.画出对应的△A′B′C′图形,直接写出点A的对应点A′的坐标;
25.某学习小组在探究三角形全等时,发现了下列两种基本图形,请给予证明.
A.3B. C.4D.
4.如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△ ,那么点A的对应点 的坐标是().
A.(-3,3)B.(3,-3)C.(-2,4)D.(1,4)
5.如图, 的斜边在 轴上, ,含 角的顶点与原点重合,直角顶点 在第二象限,将 绕原点顺时针旋转 后得到 ,则 点的对应点 的坐标是()
1.A
解析:A
【分析】
根据轴对称图形与中心对称图形的概念求解.
【详解】
解:A、是轴对称图形,不是中心对称图形,故本选项符合题意;
三、解答题
21.如图,在等腰直角三角形 中, 且 ,将 绕点C顺时针旋转 ,得到 ,连接 .
(1)判断 的形状并证明;
(2)若 ,求 的长.
西安铁一中分校九年级数学上册第三单元《旋转》检测题(含答案解析)

一、选择题1.观察下列“风车”的平面图案,其中既是轴对称又是中心对称图形的有( )A .B .C .D .2.如图,在△ABC 中,AB =AC ,∠BAC =45°,点D 在AC 边上.将△ABD 绕点A 逆时针旋转45°得到△ACD ′,且D ′、D 、B 三点在同一条直线上,则∠ABD 的大小为( )A .15°B .22.5°C .25°D .30°3.如图,将△ABC 绕点A 旋转,得到△AEF ,下列结论正确的个数是( ) ①△ABC ≌△AEF ;②AC=AE ;③∠FAB=∠EAB ;④∠EAB=∠FAC .A .1B .2C .3D .44.如图所示,ABC 中,65C =︒∠,将ABC ∆绕点A 顺时针旋转后,得到AB C ''∆,且C '在边BC 上,则B C B ''∠的度数是( )A .46°B .48°C .50°D .52°5.如图,在ABC ∆中,30,8,5BAC AB AC ∠===,将ABC ∆绕点A 顺时针旋转30得到ADE ∆连接CD ,则CD 的长是( )A .7B .8C .12D .136.如图,在平面直角坐标系中Rt △ABC 的斜边BC 在x 轴上,点B 坐标为(1,0),AC=2,∠ABC=30°,把Rt △ABC 先绕B 点顺时针旋转180°,然后再向下平移2个单位,则A 点的对应点A′的坐标为( )A .(﹣4,﹣2﹣3)B .(﹣4,﹣2+3)C .(﹣2,﹣2+3)D .(﹣2,﹣2﹣3) 7.下列图形中,既是轴对称图形又是中心对称图形的是( )A .等边三角形B .平行四边形C .正五边形D .菱形8.如图所示,在平面直角坐标系中,点A 、B 的坐标分别为(﹣2,0)和(2,0).月牙①绕点B 顺时针旋转90︒得到月牙②,则点A 的对应点A’的坐标为 ( )A .(2,2)B .(2,4)C .(4,2)D .(1,2) 9.既是中心对称图形又是轴对称图形,且只有两条对称轴的四边形是( ) A .正方形B .矩形C .菱形D .矩形或菱形10.在平面直角坐标系中,点()3,5P --关于原点对称的点的坐标是( ) A .()3,5-B .()3,5-C .()3,5D .()3,5--11.如图,在正方形ABCD 中,AB=3,点M 在CD 的边上,且DM=1,ΔAEM 与ΔADM 关于AM 所在的直线对称,将ΔADM 按顺时针方向绕点A 旋转90°得到ΔABF ,连接EF ,则线段EF 的长为( )A .3B .23C .13D .1512.如图,以点A 为中心,把△ABC 逆时针旋转120°,得到△AB'C′(点B 、C 的对应点分别为点B′、C′),连接BB',若AC'∥BB',则∠CAB'的度数为( )A .45°B .60°C .70°D .90°二、填空题13.如图,将AOB 绕点O 按逆时针方向旋转45°后得到COD △,若15AOB ∠=︒,则BOC ∠=______度.14.在ABC 中,2AB =,3AC =,以CB 为边作一个形状等边三角形BCD △,则DA 的最大值是________.15.如图,把ABC ∆绕点A 旋转,点B 旋转至BC 边的点D 位置,EAC α∠=︒,则ADE ∠的度数为_____.16.如图,点E 在正方形ABCD 的边CB 上,将DCE 绕点D 顺时针旋转90˚到ADF 的位置,连接EF ,过点D 作EF 的垂线,垂足为点H ,于AB 交于点G ,若4AG =,3BG =,则BE 的长为___________.17.如图,在ABC 中,AB =2,AC =1,∠BAC =30°,将ABC 绕点A 逆时针旋转60°得到11AB C △,连接BC 1,则BC 1的长为__________ .18.如图,点O 是等边△ABC 内一点,∠AOB =112°.将△BOC 绕点C 按顺时针方向旋转60°得△ADC ,连接OD .当α为______________度时,△AOD 是等腰三角形?19.如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转_____次,每次旋转_____度形成的.20.矩形是中心对称图形,对矩形ABCD 而言,点A 的对称点是点____.三、解答题21.有这样一个问题:探究函数的图象()()2)3(1y x x x =---与性质.小东对函数()()23()1y x x x =---的图象与性质进行了探究.下面是小东的探究过程,请补充完整:(1)函数()()23()1y x x x =---的自变量x 的取值范围是全体实数; (2)下表是y 与x 的几组对应值.x… -2 -1 0 1 2 3 4 5 6 … y…m-24-662460…m =②若()(),720,11,720M n N -为该函数图象上的两点,则n =(3)在平面直角坐标系xOy 中,如图所示,点()11,A x y 是该函数在23x ≤≤范围的图象上的最低点.①直线1y y =-与该函数图象的交点个数是②根据图象,直接写出不等式()()12()30x x x --->的解集.22.如图,在一个1010⨯的正方形网格中有一个,ABC ABC ∆∆的顶点都在格点上.(1)在网格中画出ABC ∆向下平移4个单位,再向右平移6个单位得到的111A B C ∆.(2)在网格中画出ABC ∆关于点P 成中心对称得到的222A B C ∆.(3)若可将111A B C ∆绕点О旋转得到222A B C ∆,请在正方形网格中标出点O ,连接12A A 和12B B ,请直接写出四边形2211A B A B 的面积.23.如图,四边形ABCD 中,45ABC ADC ∠=∠=︒,将BCD △绕点C 顺时针旋转一定角度后,点B 的对应点恰好与点A 重合,得到ACE △.(1)请求出旋转角的度数;(2)请判断AE 与BD 的位置关系,并说明理由.24.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.ABC 的三个顶点A ,B ,C 都在格点上,将ABC 绕点A 按顺时针方向旋转90°得到AB C ''.(1)在正方形网格中,画出AB C ''; (2)求线段CC '的长度.25.实践与探究已知:△ABC 和△DOE 都是等腰三角形,∠CAB=∠DOE=90°,点O 是BC 的中点,发现结论:(1)如图1,当OE 经过点A ,OD 经过点C 时,线段AE 和CD 的数量关系是 ,位置关系是 .(2)在图1的基础上,将△DOE 绕点O 顺时针旋转α(090α︒<<︒)得到图2,则问题(1)中的结论是否成立?请说明理由.(3)如图3在(2)的基础上,当AE=CE 时,请求出α的度数.(4)在(2)的基础上,△DOE 在旋转的过程中设AC 与OE 相交于点F ,当△OFC 为等腰三角形时,请直接写出α的度数.26.如图,在平面直角坐标系中,边长为4的正方形OABC 的顶点A 、C 分别在y 轴、x 轴的正半轴上,点O 在原点.现将正方形OABC 绕点O 按顺时针方向旋转,旋转角为θ,当点A 第一次落在直线y x =上时停止旋转,旋转过程中,AB 边交直线y x =于点M ,BC 边交x 轴于点N .(1)若30θ=︒时,求点A 的坐标;(2)设MBN △的周长为P ,在旋转正方形OABC 的过程中,P 值是否有变化?请证明你的结论;【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】根据轴对称图形和中心对称图形的两个概念对各选项分析判断即可得解. 【详解】解:A 、既是轴对称又是中心对称图形,故此项正确; B 、是轴对称,不是中心对称图形,故此项错误;C、不是轴对称,是中心对称图形,故此项错误;D、是轴对称,不是中心对称图形,故此项错误.故选:A.【点睛】本题考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.2.B解析:B【分析】由旋转的性质可得∠BAC=∠CAD'=45°,AD=AD',由等腰三角形的性质可得∠AD'D=67.5°,∠D'AB=90°,即可求∠ABD的度数.【详解】解:∵将△ABD绕点A逆时针旋转45°得到△ACD′,∴∠BAC=∠CAD'=45°,AD=AD',∴∠AD'D=1(180°-45°)=67.5°,∠D'AB=90°,2∴∠ABD=90°-67.5°=22.5°;故选:B.【点睛】本题考查了旋转的性质,等腰三角形的性质,直角三角形两锐角互余等知识;熟练运用旋转的性质和等腰三角形的性质是解题的关键.3.B解析:B【分析】由旋转的性质得到△ABC≌△AEF,再由全等三角形的性质逐项判断即可.【详解】∵△ABC绕点A旋转得到△AEF,∴△ABC≌△AEF,∴AC=AF ,不能确定AC=AE,故①正确,②错误;∵∠EAF=∠BAC,∴∠EAF-∠BAF=∠BAC-∠BAF,∴即∠EAB=∠FAC,但不能确定∠EAB等于∠FAB,故③错误,④正确;综上所述,结论正确的是①④,共2个.故选:B.【点睛】此题考查了旋转的性质.掌握旋转前后的图形全等是解答此题的关键.4.C解析:C【分析】根据旋转的性质和∠C =65°,从而可以求得∠AC′B′和∠AC′C 的度数,从而可以求得∠B′C′B 的度数. 【详解】∵将△ABC 绕点A 顺时针旋转后,可以得到△AB′C′,且C′在边BC 上, ∴AC =AC′,∠C =∠AC′B′, ∴∠C =∠AC′C , ∵∠C =65°,∴∠AC′B′=65°,∠AC′C =65°, ∴∠B′C′B =180°−∠AC′B′−∠AC′C =50°, 故选:C . 【点睛】本题考查旋转的性质,解题的关键是明确题意,找出所求问题需要的条件.5.A解析:A 【分析】过点D 作DF AC ⊥与F ,由旋转的性质可得AD=AB=8,30BAC DAB ∠=∠=︒,由直角三角形的性质可得AF=4,DF=3AF=43,由勾股定理可求解. 【详解】解:过点D 作DF AC ⊥与F ,将ABC ∆绕点A 顺时针旋转30得到ADE ∆,830AD AB BAC DAB ∴==∠=∠=︒,, 60CAD ∴∠=︒,且DF AC ⊥,AD=84343AF DF AF ∴===,,1CF ∴=,224817CD DF CF ∴=+=+=故选A ..【点睛】本题考查了旋转的性质、勾股定理,添加合适的辅助线构造直角三角形是解题的关键.6.D解析:D 【解析】解:作AD ⊥BC ,并作出把Rt △ABC 先绕B 点顺时针旋转180°后所得△A 1BC 1,如图所示.∵AC =2,∠ABC =30°,∴BC =4,∴AB =23,∴AD =AB AC BC ⋅=2324⨯=3,∴BD =2AB BC =223()=3.∵点B 坐标为(1,0),∴A 点的坐标为(4,3).∵BD =3,∴BD 1=3,∴D 1坐标为(﹣2,0),∴A 1坐标为(﹣2,﹣3).∵再向下平移2个单位,∴A ′的坐标为(﹣2,﹣3﹣2).故选D .点睛:本题主要考查了直角三角形的性质,勾股定理,旋转的性质和平移的性质,作出图形利用旋转的性质和平移的性质是解答此题的关键.7.D解析:D 【分析】根据轴对称图形与中心对称图形的概念求解. 【详解】解:A 、是轴对称图形,不是中心对称图形.故不符合题意; B 、不是轴对称图形,是中心对称图形.故不符合题意; C 、是轴对称图形,不是中心对称图形.故不符合题意; D 、是轴对称图形,也是中心对称图形.故符合题意. 故选:D . 【点睛】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.8.B解析:B 【详解】解:连接A′B ,由月牙①顺时针旋转90°得月牙②,可知A′B ⊥AB ,且A′B=AB ,由A (-2,0)、B (2,0)得AB=4,于是可得A′的坐标为(2,4).故选B.9.D解析:D【分析】根据轴对称图形与中心对称图形的概念求解.【详解】正方形是轴对称图形,也是中心对称图形,有4条对称轴;矩形是轴对称图形,也是中心对称图形,有2条对称轴;菱形是轴对称图形,也是中心对称图形,有2条对称轴.故选D.【点睛】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.10.C解析:C【解析】分析:根据关于原点对称的点的坐标特点解答.详解:点P(-3,-5)关于原点对称的点的坐标是(3,5),故选C.点睛:本题考查的是关于原点的对称的点的坐标,平面直角坐标系中任意一点P(x,y),关于原点的对称点是(-x,-y),即关于原点的对称点,横纵坐标都变成相反数.11.C解析:C【分析】连接BM.证明△AFE≌△AMB得FE=MB,再运用勾股定理求出BM的长即可.【详解】连接BM,如图,由旋转的性质得:AM=AF.∵四边形ABCD是正方形,∴AD=AB=BC=CD,∠BAD=∠C=90°,∵ΔAEM与ΔADM关于AM所在的直线对称,∴∠DAM=∠EAM.∵∠DAM+∠BAM=∠FAE+∠EAM=90°,∴∠BAM=∠EAF,∴△AFE≌△AMB∴FE=BM.在Rt△BCM中,BC=3,CM=CD-DM=3-1=2,∴2222+=+=BC CM3213∴13故选C.【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.12.D解析:D【分析】先根据旋转的性质得到∠BAB′=∠CAC′=120°,AB=AB′,根据等腰三角形的性质易得∠AB′B=30°,再根据平行线的性质由AC′∥BB′得∠C′AB′=∠AB′B=30°,然后利用∠CAB′=∠CAC′-∠C′AB′进行计算.【详解】∵以点A为中心,把△ABC逆时针旋转120°,得到△AB'C′,∴∠BAB′=∠CAC′=120°,AB=AB′,∴∠AB′B=1(180°-120°)=30°,2∵AC′∥BB′,∴∠C′AB′=∠AB′B=30°,∴∠CAB′=∠CAC′-∠C′AB′=120°-30°=90°.故选:D.【点睛】此题考查旋转的性质,等腰三角形的性质,三角形内角和定理,平行线的性质,解题关键在于掌握旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段的夹角等于旋转角.二、填空题13.60【分析】根据旋转的性质得到∠BOD=45°且∠COD=∠AOB再用∠BOD加∠COD即可【详解】∵将△AOB绕点O按逆时针方向旋转45°后得到△COD∴∠BOD=45°∠COD=∠AOB又∵∠A解析:60【分析】根据旋转的性质得到∠BOD=45°,且∠COD=∠AOB,再用∠BOD加∠COD即可.【详解】∵将△AOB绕点O按逆时针方向旋转45°后,得到△COD,∴∠BOD=45°,∠COD=∠AOB,又∵∠AOB=15°,∴∠BOC=∠BOD+∠COD=45°+15°=60°,故答案为60°.【点睛】本题考查了旋转的定义和性质,解题的关键是找准旋转角以及对应的边.14.5【分析】将△BAC绕点B逆时针旋转60º易知△ABA′为等边三角形当AA′D 三点在一线时AD最大AD最大=AA′+A′D【详解】如图以点B为旋转心将△BAC 逆时针旋转60º后的图形为△BA′D连结解析:5.【分析】将△BAC绕点B逆时针旋转60º,易知△ABA′为等边三角形,当A、A′、D三点在一线时AD 最大,AD最大=AA′+A′D.【详解】如图以点B为旋转心,将△BAC逆时针旋转60º后的图形为△BA′D,连结AA′,BA=BA′,∠ABA′=60º,∴△BAA′为等边三角形,则AA′=BA=2,A′D=AC=3,当A、A′、D三点在一线时AD最大,AD最大=2+3=5,故答案为:5.【点睛】本题考查AD 的最值问题,掌握旋转变换的性质,会用旋转变化构造等边三角形,使问题转化为两线段和最大问题使问题得以解决是关键.15.【分析】根据旋转的性质可得AB=AD ∠BAD=∠EAC=α°∠ADE=∠ABC 再根据三角形内角和定理即可求得结论【详解】解:由旋转的性质得AB=AD ∠BAD=∠EAC=α°∠ADE=∠ABC ∴∠AB 解析:1902α︒︒- 【分析】根据旋转的性质可得AB=AD ,∠BAD=∠EAC=α°,∠ADE=∠ABC ,再根据三角形内角和定理即可求得结论.【详解】解:由旋转的性质得,AB=AD ,∠BAD=∠EAC=α°,∠ADE=∠ABC ,∴∠ABD=∠ADB∴∠ABD=18019022BAD α︒-∠=︒-︒ ∴∠ADE=1902α︒-︒. 故答案为:1902α︒-︒.【点睛】此题主要考查了运用旋转的性质求解,熟练掌握旋转的性质是解答此题的关键. 16.【分析】连接EG 根据DG 垂直平分EF 即可得出EG=FG 设BE=x 则CE=7-x=AFFG=EG=11-x 再根据Rt △BEG 中BE2+BG2=EG2即可得到BE 的长【详解】解:如图所示连接EG 由旋转可 解析:5611【分析】连接EG ,根据DG 垂直平分EF ,即可得出EG=FG ,设BE=x ,则CE=7-x =AF ,FG=EG=11-x ,再根据Rt △BEG 中,BE 2+BG 2=EG 2,即可得到BE 的长.【详解】解:如图所示,连接EG ,由旋转可知DCE ≌ADF ,∴DE=AF ,CE=AF ,∵DG ⊥EF ,∴H 为EF 的中点,∴DG 垂直平分EF ,∴EG=FG , 设BE=x ,则CE=5-x =AF ,FG=EG=8-x ,∵∠B=90°,∴BE 2+BG 2=EG 2即2223(11)x x +=- 解得5611x = 故答案为:5611 【点睛】本题主要考查了正方形的性质以及旋转的性质,解题时注意:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.17.【分析】先根据旋转的定义和性质可得从而可得再利用勾股定理即可得【详解】由旋转的定义和性质得:在中故答案为:【点睛】本题考查了旋转的定义和性质勾股定理熟练掌握旋转的性质是解题关键 5【分析】先根据旋转的定义和性质可得111,60A AC C CAC ==∠=︒,从而可得190BAC ∠=︒,再利用勾股定理即可得.【详解】由旋转的定义和性质得:111,60A AC C CAC ==∠=︒,30BAC ∠=︒,1190AC BAC AC B C ∴∠=+=∠∠︒,在1Rt ABC 中,1BC ===,【点睛】 本题考查了旋转的定义和性质、勾股定理,熟练掌握旋转的性质是解题关键.18.112°或124°或136°【分析】由题意可得△COD 是等边三角形进而可得∠CDO =∠COD =60°然后分三种情况根据等腰三角形的性质和三角形的内角和定理建立方程求解即可【详解】解:∵将△BOC 绕点解析:112°或124°或136°【分析】由题意可得△COD 是等边三角形,进而可得∠CDO =∠COD =60°,然后分三种情况,根据等腰三角形的性质和三角形的内角和定理建立方程求解即可.【详解】解:∵将△BOC 绕点C 按顺时针方向旋转60°得△ADC ,∴CO =CD ,∠OCD =60°,∠ADC =α,∴△COD 是等边三角形.∴∠CDO =∠COD =60°,①若AO =AD ,则∠AOD =∠ADO ,∵∠AOD =360°﹣112°﹣60°﹣α=188°﹣α,∠ADO =α﹣60°,∴188°﹣α=α﹣60°,解得:α=124°;②若OA =OD ,则∠OAD =∠ADO .∵∠OAD =180°﹣(∠AOD +∠ADO )=180°﹣(188°﹣α+α﹣60°)=52°,∴α﹣60°=52°,∴α=112°;③若OD =AD ,则∠OAD =∠AOD .∵∠AOD =188°﹣α,∠OAD =()180602α︒--︒=120°﹣2α, ∴188°﹣α=120°﹣2α,解得:α=136°. 综上所述:当α为112°或124°或136°时,△AOD 是等腰三角形.故答案为:112°或124°或136°.【点睛】本题考查了等边三角形的判定和性质、旋转的性质、等腰三角形的性质以及三角形的内角和定理等知识,全面分类、熟练掌握上述知识是解题的关键.19.745【详解】解:利用旋转中的三个要素(①旋转中心; ②旋转方向; ③旋转角度)设计图案进而判断出基本图形和旋转次数与角度故如图所示的美丽图案可以看作是由一个三角形绕旋转中心旋转次每次旋转度形成的故 解析:7 45【详解】解:利用旋转中的三个要素(①旋转中心; ②旋转方向; ③旋转角度)设计图案,进而判断出基本图形和旋转次数与角度.故如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转7次,每次旋转45度形成的,故答案为:7;45.20.C 【分析】根据把一个图形绕某一点旋转180°如果旋转后的图形能够与原来的图形重合那么这个图形就叫做中心对称图形这个点叫做对称中心可得答案【详解】解:矩形是中心对称图形对称中心是对角线的交点点A 的对称 解析:C【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心可得答案.【详解】解:矩形是中心对称图形,对称中心是对角线的交点,点A 的对称点是点C ,故答案为C .【点睛】本题考查了中心对称图形,关键是掌握中心对称图形的性质.三、解答题21.(2)①60-;②7n =-; (3)①2;②12x <<或3x >【分析】(2)①通过观察表格,(-2,m ),(6,60)关于 (2,0)成中心对称即可; ②由于M 与N 的函数值互为相反数,()(),720,11,720M n N -关于(2,0)成中心对称,11-2=2-n 求出即可;(3)①由点()11,A x y 是该函数在23x ≤≤范围的图象的最低点,直线1y y =-与该函数图象的有一个交点()11,A x y ,与x <1部分还有一个交点即可; ②()()12()30x x x --->分四段讨论当x<1时,x-1,x-2,x-3,判断符号即可则,当1<x<2时,x-1,x-2,x-3, 判断符号即可则当2<x<3时,x-1,x-2,x-3,判断符号即可则 当x>3时,x-1,x-2,x-3,判断符号即可则即可求出 ()()12()30x x x --->的范围.【详解】(2)①通过观察表格,(-2,m ),(6,60)关于 (2,0)成中心对称,m=60-; ②()(),720,11,720M n N -为该函数图象上的两点,由于M 与N 的函数值互为相反数,()(),720,11,720M n N -关于(2,0)成中心对称,11-2=2-n ,n=-7;(3)①由点()11,A x y 是该函数在23x ≤≤范围的图象的最低点直线1y y =-与该函数图象的有一个交点()11,A x y ,与x <1部分还有一个交点,直线1y y =-与该函数图象的有一个交点有2个;②()()12()30x x x --->,分四段讨论,当x<1时,x-1<0,x-2<0,x-3<0,三负,则()()12()30x x x ---<,当1<x<2时,x-1>0,x-2<0,x-3<0,两负一正,则()()12()30x x x --->,当2<x<3时,x-1>0,x-2>0,x-3<0,两正一负,则()()12()30x x x ---<,当x>3时,x-1>0,x-2>0,x-3>0,三正,则()()12()30x x x --->,()()12()30x x x --->的范围是12x <<或3x >.【点睛】本题考查多次函数的图像与性质,根据给定的表格找出函数图像关于点(2,0)中心对称是解题关键.22.(1)画图见解析;(2)画图见解析;(3)画图见解析,10.【分析】(1)根据平移的方向和距离即可得到111A B C ∆;(2)根据中心对称变换的性质作图即可得到222A B C ∆;(3)根据各对应点的连线都经过旋转中心即可找到点O ,再根据平行四边形的面积公式可求得2211A B A B 的面积.【详解】()1如图所示,111A B C ∆即为所求.()2如图所示,222A B C ∆即为所求.()3如图所示,O 为所求点.∵11A B ∥22A B ,11A B =22A B ,∴四边形2211A B A B 为平行四边形,5210,S ∴=⨯=∴四边形2211A B A B 的面积为10.【点睛】本题考查了基本作图-平移变换、作图-中心对称变换、平行四边形的判定与性质,掌握平移变换和中心对称变换的性质,找到变换的对应点是解答的关键.23.(1)旋转角的度数为90°;(2)AE 与BD 互相垂直,理由见详解.【分析】(1)由题意易得BC=AC ,则有∠CBA=∠CAB=45°,进而问题可求解;(2)由(1)可得∠DBC=∠EAC ,如图∠1=∠2,∠2+∠DBC=90°,进而问题可求解.【详解】解:(1)由将BCD △绕点C 顺时针旋转一定角度后,点B 的对应点恰好与点A 重合,得到ACE △可得:BCD ACE ≌,∴BC=AC ,∵45ABC ADC ∠=∠=︒,∴∠CBA=∠CAB=45°,∴∠ACB=90°,即旋转角度为对应边的夹角,故旋转角为∠ACB=90°;(2)AE ⊥BD ,理由如下:如图所示,由(1)可得:BCD ACE ≌,∴∠DBC=∠EAC ,∵∠ACB=90°,∴∠2+∠DBC=90°,∵∠1=∠2,∴∠1+∠EAC=90°,∴BD ⊥AE .【点睛】本题主要考查旋转的性质,熟练掌握旋转的性质是解题的关键.24.(1)图见解析;(2)42【分析】(1)先利用网格特点和旋转的性质画出点,C B '',再顺次连接点,,A C B ''即可得; (2)利用旋转的性质、勾股定理即可得.【详解】(1)分以下三步:①先利用网格特点和旋转的性质画出点C ',②再利用旋转的性质可得,90B B A C BC AC CB '=∠'''=∠=︒,由此可画出点B ', ③顺次连接点,,A C B ''即可,如图中AB C ''即为所作:(2)由网格特点和旋转的性质得:4,90AC AC CAC ''==∠=︒, 则2242CC AC AC ''=+=,即线段CC '的长度为42【点睛】本题考查了旋转的定义和性质、勾股定理,熟练掌握旋转的性质是解题关键. 25.(1)AE=CD AE ⊥CD ;(2)成立,理由见解析;(3)45°;(4)45°或22.5°【分析】(1)证明△AOC 是等腰直角三角形即可得到结论;(2)连接AO ,延长DC 交AE 于点M ,设OE ,MD 相交于点N ,证明△AOE ≌△COD 可得AE=CD ,证明∠DME=90°可得AE ⊥CD ;(3)证明OE 是AC 的垂直平分线即可得到结论;(4)分OF=FC 和OC=CF 两种情况求解即可.【详解】解:(1)∵△ABC 是等腰三角形,∠CAB =90°,∴∠ACB=45°∵点O 是BC 的中点,∴AO ⊥BC∴△AOC 是等腰直角三角形,∴AO=CO∵△DOE 是等腰三角形,∠DOE=90°,∴EO=DO∴EO-AO=DO-CO即AE=CD∵OE 经过点A ,OD 经过点C ,∴AE ⊥CD故答案为:AE=CD AE ⊥CD(2)(1)中的结论仍然成立理由如下:连接AO ,延长DC 交AE 于点M ,设OE ,MD 相交于点N∵△ABC是等腰直角三角形,O是BC的中点∴AO=CO,AO⊥BC∴∠AOC=∠EOD=90°∴∠AOE=∠COD∵OE=OD∴△AOE≌△COD(SAS)∴AE=CD,∠AEO=∠CDO∵∠CDO+∠OND=90°,且∠OND=∠MNE∴∠AEO+∠MNE=90°∴∠DME=90°∴DM⊥AE即DC⊥AE(3)连接OA,如图3,∵AE=CE,OA=OC∴OE是AC的垂直平分线∴∠AOE=∠COE=45°∴ =45°(4)①若OF=FC时,如图4,∵△ABC 是等腰直角三角形,∠BAC=90°,∴∠ACB=45°∴∠FOC=45°∵AO ⊥BC∴∠AOC=90°∴∠AOF=90°-45°=45°,即α=45°;②当OC=FC 时,如图5,∵△ABC 是等腰直角三角形,∠BAC=90°,∴∠ACB=45°∴∠FOC=1804567.52︒-︒=︒ ∵AO ⊥BC∴∠AOC=90°∴∠AOF=90°-67.5°=22.5°,即α=22.5°;综上所述,α的度数为45°或22.5°. 【点睛】本题是几何变换综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质等知识,添加恰当辅助线构造全等三角形是本题的关键.26.(1)(2,32)不变【详解】解:(1)如图1,过A 作AD ⊥y 轴,交y 轴于点D∵AD ⊥y 轴,30θ=︒,正方形OABC 的边长是4∴AD=2,OD=23∴A 的坐标是(2,23)(2)P 值无变化.证明:延长BA 交y 轴于E 点.(如图2)在△OAE 与△OCN 中90?AOE CON OAE OCN OA OC =⎧⎪==⎨⎪=⎩∠∠∠∠ ∴△OAE ≌△OCN (AAS )∴OE=ON ,AE=CN .在△OME 与△OMN 中45?OE ON MOE MON OM OM =⎧⎪∠=∠=⎨⎪=⎩,∴△OME ≌△OMN (SAS )∴MN=ME=AM+AE ,∴MN=AM+CN ,∴P=MN+BN+BM=AM+CN+BN+BM=AB+BC=8.∴在旋转正方形OABC 的过程中,P 值无变化.【点睛】此题主要考查了一次函数的综合应用、全等三角形的判定与性质等知识,利用图形旋转的变化规律得出对应边之间关系是解题关键.。
西安铁一中分校九年级数学上册第二十三章《旋转》经典习题

一、选择题1.下列图形中,不是中心对称图形的是( )A .B .C .D . 2.如图,将△ABC 绕点A 旋转,得到△AEF ,下列结论正确的个数是( ) ①△ABC ≌△AEF ;②AC=AE ;③∠FAB=∠EAB ;④∠EAB=∠FAC .A .1B .2C .3D .4 3.如图,将△ABC 绕点C(0,1)旋转180°得到△A′B′C′,设点A 的坐标为(,)a b ,则点A′的坐标为( )A .(,)a b --B .2(),a b --+C .(),1a b --+D .(,1)a b --- 4.如图,在平面直角坐标系中,点A 的坐标为(3,1)-,将OA 绕原点O 按顺时针方向旋转90︒得到OA ',则点A '的坐标为( )A .(3,1)B .(3,1)-C .(1,3)--D .(1,3) 5.如图,将等边ABC 绕点C 逆时针旋转得到A B C '',旋转角为()060αα︒<<︒.若160BDA '∠=︒,则α的大小是( )A .20°B .40°C .60°D .80°6.下列图形中,既是轴对称图形又是中心对称图形的是( )A .B .C .D . 7.如图所示,把ABC 绕C 点旋转35︒,得到A B C ''',A B ''交AC 于点D ,若90A DC '∠=︒,则A ∠等于( )A .35︒B .65︒C .55︒D .45︒8.下列图形中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D . 9.已知等边△ABC 的边长为8,点P 是边BC 上的动点,将△ABP 绕A 逆时针转60°得到△ACQ ,点D 是AC 边的中点,连接DQ ,则DQ 的最小值是 ( )A .2B .3C .4D .不能确定 10.如图,在平面直角坐标系中,将正方形OABC 绕点O 逆时针旋转45°后得到正方形111OA B C ,依此方式,绕点O 连续旋转2020次得到正方形202020202020OA B C ,如果点A 的坐标为(1,0),那么点2020B 的坐标为( )A .(﹣1,1)B .(20)-,C .(﹣1,﹣1)D .(02)-, 11.下列命题的逆命题是真命题的是( )A .等边三角形是等腰三角形B .若22ac bc >,则a b >C .成中心对称的两个图形全等D .有两边相等的三角形是等腰三角形12.已知等边△ABC 的边长为8,点P 是边BC 上的动点,将△ABP 绕点A 逆时针旋转60°得到△ACQ ,点D 是AC 边的中点,连接DQ ,则DQ 的最小值是( )A .22B .4C .23D .不能确定 13.如图,把△ABC 绕着点A 逆时针旋转40°得到△ADE ,∠1=30°,则∠BAE =( )A .10°B .30°C .40°D .70° 14.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )A .B .C .D . 15.如图①,正方形A 的一个顶点与正方形B 的对称中心重合,重叠部分面积是正方形A 面积的12,如图②,移动正方形A 的位置,使正方形B 的一个顶点与正方形A 的对称中心重合,则重叠部分面积是正方形B 面积的( )A.12B.14C.16D.18二、填空题16.如图,将边长为6的正方形ABCD绕点A逆时针方向旋转30︒后得到正方形A B C D'''',则图中阴影部分面积为____________.17.如图,把△ABC绕点C顺时针旋转得到△A'B'C',此时A′B′⊥AC于D,已知∠A=50°,则∠B′CB的度数是_____°.18.如图,已知EAD32∠=,ADE绕着点A旋转50后能与ABC重合,则BAE∠=________度.19.如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为________ .20.如图,平行四边形ABCD 的两条对角线AC 与BD 相交于直角坐标系的原点.若点A 的坐标为(-2,3),则点C 的坐标为___________.21.如图,将一个含30°角的直角三角板ABC 绕点A 顺时针旋转α(0°<α<360°),使得点B 、A 、C ′在同一直线上,则α=______.22.如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转_____次,每次旋转_____度形成的.23.如图,在平面直角坐标系中,点1P 的坐标22,22⎛⎫ ⎪ ⎪⎝⎭,将线段1OP 绕点O 按顺时针方向旋转45°,再将其长度伸长为1OP 的2倍,得到线段2OP ;又将线段2OP 绕点O 按顺时针方向旋转45°,长度伸长为2OP 的2倍,得到线段3OP ;如此下去,得到线段4OP 、5OP ,……,n OP (n 为正整数),则点2020P 的坐标是_________.24.如图,正方形ABCD 的边长为2,BE 平分∠DBC 交CD 于点E ,将△BCE 绕点C 顺时针旋转90°得到△DCF ,延长BE 交DF 于G ,则BF 的长为_____.25.如图,把ABC ∆绕顶点C 按顺时针方向旋转得到△A B C '',当A B AC ''⊥,47A ∠=︒,128A CB ∠='︒时,B CA '∠的度数为_____.26.在平面直角坐标系中,将点P (﹣3,2)绕点Q (﹣1,0)顺时针旋转90°,所得到的对应点P '的坐标为____.三、解答题27.点O 为直线AB 上一点,过点O 作射线OC ,使65BOC ∠=︒,将一直角三角板的直角顶点放在点O 处.(1)如图1,将三角板MON 的一边ON 与射线OB 重合时,求MOC ∠的度数;(2)如图2,将三角板MON 绕点O 逆时针旋转一定角度,此时OC 是MOB ∠的角平分线,求旋转角BON ∠的度数,CON ∠的度数;(3)将三角板MON 绕点O 逆时针旋转至图3时,5NOC ∠=︒,求AOM ∠.28.(1)如图,点E 、F 分别在正方形ABCD 的边BC 、CD 上,45EAF ∠=︒,求证:EF BE FD =+;(2)如图,四边形ABCD 中,90≠︒∠BAD ,AB AD =,180B D ∠+∠=︒,点E 、F 分别在边BC 、CD 上,则当EAF ∠与BAD ∠满足什么关系时,仍有EF BE FD =+,说明理由.29.如图,在97⨯网格中的每个小正方形边长都为1个单位长度,我们把每个小正方形的顶点称为格点,,,,,A B C E F 均为格点,请按要求仅用一把无刻度的直尺作图.(1)将ABC ∆绕点O 旋转180︒得到BAD ∆,请画出点O 和BAD ∆;(2)将格点线段EF 平移至格点线段MN (点,E F 的对应点分别为,M N ),使得MN 平分四边形ABCD 的面积,请画出线段MN ;(3)在线段AD 上找一点P ,使得AOP BOD ∠=∠,请画出点P .30.已知在平面直角坐标系中,A (﹣2,0)、B (3,﹣1)、C (2,2),格中每一格表示一个单位长度,请解答以下问题:(1)求作出△ABC ;(2)将△ABC 平移,使得平移后点C 的对应点为原点,A 、B 的对应点分别为A 1,B 1,请作出平移后的△A 1B 1O ,并直接写出平移的距离为 ;(3)将△ABC 绕点A 逆时针旋转90°,得到△AB 2C 2,B 、C 的对应点分别为B 2、C 2,请作出△AB 2C 2,并求出B 2、C 2点的坐标.。
西安铁一中九年级数学上册第二十三章《旋转》基础卷(培优练)

一、选择题1.下列图形中,既是轴对称图形,又是中心对称图形的是( )A .等边三角形B .平行四边形C .圆 D .五角星C解析:C【分析】 根据轴对称图形与中心对称图形的概念求解.【详解】A 、等边三角形是轴对称图形,不是中心对称图形,故本选项不合题意;B 、平行四边形不是轴对称图形,是中心对称图形,故本选项不合题意;C 、圆既是轴对称图形,又是中心对称图形,故本选项符合题意;D 、五角星是轴对称图形,不是中心对称图形,故本选项不合题意;故选:C .【点睛】本题主要考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.2.如图,将等边ABC 绕点C 逆时针旋转得到A B C '',旋转角为()060αα︒<<︒.若160BDA '∠=︒,则α的大小是( )A .20°B .40°C .60°D .80°A解析:A【分析】 利用旋转的性质结合等边三角形的性质和三角形外角的性质,可得出答案;【详解】解:如图,∵ABC 和A B C ''均为等边三角形,∴60A A '∠=∠=︒由旋转得,旋转角为ACA α'∠=,∵160BDA '∠=︒∴160DOA A ''∠+∠=︒∴100DOA '∠=︒∵DOA COA '∠=∠,180ACA CAA COA ''∠+∠+∠=︒ ∴20ACA '∠=︒∴α的大小是20°故选:A【点睛】本题主要考查旋转的性质以及等边三角形的性质和三角形外角的性质等知识,正确掌握旋转的性质是解题关键.3.如图所示,把ABC 绕C 点旋转35︒,得到A B C ''',A B ''交AC 于点D ,若90A DC '∠=︒,则A ∠等于( )A .35︒B .65︒C .55︒D .45︒C解析:C【分析】 先根据旋转的性质可得,35A A ACA ''∠=∠∠=︒,再根据三角形的内角和定理可得A '∠的度数,由此即可得.【详解】由旋转的性质得:,35A A ACA ''∠=∠∠=︒,90A DC '∠=︒,18055A A DC ACA '''∴∠=︒-∠-∠=︒,55A A '∴∠=∠=︒,故选:C .【点睛】本题考查了旋转的性质、三角形的内角和定理,熟练掌握旋转的性质是解题关键. 4.如图,把ABC 绕点C 顺时针旋转35︒,得到A B C ''',A B ''交AC 于点D ,若105A CB '∠=︒,则ACB '∠度数为( )A .45︒B .30C .35︒D .70︒C解析:C【分析】 先根据旋转的定义可得35BCB ACA ''∠=∠=︒,再根据角的和差即可得.【详解】由旋转的定义得:BCB '∠和ACA '∠均为旋转角,35BCB ACA ''∴∠=∠=︒,105A CB '∠=︒,35ACB BCB A A CB CA '''∠=∠-∠'∴∠-=︒,故选:C .【点睛】本题考查了旋转的定义,熟练掌握旋转的概念是解题关键.5.如图,在等边ABC 中,点О在AC 上,且3,6AO CO ==,点P 是AB 上一动点,连接,OP 将线段OP 绕点О逆时针旋转60︒得到线段OD ,要使点D 恰好落在BC 上,则AP 的长是( )A .4B .5C .6D .8C解析:C【分析】 由于将线段OP 绕点O 逆时针旋转60°得到线段OD ,当点D 恰好落在BC 上时,易得:△ODP 是等边三角形,根据旋转的性质可以得到△AOP ≌△CDO ,由此可以求出AP 的长.【详解】解:当点D 恰好落在BC 上时,OP=OD ,∠A=∠C=60°,如图.∵∠POD=60°∴∠AOP+∠COD=∠COD+∠CDO=120°,∴∠AOP=∠CDO,∴△AOP≌△CDO,∴AP=CO=6.故选:C.【点睛】此题要把旋转的性质和等边三角形的性质结合求解.属探索性问题,难度较大,近年来,探索性问题倍受中考命题者青睐,因为它所强化的数学素养,对学生的后续学习意义深远.6.下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.C解析:C【分析】根据轴对称图形与中心对称图形的概念求解.【详解】解:A、不是轴对称图形,是中心对称图形,故此选项不合题意;B、是轴对称图形,不是中心对称图形,故此选项不符合题意;C、是轴对称图形,也是中心对称图形,故此选项符合题意;D、不是轴对称图形,是中心对称图形,故此选项不合题意;故选:C.【点睛】此题主要考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图形重合.7.下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.D解析:D【分析】根据轴对称图形与中心对称图形的概念求解.【详解】解:A、是轴对称图形,不是中心对称图形,故此选项错误;B、不是轴对称图形,是中心对称图形,故此选项错误;C、是轴对称图形,不是中心对称图形,故此选项错误;D、是轴对称图形,也是中心对称图形,故此选项正确.故选:D.【点睛】本题考查了轴对称与中心对称图形,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.8.已知等边△ABC的边长为8,点P是边BC上的动点,将△ABP绕点A逆时针旋转60°得到△ACQ,点D是AC边的中点,连接DQ,则DQ的最小值是( )A.22B.4 C.23D.不能确定C解析:C【分析】依据旋转的性质,即可得到∠BCQ=120°,当DQ⊥CQ时,DQ的长最小,再根据勾股定理,即可得到DQ的最小值.【详解】如图,由旋转可得∠ACQ=∠B=60°,又∵∠ACB=60°,∴∠BCQ=120°,∵点D是AC边的中点,∴CD=4,当DQ⊥CQ时,DQ的长最小,此时,∠CDQ=30°,∴CQ=1CD=2,2∴DQ=224223-=,∴DQ的最小值是23,故选:C.【点睛】此题考查旋转的性质,解题关键在于掌握对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角.9.如果齿轮A以逆时针方向旋转,齿轮E旋转的方向()A.顺时针B.逆时针C.顺时针或逆时针D.不能确定B解析:B【分析】根据图示进行分析解答即可.【详解】齿轮A以逆时针方向旋转,齿轮B以顺时针方向旋转,齿轮C以逆时针方向旋转,齿轮D 以顺时针方向旋转,齿轮E以逆时针方向旋转,故选B.【点睛】此题考查旋转问题,关键是根据图示进行解答.10.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是()A.B.C.D.D解析:D【分析】根据中心对称图形的定义和图形的特点即可求解.【详解】解:A、不是中心对称图形,故此选项错误;B、不是中心对称图形,故此选项错误;C、不是中心对称图形,故此选项错误;D、是中心对称图形,故此选项正确;故选D.【点睛】考核知识点:中心对称图形的识别.二、填空题11.如图,在ABC 中,90ABC ∠=︒,3AC =,4BC =,将ABC 绕着点B 旋转得到A BC ''△,且点A 的对应点A '落在BC 的延长线上,连接AA ',则AA '的长为________.【分析】根据勾股定理可求得AB=5根据旋转的性质得=5则=1再根据勾股定理即可求得的长【详解】解:∵∴由勾股定理得∵绕着点B 旋转得到∴=5∴=﹣BC=5﹣4=1在Rt △中由勾股定理得:故答案为:【点 10【分析】根据勾股定理可求得AB =5,根据旋转的性质得A B AB '==5,则A C '=1,再根据勾股定理即可求得AA '的长.【详解】解:∵90ABC ∠=︒,3AC =,4BC =,∴由勾股定理得2222AB AC BC 345+=+=,∵ABC 绕着点B 旋转得到A BC ''△,∴A B AB '==5,∴A C '=A B '﹣BC=5﹣4=1,在Rt △A CA '中,由勾股定理得: 22223110A A AC A C ''=+=+= 10【点睛】本题考查了勾股定理、旋转的性质,熟练掌握勾股定理和旋转的性质是解答的关键. 12.若点M (3,a ﹣2),N (b ,a )关于原点对称,则ab =_____.﹣3【分析】直接利用关于原点对称点的性质得出ab 的值即可得出答案【详解】∵点M (3a ﹣2)N (ba )关于原点对称∴b=﹣3a ﹣2=﹣a 解得:a=1则ab=1×(﹣3)=﹣3故答案为:﹣3【点睛】本题解析:﹣3【分析】直接利用关于原点对称点的性质得出a ,b 的值,即可得出答案.【详解】∵点M (3,a ﹣2),N (b ,a )关于原点对称,∴b =﹣3,a ﹣2=﹣a ,解得:a =1,则ab =1×(﹣3)=﹣3.故答案为:﹣3.【点睛】本题主要考查了关于原点对称点的性质,正确得出a ,b 的值是解题关键.13.如图,在平面直角坐标系中,将ABC 绕点A 顺时针旋转到111A B C △的位置,点B ,O (分别落在点1B ,1C 处,点1B 在x 轴上,再将11AB C △绕点1B 顺时针旋转到112A B C 的位置,点2C 在x 轴上,再将112A B C 绕点2C 顺时针旋转到222A B C △的位置,点2A 在x 轴上,依次进行下去,…,若点(3,0),(0,4),5A B AB =,则点2021B 的坐标为________.【分析】先计算出的值再根据至的变化规律得到B 点的变化规律从而得到的坐标【详解】解:由题意可得:即由上可知从纵坐标为0不变横坐标变为:∵20=8+12×∴的横坐标为故答案为(121280)【点睛】本题解析:(12128,0)【分析】先计算出13B B ,的值,再根据1B 至 3B 的变化规律,得到B 点的变化规律,从而得到2021B 的坐标.【详解】解:由题意可得:()()()123,0,3503540A B C +++,,,, ()()2335430,354350A B +++++++,,,即()()()()()12233,0,80120150,200A B C A B ,,,,,,, 由上可知,从13B B →,纵坐标为0不变,横坐标变为:1222238843520B C C A A B +++=+++=,∵20=8+12×312-,∴2021B 的横坐标为 202118128101012121282-+⨯=+⨯=, 故答案为(12128,0).【点睛】本题考查旋转的应用,根据旋转的性质找出相等的线段是解题关键. 14.如图,将OAB 绕点O 逆时针旋转70°到OCD 的位置,若40AOB ︒∠=,则AOD ∠=_______________.30°【分析】根据旋转的性质得到利用角的和差即可求解【详解】解:∵将绕点逆时针旋转70°到的位置∴∴故答案为:30°【点睛】本题考查旋转的性质明确旋转的性质是解题的关键解析:30°【分析】根据旋转的性质得到40COD AOB ∠=∠=︒,70AOC ∠=︒,利用角的和差即可求解.【详解】解:∵将OAB 绕点O 逆时针旋转70°到OCD 的位置, ∴40COD AOB ∠=∠=︒,70AOC ∠=︒,∴30AOD AOC COD ∠=∠-∠=︒,故答案为:30°.【点睛】本题考查旋转的性质,明确旋转的性质是解题的关键.15.如图,在ABC 中,4AB =, 5.8BC =,60B ∠=︒,将ABC 绕点A 顺时针旋转得到ADE ,当点B 的对应点D 恰好落在BC 边上时,则CD 的长为________.【分析】先根据旋转的性质可得再根据等边三角形的判定与性质可得然后根据线段的和差即可得【详解】由旋转的性质得:是等边三角形故答案为:【点睛】本题考查了旋转的性质等边三角形的判定与性质等知识点熟练掌握旋解析:1.8【分析】先根据旋转的性质可得AB AD =,再根据等边三角形的判定与性质可得4BD AB ==,然后根据线段的和差即可得.【详解】由旋转的性质得:4AB AD ==,60B ∠=︒,ABD ∴是等边三角形,4BD AB ∴==,5.8BC =,5.84 1.8CD BC BD ∴=-=-=,故答案为:1.8.【点睛】本题考查了旋转的性质、等边三角形的判定与性质等知识点,熟练掌握旋转的性质是解题关键.16.在Rt ABC △中,90ACB ∠=︒,将ABC 绕顶点C 顺时针旋转得到A B C '',点M 是BC 的中点,点P 是A B ''的中点,连接PM .若4BC =,30A ∠=︒,则在旋转一周的过程中线段PM 长度的最大值等于_____.6【分析】连接PC 由直角三角形的性质及旋转的性质可得根据可进行求解【详解】解:连接PC 如图所示:在Rt △ABC 中∵∠A=30°BC=4∴AB=8根据旋转的性质可得:∴∴PC=4∵CM=BM=2又∵即 解析:6【分析】连接PC ,由直角三角形的性质及旋转的性质可得8A B AB ''==,4PC =,根据PM PC CM ≤+,可进行求解.【详解】解:连接PC ,如图所示:在Rt △ABC 中,∵∠A=30°,BC=4, ∴AB=8,根据旋转的性质可得:8A B AB ''==, ∴A P B P PC ''==, ∴PC=4, ∵CM=BM=2,又∵PM PC CM ≤+,即6PM ≤, ∴PM 的最大值为6(此时P 、C 、M 共线); 故答案为6. 【点睛】本题主要考查旋转的性质及直角三角形的斜边中线定理,熟练掌握旋转的性质及直角三角形的斜边中线定理是解题的关键.17.如图,P 是等边三角形ABC 内一点,且PA =4,PB =23,PC =2,以下五个结论:①∠BPC =120°;②∠APC =120°;③S △ABC =143;④AB =28;⑤点P 到△ABC 三边的距离分别为PE ,PF ,PG ,则有PE +PF +PG =32AB ,其中正确的有_________. ②④⑤【分析】如图将△APC 绕点A 顺时针旋转60°得到△AHB 连接HP 由全等三角形的性质可得AH =AP =4BH =PC =2∠AHB =∠APC 可证△AHP 是等边三角形由勾股定理的逆定理可求∠HBP =90解析:②④⑤ 【分析】如图,将△APC 绕点A 顺时针旋转60°,得到△AHB ,连接HP ,由全等三角形的性质可得AH =AP =4,BH =PC =2,∠AHB =∠APC ,可证△AHP 是等边三角形,由勾股定理的逆定理可求∠HBP =90°,由锐角三角函数可求∠HPB =30°,可得∠AHB =120°=∠APC ,∠BPC =150°,可判断①②,由勾股定理可求AB 的长,由等边三角形的面积公式可求△ABC 的面积和PE +PF +PG 的值,即可判断③④⑤. 【详解】如图,将△APC 绕点A 顺时针旋转60°,得到△AHB ,连接HP ,∴△APC ≌△AHB ,∠HAP =60°,∴AH =AP =4,BH =PC =2,∠AHB =∠APC , ∴△AHP 是等边三角形, ∴HP =4,∠AHP =∠APH =60°, ∵HP 2=16,BH 2+BP 2=16, ∴HP 2=BH 2+BP 2, ∴∠HBP =90°, ∵HB=12HP , ∴∠HPB =30°,∴∠BHP =60°,∠APB =∠HPB +∠APH =90°, ∴∠AHB =∠AHP +∠BHP =120°=∠APC , ∴∠BPC =360°−∠APB−∠APC =150°, 故①不符合题意,②符合题意, ∵∠APB =90°, ∴AB =22161227AP BP +=+=,∴S △ABC =23734AB =, 故③不合题意,④符合题意, 如图,∵S △ABC =12AB×PG +12AC×PF +12BC×PE =3, ∴12×7×(PG +PF +PE )=3∴PG +PF +PE =372=32AB , 故⑤符合题意,故答案为:②④⑤. 【点睛】本题是三角形综合题,考查了等边三角形的性质,勾股定理的逆定理,旋转的性质,全等三角形的的性质,三角形的面积公式,添加恰当辅助线构造全等三角形是本题的关键. 18.如图,已知EAD 32∠=,ADE 绕着点A 旋转50后能与ABC 重合,则BAE ∠=________度.【分析】根据旋转对称图形的定义解答【详解】解:∵△ADE绕着点A旋转50°后能与△ABC重合∴∠BAD=50°又∵∠EAD=32°∴∠BAE=∠BAD−∠EAD=50°−32°=18°故答案为18【解析:18【分析】根据旋转对称图形的定义解答.【详解】解:∵△ADE绕着点A旋转50°后能与△ABC重合,∴∠BAD=50°,又∵∠EAD=32°,∴∠BAE=∠BAD−∠EAD=50°−32°=18°.故答案为18.【点睛】本题考查了旋转的性质,解题的关键是根据旋转对称图形的定义解答.19.在平面直角坐标系中,△OAB的位置如图所示,将△OAB绕点O顺时针旋转90°得△OA1B1;再将△OA1B1绕点O顺时针旋转90°得△OA2B2;再将△OA2B2绕点O顺时针旋转90°得△OA3B3;……依此类推,第2020次旋转得到△OA2020B2020,则项点A的对应点A2020的坐标是_______.(12)【分析】根据旋转的概率即可得出每旋转4次一个循环进而得到第2020次旋转得到△OA2020B2020则顶点A的对应点A2020的坐标与点A4的坐标相同【详解】解:将△OAB绕点O顺时针旋转9解析:(1,2)【分析】根据旋转的概率,即可得出每旋转4次一个循环,进而得到第2020次旋转得到△OA2020B2020,则顶点A的对应点A2020的坐标与点A4的坐标相同.【详解】解:将△OAB绕点O顺时针旋转90°得△OA1B1;此时,点A1的坐标为(2,-1);再将△OA1B1绕点O顺时针旋转90°得△OA2B2;此时,点A2的坐标为(-1,2);再将△OA2B2绕点O顺时针旋转90°得△OA3B3;此时,点A3的坐标为(-2,1);再将△OA3B3绕点O顺时针旋转90°得△OA4B4;此时,点A4的坐标为(1,2);∴每旋转4次一个循环,…依此类推,第2020次旋转得到△OA 2020B 2020,则顶点A 的对应点A 2020的坐标与点A 4的坐标相同,为(1,2); 故答案为:(1,2). 【点睛】本题考查了坐标与图形变化,图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.20.如图,在Rt ABC 中,5AB =,4BC =,如果ABC 绕点B 旋转,使点C 落在AB 边上的点D 处得到EBD △,则点A 到BE 的距离是__________.3【分析】连接AE 作AH ⊥BE 于H 根据勾股定理求出AC 的值根据旋转的性质可知BE=AB=5DE=AC=3然后根据等面积法求解即可【详解】解:连接AE 作AH ⊥BE 于H ∵在中∴AC=由旋转的性质得BE=解析:3 【分析】连接AE ,作AH ⊥BE 于H ,根据勾股定理求出AC 的值,根据旋转的性质可知BE=AB=5,DE=AC=3,然后根据等面积法求解即可. 【详解】解:连接AE ,作AH ⊥BE 于H , ∵在Rt ABC 中,5AB =,4BC =, ∴AC=2254=3-, 由旋转的性质得 BE=AB=5,DE=AC=3,∵1122BE AH AB DE ⋅=⋅, ∴5AH=5×3, ∴AH=3,故答案为:3.【点睛】本题考查了勾股定理,旋转的性质,等面积法求线段的长,熟练掌握各知识点是解答本题的关键.三、解答题21.如图,已知ABC 的三个顶点的坐标分别为(2,3)A -,0()6,B -,(1,0)C -.(1)将ABC 向右平移6个单位得到111A B C △.画图,写出点A 的对应点1A 的坐标. (2)将ABC 绕原点O 逆时针旋转90︒得到222A B C △.画图,写出点B 对应点2B 的坐标.(3)请直接写出:以A 、B 、C 为顶点的平行四边形的第四个顶点D 的坐标. 解析:(1)画图见解析,(4,3) (2)画图见解析,()0,6- (3)(3,3)或(7,3)-或(5,3)--【分析】(1)根据点平移的规律,找到点A 、B 、C 向右平移6个单位后点1A 、1B 、1C 点的坐标,顺次连接即可.(2)根据旋转三要素找到各点的对应点,顺次连接即可得到222A B C △,结合图像可得点2B 的坐标.(3)以BC 为对角线,AC 为对角线,AB 为对角线,三种情况入手讨论,即可得到第四个点D 的坐标. 【详解】(1)如图所示,111A B C △即为所求, 其中点1A 的坐标为(4,3).(2)如图所示,222A B C △即为所求, 其中点2B 的坐标为()0,6-.(3)如图所示:以A 、B 、C 为顶点的平行四边形的第四个顶点D 的坐标, 分别为(3,3)或(7,3)-或(5,3)--.【点睛】本题考查了作图—旋转变换,平移变换以及平行四边形的性质,最后一问的求解注意分类讨论,避免漏解.22.如图,在矩形ABCD中,AB=10,AD=6.以点A为中心,逆时针旋转矩形ABCD,得到矩形AEFG,点B,C,D的对应点分别为点E,F,G.(1)如图1,当点E落在边CD上时,求线段CE的长;(2)如图2,当点E落在线段CF上时,求证:∠EAC=∠BAC;(3)在(2)的条件下,CD与AE交于点H,求线段DH的长.解析:(1)2;(2)见解析;(3)16 5【分析】(1)由旋转的性质知AB=AE=10,由矩形的性质得出AD=BC=6,∠BAD=∠D=90°,由勾股定理得出DE=8,即可得出答案;(2)由旋转的性质知∠AEF=∠BAD=90°,AE=AB,证明Rt△ABC≌Rt△AEC(HL),即可得出结论;(3)设DH=x,由矩形的性质得出CH=CD-DH=10-x,∠DCA=∠BAC,证出∠DCA=∠EAC,得出AH=CH=10-x,在Rt△ADH中,由勾股定理得出方程,解方程即可得出答案.【详解】(1)解:由旋转的性质知:AB=AE=10,∵四边形ABCD是矩形,∴AD=BC=6,∠BAD=∠D=90°,∴DE =22AD AD -=22106-=8,∵CD =AB =10,∴CE =DC ﹣DE =10﹣8=2;(2)证明:由旋转的性质知:∠AEF =∠BAD =90°,AE =AB , ∵点E 落在线段CF 上, ∴∠AEC =∠AEF =90°, 在Rt △ABC 和Rt △AEC 中,AE ABAC AC =⎧⎨=⎩, ∴Rt △ABC ≌Rt △AEC (HL ), ∴∠EAC =∠BAC ; (3)解:设DH =x ,在矩形ABCD 中,AB ∥CD ,AB =CD =10, ∴CH =CD ﹣DH =10﹣x ,∠DCA =∠BAC , 又∵∠EAC =∠BAC , ∴∠DCA =∠EAC , ∴AH =CH =10﹣x ,在Rt △ADH 中,∵DH 2+AD 2=AH 2, ∴x 2+62=(10﹣x )2, 解得:x =165, ∴DH =165. 【点睛】本题是四边形综合题,考查了矩形的性质、旋转变换的性质、勾股定理、全等三角形的判定与性质、等腰三角形的判定等知识;熟练掌握旋转的性质和矩形的性质是解题的关键. 23.如图,点E 是正方形ABCD 的边DC 上一点,把△ADE 绕点A 顺时针旋转到△ABF 的位置,接EF .(1)求证:△AEF 是等腰直角三角形;(2)若四边形AECF 的面积为25,DE=2,求AE 的长.解析:(1)见解析;(2)AE 29 【分析】(1)由旋转的性质可得AE=AF ,∠EAF=90°,可得结论;(2)由题意可得四边形AECF 的面积等于正方形ABCD 的面积等于25,可求正方形的边长,由勾股定理可求解. 【详解】(1)∵把△ADE 绕点A 顺时针旋转90°到△ABF 的位置, ∴△ADE ≌△ABF ,∠EAF=90°, ∴AE=AF ,∴△AEF 是等腰直角三角形;(2)∵△ADE 绕点A 顺时针旋转90°到△ABF 的位置. ∴四边形AECF 的面积等于正方形ABCD 的面积等于25, ∴AD=DC=5, ∵DE=2, ∴Rt △ADE 中,AE=22225229AD DE +=+=.【点睛】本题主要考查了旋转的性质以及正方形的性质,等腰直角三角形的判定,勾股定理,正确利用旋转的性质得出对应边关系是解题关键.24.如图,在10×10的正方形方格之中,ABC 的顶点都在格点上 (1)在图1中画出ABC 关于格点O 成中心对称的A B C '''. (2)在图2中画出格点ABEF ,使得ABE A CFB SS=.解析:(1)画图见解析;(2)画图见解析. 【分析】(1)先结合网格特点,根据中心对称的定义画出点,,A B C ''',再顺次连接即可得; (2)先找出AC 的中点E ,连接BE ,再结合网格特点,根据点B 到点A 的平移方式与点E 到点F 的平移方式相同找出点F ,然后连接AF 、EF 即可得. 【详解】(1)先结合网格特点,根据中心对称的定义画出点,,A B C ''',再顺次连接即可得到A B C ''',如图所示:(2)先找出AC 的中点E ,连接BE ,再结合网格特点,根据点B 到点A 的平移方式与点E 到点F 的平移方式相同找出点F ,然后连接AF 、EF 即可得到ABEF ,且ABE A CFB SS=,如图所示:【点睛】本题考查了画中心对称图形、画平行四边形等知识点,熟练掌握中心对称的定义是解题关键.25.如图,在平面直角坐标系中,已知点()4,2A,()4,0B .(1)画出将OAB 绕原点逆时针旋转90°得到的11OA B ;(2)直接写出A 的对应点1A ( , ),B 的对应点1B ( , );(3)若点A ,1A 关于某点中心对称,则对称中心的坐标为______.解析:(1)图见解析;(2)()12,4A -,()10,4B ;(3)()1,3. 【分析】(1)先根据旋转的性质画出点11,A B ,再顺次连接点11,,A O B 即可得;(2)根据绕原点逆时针旋转90︒的点坐标变换规律即可得;(3)根据中心对称的定义可得点A ,1A 的中心对称点为线段1AA 的中点,由此即可得.【详解】(1)先根据旋转的性质画出点11,A B ,再顺次连接点11,,A O B 即可得11OA B ,如图所示:(2)绕原点逆时针旋转90︒的点坐标变换规律:先将横、纵坐标互换位置,再将横坐标变为相反数,()()4,2,4,0A B ,()()112,4,4,0B A -∴,故答案为:()()112,4,0,4A B -;(3)由中心对称的定义得:点A ,1A 的中心对称点为线段1AA 的中点, 则对称中心的坐标为4224,22-+⎛⎫⎪⎝⎭,即()1,3, 故答案为:()1,3.【点睛】本题考查了画旋转图形、找中心对称点等知识点,熟练掌握旋转的性质是解题关键.26.如图,在边长为1的正方形组成的网格中,每个正方形的顶点称为格点.已知△ABC的顶点均在格点上,建立如图所示的平面直角坐标系,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).(1)画出△ABC关于原点对称的△A1B1C1,并直接写出△A1B1C1各顶点的坐标;(2)将线段AB绕点A顺时针旋转90 °后得到AB2,画出旋转后的图形,并直接写出点B2的坐标;(3)△A1B1C1的面积为.解析:(1)图见解析;A1(-1,-1),B1(-4,-2),C1(-3,-4);(2)B2(2,-2);(3)3.5【分析】(1)先找到A、B、C关于原点对称的A1、B1、C1,再连线即可;(2)根据网格结构点A、B,找出将线段AB绕点A顺时针旋转90°的对应点B2,然后连接A B2,写出坐标即可;(3)△A1B1C1的面积即为三角形ABC的面积,利用“割补法”即可求得.【详解】解:(1)如图所示,△A1B1C1即为所求:A1(-1,-1),B1(-4,-2),C1(-3,-4);(2)如图所示,A1B2即为所求:B 2(2,-2);(3)S △ABC =11133232113222⨯-⨯⨯-⨯⨯-⨯⨯=3.5, ∴△A 1B 1C 1的面积= S △ABC =3.5,故填:3.5.【点睛】本题考查了坐标与图形变化−旋转与对称,熟练掌握网格结构,准确找出对应点的位置是解题的关键.27.实践与探究已知:△ABC 和△DOE 都是等腰三角形,∠CAB=∠DOE=90°,点O 是BC 的中点,发现结论:(1)如图1,当OE 经过点A ,OD 经过点C 时,线段AE 和CD 的数量关系是 ,位置关系是 .(2)在图1的基础上,将△DOE 绕点O 顺时针旋转α(090α︒<<︒)得到图2,则问题(1)中的结论是否成立?请说明理由.(3)如图3在(2)的基础上,当AE=CE 时,请求出α的度数.(4)在(2)的基础上,△DOE 在旋转的过程中设AC 与OE 相交于点F ,当△OFC 为等腰三角形时,请直接写出α的度数.解析:(1)AE=CD AE⊥CD;(2)成立,理由见解析;(3)45°;(4)45°或22.5°【分析】(1)证明△AOC是等腰直角三角形即可得到结论;(2)连接AO,延长DC交AE于点M,设OE,MD相交于点N,证明△AOE≌△COD可得AE=CD,证明∠DME=90°可得AE⊥CD;(3)证明OE是AC的垂直平分线即可得到结论;(4)分OF=FC和OC=CF两种情况求解即可.【详解】解:(1)∵△ABC是等腰三角形,∠CAB =90°,∴∠ACB=45°∵点O是BC的中点,∴AO⊥BC∴△AOC是等腰直角三角形,∴AO=CO∵△DOE是等腰三角形,∠DOE=90°,∴EO=DO∴EO-AO=DO-CO即AE=CD∵OE经过点A,OD经过点C,∴AE⊥CD故答案为:AE=CD AE⊥CD(2)(1)中的结论仍然成立理由如下:连接AO,延长DC交AE于点M,设OE,MD相交于点N∵△ABC是等腰直角三角形,O是BC的中点∴AO=CO,AO⊥BC∴∠AOC=∠EOD=90°∴∠AOE=∠COD∵OE=OD∴△AOE≌△COD(SAS)∴AE=CD,∠AEO=∠CDO∵∠CDO+∠OND=90°,且∠OND=∠MNE∴∠AEO+∠MNE=90°∴∠DME=90°∴DM⊥AE即DC⊥AE(3)连接OA,如图3,∵AE=CE,OA=OC∴OE是AC的垂直平分线∴∠AOE=∠COE=45°∴ =45°(4)①若OF=FC时,如图4,∵△ABC 是等腰直角三角形,∠BAC=90°,∴∠ACB=45°∴∠FOC=45°∵AO ⊥BC∴∠AOC=90°∴∠AOF=90°-45°=45°,即α=45°;②当OC=FC 时,如图5,∵△ABC 是等腰直角三角形,∠BAC=90°,∴∠ACB=45°∴∠FOC=1804567.52︒-︒=︒ ∵AO ⊥BC∴∠AOC=90°∴∠AOF=90°-67.5°=22.5°,即α=22.5°;综上所述,α的度数为45°或22.5°. 【点睛】本题是几何变换综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质等知识,添加恰当辅助线构造全等三角形是本题的关键.28.如图,在7×7的正方形网格中,选取14个格点,以其中3个格点为顶点画出△ABC .(1)请你以选取的格点为顶点再画出一个三角形,要求所画的三角形与△ABC组成的图形是中心对称图形;(2)若网格中每个小正方形的边长为1,请猜想新得到的中心对称图形是什么特殊图形(不用证明),并求出它的面积.解析:(1)如图所示见解析;(2)是平行四边形,面积是6.【分析】(1)确定出对称中心,然后根据中心对称图形的性质作出即可;(2)观察图形,根据中心对称图形的性质知新得到的图形是平行四边形,再根据格点的特点,利用三角形的面积公式即可得平行四边形的面积.【详解】(1)如图所示:所画的三角形与△ABC组成的图形是中心对称图形;(2)观察图形,根据中心对称图形的性质知新得到的图形是平行四边形,面积是:123262⨯⨯⨯=.【点睛】本题考查了利用中心对称的性质作图,平行四边形的判定,熟练掌握中心对称的性质是作图的关键,要注意对称中心的确定.。
西安铁一中滨河学校九年级数学上册第二十三章《旋转》经典复习题

一、选择题1.如图,在ABC 中,75CAB ∠=︒,在同一平面内,将ABC 绕点A 旋转到AB C ''△的位置,使得CC //AB ',则BAB '∠=( )A .30B .35︒C .40︒D .50︒2.下列图形中,不是中心对称图形的是( )A .B .C .D . 3.如图,将△ABC 绕点A 旋转,得到△AEF ,下列结论正确的个数是( ) ①△ABC ≌△AEF ;②AC=AE ;③∠FAB=∠EAB ;④∠EAB=∠FAC .A .1B .2C .3D .44.如图,在ABC 中,,90AB AC BAC =∠=︒,直角EPF ∠的顶点P 是BC 的中点,两边PE 、PF 分别交AB 、AC 于点E 、F ,当EPF ∠在ABC 内绕点P 旋转时,下列结论错误的是( )A .AE CF =B .EPF 为等腰直角三角形C .EP AP =D .2ABC AEPF S S =四边形5.如图,将△ABC 绕点C(0,1)旋转180°得到△A′B′C′,设点A 的坐标为(,)a b ,则点A′的坐标为( )A .(,)a b --B .2(),a b --+C .(),1a b --+D .(,1)a b --- 6.下列图形中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D . 7.下列图形中,是中心对称但不是轴对称的图形是( )A .平行四边形B .矩形C .菱形D .等边三角形 8.如图所示,在Rt ABC ∆中,90ACB ∠=︒,将ABC ∆绕顶点C 逆时针旋转得到A B C ∆'',M 是BC 的中点,P 是A B ''的中点,连接PM .若2BC =,30A ∠=︒,则线段PM 长的最大值是( )A .4B .3C .2D .1 9.若点P(-m ,m -3)关于原点对称的点是第二象限内的点,则m 满足( ) A .m >3 B .0<m≤3 C .m <0 D .m <0或m >3 10.下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( ) A .戴口罩讲卫生 B .勤洗手勤通风C .有症状早就医D .少出门少聚集11.下列图形:线段、等边三角形、平行四边形、矩形、菱形、正方形、直角梯形,既是轴对称图形又是中心对称图形的个数是( )A .6B .5C .4D .312.如图,Rt OCB ∆的斜边在y 轴上,3OC =30︒角的顶点与原点重合,直角顶点C 在第二象限,将Rt OCB ∆绕原点顺时针旋转120︒后得到'OC B ∆',则B 点的对应点B ′的坐标是( )A .(3,1)-B .(1,3)-C .(2,0)D .(3,0) 13.如图,点E ,F ,G ,H 分别为四边形ABCD 四条边AB 、BC 、CD 、DA 的中点,则关于四边形EFGH ,下列说法正确的是( )A .不是平行四边形B .不是中心对称图形C .一定是中心对称图形D .当AC =BD 时,它为矩形14.如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )A .3种B .4种C .5种D .6种15.在平面直角坐标系中,点()3,5P --关于原点对称的点的坐标是( )A .()3,5-B .()3,5-C .()3,5D .()3,5--二、填空题16.如图,将Rt ABC 绕点A 逆时针旋转30°,得到Rt ADE △,点E 恰好落在斜边AB 上,连接BD ,则BDE ∠=______.17.如图,四边形ABCD 是菱形,点O 是两条对角线的交点,过点O 的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线长分别为12和16时,则阴影部分面积为_________.18.已知点(,2)A m m 在直线3y x 上,则点A 关于原点对称点B 的坐标为______. 19.如图,在平面直角坐标系中,将ABC 绕点A 顺时针旋转到111A B C △的位置,点B ,O (分别落在点1B ,1C 处,点1B 在x 轴上,再将11AB C △绕点1B 顺时针旋转到112A B C 的位置,点2C 在x 轴上,再将112A B C 绕点2C 顺时针旋转到222A B C △的位置,点2A 在x 轴上,依次进行下去,…,若点(3,0),(0,4),5A B AB =,则点2021B 的坐标为________.20.如图,将ABC 绕点A 逆时针旋转得到AB C ''△.若B '落到BC 边上,50B ∠=︒,则CB C ''∠的度数为______.21.如图,在ABC 中,4AB =, 5.8BC =,60B ∠=︒,将ABC 绕点A 顺时针旋转得到ADE ,当点B 的对应点D 恰好落在BC 边上时,则CD 的长为________.22.如图,正方形AEFG 与正方形ABCD 的边长都为2,正方形AEFG 绕正方形ABCD 的顶点A 旋转一周,在此旋转过程中,线段DF 的长可取的整数值可以为______________.23.将边长为1的正方形ABCD 绕点C 按顺时针方向旋转到FECG 的位置(如图),使得点D 落在对角线CF 上,EF 与AD 相交于点H ,则HD =_________.(结果保留根号)24.如图,△ABC 、△BDE 都是等腰直角三角形,BA =BC ,BD =BE ,AC =4,DE =22.将△BDE 绕点B 逆时针方向旋转后得△BD'E',当点E'恰好落在线段AD'上时,则CE'=_______.25.如图,在平面直角坐标系中,点P (1,1),N (2,0),△MNP 和△M 1N 1P 1的顶点都在格点上,△MNP 与△M 1N 1P 1是关于某一点中心对称,则对称中心的坐标为_____.26.矩形是中心对称图形,对矩形ABCD 而言,点A 的对称点是点____.三、解答题27.(探索发现)如图①,四边形ABCD 是正方形,M ,N 分别在边CD 、BC 上,且45MAN=∠︒,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图①,将ADM ∆绕点A 顺时针旋转90︒,点D 与点B 重合,得到ABE ∆,连接AM 、AN 、MN .(1)试判断DM ,BN ,MN 之间的数量关系,并写出证明过程.(2)如图②,点M 、N 分别在正方形ABCD 的边BC 、CD 的延长线上,45MAN=∠︒,连接MN ,请写出MN 、DM 、BN 之间的数量关系,并写出证明过程.(3)如图③,在四边形ABCD 中,AB=AD ,120BAD=∠︒,180B+D=∠∠︒,点N ,M 分别在边BC ,CD 上,60MAN=∠︒,请直接写出线段BN ,DM ,MN 之间的数量关系.28.如图,点E 是正方形ABCD 的边DC 上一点,把△ADE 绕点A 顺时针旋转到△ABF 的位置,接EF .(1)求证:△AEF 是等腰直角三角形;(2)若四边形AECF 的面积为25,DE=2,求AE 的长.29.如图1,ABC 和DEF 都是等腰直角三角形, 90A ∠=︒,90E ∠=︒,DEF 的顶点D 恰好落在ABC 的斜边BC 中点,把ADEF 绕点D 旋转,始终保持线段DE 、DF 分别与线段AB 、AC 交于M 、N ,连接MN .在这个变化过程中,小明通过观察、度量,发现了一些特殊的数量关系.(1)于是他把DEF 旋转到特殊位置,验证自己的猜想.如图2,当//BC MN 时, ①通过计算BMD ∠和NMD ∠的度数,得出BMD ∠________NMD ∠(填>,<或=); ②设22BC =,通过计算AM 、MN 、NC 的长度,其中NC =____,进而得出AM 、MN 、NC 之间的数量关系是_______.(2)在特殊位置验证猜想还不够,还需要在一般位置进行证明.请你对(1)中猜想的线段AM 、MN 、NC 之间的数量关系进行证明.30.如图,ABC ∆的顶点坐标分别为()3,30,1,()),1,1(A B C ---.(1)请画出ABC ∆关于点B 成中心对称的11A BC ∆,并写出点11,A C 的坐标; (2)四边形11AC AC 的面积为 .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西安铁一中分校数学旋转几何综合中考真题汇编[解析版]一、初三数学旋转易错题压轴题(难)1.如图,四边形ABCD为正方形,△AEF为等腰直角三角形,∠AEF=90°,连接FC,G 为FC的中点,连接GD,ED.(1)如图①,E在AB上,直接写出ED,GD的数量关系.(2)将图①中的△AEF绕点A逆时针旋转,其它条件不变,如图②,(1)中的结论是否成立?说明理由.(3)若AB=5,AE=1,将图①中的△AEF绕点A逆时针旋转一周,当E,F,C三点共线时,直接写出ED的长.【答案】(1)DE=2DG;(2)成立,理由见解析;(3)DE的长为42或32.【解析】【分析】(1)根据题意结论:DE=2DG,如图1中,连接EG,延长EG交BC的延长线于M,连接DM,证明△CMG≌△FEG(AAS),推出EF=CM,GM=GE,再证明△DCM≌△DAE (SAS)即可解决问题;(2)如图2中,结论成立.连接EG,延长EG到M,使得GM=GE,连接CM,DM,延长EF交CD于R,其证明方法类似;(3)由题意分两种情形:①如图3-1中,当E,F,C共线时.②如图3-3中,当E,F,C 共线时,分别求解即可.【详解】解:(1)结论:DE=2DG.理由:如图1中,连接EG,延长EG交BC的延长线于M,连接DM.∵四边形ABCD是正方形,∴AD=CD,∠B=∠ADC=∠DAE=∠DCB=∠DCM=90°,∵∠AEF=∠B=90°,∴EF∥CM,∴∠CMG=∠FEG,∵∠CGM=∠EGF,GC=GF,∴△CMG≌△FEG(AAS),∴EF=CM,GM=GE,∵AE=EF,∴AE=CM,∴△DCM≌△DAE(SAS),∴DE=DM,∠ADE=∠CDM,∴∠EDM=∠ADC=90°,∴DG⊥EM,DG=GE=GM,∴△EGD是等腰直角三角形,∴DE=2DG.(2)如图2中,结论成立.理由:连接EG,延长EG到M,使得GM=GE,连接CM,DM,延长EF交CD于R.∵EG=GM,FG=GC,∠EGF=∠CGM,∴△CGM≌△FGE(SAS),∴CM=EF,∠CMG=∠GEF,∴CM∥ER,∴∠DCM=∠ERC,∵∠AER+∠ADR=180°,∴∠EAD+∠ERD=180°,∵∠ERD+∠ERC=180°,∴∠DCM=∠EAD,∵AE=EF,∴AE=CM,∴△DAE≌△DCM(SAS),∴DE=DM,∠ADE=∠CDM,∴∠EDM=∠ADC=90°,∵EG=GM,∴DG=EG=GM,∴△EDG是等腰直角三角形,∴DE =2DG .(3)①如图3﹣1中,当E ,F ,C 共线时,在Rt △ADC 中,AC =22AD CD +=2255+=52,在Rt △AEC 中,EC =22A AE C -=22(52)1-=7,∴CF =CE ﹣EF =6,∴CG =12CF =3, ∵∠DGC =90°, ∴DG =22CD CG -=2253-=4,∴DE =2DG =42.②如图3﹣3中,当E ,F ,C 共线时,同法可得DE =32.综上所述,DE 的长为2或2.【点睛】本题属于四边形综合题,考查正方形的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.2.已知如图1,在ABC 中,90ABC ∠=︒,BC AB =,点D 在AC 上,DF AC ⊥交BC 于F ,点E 是AF 的中点.(1)写出线段ED 与线段EB 的关系并证明;(2)如图2,将CDF 绕点C 逆时针旋转()090a α︒<<︒,其它条件不变,线段ED 与线段EB 的关系是否变化,写出你的结论并证明;(3)将CDF 绕点C 逆时针旋转一周,如果6BC =,32CF =,直接写出线段CE 的范围.【答案】(1)ED EB =,DE BE ⊥,证明见解析;(2)结论不变,理由见解析;(3)最大值22=最小值322=. 【解析】【分析】(1)在Rt △ADF 中,可得DE=AE=EF ,在Rt △ABF 中,可得BE=EF=EA ,得证ED=EB ;然后利用等腰三角形的性质以及四边形ADFB 的内角和为180°,可推导得出∠DEB=90°; (2)如下图,先证四边形MFBA 是平行四边形,再证△DCB ≌△DFM ,从而推导出△DMB 是等腰直角三角形,最后得出结论;(3)如下图,当点F 在AC 上时,CE 有最大值;当点F 在AC 延长线上时,CE 有最小值.【详解】(1)∵DF ⊥AC ,点E 是AF 的中点∴DE=AE=EF ,∠EDF=∠DFE∵∠ABC=90°,点E 是AF 的中点∴BE=AE=EF ,∠EFB=∠EBF∴DE=EB∵AB=BC ,∴∠DAB=45°∴在四边形ABFD 中,∠DFB=360°-90°-45°-90°=135°∠DEB=∠DEF+∠FEB=180°-2∠EFD+180°-2∠EFB=360°-2(∠EFD+∠EFB)=360°-2×135°=90°∴DE ⊥EB(2)如下图,延长BE 至点M 处,使得ME=EB ,连接MA 、ME 、MF 、MD 、FB 、DB ,延长MF 交CB 于点H∵ME=EB,点E是AF的中点∴四边形MFBA是平行四边形∴MF∥AB,MF=AB∴∠MHB=180°-∠ABC=90°∵∠DCA=∠FCB=a∴∠DCB=45°+a,∠CFH=90°-a∵∠DCF=45°,∠CDF=90°∴∠DFC=45°,△DCF是等腰直角三角形∴∠DFM=180°-∠DFC-∠CFH=45°+a∴∠DCB=∠DFM∵△ABC和△CDF都是等腰直角三角形∴DC=DF,BC=AB=MF∴△DCB≌△DFM(SAS)∴∠MDF=∠BDC,DB=DM∴∠MDF+∠FDB=∠BDC+∠FDB=90°∴△DMB是等腰直角三角形∵点E是MB的中点∴DE=EB,DE⊥EB(3)当点F在AC上时,CF有最大值,图形如下:∵BC=6,∴在等腰直角△ABC中,AC=62∵CF=32,∴AF=32∴CE=CF+FE=CF+12AF922=当点F在AC延长线上时,CE有最小值,图形如下:同理,CE=EF-CF322 =【点睛】本题考查三角形的旋转变换,用到了等腰直角三角形的性质和平行四边形的性质,解题关键是构造并证明△BDM是等腰直角三角形.3.综合与实践问题情境在一节数学活动课上,老师带领同学们借助几何画板对以下题目进行了研究.如图1,MN是过点A的直线,点C为直线MN外一点,连接AC,作∠ACD=60°,使AC=DC,在MN上取一点B,使∠DBN=60°.观察发现(1)根据图1中的数据,猜想线段AB、DB、CB之间满足的数量关系是;(2)希望小组认真思考后提出一种证明方法:将CB所在的直线以点C为旋转中心,逆时针旋转60°,与直线MN交于点E,即可证明(1)中的结论. 请你在图1中作出线段CE,并根据此方法写出证明过程;实践探究(3)奋进小组在继续探究的过程中,将点C绕点A逆时针旋转,他们发现当旋转到图2和图3的位置时,∠DBN=120°,线段AB、BD、CB的大小发生了变化,但是仍然满足一定的数量关系,请你直接写出这两种关系:在图2中,线段AB、DB、CB之间满足的数量关系是;在图3中,线段AB、DB、CB之间满足的数量关系是;提出问题(4)智慧小组提出一个问题:若图3中BC⊥CD于点C时,BC=2,则AC为多长?请你解答此问题.【答案】(1)AB+DB=CB;(2)见解析;(3)AB-DB=CB;DB-AB=CB;(4)23【解析】【分析】(1)根据图中数据直接猜想AB+DB=CB(2)在射线AM上一点E,使得∠ECB=60°,证明△ACE≌△DCB,推出EB=CB从而得出(1)中的结论;(3)利用旋转的性质和线段的和差关系以及全等三角形的性质得出线段关系;(4)过点C作∠BCE=60º,边CE与直线MN交于点E,设AC与BD交于点F.证明△ACE≌△DCB,得出BC=EC,结合△ECB为等边三角形,得出∠ECA=90°,在Rt△AEC中根据边长计算出AC的长度.【详解】综合与实践(1)AB+DB=CB(2)线段CE如图所示.证明:∵∠ECB=∠ACD=60º,∴∠2+∠ACB=∠1+∠ACB,∴∠2=∠1.∵∠ACD=∠DBN=60º, ∠ABD+∠DBN=180º,∴∠ABD+∠ACD=180º,∴在四边形ACDB中,∠CAB+∠3=180º.∵∠CAB+∠4=180º,∴∠4=∠3.又∵AC=DC,∴△ACE≌△DCB(ASA)∴EA=BD,EC=BC.又∵∠ECB=60°,∴△ECB为等边三角形,∴EB=CB.而EB=EA+AB=DB+AB,∴CB=DB+AB.(3) AB-DB=CB;DB-AB=CB;(4)证明:如图,过点C作∠BCE=60º,边CE与直线MN交于点E,设AC与BD交于点F.∵∠DCA=60º∴∠ECB+∠BCA=∠DCA+∠BCA即∠ECA=∠BCD∵∠DBN=120º∴∠DBA=60º又∵∠AFB=∠DFC∴∠EAF=∠BDC又∵AC=DC∴△ACE≌△DCB(ASA)∴BC=EC∴△ECB为等边三角形∴∠CEB=60º∵BC⊥CD∴∠ECA=∠BCD=90º∴在Rt△AEC中,∠CAE=30º∵BC=2,EC=BC∴AC=EC·tan60º= 3【点睛】本题考查了全等三角形的判定和性质,旋转的性质,根据题中条件适当添加辅助线构造全等三角形,利用全等的性质得出线段关系是本题的关键.4.如图1,在正方形ABCD中,点E、F分别在边BC,CD上,且BE=DF,点P是AF的中点,点Q是直线AC与EF的交点,连接PQ,PD.(1)求证:AC垂直平分EF;(2)试判断△PDQ的形状,并加以证明;(3)如图2,若将△CEF绕着点C旋转180°,其余条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.【答案】(1)证明见解析;(2)△PDQ是等腰直角三角形;理由见解析(3)成立;理由见解析.【解析】试题分析:(1)由正方形的性质得出AB=BC=CD=AD,∠B=∠ADF=90°,∠BCA=∠DCA=45°,由BE=DF,得出CE=CF,△CEF是等腰直角三角形,即可得出结论;(2)由直角三角形斜边上的中线的性质得出PD=AF,PQ=AF,得出PD=PQ,再证明∠DPQ=90°,即可得出结论;(3)由直角三角形斜边上的中线的性质得出PD=AF,PQ=AF,得出PD=PQ,再证明点A、F、Q、P四点共圆,由圆周角定理得出∠DPQ=2∠DAQ=90°,即可得出结论.试题解析:(1)证明:∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠ADF=90°,∠BCA=∠DCA=45°,∵BE=DF,∴CE=CF,∴AC垂直平分EF;(2)解:△PDQ是等腰直角三角形;理由如下:∵点P是AF的中点,∠ADF=90°,∴PD=AF=PA,∴∠DAP=∠ADP,∵AC垂直平分EF,∴∠AQF=90°,∴PQ=AF=PA,∴∠PAQ=∠AQP,PD=PQ,∵∠DPF=∠PAD+∠ADP,∠QPF=∠PAQ+∠AQP,∴∠DPQ=2∠PAD+2∠PAQ=2(∠PAD+∠PAQ)=2×45°=90°,∴△PDQ是等腰直角三角形;(3)成立;理由如下:∵点P是AF的中点,∠ADF=90°,∴PD=AF=PA,∵BE=DF,BC=CD,∠FCQ=∠ACD=45°,∠ECQ=∠ACB=45°,∴CE=CF,∠FCQ=∠ECQ,∴CQ⊥EF,∠AQF=90°,∴PQ=AF=AP=PF,∴PD=PQ=AP=PF,∴点A、F、Q、P四点共圆,∴∠DPQ=2∠DAQ=90°,∴△PDQ是等腰直角三角形.考点:四边形综合题.5.如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为. 在旋转过程中,两个正方形只有点A 重合,其它顶点均不重合,连接BE、DG.(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;(2)当点C在直线BE上时,连接FC,直接写出∠FCD 的度数;(3)如图3,如果=45°,AB =2,AE=,求点G到BE的距离.【答案】(1)证明见解析;(2)45°或135°;(3).【解析】试题分析:(1)根据正方形的性质可得AB=AD,AE=AG,∠BAD=∠EAG=90°,再求出∠BAE=∠DAG,然后利用“边角边”证明△ABE和△ADG全等,根据全等三角形对应边相等证明即可.(2)当点C在直线BE上时,可知点E与C重合或G点C与重合,据此求解即可.(3)根据和求解即可.试题解析:(1)如图2,∵四边形ABCD是正方形,∴AB=AD,∠BAE+∠EAD=90°.∵四边形AEFG是正方形,∴AE=AG,∠EAD+∠DAG=90°.∴∠BAE=∠DAG..∴△ABE≌△ADG(SAS).∴BE=DG..(2)如图,当点C在直线BE上时,可知点E与C重合或G点C与重合,此时∠FCD 的度数为45°或135°.(3)如图3,连接GB、GE.由已知α=45°,可知∠BAE=45°.又∵GE为正方形AEFG的对角线,∴∠AEG=45°.∴AB∥GE.∵,∴GE =8.∴.过点B作BH⊥AE于点H.∵AB=2,∴. ∴..设点G到BE的距离为h.∴.∴.∴点G到BE的距离为.考点:1.旋转的性质;2.正方形的性质;3.全等三角形的判定和性质;4.平行的判定和性质;5.勾股定理;6.分类思想的应用.6.(1)如图①,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,交AD于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.①求证:四边形BFDE是菱形;②直接写出∠EBF 的度数;(2)把(1)中菱形BFDE 进行分离研究,如图②,点G 、I 分别在BF 、BE 边上,且BG=BI ,连接GD ,H 为GD 的中点,连接FH 并延长,交ED 于点J ,连接IJ 、IH 、IF 、IG.试探究线段IH 与FH 之间满足的关系,并说明理由;(3)把(1)中矩形ABCD 进行特殊化探究,如图③,当矩形ABCD 满足AB=AD 时,点E 是对角线AC 上一点,连接DE 、EF 、DF ,使△DEF 是等腰直角三角形,DF 交AC 于点G.请直接写出线段AG 、GE 、EC 三者之间满足的数量关系.【答案】(1)①详见解析;②60°.(2)IH =3FH ;(3)EG 2=AG 2+CE 2.【解析】【分析】(1)①由△DOE ≌△BOF ,推出EO =OF ,∵OB =OD ,推出四边形EBFD 是平行四边形,再证明EB =ED 即可.②先证明∠ABD =2∠ADB ,推出∠ADB =30°,延长即可解决问题.(2)IH =3FH .只要证明△IJF 是等边三角形即可.(3)结论:EG 2=AG 2+CE 2.如图3中,将△ADG 绕点D 逆时针旋转90°得到△DCM ,先证明△DEG ≌△DEM ,再证明△ECM 是直角三角形即可解决问题.【详解】(1)①证明:如图1中,∵四边形ABCD 是矩形,∴AD ∥BC ,OB =OD ,∴∠EDO =∠FBO ,在△DOE 和△BOF 中,EDO FBO OD OBEOD BOF ∠∠⎧⎪⎨⎪∠∠⎩=== , ∴△DOE ≌△BOF ,∴EO =OF ,∵OB =OD ,∴四边形EBFD 是平行四边形,∵EF ⊥BD ,OB =OD ,∴EB=ED,∴四边形EBFD是菱形.②∵BE平分∠ABD,∴∠ABE=∠EBD,∵EB=ED,∴∠EBD=∠EDB,∴∠ABD=2∠ADB,∵∠ABD+∠ADB=90°,∴∠ADB=30°,∠ABD=60°,∴∠ABE=∠EBO=∠OBF=30°,∴∠EBF=60°.(2)结论:IH=3FH.理由:如图2中,延长BE到M,使得EM=EJ,连接MJ.∵四边形EBFD是菱形,∠B=60°,∴EB=BF=ED,DE∥BF,∴∠JDH=∠FGH,在△DHJ和△GHF中,DHG GHFDH GHJDH FGH∠∠⎧⎪⎨⎪∠∠⎩===,∴△DHJ≌△GHF,∴DJ=FG,JH=HF,∴EJ=BG=EM=BI,∴BE=IM=BF,∵∠MEJ=∠B=60°,∴△MEJ是等边三角形,∴MJ=EM=NI,∠M=∠B=60°在△BIF和△MJI中,BI MJB MBF IM⎧⎪∠∠⎨⎪⎩===,∴△BIF≌△MJI,∴IJ=IF,∠BFI=∠MIJ,∵HJ=HF,∵∠BFI+∠BIF=120°,∴∠MIJ+∠BIF=120°,∴∠JIF=60°,∴△JIF是等边三角形,在Rt△IHF中,∵∠IHF=90°,∠IFH=60°,∴∠FIH=30°,∴IH=3FH.(3)结论:EG2=AG2+CE2.理由:如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,∵∠FAD+∠DEF=90°,∴AFED四点共圆,∴∠EDF=∠DAE=45°,∠ADC=90°,∴∠ADF+∠EDC=45°,∵∠ADF=∠CDM,∴∠CDM+∠CDE=45°=∠EDG,在△DEM和△DEG中,DE DEEDG EDMDG DM⎧⎪∠∠⎨⎪⎩===,∴△DEG≌△DEM,∴GE=EM,∵∠DCM=∠DAG=∠ACD=45°,AG=CM,∴∠ECM=90°∴EC2+CM2=EM2,∵EG=EM,AG=CM,∴GE2=AG2+CE2.【点睛】考查四边形综合题、矩形的性质、正方形的性质、菱形的判定和性质,等边三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会转化的思想思考问题.7.(1)问题发现如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.填空:线段AD,BE之间的关系为 .如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.(3)解决问题如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.【答案】(1) AD=BE,AD⊥BE.(2) AD=BE,AD⊥BE.(3) 5-32≤PC≤5+32.【解析】【分析】(1)根据等腰三角形性质证△ACD≌△BCE(SAS),得AD=BE,∠EBC=∠CAD,延长BE交AD于点F,由垂直定义得AD⊥BE.(2)根据等腰三角形性质证△ACD≌△BCE(SAS),AD=BE,∠CAD=∠CBE,由垂直定义得∠OHB=90°,AD⊥BE;(3)作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,PC=BE,当P、E、B共线时,BE最小,最小值=PB-PE;当P、E、B共线时,BE最大,最大值=PB+PE,故5-32≤BE≤5+32.【详解】(1)结论:AD=BE,AD⊥BE.理由:如图1中,∵△ACB与△DCE均为等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ACD=90°,在Rt△ACD和Rt△BCE中AC BCACD BCECD CE⎧⎪∠∠⎨⎪⎩===∴△ACD≌△BCE(SAS),∴AD=BE,∠EBC=∠CAD延长BE交AD于点F,∵BC⊥AD,∴∠EBC+∠CEB=90°,∵∠CEB=AEF,∴∠EAD+∠AEF=90°,∴∠AFE=90°,即AD⊥BE.∴AD=BE,AD⊥BE.故答案为AD=BE,AD⊥BE.(2)结论:AD=BE,AD⊥BE.理由:如图2中,设AD交BE于H,AD交BC于O.∵△ACB与△DCE均为等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=90°,∴ACD=∠BCE,在Rt△ACD和Rt△BCE中AC BCACD BCECD CE⎧⎪∠∠⎨⎪⎩===,∴△ACD≌△BCE(SAS),∴AD=BE,∠CAD=∠CBE,∵∠CAO+∠AOC=90°,∠AOC=∠BOH,∴∠BOH+∠OBH=90°,∴∠OHB=90°,∴AD⊥BE,∴AD=BE,AD⊥BE.(3)如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,∴PC=BE,图3-1中,当P、E、B共线时,BE最小,最小值=PB-PE=5-32,图3-2中,当P、E、B共线时,BE最大,最大值=PB+PE=5+32,∴5-32≤BE≤5+32,即5-32≤PC≤5+32.【点睛】本题是几何变换综合题,考查了旋转的性质、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找三角形全等的条件,学会添加辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.8.已知,如图:正方形ABCD,将Rt△EFG斜边EG的中点与点A重合,直角顶点F落在正方形的AB边上,Rt△EFG的两直角边分别交AB、AD边于P、Q两点,(点P与点F重合),如图1所示:(1)求证:EP2+GQ2=PQ2;(2)若将Rt△EFG绕着点A逆时针旋转α(0°<α≤90°),两直角边分别交AB、AD边于P、Q两点,如图2所示:判断四条线段EP、PF、FQ、QG之间是否存在什么确定的相等关系?若存在,证明你的结论.若不存在,请说明理由;(3)若将Rt△EFG绕着点A逆时针旋转α(90°<α<180°),两直角边所在的直线分别交BA、AD两边延长线于P、Q两点,并判断四条线段EP、PF、FQ、QG之间存在何种确定的相等关系?按题意完善图3,请直接写出你的结论(不用证明).【答案】(1)见解析;(2)PF2+FQ2=EP2+GQ2;(3)四条线段EP、PF、FQ、QG之间的关系为PF2+GQ2=PE2+FQ2.【解析】【分析】(1)过点E作EH∥FG,由此可证△EAH≌△GAQ,然后根据全等三角形的性质得到EH=QG,又PQ=PH,在Rt△EPH中,EP2+EH2=PH2,由此可以得到EP2+GQ2=PQ2;(2)过点E作EH∥FG,交DA的延长线于点H,连接PQ、PH,由此可证△EAH≌△GAQ,然后根据全等三角形的性质得到EH=QG,又PH=PQ,在Rt△EPH中,EP2+EH2=PH2,即EP2+GQ2=PH2,在Rt△PFQ中,PF2+FQ2=PQ2,故PF2+FQ2=EP2+GQ2;(3)四条线段EP、PF、FQ、QG之间的关系为PE2+GQ2=PF2+FQ2,证明方法同上.【详解】(1)过点E作EH∥FG,连接AH、FH,如图所示:∵EA=AG,∠HEA=∠AGQ,∠HAE=∠GAD,∴△EAH≌△GAQ,∴EH=QG,HA=AQ,∵FA⊥AD,∴PQ=PH.在Rt△EPH中,∵EP2+EH2=PH2,∴EP2+GQ2=PQ2;(2)过点E作EH∥FG,交DA的延长线于点H,连接PQ、PH,∵EA=AG,∠HEA=∠AGQ,∠HAE=∠GAD,∴△EAH≌△GAQ,∴EH=QG,HA=AQ,∵PA⊥AD,∴PQ=PH.在Rt△EPH中,∵EP2+EH2=PH2,∴EP2+GQ2=PH2.在Rt △PFQ 中,∵PF 2+FQ 2=PQ 2,∴PF 2+FQ 2=EP 2+GQ 2.(3)四条线段EP 、PF 、FQ 、QG 之间的关系为PF 2+GQ 2=PE 2+FQ 2.【点睛】本题主要考查了旋转的性质,全等三角形的判定与性质,三线合一,勾股定理,正确作出辅助线是解答本题的关键.9.我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”。
