1993年全国大学生数学模型竞赛试题
数学建模 历年试题及论文
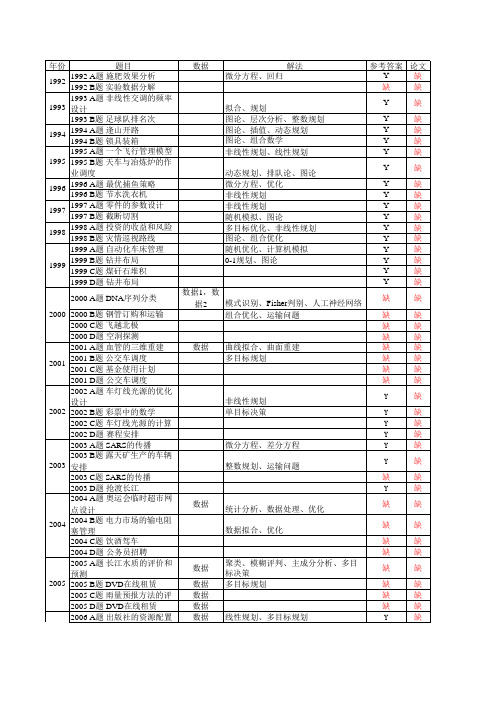
拟合、规划 图论、层次分析、整数队论、图论 微分方程、优化 非线性规划 非线性规划 随机模拟、图论 多目标优化、非线性规划 图论、组合优化 随机优化、计算机模拟 0-1规划、图论
2000 2000 B题 钢管订购和运输 缺 2000 C题 飞越北极 缺 2000 D题 空洞探测 缺 2001 A题 血管的三维重建 数据 曲线拟合、曲面重建 缺 多目标规划 2001 B题 公交车调度 缺 2001 2001 C题 基金使用计划 缺 2001 D题 公交车调度 缺 2002 A题 车灯线光源的优化设计 非线性规划 Y 2002 B题 彩票中的数学 单目标决策 Y 2002 2002 C题 车灯线光源的计算 Y 2002 D题 赛程安排 Y 2003 A题 SARS的传播 微分方程、差分方程 Y 2003 B题 露天矿生产的车辆安排 整数规划、运输问题 Y 2003 2003 C题 SARS的传播 缺 2003 D题 抢渡长江 Y 2004 A题 奥运会临时超市网点设计 数据 统计分析、数据处理、优化 缺 2004 B题 电力市场的输电阻塞管理 数据拟合、优化 缺 2004 2004 C题 饮酒驾车 缺 2004 D题 公务员招聘 缺 2005 A题 长江水质的评价和预测 数据 聚类、模糊评判、主成分分析、多目标决策 缺 2005 B题 DVD在线租赁 数据 多目标规划 缺 2005 2005 C题 雨量预报方法的评价 数据 缺 2005 D题 DVD在线租赁 数据 缺 2006 A题 出版社的资源配置 数据 线性规划、多目标规划 Y 2006 B题 艾滋病疗法的评价及疗效的预测 回归、线性规划 数据 Y 2006 2006 C题 易拉罐形状和尺寸的最优设计 缺 2006 D题 煤矿瓦斯和煤尘的监测与控制 数据 缺 2007 A题 中国人口增长预测 数据 微分、差分方程 Y 2007 B题 乘公交,看奥运 数据 图论、0-1 规划、动态规划 Y 2007 2007 C题 手机“套餐”优惠几何 数据 Y
全国大学生数学建模竞赛试题集

2002年A题……车灯线光源的优化设计安装在汽车头部的车灯的形状为一旋转抛物面,车灯的对称轴水平地指向正前方, 其开口半径36毫米,深度21.6毫米。
经过车灯的焦点,在与对称轴相垂直的水平方向,对称地放置一定长度的均匀分布的线光源。
要求在某一设计规范标准下确定线光源的长度。
该设计规范在简化后可描述如下。
在焦点F正前方25米处的A点放置一测试屏,屏与FA垂直,用以测试车灯的反射光。
在屏上过A点引出一条与地面相平行的直线,在该直线A点的同侧取B点和C点,使AC=2AB=2.6米。
要求C点的光强度不小于某一额定值(可取为1个单位),B点的光强度不小于该额定值的两倍(只须考虑一次反射)。
请解决下列问题:(1)在满足该设计规范的条件下,计算线光源长度,使线光源的功率最小。
(2)对得到的线光源长度,在有标尺的坐标系中画出测试屏上反射光的亮区。
(3)讨论该设计规范的合理性。
2002年B题……彩票中的数学近年来“彩票飓风”席卷中华大地,巨额诱惑使越来越多的人加入到“彩民”的行列,目前流行的彩票主要有“传统型”和“乐透型”两种类型。
“传统型”采用“10选6+1”方案:先从6组0~9号球中摇出6个基本号码,每组摇出一个,然后从0~4号球中摇出一个特别号码,构成中奖号码。
投注者从0~9十个号码中任选6个基本号码(可重复),从0~4中选一个特别号码,构成一注,根据单注号码与中奖号码相符的个数多少及顺序确定中奖等级。
以中奖号码“abcdef+g”为例说明中奖等级,如表一(X表示未选中的号码)。
表一10选6+1(6+1/10)中奖等级 基本号码………………特别号码 说明一等奖 Abcdef…………………g 选7中(6+1)二等奖 abcdef 选7中(6)三等奖 abcdeX……Xbcdef 选7中(5)四等奖 abcdXX……XbcdeX……XXcdef 选7中(4)五等奖 abcXXX……XbcdXX……XXcdeX……XXXdef 选7中(3)六等奖 abXXXX……XbcXXX……XXcdXX……XXXdeXXXXXef选7中(2)“乐透型”有多种不同的形式,比如“33选7”的方案:先从01~33个号码球中一个一个地摇出7个基本号,再从剩余的26个号码球中摇出一个特别号码。
1993年全国高考数学试题(理)

1993年普通高等数学招生全国统一考试(全国Ⅱ)理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.参考公式: 如果事件A 、B 互斥,那么)()()(B P A P B A P +=+如果事件A 、B 相互独立,那么)()()(B P A P B A P ⋅=⋅如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率:()(1)k kn k n n P k C P P -=-球是表面积公式24R S π=其中R 表示球的半径 球的体积公式334R V π=其中R 表示球的半径第Ⅰ卷(选择题共68分)一、选择题:本大题共17小题,每小题4分,共68分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.函数()sin cos f x x x =+的最小正周期是A .2πB. C .πD .4π 2.如果双曲线的焦距为6,两条准线间的距离为4,那么该双曲线的离心率为A .32BCD .23.和直线3450x y -+=关于x 轴对称的直线的方程为 A .3450x y +-= B .3450x y ++=C .3450x y -+-=D .3450x y -++=4.极坐标方程435cos ρθ=-所表示的曲线是A .焦点到准线距离为45的椭圆B .焦点到准线距离为45的双曲线右支C .焦点到准线距离为43的椭圆D .焦点到准线距离为43的双曲线右支5.35y x =在[1,1]-上是A .增函数且是奇函数B .增函数且是偶函数C .减函数且是奇函数D .减函数且是偶函数6.2251lim 25n n n n →∞--+的值为A .15-B .52-C .15 D .527.集合{|,}24k M x x k Z ππ==+∈,{|,}42k N x x k Z ππ==+∈,则A .M N =B .M N ⊃C .M N ⊂D .M N =∅I8.sin 20cos70sin10sin 50+oooo的值是A .14BC .12D9.参数方程|cos sin |22(02)1(1sin )2x y θθθπθ⎧=+⎪⎪<<⎨⎪=+⎪⎩表示A .双曲线的一支,这支过点1(1,)2 B .抛物线的一部分,这部分过点1(1,)2C .双曲线的一支,这支过点1(1,)2-D .抛物线的一部分,这部分过点1(1,)2- 10.若a 、b 是任意实数,且a b >,则A .22a b >B .1ba<C .lg()0a b ->D .1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭11.一动圆与两圆221x y +=和228120x y x +-+=都外切,则动圆圆心轨迹为A .圆B .椭圆C .双曲线的一支D .抛物线12.圆柱轴截面的周长l 为定值,那么圆柱体积的最大值是A .36l π⎛⎫⎪⎝⎭B .3192l π⎛⎫ ⎪⎝⎭C .34l π⎛⎫⎪⎝⎭D .324l π⎛⎫⎪⎝⎭13.451)(1)x -展开式中4x 的系数为A .40-B .10C .40D .4514.直角梯形的一个内角为45°,下底长为上底长的32,这个梯形绕下底所在的直线旋转一周所成的旋转体的全面积为(5π+,则旋转体的体积为A .2πB C D .73π15.已知1a ,2a ,…,8a 为各项都大于零的等比数列,公比1q ≠,则A .1845a a a a +>+B .1845a a a a +<+C .1845a a a a +=+D .18a a +与45a a +的大小关系不能确定16.设有如下三个命题:甲:相交两直线l ,m 都在平面α内,并且都不在平面β内.乙:l ,m 之中至少有一条与β相交.丙:α与β相交.当甲成立时 A .乙是丙的充分而不必要的条件 B .乙是丙的必要而不充分的条件C .乙是丙的充分且必要的条件D .乙既不是丙的充分条件又不是丙的必要条件17.将数字1,2,3,4填入1,2,3,4的四个方格里,每格填一个数字,则每个方格的标号与所填的数字均不相同的填法有 A .6种B .9种C .11种D .23种第Ⅱ卷(非选择题共82分)注意事项:用钢笔或圆珠笔直接答在答题卡上.二、填空题:本大题共6小题,每小题4分,共24分,把答案填在题中横线上.18.11sin(arccosarccos )23+= . 19.若双曲线2222194x y k k-=与圆221x y +=没有公共点,则实数k 的取值范围为 . 20.从1,2,…,10这十个数中取出四个数,使它们的和为奇数,共有 种取法.(用数字作答) 21.设1()42xx f x +=-,则1(0)f-= .22.建造一个容积为38m ,深为2m 的长方体无盖水池.如果池底和池壁的造价每平方米分别为120元和80元,那么水池的最低总造价为 元.23.如图,ABCD 是正方形,E 是AB 的中点,如将△DAE 和△CBE 分别沿虚线DE 和CE 折起,使AE 与BE 重合,记A 与B 重合后的点为P ,则面PCD 与面ECD 所成的二面角为 度.三、解答题:本大题共6小题,共58分,解答应写出文字说明,证明过程或演算步骤.24.(本小题满分10分)已知1()log (0,1)1a xf x a a x+=>≠-. (1)求()f x 的定义域;(2)判断()f x 的奇偶性并予以证明; (3)求使()0f x >的x 取值范围.25.(本小题满分12分)已知数列228113⋅⋅,228235⋅⋅,…,228(21)(21)n n n -+,….n S 为其前n 项和.计算得189S =,22425S =,34849S =,48081S =. 观察上述结果,推测出计算n S 的公式,并用数学归纳法加以证明.26.(本小题满分12分)已知平面αI 平面β=直线a .,αβ同垂直于平面γ,又同平行于直线b .求证: (1)a γ⊥;(2)b γ⊥.27.(本小题满分12分)在面积为1的△PMN 中,1tan 2PMN ∠=,tan 2MNP ∠=-.建立ECD PABC D E βαγab适当的坐标系,求以M ,N 为焦点且过点P 的椭圆方程.28.(本小题满分12分)设复数cos sin (0)z i θθθπ=+<<,441()1z z ω-=+,并且||ω=,arg 2πω<,求θ.数学试题参考答案一、选择题,本题考查基础知识,基本概念和基本运算能力二、填空题.本题考查基础知识,基本概念和基本运算技巧13. 14. 15. 16. 三、解答题 17.1993年普通高等学校招生全国统一考试数学试题(理工农医类)参考解答及评分标准说明:1.本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到一步应得的累加分数. 4.只给整数分数.选择题和填空题不给中间分.一、选择题:本题考查基本知识和基本运算.每小题4分,满分68分.(1)A (2)C (3)B (4)B (5)A (6)D (7)C (8)A (9)B (10)D (11)C (12)A (13)D (14)D (15)A (16)C (17)B二、填空题:本题考查基本知识和基本运算.每小题4分,满分24分.(18)6322+ (19){k ||k |>31} (20)100 (21)1 (22)1760 (23)30 三、解答题(24)本小题考查函数的奇偶性、对数函数的性质、不等式的性质和解法等基本知识及运算能力.满分12分.M NP解 (Ⅰ)由对数函数的定义知011>-+xx. ——1分 如果⎩⎨⎧>->+0101x x ,则-1<x <1;如果⎩⎨⎧<-<+0101x x ,则不等式组无解. ——4分故f (x )的定义域为(-1,1)(Ⅱ) ∵ ()()x f x xx x x f a a-=-+-=+-=-11log 11log ,∴ f (x )为奇函数. ——6分 (Ⅲ)(ⅰ)对a >1,log a 011>-+x x 等价于111>-+xx, ①而从(Ⅰ)知1-x >0,故①等价于1+x >1-x ,又等价于x >0.故对a >1,当x ∈(0,1)时有f (x )>0. ——9分(ⅱ)对0<a <1,log a011>-+x x 等价于0<111<-+xx. ② 而从(Ⅰ)知1-x >0,故②等价于-1<x <0.故对0<a <1,当x ∈(-1,0)时有f (x )>0. ——12分(25)本小题考查观察、分析、归纳的能力和数学归纳法.满分10分.解 ()()()N n n n S n ∈+-+=2212112. ——4分 证明如下:(Ⅰ)当n =1时,98313221=-=S ,等式成立. ——6分 (Ⅱ)设当n =k 时等式成立,即()().1211222+-+=k k S k ——7分 则()()()221321218++++=+k k k S S k k ()()()()()222232121812112+++++-+=k k k k k ()()()()()222232121832]112[+++++-+=k k k k k ()()()()()()22222321218323212+++++-++=k k k k k k ()()()()()222223212123212+++-++=k k k k k ()()2232132+-+=k k ()()22]112[1]112[++-++=k k 由此可知,当n =k +1时等式也成立. ——9分 根据(Ⅰ)(Ⅱ)可知,等式对任何n ∈N 都成立. ——10分 (26)本小题考查直线与平面的平行、垂直和两平面垂直的基础知识,及空间想象能力和逻辑思维能力.满分12分.证法一(Ⅰ)设α∩γ=AB ,β∩γ=AC .在γ内任取一点P 并于γ内作直线PM ⊥AB ,PN ⊥AC . ——1分 ∵ γ⊥α,∴ PM ⊥α.而 a ⊂α,∴ PM ⊥a .同理PN ⊥a . ——4分 又 PM ⊂γ,PN ⊂γ,∴ a ⊥γ. ——6分(Ⅱ)于a 上任取点Q ,过b 与Q 作一平面交α于直线a 1,交β于直线a 2.—7分∵ b ∥α,∴ b ∥a 1.同理b ∥a 2. ——8分 ∵ a 1,a 2同过Q 且平行于b ,∵ a 1,a 2重合.又 a 1⊂α,a 2⊂β,∴ a 1,a 2都是α、β的交线,即都重合于a . ——10分 ∵ b ∥a 1,∴ b ∥a .而a ⊥γ,∴ b ⊥γ. ——12分 注:在第Ⅱ部分未证明b ∥a 而直接断定b ⊥γ的,该部分不给分. 证法二(Ⅰ)在a 上任取一点P ,过P 作直线a ′⊥γ. ——1分 ∵ α⊥γ,P ∈α, ∴ a ′⊂α.同理a ′⊂β. ——3分 可见a ′是α,β的交线.因而a ′重合于a . ——5分 又 a ′⊥γ,∴ a ⊥γ. ——6分(Ⅱ)于α内任取不在a 上的一点,过b 和该点作平面与α交于直线c .同法过b 作平面与β交于直线d ——7分∵ b ∥α,b ∥β.∴ b ∥c ,b ∥d . ——8分 又 c ⊄β,d ⊂β,可见c 与d 不重合.因而c ∥d .于是c ∥β. ——9分 ∵ c ∥β,c ⊂α,α∩β=a ,∴ c ∥a . ——10分 ∵ b ∥c ,a ∥c ,b 与a 不重合(b ⊄α,a ⊂α),∴ b ∥a . ——11分 而 a ⊥γ,∴ b ⊥γ. ——12分 注:在第Ⅱ部分未证明b ∥a 而直接断定b ⊥γ的,该部分不给分.(27)本小题主要考查坐标系、椭圆的概念和性质、直线方程以及综合应用能力.满分12分. 解法一如图,以MN 所在直线为x 轴,MN 的垂直平分线为y 轴建立直角坐标系,设以M ,N 为焦点且过点P 的椭圆方程为12222=+by a x ,焦点为M (-c ,0),N (c ,0). —1分由tg M =21,tg α=tg(π-∠MNP )=2,得直线PM 和直线PN 的方程分别为y =21(x +c )和y =2(x -c ).将此二方程联立,解得x =35c ,y =34c ,即P 点坐标为(35c ,34c ). ——5分在△MNP 中,|MN |=2c ,MN 上的高为点P 的纵坐标,故.34342212c c c S MNP =⋅⋅=∆由题设条件S △MNP =1,∴ c =23,即P 点坐标为⎪⎪⎭⎫ ⎝⎛332635,. ——7分 由两点间的距离公式()3152332236352222=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=++=y c x PM , ()315332236352222=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-=+-=y c x PN .得 ()21521=+=PN PM a . ——10分 又 b 2=a 2-c 2=343415=-,故所求椭圆方程为 1315422=+y x . ——12分 解法二同解法一得23=c ,P 点的坐标为⎪⎪⎭⎫ ⎝⎛332635,. ——7分 ∵ 点P 在椭圆上,且a 2=b 2+c 2.∴13322363522222=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫⎝⎛b b .化简得3b 4-8b 2-3=0. 解得b 2=3,或b 2=31-(舍去). ——10分 又 a 2=b 2+c 2=3+41543=.故所求椭圆方程为1315422=+y x . ——12分 解法三同解法一建立坐标系. ——1分∵ ∠P =∠α-∠PMN ,∴ ()()4321212121=⨯+-=-+--=tgMN tg tgM N tg tgP ππ. ∴ ∠P 为锐角.∴ sin P =53,cos P =54.而 S △MNP =21|PM |·|PN |sin P =1,∴ |PM |·|PN |=310. ——4分∵ |PM |+|PN |=2a ,|MN |=2c ,由余弦定理,(2c )2=|PM |2+|PN |2-2|PM |·|PN |cos P =(|PM |+|PN |)2-2|PM |·|PN |(1+cos P )=(2a )2-2·310-2·310·54, ∴ c 2=a 2-3,即b 2=3. ——7分 又 sin M =51,sin N =52,由正弦定理,PMN MPN NPM sin sin sin ==,∴PMNM N PNPM sin sin sin =++.即 53251522ca =+,∴ a =5c . ——10分∴ a 2=b 2+c 2=3+52a .∴ a 2=415.① ② ③ 故所求椭圆方程为1315422=+y x . ——12分 (28)本小题考查复数的基本概念和运算,三角函数式的恒等变形及综合解题能力.满分12分. 解法一()()[][]44sin cos 1sin cos 1θθθθωi i ++-+--=()()θθθθ4sin 4cos 14sin 4cos 1i i ++----=——2分θθθθθθ2cos 2sin 22cos 22cos 2sin 22sin 222i i ++=()θθθ4cos 4sin 2tg i += ——5分 332tg 4cos 4sin 2tg ==+⋅=θθθθωi 332tg ±=θ. ——6分因πθ<<0,故有(ⅰ)当332tg =θ时,得12πθ=或127πθ=,这时都有⎪⎭⎫⎝⎛+=6sin 6cos 33ππωi ,得26arg ππω<=,适合题意. ——10分(ⅱ)当332tg -=θ时,得125πθ=或1211πθ=,这时都有⎪⎭⎫ ⎝⎛+=611sin 611cos 33ππωi , 得2611arg ππω>=,不适合题意,舍去. 综合(ⅰ)、(ⅱ)知12πθ=或127πθ=. ——2分解法二:θθ4sin 4cos 4i z +=.记θϕ4=,得()()ϕϕsin cos 44i z z-==.ϕϕϕϕωsin cos 1sin cos 1i i +++-=. ——2分()ϕϕϕϕcos sin cos 1sin i ++=()ϕϕϕcos sin 2tg i +=. ——5分 ∵ 33=ω,2arg πω<, ∴ ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥⋅>⋅=0cos 2tg 0sin 2tg 332tg ϕϕϕϕϕ ——8分当①成立时,②恒成立,所以θ应满足(ⅰ) ⎪⎪⎩⎪⎪⎨⎧≥=<<04cos 332tg 0θθπθ,或(ⅱ) ⎪⎪⎩⎪⎪⎨⎧≤-=<<04cos 332tg 0θθπθ,——10分解(ⅰ)得12πθ=或127πθ=.(ⅱ)无解.综合(ⅰ)、(ⅱ) 12πθ=或127πθ=. ——12分。
中国大学生数学建模竞赛发展史
2000网易杯全国大学生数学建模竞赛举行,27省(市、自治区)517所院校的3210队参加,其中608队参加大专组竞赛,香港城市大学有1个队首次参赛
2000.12.6~8
2000年各赛区负责人工作会议暨颁奖仪式在中山大学珠海校区举行,119队获一等奖(其中大专组23队),245队获二等奖(其中大专组55队)。
1998年全国大学生数学建模竞赛举行,26省(市、自治区)400所院校的2103队参加。
1998.12.10~13
1998年各赛区负责人工作会议暨颁奖仪式在上海华东理工大学举行,79队获一等奖,153队获二等奖。
1999.2.6~8
1999年美国大学生数学建模竞赛举行,我国参赛院校43个,占总数的19%,参赛队155个,占总数的32%,浙江大学获一项特等奖。从1999年起增加交叉学科建模竞赛(作为C题)。
2003.2
2003年美国大学生数学建模竞赛(MCM)和交叉学科竞赛(ICM)举行,我国共参加300队,占总数的47%,浙江大学、北京大学、东南大学、东华大学各一队获特等奖。
2003.9.22~25
2003高教社杯全国大学生数学建模竞赛举行,30省(市、自治区)637所院校的5406队参加。
2003.12.6~7
2003年各赛区工作会议暨颁奖仪式在厦门举行,厦门大学承办,608队获全国奖,其中本科组一等奖151队,二等奖306队,大专组一等奖48队,二等奖103队。
2004.2
2004年美国大学生数学建模竞赛(MCM)和交叉学科竞赛(ICM)举行,我国共参加398队,占总数的54%,成都电子科技大学一队获特等奖。
数学建模发展史
1992.11.27~29
1992年部分城市大学生数学模型联赛举行,这是全国性的首届竞赛,10省(市)79所院校的314队参加。
《数学建模入门》练习题1

《数学建模入门》练习题练习题1:发现新大陆!发现新大陆!人人都能做到,可是最终哥伦布做到了。
为什么哥伦布能做到呢?有兴趣、能想到、去做了、坚持到底。
练习题2:棋盘问题有一种棋盘有64个方格,去掉对角的两个格后剩下62个格(如下图),给你31块骨牌,每块是两个格的大小。
问能否用这些骨牌盖住这62个方格?不能,如图所示。
图中共有32个黄格,30个红格,而每张骨牌必定盖住一红一黄两格,那么最后两个黄格用一个骨牌无论如何也盖不上.练习题3:硬币游戏如果你和你的对手准备依次轮流地将硬币放在一个长方形桌子上,使得这些硬币不重叠。
最后放上硬币的人为胜者,在开始时你有权决定先放还是后放。
为了能赢得这场比赛,你决定先放还是后放呢?答:决定先放。
第一枚硬币放在桌子中心,随后自己放置的硬币总与对方上次放置的硬币成中心对称,如果对方能放得下,那么己方的硬币必然可以放下。
所以己方放置的硬币必然为最后一枚。
练习题4:高速问题一个人从A 地出发,以每小时30公里的速度到达B 地,问他从B 地回到A 地的速度要达到多少?才能使得往返路程的平均速度达到每小时60公里?解:设A,B两地距离为S,则有:2S/(t+T)=60.t为从A地到B地的时间,T为从B地到A地的时间。
即有○12S/(t+T)=60○2S=30t得出:T=0.即速度v=+∞但是这是不可能达到的速度。
所以此题无解。
练习题5:登山问题某人上午八点从山下的营地出发,沿着一条山间小路登山,下午五点到达山顶;次日上午八点又从山顶开始下山(沿同一条小路)返回,下午五点又到达了山下的营地。
问:是否能找到一个地点来回时刻是相同的?答:可以看做在一天,两人同时于八点分别从山顶山脚出发,,在五点到达。
看途中是否能遇到。
设f(t)为上山时的时间与位移表达式,g(t)为下山是的位移表达式,h(t)=f(t)-g(t) 为合位移,总位移为S,规定上山为正方向。
当h(t)=0,两人相遇。
以山脚为位移原点,则山脚处位移为0,山顶为S。
1993年全国高考数学试题(理)

1993年普通高等数学招生全国统一考试(全国Ⅱ)理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.参考公式: 如果事件A 、B 互斥,那么)()()(B P A P B A P +=+如果事件A 、B 相互独立,那么)()()(B P A P B A P ⋅=⋅如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率:()(1)k kn k n n P k C P P -=-球是表面积公式24R S π=其中R 表示球的半径 球的体积公式334R V π=其中R 表示球的半径第Ⅰ卷(选择题共68分)一、选择题:本大题共17小题,每小题4分,共68分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.函数()sin cos f x x x =+的最小正周期是A .2πB. C .πD .4π 2.如果双曲线的焦距为6,两条准线间的距离为4,那么该双曲线的离心率为A .32BCD .23.和直线3450x y -+=关于x 轴对称的直线的方程为 A .3450x y +-= B .3450x y ++=C .3450x y -+-=D .3450x y -++=4.极坐标方程435cos ρθ=-所表示的曲线是A .焦点到准线距离为45的椭圆B .焦点到准线距离为45的双曲线右支C .焦点到准线距离为43的椭圆D .焦点到准线距离为43的双曲线右支5.35y x =在[1,1]-上是A .增函数且是奇函数B .增函数且是偶函数C .减函数且是奇函数D .减函数且是偶函数6.2251lim 25n n n n →∞--+的值为A .15-B .52-C .15 D .527.集合{|,}24k M x x k Z ππ==+∈,{|,}42k N x x k Z ππ==+∈,则A .M N =B .M N ⊃C .M N ⊂D .M N =∅8.sin 20cos70sin10sin 50+的值是A .14BC .12D9.参数方程|cos sin |22(02)1(1sin )2x y θθθπθ⎧=+⎪⎪<<⎨⎪=+⎪⎩表示A .双曲线的一支,这支过点1(1,)2 B .抛物线的一部分,这部分过点1(1,)2C .双曲线的一支,这支过点1(1,)2-D .抛物线的一部分,这部分过点1(1,)2- 10.若a 、b 是任意实数,且a b >,则A .22a b >B .1ba<C .lg()0a b ->D .1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭11.一动圆与两圆221x y +=和228120x y x +-+=都外切,则动圆圆心轨迹为A .圆B .椭圆C .双曲线的一支D .抛物线12.圆柱轴截面的周长l 为定值,那么圆柱体积的最大值是A .36l π⎛⎫⎪⎝⎭B .3192l π⎛⎫ ⎪⎝⎭C .34l π⎛⎫⎪⎝⎭D .324l π⎛⎫⎪⎝⎭13.451)(1)x -展开式中4x 的系数为A .40-B .10C .40D .4514.直角梯形的一个内角为45°,下底长为上底长的32,这个梯形绕下底所在的直线旋转一周所成的旋转体的全面积为(5π+,则旋转体的体积为A .2πB C D .73π15.已知1a ,2a ,…,8a 为各项都大于零的等比数列,公比1q ≠,则A .1845a a a a +>+B .1845a a a a +<+C .1845a a a a +=+D .18a a +与45a a +的大小关系不能确定16.设有如下三个命题:甲:相交两直线l ,m 都在平面α内,并且都不在平面β内.乙:l ,m 之中至少有一条与β相交.丙:α与β相交.当甲成立时 A .乙是丙的充分而不必要的条件 B .乙是丙的必要而不充分的条件C .乙是丙的充分且必要的条件D .乙既不是丙的充分条件又不是丙的必要条件17.将数字1,2,3,4填入1,2,3,4的四个方格里,每格填一个数字,则每个方格的标号与所填的数字均不相同的填法有 A .6种B .9种C .11种D .23种第Ⅱ卷(非选择题共82分)注意事项:用钢笔或圆珠笔直接答在答题卡上.二、填空题:本大题共6小题,每小题4分,共24分,把答案填在题中横线上.18.11sin(arccosarccos )23+= . 19.若双曲线2222194x y k k-=与圆221x y +=没有公共点,则实数k 的取值范围为 . 20.从1,2,…,10这十个数中取出四个数,使它们的和为奇数,共有 种取法.(用数字作答) 21.设1()42xx f x +=-,则1(0)f-= .22.建造一个容积为38m ,深为2m 的长方体无盖水池.如果池底和池壁的造价每平方米分别为120元和80元,那么水池的最低总造价为 元.23.如图,ABCD 是正方形,E 是AB 的中点,如将△DAE 和△CBE 分别沿虚线DE 和CE 折起,使AE 与BE 重合,记A 与B 重合后的点为P ,则面PCD 与面ECD 所成的二面角为 度.三、解答题:本大题共6小题,共58分,解答应写出文字说明,证明过程或演算步骤.24.(本小题满分10分)已知1()log (0,1)1a xf x a a x+=>≠-. (1)求()f x 的定义域;(2)判断()f x 的奇偶性并予以证明; (3)求使()0f x >的x 取值范围.25.(本小题满分12分)已知数列228113⋅⋅,228235⋅⋅,…,228(21)(21)n n n -+,….n S 为其前n 项和.计算得189S =,22425S =,34849S =,48081S =. 观察上述结果,推测出计算n S 的公式,并用数学归纳法加以证明. 26.(本小题满分12分)已知平面α平面β=直线a .,αβ同垂直于平面γ,又同平行于直线b .求证: (1)a γ⊥;(2)b γ⊥.27.(本小题满分12分)在面积为1的△PMN 中,1tan 2PMN ∠=,tan 2MNP ∠=-.建立ECD PABC D E βαγab适当的坐标系,求以M ,N 为焦点且过点P 的椭圆方程.28.(本小题满分12分)设复数cos sin (0)z i θθθπ=+<<,441()1z z ω-=+,并且||ω=,arg 2πω<,求θ.数学试题参考答案一、选择题,本题考查基础知识,基本概念和基本运算能力二、填空题.本题考查基础知识,基本概念和基本运算技巧13. 14. 15. 16. 三、解答题 17.1993年普通高等学校招生全国统一考试数学试题(理工农医类)参考解答及评分标准说明:1.本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到一步应得的累加分数. 4.只给整数分数.选择题和填空题不给中间分.一、选择题:本题考查基本知识和基本运算.每小题4分,满分68分.(1)A (2)C (3)B (4)B (5)A (6)D (7)C (8)A (9)B (10)D (11)C (12)A (13)D (14)D (15)A (16)C (17)B二、填空题:本题考查基本知识和基本运算.每小题4分,满分24分.(18)6322+ (19){k ||k |>31} (20)100 (21)1 (22)1760 (23)30 三、解答题(24)本小题考查函数的奇偶性、对数函数的性质、不等式的性质和解法等基本知识及运算能力.满分12分.M NP解 (Ⅰ)由对数函数的定义知011>-+xx. ——1分 如果⎩⎨⎧>->+0101x x ,则-1<x <1;如果⎩⎨⎧<-<+0101x x ,则不等式组无解. ——4分故f (x )的定义域为(-1,1)(Ⅱ) ∵ ()()x f x xx x x f a a-=-+-=+-=-11log 11log ,∴ f (x )为奇函数. ——6分 (Ⅲ)(ⅰ)对a >1,log a 011>-+x x 等价于111>-+xx, ①而从(Ⅰ)知1-x >0,故①等价于1+x >1-x ,又等价于x >0.故对a >1,当x ∈(0,1)时有f (x )>0. ——9分(ⅱ)对0<a <1,log a011>-+x x 等价于0<111<-+xx. ② 而从(Ⅰ)知1-x >0,故②等价于-1<x <0.故对0<a <1,当x ∈(-1,0)时有f (x )>0. ——12分(25)本小题考查观察、分析、归纳的能力和数学归纳法.满分10分.解 ()()()N n n n S n ∈+-+=2212112. ——4分 证明如下:(Ⅰ)当n =1时,98313221=-=S ,等式成立. ——6分 (Ⅱ)设当n =k 时等式成立,即()().1211222+-+=k k S k ——7分 则()()()221321218++++=+k k k S S k k ()()()()()222232121812112+++++-+=k k k k k ()()()()()222232121832]112[+++++-+=k k k k k ()()()()()()22222321218323212+++++-++=k k k k k k ()()()()()222223212123212+++-++=k k k k k ()()2232132+-+=k k ()()22]112[1]112[++-++=k k 由此可知,当n =k +1时等式也成立. ——9分 根据(Ⅰ)(Ⅱ)可知,等式对任何n ∈N 都成立. ——10分 (26)本小题考查直线与平面的平行、垂直和两平面垂直的基础知识,及空间想象能力和逻辑思维能力.满分12分.证法一(Ⅰ)设α∩γ=AB ,β∩γ=AC .在γ内任取一点P 并于γ内作直线PM ⊥AB ,PN ⊥AC . ——1分 ∵ γ⊥α,∴ PM ⊥α.而 a ⊂α,∴ PM ⊥a .同理PN ⊥a . ——4分 又 PM ⊂γ,PN ⊂γ,∴ a ⊥γ. ——6分(Ⅱ)于a 上任取点Q ,过b 与Q 作一平面交α于直线a 1,交β于直线a 2.—7分∵ b ∥α,∴ b ∥a 1.同理b ∥a 2. ——8分 ∵ a 1,a 2同过Q 且平行于b ,∵ a 1,a 2重合.又 a 1⊂α,a 2⊂β,∴ a 1,a 2都是α、β的交线,即都重合于a . ——10分 ∵ b ∥a 1,∴ b ∥a .而a ⊥γ,∴ b ⊥γ. ——12分 注:在第Ⅱ部分未证明b ∥a 而直接断定b ⊥γ的,该部分不给分. 证法二(Ⅰ)在a 上任取一点P ,过P 作直线a ′⊥γ. ——1分 ∵ α⊥γ,P ∈α, ∴ a ′⊂α.同理a ′⊂β. ——3分 可见a ′是α,β的交线.因而a ′重合于a . ——5分 又 a ′⊥γ,∴ a ⊥γ. ——6分(Ⅱ)于α内任取不在a 上的一点,过b 和该点作平面与α交于直线c .同法过b 作平面与β交于直线d ——7分∵ b ∥α,b ∥β.∴ b ∥c ,b ∥d . ——8分 又 c ⊄β,d ⊂β,可见c 与d 不重合.因而c ∥d .于是c ∥β. ——9分 ∵ c ∥β,c ⊂α,α∩β=a ,∴ c ∥a . ——10分 ∵ b ∥c ,a ∥c ,b 与a 不重合(b ⊄α,a ⊂α),∴ b ∥a . ——11分 而 a ⊥γ,∴ b ⊥γ. ——12分 注:在第Ⅱ部分未证明b ∥a 而直接断定b ⊥γ的,该部分不给分.(27)本小题主要考查坐标系、椭圆的概念和性质、直线方程以及综合应用能力.满分12分. 解法一如图,以MN 所在直线为x 轴,MN 的垂直平分线为y 轴建立直角坐标系,设以M ,N 为焦点且过点P 的椭圆方程为12222=+by a x ,焦点为M (-c ,0),N (c ,0). —1分由tg M =21,tg α=tg(π-∠MNP )=2,得直线PM 和直线PN 的方程分别为y =21(x +c )和y =2(x -c ).将此二方程联立,解得x =35c ,y =34c ,即P 点坐标为(35c ,34c ). ——5分在△MNP 中,|MN |=2c ,MN 上的高为点P 的纵坐标,故.34342212c c c S MNP =⋅⋅=∆由题设条件S △MNP =1,∴ c =23,即P 点坐标为⎪⎪⎭⎫ ⎝⎛332635,. ——7分 由两点间的距离公式()3152332236352222=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=++=y c x PM , ()315332236352222=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-=+-=y c x PN .得 ()21521=+=PN PM a . ——10分 又 b 2=a 2-c 2=343415=-,故所求椭圆方程为 1315422=+y x . ——12分 解法二同解法一得23=c ,P 点的坐标为⎪⎪⎭⎫ ⎝⎛332635,. ——7分 ∵ 点P 在椭圆上,且a 2=b 2+c 2.∴13322363522222=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫⎝⎛b b .化简得3b 4-8b 2-3=0. 解得b 2=3,或b 2=31-(舍去). ——10分 又 a 2=b 2+c 2=3+41543=.故所求椭圆方程为1315422=+y x . ——12分 解法三同解法一建立坐标系. ——1分∵ ∠P =∠α-∠PMN ,∴ ()()4321212121=⨯+-=-+--=tgMN tg tgM N tg tgP ππ. ∴ ∠P 为锐角.∴ sin P =53,cos P =54.而 S △MNP =21|PM |·|PN |sin P =1,∴ |PM |·|PN |=310. ——4分∵ |PM |+|PN |=2a ,|MN |=2c ,由余弦定理,(2c )2=|PM |2+|PN |2-2|PM |·|PN |cos P =(|PM |+|PN |)2-2|PM |·|PN |(1+cos P )=(2a )2-2·310-2·310·54, ∴ c 2=a 2-3,即b 2=3. ——7分 又 sin M =51,sin N =52,由正弦定理,PMN MPN NPM sin sin sin ==,∴PMNM N PNPM sin sin sin =++.即 53251522ca =+,∴ a =5c . ——10分∴ a 2=b 2+c 2=3+52a .∴ a 2=415.① ② ③ 故所求椭圆方程为1315422=+y x . ——12分 (28)本小题考查复数的基本概念和运算,三角函数式的恒等变形及综合解题能力.满分12分. 解法一()()[][]44sin cos 1sin cos 1θθθθωi i ++-+--=()()θθθθ4sin 4cos 14sin 4cos 1i i ++----=——2分θθθθθθ2cos 2sin 22cos 22cos 2sin 22sin 222i i ++=()θθθ4cos 4sin 2tg i += ——5分 332tg 4cos 4sin 2tg ==+⋅=θθθθωi 332tg ±=θ. ——6分因πθ<<0,故有(ⅰ)当332tg =θ时,得12πθ=或127πθ=,这时都有⎪⎭⎫⎝⎛+=6sin 6cos 33ππωi ,得26arg ππω<=,适合题意. ——10分(ⅱ)当332tg -=θ时,得125πθ=或1211πθ=,这时都有⎪⎭⎫ ⎝⎛+=611sin 611cos 33ππωi , 得2611arg ππω>=,不适合题意,舍去. 综合(ⅰ)、(ⅱ)知12πθ=或127πθ=. ——2分解法二:θθ4sin 4cos 4i z +=.记θϕ4=,得()()ϕϕsin cos 44i z z-==.ϕϕϕϕωsin cos 1sin cos 1i i +++-=. ——2分()ϕϕϕϕcos sin cos 1sin i ++=()ϕϕϕcos sin 2tg i +=. ——5分 ∵ 33=ω,2arg πω<, ∴ ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥⋅>⋅=0cos 2tg 0sin 2tg 332tg ϕϕϕϕϕ ——8分当①成立时,②恒成立,所以θ应满足(ⅰ) ⎪⎪⎩⎪⎪⎨⎧≥=<<04cos 332tg 0θθπθ,或(ⅱ) ⎪⎪⎩⎪⎪⎨⎧≤-=<<04cos 332tg 0θθπθ,——10分解(ⅰ)得12πθ=或127πθ=.(ⅱ)无解.综合(ⅰ)、(ⅱ) 12πθ=或127πθ=. ——12分。
全国大学生数学建模竞赛赛题综合评析
社会热点
叶其孝、周义仓
开放性强、社会关注性强,突出数据来源的可靠性、结论解释的合理性
数据收集与处理、问题的分析与假设,初等数学方法、一般统计方法、多目标规划、回归分析、综合评价方法、灰色预测
2009年
A题:制动器试验台的控制方法分析
工业问题
方沛辰、刘笑羽
问题具体、专业性强,要花时间读懂、理解清楚问题
出版社的资源配置
孟大志
艾滋病疗法的评价及疗效的预测
边馥萍
易拉罐形状和尺寸的最优设计(C题)
叶其孝
煤矿瓦斯和煤尘的监测与控制(D题)
韩中庚
2007年
中国人口增长预测
唐云
乘公交,看奥运
方沛辰、吴孟达
手机“套餐”优惠几何(C题)
韩中庚
体能测试时间安排(D题)
刘雨林
2008年
数码相机定位
谭永基
高等教育学费标准探讨
叶其孝、周义仓
地面搜索(C题)
肖华勇
NBA赛程的分析与评价(D题)
姜启源
2009年
制动器试验台的控制方法分析
方沛辰、刘笑羽
眼科病床的合理安排
吴孟达、毛紫阳
卫星和飞船的跟踪测控(C题)
周义仓
会议筹备(D题)
王宏健
2010年
储油罐的变位识别与罐容表标定
韩中庚
2010年上海世博会影响力的定量评估
杨力平
输油管的布置(C题)
1
6
8
付鹂
重庆大学
1
6
9
姜启源
清华大学
4
3
10
陈叔平
浙江大学、贵州大学
2
5
11
数学建模入门基本知识

数学建模知识——之新手上路一、数学模型的定义现在数学模型还没有一个统一的准确的定义,因为站在不同的角度可以有不同的定义。
不过我们可以给出如下定义:“数学模型是关于部分现实世界和为一种特殊目的而作的一个抽象的、简化的结构。
”具体来说,数学模型就是为了某种目的,用字母、数学及其它数学符号建立起来的等式或不等式以及图表、图像、框图等描述客观事物的特征及其内在联系的数学结构表达式。
一般来说数学建模过程可用如下框图来表明:数学是在实际应用的需求中产生的,要解决实际问题就必需建立数学模型,从此意义上讲数学建模和数学一样有古老历史。
例如,欧几里德几何就是一个古老的数学模型,牛顿万有引力定律也是数学建模的一个光辉典范。
今天,数学以空前的广度和深度向其它科学技术领域渗透,过去很少应用数学的领域现在迅速走向定量化,数量化,需建立大量的数学模型。
特别是新技术、新工艺蓬勃兴起,计算机的普及和广泛应用,数学在许多高新技术上起着十分关键的作用。
因此数学建模被时代赋予更为重要的意义。
二、建立数学模型的方法和步骤1. 模型准备要了解问题的实际背景,明确建模目的,搜集必需的各种信息,尽量弄清对象的特征。
2. 模型假设根据对象的特征和建模目的,对问题进行必要的、合理的简化,用精确的语言作出假设,是建模至关重要的一步。
如果对问题的所有因素一概考虑,无疑是一种有勇气但方法欠佳的行为,所以高超的建模者能充分发挥想象力、洞察力和判断力,善于辨别主次,而且为了使处理方法简单,应尽量使问题线性化、均匀化。
3. 模型构成根据所作的假设分析对象的因果关系,利用对象的内在规律和适当的数学工具,构造各个量间的等式关系或其它数学结构。
这时,我们便会进入一个广阔的应用数学天地,这里在高数、概率老人的膝下,有许多可爱的孩子们,他们是图论、排队论、线性规划、对策论等许多许多,真是泱泱大国,别有洞天。
不过我们应当牢记,建立数学模型是为了让更多的人明了并能加以应用,因此工具愈简单愈有价值。
全国大学生数学建模竞赛试题集

选 7 中(6)
●●●●●●○
选 7 中(6) ●●●●●○……★ 选 7 中(5+1)
●●●●●○○……★ 选 7 中 ●●●●●○ (5+1)
选 7 中(5)
●●●●●○○
选 7 中(5) ●●●●○○……★ 选 7 中(4+1)
●●●●○○○……★ 选 7 中 ●●●●○○ (4+1)
选 7 中(4)
针对这种严重的道路交通情况国家质量监督检验检疫局2004月31日发布了新的车辆驾驶人员血液呼气酒精含量阈值与检验国家标准新标准规定车辆驾驶人员血液中的酒精含量大于或等于20毫克百毫升小于80毫克百毫升为饮酒驾车原标准是小于100毫克百毫升血液中的酒精含量大于或等于80毫克百毫升为醉酒驾车原标准是大于或等于100毫克百毫大李在中午12点喝了一瓶啤酒下午点检查时符合新的驾车标准紧接着他在吃晚饭时又喝了一瓶啤酒为了保险起见他呆到凌晨一次遭遇检查时却被定为饮酒驾车这让他既懊恼又困惑为什么喝同样多的酒两次检查结果会不一样呢
(1)对附件 1 所提供的一个早期的模型,评价其合理性和实用性。
(2)建立你们自己的模型,说明为什么优于附件 1 中的模型;特别要说明 怎样才能建立一个真正能够预测以及能为预防和控制提供可靠、足够的信息的模 型,这样做的困难在哪里?对于卫生部门所采取的措施做出评论,如:提前或延 后 5 天采取严格的隔离措施,对疫情传播所造成的影响做出估计。附件 2 提供的 数据供参考。
表二
-1-
中奖 等级 一等奖 二等奖 三等奖 四等奖 五等奖 六等奖 七等奖
33 选 7(7/33)
36 选 6+1(6+1/36)
基本号码……特别号码 说明 基本号码……特别号码
1993年普通高等学校招生全国统一考试.理科数学试题及答案

1993年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷4至9页,共150分.考试时间120分钟.第Ⅰ卷(选择题共68分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.3.考试结束,监考人将本试卷和答题卡一并收回.一、选择题:本大题共18小题;每小题4分,共72分.在每小题给出的四个选项中,只有一项是符合题目要求的(1)如果双曲线的实半轴长为2,焦距为6,那么该双曲线的离心率为:(A)/2 (B)/2 (C)3/2 (D)2(2)函数的最小正周期是:(A)π/4 (B)π/2 (C)π (D)2π(3)当圆锥的侧面积和底面积的比值是时,圆锥的轴截面顶角是:(A)45°(B)60°(C)90°(D)120°(4)当z=-[(1-i)/]时,z100+z50+1的值等于:(A)1 (B)-1 (C)i (D)-i(5)直线bx+ay=ab(a<0。
b<0)的倾斜角是(A)arctg(-b/a) (B)arctg(-a/b)(C)π-arctg(-b/a) (D)π-arctg(a/b)(6)在直角三角形中两锐角为A和B。
则sinAsinB(A)有最大值1/2和最小值0 (B)有最大值1/2但无最小值(C)既无最大值也无最小值 (D)有最大值1。
但无最小值(7)在各项均为正数的等比数列{a n}中,若a5a6=9,则log3a1+log3a2+…+log3a10的值为:( )(A)12 (B)10 (C)8 (D)2+log35(8)F(x)=[1+2/(2x-1)]f(x)(x≠0)是偶函数,且f(x)不恒等于零,则f(x)(A)是奇函数(B)是偶函数(C)可能是奇函数也可能是偶函数(D)不是奇函数也不是偶函数(9)曲线的参数方程为(0≤t≤5),则曲线是:(A)线段(B)双曲线的一支(C)圆弧(D)射线(10)若a、b是任意实数,且a>b,则:(A)a2>b2(B)b/a<1 (C)lg(a-b)>0 (D)(1/2)a<(1/2)b(11)已知集合E={θ│cosθ<sinθ。
全国大学生数学建模竞赛竞赛题目汇编(1992-2000)

K
产量
(t/ha) 18.98 27.35 34.86 38.52 38.44 37.73 38.43 43.87 42.77 46.22
施肥量
(kg/ha) 0 47 93 140 186 279 372 465 558 651
K
产量
(t/ha) 15.75 16.76 16.89 16.24 17.56 19.20 17.97 15.84 20.11 19.40
全国大学生数学建模竞赛 竞赛题目汇编(1992-2000)
[注]相关优秀论文已经汇编成册正式出版:全国大学生数学建模竞赛组委会编,《全国大学 生数学建模竞赛优秀论文汇编(1992-2000)》,北京:中国物价出版社,2002 年 3 月出版。
1992 年赛题
A 题 施肥效果分析 某地区作物生长所需的营养素主要是氮(N)、钾(K)、磷(P)。某作物研究所在该地区对
2.25 6.80 20.15 35.70 56.40 75.10 87.85 98.50
输入信号为 u(t) = A1 cos2πf1t + A2 cos2πf 2t + A3 cos2πf 3t ,其中 A1 = 25,A2 = 10,A3 = 45
是输入信号的振幅。对输入信号频率 f1、f2、f3 的设计要求为:
产量 (t/ha) 33.46 32.47 36.06 37.96 41.04 40.09 41.26 42.17 40.36 42.73
产量 (t/ha) 6.39 9.48 12.46 14.38 17.10 21.94 22.64 21.34 22.07 24.53
施肥量
(kg/ha) 0 47 93 140 186 279 372 465 558 651
1993美国数学建模数学竞赛试题及翻译

1993 MCM A: Optimal Composting加速餐厅剩菜堆肥的生成一家注重环境的学校餐厅正用微生物把顾客没吃完的食物再循环生成堆肥。
每天餐厅把吃剩的食物和泥浆混合,再把它们和厨房里容易弄碎的色拉菜以及少量的扯碎的纸片混合,并把混合物喂给一种真菌培养物和土壤细菌,它们把泥浆、绿叶菜、纸片消化形成有用的塔肥。
易碎的绿叶菜为真菌培养物提供氧气,而纸片则吸收过量的湿气。
但有时真菌培养物显得不能或不肯消化顾客留下的那么多的剩饭菜。
餐厅并没有因为真菌培养物没有胃口而则责怪厨师长。
餐厅收到要大量购买他们生成的堆肥的报价,所以餐厅正在研究增加堆肥产量的方法。
由于无力营建一套新的堆肥设备,因此餐厅首先寻求能加速真菌培养物活力的方法,例如,通过优化真菌培养物的环境(眼下大约是在120F和100%湿度的环境下生成堆肥的),或通过优化喂给真菌培养物的混合物统成,或同时优化两者(而达到加速真菌培养物的活力)。
试决定在喂给真菌培养物的混合物中泥浆、绿叶菜和纸片印比例与真菌培养物把混合物生成堆肥的速度间是否存在任何关系。
若你认为不存在任何关的系,试决定甚么样的比列会加速真菌培养物的活力。
除了按竞赛规则说明中规定的格式写的技术报告外,请为餐厅经理提供一页长的用非技术术语表示的实施建议。
作为数据,表93A-1列出了分别放在不同的箱子中用磅表示的混合物组成中各种原料的数量,以及把混合物喂给真菌培养物的日期以及完全生成堆肥的日期(以表示生成堆肥所需的时间)。
本题是由华盛顿大学数学系的Yves Nievegctlt 提供的,本题叙述的情况及数据来自华盛顿奶Medical Lake 地区监狱的餐厅。
他还写了一篇评论文章The outstanding optimalcompostingpapers, The UMAP Journal, v.(1993),no.3,227-288.1993 MCM B: Coal-Tipple Operations倒煤台的操作方案Aspen-Boulder煤矿公司经营一个包括一个单个的大型倒煤台在内的装煤设施。
1993年全国数学联赛

1993年全国初中数学联合竞赛决赛试题第一试一、选择题(本题共有8个小题,每小题都给出了A 、B 、C 、D 四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.)1. 多项式1612+-x x除以12-x 的余式是( )A .1B .1-C .1x +D .1x -2. 对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是( )A .Ⅰ、Ⅱ都对B .Ⅰ对、Ⅱ错C .Ⅰ错、Ⅱ对D .Ⅰ、Ⅱ都错 3. 设x 是实数,11y x x =-++.下列四个结论: Ⅰ.y 没有最小值;Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值; Ⅳ.有无穷多个x 使y 取到最小值.其中正确的是( )A .ⅠB .ⅡC .ⅢD .Ⅳ 4. 实数12345,,,,x x x x x 满足方程组12312342345345145125x x x a x x x a x x x a x x x a x x x a ++=⎧⎪++=⎪⎪++=⎨⎪++=⎪⎪++=⎩;;;;.,其中12345,,,,a a a a a 是实常数,且12345a a a a a >>>>,则12345,,,,x x x x x 的大小顺序是( )A .12345x x x x x >>>>B .42135x x x x x >>>>C .31425x x x x x >>>>D .53142x x x x x >>>> 5. 不等式21(1)37x x x -<-<+的整数解的个解( )A .等于4B .小于4C .大于5D .等于56. 在ABC △中,A O AO BC ∠=是钝角,是垂心,,则cos()OBC OCB ∠+∠的值是( ) A. BCD .12-7. 锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m , n , p,那么m :n :p 等于( )A .111a b c::; B .a b c ::C .cos cos cos A B C :: D .sin sin sin A B C ::. 8.1-可以化简成( ) A1) B1) C1 D1二.填空题9. 当x 变化时,分式22365112x x x x ++++的最小值是___________.10. 放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.11. 若方程22(1)(4)x x k --=有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.12. 锐角三角形ABC 中,30A ∠=︒.以BC 边为直径作圆,与AB , AC 分别交于D ,E ,连接DE , 把三角形ABC 分成三角形ADE 与四边形BDEC ,设它们的面积分别为12S S ,,则12S S =: ___________.第二试1. 设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积ABC HBC S S ∆∆⋅的值变小,变大,还是不变? 证明你的结论.2.ABC △中, 51213BC AC AB ===,,,在边AB ,AC 上分别取点D , E ,使线段DE将ABC △分成面积相等的两部分.试求这样的线段DE 的最小长度.3. 已知方程2200x bx c x cx b ++=++=及分别各有两个整数根12x x ,及12x x '',,且120x x >,120x x ''>. (1)求证:12120000x x x x ''<<<<,,,;(2)求证:11b c b -≤≤+;(3)求b c ,所有可能的值.。
1993年高考数学 理工农医类、全国卷 真题

1993年普通高等学校招生全国统一考试(全国卷)数学(理工农医类)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.把所选项前的字母填在题后括号内.(1)如果双曲线的实半轴长为2,焦距为6,那么该双曲线的离心率为()()()(A)45°(B)60°(C)90°(D)120°()(A)1(B)-1(C)i(D)-i(5)直线bx+ay=ab(a<0,b<0)的倾斜角是()(6)在直角三角形中两锐角为A和B,则sinAsinB()(C)既无最大值也无最小值(D)有最大值1,但无最小值(7)在各项均为正数的等比数列{an}中,若a5a6=9,则log3a1+log3a2+…+log3a10=()(A)12(B)10(C)8(D)2+log35()(A)是奇函数(B)是偶函数(C)可能是奇函数也可能是偶函数(D)不是奇函数也不是偶函数()()(10)若a、b是任意实数,且a>b,则()(11)已知集合E={θ│cosθ<sinθ,0≤θ≤2π},F={θ│tgθ<sinθ},那么E∩F为区间()(12)一动圆与两圆:x2+y2=1和x2+y2-8x+12=0都外切,则动圆圆心的轨迹为()(A)抛物线(B)圆(C)双曲线的一支(D)椭圆()(A)三棱锥(B)四棱锥(C)五棱锥(D)六棱锥(14)如果圆柱轴截面的周长l为定值,那么圆柱体积的最大值是()()(A)50项(B)17项(C)16项(D)15项(16)设a,b,c都是正数,且3a=4b=6c,那么()(17)同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则四张贺年卡不同的分配方式有()(A)6种(B)9种(C)11种(D)23种(18)已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a,b所成的角都是30°的直线有且仅有()(A)1条(B)2条(C)3条(D)4条二、填空题:把答案填在题中横线上.(20)在半径为30m的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为120°.若要光源恰好照亮整个广场,则其高度应为m(精确到0.1m).(21)在50件产品中有4件是次品,从中任意抽出5件,至少有3件是次品的抽法共种(用数字作答).(22)建造一个容积为8m3,深为2m的长方体无盖水池.如果池底和池壁的造价每平方米分别为120元和80元,那么水池的最低总造价为元.(23)设f(x)=4x-2x+1,则f-1(0)=.三、解答题:解答应写出文字说明、演算步骤.(26)如图,A1B1C1-ABC是直三棱柱,过点A1、B、C1的平面和平面ABC的交线记作l. (Ⅰ)判定直线A1C1和l的位置关系,并加以证明;(Ⅱ)若A1A=1,AB=4,BC=3,∠ABC=90°,求顶点到直线l的距离.出以M,N为焦点且过点P的椭圆方程.(29)已知关于x的实系数二次方程x2+ax+b=0有两个实数根α,β.证明: (Ⅰ)如果│α│<2,│β│<2,那么2│α│<4+b且│b│<4;(Ⅱ)如果2│α│<4+b且│b│<4,那么│α│<2,│β│<2.1993年普通高等学校招生全国统一考试(全国卷)数学(理工农医类)参考答案一、选择题:(1)C(2)B(3)C(4)D(5)C(6)B(7)B(8)A(9)A(10)D(11)A(12)C(13)D(14)A(15)B(16)B(17)B(18)B二、填空题:(19)2(20)17.3(21)4186三、解答题.(25)(26)本小题主要考查空间图形的线面关系、三棱柱的性质、空间想象能力和逻辑推理能力.解:(Ⅰ)l∥A1C1.证明如下:根据棱柱的定义知平面A1B1C1和平面ABC平行.由题设知直线A1C1=平面A1B1C1∩平面A1BC1,直线l=平面A1BC1∩平面ABC.根据两平面平行的性质定理有l∥A1C1.(Ⅱ)解法一:过点A1作A1E⊥l于E,则A1E的长为点A1到l的距离.连结AE.由直棱柱的定义知A1A⊥平面ABC.∴直线AE是直线A1E在平面ABC上的射影.又l在平面ABC上,根据三垂线定理的逆定理有AE⊥l.由棱柱的定义知A1C1∥AC,又l∥A1C1,∵l∥AC.作BD⊥AC于D,则BD是Rt△ABC斜边AC上的高,且BD=AE,在Rt△A1AE中,∵A1A=1,∠A1AE=90°,解法二:同解法一得l∥AC.由平行直线的性质定理知∠CAB=∠ABE,从而有Rt△ABC∽Rt△BEA,AE:BC=AB:AC,以下同解法一.(27)解法一:建立直角坐标系如图:以MN所在直线为x轴,线段MN的垂直平分线为y轴.(c,0)和(x0,y0).∵tgα=tg(π-∠N)=2,∴由题设知解法二:(28)(29)证法一:依题设,二次方程有两个实根α,β,所以判别式△=a2-4b≥0.平方得a2-4b<16-8a+a2,a2-4b<16+8a+a2,由此得-4(4+b)<8a<4(4+b),∴2│a│<4+b.(Ⅱ)∵2│a│<4+b,│b│<4,4±a>0;且△=a2-4b<a2-4(2│a│-4)=a2±8a+16=(4±a)2,又△≥0,∴-2<α≤β<2,得│α│<2,│β│<2.证法二:(Ⅰ)根据韦达定理│b│=│αβ│<4.因为二次函数f(x)=x2+ax+b开口向上,│α│<2,│β│<2.故必有f(±2)>0,即4+2a+b>0,2a>-(4+b);4-2a+b>0,2a<4+b.∴2│a│<4+b.(Ⅱ)由2│a│<4+b得4+2a+b>0即22+2a+b>0,f(2)>0.①及4-2a+b>0即(-2)2+(-2)a+b>0,f(-2)>0.②由此可知f(x)=0的每个实根或者在区间(-2,2)之内或者在(-2,2)之外.若两根α,β均落在(-2,2)之外,则与│b│=│αβ│<4矛盾.若α(或β)落在(-2,2)外,则由于│b│=│αβ│<4,另一个根β(或α)必须落在(-2,2)内,则与①、②式矛盾.综上所述α,β均落在(-2,2)内.∴│α│<2,│β│<2.。
1993年全国卷高考理科数学真题及答案

1993年全国卷高考理科数学真题及答案一、选择题(共17小题,每小题4分,满分68分)1.(4分)函数f(x)=sinx+cosx的最小正周期是()A.2πB.C.πD.2.(4分)如果双曲线的焦距为6,两条准线间的距离为4,那么该双曲线的离心率为()A.B.C.D.23.(4分)(2012•北京模拟)和直线3x﹣4y+5=0关于x 轴对称的直线的方程为()A.3x+4y﹣5=0 B.3x+4y+5=0 C.﹣3x+4y﹣5=0 D.﹣3x+4y+5=04.(4分)极坐标方程所表示的曲线是()A.焦点到准线距离为的椭圆B .焦点到准线距离为的双曲线右支C.焦点到准线距离为的椭圆D.焦点到准线距离为的双曲线右支5.(4分)在[﹣1,1]上是()A.增函数且是奇函数B.增函数且是偶函数C.减函数且是奇函数D.减函数且是偶函数6.(4分)的值为()A.B.C.D.7.(4分)(2002•广东)设集合M=,N=,则()A.M=N B.M⊂N C.M⊃N D.M ∩N=Φ8.(4分)sin20°cos70°+sin10°sin50°的值是()A.B.C.D.9.(4分)参数方程(0<θ<2π)表示()A.双曲线的一支,这支过点B.抛物线的一部分,这部分过C.双曲线的一支,这支过点D.抛物线的一部分,这部分过10.(4分)若a、b是任意实数,且a>b,则()A.a2>b2B.C.l g(a﹣b)>0 D.11.(4分)一动圆与两圆x2+y2=1和x2+y2﹣8x+12=0都外切,则动圆圆心轨迹为()A.圆B.椭圆C.双曲线的一支D.抛物线12.(4分)圆柱轴截面的周长l为定值,那么圆柱体积的最大值是()A.B.C.D.13.(4分)(+1)4(x﹣1)5展开式中x4的系数为()A.﹣40 B.10 C.40 D.4514.(4分)直角梯形的一个内角为45°,下底长为上底长的,这个梯形绕下底所在的直线旋转一周所成的旋转体的全面积为(5+)π,则旋转体的体积为()A.2πB.C.D.15.(4分)已知a1,a2,…,a8为各项都大于零的等比数列,公式q≠1,则()A.a1+a8>a4+a5B.a1+a8<a4+a5C.a1+a8=a4+a5D.a1+a8和a4+a5的大小关系不能由已知条件确定16.(4分)(2014•黄山一模)设有如下三个命题:甲:相交直线l、m都在平面α内,并且都不在平面β内;乙:直线l、m中至少有一条与平面β相交;丙:平面α与平面β相交.当甲成立时()A.乙是丙的充分而不必要条件B.乙是丙的必要而不充分条件C.乙是丙的充分且必要条件D.乙既不是丙的充分条件又不是丙的必要条件17.(4分)将数字1,2,3,4填入标号为1,2,3,4的四个方格里,每格填一个数字,则每个方格的标号与所填的数字均不相同的填法有()A.6种B.9种C.11种D.23种二、填空题(共6小题,每小题4分,满分24分)18.(4分)= _________ .19.(4分)若双曲线=1与圆x2+y2=1没有公共点,则实数k的取值范围为_________ .20.(4分)从1,2,…,10这十个数中取出四个数,使它们的和为奇数,共有_________ 种取法(用数字作答).21.(4分)设f (x)=4x﹣2x+1,则f﹣1(0)= _________ .22.(4分)建造一个容积为8m3,深为2m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,则水池的最低造价为_________ .23.(4分)如图,ABCD是正方形,E是AB的中点,如将△DAE和△CBE分别沿虚线DE和CE折起,使AE与BE重合,记A与B重合后的点为P,则面PCD与面ECD所成的二面角为_________ 度.三、解答题(共5小题,满分58分)24.(10分)已知f(x)=log a(a>0,a≠1).(1)求f(x)的定义域;(2)判断f(x)的奇偶性并予以证明;(3)求使f(x)>0的x取值范围.25.(12分)已知数列S n为其前n项和.计算得观察上述结果,推测出计算S n的公式,并用数学归纳法加以证明.26.(12分)已知:平面α∩平面β=直线a.α,β同垂直于平面γ,又同平行于直线b.求证:(1)a⊥γ;(2)b⊥γ.27.(12分)在面积为1的△PMN中,tan∠PMN=,tan∠MNP=﹣2.建立适当的坐标系,求以M,N为焦点且过点P的椭圆方程.28.(12分)设复数z=cosθ+isinθ(0<θ<π),,并且,,求θ.1993年全国统一高考数学试卷(理科)参考答案与试题解析一、选择题(共17小题,每小题4分,满分68分)1.(4分)函数f(x)=sinx+cosx的最小正周期是()A.2πB.C.πD.考点:三角函数中的恒等变换应用.分析:把三角函数式整理变形,变为f(x)=Asin(ωx+φ)的形式,再用周期公式求出周期,变形时先提出,式子中就出现两角和的正弦公式,公式逆用,得到结论.解答:解:∵f(x)=sinx+cosx=(=,∴T=2π,故选A点评:本题关键是逆用公式,抓住公式的结构特征对提高记忆公式起到至关重要的作用,而且抓住了公式的结构特征,有利于在解题时观察分析题设和结论等三角函数式中所具有的相似性的结构特征,联想到相应的公式,从而找到解题的切入点.2.(4分)如果双曲线的焦距为6,两条准线间的距离为4,那么该双曲线的离心率为()A.B.C.D.2考点:双曲线的简单性质.专题:计算题.分析:由双曲线的焦距为6,两条准线间的距离为4,能求出a,c,从而得到该双曲线的离心率.解答:解:由题意知,∴a2=6,c=3,∴.故选C.点评:本题考查双曲线的离心率、准线方程、焦距,要求熟练掌握双曲线的性质.3.(4分)(2012•北京模拟)和直线3x﹣4y+5=0关于x轴对称的直线的方程为()A.3x+4y﹣5=0 B.3x+4y+5=0 C.﹣3x+4y﹣5=0 D.﹣3x+4y+5=0考点:与直线关于点、直线对称的直线方程.分析:求出和直线3x﹣4y+5=0关于x轴对称的直线的斜率,再求出直线3x﹣4y+5=0和x轴的交点,可求答案.解答:解:和直线3x﹣4y+5=0关于x轴对称的直线,其斜率与直线3x﹣4y+5=0的斜率相反,设所求直线为3x+4y+b=0,两直线在x轴截距相等,所以所求直线是3x+4y+5=0.故选B.点评:本题是直线的对称问题,一般要用垂直平分解答;本题方法较多,由于对称轴是坐标轴,所以借助斜率,比较简单.4.(4分)极坐标方程所表示的曲线是()A.焦点到准线距离为的椭圆B.焦点到准线距离为的双曲线右支C.焦点到准线距离为的椭圆D.焦点到准线距离为的双曲线右支考点:简单曲线的极坐标方程.专题:计算题.分析:利用圆锥曲线统一的极坐标方程,求出圆锥曲线的离心率和焦点到准线距离,从而确定选项.解答:解:将原极坐标方程为,化成:极坐标方程为ρ=,对照圆锥曲线统一的极坐标方程得:e=>1,表示双曲线,且焦点到准线距离为.故选B.点评:本题主要考查了圆锥曲线的极坐标方程,属于基础题.5.(4分)在[﹣1,1]上是()A.增函数且是奇函数B.增函数且是偶函数C.减函数且是奇函数D.减函数且是偶函数考点:幂函数的性质.专题:数形结合.分析:做出幂函数的图象,根据幂函数的图象与性质:可得在[﹣1,1]上的单调性和奇偶性.解答:解:考查幂函数.∵>0,根据幂函数的图象与性质可得在[﹣1,1]上的单调增函数,是奇函数.故选A.点评:本题主要考查幂函数的图象与性质,幂函数是重要的基本初等函数模型之一.学习幂函数重点是掌握幂函数的图形特征,即图象语言,熟记幂函数的图象、性质.6.(4分)的值为()A.B.C.D.考点:极限及其运算.专题:计算题.分析:分子分母都除以n2,原式简化为,由此可得到的值.解答:解:==.点评:本题考查数列的极限,解题时要注意正确选用公式.7.(4分)(2002•广东)设集合M=,N=,则()A.M=N B.M⊂N C.M⊃N D.M∩N=Φ考点:集合的包含关系判断及应用.分析:从元素满足的公共属性的结构入手,首先对集合N中的k分奇数和偶数讨论,易得两集合的关系.解答:解:当k=2m(为偶数)时,N==当k=2m﹣1(为奇数)时,N===M∴M⊂N故选B点评:本题主要考查集合表示方法中的描述法.8.(4分)sin20°cos70°+sin10°sin50°的值是()A.B.C.D.考点:三角函数中的恒等变换应用.分析:从题目的结构形式来看,本题是要逆用两角和或差的正弦余弦公式,但是题目又不完全符合,因此有一个整理的过程,整理发现,刚才直观的认识不准确,要前后两项都用积化和差,再合并同类项.解答:解:原式=]==,故选A点评:在解题时观察分析题设和结论等三角函数式中所具有的相似性的结构特征,联想到相应的公式,从而找到解题的切入点.本题开始考虑时差点出错,这是解题时好多同学要经历的过程.9.(4分)参数方程(0<θ<2π)表示()A.双曲线的一支,这支过点B.抛物线的一部分,这部分过C.双曲线的一支,这支过点D.抛物线的一部分,这部分过考点:参数方程化成普通方程.专题:计算题.分析:将参数方程化为普通方程,然后再对A、B、C、D进行判断;解答:解:∵x=|cos +sin|,∴x2=1+sinθ,∵y=(1+sinθ),∴y=x2,是抛物线;当x=1时,y=;故选B.点评:此题考查参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,这也是每年高考必考的热点问题.10.(4分)若a、b是任意实数,且a>b,则()A.a2>b2B.C.l g(a﹣b)>0 D.考点:不等式比较大小.专题:综合题.分析:由题意可知a>b,对于选项A、B、C举出反例判定即可.解答:解:a、b是任意实数,且a>b,如果a=0,b=﹣2,显然A不正确;如果a=0,b=﹣2,显然B无意义,不正确;如果a=0,b=﹣,显然C,lg>0,不正确;满足指数函数的性质,正确.故选D.点评:本题考查比较大小的方法,考查各种代数式的意义和性质,是基础题.11.(4分)一动圆与两圆x2+y2=1和x2+y2﹣8x+12=0都外切,则动圆圆心轨迹为()A.圆B.椭圆C.双曲线的一支D.抛物线考点:双曲线的定义.专题:计算题.分析:设动圆P的半径为r,然后根据⊙P与⊙O:x2+y2=1,⊙F:x2+y2﹣8x+12=0都外切得|PF|=2+r、|PO|=1+r,再两式相减消去参数r,则满足双曲线的定义,问题解决.解答:解:设动圆的圆心为P,半径为r,而圆x2+y2=1的圆心为O(0,0),半径为1;圆x2+y2﹣8x+12=0的圆心为F(4,0),半径为2.依题意得|PF|=2+r|,|PO|=1+r,则|PF|﹣|PO|=(2+r)﹣(1+r)=1<|FO|,所以点P的轨迹是双曲线的一支.故选C.点评:本题主要考查双曲线的定义.12.(4分)圆柱轴截面的周长l为定值,那么圆柱体积的最大值是()A.B.C.D.考点:旋转体(圆柱、圆锥、圆台).专题:计算题;综合题.分析:设出圆柱的底面半径和高,求出体积表达式,通过求导求出体积的最大值.解答:解:圆柱底面半径R,高H,圆柱轴截面的周长L为定值:4R+2H=L,H=﹣2R,V=SH=πR2H=πR2(﹣2R)=πR2﹣2πR3求导:V'=πRL﹣6πR2令V'=0,πRL﹣6πR2=0,πR(L﹣6R)=0,L﹣6R=0,R=,当R=,圆柱体积的有最大值,圆柱体积的最大值是:V=πR2﹣2πR3=故选A.点评:本题考查旋转体的体积,导数的应用,是中档题.13.(4分)(+1)4(x﹣1)5展开式中x4的系数为()A.﹣40 B.10 C.40 D.45考点:二项式定理的应用.专题:计算题.分析:先将展开式的系数转化成几个二项展开式系数乘积的和,再利用二项展开式的通项公式求出各个二项式的系数.解答:解:展开式中x4的系数是下列几部分的和:的常数项与(x﹣1)5展开式的含x4的项的系数的乘积含x项的系数与(x﹣1)5展开式的含x3的项的系数的乘积含x2项的系数与(x﹣1)5展开式的含x2的项的系数的乘积∵展开式的通项为(x﹣1)5展开式的通项为T k+1=C5r x5﹣r(﹣1)r=(﹣1)r C5r x5﹣r∴展开式中x4的系数为C40(﹣C51)++C44(﹣C53)=45故选项为D点评:本题考查数学的等价转化的能力和二项展开式的通项公式的应用.14.(4分)直角梯形的一个内角为45°,下底长为上底长的,这个梯形绕下底所在的直线旋转一周所成的旋转体的全面积为(5+)π,则旋转体的体积为()A.2πB.C.D.考点:旋转体(圆柱、圆锥、圆台).专题:计算题.分析:由题意可知,这个几何体的面积是圆柱中一个圆加一个长方形加一个扇形的面积,而这个几何体的体积是一个圆锥加一个同底圆柱的体积.再根据题目中的条件求解即可.解答:解:这个几何体的面积是圆柱中一个圆加一个长方形加一个扇形的面积,圆的面积,直角腰为半径,长方形的面积,圆的周长为长,上底为宽,扇形的面积,圆的周长为弧长,另一腰则为扇形的半径.设上底为x,则下底为,直角腰为,另一腰为整个面积式子为,解得x=±2,因为x>0,所以x=﹣2舍去,x=2.而这个几何体的体积是一个圆锥加一个同底圆柱的体积,圆锥的高,下底减上底得圆锥的高为1,圆柱体积=Sh=h=π×12×2=2π,圆锥体积=π所以整个几何体的体积为.故选D.点评:本题考查学生的空间想象能力,和逻辑思维能力,等量之间的转换,是中档题.15.(4分)已知a1,a2,…,a8为各项都大于零的等比数列,公式q≠1,则()A.a1+a8>a4+a5B.a1+a8<a4+a5C.a1+a8=a4+a5D.a1+a8和a4+a5的大小关系不能由已知条件确定考点:等比数列.分析:用作差法比较即可.解答:解:a1+a8﹣(a4+a5)=a1(1+q7﹣q3﹣q4)=a1(1+q)(q2+q+1)(q﹣1)2(1+q2)又∵a1>0,a1,a2,…,a8为各项都大于零的等比数列∴q>0∴a1+a8﹣(a4+a5)>0故选A点评:本题考查比较法和等比数列通项公式的应用.16.(4分)(2014•黄山一模)设有如下三个命题:甲:相交直线l、m都在平面α内,并且都不在平面β内;乙:直线l、m中至少有一条与平面β相交;丙:平面α与平面β相交.当甲成立时()A.乙是丙的充分而不必要条件B.乙是丙的必要而不充分条件C.乙是丙的充分且必要条件D.乙既不是丙的充分条件又不是丙的必要条件考点:空间中直线与平面之间的位置关系;充要条件.专题:证明题;压轴题.分析:判断乙是丙的什么条件,即看乙⇒丙、丙⇒乙是否成立.当乙成立时,直线l、m中至少有一条与平面β相交,则平面α与平面β至少有一个公共点,故相交相交.反之丙成立时,若l、m中至少有一条与平面β相交,则l∥m,由已知矛盾,故乙成立.解答:解:当甲成立,即“相交直线l、m都在平面α内,并且都不在平面β内”时,若“l、m中至少有一条与平面β相交”,则“平面α与平面β相交”成立;若“平面α与平面β相交”,则“l、m中至少有一条与平面β相交”也成立故选C.点评:本题考查空间两条直线、两个平面的位置关系判断、充要条件的判断,考查逻辑推理能力.17.(4分)将数字1,2,3,4填入标号为1,2,3,4的四个方格里,每格填一个数字,则每个方格的标号与所填的数字均不相同的填法有()A.6种B.9种C.11种D.23种考点:排列、组合及简单计数问题.专题:计算题;压轴题.分析:首先计算4个数字填入4个空格的所有情况,进而分析计算四个数字全部相同,有1个数字相同的情况,有2个数字相同情况,有3个数字相同的情况数目,由事件间的相互关系,计算可得答案.解答:解:根据题意,数字1,2,3,4填入标号为1,2,3,4的四个方格里,共A44=24种填法,其中,四个数字全部相同的有1种,有1个数字相同的有4×2=8种情况,有2个数字相同的有C42×1=6种情况,有3个数字相同的情况不存在,则每个方格的标号与所填的数字均不相同的填法有24﹣1﹣8﹣6=9种,故选B.点评:本题考查排列、组合的运用,注意此类题目的操作性很强,必须实际画图操作,认真分析.二、填空题(共6小题,每小题4分,满分24分)18.(4分)= .考点:任意角的三角函数的定义.专题:计算题.分析:利用两角和正玹公式展开,利用反三角函数值的求法,即可求出答案解答:解:sin(arccos+arccos)=sin(arccos)cos(arccos)+cos(arccos)sin(arccos)==故答案为;点评:本题考查三角函数求值,不过学生对反三角函数不是很理解,希望学生能抓住实质,加大训练量.19.(4分)若双曲线=1与圆x2+y2=1没有公共点,则实数k的取值范围为{k|或} .考点:双曲线的简单性质.专题:计算题.分析:由双曲线=1与圆x2+y2=1没有公共点知圆半径的长小于双曲线的实半轴的长,由此可以求出实数k的取值范围.解答:解:∵双曲线=1与圆x2+y2=1没有公共点,∴|3k|>1,∴.解得或.实数k的取值范围为{k|或}.答案为{k|或}.点评:熟练掌握圆和双曲线的图象和性质即可顺利求解.20.(4分)从1,2,…,10这十个数中取出四个数,使它们的和为奇数,共有100 种取法(用数字作答).考点:组合及组合数公式;排列、组合的实际应用.分析:根据题意,将这10个数分为奇数与偶数两个组,每组各5个数;分析可得,若取出的四个数的和为奇数,则取出的四个数必有1个或3个奇数;分别求出两种情况下的取法情况数,相加可得答案.解答:解:根据题意,将这10个数分为奇数与偶数两个组,每组各5个数;若取出的四个数的和为奇数,则取出的四个数必有1个或3个奇数;若有1个奇数时,有C51•C53=50种取法,若有3个奇数时,有C51•C53=50种取法,故符合题意的取法共50+50=100种取法;故答案为100.点评:本题考查利用组合解决常见计数问题的方法,解本题时,注意先分组,进而由组合的方法,结合乘法计数原理进行计算.21.(4分)设f (x)=4x﹣2x+1,则f﹣1(0)= 1 .考点:反函数.专题:计算题.分析:欲求f﹣1(0),根据反函数的定义知,只要求出使等式4x﹣2x+1=0,成立的x的值即可.解答:解:∵4x﹣2x+1=0,2x(2x﹣2)=0,∴2x﹣2=0得:x=1.∴f﹣1(0)=1.故答案为1.点评:本题主要考查了反函数的概念,属于基础题之列.22.(4分)建造一个容积为8m3,深为2m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,则水池的最低造价为1760 .考点:函数模型的选择与应用.专题:应用题;压轴题.分析:欲求水池的最低造价,先设长x,则宽,列出总造价,是一个关于x的函数式,最后利用基本不等式求出此函数式的最小值即可.解答:解:设长x,则宽,造价y=4×120+4x×80+×80≥1760,当且仅当:4x×80=×80,即x=2时取等号.故答案为:1760.点评:本小题主要考查函数模型的选择与应用,属于基础题.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.23.(4分)如图,ABCD是正方形,E是AB的中点,如将△DAE和△CBE分别沿虚线DE和CE折起,使AE与BE重合,记A与B重合后的点为P,则面PCD与面ECD所成的二面角为30 度.考点:与二面角有关的立体几何综合题.专题:计算题;压轴题.分析:二面角的度量关键在于作出它的平面角,取CD的中点M,连接PM、EM,因为PD=PC,所以PM⊥CD;同理因为ED=EC,所以EM⊥CD,故∠PME即为面PCD与面ECD所成二面角的平面角.解答:解:设正方形的边长为2,取CD的中点M,连接PM、EM,∵PD=PC,∴PM⊥CD∵ED=EC,∴EM⊥CD故∠PME即为面PCD与面ECD所成二面角的平面角.在△PME中:PE=1,PM=,EM=2,∴cos∠PME=∴∠PME=30°故答案为:30.点评:本小题主要考查棱锥的结构特征,二面角和线面关系等基本知识,同时考查空间想象能力和推理、运算能力.三、解答题(共5小题,满分58分)24.(10分)已知f(x)=log a(a>0,a≠1).(1)求f(x)的定义域;(2)判断f(x)的奇偶性并予以证明;(3)求使f(x)>0的x取值范围.考点:对数函数的定义域;函数奇偶性的判断.分析:(1)求对数函数的定义域,只要真数大于0即可,转化为解分式不等式.(2)利用奇偶性的定义,看f(﹣x)和f(x)的关系,注意到和互为倒数,其对数值互为相反数;也可计算f(﹣x)+f(x)=0得到.(3)有对数函数的图象可知,要使f (x)>0,需分a>0和a<0两种境况讨论.解答:解:(1)由对数函数的定义知.如果,则﹣1<x<1;如果,则不等式组无解.故f(x)的定义域为(﹣1,1)(2)∵,∴f(x)为奇函数.(3)(ⅰ)对a>1,log a等价于,①而从(1)知1﹣x>0,故①等价于1+x>1﹣x,又等价于x>0.故对a>1,当x∈(0,1)时有f(x)>0.(ⅱ)对0<a<1,log a等价于0<.②而从(1)知1﹣x>0,故②等价于﹣1<x<0.故对0<a<1,当x∈(﹣1,0)时有f(x)>0.点评:本题考查对数函数的性质:定义域、奇偶性、单调性等知识,难度一般.25.(12分)已知数列S n为其前n项和.计算得观察上述结果,推测出计算S n的公式,并用数学归纳法加以证明.考点:数列递推式;数学归纳法.专题:证明题.分析:观察分析题设条件可知.然后再用数学归纳法进行证明.解答:解:观察分析题设条件可知证明如下:(1)当n=1时,,等式成立.(Ⅱ)设当n=k时等式成立,即则======由此可知,当n=k+1时等式也成立.根据(1)(2)可知,等式对任何n∈N都成立点评:本题考查数列性质的综合应用,解题时要注意数学归纳法的证明步骤,注意培养计算能力.26.(12分)已知:平面α∩平面β=直线a.α,β同垂直于平面γ,又同平行于直线b.求证:(1)a⊥γ;(2)b⊥γ.考点:直线与平面垂直的判定.专题:证明题;压轴题.分析:(1)在γ内任取一点P并于γ内作直线PM⊥AB,PN⊥AC,由面面垂直的性质得PM⊥α,PM⊥a;同理证明PN⊥a,这样a垂直于面γ内的2条相交直线,从而a⊥γ.(2)通过α,β同垂直于平面γ,又同平行于直线b,利用线面平行的性质定理证明,b∥a,由(1)知a⊥γ,从而证得b⊥γ.解答:证明:(1)设α∩γ=AB,β∩γ=AC.在γ内任取一点P并于γ内作直线PM⊥AB,PN⊥AC.∵γ⊥α,∴PM⊥α.而a⊂α,∴PM⊥a.同理PN⊥a.又PM⊂γ,PN⊂γ,∴a⊥γ.(2)于a上任取点Q,过b与Q作一平面交α于直线a1,交β于直线a2.∵b∥α,∴b∥a1.同理b∥a2.∵a1,a2同过Q且平行于b,∵a1,a2重合.又a1⊂α,a2⊂β,∴a1,a2都是α、β的交线,即都重合于a.∵b∥a1,∴b∥a.而a⊥γ,∴b⊥γ.点评:本题考查证明线面垂直的证明方法.27.(12分)在面积为1的△PMN中,tan∠PMN=,tan∠MNP=﹣2.建立适当的坐标系,求以M,N为焦点且过点P的椭圆方程.考点:椭圆的标准方程.专题:计算题;压轴题.分析:以MN所在直线为x轴,MN的垂直平分线为y轴建立直角坐标系,设以M,N为焦点且过点P的椭圆方程和焦点坐标,根据tanM=,tanα=tg(π﹣∠MNP)=2,得直线PM和PN的直线方程,将此二方程联立解得x和y,可知点P的坐标,根据,|MN|=2c,MN上的高为点P的纵坐标,根据三角形面积公式表示出出△MNP的面积求得c,则点P的坐标可得.由两点间的距离公式求得|PM|和|PN|,进而根据椭圆的定义求得a,进而求得b,则椭圆方程可得.解答:解:如图,以MN所在直线为x轴,MN的垂直平分线为y轴建立直角坐标系,设以M,N为焦点且过点P的椭圆方程为,焦点为M(﹣c,0),N(c,0).由tan∠PMN=,tan∠MNP=﹣2,tanα=tan(π﹣∠MNP)=2,得直线PM和直线PN的方程分别为y=(x+c)和y=2(x﹣c).将此二方程联立,解得x=c,y=c,即P点坐标为(c,c).在△MNP中,|MN|=2c,MN上的高为点P的纵坐标,故.由题设条件S△MNP=1,∴c=,即P点坐标为.由两点间的距离公式,.得.又b2=a2﹣c2=,故所求椭圆方程为.点评:本题主要考查坐标系、椭圆的概念和性质、直线方程以及综合应用能力.28.(12分)设复数z=cosθ+isinθ(0<θ<π),,并且,,求θ.考点:复数代数形式的混合运算.专题:压轴题.分析:化简ω,利用,求出θ的三角函数值,再用,来验证ω,从而求出θ的值.解答:解法一===tg2θ(sin4θ+icos4θ).,.因0<θ<π,故有(ⅰ)当时,得或,这时都有,得,适合题意.(ⅱ)当时,得或,这时都有,得,不适合题意,舍去.综合(ⅰ)、(ⅱ)知或.解法二z4=cos4θ+isin4θ.记φ=4θ,得..==.∵,,①②③∴当①成立时,②恒成立,所以θ应满足(ⅰ),或(ⅱ),解(ⅰ)得或.(ⅱ)无解.综合(ⅰ)、(ⅱ)或.点评:本题考查复数的基本概念和运算,三角函数式的恒等变形及综合解题能力;注意分类讨论思想的应用,难度较大.。
1993年中国数学奥林匹克试题解答

1.设n是奇数.试证:存在2n个整数.a1,a2,…,an;b1,b2,…,bn,使对任一整数k,0<k<n,下列3n个数a i +ai+1,ai+bi,bi+bi+k(i=1,2,…,n;其中an+1=a1,bn+j=bj,0<j<n)被3n除所得余数互不相同.证:取ai =3i,bi=3i+1(1≤i≤n),则ai+ai+1=6i+3ai+bi=6i+1显然,6i+3,6j+1,6t+3k+2,或6t+3k-3n+2,除以3余数分别为0,1,2.因此它们被3n除后余数各不相同.在1≤i≤j≤n时,(6j+3)-(6i+3)=6(j-i).因为n是奇数,0<j-i<n,所以6(j-i)不被3n整除,即6j+3与6i+3被3n除,余数不同.同样,在1≤i<j≤n时,6j+1与6i+1被3n除,余数不同.6j+3k+2或6j+3k-3n+2与6i+3k+2或6i+3k-3n+2被3n除,余数不同.因此,所取的ai ,bi(1≤i≤n)符合要求.2.给定k∈N及实数a>0,在条件k1+k2+…+k r=k(k i∈N,1≤r≤k)下,求的最大值.当且仅当k1,k2,…,k r中有r-1个1,一个为k-r+1时等号成立,所以最大值即(r-1)a+a k-r+1.3.设圆K与K1同心,半径分别为R,R1、R1>R.四边形ABCD内接于圆K,四边形A1B1C1D1内接于圆K1.点A1、B1、C1、D1分别在射线CD、DA、AB、BC上.求证:证:如图,设ABCD各边分别为a、b、c、d,AB1=x,BC1=y,CD1=z,DA1=ω.设B'D'为垂直于AC的直径,则S△ABC +S△ADC≤S△AB'C+S△AD'C即 ab+cd≤AB'2+AD'2=B'D'2=4R2同理可证ad+bc≤4R2从而结论成立.4.给定集合S={Z1,Z2,…,Z1993},其中Z1,Z2,…,Z1993为非零复数(可视为平面上非零向量).求证:可以把S中元素分成若干子集,使得(1)S中每个元素属于且仅属于一个子集;(2)每一子集中任一复数与该子集所有复数之和的夹角不超过90°;(3)将任二子集中复数分别作和,所得和数之间夹角大于90°.证:现对任意正整数n给以证明.设非零复数集S={Z1,…,Zn}.对S每个非空子集A,其中所有数之和,称为A之和.S共有2n-1个非空子集,其中必有一个子集S1,其和的模|a1|最大.若S≠S1,对S\S1,取其非空子集S2,使其和的模|a2|最大.如比等等.因S为有限集,故经若干步后,即得S的一个划分:S1,S2,…,Sk,它们的和a1,a2,…,ak的模分别是S,S\S1,S\(S1∪S2),…,S\(S1∪S2∪…∪Sk-1)的非空子集和的最大模.这样的划分,条件(1)显然满足.若某个Sr中有一元素Z与ar的夹角>90°,则如图a,|ar-Z|>|ar|.ar-Z是S\(S1U…USr-1)的非空子集Sr\{Z}之和,与Sr的选取矛盾.若ar 与at(1≤r<t≤k=的夹角≤90°,则如图(b),|ar+at|>|ar|.ar+at 是S\(S1∪…∪Sr-1)不空子集Sr∪St之和,这又与Sr选取矛盾.因此,所述划分满足条件(1)~(3).【注】因为平面上至多有三个向量,它们之间两两的夹角都大于90°,故S至多分为三个子集.5.10人到书店买书,如果已知(1)每人都买了三本书;(2)任二人所买书中都至少有一本相同,问最受欢迎的书(购买人数最多者)最少有几人购得?为什么?解:设最受欢迎的书有k人购买.每人买3本书,共买30本书.若k≤4,由于430,不可能每种书均被4人购买.设第一个人购的书为a、b、c,并且买a的人≤3个,则与第一个人的公共图书为a的,不超过2人;为b或c的,均不超过3人.从而总人数≤1+2+3+3=9,矛盾!因此k≥5.现给出一种k=5的购书法:因此,被购买人数最多的一种书,最少有5人购买.6.设函数f:R+→R+满足条件:对任意x、y∈R+,f(xy)≤f(x)f(y).试证:对任总x>0,n∈N,有证:f(x2)≤f2(x),所以f(x2)≤f(x)f1/2(x2).假设有则≥f n-1(x n)所以(1)对所有的自然数n成立.。
1993年试题全国高考数学试题及参考答案

1993年试题(理工农医类)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.把所选项前的字母填在题后括号内.(1)如果双曲线的实半轴长为2,焦距为6,那么该双曲线的离心率为【】[Key]一、选择题:本题考查基本知识和基本运算.(1)C【】[Key] (2)B(A)45°(B)60°(C)90°(D)120°【】[Key] (3)C(A)1 (B)-1 (C)i (D)-i【】[Key] (4)D(5)直线bx+ay=ab(a<0,b<0)的倾斜角是【】[Key] (5)C(6)在直角三角形中两锐角为A和B,则sinAsinB(C)既无最大值也无最小值(D)有最大值1,但无最小值【】[Key] (6)B(7)在各项均为正数的等比数列{a n}中,若a5a6=9,则log3a1+log3a2+…+log3a10=(A)12 (B)10 (C)8 (D)2+log35【】[Key] (7)B(A)是奇函数(B)是偶函数(C)可能是奇函数也可能是偶函数(D)不是奇函数也不是偶函数【】[Key] (8)A(A)线段(B)双曲线的一支(C)圆弧(D)射线【】[Key] (9)A(10)若a、b是任意实数,且a>b,则【】[Key] (10)D(11)已知集合E={θ│cosθ<sinθ,0≤θ≤2π},F={θ│tgθ<sinθ},那么E∩F为区间【】[Key] (11)A(12)一动圆与两圆:x2+y2=1和x2+y2-8x+12=0都外切,则动圆圆心的轨迹为(A)抛物线(B)圆(C)双曲线的一支(D)椭圆【】[Key] (12)C(A)三棱锥(B)四棱锥(C)五棱锥(D)六棱锥【】[Key] (13)D(14)如果圆柱轴截面的周长l为定值,那么圆柱体积的最大值是【】[Key] (14)A(A)50项(B)17项(C)16项(D)15项【】[Key] (15)B(16)设a,b,c都是正数,且3a=4b=6c,那么【】[Key] (16)B(17)同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则四张贺年卡不同的分配方式有(A)6种(B)9种(C)11种(D)23种【】[Key] (17)B(18)已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a,b所成的角都是30°的直线有且仅有(A)1条(B)2条(C)3条(D)4条【】[Key] (18)B二、填空题:把答案填在题中横线上.(20)在半径为30m的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为120°.若要光源恰好照亮整个广场,则其高度应为m(精确到0.1m).(21)在50件产品中有4件是次品,从中任意抽出5件,至少有3件是次品的抽法共种(用数字作答).(22)建造一个容积为8m3,深为2m的长方体无盖水池.如果池底和池壁的造价每平方米分别为120元和80元,那么水池的最低总造价为元.(23)设f(x)=4x-2x+1,则f-1(0)= .[Key] 二、填空题:本题考查基本知识和基本运算.(19)2 (20)17.3 (21)4186三、解答题:解答应写出文字说明、演算步骤.[Key] 三、解答题.(25)本小题考查对数函数的概念及性质,不等式的解法.(26)如图,A1B1C1-ABC是直三棱柱,过点A1、B、C1的平面和平面ABC的交线记作l.(Ⅰ)判定直线A1C1和l的位置关系,并加以证明;(Ⅱ)若A1A=1,AB=4,BC=3,∠ABC=90°,求顶点到直线l的距离.[Key] (26)本小题主要考查空间图形的线面关系、三棱柱的性质、空间想象能力和逻辑推理能力.解:(Ⅰ)l∥A1C1.证明如下:根据棱柱的定义知平面A1B1C1和平面ABC平行.由题设知直线A1C1=平面A1B1C1∩平面A1BC1,直线l=平面A1BC1∩平面ABC.根据两平面平行的性质定理有l∥A1C1.(Ⅱ)解法一:过点A1作A1E⊥l于E,则A1E的长为点A1到l的距离.连结AE.由直棱柱的定义知A1A⊥平面ABC.∴直线AE是直线A1E在平面ABC上的射影.又l在平面ABC上,根据三垂线定理的逆定理有AE⊥l.由棱柱的定义知A1C1∥AC,又l∥A1C1,∵l∥AC.作BD⊥AC于D,则BD是Rt△ABC斜边AC上的高,且BD=AE,在Rt△A1AE中,∵A1A=1,∠A1AE=90°,解法二:同解法一得l∥AC.由平行直线的性质定理知∠CAB=∠ABE,从而有Rt△ABC∽Rt△BEA,AE:BC=AB:AC,以下同解法一.出以M,N为焦点且过点P的椭圆方程.[Key] (27)本小题主要考查坐标系、椭圆的概念和性质、直线方程以及综合应用的能力.解法一:建立直角坐标系如图:以MN所在直线为x轴,线段MN的垂直平分线为y轴.(c,0)和(x0,y0).∵tgα=tg(π-∠N)=2,∴由题设知解法二:[Key] (28)本小题考查复数的基本概念和运算,三角函数式的恒等变形及综合解题能力.(29)已知关于x的实系数二次方程x2+ax+b=0有两个实数根α,β.证明:(Ⅰ)如果│α│<2,│β│<2,那么2│α│<4+b且│b│<4;(Ⅱ)如果2│α│<4+b且│b│<4,那么│α│<2,│β│<2.[Key] (29)本小题考查一元二次方程根与系数的关系,绝对值不等式的性质和证明;逻辑推理能力和分析问题、解决问题的能力.证法一:依题设,二次方程有两个实根α,β,所以判别式△=a2-4b≥0.平方得a2-4b<16-8a+a2,a2-4b<16+8a+a2,由此得-4(4+b)<8a<4(4+b),∴2│a│<4+b.(Ⅱ)∵2│a│<4+b,│b│<4,4±a>0;且△=a2-4b<a2-4(2│a│-4)=a2±8a+16=(4±a)2,又△≥0,∴-2<α≤β<2,得│α│<2,│β│<2.证法二:(Ⅰ)根据韦达定理│b│=│αβ│<4.因为二次函数f(x)=x2+ax+b开口向上,│α│<2,│β│<2.故必有f(±2)>0,即4+2a+b>0,2a>-(4+b);4-2a+b>0,2a<4+b.∴2│a│<4+b.(Ⅱ)由2│a│<4+b得4+2a+b>0即22+2a+b>0,f(2)>0. ①及4-2a+b>0即(-2)2+(-2)a+b>0,f(-2)>0. ②由此可知f(x)=0的每个实根或者在区间(-2,2)之内或者在(-2,2)之外.若两根α,β均落在(-2,2)之外,则与│b│=│αβ│<4矛盾.若α(或β)落在(-2,2)外,则由于│b│=│αβ│<4,另一个根β(或α)必须落在(-2,2)内,则与①、②式矛盾.综上所述α,β均落在(-2,2)内.∴│α│<2,│β│<2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1993年全国大学生数学模型竞赛试题
(1993年10月15日--17日)
A题非线性交调的频率设计
如果一晨线性器件输入u(t)gn 与输出y(t)的关系是 y(t)=u(t)+u2(t)(其中t 是时间),那么当输入是包含频率的信号时,输出中不公是包含输入信号,而且还会出现等新的频率成分,这些新的频率称为交调,如果交调出现在原有频率的附近,就会形成噪声干扰,因此工程设计中对交调的出现有一定的要求。
现有一SCS(非线性)系统,其输入输出关系由如下一组数据给出
输入U 0 5 10 20 30 40 50 60 80
输出Y 0 2.25 6.80 20.15 35.70 56.40 75.10 87.85 98.50
输入信号为u(t)=A1cos2πf1t+A2cos2πf2t+A3cos2πf3t,其中A1=25,A2是输入信号振幅的频率f1,f2,f3的设计要求为:
1)36≤f1≤40,41≤f2≤50,46≤f3≤53.
2)输出中的交调均不得出现在fi±5的范围内(i=1,2,3),此范围称为fi的接收带(参见下图)
3)定义输出中的信噪比SNR=10log10(Bi2(单位:分),其中是Bi输出中对应于频率为fn 信号的振幅,Cn是某一频率为的交调的振幅,若fn出现在fn=fi±6处(i=1,2,3),则对应的SNR应大于10分贝(参见上图)
4)fi不得出现在fi的接带内(i,j=1,2,3,ij)
B题足球队排名次
下表给出了我国12支足球队在1988-1989年全国足球级联赛中的成绩,要求1)设计一个依据这些成绩排出诸队名次的算法,并给出用该算法排名次的结果。
2)把算法推广到任意N个队的情况。
3)讨论:数据应具备什么样的条件,用你的方法才能够排出诸队的名次。
对下表的说明:
1)12支球队依次记作T1,T2,……,T12.
2)符号X表示两队未曾比赛。
3)数字表示两队比赛结果,如T3行与Y8列交叉处的数字表示:T3与T8比赛了2场;T3与T8的进球之比为0:1和3:1。
