专题二 函数概念与基本初等函数 第六讲函数模型及其应用答案
数学复习:第二章函数的概念、基本初等函数(Ⅰ)及函数的应用.函数模型及其应用
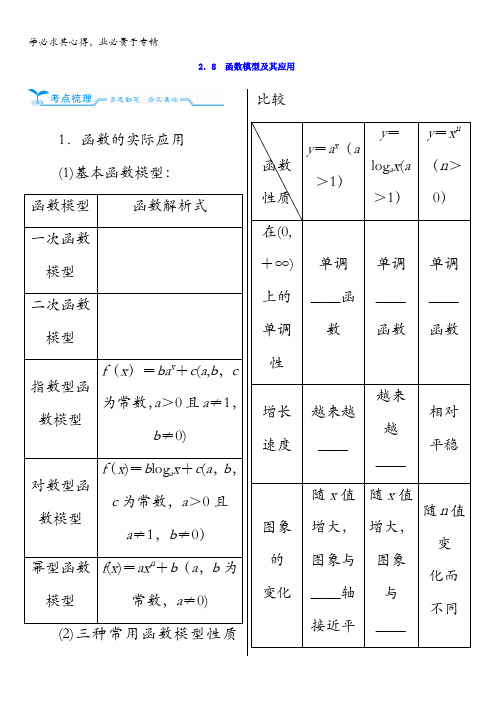
2.8 函数模型及其应用1.函数的实际应用(1)基本函数模型:函数模型函数解析式一次函数模型二次函数模型指数型函数模型f(x)=ba x+c(a,b,c 为常数,a>0且a≠1,b≠0)对数型函数模型f(x)=b log a x+c(a,b,c为常数,a>0且a≠1,b≠0)幂型函数模型f(x)=ax n+b(a,b为常数,a≠0)比较函数性质y=a x(a>1)y=log a x(a>1)y=x n(n>0)在(0,+∞)上的单调性单调____函数单调____函数单调____函数增长速度越来越____越来越____相对平稳图象的变化随x值增大,图象与____轴接近平随x值增大,图象与____随n值变化而不同行轴接近平行2。
函数建模(1)函数模型应用的两个方面:①利用已知函数模型解决问题;②建立恰当的函数模型,并利用所得函数模型解释有关现象,对某些发展趋势进行预测.(2)应用函数模型解决问题的基本过程:、、、.自查自纠1.(1)f(x)=ax+b(a,b为常数,a≠0)f(x)=ax2+bx+c(a,b,c为常数,a≠0)(2)增增增快慢y x2.审题建模解模还原手机的价格不断降低,若每隔半年其价格降低错误!,则现在价格为2 560元的手机,两年后价格可降为()A.900元B.810元C.1 440元D.160元解:半年降价一次,则两年后降价四次,其价格降为2 560×错误!错误!=810元.故选B.(错误!)某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是(参考数据:lg1.12≈0.05,lg1。
3≈0。
11,lg2≈0.30)()A.2018年B.2019年C.2020年D.2021年解:设x年后该公司全年投入的研发资金为200万元,由题可知,130(1+12%)x=200,解得x=log1。
函数概念与基本初等函数

小 题 都会 考 查 , 透 面 广. 别 是 分 渗 特 段 函数 的定 义 域 、 域 、 析 式 的 求 值 解 法 是近 几年 高 考 的热 点. 本节 知 识 作
为 工具 和 其 他 知识 结 合 起 来 命 题 的
域 与解 析 式 具 有 综合 性 ,有 时 渗 透 在解 答 题 中.2 1 江 苏 题 既 考 查 了 02 分段 函数 的解 析 式求 解 .又 考 查 了
失 分警 示 没 有 考 虑 定 义 域 的 限 制条 件 而直接 代 入 求解 是 致误 的 重要 原 因 ;多数 同 学可 能 不 知如 何
1 .考 纲 解 读
倒j (o2 1 21 ̄ ) 下列函数
中 , 满足 不 ) = ) 的是 ( )
( ) 解 函 数 的单 调 性 及 几 何 1理
概
l
宣宾 _啐0牵 羚
|
| 薯i童 1 ll |≮ | 0鼍 | l | | | | l | 0} l | 蠢_ | j l 0
| 毪Hale Waihona Puke ・|毫鬻l 黎 馨
A . )lI B = . )— I = I
1 .考 纲 解 读
本专 题 内容 主 要包 括 函数 的概念 、 图象 与 性质 , 函数 与方程 , 函数模 型及其 应用 等 , 整 是 个高 中数 学 的核 心 内容 , 同时也是 贯 穿整个 中学数 学 的一根 主线. 以函数 为基础 编 制 的考 查 能力 的试题 在历 年 的高考 试卷 中 占有 较大 的 比重.一般说来 , 择题 、 空题 主要考 查 函数 选 填 的概 念 、 单调 性 与奇偶 性 、 函数 图象 等 重要 知识 , 注 函数 知识 的应 用 以及 函数 思想 方 法 的 关 渗透 , 着力体 现概念 性 、 辨性和 应用意识.解 答题 大 多以基本初 等 函数 为载体 , 思 综合应 用 函 数、 导数 、 方程 、 不等 式等知 识 , 并与数 学 思想 方 法紧 密结合 , 函数与方 程思想 、 形结合 思 对 数 想 、 类 与整合 思想 、 限与无 限思想等进 行较为 深入 的考 查 . 分 有 体现 了能力 立意 的命 题原则.
十年高考理科数学真题 专题二 函数概念与基本初等函数 六函数综合及其应用及答案-优质
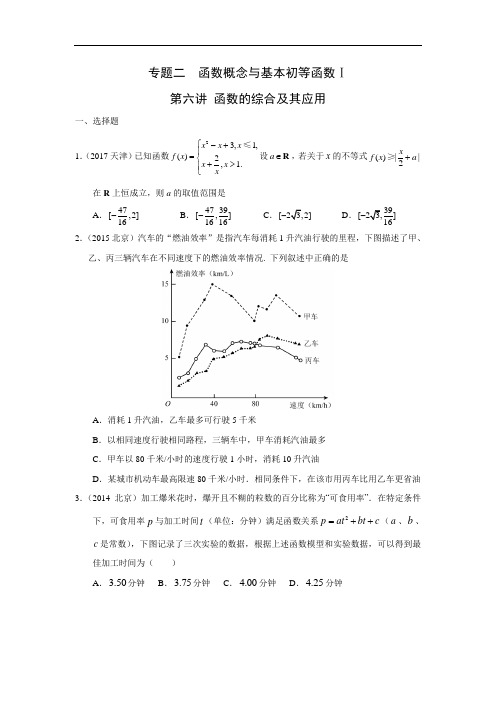
专题二 函数概念与基本初等函数Ⅰ第六讲函数的综合及其应用一、选择题1.(2017天津)已知函数23,1,()2, 1.x x x f x x x x ⎧-+⎪=⎨+>⎪⎩≤设a ∈R ,若关于x 的不等式()||2x f x a +≥在R 上恒成立,则a 的取值范围是 A .47[,2]16-B .4739[,]1616-C .[23,2]-D .39[23,]16- 2.(2015北京)汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是A .消耗1升汽油,乙车最多可行驶5千米B .以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多C .甲车以80千米/小时的速度行驶1小时,消耗10升汽油D .某城市机动车最高限速80千米/小时.相同条件下,在该市用丙车比用乙车更省油 3.(2014北京)加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率p 与加工时间t (单位:分钟)满足函数关系2p at bt c =++(a 、b 、c 是常数),下图记录了三次实验的数据,根据上述函数模型和实验数据,可以得到最佳加工时间为( )A .3.50分钟B .3.75分钟C .4.00分钟D .4.25分钟4.(2014湖南)某市生产总值连续两年持续增加,第一年的增长率为p ,第二年的增长率为q ,则该市这两年生产总值的年平均增长率为 A .2p q + B .(1)(1)12p q ++- CD1 二、填空题5.(2017山东)若函数e ()xf x (e=2.71828L ,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是 . ①()2xf x -=②2()f x x=③()3xf x -=④()cos f x x =6.(2017江苏)设()f x 是定义在R 且周期为1的函数,在区间[0,1)上,2,(),x x Df x x x D⎧∈=⎨∉⎩其中集合1{|,}n D x x n n-==∈*N ,则方程()lg 0f x x -=的解的个数是 .7.(2017新课标Ⅰ)如图,圆形纸片的圆心为O ,半径为5 cm ,该纸片上的等边三角形ABC的中心为O .D 、E 、F 为圆O 上的点,DBC ∆,ECA ∆,FAB ∆分别是以BC ,CA ,AB 为底边的等腰三角形。
高考数学第一轮复习教案-专题2函数概念与基本初等函数

反函数的定义
设函数 y f (x)(x A) 的值域是 C,根据这个函数中 x,y 的关系,用 y 把 x 表
高考数学第一轮复习教案汇总【精华】
专题二 函数概念与基本初等函数
一、考试内容: 映射、函数、函数的单调性、奇偶性. 反函数.互为反函数的函数图像间的关系. 指数概念的扩充.有理指数幂的运算性质.指数函数. 对数.对数的运算性质.对数函数. 函数的应用. 二、考试要求: (1)了解映射的概念,理解函数的概念. (2)了解函数单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法. (3)了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数. (4)理解分数指数幂的概念,掌握有理指数幂的运算性质,掌握指数函数的概念、图像 和 性质. (5)理解对数的概念,掌握对数的运算性质;掌握对数函数的概念、图像和性质. (6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题. 三、命题热点
y f 1(x)
(二)函数的性质 函数的单调性
定义:对于函数 f(x)的定义域 I 内某个区间上的任意两个自变量的值 x1,x2, ⑴若当 x1<x2 时,都有 f(x1)<f(x2),则说 f(x)在这个区间上是增函数; ⑵若当 x1<x2 时,都有 f(x1)>f(x2),则说 f(x) 在这个区间上是减函数.
奇函 数的定 义:如果 对于函 数f(x)的定 义域内 任意一 个x,都有 f(-x)=-f(x),那么 函数f(x)就叫 做奇函 数.
第2讲 函数概念与基本初等函数

第2讲函数概念与基本初等函数一.【考纲导读】(一)函数1.了解构成函数的要素,了解映射的概念,会求一些简单函数的定义域和值域.2.理解函数的三种表示法:解析法、图象法和列表法,能根据不同的要求选择恰当的方法表示简单的函数.3.了解分段函数,能用分段函数来解决一些简单的数学问题.4.理解函数的单调性,会讨论和证明一些简单的函数的单调性;理解函数奇偶性的含义,会判断简单的函数奇偶性.5.理解函数的最大(小)值及其几何意义,并能求出一些简单的函数的最大(小)值6.会运用函数图像理解和研究函数的性质.(二)指数函数1.了解指数函数模型的实际背景.2.理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.3.理解指数函数的概念,会求与指数函数性质有关的问题.4.知道指数函数是一类重要的函数模型.(三)对数函数1.理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用.2.理解对数函数的概念;会求与对数函数性质有关的问题.3.知道对数函数是一类重要的函数模型.4.了解指数函数与对数函数互为反函数.(四)幂函数1.了解幂函数的概念.2.结合函数的图像,了解它们的变化情况.(五)函数与方程1.了解函数零点的概念,结合二次函数的图像,了解函数的零点与方程根的联系.2.理解并掌握连续函数在某个区间上存在零点的判定方法。
能利用函数的图象和性质判别函数零点的个数.(六)函数模型及其应用1.了解指数函数、对数函数以及幂函数的增长特征。
知道直线上升、指数增长、对数增长等不同函数类型增长的含义.2.了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.3.能利用给定的函数模型解决简单的实际问题.二.【命题走向】分析近几年的高考试题,可以发现函数是高考数学的重点内容之一,函数的观点和思想方法贯穿整个高中数学的全过程,包括解决几何问题.在近几年的高考试卷中,选择题、填空题、解答题三种题型中每年都有函数试题,而且常考常新.以基本函数为模型的应用题和综合题是高考命题的新趋势.2015年高考热点主要有:①考查函数的表示法、定义域、值域、单调性、奇偶性、反函数和函数的图象.②函数与方程、不等式、数列是相互关联的概念,通过对实际问题的抽象分析,建立相应的函数模型并用来解决问题,是考试的热点.③考查运用函数的思想来观察问题、分析问题和解决问题,渗透数形结合和分类讨论的基本数学思想.三.【要点精讲】 1、知识网络定义定义域区间对应法则值域一元二次函数一元二次不等式映射函数性质奇偶性单调性周期性指数函数根式分数指数指数函数的图像和性质指数方程对数方程反函数互为反函数的函数图像关系对数函数对数对数的性质积、商、幂与根的对数对数恒等式和不等式常用对数自然对数对数函数的图像和性质1.2.1 对函数的进一步认识一、映射1.映射:设A 、B 是两个集合,如果按照某种对应关系f ,对于集合A 中的 元素,在集合B 中都有 元素和它对应,这样的对应叫做 到 的映射,记作 .2.象与原象:如果f :A →B 是一个A 到B 的映射,那么和A 中的元素a 对应的 叫做象, 叫做原象。
专题02 函数的概念与基本初等函数(原卷版)
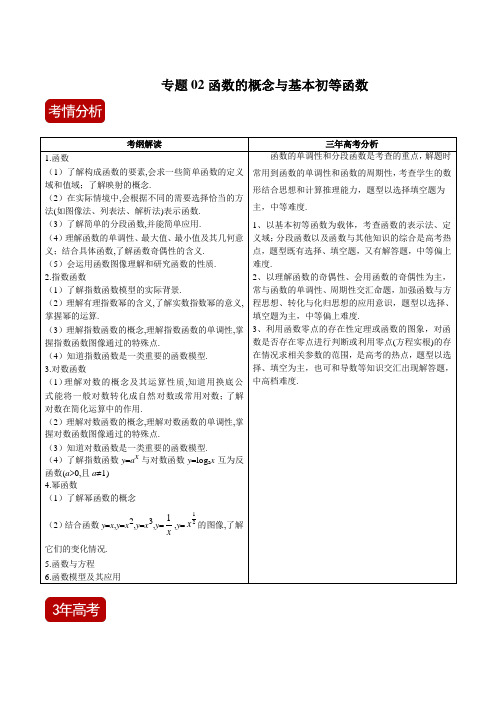
专题02函数的概念与基本初等函数1.【2019年天津文科05】已知a=log27,b=log38,c=0.30.2,则a,b,c的大小关系为()A.c<b<a B.a<b<c C.b<c<a D.c<a<b2.【2019年天津文科08】已知函数f(x)若关于x的方程f(x)x+a(a∈R)恰有两个互异的实数解,则a的取值范围为()A.[,] B.(,] C.(,]∪{1} D.[,]∪{1}3.【2019年新课标3文科12】设f(x)是定义域为R的偶函数,且在(0,+∞)单调递减,则()A.f(log3)>f(2)>f(2)B.f(log3)>f(2)>f(2)C.f(2)>f(2)>f(log3)D.f(2)>f(2)>f(log3)4.【2019年新课标2文科06】设f(x)为奇函数,且当x≥0时,f(x)=e x﹣1,则当x<0时,f(x)=()A.e﹣x﹣1 B.e﹣x+1 C.﹣e﹣x﹣1 D.﹣e﹣x+15.【2019年新课标1文科03】已知a=log20.2,b=20.2,c=0.20.3,则()A.a<b<c B.a<c<b C.c<a<b D.b<c<a6.【2019年北京文科03】下列函数中,在区间(0,+∞)上单调递增的是()A.y=x B.y=2﹣x C.y=log x D.y7.【2018年新课标2文科12】已知f(x)是定义域为(﹣∞,+∞)的奇函数,满足f(1﹣x)=f(1+x),若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=()A.﹣50 B.0 C.2 D.508.【2018年新课标1文科12】设函数f(x),则满足f(x+1)<f(2x)的x的取值范围是()A.(﹣∞,﹣1] B.(0,+∞)C.(﹣1,0)D.(﹣∞,0)9.【2018年新课标3文科07】下列函数中,其图象与函数y=lnx的图象关于直线x=1对称的是()A.y=ln(1﹣x)B.y=ln(2﹣x) C.y=ln(1+x)D.y=ln(2+x)10.【2018年北京文科05】“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献,十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于.若第一个单音的频率为f,则第八个单音的频率为()A.f B.f C.f D.f11.【2018年天津文科05】已知a,b,c,则a,b,c的大小关系为()A.a>b>c B.b>a>c C.c>b>a D.c>a>b12.【2017年北京文科05】已知函数f(x)=3x﹣()x,则f(x)()A.是偶函数,且在R上是增函数B.是奇函数,且在R上是增函数C.是偶函数,且在R上是减函数D.是奇函数,且在R上是减函数13.【2017年北京文科08】根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080,则下列各数中与最接近的是()(参考数据:lg3≈0.48)A.1033B.1053C.1073D.109314.【2017年天津文科06】已知奇函数f(x)在R上是增函数.若a=﹣f(),b=f(log24.1),c=f (20.8),则a,b,c的大小关系为()A.a<b<c B.b<a<c C.c<b<a D.c<a<b15.【2017年天津文科08】已知函数f(x),设a∈R,若关于x的不等式f(x)≥|a|在R上恒成立,则a的取值范围是()A .[﹣2,2]B .C .D .16.【2018年新课标1文科13】已知函数f (x )=log 2(x 2+a ),若f (3)=1,则a = . 17.【2018年新课标3文科16】已知函数f (x )=ln (x )+1,f (a )=4,则f (﹣a )= .18.【2018年天津文科14】已知a ∈R ,函数f (x ).若对任意x ∈[﹣3,+∞),f (x )≤|x |恒成立,则a 的取值范围是 .19.【2017年新课标2文科14】已知函数f (x )是定义在R 上的奇函数,当x ∈(﹣∞,0)时,f (x )=2x 3+x 2,则f (2)= .20.【2017年新课标3文科16】设函数f (x ),则满足f (x )+f (x )>1的x 的取值范围是 .21.【2017年北京文科11】已知x ≥0,y ≥0,且x +y =1,则x 2+y 2的取值范围是 .1.【山西省晋城市2019届高三第三次模拟考试】若函数(()sin ln f x x ax =⋅的图象关于y 轴对称,则实数a 的值为( ) A .2B .4C .2±D .4±2.【广东省东莞市2019届高三第二学期高考冲刺试题(最后一卷)】己知()f x 是定义在R 上的偶函数,在区间(]0-∞,为增函数,且()30f =,则不等式(12)0f x ->的解集为( ) A .()10-,B .()12-,C .()02,D .()2,+∞ 3.【天津市河北区2019届高三一模】已知()f x 是定义在R 上的偶函数,且()f x 在[)0,+∞内单调递减,则( )A .()()()320log 2log 3f f f <<-B .()()()32log 20log 3f f f <<-C .()()()23log 3log 20f f f -<<D .()()()32log 2log 30f f f <-<4.【天津市红桥区2019届高三二模】已知 1.22a =,52log 2=b ,1ln3c =,则( )A .a b c >>B .a c b >>C .b a c >>D .b c a >>5.【河南省八市重点高中联盟“领军考试”2019届高三第五次测评】已知函数()221log 2xf x x+=-,若()f a b =,则()4f a -=( )A .bB .2b -C .b -D .4b -6.【河南省八市重点高中联盟“领军考试”2019届高三第五次测评】已知函数()21x f x x =-,则( )A .()f x 在()0,1单调递增B .()f x 的最小值为4C .()y f x =的图象关于直线1x =对称D .()y f x =的图象关于点()1,2对称7.【山东省栖霞市2019届高三高考模拟卷(新课标I)】已知定义在R 上的奇函数()f x 满足(2)()f x f x +=-,当01x ≤≤时,2()f x x =,则(1)(2)(3)(2019)f f f f ++++=L ( )A .2019B .0C .1D .-18.【天津市红桥区2019届高三一模】若方程2121x kx x -=--有两个不同的实数根,则实数k 的取值范围是( ) A .(),1-∞-B .()1,0-C .()0,4D .()()0,11,49.【天津市部分区2019届高三联考一模】设,m n R ∈,则“m n <”是“112m n-⎛⎫> ⎪⎝⎭”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件10.【广东省2019届高考适应性考试】某罐头加工厂库存芒果()m kg ,今年又购进()n kg 新芒果后,欲将芒果总量的三分之一用于加工为芒果罐头。
高中数学专题 微专题2 基本初等函数、函数的应用

A.y=1.002x
1
C.y= x 3-5
√B.y=log7x+1
D.y=5+sin x
由题意,函数在(10,1 000)上单调递增,故D不符合题意,排除D;
1
因为当x∈(10,125)时,y=x 3-5<0,故C不符合题意,排除C;
当x=1 000时,1.0021 000≈7.37>5,故y=1.002x不符合题意,排除A;
1 2 3 4 5 6 7 8 9 10 11 12
对于D选项,当T=360,P=729时,lg P= lg 729∈(lg 102,lg 103),即lg P∈(2,3),根 据图象可知,二氧化碳处于超临界状态.
1 2 3 4 5 6 7 8 9 10 11 12
(1,+∞)上单调递减,所以由复合函数的单调性可知,f(x)在(-∞,
1)上单调递增,在(1,+∞)上单调递减.易知f(x)的图象关于直线x=1
对称,所以
c=f
6
2
=
f
2-
6
2
,
又
2 2
<2 -
6 2<
3 2
<1 ,
所以
f
2
2
<f
2-
26<f
23,所以
b>c>a.
跟则实踪数训a练的1取值(1)范(2围02是3·广东联考)已知函数f(x)=2-x,12xx≥,0x<,0,若f(a)<f(6-a),
PART TWO
热点突破
1.(2023·通州模拟)下列函数中,是奇函数且在定义域内单调递增的是
A.y=1x C.y=ex+e-x
√B.y=x3
专题二 函数概念与基本初等函数 第六讲函数综合及其应用答案

专题二 函数概念与基本初等函数Ⅰ第六讲 函数综合及其应用答案部分1.A 【解析】解法一 根据题意,作出()f x 的大致图象,如图所示x当1x ≤时,若要()||2x f x a +≥恒成立,结合图象,只需23()2x x x a -+-+≥,即2302x x a -++≥,故对于方程2302x x a -++=,21()4(3)02a ∆=--+≤,解得4716a -≥;当1x >时,若要()||2xf x a +≥恒成立,结合图象,只需22x x a x ++≥,即22x a x +≥,又222x x +≥,当且仅当22x x=,即2x =时等号成立,所以2a ≤,综上,a 的取值范围是47[,2]16-.选A . 解法二 由题意()f x 的最小值为114,此时12x =.不等式()||2xf x a +≥在R 上恒成立等价于11||24x a +≤在R 上恒成立. 当a =-12x =,111|||248x -=>,不符合,排除C 、D ; 当3916a =时,令12x =,394311||||216168x +=>,不符合,排除B .选A . 2.D 【解析】 “燃油效率”是指汽车每消耗1升汽油行驶的里程,A 中乙车消耗1升汽油,最多行驶的路程为乙车图象最高点的纵坐标值,A 错误;B 中以相同速度行驶相同路程,甲燃油效率最高,所以甲最省油,B 错误,C 中甲车以80千米/小时的速度行驶1小时,甲车每消耗1升汽油行驶的里程10km,行驶80km ,消耗8升汽油,C 错误,D 中某城市机动车最高限速80千米/小时. 由于丙比乙的燃油效率高,相同条件下,在该市用丙车比用乙车更省油,选D .3.B 【解析】由题意可知2p at bt c =++过点(3,0.7),(4,0.8)(5,0.5),代入2p at bt c =++中可解得0.2, 1.5,2a b c =-==-,∴20.2 1.52p t t =-+-= 20.2( 3.75)0.8125t --+,∴当 3.75t =分钟时,可食用率最大.4.D 【解析】设年平均增长率为x ,原生产总值为a ,则2(1)(1)(1)p q a a x ++=+,解得1x =,故选D .5.①④【解析】①()2()2x x x x e e f x e -=⋅=在R 上单调递增,故()2xf x -=具有M 性质;②()3()3x x x x e e f x e -=⋅=在R 上单调递减,故()3xf x -=不具有M 性质;③3()x x e f x e x =⋅,令3()xg x e x =⋅,则322()3(2)x x xg x e x e x x e x '=⋅+⋅=+,∴当2x >-时,()0g x '>,当2x <-时,()0g x '<,∴3()x x e f x e x =⋅在(),2-∞-上单调递减,在()2,-+∞上单调递增,故()3f x x =不具有M 性质;④2()(2)x x e f x e x =+,令()()22x g x e x =+, 则22()(2)2[(1)1]0xxxg x e x e x e x '=++⋅=++>,∴2()(2)x x e f x e x =+在R 上单调递增,故2()2f x x =+具有M 性质.6.8【解析】由于()[0,1)f x ∈,则需考虑110x ≤<的情况,在此范围内,x ∈Q 且x D ∈时,设*,,,2qx p q p p=∈≥N ,且,p q 互质, 若lg x ∈Q ,则由lg (0,1)x ∈,可设*lg ,,,2nx m n m m=∈≥N ,且,m n 互质, 因此10n mq p=,则10()nm q p =,此时左边为整数,右边为非整数,矛盾,因此lg x ∉Q ,因此lg x 不可能与每个周期内x D ∈对应的部分相等,只需考虑lg x 与每个周期x D ∉的部分的交点,画出函数图象,图中交点除外(1,0)其他交点横坐标均为无理数,属于每个周期x D ∉的部分,且1x =处11(lg )1ln10ln10x x '==<,则在1x =附近仅有一个交点,因此方程()lg 0f x x -=的解的个数为8.7.OE 交AC 于G ,由题意OE AC ⊥,设等边三角形ABC 的边长为x (05x <<),则OG x =,56GE x =-. G ODFECBA由题意可知三棱锥的高h ===底面2ABC S x ∆=,三棱锥的体积为2134V x =⨯=设45()53h x x x =-,则34()203h x x x '=-(05x <<), 令()0h x '=,解得x =x ∈时,()0h x '>,()h x 单调递增;当x ∈时,()0h x '<,()h x 单调递减,所以x =()h x取得最大值4h =所以2max 1212V ==⨯= 8.2,(,1)-∞-.【解析】①若0a =,则33,0()2,0x x x f x x x ⎧-=⎨->⎩≤,当0x >时,20x -<;当0x时,2()333(1)(1)f x x x x '=-=+-,所以函数()f x 在(,1)-∞-上单调递增,在(1,0]- 上单调递减,所以函数()f x 在(,0]-∞上的最大值为(1)2f -=. 综上函数()f x 的最大值为2.②函数33y x x =-与2y x =-的大致图象如图所示若()f x 无最大值,由图象可知22a ->,即1a <-.9.24【解析】由题意得2219248bk b e e +⎧=⎨=⎩,即1119212b k e e ⎧=⎪⎨=⎪⎩,所以该食品在33℃的保鲜时间是3311331()()193242k b k b y e e e +==⋅=⨯=.10.)+∞【解析】函数()g x 的定义域为[1,2]-,根据已知得()()()2h x g xf x +=,所以()=2()()62h x f x g x x b -=+()()hx g x >恒成立, 即62x b +>令3y x b =+,y =,则只要直线3y x b=+在半圆224(0)xy y +=≥2>,解得b >,故实数b 的取值范围是)+∞.11.160【解析】设该容器的总造价为y 元,长方体的底面矩形的长x m ,因为无盖长方体的容积为34m ,高为1m ,所以长方体的底面矩形的宽为4m x,依题意,得24420410(2)8020()8020160y x x x x ⨯=⨯++=+++⨯=≥ 12.①③④【解析】对于①,根据题中定义,()A f x ∈⇔函数()y f x =,x D ∈的值域为R ,由函数值域的概念知,函数()y f x =,x D ∈的值域为,R b R a D ⇔∀∈∃∈()f a b =,所以①正确;对于②,例如函数||1()()2x f x =的值域(0,1]包含于区间[1,1]-,所以()f x B ∈,但()f x 有最大值l ,没有最小值,所以②错误;对于③,若()()f x g x B +∈,则存在一个正数1M ,使得函数()()f x g x B +∈的值域包含于区间11[,]M M -,所以1M -≤()f x 1()g x M +≤,由()g x B ∈知,存在一个正数2M ,使得函数()g x 的值域包含于区间22[,]M M -,所以22()M g x M -≤≤,亦有 22()M g x M -≤-≤,两式相加得12()M M -+≤()f x ≤12M M +,于是()f x B ∈,与已知“.()f x A ∈”矛盾,故()()f x g x B +∉,即③正确;对于④,如果0a >, 那么,()x f x →+∞→+∞,如果0a <,那么2,()x f x →-→+∞,所以()f x 有最大值,必须0a =,此时2()1x f x x =+在区间(2,)-+∞上,有11()22f x -≤≤, 所以()f x B ∈,即④正确,故填①③④.13.【解析】(1)当030x <≤时,()3040f x =<恒成立,公交群体的人均通勤时间不可能少于自驾群体的人均通勤时间; 当30100x <<时,若40()f x <,即180029040x x+->,解得20x <(舍)或45x >; ∴当45100x <<时,公交群体的人均通勤时间少于自驾群体的人均通勤时间; (2)设该地上班族总人数为n ,则自驾人数为%n x ⋅,乘公交人数为(1%)n x ⋅-.因此人均通勤时间30%40(1%),030()1800(290)%40(1%),30100n x n x x ng x x n x n x x x n ⋅⋅+⋅⋅-⎧<⎪⎪=⎨+-⋅⋅+⋅⋅-⎪<<⎪⎩≤,整理得:240,0010()1(32.5)36.875,3010050x x g x x x ⎧-<⎪⎪=⎨⎪-+<<⎪⎩≤3, 则当(0,30](30,32.5]x ∈,即(0,32.5]x ∈时,()g x 单调递减;当(32.5,100)x ∈时,()g x 单调递增.实际意义:当有32.5%的上班族采用自驾方式时,上班族整体的人均通勤时间最短. 适当的增加自驾比例,可以充分的利用道路交通,实现整体效率提升;但自驾人数过多,则容易导致交通拥堵,使得整体效率下降.14.【解析】(1)连结PO 并延长交MN 于H ,则PH ⊥MN ,所以OH =10.θHE KGNM PO ABC D过O 作OE ⊥BC 于E ,则OE ∥MN ,所以COE θ∠=, 故40cos OE θ=,40sin EC θ=,则矩形ABCD 的面积为240cos (40sin 10)800(4sin cos cos )θθθθθ⨯+=+,CDP ∆的面积为1240cos (4040sin )1600(cos sin cos )2θθθθθ⨯⨯-=-.过N 作GN ⊥MN ,分别交圆弧和OE 的延长线于G 和K ,则10GK KN ==. 令0GOK θ∠=,则01sin 4θ=,0(0,)6πθ∈. 当0[,)2πθθ∈时,才能作出满足条件的矩形ABCD ,所以sin θ的取值范围是1[,1)4.答:矩形ABCD 的面积为800(4sin cos cos )θθθ+平方米,CDP ∆的面积为1600(cos sin cos )θθθ-,sin θ的取值范围是1[,1)4.(2)因为甲、乙两种蔬菜的单位面积年产值之比为4∶3,设甲的单位面积的年产值为4k ,乙的单位面积的年产值为3k (0)k >, 则年总产值为4800(4sin cos cos )31600(cos sin cos )k k θθθθθθ⨯++⨯-8000(sin cos cos )k θθθ=+,0[,)2πθθ∈.设()sin cos cos f θθθθ=+,0[,)2πθθ∈,则222()cos sin sin (2sin sin 1)(2sin 1)(sin 1)f θθθθθθθθ'=--=-+-=--+. 令()0f θ'=,得π6θ=, 当0(,)6πθθ∈时,()>0f θ′,所以()f θ为增函数; 当(,)62ππθ∈时,()<0f θ′,所以()f θ为减函数, 因此,当π6θ=时,()f θ取到最大值.答:当π6θ=时,能使甲、乙两种蔬菜的年总产值最大.15.【解析】(1)由21log 50x ⎛⎫+>⎪⎝⎭,得151x +>,解得()1,0,4x ⎛⎫∈-∞-+∞ ⎪⎝⎭.(2)()1425a a x a x+=-+-,()()24510a x a x -+--=, 当4a =时,1x =-,经检验,满足题意.当3a =时,121x x ==-,经检验,满足题意. 当3a ≠且4a ≠时,114x a =-,21x =-,12x x ≠. 1x 是原方程的解当且仅当110a x +>,即2a >; 2x 是原方程的解当且仅当210a x +>,即1a >. 于是满足题意的(]1,2a ∈.综上,a 的取值范围为(]{}1,23,4.(3)当120x x <<时,1211a a x x +>+,221211log log a a x x ⎛⎫⎛⎫+>+ ⎪ ⎪⎝⎭⎝⎭, 所以()f x 在()0,+∞上单调递减.函数()f x 在区间[],1t t +上的最大值与最小值分别为()f t ,()1f t +.()()22111log log 11f t f t a a t t ⎛⎫⎛⎫-+=+-+≤ ⎪ ⎪+⎝⎭⎝⎭即()2110at a t ++-≥,对任意1,12t ⎡⎤∈⎢⎥⎣⎦成立.因为0a >,所以函数()211y at a t =++-在区间1,12⎡⎤⎢⎥⎣⎦上单调递增,12t =时,y 有最小值3142a -,由31042a -≥,得23a ≥. 故a 的取值范围为2,3⎡⎫+∞⎪⎢⎣⎭.16.【解析】(1)由题意知,点M ,N 的坐标分别为()5,40,()20,2.5.将其分别代入2a y x b =+,得4025 2.5400aba b⎧=⎪⎪+⎨⎪=⎪+⎩,解得10000a b =⎧⎨=⎩.(2)①由(1)知,21000y x =(520x ≤≤),则点P 的坐标为21000,t t ⎛⎫ ⎪⎝⎭, 设在点P 处的切线l 交x ,y 轴分别于A ,B 点,32000y x '=-, 则l 的方程为()2310002000y x t t t -=--,由此得3,02t ⎛⎫A ⎪⎝⎭,230000,t ⎛⎫B ⎪⎝⎭. 故()f t ==,[]5,20t ∈. ②设()624410g t t t ⨯=+,则()6516102g t t t⨯'=-.令()0g t '=,解得t =当(t ∈时,()0g t '<,()g t 是减函数;当()t ∈时,()0g t '>,()g t 是增函数.从而,当t =()g t 有极小值,也是最小值,所以()min 300g t =,此时()min f t =答:当t =l 的长度最短,最短长度为千米.17.【解析】(Ⅰ)因为蓄水池侧面积的总成本为1002200rh rh ππ⋅=元,底面的总成本为2160r π元,所以蓄水池的总成本为(2200160rh r ππ+)元.又题意据220016012000rh r πππ+=,所以21(3004)5h r r=-,从而23()(3004)5V r r h r r ππ==-.因0r >,又由0h >可得r <故函数()V r 的定义域为. (Ⅱ)因3()(3004)5V r r r π=-,故2()(30012)5V r r π'=-.令()0V r '=,解得125,5r r ==-(因25r =-不在定义域内,舍去). 当(0,5)r ∈时,()0V r '>,故()V r 在(0,5)上为增函数;当r ∈时,()0V r '<,故()V r 在上为减函数. 由此可知,()V r 在5r =处取得最大值,此时8h =. 即当5r =,8h =时,该蓄水池的体积最大. 18.【解析】(1)当1,1,2b c n==-时,()1n f x x x =+-.∵111()(1)()10222n f f =-⨯<,∴()f x 在1(,1)2内存在零点.又当1(,1)2x ∈时,1()10n f x nx -'=+>,∴()f x 在1(,1)2上是单调递增的,∴()f x 在区间1(,1)2内存在唯一的零点;(2)解法一 由题意知1(1)1,1(1)1,f f --⎧⎨-⎩即02,20,b c b c -⎧⎨-+⎩由图像知,3b c +在点(0,2)-取得最小值6-,在点(0,0)取得最大值0.b解法二 由题意知1(1)11f b c -=++,即20b c -+.…①1(1)11f b c --=-+,即20b c --+.…②①2⨯+②得62()()30b c b c b c-++-+=+当0,2b c ==-时,36b c +=-;当0b c ==时,30b c += 所以3b c +的最小值6-,最大值0.解法三 由题意知(1)1,(1)1,f b c f b c -=-+⎧⎨=++⎩,解得(1)(1)(1)(1)2,22f f f f b c --+--==32(1)(1)3b c f f +=+--.又∵1(1)1,1(1)1,f f --⎧⎨-⎩, ∴630b c-+当0,2b c ==-时,36b c +=-;当0b c ==时,30b c += 所以3b c +的最小值6-,最大值0. (3)当2n =时,2()f x x bx c =++. 对任意12,x x [1,1]∈-都有有12()()4f x f x -等价于()f x 在[-1,1]上的最大值与最小值之差4M .据此分类讨论如下:(ⅰ)当12b>,即2b >时, (1)(1)24M f f b =--=>,与题设矛盾. (ⅱ)当102b --<,即02b <时, 2(1)()(1)422b bM f f =--=+恒成立. (ⅲ) 当012b -<,即20b -时, 2(1)()(1)422b bM f f =---=-恒成立.一线名师凭借教学实践科学分类,高质量的解析,你能感受到名家不一样的解题思路 高考押题团队客服QQ :1185941688 高考真题专项分类(理科数学) 第11页—共11页 综上可知,22b -.19.【解析】设包装盒的高为h (cm ),底面边长为a (cm ),由已知得.300),30(22260,2<<-=-==x x xh x a(1),1800)15(8)30(842+--=-==x x x ah S所以当15=x 时,S 取得最大值.(2)).20(26),30(22222x x V x x h a V -='+-== 由00=='x V 得(舍)或x =20.当)20,0(∈x 时,0;(20,30)0V x V ''>∈<当时.所以当x =20时,V 取得极大值,也是最小值. 此时1122ha =即装盒的高与底面边长的比值为12.。
函数概念与基本初等函数(最全)

函数概念与基本初等函数1.了解构成函数的要素,了解映射的概念,会求一些简单函数的定义域和值域.2.理解函数的三种表示法:解析法、图象法和列表法,能根据不同的要求选择恰当的方法表示简单的函数。
3.了解分段函数,能用分段函数来解决一些简单的数学问题。
4.理解函数的单调性,会讨论和证明一些简单的函数的单调性;理解函数奇偶性的含义,会判断简单的函数奇偶性。
5.理解函数的最大(小)值及其几何意义,并能求出一些简单的函数的最大(小)值.6.会运用函数图像理解和研究函数的性质.(二)指数函数1.了解指数函数模型的实际背景。
2.理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算。
3.理解指数函数的概念,会求与指数函数性质有关的问题。
4.知道指数函数是一类重要的函数模型。
(三)对数函数1.理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用。
2.理解对数函数的概念;会求与对数函数性质有关的问题.3.知道对数函数是一类重要的函数模型.4.了解指数函数 与对数函数互为反函数。
(四)幂函数1.了解幂函数的概念。
2.结合函数 的图像,了解它们的变化情况。
(五)函数与方程1.了解函数零点的概念,结合二次函数的图像,了解函数的零点与方程根的联系。
2.理解并掌握连续函数在某个区间上存在零点的判定方法。
能利用函数的图象和性质判别函数零点的个数.(六)函数模型及其应用1.了解指数函数、对数函数以及幂函数的增长特征。
知道直线上升、指数增长、对数增长等不同函数类型增长的含义。
2.了解函数模型(如指数函数、对数函数、幂函数、分段函数等函数模型)的广泛应用。
解答题中都有涉及,高考命题热点有以下两个方面:一是集合的运算、集合的有关述语和符号、集合的简单应用等作基础性的考查,题型多以选择、填空题的形式出现;二是以函数、方程、三角、不等式等知识为载体,以集合的语言和符号为表现形式,结合简易逻辑知识考查学生的数学思想、数学方法和数学能力,题型常以解答题的形式出现.函数是高考数学的重点内容之一,函数的观点和思想方法贯穿整个高中数学的全过程,包括解决几何问题.在近几年的高考试卷中,选择题、填空题、解答题三种题型中每年都有函数试题,而且常考常新.以基本函数为模型的应用题和综合题是高考命题的新趋势.考试热点:①考查函数的表示法、定义域、值域、单调性、奇偶性、反函数和函数的图象.②函数与方程、不等式、数列是相互关联的概念,通过对实际问题的抽象分析,建立相应的函数模型并用来解决问题,是考试的热点.③考查运用函数的思想来观察问题、分析问题和解决问题,渗透数形结合和分类讨论的基本数学思想.第1课时 函数及其表示一、映射1.映射:设A 、B 是两个集合,如果按照某种对应关系f ,对于集合A 中的 元素,在集合B 中都有 元素和它对应,这样的对应叫做 到 的映射,记作 .2.象与原象:如果f :A →B 是一个A 到B 的映射,那么和A 中的元素a 对应的 叫做象, 叫做原象。
专题02 函数概念与基本初等函数(新定义,高数观点,选填压轴题)(学生版)-2024年高考压轴专题复

专题02 函数概念与基本初等函数
(新定义,高数观点,选填压轴题)
目录
一、函数及其表示 (1)
二、函数的基本性质 (2)
三、分段函数 (4)
四、函数的图象 (5)
五、二次函数 (7)
六、指对幂函数 (7)
七、函数与方程 (8)
八、新定义题 (9)
一、函数及其表示
二、函数的基本性质
三、分段函数
四、函数的图象..
..
2023春·广东韶关·高二统考期末)
e3
cosπ
e2
x
x
x
⎫
-⎛⎫
⋅+
⎪ ⎪
+⎝⎭
⎭
部分图象大致是(
..
. .
2023春·云南楚雄·高二统考期末)函数)32e e 1
x
x x =-的部分图象大致为( )
2023春·湖北武汉·高一华中师大一附中校考期末)下列四个函数中的某个函数在区间致图象如图所示,则该函数是(
A .322x
x
x x
y --=+B .cos222x
x
x x
y -=+5.(2023春·河北沧州·高二统考期中)函数. .
. .
2023·内蒙古赤峰·统考二模)函数2
1
sin x x -
在()π,0-
A.B.
C.D.
五、二次函数
六、指对幂函数
七、函数与方程
八、新定义题A.2
=-B.
4
y x x。
第2章函数概念与基本初等函数 (6)

根据上表数据,从下列函数中选取一个函数描述西红柿种植成 本 Q 与上市时间 t 的变化关系: Q=at+b,Q=at2+bt+c,Q=a· bt,Q=a·logbt. 利用你选取的函数,求: (1)西红柿种植成本最低时的上市天数是 ________; (2)最低种植成本是 ________元/100 kg.
栏目 导引
第二章 函数概念与基本初等函 数
函数模型 对数函数模型 幂函数模型
函数解析式 f(x)=blogax+c(a,b,c 为常数,a>0 且 a≠1, b≠0) f(x)=axn+b(a,b,n 为常数,a≠0,n≠0)
栏目 导引
第二章 函数概念与基本初等函 数
2.三种函数模型性质比较 y=ax(a>1) 在(0,+∞) 上的单调性 增长速度 y=logax(a>1) y=xn(n>0)
栏目 导引
第二章 函数概念与基本初等函 数
【解析】
根据题意,要使附加税不少于 128 万元,
5 需30-2R×160×R%≥128,
整理得 R2-12R+32≤0,解得 4≤R≤8,即 R∈[4,8].
【答案】 A
栏目 导引
第二章 函数概念与基本初等函 数
角度二
构建指数函数、对数函数模型
2 a (60 - 120) +m=116, a=0.01, 解得 2 a(100-120) +m=84, m=80,
所以 Q=0.01(t-120)2+80,故当上市天数为 120 时,种植成本 取到最低值 80 元/100 kg.
答案:(1)120 (2)80
栏目 导引
栏目 导引
)
解析:选 B.根据散点图知,选择 y=a+b x最适合,故选 B.
2023年高考数学总复习第二章 函数概念与基本初等函数第6节:对数与对数函数(学生版)

2023年高考数学总复习第二章函数概念与基本初等函数第6节对数与对数函数考试要求1.理解对数的概念及其运算性质,知道用换底公式将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用;2.理解对数函数的概念及其单调性,掌握对数函数图像通过的特殊点,会画底数为2,10,12的对数函数的图像;3.体会对数函数是一类重要的函数模型;4.了解指数函数y =a x (a >0,且a ≠1)与对数函数y =log a x (a >0,且a ≠1)互为反函数.1.对数的概念一般地,如果a (a >0,a ≠1)的b 次幂等于N ,即a b =N ,那么数b 叫作以a 为底N 的对数,记作log a N =b .其中a 叫作对数的底数,N 叫作真数.2.对数的性质、运算性质与换底公式(1)对数的性质:①a log a N =N ;②log a a b =b (a >0,且a ≠1).(2)对数的运算性质如果a >0且a ≠1,M >0,N >0,那么①log a (MN )=log a M +log a N ;②log a MN =log a M -log a N ;③log a M n =n log a M (n ∈R ).(3)换底公式:log b N =log a Nlog a b(a ,b 均大于零且不等于1,N >0).3.对数函数及其性质(1)概念:函数y =log a x (a >0,且a ≠1)叫作对数函数,其中x 是自变量,函数的定义域是(0,+∞).(2)对数函数的图像与性质a >10<a <1图像性质定义域:(0,+∞)值域:R当x =1时,y =0,即过定点(1,0)当x >1时,y >0;当0<x <1时,y <0当x >1时,y <0;当0<x <1时,y >0在(0,+∞)上是增函数在(0,+∞)上是减函数4.反函数指数函数y =a x (a >0,且a ≠1)与对数函数y =log a x (a >0,且a ≠1)互为反函数,它们的图像关于直线y =x 对称.1.换底公式的两个重要结论(1)log a b =1log b a (a >0,且a ≠1;b >0,且b ≠1).(2)log a m b n =nm log a b (a >0,且a ≠1;b >0;m ,n ∈R ,且m ≠0).2.在第一象限内,不同底的对数函数的图像从左到右底数逐渐增大.3.对数函数y =log a x (a >0,且a ≠1)的图像过定点(1,0),且过点(a ,1)函数图像只在第一、四象限.1.思考辨析(在括号内打“√”或“×”)(1)log 2x 2=2log 2x .()(2)函数y =log 2(x +1)是对数函数.()(3)函数y =ln1+x1-x与y =ln(1+x )-ln(1-x )的定义域相同.()(4)当x >1时,若log a x >log b x ,则a <b .()2.(2021·全国甲卷)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量,通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L 和小数记录法的数据V 满足L =5+lg V .已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据约为(1010≈1.259)()A.1.5B.1.2C.0.8D.0.63.(2021·天津卷)设a =log 20.3,b =log 120.4,c =0.40.3,则a ,b ,c 的大小关系为()A.a <b <cB.c <a <bC.b <c <aD.a <c <b4.(易错题)函数y =log a (x -1)+2(a >0,且a ≠1)的图像恒过的定点是________.5.(易错题)已知lg x +lg y =2lg(x -2y ),则xy=________.6.若函数y =log a x (a >0,a ≠1)在[2,4]上的最大值与最小值的差是1,则a =________.考点一对数的运算1.(2020·全国Ⅰ卷)设a log 34=2,则4-a =()A.116B.19C.18D.162.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m 2-m 1=52lg E1E 2,其中星等为m k 的星的亮度为E k (k =1,2).已知太阳的星等是-26.7,天狼星的星等是-1.45,则太阳与天狼星的亮度的比值为()A.1010.1B.10.1C.lg 10.1D.10-10.13.(2021·天津卷)若2a =5b =10,则1a +1b =()A.-1B.lg 7C.1D.log 7104.计算:(1-log 63)2+log 62·log 618log 64=________.考点二对数函数的图像及应用例1(1)函数f (x )=log a |x |+1(0<a <1)的图像大致为()(2)若方程4x =log a x 0,12上有解,则实数a 的取值范围为________.训练1(1)已知函数y =log a (x +c )(a ,c 为常数,其中a >0,a≠1)的图像如图,则下列结论成立的是()A.a >1,c >1B.a >1,0<c <1C.0<a <1,c >1D.0<a <1,0<c <1(2)已知函数f (x )log 2x ,x >0,3x,x ≤0,关于x 的方程f (x )+x -a =0有且只有一个实根,则实数a 的取值范围是________.考点三解决与对数函数的性质有关的问题角度1比较大小例2(1)已知a =2-13,b =log 213,c =log 1213,则()A.a >b >cB.a >c >bC.c>b>aD.c>a>b(2)若实数a,b,c满足log a2<log b2<log c2<0,则下列关系中正确的是()A.a<b<cB.b<a<cC.c<b<aD.a<c<b(3)(2021·衡水中学检测)已知a,b=log120.2,c=a b,则a,b,c的大小关系是()A.a<b<cB.c<a<bC.a<c<bD.b<c<a角度2解对数不等式例3(1)(2022·太原质检)定义在R上的奇函数f(x),当x∈(0,+∞)时,f(x)=log2x,则不等式f(x)<-1的解集是________.(2)不等式log a(a2+1)<log a(2a)<0,则a的取值范围是________.角度3对数型函数性质的综合应用例4已知函数f(x)=log(1)若函数f(x)是R上的奇函数,求a的值;(2)若函数f(x)的定义域是一切实数,求a的取值范围;(3)若函数f(x)在区间[0,1]上的最大值与最小值的差不小于2,求实数a的取值范围.训练2(1)(2019·天津卷)已知a =log 27,b =log 38,c =0.30.2,则a ,b ,c 的大小关系为()A.c <b <aB.a <b <cC.b <c <aD.c <a <b(2)若f (x )=lg(x 2-2ax +1+a )在区间(-∞,1]上单调递减,则a 的取值范围为________.(3)已知函数f (x )=log a (8-ax )(a >0,且a ≠1),若f (x )>1在区间[1,2]上恒成立,则实数a 的取值范围是________.1.已知b >0,log 5b =a ,lg b =c ,5d =10,则下列等式一定成立的是()A.d =acB.a =cdC.c =adD.d =a +c2.(2021·濮阳模拟)已知函数f (x )=x +43x +的值域是全体实数,则实数m 的取值范围是()A.(-4,+∞)B.[-4,+∞)C.(-∞,-4)D.(-∞,-4]3.若函数f (x )=|x |+x 3,则f (lg 2)+f (lg 5)+()A.2B.4C.6D.84.(2021·新高考Ⅱ卷)已知a =log 52,b =log 83,c =12,则下列判断正确的是()A.c <b <aB.b <a <cC.a <c <bD.a <b <ca>0,且a≠1)的图像可能是5.在同一直角坐标系中,函数y=1a x,y=log()6.已知函数f(x)=log2(1-|x|),则关于函数f(x)有下列说法:①f(x)的图像关于原点对称;②f(x)的图像关于y轴对称;③f(x)的最大值为0;④f(x)在区间(-1,1)上单调递增.其中正确的是()A.①③B.①④C.②③D.②④7.(2021·济南一中检测)已知函数y=log a(2x-3)+2(a>0且a≠1)的图像恒过定点A,若点A也在函数f(x)=3x+b的图像上,则b=________.8.计算:lg25+lg50+lg2·lg500+(lg2)2=________.9.函数f(x)=log2x·log2(2x)的最小值为________.10.已知f(x)是定义在R上的偶函数,且当x≥0时,f(x)=log a(x+1)(a>0,且a≠1).(1)求函数f(x)的解析式;(2)若-1<f(1)<1,求实数a的取值范围.11.已知函数f(x)=log21+ax(a为常数)是奇函数.x-1(1)求a的值与函数f(x)的定义域;(2)若当x∈(1,+∞)时,f(x)+log2(x-1)>m恒成立,求实数m的取值范围.12.(2022·烟台模拟)某工厂产生的废气经过滤后排放,过滤过程中废气的污染物含量P(单位:mg/L)与时间t(单位:h)间的关系式为P=P0e-kt,其中P0,k为正常数.如果一定量的废气在前10h的过滤过程中污染物被消除了20%,那么污染物减少到最初含量的50%还需要经过多长时间?(结果四舍五入取整数,参考数据:ln 2≈0.693,ln5≈1.609)()A.11hB.21hC.31hD.41h13.已知函数f(x)log2(x-1),x>1,2x,x≤1,且关于x的方程f(x)-a=0有两个实数根,则实数a的取值范围为()A.(0,1)B.(0,1]C.(1,2)D.(0,2]14.(2022·郑州调研)在①f(x)+f(-x)=0,②f(x)-f(-x)=0,③f(-2)=-f(2)这三个条件中选择一个合适的补充在下面问题中,并给出解答.已知函数f(x)=log2(x2+a+x)(a∈R)满足________.(1)求a的值;(2)若函数g(x)=2f(-x)+1-x2+1,证明:g(x2-x)≤54.注:如果选择多个条件分别解答,按第一个解答计分.。
高三数学复习专题-函数与基本初等函数-第2章第6节-课件

1 高考目标导航
3 课堂典例讲练
2 课前自主导学
4 课时作业
第二章 函数与基本初等函数
走向高考 ·高考总复习 ·北师大版 ·数学
高考目标导航
第二章 函数与基本初等函数
走向高考 ·高考总复习 ·北师大版 ·数学
考纲要求
1.理解对数的概念及其 运算性质,会用换底公式将 一般对数转化成自然对数或 常用对数;了解对数在简化 运算中的作用.
∴2a+1b=2log363+log364=log3636=1.
第二章 函数与基本初等函数
走向高考 ·高考总复习 ·北师大版 ·数学
[方法总结] 对数式化简求值的基本思路: (1)利用换底公式及 logamNn=mn logaN 尽量地转化为同底的 和、差、积、商的运算; (2)利用对数的运算法则,将对数的和、差、倍数运算,转 化为对数真数的积、商、幂再运算; (3)利用约分、合并同类项,尽量地求出具体值. 提醒:对数的运算性质以及有关公式都是在式子中的所有 对数符号有意义的前提下才成立.
第二章 函数与基本初等函数
走向高考 ·高考总复习 ·北师大版 ·数学
(理)设 f(x)=2lo-gx8,1xx,∈x∈-∞1,,+1]∞,, 则满足 f(x)=14的 x 值为__________.
[答案] 3 [解析] 当 x≤1 时,令 2-x=14,则 x=2,不合题意;
当
x>1
时,令
log81x=14,则
第二章 函数与基本初等函数
走向高考 ·高考总复习 ·北师大版 ·数学
[规范解答]
2×5 5
(1)lgl2g+50l-g5l-g4l0g8=lglg54800
=lg45=1. lg4
(2)由 3a=36,4b=36 得 a=log336,b=log436.
高中数学教研活动主题集锦

高中数学教研活动主题集锦一集合与简易逻辑(一)集合(二)简易逻辑二函数概念与基本初等函数(一)函数概念及性质(二)函数图象(三)指数函数、对数函数(四)幂函数(五)函数与方程(六)函数模型与应用(七)反函数三导数及其应用(一)导数的概念及应用(二)导数在研究函数中的应用(三)定积分四三角函数、恒等变换及解三角形(一)三角函数概念(二)三角函数的图象与性质(三)三角恒等变换(四)解三角形五平面向量平面向量六复数复数七数列、极限(一)数列的概念(二)等差数列、等比数列(三)数列的综合应用(四)极限八不等式(一)不等关系与不等式的性质(二)一元二次不等式、分式不等式(三)二元一次不等式组与简单的线性规划(四)基本不等式九直线、平面、简单几何体以及空间向量(一)空间几何体(二)点、线、面的位置关系(三)空间向量的概念及运算(四)空间向量的应用十直线和圆(一)直线方程(二)圆的方程(三)直线与圆、圆与圆的位置关系十一圆锥曲线(一)椭圆(二)双曲线(三)抛物线(四)圆锥曲线的统一定义(五)直线与圆锥曲线的位置关系(六)曲线与方程十二推理与证明推理与证明十三算法算法十四统计统计十五概率初步概率初步十六概率概率十七排列组合、二项式定理(一)排列组合(二)二项式定理十八几何证明选讲几何证明选讲十九矩阵与变换矩阵与变换二十坐标系与参数方程坐标系与参数方程二十一不等式选讲不等式选讲综合专题篇(一)集合与常用逻辑用语展望(二)对函数的考点分析与高考展望(三)浅议导数的运用;(四)对三角函数的考点分析与高考展望(五)浅谈不等式恒成立问题中的交与并(六)函数思想在数列中的应用(七)向“高考试卷中立体几何命题”学习(八)对解析几何的考点分析与高考展望(九)对计数原理的考点分析及高考展望(十)对概率的考点分析与高考展望。
加练半小时高考数学江苏专用理科专题复习:6专题2 函数概念与基本初等函数 含答案

训练目标 (1)函数的概念;(2)函数的“三要素”;(3)函数的表示法.训练题型(1)函数的三种表示方法;(2)函数定义域求法;(3)函数值域的简单求法;(4)分段函数.解题策略(1)函数的核心是对应关系,任一自变量都对应唯一一个函数值;(2)若已知函数f (x )的定义域为[a ,b ],则复合函数f [g (x )]的定义域可由不等式a ≤g (x )≤b 解出;(3)分段函数是一个函数,解决分段函数的关键是根据定义域中的不同区间分类讨论.1.(2015·湖北改编)函数f (x )=4-|x |+lg x x -3的定义域为________.2.函数y =1-x +x 的定义域为________. 3.已知函数f (x )=⎩⎪⎨⎪⎧0,x >0,π,x =0,π2+1,x <0,则f {f [f (-1)]}=________.4.记函数f (x )=3-x 的定义域为A ,则A ∩N 中有________个元素.5.(2015·山东)设函数f (x )=⎩⎪⎨⎪⎧3x -b ,x <1,2x ,x ≥1.若f ⎝⎛⎭⎫f ⎝⎛⎭⎫56 =4,则b =________. 6.(2015·宁夏大学附属中学上学期期中)函数y =⎩⎪⎨⎪⎧3x ,x ∈(-∞,-1),log 2x ,x ∈[1,+∞)的值域为________.7.将长度为2的一根铁条折成长为x 的矩形,矩形的面积y 关于x 的函数关系式是y =x (1-x ),则函数的定义域是________.8.设函数y =f (x )在R 上有定义.对于给定的正数M ,定义函数f M (x )=⎩⎪⎨⎪⎧f (x ),f (x )≤M ,M ,f (x )>M ,则称函数f M (x )为f (x )的“孪生函数”.若给定函数f (x )=2-x 2,M =1,则f M (0)=________. 9.已知函数f (x +1)=x +2x ,则函数f (x )的解析式为________.10.规定记号“⊗”表示一种运算,即a ⊗b =ab +a +b (a ,b 为非负实数),若1⊗k =3,则k 的值为________;函数f (x )=k ⊗x 的值域为________.11.(2015·湖北重点中学上学期第三次月考)若函数f (x )=x 2-3x -4的定义域为[0,m ],值域为[-254,-4],则实数m 的取值范围是________.12.已知函数f (x )=1-x 2,函数g (x )=2a cos(π3x )-3a +2(a >0),若存在x 1,x 2∈[0,1],使得f (x 1)=g (x 2)成立,则实数a 的取值范围是________. 13.下列各组函数中,表示同一函数的有________个. ①y =x -1和y =x 2-1x +1;②f (x )=x 2和g (x )=(x +1)2; ③f (x )=(x )2x 和g (x )=x(x )2.14.函数y =f (x )的图象如图所示,给出下列说法: ①函数y =f (x )的定义域是[-1,5]; ②函数y =f (x )的值域是(-∞,0]∪[2,4]; ③函数y =f (x )在定义域内是增函数; ④函数y =f (x )在定义域内的导数f ′(x )>0. 其中正确的是________.答案解析1.(2,3)∪(3,4]解析 依题意,有4-|x |≥0,解得-4≤x ≤4①;x 2-5x +6x -3>0,解得x >2且x ≠3②;由①②求交集得函数的定义域为(2,3)∪(3,4]. 2.{x |0≤x ≤1}解析 由题意可知⎩⎪⎨⎪⎧1-x ≥0,x ≥0,解得0≤x ≤1.3.π解析 f (-1)=π2+1,所以f {f [f (-1)]}=f [f (π2+1)]=f (0)=π. 4.4解析 由3-x ≥0,得x ≤3,即A ={x |x ≤3},所以A ∩N ={0,1,2,3},有4个元素. 5.12解析 由题意得f ⎝⎛⎭⎫56=3×56-b =52-b . 若52-b ≥1,即b ≤32时,252-b =4,解得b =12. 若52-b <1,即b >32时,3×⎝⎛⎭⎫52-b -b =4, 解得b =78(舍去).所以b =12.6.[0,+∞)解析 当x ≥1时,log 2x ≥log 21=0;当x <-1时,0<3x <3-1=13,故函数的值域为{y |y ≥0}∪{y |0<y <13}={y |y ≥0}.7.{x |0<x <1}解析 由于矩形的长和宽均大于零,所以有x >0且2-2x2>0,得0<x <1.8.1解析 由题设f (x )=2-x 2≤1,得 当x ≤-1或x ≥1时,f M (x )=2-x 2;当-1<x <1时,f M (x )=1.∴f M (0)=1. 9.f (x )=x 2-1(x ≥1)解析 设x +1=t ,则t ≥1,x =t -1,两边平方得x =(t -1)2,∴f (t )=(t -1)2+2(t -1)=t 2-1,∴f (x )=x 2-1(x ≥1). 10.1 [1,+∞)解析 ∵a ⊗b =ab +a +b (a ,b 为非负实数), ∴1⊗k =k +1+k =3(k 为非负实数),解得k =1. 函数f (x )=k ⊗x =1⊗x =x +1+x ,设f 1(x )=x ,则f 1(x )在[0,+∞)上为增函数. 设f 2(x )=x +1,则f 2(x )在[0,+∞)上也为增函数. 由此可得f (0)=1为f (x )的最小值, 所以f (x )=x +1+x 的值域为[1,+∞). 11.[32,3]解析 函数f (x )=x 2-3x -4的图象开口向上,对称轴为直线x =32,f (32)=-254,f (0)=-4,f (3)=-4.因为所给值域中包括最小值,所以m 的取值范围是[32,3].12.[12,2]解析 当x ∈[0,1]时,f (x )=1-x 2的值域是[0,1],g (x )=2a cos(π3x )-3a +2(a >0)的值域是[2-2a,2-a ],为使存在x 1,x 2∈[0,1],使得f (x 1)=g (x 2)成立,需[0,1]∩[2-2a,2-a ]≠∅.由[0,1]∩[2-2a,2-a ]=∅,得1<-2a +2或2-a <0,解得a <12或a >2.所以,若存在x 1,x 2∈[0,1],使得f (x 1)=g (x 2)成立,则实数a 的取值范围是12≤a ≤2.13.1解析 ①中两函数的定义域不同;②中两函数的对应法则不同;③中两个函数都能化为f (x )=1(x >0),表示同一个函数. 14.①②解析①②正确;函数y=f(x)在定义域内不是增函数,因而③④错误.。
加练半小时高考数学江苏专用理科专题复习:9专题2 函数概念与基本初等函数 含答案

训练目标函数的单调性、最值、奇偶性、周期性. 训练题型 (1)判定函数的性质;(2)求函数值或解析式;(3)求参数或参数范围;(4)和函数性质有关的不等式问题.解题策略 (1)利用奇偶性或周期性求函数值(或解析式),要根据自变量之间的关系合理转换;(2)和单调性有关的函数值大小问题,先化到同一单调区间;(3)解题时可以根据函数性质作函数的草图,充分利用数形结合思想.①y =x +1;②y =-x 3;③y =1x;④y =x |x |. 2.(2015·黄冈调研)定义在R 上的函数f (x )满足f (-x )+f (x )=0,f (x )=f (x +4),且x ∈(-2,0)时,f (x )=2x +15,则f (log 220)=________. 3.已知函数f (x )=⎩⎪⎨⎪⎧x 2+1,x >0,cos x ,x ≤0,则下列结论正确的是________. ①f (x )是偶函数;②f (x )是增函数;③f (x )是周期函数;④f (x )的值域为[-1,+∞).4.若f (x )和g (x )都是奇函数,且F (x )=f (x )+g (x )+2在(0,+∞)上有最大值8,则在(-∞,0)上F (x )有最______值,为________.5.设x >y >1,0<a <1,则下列关系正确的是________.①x -a >y -a ;②ax <ay ;③a x <a y ;④log a x >log a y .6.若定义运算a ⊙b =⎩⎪⎨⎪⎧b ,a ≥b ,a ,a <b ,则函数f (x )=x ⊙(2-x )的值域为________. 7.(2015·四川成都七中零诊)对于函数f (x ),若存在常数a ≠0,使得x 取定义域内的每一个值,都有f (x )=f (2a -x ),则称f (x )为准偶函数,下列函数中是准偶函数的是________. ①f (x )=cos(x +1);②f (x )=x ;③f (x )=tan x ;④f (x )=x 3.8.(2015·安徽庐江部分示范高中第三次联考)定义域为R 的函数f (x )满足f (x +1)=2f (x ),且当x ∈[0,1]时,f (x )=x 2-x ,则当x ∈[-1,0)时,f (x )的最小值为________.9.已知函数y =f (x )是定义在R 上的奇函数,当x <0,f (x )=x +2,那么不等式2f (x )-1<0的解集是________________.10.(2015·广州综合测试一)已知幂函数f (x )=x -m 2-2m +3(m ∈Z )为偶函数,且在区间(0,+∞)上是单调增函数,则f (2)的值为________.11.定义在R 上的函数f (x )满足f (x +32)+f (x )=0,且函数y =f (x -34)为奇函数,给出下列命题:①函数f (x )的最小正周期是32; ②函数y =f (x )的图象关于点(-34,0)对称; ③函数y =f (x )的图象关于y 轴对称.其中真命题的个数是________.12.已知偶函数f (x )在区间[0,+∞)上单调递增,则满足f (2x )<f ⎝⎛⎭⎫13的x 的取值范围是________.13.已知定义在R 上的偶函数y =f (x )满足:f (x +4)=f (x )+f (2),且当x ∈[0,2]时,y =f (x )单调递减,给出以下四个命题:①f (2)=0;②直线x =-4为函数y =f (x )图象的一条对称轴;③函数y =f (x )在[8,10]上单调递增;④若关于x 的方程f (x )=m 在[-6,-2]上的两根分别为x 1,x 2,则x 1+x 2=-8.其中所有正确命题的序号为________.14.(2015·湖北武汉部分学校毕业生2月调研)已知函数f (x )=a log 2|x |+1(a ≠0),定义函数F (x )=⎩⎪⎨⎪⎧f (x ),x >0,-f (x ),x <0,给出下列命题: ①F (x )=|f (x )|;②函数F (x )是奇函数;③当a >0时,若x 1x 2<0,x 1+x 2>0,则F (x 1)+F (x 2)>0成立;④当a <0时,函数y =F (x 2-2x -3)存在最大值,不存在最小值.其中所有正确命题的序号是________.答案解析1.④解析 易知y =x |x |为奇函数,图象如下:从图知y =x |x |为增函数.2.-1解析 ∵f (-x )+f (x )=0,即f (-x )=-f (x ),∴定义在R 上的函数f (x )是奇函数.∵4=log 216<log 220<log 232=5,∴f (log 220)=f (log 220-4)=f (log 254)=-f (-log 254)=-f (log 245), ∵-2<log 245<0,∴f (log 245)=2log 245+15=1, ∴f (log 220)=-1.3.④解析 因为f (π)=π2+1,f (-π)=-1,所以f (-π)≠f (π),所以函数f (x )不是偶函数,排除A ;因为函数f (x )在(-2π,-π)上单调递减,排除B ;函数f (x )在(0,+∞)上单调递增,所以函数f (x )不是周期函数,排除C ;因为x >0时,f (x )>1,x ≤0时,-1≤f (x )≤1,所以函数f (x )的值域为[-1,+∞).4.-4解析 由题意知f (x )+g (x )在(0,+∞)上有最大值6,因为f (x )和g (x )都是奇函数,所以f (-x )+g (-x )=-f (x )-g (x )=-[f (x )+g (x )], 即f (x )+g (x )也是奇函数,所以f (x )+g (x )在(-∞,0)上有最小值-6,所以F (x )=f (x )+g (x )+2在(-∞,0)上有最小值-4.5.③解析 对于①,-a <0,幂函数f (x )=x -a 在(0,+∞)上是减函数,所以x -a <y -a ,故①不正确;对于②,x >y >1,又a >0,利用不等式的性质得ax >ay ,故②不正确;易知③正确;对于④,因为0<a <1,所以函数f (x )=log a x 在(1,+∞)上是减函数,又x >y >1,所以log a x <log a y ,故④不正确.6.(-∞,1]解析 由题意知x ⊙(2-x )表示x 与2-x 两者中的较小者,借助y =x 与y =2-x 的图象,不难得出f (x )的值域为(-∞,1].7.①解析 对于函数f (x ),若存在常数a ≠0,使得x 取定义域内的每一个值,都有f (x )=f (2a -x ),则称f (x )为准偶函数,∴函数的对称轴是直线x =a ,a ≠0,②③④中,函数没有对称轴;函数f (x )=cos(x +1),有对称轴,且x =0不是对称轴,①正确.8.-18解析 当x ∈[-1,0)时,x +1∈[0,1).∵f (x +1)=2f (x ),∴f (x )=12f (x +1)=12[(x +1)2-(x +1)]=12(x 2+x ),其图象的对称轴为直线x =-12, ∴f (x )min =f (-12)=-18. 9.{x |x <-32或0≤x <52} 解析 由题意知,函数y =f (x )的定义域是R ,当x <0时,f (x )=x +2,则当x >0时,-x <0,所以f (-x )=-x +2,又函数y =f (x )为定义在R 上的奇函数,所以f (x )=-f (-x )=x -2,即f (x )=⎩⎪⎨⎪⎧ x +2,x <0,0,x =0,x -2,x >0,因此不等式2f (x )-1<0等价于⎩⎪⎨⎪⎧ x <0,x +2<12或⎩⎪⎨⎪⎧ x =0,0<12或⎩⎪⎨⎪⎧x >0,x -2<12.解得x <-32或0≤x <52. 10.16解析 因为幂函数f (x )在区间(0,+∞)上是单调增函数,所以-m 2-2m +3>0,解得-3<m <1,因为m ∈Z ,所以m =-2或m =-1或m =0.因为幂函数f (x )为偶函数,所以-m 2-2m +3是偶数,当m =-2时,-m 2-2m +3=3,不符合,舍去;当m =-1时,-m 2-2m +3=4;当m =0时,-m 2-2m +3=3,不符合,舍去.所以f (x )=x 4,故f (2)=24=16.11.2解析 由题意可得f (x +3)=-f (x +32)=f (x ),则函数f (x )是周期函数,且其最小正周期为3,故①错误;由y =f (x -34)是奇函数,可知其图象关于原点(0,0)对称,又函数y =f (x -34)的图象向左平移34个单位长度可得函数y =f (x )的图象,则函数f (x )的图象关于点(-34,0)对称,故②正确;由②知,对于任意的x ∈R ,都有f (-34-x )=-f (-34+x ),用34+x 代换x ,可得f (-32-x )+f (x )=0,所以f (-32-x )=-f (x )=f (x +32)对于任意的x ∈R 都成立,令t =32+x ,得f (-t )=f (t ),则函数f (x )是偶函数,其图象关于y 轴对称,故③正确.综上可知,真命题的个数是2.12.⎝⎛⎭⎫-16,16 解析 偶函数满足f (x )=f (|x |),根据这个结论,有f (2x )<f ⎝⎛⎭⎫13⇔f (|2x |)<f ⎝⎛⎭⎫13, 进而转化为不等式|2x |<13,解这个不等式即得x 的取值范围是⎝⎛⎭⎫-16,16. 13.①②④解析 对于①,∵f (x +4)=f (x )+f (2),∴当x =-2时,f (-2+4)=f (-2)+f (2),∴f (-2)=0,又f (x )是偶函数,∴f (2)=0,∴①正确;对于②,∵f (x +4)=f (x )+f (2),f (2)=0,∴f (x +4)=f (x ),∴函数y =f (x )的周期T =4,又直线x =0是函数y =f (x )图象的对称轴,∴直线x =-4也为函数y =f (x )图象的一条对称轴,∴②正确;对于③,∵函数f (x )的周期是4,∴y =f (x )在[8,10]上的单调性与[0,2]上的单调性相同,∴y =f (x )在[8,10]上单调递减,∴③错误;对于④,∵直线x =-4是函数y =f (x )图象的对称轴,∴x 1+x 22=-4,x 1+x 2=-8,∴④正确. 14.②③解析 ①因为|f (x )|=⎩⎨⎧ f (x ),|x |≥2-1a ,-f (x ),0<|x |<2-1a ,而F (x )=⎩⎪⎨⎪⎧f (x ),x >0,-f (x ),x <0,这两个函数的定义域不同,不是同一函数,即F (x )=|f (x )|不成立,①错误.②当x >0时,F (x )=f (x )=a log 2|x |+1,-x <0,F (-x )=-f (-x )=-(a log 2|-x |+1)=-(a log 2|x |+1)=-F (x );当x <0时,F (x )=-f (x )=-(a log 2|x |+1),-x >0,F (-x )=f (-x )=a log 2|-x |+1=a log 2|x |+1=-F (x ).所以函数F (x )是奇函数,②正确.③当a >0时,F (x )=f (x )=a log 2|x |+1在(0,+∞)上是单调增函数.若x 1x 2<0,x 1+x 2>0,不妨设x 1>0,则x 2<0,x 1>-x 2>0,所以F (x 1)>F (-x 2)>0,又因为函数F (x )是奇函数,-F (x 2)=F (-x 2),所以F (x 1)+F (x 2)>0,③正确.④函数y =F (x 2-2x -3)=⎩⎪⎨⎪⎧ a log 2(x 2-2x -3)+1,x >3或x <-1,-a log 2(-x 2+2x +3)-1,-1<x <3,当x >3或x <-1时,因为a <0,所以y =F (x 2-2x -3)既没最大值,也没最小值,即函数y =F (x 2-2x -3)的值域为(-∞,+∞),故④错误.综上知,答案为②③.。
函数概念与基本初等函数

函数概念与基本初等函数函数概念与基本初等函数Ⅰ(一)函数1.了解构成函数的要素,了解映射的概念,会求一些简单函数的定义域和值域2.理解函数的三种表示法:解析法、图象法和列表法,能根据不同的要求选择恰当的方法表示简单的函数。
3.了解分段函数,能用分段函数来解决一些简单的数学问题。
4.理解函数的单调性,会讨论和证明一些简单的函数的单调性;理解函数奇偶性的含义,会判断简单的函数奇偶性。
5.理解函数的最大(小)值及其几何意义,并能求出一些简单的函数的最大(小)值6.会运用函数图像理解和研究函数的性质(二)指数函数1.了解指数函数模型的实际背景。
2.理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算。
3.理解指数函数的概念,会求与指数函数性质有关的问题。
4.知道指数函数是一类重要的函数模型。
(三)对数函数1.理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用。
2.理解对数函数的概念;会求与对数函数性质有关的问题3.知道对数函数是一类重要的函数模型4.了解指数函数与对数函数互为反函数()。
(四)幂函数1.了解幂函数的概念。
2.结合函数的图像,了解它们的变化情况。
(五)函数与方程1.了解函数零点的概念,结合二次函数的图像,了解函数的零点与方程根的联系。
2.理解并掌握连续函数在某个区间上存在零点的判定方法。
能利用函数的图象和性质判别函数零点的个数(六)函数模型及其应用1.了解指数函数、对数函数以及幂函数的增长特征。
知道直线上升、指数增长、对数增长等不同函数类型增长的含义。
2.了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用。
3.能利用给定的函数模型解决简单的实际问题。
根据考试大纲的要求,结合2009年高考的命题情况,我们可以预测2010年集合部分在选择、填空和解答题中都有涉及,高考命题热点有以下两个方面:一是集合的运算、集合的有关述语和符号、集合的简单应用等作基础性的考查,题型多以选择、填空题的形式出现;二是以函数、方程、三角、不等式等知识为载体,以集合的语言和符号为表现形式,结合简易逻辑知识考查学生的数学思想、数学方法和数学能力,题型常以解答题的形式出现函数是高考数学的重点内容之一,函数的观点和思想方法贯穿整个高中数学的全过程,包括解决几何问题.在近几年的高考试卷中,选择题、填空题、解答题三种题型中每年都有函数试题,而且常考常新.以基本函数为模型的应用题和综合题是高考命题的新趋势.考试热点:①考查函数的表示法、定义域、值域、单调性、奇偶性、反函数和函数的图象.②函数与方程、不等式、数列是相互关联的概念,通过对实际问题的抽象分析,建立相应的函数模型并用来解决问题,是考试的热点.③考查运用函数的思想来观察问题、分析问题和解决问题,渗透数形结合和分类讨论的基本数学思想.第1课时函数及其表示一、映射1.映射:设A、B是两个集合,如果按照某种对应关系f,对于集合A 中的元素,在集合B中都有元素和它对应,这样的对应叫做到的映射,记作.2.象与原象:如果f:A→B是一个A到B的映射,那么和A中的元素a 对应的叫做象,叫做原象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题二函数概念与基本初等函数Ⅰ第六讲函数模型及其应用答案部分1.B【解析】由()(2)f x f x=-知()f x的图像关于直线1x=对称,又函数22|23||(1)4|y x x x=--=--的图像也关于直线1x=对称,所以这两个函数图像的交点也关于直线1x=对称,不妨设12mx x x<<⋅⋅⋅<,则112mx x+=,即12mx x+=,同理212mx x-+=,……,由121mi mix x x x==++⋅⋅⋅+∑,所以121112()()()2mi m m mix x x x x x x m-==++++⋅⋅⋅++=∑,所以1miix m==∑,故选B.2.B【解析】由已知可设2(0)()2(0)-⎧≥⎪=⎨<⎪⎩xxxf xx,则2(0)()2(0)-⎧≥⎪=⎨<⎪⎩aaaf aa,因为()f x为偶函数,所以只考虑0≥a的情况即可.若()2≤bf a,则22≤a b,所以≤a b.故选B.3.B【解析】因为第一次邮箱加满,所以第二次的加油量即为该段时间内的耗油量,故耗油量48V=升.而这段时间内行驶的里程数3560035000600S=-=千米.所以这段时间内,该车每100千米平均耗油量为481008600⨯=升,故选B.4.B 【解析】采用特殊值法,若1,x y==14cz=,10az by cx++=,11ay bz cx++=,ayaz by cx++.5.B【解析】由题意可知2p at bt c=++过点(3,0.7),(4,0.8)(5,0.5),代入2p at bt c=++中可解得0.2, 1.5,2a b c=-==-,∴220.2 1.520.2( 3.75)0.8125p t t t=-+-=--+∴当 3.75t =分钟时,可食用率最大.6.D 【解析】设年平均增长率为x ,原生产总值为a ,则2(1)(1)(1)p q a a x ++=+,解得1x =,故选D .7.A 【解析】解法一 由题意可知,该三次函数满足以下条件:过点(0,0),(2,0),在(0,0)处的切线方程为y = -x ,在(2,0)处的切线方程为y = 3x -6,以此对选项进行检验.A 选项,321122y x x x =--,显然过两个定点,又2312y x x '=--, 则02|1,|3x x y y ==''=-=,故条件都满足,由选择题的特点知应选A .解法二 设该三次函数为32()f x ax bx cx d =+++,则2()32f x ax bx c '=++由题设有(0)0(2)0(0)1(2)3f f f f =⎧⎪=⎪⎨'=-⎪⎪'=⎩,解得11,,1,022a b c d ==-=-=. 故该函数的解析式为321122y x x x =--,选A . 8.A 【解析】设所求函数解析式为()y f x =,由题意知(5)2,52f f =--=(), 且(5)0f '±=,代入验证易得3131255y x x =-符合题意,故选A . 9.36π【解析】取SC 的中点O ,连接,OA OB ,因为,SA AC SB BC ==,所以,OA SC OB SC ⊥⊥.因为平面SAC ⊥平面SBC ,所以OA ⊥平面SBC .设OA r =,1112332A SBC SBC V S OA r -∆=⨯⨯=⨯⨯⨯所以31933r r =⇒=, 所以球的表面积为2436r ππ=. 10.1[,1]2【解析】由题意,22222(1)221u x y x x x x =+=+-=-+,且[0,1]x ∈, 又0x =时,221u x y =+=,12x =时,2212u x y =+=,当1x =时,221u x y =+=,所以22x y +取值范围为1[,1]2.1122221145+28=4833r r r ππππ⨯⨯⨯⨯⨯⨯⨯⨯+⨯⨯⇒=12.)+∞【解析】函数()g x 的定义域为[1,2]-, 根据已知得()()()2h x g x f x +=,所以()=2()()62h x f x g x x b -=+()()h x g x >恒成立,即62x b +>,令3y x b =+,y =,则只要直线3y x b =+在半圆224(0)x y y +=≥2>,解得b >,故实数b 的取值范围是)+∞.13.160【解析】设该容器的总造价为y 元,长方体的底面矩形的长x m ,因为无盖长方体的容积为34m ,高为1m ,所以长方体的底面矩形的宽为4m x,依题意,得24420410(28020(8020160y x x x x ⨯=⨯++=+++⨯=≥. 14.①③④【解析】对于①,根据题中定义,()A f x ∈⇔函数()y f x =,x D ∈的值域为R ,由函数值域的概念知,函数()y f x =,x D ∈的值域为,R b R a D ⇔∀∈∃∈()f a b =,所以①正确;对于②,例如函数||1()()2x f x =的值域(0,1]包含于区间[1,1]-,所以()f x B ∈,但()f x 有最大值l ,没有最小值,所以②错误;对于③,若()()f x g x B +∈,则存在一个正数1M ,使得函数()()f x g x B +∈的值域包含于区间11[,]M M -,所以1M -≤()f x ()g x M +≤,由()g x B ∈知,存在一个正数2M ,使得函数()g x 的值域包含于区间22[M -222()M g x M -≤-≤,两式相加得12()M M -+≤()f x ≤12M M +,于是()f x B ∈,与已知“.()f x A ∈”矛盾,故()()f x g x B +∉,即③正确;对于④,如果0a >,那么,()x f x →+∞→+∞,如果0a <,那么2,()x f x →-→+∞,所以()f x 有最大值,必须0a =,此时2()1x f x x =+在区间(2,)-+∞上,有11()22f x -≤≤,所以()f x B∈,即④正确,故填①③④.15.【解析】(1)由题意知,点M,N的坐标分别为()5,40,()20,2.5.将其分别代入2ayx b=+,得40252.5400abab⎧=⎪⎪+⎨⎪=⎪+⎩,解得1000ab=⎧⎨=⎩.(2)①由(1)知,21000yx=(520x≤≤),则点P的坐标为21000,tt⎛⎫⎪⎝⎭,设在点P处的切线l交x,y轴分别于A,B点,32000yx'=-,则l的方程为()2310002000y x tt t-=--,由此得3,02tΑ⎛⎫⎪⎝⎭,230000,Βt⎛⎫⎪⎝⎭.故()f t==,[]5,20t∈.②设()624410g t tt⨯=+,则()6516102g t tt⨯'=-.令()0g t'=,解得t=当(t∈时,()0g t'<,()g t是减函数;当()20t∈时,()0g t'>,()g t是增函数.从而,当t=()g t有极小值,也是最小值,所以()min300g t=,此时()minf t=答:当t=l的长度最短,最短长度为16.【解析】2160rπ元,所以蓄水池的总成本为(200π)元.又题意据220016012000rh rπππ+=,所以21(3004)5h rr=-,从而23()(3004)5V r r h r rππ==-.因0r>,又由0h>可得r<故函数()V r的定义域为.(Ⅱ)因3()(3004)5V r r rπ=-,故2()(30012)5V r rπ'=-.令()0V r'=,解得125,5r r==-(因25r=-不在定义域内,舍去).当(0,5)r∈时,()0V r'>,故()V r在(0,5)上为增函数;当r∈时,()0V r'<,故()V r在上为减函数.由此可知,()V r在5r=处取得最大值,此时8h=.即当5r=,8h=时,该蓄水池的体积最大.17.【解析】(1)当1,1,2b c n==-…时,()1nf x x x=+-.∵111()(1)(10222nf f=-⨯<,∴()f x在1(,1)2内存在零点.又当1(,1)2x∈时,1()10nf x nx-'=+>,∴()f x在1(,1)2上是单调递增的,∴()f x在区间1(,1)2内存在唯一的零点;(2)解法一由题意知1(1)1,1(1)1,ff--⎧⎨-⎩剟剟即02,20,b cb c-⎧⎨-+⎩剟剟由图像知,3b c+在点(0,2)-取得最小值6-,在点(0,0)取得最大值0.b解法二由题意知1(1)11f b c-=++剟,即20b c-+剟.…①1(1)11f b c--=-+剟,即2--?①2⨯+②得62()()30b c b c b c-++-+=+?-?,当0,2b c==-时,36b c+=-;当0b c==时,30b c+=.所以3b c+的最小值6-,最大值0.解法三由题意知(1)1,(1)1,f b cf b c-=-+⎧⎨=++⎩,解得(1)(1)(1)(1)2,22f f f f b c --+--==, 32(1)(1)3b c f f +=+--.又∵1(1)1,1(1)1,f f --⎧⎨-⎩剟剟,∴630b c -+??. 当0,2b c ==-时,36b c +=-;当0b c ==时,30b c +=.所以3b c +的最小值6-,最大值0.(3)当2n =时,2()f x x bx c =++.对任意12,x x [1,1]∈-都有有12()()4f x f x -…等价于()f x 在[-1,1]上的最大值与最小值之差4M ….据此分类讨论如下:(ⅰ)当12b >,即2b >时, (1)(1)24M f f b =--=>,与题设矛盾. (ⅱ)当102b --<…,即02b <…时, 2(1)()(1)422b b M f f =--=+…恒成立. (ⅲ) 当012b -<…,即20b -剟时, 2(1)((1)422b b M f f =---=-…恒成立. 综上可知,22b -剟.18.【解析】设包装盒的高为h (cm ),底面边长为a (cm ),由已知得.300),30(22260,2<<-=-==x x xh x a(1),1800)15(8)30(842+--=-==x x x ah S所以当15=x 时,S 取得最大值.(2)),30(22222x x h a V +-==由00=='x V 得(舍)或x =20.当)20,0(∈x 时,0;(20,30)0V x V ''>∈<当时.所以当x =20时,V 取得极大值,也是最小值. 此时1122h a =即装盒的高与底面边长的比值为12.。
