lec02
LEC评价法应用介绍

建立风险控制措施的监督和考核机制
制定明确的风险控制目标和标准 建立定期检查和评估机制 加强员工培训和意识提升 建立奖惩机制激励员工积极参与风险控制
持续改进和优化LEC评价法
定期评估:定 期对LEC评价 法进行评估确 保其准确性和
有效性
反馈机制:建 立反馈机制及 时收集和反馈 使用过程中的
问题和建议
提高效率:LEC评 价法可以帮助企业 提高工作效率减少 不必要的时间和精 力浪费。
持续改进:LEC评 价法可以帮助企业 持续改进不断提高 企业的管理水平和 竞争力。
LEC评价法未来的发展趋势和研究方向
智能化:利用大数 据和人工智能技术 提高评价的准确性 和效率
标准化:建立统一 的评价标准和规范 提高评价结果的可 比性和可信度
危险源分类:根据危险源的危害程度将其分为不同类别如重大危险源、 一般危险源等。
危险源评估:对危险源进行评估确定其风险等级如高风险、中风险、低 风险等。
制定控制措施:根据危险源的风险等级制定相应的控制措施如改进设备、 加强培训、制定应急预案等。
评价危险源的风险等级
确定危险源: 识别可能导致 事故或伤害的Байду номын сангаас
风险评估:使用LEC评价法 对危险源进行风险评估包括 风险等级、风险因素等
风险控制措施:根据风险 评估结果提出相应的风险 控制措施如加强安全管理、 改进生产工艺等
案例总结:总结案例分析 的主要发现和启示如LEC 评价法的应用效果、改进 建议等
案例二:某矿山企业安全风险评估与控制
企业背景:某大型矿山企业生产规模大员工数量多 风险评估:采用LEC评价法对矿山企业的安全风险进行评估 控制措施:根据LEC评价结果制定相应的安全风险控制措施 效果评估:实施安全风险控制措施后矿山企业的安全风险得到有效控制生产效率得到提高
麻省理工MIT(微观经济学)lec01_02_orderings and utility representation
14.123 Lectures 1-2, Page 3
Introduction
• Economics is about explaining and predicting choice. • It is assumed that economic agents choose their most desirable alternative among the set of feasible ones. – Interpret it “as if”, not necessarily “deliberate”. – “This morning I took the shuttle to MIT because this was the best possible way to come in.” Discuss. • Desirability is represented by preferences and/or utility. – Attitudes may be expressed over outcomes never experienced (Would you prefer to be Superman or Spiderman?).
14.123 Lectures 1-2, Page 6
Utility Representation
• DEF. Utility fcn u : X → represents if u(x) ≥ u(y) x y. • THM: If u represents , then is complete and transitive. ■ Follows from the same properties of ≥ on real numbers. ■ • THM: If X is finite and is complete and transitive, then there exists a utility function that represents . ■ u(x) = |{y∈X : xy}|: # of alternatives that x beats weakly.■ • THM: If X is countable and is complete and transitive, then there is a utility function with a bounded range that represents . ■ X ≡ {x1,x2,…}. Let u(x-1)=0, u(x0)=1. For all n=1,2,…, set u(xn) = [max{u(xk)|xnxk,n>k} + min{u(xk)|xkxn,n>k}]/2 .■
LEC02_PT1_CH04-round-offandtruncationerrors

LECTURE 2 -1MAE3100Prof. D.E. SmithLECTURE 2Round-Off and Truncation ErrorsMotivation:Understanding the concept of error and how it develops in numerical methods is important to the effective use of computer techniques.This study focuses on two major forms of numerical error: Round-offError and Truncation Error.Reading Assignment:Chapra Chapter 4 (required)Chapra and Canale Section 4.1 (optional)LECTURE 2 -2MAE3100Prof. D.E. SmithLECTURE 2 OBJECTIVESThe primary objective of this lecture is to provide a basicunderstanding of computational errors introduced bynumerical methods. More specifically, this lecture will:•Expose potential sources of computational errors.•Compare accuracy and precision.•Review numerical precision associated with digitalcomputing.•Provide specific calculations for evaluating error estimates.•Provide a means for estimating truncation error using theTaylor series.•Explore finite difference approximations for first and secondderivatives.MAE3100Prof. D.E. SmithLECTURE 2 -3You’ve Got A Problem•The numerical methods solution to the bungee jumper problem inChapter 1 employed an approximation to the derivative as•What is known?–Numerical error is introduced byapproximation–Approximation error depends on t–Computers have limited precision•What is needed?– A basic understanding of errors associated with computercalculations– A method for assessing the amount of error introduced withthe approximations used by numerical methodsii i i t t t v t v t v dt dv 11)()(MAE3100Prof. D.E. SmithLECTURE 2 -4Sources of Error•Errors in mathematical modelingResult from simplifying assumptions and approximations madewhen representing physical systems by mathematical equations.•BlundersResult from mathematical modeling errors and/or programmingerrors.•Errors in inputBEWARE: garbage in –garbage out•Machine errorsResult from rounding, chopping, underflow and overflow•Truncation errorsResult from simplifying assumptions and approximations madein the numerical procedureOccurs when truncating an infinite series or numericalevaluation of an improper integral. E.g.,!4!3!21432x x x x e xMAE3100Prof. D.E. SmithLECTURE 2 -5Accuracy and Precisiondata scatterdefinesimprecisionoruncertaintysystematic deviation defines inaccuracy or bias inaccurateandimpreciseaccurateandprecise MAE3100Prof. D.E. SmithLECTURE 2 -6Significant Figures•The significant digits of a number are those that can be used withconfidence.•What is the speed?–48 or 49?–48.8 or 48.9?–48.8642138?–#sig-figs = 3•What is the mileage?–87324.4 or 87324.5?–87324.46?–#sig-figs = 7•All results in MAE3100 must display appropriate units and Sig-Figs–Use no less than 3 sig-figs, 4 is preferred–Use the greatest accuracy possible during calculations–Report result with sig-figs consistent with inputMAE3100Prof. D.E. SmithLECTURE 2 -7Error Definitions•True (Absolute) ErrorNote: Issues arise when working with different orders-of-magnitude•True Percent Relative Error•Approximate Percent Relative Error (true value not always known)• A specified percent tolerance s may be used as a stopping criteria:I.e., stop with n decimal place accuracy when ionapproximat value true t E (100%) value true ionapproximat - value true (100%) value true error true t %)100(ion approximat current ionapproximat previous -ion approximat current (100%)ion approximat errore approximat a )%105.0(2n s a MAE3100Prof. D.E. SmithLECTURE 2 -8Round-Off Error•Recall that numbers are stored in binary format–16 bit integer representationRange: -32,768 to 32,767Shown: -173–Floating point representation•Single precision (32 bit)24 bit mantissa7-8 sig-figs Range: 10-38to 1039•Double precision (64 bit)15-16 sig-figsRange: 10-308to 10308Representation used by MATLAB (223210)272625242330292831….sMAE3100Prof. D.E. SmithLECTURE 2 -9Working with Computer Numbers•Computers work in base 2 making it impossible to accuratelyrepresent numbers of interest, e.g.,•MATLAB commands related to machine precision include realmax ,realmin , eps•Round-off errors can accumulate in large computations.•Loss of significant figures occurs when subtracting numbers ofsimilar magnitude:•Small numbers can be lost when added to large numbers using finitemachine precision 333100001.0107641.0107642.0...,7,,,1.0etc e 4444104000.010*******.010*******.0104000.0chopped MAE3100Prof. D.E. SmithLECTURE 2 -10Truncation Error•Taylor theorem : Any smooth function can be written as a polynomial.•Definition: The Taylor Series expansion of f (x )about x = a iswhere the remainder is•The n -th order Taylor Series with h = x –a becomes:• A Maclaurin Series is a Taylor Series expanded about a = 0 (h = x )nk nk k R a x a f k x f 0)()()(!1)(n -th order Taylor Series approximation f n (x )remainder))(()()()!1(111)1(n n n n a x O a x f n R x a nn n hn a f h a f h a f h a f a f h f !)(!3)(!2)()()()()(3)3(2 nn n xn f x f x f x f f x f !)0(!3)0(!2)0()0()0()()(3)3(2 error is ‘on the order of’(x -a )n +1a x XI (ks-eye)MAE3100Prof. D.E. SmithLECTURE 2 -11Truncation Error (cont.)•Accuracy increases as more terms are added to the Taylor Series expansionconstant)a (i.e., 0a function)linear a (i.e., 10h a a )polynomial order 2nd a (i.e.,2210h a h a a MAE3100Prof. D.E. SmithLECTURE 2 -12Taylor Series ExampleFrom Chapra Figure 4.2, pg. 68:Where) (i.e., 0about Expanded 2.125.05.015.01.0)(234x a x h a x x x x x f 0.1)0(25.0)0(2.1)0(f f f xx f 25.02.1)(1225.025.02.1)(x x x f 2.1)(0x fMAE3100Prof. D.E. SmithLECTURE 2 -13Taylor Series -ExampleDetermine the 4-th order Taylor Series of y (x ) = ln(1+x )about x = a = 0By successive differentiation we obtainThe Taylor Series for |x |≤ 1becomes:Note: The error is proportional to x 5: i.e., when x is reduced by afactor of 2, R 4decreases by a factor of 25= 32)1ln()(x x y 0)0(y x x y 11)(1)0(y 2)1(1)(x x y 1)0(y 3)3()1(2)(x x y 2)0()3(y 4)4()1(6)(x x y 6)0()4(y 4324413121)()(x x x x x y x y )()1(51120)(5555)5(4x O x x y R with 5)5()1(24)(y MAE3100Prof. D.E. SmithLECTURE 2 -14Defining the RemainderRecall that the remainder R n is defined in terms the variable asConsider a zero-order (n = 0)Taylor Seriesthen 1)1()()!1()(n n n a x n f R ha a where )()()(0a f x f x f hR f h f R 00)()(= a = x = a = x)(f xa a+hMAE3100Prof. D.E. SmithLECTURE 2 -15Defining the Remainder (cont)Recall our example y (x ) = ln(1+x )with the 4-th order Taylor Series aboutx = 0The remainder becomesCombining these equations givesFor x = 1, we obtainthen or which satisfies the condition 4432413121)(R x x x x x y 55432)1(151413121)1ln(x x x x x x 555554)1(151)0())1(ln(!51x x x dx d R x 12739.058333.0413121)(69315.0)(4324x x x x x y x y 105544)1()1(15110981.058333.069315.0)1()1(y y R MAE3100Prof. D.E. SmithLECTURE 2 -16Defining the Remainder (cont)NOTE:•Determining the number of terms required for a Taylor series torepresent a function of interest is based on the remainder.•Unfortunately, ξis not known exactly but merely lies somewherebetween a and x = a + h (or x i and x i+1).•Also, R n requires derivatives of f (x ),which are not generally known.•Despite this, R n is still useful for gaining insight into truncationerrors.•Recall that we do have control over h and can therefore assess whathappens as we change h , i.e.,1)1(1)1()!1()()()!1()(n n nn n h n f a x n f R )())((11n n n h O a x O R xa a+h hMAE3100Prof. D.E. SmithLECTURE 2 -17Using the Remainder R n1)Establish order of error (from definition)2)Verify order of error estimate*> at h = 0.5 > at h = 1.03) Provide error estimate when h is increased or reduced*at h = 0.5, we computed R 4= 0.00442344then at h = 1.0 (doubled), we estimate R 4(0.00442344)(25) = 0.141550))(()()!1()(11)1(n n n n a x O a x n f R 0.109814)1()1(44y y R 0.00442344)5.0()5.0(44y y R 2X ~25X note: 25= 32X*For y (x ) = ln(1+x )about x = 0MAE3100Prof. D.E. SmithLECTURE 2 -18Using the Remainder R n (cont)4)Calculate value of ξwhen exact function value is known*Recall for h = 1and 5)Establish upper or lower bound on error*Recall that when h = 1, we obtain and Then the upper bound of the error may becalculated as the maximum R 4over the validrange of ξas 0.109814)1()1(44y y R *For y (x ) = ln(1+x )about x = 0554)1()1(151R Equating andsolving for ξgives12739.01054)1(151R 51)1(151)1(15110max 055max 4R maxξR 4MAE3100Prof. D.E. SmithLECTURE 2 -19Numerical DifferentiationDerivatives may be evaluated numerically withthe Finite (Divided) Difference method.1.Forward Difference (error is O (h ))2.Backward Difference (error is O (h ))3.Central Difference (error is O (h 2))hx f h x f x f )()()(hh x f x f x f )()()(hh x f h x f x f 2)()()(MAE3100Prof. D.E. SmithLECTURE 2 -20Remainder w/ Finite DifferenceConsider the 1st order Taylor Series and Remainder for f (x )expandedabout a = x (note h = x )which can be rearranged to give forward differenceExample problem: consider f (x ) = sin(x ) at x = /4exact derivative:forward finite difference:error bounded by remainder:2!2)()()()(xf x x f x f x x f R 1xf x x f x x f x f 2)()()()(O (x )7071067811.0)cos()(4/x x x f 6706029729.01.0)4/sin()1.04/sin()(x f (with x = 0.1)error = 0.0370781.04/at 0.0387084/at 0.035355)(2)sin(2)(x x f。
lec评价法定义和公式

lec评价法定义和公式好的,以下是为您生成的文章:咱先来说说这“LEC 评价法”,这玩意儿在好多领域都挺有用的。
LEC 评价法,简单来讲,就是一种用来评估风险大小的方法。
那它到底咋评估的呢?这就得说到它的公式啦,LEC = L×E×C 。
这里的“L”代表事故发生的可能性,“E”呢指的是人员暴露于危险环境中的频繁程度,“C”就是一旦发生事故可能造成的后果严重程度。
比如说,咱们就拿学校里的事儿来说说。
学校要组织一场校外的实践活动,去一个农场体验生活。
那在这个活动里,怎么用 LEC 评价法来评估风险呢?先看“L”,假设当天天气不太好,有可能会下雨,导致道路湿滑,那发生交通事故的可能性就会增加。
如果天气预报说有 30%的概率会下雨,那咱们就可以把“L”的值定为 3 。
再看“E”,这次活动所有同学都要参加,而且会在农场里待上一整天,那人员暴露在这个可能有风险的环境中的频繁程度就很高,咱们可以把“E”定为 6 。
最后是“C”,要是真出了交通事故,那后果可能会很严重,比如有同学受伤,甚至可能会影响到未来的学习和生活,那“C”的值就可以定为 15 。
这样一来,通过 LEC 评价法,风险分值就等于 3×6×15 = 270 。
根据相关的标准,这个分值就表示风险处于较高的水平,那学校就得好好考虑一些应对措施,比如提前准备雨具,安排更有经验的司机,准备急救药品等等。
LEC 评价法的好处就是能把那些看起来很复杂、很模糊的风险,通过具体的数值给表现出来,让咱们能更清楚地看到风险到底有多大。
再比如说,学校里要进行化学实验课。
实验中用到一些有腐蚀性的化学试剂,如果操作不当,就可能会发生意外。
那咱们来评估一下这个风险。
对于“L”,如果实验设备老化,试剂保存不当,那发生意外的可能性就会增大,假设为 2 。
“E”呢,因为是全班同学都要参与实验,暴露的频繁程度较高,定为 5 。
“C”,要是真发生意外,被试剂腐蚀受伤,后果可能比较严重,定为 10 。
危险源辨识LEC法

1、判定准则
危险性指数大于320的,确定为A级;
危险性指数大于等于160但小于等于320的,确定为B级;
危险性指数大于等于70但小于等于159的,确定为C级;
危险性指数大于等于20但小于等于69的,为D级;
危险性指数小于20的,危险性不大不列入等级。
2、判定方法:
作业危险性是下列三个因素的乘积:
W
评价
危险源等级
>320
极危险
A
160-320
高度危险
B
70-159
很危险
C
20-69
可能危险
D
<20
不定级
10
每天在有危险的环境中工作
6
每周一次在危险环境中工作
3
每月一次在危险环境中工作
2
每年一次在危险环境中工作
1
极难出现在危险环境中工作
0.5
事故的可能后果(C)
现象
可能后果
分值
大灾难
多人死亡
100
灾难பைடு நூலகம்
数人死亡
40
非常严重
一人死亡
15
严重
严重致残
7
重大
手足伤残
6
较大
受伤较重
3
引人注目
轻伤
1
危险指数评价(W)
发生危险事件的可能性 L;
作业者在危险环境下的状况 E;
事故的可能后果 C;
危险指数 W=L*E*C
发生危险事件的可能性(L)
L
分 数
完全预料到
10
相当可能
6
不经常,但可能
3
意外,很少可能
LEC计算参数表

极不可能
实际不可能
表A.1.2 暴露于危险环境的频繁程度(E )
分数值 频繁程度 连续暴露
每天工作时间 内暴露
每周一次,或 偶然暴露
每月一次暴露 每年几次暴露 非常罕见地暴
露
表A.1.3 发生事故产生的后果(C )
分数值 后果 大灾难,许多 人死亡 灾难,数人死 亡
非常严重,一 人死亡 重伤
8
井下消防
消防设施
消防器材
火灾报警
……
9
排土场
运输
排土
平整
……
表A.1.1 事故发生的可能性(L )
分数值
事故发生的可 能性
完全可能预料
相当可能
可能,但不经 常
可能性小,完 全意外
附表5-1
LEC计算参数表
序号
主单元
岗位(设备设施 /作业活动)单
元
危险有害因素
1 开拓运输与开采
凿岩
1、凿岩机保护装置失效; 2、顶板未按规定及时支护;
事故类型 触电、顶板
L(事故可能性)
E(暴露于危险环境频 率)
C(事故后果)
完全可能预料
非常罕见地暴露
大灾难,许多人死亡
爆破
1、爆破前未检查有毒有害气 体; 2、警戒距离不符合规定;
中毒窒息、爆 破伤人
相当可能
每周一次,或偶然暴露 非常严重,一人死亡
铲装
机械伤人 很不可能,可能设想
连续暴露
轻伤
破碎
可能,但不经常 每周一次,或偶然暴露 非常严重,一人死亡
运输
可能,但不经常
每月一次暴露
非常严重,一人死亡
装卸
可能,但不经常 每周一次,或偶然暴露 非常严重,一人死亡
verilog课件 lec02_hdl

Chapter 4 <18>
单击此B处it编M辑母a版n标ip题u样l式ations: Example 2
SystemVerilog:
module mux2_8(input logic [7:0] d0, d1,
Chapter 4 <7>
单击此H处D编L辑母S版im标题u样la式tion
SystemVerilog:
module example(input logic a, b, c, output logic y);
assign y = ~a & ~b & ~c | a & ~b & ~c | a & ~b & c; endmodule
/*…*/ multiline comment
Chapter 4 <12>
单击此R处e编d辑u母c版t标io题n样O式 perators
module and8(input logic [7:0] a,
output logic
y);
assign y = &a;
// &a is much easier to write than
Chapter 4 <5>
单击此S处y编s辑te母m版标V题e样r式ilog Modules
a b c
Verilog Module
y
Two types of Modules:
– Behavioral: describe what a module does – Structural: describe how it is built from simpler
作业条件危险性分析法LEC

作业条件危险性分析法LECLEC(作业条件危险性分析法)是一种用于识别、评估和控制工作条件中潜在危险的方法。
它是一种系统性的方法,可以帮助工作场所识别并处理潜在的危险,以预防事故和职业伤害的发生。
LEC方法的核心概念是基于作业和条件危险的分析。
通过对作业职责、作业活动和作业环境的分析,可以确定出可能导致事故和伤害的危险因素。
LEC方法通过以下三个步骤来实施:前提条件、作业操作和结果条件的分析。
在LEC方法中,前提条件是指在进行具体作业之前需要满足的条件。
这些条件包括工作许可证、工作准备、培训、技能和器材等。
通过对前提条件的分析,可以确定出可能导致事故和伤害的潜在危险因素。
作业操作是指实际进行作业的过程。
在LEC方法中,对作业操作进行分析可以识别出可能导致事故和伤害的危险因素。
这些因素包括不正确的方法、低效的工具和设备、无法预测的工作环境等。
结果条件是指作业完成后可能出现的结果。
通过对结果条件进行分析,可以确定出可能导致事故和伤害的潜在危险因素。
这些因素包括错误的输出、质量问题、不良的后果等。
LEC方法的一个重要特点是风险评估。
通过对每个危险因素的评估,可以确定其潜在的严重程度和发生的可能性。
根据风险评估的结果,可以采取相应的控制措施以减少风险。
LEC方法的另一个重要特点是整体性。
它不仅考虑了独立的危险因素,还考虑了它们之间的相互作用和综合效应。
通过对整个工作系统的分析,LEC方法可以更好地理解和控制潜在的危险。
LEC方法在各种工业领域都可以应用。
它可以用于评估工厂生产线上的危险因素,也可以用于评估建筑施工现场的危险因素。
无论在哪个领域,LEC方法都可以帮助工作场所识别出潜在的危险,从而采取相应的措施保障员工的安全和健康。
综上所述,LEC方法是一种重要的工具,可以帮助工作场所识别和控制潜在的危险。
通过对作业和条件危险的分析,可以确定可能导致事故和伤害的危险因素。
通过风险评估和整体分析,可以采取相应的控制措施以减少风险。
LEC风险评价标准及风险确定准则

LEC风险评价标准及风险确定准则一、引言LEC(Lowest Effect Concentration)风险评价标准是一种用于评估化学物质对生态系统的潜在风险的方法。
该标准是基于对生物多样性和生态系统功能的保护而制定的,旨在确定化学物质在环境中的最低有效浓度,从而确保生态系统的健康和可持续发展。
二、背景随着化学物质的广泛使用和排放,对其潜在风险的评估变得越来越重要。
传统的风险评估方法主要关注高浓度下的急性毒性,而LEC风险评价标准则更注重低浓度下的慢性毒性效应。
该标准的制定旨在填补现有评估方法的不足,提供更全面、准确的风险评估结果。
三、LEC风险评价标准的主要内容1. LEC风险评价标准的基本原理LEC风险评价标准基于生态学和毒理学的原理,结合化学物质的特性和生态系统的敏感性,确定了一系列评价指标和阈值,用于评估化学物质对生态系统的潜在风险。
2. LEC风险评价标准的评估指标LEC风险评价标准主要包括以下评估指标:- 生物多样性指标:包括物种丰富度、物种多样性指数等,用于评估化学物质对生态系统中不同物种的影响。
- 生态系统功能指标:包括养分循环、能量流动等,用于评估化学物质对生态系统整体功能的影响。
- 生物标志物指标:包括生物体内的生化指标、生理指标等,用于评估化学物质对生物个体的影响。
3. LEC风险评价标准的风险等级划分LEC风险评价标准将化学物质的潜在风险划分为五个等级:极低风险、低风险、中等风险、高风险和极高风险。
根据评估指标的数值和阈值的比较,确定化学物质所属的风险等级。
四、LEC风险评价标准的应用LEC风险评价标准广泛应用于环境监测、风险管理和政策制定等领域。
具体应用包括:1. 环境监测:通过采集环境样品,测定其中化学物质的浓度,并根据LEC风险评价标准进行风险评估,为环境保护和治理提供科学依据。
2. 风险管理:基于LEC风险评价标准,制定合理的风险管理措施,包括减少化学物质的排放、采取适当的处理技术等,以降低生态系统的潜在风险。
lec02
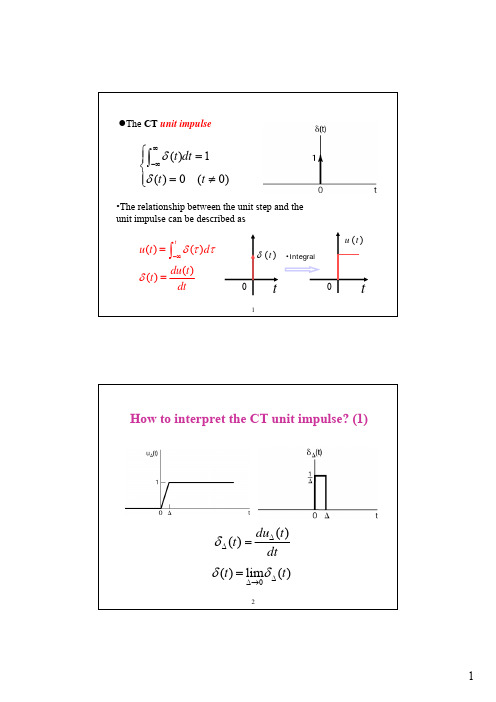
t
u (t )
(t )
0
1
•Integral
(t )
du (t ) dt
t
0
t
How to interpret the CT unit impulse? (1)
(t )
du (t ) dt
(t ) lim (t )
0
2
1
•How to interpret the CT unit impulse? (2)
y (t ) 2 x(t )
The corresponding inverse system is
w(t )
1 y (t ) 2
28
14
Is y(n) = x(2n) an invertible system?
29
Causal and Noncausal Systems
30
15
Causal or not?
1 a
(t ) dt
1 1 (t ) dt a a
11
•Example. Given the plot of a CT signal f(t), draw the plot of
its derivative.
f(t)
2 1 0 1 2 3 t
•de (t )dt 1 (t ) 0 (t 0)
•The relationship between the unit step and the unit impulse can be described as
u (t ) ( )d
17
Interconnection of Systems
lec方法危险等级划分

lec方法危险等级划分嘿,咱今儿就来聊聊 LEC 方法危险等级划分这事儿!你知道吗,这就好比给危险程度贴上不同的标签。
想象一下,危险就像一群调皮捣蛋的小精灵,在我们身边窜来窜去。
而 LEC 方法呢,就是我们用来抓住这些小精灵,给它们分分类的工具。
LEC 方法里的 L 呀,代表可能性。
就好像猜硬币正反面,正面的可能性有多大呢?这就是在看危险发生的概率。
如果一件事特别容易发生,那这个 L 的值可就高啦。
比如说,走在路上被陨石砸到,那可能性几乎趋近于零,L 值就很低咯。
但要是每天都要经过一条车水马龙的大马路,那被车碰到的可能性就大多了,L 值自然就高啦。
再来说说 E 吧,它表示暴露在危险环境中的频繁程度。
好比说你是个消防员,那天天都要和火打交道,暴露在危险中的程度就很高,E值也就大。
可要是你就是个普通上班族,每天坐在办公室里,那暴露在危险中的机会就少很多,E 值就相对较小啦。
最后这个 C 呢,是后果严重程度。
这可太重要啦!要是一个危险发生后,只是蹭破点皮,那C 值就小。
但要是会造成重伤甚至危及生命,那 C 值可就大得吓人啦!把这三个值综合起来,就能划分出不同的危险等级。
就像给学生打分一样,不同的分数段就代表着不同的等级。
低危险等级的呢,可能就像偶尔打个小喷嚏,不太碍事。
但高危险等级的,那可就得高度重视啦,就像得了重病一样,得赶紧想办法治疗。
咱举个例子哈,比如在一个化工厂里,某种化学品泄漏的可能性较大,工人经常要接触到,而且一旦泄漏后果很严重,那这危险等级肯定就很高啦。
这时候就得赶紧采取措施,加强防护,增加安全设备啥的,可不能马虎。
反过来,如果是在一个普通的办公室里,可能最大的危险就是被椅子腿绊一下,那危险等级自然就低得多啦。
你说这 LEC 方法是不是很有意思呀?它能让我们清楚地看到身边的危险程度,然后有针对性地去应对。
咱可不能小瞧了它,它就像是我们的安全卫士,帮我们把危险都看清楚,让我们能安心地生活和工作。
(麻省理工免费课程)C语言内存管理和C++面向对象编程_lec02

Recap
Pointers
Memory management
Data structures
Linked list example
Tools and tips
Goodbye
An example without pointers
What will this print?
void p r o c e s s v a r ( i n t x ) { x = 5; } void fun () { int x = 3; process var (x) ; p r i n t f ( "%d\n" , x ) ; }
Conceptually
Keep track of what memory belongs to your program, making sure
all addresses you give to other functions are valid for those
functions and
you deallocate memory you are not using while you still know
Eunsuk Kang and Jean Yang The Adventures of Malloc and New
Recap
Pointers
Memory management
Data structures
Linked list example
Tools and tips
Goodbye
Pointer syntax
Memory management
Data structures
Linked list example
lec取值标准

LEC(Likelihood of an Event)是一种用于评估事件发生概率的指标,常用于安全评价和风险管理等领域。
LEC取值标准通常由相关机构或组织制定,具体标准可能因应用领域和国家地区而异。
以下是一些常见的LEC取值标准:
1. 美国国家标准协会(ANSI)制定的LEC标准:LEC值在0到1之间,其中0表示事件不可能发生,1表示事件非常可能发生。
LEC值越高,表示事件发生的概率越大。
2. 欧洲标准化组织(CEN)制定的LEC标准:LEC值在0到1之间,其中0表示事件不可能发生,1表示事件非常可能发生。
LEC值越高,表示事件发生的概率越大。
3. 日本工业标准(JIS)制定的LEC标准:LEC值在0到1之间,其中0表示事件不可能发生,1表示事件非常可能发生。
LEC值越高,表示事件发生的概率越大。
需要注意的是,不同的应用领域和行业可能会采用不同的LEC取值标准。
在实际应用中,应根据具体情况选择合适的标准,并结合实际数据和经验进行分析和评估。
氯化二乙基铝96-10-6

4.3 及时的医疗处理和所需的特殊处理的说明和指示
如有必要,佩戴自给式呼吸器进行消防作业。
5 消防措施
5.1 灭火介质
火灾特征 无数据资料 灭火方法及灭火剂 碳氧化物,氯化氢气体,氧化铝
5.2 源于此物质或混合物的特别的危害
8 接触控制/个体防护
8.1 暴露控制
https:// 2/5
化学品安全技术说明书
适当的技术控制 全套防化学试剂工作服,阻燃防静电防护服。,防护设备的类型必须根据特定工作场所中的危险物的浓度和 数量来选择。 人身保护设备 眼/面保护 无数据资料 皮肤保护 戴手套取手套在使用前必须受检查。请使用合适的方法脱除手套(不要接触手套外部表面),避免任何皮 肤部位接触此产品.使用后请将被污染过的手套根据相关法律法规和有效的实验室规章程序谨慎处理. 请清洗并吹干双手 身体保护 遇水剧烈反应。 呼吸系统防护 如危险性评测显示需要使用空气净化的防毒面具,请使用全面罩式多功能防毒面具(US)或ABEK型 (EN14387)防毒面具筒作为工程控制的候补。如果防毒面具是保护的唯一方式,则使用全面罩式 送风防毒面具。呼吸器使用经过测试并通过政府标准如NIOSH(US)或CEN(EU)的呼吸器和零 件。
无数据资料
12.4 土壤中的迁移
无数据资料
12.5 PBT 和 vPvB的结果评价
无数据资料
12.6 其它不利的影响
无数据资料
13 废弃处置
13.1 废物处理方法
产品 无数据资料 污染了的包装物 无数据资料 进一步的说明: 无数据资料
14 运输信息
14.1 UN编号
gametheory2014Lec2

12
Extensive form: decision/game tree
-1 (17)
A
-1 (20) -1 (18) -2 (19)B -3 (18) -2 (17) -3 (16)
-2 (16) -3 (15)
A
(21)
13
Rule # 1: Backward reasoning (induction)
19
Presidential game: without Line item veto
p.42
20
Presidential game: with Line item veto
p.42
21
Hong Kong Democratic Reform game
Demo-parties
Accept Reject
Each player’s preferences are:
Being the lone surviver (best payoff = 4),
Survival with another player (the second best = 3),
All players survive (the second worst=2),
16
17
US Presidential game
Every year, the US Congress passes bill to authorize expenditures in different areas. President can sign or veto the bill depends on whether he likes it or not. When the Congress and President are controlled by different parties, there is always a flight over how money should be spent, e.g. on M (missile defense) or U (urban renewal).
LEC风险评价标准及风险确定准则

LEC风险评价标准及风险确定准则一、引言LEC(Lowest Effect Concentration)风险评价标准是一种常用的环境风险评价方法,用于评估化学物质对环境和生态系统的潜在风险。
本文将详细介绍LEC风险评价标准的基本原理和应用范围,以及风险确定准则的制定过程。
二、LEC风险评价标准的基本原理1. 毒性数据收集:收集与化学物质相关的毒性数据,包括急性毒性、亚慢性毒性、慢性毒性等。
2. 效应浓度计算:根据毒性数据,通过计算得出LEC值,即对生物体产生最低效应的浓度。
3. 风险评价指标确定:根据LEC值,将化学物质分为高风险、中风险和低风险三个等级。
三、LEC风险评价标准的应用范围1. 环境监测:通过对环境中化学物质浓度和生物效应的监测,可以评估化学物质对环境的潜在风险。
2. 毒性预测:通过LEC风险评价标准,可以预测新化学物质的潜在毒性,为环境保护和风险管理提供参考依据。
3. 毒性比较:通过比较不同化学物质的LEC值,可以评估它们对环境和生态系统的相对风险。
四、风险确定准则的制定过程1. 数据收集:收集与化学物质相关的毒性数据和环境监测数据。
2. 数据分析:对收集到的数据进行统计分析,确定LEC值和风险评价指标。
3. 风险等级划分:根据LEC值和风险评价指标,将化学物质划分为不同的风险等级。
4. 风险管理建议:根据风险等级,提出相应的风险管理建议,包括限制使用、加强监测、采取防护措施等。
五、案例分析以某化学品X为例,根据LEC风险评价标准,通过收集相关毒性数据和环境监测数据,计算得出LEC值为10 mg/L。
根据风险评价指标,将化学品X划分为中风险等级。
针对该化学品的中风险等级,建议加强对其生产、使用和排放的监管,采取必要的防护措施,减少潜在的环境和生态风险。
六、总结LEC风险评价标准是一种常用的环境风险评价方法,通过计算LEC值和划分风险等级,可以评估化学物质对环境和生态系统的潜在风险。
LEC风险评价标准及风险确定准则

LEC风险评价标准及风险确定准则一、引言LEC(Lowest Effect Concentration)风险评价标准及风险确定准则是一种用于评估化学物质对人体健康和环境的潜在风险的方法。
本文将详细介绍LEC风险评价标准的定义、原理、应用范围以及风险确定准则的制定过程。
二、LEC风险评价标准的定义LEC风险评价标准是基于慢性毒性学原理,通过确定最低效应浓度(LEC)来评估化学物质对人体健康和环境的潜在风险。
LEC是指在暴露于化学物质的情况下,引起一种明确的不良效应的最低浓度。
三、LEC风险评价标准的原理LEC风险评价标准的原理基于以下几个方面:1. 选择适当的生物标志物或效应指标,用于评估化学物质的毒性;2. 通过实验暴露动物或人群于不同浓度的化学物质,观察其对生物体的不良效应;3. 统计分析实验数据,确定LEC。
四、LEC风险评价标准的应用范围LEC风险评价标准广泛应用于以下领域:1. 环境风险评估:评估化学物质对环境生物的潜在风险,为环境管理和保护提供科学依据;2. 食品安全评估:评估食品中化学物质的安全性,保障人体健康;3. 药物安全评价:评估药物对人体的潜在毒性,为药物研发和使用提供依据;4. 职业健康评估:评估工作场所化学物质对工人健康的潜在风险。
五、风险确定准则的制定过程制定风险确定准则是为了将LEC风险评价标准转化为实际应用的指导性文件。
制定风险确定准则的过程包括以下几个步骤:1. 收集相关数据:收集与化学物质毒性、暴露途径、生物标志物等相关的数据;2. 数据分析:对收集到的数据进行统计分析,确定LEC;3. 制定风险确定准则:根据LEC和相关数据,制定适用于不同领域的风险确定准则;4. 评估和修订:将制定的风险确定准则应用于实际案例中,根据实践经验进行评估和修订。
六、总结LEC风险评价标准及风险确定准则是一种科学、可靠的方法,用于评估化学物质对人体健康和环境的潜在风险。
通过确定LEC,可以为环境管理、食品安全、药物安全和职业健康评估等领域提供科学依据。
LEC风险评价标准及风险确定准则

LEC风险评价标准及风险确定准则一、背景介绍LEC(Lowest Effect Concentration)是一种用于评估化学品对生物体的毒性效应的方法。
风险评价是指对特定活动或物质的潜在危害进行评估,并确定其对人类和环境的风险程度。
本文将详细介绍LEC风险评价标准及风险确定准则。
二、LEC风险评价标准1. LEC定义LEC是指在实验条件下,引起生物体最低效应的化学物质浓度。
它是通过实验数据统计分析得出的,可以用于评估化学品对生物体的潜在风险。
2. LEC风险评价的步骤(1)确定评估对象:确定需要评估的化学物质和受体生物体。
(2)收集数据:收集与评估对象相关的实验数据,包括化学物质的毒理学数据和生物体的敏感性数据。
(3)数据分析:对收集到的数据进行统计分析,计算出LEC值。
(4)风险评估:根据LEC值,评估化学物质对生物体的潜在风险。
3. LEC风险评价标准的制定LEC风险评价标准的制定需要考虑以下因素:(1)化学物质的毒性:根据化学物质的毒理学数据,确定不同毒性级别的划分标准。
(2)生物体的敏感性:根据生物体的敏感性数据,确定不同敏感性级别的划分标准。
(3)风险级别的划分:根据LEC值和毒性、敏感性级别的划分标准,将风险分为不同级别,如高风险、中风险和低风险。
三、风险确定准则1. 风险确定的目的风险确定是指根据风险评估结果,确定化学物质对生物体的实际风险程度。
它是制定风险管理措施和控制策略的基础。
2. 风险确定的方法(1)确定风险等级:根据风险评估结果和风险评价标准,将风险分为高风险、中风险和低风险等级。
(2)确定风险管理措施:根据风险等级,制定相应的风险管理措施,包括减少风险的措施和监测风险的措施。
(3)确定风险控制策略:根据风险等级和风险管理措施,确定适当的风险控制策略,包括技术控制、管理控制和个体防护措施。
3. 风险确定准则的制定风险确定准则的制定需要考虑以下因素:(1)风险等级的划分:根据风险评估结果和风险评价标准,确定高、中、低风险等级的划分标准。
lec打分法分级标准

lec打分法分级标准
LEC打分法是一种用于评价和分级的标准方法。
以下是该方法的分级标准:
1. 优秀(5分):表现出色,达到了超出预期的水平。
具备非常高的专业知识和技能,能够独立完成任务并给予他人指导和支持。
展现出卓越的创新能力和解决问题的能力。
2. 良好(4分):表现良好,达到了预期水平。
具备较高的专业知识和技能,能够有效地完成任务并满足要求。
展现出良好的团队合作和沟通能力。
3. 一般(3分):表现一般,达到了基本要求,但缺乏突出的表现。
具备基本的专业知识和技能,能够完成日常任务。
需要进一步提升自己的能力和技巧。
4. 需改进(2分):表现不佳,未达到基本要求。
缺乏必要的专业知识和技能,无法有效地完成任务。
需要加强学习和提高能力。
5. 不合格(1分):表现非常差,完全不能满足要求。
缺乏必要的专业知识和技能,无法胜任工作。
需要大幅改进和提高。
以上是LEC打分法的分级标准,用于评价和分析个人或团队的绩效表现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
hits/game number of games relative frequency hits/game number of games relative frequency 0 20 0.001 14 569 0.0294 1 72 0.0037 15 393 0.0203 2 209 0.0108 16 253 0.0131 3 527 0.272 17 171 0.0088 4 1048 0.541 18 97 0.005 5 1457 0.752 19 53 0.0027 6 1988 0.1026 20 31 0.0016 7 2256 0.1164 21 19 0.001 8 2403 0.124 22 13 0.0007 9 2256 0.1164 23 5 0.0003 10 1967 0.1015 24 1 0.0001 11 1509 0.0779 25 0 0 12 1230 0.0635 26 1 0.0001 13 834 0.043 27 1 0.0001
Example 1.10 Power companies need information about customer usage to obtain accurate forecasts of demands. Investigators from Wisconsin Power and Light determined energy consumption during a particular period for a sample of 90 gas-heated homes.
9-11 25 0.278
6.35 7.29 8.37 9.37 9.96 10.5 11.7 13.11 15.24
11-13 17 0.189
Continuous variables arise from making measurements.
if x is the PH of a chemical substance, then in theory x could be any number between 0 and 14; 7.0 7.03, 7.032, etc.
Selecting the Suitable Graphical Display
Figure 1.7 shows a dotplot for the O-ring temperature data introduced in example 1.1 in the previous section.
Relative frequency x = count(x)/n, n = total num of observations. Example 1.9 How unusual is a no-hitter or a one-hitter in a major league baseball game, and how frequently does a team get more than 10,15, or even 20 hits? Table 1.1 is a frequency distribution for the number of hits per team per game for all games that were played between 1989 and 1993.
Constructing a Histogram for Discrete Data
First, determine the frequency(频数)and relative frequency(相对 频数、频率)of each x value. Then mark possible x values on a horizontal scale. Above each value, draw a rectangle whose height is the relative frequency .
Pictorial and Tabular Methods in Descriptive Statistics • Describe the overall pattern of the data and any interesting departures from the pattern
– Type of data: quantitative (numerical) or categorical (groups, e.g., gender)
5.56 7.15 8 8.81 9.83 10.36 11.43 12.71 14.24
5-7 11 0.122
5.94 7.16 8.26 9.07 9.83 10.4 11.62 12.91 14.35
7-9 21 0.233
5.98 7.23 8.29 9.27 9.84 10.49 11.7 12.92 15.12
Collecting Data
Simplest Method: random sample, any particular subset of the specified size has the same chance of being selected. Alternative sampling methods: stratified sampling(分层抽样), entails separating the population units into non-overlapping groups and taking a sample from each one.
Suppose we have a numerical data set x1,x2,x3,…,xn for which each xi consists of at least two digits. A quick way to obtain an informative visual representation of the data set is to construct a stem-and-leaf display.
• Graphical summary • Numerical summary
Summarize the patterns in the observations (numerically and graphically) 1) Shape 2) Center 3) Spread 4) Unusual observations
30
40
50
60
70
80
• When the number of observations is moderately large, other graphical displays may be more useful.
Histograms(直方图)
Definition: A variable is discrete(离散的)if its set of possible values either is finite or else can be listed in an infinite sequence. A variable is continuous(连续的)if its possible values consist of an entire interval on the number line. A discrete variable x almost always results from counting.
2.97 6.8 7.73 8.61 9.6 10.28 11.12 12.31 13.47
4 6.85 7.87 8.67 9.76 10.3 11.21 12.62 13.6
1-3 1 0.011
5.2 6.94 7.93 8.69 9.82 10.35 11.29 12.69 13.96
3-5 1 0.011
0.10
0.05
0
10
20
Constructing a histogram for continuous data: equal class widths Determine the frequency and relative frequency for each class. Mark the class boundaries on a horizontal measurement axis. Above each class interval, draw a rectangle whose height is the corresponding relative frequency.
Steps for Constructing a Stem-and Leaf Display
1. Select one or more leading digits for the stem values. The trailing digits become the leaves.
2. List possible stem values in a vertical column. 3. Record the leaf for every observation beside the corresponding stem value. 4. Indicate the units for stems and leaves someplace in the display.
there are relatively few distinct data values.
As with a stem-and-leaf display, a dotplot gives information about location, spread, extremes, and gaps.
• Notation Given a data set consisting of n observations on some variable x, the individual observations will be denoted by x1,x2,x3,…,xn • Stem-and-Leaf Displays(茎叶图)
