算法流程图练习
流程图练习
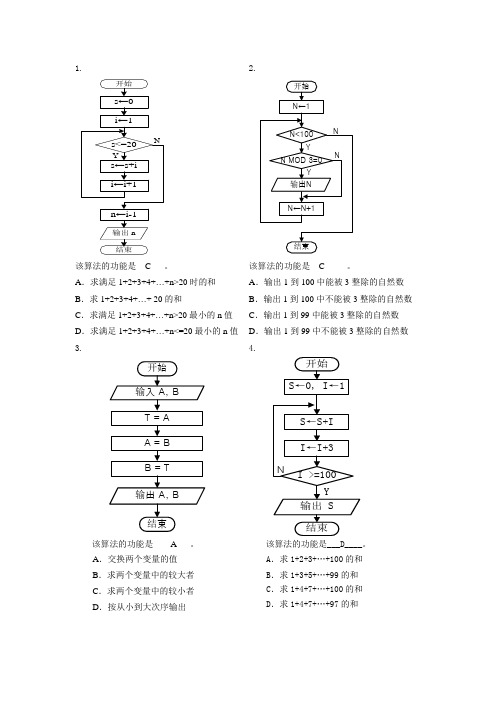
该算法的功能是__C___。
A.求满足1+2+3+4+…+n>20时的和B.求1+2+3+4+…+ 20的和C.求满足1+2+3+4+…+n>20最小的n值D.求满足1+2+3+4+…+n<=20最小的n值该算法的功能是__C_____。
A.输出1到100中能被3整除的自然数B.输出1到100中不能被3整除的自然数C.输出1到99中能被3整除的自然数D.输出1到99中不能被3整除的自然数3.该算法的功能是____A___。
A.交换两个变量的值B.求两个变量中的较大者C.求两个变量中的较小者D.按从小到大次序输出4.该算法的功能是___D____。
A.求1+2+3+…+100的和B.求1+3+5+…+99的和C.求1+4+7+…+100的和D.求1+4+7+…+97的和该算法的功能是__C___。
A.输出X的个位上的数B.输出X的万位上的数C.输出X的个位到万位上所有数的和D.把X从个位到万位上数倒过来输出该算法的功能是___A____。
A.统计输入的正数的和B.统计输入的负数的和C.求输入数中的最大数D.求输入数中的最小数7.该算法的功能是_D_____。
A.求1+4+7+10+13的值B.求4+7+10+13的值C.求1+4+7+10的值D.求4+7+10的值8.该算法的功能是___C____。
A. 输出A个位上的数B. 输出A百位上的数C. 输出A各位上所有数字的和D. 把A从个位到百位上的数字倒过来输出9.该算法的功能是____B___。
A.求1+2+3+…+N的值B.求1*2*3*…*N的值C.求1*2*3*…*(N+1)的值D.求1*2*3*…*(N-1)的值10.该算法的功能是___B____。
A.求输入的10个数中负数的个数B.求输入的11个数中负数的个数C.求输入的10个数中正数的个数D.求输入的11个数中正数的个数。
流程图练习题(三种结构)

流程图练习题(1)1.下列图形符号属于判断框的是________.2.下列关于流程线的说法①流程线表示算法步骤执行的顺序,用来连接图框;②流程线只要是上下方向就表示自上向下执行可以不要箭头;③流程线无论什么方向,总要按箭头的指向执行;④流程线是带有箭头的线,它可以画成折线.其中正确的有________.3.如图所示的流程图的输出结果是________.(第3题)(第4题)4.如上右图图的作用是交换两个变量的值并输出,则①处应为________.5.下列所画4个流程图是已知直角三角形两直角边a,b求斜边c的算法,其中正确的是________.6.如图,对本题流程图表示的算法,描述最准确的是________.①可用来判断a,b,c是否为一组勾股数;②可用来判断a,b,c之间大小顺序;③可用来判断点(a,b)是否在直线x=c上;④可用来判断点(a,b)与圆心在原点,半径为c的圆的位置关系.7.解决下列几个问题,只用顺序结构画不出其流程图的是________.①利用公式1+2+3+…+n =n (n +1)2计算1+2+3+…+100的值;②当p (x 0,y 0)及直线l :Ax +By +C =0一定时,求点p 到直线l 的距离d ; ③求函数f (x )=2x 3-3x 2-x -1当x =-1时的函数值;④求函数y =⎩⎪⎨⎪⎧x -1,x >0x 2,x ≤0当x =x 0时的函数值.8.(2011年南京高一检测)如图,该流程图的运行结果S =________.(第9题)(第8题) (第10题) 9.运行如图所示的流程图,输出的结果是________.10.下列框图用来求点p (x 0,y 0)到直线l :Ax +By +C =0的距离d ,图中①处为________.11.给出流程图如图,若输出的结果为2,则①处的处理框内应填的是________.12.下图算法的功能是________.(第11题)(第12题)13、.写出下列流程图的运行结果.(1)则x=______;(2)则ω=______;(3)若R=1,则y1=________.12.如图阅读下列两个求三角形面积的流程图,回答问题.(1)图①的流程图输出结果S是多少?图②中若输入a=4,h=3,输出的结果是多少?(2)对比一下两个流程图你有什么发现?13.下列语句表达中是算法的有________.①从济南去巴黎可以先乘火车到北京再坐飞机抵达;②利用公式S =12ah 计算底为1,高为2的三角形的面积;③12x >2x +4; ④求M (1,2)与N (-3,-5)两点连线的方程可先求MN 的斜率,再利用点斜式方程求得.14.下列四种叙述为算法的是______________.①在家里一般是妈妈做饭 ②做米饭需要刷锅、淘米、添水、加热这些步骤 ③在野外做饭叫野炊 ④做饭必须要有米15.下列各式中S 值不可以用算法求解的是________. ①S =1+2+3+4;②S =12+22+32+ (10002)③S =1+12+13+…+11000;④S =1+2+3+4+….16.已知A (-1,0),B (3,2),下面是求直线AB 的方程的一个算法,请将其补充完整:第一步,____________________________.第二步,用点斜式写出直线AB 的方程y -0=12[x -(-1)].第三步,将第二步的方程化简,得到方程x -2y +1=0. 17.结合下面的算法:第一步,输入x ;第二步,判断x 是否小于0,若是,则输出x +2,否则执行第三步; 第三步,输出x -1.当输入的x 的值为-1,0,1时,输出的结果分别为________,________,________.18.写出求方程2x +3=0的解的算法步骤:第一步____________,第二步____________,第三步____________.19.已知函数f (x )=⎩⎪⎨⎪⎧x 2-x +1 (x ≥2),x +1 (x <2),设计一个算法求函数的任一函数值.第一步 输入x ;第二步 ______________________________________; 第三步 输出x 2-x +1; 第四步 输出x +1.流程图练习题(2)1.如图所示的流程图中含有的基本结构是________.(第1题)(第4题) 2.下列函数求值算法中需要用到选择结构的是________.①f (x )=x 2-1; ②f (x )=2x +1;③f (x )=⎩⎪⎨⎪⎧x 2+1 (x >1)x 2-1 (x ≤1); ④f (x )=2x .3.某算法的程序框图如图所示,则输出量y 与输入量x 满足的关系式是________.4.①已知圆的半径,求圆的内接正三角形的边长;②求方程ax +b =0(a ,b 为常数)的根; ③求三个实数a ,b ,c 中的最小者.解决上述问题必须用选择结构的是________.5.已知函数y =2|x |,如图所示是表示给定x 的值,求其相应函数值的流程图,若输入log 122,则输出结果为______.(第5题) (第6题) 6.(改编题)指出流程图的运行结果:若输入-4,则输出结果为________.7.已知函数f (x )=⎩⎪⎨⎪⎧4x (0<x ≤5),20(5<x ≤9),56-4x (9<x <14),求f (a )(0<a <14)的算法中,需要用到条件结构,其中判断框的形式是________.8.给出一个流程图,如图所示,其作用是输入x 的值,输出相应的y 的值.若要使输入的x 的值与输出的y 的值相等,则这样的x 的值的个数有________.(第8题) (第9题)9.阅读如图所示的流程图,回答问题:若a =50.6,b =0.65,c =log 0.55,则输出的数是________.10.已知流程图:若输出的数是3,则输入的数x =________.11.(2011年盐城质检)下图的作用是判断输入数x 的奇偶性,则②处应为________.(第10题) (第11题) 12.如图流程图的功能是________.(第12题)13.画出求函数y =⎩⎪⎨⎪⎧x 2+1(x ≥0)-x 2+1(x <0)的值的流程图.解:11.已知下列算法:(1)指出其功能(用算式表示);(2)画出该算法的程序框图.①输入x ;②若x >0执行③,否则执行⑥;③y ←2x +1;④输出y ;⑤结束;⑥若x=0执行⑦;否则执行⑩;⑦y ←12;⑧输出y ;⑨结束;⑩y ←-x ;⑪输出y ;⑫结束.12.某居民区的物业部门每月向居民收取卫生费,计费方法如下:3人和3人以下的户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,并画出流程图.流程图练习题(3)1.算法中通常有三种不同的基本逻辑结构,下面说法正确的是________.①一个算法只能包含一种基本逻辑结构;②一个算法可以包含三种基本逻辑结构的任意组合;③一个算法最多可以包含两种基本逻辑结构;④一个算法必须包含三种基本逻辑结构.2.解决下列问题需用循环结构的是________.①求函数y=|x-1|的函数值;②求函数y=2x,在x=1,2,3,…,10时的函数值;③求1+2+3+…+10的值.3.(2010年高考湖南卷)如图,是求12+22+32+…+1002的值的程序框图(即流程图),则正整数n=________.(第3题)(第4题)4.算法流程图如图所示,其输出结果是________.5.已知下列说法①选择结构中,根据条件是否成立有不同的流向;②循环结构中循环体根据条件是否成立会被反复执行;③循环结构的形式只有一种.其中正确的是________.6.如图所示的流程图,若输入m=4,n=6,则输出a=________,i=________.(第6题)(第7题)7、(2010年高考天津卷改编)阅读上边的程序框图(即流程图),运行相应的程序,则输出s的值为________.8.如图是计算1+3+5+…+99的值的流程图,那么在空白的判断框中,应填入________.(第8题)(第9题)9.某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:队员i 12345 6三分球个数a1a2a3a4a5a6上图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图(即流程图),则图中判断框应填________,输出的s=________.(注:框图中的赋值符号“=”也可以写成“←”或“:=”)10.(2010年高考江苏卷)如图是一个算法流程图,则输出的S 的值是________.(第10题) (第11题)11.某流程图如图所示,该程序运行后输出的倒数第二个数是________.12.阅读如图所示的流程图,若该框图是计算“A 4+A 5+A 6”的值,那么判断框中应填________.(第12题)(第13题)13、 (2010年高考福建卷改编)阅读如图所示的程序框图(即流程图),运行相应的程序,输出的i 值等于________.14.如下图所示的四个流程图,都是为计算2222100642++++ 而设计的,正确的流程图序号为_________;图③中,输出的结果为__________________________ (只须给出算式表达式).15.现欲求12151311-++++n 的和(其中n 的值由键盘输入),下左图已给出了其流程图的一部分,则其中①应填 ,②应填 .是 否。
专题一 用流程图表示算法练习

C.29
D.7
5.(浙江高考)某算法的部分流程图如下图所示。执行这部分流程,输出 a,b 的
值分别是( )
A.5,8 C.5,11
B.4,8 D.4,11
6.(2018·6 月浙江学考)某算法的部分流程图如图所示,以下说法正确的是( )
A.该流程执行后,变量 k 的值是-1 B.该流程执行后,变量 a 的值是 16 C.该流程用于计算并输出 1+8-16 的值 D.该流程完整执行 1 次,“a<32?”共执行了 3 次 7.(2017·4 月浙江选考)某算法的部分流程图如图所示。执行这部分流程,依次 输入 3,4,-1,则输出 s 的值是( )
B.语句“k←k+2” 被执行了 14 次 C.语句“s>30”被执行了 7 次 D.该算法是求表达式 1+3+5+7+9+11+13 的值 10.某算法的部分流程图如图所示。
执行这部分流程,输入 5。流程执行结束,下列说法不.正.确.的是( ) A.i 的值为 5 B.s 的值为 6 C.语句 i←i+1 被执行了 5 次 D.条件 i≤n 与 not n>i 相当 11.某算法部分流程图如图所示,执行这部分流程,则输出 m,n,i 的值依次为 ()
A.3 14 7
B.0 20 7
C.0 15 6
D.3 15 7
12.某算法部分流程图如图所示。执行这部分流程,依次输入 12、10、2、18、
7、20、19、-1,则输出值是 ( )
A.19 20 C.2 7
B.20 19 D.7 2
13.某算法的部分流程图如图所示:
执行该流程图,输入 128,该流程图执行结束后,则下列表述正确的是( ) A.变量 f 的值为 True B.变量 t 的值为 12 C.该算法只能用流程图进行描述 D.虚线框处的流程图执行模式为循环结构
高中数学算法流程图试题与详细解析
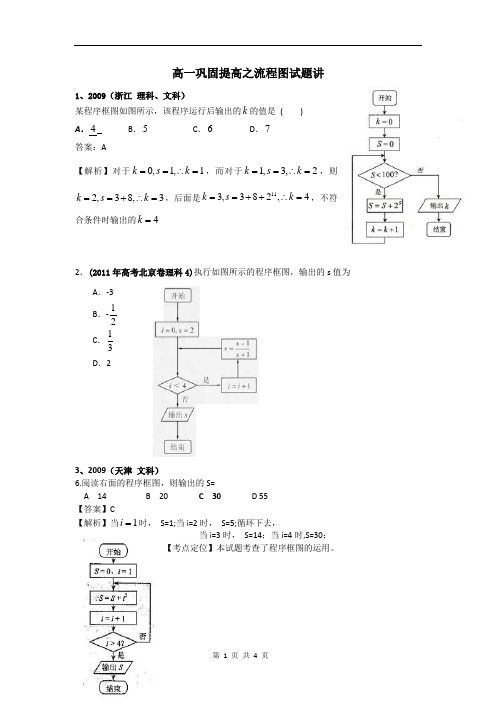
高一巩固提高之流程图试题讲1、2009(浙江 理科、文科)某程序框图如图所示,该程序运行后输出的k 的值是 ( ) A .4 B .5 C .6 D .7答案:A【解析】对于0,1,1k s k ==∴=,而对于1,3,2k s k ==∴=,则2,38,3k s k ==+∴=,后面是113,382,4k s k ==++∴=,不符合条件时输出的4k =2.(2011年高考北京卷理科4)执行如图所示的程序框图,输出的s 值为 A .-3B .-12C .13D .23、2009(天津 文科)6.阅读右面的程序框图,则输出的S=A 14B 20C 30D 55 【答案】C【解析】当1=i 时, S=1;当i=2时, S=5;循环下去,当i=3时, S=14;当i=4时,S=30;【考点定位】本试题考查了程序框图的运用。
4、2009(天津 理科)(5)阅读右图的程序框图,则输出的S=A. 26B. 35C. 40D. 57 【考点定位】本小考查框架图运算,基础题。
解:当1=i 时,2,2==S T ;当2=i 时,7,5==S T ;当3=i 时,15,8==S T ;当4=i 时,26,11==S T ;当5=i 时,40,14==S T ;当6=i ,i>5输出结果,故选择C 。
5、2009(广东 理科)随机抽取某产品n 件,测得其长度分别为12,,,n a a a ,则图3所示的程序框图输出的s = ,s 表示的样本的数字特征是 .(注:框图中的赋值符号“=”也可以写成“←”“:=”) 【解析】s =na a a n+⋅⋅⋅++21;平均数6、2009(上海 理科)某算法的程序框如右图所示,则输出量y 与输入量x 满足的关系式是____________________________ .开始输出S 结束i>5?是否S=0,i=1T=3i-1S=S+T i=i+1答案:2,12,1x x y x x ⎧≤=⎨->⎩7、2009(安徽 文科、理科)程序框图(即算法流程图)如图所示,其输出结果是_______。
高考专题专题15算法程序框图-高考数学高频考点与最新模拟(解析版)

高中数学学习材料金戈铁骑整理制作专题15 算法程序框图高频考点一 算法的设计 例1、已知函数y =⎩⎪⎨⎪⎧-2,x >0,0,x =0,2,x <0,写出求该函数函数值的算法及程序框图.高频考点二 算法的基本逻辑结构例2、设计算法求11×2+12×3+13×4+…+12 011×2 012的值,并画出程序框图.高频考点三基本算法语句例3、(1)下面程序输出的结果是________.n=5;s=0;while s<15s=s+n;n=n-1;endprint %io2,n;(2)根据如图所示的程序,当输入a,b分别为2,3时,最后输出的m的值为________.a=input “a=”;b=input“b=”;if a>bm=a;elsem=b;endprint%io2,m;答案(1)0(2)3解析(1)当s=5+4+3+2+1≥15时,停止循环,而此时,n=1-1=0.(2)本程序的功能是求两个数中较大的一个数.1.程序框图(1)通常用一些通用图形符号构成一张图来表示算法.这种图称做程序框图(简称框图).(2)基本的程序框图有起、止框、输入、输出框、处理框、判断框、流程线等图形符号和连接线构成.2.三种基本逻辑结构名称内容顺序结构条件分支结构循环结构定义最简单的算法结构,语句与语句之间,框与框之间按从上到下的顺序进行依据指定条件选择执行不同指令的控制结构根据指定条件决定是否重复执行一条或多条指令的控制结构程序框图3.基本算法语句(1)赋值语句①概念:用来表明赋给某一个变量一个具体的确定值的语句.②一般格式:变量名=表达式.③作用:计算出赋值号右边表达式的值,把该值赋给赋值号左边的变量,使该变量的值等于表达式的值.(2)输入语句①概念:用来控制输入结构的语句.②一般格式:变量名=input.③作用:把程序和初始数据分开.(3)输出语句①概念:用来控制把求解结果在屏幕上显示(或打印)的语句.②一般格式:print(%io(2),表达式).③作用:将结果在屏幕上输出.(4)条件语句①处理条件分支逻辑结构的算法语句.②条件语句的格式及框图.a.if语句最简单的格式及对应的框图b.if语句的一般格式及对应的框图(5)循环语句①算法中的循环结构是由循环语句来实现的.②循环语句的格式及框图.a.for语句b.while语句4. 在数学中,现代意义上“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成的. 5. 解决程序框图问题时应注意的问题 (1)不要混淆处理框和输入框. (2)注意区分条件分支结构和循环结构. (3)注意区分for 循环和while 循环. (4)循环结构中要正确控制循环次数. (5)要注意各个框的顺序.(2013·新课标I 理)5、执行右面的程序框图,如果输入的t ∈[-1,3],则输出的s 属于( ) A 、[-3,4] B 、[-5,2] C 、[-4,3] D 、[-2,5]【答案】A ;【解析】若[)1,1t ∈-,则[)33,3S t =∈-;若[]1,3t ∈,[]243,4S t t =-∈;综上所述[]3,4S ∈-.【学科网考点定位】本题考查算法框图,考查学生的逻辑推理能力.(2013·新课标Ⅱ理)(6)执行右面的程序框图,如果输入的N=10,那么输出的s=(A )1+ 12+ 13+…+ 110(B )1+ 12!+ 13!+…+110!(C )1+ 12+ 13+…+ 111(D )1+ 12!+ 13!+…+111!(2013·浙江理)5.某程序框图如图所示,若该程序运行后输出的值是59,则( ) A.4=a B.5=a C. 6=a D.7=a(2013·天津理)3.阅读右边的程序框图, 运行相应的程序, 若输入x的值为1, 则输出S的值为()(A) 64 (B) 73(C) 512 (D) 585(2013·陕西理)2. 根据下列算法语句, 当输入x 为60时, 输出y 的值为 ( ) (A) 25 (B) 30 (C) 31 (D) 61 【答案】C 【解析】60,250.660-50)31x y =∴=+⨯=(,故选择C 。
算法流程图(附答案)

算法流程图(附答案)选择结构直到型循环当型循环流程图——三种基本算法逻辑结构顺序结构1.该图是某算法的流程图,其输出值a是_____312. 如图所示的流程图,若输入的x=-9.5,则输出的结果为________.3. 某算法的程序框图如图,若输入a=4,b=2,c=6,则输出的结果为________.6(第1题) (第2题) (第3题)4. 一个算法的流程图如图所示,则输出的S值为______________.455.下面是一个算法的程序框图,当输入值x为8时,其输出的结果是____________.2(第4题)(第5题)6. 运行如图所示的程序框图,则输出的结果S=__________. 617. 如图所示的算法流程框图中,若输入a=4,b=48,则最后输出的a的值是__________.968. 如图,程序执行后输出的结果为_______ 64(第7题) (第8题) (第6题)9.按如图所示的流程图运算,则输出的S=2010.阅读下面的流程图,若输入a=10,b=6,则输出的结果是 211.右图是一个算法的流程图,则输出S的值是7500(第9题) (第10题) )12. 右图是一个算法的流程图,最后输出的k=_______.11 13.阅读右边的流程图,则输出S =______.3014.程序框图(即算法流程图)如图所示,其输出结果是 . 127(第13题) (第14题)15、图中是一个算法流程图,则输出的n=_______ 11 16. 右图是一个算法的流程图,最后输出的x =________.-1017.执行右边的程序框图,若15p =,则输出的n =_____________. 5(第15题) (第16题) (第17题)(第12题)18. 根据如图所示的算法流程图,可知输出的结果i 为____________.7 19. 右图是一个算法的流程图,最后输出的n =____________.100 20. 右图是一个算法的流程图,则输出a 的值是________.log 23(第18题) (第19题) (第20题)21. 已知某算法的流程图如图所示,若将输出的数组(x ,y )依次记为(x 1,y 1),(x 2,y 2),…,(x n ,y n ),…,则程序运行结束时输出的最后一个数组为________.(27,-6) 22.如图,该程序运行后输出的结果为____1623.执行右边的程序框图,若p =9,则输出的s =____________.25(第21题) (第22题) (第23题)。
算法流程图

1. 输人一个数到变量 a ,输出它的绝对值。
(要求用单分支和双分支结构分别设计算法) 单分支结构算法:(1) 输入任意数并赋值给变量 a ;(2) 判断a 是否小于0,如果a 小于0 ,取a 的相反数; (3) 输出a 。
双分支结构算法:(1) 输人任意数并赋值给变量 a ;(2) 判断a 是否小于0,如果a 小于0则输出a 的相反数,否则输出 a 。
2. 最值问题:max-x, i —1i -i+1/输出乜// 输出a /单分支结构算法流程图双分支结构算法流程医(1 )求输人的两个数中的最大值。
(开始T(3)求输入的十个数中的最大值。
「开始J x 7 /输応'」/输出b /■ /输躬](2 )求输人的三个数中的最大值。
3.循环求和(不同的控制循环方法)1.求输人20个数的和。
(知道循环次数,可以采用循环变量i来控制循环次数)计数法3.对输入的数据求和,当所求的和超过100则停止输入并输出求和结果(设此题中输人的数皆为正数)。
(没有指出输人数据的具体个数,且不能依据对输入数据的值来控制循环,控制循环的关键就在于对循环体中变量s的判断)2.求输入的若干个学生成绩的和,输入-1表示结束。
(不能确定次数,可以用输入的数据的值来进行控标志法输出a / / 输呼〃箱単b / / 輸匹输出如下图形:**************************************************A,o・o・o・o・o・ o«o»o»oeo> o»o»o«o»o> o・o・o・o・o・ o ・o・o・o・o・B•o«o»o»c»o •©•o«oeo»o •o ・o・o・o・o •o ・o・o・o・o •o ・o・o・o・o c.・o・o・o・o・o o・o・o・o・o・•o・o・o・o ・o o*o»o«o»o«•oeoooeoeo a o ・o・o・o・o・•o・o・o・o・o•o»o«o*o»oo«o*oeo>o«。
算法框图试题

算法流程图练习题1、阅读下面的程序框图,该程序输出的结果是________.第2题第3题 2、如图所示的程序框图输出的结果是 . 3、如果执行上面的程序框图,那么输出的S = (A)2450 (B)2500 (C)2550(D)265243,结果会输出________.第4题 第5题 5、执行上边的程序框图,若0.8p =,则输出的n =.6、阅读下边程序框图,若输入的n 是100,则输出的变量S 和T 的值依次是 .第6题 第7题7、阅读上图的程序框图,若输入4m =,3n =,则输出a = ,i = ;若输入4m =,6n =,则输出a =_____,i =_____.8.按如图所示的框图运算:若输入x =8,则输出k = ;若输出k =2,则输入的x 的取值范围是 .第9题9、阅读上面的程序框图,回答下列问题:若2log 3=a 、32=b 、31)21(=c ,则输出的数是______10、下面的程序框图循环体执行的次数是___ ___.第10题 第11题11、阅读上边的程序框图,请你写出y 关于x 的函数解析式 . 12、下图给出的是计算 12151311-++++n 的值的一个程序框图(其中n 的值由键盘输入),其中①处应填 ,②处应填 .第12题 第13题13、上面是一个算法的程序框图,当输入的x 值为3时,输出的y 的结果恰好是1/3,则?处的关系式是 .14、下面的程序框图,如果输入三个实数a 、b 、c ,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入 .第15题15、上面的程序框图可以计算10021(21)nn--∑的值,则在判断框中可以填写的表达式为.16、下图是计算1111223910+++⨯⨯⨯的值的算法框图,其中在判断框中应填入的条件是.第16题第17题117、给出30个数:1,2,4,7,11,……,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依此类推,要计算这30个数的和,现已给出了该问题算法的程序框图.补充上面的程序框图,使之能完成该题算法功能.。
高中数学 同步练习 课时分层作业2 流程图

课时分层作业(二) 流程图(建议用时:60分钟)[基础达标练]一、选择题1.表示判断框的图形符号是( )A.B.C.D.A [判断框用菱形表示.]2.如图所示的流程图,输出的结果是S=7,则输入的A值为( )A.2 B.3C.7 D.15B [该流程图的功能是输入A,计算2A+1的值.由2A+1=7,解得A=3.]3.下面的流程图是已知直角三角形两条直角边a,b,求斜边c的算法,其中正确的是( )A [由题意知应先输入a,b,再由公式计算c=a2+b2,最后输出c结束,B中的顺序错误;C中的起止框错误;D中的处理框错误,A正确.]4.现有如图所示的流程图,则输出的结果是( )A .12B .60C .120D .360D [该流程图的功能是求6×5×4×3的值,故输出的结果为360.] 5.如图所示的流程图运行后输出的结果为12,则输入的x 的值为( )A .-1B .22C .-1或22D .22或-22C [该流程图的作用是计算分段函数y =⎩⎪⎨⎪⎧2x, x≤0,log 12x , 0<x <14,x 2, x ≥14的函数值,当x≤0时,2x=12,则x =-1.当0<x <14时,log 12x =12,则x =22∉⎝ ⎛⎭⎪⎫0,14,舍去.当x≥14时,x 2=12,则x =22或x =-22(舍去).综上,输入的x 的值为-1或22.] 二、填空题6.编制计算y =2x 3+x 2+1的流程图,其中x =-10,-9,…,0,1,…,9,10.流程图如图所示.请将流程图填写完整.①________,②________.①x≤10 ②x←x+1 [观察循环结构,可知自变量x 的取值有规律:由小到大逐个增加1应通过累加变量体现循环.]7.执行如图所示的流程图,若输出的n 为5,则输入整数p 的最大值是________.15 [由流程图知,该算法的功能是计算20+21+22+…+2n -1的值.当输出的n 为5时,在上一次循环中S =20+21+22+23=15,此时跳出循环,故输入的p 的最大值是15.]8.执行如图所示的流程图,若输出k 的值为6,则判断框内可填入的条件是________.S >710 [第一次执行循环:S =1×910=910,k =8,S =910满足条件;第二次执行循环:S =910×89=810,k=7,S =810满足条件;第三次执行循环:S =810×78=710,k =6,正是输出的结果,故这时S =710不满足条件,结束循环.]三、解答题9.如图所示是解决某个问题而绘制的流程图,仔细分析各图框内的内容及图框之间的关系,回答下面的问题:(1)该流程图解决的是怎样的一个问题?(2)若最终输出的结果y 1=3,y 2=-2,当x 取5时输出的结果5a +b 的值应该是多大? (3)在(2)的前提下,输入的x 值越大,输出的ax +b 是不是越大?为什么?(4)在(2)的前提下,当输入的x 值为多大时,输出结果ax +b 等于0? [解] 这是一个顺序结构流程图,该流程图的作用是解决函数f(x)=ax +b 的函数值的问题.依据此函数的性质可以回答相应问题.(1)该流程图解决的是求函数f(x)=ax +b 的函数值的问题.其中输入的是自变量x 的值,输出的是x 对应的函数值.(2)y 1=3,即2a +b =3. ① y 2=-2,即-3a +b =-2.②由①②得a =1,b =1. ∴f(x)=x +1.∴当x 取5时,5a +b =f(5)=5×1+1=6. (3)输入的x 值越大, 输出的函数值ax +b 越大, 因为f(x)=x +1是R 上的增函数. (4)令f(x)=x +1=0, 得x =-1,因此当输入的x 值为-1时, 输出的函数值为0.10.在音乐唱片超市里,每张唱片售价25元.若顾客购买5张以上(含5张)唱片,则按照九折收费;若顾客购买10张以上(含10张)唱片,则按照八五折收费.请设计一个完成计费工作的算法,并画出流程图.[解] 用变量a 表示顾客购买的唱片数,用C 表示顾客要缴纳的金额,依题意应有C =⎩⎪⎨⎪⎧25a ,a<5,22.5a ,5≤a<10,21.25a ,a≥10.算法步骤如下:S1 输入a;S2 若a<5,则C←25a,否则,执行步骤S3;S3 若a<10,则C←22.5a,否则C←21.25a;S4 输出C.流程图如图所示:[能力提升练]1.下列问题的算法流程图适宜用选择结构表示的是( )①计算某次数学测试中30个学生的平均分;②解不等式ax+1>0(a≠0);③求点P(1,2)与点Q(3,4)之间的距离;④输出a,b,c中的最大数.A.①②B.①③C.②④D.③④C [②不等式ax+1>0(a≠0)在a>0与a<0不同情况下有不同的解,故要用到选择结构;④要输出a,b,c 中最大数,需要对三个数两两比较大小,故要用到选择结构;而①③分别只要代入对应公式计算即可,无需采用选择结构.]2.给出一个算法流程图如图,该流程图对应算法的功能是( )A.输出a,b,c中的最小数B.输出a,b,c中的最大数C.输出aD.输出cA [该流程图中有两个判断框,每个判断框中都是两数比较大小,如果大于号成立则执行“Y”,即用小数替换大数,最后输出较小的数.]第2题图 第3题图3.阅读如图所示的流程图,如果输出的函数值在区间⎣⎢⎡⎦⎥⎤14,12内,则输入的实数x 的取值范围是________.[-2,-1] [分析流程图可知,本题是已知分段函数的值域求自变量的取值范围的问题,其中分段函数为f(x)=⎩⎪⎨⎪⎧2x,-2≤x≤2,2,x>2或x<-2,故当值域为⎣⎢⎡⎦⎥⎤14,12时,输入的x 值的范围是[-2,-1].]4.如图所示,x 1,x 2,x 3为某次考试三个评阅人对同一道题的独立评分,p 为该题的最终得分.当x 1=6,x 2=9,p =8.5时,x 3等于________.8 [因为|x 1-x 2|=3≥2,执行输入x 3,当0<x 3<7.5时,|x 3-x 1|<|x 3-x 2|,x 2=x 3,此时p =x 1+x 32=8.5,解得x 3=11(舍去).同理,当x 3≥7.5时,解得x 3=8,符合条件.所以x 3=8.]5.某班一共有50名学生,设计一个算法,统计班上数学成绩良好(分数大于80且小于90)和优秀(分数大于或等于90)的学生人数,并画出流程图.[解] 该问题中涉及50名学生的成绩,所以要用到循环结构;每名学生的成绩需要判断是否为良好或优秀,所以还要用到选择结构.算法如下:S1 n←1,a←0,b←0;S2 输入成绩r;S3 若r>89,则a←a+1,转S5,否则执行S4;S4 若r>80,则b←b+1,转S5,否则直接执行S5;S5 n←n+1;S6 若n>50,则输出a和b,否则,转S2.流程图如图所示:。
算法与流程图习题课

N
Y min=c
Y min=b
输出min 输出
结束
1
5、设计一算法输出1~1000以内能被 整除的整数 、设计一算法输出 以内能被3整除的整数 以内能被
开始 i=0
S1:确定i的初始值为 ; :确定 的初始值为 的初始值为0;
i<1000?
否 是 i= i+1 是 3整除i? 整除i? 否 输出i 输出i
S2:判断i是否等于 :判断 是否等于 是否等于1000, , 若是则程序结束, 若是则程序结束,否则进 入S3; ; S3:使i增加 ,判断 是否 : 增加 增加1,判断i是否 能被3整除 若能输出i, 整除, 能被 整除,若能输出 , 并返回S2;否则直接返回 并返回 ; S2
结束
6、设计一个算法框图:求满足1+2 + 3 + … + n>22的最 小正整数n,并写出相应的QBASIC程序。 开始 开始 i=1,s=0 s=s+i i=i+1 否 否 s>22? 是 输出i-1 结束
算法例题选 高二数学备课组
算法知识结构: 算法知识结构:
基本思想 算 法
程序化思想 流程图
基本结构
顺序结构与条件结构
直到型 当型
循环结构
(1)顺序结构 )
A
B
(2)选择结构 ) 一 个 分 支
是 步骤1 步骤 否
条件
Y A
p
N B
两 个 步骤 分 步骤1 支
是
条件
否 步骤2 步骤
循环语句
(1)(直到型)循环 ) 直到型)
p=0,q=0,m=0,i=1,n=45 输入t 0≤t<60 N 60≤t<80 N 80≤t ≤100 N i=i+1 N i>45 Y 输出p,q,m 结束 Y m=m+1 Y Y q=q+1 p=p+1
算法与流程图

算法与流程图1.以下对算法的描画正确的有个.①对一类效果都有效;②算法可执行的步骤必需是有限的;③计算可以一步步地停止,每一步都有确切的含义;④是一种通法,只需墨守成规地做,总能失掉结果.答案 42.任何一个算法都必需有的基本结构是 .答案顺序结构3.以下效果的算法适宜用选择结构表示的是〔填序号〕.①求点P〔-1,3〕到直线l:3x-2y+1=0的距离②由直角三角形的两条直角边求斜边③解不等式ax+b>0 (a≠0)④计算100个数的平均数答案③4.以下4种框图结构中,是直到型循环结构的为〔填序号〕.答案②5.〔2020·广东理,9〕阅读下面的流程图,假定输入m=4,n=3,那么输入a= ,i= .〔注:框图中的赋值符号〝←〞也可以写成〝=〞或〝:=〞〕基础自测答案 12 3例1 点P 〔x 0,y 0〕和直线l :Ax +By +C =0,求点P 〔x 0,y 0〕到直线l 的距离d ,写出其算法并画出 流程图. 解 算法如下:第一步,输入x 0,y 0及直线方程的系数A ,B ,C . 流程图: 第二步,计算Z 1←Ax 0+By 0+C . 第三步,计算Z 2←A 2+B 2. 第四步,计算d ←21Z Z .第五步,输入d .例2 〝特快专递〞是目先人们经常运用的异地邮寄信函或托运物品的一种快捷方式,某快递公司规则甲、乙两地之间物品的托运费用依据以下方法计算:f =⎩⎨⎧>⨯-+⨯≤)100(85.0)100(6.0100)100(6.0ωωωω其中f (单位:元)为托运费,ω为托运物品的重量〔单位:千克〕.试设计计算费用f 的算法,并画出流程图.解 算法如下: S1 输入ω;S2 假设ω≤100,那么f ←0.6ω;否那么f ←100×0.6+(ω-100)×0.85; S3 输入f . 流程图为:例3 〔14分〕画出计算12-22+32-42+…+992-1002的值的流程图.解 流程图如以下图.14分1.写出求解一个恣意二次函数y =ax 2+bx +c (a ≠0)的最值的算法. 解 算法设计如下: 第一步,计算m ←ab ac 442-; 第二步,假定a >0,输入最小值m ; 第三步,假定a <0,输入最大值m .2.到银行操持团体异地汇款〔不超越100万元〕,银行收取一定的手续费,汇款额不超越100元,收取1元手续费,超越100元但不超越5 000元,按汇款额的1%收取,超越5 000元,一概收取50元手续费,试用条件语句描画汇款额为x 元时,银行收取手续费y 元的进程,画出流程图. 解 这是一个实践效果,故应先树立数学模型,y =⎪⎩⎪⎨⎧≤<≤<≤<00000010005.500005100,01.01000,1x x x x 由此看出,求手续费时,需先判别x 的范围,故运用选择结构描画. 流程图如下图:3.应用两种循环写出1+2+3+…+100的算法,并画出各自的流程图. 解 直到型循环算法: 第一步:S ←0;第二步:I←1;第三步:S←S+I;第四步:I←I+1;第五步:假设I不大于100,转第三步;否那么,输入S.相应的流程图如图甲所示.当型循环算法如下:S1 令i←1,S←0S2 假定i≤100成立,那么执行S3;否那么,输入S,完毕算法S3 S←S+iS4 i←i+1,前往S2相应的流程图如图乙所示.一、填空题1.算法:S1 输入n;S2 判别n能否是2,假定n=2,那么n满足条件,假定n>2,那么执行S3;S3 依次从2到n-1检验能不能整除n,假定不能整除n,满足上述条件的是 .答案质数2.在算法的逻辑结构中,要求停止逻辑判别,并依据结果停止不同处置的是哪种结构 . 答案选择结构和循环结构3.阅读下面的流程图,假定输入的a、b、c区分是21、32、75,那么输入的a、b、c区分是 .答案75,21,324.假设执行下面的流程图,那么输入的S = .答案 2 5505.〔2020·兴化市板桥初级中学12月月考〕如以下图的流程图输入的结果为 .答案 1326.如下图,流程图所停止的求和运算是 .答案 21+41+61+…+2017.〔2020·山东理,13〕执行下边的流程图,假定p =0.8,那么输入的n = .〔注:框中的赋值符号〝←〞,也可以写成〝=〞或〝:=〞〕答案 48.假定框图所给的顺序运转的结果为S =90,那么判别框中应填入的关于k 的判别条件是 .答案 k ≤8二、解答题9.函数f (x )=⎩⎨⎧≥-<-)0(52)0(13x x x x ,写出该函数的函数值的算法并画出流程图.解 算法如下: 第一步,输入x .第二步,假设x <0,那么使f (x )←3x -1;否那么f (x )←2-5x .第三步,输入函数值f (x ). 流程图如下:10.写出求过两点P 1(x 1,y 1),P 2(x 2,y 2)的直线的斜率的算法,并画出流程图.解 由于当x 1=x 2时,过两点P 1、P 2的直线的斜率不存在,只要当x 1≠x 2时,依据斜率公式 k =1212x x y y --求出,故可设计如下的算法和流程图.算法如下:第一步:输入x 1,y 1,x 2,y 2;第二步:假设x 1=x 2,输入〝斜率不存在〞,否那么,k ←1212x x y y --;第三步:输入k . 相应的流程图如下图:11.画出求211⨯+321⨯+431⨯+…+100991⨯的值的流程图.解 流程图如下图:12.某企业2007年的消费总值为200万元,技术创新后估量以后的每年的消费总值将比上一年添加5%,问最早哪一年的年消费总值将超越300万元?试写出处置该效果的一个算法,并画出相应的流程图. 解 算法设计如下:第一步,n ←0,a ←200,r ←0.05. 第二步,T ←ar (计算年增量). 第三步,a ←a +T 〔计算年产量〕.第四步,假设a ≤300,那么n ←n +1,重复执行第二步. 假设a >300,那么执行第五步. 第五步,N ←2 007+n . 第六步,输入N . 流程图如下: 方法一方法二§13.2 基本算法语句、算法案例1.下面是一个算法的操作说明:①初始值为n←0,x←1,y←1,z←0;②n←n+1;③x←x+2;④y←2y;⑤z←z+xy;⑥假设z>7 000,那么执行语句⑦;否那么回到语句②继续执行;⑦打印n,z;⑧顺序终止.由语句⑦打印出的数值为、.答案8 7 6822.依照下面的算法停止操作:S1 x←2.35S2 y←Int〔x〕S3 Print y最后输入的结果是 .答案 23.读下面的伪代码:Read xIf x>0 ThenPrint xElsePrint -xEnd If这个伪代码表示的算法的功用是 .答案输入一个数,输入其相对值4.下面是一个算法的伪代码.假设输入的x的值是20,那么输入的y的值是 . 答案150基础自测5.与以下伪代码对应的数学表达式是 .Read ne←0S←1For I From 1 To n Step 1S←S×Ie←e+1/SEnd forPrint e答案S=1+!21+!31+…+!1n例1设计算法,求用长度为l的细铁丝区分围成一个正方形和一个圆时的面积.要求输入l的值,输入正方形和圆的面积.解伪代码如下:Read lS1←(l×l)/16S2←(l×l)/(4×3.14)Print S1Print S2End例2 〔14分〕分段函数y=⎪⎩⎪⎨⎧>+=<+-,1,0,1xxxxx,编写伪代码,输入自变量x的值,输入其相应的函数值,并画出流程图.解伪代码如下:流程图如下图:Read xIf x<0 Theny ←-x+1ElseIf x=0 Theny←0Elsey←x+1End IfEnd IfPrint yEnd 7分例3 编写一组伪代码计算1+21+31+…+00011,并画出相应的流程图.解 伪代码如下: i ←1 S ←0While i ≤1 000 S ←S +1/i i ←i +1 End While Print S End流程图如下图:1.下面的表述: ①6←p ; ②t ←3×5+2; ③b +3←5;④p ←((3x +2)-4)x +3; ⑤a ←a 3; ⑥x ,y ,z ←5; ⑦ab ←3; ⑧x ←y +2+x .其中正确表述的赋值语句有 . 〔注:要求把正确的表述的序号全填上〕 答案 ②④⑤⑧2.某百货公司为了促销,采用打折的优惠方法: 每位顾客一次购物①在100元以上者〔含100元,下同〕,按九五折优惠; ②在200元以上者,按九折优惠; ③在300元以上者,按八五折优惠; ④在500元以上者,按八折优惠.试写出算法、画出流程图、伪代码,以求优惠价. 解 设购物款为x 元,优惠价为y 元, 那么优惠付款公式为y =⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<≤<500,8.0500300,85.0300200,9.0200100,95.0100,x x x x x x x x x x 算法剖析: S1 输入x 的值;S2 假设x <100,输入y ←x ,否那么转入S3; S3 假设x <200,输入y ←0.95x ,否那么转入S4; S4 假设x <300,输入y ←0.9x ,否那么转入S5; S5 假设x <500,输入y ←0.85x ,否那么转入S6; S6 输入y ←0.8x .3.某玩具厂1996年的消费总值为200万元,假设年消费增长率5%,计算最早在哪一年消费总值超越300万元.试写出伪代码. 解 伪代码如下: n ←1 996 p ←1.05 a ←200 While a ≤300a←a×pn←n+1End WhilePrint nEnd一、填空题1.伪代码a←3b←5Print a+b的运转结果是 .答案82.为了在运转下面的伪代码后输入y=16,应输入的整数x的值是 . Read xIf x<0 Theny←(x+1)2Elsey←1-x2End IfPrint y答案-53.写出以下伪代码的运转结果.图1 图2〔1〕图1的运转结果为;〔2〕图2的运转结果为 .答案〔1〕7 〔2〕64.以下给出的是用条件语句编写的一个伪代码,该伪代码的功用是 .答案 求以下函数当自变量输入值为x 时的函数值f (x ),其中f 〔x 〕=⎪⎩⎪⎨⎧>-=<3,13,23,22x x x x x 5.下面是一个算法的伪代码,其运转的结果为 .答案 2 5006.如下图,该伪代码表示的作用是 .答案 求三个数中最大的数7.如图〔1〕是某循环流程图的一局部,假定改为图〔2〕,那么运转进程中I 的值是.答案 18.图中算法执行的循环次数为 .答案333二、解答题9.用条件语句描画下面的算法流程图.解Read xIf x<0 Theny←2×x+3ElseIf x>0 Theny←2×x-5Elsey←0End IfEnd IfPrint yEnd10.请设计一个效果,使得该效果的算法如的伪代码所示.解 圆O 内有一个边长为a 的圆的内接正方形,求圆的面积比正方形的面积大多少? 11.有一个算法如下: S1 输入x ; S2 判别x >0是:z ←1;否:z ←-1; S3 z ←1+z ; S4 输入z .试写出上述算法的流程图及相应的伪代码. 解12.一个小冤家在一次玩皮球时,偶然发现一个现象:球从某高度落下后,每次都反弹回原高度的31,再落下,再反弹回上次高度的31,如此重复.假定球从100 cm 处落下,那么第10次下落的高度是多少?在第10次落地时共经过多少路程?试用伪代码表示其算法. 解 伪代码如下图:Read a r ←2a /2 S ← ×r ×r -a ×a Print S EndRead xIf x >0 Thenz ←1 Elsez ←-1 End If z ←z +1 Print z Endh ←100 s ←100 i ←2While i ≤10h ←h /3 s ←s +2×h i ←i +1 End WhilePrint 〝第10次下落的高度为:〞;hPrint 〝第10次落地时共经过的路程为:〞;s End。
算法流程图(附答案)
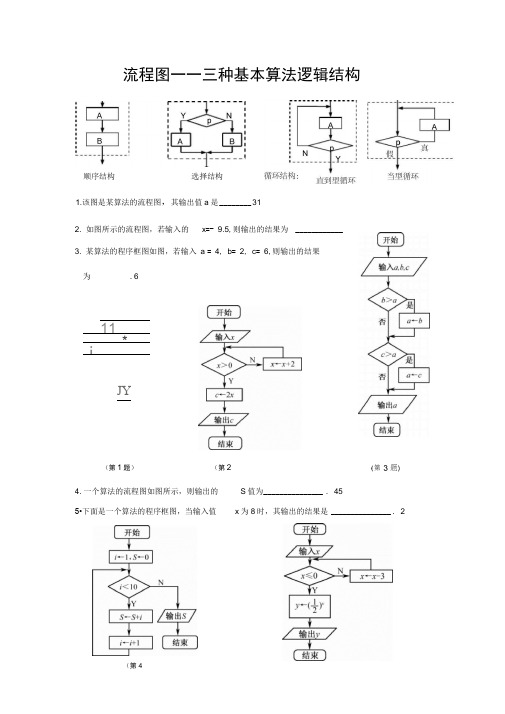
1.该图是某算法的流程图,其输出值a是________ 312. 如图所示的流程图,若输入的x=- 9.5,则输出的结果为 ____________3. 某算法的程序框图如图,若输入a = 4, b= 2, c= 6,则输出的结果为.611*iJY(第1题)4. 一个算法的流程图如图所示,则输出的5•下面是一个算法的程序框图,当输入值S值为_______________ . 45x为8时,其输出的结果是_______________ . 2流程图一一三种基本算法逻辑结构顺序结构选择结构(第2题)(第4题)6. 运行如图所示的程序框图,则输出的结果 S = ___________ . 617. 如图所示的算法流程框图中, 若输入a = 4,b = 48,则最后输出的a 的值是 ________________ .96 8. 如图,程序执行后输出的结果为 _________ 6410.阅读下面的流程图,若输入______________a = 10, b = 6,则输出的结果是 211. _____________________________________________ 右图是一个算法的流程图,则输出 S 的值是 _________________________________________________ 7500开始/输出P/ 卩/9•按如图所示的流程图运算 ,则输出的S 二 _________20 (第6题)(第7题)I —12. ___________________________________________ 右图是一个算法的流•程图,最后输出的k= _________________ . 1113•阅读右边的流程图,则输出S= ________ . 3015、图中是一个算法流程图,则输出的n= ______ 1116. 右图是一个算法的流程图,最后输出的x= ________ .-1017.执行右边的程序框图,若p =15,则输出的n二fT-li S^-0(第16题)5/输入/n=l,S=0沪針严/5丽7ZE~~TM=n+1 [结束](第15题)(第17题))如图所示,其输出结果是127开始(第14 题)结束14•程序框图(即算法流程图(第12题)(第13题)c-2cr+'l/输出口/18. 根据如图所示的算法流程图,可知输出的结果i为______________ .719. 右图是一个算法的流程图,最后输出的n = ____________ .10020. 右图是一个算法的流程图,则输出a的值是_____________. log2321. 已知某算法的流程图如图所示,若将输出的数组(x, y)依次记为(X1, y1), (X2, y2),…, (X n, y n),…,则程序运行结束时输出的最后一个数组为22. _________________________________ 如图,该程序运行后输出的结果为______________________________ 1623•执行右边的程序框图,若p= 9,则输出的s= _(第19题)(第18题)(开始〕1 rm2托(第20题)(第22 题)—• (27,—6)2.5苏州市第六中学2014数学必修三(算法)。
算法流程图试题(6页)

整个过程I永远是1,所以只要执行到步骤3就会再跳到步骤2
20(C)
一流程图如下图所示,依流程顺利执行后,打印B的值为何?
(A)34 (B)40 (C)45 (D)49。
解析
21(C)
依据下列流程图,变量a之输出值为多少?
(A)68 (B)84 (C)104 (D)124。
解析
22(B)
下图为从1开始循序累加的算法,请问最终的累加结果会印出
步骤3:A = A + 1
步骤4:跳至步骤2
步骤5:输出SUM
步骤6:结束
(A)指令不够明确(B)输出的整数值个数较设定的初始值个数少(C)算法无法在有限步骤之内结束(D)设定1个以上的初始值
解析
只要执行到步骤4就跳到步骤2,之间没有设定离开的条件
19(C)
下列算法所犯的错误为何?
(A)指令不够明确(B)输出的整数值个数较设定的初始值个数少(C)算法无法在有限步骤之内结束(D)设定1个以上的初始值
解析
CA课本p351表5-20
讲义p6算法─(3)流程图表示法─常用符号
9(B)
在流程图中符号 表示何种意义?
(A)输出/输入(B)处理(C)决策判断(D)开始
解析
CA课本p351表5-20
讲义p6算法─(3)流程图表示法─常用符号
10(C)
在流程图中符号 表示何种意义?
(A)输出/输入(B)处理(C)决策判断(D)开始
(A)SUM = 55 (B)SUM = 45 (C)SUM = 0 (D)SUM = 66。
解析
23(A)
下列何者不是程序的基本结构?
(A)平行结构(B)循序结构(C)条件结构(D)重复结构
高一数学-高一数学程序框图1 精品

变式练习1.确定线段AB 的5等分点,是指在线段AB 上确定一点M ,使得AM =51AB .画出这个算法的流程图.答案:连结D B 过点C 交于A B A B 的2.高中某班一共有40名学生,(分数>80)和优秀(分数>90)的学生人数.答案:是 是 是 否否i =i +1m =m +1n =n +1i >40?3.设计算法流程图,输出2000以内除以3余1答案:开始n =14.设计算法流程图,答案:5.设计一个算法计算正整数的前n 答案:是结束输出s u m +1u m +i i =n <?6.函数y =⎪⎩⎪⎨⎧<+=>+-0. 3,0, 0,0, 1x x x x x ,,输出函数值.答案:7.一个三位数,各位数字互不相同,十位数字比个位、百位数字之和还要大,且十位、百位数字不是素数.设计算法,找出所有符合条件的三位数,要求画出流程图.答案:否结束8.1165km,北京到兰州为1813 km,答案:分析:用C 1来代表每天,C 2代表北京到西安的总千米数,C 3人长跑累计千米数. 只需用C 与C 2、C 3比较,当间P =0,西安到兰州之间P =1;S1 C 1=32×1000/1000 S2 P =0 S3 C =0 S4 I =1 S5 C 2=1165S6 C 3=1813S7 C=C+C1S8 输出I,CS9 如果C>=C3,则执行S16 S10 如果P=1,则执行S14 S11 如果C<C2,则执行S14 S12 输出“到西安”S13 P=1S14 I=I+1S15 执行S7S16 输出“到兰州”S17 结束流程图如下:。
用传统流程图表示求解以下问题的算法。1.有两个瓶子A和B,分别盛放醋和酱油,要求将他们互换。。。

⽤传统流程图表⽰求解以下问题的算法。
1.有两个瓶⼦A和B,分别盛放醋和酱油,要求将他们互换。
⽤传统流程图表⽰求解以下问题的算法。
1. 有两个瓶⼦A和B,分别盛放醋和酱油,要求将他们互换(即A瓶原来盛醋,现在盛酱油,B瓶则相反)。
解析:⽤两个瓶⼦显然很难实现,可以借助⼀个空瓶⼦C作为中转,先将A中醋导⼊C中,然后将B中的酱油导⼊A中,最后将C中的醋导⼊B 中即可实现交换。
2. 依次将10个数输⼊,要求输出其中最⼤的数。
解析:先输⼊10个整数,将第⼀个整数给max,然后依次取剩余整数与max进⾏⽐较,如果某个整数⼤于max,将该整数交给max,直到所有剩余整数全部⽐较完,max中保存的即为最⼤整数,将max值输出。
3. 有3个数a,b,c, 要求按⼤⼩顺序把他们输出。
解析:i:先⽤a和b⽐较,如果a⼤于b,将a与b内容交换,否则进⾏iiii:⽤c和a⽐较,如果c⼤于a,将a和c交换,否则进⾏iviii:⽤c和b⽐较,如果c⼤于b,将c和b进⾏交换,否则进⾏iviv:输出a、b、c,结束4. 求1 + 2 + 3 + ... + 100。
解析:给定N为1,sum为0,如果N ⼩于等于100时,进⾏sum += N,直到N超过100,循环操作完成后sum即为从1加到100的结果。
5. 判断⼀个数n能否同时被3和5整除。
解析:i:输⼊数据nii:如果n能被3整数,进⾏iii,否则输出n不能被3和5整数iii:如果n能被5整数,输出n能被3和5整数,否则n不能被3和5整数6. 将100~200之间的素数输出素数:即数学中的质数,因⼦只有1和其本⾝的数字称为质数。
对100和200之间的每个数进⾏⼀下操作:该数能否被2~该数之间的所有数整除,是则是素数输出,否则取下⼀个数字。
7. 求两个数m和n的最⼤公约数解析:辗转相除法a. 如果m⼤于n,交换m和nb. 循环进⾏⼀下操作:n是否为0?是则最⼤公约数为m,输出m结束。
(完整版)高考算法程序框图真题练习及答案详解

(完整版)高考算法程序框图真题练习及答案详解1. 该算法程序框图的功能是什么?A. 求a,b,c三数的最大数B. 求a,b,c三数的最小数C. 将a,b,c按从小到大排列2. 该算法程序框图的功能是什么?A. 求输出a,b,c三数的最大数B. 求输出a,b,c三数的最小数C. 将a,b,c按从小到大排列3. 该算法程序框图的功能是什么?A. 找出a、b、c三个数中最大的数B. 找出a、b、c三个数中最小的数C. 找出a、b、c三个数中第二大的数4. 程序框图表示的算法的运行结果是什么?A. 5B. 6C. 75. 程序框图中所表示的算法是什么?A. 求x的绝对值B. 求x的相反数C. 求x的平方根6. 运行图中所示程序框图所表达的算法,输出的结果是什么?A. 3B. 7C. 157. 程序框图(算法流程图)的输出结果是什么?A. 6B. 5C. 48. 运行相应的程序,输出的结果为什么?A. 676B. 26C. 59. 运行相应的程序,输出的结果是什么?A. 1B. 2C. 310. 运行相应的程序,输出的S的值等于什么?A. 18B. 2C. 2111. 当m=7,n=3时,执行如图所示的程序框图,输出的S的值为什么?A. 7B. 42C. 21012. 执行如图所示的程序框图,若输入n=10,则输出的S=什么?A.B.C.13. 运行相应的程序,当输入x的值为-25时,输出x的值为什么?A. -1B. 1C. 314. 运行相应的程序,输出s值等于什么?A. -3B. -10C.15. 执行如图所示的程序框图,若输入n的值为6,则输出s的值为什么?A. 105B.C. 1516. 执行如图所示的程序框图,则输出的S的值是什么?A.B. 16C.D. 1A.9B.10C.11D.12考点:循环结构.专题:程序框图.分析:根据程序框图,计算每次循环后变量a的值,直到不满足循环条件,输出结果.解答:解:根据程序框图,计算每次循环后变量a的值,直到不满足循环条件,输出结果.第一次循环:a=3+2=5第二次循环:a=5+3=8第三次循环:a=8+4=12第四次循环:a=12+5=17第五次循环:a=17+6=23第六次循环:a=23+7=30第七次循环:a=30+8=38第八次循环:a=38+9=47第九次循环:a=47+10=57此时不满足循环条件,输出a的值,为57-9=48,故选A.点评:本题考查了应用程序框图进行简单的计算问题,是基础题.并在满足条件时跳出循环,输出S的值.当k=3时,不满足条件k≥n,跳出循环,输出S=7×6×5×4=840.故选D.点评:本题考查了直到型循环结构的程序框图,根据框图的流程判断算法的功能是解题的关键.同时,需要注意条件的判断和循环变量的变化过程.解:$k=1$,满足判断框,第1次循环,$s=1$,$k=2$;第2次判断后循环,$s=0$,$k=3$;第3次判断并循环$s=-3$,$k=4$,第3次判断退出循环,输出$s=-3$。
(完整版)高考算法程序框图真题练习及答案详解
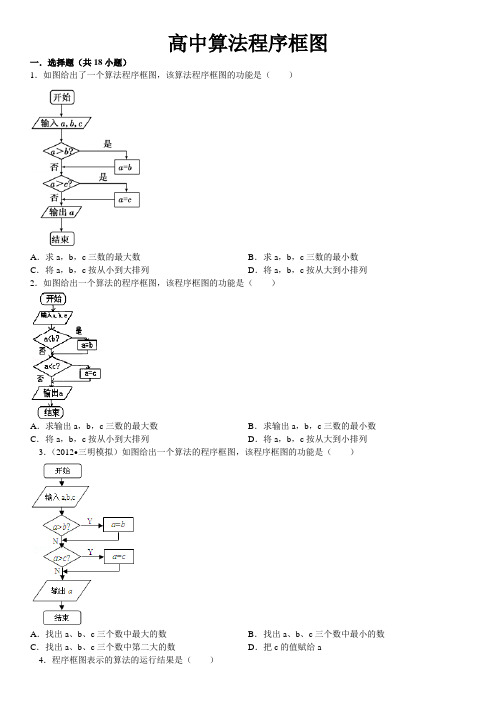
高中算法程序框图一.选择题(共18小题)1.如图给出了一个算法程序框图,该算法程序框图的功能是()A.求a,b,c三数的最大数B.求a,b,c三数的最小数C.将a,b,c按从小到大排列D.将a,b,c按从大到小排列2.如图给出一个算法的程序框图,该程序框图的功能是()A.求输出a,b,c三数的最大数B.求输出a,b,c三数的最小数C.将a,b,c按从小到大排列D.将a,b,c按从大到小排列3.(2012•三明模拟)如图给出一个算法的程序框图,该程序框图的功能是()A.找出a、b、c三个数中最大的数B.找出a、b、c三个数中最小的数C.找出a、b、c三个数中第二大的数D.把c的值赋给a4.程序框图表示的算法的运行结果是()A.5B.6C.7D.85.程序框图中所表示的算法是()A.求x的绝对值B.求x的相反数C.求x的平方根D.求x的算术平方根6.(2014•泉州一模)运行图中所示程序框图所表达的算法,输出的结果是()A.3B.7C.15 D.317.(2013•合肥二模)如图所示,程序框图(算法流程图)的输出结果是()A.6B.5C.4D.3 8.阅读如图所示的程序框图,运行相应的程序,输出的结果为()A.676 B.26 C.5D.2 9.阅读如图所示的程序框图,运行相应的程序,输出的结果是()A.1B.2C.3D.4 10.(2014•福建)阅读如图所示的程序框图,运行相应的程序,输出的S的值等于()A.18 B.20 C.21 D.40 11.(2014•北京)当m=7,n=3时,执行如图所示的程序框图,输出的S的值为()A.7B.42 C.210 D.840 12.(2013•辽宁)执行如图所示的程序框图,若输入n=10,则输出的S=()A.B.C.D.13.(2012•天津)阅读程序框图,运行相应的程序,当输入x的值为﹣25时,输出x的值为()A.﹣1 B.1C.3D.9 14.(2012•福建)阅读如图所示的程序框图,运行相应的程序,输出s值等于()A.﹣3 B.﹣10 C.0D.﹣2 15.(2012•广东)执行如图所示的程序框图,若输入n的值为6,则输出s的值为()A.105 B.16 C.15 D.1 16.(2012•辽宁)执行如图所示的程序框图,则输出的S的值是()A.4B.C.D.﹣1 17.(2011•北京)执行如图所示的程序框图,若输入A的值为2,则输入的P值为()A.2B.3C.4D.5 18.(2011•北京)执行如图所示的程序框图,输出的s值为()C.D.2 A.﹣3 B.﹣二.填空题(共9小题)19.程序框图(如图所示),则该程序框图表示的算法的功能是:_________.20.有如图程序框图,则该程序框图表示的算法功能是_________.21.如图所示的程序框图,其算法功能是_________.22.(2014•许昌三模)如图所示,程序框图(算法流程图)的输出结果是_________.23.如图所示的程序框图表示的算法的结果是_________.24.某算法的程序框图如图所示,则程序输出y的值是_________.25.(2011•江西)下图是某算法的程序框图,则程序运行后所输出的结果是_________.26.(2014•惠州模拟)如图所示,程序框图(算法流程图)的输出结果为_________.27.阅读如图所示的程序框图,运行相应的程序,则输出的s值等于_________.三.解答题(共1小题)28.如图所示,程序框图(算法流程图)的输出结果是_________.参考答案与试题解析一.选择题(共18小题)1.如图给出了一个算法程序框图,该算法程序框图的功能是()A.求a,b,c三数的最大数B.求a,b,c三数的最小数C.将a,b,c按从小到大排列D.将a,b,c按从大到小排列考点:设计程序框图解决实际问题.专题:操作型.分析:逐步分析框图中的各框语句的功能,第一个条件结构是比较a,b的大小,并将a,b中的较小值保存在变量a中,第二个条件结构是比较a,c的大小,并将a,c中的较小值保存在变量a中,故变量a的值最终为a,b,c中的最小值.由此不难推断程序的功能.解答:解:逐步分析框图中的各框语句的功能,第一个条件结构是比较a,b的大小,并将a,b中的较小值保存在变量a中,第二个条件结构是比较a,c的大小,并将a,c中的较小值保存在变量a中,故变量a的值最终为a,b,c中的最小值.由此程序的功能为求a,b,c三个数的最小数.故答案选B点评:算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.要判断程序的功能就要对程序的流程图(伪代码)逐步进行分析,分析出各变量值的变化情况,特别是输出变量值的变化情况,就不难得到正确的答案.2.如图给出一个算法的程序框图,该程序框图的功能是()A.求输出a,b,c三数的最大数B.求输出a,b,c三数的最小数C.将a,b,c按从小到大排列D.将a,b,c按从大到小排列考点:程序框图.专题:算法和程序框图.分析:根据框图的流程判断,第一个环节的功能是输出的a是a,b之间的最大数,第二个环节功能是输出a,c 之间的最大数,由此可得答案.解答:解:由程序框图知:第一个环节是比较a,b,输出的a是a,b之间的最大数;第二个环节是比较a,c,输出的a是a,c之间的最大数.∴算法的功能是输出a,b,c三数的最大数.故选:A.点评:本题考查了排序程序框图,根据框图的流程判断算法的功能是关键.3.(2012•三明模拟)如图给出一个算法的程序框图,该程序框图的功能是()A.找出a、b、c三个数中最大的数B.找出a、b、c三个数中最小的数C.找出a、b、c三个数中第二大的数D.把c的值赋给a考点:程序框图.专题:阅读型.分析:再输入了三个实数a、b、c后,首先对其中的两个数a、b的大小加以判断,二者取小的数,然后再比较取得的数与c的大小,再取小的数输出.解答:解:输入框中输入了三个实数a、b、c,然后首先判断a与b的大小,若a>b成立,则用b替换a,若a≤b,不进行替换,这样再用两者之间的小的数和c比较,若a>c,用c替换a,输出a,否则,直接输出小的数a所以程序框图的功能是找出a、b、c三个数中最小的数.故选B.点评:本题考查了程序框图中的条件结构,条件结构有两个路径,满足条件执行一个路径,不满足条件,执行另一个路径,解答本题时,一定要注意“=”的意义,是用后者替换前者.4.程序框图表示的算法的运行结果是()A.5B.6C.7D.8考点:程序框图.专题:计算题.分析:由判断框可知:只要s≤20,则程序就执行“是”,否则就跳出循环程序,执行“否”,并输出i.据此可得出答案.解答:解:由判断框可知:只要s≤20,则程序就执行“是”,否则就跳出循环程序,执行“否”,并输出i.当s=1+2+3+4+5=15<20,应继续执行“是”,则s=15+6=21>20,此时i=6+1=7,要跳出循环,输出7.故选C.点评:理解循环结构的工作原理并会计算s与i是解决问题的关键.5.程序框图中所表示的算法是()A.求x的绝对值B.求x的相反数C.求x的平方根D.求x的算术平方根考点:选择结构.专题:图表型.分析:写出经过选择结构得到的结果,得到求的y的值的形式,即可判断出框图的功能.解答:解:逐步分析框图中的各框语句的功能,该程序框图表示算法的功能是求函数y=的值,即y=|x|,故选A.点评:本题考查解决程序框图中的选择结构时,常采用写出前几次选择的结果,找规律.6.(2014•泉州一模)运行图中所示程序框图所表达的算法,输出的结果是()A.3B.7C.15 D.31考点:程序框图.专题:算法和程序框图.分析:由算法的程序框图,计算各次循环的结果,满足条件,结束程序.解答:解:根据算法的程序框图知,第一次循环得a=2×1+1=3,第二次循环得a=2×3+1=7,第三次循环得a=2×7+1=15,结束循环,故选C,点评:本题考查了应用程序框图进行简单的计算问题,是基础题.7.(2013•合肥二模)如图所示,程序框图(算法流程图)的输出结果是()A.6B.5C.4D.3考点:循环结构.专题:图表型.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算i值,并输出满足条件S>20的第一个i值,模拟程序的运行过程,用表格将程序运行过程中变量k的值的变化情况进行分析,不难给出答案.解答:解:程序在运行过程中各变量的值如下表示:s i 是否继续循环循环前 1 1/第一圈 1 2 是第二圈 2 3 是第三圈 6 4 是第四圈24 5 否故最后输出的i值为:5,故选B.点评:根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.8.阅读如图所示的程序框图,运行相应的程序,输出的结果为()A.676 B.26 C.5D.2考点:循环结构.专题:图表型.分析:根据已知中的流程图,我们模拟程序的运行结果,看变量a的值是否满足判断框的条件,当判断框的条件不满足时执行循环,满足时退出循环,即可得到输出结果.解答:解:a=1,满足条件a<15,执行循环,a=2,满足条件a<15,执行循环,a=5,满足条件a<15,执行循环,a=26,不满足条件a<15,退出循环,执行输出语句,输出a=26.故选B.点评:本题主要考查的知识点是程序框图,模拟循环的执行过程是解答此类问题常用的办法,属于基础题.9.阅读如图所示的程序框图,运行相应的程序,输出的结果是()A.1B.2C.3D.4考点:程序框图.专题:图表型.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算S值重新为2时变量n的值,并输出,模拟程序的运行过程,即可得到答案.解答:解:程序在运行过程中各变量的值如下表示:S n 是否继续循环循环前 2 1/第一圈﹣1 2 是第二圈 3 是第三圈 2 4 否则输出的结果为4故选D点评:本题考查的知识点是程序框图,在写程序的运行结果时,模拟程序的运行过程是解答此类问题最常用的办法.10.(2014•福建)阅读如图所示的程序框图,运行相应的程序,输出的S的值等于()A.18 B.20 C.21 D.40考点:循环结构.专题:计算题;算法和程序框图.分析:算法的功能是求S=21+22+…+2n+1+2+…+n的值,计算满足条件的S值,可得答案.解答:解:由程序框图知:算法的功能是求S=21+22+…+2n+1+2+…+n的值,∵S=21+22+1+2=2+4+1+2=9<15,S=21+22+23+1+2+3=2+4+8+1+2+3=20≥15.∴输出S=20.故选:B.点评:本题考查了直到型循环结构的程序框图,根据框图的流程判断算法的功能是解题的关键.11.(2014•北京)当m=7,n=3时,执行如图所示的程序框图,输出的S的值为()A.7B.42 C.210 D.840考点:循环结构.专题:计算题;算法和程序框图.分析:算法的功能是求S=7×6×…×k的值,根据条件确定跳出循环的k值,计算输出S的值.解答:解:由程序框图知:算法的功能是求S=7×6×…×k的值,当m=7,n=3时,m﹣n+1=7﹣3+1=5,∴跳出循环的k值为4,∴输出S=7×6×5=210.故选:C.点评:本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是解答本题的关键.12.(2013•辽宁)执行如图所示的程序框图,若输入n=10,则输出的S=()A.B.C.D.考点:循环结构.专题:计算题;图表型.分析:框图首先给累加变量S和循环变量i分别赋值0和2,在输入n的值为10后,对i的值域n的值大小加以判断,满足i≤n,执行,i=i+2,不满足则跳出循环,输出S.解答:解:输入n的值为10,框图首先给累加变量S和循环变量i分别赋值0和2,判断2≤10成立,执行,i=2+2=4;判断4≤10成立,执行=,i=4+2=6;判断6≤10成立,执行,i=6+2=8;判断8≤10成立,执行,i=8+2=10;判断10≤10成立,执行,i=10+2=12;判断12≤10不成立,跳出循环,算法结束,输出S的值为.故选A.点评:本题考查了循环结构中的当型循环,即先判断后执行,满足条件,执行循环,不满足条件跳出循环,算法结束,是基础题.13.(2012•天津)阅读程序框图,运行相应的程序,当输入x的值为﹣25时,输出x的值为()A.﹣1 B.1C.3D.9考点:循环结构.专题:计算题.分析:根据题意,按照程序框图的顺序进行执行,当|x|≤1时跳出循环,输出结果.解答:解:当输入x=﹣25时,|x|>1,执行循环,x=﹣1=4;|x|=4>1,执行循环,x=﹣1=1,|x|=1,退出循环,输出的结果为x=2×1+1=3.故选:C.点评:本题考查循环结构的程序框图,搞清程序框图的算法功能是解决本题的关键,按照程序框图的顺序进行执行求解,属于基础题.14.(2012•福建)阅读如图所示的程序框图,运行相应的程序,输出s值等于()A.﹣3 B.﹣10 C.0D.﹣2考点:循环结构.专题:计算题.分析:通过循环,计算s,k的值,当k=4时退出循环,输出结果即可.解答:解:k=1,满足判断框,第1次循环,s=1,k=2,第2次判断后循环,s=0,k=3,第3次判断并循环s=﹣3,k=4,第3次判断退出循环,输出S=﹣3.故选A.点评:本题考查循环结构,注意循环条件的判断,循环计算的结果,考查计算能力.15.(2012•广东)执行如图所示的程序框图,若输入n的值为6,则输出s的值为()A.105 B.16 C.15 D.1考点:循环结构.专题:计算题;压轴题.分析:本循环结构是当型循环结构,它所表示的算式为s=1×3×5×…×(2i﹣1),由此能够求出结果.解答:解:如图所示的循环结构是当型循环结构,它所表示的算式为s=1×3×5×…×(2i﹣1)∴输入n的值为6时,输出s的值s=1×3×5=15.故选C.点评:本题考查当型循环结构的性质和应用,是基础题.解题时要认真审题,仔细解答.16.(2012•辽宁)执行如图所示的程序框图,则输出的S的值是()A.4B.C.D.﹣1考点:循环结构.专题:阅读型.分析:根据流程图,先进行判定条件,满足条件则运行循环体,一直执行到不满足条件即跳出循环体,求出此时的S即可.解答:解:第一次运行得:S=﹣1,i=2,满足i<6,则继续运行第二次运行得:S=,i=3,满足i<6,则继续运行第三次运行得:S=,i=4,满足i<6,则继续运行第四次运行得:S=4,i=5,满足i<6,则继续运行第五次运行得:S=﹣1,i=6,不满足i<6,则停止运行输出S=﹣1,故选D.点评:本题主要考查了当型循环结构,循环结构有两种形式:当型循环结构和直到型循环结构,当型循环是先判断后循环,直到型循环是先循环后判断,属于基础题.17.(2011•北京)执行如图所示的程序框图,若输入A的值为2,则输入的P值为()A.2B.3C.4D.5考点:循环结构.专题:图表型.分析:根据输入A的值,然后根据S进行判定是否满足条件S≤2,若满足条件执行循环体,依此类推,一旦不满足条件S≤2,退出循环体,求出此时的P值即可.解答:解:S=1,满足条件S≤2,则P=2,S=1+=满足条件S≤2,则P=3,S=1++=满足条件S≤2,则P=4,S=1+++=不满足条件S≤2,退出循环体,此时P=4故选:C点评:本题主要考查了当型循环结构,循环结构有两种形式:当型循环结构和直到型循环结构,当型循环是先判断后循环,直到型循环是先循环后判断.18.(2011•北京)执行如图所示的程序框图,输出的s值为()A.﹣3 B.C.D.2﹣考点:循环结构.专题:图表型.分析:i=0,满足条件i<4,执行循环体,依此类推,当i=4,s=2,此时不满足条件i<4,退出循环体,从而得到所求.解答:解:i=0,满足条件i<4,执行循环体,i=1,s=满足条件i<4,执行循环体,i=2,s=﹣满足条件i<4,执行循环体,i=3,s=﹣3满足条件i<4,执行循环体,i=4,s=2不满足条件i<4,退出循环体,此时s=2故选:D点评:根据流程图计算运行结果是算法这一模块的重要题型,处理的步骤一般为:分析流程图,从流程图中即要分析出计算的类型,又要分析出参与计算的数据建立数学模型,根据第一步分析的结果,选择恰当的数学模型解模.算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.二.填空题(共9小题)19.程序框图(如图所示),则该程序框图表示的算法的功能是:计算并输出使1×3×5×7×…>10000成立的最小整数.考点:循环结构.专题:图表型.分析:写出经过几次循环得到的结果,得到求的s的形式,判断出框图的功能.解答:解:经过第一次循环得到s=1×3,i=5经过第二次循环得到s=1×3×5,i=7经过第三次循环得到s=1×3×5×7,i=8…s=1×3×5×7×…>10000该程序框图表示算法的功能是求计算并输出使1×3×5×7×…>10000成立的最小整数故答案为计算并输出使1×3×5×7×…>10000成立的最小整数点评:本题考查程序框图,考查了循环体以及循环次数两个具体问题,常采用写出前几次循环的结果,找规律.属于基础题.20.有如图程序框图,则该程序框图表示的算法功能是求使不等式1×3×5×…×i≥10000成立的最小i值.考点:程序框图.专题:算法和程序框图.分析:根据框图的流程可得i的值与S的值的变化规律,再根据跳出循环的条件与输出的值,可得算法的功能.解答:解:由框图的流程知:i的值依次为3、5、7、…,∴S的值依次为1,1×3,1×3×5,…,1×3×5×…,根据退出循环的条件是S≥10000得:条件是满足不等式1×3×5×…×i≥10000,∵输出i﹣2,∴算法的功能是求使不等式1×3×5×…×i≥10000成立的最小i值.故答案为:求使不等式1×3×5×…×i≥10000成立的最小i值.点评:本题考查了循环价格的垂线框图,根据框图的流程判断i值与S值的变化规律是关键.21.如图所示的程序框图,其算法功能是计算并输出使1×3×5×7×…>1000成立的最小整数.考点:循环结构.专题:阅读型.分析:写出经过几次循环得到的结果,得到求的s的形式,判断出框图的功能.解答:解:经过第一次循环得到s=1×3,i=5经过第二次循环得到s=1×3×5,i=7经过第三次循环得到s=1×3×5×7,i=9…s=1×3×5×7×…>1000该程序框图表示算法的功能是求计算并输出使1×3×5×7×…>1000成立的最小整数故答案为:计算并输出使1×3×5×7×…>1000成立的最小整数点评:本题考查程序框图,考查了循环体以及循环次数两个具体问题,常采用写出前几次循环的结果,找规律.属于基础题.22.(2014•许昌三模)如图所示,程序框图(算法流程图)的输出结果是﹣2.考点:程序框图.专题:操作型.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算并输出y值,模拟程序的运行过程,可得答案.解答:解:当x=1时,满足循环条件,此时x=2,y=0当x=2时,满足循环条件,此时x=4,y=﹣1当x=4时,满足循环条件,此时x=8,y=﹣2当x=8时,不满足循环条件,退出循环故输出结果为﹣2故答案为:﹣2点评:根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.23.如图所示的程序框图表示的算法的结果是127.考点:程序框图.专题:算法和程序框图.分析:根据框图的流程依次计算程序运行的结果,直到满足条件a>100,跳出循环,确定输出a的值.解答:解:由程序框图知:第一次循环a=2×1+1=3;第二次循环a=2×3+1=7;第三次循环a=2×7+1=15;第四次循环a=2×15+1=31;第五次循环a=2×31+1=63;第六次循环a=63×2+1=127.满足条件a>100,跳出循环,输出a=127.故答案为:127.点评:本题考查了循环结构的程序框图,根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法.24.某算法的程序框图如图所示,则程序输出y的值是﹣1.考点:选择结构.专题:函数的性质及应用.分析:由题意,x=﹣1,执行函数y=3x+2,代入计算可得结论.解答:解:由题意,x=﹣1,执行函数y=3x+2,代入计算可得y=﹣1故答案为:﹣1点评:本题考查选择结构,考查学生的计算能力,属于基础题.25.(2011•江西)下图是某算法的程序框图,则程序运行后所输出的结果是27.考点:程序框图.专题:计算题;阅读型.分析:根据s=0,n=1,s=(0+1)×1=1,n=1+1=2,不满足条件n>3,执行循环体;依此类推,当n=4,满足条件n>3,退出循环体,得到输出结果即可.解答:解:s=0,n=1,s=(0+1)×1=1,n=1+1=2,不满足条件n>3,执行循环体;s=(1+2)×2=6,n=1+2=3,不满足条件n>3,执行循环体;s=(6+3)×3=27,n=1+3=4,满足条件n>3,退出循环体,则输出结果为:27故答案为:27点评:本题主要考查了直到型循环结构,循环结构有两种形式:当型循环结构和直到型循环结构,当型循环是先判断后循环,直到型循环是先循环后判断,属于基础题之列.26.(2014•惠州模拟)如图所示,程序框图(算法流程图)的输出结果为.考点:程序框图.专题:算法和程序框图.分析:根据框图的流程依次计算运行的结果,直到条件不满足,计算输出s的值.解答:解:由程序框图知:第一次循环:s=0+,n=2+2=4;第二次循环:s=+=,n=4+2=6;第三次循环:s=+=,n=6+2=8;不满足条件n<8,程序运行终止,输出s=.故答案为:.点评:本题考查了循环结构的程序框图,根据框图的流程依次计算运行的结果是解答此类问题的常用方法.27.阅读如图所示的程序框图,运行相应的程序,则输出的s值等于46.考点:程序框图.专题:计算题.分析:①i←1,s←1,i←1+1,s←2×(1+1),判断“i>4”,应执行“否”;…;直到“i>4”成立即可跳出循环结构,输出s的值.解答:解:①i←1,s←1,i←1+1,s←2×(1+1),判断“i>4”,应执行“否”;②i←2+1,s←2×(4+1),判断“i>4”,应执行“否”;③i←3+1,s←2×(10+1),判断“i>4”,应执行“否”;④i←4+1,s←2×(22+1),判断“i>4”,应执行“是”.输出s←46.故答案为46.点评:本题考查了循环结构的功能,属于基础题.三.解答题(共1小题)28.如图所示,程序框图(算法流程图)的输出结果是.考点:程序框图.专题:算法和程序框图.分析:根据程序框图,程序的功能是求和由此可得结论.解答:解:根据程序框图,程序的功能是求和故答案为:.点评:本题考查循环结构,考查数列的求和,考查学生的计算能力,属于基础题.。
算法流程图练习

算法及算法的表示检测一、选择题(题型注释)1.某算法要实现0到100的偶数之和,流程图如图所示。
则i i+2被执行的次数是A.50 B.51 C.100 D.1012.某算法的部分流程图如右图所示,执行这部分流程后,变量x的值是A.0B.1C.2D.33.某商品团购优惠策略的流程图如图所示当n为100、p为10时,实付金额s的值是( )。
A. 1000B. 950C. 850D.7504.写出下面流程图所表述的算法的功能▁▁▁▁A. 降序排序B. 求最大值C. 交换输出D. 判断是否是偶数5.以下流程图的运行结果是_______。
A.4 9 B.5 9 C.4 5 D.9 56.若输入两数1,-4,输出结果_______A.-5 B.-3 C.5 D.37.如图所示,是求绝对值的算法,其描述方式分别是()A.自然语言、流程图 B.伪代码、流程图C.自然语言、伪代码D.流程图、自然语言8.将两位同学的身高放入变量a和b中,比较这两个变量的大小,最后把其中较大的数放到变量c中并输出,流程图如图所示。
①中应填()A.a<b B.a>b C.a=b D.a<>b9.求[0,100]之间所有偶数之和s的算法流程图如图所示。
为了实现此算法,图中判断框①和处理框②处可填入的是()A.① x ≤ 100?② x←x+2B. ① x ≤ 100?② x←x+1C.① x ≥ 100?② x←x+2D. ① x ≥ 100?② x←x+110.某算法流程图如图所示,执行该算法后,“s←s+i”共被执行的次数是()开始A.0 B.6 C.7 D.811.某算法的流程图如下所示:当输入a、b、c的值分别为5、2、8时,该算法的输出结果为()A. 8B. 2C. 5D. 7。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法及算法的表示检测
一、选择题(题
型注释)
1.某算法要实现0到100的偶数之和,流程图如图所示。
则i i+2被执行的次数是
A.50 B.51 C.100 D.101
2.某算法的部分流程图如右图所示,执行这部分流程后,变量x的值是
A.0
B.1
C.2
D.3
3.某商品团购优惠策略的流程图如图所示
当n为100、p为10时,实付金额s的值是( )。
A. 1000
B. 950
C. 850
D.750
4.写出下面流程图所表述的算法的功能▁▁▁▁
A. 降序排序
B. 求最大值
C. 交换输出
D. 判断是否是偶数
5.以下流程图的运行结果是_______。
A.自然语言、流程图B.伪代码、流程图
C.自然语言、伪代码D.流程图、自然语言
8.将两位同学的身高放入变量a和b中,比较这两个变量的大小,最后把其中较大的数放到变量c中并输出,流程图如图所示。
①中应填()
A.a<b B.a>b C.a=b D.a<>b
9.求[0,100]之间所有偶数之和s的算法流程图如图所示。
