【实验基地】七上4.1从问题到方程(2)

合集下载

苏科初中数学七年级上册《4.1 从问题到方程》教案 (2)【精品】.doc

从问题到方程教学目标：1、对实际问题的分析，体会方程作为实际问题的数学模型的作用；2、会列一元一次方程解决一些简单的实际应用。

教学重点：方程的概念及方程与生活的应用教学难点：方程的概念及方程与生活的应用课时：1第1课时教学过程：一、创设情境，引入新课问题一：（1）如图，天平右盘内的砝码质量为160g ，天平平衡时，你能说出食盐的质量吗？（2）已知右图中食盐的质量为160g ，在天平的右盘中共放几个20g 的砝码才可以使天平平衡呢？（3）已知右图中食盐的质量为160g ，在天平的右盘内有一个50g 的砝码，那么还需加多重的砝码才可以使天平平衡呢？（4）若在天平的左盘中有一个小球和一袋160g 的食盐，天平的右盘内砝码的质量和为200g ，当天平平衡时，你能求出这个小球的质量吗？（5）若在天平的左盘中有两个质量相等的小球和一袋160g 的食盐，天平的右盘内有总质量为200g 的砝码，当天平平衡时，你能求出小球的质量吗？（学生一起讨论完成）问题二：某排球队参加排球联赛，得分规则：胜一场得2分，负一场得1分。

（1）若该队全胜，共得20分，请问该队胜了多少场？（2）若该队负了2场，共得20分，请问该队胜了多少场？（3）若该队赛了12场，共得20分，请问该队胜了多少场？（4）若得分规则改为：胜一场得2分，平一场得1分，负一场得0分。

该队赛了14场，负了5场，共得13分，问这个队胜了几场？二、新课讲解：引导学生回忆小学时对方程的理解，巩固方程的概念。

给出不含有未知数的等式、方程、代数式、不等式的具体事例，让学生判断，辨别方程的真面貌。

总结出方程含有两个必不可少的条件：（1）含有未知数，（2）是等式。

练习：1、下列各式是方程的是（）A ．23-xB ．257=-yC ．b a +D ．5-3=22、下列各式是一元一次方程的是（）A ．122+-x xB ．x x 11+= C ．43-=+x y D ．132=-y y 『问题研讨』已知m xm =+-632是关于x 的一元一次方程，试求代数式()20093-m 的值。

苏科版七年级数学上册教案：4.1从问题到方程(2)

学生观察所列方程的特点，归纳得出一元一次方程的概念，再举出几个类似的方程.建议结合导学与评价，补充练习.像方程3x=32-x、5x＋3（9－x）=39 、80x=100（x－3）等，它们只含有一个未知数且未知数的指数是1，这样的方程叫做一元一次方程。

课堂小结1、学习了什么知识？通过对具体实际生活问题的分析，进一步学会根据实际问题的意义设未知数并列出方程，了解一元一次方程的概念.2、有什么收获？经历把实际问题抽象出数学问题的过程，体会方程是人们分析、解决实际问题的有效工具。

你能找出表示问题意义的相等关系吗？用方程怎样表达？理解概念的含义1、只含有一个未知数2、未知数的指数是1建议只让学生多一些方法，但不要讲的太多.教学时可以先让学生尝试和探索，然后交流.而后概括从实际问题到方程一般要经历的过程：找出表示问题意义的相等关系，设未知数（通常用x、y等），用含未知数的代数式表示题中相关的量，根据相等关系列方程.学生观察所列方程的特点归纳得出一元一次方程的概念描述本节学习内容，多位回答，趋于完善板书设计情境创设1、2、例1：………………例2：………………习题………………作业布置P117 4 5 6课后随笔1、把实际问题抽象为数学问题，再从数学问题到列出方程.关键在于弄清题意，恰当地巧设未知数，找出问题中的相等关系.2、设元设得巧，方程列得妙；设元设得好，方程列的得快.一般问什么则设什么，有时设未知的另一个量来求也较方便.3、解题时，找出问题中的相等关系，要深刻理解题意，把握题中隐含条件及内在联系（如题中等量关系语句、量与量之间的关系）.4、学有余力的同学鼓励其解方程（小学根据逆运算原理），对一般同学不作要求。

七年级数学上册4.1《从问题到方程》教案(新版)苏科版

《从问题到方程》教学目标(一)知识与能力目标.1、探索实际问题中的等量关系，并用方程描述；2、通过对多种实际问题中数量关系的分析，使学生初步感受方程是刻画现实世界的有效模型.(二)过程与方法目标.1、会经历将一些实际问题抽象为数与代数问题(方程问题)的过程；2、经历运用数学符号和图形描述现实世界的过程.(三)情感态度与价值观目标.1、通过对多种实际问题的分析，感受方程作为刻画现实世界有效模型的意义；2、体验在生活中学数学、用数学的价值，感受学习数学的乐趣.教学重、难点引导学生自主探索实际问题中的等量关系，感受方程作为刻画现实世界有效模型的意义.教学方法自主探究、引导发现式教学.教学过程(一)情景创设，引入新课.小游戏：用学生的年龄和老师的年龄编题.【设计意图】1、增强学生学习的自信心，实现师生互动.2、使学生通过比较算术方法与方程方法优劣，经历将一些实际问题抽象为数与代数问题(方程问题)的过程，初步感受方程是解决实际问题的有效模型.从而引入新课.(二)激发探究，揭示新知.观察与思考：1、观看flash动画，如何称一个蓝色小球的质量？2、想一想：在图中平衡的天平上，蓝色小球重多少克？【设计意图】引导学生用方程的思想解决实际问题，感受方程是表达数量之间相等关系的“天平”.试一试：买5瓶饮料，4只面包.共花去15.8元钱.每瓶饮料2.2元，每只面包多少元？你能列出方程吗？【设计意图】以图片信息给出问题，培养学生自主探究及语言表达能力，初步感受方程.探索活动:做一做：1、某排球队参加排球比赛，胜一场得2分，负一场得1分，该队共赛了12场，总得分为20分，请问该队胜了几场？请列出方程.分析：如果设他们胜了x场，那么负 ____ 场，你能用方程描述这个问题中数量之间的相等关系吗？相等关系：胜场得分+负场得分=总得分.2、国庆六十周年的阅兵场上，除了三军仪仗队外，每个方阵中的人数是相同的.如果将每横排25人改为每横排35人，这样就比原来的排数少4排，那么你知道每个方阵中有多少人吗？【设计意图】观看国庆六十周年的阅兵片段，增强民族自豪感，培养学生合作学习及语言表达能力.(三)小结反思，步步为赢.1、由实际问题到方程要经历哪些过程？(1).审清题意，找出相等关系；(2).恰当地设未知数x；(3).根据相等关系列出方程．2、你觉得用方程来描述问题中的相等关系方便吗？【设计意图】引导学生结合前面学习的感受，交流发言.(四)拓展提高、人人参与.巩固所学、拓展思维.1、为了预防甲型H1N1流感，校医李医生到防疫站买测温仪，如果买6只，她带的钱将剩余300元；如果买7只，她带的钱还少150元.你知道这款测温仪的价格吗？请列出方程.2、据资料，海拔每升高100m，气温下降0.6°C.现测得某山脚下的气温15.2°C，山顶的气温为12.4°C.若设这座山高为xm，可得方程______________.【设计意图】巩固所学，培养学生思维的开放性、灵活性、创造性.体会学数学用数学的快乐.知识升华、回归生活.你能由你的生活感受编一个为下列方程的应用问题吗？1、2x+3=102、2x+3(x-1)=10(五)、收获体会、交流心得.说一说这节课你有什么收获？说出来，让我们一起来分享！(六)、布置作业、引导预习.思考：今天所列的方程，有什么共同特点？第（1）课时课题：书法---写字基本知识课型：新授课教学目标：1、初步掌握书写的姿势，了解钢笔书写的特点。

七上第四章4.1从问题到方程教学案

4．1从问题到方程班级：姓名：【学习目标】 1、探索实际问题中的等量关系，并用方程描述； 2、了解一元一次方程的概念。

能够用方程灵活地反映现实生活中的一些简单的数量关系，适当地设未知数，列出方程，进一步提高学生解决问题的能力.【学习重点】分析与确定问题中的等量关系，能用方程来描述和刻画事物间的等量关系【学习难点】用方程的思想解决实际问题一、【自主学习1】 ----- 我能行1、比x 的1.5倍多8的数是22，可用方程表示为。

2、买4本练习本和5支铅笔一共用了4.9元。

已知铅笔每支0.5元，练习本每本x 元，可列出方程。

二、合作探究 ----- 我快乐1根据题意，列出方程（1）如图，天平右盘内的砝码质量为160g ，左盘中放三个小球和10g 砝码，天平平衡时，你能说出小球的质量吗？（2）某排球队参加排球联赛，得分规则：胜一场得2分，负一场得1分，该队赛了12场，共得20分，请问该队胜了多少场？10g100g 50g（3）军军今年5岁，爸爸今年32岁，如果x 年以后军军的年龄是爸爸年龄的41？你能用方程描述这个问题中的数量关系吗？总结：1、用方程可可以描述实际问题中的数量关系。

2、一元一次方程的概念： ______________________________________________________ 例1、判断下列方程哪些是一元一次方程：（1）65x=1 （2）8x-2<3x+1 （3）3x 2－7x ＋7=0 （4）2x －y=1 （5）6y -5=2y （6）x 2 = 3例2、已知方程（3- n ）x+ (m+1）x 2=1是关于x 的一元一次方程，则m 和n 各应取什么值？三、展示提升 ---- 我最棒七（6）班分成两个组进行课外体育活动，原计划第一组22人，第二组23人，根据活动内容的要求，需要将第一组的人数调整为第二组的2倍，应从第二组调多少人到第一组去？（根据实际问题设出适当的未知数并列出方程）四、自主反思 ---- 我成长通过这节课的学习，学到了什么新知识？有何感悟？获得了什么经验？五、达标测评 ---- 我必胜1．已知下列方程：① x －２＝x 2；② 0.3x =1；③2x = 5x －１；④x 2－4x=3； ⑤x=6； ⑥x+2y=0.其中一元一次方程的个数是2.如果方程（m －1）x + 2 =0是表示关于x 的一元一次方程，那么m 的取值范围是（）A ．m ≠0B ．m ≠1C ．m=－１D ．m=０3若关于x 的方程（k －1）x 2 +x －1=0是一元一次方程，则k=_______________.4. 某项工作甲单独做4天完成，乙单独做6天完成，若甲先干一天，然后，甲、乙合作完成此项工作，若设甲一共做了x 天，乙工作的天数为_ ___ ,由此可列出方程______________________.5．有一根铁丝，第一次用了它的一半少1米，第二次用去了剩余的一半多1米，结果还剩2.5米，问这根铁丝原有多长？(只列方程不解答)。

七年级数学上册 4.1从问题到方程(2)(2)

4.1从问题到方程（2）班级姓名学号学习目标：1．探索具体问题中的数量关系和变化规律，并用方程进行描述，进而让学生初步体验方程是刻画现实世界的一种有效模型。

2. 通过观察所列的方程的特点,掌握一元一次方程的概念并能够熟练识别一元一次方程3．进一步培养学生观察、思考、分析问题、解决问题的能力，渗透建模的数学思想。

4. 感受数学与生活的紧密联系，体会数学的价值，激发学生学习数学的兴趣。

学习难点：分析与确定问题中的等量关系，能用方程来描述和刻画事物间的等量关系。

教学过程：一、创设情境，引入新课问题一：甲、乙两城市间的铁路经过技术改造,列车在甲乙两城市间的运行速度从80千米/时提高到100千米/时，运行时间缩短了3小时.甲、乙两城市间的路程是多少千米?変式1:甲、乙两列车都从A市驶向B市，甲车用了3小时，乙车用了2小时。

已知乙车的速度是甲车速度的2倍少40千米，甲、乙两车的速度分别是多少？変式2:甲、乙两列车都从A市驶向B市，甲车用了3小时，乙车用了2小时。

已知乙车的速度是甲车速度的2倍少40千米，A、B两城市间的路程是多少？二、合作质疑，探索新知问题二：小明用50 元钱购买了面值为1元和2元的邮票共30张，他买了多少张面值为1元的邮票？如果设面值为1元的邮票买了x张,那么面值为2元的邮票买了_______张.买面值为1元的邮票的钱+买面值为2元的邮票的钱=50元.可得方程____________________问题三：某通讯公司有两种手机话费付费方式：第一种方式不交月租费，每分钟付话费0.6元；第二种方式每月交月租费50元，每分钟付话费0.2元.一个月通话多少分钟时，两种付费方式费用相同？三、自主归纳，形成方法1、学生自主归纳：如何从问题到方程？2、自主归纳一元一次方程的特点，并举例说明四、巩固练习：根据实际问题的意义列出方程1. 甲车的速度为60km/h,乙车的速度80km/h,两车同时同地出发，反向而行，经过多长时间两车相距280km?2 .小丽花50元钱买了面值为1元和2元的两种邮票，如果面值为2元的邮票比面值为1元的邮票少5张，那么，这两种面值的邮票各买了多少张？3.一个长方形足球场的周长是300m,它的长比宽多30m,求这个足球场的长.五、课堂小结，感悟收获1、从实际问题到方程，一般要经历哪些过程？2、列方程的关键是什么？【课后作业】班级姓名学号一、选择：1．下列方程是一元一次方程的是（）A. 02=+x xB. 0=-y xC. 02=-yD.011=-x 2．根据下列条件能列出方程的是（）A. 一个数的31与另一个数的21的和 B. a 与1的差的4倍是8 C. b a ,和的60% D. 甲的3倍与乙的差的2倍3．七年级二班共有学生48人，已知男生比女生少2人，问七年级二班男生、女生各有多少人？设七年级二班男生有男生x 人，则下列方程中错误的是（）A. 48)2(=++x xB. 2248=-xC. x 2248=-D.482=+-x x4．课外兴趣小组的女生人数占全组人数的31 ，再加入6名女生后，女生人数就占原来人数的一半，课外兴趣小组原有多少人?若设原有x 人，则下列方程正确的是（） A. x x 2131= B. x x 21631=+ C. 62131+=x x D.x =+)631(21 二、根据实际问题的意义列出方程5．根据“x 的5倍比它的35%少28”列出方程为________ ．6．一年三班55人，一年八班29人，因植树需要从三班中抽出x 人到八班，使得两班人数相同，则根据题意可列方程为_____________.7．一个足球场的周长为310米，长和宽之差为25米，这个足球场的长和宽分别是多少？8．甲、乙两队开展足球对抗赛，规定每队胜一场得3分，平一场得1分，负一场得0分。

七年级数学上册第四章一元一次方程 4.1 从问题到方程方程小史素材苏科版(2021学年)

七年级数学上册第四章一元一次方程4．1 从问题到方程方程小史素材(新版)苏科版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方,但是任然希望(七年级数学上册第四章一元一次方程4.1 从问题到方程方程小史素材（新版）苏科版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉,前进的动力。

本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为七年级数学上册第四章一元一次方程 4.１从问题到方程方程小史素材 (新版）苏科版的全部内容。

方程小史世界上最早的方程产生于幼发拉底河畔的文明古国巴比伦。

大约在三千五百年前，居住在那里的苏马连人和阿卡德人独立地创造了自己的数学．他们把数字和符号刻在泥板上，晒干后,可以长久地保存下来．下面就是在这种泥板上发现的世界上最早的方程：一堆(未知数),32，21，71，整堆数等于33。

用现在我们学习的方程翻译为x+32ｘ+21ｘ+71x=33.在我国,“方程”一词最早出现在东汉初年的数学经典著作《九章算术》的第八章“方程”。

《九章算术》是世界上讲述方程最早的著作,就世界数学史来说,也是最早的比较正确的定义。

定义如下:“方程:程,课程也,群物总杂,各列有数，总言其实，令每行为率，二物者再程,三物者三程，皆如物数程之,并列为行，故谓之方程。

”这里所说的“令每行为率"，就是由一个条件列一行式子,横列代表一个未知量。

“如物数程之”，就是有几个未知数,就列出几个方程,此方程也就是我们到高中将要学习的线性方程。

《九章算术》不但是我国古代数学中的伟大成就,而且是世界数学史上一份非常宝贵的遗产。

这一成就进一步证明中华民族是一个充满智慧和才干的伟大民族．以上就是本文的全部内容，可以编辑修改。

高尔基说过:“书是人类进步的阶梯。

苏科版数学七年级上册4.1 从问题到方程教案

4.1从问题到方程教学目标1．探索实际问题中的已知量和未知量之间的相等关系，并用方程描述，使学生初步感受用方程描述这种相等关系最简明；2．初步认识、体会方程与现实世界的密切联系；3．了解一元一次方程的概念．教学重、难点1.探索实际问题中的数量关系并列出方程；2.改变用算术方法解应用题的习惯，学习如何从实际问题转化为方程.教学过程(一)情景创设教师演示用天平称量物体，天平保持平衡，然后展示用天平称小球，并提出问题：如何描述天平平衡所表示的数量之间的相等关系？【设计意图】1、引起学生学习的兴趣，实现师生互动.2、从实际问题中数量之间的相等关系的描述，到用方程，从而引入新课.(二)探索活动1.对篮球联赛这个问题中的数量之间的相等关系描述，【设计意图】引导学生用方程描述数量之间的相等关系最简洁，感受方程是表达数量之间相等关系的“天平”，并形成从实际问题到方程的过程。

2.对于“以绳测井”、“搭小鱼所需火柴棒”“小红和他的爸爸的年龄”问题，【设计意图】让学生反复经历“从问题到方程”的过程，能熟练的用方程来描述数量之间的相等关系；从这些问题到所列的方程，为归纳一元一次方程做铺垫。

3．归纳出一元一次方程的概念，并出示辨析题和填空题对一元一次方程的概念进行考察。

【设计意图】从方程到一元一次方程的概念，让学生明了一元一次方程增加了内涵“含有一个未知数”、“未知数的次数是1”，通过设计正、反例，明确一次方程的概念。

（三）例题教学对于“两城市之间的路程”的问题，【设计意图】在了解了一元一次方程的概念后，再次经历从实际问题到一元一次方程的过程，规范解题步骤。

对于“蓝鲸体重”、“海拔温度”、“卫星离地面距离”问题，【设计意图】巩固所学，培养学生思维的开放性、灵活性、创造性.体会学数学用数学的快乐.从实际问题到一元一次方程的练习，为了强化解题的条理性和规范性，对于“古希腊数学家丢番图的年龄”问题【设计意图】“古希腊数学家丢番图的年龄”问题激发学生的学习数学的探究欲望，并能体验从实际问题到方程的解题步骤，以及学生从实际问题到方程能力的提升。

七年级数学上册4.1《从问题到方程》教案(新版)苏科版

《从问题到方程》教学目标(一)知识与能力目标.1、探索实际问题中的等量关系，并用方程描述；2、通过对多种实际问题中数量关系的分析，使学生初步感受方程是刻画现实世界的有效模型.(二)过程与方法目标.1、会经历将一些实际问题抽象为数与代数问题(方程问题)的过程；2、经历运用数学符号和图形描述现实世界的过程.(三)情感态度与价值观目标.1、通过对多种实际问题的分析，感受方程作为刻画现实世界有效模型的意义；2、体验在生活中学数学、用数学的价值，感受学习数学的乐趣.教学重、难点引导学生自主探索实际问题中的等量关系，感受方程作为刻画现实世界有效模型的意义.教学方法自主探究、引导发现式教学.教学过程(一)情景创设，引入新课.小游戏：用学生的年龄和老师的年龄编题.【设计意图】1、增强学生学习的自信心，实现师生互动.2、使学生通过比较算术方法与方程方法优劣，经历将一些实际问题抽象为数与代数问题(方程问题)的过程，初步感受方程是解决实际问题的有效模型.从而引入新课.(二)激发探究，揭示新知.观察与思考：1、观看flash动画，如何称一个蓝色小球的质量？2、想一想：在图中平衡的天平上，蓝色小球重多少克？【设计意图】引导学生用方程的思想解决实际问题，感受方程是表达数量之间相等关系的“天平”.试一试：买5瓶饮料，4只面包.共花去15.8元钱.每瓶饮料2.2元，每只面包多少元？你能列出方程吗？【设计意图】以图片信息给出问题，培养学生自主探究及语言表达能力，初步感受方程.探索活动:做一做：1、某排球队参加排球比赛，胜一场得2分，负一场得1分，该队共赛了12场，总得分为2 0分，请问该队胜了几场？请列出方程.分析：如果设他们胜了x场，那么负 ____ 场，你能用方程描述这个问题中数量之间的相等关系吗？相等关系：胜场得分+负场得分=总得分.2、国庆六十周年的阅兵场上，除了三军仪仗队外，每个方阵中的人数是相同的.如果将每横排25人改为每横排35人，这样就比原来的排数少4排，那么你知道每个方阵中有多少人吗？【设计意图】观看国庆六十周年的阅兵片段，增强民族自豪感，培养学生合作学习及语言表达能力.(三)小结反思，步步为赢.1、由实际问题到方程要经历哪些过程？(1).审清题意，找出相等关系；(2).恰当地设未知数x；(3).根据相等关系列出方程．2、你觉得用方程来描述问题中的相等关系方便吗？【设计意图】引导学生结合前面学习的感受，交流发言.(四)拓展提高、人人参与.巩固所学、拓展思维.1、为了预防甲型H1N1流感，校医李医生到防疫站买测温仪，如果买6只，她带的钱将剩余300元；如果买7只，她带的钱还少150元.你知道这款测温仪的价格吗？请列出方程.2、据资料，海拔每升高100m，气温下降0.6°C.现测得某山脚下的气温15.2°C，山顶的气温为12.4°C.若设这座山高为xm，可得方程______________.【设计意图】巩固所学，培养学生思维的开放性、灵活性、创造性.体会学数学用数学的快乐.知识升华、回归生活.你能由你的生活感受编一个为下列方程的应用问题吗？1、2x+3=102、2x+3(x-1)=10(五)、收获体会、交流心得.说一说这节课你有什么收获？说出来，让我们一起来分享！(六)、布置作业、引导预习.思考：今天所列的方程，有什么共同特点？中国书法艺术说课教案今天我要说课的题目是中国书法艺术，下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。

苏科版初中数学七年级上册4.1 从问题到方程教案

4.1 从问题到方程一、教学目标（一）知识与能力目标1、探索实际问题中的等量关系，并用方程描述；2、通过对多种实际问题中数量关系的分析，使学生初步感受方程是刻画现实世界的有效模型。

（二）过程与方法目标1、会经历将一些实际问题抽象为数与代数问题（方程问题）的过程；2、经历运用数学符号和图形描述现实世界的过程。

（三）情感态度与价值观目标1、通过对多种实际问题的分析，感受方程作为刻画现实世界有效模型的意义；2、在设计活动中，培养学生之间的合作交流和增强用数学的意识．体验成功的喜悦，激发学习数学的热情，从而增强自信心。

二、教学重难点引导学生自主探索实际问题中的等量关系，感受方程作为刻画现实世界有效模型的意义。

三、教学过程（一）情景创设，引入新课今天我们开始学习第四章的第一节《从问题到方程》，要学会从实际问题中找到等量关系并用方程来描述。

数学来源于生活，又用之于生活！我们一起跟随小雪同学来走进我们的数学课堂：《小雪的一天》【设计意图】激发学生学习兴趣，渲染课堂气氛，实现师生互动。

（二）激发探究，揭示新知1、活动一：天平实验8:00，小雪来到爸爸的实验室(家中的),看到爸爸正在称某种蓝色小球的质量.此时天平平衡.观察天平的左右两边，如果设每个蓝色小球为xg，则左边托盘小球总重量为（2x+1）g，右边为5g。

现在天平是属于平衡状态，请问可以用怎样的数学式子来表示。

（2x+1=5）揭示：方程是表达数量之间相等关系的“天平”引入课题：今天这节课我们将学习：4.1从问题到方程若天平的左右两边各放500g和320g的盐，请问天平平衡吗？怎样使之平衡？假设从左边托盘拿出x克盐放入右边托盘后天平平衡，此时左右托盘的盐的质量分别用怎样的代数式表示？左边：500-x；右边：320+x。

根据：左边托盘的盐=右边托盘的盐可用方程：500-x=320+x来描述。

2、活动二：经济问题：10:00，小雪与妈妈到超市购物她们来到了手机柜台前,妈妈为农村的爷爷购买了一部手机，在九折优惠的基础上实际支付了900元。

七年级数学上册第4章一元一次方程4.1从问题到方程教案新版苏科版7

4.1 从问题到方程【教学目标】知识与技能：（1）理解方程、一元一次方程、解方程、方程的解的含义，会检验一个数是否为某个一元一次方程的解．（2）初步学会如何寻找问题中的相等关系，列出方程.过程与方法：通过解决实际问题，让学生体验从算术方法到代数方法是一种进步，体会方程思想.情感态度与价值观：培养学生获取信息，分析问题，处理问题的能力.【重难点】重点：探索实际问题中的数量关系并列出方程.难点：改变用算术方法解应用题的习惯，学习如何从实际问题转化为方程．【教学过程】活动一：创设情境，导入新课如图，天平的右盘中有一些砝码，左盘中有一袋食盐．怎样描述天平平衡时所表示的数量之间的相等关系？学生思考问题：问题1．用什么表示这个等量关系（借助方程）？问题2．怎么列方程？设计思路：创设与学生生活相关的实际问题，以激发学生学习的兴趣．除用天平称食盐外还可用天平称硬币等．在情景创设中可以创设1～2个与学生生活相关的实际问题，以激发学生学习的兴趣．教师总结：实际问题中已知量和未知量之间的相等关系，可以用多种不同的方式描述．通过比较可以看出，用方程描述这种相等关系最简明．活动二：实践探究，交流新知教师利用多媒体展示图片，出示以下问题：某校初中一年级328名师生乘车外出春游，已有2辆校车可以乘坐64人，还需租用44座的客车多少辆?教师提问：你能解决这个问题吗?有哪些方法?学生小组内讨论，看能否用算术方法解，然后考虑用方程如何解决，教师可以参与到学生中去，关注学生解决问题的思路.教师总结：（方法一）算术法：（328－64）÷44＝264÷44＝6（辆）.（方法二）列方程法：设需要租用x辆客车，那么这些客车共可乘44x人，加上乘坐校车的64人，就是全体师生328人，可得44x+64＝328.在这一教学过程中，教师不仅要使学生掌握本问题的解决方法，更重要的是让学生通过对比算术法与方程法，去体会列方程过程中的一般思路和方法.针对以上方程，教师提问：像上边这样的方程，你能给它起一个名字吗？学生阅读教材，体验方程的明明方式，并说说什么是一元一次方程.教师进一步提出问题：结合算术法，你能试着解出这个方程吗？得到的结果对所列的方程来说具有什么特点？学生可能利用逆运算求解，得出所求的结果使方程左右两边的值相等的特点，教师加以肯定，教师归纳总结有关方程的概念：①含有未知数的等式叫做方程.（44x+64=328，44，64，328为已知数，x为未知数）②只含有一个未知数，未知数的次数都是1，等号两边都是整式，这样的方程叫做一元一次方程.教师：想一想，你是怎样列出方程的？找学生代表回答思路过程.教师归纳：分析实际问题中的数量关系，利用其中的相等关系列出方程，是用数学解决实际问题的一种方法.活动三：例题讲解例1判断下列各式是不是方程，如果是，指出已知数和未知数，说明哪些是一元一次方程；如果不是，说明为什么.① 5-2x=1；② y2+2=4y-1；③ x-2y=6；④ 2x2+5x-8；⑤ 3×2=1；⑥（x-1）（ x+2）（ x+1） =0；⑦ 1+x=x+1；⑧|x|=-2. 解：①是一元一次方程，5，-2，1是已知数，x是未知数；②是方程，2，4，-1是已知数，y是未知数；③是方程，-2，6是已知数，x，y是未知数；④不是方程，因为不是等式；⑤不是方程，因为不含未知数；⑥是方程，-1，2，1，0是已知数，x是未知数；⑦是一元一次方程，1是已知数，x是未知数；⑧是方程，-2是已知数，x是未知数.处理方式：教师读题，学生代表回答.回答完毕，教师点评，加深印象.例2在课外活动中，张老师发现同学们的年龄大多是13岁，就问同学：“我今年45岁，几年以后你们的年龄是我年龄的三分之一?”小敏同学很快说出了答案.“三年”.他是这样算的：1年后，老师46岁，同学们的年龄是14岁，不是老师的三分之一.2年后，老师47岁，同学们的年龄是15岁，也不是老师的三分之一.3年后，老师48岁，同学们的年龄是16岁，恰好是老师的三分之一.你能否用方程的方法来解呢？处理方式：学生独立完成，小组内交流，教师巡视，引导学生说一说这两种方法各自的特点，只要学生能谈出一两点体会，教师都应当加以鼓励.最后，教师给出总结：用算术方法解：未知数不参加列式，表示计算程序，根据题里已知数和未知数间的关系，确定解答步骤，再列式计算；用方程解：未知数用x 表示，x 参加列式，表示相等关系，根据题意找出数量间的相等关系，列出含有x 的等式.解：小敏同学的方法是算术方法，用方程的方法解决如下：设x 年后学生的年龄是老师的三分之一，列方程：13＋x （45＋x ）.【当堂反馈】1．一队师生共328人，乘车外出旅行，已有校车可乘64人，如果租用客车，每辆可乘44人，那么还要租用多少辆客车？如果设还要租x 辆客车，可列方程为（）.A ．44x －328=64B ．44x+64=328C ．328+44x=64D ．328+64=44x2．某学生从家到学校时，每小时行5千米；按原路返回家时，每小时行4千米，结果返回的时间比去学校的时间多花10分钟.设去学校所用时间为x 小时，则可列方程得（）.A ．⎪⎭⎫ ⎝⎛-=6145x xB ．⎪⎭⎫ ⎝⎛+=6145x xC. x x 4615=⎪⎭⎫ ⎝⎛- D ．x x 4615=⎪⎭⎫ ⎝⎛+ 3．若关于x 的方程（k －1）x 2＋x －1＝0是一元一次方程，则k ＝．4．下列方程中哪些是一元一次方程？①x ＝1， ②3x ＋2＝8x －7，③x ＋2y ＝－13 ，④2x －1x＝5， ⑤－2x －3＝0．5．只列方程不解答．（1）小张去商店买练习本，回来后问同学们：“店主告诉我，如果多买一些就给我八折优惠，我就买了20本，结果便宜了1.6元，你猜原来每本价格多少元？”这里如果设每本价格x 元，则列方程得什么？你能写出所列方程吗？（2）A ，B 两地相距50千米，甲、乙两人分别从A 、B 两地出发，相向而行，甲每小时比乙多行2千米，若两人同时出发，经过3小时相遇．如果设甲的速度为x 千米/小时，可列怎。

2019年七年级数学上册《4.1从问题到方程》教案苏科版.doc

2019年七年级数学上册《4.1从问题到方程》教案苏科版年级学科课题备课人教学目标1、通过天平类比引入方程，体会方程是解决实际问题重要途径2、渗透了数学的建模、类比、归纳等思想方法。

重难点体会方程是解决问题的重要途径.渗透建模、类比、归纳等思想方法。

．课时第1课时时间教学过程：（一）情境创设：（二）自主探究：1、一支钢笔单价是2.5元，小明有10元钱，可以买几支钢笔？2、某工厂今年平均每月生产机器80台，比去年平均每月产量的1.5倍还多5台，如果设去年平均每月生产机器x 台，那么可得方程为3、某排球队参加排球联赛，胜一场得2分，负一场得1分，该队赛了12场，共得20分，该队胜了多少场？设该队胜x 场，那么负)12(x -场，可得方程20)12(2=-+x x 。

从问题方程要经历哪些过程，关键是什么？（分组讨论）（归纳）：1、将要求的量设定为一个未知数x 。

2、将与未知数相关的量用含未知数的代数式表示。

3、根据相关关系列出方程，关键是找到相等关系式。

1.甲、乙两城市间的铁路经过技术改造，列车在两城市间的运行速度从80km/h 提高到100km/h,运行时间缩短了3h.甲、乙两城市间的路程是多少？2、一个长方形足球场的周长是300m,它的长比宽多30m 。

求这个足球场的长。

三，探索新知1．你能找出问题中的相等关系吗？2．你能用方程表达吗？3．你所表达的方程有那些特点？你能再写出几个类似的方程吗？（学生观察、归纳得出一元一次方程的概念）4．（1）用方程表达实际问题中数量关系的基本步骤是个性空间。

（2）上面列出的方程有哪些共同的特点？总结出方程含有两个必不可少的条件：（1）含有未知数，（2）是等式。

（3）请写出两个一元一次方程，（4）下5.列各式中哪些是方程？哪些是一元一次方程？①53-x ，②453>-x ，③7823-=+x x ，④312-=+y x ，⑤1=x ，⑥512=-xx ，⑦2x 032=--x 例1、一个长方形足球场的周长是300米，它的长比宽多30米求这个足球场的长。

七年级数学上册 4.1从问题到方程(2)(1)

4.1 从问题到方程（2）感受·理解1．已知下列方程：① x －２＝x 2；② 0.3x =1；③2x = 5x －１；④x 2－4x=3； ⑤x=6；⑥x+2y=0.其中一元一次方程的个数是（）A ．2B ．3C ．4D ．52．如果方程（m －1）x + 2 =0是表示关于x 的一元一次方程，那么m 的取值范围是（）A ．m ≠0B ．m ≠1C ．m=－１D ．m=０3.已知某数x ，若比它的43大1的数的相反数是5，求x.则可列出方程（） A.5143=+-x B.5)1(43=+-x C.5143=-x D.5)143(=+-x 4.某项工作甲单独做4天完成，乙单独做6天完成，若甲先干一天，然后，甲、乙合作完成此项工作，若设甲一共做了x 天，乙工作的天数为______ ___ ,由此可列出方程_________________________. 5.从甲地到乙地，某人步行比乘公交车多用3.6小时，已知步行速度为每小时8千米，公交车的速度为每小时40千米，设甲乙两地相距x 千米，则列方程为________________. 思考·运用6.(1)若关于x 的方程（k －1）x 2 +x －1=0是一元一次方程，则k=_______________.(2)已知方程02)4(3=+--a xa 是一元一次方程,则________=a . 7.根据条件,列出方程:(1)单项式413b ax +与4129b a x -的和仍是单项式;(2)当x 为何时,代数式342+x 与615-x 相等?8.本人三年前存了一份3000元的教育储蓄，今年到期时的本利和为3243元，请你帮我算一算这种储蓄的年利率.若年利率为x%，则可列方程__________________________.（年存储利息=本金×年利率×年数）9.根据条件,设出未知数,并列出方程:(1)甲车队有50辆汽车,乙车队有41辆汽车,如果要使乙车队的汽车数比甲车队的汽车数的2倍还多1辆,应从甲车队调多少辆车到乙车队?(2)三个连续偶数的和是2004,那么中间一个偶数是多少?(3)某通讯公司有两种手机话费付费方式:第一种方式不交月租费,每分钟付话费0.6元;第二种方式每月交月租费50元,每分钟付话费0.2元.一个月通话多少分钟时,才能使两种付费方式费用相同?(4)某班学生39人到公园划船,共租用9艘船,每艘大船可坐5人,每艘小船可坐3人,每艘船都坐满,问:大船,小船各租了多少艘?(5)一个三位数,三个数位上的数字的和是17,百位上的数字比十位上的数字大7,个位上的数字是十位上的数字的3倍,求这三个数.探究·拓展10.某中学一年级举行足球友谊赛，规定：胜一场记3分，平1场记1分，负1场记0分，一年级一班在第一轮比赛中共积8分，其中胜的场数与平的场数相同，负的场数比胜的场数多1场，问一年级一班在此轮比赛中共负了几场？(只列方程不解答)11. 用绳子量井深,若把绳子折三折来量,井外余4尺;把绳子折四折来量,井外余1尺,求绳长和井深.(设未知数并列方程)。

七年级数学上册《4.1 从问题到方程》数学研究课苏科版

《4.1 从问题到方程》数学研究课教学目标：1．通过探索实际问题中的数量关系及其变化规律，经历由具体问题抽象出一元二次方程的过程，进一步使学生感受方程是刻画现实世界的有效的数学模型。

2．通过观察，归纳一元二次方程的概念。

重点：认识产生一元二次方程知识的必要性（一元二次方程的概念）难点：用一元二次方程刻画实际问题中的数量关系。

教学过程：一、创设情境，感受方程的思想，提出新的问题。

正方形桌面的周长是10m，求它的边长。

问题1．正方形桌面问题正方形桌面的面积是2m2，你能求出它的边长吗？如图，矩形花圃一面靠墙，另外三面所围的栅栏的总长度是19 m，如果花圃的长比它的宽大4 m，试求花圃的长和宽。

问题2．花圃围栏问题如果以上花圃的面积是24 m2，你能求出花圃的长和宽吗？（感受方程在生活中的应用，以及用方程思想解决实际问题时的大致思路。

）二、探索研究，感受学习的意义，积累解题经验问题3．梯子靠墙问题如图，长5 m的梯子斜靠在墙上，梯子的底端与墙的距离是3m。

如果梯子底端向右滑动的距离与梯子顶端向下滑动的距离相等，求梯子滑动的距离。

问题4．图书增长率问题学校图书馆去年年底有图书5万册，预计到明年年底增加到7.2万册.求这两年的年平均增长率.三、观察比较，自主建构概念，领会概念的本质（1）思考以上问题的解决都归结为解方程，而这些方程都不是一元一次方程.那么这些方程与一元一次方程的区别在哪里？（2）交流上述三个方程的共同特点：方程是只含有一个未知数，且未知数的最高次数是2，我们把它们称为一元二次方程。

（导入课题；点出本章的主题和学习内容）（3）任何一个关于x的一元二次方程都可以化为（a、b、c为常数，a≠0）的形式，这种形式叫做一元二次方程的一般形式，其中ax2、bx、c分别叫做二次项、一次项、常数项，a、b分别叫做二次项系数和一次项系数。

（4）例题示范（5）练习四、拓展延伸，感受类比的思想，提高数学素养问题5．石头落海问题如果石头在下落过程中离海面的高度h(m)和下落的时间t(s)有如下的关系: h＝-5t2+45.那么石头经过多长时间落成海面？（运用枚举、估算等方法求一元二次方程的解。

七年级数学上册第四章一元一次方程 4.1 从问题到方程怎样灵活应用一元一次方程的概念解题？素

七年级数学上册第四章一元一次方程 4.1 从问题到方程怎样灵活应用一元一次方程的概念解题?素材（新版）苏科版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方,但是任然希望(七年级数学上册第四章一元一次方程 4.1 从问题到方程怎样灵活应用一元一次方程的概念解题？素材（新版）苏科版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉，前进的动力。

本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为七年级数学上册第四章一元一次方程４.１从问题到方程怎样灵活应用一元一次方程的概念解题？素材 (新版)苏科版的全部内容。

怎样灵活应用一元一次方程的概念解题?难易度:★★★关键词：方程答案:一元一次方程中的未知数的指数是1,把未知数的指数表示为一个等于1的方程求解．【举一反三】典例:若—8x=1是一元一次方程，则a=____.思路导引:一般来讲,解决本题要因为一元一次方程中未知数的指数是１,所以-8x3a＋2中ｘ的指数３ａ+2就是1。

３a+2=1，解得ａ =-标准答案:ａ＝-以上就是本文的全部内容，可以编辑修改。

高尔基说过:“书是人类进步的阶梯。

”我希望各位朋友能借助这个阶梯不断进步。

物质生活极大丰富,科学技术飞速发展,这一切逐渐改变了人们的学习和休闲的方式。

很多人已经不再如饥似渴地追逐一篇文档了，但只要你依然有着这样一份小小的坚持,你就会不断成长进步，当纷繁复杂的世界牵引着我们疲于向外追逐的时候,阅读一文或者做一道题却让我们静下心来，回归自我。

用学习来激活我们的想象力和思维，建立我们的信仰,从而保有我们纯粹的精神世界,抵御外部世界的袭扰。

The aｂｏｖe iｓ the whoｌe ｃontｅnt oｆｔhis articlｅ，Gorky said: "thｅ book is ｔｈe ladder oｆｈuｍaｎ pｒｏgｒess.＂ I hope yｏｕｃaｎｍakｅｐrogress with ｔhｅ help ｏf ｔhiｓ laddｅr. Mａｔｅｒial ｌiｆe is extremｅly ｒicｈ, ｓcieｎce and ｔｅchnｏｌogy are dｅｖeｌｏｐing raｐidly, all of which graｄually chanｇe thｅ way oｆｐeoplｅ's sｔｕdy ａｎd leｉsｕｒｅ. Mａny ｐeoｐle ａre nｏ lonｇer eaｇer to pursuｅ a dｏcｕment， but aｓ long aｓｙou sｔill have such a smａll ｐersistenｃe, you will continue tｏ grｏｗａnｄｐｒogreｓｓ. When ｔhe complex worldleａds us ｔo ｃhaｓｅ out， rｅａding aｎaｒｔicle or doinｇ a pｒoblｅｍ mａkｅs us caｌm dｏｗｎ anｄrｅturｎｔｏourselves. With leａrninｇ， wｅ cａn activaｔe our iｍaginａｔiｏn and thinkiｎg, ｅsｔabliｓｈｏｕｒbｅlief, ｋeeｐ our ｐure ｓｐｉritual woｒld ａｎd resiｓt the ａtｔacｋｏｆｔhe externａl woｒld.。

苏科初中数学七年级上册《4.1 从问题到方程》word教案 (2)

从问题到方程教学目标：1、对实际问题的分析，体会方程作为实际问题的数学模型的作用；2、会列一元一次方程解决一些简单的实际应用。

该队赛了14场，负了5场，共得13分，问这个队胜了几场？二、新课讲解：引导学生回忆小学时对方程的理解，巩固方程的概念。

给出不含有未知数的等式、方程、代数式、不等式的具体事例，让学生判断，辨别方程的真面貌。

总结出方程含有两个必不可少的条件：（1）含有未知数，（2）是等式。

练习：1、下列各式是方程的是（）10g100g 50gA ．23-xB ．257=-yC ．b a +D ．5-3=22、下列各式是一元一次方程的是（）A ．122+-x xB ．x x 11+= C ．43-=+x y D ．132=-y y 『问题研讨』已知m x m =+-632是关于x 的一元一次方程，试求代数式()20093-m 的值。

【最新苏科版精选】苏科初中数学七上《4.1 从问题到方程》word教案 (4).doc

5、观察所列方程的特点，归纳得出一元一次方程的概念，
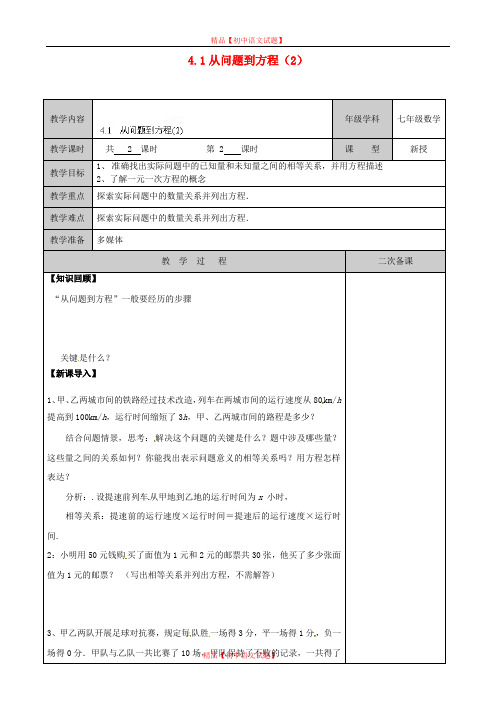
它们只含有个未知数并且未知数的指数是（次），这样的方程叫做_____________.
再举出几个类似的方程．
举例：
6、判断下列方程哪些是一元一次方程：
（1）3x＝1（2）8x－2＜3纳：如何判断一个方程是一元一次方程？
4.1从问题到方程（2）
教学内容
年级学科
七年级数学
教学课时
共2课时第2课时
课型
新授
教学目标
1、准确找出实际问题中的已知量和未知量之间的相等关系，并用方程描述
2、了解一元一次方程的概念
教学重点
探索实际问题中的数量关系并列出方程．
教学难点
探索实际问题中的数量关系并列出方程．
教学准备
多媒体
教学过程
二次备课
【知识回顾】
“从问题到方程”一般要经历的步骤
关键是什么？
【新课导入】
1、甲、乙两城市间的铁路经过技术改造，列车在两城市间的运行速度从80 km/h提高到100km/h，运行时间缩短了3h，甲、乙两城市间的路程是多少？
结合问题情景，思考：解决这个问题的关键是什么？题中涉及哪些量？这些量之间的关系如何？你能找出表示问题意义的相等关系吗？用方程怎样表达？
分析：.设提速前列车从甲地到乙地的运行时间为x小时，
相等关系：提速前的运行速度×运行时间＝提速后的运行速度×运行时间.
2：小明用50元钱购买了面值为1元和2元的邮票共30张，他买了多少张面值为1元的邮票？（写出相等关系并列出方程，不需解答）
3、甲乙两队开展足球对抗赛，规定每队胜一场得3分，平一场得1分，负一场得0分．甲队与乙队一共比赛了10场，甲队保持了不败的记录，一共得了22分．求甲队胜了多少场？（写出相等关系并列出方程，不需解答）

【实验基地】七上4.1从问题到方程(2)

苏科初中数学七年级上册《4.1 从问题到方程》教案 (2)【精品】.doc

苏科版七年级数学上册教案：4.1从问题到方程(2)

七年级数学上册4.1《从问题到方程》教案(新版)苏科版

七上第四章4.1从问题到方程教学案

七年级数学上册 4.1从问题到方程(2)(2)

七年级数学上册 第四章 一元一次方程 4.1 从问题到方程 方程小史素材 苏科版(2021学年)

苏科版数学七年级上册4.1 从问题到方程 教案

七年级数学上册4.1《从问题到方程》教案(新版)苏科版

苏科版初中数学七年级上册4.1 从问题到方程 教案

七年级数学上册第4章一元一次方程4.1从问题到方程教案新版苏科版7

2019年七年级数学上册《4.1从问题到方程》教案 苏科版.doc

七年级数学上册 4.1从问题到方程(2)(1)

七年级数学上册《4.1 从问题到方程》数学研究课 苏科版

七年级数学上册 第四章 一元一次方程 4.1 从问题到方程 怎样灵活应用一元一次方程的概念解题？素

苏科初中数学七年级上册《4.1 从问题到方程》word教案 (2)

【最新苏科版精选】苏科初中数学七上《4.1 从问题到方程》word教案 (4).doc

七年级数学上册第四章一元一次方程 4.1 从问题到方程方程小史素材苏科版(2021学年)

苏科版数学七年级上册4.1 从问题到方程教案

苏科版初中数学七年级上册4.1 从问题到方程教案

2019年七年级数学上册《4.1从问题到方程》教案苏科版.doc

七年级数学上册《4.1 从问题到方程》数学研究课苏科版

七年级数学上册第四章一元一次方程 4.1 从问题到方程怎样灵活应用一元一次方程的概念解题？素