焦作市2016-2017学年高二数学(理)上学期期中考试试题 答案版
2016-2017学年高二上学期期中考试数学试题 Word版含答案

2016-2017学年高二上学期期中考试数学试题一、选择题(本大题共8小题,每小题5分,共40分)1.某产品共有三个等级,分别为一等品、二等品和不合格品.从一箱产品中随机抽取1件进行检测,设“抽到一等品”的概率为0.65,“抽到二等品”的概率为0.3,则“抽到不合格品”的概率为( )A .0.05B .0.35C .0.7D .0.95 2.全称命题“2,54x R x x ∀∈+=”的否定是( )A .2000,54x R x x ∃∈+=B .2,54x R x x ∀∈+≠C .2000,54x R x x ∃∈+≠D .以上都不正确3.在如图所示的茎叶图中,若甲组数据的众数为14,则乙组数据的中位数为( )A .6B .8C .10D .144.某程序框图如图所示,若输出的结果是62,则判断框中可以是( ) A .7?i ≥ B .6?i ≥ C .5?i ≥ D .4?i ≥5.对于实数,,a b c ,“a b >”是“22ac bc >”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.已知椭圆22221(0)x y a b a b+=>>的一个焦点是圆22680x y x +-+=的圆心,且短轴长为8,则椭圆的左顶点为( )A .(2,0)-B .(3,0)-C .(4,0)-D .(5,0)- 7.点P 在边长为1的正方形ABCD 内运动,则动点P 到 定点A 的距离|PA |1<|的概率为( )A.πB.2π C.4π D .6π8.若点O 和点F 分别为椭圆22143x y +=的中心和左焦点,点P 为椭圆上的任意一点,则OP FP ⋅ 的最大值为( ) A .2 B .3 C .6 D .8二、填空题(每题5分,共6个小题,满分30分) 9.某课题组进行城市空气质量调查,按地域把24个城市分 成甲、乙、丙三组,对应城市数分别为 4、12、8.若用分层 抽样方法抽取6个 城市,则甲组中应抽取的城市数为________.10.执行如图所示的程序框图,若输入的x 的值为1, 则输出的n 的值为________.11.有一个容量为200的样本,其频率分布直方图如图所示, 据图知,样本数据在[8,10)内的频数为 12.已知点M 是圆224x y +=上任意一点,过点M 向x 轴作垂线,垂足为N ,则线段MN (包括MN 重合) 的中点的轨迹方程为13.在平面直角坐标系xoy 中,椭圆C 的中心为原点,焦点12,F F 在x轴上,离心率为2.过点1F 的直线L 交C 于,A B 两点,且2ABF ∆的周长为16,那么C 的方程为 . 14.有下列命题:①“若0x y +>,则00x y >>且”的否命题; ②“矩形的对角线相等”的否命题;③“若1m ≥,则22(m 1)x m 30mx -+++>的解集是R ”的逆命题; ④“若7a +是无理数,则a 是无理数”的逆否命题. 其中正确命题的序号是三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)15.(满分13分)设命题p :x y c =为R 上的减函数,命题q :函数2(x)234f x x c =-+>在1,22x ⎡⎤∈⎢⎥⎣⎦上恒成立.若p q ∨为真命题,p q ∧为假命题,求c 的取值范围.第18题图16.(满分13分)某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查,调查问卷共10道题,答题情况如下表所示.(1)如果出租车司机答对题目数大于等于9,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率率;(2)从答对题目数小于8的出租车司机中任选出2人做进一步的调查,求选出的2人中至少有一名女出租车司机的概率.17.(满分13分)在如图所示的几何体中,面CDEF 为正方形,面ABCD 为等腰梯形,AB //CD,AC ,22AB BC ==,AC FB ⊥.(1)求证:⊥AC 平面FBC ;(II )线段AC 的中点为M ,求证EA //平面FDM18(满分14分).随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.(Ⅰ)根据茎叶图判断哪个班的平均身高较高; (Ⅱ)计算甲班的样本方差;(Ⅲ)现从乙班这10名同学中随机抽取两名身高不低于173cm 的同学,求身高为176cm 的同学被抽中的概率.19.(满分14分)某同学利用国庆节期间进行社会实践活动,在[25,55]岁的人群中随机抽取n 人进行了一次生活习惯是否符合低碳生活的调查,若生活习惯符合低碳生活的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数的频率分布直方图:(1)补全频率分布直方图,并求,,n a p 的值;(2)从年龄在[40,50)岁的“低碳族”中采用分层抽样的方法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.20.(满分14分)已知椭圆的标准方程为:22221(0)43x y a a a+=>(1)当1a =时,求椭圆的焦点坐标及椭圆的离心率; (2)过椭圆的右焦点2F 的直线与圆222:4(0)C x y a a +=>常数交于,A B 两点,求22|F ||F |A B ⋅的值.2016-2017学年高二上学期期中考试数学试题答案一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.某产品共有三个等级,分别为一等品、二等品和不合格品.从一箱产品中随机抽取1件进行检测,设“抽到一等品”的概率为0.65,“抽到二等品”的概率为0.3,则“抽到不合格品”的概率为( )A .0.95B .0.7C .0.35D .0.05解析:“抽到一等品”与“抽到二等品”是互斥事件,所以“抽到一等品或二等品”的概率为0.65+0.3=0.95,“抽到不合格品”与“抽到一等品或二等品”是对立事件,故其概率为1-0.95=0.05.答案:D2.全称命题“∀x ∈R ,x 2+5x =4”的否定是( )A .∃x 0∈R ,x 20+5x 0=4 B .∀x ∈R ,x 2+5x ≠4 C .∃x 0∈R ,x 20+5x 0≠4 D .以上都不正确解析:选C 全称命题的否定为特称命题.3.在如图所示的茎叶图中,若甲组数据的众数为14,则乙组数据的中位数为( )A .6B .8C .10D .14解析:由甲组数据的众数为14得x =y =4,乙组数据中间两个数分别为6和14,所以中位数是6+142=10.答案:C4.某程序框图如图所示,若输出的结果是126,则判断框中可以是( )A .i >6?B .i >7?C .i ≥6?D .i ≥5?解析:根据题意可知该程序运行情况如下: 第1次:S =0+21=2,i =1+1=2; 第2次:S =2+22=6,i =3; 第3次:S =6+23=14,i =4; 第4次:S =14+24=30,i =5; 第5次:S =30+25=62,i =6; 第6次:S =62+26=126,i =7;此时S =126,结束循环,因此判断框应该是“i >6?”.答案:A5.“a <0”是“方程ax 2+1=0至少有一个负根”的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件解析:选C 方程ax 2+1=0至少有一个负根等价于x 2=-1a,故a <0,故选C.6.已知椭圆22221(0)x y a b a b+=>>的一个焦点是圆22680x y x +-+=的圆心,且短轴长为8,则椭圆的左顶点为( )A .(2,0)-B .(3,0)-C .(4,0)-D .(5,0)-【解析】圆心坐标为(3,0),∴c =3,又b =4,∴5a =. ∵椭圆的焦点在x 轴上,∴椭圆的左顶点为(-5,0). 【答案】 D7.点P 在边长为1的正方形ABCD 内运动,则动点P 到定点A 的距离|PA |<1的概率为( )A.14B.12C.π4D .π 解析:如图所示,动点P 在阴影部分满足|PA |<1,该阴影是半径为1,圆心角为直角的扇形,其面积为S ′=π4,又正方形的面积是S =1,则动点P到定点A 的距离|PA |<1的概率为S ′S =π4. 答案:C 8.直线l 经过椭圆的一个短轴顶点顶点和一个焦点,若椭圆中心到l 的距离为其短轴长的14,则该椭圆的离心率为( )A .13B .12C .23D .34解析:选B 不妨设直线l 经过椭圆的一个顶点B (0,b )和一个焦点F (c,0),则直线l 的方程为x c +yb=1,即bx +cy -bc =0.由题意知|-bc |b 2+c 2=14×2b ,解得c a =12,即e =12.故选B .二、填空题(每题5分,共6个小题,满分30分)9.某课题组进行城市空气质量调查,按地域把24个城市分成甲、乙、丙三组,对应城市数分别为4、12、8.若用分层抽样方法抽取6个城市,则甲组中应抽取的城市数为________.答案:110.执行如图所示的程序框图,若输入的x 的值为1, 则输出的n 的值为________.答案:311.有一个容量为200的样本,其频率分布直方图如图所示,据图知,样本数据在[8,10)内的频数为( )A .38B .57C .76D .95 答案:C12.已知点M 是圆224x y +=上任意一点,过点M 向x 轴作垂线,垂足为N ,则线段MN (包括MN 重合)的中点的轨迹方程为2214x y += 13.在平面直角坐标系xoy 中,椭圆C 的中心为原点,焦点12,F F 在x 轴上,离心率为2.过点1F 的直线L 交C 于,A B 两点,且2ABF ∆的周长为16,那么C 的方程为_________.【答案】221168x y +=14.有下列命题:①“若x +y >0,则x >0且y >0”的否命题; ②“矩形的对角线相等”的否命题;③“若m ≥1,则mx 2-2(m +1)x +m +3>0的解集是R ”的逆命题; ④“若a +7是无理数,则a 是无理数”的逆否命题. 其中正确的是 ①③④三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)15.(满分13分)设命题p :x y c =为R 上的减函数,命题q :函数2(x)234f x x c =-+>在1,22x ⎡⎤∈⎢⎥⎣⎦上恒成立.若p q ∨为真命题,p q ∧为假命题,求c 的取值范围.解:由p ∨q 真,p ∧q 假,知p 与q 为一真一假,对p ,q 进行分类讨论即可. 若p 真,由y =c x为减函数,得0<c <1. .....................3分 当1,22x ⎡⎤∈⎢⎥⎣⎦时,由不等式2(x 1)22-+≥(x =1时取等号)知(x)f 在1,22⎡⎤⎢⎥⎣⎦上的最小值为2 ......................6分若q 真,则42c <,即12c < .......................8分 若p 真q 假,则112c ≤<; .......................10分 若p 假q 真,则0c ≤. ......................12分 综上可得,(]1,0,12c ⎡⎫∈-∞⎪⎢⎣⎭......................13分16.(满分13分)某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查,调查问卷共10道题,答题情况如下表所示.(1)如果出租车司机答对题目数大于等于9,就认为该司机对新法规的知晓情况比较好,计算被调查的出租车司机对新法规知晓情况比较好的频率;(2)从答对题目数小于8的出租车司机中任选出2人做进一步的调查,求选出的2人中至少有一名女出租车司机的概率.解:(1)答对题目数小于9的人数为55,记“答对题目数大于等于9”为事件A ,P (A )=1-55100=0.45. .......................6分 (2)记“选出的2人中至少有一名女出租车司机”为事件M ,设答对题目数小于8的司机为A ,B ,C ,D ,E ,其中A ,B 为女司机,任选出2人包含AB ,AC ,AD ,AE ,BC ,BD ,BE ,CD ,CE ,DE ,共10种情况,.......................9分(3)至少有一名女出租车司机的事件为AB ,AC ,AD ,AE ,BC ,BD ,BE ,共7种 ..12分则P (M )=710=0.7. ......13分16.(满分14分)在如图所示的几何体中,面CDEF 为正方形,面ABCD 为等腰梯形,AB //CD,AC ,22AB BC ==,AC FB ⊥.(1)求证:⊥AC 平面FBC ;(II )线段AC 的中点为M ,求证EA //平面FDM第3题图17.(本小题满分14分) (Ⅰ)证明:在△ABC 中,因为AC =,2AB =,1BC =,所以 BC AC ⊥. ………………3分 又因为 AC FB ⊥, 因为BC FB B =所以 ⊥AC 平面FBC . ………………6分 (Ⅱ)M 为AC 中点时,连结CE ,与DF 交于点N ,连结MN .因为 CDEF 为正方形,所以N 为CE 中点. ……………8分 所以 EA //MN . ……………10分 因为 ⊂MN 平面FDM ,⊄EA 平面FDM , ………12分 所以 EA //平面FDM . …………13分18(满分14分).随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.(Ⅰ)根据茎叶图判断哪个班的平均身高较高; (Ⅱ)计算甲班的样本方差;(Ⅲ)现从乙班这10名同学中随机抽取两名身高不低于173cm 的同学,求身高为176cm 的同学被抽中的概率. 规范解答不失分 (Ⅰ)由茎叶图可知:甲班身高集中于160179:之间, 而乙班身高集中于170180: 之间.因此乙班平均身高高于甲班 ...............4分 (Ⅱ)158162163168168170171179182170.10x ++++++++==...............6分 甲班的样本方差为:222222222221(158170)(162170)(163170)(168170)10(168170)(170170)(171170)(179170)(179170)(182170)57.2.s ⎡=-+-+-+-⎣+-+-+-+-+-+-=...............8分(Ⅲ)设身高为176cm的同学被抽中的事件为A;从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173)(181,176)(181,178)(181,179)(179,173)(179,176)(179,178)(178,173)(178, 176) (176,173)共10个基本事件,...............10分而事件A含有4个基本事件;...............12分所以42().105P A ...............14分19.(满分14分)某同学利用国庆节期间进行社会实践活动,在[25,55]岁的人群中随机抽取n人进行了一次生活习惯是否符合低碳生活的调查,若生活习惯符合低碳生活的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数的频率分布直方图:(1)补全频率分布直方图,并求n,a,p的值;(2)从年龄在[40,50)岁的“低碳族”中采用分层抽样的方法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.解:(1)第二组的概率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,所以频率组距=0.35=0.06.............2分 频率分布直方图如下:............4分第一组的人数为1200.6=200,频率为0.04×5=0.2, 所以n =2000.2=1 000 .............6分 因为第二组的频率为0.3,所以第二组的人数为1 000×0.3=300,所以p =195300=0.65. 第四组的频率为0.03×5=0.15,所以第四组的人数为1 000×0.15=150.所以a =150×0.4=60 .............8分(2)因为年龄在[40,45)岁的“低碳族”与[45,50)岁的“低碳族”的人数的比为60∶30=2∶1,所以采用分层抽样法抽取6人,[40,45)中有4人,[45,50)中有2人.设[40,45)中的4人为a ,b ,c ,d ,[45,50)中的2人为m ,n ,则选取2人作为领队的情况有(a ,b ),(a ,c ),(a ,d ),(a ,m ),(a ,n ),(b ,c ),(b ,d ),(b ,m ),(b ,n ),(c ,d ),(c ,m ),(c ,n ),(d ,m ),(d ,n ),(m ,n ),共15种, ............10分(3)其中恰有1人年龄在[40,45)岁的情况有(a ,m ),(a ,n ),(b ,m ),(b ,n ),(c ,m ),(c ,n ),(d ,m ),(d ,n ),共8种, ............12分(4)所以选取的2名领队中恰有1人年龄在[40,45)岁的概率P =815.............14分 20.(满分14分)已知椭圆的标准方程为:22221(0)43x y a a a+=> (1)当1a =时,求椭圆的焦点坐标及离心率;(2)过椭圆的右焦点2F 的直线与圆222:4(0)C x y a a +=>常数交于,A B 两点,证明22|F ||F |A B ⋅为定值. 解:(1)焦点坐标12(1,0),F (1,0)F - ..........2分离心率12e = ..........3分(2)当斜率不存在时11|||F B |F A ===此时212|FA ||F B|3a ⋅= 5分当斜率不存在=时,设1122(x ,y ),B(x ,y )A:()AB y k x a =-由222(x a)x 4y k y a =-⎧⎨+=⎩ 得222222(1k )x 240ak x k a a +-+-= 7分 222212122224,11ak k a a x x x x k k -+==++ 9分11|FA |x a |==-22|F A |x a |==-所以22111212|FA||FB|(1)|x x a(x )a |k x ⋅=+-++ 12分 22222222242(1k )|a |11k a a a k k k -=+-+++23a = 13分 所以 22|F ||F |A B ⋅为定值23a .。
河南省焦作市2016-2017学年上学期高三期中数学(理科)考试题Word版含答案.doc

焦作市2016-2017学年(上)高三年级期中学业水平测试数学试卷(理)一 选择题:每小题5分,共12小题,共60分。
1.已知i 为虚数单位,复数z 满足i z i +=--1)1)(1(,则z 的共轭复数为( ) A.-1-i B.1-i C.1+i D.-1+i2.设集合M={1,9,a},集合P={1,a2},若P ⊆M,则实数a 的取值个数为( ) A.0个 B.1个 C.2个 D.3个3.某校高三年级有1221名同学,现采用系统抽样方法舟曲37名同学做问卷调查,将1221名同学按1,2,3,4,...,1221随机编号,则抽取的37名同学中,标号落入区间[496,825]的人数有( )A.12人B.11人C.10人D.9分 4.已知奇函数f(x)在R 上为增函数,且f(1)=21,若实数a 满足1)31(log )3(log ≤-a a f f ,则实数a 的取值范围为( ) A.310≤<a B.31≤a C.131<≤a D.103<<≥a a 或 5.已知A 1、A 2分别是椭圆C:)0(12222>>=+b a by ax 的左、右顶点,点P 为椭圆C 上一点(与A 1、A 2不重合),若直线PA 1与PA 2的斜率乘积是43-,则椭圆C 的离心率为( ) A.41 B.3 C.23D.21 6.直线下面的程序框图,如果输入的N 是9,那么输出的S 是( ) A.2 B.21C.-1D.07.已知函数f(x)=2cos(ϕω+x )的部分图象如图所示,其中ω>0,2πϕ<,则f(41)的值为( )A.3-B.-1C.21 D.23-8.已知棱长都是2的直三棱柱的视图是一个正三角形,则该直三棱柱的主视图的面积不可能等于( )A.4B.32C.519D.23 9.若⎰=-=123)()(dt t g x x g ,则g(x)=( ) A.x+1 B.x-1 C.x-2 D.x-23 10.若F1、F2是双曲线15422=-y x 的左右焦点,M 是双曲线右支上一动点,则1211MF MF -的最大值为( ) A.43 B.54C.1D.45 11.若a 、b 、m ∈Z(m>0),且a 、b 除以m 所得的余数相同,则a 、b 是m 的同余数.已知201720172017220172120172...22C C C x +++=,且x 、y 是10的同余数,则y 的值可以是( )A.2012B.2019C.2016D.2013 12.在△ABC 中,内角A=3π,P 为△ABC 的外心,若AC AB AP 212λλ+=,其中1λ与2λ为实数,则1λ+2λ的最大值为( ) A.21 B.231- C.43 D.231+ 二 填空题:每小题5分,共4小题,共20分。
2016-2017年第一学期高二数学期中试题及答案

2
3
4
5
6
7
8
9
10
11
12
礼券额
20
40
60
80
100
120
100
80
60
40
20
方案3总点数为2和12时的礼券最多,都为120元;点数从2到7递增或从12到7递减时,礼券都依次减少20元.
总点数
2
3
4567891011
12
礼券额
120
100
80
60
40
20
40
60
80
100
120
如果你是该公司老总,你准备怎样去选择促销方案?请你对以上三种方案给出裁决.
17.(10分)用秦九韶算法求多项式
当 时的值。
18.(12分)为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为 ,第二小组频数为12.
(1)第二小组的频率是多少?样本容量是多 少?
(2)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为 时的销售价格.
21.(12分)甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头,它们在一昼夜内任何时刻到达是等可能的.
(1)如果甲船和乙船的停泊的时间都是4小时,求它们中的任何一条船不需要等待码头空出的概率;
(2)如果甲船的停泊时间为4小时,乙船的停泊时间为2小时,求它们中的任何一条船不需要等待码头空出的概率.
(2)记“3个矩形颜色都不同”为事件B,由图可知,事件B的基本事件有2×3=6个,故P
2017年河南省焦作市高二上学期数学期中试卷和解析(理科)

2016-2017学年河南省焦作市高二(上)期中数学试卷(理科)一、选择题(共12小题,每小题5分,满分60分)1.(5分)设集合A={x|x2﹣4x+3<0},B={x|2x﹣3>0},则A∩B=()A.(﹣3,﹣)B.(﹣3,)C.(1,)D.(,3)2.(5分)已知向量=(1,m),=(3,﹣2),且(+)⊥,则m=()A.﹣8 B.﹣6 C.6 D.83.(5分)设0<a<b,则下列不等式中正确的是()A.B.C.D.4.(5分)在△ABC中,已知a2tanB=b2tanA,则△ABC该的形状为()A.等腰三角形B.直角三角形C.正三角形D.等腰或直角三角形5.(5分)已知S n为等差数列{a n}的前n项的和,a2+a5=4,S7=21,则a7的值为()A.6 B.7 C.8 D.96.(5分)某三棱锥的三视图如图所示,则该三棱锥的体积为()A.B.C.D.17.(5分)在△ABC中,已知a=,b=2,B=45°,则角A=()A.30°或150°B.60°或120°C.60°D.30°8.(5分)若执行如图所示的框图,输入x1=1,x2=2,x3=3,=2,则输出的数等于()A.B.C.D.9.(5分)已知过点P(2,2)的直线与圆(x﹣1)2+y2=5相切,且与直线ax﹣y+1=0垂直,则a=()A.B.1 C.2 D.10.(5分)已知方程|x2﹣a|﹣x+2=0(a>0)有两个不等的实数根,则实数a的取值范围是()A.(0,4) B.(4,+∞)C.(0,2) D.(2,+∞)11.(5分)已知偶函数f(x)在区间[0,+∞)上为增函数,且f(﹣1)=,若实数a满足f(log a3)+f()≤1,则实数a的取值范围为()A.0<a≤B.a≥3,或0<a<C.a≥3,或0<a≤D.a≥3 12.(5分)已知数列{a n}满足a n+2﹣a n+1=a n+1﹣a n,n∈N*,且a5=,若函数f (x)=sin2x+2cos2,记y n=f(a n),则数列{y n}的前9项和为()A.0 B.﹣9 C.9 D.1二、填空题(共4小题,每小题5分,满分20分)13.(5分)不等式的解集为.14.(5分)已知x>0,y>0,且+=1,若x+2y≥a恒成立,则实数a的范围为.15.(5分)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为元.16.(5分)已知函数f(x)=2cos(ωx+φ)的部分图象如图所示,其中ω>0,|φ|<,则f(sin)的值为.三、解答题(共6小题,满分70分)17.(10分)设数列{a n}的前n项和为S n,a1=1,a n+1=S n+1,等差数列{b n}中,b1=a1,b2=2a2.(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)求数列{a n•b n}的前n项和T n.18.(12分)我国是世界上严重缺水的国家,某市政府为了制定合理的节水方案,对居民用水进行了调查,通过抽样,获得了100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.(Ⅰ)求直方图中a的值;(Ⅱ)估计居民月均用水量的中位数;(Ⅲ)若居民用水量小于0.5吨,将被授予“节水达人”称号,在[0,0.5)、[4,4.5]两组种任选两人,求至少有一位“节水达人”的概率.19.(12分)如图所示,在四棱锥P﹣ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是CD上的点且DF=AB,PH为△PAD中AD边上的高.(Ⅰ)证明:EF∥平面PAD;(Ⅱ)若PH=1,AD=,FC=2,求三棱锥E﹣BCF的体积.20.(12分)在平面直角坐标系xOy中,曲线y=x2﹣6x+1与坐标轴的交点都在圆C上.(1)求圆C的方程;(2)若圆C与直线x﹣y+a=0交于A,B两点,且OA⊥OB,求a的值.21.(12分)设函数f(x)=sinx+cos(x+),x∈R(Ⅰ)求函数f(x)的最小正周期及其在区间[0,]上的值域;(Ⅱ)记△ABC的内角A,B,C的对边分别为a,b,c,若f(A)=,且a=,求角B的大小.22.(12分)已知各项均不相等的等差数列{a n}的前四项和S4=14,且a1,a3,a7成等比数列.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设T n为数列{}的前n项和,若T n≤λa n对∀n∈N*恒成立,求实+1数λ的最小值.2016-2017学年河南省焦作市高二(上)期中数学试卷(理科)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)设集合A={x|x2﹣4x+3<0},B={x|2x﹣3>0},则A∩B=()A.(﹣3,﹣)B.(﹣3,)C.(1,)D.(,3)【解答】解:∵集合A={x|x2﹣4x+3<0}=(1,3),B={x|2x﹣3>0}=(,+∞),∴A∩B=(,3),故选:D.2.(5分)已知向量=(1,m),=(3,﹣2),且(+)⊥,则m=()A.﹣8 B.﹣6 C.6 D.8【解答】解:∵向量=(1,m),=(3,﹣2),∴+=(4,m﹣2),又∵(+)⊥,∴12﹣2(m﹣2)=0,解得:m=8,故选:D.3.(5分)设0<a<b,则下列不等式中正确的是()A.B.C.D.【解答】解:令a=1,b=4则=2,=,∵1<2<<4∴.故选:B.4.(5分)在△ABC中,已知a2tanB=b2tanA,则△ABC该的形状为()A.等腰三角形B.直角三角形C.正三角形D.等腰或直角三角形【解答】解:∵△ABC中,b2tanA=a2tanB,∴由正弦定理得:,在三角形中,sinA≠0,sinB≠0,∴,∴sinAcosA=sinBcosB,即sin2A=sin2B,则sin2B=sin2A,∴A=B或2A=π﹣2B,∴A=B或A+B=,∴△ABC为等腰三角形或直角三角形.故选:D.5.(5分)已知S n为等差数列{a n}的前n项的和,a2+a5=4,S7=21,则a7的值为()A.6 B.7 C.8 D.9【解答】解法一:等差数列{a n}中,a2+a5=4,S7=21根据等差数列的性质可得a3+a4=a1+a6=4①根据等差数列的前n项和公式可得,所以a1+a7=6②②﹣①可得d=2,a1=﹣3所以a7=9解法二:S6=()×6=12a7=S7﹣S6=9故选D6.(5分)某三棱锥的三视图如图所示,则该三棱锥的体积为()A.B.C.D.1【解答】解:由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱锥,棱锥的底面面积S=×1×1=,高为1,故棱锥的体积V==,故选:A.7.(5分)在△ABC中,已知a=,b=2,B=45°,则角A=()A.30°或150°B.60°或120°C.60°D.30°【解答】解:∵a=,b=2,B=45°,∴由正弦定理,得可得sinA==∴A=30°或150°∵a<b,可得A<B,∴A=30°故选:D.8.(5分)若执行如图所示的框图,输入x1=1,x2=2,x3=3,=2,则输出的数等于()A.B.C.D.【解答】解:S=0+(1﹣2)2=1,i=1,满足条件i<3,执行循环体,i=2S=1+(2﹣2)2=1,i=2,满足条件i<3,执行循环体,i=3S=1+(3﹣2)2=2,i=3,不满足条件i<3,退出循环体,则S=×2=.故选:B.9.(5分)已知过点P(2,2)的直线与圆(x﹣1)2+y2=5相切,且与直线ax﹣y+1=0垂直,则a=()A.B.1 C.2 D.【解答】解:因为点P(2,2)满足圆(x﹣1)2+y2=5的方程,所以P在圆上,又过点P(2,2)的直线与圆(x﹣1)2+y2=5相切,且与直线ax﹣y+1=0垂直,所以切点与圆心连线与直线ax﹣y+1=0平行,所以直线ax﹣y+1=0的斜率为:a==2.故选:C.10.(5分)已知方程|x2﹣a|﹣x+2=0(a>0)有两个不等的实数根,则实数a的取值范围是()A.(0,4) B.(4,+∞)C.(0,2) D.(2,+∞)【解答】解:∵方程|x2﹣a|﹣x+2=0(a>0)有两个不等的实数根,∴函数y=|x2﹣a|(a>0)与函数y=x﹣2的图象有两个交点,作函数y=|x2﹣a|(a>0)与函数y=x﹣2的图象如下,结合图象可得,存在x>2时,x2﹣a=0,即a=x2>4;实数a的取值范围是(4,+∞)故选:B.11.(5分)已知偶函数f(x)在区间[0,+∞)上为增函数,且f(﹣1)=,若实数a满足f(log a3)+f()≤1,则实数a的取值范围为()A.0<a≤B.a≥3,或0<a<C.a≥3,或0<a≤D.a≥3【解答】解:由偶函数f(x)在区间[0,+∞)上为增函数,且可知:函数f(x)在区间(﹣∞,0]上为减函数,且,整理求解题中所给的不等式:f(log a3)+f(log a)=f(loga3)+f(﹣loga3)=2f(loga3)⩽1,∴,结合函数的单调性和奇偶性有:|log a3|≤1,解得a≥3,或0<a≤.故选:C.12.(5分)已知数列{a n}满足a n+2﹣a n+1=a n+1﹣a n,n∈N*,且a5=,若函数f (x)=sin2x+2cos2,记y n=f(a n),则数列{y n}的前9项和为()A.0 B.﹣9 C.9 D.1【解答】解:∵数列{a n}满足a n+2﹣a n+1=a n+1﹣a n,n∈N*,∴数列{a n}是等差数列,∵a5=,∴a1+a9=a2+a8=a3+a7=a4+a6=2a5=π,∵f(x)=sin2x+2cos2,∴f(x)=sin2x+cosx+1,∴f(a1)+f(a9)=sin2a1+cosa1+1+sin2a9+cosa9+1=2,同理f(a2)+f(a8)=f(a3)+f(a7)=f(a4)+f(a6)=2,∵f(a5)=1,∴数列{y n}的前9项和为9.故选:C.二、填空题(共4小题,每小题5分,满分20分)13.(5分)不等式的解集为{x|} .【解答】解:不等式的解集可转化成即等价于解得:故不等式的解集为{x|}故答案为:{x|}14.(5分)已知x>0,y>0,且+=1,若x+2y≥a恒成立,则实数a的范围为(﹣∞,8] .【解答】解:x>0,y>0,且+=1,可得x+2y=(x+2y)(+)=4++≥4+2=8,当且仅当x=2y=4,取得最小值8.由x+2y≥a恒成立,可得a≤8,故答案为:(﹣∞,8].15.(5分)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为216000元.【解答】解:(1)设A、B两种产品分别是x件和y件,获利为z元.由题意,得,z=2100x+900y.不等式组表示的可行域如图:由题意可得,解得:,A(60,100),目标函数z=2100x+900y.经过A时,直线的截距最大,目标函数取得最大值:2100×60+900×100=216000元.故答案为:216000.16.(5分)已知函数f(x)=2cos(ωx+φ)的部分图象如图所示,其中ω>0,|φ|<,则f(sin)的值为﹣1.【解答】解:由图象可得:,∴T=1,,∴ω=2π,那么:f(x)=2cos(2πx+φ).∵图象过(),可得图象过(,﹣2)∴cos(2+φ)=﹣1,∵|φ|<,∴φ=∴f(x)=2cos(2πx+).∵sin==.那么:f(sin)=f()=2cos(2)=﹣2cos=﹣1.故答案为:﹣1.三、解答题(共6小题,满分70分)17.(10分)设数列{a n}的前n项和为S n,a1=1,a n+1=S n+1,等差数列{b n}中,b1=a1,b2=2a2.(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)求数列{a n•b n}的前n项和T n.【解答】解:(I)a n=S n+1,n≥2时,a n=S n﹣1+1.+1﹣a n=a n,即a n+1=2a n.∴a n+1∴数列{a n}是等比数列,公比为2,首项为1.∴a n=2n﹣1.等差数列{b n}中,b1=a1=1,b2=2a2=4.∴公差d=4﹣1=3.∴b n=1+3(n﹣1)=3n﹣2.(Ⅱ)a n•b n=(3n﹣2)•2n﹣1.∴T n=1+4×2+7×22+…+(3n﹣2)•2n﹣1.∴2T n=2+4×22+…+(3n﹣5)•2n﹣1+(3n﹣2)•2n,∴﹣T n=1+3(2+22+…+2n﹣1)﹣(3n﹣2)•2n=1+3×﹣(3n﹣2)•2n,可得:T n=(3n﹣5)•2n+5.18.(12分)我国是世界上严重缺水的国家,某市政府为了制定合理的节水方案,对居民用水进行了调查,通过抽样,获得了100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.(Ⅰ)求直方图中a的值;(Ⅱ)估计居民月均用水量的中位数;(Ⅲ)若居民用水量小于0.5吨,将被授予“节水达人”称号,在[0,0.5)、[4,4.5]两组种任选两人,求至少有一位“节水达人”的概率.【解答】解:(Ⅰ)由频率统计相关知识,各组频率之和为1,∴0.5×(0.08+0.16+a+0.4+0.52+a+0.12+0.08+0.04)=1,解得a=0.8;(Ⅱ)由频率分布直方图知,(0.08+0.16+0.30+0.40)×0.5=0.47<0.5,0.47+0.52×0.5=0.73>0.5,∴中位数在[2,2.5)内,设为x,则(x﹣2)×0.52+0.47=0.5,解得x≈2.06,估计全市月均用水量的中位数是2.06吨.(Ⅲ)月均用水量低于0.5吨的人数为100×0.08×0.5=4人,月均用水量在[4,4.5)之间有100×0.04×0.5=2人,从这6人中取出2人,共有=15种不同取法,都在[4,4.5)的取法是=1种,故至少有一位“节水达人”的概率为P=1﹣=.19.(12分)如图所示,在四棱锥P﹣ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是CD上的点且DF=AB,PH为△PAD中AD边上的高.(Ⅰ)证明:EF∥平面PAD;(Ⅱ)若PH=1,AD=,FC=2,求三棱锥E﹣BCF的体积.【解答】(Ⅰ)证明:取PA中点M,连接DM,EM,∵E是PB的中点,∴EM∥AB,且EM=,又AB∥CD,且DF=AB,∴EM∥DF,且EM=DF,则四边形EFDM为平行四边形,∴EF∥DM,∵DM⊂平面PAD,EF⊄平面PAD,∴EF∥平面PAD;(Ⅱ)解:∵AB⊥平面PAD,∴AB⊥AD,又AB∥CD,∴AD⊥CD,连接BH,取BH中点G,连接EG,∵E是PB的中点,∴EG∥PH,∵PH⊥平面ABCD,∴EG⊥平面ABCD,则EG=PH=,=S△BCF•EG=••FC•AD•EG=.∴V E﹣BCF20.(12分)在平面直角坐标系xOy中,曲线y=x2﹣6x+1与坐标轴的交点都在圆C上.(1)求圆C的方程;(2)若圆C与直线x﹣y+a=0交于A,B两点,且OA⊥OB,求a的值.【解答】解:(1)圆x2+y2+Dx+Ey+F=0,x=0,y=1有1+E+F=0y=0,x2 ﹣6x+1=0与x2+Dx+F=0是同一方程,故有D=﹣6,F=1,E=﹣2,即圆方程为x2+y2﹣6x﹣2y+1=0;(2)设A(x1,y1),B(x2,y2),其坐标满足方程组消去y,得到方程2x2+(2a﹣8)x+a2﹣2a+1=0,由已知可得判别式△=56﹣16a ﹣4a2>0.在此条件下利用根与系数的关系得到x1+x2=4﹣a,x1x2=…①由于OA⊥OB可得x1x2+y1y2=0,又y1=x1+a,y2=x2+a,所以可得2x1x2+a(x1+x2)+a2=0…②由①②可得a=﹣1,满足△=56﹣16a﹣4a2>0.故a=﹣1.21.(12分)设函数f(x)=sinx+cos(x+),x∈R(Ⅰ)求函数f(x)的最小正周期及其在区间[0,]上的值域;(Ⅱ)记△ABC的内角A,B,C的对边分别为a,b,c,若f(A)=,且a=,求角B的大小.【解答】解:(Ⅰ)函数f(x)=sinx+cos(x+),x∈R.化简可得:f(x)=sinx+cosxcos﹣sinxsin=sinx+cosx=sin(x+),∴函数f(x)的最小正周期T=,∵x∈[0,],∴,sin(x+)≤1,∴x∈[0,]上f(x)的值域为[,1];(Ⅱ)由f(A)=,即sin(A+)=,∵0<A<π,∴<A<,则A+=,可得:A=,∵a=,由正弦定理:,可得sinB=1,∵0<B<π,∴B=.22.(12分)已知各项均不相等的等差数列{a n}的前四项和S4=14,且a1,a3,a7成等比数列.(Ⅰ)求数列{a n}的通项公式;对∀n∈N*恒成立,求实(Ⅱ)设T n为数列{}的前n项和,若T n≤λa n+1数λ的最小值.【解答】解:(I)设公差为d,由已知得:,即,解得:d=1或d=0(舍去),∴a1=2,故a n=2+(n﹣1)=n+1;(II)∵==﹣,∴T n=﹣+﹣+…+﹣=﹣=,对∀n∈N*恒成立,即≤λ(n+2),λ≥∀n∈N*恒成∵T n≤λa n+1立,又=≤=,∴λ的最小值为.赠送初中数学几何模型【模型三】双垂型:图形特征:60°运用举例:1.在Rt△ABC中,∠ACB=90°,以斜边AB为底边向外作等腰三角形PAB,连接PC.(1)如图,当∠APB=90°时,若AC=5,PC=,求BC的长;(2)当∠APB=90°时,若AB=APBC的面积是36,求△ACB的周长.2.已知:如图,B、C、E三点在一条直线上,AB=AD,BC=CD.(1)若∠B=90°,AB=6,BC=23,求∠A的值;(2)若∠BAD+∠BCD=180°,cos∠DCE=35,求ABBC的值.3.如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°,(1)若AB=3,BC+CD=5,求四边形ABCD的面积(2)若p= BC+CD,四边形ABCD的面积为S,试探究S与p之间的关系。
2016-2017年高二数学(理)期中试卷及答案

∴它们所围成的三角形面积为: ……(10分)
18.证明:以D为原点,分别以DA、DC、DD1为x轴、y轴、z轴建立空间直角坐标系,则A(a,0,0),B(a,2a,0),C(0,2a,0),D1(0,0,a),E(a,2a,0),
图2
∵M、N分别为AE、CD1的中点,
A.必在圆x2+y2=2内B.必在圆x2+y2=2上
C.必在圆x2+y2=2外D.以上三种情形 都有可能
.
二、填空题(本大题共4小题,每小题5分,共20分,把答案 填在答题卷的横线上。)
13、已知双曲线 上一点M的横坐标为4,则点M到左焦点的距离是14.设双曲线 的一条渐近线与抛物线y=x +1只有一个公共点,则双曲线的离心率为
三、解 答题(本大题共6小题,满分70分,解答应写出文字说明、证明过程或演算步骤。)
17.(本小题满分10分)
抛物线 的焦点与双曲线 的右焦点重合.
(Ⅰ)求抛物线的方程;(Ⅱ)求抛物线的准线与双曲线的渐近线围成的三角形的面积.
18.(本小题满分12分)如图 ,已知长方体ABCD-A1B1C1D1中,E、M、N分别是BC、AE、CD1的中点,AD=AA1=a,AB=2a.求证:MN∥平面ADD1A1.
∴M(a,a,0),N(0,a,).
∴=(-a,0,).……(6分)
取n=(0,1,0),……(8分)显然n⊥平面A1D1DA,且·n=0,
∴⊥n.又MN⊄平面ADD1A1.
∴MN∥平面ADD1A1………(12分)
19.证明:以C为坐标原点,建立如图4所示的空间直角坐标系,则A(,,0),B(0,,0),D(,0,0),F(,,1),M(,,1).
2016-2017年河南省焦作市高二(上)期中数学试卷和参考答案(文科)

第 3 页(共 19 页)
女生 男生 (1)请完成此统计表; (2)试估计高二年级学生“同意”的人数;
4 2
(3)从被调查的女生中选取 2 人进行访谈,求选到的两名学生中,恰有一人“同 意”一人“不同意”的概率. 19. (12 分)如图所示,在四棱锥 P﹣ABCD 中,AB⊥平面 PAD,AB∥CD,PD=AD, E 是 PB 的中点,F 是 DC 上的点且 DF= AB,PH 为△PAD 中 AD 边上的高. (1)证明:PH⊥平面 ABCD; (2)若 PH=1,AD= ,FC=2,求三棱锥 E﹣BCF 的体积;
11. (5 分)已知数列{an}: , + , 若 bn= A.2﹣ C.
,那么数列{bn}的前 n 项和 Sn 等于( B.3﹣ D .4﹣
12. (5 分)已知函数 f(x)=2cos(ωx+φ)的部分图象如图所示,其中 ω>0,|φ| < ,则 f(sin )的值为( )
第 2 页(共 19 页)
)
A.9
B.18 C.20 D.35
9. (5 分)已知方程|x2﹣a|﹣x+2=0(a>0)有两个不等的实数根,则实数 a 的 取值范围是( )
A. (0,4) B. (4,+∞) C. (0,2) D. (2,+∞) 10. (5 分)在△ABC 中,三个内角 A,B,C 所对的边为 a,b,c,若 S△ABC=2 a+b=6, c=( A.2 ) B.4 C.2 D.3 ,…, ) ,…, =2cosC,则 ,
,其中[x]表示不超过 x 的最大整数,则方 .
三、解答题(共 6 小题,满分 70 分) 17. (10 分)设{an}为等差数列,a1=2,a2+a4=8. (1)求数列{an}的通项公式; (2)设 bn=2(an+ ) ,求数列{bn}的前 n 项和 Sn.
2016-2017学年高二上学期期中考试数学试题Word版含答案
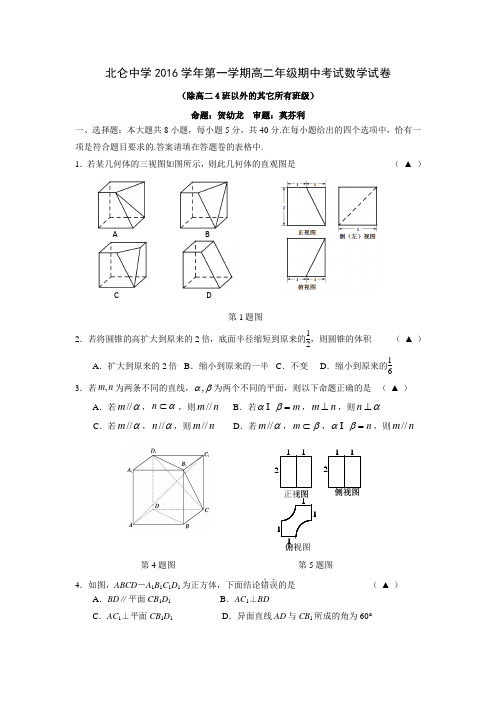
北仑中学2016学年第一学期高二年级期中考试数学试卷(除高二4班以外的其它所有班级) 命题:贺幼龙 审题:莫芬利一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,恰有一项是符合题目要求的.答案请填在答题卷的表格中.1.若某几何体的三视图如图所示,则此几何体的直观图是 ( ▲ )第1题图2.若将圆锥的高扩大到原来的2倍,底面半径缩短到原来的12,则圆锥的体积 ( ▲ )A .扩大到原来的2倍B .缩小到原来的一半C .不变D .缩小到原来的163.若,m n 为两条不同的直线,,αβ为两个不同的平面,则以下命题正确的是 ( ▲ ) A .若α//m ,α⊂n ,则n m // B .若m =βα ,n m ⊥,则α⊥nC .若α//m ,α//n ,则n m //D .若α//m ,β⊂m ,n =βα ,则n m //第4题图 第5题图4.如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错误..的是 ( ▲ )A .BD ∥平面CB 1D 1 B .AC 1⊥BDC .AC 1⊥平面CB 1D 1 D .异面直线AD 与CB 1所成的角为60°A BC D5.某几何体三视图如图所示,则该几何体的体积为 ( ▲ ) A .82π- B .8π- C .82π- D .84π-6.如果一个水平放置的图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是 ( ▲ )A .2+2 B.1+22 C.2+22D .1+ 27.下列四个命题中正确的命题有 ( ▲ ) ①过空间任何一点P 可以作无数条直线与已知的异面直线b a ,都相交; ②三个平面两两相交,有三条交线,则此三条交线或交于一点,或互相平行;③直线a α⊥平面,直线b β⊥平面,则直线b a ,所成角与平面βα,所成角相等或互补; ④αβ⊥平面平面,,,m n m n αβ⊂⊂⊥,则β⊥m 或α⊥n .A.1个B.2个C.3个D.4个8.如图,正方体1111ABCD A B C D -的棱长为1,点A 在平面α内,点E 是底面ABCD 的中心.若1C E ⊥平面α,则1C AB ∆在平面α内的射影的面积为 ( ▲ )ABCD第8题图 第11题图 第12题图二、填空题:本大题共7小题,前4题每空3分,后3题每空4分,共36分.将正确答案填在答题卷的横线上.9.正方体1111ABCD A B C D -的棱长为1,则其表面积为 ▲ ,其内切球的体积为 ▲ . 10.将一个边长分别是2 cm 和3 cm ,两邻边夹角为60°的平行四边形绕其3 cm 边上的高所在直线旋转一周形成的简单几何体是 ▲ ,其体积为 ▲ cm 3.11.如图,P 是正方形ABCD 外一点,且PA ABCD ⊥平面,则此几何体的5个面中互相垂直的面有 ▲ 对;若PA AB =,则直线PC 与平面PAB 所成角的正切值为 ▲ .1C 1A 1D 1B CDABαE12.一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体体积为 ▲ ,表面积为 ▲ .第13题图 第15题图13.如图,已知正三棱锥A —BCD 侧面的顶角为45°,侧棱长为a ,动点E 在侧棱AC 上运动,则线段BE 、ED 长度和的最小值为 ▲ .14,a b ,则a,b 所满足的等量关系式是 ▲ .15.如图,已知平面⊥α平面β,、A B 是平面α与β的交线上的两个定点,β⊂DA ,β⊂CB ,且6,8,4,,===⊥⊥AB BC AD CB DA αα,在平面α上有一个动点P ,使得BPC APD ∠=∠,则PAB ∆的面积的最大值为 ▲ .三、解答题:本大题共5小题,共74分.解答应写出文字说明,证明过程或演算步骤.16.(本题满分14的正四棱锥P -ABCD 中,侧棱与底面所成角的大小为60°. (1)求侧棱的长度;(2)求正四棱锥P -ABCD 的外接球的表面积.第16题图 第17题图17.(本题满分15分)如图所示,在直三棱柱ABC -A 1B 1C 1中,AB =BC =AA 1=1,∠ABC=PDCBABCDAE90°. 点E 、F 分别是棱AB 、BB 1的中点. (1)求三棱锥B -AFC 的体积; (2)求异面直线EF 和BC 1所成的角.18.(本题满分15分)如图1,平面四边形 ABCD 关于直线AC 对称,2=CD ,60,90,A C ︒︒∠=∠=把ABD ∆沿BD 折 起(如图2)使二面角C BD A --的余弦值 为33.对于图2 (1)求AC 的长;(2)证明:⊥AC 平面BCD ;(3)求直线AC 与平面ABD 所成角的正弦值.第18题图19.(本题满分15分)如图,两矩形ABCD ,ABEF 所在平面互相垂直,DE 与平面ABCD 及平面ABEF 所成角分别为0030,45,N M ,分别为DB DE 、的中点,且1=MN . (1)求证:⊥MN 平面ABCD ; (2)求二面角B DE A --的正弦值.第19题图 第20题图20.(本题满分15分)如图,矩形ABCD 所在的半平面和直角梯形CDEF 所在的半平面 成60的二面角,.45,6,23,2,,// =∠===⊥CFE CF EF AD DE CD CF DE (1)求证:BF ∥平面ADE ;A CDB图1CABD图2FACB ED(2)试问在线段CF 上是否存在一点G ,使锐二面角D EG B --的余弦值为41.若存在,请求出CG 的值;若不存在,请说明理由.北仑中学2016学年第一学期高二年级期中考试数学参考答案(除高二4班以外的其它所有班级)一.选择题二.填空题9._____6______ ___6π____ 10.__圆台_____ ___3319π__ 11.______5_____ ____22___ 12.___ 31____ ____32+__13. 14. 822=+b a15. 12三.解答题16.(本题满分14分) (1)2 (2)316π17. (本题满分15分)PDCBA(1)1/12(2)318.(本题满分15分)解:(Ⅰ)取的中点,连接,由,得:就是二面角的平面角,在中,(Ⅱ)由,,又平面(Ⅲ)方法一:由(Ⅰ)知平面平面∴平面平面平面平面,作交于,则平面,就是与平面所成的角方法二:设点到平面的距离为,∵于是与平面所成角的正弦为.19. (本题满分15分)(1)证明:∵平面ABCD⊥平面ABEF,且平面ABCD∩平面ABEF=AB,EB ⊥AB,∴EB⊥平面ABCD,又MN∥EB,∴MN⊥面ABCD.(2)解:过B作BO⊥AE于O点,过O作OH⊥DE于H,连BH,∵AD⊥平面ABEF,BO面ABEF,∴BO⊥平面ADE,∴OH为BH在平面ADE内的射影,∴BH⊥DE,即∠BHO为所求二面角的平面角,在Rt△ABE中,BO=,在Rt△DBE中,由BH·DE=DB·OE得BH=,∴sin∠BHO= .MOGFACBEDHOH20. (本题满分15分)证明:(1)∵在矩形ABCD 中BC ∥AD , AD ⊂平面ADE BC ⊄平面ADE , ∴BC ∥平面ADE , 同理CF ∥平面ADE , 又∵BC∩CF=C , ∴平面BCF ∥平面ADE , 而BF ⊂平面BCF , ∴BF ∥平面ADE . (2)∵CD ⊥AD ,CD ⊥DE∴∠ADE 即为二面角A-CD-F 的平面角, ∴∠ADE=60° 又∵AD∩DE=D , ∴CD ⊥平面ADE , 又∵CD ⊂平面CDEF ∴平面CDEF ⊥平面ADE ,作AO ⊥DE 于O ,则AO ⊥平面CDEF .过O 作EH OH ⊥于H,连接BH,易得BHO ∠是锐二面角D EG B --的平面角 因为3=BO ,易求得55=OH 取CF 中点M,易知OHG ∆与EMG ∆相似,设x OG =(x>0),则EGEMOG OH =,即2)2(9355x x -+=,解得21=x 或2213-=x (舍)因此存在符合题意的点G,使得CG=23.。
河南省焦作市高二数学上学期期中试题 理(扫描版)

河南省焦作市2016-2017学年高二数学上学期期中试题理(扫描版)高二理科参考答案一、选择题DDBDD ADBDB CC 二、填空题13. 3|24x x ⎧⎫≤<⎨⎬⎩⎭14. (,8]-∞ 15. 216000 16. 三、解答题 17. (1) a n =2n -1,b n =1+3(n -1)=3n -2……………………………………………………4分(2)设数列{a n b n }的前n 项和为T n ,a n b n =(3n -2)·2n -1,∴T n =1·1+4·21+7·22+…+(3n -2)·2n -1.①∴2T n =1·21+4·22+7·23+…+(3n -5)·2n -1+(3n -2)·2n.②①-②得-T n =1·1+3·21+3·22+…+3·2n -1-(3n -2)·2n=1+3·2·(1-2n -1)1-2-(3n -2)·2n.整理得T n =(3n -5)·2n+5. ……………………………………10分18. .(Ⅰ)由频率分布直方图,可知:月用水量在[0,0.5]的频率为0.08×0.5=0.04.[来同理,在[0.5,1),(1.5,2],[2,2.5),[3,3.5),[3.5,4),[4,4.5)等组的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.由1–(0.04+0.08+0.20+.026+0.06+0.04+0.02)=0.5×a +0.5×a , 解得a =0.30. …………………………………………5分 (Ⅱ)设中位数为x 吨.因为前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73>0.5, 而前4组的频率之和为0.04+0.08+0.15+0.20=0.47<0.5所以2≤x <2.5. 由0.52×(x –2)=0.5–0.47,解得x ≈2.06.故可估计居民月均用水量的中位数为2.06吨. ……………………………9分 (Ⅲ)用水量在[0,0.5)的共有100⨯0.04=4人,设为A 、B 、C 、D ; 用水量在[4,4.5)的共有100⨯0.02=2人,设为a ,b ,从中选出两人共有(A,B ),(A,C),(A,D),(A,a),(A,b),(B,C),(B,D),(B,a),(B,b),(C,D),(C,a),(C,b),(D,a),(D,b),(a,b )共15种方法;其中都不是节水达人的只有一种,所以至少有一位节水达人的概率为1514.…………………………………………12分 19. (1) 取AP 的重点M ,因为E 为PB 中点,所以1//2ME AB ,又1//2DF AB所以//ME DF ,所以EG ∥DM ,所以EF//平面PAD ………………………………………5分(2)连接BH ,取BH 的中点G ,连接EG .因为E 是PB 的中点,所以EG ∥PH ,且EG =12PH =12.因为AB ⊥平面PAD ,PH ⊂平面PAD , 所以PH ⊥AB .因为PH 为△PAD 中AD 边上的高,所以PH ⊥AD . 因为AB ∩AD =A ,AB ,AD ⊂平面ABCD , 所以PH ⊥平面ABCD . 所以EG ⊥平面ABCD .因为AB ⊥平面PAD ,AD ⊂平面PAD , 所以AB ⊥AD ,所以底面ABCD 为直角梯形, 从而△BCF 以CF 为底边的高为AD ,所以V E-BCF =13S △BCF ·EG =13·12·FC ·AD ·EG =. ……………………………………12分20.解:(Ⅰ)曲线162+-=x x y 与y 轴的交点为(0,1),与x 轴的交点为().0,223(),0,223-+故可设C 的圆心为(3,t ),则有,)22()1(32222t t +=-+解得t =1.则圆C 的半径为.3)1(322=-+t所以圆C 的方程为.9)1()3(22=-+-y x ………………………………5分 (Ⅱ)设A (11,y x ),B (22,y x ),其坐标满足方程组:⎪⎩⎪⎨⎧=-+-=+-.9)1()3(,022y x a y x 消去y ,得到方程.012)82(222=+-+-+a a x a x ………………………………7分由已知可得,判别式2561640.a a ∆=-->21212214,2a a x x a x x -++=-=.①由于OA ⊥OB ,可得12120x x y y +=. 又,,2211a x y a x y +=+= 所以.0)(222121=+++a x x a x x②由①,②得1-=a ,满足,0>∆故.1-=a ………………………………12分∴)(x f 的最小正周期为π2. ………………………………………….4分所以)(x f 的值域为分 (2)由(1)可知分1112分22. 试题解析:(Ⅰ)设公差为d ,由已知得⎩⎨⎧+=+=+)6()2(,146411211d a a d ad a 解得1=d 或0=d (舍去), 21=∴a ,故1+=n a n . …………………………………… 4分…………………………………… 6分8分 1+≤n na T λ ,,即λ的最小值为……………………………………12分。
河南省焦作市高二上学期期中数学试卷(理科)

河南省焦作市高二上学期期中数学试卷(理科)姓名:________班级:________成绩:________一、 选择题 (共 12 题;共 24 分)1. (2 分) 设 和 为双曲线 的三个顶点,则双曲线的离心率为 ( )的两个焦点, 若 , ,是正三角形A.B. C.2 D.3 2. (2 分) (2020·宝鸡模拟) 已知直线 y=k(x+1)(k>0)与抛物线 C 焦点,若|FA|=2|FB|,则|FA| =( ) A.1 B.2 C.3 D.4相交于 A , B 两点,F 为 C 的3. (2 分) (2018 高二上·桂林期中) 设为实数,则“A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件4. (2 分) (2018·衡阳模拟) 下列说法正确的是( )A . 命题“若,则.”的否命题是“若第 1 页 共 18 页”是“”的( ),则.”B.是函数C.在定义域上单调递增的充分不必要条件D . 若命题,则5. (2 分) (2019 高二上·延吉期中) 下列有关命题的说法正确的是( )A . 命题“若,则”的否命题为:“若则”B.为假命题,则均为假命题C . 命题“若 D . 命题“若成等比数列,则”的逆命题为真命题,则”的逆否命题为真命题6. (2 分) (2019 高二上·西安月考) 长方体中中点,则异面直线与 所成角的余弦值为( ),为的A. B.C.D. 7. (2 分) (2018 高三上·南阳期末) 已知双曲线 的一条渐近线的方程是:过点,则双曲线 的方程是( )第 2 页 共 18 页,且该双曲线 经A.B. C.D. 8. (2 分) (2018 高二上·哈尔滨期中) 过抛物线 不同的两点 、 ,则弦长 的值为( ) A. B.的焦点 ,且倾斜角为的直线交抛物线于C. D.9. (2 分) (2018 高二下·沈阳期中) 若向量 为( ),,,则实数 的值A. B.C. D.10. (2 分) 双曲线的一个焦点坐标为, 则双曲线的渐近线方程为( )A.B.C.第 3 页 共 18 页D.11. (2 分) (2017 高二下·汪清期末) 如图,长方形的面积为 1,将 100 个豆子随机地撒在长方形内,其中 恰好有 20 个豆子落在阴影部分,则用随机模拟的方法可以估计图中阴影部分的面积为( )A. B. C. D.12. (2 分) 过原点的直线与双曲线(a>0,b>0)交于 M,N 两点,P 是双曲线上异于 M,N 的一点,若直线 MP 与直线 NP 的斜率都存在且乘积为 , 则双曲线的离心率为( )A.B.C. D.2二、 填空题 (共 4 题;共 4 分)13. (1 分) 已知到直线 AB 中点的距离为 3,其中 A(3,5,-7)、B(-2,4,3),则 z=________.14. (1 分) (2017 高一上·长宁期中) 命题“如果 x>2 且 y>2,那么 x+y>4”的否命题是________.15. (1 分) (2015 高二上·菏泽期末) 设抛物线 C:y2=2x 的焦点为 F,直线 l 过 F 与 C 交于 A,B 两点,若 |AF|=3|BF|,则 l 的方程为________.16. (1 分) (2015 高二上·宝安期末) 已知命题 p:∀ x∈R,x2+1>m;命题 q:指数函数 f(x)=(3﹣m)x第 4 页 共 18 页是增函数.若“p∧q”为假命题且“p∨q”为真命题,则实数 m 的取值范围为________.三、 解答题 (共 6 题;共 55 分)17. (10 分) (2016 高二上·沭阳期中) 某校举行“青少年禁毒”知识竞赛网上答题,高二年级共有 500 名 学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了 100 名学生的成绩进行统计.请你解答下列问题:(1) 根据下面的频率分布表和频率分布直方图,求出 a+d 和 b+c 的值;(2) 若成绩不低于 90 分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人?分组 频数 频率[60,70) 100.1[70,80) 220.22[80,90) a0.38[90,100] 30c合计100d18. (10 分) (2020·聊城模拟) 已知椭圆 上的点到点 F 的距离的最小值与最大值的积为 1,圆的长轴长为 4,右焦点为 F,且椭圆 C与 轴交于两点.(1) 求椭圆 C 的方程;(2) 动直线 的面积乘积的取值范围.与椭圆 C 交于两点,且直线 l 与圆 O 相切,求的面积与19. (10 分) (2019 高二上·集宁月考) 已知双曲线的中心在原点,焦点且过点.第 5 页 共 18 页在坐标轴上,离心率为 ,(1) 求双曲线的方程;(2) 若点在双曲线上,求的面积.20. (10 分) (2019 高二下·宝山期末) 如图,在 正半轴上的 点有一只电子狗,B 点有一个机器人,它们运动的速度确定,且电子狗的速度是机器人速度的两倍,如果同时出发,机器人比电子狗早到达或同时到达某点,那么电子狗将被机器人捕获,电子狗失败,这一点叫失败点,若.(1) 求失败点组成的区域; (2) 电子狗选择 正半轴上的某一点 ,若电子狗在线段 上获胜,问点 应在何处?21. (5 分) (2019 高二上·北京期中) 已知椭圆为.(Ⅰ)求椭圆 C 的标准方程;长轴是短轴的 倍,且右焦点(Ⅱ)直线 的面积.交椭圆 于两点,若线段 中点的横坐标为,求直线 的方程及22. (10 分) (2017 高二上·中山月考) 已知椭圆 C: , 的距离的和是 6.( ) 上一点 到它的左右焦点(1) 求椭圆 C 的离心率的值;(2) 若轴,且 在 轴上的射影为点 ,求点 的坐标.第 6 页 共 18 页一、 选择题 (共 12 题;共 24 分)答案:1-1、 考点:参考答案解析: 答案:2-1、 考点: 解析:第 7 页 共 18 页答案:3-1、 考点:第 8 页 共 18 页解析:答案:4-1、 考点: 解析:答案:5-1、 考点: 解析:答案:6-1、 考点: 解析:第 9 页 共 18 页答案:7-1、 考点: 解析:答案:8-1、 考点: 解析:第 10 页 共 18 页答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共55分)答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、考点:解析:答案:22-1、答案:22-2、考点:解析:。
河南省焦作市高二上学期期中数学试卷

河南省焦作市高二上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共8题;共16分)1. (2分)“过点的直线与双曲线有且仅有一个公共点”是“直线的斜率的值为”的()A . 充分必要条件B . 充分但不必要条件C . 必要但不充分条件D . 既不充分也不必要条件2. (2分) (2017高一下·长春期末) 如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的体积是()A .B .C .D .3. (2分)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为()A . 10B . 12C . 14D . 164. (2分)对于两条不相交的空间直线a和b,必定存在平面,使得()A .B .C .D .5. (2分)如图,在正方体ABCD﹣A1B1C1D1中,若平面A1BCD1上一动点P到AB1和BC的距离相等,则点P 的轨迹为()A . 椭圆的一部分B . 圆的一部分C . 一条线段D . 抛物线的一部分6. (2分)已知m,n是两条不同的直线,是两个不同的平面,则下列命题中的真命题是()A . 若,则B . 若,则C . 若,则D . 若,则7. (2分)已知四棱锥P﹣ABCD的底面是正方形,PA⊥底面AC,PA=2AD=2,则它外接球表面积为()A . πB . 6πC . πD . π8. (2分)下图中属于棱柱的有()A . 2个B . 3个C . 4个D . 5个二、填空题 (共7题;共7分)9. (1分) (2018高一下·长阳期末) 下列命题正确的是________.①每条直线都有唯一一个倾斜角与之对应,也有唯一一个斜率与之对应;②倾斜角的范围是: ,且当倾斜角增大时,斜率不一定增大;③直线过点,且横截距与纵截距相等,则直线的方程一定为;④过点 ,且斜率为1的直线的方程为 .10. (1分) (2016高二上·江阴期中) 已知一个球与一个正三棱柱的三个侧面和两个底面都相切,若这个球的表面积为12π,则这个正三棱柱的体积为________.11. (1分) (2018高二下·赤峰期末) 在直三棱柱中, .有下列条件:① ;② ;③ .其中能成为的充要条件的是________.(填上序号)12. (1分)三棱锥P﹣ABC中,平面PAC⊥平面ABC,PA=PC=AB=2, AC=4,∠BAC=30°.若三棱锥P﹣ABC 的四个顶点都在同一球面上,则该球的表面积为________13. (1分) (2016高二下·泰州期中) 设异面直线l1 , l2的方向向量分别为 =(1,1,0), =(1,0,﹣1),则异面直线l1 , l2所成角的大小为________.14. (1分)(2017·山东) 由一个长方体和两个圆柱体构成的几何体的三视图如图,则该几何体的体积为________.15. (1分)(2017·奉贤模拟) 如图,一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边成为1,那么这个几何体的表面积是________.三、解答题 (共5题;共40分)16. (5分)(2017·桂林模拟) 如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且.(Ⅰ)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面ECF平行,要求保留作图痕迹,但不要求证明.(Ⅱ)求直线EB与平面ECF所成角的正弦值.17. (10分)(2020·晋城模拟) 在直角坐标系中,曲线的参数方程为(为参数),以坐标原点为极点,以轴正半轴为极轴,建立极坐标系,直线的极坐标方程为 .(1)求的普通方程和的直角坐标方程;(2)直线与轴的交点为,经过点的直线与曲线交于两点,若,求直线的倾斜角.18. (10分)(2018高二下·孝感期中) 如图,四边形是矩形,四边形是梯形,,平面平面,,点是的中点.(1)求证:∥平面;(2)求二面角的余弦值.19. (10分) (2016高二上·黑龙江期中) 如图,在棱长为3的正方体ABCD﹣A1B1C1D1中,A1E=CF=1.(1)求两条异面直线AC1与D1E所成角的余弦值;(2)求直线AC1与平面BED1F所成角的正弦值.20. (5分)(2017·仁寿模拟) 如图,在四棱锥P﹣ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.(Ⅰ)若 AF=1,求证:CE∥平面 BDF;(Ⅱ)若 AF=2,求平面 BDF 与平面 PCD所成的锐二面角的余弦值.参考答案一、选择题 (共8题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共7题;共7分)9-1、10-1、11-1、12-1、13-1、14-1、15-1、三、解答题 (共5题;共40分)16-1、17-1、17-2、18-1、18-2、19-1、19-2、。
河南省焦作市高二上学期期中数学试卷(理科)

河南省焦作市高二上学期期中数学试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2020高二上·青铜峡期末) 已知数列是无穷数列,则“ ”是“数列为等差数列”的()A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件2. (2分)命题“,”的否定为()A . ,B . ,C . ,D . ,3. (2分) (2016高三上·日照期中) 下列说法正确的是()A . “x2+x﹣2>0”是“x>1”的充分不必要条件B . “若am2<bm2 ,则a<b”的逆否命题为真命题C . 命题“∃x∈R,使得2x2﹣1<0”的否定是“∀x∈R,均有2x2﹣1>0”D . 命题“若x= ,则tanx=1”的逆命题为真命题4. (2分) (2016高一下·仁化期中) 已知a、b为直线,α,β,γ为平面,有下列四个命题:①a∥α,b∥α,则a∥b②α⊥β,β⊥γ,则α∥β③a∥α,a∥β,则α∥β④a∥b,b⊂α,则a∥α其中正确命题的个数是()A . 0B . 1C . 2D . 35. (2分)命题“对任意x∈R,都有x2≥0”的否定为()A . 对任意x∈R,使得x2<0B . 不存在x∈R,使得x2<0C . 存在x0∈R,都有D . 存在x0∈R,都有6. (2分) (2016高二上·郑州期中) 已知命题p:1∈{x|(x+2)(x﹣3)<0},命题q:∅={0},则下面判断正确的是()A . p假q真B . “p∨q”为真C . “p∧q”为真D . “¬q”为假7. (2分)(2017·山西模拟) 已知F1 , F2分别是椭圆mx2+y2=m(0<m<1)的左、右焦点,P为椭圆上任意一点,若的最小值为,则椭圆的离心率是()A .B .C .D .8. (2分)(2018·石嘴山模拟) 已知双曲线的左、右焦点分别为,以为直径的圆与双曲线渐近线的一个交点为,则双曲线的方程为()A .B .C .D .9. (2分)(2016·铜仁) 以双曲线的焦点为顶点,顶点为焦点的椭圆标准方程为()A .B .C .D .10. (2分)(2018·南宁模拟) 抛物线的焦点F已知点A和B分别为抛物线上的两个动点.且满足,过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则的最大值为()A .B .C .D .11. (2分)若直线y=kx+1与圆x2+y2+kx﹣y﹣9=0的两个交点恰好关于y轴对称,则k等于()A . 0B . 1C . 2D . 312. (2分) (2017高三上·红桥期末) 已知双曲线﹣ =1(a>0,b>0)的两条渐近线与抛物线y2=2px (p>0)的准线分别交于O、A、B三点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为,则p=()A . 1B .C . 2D . 3二、填空题 (共4题;共4分)13. (1分) (2019高二上·兴庆期中) 过抛物线的焦点作直线与抛物线交于两点,当此直线绕焦点旋转时,弦中点的轨迹方程为________.14. (1分) (2017高三下·赣州期中) 点P在双曲线﹣ =1(a>0,b>0)的右支上,其左、右焦点分别为F1 , F2 ,直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 ,则该双曲线的渐近线的斜率为________.15. (1分)过点(,0)引直线l与曲线y= 相交于A,B两点,则直线l斜率的取值范围是________.16. (1分) (2015高二下·双流期中) 如图,椭圆的中心在坐标原点,F为左焦点,A、B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“优美椭圆”;类比“优美椭圆”,可推出“优美双曲线”的离心率为________.三、解答题 (共6题;共50分)17. (10分) (2018高二上·哈尔滨月考) 一动圆与圆外切,与圆内切.(1)求动圆圆心的轨迹的方程.(2)设过圆心的直线与轨迹相交于两点,(为圆的圆心)的内切圆的面积是否存在最大值?若存在,求出这个最大值及直线的方程,若不存在,请说明理由.18. (5分)已知p:2x2﹣3x+1≤0,q:x2﹣(2a+1)x+a(a+1)≤0(1)若a=,且p∧q为真,求实数x的取值范围.(2)若p是q的充分不必要条件,求实数a的取值范围.19. (5分) (2017高三上·张家口期末) 已知M是直线l:x=﹣1上的动点,点F的坐标是(1,0),过M的直线l′与l垂直,并且l′与线段MF的垂直平分线相交于点N(Ⅰ)求点N的轨迹C的方程(Ⅱ)设曲线C上的动点A关于x轴的对称点为A′,点P的坐标为(2,0),直线AP与曲线C的另一个交点为B(B与A′不重合),直线P′H⊥A′B,垂足为H,是否存在一个定点Q,使得|QH|为定值?若存在,求出点Q 的坐标;若不存在,请说明理由.20. (10分)(2017·包头模拟) 已知F1、F2分别是椭圆C: +y2=1的左、右焦点.(1)若P是第一象限内该椭圆上的一点,• =﹣,求点P的坐标;(2)设过定点M(0,2)的直线l与椭圆交于不同的两点A,B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.21. (10分)已知圆C:x2+y2+2x-4y+3=0.(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程.①当切线在两坐标轴上的截距为零时,设切线方程为y=kx,则,解得k=2± ,从而切线方程为y=(2± )x.②当切线在两坐标轴上的截距不为零时,设切线方程为x+y-a=0,则,解得a=-1或3,从而切线方程为x+y+1=0或x+y-3=0.综上,切线方程为(2+)x-y=0或(2-)x-y=0或x+y+1=0或x+y-3=0(2)点P在直线l:2x-4y+3=0上,过点P作圆C的切线,切点记为M,求使|PM|最小的点P的坐标.22. (10分) (2017高二上·江苏月考) 已知椭圆:的离心率为,其中左焦点为.(1)求椭圆的方程;(2)若直线与椭圆交于不同的两点、,且线段的中点在圆上,求的值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共50分)17-1、17-2、18-1、20-1、20-2、21-1、21-2、22-1、22-2、。
河南省焦作市2017届高三上学期期中考试(图片)——数学

参考答案D(13) 1 (14)(15) 39 (16)三、解答题(17)解:(Ⅰ)设等差数列的的公差为,则由,知∴()61228n a n n =-+-⨯=- ┈┈┈┈┈┈┈3分设等比数列的的公比为,则由,得,∴,或,又∵为等比数列,∴∴,∴┈┈┈┈7分(Ⅱ)212311111114121132232k k k k S b b b b -⎛⎫⎛⎫⎛⎫=++++=++++=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ∴, 又∵∴不存在正整数,使得数列的前项和大于┈┈┈┈12分(18)解:(Ⅰ)如图,在 内过点作于点,由四边形为等腰梯形,111=4=2BC B C C C =,,所以,,在中,知,所以 ,可得,所以,又因,11BCC B ABCD ⊥平面平面,11BCC B ABCD BC =平面平面,所以,因为 所以,又因, 所以┈┈┈┈┈5分(Ⅱ)延长知相交于一点,记该点为,取中点,在四棱台中, ,又因11BCC B ABCD ⊥平面平面,所以,取中点,知,且,所以以为坐标原点,向量的方向分别为轴,轴,轴的正方向,建立空间直角坐标系,则()()()(3,2,0,0,2,0,0,2,0,A B C P -- , 所以()()()10,3,3,3,2,23,0,4,0BC PA AD BC =-=--==-设平面的法向量为,则 00n PA n AD ⎧∙=⎪⎨∙=⎪⎩,得000032040x y y ⎧--=⎪⎨-=⎪⎩,可取 所以11121cos ,14n BC n BC n BC ∙== 故直线与平面所成的角的正弦值为┈┈┈┈┈12分(19)解:(Ⅰ)因为国庆节当日客流量超过5万人的概率为所以未来连续3年国庆节当日中,恰好有年国庆节当日客流量超过5万人的概率为 ┈┈┈┈┈3分(Ⅱ)当投入1艘游船时,因客流量总大于1所以当投入2艘游船时,若,则,此时()521132105P Y P X ⎛⎫==<<== ⎪⎝⎭ 若X≥3,则,此时 54)5()53()6(=+≤≤== X P X P Y P 故()51453625510E Y =⨯+⨯= ┈┈┈┈┈7分 当投入3艘游船时,若,则若,则,若,则此时的分布列如下表此时()12952555EY =⨯+⨯+⨯= 由于所以该水面游览中心在国庆节当日应投入艘游船可使该水面游览中心在国庆节当日效益最佳. ┈┈┈┈┈12分(20)解:(Ⅰ)设动圆圆心的坐标为则,=,可知所以动圆圆心的轨迹的方程 ┈┈┈┈┈4分(Ⅱ)直线的斜率一定存在,设的方程为,由2214y kx y x =-⎧⎪⎨=-⎪⎩,得,设两点的坐标分别为, 则12124,8x x k x x +=-=-,设直线方程为,由112y yy x x =⎧⎪⎨=⎪⎩,得的横坐标 同理得的横坐标,所以()12128C D x x CD x x x x -=-== (11112242S CD y kx =-=-(2224S kx =- ())(21212882S S k x x k +=-+=+ ┈┈┈┈┈10分令,则)231228S S k t +=+=令,则,时,所以是的增函数,所以()f t f =…即的最小值为 ┈┈┈┈┈12分(21)解:(Ⅰ),由,得,此时在为增函数,在为减函数,所以在时存在极大值.所以.┈┈┈┈┈3分(Ⅱ)当,时,当时由(Ⅰ)知,,,所以,,显然不成立.故,此时,当时,可转化为,()1ln 10bx b x x --+-< 令()()11ln 1g x bx b x x =--+-,则()'11ln 1b g x b x b x+=+-+ 令,则()'222111b x b b b g x x x x ⎛⎫++ ⎪+⎝⎭=+= ①若,当时,得所以为上的增函数,故存在,使与相矛盾,故时,不能使成立;②若,当时,1110,(1)0x b x b b++>++<,即,得, 所以为上的减函数,故所以成立,综上所述,实数的取值范围是.┈┈┈┈┈12分(22)解:证明:(Ⅰ)如图, 设与交于点, 则,,CFE CDF DCF ∠=∠+∠DEC EDA ∠=∠+∠又因为圆的切线,所以,又因为的平分线,所以,所以即,,所以为等腰三角形,又因为的平分线,所以,即┈┈┈┈┈5分(Ⅱ)因为圆的切线,所以 ,又因为的平分线,所以,所以即.┈┈┈┈┈10分(23)解:(Ⅰ)曲线的普通方程为化为极坐标方程为┈┈┈┈┈5分 (Ⅱ)由,得cos 0ρθθ+=化为直角坐标方程为,由()2222140x y x y x ⎧-+=⎪⎨+++=⎪⎩得0,x y =⎧⎪⎨=⎪⎩ 化为极坐标为或.┈┈┈┈┈10分(24)解:(Ⅰ) 由得可化为,111144,,771414121444x x x x x x ⎧⎧≥≤<<⎧⎪⎪⎪⎪⎪⎨⎨⎨-<⎪⎪⎪-<+<⎩⎪⎪⎩⎩或或 得,所以的解集为┈┈┈┈┈┈┈6分 (Ⅱ)因为 所以3)(2222=++≥+++++c b a c ca b b c a a b 所以┈┈┈┈┈┈┈10分。
河南省焦作市高二数学上学期第二次月考试题 理(1)

河南省焦作市2016-2017学年高二数学上学期第二次月考试题 理(时间:120分钟 满分:150分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.命题:若a >0,则a 2>0的逆命题为( )A .若a >0,则a 2≤0 B .若a 2>0,则a >0 C .若a ≤0,则a 2>0D .若a ≤0,则a 2>02.设点B (-4,0),C (4,0),若△ABC 的周长为18,则动点A 的轨迹方程是( )A.x 225+y 29=1(y ≠0) B.y 225+x 29=1(y ≠0) C.x 225+y 216=1(x ≠0) D.y 216+x 29=1(x ≠0) 3.在△ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,则“a ≤b ”是“sin A ≤sin B ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知1F 、2F 是椭圆2221x a b2y +=(a>b>0)的两个焦点,以线段1F 2F 为边作正三角形M 1F 2F ,若边M 1F 的中点在椭圆上,则椭圆的离心率是A B 1 C D 1 5.命题“∃x 0∈R,2x 0-3>1”的否定是( )A .∃x 0∈R,2x 0-3≤1B .∀x ∈R,2x -3>1C .∀x ∈R,2x -3≤1D .∃x 0∈R,2x 0-3>16.曲线192522=+y x 与曲线)9(192522<=-+-k ky k x 的()A . 长轴长相等B . 短轴长相等 C.离心率相等 D. 焦距相等 7.抛物线y =ax 2的准线方程是y =2,则a 的值为( )A .18B .-18C .8 D .-88.正三角形的一个顶点位于原点,另外两个顶点在抛物线)0(22>=p px y 上,则这个正三角形的边长是()A.p )23(2+B.p )32(2—C.p p )32(2)23(2—或+D. p 349.已知椭圆C 的方程为x 216+y 2m 2=1(m >0),如果直线y =22x 与椭圆的一个交点M 在x 轴上的射影恰好为椭圆的右焦点F ,则m 的值为( )A .1 B. 2 C .2D .2 210.已知F 1(-3,0),F 2(3,0)是椭圆x 2m +y 2n=1的两个焦点,点P 在椭圆上,∠F 1PF 2=α.当α=2π3时,△F 1PF 2面积最大,则m +n 的值是( )A .41B .15C .9D .111.若直线m x y +-=与曲线2415x y -=只有一个公共点,则m 的取值范围是( ) A. 22m -≤< B .5252≤≤-m C .522=<≤-m m 或 D .55252=<≤-m m 或12.如图,在正三棱柱ABC —A 1B 1C 1中,若AB =2BB 1,则AB 1与C 1B 所成角的大小为( )A .60°B .90°C .105°D .75°二、填空题(本大题共4个小题,每小题4分,共16分,将正确答案填在题中横线上)13. 过点P (-2, -4)的抛物线的标准方程为___________14.方程22sin cos 1,0,x y αααπ-=<<表示焦点在y 轴上的椭圆,则α的取值范围是___________15.已知正四棱锥的体积为12,底面对角线的长为26,则侧面与底面所成的二面角等于________.16.椭圆x 2a 2+y 2b2=1(a >b >0)的右顶点是A (a,0),其上存在一点P ,使∠APO =90°,椭圆离心率的取值范围是________三、解答题(本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)给定两个命题,p :对任意实数x 都有2x +ax +1>0恒成立;q :函数y =log a x (a>0且a ≠1)为增函数,若p 假q 真,求实数a 的取值范围.18..(本小题满分12分)在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC ⊥BC ,AC =BC =BD =2AE ,M 是AB 的中点,建立适当的空间直角坐标系,解决下列问题:(1)求证:CM ⊥EM ;(2)求CM 与平面CDE 所成角的大小.19.(本小题满分12分)设递增等比数列{n a }的前n 项和为n S ,且2a =3,3S =13,数列{n b }满足1b =1a ,点P (n b ,1n b +)在直线x -y +2=0上,n ∈N ﹡. (Ⅰ)求数列{n a },{n b }的通项公式; (Ⅱ)设n c =nnb a ,数列{nc }的前n 项和n T ,若n T >2a -1恒成立(n ∈N ﹡),求实数a 的取值范围.20.(本小题满分12分)已知点P 是圆O :x 2+y 2=9上的任意一点,过P 作PD 垂直x 轴于D ,动点Q 满足DQ =23DP .(1)求动点Q 的轨迹方程;(2)已知点E (1,1),在动点Q 的轨迹上是否存在不重合的两点M ,N ,使OE =12(OM +ON )(O 是坐标原点),若存在,求出直线MN 的方程,若不存在,请说明理由.21.(本小题满分12分)如图,在四棱柱ABCD -A 1B 1C 1D 1中,侧棱A 1A ⊥底面ABCD ,AB ⊥AC ,AB =1,AC =AA 1=2,AD =CD =5,且点M 和N 分别为B 1C 和D 1D 的中点.(1)求证:MN ∥平面ABCD ; (2)求二面角D 1-AC -B 1的正弦值;(3)设E 为棱A 1B 1上的点.若直线NE 和平面ABCD 所成角的正弦值为13,求线段A 1E 的长.22.(本小题满分12分)已知椭圆的中心在坐标原点O ,长轴长为,离心率e, 过右焦点F 的直线l 交椭圆于P 、Q 两点. (Ⅰ)求椭圆的方程;(Ⅱ)若OP 、OQ 为邻边的平行四边形是矩形,求满足该条件的直线l 的方程.2016—2017学年高二上期第二次月考理科数学 参考答案一、选择题:本大题12个小题,每小题5分,共60分二、填空题(本大题共4个小题,每小题5分,共20分) 13.28y x =-或2x y =-14 3.24ππα∴<<;15π3; 16. ∴22<e <1.17题解:对任意实数x 都有012>++ax x 恒成立,则042<-=∆a ;即22<<-a .……………………………………3分 函数x y a log =,(1a 0≠>且a )为则增函数,所以1>a . …………………………6分因为p 假q 真,所以22,1,a a a ≤-≥⎧⎨>⎩或………………………8分∴2≥a . …………………………10分18.(12分)解:(1)证明:分别以CB ,CA 所在直线为x ,y 轴,过点C 且与平面ABC 垂直的直线为z 轴,建立如图所示的空间直角坐标系.设AE =a ,则M (a ,-a,0),E (0,-2a ,a ),D (2a,0,2a ),所以CM =(a ,-a,0),EM =(a ,a ,-a ),所以CM ·EM =a ×a +(-a )×a +0×(-a )=0, 所以CM ⊥EM .(2)CE =(0,-2a ,a ),CD =(2a,0,2a ), 设平面CDE 的法向量n =(x ,y ,z ),则有⎩⎪⎨⎪⎧-2ay +az =0,2ax +2az =0,即⎩⎪⎨⎪⎧z =2y ,x =-z ,令y =1,则n =(-2,1,2),cos 〈CM ,n 〉=CM ·n|CM ||n |=a -+-a +0×22a ×3=-22,所以直线CM 与平面CDE 所成的角为45°.19. 解:(Ⅰ)由231233,13,a S a a a =⎧⎨=++=⎩可得313或=q ,因为数列{}n a 为递增等比数列,所以3=q ,11=a .故{}n a 是首项为1,公比为3的等比数列.所以13n n a -=.…………3分 由点1(,)n n P b b +在直线20x y -+=上,所以12n n b b +-=.则数列{}n b 是首项为1,公差为2的等差数列.则1(1)221n b n n =+-⋅=-. ………5分(Ⅱ)因为1213n n n n b n c a --==,所以0121135213333n n n T --=++++. 则122111352321333333n n n n n T ---=+++++,………………………7分 两式相减得:211122222113333311[1()]2112133122().133313n n n n n n n n T n n ----=++++----=+⨯-=---…………8分 所以2112132323n n n n T ---=--⋅⋅1133n n -+=-. ………………………………9分,031231332311>+=++-+-=--+nn n n n n n n T T ∴11=≥T T n . 若12.->a T n 恒成立,则121->a ,∴1<a . ……………12分20解:(1)设P (x 0,y 0),Q (x ,y ),依题意,得点D 的坐标为D (x 0,0),DQ =(x -x 0,y ),DP =(0,y 0),又DQ =23DP ,∴⎩⎪⎨⎪⎧x -x 0=0,y =23y 0,即⎩⎪⎨⎪⎧x 0=x ,y 0=32y ,∵点P 在圆O 上,故x 20+y 20=9, ∴x 29+y 24=1,∴动点Q 的轨迹方程为x 29+y 24=1.(2)假设椭圆x 29+y 24=1上存在不重合的两点M (x 1,y 1),N (x 2,y 2)满足OE =12(OM +ON ),则E (1,1)是线段MN 的中点,且有⎩⎪⎨⎪⎧x 1+x22=1,y 1+y22=1,即⎩⎪⎨⎪⎧x 1+x 2=2,y 1+y 2=2,又M (x 1,y 1),N (x 2,y 2)在椭圆x 29+y 24=1上,∴⎩⎪⎨⎪⎧x 219+y 214=1,x 229+y 224=1,两式相减,得x 1-x 2x 1+x 29+y 1-y 2y 1+y 24=0,∴k MN =y 1-y 2x 1-x 2=-49, ∴直线MN 的方程为4x +9y -13=0,∴椭圆上存在点M ,N 满足OE =12(OM +ON ),此时直线MN 的方程为4x +9y -13=021.如图,以A 为原点建立空间直角坐标系,依题意可得A (0,0,0),B (0,1,0),C (2,0,0),D (1,-2,0),A 1(0,0,2),B 1(0,1,2),C 1(2,0,2),D 1(1,-2,2),又因为M ,N 分别为B 1C 和D 1D 的中点,得M ⎝⎛⎭⎪⎫1,12,1,N (1,-2,1).(1)依题意,可得n =(0,0,1)为平面ABCD 的一个法向量,MN ―→=⎝ ⎛⎭⎪⎫0,-52,0, 由此可得,MN ―→·n =0,又因为直线MN ⊄平面ABCD , 所以MN ∥平面ABCD .(2)AD 1―→=(1,-2,2),AC ―→=(2,0,0), 设n 1=(x 1,y 1,z 1)为平面ACD 1的法向量,则⎩⎪⎨⎪⎧n 1·AD ―→=0n 1·AC ―→=0,即⎩⎪⎨⎪⎧x 1-2y 1+2z 1=02x 1=0,不妨设z 1=1,可得n 1=(0,1,1),设n 2=(x 2,y 2,z 2)为平面ACB 1的一个法向量, 则⎩⎪⎨⎪⎧n 2·AB 1―→=0n 2·AC ―→=0,又AB 1―→=(0,1,2),得⎩⎪⎨⎪⎧y 2+2z 2=02x 2=0,不妨设z 2=1,可得n 2=(0,-2,1).因此有cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=-1010,于是sin 〈n 1,n 2〉=31010,所以二面角D 1-AC -B 1的正弦值为31010.(3)依题意,可设A 1E ―→=λA 1B 1―→,其中λ∈,则E (0,λ,2),从而NE ―→=(-1,λ+2,1),又n =(0,0,1)为平面ABCD 的一个法向量,由已知得cos 〈NE ―→,n 〉=NE ―→·n|NE ―→||n |=1-2+λ+2+12=13,整理得λ2+4λ-3=0, 又因为λ∈,解得λ=7-2, 所以线段A 1E 的长为7-2.22.解:(1)由已知,椭圆方程可设为()222210x y a b a b+=>>.∵长轴长为,离心率e =即2c a e a ===.∴1a b c ===.所求椭圆方程为2212x y +=. ………… 4分(2)当直线l 与x 轴垂直时,直线l 的方程为1x =,此时POQ ∠小于90,,OP OQ 为邻边的平行四边形不可能是矩形. ……………5分当直线l 与x 轴不垂直时,设直线l 的方程为()1y k x =-.由 ()2222,1,x y y k x ⎧+=⎪⎨=-⎪⎩ 可得()2222124220k x k x k +-+-=.∴由求根公式可得:2222,121222kk k x ++±=. ∴22121222422,1212k k x x x x k k-+==++.……………………7分 11(1)y k x =-,22(1)y k x =-.222121212122(1)(1)[()1]12k y y k x x k x x x x k -∴=--=-++=+. 因为以,OP OQ 为邻边的平行四边形是矩形,所以OP OQ ⊥, 所以.0=⋅.由021212222222121=+-++-=+=⋅kk k k y y x x ,得22k =,k ∴=. …………………………………………10分∴所求直线的方程为1)y x =-.………………1 2分。
河南省焦作市高二上学期期中数学试卷(理科)

河南省焦作市高二上学期期中数学试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2016高一上·包头期中) 三个数60.7 , 0.76 , log0.76的大小顺序是()A . 0.76<60.7<log0.76B . 0.76<log0.76<60.7C . log0.76<60.7<0.76D . log0.76<0.76<60.72. (2分)已知等差数列{an}中,an=﹣3n+1,则首项a1和公差d的值分别为()A . 1,﹣3B . ﹣2,﹣3C . 2,3D . ﹣3,13. (2分)数列前n项和为,已知,且对任意正整数,都有,若恒成立,则实数的最小值为()A .B .C .D . 44. (2分) (2016高一下·定州期末) 在△ABC中,内角A,B,C所对的边分别为a,b,c,若b2+c2=2,则△ABC的面积的最大值为()A .B .C .D . 15. (2分) (2019高二上·城关期中) 在△ABC中,角A、B、C所对的边分别为a、b、c,若acosA=bcosB,则△ABC的形状为()A . 等腰三角形B . 直角三角形C . 等腰三角形或直角三角形D . 等腰直角三角形6. (2分) (2017高三上·长沙开学考) 已知等差数列{an}的前n项和为Sn ,若a4+a12﹣a8=8,a10﹣a6=4,则S23=()A . 23B . 96C . 224D . 2767. (2分)不等式的解集为()A . {x|或}B .C . {x|或}D .8. (2分)设变量x,y满足约束条件,则目标函数的最大值和最小值分别为()A .B .C .D .9. (2分)已知等比数列{an}中,a3a11=4a7 ,数列{bn}是等差数列,且b7=a7 ,则b5+b9等于()A . 2B . 4C . 8D . 1610. (2分) (2019高一上·台州期中) 若函数,,则函数的值域()A . [4,5]B . [4,]C . [,5]D . [1,3]11. (2分)在各项均为正数的等比数列中,若,则()A . 12B . 10C . 15D .12. (2分) (2016高一下·南平期末) 已知Sn为等差数列{an}的前n项和,a1=﹣1,S4=14,则a4等于()A . 2B . 4C . 6D . 8二、填空题 (共4题;共4分)13. (1分) (2016高二上·洛阳期中) 若实数x,y满足约束条件,则的最小值为________.14. (1分)等差数列{an},{bn}的前n项和分别为Sn、Tn ,若=,则=________15. (1分) (2016高二上·灌云期中) 已知直角三角形ABC中,∠C=90°,D为斜边AB上一点且D到两直角边AC,BC的距离分别为1和2,则三角形ABC的面积最小值为________.16. (1分)(2018·黄山模拟) 已知直线过点,若可行域的外接圆直径为20,则 ________.三、解答题 (共6题;共45分)17. (5分) (2017高一上·金山期中) 已知集合A={x|x2﹣px﹣2=0},B={x|x2+qx+r=0},若A∪B={﹣2,1,5},A∩B={﹣2},求p+q+r的值.18. (5分) (2017高三上·韶关期末) 设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13.(Ⅰ)求{an}、{bn}的通项公式;(Ⅱ)求数列的前n项和Sn .19. (10分)(2017·新课标Ⅰ卷文) 记Sn为等比数列{an}的前n项和.已知S2=2,S3=﹣6.(12分)(1)求{an}的通项公式;(2)求Sn,并判断Sn+1,Sn,Sn+2是否能成等差数列.20. (10分)(2020·阜阳模拟) 的内角,,的对边分别为,,,已知,点为边的中点,且 .(1)求;(2)若,求的面积.21. (5分) (2018高一下·攀枝花期末) 已知数列满足,.(Ⅰ)求数列的通项公式;(Ⅱ)设,求.22. (10分)某小区现有一块草坪ABCD呈平行四边形形状,AB=3,AD=2,∠BAD=60°,为了改善居民的生活环境,决定将原草坪扩建成三角形PAQ形状,点A,D,P共线,Q,C,P共线,A,B,Q共线,设AP=x,BQ=y.(1)求y关于x的函数关系式;(2)求△APQ面积最小值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共45分) 17-1、18-1、19-1、19-2、20-1、20-2、21-1、22-1、22-2、。
河南省焦作市高二上学期期中数学试卷

河南省焦作市高二上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共14分)1. (1分) (2016高一下·苏州期中) 在等差数列{an}中,当a2+a9=2时,它的前10项和S10=________.2. (1分)(2017·合肥模拟) 等比数列{an}满足an>0,且a2a8=4,则log2a1+log2a2+log2a3+…+log2a9=________.3. (1分)(2017·新课标Ⅱ卷理) 等差数列{an}的前n项和为Sn , a3=3,S4=10,则 =________.4. (1分)若三个数5+2, m,5﹣2成等比数列,则m=________5. (1分)若数列{an};满足:,则其前n 项和Sn=________6. (1分) (2017高一下·淮安期末) 已知{an}是等差数列,a1=1公差d≠0,Sn为其前n项的和,若a1 ,a2 , a5成等比数列,S10=________.7. (1分)单调递增数列数列{an}的通项公式为an=n2+bn,则实数b的取值范围为________.8. (1分) (2018高一下·长阳期末) 在如下数表中,已知每行、每列中的数都成等差数列,那么,位于下表中的第行第列的数是________.9. (1分)(2017·吉林模拟) 艾萨克•牛顿(1643年1月4日﹣1727年3月31日)英国皇家学会会长,英国著名物理学家,同时在数学上也有许多杰出贡献,牛顿用“作切线”的方法求函数f(x)零点时给出一个数列{xn}:满足,我们把该数列称为牛顿数列.如果函数f(x)=ax2+bx+c(a>0)有两个零点1,2,数列{xn}为牛顿数列,设,已知a1=2,xn>2,则{an}的通项公式an=________.10. (1分)在等差数列{an}中,Sn为其前n项和,若且A,B,C三点共线,则S2013=________.11. (1分) (2016高二上·嘉定期中) 用数学归纳法证明等式:1+a+a2+…+an+1= (a≠1,n∈N*),验证n=1时,等式左边=________.12. (1分) (2018高一下·重庆期末) 等比数列中,为其前项和,若,则实数的值为________.13. (1分) (2016高一下·惠阳期中) 已知数列{an}的前n项和Sn=n2+n+1,那么它的通项公式为an=________14. (1分) (2016高三上·湖北期中) 已知Sn为数列{an}的前n项和,若Sn=nan+1+2n ,则数列{ }的前n项和Tn=________.二、选择题 (共4题;共8分)15. (2分) (2018高一下·双鸭山期末) 在等差数列中,,则()A . 8B . 12C . 16D . 2016. (2分) (2019高二上·上海月考) 设等差数列前项和为,且满足,,则、、、、中,最大项为()A .B .C .D .17. (2分) (2016高三上·崇礼期中) 设等比数列{an}的前n项和为Sn ,若a1=3,a4=24,则S6=()A . 93B . 189C . 99D . 19518. (2分) (2016高二上·宝安期中) 已知等比数列{an}的前三项依次为a﹣2,a+2,a+8,则an=()A .B .C .D .三、解答题 (共5题;共35分)19. (10分) (2018高二下·湖南期末) 等比数列的各项均为正数,且, .(1)求数列的通项公式;(2)设,求数列的前项和 .20. (5分)(2018高二下·如东月考) 已知函数,对任意正整数,有,求方程的所有解.21. (10分) (2015高一上·腾冲期末) 某军工企业生产一种精密电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)= 其中x是仪器的月产量.(1)将利润表示为月产量的函数;(2)当月产量为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润.)22. (5分)(2017·泉州模拟) 在数列{an}中,a1=4,nan+1﹣(n+1)an=2n2+2n.(Ⅰ)求证:数列是等差数列;(Ⅱ)求数列的前n项和Sn .23. (5分)已知数列{an}的前n项和为Sn ,且an是Sn与2的等差中项,数列{an}中,b1=1,点P(bn ,bn+1)在直线x﹣y+2=0上.(Ⅰ)求数列{an},{bn}的通项公式an和bn;(Ⅱ)设cn=an•bn ,求数列{cn}的前n项和Tn .参考答案一、填空题 (共14题;共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、选择题 (共4题;共8分)15-1、16-1、17-1、18-1、三、解答题 (共5题;共35分) 19-1、19-2、20-1、21-1、21-2、22-1、23-1、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二理科参考答案
一、选择题
DDBDD
ADBDB CC
二、填空题13.3|24x x ⎧⎫≤<⎨⎬⎩⎭
14.(,8]-∞15.21600016.3
-三、解答题17.(1)a n =2n -
1,b n =1+3(n -1)=3n -2……………………………………………………4分(2)设数列{a n b n }的前n 项和为T n ,a n b n =(3n -2)·2n -
1,∴T n =1·1+4·21+7·22+…+(3n -2)·2n -
1.①∴2T n =1·21+4·22+7·23+…+(3n -5)·2n -
1+(3n -2)·2n .②①-②得-T n =1·1+3·21+3·22+…+3·2n -1-(3n -2)·2n
=1+3·2·(1-2n -1)1-2
-(3n -2)·2n .整理得T n =(3n -5)·2n +5.……………………………………10分18..(Ⅰ)由频率分布直方图,可知:月用水量在[0,0.5]的频率为0.08×0.5=0.04.[来
同理,在[0.5,1),(1.5,2],[2,2.5),[3,3.5),[3.5,4),[4,4.5)等组的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1–(0.04+0.08+0.20+.026+0.06+0.04+0.02)=0.5×a +0.5×a ,
解得a =0.30.…………………………………………5分
(Ⅱ)设中位数为x 吨.
因为前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73>0.5,
而前4组的频率之和为0.04+0.08+0.15+0.20=0.47<0.5
所以2≤x <2.5.由0.52×(x –2)=0.5–0.47,解得x ≈2.06.
故可估计居民月均用水量的中位数为2.06吨.……………………………9分
(Ⅲ)用水量在[0,0.5)的共有100⨯0.04=4人,设为A 、B 、C 、D ;用水量在[4,4.5)的共有100⨯0.02=2人,设为a ,b ,从中选出两人共有(A,B ),(A,C),(A,D),(A,a),(A,b),(B,C),(B,D),(B,a),(B,b),(C,D),(C,a),(C,b),(D,a),(D,b),(a,b )共15种方法;其中都不是节水达人的只有一种,所以至少有一位节水达人的概率为
1514.…………………………………………12分19.(1)取AP 的重点M ,因为E 为PB 中点,所以1//2ME AB ,又1//2
DF AB 所以//ME DF ,所以EG ∥DM ,所以EF//平面PAD ………………………………………5分
(2)连接BH ,取BH 的中点G ,连接EG .因为E 是PB 的中点,
所以EG ∥PH ,且EG =12PH =12
.因为AB ⊥平面PAD ,PH ⊂平面PAD ,
所以PH ⊥AB .
因为PH 为△PAD 中AD 边上的高,所以PH ⊥AD .
因为AB ∩AD =A ,AB ,AD ⊂平面ABCD ,
所以PH ⊥平面ABCD .
所以EG ⊥平面ABCD .
因为AB ⊥平面PAD ,AD ⊂平面PAD ,
所以AB ⊥AD ,所以底面ABCD 为直角梯形,
从而△BCF 以CF 为底边的高为AD ,
所以V E-BCF =13S △BCF ·EG =13·12
·FC ·AD ·EG
=.……………………………………12分20.解:(Ⅰ)曲线162+-=x x y 与y 轴的交点为(0,1),与x 轴的交点为().
0,223(),0,223-+故可设C 的圆心为(3,t ),则有,)22()1(32222t t +=-+解得t =1.则圆C 的半径为.
3)1(32
2=-+t 所以圆C 的方程为.9)1()3(22=-+-y x ………………………………5分(Ⅱ)设A (11,y x ),B (22,y x ),其坐标满足方程组:⎪⎩
⎪⎨⎧=-+-=+-.9)1()3(,022y x a y x 消去y ,得到方程.012)82(22
2=+-+-+a a x a x ………………………………7分由已知可得,判别式2561640.a a ∆=-->21212214,2
a a x x a x x -++=-=.①
由于OA ⊥OB ,可得12120x x y y +=.
又,
,2211a x y a x y +=+=所以.0)(222121=+++a x x a x x ②
由①,②得1-=a ,满足,0>∆故.1-=a ………………………………12分21.)3
sin(cos 23sin 216
sin sin 6cos cos sin )6cos(sin )()1(:.ππππ+=+=-+=++=x x x x x x x x x f 解∴)(x f 的最小正周期为π2.………………………………………….4分因为]65,3[3],2,0[ππππ∈+∈x x 所以,所以)(x f 的值域为[1,2
1].……7分(2)由(1)可知,23)3sin()3sin()(=+∴+
=ππA A A f 0A <<Q 3
433ππππ<+<∴A ,323ππ=+∴A 得到3π=A .………………………………………………9分3,2sin sin a b a b A B
==Q 11分
................................................................1sin sin 23
23=∴=∴B B b b 0B π<<Q 2
π=∴B ………………………………12分22.试题解析:(Ⅰ)设公差为d ,由已知得⎩⎨⎧+=+=+)
6()2(,146411211d a a d a d a 解得1=d 或0=d (舍去),21=∴a ,故1+=n a n .
……………………………………4分(Ⅱ)2
111)2)(1(111+-+=++=+n n n n a a n n ……………………………………6分
)
2(22121211141313121+=+-=+-+++-+-=∴n n n n n T n ………………………8分1+≤n n a T λ ,)2()2(2+≤+∴
n n n λ,2)2(2+≥n n λ,44212++⋅≥n n n λ即44121++⋅≥n n λ恒成立.…………………………………10分
161≥λ ,即λ的最小值为161.……………………………………12分。
