第五章 频率响应法5_1
第五章 放大电路的频率响应-new

1 ZC = jωC
C1
& Ib I& c
& Ib
V&O
前面分析, 前面分析 隔直电容 处理为:直流开路 交流短路 处理为 直流开路,交流短路 直流开路
f 1Hz 10Hz 100Hz 1kHz 10kHz
60 40
带宽 20 0 2
2. 频率响应的分析任务
20 fL
2× 102
2× 103
2× 104 fH
f/Hz
(1)频率响应表达式 AV = AV (ω )∠ϕ (ω ) )频率响应表达式: & 下限频率f (2)带宽 )带宽BW、上限频率 f H、下限频率 L 、
继续
3. AV随 f 变化的原因
继续
(1)高通电路:频率响应 )高通电路:
fL
& Uo jωRC & = Au = & U i 1 + jωRC
1 & = j f fL 令f L = ,则Au 2 πRC 1 + j f fL
f>>fL时放大 倍数约为1 倍数约为
f fL & Au = 1 + ( f f L )2 ϕ = 90° − arctan( f f L )
由于放大电路中耦合电容、旁路电容、 由于放大电路中耦合电容、旁路电容、半导体器 耦合电容 极间电容的存在 使放大倍数为频率的函数。 的存在, 件极间电容的存在,使放大倍数为频率的函数。
继续
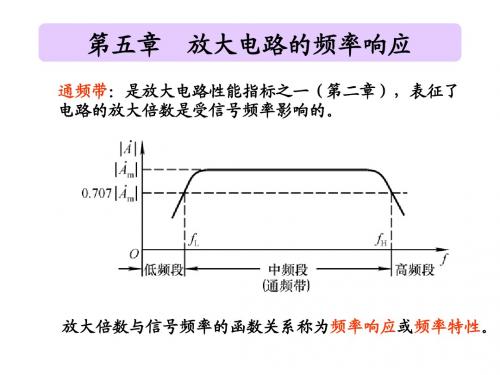
5.1 频率响应概述
频率响应——放大器的电压放大倍数 放大器的电压放大倍数 频率响应 与频率的关系
自动控制原理第五章

KT j 1 2T 2
0 : U(0) K
V (0) 0
1: T
:
U(1) K T2
U() 0
V(1) K T2
V() 0
●
●
K
●
0.707K
V(ω)
K/2 K
●
●
U(ω)
-K/2
●
10
3 由零、极点分布图绘制
1)在[s]上标出开环零极点;
G( j ) K K / T 1 jT j 1 / T
低频段 1
T
L( ) 20lg A( ) 20lg () arctgT 0
10
高频段
1
T
20lg A() 20lgT ( ) arctgT 900
转折频率 1
T
20lg A( ) 20lg 2 3.01 0db
( ) arctgT 450
15
20 0 -20 -40 -60 90 45 0 -45 -90
3) 振荡环节
1
G(s) (s / n )2 2 (s / n ) 1
n
1 T
0
4) 一阶微分 G(s) Ts 1 (T>0)
0 1
5) 二阶微分 G(s) (s / n )2 2 (s / n ) 1 (n 0, 0 1)
6) 纯滞后环节 G(s) e s
19
5-3-2 最小相位典型环节的频率特性
0.01
0.1
T
10
T
●
●
●
●
0.1
1/T1
10
T 0.1 () arctg0.1 5.70
T 1 ( ) arctg10 84.30
第五章 放大电路的频率响应
1 fH 2 RC
1 fL 2 RC
当信号频率等于上(下)限频率时,放大电路的 增益下降3dB,且产生±45°相移
近似分析时,可用折线化的波特图表示电路的频 率特性
一个电容对应的渐进线斜率为20dB/十倍频
简单 RC 电路的频率特性
Ui
•
R C
Uo
•
Ui
•
C R
Uo
•
RC 低通电路
RC 高通电路
Au
• |Au |
1 0.707
1 f 1 j fH
1 0.707
Au
1 fL 1 j f
|Au |
fL
f
•
O
fH f
f
O
O –45° –90°
90° 45° O
f
研究频率响应的方法 (1) 三个频段的划分 1) 中频区(段) 特点:Aus与f无关
与f无关
5.4 单管放大电路的频率响应
本节以单管共射电路为例,介绍频率响应的一般 分析方法。
5.4.1 单管共射放大电路的频率响应
1、画出全频段的微变等效电路
+VCC RB C1 + . Ui VT RL . Uo RC C2 + + . Ui _ RB rb′e
C1
rbb′ . gmUb'e Cπ′
C2 + RC . RL U o _
R
fL
L 1 1 下限截止频率 2 2 2 RC
Au பைடு நூலகம்
1
L 1 j
1 fL 1 jf
f j fL f 1 j fL
1、RC高通电路的频率响应
自动控制原理(第三版)第五章频率响应法

示。 这两条线相交处的交接频率ω=1/T, 称为振荡环节的无阻尼
自然振荡频率。在交接频率附近, 对数幅频特性与渐近线存在
一定的误差, 其值取决于阻尼比ζ的值, 阻尼比越小, 则误差越大, 如表5-4所示。当ζ<0.707时, 在对数幅频特性上出现峰值。根
一个单位长度。设对数分度中的单位长度为L, ω0为参考点, 则 当ω以ω0为起点, 在10倍频程内变化时, 坐标点相对于ω0的距离
为表5-1中的第二行数值乘以L。
第五章 频 率 响 应 法
图 5-4 对数分度和线性分度
第五章 频 率 响 应 法
表 5-1 10倍频程内的对数分度
第五章 频 率 响 应 法
第五章 频 率 响 应 法
图 5-7 比例环节的伯德图
第五章 频 率 响 应 法
2. 积分环节 积分环节的频率特性为
其幅频特性和相频特性为
(5.18)
(5.19)
由式(5.19)可见,它的幅频特性与角频率ω成反比, 而相频特性恒
为-90°。对数幅频特性和相频特性为
(5.20)
第五章 频 率 响 应 法
T), 则有
因此有
这表明φ(ω)是关于ω=1/T, φ(ω)=-45°这一点中心对称的。 用
MATLAB画出的惯性环节的伯德图如图5-14所示(T=1)。
第五章 频 率 响 应 法
图 5-14 MATLAB绘制的惯性环节的伯德图
第五章 频 率 响 应 法
5. 一阶微分环节 一阶微分环节的频率特性为 幅频特性和相频特性为
即 所以, 惯性环节的奈氏图是圆心在(0.5, 0), 半径为0.5的半圆 (
见图5-12)。 对数幅频特性和相频特性为
第五章 频率响应

4、下限频率fL
f L 1 .1 f
5、上限频率fH
2 L1
f
2 L2
f
2 Ln
1 fH
1 .1
1 f
2 H1
1 f
2 H2
1 f
2 Hn
6、通频带BW0.7↓=fH↓-fL↑
第五章 放大器的频率响应
5.1 频率响应概述
5.2 共射放大器的频率响应 5.4 多级放大器的频率响应
5.1 频率响应概述
频率响应:放大器的放大倍数是输入 信号频率的函数。
观察一组实验(阻容耦合共基)
实验条件:输入信号Ui= Uimsint
Uim不变, 改变
ui
ui
uo
uo
ui
ui uo
பைடு நூலகம்uo
三、频率响应的表示
1、基本思想:
波特图 幅频特性:纵轴——用分贝表示放大倍 数:20lg|Au| 相频特性:纵轴—— ( f )
频率采用对数分度
工程上采用渐近直线来近似。
2、 RC低通电路
+
+
R1 Ui
_
C1
Uo
_
+
+
RC低通电路
Ui
_
R1
C1
Uo
_
电压传递函数为:
Uo 1 Au U i 1 j( f / f H )
L1
/ f ) 1 j ( f L2 / f )
f L2 1 2 ( RC RL ) C 2
Ausm
式中: f L1
1 2 ( RS Ri ) C 1
共射基本放大器低频段源电压增益有 两个转折频率fL1和fL2 。如果两者的比值 在四倍以上,可取较大的值作为放大电路 的下限频率fL 。
第5章 放大电路的频率响应

由微变等效分析可知:
根据式(5.2.4), 将混合 П 型等效电路中c、e输出端短路, 则得图5.2.4。
第5章 放大电路的频率响应 图5.2.4 计算̇β=̇Ic/̇Ib 的等效电路
第5章 放大电路的频率响应
其幅频特性和相频特性的表达式为
式中 可见β为具有一个转折频率fβ的频率特性曲线, 如图5.2.5所示。fβ称为共射极 截止频率, 其值主要决定于管子的结构。
式中,ω 为输入信号的角频率, R1C1为回路的时间常数τ,
第5章 放大电路的频率响应 图5.1.2 用来模拟放大电路高频 特性的RC低通电路
第5章 放大电路的频率响应
令 则式(5.1.2)变为
AuH为高频电压增益, 其幅值|̇AuH|和相角φH分别为
第5章 放大电路的频率响应
1) 幅频特性 幅频响应波特图可按式(5.1.5)由下列步骤画出: 当f≪fH时,
第5章 放大电路的频率响应 图5.2.3 低频等效电路
第5章 放大电路的频率响应
晶体管放大电路的高频特性决定于混合 Π 型等效电路的参数gm、rbb'、 rb'e、 Cb'e及Cb'c。这些参数可用β、rbe、fT及Cob来表示。因此, 可用β、rbe、fT 及Cob来衡量晶体管的高频性能。
第5章 放大电路的频率响应
可求得̇A'u的表达式如下:
第5章 放大电路的频率响应
因为Cb‘c很小,β)re=(1+β)UT/IE。Cb'e为发射结电容。
3) 集电结参数rb'c和Cb'c
rb'c表示集电结的结电阻, 由于集电结工作时处于反向偏置。Cb'c为集电结电
五章节频率响应法

G (jc s)(st )G (a ) e ej jt( )aejt
频率特性:
系统对正弦输入信号的稳态响应特性。
G (j) G (j)e j G (j ) G () e j( )
其振幅比依赖于角频率的函数G()称为
系统的幅频特性;
其稳态输出信号对正弦输入信号的相移
f()称为系统的相频特性。
一、 频率特性的极坐标图
G k(s)b a 00 ssm n b a 1 1 ssm n 1 1 b am n 1 1s s a bn m
K
1 sv
h i1
1
(Tis 1)
1(nvh) 2
(Ti2
1
2
s 2iTis 1)
i1
L
1(mL) 2
( j 1)
( 2j s2 2 j js 1)
例5-2系统开环传递函数是
G(s)H(sG )=(js)(H TsK(j1))j,试(T绘Kj制其1奈) 氏图。
-KT
Im 0 Re
当 l渐 i0 近 R 当幅相m 线 G 值 角幅 相横 (e : :j值 角 坐0): :时H 标时(:j 0 G ) ( lG 9 i)0 (9 H T 0m 0 0)2 (H 9 K 4() 0 )0 T 2 0 1 K 8T
开环系统的频率特性通常是若干典型环节频率特性的乘积
n
G (j) G 1 (j)G 2 (j) G n (j) G i(nj)
极坐标形式:G (j
n
)G ( )ej()
i 1 j i()
G i( )ei1
i1
求系统的开环幅相特性: 分别求出系统各串联环节频率特性的幅值及相角, 然后算出不同频率下开环系统频率特性的幅值及 相角,从而就可绘制极坐标图。
自动控制原理第五章-1

积分环节:G(s)=1/s
微分环节:G(s)=s 惯性环节:G(s)=1/(Ts+1) 一阶微分环节:G(s)=Ts+1 振荡环节 1/(s 2 / n2 2s / n 1)
二阶微分环节 s 2 / 2 2s / 1 n n
比例环节:G(s)=K (K<0)
惯性环节:G(s)=1/(1-Ts)
系统开环传函由多个典型环节相串联 :
G(s) H (s) G1 (s)G2 (s)Gr (s)
那么,系统幅相特性为:
G ( jw) H ( jw) G1 ( jw)G2 ( jw) Gr ( jw) A1 ( w)e
j1 ( w )
A2 ( w)e k ( w )
k 1 r
A A A ( s j ) s j G( j ) ( s j ) s j G( j ) ( s j )(s j ) 2j s2 2
a G( s)
A A A ( s j ) s j G( j ) ( s j ) s j G( j ) s2 2 ( s j )(s j ) 2j
幅频特性 相频特性
线性系统的稳态输出是和输入具有相同频率的正弦信号, 其输出与输入的幅值比为 输出与输入的相位差
A() G( j)
( )
G ( j )
(1)、频率响应 在正弦输入信号作用下,系统输出的稳态值称为系统的 频率响应, 记为css(t)
(2)、频率特性
幅频特性A(): 稳态输出信号的幅值与输入信号的幅值之比: Ac A( ) G ( j ) A 相频特性(): 稳态输出信号的相角与输入信号相角之差: ( ) G ( j ) 幅相频率特性G(j) : G(j) 的幅值和相位均随输入正弦信 号角频率的变化而变化。 G( j ) A(w)e j ( ) 在系统闭环传递函数G(s)中,令s= j,即可得到系统的频率 特性。
模拟电子技术基础 第五章 频率响应PPT课件

第5章 频率响应
UCRUCRUCRsississisCrCrRbCrRbbRbebsebseesee((rr(RCrrbRbCrrbRbCbbSbeMbSeMbSeMrrrrbbrrbCbbeCbbCebebb)Ub)Ub)Ueeesss((1(1R1RRssrgsrbgrbgbmemermeRrbrRbRebeLeLUL)U)UC)CsCsbsbbeee
U1 -
Z1
Z
N
A(jω) =
U2 U1
(a)
I2 +
U2 -
Z2
图5–7 (a)原电路;
(b)等效后的电路
I1 +
U1 -
N
Z1
A(jω) =
U2 U1
第5章 频率响应
I2 +
Z2
U2
-
(b)
图5–7 (a)原电路;
(b)等效后的电路
第5章 频率响应
Z1Z1ZU11IU1I1 11UUII1111 UU 1U1UUZZ1U11ZU1UUZ1U12U2221111ZUUZ2ZZUU2UU12U2U2121212 111Z1ZAZAuZAu Au u
(5–1) (5–2a) (5–2b)
第5章 频率响应
图5–2给出了不产生线性失真的振幅频率响应和相 位频率响应,称之为理想频率响应。
|Au(jω)|
(jω)
K
0
0
ω
ω
∞ω
(a)
(b)
图5–2 (a)理想振幅频率响应;(b)理想相位频率响应
第5章 频率响应
5–1–2实际的频率特性及通频带定义 实际的振幅频率特性一般如图5–3所示。在低频和
三、高频增益表达式及上限频率
第5章 频率响应
第五章 系统频率响应分析

第五章 系统频率响应分析 5.1.2 频率特性的特点和作用 1. 频率特性可通过频率响应试验求取
根据频率特性的定义,首先改变输入正弦信号 Xie jt 的频率 并测出与此相应的输出幅值Xo ()与相移 ()。然后作出幅值比 Xo () / Xi 对频率 的函数曲线,此即幅频特性曲线;作出相移 () 对频率 的函数曲线,此即相频特性曲线。
e tT
Xi K sin(t arctanT) 1 T 2 2
1/T 为 G(s) 的极点或系统微分方程的特征根,因 si为负值, 所以系统是稳定的,随着时间的推移,即t→∞时,瞬态分 量迅速衰减至零,此时系统只剩下稳态输出
x o (t) = Xi K sin(t arctanT) 1 T 2 2
第五章 系统频率响应分析
待定系数 B和B*
B
G(
s)
(s
Xi j )( s
j)
(s
j)
s j
G(s) Xi s j
s j
G(
j)
Xi 2j
G( j) e jG( j) Xi 2j
B*
s j
G( j)
Xi 2j
G( j) ejG( j) Xi 2j
将 B和B*代入(5.9)中,则系统的稳态响应为
(5.12)
式中 u()是频率特性的实部,称为实频特性;
v()是频率特性的虚部,称为虚频特性。
综上所述,一个系统可以用微分
微分方程 dtd
s
dt d
jω
方程或传递函数来描述,也可以用频
系统
率特性来描述。他们之间的相互关系 如图5.3所示。
传递函数 s
频率特性 jω
图5.3 系统的微分方程,传递函数和 频率特性相互转换
频率响应法

第五章 频域响应法5-1 频率特性一. 频率特性的基本概念1. 所谓频率特性,即在零初始条件下,系统输入在正弦信号的控制下,其稳态输出C(t) 的被控制量信号的幅值A(ω)和相角ψ(ω)随r(t)信号的角频率ω变化的规律,记为G(j ω)。
G(j ω)=G(S)| s=j ω C(j ω) C(s)G(j ω)== R(j ω) R(s)| s=j ωb 0(j ω) m +b 1(j ω) 1+m +……+b 1-m (j ω)+b m G(j ω)=( j ω) n +a 1(j ω) 1-n +……a 1-n (j ω)+a n2、G(j ω)的数模表达式有两种标准式: (1)Nyquist 标准式:G(j ω)=︱G(j ω)︱e)(jw G j ∠=u(ω)+jv(ω)其中A(j ω)= ︱G(j ω)︱称为幅频特性,是ω的偶函数。
ψ(ω)= ∠G(j ω) 称为相频特性,是ω的奇函数。
u(ω)=Re [G(j ω)]为实部; v(ω)=Im [G(j ω)]为虚部。
(2)Bode 表达式:L (ω)=20lg [A(j ω) ] 称为对数幅频,ψ(ω)= ∠G(j ω) 称为对数相频。
二. 频率特性的图解表示法在工程分析和设计中,通常把频率特性画成曲线,从这些频率特性曲线出发研究。
现以RC 网络为例。
如图5-2。
其频率特性为G(j ω)=)(11jw T +(T=RC )。
A(ω)= G(j ω)=2)(11TW +;ψ(ω)=-arctg(T ω)1.极坐标图----Nyquist图当ω=0→∞变化时,A(ω)和φ(ω)随ω而变,以A(ω)作幅值,φ(ω)作相角的端点在s平面上形成的轨迹,称Nyquist曲线(幅相频率特性曲线)简称幅相曲线即Nyquist图,是频率响应法中常用的一种曲线。
2、对数坐标图----Bode图对数频率特性曲线又称Bode曲线,包括对数幅频和对数相频两条曲线。
自动控制原理(第二版)第五章频率响应法

发展多变量频率响应法
针对多输入多输出系统,需要发展多变量频率响 应法,以便更好地处理复杂系统的分析问题。
深入研究非最小相位系统
针对非最小相位系统的稳定性判断问题,需要深 入研究其频率响应特性,并寻求有效的解决方法 。
06
CATALOGUE
结论
总结频率响应法的要点与重点
01 02 03 04
频率响应法是一种通过分析线性定常系统对正弦输入信号的稳态响应 来评价系统性能的方法。
频率响应法的优势与局限性
优势
频率响应法能够提供系统在整个频率范围内的动态性能信息,有助于全面了解 系统的性能特点;通过分析频率特性,可以更容易地识别系统的稳定性和潜在 的谐振问题。
局限性
频率响应法主要适用于线性定常系统,对于非线性或时变系统,其应用可能受 到限制;此外,频率响应法无法提供系统的时域信息,如瞬态响应和稳定性。
05
CATALOGUE
频率响应法的局限性与改进方法
频率响应法的局限性
01
频率响应法主要适用于线性时不 变系统,对于非线性或时变系统 ,频率响应法可能不适用。
02
频率响应法只能给出系统在正弦 输入下的稳态输出,无法反映系
统的动态行为。
频率响应法无法处理多输入多输 出系统,对于复杂的多变量系统 ,需要采用其他方法进行分析。
02
CATALOGUE
频率响应的基本概念
频率特性的定义
频率特性
系统对正弦输入信号的稳态输出与输入之比,用复数表示的频率 函数。
频率特性与传递函数
传递函数是系统在零初始条件下,频率特性的解析表达式。
频率特性与系统性能
频率特性直接反映系统在不同频率的正弦输入信号下的响应特性 ,与系统的动态和稳态性能密切相关。
第五章频率响应

分析滤波电路,就是求解电路的频率特性,即求解Au (Aup (通带放大倍数) ) 、 fp和过渡带的斜率 。
滤波电路的分类:
无源滤波电路:仅有无源元件(R、C、L) 组成
有源滤波电路:有无源元件和有源元件(双 击型晶体管、单级型管、集成运放)共同组 成
1.无源低通滤波器:
信号频率趋于零时,电容容抗 趋于无穷大(开路),通带放 大倍数:
切比雪夫(Chebyshev) 贝塞尔(Bessel)
图7.4.15三种类型二阶LPF幅频特性
7.4.3 其它滤波电路
一、高通滤波电路
高通滤波电路与低通滤波电路具有对称性
1.压控电压源二阶 高通滤波电路
2.无限增益多路反馈 二阶高通滤波电路
图7.4.16二阶高通滤波电路
二阶有源高通滤波器
A u
时域(t)变量t是实数, 复频域F(s)变量s是复数。变 量s又称“复频率”。
拉氏变换建立了时域与复频域(s域)之间的联系。 s=jw,当中的j是复数单位,所以使用的是复频域。
通俗的解释方法是,因为系统中有电感X=jwL、电 容X=1/jwC,物理意义是,系统H(s)对不同的频率分 量有不同的衰减,即这种衰减是发生在频域的,所 以为了与时域区别,引入复数的运算。 在复频域计算的形式仍然满足欧姆定理、KCL、 KVL、叠加法。
A
R 1
u 1 ( f )2 j3 f
f
f
0
0
图7.4.8简单二阶低通电路的幅频特性
二、反相输入低通滤波器
1.一阶电路
令信号频率=0,求出 通带放大倍数
A
R 2
up
R
1
电路的传递函数
图7.4.11反相输入一阶
第5章 放大电路的频率响应(1)

例1: 已知某电路的波特图如图所示。 (1)电路的中频电压增益 = -32 。 = 30 dB, A um
(2)电路的下限频率fL≈ 10 Hz,上限频率fH≈ 100 kHz。
(3)电路的电压放大倍数 = 的表达式 A u
A u 32 (1 10 f )( 1 j 5 ) jf 10 或A u 3.2 jf f f ( 1 j )( 1 j 5 ) 10 10
5 - 1 - 34
例3(p243 自测题一)选择正确答案填入空内。
( 3)当信号频率等于放大电路的fL 或 fH时,放大倍数 的值约下降到中频时的 B 。 A.0.5倍 B.0.7倍 C.0.9倍 即增益下降 A 。 A.3dB B.4dB C.5dB (4)对于单管共射放大电路,当f = fL时,输出与输 入相位关系是 C 。 A.+45˚ B.-90˚ C.-135˚ 当f = fH时,输出与输入的相位关系是 C 。 A.-45˚ B.-135˚ C.-225˚
模拟电子技术基础
第十七次课
河北科技大学信息学院
基础电子教研室
5-1-1
第五章 放大电路的频率响应
. 频率响应概述
. 晶体管的高频等效模型 . 放大电路的频率响应
5-1-2
5.1 频率响应概述
一、 频率响应的概念: 在放大电路中,放大倍数与信号频率的函数关系, 称为频率响应或频率特性。
放大电路中由于C,L及晶体管极间电容的存在,电路对不 同频率的信号具有不同的放大能力。 在第二章中2.1介绍电路性能时,简单说明了通频带的概念。 指出放大电路对某一频率范围的信号能正常放大,这个频率范围 称为通频带。 了解电路对不同频率信号的放大能力,在使用电路前应查阅 资料,了解通频带,确定电路的适用范围。
自动控制原理期末考试题5

第五章 频率响应法习题及解答5-1 设系统开环传递函数为1)(+=Ts K s G今测得其频率响应,当ω=1rad/s 时,幅频2/12)(=j G ,相频︒-=45)(j ϕ。
试问放大系数K 及时间常数T 各为多少? 解:已知系统开环传递函数()1K G s Ts =+则频率特性:()1K G j Tj ωω=+幅频特性:()G j ω=相频特性:()arctan T ϕωω=-当1/rad s ω=时,()G j ==()arctan 45j T ϕ=-=-则有12K =,1T =。
5-2 设单位反馈系统的开环传递函数为11)(+=s s G当闭环系统作用有以下输入信号时,试求系统的稳态输出。
(1) t t r sin )(= (2))2cos(2)(t t r =(3) )2cos(2sin )(t t t r -=解:系统闭环传递函数为:1()2s s φ=+频率特性:2212()244j j j ωφωωωω-==++++幅频特性:()j φω=相频特性:()arctan()2ωϕω=- (1) 当()sin r t t =时,则1ω=,11R =则 1()0.45j ωφω===,1(1)arctan()26.52j ϕ=-=-[]1()(1)sin (1)0.45sin(26.5)s C t R j t j t φϕ=⋅+=-(2) 当()2cos(2)r t t =时,则2ω=,22R =则1(2)0.35j ωφ===,2(2)arctan()452j ϕ=-=-[]2()(2)cos 2(2)0.7cos(245)s C t R j t j t φϕ=⋅+=-(3) 当()sin 2cos 2r t t t =-时,[][]12()(1)sin (1)(2)cos 2(2)s C t R j t j R j t j φϕφϕ=+-+0.45sin(26.5)0.7cos(245)t t =---5-3 若系统单位阶跃响应为t t e e t h 948.08.11)(--+-=0≥t试求系统的频率特性。
自动控制原理第五章--频率法

G(s) T 2s2 2Ts 1
频率特性分别为:
G( j ) j G( j ) 1 jT G( j ) 1 T 2 2 j2T
① 纯微分环节: G( j ) j
A() , ()
2
P() 0, Q()
微分环节的极坐标图为 正虚轴。频率从0→∞ 特性曲线由原点趋向虚 轴的+∞。
当 o 时,误差为:2 20lg 1 T 22 20lgT
T L(),dB 渐近线,dB0.1 0.2来自0.5 1 2 510
-0.04 -0.2 -1 -3 -7 -14.2 -20.04
0
0
0 0 -6 -14
-20
最大误差发生在
o
处,为
1 T
误差,dB
0 -1
-0.04 -0.2 -1 -3 -1 -0.2
时:A() 0,() 90
P() 0,Q() 0
2. 对数频率特性
A( ) K 1 T 2 2
G(s) K Ts 1
G( j ) K jT 1
( ) tg1T
①对数幅频特性:L() 20lg A() 20lg K 20lg 1 T 2 2
为了图示简单,采用分段直线近似表示。
二、频率特性的表示方法:
工程上常用图形来表示频率特性,常用的有:
1.幅相频率特性图,极坐标图,也称乃奎斯特(Nyquist) 图。是以开环频率特性的实部为直角坐标横坐标,以其
虚部为纵坐标,以 为参变量的幅值与相位的图解表示
法。
它是在复平面上用一条曲线表示 由 0 时的频
率特性。即用矢量 G( j)的端点轨迹形成的图形。 是
R Ar0o ,C Ac
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:传递函数零极点的分布如图所示,令
S j2
10( j 2 1) G( j 2) ( j 2 2 j3)( j。 2 2 j3)
10 563.4 2968.2 5 26.6 1.85721.8
图 传递函数零极点的分 布
图5-7频率响应曲线
E2 ( s ) 1 E1 ( s ) 1 RCS
令:RC T , 则上式可以变为: E2 ( s ) 1 E1 ( s) 1 Ts
设输入
e1 A sin t
其拉氏变换为
A E1 ( s ) 2 s 2
则输出 e 2的拉氏变换为
求拉氏反变换,得
1 A E2 ( s ) 2 2 Ts 1 s
数据见书上表5-1
4. 证明一般情况(自学) 设线性系统的传递函数为:
C (s) U (s) G( s) R( s ) V ( s)
当 r (t ) A sin t
C ( s)
R( s)
A 时, 其输出为: 2 2 s
U (s) A 2 2 V (s) s
暂态分量
t T
稳态分量
AT e2 e 2 2 1 T
其中
A 1 T
2 2
sin(t )
Hale Waihona Puke arctgTRC电路的频率响应为 A lim e2 sin(t ) t 1 T 2 2 1 1 A sin(t ) 1 jT 1 jT 1 RC电路的频率特性为 G ( j ) A( )e j ( ) 1 jT 1 1 式中 A( ) 为幅频特性 2 2 1 jT 1 T 1 ( ) ( ) arct anT 为相频特性 1 jT
G( j) P() jQ() G( j) e G( j) G( j) e j ( )
j ( )
c(t ) A G( j)
e
j [t ( )]
e 2j
j[t ( )]
A G( j) sin(t )
三.频率特性 定义
在正弦输入下,线性定常系统或环节,其输出
的稳态分量与输入的复数比,称为系统或环节的频 率特性,记为:
C ( j ) G ( j ) R( j )
G( j) G( j) e
j ( )
在正弦输入下,线性定常系统或环节,其稳态输出的幅值 与输入幅值之比,称为系统或环节的幅频特性,记为:
g ()
2.物理意义 在 线性系统中,加入一个正弦信号,其稳态输出具有与输 入同一频率的正弦信号。 当输入量的 改变时,输出量的 与之同频,但幅值及相位随 变化,这种基于 的输出与输 入复数之比关系为系统的频率特性。
3.RC电路的频率特性
如图所示电路图,可以得出传递函数为:
•典型环节及系统开环频率特性的奈氏图、波 特图的绘制和分析方法 •控制系统稳定性的频域分析法
•系统稳定裕度的概念和求法
•频率法:工程研究方法
•根据系统的频率特性
1)分析系统的动、静态性能;
2)判断系统参数对性能的影响,并指出改进 的方向。
•优点:其频率特性可由实验测的
第一节
一、基本概念 1. 实验
C ( j ) G( j ) A() R( j )
在正弦输入下,线性定常系统或环节,其稳态输出的相位 与输入相位之差,称为系统或环节的相频特性,记为:
G( j) ()
(1)幅频特性反映系统对不同频率正弦信号
的稳态衰减(或放大)特性.
(2)相频特性表示系统在不同频率正弦信号 (3)已知系统的传递函数,令 s j ,可 得系统的频率特性。 (4)频率特性包含了系统的全部动态结构参 数,反映了系统的内在性质.
U ( s)
(s p )
i 1 i
n
A s2 2
式中: pi 为 G ( s ) 的极点,对于稳定系统,为简单起见, 令这些极点为不相等的负实数极点。
n bi a a C ( s) s j s j i 1 (s pi )
其中:
a 、a
、 bi 均为待定系数。
第五章 频率法(12+2学时)
第一节 频率特性的基本概念 第二节 对数坐标图 第三节 极坐标图 第四节 传递函数的实验确定 第五节 奈奎斯特稳定判据 第六节 相对稳定性 第七节 频域性能指标与时域性能指标间的关 系 第八节 MATLAB在频率法中的应用
本章重点
•频率特性的概念与性质
对上式取拉氏反变换,得
c(t ) ae
稳态分量为:
jt
ae
jt
bi e
i 1
n
pi t
c(t ) ae
jt
ae
jt
式中待定系数:
A a G ( j ) 2j A a G ( j ) 2j A jt A jt c(t ) G ( j ) e G ( j ) e 2j 2j
系统的频率特性由系统的结构和参数决定,与输入信号的幅值 与相位无关。
幅频特性
相频特性
图 R-C电路的频率特性
二、由传递函数确定系统的频率响应
例5-1 G( s)
10( S 1) 10( S 1) S 2 4S 13 ( S 2 j3)(S 2 j3)
试绘制系统的幅频和相频特性曲线。
2.对数频率特性 3. 对数幅相频率特性
半对数坐标图(Bode 伯德图) (尼科尔斯图)
纵坐标为L(ω),横坐标为 ( )
0
),传递函数 G ( s ) 变为频率特性 G ( j )
频率特性可当作是传递函数的一个特例,它反映了系 统在复频率
j 下的输入输出传递函数关系。
3)通过实验测得
五、频率特性的几种图示法 工程上: 采用图解法 分析系统性能 ,并得到改善系
统性能的途径
特点:直观
每一种图解法都基于某一形式的坐标图表示法 1. 幅相频率特性 极坐标图(Nyqust 乃氏图)
下输出的相位移.
d s dt
传递函数
微分方程
系统
s j
频率特性
d j dt
四、频率特性的求取方法
1)由系统的微分方程求取
r (t ) 为正弦函数
c(t )
的稳态解
取输出的稳态分量与输入的复数比,即得频率特性。 2)由系统的传递函数求取 当取复变量 取
s j
时(定义 s j ,
信号 发生器
频率特性
双踪 被测电路
R
示波器
e1 (t ) A sin t
C
稳态时 : e2 (t ) U om sin(t )
A
U om
U om f ()
A 1 (T)2
g () tg 1T
可见:
1) 输出为同频正弦量 2) 3)
Uom f () Uom
