六校2015届高三第三次联合考试(理数)
广东省六校联盟2015届高三第三次联考数学(理)试题及答案

2015届广东六校联盟第三次联考试题数学(理科)(满分150分) 考试时间:120分钟参考公式:柱体的体积公式V Sh =,锥体的体积公式13V Sh =.一、选择题:(本大题共8小题,每小题5分,共计40分.每小题只有一个正确答案,请把正确答案填涂在答题卡相应位置) 1. 设集合{}{}{}1,2,3,4,5,2,3,4,3,5U A B ===,则图中阴影部分所表示的集合为( )A.{}2,3B.{}1,4C.{}5D.{}6 2. 已知复合命题()p q ∧⌝是真命题,则下列命题中也是真命题的是( )A.()p q ⌝∨B.p q ∨C.p q ∧D.()()p q ⌝∧⌝ 3. 已知向量()()()5,2,4,3,,a b c x y ==--=,若320a b c -+=,则c =( )A.()23,12--B.()23,12C.()7,0D.()7,0-4. 下列函数中,在其定义域上为奇函数的是( )A.xxy e e -=+B.y =C.tan y x =D.1ln1xy x+=- 5. 某几何体的三视图如图所示,该几何体的体积为( )A.263 B.83π+ C.143π D.73π 6. 已知等差数列{}n a 中,10,0a d >>,前n 项和为n S ,等比数列{}n b 满足11b a =,44b a =,前n 项和为n T ,则( ) A.44S T >B.44S T <C.44S T =D.44S T ≤7. 已知直线()1:2110l ax a y +++=,()()2:110l a x a y ++-=,若12l l ⊥,则a =( )A.2或12 B.13或1- C.13D.1- 8. 已知函数()f x 的定义域为D ,如果存在实数M ,使对任意的x D ∈,都有()f x M ≤,则称函数()f x 为有界函数,下列函数: ①()2,xf x x R -=∈ ②()()ln ,0,f x x x =∈+∞③()()()2,,00,1xf x x x =∈-∞+∞+; ④()()sin ,0,f x x x x =∈+∞U AB主视图 侧视图俯视图为有界函数的是( ) A.②④ B.②③④C.①③D.①③④二、填空题:(本大题共6小题,每小题5分,共计30分.)9. 函数()ln f x x x =在点()(),e f e 处的切线方程为___________________. 10. 在ABC ∆中,45,75,2A B c =︒=︒=,则此三角形的最短边的长度是________. 11. 已知递增的等差数列{}n a 满足21252,6a a a ==+,则n a =___________.12. 已知圆2220x y x +-=上的点到直线:2l y kx =-的最近距离为1,则k =______. 13. 如图,为了测量两座山峰上两点P 、Q 之间的距离,选择山坡上一段长度为P,Q 两点在同一平面内的路段AB 的 两个端点作为观测点,现测得四个角的大小分别是90PAB ∠=︒,60PAQ PBA PBQ ∠=∠=∠=︒,可求得P 、Q 两点间的距离为 米.14. 已知(){}:,23p M x y x x ∈+-+;()(){}()222:,10q M x y x y r r ∈-+<>如果p 是q 的充分但不必要条件,则r 的取值范围是_ .三、解答题(本大题共六个小题,共80分.解答应写出文字说明、证明过程和演算步骤) 15.(本小题满分12分)已知函数()sin 1f x x x ωω=+(其中0,x R ω>∈)的最小正周期为6π. (1)求ω的值; (2)设,0,2παβ⎡⎤∈⎢⎥⎣⎦,13217f πα⎛⎫-= ⎪⎝⎭,()1135f βπ+=,求()cos αβ+的值. 16.(本小题满分12分)寒假期间校学生会拟组织一次社区服务活动,计划分出甲、乙两个小组,每组均组织①垃圾分类宣传,②网络知识讲座,③现场春联派送三项活动,甲组计划12的同学从事项目①,14的同学从事项目②,最后14的同学从事项目③;乙组计划15的同学从事项目①,另15的同学从事项目②,最后35的同学从事项目③,每个同学最多只能参加一个小组的一项活动,从事项目①的总人数不得多于20人,从事项目②的总人数不得多于10人,从事项目③的总人数不得多于18人,求人数足够的情况下,最多有多少同学能参加此次的社区服务活动?17.(本小题满分14分)如图,将长为4,宽为1的长方形折叠成长方体ABCD-A 1B 1C 1D 1的四个侧面,记底面上一边(),02AB t t =<<,连接A 1B,A 1C,A 1D.(1)当长方体ABCD-A 1B 1C 1D 1的体积最大时,求二面角B-A 1C-D 的值;(2)线段A 1C 上是否存在一点P ,使得A 1C ⊥平面BPD ,若有,求出P 点的位置,没有请说明理由.18.(本小题满分14分)已知数列{}n a 中,1141,13n n a a a +==-+ ,数列{}n b 满足()*1,1n n b n N a =∈+. (1)求数列{}n b 的通项公式; (2)证明:222121117n b b b +++<. 19.(本小题满分14分)已知直角坐标系中,圆O 的方程为222x y r +=()0r >,两点()()4,0,0,4A B ,动点P 满足(),01AP AB λλ=≤≤. (1)求动点P 的轨迹C 方程;C 1A BCD A 1B 1D 1(2)若对于轨迹C 上的任意一点P ,总存在过点P 的直线l 交圆O 于M,N 两点,且点M 是线段PN 的中点,求r 的取值范围.20.(本小题满分14分)已知函数()()ln f x x a ax =++. (1)求函数()f x 的单调区间和极值;(2)若()1,0a ∈-,函数()()g x a f x '=的图像上存在12,P P 两点,其横坐标满足1216x x <<<, 且()g x 的图像在此两点处的切线互相垂直,求a 的取值范围.六校联盟第三次联考理科数学参考答案及评分标准一、选择题:CBAD DABC二、填空题:9.20x y e --=; 10.3; 11.2n 12.0或者43-; 13. 900;14. r >)r ∈+∞或者直接)+∞均可三、解答题:15. 解:⑴ ()sin 12sin()13f x x x x πωωω=+=-+ …………3分26T ππω==,所以13ω=. ………………………………………………6分 ()12sin()133f x x π=-+注:如果()2cos()16f x x πω=-++等正确结果的话相应给分即可.⑵1132sin (3)12sin 12cos 12323217f ππππαααα⎛⎫⎛⎫⎛⎫-=--+=-+=-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 所以8cos 17α= ………………………………………………………………7分()11132sin (3)12sin 1335f πβπβπβ⎛⎫+=+-+=+= ⎪⎝⎭所以3sin 5β= …………………………………………………………………8分因为,0,2παβ⎡⎤∈⎢⎥⎣⎦,所以154sin ,cos 175αβ====,10分所以()13cos cos cos sin sin 85αβαβαβ+=-=-. …………………………12分 16.解:设甲组x 名同学,乙组y 名同学,根据题意有:……………………1分1120251110451318450,0x y x y x y x y ⎧+≤⎪⎪⎪+≤⎪⎨⎪+≤⎪⎪⎪≥≥⎩ 整理得: 52200542005123600,0x y x y x y x y +≤⎧⎪+≤⎪⎨+≤⎪⎪≥≥⎩ 可行域如图: 参加活动的总人数z x y =+,变形为y x z =-+,当经过可行域内的点,斜率为1-的直线在y 轴上 截距最大时,目标函数z x y =+取得最大值. 由可行域图像可知,直线y x z =-+经过54200x y +=和512360x y +=的交点A 时,在y 轴上截距最大. ……………8分解方程组54200512360x y x y +=⎧⎨+=⎩得:24,20x y == ……………………………………10分所以max 242044z x y =+=+= …………………………………………………11分答:甲组24名同学参加,乙组20名同学参加,此时总人数达到最大值44人.………12分 17.解:法一:⑴ 根据题意,长方体体积为()()2221212t t V t t t t +-⎛⎫=-⨯=-≤= ⎪⎝⎭……2分当且仅当2t t =-,即1t =时体积V 有最大值为1所以当长方体ABCD-A 1B 1C 1D 1的体积最大时,底面四边 形ABCD 为正方形 ……4分作BM ⊥A 1C 于M ,连接DM ,BD ……………5分因为四边形ABCD 为正方形,所以1A BC ∆与1A DC ∆全等,故DM ⊥A 1C ,所以BMD ∠即为所求二面角的平面角 ……6分因为BC ⊥平面AA 1B 1B ,所以1A BC ∆为直角三角形 又11AB AC =,所以11A B BC BM AC ⨯===DM = Ox y54200x y +=52200x y +=512360x y +=y x =- A (24,20)………7分,约束条件和图像各3分,不化简不扣分 AB C DA 1B 1C 1DM在∆BMD中,根据余弦定理有:6621cos 2BMD +-∠==- ………………8分因为()0,180BMD ∠∈︒︒,所以120BMD ∠=︒即此时二面角B-A 1C-D 的值是120︒. ……………………………………………………9分 ⑵ 若线段A 1C 上存在一点P ,使得 A 1C ⊥平面BPD ,则A 1C ⊥BD ………………10分 又A 1A ⊥平面ABCD,所以A 1A ⊥BD ,所以BD ⊥平面A 1AC所以BD ⊥AC ……………………………………………………………………12分底面四边形ABCD 为正方形,即只有ABCD 为正方形时,线段A 1C 上存在点P 满足要求,否则不存在由⑴知,所求点P 即为BM ⊥A 1C 的垂足M此时,21113A B A P AC ===……………………………………………………14分 法二:根据题意可知,AA 1, AB,AD 两两垂直,以AB 为x 轴,AD 为y 轴,AA 1为z 轴建立如图所示的空间直角坐标系:⑴长方体体积为()()2221212t t V t t t t +-⎛⎫=-⨯=-≤= ⎪⎝⎭………………………2分当且仅当2t t =-,即1t =时体积V 有最大值为1 …………………………………3分所以当长方体ABCD-A 1B 1C 1D 1的体积最大时,底面四边形ABCD则()()()()()110,0,1,1,0,0,1,1,0,1,0,1,0,1,0A B C A B BC =-=,设平面A 1BC 的法向量(),,m x y z =,则00x z y -=⎧⎨=⎩取1x z ==,得:()1,0,1m = ………………6分同理可得平面A 1CD 的法向量()0,1,1n = ……7分 所以,1cos ,2m n m n m n⋅==⋅ ………………8分 又二面角B-A 1C-D 为钝角,故值是120︒.…………9分(也可以通过证明B 1A ⊥平面A 1BC 写出平面A 1BC 的法向量)⑵ 根据题意有()()(),0,0,,2,0,0,2,0B t C t t D t --,若线段A 1C 上存在一点P 满足要求,不妨11A P AC λ=,可得()(),2,1P t t λλλ-- ()()(),2,1,,2,0BP t t t BD t t λλλ=---=--1100BP AC BD AC ⎧⋅=⎪⎨⋅=⎪⎩ 即:()()()()22221020t t t t t t λλλ⎧-+---=⎪⎨-+-=⎪⎩…………………………11分解得:21,3t λ==…………………………………………………………13分 即只有当底面四边形是正方形时才有符合要求的点P ,位置是线段A 1C 上1:2:1A P PC =处. ………………………………………………………14分18.解:⑴ 12241233nn n n a a a a +++=-=++ …………………………………………2分 ()()11123111112221122n n n n n n n n a a b b a a a a +++++====+=+++++ …………………6分又112b =,所以数列{}n b 是首项为12,公差为12的等差数列,2n nb = …………8分(也可以求出12341234,,,2222b b b b ====,猜想并用数学归纳法证明,给分建议为计算前2项1分,计算前3项或者更多2分,猜想通项公式2分,数学归纳法证明4分数学归纳法证明过程如下:① 当1n =时,112b =符合通项公式2n nb =;② 假设当n k =时猜想成立,即112k k kb a ==+,21k a k =-那么当1n k =+时12111123113k k k a k k a a k k +----===++-+,1111111211k k k b k a k+++===-+++ 即1n k =+时猜想也能成立综合①②可知,对任意的*n N ∈都有2n n b =.⑵ 当1n =时,左边=21147b =<不等式成立;……………………………………9分当2n =时,左边=2212114157b b +=+=<不等式成立; …………………………10分当3n ≥时,()2214411411n b n n n n n ⎛⎫=<=- ⎪--⎝⎭ 左边=22212111111111414()23341n b b b n n+++<++-+-++-- 11454()772n n=+-=-<不等式成立 …………………………………………………………………………14分19.解:⑴ 设(),P x y ,因为(),01AP AB λλ=≤≤,所以444x y λλ-=-⎧⎨=⎩消去λ并注意到01λ≤≤可得动点P 的轨迹C 即为线段AB ,方程为:()40,04x y x +-=≤≤ ……5分,不写出x 的范围扣1分⑵ 设()()()00,,,4,04N x y P t t t -≤≤,则004(,)22x t y tM ++- 方程组22200222004()()22x y r x t y t r ⎧+=⎪⎨++-+=⎪⎩即2220022200()(4)4x y r x t y t r ⎧+=⎪⎨+++-=⎪⎩有解 ……7分 法一:将方程组两式相减得:()()22200224430tx t y t t r +-++--= ………8分原方程组有解等价于点()0,0到直线()()222:224430l tx t y t t r +-++--=的距离小于或等于rr ≤ …………………………………………………………9分整理得:()()()22222221683444t t rt t r +--≤+-即()()22222816281690t t rtt r -+--+-≤也就是,22228169r t t r ≤-+≤对任意的04t ≤≤恒成立 ……………………10分根据二次函数22816y t t =-+的图像特征可知,在区间[]0,4上,当0t =或者4t =时,()2m a x281616tt -+=;当2t =时,()2min28168t t -+= …………………………12分所以21689r ≤≤,43r≤≤ ……………………………………………………13分 特别的,当r =228x y +=与40x y +-=切于点()2,2,此时过C 上的点()2,2P没有合乎要求的直线,故r ≠,即所求r 的范围为43r ⎡∈⎢⎣. ……14分法二:上述方程组有解即以()0,0为圆心,r 为半径的圆与以(),4t t --为圆心,2r 为半径的圆有公共点,故对于任意的04t ≤≤都有3r r ≤≤成立 ……9分整理得:22228169r t t r ≤-+≤对任意的04t ≤≤恒成立 ……………………10分根据二次函数22816y t t =-+图像特征可知,在区间[]0,4上,当0t =或者4t =时,()2m a x281616tt -+=;当2t =时,()2min28168t t -+= …………………………12分所以21689r ≤≤,43r≤≤ ……………………………………………………13分 特别的,当r =228x y +=与40x y +-=切于点()2,2,此时过C 上的点()2,2P没有合乎要求的直线,故r ≠,即所求r 的范围为43r ⎡∈⎢⎣. ……14分20.解:⑴函数()()ln f x x a ax =++的定义域为(),a -+∞,()1f x a x a'=++ ……1分当0a >时,原函数在区间(),a -+∞上有()0f x '>,()f x 单调递增,无极值; 当0a =时,原函数在区间()0,+∞上有()0f x '>,()f x 单调递增,无极值;……2分当0a <时,令()10f x a x a '=+=+得:1x a a=-- ………………………………3分 当1(,)x a a a ∈---时,()0f x '>,原函数单调递增;当1(,)x a a∈--+∞时,()0f x '<,原函数单调递减 …………………………………………………………………………………4分所以()f x 的极大值为()21ln 1f a a a a ⎛⎫--=---- ⎪⎝⎭ ………………………………5分 ⑵ 由⑴知,当()1,0a ∈-时()()221,(,)11,(,)a a x a a x a ag x a f x a a a x a a x a x aa ⎧+∈---⎪⎪+'==+=⎨+⎪--∈--+∞⎪+⎩ ……………………6分函数图像上存在符合要求的两点,必须12116x a x a<<--<<,得:13a -<<-+………………………………………………………………………8分 当1(,)x a a a∈---时,()2a g x a x a =++,函数在点1P 处的切线斜率为()121a k x a =-+; 当1(,)x a a ∈--+∞时,()2a g x a x a =--+,函数在点2P 处的切线斜率为()222ak x a =+; ………………………………………………………………10分 函数图像在两点处切线互相垂直即为:()()22121aax a x a ⋅=++,即()()22212x a x a a ++= ………………………………11分因为121016a x a x a a a<+<+<-<+<+,故上式即为()()12x a x a a ++=- …12分 所以()()1116a a a a a a⎧-+<-⎪⎪⎨⎪-+>-⎪⎩,解得:2a -<<综合得:所求a的取值范围是(a ∈-. ………………………………14分。
2015届第三次高考适应性考试数学试卷(理科)

2015届第三次高考适应性考试数学试卷(理科)【试卷综析】这套试题,具体来说比较平稳,基本符合高考复习的特点,稳中有变,变中求新,适当调整了试卷难度,体现了稳中求进的精神.考查的知识涉及到函数、三角函数、数列、解析几何、立体几何、概率、复数等几章知识,重视学科基础知识和基本技能的考察,同时侧重考察了学生的学习方法和思维能力的考察,有相当一部分的题目灵活新颖,知识点综合与迁移.试卷的整体水准应该说可以看出编写者花费了一定的心血.但是综合知识、创新题目的题考的有点少.这套试题以它的知识性、思辨性、灵活性,基础性充分体现了考素质,考基础,考方法,考潜能的检测功能.试题中无偏题,怪题,起到了引导高中数学向全面培养学生数学素质的方向发展的作用.【题文】第I卷共10小题。
【题文】一、选择题:本大题共10小题,每题5分,共50分·在每个小题给出的四个选项中,只有一项是符合题目要求的.【题文】1.设集合M满足{1,2}{1,2,3,4},则满足条件的集合M的个数为()A.1 B .2 C .3. D. 4【知识点】子集与真子集A1【答案】【解析】C 解析:根据子集的定义,可得集合M必定含有1、2两个元素,而且含有1,2,3,4中的至多三个元素.因此,满足条件{1,2}⊆M⊈{1,2,3,4}的集合M有:{1,2}、{1,2,3}、{1,2,4},共3个.故选:C.【思路点拨】根据集合包含关系的定义,将满足条件的集合逐个列出,即可得到本题答案.【题文】2.已知点A(1,3),B(4,一1),则与向量AB的方向相反的单位向量是()A、(-35,45)B、(-45,35)C、(35,-45)D、(45,-35)【知识点】单位向量F1【答案】【解析】A 解析:AB=(4,﹣1)﹣(1,3)=(3,﹣4),|AB |==5.∴与向量AB的方向相反的单位向量()3,434,555ABAB-⎛⎫-=-=- ⎪⎝⎭.故选:A.【思路点拨】利用与向量的方向相反的单位向量ABAB-即可得出.【题文】3.函数2()f x x=+bx的图象在点A(l,f(1))处的切线与直线3x - y+2=0平行,若数列{1()f n}的前n项和为Sn,则S2015=()A、1B、20132014C、20142015D、20152016【知识点】数列的求和;二次函数的性质.B5 D4【答案】【解析】D 解析:f′(x)=2x+b,由直线3x﹣y+2=0可知其斜率为3,根据题意,有f′(1)=2+b=3,即b=1,所以f(x)=x2+x,从而数列{1 () f n}的通项为,所以S2015==,故选:D.【思路点拨】由f′(1)与直线斜率相等可得f(x)的解析式,从而可得数列{1()f n}的通项公式,计算可得答案.【题文】4.某锥体三视图如右,根据图中所标数据,该锥体的各侧面中,面积最大的是()A. 3B. 25C. 6D. 8【知识点】由三视图求面积、体积.G2【答案】【解析】C 解析:因为三视图复原的几何体是四棱锥,顶点在底面的射影是底面矩形的长边的中点,底面边长分别为4,2,后面是等腰三角形,腰为3,所以后面的三角形的高为:=,所以后面三角形的面积为:×4×=2.两个侧面面积为:×2×3=3,前面三角形的面积为:×4×=6,四棱锥P﹣ABCD的四个侧面中面积最大的是前面三角形的面积:6.故选C.【思路点拨】三视图复原的几何体是四棱锥,利用三视图的数据直接求解四棱锥P﹣ABCD 的四个侧面中面积,得到最大值即可.【题文】5.已知圆C1:(x一2)2+(y-3 )2 =1 ,圆C2 : (x -3)2+(y-4).2 =9,M,N分别是Cl ,C2上的动点,P为x轴上的动点,则|PM |+ |PN|的最小值为()A. 17-1B、6-22C、52-4D .17【知识点】圆与圆的位置关系及其判定.H4【答案】【解析】C 解析:如图圆C1关于x轴的对称圆的圆心坐标A(2,﹣3),半径为1,圆C2的圆心坐标(3,4),半径为3,由图象可知当P,C2,C3,三点共线时,|PM|+|PN|取得最小值,|PM|+|PN|的最小值为圆C3与圆C2的圆心距减去两个圆的半径和,即:|AC2|﹣3﹣1=﹣4=﹣4=5﹣4.故选:C.【思路点拨】求出圆C1关于x轴的对称圆的圆心坐标A,以及半径,然后求解圆A与圆C2的圆心距减去两个圆的半径和,即可求出|PM|+|PN|的最小值.【题文】6.函数恰有两个零点,则实数k的范围是()A.(0,1)B.(0,l)U(1,2)C. (1,+oo)D、(一oo,2)【知识点】函数的零点与方程根的关系.B9【答案】【解析】B 解析:由题意,令f(x)=0,则211xkx x-= -令2111xyx-=-,2y kx=,则y1==,图象如图所示2y kx =表示过点(0,0)的直线,结合图像以及斜率的意义,∴k 的取值范围是(0,1)∪(1,2), 故选B.【思路点拨】令f (x )=0,则211x kxx -=-,构建函数,作出函数的图象,即可求得k 的取值范围.【题文】7.已知抛物线22(0)y px p =>上一点M (1,m )(m >0)到其焦点的距离为5,双曲线2221x y a -=的左顶点为A ,若双曲线一条渐近线与直线AM 平行、则实数a 等于( ) A 、19 B 、14 C 、13 D 、12【知识点】双曲线的简单性质;抛物线的简单性质.H6 H7【答案】【解析】A 解析:抛物线y2=2px (p >0)的准线方程为x=﹣, 由抛物线的定义可得5=1+,可得p=8,即有y2=16x ,M (1,4),双曲线﹣y2=1的左顶点为A (﹣,0),渐近线方程为y=±x ,直线AM 的斜率为,由双曲线的一条渐近线与直线AM 平行,可得=,解得a=,故选A .【思路点拨】求得抛物线的准线方程,再由抛物线的定义可得p=8,求出M 的坐标,求得双曲线的左顶点和渐近线方程,再由斜率公式,结合两直线平行的条件:斜率相等,计算即可得到a 的值. 【题文】8.函数在x =1和x =-1处分别取得最大值和最小值,且对于,则函数f (x +1)一定是( )A .周期为2的偶函数 B.周期为2的奇函数C.周期为4的奇函数D.周期为4的偶函数 【知识点】正弦函数的图象.B4 【答案】【解析】C 解析:由题意可得,[﹣1,1]是f (x )的一个增区间,函数f (x )的周期为2×2=4, ∴=4,ω=,∴f (x )=Asin (x+φ).再根据f (1)=Asin (ω+φ)=A ,可得sin (+φ)=cosφ=1,故φ=2kπ,k ∈z ,f (x )=Asin x ,故f (x )是周期为4的奇函数,故选:C .【思路点拨】由题意可得函数f (x )的周期为4,由此求得ω 的值,再根据f (1)=A ,求得φ 的值,可得f (x )的解析式,从而得出结论. 【题文】9.已知正方体ABCD 一A1B1C1D1,,下列命题:③向量1AD 与向量1A B 的夹角为600④正方体ABCD 一A1B1C1D1的体积为1||AB AA AD ,其中正确命题序号是A.①③B.①②③C.①④D.①②④. 【知识点】空间向量及应用F1 【答案】【解析】A 解析:如图所示:以点D 为坐标原点,以向量,,所在直线分别为x ,y ,z 轴,建立空间直角坐标系,设棱长为1,则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),D1(0,0,1),对于①:,∴,,∴,∴||=,||=1,∴①正确;对于②:,,∴=2.∴②错误;对于③:,,∴,∴③正确;对于④:∵,∴④错误,故选A.【思路点拨】结合图形,以点D为坐标原点,以向量,,所在直线分别为x,y,z轴,建立空间直角坐标系,然后结合空间向量的坐标运算,对四个命题进行逐个检验即可.【题文】10.已知函数,则关于x的方程有5个不同实数解的充要条件是()A. b<一2且c>0B. b>一2且c<0C. b<一2且c=0D. b≤一2且c=0【知识点】充要条件.A2【答案】【解析】C 解析:∵方程f2(x)+af(x)+b=0有且只有5个不同实数解,∴对应于f(x)等于某个常数有4个不同实数解,由题意作出f(x)的简图:由图可知,只有当f(x)=0时,它有﹣个根.且f(x)=﹣b时有四个根,由图可知﹣b>2,∴b<﹣2.故所求充要条件为:b<﹣2且c=0,故选C.【思路点拨】作出f(x)的简图,数形结合可得.【题文】 第II 卷(非选择题,满分100分)【题文】二、填空题:本大题共5小题,每小题5分,共25分. 【题文】11、若复数x =(1+ai )(2+i )的实部与虚部相等,则实数a = 【知识点】复数的基本概念;复数代数形式的乘除运算.L4【答案】【解析】13 解析: ()()()12221x ai i a a i=-++=++,因为实部与虚部相等,所以221a a -=+,解得13a =,故答案为13【思路点拨】利用两个复数代数形式的乘法,虚数单位i 的幂运算性质,把复数化为最简形式,由实部和虚部相等,求出实数a .【题文】12.93()3x x -的展开式中常数项等于 【知识点】二项式系数的性质.J3【答案】【解析】289-解析:93()3x x -的展开式的通项公式为Tr+1=••(﹣3)r•,令=0,求得r=3,可得展开式中常数项等于••(﹣3)3=﹣,故答案为:289-.【思路点拨】先求出二项式展开式的通项公式,再令x 的幂指数等于0,求得r 的值,即可求得展开式中的常数项的值.【题文】13.7个身高各不相同的学生排成一排照相,高个子站中间,从中间到左边一个比一个矮,从中间到右边也一个比一个矮,则共有 种不同的排法(结果用数字作答). 【知识点】排列、组合及简单计数问题.J3 【答案】【解析】20 解析:最高个子站在中间,只需排好左右两边,第一步:先排左边,有=20种排法,第二步:排右边,有=1种,根据分步乘法计数原理,共有20×1=20种,故答案为:20.【思路点拨】最高个子站在中间,只需排好左右两边,第一步:先排左边,有=20种排法,第二步:排右边,有=1种,根据分步乘法计数原理可得结论.【题文】14.阅读右边框图,为了使输出的n=5,则输人的整数P的最小值为【知识点】程序框图.L1【答案】【解析】8 解析:程序在运行过程中各变量的值如下表示:是否继续循环S n循环前/0 1第一圈是 1 2第二圈是 3 3第三圈是7 4第四圈是15 5第五圈否故S=7时,满足条件S<pS=15时,不满足条件S<p故p的最小值为8故答案为:8【思路点拨】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算变量S的值,并输出满足退出循环条件时的k值,模拟程序的运行,用表格对程序运行过程中各变量的值进行分析,不难得到输出结果.【题文】15.平面内两定点M(0,一2)和N(0,2),动点P(x,y)满足,动点P的轨迹为曲线E,给出以下命题:①∃m,使曲线E过坐标原点;②对∀m,曲线E与x轴有三个交点;③曲线E只关于y轴对称,但不关于x轴对称;④若P、M、N三点不共线,则△PMN周长的最小值为2m+4;⑤曲线E上与M,N不共线的任意一点G关于原点对称的另外一点为H,则四边形GMHN的面积不大于m。
2015年高考模拟试题三模试题_河南省重点高中联考2015年高三年级第三次质量检测数学理科试题二

河南省重点高中联考2015年高三年级第三次质量检测试题数学试题注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至3页,第Ⅱ卷3至5页。
2. 答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3. 全部答案在答题卡上完成,答在本试题上无效。
4. 考试结束,将本试题和答题卡一并交回。
题号 一 二 三 总分 分数第I 卷1、已知=+-=+ni m i n m ni im是虚数单位,则是实数,,,其中11( ) (A)1+2i (B) 1-2i (C)2+i (D)2- i 2、下列命题中,真命题是( )(A )m R ∃∈,使函数2()()f x x mx x R =+∈是偶函数 (B )m R ∃∈,使函数2()()f x x mx x R =+∈是奇函数 (C )m R ∀∈,函数2()()f x x mx x R =+∈都是偶函数(D )m R ∀∈,函数2()()f x x mx x R =+∈都是奇函数 3、已知随机变量x ,y 的值如下表所示:如果y 与x 线性相关且回归 直线方程为y =bx +72,则实数b =( ) A .-12 B .12 C .-110 D .1104、执行右边的程序框图,若t ∈[-1,2],则s ∈( )A .[-1,1)B .[0,2]C .[0,1)D .[-l ,2]5、为了得到函数sin 3cos3y x x =+的图象,可以将函数2sin3y x =的图象( )阅卷人 得分x2 3 4 y546A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位6、正项等比数列{n a }的公比q ≠1,且2a ,321a ,1a 成等差数列,则5443a a a a ++的值为( )A. 215-B.215+C.215+或215- D.251- 7、下列命题正确的个数是( )①命题“020031,x x R x >+∈∃”的否定是“x x R x 31,2≤+∈∀”;②“函数ax ax x f 22sin cos )(-=的最小正周期为π”是“1=a ”的必要不充分条件; ③ax x x ≥+22在]2,1[∈x 上恒成立max min 2)()2(ax x x ≥+⇔在]2,1[∈x 上恒成立; ④“平面向量a 与b 的夹角是钝角”的充分必要条件是“0<⋅b a ”.A .1B .2C .3D .4 8、一个几何体的三视图如图所示,则该几何体的体积为( )A .π+33B .2π+3C .π+3D .2π+339、已知x >0,y >0,x+2y+2xy=8,则x+2y 的最小值是( ) A . 3B . 4C .D .10、已知M 是ABC ∆内一点,且23,30,AB AC BAC ⋅=∠=若MBC ∆、MAB ∆、MAC ∆的面积分别为12、x y 、, 则14x y+的最小值是( )A .9 B. 16 C. 18 D. 2011、已知双曲线2221x a b2y -=(a >0,b >0),过其右焦点且垂直于实轴的直线与双曲线交于M ,N 两点,O 为坐标原点.若OM ⊥ON ,则双曲线的离心率为( ) A .133-+ B .132+ C .152-+ D .152+12、设函数f (x )=[],0,(0.x x x f x x ⎧⎨⎩-≥+1),<其中[x]表示不超过x 的最大整数,如[-1,1]=-2, [π]=3.若直线y =kx +k (k >0)与函数f (x )的图象恰好有3个不同的交点,则实数k 的取值范围是( ) A .(0,14) B .[14,13) C .(13,1) D .[14,1) 第Ⅱ卷本卷包括必考题和选考题两部分。
广东省六校2015届高三第三次联合考试

语文试卷一、本大题4小题,每小题3分,共12分。
1.下列词语中加点字的读音,都不相同的一组是()A.诅.咒/龃.龉惬.意/怯.懦降.解/降.龙伏虎B.眼睑./敛.财亵.渎/楔.子角.色/群雄角.逐C.发酵./咆哮.觊觎./墙隅.弹劾./言简意赅.D.创.伤/悲怆.绯.闻/斐.然羁縻./靡.日不思2.下面文段中,加点的词语使用不恰当的一句是()当然,对于在现代化坐标中登攀高点的中国人而言,“回到孔子”不仅仅出于为解决现实问题提供精神资源这个功利目的,它更意味着一个古老民族在价值和情感上的回归。
当越来越多的人痛.心疾首....的传统典籍中找到此心安处,当一个国家把建设文化...于“故乡沦陷”,满心渴望从浩如烟海强国、塑造核心价值观上升为国家战略,这些都表达着上至庙堂、下及万民的共同诉求..:中国越是在现代化道路上狂飙突进,就越需要仰望历史星空瞄准..价值罗盘、补充精神给养。
A.痛心疾首 B.浩如烟海 C.诉求 D.瞄准3.下列各句中,没有语病的一句是()A.奥巴马作为美国第一位非洲裔总统,本来被舆论解读为种族和解的象征,但是弗格森事件表明,美国并未进入“后种族时代”,种族矛盾依旧是美国的突出问题。
B.数据显示,A股上市公司前三季度的增幅为9.67%,基本与上半年8.5%的业绩增速持平,如果剔除金融类上市公司后,同比增长率仅为不足8%。
C.与此同时,博物馆融入社会的步伐在日益加快,服务社会的功能在日益凸显,以陈列展览和社会教育核心的公共文化服务功能正发挥着日益重要的作用。
D.11月30日,中国首次出口了最高速度的米轨动车组在南车株洲电力机车有限公司下线,预计明年底前在马来西亚吉隆坡至怡保200多公里的线路上运营。
4.把下列句子组成语意连贯的语段,排序最恰当的一项是()①但是,这却不影响它会建构一个信仰中心。
②儒教信仰缺乏宗教化的制度支撑,却制约于国家设置的宗教制度。
③这一信仰中心,它能够囊括所有中国人的信仰。
福建省四地六校2015届高三上学期第三次月考试卷数学(理)

福建省四地六校2015届高三上学期第三次月考试卷数学(理)时间:120分钟 满分:150分一、选择题:本大题共10小题,每小题5分,满分50分,只有一项是符合题目要求的。
1、已知R 为实数集,}02{2<-=x x x M ,}1{-==x y x N ,则=)(N C M R ( )A .{x|0<x<1}B .{x|x<2}C .{x|0<x<2}D .∅2.设)cos ,21(),1,(sin x x ==,且b a //,则锐角x 为( ) A .3π B . 4πC .6π D .12π3.棱长为a 的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为( )A .33a B. 43a C. 63a D. 123a4.在等比数列}{n a 中,b a a a a a a =+≠=+161565),0(,则2625a a +的值是( )A .a bB .22ab C.a b 2 D .2a b5.在各项都为正数的等差数列}{n a 中,若a 1+a 2+…+a 10=30,则a 5·a 6的最大值等于( ) A . 3 B . 6 C .9 D . 36 6.设l ,m ,n 表示三条直线,α,β,γ表示三个平面,给出下列四个命题:①若l ⊥α,m ⊥α,则l ∥m ; ②若m ⊂β,n 是l 在β内的射影,m ⊥l ,则m ⊥n ; ③若m ⊂α,m ∥n ,则n ∥α;④若α⊥γ,β⊥γ,则α∥β. 其中真命题为( )A .①②B .①②③C .①②③④D .③④7.将函数x x y sin cos 3-=的图像向右平移n 个单位后所得图像关于y 轴对称,则n 的最小正值是( )A .6π B .2πC .67πD .3π 8.如图,正方体ABCD —A 1B 1C 1D 1中,O 为底面ABCD 的中心, M 为棱BB 1的中点,则下列结论中错误..的是( ) A .D 1O ∥平面A 1BC 1 B . D 1O ⊥平面AMCC .异面直线BC 1与AC 所成的角等于60°D .二面角M -AC -B 等于45°9.已知函数f (x )=201543212015432x x x x x +⋯+-+-+,则下列结论正确的是 A . f (x )在(0,1)上恰有一个零点 B . f (x )在(-1,0)上恰有一个零点C . f (x )在(0,1)上恰有两个零点D . f (x )在(-1,0)上恰有两个零点34 2 俯视图主视图 左视图 1 2 3 4 5 6 7 8 9 10 …………第14题图10.某同学在研究函数()1xf x x=+ (x ∈R ) 时,分别给出下面几个结论: ①等式()()0f x f x -+=在x R ∈时恒成立;②函数 f (x ) 的值域为 (-1,1);③若x 1≠x 2,则一定有f (x 1)≠f (x 2); ④函数()()g x f x x =-在R 上有三个零点. 其中正确结论的序号是( ) A .①② B .①②③ C . ①③④ D .①②③④二、填空题:本大题共5小题,每小题4分,满分20分。
2015六校联考 浙江省六校2015届高三联考数学理试题 Word版含答案

浙江省六校2015届高三年级联考数学(理)试题本试题卷分选择题和非选择题两部分,考试时间为120分钟.参考公式:柱体的体积公式V Sh = 其中S 表示柱体的底面积,h 表示柱体的高锥体的体积公式V =13Sh . 其中S 表示锥体的底面积,h 表示锥体的高台体的体积公式V =13h 12()S S + 其中S1,S2分别表示台体的上,下底面积球的表面积公式S =4πR 2 其中R 表示球的半径,h 表示台体的高 球的体积公式343V R π= 其中R 表示球的半径选择题部分(共40分) 一、选择题1.若全集U=R ,集合22{|20},{|1log (3),}A x x x B y y x x A =+-≤==+∈,则集合()U A C B =A .{|20}x x -≤<B .{|01}x x ≤≤C .{|32}x x -<≤-D .{|3}x x ≤- 2. 已知直线l :y=kx 与圆O :x 2+y 2=1相交于A ,B 两点,则“k=1”是“△OAB 的面积为12”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分又不必要条件3.△ABC的内角A、B 、C 的对边分别是a 、b 、c , 若则c=A .B .2CD .14.设,,αβγ是三个不重合的平面,m,n 是两条不重合的直线,下列判断正确的是A .若α⊥β,则β⊥γ ,则α∥γB .若α⊥β,l ∥β,则l ⊥αC .若则m ⊥α, n ⊥α, m ∥nD .若m ∥α,n ∥α,则m ∥n5. 已知函数f (x)=Asin ()(0)36x A ππ+>在它的一个最小正周期内的图象上,最高点与最低点的距离是,则A 等于 A .1 B .2C .4D . 8 6. 已知向量是单位向量,a b ,若a ·b =0,且|||2|5c a c b -+-=,则|2|c a +的取值范围是A .[1,3]B .[] C .D .7.已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为F 1, F 2, P 为双曲线上任一点,且1PF ·2PF 最小值的取值范围是2231[,]42c c --,则该双曲线的离心率的取值范围为 A.( B.2⎤⎦ C.( D .[)2,+∞8.已知2(),()|1|f x x g x x ==-,令11()(()),()(())n n f x g f x f x g f x +==,则方程2015()1f x =解的个数为 A .2014 B . 2015 C . 2016D .2017非选择题部分(共110分) 二、填空题9. 函数()sin cos f x x x =+的单调增区间为 ,已知3sin 5α=,且(0,)2πα∈,则()12f πα-= . 10.设公差不为零的等差数列{a n }满足: a 1=3, a 4+5是a 2+5和a 8+5的等比中项,则a n = ,{a n }的前n 项和S n =_________.11.某空间几何体的三视图(单位:cm )如图所示,则其体积是cm 3, 表面积是 ____ cm 2.12.已知变量x ,y 满足430401x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩,点(x ,y )对应的区域的面积__________,22x y xy+的取值范围为__________. 13.已知F 为抛物线C: y 2=2px(p >0)的焦点,过F 作斜率为1的直线交抛物线C 于A 、B 两点,设||||FA FB >,则 ||||FA FB = . 14.若实数a 和b 满足2×4a -2a ·3b +2×9b =2a +3b +1,则2a +3b 的取值范围为__________________.15.已知正方体ABC D -A 1B 1C 1D 1A 为球心,2为半径作一个球,则球面与正方体的表面相交所得到的曲线的长等于________.三、解答题:本大题共5小题,共74分.解答请写在答卷纸上,应写出文字说明,证明过程或演算步骤.16.(本题15分)如图,在△ABC 中,已知3B π=,AC=为BC 边上一点.(I )若AD=2,S △DAC =DC 的长;(II )若AB=AD ,试求△ADC 的周长的最大值.17.(本题15分)如图,在三棱锥A-BCD 中, AB ⊥平面BCD,BC ⊥CD,∠CBD=60°,BC=2. (I )求证:平面ABC ⊥平面ACD ;(II )若E 是BD 的中点,F 为线段AC 上的动点,EF 与平面ABC 所成的角记为θ,当tan θ的最大值为2,求二面角A-CD-B 的余弦值.18. (本题15分)已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为F 1、F 2,该椭圆的A 是椭圆上一点,AF 2⊥F 1F 2,原点O 到直线AF 1的距离为13.(I )求椭圆的方程; (II )是否存在过F 2的直线l 交椭圆于A 、B 两点,且满足△AOB 的面积为23,若存在,求直线l 的方程;若不存在,请说明理由.19.(本题15分)已知数列{a n }的前n 项和为S n ,S n *3()2n a n n N =-∈. (I )求证{a n +1}是等比数列,并求数列{a n }的通项公式;(II )证明:20.(本题14分)已知函数 f (x )=x 2+4|x -a |(x ∈R ).(I )存在实数x 1、x 2∈ [-1,1],使得f (x 1)=f (x 2)成立,求实数a 的取值范围; (II )对任意的x 1、x 2∈ [-1,1],都有|f (x 1)-f (x 2)|k ≤成立,求实数k 的最小值.参考答案。
江苏大联考2015届高三第三次联考数学(理)试卷 含答案

江苏大联考2015届高三第三次联考·数学试卷考生注意:1。
本试卷共160分.考试时间120分钟。
2。
答题前,考生务必将密封线内的项目填写清楚。
3。
请将各题答案填在试卷后面的答题卷上.4.交卷时,可根据需要在加注“”标志的夹缝处进行裁剪。
5.本试卷主要考试内容:前2次联考内容+数列+不等式。
一、填空题:本大题共14小题,每小题5分,共70分。
把答案填在答题卷中的横线上。
1.设集合M={x|x2+x-6〈0},N={x|1≤x≤3},则M∩N=▲.2。
已知数列{a n}为等差数列,其前9项和为S9=54,则a5=▲.3。
用12米的绳子围成一个矩形,则这个矩形的面积最大值为▲.4.在等比数列{a n}中,a1=2,若a1,2a2,a3+6成等差数列,则a n=▲ .5。
若tan θ=1,则cos 2θ=▲。
,则a10+a13=6。
已知在等比数列{a n}中,a3+a6=4,a6+a9=12▲。
=7。
已知a>0,b〉0,ab=4,当a+4b取得最小值时,ab▲。
8.已知平面向量a、b,|a|=3,|b|=2√3且a—b与a垂直,则a与b的夹角为▲。
9。
设变量x,y满足约束条件{x+y≥3,则目标函数z=2x+3y的最小值与x-y≥-12x-y≤3最大值的和为▲。
10.若对于任意的x〉0,不等式x≤a恒成立,则实数a的取值范围x2+2x+4为▲.11.已知在各项为正的等比数列{a n}中,a2与a8的等比中项为8,则4a3+a7取最小值时首项a1= ▲.12。
下面图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第16个图形中小正方形的个数是▲.13.在数列{a n}中,若存在一个确定的正整数T,对任意n∈N*满足a n+T=a n,则称{a n}是周期数列,T叫做它的周期。
已知数列{x n}满足x1=1,x2=a(a≤1),x n+2=|x n+1—x n|,若数列{x n}的周期为3,则{x n}的前100项的和为▲.的取值范围是14。
2015年高三三模试卷理科数学附答案

O ππ3π6112015年高三三模试卷理科数学一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题意要求的.)1、设复数11221,2,z z i z ai z =+=+若为纯虚数,则实数a =( )A .-2B .2C .-1D .12、 已知命题x x R x p lg 2,:>-∈∃,命题:1,ln(1)x q x e x ∀>->+,则( ) A.命题q p ∨是假命题 B.命题q p ∧是真命题 C.命题)(q p ⌝∧是真命题 D.命题)(q p ⌝∨是假命题3、已知某随机变量X 的概率密度函数为P (x )=⎩⎨⎧>≤-0,0,0x e x x ,则随机变量X 在区间(1,2)内的概率为( )A .e 2+eB .21e e + C .e 2-e D .21ee - 4.下列命题中正确的是( )A.如果两条直线都平行于同一个平面,那么这两条直线互相平行B.过已知平面的一条斜线有且只有一个平面与已知平面垂直C.平面α不垂直平面β,但平面α内存在直线垂直于平面βD.若直线l 不垂直于平面α,则在平面α内不存在与l 垂直的直线 5.设0>ω,函数)sin(ϕω+=x y )(πϕπ<<-的图象向左平移3π个单位后,得到下面的图像,则ϕω,的值为( )(A )32,1πϕω== (B )32,2πϕω== (C )3,1πϕω-== (D )3,2πϕω-==6、ABCDEF 6个同学和1个数学老师站成一排合影留念,数学老师穿白色文化衫,A,B 和C,D 同学分别穿着白色和黑色文化衫,E 和F 分别穿着红色和橙色的文化衫.若老师站中间,穿着白色文化衫的不相邻,则不同的站法种数为( )A.72B.192C. 112D.1607、 设函数)(x f 的导函数为)(x f ',对任意∈x R 都有)()(x f x f >'成立,则( )A .3(ln 2)2(ln3)f f > B.3(ln 2)2(ln 3)f f =C .3(ln 2)2(ln3)f f < D.3(ln 2)2(ln3)f f 与的大小不确定8、过双曲线2222x y a b-=1(a >0,b >0)的左焦点F 引圆x 2+y 2=a 2的切线,切点为T ,延长FT 交双曲线右支于点P ,若T 为线段FP 的中点,则该双曲线的渐近线方程为( ) A .x ±y =0B .2x ±y =0C .4x ±y =0D .x ±2y =09、已知,40,tan 12sin sin 22πθθθθ<<=++k 则)4sin(πθ-的值( ) A .随着k 的增大而增大 B .有时随着k 的增大而增大,有时随着k 的增大而减小 C .随着k 的增大而减小 D .是一个与k 无关的常数10、已知符号函数1,0sgn()0,01,0x x x x >⎧⎪==⎨⎪-<⎩,则函数1()sgn(ln )(23)x f x x -=--的零点个数为( ) A.1 B.2 C.3 D.411、平面α、β、γ两两互相垂直,点A ∈α,点A 到β、γ的距离都是3,P 是α内的动点,P 到β的距离是到点A 距离的2倍,则点P 的轨迹上的点到γ的距离的最小值是( ) A . 3- 3B .3+ 3C .1D .312、定义在R 上的函数)(x f y = 是增函数,且函数)3(-=x f y 的图像关于(3,0)成中心对称,若t s ,满足不等式22(2)(2)0f s s f t t -+-≥,则当14s ≤≤时,3t s +的取值范围是( ) A .]10,2[- B .[4,16] C .]10,4[ D .]16,2[-第II 卷二、填空题(本大题共4小题,每小题5分,共20分).13、右面程序框图中,已知f 0(x)=xe x ,则输出的结果是___ __;14、已知{x 1, x 2, x3, x 4}⊆{x >0|(x -3)sinπx =1}, 则x 1+x 2+x 3+x 4的最小值为___ __;15、ABC ∆内接于以O 为圆心,1为半径的圆,且3450OA OB OC ++=,则该ABC ∆的面积___ __;16、某几何体的三视图如图,若该几何体的各顶点都在一个球面上,则此球的表面积为___ __;(2sin aR A=,其中R 为三角形外接圆半径)三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.) 17、(本小题满分12分)在各项均为正数的等比数列{}n a 中, 已知3212+=a a , 且23a ,4a ,35a 成等差数列.(1)求数列{}n a 的通项公式; (2)设n n a b 3log =,求数列{}n n b a 的前n 项和n S .18.(本小题满分12分)已知某几何体直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,60°3388主视图侧视图(1)求证:BN 11C B N ⊥平面; (2)11sin C N CNB θθ设为直线与平面所成的角,求的值; (3)设M 为AB 中点,在BC 边上找一点P ,使MP //平面1CNB 并求BPPC的值 19、(本小题满分12分)一个盒子装有六张卡片,上面分别写着如下六个函数:31()f x x =,2()5xf x =,3()2f x =,421()21x xf x -=+,5()sin()2f x x π=+,6()cos f x x x =. (Ⅰ)从中任意拿取2张卡片,若其中有一张卡片上写着的函数为奇函数。
安徽省宿州市2015届高三第三次质量检测数学理试题 Word版含答案
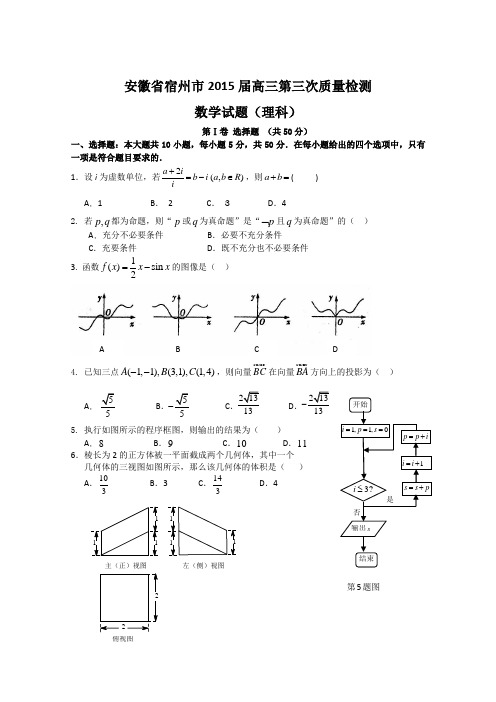
安徽省宿州市2015届高三第三次质量检测数学试题(理科)第Ⅰ卷 选择题 (共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设i 为虚数单位,若2(,)a ib i a b R i+=-∈,则a b +=( ) A .1 B . 2 C . 3D .42. 若,p q 都为命题,则“p 或q 为真命题”是“p ⌝且q 为真命题”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件3. 函数1()sin 2f x x x =-的图像是( )4. 已知三点(1,1),(3,1),(1,4)A B C --,则向量BC 在向量BA 方向上的投影为( )A .5 B.5- CD. 5. 执行如图所示的程序框图,则输出的结果为( )A .8B .9C .10D .11 6.棱长为2的正方体被一平面截成两个几何体,其中一个 几何体的三视图如图所示,那么该几何体的体积是( )A .310B .3C .314D .4俯视图左(侧)视图主(正)视图第5题图A B C D7.若实数,x y 满足约束条件42401x y x y x +≤⎧⎪--≤⎨⎪≥⎩,则点(,)P x y 落在圆22(1)(3)4x y -+-=内的概率为( )A .27π B .227π C .9π D .29π 8.若函数()2sin()3f x x πω=+,且()2,()0f f αβ=-=,αβ-的最小值是2π,则()f x 的单调递增区间是( )A. 5[,]()1212k k k Z ππππ-+∈ B . [,]()36k k k Z ππππ-+∈ C .2[2,2]()33k k k Z ππππ-+∈ D . 5[2,2]()66k k k Z ππππ-+∈ 9. 已知抛物线2:2(0)C y px p =>的焦点为F ,准线为l ,动点M 在直线l 上,线段MF 的中垂线为m ,则直线m 与抛物线C 交点的个数为( )A .0B .1C .2D .无法确定10.各位数字之和为8的正整数(如:8,17,224)按从小到大的顺序构成数列{}n a ,若2015n a =,则=n ( )A. 56 B .72 C .83 D .124第Ⅱ卷 非选择题(共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人.为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的青年职工有7人,则该样本容量为 人.12.在极坐标系中,圆3ρ=上的点到直线sin )2ρθθ-=的距离的最大值为 .13.设22cos a xdx ππ-=⎰,则二项式6(展开式中含 2x 项的系数是 . 14. 已知数列{}n a 满足151=a ,12n n a a n+-=,则n an 的最小值为 .15.定义:如果函数()f x 在给定区间][b a ,上存在0(,)x a b ∈,满足ab a f b f x f --=)()()(0,则称函数()f x 是][b a ,上的“斜率等值函数”,0x 是函数()f x 的一个等值点.例如函数2()f x x =是]22[,-上的“斜率等值函数”,0是它的一个等值点.给出以下命题: ①函数1cos )(-=x x f 是]22[ππ,-上的“斜率等值函数”;②若()f x 是][b a ,上的偶函数,则它一定是][b a ,上的“斜率等值函数”; ③若()f x 是][b a ,上的“斜率等值函数”,则它的等值点x 0≥2ba +; ④若函数1)(2--=mx x x f 是]11[,-上的“斜率等值函数”,则实数m 的取值范围是)20(,;⑤若()ln f x x =是区间[a ,b ] (b >a ≥1)上的“斜率等值函数”,0x 是它的一个等值点,则0ln x <. 其中的真命题有 .(写出所有真命题的序号)三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤. 16. (本小题满分12分)在ABC ∆中,角,,A B C 的对边分别是,,a b c cos 2cos C b A =().(Ⅰ)求角A 的大小; (Ⅱ)求25cos()2sin 22CB π--的取值范围.17. (本小题满分12分)宿州市在举办奇石文化艺术节期间,为了提升与会者的赏石品味,组委会把聘请的6位专家随机的安排在“奇石公园”与“奇石展览中心”两个不同地点作指导,每一地点至少安排一人. (Ⅰ)求6位专家中恰有2位被安排在“奇石公园”的概率;(Ⅱ)设,x y 分别表示6位专家被安排在“奇石公园”和“奇石展览中心”的人数,记X x y =-,求随机变量X 的分布列和数学期望EX .18. (本小题满分12分)设函数321()3f x x x ax =++,a R ∈. (Ⅰ)若()f x 在区间3(,)2-∞-上存在单调递减区间,求a 的取值范围;(Ⅱ)当40a -<<时,()f x 在区间[]0,3上的最大值为15,求()f x 在[]0,3上的最小值.19. (本小题满分13分)如图(1)所示,以线段BD 为直径的圆经过,A C 两点,且1AB BC ==,2BD =,延长,DA CB交于点P ,将PAB ∆沿AB 折起,使点P 至点P '位置得到如图(2)所示的空间图形,其中点P '在平面ABCD 内的射影恰为线段AD 的中点Q .(Ⅰ)若线段,P B P C ''的中点分别为,E F ,试判断,,,A D E F 四点是否共面?并说明理由; (Ⅱ)求平面P AB '与平面P CD '的夹角的余弦值.20. (本小题满分13分)已知椭圆2222:1(0)x y C a b a b +=>>.(Ⅰ)求椭圆C 的方程;(Ⅱ)过点(3,2)M 的直线与椭圆C 相交于两不同点A 、B ,且AM BM λ=.在线段AB 上取点N ,若AN BN λ=-,证明:动点N 在定直线上.21.(本小题满分13分)已知数列{}n a 满足101a <<,1ln(1)n n n a a a +=-+ ;数列{}n b 满足1111,(1)22n n b b n b +==+. (Ⅰ)求证:101n n a a +<<<;'(Ⅱ)若221=a 且1+n a <22n a ,则当2n ≥时,求证:!n n b a n >⋅.试题答案第Ⅰ卷 选择题 (共50分)一、 选择题:本大题共10小题,每小题5分,共50分.二、填空题:本大题共5小题,每小题5分,共25分. 11.15; 12. 4; 13. -192; 14.274; 15. ①④⑤. 三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.16. 解:(Ⅰ)由正弦定理可得,cos 2sin cos cos A C B A C A =)2sin cos A C B A +=, 即sin 2sin cos B B A =又B 为三角形的内角,所以sin 0B ≠,于是cos A =, 又A 亦为三角形内角,因此,=6A π. …………6分(Ⅱ)255cos()2sin sin cos 1sin cos()1226C B B C B B ππ--=+-=+-- 55sin cos cos sin sin 166B B B ππ=++-3sin cos 1)1226B B B π=--=-- 由=6A π可知,5(0,)6B π∈,所以2(,)663B πππ-∈-,从而1sin(),162B π⎛⎤-∈- ⎥⎝⎦,)116B π⎛⎤--∈ ⎥ ⎝⎦,故25cos()2sin 22C B π--的取值范围为1⎛⎤ ⎥ ⎝⎦. …………12分17.解:(Ⅰ)设6位专家中恰有i 名被安排在“奇石公园”的事件为i A ,(1,2,3,4,5)i =,则24642615()2262C C P A ==-. …………4分(Ⅱ)X 的所有可能取值是0,2,4.()33633610(0)2231C C P X P A =-===()()24426462246615(2)+222231C C C C P X P A P A --==+==;()()155********(4)+222231C C C P X P A P A --==+==.则随机变量X 的分布列为则X 的数学期望()=0+2+431313131E X ⨯⨯⨯= ………………12分18. 解:(Ⅰ)由条件知导函数()'22f x x x a =++在3(,)2-∞-上存在函数值小于零的区间,只需2'33320222f a ⎛⎫⎛⎫⎛⎫-=-+⨯-+< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得34a <,故a 的取值范围为3(,)4-∞. …………5分(Ⅱ)()'22fx x x a =++ 的图像开口向上,且对称轴1x =-,()'00,f a =<()'396150,f a a =++=+>所以必存在一点0(0,3),x ∈使得(),00'=x f 此时函数()x f 在[]00,x 上单调递减,在[]0,3x 单调递增,又由于()00f =,()()3991800f a a f =++=+>=所以()31815f a =+=,即3a =-,此时, 由()()'200002301-3fx x x x =+-=⇒=或舍去,所以函数()()min 513f x f ==-. …………12分19. 解:(Ⅰ)假设,,,A D E F 四点共面. 因为//,EF BC BC ⊄平面AEFD ,所以//BC 平面AEFD ,又平面AEFD平面ABCD AD =,且BC ⊆平面ABCD ,所以//BC AD ,这就与已知图(1)中BC AD P =矛盾,所以,,,,A D E F 四点不共面. …………5分 (Ⅱ)因为BD 为圆的直径,所以2BAD BCD π∠=∠=,在Rt ABD ∆和Rt BCD ∆中,由1,2AB BC BD ===,可得AD CD = 且6ADB BDC π∠=∠=,所以3ADC π∠=,连接AC ,则有ACD ∆为正三角形,又Q 为AD 的中点,连接CQ 可知CQ AD ⊥,又P Q '⊥底面ABCD ,所以,,QC QD QP '两两垂直.以Q 为坐标原点,分别以,,QC QD QP '为,,x y z 轴建立空间直角坐标系Q xyz -,则有3(0,(1,(,0,0),2A B C3(0,0,)2D P ' 设平面P AB '的一个法向量为1(,,)n x y z =,则12(,,)(1,0,0)033(,,)(0,)022n AB x y z x n PA x y z y z ⎧⋅=⋅==⎪⎨⋅=⋅-=-=⎪⎩ 令1z =,可得1(0,)n =,同理可求得平面P CD '的一个法向量为2(1)n =, 1212125cos ,5n n n n n n ⋅<>==⨯…………13分 因此,平面P AB '与平面P CD '的夹角的余弦值为5. 20. 解:(Ⅰ)由题意:22222211c aa b c a b⎧=⎪⎪⎪+=⎨⎪⎪⎪=+⎩,解得224,2a b ==,所求椭圆方程为22142x y +=. …………4分(Ⅱ)设点,,Q A B 的坐标分别为1122(,),(,),(,)x y x y x y .由题意得,记1122(3,2)(3,2)x y x y λ--=--,1122(,)(,)x x y y x x y y λ--=---,于是有 123(1)x x λλ-=- ① 122(1)y y λλ-=- ② 12(1)x x x λλ+=+ ③ 12(1)y y y λλ+=+ ④①⨯③得 222123(1)x x x λλ-=- ⑤ ②⨯④得 222122(1)y y y λλ-=- ⑥由点,A B 在椭圆C 上,得221124,x y += 222224,x y +=⑤+2⨯⑥得 224(1)(34)(1)x y λλ-=+- 由题意知0λ>且1λ≠,所以344x y +=,故点N 在定直线3440x y +-=上. …………13分 21.证明:(Ⅰ)先用数学归纳法证明01n a <<. ①当1n =时,由已知得结论成立②假设n k =()k N +∈时01k a <<成立,则当1n k =+时,设)1ln()(+-=x x x f , 于是1()11f x x '=-+在(0,1)上恒有()0f x '>,所以)(x f 在(0,1)上递增, 所以(0)()(1)1ln 21k f f a f <<=-<,又(0)0f =,从而101k a +<<, 这就是说当1n k =+时命题成立, 由①②知01n a <<成立又1ln(1)0n n n a a a +-=-+<,即1n n a a +<,综上可得,101n n a a +<<<,n N +∈. …………6分 (Ⅱ)因为211=b ,n n b n b )1(211+=+,所以211+=+n b b n n ,所以2≥n 时,1211211!2n n n n n n b b b b b n b b b ---=⋅⋅⋅⋅=⋅ 因为221n n a a <+ , 0n a >,所以21n n n a a a <+, 从而2≥n 时312121121222n n n n a a a a a a a a a a a --=⋅⋅<⋅⋅, 因为221=a ,当2≥n 时,101n n a a -<<< 所以2112111122222n n n n a a aa a a --<⋅⋅⋅<=,又1!2n n b n =⋅,因此当2n ≥时,!n n b a n >⋅. …………13分。
安徽省江淮名校2015届高三第三次联考数学(理)试题 扫描版含答案

数学(理科)试卷满分:150分 考试时间:120分钟第Ⅰ卷(选择题 满分50分)一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.选A解析:{|2},{|13},{|31}{|1}R R A x x B x x C B x x A C B x x =<=<<=≥≤=≤或,,2.C3.D4.选C解析:22(1,0)3)2,3)O C O A O B λλλλ=-+=-+=,即()C λ-,又120AOC ∠=所以3tan120=1λ= , 5.D6.A 解析:由41a a <得31q >即1q >,由53a a <得21q >即1q >或1q <-7.B解析:211334214322144C C C C A A ∙∙= 8.选D解析:03(1)3(1)ay a y z x x -==∙+--表示阴影部分内的点P 到点(A 连线斜率的3a 倍,由图可知连线斜率恒大于或等于0,故当P 为(0,1)时z 的最大值为18,所以10130(1)8a -=--得38a =, 9.D 解析:作出()y f x =的图像如下所示,则()()F x f x a =-的零点即为函数()y f x =与y a =图像交点的横坐标,由图可知共有五个零点,不妨设为12345,,,,x x x x x 且12345x x x x x <<<<,从图中可看出1x 与2x 关于直线3x =-对称,4x 与5x 关于直线3x =对称,故12452(3)230x x x x +++=⨯-+⨯=,当(1,0)x ∈-时12()log (1)f x x =--+,因此由12log (1)x a --+=解得312a x =-,故1234512a x x x x x ++++=-10.选B . 由()cos sin 0f x x x x '=-=得cos sin 0x x x -=,显然cos 0x ≠所以1tan x x=,易知方程1tan x x =的实根就是()f x 的极值点。
2015届高三统测(三)理科答案

高三统测试卷(三)答案 理科第Ⅰ卷一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合}02|{≥-=x x A ,|{x B =0<x 2log <2},则)(B A C R ⋂是( )A .|{x 2<x <4}B .}2|{≥x xC .}4,2|{≥≤x x x 或D . ,2|{〈x x 或}4≥x 2. 在ABC ∆中,“3π=A ”是“1cos 2A =”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件3.设函数22()cos ()sin (),44f x x x x R ππ=+-+∈,则函数()f x 是( )A .最小正周期为2π的奇函数 B .最小正周期为π的奇函数C .最小正周期为2π的偶函数 D .最小正周期为π的偶函数4.已知)4sin(cos 22sin ,2,21)4tan(2παααπαππα--<<-=+则且等于( )A .552- B .1053- C .552 D .101035. 下列函数中,图像的一部分如右图所示的是( )A .sin()6y x π=+ B. sin(2)6y x π=- C. cos(4)3y x π=- D. cos(2)6y x π=-6.由直线x =1,x =2,曲线1y x =及x 轴所围图形的面积为( )A .47B .411C .ln2D .2ln 27. 为了得到函数sin 26y x π⎛⎫=- ⎪⎝⎭的图象,可以将函数cos 2y x =的图象( )A. 向左平移3π个单位 B. 向右平移6π个单位 C. 向右平移3π个单位 D. 向左平移6π个单位 8. 定义在R 上的偶函数,f (x )满足:对任意的x 1, x 2∈(],0-∞(x 1≠x 2), 有(x 1-x 2)[f (x 2)-f (x 1)]>0,则当n *N ∈时,有( )A .f (-n)<f (n-1)<f (n+1) B. f (n -1)<f (-n )<f (n +1)C. f (n +1)<f (-n )<f (n -1)D. f (n +1)<f (n -1)<f (-n )9. 函数1|log |3)(21-=x x f x的零点个数为( )A .0B .1C .4D .210.函数12,41()),3),7),2(2),4x x f x a f b f c f x f x x ⎧->⎪====⎨⎪+≤⎩记 则( )A .a >c >bB .b <a <cC .a <c <bD .a >b >c11. )0)()((),(≠x g x g x f 分别是定义在R 上的奇函数和偶函数,当0x <时,()()()()f x g x f x g x ''<,且0)()(,0)3(<=-x g x f f的解集为( )A .(-∞,-3)∪(3,+∞)B .(-3,0)∪(0,3)C .(-3,0)∪(3,+∞)D .(-∞,-3)∪(0,3)12.已知定义在R 上的偶函数f (x )在[0,+∞]上是增函数,不等式f (ax + 1)≤f (x –2) 对任意x ∈[21,1]恒成立,则实数a 的取值范围是( )A .[–3,–1]B .[–2,0]C .[–5,1]D .[–2,1]第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.13. 设定义在R 上的函数f (x )满足7)()2(=∙+x f x f ,若f (1)=2,则f (107)=__________.14.已知直线y =2x +1与曲线)ln(a x y +=相切,则a 的值为 .15. 下列几个命题:①函数y =是偶函数,但不是奇函数;②“⎩⎨⎧≤-=∆>0402ac b a ”是“一元二次不等式ax 2+bx +c ≥0的解集为R ”的充要条件; ③ 设函数()y f x =定义域为R ,则函数(1)y f x =-与(1)y f x =-的图象关于y 轴对称; ④若函数)0)(cos(≠+=A x A y ϕω为奇函数,则)(2Z k k ∈+=ππϕ;⑤已知x ∈(0,π),则y =sin x +xsin 2的最小值为。
广东省“六校联盟”2015-2016学年高三(上)第三次联考数学试卷(解析版)(理科)

2015-2016学年广东省“六校联盟”高三(上)第三次联考数学试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={x∈R|},N={x∈R|y=ln(x﹣1)},则M∩N()A.∅B.{x|x≥1}C.{x|x>1}D.{x|x≥1或x<0} 2.已知两条直线m,n,两个平面α,β,给出下面四个命题:①m∥n,m⊥α⇒n⊥α②α∥β,m⊂α,n⊂β⇒m∥n③m∥n,m∥α⇒n∥α④α∥β,m∥n,m⊥α⇒n⊥β其中正确命题的序号是()A.①③B.②④C.①④D.②③3.下列四个条件中,p是q的必要不充分件的是()A.p:a>b,q:a2>b2B.p:a>b,q:2a>2bC.p:非零向量与夹角为锐角,q:D.p:ax2+bx+c>0,q:﹣+a>04.设函数f(x)=x﹣lnx﹣,则函数y=f(x)()A.在区间(),(1,e)内均有零点B.在区间(),(1,e)内均无零点C.在区间()内有零点,在区间(1,e)内无零点D.在区间()内无零点,在区间(1,e)内有零点5.要得到函数y=cosx的图象,需将函数y=sin(2x+)的图象上所有的点的变化正确的是()A.横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度B.横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度C.横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动个单位长度D.横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动个单位长度=()6.已知{a n}是等比数列,a2=,a5=4,则a1a2+a2a3+…+a n a n+1A.(2n﹣1)B.(2n+4)C.(4n﹣1)D.(4n﹣2)7.如果点P在平面区域,点Q在曲线x2+(y+2)2=1上,那么|PQ|的最小值为()A.﹣1 B.2﹣1 C.2 D.﹣18.已知函数y=f(x)是定义在R上的奇函数,当x≤0时f(x)=2﹣x+m﹣1(m∈R),a=f (log45),b=(log23),c=f(m),则a,b,c的大小关系为()A.a<b<c B.b<a<c C.c<a<b D.c<b<a9.在△ABC中,己知D是AB边上一点,若=λ,=+μ(λ,μ∈R),则λ=()A.﹣2 B.﹣1 C.1 D.210.已知函数f(x)=f′(1)x2+2x f(x)dx+1在区间(a,1﹣2a)上单调递增,则实数a的取值范围是()A.(,)B.[,)C.(﹣∞,)D.[,+∞)11.一个正三棱锥的四个顶点都在直径为2的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是()A.2B.C.D.12.已知定义在(0,+∞)上的连续函数y=f(x)满足:xf′(x)﹣f(x)=xe x且f(1)=﹣3,f(2)=0.则函数y=f(x)()A.有极小值,无极大值B.有极大值,无极小值C.既有极小值又有极大值D.既无极小值又无极大值二、填空题:本大题共4小题,每小题5分,满分20分13.在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2﹣c2=3b,且sinAcosC=2cosAsinC,则b=.14.已知数列{a n}的前n项和为S n,且满足S n=2a n﹣1(n∈N*),则数列{na n}项和T n.15.已知某个几何体的三视图如图,根据图中标出的尺寸,可得这个几何体的体积等于,全面积为.16.若不等式(﹣1)n a<n+对任意n∈N*恒成立,则实数a的取值范围是.三、解答题:包括必做题和选做题,第17题到第21题为必做题,解答应写出文字说明,证明过程或演算步骤.17.已知函数f(x)=cos(2x﹣)+2sin(x﹣)sin(x+).(1)求函数f(x)的最小正周期和图象的对称轴方程;(2)求函数f(x)在区间[﹣,]上的最值.18.等差数列{a n}各项均为正数,其前n项和为S n,a2S3=75且a1,a4,a13成等比数列.(1)求数列{a n}的通项公式a n;(2)若数列{a n}为递增数列,求证:≤.19.如图,在三棱锥P﹣ABC中,PA⊥平面ABC,底面ABC是直角三角形,PA=AB=BC=4,O是棱AC的中点,G是△AOB的重心,D是PA的中点.(1)求证:BC⊥平面PAB;(2)求证:DG∥平面PBC;(3)求二面角A﹣PC﹣B的大小.20.已知点P是圆O:x2+y2=1上任意一点,过点P作PQ⊥y轴于点Q,延长QP到点M,使.(1)求点M的轨迹的方程;(2)过点C(m,0)作圆O的切线l,交(1)中曲线E于A,B两点,求△AOB面积的最大值.21.已知函数f(x)=ln(x+1)+ax2﹣x(a∈R).(1)若a=,求曲线y=f(x)在点(0,f(0))处的切线方程;(2)讨论函数y=f(x)的单调性;(3)若存在x0∈[0,+∞),使f(x)<0成立,求实数a的取值范围.请考生在第(22),(23),(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分,作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑.选修4-1:几何证明选讲22.如图,已知圆O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是圆O的直径.过点C作圆O的切线交BA的延长线于点F.(Ⅰ)求证:ACBC=ADAE;(Ⅱ)若AF=2,CF=2,求AE的长.选修4-4:坐标系与参数方程.23.在平面直角坐标系xOy中,直线l的参数方程为(t为参数).在以原点O为极点,x轴正半轴为极轴的极坐标中,圆C的方程为ρ=2sinθ.(1)写出直线l的普通方程和圆C的直角坐标方程;(2)设点P(3,),直线l与圆C相交于A、B两点,求+的值.选修4-5:不等式选讲.24.已知函数f(x)=的定义域为R.(1)求实数m的取值范围;(2)若实数m的最大值为n,正数a,b满足=n,求4a+3b的最小值.2015-2016学年广东省“六校联盟”高三(上)第三次联考数学试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={x∈R|},N={x∈R|y=ln(x﹣1)},则M∩N()A.∅B.{x|x≥1}C.{x|x>1}D.{x|x≥1或x<0}【考点】交集及其运算.【分析】求出M中x的范围确定出M,求出N中x的范围确定出N,找出两集合的交集即可.【解答】解:由M中,解得x<0或x≥1,得到M={x|x<0或x≥1},由N中y=ln(x﹣1),得到x﹣1>0,解得:x>1,即N={x|x>1},则M∩N={x|x>1},故选:C.【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.已知两条直线m,n,两个平面α,β,给出下面四个命题:①m∥n,m⊥α⇒n⊥α②α∥β,m⊂α,n⊂β⇒m∥n③m∥n,m∥α⇒n∥α④α∥β,m∥n,m⊥α⇒n⊥β其中正确命题的序号是()A.①③B.②④C.①④D.②③【考点】空间中直线与平面之间的位置关系.【分析】由题意用线面垂直和面面平行的定理,判断线面和面面平行和垂直的关系.【解答】解:用线面垂直和面面平行的定理可判断①④正确;②中,由面面平行的定义,m,n可以平行或异面;③中,用线面平行的判定定理知,n可以在α内;故选C.【点评】本题考查了线面垂直和面面平行的定理,及线面、面面位置关系的定义,属于基础题.3.下列四个条件中,p是q的必要不充分件的是()A.p:a>b,q:a2>b2B.p:a>b,q:2a>2bC.p:非零向量与夹角为锐角,q:D.p:ax2+bx+c>0,q:﹣+a>0【考点】必要条件、充分条件与充要条件的判断.【分析】对四个选项逐个分析知A.p不是q的充分条件,也不是必要条件;B.p是q的充要条件;C.p是q的充分条件,不是必要条件;【解答】解:A.p不是q的充分条件,也不是必要条件;B.p是q的充要条件;C.p是q的充分条件,不是必要条件;D.正确故选:D.【点评】判断一个命题是另一个命题的什么条件,应该先确定出条件角色,然后两边相互推一下,利用充要条件的定义得出结论.4.设函数f(x)=x﹣lnx﹣,则函数y=f(x)()A.在区间(),(1,e)内均有零点B.在区间(),(1,e)内均无零点C.在区间()内有零点,在区间(1,e)内无零点D.在区间()内无零点,在区间(1,e)内有零点【考点】利用导数研究函数的单调性.【分析】由导数判断f (x )在(),(1,e )上均为单调函数,结合f ()>0,f(1)<0,f (e )>0得答案.【解答】解:由f (x )=x ﹣lnx ﹣,得f ′(x )=1﹣=,当x ∈(0,1)时,f ′(x )<0,当x ∈(1,+∞)时,f ′(x )>0, ∴f (x )在(),(1,e )上均为单调函数,又,f (1)=1﹣ln1﹣=<0,f (e )=e﹣lne ﹣=e ﹣>0,∴函数y=f (x )在区间(),(1,e )内均有零点,故选:A .【点评】本题考查利用导数研究函数的单调性,考查函数零点判定定理,是中档题.5.要得到函数y=cosx 的图象,需将函数y=sin (2x +)的图象上所有的点的变化正确的是( )A .横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度B .横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度C .横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动个单位长度D .横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动个单位长度【考点】函数y=Asin (ωx +φ)的图象变换.【分析】由条件利用诱导公式以及y=Asin (ωx +φ)的图象变换规律,可得结论.【解答】解:将函数y=sin (2x +)的图象上所有的点横坐标伸长到原来的2倍(纵坐标不变),可得函数y=sin (x +)=cos [﹣(x +)]=cos (x ﹣)的图象;再把所得图象向左平行移动个单位长度,可得函数y=cosx 的图象,故选:C .【点评】本题主要考查诱导公式的应用,利用了y=Asin (ωx +φ)的图象变换规律,统一这两个三角函数的名称,是解题的关键,属于基础题.6.已知{a n }是等比数列,a 2=,a 5=4,则a 1a 2+a 2a 3+…+a n a n +1=( )A .(2n ﹣1)B .(2n +4)C .(4n ﹣1)D .(4n ﹣2)【考点】等比数列的通项公式.【分析】利用等比数列的通项公式可得公比q ,再利用等比数列的通项公式与求和公式即可得出.【解答】解:设等比数列{a n }的公比为q ,∵a 2=,a 5=4,∴,解得q=2.∴a n ==2n ﹣3,∴a n a n +1=2n ﹣32n ﹣2=22n ﹣5.则a 1a 2+a 2a 3+…+a n a n +1=+2+…+22n ﹣5==.故选:C .【点评】本题考查了等比数列的通项公式与求和公式,考查推理能力与计算能力,属于中档题.7.如果点P 在平面区域,点Q 在曲线x 2+(y +2)2=1上,那么|PQ |的最小值为( )A.﹣1 B.2﹣1 C.2 D.﹣1【考点】简单线性规划.【分析】画出平面区域以及Q在的曲线,利用圆上的点到区域内点的距离求最小值.【解答】解:P所在的平面区域如图:过圆心(0,﹣2)作直线x+y﹣2=0的垂线,垂直为Q,与圆交于P,则|PQ|所求,由点到直线的距离得到|PQ|=;故选B.【点评】本题考查了简单线性规划问题,求线段长度的最小值,关键|PQ|的几何意义得到最小值的位置.8.已知函数y=f(x)是定义在R上的奇函数,当x≤0时f(x)=2﹣x+m﹣1(m∈R),a=f (log45),b=(log23),c=f(m),则a,b,c的大小关系为()A.a<b<c B.b<a<c C.c<a<b D.c<b<a【考点】函数奇偶性的性质.【分析】求出m,确定函数y=f(x)是在R上单调递减,0<log45<log23,即可得出结论.【解答】解:由题意,f(0)=0,∴2m﹣1=0,∴m=0,∴当x≤0时f(x)=2﹣x﹣1,单调递减,∵函数y=f(x)是定义在R上的奇函数,∴函数y=f(x)是在R上单调递减,∵0<log45<log23,∴f(0)>f(log45)>f(log23),∴c>a>b,故选:B.【点评】本题考查函数的奇偶性,单调性,考查学生分析解决问题的能力,属于中档题.9.在△ABC中,己知D是AB边上一点,若=λ,=+μ(λ,μ∈R),则λ=()A.﹣2 B.﹣1 C.1 D.2【考点】向量加减混合运算及其几何意义.【分析】用表示出,结合已知条件列出方程解出λ.【解答】解:=+=+=+()=,∴,解得λ=2.故选:D.【点评】本题考查了平面向量加减运算的几何意义,是基础题.10.已知函数f(x)=f′(1)x2+2x f(x)dx+1在区间(a,1﹣2a)上单调递增,则实数a的取值范围是()A.(,)B.[,)C.(﹣∞,)D.[,+∞)【考点】定积分.【分析】先设f(x)dx=c,再求导得到f(x)=f′(1)x2+2cx+1,令x﹣1,得到f′(1)=﹣2c,继而得到f(x),再根据定积分的计算,求出c的值,继而求出f(x)=﹣3x2+3x+1,根据二次函数的性质即可求出a的取值范围.【解答】解:设f(x)dx=c,∴f(x)=f′(1)x2+2cx+1,∴f′(x)=f′(1)2x+2c,∴f′(1)=2f′(1)+2c,∴f′(1)=﹣2c,∴f(x)=﹣2cx2+2cx+1,∴f(x)dx=(﹣2cx2+2cx+1)dx=(﹣cx3+cx2+x)|=﹣c+c+1=c,解得c=,∴f′(1)=﹣2c=﹣3,∴f(x)=﹣3x2+3x+1,∴函数f(x)的对称轴为x=,且开口向下,∴f(x)在(﹣∞,)上单调递增,∵f(x)在区间(a,1﹣2a)上单调递增,∴,解得≤a<,故选:B.【点评】本题考查了定积分的计算,二次函数的单调性,关键是换元,属于中档题.11.一个正三棱锥的四个顶点都在直径为2的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是()A.2B.C.D.【考点】棱柱、棱锥、棱台的体积.【分析】正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,所以球心是底面三角形的中心.然后求出三角形的边长,再求体积.【解答】解:正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,所以球心是底面三角形的中心.设球的半径为R=1,底面三角形的边长为a,=1⇒a=该正三棱锥的体积:=故选:C【点评】本题考查了正棱锥体积公式、三角形重心定理、球大圆的定义等相关知识点,属基础题.12.已知定义在(0,+∞)上的连续函数y=f(x)满足:xf′(x)﹣f(x)=xe x且f(1)=﹣3,f(2)=0.则函数y=f(x)()A.有极小值,无极大值B.有极大值,无极小值C.既有极小值又有极大值D.既无极小值又无极大值【考点】利用导数研究函数的极值.【分析】由题意可得在(0,+∞)上是增函数,从而可得f′(x)在(0,+∞)上是增函数,从而解得.【解答】解:∵==>0,∴在(0,+∞)上是增函数,∵xf′(x)﹣f(x)=xe x,∴f′(x)=+e x,∵y=e x在(0,+∞)上是增函数,∴f′(x)在(0,+∞)上是增函数,又∵f′(1)=﹣3+e<0,f′(2)=0+e2>0,故f′(x)在(0,+∞)上先负值,后正值;故函数y=f(x)有极小值,无极大值,故选A.【点评】本题考查了导数的综合应用,关键在于构造函数.二、填空题:本大题共4小题,每小题5分,满分20分13.在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2﹣c2=3b,且sinAcosC=2cosAsinC,则b=9.【考点】正弦定理.【分析】利用正余弦定理求解即可.sinAcosC=2cosAsinC,可得acosC=2ccosA,再由余弦定理:cosC=,cosA=,a2﹣c2=3b,带入即可求解.【解答】解:由余弦定理:cosC=,cosA=,由题意:∵sinAcosC=2cosAsinC,∴acosC=2ccosA,则:=2×∵a2﹣c2=3b,所以有:=b﹣3解得:b=9故答案为9.【点评】本题考查了利用正余弦定理运用能力和计算能力.属于基础题.14.已知数列{a n}的前n项和为S n,且满足S n=2a n﹣1(n∈N*),则数列{na n}项和T n(n ﹣1)2n+1.【考点】数列的求和.【分析】由S n=2a n﹣1(n∈N*),可得:n=1时,a1=2a1﹣1,解得a1;n≥2时,a n=S n﹣S n﹣1,化为a n=2a n﹣1,利用等比数列的通项公式可得a n,于是na n=n2n﹣1.再利用“错位相减法”、等比数列的求和公式即可得出.【解答】解:∵S n=2a n﹣1(n∈N*),∴n=1时,a1=2a1﹣1,解得a1=1;n≥2时,a n=S n﹣S n﹣1=2a n﹣1﹣(2a n﹣1﹣1),化为a n=2a n﹣1,∴数列{a n}为等比数列,a n=2n﹣1.∴na n=n2n﹣1.则数列{na n}项和T n=1+2×2+3×22+…+n2n﹣1.∴2T n=2+2×22+…+(n﹣1)×2n﹣1+n2n,∴﹣T n=1+2+22+…+2n﹣1﹣n2n=﹣n2n=(1﹣n)2n﹣1,∴T n=(n﹣1)2n+1.故答案为:=(n﹣1)2n+1.【点评】本题考查了“错位相减法”、等比数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.15.已知某个几何体的三视图如图,根据图中标出的尺寸,可得这个几何体的体积等于,全面积为2(3++).【考点】构成空间几何体的基本元素.【分析】根据几何体的三视图,得出该几何体是底面为正方形的直四棱锥,结合图中数据求出它的体积与全面积.【解答】解:(1)根据几何体的三视图,得;该几何体是底面为正方形的直四棱锥,底面边长为2,高为2,如图所示;∴该四棱锥的体积为V=×22×2=;四棱锥(2)该四棱锥的全面积为=22+×2×2+2××2×+×2×2S全面积=4+2+2+2=.故答案为:,2(3++).【点评】本题考查了空间几何体的三视图的应用问题,解题的关键是根据几何体的三视图得出该几何体的结构特征是什么,是基础题目.16.若不等式(﹣1)n a<n+对任意n∈N*恒成立,则实数a的取值范围是().【考点】函数恒成立问题.【分析】按照n为奇数,偶数两种情况讨论,分离出参数a后化为函数最值问题求解即可.【解答】解:①当n为奇数时,设n=2k﹣1(k∈N*)那么(﹣1)n a<n+转化为:﹣a<(2k﹣1)+∴﹣a<2k﹣1+,(k∈N*)a>1﹣(2k)∵2k,当且仅当k=时取等号,又∵k∈N*∴当k=1时,2k=当k=2时,2k=可见当k=2时,取得最小值.∴a>1﹣=所以a>恒成立.②当n为偶数时,设n=2k(k∈N*)那么(﹣1)n a<n+转化为:a<2k﹣∴a<2k+1﹣﹣1,(k∈N*)2k+1﹣≥0,所以a<﹣1时恒成立.综上所述:a的取值范围是()故答案为()【点评】本题考查了函数恒成立,不等式知识点,考查转化思想,分类讨论思想.属于中档题.三、解答题:包括必做题和选做题,第17题到第21题为必做题,解答应写出文字说明,证明过程或演算步骤.17.已知函数f(x)=cos(2x﹣)+2sin(x﹣)sin(x+).(1)求函数f(x)的最小正周期和图象的对称轴方程;(2)求函数f(x)在区间[﹣,]上的最值.【考点】三角函数中的恒等变换应用;正弦函数的图象.【分析】(1)利用积化和差和和差化积公式将已知函数转化为正弦函数,由此来求函数f (x)的最小正周期和图象的对称轴方程;(2)利用(1)中的结果和正弦函数的单调性进行解答.【解答】解:(1)∵f(x)=cos(2x﹣)+2sin(x﹣)sin(x+)=cos2x+sin2x+(sinx﹣cosx)(sinx+cosx)=cos2x+sin2x+sin2x﹣cos2x=cos2x+sin2x﹣cos2x=sin(2x﹣),∴T==π.由2x﹣=+kπ,k∈Z得,x=+,k∈Z,∴对称轴方程为x=+,k∈Z;(2)∵,∴.∵f(x)=sin(2x﹣)在区间[﹣,]上单调递增,在区间[,]上单调递减,∴当x=时,f(x)max=1.又∵,∴当x=﹣时,f(x)min=﹣1.【点评】本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.18.等差数列{a n}各项均为正数,其前n项和为S n,a2S3=75且a1,a4,a13成等比数列.(1)求数列{a n}的通项公式a n;(2)若数列{a n}为递增数列,求证:≤.【考点】数列与不等式的综合;等差数列的通项公式;数列的求和.【分析】(1)设数列{a n}的公差为d(d≥0),由已知列式求得首项和公差,则等差数列的通项公式可求;(2)由(Ⅰ)求出等差数列的通项公式,进一步求得前n项和,取倒数后利用裂项相消法求出数列前n项和的倒数和,即可证得不等式右边,再由数列的函数特性证明左边得答案.【解答】(1)解:设数列{a n}的公差为d(d≥0),由已知,则有,∵a n>0,∴,即,解得,或.a n=5或a n=2n+1;(2)∵数列{a n}为递增数列,∴由(Ⅰ)知a n=2n+1,∴,n∈N*,∴,∴=,记由,则T n关于n递增.∴.综上可得:≤.【点评】本题考查数列递推式,考查了裂项相消法求数列的前n项和,训练了利用数列的函数特性求最值,是中档题.19.如图,在三棱锥P﹣ABC中,PA⊥平面ABC,底面ABC是直角三角形,PA=AB=BC=4,O是棱AC的中点,G是△AOB的重心,D是PA的中点.(1)求证:BC⊥平面PAB;(2)求证:DG∥平面PBC;(3)求二面角A﹣PC﹣B的大小.【考点】二面角的平面角及求法;直线与平面平行的判定;直线与平面垂直的判定.【分析】(1)证明PA⊥BC,BC⊥AB,即可证明BC⊥平面PAB;(2)连结OG并延长交AB于点E,连结DO,DE,证明平面DOE∥平面PBC,即可证明DG∥平面PBC;(3)过点O作OQ∥PC于点Q,连结BQ,证明∠OQB为二面角A﹣PC﹣B的平面角,即可求二面角A﹣PC﹣B的大小.【解答】(1)证明:∵PA⊥平面ABC,∴PA⊥BC,∵底面ABC是直角三角形,AB=BC,∴BC⊥AB,∵PA∩AB=A,∴BC⊥平面PAB;…(2)证明:连结OG并延长交AB于点E,连结DO,DE∵G是△AOB的重心,∴OE为AB边上的中线,∴E为AB边上的中点,又有D为PA边上的中点,∴DE∥PB,同理可得DO∥PC,且DE∩DO=D,∴平面DOE∥平面PBC,又有DG⊂平面DOE,∴DG∥平面PBC …(3)解:过点O作OQ∥PC于点Q,连结BQ,∵AB=BC且O是棱AC的中点,∴BO⊥AC.∵PA⊥平面ABC,∴平面PAC⊥平面ABC.又有平面PAC∩平面ABC=AC,且BO⊂平面ABC,∴BO⊥平面PAC,又有OQ⊥PC,∴由三垂线定理得BQ⊥PC,∴∠OQB为二面角A﹣PC﹣B的平面角.…由已知得OB=OC=2,PC==4,∵△PAC∽△OQC,∴,∴OQ=,∴tan∠OQB=,∴∠OQB=60°,即二面角A﹣PC﹣B的大小为60°.…【点评】本题考查了二面角A﹣PC﹣B的大小,考查了线面平行与线面垂直的证明,考查了学生的空间想象能力与推理论证能力.20.已知点P是圆O:x2+y2=1上任意一点,过点P作PQ⊥y轴于点Q,延长QP到点M,使.(1)求点M的轨迹的方程;(2)过点C(m,0)作圆O的切线l,交(1)中曲线E于A,B两点,求△AOB面积的最大值.【考点】椭圆的简单性质;轨迹方程.【分析】(1)设点M(x,y),由,可得P为QM的中点,又有PQ⊥y轴,可得P,把点P代入圆:x2+y2=1即可得出.(2)由题意可知直线l不与y轴垂直,故可设l:x=ty+m,t∈R,A(x1,y1),B(x2,y2),由l与圆O:x2+y2=1相切,可得=1,即m2=t2+1,直线方程与椭圆方程联立化为:(t2+4)y2+2mty+m2﹣4=0,利用根与系数的关系可得:=,把根与系数的关系代入化简即可得出S,再利用△OAB基本不等式的性质即可得出.【解答】解:(1)设点M(x,y),∵,∴P为QM的中点,又有PQ⊥y轴,∴P,∴点P是圆:x2+y2=1上的点,∴有=1,即点M的轨迹E的方程为: +y2=1.(2)由题意可知直线l不与y轴垂直,故可设l:x=ty+m,t∈R,A(x1,y1),B(x2,y2),∵l与圆O:x2+y2=1相切,∴=1,即m2=t2+1,①由消x并整理得:(t2+4)y2+2mty+m2﹣4=0,其中△=4m2t2﹣4(t2+4)(m2﹣4)=48>0,又有y1+y2=,y1y2=.②∴=,将①②代入上式得|AB|==,|m|≥1.∴,当且仅当即时,等号成立.∴(S)max=1.△AOB【点评】本题考查了椭圆与圆的标准方程及其性质、直线与椭圆相交问题、直线与圆相切的性质、一元二次方程的根与系数的关系、两点之间的距离公式、点到直线的距离公式、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.21.已知函数f(x)=ln(x+1)+ax2﹣x(a∈R).(1)若a=,求曲线y=f(x)在点(0,f(0))处的切线方程;(2)讨论函数y=f(x)的单调性;(3)若存在x0∈[0,+∞),使f(x)<0成立,求实数a的取值范围.【考点】利用导数求闭区间上函数的最值;利用导数研究曲线上某点切线方程.【分析】(1)根据导数的几何意义即可求出答案,(2)根据导数和函数的单调性关系,再分类讨论,即可得到函数的单调区间,(3)存在x∈[0,+∞),使x∈[0,+∞)成立”的非命题为“对任意x∈[0,+∞),都有f (x)≥0成立”根据(2)即可得到a的取值范围.【解答】解:(1)当a=时,f(x)=ln(x+1)+x2﹣x,∴f′(x)=+x﹣1,∴f(0)=0,f'(0)=0,∴切点为(0,0),切线斜率k=f'(0)=0,∴在点(0,f(0))处切线方程为:y=0…(2)由已知得当a≤0时,∵x>﹣1,∴x+1>0,∴2ax+2a﹣1=2a(x+1)﹣1≤﹣1<0,∴x∈(﹣1,0)时,f'(x)>0,x∈(0,+∞)时,f'(x)<0,此时,f(x)在(﹣1,0)上单调递增,在(0,+∞)上单调递减.…当a>0时,由f'(x)=0得,∵a>0,∴=…若,则,∴,此时,f(x)在(﹣1,+∞)上单调递增;…若,则x1<x2,f(x),f'(x)的变化如下表x (﹣1,x1)x1(x1,x2)x2(x2,+∞)f'(x)+0 ﹣0 +f(x)单调递增单调递减单调递增此时f(x)在(﹣1,x1)和(x2,+∞)上单调递增,在(x1,x2)上单调递减.…若a>则x1>x2,f(x),f'(x)的变化如下表x (﹣1,x2)x2(x2,x1)x1(x1,+∞)f'(x)+0 ﹣0 +f(x)单调递增单调递减单调递增此时f(x)在(﹣1,x2)和(x1,+∞)上单调递增,在(x2,x1)上单调递减…综上所述:当a≤0时,f(x)在(﹣1,0)上单调递增,在(0,+∞)上单调递减;当时,f(x)在(﹣1,0)和上单调递增,在上单调递减;当时,f(x)在(﹣1,+∞)上单调递增;当时,f(x)在和(0,+∞)上单调递增,在上单调递减;…(3)“存在x∈[0,+∞),使x∈[0,+∞)成立”的非命题为“对任意x∈[0,+∞),都有f (x)≥0成立”由(2)得,当时,f(x)在[0,+∞)上单调递增,当时,一定存在区间(0,m)⊆[0,+∞)(m>0),有f(x)在(0,m)上单调递减又有f(0)=0,∴当且仅当对时,“任意x∈[0,+∞),都有f(x)≥f(0)=0成立”即若对任意x∈[0,+∞),都有f(x)≥0成立,则实数a的取值范围是.【点评】本题考查了导数和函数的单调性和最值的关系,以及不等式恒成立的问题和参数的取值范围,属于难题.请考生在第(22),(23),(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分,作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑.选修4-1:几何证明选讲22.如图,已知圆O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是圆O的直径.过点C作圆O的切线交BA的延长线于点F.(Ⅰ)求证:ACBC=ADAE;(Ⅱ)若AF=2,CF=2,求AE的长.【考点】与圆有关的比例线段.【分析】(I)如图所示,连接BE.由于AE是⊙O的直径,可得∠ABE=90°.利用∠E与∠ACB都是所对的圆周角,可得∠E=∠ACB.进而得到△ABE∽△ADC,即可得到.(II)利用切割线定理可得CF2=AFBF,可得BF.再利用△AFC∽△CFB,可得AF:FC=AC:BC,进而根据sin∠ACD=sin∠AEB,AE=,即可得出答案.【解答】证明:(I)如图所示,连接BE.∵AE是⊙O的直径,∴∠ABE=90°.又∠E与∠ACB都是所对的圆周角,∴∠E=∠ACB.∵AD⊥BC,∠ADC=90°.∴△ABE∽△ADC,∴AB:AD=AE:AC,∴ABAC=ADAE.又AB=BC,∴BCAC=ADAE.解:(II)∵CF是⊙O的切线,∴CF2=AFBF,∵AF=2,CF=2,∴(2)2=2BF,解得BF=4.∴AB=BF﹣AF=2.∵∠ACF=∠FBC,∠CFB=∠AFC,∴△AFC∽△CFB,∴AF:FC=AC:BC,∴AC==.∴cos∠ACD=,∴sin∠ACD==sin∠AEB,∴AE==【点评】本题考查了圆的性质、三角形相似、切割线定理,属于中档题.选修4-4:坐标系与参数方程.23.(2015秋广东月考)在平面直角坐标系xOy中,直线l的参数方程为(t为参数).在以原点O为极点,x轴正半轴为极轴的极坐标中,圆C的方程为ρ=2sinθ.(1)写出直线l的普通方程和圆C的直角坐标方程;(2)设点P(3,),直线l与圆C相交于A、B两点,求+的值.【考点】参数方程化成普通方程.【分析】(1)把直线l的参数方程消去参数t可得,它的直角坐标方程;把圆C的极坐标方程依据互化公式转化为直角坐标方程.(2)把直线l的参数方程代入圆C的直角坐标方程,得,即,结合根与系数的关系进行解答.【解答】解:(1)由得直线l的普通方程为.又由得圆C的直角坐标方程为即;(2)把直线l的参数方程代入圆C的直角坐标方程,得,即,由于,故可设t1,t2是上述方程的两实数根,所以,∴t1>0,t2>0…又有直线l过点,A、B两点对应的参数分别为t1,t2所以|PA|=t1,|PB|=t2所以.【点评】本题重点考查了直线的参数方程和普通方程的互化、极坐标方程和直角坐标方程的互化、直线与圆的位置关系等知识,属于中档题.选修4-5:不等式选讲.24.(2015秋牡丹江校级期末)已知函数f(x)=的定义域为R.(1)求实数m的取值范围;(2)若实数m的最大值为n,正数a,b满足=n,求4a+3b的最小值.【考点】基本不等式在最值问题中的应用.【分析】(1)由函数定义域为R,可得|x+2|+|6﹣x|≥m恒成立,设函数g(x)=||x+2|+|6﹣x||,利用绝对值不等式的性质求出其最小值即可;(2)由(1)知n=8,变形,利用基本不等式的性质即可得出.【解答】解:(1)因为函数f(x)的定义域为R.所以|x+2|+|6﹣x|≥m恒成立;设g(x)=|x+2|+|6﹣x|,则g(x)min≥m.又|x+2|+|6﹣x|≥|(x+2)+(6﹣x)|=8,当且仅当﹣2≤x≤6时,g(x)min=8所以m≤8.(2)有(1)可知,n=8,∴,即,有由于a,b均为正数,所以4a+3b=(4a+3b)(+),= [(3a+b)+(a+2b)](+),= [5++]≥(5+4)=,当且2(a +2b )=3a +b ,即时,上式等号成立.所以4a +3b 的最小值是.【点评】本题考查了函数的定义域、绝对值不等式的性质、基本不等式的性质、“乘1法”,考查了推理能力与计算能力,属于中档题.。
全国大联考2015届高三第三次联考(山东版)数学【理】试卷(Word版)

【学易大联考】2015年第三次全国大联考【山东卷】理科数学试卷注意事项:1.本试卷分第Ⅰ卷和第Ⅱ卷两部分。
满分150分,考试时间120分钟2.答题前考生务必用05毫米黑色墨水签字笔填写好自己的姓名、班级、考号等信息 3.考试作答时,请将答案正确填写在答题卡上。
第一卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;第Ⅱ卷请用直径05毫米的黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸......................上作答无效.....第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共00分在每小题给出的四个选项中,只有一项是符合题目要求的1.设集合{||1|3}P x x =+≤,1{|(),(2,1)}3xQ y y x ==∈-,则PQ =( )A. 1(4,)9-B. 1(,2]9C. 1(,2]3D. 1(,2)32.已知,x y R ∈,i 是虚数单位.若2xi +与31yi i++互为共轭复数,则2()x yi +=( ) A. 3i B. 32i +C.2i -D.2i3.函数()f x =的定义域为( ) A. 1(,)3+∞ B. 1[,2)(2,)3+∞ C. 1(,2)(2,)3+∞D. 1[,)3+∞4.用反证法证明命题:“设a 为实数,则函数2()ln f x x a x =-至多有两个零点”时,要做的假设是( )A. 函数2()ln f x x a x =-至少有三个零点 B. 函数2()ln f x x a x =-只有两个零点 C. 函数2()ln f x x a x =-至少有两个零点 D. 函数2()ln f x x a x =-没有零点 5.若正实数,a b 满足2a b ab +=,则a b +的最小值为( )A.5B.C. 3+D. 3+6.曲线3y x =与22y x x =-在第一象限内所围成的封闭图形的面积为( )A.512B.712C.12D.137.某中学为了解高三学生数学课程的学习情况,从从一模考试成绩中随机抽取部分学生的考试成绩进行统计分析,得到如下的样本的频率分布直方图,已知成绩在[80,90)的学生共有40人,则样本中成绩在[60,80)内的人数为( )A.102B.104C.112D.1148.已知变量,x y 满足226y x x y x y ⎧⎪+⎨⎪+≤⎩≤≥,则2z x y =-的最大值为( )A.2B.10C.1D.129.如图,角θ的终边与单位圆O 交于点P ,过点(1,0)A 作OP 的垂线AQ ,垂足为Q ,将点Q 到x 轴的距离表示成θ的函数()f θ,则()y f θ=在区间[,]22ππ-上的图象大致为( )A B C D10.已知抛物线2:4C y x =的焦点为F ,过点F 的直线l 与C 交于,P Q 两点,且30FP FQ +=,则OPQ ∆的面积S 等于( )B.C.3D.3第Ⅱ卷(共90分)二、填空题(每题5分,满分25分,将答案填在答题纸上)11.执行如图所示的程序框图,若4m =,则输出的结果 为 . 12.在ABC ∆中,已知,,A B C 分别为边,,a b c 所对的角,已知2CA CB ⋅=,a b ab +=,其面积S =则边c =.13.四棱锥P ABCD -的底面ABCD 为平行四边形,且23PN PB =,则三 棱锥C BND -与三棱锥P ABC -的体积比等于 .14.4()(21)ax x x-+的展开式中各项系数的和为81-,则该展开式中常数项为 .15.在实数集R 中,我们定义的大小关系“>”为全体实数排了一个“序”.类似实数排序的定义,我们定义“点序”记为“”:已知11(,)M x y 和22(,)N x y ,MN ,当且仅当“12x x >”或“12x x =且12y y >”.定义两点的“⊕”与“⊗”运算如下:1212(,)M N x x y y ⊕=++,1212M N x x y y ⊗=+.则下面四个命题:①已知(2015,2014)P 和(2014,2015)Q ,则P Q ;②已知(2015,2014)P 和(,)Q x y ,若P Q ,则2015x ≤,且2014y ≤;③已知P Q ,Q M ,则P M ;④已知P Q ,则对任意的点M ,都有P M Q M ⊕⊕;⑤已知PQ ,则对任意的点M ,都有P M Q M ⊗>⊗.其中真命题的序号为 (把真命题的序号全部写出).三、解答题 (本大题共6小题,共75分解答应写出文字说明、证明过程或演算步骤)16.(本小题满分12分)已知函数()cos cos )f x x x x ωωω=-(0ω>)的两条对称轴之间的最小距离为2π. (Ⅰ)求ω的值以及()f x 的最大值;(Ⅱ)已知ABC ∆中,cos 0A <,若()f A m ≥恒成立,求实数m 的取值范围.17.(本小题满分12分)2015年山东省参加自主招生大学仍然只有三所:山东大学、中国石油大学(华东)与中国海洋大学,据有关消息透露2015年山东大学自主招生将测试脱离“北约”联盟统一测试,自己单独命题.已知某校高三8班甲、乙、丙、丁四名同学报考山东大学自主招生的概率分别为13,14,16,13,并且四名学生报考自主招生学校之间互不影响. (Ⅰ)求这四名同学至少有一名同学报考山东大学的概率;(Ⅱ)若用X 表示该班这四名同学报考山东大学自主招生的人数,求X 的分布列与期望. 18.(本小题满分12分)如图,平行四边形ABCD 与直角梯形ABEF 所在的平面相互垂直,且112AB BE AF ===,//BE AF ,且 AB AF ⊥,4CBA π∠=,BC =P 为DF 的中点. (Ⅰ)求证://PE 平面ABCD ;(Ⅱ)求平面DEF 与平面ABCD 所成的二面角(锐角)的余弦值.19.(本小题满分12分)已知数列{}n a 的前n 项和22n S n n =+,正项等比数列{}n b 满足:111b a =-,且4232b b b =+.(Ⅰ)求数列{}n a 和{}n b 的通项公式; (Ⅱ)若数列{}n c 满足:nn na cb =,其前n 项和为n T ,证明:352n T ≤<.20.(本小题满分13分)设函数2()ln f x ax x x =-+()a R ∈. (Ⅰ)试讨论函数()f x 的单调区间;(Ⅱ)设1()1x g x xe -=-,若对于任意给定的(]00,x e ∈,方程0()()f x g x =在(]0,e 内有两个不同的根,求实数a 的取值范围.21.(本小题满分14分)如图,已知椭圆M :22221(0)x y a b a b+=>>的离心率为12,1A 、2A 、1B 、2B 是其四个顶点,且四边形1122A B A B 的面积为4.(Ⅰ)求椭圆的方程;(Ⅱ)已知直线l 与椭圆M 交于P 、Q 两点,(ⅰ)若直线l 过点(0,2)D ,则是否存在直线l ,使得以PQ 为直径的圆经过点(1,0)E ?求直线l 的方程;如果存在求出直线l 的方程;如果不存在,是说明理由.(ⅱ)若12k =,且坐标原点在以PQ 为直径的圆外,求该直线在y 轴上的截距的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六校2015届高三第三次联合考试数学(理科)(满分150分) 考试时间:120分钟参考公式:柱体的体积公式V Sh =,锥体的体积公式13V Sh =.一、选择题:(本大题共8小题,每小题5分,共计40分.每小题只有一个正确答案,请把正确答案填涂在答题卡相应位置)1.设集合{}{}{}1,2,3,4,5,2,3,4,3,5U A B ===,则图中阴影部分所表示的集合为( )A.{}2,3B.{}1,4C.{}5D.{}62.已知复合命题()p q ∧⌝是真命题,则下列命题中也是真命题的是( ) A.()p q ⌝∨B.p q ∨C.p q ∧D.()()p q ⌝∧⌝3.已知向量()()()5,2,4,3,,a b c x y ==--=,若320a b c -+=,则c =( ) A.()23,12--B.()23,12C.()7,0D.()7,0-4.下列函数中,在其定义域上为奇函数的是( ) A.xxy e e -=+B.y =C.tan y x =D.1ln1xy x+=- 5.某几何体的三视图如图所示,该几何体的体积为( ) A.263 B.83π+ C.143π D.73π 6.已知等差数列{}n a 中,10,0a d >>,前n 项和为n S ,等比数列{}n b 满足11b a =,44b a =,前n 项和为n T ,则( ) A.44S T >B.44S T <C.44S T =D.44S T ≤7.已知直线()1:2110l ax a y +++=,()()2:110l a x a y ++-=,若12l l ⊥,则a =( )A.2或12B.13或1- C.13D.1- U AB主视图 侧视图俯视图8.已知函数()f x 的定义域为D ,如果存在实数M ,使对任意的x D ∈,都有()f x M ≤,则称函数()f x 为有界函数,下列函数:①()2,xf x x R -=∈ ②()()ln ,0,f x x x =∈+∞③()()()2,,00,1xf x x x =∈-∞+∞+; ④()()sin ,0,f x x x x =∈+∞为有界函数的是( ) A.②④B.②③④C.①③D.①③④二、填空题:(本大题共6小题,每小题5分,共计30分.)9.函数()ln f x x x =在点()(),e f e 处的切线方程为___________________. 10.在ABC ∆中,45,75,2A B c =︒=︒=,则此三角形的最短边的长度是________. 11.已知递增的等差数列{}n a 满足21252,6a a a ==+,则n a =___________. 12.已知圆2220x y x +-=上的点到直线:2l y kx =-的最近距离为1,则k =______.13.如图,为了测量两座山峰上两点P 、Q 之间的距离,选择山坡上一段长度为米且和P,Q 两点在同一平面内的路段AB 的两个端点作为观测点,现测得四个角的大小分别是90PAB ∠=︒,60PAQ PBA PBQ ∠=∠=∠=︒, 可求得P 、Q 两点间的距离为 米.14.已知(){}:,23p M x y x x ∈+-+;()(){}()222:,10q M x y x y r r ∈-+<>如果p 是q 的充分但不必要条件,则r 的取值范围是_三、解答题(本大题共六个小题,共80分.解答应写出文字说明、证明过程和演算步骤)15.(本小题满分12分)已知函数()sin 1f x x x ωω=+(其中0,x R ω>∈)的最小正周期为6π.⑴ 求ω的值; ⑵ 设,0,2παβ⎡⎤∈⎢⎥⎣⎦,13217f πα⎛⎫-= ⎪⎝⎭,()1135f βπ+=,求()cos αβ+的值.16.(本小题满分12分)寒假期间校学生会拟组织一次社区服务活动,计划分出甲、乙两个小组,每组均组织①垃圾分类宣传,②网络知识讲座,③现场春联派送三项活动,甲组计划12的同学从事项目①,14的同学从事项目②,最后14的同学从事项目③;乙组计划15的同学从事项目①,另15的同学从事项目②,最后35的同学从事项目③,每个同学最多只能参加一个小组的一项活动,从事项目①的总人数不得多于20人,从事项目②的总人数不得多于10人,从事项目③的总人数不得多于18人,求人数足够的情况下,最多有多少同学能参加此次的社区服务活动?17.(本小题满分14分)如图,将长为4,宽为1的长方形折叠成长方体ABCD-A 1B 1C 1D 1的四个侧面,记底面上一边(),02AB t t =<<,连接A 1B,A 1C,A 1D.⑴ 当长方体ABCD-A 1B 1C 1D 1的体积最大时,求二面角B-A 1C-D 的值;⑵ 线段A 1C 上是否存在一点P ,使得A 1C ⊥平面BPD ,若有,求出P 点的位置,没有请说明理由.18.(本小题满分14分)已知数列{}n a 中,1141,13n n a a a +==-+ ,数列{}n b 满足()*1,1n n b n N a =∈+. ⑴ 求数列{}n b 的通项公式; ⑵ 证明:222121117nb b b +++<.19.(本小题满分14分)已知直角坐标系中,圆O 的方程为222x y r +=()0r >,两点()()4,0,0,4A B ,动点P 满足(),01AP AB λλ=≤≤.⑴ 求动点P 的轨迹C 方程;⑵ 若对于轨迹C 上的任意一点P ,总存在过点P 的直线l 交圆O 于M,N 两点,且点M 是线段PN 的中点,求r 的取值范围.20.(本小题满分14分)已知函数()()ln f x x a ax =++. ⑴ 求函数()f x 的单调区间和极值;⑵ 若()1,0a ∈-,函数()()g x a f x '=的图像上存在12,P P 两点,其横坐标满足1216x x <<<,且()g x 的图像在此两点处的切线互相垂直,求a 的取值范围.数学(理科)参考答案一、选择题: CBAD DABC 二、填空题:9.20x y e --=; 10.3; 11.2n 12.0或者43-; 13. 900;14. r >)r ∈+∞或者直接)+∞均可三、解答题:15. 解:⑴ ()sin 12sin()13f x x x x πωωω=+=-+ …………3分26T ππω==,所以13ω=. ………………………………………………6分 ()12sin()133f x x π=-+注:如果()2cos()16f x x πω=-++等正确结果的话相应给分即可.⑵1132sin (3)12sin 12cos 12323217f ππππαααα⎛⎫⎛⎫⎛⎫-=--+=-+=-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 所以8cos 17α=………………………………………………………………7分 ()11132sin (3)12sin 1335f πβπβπβ⎛⎫+=+-+=+= ⎪⎝⎭所以3sin 5β=…………………………………………………………………8分因为,0,2παβ⎡⎤∈⎢⎥⎣⎦,所以154sin ,cos 175αβ====,10分 所以()13cos cos cos sin sin 85αβαβαβ+=-=-. …………………………12分 16.解:设甲组x 名同学,乙组y 名同学,根据题意有:……………………1分1120251110451318450,0x y x y x y x y ⎧+≤⎪⎪⎪+≤⎪⎨⎪+≤⎪⎪⎪≥≥⎩ 整理得: 52200542005123600,0x y x y x y x y +≤⎧⎪+≤⎪⎨+≤⎪⎪≥≥⎩ 可行域如图: 参加活动的总人数z x y =+,变形为y x z =-+,当经过可行域内的点,斜率为1-的直线在y 轴上截距最大时,目标函数z x y =+取得最大值.由可行域图像可知,直线y x z =-+经过54200x y +=和512360x y +=的交点A 时,在y 轴上截距最大. …………………………………………………………………8分解方程组54200512360x y x y +=⎧⎨+=⎩得:24,20x y == …………………………………10分所以max 242044z x y =+=+= ………………………………………………11分 答:甲组24名同学参加,乙组20名同学参加,此时总人数达到最大值44人.………12分17.解:法一:⑴ 根据题意,长方体体积为()()2221212t t V t t t t +-⎛⎫=-⨯=-≤= ⎪⎝⎭……2分当且仅当2t t =-,即1t =时体积V 有最大值为1 所以当长方体ABCD-A 1B 1C 1D 1的体积最大时,底面四边 形ABCD 为正方形 ……4分作BM ⊥A 1C 于M ,连接DM ,BD ……………5分因为四边形ABCD 为正方形,所以1A BC ∆与1A DC ∆全等,故DM ⊥A 1C ,所以BMD ∠即为所求二面角的平面角 ……6分Oxy54200x y +=52200x y +=512360x y +=y x =-A (24,20)………7分,约束条件和图像各3分,不化简不扣分A BCDA 1B 1C 1DM因为BC ⊥平面AA 1B 1B ,所以1A BC ∆为直角三角形又11AB AC =113A B BC BM AC ⨯===DM = 在∆BMD中,根据余弦定理有:6621cos 2BMD +-∠==- ……………8分 因为()0,180BMD ∠∈︒︒,所以120BMD ∠=︒即此时二面角B-A 1C-D 的值是120︒. …………………………………………………9分 ⑵ 若线段A 1C 上存在一点P ,使得 A 1C ⊥平面BPD ,则A 1C ⊥BD ……………10分 又A 1A ⊥平面ABCD,所以A 1A ⊥BD ,所以BD ⊥平面A 1AC所以BD ⊥AC …………………………………………………………………12分 底面四边形ABCD 为正方形,即只有ABCD 为正方形时,线段A 1C 上存在点P 满足要求,否则不存在由⑴知,所求点P 即为BM ⊥A 1C 的垂足M此时,2111A B A P AC ===……………………………………………………14分 法二:根据题意可知,AA 1, AB,AD 两两垂直,以AB 为x 轴,AD 为y 轴,AA 1为z 轴建立如图所示的空间直角坐标系:⑴长方体体积为()()2221212t t V t t t t +-⎛⎫=-⨯=-≤= ⎪⎝⎭……………………2分当且仅当2t t =-,即1t =时体积V 有最大值为1 ………………………………3分 所以当长方体ABCD-A 1B 1C 1D 1的体积最大时,底面四边形ABCD 为正方形 ……4分 则()()()()(110,0,1,1,0,0,1,1,0,1,0,1,A B C A B BC =-=设平面A 1BC 的法向量(),,m x y z =,则00x z y -=⎧⎨=⎩取1x z ==,得:()1,0,1m = ………………6分 同理可得平面A 1CD 的法向量()0,1,1n = ……7分所以,1cos ,2m n m n m n⋅==⋅ ………………8分 又二面角B-A 1C-D 为钝角,故值是120︒.…………9分(也可以通过证明B 1A ⊥平面A 1BC 写出平面A 1BC 的法向量)⑵ 根据题意有()()(),0,0,,2,0,0,2,0B t C t t D t --,若线段A 1C 上存在一点P 满足要求,不妨11A P AC λ=,可得()(),2,1P t t λλλ--()()(),2,1,,2,0BP t t t BD t t λλλ=---=--1100BP AC BD AC ⎧⋅=⎪⎨⋅=⎪⎩ 即:()()()()22221020t t t t t t λλλ⎧-+---=⎪⎨-+-=⎪⎩…………………………11分 解得:21,3t λ== …………………………………………………………13分即只有当底面四边形是正方形时才有符合要求的点P ,位置是线段A 1C 上1:2:1A P PC =处. ………………………………………………………14分18.解:⑴ 12241233nn n n a a a a +++=-=++ ……………………………………2分 ()()11123111112221122n n n n n n n n a a b b a a a a +++++====+=+++++ …………………6分又112b =,所以数列{}n b 是首项为12,公差为12的等差数列,2n nb = …………8分(也可以求出12341234,,,2222b b b b ====,猜想并用数学归纳法证明,给分建议为计算前2项1分,计算前3项或者更多2分,猜想通项公式2分,数学归纳法证明4分数学归纳法证明过程如下: ① 当1n =时,112b =符合通项公式2n n b =;② 假设当n k =时猜想成立,即112k k kb a ==+,21k a k =-那么当1n k =+时1211113113k k k a k k a a k k +----===++-+,1111111211k k k b k a k+++===-+++即1n k =+时猜想也能成立综合①②可知,对任意的*n N ∈都有2n n b =. ⑵ 当1n =时,左边=21147b =<不等式成立;……………………………………9分 当2n =时,左边=2212114157b b +=+=<不等式成立; …………………………10分 当3n ≥时,()2214411411n b n n n n n ⎛⎫=<=- ⎪--⎝⎭左边=22212111111111414()23341n b b b n n+++<++-+-++-- 11454()772n n=+-=-<不等式成立 …………………………………………………………………………14分19.解:⑴ 设(),P x y ,因为(),01AP AB λλ=≤≤,所以444x y λλ-=-⎧⎨=⎩ 消去λ并注意到01λ≤≤可得动点P 的轨迹C 即为线段AB ,方程为:()40,04x y x +-=≤≤ ……5分,不写出x 的范围扣1分⑵ 设()()()00,,,4,04N x y P t t t -≤≤,则004(,)22x t y tM ++- 方程组22200222004()()22x y r x t y t r ⎧+=⎪⎨++-+=⎪⎩即2220022200()(4)4x y r x t y t r ⎧+=⎪⎨+++-=⎪⎩有解 ……7分 法一:将方程组两式相减得:()()22200224430tx t y t t r +-++--= ………8分 原方程组有解等价于点()0,0到直线()()222:224430l tx t y t t r +-++--=的距离小于或等于r r ≤ ……………………………………9分整理得:()()()22222221683444t t r t t r +--≤+-即()()22222816281690t t rtt r -+--+-≤也就是,22228169r t t r ≤-+≤对任意的04t ≤≤恒成立 …………………10分根据二次函数22816y t t =-+的图像特征可知,在区间[]0,4上,当0t =或者4t =时,()2max281616tt -+=;当2t =时,()2min28168t t -+= ………………………12分所以21689r ≤≤,43r ≤≤ ……………………………………………………13分特别的,当r =228x y +=与40x y +-=切于点()2,2,此时过C 上的点()2,2P 没有合乎要求的直线,故r ≠,即所求r 的范围为43r ⎡∈⎢⎣. ……14分法二:上述方程组有解即以()0,0为圆心,r 为半径的圆与以(),4t t --为圆心,2r 为半径的圆有公共点,故对于任意的04t ≤≤都有3r r 成立 ……9分整理得:22228169r t t r ≤-+≤对任意的04t ≤≤恒成立 ……………………10分根据二次函数22816y t t =-+图像特征可知,在区间[]0,4上,当0t =或者4t =时,()2max281616tt -+=;当2t =时,()2min28168t t -+= …………………………12分所以21689r ≤≤,43r ≤≤ ……………………………………………………13分特别的,当r =228x y +=与40x y +-=切于点()2,2,此时过C 上的点()2,2P 没有合乎要求的直线,故r ≠,即所求r 的范围为43r ⎡∈⎢⎣. ……14分20.解:⑴函数()()ln f x x a ax =++的定义域为(),a -+∞,()1f x a x a'=++ ……1分当0a >时,原函数在区间(),a -+∞上有()0f x '>,()f x 单调递增,无极值; 当0a =时,原函数在区间()0,+∞上有()0f x '>,()f x 单调递增,无极值;…2分 当0a <时,令()10f x a x a '=+=+得:1x a a=-- …………………………3分11 当1(,)x a a a ∈---时,()0f x '>,原函数单调递增;当1(,)x a a∈--+∞时,()0f x '<,原函数单调递减 …………………………………………………………4分 所以()f x 的极大值为()21ln 1f a a a a ⎛⎫--=---- ⎪⎝⎭…………………………5分 ⑵ 由⑴知,当()1,0a ∈-时 ()()221,(,)11,(,)a a x a a x a a g x a f x a a a x a a x a x aa ⎧+∈---⎪⎪+'==+=⎨+⎪--∈--+∞⎪+⎩ ………………6分 函数图像上存在符合要求的两点,必须12116x a x a<<--<<,得:132a -<<-……8分 当1(,)x a a a ∈---时,()2a g x a x a=++,函数在点1P 处的切线斜率为()121ak x a =-+; 当1(,)x a a ∈--+∞时,()2a g x a x a=--+,函数在点2P 处的切线斜率为()222ak x a =+; ………………………………………………………………10分 函数图像在两点处切线互相垂直即为:()()22121a a x a x a ⋅=++,即()()22212x a x a a ++= …………………………11分 因为121016a x a x a a a <+<+<-<+<+,故上式即为()()12x a x a a ++=- …12分 所以()()1116a a a a a a⎧-+<-⎪⎪⎨⎪-+>-⎪⎩,解得:122a -<< 综合得:所求a的取值范围是(a ∈-. ………………………………14分。
