高三上期文科数学周末辅导七

合集下载

高三文科详细学习计划时间

高三文科详细学习计划时间一、时间管理作为高三学生，时间管理是非常重要的。

我计划每天早上6:30起床，进行早晨锻炼和自习。

8:00-12:00上午进行课堂学习，12:00-1:30午餐休息时间。

下午2:00-5:00进行课外补习或者自主学习。

晚上6:00-7:30进行晚餐时间和休息。

7:30-9:30再次进行自习。

然后10:00之前进行休息和睡眠。

周末时间进行复习并且利用时间进行课外辅导。

二、科目学习计划1. 语文语文是高考文科生考试的一门重要科目。

我准备每周进行写作和阅读的练习。

每天坚持阅读一些名著和经典作品，扩大自己的文学视野。

每周末进行一次语文模拟考试，查漏补缺。

2. 数学数学是文科生的一大难题。

我计划每周进行两次的数学补习课，利用课下时间进行习题的练习。

每周末进行一次数学模拟考试，复习所学知识。

3. 英语英语是我们与全球交流的工具，也是高考文科的必考科目之一。

我计划每天进行英语听力和口语练习，提高自己的英语水平。

每周末进行一次英语模拟考试，针对性的查漏补缺。

4. 历史历史是高考文科生的一大挑战。

我计划每周进行一次历史课外辅导，加深对历史知识的理解。

课下时间进行历史知识的总结和整理。

每周末进行一次历史模拟考试，巩固所学知识。

5. 政治政治是文科生的一大难点，我计划每周进行一次政治课外辅导，提高对政治知识的理解。

课下时间进行政治知识的总结和整理。

每周末进行一次政治模拟考试，巩固所学知识。

三、课外活动在学习之余，我也准备参加一些课外活动来放松自己。

比如参加学生社团，参加学校的辩论赛或者朗诵比赛。

此外，我也计划每天进行半小时的户外运动，保持良好的身体状况。

四、备考规划在备考阶段，我将针对各科目进行有针对性的复习，每周末进行一次模拟考试，针对性的查漏补缺，并进行错误分析和总结。

在备考阶段，我也准备参加一些模拟考试和模拟面试，提前适应高考的考试环境。

五、心理调适在备考期间，我也需要注意心理调适，保持乐观的心态，不要给自己太大的压力。

2021年高三上学期数学周练试题(文科实验班1.17) 含答案

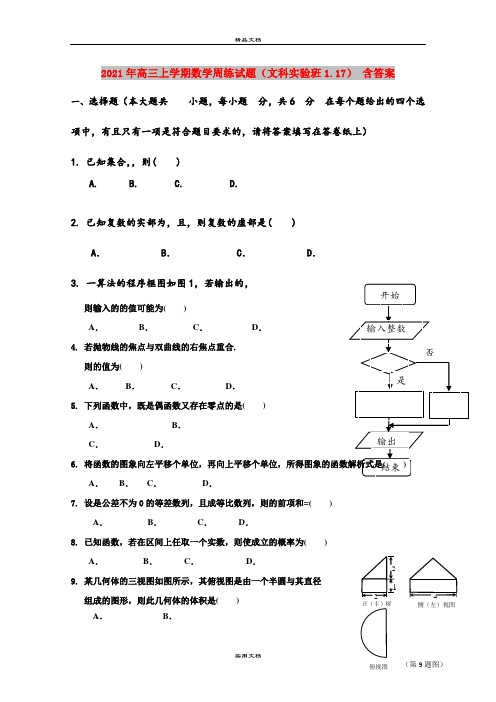
开始输入整数是否输出结束侧（左）视图4212正（主）视2021年高三上学期数学周练试题（文科实验班1.17）含答案一、选择题（本大题共小题，每小题分，共6分在每个题给出的四个选项中，有且只有一项是符合题目要求的，请将答案填写在答卷纸上） 1. 已知集合，，则( )A. B. C. D.2. 已知复数的实部为，且，则复数的虚部是( ) A ． B ． C ． D ．3. 一算法的程序框图如图1，若输出的，则输入的的值可能为( )A ．B ．C ．D ． 4. 若抛物线的焦点与双曲线的右焦点重合, 则的值为( )A ．B ．C ．D ． 5. 下列函数中，既是偶函数又存在零点的是( ) A ． B ． C ． D ．6. 将函数的图象向左平移个单位，再向上平移个单位，所得图象的函数解析式是( )A ．B ．C ．D ．7. 设是公差不为0的等差数列，且成等比数列，则的前项和=( ) A ． B ． C ．D ．8. 已知函数，若在区间上任取一个实数，则使成立的概率为( ) A ． B ． C ．D ．9. 某几何体的三视图如图所示，其俯视图是由一个半圆与其直径组成的图形，则此几何体的体积是( )A ．B ．C．D．10. 已知是内的一点，且，，若，和的面积分别为，则的最小值是( )A．B．C．D．11.如图，椭圆与双曲线有公共焦点、，它们在第一象限的交点为,且，，则椭圆与双曲线的离心率的倒数和为( )A．2B．C．D．12.已知函数, 则12340292015201520152015f f f f⎛⎫⎛⎫⎛⎫⎛⎫++++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的值为A．B．C．D．二、填空题：（本大题共4小题，每小题5分，满分20分）13.曲线在处的切线方程为_____________．14. 若满足且的最小值为，则的值为________．15. 已知三棱锥,,, 且，则三棱锥的外接球的表面积为________．16. ．函数，，，，对任意的，总存在，使得成立，则的取值范围为．三、解答题(本大题共6小题，共70分)17.（本小题满分12分）设等差数列的前n项和为，数列的前n项和为满足(I)求数列的通项公式及数列的前n项和；(Ⅱ)是否存在非零实数，使得数列为等比数列？并说明理由18.（本小题满分12分）高三某班男同学有名，女同学有名，老师按照性别进行分层抽样组建了一个人的课外兴趣小组．（1）经过一个月的学习、讨论，这个兴趣小组决定选出两名同学做某项实验，方法是先从小组里选出一名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率；（2）试验结束后，第一次做试验的同学得到的试验数据为，第二次做试验的同学得到的试验数据为，请问哪位同学的实验更稳定？并说明理由．19.（本小题满分12分）如图,四棱锥,侧面是边长为的正三角形,且与底面垂直, 底面是的菱形,为的中点.(1) 在棱上是否存在一点,使得?若存在,指出点的位置并证明；若不存在,请说明理由； (2) 求点到平面的距离．20.（本小题满分12分）已知圆：关于直线对称的圆为．（1）求圆的方程；（2）过点作直线与圆交于两点，是坐标原点.设，是否存在这样的直线，使得四边形的对角线相等？若存在，求出所有满足条件的直线的方程；若不存在，请说明理由.21．（本题满分12分）设函数，．其中（1）设，求函数在上的值域；（2）证明：对任意正数，存在正数，使不等式成立．请考生从第（22）、（23）二题中任选一题作答。

2021年高三第7周综合练习卷数学文试题含答案

2021年高三第7周综合练习卷数学文试题含答案一、选择题（本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1、函数的定义域为（）A． B． C． D．2、已知复数（其中，，是虚数单位），则的值为（）A．B．C．D．3、如果函数的最小正周期为，则的值为（）A．B．C．D．4、在中，，，，在上任取一点，使为钝角三角形的概率为（）A．B．C．D．5、如图是一个空间几何体的三视图，则该几何体的侧面积为（）A．B．图1 C．D．6、在平面直角坐标系中，若不等式组表示的平面区域的面积为，则实数的值为（）A．B．C．D．7、已知幂函数在区间上单调递增，则实数的值为（）A．B．C．或D．或8、已知两个非零向量与，定义，其中为与的夹角．若，，则的值为（）A．B．C．D．9、已知函数，对于任意正数，是成立的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件10、已知圆，点是圆内一点，过点的圆的最短弦所在的直线为，直线的方程为，那么（）A．，且与圆相离B．，且与圆相切C．，且与圆相交D．，且与圆相离二、填空题（本大题共5小题，考生作答4小题，每小题5分，满分20分．）（一）必做题（11～13题）11、若函数是偶函数，则实数的值为． 12、已知集合，，若，则实数的取值范围为．13、两千多年前，古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题，他们在沙滩上画点或用小石子来表示数，按照点或小石子能排列的形状对数进行分类，如图中的实心点个数，，，，，被称为五角形数，其中第个五角形数记作，第个五角形数记作，第个五角形数记作，第个五角形数记作，，若按此规律继续下去，则，若，则．（二）选做题（14、15题，考生只能从中选做一题）14、（几何证明选讲选做题）如图，圆的半径为，点是弦的中点，，弦过点，且，则的长为． 15、（坐标系与参数方程选做题）在平面直角坐标系中，已知直线与曲线的参数方程分别为（为参数）和（为参数），若与相交于、两点，则．三、解答题（本大题共2小题，共26分．解答应写出文字说明、证明过程或演算步骤．） 16、（本小题满分12分）已知函数．求的值；若，求的值．5 12 122 图217、（本小题满分14分）如图所示，在三棱锥中，，平面平面，于点，，，．求三棱锥的体积；证明：为直角三角形．图4高三文科数学综合练习卷（7）参考答案一、选择题（本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．）（一）必做题（11～13题）11、12、13、（二）选做题（14、15题，考生只能从中选做一题）14、15、三、解答题（本大题共2小题，共26分．解答应写出文字说明、证明过程或演算步骤．）16、（1）解：……………………………………………………1分 (3)分．…………………………………………………4分（2）解法1：因为……………………………………5分……………………………………6分．………………………………………7分所以，即．①因为，②由①、②解得．…………………………………………………………9分所以……………………………………………………11分．……………………………………………12分解法2：因为……………………………5分……………………………………………6分．…………………………………………7分所以…………………………………………………9分……………………………………………………10分……………………………………………………11分．…………………………………………………12分17、（1）证明：因为平面平面，平面平面，平面，，所以平面．………………………………………2分记边上的中点为，在△中，因为，所以．因为，，所以．……………………………………4分所以△的面积．……………………………………5分因为，所以三棱锥的体积．………7分（2）证法1：因为，所以△为直角三角形．因为，，所以．………9分连接，在△中，因为，，，所以．……10分由（1）知平面，又平面，所以．在△中，因为，，，所以．……………………………………12分在中，因为，，，所以．……………………………………………………………13分所以为直角三角形．…………………………………………………………14分证法2：连接，在△中，因为，，，所以．…………8分在△中，，，，所以，所以．……10分由（1）知平面，因为平面，所以．因为，所以平面．………………………………………………………………12分因为平面，所以．所以为直角三角形．……………………………………………………14分32248 7DF8 緸34396 865C 虜N22256 56F0 困28954 711A 焚32079 7D4F 絏27614 6BDE 毞20024 4E38 丸Rs26444 674C 杌21894 5586 喆。

高三上期数学周训7

高三上期数学周训7蔺阳中学高2019级高三上期数学（文）周训七（考试时间：2019年10月22日；考试用时：60分钟）命题人：屈中兴注意事项：1、本试卷共75分，所有班级都应该作答；2、请将选择题、填空题的答案答在对应的答题卡上，没答在规定的地方不给分．一、选择题：（每小题5分，共30分） 1．已知集合{}2|540A x N xx =∈-+≤，{}2|40B x x=-=，下列结论成立的是（）A ．B A ⊆ B ．AB A= C ．AB A= D ．{}2AB =2．已知命题p ：x R ∃∈，20x ->，命题q ：x R ∀∈，x x<，则下列说法中正确的是（）A 、命题p q ∨是假命题B 、命题p q∧是真命题 C 、命题()p q ∧⌝是真命题 D 、命题()p q ∨⌝是假命题3. 等差数列{a n }中的a 4、a 4030是函数的两个极值点，则log 2（a 2019）=（） A ．2 B ．3C ．4D ．54．已知定义在R 上的奇函数f （x ）满足f （x+3）=f （x ），且当x ∈[0，）时，f （x ）=﹣x 3，．则f （）=（）A ．﹣B ．C ．﹣D ．5．设函数()f x 的导函数为()f x '，若()f x 为偶函数，且在()0,1上(1)求a的值及f（x）的单调区间；(2)若关于x的方程f（x）=kx2﹣2（k＞2）存在两个不相等的正实数根x1，x2，证明：|x1﹣x2|＞ln（）．考号：班级：姓名：总分：选择题、填空题答题卡：1 2 3 4 5 67．；8．；9．；10．．三．解答题：（11题12分；12题13分；共25分）11．若函数f(x)＝ax3－bx＋4，当x＝2时，函数f(x)有极值－4 3．(1)求曲线y=f(x)在点（1，f(1)）处的切线方程．(2)若方程f(x)＝k有3个不同的根，求实数k的取值范围．11．12．已知函数f（x）=xe x﹣ae x﹣1，且f′（1）=e．(1)求a的值及f（x）的单调区间；(2)若关于x的方程f（x）=kx2﹣2（k＞2）存在两个不相等的正实数根x1，x2，证明：|x1﹣x2|＞ln（）．12．蔺阳中学高2019级高三上期数学（文）周训七参考答案一、选择题题号 1 2 3 4 5 6选项D C A B C B二填空题 7.22+ 8．3 9． (]32，10．(－2,0)∪(2，＋∞) 三．解答题11. 解(1)f ′(x )＝3ax 2－b .(1)由题意得⎩⎪⎨⎪⎧f ′（2）＝12a －b ＝0，f （2）＝8a －2b ＋4＝－43，解得⎩⎪⎨⎪⎧a ＝13，b ＝4，故所求函数的解析式为f (x )＝13x 3－4x ＋4.f ′(x )＝x 2－4，f ′(1)＝－3,f (1)＝13.y=f(x)在点（1，f(1)）处的切线方程为：y-13=－3(x-1),即9x+3y-10=0.(2)由(1)可得f ′(x )＝x 2－4＝(x －2)(x ＋2)，令f ′(x )＝0，得x ＝2或x ＝－2. 当x 变化时，f ′(x )，f (x )的变化情况如下表：x (－∞，－2)－2(－2，2)2(2，＋∞)f ′(x ) ＋－＋f (x )错误－43因此，当x ＝－2时，f (x )有极大值283，当x ＝2时，f (x )有极小值－43，作出函数f (x )＝13x 3－4x ＋4的图象大致所示．若f (x )＝k 有3个不同的根，则直线y ＝k 与函数f (x )的图象有3个交点，所以－43<k <283. 即428,33k ⎫⎛∈- ⎪⎝⎭12、【解答】（1）解：f′（x ）=e x +xe x ﹣ae x ﹣1，∴f′（1）=e+e﹣a=e．解得a=e．∴f′（x）=e x+xe x﹣ee x﹣1=xe x．∴x＞0时，f′（x）＞0，函数f（x）单调递增；x＜0时，f′（x）＜0，函数f（x）单调递减．即函数f（x）单调递增区间为（0，+∞）；函数f（x）单调递减区间为（﹣∞，0]．（2）证明：方程f（x）=kx2﹣2（k＞2），即（x﹣1）e x﹣（kx2﹣2）=0，令g（x）=（x﹣1）e x﹣（kx2﹣2），g′（x）=xe x﹣2kx=x（e x﹣2k），令g′（x）=0，解得x=0或ln（2k）．∵k＞2，∴ln（2k）＞1．g（0）=1，g（1）=2﹣k＜0，g（ln（2k））＜0．x→+∞时，g（x）→+∞．因此关于x的方程f（x）=kx2﹣2（k＞2）存在两个不相等的正实数根x1，x2，不妨设x1＜x2．可得：0＜x1＜1＜ln（2k）＜x2．∴|x1﹣x2|＞ln（2k）﹣1=＞ln（）．。

高三上期文科数学周末辅导一

周末辅导（一）1.已},6|{},1|{2≤+=<=x x x B x x A 则A B = ( ) A 、(]2,1 B 、[)1,3- C 、(]3,-∞- D 、(]2,∞-2. 函数)6(log 3)(2x x x f -++=的定义域是（） A ．{}|6x x > B ．{}|36x x -<< C ．{}|3x x >- D ．{}|36x x -<≤3.“p 或q 是假命题”是“非p 为真命题”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件4.函数[]3,0,342∈+-=x x x y 的值域是[ ] A. []3,0 B. []0,1- C. []3,1- D. []2,05、设1>a ，函数x x f a log )(=在区间[]a a 2,上的最大值与最小值之差为21，则a =（）A ．4 C ．．26、已知函数[]⎩⎨⎧<+≥-=10,)5(10,3)(x x f f x x x f ，其中x N ∈，则=)8(f （） A ．2 B ．4 C ．6D ．7 7.已知函数2)(xx e e x f --=，则下列判断中正确的是( ) A ．奇函数，在R 上为增函数 B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数8.函数f (x )＝ln 1－x 1＋x的图象只可能是__________．9．已知函数f (x )的定义域为[a ，b ]，函数y ＝f (x )的图象如下图所示，则函数f (|x |)的图象是( )10.函数)32(log )(221++-=x x x f 的单调递增区间为_______11，设)(x f 是周期为2的奇函数，当0≤x ≤1时，)(x f =)1(2x x -，)25(-f =_____. 12．91log 161log 25log 532∙∙=_____. 13. 已知集合{}73|<≤=x x A ,{}102|<<=x x B ,{}a x a x C <<-=5|.（1）求B A ⋃,B A C R ⋂)(; （2）若)(B A C ⋃⊆,求a 的取值范围.14.已知p: 311--x ≤2,q: 2212m x x -+-≤0(m>0).若¬p 是¬q 的充分不必要条件,求实数m 的取值范围.。

高三文科数学学习辅导计划

高三文科数学学习辅导计划
十一月份
第一节
三角函数的图像与性质
三角恒等变换
第二节
正、余弦定理
解三角形
第三节
平面向量的概念及线性运算
平面向量基本定理及坐标表示、
平面向量的数量积和应用
第四节
立体几何
第五节
等差、等比数列{an}的求法
等差、等比数列前n项和的求法
第六节
等差、等比数列的综合性题目
第七节
不等关系与不等式
一元二次不等式及其解法
第八节
简单的线性规划
基本不等式及其应用十二月份第九节导数的概念及其运算
导数的综合应用
第十节
坐标系与参数方程
第十一节
概率与统计
第十二节
直线与圆
椭圆及其性质
第十三节
双曲线、抛物线
直线与圆锥曲线的位置关系

石家庄精英中学高三课程表安排

石家庄精英中学高三课程表安排一、前言作为学生，每一个人都经历过高三这个阶段。

在这一年里，学生们需要面对着繁重的学习压力和备战高考的挑战，高三的课程安排显得格外重要。

而石家庄精英中学作为一所知名的学府，其高三课程表安排自然也备受关注。

在本文中，我将共享我对石家庄精英中学高三课程表安排的深入理解和个人观点，希望能够为大家提供一些参考。

二、整体评估石家庄精英中学的高三课程表安排是十分紧凑和有规律的。

从周一到周五，上午有四节课，下午有两节课。

除了正常的课程外，还有晚自习和周末的复习课安排。

课程设置包括语文、数学、英语、物理、化学、生物、政治、历史、地理等，覆盖了文科和理科的所有学科。

这种全面而有规律的安排，有助于学生们系统地复习和掌握知识点，提高学习效率。

三、深度探讨对于高中生来说，学业压力是不可避免的。

高三课程安排不仅仅是简单地排列课程和时间，更是对学生复习进度和能力的考量。

在石家庄精英中学的高三课程表安排中，我发现学校在布置作息时间上是很有章法的。

早上的第一节课通常是数学或语文，这两门学科可以激活学生的思维和逻辑能力，为一天的学习奠定基础。

而晚上的自习课则充分利用了学生的黄金学习时间，有利于弥补白天课程安排可能存在的遗漏。

除了正常的学科课程，石家庄精英中学还为学生安排了专门的复习课。

这些复习课程通常会覆盖高考大纲中重点和难点部分，有针对性地帮助学生查漏补缺。

数学有8点到10点的强化课，在晚自习结束后还会有一节30分钟的考试分析课。

这种安排能够有效地帮助学生梳理知识结构，找到自己的薄弱环节，并及时进行补充和突破。

四、总结和回顾石家庄精英中学高三课程表安排紧凑而有序，是对学生高考复习期的科学安排。

课程设置全面，安排合理，有针对性的复习课更能够满足学生的实际需求。

学生们在这样的课程表安排下，不仅能够有序地进行复习备考，也能够培养良好的学习习惯和高效的学习方式。

五、个人观点和理解从我个人的观点来看，石家庄精英中学的高三课程表安排是非常合理和科学的。

高三数学上学期周考七文试题

信丰中学2021届高三数学上学期周考七文本卷贰O 贰贰年贰月捌日编写；出题人：令狐学复；欧阳化语；令狐理总。

一、选择题〔本大题一一共8小题，每一小题5分，一共40分〕1.以下各组向量中，可以作为基底的是〔〕 A.），（），（2-1e 0,0e 21== B. ）（），（7,5e 2,1-e 21== C.）（），（10,6e 5,3e 21== D. ），（），，（43-21e 3-2e 21== 2．设数列2，5，22，11，…，那么215是这个数列的〔〕A ．第6项B ．第7项C ．第8项D ．第9项3．如下图，△ABC 中，点D 是线段BC 的中点，E 是线段AD 的靠近A 的三等分点，那么AC =〔〕A. 43AD BE + B.4132AD BE + C. 53AD BE + D. 5132AD BE + 4．等差数列{a n }的前n 项和S n ，假设12018OB a OA a OC =+，且A 、B 、C 三点一共线〔该直线不过原点〕，2018S =〔〕A. 1008B. 1009C. 2021D. 20215.ABC ∆中，,2,60a x b B ==∠=，那么当ABC ∆有两个解时，x 的取值范围是〔〕〔A 〕43x >〔B 〕432x x <>或〔C 〕2x < 〔D 〕432x <<6．如图设点O 在△ABC 内部,且有230OA OB OC ++=,那么△ABC 的面积与△AOC 的面积的比为( )A. 2B. 32C. 3D. 537.在数列{a n }中，a 1＝2，a n ＋1＝a n ＋ln ⎝ ⎛⎭⎪⎫1＋1n ，那么a n 等于( )A.2＋ln nB.2＋(n －1)ln nC.2＋n ln nD.1＋n ＋ln n8.在△ABC 中，点D 是AC 上一点，且AD AC 4=，P 为BD 上一点，向量)0,0(>>+=μλμλAC AB AP ，那么μλ14+的最小值为〔〕A ．16B ．8C ．4D ．2二．填空题〔本大题一一共4小题，每一小题5分，一共20分〕9．向量()()()12311a b c λ===，，，，，.假设2a b -与c 一共线，那么a 在c 方向上的投影为______________.10.S n 为数列{a n }的前n 项和，且log 2(S n ＋1)＝n ＋1，那么数列{a n }的通项公式为________________.11..函()21,23,x 21x x f x x ⎧-<⎪=⎨≥⎪-⎩设方程()0f x a -=有三个不同实数根，那么实数a 的取值范围___._______12..在ABC ∆中，060A ∠= ，M 是AB 的中点，假设2,23AB BC ==，D 在线段AC 上运动，那么下面结论正确的选项是___._______.③ ABC ∆是直角三角形； ②DB DM ⋅的最小值为2316；③DB DM ⋅的最大值为2； ④存在[]0,1λ∈使得(1)BD BA BC λλ=+-三．解答题〔本大题一一共2小题，一共24分〕13.()cos ,sin a αα=，()cos ,sin b ββ=，0βαπ<<<。

山西省平遥县和诚中学2020届高三数学上学期7月周练暑期补习试题文及参考答案

和诚中学2019-2020学年度高三7月周练文科数学试题（一）满分：100分考试时间：60分钟一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.不等式()()120x x +->的解集是（） A ．{}1x x >- B ．{}1x x <C ．{}12x x -<< D ．{}12x x x <->或2.如果0<<b a ，那么下列各式一定成立的是（） A ．0>-b a B ．bc ac < C ．22b a > D ．ba 11< 3.已知全集U =R ，集合307x A xx ⎧-⎫=≤⎨⎬-⎩⎭，{}27100B x x x =-+<，则=( )A.()(),35,-∞+∞UB.()[),35,-∞+∞UC.(][),35,-∞+∞UD.(](),35,-∞+∞U4.若0<x<y ，则下列各式正确的是( )A.33x y < B.1133log log x y < C.1133x y⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭ D.33x y <5．已知函数()20y ax bx c a =++≠的图象经过()1,3-和()1,1两点，若01c <<，则a 的取值范围是 ( )A ．()1,3B ．()1,2C ．[)2,3D ．[]1,3 6. 已知x R ∈，则“230x x -≤”是“()()120x x --≤成立”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 7. 若关于x 的不等式有实数解，则实数m 的取值范围是（）A.(,4)(2,)-∞-+∞UB.(][),42,-∞-+∞UC.)2,4(-D.(][),24,-∞-+∞U8.已知集合{}2230A x x x =+-≤，()(){}2210B x x a x a ⎡⎤⎣--+⎦=≤，且A B ⊂≠，则实数a 的取值范围是 ( )A.3,2⎡⎫-+∞⎪⎢⎣⎭B.3,2⎛⎫-+∞ ⎪⎝⎭C.3,2⎛⎤-∞- ⎥⎝⎦D.3,2⎛⎫-∞- ⎪⎝⎭ 9．已知函数()21f x x mx =--+，若对于任意[],1x m m ∈+，都有()0f x >成立，则实数m 的取值范围是（） A ．2,02⎡⎤-⎢⎥⎣⎦ B ．2,02⎛⎫- ⎪ ⎪⎝⎭ C ．20,2⎡⎤⎢⎥⎣⎦ D ．20,2⎛⎫⎪ ⎪⎝⎭10.任意x ∈R ，函数24y ax x a =++的图象恒在212y x =-图象的上方，则实数a 的取值范围是 ( ) A.()2,+∞B.()2,-+∞C.()(),32,-∞-+∞UD.()(),32,-∞--+∞U11.己知,a b 均为正实数，且直线60ax by +-=与直线()3250b x y --+=互相垂直，则23a b +的最小值为( )A.12B.13C.24D.2512.若关于x 的不等式23x a x -->至少有一个负数解，则实数a 的取值范围是（） A ．1334a -<<B ．131344a -<< C ．33a -<< D ．1334a -<< 二、填空题(每小题7分，共28分) 13.设322a =27b =,a b 的大小关系为．14.不等式220ax bx -+>的解集为1123x x ⎧⎫-<<⎨⎬⎩⎭，则a b += ．15. 已知不等式组的解集是不等式2x 2﹣9x+a ＜0的解集的子集，则实数a的取值范围是．16. 若不等式()0()f x x R ≤∈的解集为[]1,2-，则不等式(lg )0f x >的解集为__________.三、解答题(共12分)17.(本题满分12分) 已知函数f x ()=x 2+ax +6. （1）当a =5时，求不等式f x ()<0的解集；（2）若不等式f x ()>0的解集为R ，求实数a 的取值范围.和诚中学2019-2020学年度高三7月周练文科数学答题卡班级姓名考号一、选择题（本大题共12小题，每小题5分，共60分）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题（每小题7分，共28分）13. ______________ 14. ______________ 15.______________ 16. ______________ 三、解答题（共12分） 17.第三章不等式单元测试参考答案及解析1. 【答案】D【解析】根据题意可得x <-1或x >2，故选D. 2. 【答案】C【解析】A 中应为a -b <0，B 中当c =0时不成立，D 应为1a >1b，故选C. 3. 【答案】B 【解析】因为A =x 3£x <7{}，B =x 2<x <5{}，所以，所以.4. 【答案】A【解析】由不等式的基本性质可得A 正确；函数y =log 13x 在0,+¥()上为减函数，且0<x<y ，所以log 13x >log 13y ，B 错误；函数y =13æèçöø÷x 在0,+¥()上为减函数，所以13æèçöø÷x >13æèçöø÷y，C错误；函数y =3x在0,+¥()上为减函数，所以3x >3y ，D 错误.5. 【答案】B【解析】由题意得a -b +c =3,a +b +c =1,ìíî\a +c =2,c =2-a ,\0<2-a <1,1<a <2. 6. 【答案】B【解析】解230x x -≤得其解集{|03}A x x =≤≤，解()()120x x --≤得{|12}B x x =≤≤，因为B A ⊆，所以，230x x -≤”是“()()120x x --≤成立”的必要不充分条件，选B . 7. 【答案】A 【解析】试题分析：将不等式22292x x m m +++＜转化为不等式222920x x m m ++--＜，则2224920m m ∆=---（）＞，然后求出m 的值即可;∵不等式22292x x m m +++＜等价于222920x x m m ++--＜，故不等式22292x x m m+++＜有实数解，则2224920m m ∆=---（）＞，22804m m m ∴+-∴-＞，＜或m ＞2．故答案为：A8. 【答案】C【解析】因为集合A =x x 2+2x -3£0{}=x -3£x £1{}，B =x x -2a ()x -a 2+1()éëùû£0{}=x 2a £x £a 2+1{}，又集合A 是B 的真子集，所以2a £-3,a 2+1³1,ìíî且两个等号不能同时取到，解得a £-32，则实数a 的取值范围是-¥,-32æèçùûú.9. 【答案】B 【解析】10. 【答案】A 【解析】函数y =ax 2+4x +a 的图象恒在y =1-2x 2图象的上方，则ax 2+4x +a>1-2x2，即a +2()x2+4x +a -1>0在R 上恒成立，当a +2=0时，不等式不恒成立；当a +2¹0时，有()()20,164210,a a a +>⎧⎪⎨∆=-+-<⎪⎩解得a >2.综上，a 的取值范围是2,+¥(). 11. 【答案】D【解析】由两直线互相垂直可得a b -3()-2b =0，即2b +3a =ab ，则2a +3b=1.又a ,b 为正数，所以2a +3b =2a +3b ()2a +3b æèçöø÷=13+6a b +6b a ³13+26a b ´6ba =25，当且仅当a =b 时取等号，故2a +3b 的最小值为25.12. 【答案】D【解析】3-x -a >x 2，即x -a <3-x 2，且3-x 2>0，在同一坐标系中，画出y =3-x2和y =x -a 的图象，当函数y =x -a 的图象的左支经过点0,3()时，求得a =3，当函数y =x -a 的图象的右支和y =3-x 2的图象相切时，方程组y =x -a ,y =3-x2ìíî有唯一的解，即x 2+x -a -3=0有唯一的解，故D =1-4(-a -3)=0，解得a =-134，所以实数a 的取值范围是-134<a <3，故选D ．13. 【答案】a <b 【解析】∵a 2=11+46,b 2=11+47，\a 2<b 2,\a <b ．14. 【答案】-10【解析】由一元二次方程与一元二次不等式之间的关系可知，方程ax 2-bx +2=0的两根是-12,13，所以x 1+x 2=b a =-16,x 1×x 2=2a =-16,因此a =-12,b =2,\a +b =-10. 考点：一元二次方程与一元二次不等式之间的关系. 15. 【答案】（﹣∞，9].16.【答案】110x x x ⎧⎫<<>⎨⎬⎩⎭|0或100 【解析】因为不等式()0()f x x R ≤∈的解集为[]1,2-，则()0f x >的解集为，()(),12,-∞-⋃+∞，则不等式(lg )0f x >的解集为lg 10x x <-⎧⎨>⎩或lg 2x x >⎧⎨>⎩，即110x x x ⎧⎫<<>⎨⎬⎩⎭|0或100.17. 【答案】（1）x -3<x <-2{} （2）-26,26()【解析】（1）当a =5时，f x ()=x 2+5x +6.由f x ()<0，得x 2+5x +6<0，即x +2()x +3()<0，所以-3<x <-2.（2）不等式f x ()>0的解集为R ，则有D =a 2-4´6<0，解得-26<a <26，即实数a 的取值范围是-26,26().。

高三数学上学期周末练习试题(7)试题

心尺引州丑巴孔市中潭学校塘栖2021届高三数学上学期周末练习试题一、选择题〔05510'='⨯〕1、以下函数中，既是偶函数又存在零点的是〔〕〔A 〕ycos x = 〔B 〕y sin x = 〔C 〕y ln x = 〔D 〕21y x =+2、设函数211log (2),1,()2,1,x x x f x x -+-<⎧=⎨≥⎩,2(2)(log 12)f f -+= ( )A ．3B ．6C ．9D ．12 3、全集R U =，{}22≤≤-=x x M ，{}1<=x x N ，那么=N M ( )A ．{}12<≤-x x B ．{}12<<-x x C ．{}2-<x x D ．{}2≤x x4、设a 、b 、c 是△ABC 的三边，那么“a ＞b 〞是“cosA ＜cosB 〞的 ( ) A ．充分不必要条件 B.必要不充分条件 C ．充要条件 D.既不充分也不必要条件5、设{}n a 是等差数列. 以下结论中正确的选项是〔〕A ．假设120a a +>，那么230a a +>B ．假设130a a +<，那么120a a +<C ．假设120a a <<，那么2a >D ．假设10a <，那么()()21230a a a a -->6、{}n a 是等差数列，公差d 不为零，前n 项和是n S ，假设3a ，4a ，8a 成等比数列，那么〔〕 A ．140,0a ddS >> B. 140,0a d dS << C. 140,0a d dS >< D. 140,0a d dS <>7、⎩⎨⎧≥+<=0,10,1)(2x x x x f ，那么不等式)2()1(2x f x f =-的解集是〔〕 A ．{}1-≤x x B ． {}211+-=-≤x x x 或C ．{}21+- D ．{}211+-=-<x x x 或8、函数3)11(log )2121()(2++-++-=x x a b x f xX (a 、b 为常数),假设)(x f 在定义域上的最大和最小值分别是M ，N ，求M+N= 〔〕A.6B.3C.0D.-39、函数()cos 3f x x πω⎛⎫=+ ⎪⎝⎭(,0)x R ω∈>的最小正周期为π，为了得到()f x 的图象，只需将函数()sin 3gx x πω⎛⎫=+⎪⎝⎭的图象向右平移几个单位〔〕〔A 〕2π〔B 〕23π 〔C 〕4π〔D 〕43π10、方程0|1|lg 122=-+--x x x 的所有实根的和是 ( )A ．2B ．4C ．6D ．8二、填空题〔8247'='⨯〕11、不等式225--x x1>的解集为 12、求sin15cos165的值是__________；13、函数)1(+x f 是偶函数，当112>>x x 时，0))](()([1212>--x x x f x f 恒成立，设)5.0(-=f a ，)2(f b =，)3(f c =，那么a ，b ，c 的大小关系为14、设ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，假设a = 1sin 2B =，6C =π，那么b= .15、定义在R 上的偶函数0),(≥x x g 当时，)(x g 单调递减，假设)2()12(+<-m g m g ，那么实数m的取值范围是16、3cos()45πα+=，322ππα≤<，那么αcos =_____ ____． 17、假设函数)4(log )(2a x x x f a ++=有最小值，求a 的取值范围三、简答题〔5151414141'+'+'+'+'〕18、C ∆AB 的内角A ，B ，C 所对的边分别为a ，b ，c ．向量(),3m a b=与()cos ,sin n =A B 平行．〔I 〕求A ；〔II 〕假设a=2b =求C ∆AB 的面积．19、在△ABC 中，满足AB 与AC 的夹角为 60，M是AB 的中点，〔1AB +2AC 与AB 的夹角的余弦值；〔2232，点D 在边AC 上且AC AD λ=，如果0=⋅AC MD ，求λ的值。

高三数学上学期周末巩固训练一文试题

卜人入州八九几市潮王学校信丰2021届高三数学上学期周末稳固训练一文一、选择题：〔本大题一一共12小题，每一小题5分，一共60分，在每一小题给出的四个选项里面，只有一项为哪一项哪一项符合题目要求的〕 1.i 为虚数单位，假设复数2)1(1i z -+=,那么=||z 〔〕A.1B. 2C.2 D.52.设集合{}A x x a =<，{}2320B x xx =-+<，假设A B B ⋂=，那么实数a 的取值范围是〔〕A.1a <B.1a ≤C.2a >D.2a ≥3.以下选项里面，说法正确的选项是〔〕 A.2,0x R x x ∃∈-≤〞的否认是“2,0x R x x ∃∈->〞B.p q ∨p q ∧为真〞的充分不必要条件C.22am bm <，那么a b <D.ABC ∆中，假设1sin 2A <,那么6A π< 4.()xx x x p 1sin ,,0:+≥+∞∈∀:,1x q x R e ∃∈<〕 A ．()p q ∧⌝B ．()()p q ⌝∧⌝C ．()p q ⌝∧D ．p q ∧5.设214-=a ，31log 21=b，2log 3=c ，那么a,b,c 的大小关系是〔〕 A ．c b a <<B ．b c a <<C ．b a c <<D ．a b c <<6.我国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一直角边为股，斜边为弦。

假设c b a ,,为直角三角形的三边.其中c 为斜边，那么222c b a =+，称这个定理为勾股定理.现将这一定理推广到立体几何中：在四面体0-ABC 中，090=∠=∠=∠AOC BOC AOB.S 为顶点0所对面的面积，321,,S S S 分别为侧面OBC OAC OAB ∆∆∆,,的面积，那么以下选项里面对于321,,S S S 满足的关系描绘正确的为()A.321S S S S++= B.2322212111S S S S ++=C.2222321S S S S++= D.321111S S S S ++=7.定义在R 上的函数()f x 满足),()(x f x f -=-)1()1(x f x f -=+,且当[]1,0∈x时,)1(log )(2+=x x f ，那么 =)31(f 〔〕A.0B.-121)(x ex x f -=的图象大致是〔〕x a x x f 2sin )(+=在]4,0[π上单调递增，那么a 的取值范围是()A.]0,21[-B.],21[+∞-C.],1[+∞-D.]21,[--∞ 10.函数()f x 是定义在R 上的奇函数，且在区间(,0]-∞上单调递减，(1)1f =-，设2()log (3)g x x =+，那么满足()()f x g x ≥的x 的取值范围是〔〕A ．(3,1]--B ．[1,)-+∞C ．(,1]-∞-D ．(3,1]-11.函数f(x)的定义域为]5,1[-，局部对应值如下表。

2021年高三上学期第七次周练数学(文)试题含答案

2021年高三上学期第七次周练数学（文）试题含答案一、选择题（每题10分）1．若关于的不等式的解集为，且中只有一个整数，则实数的取值范围是（）A. B.C. D.2．函数的图象可能是（）A．（1）（3） B．（1）（2）（4）C．（2）（3）（4） D．（1）（2）（3）（4）3．设函数，对任意，不等式恒成立，则正数的取值范围是（）A． B． C． D．4．设函数=,其中，若存在唯一的整数，使得＞0，则的取值范围是（）A．[，1） B．[错误！未指定书签。

，错误！未指定书签。

） C．[错误！未指定书签。

，错误！未指定书签。

） D．[错误！未指定书签。

，1）5．已知函数，对，使得，则的最小值为（）A． B． C． D．二、填空题（每题10分）6．若函数在其定义域内的一个子区间内存在极值，则实数的取值范围．7．函数，对任意的时，恒成立，则a的范围为8．已知，若对任意两个不等的正实数都有恒成立，则的取值范围是 .三、解答题（每题20分）9．已知函数.（1）若函数的图象关于点对称，直接写出的值；（2）求函数的单调递减区间；（3）若在区间上恒成立，求的最大值.10．已知函数（1）当时，求的单调递减区间；（2）若当时，恒成立，求的取值范围；（3）求证：1111ln(1)()35721n n Nn* +>++++∈+高三年级第七周周练试卷数学（文科）参考答案考试时间：45分钟；张正友；总分：120分一、选择题（每题10分）1．若关于的不等式的解集为，且中只有一个整数，则实数的取值范围是（）A. B.C. D.【答案】B2．函数的图象可能是（）A．（1）（3） B．（1）（2）（4）C．（2）（3）（4） D．（1）（2）（3）（4）【答案】C3．设函数，对任意，不等式恒成立，则正数的取值范围是（）A． B． C． D．【答案】B4．设函数=,其中，若存在唯一的整数，使得＞0，则的取值范围是（）A．[，1） B．[错误！未指定书签。

2021年高三上学期第7周周六考试数学文试题

2021年高三上学期第7周周六考试数学文试题注意：本卷满分150分，考试时间120分钟．答案应填（涂）在答题卷相应的位置上，否则无效．考试结束后，试卷自己带回保存，只交答题卷．参考公式：锥体的体积公式，其中是锥体的底面积，是锥体的高．一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的．）1、已知集合，，则（）A． B． C． D．2、在复平面内，复数对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限3、若关于的方程有两个不相等的实数根，则实数的取值范围是（）A．B．C．D．4、一个几何体的正视图、侧视图和俯视图形状都相同，大小均相等，则这个几何体不可以是（）A．球B．三棱锥C．正方体D．圆柱5、已知向量，，且，则（）A．B．C．D．6、等比数列中，，，则（）A．B．C．或D．或7、若实数，满足条件，则目标函数的最大值是（）A．B．C．D．8、下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行9、已知双曲线（，）的离心率为，一个焦点与抛物线的焦点相同，则双曲线的渐近线方程是（）A．B．C．D．10、对任意实数，，定义运算，其中，，为常数，等号右边的运算是通常意义的加、乘运算．现已知，，且有一个非零实数，使得对任意实数，都有，则（）A．B．C．D．二、填空题（本大题共5小题，考生作答4小题，每小题5分，满分20分．）（一）必做题（11～13题）11、若为偶函数，则实数．12、阅读如图所示的程序框图，若输入，则输出的值是．13、在长为的线段上任取一点，现作一矩形，邻边长分别等于线段，的长，则该矩形面积大于的概率是．（二）选做题（14～15题，考生只能从中选做一题）14、（坐标系与参数方程选做题）以平面直角坐标系的原点为极点，轴的正半轴为极轴建立极坐标系，已知曲线的参数方程为（其中为参数，且），则曲线的极坐标方程是．15、（几何证明选讲选做题）如图，在中，，，，、为垂足，若，，则．三、解答题（本大题共6小题，共80分．解答应写出文字说明、演算步骤或推理过程．）16、（本小题满分12分）已知函数（，）的最小正周期为．求的值；设，，，，求的值．17、（本小题满分12分）从一批柚子中，随机抽取个，获得其重量（单位：克）数据按照区间，，，进行分组，得到频率分布直方图，如图．根据频率分布直方图计算抽取的个柚子的重量众数的估计值；用分层抽样的方法从重量在和的柚子中共抽取个，其中重量在的有几个？在中抽出的个柚子中，任取个，求重量在的柚子最多有个的概率．18、（本小题满分14分）如图，在三棱锥中，底面为等腰直角三角形，，棱垂直底面，，，，是的中点．证明：平面；证明：平面；求四棱锥的体积．19、（本小题满分14分）已知各项均为正数的等比数列的首项，为其前项和，若，，成等差数列．求数列的通项公式；设，，记数列的前项和．若对，恒成立，求实数的取值范围．20、（本小题满分14分）已知椭圆过点，离心率．求椭圆的方程；若直线与该椭圆有两个交点，，当线段的中点在直线上时，求的取值范围．21、（本小题满分14分）已知函数，．设，讨论函数的单调性；若函数有唯一的零点，求的取值范围．凤翔中学xx －xx 学年度第一学期第7周周六考试高三文科数学试卷参考答案（一）必做题11、 12、 13、（二）选做题14、 15、三、解答题：16、解：函数的最小正周期为 …………………1分解得：…………………2分…………………3分3132sin 2sin 23263f ππππ⎛⎫⎛⎫=⨯-== ⎪ ⎪⎝⎭⎝⎭…………………5分 11032sin 32sin 232613f πππααα⎡⎤⎛⎫⎛⎫+=+-==- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ …………………6分()()16322sin 322sin 2cos 3625f ππβπβπββ⎡⎤⎛⎫+=+-=+== ⎪⎢⎥⎣⎦⎝⎭ …………………7分，…………………9分4sin 5β===-…………………10分 ()1235416cos cos cos sin sin 13513565αβαβαβ⎛⎫⎛⎫+=-=⨯--⨯-= ⎪ ⎪⎝⎭⎝⎭………………12分17、解：众数的估计值为最高的矩形的中点，即众数的估计值等于（克）…………………2分从图中可知，重量在的柚子数（个）…………………3分重量在的柚子数（个）…………4分从符合条件的柚子中抽取个，其中重量在的个数为（个）…………………6分由知，重量在的柚子个数为3个，设为，，，重量在的柚子个数为2个，设为，．…………………7分在中抽出的个柚子中，任取个，有10种，分别是，，，，，，，，，…………………9分重量在的柚子最多有1个，有7种，分别是，，，，，，…………………11分设事件“重量在的柚子最多有1个”，则答：重量在的柚子最多有1个的概率是…………………12分18、证明：∵，∴…………………1分∴…………………2分又∵平面ABC，平面ABC∴平面ABC…………………3分证明：∵PA⊥平面ABC，BC⊂平面ABC，∴BC⊥PA…………………4分∵∴即BC⊥AC…………………5分又∵∴平面…………………7分∵为等腰直角三角形，F是AB的中点∴∴的面积…………………8分过D作于，则，∴平面，且三棱锥的高…………………9分又∴…………………10分∴三棱锥的体积…………………11分又三棱锥的体积1111116.424332323P ABC ABC V S PA AB CF PA -∆==⨯⋅⋅=⨯⨯⨯⨯=…………………13分 ∴四棱锥的体积…………………14分19、解：，，成等差数列………………1分即化简得：………………2分解得：或………………3分数列的各项均为正数不合题意………………4分的通项公式为：………………5分由得：………………6分………………7分………………8分对，恒成立………………11分当且仅当，即时等号成立………………12分………………13分的取值范围是………………14分20、解：依题意：∴…………………………………………1分由，得……………………………………………………2分∴…………………………………………………………………3分∴所求椭圆方程为……………………………………………………4分设坐标分别为，将代入椭圆方程，整理得：…………………6分∴（*） ……………………………………8分要令为中点，则∴∴ ………………………………………………………………9分代入（*）得：0]19)13()[13(129)13(3622222222>-++-+⋅k k k k k k ……………10分…………12分∴或…………13分∴的取值范围是……………………………………14分21、解：，定义域为………………1分………………2分令，判别式当，即时，，，此时在上单调递增………………4分（注：如果是分开，，其讨论各占1分）当，即或时，由得：，………………5分若，则，又，所以，故在上恒成立所以在上单调递增………………6分若，则，又，所以此时，当时，，当时，，当时，故在，上单调递增，在上单调递减………………7分综上，当时，在上单调递增；当时，在，上单调递增，在上单调递减………………8分（注：先不写定义域，但后续单调性中体现了定义域特征不扣分；没有“综上”这一整合过程扣1分）问题等价于有唯一实根显然，则关于的方程有唯一实根………………10分构造函数，则由，得当时，，单调递减当时，，单调递增所以的极小值为………………12分如图，为函数的图象，则要使有唯一实根，只需直线与有唯一交点，则或解得：或故的取值范围是或………………14分（注：有分离思想，给2分，构造函数（有用）并求导正确给1分）s29952 7500 甀27720 6C48 汈aH28166 6E06 渆32547 7F23 缣34417 8671 虱$Ke24956 617C 慼H"<。

2021年高三上学期补习班数学周练试题(文科1.12) 含答案

2021年高三上学期补习班数学周练试题（文科1.12）含答案一、选择题1．已知全集，集合，则为（）A． B． C． D．2．复数的虚部为（）A. 0B.C. 1D.3．设等比数列中，公比，前项和为，则的值为（）A． B． C． D．4．幂函数的图象经过点（）A. B. C. D.5．已知向量，若2-与垂直，则（）.A． B． C． D．46．如右图所示的程序框图的输出值，则输入值 ( ▲ )A． B．C． D．7．设，是两条不同的直线，是一个平面，则下列命题正确的是（）A．若，，则B．若，，则C．若，，则D．若，，则8．为三角形的内角，则的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件9．数列1，2，2，3，3，3，4，4，4，4，……的第50项（）A．8 B．9 C．10 D．1110．若直线与曲线有公共点，则的取值范围是（）（A）（B）（C）（D）11．已知函数的图像过点，为函数的导函数，为自然对数的底数，若，恒成立，则不等式的解集为（）A． B． C． D．12．下列结论：①函数有最大值；②函数有最大值10；③若，则．正确的序号是A．① B．①③ C．②③ D．①②③二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）13．已知不论a 为何正实数，的图象恒过定点，则这个定点的坐标是______．14．函数f (θ)=的最大值为_________，最小值为_________15．已知双曲正弦函数和双曲作弦函数与我们学过的正弦函数和余弦函数有许多类似的性质，请类比正弦函数和余弦函数的和角或差角．．．．．公式，写出双曲正弦或双曲余弦函数的一个．．类似的正确结论______________.16．给出定义：若(其中为整数)，则叫做离实数最近的整数，记作，即.在此基础上给出下列关于函数的四个命题：①的定义域是，值域是；②点是的图像的对称中心，其中； ③函数的最小正周期为；④函数在上是增函数．则上述命题中真命题的序号是．一、选择题（本大题共12小题，每小题5分，共60分）二、填空题（本大题共4小题，每小题5分，共20分）三、解答题17．已知正方形ABCD 的边长是13，平面ABCD 外一点P 到正方形各顶点的距离都为13，M 、N 分别是PA 、BD 上的点且PM ：MA=BN ：ND=5：8，如图．（1）求证：直线MN ∥平面PBC ；（2）求线段MN 的长．题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 13.____________14.______________15.__________________16.______________18．已知函数（1）当时，求函数的单调区间；（2）若函数对恒成立，求实数的取值范围．19．已知函数图像上一点处的切线方程为(1)求的值；(2)若方程在区间内有两个不等实根，求的取值范围；(3)令如果的图像与轴交于两点，的中点为，求证：一、选择题（本大题共12小题，每小题5分，共60分）二、填空题（本大题共4小题，每小题5分，共20分）13．14．,0 15．16．①③三．解答题17．（1）连结AN并延长和BC交于E点，由条件证明MN∥PE，再利用直线和平面平行的判定定理证明MN∥平面PBC；（2）由于△PBC是边长为13的等边三角形，利用余弦定理求得PE的值，根据△AMN 与△APE的相似比为，可得MN=PE的值试题解析：（1）证明：连结AN并延长和BC交于E点，由PM：MA=BN：ND=5：8，可得EN：NA=BN：ND=MP：MA=5：8，即 =，∴MN∥PE，而MN⊄平面PBC，PE⊂面PBC，∴MN∥平面PBC．（2）解：由于△PBC是边长为13的等边三角形，余弦定理求得PE2=PB2+BE2﹣2PB•EBcos60°=132+﹣2×13××=，∴PE=．由于△AMN 与△APE的相似比为，∴MN=PE=7．18．（1）把代入函数中，对进行求导，解得的解集是减区间，的解集是增区间；（2）构造函数1ln)1(1)()(2+-+-=+-=xxxaxxfxg，函数对恒成立既是在上的最大值．对进行求导，得出在上的单调性，从而找出的最大值．再令，即可得出的范围．试题解析：（1），，（x＞0）f＇（x）xxxxxxxx2)1)(2(22121212+--=++-=++-=，当0＜x ＜2时，f＇（x）＞0，f（x）在（0，2）单调递增；当x＞2时，f＇（x）＜0，f（x）在单调递减；所以函数的单调递增区间是（0，2），单调递减区间是．（2）由题意得对恒成立，设，，则，求导得22ax(21)1(21)(1)'()a x ax xg xx x-++--==，当时，若，则，所以在单调递减成立，得；当时，，在单调递增，题号1 2 3 4 5 6 7 8 9 10 11 12答案 C D A C C D B A C D B B所以存在，使，则不成立；当时，，则在上单调递减，单调递增，则存在，有01ln 111ln )11()1(2>-+-=+-+-=a a aa a a a g ，所以不成立．综上得．19．(1),,.∴,且.解得a ＝2,b ＝1. . (4分)(2),设,则,令,得x ＝1(x ＝－1舍去).当x ∈时,, h(x)是增函数；当x ∈时,, h(x)是减函数. 则方程在内有两个不等实根的充要条件是. (8分)(3),.假设结论成立,①－②,得.∴.由④得,于是有,∴,即.⑤ 令, (0＜t ＜1),则＞0.∴在0＜t ＜1上是增函数,有,∴⑤式不成立,与假设矛盾. ∴. (12分)g28783 706F 灯X z34418 8672 虲40392 9DC8 鷈xX 37544 92A8 銨32270 7E0E 縎37713 9351 鍑25296 62D0 拐。

2021年高三上学期补习班周练数学试题(文科1.6) 含答案

2021年高三上学期补习班周练数学试题（文科1.6）含答案一、选择题1．在复平面内，复数对应的点位于（）A．第一象限 B．第二象限 C．第三象限 D．第四象限2．某单位有老年人28人，中年人54人，青年人81人．为了调查他们的身体状况，需从他们中抽取一个容量为36的样本，最适合抽取样本的方法是( )A．简单随机抽样B．系统抽样C．分层抽样D．先从老年人中剔除一人，然后分层抽样3．若命题“使得”为假命题，则实数的取值范围是（）A．[2，6] B．[-6，-2] C．（2，6）D．（-6，-2）4．等比数列的各项均为正数，且，则（）A. B. C. D.5．如图是某几何体的三视图，则此几何体的体积是（）A．36 B．108 C．72 D．1806．已知，则的值是A． B． C． D．7．函数（其中）的图象如图所示，为了得到的图象，则只要将的图象( )A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度8．已知A、B、C三点共线，O是该直线外的一点，且满足,则的值为( )A．1 B．2 C． D．9．设函数的定义域为,值域为,若的最小值为,则实数a的值为( )A. B. 或 C. D. 或10．已知数列满足，则A． B． C． D．11．设均为正实数，且，则的最小值为A．4 B． C．9 D．1612．已知直线y＝mx与函数的图象恰好有3个不同的公共点，则实数m的取值范围是（）A．（，4） B．（，＋∞） C．（，5） D．（，）二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）13．函数的值域是__________.14．若向量、的夹角为，==1，则= ．15．设实数x，y满足约束条件，若目标函数（）的最大值为8，则的最小值为 . 16．定义在上的可导函数满足：且,则的解集为。

一、选择Array题（本大题共12小题，每小题5分，共60分）二、填空题（本大题共4小题，每小题5分，共20分）13.____________14.______________15.__________________16.______________三、解答题17．如图，平面，矩形的边长，，为的中点．（1）证明：；（2）如果异面直线与所成的角的大小为，求的长及点到平面的距离．18．为了调查学生星期天晚上学习时间利用问题，某校从高二年级1000名学生（其中走读生450名，住宿生550名）中，采用分层抽样的方法抽取名学生进行问卷调查，根据问卷取得了这名同学每天晚上学习时间（单位：分钟）的数据，按照以下区间分为八组①，②，③，④，⑤，⑥，⑦，⑧，得到频率分布直方图如下，已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人：（1）求的值并补全下列频率分布直方图；学生，完成下列列联表：利用时间充分利用时间不充分总计走读生住宿生10总计据此资料，你是否认为学生“利用时间是否充分”与走读、住宿有关？参考公式：19．已知函数．（1）求函数在区间上的最值；（2）若（其中为常数），当时，设函数的3个极值点为，且，证明：．一、选择题（本大题共12小题，每小题5分，共60分）题号1 2 3 4 5 6 7 8 9 10 11 12答案 C D A B B D A A D C D B二、填空题（本大题共4小题，每小题5分，共20分）13． 14． 15．4 16．三．解答题 17．（1）证明：连接，由，得，同理得，，，由勾股定理得， ∵平面，∴．又，∴平面， ∴．（2）取的中点，的中点，连 ∴∥，∥，∴的大小等于异面直线与所成的角或其补角的大小，即或（或者由观察可知，，不需分类讨论）设，则，，．若，由，得． ∴．在中，，，∴∴点到平面的距离为．若，由，显然不适合题意．综上所述，，点到平面的距离为．18．(1)设第组的频率为,∴学习时间少于60分钟的频率为，由题意知：，所以又因为所以，所以第④组的高度为: ．频率分布直方图如图：（注：未标明高度1/250扣1分）（2）由频率分布直方图可知，在抽取的100人中，“走读生”有45人，利用时间不充分的有40人，从而列联表如下：11/1/1/11/11/将列联表中的数据代入公式计算，得因为，所以没有理由认为学生“利用时间是否充分”与走读、住宿有关．19．（1）函数的定义域为，，令可得，当时，，函数单调递减；当时，，函数单调递增．，又且，所以函数的最小值为，最大值为．（2）由题意得,,令，有，所以函数在上单调递减，在上单调递增．因为函数有三个极值点从而当时，，从而3个极值点中，有一个为，有一个小于，有一个大于1．又，即，故．21932 55AC 喬_38899 97F3 音27737 6C59 汙20677 50C5 僅O 40323 9D83 鶃36305 8DD1 跑-23718 5CA6 岦F33010 80F2 胲。

2021年高三上学期补习班数学周练试卷(文科12.15) 含答案

2021年高三上学期补习班数学周练试卷（文科12.15）含答案一选择题1、平行六面体ABCD﹣A1B1C1D1中，既与AB共面也与CC1共面的棱的条数为（）A 3B 4 C．5 D 62、下列说法中正确的是（） A．三点确定一个平面 B．两条直线确定一个平面 C．两两相交的三条直线一定在同一平面内 D．过同一点的三条直线不一定在同一平面内3、若直线，，则直线与的位置关系是（）A．异面 B．相交 C．平行 D．异面或相交4、给出下列四个命题：①分别与两条异面直线都相交的两条直线一定是异面直线；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中为真命题的是（）A．①和② B．②和③ C．③和④ D．②和④5、如图，在正四棱柱中，、分别是、的中点，则下列结论不成立的是 ( )A．与垂直 B．与垂直C．与异面 D．与异面6、．直三棱柱ABC﹣A1B1C1中，若∠BAC=90°，AB=AC=AA1，则异面直线BA1与AC1所成的角等于（）A． 30° B． 45° C． 60° D． 90°7、如图,若是长方体被平面截去几何体后得到的几何体,其中E为线段上异于的点，F为线段上异于的点，且∥，则下列结论中不正确的是（）A. ∥B.四边形是矩形C. 是棱柱D. 是棱台8、已知在空间四边形ABCD中，AD⊥BC，AD⊥BD，且△BCD是锐角三角形，则必有( )A．平面ABD⊥平面ADC B．平面ABD⊥平面ABCC．平面ADC⊥平面BDC D．平面ABC⊥平面BDC9、如图，正方体ABCD﹣A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F，且EF=则下列结论中错误的是（）A． AC⊥BE B． EF∥平面ABCDC．三棱锥A﹣BEF的体积为定值 D．△AEF的面积与△BEF的面积相等10、在正方体AC1中，E、F分别为AB和CD的中点，则异面直线A1E与BF所成角的余弦值为（） A．－ B． C．－或 D．11、设α、β、γ为平面，为直线，则的一个充分条件是（）A． B．C． D．12、若P是两条异面直线l、m外的任意一点，则A.过点P有且仅有一条直线与l、m都平行B.过点P有且仅有一条直线与l、m都垂直C.过点P有且仅有一条直线与l、m都相交D.过点P有且仅有一条直线与l、m都异面二、填空题13、在棱长为1的正方体ABCD﹣A1B1C1D1中，若点P是棱上一点，则满足|PA|+|PC1|=2的点P的个数为14、三棱锥中，⊥底面，＝3，底面是边长为2的正三角形，则三棱锥的体积等于________．15、已知在长方体ABCDA1B1C1D1中，底面是边长为2的正方形，高为4，则点A1到截面AB1D1的距离是________．16、，，是空间中的三条直线，下面给出三个命题：①若，，则；②若与相交，与相交，则与相交；③若，与成等角，则．上述命题中正确的命题是（只填序号）．丰城中学xx学年上学期高四周练答题卡班级: _____ 姓名：__________学号：_______ 得分：_______题号1 2 3 4 5 6 7 8 9 10 11 12答案13． 14． 15． 16．三、解答题：17、如图所示，是正方形，，是的中点（1）求证：；（2）若，求三棱锥的体积．18、如图，正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD，AB ＝AD＝2，CD＝4，M为CE的中点．(1)求证：BM∥平面ADEF； (2)求证：平面BDE⊥平面BEC.19（附加题）、在四边形ABCD中，BC∥AD，BC⊥CD，AD＝4，BC＝CD＝2，E，P 分别为AD，CD的中点(如图K4510(1)所示)，将△ABE沿BE折起，使二面角A BE C为直二面角，如图(2)，在线段AE上，是否存在一点M，使得PM∥平面ABC？若存在，请指出点M的位置，并证明你的结论；若不存在，请说明理由．参考答案(12.15)题号1 2 3 4 5 6 7 8 9 10 11 12答案C D D D D C D C D B D B中横线上）13．6． 14．15．16．①三、简答题17、（1）略（2）∵，∴是三棱锥的高，∵是正方形，是的中点，∴是等腰直角三角形，故,故18. 1)证明：延长DA与CB相交于P，∵AB＝AD＝2，CD＝4，AB∥CD，∴B为PC的中点，又M为CE的中点，∴BM∥EP，∵BM⊄平面ADEF，EP⊂平面ADEF，∴BM∥平面ADEF.∴BD2＋BC2＝CD2，∴BD⊥BC.又平面ADEF⊥平面ABCD，ED⊥AD，∴ED⊥平面ABCD，∴ED⊥BC，∵ED∩BD＝D，∴BC⊥平面BDE，又BC⊂平面BEC，∴平面BDE⊥平面BEC.19.存在点M，当M为线段AE的中点时，PM∥平面ABC，理由略38842 97BA 鞺 34377 8649 虉26786 68A2 梢";$21803 552B 唫21357 536D 卭38239 955F 镟 40387 9DC3 鷃25653 6435 搵2。