中学数学 解读高斯正十七边形的作法 教案
高斯与正十七边形

高斯与正十七边形数学就象一棵美丽的星球,他那博大精深、简明透彻的数学美就是他的引力场。
许许多多人类的精英被他的引力所吸引,投入他的怀抱为他献出了自己毕生的精力。
被誉为“数学王子”的伟大数学家高斯就是其中之一。
高斯是个数学天才,幼年时巧妙地计算1+2+3+…+100为101×50=5050的故事几乎尽人皆知。
其实,学生日期的高斯不仅数学成绩优异,而且各科成绩都名列前茅。
小学毕业后,高斯考了文科学校。
由于他古典文学成绩突出,入学后直接上了二年级。
两年以后高斯又升入了高中哲学班。
15岁时,高斯在一位公爵的资助下上了大学-卡罗琳学院。
在那里,他掌握了希腊文、拉丁文、法文、英文有丹麦文,又学会了代数、几何、微积分。
语言学和数学是他最喜爱的两门课程。
18岁时,高斯进入了哥廷根大学深造。
这时,高斯面临着一个非常痛苦的选择:是把语言学作为自己的终生事业?还是把数学作为自己的终生事业?两棵下不了决心进行最后的选择。
后来,一次数学研究上的突破改变了两个引力场的均衡。
高斯终于下定决心,飞向了数学之星。
事情是这样的,尺规作图是几何学的重要内容之一,从古希腊开始,人们一直认为正多边形是最美的图形,因此,用尺规作图法能够作出哪些正多边形,历来就是一个极具魅力的问题。
到高斯的时代,人们已经解决了边数是n 23•、n 24•、n 25•、n 253••(=n 0,1,2,3……)的正多边形的尺规作图问题。
但是,还没有人能作出正7边形、正11边形、正17边形等等。
很多人认为,当边数是大于5的素数时,那样的正多边形是不可以用尺规作图完成的。
高斯一直对正多边形尺规作图问题非常着迷。
经过持久地,如醉如痴的思考与画图,于1796年3月30日,19岁的高斯出人意料地作出了正17边形。
并且,他把正多边形作图问题与高次方程联系起来,彻底解决了哪些正多边形能作出,哪些正多边形不能作出。
他证明了一切边数形如122+t(=t 0,1,2,3,……)的正多边形都只可以作出,而边数为7、11、14,……的正多边形是作不出的。
正十七边形

正十七边形尺规作法(无刻度)步骤一:给一圆O,作两垂直的半径OA、OB,作C点使OC=1/4OB,作D点使∠OCD=1/4∠OCA,作AO延长线上E点使得∠DCE=45度。
步骤二:作AE中点M,并以M为圆心作一圆过A点,此圆交OB于F点,再以D为圆心,作一圆过F点,此圆交直线OA于G4和G6两点。
步骤三:过G4作OA垂直线交圆O于P4,过G6作OA垂直线交圆O于P6,则以圆O为基准圆,A为正十七边形之第一顶点P4为第四顶点,P6为第六顶点。
连接P4P6,以1/2弧P4P6为半径,在圆上不断截取,即可在此圆上截出正十七边形的所有顶点。
历史最早的十七边形画法创造人为高斯。
高斯(1777~1855年),德国数学家、物理学家和天文学家。
在童年时代就表现出非凡的数学天才。
三岁学会算术,八岁因发现等差数列求和公式而深得老师和同学的钦佩。
1799年以代数基本定理的四个漂亮证明获得博士学位。
高斯的数学成就遍及各个领域,其中许多都有着划时代的意义。
同时,高斯在天文学、大地测量学和磁学的研究中也都有杰出的贡献。
1801年,高斯证明:如果k是质数的费马数,那么就可以用直尺和圆规将圆周k 等分。
高斯本人就是根据这个定理作出了正十七边形,解决了两千年来悬而未决的难题。
道理当时,如果高斯的老师告诉了高斯这是道2000多年没人解答出来的题目,高斯就不会画出这个正十七边形。
这说明了你不怕困难,困难就会被攻克,当你惧怕困难,你就不会胜利。
正十七边形的证明方法正十七边形的尺规作图存在之证明:设正17边形中心角为a,则17a=360度,即16a=360度-a故sin16a=-sina,而sin16a=2sin8acos8a=4sin4acos4acos8a=16sinaco sacos2acos4acos8a因sina不等于0,两边除之有:16cosacos2acos4acos8a=-1又由2cosacos2a=cosa+cos3a等,有2(cosa+cos2a+…+cos8a)=-1注意到cos15a=cos2a,cos12a=cos5a,令x=cosa+cos2a+cos4a+cos8№ay=cos3a+cos5a+cos6a+cos7a有:x+y=-1/2又xy=(cosa+cos2a+cos4a+cos8a)(cos3a+cos5a+co s6a+cos7a)=1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a)经计算知xy=-1又有x=(-1+根号17)/4,y=(-1-根号17)/4其次再设:x1=cosa+cos4a,x2=cos2a+cos8ay1=cos3a+cos5a,y2=cos6a+cos7a故有x1+x2=(-1+根号17)/4y1+y2=(-1-根号17)/4最后,由cosa+cos4a=x1,cosacos4a=(y1)/2可求cosa之表达式,它是数的加减乘除平方根的组合, 故正17边形可用尺规作出数学未解之谜一数学基础问题。
解读数学王子高斯正十七边形的作法-上

解读“数学王子”高斯正十七边形的作法(上)江苏省泰州市朱庄中学曹开清 225300一、高斯的传奇故事高斯(Carl Friedrich Gauss 1777.4.30~1855.2.23),德国数学家、物理学家、天文学家。
有一天,年幼的高斯在一旁看著作水泥工厂工头的父亲计算工人们的周薪。
父亲算了好一会儿,终于将结果算出来了。
可是万万没想到,他身边传来幼嫩的童音说:“爸爸,你算错了,总数应该是……”父亲感到很惊异,赶忙再算一遍,结果证实高斯的答案是对的。
这时的高斯只有3岁!高斯上小学了,教他们数学的老师布特勒(Buttner)是一个态度恶劣的人,他讲课时从不考虑学生的接受能力,有时还用鞭子惩罚学生。
有一天,布德勒让全班学生计算1+2+3+4+5+……+98+99+100=?的总和,并且威胁说:“谁算不出来,就不准回家吃饭!”布德勒说完,就坐在一旁独自看起小说来,因为他认为,做这样一道题目是需要些时间的。
小朋友们开始计算:“1 +2 =3,3+3=6,6+4=10,……”数越来越大,计算越来越困难。
但是不久,高斯就拿着写着解答的小石板走到布德勒的身边。
高斯说:“老师,我做完了,你看对不对?“做完了?这么快就做完了?肯定是胡乱做的!”布德勒连头都没抬,挥挥手说:“错了,错了!回去再算!”高斯站着不走,把小石板往前伸了伸说:“我这个答案是对的。
”布德勒抬头一看,大吃一惊。
小石板上写着5050,一点也没有错!高斯的算法是1 +2 +3+……+98+99+100100+99+98+……+3+2+1101+101+101+……+101+101+101=101×100=1010010100÷2=5050高斯并不知道,他用的这种方法,其实就是古代数学家经过长期努力才找出来的求等差数列和的方法,那时他才八岁!1796年的一天,德国哥廷根大学。
高斯吃完晚饭,开始做导师给他单独布置的三道数学题。
前两道题他不费吹灰之力就做了出来了。
高斯仅用没有刻度的尺子与圆规便构造出了正17边形

高斯仅用没有刻度的尺子与圆规便构造出了正17边形解法一:将你要画的正17边形的边长为d,它的外接圆的半径为R。
则d和R的关系是Sin(360度/(17*2))=d/(2R)正17边形的边对应的圆心角度数为360/17,正17边形的一条边和其两个端点与圆心连接的半径成为一个等边三角形;然后从圆心作出一条垂线到边上,就能得出一个直角三角形,圆心的那个角是圆心角的一半,即360度/(17*2),对边是d/2,斜边是R,所以得出Sin(360度/(17*2))=d/(2R)最后,根据该公式,如果你想画出一个边长为1厘米的正17边形,则把d=1代入公式,得出R的值。
1、先画一个R半径的圆;2、用圆规支脚支在圆周的一个点上,取d为半径,交圆周于一点,然后把这两点连起来,就是17边形的一条边了;3、如此类推,把17条边画完就是一个正17边形了解法二:在与圆O的直径AB垂直的半径OC上,作出OC的中点D,在OB上作一点E,使OE等于半径的1/8;以E为圆心,ED长为半径作弧,与OA、OB分别交于F、G;以F为圆心,FD 长为半径作弧,交OA延长线于H,以G为圆心,GD长为半径作弧,交OA于I;作OB中点J,以线段IJ为直径作圆,交OC于K;过K作AB的平行线,与以线段OH为直径的圆交于远端L,过L作OC的平行线,与圆O交于M。
弧AM就是圆O的1/17,依次连结各点就行了解法三:将你要画的正17边形的边长为d,它的外接圆的半径为R。
则d和R的关系是Sin(360度/(17*2))=d/(2R) 正17边形的边对应的圆心角度数为360/17,正17边形的一条边和其两个端点与圆心连接的半径成为一个等边三角形;然后从圆心作出一条垂线到边上,就能得出一个直角三角形,圆心的那个角是圆心角的一半,即360度/(17*2),对边是d/2,斜边是R,所以得出Sin(360度/(17*2))=d/(2R) 最后,根据该公式,如果你想画出一个边长为1厘米的正17边形,则把d=1代入公式,得出R的值。
高斯正17边形的尺规作图方法
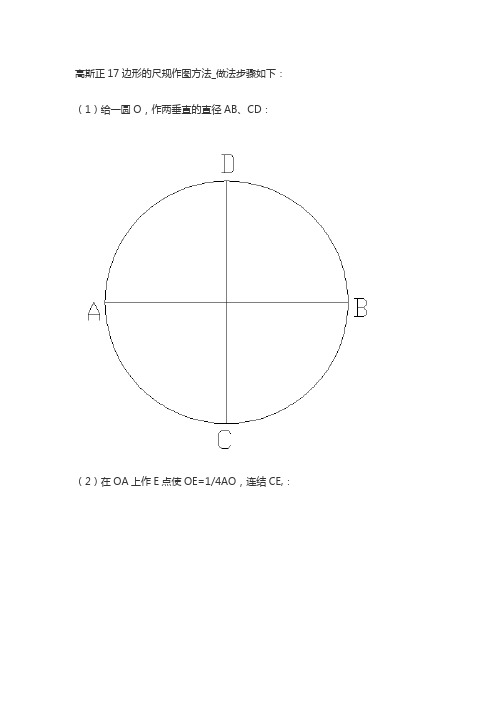
高斯正17边形的尺规作图方法_做法步骤如下:(1)给一圆O,作两垂直的直径AB、CD:
(2)在OA上作E点使OE=1/4AO,连结CE,:
(3)作∠CEB的平分线EF:
(4)作∠FEB的平分线EG,交CO于P:
(5)作∠GEH=45°,交CD于Q:
(6)以CQ为直径作圆,交OB于K:
(7)以P为圆心,PK为半径作圆.交CD于L、M:
(8)分别过M、L作CD的垂线,交圆O于N、R:
(9)作弧NR的中点S,以SN为半径将圆O分成17等份:
最后几何作图如下:
简易作法
因为360°/17≈21°10′,利用sinA 21°6′=0.3600可得近似角。
用该方法作正十七边形总误差为17*4′=68′,在不要求十分精确的情况下还是可行的。
作法如下:
1.先画一条直线,用圆规在上面截取5条相等线段,(尽量越短越好),再截
取之前四条线段的和,接续之前画的线段。
这样,如果每条小线段算作
0.1的话,那么整条线段就是1.8。
2.用圆规截取之前5条小线段的长,画5次,这样这条线段就是5。
1.8/5=0.36。
准备工作完毕!
3.另作一条直线,作垂线,1.8的线段作为对边,5的线段作为斜边,那个
最小的锐角即是近似的360°/17的角。
以其顶点为圆心,重复作角直至闭合。
画一大圆,连接其与17条射线的交点,即可。
GAUSS与正十七边形

GAUSS与正十七边形用直尺和圆规作出圆内接正七、正九、正十一、正十三、正十七边形, 是从古希腊以来两千多年悬而未决的著名数学难题; 它困扰了许多著名的数学家,有的甚至为之付出终身的努力,却毫无所获. 但是,此难题却被18岁的高斯在1796年3月30日功克.高斯是18~19世纪最伟大的数学家, 近代数学的奠基人之一. 他被称为〝数学王子〞, 〝数学巨人〞. 假设说世界上有神童的话, 那么高斯就是其中的一位. 听说他三岁就发现了他父亲算帐时出现的错误, 10岁时已表现出超群的数学思想才干.有一次,教员出了一道题: 把1到100的整数全部加起来. 其他同窗都拿起笔来一个一个地加, 高斯却坐在那一动也不动. 教员走到跟前问他为什么不做, 他却立刻报出了答案: 5050. 他的做法是: 把1和100相加得101, 2和99相加也是101, 3和97相加还是101; 如此下去, 共有50个101. 因此, 得数为101×50 = 5050. 教员慨叹地说〝他曾经超越我了, 我没有什么可以教他的了〞.15岁时, 高斯进入了卡罗琳学院, 学习了牛顿, 拉格郎日, 欧拉等人的著作, 很快掌握了微积分实际.18岁时, 高斯进入哥廷根大学. 在一次偶然的阅读中, 他知道了用直尺和圆规作出圆内接正七边形的难题. 这使他十分着迷, 并决计要功克它. 他首先查找出先人的作图方法, 细心研讨他们失败的缘由, 经过半年多的努力, 他终于作出了正七边形; 接着, 正九、正十一、正十三边形都被他逐一克制. 没多久, 正十七边形也被他功克.面对第一次取得的成功, 高斯异常兴奋, 决计把自己的终身献给数学. 1801年, 他宣布了<<算术研讨>>,论述了数论和初等代数的一些效果. 高斯对数学的研讨触及很多方面,除了在复变函数\\统计数学\\椭圆函数论上有突出贡献外, 他在向量剖析\\正态散布的正轨曲线\\质数定理的验算研讨上也取得了效果.在高斯逝世后, 哥廷根大学为他建造了一个以正十七边形棱柱为底座的纪念像, 以纪念他终身中的第一个严重发现.。
正十七边形尺规作图及证明

正十七边形尺规作图及证明正十七边形样本图正十七边形作法:第一步:在给定直线l上作一个圆O交直线于点A,B,分别以A,B为圆心,AB,BA为半径作弧,两弧交于点C,D,连接CD;第二步:以C为半径,CO为半径作弧交圆于点E,F,连接EF交CD于点K,再分别以K,O为圆心,KO,OK为半径作弧,两弧交于点G,H,连接GH交直线CD于点P,连接PB;第三步:再以P为圆心,小于PB的长度为半径作弧U,分别交AB,CD于点M,N,再分别以M,N为圆心,MN,NM为半径作弧,两弧圆外的交点为Q,连接QP交圆于点T,再分别以T,M为圆心,TM,MT为半径作弧,两弧圆外的交点为R,连接PR交弧U于上面的点S,下面的点W;第四步:连接S,W,再分别以S,W为圆心,SW,WS为半径作弧交于圆外的点Y,连接PY交弧U于点X,再分别以X,S为圆心SX,XS为半径作弧,两弧圆外的交点为Z,连接PZ;第五步:PZ交AB于点A₁,再分别以A₁,B为圆心,A₁B,B A₁作弧交于点A ₂,B₁,连接A₂,B₁交AB于点B₂,交圆于点C₁,连接B₂,C₁;第六步:再最后的C₁B依次戴取分点,直到最后作出十七个分点后连接,便是正十七边形。
正十七边形证明我们知道,一个正多边形的中心角的余弦值如果不是超越数,就可以用尺规作出该正多边形,求出的中心角的三角函数值代数式也就是包含了过程。
计算360cos 17⎛⎫︒ ⎪⎝⎭设正十七边形的中心角为α,则17360α=︒即16360αα=︒-亦即()sin16sin 360sin ααα=︒-=-由诱导公式()cos 2cos παα-=,我们发现:()()()()()()()()()()()()cos cos 360cos 17cos16cos 2cos 3602cos 172cos15cos3cos 3603cos 173cos14cos 4cos 3604cos 174cos13cos5cos 3604cos 175cos12cos 6cos 3606cos 176cos11cos 7ααααααααααααααααααααααααααααααα=︒-=-==︒-=-==︒-=-==︒-=-==︒-=-==︒-=-=()()()()cos 3607cos 177cos10cos8cos 3608cos 178cos9ααααααααα=︒-=-==︒-=-=因此我们有结论1:cos cos16cos 2cos15cos3cos14cos 4cos13cos5cos12cos 6cos11cos 7cos10cos8cos9αααααααααααααααα======== 该结论我们以后使用。
沉思启智之“心态”主题故事:高斯的正十七边形

高斯的正十七边形1796年的一天,德国哥廷根大学,一个很有数学天赋的 19岁青年吃完晚饭,开始做导师单独布置给他的每天例行的三道数学题。
前两道题在两个小时内就顺利完成了。
第三道题写在另一张小纸条上:要求只用圆规和一把没有刻度的直尺,画出一个正十七边形。
他感到非常吃力。
时间一分一秒地过去了,第三道题竟毫无进展。
这位青年绞尽脑汁,但他发现,自己学过的所有数学知识似乎对解开这道题都没有任何帮助。
困难反而激起了他的斗志:我一定要把它做出来!他拿起圆规和直尺,一边思索一边在纸上画着,尝试着用一些超常规的思路去寻求答案。
当窗口露出曙光时,青年长舒了一口气,他终于完成了这道难题。
见到导师时,青年有些内疚和自责。
他对导师说:“您给我布置的第三道题,我竟然做了整整一个通宵,我辜负了您对我的栽培……”导师接过学生的作业一看,当即惊呆了。
他用颤抖的声音对青年说:“这是你自己做出来的吗?”青年有些疑惑地看着导师,回答道:“是我做的。
但是,我花了整整一个通宵。
”导师请他坐下,取出圆规和直尺,在书桌上铺开纸,让他当着自己的面再做出一个正十七边形。
青年很快做出了一个正十七边形。
导师激动地对他说:“你知不知道?你解开了一桩有两千多年历史的数学悬案!阿基米德没有解决,牛顿也没有解决,你竟然一个晚上就解出来了。
你是一个真正的天才!”原来,导师也一直想解开这道难题。
那天,他是因为失误,才将写有这道题目的纸条交给了学生。
每当这位青年回忆起这一幕时,总是说:“如果有人告诉我,这是一道有两千多年历史的数学难题,我可能永远也没有信心将它解出来。
”这位青年就是数学王子高斯。
【引领点】那一年,高斯还仅仅是一个 19岁的大学生,与世界级数学大师还相差甚远。
可他却在不知情的情况下,用平常心解决了一道拥有两千多年历史的数学难题。
不可否认,他在数学方面极具天赋,但是连他都承认了:“如果有人告诉我,这是一道有两千多年历史的数学难题,我可能永远也没有信心将它解出来!”这说明什么问题?有时候制约我们发挥潜力的因素,不是客观的外部条件,而是来自于对未知困难的恐惧和胆怯。
中学数学 解读高斯正十七边形的作法 教案
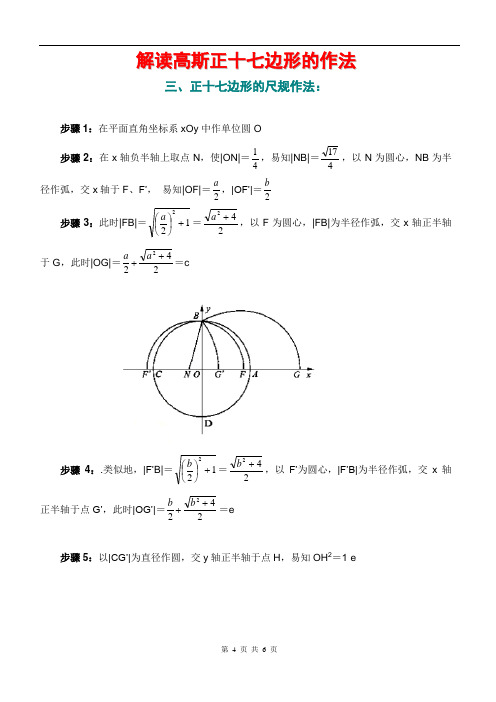
解读高斯正十七边形的作法三、正十七边形的尺规作法:步骤1:在平面直角坐标系xOy 中作单位圆O 步骤2:在x 轴负半轴上取点N ,使|ON|=41,易知|NB|=417,以N 为圆心,NB 为半径作弧,交x 轴于F 、F’, 易知|OF|=2a ,|OF’|=2b步骤3:此时|FB|=122+⎪⎭⎫⎝⎛a =242+a ,以F 为圆心,|FB|为半径作弧,交x 轴正半轴于G ,此时|OG|=2422++a a =c步骤4:.类似地,|F’B|=122+⎪⎭⎫⎝⎛b =242+b ,以F’为圆心,|F’B|为半径作弧,交x 轴正半轴于点G’,此时|OG’|=2422++b b =e步骤5:以|CG’|为直径作圆,交y 轴正半轴于点H ,易知OH 2=1·e步骤6:以H 为圆心,21|OG|为半径作弧,交x 轴正半轴于点K ,则有|OK|=222OH OG -⎪⎭⎫ ⎝⎛=222e c -⎪⎭⎫ ⎝⎛=242e c - 步骤7:以K 为圆心,|KH|=21|OG|为半径作弧,交x 轴正半轴于点L ,则|OL|=242ec c -+步骤8:取OL 的中点M ,则|OM|=442e c c -+= cos 172π步骤9:过点M 作y 轴的并行线交单位圆O 于两点A 2和A 17,则Α为正十七边形的第一个顶点,A 2为第二个顶点,A 17为第十七个顶点,从而作出正十七边形。
四、正十七边形边长的表达式在上面得到的一系列等式:a =2171+-,b =2171-- ,c =242++a a , e =242++b b ,cos 172π=442e c c -+中,依次求出c =417234171-++-,e =417234171++--。
从而求出cos172π的其它表达式:可以验证,它们在数值上是相等的,其中以第二个表达式为最优。
在单位圆中,根据余弦定理,得正十七边形的边长为 172cos22π-,将cos 172π的值代入,即可求出正十七边形的边长。
正十七边形尺规作图与详解.docx

实用标准文档解读“数学王子”高斯正十七边形的作法一、高斯的传奇故事高斯 (Carl Friedrich Gauss1777.4.30~1855.2.23),德国数学家、物理学家、天文学家。
有一天,年幼的高斯在一旁看著作水泥工厂工的父算工人的周薪。
父算了好一会儿,于将果算出来了。
可是万万没想到,他身来幼嫩的童音:“爸爸,你算了,数是⋯⋯”父感到很惊异,赶忙再算一遍,果高斯的答案是的。
的高斯只有 3 !高斯上小学了,教他数学的老布特勒(Buttner)是一个度劣的人,他从不考学生的接受能力,有用鞭子学生。
有一天,布德勒全班学生算1+2+3+4+5+⋯⋯+98+99+100=?的和,并且威:“ 算不出来,就不准回家吃!”布德勒完,就坐在一旁独自看起小来,因他,做一道目是需要些的。
小朋友开始算:“ 1 + 2=3,3+3=6,6+4=10,⋯⋯”数越来越大,算越来越困。
但是不久,高斯就拿着写着解答的小石板走到布德勒的身。
高斯:“老,我做完了,你看不?“做完了?么快就做完了?肯定是胡乱做的!”布德勒都没抬,手:“ 了,了!回去再算!”高斯站着不走,把小石板往前伸了伸:“我个答案是的。
”布德勒抬一看,大吃一惊。
小石板上写着5050 ,一点也没有!高斯的算法是1+ 2 + 3+⋯⋯+ 98 +99 + 100100+99 +98+⋯⋯+3+ 2+1101+ 101 + 101 +⋯⋯+101 +101 + 101 =101 ×100 =1010010100 ÷2= 5050高斯并不知道,他用的种方法,其就是古代数学家期努力才找出来的求等差数列和的方法,那他才八!1796 年的一天,德国哥廷根大学。
高斯吃完晚,开始做他独布置的三道数学。
前两道他不吹灰之力就做了出来了。
第三道写在另一小条上:要求只用和没有刻度的直尺,作出一个正十七形。
道把他住了——所学的数学知竟然解出道没有任何帮助。
一分一秒的去了,第三道竟毫无展。
正十七边形尺规作图与详细讲解

解读“数学王子”高斯正十七边形的作法一、高斯的传奇故事高斯(Carl Friedrich Gauss 1777.4.30~1855.2.23),德国数学家、物理学家、天文学家。
有一天,年幼的高斯在一旁看著作水泥工厂工头的父亲计算工人们的周薪。
父亲算了好一会儿,终于将结果算出来了。
可是万万没想到,他身边传来幼嫩的童音说:“爸爸,你算错了,总数应该是……”父亲感到很惊异,赶忙再算一遍,结果证实高斯的答案是对的。
这时的高斯只有3岁!高斯上小学了,教他们数学的老师布特勒(Buttner)是一个态度恶劣的人,他讲课时从不考虑学生的接受能力,有时还用鞭子惩罚学生。
有一天,布德勒让全班学生计算1+2+3+4+5+……+98+99+100=?的总和,并且威胁说:“谁算不出来,就不准回家吃饭!”布德勒说完,就坐在一旁独自看起小说来,因为他认为,做这样一道题目是需要些时间的。
小朋友们开始计算:“1 + 2 =3,3+3=6,6+4=10,……”数越来越大,计算越来越困难。
但是不久,高斯就拿着写着解答的小石板走到布德勒的身边。
高斯说:“老师,我做完了,你看对不对?“做完了?这么快就做完了?肯定是胡乱做的!”布德勒连头都没抬,挥挥手说:“错了,错了!回去再算!”高斯站着不走,把小石板往前伸了伸说:“我这个答案是对的。
”布德勒抬头一看,大吃一惊。
小石板上写着5050,一点也没有错!高斯的算法是1 +2 +3+……+98+99+100100+99+98+……+3+2+1101+101+101+……+101+101+101=101×100=1010010100÷2=5050高斯并不知道,他用的这种方法,其实就是古代数学家经过长期努力才找出来的求等差数列和的方法,那时他才八岁!1796年的一天,德国哥廷根大学。
高斯吃完晚饭,开始做导师给他单独布置的三道数学题。
前两道题他不费吹灰之力就做了出来了。
第三道题写在另一张小纸条上:要求只用圆规和没有刻度的直尺,作出一个正十七边形。
正十七边形尺规作图与详解

解读“数学王子”高斯正十七边形的作法一、高斯的传奇故事高斯(Carl Friedrich Gauss 1777.4.30~1855.2.23),德国数学家、物理学家、天文学家。
有一天,年幼的高斯在一旁看著作水泥工厂工头的父亲计算工人们的周薪。
父亲算了好一会儿,终于将结果算出来了。
可是万万没想到,他身边传来幼嫩的童音说:“爸爸,你算错了,总数应该是……”父亲感到很惊异,赶忙再算一遍,结果证实高斯的答案是对的。
这时的高斯只有3岁!高斯上小学了,教他们数学的老师布特勒(Buttner)是一个态度恶劣的人,他讲课时从不考虑学生的接受能力,有时还用鞭子惩罚学生。
有一天,布德勒让全班学生计算1+2+3+4+5+……+98+99+100=?的总和,并且威胁说:“谁算不出来,就不准回家吃饭!”布德勒说完,就坐在一旁独自看起小说来,因为他认为,做这样一道题目是需要些时间的。
小朋友们开始计算:“1 + 2 =3,3+3=6,6+4=10,……”数越来越大,计算越来越困难。
但是不久,高斯就拿着写着解答的小石板走到布德勒的身边。
高斯说:“老师,我做完了,你看对不对?“做完了?这么快就做完了?肯定是胡乱做的!”布德勒连头都没抬,挥挥手说:“错了,错了!回去再算!”高斯站着不走,把小石板往前伸了伸说:“我这个答案是对的。
”布德勒抬头一看,大吃一惊。
小石板上写着5050,一点也没有错!高斯的算法是1 +2 +3+……+98+99+100100+99+98+……+3+2+1101+101+101+……+101+101+101=101×100=1010010100÷2=5050高斯并不知道,他用的这种方法,其实就是古代数学家经过长期努力才找出来的求等差数列和的方法,那时他才八岁!1796年的一天,德国哥廷根大学。
高斯吃完晚饭,开始做导师给他单独布置的三道数学题。
前两道题他不费吹灰之力就做了出来了。
第三道题写在另一张小纸条上:要求只用圆规和没有刻度的直尺,作出一个正十七边形。
高斯和他的正十七边形

导师接过学生的作业一看,当即惊呆了。他用颤抖的声音对 青年说:“这是你自己做出来的吗?”青年有些疑惑地看着导师,
回答道:“是我做的。但是,我花了整整一个通宵。”导师请他
坐下,取出圆规和直尺,在书桌上铺开纸,让他当着自己的面再
做出一个正17边形。青年很快做出了一个正17边形。
导师激动地对他说:“你知不知道?你解开了一桩有两千多 年历史的数学悬案!阿基米德没有解决,牛顿也没有解决,你竟 然一个晚上就解出来了。你是一个真正的天才!”
原来,导师也一直想解开这道难题。那天,他是因为失误,才将写
有这道题目的纸条交给了学生。每当这位青年回忆起这一幕时,总是说:
“如果有人告诉我,这是一道有两千多年历史的数学难题,我可能永远
也没有信心将它解出来”。这位青年就是数学王子高斯。
这个问题是高斯用代数的方法解决的,他也视此为生平
得意之作,还交待要把正十七边形刻在他的墓碑上,但后来
尺规作图对于学过几何的人来说都不陌生,它是指用没有 刻度的直尺和圆规作图。你也许可以用尺规作图作出正三
角形、正方形、正六边形等,但是你有没有想过用尺规作
图作正十七边形,甚至正十七边能不能用尺规作图作出来。
其实这一问题早在1796年就由德国著名的数学家高斯在他
19岁时解决,这其中还有一段趣闻:,一个很有数学天赋的 19岁青 年吃完晚饭,开始做导师单独布置给他的每天例行的三道数学题。 前两道题在两个小时内就顺利完成了。第三道题写在另一张小纸条 上:要求只用圆规和一把没有刻度的直尺,画出一个正17边形。他 感到非常吃力。时间一分一秒的过去了,第三道题竟毫无进展。这 位青年绞尽脑汁,但他发现,自己学过的所有数学知识似乎对解开 这道题都没有任何帮助。困难反而激起了他的斗志:我一定要把它 做出来!他拿起圆规和直尺,他一边思索一边在纸上画着,尝试着 用一些超常规的思路去寻求答案。 当窗口露出曙光时,青年长舒了一口气,他终于完成了这道难 题。见到导师时,青年有些内疚和自责。他对导师说:“您给我布 置的第三道题,我竟然做了整整一个通宵,我辜负了您对我的栽 培……”
仅有尺规做正17边形

正十七边形编辑正十七边形是指有17条边的正边形,最早画出该形状的是德国大学者高斯。
[活动]“你好,地球”百科大神之巅峰对决!目录1简介2步骤一3步骤二4步骤三5简易作法6历史1简介最早的十七边形画法创造人是高斯。
高斯(1777─1855年)德国数学家、物理学家和天文学家。
高斯在童年时代就表现出非凡的数学天才。
年仅三岁,就学会了算术,八岁因运用等差数列求和公式而深得老师和同学的钦佩。
大学二年级时得出正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件。
解决了两千年来悬而未决的难题,1799年以代数基本定理的四个漂亮证明获博士学位。
高斯的数学成就遍及各个领域,在数学许多方面的贡献都有着划时代的意义。
并在天文学,大地测量学和磁学的研究中都有杰出的贡献。
下附正十七边形作法先计算或作出cos(360°/17)设正17边形中心角为a,则17a=360°,即16a=360°-a故sin16a=-sina,而sin16a=2sin8acos8a=4sin4acos4acos8a=16sinacosacos2acos4acos8a因sina不等于0,两边除之有:16cosacos2acos4acos8a=-1又由2cosacos2a=cosa+cos3a(三角函数积化和差公式)等注意到cos15a=cos2a,cos12a=cos5a(诱导公式)等,有2(cosa+cos2a+…+cos8a)=-1令x=cosa+cos2a+cos4a+cos8ay=cos3a+cos5a+cos6a+cos7a有:x+y=-1/2又xy=(cosa+cos2a+cos4a+cos8a)(cos3a+cos5a+cos6a+cos7a)=1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a)经计算知xy=-1因而:x=(-1+√17)/4,y=(-1-√17)/4其次再设:x1=cosa+cos4a,x2=cos2a+cos8ay1=cos3a+cos5a,y2=cos6a+cos7a故有x1+x2=(-1+√17)/4y1+y2=(-1-√17)/4最后,由cosa+cos4a=x1,cosacos4a=(y1)/2可求cosa之表达式,它是数的加减乘除平方根的组合, 故正17边形可用尺规作出2步骤一给一圆O,作两垂直的半径OA、OB,在OB上作C点使OC=1/4OB,在OA上作D点使∠OCD=1/4∠OCA 作AO延长线上E点使得∠DCE=45度。
数学家高斯正17边形的故事

数学家高斯正17边形的故事朋友,今天我跟你唠唠咱数学界的一个传奇人物——高斯和他的正17边形。
说起高斯啊,他那脑子聪明得像开了光似的。
话说有一天,这高斯才20岁,正值人生的大好年华。
你可能在琢磨,这大数学家难道青春期不折腾点别的么?嘿,他可不走寻常路,偏偏在数圈儿里找乐子。
听说那年春天,花儿正开得烂漫,高斯突然眉头一挑,心里头就有了个大想法:我得解开这17边形的秘密啊!这正17边形,可是个难啃的硬骨头呀。
之前的数学家们都抓耳挠腮,愁着哪里下手。
不过,高斯这小子不一般,他的聪明劲儿就像老张头果园里的水蜜桃一样,透着灵光闪闪。
一天傍晚,他一个人在屋里来回踱步,心思深沉,就像个大哲学家思考人生。
就在这会儿,他的灵光乍现,像水蜜桃熟透了,突然间“啪”地掉下来开花。
高斯用他的绝顶聪明,找到了一种能构造正17边形的方法!朋友,你知道吗?这可是从古希腊起,经过了一千多年的数学难题啊。
我当时要是在现场,简直要为他拍手叫绝。
高斯这小子厉害吧,解开个17边形,不光是数学上的伟大突破,还让其他数学家都倒吸一口凉气。
他那时候心情就跟村儿里过大年的时候似的,特别的喜气洋洋。
当然了,这故事不仅仅是个关于几何的胜利,更是高斯这人,不管多难的题,敢于挑战的勇气和信心。
他用这种精神灌注到整个数学界,引得后来的学者们纷纷效仿。
想想看,就像高斯打破了人们对几何的禁锢,人生也得学会打破束缚,就如同品尝一个不同寻常的水蜜桃,你永远不知道会爆出什么样的惊喜。
至于正17边形怎么画呢,嘿,咱就交给那些数学高手们去琢磨吧,咱就享受这傻乐呵的快乐就好啦。
朋友,你要是对数学或者高斯这小子的其他故事有兴趣,也欢迎来跟我一起聊聊。
咱也许不能像高斯那样聪明绝顶,但一定能从这些传奇故事里汲取到些许智慧,过好咱自己的小日子。
提高计算准确率——高中数学正多边形计算教案

提高计算准确率——高中数学正多边形计算教案。
一、教学目标1、掌握正多边形的性质,理解正n边形划分成n个小三角形的规律;2、学习正多边形的计算方法,掌握正多边形的面积、周长、内角和外角的计算方法;3、培养学生的逻辑思维能力和计算准确性,激发学生的兴趣和自信心。
二、教学重点1、正n边形的划分规律;2、正多边形的面积、周长、内角和外角的计算方法。
三、教学方法1、运用多媒体教学法,通过图片、视频等形式直观展示正多边形的性质和计算方法;2、运用小组合作学习法,让学生相互讨论、交流和合作,加强学生的合作意识和思考能力;3、运用巩固练习法,让学生通过大量的联系和练习巩固所学知识,提高计算准确率。
四、教学步骤第一步:引入通过讲解正多边形的性质和重要计算方法,激发学生的学习兴趣和自信心。
第二步:正n边形的划分规律1、将正n边形划分成n个小三角形的规律:以正六边形为例,将正六边形分割为6个小三角形,每个小三角形的面积都相等,且都等于正六边形的面积除以6。
2、以此类推,正n边形被划分成n个相等的小三角形。
第三步:正多边形的面积计算方法1、公式法:以正五边形为例,设正五边形的边长为a,则正五边形的面积S=5/4a^2 cot(π/5)。
2、证明法:以正六边形为例,将正六边形划分为6个小三角形,每个小三角形的面积为1/2×边长×高。
由于正六边形的高等于边长,因此正六边形的面积为3√3/2×a^2。
3、以上两种方法计算正n边形的面积都有其特定的公式和证明方法。
第四步:正多边形的周长计算方法以正五边形为例,设正五边形的边长为a,则正五边形的周长L= 5a。
其它正n边形的周长计算方法可类似推导。
第五步:正多边形的内角计算方法以正五边形为例,设正五边形的内角为x,则由正五边形的熟知公式可推导出:5x-360=0,解得x=108度。
其它正n边形的内角计算方法可类似推导。
第六步:正多边形的外角计算方法以正五边形为例,设正五边形的外角为y,则由正五边形的熟知公式可推导出:y=360/5=72度。
高斯正十七边形故事

高斯正十七边形故事篇一嗨,亲爱的朋友,今天我要给你讲讲高斯正十七边形的故事。
我还记得那是一个阳光灿烂的日子,我正百无聊赖地在教室里发呆。
突然,我们那严肃又有点可爱的数学老师走进了教室,他神秘兮兮地在黑板上写下了“高斯正十七边形”这几个大字。
“同学们,今天咱们来聊聊这个神奇的高斯正十七边形。
”老师的眼睛里闪烁着光芒。
我当时心里就嘀咕:“这能有多神奇呀?”同桌小李凑过来悄悄说:“我看呀,准又是一堆复杂的公式和计算。
”可老师接下来的话,让我们都瞪大了眼睛。
他说:“当年啊,高斯还是个十几岁的少年,就解决了这个困扰了数学家们两千多年的难题。
”“哇!”大家都忍不住惊叹起来。
老师接着讲:“高斯这孩子,从小就聪明得很。
那天他也是像咱们现在这样坐在教室里,老师布置了一个任务,让大家把正十七边形用尺规作图作出来。
其他同学都觉得这简直是不可能完成的任务,一个个愁眉苦脸的。
可高斯呢,他就闷头在那琢磨。
”我忍不住问老师:“那他到底是怎么琢磨出来的呀?”老师笑了笑说:“他呀,就靠他那聪明的脑袋和不服输的劲儿。
别人都放弃了,他还在那不停地尝试,不停地思考。
”“然后呢?然后呢?”同学们都着急地问。
老师清了清嗓子:“然后啊,经过一夜的努力,高斯终于画出了正十七边形!这一下子,可把大家都惊呆了。
”这时候,平时最调皮的小王站起来说:“老师,那高斯是不是从此就成了大数学家啦?”老师点了点头:“没错,高斯因为这个发现,从此走上了数学的巅峰之路。
”下课铃响了,可我们还沉浸在高斯的故事里。
我心里想:“高斯可真厉害,我也要像他一样,不怕困难,努力去解决问题。
”这就是我给你讲的高斯正十七边形的故事,是不是挺有意思的?篇二嘿,朋友,让我再给你讲讲高斯正十七边形的故事。
有一天,我跟几个朋友在公园里闲逛,聊着各种稀奇古怪的事儿。
不知怎么的,就说到了数学上的难题,然后就提到了高斯正十七边形。
我朋友小张一脸迷茫地问:“啥是高斯正十七边形啊?我咋从来没听说过。
正十七边形

正十七边形尺规作法(无刻度)步骤一:给一圆O,作两垂直的半径OA、OB,作C点使OC=1/4OB,作D点使∠OCD=1/4∠OCA,作AO延长线上E点使得∠DCE=45度。
步骤二:作AE中点M,并以M为圆心作一圆过A点,此圆交OB于F点,再以D为圆心,作一圆过F点,此圆交直线OA于G4和G6两点。
步骤三:过G4作OA垂直线交圆O于P4,过G6作OA垂直线交圆O于P6,则以圆O为基准圆,A为正十七边形之第一顶点P4为第四顶点,P6为第六顶点。
连接P4P6,以1/2弧P4P6为半径,在圆上不断截取,即可在此圆上截出正十七边形的所有顶点。
历史最早的十七边形画法创造人为高斯。
高斯(1777~1855年),德国数学家、物理学家和天文学家。
在童年时代就表现出非凡的数学天才。
三岁学会算术,八岁因发现等差数列求和公式而深得老师和同学的钦佩。
1799年以代数基本定理的四个漂亮证明获得博士学位。
高斯的数学成就遍及各个领域,其中许多都有着划时代的意义。
同时,高斯在天文学、大地测量学和磁学的研究中也都有杰出的贡献。
1801年,高斯证明:如果k是质数的费马数,那么就可以用直尺和圆规将圆周k 等分。
高斯本人就是根据这个定理作出了正十七边形,解决了两千年来悬而未决的难题。
道理当时,如果高斯的老师告诉了高斯这是道2000多年没人解答出来的题目,高斯就不会画出这个正十七边形。
这说明了你不怕困难,困难就会被攻克,当你惧怕困难,你就不会胜利。
正十七边形的证明方法正十七边形的尺规作图存在之证明:设正17边形中心角为a,则17a=360度,即16a=360度-a故sin16a=-sina,而sin16a=2sin8acos8a=4sin4acos4acos8a=16sinaco sacos2acos4acos8a因sina不等于0,两边除之有:16cosacos2acos4acos8a=-1又由2cosacos2a=cosa+cos3a等,有2(cosa+cos2a+…+cos8a)=-1注意到cos15a=cos2a,cos12a=cos5a,令x=cosa+cos2a+cos4a+cos8№ay=cos3a+cos5a+cos6a+cos7a有:x+y=-1/2又xy=(cosa+cos2a+cos4a+cos8a)(cos3a+cos5a+co s6a+cos7a)=1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a)经计算知xy=-1又有x=(-1+根号17)/4,y=(-1-根号17)/4其次再设:x1=cosa+cos4a,x2=cos2a+cos8ay1=cos3a+cos5a,y2=cos6a+cos7a故有x1+x2=(-1+根号17)/4y1+y2=(-1-根号17)/4最后,由cosa+cos4a=x1,cosacos4a=(y1)/2可求cosa之表达式,它是数的加减乘除平方根的组合, 故正17边形可用尺规作出数学未解之谜一数学基础问题。
