巧算题天平及其他

合集下载

三年级奥数第四讲—砝码问题与混合运算竞赛

一、砝码问题
例1、有1克、2克、4克、8克、16克砝码若干个，要在天平上一次秤出23克
物品、请写出五种使用砝码的不同方法。

例2、有一架天平和一个50克的砝码，如果要得到150克的糖果，只许秤两次，应该如何秤？
例3、有八个西瓜，期中一个是有毒瓜，有毒瓜比没毒瓜重0.1千克。

有一架
天平，你只能秤两次，你能秤出哪个瓜有毒？
二、加减法的混合巧算竞赛-老师在黑板上出题
竞赛规则：小伙伴们自愿分成常规队和巧算队，分别选出一名队长。

题目有10题，分数分别为1分、2分、3分、4分、5分，每名小伙伴最多只能答3题，参赛的小伙伴由队里推荐，最后得分最多的为赢家！
先来一波题热身下：
（1）497＋28 （2）750＋1002 （3）574－397 （4）472―203
（5）208＋494―498―95 （6）9999＋999＋99＋9
（7）321＋127＋79＋73 （8）483＋254－183
（9）487＋（213－92）（10）812＋（188－123）
（11）1000―90―10―80―20―70―30―60―40―50―50
回家作业
小英雄们，课后要不来挑战下哇哇哇！！！
1. 砝码问题
有6个形状相同的零件，其中有一个次品的重量轻一些，你能不能用一架天平秤两次就把次品找出来呢？
2.六宫格。

巧用天平称物体的重量

４．３０（专一素）青２７０（个）５・乙队：１８２人；甲队：３３６ —１８２ｌ５４（人）
０Ｑ
链２０颗一串。一位顾客问： “ 一颗黑珠子重，还是一颗白珠子重？” 柜台里面有一架没有砝码的天平，你能想办法称出是哪一种珠子重吗？
‘ 呻＋十＋ ÷＋＋十士枷 ÷ ・；ｆ． ÷÷＋卜－十÷－ｉ曲－｝÷・卜－Ｆｑ斗 ÷寻十・ｌ・・｝扣｝‘ ， ‘ ・ｔ ÷一｛，＋－一十牛・卜 ÷・：斗 ‘ 一・；ｔ ÷ ｑ・ ÷÷
村｛遇点可看作植树点。因此，首先要设法弄清 “ 株距 ” ，也就是货车司机连
续遇到两辆公共汽车的时间间隔。把公共汽车每分钟行的路程看作１份，
两车之间的和是两份，行
同的重量。
《 “ 对应 ” 十法》 “ 练一练 ” 参考答案：
Ｉ．男工人数９６．Ａ，女工人数：８０Ａ２．３６＋（１一争：６ｏ（公顷）３．（２１＋４＋９４卜（１一吉一吉）＝ｌ６８（米）
的珠子数。把２串黑珠子链、３串白珠子链分别放在天平的两端，就能比较出哪种珠子重了。
【例２】小亮有糖果３００克，一架天平只有３０克、５克两个砝码，用这架
天平最少称几次可以将糖果分成两份，使一份重ｌ００克，一份重２００克？【分析与解我们可以把称出的物体作砝码用。第一次用３０克和５克的砝码称Ｌ｛Ｊ３５克的糖果。第二次用３０克的砝码和３５克的糖果称出６５克的糖果。６５＋３５＝１００（克），３００－ｌ００＝２００（克）。所以最少要称２次。

一年级奥数培训教材：第六章算一算(二)第二讲天平平衡

一年级奥数培训教材：第六章算一算（二）第二讲天平平衡目录第一章：数一数第一讲看图数一数第二讲有几种走法第二章：比一比、看一看第一讲变与不变第二讲移多补少单元练习（一）第三章：算一算（一）第一讲单数和双数第二讲算式猜谜第三讲巧算速算（一）第四讲＋、－和（）单元练习（二）第四章：简单应用（一）第一讲没有那么简单第二讲简单的判断第三讲小兔吃萝卜第四讲猫和老鼠单元练习（三）第五章：找规律第一讲按规律填下去第六章：算一算（二）第一讲合理分组第二讲天平平衡第三讲巧算速算（二）单元练习（四）第七章：简单应用（二）第一讲摸彩球第二讲付钱的方法第三讲鸡兔同笼单元练习（五）第八章：趣味数学第一讲火柴棒游戏（一）第二讲火柴棒游戏（二）第三讲趣味问题单元练习（六）综合练习（一）综合练习（二）第六章算一算（二）第二讲天平平衡【知识导航】小朋友，通过前面的学习，我们已经掌握了比较简单的推理题，例如：这就是最简单的推理题。

学会推理，我们的思路会越来越开阔，头脑会越来越灵活根据已经知道的一些图形条件和一些等式，通过分析、判断、推理，最后得出结论，这个过程就是“逻辑推理”【典型例题】【例1】下面三个天平都不平衡，你能动脑筋，想办法使它们平衡吗？【例2】观察下面两幅图，比较一个梨和一个草莓哪个重？【例3】看图分析，每个乒乓球重多少克？【例4】1只西瓜+1只菠萝=8千克1只西瓜+1串香蕉=9千克1只菠萝+1串香蕉=5千克1只西瓜=（）千克1只菠萝=（）千克1串香蕉=（）千克过关训练1、如下图，左边有5个书包，右边有3个书包，要使左右书包个数相等，你能想出什么办法（一共只有8个书包）？2、观察下面两幅图，比较一个梨和一个草莓哪个重？（）重。

3、红球+黑球=20个红球+白球=16个黑球+白球=12个红球=（）个黑球=（）个白球=（）个4、看算式填空。

★=◎+◎+◎◎=△+△★=（）个△5、你能使下面两个天平都平衡吗？6、观察下面两幅图，比较一个梨和一个草莓哪个重？7、观察下面两幅图，比较一个梨和一个草莓哪个重？8、1只鸡+1只鸭=7千克1只鸡+1只鹅=8千克1只鸭+1只鹅=9千克1只鸡=（）千克1只鸭=（）千克1只鹅=（）千克拓展题。

三年级趣味数学题

三年级趣味数学题1.请问几分钟时，盒内为半满状态有一个魔术盒子，里面装有鸡蛋，魔法一施展，每分钟鸡蛋的数目就增加一倍，10分钟后，盒内盛满了鸡蛋，请问几分钟时，盒内为半满状态2.请问最少要拿出几只袜子抽屉中有十只黑袜子和十只白袜子，假若你在黑暗中开抽屉，伸手拿袜子;请问最少要拿出几只袜子，才能确定拿到了一双3.它何时才能爬出枯井一只猴子陷落在一口三十尺深的枯井中，如果它每天能够向上爬三尺，再向下滑一尺，以这种速度，它何时才能爬出枯井4.最高要化费多少分钟假设三只猫能在三分钟内杀死三鼠，请问一百只猫杀死一百只老鼠，最高要化费多少分钟5.他们谁最大谁最小扎扎比菲菲大，但比胡安小.菲菲比乔乔和马修大。

马修比卡罗斯和乔乔小。

胡安比菲菲和马修大，但比卡罗斯小。

他们谁最大谁最小6.请用+、-、×、÷、( )等运算符号1.请用+、-、×、÷、( )等运算符号把五个3连接起来，组成算式，使它们的得数分别是0、1、2、3、4、5、6、7、8、9、10。

2.请你在四个5之间添上运算符号，使运算结果分别等于0、1、2、3、4、5、6、7。

3.下面的算式只写了数字，忘记写运算符号，请你选用+、-、×、÷、( )、[ ]这几种符号填进算式之中，使等式成立。

1 2 3=11 2 3 4=11 2 3 4 5=11 2 3 4 5 6=11 2 3 4 5 6 7=11 2 3 4 5 6 7 8=11 2 3 4 5 6 7 8 9=17.这只狗共奔跑了多少千米路甲和乙从东西两地同时出发，相对而行，两地相距10千米。

甲每小时走3千米，乙每小时走2千米，几小时两人相遇如果甲带了一只狗，和甲同时出发，狗以每小时5千米的速度向乙奔去，遇到乙后即回头向甲奔去;遇到甲又回头向乙奔去，直到甲乙两人相遇时狗才停住。

问这只狗共奔跑了多少千米路8.下面算式里“华杯”代表的两位数是多少华罗庚是1910年出生的，下面算式里“华杯”代表的两位数是多少1910+ 华杯9.赛马场有这幺一个赛马场，跑道上A马一分钟可跑2圈，B马能跑3圈，C马则跑4圈。

拓展思维能力：有趣的思考题

拓展思维能力：有趣的思考题思维能力是我们在解决问题和面对挑战时的重要工具。

拥有强大的思维能力能够帮助我们更好地分析和理解复杂的情况，并提供创新和独特的解决方案。

为了拓展思维能力，我们可以通过尝试解决一些有趣的思考题来锻炼我们的大脑。

这些思考题可以激发我们的想象力和创造力，让我们思考问题的多个角度。

在本文中，我们将介绍一些有趣的思考题，帮助你锻炼思维能力并开拓思维的边界。

思考题一：鸡蛋和楼梯想象一下，你手里有两个鸡蛋，你现在站在一个十层的楼梯前。

你希望找到一个最高的楼层，使得当你把鸡蛋从这个楼层上扔下去时，它们刚好不会破裂。

在此过程中，你只能使用两个鸡蛋。

你能找到这个楼层吗？要如何确定这个楼层？这个问题看似简单，但是实际上需要一些巧妙的思考。

首先，我们可以尝试从第一层开始逐层往上扔鸡蛋。

但是如果第一个鸡蛋在某一层破碎了，我们就不能确定最高楼层是哪一层，因为第二个鸡蛋已经用完了。

所以需要找到一种更高效的方法。

一个可行的策略是使用二分法。

首先在第5层扔一个鸡蛋，如果鸡蛋没有破裂，我们再去第8层扔一个鸡蛋。

如果第一个鸡蛋在第5层破裂了，我们就可以确定最高楼层不会超过第4层，然后我们再在第1到第4层中逐层扔鸡蛋，一旦鸡蛋破裂，我们就可以确定最高楼层。

同样的，如果第二个鸡蛋也没在第8层破裂，我们就可以确定最高楼层在第6或第7层，然后逐层扔鸡蛋即可。

这道题目考察了我们对于搜索和判断的能力，需要我们巧妙地使用限制条件来缩小搜索范围，从而找到最优解。

思考题二：三门问题假设你在一个游戏节目中，面前有三扇关闭了的门，其中一扇门后面有一辆汽车，另外两扇门后面是山羊。

主持人让你选择一扇门作为你的答案，并且告诉你，在你做出选择之前，他会打开一扇门，门后面是山羊。

现在，主持人问你，你是否希望改变你的选择，选择另一扇门。

你应该怎么做？这个问题看似微不足道，但是答案却有些令人吃惊。

虽然这个问题一开始可能认为改变选择并没有什么影响，因为主持人打开的门后面一定是山羊。

数学与天平的妙用

数学与天平的妙用A组:1.9个硬币有一个是假的,用天平最少称几次可找出假的?(假币比真币轻)2.27个硬币中有一个是假的,用天平最少称几次可找出假的?(假币比真币轻)3.有一次一个工人生产了81个零件。

后来,他发现有一个内部有空洞的原材料也做成了成品,可从外表看不出来。

他想,这个内部有空洞的零件稍为轻一点,一定可以用天平称出来。

于是他想了一个办法,利用一架没有砝码的天平,一共只称4次就把废品找出来了。

你知道他是怎样称法的吗?4.一杆秤,最多能称4斤重的东西。

有一根铁棍近7斤重,怎样称?5.有根木头超过304克,怎样称出它的准确重量呢?现在,这里有许多秤,但是,每个台秤只能称出10千克的重量。

小浩说:把木头锯断。

小美不同意,她想出了一个更简单的办法。

她是怎样称的?6.有一个带托盘的大天平,两边托盘放上重量相等的东西时,天平正好平衡,但天平本身没有重量刻度。

现有140公斤的食盐和7公斤及2公斤的砝码各1个,使用3次天平,如何把食盐分成90公斤和50公斤呢?7.3袋麦子,不许一袋一袋称,三次要称出各袋的重量,怎么称法?8.一台天平秤,只有一只20克的砝码。

现有70克的药粉,如何用这台天平称两次从中称出5克药粉?B组:9.一位科学家忘记了拿全部的砝码,他手头只有2块橡皮泥,一块重3克,另一块重10克,他利用天平把2块橡皮泥做成了3个砝码,用这3个砝码可以称出从1克到13克的任何整克数的物体。

这3个砝码各重多少?他是怎样称的?10.有一个铅块重121克,要把它熔成若干个小砝码,以便放在天平上来称121克以内各种整克数重量的物品,至少要熔成几个?每个重量多少克?11.需要多少砝码?有一系列重量分别在1到40克(重量为整数)的物体,现用天平称它们的重量。

如果限制砝码只能放在天平的一端,至少需要几个重量不同的砝码?如果天平两端均可以放砝码,则至少需要几个重量不同的砝码?12.用天平称1~160克之间的任何分量,至少要具备哪8种砝码?13.81个物体,重量分别是1~81克中的整数,如果用天平称量它们中的任意一个物体的重量,试问最少需要几个砝码?每个砝码各多少克?C组:14.某仓库进了10箱菠萝罐头,其中有一箱每筒都少装了一片,每片重50克。

五年级上册数学学案带单元检测题12-2期巧解简易方程,全国通用版同步学案练习题

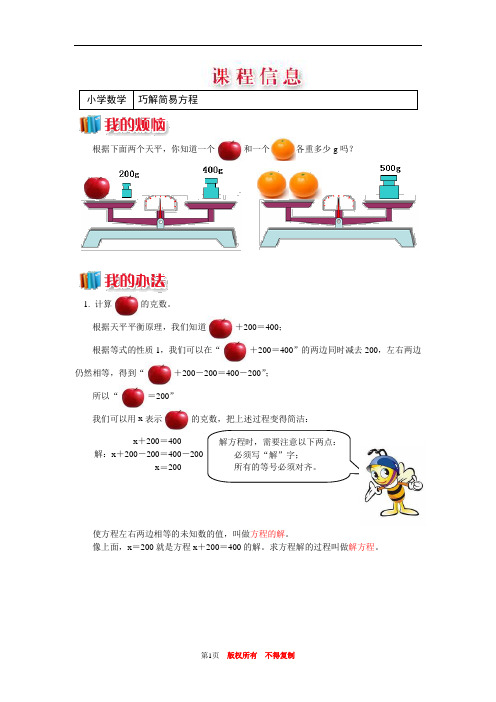
小学数学巧解简易方程根据下面两个天平，你知道一个和一个各重多少g 吗？1. 计算的克数。

根据天平平衡原理，我们知道＋200＝400；根据等式的性质1，我们可以在“＋200＝400”的两边同时减去200，左右两边仍然相等，得到“＋200－200＝400－200”；所以“＝200”我们可以用x 表示的克数，把上述过程变得简洁：x＋200＝400 解：x ＋200－200＝400－200 x ＝200解方程时，需要注意以下两点：必须写“解”字；所有的等号必须对齐。

使方程左右两边相等的未知数的值，叫做方程的解。

像上面，x ＝200就是方程x ＋200＝400的解。

求方程解的过程叫做解方程。

x＝200是不是正确的答案呢？我们可以检验一下：检验：方程左边＝x＋200＝200＋200＝400＝方程右边所以，x＝200是方程的解。

注意：检验时，如果方程左边不等于方程的右边，就说明这个值不是方程的解。

2. 计算的克数。

按照上面的方法，我们同样用x表示的克数，所以：所以的克数是250g。

1. 形如bax=±的方程的解法：bax=+bax=-解：abaax-=-+… 等式的性质1… 解：abaax+=+-abx-=abx+=2. 形如)0(≠=abax的方程的解法：bax=解：abaax÷=÷… 等式的性质2abx÷=补充：形如()0≠=÷abax的方程的解法与bax=的解法基本相同：bax=÷解：abaax⨯=⨯÷… 等式的性质2abx=3. 扩展：形如bxa=-和bxa=÷的方程的解法：bxa=-bxa=÷解：xbxxa+=+-… 等式的性质1 解：xbxxa⨯=⨯÷…等式性质2xba+=xba⨯=axb=+… 等式左右交换位置axb=⨯…等式左右交换位置babxb-=-+… 等式的性质1 babxb÷=÷⨯…等式的性质2bax-=bax÷=解方程时需要注意的问题：①首先要写“解”字；②根据等式的性质解方程；③所有的等号要对齐；④求出方程的解后，要检验，检验的格式与解方程的格式相同，等号对齐。

天平平衡问题

天平平衡问题巧解“天平平衡”问题一、天平平衡问题的解题思路解有关天平问题的基本思路是：加入左右两盘容器里的物质的质量与离开容器（主要以气体形式离开）的物质的质量之差就是烧杯内反应前后变化（增加或减少）的质量。

若变化的质量相等，则天平平衡；不等时，天平指针向质量大的一边偏转。

二、综合归纳：解答有关天平平衡的问题注意以下规律：（1）当题中给出两个反应物的质量，计算时选不足量。

（2）当天平两边加入的反应物质量相同时，天平是否平衡，取决于跑出的气体质量。

即跑出的气体相等，天平平衡，跑出的气体质量不相等，天平不平衡。

（3）当天平两边加入的反应物质量不相同，天平是否平衡，取决于变化的质量（即增加的质量）是否相同。

变化的质量相同，天平平衡；变化的质量不相同，天平不平衡。

1、天平两托盘上的烧杯中，分别放有足量的等质量、等溶质质量分数的稀硫酸，调整天平至平衡后，向天平左端烧杯中加入4.4克氧化铁，欲保持天平平衡，应向右端的烧杯中加入（）A. 4.5克Ag B.5.4克Al C.4.3克Zn D. 4.8克Mg2．在天平两边各放置一个盛有相同浓度的等体积的足量盐酸的烧杯，把天平调至平衡，在左边烧杯中放入3.60克铝粉，为了使天平最终保持平衡，右边烧杯中应放入镁粉的质量为（）A、3.49克B、3.60克C、3.70克D、3.81克3.在托盘天平的两盘上各放一只质量相同的烧杯，分别注入100g7.3%的稀盐酸，天平平衡，向左盘烧杯中投入一定质量的碳酸钙粉末，向右盘烧杯中投入一定量的镁粉，均恰好完全反应，天平指针发生偏转。

则下列各项正确的是_____A 在左盘上放4g砝码B 在左盘上放6g砝码C移动游码至3.4g刻度 D 移动游码至7.6g刻度4．在托盘天平两盘上各放一只烧杯，两烧杯中盛有等质量百分比浓度的足量的盐酸，使两边保持平衡。

此时向左边烧杯中加入11.2克CaO，若要使两边再次保持平衡，需向右边烧杯中加入CaCO3的质量是（）A.11.2克B.17.6克C.20克D.22.4克5. 在托盘天平的两边各放一只盛有足量相同质量、相同质量分数稀盐酸的烧杯，调至平衡，然后向左边烧杯中加入5.6g铁，欲使天平再次保持平衡；应向右边烧杯中加入（）A. 6g 镁B. 5.6g铜C. 5.4g氧化钙D. 10g碳酸钙6.在天平两端的烧杯中，分别盛有足量等质量、等浓度的稀硫酸，天平平衡后，往天平两端的烧杯中，分别加入等质量的镁和铜、铝合金，恰好完全反应，且天平仍保持平衡，则铜、铝合金中铜和铝的质量比为（）A. 1:1B. 1:2C. 1:3D. 2 :37.在天平的两盘分别放入质量相等的烧杯,烧杯中各盛100克9.8%的硫酸溶液,向两个烧杯中同时放入哪组金属,反应终止时天平仍保持平衡（）(A)锌、铁各7克（B）锌、铁各5克（C）锌、铁各4克（D）锌、铁各3克8.托盘天平两端分别放一个质量相等的烧杯，烧杯中各盛有100g质量分数为9.8％的稀硫酸，向两个烧杯中分别加入下列各组物质中的一种，反应终止后天平仍然保持平衡的是（）A. Fe、Zn各3gB. Cu、Fe各4gC. Fe、Zn各7gD. Zn、ZnO各5g 9.在已调好零点的天平两边托盘上各放一质量相同的烧杯，分别盛放等质量、等质量分数的稀盐酸。

小学数学趣题巧算全集

小学数学趣题巧算（一）1．钟声小明家离火车站很近，他每天都可以根据车站大楼的钟声起床。

车站大楼的钟，每敲响一下延时3秒，间隔1秒后再敲第二下。

假如从第一下钟声响起，小明就醒了，那么到小明确切判断出已是清晨6点，前后共经过了几秒钟？2．越减越多同学们对这样的问题可能并不陌生：“一个长方形被切去1个角，还剩几个角？”这种题的最大特点是答案不唯一，要根据去掉的这个角的不同情况来确定“剩角”的多少。

图1以上3幅示意图，表明了3种不同情况的3种不同答案。

其中第3种情况最有趣，长方形原有4个角，切去了1个角，反而多了1个角，出现了越减越多的情况。

下面一道题的思考方法与上题类似，看你能否正确回答。

“一个正方体，锯掉一个角，还剩几个角？”请注意，这里的“角”是立体的“角”，它不同于平面上的角。

3．数一数如果有人问你“会数数儿吗？”，你会不屑一顾地说：“这么大了，还不会数数儿！”其实，数数儿的学问还是很大的。

不信，请你数出下面几何图形的个数。

图24．画一画下面这些图形你能一笔画出来吗？（不重复画）图35．最短的路线养貂专业户养殖场内安置了9个貂笼（如下图）。

为了节省每次喂食的时间，他必须走一条最短的路，但又不能漏掉一个貂笼，喂完食后还要回到原出发点。

你能替他设计一条最短的路线吗？并算出每喂食一次，至少要走多少米的路。

6．切西瓜六（1）班召开夏夜乘凉晚会，买来了许多西瓜。

班主任李老师说：“今天买来了许多西瓜请大家吃。

在吃以前我先要以切西瓜为名请大家做一道数学题。

我规定，西瓜只能竖切，不能横剖。

大家知道，切一刀最多分成2块，切2刀最分成多4块，那么切3刀最多能分成几块？切4刀、切5刀、切6刀呢？这中间有没有规律？如果有规律，请同学们找出来。

”李老师刚说完，同学们就七嘴八舌地讨论起来。

请你也参加他们的讨论吧。

7．均分承包田有一块等腰梯形菜地（如下图），地边有一口水井。

现在3户种菜专业户都提出要承包这块地。

经研究，决定让这3户共同承包这块地，因此必须把这块地分成面积相等、形状相同且与这口水井的距离也要相等的3块地。

第14讲智巧问题-四年级奥数下册同步精讲精练(西师大版)

第十四讲智巧问题ʌ知识概述ɔ在日常生活中,我们经常会遇到一些非常有趣的数学题目㊂解答这类问题,常常不需要复杂的计算,而是要认真读题,理解题目中的条件,开动脑筋想一想,用巧妙的方法来解答,有的不列算式就可以知道答案了,我们把这类问题称为智巧问题㊂例题精学例1池塘里的睡莲的面积每天长大一倍,经过20天就可以长满整个池塘㊂问需要经过多少天,这些睡莲能长满半个池塘?ʌ思路点拨ɔ睡莲长满半个池塘的时间只比长满整个池塘的时间少1天,因为池塘里的睡莲的面积每天长大一倍,所以需要经过19天,这些睡莲就能长满半个池塘㊂同步精练1.一种荷叶每天长大1倍,第12天把池塘盖满,求盖满池塘的一半时是第几天?2.密封的瓶中,如果放进一个细菌,2分钟后瓶中就充满了细菌㊂已知每个细菌每秒钟分裂成2个,两秒钟就分裂成4个,三秒钟就分裂成8个 ,如果开始时放进两个细菌,要使瓶中充满细菌,需要多长时间?3.一杯咖啡,王老师先喝了半杯,然后加满水,又喝了半杯,再加满水,最后全部喝完,王老师咖啡喝得多,还是水喝得多?224225例2 一只蜗牛从深12米的井底沿井壁向上爬,白天向上爬3米,晚上向下滑2米㊂求这只蜗牛几天能爬到井口?ʌ思路点拨ɔ 每天实际向上爬了多少米?这只蜗牛是不是12天爬到井口?如果你认为要12天才爬到井口就错了,原因是当蜗牛最后一天爬3米,就到了井口,而前面的12-3=9(米)才是每天爬1米所爬的米数,这样可先求出爬了几天后,最后一天爬3米就到了井口㊂同步精练1.一只蜗牛从墙脚沿墙壁向10米高的墙头爬去,白天向上爬4米,到夜里往下滑3米,求这只蜗牛什么时候爬到墙头?2.用蘸水钢笔每画一个正方形需蘸一次墨水,要画好图中的图形需要蘸几次墨水?3.一只蜗牛从深14米的井底沿井壁向上爬,白天向上爬3米,晚上向下滑2米,求这只蜗牛几天能爬到井口?例3有一次,一个工人生产了81个零件㊂后来,他发现有一个内部有空洞的零件稍微轻一些,一定可以用天平称出来㊂于是他想了一个办法,利用一架没有砝码的天平,一共只称4次就把废品找出来㊂你知道他是怎样称的吗?ʌ思路点拨ɔ由于这架天平没有砝码,不可能一个一个去称出零件的重量,所以应相应地分为3堆,每堆27个,把其中两堆放在天平两端,若天平平衡了,另一堆里有一个零件是空的;若有一堆在天平的一端翘起来,则这堆里有一个零件是空的㊂把有空的这堆再平均分成3份,每份27ː3=9(个)㊂像第一次那样称出一堆有空的,再把一堆9个平均分成3堆,每堆9ː3=3(个),利用第一次的称法,称出一堆中的3个有空洞的零件,再把3个零件分成3份,必得到其中一个有空洞的零件㊂同步精练1.某工厂生产27只形状相同的零件,正品重量相同,可其中混杂了一只次品,次品的重量比正品轻,你能不用砝码,用一架天平称3次把次品找出来吗?2.有一个带托盘的天平,在两边托盘上有质量相等的物品时,天平正好平衡,但天平本身没有质量刻度㊂现有质量140千克的食盐和7千克及2千克的砝码各一个,使用3次天平,如何把食盐分成90千克和50千克?3.一台天平秤,只有一只20克重的砝码㊂现有70克的药粉,如何用这台天平称2次从中称出5克药粉?226例4小明的棋子在125~165之间,如果8个装一盒,那么有一盒多5个;如果12个装一盒,那么有三盒各少一个㊂问小明有多少个棋子?ʌ思路点拨ɔ由于两种情形中到底各有多少盒不明确,这时的一多一少给同学们解题增加了难度,为了避免多与少的复杂性,我们采用借来还去的策略,先借来3个棋子参加分配,使条件变为8个一盒不多也不少,12个一盒不多也不少,这时棋子数既是8的倍数又是12的倍数,这些数是24㊁48㊁72㊁96㊁120㊁144㊁168…,其中满足条件的是144,还去借来的3个棋子,可知小明有棋子141个㊂同步精练1.一天,有个地主给三个长工出了道难题: 你们到山上,每人抬两根圆木回来,但一共只能是三根㊂如果办不到,今天甭想吃饭! 三个长工一合计,轻松地办到了㊂你猜猜看,他们是怎样做的?2.两人坐在圆桌旁,相继轮流往桌上放同样大小的棋子,条件是棋子一定要平放在桌面上,不能使后放的棋子压在已放的棋子上,这样继续下去,最后桌面上只剩下一个位置时,谁放下最后一枚,谁就算胜了㊂如果两人都是高手,怎样放才能保证胜利?227练习卷一㊁填空题㊂1.密封的瓶中,如果放进一个细菌,1分钟后瓶中就充满了细菌㊂已知每个细菌每秒分裂成2个,两秒就分裂成4个, ,如果开始时放进两个细菌,要使瓶中充满细菌需要()秒㊂2.把一个大正方形平均分成9个小正方形,第一个正方形里放1粒米,第二个放2粒米,第三个放4粒米,然后每一个正方形里都放比前一个正方形多一倍的米;9个正方形放完,一共要放()粒米㊂3.房间里有一些猫:两只在后,一只在前;一只在后,两只在前;一只在中间,房间里共有()只猫㊂二㊁解决问题㊂1.如果5只猫在5分钟内可以抓到5只老鼠,那么,100分钟抓100只老鼠需要几只猫?2.王欣和李媛都想买‘葫芦岛历险记“,两人一道来到新华书店才发现,王欣缺1分钱,李媛缺2元4角钱,用她们两人的钱合买一本,钱还是不够,这本书多少钱?想一想:你能看出李媛带了多少钱吗?为什么?2283.有一个猎人带了一条狼狗,一只兔子和一筐青菜,要乘船到河对面去㊂河里只有一条小船㊂因为船小,猎人一次只能带一样东西㊂但是他不在时,狼狗会咬兔子,兔子又会吃青菜㊂请同学们帮他想一想,应该怎样安排过河?4.请将16个棋子分放在边长30厘米㊁20厘米㊁10厘米的3个正方形盒子里,使大盒子里的棋子数是中盒子里棋子数的2倍,中盒子里的棋子数是小盒子里棋子数的2倍㊂问应当如何放置?5.今有101枚硬币,其中有100枚同样的真币和1枚伪币,伪币与真币的重量不同㊂现需弄清楚伪币究竟比真币轻,还是比真币重,但只有一架没有砝码的天平㊂那么怎样利用这架天平称两次,来达到目的?229230三㊁操作题㊂1.有5整杯和5个半杯的牛奶,还有5个空杯子,既不能称也不能倒,你能把牛奶和杯子平均分成三等份吗?2.体育兴趣小组有24人,排成六行,每行5人,以便开展体育游戏㊂体育委员怎么也排不出来,你能为他想个办法吗?3.用铁丝制成左下图的铁丝网,重量是30克㊂用同型号的铁丝制成右下图的铁丝网,重量是多少克?四㊁问答题㊂1.有一艘军舰停靠在港口,军舰的外弦有一梯子㊂梯子的第三级正好挨着海面,往上每隔25厘米有一级㊂这时海水也正巧以每小时25厘米的速度涨潮㊂求经过多长时间海水涨到梯子的第四级?2.一个仓库里堆满了底面完全一样的长方体形状的纸箱,每只纸箱的重量都是整千克数,其中最轻的重1千克,最重的重100千克㊂仓库保管员整理仓库,将轻的箱子放到重的箱子上面,但每只箱子上面的总重量不能超过自己的重量㊂在1~100千克的箱子都有的情况下,这些箱子最多能堆几层?3.虹桥宾馆要把洗好的100条毛巾,用夹子夹在一条直绳子上晒干㊂每条毛巾的两边都必须用夹子夹住,同一个夹子可以夹在相邻的两条毛巾的两边㊂求至少需要多少个夹子?4.中午放学的时候,还在下雨,大家都盼着天晴㊂小聪对小明说: 已经连续三天下雨了,你说再过36小时会出太阳吗? 同学,你说呢?231第十四讲智巧问题例1解:经过19天,这些睡莲就能长满半个池塘㊂答:需要经过19天㊂[同步精练]1.由于荷叶每天长大1倍,第12天把池塘盖满,所以盖满池塘的一半时是第11天㊂2.1分59秒3.一样多例2解:(1)这只蜗牛每天实际向上爬了多少米?3-2=1(米)(2)几天爬到井口?(12-3)ː1+1=10(天)答:这只蜗牛10天能爬到井口㊂[同步精练]1.(10-4)ː(4-3)+1=7(天)2.画一个正方形,要画4条相等的线段,而图中共有线段2ˑ6= 12(条),即有12ː4=3(个)小正方形形成的段数,因此画好这个图形,需要蘸三次墨水㊂3.(14-3)ː(3-2)+1=12(天)例3详解见思路点拨㊂[同步精练]1.参照例3,只要用天平称3次就可把次品找出来㊂2.第一次先把7千克和2千克的砝码放在天平的一端,在另一端称出9千克的盐;第二次再把9千克盐和7千克砝码放在天平一端,在另一端称出9+7=16(千克)的盐;第三次在天平的一端放上9+16=25(千339克)的盐,另一端放上25千克的盐,这时天平的两端共有25+25=50(千克)的盐,此时还剩下90千克,这样便可得到90千克和50千克的盐㊂(答案不唯一)3.①把20克的砝码和70克药粉混合放在一起,放在天平的两端,便可称出20+25=45(克)这样的两堆;②再把25克的药粉这一堆取20克与20克的砝码分别放在天平的两端,剩下的便为5克的药粉㊂例4144-3=141(个)[同步精练]1.他们把3根圆木摆成三角形,每人抬一角㊂2.如果退,退到这张桌子只能放下一枚棋子,当然是先放的人胜利㊂让圆桌变大,由于圆桌有对称中心,那么问题便迎刃而解了还是先放的获胜㊂方法是先放的人在对称中心处放第一枚棋子㊂根据平面内其他各点以中心点呈对称性可知,只要后放的人有位置放棋子,必然留下另一空位给先放的人,直到后放的不能再放为止㊂所以先放的人必定取胜㊂练习卷一㊁1.592.511提示:1+2+4+8+16+32+64+128+256=511(粒)3.3二㊁1.我们不妨直接来想:5只猫在5分钟内可以捉5只老鼠,那么5只猫在5ˑ2=10(分钟)内可以捉到5ˑ2=10(只)老鼠,在5ˑ4=20(分钟)内可以捉到5ˑ4=20(只)老鼠,因此,5ˑ20=100(分钟)抓5ˑ20=100 (只)老鼠,由于时间多用了20倍,因此抓老鼠的只数也相应地扩大20倍,但猫的只数没有变,所以,100分钟抓100只老鼠需要5只猫㊂3402.因为王欣买‘葫芦岛历险记“只缺1分钱,所以只要李媛带了1分或多于1分的钱,则两人的钱合起来肯定够买一本书,这说明李媛没带钱㊂李媛所缺的2元4角钱,就是这本书的价钱㊂3.想一想:狼狗㊁兔子和青菜,谁和另外二者都不能离开猎人而单独在一起?猎人不在时,兔子既不能和狼狗在一起,也不能和青菜在一起㊂猎人可以经过4个来回,将狼狗㊁兔子和青菜全部安全带过河去,方法如下:(1)先把兔子带过河去,猎人独自划船返回;(2)再把狼狗(或青菜)带过河去,猎人划船将兔子带回;(3)将青菜(或狼狗)带过河去,猎人独自划船返回;(4)将兔子带过河去㊂4.把小盒子放进中盒子里,最后一起放入大盒子里,小盒里放4个,中盒里放4个,大盒里放8个㊂5.分成50㊁50㊁1三堆:第一次称两个50,如果平了,第二次从这100个中任意拿1个(当然是真的)与第三堆的1个称,自然会得出结果;第一次称两个50不平是正常的,第二次我们把其中一堆(或重的或轻的都行)分成25㊁25称第二次;①把轻的分成25㊁25,如果平了,说明那堆重的有假,当然假的是超重;如果不平,说明这50个轻的有假,假的是轻了;②把重的分成25㊁25,道理同上㊂所以两次可以发现轻重,但是找不出哪个是假的㊂三㊁1.每份为2杯半牛奶㊂第一份:2整杯,1半杯,2空杯第二份:2整杯,1半杯,2空杯341第三份:1整杯,3半杯,1空杯2.排成六边形,一人在角上当两人用㊂每行5人㊂3.每个铁丝网重30克,而每个铁丝网共用铁丝所在的线段有2ˑ6 =12(条)㊂而由同型号的铁丝制成的右下图的铁丝网,共用线段条数4ˑ10=40(条),每2条为一组,左边图形有12ː2=6(组),每组重30ː6 =5(克),右边图形有40ː2=20(组),一共重5ˑ20=100(克)㊂四㊁1.因为水涨船高,所以水在涨高,船也在涨高,船上的梯子也随着船升高而升高,不管水怎样涨,永远都是第三级㊂2.列表如下:(叠法不唯一)层数重量第一层1千克第二层2千克第三层3千克第四层6千克第五层12千克第六层24千克第七层48千克第八层96千克第九层192千克因为192千克>100千克㊂而96千克<100千克,所以这些箱子最多只能堆八层㊂3.根据植树原理,100条毛巾用夹子夹在绳子上晒干,由于两头都342夹,同一个夹子可以夹在相邻的两条毛巾的两边,夹子数要比毛巾数多1个,即101个㊂4.由于是中午在谈话,小聪说的是再过36小时会不会出太阳;再过24小时是第二天中午,此时还有12小时,到第36小时应该是半夜,不管天气是否晴朗,还是不会出太阳㊂综合调研卷(一)一㊁1.222.36723.404.62195.306.367.108.2500 9.120提示:从100至199的整数中,每个数的百位上都是1,所以1出现的次数为100+20=120(次)㊂10.173提示:用和分别减去个位㊁十位上错误的数值,加上正确的数值即得:201-7-90+9+60=17311.36二㊁4321+3214+2143+1432,从个位算起,每个数位上都是1+2+3+4 =10,所以原式=11110101ˑ101-101=101ˑ(101-1)=101ˑ100=101006300ː25=63ˑ(100ː25)=63ˑ4=252117000ː125=117ˑ(1000ː125)=117ˑ8=936199+99ˑ99=100+99ˑ(99+1)=100+99ˑ100=100ˑ(99+1) =1000099ˑ7+11ˑ37=11ˑ63+11ˑ37=11ˑ100=1100三㊁长方形的面积是9ˑ4=36,因为6ˑ6=36,所以正方形的边长应该是6厘米㊂如图所示:343。

天平称量数学问题

天平称量数学问题
天平称量的数学问题通常涉及到如何使用最少的称量次数来确定一组物品中的特殊物品。

这里有两个经典的问题：
次品问题：假设有N个小球，其中有一个是次品，质量与其他小球不同。

问题是，使用天平最少需要称量几次才能找出这个次品。

砝码问题：假设有一组砝码，每个砝码的质量都是3的整数次幂（例如1克、3克、9克、27克等）。

问题是，如何使用这些砝码以及天平来称量任意整数克的重量。

对于第一个问题，如果已知次品比正常小球重，那么经过k次称重，最多可以从3k个小球中找出次品。

如果次品的轻重未知，那么经过k次称重，最多可以从23k−3个小球中找出次品。

对于第二个问题，例如称量14克，需要27克砝码，27- (9+3+1)=14，以此类推。

四年级奥数巧解智巧巧问题

巧解智巧巧问题巧点晴——方法和技巧用“枚举法”、“类比法”、“极端性原则”、“正难则反”等方法解决非常问题。

巧指导——例题精讲A级冲刺名校·基础点晴【例1】有一只圆桶，里面盛了一些水。

小明说桶里的水超过半桶，小红却说不到半桶。

当时又没有任何测量器具，怎样才能判定谁说的对呢？甲乙丙做一做1一城镇共有5000户居民，每户居民的子女都不超过2个，一部分家庭有1个孩子，余下的家庭一半每家有2个孩子，另一半没有孩子，问这个城镇共有多少个孩子？【例2】小燕在少年宫猜谜室里发现一个有趣的图形，9盏绿灯纵横交错地排成十行，而且每行都是3盏灯。

请画出它的排列方式。

（上海“金钥匙”少年数学竞赛四年级试题）分析与解9盏绿灯纵横交错地排成十行，而且每行都有3盏灯，这里每盏灯都被重复计算，否则是不可能的。

可画图试验，确定正确的排列方法，右图是其中方法之一。

做一做2 五年级同学把10棵树平均种成5行，每行都是4棵。

他们是怎样种的？请你画图表示出来。

【例3】某食堂买回100个鸡蛋，每袋装10个，其中9个袋里的鸡蛋，每个都是50克重，另一个袋里装的每个都是40克重，将这10袋混在一起，只准用秤称一次，就能找出哪个袋里装的每个是40克重的鸡蛋。

请问是怎么办到的？做一做3 16个外表一样的球，有10克和9克两种重量。

现在用一台天平来测定每种球各几个。

先取两个球，天平两边各放一个。

结果天平不平衡，就拿这两个球作标准，将余下的14个球分成7对，用天平与这对标准球逐一比较，结果3对较重，2对较轻，2对与标准球一样重。

那么这16个球的总重量是多少克？B级培优竞赛·更上层楼【例4】今有8升牛奶一瓶，要用5升和3升的两种容器分成4升一份的两份牛奶，怎么分？分析与解要解答本题，需要仔细设计操作方法，下面给出一个操作程序表，请读者由开始逐步分析操作的意义，直到最后得到解答，是很有趣的。

做一做4两个汽车驾驶员要平分12千克的大桶汽油，身边只有能装9千克和5千克的两只空桶。

小学数学趣题巧算-六年级分册

一、百题１．钟声小明家离火车站很近，他每天都可以根据车站大楼的钟声起床。

车站大楼的钟，每敲响一下延时３秒，间隔１秒后再敲第二下。

假如从第一下钟声响起，小明就醒了，那么到小明确切判断出已是清晨６点，前后共经过了几秒钟？２．越减越多同学们对这样的问题可能并不陌生：“一个长方形被切去１个角，还剩几个角？”这种题的最大特点是答案不唯一，要根据去掉的这个角的不同情况来确定“剩角”的多少。

图１以上３幅示意图，表明了３种不同情况的３种不同答案。

其中第３种情况最有趣，长方形原有４个角，切去了１个角，反而多了１个角，出现了越减越多的情况。

下面一道题的思考方法与上题类似，看你能否正确回答。

“一个正方体，锯掉一个角，还剩几个角？”请注意，这里的“角”是立体的“角”，它不同于平面上的角。

３．数一数如果有人问你“会数数儿吗？”，你会不屑一顾地说：“这么大了，还不会数数儿！”其实，数数儿的学问还是很大的。

不信，请你数出下面几何图形的个数。

图２４．画一画下面这些图形你能一笔画出来吗？（不重复画）图３５．最短的路线养貂专业户养殖场内安置了９个貂笼（如下图）。

为了节省每次喂食的时间，他必须走一条最短的路，但又图４不能漏掉一个貂笼，喂完食后还要回到原出发点。

你能替他设计一条最短的路线吗？并算出每喂食一次，至少要走多少米的路。

６．切西瓜六（１）班召开夏夜乘凉晚会，买来了许多西瓜。

班主任李老师说：“今天买来了许多西瓜请大家吃。

在吃以前我先要以切西瓜为名请大家做一道数学题。

我规定，西瓜只能竖切，不能横剖。

大家知道，切一刀最多分成２块，切２刀最分成多４块，那么切３刀最多能分成几块？切４刀、切５刀、切６刀呢？这中间有没有规律？如果有规律，请同学们找出来。

”李老师刚说完，同学们就七嘴八舌地讨论起来。

请你也参加他们的讨论吧。

７．均分承包田有一块等腰梯形菜地（如下图），地边有一口水井。

现在３户种菜专业户都提出要承包这块地。

经研究，决定让这３户共同承包这块地，因此必须把这块地分成面积相等、形状相同且与这口水井的距离也要相等的３块地。

初三物理巧解托盘天平测量题

初三物理巧解托盘天平测量题实验中学任多佳使用托盘天平测量物体质量的实验操作过程相对于其他测量仪器要来得复杂，且对每一步操作的先后顺序都有严格的要求，稍有差池就会对测量结果造成严重，可能使测量结果偏大或偏小。

而由此延伸出的“分析天平的测量结果偏差问题”，由于题目把戏较多，没有统一的做法，给同学们制造了不少麻烦。

本文将介绍一种此类问题的巧解方法，希望能给同学们的解题带来便利。

首先回忆一下使用托盘天平测量物体质量的步骤：0.估测被测物体质量，选择适宜量程(称量)和分度值(感量)的天平，观察铭牌。

1.将托盘天平放在水平桌面(或实验台)上。

水平放置2.将游码拨至标尺左端的零刻线处。

3.调节平衡螺母，使横梁平衡。

平衡螺母4.把被测物体放在左盘内，按“先大后小”顺序选择适当砝码，用镊子向右盘里增减砝码并调节游码在标尺上的位置，直到横梁平衡。

左物右码5.盘里砝码的总质量加上游码所对的刻度值，就等于被测物体的质量。

6.取下物体，用镊子将砝码放回盒中，游码归零，实验完毕。

注：判断横梁平衡方法：a.指针指在分度盘的中线处；b.指针左右摆动幅度相同。

(黑体字为口诀)例1、测量前，天平未调平衡，横梁左倾，其他操作正确，便开始测量，测量结果。

(选填“偏大”、“偏小”、“正常”) 巧解方法：无论是测量前调节平衡螺母，还是测量开始后放置砝码、调节游码位置，目的都是为了使横梁平衡。

如果测量前横梁未平衡，可采用这样的方法分析——横梁左倾，那么相当于左盘沉，应在右盘放一个适宜的小砝码使横梁恰好平衡，甚至我们可以假设这个小砝码的质量就是1g。

接下来假设左盘放一个100g的物体，右盘放一个100g的砝码，这样横梁会依然平衡。

那么左盘物体质量的测量值=砝码值总和=100+1=101g，而其实际质量是100g，所以测量值偏大。

本方法实际上就是取特殊值，一般情况成立，取特殊值也一定成立。

特殊值也不一定非取100g、1g，只是为了分析方便而已。

苏教版小学奥数三年级巧算

苏教版小学奥数三年级巧算一、拓展提优试题1．数一数图中，带有☆的正方形有个．2．有一个挂钟，3时敲3下，要用6秒．这个挂钟12时敲12下，需要用秒．3．甲、乙、丙、丁4个小朋友进行象棋比赛，没两个都比赛一场，规定胜者得3分，平局得1分，输者得0分．结果丁得6分，乙得4分，丙得2分，那么甲得分．4．一天中午，孙悟空吃了10个桃子，猪八戒吃了25个包子，孙悟空说猪八戒太能吃了，但猪八戒说自己的包子比桃子小得多，还是孙悟空吃得多．聪明的沙僧用天平得到了如图所示的两种情况（圆圈是桃子，三角是包子长方形表示重量为所标数值的砝码），那么1个桃子和1个包子共重克．5．妹妹今年18岁，姐姐今年26岁，当两人年龄之和是20岁时，姐姐岁．6．只用2，3，5三个数（可重复使用）填在右图中的○内，使得每个三角形三个顶点上的三个数的和都相等．7．一些糖果，如果每天吃3个，十多天吃完，最后一天只吃了2个，如果每天吃4个，不到10天就吃完了，最后一天吃了3个．那么，这些糖果原来有（）个．A．32B．24C．35D．368．一个不透明的布袋中有黑、白、黄三种颜色的筷子各10根，最少拿出根筷子就能保证有一双是同样颜色的筷子．9．传说，能在三叶草中找到四叶草的人，都是幸运之人．一天，佳佳在大森林中摘取三叶草，当她摘到第一颗四叶草时，发现摘到的草刚好共有100片叶子，那么，她已经有颗三叶草．10．在一根绳子上依次穿入5颗红珠、4颗白珠、3颗黄珠和2颗蓝珠，并按照此方式不断重复，如果从头开始一共穿了2014颗珠子，那么第2014颗珠子的颜色是色．【参考答案】一、拓展提优试题1．解：由分析得出小鸟在不同的正方形的个数：1+4+4+1＝10（个），故答案为：10．2．解：6÷（3﹣1）×（12﹣1），＝6÷2×11，＝3×11，＝33（秒），答：需要33秒；故答案为：33．3．解：每两个人赛一局，说明一共赛6局，每人都赛三局；丁得六分说明：赢两局输一局（3+3+0＝6）；乙得四分说明：赢一局平一局输一局（3+1+0＝4）；丙得两分说明：平两局输一局（1+1+0＝2）；胜负平分别三局说明：六场比赛总得分应该是（3+0）+（3+0）+（3+0）+（1+1）+（1+1）+（1+1）＝12分；甲得分：12﹣6﹣4﹣2＝0（分）；答：那么甲得0分；故答案为：0．4．解：由图可知：○＝2△+40克①○+80克＝△+200克②由②可知：○＝△+120克③把③带入①得：△+120克＝2△+40克△+120克﹣40克＝2△+40克﹣40克△+80克＝2△△+80克﹣△＝2△﹣△△＝80克把△＝80克带入③得：○＝200克200+80＝280（克）答：1个桃子和1个包子共重280克．故答案为：280．5．解：（20+8）÷2，＝28÷2，＝14（岁）；答：当两人年龄之和是20岁时，姐姐14岁．故答案为：14．6．解：这个幻方可以是（答案不唯一）：7．解：糖每天吃3个，最少吃11天，最后一天2个，糖至少有10×3+2＝32（个）糖最多吃9天，最后一天吃3个，最多8×4+3＝35个．∴在32，33，34，35这几个数中满足除以3余数是2，除以4余数是3的只有35．故选：C．8．解：把三种颜色的筷子构造为三个抽屉，分别放黑、白、黄不同颜色的筷子．从最不利情况考虑，拿了3根，颜色各不同放到三个抽屉里，此时再任意拿1根，即可出现一个抽屉里能放了2根筷子．即出现一个抽屉里2根，另外两个抽屉里各1根筷子的情况，共计2+1+1＝4根．故答案为：4．9．解：（100﹣4）÷3＝96÷3＝32（棵）答：她已经有了32棵三叶草．故答案为：32．10．解：5+3+4+2＝14（个）2014÷14＝143…12，所以第2014颗珠子是第144周期的第12个，是黄颜色；答：第2014颗珠子的颜色是黄色．故答案为：黄．。