八年级数学第十一章

合集下载

第十一章三角形第一课时三角形的边课件八年级数学人教版上册

△DBE、△CBE、
( C ) 困，你是人类艺术的源泉，你将伟大的灵感赐予诗人。
△ABC、△ABD、△ACE、△ADE 天才是由于对事业的热爱感而发展起来的，简直可以说天才。
△ABC、△ABD、△ACE、△ADE 1 与三角形有关的线段 1 与三角形有关的线段天才是由于对事业的热爱感而发展起来的，简直可以说天才。
共_4__个等腰三角形为__△__A__B_C__、__△__A__B_D__、__△__A__C_E__、__△__A__D_E__，有__1__个等边三角形．
三角形的三边关系
【2020·徐州】若一个三角形的两边长分别为 3 cm、6 cm，
则它的第三边的长可能是( C )
A．2 cm
B．3 cm
丈夫志不大，何以佐乾坤。一个人如果胸无大志，既使再有壮丽的举动也称不上是伟人。
∵a、b、c 是△ABC 的三边长，根据两边之和大于第儿童有无抱负，这无关紧要，可成年人则不可胸无大志。
鹰爱高飞，鸦栖一枝。鸟贵有翼，人贵有志。有志不在年高，无志空活百岁。困，你是人类艺术的源泉，你将伟大的灵感赐予诗人。
1△D与BE三、角△形C有BE关、的线段
天△才AB是C由、于△对AB事D业、的△热AC爱E感、而△发AD展E起来的，简直可以说天才。
儿△童DB有E、无△抱C负B，E、这无关紧要，可成年人则不可胸无大志。
△ABD、△ABE、△ABC
△ABD、△ABE、△ABC
△ABD、△ABE、△ABC
△DBE、△CBE、
C．6 cm
D．9 cm
名师点评：三角形的三边关系是判断线段能否组成三角形的依据，一般只需判断三角形的最长边是否小于其余两边之和即可，不必每个都验证．

人教版八年级上册数学第十一章三角形全章课件

B
D
A DC
C
锐角三角形的三条高
每人画一个锐角三角形. (1) 你能画出这个三角形的三条高吗? (2) 这三条高之间有怎样的位置关系？
将你的结果与同伴进行交流.
锐角三角形的三条高是
B
在三角形的内部还是外部?
A
F
OE
C D
锐角三角形的三条高交于同一点. 锐角三角形的三条高都在三角形的内部.
直角三角形的三条高
(2)它们所在的直线交于一点吗？ D
将你的结果与同伴进行交流.
钝角三角形的三条高不相交于一点. 钝角三角形的三条高所在直线交于一点.
O
F
B
C
E
从三角形中的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形这边的高.
三角形的三条高的特性：
•锐角三角形 •直角三角形 •钝角三角形
E,F为AB上一点,CF⊥AD于H,判断下列说法哪些是正确的,
哪些是错误的. A
①AD是△ABE的角平分线( × )
②BE是△ ABD边AD上的中线( × ) ③BE是△ ABC边AC上的中线( × ) F
12 E G
④CH是△ ACD边AD上的高( √ ) B
H
D
C
三角形的高、中线与角平分线都是线段.
3.(滨州中考)若某三角形的两边长分别为3和4，则下列
长度的线段能作为其第三边的是(
)
A.1
B.5
C.7
D.9
【解析】选B.设第三边为x，则1＜x＜7.
4.若△ABC的三边为a，b，c，则化简︱a+b-c︱+︱ba-c︱的结果是（）. A. 2a-2b B.2a+2b+2c C. 2a D. 2a-2c

l八年级上册数学第十一章知识点

l八年级上册数学第十一章知识点八年级上册数学第十一章知识点八年级上册数学第十一章主要讲述了平面直角坐标系、平面图形的性质以及对称性等内容，以下是本章的具体知识点。

一、平面直角坐标系平面直角坐标系是用两条数轴来确定平面上任一点的位置关系，称为点的坐标。

其中，横坐标表示在横轴上的距离，纵坐标表示在纵轴上的距离。

坐标轴上的交点被称为原点，坐标轴正方向由左往右、由下往上标出。

二、平面图形的性质1. 直线的性质：直线是由无数个点组成，图中的点有无数个，且在直线上。

除此之外，它是平面中最短的路径，两点都在这个路径上。

2. 角的性质：角是两个不同的线段之间的空间，其中两端点相交的点被称为角的顶点。

根据顶点不同，角可分为锐角、直角、钝角等。

3. 三角形的性质：三角形是由三个线段组成的图形，共有三个顶点和三个内角，角度之和为180度。

可分类为等边三角形、等腰三角形、直角三角形等。

4. 四边形的性质：四边形是由四个线段组成的图形，共有四个顶点和四个内角，角度之和为360度。

可分类为平行四边形、矩形、正方形等。

5. 圆的性质：圆是由所有围绕圆心等距离的点组成的图形。

圆心是圆上最中间的点，直径是连接圆上任意两点的线段的长度。

该图形特点是半径相等。

三、对称性对称性是指一个图形绕某一直线或点旋转、翻折或滑动后，它和原来的图形完全重合。

一般有以下两种类型：1. 线对称性：指线对称轴上的任意一个点与该图形对称轴另一侧的一个点相互对称，如镜子对称。

2. 点对称性：指点对称中心与图形上任意一点的交点与该图形对称中心的另一点相互对称，如旋转对称。

以上是本章的主要知识点，掌握这些知识点，将对接下来的学习有很大的帮助。

八年级数学上册知识梳理(11—12章)

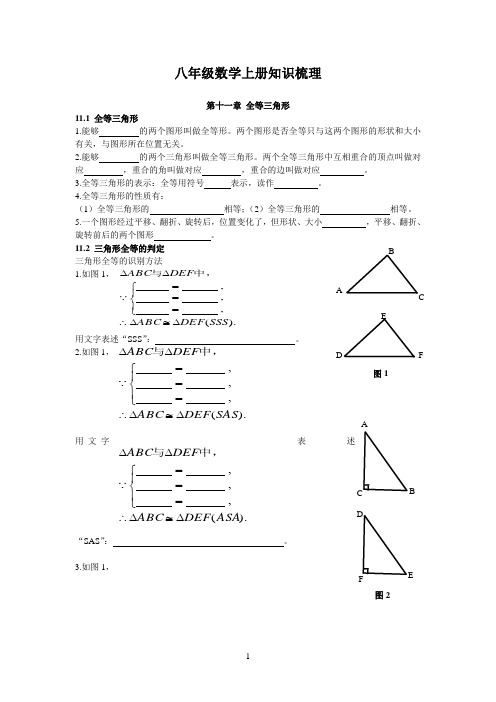
).(, ,, SAS DEF ABC DEF ABC ∆≅∆∴⎪⎩⎪⎨⎧===∆∆ 中，与).(, , ,ASA DEF ABC DEF ABC ∆≅∆∴⎪⎩⎪⎨⎧===∆∆ 中，与 AC BFED图2八年级数学上册知识梳理第十一章全等三角形11.1 全等三角形1.能够的两个图形叫做全等形。

两个图形是否全等只与这两个图形的形状和大小有关，与图形所在位置无关。

2.能够的两个三角形叫做全等三角形。

两个全等三角形中互相重合的顶点叫做对应，重合的角叫做对应，重合的边叫做对应。

3.全等三角形的表示：全等用符号表示，读作。

4.全等三角形的性质有：（1）全等三角形的相等；（2）全等三角形的相等。

5.一个图形经过平移、翻折、旋转后，位置变化了，但形状、大小，平移、翻折、旋转前后的两个图形。

11.2 三角形全等的判定三角形全等的识别方法 1.如图1，用文字表述“SSS ”：。

2.如图1，用文字表述“SAS ”：。

3.如图1，).(, , , SSS DEF ABC DEF ABC ∆≅∆∴⎪⎩⎪⎨⎧===∆∆ 中，与 A F E D C B 图1).(, , ,AAS DEF ABC DEF ABC ∆≅∆∴⎪⎩⎪⎨⎧===∆∆ 中，与用文字表述“ASA ”：。

4.如图1，用文字表述“AAS ”：。

5.如2，用文字表述“HL ”：。

判断两个三角形全等的常见思路如下表：11.3角平分线的性质1.定义：角平分线是把一个角分成两个相等的角的射线。

2.角平分线的尺规作图作法。

（见课本P19）3.角平分线的性质（1）性质：角的平分线上的点到两边的相等。

（2）符号语言：如图3，).(, , HL DEF ABC DEF Rt ABC Rt ∆≅∆∴⎩⎨⎧==∆∆ 中，与ODCPBA图3).( D,OB PD C OP AOB 角平分线的性质于，于上，在射线，点平分∴⊥⊥∠OA PC P OP（3）应用角平分线性质解题的格式的两边的距离相等）。

新人教版八年级数学上册课件《第11章三角形》(全章)PPT教学课件

解：（1）不能，因为3cm+4cm<8cm；（2）不能，因为5cm+6cm=11cm；（3）能，因为5cm+6cm>10cm.
归纳判断三条线段是否可以组成三角形，只需说明两条较短线段之和大于第三条线段即可.
针对训练一根木棒长为7，另一根木棒长为2，那么用长度为4 的木棒能和它们拼成三角形吗？长度为11的木棒呢？若不能拼成，则第三条边应在什么范围呢？解：设第三边长为x，则应有
定义：由不在同一条直线上的三条线段首尾顺次相接
所组成的图形叫做三角形.
A
B
C
问题2：三角形中有几条线段?有几个角?
有三条线段，三个角
边：线段AB，BC，CA是三角形的边. 顶点：点A，B，C是三角形的顶点，角：∠A，∠B，∠C叫做三角形的内角，简称三角形的角.
记法：三角形ABC用符号表示_△__A_B__C__.
△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC，顶点C所对应的边为BD，顶点D所对应的边为BC.
二三角形的分类
问题1：按照三角形内角的大小，三角形可以分为哪几类？锐角三角形、直角三角形、钝角三角形.
问题2：如果以三角形边的元素的不同，三角形该如何分类பைடு நூலகம்？ (1)等腰三角形和等边三角形的区别是什么?
基本要素：三角形的边：边AB、BC、CA；三角形的顶点：顶点A、B、C；三角形的内角(简称为三角形的角）：∠ A、 ∠ B、 ∠ C.
特别规定：三角形ABC的三边,一般的顶点A所对的边记作a,顶点 B所对的边记作b,顶点C所对的边记作c.
找一找：(1)图中有几个三角形？用符号表示出这些三角形？
7-2<x<7+2，即5<x<9. 则用长度为4的木棒不能和它们拼成三角形，长度为11的木棒也不能和它们拼成三角形.第三边长的范围为5<x<9.

人教版八年级数学上册电子书第十一章相似三角形

人教版八年级数学上册电子书第十一章
相似三角形
相似三角形是几何学中的一个重要概念，本章将介绍相似三角形的定义、性质以及相似三角形的判定方法。

一、相似三角形的定义
相似三角形是指具有相等或成比例的对应角度，并且对应边成比例的两个三角形。

当两个三角形的形状相似时，它们的所有对应角度都相等，对应边的长度成比例。

二、相似三角形的性质
1. 相似三角形的对应边成比例。

设两个相似三角形中的对应边分别为a、b和c、d，如果它们相似，则有a/b = c/d。

2. 相似三角形的对应角度相等。

设两个相似三角形中的对应角分别为∠A、∠B和∠C、∠D，如果它们相似，则有∠A = ∠C，∠B = ∠D。

3. 相似三角形的周长成比例。

设两个相似三角形的对应边长分
别为a、b和c、d，如果它们相似，则周长之比为a+b+c : c+d。

三、相似三角形的判定方法
1. AA判定法：如果两个三角形的两个角分别相等，则它们相似。

2. AAA判定法：如果两个三角形的每个角都相等，则它们相似。

3. SAS判定法：如果两个三角形的一个角相等，且两个角的对
边成比例，则它们相似。

4. SSS判定法：如果两个三角形的对应边成比例，则它们相似。

这些判定方法是判断两个三角形是否相似的基本依据，可以帮
助我们在几何学中进行相似三角形的判断和推导。

以上是人教版八年级数学上册电子书第十一章相似三角形的内容简介。

通过学习相似三角形的定义、性质以及判定方法，我们可以更好地理解几何学中的相似三角形概念，并应用于实际问题的解决中。

八上数学十一章到十五章知识点

八上数学十一章到十五章知识点以下是八年级上册数学第十一章到第十五章的知识点总结：第十一章：全等三角形1. 全等三角形的定义和性质：全等三角形是两个能够完全重合的三角形，具有一些特定的性质。

2. 全等三角形的判定定理：SSS（三边全等）、SAS（两边和夹角全等）、ASA（两角和一边全等）、AAS（两角和非夹角全等）和HL（直角边斜边公理）。

3. 全等三角形的证明方法：通过使用判定定理来证明两个三角形全等。

4. 全等三角形的应用：在几何图形、测量、工程等领域有着广泛的应用。

第十二章：轴对称1. 轴对称的定义和性质：如果一个图形沿一条直线折叠后与另一个图形完全重合，则这两个图形关于这条直线对称。

2. 轴对称的判定定理：通过观察图形的形状和大小来判断是否关于某条直线对称。

3. 轴对称的应用：在艺术、设计、建筑等领域有着广泛的应用。

第十三章：实数1. 无理数和有理数的定义：无理数是不能表示为两个整数的比的数，而有理数则可以表示为两个整数的比。

2. 实数的定义和性质：实数是包括有理数和无理数在内的所有数的集合，具有一些基本的性质。

3. 平方根和立方根的定义和性质：平方根是一个数的非负的平方根，立方根是一个数的立方等于给定值的数。

4. 实数的运算：实数可以进行加、减、乘、除等基本运算，并遵循运算规则。

第十四章：一次函数1. 函数的概念和性质：函数是定义在某个数集上的一种特殊的对应关系，具有一些基本性质。

2. 一次函数的定义和性质：一次函数是函数的一种，其图像为一条直线。

3. 一次函数的解析式和图像：一次函数的一般形式为y=kx+b，其中k和b 是常数。

通过解析式可以确定函数的图像，并通过图像研究函数的性质。

4. 一次函数的实际应用：一次函数在经济学、工程学、物理学等领域有着广泛的应用。

第十五章：整式的乘除与因式分解1. 整式的乘法规则：通过单项式乘以单项式、单项式乘以多项式、多项式乘以多项式等规则来进行整式的乘法运算。

人教版数学八年级上册课件第11章第8课时多边形的外角和

又∵多边形的外角和为 360°，
∴∠1＋∠2＋∠3＋∠4＝360°－∠5＝300°.
小结：将已知角转化到外角中去，再利用外角和定理求解.
★16.如图，∠α，∠β 分别是四边形 ABCD 的外角，求证： ∠α＋∠β＝∠A＋∠C.
证明：∵∠α 与∠ADC 是邻补角，∠β 与∠ABC 是邻补角， ∴∠α＝180°－∠ADC，∠β＝180°－∠ABC， ∴∠α＋∠β＝360°－(∠ADC＋∠ABC)． ∵∠A，∠ABC，∠C，∠ADC 是四边形 ABCD 的内角， ∴∠A＋∠C＝360°－(∠ADC＋∠ABC)． ∴∠α＋∠β＝∠A＋∠C.
知识点二：运用多边形的外角和进行相关计算 (1)已知一个正多边形的一个外角，求该多边形的边数； (2)已知一个正多边形的边数，求该多边形的每一个外角； (3)注：①正多边形的外角和等于 360°； ②正 n 边形的每个顶点处各取一个外角，则有 n 个外角； ③正多边形的每一个外角都相等．
3.正十边形的外角和为 360° . 4．一个正 n 边形的一个外角等于 90°，则 n 的值等于 4 . 5．正六边形的每一个外角的度数都是 60° .
关系，构建方程.
15.(2019 鞍山)如图，某人从点 A 出发，前进 8m 后向右转 60°，再前进 8 m 后又向右转 60°，…，按照这样的方式一直走下去，当他第一次回到出发点 A 时，共走了( D )
A．24m C．40m
B.32 m D.48m
解：如图，由题意得∠5＝180°－∠EAB＝60°，
变式练习
13.一个边形的每一个外角都等于 45°，则这个多边形的内角
和为( B )
A．1260°
B.1080°
C．1620°
D.360°

八年级上册数学第十一章笔记

八年级上册数学第十一章笔记八年级上册数学第十一章三角形一、三角形的概念1. 定义由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

三角形有三条边、三个顶点和三个角。

2. 表示方法三角形用符号“△”表示，顶点是A、B、C的三角形记作“△ABC”，读作“三角形ABC”。

二、三角形的分类1. 按角分类锐角三角形：三个角都是锐角的三角形。

直角三角形：有一个角是直角的三角形。

直角三角形可以用“Rt△”表示，直角所对的边称为斜边，夹直角的两条边称为直角边。

钝角三角形：有一个角是钝角的三角形。

2. 按边分类不等边三角形：三边都不相等的三角形。

等腰三角形：有两边相等的三角形。

相等的两边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。

等边三角形：三边都相等的三角形，等边三角形是特殊的等腰三角形，它的三个角都相等，并且每个角都等于60°。

三、三角形的三边关系1. 定理三角形两边的和大于第三边。

三角形两边的差小于第三边。

2. 应用判断三条线段能否组成三角形：只需判断较短的两条线段之和是否大于最长的线段。

已知三角形两边的长度，求第三边的取值范围：设三角形的两边长分别为a、b （a>b），则第三边c的取值范围是a b < c < a + b。

四、三角形的高、中线与角平分线1. 三角形的高定义：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形的高。

性质：三角形的三条高所在的直线相交于一点。

锐角三角形的三条高都在三角形内部；直角三角形的两条直角边是它的两条高，另一条高在三角形内部；钝角三角形的高，一条在三角形内部，另外两条在三角形外部。

2. 三角形的中线定义：在三角形中，连接一个顶点和它对边中点的线段叫做三角形的中线。

性质：三角形的三条中线相交于一点，这点称为三角形的重心。

三角形的一条中线将三角形分成两个面积相等的三角形，因为等底同高的三角形面积相等。

八年级上册数学第十一章知识点

八年级上册数学第十一章知识点稿子一
嘿，亲爱的小伙伴们！今天咱们来聊聊八年级上册数学第十一章那些有趣的知识点哈。

先说三角形，这可是个重要角色！三角形的内角和知道不？那可是 180 度哦，不管它是啥形状，这个度数都不变，神奇吧？还有三角形的外角，它等于和它不相邻的两个内角的和呢。

三角形的三边关系也很关键哟！两边之和得大于第三边，两边之差得小于第三边。

不然可组不成三角形啦。

再说说全等三角形，这就像是双胞胎一样，形状大小都一模一样。

全等三角形的判定条件可不少，什么“边边边”“边角边”“角边角”“角角边”，记清楚这些，判断起来就轻松多啦。

等腰三角形也很有意思。

等腰三角形两腰相等，两个底角也相等。

要是等边三角形，那就更特别啦，三个角都 60 度，三条边都一样长。

怎么样，这些知识点是不是还挺好玩的？好好学，数学可有趣着呢！
稿子二
嗨呀，小伙伴们！咱们一起来瞧瞧八年级上册数学第十一章的知识点哟。

三角形，那可是常见的图形。

比如说直角三角形，有个直角在那，它的两条直角边的平方和等于斜边的平方，这就是大名鼎鼎的勾股定理。

三角形的稳定性也很厉害，不像四边形容易变形，三角形可牢固啦。

还有三角形的中线、高线、角平分线，可别弄混了。

中线把三角形分成面积相等的两部分，高线是从顶点到对边的垂线，角平分线把角分成相等的两份。

全等三角形在解题中用处可大啦。

全等之后，对应的边和角都相等，能帮咱们求出好多未知的东西。

在等腰三角形里，对称轴特别重要，沿着对称轴对折，两边能完全重合。

这第十一章的知识点虽然不少，但只要咱们用心，都能掌握得妥妥的，加油哦！。

八年级数学上册知识点总结第十一章

第十一章全等三角形
一、全等形
能够完全重合的两个图形叫做全等形。

二、全等三角形
１．全等三角形：能够完全重合的两个三角形叫做全等三角形。

(两个三角形全等，互相重合的顶点叫做对应点，互相重合的边叫做对应边，互相重合的角叫做对应角。

)
２．全等三角形的符号表示、读法：△ＡＢＣ与△Ａ′Ｂ′Ｃ′全等记作△ＡＢＣ≌△Ａ′Ｂ′Ｃ′，“≌”读作“全等于”。

(两个三角形全等时，通常把对应顶点的字母写在对应的位置上，这样对应的两个字母为端点的线段是对应边；对应的三个字母表示的角是对应角）。

３．全等三角形的性质：全等三角形的对应边相等，对应角相等。

二、三角形全等的判定：
1．三边对应相等的两个三角形全等，简写成“边边边”或“ＳＳＳ”。

2．两边和他们的夹角对应相等的两个三角形全等，简写成“边角边”或“ＳＡＳ”。

3．两角和他们的夹边对应相等的两个三角形全等，简写成“角边角”或“ＡＳＡ”。

4．两个角和其中一个角的对边对应相等的两个三角形全等，简写成“角角边”或“Ａ
ＡＳ”。

5．斜边和一条直角边对应相等的两个直角三角形全等，简写成“斜边、直角边”或“ＨＬ”。

(ＳＳＡ、ＡＡＡ不能识别两个三角形全等，识别两个三角形全等时，必须有边的参与，如果有两边和一角对应相等时，角必须是两边的夹角。

)
三、角的平分线的性质
1.性质：角平分线上的点到角的两边距离相等。

2．逆定理：在角的内部，到角的两边距离相等的点在角平分线上。

3.三角形的内心：利用角的平分线的性质定理可以导出：三角形的三个内角的角平分线交于一点，此点叫做三角形的内心，它到三边的距离相等。

新人教版八年级上册数学第十一章知识点

可编辑范本第十一章三角形一、知识框架：二、知识概念：1.三角形：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.三边关系：三角形任意两边的和大于第三边，任意两边的差小于第三边.3.高：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足间的线段叫做三角形的高.4.中线：在三角形中，连接一个顶点和它对边中点的线段叫做三角形的中线.5.角平分线：三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线.6.三角形的稳定性：三角形的形状是固定的，三角形的这个性质叫三角形的稳定性.7.多边形：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形.8.多边形的内角：多边形相邻两边组成的角叫做它的内角.9.多边形的外角：多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.10.多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线.11.正多边形：在平面内，各个角都相等，各条边都相等的多边形叫正多边形.12.平面镶嵌：用一些不重叠摆放的多边形把平面的一部分完全覆盖，叫做用多边形覆盖平面，13.公式与性质：⑴三角形的内角和：三角形的内角和为180°⑵三角形外角的性质：性质1：三角形的一个外角等于和它不相邻的两个内角的和.性质2：三角形的一个外角大于任何一个和它不相邻的内角.⑶多边形内角和公式：n 边形的内角和等于(2)n -·180°⑷多边形的外角和：多边形的外角和为360°.⑸多边形对角线的条数：①从n 边形的一个顶点出发可以引(3)n -条对角线，把多边形分成(2)n -个三角形.②n 边形共有(3)2n n -条对角线.。

人教版八年级上册数学第11章多边形1(18页)

知识讲授
多边形的定义及相关概念问题1 什么是三角形？由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
问题2 观察画某多边形的过程，类比三角形的概念，你能说出什么是多边形吗？
在平面内，由一些线段首尾顺次相接组成的封闭图形叫做多边形.
思考：比较多边形的定义与三角形的定义，为什么要强调“在平面内”呢？怎样命名多边形呢？
n边形有n个顶点，顶点
n条边，n个内角， 2n个外角．
边
外角：多边形的边与它的邻边的延长线组成的角.
多边形按它的边数可分为：三角形，四边形，五边形等等.其中三角形是最简单的多边形.
问题4 请分别画出下列两个图形各边所在的直线,你能得到什么发现？
D
E
A
C
G
B （1）
F （2） H
此类多边形被一条边所在的直线分成了两部分，不在这条直线同侧是凹多边形.
第十一章三角形 11.3 多边形及其内角和
11.3.1 多边形
学习目标
1.掌握多边形的定义及有关概念，能区分凹凸多边形. 2.掌握正多边形的概念.（重点） 3.会求多边形的对角线的条数.（难点）
情境导入
在实际生活当中，除了三角形，还有许多由线段围成的图形.观察以下图片，你能找到由一些线段围成的图形吗？
如图（1）这样，画出多边形的任何一条边所在的直线，
整个多边形都在这条直线的同一侧，那么这个多边形就
是凸多边形.本节我们只讨论凸多边形.
典例分析
例1 凸六边形纸片剪去一个角后，得到的多边形的边数可能是多少？画出图形说明．解：∵六边形截去一个角的边数有增加1、减少1、不变三种情况， ∴新多边形的边数为7、5、6三种情况，如图所示.

八上数学第十一章知识点

八上数学第十一章知识点哎呀，提起八年级上册数学第十一章，那可真是让我又爱又恨呐！这第十一章讲的是三角形。

三角形，就像我们生活中的好多东西，比如屋顶的形状、自行车的车架，它们不都是三角形的嘛！这三角形可是有着好多神奇的知识点呢！先来说说三角形的边。

三角形的三边关系，那可是相当重要！任意两边之和大于第三边，任意两边之差小于第三边。

这就好比我们三个人手拉手，两边的人胳膊加起来一定要比中间那个人的胳膊长，不然怎么能拉得住呢？再讲讲三角形的角。

内角和是180 度，这可是铁打的定律！就像一个完整的蛋糕切成三块，三块加起来还是那个完整的蛋糕呀！还有外角，外角等于不相邻的两个内角之和。

这就好像我有三个好朋友，我和其中两个的关系好，加起来就等于和第三个的关系，神奇吧？然后是三角形的重要线段，像中线、高线和角平分线。

中线把三角形分成面积相等的两部分，这多有用呀！就好像把一块大蛋糕平均分成两份，大家都能吃得一样多。

高线呢，就是从三角形的一个顶点向它的对边作垂线，顶点和垂足之间的线段。

角平分线就更好理解啦，把一个角平分成两个相等的角。

在学习这些知识的时候，我和同学们可没少讨论。

有一次，我和同桌小李就为了一道关于三角形内角和的题目争得面红耳赤。

我说：“这道题肯定是180 度，内角和不一直都是180 度嘛！”小李却不服气：“你再好好想想，万一有特殊情况呢？”最后还是老师出马，给我们讲明白了。

还有一次，小组讨论三角形的中线问题，小王说：“中线不就是中间的那条线嘛，有啥难的。

”小赵立刻反驳：“你可别乱说，中线是能把三角形分成面积相等的两部分的线！”大家你一言我一语，讨论得可热闹了。

学完这一章，我算是明白了，三角形的世界真是丰富多彩。

它不仅在数学书里，还在我们的生活中无处不在。

我们得好好掌握这些知识，才能在数学的海洋里畅游呀！总之，八年级上册数学第十一章的三角形知识，既有趣又有用，我们可得把它学好！。