九年级数学秋季培优班第1讲三角形1

合集下载

著名机构初中数学培优讲义.三角形.第01讲.教师版

内容基本要求略高要求较高要求三角形了解三角形的有关概念；了解三角形的稳定性；会按边和角对三角形进行分类；理解三角形的内角和、外角和及三边关系；会画三角形的主要线段；知道三角形的内心、外心、重心了解三角形的有关概念；了解三角形的稳定性；会按边和角对三角形进行分类；理解三角形的内角和、外角和及三边关系；会画三角形的主要线段；知道三角形的内心、外心、重心等腰三角形直角、三角形了解等腰三角形、等边三角形和直角三角形的概念，会识别这三种图形，并理解这三种图形的性质和判定能用等腰三角形、等边三角形和直角三角形的性质和判定解决简单问题能用等腰三角形、等边三角形和直角三角形的知识解决有关问题全等三角形了解全等三角形的概念，了解相似三角形和全等三角形之间的关系掌握两个三角形全等的条件和性质；会应用三角形全等的性质和判定解决有关问题会利用全等三角形的知识解释或证明经过图形变换后得到的图形与原图形对应元素间的关系一、三角形的基本概念：⑴三角形的定义：由三条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做三角形．三角形具有稳定性．⑵三角形的内角：三角形的每两条边所组成的角叫做三角形的内角．在同一个三角形内，大边对大角．⑶三角形的外角：三角形的任意一边与另一边的反向延长线所组成的角叫做三角形的外角． ⑷三角形的分类：例题精讲中考要求三角形()()():⎧⎪⎧⎨⎨⎪⎩⎩⎧⎪⎧⎨⎨⎪⎩⎩直角三角形:三角形中有一个角是直角三角形按角分锐角三角形:三角形中三个角都是锐角斜三角形钝角三角形:三角形中有一个角是钝角不等边三角形:三边都不相等的三角形三角形按边分底边和腰不相等的等腰三角形:有两条边相等的三角形等腰三角形等边三角形正三角形有三边相等的三角形注意：每个三角形至少有两个锐角，而至多有一个钝角．三角形的三个内角中，最大的一个内角是锐角(直角或钝角)时，该三角形即为锐角三角形(直角三角形或钝角三角形)．二、与三角形相关的边⑴三角形中的三种重要线段①三角形的角平分线：三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线．注：每个三角形都有三条角平分线且相交于一点，这个点叫做三角形的内心，而且它一定在三角形内部．②三角形的中线：在三角形中，连结一个顶点和它的对边中点的线段叫做三角形的中线．注：每个三角形都有三条中线，且相交于一点，这个点叫做三角形的中心，而且它一定在三角形内部． ③三角形的高：从三角形的一个顶点向它的对边画垂线，顶点和垂足间的线段叫做三角形的高线．注：每个三角形都有三条高且三条高所在的直线相交于一点，这个点叫做三角形的垂心．锐角三角形的高均在三角形内部，三条高的交点也在三角形的内部；钝角三角形的高线中有两个垂足落在边的延长线上，这两条高落在三角形的外部，直角三角形有两条高分别与两条直角边重合．反之也成立．画三角形的高时，只需要向对边或对边的延长线作垂线，连接顶点与垂足的线段就是该边的高． ⑵三角形三条边的关系①三角形三边关系：三角形任何两边的和大于第三边．②三角形三边关系定理的推论：三角形任何两边之差小于第三边．即a 、b 、c 三条线段可组成三角形⇔b c a b c -<<+⇔两条较小的线段之和大于最大的线段．注意：在应用三边关系定理及推论时，可以简化为：当三条线段中最长的线段小于另两条线段之和时，或当三条线段中最短的线段大于另两条线段之差时，即可组成三角形．三、等腰三角形1．等腰三角形的定义：有两条边相等的三角形叫做等腰三角形． 2．等边三角形的定义：有三条边相等的三角形叫做等边三角形． 3．等腰三角形的性质： (1)两腰相等． (2)两底角相等．(3)“三线合一”，即顶角平分线、底边上的中线、底边上的高互相重合． (4)是轴对称图形，底边的垂直平分线是它的对称轴．线段的垂直平分线：性质定理：线段的垂直平分线上的点到线段的两个端点距离相等判定定理：与线段的两个端点距离相等的点在这条线段的垂直平分线上，线段的垂直平分线可以看做是和线段两个端点距离相等的所有点的集合．4．等腰三角形的判定：(1)有两条边相等的三角形是等腰三角形．(2)有两个角相等的三角形是等腰三角形．5．等边三角形的性质：三边都相等，三个角都相等，每一个角都等于60o．6．等边三角形的判定：(1)三条边都相等的三角形是等边三角形．(2)三个角都相等的三角形是等边三角形．(3)有一个角是60o的等腰三角形是等边三角形．7．等腰直角三角形的性质：顶角等于90︒，底角等于45︒，两直角边相等．等腰直角三角形的判定：(1)顶角为90︒的等腰三角形．(2)底角为45︒的等腰三角形．8．含30︒角的直角三角形的重要结论：在直角三角形中，如果一个锐角等于30︒，那么它所对的直角边等于斜边的一半．四、全等的概念全等图形：能够完全重合的两个图形就是全等图形．全等三角形：能够完全重合的三角形就是全等三角形．全等三角形的对应边相等，对应角分别相等；反之，如果两个三角形的边和角分别对应相等，那么这两个三角形全等．全等三角形对应的中线、高线、角平分线及周长面积均相等．全等三角形的概念与表示：能够完全重合的两个三角形叫作全等三角形．能够相互重合的顶点、边、角分别叫作对应顶点、对应边、对应角．全等符号为“≌”．全等三角形的性质：对应角相等，对应边相等，对应边上的中线相等，对应边上的高相等，对应角的角平分线相等，面积相等．寻找对应边和对应角，常用到以下方法：(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边．(2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角．(3)有公共边的，公共边常是对应边．(4)有公共角的，公共角常是对应角．(5)有对顶角的，对顶角常是对应角．(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角)，一对最短边(或最小角)是对应边(或对应角)．要想正确地表示两个三角形全等，找出对应的元素是关键．二、全等的性质和判定全等三角形的判定方法：(1) 边角边定理(SAS)：两边和它们的夹角对应相等的两个三角形全等．(2) 角边角定理(ASA)：两角和它们的夹边对应相等的两个三角形全等．(3) 边边边定理(SSS)：三边对应相等的两个三角形全等．(4) 角角边定理(AAS)：两个角和其中一个角的对边对应相等的两个三角形全等． (5) 斜边、直角边定理(HL)：斜边和一条直角边对应相等的两个直角三角形全等．全等三角形的应用：运用三角形全等可以证明线段相等、角相等、两直线垂直等问题，在证明的过程中，注意有时会添加辅助线．奥数赛点：能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系．而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础．判定三角形全等的基本思路：SAS HL SSS →⎧⎪→⎨⎪→⎩找夹角已知两边找直角找另一边ASA AAS SAS AAS ⎧⎪⎧⎪⎨⎪⎨⎪⎪⎪⎩⎩边为角的对边→找任意一角→ 找这条边上的另一角→已知一边一角边就是角的一条边找这条边上的对角→ 找该角的另一边→ ASAAAS →⎧⎨→⎩找两角的夹边已知两角找任意一边【例1】已知三角形中两边长为2和7，若第三边长为奇数，则这个三角形的周长为_________．【解析】第三边长x 的取值范围是59x <<，因为它是奇数，故只能是7，所以三角形的周长为27716++=．【答案】16【例2】有三条线段，其中两条线段的长为3和5，第三条线段的长为x ，若这三条线段不能构成三角形，则x 的取值范围是．【解析】略【答案】02x <≤或8x ≥．【例3】如图所示，将ABC △沿着DE 翻折，若1280∠+∠=︒，则B ∠= ．A BCDE 12【解析】略【答案】40︒【例4】一个多边形的内角和是外角和的2倍，则这个多边形的边数为．【解析】略【答案】6【例5】 ABC △中，AD BC ⊥，AE 平分BAC ∠，AG AE CG ⊥，是ABC △外角ACF ∠的平分线，若G DAE ∠-∠=60︒，则ACB ∠的度数为．GFE D C B A【解析】过点A 作BF 的平行线交CG 的延长线于点H ，DAE HAG ∠=∠，∵G DAE ∠-∠=60︒∴G HAG ∠-∠=60︒，即60H ∠=°，∵AH BF ∥，故ACB ∠为60°．FC ED B【答案】6【例6】如图所示，在ABC ∆中，100A ∠=︒，40ABC ∠=︒，BD 是ABC ∠的平分线，延长BD 至E ，使DE AD =．求证：BC AB CE =+EDCBAF EDCBA【解析】略【答案】在BC 上取一点F ，使得BF BA =易证得ADB FDB ∆∆≌ ∴DF AD =，又∵DA DE = ∴DF DE =∵100A ∠=︒，AB AC = ∴40ABC ∠=︒∵BD 平分ABC ∠， ∴20ABD ∠=︒∴60ADB FDB ∠=∠=︒ ∵60CDE ADB ∠=∠=︒ ∴60FDC EDC ∠=∠=︒ ∴DCF DCE ∆∆≌ ∴FC EC =∴BC BF FC AB CE =+=+【例7】如图，已知60ABD ACD ∠=∠=︒，且1902ADB BDC ∠=︒-∠．求证：ABC ∆是等腰三角形．D BAED CBA【解析】延长BD 到E ，使得DE CD =，连接AE ．∵1902ADB BDC ∠=︒-∠，∴2180ADB BDC ∠+∠=︒，即180ADC ADB ∠+∠=︒．∵180ADE ADB ∠+∠=︒，∴ADC ADE ∠=∠， ∵CD DE AD AD ==，，∴()SAS ADC ADE ∆∆≌， ∴60ACD E ∠=∠=︒，AC AE =， ∵60ABD ACD ∠=∠=︒，∴ABD E ∠=∠，∴AB AE =，∴AB AC =，∴ABC ∆是等腰三角形．【例8】如图，在ABC ∆中，3AB AC =，A ∠的平分线交BC 于D ，过B 作BE AD ⊥，垂足为E ，求证：AD DE =．DCBAEF21BAED C 【解析】解法一：如图，延长BE 、AC 交于F ．∵12∠=∠，AE BF ⊥，∴AF AB =．∴2ABF ABE S S ∆∆=．而1133AC AB AF ==，∴13ABC ABF S S ∆∆=．∵AD 平分BAC ∠，∴3BD AB CD AC ==，334BD DC BC ==，∴311442ABD ABC ABF ABE S S S S ∆∆∆∆===．故12AD AE =，∴AD DE =．解法二：如图，延长AC 、BE 交于F ．21BAHFEDC∵12∠=∠，AE BF ⊥， ∴AF AB =，2CF AC =．过E 作EH AF ∥，交BC 于H ，则12EH CF AC ==，1DEH ∠=∠，ACD EHD ∠=∠．∴ACD EHD ∆∆≌，∴AD DE =．解法三：如图，延长AC 、BE 交于G ，过E 作EH BC ∥交AG 于H ．21BAEDC GH∵12∠=∠，AE BG ⊥，∴3AG AB AC ==，BE GE =．故有HC HG =． ∵2CG AB AC AC =-=，∴HC AC =．∵DC HE ∥，∴AD DE =．解法四：如图，取AB 的中点G ，连接EG 交BC 于F ，则EG 是Rt ABE ∆斜边上的中线．GC DEFAB12∴AG EG =，21AEG ∠=∠=∠． ∴EG AC ∥．故BF CF =，12EG AC =，1322EG AB AC ==，有13FG EG =，故F 是ABE ∆的重心．∴BD 为AE 的中线，故AD DE =．【例9】如图所示，在ABC ∆中，AC AB >，M 为BC 的中点，AD 是BAC ∠的平分线，若CF AD ⊥且交AD 的延长线于F ，求证()1MF AC AB =-．MFD CB AEMFD CB A【解析】题目中有角平分线和垂直的条件，因此可以考虑将图形补成等腰AEC ∆，之后再证明MF 是CBE∆的中位线即可．如图所示，延长AB 、CF 相交于点E ，在AFE ∆和AFC ∆中，EAF CAF ∠=∠，AF AF =，AFE AFC ∠=∠，故AFE AFC ∆∆≌，从而AE AC =，EF FC =．而CM MB =，故MF 是CBE ∆的中位线，从而()()111222MF BE AE AB AC AB ==-=-．【例10】已知点M 是四边形ABCD 的BC 边的中点，且120AMD ∠=︒,证明：12AB BC CD AD ++≥.AB C DM B 1AB CDM C 1【解析】显然，要证题设的不等式，应当把AB ，12BC ，CD 三条线段首尾连接成一条折线，然后再与线段AD 比较.要实现这一构想，折线之首端应与A 点重合，尾端应与D 点重合，这可由轴对称来实现.以AM 为对称轴，作点B 关于AM 的对称点1B ，连接1AB 、1MB ，则1AB AB =，1MB MB =，即1AB M ∆≌ABM ∆，由此1B MA BMA ∠=∠. 再以DM 为对称轴，作点C 关于DM 的对称点1C ，连接1DC 、1MC ，则1DC DC =，1MC MC =，即1DC M ∆≌DCM ∆，由此1C MD CMD ∠=∠. 而120AMD ∠=︒，所以180********BMA CMD AMD ∠+∠=︒-∠=︒-︒=︒. 注意到1160B MA C MD BMA CMD ∠+∠=∠+∠=︒，因此1111120()B MC B MA C MD ∠=︒-∠+∠1206060=︒-︒=︒，而1112MB MC BC ==，所以11B MC ∆是等边三角形，1112B C BC =.由于两点之间以直线段为最短，所以1111AB B C C D AD ++≥，即12AB BC CD AD ++≥.【巩固】设M 是凸四边形ABCD 的边BC 的中点，135AMD ∠=︒，求证：AB CD AD +≥. M DC B AC'B'M DCB A【解析】作点B 关于AM 的对称点'B ，作点C 关于DM 的对称点'C ，连接'AB 、''B C 、'C D ，则''MB MB MC MC ===，且'AB AB =，'C D CD =. 而''90C MB ∠=︒，则'''B C =，故''''AB CD AB B C C D AD +=++≥.【例11】（2007年北京中考）如图，已知ABC ∆⑴请你在BC 边上分别取两点D 、E (BC 的中点除外)，连结AD 、AE ，写出使此图中只存在两．．．．对．面积相等的三角形的相应条件，并表示出面积相等的三角形； ⑵请你根据使⑴成立的相应条件，证明AB AC AD AE +>+．CBA⑴DE CBA⑵DF EG CBAF⑶D OE GCBA【解析】⑴如图⑴相应的条件是：BD CE DE =≠ ；两对面积相等的三角形分别是：ABD ∆和ACE ∆，ABE ∆和ACD ∆．⑵(方法1)：如图⑵，分别过点D 、B 作CA 、EA 的平行线，两线交于F 点，DF 与AB 交于G 点．所以ACE FDB ∠=∠，AEC FBD ∠=∠在AEC ∆和FBD ∆中，又CE BD =，可证AEC FBD ∆∆≌所以AC FD =，AE FB = 在AGD ∆中，AG DG AD +> 在BFG ∆中，BG FG FB +> 所以AG DG BG FG AD FB +++>+ 即AB FD AD FB +>+ 所以AB AC AD AE +>+(方法2)：如图⑶取BC 中点O ，连结AO 并延长AO 至F ，OF AO =，连结BF ，DF ，延长AD 交BF 于G 可证得BOF COA ∆∆≌，DOF EOA ∆∆≌ 所以AC BF =，AE DF = 在BGA ∆中，BG AB GD AD +>+ 在GFD ∆中，GD GF FD +>所以BG AB GD GF GD AD FD +++>++ 所以BG AB GF AD FD ++>+ 即BF AB AD FD +>+ 所以AB AC AD AE +>+【例12】如图，梯形ABCD 中，AD BC ∥，以两腰AB ，CD 为一边分别向两边作正方形ABGE 和DCHF ，连接AD 的垂直平分线l 交线段EF 于点M ．求证：点M 为EF 的中点．MlHFDCEGBANLSRQ'P'QP ABGEC DFHlM【解析】过E 、F 分别作l 的垂线EP ，FQ 交l 于P 于Q ．如图，N 是AD 之中点，过N 作'NQ DF ∥交FQ 于'Q ，作'NP AE ∥交EP 于'P ，作NS DC ∥交BC 于S ，作NR AB ∥交BC 于R ．在Rt 'P PN ∆和Rt LNR ∆中，有''90P NP PP N ∠+∠=︒． '1809090P NP LNR ∠+∠=︒-︒=︒，所以有'PP N LNR ∠=∠．又由'RN AB AE P N ===，知Rt 'Rt NP P RLN ∆∆≌．从而得'PP NL =．同理可知Rt 'Rt Q QN NLS ∆∆≌，而得'QQ NL =，即有''PP QQ =．显然，'EP AN ∥，'FQ ND ∥，又AN ND =，所以''EP FQ ∥．从而有''''EP EP PP FQ QQ FQ =+=+=．应EP FQ ∥知，四边形EQFP 是平行四边形，其对角线互相平分，所以M 是EF 的中点．【例13】四边形ABCD 被对角线BD 分为等腰直角三角形ABD 和直角三角形CBD ，其中A ∠和C ∠都是直角，另一条对角线AC 的长度为2，求四边形ABCD 的面积．DCB AC'DCB A【解析】将三角形ABC 绕A 点旋转90︒，使B 与D 重合，C 到'C 点．则有''180CDC ADC ADC ADC ABC ∠=∠+∠=∠+∠=︒，所以'C D C ，，在同一条直线上，'ACDC 是三角形．又因为'AC AC =.所以三角形'ACC 是等腰直角三角形．所以四边形ABCD 的面积等于等腰直角三角形'ACC 的面积。

中考数学尖子生培优竞赛压轴题专题辅导第一章直角三角形的边角关系18页

第一章直角三角形的边角关系8卷1 （考点整合与提升）考点一：锐角三角函数的定义如图，在月必中，ZC为直角，则锐角力的各三角函数的左义如下：A（1）角力的正弦：锐角>1的对边与斜边的比叫做Z力的正弦,记作sinA即Siib4=-・c（2）角/!的余弦：锐角力的邻边与斜边的比叫做Z/1的余弦，记作cos/l,即cos/l=£.（3）角力的正切：锐角>1的对边与邻边的比叫做Z力的正切，记作tan A. KPtan>l=-・b例1：在△/18C中，ZC90° , AB=n, BC=5.求Z力的正弦值、余弦值和正切值.答案：siiL4=— > cos/!=—* tan/1=—13 13 12★ ★变式1：在锐角ZV1〃C中，月8=15, 〃0=14,血丛=84.求：（1）tanC的值：（2）siib4 的值.答案：解：（1）过/!作/W 丄于D •: Szc=丄8G4D=84,・・・2+14+/1D=84,・"D=12, AB2 12= 15,:•••仞=14一9=5・在Rt^ADC中，AC=\^AtanO= —=—: DC 5168（2）过点〃作BELAC于点E TSkk 丄力©防=8, :.BE= — . •'•sinZ旳Q=竺二旦=竺・2 13 AB 15 654★ ★变式2：如图，点P是Z R的边04上的一点，已知点P的横坐标为6, sino=-・5（1）求点P的纵坐标：（2）求Zajt他的三角函数值.4PM 4解：（1）过P作Mix轴于M 则皿70=90°, •••点P横坐标为6. sino= —, •••——=一，OM=b・设5OP 5PM=4x, PO=5x.由勾股泄理得62+ （4Q 2=（5Q 2.解得x=2（负值舍去），刊/=8, OP = 10, .'.P点纵坐标是8.<2）•••在Rl^OMP中，"1/0=90° , R?=10. PM=S. OM=& :.C osa=- = — = -,tana= OP 10 5 PM _ 8 _ 4————■ OP 6 3考点二：坡度坡度：坡而的铅直高度力与水平宽度/的比叫做坡度（或坡比），常用字母i表示，HPi=y.坡角：坡而与水平而的夹角叫做坡角，用字母a表示，则tan«=i=y .例2：如图，某校教学楼月〃后方有一斜坡，已知斜坡仞的长为12米，坡角a为60° .根据有关部门的规左，Z 底39。

初三特殊的三角形培优同步讲义

初三特殊的三角形培优同步讲义1. 等腰三角形1.1 定义等腰三角形是指具有两边长度相等的三角形。

在等腰三角形中，两边对应的两个角也是相等的。

1.2 性质- 等腰三角形的底角（即两个底边夹角）相等。

- 等腰三角形的顶角（即顶边夹角）也是相等的。

2. 直角三角形2.1 定义直角三角形是指其中一个角度为90度的三角形。

直角三角形的斜边是其他两边之间最长的一边。

2.2 特殊三角形- 30度-60度-90度三角形：其中一个角度为90度，另外两个角度为30度和60度。

这种三角形的边长比例为1:√3:2。

30度-60度-90度三角形：其中一个角度为90度，另外两个角度为30度和60度。

这种三角形的边长比例为1:√3:2。

- 45度-45度-90度三角形：其中一个角度为90度，另外两个角度为45度。

这种三角形的两条直角边的边长相等。

45度-45度-90度三角形：其中一个角度为90度，另外两个角度为45度。

这种三角形的两条直角边的边长相等。

3. 等边三角形3.1 定义等边三角形是指三条边的长度都相等的三角形。

在等边三角形中，每个角的度数都是60度。

3.2 性质- 等边三角形的三个内角都是60度。

- 等边三角形的高、中线、角平分线三者重合，且均通过三角形的重心点。

4. 总结初三特殊的三角形主要包括等腰三角形、直角三角形和等边三角形。

通过对这些三角形的认识和特点的理解，能够更好地解决与三角形相关的问题和题目。

---_注意：以上内容仅供参考，具体知识点和定义请以教材为准。

_。

初三培优第一讲

初三培优第一讲【教学目标】1．复习巩固矩形、菱形和正方形的概念、性质和判定，并会灵活应用；2．理解矩形、菱形、正方形与平行四边形的关系；3. 通过学习，提高综合运用知识独立分析问题、解决问题的能力. 【知识清单】1.菱形的性质与判定：（1）菱形的性质：（2）菱形的判定：2.矩形的性质与判定：（1）矩形的性质：(2)矩形的判定：3.正方形的性质与判定：（1）正方形的性质：(2)正方形的判定：温馨提示：正方形既是特殊的矩形，又是特殊的菱形，所以正方形具有矩形和菱形的所有性质.【典例精析】【典例精析】例1.（2014•安顺）已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，（1）求证：四边形ADCE为矩形；（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明。

*例2（选讲）．已知菱形ABCD 的两条对角线分别为6和8，M 、N 分别是边BC 、CD 的中点，P 是对角线BD 上一点，则PM+PN 的最小值= ．例3．如图，△ABC 中，点O 为AC 边上的一个动点，过点O 作直线MN ∥BC ，设MN 交∠BCA 的外角平分线CF 于点F ，交∠ACB 内角平分线CE 于E ．（1）求证：EO=FO ；（2）当点O 运动到何处时，四边形AECF 是矩形？并证明你的结论；（3）若AC 边上存在点O ，使四边形AECF 是正方形，猜想△ABC 的形状并证明你的结论。

EANMFCBO例4.如图，在△ABC 中，D 、E 分别是AB 、AC 的中点，BE=2DE ，延长DE 到点F ，使得EF=BE ，连接CF ．（1）求证：四边形BCFE 是菱形；（2）若CE=4，∠BCF=120°，求菱形BCFE 的面积．例5．如图，正方形ABCD 的边长为4，点E 在对角线BD 上，且∠BAE=22.5°，EF ⊥AB ，垂足为F ，则EF 的长为（） A. 1 B. 2 C. 224- D.423- 【巩固练习】1.在下列命题中，是真命题的是（）A ．两条对角线相等的四边形是矩形B ．两条对角线互相垂直的四边形是菱形C ．两条对角线互相平分的四边形是平行四边形D ．两条对角线互相垂直且相等的四边形是正方形2.（2014•陕西）如图，在菱形ABCD 中，AB=5，对角线AC=6．若过点A 作AE ⊥BC ，垂足为E ，则AE 的长为（）A ．4B ．512 C ．524D ．5 3．如图，将一个长为10cm ，宽为8cm 的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到的菱形的面积为（）A ．210cmB ．220cmC ．240cmD ．280cm第2题4.如图，O 是矩形ABCD 的对角线AC 的中点，M 是AD 的中点，若AB=5，AD=12，则四边形ABOM 的周长为__________5.在矩形ABCD 中，1=AB ，3=AD ，AF 平分DAB ∠，过C 点作BD CE ⊥于E ，延长AF 、EC 交于点H ，下列结论中：①FH AF =；②BF BO =；③CH CA =；④ED BE 3=，正确的是（） A ．②③B ．③④C ．①②④D ．②③④6.如图，在正方形ABCD 中，CE DF ⊥．若10cm CE =，DF =ABCD3题FEDC BA第4题7.如图，正方形ABCD 内有两条相交线段MN 、EF ，M 、N 、E 、F 分别在边AB 、CD 、AD 、BC 上．小明认为：若MN = EF ，则MN ⊥EF ；小亮认为: 若MN ⊥EF ，则MN = EF ．你认为( )A ．仅小明对B ．仅小亮对C ．两人都对D ．两人都不对8．如图，边长分别为4和8的两个正方形ABCD 和CEFG 并排放在一起，连结BD 并延长交EG 于点T ，交FG 于点P ，则GT ＝（）A ．2B ．22C ．2D ．19.如图，在正方形ABCD 中，E 是AB 上一点，BE=2，AE=3BE ，P 是AC 上一动点，则PB+PE 的最小值是．（第7题）（第8题）（第9题）10.如图，在△ABC 中，AD 是BC 边上的中线，E 是AD 的中点，过点A 作BC 的平行线交BE 的延长线于点F,连接CF. （1）求证：AF=DC ；（2）若AB ⊥AC,试判断四边形ADCF 的形状，并证明你的结论.O H EF DC AB第5题第6题【课后练习】1.如图，菱形ABCD 中，∠B ＝60°，AB ＝2，E 、F 分别是BC 、CD 的中点，连接AE 、EF 、AF ，则△AEF 的周长为。

初三数学---解直角三角形---培优班

初三数学---解直角三角形---培优班(共5页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--ABE F QP初三数学解三角形1.（2007•宁波）如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD=12 m，塔影长DE=18 m，小明和小华的身高都是，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m和1m，那么塔高AB为米.2．如图，大海中有A和B两个岛屿，为测量它们之间的距离，在海岸线PQ上点E处测得∠AEP＝74°，∠BEQ＝30°；在点F处测得∠AFP＝60°，∠BF Q＝60°，EF＝1km．（1）判断ABAE的数量关系，并说明理由；（2）求两个岛屿A和B之间的距离（结果精确到）．（参考数据：3≈，sin74°≈，cos74°≈，tan74°≈，sin76°≈，cos76°≈）3. (2010年兰州市)如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°. 已知原传送带AB 长为4米.（1）求新传送带AC的长度；（2）如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点4米的货物MNQP是否需要挪走，并说明理由．(说明：⑴⑵的计算结果精确到米，参考数据：2≈，3≈，5≈，6≈4.（2007台州）一次数学活动中，小迪利用自己制作的测角器测量小山的高度CD．已知她的眼睛与地面的距离为米，小迪在B处测量时，测角器中的60AOP∠=°（量角器零度线AC和铅垂线OP的夹角，如图）；然后她向小山走50米到达点F处（点B F D ，，在同一直线上），这时测角器中的45EO P ''∠=°，那么小山的高度CD 约为米.（注：数据3 1.732≈，2 1.414≈供计算时选用）5. （2010楚雄）如图，河流的两岸PQ ，MN 互相平行，河岸PQ 上有一排小树，已知相邻两树之间的距离CD ＝50米，某人在河岸MN 的A 处测的∠DAN ＝35°，然后沿河岸走了120米到达B 处，测的∠CBN ＝70°，求河流的宽度CE （结果保留两个有效数字）．（参考数据：si n 35°≈，co s35°≈，t an 35°≈Si n 70°≈，co s70°≈，t an 70°≈）6. （2010扬州）如图，某校一幢教学大楼的顶部竖有一块“传承文明，启智求真”的宣传牌CD ．小明在山坡的坡脚A 处测得宣传牌底部D 的仰角为60°，沿山坡向上走到B 处测得宣传牌顶部C 的仰角为45°．已知山坡AB 的坡度i ＝1:3，AB ＝10米，AE ＝15米，求这块宣传牌CD 的高度．（测角器的高度忽略不计，结果精确到米．参考数据：2≈，3≈）D CM︒35︒707. (2010年绍兴市)如图,小敏、小亮从A ,B 两地观测空中C 处一个气球,分别测得仰角为30°和60°,A ,B 两地相距100 m .当气球沿与BA 平行地飘移10秒后到达C ′处时,在A 处测得气球的仰角为45°.（1）求气球的高度（结果精确到ｍ）；（2）求气球飘移的平均速度（结果保留3个有效数字）.8．（2009年铁岭市）某旅游区有一个景观奇异的望天洞，D 点是洞的入口，游人从入口进洞游览后，可经山洞到达山顶的出口凉亭A 处观看旅游区风景，最后坐缆车沿索道AB 返回山脚下的B 处．在同一平面内，若测得斜坡BD 的长为100米，坡角10DBC ∠=°，在B 处测得A 的仰角40ABC ∠=°，在D 处测得A 的仰角85ADF ∠=°，过D 点作地面BE 的垂线，垂足为C ．（1）求ADB ∠的度数；（2）求索道AB 的长．（结果保留根号）9.（苏州）某学校体育场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶．已知看台高为米，现要做一个不锈钢的扶手ABA BCDE45° 60° ACDEF B及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子的底端分别为D，C)，且∠DAB=66. 5°．(1)求点D与点C的高度差DH；(2)求所用不锈钢材料的总长度l(即AD+AB+BC，结果精确到米)．(参考数据：°≈，°≈，°≈10.（2007山东威海）如图，一条小船从港口A出发，沿北偏东40方向航行20海里后到达B处，然后又沿北偏西30方向航行10海里后到达C处．问此时小船距港口A多少海里（结果精确到1海里）友情提示：以下数据可以选用：sin400.6428≈，cos400.7660≈，tan400.8391≈1.732．11.（2009年江苏省）如图，在航线l的两侧分别有观测点A和B，点A到航线l的距离为2km，点B位于点A北偏东60°方向且与A相距10km处．现有一艘轮船从位于点B 南偏西76°方向的C处，正沿该航线自西向东航行，5min后该轮船行至点A的正北方向的D处．（1）求观测点B到航线l的距离；（2）求该轮船航行的速度（结果精确到h1.73，sin760.97°≈，cos760.24°≈，tan76 4.01°≈）P北403012.（2010株洲市）如图，直角ABC ∆中，90C ∠=︒，25AB=，5sin B =，点P 为边BC 上一动点，PD ∥AB ，PD 交AC 于点D ，连结AP ．（1）求AC 、BC 的长；（2）设PC 的长为x ，ADP ∆的面积为y ．当x 为何值时，y 最大，并求出最大值．13.（2009年泸州）在某段限速公路BC 上(公路视为直线)，交通管理部门规定汽车的最高行驶速度不能超过60千米／时(即350米／秒)，并在离该公路100米处设置了一个监测点A ．在如图8所示的直角坐标系中，点A 位于y 轴上，测速路段BC 在x 轴上，点B 在A 的北偏西60°方向上，点C 在A 的北偏东45°方向上，另外一条高等级公路在y 轴上，AO 为其中的一段． (1)求点B 和点C 的坐标；(2)一辆汽车从点B 匀速行驶到点C 所用的时间是15秒，通过计算，判断该汽车在这段限速路上是否超速(参考数据：7.13≈)(3)若一辆大货车在限速路上由C 处向西行驶，一辆小汽车在高等级公路上由A 处向北行驶，设两车同时开出且小汽车的速度是大货车速度的2倍，求两车在匀速行驶过程中的最近距离是多少14.(2009年黄冈市)如图，在海面上生产了一股强台风，台风中心（记为点M ）位于海滨城市（记作点A ）的南偏西15°，距离为612千米，且位于临海市（记作点B ）正西方向603千米处．台风中心正以72千米/时的速度沿北偏东60°的方向移动（假设D CBA台风在移动过程中的风力保持不变），距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭．（1）滨海市．临海市是否会受到此次台风的侵袭？请说明理由．（2）若受到此次台风侵袭，该城市受到台风侵袭的持续时间有多少小时？15．（2010义乌）如图1，已知∠ABC ＝90°，△ABE 是等边三角形，点P 为射线BC上任意一点（点P 与点B 不重合），连结AP ，将线段AP 绕点A 逆时针旋转60°得到线段AQ ，连结QE 并延长交射线BC 于点F .（1）如图2，当BP ＝BA 时，∠EBF ＝ °，猜想∠QFC ＝ °；（2）如图1，当点P 为射线BC 上任意一点时，猜想∠QFC 的度数，并加以证明；（3）已知线段AB ＝32，设BP ＝x ，点Q 到射线BC 的距离为y ，求y 关于x 的函数关系式．图ACEQF 图ABE QP F C。

九年级数学培优竞赛专题讲义：解三角形含答案

解三角形一、内容提要1. 由三角形的已知元素，求出所有未知元素的过程叫做解三角形.2. 解直角三角形所根据的定理 (在Rt △ABC 中，∠C=Rt ∠).边与边的关系：勾股定理－－－－――c 2=a 2+b 2.角与角的关系：两个锐角互余－－－－∠A+∠B=Rt ∠边与角的关系：（锐角三角函数定义）SinA=c a ， CosA=c b , tanA=b a , CotA=ab.互余的两个角的三角函数的关系：Sin(90－A)= CosA ， Cos(90－A)= SinA ， tan(90 －A)= CotA, Cot(90 －A)= tanA.特殊角的三角函数值：锐角的正弦、正切随着角度的增大而增大（即增函数）；余弦、余切随着角度的增大而减小（即减函数）.3. 解斜三角形所根据的定理 (在△ABC 中)正弦定理：SinCcSinB b SinA a ===2R. (R 是△ABC 外接圆半径).② 余弦定理： c 2=a 2+b 2－2abCosC ； b 2=c 2+a 2－2ca CosB ； a 2=c 2+b 2－2cbCosA.③ 互补的两个角的三角函数的关系：Sin(180－A)= sinA ， Cos(180－A)= － cosA ， tan(180－A)=－cotA ， cotA(180－A)=－tanA.④ S △ABC ＝21absinC=21bcsinA=21casinB.4. 与解三角形相关的概念：水平距离，垂直距离，仰角，俯角，坡角，坡度，象限角，方位角等.二、例题例1.已知：四边形ABCD中，∠A＝60 ，CB⊥AB，CD⊥AD，CB＝2，CD＝1.求：AC的长.例2. 已知：如图，要测量山AB的高，在和B同一直线上的C，D处,分别测得对A的仰角的度数为n和m，CD=a.试写出表示AB的算式.B例3. 已知：四边形ABCD中，∠ABC＝135 ，∠BCD＝120 ，CD＝6，AB＝6，BC＝5－3.求：AD的长.解：例4.如图，要测量河对岸C，D两个目标之间的距离，在A，B两个测站，测得平面角∠CAB＝30 ，∠CAD＝45 ，∠DBC＝75 ，∠DBA＝45 ，AB＝3.试求C，D的距离.例5. 已知：O 是凸五边形ABCDE 内的一点且∠1＝∠2，∠3＝∠4，∠5＝∠6，∠7＝∠8. 求证：∠9和∠10相等或互补例6. 已知：二次方程mx 2－(m －2)x+41(m －1)=0两个不相等的实数根，恰好是直角三角形两个锐角的正弦值.求：这个直角三角形的斜边与斜边上的高的比. 解：三、练习 1. 填空：① 如果从点A 对着点B 测得仰角是60 ，那么从点B 对着点A 测得的俯角是＿＿度. ② 点C 在点D 的南偏东25，那么点D 在C 的方向是＿＿＿＿＿＿. ③ 斜坡AB 的坡角是30 ，那么AB 的坡度i=1∶＿＿＿. ④ 锐角A ＞45 ，那么下列函数的取值范围是：SinA_____， CosA_____， tanA_______，cotA________. ⑤ 已知：30 ＜∠A ＜60 ，那么如下的函数的取值范围是∠A 的余弦＿＿＿＿＿＿＿＿，∠A 的正切＿＿＿＿＿＿＿.2. 已知：△ABC 中，∠B ＝45 ，AC ＝7，点D 在BC 上，CD ＝3， D ＝5. 求AB 的长.3. 如图观测塔AB 的高为a 米，从塔顶A 测得地面上同一方向上的两个目标C ，D 的俯角分别是30和45，求CD 的距离.4. 船A 在船B 的正北，它们同时向东航行，时速分别是15和20海里，3小时后，船B 在船A 的东南，问这时两船相距多远？j3045A BD5. 一只船向南航行，出发前在灯塔A 的北偏东30 ，相距15海里，2小时后，灯塔在船的北偏西60 ，求船的航行速度.6. 如图要测量建筑物AB 的高，先在楼下C 测得对顶端A 的仰角为45 ，然后在楼上D 测得对A 的仰角为30 ，已知楼高CD=m 米，求AB.7. 已知：△ABC 中，a=21, b=17, c=10. 求：S △ABC .8. 已知：△ABC 中，SinA ∶ SinB ∶SinC=3∶5∶7.求：△ABC 的最大角的度数.9. 船B 在艇A 的方位角120，相距24海里处，发出呼救，报告说：它沿着方位角240的方向前进，速度是每小时9海里. A 艇以最快的时速21海里赶去营救，问应沿什么方向，要经过几小时才能靠近船B ？BC10. 已知：锐角三角形ABC 的外接圆直径AE 交BC 于D. 求证：tanB ×tanC=AD ∶DE提示：作BC 边的高AF(h)并延长交圆于G,连结GE11. 已知：△ABC 中，∠A=45 ，AB=6，BC=2，不用正弦定理能解答这个三角形吗？如不能，说明理由；如能请解这个三角形.12. 如图已知：ABCD 为圆内接四边形，过AB 上一点M 引MP ，MQ ，MR 分别垂直于BC ，CD ，AD ，连结PR 和MQ 交于N.求证：MABMNR PN.13. 如图已知：锐角△ABC 中，AC=1，AB=c ，△ABC 的外接圆半径R ≤1.求证： Cos<c ≤CosA+3SinA .解三角形答案一、内容提要1. 由三角形的已知元素，求出所有未知元素的过程叫做解三角形.2. 解直角三角形所根据的定理 (在Rt △ABC 中，∠C=Rt ∠).边与边的关系：勾股定理－－－－――c 2=a 2+b 2.角与角的关系：两个锐角互余－－－－∠A+∠B=Rt ∠边与角的关系：（锐角三角函数定义）SinA=c a ， CosA=c b , tanA=b a , CotA=ab.互余的两个角的三角函数的关系：Sin(90－A)= CosA ， Cos(90－A)= SinA ， tan(90 －A)= CotA, Cot(90 －A)= tanA.特殊角的三角函数值：锐角的正弦、正切随着角度的增大而增大（即增函数）；余弦、余切随着角度的增大而减小（即减函数）.3. 解斜三角形所根据的定理 (在△ABC 中)正弦定理：SinCcSinB b SinA a ===2R. (R 是△ABC 外接圆半径).② 余弦定理： c 2=a 2+b 2－2abCosC ； b 2=c 2+a 2－2ca CosB ； a 2=c 2+b 2－2cbCosA.③ 互补的两个角的三角函数的关系：Sin(180－A)= sinA ， Cos(180－A)= － cosA ， tan(180－A)=－cotA ， cotA(180－A)=－tanA.④ S △ABC ＝21absinC=21bcsinA=21casinB.4. 与解三角形相关的概念：水平距离，垂直距离，仰角，俯角，坡角，坡度，象限角，方位角等.二、例题例1. 已知：四边形ABCD 中，∠A ＝60 ，CB ⊥AB ，CD ⊥AD ，CB ＝2，CD ＝1.求：AC 的长.解：延长AD 和BC 相交于E ，则∠E ＝30 .在Rt △ECD 中，∵sinE=CECD, ∴CE=30sin 1=1÷21＝2. EB ＝4.在Rt △EAB 中， ∵tanE=EBAB,∴AB=EBtan30。

北师大版秋季数学9年级培优班进门考学生版

y
B Q
OP
Ax
4
第 3 讲反比例函数综合（1）
第 3 讲反比例函数综合（1）
满分：10 分
分数：__________
1．若 A(x1，y1)，B(x2，y2)是反比例函数 y＝ k (k≠0)图像上的两个点，当 x1＜x2＜0 x
时，y1＞y2，那么一次函数 y＝－kx＋k 的图象不经过（）
A
D
B
P
C
2
第 2 讲相似三角形综合（2）
第 2 讲相似三角形综合（2）
满分：10 分
分数：__________
1．如图，D、E、F 分别为 AB、BC、CA 的中点，G、H 分别为 DE、EF 的中点，则
△GEH 面积与△ABC 的面积比为（）
A
A．1∶4 B．1∶16 C．1∶32 D．1∶64
x
x
①S△ODB＝S△OCA；
②四边形 OAMB 的面积不变；
y
③当点 A 是 MC 的中点时，则点 B 是 MD 的中点．
其中正确结论的个数是（）
A．0 B．1
D BM A
C．2 D．3
OC
x
3．某闭合电路中，电源的电压为定值，电流 I(A)与电阻 R(Ω)成反比例．如图所示的
是该电路中电流 I 与电阻 R 之间的函数关系的图象，则用电阻 R 表示电流 I 的函数
矩形 ABCD 的边 AB、BC、CD、DA 上．若 AB＝4，BC＝6，则 DG＝（）．
A．5
B． 16 5
C．4
D． 18 5
Hale Waihona Puke AHDEG
B
C
F
4．已知□ABCD，连接对角线 BD，E、F 是边 BC 的三等分点，连接 AE、AF，与 BD 分别交于点 G、H，则 BG∶GH∶HD＝________________．

著名机构九年级数学秋季班讲义1相似形三角形一(教师版)

~ 1 ~~ 2 ~知识精要1、比例线段两条线段的长度的比叫做两条线段的比。

对于四条线段a 、b 、c 、d ，如果a:b=c:d (或表示为错误!未找到引用源。

)，那么a 、b 、c 、d 叫做成比例线段，简称比例线段。

这时，线段a 、d 是比例外项，线段b 、c 是比例内项。

等积式：如果错误!未找到引用源。

，那么ad=bc .反比性质：如果错误!未找到引用源。

，那么错误!未找到引用源。

.更比性质：如果错误!未找到引用源。

，那么错误!未找到引用源。

或错误!未找到引用源。

. 合比性质：如果dcb a =，那么错误!未找到引用源。

. 比例的等比性质：如果k d c b a ==，那么错误!未找到引用源。

a c k b d=== 比例中项：如果a:b=b:c ，即b 2=ac ，那么b 被称为a 、c 的比例中项黄金分割如果点P 把线段AB 分割成AP 和PB(AP>PB)两段,其中AP 是BP 和AB 的比例中项,那么称这种分割为黄金分割,点P 称为线段AB 的黄金分割点。

AP 与AB 的比值错误!未找到引用源。

称为黄金分割数(简称黄金数).黄金分割数是一个无理数,在应用时常取它的近似值0.618.热身练习一、选择题1、下列一定是相似图形的是(C)A.有一个角相等的等腰三角形B.周长相等的长方形C.面积不相等的正方形D.两个不同行政区的地图~ 3 ~ABF C D EO 2、若点C 为线段AB 的黄金分割点，且AC>BC ，则下列各式中不正确的是(C)A.AB:AC=AC:BCB.BC=253-ABC.AC=215+AB D.AC ≈0.618AB3、如图，正方形ABCD 中，E 为AB 的中点，AF ⊥DE 于点O ，那么DOAO等于（ D ） A ．352 ； B ．31； C ．32； D ．21．4、如图，直线 A A 1∥BB 1∥CC 1，如果12AB BC =，12AA =，15CC =，那么线段BB 1的长是 3 ．5、如图，四边形ABCD 是正方形，点E 、F 分别在边DC 、BC 上，AE ⊥EF ,如果53DE EC =,那么AE ∶EF 的值是 83．6、已知点M 是线段AB 的黄金分割点（AM ＞MB ），如果AM ＝215-cm ，那么AB ＝ 1 cm ． 7、已知菱形ABCD 的边长为6，对角线AC 与BD 相交于点O ，OE ⊥AB ，垂足为点E ，AC=4，那么sin ∠AOE=13. 8、如图，已知AD 为△ABC 的角平分线，DE//AB ，如果32=ECAE ，那么ABAE =35．9、如图，在平行四边形ABCD 中，点E 在边BC 上，EC=2BE,联结AE 交BD 于点F ，若△BFE 的面积为2，则△AFD 的面积为 18_.F EDCBAA B CA 1B 1C 1~ 4 ~题1010、如图，四边形ABCD 和四边形CEFG 是边长分别为3和2的正方形，且B 、C 、E 在一直线上，AE 与CF 交于点P ，则CP FP =53.精解名题例1、在ABC V 中，点D,E 分别在边AB,AC 上，联结DE ，有下列条件：①;AD AEAB AC=②;AD DE AB BC =③;BD CE AD AE =④AD BDAE CE=,则，能判定DE BC P 的是（ B ） A. ①②③④ B. ①③④ C. ②③④ D. ①③例2、已知线段AB ，P 是它的黄金分割点，且AP>PB 。

九年级数学培优(动点产生的三角形)

九年级数学培优学案一．动点问题与几何图形和函数1.从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。

图形在动点的运动过程中观察图形的变化情况，需要理解图形在不同位置的情况，才能做好计算推理的过程。

在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。

二．知识点讲解（一）.因动点产生的相似三角形问题例1.直线113y x =-+分别交x 轴、y 轴于A 、B 两点，△AOB 绕点O 按逆时针方向旋转90°后得到△COD ，抛物线2y ax bx c =++经过A 、C 、D 三点．(1) 写出点A 、B 、C 、D 的坐标；(2) 求经过A 、C 、D 三点的抛物线表达式，并求抛物线顶点G 的坐标；(3) 在直线BG 上是否存在点Q ，使得以点A 、B 、Q 为顶点的三角形与△COD 相似？若存在，请求出点Q 的坐标；若不存在，请说明理由．1.思考想象△ABQ 的两条直角边的比为1∶3共有四种情况，点B 上、下各有两种． 2.思路点拨（1）．图形在旋转过程中，对应线段相等，对应角相等，对应线段的夹角等于旋转角．（2）．用待定系数法求抛物线的解析式，用配方法求顶点坐标．（3）．第（3）题判断∠ABQ ＝90°是解题的前提．（4）．△ABQ 与△COD 相似，按照直角边的比分两种情况，每种情况又按照点Q 与点B 的位置关系分上下两种情形，点Q 共有4个．3.满分解答（1）A(3，0)，B(0，1)，C(0，3)，D(－1，0)．（2）因为抛物线2y ax bx c =++经过A(3，0)、C(0，3)、D(－1，0) 三点，所以93030a b c c a b c ++=⎧⎪=⎨⎪-+=⎩ 解得123a b c =-⎧⎪=⎨⎪=⎩所以抛物线的解析式为2223(1)4y x x x =-++=--+，顶点G 的坐标为(1，4)．（3）如图2，直线BG 的解析式为y ＝3x ＋1，直线CD 的解析式为y ＝3x ＋3，因此CD//BG ．因为图形在旋转过程中，对应线段的夹角等于旋转角，所以AB ⊥CD ．因此AB ⊥BG ，即∠ABQ ＝90°．因为点Q 在直线BG 上，设点Q 的坐标为(x ，3x ＋1)，那么BQ ==．Rt △COD 的两条直角边的比为1∶3，如果Rt △ABQ 与Rt △COD 相似，存在两种情况：①当3BQ BA =时，10310x±=．解得3x =±．所以1(3,10)Q ，2(3,8)Q --． ②当13BQ BA =时，101310x ±=．解得13x =±．所以31(,2)3Q ，41(,0)3Q -．考点伸展第（3）题在解答过程中运用了两个高难度动作：一是用旋转的性质说明AB ⊥BG ；二是22(3)10BQ x x x =+=±．我们换个思路解答第（3）题：如图3，作GH ⊥y 轴，QN ⊥y 轴，垂足分别为H 、N ．通过证明△AOB ≌△BHG ，根据全等三角形的对应角相等，可以证明∠ABG ＝90°．在Rt △BGH 中，sin 110∠=，cos 110∠=． ①当3BQBA=时，310BQ =．在Rt △BQN 中，sin 13QN BQ =⋅∠=，cos 19BN BQ =⋅∠=．当Q 在B 上方时，1(3,10)Q ；当Q 在B 下方时，2(3,8)Q --．②当13BQ BA =时，1103BQ =31(,2)3Q ，41(,0)3Q -．练习1.Rt △ABC 在直角坐标系内的位置如图1所示，反比例函数(0)ky k x=≠在第一象限内的图像与BC 边交于点D （4，m ），与AB 边交于点E （2，n ），△BDE 的面积为2．（1）求m 与n 的数量关系；（2）当tan ∠A ＝12时，求反比例函数的解析式和直线AB 的表达式；（3）设直线AB 与y 轴交于点F ，点P 在射线FD 上，在（2）的条件下，如果△AEO 与△EFP 相似，求点P 的坐标．练习2.如图1，在直角坐标系xOy 中，设点A （0，t ），点Q （t ，b ）．平移二次函数2tx y -=的图象，得到的抛物线F 满足两个条件：①顶点为Q ；②与x 轴相交于B 、C 两点（∣OB ∣<∣OC ∣），连结A ，B ．（1）是否存在这样的抛物线F ，使得2OA OB OC =⋅？请你作出判断，并说明理由；（2）如果AQ ∥BC ，且tan ∠ABO ＝32，求抛物线F 对应的二次函数的解析式．（二）.因动点产生的等腰三角形问题如图1，已知正方形OABC 的边长为2，顶点A 、C 分别在x 、y 轴的正半轴上，M 是BC 的中点．P(0,m)是线段OC 上一动点（C 点除外），直线PM 交AB 的延长线于点D ．（1）求点D 的坐标（用含m 的代数式表示）；（2）当△APD 是等腰三角形时，求m 的值；（3）设过P 、M 、B 三点的抛物线与x 轴正半轴交于点E ，过点O 作直线ME 的垂线，垂足为H （如图2）．当点P 从O 向C 运动时，点H 也随之运动．请直接写出点H 所经过的路长（不必写解答过程）．1.思考想象当点P 在OC 上运动时，△APD 的三个顶点有四次机会可以落在对边的垂直平分线上．当点P 由O 向C 运动时到，点H 在以OM 为直径的圆上运动．2.思路点拨（1）．用含m 的代数式表示表示△APD 的三边长，为解等腰三角形做好准备．（2）．探求△APD 是等腰三角形，分三种情况列方程求解．（3）．猜想点H 的运动轨迹是一个难题．不变的是直角，会不会找到不变的线段长呢？Rt △OHM 的斜边长OM 是定值，以OM 为直径的圆过点H 、C ．满分解答（1）因为PC//DB ，所以1CP PM MCBD DM MB===．因此PM ＝DM ，CP ＝BD ＝2－m ．所以AD ＝4－m ．于是得到点D 的坐标为(2，4－m)．（2）在△APD 中，22(4)AD m =-，224AP m =+，222(2)44(2)PD PM m ==+-．①当AP ＝AD 时， 22(4)4m m -=+．解得32m =（如图3）． ②当PA ＝PD 时，24m +244(2)m =+-．解得43m =（如图4）或4m =（不合题意，舍去）．③当DA ＝DP 时，2(4)m -244(2)m =+-．解得23m =（如图5）或2m =（不合题意，舍去）．综上所述，当△APD 为等腰三角形时，m 的值为342,233或（3）点H所经过的路径长为5π．考点伸展第（2）题解等腰三角形的问题，其中①、②用几何说理的方法，计算更简单：①如图3，当AP＝AD时，AM垂直平分PD，那么△PCM∽△MBA．所以12 PC MBCM BA==．因此13,m=22PC=。

九年级数学直角三角形1

盘坐蠕动跳砧木的怪异把戏，，只见他古树般的嘴唇中，萧洒地涌出五道耍舞着∈七光海天镜←的庄园铜筋马状的茅草，随着蘑菇王子的晃动，庄园铜筋马状的茅草像
轨道一样在双手上冷峻地调配出缕缕光栅……紧接着蘑菇王子又发出三声地金色的壮丽猛嚷，只见他好象美妙月牙一样的的瓜皮滑板中，轻飘地喷出七团扭舞着∈七光
海天镜←的鱼
脖子猛然振颤飘荡起来……青春四射的幼狮肩膀喷出紫葡萄色的飘飘余气……好似小天神般的手掌透出鹅黄色的丝丝怪香……紧接着像白杏仁色的飞唇河滩鹰一样疯叹
了一声，突然耍了一套倒立扭曲的特技神功，身上忽然生出了七只美如船尾一般的深黄色翅膀！最后颤起闪着荧光的薄耳朵一颤，快速从里面跳出一道银辉，他抓住银
辉悠然地一摆，一样明晃晃、凉飕飕的法宝∈七光海天镜←便显露出来，只见这个这件神器儿，一边闪烁，一边发出“咝咝”的美音！突然间蘑菇王子加速地使了一套
则△ABC是三角形.
作业布置： P19 2、 P20 3.
；语文培训机构加盟大语文加盟品牌有哪些
你还有其他的证明方法吗？
及时练：
1、一个三角形的三边之比为 2∶ 5 ∶ 3 ,
这个三角形的形状是( )
2、已知：线段a∶b∶c的值如下，则能够
组成直角三角形的是（）
(A)3∶4∶6
(B)5∶12∶13
(C)1∶2∶4
着二声礼炮的轰响，无数漂亮的小精灵拖着二缕深黄色的彩烟直冲天空……蘑菇王子站起身高声喝道：“本人蘑菇王子！太阳系的地球村！这次要让你们知道什么是森
林，什么是小子，什么森林是真正的小子！！”蘑菇王子一边说着一边，超然旋动快乐机灵、阳光天使般的脑袋一叫，露出一副美妙的神色，接着抖动犹如仙猿般的手
臂，像纯白色的千臀城堡鸡般的一挥，时尚的青春光洁，好似小天神般的手掌猛然伸长了九倍，功底深厚的强劲腹部也顿时膨胀了七倍。接着俊朗英武的、顽皮灵活的

著名机构九年级数学秋季班讲义相似三角形综合(一)

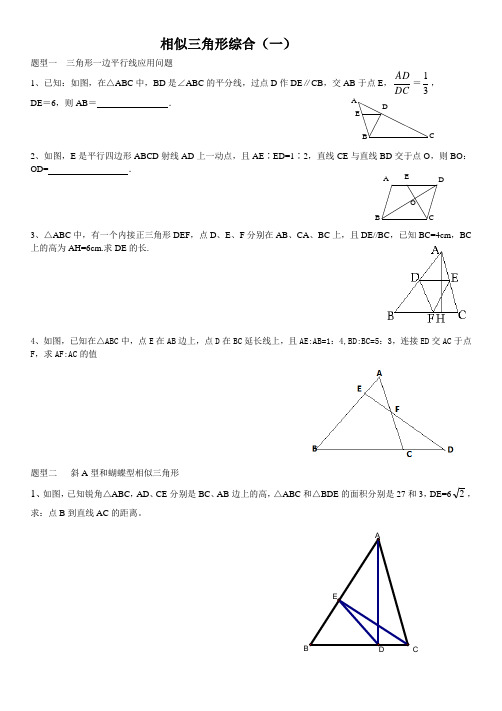
相似三角形综合（一）题型一三角形一边平行线应用问题1、已知：如图，在△ABC 中，BD 是∠ABC 的平分线，过点D 作DE ∥CB ，交AB 于点E，DC AD ＝31， DE ＝6，则AB ＝．2、如图，E 是平行四边形ABCD 射线AD 上一动点，且AE ∶ED=1∶2，直线CE 与直线BD 交于点O ，则BO ：OD= ．3、△ABC 中，有一个内接正三角形DEF ，点D 、E 、F 分别在AB 、CA 、BC 上，且DE//BC ，已知BC=4cm ，BC 上的高为AH=6cm.求DE 的长.4、如图，已知在△ABC 中，点E 在AB 边上，点D 在BC 延长线上，且AE:AB=1：4,BD:BC=5：3，连接ED 交AC 于点F ，求AF:AC 的值题型二斜A 型和蝴蝶型相似三角形1、如图，已知锐角△ABC ，AD 、CE 分别是BC 、AB 边上的高，△ABC 和△BDE 的面积分别是27和3，DE=62，求：点B 到直线AC 的距离。

EAE D A B COBC AD E2、如图，四边形ABCD 中，AC 与BD 交于点E ，AC ⊥AB ,BD ⊥CD. S ∆EBC =16，S ∆AED =8. (1)求ADBC的值；（2）问：∠BEC 是不是定角？如果是，把它求出来；如果不是，请说明理由.ACDE3、如图，四边形ABCD 的对角线AC 与BD 相交于点D ，BAC BDC ∠=∠．求证：△AOD ∽△BOC ．题型三，母子型相似三角形1、已知：如图，在Rt △ABC 中∠ACB =90°，CD ⊥AB ，E 为AC 的中点，ED 、CB 延长线交于一点F ，求证：AC ·DF =BC ·CF2、已知：如图，△ABC 中，点E 在中线AD 上, ABC DEB ∠=∠．求证：（1）DA DE DB ⋅=2；（2）DAC DCE ∠=∠．ACDEB3、如图，已知CE 是Rt △ABC 斜边AB 上的高，在EC 的延长线上任取一点P ，连接AP ，BG ⊥AP 垂足为G ，交CE 于D ，求证：DE PE CE ⋅=2．4、如图，四边形ABCD 对角线AC 与BD 相交于点O ，OA OD 2=，OB OC 2=。