第二十六章二次函数测试题

合集下载

九年级第二十六章二次函数测试题

第二十六章二次函数测试题一、选择题（每题3分，共30分）1，函数y ＝x 2－4的图象与y 轴的交点坐标是（）A.（2，0）B.（－2，0）C.（0，4）D.（0，－4）2，在平面直角坐标系中，抛物线21y x =-与x 轴的交点的个数是（） A ．3 B ．2 C ．1 D ．03，抛物线经过第一、三、四象限，则抛物线的顶点必在（）A.第一象限B.第二象限C.第三象限D.第四象限4，二次函数362+-=x kx y 的图象与x 轴有交点，则k 的取值范围是【】 A ．3<k B ．03≠<k k 且 C ．3≤k D ．03≠≤k k 且 5，已知反比例函数y ＝kx 的图象在每个象限内y 随x 的增大而增大，则二次函数y ＝2kx 2－x +k 2的图象大致为如图2中的（）6，二次函数y ＝ax 2+bx +c 的图象如图3，则点（b ，ca）在（）A.第一象限B.第二象限C.第三象限D.第四象限7，某公司的生产利润原来是a 元，经过连续两年的增长达到了y 万元，如果每年增长的百分数都是x ，那么y 与x 的函数关系是（）A.y ＝x 2+aB.y ＝a (x －1)2C.y ＝a (1－x )2D.y ＝a (l+x )28，若二次函数y ＝ax 2+bx +c ，当x 取x 1，x 2（x 1≠x 2）时，函数值相等，则当x 取（x 1+x 2）时，函数值为（）A.a +cB.a －cC.－cD.c 9，不论m 为何实数，抛物线y ＝x 2－mx ＋m －2（）A.在x 轴上方B.与x 轴只有一个交点C.与x 轴有两个交点D.在x 轴下方10，若二次函数y ＝x 2－x 与y ＝－x 2+k 的图象的顶点重合，则下列结论不正确的是（）A.这两个函数图象有相同的对称轴B.这两个函数图象的开口方向相反C.方程－x 2+k ＝0没有实数根D.二次函数y ＝－x 2＋k 的最大值为12二、填空题（每题3分，共30分）11，顶点为（－2，－5）且过点（1，－14）的抛物线的解析式为＿＿＿. 12，若点A (2，m )在抛物线y ＝x 2上，则点A 关于y 轴对称点的坐标是＿＿＿.13，二次函数y ＝2x 2+bx +c 的顶点坐标是(1，－2).则b ＝＿＿＿，c ＝＿＿＿.14，已知二次函数y ＝ax 2+bx +c (a ≠0）与一次函数y ＝kx +m (k ≠0）的图象相交于点A （－2，4），B (8，2)，如图4所示，能使y 1＞y 2成立的x 取值范围是＿＿＿.15，y 与x 的函数表达式为＿＿＿.16，平移抛物线y ＝x 2+2x －8，使它经过原点，写出平移后抛物线的一个解析式＿＿＿.17，抛物线y ＝ax 2+bx+c 中，已知a∶b ∶c ＝l ∶2∶3，最小值为6，则此抛物线的解析式为＿＿＿.18，把一根长100cm 的铁丝分为两部分，每一部分均弯曲成一个正方形，它们的面积和最小是＿＿＿.19．已知二次函数2)(22＋－＋＝x m m mx y 的图象关于y 轴对称，则m ＝________．20．一男生推铅球，铅球行进高度y （m ）与水平距离x （m ）之间的关系是y ＝－2121x＋x32＋35，则铅球推出的水平距离为______________m ．图4图2图3图1三、解答题21，已知抛物线与x轴交于点(1，0)和(2，0)且过点 (3，4).求抛物线的解析式.22，当x＝4时，函数y＝ax2+bx+c的最小值为－8，抛物线过点（6，0）．求：（1）顶点坐标和对称轴；（2）函数的表达式；（3）x取什么值时，y随x的增大而增大；x取什么值时，y随x增大而减小.23．已知抛物线y＝－x2＋5x＋n经过点A（1，0），与y轴交于B点，（1）求抛物线解析式；（2）P是y轴正半轴上一点，且△PAB是以AB为腰的等腰三角形，求P点坐标．24，某通讯器材公司销售一种市场需求较大的新型通讯产品．已知每件产品的进价为40元，每年销售该种产品的总开支（不含进价）总计120万元．在销售过程中发现，年销售量y（万件）与销售单价x（元）之问存在着如图6所示的一次函数关系.（1）求y关于x的函数关系式；（2）试写出该公司销售该种产品的年获利z（万元）关于销售单价x（元）的函数关系式（年获利＝年销售额一年销售产品总进价一年总开支）．当销售单价x为何值时，年获利最大？并求这个最大值；25已知，如图二次函数的图象与x轴两交点A，B间的距离为8，顶点为C，此二次函数的图象与y轴的交点的纵坐标为6，且△ABC的面积为32，求此二次函数的解析式．图6)(第25题)26、已知二次函数的图像过点（3，-8），对称轴为直线x=-2，函数与x 轴的两个交点的距离为6，求：（1）图像与x轴的两个交点A、B（A在B的左边）的坐标（2）函数图像与y轴交点C的坐标及顶点P的坐标（3）求四边形PABC的面积27、抛物线y=ax2-5ax+4a与x轴相交于点A、B，且过点C（5,4）（1）求a的值和抛物线顶点P的坐标（2）请你设计一种平移的方法，使平移后抛物线的顶点落在第二象限，并写出平移后抛物线的解析式28、在平面直角坐标系中，抛物线过A（-1,0），B（3,0）C（0，-1）三点。

2023年华东师大版九年级数学下册第二十六章《二次函数》复习检测卷附答案解析

2023年九年级数学下册第二十六章《二次函数》复习检测卷一、单项选择。

1．在平面直角坐标系中，将二次函数y＝(x－1)2＋1的图象向左平移1个单位长度，再向下平移2个单位长度，所得函数的表达式为()A．y＝(x－2)2－1B．y＝(x－2)2＋3C．y＝x 2＋1D．y＝x 2－12．关于二次函数y＝－3x 2＋6x＋1，下列说法错误的是()A．图象与y 轴的交点坐标为(0，1)B．图象的对称轴在y 轴的右侧C．当x＞0时，y 的值随x 值的增大而减小D．y 的最大值为43．如图，抛物线L 1：y＝ax 2＋bx＋c(a≠0)与x 轴只有一个公共点A(1，0)，与y 轴交于点B(0，2)，虚线为其对称轴，若将抛物线向下平移两个单位长度得抛物线L 2，则图中两个阴影部分的面积和为()A．1B．2C．3D．44．如图，抛物线y＝ax 2＋bx＋c 与x 轴相交于点A(－2，0)，B(6，0)，与y 轴相交于点C，小红同学得出了以下结论：①b 2－4ac＞0；②4a＋b＝0；③当y＞0时，－2＜x＜6；④a＋b＋c＜0.其中正确的个数为()A．4B．3C．2D．15．抛物线y＝ax 2＋bx＋c 上部分点的横坐标x，纵坐标y 的对应值如下表：下列结论不正确的是()x －2－101y466A．抛物线的开口向下B．抛物线的对称轴为直线x＝12C．抛物线与x 轴的一个交点坐标为(2，0)D．函数y＝ax 2＋bx＋c 的最大值为2546．若函数y＝mx 2＋(m＋2)x＋12m＋1的图象与x 轴只有一个交点，那么m 的值为()A．0B．0或2C．2或－2D．0，2或－27．已知二次函数y＝ax 2＋2ax＋3a 2＋3(其中x 是自变量)，当x≥2时，y 随x 的增大而增大，且－2≤x ≤1时，y 的最大值为9，则a 的值为()A．1或－2B．－2或2C．2D．18．二次函数y＝ax 2＋bx＋c 的部分图象如图所示，则下列选项错误的是()A.若(－2，y 1)，(5，y 2)是图象上的两点，则y 1＞y 2B．3a＋c＝0C．方程ax 2＋bx＋c＝－2有两个不相等的实数根D.当x≥0时，y 随x 的增大而减小9.二次函数y＝ax 2＋bx＋c 的图象如图所示，对称轴是直线x＝－1，有以下结论：①abc＞0；②4ac＜b 2；③2a＋b＝0；④a－b＋c＞2.其中正确的结论的个数是()A．1个B．2个C．3个D．4个10．如图，函数y＝ax 2－2x＋1和y＝ax－a(a 是常数，且a≠0)在同一平面直角坐标系的图象可能是()11．已知二次函数y＝x 2－2ax＋a 2－2a－4(a 为常数)的图象与x 轴有交点，且当x＞3时，y 随x 的增大而增大，则a 的取值范围是()A．a≥－2B．a＜3C．－2≤a＜3D．－2≤a≤312.若二次函数y＝x 2－6x＋c 的图象经过A(－1，y 1)，B(2，y 2)，C(3＋2，y 3)三点，则关于y 1，y 2，y 3大小关系正确的是()A．y 1＞y 2＞y 3B．y 1＞y 3＞y 2C．y 2＞y 1＞y 3D．y 3＞y 1＞y 213．已知a＞1，点A(a－1，y 1)，B(a，y 2)，C(a＋1，y 3)都在二次函数y＝12－x 2的图象上，则()A．y 1＞y 2＞y 3B．y 1＞y 3＞y 2C．y 2＞y 1＞y 3D．y 3＞y 1＞y 214．已知y＝ax 2＋k 的图象上有三点A(－3，y 1)，B(1，y 2)，C(2，y 3)，且y 2＜y 3＜y 1，则a 的取值范围是()A．a＞0B．a＜0C．a≥0D．a≤015.如图，二次函数y＝ax 2＋bx(a≠0)的图象过点(2，0)，下列结论错误的是()A．b＞0B．a＋b＞0C．x＝2是关于x 的方程ax 2＋bx＝0(a≠0)的一个根D．点(x 1，y 1)，(x 2，y 2)在二次函数的图象上，当x 1＞x 2＞2时，y 2＜y 1＜0二、填空题。

第二十六章二次函数测试题

第二十六章二次函数测试题Revised by Jack on December 14,2020第二十六章二次函数一、填空题1．抛物线y ＝－x 2＋2的顶点坐标是________，对称轴是________，开口向________． 2．把抛物线y ＝3x 2 沿x 轴向________平移________个单位即可得到抛物线y ＝3(x －1)2；把抛物线y ＝3x 2 沿y 轴向________平移________个单位即可得到抛物线y ＝3x 2＋2．3．抛物线y ＝x 2－3x 与x 轴的交点坐标是________________________．抛物线y ＝－x 2＋3x －5与y 轴的交点坐标是____________．4．抛物线y ＝2(x －3)2＋5，当x ＜________时，y 的值随x 值的增大而________，当x ＞________时，y 的值随 x 值的增大而________；当x ＝________时，y 取得最________值，最________值＝________．5．已知二次函数y ＝－4x 2－2mx ＋m 2与反比例函数y ＝xm 42 的图象在第二象限内的一个交点的横坐标是－2，则m 的值是．6．函数362＋－＝x x y k 的图象与x 轴有交点，则k 的取值范围是． 7．抛物线y ＝ax 2＋bx ＋c (a ≠0)过第二，三，四象限，则a 0，b 0，c 0． 8．顶点为（－2，－5）且过点（1，－14）的抛物线的解析式为．9．对称轴是y 轴且过点A （1，3），点B （－2，－6）的抛物线的解析式为．顶点坐标为______________．10．已知二次函数232)1(2－＋＋－＝m mx x m y ，则当m ＝时，其最大值为0． 11．若二次函数2223m m x mx y －＋－＝的图象经过原点，则m ＝_________． 12．已知二次函数2)(22＋－＋＝x m m mx y 的图象关于y 轴对称，则m ＝________．13．抛物线y ＝3x 2－6x ＋5化成顶点式是______________，当x _____时，y 随x 的增大而减少；当x _____时，y 随x 的增大而增大．14．一男生推铅球，铅球行进高度y （m ）与水平距离x （m ）之间的关系是y ＝－2121x ＋x 32＋35，则铅球推出的水平距离为______________m ．二、选择题1．二次函数y ＝x 2－(12－k )x ＋12，当x ＞1时，y 随着x 的增大而增大，当x ＜1时，y 随着x 的增大而减小，则k 的值应取（）．A ．12B ．11C ．10D ．92．下列四个函数中，y 的值随着x 值的增大而减小的是（）． A ．y ＝2xB ．xy 1＝(x ＞0)C ．1＋＝x yD ．2x y ＝(x ＞0)3．如果抛物线y ＝x 2－6x ＋c －2的顶点到x 轴的距离是3，那么c 的值等于（）． A ．8B ．14C ．8或14D ．－8或－144．当a ＞0，b ＜0，c ＞0时，下列图象有可能是抛物线y ＝ax 2＋bx ＋c 的是（）．5．不论x 为何值，函数y ＝ax 2＋bx ＋c （a ≠0）的值恒大于0的条件是（）． A ．a ＞0，Δ＞0B ．a ＞0，Δ＜0C ．a ＜0，Δ＜0D ．a ＜0，Δ＜0 6．二次函数y ＝ax 2＋bx ＋c 的图象如图所示，则abc ，b 2－4ac ，2a ＋b ，a ＋b ＋c 这四个式子中，值为正数的有（）．A ．4个B ．3个C ．2个D ．1个三、解答题1．根据条件求二次函数的解析式：(第6题)（1）抛物线过（－1，0），（3，0），（1，－5）三点，并求出x在2≤x≤4范围内的最大或最小值．（2）抛物线在x轴上截得的线段长为4，且顶点坐标是（3，－2）．（3）二次函数的图象经过点（－1，0），（3，0），且最大值是3．2．已知点A（－2，－c）向右平移8个单位得到点A'，A与A'两点均在抛物线y＝ax2＋bx＋c上，且这条抛物线与y轴的交点的纵坐标为－6，求这条抛物线的顶点坐标．3．如图有一座抛物线形拱桥，桥下面的正常水位时AB宽20 m，水位上升3 m就达到警戒线CD，这时水面宽度为10 m．（1）在如图的坐标系中求抛物线的解析式．（2）若洪水到来时，水位以每小时0.2 m的速度上升，从警戒线开始，再持续多少小时水到拱桥顶(第3题)4．已知抛物线y＝－x2＋5x＋n经过点A（1，0），与y轴交于B点，（1）求抛物线解析式；（2）P是y轴正半轴上一点，且△PAB是以AB为腰的等腰三角形，求P点坐标．(第4题)5．已知，如图二次函数的图象与x轴两交点A，B间的距离为8，顶点为C，此二次函数的图象与y轴的交点的纵坐标为6，且△ABC的面积为32，求此二次函数的解析式．(第5题)6．如图，对称轴为直线x＝的抛物线经过点A（6，0）和B（0，4）．（1）求抛物线解析式及顶点坐标；（2）设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形．求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；①当平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形②是否存在点E，使平行四边形OEAF为正方形若存在，求出点E的坐标；若不存在，请说明理由．(第6题)第二十六章二次函数参考答案一、填空题：1．（0，2），y 轴，下．解析：顶点坐标x ＝－）（120-⨯＝0，y ＝)1(42)1(4-⨯⨯-⨯＝2，a ＝－1＜0，开口向下．2．右，1，上，2．解析：由y ＝3(x －1)2可知将y ＝3x 2的图像右移1个单位即可得到；y ＝3x 2＋2可由 y ＝3x 2的图像向上平移2个单位即得．3．（0，0），（3，0），（0，－5）．解析：令y ＝0，x 2－3x ＝0，x 1＝0，x 2＝3；与x 轴的交点（0，0），（3，0）；当x ＝0时，y ＝－5，与y 轴的交点（0，－5）．4．3，减小，3，增大，3，小，小，5．解析：该抛物线的开口向上，对称轴为x ＝3，当x ＜3时y 随x 的增大而减小；当x ＞3时y 随x 的增大而增大；x ＝3时，y 有最小值5．5．－7．解析：y ＝242-＋m ，y ＝－4×(－2) 2－2m (－2)＋m 2，∵ y 1＝y 2，化简得m 2＋5m －14＝0，∴ m 1＝－7，m 2＝2，反比例函数在第二，四象限，2m ＋4 ＜0，∴ m ＝2舍去．6．k ≤3．解析：Δ＝36－12k ≥0． 7．＜，＜，＜．解析：抛物线开口向下，则a ＜0，而－ab2＜0，则b ＜0，c ＜0． 8．y ＝－(x ＋2)2－5＝－x 2－4x －9．解析：y ＝a (x ＋2)2－5，当x ＝1时，y ＝－14，－14＝9a －5，a ＝－1． 9．y ＝－3x 2＋6，（0，6）．解析：设y ＝ax 2＋k ，a ＋k ＝3，4a ＋k ＝－6可解得a ＝－3，k ＝6，y ＝－3x 2＋6． 10．21．解析：)1(4)2()23)(1(42----m m m m ＝0，m 1＝21，m 2＝2，又m －1＜0， ∴ m ＜1，∴ m ＝21． 11．2．解析：当x ＝0时，y ＝0，2m －m 2＝0，m 1＝0（舍去），m 2＝2． 12．1．解析：抛物线关于y 轴对称，则b ＝0. 令m 2－m ＝0得m ＝1或m ＝0（舍去）． 13．y ＝3(x －1)2＋2，＜1，＞1．解析：y ＝3x 2－6x ＋5＝3(x －1)2＋2 ，对称轴：直线x ＝1． 14．10．解析：当y ＝0时，－121x 2＋32x ＋35＝0，x 1＝10，x 2＝－2（舍去）．二、选择题 1．C 解析：∵ a b2-＝－2)12(k --＝212k -＝1，∴ k ＝10． 2．B解析：参考4个函数的图象，y ＝x1(x ＞0)满足要求． 3．C解析：y ＝(x －3)2＋c －11，∴ 11-c ＝3，∴ c 1＝14或c 2＝8． 4．A解析：∵ a ＞0，b ＜0， ∴ －a b2＞0，抛物线的顶点可能在第一或第四象限，而c ＞0，则A 图满足条件．5．B解析：图象开口向上，且与x 轴无交点，所以a ＞0且Δ＜0． 6．B解析：∵ a ＞0，a b 2-＞0，c ＜0．∴ a ＞0，b ＜0，c ＜0，∴ abc ＞0，又∵ ab2-＜1， ∴ab2＞－1，b ＞－2a ，即2 a ＋b ＞0．又图像与x 轴有两个交点，∴Δ＞0．当x ＝1时，y ＝a ＋b ＋c ＜0． ∴ 四个式子中，值为正数的有3个．三、解答题1．（1）解：设抛物线解析式为y ＝a (x ＋1)(x ＋3)． ∵ 当x ＝1时，y ＝－5， ∴（1＋1）（1－3）a ＝－5， ∴ a ＝45．∴ y ＝45(x ＋1)(x －3)＝45x 2－25x －415＝45(x －1) 2－5．当x ＞1时，y 随x 增大而增大． ∴ 当x ＝2时，y 最小＝－415；当x ＝4时，y 最大＝425． ∴ 当2≤x ≤4时，函数最小值为－415，最大值为425．（2）解：设抛物线与x 轴交于点A （x 1，0）B (x 2，0)，x 1＜x 2． ∵ 顶点（3，－2），AB ＝4， ∴ A （1，0），B （5，0）．设抛物线y ＝a (x －1)(x －5) ．当x ＝3时，y ＝－2． ∴ a (3－1)(3－5)＝－2． ∴ a ＝21．∴ y ＝21（x －1）（x －5）＝21x 2－3x ＋25．（3）解：∵ 二次函数图像经过点（－1，0），（3，0）， ∴ 对称轴是直线 x ＝231+-＝1． ∴ 顶点坐标是（1，3）．设抛物线解析式为y ＝a (x －1) 2＋3． ∵ 当 x ＝－1时，y ＝0， ∴ (－1－1) 2a ＋3＝0． ∴ a ＝－43，∴ y ＝－43(x －1) 2＋3．2．解：由题意：A ′（－2＋8，－c ）即A ′（6，－c ）． ∴ 4a －2b ＋c ＝－c ，36a ＋6b ＋c ＝－c ，c ＝－6，解得a ＝1，b ＝－4，c ＝－6． ∴ y ＝x 2－4x －6＝(x －2) 2－10． ∴ 顶点坐标是（2，－10）．3．解：（1）设AB ，CD 分别交y 轴于点E ，F ．则DF ＝21CD ＝5，EB ＝21AB ＝10．设D （5，m ），则B （10，m －3）．设抛物线解析式为y ＝ax 2（a ≠0）． ∴ 25a ＝m ，100a ＝m －3． ∴ a ＝－251，m ＝－1． ∴ y ＝－251x 2．（2）由（1）得m ＝－1，∴ OF ＝1，2.01＝5（小时）．答：从警戒线开始，再持续5小时水到拱桥顶． 4．解：（1）∵ 抛物线过线A （1，0），∴ －1＋5＋n ＝0．∴ n ＝－4．∴ y ＝－x 2＋5x －4．（2）由（1）得：B （0，－4），∵ P 是y 轴正半轴上一点， ①若AP ＝AB ，则OP ＝OB ＝4，∴ P 1（0，4）．②若BA ＝BP ，则BP ＝2241 ＝17，∴ OP ＝17－4，∴ P 2（0，17－4）．∴ P 1（0，4），P 2（0，17－4）为所求P 点．5．解：设顶点C （h ，k ）．∵ S △ABC ＝32，∴ 21A B ×EC ＝32．∴ 21×8×（－k ）＝32，k ＝－8．∵ A ，B 间的距离是8，∴ A （h －4，0），B （h ＋4，0）．设抛物线为y ＝a (x －h ) 2＋k ．则y ＝a (x －h ) 2－8．∵ 点A 在抛物线上，∴ a (h －4－h ) 2－8＝0．∴ a ＝21．∴ y ＝21(x －h ) 2－8．又∵ D (0，6)是抛物线与y 轴的交点，∴ 21h 2－8＝6，∴ h ＝±27．∵ h ＞0，∴ h ＝27．∴ y ＝21(x －27)2－8．6．解：（1）设抛物线y ＝ax 2＋bx ＋c (a ≠0)．由题意得－a b 2＝27，36a ＋6b ＋c ＝0，c ＝4． ∴ a ＝32，b ＝－314，c ＝4． ∴ y ＝32x 2－314x ＋4＝32(x －27)2－625． ∴ 顶点坐标（27，－625）．（2）∵点E （x ，y ）在抛物线上，位于第四象限，且坐标适合y ＝32(x －27)2－625， ∴ y ＜0，即－y ＞0，－y 表示点E 到OA 的距离．∵ OA 是平行四边形OEAF 的对角线，∴ S ＝2S △OAE ＝2×21OA ×y ＝－6y ＝－4(x －27)2＋25． ∵ 抛物线与x 轴交于（1，0），（6，0），∴ 0＜x ＜6．当S ＝24时，－4(x －27)2＋25＝24．解得x 1＝3，x 2＝4．∴ E 1（3，－4），E 2（4，－4）．①当E 1（3，－4）时，OE ＝AE ，∴平行四边形OEAF 是菱形．当E 2（4，－4）时，OE ≠AE ，∴平行四边形OEAF 不是菱形． ②不存在．当OA ⊥EF 且OA ＝EF 时，平行四边形OEAF 是正方形．此时点E 的坐标只能是（3，－3），但点（3，－3）不在抛物线上，∴ 不存在这样的点，使平行四边形OEAF 是正方形．。

九年级第26章《二次函数》测试题(含答案)

第26章《二次函数》检测题（全卷共五个大题，满分150分，考试时间120分钟）抛物线)0(2≠++=a c bx ax y 的顶点坐标为)44,2(2a b ac a b --一、选择题（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将正确答案的代号填在答题卷中相应的位置上.1．由二次函数1)3(22+-=x y ，可知（）A ．其图象的开口向下B ．其图象的对称轴为直线3-=xC ．其最小值为1D ．当3<x 时，y 随x 的增大而增大2、k 为任何实数，则抛物线y ＝2(x ＋k)2－k 的顶点在（）上A 、直线y=x 上，B 、直线y= -xC 、x 轴D 、y 轴3、0=+q p ，抛物线q px x y ++=2必过点（）A 、（-1，1）B 、（1，-1）C 、（-1，-1）D 、（1，1） 4、已知点(3，1y ),(4，2y ), (5，3y )在函数y=2x 2+8x+7的图象上,则y 1,y 2,y 3的大小关系是( )A 、y 1>y 2>y 3B 、y 2> y 1> y 3C 、y 2>y 3> y 1D 、y 3> y 2> y 15．将抛物线23y x =向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（）A ．23(2)3y x =++B ．23(2)3y x =-+C ．23(2)3y x =+-D ．23(2)3y x =--6、抛物线234y x x =--+与坐标轴的交点个数是（）A ． 0B ．1C ． 2D ． 37、若点(2，5)，(4，5)在抛物线y ＝ax 2＋bx ＋c 上，则它的对称轴是( )A ．ab x -= B ．x ＝1 C ．x ＝2 D ．x ＝3 8．二次函数c bx ax y ++=2的图象如右上图所示，则abc ，ac b 42-，b a +2，cb a ++这四个式子中，值为正数的有（）A ． 4个B ．3个C ．2个D ．1个 9、如图是二次函数y=ax 2+bx+c 的部分图象，由图象可知不等式ax 2+bx+c ＜0的解集是（）A．﹣1＜x＜5 B．x＞5 C．x＜﹣1且x＞5 D．x＜﹣1或x＞5 10．已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（﹣1，0），（3，0）．对于下列命题：①b﹣2a=0；②abc＜0；③a﹣2b+4c＜0；④8a+c＞0．其中正确的有（）A．3个B．2个C．1个D．0个卷相应位置的横线上．11：抛物线422-+=xxy的对称轴是________,顶点坐标是_________；12．已知二次函数2(0)y ax bx c a=++≠的顶点坐标(1, 3.2)--及部分图象（如图1所示），由图象可知关于x的一元二次方程20ax bx c++=的两个根分别是11.3x=和2x=。

九年级数学第26章二次函数单元检测题

九年级数学第26章二次函数单元检测题某某学号一、选择题：（每题3分，共30分） 1、下列函数中,是二次函数的是( )A.y=x 2+1 B.y=-x+1; C.y=8x D.y=21x2、开口向上，顶点坐标为（－9,3）的抛物线为（）。

A 、y=2(x －9)2+3B 、y=2(x+9)2+3C 、y=－2(x －9)2－3D 、y=－2(x+9)2+33、把抛物线y=3x 2先向上平移2个单位，再向右平移3个单位，所得抛物线的解析式是（）（A ）y=3（x+3）2 -2 （B ）y=3（x+2）2+3 （C ）y=3（x-3）2 -2 （D ）y=3（x-3）2+24、二次函数y=x 2＋4x ＋a 的最小值是2，则a 的值是（） A 、4 B 、5 C 、6 D 、75、抛物线122+-=x x y 则图象与x 轴交点个数为（） A ． 1个 B ． 2个 C ． 0个 D ．不能确定6、二次函数c bx ax y ++=2的图象如右图所示，则下列结论中正确的是：（）A a>0 b<0 c>0B a<0 b<0 c>0C a<0 b>0 c<0D a<0 b>0 c>0 7、二次函数y=x 2－4x+3的图象交x 轴于A 、B 两点，交y 轴于C 点，则△ABC 的面积是（） A 、6 B 、4 C、3 D 、18、二次函数y=ax2+bx+c 的值永远为正值的条件是( )A.a>0,b 2-4ac<0B.a<0,b 2-4ac>0C.a>0,b 2-4ac>0D.a<0,b 2-4ac<09、已知二次函数2(0)y ax bx c a =++≠的图象如右图所示，给出以下结论： ① 0a b c ++<；② 0a b c -+<；③20b a +<；④0abc >.其中所有正确结论的序号是（）A. ③④B. ②③C. ①④D. ①②10、在同一坐标系中一次函数y ax b =+和二次函数2二、填空题（每题3分，共30分）11．若72)3(--=m x m y 是二次函数，则m=。

第26章二次函数单元测试(人教版九年级)!.docx

第二十六章检测二次函数时间：90分钟满分：100分一、选择题（每小题3分，共30分）（2010,金华中考）已知抛物线）,=0?+加的开口向下，顶点坐标为（2,宁夏中考）把抛物线j = -^2向左平移1个单位，然后向上平移3个单位，则平移后抛物线的表达式（） -3），那么该抛物线有（ A.最小值一3 ）B.最大值一3C.最小值2D.最大值22、（2010,安徽中考）若二次函数y =川+加+ 5配方后为〉,=（兀_ 2尸+ R ,则b 、比的值分别为（ A 、0. 5 0. 13、（2010,河北中考）如图5,已知抛物线y = x 2+bx + c 的对称轴为"2,点力, 2均在抛物线上，且〃〃与x 轴平行，其中点力的坐标为（0, 3）,则点〃的坐标为A. （2, 3）B. （3, 2）C. （3, 3）D. （4, 3）4、（2010,芜湖中考）二次函数y 二曰#+bx+c 的图象如图所示，反比例函数尸纟与正比例函数y 二（b+c ）x 在同一坐 )C 、一4. 5D 、一4. 12y 万元，则y 与x Z 间的函数表达式为（）A. y 二60 （1-x ） 2B. y=60 （1一x ）C. y=60-x 2D. y=60 （1 + 7、某幢建筑物，从10m 高的窗口 A 用水管向外喷水，喷出的水成抛物线状（抛物线所在平面与地面垂直）。

如果抛物线的最高40 lm ,离地面—则水流落地点离墙的距离0B 为 3 点M 离墙 ( )A. 2mB. 3mC. 4mD. 5m x) 21、 8、 (2010,B A I I y ：x = 2 O 图5是（）A. y=^2x +x+2B. y^x +3x+2C. y^x~2x+3D. y=x~3x+2.6、一台机器原价为60万元，如果每年的折旧率为x,两年后这台机器的价位为A. y = —(x_l)_+3B. y =—(兀 + 1)_+3C. y = _(无一1)~—3D. y = —(x +1)~ ~ 39、已知二次函数y = x 2 - 2twc + m- 1的图象经过原点，与兀轴的另一个交点A,抛物线的顶点为B,则AOAB 的面积为（）3 1A 、一B 、 2C 、 1D 、一 2 210、已知函数尸2x — 2的图象如图示，根据其中提供的信息，可求得使成立的x 的取值范围是（）A 、一1W/W3B 、一3MW1C 、心一3D 、穴一1 或心3.二、填空题（每题3分，共30分）11 > 把y=£-4x-4转化成 y = a(x- h)2 + k 形式 _________12、 ____________________________________________________ 抛物线y = x 2-4x + m 与x 轴只有一个交点，则in 二 __________________________ 。

华师大版九年级数学下《第26章二次函数》测试题含答案

二次函数测试题一、选择题（每小题3分，共30分）1. 下列函数不属于二次函数的是（）A.y=(x －1)(x+2)B.y=21(x+1)2 C. y=1－3x 2D. y=2(x+3)2－2x 22．给出下列四个函数：x y 2-=，12-=x y ，32+-=x y （x >0），其中y 随x •的增大而减小的函数有（）A ．3个B ．2个C ．1个D ．0个 3. 把二次函数2114y x x =+-化为()k h x a y ++=2的形式是（） A ．21(1)24y x =++ B ．21(2)24y x =+-C ．21(2)24y x =-+D ．21(2)24y x =--4. 下列说法错误的是（）A ．二次函数y=3x 2中，当x>0时，y 随x 的增大而增大 B ．二次函数y=－6x 2中，当x=0时，y 有最大值0 C ．a 越大图象开口越小，a 越小图象开口越大D ．不论a 是正数还是负数，抛物线y=ax 2(a ≠0)的顶点一定是坐标原点 5．二次函数227y x x =-＋，当y=8时，对应的x 的值是（）A.3B.5C.－3或 5D.3和－56．二次函数24y x x =－的对称轴是（）A ．2x =-B ．4x =C ．2x =D ．4x =-7．如果将抛物线22y x =+向下平移1个单位，那么所得新抛物线的解析式是（）A. 2(1)2y x =-+ B. 2(1)2y x =++ C. 21y x =+ D. 23y x =+8. 若二次函数2()1y x m =--．当x ≤l 时，y 随x 的增大而减小，则m 的取值范围是（） A ．m =l B ．m >l C ．m ≥l D ．m ≤l9．如图，两条抛物线12121+-=x y 、12122--=x y 与分别经过点(-2，0)，(2，0)且平行于y 轴的两条平行线圈成的阴影部分的面积为 ( ) A ．6 B.8 C.10 D.1210．函数y=x 2+bx+c 与y=x 的图象如图所示，有以下结论：①b 2﹣4c ＞0；②b+c+1=0；③3b+c+6=0； ④当1＜x ＜3时，x 2+（b ﹣1）x+c ＜0．其中正确的个数为（）A ．1 B.2 C.3 D.4二、填空题（每小题4分，共32分）11.已知抛物线 82++=kx x y 过点（2，-8)，则=k . 12.抛物线21(4)52y x =-+的顶点坐标是 . 13.已知一圆的周长为x cm ，该圆的面积为y cm 2，则y 与x 函数关系式是． 14．二次函数y =－x 2＋6x －5，当x 时， 0<y ，且y 随x 的增大而减小． 15．二次函数2y ax bx c =++的部分对应值如下表：当x =2时，对应的函数值y =．16．如图是二次函数2)1(2++=x a y 图像的一部分，该图在y 轴右侧与x 轴交点的坐标是17．二次函数y ＝2x 2＋bx ＋2的图象如图所示，则b = ．18．如图，Rt△OAB 的顶点A （－2，4）在抛物线2y ax =上，将Rt△OAB 绕点O 顺时针旋转90°，得到△OCD ，边CD 与该抛物线交于点P ，则点P 的坐标为．三、解答题（共58分）19．（8分）函数2ax y =（a ≠0）的图象与直线2--=x y 交于点A （2，m ），求a 和m 的值．20．（8分）已知函数3522+--=x x y 。

新人教版26章二次函数试题(含参考答案及评析)

新人教版九年级下第26章《二次函数》试题班级姓名得分一．选择题（共10小题）1．（2013•遵义）二次函数y=ax2+bx+c（a≠0）的图象如图如图所示，若M=a+b﹣c，N=4a﹣2b+c，P=2a﹣b．则M，N，P中，值小于0的数有（）23．（2013•岳阳）二次函数y=ax2+bx+c的图象如图所示，对于下列结论：①a＜0；②b＜0；③c＞0；④b+2a=0；⑤a+b+c ＜0．其中正确的个数是（）4．（2013•烟台）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（，y2）是抛物线上两点，则y1＞y2．其中说法正确的是（）26．（2013•攀枝花）二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，则函数y=与y=bx+c 在同一直角坐标系内的大致图象是（）．C D ．7．（2013•南昌）若二次函数y=ax 2+bx+c （a ≠0）的图象与x 轴有两个交点，坐标分别为（x 1，0），（x 2，0），且x 18．（2013•牡丹江）抛物线y=ax 2+bx+c （a ＜0）如图所示，则关于x 的不等式ax 2+bx+c ＞0的解集是（）210．（2012•泰安）设A （﹣2，y 1），B （1，y 2），C （2，y 3）是抛物线y=﹣（x+1）2+a 上的三点，则y 1，y 2，y 3的二．填空题（共10小题）11．（2013•宿迁）若函数y=mx 2+2x+1的图象与x 轴只有一个公共点，则常数m 的值是 _________ ．12．（2013•牡丹江）抛物线y=ax 2+bx+c （a ≠0）经过点（1，2）和（﹣1，﹣6）两点，则a+c= _________ ．13．（2012•扬州）如图，线段AB 的长为2，C 为AB 上一个动点，分别以AC 、BC 为斜边在AB 的同侧作两个等腰直角三角形△ACD 和△BCE ，那么DE 长的最小值是 _________ ．14．（2012•新疆）当x= _________ 时，二次函数y=x 2+2x ﹣2有最小值．15．（2011•资阳）将抛物线y=2x2﹣1沿x轴向右平移3个单位后，与原抛物线交点的坐标为_________．16．（2010•镇江）已知实数x，y满足x2+3x+y﹣3=0，则x+y的最大值为_________．17．（2010•扬州）抛物线y=2x2﹣bx+3的对称轴是直线x=1，则b的值为_________．18．（2008•青海）二次函数y=ax2+bx+c图象如图所示，则点A（b2﹣4ac，﹣）在第_________象限．19．（2007•眉山）如图，已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米，AC与MN在同一直线上，开始时点A与点N重合，让△ABC以每秒2厘米的速度向左运动，最终点A与点M重合，则重叠部分面积y（厘米2）与时间t（秒）之间的函数关系式为_________．20．（2007•黄石）二次函数y=a（x﹣1）2+bx+c（a≠0）的图象经过原点的条件是_________．三．解答题（共5小题）21．（2010•双鸭山）已知二次函数的图象经过点（0，3），（﹣3，0），（2，﹣5），且与x轴交于A、B两点．（1）试确定此二次函数的解析式；（2）判断点P（﹣2，3）是否在这个二次函数的图象上？如果在，请求出△PAB的面积；如果不在，试说明理由．22．（2013•泉州）已知抛物线y=a（x﹣3）2+2经过点（1，﹣2）．（1）求a的值；（2）若点A（m，y1）、B（n，y2）（m＜n＜3）都在该抛物线上，试比较y1与y2的大小．23．（2013•牡丹江）如图，已知二次函数y=x2+bx+c过点A（1，0），C（0，﹣3）（1）求此二次函数的解析式；（2）在抛物线上存在一点P使△ABP的面积为10，请直接写出点P的坐标．24．已知：二次函数的图象与一次函数y=4x﹣8的图象有两个公共点P（2，m）、Q（n，﹣8）．如果抛物线的对称轴是x=﹣1，（1）求二次函数的解析式；（2）当x为何值时，y随x增大而增大，当x为何值时，抛物线在x轴上方．25．（2012•新疆）如图1，在直角坐标系中，已知△AOC的两个顶点坐标分别为A（2，0），C（0，2）．（1）请你以AC的中点为对称中心，画出△AOC的中心对称图形△ABC，此图与原图组成的四边形OABC的形状是_________，请说明理由；（2）如图2，已知D（，0），过A，C，D的抛物线与（1）所得的四边形OABC的边BC交于点E，求抛物线的解析式及点E的坐标；（3）在问题（2）的图形中，一动点P由抛物线上的点A开始，沿四边形OABC的边从A﹣B﹣C向终点C运动，连接OP交AC于N，若P运动所经过的路程为x，试问：当x为何值时，△AON为等腰三角形（只写出判断的条件与对应的结果）？新人教版九年级下第26章《二次函数》试题参考答案与试题解析一．选择题（共10小题）1．（2013•遵义）二次函数y=ax2+bx+c（a≠0）的图象如图如图所示，若M=a+b﹣c，N=4a﹣2b+c，P=2a﹣b．则M，N，P中，值小于0的数有（）＞﹣23．（2013•岳阳）二次函数y=ax2+bx+c的图象如图所示，对于下列结论：①a＜0；②b＜0；③c＞0；④b+2a=0；⑤a+b+c ＜0．其中正确的个数是（）=1=14．（2013•烟台）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：①abc ＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（，y2）是抛物线上两点，则y1＞y2．其中说法正确的是（）=26．（2013•攀枝花）二次函数y=ax2+bx+c（a≠0）的图象如图所示，则函数y=与y=bx+c在同一直角坐标系内的大致图象是（）．C D．y=（2013•南昌）若二次函数y=ax2+bx+c（a≠0）的图象与x轴有两个交点，坐标分别为（x1，0），（x2，0），且x17．8．（2013•牡丹江）抛物线y=ax2+bx+c（a＜0）如图所示，则关于x的不等式ax2+bx+c＞0的解集是（）2，在对10．（2012•泰安）设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y=﹣（x+1）2+a上的三点，则y1，y2，y3的二．填空题（共10小题）11．（2013•宿迁）若函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是0或1．12．（2013•牡丹江）抛物线y=ax2+bx+c（a≠0）经过点（1，2）和（﹣1，﹣6）两点，则a+c=﹣2．13．（2012•扬州）如图，线段AB的长为2，C为AB上一个动点，分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE，那么DE长的最小值是1．CE=x（14．（2012•新疆）当x=﹣1时，二次函数y=x2+2x﹣2有最小值．15．（2011•资阳）将抛物线y=2x2﹣1沿x轴向右平移3个单位后，与原抛物线交点的坐标为（，）．，解得，16．（2010•镇江）已知实数x，y满足x2+3x+y﹣3=0，则x+y的最大值为4．17．（2010•扬州）抛物线y=2x2﹣bx+3的对称轴是直线x=1，则b的值为4．，即﹣=1，．18．（2008•青海）二次函数y=ax2+bx+c图象如图所示，则点A（b2﹣4ac，﹣）在第四象限．x=＜，﹣）在第四象限．19．（2007•眉山）如图，已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米，AC与MN在同一直线上，开始时点A与点N重合，让△ABC以每秒2厘米的速度向左运动，最终点A与点M重合，则重叠部分面积y（厘米2）与时间t（秒）之间的函数关系式为y=（20﹣2t）2．y=（20．（2007•黄石）二次函数y=a（x﹣1）2+bx+c（a≠0）的图象经过原点的条件是a+c=0．三．解答题（共5小题）21．（2010•双鸭山）已知二次函数的图象经过点（0，3），（﹣3，0），（2，﹣5），且与x轴交于A、B两点．（1）试确定此二次函数的解析式；（2）判断点P（﹣2，3）是否在这个二次函数的图象上？如果在，请求出△PAB的面积；如果不在，试说明理由．；×22．（2013•泉州）已知抛物线y=a（x﹣3）2+2经过点（1，﹣2）．（1）求a的值；（2）若点A（m，y1）、B（n，y2）（m＜n＜3）都在该抛物线上，试比较y1与y2的大小．23．（2013•牡丹江）如图，已知二次函数y=x2+bx+c过点A（1，0），C（0，﹣3）（1）求此二次函数的解析式；（2）在抛物线上存在一点P使△ABP的面积为10，请直接写出点P的坐标．，24．已知：二次函数的图象与一次函数y=4x﹣8的图象有两个公共点P（2，m）、Q（n，﹣8）．如果抛物线的对称轴是x=﹣1，（1）求二次函数的解析式；（2）当x为何值时，y随x增大而增大，当x为何值时，抛物线在x轴上方．，得到﹣25．（2012•新疆）如图1，在直角坐标系中，已知△AOC的两个顶点坐标分别为A（2，0），C（0，2）．（1）请你以AC的中点为对称中心，画出△AOC的中心对称图形△ABC，此图与原图组成的四边形OABC的形状是正方形，请说明理由；（2）如图2，已知D（，0），过A，C，D的抛物线与（1）所得的四边形OABC的边BC交于点E，求抛物线的解析式及点E的坐标；（3）在问题（2）的图形中，一动点P由抛物线上的点A开始，沿四边形OABC的边从A﹣B﹣C向终点C运动，连接OP交AC于N，若P运动所经过的路程为x，试问：当x为何值时，△AON为等腰三角形（只写出判断的条件与对应的结果）？，的坐标为（，﹣﹣2或。

数学：第二十六章《二次函数》综合测试卷

数学：第二十六章《二次函数》综合测试卷一、填空：(30分)1．二次函数的图象经过三个定点（2，0），（3，0），（•0，-•1），则它的解析式为________，该图象的顶点坐标为__________．2．当k=________时，直线x+2y+k+1=0和2x+y+2k=0的交点在抛物线y=-x2上．3．已知二次函数y=x2-2（k+1）x+k2+2的图象与x轴交点的横坐标分别为x1，x2，且（x1+1）（x2+1）=8，则k的值为__________．4．如果y与x2成正比例，并且它的图象上一点P的横坐标a和纵坐标b分别是方程x2-x-6=0的两根，那么这个函数的解析式为_________．5．抛物线y=x2-4x+11的对称轴是直线________，顶点坐标为________．6．如果抛物线y=-23x2+（m+2）x+27m的对称轴为直线x=32，则m的值为_________．7．把函数y=5x2+10mx+n的图象向左平移2个单位，向上平移3个单位，•所得图象的函数解析式为y=5x2+30x+44，则m=_______，n=_______．8．二次函数y=ax2+bx+c中的a、b、c满足条件________时，•它的图象经过坐标系中的四个象限．9．开口向下的抛物线y=a（x+1）（x-4）与x轴交于A、B两点，与y•轴交于点C．•若∠ACB=90°，则a的值为________．10．如图，二次函数y=x2-ax+a-5的图象交x轴于点A和B，交y轴于点C，当线段AB•的长度最短时，点C的坐标为________．二、选择题：(20分)11．在同一直角坐标系内，二次函数y1=ax2+bx+c与y2=cx2+bx+a的图象大致为（）12．在同一直角坐标系内，函数y=ax2+bx与y=bx（b≠0）的图象大致为（）13．给出下列四个函数：y=-2x，y=2x-1，y=3x（x>0），y=-x2+3（x>0），其中y随x•的增大而减小的函数有（）A．3个 B．2个 C．1个 D．0个14．当m取任何实数时，抛物线y=-2（x-m）2-m的顶点所在的直线为（）A．x轴 B．y轴 C．y=x D．y=-x15．当m取任何实数时，抛物线y=-2（x+m）2-m2的顶点所在的曲线为（）A．y=x2 B．y=-x2 C．y=x2（x>0） D．y=-x2（x>0）16．已知抛物线y=ax2+bx+c（a≠0）与抛物线y=x2-4x+3关于x轴对称，则a、b、c•的值分别是（）A．-1，4，-3 B．-1，-4，-3 C．-1，4，3 D．-1，-4，317．已知抛物线y=ax2+bx+c（a≠0）与抛物线y=x2-4x+3关于y轴对称，则函数y=ax2+bx+c的解析式为（） A．y=x2+4x+3 B．y=x2-4x-3 C．y=x2+4x-3 D．y=-x2-4x+318．从一张矩形纸片ABCD的较短边AD上找一点E，过这点剪下两个半圆，它们的直径分别是AE、DE，要使剪下的两个半圆的面积和最小，点E应选在（）A．边AD的中点外 B．边AD的13处 C．边AD的14处 D．边AD的15处19．对某条路线的长度进行n次测量，得到n个结果x1，x2，…，x n，如果用x作为这条路线长度的近似值，当x=p时，（x-x1）2+（x-x2）2+…+（x-x n）2最小，则p的值为（）A．1n（x1+x2+…+x n） B．1n（x1-x2-…-x n）C．1nn+（x1+x2+…+x n） D．1nn+（x1+x2+…+x n）20．已知函数y=-（x-1）2-（x-3）2-（x-5）2-（x-7）2，当x=p时，函数y取得最大值，则p•的值为（） A．4 B．8 C．10 D．16三、解答题：(90分)1．如图，△OAB是边长为2的等边三角形，直线x=t•截这个三角形所得位于直线左方的图形面积为y．（1）写出以自变量为t的函数y的解析式；（2）画出（1）中函数y的图象．2．如图，AB是半径为R的圆的直径，C为直径AB上的一点，•过点C•剪下两个正方形ADCE和BFCG，它们的对角线分别是AC、CB．要使剪下的两个正方形的面积和最小，•点C应选在何处？3．已知一个二次函数的图象过点A（-1，10），B（1，4），C（2，7），点D和B•关于抛物线的对称轴对称，问是否存在与抛物线只有一个公共点D的直线？如果存在，求出符合条件的直线；如不存在，请说明理由．4．如图，在直角坐标系xOy中，A、B是x轴上的两点，以AB为直径的圆交y轴于C，设过A、B、C三点的抛物线的解析式为y=x2-mx+n，方程x2-mx+n=0的两根倒数和为-2．（1）求n的值；（2）求此抛物线的解析式；（3）设平行于x轴的直线交此抛物线于E、F两点，问是否存在此线段EF•为直径的圆恰好与x轴相切，若存在，求出此圆的半径；若不存在，说明理由．5．某电厂规定，该厂家属区的每户居民如果一个月的用电量不超过x度，•那么这个月这户居民只交10元用电费．如果超过x度，这个月除了要交10元用电费外，超过部分按每度元交费．（1）该厂某户居民1月份用电90度，超过了x度的规定，试用x的代数式表示超过部分应交的电费（元）；（2）下表是这户居民2月、3月的用电情况和交费情况，请根据表中的数据，•求出电厂规定的这个月份用电量（度）交电费总数（元） 2月 80 25 3月 45106．如图（1），平面直角坐标系中有一张矩形纸片OABC ，O 为坐标原点，A•点坐标为（10，0），C 点坐标为（0，6）．D 是BC 边上的动点（与点B 、C 不重合），现将△COD 沿OD 翻折，得到△FOD ；再在AB 边上选取适当的点E ，使△BDE 沿DE 翻折，得到△GDE ，并使直线DG ，DF 重合．（1）如图②，若翻折后点F 落在OA 边上，求直线DE 的函数关系式；（2）设D （a ，6），E （10，b ），求b 关于a 的函数关系式，并求b 的最小值；（3）一般地，请你猜想直线DE 与抛物线y=-124x 2+6的公共点的个数，•在图②的情形中通过计算验证你的猜想；如果直线DE 与抛物线y=-124x 2+6始终有公共点，请在图①中作出这样的公共点．附加题： (10分)当抛物线的解析式中含有字母系数时，随着系数中字母取值的不同，抛物线的顶点坐标也将发生变化．例如：由抛物线y=x 2-2mx+m 2+3m-2． ① 得y=（x-m ）2+3m-2 ②抛物线的顶点坐标为（m ，3m-2），即32x m y m =⎧⎨=-⎩当m 的值变化时，x ，y 的值也随之变化，•因而y值也随x 值的变化而变化．将③代入④，得y=3x-2 ⑤可见不论m 取任何实数抛物线顶点的纵坐标y 和横坐标x 都满足关系式y=3x-2，即抛物线①的顶点总在直线y=3x-2上．在上述过程中，由①到②所用的数学方法是__________；由③、④到⑤所用的数学方法是________．请解答:求出抛物线y=x 2-4mx+4m 2-2m•的顶点的纵坐标y 和横坐标x 之间的关系式．答案:1．y=-16x2+56x-1 （52，124）2．13±633．14．y=-29x2和y=34x25．x=2 （2，7） 6．0 7．1 18．a、c异号，b为任何实数 9．-10．（0，-3）（设A（x1，0），B（x2，0）．（x1-x2）2=（x1+x2）2-4x1x2=a2-4a+20=（a-2）2+16．当a=2时，•线段AB的长度最短为4，此时y=x2-2x-3，点C的坐标为（0，-3）二、选择题：11．D 12．D 13．A 14．D 15．B 16．A 17．A 18．A 19．A 20．A 三、解答题：1．（1）y=223(01)23(2)3(2)2t tt t⎧≤≤⎪⎪⎨⎪--+≤≤⎪⎩（2）如第1题图.2．设AC长为x，BC长为2R-x，S正方形ADCE=12x2，S正方形BFCG=12（2R-x）2．两个正方形面积之和为y=12x2+12（2R-x）2=x2-2Rx+2R2=（x-R）2+R2，当x=R时，两个正方形面积之和有最小值R2，此时点C应选在AB•的中点处，即圆心．3．过点A、B、C的抛物线的解析式为y=2x2-3x+5，其对称轴为直线x=34．因D和B关于直线x=34对称，所以D点坐标为（12，4）．与抛物线只有一个公共点D 的直线有两条：（1）平行于y 轴，即直线x=12．（2）不平行于y 轴，设直线为y=kx+b ，因为过D 点，所以4=12k+b ．即k=8-2b ，（8-2b ）x+b=2x 2-3x+5．2x 2+（2b-11）x+5-b=0．方程有两个相等的实数根，△=（2b-11）2-8（5-b ）=0，解得b=92，k=-1．所以y=-x+92．符合条件的直线为y=-x+92和x=12． 4．（1）设A （x 1，0），B （x 2，0），则OA=-x 1，OB=x 2．因为AB 是直径，OC⊥AB，所以CO 2=OA·OB，•即n 2=-x 1x 2．又x 1x 2=n ，所以n 2=-n ，n=-1，n=0（舍去）．（2）11x +21x =1212x x x x +=-2，又x 1+x 2=m ，x 1x 2=-1，1m -=-2，m=2，所求的抛物线的解析式为y=x 2-2x-1．（3）由（2）得抛物线的对称轴为x=1．设满足条件的圆的半径为│a │，则点F•的坐标为（1+│a │，a ），点F 在抛物线上，a=（1+│a │）2-2（1+│a │）-1，即a 2-a-2=0，a 1=2，a 2=-1，所求的圆的半径为1或2，故存在以EF 为直径的圆，恰好与x 轴相切． 5．（1）100x（90-x ）元（2）表格中的数据告诉我们，这户居民2月份用电超标，3•月份用电不超标，可见45≤x<80，列出方程10+100x （80-x ）=25，即x 2-80x+150=0，解得x 1=30，x 2=50．因45≤x<80，所以x=30，电厂规定的标准是30度．6．（1）解：根据题意，可知D （6，6），E （10，2），直线DE 的函数关系式为y=-x+12．（2）解：根据题意，可知∠CDO=∠ODF ，∠BDE=∠GDE ．∠CDO+∠ODF+∠BDE+∠GDE=180°，•∠CDO+∠BDE=90°，∠COD+∠CDO=90°，∠COD=∠BDE ．又∠COD=∠DBE=90°，△COD ≌△BDE ．CE COBE BD=．根据题意，可知BE=6-b ，BD=10-a ，6610a b a =--，b+16a 2-53a+6=16（a-5）2+116．当a=5时，b 最小值=116．（3）猜想：直线DE 与抛物线y=-124x 2+6只有1个公共点．证明:由（1）可知，DE所在直线为y=-124x+12．代入抛物线y=-x2+6，消去y，得-124x2+6=-x+12．化简，得x2-24x+144=0，△=0．直线DE与抛物线y=-124x2+6只有1个公共点．作法一：延长OF交DE于点H，作法二：在DB上取点M，使DM=CD，过M作MH⊥BC，交DE于点H．附加题：配方法; 消元法; y=-4x.。

第26章《二次函数》测试题

第26章《二次函数》测试题一、选择题（每小题2分，共20分）1．若抛物线c bx ax y ++=2的顶点在第一象限，与x 轴的两个交点分布在原点两侧，则点（a ，ac）在（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 2．若双曲线)0(≠=k xky 的两个分支在第二、四象限内，则抛物线222k x kx y +-= 的图象大致是图中的（）xyOxyO xyO O yx DCBA3．如图是二次函数c bx ax y ++=2的图象，则一次函数bc ax y +=的图象不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限第3题图第6题图4．若点（2，5），（4，5）是抛物线c bx ax y ++=2上的两个点，那么这条抛物线的对称轴是（） A ．直线1=x B ．直线2=x C ．直线3=x D ．直线4=x 5．已知函数772--=x kx y 的图象与x 轴有交点，则k 的取值范围是（）A ．47-k B ．047≠-≥k k 且 C ．47-≥k D ．047≠-k k 且 6．函数y=ax 2+bx+c 的图象如图所示，那么关于一元二次方程ax 2+bx+c-3=0的根的情况是（）A ．有两个不相等的实数根B ．有两个异号的实数根C ．有两个相等的实数根D ．没有实数根 7．现有A ，B 两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6），用小莉掷A 立方体朝上的数字为x ，小明掷B 立方体朝上的数字为y 来确定点P （x ，y ），那么他们各掷一次所确定的点P 落在已知抛物线y=－x 2+4x 上的概率为（） A ．118 B ．112C ．19D ．168．已知a<－1，点（a －1，y 1），（a ，y 2），（a+1，y 2）都在函数y=x 2的图象上，则（） A ．y 1<y 2<y 3 B ．y 1<y 3<y 2 C ．y 3<y 2<y 1 D ．y 2<y 1<y 3 9．已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，给出以下结论：①a+b+c<0；②a －b+c<0；③b+2a<0；④abc>0，其中所有正确结论的序号是（）A ．③④B ．②③C ．①④D ．①②③ 第9题图 10．把抛物线y=x 2+bx+c 的图象向右平移3个单位，再向下平移2个单位，所得图象的Oyx解析式是y=x 2－3x+5，则有（）A ．b=3，c=7B ．b=－9，c=－15C ．b=3，c=3D ．b=－9，c=21二、填空题（每小题3分，共30分）11．如图所示，矩形的窗户分成上、下两部分，用9米长的塑钢制作这个窗户的窗框（包括中间档），设窗宽x （米），则窗的面积y （平方米）用x 表示的函数关系式为_____________________________；要使制作的窗户面积最大，那么窗户的高是________米，窗户的最大面积是_______________平方米。

数学九年级下人教新课标第二十六章《二次函数》测试题D

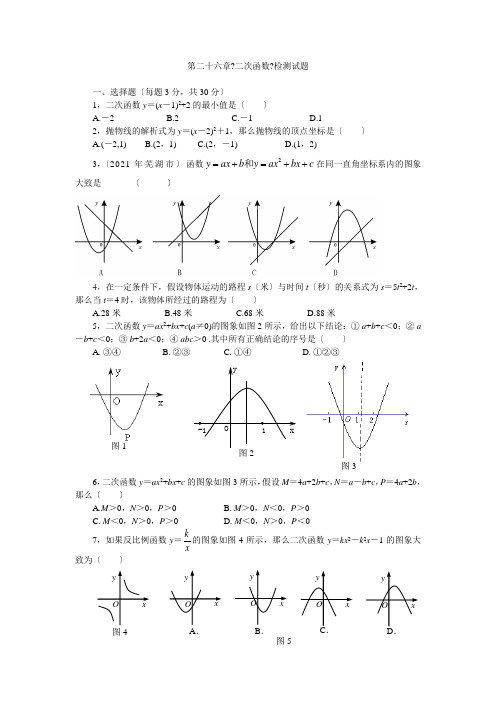
第二十六章?二次函数?检测试题一、选择题〔每题3分，共30分〕1，二次函数y ＝(x －1)2+2的最小值是〔〕A.－2B.2C.－1D.12，抛物线的解析式为y ＝(x －2)2＋1，那么抛物线的顶点坐标是〔〕A.(－2,1)B.(2，1)C.(2，－1)D.(1，2)3，〔2021年芜湖市〕函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是〔〕4，在一定条件下，假设物体运动的路程s 〔米〕与时间t 〔秒〕的关系式为s ＝5t 2+2t ，那么当t ＝4时，该物体所经过的路程为〔〕A.28米B.48米C.68米D.88米5，二次函数y ＝ax 2+bx +c (a ≠0)的图象如图2所示，给出以下结论：① a +b +c ＜0；② a －b +c ＜0；③ b +2a ＜0；④ abc ＞0 .其中所有正确结论的序号是〔〕A. ③④B. ②③C. ①④D. ①②③6，二次函数y ＝ax 2+bx +c 的图象如图3所示，假设M ＝4a +2b +c ，N ＝a －b +c ，P ＝4a +2b ，那么〔〕A.M ＞0，N ＞0，P ＞0B. M ＞0，N ＜0，P ＞0C. M ＜0，N ＞0，P ＞0D. M ＜0，N ＞0，P ＜07，如果反比例函数y ＝k x 的图象如图4所示，那么二次函数y ＝kx 2－k 2x －1的图象大致为〔〕图3 y x O 图4 y x O A ．y x O B ．y x O y x O 图5 x -11yO 图2 图18，用列表法画二次函数y ＝x 2+bx +c 的图象时先列一个表，当表中对自变量x 的值以相等间隔的值增加时，函数y 所对应的函数值依次为：20，56，110，182，274，380，506，650.其中有一个值不正确，这个不正确的值是( )A. 506B.380C.274D.189，二次函数y ＝x 2的图象向上平移2个单位，得到新的图象的二次函数表达式是〔〕A. y ＝x 2－2B. y ＝(x －2)2C. y ＝x 2+2D. y ＝(x +2)210，如图6，小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数h ＝3.5t －4.9t 2〔t 的单位：s ，h 的单位：m 〕可以描述他跳跃时重心高度的变化，那么他起跳后到重心最高时所用的时间是〔〕A.0.71sB.0.70sC.0.63sD.0.36s二、填空题〔每题3分，共24分〕11，形如y ＝＿＿＿ (其中a ＿＿＿，b 、c 是_______ )的函数，叫做二次函数.12，抛物线y ＝(x –1)2–7的对称轴是直线 .13，如果将二次函数y ＝2x 2的图象沿y 轴向上平移1个单位，那么所得图象的函数解析式是 .14，平移抛物线y ＝x 2+2x －8，使它经过原点，写出平移后抛物线的一个解析式______ . 15，假设二次函数y ＝x 2－4x ＋c 的图象与x 轴没有交点，其中c 为整数，那么c ＝____(只要求写出一个).16，现有A 、B 两枚均匀的小立方体〔立方体的每个面上分别标有数字1，2，3，4，5，6〕.用小莉掷A 立方体朝上的数字为x 、小明掷B 立方体朝上的数字为y 来确定点P 〔x ，y 〕，那么它们各掷一次所确定的点P 落在抛物线y ＝－x 2+4x 上的概率为＿＿＿.17，二次函数y ＝ax 2+bx +c 的图像如图7所示，那么点A (a ，b )在第＿＿＿象限.18，抛物线y ＝x 2－6x +5的局部图象如图8，那么抛物线的对称轴为直线x ＝，满足y ＜0的x 的取值范围是 .三、解答题〔共66分〕19，抛物线y ＝ax 2经过点(1，3)，求当y ＝4时，x 的值.20，一抛物线与x 轴的交点是)0,2( A 、B 〔1，0〕，且经过点C 〔2，8〕。

第二十六章二次函数单元检测试卷含答案解析

数学人教九年级下第二十六章二次函数单元检测(时间：45分钟，满分：100分)一、选择题(每小题4分，共32分) 1．把二次函数y ＝215322x x ++的图象向右平移2个单位后，再向上平移3个单位，所得函数图象的顶点是( )．A ．(－5,1)B ．(1，－5)C ．(－1,1)D ．(－1,3)2．若点(2,5)，(4,5)在抛物线y ＝ax 2＋bx ＋c 上，则它的对称轴是( )．A ．x ＝b a-B ．x ＝1C ．x ＝2D ．x ＝33．已知二次函数的图象(0≤x ≤3)如图所示，关于该函数在所给自变量取值范围内，下列说法正确的是( )．A ．有最小值0，有最大值3B ．有最小值－1，有最大值0C ．有最小值－1，有最大值3D ．有最小值－1，无最大值4．把抛物线y ＝x 2＋bx ＋c 的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式为y ＝x 2－3x ＋5，则( )．A ．b ＝3，c ＝7B ．b ＝6，c ＝3C ．b ＝－9，c ＝－5D ．b ＝－9，c ＝215．已知二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象如图所示，则下列结论：①a c ＞0；②方程ax 2＋bx ＋c ＝0的两根之和大于0；③y 随x 的增大而增大；④a －b ＋c ＜0，其中正确的有( )．A ．4个B ．3个C ．2个D ．1个6．二次函数y ＝ax 2＋bx ＋c 的图象如图所示，若点A (1，y 1)，B (2，y 2)是图象上的两点，则y 1与y 2的大小关系是( )．A ．y 1＜y 2B ．y 1＝y 2C ．y 1＞y 2D ．不能确定7．如图，从地面竖直向上抛出一个小球，小球的高度h (单位：m)与小球运动时间t (单位：s)之间的关系式为h ＝30t －5t 2，那么小球从抛出至回落到地面所需要的时间是( )．A ．6 sB ．4 sC ．3 sD ．2 s8．二次函数y ＝ax 2＋bx ＋c 的图象如右图所示，反比例函数y ＝ax与正比例函数y ＝bx 在同一坐标系内的大致图象是( )．二、填空题(每小题4分，共20分)9．若抛物线y ＝x 2＋bx ＋c 与y 轴交于点A ，与x 轴正半轴交于B ，C 两点，且BC ＝2，S △ABC ＝3，则b ＝__________.10．二次函数y ＝x 2－6x ＋c 的图象的顶点与原点的距离为5，则c ＝__________.11．二次函数y ＝21222x x --的图象在坐标平面内绕顶点旋转180°，再向左平移3个单位，向上平移5个单位后图象对应的二次函数解析式为__________．12．已知抛物线y ＝212x bx +经过点A (4,0)．设点C (1，－3)，请在抛物线的对称轴上确定一点D ，使得|AD －CD |的值最大，则D 点的坐标为______．13．如图，已知⊙P 的半径为2，圆心P 在抛物线y ＝2112x -上运动，当⊙P 与x 轴相切时，圆心P 的坐标为__________．三、解答题(共48分)14．(10分)下表给出了代数式x 2＋bx ＋c 与x 的一些对应值.x … 0 1 2 3 4 … x 2＋bx ＋c … 3 －1 3 …(1)(2)设y ＝x 2＋bx ＋c ，则当x 取何值时，y ＞0?(3)请说明经过怎样平移函数y ＝x 2＋bx ＋c 的图象得到函数y ＝x 2的图象？15．(12分)已知抛物线y ＝－x 2＋4x －3与x 轴相交于A ，B 两点(A 点在B 点的左侧)，顶点为P .(1)求A ，B ，P 三点的坐标；(2)在给出的直角坐标系内画出此抛物线的简图，并根据简图写出当x 取何值时，函数值y 大于零；(3)确定此抛物线与直线y ＝－2x ＋6公共点的个数，并说明理由．16．(12分)2011年春节期间某水库养殖场为适应市场需求，连续用20天时间，采用每天降低水位以减少捕捞成本的办法，对水库中某种鲜鱼进行捕捞、销售．九(1)班数学建模兴趣小组根据调查，整理出第x 天(1≤x ≤20，且x 为整数)的捕捞与销售的相关信息如下：鲜鱼销售单价/元·kg －1 20单位捕捞成本/元·kg －155x捕捞量/kg 950－10x(1)(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失，且能在当天全部售出，求第x 天的收入y (元)与x (天)之间的函数关系式．(当天收入＝日销售额－日捕捞成本)(3)试说明(2)中的函数y 随x 的变化情况，并指出在第几天y 取得最大值，最大值是多少？17．(14分)如图甲，Rt △PMN 中，∠P ＝90°，PM ＝PN ，MN ＝8 cm ，矩形ABCD 的长和宽分别为8 cm 和2 cm ，C 点和M 点重合，BC 和MN 在一条直线上．令Rt △PMN 不动，矩形ABCD 沿MN 所在直线向右以1 cm/s 的速度移动(如图乙)，直到C 点与N 点重合为止．设移动x 秒后，矩形ABCD 与△PMN 重叠部分的面积为y cm 2.求y 与x 之间的函数关系式．参考答案1. 答案：C2. 答案：D3. 答案：C4. 答案：A 本题可以从y ＝x 2－3x ＋5开始先向上平移2个单位，再向左平移3个单位得y ＝(x ＋3)2－3(x ＋3)＋5＋2＝x 2＋3x ＋7，即y ＝x 2＋bx ＋c ＝x 2＋3x ＋7，所以b ＝3，c ＝7.5. 答案：C 由图象显然有a ＜0，c ＞0，所以ac ＞0不成立；由于对称轴在y 轴的右侧，所以2ba-＞0，又a ＜0，所以b ＞0，方程ax 2＋bx ＋c ＝0的两根之和大于0，y 随x 的增大而增大也不成立；由图象可知当x ＝－1时，y ＜0，即a －b ＋c ＜0正确，故选C.6. 答案：C 由图象可知对称轴的右侧y 随x 的增大而减小，随着x 由1到2的增大，y 值减小，即y 1＞y 2.7. 答案：A 小球抛出离手前的瞬间距地面0 m ，小球抛出后经历一段时间落地又距地面0 m ，由此设h ＝0，得30t －5t 2＝0，解得t ＝0或6,6－0＝6(s)，所以选A.8. 答案：B 由二次函数的图象可知，a ＜0，b ＜0. 9. 答案：－4 10. 答案：5或13 11. 答案：y ＝21122x x --+ 12. 答案：(2，－6)13. 答案：(6±，2) 半径为2的圆与x 轴相切，则圆心P 到x 轴的距离为2，所以y P ＝±2. 又抛物线开口向上，它的顶点为(0，－1)，所以P 只能在x 轴的上方．则y P ＝2，即2＝2112x -，解得x ＝6±. 所以圆心P 的坐标为(6，2)．14. 解：(1)由表格中数据可知：当x ＝0时，y ＝3，当x ＝4时，y ＝3.代入代数式得3,1643,c b c =⎧⎨++=⎩解得3,4.c b =⎧⎨=-⎩表内空格中应填：0 0(2)函数y ＝x 2－4x ＋3开口向上，当x ＝1和x ＝3时，y ＝0，则当x ＜1或x ＞3时，y ＞0，也可由图象观察得到结果．(3)把函数y ＝x 2－4x ＋3化为顶点式y ＝(x －2)2－1，由函数y ＝(x －2)2－1的图象向左平移2个单位得y ＝x 2－1的图象，再向上平移1个单位得函数y ＝x 2的图象．15. 解：(1)令y ＝0，解方程－x 2＋4x －3＝0，则x 1＝1，x 2＝3，则A (1,0)，B (3,0)．将y＝－x 2＋4x －3配方得y ＝－(x －2)2＋1，得顶点P (2,1)．(2)如图，当1＜x ＜3时，y ＞0.(3)由题意列方程组243,26,y x x y x ⎧=-+-⎨=-+⎩转化为一元二次方程，得x 2－6x ＋9＝0，由Δ＝0，故方程的两根相等，方程只有一组解．因此抛物线与直线有唯一的公共点． 16. 解：(1)该养殖场每天的捕捞量与前一天的捕捞量相比每天减少了10 kg. (2)由题意，得y ＝20(950－10x )－5(95010)5x x ⎛⎫-- ⎪⎝⎭＝－2x 2＋40x ＋14 250. (3)∵－2＜0，y ＝－2x 2＋40x ＋14 250＝－2(x －10)2＋14 450，又1≤x ≤20，且x 为整数，∴当1≤x ≤10时，y 随x 的增大而增大；当10≤x ≤20时，y 随x 的增大而减小；当x ＝10时，即在第10天，y 取得最大值，最大值为14 450元． 17. 解：在Rt △PMN 中， ∵PM ＝PN ，∠P ＝90°， ∴∠PMN ＝∠PNM ＝45°.延长AD ，分别交PM ，PN 于点G ，H ，过G 作GF ⊥MN 于点F ，过H 作HT ⊥MN 于点T .∵DC ＝2 cm ，∴MF ＝GF ＝2 cm ，TN ＝HT ＝2 cm. ∵MN ＝8 cm ，∴MT ＝6 cm ，因此，矩形ABCD 以1 cm/s 的速度由开始向右移动到停止，与Rt △PMN 重叠部分的形状，可分为下列三种情况：(1)当C 点由M 点运动到F 点的过程中(0≤x ≤2)，如图①所示，设CD 与PM 交于点E ，则重叠部分图形是Rt △MCE ，且MC ＝EC ＝x ，图①∴y ＝12MC ·EC ，即y ＝212x (0≤x ≤2)． (2)当C 点由F 点运动到T 点的过程中(2＜x ≤6)，如图②所示，重叠部分图形是直角梯形MCDG .∵MC ＝x ，M F ＝2，∴FC ＝DG ＝x －2，且DC ＝2， ∴y ＝12(MC ＋GD )·DC ＝2x －2(2＜x ≤6)．图②(3)当C 点由T 点运动到N 点的过程中(6＜x ≤8)，如图③所示，图③设CD 与PN 交于点Q ，则重叠部分图形是五边形MCQHG .∵MC ＝x ，∴CN ＝CQ ＝8－x ，且DC ＝2，∴y ＝12(MN ＋GH )·DC －12CN ·CQ ＝12(x －8)2＋12(6＜x ≤8)．。

第26章《二次函数》的测试题

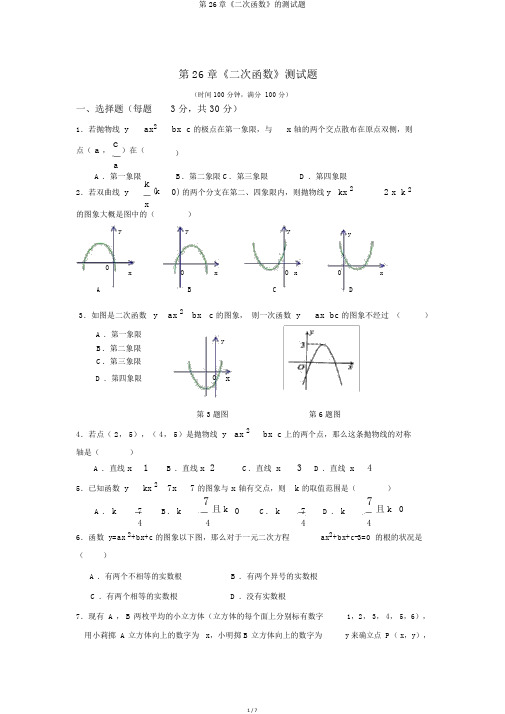
第26章《二次函数》测试题（时间 100 分钟，满分 100 分）一、选择题（每题3 分，共 30 分）1．若抛物线 y ax 2bx c 的极点在第一象限，与x 轴的两个交点散布在原点双侧，则点（ a ，c）在（）aA ．第一象限B ．第二象限C ．第三象限D ．第四象限2．若双曲线 yk(k 0) 的两个分支在第二、四象限内，则抛物线y kx 22 x k 2x的图象大概是图中的（）yyyyOxO xO xOxABCD3．如图是二次函数 y ax 2 bx c 的图象，则一次函数 yax bc 的图象不经过（）A ．第一象限yB ．第二象限C ．第三象限D ．第四象限O x第 3题图第 6题图4．若点（ 2， 5），（ 4， 5）是抛物线 y ax 2 bx c 上的两个点，那么这条抛物线的对称轴是（）A ．直线 x 1B ．直线 x 2C ．直线 x 3D ．直线 x 45．已知函数 ykx 2 7x 7 的图象与 x 轴有交点，则 k 的取值范围是（）A ． k7 B ． k7且 k 0 C ． k7D ． k7且 k 044446．函数 y=ax 2+bx+c 的图象以下图，那么对于一元二次方程 ax 2+bx+c-3=0 的根的状况是（）A ．有两个不相等的实数根B ．有两个异号的实数根C ．有两个相等的实数根D ．没有实数根7．现有 A ， B 两枚平均的小立方体（立方体的每个面上分别标有数字 1，2， 3， 4， 5，6），用小莉掷 A 立方体向上的数字为 x ，小明掷 B 立方体向上的数字为y 来确立点 P （ x ，y ），那么他们各掷一次所确立的点P 落在已知抛物线 y= － x 2+4x 上的概率为（）111D ．1A ．B ．C ．618129122y=x 2 的图象上，则（）8．已知 a<－1，点（ a － 1， y ），（ a ， y ），（ a+1，y ）都在函数A ． y <y <y3B ． y <y <y2C ． y <y <y1 D ． y <y <y 3121 33 2 2 19．已知二次函数 y=ax 2+bx+c （ a ≠ 0）的图象以下图，给出以下结论：① a+b+c<0 ；② a － b+c<0 ；③ b+2a<0；④ abc>0，此中全部正确结论的序号是（）A ．③④B ．②③C ．①④D ．①②③第 9题图10．把抛物线 y=x 2 +bx+c 的图象向右平移 3 个单位，再向下平移 2 个单位，所得图象的分析式是 y=x 2－ 3x+5 ，则有（）A ． b=3， c=7B ． b=－9， c=－ 15C ． b=3 ， c=3D ． b=－ 9， c=21二、填空题（每题 3 分，共 18 分）11、圆的半径为 3，若半径增添 x ，则面积增添 y 。

第26章二次函数(26.1)水平测试(含答案).doc

26.1 二次函数（时间45分钟满分100分）班级 _____________ 学号姓名 ________ 得分____一、选择题（本大题共10小题，每小题３分，共30分）1．下列函数不属于二次函数的是（ D ）A.y=(x －1)(x+2)B.y=21(x+1)2C. y=1－3x 2D. y=2(x+3)2－2x 22. 函数y=－x 2－4x+3图象顶点坐标是（ A ）A.（2，－1）B.（－2，1）C.（－2，－1）D.（2， 1）3. 抛物线()12212++=x y 的顶点坐标是（ B ） A ．（2，1） B ．（－2，1） C ．（2，－1） D ．（－2，－1）4. y=(x －1)2＋2的对称轴是直线（ B ）A ．x=－1B ．x=1C ．y=－1D ．y=15．已知二次函数)2(2-++=m m x mx y 的图象经过原点，则m 的值为（ C ）A ． 0或2B ． 0C ． 2D ．无法确定6. 二次函数y ＝x 2的图象向右平移3个单位，得到新的图象的函数表达式是（ D ）A. y ＝x 2＋3B. y ＝x 2－3C. y ＝(x ＋3)2D. y ＝(x －3)27．函数y=2x 2－3x+4经过的象限是（ B ）A.一、二、三象限B.一、二象限C.三、四象限D.一、二、四象限8．下列说法错误的是（ C ）A ．二次函数y=3x 2中，当x>0时，y 随x 的增大而增大B ．二次函数y=－6x 2中，当x=0时，y 有最大值0C ．a 越大图象开口越小，a 越小图象开口越大D ．不论a 是正数还是负数，抛物线y=ax 2(a ≠0)的顶点一定是坐标原点9．如图，小芳在某次投篮中，球的运动路线是抛物线y ＝－15x 2＋3.5的一部分，若命中篮圈中心，则他与篮底的距离l 是（ B ）A ．3.5mB ．4mC ．4.5mD ．4.6m10．二次函数y=ax 2＋bx ＋c 的图象如图所示，下列结论错误的是（ B ）A ．a ＞0．B ．b ＞0．C ．c ＜0．D ．abc ＞0．(第9题) (第10题) 2.5m 3.05m l x yO二、填空题（本大题共4小题，每小题３分，共12分）11．一个正方形的面积为16cm 2，当把边长增加x cm 时，正方形面积为y cm 2，则y 关于x的函数为 y= (x+4)2 。

第二十六章二次函数测试题

九年级第二十六章二次函数测试题

2023年华东师大版九年级数学下册第二十六章《二次函数》复习检测卷附答案解析

第二十六章二次函数测试题

九年级第26章《二次函数》测试题(含答案)

九年级数学第26章二次函数单元检测题

第26章二次函数单元测试(人教版九年级)!.docx

华师大版九年级数学下《第26章二次函数》测试题含答案

新人教版26章 二次函数试题(含参考答案及评析)

数学：第二十六章《二次函数》综合测试卷

第26章《二次函数》测试题

数学九年级下人教新课标第二十六章《二次函数》测试题D

第二十六章二次函数单元检测试卷含答案解析

第26章《二次函数》的测试题

第26章 二次函数(26.1)水平测试(含答案).doc

新人教版26章二次函数试题(含参考答案及评析)

第26章二次函数(26.1)水平测试(含答案).doc