双曲线定义(带动画)
双曲线及其标准方程(带动画)很好

x
方程
x y 2 1 2 a b
F ( ±c, 0)
2
2
y2 x2 2 1 2 a b
F(0, ± c)
2 2
焦点 a.b.c 的关 系
c a b
2
(c a ) x a y a (c a )
2 2 2 2 2 2 2 2
令c2-a2=b2
x y 2 1 2 a b
2
2
双曲线的标准方程
焦点在x轴上
y
M
焦点在y轴上
y
F2
M x
F
1
O
F
2
x
O
F1
2 2 x y y x 2 1 2 1 2 2 a b a b 2 2 2 (a 0,b 0)并且c =a b
焦点
F(±c,0)
F(±c,0)
F(0,±c)
a.b.c的关 系
F(0,±c)
a>0,b>0,但a不一 定大于b,c2=a2+b2
a>b>0,a2=b2+c2
小结 ----双曲线定义及标准方程
定义
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
y
M
M F2
y
图象
F1
o
F2
x
F1
椭
定义 方程
圆
双曲线
||MF1|-|MF2||=2a
x2 y 2 2 1(a 0, b 0) 2 a b y 2 x2 2 1(a 0, b 0) 2 a b
|MF1|+|MF2|=2a
x2 y2 2 1(a b 0) 2 a b y 2 x2 2 1(a b 0) 2 a b
三种圆锥曲线统一定义及动画演示

抛物线的定义 :
平面内到一个定点F和一条定直线L(F不在L 上)的距离相等的点轨迹叫做抛物线,定点F叫做 抛物线的焦点,定直线L叫做抛物线的准线.
(2)与椭圆、双曲线不同, 抛物线只有一个焦点和一条准线
可以用数学表达式来体现: 设平面内的动点为M ,有 MF=d(d为动点M到
直线L的ቤተ መጻሕፍቲ ባይዱ离)
抛物线的定义:
▪ 平面内与一个定点F的距离和一条定直线l (F不在l上)的距离相等的点的轨迹叫做抛物 线,定点F叫做抛物线的焦点,定直线l叫 做抛物线的准线
说明:(1)点F不能在直线l上, 否则其轨迹是过点F且与l垂直的直线
关于椭圆、双曲线、抛物线你了解多少? 在我们的实际生活中有这些曲线吗? 它们分别给我们什么印象?
椭圆?
汽车贮油罐的横截面的外轮廓线 的形状像椭圆.
北京摩天大楼
巴西利亚大教堂
法拉利主题公园
花瓶
椭圆
双曲线
抛物线
椭圆的定义
平面内到两定点 F1 ,F2的距离之和 为常数(大于F1 F2 距离)的点的轨迹 叫椭圆,两个定点 叫椭圆的焦点,两 焦点的距离叫做椭 圆的焦距.
说明: 若动点M到的距离之和为2a , | F1 F2| = 2c 则当a>c>0时,动点M的轨迹是椭圆; 当a = c>0时,动点M的轨迹是线段F1 F2 ; 当 0 < a < c时,动点M无轨迹
双曲线的定义 :
双曲线定义与方程(带动画)

F
1
M
o
F
2
3.双曲线的标准方程
1. 建系. 以F1,F2所在的直线为X轴, 如何求这优美的曲线的方程? 线段F1F 2的中点为原点建立直角坐 标系 2.设点. 设M(x , y),双曲线的焦 距为2c(c>0),F1(-c,0),F2(c,0) 3.列式. |MF1|
平面内与两个定点F1,F2的距离的差的绝对值 等于常数2a (小于︱F1F2︱) 的点的轨迹叫做双曲线. ① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距. 注意
M
(1)距离之差的绝对值
| |MF1| - |MF2| | = 2a
|MF1| - |MF2| = 2a
F
1
o
F2
x2 y2 2.已知方程 1 9k k 3 3 k 9且 k 6; (1)方程表示椭圆,则 k的取值范围是 __________ ______
小结 ----双曲线定义及标准方程
定义
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
y
M
M F2
y
图象
F1
o
F2
x
2 2
2
(c a ) x a y a (c a )
2 2 2 2 2 2 2 2
令c2-a2=b2
x y 2 1 2 a b
2
2
双曲线的标准方程
y
M
y
M F2 x
F
O
1
F
2
x
O
双曲线第一课定义(带动画)_图文

上面 两条合起来叫做双曲线
根据实验及椭圆定义,你能给双曲线下定义吗?
回2.忆双椭曲圆线的定义
等值于平(常面大数平内于面(与︱内小F两1与于F个2两︱︱定个)F点1定F的F2点1︱点,F)的F1,2轨的的F迹距点2的叫离的距做的轨离椭差迹的圆的叫和绝做为对双一值曲个线定.
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
M
注意 (1)距离之差的绝对值
| |MF1| - |MF2| | = 2a
F1 o F2
(2)常数要小于|F1F2|大于0
0<2a<2c
ቤተ መጻሕፍቲ ባይዱ
令c2-a2=b2
y
M
F1
o
双曲线的标准方程
y
M
y M
F1 O F2 x
F2 x
O
F1
思考:如何由双曲线的标准方程来判断它的焦点 是在X轴上还是Y轴上?
双曲线第一课定义(带动画)_图文.ppt
北京摩天大楼
巴西利亚大教堂
法拉利主题公园
花瓶
反比例函数的图像
冷却塔
罗兰导航系统原理
画双曲线
演示实验:用拉链画双曲线
①如图(A), |MF1|-|MF2|=|F2F|=2a
②如图(B), |MF2|-|MF1|=|F1F|=2a
由①②可得: | |MF1|-|MF2| | = 2a
判断:
与
的焦点位置?
结论:看
前的系数,哪一个为正,则
焦点在哪一个轴上。
双曲线的标准方程与椭圆的 标准方程有何区别与联系?
椭圆、双曲线、抛物线的统一定义以及动画演示

双曲线的定义 :
平面内与两定点F1、F2的距离的差的绝对 值是常数(小于|F1F2|)的点的轨迹叫做双 曲线.这两个定点F1、F2叫做双曲线的 焦点,两个焦点之间的距离叫做焦距.
说明:若动点M到两定点的距离之差的 绝对值为2a ,| F1 F2| = 2c 当c > a >0时,动点M的轨迹是双曲线; 当a = c>0时,动点M的轨迹是两条射线; 当 0 < c < a时,动点M无轨迹
关于椭圆、双曲线、抛物线你了解多少? 在我们的实际生活中有这些曲线吗? 它们分别给我们什么印象?
椭圆?
汽车贮油罐的横截面的外轮廓线 的形状像椭圆.
北京摩天大楼
巴西利亚大教堂
法拉利主题公园
花瓶
椭圆定点 F1 ,F2的距离之和 为常数(大于F1 F2 距离)的点的轨迹 叫椭圆,两个定点 叫椭圆的焦点,两 焦点的距离叫做椭 圆的焦距.
的点的轨迹叫做抛物线.
· N M
定点F叫做抛物线的焦点.
·F
定直线l 叫做抛物线的准线.
即:
若
︳MF ︳MN
︳ ︳ 1,
则 点M的
轨迹
是
抛物线
。
椭圆的定义:
平面内到两定点F1、F2的距离之和等于 常数(大于|F1F2|)的点的轨迹叫做椭圆. 这两个定点叫做椭圆的焦点,两焦点 间的距离叫做焦距.
说明: 若动点M到的距离之和为2a , | F1 F2| = 2c 则当a>c>0时,动点M的轨迹是椭圆; 当a = c>0时,动点M的轨迹是线段F1 F2 ; 当 0 < a < c时,动点M无轨迹
抛物线的定义 :
平面内到一个定点F和一条定直线L(F不在L 上)的距离相等的点轨迹叫做抛物线,定点F叫做 抛物线的焦点,定直线L叫做抛物线的准线.
双曲线ppt

谢谢
定义2:平面内,到给定一点及一直线的距离之比为常数e(e>1,即为双曲线的离心率; 定点不在定直线上)的点的轨迹称为双曲线。定点叫双曲线的焦点,定直线叫双曲线的 准线。
定义3:一平面截一圆锥面,当截面与圆锥面的母线不平行也不通过圆锥面顶点,且与 圆锥面的两个圆锥都相交时,交线称为双曲线。
定义4:在平面直角坐标系中,二元二次方程 F(x,y)=Ax2+2Bxy+Cy2+2Dx+2Ey+F=0满足以下条件时,其图像为双曲线。
双曲线ppt
演讲人
一般的,双曲线(希腊语“Υπερβολία” ,字面意思是“超过”或“超出”)是定 义为平面交截直角圆锥面的两半的一类圆锥曲线。
它还可以定义为与两个固定的点(叫做焦点)的距离差是常数的点的轨迹。这个固 定的距离差是a的两倍,这里的a是从双曲线的中心到双曲线最近的分支的顶点的距 离。a还叫做双曲线的实半轴。焦点位于贯穿轴上,它们的中间点叫做中心,中心一 般位于原点处。
名称定义
播报
编辑
我们把平面内与两个定点F1,F2的距离的差的绝对值等于一个常数(常数为2a,小于 |F1F2|)的轨迹称为双曲线;平面内到两定点的距离差的绝对值为定长的点的轨迹叫做 双曲线。
即:||PF1|-|PF2||=2a
定义1:
平面内,到两个定点的距离之差的绝对值为常数2a(小于这两个定点间的距离)的点 的轨迹称为双曲线。定点叫双曲线的焦点,两焦点之间的距离称为焦距,用2c表示。
双曲线的每个分支具有从双曲线的中心进一步延伸的更直(较低曲率)的两个臂。 对角线对面的手臂,一个从每个分支,倾向于一个共同的线,称为这两个臂的渐近 线。所以有两个渐近线,其交点位于双曲线的对称中心,这可以被认为是每个分支 反射以形成另一个分支的镜像点。在曲线的情况下,渐近线是两个坐标轴。
双曲线的定义和性质

双曲线的定义和性质
双曲线(Hyperbolic Curve)是数学中一种特殊的曲线,它具有两条反曲线(Hyperbolic curve),沿着直线封闭,它被认为是一种极限曲线,可以收敛到两个不同
的焦点。
虽然双曲线也称为平行双曲线,但它们可以按照任意方向曲折,但不会超过可以
认为是一个自治空间内的某个最大距离。
双曲线常用来描述流动的几何形状,可以用来解
释力的重力学传播效应。
(1)双曲线的最重要的性质就是它收敛到两个焦点,且这两个焦点之间的距离可以
通过一个称为双曲线的焦距的值来衡量。
(2)另外,双曲线完全由两个反曲线(Hyperbolic curves)组成,沿着直线封闭,
且双曲线具有节点,这些节点与直线联系在一起,称为切点,切点与双曲线的凹角相关联。
(3)此外,双曲线还具有两个定点,它们位于曲线上,且称为双曲线的交点,即双
曲线截止点。
双曲线的曲率(Curvature)取决于双曲线的焦距,曲率越大,双曲线的弯
曲越明显。
(4)双曲线的面积是负的,这意味着它的形状并不完全似圆,而是更加具有弯曲性,因此它在空间中形状更复杂。
(5)双曲线具有相反性,也就是说,当它在一个方向运行时,它会在相反的方向运行。
(6)另外,双曲线的拉伸性也很高,可以曲折的的角度和弯曲程度要比普通圆弧更大,这也使它具有很多实用价值。
(7)双曲线可以用于许多不同的几何计算,如极限几何的计算,倒立曲线的计算以
及复杂的曲面的几何计算。
双曲线的定义-高中数学知识点讲解

双曲线的定义1.双曲线的定义【定义】双曲线(Hyperbola)是指与平面上到两个定点的距离之差的绝对值为定值的点的轨迹,也可以定义为到定点与定直线的距离之比是一个大于 1 的常数的点之轨迹.双曲线是圆锥曲线的一种,即圆锥面与平面的交截线.双曲线在一定的仿射变换下,也可以看成反比例函数.两个定点F1,F2 叫做双曲线的焦点(focus),定直线是双曲线的准线,常数e 是双曲线的离心率.【标准方程】푥2푎2①―푦2푏2=1(a,b>0),表示焦点在x 轴上的双曲线;푦2푎2②―푥2푏2=1(a,b>0),表示焦点在y 轴上的双曲线.【性质】푥2푎2这里的性质以―푦2푏2=1(a,b>0)为例讲解:푎2①焦点为(±c,0),其中c2=a2+b2;②准线方程为:x=±;③离心率e =푐푐푏푎>1;④渐近线:y=±푎x;⑤焦半径公式:左焦半径:r=|ex+a|,右焦半径:r=|ex﹣a|.【实例解析】푥2例 1:双曲线4―푦216= 1 的渐近线方程为푥2解:由4―푦216푥2= 0 可得y=±2x,即双曲线4―푦216= 1 的渐近线方程是y=±2x.故答案为:y=±2x.这个小题主要考察了对渐近线的理解,如果实在记不住,可以把那个等号后面的 1 看成是 0,然后因式分解得到的两个式子就是它的渐近线.例 2:已知双曲线的一条渐近线方程是x﹣2y=0,且过点P(4,3),求双曲线的标准方程解:根据题意,双曲线的一条渐近线方程为x﹣2y=0,1/ 2푥2设双曲线方程为4―y2=λ(λ≠0),∵双曲线过点P(4,3),424∴― 32=λ,即λ=﹣5.푥2∴所求双曲线方程为4―y2=﹣5,푦2即:5―푥220= 1.一般来说,这是解答题的第一问,常常是根据一些性质求出函数的表达式来,关键是找到a、b、c 三者中的两者,最后还要判断它的焦点在x 轴还是y 轴,知道这些参数后用待定系数法就可以直接写出函数的表达式了.【考点点评】这里面的两个例题是最基本的,必须要掌握,由于双曲线一般是在倒数第二个解答题出现,难度一般也是相当大的,在这里可以有所取舍,对于基础一般的同学来说,尽量的把这些基础的分拿到才是最重要的,对于还剩下的部分,尽量多写.2/ 2。
双曲线的定义及其基本性质

双曲线的定义及其基本性质
一、双曲线的定义:
(1)到两个定点F 1与F 2的距离之差的绝对值等于定长(<
2
1F F )的点的轨迹。
两定点叫双曲线的焦点。
a PF PF 221=-<2
1F F
(2)动点P 到定点F 的距离与到一条定直线的距离之比是常数e (e >1)时,这个动点的轨迹是双曲线。
这定点叫做双曲线的焦点,定直线l 叫做双曲线的准线。
二、双曲线的方程: 双曲线标准方程的两种形式:
①
12
222=-b y a x ,2
2b a c +=,
F 1(-c,0),F 2(c,0) 三、双曲线的性质:
(1)焦距F 1F 2=2c,实轴长A 1A 2=2a,虚轴长(2)双曲线的离心率为e=a
c
,e>1(3)焦点到渐近线的距离:虚半轴长b (4)有两条准线,c a x l 21:-=x l 2:=四、双曲线的渐近线:
(1)若双曲线为12222=-b y a x ⇒渐近线方程为x a
b
y ±=,
(2)若已知某双曲线与12222=-b y a x 有公共渐近线,则可设此双曲线为λ=-22
22b
y a x ,
(3)特别地当a=b 时⇔2=e ⇔两渐近线互相垂直,分别为y =±x ,此时双曲线为等轴双曲线
五、共轭双曲线:
双曲线A 的实轴为双曲线B 的虚轴,双曲线A 的虚轴为双曲线B 的实轴,即11
122=+B
A e e 。
2.3.1双曲线及其标准方程(自带动画不需另下,绝对好)
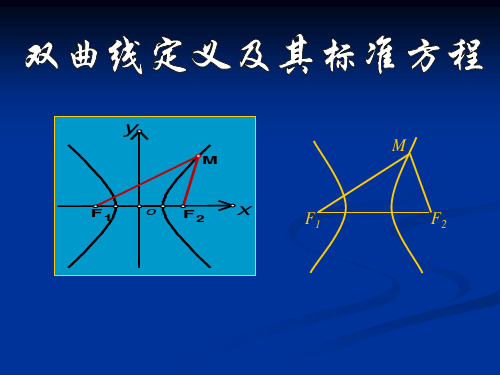
双曲线标准方程的推导
5
一、建立坐标系;设动点为 P(x,y)
P(x,y)
注:设两焦点之间的距离为 2c(c>0), 即焦点F 1(c,0),F 2(-c,0)
-5
F1(-c,0)
F2(c,0)
5
二、根据双曲线的定义找出P点 满足的几何条件。
-5
| PF1 | | PF2 | 2a 0 a c
y
M
M F2
焦点在Y轴上
y
图象
F1 o F2
x
F1
x
方程
焦点
a.b.c 的关系
x y 2 1 2 a b
F ( ±c, 0)
2 2
2
2
y x 2 1 2 a b
F(0, ± c)
2
2
2
c a b
椭 定义 方程
圆 y2
b2
双曲线
||MF1|-|MF2||=2a
2 x2 - y = 1 2 2 a b
|MF1|+|MF2|=2a
x2
a2
+
=1
y2 x2 =1 2 + 2 a b
椭圆以大小论长短
y2 a2
x2 = 1 2 b
F(±c,0) F(0,±c)
双曲线以正负定实虚
焦点
F(±c,0) F(0,±c)
a.b.c的 关系
a>b>0,a2=b2+c2
a>0,b>0,但a不一定 大于b,c2=a2+b2
三、将几何条件化为代数条件:
根据两点的间的距离公式得:
( x c) y
2
2
双曲线的性质课件(PPT 15页)

y
B2
A1 F1 O
F2 A2
x
B1
y C3C2 C1
O
x
焦点在x轴上的双曲线图像
y 渐进线方程: b x a
Y x2 y2 1 a2 b2
B2
F1
A1
A2 F2 X B1
离心率对双曲线形状的影响
焦点在y轴上的双曲线图
像
Y
y2 a2
x2 b2
1
F2
A2
B1
O
B2
X
A1
F1
焦点在y轴上的双曲线的几何性质
2、对称性:关于x轴,y轴,
原点对称。 3、顶点 A1(-a,0),A2(a,0)
F1 A1 O
A2 F2
x
4、轴:实轴 A1A2 虚轴 B1B2
B1
|A1A2|=2ca,|B1B2|=2b 5、离心率:e= a
根据以上几何性质能够
根据以上几何性质能否
较准确地画出椭圆的图形? 较准确地画出双曲线的图形呢?
双曲线标准方程:y 2 x 2 1 双曲线性质: a 2 b2
Y
1、范围:y≥a或y≤-a
F2
2、对称性:关于x轴,y轴,原点对称。
A2
3、顶点 A1(0,-a),A2(0,a)
4、轴:实轴 A1A2 ; 虚轴 B1B2 B1
5、渐近线方程: y a x
o
b
6、离心率:e=c/a
A1
F2
B2 X
Y
F1
B2
F’1 A1 o
B1
X
A2 F’2
F2
证明:(1)设已知双曲线的方程是:
x2 a2
y2 b2
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cx a2 a (x c)2 y2
F1
(c2 a2 )x2 a2y2 a2(c2 a2)
令c2-a2=b2
x2 a2
y2 b2
1
y
M
o
双曲线的标准方程
y
M
y M
F
1
OF
2
x
F2 x
O
F1
x2 a2
y2 b2
1
y2 x2 a2 b2 1
(a 0,b 0)
思考:如何由双曲线的标准方程来判断它的焦点 是在X轴上还是Y轴上?
三、例题选讲
例1 已知两定点 F1 5,0, F25,0 ,动点 P 满
足 PF1 PF2 6 ,求动点P 的轨迹方程
解:∵ F1F2 10 >6, PF1 PF2 6
∴由双曲线的定义可知,点 P 的轨迹是一条双曲线,
∵焦点为 F1(5, 0), F2(5, 0)
∴可设所求方程为:
x2 a2
判断:x2
16
y2 9
1与
y2 9
x2 16
1的焦点位置?
结论:看 x2 , y 2前的系数,哪一个为正,则
焦点在哪一个轴上。
双曲线的标准方程与椭圆的 标准方程有何区别与联系?
双曲线与椭圆之间的区别与联系
椭圆
双曲线
定义 方程
|MF1|+|MF2|=2a
x2 a2
y2 b2
1(a
b
0)
y2 a2
课堂巩固
已知双曲线的焦点为F1(-5,0), F2(5,0)双曲线上一点到焦点的距离差 的绝对值等于6,则
3 5 (1) a=_______ , c =_______ , b =_______
4
(2) 双曲线的标准方程为______________
(3)双曲线上一点P, |PF1|=10, 则|PF2|=_4_或__1_6____
说明: 0<2a<2c ;
F
1
oF
2
x
思考:
(1)若2a=2c,则轨迹是什么? (1)两条射线
(2)若2a>2c,则轨迹是什么? (2)不表示任何轨迹 (3)若2a=0,则轨迹是什么? (3)线段F1F2的垂直平分线
3.双曲线的标准方程
1.段建F系1F.2的以如中F何1点,F求2为所这原在优点的美建直的立线曲直为线角X的轴坐方,标程线? 系
北京摩天大楼
巴西利亚大教堂
法拉利主题公园
花瓶
反比例函数的图像
冷却塔
罗兰导航系统原理
画双曲线
演示实验:用拉链画双曲线
画双曲线
演示实验:用拉链画双曲线
①如图(A), |MF1|-|MF2|=|F2F|=2a
②如图(B), |MF2|-|MF1|=|F1F|=2a
由①②可得: | |MF1|-|MF2| | = 2a
1 ①a=4,xb2=3,y焦2 点在x轴上; 16 9
②焦点为(0,-6),(0,6),经过点(2,-5)
1 y2
x2
20 16
1 2.已知方程 x2
y2
2m m1
表示焦点在y轴的
双曲线,则实数m的取值范围是___m__<__-_2______
变式: 上述方程表示双曲线,则m的取值范围是 ___m_<__-__2_或__m__>__-__1_
x2 b2
1(a
b
0)
||MF1|-|MF2||=2a
x2 y2 1(a 0, b 0) a2 b2 y2 x2 1(a 0,b 0) a2 b2
焦点
a.b.c的关 系
F(±c,0) F(0,±c)
a>b>0,a2=b2+c2
F(±c,0) F(0,±c)
a>0,b>0,但a不一 定大于b,c2=a2+b2
y2 b2
1
(a>0,b>0).
∵2a=6,2c=10,∴a=3,c=5.∴b2=52-32=16.
所以点 P 的轨迹方程为 x2 y2 1 . 9 16设ຫໍສະໝຸດ 一:设法二:设法三:
变式 已知双曲线上的两点P1、P2的坐标分别为
(
2,
3),(
15 3
,
2),求双曲线的
标准方程。
小结 ----双曲线定义及标准方程
2.设点.设M(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
F1
3.列式.|MF1| - |MF2|= 2a
y
M
o F2 x
即 (x+c)2 + y2 - (x-c)2 + y2 = +_ 2a
4.化简.
(x c)2 y2 (x c)2 y2 2a
( (x c)2 y2 )2 ( (x c)2 y2 2a)2
讨论: 当 m、n 取何值时,方程 mx 2 ny 2 1 表示椭圆,双
曲线,圆 。
解:由各种方程的标准方程知,
当m 0, n 0, m n 时方程表示的曲线是椭圆
当m n 0 时方程表示的曲线是圆 当m n 0 时方程表示的曲线是双曲线
随堂练习
1.求适合下列条件的双曲线的标准方程
定义 图象
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
y
y
M M
F2
F1 o F2 x
x
F1
方程
焦点
a.b.c 的关 系
x2 a2
y2 b2
1
y2 x2 a2 b2 1
F ( ±c, 0)
F(0, ± c)
c2 a2 b2
(差的绝对值)
上面 两条合起来叫做双曲线
根据实验及椭圆定义,你能给双曲线下定义吗?
一、 双曲线定义(类比椭圆)
平面内与两个定点F1,F2的距离的差的绝对值 等于常数(小于︱F1F2︱)的点的轨迹叫做双y 曲线.
| |MF1| - |MF2| | = 2a
① 两个定点F1、F2——双曲线的焦点;
M
② |F1F2|=2c ——焦距.
