《三角形》培优题

合集下载

三角形培优精选题---思维能力提升

11.在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为12CM和15CM两部分,求三角形的各边长?
12.五种基本图形(必会)：写出∠BOC与∠A之间的数量关系。
(1)如图1,∠BOC=____________ (2)如图2,八字形的结论______________
(3)如图3若OB,OC分别平分∠ABC,∠ACB,则∠BOC=___________
A、0 B、 C、 D、
37.若a、b、c是△ABC的三边，化简 + + =( )
A、a+b-c B. a-b+c C. a+b+c D. a-b-c
41.如图所示，在△ABC中，CD、BE分别是AB、AC边
上的高，并且CD、BE交于，点P，若∠A=500，则∠BPC等于（）
A、90°B、130°C、270°D、315°
(4)如图4若OB,OC分别平分∠CBF,∠ECB,则∠BOC=____________
(5)如图5若OB,OC分别平分∠ABC,∠ACD,则∠BOC=_____________
13.已知等腰三角形的两个内角的度数比为1:2,求这个等腰三角形的顶角是多少度?
14.如图,求∠A+∠B+∠C+∠D+∠E=?
BE与CE交于G，若∠BDC=140O,∠BGC=110O,则∠A的
度数为（）
A.50OB.55OC.800D.700
23、如图1，线段AB、CD相交于点O,连接AD、CB，我们把形如图1的图形称之为“8字形”.
如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N.试解答下列问题：
问题(3)：若点是内角∠ 、外角∠ 的平分线的交点，试探索：∠ 与∠ 的数量关系，并说明理由．

(人教版)广州八年级数学上册第十一章《三角形》经典测试卷(提高培优)

一、选择题1．如图，在ABC 中，AB 边上的高为（）A ．CGB ．BFC ．BED ．AD 2．下列四组线段中，不可以构成三角形的是（）A ．4，5，6B ．1.5，2，2.5C ．13，14，15D ．1，2，3 3．如图，AB 和CD 相交于点O ，A C ∠=∠，则下列结论中不正确的是（）．A ．B D ∠=∠B ．1A D ∠=∠+∠C ．2D ∠>∠D ．C D ∠=∠ 4．若一个三角形的三边长分别为3，7，x ，则x 的值可能是（） A ．6B ．3C ．2D ．11 5．如果一个三角形的三边长分别为5,8,a ．那么a 的值可能是（） A ．2B ．9C ．13D ．15 6．如图，ABC 中，55,B D ∠=︒是BC 延长线上一点，且130ACD ∠=︒，则A ∠的度数是（）A ．50︒B ．65︒C ．75︒D ．85︒7．一个多边形的内角和外角和之比为4：1，则这个多边形的边数是（）A ．7B ．8C ．9D ．108．下列命题是真命题的个数为（）①两条直线被第三条直线所截，内错角相等．②三角形的内角和是180°．③在同一平面内平行于同一条直线的两条直线平行．④相等的角是对顶角．⑤两点之间，线段最短．A ．2B ．3C ．4D ．59．如图，D 是ABC 的边BC 上任意一点，E 、F 分别是线段AD CE 、的中点，且ABC 的面积为220cm ，则BEF 的面积是（）2cmA ．5B ．6C ．7D ．8 10．用下列长度的三根木棒首尾相接，能做成三角形框架的是（） A ．2,2,4 B ．3,4,5 C ．1,2,3 D ．2,3,6 11．如图，在ABC ∆中，AD 是ABC ∆的角平分线，DE AC ⊥，若40,60B C ︒︒∠=∠=，则ADE ∠的度数为（）A ．30︒B ．40︒C ．50︒D ．60︒ 12．如果一个三角形的两边长分别为4和7，则第三边的长可能是（）A ．3B ．4C ．11D ．12 13．如图，已知,,90,//AD BC FG BC BAC DE AC ⊥⊥∠=︒．则结论①//FG AD ；②DE 平分ADB ；③B ADE ∠=∠；④CFG BDE ∠+∠90=︒．正确的是（）A ．①②③B ．①②④C ．①③④D ．②③④ 14．如图，盖房子时，在窗框没有安装之前，木工师傅常常先在窗框上斜钉一根木条，使其不变形，这种做法的根据是（）A ．两点之间线段最短B ．长方形的对称性C ．长方形四个角都是直角D ．三角形的稳定性 15．如图，在ABC 中，70B ∠=，D 为BC 上的一点，若ADC x ∠=，则x 的度数可能为（）A ．30°B ．60°C ．70°D ．80°二、填空题16．如图1，ABC 纸片面积为24，G 为ABC 纸片的重心，D 为BC 边上的一个四等分点（BD CD <）连结CG ，DG ，并将纸片剪去GDC ，则剩下纸片（如图2）的面积为__________．17．如果一个多边形所有内角和与外角和共为2520°，那么从这个多边形的一个顶点出发共有_________条对角线18．多边形每一个内角都等于108°，多边形一个顶点可引的对角线的条数是________条． 19．如图，已知ABC 中，90,50ACB B D ︒︒∠=∠=，为AB 上一点，将BCD △沿CD 折叠后，点B 落在点E 处，且//CE AB ，则ACD ∠的度数是___________．20．如图，飞机P 在目标A 的正上方，飞行员测得目标B 的俯角为30°，那么APB ∠的度数为______°．21．如图，∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H 的度数为___________．22．如图：70B ∠=︒，60A ∠=︒，将ABC 沿一条直线MN 折叠，使点C 落到1C 位置，则12∠-∠=______．23．如图，将长方形纸片的一角折叠，使顶点A 落在F 处，折痕为BC ，FBD ∠的角平分线为BE ，将FBD ∠沿BF 折叠使BE ，BD 均落在FBC ∠的内部，且BE 交CF 于点M ，BD 交CF 于点N ，若BN 平分CBM ∠，则ABC ∠的度数为_________．24．如图，在ABC 中，已知66ABC ∠=︒，54ACB ∠=︒，BE 是AC 上的高，CF 是AB 上的高，H 是BE 和CF 的交点，EHF ∠的度数是________．25．一块含45°角的直角三角板如图放置，其中，直线//a b ，185∠=︒，则2∠=______度．26．如图，若//AB CD ，BF 平分ABE ∠，DF 平分CDE ∠，90BED ∠=，则BFD ∠=______．三、解答题27．如图，BP 平分ABC ∠，交CD 于点F ，DP 平分ADC ∠交AB 于点E ，AB 与CD 相交于点G ，42A ∠=︒．（1）若60ADC ∠=︒，求AEP ∠的度数；（2）若38C ∠=︒，求P ∠的度数．28．已知AB ∥CD ，CF 平分∠ECD ．（1）如图1，若∠DCF =25°，∠E =20°，求∠ABE 的度数．（2）如图2，若∠EBF =2∠ABF ，∠CFB 的2倍与∠CEB 的补角的和为190°，求∠ABE 的度数．29．如图，在ABC 中，90ACB ∠=︒．（1）作出AB 边上的高CD ．（2）5AC =，12BC =，13AB =，求高CD 的长．30．一个多边形的每个外角都等于40°，求这个多边形的内角和．。

新人教版八上第十一章《三角形》培优练习

第十一章三角形习题集第1课时三角形的边——三边关系姓名：___________☆知识导学1．若三角形的两边长分别为a，b(a＞b)，则第三边长x的取值范围是_______________________．2．三角形具有___________，四边形具有_____________．☆习题演练1．已知三角形ABC三边a、b、c满足（a-b）2+|b-c|=0，则△ABC的形状是（）A．钝角三角形B．直角三角形C．等边三角形D．以上都不对2．不能组成一个三角形的三条线段的长度是（）A．3，3，3 B．3，6，2 C．3，4，3 D．3，5，73．（2012•海南）一个三角形的两边长分别为3cm和7cm，则此三角形的第三边的长可能是（）A．3cm B．4cm C．7cm D．11cm4．（2013•南通）有3cm，6cm，8cm，9cm的四条线段，任选其中的三条线段组成一个三角形，则最多能组成三角形的个数为（）A．1 B．2 C．3 D．45．（2012•肇庆）等腰三角形两边长分别为4和8，则这个等腰三角形的周长为（）A．16 B．18 C．20 D．16或206．下列说法中正确的是（）A．三角形的内角中至少有两个锐角B．三角形的内角中至少有两个钝角C．三角形的内角中至少有一个直角D．三角形的内角中至少有一个钝角7．图中有______个三角形，用符号表示这些三角形：__________________________．第7题图第13题图8．在△ABC中，已知两条边a=6，b=7，则第三条边c的取值范围是_________________．9．若三角形的两边长分别为3和5，且周长为奇数，则第三边可以是________（只填符合条件的一个即可）．10．（2012•哈尔滨）一个等腰三角形的两边分别为5和6，则这个等腰三角形的周长是________________．11．若三角形的两边长分别为3和5，则它的周长l的取值范围是________________．12．（提高题）△ABC的边长均为整数，且最大边的边长为7，那么这样的三角形共有________个．13．如图，木工师傅在做完门框后，为防止变形常常像图中所示那样钉上两条斜拉的木条（图中的AB，CD两根木条），这样做的数学道理是_____________________________．14．用一条长为20cm的铁丝围成一个等腰三角形能围成有一边长为6cm的等腰三角形吗？为什么？第2课时三角形的高、中线与角平分线姓名：___________ ☆知识导学如图，完成下面几何语言的表达：（1）∵AD是△ABC的高（已知）∴AD⊥BC，∠______=∠______=90º．（2）∵AE是△ABC的中线（已知）∴______=______=21______，______=2______=2______．（3）∵AF是△ABC的角平分线（已知）∴∠______=∠______=21∠______，∠______=2∠______=2∠______．☆习题演练1．如图所示的△ABC中，线段BE是三角形AC边上的高的是（）A．B．C．D．2．下列说法正确的是（）①三角形的三条中线都在三角形内部；②三角形的三条角平分线都在三角形内部；③三角形三条高都在三角形的内部．A．①②③B．①②C．②③D．①③3．如图，已知BD是△ABC的中线，AB=5，BC=3，△ABD和△BCD的周长的差是（）A．2 B．3 C．6 D．不能确定4．如图，△ABC的角平分线AD、中线BE相交于点O，则①AO是△ABE的角平分线；②BO是△ABD 的中线；③DE是△ADC的中线；④S△ADE= S△CDE，其中结论正确的有（）A．1个B．2个C．3个D．4个5．三角形中的角平分线、中线、高都是三条特殊的__________（填直线、射线、线段）．6．如图，在边长为1的正方形网格中，△ABC的顶点B的坐标是（1，-4），过点B作AC边上的高线，则垂足D点的坐标是________．AB CD EF第3题图第4题图第6题图8．如图，在△ABC中，已知CD是角平分线，∠A=70°，∠B=50°，求∠BCD的度数．9．如图，AD是△ABC的角平分线，CE是△ABC的高，∠BAC=60°，∠BCE=40°，求∠ADB的度数．10．如图，△ABC的边BC上的高为AD，且BC=9cm，AD=2cm，AB=6cm．（1）画出AB边上的高CE；（2）求CE的长．11．如图，D，E分别是△ABC的边BC和AB上的点，△ABD与△ACD的周长相等，△CAE与△CBE 的周长相等．设BC=a，AC=b，AB=c．求AE，BD的长（用含a，b，c的代数式表示）．AB CD第3课时三角形的内角姓名：___________☆知识导学如图，延长BC 至D ，过点C 作CE//AB ∵CE//AB∴∠ECD=∠______（_________________________________________） ∠ECA=∠______（_________________________________________）∵∠ECD+∠ECA+∠ACB=180°（___________________） ∴∠A+∠B+∠ACB=180°（等量代换）归纳：三角形的内角和等于____________． ☆习题演练 1．在△ABC 中，（1）若∠A=40°，∠C=35°，则∠B=_______，△ABC 是__________三角形．（2）若∠A=70°，∠B=∠C ，则∠B=_______°．（3）若∠A ∶∠B ∶∠C=1∶1∶2，则△ABC 是__________三角形．2．如图，AD 是△ABC 的角平分线，点O 在AD 上，且OE ⊥BC 于点E ，∠BAC=60°，∠C=80°，则∠EOD 的度数为（）A ．20°B ．30°C ．10°D ．15°第2题图第4题图第5题图 3．在△ABC 中，∠B 与∠C 的角平分线交于O 点，若∠A=50°，则∠BOC=（） A ．130° B ．50° C ．25° D ．115°4．将一副直角三角板如图所示放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合，则∠1的度数为（）A ．45°B ．60°C ．75°D ．85°5．（2012•梅州）如图，在折纸活动中，小明制作了一张△ABC 纸片，点D 、E 分别是边AB 、AC 上，将△ABC 沿着DE 折叠压平，A 与A′重合，若∠A=75°，则∠1+∠2=（） A ．150° B ．210° C ．105° D ．75°6．（2005•长沙）在△ABC 中，若∠A=38°36′，∠B=57°36′，则∠C=_________度． 7．已知△ABC 中，∠A=2（∠B+∠C ），则∠A 的度数为________度．8．（2013•上海）当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内ABC DE9．如图，在△ABC 中，∠ABC=∠C ，BD 平分∠ABC ，∠A=36º，求∠BDC 的度数．10．如图，在△ABC 中，∠ABC=66°，∠ACB=54°，BE 是AC 上的高，CF 是AB 上的高，H 是BE 和CF 的交点，求∠ABE 、∠ACF 和∠BHC 的度数．11．如图，在△ABC 中，∠ACB=90°，CD 为AB 边上的高，BE 平分∠ABC ，分别交CD 、AC 于点F 、E ．求证：∠CFE=∠CEF ．12．如图，有一块直角三角板XYZ 放置在△ABC 上，恰好三角板XYZ 的两条直角边XY 、XZ 分别经过点B 、C ．△ABC 中，∠A=40°，求∠XBA+∠XCA 的度数． EFABCD13．如图，B岛在A岛的南偏西45°方向，C岛在A岛的南偏东15°方向，C岛在B岛的北偏东80°方向．从C岛看A，B两岛的视角∠ACB是多少度？14．如图，AD是△ABC的BC边上的高，AE是∠BAC的角平分线，（1）若∠B=47°，∠C=73°，求∠DAE的度数．（2）若∠B=α，∠C=β，（α＜β），求∠DAE的度数（用含α、β的代数式表示）15．已知，如图，在△ABC中，AD平分∠BAC，DE，DF分别是△ADC的高和角平分线（∠C＞∠DAC），若∠B=80°，∠C=40°．（1）求∠DAE的度数；（2）试猜想∠EDF、∠C与∠DAC有何关系？并说明理由．第4课时三角形的外角姓名：___________☆知识导学1．如图，延长QR 至T ，∵∠PRQ+∠P+∠Q=180º（__________________________）又∵∠PRQ+∠PRT=180º（__________________________） ∴∠PRT =∠P+∠Q可得：三角形的一个外角等于__________________的两个内角的和．∵∠PRT =∠P+∠Q∴∠PRT ＞∠P ，∠PRT ＞∠Q可得：三角形的一个外角大于_______________________________．2．如图，∵∠1=∠XYZ+∠YZX ，∠2=_______+_______，∠3=_______+_______．∴∠1+∠2+∠3=（∠XYZ+∠YZX ）+（______+______）+（______+______） =2（_____+______+______）=2×_____°=_____°．归纳：三角形的外角和等于____________． ☆习题演练1．如图，（1）若∠A=50º，∠B=70º，则∠ACD=_________．（2）若∠A=40º，∠ACD =130º，则∠B =_________．（3）若∠B=80º，∠ACD =135º，则∠A =_________． 2．将一副三角板按如图所示摆放，图中∠α的度数是（） A ．75° B ．90° C ．105° D ．120°第2题图第3题图第4题图第5题图 3．一副三角板有两个直角三角形，如图叠放在一起，则∠α的度数是（） A ．165° B ．120° C ．150° D ．135°4．如图，∠BDC=98°，∠C=38°，∠B=23°，∠A 的度数是（） A ．61° B ．60° C ．37° D ．39° 5．如图，∠1、∠2、∠3的大小关系为（）A ．∠2＞∠1＞∠3B ．∠1＞∠3＞∠2C ．∠3＞∠2＞∠1D ．∠1＞∠2＞∠3 6．如图，直线MA ∥NB ，∠A=70°，∠B=40°，则∠P=_______度．第6题图第7题图第8题图第9题图PQRTαABC DN A BM PEAB DCABCDXYZ 12 38．三角形三个内角之比为3∶4∶5，则它的三个外角之比为____________．9．如图，在△ABC 中，∠ACB=90°，∠A=50°，将其折叠，使点A 落在边BC 上E 处，折痕为CD ，则∠EDB=_________°．10．如图，在△ABC 中，∠A=α．∠ABC 与∠ACD 的平分线交于点A 1，得∠A 1；∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得∠A 2； …；∠A 2011BC 与∠A 2011CD 的平分线相交于点A 2012，得∠A 2012，则∠A 2012=____________．11．如图，已知D 为△ABC 边BC 延长线一点，DF ⊥AB 于F ，且交AC 于E ，∠A=34°，∠D=42°．求∠ACD 的度数．12．一个零件的形状如图中阴影部分．按规定∠A 等于90°，∠B 、∠C 应分别等于29°和21°．（1）检验人员度量得∠BDC=141°，就断定这个零件不合格．你能说明理由吗？（2）你知道∠B 、∠C 、∠BDC 三个角之间有何关系吗？请写出你的结论．（不需说明理由）13．如图，在△ABC 中，∠1=100°，∠C=80°，∠2=21∠3，BE 平分∠ABC ．求∠4的度数．14．如图，已知∠BAD=∠CBE=∠ACF ，∠FDE=48°，∠DEF=64°，求△ABC 各内角的度数．15．如图，∠ACD 是△ABC 的外角，BE 平分∠ABC ，CE 平分∠ACD ，且BE 、CE 交于E 点．求证：∠E=21∠A ．16．如图①，A 、B 两点同时从原点O 出发，点A 以每秒m 个单位长度沿x 轴的正方向运动，点B 以每秒n 个单位长度沿y 轴正方向移动．（1）若|m+2n-5|+|2m-n|=0，试分别求出1秒后，A 、B 两点的坐标；（2）如图②，设∠4的邻补角和∠3的邻补角的平分线相交于点P ．试问：在点A 、B 运动的过程中，∠P 的大小是否会发生变化？若不发生变化，请求出其值；若发生变化，请说明理由．17．已知：在△ABC 和△XYZ 中，∠A=40°，∠Y+∠Z=95°，将△XYZ 如图摆放，使得∠X 的两条边分别经过点B 和点C ．（1）当将△XYZ 如图1摆放时，则∠ABX+∠ACX=_______度；（2）当将△XYZ 如图2摆放时，请求出∠ABX+∠ACX 的度数，并说明理由；（3）能否将△XYZ 摆放到某个位置时，使得BX 、CX 同时平分∠ABC 和∠ACB ？为什么？ ABXA ZCX ZYB图1图24 A3OAx1 2 BB Px y y O 图2第5课时多边形的内角和、外角和姓名：___________☆知识导学1．过点A 作出下列多边形的对角线，各将多边形分成几个三角形？完成表格：归纳：（1）从n 边形的一个顶点出发可以引_______条对角线，把n 边形分成________个三角形．（2）n 边形的内角和等于___________．（其中n ≥3）2．从与每个内角相邻的两个外角中分别取1个相加，得到的和称为多边形的外角和．∠1＋∠2＋∠3=________°， ∠1＋∠2＋∠3＋∠=________°归纳：n 边形的外角和等于__________． ☆习题演练1．八边形的内角和是（）A ．540°B ．720°C ．900°D ．1080° 2．一个多边形的内角和等于720°，这个多边形的边数是（） A ．9 B ．8 C ．7 D ．6 3．下列各角不是多边形的内角和的是（）A ．1800°B ．540°C ．1900°D ．1440° 4．正六边形的每个内角都是（）A ．60°B ．80°C ．100°D ．120° 5．一个多边形的每个外角都等于72°，则这个多边形的边数为（） A ．5 B ．6 C ．7 D ．86．把一张形状是多边形的纸片剪去其中某一个角，剩下的部分是一个四边形，则这张纸片原来的形状不可能是（）A ．六边形B ．五边形C ．四边形D ．三角形 7．一个多边形的各个内角都等于108°，它是_______边形．8．一个多边形的内角和是1440°，则这个多边形是______边形，过其中一个顶点可以作_______条对角线，AAAA123 12349．如果一个多边形的边数增加一条，那么这个多边形的内角和增加_______，外角和__________．10．（2013•乐山）如图，在四边形ABCD中，∠A=45°．直线l与边AB，AD分别相交于点M，N，则∠1+∠2=_________．第9题图第10题图11．如图所示，将多边形分割成三角形、图（1）中可分割出2个三角形；图（2）中可分割出3个三角形；图（3）中可分割出4个三角形；由此你能猜测出，n边形可以分割出______个三角形．12．已知一个多边形的内角和是1440°，求这个多边形的边数．13．若两个多边形的边数之比为1∶2，内角和的度数之比为1∶3，求这两个多边形的边数．14．已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数．15．如图，四边形ABCD中，如果∠A与∠C互为补角，求证：∠B与∠D也互为补角．16．如图，五边形ABCDE的内角都相等，且∠1=∠2，∠3=∠4，求x的值．17．如图，求∠A+∠B+∠C+∠D+∠E+∠F的度数和．18．已知一个多边形的最小的一个内角是120°，比它稍大的一个内角是125°以后依次每一个内角比前一个内角多5°，且所有内角的和与最大的内角的度数之比是63∶8，试求这个多边形的边数．19．如图所示，小明从A点出发，沿直线前进8米后左转40°，再沿直线前进8米，又左转40°，照这样走下去，他第一次回到出发点A时，（1）整个行走路线是什么图形？（2）一共走了多少米？20．如图，BC⊥CD，∠1=∠2=∠3，∠4=70°，∠5=∠6．（1）求证：AC⊥BD；（2）求四边形ABCD各内角的度数；（3）若AC=8，BD=6，求四边形ABCD的面积．。

人教版数学八年级上册第11章《三角形》培优测试题（含答案）

第11章《三角形》培优测试题一．选择题（共10小题）1．下面分别是三根小木棒的长度，能摆成三角形的是（）A．5cm，8cm，2cm B．5cm，8cm，13cmC．5cm，8cm，5cm D．2cm，7cm，5cm2．如图，在△ABC中，∠ACB=100°，∠A=20°，D是AB上一点，将△ABC沿CD 折叠，使B点落在AC边上的B′处，则∠ADB′等于（）A．40°B．20°C．55°D．30°3．如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1=30，∠2=20°，则∠B=（）A．20°B．30°C．40°D．50°4．三角形的三个内角的度数之比为2：3：7，则这个三角形最大内角一定是（）A．75°B．90°C．105°D．120°5．在△ABC中，若AB=9，BC=6，则第三边CA的长度可以是（）A．3B．9C．15D．166．如图，AD，CE为△ABC的角平分线且交于O点，∠DAC=30°，∠ECA=35°，则∠ABO等于（）A．25°B．30°C．35°D．40°7．若正多边形的一个外角是60°，则该正多边形的内角和为（）A．360°B．540°C．720°D．900°8．如图，图中直角三角形共有（）A．1个B．2个C．3个D．4个9．有公共顶点A，B的正五边形和正六边形按如图所示位置摆放，连接AC交正六边形于点D，则∠ADE的度数为（）A．144°B．84°C．74°D．54°10．如图，AE平分△ABC外角∠CAD，且AE∥BC，给出下列结论：①∠DAE=∠CAE；②∠DAE=∠B；③∠CAE=∠C；④∠B=∠C；⑤∠C+∠BAE=180°，其中正确的个数有（）A．5个B．4个C．3个D．2个二．填空题（共8小题）11．三角形三边长分别为3，2a﹣1，4．则a的取值范围是．12．如图，在△ABC中，D、E分别是AB、AC上的点，点F在B C的延长线上，DE∥BC，∠A=44°，∠1=57°，则∠2= ．13．在△ABC中，BO平分∠ABC，CO平分∠ACB，当∠A=50°时，∠BOC= ．14．一个n边形的每个内角都为144°，则边数n为．15．在△ABC中，∠C=∠A=∠B，则∠A= 度．16．如图，AE是△ABC的角平分线，AD⊥BC于点D，若∠BAC=128°，∠C=36°，∠DAE 度．17．如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1=40°，∠2=20°，则∠B= ．18．如图，在△ABC中，点M、N是∠ABC与∠ACB三等分线的交点，若∠A=60°，则∠BMN的度数是．三．解答题（共7小题）19．（1）已知三角形三个内角的度数比为1：2：3，求这个三角形三个外角的度数．（2）一个正多边形的内角和为1800°，求这个多边形的边数．20．如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于E，∠BAC=60°，∠ABE=25°．求∠DAC的度数．21．如图①所示，为五角星图案，图②、图③叫做蜕变的五角星．试回答以下问（1）在图①中，试证明∠A+∠B+∠C+∠D+∠E=180°；（2）对于图②或图③，还能得到同样的结论吗？若能，请在图②或图③中任选其一证明你的发现；若不能，试说明理由．22．如图，已知△ABC中，高为AD，角平分线为AE，若∠B=28°，∠ACD=52°，求∠EAD的度数．23．如图，在△ABC中，AD平分∠BAC交BC于点D，AE⊥BC，垂足为E，且CF∥AD．（1）如图1，若△ABC是锐角三角形，∠B=30°，∠ACB=70°，则∠CFE= 度；（2）若图1中的∠B=x，∠ACB=y，则∠CFE= ；（用含x、y的代数式表示）（3）如图2，若△ABC是钝角三角形，其他条件不变，则（2）中的结论还成立吗？请说明理由．24．如图，BG∥EF，△ABC的顶点C在EF上，AD=BD，∠A=23°，∠BCE=44°，求∠ACB的度数．25．【探究】如图①，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点P．（1）若∠ABC=50°，∠ACB=80°，则∠A= 度，∠P= 度（2）∠A与∠P的数量关系为，并说明理由．【应用】如图②，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点P．∠ABC的外角平分线与∠ACB的外角平分线相交于点Q．直接写出∠A与∠Q的数量关系为．参考答案一．选择题1． C．2． A．3． D．4． C．5． B．6． A．7． C．8． C．9． B．10． A．二．填空题11． 1＜a＜4．12．101°．13．115°．14． 10．15．60．16． 10．17．30°．18．50°．三．解答题19．解：（1）设此三角形三个内角的比为x，2x，3x，则x+2x+3x=180，6x=180，x=30，则三个内角分别为30°、60°、90°，相应的三个外角分别为150°、120°、90°．（2）设这个多边形的边数是n，则（n﹣2）•180°=1800°，解得n=12．故这个多边形的边数为12．20．解：∵BE平分∠ABC，∴∠ABC=2∠ABE=2×25°=50°，∵AD是BC边上的高，∴∠BAD=90°﹣∠ABC=90°﹣50°=40°，∴∠DAC=∠BAC﹣∠BAD=60°﹣40°=20°．21．解：（1）证明：如图①，设BD、AD与CE的交点为M、N；△MBE和△NAC中，由三角形的外角性质知：∠DMN=∠B+∠E，∠DNM=∠A+∠C；△DMN中，∠DMN+∠DNM+∠D=180°，故∠A+∠B+∠C+∠D+∠E=180°．（2）结论仍然成立，以图③为例；延长CE交AD于F，设CE与BD的交点为M；同（1）可知：∠DMF=∠B+∠E，∠DFM=∠A+∠C；在△DMF中，∠D+∠DMF+∠DFM=180°，∴∠A+∠B+∠C+∠D+∠E=180°．22．解：∵AD为高，∠B=28°，∴∠BAD=62°，∵∠ACD=52°，∴∠BAC=∠ACD﹣∠B=24°，∵AE是角平分线，∴∠BAE=BAC=12°，∴∠EAD=∠BAD﹣∠BAE=50°．23．解：（1）∵∠B=30°，∠ACB=70°，∴∠BAC=180°﹣∠B﹣∠ACB=80°，∵AD平分∠BAC，∴∠BAD=40°，∵AE⊥BC，∴∠AEB=90°∴∠BAE=60°∴∠DAE=∠BAE﹣∠BAD=60°﹣40°=20°，∵CF∥AD，∴∠CFE=∠DAE=20°；故答案为：20；（2）∵∠BAE=90°﹣∠B，∠BAD=∠BAC=（180°﹣∠B﹣∠BCA），∴∠CFE=∠DAE=∠BAE﹣∠BAD=90°﹣∠B﹣（180°﹣∠B﹣∠BCA）=（∠BCA ﹣∠B）=y﹣x．故答案为： y﹣x；（3）（2）中的结论成立．∵∠B=x，∠ACB=y，∴∠BAC=180°﹣x﹣y，∵AD平分∠BAC，∴∠DAC=∠BAC=90°﹣x﹣y，∵CF∥AD，∴∠ACF=∠DAC=90°﹣x﹣y，∴∠BCF=y+90°﹣x﹣y=90°﹣x+y，∴∠ECF=180°﹣∠BCF=90°+x﹣y，∵AE⊥BC，∴∠FEC=90°，∴∠CFE=90°﹣∠ECF=y﹣x．24．解：∵AD=BD，∠A=23°，∴∠ABD=∠A=23°，∵BG∥EF，∠BC E=44°，∴∠DBC=∠BCE=44°，∴∠ABC=44°+23°=67°，∴∠ACB=180°﹣67°﹣23°=90°．25．解：（1）∵∠ABC=50°，∠ACB=80°，∴∠A=50°，∵∠ABC的平分线与∠ACB的平分线相交于点P，∴∠CBP=∠ABC，∠BCP=∠ACB，∴∠BCP+∠CBP=（∠ABC+∠ACB）=×130°=65°，∴∠P=180°﹣65°=115°，故答案为：50，115；（2）．证明：∵BP、CP分别平分∠ABC、∠ACB，∴，，∵∠A+∠ABC+∠ACB=180°∠P+∠PBC+∠PCB=180°，∴，∴，∴；（3）．理由：∵∠ABC的外角平分线与∠ACB的外角平分线相交于点Q，∴∠CBQ=（180°﹣∠ABC）=90°﹣∠ABC，∠BCQ=（180°﹣∠ACB）=90°﹣∠ACB，∴△BCQ中，∠Q=180°﹣（∠CBQ+∠BCQ）=180°﹣（90°﹣∠ABC+90°﹣∠ACB）=（∠ABC+∠ACB），又∵∠ABC+∠ACB=180°﹣∠A，∴∠Q=（180°﹣∠A）=90°﹣∠A．。

三角形培优专题 - 参考答案

《三角形培优专题》参考答案【例题讲解】例题1．已知等腰三角形的周长为24，试求腰长x 的取值范围和底边长y 的取值范围．【解答】解：依题意有2x +y = 24 ；对于腰长，有：y < 2x < 24 ，即：24 - 2x < 2x < 24 ，解得：6 <x < 12 ；对于底长，有：0 <y < 2x ，即：0 <y < 24 -y ，解得：0 <y < 12 ．故腰长x 的取值范围是 6 <x < 12 ，底边长y 的取值范围是0 <y < 12 ．例题2．如图，已知∠B =∠C =∠BAD ，∠ADC =∠DAC ，AE ⊥BC ，求∠DAE 的度数．【解答】解： ∠ADC =∠B +∠BAD ，∠B =∠C =∠BAD ，∠ADC =∠DAC ，∴∠B +∠C +∠BAD +∠DAC = 180︒，∴ 5∠B = 180︒，解得∠B = 36︒，∴∠ADC = 72︒．AE ⊥BC ，∴∠DAE = 90︒-∠ADE = 90︒- 72︒= 18︒．例题3．（1）如图1，这是一个五角星ABCDE，你能计算出∠A+∠B+∠C+∠D+∠E的度数吗？为什么？（必须写推理过程）（2）如图2，如果点B 向右移动到AC 上，那么还能求出∠A +∠DBE +∠C +∠D +∠E 的大小吗？若能结果是多少？（可不写推理过程）（3）如图，当点 B 向右移动到AC 的另一侧时，上面的结论还成立吗？（4）如图4，当点B 、E 移动到∠CAD 的内部时，结论又如何？根据图3 或图4，说明你计算的理由．【解答】解：（1）如图，由三角形的外角性质，∠A+∠C=∠1，∠B+∠D=∠2，∠1 +∠2 +∠E = 180︒，∴∠A +∠B +∠C +∠D +∠E = 180︒；（2）如图，由三角形的外角性质，∠A +∠D =∠1 ，∠1 +∠DBE +∠C +∠E = 180︒，∴∠A +∠DBE +∠C +∠D +∠E = 180︒；（3）如图，由三角形的外角性质，∠A +∠C =∠1，∠B +∠D =∠2 ，∠1 +∠2 +∠E = 180︒，∴∠A +∠B +∠C +∠D +∠E = 180︒；（4）如图，延长CE 与AD 相交，由三角形的外角性质，∠A +∠C =∠1，∠B +∠E =∠2 ， ∠1 +∠2 +∠D = 180︒，∴∠A +∠B +∠C +∠D +∠E = 180︒．例题4．Rt∆ABC 中，∠C = 90︒，点D 、E 分别是∆ABC 边AC 、BC 上的点，点P 是一动点．令∠PDA =∠1，∠PEB =∠2 ，∠DPE =∠α．（1）若点 P 在线段 AB 上，如图（1）所示，且∠α= 50︒，则∠1 +∠2 =140 ︒；（2）若点P 在边AB 上运动，如图（2）所示，则∠α、∠1、∠2 之间有何关系？（3）若点P 在Rt∆ABC 斜边BA 的延长线上运动(CE <CD) ，则∠α、∠1、∠2 之间有何关系？猜想并说明理由．【解答】解：（1）如图，连接PC ，由三角形的外角性质，∠1 =∠PCD +∠CPD ，∠2 =∠PCE +∠CPE ，∴∠1+∠2 =∠PCD +∠CPD +∠PCE +∠CPE =∠DPE +∠C ，∠DPE =∠α= 50︒，∠C = 90︒，∴∠1+∠2 = 50︒+ 90︒=140︒，故答案为：140︒；（2）连接PC ，由三角形的外角性质，∠1 =∠PCD +∠CPD ，∠2 =∠PCE +∠CPE ，∴∠1+∠2 =∠PCD +∠CPD +∠PCE +∠CPE =∠DPE +∠C ，∠C = 90︒，∠DPE =∠α，∴∠1+∠2 = 90︒+∠α；（3）如图1，由三角形的外角性质，∠2 =∠C +∠1+∠α，∴∠2 -∠1 = 90︒+∠α；如图2，∠α= 0︒，∠2 =∠1+ 90︒；如图3，∠2 =∠1-∠α+∠C ，∴∠1-∠2 =∠α- 90︒．例题 5．如图 1，在 ∆ABC 中， BE 平分∠ABC ，CE 平分∠ACB ，若∠A = 82︒，则∠BEC = 131︒；若∠A =a︒，则∠BEC = ．【探究】（1）如图2，在∆ABC 中，B D ，B E 三等分∠ABC ，CD ，CE 三等分∠ACB ，若∠A =a︒，则∠BEC = ；（2）如图3，O 是∠ABC 与外角∠ACD 的平分线BO 和CO 的交点，试分析∠BOC 和∠A 有怎样的关系？请说明理由；（3）如图4，O 是外角∠DBC 与外角∠BCE 的平分线BO 和CO 的交点，则∠BOC 与∠A 有怎样的关系？请说明理由．【解答】解： ∠A = 82︒，∴∠ABC +∠ACB = 180︒-∠A = 180︒- 82︒= 98︒， BE 平分∠ABC ，CE 平分∠ACB ，∴∠EBC =1∠ABC ，∠ECB =1∠ACB ，2 2∴∠EBC +∠ECB =1(∠ABC +∠ACB) =1⨯ 98︒= 49︒，2 2∴∠BEC = 180︒- (∠EBC +∠ECB) = 180︒- 49︒= 131︒；由三角形的内角和定理得，∠ABC +∠ACB = 180︒-∠A = 180︒-a︒， BE 平分∠ABC ，CE 平分∠ACB ，∴∠EBC =1∠ABC ，∠ECB =1∠ACB ，2 2∴∠EBC +∠ECB =1(∠ABC +∠ACB) =1⨯ (180︒-a︒) = 90︒-1a︒，2 2 2∴∠BEC = 180︒- (∠EBC +∠ECB) = 180︒- (90︒-1a︒) = 90︒+1a︒；2 2故答案为：131︒，90︒+1a︒；2探究：（1）由三角形的内角和定理得，∠ABC+∠ACB=180︒-∠A=180︒-a︒， BD ，BE 三等分∠ABC ，CD ，CE 三等分∠ACB ，∴∠EBC =2∠ABC ，∠ECB =2∠ACB ，3 3∴∠EBC +∠ECB =2(∠ABC +∠ACB) =2⨯ (180︒-a︒) = 120︒-2a︒，3 3 3∴∠BEC = 180︒- (∠EBC +∠ECB) = 180︒- (120︒-2a︒) = 60︒+2a︒；3 3故答案为：60︒+2a︒；3（2）∠BOC =1∠A ．2理由如下：由三角形的外角性质得，∠ACD =∠A +∠ABC ，∠OCD =∠BOC +∠OBC ，O 是∠ABC 与外角∠ACD 的平分线BO 和CO 的交点，∴∠ABC = 2∠OBC ，∠ACD = 2∠OCD ，∴∠A +∠ABC = 2(∠BOC +∠OBC ) ，∴∠A = 2∠BOC ，∴∠BOC =1∠A ；2（3）∠BOC = 90︒-1∠A ．2理由如下： O 是外角∠DBC 与外角∠BCE 的平分线BO 和CO 的交点，∴∠OBC =1(180︒-∠ABC) = 90︒-1∠ABC ，∠OCB =1(180︒-∠ACB) = 90︒-1∠ACB ，2 2 2 2在∆OBC 中，∠BOC =180︒-∠OBC -∠OCB =180︒- (90︒-1∠ABC) - (90︒-1∠ACB) =1(∠ABC +∠ACB) 2 2 2，由三角形的内角和定理得，∠ABC +∠ACB = 180︒-∠A ，∴∠BOC =1(180︒-∠A) = 90︒-1∠A ．2 2【巩固练习】1．已知线段AB = 3cm ，BC =1cm ，则线段AC 的长度为( )A ．一定是4cmB ．一定是2cmC ．一定是2cm 或4cmD ．以上都不对【解答】选：D．2．如图，∠ABC =∠ACB ，AD ，BD ，CD 分别平分∆ABC 的外角∠EAC 、内角∠ABC 、外角∠ACF ．以下结论：①AD / / B C ；②∠ACB = 2∠ADB ；③DB 平分∠ADC ；④∠ADC = 90︒-∠ABD ；⑤∠BDC =1∠BAC ．其中正确的结论有( ) 2A．1 个B．2 个C．3 个D．4 个【解答】解： AD 平分∠EAC ，∴∠EAC = 2∠EAD ，∠EAC =∠ABC +∠ACB ，∠ABC =∠ACB ，∴∠EAD =∠ABC ，∴AD / / BC ，∴①正确；AD / / BC ，∴∠ADB =∠DBC ，BD 平分∠ABC ，∠ABC =∠ACB ，∴∠ABC =∠ACB = 2∠DBC ，∴∠ACB = 2∠ADB ，∴②正确；BD 平分∠ABC ，∴∠ABD =∠DBC ，∠ADB =∠DBC ，∠ADC = 90︒-1∠ABC ，2∴∠ADB 不等于∠CDB ，∴③错误； AD 平分∠EAC ，CD 平分∠ACF ，∴∠DAC =1∠EAC ，∠DCA =1∠ACF ，2 2∠EAC =∠ACB +∠ACB ，∠ACF =∠ABC +∠BAC ，∠ABC +∠ACB +∠BAC = 180︒，∴∠ADC = 180︒- (∠DAC +∠ACD)= 180︒-1(∠EAC +∠ACF ) 2= 180︒-1(∠ABC +∠ACB +∠ABC +∠BAC) 2= 180︒-1(180︒+∠ABC) 2= 90︒-1∠ABC ，∴④正确；2∠BDC =∠DCF -∠DBF =1∠ACF -1∠ABC =1∠BAC ，∴⑤正确，2 2 2故选：D ．3．如图，要使六边形木架（用六根木条钉成）不变形，至少要再钉上木条的根数是( )A ．1B ．2C ．3D ．4【解答】解：过六边形的一个顶点作对角线，有6 - 3 = 3 条对角线，所以至少要钉上 3 根木条．故选： C ．4．如图，在 ∆ABC 中， ∠ABC 的平分线与 ∠ACD 的平分线交于点 A 1 ， ∠A 1BC 的平分线与∠A CD 的平分线交于点 A ，依此类推．已知∠A = α，则∠A 的度数为α（用含12n 、α的代数式表示）．n2n【解答】解： ∆ABC 中， ∠A = ∠ACD - ∠ABC ， A 1 是 ∠ABC 角平分与 ∠ACD 的平分线的交点， ∠A = α，∴∠A = ∠A CD - ∠A BC = 1 (∠ACD - ∠ABC ) = 1∠A ；1 1 12 2同理可得， ∠A = 1 ∠A = 1∠A ，22 1 22∠A = 1 ∠A = 1∠A ， 32 2 23依此类推， ∠A = 1∠A ，即∠A = α ．n 2n 故答案为： α．2nn2n5．如图，线段 AB 、CP 相交于点O ，连接 AD 、CB ， ∠DAB 、∠BCD 的平分线 AP 、CP 相交于点 P ，并且为CD 、 AB 分别相交于 M 、N 两点，若∠D = 40︒ ，∠B = 30︒ ，则∠P 的度数为 35︒ ．【解答】解：在∆AOD 中，∠AOD =180︒-∠OAD -∠D ，在∆BOC 中，∠BOC = 180︒-∠B -∠OCB ，∠AOD=∠BOC（对顶角相等），∴180︒-∠OAD -∠D = 180︒-∠B -∠OCB ，∴∠OAD +∠D =∠B +∠OCB ，∠D = 40︒，∠B = 30︒，∴∠OAD + 40︒=∠OCB + 30︒，∴∠OCB -∠OAD = 10︒，AP 、CP 分别是∠DAB 和∠BCD 的角平分线，∴∠1 =1∠OAD ，∠3 =1∠OCB ，2 2又 ∠1 +∠D =∠3 +∠P ，∴∠P =∠1 +∠D -∠3 =1(∠OAD -∠OCB) +∠D =1⨯ (-10︒) + 40︒= 35︒．2 2故答案为：35︒．6．在∆ABC 中，AB =AC ，AC 边上的中线BD 把三角形ABC 的周长分为9cm 和12cm 的两部分，求三角形各边的长．【解答】解：根据题意画出图形，如图，设等腰三角形的腰长AB =AC = 2x ，BC =y ，BD 是腰上的中线，∴AD =DC =x ，若AB +AD 的长为12，则2x +x = 12 ，解得x = 4cm ，则x +y = 9 ，即 4 +y = 9 ，解得y = 5cm ；若AB +AD 的长为9，则2x +x = 9 ，解得x = 3cm ，则x +y = 12 ，即3 +y = 12 ，解得y = 9cm ；所以等腰三角形的腰长为8 厘米，底边长为 5 厘米．或腰长为6cm ，底长为9cm ．7．已知a，b，c 是△ABC 的三边长，a=4，b=6，设三角形的周长是x．（1）直接写出c 及x 的取值范围；（2）若x 是小于18 的偶数①求c 的长；②判断△ABC 的形状．【解答】解：（1）因为a=4，b=6，所以2＜c＜10．故周长x 的范围为12＜x＜20．（2）①因为周长为小于18 的偶数，所以x=16 或x=14．当x 为16 时，c=6；当x 为14 时，c=4．②当c=6 时，b=c，△ABC 为等腰三角形；当c=4 时，a=c，△ABC 为等腰三角形．综上，△ABC 是等腰三角形．8．如图，四边形ABCD 中，BE 、CF 分别是∠B 、∠D 的平分线．且∠A =∠C = 90︒，试猜想BE 与DF 有何位置关系？请说明理由．【解答】解：BE / / DF ，理由是：四边形内角和等于360︒，∠A =∠C = 90︒，∴∠ABC +∠ADC = 180︒，BE 、CF 分别是∠B 、∠D 的平分线，∴∠1 =1∠ABC ，∠2 =1∠ADC ，2 2∴∠1 +∠2 = 90︒，在Rt∆DCF 中，∠3 +∠2 = 90︒，∴∠1 =∠3 ，∴BE / / DF ．9．如图，∆ABC 中，三条内角平分线AD 、BE 、CF 相交于点O ，OG ⊥BC 于点G ．（1）若∠ABC = 40︒，∠BAC = 60︒，求∠BOD 和∠COG 的度数．（2）若∠ABC =α，∠BAC =β，则∠BOD 和∠COG 相等吗？请说明理由．【解答】解：（1）∠BOD=∠OAB+∠OBA=1∠BAC +1∠ABC = 50︒2 2∠COG = 90︒-∠OCG= 90︒-1(180︒-∠ABC -∠BAC) 2= 90︒- 40︒= 50︒；（2）∠BOD 和∠COG相等．理由： ∠BOD =∠OAB +∠OBA=1∠BAC +1∠ABC 2 2=1(α+β) 2=1(180︒-∠ACB) 2= 90︒-1∠ACB 2= 90︒-∠OCG =∠COG ．10．如图1 ，在∆ABC 中，∠B = 90︒，分别作其内角∠ACB 与外角∠DAC 的平分线，且两条角平分线所在的直线交于点 E ．（1）∠E = 45 ︒；（2）分别作∠EAB 与∠ECB 的平分线，且两条角平分线交于点F ．①依题意在图1 中补全图形；②求∠AFC 的度数；（3）在（2）的条件下，射线FM 在∠AFC 的内部且∠AFM =1∠AFC ，设3EC 与AB 的交点为H ，射线HN 在∠AHC 的内部且∠AHN =1∠AHC ，射线3HN 与 FM 交于点 P ，若∠FAH ，∠FPH 和∠FCH 满足的数量关系为∠FCH =m∠FAH +n∠FPH ，请直接写出m ，n 的值．【解答】解：（1）如图 1 ， EA平分∠DAC ，EC 平分∠ACB ，∴∠CAF =1∠DAC ，∠ACE =1∠ACB ，2 2设∠CAF =x ，∠ACE =y ，∠B = 90︒，∴∠ACB +∠BAC = 90︒，∴ 2 y +180 - 2x = 90，x -y = 45，∠CAF =∠E +∠ACE ，∴∠E =∠CAF -∠ACE =x -y = 45︒，故答案为： 45 ；（2）①如图 2 所示，②如图 2 ， CF 平分∠ECB ，∴∠ECF = 1 y ， 2∠E + ∠EAF = ∠F + ∠ECF ，∴ 45︒ + ∠EAF = ∠F + 1 y ①， 2同理可得： ∠E + ∠EAB = ∠B + ∠ECB ， ∴ 45︒ + 2∠EAF = 90︒ + y ，∴∠EAF = 45 + y ②，2把②代入①得： 45︒ + 45 + y = ∠F + 1 y ，2 2∴∠F = 67.5︒，即∠AFC = 67.5︒ ；（3）如图 3 ，设∠FAH =α，AF 平分∠EAB ，∴∠FAH = ∠EAF =α，∠AFM = 1∠AFC = 1⨯ 67.5︒ = 22.5︒ ，3 3 ∠E + ∠EAF = ∠AFC + ∠FCH ，∴45 +α= 67.5 + ∠FCH ，∴∠FCH =α- 22.5①，∠AHN = 1 ∠AHC = 1 (∠B + ∠BCH ) = 1 (90 + 2∠FCH ) = 30 + 2∠FCH ， 3 3 3 3 ∠FAH + ∠AFM = ∠AHN + ∠FPH ，∴α+ 22.5 = 30 + 2∠FCH + ∠FPH ，②3 把①代入②得： ∠FPH = α+ 22.5 ，3∠FCH = m ∠FAH+ n ∠FPH ，α- 22.5 = m α+ n α+ 22.5 ，3解得： m = 2 ， n = -3．。

八年级数学上册第十一章【三角形】提高练习(培优专题)

一、选择题1．下列每组数分别是三根小木棒的长度，不能用它们搭成三角形的是（）A ．1cm ，2cm ，3cmB ．2cm ，3cm ，4cmC ．3cm ，4cm ，5cmD ．5cm ，6cm ，7cm2．若一个正多边形的内角和等于其外角和的3倍，则这个正多边形是（）A ．5边形B ．6边形C ．7边形D ．8边形3．若过六边形的一个顶点可以画n 条对角线，则n 的值是（）A ．1B ．2C ．3D ．44．用若干根等长的小木棍搭建等边三角形（三边相等的三角形），搭建1个等边三角形最少需要3根小木棍，搭建2个等边三角形最少需要5根小木棍，搭建4个等边三角形最少需要小木棍的根数是（）A ．12B ．10C ．9D ．65．已知长度分别为3cm ，4cm ，xcm 的三根小棒可以摆成一个三角形，则x 的值不可能是（）A ．2.4B ．3C ．5D ．8.56．如图，在ABC ∆中，AD 是ABC ∆的角平分线，DE AC ⊥，若40,60B C ︒︒∠=∠=，则ADE ∠的度数为（）A ．30︒B ．40︒C ．50︒D ．60︒7．做一个三角形的木架，以下四组木棒中，符合条件的是（）A ．4cm, 5cm,9cmB ．4cm, 5cm, 6cmC ．5cm,12cm,6cmD ．4cm,2cm,2cm8．现有两根木棒，长度分别为5cm 和13cm ，若不改变木棒的长度，要钉成一个三角形木架，则应在下列四根木棒中选取（）A ．20cm 的木棒B ．18cm 的木棒C ．12cm 的木棒D ．8cm 的木棒 9．以下列长度的各组线段为边，能组成三角形的是（）A ．2cm ，3cm ，6cmB ．3cm ，4cm ，8cmC ．5cm ，6cm ，10cmD ．5cm ，6cm ，11cm10．下列四个图形中，线段CE 是ABC 的高的是（）A ．B ．C ．D ． 11．如图，王师傅用六根木条钉成一个六边形木框，要使它不变形，至少还要再钉上________根木条（）A ．2B ．3C ．4D ．5二、填空题12．如图1，△ABC 中，有一块直角三角板PMN 放置在△ABC 上（P 点在△ABC 内），使三角板PMN 的两条直角边PM 、PN 恰好分别经过点B 和点C .若∠A ＝52°，则∠1＋∠2＝__________；13．将正三角形、正四边形、正五边形按如图所示的位置摆放．如果147∠=︒，220∠=︒，那么3∠= __________．14．如图，在ABC 中，CE AB ⊥于点E ，AD BC ⊥于点D ，且3AB =，6BC =，5CE =，则AD =_________．15．一个正多边形的每个内角为108°，则这个正多边形所有对角线的条数为_____． 16．已知ABC 的高为AD ，65BAD ∠=︒，25CAD ∠=︒，则BAC ∠的度数是_______． 17．如图，在ABC 中，已知66ABC ∠=︒，54ACB ∠=︒，BE 是AC 上的高，CF 是AB 上的高，H 是BE 和CF 的交点，EHF ∠的度数是________．18．已知等腰三角形的一边长等于11cm ，一边长等于5cm ，它的周长为______． 19．已知//AB CD ，点P 是平面内一点，若30,20BPD PBA ∠=︒∠=︒，则CDP ∠=___________度．20．如图，把正三角形、正四边形、正五边形按如图所示的位置摆放，若150,222∠=︒∠=︒，则3∠=_______．21．如图，在ABC 中，E 、D 、F 分别是AD 、BF 、CE 的中点，若DEF 的面积是1，则ABC S =______．三、解答题22．如图，BP 平分ABC ∠，交CD 于点F ，DP 平分ADC ∠交AB 于点E ，AB 与CD 相交于点G ，42A ∠=︒．（1）若60ADC ∠=︒，求AEP ∠的度数；（2）若38C ∠=︒，求P ∠的度数．23．已知，a ，b ，c 为ABC 的三边，化简|a ﹣b ﹣c|﹣2|b ﹣c ﹣a|+|a+b ﹣c|． 24．如图，//AE DF ，BE DF ⊥于点G ，190B ∠+∠=︒．（1）判断CD 与AB 的位置关系，并说明理由．（2）若50A ∠=︒，求出DEG ∠的度数．25．如图，ABC 中，AD 是高，,AE BF 是角平分线，它们相交于点,80O CAB ∠=︒，60C ∠=°，求DAE ∠和BOA ∠的度数．一、选择题1．随着人们物质生活的提高，玩手机成为一种生活中不可缺少的东西，手机很方便携带，但唯一的缺点就是没有固定的支点，为了解决这一问题，某工厂研制生产了一种如图所示的手机支架．把手机放在上面就可以方便地使用手机，这是利用了三角形的哪一个性质（）A ．三角形两边之和大于第三边B ．三角形具有稳定性C ．三角形的内角和是180D ．直角三角形两个锐角互余2．将一副直角三角板如图放置，使两直角重合DFB ∠的度数为（）A ．145︒B ．155︒C ．165︒D ．175︒3．已知三角形的两边长分别为1和4，则第三边长可能是（）A ．3B ．4C ．5D ．64．若一个多边形的每个内角都等于160°，则这个多边形的边数是（）A ．18B ．19C ．20D ．215．如图，D 是ABC 的边BC 上任意一点，E 、F 分别是线段AD CE 、的中点，且ABC 的面积为220cm ，则BEF 的面积是（）2cmA ．5B ．6C ．7D ．86．在ABC 中，若一个内角等于另两个内角的差，则（）A ．必有一个内角等于30°B ．必有一个内角等于45°C ．必有一个内角等于60°D ．必有一个内角等于90°7．如图，△ABC 中AC 边上的高是哪条垂线段．（）A ．AEB ．CDC ．BFD ．AF8．如图，直线//BC AE ，CD AB ⊥于点D ，若150∠=︒，则BCD ∠的度数是（）A ．60°B ．50°C ．40°D ．30°9．现有两根木棒，长度分别为5cm 和13cm ，若不改变木棒的长度，要钉成一个三角形木架，则应在下列四根木棒中选取（）A ．20cm 的木棒B ．18cm 的木棒C ．12cm 的木棒D ．8cm 的木棒 10．下列长度的三条线段，能组成三角形的是（）A ．3，5，6B ．3，2，1C ．2，2，4D ．3，6，10 11．下列说法正确的个数为（）①过两点有且只有一条直线；②两点之间，线段最短；③若ax ay =，则x y =；④若A 、B 、C 三点共线且AB BC =，则B 为AC 中点；⑤各边相等的多边形是正多边形． A ．①②④ B ．①②③ C ．①④⑤ D ．②④⑤二、填空题12．如图，已知//,AB CD E 是直线AB 上方一点，G 为直线AB 下方一点，F 为直线CD 上一点，148EAF ︒∠=，3BAF BAG ∠=∠，3DCE DCG ∠=∠，则E ∠和G ∠的数量关系为___________．13．如图，C 为∠AOB 的边OA 上一点，过点C 作CD ∥OB 交∠AOB 的平分线OE 于点F ，作CH ⊥OB 交BO 的延长线于点H ，若∠EFD ＝α，现有以下结论：①∠COF ＝α；②∠AOH ＝180°﹣2α；③CH ⊥CD ；④∠OCH ＝2α﹣90°．其中正确的是__（填序号）．14．如图，在△ABC 中，点O 是△ABC 内一点，且点O 到△ABC 三边的距离相等，若∠A ＝70°，则∠BOC ＝________．15．将正三角形、正四边形、正五边形按如图所示的位置摆放．如果147∠=︒，220∠=︒，那么3∠= __________．16．如图，∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H 的度数为___________．17．如图，△ABC 的面积为1，分别倍长（延长一倍）AB ，BC ，CA 得到△A 1B 1C 1，再分别倍长A 1B 1，B 1C 1，C 1A 1得到△A 2B 2C 2．…按此规律，倍长2020次后得到的△A 2020B 2020C 2020的面积为_____．18．多边形每一个内角都等于90︒，则从此多边形一个顶点出发的对角线有____条． 19．如图，△ABC 中，D 为BC 边上的一点，BD ：DC=2：3，△ABC 的面积为10，则△ABD 的面积是_________________20．如图，AB BE ,分别是ABC 中,BC AC 边上的高，6cm BC ，4cm AC =，若3cm =AD ，则BE 的长为__________cm ．21．一个三角形的三个内角度数之比为2:3:5，那这个三角形一定是三角形__________．三、解答题22．如图，已知在ABC 中，CE 是外角ACD ∠的平分线，BE 是ABC ∠的平分线．（1）求证：2A E ∠=∠．（2）若A ABC ∠=∠，求证：//AB CE ．23．题情景：在三角形纸片内部给定－些点，满足这些点连同三角形三个顶点没有三个点在一条直线上，以这些点为顶点，将纸片剪成－些小三角形纸片，一共能得到几个小三角形？问题解决：甲同学绘制了如下三个图，分别在三角形内部取1个点、2个点，如下图所示：继续探究：在三角形内部取三个点，画出分割的图形，并经过观察计数完成表格：内部点的个数1 2 3 n 得到三角形个数 3 5拓展联系：当纸片是四边形时，探究此时内部所取点的个数与得到三角心个数的关系，完成表格：内部点的个数1 2 3 n 得到三角形个数概括提升：设纸片的边数为m ，内部点的个数为n ，得到三角形的个数是x ，请直接写出x 与m 、n 的关系：______________．24．如图BC 平分∠ABE ，DC 平分∠ADE ，求证：∠E+∠A=2∠C25．已知：180,BDG EFG B DEF ∠+∠=︒∠=∠．（1）如图1，求证：//DE BC ．（2）如图2，当90A EFG ∠=∠=︒时，请直接写出与C ∠互余的角．一、选择题1．将一副直角三角板如图放置，使两直角重合DFB ∠的度数为（）A ．145︒B ．155︒C ．165︒D ．175︒ 2．一个多边形的外角和是360°，这个多边形是（）A ．四边形B ．五边形C ．六边形D ．不确定 3．若一个正多边形的内角和等于其外角和的3倍，则这个正多边形是（） A ．5边形 B ．6边形 C ．7边形 D ．8边形 4．下列长度（单位：cm ）的三条线段能组成三角形的是（）A ．13，11，12B ．3，2，1C ．5，12，7D ．5，13，5 5．如图，D 是ABC 的边BC 上任意一点，E 、F 分别是线段AD CE 、的中点，且ABC 的面积为220cm ，则BEF 的面积是（）2cmA ．5B ．6C ．7D ．86．下列长度的线段能组成三角形的是（）A ．2，3，5B ．4，6，11C ．5，8，10D ．4，8，4 7．在下列长度的四根木棒中，能与2m 、5m 长的两根木棒钉成一个三角形的是（） A ．2m B ．3m C ．5m D ．7m8．如图，直线//BC AE ，CD AB ⊥于点D ，若150∠=︒，则BCD ∠的度数是（）A ．60°B ．50°C ．40°D ．30°9．设四边形的内角和等于a ，五边形的外角和等于b ，则a 与b 的关系是（）． A ．a b = B ．180a b =+° C ．180b a =+︒ D ．360b a =+︒ 10．下列说法正确的个数为（）①过两点有且只有一条直线；②两点之间，线段最短；③若ax ay =，则x y =；④若A 、B 、C 三点共线且AB BC =，则B 为AC 中点；⑤各边相等的多边形是正多边形． A ．①②④ B ．①②③ C ．①④⑤ D ．②④⑤ 11．如图，105DBA ∠=︒，125ECA ∠=︒，则A ∠的度数是（）A ．75°B ．60°C ．55°D ．50°二、填空题12．从n 边形的一个顶点出发，连接其余各顶点，可以将这个n 边形分割成17个三角形，则n ＝______．13．在△ABC 中，∠A 是钝角，∠B =30°，设∠C 的度数是α，则α的取值范围是___________14．如图，已知ABC 中，90,50ACB B D ︒︒∠=∠=，为AB 上一点，将BCD △沿CD折叠后，点B 落在点E 处，且//CE AB ，则ACD ∠的度数是___________．15．若,,a b c 是△ABC 的三边长,试化简a b c a c b +-+--= __________． 16．如果三角形两条边分别为3和5，则周长L 的取值范围是________17．如果点G 是ABC ∆的重心，6AG =，那么BC 边上的中线长为_______________________．18．如图，△ABC 的两条中线AD 、BE 相交于点G ，如果S △ABG ＝2，那么S △ABC ＝_____．19．如图，在一个四边形ABCD 中，AE 平分∠BAD ，DE 平分∠ADC ，且∠ABC=80°，∠BCD=70°，则∠AED=_________．20．如图中，36B ∠=︒，76C ∠=︒，AD 、AF 分别是ABC 的角平分线和高，DAF ∠=________．21．如图，ABC ∆的面积是2，AD 是BC 边上的中线，13AE AD =，12BF EF =．则DEF ∆的面积为_________．三、解答题22．如图，在ABC ∆中，48,A CE ∠=︒是ACB ∠的平分线， B C D 、、在同一直线上，,40.BEC BFD D ∠=∠∠=︒（1）求BCE ∠的度数；（2）求B 的度数． 23．如图，BM 是ABC 的中线，AB ＝5cm ，BC ＝3cm ，那么ABM 与BCM 的周长的差是多少？24．已知一个多边形的内角和比它的外角和的3倍还多180度．（1）求这个多边形的边数；（2）求这个多边形的对角线的总条数．25．平面内，四条线段AB，BC，CD，DA首尾顺次连接，∠ABC=24°，∠ADC=42°．（1）∠BAD和∠BCD的角平分线交于点M（如图1），求∠AMC的大小．（2）点E在BA的延长线上，∠DAE的平分线和∠BCD平分线交于点N（如图2），求∠ANC．。

人教版八年级上册三角形培优卷

三角形单元测试题一、选择题（每空3分，共30分）1、如果三角形的两边分别为3和5，那么这个三角形的周长可能是（）A．15 B．16 C．8 D．72、下列说法中，正确的个数为（）①三角形的三条高都在三角形内，且都相交于一点.②三角形的中线都是过三角形的某一个顶点，且平分对边的直线.③在△ABC中，若∠A= ∠B= ∠C，则△ABC是直角三角形.④一个三角形的两边长分别是8和10，那么它的最短边的取值范围是2<b<18.A．1个 B．2个 C．3个 D．4个3、三角形的三条高所在的直线相交于一点，则这个交点的位置（）A．在三角形外 B．在三角形内 C．在三角形边上D．要根据三角形的形状才能定4、有五条线段，长度分别为1、4、5、6、8，从中任取3条，一定能构成三角形的可能性是（）A．20％ B．30％ C．40％ D．50％5、如图，将矩形ABCD纸片沿对角线BD折叠，使点C落在C’处，BC’交AD于E，若∠DBC=22.5°，则在不添加任何辅助线的情况下，图中45°的角（虚线也视为角的边）有（）A．6个 B．5个 C．4个 D．3个6、在△ABC中，AB=6，AC=3，则∠B的最大值为（）A．30° B．45° C．60° D．90°7、希腊人常用小石子在沙滩上摆成各种形状来研究数，例如：他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数;类似地，称图2中的1，4，9，16…这样的数成为正方形数。

下列数中既是三角形数又是正方形数的是（）A.289B.1024C.1225D.13788、图①是一块边长为1，周长记为P1的正三角形纸板，沿图①的底边剪去一块边长为的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪如图掉正三角形纸板边长的）后，得图③，④，…，记第n(n≥3) 块纸板的周长为Pn ，则Pn-Pn-1的值为（）A． B．C． D．9、如图，已知△ABC是等腰直角三角形，∠A=90°，BD是∠ABC的平分线，DE⊥BC于E，若BC=10cm，则△DEC的周长为（）A．8cm B．10cm C．12cm D．14cm10、如图，在边长为4的等边三角形ABC中，AD是BC边上的高，点E、F是AD上的两点，则图中阴影部分的面积是（）A．4B．3C．2D．二、填空题（每空3分，共18分）11、如图，三角形纸片ABC中，∠A＝65°，∠B＝75°，将纸片的一角折叠，使点C落在△ABC 内，若∠1＝20°，则∠2=___ ___。

第十一章三角形同步培优专项习题(一)人教版八年级数学上册

第十一章《三角形》同步培优专项习题（一）1．如图，AE，DE分别平分∠BAC和∠BDC，∠B＝∠BDC＝45°，∠C＝51°，求∠E的度数．2．已知，如图，在△ABC中，AD，AE分别是△ABC的高和角平分线．（1）若∠ABC＝30°，∠ACB＝60°，求∠DAE的度数；（2）写出∠DAE与∠C﹣∠B的数量关系，并证明你的结论．3．如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B＝70°，∠C＝30°．（1）求∠BAE的度数；（2）求∠DAE的度数；（3）探究：小明认为如果只知道∠B﹣∠C＝40°，也能得出∠DAE的度数？你认为可以吗？若能，请你写出求解过程；若不能，请说明理由．4．（1）已知：如图1，P是直角三角板ABC斜边AB上的一个动点，CD、CE分别是∠ACP 和∠BCP的平分线，试探究：当点P在斜边AB上移动时，∠DCE的大小是否会发生变化，请说明你的理由．（2）把直角三角板的直角顶点C放在直尺的一边MN上，点A和点B在直线MN的上方（如图2），此时∠ACM与∠BCN的数量关系是∠ACM+∠BCN＝；当把这把直角三角板绕顶点C旋转到点A在直线MN的下方，点B仍然在直线MN的上方时（如图3），∠ACM 与∠BCN的数量关系是；当把这把直角三角板绕顶点C旋转到点A和点B都在直线MN的下方时（如图4），∠ACM与∠BCN的数量关系是．5．如图，在△ABC中，∠B＝30°，∠C＝66°，AE⊥BC于E，AD平分∠BAC，求∠DAE的度数．6．如图：在直角坐标系中，已知B（b，0），C（0，c），且|b+3|+（2c﹣8）2＝0．（1）求B、C的坐标；（2）点A、D是第二象限内的点，点M、N分别是x轴和y轴负半轴上的点，∠ABM＝∠CBO，CD∥AB，MC、NB所在直线分别交AB、CD于E、F，若∠MEA＝70°，∠CFB＝30°．求∠CMB﹣∠CNB的值；（3）如图：AB∥CD，Q是CD上一动点，CP平分∠DCB，BQ与CP交于点P，给出下列两个结论：①的值不变；②的值改变．其中有且只有一个是正确的，请你找出这个正确的结论并求其定值．7．如图，AD是△ABC边BC上的高，BE平分∠ABC交AD于点E．若∠C＝60°，∠BED＝70°．求∠ABC和∠BAC的度数．8．已知：如图A，△ABC各角的平分线AD，BE，CF交于点O．（1）试说明∠BOC＝90°+∠BAC；（2）如图B，过点O作OG⊥BC于G，试判断∠BOD与∠COG的大小关系（大于，小于或等于），并说明理由．9．（1）探究：如图1，求证：∠BOC＝∠A+∠B+∠C．（2）应用：如图2，∠ABC＝100°，∠DEF＝130°，求∠A+∠C+∠D+∠F的度数．10．一个多边形的内角和与外角和的差为1260°，求它的边数．11．（1）如图，已知△ABC中，O为∠ABC和∠ACB的平分线BO，CO的交点．试猜想∠BOC 和∠A的关系，并说明理由；（2）如图，若O为∠ABC和∠ACB外角的平分线BO，CO的交点，则∠BOC与∠A的关系又该怎样？为什么？12．如图，在△ABC中，∠ABC、∠ACB的平分线相交于点O．（1）若∠ABC＝40°、∠ACB＝50°，则∠BOC＝；（2）若∠ABC+∠ACB＝116°，则∠BOC＝；（3）若∠A＝76°，则∠BOC＝；（4）若∠BOC＝120°，则∠A＝；（5）请写出∠A与∠BOC之间的数量关系（不必写出理由）．13．如图，在△ABC中，点D在BC上，点E在AC上，AD交BE于F．已知EG∥AD交BC于G，EH⊥BE交BC于H，∠HEG＝55°．（1）求∠BFD的度数．（2）若∠BAD＝∠EBC，∠C＝44°，求∠BAC的度数．14．如图①，△ABC的角平分线BD、CE相交于点P．（1）如果∠A＝80°，求∠BPC的度数；（2）如图②，过P点作直线MN，分别交AB和AC于点M和N，且MN平行于BC，则有∠MPB+∠NPC＝90°﹣∠A．若将直线MN绕点P旋转，（ⅰ）如图③，试探索∠MPB、∠NPC、∠A三者之间的数量关系是否依然成立，并说明理由；（ⅱ）当直线MN与AB的交点仍在线段AB上，而与AC的交点在AC的延长线上时，如图④，试问（ⅰ）中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立？若不成立，请给出∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由．15．如图，已知在△ABC中，CE是外角∠ACD的平分线，BE是∠ABC的平分线．（1）求证：∠A＝2∠E；（2）若∠A＝∠ABC，求证：AB∥CE．16．如图，在△ABC中，∠BAC＝50°，∠B＝60°，AE⊥BC于点E，CD平分∠ACB且分别与AB、AE交于点D、F，求∠AFC的度数．17．已知如图，△ABC过点A做∠DAE＝∠BAC，且AD∥BC，∠1＝∠2．（1）求证AB∥DE；（2）若已知AE平分∠BAC，∠C＝35°，求∠BAD的度数．18．已知如图①，BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线，BQ、CQ分别是∠PBC、∠PCB的角平分线，BM、CN分别是∠PBD、∠PCE的角平分线，∠BAC＝α．（1）当α＝40°时，∠BPC＝°，∠BQC＝°；（2）当α＝°时，BM∥CN；（3）如图②，当α＝120°时，BM、CN所在直线交于点O，求∠BOC的度数；（4）在α＞60°的条件下，直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系：．。

《三角形》全章复习与巩固(培优篇)(含答案)

《三角形》全章复习与巩固（培优篇）（含答案）一、单选题1.如图，ZkABC的面积为3（）C∏Λ AE=ED, BD=2DC,则图中四边形EDCF的面积等于（）A. 8.5B. 8C. 9.5D. 92.如图，41/,。

“平分/^位＞和/88,若/8 = 34。

，/0 = 42。

，则NΛ∕=（）A. 34oB. 38oC. 40oD. 42°3.已知MBC中，CD是A8边上的高，C£平分ZAC8.若NA =机。

，ZB = ∕ιo, m≠n,则NQCE的度数等于（）A. -m oB. -n oC. ，（〃?。

一〃。

）D. -∖m o-n o2 2 2v f2l4.如图，AD∕∕BC,N力=NA8C,点E是边力。

上一点，连接4E交5C的延长线于点儿点尸是边A8上一点，使得NFBE= ∕FEB,作NFE"的角平分线EG交5〃于点G.若N8EG=40。

，则NOE”的度数为（）A. 50oB. 75oC. 100oD. 125°5.如图，在第1个4A∕3C中，ZB=3（）o, A1B=CB,在边A/3上任取一点力，延长C4/到使A∕A2=A∕O,得到第2个△ A lΛ2D i在边4。

上任取一点E,延长4/2到4,使A2A3=A2E,得到第3个AA2λ3E,…按此做法继续下去,则第2021个三角形中以A2O2O为顶点的底角度数是（）7 .如图，在四边形A5CO 中，AD//BC,若ND45的角平分线A£交。

于E,连接8E,且8E 边平分NABC,得到如下结论：(l)ZAEB=90o ；(2)I3C+AD=AB ；③BE=^CD ； ®BC=CE-⑤若 A8=x,则 BE 的取值范围为 0<3EVx,那么以 8 .如图，已知AB = AC,点。

、E 分别在AC 、A8上且ΛE = AD,连接EC, BD, EC 交BD 于点、M,连接AM,过点A 分别作AE_LC£AG_L8O,垂足分别为F 、G,卜.列结论：①.EBM 咨&DCM ；②NEMB = NFAG ；③M4平分NEMD ；④如果 S.BEM =S,ADM ,则E 是的中点；其中正确结论的个数为（）9 .“经过已知角一边上的一点作“个角等于已知角”的尺规作图过程如下:A. (!) 2020∙75oB.弓)2020∙65oC. (；) 2021 ∙75D. (!) 2021 ∙6506.如图所示，锐角^ABC 中，D, E 分别是AB, AC 边上的点，2∖ADC/ z √iOC, ∆AEB^ ^AEB ,, 且C'D∕∕EB f "BC, BE 、CD 交于点F,若NBAO40。

2020年中考数学考点过关培优训练卷：《三角形》(附答案)

2020年中考数学考点过关培优训练卷：《三角形》一．选择题（每小题4分，共40分）1．如图，在△ABC中，AB＝AC，∠A＝40°，DE垂直平分AC，则∠BCD的度数等于（）A．20°B．30°C．40°D．50°2．如图，△ABC的中线BE与CD交于点G，连接DE，下列结论不正确的是（）A．点G是△ABC的重心B．DE∥BCC．△ABC的面积＝2△ADE的面积D．BG＝2GE3．在平面直角坐标系中，点A的坐标为（1，1），在坐标轴上找到一点P，使△AOP为等腰三角形，这样的点P个数为（）A．8个B．7个C．6个D．5个4．如图，∠BAC的平分线与BC的垂直平分线DG相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB＝11，AC＝5，则BE的长（）A．3B．2C．5D．45．若等腰△ABC中有一个内角为40°，则这个等腰三角形的一个底角的度数为（）A．40°B．100°C．40°或100°D．40°或70°6．如图，在△ABC中，AC＝4，BC边上的垂直平分线DE分别交BC、AB于点D，若△A EC 的周长是11，则AB＝（）A．28B．18C．10D．77．如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，DE⊥AB于点E，则下列结论：①AD平分∠CDE；②∠BAC＝∠BDE；③DE平分∠ADB；④若A C＝4BE，则S△ABC ＝8S△BDE．其中正确的有（）A．1个B．2个C．3个D．4个8．如图，长方体的底面是边长为6的正方形，高为8，点A离点C的距离是3，点B离点D的距离是2．一只蚂蚁沿长方体表面从点A爬到点B，其最短距离是（）A．5B．3C．D．109．下列四组数中不是勾股数的一组是（）A．4，5，6B．7，24，25C．5，12，13D．11，60，61 10．如图，四边形ABCD中，点E、F、G、H分别是线段AB、CD、AC、BD的中点，则四边形EGFH的周长（）A．只与AB、CD的长有关B．只与AD、BC的长有关C．只与AC、BD的长有关D．与四边形ABCD各边的长都有关．二．填空题（每小题4分，共20分）11．已知等腰△ABC中，顶角∠A为36°，BD平分∠ABC交AC于D，那么AD：AC＝．12．已知△ABC是等腰三角形，其边长为3和7，△DEF≌△ABC，则△DEF的周长是．13．在△ABC中，AC＝2BC，BC边上的中线AD把△ABC的周长分成60和40两部分，则AC＝，AB＝．14．如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD＝CE，连结DE 并延长至点F，使EF＝AE，连结AF、BE和CF．则图中全等三角形共有对．15．如图，Rt△ABC中，∠ACB＝90°，AC＝BC＝4，点P1，P2，P3，…，P n﹣1将AC分成n等份，过点P1，P2，P3，……，P n﹣1分别作AC的垂线，交AB于点N1，N2，N3，……，N n﹣1，用S1，S2，S3，……，S n分别表示△CBN2，△P1N1N2，△P2N2N3，…△P n﹣1N n﹣1A的面积，则S1+S2+S3+……+S n＝．三．解答题（每题8分，共40分）16．如图，将一张长方形的纸条ABCD 沿EF 折叠，若折叠后∠AGC ′＝48°，AD 交EC ′于点G ．（1）求∠CEF 的度数；（2）求证：△EFG 是等腰三角形．17．如图，平面直角坐标系中，点O 为坐标原点，点A 在x 轴的负半轴上，点B 在x 轴的正半轴上，以AB 为斜边向上作等腰直角△ABC ，BC 交y 轴于点D ，C （﹣2，4）．（1）如图1，求点B 的坐标；（2）如图2，动点E 从点O 出发以每秒1个单位长度的速度沿y 轴的正半轴运动，设运动时间为t 秒，连接CE ，设△ECD 的面积为S ，请用含t 的式子来表示S ；（3）如图3，在（2）的条件下，当点E 在OD 的延长线上时，点F 在直线CE 的下方，且CF ⊥CE ，CF ＝CE ．连接AD ，取AD 的中点M ，连接FM 并延长交AO 于点N ，连接FO ，当S △NFO ＝10S △AMN 时，求S 的值．18．如图，在△ABC中，AB＝AC，CD是∠ACB的平分线，DE∥BC，交AC于点E．（1）求证：DE＝CE．（2）若∠CDE＝25°，求∠A的度数．19．已知如图1，在△ABC中，∠ACB＝90°，BC＝AC，点D在AB上，DE⊥AB交BC于E，点F是AE的中点．（1）线段FD与线段FC的数量关系，位置关系；（2）如图2，将△BDE绕点B逆时针旋转a（0°＜a＜90°），其它条件不变，线段FD 与线段FC的关系是否变化，写出你的结论并证明；（3）将△BDE绕点B逆时针旋转一周，如果BC＝4，BE＝2，直接写出线段BF的范围．20．在平面直角坐标系中，A（2，2），AB⊥y轴于点B，AC⊥x轴于点C．（1）如图1，求证：OA平分∠BOC；（2）如图2，点E、F分别在y轴、x轴的正半轴上，且AE⊥AF，EF交AC于点G，DG ∥x轴交OA于点D，连DE，求∠DEF的度数；（3）如图3，点E、D分别在y轴、x轴的正半轴上，且AC＝CD，F为EC的中点，连BF，过F作FK⊥BF交AD于点K，求∠KBF的度数．参考答案一．选择题1．解：∵AB＝AC，∠A＝40°，∴∠ABC＝∠ACB＝70°．∵DE垂直平分AC，∴AD＝CD，∴∠A＝∠ACD＝40°∴∠BCD＝∠ACB﹣∠ACD＝30°．故选：B．2．解：∵△ABC的中线BE与CD交于点G，∴点G是△ABC的重心，∴DE∥BC且DE＝BC，所以选项A、B正确；∵点G是△ABC的重心，根据重心性质或利用三角形相似可得BG＝2GE，∴选项D正确；由△ADE∽△ABC，可知△ABC的面积＝4△ADE的面积，所以选项C错误．故选：C．3．解：如图所示，AO为底边时，点P可以有两个位置，AO为腰长时，点P可以有6个位置，所以，符合条件的点P共有8个．故选：A．4．解：如图，连接CD，BD，∵AD是∠BAC的平分线，DE⊥AB，DF⊥AC，∴DF＝DE，∠F＝∠DEB＝90°，∠ADF＝∠ADE，∴AE＝AF，∵DG是BC的垂直平分线，∴CD＝BD，在Rt△CDF和Rt△BDE中，，∴Rt△CDF≌Rt△BDE（HL），∴BE＝CF，∴AB＝AE+BE＝AF+BE＝AC+CF+BE＝AC+2BE，∵AB＝11，AC＝5，∴BE＝（11﹣5）＝3．故选：A．5．解：当40°的角为等腰三角形的顶角时，底角的度数＝＝70°；当40°的角为等腰三角形的底角时，其底角为40°，故它的底角的度数是70°或40°．故选：D．6．解：∵DE是BC的中垂线，∴BE＝EC，则AB＝EB+AE＝CE+EA，又∵△ACE的周长为11，故AB＝11﹣4＝7，故选：D．7．解：∵AD 平分∠BAC ，∴∠DAC ＝∠DAE ，∵∠C ＝90°，DE ⊥A B ，∴∠C ＝∠E ＝90°，∵AD ＝AD ，∴△DAC ≌△DAE （AAS ），∴∠CDA ＝∠EDA ，∴①AD 平分∠CDE 正确；无法证明∠BDE ＝60°，∴③DE 平分∠ADB 错误；∵BE +AE ＝AB ，AE ＝AC ，∵AC ＝4BE ，∴AB ＝5BE ，AE ＝4BE ，∴S △ADB ＝5S △BDE ，S △ADC ＝4S △BDE ，∴S △ABC ＝9S △BDE ，∴④错误；∵∠BDE ＝90°﹣∠B ，∠BAC ＝90°﹣∠B ，∴∠BDE ＝∠BAC ，∴②∠BAC ＝∠BDE 正确．故选：B ．8．解：如图1，AB ＝＝；如图2，AB ＝＝＝3， ∵， ∴一只蚂蚁沿长方体表面从点A 爬到点B ，其最短距离是3，故选：B ．9．解：A、∵42+52≠62，∴4，5，6不是勾股数，故本选项符合题意；B、∵72+242＝252，∴7，24，25是勾股数，故本选项不符合题意；C、∵52+122＝132，∴5，12，13是勾股数，故本选项不符合题意；D、∵112+602＝612，∴11，60，61是勾股数，故本选项不符合题意；故选：A．10．解：∵点E、F、G、H分别是线段AB、CD、AC、BD的中点，∴四边形EGFH的周长＝FG+GE+EH+FH＝，故选：B．二．填空题（共5小题）11．解：假设AB＝AC＝1，那么在△ACB和△BCD中，∠C＝∠C，∠A＝∠CBD＝36°，∴△ACB∽△BCD，∴AC：BC＝BC：DC，∴AC：BC＝BC：DC，而BC＝BD＝DA（等腰的性质）所以设AD＝x，那么CD＝1﹣x，1：x＝x：（1﹣x），所以舍负根，得到：x＝，∴AD：AC＝．12．解：当3为腰时，3+3＝6，∵6＜7，∴3、3、7不能组成三角形；当7为腰时，3+7＝10，∵7＜10，∴3、7、7能组成三角形．∴△ABC的周长为3+7+7＝17．又∵△DEF≌△ABC，∴△DEF的周长是17．故答案为：17．13．解：∵AD是BC边上的中线，AC＝2BC，∴BD＝CD，设BD＝CD＝x，AB＝y，则AC＝4x，分为两种情况：①AC+CD＝60，AB+BD＝40，则4x+x＝60，x+y＝40，解得：x＝12，y＝28，即AC＝4x＝48，AB＝28；②AC+CD＝40，AB+BD＝60，则4x+x＝40，x+y＝60，解得：x＝8，y＝52，即AC＝4x＝32，AB＝52，BC＝2x＝16，此时不符合三角形三边关系定理；综合上述：AC＝48，AB＝28．故答案为：48；28．14．解：∵△ABC是等边三角形，∴∠BAC＝∠ACB＝60°，AB＝AC，又∵CD＝CE，∴△CDE是等边三角形，AE＝BD，∴CD＝CE＝DE，∠DEC＝∠AEF＝60°，又∵AE＝EF，∴△AEF是等边三角形，∴∠CAF＝60°，AE＝AF＝EF，∴BD＝EF，∴DF＝CB，∴△ABE≌△ACF（SAS），△BCE≌△FDC（SAS），△BDE≌△FEC（SSS），∴图中全等三角形共有3对，故答案为：3．15．解：如图，由题意S1＝8×＝8×，S2＝8×，S3＝8×，…，S n＝8×，∴S1+S2+S3+……+S n＝8×[]＝8×＝，故答案为．三．解答题（共5小题）16．（1）解：∵四边形ABCD是矩形，∴AD∥BC，∴∠BEG＝∠AGC'＝48°，由折叠的性质得：∠CEF＝∠C'EF，∴∠CEF＝（180°﹣48°）＝66°；（2）证明：∵四边形ABCD是矩形，∴AD∥BC，∴∠GFE＝∠CEF，由折叠的性质得：∠CEF＝∠C'EF，∴∠GFE＝∠C'EF，∴GE＝GF，即△EFG是等腰三角形．17．解：（1）如图1中，作CH⊥AB于H．∵C（﹣2，4），∴CH＝4，OH＝2，∵AC﹣BC，∠ACB＝90°，∴AH＝CH＝BH＝4，∴OB＝OH＝2，∵OD∥CH，∴CD＝DB，∴OD＝CH＝2，∴D（0，2），B（2，0）．（2）由（1）可知D（0，2），所以当0≤t＜2时，当t＞2时，，综上所述，S＝．（3）如图3中，延长AC交y轴于H，连接FD，AF．FO．∵C（﹣2，4），△ABC是等腰直角三角形，∴AB＝8，由（1）知B（2，0），∴OB＝2，OA＝6，∵△ABC是等腰直角三角形，∴∠ACB＝90°，∴∠CAB＝45°，∵∠AOH＝90°，∴∠CHE＝∠CAB＝45°，∴OH＝OA＝6，∵∠ACB＝90°，∴∠DCH＝90°，∵∠CHE＝45°，∴∠CDH＝∠CHE＝45°，∴CH＝CD，∵CF⊥CE，∴∠DCF+∠ECD＝90°，∵∠ACB＝90°，∴∠HCE+∠ECD＝90°，又∵CF ＝CE ，∴△HCE ≌△DCF （SAS ），∴HE ＝FD ＝6﹣t ，∠CDF ＝∠CHE ＝45°，∵∠CBA ＝45°，∴∠CDF ＝∠CBA ，∴FD ∥AB ，∴∠FDM ＝∠NAM ，∵M 是AD 中点，∴DM ＝AM ，又∵∠FMD ＝∠NMA ，∴△DMF ≌AMN （ASA ），∴AN ＝FD ＝6﹣t ，∵DM ＝AM ，∴S △DMF ＝S △AMF∵△DMF ≌△AMN ，∴S △DMF ＝S △AMN ，∴S △NF A ＝2S △AMN∵S △NFO ＝10S △AMN∴S △NFO ＝5S △NF A ，∴5AN ＝ON ，∵OA ＝6，∴AN ＝1，∴AN ＝6﹣t ＝1，∴t ＝5，∴S ＝t ﹣2＝5﹣2＝3．18．（1）证明：∵CD 是∠ACB 的平分线，∴∠BCD ＝∠ECD ，∵DE ∥BC ，∴∠EDC ＝∠BCD ，∴DE＝CE．（2）解：∵∠ECD＝∠EDC＝25°，∴∠ACB＝2∠ECD＝50°，∵AB＝AC，∴∠ABC＝∠ACB＝50°，∴∠A＝180°﹣50°﹣50°＝80°．19．解：（1）如图1中，∵∠ADE＝∠ACE＝90°，AF＝FE，∴DF＝AF＝EF＝CF，∴∠F AD＝∠FDA，∠F AC＝∠FCA，∴∠DFE＝∠FDA+∠F AD＝2∠F AD，∠EFC＝∠F AC+∠FCA＝2∠F AC，∵CA＝CB，∠ACB＝90°，∴∠BAC＝45°，∴∠DFC＝∠EFD+∠EFC＝2（∠F AD+∠F AC）＝90°，∴DF＝FC，DF⊥FC，故答案为：DF＝FC，DF⊥FC．（2）结论不变．理由：如图2中，延长AC到M使得CM＝CA，延长ED到N，使得DN＝DE，连接BN、BM．EM、AN，延长ME交AN于H，交AB于O．∵BC⊥AM，AC＝CM，∴BA＝BM，同法BE＝BN，∵∠ABM＝∠EBN＝90°，∴∠NBA＝∠EBM，∴△ABN≌△MBE，∴AN＝EM，∴∠BAN＝∠BME，∵AF＝FE，AC＝CM，∴CF＝EM，FC∥EM，同法FD＝AN，FD∥AN，∴FD＝FC，∵∠BME+∠BOM＝90°，∠BOM＝∠AOH，∴∠BAN+∠AOH＝90°，∴∠AHO＝90°，∴AN⊥MH，FD⊥FC．（3）如图3中，当点E落在AB上时，BF的长最大，最大值＝3如图4中，当点E落在AB的延长线上时，BF的值最小，最小值＝．综上所述，≤BF≤3．20．（1）证明：∵A（2，2），AB⊥y轴于点B，AC⊥x轴于点C．∠BOC＝90°，∴AB＝AC＝2，四边形ABOC是矩形，∴四边形ABOC是正方形，∴OA平分∠BOC；（2）解：∵四边形ABOC是正方形，∴∠BAC＝90°，∠OAC＝45°，∵AE⊥AF，∴∠EAF＝90°，∴∠EAF+∠BOC＝180°，∴A、E、O、F四点共圆，∴∠OAE＝∠OFE，∵DG∥x轴，∴∠DGE＝∠OFE，∴∠OAE＝∠DGE，∴A、E、D、G四点共圆，∴∠DEF＝∠OAC＝45°；（3）解：延长BF交AC于G，连接KG，作KM⊥AB于M，KN⊥AC于N，如图3所示：∵四边形ABOC是正方形，∴OB∥AC．∴∠EBF＝∠CGF，∠BEF＝∠GCF．∵F是CE的中点，∴EF＝CF．在△BEF和△GCF中，，∴△BEF≌△GCF（AAS），∴BF＝GF．∵BF⊥FK，∴∠BFK＝∠GFK＝90°．在△BFK和△GFK中，，∴△BFK≌△GFK（SAS），∴BK＝GK．∵AC＝CD，∠ACD＝90°，∴△ACD是等腰直角三角形，∴∠CAD＝45°．∵KN⊥AC，∴∠ANK＝90°，∴∠AKN＝45°，∴AN＝KN，∵KM⊥AB，∴四边形AMKN是正方形，∴KM＝KN．∠M＝∠GNK＝90°，AM∥KN．在Rt△BKM和Rt△GKN中，，∴Rt△BKM≌Rt△GKN（HL），∴∠MBK＝∠NGK．∠GKN＝∠BKM．∵AM∥KN，∴∠BKN＝∠MBK．∵∠BKM+∠BKN＝90°，∴∠GKN+∠BKN＝90°，即∠BKG＝90°．∵BK＝GK，∴△BKG是等腰直角三角形．∴∠KBF＝45°．。

全等三角形经典培优题型(含标准答案)

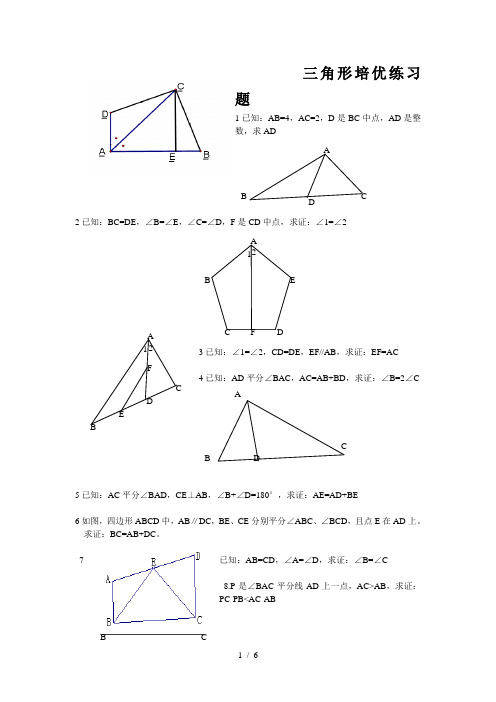
三角形培优练习题1已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC4已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C5已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE6如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

已知：AB=CD ，∠A=∠D ，求证：∠B=∠C78.P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-ABCDBA BC DEF 2 1ADBCA B CD ABACDF2 1 E9已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC10．如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．11如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠B12如图：AE 、BC 交于点M ，F点在AM 上，BE∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

13已知：如图，AB =AC ，BD ⊥AC ，CE ⊥AB ，垂足分别为D 、E ，BD 、CE 相交于点F 。

求证：BE =CD ．14在△ABC 中，︒=∠90ACB ，BC AC =，直线MN 经过点C ，且MN AD ⊥于D ，MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时，求证： ①ADC ∆≌CEB ∆；②BE AD DE +=；(2)当直线MN 绕点C 旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由.15如图所示，已知AE ⊥AB ，AF ⊥AC ，AE=AB ，AF=AC 。

福州市三牧中学八年级数学上册第十一章《三角形》(培优)

一、选择题1．一个多边形的外角和是360°，这个多边形是（）A ．四边形B ．五边形C ．六边形D ．不确定 2．下列每组数分别是三根小木棒的长度，不能用它们搭成三角形的是（） A ．1cm ，2cm ，3cmB ．2cm ，3cm ，4cmC ．3cm ，4cm ，5cmD ．5cm ，6cm ，7cm 3．若一个三角形的三边长分别为3，7，x ，则x 的值可能是（） A ．6B ．3C ．2D ．11 4．如图，在ABC 中，55A ∠=︒，65C =︒∠，BD 平分ABC ∠，//DE BC ，则BDE∠的度数是（）A ．50°B ．25°C ．30°D ．35° 5．已知长度分别为3cm ，4cm ，xcm 的三根小棒可以摆成一个三角形，则x 的值不可能是（）A ．2.4B ．3C ．5D ．8.56．内角和为720°的多边形是（）．A ．三角形B ．四边形C ．五边形D ．六边形7．一个多边形的内角和外角和之比为4：1，则这个多边形的边数是（）A ．7B ．8C ．9D ．108．下列命题是真命题的个数为（）①两条直线被第三条直线所截，内错角相等．②三角形的内角和是180°．③在同一平面内平行于同一条直线的两条直线平行．④相等的角是对顶角．⑤两点之间，线段最短．A ．2B ．3C ．4D ．59．如图，D 是ABC 的边BC 上任意一点，E 、F 分别是线段AD CE 、的中点，且ABC 的面积为220cm ，则BEF 的面积是（）2cmA ．5B ．6C ．7D ．8 10．在下列长度的四根木棒中，能与2m 、5m 长的两根木棒钉成一个三角形的是（）A ．2mB ．3mC ．5mD ．7m 11．长度分别为2，3，4，5的四根细木棒首尾相连，围成一个三角形（木棒允许连接，但不允许折断），得到的三角形的最长边长为（）A ．8B ．5C ．6D ．712．如图，为估计池塘岸边A 、B 的距离，小方在池塘的一侧选取一点O ，测得OA ＝15米，OB=10米，A 、B 间的距离不可能是（）A ．20米B ．15米C ．10米D ．5米 13．一个多边形的内角和是外角和的4倍，则这个多边形的边数为（） A ．10B ．8C ．6D ．4 14．下列长度的四根木棒，能与3cm ，7cm 长的两根木棒钉成一个三角形的是（） A ．3cmB ．10cmC ．4cmD ．6cm 15．设四边形的内角和等于,a 五边形的外角和等于,b 则a 与b 的关系是（）A ．a b =B ．120a b =+C ．180b a =+︒D ．360b a =+︒ 二、填空题16．设三角形三内角的度数分别为,,x y z ︒︒︒，如果其中一个角的度数是另一个角的度数的2倍、那我们称数对(,)()y z y z <是x 的和谐数对，当150x =时，对应的和谐数对有一个，它为(10,20)；当66x =时，对应的和谐数对有二个，它们是__________．当对应的和谐数对(,)y z 有三个时，请写出此时x 的范围_______．17．从一个多边形的一个顶点出发，一共可作9条对角线，则这个多边形的内角和是_________度．18．如图，ACD ∠是ABC 的外角，ABC ∠的平分线与ACD ∠的平分线交于点1A ，1A BC ∠的平分线与1A CD ∠的平分线交于点2A ，…，1n A BC -∠的平分线与1n A CD -∠的平分线交于点n A ，设=A θ∠，则2=A ∠___________，=n A ∠___________．19．如果点G 是ABC ∆的重心，6AG =，那么BC 边上的中线长为_______________________．20．如图所示，在ABC 中，80A ∠=︒，延长BC 到D ，ABC ∠与ACD ∠的平分线相交于1A 点，1A BC ∠与1A CD ∠的平分线相交于A 点，依此类推，4A BC ∠与4A CD ∠的平分线相交于5A 点，则5A ∠的度数是_________．21．如图，在ABC 中，点,,D E F 分别在三边上，点E 是AC 的中点，,,AD BE CF 交于一点,283BGD AGE G BD DC S S ===，，，则ABC 的面积是________．22．如图，则∠A+∠B+∠C+∠D+∠E+∠F+∠G ＝_____．23．鹿鸣社区里有一个五边形的小公园，如图所示，王老师每天晚饭后都要到公园里去散步，已知图中的∠1=95︒，王老师沿公园边由A 点经B→C→D→E ，一直到F 时，他在行程中共转过了_____度．24．如图，已知AE 是ABC 的边BC 上的中线，若8AB cm =，ACE △的周长比AEB △的周长多2cm ，则AC =______cm ．25．如图中，36B ∠=︒，76C ∠=︒，AD 、AF 分别是ABC 的角平分线和高，DAF ∠=________．26．如图，ABC 面积为1，第一次操作：分别延长,,AB BC CA 至点111,,A B C 使111,,A B AB B C BC C A CA ===顺次结111,,A B C ，得到111A B C △，第二次操作：分别延长111111,,A B B C C A 至点222A B C ，使211121112111,,A B A B B C B C C A C A ===，顺次连结222,,A B C ，得到222A B C △…，按此规律，则333A B C △的面积为_______．三、解答题27．△ABC 中，AD 是∠BAC 的角平分线，AE 是△ABC 的高．（1）如图1，若∠B ＝40°，∠C=60°，求∠DAE 的度数；（2）如图2，∠B ＜∠C ，则DAE 、∠B ，∠C 之间的数量关系为___________；（3）如图3，延长AC 到点F ，∠CAE 和∠BCF 的角平分线交于点G ，求∠G 的度数．28．如图，在ABC 中，AD 为高，AE 为BAC ∠的平分线，若28B ∠=︒，52ACD ∠=°，求EAD ∠的度数．29．如图ABC 中，45B ∠=︒，70ACB ∠=︒，AD 是ABC 的角平分线，F 是AD 上一点EF AD ⊥，交AC 于E ，交BC 的延长线于G ．求G ∠的度数．30．已知22a m n =+，2b m =，c mn =，且m >n >0．（1）比较a ，b ，c 的大小；（2）请说明以a ，b ，c 为边长的三角形一定存在．。

八年级上数学几何培优试题分类解析

八年级上数学培优练习（一）: 三角形（1） 1、△ABC 的内角为∠A ，∠B ，∠C ，且∠1=∠A+∠B ，∠2=∠B+∠C ，∠3=∠A+∠C ，则∠1、∠2、∠3中( )A ．至少有一个锐角；B ．一定都是钝角；C ．至少有两个钝角；D ．可以有两个直角；2、如图，在等腰△ABC 中，AB=AC ，∠A=130°，将它向右平移到△DEF 的位置，使AB=BE ，若BD 和AF 相交于点M ，则∠BMF 等于( ) A ．130° B ．142.5° C ．150° D ．1553.如上图，在四边形ABCD 中，AB ∥CD ，AD ∥BC ，点E 是AD 中点，点F 是CD 上一点，若8=∆ABE S ， 3=∆DEF S ，则___________=∆BEF S 4.△ABC 中，AB=BC ，在BC 上取点N 和M (N 比M 更靠近B)，使得NM=AM 且∠MAC=∠BAN ，则∠CAN=( )A ．30°B ．45°C ．60°D ．75°5.周长为P 的三角形中，最长边m 的取值范围是 ( )A ．23P m P <≤B ．23P m P <<C ．23P m P ≤<D ．23P m P ≤≤ 6．各边长均为整数且三边各不相等的三角形的周长小于13，这样的三角形个数共有( ) A ．5个 B ．4个 C ．3个 D ．2个7．等腰三角形的周长为24cm ，腰长为xcm ，则x 的取值范围是________．8．不等边三角形中，如果有一条边长等于另外两条边长的平均值，那么，最大边上的高与最小边上的高的比值k 的取值范围是( )A ．143<<kB ．131<<kC ． 1<k<2D ．121<<k 9．已知三角形的三边的长a 、b 、c 都是整数，且a ≤b<c ，若b=7，则这样的三角形有( )A ．14个B ．28个C ．21个D ．49个10．如果三角形的一个外角大于这个三角形的某两个内角的2倍，那么这个三角形一定是( )A ．锐角三角形B ．钝角三角形C ．直角三角形D ．直角或钝角三角形11.如下图，在△ABC 中，BC>AC ，∠A=60°，D 、E 分别为AB 、AC 的中点，若PC 平分∠ACB ，PD 平分∠ADE ，则∠DPC=___________B A F12.如上图，在直角三角形ABC的两直角边AC、BC上分别作正方形ACDE和CBFG，连接DG，连接AF交BC于W，连接GW。

《易错题》初中八年级数学上册第十一章《三角形》经典题(培优专题)

一、选择题1．若一个三角形的三边长分别为3，7，x ，则x 的值可能是（）A ．6B ．3C ．2D ．11A解析：A【分析】根据三角形的三边关系列出不等式，即可求出x 的取值范围，得到答案．【详解】解：∵三角形的三边长分别为3，7，x ，∴7-3＜x ＜7+3，即4＜x ＜10，四个选项中，A 中，4＜6＜10，符合题意．故选：A ．【点睛】本题主要考查了三角形的三边关系，即任意两边之和大于第三边，任意两边之差小于第三边．2．已知三角形的两边长分别为1和4，则第三边长可能是（）A ．3B ．4C ．5D ．6B 解析：B【分析】根据三角形的三边关系“第三边大于两边之差，而小于两边之和”，求得第三边的取值范围．【详解】解：根据三角形的三边关系，设第三边的长为x ，∵三角形两边的长分别是1和4，∴4-1＜x ＜4+1，即3＜x ＜5．故选：B ．【点睛】此题考查了三角形的三边关系，关键是正确确定第三边的取值范围．3．如图，ABC 中，将A ∠沿DE 翻折，若30A ∠=︒，25BDA '∠=︒，则CEA '∠多少度（）A ．60°B ．75°C ．85°D ．90°C解析：C【分析】根据折叠前后对应角相等可得ADE A DE '∠=∠，AED A ED '∠=∠，再运用平角的定义和三角形内角和定理依次求得ADE ∠、AED ∠，再次运用平角的定义即可求得CEA '∠．【详解】解：∵将A ∠沿DE 翻折，∴ADE A DE '∠=∠，AED A ED '∠=∠，∵D 是线段AB 上的点，25BDA '∠=︒，∴180ADE A D B E DA '∠+∠-'∠=︒，即251280ADE ︒=∠-︒，解得102.5ADE ∠=︒，∵30A ∠=︒，180A AED ADE ∠+∠+∠=︒，∴180180102.53047.5AED ADE A ∠=︒-∠-∠=︒-︒-︒=︒，∴18018047.547.585CEA AED A ED ''∠=︒-∠-∠=︒-︒-︒=︒．故选：C ．【点睛】本题考查折叠的性质，三角形内角和定理，平角的定义．理解折叠前后对应角相等是解题关键．4．下列长度（单位：cm ）的三条线段能组成三角形的是（）A ．13，11，12B ．3，2，1C ．5，12，7D ．5，13，5A 解析：A【分析】根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”进行分析．【详解】解：根据三角形的三边关系，A 、11+12＞13，能组成三角形，符合题意；B 、1+2=3，不能组成三角形，不符合题意；C 、5+7=12，不能组成三角形，不符合题意；D 、5+5＜13，不能组成三角形，不符合题意；故选A ．【点睛】此题考查了三角形的三边关系．判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数．5．如图，,AD CE 分别是ABC 的中线与角平分线，若,40B ACB BAC ∠=∠∠=︒，则ACE ∠的度数是（）A ．20︒B ．35︒C ．40︒D ．70︒B解析：B【分析】由,40B ACB BAC ∠=∠∠=︒，再利用三角形的内角和定理求解ACB ∠，结合三角形的角平分线的定义，从而可得答案．【详解】解： ,B ACB ∠=∠40BAC ∠=︒，18040702B ACB ︒-︒∴∠=∠==︒， CE 是ABC 角平分线，1352ACE ACB ∴∠=∠=︒，故选：.B【点睛】本题考查的是三角形的角平分线的定义，三角形的内角和定理，掌握以上知识是解题的关键．6．下列长度的三条线段，能组成三角形的是（）A ．3，5，6B ．3，2，1C ．2，2，4D ．3，6，10A解析：A【分析】根据三角形三边长关系，逐一判断选项，即可得到答案．【详解】A. ∵3+5＞6，∴长度为3，5，6的三条线段能组成三角形，故该选项符合题意，B. ∵1+2=3，∴长度为3，2，1的三条线段不能组成三角形，故该选项不符合题意，C. ∵2+2=4，∴长度为2，2，4的三条线段不能组成三角形，故该选项不符合题意，D. ∵3+6＜10，∴长度为3，6，10的三条线段不能组成三角形，故该选项不符合题意，故选A【点睛】本题主要考查三角形三边长的关系，掌握三角形任意两边之和大于第三边，是解题的关键．7．如图，在ABC ∆中，80,BAC ∠=︒点D 在BC 边上，将ABD △沿AD 折叠，点B 恰好落在AC 边上的点'B 处，若'20B DC ∠=．则C ∠的度数为（）A ．20B ．25C ．35D ．40D解析：D【分析】由折叠的性质可求得'B AB D ∠=∠，利用三角形内角和及外角的性质列方程求解．【详解】解：由题意可得'B AB D ∠=∠∵80,BAC ∠=︒∴∠B+∠C=100°又∵'='=20B AB D C B DC C ∠=∠+∠+∠∠，∴∠C+20°+∠C=100°解得：∠C=40°故选：D ．【点睛】本题考查三角形内角和及外角的性质，找准角之间的等量关系列出方程正确计算是解题关键．8．如图，在七边形ABCDEFG 中，AB ，ED 的延长线交于点O ．若1,2,3,4∠∠∠∠的外角和于210°，则BOD ∠的度数为（）A ．30°B ．35°C ．40°D ．45°A解析：A【分析】由外角和内角的关系可求得∠1、∠2、∠3、∠4的和，由五边形内角和可求得五边形OAGFE 的内角和，即可求得∠BOD ．【详解】解：∵∠1、∠2、∠3、∠4的外角的角度和为210°，∴∠1+∠2+∠3+∠4+210°=4×180°，∴∠1+∠2+∠3+∠4=510°，∵五边形OAGFE 内角和=（5-2）×180°=540°，∴∠1+∠2+∠3+∠4+∠BOD=540°，∴∠BOD=540°-510°=30°．故选：A.【点睛】本题主要考查多边形的内角和，利用内角和外角的关系求得∠1、∠2、∠3、∠4的和是解题的关键．9．如图，在ABC 中，70B ∠=，D 为BC 上的一点，若ADC x ∠=，则x 的度数可能为（）A ．30°B ．60°C ．70°D ．80°D解析：D【分析】根据三角形的外角的性质得到∠ADC=∠B+∠BAD ，得到x ＞70°，根据平角的概念得到x ＜180°，计算后进行判断得到答案．【详解】解：∵∠ADC=∠B+∠BAD ，∴x ＞70°，又x ＜180°，∴x 的度数可能为80°，故选：D ．【点睛】本题考查的是三角形的外角的性质，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．10．如图，105DBA ∠=︒，125ECA ∠=︒，则A ∠的度数是（）A ．75°B ．60°C ．55°D ．50°D解析：D【分析】根据邻补角的定义可求得ABC ∠和ACB ∠，再根据三角形内角和为180°即可求出A ∠．【详解】解：105DBA ∠=︒，125ECA ∠=︒，18010575ABC ∴∠=︒-︒=︒，18012555ACB ∠=︒-︒=︒．180755550A ∴∠=︒-︒-︒=︒．故选D ．【点睛】本题考查了邻补角和三角形内角和定理，识记三角形内角和为180°是解题的关键．二、填空题11．如图是一块正多边形的碎瓷片，经测得30ACB ∠=︒，则这个正多边形的边数是_________．12【分析】根据瓷片为正多边形及可知正多边形的外角为进而可求得正多边形的边数【详解】如图延长BC 可知∠1为正多边形的外角∵瓷片为正多边形∴AD=DB=BC ∠ADB=∠DBC ∴四边形ACBD 为等腰梯形解析：12【分析】根据瓷片为正多边形及=30ACB ∠︒，可知正多边形的外角为30︒，进而可求得正多边形的边数．【详解】如图，延长BC ，可知∠1为正多边形的外角，∵瓷片为正多边形，∴AD=DB=BC ，∠ADB=∠DBC ，∴四边形ACBD 为等腰梯形，∴BD ∥AC ，∴∠1==30ACB ∠︒，∴正多边形的边数为：360=1230︒︒，故答案为：12．【点睛】本题考查正多边形的外角和，掌握相关知识点是解题的关键．12．在△ABC 中，∠A 是钝角，∠B =30°，设∠C 的度数是α，则α的取值范围是___________【分析】依据三角形的内角和定理表示∠A 根据它是钝角列出不等式组求解即可【详解】解：∵∠A+∠B+∠C=180°∴∠A=180°-30°-α=150°-α∵∠A 是钝角∴即故答案为：【点睛】本题考查解不解析：3060α︒<<︒【分析】依据三角形的内角和定理表示∠A ，根据它是钝角列出不等式组，求解即可．【详解】解：∵∠A+∠B+∠C=180°，∴∠A=180°-30°-α=150°-α．∵∠A 是钝角，∴90150180α︒<︒-<︒，即3060α︒<<︒，故答案为：3060α︒<<︒．【点睛】本题考查解不等式组，三角形内角和定理．能正确表示∠A 及利用它的大小关系列出不等式是解题关键．13．如图，则A B C D E ∠+∠+∠+∠+∠的度数为________．180°【分析】两次运用三角形的外角定理求出∠B+∠C+∠D=∠2再通过三角形的内角和定理即可求解【详解】解：如图∵∠1是△CDF 外角∴∠C+∠D=∠1∵∠2是三角形BFG 外角∴∠B+∠1=∠2∴∠解析：180°【分析】两次运用三角形的外角定理求出∠B+∠C+∠D=∠2，再通过三角形的内角和定理即可求解【详解】解：如图，∵∠1是△CDF 外角，∴∠C+∠D=∠1，∵∠2是三角形BFG 外角，∴∠B+∠1=∠2，∴∠B+∠C+∠D=∠2，∴=2180A B C D E A E ∠+∠+∠+∠+∠∠+∠+∠=︒．故答案为：180°【点睛】本题考查了三角形的外角定理、内角和定理，通过三角形的外角定理将∠B+∠C+∠D 转化为∠2是解题关键．14．七边形的外角和为________．360°【分析】根据多边形的外角和等于360°即可求解；【详解】∵多边形的外角和都是360°∴七边形的外角和为360°故答案为：360°【点睛】本题考查了多边形的外角的性质掌握多边形的外角和等于36 解析：360°【分析】根据多边形的外角和等于360°即可求解；【详解】∵ 多边形的外角和都是360°，∴七边形的外角和为360°，故答案为：360°．【点睛】本题考查了多边形的外角的性质，掌握多边形的外角和等于360°是解题的关键； 15．用边长相等的正三角形和正六边形铺满地面，一个结点周围有m 块正三角形，n 块正六边形，则m+n ＝______．4或5【分析】先求出正三角形和正六边形的内角大小然后列出关于mn 的二元一次方程然后确定mn 的值最后求m+n 即可【详解】解：∵正三边形和正六边形内角分别为60°120°∴60°m+120°n=360°解析：4或5【分析】先求出正三角形和正六边形的内角大小，然后列出关于m 、n 的二元一次方程，然后确定m 、n 的值，最后求m+n 即可．【详解】解：∵正三边形和正六边形内角分别为60°、120°∴60°m+120°n=360°，即m+2n=6∴当n=1时，m=4；当n=2时，m=2；∴m+n=5或m+n=4．故答案为：4或5．【点睛】本主要考查了正多边形的组合能否进行平面镶嵌，掌握位于同一顶点处的几个角之和能否为360°成为解答本题的关键．16．一个正多边形的每个内角为108°，则这个正多边形所有对角线的条数为_____．【分析】先根据多边形的内角度数得出每个外角的度数再根据外角和为360°求出多边形的边数最后根据n边形多角线条数为求解即可【详解】∵一个正多边形的每个内角为108°∴每个外角度数为180°﹣108°=解析：【分析】先根据多边形的内角度数得出每个外角的度数，再根据外角和为360°求出多边形的边数，最后根据n边形多角线条数为(3)2n n-求解即可．【详解】∵一个正多边形的每个内角为108°，∴每个外角度数为180°﹣108°=72°，∴这个正多边形的边数为360°÷72°=5，则这个正多边形所有对角线的条数为(3)2n n-=5(53)2⨯-=5，故答案为：5．【点睛】本题主要考查多边形内角与外角、多边形的对角线，解题的关键是掌握多边形外角和度数为360°，n边形多角线条数为()32n n-．17．一副直角，三角板有一个角的顶点如图所示重合，则下列说法中正确的有_________．①如图 1，若 AB⊥AE，则∠BFC=75°；②图 2 中 BD过点C，则有∠DAE+∠DCE=45°；③图 3中∠DAE+∠DFC等于 135°；④保持重合的顶点不变，改变三角板BAD的摆放位置，使得D在边AC上，则∠BAE=105°．①②③④【分析】由可得：再结合：从而可求解于是可得可判断①；由可得：再利用：求解可判断②；由再利用角的和差可得：可判断③；由图4可得：可判断④【详解】解：如图1故①正确；如图2故②正确；如图3故③正解析：①②③④．【分析】由,AB AE ⊥可得：90BAC CAD DAE ∠+∠+∠=︒，再结合：2105BAC CAD DAE ∠+∠+∠=︒，从而可求解CAD ∠，于是可得BFC ∠，可判断①；由90ADB ，∠=︒可得：90DAC ACD ∠+∠=︒，再利用：180CAE E ACE ∠+∠+∠=︒， 45E ∠=°，求解DAE DCE ∠+∠，可判断②；由,DFC D DAF ∠=∠+∠再利用角的和差可得：135DFC DAE D CAE ∠+∠=∠+∠=︒，可判断③；由图4可得：105BAE BAC CAE ∠=∠+∠=︒，可判断④．【详解】解：如图1，,AB AE ⊥90BAC CAD DAE ∴∠+∠+∠=︒，60BAD BAC CAD ∠=∠+∠=︒，45CAE CAD DAE ∠=∠+∠=︒，2105BAC CAD DAE ∴∠+∠+∠=︒，15CAD ∴∠=︒，90ADB ∠=︒，901575BFC AFD ∴∠=∠=︒-︒=︒，故①正确；如图2，90ADB ∠=︒，90DAC ACD ∴∠+∠=︒，180CAE E ACE ∠+∠+∠=︒， 45E ∠=°，90ACE ∠=︒， 180CAD DAE ACD DCE E ∴∠+∠+∠+∠+∠=︒，()()180180904545DAE DCE CAD ACD E ∴∠+∠=︒-∠+∠+∠=︒-︒+︒=︒，故②正确；如图3，,DFC D DAF ∠=∠+∠9045135DFC DAE D DAF DAE D CAE ∴∠+∠=∠+∠+∠=∠+∠=︒+︒=︒，故③正确；如图4，6045BAD CAE ∠=︒∠=︒，，6045105BAE ∴∠=︒+︒=︒，故④正确．故答案为：①②③④．【点睛】本题考查的是三角形的内角和定理，三角形的外角的性质，角的和差，掌握以上知识是解题的关键．18．如图，已知AE 是ABC 的边BC 上的中线，若8AB cm =，ACE △的周长比AEB △的周长多2cm ，则AC =______cm ．10【分析】依据AE 是△ABC 的边BC 上的中线可得CE=BE 再根据AE=AE △ACE 的周长比△AEB 的周长多2cm 即可得到AC 的长【详解】解：∵AE 是△ABC 的边BC 上的中线∴CE=BE 又∵AE=A解析：10【分析】依据AE 是△ABC 的边BC 上的中线，可得CE=BE ，再根据AE=AE ，△ACE 的周长比△AEB 的周长多2cm ，即可得到AC 的长．【详解】解：∵AE 是△ABC 的边BC 上的中线，∴CE=BE ，又∵AE=AE ，△ACE 的周长比△AEB 的周长多2cm ，∴AC-AB=2cm ，即AC-8=2cm ，∴AC=10cm ，故答案为：10；【点睛】本题考查了三角形的角平分线、中线和高，求出两个三角形的周长的差等于两边的差是解题的关键．19．如图，∠BAK ＋∠B ＋∠C ＋∠CDE ＋∠E ＋∠F ＋∠MGN ＋∠H ＋∠K ＝________．540°【分析】连接AGGD 先根据∠H+∠K=∠HGA+∠KAG ∠E+∠F=∠EDG+∠FGD 最后根据多边形的面积公式解答即可【详解】解：连接AGGD ∵∠H+∠K+∠HMK=180°∠HGA+∠KA解析：540°【分析】连接AG 、GD ，先根据∠H+∠K=∠HGA+∠KAG, ∠E+∠F=∠EDG+∠FGD,最后根据多边形的面积公式解答即可．【详解】解：连接AG 、GD ，∵∠H+∠K+∠HMK=180°，∠HGA+∠KAG +∠AMG=180°，∠HMK=∠AMG∴∠H+∠K=∠HGA+∠KAG；同理：∠E+∠F=∠EDG+∠FGD∴∠BAK＋∠B＋∠C＋∠CDE＋∠E＋∠F＋∠MGN＋∠H＋∠K=∠BAK＋∠B＋∠C＋∠CDE＋∠EDG+∠FGD＋∠MGN＋∠HGA+∠KAG=五边形的内角和=（5-2）×180°=540°故答案为540°．【点睛】本题考查了三角形内角和定理和多边形内角和定理，根据题意正确作出辅助线成为解答本题的关键．∆的高线和中线，则线段AM，AN的大小关系是20．若线段AM，AN分别是ABCAM_______AN（用“≤”，“≥”或“=”填空）．；【分析】根据三角形的高的概念得到AM⊥BC根据垂线段最短判断【详解】解：如图∵线段AM是△ABC边BC上的高∴AM⊥BC由垂线段最短可知AN≥AM故答案为：【点睛】本题考查的是中线和高的概念掌握垂解析：≤；【分析】根据三角形的高的概念得到AM⊥BC，根据垂线段最短判断．【详解】解：如图，∵线段AM是△ABC边BC上的高，∴AM⊥BC，由垂线段最短可知，AN≥AM，故答案为：≤．【点睛】本题考查的是中线和高的概念，掌握垂线段最短是解题的关键．三、解答题21．如图，将△ABC 沿着平行于BC 的直线DE 折叠，点A 落到点A ′，若∠C ＝125°，∠A ＝20°，求∠BD A ′的度数.解析：110°【分析】利用翻折变换的性质以及三角形内角和定理求出∠BDE ，∠A′DE ，即可解决问题．【详解】∵∠A ＋∠B ＋∠C ＝180°，∠A ＝20°，∠C ＝125°，∴∠B ＝35°，∵DE ∥BC ，∴∠ADE ＝∠B ＝35°，∠BDE ＋∠B ＝180°，∴∠BDE ＝180−∠B ＝180°−35°＝145°，∵△ADE 沿DE 折叠成△A′DE ，∴∠A′DE ＝∠ADE ＝35°，∴∠BDA′＝∠BDE−∠A′DE ＝145°−35°＝110°．【点睛】本题考查三角形内角和定理，翻折变换的性质以及平行线的性质，解题的关键是熟练掌握翻折变换的性质，属于中考常考题型．22．已知AD 是ABC 的角平分线，CE 是AB 边上的高，AD ，CE 相交于点P ，BCE 40,APC 123∠∠=︒=︒，求ADC ∠和ACB ∠的度数．解析：∠ADC 83=︒，∠ACB 64=︒．【分析】由CE 是AB 边上的高，可得∠AEC=90︒，再利用三角形的外角性质可得∠ADC ，∠EAP ，∠B 的度数，再根据AD 是ABC 的平分线，可得∠BAC 的度数，再利用三角形的内角和定理即可得到∠ACB 的度数．【详解】∵CE 是AB 边上的高，∴CE ⊥AB ，即∠AEC=90︒，∵∠APC=∠BCE+∠ADC=123︒，∠BCE=40︒，∴∠ADC=123︒-4083︒=︒，∵∠APC=∠AEP+∠EAP=123︒，∴∠EAP=1239033︒-︒=︒，∵AD 是ABC 的角平分线，∴∠BAC=2∠EAP=23366⨯︒=︒，∵∠ADC=∠BAD+∠B ，∴∠B=833350︒-︒=︒，∵∠B+∠BAC+∠ACB=180︒，∴∠ACB=180665064︒-︒-︒=︒，即∠ADC 83=︒，∠ACB 64=︒．【点评】本题考查了三角形的角平分线、高线，三角形的外角性质和三角形的内角和定理．熟记性质并准确识图是解题的关键．23．()1若n 边形的内角和等于它外角和的3倍，求边数n ．()2已知a ，b ，c 为三角形三边的长，化简：a b c b c a --+--．解析：()18；()22c ．【分析】（1）根据多边形的内角和与外角和公式列出方程即可求解；（2）根据三角形的三边关系可得a c b +>，b c a +>，再根据化简绝对值的方法即可求解．【详解】解：()1由题意得：()18023603n ︒-=︒⨯，解得：8n =．()2∵a ，b ，c 为三角形三边的长，∴a c b +>，b c a +>， ∴a b c b c a --+--()()2a b c b c a b c a a c b c =-++-+=+-++-=．【点睛】此题主要考查多边形的内角和与外角和、三角形的三边关系的应用，解题的关键是熟知多边形的性质及去绝对值的方法．24．已知一个多边形的内角和比它的外角和的3倍还多180度．（1）求这个多边形的边数；（2）求这个多边形的对角线的总条数．解析：（1）9；（2）27【分析】（1）利用多边形的外角和为360°，根据内角和与外角和的关系及多边形内角和公式求出边数即可得答案；（2）根据多边形对角线条数公式计算即可得答案．【详解】（1）设多边形的边数为n，∵多边形的外角和为360°，内角和比它的外角和的3倍还多180度，∴此多边形的内角和为360°×3+180°=1260°，∴（n-2）×180°=1260，解得：n=9，答：这个多边形的边数是9．（2）由（1）可知此多边形为9边形，∴从一个顶点可引出对角线9-3=6（条），∴这个多边形的对角线的总条数为6×9÷2=27（条），答：这个多边形的对角线的总条数为27条．【点睛】本题考查了多边形的内角与外角、多边形的对角线，掌握多边形的内角和定理、多边形的对角线的条数的计算公式是解题的关键．25．如图所示，已知AD，AE分别是△ABC的高和中线，AB=3cm，AC=4 cm，BC=5 cm，∠CAB=90°．(1)求AD的长．(2)求△ABE的面积．解析：（1）125cm；（2）3cm2【分析】（1）利用“面积法”来求线段AD的长度；（2）△AEC与△ABE是等底同高的两个三角形，它们的面积相等【详解】解：∵∠BAC=90°，AD是边BC上的高，∴12AB•AC=12BC•AD，∴341255AB AC AD BC ⋅⨯===（cm ），即AD 的长度为125cm ；（2）如图，∵△ABC 是直角三角形，∠BAC=90°，AB=3cm ，AC=4cm ， ∴S △ABC =12AB•AC=12×3×4=6（cm 2）．又∵AE 是边BC 的中线，∴BE=EC ，∴12BE•AD=12EC•AD ，即S △ABE =S △AEC ， ∴S △ABE=12S △ABC =3（cm 2）． ∴△ABE 的面积是3cm 2．【点睛】本题考查了中线的性质．解题的关键是利用三角形面积的两个表达式相等，求出AD ． 26．已知：180,BDG EFG B DEF ∠+∠=︒∠=∠．（1）如图1，求证：//DE BC ．（2）如图2，当90A EFG ∠=∠=︒时，请直接写出与C ∠互余的角．解析：（1）证明见解析；（2）,,B ADE DEF ∠∠∠．【分析】（1）先根据角的和差、等量代换可得EFG ADG ∠=∠，再根据平行线的判定可得//EF AB ，然后根据平行线的性质可得ADE DEF ∠=∠，从而可得B ADE ∠=∠，最后根据平行线的判定即可得证；（2）根据直角三角形的两锐角互余、等量代换即可得．【详解】（1）180,180BDG EFG BDG ADG ∠+∠=︒∠+∠=︒，EFG ADG ∴∠=∠，//EF AB ∴，ADE DEF ∴∠=∠，B DEF ∠=∠，B ADE ∴∠=∠，//DE BC ∴；（2）90A ∠=︒，90B C ∴∠+∠=︒，B DEF ∠=∠，90DEF C ∴∠+∠=︒，由（1）可知，B ADE ∠=∠，90ADE C ∴∠+∠=︒，综上，与C ∠互余的角有,,B ADE DEF ∠∠∠．【点睛】本题考查了直角三角形的两锐角互余、平行线的判定与性质等知识点，熟练掌握平行线的判定与性质是解题关键．27．（问题引入）（1）如图1，△ABC ，点O 是∠ABC 和∠ACB 相邻的外角平分线的交点，若∠A=40°，请求出∠BOC 的度数．（深入探究）（2）如图2，在四边形ABDC 中，点O 是∠BAC 和∠ACD 的角平分线的交点，若∠B+∠D=110°，请求出∠AOC 的度数．（类比猜想）（3）如图3，在△ABC 中，∠CBO=13∠DBC ，∠BCO= 13∠ECB ，∠A=α，则∠BOC=___（用α的代数式表示，直接写出结果，不需要写出解答过程）．（4）如果BO ，CO 分别是△ABC 的外角∠DBC ，∠ECB 的n 等分线，它们交于点O ，∠CBO=∠1n DBC ∠BCO=1n∠ECB ，则∠BOC=___（用n 、a 的代数式表示，直接写出结果，不需要写出解答过程）．解析：（1）70°；（2）55°；（3）120°-13α；（4）()11801n n nα-⨯︒- 【分析】（1）由三角形内角和定理可求得∠ABC+∠ACB ，再利用邻补角可求得∠DBC+∠ECB ，根据角平分线的定义可求得∠OBC+∠OCB ，在△BOC 中利用三角形内角和定理可求得∠BOC ；（2）根据三角形内角和等于180°，四边形内角和等于360°，结合角平分线的定义即可得到∠AOC 与∠B+∠D 之间的关系；（3）根据三角形的内角和等于180°以及三角形的外角性质列式整理即可得∠BOC=120°-3α；（4）根据三角形的内角和等于180°以及三角形的外角性质列式整理即可得∠BOC=()11801n n nα-⨯︒-．【详解】（1）∵∠A=40°，∴∠ABC+∠ACB=180°-∠A=140°，∴∠DBC+∠ECB=180°-∠ABC+180°-∠ACB=360°-(∠ABC+∠ACB)=360°-140°=220°，∵BO 、CO 分别平分∠DBC 和∠ECB ，∴∠OBC+∠OCB=12(∠DBC+∠ECB) =12×220°=110°， ∴∠BOC=180°-（∠OBC+∠OCB ）=180°-110°=70°；（2）∵点O 是∠BAC 和∠ACD 的角平分线的交点，∴∠OAC=12∠CAB ，∠OCA=12∠ACD ， ∴∠AOC=180°-(∠OAC+∠OCA) =180°-12(∠CAB+∠ACD) =180°-12(360°-∠B-∠D) =12(∠B+∠D)， ∵∠B+∠D=110°， ∴∠AOC=12(∠B+∠D)=55°；（3）在△OBC 中，∠BOC=180°-(∠OBC+∠OCB)=180°-13(∠DBC+∠ECB) =180°-13(∠A+∠ACB+∠A+∠ABC) =180°-13(∠A+180°) =120°-13α；故答案为：120°-13α；（4）在△OBC 中，∠BOC=180°-(∠OBC+∠OCB)=180°-1n(∠DBC+∠ECB) =180°-1n(∠A+∠ACB+∠A+∠ABC) =180°-1n (∠A+180°) =()11801n n nα-⨯︒-．故答案为：()11801n n nα-⨯︒-．【点睛】本题考查了三角形的内角和定理，三角形的外角性质，角平分线的定义，整体思想的利用是解题的关键．28．如图，有一块直角三角板XYZ 置在ABC 上，恰好三角板XYZ 的两条直角边XY 、XZ 分别经过点B 、C ．ABC 中，30A ∠=︒．（1）ABC ACB ∠+∠=________．（2）ABX ACX ∠+∠=________．（说明理由）解析：（1）150︒ （2）60︒；理由见解析【分析】（1）根据三角形的内角和定理即可求得答案；（2）先求得XBC XCB ∠+∠=90°，再根据ABX ACX ∠+∠()()ABC ACB XBC XCB =∠+∠-∠+∠即可求得答案．【详解】解：（1）∵180ABC ACB A ∠+∠+∠=︒，30A ∠=︒，∴180ABC ACB A ∠+∠=︒-∠18030=︒-︒150=︒，故答案为：150°；（2）60ABX ACX ∠+∠=︒，理由如下：∵180XBC XCB X ∠+∠+∠=︒，90X ∠=︒， ∴180XBC XCB X ∠+∠=︒-∠18090=︒-︒90=︒，∴ABX ACX ∠+∠ABC XBC ACB XCB =∠-∠+∠-∠()()ABC ACB XBC XCB =∠+∠-∠+∠15090=︒-︒60=︒，故答案为：60°．【点睛】本题考查了三角形的内角和定理，熟练掌握三角形的内角和定理是解决本题的关键．。

【教师卷】初中数学八年级数学上册第十一章《三角形》经典题(培优)

一、选择题1．如图，在△ABC 中，∠ACB=90°，D 在AB 上，将△ABC 沿CD 折叠，点B 落在AC 边上的点B′处，若'20ADB ∠=︒，则∠A 的度数为（）A ．25°B ．30°C ．35°D ．40°C解析：C【分析】利用翻折不变性，三角形内角和定理和三角形外角的性质即可解决问题．【详解】∵∠ACB ＝90°，∴∠A ＋∠B ＝90°，∵△CDB′是由△CDB 翻折得到，∴∠CB′D ＝∠B ，∵∠CB′D ＝∠A ＋∠ADB′＝∠A ＋20°，∴∠A ＋∠A ＋20°＝90°，解得∠A ＝35°．故选：C ．【点睛】本题考查三角形内角和定理和三角形外角的性质，翻折变换等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．2．用若干根等长的小木棍搭建等边三角形（三边相等的三角形），搭建1个等边三角形最少需要3根小木棍，搭建2个等边三角形最少需要5根小木棍，搭建4个等边三角形最少需要小木棍的根数是（）A ．12B ．10C ．9D ．6D解析：D【分析】要先根据题意，画出图形，通过对图形观察，思考，得出需要小木棍的根数，然后图形对比，选出最少需要小木棍的根数．【详解】图1没有共用部分，要6根小木棍，图2有共用部分，可以减少小木棍根数，仿照图2得到图3，要7根小木棍，同法搭建的图4，要9根小木棍，如按图5摆放，外围大的等边三角形，可以得到5个等边三角形，要9根小木棍，如按图6摆成三棱锥(西面体)就可以得到4个等边三角形，∴搭建4个等边三角形最少需要小木棍6根．故选：D【点睛】此题考查的是组成图形的边的条数，解答此题需要灵活利用立体空间思维解答． 3．下列每组数分别三根小木棒的长度，用它们能摆成三角形的是（）A ．3,4,8cm cm cmB ．7,8,15cm cm cmC ．12,13,22cm cm cmD ．10,10,20cm cm cm C解析：C【分析】根据三角形两边之和大于第三边，两边之差小于第三边计算判断即可.【详解】∵3+4＜8，∴A 选项错误；∵7+8=15，∴B 选项错误；∵12+13＞22，∴C 选项正确；∵10+10=20，∴D 选项错误；故选C.【点睛】本题考查了三角形的存在性，熟练掌握三角形的三边关系定理是解题的关键.4．一个多边形的内角和是外角和的4倍，则这个多边形的边数为（）A ．10B ．8C ．6D ．4A【分析】设这个多边形的边数为n ，根据内角和公式以及多边形的外角和为360°即可列出关于n 的一元一次方程，解方程即可得出结论．【详解】解：设这个多边形的边数为n ，则该多边形的内角和为（n-2）×180°，依题意得：（n-2）×180°=360°×4，解得：n=10，∴这个多边形的边数是10．故选：A【点睛】本题考查了多边形内角与外角，解题的关键是根据多边形内角和公式得出方程（n-2）×180°=360°×4．5．小红有两根长度分别为4cm 和8cm 的木棒，他想摆一个三角形，现有长度分别为3cm ，4cm ，8cm ，15cm 四根木棒，则他应选择的木棒长度为（）．A ．3cmB ．4cmC ．8cmD ．15cm C解析：C【分析】设选择的木棒长为x ，根据第三边大于两边之差小于两边之和即可求出范围，再结合选项即可得出答案．【详解】由题意得，设选择的木棒长为x ，则8448x -<<+，即412x <<， ∴选择木棒长度为8cm ．故选C ．【点睛】本题考查了三角形三边关系的应用，熟练掌握三边关系是解题的关键．6．以下列长度的各组线段为边，能组成三角形的是（）A ．2cm ，3cm ，6cmB ．3cm ，4cm ，8cmC ．5cm ，6cm ，10cmD ．5cm ，6cm ，11cm C解析：C【分析】根据三角形三边关系解答．【详解】A 、∵2+3<6，∴以此三条线段不能组成三角形；B 、3+4<8，∴以此三条线段不能组成三角形；C 、∵5+6>10，∴以此三条线段能组成三角形；D 、∵5+6=11，∴以此三条线段不能组成三角形；故选：C ．此题考查三角形的三边关系：三角形两边的和大于第三边．7．下列四个图形中，线段CE是ABC的高的是（）A．B．C．D． B解析：B【分析】利用三角形高的定义逐一判断选项，可得答案．【详解】A．CE不垂直AB，故CE不是ABC的高，不符合题意，B．CE是ABC中AB边上的高，符合题意，C．CE不是ABC的高，不符合题意，D．CE不是ABC的高，不符合题意．故选B．【点睛】此题主要考查了三角形的高，关键是掌握从三角形的一个顶点向对边作垂线，垂足与顶点之间的线段叫做三角形的高．8．下列长度的三条线段，能组成三角形的是（）A．3，5，6 B．3，2，1 C．2，2，4 D．3，6，10A解析：A【分析】根据三角形三边长关系，逐一判断选项，即可得到答案．【详解】A. ∵3+5＞6，∴长度为3，5，6的三条线段能组成三角形，故该选项符合题意，B. ∵1+2=3，∴长度为3，2，1的三条线段不能组成三角形，故该选项不符合题意，C. ∵2+2=4，∴长度为2，2，4的三条线段不能组成三角形，故该选项不符合题意，D. ∵3+6＜10，∴长度为3，6，10的三条线段不能组成三角形，故该选项不符合题意，故选A【点睛】本题主要考查三角形三边长的关系，掌握三角形任意两边之和大于第三边，是解题的关键．9．以下列各组线段为边，能组成三角形的是（）A．1，2，3 B．2，3，4 C．2，5，8 D．6，3，3B解析：B【分析】根据三角形的三边关系定理：两边之和大于第三边，即两条较短的边的长大于最长的边即可．【详解】A 、1+2=3，不能构成三角形， A 错误；B 、2+3=5>4可以构成三角形，B 正确；C 、2+5=7＜8，不能构成三角形， C 错误；D 、3+3=6，不能构成三角形，D 错误．故答案选：B ．【点睛】本题主要考查三角形的三边关系，比较简单，熟记三边关系定理是解决本题的关键． 10．下列说法正确的个数为（）①过两点有且只有一条直线；②两点之间，线段最短；③若ax ay =，则x y =；④若A 、B 、C 三点共线且AB BC =，则B 为AC 中点；⑤各边相等的多边形是正多边形． A ．①②④B ．①②③C ．①④⑤D ．②④⑤A解析：A【分析】根据直线的性质、两点间的距离、等式的性质、线段中点定义、多边形的定义依次判断．【详解】①过两点有且只有一条直线，故①正确；②两点之间，线段最短，故②正确；③若ax ay =，当0a =时，x 不一定等于y ，故③错误；④若A ，B ，C 三点共线且AB BC =，则B 为AC 中点，故④正确；⑤各角都相等且各边相等的多边形是正多边形，故⑤错误．∴正确的有①②④，故选：A ．【点睛】此题考查理解能力，正确掌握直线的性质、两点间的距离、等式的性质、线段中点定义、正多边形的定义是解题的关键．二、填空题11．如图，BF 平分∠ABD ，CE 平分∠ACD ，BF 与CE 交于G ，若130,90BDC BGC ∠=︒∠=︒，则∠A 的度数为_________．50°【分析】连接BC 根据三角形内角和定理可求得∠DBC ＋∠DCB 的度数再利用三角形内角和定理及角平分线的定义可求得∠ABC ＋∠ACB 的度数即可求得∠A 的度数【详解】解：连接BC ∵∠BDC ＝130° 解析：50°【分析】连接BC，根据三角形内角和定理可求得∠DBC＋∠DCB的度数，再利用三角形内角和定理及角平分线的定义可求得∠ABC＋∠ACB的度数，即可求得∠A的度数．【详解】解：连接BC，∵∠BDC＝130°，∴∠DBC＋∠DCB＝180°−∠BDC＝50°，∵∠BGC＝90°，∴∠GBC＋∠GCB＝180°−∠BGC＝90°，∴∠GBD＋∠GCD＝（∠GBC＋∠GCB）−（∠DBC＋∠DCB）＝40°，∵BF平分∠ABD，CE平分∠ACD，∴∠ABD＋∠ACD＝2∠GBD＋2∠GCD＝80°，∴∠ABC＋∠ACB＝（∠ABD＋∠ACD）＋（∠DBC＋∠DCB）＝130°，∴∠A＝180°−（∠ABC＋∠ACB）＝180°−130°＝50°．故答案为：50°．【点睛】本题主要考查了与角平分线有关的三角形内角和问题，根据题意作出辅助线，构造出三角形是解答此题的关键．12．2016年2月6日凌晨，宝岛高雄发生6.7级地震，得知消息后，中国派出武警部队探测队，探测队探测出某建筑物下面有生命迹象，他们在生命迹象上方建筑物的一侧地面上的,A B两处，用仪器探测生命迹象C，已知探测线与地面的夹角分别是30︒和60︒（如∠的度数是_________．图)，则C【分析】先由题意得CAB=30°∠ABD=60°再由三角形的外角性质即可得出答案【详解】解：∵探测线与地面的夹角为30°和60°∴∠CAB=30°∠ABD=60°∵∠ABD=∠CAB+∠C∴∠C=6解析：30︒【分析】先由题意得CAB=30°，∠ABD=60°，再由三角形的外角性质即可得出答案．【详解】解：∵探测线与地面的夹角为30°和60°，∴∠CAB=30°，∠ABD=60°，∵∠ABD=∠CAB+∠C，∴∠C=60°-30°=30°，故答案为：30°．【点睛】本题考查了三角形的外角的性质，对顶角，解题的关键是熟练掌握三角形的外角性质，比较简单．13．七边形的外角和为________．360°【分析】根据多边形的外角和等于360°即可求解；【详解】∵多边形的外角和都是360°∴七边形的外角和为360°故答案为：360°【点睛】本题考查了多边形的外角的性质掌握多边形的外角和等于36 解析：360°【分析】根据多边形的外角和等于360°即可求解；【详解】∵多边形的外角和都是360°，∴七边形的外角和为360°，故答案为：360°．【点睛】本题考查了多边形的外角的性质，掌握多边形的外角和等于360°是解题的关键；的度14．如图，飞机P在目标A的正上方，飞行员测得目标B的俯角为30°，那么APB数为______°．60【分析】先由题意得到∠A=∠B=根据直角三角形两锐角互余求得结果【详解】∵飞机P在目标A的正上方飞行员测得目标B的俯角为30°∴∠A=∠CPB=∵CP∥AB∴∠B=∠CPB=∴=-∠B=故答案为解析：60【分析】先由题意得到∠A=90︒，∠B=30，根据直角三角形两锐角互余求得结果．【详解】∵飞机P在目标A的正上方，飞行员测得目标B的俯角为30°，∴∠A=90︒，∠CPB=30,∵CP∥AB，∴∠B=∠CPB=30,∠=90︒-∠B=60︒,∴APB故答案为：60．【点睛】此题考查直角三角形两锐角互余的性质，理解飞行员测得目标B的俯角为30°得到∠B=30是解题的关键．15．如图，△ABC的两条中线AD、BE相交于点G，如果S△ABG＝2，那么S△ABC＝_____．6【分析】根据DE分别是三角形的中点得出G是三角形的重心再利用重心的概念可得：2GD＝AG进而得到S△ABG：S△ABD＝2：3再根据AD是△ABC的中线可得S△ABC＝2S△ABD进而得到答案【详解析：6【分析】根据D，E分别是三角形的中点，得出G是三角形的重心，再利用重心的概念可得：2GD＝AG进而得到S△ABG：S△ABD＝2：3，再根据AD是△ABC的中线可得S△ABC＝2S△ABD进而得到答案．【详解】解：∵△ABC的两条中线AD、BE相交于点G，∴2GD＝AG，∵S△ABG＝2，∴S△ABD＝3，∵AD是△ABC的中线，∴S △ABC ＝2S △ABD ＝6．故答案为：6．【点睛】此题主要考查了重心的概念和性质：三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的两倍．16．如图，ABC 的三边的中线AD ，BE ，CF 的公共点为G ，且21AG GD =：：．若12ABC S =△，则图中阴影部分的面积是________． 4【分析】根据三角形的中线把三角形的面积分成相等的两部分知△ABC 的面积即为阴影部分的面积的3倍【详解】解：∵△ABC 的三条中线ADBECF 交于点GAG ：GD=2：1∴AE=CE ∴S △CGE=S △A解析：4【分析】根据三角形的中线把三角形的面积分成相等的两部分，知△ABC 的面积即为阴影部分的面积的3倍．【详解】解：∵△ABC 的三条中线AD 、BE ，CF 交于点G ，AG ：GD=2：1，∴AE=CE ，∴S △CGE =S △AGE =13S △ACF ，S △BGF =S △BGD =13S △BCF ， ∵S △ACF =S △BCF =12S △ABC =12×12=6， ∴S △CGE =13S △ACF =13×6=2，S △BGF =13S △BCF =13×6=2， ∴S 阴影=S △CGE +S △BGF =4．故阴影部分的面积为4．故答案为：4．【点睛】本题考查了三角形的面积，三角形中线的性质，正确的识别图形是解题的关键． 17．如图，在ABC ∆中，4ACB A ∠=∠，点D 在边AC 上，将BDA ∆沿BD 折叠，点A 落在点A '处，恰好BA AC '⊥于点E 且//BC DA '，则BDC ∠的度数为__________度．54°【分析】根据折叠的性质及题意可在Rt △BEC中求解∠C 及∠CBE 的度数从而计算∠ABD 的度数则∠BDC=∠A+∠ABD 即可计算出结果【详解】由题意可得：∠A=∠∠=∠CBE ∴则在Rt △BEC 中解析：54°【分析】根据折叠的性质及题意，可在Rt △BEC 中求解∠C 及∠CBE 的度数，从而计算∠ABD 的度数，则∠BDC=∠A+∠ABD ，即可计算出结果．【详解】由题意可得：∠A=∠A '，∠A '=∠CBE ，∴44ACB A CBE ∠=∠=∠，则在Rt △BEC 中，∠C+∠CBE=90°，即：5∠CBE=90°，∠CBE=18°，∴∠A=18°，∠C=72°，∠ABC=90°，∴72ABA ABC CBE '=-=︒∠∠∠，由折叠性质可知，ABD A BD '∠=∠，∴=36ABD A BD '∠=∠︒，∴54BDC ABD A ∠=∠+∠=︒故答案为：54°．【点睛】本体三角形的折叠问题，平行线的性质及三角形的外角定理，理解图形变化中的特点，准确结合题意计算是解题关键．18．一个三角形的两边长分别是3和7，且第三边长为奇数，这样的三角形的周长最大值是___________，最小值是___________．15【分析】记三角形的第三边为c 先根据三角形的三边关系确定c 的取值范围进而可得三角形第三边的最大值与最小值进一步即可求出答案【详解】解：记三角形的第三边为c 则7－3＜c ＜7+3即4＜c ＜10因为第三解析：15【分析】记三角形的第三边为c ，先根据三角形的三边关系确定c 的取值范围，进而可得三角形第三边的最大值与最小值，进一步即可求出答案．【详解】解：记三角形的第三边为c ，则7－3＜c ＜7+3，即4＜c ＜10，因为第三边长为奇数，所以三角形第三边长的最大值是9，最小值是5，所以三角形的周长最大值是3+7+9=19；最小值是3+7+5=15；故答案为：19，15．【点睛】本题考查了三角形的三边关系与不等式组的整数解，属于基础题型，正确理解题意、掌握解答的方法是关键．19．AD 为ABC 的中线，AE 为ABC 的高，ABD △的面积为14，7,2AE CE ==则DE 的长为_________．2或6【分析】利用面积法求出BD 即可求得CD 再分AE 在内部和外部求出DE 即可【详解】解：为的高△ABD 的面积为14AE=7∴∵为的中线∴CD=BD=4当AE 在内部时∵CE=2∴DE=CD-CE=2当解析：2或6【分析】利用面积法求出BD ，即可求得CD ，再分AE 在ABC 内部和外部，求出DE 即可．【详解】解：AE 为ABC 的高，△ABD 的面积为14，AE=7， 1142∴⋅⋅=BD AE ， ∴2828=4,B 7D ==AE ∵AD 为ABC 的中线，∴CD=BD=4，当AE 在ABC 内部时∵CE=2，∴DE=CD-CE=2，当AE 在ABC 外部时∵CE=2，∴DE=CD+CE=6，故答案为：2或6【点睛】本题考查三角形的高、中线和面积，注意高可在三角形的内部和外部是解题的关键． 20．如图，若//AB CD ，BF 平分ABE ∠，DF 平分CDE ∠，90BED ∠=，则BFD ∠=______．45°【分析】如图作射线BF 与射线BE 根据平行线的性质和三角形的外角性质可得∠ABE+∠EDC ＝90°然后根据角平分线的定义和三角形的外角性质即可求出答案【详解】解：如图作射线BF 与射线BE ∵AB ∥ 解析：45°【分析】如图，作射线BF 与射线BE ，根据平行线的性质和三角形的外角性质可得∠ABE +∠EDC ＝90°，然后根据角平分线的定义和三角形的外角性质即可求出答案．【详解】解：如图，作射线BF 与射线BE ，∵AB ∥CD ，∴∠ABE ＝∠4，∠1＝∠2，∵∠BED ＝90°，∠BED ＝∠4+∠EDC ，∴∠ABE +∠EDC ＝90°，∵BF 平分∠ABE ，DF 平分∠CDE ，∴∠1+∠3＝12∠ABE +12∠EDC ＝45°， ∵∠5＝∠2+∠3，∴∠5＝∠1+∠3＝45°，即∠BFD ＝45°，故答案为：45°．【点睛】本题考查了平行线的性质、角平分线的定义和三角形的外角性质，属于常考题型，熟练掌握上述知识是解题的关键．三、解答题21．如图，在平面内有三个点、、A B C（1）根据下列语句画图：①连接AB ；②作直线BC ；③作射线AC ，在AC 的延长线上取一点D 使得CD CB =，连接BD ；（2）比较,,AB BD AB BC CD AD +++的大小关系．解析：（1）见解析；（2）AB BC CD AB BD AD ++>+>【分析】（1）①按要求作图；②按要求作图；③按要求作出射线AC ，然后以点C 为圆心，BC 为半径画弧，交射线AC 于点D ，连接BD ；（2）结合图形，根据三角形两边之和大于第三边进行分析比较．【详解】解：（1）①如图，线段AB 即为所求；②如图，直线BC 即为所求；③如图，射线AC ，点D ，线段BD 即为所求（2）如图，在△BCD 中，BC+CD ＞BD∴AB BC CD AB BD ++>+在△ABD 中，AB+BD ＞AD∴AB BC CD AB BD AD ++>+>【点睛】本题考查基本作图及三角形三边关系，正确理解几何语言并掌握三角形三边关系是解题关键．22．已知：在RT △ABC 中，∠ACB ═90°，CD ⊥AB ，AE 是∠CAB 的角平分线，AE 与CD 交于点F ．（1）如图1，求证：∠CEF ＝∠CFE ．（2）如图2，过点E 作EG ⊥AB 于点G ，请直接写出图中与∠CAE 互余的所有角．解析：（1）见解析；（2）图中与∠CAE 互余的角有∠CEA ，∠GEA ，∠CFE ，∠DFA ．【分析】（1）根据角平分线的定义可得∠DAF ＝∠CAE ，再根据等角的余角相等、对顶角相等，可得∠CEF ＝∠CFE ；（2）根据互余的两个角的和为90°求解即可．【详解】（1）证明：∵∠ACB ═90°，CD ⊥AB ，∴∠DAF +∠AFD ＝90°，∠CAE +∠CEF ＝90°，又∵AE 是∠CAB 的角平分线，∴∠DAF ＝∠CAE ，∴∠AFD ＝∠CEF ，又∵∠AFD ＝∠CFE ，∴∠CEF ＝∠CFE ；（2）∵EG ⊥AB 于点G ，∴∠DAF +∠GEA ＝90°，由（1）可知∠DAF ＝∠CAE ，∠CAE +∠CEF ＝90°，∠CEF ＝∠CFE ＝∠DFA ，∴图中与∠CAE 互余的角有∠CEA ，∠GEA ，∠CFE ，∠DFA ．【点评】本题考查了角平分线的定义和余角的定义，解决本题的关键是熟记余角的定义． 23．如图，在ABC 中，AD 为高，AE 为BAC ∠的平分线，若28B ∠=︒，52ACD ∠=°，求EAD ∠的度数．解析：50°【分析】由AD 为高，28B ∠=︒，求出52ACD ∠=°，利用外角性质求出24BAC ACD B ∠∠∠=-=︒，根据AE 是角平分线，求出1122BAE BAC ∠∠==︒，即可求出EAD ∠的度数.【详解】解：∵AD 为高，28B ∠=︒，∴62BAD ∠=︒．∵52ACD ∠=°，∴24BAC ACD B ∠∠∠=-=︒．∵AE 是角平分线，∴1122BAE BAC ∠∠==︒， ∴50EAD BAD BAE ∠=∠-∠=︒.【点睛】此题考查三角形的角平分线的性质，直角三角形两锐角互余的性质，三角形的外角等于与它不相邻的两个内角的和.24．如图，已知1,23180BDE ︒∠=∠∠+∠=．（1）证明：//AD EF ．（2）若DA 平分BDE ∠，FE AF ⊥于点F ，140∠=︒，求BAC ∠的度数．解析：（1）见解析；（2）70°【分析】（1）根据平行线的判定得出AC//DE ，根据平行线的性质得出∠2=∠ADE ，求出∠3+∠ADE=180°，根据平行线的判定得出即可；（2）求出∠BDE 的度数，求出∠2的度数，求出∠3的度数，根据四边形的内角和定理求出∠B ，再根据三角形内角和定理求出即可．【详解】（1）证明：∵∠1=∠BDE ，∴AC//DE ，∴∠2=∠ADE ，∵∠2+∠3=180°，∴∠3+∠ADE=180°，∴AD//EF ；（2）∵∠1=∠BDE ，∠1=40°，∴∠BDE=40°，∵DA 平分∠BDE ，∴∠ADE=12∠BDE=20°， ∴∠2=∠ADE=20°，∵∠2+∠3=180°∴∠3=160°，∵FE ⊥AF ，∴∠F=90°，∴∠B=360°-90°-160°-40°=70°，在△ABC 中，∠BAC=180°-∠1-∠B=180°-40°-70°=70°．【点睛】本题考查了平行线的性质和判定，多边形的内角和定理，角平分线的定义，能灵活运用知识点进行推理和计算是解此题的关键．25．如图，已知在ABC 中，90C ∠=︒，BE 平分ABC ∠，且//BE AD ，20BAD ∠=︒，求AEB ∠的度数．解析：110°【分析】根据平行线的性质和三角形外角的性质即可得到结论．【详解】∵BE ∥AD ，∴∠ABE=∠BAD=20°，∵BE 平分∠ABC ，∴∠EBC=∠ABE=20°，∵∠C=90°，∴∠AEB=∠C+∠CBE=90°+20°=110°．【点睛】考查了三角形的外角的性质、平行线的性质和角平分线的定义，解题关键是正确识别图形得出图中角之间的关系．26．如图所示，AD 、AE 分别是△ABC 的高和角平分线，∠B=20°，∠C=80°，求∠EAD 的度数．解析：30°【分析】由三角形的内角和可求得∠BAC ，则由角平分线定义可求得∠EAC ，三角形的内角和可求得∠DAC 即可．【详解】解：在△ABC 中∵∠B=20°，∠C=80°∴∠BAC=180°－∠B －∠C=180°－20°－80°=80°；∵AE 是△ABC 的角平分线，∴∠EAC=12∠BAC=12×80°=40°； ∵AD 是△ABC 的高∴∠ADC=90°；又∵在△ADC 中，∠C=80°∴∠DAC=180°－∠C －∠ADC=180°－80°－90°=10°；∴∠EAD=∠EAC －∠DAC=40°－10°=30°；【点睛】本题考查了角平分线定义，三角形内角和定理的应用，题目比较好，难度适中． 27．如图，在ABC 中，AD 是高，AE 、BF 是角平分线，它们相交于点O ，60BAC ∠=︒，70C ∠=︒．求EAD ∠和∠BOE 的度数．解析：10EAD ∠=︒，55BOE ∠=︒【分析】根据三角形内角和定理求出∠BAC=180°-60°-70°=50°，再由AE 是角平分线，求出∠EAC=12∠BAC=30°，由AD 是高，求出∠CAD=90°-∠C=20°，最后即可求出∠EAD=∠EAC-∠CAD=10°；根据角平分线的性质，得∠OAB=12∠BAC ，∠OBA=12∠ABC ，所以∠BOE=∠OAB+∠OBA=12（∠BAC+∠ABC ）=12（180°-∠C ）=12×（180°-70°）=55°．【详解】解：∠B AC =60°，∠C =70°∴∠ABC =180°−∠ABC −∠C =180°−60°-70°=50°，∵AE 是角平分线，∴∠EAC =12∠BAC =12×60°=30°， ∵AD 是高，∴∠ADC =90°，∴∠CAD =90°−∠C =90°−70°=20°，∴∠DAE =∠EAC −∠CAD =30°−20°=10°；∵AE ，BF 是角平分线，∴∠OAB =12∠BAC ,∠OBA =12∠ABC ， ∴∠BOE =∠OAB +∠OBA =12(∠BAC +∠ABC )=12(180°−∠C )=12×(180°−70°) =55°．【点睛】本题考查了三角形内角和定理、角平分线性质，解题的关键是明确题意，找出所求问题需要的条件．28．如图，CAD ∠与CBD ∠的角平分线交于点P ．（1）若35C ∠=︒，29D ∠=︒，求P ∠的度数；（2）猜想D ∠，C ∠，P ∠的等量关系．解析：（1）32°；（2）()12P C D ∠=∠+∠．【分析】（1）根据对顶角相等可得∠AFC=∠BFP ，∠BED =∠AEP ，利用三角形的内角和定理可得∠C ＋∠CAF=∠P ＋∠PBF①，∠D ＋∠DBE=∠P ＋∠PAE②，两式相加并利用角平分线的定义和等式的基本性质变形可得∠C ＋∠D=2∠P ，从而求出∠P ；（2）根据对顶角相等可得∠AFC=∠BFP ，∠BED =∠AEP ，利用三角形的内角和定理可得∠C ＋∠CAF=∠P ＋∠PBF①，∠D ＋∠DBE=∠P ＋∠PAE②，两式相加并利用角平分线的定义和等式的基本性质变形可得∠C ＋∠D=2∠P ，从而证出结论．【详解】解：（1）∵∠AFC=∠BFP ，∠BED =∠AEP∴180°－（∠C ＋∠CAF ）=180°－（∠P ＋∠PBF ），180°－（∠D ＋∠DBE ）=180°－（∠P ＋∠PAE ）∴∠C ＋∠CAF=∠P ＋∠PBF①，∠D ＋∠DBE=∠P ＋∠PAE②①＋②，得∠C ＋∠CAF ＋∠D ＋∠DBE=∠P ＋∠PBF ＋∠P ＋∠PAE∵CAD ∠与CBD ∠的角平分线交于点P∴∠CAF=∠PAE ，∠DBE=∠PBF∴∠C ＋∠D=2∠P∴∠P=()12C D ∠+∠=()135292︒+︒=32°；（2）()12P C D ∠=∠+∠，理由如下 ∵∠AFC=∠BFP ，∠BED =∠AEP ∴180°－（∠C ＋∠CAF ）=180°－（∠P ＋∠PBF ），180°－（∠D ＋∠DBE ）=180°－（∠P ＋∠PAE ）∴∠C ＋∠CAF=∠P ＋∠PBF①，∠D ＋∠DBE=∠P ＋∠PAE②①＋②，得∠C ＋∠CAF ＋∠D ＋∠DBE=∠P ＋∠PBF ＋∠P ＋∠PAE∵CAD ∠与CBD ∠的角平分线交于点P∴∠CAF=∠PAE ，∠DBE=∠PBF∴∠C ＋∠D=2∠P∴∠P=()12C D ∠+∠．【点睛】此题考查的是三角形的内角和定理和角的和与差，掌握三角形的内角和定理和角平分线的定义是解题关键．。

人教版八年级上册数学第11章三角形同步培优专项习题

人教版八年级上册数学第11章三角形同步培优专项习题1．如图，在三角形ABC中，∠B＝60°，∠C＝α，点D是AB上一点，E是AC上一点，∠ADE＝60°，点F为线段BC上一点，连接EF，过D作DG∥AC交EF于点G，（1）若α＝40°，求∠EDG的度数；（2）若∠FEC＝2∠DEF，∠DGF＝∠BFG，求α．2．如图，在△ACB中，∠ACB＝90゜，CD⊥AB于D．（1）求证：∠ACD＝∠B；（2）若AF平分∠CAB分别交CD、BC于E、F，求证：∠CEF＝∠CFE．3．已知，如图，在△ABC中，AD，AE分别是△ABC的高和角平分线．（1）若∠ABC＝30°，∠ACB＝60°，求∠DAE的度数；（2）写出∠DAE与∠C﹣∠B的数量关系，并证明你的结论．4．阅读下面的材料，并解决问题．（1）已知在△ABC中，∠A＝60°，图1﹣3的△ABC的内角平分线或外角平分线交于点O，请直接求出下列角度的度数．如图1，∠O＝；如图2，∠O＝；如图3，∠O＝；如图4，∠ABC，∠ACB的三等分线交于点O1，O2，连接O1O2，则∠BO2O1＝．（2）如图5，点O是△ABC两条内角平分线的交点，求证：∠O＝90°+∠A．（3）如图6，△ABC中，∠ABC的三等分线分别与∠ACB的平分线交于点O1，O2，若∠1＝115°，∠2＝135°，求∠A的度数．5．如图1，已知两条直线AB，CD被直线EF所截，分别交于点E，点F，EM平分∠AEF交CD于点M，且∠FEM＝∠FME．（1）直线AB与直线CD是否平行，说明你的理由；（2）如图2，点G是射线MD上一动点（不与点M，F重合），EH平分∠FEG交CD于点H，过点H作HN⊥EM于点N，设∠EHN＝α，∠EGF＝β．①当点G在点F的右侧时，若β＝60°，求α的度数；②当点G在运动过程中，α和β之间有怎样的数量关系？请写出你的猜想，并加以证明．6．如图所示，在△ABC中，BO，CO分别平分∠ABC和∠ACB；BD、CD分别平分∠ABC和∠ACB的外角．（1）若∠BAC＝70°，求：∠BOC的度数；（2）探究∠BDC与∠A的数量关系．（直接写出结论，无需说明理由）7．发现：已知△ABC中，AE是△ABC的角平分线，∠B＝72°，∠C＝36°（1）如图1，若AD⊥BC于点D，求∠DAE的度数；（2）如图2，若P为AE上一个动点（P不与A、E重合），且PF⊥BC于点F时，∠EPF＝°．（3）探究：如图2△ABC中，已知∠B，∠C均为一般锐角，∠B＞∠C，AE是△ABC的角平分线，若P为线段AE上一个动点（P不与E重合），且PF⊥BC于点F时，请写出∠EPF与∠B，∠C的关系，并说明理由．8．如图①，在△ABC中，∠BAC＝90°，AD是BC边上的高．（1）求证：∠DAC＝∠ABC；（2）如图②，△ABC的角平分线CF交AD于点E，求证：∠AFE＝∠AEF．9．问题引入：（1）如图①所示，△ABC中，点O是∠ABC和∠ACB的平分线的交点，若∠A＝α，则∠BOC＝（用α表示）：不用说明理由，直接填空．如图②所示，∠OBC＝∠ABC，∠OCB＝∠ACB，若∠A＝α，则∠BOC＝（用α表示），不用说明理由，直接填空．（2）如图③所示，∠OBC＝∠DBC，∠OCB＝∠ECB，若∠A＝α，则∠BOC＝（用α表示），填空并说明理由．10．如图，∠CAD与∠CBD的角平分线交于点P．（1）若∠C＝35°，∠D＝29°，求∠P的度数；（2）猜想∠D，∠C，∠P的等量关系．11．已知在四边形ABCD中，∠A＝∠C＝90°．（1）如图1，若BE平分∠ABC，DF平分∠ADC的邻补角，请写出BE与DF的位置关系，并证明；（2）如图2，若BF、DE分别平分∠ABC、∠ADC的邻补角，判断DE与BF位置关系，并证明；（3）如图3，若BE、DE分别五等分∠ABC、∠ADC的邻补角，（即∠CDE＝∠CDN，∠CBE＝∠CBM），求∠E度数．12．完成下面的证明：已知：如图，四边形ABCD中，∠A＝106°﹣α，∠ABC＝74°+α，BD⊥DC于点D，EF⊥DC于点F．求证：∠1＝∠2．证明：∵∠A＝106°﹣α，∠ABC＝74°+α（已知），∴∠A+∠ABC＝180°．∴AD∥（）．∴∠1＝．∵BD⊥DC，EF⊥DC（已知），∴∠BDF＝∠EFC＝90°（）．∴BD∥（）．∴∠2＝（）．∵∠1＝（已证），∴∠1＝∠2（）．13．已知点A在射线CE上，∠BDA＝∠C．（1）如图1，若AC∥BD，求证：AD∥BC；（2）如图2，若BD⊥BC，请证明∠DAE+2∠C＝90°；（3）如图3，在（2）的条件下，∠BAC＝∠BAD，过点D作DF∥BC交射线CE于点F，当∠DFE＝8∠DAE时，求∠BAD的度数．（直接写出结果）14．在△ABC中，∠A＝70°，点D、E分别是边AC、AB上的点（不与A、B、C重合），点P是平面内一动点（P与D、B不在同一直线上），设∠PEB＝∠1，∠DPE＝∠2，∠PDC＝∠3．（1）若点P在边BC上运动（不与点B和点C重合），如图（1）所示，则∠2＝；（用含有∠1、∠3的代数式表示）（2）若点P在△ABC的外部，如图（2）所示，则∠1、∠2、∠3之间有何关系？写出你的结论，并说明理由．∠3之间的关系式．（不需要证明）15．如图，已知∠DAE+∠CBF＝180°，CE平分∠BCD，∠BCD＝2∠E．（1）CD与EF是否平行，请说明理由．（2）若DF平分∠ADC，求∠DOC的度数（注：三角形的三个内角和等于180°）．16．如图，在△ABC中，BE是△ABC角平分线，点D是AB上的一点，且满足∠DEB＝∠DBE．（1）DE与BC平行吗？请说明理由；（2）若∠C＝50°，∠A＝45°，求∠DEB的度数．17．如图①，△ABC中，BD平分∠ABC，且与△ABC的外角∠ACE的角平分线交于点D．（1）若∠ABC＝70°，∠ACB＝40°，求∠D的度数；（2）若把∠A截去，得到四边形MNCB，如图②，猜想∠D、∠M、∠N的关系，并说明理由．18．在△ABC中，CD平分∠ACB交AB于点D，AH是△ABC边BC上的高，且∠ACB＝70°，∠ADC＝80°，求：（1）直接写出∠BAC＝．（2）求∠BAH的度数．19．如图，在四边形ABCD中，∠A与∠C互补，BE、DF分别平分∠ABC、∠ADC，EG∥AB与BC相交于点G．（1）∠1与∠2有怎样的数量关系？说明理由；（2）若∠A＝108°，∠1＝46°，求∠CEG的度数．20．如图，在四边形ABCD中，∠A＝140°，∠D＝80°．（1）如图1，若∠B＝∠C，则∠C＝度；（2）如图2，若∠ABC的角平分线BE交DC于点E，且BE∥AD，试求出∠C的度数；（3）①如图3，若∠ABC和∠DCB的角平分线交于点E，试求出∠BEC的度数；②在①的条件下，若延长BA、CD交于点F（如图4）．将原来条件“∠A＝140°，∠D＝80°”改为“∠F ＝40°”．其他条件不变．则∠BEC的度数为．。

上海华东师范大学第四附属中学八年级数学上册第十一章《三角形》经典练习卷(培优提高)

一、选择题1．若过六边形的一个顶点可以画n 条对角线，则n 的值是（）A ．1B ．2C ．3D ．4C 解析：C【分析】根据从一个n 边形一个顶点出发，可以连的对角线的条数是n-3进行计算即可．【详解】解：6-3=3（条）．答：从六边形的一个顶点可引出3条对角线．故选：C ．【点睛】本题考查了多边形的对角线，解答此类题目可以直接记忆：一个n 边形一个顶点出发，可以连的对角线的条数是n-3．2．内角和为720°的多边形是（）．A ．三角形B ．四边形C ．五边形D ．六边形 D解析：D【分析】根据多边形内角和的计算方法（n-2）•180°，即可求出边数．【详解】解：依题意有（n-2）•180°=720°，解得n=6．该多边形为六边形，故选：D ．【点睛】本题考查了多边形的内角和，利用多边形的内角和计算公式正确计算是解题关键． 3．如图，ABC 中，55,B D ∠=︒是BC 延长线上一点，且130ACD ∠=︒，则A ∠的度数是（）A．50︒B．65︒C．75︒D．85︒C解析：C【分析】根据三角形的外角性质求解．【详解】解：由三角形的外角性质可得：∠ACD=∠B+∠A，∴∠A=∠ACD-∠B=130°-55°=75°，故选C．【点睛】本题考查三角形的外角性质，熟练掌握三角形的外角性质定理并能灵活运用是解题关键．4．在多边形的一边上任取一点（不是顶点），将这个点与多边形的各顶点连接起来，可以将多边形分割成8个三角形，则该多边形的边数为（）A．8 B．9 C．10 D．11B解析：B【分析】逐一探究在三角形，四边形，五边形一边上任取一点（不是顶点），将这个点与多边形的各顶点连接起来，得到分割成的三角形的数量，再总结规律，运用规律列方程即可得到答案．【详解】解：如图，探究规律：在三角形的一边上任取一点（不是顶点），将这个点与三角形的各顶点连接起来，可以将三角形分割成2个三角形，在四边形的一边上任取一点（不是顶点），将这个点与四边形的各顶点连接起来，可以将四边形分割成3个三角形，在五边形的一边上任取一点（不是顶点），将这个点与五边形的各顶点连接起来，可以将五边形分割成4个三角形，总结规律：在n 边形的一边上任取一点（不是顶点），将这个点与n 边形的各顶点连接起来，可以将n 边形分割成()1n -个三角形，应用规律：由题意得：18,n -=9.n ∴=故选：.B【点睛】本题考查的是规律探究及规律运用，探究“在n 边形的一边上任取一点（不是顶点），将这个点与n 边形的各顶点连接起来，把n 边形分割成的三角形的数量”是解题的关键． 5．如图，在ABC 中，B C ∠=∠，D 为BC 边上的一点，点E 在AC 边上，ADE AED ∠=∠，若10CDE ∠=︒，则BAD ∠的度数为（）A ．20°B ．15°C ．10°D ．30°A解析：A【分析】先根据三角形外角的性质得出∠ADC=∠B+∠BAD ，∠AED=∠C+∠EDC ，再根据∠B=∠C ，∠ADE=∠AED 即可得出结论．【详解】解：∵∠ADC 是△ABD 的外角，∴∠ADC=∠B+∠BAD ，∴∠ADE=∠ADC-∠CDE=∠B+∠BAD-∠CDE∵∠AED 是△CDE 的外角，∴∠AED=∠C+∠EDC ，∵∠ADE=∠AED ，∴∠B+∠BAD-∠CDE=∠C+∠EDC ，∵∠B=∠C ，∴∠BAD=2∠EDC ，∵10CDE ∠=︒∴∠BAD=20°；故选：A【点睛】本题考查的是三角形外角的性质，熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键．6．下列长度的三条线段能组成三角形的是（）A ．3，3，4B ．7，4，2C ．3，4，8D ．2，3，5A解析：A【分析】看哪个选项中两条较小的边的和大于最大的边即可．【详解】解：A 、3+3＞4，能构成三角形，故此选项正确；B 、4+2＜7，不能构成三角形，故此选项错误；C 、3+4＜8，不能构成三角形，故此选项错误；D 、2+3=5，不能构成三角形，故此选项错误．故选：A ．【点睛】此题主要考查了三角形的三边关系，在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．7．如图，在ABC 中，AD 是角平分线，AE 是高，已知2BAC B ∠=∠，2B DAE ∠=∠，那么C ∠的度数为（）A ．72°B ．75°C ．70°D ．60°A解析：A【分析】利用角平分线的定义和三角形内角和定理，余角即可计算．【详解】由图可知DAE DAC EAC ∠=∠-∠，∵AD 是角平分线． ∴12DAC BAC ∠=∠， ∴12DAE BAC EAC ∠=∠-∠， ∵90EAC C ∠=︒-∠， ∴1(90)2DAE BAC C ∠=∠-︒-∠ ∵2BAC B ∠=∠，2B DAE ∠=∠，∴14(90)2DAE DAE C ∠=⨯∠-︒-∠， ∴90DAE C ∠=︒-∠∵180C B BAC ∠=︒-∠-∠， ∴18024C DAE DAE ∠=︒-∠-∠，∴1802(90)4(90)C C C ∠=︒-︒-∠-︒-∠，∴72C ∠=︒．故选：A ．【点睛】本题主要考查了角平分线的定义和三角形的内角和定理以及余角．根据题意找到角之间的数量关系是解答本题的关键．8．若多边形的边数由3增加到n （n 为大于3的正整数），则其外角和的度数（） A ．不变B ．减少C ．增加D ．不能确定A解析：A【分析】利用多边形的外角和特征即可解决问题．【详解】解：因为多边形外角和固定为360°，所以外角和的度数是不变的．故选：A ．【点睛】此题考查多边形内角与外角的性质，容易受误导，注意多边形外角和等于360°． 9．一个多边形的内角和是外角和的4倍，则这个多边形的边数为（）A ．10B ．8C ．6D ．4A 解析：A【分析】设这个多边形的边数为n ，根据内角和公式以及多边形的外角和为360°即可列出关于n 的一元一次方程，解方程即可得出结论．【详解】解：设这个多边形的边数为n ，则该多边形的内角和为（n-2）×180°，依题意得：（n-2）×180°=360°×4，解得：n=10，∴这个多边形的边数是10．故选：A【点睛】本题考查了多边形内角与外角，解题的关键是根据多边形内角和公式得出方程（n-2）×180°=360°×4．10．如图，王师傅用六根木条钉成一个六边形木框，要使它不变形，至少还要再钉上________根木条（）A．2 B．3 C．4 D．5B解析：B【分析】根据三角形的稳定性，要使它不变形，只需每一条边都分别在一个三角形之中即可【详解】解：要使六边形木框不变形，则需每一条边都分别在一个三角形之中，观察图形可得，至少还需要再钉上3根木条故选：B【点睛】本题考查了三角形的稳定性，观察图形如何使每一条边都分别在一个三角形之中是解决本题的关键二、填空题11．如图，BF平分∠ABD，CE平分∠ACD，BF与CE交于G，若130,90∠=︒∠=︒，则∠A的度数为_________．BDC BGC50°【分析】连接BC根据三角形内角和定理可求得∠DBC＋∠DCB的度数再利用三角形内角和定理及角平分线的定义可求得∠ABC ＋∠ACB的度数即可求得∠A的度数【详解】解：连接BC∵∠BDC＝130°解析：50°【分析】连接BC，根据三角形内角和定理可求得∠DBC＋∠DCB的度数，再利用三角形内角和定理及角平分线的定义可求得∠ABC＋∠ACB的度数，即可求得∠A的度数．【详解】解：连接BC，∵∠BDC ＝130°，∴∠DBC ＋∠DCB ＝180°−∠BDC ＝50°，∵∠BGC ＝90°，∴∠GBC ＋∠GCB ＝180°−∠BGC ＝90°，∴∠GBD ＋∠GCD ＝（∠GBC ＋∠GCB ）−（∠DBC ＋∠DCB ）＝40°，∵BF 平分∠ABD ，CE 平分∠ACD ，∴∠ABD ＋∠ACD ＝2∠GBD ＋2∠GCD ＝80°，∴∠ABC ＋∠ACB ＝（∠ABD ＋∠ACD ）＋（∠DBC ＋∠DCB ）＝130°，∴∠A ＝180°−（∠ABC ＋∠ACB ）＝180°−130°＝50°．故答案为：50°．【点睛】本题主要考查了与角平分线有关的三角形内角和问题，根据题意作出辅助线，构造出三角形是解答此题的关键．12．如图，五边形ABCDE 中，//AE BC ，则C D E ∠+∠+∠的度数为__________．【分析】根据求出根据多边形内角和公式求出五边形的内角和即可得到答案【详解】∵∴∵五边形内角和=∴==故答案为：【点睛】此题考查两直线平行同旁内角互补多边形内角和公式熟记多边形内角和计算公式是解题的关键解析：360︒【分析】根据//AE BC 求出180A B ∠+∠=︒，根据多边形内角和公式求出五边形ABCDE 的内角和，即可得到答案．【详解】∵//AE BC ，∴180A B ∠+∠=︒，∵五边形内角和=5218540(0)-⨯︒=︒，∴C D E ∠+∠+∠=540180︒-︒=360︒，故答案为：360︒．【点睛】此题考查两直线平行同旁内角互补，多边形内角和公式，熟记多边形内角和计算公式是解题的关键．13．如果三角形的三边长分别为5，8，a ，那么a 的取值范围为__．3<a<13【分析】根据三角形的三边关系解答【详解】由题意得：8-5<a<8+5∴3<a<13故答案为：3<a<13【点睛】此题考查三角形的三边关系：三角形任意两边的和大于第三边解析：3<a<13【分析】根据三角形的三边关系解答．【详解】由题意得：8-5<a<8+5，∴3<a<13，故答案为：3<a<13．【点睛】此题考查三角形的三边关系：三角形任意两边的和大于第三边．14．已知三角形三边长分别为m ，n ，k ，且m 、n 满足2|9|(5)0n m -+-=，则这个三角形最长边k 的取值范围是________．【分析】根据求出mn 的长根据三角形三边关系求出k 的取值范围再根据k 为最长边进一步即可确定k 的取值【详解】解：由题意得n-9=0m-5=0解得m=5n=9∵mnk 为三角形的三边长∴∵k 为三角形的最长边解析：914k ≤<【分析】根据2|9|(5)0n m -+-=求出m 、n 的长，根据三角形三边关系求出k 的取值范围，再根据k 为最长边进一步即可确定k 的取值．【详解】解：由题意得n-9=0，m-5=0，解得 m=5，n=9，∵m ，n ，k ，为三角形的三边长，∴414k ≤<，∵k 为三角形的最长边，∴914k ≤<．故答案为：914k ≤<【点睛】本题考查了绝对值、偶次方的非负性，三角形的三边关系，根据题意求出m 、n 的长是解题关键，确定k 的取值范围时要注意k 为最长边这一条件．15．如图，已知ABC 中，90,50ACB B D ︒︒∠=∠=，为AB 上一点，将BCD △沿CD 折叠后，点B 落在点E 处，且//CE AB ，则ACD ∠的度数是___________．25°【分析】先求出∠A 的度数再根据折叠的性质可得∠E 的度数根据平行线的性质求出∠ADE 的度数进而即可求解【详解】∵∴∠A=40°∵沿折叠后点B 落在点E 处∴∠E=∠B=50°∵∴∠ADE=∠E=50解析：25°【分析】先求出∠A 的度数，再根据折叠的性质可得∠E 的度数，根据平行线的性质求出∠ADE 的度数，进而即可求解．【详解】∵90,50ACB B ︒︒∠=∠=， ∴∠A=40°，∵BCD △沿CD 折叠后，点B 落在点E 处，∴∠E=∠B=50°，∵//CE AB ，∴∠ADE=∠E=50°，∴∠BDC=∠EDC=（180°-50°）÷2=65°，∴∠ACD=∠BDC-∠A=65°-40°=25°，故答案是：25°．【点睛】本题主要考查折叠的性质，三角形外角的性质，平行线的性质，直角三角形的性质，掌握平行线的性质以及三角形外角的性质，是解题的关键．16．将正三角形、正四边形、正五边形按如图所示的位置摆放．如果147∠=︒，220∠=︒，那么3∠= __________．35°【分析】先求出等边三角形正方形正五边形的内角度数再根据三角形的外角和为360°即可求解【详解】∵等边三角形的内角度数是60°正方形的度数是90°正五边形的度数是∴∠3=360°-60°-90°解析：35°【分析】先求出等边三角形，正方形，正五边形的内角度数，再根据三角形的外角和为360°，即可求解．【详解】∵等边三角形的内角度数是60°，正方形的度数是90°，正五边形的度数是(52)1801085-⨯︒=︒， ∴∠3=360°-60°-90°-108°-∠1-∠2=360°-60°-90°-108°-47°-20°=35°，故答案是：35°【点睛】本题主要考查正多边形的内角和以及外角和定理，准确分析图形中角的数量关系，是解题的关键．17．如图，六边形ABCDEF 中，AB ∥DC ，∠1、∠2、∠3、∠4分别是∠BAF 、∠AFE 、∠FED 、∠EDC 的外角，则∠1+∠2+∠3+∠4＝_____．180°【分析】根据多边形的外角和减去∠B 和∠C 的外角的和即可确定四个外角的和【详解】解：∵AB ∥DC ∴∠B+∠C ＝180°∴∠B 的外角与∠C 的外角的和为180°∵六边形ABCDEF 的外角和为360解析：180°【分析】根据多边形的外角和减去∠B 和∠C 的外角的和即可确定四个外角的和．【详解】解：∵AB ∥DC ，∴∠B +∠C ＝180°，∴∠B 的外角与∠C 的外角的和为180°，∵六边形ABCDEF 的外角和为360°，∴∠1+∠2+∠3+∠4＝180°，故答案为：180°．【点睛】本题考查了多边形的外角和定理，解题的关键是发现∠B 和∠C 的外角的和为180° 18．如图，在ABC 中，已知66ABC ∠=︒，54ACB ∠=︒，BE 是AC 上的高，CF 是AB 上的高，H 是BE 和CF 的交点，EHF ∠的度数是________．120°【分析】先根据三角形内角和定理求出∠A 的度数再根据CF是AB 上的高得出∠ACF 的度数再由三角形外角的性质即可得出结论【详解】解：∵∠ABC=66°∠ACB=54°∴∠A=60°∵CF 是AB 上解析：120°【分析】先根据三角形内角和定理求出∠A 的度数，再根据CF 是AB 上的高得出∠ACF 的度数，再由三角形外角的性质即可得出结论．【详解】解：∵∠ABC=66°，∠ACB=54°，∴∠A=60°，∵CF 是AB 上的高，∴在△ACF 中，∠ACF=180°-∠AFC-∠A=30°，在△CEH 中，∠ACF=30°，∠CEH=90°，∴∠EHF=∠ACF+∠CEH=30°+90°=120°．故答案为120°．【点睛】本题考查的是三角形内角和定理及三角形外角的性质、三角形的高线等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．19．一副直角，三角板有一个角的顶点如图所示重合，则下列说法中正确的有_________．①如图 1，若 AB ⊥AE ，则∠BFC=75°；②图 2 中 BD 过点C ，则有∠DAE+∠DCE=45°；③图 3中∠DAE+∠DFC 等于 135°；④保持重合的顶点不变，改变三角板BAD 的摆放位置，使得D 在边AC 上，则∠BAE=105°．①②③④【分析】由可得：再结合：从而可求解于是可得可判断①；由可得：再利用：求解可判断②；由再利用角的和差可得：可判断③；由图4可得：可判断④【详解】解：如图1故①正确；如图2故②正确；如图3故③正解析：①②③④．【分析】由,AB AE ⊥可得：90BAC CAD DAE ∠+∠+∠=︒，再结合：2105BAC CAD DAE ∠+∠+∠=︒，从而可求解CAD ∠，于是可得BFC ∠，可判断①；由90ADB ，∠=︒可得：90DAC ACD ∠+∠=︒，再利用：180CAE E ACE ∠+∠+∠=︒， 45E ∠=°，求解DAE DCE ∠+∠，可判断②；由,DFC D DAF ∠=∠+∠再利用角的和差可得：135DFC DAE D CAE ∠+∠=∠+∠=︒，可判断③；由图4可得：105BAE BAC CAE ∠=∠+∠=︒，可判断④．【详解】解：如图1，,AB AE ⊥90BAC CAD DAE ∴∠+∠+∠=︒，60BAD BAC CAD ∠=∠+∠=︒，45CAE CAD DAE ∠=∠+∠=︒，2105BAC CAD DAE ∴∠+∠+∠=︒，15CAD ∴∠=︒，90ADB ∠=︒，901575BFC AFD ∴∠=∠=︒-︒=︒，故①正确；如图2，90ADB ∠=︒，90DAC ACD ∴∠+∠=︒，180CAE E ACE ∠+∠+∠=︒， 45E ∠=°，90ACE ∠=︒， 180CAD DAE ACD DCE E ∴∠+∠+∠+∠+∠=︒，()()180180904545DAE DCE CAD ACD E ∴∠+∠=︒-∠+∠+∠=︒-︒+︒=︒，故②正确；如图3，,DFC D DAF ∠=∠+∠9045135DFC DAE D DAF DAE D CAE ∴∠+∠=∠+∠+∠=∠+∠=︒+︒=︒，故③正确；如图4，6045BAD CAE ∠=︒∠=︒，，6045105BAE ∴∠=︒+︒=︒，故④正确．故答案为：①②③④．【点睛】本题考查的是三角形的内角和定理，三角形的外角的性质，角的和差，掌握以上知识是解题的关键．20．如图，线段AD ，BE ，CF 两两相交于点H ，I ，G ，分别连接AB ，CD ，EF ．则A B C D E F ∠+∠+∠+∠+∠+∠=____．360°【分析】根据三角形的外角性质和三角形的内角和求出即可【详解】解：∵∠BHI=∠A+∠B∠DIF=∠C+∠D∠FGH=∠E+∠F∴∠BHI+∠DIF+∠FGH=∠A+∠B +∠C+∠D+∠E+∠解析：360°【分析】根据三角形的外角性质和三角形的内角和求出即可．【详解】解：∵∠BHI=∠A+∠B，∠DIF=∠C+∠D，∠FGH=∠E+∠F，∴∠BHI+∠DIF+∠FGH=∠A+∠B+∠C+∠D+∠E+∠F，∵∠BHI+∠DIF+∠FGH=360°，∴∠A+∠B+∠C+∠D+∠E+∠F=360°，故答案为：360°．【点睛】本题考查了三角形的外角和定理，三角形的外角性质的应用，主要考查学生运用定理进行推理的能力，注意：三角形的一个外角等于和它不相邻的两个内角的和，三角形的外角和等于360°．三、解答题21．图①、图②、图③都是5×5的网格，每个小正方形的顶点称为格点，△ABC的顶点均在格点上，在图①、图②、图③给定网格中，仅用无刻度的直尺，按下列要求完成画图，并保留作图痕迹．（1）在图①中边AB上找到格点D，并连接CD，使CD将△ABC面积两等分；（2）在图②中△ABC的内部找到格点E，并连接BE、CE，使△BCE是△ABC面积的14．（3）在图③中△外部画一条直线l，使直线l上任意一点与B、C构成的三角形的面积是△ABC的18．解析：（1）见解析图；（2）见解析图；（3）见解析图【分析】（1）根据三角形中线的性质可知，当CD为△ABC在AB边上的中线时，可将其面积平分，即找到AB的中点，连接AE即可；（2）可按照△BCE与△ABC都以BC为底边进行分析，当都以BC为底边时，△ABC 的高为4，从而使得△BCE的高为1即可；（3）延续（2）的解题思路，都以BC为底边，要使得构成的三角形的面积是△ABC的1 8，则让构成的三角形的高为12即可，则在BC下方12个单位处作平行于BC的直线即为所求．【详解】如图所示：（1）D在格点上，也为AB的中点，故CD即为所求；（2）当点E在直线m上，且三角形内部时，均满足题意，如图△BCE，此时答案不唯一，符合要求即可；（3）如图，直线l即为所求．【点睛】本题主要考查作图－应用与设计作图，充分理解三角形中线的性质，以及灵活运用底相等时，面积之比等于高之比进行图形构造是解题关键．22．如图，所有小正方形的边长都为1个单位，A、B、C均在格点上．（1）过点A 画线段BC 的垂线，垂足为E ；（2）过点A 画线段AB 的垂线，交线段CB 的延长线于点F ；（3）线段BE 的长度是点到直线的距离；（4）线段AE 、BF 、AF 的大小关系是．（用“＜”连接）解析：（1）见解析；（2）见解析；（3）B ，AE ；（4）AE ＜AF ＜BF【分析】（1）根据垂线的做法画出图象；（2）根据垂线的做法画出图象；（3）根据点到直线距离的定义填空；（4）利用直角三角形的斜边和直角边的大小关系，得出结果．【详解】(1)如图所示；(2)如图所示；(3) ∵BE AE ⊥，∴线段BE 的长度是点B 到直线AE 的距离，故答案是：B ，AE ；(4)∵AE 是直角三角形AEF 的直角边，AF 是直角三角形AEF 的斜边，∴AE AF <，∵BF 是直角三角形ABF 的斜边，AF 是直角三角形ABF 的直角边，∴AF BF <，∴AE AF BF <<，故答案是：AE AF BF <<．【点睛】本题考查作垂线和直角三角形的性质，解题的关键是掌握作垂线的方法和直角三角形的直角边和斜边的大小关系．23．在ABC ∆中，已知3,7AB AC ==，若第三边BC 的长为偶数，求ABC ∆的周长．解析：周长为16或18．【分析】利用三角形三边关系定理，先确定第三边的范围，再根据第三边BC 的长为偶数求出符合条件的BC 值，即可求出周长．【详解】解：在ABC ∆中，3,7AB AC ==，∴第三边BC 的取值范围是：410,BC <<∴符合条件的偶数是6或8，∴当6BC =时，ABC ∆的周长为：36716++=；当8BC =时，ABC ∆的周长为：37818++=．ABC ∆∴的周长为16或18．【点睛】此题主要考查了三角形三边关系，要注意三角形形成的条件：任意两边之和大于第三边，任意两边之差小于第三边．24．如图，在ABC 中，D 是AB 上一点，且AD AC =，连结CD ．请在下面空格中用“>”，“<”或“=”填空．（1）AB________AC BC +；（2）2AD________CD ；（3）BDC ∠________A ∠．解析：（1）<；（2）>；（3）>【分析】（1）根据三角形的三边关系解答；（2）根据三角形的三边关系解答；（3）根据三角形的外角性质解答．【详解】（1）在△ABC 中，AB<AC+BC ，故答案为：<；（2）在△ACD 中，AD+AC>CD,∵AD AC =,∴2AD>CD ，故答案为：>；（3）∵∠BDC 是△ACD 的外角，∴∠BDC>∠A ，故答案为：>．【点睛】此题考查三角形的三边关系：两边之和大于第三边，三角形的外角性质三角形的外角大于每一个与它不相邻的内角．25．如图1，已知线段AB、CD相交于点O，连接AC、BD，则我们把形如这样的图形称为“8字型”．(1)在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：；(2)如图2，若∠CAB和∠BDC的平分线AP和DP相交于点P，且与CD、AB分别相交于点M、N．①以线段AC为边的“8字型”有个，以点O为交点的“8字型”有个；②若∠B＝100°，∠C＝120°，求∠P的度数；③若角平分线中角的关系改为“∠CAP＝13∠CAB，∠CDP＝13∠CDB”，请直接写出∠P与∠B、∠C之间存在的数量关系．解析：（1）∠A+∠C＝∠B+∠D；（2）①3，4；②110°；③3∠P=∠B+2∠C．【分析】（1）根据三角形的内角和即可得到结论；（2）①以线段AC为边的“8字型”有3个，以点O为交点的“8字型”有4个；②根据角平分线的定义得到∠CAP=∠BAP，∠BDP=∠CDP，再根据三角形内角和定理得到∠CAP+∠C=∠CDP+∠P，∠BAP+∠P=∠BDP+∠B，两等式相减得到∠C-∠P=∠P-∠B，即∠P=12（∠C+∠B），然后把∠C=120°，∠B=100°代入计算即可；③与②的证明方法一样得到3∠P=∠B+2∠C．【详解】（1）证明：在图1中，有∠A+∠C=180°-∠AOC，∠B+∠D=180°-∠BOD，∵∠AOC=∠BOD，∴∠A+∠C=∠B+∠D；（2）解：①以线段AC为边的“8字型”有3个：以点O 为交点的“8字型”有4个：故答案为：3，4；②以M 为交点“8字型”中，有∠P+∠CDP=∠C+∠CAP ，以N 为交点“8字型”中，有∠P+∠BAP=∠B+∠BDP∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP ，∵AP 、DP 分别平分∠CAB 和∠BDC ，∴∠BAP=∠CAP ，∠CDP=∠BDP ，∴2∠P=∠B+∠C ，∵∠B=100°，∠C=120°，∴∠P=12（∠B+∠C ）=12（100°+120°）=110°； ③3∠P=∠B+2∠C ，其理由是：∵∠CAP=13∠CAB ，∠CDP=13∠CDB ， ∴∠BAP=23∠CAB ，∠BDP=23∠CDB ，以M 为交点“8字型”中，有∠P+∠CDP=∠C+∠CAP ，以N 为交点“8字型”中，有∠P+∠BAP=∠B+∠BDP∴∠C-∠P=∠CDP-∠CAP=13（∠CDB-∠CAB ）， ∠P-∠B=∠BDP-∠BAP=23（∠CDB-∠CAB ）． ∴2（∠C-∠P ）=∠P-∠B ，∴3∠P=∠B+2∠C ．【点睛】本题考查了三角形内角和定理：三角形内角和是180°．也考查了角平分线的定义． 26．如图，四边形ABCD 中，ABC ∠和BCD ∠的平分线交于点O ．（1）如果130A ∠=︒，110D ∠=︒，求BOC ∠的度数；（2）请直接写出BOC ∠与A D ∠+∠的数量关系．解析：（1）120°；（2）1()2BOC A D ∠=∠+∠ 【分析】（1）先由四边形内角和定理求出∠ABC+∠DCB=120°，再由角平分线定义得出∠OBC+∠OCB=60°，最后根据三角形内角和定理求出∠O=120°即可；（2）方法同（1）【详解】解：（1）∵∠A+∠ABC+∠BCD+∠D=360°，且∠A+∠D=130°+110°=240°，∴∠ABC+∠BCD=360°-（∠A+∠D ）=360°-240°=120°，∵OB ，OC 分别是∠ABC 和∠BCD 的平分线，∴∠OBC+∠OCB=111(221)1206220AB ABC DC C BCD B ∠+∠=⨯+∠︒=∠=︒ ， ∴∠O=180°-（∠OBC+∠OCB ）=180°-60°=120°；（2）1()2BOC A D ∠=∠+∠ 证明：在四边形ABCD 中，360A B C D ∠+∠+∠+∠=︒∴360()ABC DCB A D ∠+∠=︒-∠+∠∵OB ，OC 分别是∠ABC 和∠BCD 的平分线，∴∠OBC+∠OCB=1111((222)180)2ABC BCD AB D A C D CB ∠+∠=︒-∠∠=+∠∠+ ∴180(1)()2O BOC BC OCB A D ∠+∠=︒-∠=∠+∠ 【点睛】此题主要考查了四边形内角和定理，三角形的内角和定理以及角平分线的性质和应用，要熟练掌握，解答此题的关键是要明确：三角形的内角和是180°；一个角的角平分线把这个角分成两个大小相等的角．27．如图BC 平分∠ABE ，DC 平分∠ADE ，求证：∠E+∠A=2∠C解析：证明见解析．【分析】如图（见解析），先根据角平分线的定义可得12,34∠=∠∠=∠，再根据三角形的外角性质可得13,42A C E C ∠+∠=∠+∠∠+∠=∠+∠，然后两式相加化简即可得．【详解】如图，BC 平分ABE ∠，DC 平分ADE ∠，12,34∴∠=∠∠=∠，由三角形的外角性质得：153462A C E C ∠+∠=∠=∠+∠⎧⎨∠+∠=∠=∠+∠⎩，即1342A C E C ∠+∠=∠+∠⎧⎨∠+∠=∠+∠⎩，两式相加得：14223A E C ∠+∠+∠+∠=∠+∠+∠，14214A E C ∴∠+∠+∠+∠=∠+∠+∠，2E A C ∴∠+∠=∠．【点睛】本题考查了角平分线的定义、三角形的外角性质等知识点，熟练掌握三角形的外角性质是解题关键．28．阅读材料在平面中，我们把大于180︒且小于360︒的角称为优角．如果两个角相加等于360︒，那么称这两个角互为组角，简称互组．（1）若1∠，2∠互为组角，且1135∠=︒，则2∠=______．习惯上，我们把有一个内角大于180︒的四边形俗称为镖形．（2）如图，在镖形ABCD 中，优角BCD ∠与钝角BCD ∠互为组角，试探索内角A ∠，B ，D ∠与钝角BCD ∠之间的数量关系，并至少用两种以上的方法说明理由．解析：（1）225°；（2）钝角∠BCD=∠A+∠B+∠D ，理由见解析．【分析】（1）根据互为组角的定义可知∠2=360°-∠1，代入数据计算即可；（2）理由①：根据四边形内角和定理可得∠A+∠B+优角∠BCD+∠D=360°，根据周角的定义可得优角∠BCD+钝角∠BCD=360°´，再利用等式的性质得出钝角∠BCD=∠A+∠B+∠D；理由②：连接AC并延长，根据三角形外角的性质即可得出结论．【详解】解：（1）∵∠1、∠2互为组角，且∠1=135°，∴∠2=360°-∠1=225°，故答案为：225°；（2）钝角∠BCD=∠A+∠B+∠D．理由如下：理由①：∵在四边形ABCD中，∠A+∠B+优角∠BCD+∠D=360°，又∵优角∠BCD+钝角∠BCD=360°´，∴钝角∠BCD=∠A+∠B+∠D；理由②：如下图，连接AC并延长，∵∠BAC+∠B=∠BCE，∠DAC+∠D=∠DCE（三角形外角的性质），∴钝角∠BCD=∠BCE+∠DCE=∠BAC+∠B+∠DAC+∠D=∠A+∠B+∠D．【点睛】本题考查三角形的外角，四边形内角和．能正确作出辅助线，将四边形分成两个三角形是理由②的关键．。

八年级数学上册第十一章《三角形》经典习题(课后培优)

一、选择题1．如图，在△ABC 中，∠ACB=90°，D 在AB 上，将△ABC 沿CD 折叠，点B 落在AC 边上的点B′处，若'20ADB ∠=︒，则∠A 的度数为（）A ．25°B ．30°C ．35°D ．40°2．如图，//,40,50,AB CD B C ∠=︒∠=︒则E ∠的度数为（）A ．70︒B ．80︒C ．90︒D ．100︒ 3．如图，ABC 中，BC 边上的高是（）A ．AEB ．ADC ．CD D ．CF 4．如图，//AB CD ，40C ∠=︒，60A ∠=︒，则F ∠的度数为（）A ．10°B ．20°C ．30°D ．40° 5．已知三角形的两边长分别为1和4，则第三边长可能是（） A ．3B ．4C ．5D ．6 6．如图，ABC 中，55,B D ∠=︒是BC 延长线上一点，且130ACD ∠=︒，则A ∠的度数是（）A ．50︒B ．65︒C ．75︒D ．85︒ 7．将一个多边形纸片剪去一个内角后得到一个内角和是外角和4倍的新多边形，则原多边形的边数为（）A ．9B ．10C ．11D ．以上均有可能 8．下列命题是真命题的个数为（）①两条直线被第三条直线所截，内错角相等．②三角形的内角和是180°．③在同一平面内平行于同一条直线的两条直线平行．④相等的角是对顶角．⑤两点之间，线段最短．A ．2B ．3C ．4D ．59．如图，,AD CE 分别是ABC 的中线与角平分线，若,40B ACB BAC ∠=∠∠=︒，则ACE ∠的度数是（）A ．20︒B ．35︒C ．40︒D ．70︒ 10．一副透明的三角板，如图叠放，直角三角板的斜边AB 、CE 相交于点D ，则BDC∠的度数是（）A ．65︒B ．75︒C ．85︒D ．105︒ 11．如果一个三角形的两边长分别为4和7，则第三边的长可能是（）A ．3B ．4C ．11D ．1212．长度分别为2，3，4，5的四根细木棒首尾相连，围成一个三角形（木棒允许连接，但不允许折断），得到的三角形的最长边长为（）A ．8B ．5C ．6D ．713．如图，为估计池塘岸边A 、B 的距离，小方在池塘的一侧选取一点O ，测得OA ＝15米，OB=10米，A 、B 间的距离不可能是（）A ．20米B ．15米C ．10米D ．5米 14．设四边形的内角和等于a ，五边形的外角和等于b ，则a 与b 的关系是（）． A ．a b =B ．180a b =+°C ．180b a =+︒D ．360b a =+︒ 15．某多边形的内角和是其外角和的3倍，则此多边形的边数是（）A ．5B ．6C ．7D ．8 二、填空题16．如图，点D 在ABC 的边BA 的延长线上，点E 在BC 边上，连接DE 交AC 于点F ，若3117DFC B ∠∠==︒，C D ∠=∠，则BED ∠=________．17．如图，将一副直角三角尺按图③放置，使三角尺①的长直角边与三角尺②的某直角边在同一条直线上，则图③中的∠1=______°．18．如图，△ABC 的两条中线AD 、BE 相交于点G ，如果S △ABG ＝2，那么S △ABC ＝_____．19．如图，在ABC 中，点D 、E 、F 分别是边BC 、AD 、CE 上的中点，则6ABC S =，则BEF S =△______．20．如图，则∠A+∠B+∠C+∠D+∠E+∠F+∠G ＝_____．21．如图，六边形ABCDEF 中，AB ∥DC ，∠1、∠2、∠3、∠4分别是∠BAF 、∠AFE 、∠FED 、∠EDC 的外角，则∠1+∠2+∠3+∠4＝_____．22．鹿鸣社区里有一个五边形的小公园，如图所示，王老师每天晚饭后都要到公园里去散步，已知图中的∠1=95︒，王老师沿公园边由A 点经B→C→D→E ，一直到F 时，他在行程中共转过了_____度．23．一个多边形的内角和比它的外角和的3倍还多180°，则它是___________边形，从该多边形的一个顶点，可以引__________条对角线．24．如图，已知AE 是ABC 的边BC 上的中线，若8AB cm =，ACE △的周长比AEB △的周长多2cm ，则AC =______cm ．25．已知//AB CD ，点P 是平面内一点，若30,20BPD PBA ∠=︒∠=︒，则CDP ∠=___________度．26．如图，P 为正五边形ABCDE 的边AE 上一点，过点P 作PQ //BC ，交DE 于点Q ，则∠EPQ 的度数为_____．三、解答题27．如图，已知点D ，E 分别在ABC 的边AB ，AC 上，//DE BC ．（1若80ABC ∠=︒，40AED ∠=︒，求A ∠的度数：（2）若180BFD CEF ∠+∠=︒，求证：EDF C ∠=∠．28．如图，AF ，AD 分别是ABC 的高和角平分线，且34B ∠=︒，76C ∠=︒，求DAF ∠的度数．29．如图①，ABC 中，BD 平分ABC ∠，且与ABC 的外角ACE ∠的角平分线交于点D ．（1）若75ABC ∠=︒，45ACB ∠=︒，求D ∠的度数；（2）若把A ∠截去，得到四边形MNCB ，如图②，猜想D ∠、M ∠、N ∠的关系，并说明理由．30．如图，已知BP 是△ABC 的外角∠ABD 的平分线，延长CA 交BP 于点P ．射线CE 平分∠ACB 交BP 于点E ．（1）若∠BAC=80°，求∠PEC 的度数；（2）若∠P=20°，分析∠BAC 与∠ACB 的度数之差是否为定值？（3）过点C 作CF ⊥CE 交直线BP 于点F ．设∠BAC=α，求∠BFC 的度数（用含α的式子表示）．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《三角形》培优题一、选择题：1、图中三角形的个数是（）A、8B、9C、10D、11（第一题）（第三题）2、在△ABC中，∠ACB是钝角，让点C在射线BD上向右移动，则（）A、△ABC将先变成直角三角形，然后再变成锐角三角形，而不会再是钝角三角形B、△ABC将变成锐角三角形，而不会再是钝角三角形C、△ABC将先变成直角三角形，然后再变成锐角三角形，接着又由锐角三角形变为钝角三角形D、△ABC先由钝角三角形变为直角三角形，再变为锐角三角形，接着又变为直角三角形，然后再次变为钝角三角形3、如图，在三角形ABC中，∠1=∠2，G为AD的中点，延长BG交AC于E．F为AB上的一点，CF ⊥AD于H．下列判断正确的有（）（1）AD是三角形ABE的角平分线；（2）BE是三角形ABD边AD上的中线；（3）CH为三角形ACD 边AD上的高．A、1个B、2个C、3个D、0个4、三角形两边长为4和6，则第三边上的中线x的取值范围是（）A、2＜x＜10B、1＜x＜5C、x＞5D、不能确定6、下列说法错误的是（）A、三角形的三条高一定在三角形内部交于一点B、三角形的三条中线一定在三角形内部交于一点C、三角形的三条角平分线一定在三角形内部交于一点D、三角形的三条高可能相交于外部一点7、如图，在△ABC中，∠ACB=90°，CD⊥AD，垂足为点D，有下列说法：①点A与点B的距离是线段AB的长；②点A到直线CD的距离是线段AD的长；③线段CD是△ABC边AB上的高；④线段CD是△BCD边BD上的高．上述说法中，正确的个数为（）A、1个B、2个C、3个D、4个（第七题）（第八题）（第九题）8、如图，在△ABC中E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC，△ADF，△BEF的面积分别为S△ABC，S△ADF，S△BEF，且S△ABC=12，则S△ADF-S△BEF=（）A、1B、2C、3D、49、如图，将四个全等的矩形分别等分成四个全等的小矩形，其中阴影部分面积相等的是（）A、只有①和②相等B、只有③和④相等C、只有①和④相等D、①和②，③和④分别相等10、如图所示，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=4cm2，则S 阴影等于（）A、2cm22B、1 cm2C、cm2D、cm2（第十题）（第十一题）11、如图，△ABC中，点D是BC上的一点，点E是AD上的一点，若BD：CD=2：3，DE：AE=1：4，△ABC的面积是8，则△DEC的面积为（）A、B、1 C、D、12、锐角三角形中，最大角α的取值范围是（）A、60°≤α＜90°B、60°＜α＜180°C、60°＜α＜90°D、0°＜α＜90°二、填空题12、如图，一个直角三角形纸片，剪去直角后，得到一个四边形，则∠1+∠2=____________（第十二题）（第十四题）13、已知△ABC中，∠A=60°，∠ABC、∠ACB的平分线交于点O，则∠BOC的度数为____________若△ABC中，∠A+∠B=∠C，则此三角形是____________三角形．14、一副三角板，如图叠放在一起，∠1的度数是____________15、如图所示，AB∥CD，∠ABE=66°，∠D=54°，则∠E的度数为____________（第十五题）（第十六题）16、如图所示，∠BDC=148°，∠B=34°，∠C=38°，那么∠A=____________17、如图，在△ABC中，∠A=α，∠ABC的平分线与∠ACD的平分线交于点A1得∠A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，得∠A2，…，∠A2008BC的平分线与∠A2008CD的平分线交于点A2009，得∠A2009，则∠A2009=____________18．一个三角形三边之比为3：4：5，那么这三边上的高的比为。

19．如图，S△ABC=60，BE：CE=1：2，AD：CD=3：1，则S四边形DOEC= 。

20、如图，D，E分别是△ABC边AB，BC上的点，AD=2BD，BE=CE，设△ADC的面积为S1，△ACE的面积为S2，若S△ABC=6，则S1-S2的值为。

21．已知：如图△ABC中，点D、E、F分别在三边上，E是AC的中点，AD，BE，CF交于一点G，BD=2DC，S△BGD=8，S△AGE=3，则△ABC的面积是。

22、在△ABC中，点D，E分别在AB，AC上，且CD与BE相交于点F，已知△BDF的面积为10，△BCF的面积为20，△CEF的面积为16，则四边形区域ADFE的面积等于。

23、设△ABC中，边BC上一点D满足BC：CD=4，边CA上一点E满足CA：AE=5，边AB上一点F满足AB：BF=6，那么△DEF的面积：△ABC的面积= 。

24、一个凸n边形的内角中，恰有5个钝角。

问n的最大值是25、已知等腰三角形的周长为10，其各边长为整数，这个三角形的底边长为26、如图，任意四边形ABCD中，AC和BD相交于点O，把△AOB、△AOD、△COD、△BOC的面积分别记作S1、S2、S3、S4，则下列各式成立的是（）A 、S1+S3=S2+S4B．S3-S2=S4-S1C．S1•S4=S2•S3 D．S1•S3=S2•S427、如右图，△ABC中，A1，A2，A3，…，An为AC边上不同的n个点，若连接BA1、BA2 、BA3、……一直连接到An，则图中共有个三角形．三、计算题：1、在⊿ABC中，AB = AC，周长为20cm，D是AC上一点，⊿ABD与⊿BCD面积相等且周长差为3cm，求⊿ABC各边的长。

2．观察并探求下列各问题，写出你所观察得到的结论，并说明理由。

（1）如图①，△ABC 中，P 为边BC 上一点，试观察比较BP + PC 与AB + AC 的大小，并说明理由。

C图①（2）将（1）中点P 移至△ABC 内，得图②，试观察比较△BPC 的周长与△ABC 的周长的大小，并说明理由。

C B AP图②（3）将（2）中点P 变为两个点P 1、P 2得图③，试观察比较四边形BP 1P 2C 的周长与△ABC 的周长的大小，并说明理由。

C BAP 1P 2图③（4）将（3）中的点P 1、P 2移至△ABC 外，并使点P 1、P 2与点A 在边BC 的异侧，且∠P 1BC ＜∠ABC ，∠P 2CB ＜∠ACB ，得图④，试观察比较四边形BP 1P 2C 的周长与△ABC 的周长的大小，并说明理由。

图④C B A P 1P 243P 21CB A A B CDE PF（5）若将（3）中的四边形BP 1P 2C 的顶点B 、C 移至△ABC 内，得四边形B 1P 1P 2C 1，如图⑤，试观察比较四边形B 1P 1P 2C 1的周长与△ABC 的周长的大小，并说明理由。

C B AP 1P 2B 1C 1图⑤3、如图，ABCD 是凸四边形，AB=2，BC=4，CD=7，求线段AD 的取值范围．4、如图，若AB∥CD，EF 与AB 、CD 分别相交于E 、F ，EP⊥EF，∠EFD 的平分线与EP 相交于点P ，且∠BEP＝40°。

求∠P 的度数。

5、如图，已知：D , E 分别是△ABC 的边BC 和边AC 的中点，连接DE,AD 若S ABC △=24cm 2,求△DEC 的面积。

6、如图所示,已知∠1=∠2,∠3=∠4,∠C=32°,∠D=28°,求∠P 的度数.AD CBE12A D C B E 12A D CB E y°x°ADCB E7．如图：△ABC 被通过它的三个顶点与一个内点的三条直线分为六个小的三角形，其中四个小三角形的面积已在图中标出，试求△ABC 的面积。

8、探究：（1）如图①∠1＋∠2与∠B ＋∠C 有什么关系？为什么？（2）把图①△ABC 沿DE 折叠，得到图②，填空：∠1＋∠2_______∠B ＋∠C(填“＞”“＜”“=”)，当∠A ＝40°时，∠B ＋∠C ＋∠1＋∠2＝______（3）如图③，是由图①的△ABC 沿DE 折叠得到的，如果∠A ＝30°，则x ＋y ＝360°－（∠B ＋∠C ＋∠1＋∠2）＝360°－＝ ,猜想∠BDA ＋∠CEA 与∠A 的关系为图① 图② 图③9、如图，在△ABC 中，三个内角的角平分线交于点O ，OE ⊥BC 于点E ．（1）求∠ABO+∠BCO+∠CAO 的度数；（2）求证：∠BOD=∠COE ．10、如图，在△ABC 中，AD 平分∠BAC ，P 为线段AD 上的一个动点，PE ⊥AD 交直线BC 于点E ．（1）若∠B=35°，∠ACB=85°，求∠E 的度数；（2）当P 点在线段AD 上运动时，猜想∠E 与∠B 、∠ACB 的数量关系，写出结论无需证明．11、在△ABC 中，AB ＝2AC 。

问：（1）、△ABC 中哪条边是最小边？（2）、证明：△ABC 中最小边大于周长的61并且小于周长的41。

12、已知如图，△ABC ．（1）如图①，若P 点是∠ABC 和∠ACB 的角平分线的交点，点E 是外角∠MBC ，∠BCN 的角平分线的交点；（2）如图②，若P 点是∠ABC 和∠ACB 的角平分线的交点，点E 是∠ABC 和外角∠ACH 的角平分线的交点；（3）如图③，若P 点是∠ABC 和外角∠ACH 的角平分线的交点，点E 是外角∠MBC ，∠BCN 的角平分线的交点．请猜测三种情况下，∠BPC 与∠E 的数量关系，并选择其中两种情况说明理由．13、在如图1至图3中，△ABC的面积为a（1）如图1，延长△ABC的边BC到点D，使CD=BC，连接DA．若△ACD的面积为S1，则S1=_________（用含a的代数式表示）；（2）如图2，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连接DE．若△DEC 的面积为S2，则S2=__________（用含a的代数式表示），并写出理由；（3）在图2的基础上延长AB到点F，使BF=AB，连接FD，FE，得到△DEF（如图3）．若阴影部分的面积为S3，则S3= __________（用含a的代数式表示）．发现：像上面那样，将△ABC各边均顺次延长一倍，连接所得端点，得到△DEF（如图3），此时，我们称△ABC 向外扩展了一次．可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的_____倍．应用：去年在面积为10m2的△ABC空地上栽种了某种花卉．今年准备扩大种植规模，把△ABC向外进行两次扩展，第一次由△ABC扩展成△DEF，第二次由△DEF扩展成△MGH（如图4）．求这两次扩展的区域（即阴影部分）面积共为多少m2？。