2013届高三文科数学考点专练三角函数1
2013年全国各省市高考真题——三角函数(带答案)
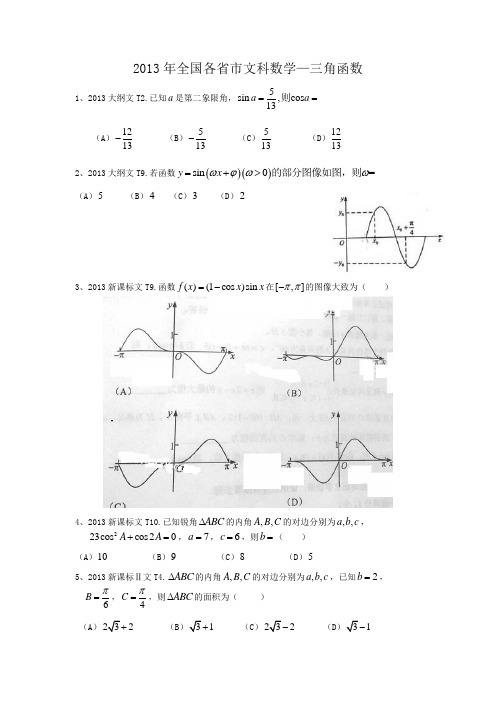
2013年全国各省市文科数学—三角函数1、2013大纲文T2.已知a 是第二象限角,5sin ,cos 13a a ==则 (A )1213-(B )513- (C )513 (D )12132、2013大纲文T9.若函数()()sin 0=y x ωϕωω=+>的部分图像如图,则(A )5 (B )4 (C )3 (D )23、2013新课标文T9.函数()(1cos )sin f x x x =-在[,]ππ-的图像大致为( )4、2013新课标文T10.已知锐角ABC ∆的内角,,A B C 的对边分别为,,a b c ,223cos cos 20A A +=,7a =,6c =,则b =( )(A )10(B )9(C )8(D )55、2013新课标Ⅱ文T4.ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知2b =,6B π=,4C π=,则ABC ∆的面积为( )(A )2 (B 1 (C )2 (D 16、2013新课标Ⅱ文T6.已知2sin 23α=,则2cos ()4πα+=( ) (A )16 (B )13 (C )12 (D )237、2013辽宁文T6.在ABC ∆,内角,,A B C 所对的边长分别为,,.a b c1sin cos sin cos ,2a B C c B Ab +=,a b B >∠=且则A .6π B .3πC .23πD .56π8、2013山东文T7.ABC ∆的内角A B C 、、的对边分别是a b c 、、, 若2B A =,1a =,b =,则c =(A)(D)19、2013山东文T9.函数x x x y sin cos +=的图象大致为10、2013北京文T5.在ABC ∆中,3a =,5b =,1sin 3A =,则sin B =( ) A .15 B .59CD .111、2013四川文T6.函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是( )(A )2,3π-(B )2,6π-(C )4,6π-(D )4,3π12、2013天津文T6. 函数()sin 24f x x π⎛⎫=- ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值是(A) 1- (B) (D) 0 13、2013浙江文T6.函数f(x)=sin xcos x+32cos 2x 的最小正周期和振幅分别是 A 、π,1 B 、π,2 C 、2π,1 D 、2π,2 14、2013福建文T9.将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象,若)(),(x g x f 的图象都经过点)23,0(P ,则ϕ的值可以是( ) A .35π B .65π C .2π D .6π 15、2013广东文T4.已知51sin()25πα+=,那么cos α= A .25-B .15-C .15D .2516、2013安徽文T9. 设ABC ∆的内角,,A B C 所对边的长分别为,,a b c ,若2,3sin 5sin b c a A B +==,则角C =(A)3π (B) 23π (C) 34π (D) 56π 17、2013陕西文T9. 设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=, 则△ABC 的形状为 (A) 直角三角形(B) 锐角三角形(C) 钝角三角形(D) 不确定18、2013湖南文T5.在锐角∆ABC 中,角A ,B 所对的边长分别为a ,b. 若2sinB=3b ,则角A 等于A.3π B.4π C.6πD.12π19、2013湖北文T6.将函数sin ()y x x x =+∈R 的图象向左平移(0)m m >个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是 A .π12 B .π6C .π3D .5π620、2013江西文T3. sincos 2αα==若 ( ) A. 23-B. 13-C. 13D.2321、2013新课标文T16.设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=______.22、2013新课标Ⅱ文T16.函数cos(2)()y x ϕπϕπ=+-≤≤的图象向右平移2π个单位后,与函数sin(2)3y x π=+的图象重合,则ϕ=_________。
2013年三角函数精选高考题

实战化训练---2013年高考题三角函数1、(广东卷理)已知函数()12f x x π⎛⎫=-⎪⎝⎭,x ∈R . (Ⅰ) 求6f π⎛⎫- ⎪⎝⎭的值; (Ⅱ) 若3cos 5θ=,3,22πθπ⎛⎫∈ ⎪⎝⎭,求23f πθ⎛⎫+ ⎪⎝⎭.2、(广东卷文)已知函数(),12f x x x R π⎛⎫=-∈ ⎪⎝⎭. (Ⅰ) 求3f π⎛⎫ ⎪⎝⎭的值;(Ⅱ) 若33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭. 3、(湖南卷理)已知函数2()sin()cos(),()2sin 632x f x x x g x ππ=-+-=。
(I )若α是第一象限角,且()f α=()g α的值;(II )求使()()f x g x ≥成立的x 的取值集合。
4、(湖南卷文)已知()cos cos()3f x x x π=-(I )求2()3f π的值;(II )求使 1()4f x <成立的x 的取值集合 5、(北京卷文)已知函数21(2cos 1)sin 2cos 42f x x x x =-+()(I )求f x ()的最小正周期及最大值; (II )若(,)2παπ∈,且f α=(),求α的值.6、(天津卷理)已知2()26sin cos 2cos 41,f x x x x x x π⎛⎫=++- ⎪+⎝⎭∈R . (Ⅰ) 求f (x )的最小正周期; (Ⅱ) 求f (x )在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.7、(山东卷文)设函数2()sin cos (0)f x x x x ωωωω=->,且()y f x = 的图象的一个对称中心到最近的对称轴的距离为4π, (Ⅰ)求ω的值 (Ⅱ)求()y f x =在区间3,2ππ⎡⎤⎢⎥⎣⎦上的最大值和最小值 8、(安徽卷理)已知函数()4cos sin (0)4f x x x πωωω⎛⎫=⋅+> ⎪⎝⎭的最小正周期为π。
山东省各地市2013届高三文科数学试题分类汇编3:三角函数_Word版含答案

山东省各地市2013届高三文科数学试题分类汇编3:三角函数一、选择题1 .(【解析】山东省泰安市2013届高三上学期期末考试数学文)函数()()sin f x A x ωϕ=+(其中0,2A πϕ><)的图象如图所示,为了得到()sin 2g x x =的图象,则只需将()f x 的图象( )A .向右平移6π个长度单位 B .向右平移12π个长度单位 C .向左平移6π个长度单位D .向左平移12π个长度单位【答案】A 【解析】由图象可知1A =,741234T πππ=-=,即周期2T ππω==,所以2ω=,所以函数为()()sin 2f x x ϕ=+.又77()sin(2)11212f ππϕ=⨯+=-,即sin()16πϕ+=,所以2,62k k Z ππϕπ+=+∈,即2,3k k Z πϕπ=+∈,因为2πϕ<,所以当0k =时,3πϕ=,所以()sin(2)3f x x π=+.()sin 2sin[2()]63g x x x ππ==-+,所以只需将()f x 的图象向右平移6π,即可得到()sin 2g x x =的图象,所以选A .2 .(【解析】山东省潍坊市2013届高三第一次模拟考试文科数学)定义12142334a a a a a a a a =-,若函数sin 2 cos2x () 1 x f x =,则将()f x 的图象向右平移3π个单位所得曲线的一条对称轴的方程是( )A .6x π=B .4x π=C .2x π=D .x π=【答案】A 由定义可知,()2cos 22sin(2)6f x x x x π=-=-,将()f x 的图象向右平移3π个单位得到52sin[2()]2sin(2)366y x x πππ=--=-,由52,62x k k Z πππ-=+∈得对称轴为2,32k x k Z ππ=+∈,当1k =-时,对称轴为2326x πππ=-=,选A .3 .(【解析】山东省潍坊市2013届高三第一次模拟考试文科数学)已知,(0,)2παβ∈,满足tan()4tan αββ+=,则tan α的最大值是( )A .14B .34CD .32【答案】B 由tan()4tan αββ+=tan tan 4tan 1tan tan αββαβ+=-,得23tan tan 14tan βαβ=+,因为(0,)2πβ∈,所以tan 0β>.所以33tan 144tan tan αββ=≤=+,当且仅当14tan tan ββ=,即21tan 4β=,1tan 2β=时,取等号,所以tan α的最大值是34,所以选 B .4 .(【解析】山东省潍坊市2013届高三第一次模拟考试文科数学)设曲线sin y x =上任一点(,)x y 处切线斜率为()g x ,则函数2()y x g x =的部分图象可以为.【答案】C 'cos y x =,即()cos g x x =,所以22()cos yx g x x x ==,为偶函数,图象关于y 轴对称,所以排除A, B .当2cos 0y x x ==,得0x =或,2x k k Z ππ=+∈,即函数过原点,所以选 C .5 .(【解析】山东省泰安市2013届高三第一轮复习质量检测数学(文)试题)在,2ABC AB ∆∠=中,A=60,且ABC ∆,则BC 的长为 ( )AB .3CD .7【答案】 A11sin 60222S AB AC AC =⨯⋅=⨯=,所以1AC =,所以2222cos 603BC AB AC AB AC =+-⋅= ,,所以BC =,选A .6 .(【解析】山东省潍坊市2013届高三上学期期末考试数学文(a ))函数x x y sin =在[]ππ,-上的图象是【答案】A 【解析】函数x x y sin =为偶函数,所以图象关于y 对称,所以排除D .当2x π=时,02y π=>,排除 B .当34x π=时,3sin 44422y πππππ===<,排除C,选A .7 .(山东省烟台市2013届高三3月诊断性测试数学文)设ω是正实数,函数f(x)=2cos x ω在x∈20,3π⎡⎤⎢⎥⎣⎦上是减函数,那么ω的值可以是 ( )A .12B .2C .3D .4【答案】因为函数在[0,]4T 上递增,所以要使函数f(x)=2cos )0(>ωωx 在区间20,3π⎡⎤⎢⎥⎣⎦上单调递减,则有234T π≤,即83T π≥,所以283T ππω=≥,解得34ω≤,所以ω的值可以是12,选 ( )A .8 .(【解析】山东省青岛一中2013届高三1月调研考试文科数学)ABC ∆中,三边长a ,b ,c 满足333c b a =+,那么ABC ∆的形状为 ( )A .锐角三角形B .钝角三角形C .直角三角形D .以上均有可能【答案】A 【解析】由题意可知,c a c b >>,即角C 最大.所以332222a b a a b b ca cb +=+<+,即322c ca cb <+,所以222c a b <+.根据余弦定理得222cos 02a b c C ab +-=>,所以02C π<<,即三角形为锐角三角形,选A .9 .(山东省淄博市2013届高三复习阶段性检测(二模)数学(文)试题)已知ABC ∆中,三个内角A,B,C 的对边分别为a,b,c,若ABC ∆的面积为S,且()222,tan S a b c C =+-则等于 ( )A .34 B .43 C .43-D .34-【答案】C 由()222S a b c =+-得22222S a b ab c =++-,即22212sin 22ab C a b ab c ⨯=++-,所以222sin 2ab C ab a b c -=+-,又222sin 2sin cos 1222a b c ab C ab CC ab ab +--===-,所以sin cos 12C C +=,即22cos sin cos 222C C C =,所以tan 22C =,即222tan2242tan 1231tan 2CC C ⨯===---,选C .10.(【解析】山东省实验中学2013届高三第一次诊断性测试数学(文)试题)将函数sin y x =的图象向左平移(02)ϕϕπ≤<个单位后,得到函数sin()6y x π=-的图象,则ϕ等于( )A .6πB .56π C .76π D .116π【答案】D 【解析】将函数sin y x =的图象向左平移(02)ϕϕπ≤<个单位后,得到函数sin()6y x π=-的图象,即将sin()6y x π=-向右平移(02)ϕϕπ≤<吗,得到sin()sin 6y x x πϕ=--=,所以26k πϕπ+=,所以2,6k k Z πϕπ=-∈,又02ϕπ≤<,定义当1k =时,11266ππϕπ=-=,选 D . 11.(【解析】山东省烟台市2013届高三上学期期末考试数学(文)试题)已知1sin()23πα+=,则cos(2)πα+的值为 ( )A .79-B .79C .29D .23-【答案】B 【解析】由1sin()23πα+=得1sin()cos 23παα+==.所以227cos(2)cos 2(2cos 1)12cos 9παααα+=-=--=-=,选B . 12.(【解析】山东省滨州市2013届高三第一次(3月)模拟考试数学(文)试题)函数sin ((,0)(0,))xy x x=∈-π⋃π的图象大致是【答案】A 函数为偶函数,所以图像关于y 轴对称,排除B,C .当x π→时, sin 0xy x=→,所以选A .13.(【解析】山东省滨州市2013届高三第一次(3月)模拟考试数学(文)试题)把函数sin y x =的图象上所有点的横坐标缩小到原来的一半,纵坐标保持不变,再把所得函数图象向左平移4π个单位长度,得到的函数图象对应的解析式是 ( )A .cos2y x =B .sin 2y x =-C .sin(2)4y x π=-D .sin(2)4y x π=+【答案】A 把函数sin y x =的图象上所有点的横坐标缩小到原来的一半,纵坐标保持不变,得到sin 2y x =,再把所得函数图象向左平移4π个单位长度,得到的函数图象对应的解析式sin 2()sin(2)cos 242y x x x ππ=+=+=,选A .14.(【解析】山东省济南市2013届高三3月高考模拟文科数学)已知函数)0)(6sin(2)(>-=ωπωx x f 的最小正周期为π,则)(x f 的单调递增区间 ( )A .)](65,3[Z k k k ∈++ππππ B .)](32,62[Z k k k ∈+-ππππC .)](6,3[Z k k k ∈+-ππππD .)](3,6[Z k k k ∈+-ππππ【答案】D因为2T ππω==,所以2ω=,所以函数为()2sin(2)6f x x π=-,由222262k x k πππππ-+≤-≤+,得63k x k ππππ-+≤≤+,即函数的单调递增区间是[,]()63k k k Z ππππ-++∈,选D .15.(【解析】山东省潍坊市2013届高三上学期期末考试数学文(a ))已知,54cos ,23,-=⎪⎭⎫ ⎝⎛∈αππα则)4tan(απ-等于( )A .7B .71C .71-D .7- 【答案】B 【解析】因为34(,),cos ,25αππα∈=-所以sin 0α<,即33sin tan 54αα=-=,.所以311tan 14tan()341tan 71+4πααα---===+,选 B . 16.(【解析】山东省潍坊市2013届高三上学期期末考试数学文(a ))要得到函数)23sin(-=x y 的图象,只要将函数x y 3sin =的图象 ( )A .向左平移2个单位B .向右平移2个单位C .向左平移32个单位 D .向右平移32个单位 【答案】D 【解析】因为2sin(32)sin 3()3y x x =-=-,所以只需将函数x y 3sin =的图象向右平移32个单位,即可得到)23sin(-=x y 的图象,选 D .17.(【解析】山东省临沂市2013届高三5月高考模拟文科数学)函数ln sin (,0)y x x x =-≠∣∣π<<π且的图象大致是( )A .B .C .D .【答案】C 因为sin 1x ≤且sin 0x ≠,所以ln sin 0x ≤,所以选C .18.(【解析】山东省泰安市2013届高三上学期期末考试数学文)设向量()()cos ,1,2,sin a b αα=-=,若a b ⊥ ,则tan 4πα⎛⎫- ⎪⎝⎭等于( )A .13-B .13C .3-D .3【答案】B 【解析】因为a b ⊥ ,所以2cos sin 0a b αα=-=,即tan 2α=.所以tan 1211tan()41tan 123πααα---===++,选 B .19.(【解析】山东省实验中学2013届高三第二次诊断性测试数学文试题)已知53)4cos(=-x π,则x 2sin = ( )A .2518 B .257 C .-257 D .2516-【答案】C 【解析】因为2sin 2cos(2)cos 2()2cos ()1244x x x x πππ=-=-=--,所以23187sin 22()1152525x =⨯-=-=-,选 C .20.(山东省青岛即墨市2013届高三上学期期末考试 数学(文)试题)函数x xy sin 3+=的图象大致是【答案】C 解:函数()sin 3xy f x x ==+为奇函数,所以图象关于原点对称,排除B .当x →+∞时,0y >,排除 D .1'()cos 3f x x =+,由1'()cos 03f x x =+=,得1cos 3x =-,所以函数()sin 3xy f x x ==+的极值有很多个,所以选C . 21.(【解析】山东省泰安市2013届高三上学期期末考试数学文)函数212sin 4y x π⎛⎫=--⎪⎝⎭是 ( ) A .最小正周期为π的偶函数 B .最小正周期为π的奇函数 C .最小正周期为2π的偶函数D .最小正周期为2π的奇函数【答案】B 【解析】212sin ()cos 2()cos(2)sin 2442y x x x x πππ=--=-=-=,所以周期222T πππω===,所以函数为奇函数,所以选 B .22.(【解析】山东省青岛市2013届高三第一次模拟考试文科数学)下列函数中周期为π且为偶函数的是( )A .)22sin(π-=x yB .)22cos(π-=x yC .)2sin(π+=x yD .)2cos(π+=x y【答案】A sin(2)cos 22y x x π=-=-为偶函数,且周期是π,所以选( )A .23.(【解析】山东省临沂市2013届高三3月教学质量检测考试(一模)数学(文)试题)在△ABC 中,角A,B,C所对的边分别为a,b,c,若222sin A sin C sin B A sinC +-=,则角B 为( )A .6πB .3π C .23π D .56π 【答案】A由正弦定理可得222a cb +-=,所以222cos 2a c b B ac +-===,所以6B π=,选 ( )A .24.(【解析】山东省实验中学2013届高三第二次诊断性测试数学文试题)已知21)4tan(-=+πα,且παπ<<2,则)4sin(cos 22sin 2πααα--等于( )A .552 B .1053-C .552-D .10103-【答案】C【解析】2sin 22cos sin()4αααπα--,由21)4tan(-=+πα得tan 11=1tan 2αα+--,解得tan =3α-,因为παπ<<2,所以解得cos =α,所以2sin 22cos cos (sin()4αααπα--,选 C .25.(【解析】山东省泰安市2013届高三第一轮复习质量检测数学(文)试题)当4x π=时,函数()()()sin 0f x A x A ϕ=+>取得最小值,则函数34y f x π⎛⎫=- ⎪⎝⎭是( )A .奇函数且图像关于点,02π⎛⎫⎪⎝⎭对称 B .偶函数且图像关于点(),0π对称C .奇函数且图像关于直线2x π=对称 D .偶函数且图像关于点,02π⎛⎫⎪⎝⎭对称 【答案】C 当4x π=时,函数()()()sin 0f x A x A ϕ=+>取得最小值,即2,42k k Z ππϕπ+=-+∈,即32,4k k Z πϕπ=-+∈,所以()()3sin()04f x A x A π=->,所以333()sin()sin 444y f x A x A x πππ=-=--=-,所以函数为奇函数且图像关于直线2x π=对称,选C .26.(【解析】山东省枣庄市2013届高三3月模拟考试 数学(文)试题)△ABC 中,21cos 2,A A =-则A 的值为 ( )A .23π B .6πC .4πD .3π【答案】D 由21cos 2,A A =-得22cos 1cos 21(12sin )2sin A A A A A =-=--=,sin A A =,即tan A =所以3A π=,选 D .27.(山东省威海市2013届高三上学期期末考试文科数学)函数()sin(2),(||)2f x x πϕϕ=+<向左平移6π个单位后是奇函数,则函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的最小值为 ( )A .B .12-C .12D 【答案】【答案】A 函数()sin(2),(||)2f x x πϕϕ=+<向左平移6π个单位后得到函数为()sin[2()]sin(2)663f x x x πππϕϕ+=++=++,因为此时函数为奇函数,所以,3k k Z πϕπ+=∈,所以,3k k Z πϕπ=-+∈.因为||2πϕ<,所以当0k =时,3πϕ=-,所以()sin(2)3f x x π=-.当02x π≤≤,所以22333x πππ-≤-≤,即当233x ππ-=-时,函数()sin(2)3f x x π=-有最小值为sin()3π-=,选 ( )A .28.(【解析】山东省济宁市2013届高三第一次模拟考试文科数学 )若函数3f (x )sin(x )πω=+的图象向右平移3π个单位后与原函数的图象关于x 轴对称,则ω的最小正值是( )A .12B .1C .2D .3【答案】D 【解析】若函数向右平移3π个单位后与原函数的图象关于x 轴对称,则平移的大小为23T π=,所以23T π=,所以223T ππω==,即3ω=,所以选 D .29.(【解析】山东省烟台市2013届高三上学期期末考试数学(文)试题)函数()sin()f x A x ωϕ=+其中(02A πϕ><,)的图象如图所示,为了得到()sin 2g x x =的图象,则只需将()f x 的图象( )A .向右平移6π个长度单位 B .向右平移3π个长度单位 C .向左平移6π个长度单位D .向左平衡3π个长度单位【答案】A 【解析】由图象可知71,41234T A πππ==-=,即T π=,又2T ππω==,所以2ω=,所以()sin(2)f x x ϕ=+,由77()sin(2)11212f ππϕ=⨯+=-,得7in()16πϕ+=-,即73262k ππϕπ+=+,即23k πϕπ=+,因为2πϕ<,所以3πϕ=,所以()sin(2)3f x x π=+.因为()sin 2sin[2()]63g x x x ππ==-+,所以只需将()f x 的图象向右平移6π个长度单位,即可得到()sin 2g x x =的图象,所以选( )A .30.(【解析】山东省烟台市2013届高三5月适应性练习(一)文科数学)将函数f(x)=3sin(4x+6π)图象上所有点的横坐标伸长到原来的2倍,再向右平移6π个单位长度,得到函数y= g(x)的图象,则y=g(x)图象的一条对称轴是 ( )A .x=12πB .x=6πC .x=3πD .x=23π【答案】【解析】将函数f(x)=3sin(4x+6π)图象上所有点的横坐标伸长到原来的2倍,得到函数3sin(2)6y x π=+,再向右平移6π个单位长度,得到3sin[2()]3sin(2)666y x x πππ=-+=-,即()3sin(2)6g x x π=-.当3x π=时,()3sin(2)3sin 33362g ππππ=⨯-==,所以3x π=是一条对称轴,选C .31.(【解析】山东省实验中学2013届高三第一次诊断性测试数学(文)试题)在△ABC 中,内角 ( )A .B .C 的对边分别为a 、b 、c,且222222c a b ab =++,则△ABC是( )A .钝角三角形B .直角三角形C .锐角三角形D .等边三角形【答案】A 【解析】由222222c a b ab =++得,22212a b c ab +-=-,所以222112cos 0224aba b c C ab ab -+-===-<,所以090180C << ,即三角形为钝角三角形,选 ( )A .32.(山东省青岛即墨市2013届高三上学期期末考试 数学(文)试题)已知53)4sin(=+x π,则x 2sin 的值为 ( )A .2524-B .2524 C .257-D .257 【答案】C 解:27sin 2sin[2()]cos 2()[12sin ()]424425x x x x ππππ=+-=-+=--+=-,选C .33.(山东省淄博市2013届高三复习阶段性检测(二模)数学(文)试题)函数()2tan 22f x x x ππ⎛⎫=--⎪⎝⎭在,上的图象大致为【答案】C 函数()2tan f x x x =-为奇函数,所以图象关于原点对称,所以排除A,B .当2x π→时,0y <,所以排除D,选C .34.(【解析】山东省德州市2013届高三3月模拟检测文科数学)函数2cos ()4y x π=+的图象沿x 轴向右平移a 个单位(0)a >,所得图象关于y 轴对称,则a 的最小值为 ( )A .πB .34πC .2πD .4π【答案】D 21cos(2)1sin 2112cos ()sin 242222x x y x x ππ++-=+===-,函数向右平移a 个单位得到函数为1111sin 2()sin(22)2222y x a x a =--=--,要使函数的图象关于y 轴对称,则有2,2a k k Z ππ-=+∈,即,42k a k Z ππ=--∈,所以当1k =-时,得a 的最下值为4π,选 D .35.(山东省青岛即墨市2013届高三上学期期末考试 数学(文)试题)设a,b 是不同的直线,βα、是不同的平面,则下列命题:①若βα//,//,b a b a 则⊥ ②若ββαα⊥⊥a a 则,,// ③若αβαβ//,,a a 则⊥⊥ ④若βαβα⊥⊥⊥⊥则,,,b a b a 其中正确命题的个数是( )A .0B .1C .2D .3【答案】B 解:①当,//,a b a α⊥时b 与β可能相交,所以①错误.②中a β⊥不一定成立.③中a α⊂或//a α,所以错误.④正确,所以正确的个数有1个,所以选 B .36.(【解析】山东省临沂市2013届高三5月高考模拟文科数学)将函数sin y x =的图象向右平移2π个单位长度,再向上平移1个单位长度,则所得的图象对应的解析式为 ( )A .1sin y x =-B .1sin y x =+C .1cos y x =-D .1cos y x =+【答案】C 函数sin y x =的图象向右平移2π个单位长度,得到函数为sin()2y x π=-,再向上平移1个单位长度,得到sin()11cos 2y x x π=-+=-,选C .37.(【解析】山东省济南市2013届高三上学期期末考试文科数学)在ABC ∆中,若ab b c a 3222=+-,则C=( )A .30°B .45°C .60°D .120°【答案】A 解:由ab b c a 3222=+-得,222cos 2a b c C ab +-===,所以30C =,选( )A .38.(【解析】山东省济南市2013届高三上学期期末考试文科数学)把函数sin y x =的图象上所有的点向左平行移动6π个单位长度,再把所得图象上所有点的横 坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数解析式是( )A .sin 23y x π⎛⎫=-⎪⎝⎭B.sin 26x y π⎛⎫=+ ⎪⎝⎭C .sin(2)6y x π=-D .sin(2)6y x π=+【答案】D 解:函数sin y x =的图象上所有的点向左平行移动6π个单位长度,得到sin()6y x π=+,再把所得图象上所有点的横坐标缩短到原来的12倍,得到sin(2)6y x π=+,选 D .二、填空题39.(【解析】山东省潍坊市2013届高三上学期期末考试数学文(a ))已知三角形的一边长为4,所对角为60°,则另两边长之积的最大值等于_______.【答案】16【解析】设另两边为,a b ,则由余弦定理可知22242cos 60a b ab =+-,即2216a b ab =+-,又22162a b ab ab ab ab =+-≥-=,所以16ab ≤,当且仅当4a b ==时取等号,所以最大值为16.40.(【解析】山东省济宁市2013届高三1月份期末测试(数学文)解析)在ABC ∆中,a,b,c 分别是角A,B,C的对边,若21,3b c C π==∠=,则ABC S ∆=____.解:因为c b >,所以B C <所以由正弦定理得sin sin b c B C =,即12sin B ==,即1sin 2B =,所以6B π=,所以2636A ππππ=--=.所以111sin 222ABC S bc A ∆===41.(【解析】山东省枣庄市2013届高三3月模拟考试 数学(文)试题)设()y f t =是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t 与水深y 的关系:经长期观察,函数y=f(t)的图象可以近似地看成函数sin()y h A x ωφ=++的图象.最能近似表示表中数据间对应关系的函数是_______.【答案】 5.0 2.5sin6y t π=+由数据可知函数的周期12T =,又212T πω==,所以6πω=.函数的最大值为7.5,最小值为2.5,即7.5, 2.5h A h A +=-=,解得 5.0, 2.5h A ==,所以函数为() 5.0 2.5sin()6y f x t πφ==++,又(3) 5.0 2.5sin(3)7.56y f πφ==+⨯+=,所以sin()cos 12πφφ+==,即2,k k Z φπ=∈,所以最能近似表示表中数据间对应关系的函数是5.0 2.5sin6y t π=+.42.(【解析】山东省烟台市2013届高三5月适应性练习(一)文科数学)已知cos4α-sin 423α=,(0,)2πα∈,则cos(2)3πα+=___________.【答案】【解析】由cos4α-sin423α=得2cos23α=,所以sin2α=,所以112cos(2)cos2sin23223πααα+==⨯.43.(【解析】山东省德州市2013届高三3月模拟检测文科数学)已知锐角,αβ满足3tan tan()ααβ=+,则tanβ的最大值为___________.【答案】因为tan()tantan tan()1tan()tanαβαβαβααβα+-=+-=++,所以2tan()tan2tantan1tan()tan13tanαβααβαβαα+-==+++,即2tan13tantanβαα=+,因为(0,)2πα∈,所以tan0α>.所以2tan13tantanβαα=≤=+,当且仅当13tantanαα=,即21tan3α=,tanα=时,取等号,所以tanβ.44.(【解析】山东省实验中学2013届高三第三次诊断性测试文科数学)已知函数)(xgy=的图象由xxf2sin)(=的图象向右平移)0(πϕϕ<<个单位得到,这两个函数的部分图象如图所示,则ϕ=____________.【答案】3π【解析】函数xxf2sin)(=的图象在y轴右侧的第一个对称轴为22xπ=,所以4xπ=.8π关于4xπ=对称的直线为38xπ=,由图象可知,通过向右平移之后,横坐标为38xπ=的点平移到1712xπ=,所以1732483πππϕ=-=.45.(【解析】山东省实验中学2013届高三第三次诊断性测试文科数学)已知角α的终边上一点的坐标为)65cos,65(sinππ,则角α的最小正值为_____________.【答案】32π【解析】因为点的坐标为1(,2,所以tan α=,即,3k k Z παπ=-+∈,所以当1k =时,得角α的最小正值为233πππ-+=. 46.(【解析】山东省临沂市2013届高三5月高考模拟文科数学)若△ABC 的边,,a b c 满足2224a b c +-=,且C =60°,则ab 的值为_________.【答案】4 由余弦定理得222cos 2a b c C ab +-=,即1422ab=,解得4ab =.47.(【解析】山东省枣庄市2013届高三3月模拟考试 数学(文)试题)已知一个半径为Im 的半圆形工件,未搬动前如图所示(直径平行于地面放置),搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移40m,则圆心D 所经过的路线长是_______m.【答案】40π+开始到直立圆心O 的高度不变,所走路程为14圆弧,从直立到扣下正好是一个旋转的过程,所以从开始到直立可以设想为一个球的球心在转动过程中是平直前进的, O 走的是线段,线段长为14圆弧,从直立到扣下,球心走的是14即球在无滑动旋转中通过的路程为12圆弧,为π;再将它沿地面平移40米,则圆心O 所经过的路线长是:(π+40)米.48.(【解析】山东省烟台市2013届高三上学期期末考试数学(文)试题)设△ABC 的内角A 、B 、C 的对边分别为a 、b 、c,且a=1,b=2,1cos 4C =,则sinB 等于 _________【答案】【解析】,由余弦定理得2222cos 4c a b ab C =+-=,即2c =.由1cos 4C =得,sin C =.由正弦定理得sin sin b cB C=,得sin 2sin 2b C B c ===.(或者因为2c =,所以2b c ==,即三角形为等腰三角形,所以sin sin B C ==49.(【解析】山东省潍坊市2013届高三第二次模拟考试文科数学)在ABC ∆中,角A,B,C 新对的边分别为a,b,c,若cos cos sin a B b A c C +=,222b c a +-=,则角B=________.【答案】60由222b c a +-=得222cos 2b c a A bc +-===,所以30A = .由正弦定理得sin cos sin cos sin sin A B B A C C +=,即sin()sin sin sin A B C C C +==,解得sin 1C =,所以90C = ,所以60B = .50.(【解析】山东省实验中学2013届高三第二次诊断性测试数学文试题)已知81cos sin =⋅θθ,且24πθπ<<,则θθsin cos -的值为___________【答案】【解析】当24πθπ<<时,sin cos θθ>,所以cos sin 0θθ-<,又213(cos sin =12sin cos =1=44θθθθ---),所以cos sin =θθ-. 51.(【解析】山东省德州市2013届高三上学期期末校际联考数学(文))设tan ,tan a b 是方程2450x x --=的两个根,则tan()a b +的值为________.【答案】23解:由题意知tan tan 4,tan tan 5a b a b +==-,所以tan tan 442tan()1tan tan 1(5)63a b a b a b ++====---.52.(【解析】山东省实验中学2013届高三第一次诊断性测试数学(文)试题)在△ABC 中,角A,B,C 的对边为a,b,c,若45a b B ===︒,则角A=_______.【答案】60 或120【解析】由正弦定理可知sin sin a bA B=,2==,所以sin A =,因为a b >,所以45A > ,所以60A = 或120A = .53.(山东省青岛即墨市2013届高三上学期期末考试 数学(文)试题)已知函数⎥⎦⎤⎢⎣⎡∈--+=2,412cos 3)4(sin 2)(2πππx x x x f ,则)(x f 的最小值为_________.【答案】1解:2()2sin ()211cos 2()2144f x x x x x ππ=+-=-+--cos(2)2sin 222sin(2)23x x x x x ππ=-+=-=-,因为42x ππ≤≤,所以22633x πππ≤-≤,所以sinsin(2)sin632x πππ≤-≤,即1sin(2)123x π≤-≤,所以12sin(2)23x π≤-≤,即1()2f x ≤≤,所以)(x f 的最小值为1.三、解答题54.(【解析】山东省潍坊市2013届高三上学期期末考试数学文(a ))已知函数),0(sin )6cos()6cos()(R x x x x x f ∈>--++=ωωπωπω的最小正周期为π2.(I)求函数)(x f 的对称轴方程;(II)若36)(=θf ,求)23cos(θπ+的值. 【答案】55.(【解析】山东省实验中学2013届高三第三次诊断性测试文科数学)在ABC ∆内,c b a ,,分别为角CB A ,,所对的边,c b a ,,成等差数列,且c a 2=.(Ⅰ)求A cos 的值;(Ⅱ)若4153=∆ABC S ,求b 的值. 【答案】解(Ⅰ)因为a,b,c 成等差数列,所以a+c=2b,又c a 2=,可得c b 23=, 所以412324492cos 2222222-=⨯-+=-+=c c c c bc a c b A , (Ⅱ)由(Ⅰ)41cos -=A ,),(π0∈A ,所以415sin =A ,因为,sin 214153A bc S S ABC ABC ==∆∆,所以41534152321sin 212=⨯==∆c A bc S ABC , 得42=c ,即3,2==b c56.(【解析】山东省青岛市2013届高三第一次模拟考试文科数学)已知a b c ,,为ABC △的内角A B C,,的对边,满足A CB AC B cos cos cos 2sin sin sin --=+,函数()sin f x x ω=(0)ω>在区间[0,]3π上单调递增,在区间2[,]33ππ上单调递减.(Ⅰ)证明:a c b 2=+;(Ⅱ)若A f cos )9(=π,证明ABC △为等边三角形.【答案】解:(Ⅰ)ACB AC B cos cos -cos -2sin sin sin =+ ∴sin cos sin cos 2sin -cos sin -cos sin B A C A A B A C A += ∴sin cos cos sin sin cos cos sin 2sin B A B A C A C A A +++=sin ()sin ()2sin A B A C A +++=sin sin 2sin C B A += 所以2b c a +=(Ⅱ)由题意知:由题意知:243ππω=,解得:32ω=, 因为1()sin cos 962f A ππ===, (0,)A π∈,所以3A π=由余弦定理知:222-1cos 22b c a A bc +==所以222-b c a bc += 因为2b c a +=,所以222-()2b c b c bc ++=, 即:22-20b c bc +=所以b c = 又3π=A ,所以ABC △为等边三角形57.(【解析】山东省烟台市2013届高三上学期期末考试数学(文)试题)已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点1)P -. (1)求sin 2tan αα-的值:(2)若函数()sin 2cos cos 2sin f x x x αα=+g g ,求()f x 在20,3π⎡⎤⎢⎥⎦⎣上的单调递增区间. 【答案】58.(【解析】山东省临沂市2013届高三3月教学质量检测考试(一模)数学(文)试题)已知函数32f (x )cos(x )sin(x )ππ=---.(I)求函数f (x )的最小正周期;(Ⅱ)若02(,)πα∈,且365f ()πα+=,求2f ()α的值. 【答案】59.(【解析】山东省济宁市2013届高三1月份期末测试(数学文)解析)已知函数()2cos 2sin 1,.f x x x x x R =+-∈(I)求函数()f x 的最小正周期和单调递增区间;(II)将函数()y f x =的图象上各点的纵坐标保持不变,横坐标缩短到原来的12,再把所得到的图象向左平移6π个单位长度,得到函数()y g x =的图象,求函数()y g x =在区间,612ππ⎡⎤-⎢⎥⎣⎦上的值域. 【答案】60.(山东省威海市2013届高三上学期期末考试文科数学)在ABC ∆中,角,,A B C 所对应的边分别为c b a ,,,,A B 为锐角且B A <,sin A =3sin 25B =.(Ⅰ)求角C 的值;(Ⅱ)若1b c +=+,求c b a ,,的值.【答案】解:(Ⅰ)∵A 为锐角,sinA =∴cos A ==∵B A <,sin A =<,∴45B <∵3sin 25B =,∴4cos 25B ==∴cosB ==,sin B =cos cos()cos cos sin sinC A B A B A B =-+=-+==∴135C =(Ⅱ)由正弦定理sin sin sin a b ck A B C===∴b c k +=+,解得k =∴1,a b c ===61.(【解析】山东省实验中学2013届高三第三次诊断性测试文科数学)已知函数x x x f cos sin 1)(+=.(Ⅰ)求函数)(x f 的最小正周期和单调递减区间; (Ⅱ)若2tan =x ,求)(x f 的值.【答案】解:(Ⅰ)已知函数即ππ==∴+=22,2sin 211)(T x x f , 令)(223222Z k k x k ∈+<<+ππππ,则)(434Z k k x k ∈+<<+ππππ, 即函数)(x f 的单调递减区间是)](43,4[Z k k k ∈++ππππ;(2)由已知1tan 1tan tan cos sin cos cos sin sin 222222+++=+++=x x x x x x x x x y , ∴当2tan =x 时,571212222=+++=y 62.(【解析】山东省青岛一中2013届高三1月调研考试文科数学)已知函数()1sin cos f x x x =+.(1)求函数()f x 的最小正周期和单调递减区间; (2)若tan 2x =,求()f x 的值.【答案】解答:(1)已知函数1()1sin 22f x x =+,∴22T ππ==, 令322222k x k ππππ+≤≤+,则3()44k x k k Z ππππ+≤≤+∈,即函数()f x 的单调递减区间是3[,]()44k k k ππππ++∈Z ;(2)由已知222222sin sin cos cos tan tan 1sin cos tan 1x x x x x x y x x x ++++==++,∴当tan 2x =时,222217521y ++==+ 63.(【解析】山东省实验中学2013届高三第二次诊断性测试数学文试题)已知函数x x x x f cos sin sin 3)(2+-=(1)求)625(πf 的值. (2)设2341)2(0-=∈απαf ),,(,求αsin 的值 【答案】64.(【解析】山东省滨州市2013届高三第一次(3月)模拟考试数学(文)试题)已知函数2()22cos 1,f x x x x =--∈R .(Ⅰ)求函数()f x 的最小正周期和最小值;(Ⅱ)在ABC 中,,,A B C 的对边分别为,,a b c ,已知()0,sin 2sin c f C B A ===,求,a b 的值.【答案】65.(【解析】山东省实验中学2013届高三第二次诊断性测试数学文试题)已知角α终边经过点)0)(2,(≠-x x p 且x 63cos =α,求ααtan ,sin 的值 【答案】66.(【解析】山东省烟台市2013届高三5月适应性练习(一)文科数学)在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,且满足b 2 +C 2 -a 2= bc.(1)求角A 的值;(2)若,设角B 的大小为x,△ABC 周长为y,求y=f(x)的最大值.【答案】67.(【解析】山东省济宁市2013届高三第一次模拟考试文科数学 )在△ABC 中,已知A=4π(I)求cosC 的值;(Ⅱ)若为AB 的中点,求CD 的长.【答案】解:(Ⅰ)552cos =B 且(0,)B π∈,∴55cos 1sin 2=-=B B )43cos()cos(cos B B A C -=--=ππ 1010552255222sin 43sin cos 43cos-=⋅+⋅-=+=B B ππ (Ⅱ)由(Ⅰ)可得10103)1010(1cos 1sin 22=--=-=C C 由正弦定理得sin sin BC AB A C =,即101032252AB=,解得6=AB 在BCD ∆中,55252323)52(222⨯⨯⨯-+=CD 5=, 所以5=CD68.(【解析】山东省潍坊市2013届高三第一次模拟考试文科数学)已知函数2()cossin (0,0)2222x x x f x ωϕωϕωϕπωϕ+++=+><<.其图象的两个相邻对称中心的距离为2π,且过点(,1)3π.(I) 函数()f x 的达式;(Ⅱ)在△ABC 中.a 、b 、c 分别是角A 、B 、C 的对边,a =,ABC S ∆=,角C 为锐角.且满7()2126C f π-=,求c 的值.【答案】解:(Ⅰ)1())[1cos()]2f x x x ωϕωϕ++-+ π1sin()62x ωϕ=+-+两个相邻对称中心的距离为π2,则πT =, 2ππ,0,2,||ωωω∴=>∴= 又()f x 过点π(,1)3,2ππ1π1sin 1,sin 36222j j 骣骣鼢珑\-++=+=鼢珑鼢珑桫桫即, 1cos 2j \=, πππ10,,()sin(2)2362f x x j j <<\=\=++Q(Ⅱ)πππ117sin sin 21266226C f C C 骣骣鼢珑-=-++=+=鼢珑鼢珑桫桫, 2sin 3C \=,π0,cos 2C C <<\=Q又112sin 223ABC a S ab C b D ===?,6b \=,由余弦定理得2222cos 21c a b ab C =+-=,c \=69.(山东省烟台市2013届高三3月诊断性测试数学文)已知函数sin2x-cos 2x-12,x∈R . (1)求函数f(x)的最小值,及取最小值时x 的值;(2)设△ABC 的内角A,B,C 的对边分别为a,b,c 且,f(C)=0,若sinB=2sinA,求a,b 的值.【答案】70.(山东省淄博市2013届高三复习阶段性检测(二模)数学(文)试题)已知函数()()21cos cos 02f x x x x ωωωω=+-> ,其最小正周期为.2π(I)求()f x 的表达式;(II)将函数()f x 的图象向右平移8π个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数()y g x =的图象,若关于x 的方程()0g x k +=,在区间0,2π⎡⎤⎢⎥⎣⎦上有且只有一个实数解,求实数k 的取值范围.【答案】解:(I)21()cos cos 2f x x x x ωωω=⋅+-cos2112sin(2)226x x x ωπωω+=+-=+ 由题意知)(x f 的最小正周期2T π=,222T πωπωπ===所以2=ω 所以()sin 46f x x π⎛⎫=+⎪⎝⎭(Ⅱ)将()f x 的图象向右平移个8π个单位后,得到)34sin(π-=x y 的图象,再将所得图象所有点的横坐标伸长到原来的2倍,纵坐标不变,得到)32sin(π-=x y 的图象.所以)32sin()(π-=x x g因为02x π≤≤,所以22333x πππ-≤-≤()0g x k +=在区间0,2π⎡⎤⎢⎥⎣⎦上有且只有一个实数解,即函数()y g x =与y k =-在区间0,2π⎡⎤⎢⎥⎣⎦上有且只有一个交点,由正弦函数的图象可知k ≤-<或1k -=所以k <≤或1k =- 71.(【解析】山东省泰安市2013届高三第一轮复习质量检测数学(文)试题)已知()sin ,,,,334x x m A A n f x m n f π⎛⎫⎫⎛⎫===⋅=⎪⎪ ⎪⎝⎭⎭⎝⎭且(1)求A 的值; (II)设α、()()30780,,3,3,cos 21725f f πβαπβπαβ⎡⎤⎛⎫∈+=-=-+ ⎪⎢⎥⎣⎦⎝⎭求的值.【答案】72.(【解析】山东省济南市2013届高三3月高考模拟文科数学)在ABC ∆中,边a 、b 、c 分别是角A 、B 、C 的对边,且满足cos (3)cos b C a c B =-.(1)求B cos ;(2)若4BC BA ⋅=,b =,求边a ,c 的值.【答案】解:(1)由正弦定理和cos (3)cos b C a c B =-,得sin cos (3sin sin )cos B C A C B =-,化简,得sin cos sin cos 3sin cos B C C B A B +=即sin3sin cos B C A B +=(), 故sin 3sin cos A A B =.所以1cos =3B (2)因为4BC BA ⋅=, 所以4cos ||||=⋅⋅=⋅B BA BC BA BC所以12BC BA ⋅=,即12ac =. (1) 又因为2221cos =23a cb B ac +-=, 整理得,2240a c +=. (2)联立(1)(2) 224012a c ac ⎧+=⎨=⎩,解得26a c =⎧⎨=⎩或62a c =⎧⎨=⎩73.(【解析】山东省德州市2013届高三3月模拟检测文科数学)在△ABC 中,角A,B,C 的对边分别为a,b,c,已知角,sin 3sin .3A B C π==(1)求tan C 的值;(2)若a =求△ABC 的面积.【答案】74.(【解析】山东省实验中学2013届高三第一次诊断性测试数学(文)试题)设函数().,(2cos 1),(cos 2),f x a b a x b x x x R ===∈其中向量(1)求函数()f x 的单调减区间; (2)若[,0]4x π∈-,求函数()f x 的值域;【答案】75.(【解析】山东省泰安市2013届高三上学期期末考试数学文)ABC ∆的内角A 、B 、C 所对的边分别为,,a b c且sin sin sin sin a A b B c C B += (I)求角C;(II)cos 4A B π⎛⎫-+⎪⎝⎭的最大值. 【答案】76.(山东省青岛即墨市2013届高三上学期期末考试 数学(文)试题)已知ABC ∆的角A 、B 、C,所对的边分别是a 、b 、c,且3π=C ,设向量m (a,b),n (sin B,sin A),p=b-2,a-2)==(.(1)若m //n,求B;(2)若ABC m p,S ∆⊥=求边长c.【答案】证明:(1)B b A a n m sin sin ,//=∴由正弦定理得b a b a ==即22又3π=c3π=∆∴B ABC 为等边三角形由题意可知0)2()2(,0.=-+-=a b b a p m 即ab b a =+∴①由正弦定理和①②得,ab c .sin .213=23sin ,3=∴=C C π4=∴ab ②2412163)(2222=∴=-=-+=-+=∴c ab b a ab b a c77.(【解析】山东省潍坊市2013届高三第二次模拟考试文科数学)已知函数())cos()cos 44f x x x x x ππ=+-+.(I)求()f x 的最小正周期和最大值;(Ⅱ)在给出的坐标系中画出函数()y f x =在[]0,π上的图象,并说明()y f x =的图象 是由sin 2y x =的图象怎样变换得到的.【答案】78.(【解析】山东省济南市2013届高三上学期期末考试文科数学)已知向量1sin ,,cos 2x x ⎛⎛⎫= ⎪ ⎝⎭⎝ a =b ,()f x =⋅ a b .(1)求函数()y f x =的解析式;(2)求函数()y f x =的单调递增区间.【答案】解:(1)()f x =⋅a b 1sin 2x x =+sin coscos sin33x x ππ=+sin()3x π=+(2)由22232k x k πππππ-+≤+≤+,k Z ∈得52266k x k ππππ-+≤≤+,k Z ∈ ∴函数()y f x =的单调递增区间是5[2,2]66k k ππππ-++,k Z ∈79.(【解析】山东省德州市2013届高三上学期期末校际联考数学(文))若函数2()22cos f x x x m =++在区间[0,]2π上的最大值为2,将函数()f x 图象上所有点的横坐标伸长为原来的2倍(纵坐标保持不变),再将图象上所有的点向右平移6π个单位,得到函数()g x 的图象. (1)求函数()f x 解析式;(2)在△ABC 中,角A 、B 、C 所对的边分别是a 、b 、c,又8(),225g A b π-==,△ABC 的面 积等于3,求边长a 的值, 【答案】80.(【解析】山东省枣庄市2013届高三3月模拟考试 数学(文)试题)已知函数()sin(),0,||.2f x x πωϕωϕ=+><其中(l)若3cossin()sinsin 0,424πππϕϕϕ+-=求的值; (2)在(1)的条件下,若函数f(x)的图象的两条相邻对称轴之间的距离等于3π,求函数f(x)的解析式;并求最小的正实数m,使得函数f(x)的图象向右平移m 个单位后所对应的函数是偶函数.【答案】81.(【解析】山东省临沂市2013届高三5月高考模拟文科数学)已知2,0(1,sin()),(cos sin ),2x x x x ωωωωπ∈=+=R >,u v 函数1()2=⋅-f x u v 的最小正周期为π. (Ⅰ)求ω的值;(Ⅱ)求函数()f x 在区间[0,]2π上的值域.【答案】解:(Ⅰ)依据题意,211()(1,sin())(cos )222f x x x x ωωω=-=+⋅- πu v21cos cos 2x x x ωωω=+⋅-1cos 212221cos 222x x x x ωωωω+=+-=+sin(2)6x ω=+π.0ω >,函数的最小正周期T =π,。
2013高考数学考前大冲关专题01三角函数(上)

【2013命题趋势预测】通过对近三年高考中三角函数的题型分析,编者在此对2013三角函数的命题做出如下预测,欢迎各个老师进行讨论、指导;1、 相对于其他一些考点而言,三角函数近三年的考查趋势较为稳定,所谓“稳定”,是指三角函数出题形式相对比较传统,难度较低,位置靠前,但重点突出,易于学生把握,能够很好的考查了学生对基础知识的掌握程度,所以预测在2013年的高考中三角函数问题仍然将会保持“稳定”的一个趋势;2、 大部分的省市对三角函数的出题分为两个部分,一是选择、填空中的三角函数问题,二是解答题中基本三角问题的考查,通过两个部分,来了解学生对三角函数问题的掌握程度;因此,我们可以预测,在2013年的高考中,大部分高考试卷会延续“选择+大题”或者“填空+大题”的考题形式,少部分试卷仅在解答题中考查三角函数问题;3、 三角函数的考点屈指可数,但可以灵活交汇,因此对编者根据对考试大纲的解读,预测2013年高考中,在选择题、填空题中,针对性的考查三角函数的知识点(如三角函数性质、平面向量数量积),解答题一般有四个命题方向;一是考查三角函数图像和性质为主;二是把解三角形与三角函数性质、三角恒等变换等进行“内部交汇”;三是考查解三角形或解三角形在实际问题中的应用;四是三角函数与平面向量、数列、解析几何的交汇.【高考冲刺押题】【押题1】在△ABC 中,角A, B, C 的对边分别为,,,c b a 且满足(2)cos 0.c a cosB b A --= (1)若7,13b a c =+=,求此三角形的面积;(2()6A sin C π+-的取值范围.名师押题理由:本题综合性强,考查了三角函数与解三角形问题中的多个知识点:1、 正弦定理、余弦定理的使用;2、三角形面积公式的选用;3、三角形内角和公式的应用;4、三角恒等变换公式;5、定区间上求三角函数的值域.【押题2】设函数a x x x x f ++=2cos cos sin 3)((1) 写出函数)(x f 的最小正周期及单调递减区间;(2)(2)已知当⎥⎦⎤⎢⎣⎡-∈3,6ππx 时,函数)(x f 的最大值与最小值的和为23,求不等式1)(>x f的解集.【深度剖析】 押题指数:★★★★★名师思路点拨:(1)先利用二倍角公式将sin cos x x 与2cos x 转化为二倍角,然后再利用三角恒等变换公式得到()f x 1sin(2)62x a π=+++,即可求出函数的周期与单调区间;(2)可以当⎥⎦⎤⎢⎣⎡-∈3,6ππx 时()f x 的最大值与最小值,进而得到0a =,所以将不等式为1sin(2)62x π+>,结合三角函数的图像解出不等式,注意k Z ∈.名师押题理由:本题综合性较强,考查了三角函数中的多个知识点:1、二倍角公式;2、三角很等变换公式;3、三角函数的周期性;4、三角函数的单调区间;5、定区间上求三角函数的最值;6、解三角函数不等式.【押题3】在锐角ABC ∆中,已知内角A 、B 、C 所对的边分别为,,a b c ,向量2(2sin(),3),(cos 2,2cos 1)2Bm A C n B =+=-,且向量//m n . (1)求角B 的大小;(2)如果1b =,求ABC ∆的面积ABC S ∆的最大值.【深度剖析】 押题指数:★★★★★名师思路点拨:(1)利用向量平行的坐标形式以及三角的内角和公式可以得到sin 22B B =,所以转化为正切以后再结合角度的取值范围可以求出B ;(2)因为1sin 2ABC S ac B ∆=,可以先利用余弦定理得到221a c =+,再利用基本不等式得到2ac ≤,最后代入面积公式即可.名师押题理由:本题综合性较强,试题涉及众多考点:1、向量平行的坐标形式;2、三角形内角和的转化;3、二倍角公式;4、三角函数求值;5、余弦定理;6、基本不等式;7、三角形的面积公式.【押题4(Ⅰ)求 函 数()f x 的 解 析 式;(Ⅱ)在△ABC 中,角C B A 、、的 对 边 分 别的 取 值 范 围.押题指数:★★★★★名师思路点拨:(1)由最高点的纵坐标可以看出M 的大小,由图形可以看出54126T ππ=-,进而定出ω,由特殊点坐标(,1)6π可以定出ϕ的大小;(2)由于所给的条件是边角混合的形式,所以先利用正弦定理实现角化边,然后结合三角形的内角和公式,得到A CB B A sin )sin(cos sin 2=+=,求出3B π=,将求()f A 的取值范围转化为定区间上的求三角函数的最值问题进行探究.名师押题理由:本题考查的知识点较为广泛,综合性较强:1、求()sin()f x A x ωϕ=+的函数解析式;2、三角函数的图形与性质;3、正弦定理;4、两角和的正弦公式;5、三角形的内角和公式;6、定区间上的最值问题.【押题5】已知向量(sin1)(3coscos )(00)222xx Am n A x A ωωωω==>>,,,,,函数 ()f x m n =的最大值为6,最小正周期为π.(1)求A ,ω的值;(2)将函数()y f x =的图像向左平移12π个单位,再向上平移1个单位,得到函数()y g x =的图像;求5()6g x π在[0,]上的值域.【深度剖析】 押题指数:★★★★★名师思路点拨:(1)先利用向量的数量积公式求出1()cos )2f x A x x ωω=+,然后在利用两角和的正弦公式对上式进行化简,得到()sin()6f x A x πω=+,再利用题设给出的最值与周期的条件可以得到()f x 的函数解析式;(2)根据函数图像的平移原理,得到平移以后的函数解析式为()6sin(2)13g x x π=++,由于5[0,]6x π∈,则将第(2)问转化为求定区间上的最值问题进行求解.名师押题理由:本题属于向量背景下的三角函数问题,试题较为基础,主要考查: 1、向量的数量积公式;2、三角函数的恒等变换;3、三角函数的性质; 4、函数图像的平移与伸缩;5、定区间上的最值问题.【名校试题精选】【模拟训练1】在锐角△ABC 中,内角A 、B 、C 的对边分别为a b c 、、,已知226cos a b ab C +=且2sin 2sin sin C A B =.(1)求角C 的值; (2)设函数()sin()cos (0)6f x x x πωωω=-->,且()f x 图象上相邻两最高点间的距离为π,求()f A 的取值范围.【深度剖析】名校试题来源:2012-2013山东省菏泽一中高三上学期期末考 难度系数:★★ 综合系数:★★★★★名师思路点拨:(1)利用余弦定理化简“226cos a b ab C +=”,再利用正弦定理化简“2sin 2sin sin C A B =”,两式联立可以求出cos C ;(2)可以求出“2ω=”,再利用三角函数的恒等变化化简()f x ,再求出()f A 的取值范围.【模拟训练2】在△ABC 21cos 2B B =-. (1)求角B 的值; (2)若2BC =,4A π=,求△ABC 的面积.【深度剖析】名校试题来源:2012-2013北京市西城区高三第一学期期末测试 难度系数:★ 综合系数:★★★★★名师思路点拨:(1)思路1:将题设等式利用二倍角公式展开得到“2cos 2sin B B B =”,进而计算出B ;思路2:利用辅助角公式将等式转化为“2sin(2)16B π+=”,结合B 的取值范围,算出B 的大小;(2)思路1:两角一边问题,先求出第三个角,利用正弦定理解三角形,在利用面积公式求出S ;思路2:利用正弦定理和余弦定理配合解题,再利用面积公式求出S.【模拟训练3】ABC ∆中,c b a ,,分别是角A,B,C的对边,已知),cos 1,(sin ),sin 2,3(A A n A m +==满足n m //,且a b c =-)(7(1)求角A 的大小; (2)求)6cos(π-C 的值【深度剖析】名校试题来源:2012-2013山西省晋中市“四大名校”高三上学期期末联考 难度系数:★★★ 综合系数:★★★★★名师思路点拨:(1)利用两向量平行的坐标形式和同角三角函数的基本关系可以求出角A 的大小;(2)利用“a b c =-)(7”和余弦定理得到角B 和角C 的关系,然后再与sin )sin C B A -==”联立可以求出sin cos C C 、,最后使用两角差的余弦公式可以求出)6cos(π-C 的值.【模拟训练4】已知函数3())2sin()2f x x x ππ=-++ (1)若[0,],x π∈求()f x 的值域;(2)若0x 为函数()y f x =的值.方法三:0x 为函数()y f x =的一个零点【模拟训练5】已知ABC ∆中三个内角C B A ,,的对边分别为c b a ,,,满足ccb B A B A +=+-tan tan tan tan . (1)求A ∠的值; (2)若3=a ,求ABC S ∆的最大值.【详细解析】(1)tan tan sin sin sin cos cos sin tan tan sin sin cos cos sin A B B C A B A BA B C A B A B-+-=⇒++【深度剖析】名校试题来源:2012-2013江西省景德镇市高三上学期期末考试 难度系数:★★ 综合系数:★★★★★名师思路点拨:(1)利用正弦定理和同角三角函数的商数关系对“ccb B A B A +=+-tan tan tan tan ”进行化简,在利用两角和的公式对其重新组合得到A ∠的值;(2)利用1sin 2ABC S bc A ∆=来求面积的最大值,再使用余弦定理和基本不等式定出bc 的取值范围即可.【模拟训练6】设函数2()sin sin()cos 2f x x x x π=++,在△ABC 中,角A 、B、C的对边分别为a,b,c(1)求()f x 的最大值;(2)若()1f A =,712A B π+=,b =求A 和a 。
2013文科高考汇编01:三角函数与解三角形

高考真题汇编:三角函数与解三角形
第 11 题、文科 2013 年浙江卷 18 题
在锐角△ABC 中,内角 A,B,C 的对边分别为 a,b,c,且 2asin B= 3 b.
⑴求角 A 的大小;⑵若 a=6,b+c=8,求△ABC 的面积.
解析:⑴由 2asin B= 3 b 及正弦定理 a b sin A sin B
解析:⑴由已知得 sin Asin B+sin Bsin C=2sin2B, 因为 sin B≠0,所以 sin A+sin C=2sin B. 由正弦定理,有 a+c=2b,即 a,b,c 成等差数列.
⑵由 C 2π ,c=2b-a 及余弦定理得(2b-a)2=a2+b2+ab, 3
即有 5ab-3b2=0,所以 a 3 . b5
5
令 g(x)=0,得 x=kπ+
3
或 x=kπ+
(k Z).
12
4
因为[a,a+10π]恰含 10 个周期,所以,
当 a 是零点时,在[a,a+10π]上零点个数为 21;
当 a 不是零点时,a+kπ(kZ)也都不是零点,区间[a+kπ,a+(k+1)π]上恰有两个零点,
故在[a,a+10π]上有 20 个零点.
2
2
F( )=2
2
,
F
(
)
=0,
F
(
)
≠
F
(
)
,
F
(
)
≠-
F
(
)
.
4
4
44
4
4
所以,F(x)既不是奇函数,也不是偶函数.
⑵f(x)=2sin2x,
2013年高考试题分类汇编(三角函数)

2013年高考试题分类汇编(三角函数)考点1 任意角的三角函数考法1 三角函数的定义1.(2013·全国大纲卷·理科)已知a 是第三象限角,1sin 3a =-,则cot a = .2.(2013·全国大纲卷·文科)已知a 是第二象限角,5sin 13a =,则cos a =A.1213-B.513- C.513 D.12133.(2013·全国卷Ⅱ·理科)设θ为第二象限角,若1tan()42πθ+=,则s i nc o s θθ+ =______.考法2 三角函数的图像1.(2013·全国卷Ⅱ·文科)函数cos(2) ()y x ϕπϕπ=+-≤<的图像向右平移2π个单位后,与函数sin(2)3y x π=+的图像重合,则ϕ=____.2.(2013·湖北卷·理科)将函数sin y x x =+(x R ∈)的图象向左平移(0)m m >个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是A .12π B .6π C .3π D .5π 3.(2013·全国大纲卷·文科)若函数()(sin y x ωϕω=+的部分图像如图,则ω= A.5 B.4 C.3 D.24.(2013·福建卷·文科)将函数()sin(2)f x x θ=+(22ππθ-<<)的图像向右平移(1)ϕϕ>单位长度后得到函数()g x 的图像,若()(),f x g x 的图像都经过(02P ,,则ϕ的一个值可以是A .53π B .56π C .2π D .6π 5.(2013·安徽卷·文科)设函数()sin sin()3f x x x π=++.(Ⅰ)求()f x 的最小值,并求使()f x 取得最小值的x 的集合;(Ⅱ)不画图,说明函数()y f x =的图像可由sin y x =的图象经过怎样的变化的到.6.(2013·四川卷·理科)函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则ω,ϕ的值分别是A.2,3π-B.2,6π-C.4,6π-D.4,3π考法3 三角函数的性质1.(2013·天津卷·文科)函数()sin(2)4f x x π=-在区间[0,]2π上的最小值是A.1-B.D. 0 2.(2013·江苏卷)函数)2sin(3π+=x y 的最小正周期为 .4.(2013·江西卷·理科)定义域为R 的四个函数3y x =,2x y =,2+1y x =,2sin y x =中,奇函数的个数是A. 4B.3C. 2D.15.(2013·全国大纲卷·理科)已知函数()=cos sin 2f x x x ,下列结论错误的是 A.()f x 的图像关于点(),0π中心对称 B.()f x 的图像关于2x π=对称C.()f x 的最大值为()f x 既是奇函数又是周期函数 6.(2013·重庆卷·文科)已知函数3()sin 4(,)f x ax b x a b R =++∈,2(lg(log 10))5f =,则(lg(lg 2))f =A.5-B.1-C.3D.47.(2013·浙江卷·理科)已知函数()cos()f x A x ωϕ=+(0A >,0ω>,R ϕ∈),则“()f x 是奇函数”是“2πϕ=”的A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件8.(2013·浙江卷·文科)若R α∈,则“0α=”是“sin cos αα<”的 A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件9. (2013·北京卷·理科)“ϕπ=”是“曲线sin(2)y x ϕ=+过坐标原点的” A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件10.(2013·浙江卷·文科)函数()sin cos 2f x x x x =的最小正周期和振幅分别是A. 1π,B. 2π,C. 2 1π,D.2 2π,11.(2013·辽宁卷·理科)设向量,sin )a x x = ,(cos ,sin )b x x = ,[0,]2x π∈.(Ⅰ)若a b =r r,求x 的值;(Ⅱ)设函数()f x a b =⋅r r,求()f x 的最大值.12.(2013·湖南卷·理科)已知函数()sin()cos()63f x x x ππ=-+-,2()2sin 2xg x =(Ⅰ)若α是第一象限角,且()f α=求()g α的值; (Ⅱ)求使()()f x g x ≥成立的x 的取值集合.13.(2013·广东卷·理科)已知函数())12f x x π=-,x R ∈.(Ⅰ)求() 6f π-的值;(Ⅱ)若3cos 5θ=,3(,2)2πθπ∈,求(2)3f πθ+.考点2 三角函数的恒等变换1.(2013·江西卷·文科)若sin2α=,则cos α= A. 23- B. 13- C. 13 D. 232.(2013·广东卷·文科)已知51sin()25πα+=,那么cos α=A. 25-B. 15-C. 15D. 253.(2013·江西卷·文科)设()sin 3cos 3f x x x =+,若对任意实数x 都有()f x a ≤,则实数a 的取值范围是 .4.(2013·全国卷Ⅰ·文理)设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=____ _.5.(2013·全国卷Ⅱ·文科)已知2sin 23α=,则2cos ()4πα+= A. 16 B. 13 C. 12 D. 236.(2013·浙江卷·理科)已知函数R α∈,sin 2cos 2αα+=,则tan 2α= A.43 B. 34 C. 34- D. 43- 7.(2013·四川卷·文科)设sin 2sin αα=-,(,)2παπ∈,则t an 2α的值是_____. 8.(2013·重庆卷·理科)4cos50tan 40-=1 9.(2013·浙江卷·理科)在ABC ∆中,90C ∠= ,M 是BC 的中点,若sin BAM ∠13=,则sin BAC ∠= . 10.(2013·湖南卷·文科)已知函数()cos cos()3f x x x π=-(Ⅰ)求2()3f π的值;(Ⅱ)求使 1()4f x <成立的x 的取值集合.11.(2013·山东卷·文科)设函数2()sin cos f x x x x ωωω=-,0ω>, 且()y f x =的图象的一个对称中心到最近的对称轴的距离为4π. (Ⅰ)求ω的值; (Ⅱ)求()f x 在区间3[,]2ππ上的最大值和最小值.12.(2013·安徽卷·理科)已知函数()4cos sin()(0)4f x x x πωωω=⋅+>的最小正周期为π. (Ⅰ)求ω的值;(Ⅱ)讨论()f x 在区间[]0,2上的单调性.13.(2013·北京卷·文科)已知函数21()(2cos 1)sin2cos42f x x x x =-+ (Ⅰ)求()f x 的最小正周期及最大值;(Ⅱ)若(,)2παπ∈且()2f α=,求α的值.14.(2013·天津卷·理科)已知函数())6sin cos 4f x x x x π=++22cos x -1+,x R ∈.(Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在区间[0,]2π上的最大值和最小值.15. (2013·陕西卷·理科)已知向量1(cos ,)2a x =- , ,cos2)b x x = ,x R ∈,设函数()f x a b =⋅.(Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在[0,]2π上的最大值和最小值.考点3 解三角形考法1 正弦定理1.(2013·北京卷·文科)在ABC ∆中,3a =,5b =,1sin 3A =,则sin B =A. 15B.592.(2013·湖南卷·理科)在锐角中ABC ∆,角,A B 所对的边长分别为,a b .若2sin a B =,则A 等于 A .12π B .6π C .4π D .3π3.(2013·山东卷·文科)ABC ∆的内角,,A B C 的对边分别是,,a b c ,若2B A =,1a =,b =c =A.4.(2013·辽宁卷·理科)在ABC ∆,内角,,A B C 所对的边长分别为,,a b c .1sin cos sin cos 2a B C c B Ab +=,且a b >,则B ∠=A .6πB .3π C .23π D .56π5.(2013·陕西卷·理科)设ABC ∆的内角,,A B C 所对的边分别为,,a b c , 若cos cos sin b C c B a A +=, 则ABC ∆的形状为A. 锐角三角形B. 直角三角形C.钝角三角形D. 不确定考法2 余弦定理1.(2013·全国卷Ⅰ·文科)已知锐角ABC ∆的内角,,A B C 的对边分别为,,a b c ,223cos cos 20A A +=,7a =,6c =,则b =A.10B. 9C.8D.52.(2013·福建卷·理科)如图,在ABC ∆中,已知点D 在BC 边上,AC AD ⊥,sin 3BAC ∠=,AB =3AD =, 则BD 的长为. 3.(2013·江西卷·理科)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,已知cos (cos )cos 0C A A B +=. (Ⅰ)求角B 的大小;(Ⅱ)若1a c +=,求b 的取值范围.4.(2013·四川卷·文科)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且3cos()cos sin()sin()5A B B A B A C ---+=-.(Ⅰ)求sin A 的值;(Ⅱ)若a =5b =,求向量BA 在BC方向上的投影.5.(2013·四川卷·理科)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且22cos cos sin()sin 2A B B A B B ---3cos()5A C ++=-.(Ⅰ)求cos A 的值;ABCD(Ⅱ)若a =5b =,求向量BA 在BC方向上的投影.7.(2013·重庆卷·理科)在ABC ∆中,内角A 、B 、C 的对边分别是a 、b 、c ,且222a b c ++=. (Ⅰ)求C ;(Ⅱ)设cos cos A B =,2cos()cos()cos A B ααα++=,求tan α的值. 8.(2013·全国大纲卷·理科)设ABC ∆的内角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=,(Ⅰ)求B ;(Ⅱ)若sin sin A C =,求C . 考法3 正弦定理、余弦定理、面积公式综合应用1.(2013·天津卷·文科)在ABC ∆中, 4ABC π∠=,AB =,3BC =,则sin BAC ∠=B.2.(2013·安徽卷·文科)设ABC ∆的内角,,A B C 所对边的长分别为,,a b c ,若2b c a +=,3sin 5sin A B =,则角C =A.3π B. 23π C. 34π D. 56π3.(2013·安徽卷·理科)设ABC ∆的内角,,A B C 所对边的长分别为,,a b c ,若2b c a +=,则3sin 5sin A B =,则角C =_____.4.(2013·全国卷Ⅱ·文科)ABC ∆的内角,,A B C 的对边分别是,,a b c ,已知2b =,6B π=,4C π=,则ABC ∆的面积为A.2 1 C. 215.(2013·浙江卷·文科)在锐角ABC ∆中,内角,,A B C 的对边分别为,,a b c ,且2sin a B =. (Ⅰ)求角A 的大小;(Ⅱ)若6a =,8b c +=,求ABC ∆的面积.6.(2013·江西卷·文科)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,已知sin sin sin sin cos 21A B B C B ++=.(Ⅰ)求证:,,a b c 成等差数列; (Ⅱ)若2C 3π=,求ab的值. 7.(2013·湖北卷·理科)在ABC ∆中,角,,A B C 对应的边分别是,,a b c . 已知cos 23cos()1A B C -+=.(Ⅰ)求角A 的大小;(Ⅱ)若ABC ∆的面积S =5b =,求sin sin B C 的值.8.(2013·北京卷·理科)在ABC ∆中,3a =, b =,2B A ∠=∠. (Ⅰ)求cos A 的值; (Ⅱ)求c 的值.9.(2013·天津卷·文科)ABC ∆的内角,,A B C 的对边分别是,,a b c .已知sin 3sin b A c B =,3a =,2cos 3B =. (Ⅰ)求b 的值;(Ⅱ)求sin(2)3B π-的值.10.(2013·全国卷Ⅱ·理科)ABC ∆在内角,,A B C 的对边分别为,,a b c ,已知cos sin a b C c B =+.(Ⅰ)求B ;(Ⅱ)若2b =,求ABC ∆面积的最大值.11.(2013·山东卷·理科)设ABC ∆的内角,,A B C 所对的边分别为,,a b c ,且6a c +=,2b =,7cos 9B =. (Ⅰ)求,a c 的值; (Ⅱ)求sin()A B -的值.。
2013高考数学必考点之三角函数——解答题1

1在△ABC 中,角A 、B 、C 所对的边分别是a ,b ,c ,且.21222ac b c a =-+(1)求B C A 2cos 2sin 2++的值;(2)若b=2,求△ABC 面积的最大值. 解:(1) 由余弦定理:conB=14sin22A B ++cos2B= -14(2)由.415sin ,41cos ==B B 得 ∵b=2,a 2+c 2=12ac+4≥2ac,得ac ≤38,S △ABC =12acsinB ≤315(a=c 时取等号) 故S △ABC 的最大值为3152在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且.cos cos 3cos B c B a C b -=(I )求cosB 的值;(II )若2=⋅BC BA ,且22=b ,求c a 和b 的值.解:(I )由正弦定理得C R c B R b A R a sin 2,sin 2,sin 2===,,0sin .cos sin 3sin ,cos sin 3)sin(,cos sin 3cos sin cos sin ,cos sin cos sin 3cos sin ,cos sin 2cos sin 6cos sin 2≠==+=+-=-=A B A A B A C B B A B C C B B C B A C B B C R B A R C B R 又可得即可得故则因此.31cos =B …………6分(II )解:由2cos ,2==⋅B a BC BA 可得,,,0)(,12,cos 2,6,31cos 222222c a c a c a B ac c a bac B ==-=+-+===即所以可得由故又所以a =c = 63已知向量m =()B B cos 1,sin -, 向量n = (2,0),且m 与n 所成角为π3,其中A 、B 、C 是ABC ∆的内角。
(1)求角B 的大小;(2)求 C A sin sin +的取值范围。
高考复习文科数学之三角函数(1)

各地解析分类汇编:三角函数(1)1 【山东省师大附中2013届高三上学期期中考试数学文】已知()cos tan 2,cos 2πααπα+=⎛⎫+ ⎪⎝⎭则的值为A.12-B.2-C.12D.2【答案】C 【解析】()cos cos 11sin tan 2cos 2πααπααα+-===-⎛⎫+ ⎪⎝⎭,选C.2 【山东省临沂市2013届高三上学期期中考试数学文】已知cos()||,tan 222ππϕϕϕ+=-<则=A.3-B.3C.D【答案】D【解析】由cos()22πϕ+=-得sin 2ϕ=,所以,3πϕ=所以tan ϕ= D. 3 【山东省临沂市2013届高三上学期期中考试 数学文】若△ABC 的内角A 、B 、C 满足s i n :s i n:s i n 2:3:3,A B C B =则A .14 B .13C .12D .23【答案】B【解析】根据正弦定理知sin :sin :sin ::2:3:3A B C a b c ==,不妨设2,0a k k =>,则3b c k ==,所以22222224991cos 2123a cb k k k B ac k +-+-===,选B.4 【山东省聊城市东阿一中2013届高三上学期期初考试 】若0sin2<θ,则角θ是( )A.第一或第二象限角B.第二或第三象限角C.第三或第四象限角D.第二或第四象限角 【答案】D【解析】因为sin22sin cos 0θθθ=<,则角θ是第二或第四象限角,选D5 【山东省师大附中2013届高三12月第三次模拟检测文】在,,ABC A B C ∆中,的对边分别为,,a b c ,若cos ,cos ,cos a C b B c A 成等差数列,则B =A.6π B. 4π C. 3π D. 23π【答案】C【解析】因为cos ,cos ,cos a C b B c A 成等差数列,所以cos cos 2cos a C c A b B +=,根据正弦定理可得sin cos sin cos 2sin cos A C CA BB +=,即s i n()2s i n c o s A C B B+=,即s i n2s i n c o s B B B =,所以1cos 2B =,即3B π=,选C. 6.【山东省济南外国语学校2013届高三上学期期中考试 文科】 若点(,9)a 在函数3xy =的图象上,则tan 6πa 的值为( )【答案】D【解析】因为点(,9)a 在函数3xy =的图象上,所以39a =,解得2a =,所以2tantan 33a ππ== D. 7 【山东省济南外国语学校2013届高三上学期期中考试 文科】已知函数()2sin(),,f x x x R ωϕ=+∈其中0,.ωπϕπ>-<≤若()f x 的最小正周期为6π,且当2x π=时, ()f x 取得最大值,则( )A. ()f x 在区间[2,0]π-上是增函数B. ()f x 在区间[3,]ππ--上是增函数C. ()f x 在区间[3,5]ππ上是减函数D. ()f x 在区间[4,6]ππ上是减函数 【答案】A 【解析】由26T ππω==,所以13ω=,所以函数1()2sin()3f x x ϕ=+,当2x π=时,函数取得最大值,即12322k ππϕπ⨯+=+,所以23k πϕπ=+,因为πϕπ-<≤,所以3πϕ=,1()2sin()33f x x π=+,由1222332k x k πππππ-+≤+≤+,得56622k x k ππππ-+≤≤+,函数的增区间为5[6,6]22k k ππππ-++,当0k =时,增区间为5[,]22ππ-,所以()f x 在区间[2,0]π-上是增函数,选A.8 【山东省德州市乐陵一中2013届高三10月月考数学(文)】如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。
2013年广东省高考数学考前专题训练:三角函数

2013年广东省高考数学考前专题训练三角函数近几年广东省高考数学试题中,解答题第1题,即试题的第16题都是三角函数试题,由于试题结构具有相对稳定性,估计2013年广东高考数学解答题第1题还是考查三角函数,,因此,三角函数的知识应该充分训练,力争高考中拿下满分12分。
本节内容目录一、近三年高考试题回顾 二、三角函数及其图象试题 三、三角函数与平面向量试题 四、三角函数与解三角形试题五、三角函数与三角恒等变换试题六、三角函数应用题一、近三年高考试题回顾1、(2012广东数学文)已知函数()cos()()46x f x A x R π=+∈,且()23f π=。
(1)求A 的值; (2)设,[0,]2παβ∈,43028(4),(4)31735f f ππαβ+=--=;求cos()αβ+的值【解析】(1)()2cos 2234f A A ππ=⇔=⇔=(2)43015158(4)cos()sin ,cos 3172171717f ππαααα+=-⇔+=-⇔==2843(4)c o s ,s i n 3555f πβββ-=⇔==4831513c o s ()c o s c o s s i n s i n 51751785αβαβαβ+=-=⨯-⨯=- 2、(2011广东数学文)已知函数1()2sin()36f x x π=-,x ∈R .(1)求(0)f 的值;(2)设,0,2παβ⎡⎤∈⎢⎥⎣⎦,10(3)213f πα+=,6(32)5f βπ+=,求sin()αβ+的值.解:(1)(0)2sin()16f π=-=-(2)110(3)2sin[(3)]2sin 232613f πππααα+=+-==,即5sin 13α= 16(32)2sin[(32)]2sin()3625f ππβπβπβ+=+-=+=,即3cos 5β=∵,0,2παβ⎡⎤∈⎢⎥⎣⎦,∴212cos 1sin 13αα=-=,24sin 1cos 5ββ=-=∴5312463sin()sin cos cos sin 13513565αβαβαβ+=+=⨯+⨯=3、(2010广东数学文)设函数()3sin 6f x x πω⎛⎫=+⎪⎝⎭,0ω>,(),x ∈-∞+∞,且以2π为最小正周期.(1)求()0f ;(2)求()f x 的解析式;(3)已知94125f απ⎛⎫+= ⎪⎝⎭,求sin α的值. 解:(1)由已知可得:236sin3)0(==πf(2)∵)(x f 的周期为2π,即22πωπ=∴4=ω 故)64sin(3)(π+=x x f (3)∵]6)124(4sin[3)124(πππ++⨯=+a a f )2sin(3π+=a a cos 3=∴由已知得:59cos 3=a 即53cos =a∴54)53(1cos 1sin 22±=-±=-±=a a 故a sin 的值为54或54-二、三角函数及其图象试题 1、已知,αβ均为锐角,且3sin 5α=,1tan()3αβ-=-.(1)求sin()αβ-的值; (2)求cos β的值.2.已知函数()())2,0,0(sin πϕωϕω<>>+=A x A x f 的图象的一部分如图所示.(Ⅰ)求函数()x f 的解析式; (Ⅱ)求函数())44cos(2ππ++=x x f y ])32,6[(--∈x 的最大值和最小值.3、已知函数sin 2(sin cos )()cos x x x f x x+=.(Ⅰ)求)(x f 的定义域及最小正周期;(Ⅱ)求)(x f 在区间⎥⎦⎤⎢⎣⎡-46ππ,上的最大值和最小值.4、已知函数.20,0,),3sin()(πϕϕπ<<>∈+=A R x x A x f ,y=f(x)的部分图像如图所示,点是该图象上的一点,P,Q 分别为该图像在y 轴右侧的第一个最高点和第一个最低点,且 =1.(1) 求ϕ和A 的值;(2)若,求的値.5、已知函数()sin()(0,0,||)2f x A x A πωϕωϕ=+>><的部分图象如图所示。
2013高考数学专题复习--三角函数

2013高考数学——三角函数专题复习(文科)★ 知 识 梳理 ★1. 内角和定理:在ABC ∆中,A B C ++=π;sin()A B +=sin C ;cos()A B +=cos C - cos 2A B +=sin 2C 2.面积公式:1sin 2ABC S ab C ∆== 1sin 2bc A =1sin 2ca B 3.正弦定理:在一个三角形中,各边和它的所对角的正弦的比相等. 形式一:R Cc B b A a 2sin sin sin === (解三角形的重要工具) 形式二:⎪⎩⎪⎨⎧===C R c B R b A R a sin 2sin 2sin 2 (边角转化的重要工具)4.余弦定理:三角形任何一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍..形式一:2222cos a b c bc A =+-2222cos b c a ca B =+- (解三角形的重要工具)2222cos c a b ab C =+-形式二:cos A =bc a c b 2222-+ ; cos B =ca b a c 2222-+ ; cos C =ab c b a 2222-+ 1 在△ABC 中,,则等于( ) ABCD2 在△ABC 中,若cos A cos B =b a ,则△ABC 的形状是.( )A.等腰直角三角形B.直角三角形C.等腰或直角三角形D.等边三角形3 在△ABC 中,若0030,6,90===B a C ,则b c -等于( )A 1B 1-C 32D 32-4.【台州市·理】6.在ABC ∆中,若a =1,C=︒60, c =3则A 的值为A .︒30B .︒60C .30150︒︒或D .60120︒︒或 5 在△ABC 中,若B a b sin 2=,则A 等于( )A 006030或B 006045或C 0060120或D 0015030或6.在△ABC 中,若3a =2b sin A ,则B 为( )A .3πB .6πC .3π或32πD .6π或65π7.在ABC ∆中,a ,b ,c 分别为角A ,B ,C 所对边,若C b a cos 2=,则此三角形一定是( )A.等腰直角三角形B. 直角三角形C. 等腰三角形D. 等腰或直角三角形8在△ABC 中,A =60°,B =75°,a =10,则c 等于_________.9在△ABC 中,a =3,b =1,c =2,则A 等于________.10在△ABC 中,a =32,b =23,cos C =13,则△ABC 的面积为________.11.(本小题满分12分) 函数()()()πϕωϕω≤>>+=,0,0sin A x A x f 在一个周期内,当6x π=时,y 取最小值3-;当23x π=时,y 最大值3. (I)求()f x 的解析式; (II)求()f x 在区间⎥⎦⎤⎢⎣⎡ππ,2上的最值.12.在△ABC 中,设内角A 、B 、C 的对边分别为a 、b 、c ,22)4cos()4cos(=-++ππC C (Ⅰ)求角C 的大小;(Ⅱ)若32=c 且B A sin 2sin =,求ABC ∆的面积.13,(陕西)(本小题满分12分) 函数()sin()16f x A x πω=-+(0,0A ω>>)的最大值为3, 其图像相邻两条对称轴之间的距离为2π, (Ⅰ)求函数()f x 的解析式; (Ⅱ)设(0,)2πα∈,则()22f α=,求α的值。
2013届高三文科数学三角函数概念恒等变换

2013届高三文科数学练习——三角函数概念、三角恒等变换班别:高三( )班 姓名: 座号:一、选择题: 1.已知4sin 5α=,并且α是第二象限的角,那么tan α的值等于( ) A .43- B .34- C .43 D .342.若角0600的终边上有一点()a ,4-,则a 的值是( )A .34B .34-C .34±D .33.设00sin14cos14a =+,00sin16cos16b =+,c =,则,,a b c 大小关系( ) A .a b c << B .b a c <<C .c b a <<D .a c b << 4.(2007江西文4)若tan 3α=,4tan 3β=,则tan()αβ-等于( ) A.3-B.13-C.3 D.135.化简0sin 600的值是( )A .0.5B .0.5-C .2 D .2-6.如果1弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( )A .5.0sin 1B .sin 0.5C .2sin 0.5D .tan 0.57.若θ为锐角且2cos cos 1-=--θθ,则θθ1cos cos -+的值为( ) A .22 B .6 C .6 D .48.设5sin7a π=,2cos 7b π=,2tan 7c π=,则( ) A .a b c << B .a c b << C .b c a << D .b a c <<9.函数x x y 24cos sin +=的最小正周期为( )A .4π B .2πC .πD .2π 10.△ABC 中,090C ∠=,则函数2sin 2sin y A B =+的值的情况( )A .有最大值,无最小值B .无最大值,有最小值C .有最大值且有最小值D .无最大值且无最小值11.0000(1tan 21)(1tan 22)(1tan 23)(1tan 24)++++ 的值是( )A . 16B . 8C . 4D . 212.当04x π<<时,函数22cos ()cos sin sin xf x x x x=-的最小值是( )A .4B .12C .2D .1413.已知函数R x x x x f ∈+=,sin )2cos 1()(2,则)(x f 是( )A .最小正周期为π的奇函数 B. 最小正周期为π的偶函数C. 最小正周期为2π的奇函数 D. 最小正周期为2π的偶函数 14.函数2()sin cos f x x x x =在区间,42ππ⎡⎤⎢⎥⎣⎦上的最大值是( . )A.1B.12+ C. 3215.函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是( )二、填空题16.已知角α终边上一点P 的坐标是(2sin2,-2cos2),则sin α= .17.已知sin α=55,则sin 4α-cos 4α的值为 .18.(2008·浙江理)若cos α+2sin α=-5,则tan α= .19.(2008·山东理)已知cos ⎪⎭⎫⎝⎛-6πα+sin α=354,则sin ⎪⎭⎫ ⎝⎛+67πα的值是 .20.sin163°·sin223°+sin253°·sin313°= .三.解答题xxA .B .C .D .21 已知tan α=2,求下列各式的值: (1)ααααcos 9sin 4cos 3sin 2--;(2)αααα2222cos 9sin 4cos 3sin 2--;(3)4sin 2α-3sin αcos α-5cos 2α.22.已知cos(π+α)=-21,且α是第四象限角,计算: (1)sin(2π-α); (2) [][])2cos()2sin()12(sin )12(sin παπαπαπαn n n n -∙++-+++ (n ∈Z ).23.求值:(1)已知cos ⎪⎭⎫⎝⎛-2βα =-54,sin ⎪⎭⎫ ⎝⎛-2αβ=135,且2π<α<π,0<β<2π,求cos2βα+的值;(2)已知tan α=43,cos(α+β)=-1411, α、β均为锐角,求cos β的值.24.已知函数2πππ()12sin 2sin cos 888f x x x x ⎛⎫⎛⎫⎛⎫=-++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.求: (I )函数()f x 的最小正周期;(II )函数()f x 的单调增区间.2013届高三文科数学练习——三角函数概念、三角恒等变换班别:高三( )班 姓名: 座号:一、选择题: 1.已知4sin 5α=,并且α是第二象限的角,那么 tan α的值等于( A )A .43-B .34- C .43 D .342.若角0600的终边上有一点()a ,4-,则a 的值是( B )A .34B .34-C .34±D .33.设00sin14cos14a =+,00sin16cos16b =+,c =, 则,,a b c 大小关系( D ) A .a b c << B .b a c <<C .c b a <<D .a c b << 4.(2007江西文4)若tan 3α=,4tan 3β=,则tan()αβ-等于( D ) A.3-B.13-C.3 D.135.化简0sin 600的值是( D )A .0.5B .0.5-C .2 D .2-6.如果1弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( A )A .5.0sin 1B .sin 0.5C .2sin 0.5D .tan 0.57.若θ为锐角且2cos cos 1-=--θθ,则θθ1cos cos -+的值为( A ) A .22 B .6 C .6 D .4 8.设5sin7a π=,2cos 7b π=,2tan 7c π=,则( D ) A .a b c << B .a c b << C .b c a <<D .b a c <<9.函数x x y 24cos sin +=的最小正周期为( B )A .4π B .2πC .πD .2π 10.△ABC 中,090C ∠=,则函数2sin 2sin y A B =+的值的情况( D )A .有最大值,无最小值B .无最大值,有最小值C .有最大值且有最小值D .无最大值且无最小值11.0000(1tan 21)(1tan 22)(1tan 23)(1tan 24)++++ 的值是( C )A . 16B . 8C . 4D . 212.当04x π<<时,函数22cos ()cos sin sin xf x x x x=-的最小值是( A )A .4B .12 C .2 D .1413.已知函数R x x x x f ∈+=,sin )2cos 1()(2,则)(x f 是( D )A .最小正周期为π的奇函数 B. 最小正周期为π的偶函数C. 最小正周期为2π的奇函数 D. 最小正周期为2π的偶函数 14.函数2()sin cos f x x x x =在区间,42ππ⎡⎤⎢⎥⎣⎦上的最大值是( C. )A.1C. 3215.函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是( A )二、填空题16.已知角α终边上一点P 的坐标是(2sin2,-2cos2),则sin α= . 答案 -cos2 17.已知sin α=55,则sin 4α-cos 4α的值为 . 答案 53-xxA .B .C .D .18.(2008·浙江理)若cos α+2sin α=-5,则tan α= . 答案 219.(2008·山东理)已知cos ⎪⎭⎫⎝⎛-6πα+sin α=354,则sin ⎪⎭⎫ ⎝⎛+67πα的值是 . 答案 54-20.sin163°·sin223°+sin253°·sin313°= .答案 21 三.解答题21 已知tan α=2,求下列各式的值: (1)ααααcos 9sin 4cos 3sin 2--;(2)αααα2222cos 9sin 4cos 3sin 2--;(3)4sin 2α-3sin αcos α-5cos 2α. 解 (1)原式=19243229tan 43tan 2-=-⨯-⨯=--αα.(2)759243229tan 43tan 2cos 9sin 4cos 3sin 222222222=-⨯-⨯=--=--αααααα. (3)∵sin 2α+cos 2α=1, ∴4sin 2α-3sin αcos α-5cos 2α=αααααα2222cos sin cos 5cos sin 3sin 4+--=114523441tan 5tan 3tan 422=+-⨯-⨯=+--ααα22.已知cos(π+α)=-21,且α是第四象限角,计算: (1)sin(2π-α); (2)[][])2cos()2sin()12(sin )12(sin παπαπαπαn n n n -∙++-+++ (n ∈Z ).解 ∵cos(π+α)=-21,∴-cos α=-21,cos α=21,又∵α是第四象限角,∴sin α=-23cos 12-=-α. (1)sin(2π-α)=sin [2π+(-α)]=sin(-α)=-sin α=23. (2)[][])2cos()2sin()12(sin )12(sin παπαπαπαn n n n -∙++-+++=)2cos()2sin()2sin()2sin(απαπαππαππ+-∙++--+++n n n n=αααπαπcos sin )sin()sin(∙+-++=αααπαcos sin )sin(sin ∙---=αααcos sin sin 2∙-=αcos 2-=-4.23.求值:(1)已知cos ⎪⎭⎫⎝⎛-2βα =-54,sin ⎪⎭⎫ ⎝⎛-2αβ=135,且2π<α<π,0<β<2π,求cos2βα+的值;(2)已知tan α=43,cos(α+β)=-1411, α、β均为锐角,求cos β的值. 解 (1)⎪⎭⎫ ⎝⎛-2βα+⎪⎭⎫ ⎝⎛-2αβ =2βα+,∵2π<α<π,0<β<2π. ∴2βα-∈⎪⎭⎫⎝⎛ππ,4,2αβ-∈⎪⎭⎫ ⎝⎛-4,2ππ∴sin ⎪⎭⎫ ⎝⎛-2βα=)2(cos 12βα--=53,cos ⎪⎭⎫ ⎝⎛-2αβ=1312)2(sin 12=--αβ,∴cos 2βα+=cos ⎥⎦⎤⎢⎣⎡-+-)2()2(αββα=cos ⎪⎭⎫⎝⎛-2βαcos ⎪⎭⎫ ⎝⎛-2αβ-sin ⎪⎭⎫ ⎝⎛-2βαsin ⎪⎭⎫ ⎝⎛-2αβ=)54(-×1312-135×53=-6563.(2)∵tan α=43,且α为锐角, ∴34cos sin =αα,即sin α=43cos α,又∵sin 2α+cos 2α=1, ∴sin α=734,cos α=71.∵0<α,β<2π,∴0<α+β<π,∴sin(α+β)=)(cos 12βα+-=1435.而β=(α+β)-α, ∴cos β=cos [(α+β)-α]=cos(α+β)cos α+sin(α+β)sin α=⎪⎭⎫ ⎝⎛-1411×71+1435×734=21.24.已知函数2πππ()12sin 2sin cos 888f x x x x ⎛⎫⎛⎫⎛⎫=-++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.求: (I )函数()f x 的最小正周期;(II )函数()f x 的单调增区间.解:ππ()cos(2)sin(2)44f x x x =+++πππ))2442x x x =++=+=.(I )函数()f x 的最小正周期是2ππ2T ==;(II )当2ππ22πk x k -≤≤,即πππ2k x k -≤≤(k ∈Z )时,函数()f x x=是增函数,故函数()f x 的单调递增区间是π[ππ]2k k -,(k ∈Z ).。
2013年全国各地高考文:三角函数-推荐下载

对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置各试时类卷,管调需路控要习试在题验最到;大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资,常料要工试加况卷强下安看与全22过,22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
2013届高考冲刺押题(数学文)专题01三角函数(下)

2013届高考冲刺押题(数学文)专题01三角函数(下)【名师备考建议】鉴于三角函数问题具有基础性强、容易入手、必须拿分的特点,名师给出以下四点备考建议:主观形成三角函数的知识结构;对三角函数知识的记忆有助于学生对考题的理解,在高考复习的最后时期,学生应该形成自身的关于三角函数的知识体系,熟练掌握各个知识点的常见问题,因此在复习过程中,既要注重三角知识的基础性,突出三角函数的图像、周期性、单调性、奇偶性、对称性等性质,以及化简、求值和最值等重点内容的复习,又要注重三角知识的工具性,突出三角与代数、几何、向量的综合联系,以及三角知识的应用意识;熟练记忆三角函数的各种公式;三角函数考题对公式的使用较为频繁,在一个考题中通常呈现出四、五个公式的套用,因此能够熟练的使用三角函数的公式是旗开得胜的必要条件;三角函数的公式大致分为定义式、诱导公式、两角和差公式、倍角半角公式以及恒等变换的公式等,其中三角函数的恒等变换一直作为高考的重点进行考查,因此,在记忆公式的基础上还要充分的理解公式的用途,可以针对性的以一两个问题为铺垫,实现公式与考题的配合记忆;灵活处理三角函数的交汇问题;三角函数的交汇是高考的一个方向,近三年来,高考试题中既出现过三角函数自身的交汇,即三角函数与解三角形问题的交汇,也出现过三角函数同其他知识的交汇,例如三角函数与向量、数列、解析几何、不等式的交汇;因此,学生在复习三角函数问题的同时,也应该提高自身处理综合问题的能力,这样才能使自己立于不败之地;增强处理三角函数的信心状态;由于三角函数的问题常常作为各省解答题的第一题出现,因此能否做好三角函数问题往往对考生的心态有着极大的影响;因此,在面对三角函数的问题之时,学生应当冷静思考,认真计算,切勿因为问题简单而显得浮躁、盲目的自信,这样在考试的过程中就容易造成计算失误,进而信心受挫.【高考冲刺押题】【押题6】已知函数()cos2sin2 f x x x=+(1)求()f x的最大值和最小正周期;(2)设,[0,]2παβ∈,(),()2822f fαπβπ+=+=sin()αβ+的值【深度剖析】押题指数:★★★★★名师思路点拨:(1)使用三角很等变换公式将sin 2cos2x x +)4x π+,然后可以求出最大值和周期;(2)利用(),0,2822f αππα⎡⎤+=∈⎢⎥⎣⎦,可以求出cos α、sin α;利用()0,22f βππβ⎡⎤+=∈⎢⎥⎣⎦)4πβ+=4πβ=,然后利用两角和的正弦公式可以求出sin()αβ+的值.名师押题理由:本题基础性较强,考查了一下的知识点:1、三角恒等变换公式;2、三角函数的基本性质;3、三角函数的诱导公式;4、三角函数的基本运算;5、两角和的正弦公式.【押题7】在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,已知c b aB A 2cos cos +-=. (Ⅰ)求角A 的大小;(Ⅱ)求C B sin sin 的最大值.【】∵30π<<B ,∴65626πππ<+<B ,【深度剖析】押题指数:★★★★★名师押题理由:本题是三角函数以及解三角新的综合题,解法中渗透一题多解的思想,主要考点如下: 1、正弦定理、余弦定理的应用;2、两角和的正弦公式;3、三角形的内角和公式; 4、定区间上的最值问题;5、三角恒等变换公式;6、构造角度的思想.【押题8】已知函数(cos 2,1),(1,cos(2)),3a x b x π=-=-设()1f x a b =+, (1)求函数()f x 的最小正周期及单调递减区间;【】(2)设x 为三角形的内角,且函数2()y f x k =+恰有两个零点,求实数k 的取值范围.[【深度剖析】押题指数:★★★★★名师思路点拨:(1)先利用向量的数量积公式求出()f x ,再利用三角恒等变换公式对()f x 进行化简,得到()f x cos(2)13x π=++,然后可以求出函数的周期与单调递减区间;(2)可以得到2cos(2)23y x kπ=+++有两个零点,即方程2cos(2)203x k π+++=有两个实数根,可以利用分离参数的方法,进行求解.名师押题理由:本题综合性较强,体现了三角函数与函数零点的交汇:1、向量的数量积运算;2、三角恒等变换公式;3、三角函数的性质;4、函数的零点转化;5、三角函数的图像;6、不等式的基本解法.【押题9】在一个特定时段内,以点E 为中心的7海里以内海域被设为警戒水域.点E 正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A 北偏东45且与点A 相距海里的位置B ,经过40分钟又测得该船已行驶到点A 北偏东45+θ(其中sin θ=,090θ<<)且与点A 相距C.(1)求该船的行驶速度(单位:海里/小时);(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15. 过点E作EP ⊥BC于点P,则EP为点E到直线BC的距离.在RtQPE∆中,PE=QE·sin sin sin(45)PQE QE AQC QE ABC∠=⋅∠=⋅-∠=157.=所以船会进入警戒水域.【深度剖析】押题指数:★★★★★名师思路点拨:(1)已知sin26θ=,利用同角三角函数的基本关系可以求出cosθ,然后【押题10】如图,在平面直角坐标系中,锐角α、β的终边分别与单位圆交于A,B两点.(1)如果3tan4α=,B点的横坐标为513,求()cosαβ+的值;(2)若角αβ+的终边与单位圆交于C点,设角α、β、αβ+的正弦线分别为MA、NB、PC,求证:线段MA、NB、PC能构成一个三角形;(3)探究第(Ⅱ)小题中的三角形的外接圆面积是否为定值?若是求出出该定值;若不是,请说明理由.【深度剖析】押题指数:★★★★★ 名师思路点拨:(1)因为3tan 4α=,可以利用同角三角函数的基本关系求出sin α和cos α,根据单位圆上三角函数的定义,可以求出sin β和cos β,然后使用两角和的余弦公式,求出()cos αβ+;(2)若线段sin MA α=,sin NB β=,sin()PC αβ=+能构成一个三角形,则其中两边之和必定大于第三边,即证sin()sin sin αβαβ+<+、sin sin()sin βαβα<++、sin sin()sin ααββ<++成立即可,将两角和的正弦公式展开,再利用三角函数的有界性即可证明;【名校试题精选】【模拟训练1】已知函数()sin(3)(0,,0)f x A x A x R ϕϕπ=+>∈<<在12x π=时取得最大值4.(1) 求()f x 的最小正周期;【】 (2)求()f x 的解析式;(3)若f (23α +12π)=125,求sin α.【详细解析】【深度剖析】名校试题2012-2013陕西省西安一中高三上学期期末测试 难度系数:★★综合系数:★★★★★名师思路点拨:(1)利用2T πω=进行求解;(2)利用()412f π=定出ϕ的取值范围;(3)将角拆分成,利用二倍角公式进行计算.【模拟训练2】已知函数f(x)=)0,0)(cos()sin(3><<+-+ωϕϕωϕωπx x 为偶函数,且函数y =f(x)图象的两相邻对称轴间的距离为.2π (1)求f(8π)的值;(2)将函数y =f(x)的图象向右平移6π个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y =g(x)的图象,求g(x)的单调递减区间.【深度剖析】名校试题2012-2013山东省济南市高三上学期期末模拟测试 难度系数:★★★★★ 综合系数:★★★★★名师思路点拨:(1)利用辅助角公式对()f x 进行化简,再利用“周期”以及“偶函数”的条件求出()f x ,进而求出()8f π;(2)先利用函数的平移以及伸缩变换得到()g x 的函数解析式,然后求出递减区间.【模拟训练3】已知函数x xx x x f sin 2sin )cos (sin )(-=(1)求f(x)的定义域及最小正周期;(2)求f(x)的单调递增区间.【深度剖析】名校试题2012-2013山西省晋中市部分达标中学高三上学期期末 难度系数:★★综合系数:★★★★★名师思路点拨:(1)利用二倍角公式、半角公式以及辅助角公式对()f x 进行化简,得到()f x 的最简形式,再求出周期;(2)套用正弦函数的单调增区间进行求解.【模拟训练4】设锐角ABC ∆的三个内角C B A 、、的对边分别为c b a 、、,已知c b a ,,成等比数列,且43sin sin =C A(1) 求角B 的大小;(2) 若),0[π∈x ,求函数x B x x f sin )sin()(+-=的值域.【模拟训练5】在ABC ∆中a 、b 、c 分别内角A 、B 、C 的对边,已知向量(,)m c b =,(sin 2,sin )n B C =,且m n ⊥。
2013年高考试题分项版解析数学(文) 专题04 三角函数与解三角形(Word精析版)

第四章 三角函数与解三角形 一.基础题组1.【2013年普通高等学校招生全国统一考试(江西卷)文科】若sin 2a =,则cos a =( ) A .23-B .13-C .13D .23[答案]C[解析]221cos 12sin 12..23C αα=-=-⨯=∴选 [考点定位]此题主要考查三角恒等变换里面的二倍角余弦公式、三角函数求值问题. 2.【2013年普通高等学校统一考试试题大纲全国文科】已知a 是第二象限角,5sin ,13a =则cos a =( )(A )1213- (B )513- (C )513 (D )1213【答案】A【解析】∵a 是第二象限角,∴12cos 13α===-.故选A. 【考点定位】三角求值3.【2013年普通高等学校招生全国统一考试(广东卷)文科】已知51sin()25πα+=,那么cos α=( )A .25-B .15-C .15D .25【答案】C 【解析】51sin()sin(2+)sin cos 2225πππαπααα⎛⎫+=+=+== ⎪⎝⎭,选C. 【考点定位】三角函数诱导公式.4.【2013年普通高等学校统一考试试题大纲全国文科】若函数()()sin 0y x ωϕω=+>的部分图像如图,则=ω( )(A )5 (B )4 (C )3 (D )2 【答案】B【解析】∵由题中图像可知0042T x x π+-=.∴2T π=.∴22ππω=.∴4ω=.故选B. 【考点定位】三角函数的图像与解析式.5.【2013年普通高等学校招生全国统一考试(四川卷)文科】函数()2s i n ()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是( ) (A )2,3π- (B )2,6π-(C )4,6π-(D )4,3π【答案】A【解析】由图知,周期T 满足111521212T ππ=-,∴T π=,又0ω>,∴2ω=,故()2sin(2)f x x ϕ=+,图象的最高点为5,212π⎛⎫⎪⎝⎭,于是由“五点法”作图,知52122ππϕ⨯+=,解得3πϕ=-,选A.【易错点】注意求初相ϕ的值时,图象的最高点坐标与五个关键点坐标的对应关系最容易代错!【考点定位】本题考查正弦型函数()sin()f x A x ωϕ=+的图象与性质,难点是确定初相ϕ的值,关键是理解“五点法”作图.6.【2013年高考新课标Ⅱ数学(文)卷】 已知sin2α=错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12届高三文科数学考点专练——三角函数
1、 如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A ,B 两点.
(1)如果A 、B 两点的纵坐标分别为
45、1213
,求c o s α和sin β; (2)在⑴的条件下,求c o s ()βα-的值;
(3)已知点C (1-,求函数()f O A O C
α=⋅ 的值域.
2、已知函数2()sin cos f x x x x =+,π[,π]2
x ∈.
(Ⅰ)求()f x 的零点;(Ⅱ)求()f x 的最大值和最小值及取得最值时x 的值.
3、 已知函数2()cos 2cos 2.f x x x x =-+
( I )求()f x 的单调递增区间;
(Ⅱ)若()2f x m -<对一切x ∈[0,
2
π]均成立,求实数m 的取值范围.
4、设2,sin ),(1,cos )a x x b x ωωω== (其中0ω>),已知()f x a b =⋅ 且()f x 最小正周期为2.π
(1)求ω的值及()y f x =的表达式;
(2)设2(
,),63ππα∈5(,),63ππβ∈--34(),().cos()55
f f αβαβ==--求的值
5、已知函数R x x x x x f ∈--=,2
1cos cos sin 3)(2 (1)求函数()f x 的最小值和最小正周期;
(2)已知ABC ∆内角A 、B 、C 的对边分别为a 、b 、c 且c=3,0)(=C f ,若向量)sin ,1(A m = 与)sin ,2(B n = 共线,求实数a 、b 的值。
6、已知),,(cos ),1,sin 32cos 2(y x x x -=+=满足.0=∙
(1)将y 表示为x 的函数)(x f ,并求)(x f 的最小正周期;
(2)已知c b a ,,分别为ABC ∆的三个内角C B A ,,对应的边长,若,3)2
(=A f
且2=a ,求c b +的取值范围。
12届高三文科数学考点专练——三角函数答案
1-5ACCDA 6-8CCA
9、135
10.
43 解:222tan 4tan 2,tan 2.11tan 3
αααα-==-∴==- 11.725- 解:由3sin()25πθ+=得3cos 5θ=;2237cos 22cos 12()1525
θθ=-=⨯-=- 12.10 解:2105T ππωω==⇒= 13
解:解法一:
2222sin 13sin cos 31tan cot sin 22sin cos 22x x x y x x x x x ++===+≥= 三、解答题
1、根据三角函数的定义,得4sin 5α=,12sin 13β=. 又α是锐角,所以3cos 5α=
( 4分) (2)由(1)知12sin 13β=.因为β是钝角,所以5cos 13
β=-. 所以5312433c o s ()c o s c o ss i n s i n ()13565βαβαβα-=+=-⨯+
⨯=. ( 8分) (3)由题意可知,(c o s s i n)O A αα= ,,(O C . 所以()i nc o s 2s i n ()6f O A π
αααα
=⋅-=- , 因为0
2πα<<,所以663πππα-<-<,1s i
n ()26a π-<- 从而1()f α-<
()f O A O C α=⋅ 的值域为(-. ( 12分)
2、【解析】法一:(Ⅰ):令()0f x =,得 sin cos )0x x x ⋅+=,……1分
得 πsin(2)3x -=……4分因为π[,π]2x ∈,所以π2π5π2[]333x -∈,.…………5分 所以,当π4π233x -=,或π5π233
x -=时,()0f x =.……7分 即 5π6x =或πx =时,()0f x =.综上,函数)(x f 的零点为5π6
或π.………9分
(Ⅱ):由(Ⅰ)可知,当π2π233
x -=,即π2x =时,)(x f 11分
当π3π232x -=,即11π12x =时,)(x f 的最小值为12
-+. ………………13分 3、【解析】1)62sin(212cos 2sin 3)(+-=+-=
πx x x x f . (Ⅰ)由ππ
π
ππ
k x k 226222+≤-≤+-,解得Z k k x k ∈+≤≤+-,36ππ
ππ
.
所以,)(x f 的递增区间为]3,6[ππ
ππ
k k ++-Z ∈k ,. ……………(5分)
(Ⅱ)由()2f x m -<,得()x f m >+2对一切]2,0[π
∈x 均成立.
4、
5、(1)211()cos cos 2cos 2122
f x x x x x x =--=--sin(2)16x π=-- ∴ ()f x 的最小值为2-,最小正周期为π.…………5分
(2)∵ ()sin(2)106
f C C π=-
-=, 即sin(2)16C π
-= ∵ 0C π<<,112666C πππ-<-<,∴ 262C ππ-=,∴ 3C π=. ……7分 ∵ m 与n 共线,∴ sin 2sin 0B A -=.由正弦定理 sin sin a b A B =, 得2,b a = ①…9分。
