第4章6节 高斯求积公式
合集下载
高斯求积公式
x xj xi xj
ji
高斯求积公式具有较高的代数精度((2n+1)阶）, 并且是数值稳定的.
三、几种常见的高斯求积公式
1.高斯-勒让德求积公式
取( x) 1,积分区间为[1,1]上的高斯求积公式
称为高斯－勒让德公式。
1
f ( x)dx
1
n
i f ( xi )
i0
xi 勒让德多项式的零点
式 Ln( x)，
由插值原理，可用插值多项式Ln( x)作为 f ( x)的近似，由于多项式求导较为简单，
f (k ) ( x) L(nk ) ( x) (k 1,2, , n) 这 样 建 立 的 数 值 微 分 公式 称 为 插 值 型 数 值 微分公式。
应当指出，即使 f (x) 与 Ln( x)处处相差不多， f ( x) 与 Ln ( x) 在某些点仍然可能出入很大.
f
( x0 )
+
1
f
( x1 )
令f ( x) 1, x, x 2 , x 3 使上式成立，得非线性方程组
0＋1＝2
0
x0
+ 1 x1
0
0
x
2 0
0
x03
+ 1 x12 + 1 x13
2
3 0
0 1
1 1
x0
3 3
x1
3 3
由此得两点公式
1
f ( x)dx f (
3)+ f(
以高斯点 xk (k 0,1, , n)为零点的 n+1次多项式，
pn+1( x) ( x x0 )( x x1 ) ( x xn )
称为勒让德(Legendre)多项式。
高斯求积公式
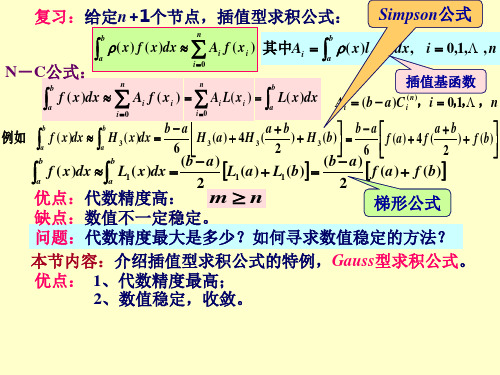
定理4 求积公式(2.2)是Gauss型的 Gauss点a<x0<…<xn <b
是[a,b]上关于权 ( x)的n+1次正交多项式的根。
分析：“充分性”即是引理1的结论。以下只证必要性
“必要性”，即Gauss点作为节点正是n+1次正交多项式的根。
只需证 n1(x) 关于( x) 正交。 证明：取2n 1次多项式f ( x) n1( x)q( x) ( x x0 ) ( x xn )q( x)，
q( x)为次数 n的多项式。
则有
b
Gauss点 的 定 义
a ( x)n1( x)q( x)dx
n
Akn1 ( xk )q( xk ) 0，
k 0
由于左端等于0，即( n1 ( x)，q( x)) 0,
n1 ( x)在a, b上关于权 ( x)是n 1次正交多项式，
则 x（k k 0，1， ，n）是n 1次正交多项式 n1( x)的根。
max
a
a
2、收敛性 引理2 对于有限闭区间[a, b] 上的任何连续函数 f ( x)有
lim R[ f ] 0
(2.4)
n
证明 : [a, b] 上的连续函数 f ( x) 可以用代数多项式一致逼近,
对任意给定的
max |
a xb
f
0,
(x
存在某个多项式
) qm ( x) | b
2 (
qm (x x)dx
由
b
a ( x)H2n1( x)dx
n
Ak H 2n1( xk )
k0
b
n
Ak f ( xk ) (
k0
b
( x) f ( x)dx I( f ))
第4章6节+高斯求积公式
f
(
1 ), 3
19
令它对 f (x) 1, x 都准确成立，有
A0 A0
A1 1 3
2;
A1
1 0. 3
由此解出 A0 A1 1, 从而得到两点高斯-勒让德求积公式
1
1
1
f (x)dx f ( ) f ( ).
0.0000000 0.8611363
0.3399810 0.9061798
0.5384693
0.0000000
Ak 2.0000000
1.0000000 0.5555556
0.8888889 0.3478548
0.6521452 0.2369269
0.4786287
0.5688889
1
3
3
三点高斯-勒让德公式的形式是
1 f (x)dx 5 f ( 15 ) 8 f (0) 5 f ( 15 ).
1
9
59
95
表4-7列出了高斯-勒让德求积公式的节点和系数.
20
n 0 1 2
3
4
表4 - 7
xk 0.0000000
0.5773503 0.7745967
证：令g(x)=(x-x0)2…(x-xn)2
I (g)
b
(x)g(x)dx 0
a
n
In Ak g(xk ) 0( g(xk ) 0) k 0
对2n 2次多项式不精确成立。
4
定义 若n+1个互异节点的插值型求积公式 的代数精度达到2n+1次，则称此n+1个互 异节点为高斯点， 此求积公式为高斯型 求积公式。
(
1 ), 3
19
令它对 f (x) 1, x 都准确成立，有
A0 A0
A1 1 3
2;
A1
1 0. 3
由此解出 A0 A1 1, 从而得到两点高斯-勒让德求积公式
1
1
1
f (x)dx f ( ) f ( ).
0.0000000 0.8611363
0.3399810 0.9061798
0.5384693
0.0000000
Ak 2.0000000
1.0000000 0.5555556
0.8888889 0.3478548
0.6521452 0.2369269
0.4786287
0.5688889
1
3
3
三点高斯-勒让德公式的形式是
1 f (x)dx 5 f ( 15 ) 8 f (0) 5 f ( 15 ).
1
9
59
95
表4-7列出了高斯-勒让德求积公式的节点和系数.
20
n 0 1 2
3
4
表4 - 7
xk 0.0000000
0.5773503 0.7745967
证：令g(x)=(x-x0)2…(x-xn)2
I (g)
b
(x)g(x)dx 0
a
n
In Ak g(xk ) 0( g(xk ) 0) k 0
对2n 2次多项式不精确成立。
4
定义 若n+1个互异节点的插值型求积公式 的代数精度达到2n+1次，则称此n+1个互 异节点为高斯点， 此求积公式为高斯型 求积公式。
第四节 高斯公式
分析：由于 p( x) ( x)是次数不高于 2 n 1的多项式，因而高斯公式准确成立。有
1
－1
p( x) ( x)dx Ak p( xk ) ( xk ) 0
k 1
n
内江师范学院数学与信息科学学院 吴开腾 制作
注释：利用正交的线性性质。把 P( x)
i a x i 用 i 0
n 1
P( x) xk , k 0,1,
定理* 节点 xk (k 1, 2,
1
, n 1
进行表示，于是有
, n) 是高斯点的充分必要条件是多
项式 x j 与一切次数 n 1 的多项式 ( x) 正交，即成立
－1
x j ( x)dx 0, j 0,1,
, n 1
内江师范学院数学与信息科学学院 吴开腾 制作
求解上述非线性方程有：
1 x2 x1 3 A 1 A 2 1
二点高斯公式的具体形式为
1
－1
1 1 f x dx f ( ) f ( ) 3 3
内江师范学院数学与信息科学学院 吴开腾 制作
4、任意区间上二点高斯公式
内江师范学院数学与信息科学学院 吴开腾 制作
一、高精度的求积公式
1、高斯公式（Gauss）的定义
设 ห้องสมุดไป่ตู้ 1, b 1 ，有求积公式
1
1
f ( x)dx Ak f ( xk )
k 1
n
(30)
高斯公式（Gauss）的定义：对于插值型求积公式（30），
适当地选取求积节点 xk (k 1, 2,
三点高斯公式为
1
1
－1
p( x) ( x)dx Ak p( xk ) ( xk ) 0
k 1
n
内江师范学院数学与信息科学学院 吴开腾 制作
注释：利用正交的线性性质。把 P( x)
i a x i 用 i 0
n 1
P( x) xk , k 0,1,
定理* 节点 xk (k 1, 2,
1
, n 1
进行表示，于是有
, n) 是高斯点的充分必要条件是多
项式 x j 与一切次数 n 1 的多项式 ( x) 正交，即成立
－1
x j ( x)dx 0, j 0,1,
, n 1
内江师范学院数学与信息科学学院 吴开腾 制作
求解上述非线性方程有：
1 x2 x1 3 A 1 A 2 1
二点高斯公式的具体形式为
1
－1
1 1 f x dx f ( ) f ( ) 3 3
内江师范学院数学与信息科学学院 吴开腾 制作
4、任意区间上二点高斯公式
内江师范学院数学与信息科学学院 吴开腾 制作
一、高精度的求积公式
1、高斯公式（Gauss）的定义
设 ห้องสมุดไป่ตู้ 1, b 1 ，有求积公式
1
1
f ( x)dx Ak f ( xk )
k 1
n
(30)
高斯公式（Gauss）的定义：对于插值型求积公式（30），
适当地选取求积节点 xk (k 1, 2,
三点高斯公式为
1
数值分析课件_高斯求积公式
b
a
f ( x ) ( x )dx Ak f ( xk )
k 0
b b
n
2
a
f ( x ) ( x )dx p( x ) ( x )dx
a
b
a
p( x ) ( x )dx Ak p( xk )
k 0
n
n
0
2
m 2n 1
Ak p( xk ) Ak f ( xk )
证明：由Weierstrass定理知
f p max f p
a xb
则Gauss型求积公式（*）是收敛的。 对
0
b
存在m次多项式
下证
p( x ) 满足
fp
n
N ,
当n
N时
k 0
2 ( x )dx
a
b
a
f ( x ) ( x )dx Ak f ( xk )
的插值型求积公式的代数精度最高不超过2n+1次。 只需证明：对于上述插值型求积公式，存在一个 2n+2次多项式，使得求积公式不能精确成立。
2 n1
令 f ( x)
因为
b
( x)
b a
其中 n 1 ( x ) ( x xk )
k 0
n
f ( x)dx 而 A f (x ) 0
k 0
n
与任何不超过n次的多项式 p( x ) 带权正交:
b a
p( x )n1 ( x ) ( x )dx 0
证明： 必要性 设
p( x ) H n
高数高斯公式
R z
)dv
Pdydz
Qdzdx
Rdxdy
2、高斯公式的实质
（1）应用的条件
（2）物理意义 divAdv AdS
21
习题10 6
P174
高斯 ( Gauss ) 公 式25
1(2)(3)(4),2(3),3(2)
22
1
3
x2 y2 dxdy
Dxy
2
d
R
r rdr
2 R3
0
0
3
1
1
1
高斯
1 4 R3 2 R3 4 R3
( Gauss ) 公 式10
23
3
3
9
例 3 计算曲面积分
高斯
( x2 cos y2 cos z2 cos )ds,其中Σ为
( Gauss ) 公 式11
解 P ( y z)x, Q 0, x R x y,
1
3
z
o1
y
5
P y z, Q 0, R 0,
x
y
z
z
高斯 ( Gauss ) 公
式7
1
3
原式 ( y z)dxdydz
(利用柱面坐标得)
(r sin z)rdrddz
o1
y
x
2
1
3
0 d 0 rdr 0 (r sin z)dz
A( x, y, z) P( x, y, z)i Q( x, y, z) j R( x, y, z)k
沿场中某一有向曲面Σ的第二类曲面积分为
AdS Pdydz Qdzdx Rdxdy
如E为称电为场向强量 度,场单A位(时x,间y,通z)过向正的侧电穿通过量曲面I Σ的E通dS量.
高斯求积公式范文
高斯求积公式范文高斯求积公式，也称为高斯–勒让德求积公式（Gauss-Legendre Quadrature），是数值计算中一种常见的数值积分方法。
它通过选择适当的节点和权重来近似计算一个确定积分的值。
高斯求积公式的基本思想是通过选取合适的节点，使得积分节点上的函数值和求积公式的节点值与相应的权重值的乘积之和等于被积函数的积分。
要了解高斯求积公式，首先需要了解勒让德多项式（Legendre Polynomials）。
勒让德多项式是定义在区间[-1,1]上的一个连续函数系列，它们具有许多重要的性质。
其中最为重要的性质是勒让德多项式是在[-1,1]上正交的，即在区间[-1,1]上的积分为0，除非两个不同的多项式相乘。
高斯求积公式可以通过使用勒让德多项式的正交性质来推导。
假设我们要计算函数f(x)在区间[-1,1]上的积分，可以通过勒让德多项式来近似这个积分。
具体的做法是，首先选择一个适当的正整数n，计算n个勒让德多项式。
然后，在区间[-1,1]上选择n个互不相同的节点x_i，通过求解勒让德多项式的根来得到这些节点。
接下来，计算n个权重w_i，使得求积公式的节点值与权重值之积的和等于被积函数在区间[-1,1]上的积分。
对于一个给定的n，高斯求积公式的节点和权重可以通过一系列的计算得到。
首先，通过求解勒让德多项式的根来得到节点。
勒让德多项式的根是对应于勒让德多项式的零点的x值。
然后，通过求解勒让德多项式的导数来得到权重。
通过这些计算，我们可以得到一组称为高斯节点和权重的数值。
利用高斯节点和权重，我们可以将原始的积分问题转化为一组简单的加权求和问题。
具体地，我们可以将被积函数f(x)展开为勒让德多项式的级数形式，然后将这个级数代入原始积分的公式中，使用高斯节点和权重来计算每一项的值，最后将这些值相加得到积分的数值近似值。
1.高准确性：高斯求积公式可以提供非常精确的数值积分结果。
2.高效性：高斯求积公式可以通过选择适当的节点和权重，使计算量最小化。
高斯求积公式
总结
1：梯形求积公式和抛物线求积公式是低精度的方法，但对于光滑 性较差的函数有时比用高精度方法能得到更好的效果。复化梯形 公式和抛物线求积公式，精度较高，计算较简，使用非常广泛。 2：Romberg求积方法，算法简单，当节点加密提高积分近似程度 时，前面的计算结果可以为后面的计算使用，因此，对减少计算 量很有好处。并有比较简单的误差估计方法。 3。Gauss型求积，它的节点是不规则的，所以当节点增加时，前 面的计算的函数值不能被后面利用。计算过程比较麻烦，但精度 高，特别是对计算无穷区间上的积分和旁义积分，则是其他方法 所不能比的。
n
证明： 时代入公式， 证明：分别取 f(x)=1, x，x2，...xn 时代入公式，并让其成为等式得 ，
A1 + A2 + …… + An =∫ab1dx.= b-a +xn An =∫abxdx.= （b2-a 2)/2 ...... x1 rA1 + x2 rA2+ …… +xn rAn =∫abxr dxr =(br+1-a r+1)/ (r+1) 等式， 个待定系数 变元),要想如上方程组有唯一解 个待定系数(变元 要想如上方程组有唯一解， 上式共有 r 个 等式，2n个待定系数 变元 要想如上方程组有唯一解，应有方 程组中方程的个数等于变元的个数,即 程组中方程的个数等于变元的个数 即 r=2n,这样求出的解答应的求积公式的代 这样求出的解答应的求积公式的代 数精度至少是2n-1,下面证明代数精度只能是2n-1. 下面证明代数精度只能是 数精度至少是 下面证明代数精度只能是 [ 如果事先已选定 ，b]中求积节点 k如下a≤x1 ≤…x n≤b,上式成为 个未知 如果事先已选定[a 中求积节点x 上式成为n个未知 中求积节点 如下 ≤ 上式成为 元线性方程组， 时方程组有唯一解 有唯一解] 数 A1、...An的n元线性方程组，此时要 元线性方程组 此时要r=n 时方程组有唯一解 、 x1 A1 + x2 A2+ ……
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
b a
b
n
f ( xk ).
12
可见求积公式对一切次数不超过 确成立. 因此， xk (k
2n 1
的多项式均精
0,1, , n)为高斯点.
定理表明在 [ a, b]上带权 ( x )的 零点就是求积公式的高斯点. 有了求积节点
次正交多项式的 n 1
xk (k 0,1, , n)，再利用
2 9
7
; ;
.
由此解出
x0 x1
5 21
,
x0 x1
10 9
,
从而
8
1
0
x f ( x)dx A0 f ( x0 ) A f ( x1 ). 1
x0 0.821162, A0 0.389111,
m 这样，高斯公式是 A x
x1 0.289949; A 0.277556. 1
~
n1
( x) 是最高项系数为1的勒让德多项式.
~ Pn ( x)
n!
d
n n
[( x
2
1) ].
n
( 2n)! dx
n
1
1
m n; 0, f ( xn ( x) Pm ( x )dxk xk 2. A f( ) 1 P)dx m n. k 0 2n 1
a
2 n 1
故成立.
n1
b 对于 x)f ( x1x) ( x)用 0.( x) 除 充分性. P( n ) ( H , dx
f ( x)
， ,
记商为 P ( x ), 余式为
q ( x ),
即
f ( x) P( x)n 1 ( x) q( x)
其中 P( x), q( x) H n.
[1,1]
上辛普森公式的余项
1
1
f ( x)dx f (
三点高斯-勒让德公式的形式是
1 1
f ( x)dx
5 9
f (
15 5
)
8 9
f (0)
5 9
f(
15 5
).
表4-7列出了高斯-勒让德求积公式的节点和系数.
20
表4 - 7 n 0 1 2 0. 0000000 0. 8611363 3 0. 3399810 0. 9061798 0. 5384693 0. 0000000 0. 8888889 0. 3478548 0. 6521452 0.2369269 0.4786287 0. 5688889 xk 0. 0000000 0. 5773503 0. 7745967 Ak 2. 0000000 1 0000000 . 0. 5555556
b
I
b
f ( x) ( x)dx,
a
f ( x ) ( x )dx
a
A
k 0
n
k
f ( xk ),
的求积系数. Ak (k 0,1, , n) 为不依赖于 f ( x ) 为求积节点， xk (k 0,1 , n) , 适当选取 使其具有最高 次代数精度
xk 及Ak
b
a
P( x)n 1) ) )dxdx q( x) ( x)dx. f ( x ( x ( x ( x) 0.
b b a a
11
由于求积公式是插值型的， 即
它对于q( x) H
n
是精确的，
b
a
P( x) n 1 ( x) ( x)dx 0.
b
再注意到
f ( x) P( x)n1 ( x) 精确成立，即有
因
b
a
n P ( x )n 1 ( x ) ( x ) dx b
f ( x ) ( x )dx
a
k 0
A P x ), ( x A f (
k
kk 0 k
n
k
)n 1 ( xk ).
n 1 ( xk ) 0(k 0,1, , n),
4
21
余项
( 2 n 2) b f f ( ) ( ) 2 1 ~ 2 Rn [ f ] f ] Pn x)) x Rn [ a)! n 1 ( x)1 (( xddx. [1,1], 1 (2n 2)! 2 ( 2n ( 2 n 2)
这里 P
2
n
x xj
k
xj
,
它是 n次多项式， 因而
故高斯求积 l k ( x ) 是 2n次多项式，
公式对于它能准确成立，即有
0
b
a
lk ( x ) ( x )dx
2
Al
i i 0
n
2 k
( xi ).
注意到
lk ( xi ) ki , 上式右端实际上即等于 Ak ,
从而有
3
定理 n+1个节点的插值型求积公式的代数精度 不超过2n+1. 证：令g(x)=(x-x0)2…(x-xn)2
I (g)
n
b
( x) g ( x)dx 0
a
I n Ak g ( xk ) 0( g ( xk ) 0)
k 0
对2n 2次多项式不精确成立。
4
1
22
得
Rn [ f ] 2
2 n 3
[( n 1)!]
4 3
(2n 3)[( 2n 2)!]
f
( 2 n 2)
( )
(1,1).
当 n 1 时，有
R1[ f ] 1 135 R1[ f ] 1 90 f
( 4)
f
( 4)
( ). ( )
它比区间
1 3
) A f ( 1
),
令它对
f ( x) 1, x
都准确成立，有
A0 A 2; 1 1 1 A0 A 0. 1 3 3
由此解出
A0 A 1, 1
从而得到两点高斯-勒让德求积公式
1 3 ) f ( 1 3 ).
Rn [ f ] I Ak f ( xk )
k 0 n
b
f
( 2 n 2)
( )
a
(2n 2)!
2 n 1 ( x) ( x)dx.
由于
2 n 1
( x) ( x) 0,
由积分中值定理得为
Rn [ f ]
b
f
( 2 n 2)
( )
(2n 2)!
解 令公式(5.3)对于 f ( x) 1, x, x 2 , x 3 准确成立，
得
2 A0 A ; 1 3 x A x A 0 0 0 0 2 2 1 x0 A0 x1 A 3 3 x0 A0 x1 A 1 2 5 2 7
而从分析高斯点的特性来构造高斯求积公式.
9
b
f ( x ) ( x )dx
a
A
k 0
n
k
f ( xk ),
定理5 插值型求积公式的节点
a x0 x1 xn b
是高斯点的充分必要条件是以这些节点为零点的多项式
n 1 ( x) ( x x0 )( x x1 ) ( x xn )
m 0,1, ,2n 1.
n
k
k
k 0 1
b
x ( x)dx,
m
a
x f ( x)dx 0.389111 f (0.821162)
0
0.277556 f (0.289949).
由于非线性方程组较复杂， 故一般不通过解方程
通常 n 2就很难求解.
求xk 及Ak (k 0,1,, n) ，
定义 若n+1个互异节点的插值型求积公式 的代数精度达到2n+1次，则称此n+1个互 异节点为高斯点， 此求积公式为高斯型 求积公式。
5
根据定义要使求积公式具有 2n 1次代数精度，只要对
f ( x) x
m
(m 0,1, ,2n 1),
令
b
f ( x ) ( x )d x
与任何次数不超过 n 的多项式 P ( x )带权 ( x ) 正交，即
b
a
P( x) n 1 ( x) ( x)dx 0.
证明 必要性. 设 P( x) H n , 则 P( x) n1 ( x) H 2 n1 ,
10
因此，如果
x0 , x1 , , xn
是高斯点，则求积公式对于
a k k k 0
b
n
Ak (k 0,1, , n).
下面讨论高斯求积公式的余项. 利用
H 2 n1 ,
f ( x ) 在节点 xk (k 0,1, , n) 的埃尔米特插值
即
H 2 n1 ( xk ) f ( xk ), k 0,1,, n.
H 2 n1 ( xk ) f ( xk ),
§6
高斯求积公式
1
1.
求积公式
b
一般理论
n
f ( x )dx
a
A
k 0
k
f ( xk )
含有 2n 2个待定参数 当
xk , Ak (k 0,1, , n).
x k为等距节点时得到的插值求积公式其代数精度至
b
n
f ( xk ).
12
可见求积公式对一切次数不超过 确成立. 因此， xk (k
2n 1
的多项式均精
0,1, , n)为高斯点.
定理表明在 [ a, b]上带权 ( x )的 零点就是求积公式的高斯点. 有了求积节点
次正交多项式的 n 1
xk (k 0,1, , n)，再利用
2 9
7
; ;
.
由此解出
x0 x1
5 21
,
x0 x1
10 9
,
从而
8
1
0
x f ( x)dx A0 f ( x0 ) A f ( x1 ). 1
x0 0.821162, A0 0.389111,
m 这样，高斯公式是 A x
x1 0.289949; A 0.277556. 1
~
n1
( x) 是最高项系数为1的勒让德多项式.
~ Pn ( x)
n!
d
n n
[( x
2
1) ].
n
( 2n)! dx
n
1
1
m n; 0, f ( xn ( x) Pm ( x )dxk xk 2. A f( ) 1 P)dx m n. k 0 2n 1
a
2 n 1
故成立.
n1
b 对于 x)f ( x1x) ( x)用 0.( x) 除 充分性. P( n ) ( H , dx
f ( x)
， ,
记商为 P ( x ), 余式为
q ( x ),
即
f ( x) P( x)n 1 ( x) q( x)
其中 P( x), q( x) H n.
[1,1]
上辛普森公式的余项
1
1
f ( x)dx f (
三点高斯-勒让德公式的形式是
1 1
f ( x)dx
5 9
f (
15 5
)
8 9
f (0)
5 9
f(
15 5
).
表4-7列出了高斯-勒让德求积公式的节点和系数.
20
表4 - 7 n 0 1 2 0. 0000000 0. 8611363 3 0. 3399810 0. 9061798 0. 5384693 0. 0000000 0. 8888889 0. 3478548 0. 6521452 0.2369269 0.4786287 0. 5688889 xk 0. 0000000 0. 5773503 0. 7745967 Ak 2. 0000000 1 0000000 . 0. 5555556
b
I
b
f ( x) ( x)dx,
a
f ( x ) ( x )dx
a
A
k 0
n
k
f ( xk ),
的求积系数. Ak (k 0,1, , n) 为不依赖于 f ( x ) 为求积节点， xk (k 0,1 , n) , 适当选取 使其具有最高 次代数精度
xk 及Ak
b
a
P( x)n 1) ) )dxdx q( x) ( x)dx. f ( x ( x ( x ( x) 0.
b b a a
11
由于求积公式是插值型的， 即
它对于q( x) H
n
是精确的，
b
a
P( x) n 1 ( x) ( x)dx 0.
b
再注意到
f ( x) P( x)n1 ( x) 精确成立，即有
因
b
a
n P ( x )n 1 ( x ) ( x ) dx b
f ( x ) ( x )dx
a
k 0
A P x ), ( x A f (
k
kk 0 k
n
k
)n 1 ( xk ).
n 1 ( xk ) 0(k 0,1, , n),
4
21
余项
( 2 n 2) b f f ( ) ( ) 2 1 ~ 2 Rn [ f ] f ] Pn x)) x Rn [ a)! n 1 ( x)1 (( xddx. [1,1], 1 (2n 2)! 2 ( 2n ( 2 n 2)
这里 P
2
n
x xj
k
xj
,
它是 n次多项式， 因而
故高斯求积 l k ( x ) 是 2n次多项式，
公式对于它能准确成立，即有
0
b
a
lk ( x ) ( x )dx
2
Al
i i 0
n
2 k
( xi ).
注意到
lk ( xi ) ki , 上式右端实际上即等于 Ak ,
从而有
3
定理 n+1个节点的插值型求积公式的代数精度 不超过2n+1. 证：令g(x)=(x-x0)2…(x-xn)2
I (g)
n
b
( x) g ( x)dx 0
a
I n Ak g ( xk ) 0( g ( xk ) 0)
k 0
对2n 2次多项式不精确成立。
4
1
22
得
Rn [ f ] 2
2 n 3
[( n 1)!]
4 3
(2n 3)[( 2n 2)!]
f
( 2 n 2)
( )
(1,1).
当 n 1 时，有
R1[ f ] 1 135 R1[ f ] 1 90 f
( 4)
f
( 4)
( ). ( )
它比区间
1 3
) A f ( 1
),
令它对
f ( x) 1, x
都准确成立，有
A0 A 2; 1 1 1 A0 A 0. 1 3 3
由此解出
A0 A 1, 1
从而得到两点高斯-勒让德求积公式
1 3 ) f ( 1 3 ).
Rn [ f ] I Ak f ( xk )
k 0 n
b
f
( 2 n 2)
( )
a
(2n 2)!
2 n 1 ( x) ( x)dx.
由于
2 n 1
( x) ( x) 0,
由积分中值定理得为
Rn [ f ]
b
f
( 2 n 2)
( )
(2n 2)!
解 令公式(5.3)对于 f ( x) 1, x, x 2 , x 3 准确成立，
得
2 A0 A ; 1 3 x A x A 0 0 0 0 2 2 1 x0 A0 x1 A 3 3 x0 A0 x1 A 1 2 5 2 7
而从分析高斯点的特性来构造高斯求积公式.
9
b
f ( x ) ( x )dx
a
A
k 0
n
k
f ( xk ),
定理5 插值型求积公式的节点
a x0 x1 xn b
是高斯点的充分必要条件是以这些节点为零点的多项式
n 1 ( x) ( x x0 )( x x1 ) ( x xn )
m 0,1, ,2n 1.
n
k
k
k 0 1
b
x ( x)dx,
m
a
x f ( x)dx 0.389111 f (0.821162)
0
0.277556 f (0.289949).
由于非线性方程组较复杂， 故一般不通过解方程
通常 n 2就很难求解.
求xk 及Ak (k 0,1,, n) ，
定义 若n+1个互异节点的插值型求积公式 的代数精度达到2n+1次，则称此n+1个互 异节点为高斯点， 此求积公式为高斯型 求积公式。
5
根据定义要使求积公式具有 2n 1次代数精度，只要对
f ( x) x
m
(m 0,1, ,2n 1),
令
b
f ( x ) ( x )d x
与任何次数不超过 n 的多项式 P ( x )带权 ( x ) 正交，即
b
a
P( x) n 1 ( x) ( x)dx 0.
证明 必要性. 设 P( x) H n , 则 P( x) n1 ( x) H 2 n1 ,
10
因此，如果
x0 , x1 , , xn
是高斯点，则求积公式对于
a k k k 0
b
n
Ak (k 0,1, , n).
下面讨论高斯求积公式的余项. 利用
H 2 n1 ,
f ( x ) 在节点 xk (k 0,1, , n) 的埃尔米特插值
即
H 2 n1 ( xk ) f ( xk ), k 0,1,, n.
H 2 n1 ( xk ) f ( xk ),
§6
高斯求积公式
1
1.
求积公式
b
一般理论
n
f ( x )dx
a
A
k 0
k
f ( xk )
含有 2n 2个待定参数 当
xk , Ak (k 0,1, , n).
x k为等距节点时得到的插值求积公式其代数精度至