四年级数学数阵图(二)例题讲解
四年级下册数学讲义-奥数专题讲练:第十讲 有趣的数阵图(二)(例题解析版)全国通用

第十讲有趣的数阵图(二)下面我们继续研究有关数阵图的问题.例1 将1~7这七个自然数分别填入右图的7个小圆圈中,使三个大圆圆周上及内部的四个数之和都等于定数S,并指出这个定数S的取值范围,最小是多少,最大是多少?并对S最小值填出数阵.分析为了叙述方便,用字母表示圆圈中的数.通过观察,我们发现,三个大圆上,每个大圆上都有4个小圆,由题设每个大圆上的4个小圆之和为S.从图中不难看出:B是三个圆的公共部分,A、C、D分别是两个圆的公共部分而E、F、G仅各自属于一个圆.这样三个大圆的数字和为:3S=3B+2A+2C+2D+E+F+G,而A、B、…、F、G这7个数的全体恰好是1、2、…、6、7.∴3S=1+2+3+4+5+6+7+2B+A+C+D.3S=28+2B+A+C+D.如果设2B+A+C+D=W,要使S等于定数即W最小发生于B=1、A=2、C=3、D=4W最大发生于B=7、A=6、C=5、D=4,综上所述,得出:13≤S≤19即定数可以取13~19中间的整数.本题要求S=13,那么A=2、B=1、C=3、D=4、E=5、F=6、G=7.注意:解答这类问题常常抓两个要点,一是某种共同的“和数”S.(同一条边上各数和,同一三角形上各数和,同一圆上各数和等等).二是全局考虑数阵的各数被相加的“次”数.主要突破口是估算或确定出S 的值.从“中心数”B处考虑.(B是三个大圆的公共部分,常根据S来设定B的可能值.这里重视B不是简单地看到B处于几何中心,主要因为B参与相加的次数最多)此处因为定数是13,中心数可从1开始考虑.确定了S和中心数B,其他问题就容易解决了.解:例2 把20以内的质数分别填入右图的八个圆圈中,使圈中用箭头连接起来的每条路上的四个数之和都相等.分析观察右图,我们发现:①有3条路,每条路上有4个数,且4个数相加的和要相等.②图形两端的两个数是三条路的公共起点和终点.因此只要使三条路上其余两个数的和相等,就可以确保每条路上的四个数的和相等.③20以内的质数共有8个,依次是2、3、5、7、11、13、17、19.如果能从这八个数中选出六个数凑成相等的三对数,问题就可迎刃而解.如要分析,设起点数为X,终点数为y,每条路上4个数之和为S,显然有:3S=2x+2y+2+3+5+7+11+13+17+19=2x+2y+77.即S最小=29,此时x=2,y=3但这时,中间二个质数之和为47-(19+13)=15,但17>15,17无处填.所以S=47是无法实现的.这题还另有一个独特的分析推理.即惟一的偶质数必处于起点或终点位上.不然,其他路上为4个质数之和,2处于中间位的路上.这条路为3奇1偶相加,另两条路上为4个奇相加,形成矛盾.再进一步分析,(终点,始点地位对称)始点放上2,终点放上另一个质数,其他6个质数之和必为3的倍数.而经试算,只有终点放上3,而可满足的解法只有一种(已在下图中表出).解:这样,轻而举地可得到:5+19=24,7+17=24,11+13=24.例3 把1、2、3、4、5、6、7、8这八个数分别填入右图中的正方形的各个圆圈中,使得正方形每边上的三个数的和相等.分析和解假设每边上的三数之和为S,四边上中间圆圈内所填数分别为a、b、c、d,那么:a+c=b+d=(1+2+…+8)-2S=36-2S∴2S=36-(a+C)=36-(b+d)①_x0001_S=15,则a+c=b+d=6,又1+5=2+4=6,试验可得下图②若S=14,则a+c=b+d=8,又1+7=2+6=3+5=8,试验可得下两图③若S=13,则a+c=b+d=10,又2+8=3+7=4+610,试验可得下两图④若S=12,则a+c=b+d=12,又4+8=5+7=12,试验可得下图例4 在一个立方体各个顶点上分别填入1~9这九个数中的八个数,使得每个面上四个顶点所填数字之和彼此相等,并且这个和数不能被那个没有被标上的数字整除.试求:没有被标上的数字是多少?并给出一种填数的方法.分析为了叙述方便,设没有被标上的数字为a,S是每个面上的四个顶点上的数字之和.由于每个顶点数都属于3个面,所以得到:6S=3×(1+2+3+4+5+6+7+8+9)-3a6S=3×45-3a2S=45-a (1)根据(1)式可看出:因为左边2S是偶数,所以右边45-a也必须是偶数,故a必须是奇数.又因为根据题意,S不能被a整除,而2与a互质,所以2S不能被a整除,45也一定不能被a整除.”在奇数数字1、3、5、7、9中,只有7不能整除45,所以可以确定a=7.这就证明正方体每个面上四个顶点所填数字之和是19,解法如图.例5 将1~8这八个数标在立方体的八个顶点上,使得每个面的四个顶点所标数字之和都相等.分析观察下图,知道每个顶点属于三个面,正方体有6个面,所以每个面的数字之和为:(1+2+3+4+5+6+7+8)×3÷6=18.这就是说明正方体每个面上四个顶点所填数字之和是18.下面有3种填法的提示,作为练习,请读者补充完整.解:例6 在下左图中,将1~9这九个数,填人圆圈内,使每个三角形三个顶点的数字之和都相等.分析为了便于叙述说明,圆圈内应填的数,先由字母代替.设每个三角形三个顶点圆圈内的数字和为S.即:A+B+C=S、D+E+F=S、G+H+I=S、C+G+E=S、A+G+D=S、B+H+E=S、C+I+F=S.将上面七个等式相加得到:2(A+B+C+D+E+F+G+H+I)+C+G+E=7S.即:A+B+C+D+E+F+G+H+I=3S又∵A、B、C、D、E、F、G、H、I,分别代表1~9这九个数.即:1+2+3+4+5+6+7+8+9=45.3S=45S=15.这15就说明每个三角形三个顶点的数字之和是15.在1~9九个数中,三个数的和等于15的组合情况有以下8种即:(1、9、5);(1、8、6);(2、9、4);(2、8、5);(3、7、5);(2、7、6);(3、8、4);(4、5、6);观察九个数字在上述8种情况下出现的次数看,数字2、4、5、6、8都均出现了三次,其他数字均只出现两次,所以,符合题意的组合中的2、8、5和4、5、6可填入图中的圆圈内,这样就得到本题的两个解.解:例7 在有大小六个正方形的方框下左图中的圆圈内,填入1~9这九个自然数,使每一个正方形角上四个数字之和相等.分析为了叙述方便,我们将各个圆圈内填入字母,如上右图所示.如果设每个正方形角上四个数字之和为S,那么图中六个正方形可得到:a1+a2+b1+b2=S,a2+b2+a3+b3=S,b1+b2+c1+b2=S,a2+b3+b2+b1=S,b2+b2+b3+c3=S,a1+a3+c3+c1=S.将上面的六个等式相加可得到:2(a1+a3+c3+c1)+3(a2+b3+b2+b1)+4b2=6S.则4b2=S4(a1+a3+c3+c1)+4(a2+b3+b2+b1)+4b2=9S.于是有:4(a1+a2+a3+b1+b2+b3+c1+b2+c3)=4×45=9S.9S=4×45S=20.这就说明每个正方形角上四个数字之和为20.所以:b2=5.从而得到:a1+a2+b1=a2+a3+b3=15,b1+c1+b2=b2+c3+b3=15.由上面两式可得:a1+b1=a3+b3,b1+c1=b3+c3.如果a2为奇数,则a1+b1和a3+b3均为偶数.①若a1为奇数,a3为偶数,则b1为奇数,b3为偶数.因为a2+b3+b2+b1=20,所以b2为偶数,则c1为偶数,c3为奇数.但是a1+a2+5+b1=20,而奇数1、3、5、7、9中含有5的任意四个奇数的和不等于20,有矛盾.②若a1为偶数,a3为偶数,则b1也为偶数,b3也为偶数.因为a2+b3+b2+b1=20,所以b2为奇数,则c1为偶数,c3为偶数,但1~9中只有4个偶数,有矛盾.③若a1为奇数,a3为奇数,则b1、b3也为奇数,这样1~9中有六个奇数,有矛盾.④若a1为偶数,a3为奇数,情况与①相同.综合上述,a2必为偶数.由对称性易知:b2、b2、b1也为偶数.因此a1、a3、c3、c1全为奇数.这样,就比较容易找到此解.解:注:也可以这样想:因为1+2+3+4+5+6+7+8+9=45,中心数用5试填后,余下40,那么大正方形、中正方形对角数字之和一定为10,比如:2+8=10、3+7=10、1+9=10、4+6=10.再利用小正方形调整一下,便可以凑出结果了.习题十1.将1~6六个自然数字分别填入下图的圆圈内,使三角形每边上的三数之和都等于定数S,指出这个定数S的取值范围.并对S=11时给出一种填法.2.将1~10这十个自然数分别填入下左图中的10个圆圈内,使五边形每条边上的三数之和都相等,并使值尽可能大.3.将1~8填入上右图中圆圈内,使每个大圆周上的五个数之和为21.。
小学数学解题方法解题技巧之数阵图

第一章小学数学解题方法解题技巧之数阵图【方阵】例1 将自然数1至9,分别填在图5.17的方格中,使得每行、每列以及两条对角线上的三个数之和都相等。
(长沙地区小学数学竞赛试题)讲析:中间一格所填的数,在计算时共算了4次,所以可先填中间一格的数。
(l+2+3+……+9)÷3=15,则符合要求的每三数之和为15。
显然,中间一数填“5”。
再将其它数字顺次填入,然后作对角线交换,再通过旋转(如图5.18),便得解答如下。
例2 从1至13这十三个数中挑出十二个数,填到图5.19的小方格中,使每一横行四个数之和相等,使每一竖列三个数之和又相等。
(“新苗杯”小学数学竞赛试题)讲析:据题意,所选的十二个数之和必须既能被 3整除,又能被 4整除,(三行四列)。
所以,能被12整除。
十三个数之和为91,91除以12,商7余7,因此,应去掉7。
每列为(91—7)÷4=21而1至13中,除7之外,共有六个奇数,它们的分布如图5.20所示。
三个奇数和为21的有两种:21=1+9+11=3+5+13。
经检验,三个奇数为3、5、13的不合要求,故不难得出答案,如图5.21所示。
例3 十个连续自然数中,9是第三大的数,把这十个数填到图5.22的十个方格中,每格填一个,要求图中三个2×2的正方形中四数之和相等。
那么,这个和数的最小值是______。
(1992年全国小学数学奥林匹克初赛试题)讲析:不难得出十个数为:2、3、4、5、6、7、8、9、10、11。
它们的和是65。
在三个2×2的正方形中,中间两个小正方形分别重复了两次。
设中间两个小正方形分别填上a和b,则(65+a+b)之和必须是 3的倍数。
所以,(a+b)之和至少是7。
故,和数的最小值是24。
【其他数阵】例1 如图5.23,横、竖各12个方格,每个方格都有一个数。
已知横行上任意三个相邻数之和为20,竖列上任意三个相邻数之和为21。
图中已填入3、5、8和“×”四个数,那么“×”代表的数是______。
四年级秋季第16讲_数阵图(四年级学生用) 2
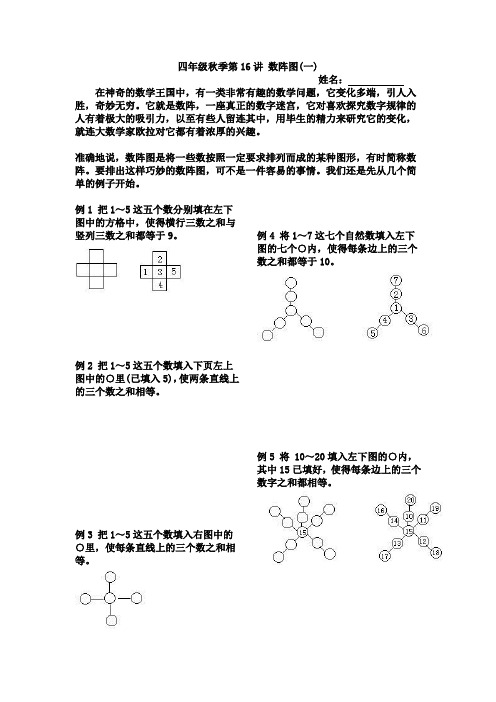
四年级秋季第16讲数阵图(一)姓名:在神奇的数学王国中,有一类非常有趣的数学问题,它变化多端,引人入胜,奇妙无穷。
它就是数阵,一座真正的数字迷宫,它对喜欢探究数字规律的人有着极大的吸引力,以至有些人留连其中,用毕生的精力来研究它的变化,就连大数学家欧拉对它都有着浓厚的兴趣。
准确地说,数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵。
要排出这样巧妙的数阵图,可不是一件容易的事情。
我们还是先从几个简单的例子开始。
例1 把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
例2 把1~5这五个数填入下页左上图中的○里(已填入5),使两条直线上的三个数之和相等。
例3 把1~5这五个数填入右图中的○里,使每条直线上的三个数之和相等。
例4 将1~7这七个自然数填入左下图的七个○内,使得每条边上的三个数之和都等于10。
例5 将 10~20填入左下图的○内,其中15已填好,使得每条边上的三个数字之和都相等。
例6 将1~8这八个数分别填入右图的○中,使两个大圆上的五个数之和都等于21。
例7 将1~6这六个自然数分别填入右图的六个○内,使得三角形每条边上的三个数之和都等于11。
例8 将1~6这六个自然数分别填入上图的六个○中,使得三角形每条边上的三个数之和都相等。
例9将2~9这八个数分别填入右图的○里,使每条边上的三个数之和都等于18。
练习161. 将1~7这七个数分别填入左下图中的○里,使每条直线上的三个数之和都等于12。
如果每条直线上的三个数之和等于10,那么又该如何填?2.将1~9这九个数分别填入右上图中的○里(其中9已填好),使每条直线上的三个数之和都相等。
如果中心数是5,那么又该如何填?3.将1~9这九个数分别填入右图的小方格里,使横行和竖列上五个数之和相等。
(至少找出两种本质上不同的填法)4.将3~9这七个数分别填入左下图的○里,使每条直线上的三个数之和等于20。
数阵图(二)例题讲解.doc

第17讲数阵图(二)例1在右图的九个方格中填入不大于12且互不相同的九个自然数(其中已填好一个数),使得任一行、任一列及两条对角线上的三个数之和都等于21。
解:由上一讲例4知中间方格中的数为7。
再设右下角的数为x,然后根据任一行、任一列及每条对角线上的三个数之和都等于21,如下图所示填上各数(含x)。
因为九个数都不大于12,由16-x≤12知4≤x,由x+2≤12知x≤10,即4≤x≤10。
考虑到5,7,9已填好,所以x只能取4,6,8或10。
经验证,当x=6或8时,九个数中均有两个数相同,不合题意;当x=4或10时可得两个解(见下图)。
这两个解实际上一样,只是方向不同而已。
例2将九个数填入右图的空格中,使得每行、每列、每条对角线上的三个数之和都相等,则一定有证明:设中心数为d。
由上讲例4知每行、每列、每条对角线上的三个数之和都等于3d。
由此计算出第一行中间的数为2d——b,右下角的数为2d-c(见下图)。
根据第一行和第三列都可以求出上图中★处的数由此得到3d-c-(2d-b)=3d-a-(2d-c),3d-c-2d+b=3d-a-2d+c,d——c+b=d——a+c,2c=a+b,a+bc=2。
值得注意的是,这个结论对于a和b并没有什么限制,可以是自然数,也可以是分数、小数;可以相同,也可以不同。
例3在下页右上图的空格中填入七个自然数,使得每一行、每一列及每一条对角线上的三个数之和都等于90。
解:由上一讲例4知,中心数为90÷3=30;由本讲例2知,右上角的数为(23+57)÷2=40(见左下图)。
其它数依次可填(见右下图)。
例4在右图的每个空格中填入个自然数,使得每一行、每一列及每条对角线上的三个数之和都相等。
解:由例2知,右下角的数为(8+10)÷2=9;由上一讲例4知,中心数为(5+9)÷2=7(见左下图),且每行、每列、每条对角线上的三数之和都等于7×3=21。
四年级奥数:数阵图

四年级奥数:数阵图(一)我们在三年级已经学习过辐射型和封闭型数阵,其解题的关键在于“重叠数”.本讲和下一讲,我们学习三阶方阵,就是将九个数按照某种要求排列成三行三列的数阵图,解题的关键仍然是“重叠数”.我们先从一道典型的例题开始.例1把1~9这九个数字填写在右图正方形的九个方格中,使得每一横行、每一竖列和每条对角线上的三个数之和都相等.分析与解:我们首先要弄清每行、每列以及每条对角线上三个数字之和是几.我们可以这样去想:因为1~9这九个数字之和是45,正好是三个横行数字之和,所以每一横行的数字之和等于45÷3=15.也就是说,每一横行、每一竖列以及每条对角线上三个数字之和都等于15.在1~9这九个数字中,三个不同的数相加等于15的有:9+5+1,9+4+2,8+6+1,8+5+2,8+4+3,7+6+2,7+5+3,6+5+4.因此每行、每列以及每条对角线上的三个数字可以是其中任一个算式中的三个数字.因为中心方格中的数既在一个横行中,又在一个竖列中,还在两对角线上,所以它应同时出现在上述的四个算式中,只有5符合条件,因此应将5填在中心方格中.同理,四个角上的数既在一个横行中,又在一个竖列中,还在一条对角线上,所以它应同时出现在上述的三个算式中,符合条件的有2,4,6,8,因此应将2,4,6,8填在四个角的方格中,同时应保证对角线两数的和相等.经试验,有下面八种不同填法:上面的八个图,都可以通过一个图的旋转和翻转得到.例如,第一行的后三个图,依次由第一个图顺时针旋转90°,180°,270°得到.又如,第二行的各图,都是由它上面的图沿竖轴翻转得到.所以,这八个图本质上是相同的,可以看作是一种填法.例1中的数阵图,我国古代称为“纵横图”、“九宫算”.一般地,将九个不同的数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列和每条对角线上的三个数之和都相等,那么这样的图称为三阶幻方.在例1中如果只要求任一横行及任一竖列的三数之和相等,而不要求两条对角线上的三数之和也相等,则解不唯一,这是因为在例1的解中,任意交换两行或两列的位置,不影响每行或每列的三数之和,故仍然是解.例2用11,13,15,17,19,21,23,25,27编制成一个三阶幻方.分析与解:给出的九个数形成一个等差数列,对照例1,1~9也是一个等差数列.不难发现:中间方格里的数字应填等差数列的第五个数,即应填19;填在四个角上方格中的数是位于偶数项的数,即13,17,21,25,而且对角两数的和相等,即13+25=17+21;余下各数就不难填写了(见右图).与幻方相反的问题是反幻方.将九个数填入3×3(三行三列)的九个方格中,使得任一行、任一列以及两条对角线上的三个数之和互不相同,这样填好后的图称为三阶反幻方.例3将前9个自然数填入右图的9个方格中,使得任一行、任一列以及两条对角线上的三个数之和互不相同,并且相邻的两个自然数在图中的位置也相邻.分析与解:题目要求相邻的两个自然数在图中的位置也相邻,所以这9个自然数按照大小顺序在图中应能连成一条不相交的折线.经试验有下图所示的三种情况:按照从1到9和从9到1逐一对这三种情况进行验算,只有第二种情况得到下图的两个解.因为第二种情况是螺旋形,故本题的解称为螺旋反幻方.例4将九个数填入左下图的九个空格中,使得任一行、任一列以及两条证明:因为每行的三数之和都等于k,共有三行,所以九个数之和等于3k.如右上图所示,经过中心方格的有四条虚线,每条虚线上的三个数之和都等于k,四条虚线上的所有数之和等于4k,其中只有中心方格中的数是“重叠数”,九个数各被计算一次后,它又被重复计算了三次.所以有九数之和+中心方格中的数×3=4k,3k+中心方格中的数×3=4k,注意:例4中对九个数及定数k都没有特殊要求.这个结论对求解3×3方格中的数阵问题很实用.在3×3的方格中,如果要求填入九个互不相同的质数,要求任一行、任一列以及两条对角线上的三个数之和都相等,那么这样填好的图称为三阶质数幻方.例5求任一列、任一行以及两条对角线上的三个数之和都等于267的三阶质数幻方.分析与解:由例4知中间方格中的数为267÷3=89.由于在两条对角线、中间一行及中间一列这四组数中,每组的三个数中都有89,所以每组的其余两数之和必为267-89=178.两个质数之和为178的共有六组:5+173=11+167=29+149=41+137=47+131=71+107.经试验,可得右图所示的三阶质数幻方.练习161.将九个连续自然数填入3×3的方格内,使得每一横行、每一竖列及两条对角线上的三个数之和都等于66.2.将1,3,5,7,9,11,13,15,17填入3×3的方格内,使其构成一个幻方.3.用2,4,6,12,14,16,22,24,26九个偶数编制一个幻方.4.在下列各图空着的方格内填上合适的数,使每行、每列及每条对角线上的三数之和都等于27.5.将右图中的数重新排列,使得每行、每列及两条对角线上的三个数之和都相等.6.将九个质数填入3×3的方格内,使得每一横行、每一竖列及两条对角线上的三个数之和都等于21.7.求九个数之和为657的三阶质数幻方.第17讲数阵图(二)例1在右图的九个方格中填入不大于12且互不相同的九个自然数(其中已填好一个数),使得任一行、任一列及两条对角线上的三个数之和都等于21.解:由上一讲例4知中间方格中的数为7.再设右下角的数为x,然后根据任一行、任一列及每条对角线上的三个数之和都等于21,如下图所示填上各数(含x).因为九个数都不大于12,由16-x≤12知4≤x,由x+2≤12知x≤10,即4≤x≤10.考虑到5,7,9已填好,所以x只能取4,6,8或10.经验证,当x=6或8时,九个数中均有两个数相同,不合题意;当x=4或10时可得两个解(见下图).这两个解实际上一样,只是方向不同而已.例2将九个数填入右图的空格中,使得每行、每列、每条对角线上的三个数之和都相等,则一定有证明:设中心数为d.由上讲例4知每行、每列、每条对角线上的三个数之和都等于3d.由此计算出第一行中间的数为2d——b,右下角的数为2d-c(见下图).根据第一行和第三列都可以求出上图中★处的数由此得到3d-c-(2d-b)=3d-a-(2d-c),3d-c-2d+b=3d-a-2d+c,d——c+b=d——a+c,2c=a+b,a+bc=2.值得注意的是,这个结论对于a和b并没有什么限制,可以是自然数,也可以是分数、小数;可以相同,也可以不同.例3在下页右上图的空格中填入七个自然数,使得每一行、每一列及每一条对角线上的三个数之和都等于90.解:由上一讲例4知,中心数为90÷3=30;由本讲例2知,右上角的数为(23+57)÷2=40(见左下图).其它数依次可填(见右下图).例4在右图的每个空格中填入个自然数,使得每一行、每一列及每条对角线上的三个数之和都相等.解:由例2知,右下角的数为(8+10)÷2=9;由上一讲例4知,中心数为(5+9)÷2=7(见左下图),且每行、每列、每条对角线上的三数之和都等于7×3=21.由此可得右下图的填法. 例5在下页上图的每个空格中填一个自然数,使得每行、每列及每条对角线上的三个数之和都相等.解:由例2知,右下角的数为(6+12)÷2=9(左下图).因为左下图中两条虚线上的三个数之和相等,所以,“中心数”=(10+6)-9=7.其它依次可填(见右下图).由例3~5看出,在解答3×3方阵的问题时,上讲的例4与本讲的例2很有用处.练习171.在左下图的每个空格中填入一个数字,使得每行、每列及每条对角线上的三个数之和都相等.2.在右上图的每个空格中填入一个数字,使得每行、每列及每条对角线上的三个数之和都等于24.3.下列各图中的九个小方格内各有一个数字,而且每行、每列及每条对角线上的三个数之和都相等,求x.4.在左下图的空格中填入七个自然数,使得每行、每列、每条对角线上的三个数之和都等于48.5.在右上图的每个空格中填入一个自然数,使得每行、每列及每条对角线上的三个数之和都相等.6.在右图的每个空格中填入不大于12且互不相同的九个自然数,使得每行、每列、每条对角线上的三个数之和都等于21.第18讲数阵图(三)数阵问题是多种多样的,解题方法也是多种多样的,这就需要我们根据题目条件灵活解题.例1把20以内的质数分别填入下图的一个○中,使得图中用箭头连接起来的四个数之和都相等.分析与解:由上图看出,三组数都包括左、右两端的数,所以每组数的中间两数之和必然相等.20以内共有2,3,5,7,11,13,17,19八个质数,两两之和相等的有5+19=7+17=11+13,于是得到下图的填法.例2在右图的每个方格中填入一个数字,使得每行、每列以及每条对角线上的方格中的四个数字都是1,2,3,4.分析与解:如左下图所示,受列及对角线的限制,a处只能填1,从而b处填3;进而推知c处填4,d处填3,e处填4,……右下图为填好后的数阵图.例3将1~8填入左下图的○内,要求按照自然数顺序相邻的两个数不能填入有直线连接的相邻的两个○内.分析与解:因为中间的两个○各自只与一个○不相邻,而2~7中的任何一个数都与两个数相邻,所以这两个○内只能填1和8.2只能填在与1不相邻的○内,7只能填在与8不相邻的○内.其余数的填法见右上图.例4在右图的六个○内各填入一个质数(可取相同的质数),使它们的和等于20,而且每个三角形(共5个)顶点上的数字之和都相等.分析与解:因为大三角形的三个顶点与中间倒三角形的三个顶点正好是图中的六个○,又因为每个三角形顶点上的数字之和相等,所以每个三角形顶点上的数字之和为20÷2=10.10分为三个质数之和只能是2+3+5,由此得到右图的填法.例5在右图所示立方体的八个顶点上标出1~9中的八个,使得每个面上四个顶点所标数字之和都等于k,并且k不能被未标出的数整除.分析与解:设未被标出的数为a,则被标出的八个数之和为1+2+…+9-a=45-a.由于每个顶点都属于三个面,所以六个面的所有顶点数字之和为6k=3×(45-a),2k=45-a.2k是偶数,45-a也应是偶数,所以a必为奇数.若a=1,则k=22;若a=3,则k=21;若a=5,则k=20;若a=7,则k=19;若a=9,则k=18.因为k不能被a整除,所以只有a=7,k=19符合条件.由于每个面上四个顶点上的数字之和等于19,所以与9在一个面上的另外三个顶点数之和应等于10.在1,2,3,4,5,6,8中,三个数之和等于10的有三组:10=1+3+6=1+4+5=2+3+5,将这三组数填入9所在的三个面上,可得右图的填法.练习181.将1~6这六个数分别填入左下图中的六个○内,使得三条直线上的数字的和都相等.2.将1~8这八个数分别填入右上图中的八个方格内,使上面四格、下面四格、左边四格、右边四格、中间四格及四角四格内四个数相加的和都是18.3.在下页左上图的每个方格中填入一个数字,使得每行、每列以及每条对角线上的方格中的四个数都是1,2,3,4.4.将1~8填入右上图的八个空格中,使得横、竖、对角任何两个相邻空格中的数都不是相邻的两个自然数.5.20以内共有10个奇数,去掉9和15还剩八个奇数.将这八个奇数填入右图的八个○中(其中3已填好),使得用箭头连接起来的四个数之和都相等.6.在左下图的七个○内各填入一个质数,使每个小三角形(共6个)的三个顶点数之和都相等,且为尽量小的质数.7.从1~13中选出12个自然数填入右上图的空格中,使每横行四数之和相等,每竖列三数之和也相等.答案练习16练习173.(1)11;(2)9.提示:(1)右下角的数为(3+7)÷2=5,所以x=8×2-5=11.(2)右下角的数为(5+9)÷2=7,中心数为(6+9)-7=8,所以x=8×2-7=9提示:左下角的数为(13+27)÷2=20,中心数为48÷3=16.提示:右下角的数为(20+16)÷2=18,中心数为(8+18)÷2=13.提示:与例1类似.练习181.有下面四个基本解.。
数阵问题 整理版

数阵趣味导读:有些数按照一定的要求排列成各种各样的图形,就叫做数阵图,数阵填数的游戏是非常有趣的,有时也有一定的难度。
不过它能促使我们积极地思考问题,分析问题,拓展我们的能力。
有的同学说:这样的数阵图填写时只能采取试的方法,没有其他捷径好走。
其实这话不对。
填写数阵图时,我们应抓住数阵中的关键位置(例如两种线的交点,长方形和正方形的顶点),再根据题目的要求,进行必要的计算,先填写这些关键位置的数,再填写出其他位置的数。
一些数按照一定的规则,填在某一特定图形的规定位置上,这种图形,我们称它为“数阵图”,数阵图的种类繁多,绚丽多彩,这里只向大家介绍三种数阵图,即封闭型数阵图、辐射型数阵图和复合型数阵图。
在解答这类问题时,要善于确定所求的和与关键数字间的关系式,用试验的方法,找到相等的和与关键数字:要会对基本解中的数进行适当调整,得到其他的解,从而培养自己的观察能力,思维的灵活性和严密性。
【解法总结】:做数阵题目,我们的一般步骤是:①.先观察在图中有哪些格子重复了,重复了几次。
②.根据题中给出的数字以及图形来发现重复的这几个数有什么特点。
③.看看在给出的数中有哪些数符合我们特点,再通过试算,确定每个格子中的数。
【例题1】将1,2,3,4,5这五个数分别填入下图的各正方形中,组成一个“十字数阵图”使图中横行三个数的和与竖行三个数据的和相等。
解析:根据图形的特点,中间那个数是横行与竖行共用的,要使横行与竖行三个数的和相等,可以先确定中间的数,再让左右两数的和与上、下两数的和相等。
①中间填1,则剩下2,3,4,5,而2+5=4+3,共有8种填法。
②中间填2,则剩下1,3,4,5而这四个数无法组成□+□=□+□的形式所以中间不可填?③中间填3,则剩下1,2,4,5,而1+5=2+4,共有8种填法:④中间填4,则剩下1,2,3,5而这四个数无法组成□+□=□+□的形式所以中间可能填4。
⑤中间填5,则剩下1,2,3,4,1+4=2+3共有8种填法。
四年级奥数详解答案-第3讲-数阵图

四年级奥数详解答案 第3讲第三讲 数阵图一、知识概要1. 数阵图就是把一些数字填入图形的某种位置上,并使数字满足一定的条件。
2. 数阵图的种类,大致分为三种:①封闭型数阵图;②开放型数阵图;③复合型数阵图3. 解数阵图的一般方法:(1) 分析隐含的数量关系和数字的位置关系,以特殊的位置为突破口,一般选用使用次数多的数作为关健数。
(2) 依据图中条件,建立所求的和与关健数的关系式,并通过讨论最大值与最小值,以及试验的方法确定关键数的数值及相等的和。
(3) 对其他部位上的数字一般都是作尝试选填,直至符合题为止二、典型例题精讲 1. 把1~6这6个数分别填在图中的○内,使每多边上三个○内的数字和相等。
分析指导: 21654321=+++++∴21+(a+b+c)=(a+d+b)+(b+f+c)+(a+e+c)a+d+b=b+f+c=a+e+c,且设a+d+b=k∴有:21+(a+b+c)=3k当a+b+c 为最小值,即1+2+3=6时,k=9当a+b+c 为最大值,即6+5+4=15时,k=12这样就可以确定,三角形每边上的三个○内的数字和在9~12之间解:(1)当k=9时,a+b+c=6,令a=1,b=2,c=3则:d=9-(2+1)=6 e=9-1-3=5 f=9-2-3=4其结果如以下图所示:(2)当k=10时,a+b+c=9, 则:a.b.c 的取值有三种可能:①a=1,b=2,c=6 ②a=1,b=3,c=5 ③a=2,b=3,c=4-----①种情况,a=1,b=2,c=6,则d=10-1-2=7 (不合题意,舍去)-----②种情况,a=1,b=3,c=5,则d=10-1-3=6,e=10-1-5=4;f=10-3-5=2,所以结果如下图。
------③种情况,a=2,b=3,c=4,则d=10-2-3=5,e=10-2-4=6, f=10-3-4=3, 与b=3重复,不合题意,舍去。
四年级数学趣的数阵图课件

11 7 3
6
9
8
5
10
例2 在下面图中的 里,填上适当的 数,使每条线上3个 里的数的和等于13。
8 1 4 3 2 7
6
猴博士考考你
把10到20这11个数填在图中的 使每条线段上的3个数的和等于45。
20
16 14 15 13 17 12 10 11 19
里,
18
例3、把1、2、3、4、5这5个自然数 填入到图中的 里,使每条线段上的3个 数的和相等。
有趣的数阵图
四年级上学期 《数学探究 我快乐》第51页~54页
金坛市金城镇中心小学
丁国新
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形,通常叫做数阵图。
例1 在下面的三角形数阵图的 里, 填入适当的数,使三边上3个 里的数的和 是12。
5
1
3 2
4
6
猴博士考考你
在正方形数阵图中的 里填入适当的 数,使每条线上的3个数的和等于21。
1
5博士送你一句数学家名言:
数学好玩!
陈省身
谢谢各位!
; / 聚星娱乐
mqx93jop
递给耿英。耿英接过毛巾刚端起脸盆儿,耿兰就进来了。她从姐姐手里接过脸盆儿,说:“俺去倒水,你们快去吃饭哇!” 26 第百十六回 但愿今日亲人归|(大壮青山归来后,意外发现骡和车;匆匆回家问仔细,但愿今日亲人归。)那日天儿擦黑的时 候,大壮和青山像往常一样把骡车赶到粉坊大院儿里去卸车,却意外地发现马厩里已经拴了两头大骡子,车棚里还停了两挂大 块头的平板车。青山赶快跑进粉坊一看,爹和弟弟已经回家去了,就问了那两个雇佣的伙计,才知道今儿上午回来了两挂车, 五个人。青山马上想到是不是盼望已久的耿家父子们回来了!不及细想,他高兴地转身出来,一边跑一边语无伦次地对大壮说: “俩,俩伙计说,今儿,今儿个上午回来了两挂车,五,五个人,大概是耿伯他们!”大壮一听,牵着骡子缰绳的手开始颤抖 了„„但转念一想,结结巴巴地说:“不,不对呀,怎么会,会是五,五个人哇!”青山说:“别多想了,咱们赶快回家问个 究竟去!”于是,俩人开始手忙脚乱地卸车,伺候辛苦一天的大骡子„„当大壮风风火火地往马厩里牵枣红色大骡子时,青山 说:“拴远点儿哇,免得它们咬槽!”可路过那两头骡子时,任凭大壮怎么拽,枣红大骡就是不愿意走了。而那两头骡子也很 是示好,都“嗬儿嗬儿”地轻轻欢啸呢!于是大壮不再硬拽它了,但没有想到这畜生径自进了马厩内,而且三个大家伙竟然互 相蹭开了脖子!青山见了,忍不住哈哈大笑起来,说:“把它们拴在一起哇!你看它们那个亲热劲儿,活像是多年不见的亲兄 弟似的!”大壮无可奈何地说:“看来,也只能这样了!”大壮把枣红色大骡子拴好了,提桶清水,并撒些草节什么的过来给 它喝,旁边的那两头骡子也先后伸过嘴巴来喝了几口。在水桶里撒一些草节可以避免牲畜喝得太快,从而引起所谓的“炸肺”, 实际上是怕冷水喝得太快,导致伤了它们的肠胃。大壮刚把喝剩的水提出来放到一边,青山已经拿个大笸箩把草料端来了。他 一边添草料,一边对骡子们说:“待会儿你们要是不和气了,可莫怪俺们啊!”伺候完了骡子们,俩人赶快大步回家去了。听 到耿憨和青海回来了,耿正赶快走出秀儿的闺房,来到隔壁的堂屋里陪耿憨和青海说话。三个人围坐在大大的餐桌边说了没几 句话,裴氏和秀儿就摆上碗筷来了。耿憨笑着对妻子说:“这早就吃晚饭啦?”裴氏说:“早点儿吃哇,吃了好让正儿回去歇 息!娃儿今儿个累呢!”话音刚落,忽然听到院子里一阵急促的脚步声响起,原来是青山急匆匆地赶回来了。他人还没有进了 屋里,就大声问道:“爹,俺和大壮哥看到咱粉坊院儿里的两头骡子和两挂平车了,问伙计,可他们说回来了五个人,怎么回 事?是不是„„”青山的话还没有问完,耿正已经冲出了
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“中心数”=(10+6)-9=7。 其它依次可填(见右下图)。 由例 3~5 看出,在解答 3×3 方阵的问题时,上讲的例 4 与本讲的例 2 很有用处。
例 2 将九个数填入右图的空格中,使得每行、每列、每条对角线上的三个 数之和都相等,则一定有
证明:设中心数为 d。由上讲例 4 知每行、每列、每条对角线上的三个数 之和都等于 3d。由此计算出第一行中间的数为 2d——b,右下角的数为 2d-c(见下图)。
根据第一行和第三列), 3d-c-2d+b=3d-a-2d+c, d——c+b=d——a+c, 2c=a+b, a+b c=2。
值得注意的是,这个结论对于 a 和 b 并没有什么限制,可以是自然数, 也可以是分数、小数;可以相同,也可以不同。 例 3 在下页右上图的空格中填入七个自然数,使得每一行、每一列及每一 条对角线上的三个数之和都等于 90。
解:由上一讲例 4 知,中心数为 90÷3=30;由本讲例 2 知,右上角的数 为(23+57)÷2=40(见左下图)。其它数依次可填(见右下图)。
因为九个数都不大于 12,由 16-x≤12 知 4≤x,由 x+2≤12 知 x≤10, 即 4≤x≤10。考虑到 5,7,9 已填好,所以 x 只能取 4,6,8 或 10。经 验证,当 x=6 或 8 时,九个数中均有两个数相同,不合题意;当 x=4 或 10 时可得两个解(见下图)。这两个解实际上一样,只是方向不同而 已。
第 17 讲 数阵图(二) 例 1 在右图的九个方格中填入不大于 12 且互不相同的九个自然数(其中 已填好一个数),使得任一行、任一列及两条对角线上的三个数之和都等 于 21。
解:由上一讲例 4 知中间方格中的数为 7。再设右下角的数为 x,然后根 据任一行、任一列及每条对角线上的三个数之和都等于 21,如下图所示 填上各数(含 x)。
例 4 在右图的每个空格中填入个自然数,使得每一行、每一列及每条对角 线上的三个数之和都相等。
解:由例 2 知,右下角的数为
(8+10)÷2=9;由上一讲例 4 知,中心数为(5+9)÷2=7(见左 下图),且每行、每列、每条对角线上的三数之和都等于 7×3=21。由此 可得右下图的填法。 例 5 在下页上图的每个空格中填一个自然数,使得每行、每列及每条对角 线上的三个数之和都相等。
