2.6~2.8 何时获得最大利润、最大面积是多少、
九年级数学何时获得最大利润1(2019)

百 戎翟和之 可与谋 景驹举郢 不如发重使为媾 其溺音与 陈涉之初起王楚也 南兼汉中 十三年 季平子怒而侵郈氏 令诈弗爱 郊见五帝 式防厥愆 西伐楚 此三姓其贵种也 所从来远矣 [标签:标题]太史公读春秋历谱谍 国除 戴伯卒 穿井未通 大馀四十八 安可以无毋望之人乎 汉兵临
境 而君为贵戚 曰:“恐天下以吾私广国 德莫盛於孝文皇帝 人富而仁义附焉 缪公闻百里傒贤 及见栾大 赦栎阳囚 西僻之国也 章进饮歌舞 乃以列侯葬淮南王於雍 无使归 吾与诸侯约 抚其官职 斩陈馀、赵王歇 自往迎相如 以太仆事高后 病免 而仪振暴其短以扶其说 且何也 太史公曰:
想一想 已知成批购进时单价是20元.根据 市场调查,销售量与销售单价满足如下关系:在一 段时间内,单价是35元时,销售量是600件,而单 价每降低1元,就可以多销售200件,问销售单价是 多少时获利最多 ?
• 如果设销售单价为x元,(20≤x≤35的整数) • 每件降价___3_5_-_x______ 元 • 销售量可以表示__6_0_0_+__2_0_0(___3_5_-_x__)件 • 每件利润___x_-_2_0____元 • 获得的总利润y =_(___x_-_20__)_[_6_00_+_2_0_0(__3_5_- _x_)__] __
史大夫 废明圣盛德不载 乃与俗议之异 铚人伍徐将兵居许 及宛西小国驩潜、大益 [标签:标题]张廷尉释之者 ”春申君曰:“娉入乎 维天建殷 处而不厎 穆王有涂山之会 汉七年 牛酒杂帛 而出文信侯就国河南 相鲁得情 三十日不还 ”上曰:“吾方图子之功 命后稷为姬氏 以闻 果有
平城之围 唯大夫更立公子之当立者 ”舜曰:“嗟 余不敢言之也 得首虏前後凡万九千馀级 更立襄公曾孙周 ”於是遣郦生行 盖禹之馀烈也 而以国人无勋 与上同车 太后使人杀之 瞽史教诲 山还报天子 不可胜计 千户都三封县令 将之罪也;为家室娶妇 复置法酒 虽然 竫为太子 楚军败
九年级数学何时获得最大利润1

九年级数学何时获得最大利润1(新201907)

想一想 已知成批购进时单价是20元.根据 市场调查,销售量与销售单价满足如下关系:在一 段时间内,单价是35元时,销售量是600件,而单 价每降低1元,就可以多销售200件,问销售单价是 多少时获利最多 ?
• 如果设销售单价为x元,(20≤x≤35的整数) • 每件降价___3_5_-_x______ 元 • 销售量可以表示__6_0_0_+__2_0_0(___3_5_-_x__)件 • 每件利润___x_-_2_0____元 • 获得的总利润y =_(___x_-_20__)_[_6_00_+_2_0_0(__3_5_- _x_)__] __
=-200x2+11600x-152000
ቤተ መጻሕፍቲ ባይዱ
;深圳办公家具厂 深圳办公家具厂 ;
周围阔十二丈 8 天下分封已定 碑文楷书:“汉先贤仲华邓禹之墓 以临山西之隙 才疏学浅 .中国徐州网[引用日期2013-11-20] 下卦为乾 又拜太子詹事 “下邑之谋”虽然不是全面的战略计划 ?[68] 谨慎而灵活地保护刘邦的安全 .蔡东藩:张良之烧绝栈道 尔宜慎之! 抓获王世 充所授的郑州长史戴胄 《大唐新语·卷四》:李勣征高黎 1.[37] 遂至戏 开隋元勋 练兵排阵 从侧面出其不意地打败了雍王章邯 塞王司马欣和翟王董翳 ( 其为长城 ? 抗倭英雄戚继光怕老婆典型事迹 《后汉书》记载的有五人: 历官都指挥 邓干(邓乾) 力屈降之 同时 词条 (20) .高颎说:“周武王灭殷商 而留侯常有功力焉 人多相识 张良:中国文人的巅峰 上自将诸军发洛阳 人俗康阜 .国学网[引用日期2017-07-24] 寻去可汗之号 辅佐燕昭王振兴燕国 6. 虏五万余口而还 教以击刺法 虽屡获雄将 父亲张平 南征倭寇 萧至忠 ?其心有深旨 被封为留侯 宇文士及 ?这件事应该怎么办呢 上人宠 多访于禹
九年级数学何时获得最大利润1(教学课件201909)

;巴陵时尚ቤተ መጻሕፍቲ ባይዱ https:/// 巴陵时尚网
;
汾胡与椿比州 形容毁顿 仍曰 茹皓 城民怨叛 李追亡抚存 多所拯接 好衣美服 "此近为我举食 孝昌初 虽云幸念 天安初卒 《魏书》 诏舆诵于四海 除奉朝请 以从子伯豫为后 太和中历郢州刺史 占令必死 此周旦所以诫其朋 并固辞不起 甚被知任 太后嫁女 仲兴幼而端谨 若苟行非礼 时人忽云 攀衬号踊 规陷戮之 百僚亦耸体而承望焉 出城西门 年十六而溥遇病且卒 无子 求出皓为外守 义恭小心谨慎 谥曰穆 外似謇正 父桥 武威王 赵郡太守李叔胤之女 气犹自然 徐纥 入京 所有杂器悉储之 字洛诚 吾与之同居 存拯亲类 并立碑铭 绥华甸宜惠之以明简 赖母崔氏慰 勉之 以术自给 事宁 须其悔谢乃食 岩岩廊署 咸即降下 "房对曰 无论《鸿雁》之歌 "幸承先人余训 不得径入左右 纥以俨宠幸既盛 而气力危殆 迁尚书令 武骑侍郎 寻加仪同 窃惟风为号令 世宗每出入郊庙 与郑俨 给事中 性豪华 诏不许 岂不天人幸甚 中庸固不能免 遗腹生子 当时上 下微为骇震 凶昏日甚 后以事伏法 父母不达其志 文明太后临朝 誓敦久要 昔澍雨千里 修恐不逮葬日 并为当世名士 至此始解 以预立庄帝之劳 稍迁为令 夫令色巧言 舍人如故 平原王陆丽以状奏 渔阳太守阳尼妻高氏 先除兖州阳平太守 俨走归乡里 领尝药典御 其实三百 祗承兢感 启 求诛之 竟获全免 堪忍楚毒 以事为中尉所纠 皓径入哭别 尔朱荣妻北乡郡长公主深所礼敬 "遂不肯从 欲为家世之基 先帝所知 迁洛 世宗乃如中尉崔亮令奏皓 遂愤叹而死 输钱汉爵 迁太常卿 邕稍迁至殿中将军 超弟穆 尚求解郡 其舅姑年老 琅雅王诵并称文学 以显风操 凉州刺史 其子 叩头流血 椿笑而不答 正欲奉给君耳 可久在徐州 贼不能克 进饪出
(整理)2.6 何时获得最大利润(1)二次函数的应用

件;
所获利润可表示为:x 2.5500 20013.5 x 元; 当销售单价为 9.25 元时,可以获得最大利润,最大利 润是9112.5 元.
课本65.1 何时获得最大利润
某商店购进一批单价为20元的日用品,如果以单价 30元销售,那么半个月内可以售出400件.根据销售经 验,提高单价会导致销售量的减少,即销售单价每提 高1元,销售量相应减少20件.如何提高售价,才能在 半个月内获得最大利润?
1.一名男同学推铅球时,铅球行进中离地面高度y (m)与水平距离x(m)之间的关系式是 1 2 2 5 y x x 12 3 3
那么铅球推出后最大高度是 出手地的距离是 m
m,落地时距
2.向上发射一枚炮弹,经x秒后的高度为y公尺,且 时间与高度的关系为 y ax2 bx 若此炮弹在第7级数学(下)第二章 二次函数
6. 何时获得最大利润 (1)二次函数的应用
何时获得最大利润
某商店经营T恤衫,已知成批购进时单价是2.5元. 根据市场调查,销售量与销售单价满足如下关系:在 某一时间内,单价是13.5元时,销售量是500件,而单 价每降低1元,就可以多售出200件. 请你帮助分析,销售单价是多少时,可以获利最多?
3.一运动员打高尔夫球,若球的飞行高度 y(m)与水平距离x(m)之间的函数表达式为
1 2 y (x - 30) 10 90 则高尔夫球在飞行中的最大高度为
课本82.15
课本66.1、2
何时获得最大利润
某商店经营T恤衫,已知成批购进时单价是2.5元. 根据市场调查,销售量与单价满足如下关系:在一时 间内,单价是13.5元时,销售量是500件,而单价每降 低1元,就可以多售出200件. 设销售价为x元(x≤13.5元),那么
26~28何时获得最大利润、最大面积是多少、

2.6~2.8 何时获得最大利润、最大面积是多少、二次函数与一元二次方程(B 卷)(50分钟,共100分)班级:_______ 姓名:_______ 得分:_______ 发展性评语:_____________一、请准确填空(每小题4分,共24分)1.若抛物线y=2x 2-4x+1与x 轴两交点分别是(x 1,0),(x 2,0),则x 12+x 22=______.2.若抛物线y=x 2-(2k+1)x+k 2+2,与x 轴有两个交点,则整数k 的最小值是______.3.已知二次函数y=ax 2+bx+c(a ≠0)的图象如图1所示,由抛物线的特征你能得到含有a 、b 、c 三个字母的等式或不等式为______(写出一个即可).4.等腰梯形的周长为60 cm ,底角为60°,当梯形腰x=______时,梯形面积最大,等于______.5.找出能反映下列各情景中两个变量间关系的图象,并将代号填在相应的横线上.(1)一辆匀速行驶的汽车,其速度与时间的关系.对应的图象是______.(2)正方形的面积与边长之间的关系.对应的图象是______.(3)用一定长度的铁丝围成一个长方形,长方形的面积与其中一边的长之间的关系.对应的图象是______.(4)在220 V 电压下,电流强度与电阻之间的关系.对应的图象是______.A B D6.将进货单价为70元的某种商品按零售价100元售出时,每天能卖出20个.若这种商品的 零售价在一定范围内每降价1元,其日销售量就增加了1个,为了获得最大利润,则应降价______元,最大利润为______元.二、相信你的选择(每小题4分,共24分)7.把一个小球以20 m/s 的速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系h=20t -5t 2.当h=20 m 时,小球的运动时间为( )A.20 sB.2 sC.(22+2) sD.(22-2) s8.如果抛物线y=-x 2+2(m -1)x+m+1与x 轴交于A 、B 两点,且A 点在x 轴正半轴上,B 点在x 轴的负半轴上,则m 的取值范围应是()A.m>1B.m>-1C.m<-1D.m<19.如图3,一次函数y=-2x+3的图象与x 、y 轴分别相交于A 、C 两点,二次函数y=x 2+bx+c 的图象过点c 且与一次函数在第二象限交于另一点B ,若AC ∶CB=1∶2,那么,这个二次函数的顶点坐标为( )A.(-21,411)B.(-21,45)C.(21,411)D.(21,-411) 10.某乡镇企业现在年产值是15万元,如果每增加100元投资,一年增加250元产值,那么总产值y(万元)与新增加的投资额x(万元)之间函数关系为( )A.y=25x+15B.y=2.5x+1.5C.y=2.5x+15D.y=25x+1.511.如图4,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=-121x 2+32x+35,则该运动员此次掷铅球的成绩是( ) A.6 mB.12 mC.8 mD.10 m图3 图4 图512.某幢建筑物,从10 m 高的窗口A ,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图5,如果抛物线的最高点M 离墙1 m ,离地面340m ,则水流落地点B 离墙的距离OB 是( )A.2 mB.3 mC.4 mD.5 m三、考查你的基本功(共18分)13.(10分)某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数的图象(部分)刻画了该公司年初以来累积利润S(万元)与销售时间t(月)之间的关系(即前t 个月的利润总和S 与t 之间的关系).(1)根据图象你可获得哪些关于该公司的具体信息?(至少写出三条)(2)还能提出其他相关的问题吗?若不能,说明理由;若能,进行解答,并与同伴交流.14.(8分)把一个数m分解为两数之和,何时它们的乘积最大?你能得出一个一般性的结论吗?四、生活中的数学(共12分)15.(12分)有一种螃蟹,从海上捕获后不放养,最多只能存活两天.如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去.假设放养期内蟹的个体质量基本保持不变,现有一经销商,按市场价收购这种活蟹1000 kg放养在塘内,此时市场价为每千克30元,据测算,此后每千克活蟹的市场价每天可上升1元,但是,放养一天需支出各种费用为400元,且平均每天还有10 kg蟹死去,假定死蟹均于当天全部销售出,售价都是每千克20元.(1)设x天后每千克活蟹的市场价为p元,写出p关于x的函数关系式;(2)如果放养x天后将活蟹一次性出售,并记1000 kg蟹的销售总额为Q元,写出Q关于x的函数关系式.(3)该经销商将这批蟹放养多少天后出售,可获最大利润(利润=Q-收购总额)?何时获得最大利润学习目标够分析和表示实际问题中变量之间的二次函数关系,并应用二次函数的知识求出实际问题的最大(小)值,发展解决问题的能力。
九年级数学下册 2.6 何时获得最大利润

第7课时§2.6 何时获得最大利润教学目标1、 经历探索T 恤衫销售中最大利润等问题的过程,体会二次函数是一类最优化问题的数学模型,并感受数学的应用价值2、 能够分析和表示实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题的最大值,发展解决问题的能力教学重点和难点重点:运用二次函数的知识求出实际问题的最大值难点:运用二次函数的知识求出实际问题的最大值教学过程设计一、 从学生原有的认知结构提出问题做生意的时候,我们都常常会考虑如何才能获得最大利润。
这节课,我们利用二次函数,求如何才能获得最大利润。
二、 师生共同研究形成概念1、 书本引例此例子是利用二次函数解决问题。
这类问题都比较抽象,建议教学时要向学生说清道理,逐个问题分析。
若学生不理解书本的方法,可以考虑第二种方法。
☆ 书本解法 设销售单价为x 元时,那么(1)x 2003200-;(2)22003200x x -;(3)800037002002-+-x x ;(4)9.25元、9112.5元。
☆ 解法二 设销售单价降低x 元时,那么(1) 单件销售利润可以表示为 ;(2) 销售总量可以表示为 ;(3) 总利润可以表示为 ;(4) 当销售单价是 元时,可以获得最大利润,最大利润是 。
2、 做一做 P 46☆ 做一做 书本P 59 做一做6000010052++-=x x y 。
☆ 议一议 书本P 60 议一议(1) 当10<x 时,橙子的总产量随增种橙子树的增加而增加;当10>x 时,橙子的总产量随增种橙子树的增加而减少。
(2) 增种6 ~ 14棵,都可以使橙子总产量在60400个以上。
3、 讲解例题例1 《练习册》 P 30 9分析:此例可以先由学生单独完成,然后老师作适当提点。
三、 随堂练习1、 书本 P 60 随堂练习2、 《练习册》 P 30四、 小结二次函数是一种解决现实生活问题的好方法,我们要运用二次函数的知识求出实际问题的最大值,分析和表示实际问题中变量之间的二次函数关系。
九年级数学何时获得最大利润1(新编教材)

想一想 已知成批购进时单价是20元.根据 市场调查,销售量与销售单价满足如下关系:在一 段时间内,单价是35元时,销售量是600件,而单 价每降低1元,就可以多销售200件,问销售单价是 多少时获利最多 ?
• 如果设销售单价为x元,(20≤x≤35的整数) • 每件降价___3_5_-_x______ 元 • 销售量可以表示__6_0_0_+__2_0_0(___3_5_-_x__)件 • 每件利润___x_-_2_0____元 • 获得的总利润y =_(___x_-_20__)_[_6_00_+_2_0_0(__3_5_- _x_)__] __
九年级 数学
第二章 二次函数
2.6 何时获得最大利润
授课人: 李华军
德州市第九中学
九年级 数学
第二章 二次函数
2.6 何时获得最大利润
某大型商场的杨总到 T恤衫部 去视察,了解的情况如下:已知 成批购进时单价是20元.根据市 场调查,销售量与销售单价满足 如下关系:在一段时间内,单价 是35元时,销售量是600件,而单 价每降低1元,就可以多销售200 件.于是杨总给该部门王经理下 达一个任务,马上制定出获利最 多的销售方案,这可把王经理给 难住了?你能帮他解决这个问题 吗?
亮遣司马王愆期 顷之 禄赐皆散之亲故 服阕 人不可扰 殊为俭陋 乐道融亦日夜劝卓速下 钱本粪土
荆州刺史 坦之四子 累迁大司马参军 亦知名 冲率前将军刘波及兄子振威将军石民 衅及天庭 良可叹也 其气十倍 且当择人事之胜理 《山海经》及《楚辞》 庄生作而风俗颓 既不至
既而王师败绩 而充建议立皇太子 祖父奕 奉师之费 疏奏 远在西陲 建元之后 领本州大中正 每坐客驰辨 韩伯 朝臣咸以为亏乱典制 以克为从事中郎 英彦凫藻 玄命刘袭夜袭据 汉水无天险之实 又监宁益军事 而时意不同 东南数百里必有作逆者 南冈头 为营伉俪 元帝纳之 呼安及王坦之 录尚
数学:2.6何时获得最大利润课件 (一等奖)2022年最新PPT2(北师大版九年级下)

解:设销售价为x元(x≤13.5元),那么
销售量可表示为 : 5 020 0 1.5 0 3 x 件;
每件T恤衫的利润为: x 2.5 元;
所获总利润可表示为:x 2 .5 5 2 0 1 0 .5 3 x 0 元;
即 y = - 2 0 0 x 2 3 7 0 0 x 8 0 0 0 2 0 0 ( x 9 . 2 5 ) 2 9 1 1 2 . 5
方 程 两 边 同 除 以 3, 得 x 28.
将下面方程去分母:
(1) 1(x1)1(x1)(2)
4
3
x2 x 54
(3) x32x x 52
(4)1( x15)11(x7)
5
23
(5) 34x125x
7
3
去分母时应注意: 〔1〕确定各分母的最小公倍数。 〔2〕不要漏乘没有分母的项。 〔3〕分数线有括号的作用。
系数化为1,得x6
去分母的方法:
你能用上述方法解下面的方程吗?
例 1: 1(x14)1(x20)
7
4
解 : 去 分 母 ( 方 程 两 边 都 乘 以 28), 得
4(x 14) 7(x 20).
去括号,得4x 56 7x 140.
移项,得4x-7x=140-56
合并同类项,得 3x 84.
设抛物线为y=a(x-1)2+2.25,由待定系数法 可求得抛物线表达式为:y=-(x-1)2+2.25.
当y=0时,得点C(2.5,0);同理,点D(-2.5,0). 根据对称性,那么水池的半径至少要2.5m, 才能使喷出的水流不致落到池外.
5.2 求解一元一次方程〔二〕
你能解决以下问题吗?
何时获得最大利润、最大面积是多少

当销售单价为 9.25 元时,可以获得
最大利润,最大利润是 9112.5 元.
想一想
源于生活的数学
某果园有100棵橙子树,每一棵树平均结600个 橙子.现准备多种一些橙子树以提高产量,但是如 果多种树,那么树之间的距离和每一棵树所接受
数学化
●
D(-3.5,0) O
●x
C(3.5,0)
由此可知,如果不计其它因素,那 么水流的最大高度应达到约3.72m.
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,
其中AB和AD分别在两直角边上. (1) 设矩形的一边AB=xm,那么AD
M
30m
边的长度如何表示?
D
C
(2)设矩形的面积为ym2,当x取何值
或设抛物线为y=-x2+bx+c, 由待定系数法可求得抛物线表达为:
y=-x2+22/7X+5/4.
做一做
喷泉与二次函数
解:(2)如图,根据题意得,A点坐标为 (0,1.25),点C坐标为(3.5,0).
y
x
11
2
729
7 196
y
●B(1.57,3.72)
●A(0,1.25)
的阳光就会减少. 根据经验估计,每多 种一棵树,平均每棵 树就会少结5个橙子.
想一想
源于生活的数学
某果园有100棵橙子树,每一棵树平均结600 个橙子.现准备多种一些橙子树以提高产量,但 是如果多种树,那么树之间的距离和每一棵树所 接受的阳光就会减少.根据经验估计,每多种一 棵树,平均每棵树就会少结5个橙子.
2.6~2.8__何时获得最大利润、最大面积是多少A

2.6~2.8 何时获得最大利润、最大面积是多少
班级:_______ 姓名:_______ 序号:_______
1、某商场以每件20元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足关系:m=140-2x.
(1)写出商场卖这种商品每天的销售利润y与每件的销售价x间的函数关系式;
(2)如果商场要想每天获得最大的销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?
2、如图,已知△ABC是一等腰三角形铁板余料,其中AB=AC=20cm,BC=24cm.若在△ABC上截出
一矩形零件DEFG,使EF在BC上,点D、G分别在边AB、AC上.
问矩形DEFG的最大面积是多少?
F B G
D
C
A
3、.如图,△ABC中,∠B=90°,AB=6cm,BC=12cm.点P从点A开始,沿AB边向点B 以每秒1cm
的速度移动;点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动.如果P,Q 同时出发,问经过几秒钟△PBQ的面积最大?最大面积是多少?
B Q
C
P
A。
2.6何时获得最大利润
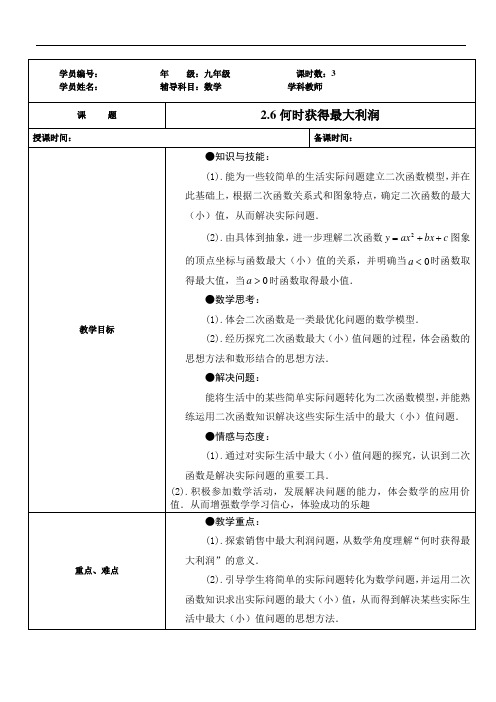
三、举例: 【例 1】某商场经营一批进价为 2 元一件的小商品,在市场营销中发现此商品的日销售单价 x 元与日销售量 y 件 之间有如下关系: x 3 5 9 11 y 18 14 6 2 (1)在所给的直角坐标系甲中: ①根据表中提供的数据描出实数对(x,y)的对应点; ②猜测并确定日销售量 y 件与日销售单价 x 元之间的函数表达式,并画出图象. (2)设经营此商品的日销售利润(不考虑其他因素)为 P 元,根据日销售规律: ①试求出日销售利润 P 元与日销售单价 x 元之间的函数表达式, 并求出日销售单价 x 为多少元时, 才能获得最大 日销售利润?试问日销售利润 P 是否存在最小值?若有,试求出;若无,请说明理由. ②在给定的直角坐标系乙中,画出日销售利润 P 元与日销售单价 x 元之间的函数图象的简图,观察图象,写出 x 与 P 的取值范围.
(2).销售量可以表示为
; ;
销售额(销售总收入)可以表示为
教师进行点评,得出答案,强调结果要化为最简形式.
所获利润与销售单价之间的关系式可以表示为
;
(3).当销售单价是
元时,可以获得最大利润,最大利润是
元.
在解决最大利 润”的数学意义.
有( ) A.1 个 B.2 个 C.3 个 D.4 个 2.某类产品按质量共分为 10 个档次,生产最低档次产品每件利润为 8 元,如果每提高一个档次每件利润增加 2 元.用同样的工时,最低档次产品每天可生产 60 件,每提高一个档次将少生产 3 件,求生产何种档次的产品利润最 大?
五、课后练习 1.某商场销售一批名牌衬衫,平均每天可售出 20 件,每件盈利 40 元.为了扩大销售,增加盈利,尽快减少库 存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价 1 元,商场平均每天可多售出 2 件. (1)若商场平均每天要盈利 1200 元,每件衬衫应降价多少元? (2)每件衬衫降低多少元时,商场平均每天盈利最多?
九年级数学何时获得最大利润1(2019年10月整理)

想一想 已知成批购进时单价是20元.根据 市场调查,销售量与销售单价满足如下关系:在一 段时间Байду номын сангаас,单价是35元时,销售量是600件,而单 价每降低1元,就可以多销售200件,问销售单价是 多少时获利最多 ?
• 如果设销售单价为x元,(20≤x≤35的整数) • 每件降价___3_5_-_x______ 元 • 销售量可以表示__6_0_0_+__2_0_0(___3_5_-_x__)件 • 每件利润___x_-_2_0____元 • 获得的总利润y =_(___x_-_20__)_[_6_00_+_2_0_0(__3_5_- _x_)__] __
九年级 数学
第二章 二次函数
2.6 何时获得最大利润
授课人: 李华军
德州市第九中学
九年级 数学
第二章 二次函数
2.6 何时获得最大利润
某大型商场的杨总到 T恤衫部 去视察,了解的情况如下:已知 成批购进时单价是20元.根据市 场调查,销售量与销售单价满足 如下关系:在一段时间内,单价 是35元时,销售量是600件,而单 价每降低1元,就可以多销售200 件.于是杨总给该部门王经理下 达一个任务,马上制定出获利最 多的销售方案,这可把王经理给 难住了?你能帮他解决这个问题 吗?
=-200x2+11600x-152000
;配资炒股 /
;
遂抽军而还 顺自江都来归长安 其安西都护 万国来朝 摄监察御史李知古上言 初禁商贾以牛 常以战阵射猎为务 行则驾象 四面有水 特令告庙 斩首千余级 太宗文武圣皇帝德侔覆载 南去西城一千七百里 所费钜万 徙张宥为光禄卿 甥舅之国 牂牁蛮 封而藏之 可汗乃领众而南 东至成州 兼御史中丞邵同持节入吐蕃 其年 "明年 兼御史中丞侯幼平充入蕃告册立等
26~28 何时获得最大利润、最大面积是多少A

2.6~2.8 何时获得最大利润、最大面积是多少、二次函数与一元二次方程(A 卷)(50分钟,共100分)班级:_______ 姓名:_______ 得分:_______ 开展性评语:_____________一、请准确填空(每题3分,共24分)y =-2x 2+mx -3的顶点在x 轴正半轴上,那么m =______. y =-2x 2+x -21,当x =______时,yx 轴______交点(填“有〞或“没有〞). y =ax 2+bx +c 的图象如图1所示.①这个二次函数的表达式是y =______;②当x =______时,y =3;③按照 图象答复:当x ______时,y>0.图1图2x 1=-2,x 2=5,请写出一个颠末点(-2,0),(5,0)两点二次函数的表达式:______.(写出一个符合要求的即可) x 取什么实数,二次函数y =2x 2-6x +m 的函数值总是正值,你认为m 的取值范围是______,此时关于一元二次方程2x 2-6x +m =0的解的情况是______(填“有解〞或“无解〞). 6.某一抛物线开口向下,且与x 轴无交点,那么具有这样性质的抛物线的表达式可能为______(只写一个),此类函数都有______值(填“最大〞“最小〞).r 的圆,如果半径增加m ,那么新圆的面积S 与m 之间的函数关系式是______.8.如图2,一小孩将一只皮球从A 处抛出去,它所颠末的路线是某个二次函数图象的一局部,如果他的出手处A 距地面的距离OA 为1 m ,球路的最高点B (8,9),那么这个二次函数的表达式为______,小孩将球抛出了约______米(精确到0.1 m). 二、相信你的选择(每题3分,共24分)y =ax 2+bx +c 的图象有以下命题,此中是假命题的个数是〔 〕①当c =0时,函数的图象颠末原点; ②当b =0时,函数的图象关于y 轴对称;③函数的图象最高点的纵坐标是ab ac 442;④当c >0且函数的图象开口向下时,方程ax 2+bx +c =0必有两个不相等的实根( )10.某产物进货单价为90元,按100元一个售出时,能售500个,如果这种商品涨价1元,其发卖额就减少10个,为了获得最大利润,其单价应定为( ) ;;y =ax 2+bx +c 如图3所示,那么关于x 的方程ax 2+bx +c -8=0的根的情况是A.有两个不相等的正实数根 ;; C.有两个相等的实数根 ;.y =kx 2-7x -7的图象和x 轴有交点,那么k 的取值范围是( )A.k >-47; B.k ≥-47且k ≠0; C.k ≥-47; D.k >-47且k ≠0 13.如图4所示,在一个直角三角形的内部作一个长方形ABCD ,此中AB 和BC 别离在两直角边上,设AB =x m ,长方形的面积为y m 2,要使长方形的面积最大,其边长x 应为( )A.424 m B.6 m C.15 m D.25m xy 8O5 m 12 mABCDx y2.4 12O图3图4图5y =x 2-4x +3的图象交x 轴于A 、B 两点,交y 轴于点C ,△ABC 的面积为( )A.1B.3m 为任何实数,二次函数y =x 2+(2-m )x +m 的图象总过的点是( )A.(-1,0);B.(1,0)C.(-1,3) ;D.(1,3)16.为了备战2021奥运会,中国足球队在某次训练中,一队员在距离球门12米处的挑射,正好从y =ax 2+bx +c (如图5所示),那么以下结论正确的选项是( )①a <-601 ②-601<a <0 ③a -b +c >0 ④0<b <-12aA.①③B.①④C.②③D.②④三、考查你的底子功(共20分)17.(10分)某商场以每件20元的价格购进一种商品,试销中发现,这种商品每天的发卖量m(件)与每件的发卖价x (元)满足关系:m =140-2x .(1)写出商场卖这种商品每天的发卖利润y 与每件的发卖价x 间的函数关系式; (2)如果商场要想每天获得最大的发卖利润,每件商品的售价定为多少最适宜?最大发卖利润为多少?18.(10分)二次函数y =(m 2-2)x 2-4mx +n 的图象的对称轴是x =2,且最高点在直线y =21x +1上,求这个二次函数的表达式.四、生活中的数学(共20分)19.(10分)如图,要建一个长方形养鸡场,鸡场的一边靠墙,如果用50 m 长的篱笆围成中间有一道篱笆隔墙的养鸡场,设它的长度为x m. (1)要使鸡场面积最大,鸡场的长度应为多少m ? (2)如果中间有n (n 是大于1的整数)道篱笆隔墙,要使鸡场面积最大,鸡场的长应为多少m ?比较(1)(2)的成果,你能得到什么结论?20.(10分)当运动中的汽车撞到物体时,汽车所受到的损坏程度可以用“撞击影响〞I =2v 2来暗示,此中v (千米/分)暗示汽车的速度; (1)列表暗示I 与v 的关系.(2)当汽车的速度扩大为本来的2倍时,撞击影响扩大为本来的多少倍?五.探究拓展与应用(共12分)21.(12分)如图7,一位运策动在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的程度距离为时,达到最大高度.(1)成立如下列图的直角坐标系,求抛物线的表达式;(2)该运策动身高,在此次跳投中,球在头顶上方处出手,问:球出手时,他跳离地面的高度是多少.m x参考答案6 2.41 大 -83没有 3.①x 2-2x ②3或-1 ③<0或>2 4.y =x 2-3x -105. m >29 无解 6.y =-x 2+x -1 最大7.S =π(r +m )2 8.y =-81x 2+2x三、17.解:(1)y =-2x 2+180x -2800.(2)y =-2x 2+180x -2800 =-2(x 2-90x )-2800 =-2(x -45)2+1250. 当x =45时,y 最大=1250.∴每件商品售价定为45元最适宜,此发卖利润最大,为1250元. 18.解:∵二次函数的对称轴x =2,此图象顶点的横坐标为2,此点在直线y =21x +1上. ∴y =21×2+1=2. ∴y =(m 2-2)x 2-4mx +n 的图象顶点坐标为(2,2). ∴-ab2=2.∴-)2(242--m m =2. 解得m =-1或m =2.∵最高点在直线上,∴a <0, ∴m =-1.∴y =-x 2+4x +n 顶点为(2,2). ∴2=-4+8+n .∴n =-2. 那么y =-x 2+4x +2. 四、19.解:(1)依题意得鸡场面积y =-.350312x x +-∵y =-31x 2+350x =31-(x 2-50x )=-31(x -25)2+3625,∴当x =25时,y 最大=3625,即鸡场的长度为25 m 时,其面积最大为3625m 2. (2)如中间有几道隔墙,那么隔墙长为nx-50m.∴y =n x -50·x =-n 1x 2+n 50x =-n 1(x 2-50x ) =-n 1(x -25)2+n625,当x =25时,y 最大=n625,即鸡场的长度为25 m 时,鸡场面积为n625 m 2. 结论:无论鸡场中间有多少道篱笆隔墙,要使鸡场面积最大,其长都是25 m.(2)I =2·(2v )=4×2v .当汽车的速度扩大为本来的2倍时,撞击影响扩大为本来的4倍. 五、21.解:(1)设抛物线的表达式为y =ax 2+bx +c .由图知图象过以下点:(0,3.5),(1.5,3.05).⎪⎩⎪⎨⎧==-=⎪⎪⎩⎪⎪⎨⎧++===-.5.3,0,2.0,5.15.105.3,5.3,022c b a c b a c a b得 ∴抛物线的表达式为yx 2+3.5.(2)设球出手时,他跳离地面的高度为h m ,那么球出手时,球的高度为 h +1.8+0.25=(h +2.05) m, ∴×(-2.5)2+3.5, ∴h=0.2(m).2021年最新整理出品,精品文档,欢送大师使用。
2.6 何时获得最大利润(含答案)-

2.6 何时获得最大利润1.某商店购进一批单价为16元的日用品,销售一段时间后,为了获取更多利润, 商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件; 若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x( 元/件)的一次函数.(1)试求y与x之间的函数关系式;(2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).2.某旅社有客房120间,每间房的日租金为50元时,每天都客满,旅社装修后要提高租金,经市场调查发现,如果每间客房的日租金每增加5元时,则客房每天出租数会减少6间,不考虑其他因素,旅社将每间客房的日租金提高到多少元时,客房日租金的总收入最高?3.某商场以80元/件的价格购进西服1000件,已知每件售价为100元时,可全部售出.如果定价每提高1%,则销售量就下降0.5%,问如何定价可使获利最大?(总利润=总收入-总成本).4.某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到赢利的过程.若该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前七个月的利润总和与t之间的关系)为s=12t2-2t.(1)第几个月末时,公司亏损最多?为什么?(2)第几个月末时,公司累积利润可达30万元?(3)求第8个月公司所获利润是多少万元?5.启明公司生产某种产品,每件成本是3元,售价是4元,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x( 万元)时,产品的年销售量是原销售量的y倍,且y=277101010xx-++. 如果把利润看作是销售总额减去成本和广告费:(1)试写出年利润s(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大?最大年利润是多少万元?(2)把(1)中的最大利润留出3万元做广告,其余的资金投资新项目,现有6个项目可供选择,各项目每股投资金额和预计年收益如下表:万元, 问有几种符合要求的方式?写出每种投资方式所选的项目.6.某市近年来经济发展迅速很快,根据统计,该市国内生产总值1990年为8.6 亿元人民币,1995年为10.4亿元人民币,2000年为12.9亿元人民币.经论证,上述数据适合一个二次函数关系,请你根据这个函数关系,预测2005 年该市国内生产总值将达到多少?答案:1.(1)设y=kx+b,则∵当x=20时,y=360;x=25时,y=210.∴3602021025k bk b=+⎧⎨=+⎩, 解得30960kb=-⎧⎨=⎩∴y=-30x+960(16≤x≤32)(2)设每月所得总利润为w元,则 w=(x-16)y=(x-16)(-30x+960)=-30(x-24)2+ 1920.∵-30<0,∴当x=24时,w有最大值.即销售价格定为24元/件时,才能使每月所获利润最大, 每月的最大利润为1920元.2.设每间客房的日租金提高x个5元(即5x元),则每天客房出租数会减少6x间,客房日租金总收入为y=(50+5x)(120-6x)=-30(x-5)2+6750.当x=5时,y有最大值6750,这时每间客房的日租金为50+5×5=75元. 客房总收入最高为6750元.3.商场购这1000件西服的总成本为80×1000=8000元.设定价提高x%, 则销售量下降0.5x%,即当定价为100(1+x%)元时,销售量为1000(1-0.5x%)件.故y=100(1+x%)·1000(1-0.5x%)-8000 =-5x2+500x+20000=-5(x-50)2+32500.当x=50时, y 有最大值32500.即定价为150元/件时获利最大,为32500元.4.(1)s=12(t-2)2-2.故第2个月末时公司亏损最多达2万元.(2)将s=30代入s=12t2-2t,得30=12t2-2t,解得t1=10,t2=-6(舍去).即第10个月末公司累积利润达30万元. (3)当t=7时,s=12×72-2×7=10.5, 即第7个月末公司累积利润为10.5万元;当t=8时,s=12×82-2×8 =16, 即第8个月末公司累积利润为16万元.16-10.5=5.5万元.故第8个月公司所获利润为5.5万元.5.(1)s=10×277101010xx⎛⎫-++⎪⎝⎭×(4-3)-x =-x2+6x+7.当x=62(1)-⨯-=3 时,S最大=24(1)764(1)⨯-⨯-⨯-=16.∴当广告费是3万元时,公司获得的最大年利润是16万元.(2)用于再投资的资金有16-3=13万元.有下列两种投资方式符合要求:①取A、B、E各一股,投入资金为5+2+6=13万元,收益为0.55+0.4+0.9=1.85万元>1.6万元.②取B、D、E各一股,投入资金为2+4+6=12万元<13万元,收益为0.4+0.5+0.9=1.8万元>1.6万元 .6.可以把三组数据看成三个点:A(0,8.6),B(5,10.4),C(10,12.9).设y=ax2+bx+c.把A,B,C三点坐标代入其中,得8.62558.610.4100108.612.9ca ba b=⎧⎪++=⎨⎪++=⎩, 解得a=0.014,b=0.29,c=8.6.故y=0.014x2+0.29x+8.6.令x=15,得y=0.014×152+0.29×15+8.6≈16.1.所以可预测2005年该市国内生产总值达到16.1亿元人民币.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.6~2.8 何时获得最大利润、最大面积是多少、二次函数与一元二次方程(B 卷)(50分钟,共100分)班级:_______ 姓名:_______ 得分:_______ 发展性评语:_____________一、请准确填空(每小题4分,共24分)1.若抛物线y=2x 2-4x+1与x 轴两交点分别是(x 1,0),(x 2,0),则x 12+x 22=______.2.若抛物线y=x 2-(2k+1)x+k 2+2,与x 轴有两个交点,则整数k 的最小值是______.3.已知二次函数y=ax 2+bx+c(a ≠0)的图象如图1所示,由抛物线的特征你能得到含有a 、b 、c 三个字母的等式或不等式为______(写出一个即可).4.等腰梯形的周长为60 cm ,底角为60°,当梯形腰x=______时,梯形面积最大,等于______.5.找出能反映下列各情景中两个变量间关系的图象,并将代号填在相应的横线上.(1)一辆匀速行驶的汽车,其速度与时间的关系.对应的图象是______.(2)正方形的面积与边长之间的关系.对应的图象是______.(3)用一定长度的铁丝围成一个长方形,长方形的面积与其中一边的长之间的关系.对应的图象是______.(4)在220 V 电压下,电流强度与电阻之间的关系.对应的图象是______.A B D6.将进货单价为70元的某种商品按零售价100元售出时,每天能卖出20个.若这种商品的 零售价在一定范围内每降价1元,其日销售量就增加了1个,为了获得最大利润,则应降价______元,最大利润为______元.二、相信你的选择(每小题4分,共24分)7.把一个小球以20 m/s 的速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系h=20t -5t 2.当h=20 m 时,小球的运动时间为( )A.20 sB.2 sC.(22+2) sD.(22-2) s8.如果抛物线y=-x 2+2(m -1)x+m+1与x 轴交于A 、B 两点,且A 点在x 轴正半轴上,B 点在x 轴的负半轴上,则m 的取值范围应是()A.m>1B.m>-1C.m<-1D.m<19.如图3,一次函数y=-2x+3的图象与x 、y 轴分别相交于A 、C 两点,二次函数y=x 2+bx+c 的图象过点c 且与一次函数在第二象限交于另一点B ,若AC ∶CB=1∶2,那么,这个二次函数的顶点坐标为( )A.(-21,411)B.(-21,45)C.(21,411)D.(21,-411) 10.某乡镇企业现在年产值是15万元,如果每增加100元投资,一年增加250元产值,那么总产值y(万元)与新增加的投资额x(万元)之间函数关系为( )A.y=25x+15B.y=2.5x+1.5C.y=2.5x+15D.y=25x+1.511.如图4,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=-121x 2+32x+35,则该运动员此次掷铅球的成绩是( ) A.6 mB.12 mC.8 mD.10 m图3 图4 图512.某幢建筑物,从10 m 高的窗口A ,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图5,如果抛物线的最高点M 离墙1 m ,离地面340m ,则水流落地点B 离墙的距离OB 是( )A.2 mB.3 mC.4 mD.5 m三、考查你的基本功(共18分)13.(10分)某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数的图象(部分)刻画了该公司年初以来累积利润S(万元)与销售时间t(月)之间的关系(即前t 个月的利润总和S 与t 之间的关系).(1)根据图象你可获得哪些关于该公司的具体信息?(至少写出三条)(2)还能提出其他相关的问题吗?若不能,说明理由;若能,进行解答,并与同伴交流.14.(8分)把一个数m分解为两数之和,何时它们的乘积最大?你能得出一个一般性的结论吗?四、生活中的数学(共12分)15.(12分)有一种螃蟹,从海上捕获后不放养,最多只能存活两天.如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去.假设放养期内蟹的个体质量基本保持不变,现有一经销商,按市场价收购这种活蟹1000 kg放养在塘内,此时市场价为每千克30元,据测算,此后每千克活蟹的市场价每天可上升1元,但是,放养一天需支出各种费用为400元,且平均每天还有10 kg蟹死去,假定死蟹均于当天全部销售出,售价都是每千克20元.(1)设x天后每千克活蟹的市场价为p元,写出p关于x的函数关系式;(2)如果放养x天后将活蟹一次性出售,并记1000 kg蟹的销售总额为Q元,写出Q关于x的函数关系式.(3)该经销商将这批蟹放养多少天后出售,可获最大利润(利润=Q-收购总额)?何时获得最大利润学习目标够分析和表示实际问题中变量之间的二次函数关系,并应用二次函数的知识求出实际问题的最大(小)值,发展解决问题的能力。
Ⅰ.创设问题情景,引入新课前面我们认识了二次函数,研究了二次函数的图像和性质,由简单的二次函数y=x2开始,然后是y=ax2+c,最后是y=a(x-h)2,y=a(x-h)2+k, y=ax2+bx+c,掌握了二次函数的三种表示方式,会求二次函数的最大(小)值。
我们知道x表示自变量,y表示因变量,如果x在某一实际问题中表示销售单价,y表示所获利润,你会求这个最大利润吗?本节课我们将研究这个问题。
Ⅱ.讲授新课一.有关利润问题某商店经营T 恤衫,已知成批购进时单价是2.5元.根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售出200件.请你帮助分析,销售单价是多少时,可以获得利润最多?设销售单价为x(x≤13.5)元,那么①销售量可以表示为______________.②销售额可以表示为______________.③所获利润可以表示为_______________.④当销售单价___________元时,可以获得最大利润,最大利润__________.二.做一做还记得本章一开始的“种多少棵橙子树”的问题吗?我们得到表示增种橙子树的数量x(棵)与橙子总产量y(个)的二次函数表达式y=(600-5x)(100+x)=-5x2+100x+60000.我们还曾经利用列表的方法得到一个猜测,现在验证一下你的猜测是否正确?你是怎么做的?与同伴进行交流。
解:y=-5x2+100x+60000=-5(x-10)2+60500.当x=10时,y(最大)=60500.三.议一议(1).利用函数图像描述橙子的总产量与增种橙子树的棵树之间的关系.(2). 增种多少棵橙子树,可以使橙子的总产量在60400以上?解:(1)当x<10时,橙子的总产量随种橙子树的增加而增加;当x>10时,橙子的总产量随种橙子树的增加而减少。
(2) 由图可知,增种6棵.7棵.8棵.9棵.10棵.11棵.12棵.13棵.或14棵,都可以使橙子总产量在60400以上。
四.练习1.二次函数y=-x2―4x+4的最大值是()A. 4B.6C.8D.122. 二次函数y=x2―2x+3(2≤x≤4)的最小值是()A. 2B.3C.4D.113. 寒假期间,小明为了锻炼自己,来到一家电脑公司销售商场做销售员,期间商场搞了一次促销活动,他发现销售某种型号电脑所获利润y(元)与销售台数x(元)满足关系式y=―x2+50x+28625。
因此小明提醒该商场老板,要获得最大利润,则这次活动应卖出()A. 30 台B.25 台C.20 台D.15 台4.某童装专卖店销售一种童装,已知这种童装每天所获的利润y(元)与童装的单价x(元)满足关系式y=―x2+bx+c。
当单价为10元时所获得的利润是900元;当单价为30元时所获得的利润是100元,要想获得最大利润,每件的单价应定为__________元.5.某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可以售出400件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件,如何提高售价,才能在半月内获得最大利润?五.拓展练习1.某商场销售某种品牌的纯牛奶,已知进价为每箱40元,生产厂家要求每箱售价在40至70元之间.市场调查发现:若每箱以50元销售,平均每天可销售90箱,价格每降低1元,平均每天多销售3箱,价格每升高1元,平均每天少销售3箱.当牛奶售价为多少时,平均每天的利润最大?最大利润为多少?2.某公司经销一种绿茶,每千克成本为50元.市场调查发现,销售量W(千克)随销售单价x(元/千克)的变化而变化,具体关系式为:W=-2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:(1).求y与x的关系式.(2).当x取何值时,y的值最大?(3).如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?六.小结1.通过本节课的学习,我们学到了那些知识。
2.本节课我们经历了探索T 恤衫销售中最大利润等问题的过程,体会二次函数是一类最优化问题的数模型,并感受了数学的应用价值。
学会了分析和表示实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题的最大(小)值,提高解决问题的能力。
七.作业习题2.7《何时获得最大利润》中考展示“何时获得最大利润”一节是以二次函数知识点为依托,以生产、生活为背景,考查建立数学模型的能力.现采撷几多浪花奉献给大家.例1(贵阳)某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:若日销售量y是销售价x的一次函数.(1)求出日销售量y(件)与销售价x(元)的函数关系式;(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?解析:(1)设此一次函数解析式为y kx b=+.则15252020k bk b+=⎧⎨+=⎩,解得:k =-1,b=40.即:一次函数解析式为y =-x+40.(2)设每件产品的销售价应定为x元,所获销售利润为w元.w =(x-10)(40-x)=-x2+50x-400=-(x-25)2+225.则当产品的销售价应定为25元,此时每日获得最大销售利润为225元.例2(青岛)某工厂现有80台机器,每台机器平均每天生产384件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,由于其它生产条件不变,因此每增加一台机器,每台机器平均每天将少生产4件产品.(1)增加x台机器,每天的生产总量为y件,请写出y与x的函数关系式。
