2017年春季新版北师大版九年级数学下学期3.7、切线长定理同步练习4
九年级数学下册 3.7 切线长定理特色训练 北师大版(2021学年)

2017春九年级数学下册 3.7 切线长定理特色训练(新版)北师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017春九年级数学下册3.7 切线长定理特色训练(新版)北师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017春九年级数学下册3.7 切线长定理特色训练(新版)北师大版的全部内容。
切线长定理以上就是本文的全部内容,可以编辑修改。
高尔基说过:“书是人类进步的阶梯。
”我希望各位朋友能借助这个阶梯不断进步。
物质生活极大丰富,科学技术飞速发展,这一切逐渐改变了人们的学习和休闲的方式。
很多人已经不再如饥似渴地追逐一篇文档了,但只要你依然有着这样一份小小的坚持,你就会不断成长进步,当纷繁复杂的世界牵引着我们疲于向外追逐的时候,阅读一文或者做一道题却让我们静下心来,回归自我。
用学习来激活我们的想象力和思维,建立我们的信仰,从而保有我们纯粹的精神世界,抵御外部世界的袭扰。
The above is the wholecontent ofthis article,Gorkysaid: "thebook is the ladder of humanprogress." Ihopeyou canmake progresswiththe help of this ladder. Material life is extremelyrich, science and technology are developing rapidly, all of which gradually change the way of people'sstudy and leisure. Manypeopleare no longer eagerto pursueadocument,but as long as you stillhave sucha small persistence, youwill continuetogrow and progress.Wh en the complex world leads us tochase out, reading anarticl eordoing a problem makes us calm down and return to ourselves. With learning, we canactivate our imagination and thinking,establish our belief, keep our pure spiritual world and resist theattack of theexternalworld.。
【数学九年级下】北师大版 单元练习 切线长定理 同步测试题(答案}
11. 若圆外切四边形 䉨⇔侐 的面积为 平方厘米, 侐 䉨⇔ ൌ 厘米,则该圆半径为 ________.
12. 如图, 与 侐 的边 侐 相切于点 ⇔,与 侐、 的延长线切于 、䉨 两点,已
知
ൌ ,则 侐 的周长为________.
13. 如图, 䉨, 侐,侐⇔ 与半圆 均相切, 侐 䉨⇔, 䉨 ,⇔侐 ,则
5. 如图, 内切于四边形 䉨⇔侐, 䉨 ൌ ,䉨⇔ ⣀,⇔侐 ,则 侐 的长度为( )
A.
B.
C.ൌ
D.ൌൌ
6. 如图,四边形 䉨⇔侐 的边 䉨、䉨⇔、⇔侐、侐 和 分别相切于点 、 、 、 .若
四边形 䉨⇔侐 的周长为 ,则 䉨 ⇔侐 等于( )
A.
B.
C.ൌ
D.ൌ
7. 如图, , 䉨 分别与 相切于点 ,䉨,过圆上点 ⇔ 作
侐 ൌ,那么 䉨⇔ 的长为________. 20. 如图: 、 䉨 切 于 、䉨,过点 ⇔ 的切线交 、 䉨 于 侐、 ,
ൌ ܤ,则
侐 的周长为________.
三、 解答题 (本题共计 6 小题 ,共计 60 分 , )
21. 如图, 、 䉨 是 的切线, 、䉨 为切点, ⇔ 是 的直径, 䉨 ⇔
C.
D.
3. 已知四边形 䉨⇔侐 是梯形,且 侐 䉨⇔, 侐 䉨⇔,又 与 䉨、 侐、⇔侐 分别相 切于点 、 、 ,圆心 在 䉨⇔ 上,则 䉨 ⇔侐 与 䉨⇔ 的大小关系是( )
A.大于
B.等于
C.小于
D.不能确定
4. 如图, 为 外一点, , 䉨 分别切 两点,若
,则 䉨 ( )
A.
B.
C.
D.
①求
的周长;
北师大版九年级数学下册 3.7 切线长定理 同步测试题

真情提示:题号得分43. 如图,一圆内切四边形50A.5A.4B.5C.6D.无法确定6. 如图所示,已知、切于、两点,是上一动点,过作的切线交PA PB ⊙O A B C ^AB C ⊙O 于点,交于点,已知,则 PA M PB N ∠P =56∘∠MON =()A.56∘ B.60∘ C.62∘ D.不可求7. 如图,,分别切于点和点,是上任一点,过的切线分别交,PA PB ⊙O A B C ^AB C PA 于,.若的半径为,,则的周长是( )PB D E ⊙O 6PO =10△PDEA.16B.14C.12D.108. 如图,是一张周长为的三角形的纸片,,是它的内切圆,△ABC 17cm BC =5cm ⊙O 小明准备用剪刀在的右侧沿着与相切的任意一条直线剪下,则剪下⊙O ⊙O MN △AMN 的三角形的周长为( )A. B.12cm 7cmC. D.随直线的变化而变化6cm MN9. 如图,从外一点引圆的两条切线、,切点为、,点是劣弧上一点,⊙O P PA PB A B C AB 过的切线交、分别于、,若的半径为,,则的周长为C PA PB M N ⊙O 2∠P =60∘△PMN ( )12. 如图所示,⊙△AEF∠C345⊙O所对的边长依次为,,,则的半径是________.PA PB EF⊙O A B D PA=10cm△PEF15. 如图,、、分别切于、、,若,则的周长是cm∠P=35∘∠AOB=∠EOF=________ ,若,则________(度),________(度).PA PB⊙O A B CD AB E16. 如图,、是的两条切线,、是切点,切劣弧于点,已知切线PA6cm△PCD cm的长为,则的周长为________.⊙O3cm P6cm P⊙O17. 如图,的半径为,点到圆心的距离为,经过点引的两条切线,这两条切线的夹角为________度.P⊙O PA PB⊙O A B CD⊙O E18. 如图所示,为外一点,、分别切于、,切于点,分别PA PB C D PA=15△PCD交、于点、,若,则的周长为________.PA PB CD⊙O A B E PA=10△PCD19. 如图,、、为的切线,、、为切点,,则的周长为________.PA PB O A B O CD C D20. 如图,,分别切圆于,,并与圆的切线分别相交于,,已知三、解答题(本题共计PA PB⊙O A B Q AB Q 24. 已知:如图,、是的切线,切点分别是、,为上一点,过点作⊙O PA PB E F PA=10cm△PEF的切线,交、于、点,已知,求的周长.∠APB=52∘PA PB DE⊙O A B F 25. 如图,,、、都为的切线,切点分别为、、,且PA=6.△PDE(1)求的周长;∠DOE(2)求的度数.PA PB⊙O A B EF⊙O26. 如图,、是的切线,切点分别是、,直线也是的切线,切点为Q PA PB E F PA=12cm∠P=40∘,交、于点、,已知,△PEF①求的周长;∠EOF②求的度数.。
北师大版初三数学下册《3.7切线长定理》习题课件(附答案)

(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
(1)证明:如图,连接OC. ∵BD是⊙O的切线, ∴∠ABD=90°.
∵AB是⊙O的直径,∴∠ACB=90°.
∴∠ACO+∠BCO=90°,∠BCD=90°. ∵点E是BD的中点, 1 ∴CE= BD=BE. 2 ∴∠BCE=∠CBE. ∵∠CBE+∠ABC=90°,
∵DF是⊙O的切线,
∴OD⊥DF. ∴∠EDF=90°-60°=30°. ∴∠DFE=90°. ∴DF⊥CE.
∴CF=EF.
(2)解: 相等.理由如下:
当点E运动至与点B重合时,BC是⊙O的切线, ∵⊙O的切线DF交BC于点F,
∴BF=DF.
∴∠BDF=∠DBF. ∵AB是直径, ∴∠ADB=∠BDC=90°. ∴∠FDC=∠C. ∴DF=CF. ∴BF=CF.
DH=BC+AD,
即AB+CD=BC+AD. (2)过点B作⊙O的切线,交AD于点M. 由(1)可知BM+CD=BC+MD. ∵AB<AM+BM,
∴AB+BM+CD<AM+BM+BC+MD,
即AB+CD<BC+AD.
∵AB=2,∴OE=DE.
∴△ODE是等边三角形. ∴∠ODE=∠OED=60°. ∵DE∥AB, ∴∠AOD=∠ODE=60°,∠EOB=∠OED=60°.
∴△AOD和△BOE是等边三角形.
∴∠OAD=∠OBE=60°.
∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°. ∴△CDE是等边三角形.
BD BC 2 1 , ∵tan A= AB AC 4 2 1 1 5 . ∴BD= AB 5. CE BD 2 2 2
12.【中考•泸州】如图,⊙O与Rt△ABC的直角边AC和斜 边AB分别相切于点C,D,与边BC相交于点F,OA与 CD相交于点E,连接FE并延长交AC边于点G. (1)求证:DF∥AO;
北师大版数学九年级下册第3章第7节切线长定理同步检测.docx

初中数学试卷桑水出品北师大版数学九年级下册第3章第7节切线长定理同步检测一、选择题1.如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为()A.32 B.34 C.36 D.38答案:B解析:解答:由题意可得圆外切四边形的两组对边和相等,所以四边形的周长=2×(7+10)=34.故选:B.分析:根据切线长定理,可以证明圆外切四边形的性质:圆外切四边形的两组对边和相等,从而可求得四边形的周长.2.如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为()A.15 B.12 C.20 D.30答案:D解析:解答:∵P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,∴AC=EC,BD=DE,AP=BP,∵PA=15,∴△PCD的周长为:PA+PB=30.故选:D.分析:直接利用切线长定理得出AC=EC,BD=DE,AP=BP,进而求出答案.3.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为()A.20cm B.15cm C.10cm D.随直线MN的变化而变化答案:A解析:解答:如图:∵△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,AD=10cm,∴设E、F分别是⊙O的切点,故DM=MF,FN=EN,AD=AE,∴AM+AN+MN=AD+AE=10+10=20(cm).故选:A.分析:利用切线长定理得出DM=MF,FN=EN,AD=AE,进而得出答案.4.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为()A.8 B.9 C.10 D.11答案:D解析:解答:∵⊙O内切于四边形ABCD,∴AD+BC=AB+CD,∵AB=10,BC=7,CD=8,∴AD+7=10+8,解得:AD=11.故选:D.分析:根据圆外切四边形的性质对边和相等进而得出AD的长.5.圆外切等腰梯形的一腰长是8,则这个等腰梯形的上底与下底长的和为()A.4 B.8 C.12 D.16答案:D解析:解答:∵圆外切等腰梯形的一腰长是8,∴梯形对边和为:8+8=16,则这个等腰梯形的上底与下底长的和为16.故选:D.分析:直接利用圆外切四边形对边和相等,进而求出即可.6.如图,⊙O是△ABC的内切圆,点D、E分别为边AB、AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是()A.7 B.8 C.9 D.16答案:A解析:解答:∵AB、AC、BC、DE都和⊙O相切,∴BI=BG,CI=CH,DG=DF,EF=EH.∴BG+CH=BI+CI=BC=9,∴△ADE的周长=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=△ABC的周长-(BG+EH+BC)=25-2×9=7.故选A.分析:根据切线长定理,可得BI=BG,CI=CH,DG=DF,EF=EH,△ADE的周长=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=△ABC的周长-(BG+EH+BC),据此即可求解.7.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB 的长是()A.4 B.8 C.4√3 D.8√3答案:B解析:解答:∵PA、PB都是⊙O的切线,∴PA=PB,又∵∠P=60°,∴△PAB是等边三角形,即AB=PA=8,故选B.分析:根据切线长定理知PA=PB,而∠P=60°,所以△PAB是等边三角形,由此求得弦AB的长.8.如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为()A.35° B.45° C.60° D.70°答案:D解析:解答:根据切线的性质定理得∠PAC=90°,∴∠PAB=90°-∠BAC=90°-35°=55°.根据切线长定理得PA=PB,所以∠PBA=∠PAB=55°,所以∠P=70°.故选D.分析:根据切线长定理得等腰△PAB,运用内角和定理求解.9.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为()A.130° B.120° C.110° D.100°答案:C解析:解答:∵AB、AC是⊙O的两条切线,B、C是切点,∴∠B=∠C=90°,∠BOC=180°-∠A=110°.故选C.分析:利用切线的性质可得,∠B=∠C=90°,再用四边形的内角和为360度可解.10.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=23,那么∠AOB等于()A.90° B.100° C.110° D.120°答案:D解析:解答:∵△APO≌△BPO(HL),∴∠AOP=∠BOP.∵sin∠AOP=AP:OP=23:4= 3:2,∴∠AOP=60°.∴∠AOB=120°.故选D.分析:由切线长定理知△APO≌△BPO,得∠AOP=∠BOP.可求得sin∠AOP= 3:2,所以可知∠AOP=60°,从而求得∠AOB的值.11.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,错误的是()A.∠1=∠2 B.PA=PB C.AB⊥OP D.PA2=PC•PO答案:D解析:解答:连接OA、OB,AB,∵PA切⊙O于A,PB切⊙O于B,由切线长定理知,∠1=∠2,PA=PB,∴△ABP是等腰三角形,∵∠1=∠2,∴AB⊥OP(等腰三角形三线合一),故A,B,C正确,根据切割线定理知:PA2=PC•(PO+OC),因此D错误.故选D.分析:由切线长定理可判断出A、B选项均正确.易知△ABP是等腰三角形,根据等腰三角形三线合一的特点,可求出AB⊥OP,故C正确.而D选项显然不符合切割线定理,因此D错误.12.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为()A.5,12(90°+∠P) B.7,90°+12C.10,90°-12∠P D.10,90°+12∠P答案:C解析:解答:∵PA、PB切⊙O于A、B,CD切⊙O于E,∴PA=PB=10,ED=AD,CE=BC;∴△PCD的周长=PD+DE+PC+CE=2PA,即△PCD的周长=2PA=10,;如图,连接OA、OE、OB.由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,∵AO=OE=OB,易证△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),∴∠AOC=∠EOC,∠EOD=∠BOD,∴∠COD=12∠AOB,∴∠AOB=180°-∠P,∴∠COD=90°-12∠P.故选:C.分析:根据切线长定理,即可得到PA=PB,ED=AD,CE=BC,从而求得三角形的周长=2PA;连接OA、OE、OB根据切线性质,∠P+∠AOB=180°,再根据CD为切线可知∠COD=12∠AOB.A.4 B.6 C.8 D.10答案:C解析:解答:如图,设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,∴MN=12(AB+CD),根据切线长定理得:DE=DH,CF=CH,并且等腰梯形和圆都是轴对称图形,∴CD=DH+CH=DE+CF=12(AB+CD),∴CD=MN,而MN=8,∴CD=8.故选C.分析:如图,设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,根据中位线定理可以得到上下底之和,然后利用切线长定理可以得到一腰长等于中位线,由此即可解决问题.14.如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为()A.9 B.7 C.11 D.8答案:C解析:解答:如图:设AB,AC,BC和圆的切点分别是P,N,M,CM=x,根据切线长定理,得CN=CM=x,BM=BP=9-x,AN=AP=10-x.则有9-x+10-x=8,解得:x=5.5.所以△CDE的周长=CD+CE+QE+DQ=2x=11.故选:C.分析:设AB,AC,BC和圆的切点分别是P,N,M.根据切线长定理得到NC=MC,QE=DQ.所以三角形CDE 的周长即是CM+CN的值,再进一步根据切线长定理由三角形ABC的三边进行求解即可.15.已知四边形ABCD是梯形,且AD∥BC,AD<BC,又⊙O与AB、AD、CD分别相切于点E、F、G,圆心O在BC上,则AB+CD与BC的大小关系是()A.大于 B.等于 C.小于 D.不能确定答案:A解析:解答:连接OF,∵AD是切线,∴OF⊥AD,又∵AD∥BC,∴AB≥OF,CD≥OF,又∵AD<BC,∴AB≥OF,CD≥OF最多有一个成立.∴AB+CD>2OF,∵BC=2OF,∴AB+CD>BC.故选A,分析:连接OF,则OF是梯形的高,则AB≥OF,CD≥OF,而两个式子不能同时成立,据此即可证得.二、填空题16.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD的周长等于10cm,则PA= cm.答案:5解析:解答:如图,设DC与⊙O的切点为E;∵PA、PB分别是⊙O的切线,且切点为A、B;∴PA=PB;同理,可得:DE=DA,CE=CB;则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm);∴PA=PB=5cm,故答案为:5.分析:由于DA、DC、BC都是⊙O的切线,可根据切线长定理,将△PCD的周长转换为PA、PB的长,然后再进行求解.17.如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8cm,那么△PDE的周长为答案:16解析:解答:∵PA、PB、DE分别切⊙O于A、B、C,∴PA=PB,DA=DC,EC=EB;∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=8+8=16;∴△PDE的周长为16.故答案为16.分析:由于PA、PB、DE都是⊙O的切线,可根据切线长定理将切线PA、PB的长转化为△PDE的周长.18.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,若⊙O的半径为r,△PCD的周长等于3r,则tan 12∠APB的值是答案:2 3解析:解答:连接PO,AO,∵PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,∴∠APO=∠BPO,AC=EC,DE=BD,PA=PB,∴PA+PB=△PCD的周长=3r,∴PA=PB=1.5r,∴tan 12∠APB=AO: PA =r :1.5r =23,故答案为:2 3.分析:利用切线长定理得出PA=PB=1.5r,再结合锐角三角函数关系得出答案.19.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为答案:8cm解析:解答:连接OD、OE,∵⊙O是Rt△ABC的内切圆,∴OD⊥AB,OE⊥BC,∵∠ABC=90°,∴∠ODB=∠DBE=∠OEB=90°,∴四边形ODBE是矩形,∵OD=OE,∴矩形ODBE是正方形,∴BD=BE=OD=OE=4cm,∵⊙O切AB于D,切BC于E,切MN于P,NP与NE是从一点出发的圆的两条切线,∴MP=DM,NP=NE,∴Rt△MBN的周长为:MB+NB+MN=MB+BN+NE+DM=BD+BE=4cm+4cm=8cm,故答案为:8cm.分析:连接OD、OE,求出∠ODB=∠DBE=∠OEB=90°,推出四边形ODBE是正方形,得出BD=BE=OD=OE=4cm,根据切线长定理得出MP=DM,NP=NE,代入MB+NB+MN得出BD+BE,求出即可.20.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是答案:14解析:解答:根据切线长定理,得AD=AE,BC=BE,所以梯形的周长是5×2+4=14,故答案为:14.分析:由切线长定理可知:AD=AE,BC=BE,因此梯形的周长=2AB+CD,已知了AB和⊙O的半径,由此可求出梯形的周长.三、计算题21.已知四边形ABCD外切于⊙O,四边形ABCD的面积为24,周长24,求⊙O的半径.答案:2解析:解答:设四边形ABCD是⊙O的外切四边形,切点分别为:F,G,M,E,连接FO,AO,OG,CO,OM,DO,OE,四边形ABCD的面积为:1 2×EO×AD+12OM×DC+12GO×BC+12FO×AB=12EO(AD+AB+BC+DC)=12EO×24=24,解得:EO=2.故r=2.分析:利用切线的性质进而利用三角形面积求法得出⊙O的半径.22.如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,求CE.答案:2解析:解答:∵CD、CE分别与⊙O相切于点D、E,∴CD=CE,∵∠DAC=∠DCA,∴AD=CD,∴AD=CE,∵AD=2,∴CE=2.故答案为:2.分析:由条件可得AD=CD,再由切线长定理可得:CD=CE,所以AD=CE,问题得解.23.如图,已知PA、PB分别切⊙O于点A、B,∠P=90°,PA=3,求⊙O的半径.答案:3解析:解答:连接OA、OB,则OA=OB(⊙O的半径),∵PA、PB分别切⊙O于点A、B,∴PA=PB,∠OAP=∠OBP=90°,已知∠P=90°,∴∠AOB=90°,∴四边形APBO为正方形,∴OA=OB=PA=3,则⊙O的半径长是3,故答案为:3.分析:连接OA、OB,已知PA、PB分别切⊙O于点A、B,由切线的性质及切线长定理可得:PA=PB,∠OAP=∠OBP=90°,再由已知∠P=90°,所以得到四边形APBO为正方形,从而得⊙O的半径长即PA的长.24.如图,P是⊙O的直径AB的延长线上一点,PC、PD切⊙O于点C、D.若PA=6,⊙O的半径为2,求∠CPD.答案:60°解析:解答:∵PA=6,⊙O的半径为2,∴PB=PA-AB=6-4=2,∴OP=4,∵PC、PD切⊙O于点C、D.∴∠OPC=∠OPD,∴CO⊥PC,∴sin∠OPC=2: 4 =0.5 ,∴∠OPC=30°,∴∠CPD=60°,故答案为:60°.分析:根据切线的性质定理和切线长定理求出OP=4,∠OPC=∠OPD,再利用解直角三角形的知识求出∠OPC=30°,即可得出答案.25.如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,求⊙O的半径.答案:2解析:解答:连接OD、OE,∵⊙O与△ABC中AB、AC的延长线及BC边相切,∴AF=AD,BE=BF,CE=CD,OD⊥AD,OE⊥BC,∵∠ACB=90°,∴四边形ODCE是正方形,设OD=r,则CD=CE=r,∵BC=3,∴BE=BF=3-r,∵AB=5,AC=4,∴AF=AB+BF=5+3-r,AD=AC+CD=4+r,∴5+3-r=4+r,r=2,则⊙O的半径是2.故答案为:2.分析:先连接OD、OE根据⊙O与△ABC中AB、AC的延长线及BC边相切,得出AF=AD,BE=BF,CE=CD,再根据OD⊥AD,OE⊥BC,∠ACB=90°,得出四边形ODCE是正方形,最后设OD=r,列出5+3-r=4+r,求出r=2即可.。
北师大版九年级数学下册3.7切线长定理同步练习
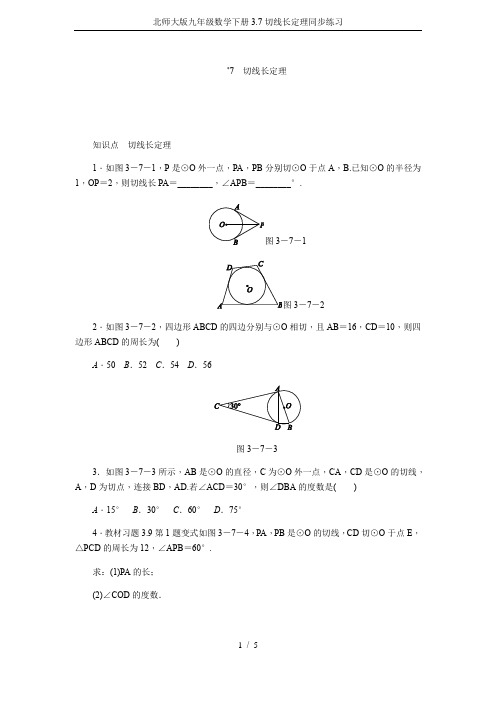
*7切线长定理知识点切线长定理1.如图3-7-1,P是⊙O外一点,PA,PB分别切⊙O于点A,B.已知⊙O的半径为1,OP=2,则切线长PA=________,∠APB=________°.3-7-13-7-22.如图3-7-2,四边形ABCD的四边分别与⊙O相切,且AB=16,CD=10,则四边形ABCD的周长为()A.50 B.52 C.54 D.56图3-7-33.如图3-7-3所示,AB是⊙O的直径,C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的度数是()A.15°B.30°C.60°D.75°4.教材习题3.9第1题变式如图3-7-4,PA,PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)PA的长;(2)∠COD的度数.图3-7-45.如图3-7-5,PA ,PB 切⊙O 于A ,B 两点,CD 切⊙O 于点F 且分别交PA ,PB 于点C ,D ,若⊙O 的半径为r ,△PCD 的周长为3r ,连接OA ,OP ,则OAPA的值是( )A .213 13B .125C .32D .233-7-53-7-66.如图3-7-6,正方形ABCD 的边长为4 cm ,以正方形的一边BC 为直径在正方形ABCD 内作半圆,过点A 作半圆的切线,与半圆相切于点F ,与DC 相交于点E ,则△ADE 的面积为( )A .12 cm 2B .24 cm 2C .8 cm 2D .6 cm 2图3-7-77.如图3-7-7,△ABC 的周长为16,∠A =60°,BC =6.若⊙O 与BC ,AC ,AB 三边分别切于点E ,F ,D ,则DF 的长为________.8.[2017·孝感模拟]如图3-7-8,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,OB=6 cm,OC=8 cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.图3-7-8详解详析1.3602.B[解析] 根据切线长定理可证AB+CD=AD+BC,∴四边形ABCD的周长=2×(16+10)=52.故选B.3.D [解析] 连接OD .∵CA ,CD 是⊙O 的切线, ∴OA ⊥AC ,OD ⊥CD ,∴∠OAC =∠ODC =90°.∵∠ACD =30°,∴∠AOD =360°-∠C -∠OAC -∠ODC =150°.∵OB =OD ,∴∠DBA =∠ODB =12∠AOD =75°.故选D.4.解:(1)∵CA ,CE 都是⊙O 的切线,∴CA =CE . 同理DE =DB ,P A =PB ,∴△PCD 的周长=PD +CD +PC =PD +PC +CA +BD =P A +PB =2P A =12,∴P A =6. (2)∵∠P =60°,∴∠PCE +∠PDE =120°, ∴∠ACD +∠CDB =360°-120°=240°. ∵CA ,CE 是⊙O 的切线, ∴∠OCE =∠OCA =12∠ACD .同理∠ODE =12∠CDB ,∴∠OCE +∠ODE =12(∠ACD +∠CDB )=120°,∴∠COD =180°-120°=60°.5.D [解析] ∵P A ,PB 切⊙O 于A ,B 两点,CD 切⊙O 于点F 且分别交P A ,PB 于点C ,D ,∴CA =CF ,DF =DB ,P A =PB ,∴PC +CF +DF +PD =P A +PB =2P A =3r , ∴P A =32r ,∴OA P A =r 32r =23.故选D.6.D [解析] 设DE =x cm ,则CE =(4-x )cm ,根据题意知EF =CE =(4-x )cm ,AF =AB =4 cm ,∴AE =(8-x )cm.在Rt △ADE 中,AD 2+DE 2=AE 2,即42+x 2=(8-x )2,解得x =3.∴△ADE 的面积=12×AD ×DE =12×4×3=6(cm 2).7.2.8.解:(1)如图,连接OF .根据切线长定理,得BE =BF ,CF =CG ,∠OBF =∠OBE ,∠OCF =∠OCG .∵AB ∥CD ,∴∠ABC +∠BCD =180°, ∴∠OBF +∠OCF =90°, ∴∠BOC =90°.(2)由(1)知,∠BOC =90°. ∵OB =6 cm ,OC =8 cm ,∴由勾股定理,得到BC =OB 2+OC 2=10 cm , ∴BE +CG =BC =10 cm.(3)由(1)知,OF ⊥BC ,OB ⊥OC , ∴OF =OB ·OCBC =4.8 cm.即⊙O 的半径为4.8 cm.。
北师大版九年级数学下册试题3.7切线长定理

初中数学试卷3.7切线长定理一、选择题1. 一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( )A.21 B.20 C.19 D.182. 如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角(不包括∠PAB本身)有( )A.1个 B.2个 C.3个 D.4个3. 如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的 ( )A.三条中线的交点B.三条高的交点C.三条角平分线的交点D.三条边的垂直平分线的交点4.△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是()A.120° B.125° C.135° D.150°5.一个钢管放在V形架内,右图是其截面图,O为钢管的圆心.如果钢管的半径为25 cm ,∠MPN = 60,则OP =( )A .50 cmB .253cm C.3350cm D .503cm 6.如图1,PA 、PB 分别切圆O 于A 、B 两点,C 为劣弧AB 上一点,∠APB=30°,则∠ACB=( ).A .60°B .75°C .105°D .120°(1) (2)7.圆外一点P ,PA 、PB 分别切⊙O 于A 、B ,C 为优弧AB 上一点,若∠ACB=a ,则∠APB=( )A .180°-aB .90°-aC .90°+aD .180°-2a 二、填空题8. 如图,在△ABC 中,5cm AB AC ==,cosB 35=.如果⊙O 的半径为10cm ,且经过点B 、C ,那么线段AO= cm .9.如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,且ο60=∠AEB ,则=∠P __ ___度.BC DPO BAC P O10. 如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,则△ABC的周长是.11. 如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC= 12,∠P=60o,弦AB的长为------.三、解答题:12. 如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.13. 如图,已知AB为⊙O的直径,AD、BC、CD为⊙O的切线,切点分别是A、B、PBAOE ,则有一下结论:(1)CO ⊥DO ;(2)四边形OFEG 是矩形.试说明理由.14. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°.(1)求∠APB 的度数; (2)当OA =3时,求AP 的长.15. 如图,在△ABC 中,已知∠ABC=90o ,在AB 上取一点E ,以BE 为直径的⊙O 恰与AC 相切于点D ,若AE=2 cm ,AD=4 cm . (1)求⊙O 的直径BE 的长; (2)计算△ABC 的面积.参考答案1. C2. B (提示:②④错误)3. D (提示:AD=AF,BD=BE,CE=CF ∴周长=821218⨯+⨯=)4. CGFECB5. D6. C7.D8. A(提示:∠MPN=600可得∠OPM=300可得OP=2OM=50)9.(提示:连接OB,易得:∠ABC=∠AOB ∴cos∠AOB=cos∠3 5=OBOA AO)os300=ABAC∴AB=10. ∠P=60011. 760(提示:连接ID,IF ∵∠DEF=520∴∠DIF=1040∵D、F是切点∴DI⊥AB,IF⊥AC∴∠ADI=∠AFI=900∴∠A=1800-1040=760)12. 52 (提示:AB+CD=AD+BC)13. 1150(提示:∵∠A=500∴∠ABC+∠ACB=1300∵OB,OC分别平分∠ABC,∠ACB ∴∠OBC+∠OCB=650∴∠BOC=1800-650=1150)14. 解:∵AD,AE切于⊙O于D,E ∴AD=AE=20 ∵AD,BF切于⊙O于D,F ∴BD=BF 同理:CF=CE∴C△ABC=AB+BC+AC=AB+BF+FC+AC=AB+BD+EC+AC=AD+AE=4014 解:(1)∵在△ABO中,OA=OB,∠OAB=30°∴∠AOB=180°-2×30°=120°∵PA、PB是⊙O的切线∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°∴在四边形OAPB中,∠APB=360°-120°-90°-90°=60°.(2)如图①,连结OP∵PA 、PB 是⊙O 的切线∴PO 平分∠APB ,即∠APO =12∠APB =30°又∵在Rt △OAP 中,OA =3, ∠APO =30°∴AP =tan 30OA°=15 解:(1)连接OD ∴OD ⊥AC ∴△ODA 是Rt △设半径为r ∴AO=r+2 ∴(r+2)2—r 2=16 解之得:r=3 ∴BE=6(2) ∵∠ABC=900 ∴OB ⊥BC ∴BC 是⊙O 的切线 ∵CD 切⊙O 于D ∴CB=CD 令CB=x∴AC=x+4,BC=4,AB=x ,AB=8 ∵2228(4)x x +=+ ∴6x =∴S △ABC =186242⨯⨯=。
北师大版九年级数学下册3.7:切线长定理课后练习题(无答案)

定理课后练习题(无答案)北师大版九年级数学下册3.7:切线长定理课后练习题(无答案)3.7切线长定理课后练习一、选择题1.矩形ABCD中,AB=4,AD=3,以AB为直径在矩形内作半圆.DE切⊙O于点E(如图),则tan∠CDF的值为()A.B.C.D.2.如图,在平面直角坐标系xOy中,直线AB经过点A(6,0)、B(0,6),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为()A.B.3 C.3D.3.如图,PA、PB切⊙O于点A、B,直线FG切⊙O于点E,交PA于F,交PB于点G,若PA=8cm,则△PFG的周长是()A.8cm B.12cm C.16cm D.20cm定理课后练习题(无答案)北师大版九年级数学下册3.7:切线长定理课后练习题(无答案)4.如图,AD、AE、CB均为⊙O的切线,D、E、F分别为切点,AD=8,则△ABC的周长为()A.8 B.10 C.12 D.165.如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的有()个:①AF=BG;②CG=CH;③AB+CD=AD+BC;④BG<CG.A.1 B.2 C.3 D.46.如图,从⊙O外一点P引圆的两条切线PA、PB,切点分别是A、B,如果∠APB=60°,线段PA=10,那么弦AB的长是()A.10 B.12 C.5D.107.如图,PA、PB分别切⊙O于A、B,PA=10cm,C是劣弧AB上的点(不与点A、B 重合),过点C的切线分别交PA、PB于点E、F.则△PEF的周长为()定理课后练习题(无答案)北师大版九年级数学下册3.7:切线长定理课后练习题(无答案)A.10cm B.15cm C.20cm D.25cm8.如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有()个①AF=BG②CG=CH③AB+CD=AD+BC④BG<CG.A.1 B.2 C.3 D.49.如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为()A.12 B.6 C.8 D.410.如图,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC、CD、DA相切,若BC=2,DA=3,则AB的长()定理课后练习题(无答案)北师大版九年级数学下册3.7:切线长定理课后练习题(无答案)A.等于4 B.等于5 C.等于6 D.不能确定11.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C,且在上的动点,则∠BPC的度数是()A.65°B.115°C.115°或65°D.130°或65°12.如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是()A.7 B.8 C.9 D.16二、填空题13.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是cm.14.如图,MA、MB是⊙O的两条切线,A、B为切点,若∠AMB=60°,AB=1,则⊙O 的直径等于.定理课后练习题(无答案)北师大版九年级数学下册3.7:切线长定理课后练习题(无答案)15.如图,PA、PB分别切⊙O于A、B,并与⊙O的另一条切线分别相交于D、C两点,已知PA=7,则△PCD的周长=.16.如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于.三、解答题17.如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC =8cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.18.如图所示,PA,PB是⊙O的两条切线,A,B为切点,连接PO,交⊙O于点D,交定理课后练习题(无答案)北师大版九年级数学下册3.7:切线长定理课后练习题(无答案)AB于点C,根据以上条件,请写出三个你认为正确的结论,并对其中的一个结论给予证明.。
北师大版九年级数学下册 3.7 切线长定理 同步测试题

3.7 切线长定理同步测试题(满分120分;时间:90分钟)一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为()A.32B.34C.36D.382. PA,PB切⊙O于点A,B,PA=10,CD切⊙O于点E,交PA,PB于C,D两点,则△PCD的周长是()A.10B.18C.20D.223. 已知四边形ABCD是梯形,且AD // BC,AD<BC,又⊙O与AB、AD、CD分别相切于点E、F、G,圆心O在BC上,则AB+CD与BC的大小关系是()A.大于B.等于C.小于D.不能确定4. 如图,P为⊙O外一点,PA,PB分别切⊙O两点,若PA=3,则PB=()A.5B.4C.3D.25. 如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为()A.8B.9C.10D.116. 如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于点L、M、N、P.若四边形ABCD的周长为20,则AB+CD等于()A.5B.8C.10D.127. 如图,PA,PB分别与⊙O相切于点A,B,过圆上点C作⊙O的切线EF分别交PA,PB于点E,F,若PA=4,则△PEF的周长是()A.4B.8C.10D.12̂上任一点,过C的切线分别交PA,PB 8. 如图,PA,PB分别切⊙O于点A和点B,C是AB于D,E.若⊙O的半径为6,PO=10,则△PDE的周长是()A.16B.14C.12D.109. 如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有()个①AF=BG②CG=CH③AB+CD=AD+BC④BG<CG.A.1B.2C.3D.410. 如图,从⊙O外一点P引圆的两条切线PA、PB,切点为A、B,点C是劣弧AB上一点,过C的切线交PA、PB分别于M、N,若⊙O的半径为2,∠P=60∘,则△PMN的周长为()A.4B.6C.4√3D.6√3二、填空题(本题共计10 小题,每题3 分,共计30分,)11. 若圆外切四边形ABCD的面积为20平方厘米,AD+BC=10厘米,则该圆半径为________.。
北师大版九年级数学下册 3.7切线长定理 同步练习题(含答案)
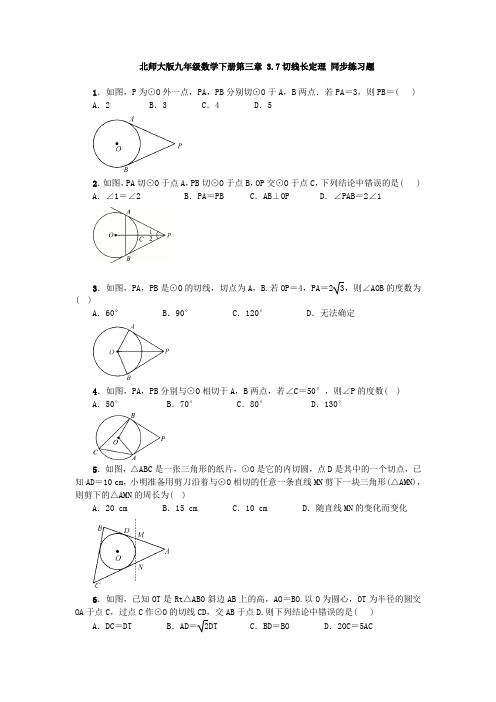
北师大版九年级数学下册第三章 3.7切线长定理同步练习题1.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB=( ) A.2 B.3 C.4 D.52.如图,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中错误的是( ) A.∠1=∠2 B.PA=PB C.AB⊥OP D.∠PAB=2∠13.如图,PA,PB是⊙O的切线,切点为A,B.若OP=4,PA=23,则∠AOB的度数为( )A.60°B.90°C.120° D.无法确定4.如图,PA,PB分别与⊙O相切于A,B两点,若∠C=50°,则∠P的度数( )A.50° B.70° C.80° D.130°5.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10 cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )A.20 cm B.15 cm C.10 cm D.随直线MN的变化而变化6.如图,已知OT是Rt△ABO斜边AB上的高,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( ) A.DC=DT B.AD=2DT C.BD=BO D.2OC=5AC7.如图,在△MBC中,∠B=90°,∠C=60°,MB=23,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为( )A. 2B. 3 C.2 D.38.如图,一圆内切于四边形ABCD,AB=16,CD=10,则四边形ABCD的周长为( )A.50 B.52 C.54 D.569.如图,AB,AC,BD是⊙O的切线,P,C,D为切点.如果AB=5,AC=3,那么BD 的长为______.10.如图,在菱形ABCD中,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径为______.11.如图,AB为⊙O的直径,点C在AB的延长线上,CD,CE分别与⊙O相切于点D,E.若AD=2,∠DAC=∠DCA,则CE=______.12.如图,P为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E且分别交PA,PB 于点C ,D.若PA =4,则△PCD 的周长为______.13.如图,菱形ABOC 的边AB ,AC 分别与⊙O 相切于点D ,E.若点D 是AB 的中点,则∠DOE =______.14.如图,PA ,PB 是⊙O 的切线,A ,B 为切点,AC 是⊙O 的直径,∠P =60°,OA =2,求BC 的长.B 组(中档题)15.如图,菱形ABCD 的边AB =20,面积为320,∠BAD <90°,⊙O 与边AB ,AD 都相切.若AO =10,则⊙O 的半径长为______.16.如图,AB 为半圆O 的直径,AD ,BC 分别切⊙O 于A ,B 两点,CD 切⊙O 于点E ,AD 与CD 相交于点D ,BC 与CD 相交于点C ,连接OD ,OC ,对于下列结论:①OD 2=DE ·CD ;②AD +BC =CD ;③OD =OC ;④S 梯形ABCD =12CD ·OA ;⑤∠DOC =90°.其中正确的是______.(只需填上正确结论的序号)17.如图,PA,PB分别切⊙O于点A,B,连接PO,与AB相交于D,C是⊙O上一点,∠C=60°.(1)求∠APB的大小;(2)若PO=20 cm,求△AOB的面积.18.在一个夹角为120°的墙角放置了一个圆柱体的容器,俯视图如图,在俯视图中圆与两边的墙分别切于B,C两点(圆柱体容器的直径不易直接测量).(1)写出此图中相等的线段;(2)请你设计一种可以通过计算求出直径的测量方法(写出主要解题过程).19.如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F点在AD上,BE是⊙O的弦,求△CDF的面积.C组(综合题)20.如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6 cm,CO=8 cm.(1)求证:BO⊥CO;(2)求BE和CG的长.21.如图,P为⊙O外一点,PA,PB均为⊙O的切线,A和B是切点,BC是直径.求证:(1)∠APB=2∠ABC;(2)AC∥OP.22.如图,AB是⊙O的直径,AM和BN是它的两条切线,过⊙O上一点E作直线DC,分别交AM,BN于点D,C,且DA=DE.求证:(1)直线CD是⊙O的切线;(2)OA2=DE·CE.参考答案2020-2021学年北师大版九年级数学下册第三章 3.7切线长定理同步练习题A组(基础题)1.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB=(B) A.2 B.3 C.4 D.52.如图,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中错误的是(D) A.∠1=∠2 B.PA=PB C.AB⊥OP D.∠PAB=2∠13.如图,PA,PB是⊙O的切线,切点为A,B.若OP=4,PA=23,则∠AOB的度数为(C)A.60°B.90°C.120° D.无法确定4.如图,PA,PB分别与⊙O相切于A,B两点,若∠C=50°,则∠P的度数(C)A.50° B.70° C.80° D.130°5.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10 cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为(A)A.20 cm B.15 cm C.10 cm D.随直线MN的变化而变化6.如图,已知OT是Rt△ABO斜边AB上的高,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是(D) A.DC=DT B.AD=2DT C.BD=BO D.2OC=5AC7.如图,在△MBC中,∠B=90°,∠C=60°,MB=23,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为(C)A. 2B. 3 C.2 D.38.如图,一圆内切于四边形ABCD,AB=16,CD=10,则四边形ABCD的周长为(B)A.50 B.52 C.54 D.569.如图,AB,AC,BD是⊙O的切线,P,C,D为切点.如果AB=5,AC=3,那么BD 的长为2.10.如图,在菱形ABCD中,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径11.如图,AB为⊙O的直径,点C在AB的延长线上,CD,CE分别与⊙O相切于点D,E.若AD=2,∠DAC=∠DCA,则CE=2.12.如图,P为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E且分别交PA,PB于点C,D.若PA=4,则△PCD的周长为8.13.如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE=60°.14.如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P=60°,OA=2,求BC的长.解:∵PA ,PB 是⊙O 的切线,∴AP =BP. 又∵∠P =60°,∴△ABP 是等边三角形. ∴∠PAB =60°. ∵PA 是⊙O 的切线, ∴∠PAC =90°.∴∠BAC =90°-60°=30°. 又∵AC 是⊙O 的直径, ∴∠ABC =90°. ∴BC =12AC =OA =2.B 组(中档题)15.如图,菱形ABCD 的边AB =20,面积为320,∠BAD <90°,⊙O 与边AB ,AD 都相切.若AO =10,则⊙O 的半径长为25.16.如图,AB 为半圆O 的直径,AD ,BC 分别切⊙O 于A ,B 两点,CD 切⊙O 于点E ,AD 与CD 相交于点D ,BC 与CD 相交于点C ,连接OD ,OC ,对于下列结论:①OD 2=DE ·CD ;②AD +BC =CD ;③OD =OC ;④S 梯形ABCD =12CD ·OA ;⑤∠DOC =90°.其中正确的是①②⑤.(只需填上正确结论的序号)17.如图,PA ,PB 分别切⊙O 于点A ,B ,连接PO ,与AB 相交于D ,C 是⊙O 上一点,∠C =60°.(1)求∠APB 的大小;(2)若PO =20 cm ,求△AOB 的面积.解:(1)∵∠C =60°, ∴∠AOB =120°.∵PA ,PB 分别切⊙O 于点A ,B , ∴∠PAO =∠PBO =90°.∴∠APB =360°-90°-90°-120°=60°. (2)∵PA ,PB 分别切⊙O 于点A ,B ,∴PA =PB.∴点P 在AB 的垂直平分线上. 同理,点O 在AB 的垂直平分线上. ∴PO 垂直平分AB.∵∠APB =60°,∠AOB =120°,∴∠OPB =∠OPA =30°,∠POB =∠POA =60°. ∵PO =20 cm ,∴OB =10 cm. ∴OD =OB ·cos ∠POB =5 cm , BD =OB ·sin ∠POB =5 3 cm. ∴AB =2BD =10 3 cm.∴S △AOB =12×103×5=253(cm 2).18.在一个夹角为120°的墙角放置了一个圆柱体的容器,俯视图如图,在俯视图中圆与两边的墙分别切于B ,C 两点(圆柱体容器的直径不易直接测量).(1)写出此图中相等的线段;(2)请你设计一种可以通过计算求出直径的测量方法(写出主要解题过程).解:(1)根据切线长定理,知AB =AC. (2)连接OB ,OA. ∵∠BAC =120°, ∴∠OAB =60°. 在Rt △AOB 中,OB =AB ·tan ∠OAB =3AB. ∴圆的直径为23AB.故只需测得AB 的长,就可求得圆的直径.19.如图,边长为1的正方形ABCD 的边AB 是⊙O 的直径,CF 是⊙O 的切线,E 为切点,F 点在AD 上,BE 是⊙O 的弦,求△CDF 的面积.解:设AF =x.∵四边形ABCD 是正方形, ∴∠DAB =∠CBA =90°. ∴DA ⊥AB ,CB ⊥AB.又∵OA ,OB 是⊙O 的半径, ∴AD ,BC 是⊙O 的切线.∵CF 是⊙O 的切线,E 为切点,∴EF =AF =x ,CE =CB =1.∴FD =1-x ,CF =CE +EF =1+x.在Rt △CDF 中,由勾股定理,得CF 2=CD 2+DF 2,即(1+x)2=1+(1-x)2,解得x =14. ∴DF =1-x =34. ∴S △CDF =12×1×34=38.C 组(综合题)20.如图,AB ,BC ,CD 分别与⊙O 相切于点E ,F ,G ,且AB ∥CD ,BO =6 cm ,CO =8 cm.(1)求证:BO ⊥CO ;(2)求BE 和CG 的长.解:(1)证明:∵AB ∥CD ,∴∠ABC +∠BCD =180°.∵AB ,BC ,CD 分别与⊙O 相切于点E ,F ,G ,∴BO 平分∠ABC ,CO 平分∠DCB.∴∠OBC =12∠ABC ,∠OCB =12∠DCB. ∴∠OBC +∠OCB =12(∠ABC +∠DCB)=12×180°=90°. ∴∠BOC =90°.∴BO ⊥CO.(2)连接OF ,则OF ⊥BC ,∴Rt △BOF ∽Rt △BCO.∴BF BO =BO BC. ∵在Rt △BOC 中,BO =6 cm ,CO =8 cm ,∴BC =BO 2+CO 2=10(cm).∴BF 6=610. ∴BF =3.6 cm.∵AB ,BC ,CD 分别与⊙O 相切,∴BE =BF =3.6 cm ,CG =CF.∴CG =CF =BC -BF =6.4 cm.21.如图,P 为⊙O 外一点,PA ,PB 均为⊙O 的切线,A 和B 是切点,BC 是直径.求证:(1)∠APB =2∠ABC ;(2)AC ∥OP.证明:(1)连接AO ,∵PA ,PB 均为⊙O 的切线,A 和B 是切点,∴∠APO =∠BPO ,OA ⊥AP ,PA =PB.∴∠APB =2∠BPO ,∠OBP =90°,PO ⊥AB.∴∠OBA +∠ABP =90°,∠ABP +∠BPO =90°.∴∠OBA =∠BPO.∴∠APB =2∠ABC.(2)设AB 交OP 于点F ,由(1)知,PO ⊥AB ,∴∠AFP =90°.∵BC 是⊙O 直径,∴∠CAB =90°.∴∠CAB =∠AFP.∴AC ∥OP.22.如图,AB 是⊙O 的直径,AM 和BN 是它的两条切线,过⊙O 上一点E 作直线DC ,分别交AM ,BN 于点D ,C ,且DA =DE.求证:(1)直线CD 是⊙O 的切线;(2)OA 2=DE ·CE.证明:(1)连接OE ,OD ,∵DA 是⊙O 的切线,∴∠OAD =90°.∵OA =OE ,DA =DE ,OD =OD ,∴△AOD ≌△EOD(SSS).∴∠OAD =∠OED =90°.∴OE ⊥CD.又∵OE 是⊙O 的半径,∴CD 是⊙O 的切线.(2)连接OC ,∵AM ,BN ,DC 是⊙O 的切线,∴∠OAD =∠OBC =∠DEO =∠OEC =90°,CE =CB ,OD 平分∠ADE ,OC 平分∠BCE. ∴AM ∥BN.∴∠ADE +∠BCE =180°.∴∠ODE +∠OCE =12(∠ADE +∠BCE)=12×180°=90°. 又∵∠ODE +∠DOE =90°,∴∠OCE =∠DOE.∴△DEO ∽△OEC.∴OECE=DEOE.∴OE2=DE·CE.又∵OA=OE,∴OA2=DE·CE.。
北师大版九年级数学下册3.7切线长定理同步练习

北师大版九年级数学下册3.7切线长定理同步练习*7切线长定理知识点切线长定理1.如图3-7-1,P是⊙O外一点,PA,PB分别切⊙O于点A,B.已知⊙O的半径为1,OP=2,则切线长PA=________,∠APB=________°.图3-7-13-7-22.如图3-7-2,四边形ABCD的四边分别与⊙O相切,且AB=16,CD=10,则四边形ABCD的周长为()A.50 B.52 C.54 D.56图3-7-33.如图3-7-3所示,AB是⊙O的直径,C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的度数是()4 cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过点A作半圆的切线,与半圆相切于点F,与DC相交于点E,则△ADE的面积为()A.12 cm2B.24 cm2C.8 cm2D.6 cm2图3-7-77.如图3-7-7,△ABC的周长为16,∠A=60°,BC=6.若⊙O与BC,AC,AB三边分别切于点E,F,D,则DF的长为________.8.[2019·孝感模拟]如图3-7-8,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,OB=6 cm,OC=8 cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.图3-7-8详解详析1.3602.B[解析] 根据切线长定理可证AB+CD=AD+BC,∴四边形ABCD的周长=2×(16+10)=52.故选B.3.D[解析] 连接OD.∵CA,CD是⊙O 的切线,∴OA⊥AC,OD⊥CD,∴∠OAC=∠ODC =90°.∵∠ACD=30°,∴∠AOD=360°-∠C -∠OAC-∠ODC=150°.∵OB=OD,∴∠DBA=∠ODB=12∠AOD=75°.故选D.4.解:(1)∵CA,CE都是⊙O的切线,∴CA=CE.同理DE=DB,PA=PB,∴△PCD的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,∴PA=6.(2)∵∠P=60°,∴∠PCE+∠PDE=120°,∴∠ACD+∠CDB=360°-120°=240°.∵CA ,CE 是⊙O 的切线,∴∠OCE =∠OCA =12∠ACD . 同理∠ODE =12∠CDB ,∴∠OCE +∠ODE =12(∠ACD +∠CDB )=120°, ∴∠COD =180°-120°=60°.5.D [解析] ∵PA ,PB 切⊙O 于A ,B 两点,CD 切⊙O 于点F 且分别交PA ,PB 于点C ,D ,∴CA =CF ,DF =DB ,PA =PB ,∴PC +CF +DF +PD =PA +PB =2PA =3r ,∴PA =32r ,∴OA PA =r 32r =23.故选D. 6.D [解析] 设DE =x cm ,则CE =(4-x )cm ,根据题意知EF =CE =(4-x )cm ,AF =AB =4 cm ,∴AE =(8-x )cm.在Rt△ADE中,AD2+DE2=AE2,即42+x2=(8-x)2,解得x=3.∴△ADE的面积=12×AD×DE=12×4×3=6(cm2).7.2.8.解:(1)如图,连接OF.根据切线长定理,得BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG.∵AB∥CD,∴∠ABC+∠BCD=180°,∴∠OBF+∠OCF=90°,∴∠BOC=90°.(2)由(1)知,∠BOC=90°.∵OB=6 cm,OC=8 cm,∴由勾股定理,得到BC=OB2+OC2=10 cm,∴BE+CG=BC=10 cm.(3)由(1)知,OF⊥BC,OB⊥OC,∴OF=OB·OCBC=4.8 cm.即⊙O的半径为4.8 cm.。
北师大版九年级数学下册3.7:切线长定理 同步测试

3.7 切线长定理同步测试一、选择题1.如图,直线AB 与半径为2的⊙O 相切于点C ,点D ,E ,F 是⊙O 上三个点,EF ∥AB ,若EF=2 3,则∠EDC 的度数为( )A. 60°B. 90°C. 30°D. 75°2.如图,PA 、PB 分别切⊙O 于点A 、B ,AC 是⊙O 的直径,连结AB 、BC 、OP ,则与∠PAB 相等的角(不包括∠PAB 本身)有( )A .1个B .2个C .3个D .4个3.如图,在Rt △ABC 中,∠ABC =90°,AB ==2,以AB 的中点O 为圆心,OA 的长为半径作半圆交AC 于点D,则图中阴影部分的面积为( )2π 2π C.π D.2π4.边长分别为3,4,5的三角形的内切圆半径与外接圆的半径之比为( ).A.1:5B.2:5C.3:5D. 4:55.一个钢管放在V形架内,右图是其截面图,O为钢管的圆心.如果钢管的半径为25 cm,∠MPN = 60 ,则OP =( )A.50 cm B.25cm C.cm D.50cm6. 一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( )A.21 B.20 C.19 D.187.如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为()A.40°B.50°C.60°D.20°8.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( )A.21 B.20 C.19 D.189.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与图中4×7方格中的格点的连线中,能够与该圆弧相切的格点个数有()A.1个B.2个C.3个D. 4个10.如图,AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC.若∠P=20°,则∠B的度数是()A. 20°B. 25°C. 30°D. 35°二、填空题11.如图,在△ABC中,,cos B.如果⊙O的半径为cm,且经过点B、C,那么线段AO= cm.12.如图,PA、PB是⊙O的两条切线,切点分别是A、B,如果AP=4, ∠APB= 40 ° ,则∠APO= ,PB= .13.如图,已知点O是△ABC 的内心,且∠ABC= 60 °, ∠ACB= 80 °,则∠BOC= .14.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.15.如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠ACB=70°,那么∠OPA的度数是________度.三、综合题16. 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.(1)求∠APB的度数;(2)当OA=3时,求AP的长.17.如图,AB是 O的直径,点P是BA延长线上一点,过点P作 O的切线PC,切点是C,过点C作弦CD⊥AB于E,连接CO,CB.(1)求证:PD是 O的切线;(2)若AB=10,tanB=1,求PA的长;218.如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.(1)求证:∠ABC=∠CBD;(2)若BC=45,CD=4,则⊙O的半径是.19.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G 三点,过点D作⊙O的切线交BC于点M,切点为N,求DM的长.3.7 切线长定理同步测试答案一、选择题1.A2.C3.A4.C5.D6.B7.C8.C9.D 10.B二、填空题11.12.200 4 13.110014.5215.200三、综合题 16.解:(1)∵在△ABO 中,OA =OB ,∠OAB =30°∴∠AOB =180°-2×30°=120°∵PA 、PB 是⊙O 的切线∴OA ⊥PA ,OB ⊥PB .即∠OAP =∠OBP =90°∴在四边形OAPB 中,∠APB =360°-120°-90°-90°=60°.(2)如图①,连结OP∵PA 、PB 是⊙O 的切线∴PO 平分∠APB ,即∠APO =21∠APB =30° 又∵在Rt △OAP 中,OA =3, ∠APO =30°∴AP ==3.17.解:(1)连接OD,∵CD ⊥AB,∴CE =ED,∴PC =PD,∵OC =OD,∴△POC ≌△POD,∴∠PDO =∠PCO,∵PC 是 O 的切线,∴PC ⊥OC,∠PCO =90°,∴∠PDO =90°,∴PD ⊥DO,∴PD 是 O 的切线;(2)连接AC,∵tanB =12,∴设AC =x,则BC =2x,∵AB =10,∴AO =CO =5,在Rt △ABC 中,由勾股定理可求得:AC =25,BC =45,∴CE =4,EO =3,∵△COE ∽△POC,∴PO =253,∴AP =PO -AO =103; 18.(1)证明:连接OC ,∵MN 为⊙O 的切线,∴OC ⊥MN ,∵BD ⊥MN ,∴OC ∥BD ,∴∠CBD =∠BCO .又∵OC =OB ,∴∠BCO =∠ABC ,∴∠CBD =∠ABC .;(2)解:连接AC ,在Rt △BCD 中,BC =45,CD =4,∴BD =8,∵AB 是⊙O 的直径,∴∠ACB =90°,∴∠ACB =∠CDB =90°,∵∠ABC =∠CBD ,∴△ABC ∽△CBD , ∴BD CB BC AB ,即54AB =854,∴AB =10,∴⊙O 的半径是5,故答案为5.19.解:连接OE ,OF ,ON ,OG .∵四边形ABCD 是矩形,∴∠A =∠B =90°,CD =AB =4.∵AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,∴∠AEO =∠AFO =∠OFB =∠BGO =90°,OE =OF =OG ,∴四边形AFOE ,FBGO 是正方形,∴AF =BF =AE =BG =2,∴DE =3.∵DM 是⊙O 的切线,∴DN =DE =3,MN =MG ,∴CM =BC -BG -MG =5-2-MN =3-MN .在Rt △DMC 中,DM 2=CD 2+CM 2,∴(3+MN )2=42+(3-MN )2,∴MN =43,∴DM =3+43=133.。
北师大九年级下《3.7切线长定理》课时练习含答案解析

北师大版数学九年级下册第3章第7节切线长定理同步检测一、选择题1.如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为()A.32 B.34 C.36 D.38答案:B解析:解答:由题意可得圆外切四边形的两组对边和相等,所以四边形的周长=2×(7+10)=34.故选:B.分析:根据切线长定理,可以证明圆外切四边形的性质:圆外切四边形的两组对边和相等,从而可求得四边形的周长.2.如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为()A.15 B.12 C.20 D.30答案:D解析:解答:∵P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,∴AC=EC,BD=DE,AP=BP,∵PA=15,∴△PCD的周长为:PA+PB=30.故选:D.分析:直接利用切线长定理得出AC=EC,BD=DE,AP=BP,进而求出答案.3.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为()A.20cm B.15cm C.10cm D.随直线MN的变化而变化答案:A解析:解答:如图:∵△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,AD=10cm,∴设E、F分别是⊙O的切点,故DM=MF,FN=EN,AD=AE,∴AM+AN+MN=AD+AE=10+10=20(cm).故选:A.分析:利用切线长定理得出DM=MF,FN=EN,AD=AE,进而得出答案.4.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为()A.8 B.9 C.10 D.11答案:D解析:解答:∵⊙O内切于四边形ABCD,∴AD+BC=AB+CD,∵AB=10,BC=7,CD=8,∴AD+7=10+8,解得:AD=11.故选:D.分析:根据圆外切四边形的性质对边和相等进而得出AD的长.5.圆外切等腰梯形的一腰长是8,则这个等腰梯形的上底与下底长的和为()A.4 B.8 C.12 D.16答案:D解析:解答:∵圆外切等腰梯形的一腰长是8,∴梯形对边和为:8+8=16,则这个等腰梯形的上底与下底长的和为16.故选:D.分析:直接利用圆外切四边形对边和相等,进而求出即可.6.如图,⊙O是△ABC的内切圆,点D、E分别为边AB、AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是()A.7 B.8 C.9 D.16答案:A解析:解答:∵AB、AC、BC、DE都和⊙O相切,∴BI=BG,CI=CH,DG=DF,EF=EH.∴BG+CH=BI+CI=BC=9,∴△ADE的周长=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=△ABC的周长-(BG+EH+BC)=25-2×9=7.故选A.分析:根据切线长定理,可得BI=BG,CI=CH,DG=DF,EF=EH,△ADE的周长=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=△ABC的周长-(BG+EH+BC),据此即可求解.7.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是()A.4 B.8 C.4D.8答案:B解析:解答:∵PA、PB都是⊙O的切线,∴PA=PB,又∵∠P=60°,∴△PAB是等边三角形,即AB=PA=8,故选B.分析:根据切线长定理知PA=PB,而∠P=60°,所以△PAB是等边三角形,由此求得弦AB 的长.8.如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为()A.35° B.45° C.60° D.70°答案:D解析:解答:根据切线的性质定理得∠PAC=90°,∴∠PAB=90°-∠BAC=90°-35°=55°.根据切线长定理得PA=PB,所以∠PBA=∠PAB=55°,所以∠P=70°.故选D.分析:根据切线长定理得等腰△PAB,运用内角和定理求解.9.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为()A.130° B.120° C.110° D.100°答案:C解析:解答:∵AB、AC是⊙O的两条切线,B、C是切点,∴∠B=∠C=90°,∠BOC=180°-∠A=110°.故选C.分析:利用切线的性质可得,∠B=∠C=90°,再用四边形的内角和为360度可解.10.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=23,那么∠AOB等于()A.90° B.100° C.110° D.120°答案:D解析:解答:∵△APO≌△BPO(HL),∴∠AOP=∠BOP.∵sin∠AOP=AP:OP=23:4= 3:2,∴∠AOP=60°.∴∠AOB=120°.故选D.分析:由切线长定理知△APO≌△BPO,得∠AOP=∠BOP.可求得sin∠AOP= 3:2,所以可知∠AOP=60°,从而求得∠AOB的值.11.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,错误的是()A.∠1=∠2 B.PA=PB C.AB⊥OP D.=PC•PO答案:D解析:解答:连接OA、OB,AB,∵PA切⊙O于A,PB切⊙O于B,由切线长定理知,∠1=∠2,PA=PB,∴△ABP是等腰三角形,∵∠1=∠2,∴AB⊥OP(等腰三角形三线合一),故A,B,C正确,根据切割线定理知:=PC•(PO+OC),因此D错误.故选D.分析:由切线长定理可判断出A、B选项均正确.易知△ABP是等腰三角形,根据等腰三角形三线合一的特点,可求出AB⊥OP,故C正确.而D选项显然不符合切割线定理,因此D错误.12.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为()A.5,12(90°+∠P)B.7,90°+12C.10,90°-12∠P D.10,90°+12∠P答案:C解析:解答:∵PA、PB切⊙O于A、B,CD切⊙O于E,∴PA=PB=10,ED=AD,CE=BC;∴△PCD的周长=PD+DE+PC+CE=2PA,即△PCD的周长=2PA=10,;如图,连接OA、OE、OB.由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,∵AO=OE=OB,易证△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),∴∠AOC=∠EOC,∠EOD=∠BOD,∴∠COD=12∠AOB,∴∠AOB=180°-∠P,∴∠COD=90°-12∠P.故选:C.分析:根据切线长定理,即可得到PA=PB,ED=AD,CE=BC,从而求得三角形的周长=2PA;连接OA、OE、OB根据切线性质,∠P+∠AOB=180°,再根据CD为切线可知∠COD=12∠AOB.13.圆外切等腰梯形的中位线等于8,则一腰长等于()A.4 B.6 C.8 D.10答案:C解析:解答:如图,设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,∴MN=12(AB+CD),根据切线长定理得:DE=DH,CF=CH,并且等腰梯形和圆都是轴对称图形,∴CD=DH+CH=DE+CF=12(AB+CD),∴CD=MN,而MN=8,∴CD=8.故选C.分析:如图,设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,根据中位线定理可以得到上下底之和,然后利用切线长定理可以得到一腰长等于中位线,由此即可解决问题.14.如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为()A.9 B.7 C.11 D.8答案:C解析:解答:如图:设AB,AC,BC和圆的切点分别是P,N,M,CM=x,根据切线长定理,得CN=CM=x,BM=BP=9-x,AN=AP=10-x.则有9-x+10-x=8,解得:x=5.5.所以△CDE的周长=CD+CE+QE+DQ=2x=11.故选:C.分析:设AB,AC,BC和圆的切点分别是P,N,M.根据切线长定理得到NC=MC,QE=DQ.所以三角形CDE的周长即是CM+CN的值,再进一步根据切线长定理由三角形ABC的三边进行求解即可.15.已知四边形ABCD是梯形,且AD∥BC,AD<BC,又⊙O与AB、AD、CD分别相切于点E、F、G,圆心O在BC上,则AB+CD与BC的大小关系是()A.大于B.等于C.小于D.不能确定答案:A解析:解答:连接OF,∵AD是切线,∴OF⊥AD,又∵AD∥BC,∴AB≥OF,CD≥OF,又∵AD<BC,∴AB≥OF,CD≥OF最多有一个成立.∴AB+CD>2OF,∵BC=2OF,∴AB+CD>BC.故选A,分析:连接OF,则OF是梯形的高,则AB≥OF,CD≥OF,而两个式子不能同时成立,据此即可证得.二、填空题16.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD 的周长等于10cm,则PA= cm.答案:5解析:解答:如图,设DC与⊙O的切点为E;∵PA、PB分别是⊙O的切线,且切点为A、B;∴PA=PB;同理,可得:DE=DA,CE=CB;则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm);∴PA=PB=5cm,故答案为:5.分析:由于DA、DC、BC都是⊙O的切线,可根据切线长定理,将△PCD的周长转换为PA、PB的长,然后再进行求解.17.如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O 的切线长为8cm,那么△PDE的周长为答案:16解析:解答:∵PA、PB、DE分别切⊙O于A、B、C,∴PA=PB,DA=DC,EC=EB;∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=8+8=16;∴△PDE的周长为16.故答案为16.分析:由于PA、PB、DE都是⊙O的切线,可根据切线长定理将切线PA、PB的长转化为△PDE的周长.18.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,若⊙O的半径为r,△PCD的周长等于3r,则tan 12∠APB的值是答案:2 3解析:解答:连接PO,AO,∵PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,∴∠APO=∠BPO,AC=EC,DE=BD,PA=PB,∴PA+PB=△PCD的周长=3r,∴PA=PB=1.5r,∴tan 12∠APB=AO: PA =r :1.5r =23,故答案为:2 3.分析:利用切线长定理得出PA=PB=1.5r,再结合锐角三角函数关系得出答案.19.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为答案:8cm解析:解答:连接OD、OE,∵⊙O是Rt△ABC的内切圆,∴OD⊥AB,OE⊥BC,∵∠ABC=90°,∴∠ODB=∠DBE=∠OEB=90°,∴四边形ODBE是矩形,∵OD=OE,∴矩形ODBE是正方形,∴BD=BE=OD=OE=4cm,∵⊙O切AB于D,切BC于E,切MN于P,NP与NE是从一点出发的圆的两条切线,∴MP=DM,NP=NE,∴Rt△MBN的周长为:MB+NB+MN=MB+BN+NE+DM=BD+BE=4cm+4cm=8cm,故答案为:8cm.分析:连接OD、OE,求出∠ODB=∠DBE=∠OEB=90°,推出四边形ODBE是正方形,得出BD=BE=OD=OE=4cm,根据切线长定理得出MP=DM,NP=NE,代入MB+NB+MN得出BD+BE,求出即可.20.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是答案:14解析:解答:根据切线长定理,得AD=AE,BC=BE,所以梯形的周长是5×2+4=14,故答案为:14.分析:由切线长定理可知:AD=AE,BC=BE,因此梯形的周长=2AB+CD,已知了AB和⊙O 的半径,由此可求出梯形的周长.三、计算题21.已知四边形ABCD外切于⊙O,四边形ABCD的面积为24,周长24,求⊙O的半径.答案:2解析:解答:设四边形ABCD是⊙O的外切四边形,切点分别为:F,G,M,E,连接FO,AO,OG,CO,OM,DO,OE,四边形ABCD的面积为:1 2×EO×AD+12OM×DC+12GO×BC+12FO×AB=12EO(AD+AB+BC+DC)=12EO×24=24,解得:EO=2.故r=2.分析:利用切线的性质进而利用三角形面积求法得出⊙O的半径.22.如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,求CE.答案:2解析:解答:∵CD、CE分别与⊙O相切于点D、E,∴CD=CE,∵∠DAC=∠DCA,∴AD=CD,∴AD=CE,∵AD=2,∴CE=2.故答案为:2.分析:由条件可得AD=CD,再由切线长定理可得:CD=CE,所以AD=CE,问题得解.23.如图,已知PA、PB分别切⊙O于点A、B,∠P=90°,PA=3,求⊙O的半径.答案:3解析:解答:连接OA、OB,则OA=OB(⊙O的半径),∵PA、PB分别切⊙O于点A、B,∴PA=PB,∠OAP=∠OBP=90°,已知∠P=90°,∴∠AOB=90°,∴四边形APBO为正方形,∴OA=OB=PA=3,则⊙O的半径长是3,故答案为:3.分析:连接OA、OB,已知PA、PB分别切⊙O于点A、B,由切线的性质及切线长定理可得:PA=PB,∠OAP=∠OBP=90°,再由已知∠P=90°,所以得到四边形APBO为正方形,从而得⊙O的半径长即PA的长.24.如图,P是⊙O的直径AB的延长线上一点,PC、PD切⊙O于点C、D.若PA=6,⊙O 的半径为2,求∠CPD.答案:60°解析:解答:∵PA=6,⊙O的半径为2,∴PB=PA-AB=6-4=2,∴OP=4,∵PC、PD切⊙O于点C、D.∴∠OPC=∠OPD,∴CO⊥PC,∴sin∠OPC=2: 4 =0.5 ,∴∠OPC=30°,∴∠CPD=60°,故答案为:60°.分析:根据切线的性质定理和切线长定理求出OP=4,∠OPC=∠OPD,再利用解直角三角形的知识求出∠OPC=30°,即可得出答案.25.如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C 所对的边长依次为3,4,5,求⊙O的半径.答案:2解析:解答:连接OD、OE,∵⊙O与△ABC中AB、AC的延长线及BC边相切,∴AF=AD,BE=BF,CE=CD,OD⊥AD,OE⊥BC,∵∠ACB=90°,∴四边形ODCE是正方形,设OD=r,则CD=CE=r,∵BC=3,∴BE=BF=3-r,∵AB=5,AC=4,∴AF=AB+BF=5+3-r,AD=AC+CD=4+r,∴5+3-r=4+r,r=2,则⊙O的半径是2.故答案为:2.分析:先连接OD、OE根据⊙O与△ABC中AB、AC的延长线及BC边相切,得出AF=AD,BE=BF,CE=CD,再根据OD⊥AD,OE⊥BC,∠ACB=90°,得出四边形ODCE是正方形,最后设OD=r,列出5+3-r=4+r,求出r=2即可.。
九年级数学下册第三章圆3.7切线长定理同步练习新版北师大版1.doc

课时作业(二十七)[第三章*7 切线长定理]一、选择题1.2017·红桥区期末如图K-27-1,PA,PB分别切⊙O于点A,B,PA=10,CD切⊙O 于点E,与PA,PB分别交于C,D两点,则△PCD的周长是链接听课例1归纳总结( )图K-27-1A.10 B.18 C.20 D.222.如图K-27-2,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O与AB,BC,AC分别切于点D,E,F,则AF的长为()图K-27-2A.5 B.10 C.7.5 D.43.已知⊙O的半径是4,P是⊙O外一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB的长为()A.4 B.4 2 C.4 3 D.2 34.如图K-27-3,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中,错误的是( )链接听课例2归纳总结图K-27-3A.∠1=∠2 B.PA=PBC.AB⊥OP D.PA2=PC·PO5.如图K-27-4,AB为半圆O的直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD,OC.下列结论:①∠DOC=90°;②AD+BC=CD;③S△AOD∶S△BOC=AD2∶AO2;④OD∶OC=DE∶EC;⑤OD2=DE·CD.其中正确的有( )图K-27-4A.2个 B.3个C.4个 D.5个二、填空题6.如图K-27-5,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为________.图K-27-57.2017·昌平区期末如图K-27-6所示,在Rt△ABC中,∠C=90°,AC长为8,BC 长为15,则△ABC的内切圆⊙O的直径是________.图K-27-68.如图K-27-7,P是⊙O的直径AB的延长线上的一点,PC,PD分别切⊙O于点C,D.若PA=6,⊙O的半径为2,则∠CPD=________°.图K-27-79.如图K-27-8所示,已知PA,PB,EF分别切⊙O于点A,B,D,若PA=15 cm,则△PEF的周长是________ cm;若∠P=50°,则∠EOF=________°.链接听课例1归纳总结图K-27-810.如图K-27-9所示,⊙O与△ABC中AB,AC的延长线及BC边相切,且∠ACB=90°,∠A,∠ABC,∠ACB所对的边长依次为3,4,5,则⊙O的半径是________.图K-27-9三、解答题11.如图K-27-10,PA,PB分别切⊙O于点A,B,连接PO与⊙O相交于点C,连接AC,BC.求证:AC=BC.链接听课例2归纳总结图K-27-1012.2017·孝感模拟如图K-27-11,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,OB=6 cm,OC=8 cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.链接听课例1归纳总结图K-27-1113.如图K-27-12,△ABC外切于⊙O,切点分别为D,E,F,∠A=60°,BC=7,⊙O的半径为 3.求:(1)BF+CE;(2)△ABC的周长.图K-27-1214.如图K-27-13,AB为⊙O的直径,∠DAB=∠ABC=90°,DE与⊙O相切于点E,⊙O的半径为5,AD=2.(1)求BC的长;(2)延长AE交BC的延长线于点G,求EG的长.图K-27-13探究存在题如图K-27-14,以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E.(1)求证:EB=EC=ED.(2)在线段DC上是否存在点F,使得BC2=4DF·DC?若存在,求出点F,并予以证明;若不存在,请说明理由.图K-27-14详解详析【课时作业】 [课堂达标]1.[解析] C ∵PA ,PB 分别切⊙O 于点A ,B ,CD 切⊙O 于点E , ∴PA =PB =10,CA =CE ,DE =DB ,∴△PCD 的周长是PC +CD +PD =PC +AC +DB +PD =PA +PB =10+10=20.故选C.2.[解析] A 设AF =x ,根据切线长定理得AD =x ,BD =BE =9-x ,CE =CF =CA -AF =6-x ,则有9-x +6-x =5,解得x =5,即AF 的长为5.3.[解析] C 如图,PA ,PB 分别切⊙O 于A ,B 两点.∵OA =4,PO =8,∴AP =82-42=43,∠APO =30°,∴∠APB =2∠APO =60°, ∴△PAB 是等边三角形,∴AB =AP =4 3.4.[解析] D 如图,连接OA ,OB .∵PA 切⊙O 于点A ,PB 切⊙O 于点B ,∴PA =PB , ∴△ABP 是等腰三角形.易证∠1=∠2,∴AB ⊥OP .故A ,B ,C 均正确.设OP 交AB 于点D ,易证△PAD ∽△POA ,∴PA ∶PO =PD ∶PA ,∴PA 2=PD ·PO .故D 错误.5.[解析] C 连接OE .∵AD ,BC ,CD 分别与⊙O 切于点A ,B ,E ,∴OA ⊥AD ,OB ⊥BC ,OE ⊥CD ,DA =DE ,EC =BC ,∠ADO =∠EDO ,∠ECO =∠BCO ,∴∠OAD =∠OED =∠OEC =∠OBC =90°,∴∠AOD =∠EOD ,∠BOC =∠EOC .①∵∠AOD +∠EOD +∠BOC +∠EOC =180°,∴∠DOC =∠EOD +∠EOC =90°,∴①正确;②∵DA =DE ,EC =BC ,∴AD +BC =DE +EC =CD ,∴②正确;③∵∠AOD +∠BOC =90°,∠AOD +∠ADO =90°,∴∠BOC =∠ADO .又∵∠OAD =∠CBO =90°,∴△OAD ∽△CBO ,∴S △AOD ∶S △BOC =AD 2∶BO 2=AD 2∶AO 2,∴③正确;④∵△OAD ∽△CBO ,∴OD OC =AD OB =DEOB.∵OB ≠EC ,∴④不正确;⑤∵∠DOC =∠OED =90°,∴∠EOD +∠EDO=90°,∠CDO +∠DCO =90°,∴∠EOD =∠DCO ,∴△OED ∽△COD ,∴OD CD =DEOD,即DE ·CD =OD 2,∴⑤正确.综上,正确的有①②③⑤.故选C.6.[答案] 44[解析] ∵四边形ABCD 是⊙O 的外切四边形,∴AD +BC =AB +CD =22,∴四边形ABCD 的周长=AD +BC +AB +CD =44. 7.[答案] 6[解析] ∵∠C =90°,AC =8,BC =15,∴AB =AC 2+BC 2=17,∴△ABC 的内切圆⊙O的直径为15×817+15+8×2=6.故答案为6.8.[答案] 60[解析] 连接OC .∵PA =6,⊙O 的半径为2,∴OP =PA -OA =6-2=4.∵PC ,PD 分别切⊙O 于点C ,D ,∴∠OPC =∠OPD ,OC ⊥PC ,∴sin ∠OPC =24=12,∴∠OPC =30°,∴∠CPD =60°.9.[答案] 30 65[解析] ∵PA ,PB ,EF 分别切⊙O 于点A ,B ,D , ∴PA =PB =15 cm ,ED =EA ,FD =FB ,∴PE +EF +PF =PE +ED +PF +FD =PA +PB =30 cm ,即△PEF 的周长是30 cm ;连接OA ,OB ,OD .∵PA ,PB 为⊙O 的切线,∴∠PAO =∠PBO =90°,而∠P =50°,∴∠AOB =360°-90°-90°-50°=130°.易证得Rt △OAE ≌Rt △ODE ,Rt △OFD ≌Rt △OFB ,∴∠1=∠2,∠3=∠4,∴∠2+∠3=12∠AOB =65°,即∠EOF =65°.10.[答案] 2[解析] 如图,设⊙O 与AB ,AC 的延长线及BC 边分别相切于点F ,D ,E .连接OD ,OE .∵⊙O 与△ABC 中AB ,AC 的延长线及BC 边相切,∴AF =AD ,BE =BF ,CE =CD ,OD ⊥AD ,OE ⊥BC .∵∠ACB =90°,∴四边形ODCE 是正方形.设OD =r ,则CD =CE =r .∵BC =3,∴BE =BF =3-r .∵AB =5,AC =4,∴AF =AB +BF =5+3-r ,AD =AC +CD =4+r ,∴5+3-r =4+r ,解得r =2,则⊙O 的半径是2.11.证明:∵PA ,PB 分别切⊙O 于点A ,B , ∴PA =PB ,∠APC =∠BPC .又∵PC =PC ,∴△APC ≌△BPC ,∴AC =BC .12.解:(1)连接OF .根据切线长定理,得BE =BF ,CF =CG ,∠OBF =∠OBE ,∠OCF =∠OCG .∵AB ∥CD ,∴∠ABC +∠BCD =180°,∴∠OBF +∠OCF =90°, ∴∠BOC =90°.(2)由(1)知,∠BOC =90°. ∵OB =6 cm ,OC =8 cm ,∴由勾股定理,得BC =OB 2+OC 2=10 cm , ∴BE +CG =BC =10 cm.(3)∵OF ⊥BC ,由三角形的面积公式,得12OB ·OC =12BC ·OF ,∴OF =OB ·OCBC =4.8 cm.13.解:(1)∵△ABC 外切于⊙O ,切点分别为D ,E ,F ,∴BF =BD ,CE =CD ,∴BF +CE =BD +CD =BC =7.(2)如图,连接OE ,OF ,OA .∵△ABC 外切于⊙O ,切点分别为D ,E ,F , ∴∠OEA =90°,∠OAE =12∠BAC =30°,∴OA =2OE =2 3.由勾股定理,得AF =AE =OA 2-OE 2=3,∴△ABC 的周长是AB +BC +AC =AF +AE +CE +BF +BC =3+3+7+7=20, 即△ABC 的周长是20.14.[解析] (1)过点D 作DF ⊥BC 于点F ,由切线长定理可得DE =AD =2,CE =BC .设BC =x ,在Rt △DCF 中,DC 2=CF 2+DF 2,即可得方程(2+x )2=(x -2)2+(2 5)2,解此方程即可求得答案;(2)易证得△ADE ∽△GCE ,由相似三角形的对应边成比例,可得AE ∶EG =4∶5,由勾股定理即可求得AG 的长,继而求得答案.解:(1)过点D 作DF ⊥BC 于点F . ∵∠DAB =∠ABC =90°,∴四边形ABFD 是矩形,AD 与BC 是⊙O 的切线,∴DF =AB =2 5,BF =AD =2. ∵DE 与⊙O 相切, ∴DE =AD =2,CE =BC .设BC =x ,则CF =BC -BF =x -2,DC =DE +CE =2+x .在Rt △DCF 中,DC 2=CF 2+DF 2,即(2+x )2=(x -2)2+(2 5)2,解得x =52,即BC =52.(2)∵∠DAB +∠ABC =180°,∴AD ∥BC ,∴△ADE ∽△GCE , ∴AD GC =DE CE ,AE EG =ADGC.∵AD =DE =2,∴GC =CE =BC =52,∴BG =BC +CG =5,AE EG =45.在Rt △ABG 中,AG =AB 2+BG 2=3 5,∴EG =59AG =535.[点评] 此题考查了切线的性质与判定、切线长定理以及勾股定理等知识,难度适中,注意掌握辅助线的作法与方程思想的应用.[素养提升][解析] (1)连接BD ,已知ED ,EB 都是⊙O 的切线,由切线长定理可证得OE 垂直平分BD ,而BD ⊥AC (圆周角定理),则OE ∥AC .由于O 是AB 的中点,可证得OE 是△ABC 的中位线,即E 是BC 的中点,那么在Rt △BDC 中,DE 就是斜边BC 的中线,由此可证得所求的结论.(2)由(1)知:BC =2BE =2DE ,则所求的比例关系式可转化为(BC 2)2=DF ·DC ,即DE 2=DF ·DC ,那么只需作出与△DEC 相似的△DFE 即可,这两个三角形的公共角为∠CDE ,只需作出∠DEF =∠C 即可.①当∠DEC >∠C ,即180°-2∠C >∠C ,0°<∠C <60°时,∠DEF 的EF 边与线段DC 相交,那么交点即为所求的点F ;②当∠DEC =∠C ,即180°-2∠C =∠C ,∠C =60°时,点F 与点C 重合,点F 仍在线段DC 上,此种情况也成立;③当∠DEC <∠C ,即180°-2∠C <∠C ,60°<∠C <90°时,∠DEF 的EF 边与线段DC 的延长线相交,与线段CD 没有交点,所以在这种情况下不存在符合条件的点F .解:(1)证明:连接BD .∵ED ,EB 是⊙O 的切线,由切线长定理,得ED =EB ,∠DEO =∠BEO , ∴OE 垂直平分BD . 又∵AB 是⊙O 的直径, ∴AD ⊥BD ,∴AD ∥OE ,即OE ∥AC . 又O 为AB 的中点,∴OE 为△ABC 的中位线, ∴EB =EC ,∴EB =EC =ED .(2)存在.在△DEC 中,∵ED =EC , ∴∠C =∠CDE ,∴∠DEC =180°-2∠C .①当∠DEC >∠C 时,有180°-2∠C >∠C ,即0°<∠C <60°时,在线段DC 上存在满足条件的点F .在∠DEC 内,以ED 为一边,作∠DEF ,使∠DEF =∠C ,且EF 交DC 于点F ,则点F 即为所求.证明:在△DCE 和△DEF 中,∠CDE =∠EDF ,∠C =∠DEF ,∴△DEF ∽△DCE ,∴DE DC =DF DE, ∴DE 2=DF ·DC ,即(12BC )2=DF ·DC ,∴BC 2=4DF ·DC .②当∠DEC =∠C 时,△DEC 为等边三角形,即∠DEC =∠C =60°,此时,点C 即为满足条件的点F , 于是,DF =DC =DE ,仍有BC 2=4DE 2=4DF ·DC . ③当∠DEC <∠C ,即180°-2∠C<∠C,60°<∠C<90°时,所作的∠DEF>∠DEC,此时点F在DC的延长线上,故线段DC上不存在满足条件的点F.。
九年级数学下册 3.7 切线长定理特色训练 北师大版(2021年整理)

2017春九年级数学下册3.7 切线长定理特色训练(新版)北师大版编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017春九年级数学下册3.7 切线长定理特色训练(新版)北师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017春九年级数学下册3.7 切线长定理特色训练(新版)北师大版的全部内容。
切线长定理。
北师大版九年级数学下册【同步练习】《切线长定理》

《切线长定理》同步练习1.如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为()A.32 B.34 C.36 D.382.如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为()A.15 B.12 C.20 D.303.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为()A.20cm B.15cm C.10cm D.随直线MN的变化而变化4.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为()A.8 B.9 C.10 D.115.圆外切等腰梯形的一腰长是8,则这个等腰梯形的上底与下底长的和为()A.4 B.8 C.12 D.16◆选择题6.如图,⊙O是△ABC的内切圆,点D、E分别为边AB、AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是()A.7 B.8 C.9 D.167.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是()A.4 B.8 C.4D.88.如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为()A.35°B.45°C.60°D.70°9.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为()A.130° B.120° C.110° D.100°10.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=23,那么∠AOB等于()A.90° B.100° C.110° D.120°11.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,错误的是()A.∠1=∠2 B.PA=PB C.AB⊥OP D.=PC•PO12.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为()A.5,12(90°+∠P)B.7,90°+12C.10,90°-12∠P D.10,90°+12∠P13.圆外切等腰梯形的中位线等于8,则一腰长等于()A.4 B.6 C.8 D.1014.如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为()A.9 B.7 C.11 D.815.已知四边形ABCD是梯形,且AD∥BC,AD<BC,又⊙O与AB、AD、CD分别相切于点E、F、G,圆心O在BC上,则AB+CD与BC的大小关系是()A.大于B.等于C.小于D.不能确定◆填空题16.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD 的周长等于10cm,则PA= cm.17.如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O 的切线长为8cm,那么△PDE的周长为18.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,若⊙O的半径为r,△PCD的周长等于3r,则tan 12∠APB的值是19.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为20.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是◆解答题21.已知四边形ABCD外切于⊙O,四边形ABCD的面积为24,周长24,求⊙O的半径.22.如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,求CE.23.如图,已知PA、PB分别切⊙O于点A、B,∠P=90°,PA=3,求⊙O的半径.24.如图,P是⊙O的直径AB的延长线上一点,PC、PD切⊙O于点C、D.若PA=6,⊙O 的半径为2,求∠CPD.25.如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C 所对的边长依次为3,4,5,求⊙O的半径.【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
北师大版九年级数学下册试题3.7切线长定理

初中数学试卷3.7切线长定理一、选择题1. 一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( )A.21 B.20 C.19 D.182. 如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角(不包括∠PAB本身)有( )A.1个 B.2个 C.3个 D.4个3. 如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的 ( )A.三条中线的交点B.三条高的交点C.三条角平分线的交点D.三条边的垂直平分线的交点4.△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是()A.120° B.125° C.135° D.150°5.一个钢管放在V形架内,右图是其截面图,O为钢管的圆心.如果钢管的半径为25 cm ,∠MPN = 60︒,则OP =( ) A .50 cm B .253cm C.3350cm D .503cm 6.如图1,PA 、PB 分别切圆O 于A 、B 两点,C 为劣弧AB 上一点,∠APB=30°,则∠ACB=( ).A .60°B .75°C .105°D .120°(1) (2)7.圆外一点P ,PA 、PB 分别切⊙O 于A 、B ,C 为优弧AB 上一点,若∠ACB=a ,则∠APB=( )A .180°-aB .90°-aC .90°+aD .180°-2a 二、填空题8. 如图,在△ABC 中,5cm AB AC ==,cosB 35=.如果⊙O 的半径为10cm ,且经过点B 、C ,那么线段AO= cm .9.如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,且ο60=∠AEB ,则=∠P __ ___度.BC DPO BAC P O10. 如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,则△ABC的周长是.11. 如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC= 12,∠P=60o,弦AB的长为------.三、解答题:12. 如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.13. 如图,已知AB为⊙O的直径,AD、BC、CD为⊙O的切线,切点分别是A、B、PBAOE ,则有一下结论:(1)CO ⊥DO ;(2)四边形OFEG 是矩形.试说明理由.14. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°.(1)求∠APB 的度数; (2)当OA =3时,求AP 的长.15. 如图,在△ABC 中,已知∠ABC=90o ,在AB 上取一点E ,以BE 为直径的⊙O 恰与AC 相切于点D ,若AE=2 cm ,AD=4 cm . (1)求⊙O 的直径BE 的长; (2)计算△ABC 的面积.参考答案1. C2. B (提示:②④错误)3. D (提示:AD=AF,BD=BE,CE=CF ∴周长=821218⨯+⨯=)GFECB4. C5. D6. C7.D8. A(提示:∠MPN=600可得∠OPM=300可得OP=2OM=50)9.3(提示:连接OB,易得:∠ABC=∠AOB ∴cos∠AOB=cos∠3 5=OBOA AO)os300=ABAC∴AB=10. ∠P=60011. 760(提示:连接ID,IF ∵∠DEF=520∴∠DIF=1040∵D、F是切点∴DI⊥AB,IF⊥AC∴∠ADI=∠AFI=900∴∠A=1800-1040=760)12. 52 (提示:AB+CD=AD+BC)13. 1150(提示:∵∠A=500∴∠ABC+∠ACB=1300∵OB,OC分别平分∠ABC,∠ACB ∴∠OBC+∠OCB=650∴∠BOC=1800-650=1150)14. 解:∵AD,AE切于⊙O于D,E ∴AD=AE=20 ∵AD,BF切于⊙O于D,F ∴BD=BF 同理:CF=CE∴C△ABC=AB+BC+AC=AB+BF+FC+AC=AB+BD+EC+AC=AD+AE=4014 解:(1)∵在△ABO中,OA=OB,∠OAB=30°∴∠AOB=180°-2×30°=120°∵PA、PB是⊙O的切线∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°∴在四边形OAPB中,∠APB =360°-120°-90°-90°=60°. (2)如图①,连结OP∵PA 、PB 是⊙O 的切线∴PO 平分∠APB ,即∠APO =12∠APB =30°又∵在Rt △OAP 中,OA =3, ∠APO =30°∴AP =tan 30OA°=15 解:(1)连接OD ∴OD ⊥AC ∴△ODA 是Rt △设半径为r ∴AO=r+2 ∴(r+2)2—r 2=16 解之得:r=3 ∴BE=6(2) ∵∠ABC=900 ∴OB ⊥BC ∴BC 是⊙O 的切线 ∵CD 切⊙O 于D ∴CB=CD 令CB=x∴AC=x+4,BC=4,AB=x ,AB=8 ∵2228(4)x x +=+ ∴6x =∴S △ABC =186242⨯⨯=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线和圆的位置关系
一、选择题
1.如图,从圆O 外一点P 引圆O 的两条切线PA ,PB ,切点分别为A ,B .如果∠APB=60°,PA=8,那么弦AB 的长是( )
A .4
B .8
C .43
D .83
2如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,且∠AEB=60°,则∠P 的度数是( )
A .60°
B .120°
C .50°
D .30°
3.如图,P 是⊙O 外一点,PA ,PB 分别和⊙O 切于A ,B 两点,C 是弧AB 上任意一点,过C 作⊙O 的切线分别交PA ,PB 于D ,E .若△PDE 的周长为12,则PA 的长为( )
A .12
B .6
C .8
D .4
4.如图,边长为a 的正三角形的内切圆半径是( )
A
B
a C
D
5.在△AB C 中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是( )
A .5
B .7
C .2
D .1
6.如图,点O 是△ABC 的内切圆的圆心,若∠BAC=80°,则∠
BOC=( )
A.130° B.100° C.50° D.65°
7.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=,那么∠AOB的度
数为( )
A.90° B.100° C.110° D.120°
8.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为()
A.r B.3
2
r C.2r D.
5
2
r
二、填空题
9.如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO=__________.
10.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB 均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是_________.
11.如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则
∠BAC= .
12.如图,PA ,PB 是⊙O 的切线,切点分别为A ,B ,PO 交⊙O 于D 、E ,交AB 于C ,则下面的结论正确的有 .
①PA=PB ;②∠APO=∠BPO ;③OP ⊥AB ;④»»A D B D ;⑤∠PAB=∠PBA ;⑥PO=2AO ;⑦AC=BC .
13.如图,在△ABC 中,点P 是△ABC 的内心,则∠PBC+∠PCA+∠PAB= .
14.P 为⊙O 外一点,PA ,PB 是⊙O 的切线,切点分别为A ,B ,∠AP B=50°,点C 为⊙O 上一点(不与A ,B 重合),则∠ACB 的度数为 .
15.如图,点O 为△ABC 的外心,点I 为△ABC 的内心,若∠BOC=140°,则∠BIC 的度数为 .
三、解答题
16.已知正方形ABCD 的边长为2,点M 是BC 的中点,P 是线段
MC 上的一个动点,P 不与M 和C 重合,以AB 为直径作⊙O ,过点P 作⊙O 的切线交AD 于点F ,切点为E .求四边形CDFP 的周长.
17.如图,是一个不倒翁图案,不倒翁的圆形脸恰好与帽子边沿PA 、PB 分别相切于点A 、B ,
A
B C I O
B
不倒翁的鼻尖正好是圆心O ,若∠OAB=25°,求∠APB 的度数.
18.已知:如图,在直角△ABC 中,∠ABC =90°,以AB 上的点O 为圆心,OB 的长为半径的圆与AB 交于点E ,与AC 切于点D .
(1)求证:BC =CD ;(2)求证:∠ADE =∠ABD .
19.如图,AO 是△ABC 的中线,⊙O 与AB 相切于点D .
(1)要使⊙O 与边AC 也相切,应增加条件 (任写一个);
(2)增加条件后,请你说明⊙O 与边AC 相切的理由.
20.如图,已知AB 为O ⊙的直径,PA PC ,是O ⊙的切线,A C ,为切点,30BAC ∠=°.
(1)求P ∠的大小;(2)若2AB =,求PA 的长.
∙A B C D
E O。
