勾股定理培优2

合集下载

八年级下册第17章勾股定理培优试题(含答案)

人教版数学八年级下册第17章勾股定理培优试题一．选择题（共10小题）1．在△ABC 中，∠B=90°,若BC=3,AC=5，则AB 等于（）A ．2B ．3C ．4D ．342．如图，有一长方形空地ABCD,如果AB=6米，AD=8米，要从A 走到C ，至少要走（） A ．6米 B ．8米 C ．10米 D ．14米3．以下各组数为三角形的三边长，其中不能够构成直角三角形的是（）A ．32、42、52B ．7、24、25C ．0.3、0.4、0.5D ．9、12、154．“折竹抵地”问题源自《九章算术》中，即：今有竹高一丈，末折抵地，去本四尺，问折者高几何？意思是：一根竹子，原高一丈，一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部4尺远（如图），则折断后的竹子高度为多少尺？（1丈=10尺）（） A ．3 B ．5 C ．4.2 D ．45．某直角三角形的一直角边长为8，另一直角边长与斜边长的和为32，则斜边的长为（） A ．8 B ．10 C ．15 D ．176．满足下列条件的△ABC,不是直角三角形的是（）A ．∠C=∠A+∠BB ．∠C=∠A-∠BC ．a ：b ：c=3：4：5D ．∠A ：∠B ：∠C=3：4：57．小明想知道学校旗杆的高度，她发现旗杆上的绳子刚好垂到地面，当她把绳子的下端拉开5米后，发现绳子下端距离地面1米，则旗杆的高是（）A ．8米B ．10米C ．12米D ．13米8．下列各组数中，不是勾股数的是（）A ．9,12,15B ．8,15,17C ．12,18,22D ．5,12,13 9．下列结论中，错误的有（）①在Rt △ABC 中，已知两边长分别为3和4，则第三边的长为5；②△ABC 的三边长分别为AB,BC,AC,若BC 2+AC 2=AB 2,则∠A=90°;③在△ABC 中，若∠A ：∠B ：∠C=1：5：6，则△ABC 是直角三角形；④若三角形的三边长之比为3：4：5，则该三角形是直角三角形；A ．0个B ．1个C ．2个D ．3个10．如图,△ABC 中，AB=AC,AB=5,BC=8,AD 是∠BAC 的平分线，则AD 的长为（） A ．5 B ．4 C ．3 D ．2二．填空题（共6小题）11．已知一个直角三角形的两直角边长分别是1和2，则斜边长为．12．如图，在△ABC 中，∠C=90°,AD 平分∠CAB,DE ⊥AB 于E ，且DE=15cm,BE=8cm,则 BC= cm ．13．平面直角坐标系上有点A(-3,4),则它到坐标原点的距离为．14．如图，分别以直角△ABC 的三边为直径作半圆，若两直角边分别为6,8,则阴影部分的面积是．15．定义：如图，点P 、Q 把线段AB 分割成线段AP 、PQ 和BQ ，若以AP 、PQ 、BQ 为边的三角形是一个直角三角形，则称点P 、Q 是线段AB 的勾股分割点．已知点P 、Q 是线段AB的勾股分割点，如果AP=8,PQ=12(PQ>BQ),那么BQ= ．16．如图，一架长5米的梯子A1B1斜靠在墙A1C上,B1到墙底端C的距离为3米，此时梯子的高度达不到工作要求，因此把梯子的B1端向墙的方向移动了1.6米到B处，此时梯子的高度达到工作要求，那么梯子的A1端向上移动了米．三．解答题（共8小题）17．如图，在正方形网格中，小正方形的边长为1,A,B,C为格点（1）判断△ABC的形状，并说明理由．（2）求BC边上的高．18．已知：如图，在△ABC中，AB=13,AC=20,AD=12，且AD⊥BC,垂足为点D，求BC的长．19．我市鸭绿江边的景观区内有一块四边形空地，如图所示，景区管理人员想在这块空地上铺满观赏草坪，需要测量其面积，经技术人员测量∠ABC=90°,AB=20米，BC=15米，CD=7米，AD=24米．（1）请你帮助管理人员计算出这个四边形对角线AC的长度；（2）请用你学过的知识帮助管理员计算出这块空地的面积．20．某广场内有一块空地ABCD如图所示，现计划在空地上种草皮，经测量，∠B=90°,AB=6m,BC=8m,CD=26m,AD=24m．求四边形ABCD空地的面积．21．在△ABC中，CD是AB边上的高，AC=4,BC=3,DB=1.8．（1）求CD的长；（2）求AB的长；(3)△ABC是直角三角形吗？请说明理由．22．如图，小巷左石两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离BC 为0.7米，梯子顶端到地面的距离AC 为2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离A ′D 为1.5米，求小巷有多宽．23．如图，长7.5m 的梯子靠在墙上，梯子的底部离墙的底端4.5m ．（1）求梯子的顶端到地面的距离；（2）由于地面有水，梯子底部向右滑动1.5m,则梯子顶端向下滑多少米？24．阅读下列一段文字，然后回答下列问题．已知在平面内有两点P 1()x 1,y 1、P 2()x 2,y 2,其两点间的距离P 1P 2=()x 1-x 22+()y 1-y 22,同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可化简为|x 2-x 1|或|y 2-y 1|．（1）已知A(2,4)、B(-3,-8),试求A、B两点间的距离;（2）已知M、N在平行于y轴的直线上，点M的纵坐标为4，点N的纵坐标为-1，试求M、N两点的距离为;（3）已知一个三角形各顶点坐标为D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗？说明理由．答案：1-5 CCACD6-10 DDCCC11.12.3213.514.2415.416.0.817. 解：（1）结论：△ABC是直角三角形．理由：∵BC2=12+82=65，AC2=22+32=13，AB2=62+42=52，∴AC2+AB2=BC2，∴△ABC是直角三角形．（2）设BC边上的高为h．则有•AC•AB=•BC•h，∵AC=,AB=2,BC=∴h=18.解：∵AB=13，AC=20，AD=12，AD⊥BC，∴Rt△ABD中，BD===5，Rt△ACD中，CD===16，∴BC=BD+CD=5+16=21．19.解：（1）连接AC．在Rt△ABC中，∵∠ABC=90°，AB=20，BC=15，∴AC===25（米）．∴这个四边形对角线AC的长度为25米．（2）在△ADC中，∵CD=7，AD=24，AC=25，∴AD2+CD2=242+72=252=AC2，∴△ADC为直角三角形，∠ADC=90°，∴S四边形ABCD=S△ADC+S△ABC=×15×20+×7×24=234（平方米），∴四边形ABCD的面积为234平方米．20. 解：连接AC，在Rt△ABC中，AC2=AB2+BC2=62+82=102，∴AC=10．在△DAC中，CD2=262，AD2=242，而242+102=262，即AC2+AD2=CD2，∴∠DCA=90°，S四边形ABCD=S△BAC+S△DAC=•BC•AB+DC•AC，=×8×6+×24×10=144（m）2，答：四边形ABCD空地的面积是144m2．21.解：（1）∵CD是AB边上的高，∴△BDC是直角三角形，∴CD=＝＝2.4；（2）同（1）可知△ADC也是直角三角形，∴AD=＝＝3.2，∴AB=AD+BD=3.2+1.8=5；（3）△ABC是直角三角形，理由如下：又∵AC=4，BC=3，AB=5，∴AC2+BC2=AB2，∴△ABC是直角三角形．22.解：在Rt△ACB中，∵∠ACB=90°，BC=0.7米，AC=2.4米，∴AB2=0.72+2.42=6.25．在Rt△A′BD中，∵∠A′DB=90°，A′D=2米，BD2+A′D2=A′B′2，∴BD2+1.52=6.25，∴BD2=4．∵BD＞0，∴BD=2米．∴CD=BC+BD=0.7+2=2.7米．答：小巷的宽度CD为2.7米．23.解：（1）如图，在Rt△ABC中，AC2=AB2-BC2，∵AB=7.5m，BC=4.5m，∴AC==6（m），答：梯子的顶端到地面的距离为6m；（2）如图，∵BF=1.5m，∴CF=6m，∴EC==4.5（m），∴AE=1.5，答：梯子顶端向下滑1.5米．24.解：（1）AB==13，故答案为：13；（2）MN=4-（-1）=5；故答案为：5；（3）△ABC为等腰三角形．理由如下：∵DE=5，EF=4-（-2）=6，DF==5，∴DE=DF，∴△DEF为等腰三角形；。

著名机构初中数学培优讲义勾股定理逆定理.第02讲(A级).教师版

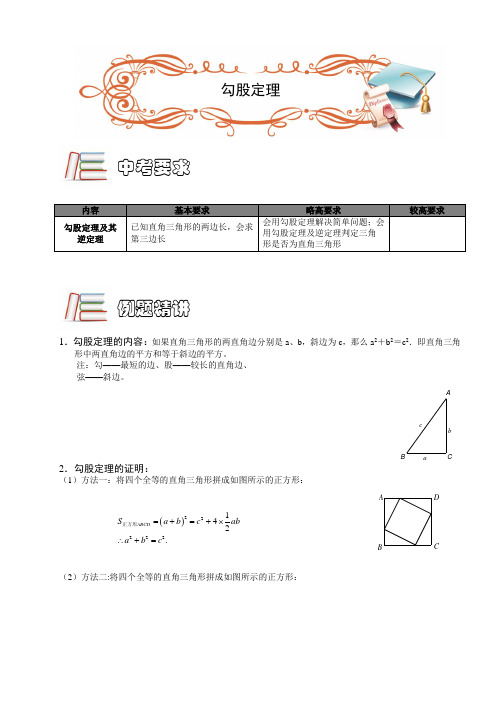
内容基本要求略高要求较高要求勾股定理及其逆定理已知直角三角形的两边长，会求第三边长会用勾股定理解决简单问题；会用勾股定理及逆定理判定三角形是否为直角三角形1．勾股定理的内容：如果直角三角形的两直角边分别是a 、b ，斜边为c ，那么a 2＋b 2＝c 2．即直角三角形中两直角边的平方和等于斜边的平方。

注：勾——最短的边、股——较长的直角边、弦——斜边。

CAB cba2．勾股定理的证明：（1）方法一：将四个全等的直角三角形拼成如图所示的正方形：()22222142.ABCD S a b c aba b c =+=+⨯∴+=正方形DCB A（2）方法二:将四个全等的直角三角形拼成如图所示的正方形：例题精讲中考要求勾股定理如果三角形中两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

即222,,ABC AC BC AB ABC ∆+=∆在中如果那么是直角三角形。

4．勾股数：满足a 2 +b2=c 2的三个正整数，称为勾股数．勾股数扩大相同倍数后，仍为勾股数．常用勾股数：3、4、5；5、12、13；7、24、25；8、15、17。

模块一勾股定理的逆定理【例1】在△ABC 中，AB=6，AC=8，BC=10，则该三角形为（）A 、锐角三角形B 、直角三角形C 、钝角三角形D 、等腰直角三角形【解析】欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．在△ABC 中，AB=6，AC=8，BC=10，推断出62+82=102，由勾股定理的逆定理得此三角形是直角三角形，【答案】B ．【巩固】下列由线段a 、b 、c 组成的三角形，不是直角三角形的是（）A 、a=3，b=4，c=5B 、a=1，b=43，c= 53C 、a=9，b=12，c=15D 、b=2，【解析】略【答案】D ．【巩固】已知a 、b 、c 是△ABC 的三边，且a 4-b 4=a 2c 2-b 2c 2，请判断△ABC 的形状．【解析】∵a 4-b 4=a 2c 2-b 2c 2∴a 4-b 4-a 2c 2+b 2c 2=0即：（a2+b2-c2）（a2-b2）=0则a2+b2-c2=0或a2-b2=0可得a2+b2=c2或a=b．【答案】△ABC是等腰三角形或直角三角形．【例2】如图，△ABC中，CD⊥AB于D，一定能确定△ABC为直角三角形的条件的个数是（）①∠1=∠A；②CD DBAD CD=；③∠B+∠2=90°；④BC：AC：AB=3：4：5；⑤AC•BD=AD•CDA、1B、2C、3D、4【解析】①因为∠A+∠2=90°，∠1=∠A，所以∠1+∠2=90°，即△ABC为直角三角形，故正确；②根据CD2=AD•DB得到CD DBAD CD=，再根据∠ADC=∠CDB=90°，则△ACD∽△CBD，∴∠1=∠A，∠2=∠B，根据三角形内角和定理可得：∠ACB=90°，故正确；③因为∠B+∠2=90°，∠B+∠1=90°，所以推出∠1=∠2，无法得到两角和为90°，故错误；④设BC的长为3x，那么AC为4x，AB为5x，由9x2+16x2=25x2，符合勾股定理的逆定理，故正确；⑤由三角形的相似无法推出AC•BD=AD•CD成立，所以△ABC不是直角三角形，故错误．所以正确的有三个．【答案】C．【巩固】如图，已知正方形ABED与正方形BCFE，现从A，B，C，D，E，F六个点中任取三个点，使得这三个点能作为直角三角形的三个顶点，则这样的直角三角形共有（）A、10B、12C、14D、16【解析】可得到14个直角三角形，分别为△ABE、△ADE、△ABD、△BED、△BCE、△CFE、△BCF、△BEF、△ACF、△ADF、△ACD、△CDF、△AEC、△DBF．【答案】C．【例3】已知△ABC的三边长分别为5，13，12，则△ABC的面积为（）A、30B、60C、78D、不能确定【解析】∵52+122=132，∴三角形为直角三角形，∵长为5，12的边为直角边，∴三角形的面积= 12×5×12=30．【答案】A．【巩固】如图所示的一块地，已知AD=4m，CD=3m，AD⊥DC，AB=13m，BC=12m，求这块地的面积．【解析】连接AC．∵AD=4m，CD=3m，AD⊥DC∴AC=5m∵122+52=132∴△ACB为直角三角形∴S△ACB= 12×AC×BC= 12×5×12=30m2，∴这块地的面积=S△ACB-S△ACD=30-6=24m2．【答案】24【例4】如图，已知CA⊥AB，DB⊥AB，AC=BE，AE=BD．（1）试猜想线段CE与DE的大小与位置关系，并说明你的结论；（2）若AC=5，BD=12，求CE的长．（提示：连接CD）【解析】（1）利用三角形判定全等的方法先求出△AEC≌△BDE，在利用全等的性质得出数量关系和位置关系；（2）直接利用（1）中的全等找到三角形ACE中的边长，用勾股定理求解即可．【答案】（1）CE=DE，CE⊥DE．∵CA⊥AB，DB⊥AB，∴∠A=∠B．∵AC=BE，AE=BD，∴△AEC≌△BDE（SAS）．∴CE=DE，∠CEA=∠BDE．∵∠BED+∠BDE=90°，∴∠CEA+∠BED=90°．∴CE⊥DE．（2）由（1）可知AC=5，AE=BD=12，∴CE=13．【巩固】如图所示，在△ABC中，AB：BC：CA=3：4：5，且周长为36，点P从点A开始沿AB边向B点以每秒1cm的速度移动；点Q从点B沿BC边向点C以每秒2cm的速度移动，如果同时出发，则过3秒时，△BPQ的面积为（）cm2．【解析】设AB为3x，BC为4x，AC为5x∵周长为36AB+BC+AC=36，∴3x+4x+5x=36得x=3∴AB=9，BC=12，AC=15∵AB2+BC2=AC2，∴△ABC是直角三角形过3秒时，BP=9-3=6，BQ=2×3=6∴S△PBQ=12BP•BQ=12×（9-3）×6=18cm2．【答案】18cm2【例5】阅读理解题：（1）如图所示，在△ABC中，AD是BC边上的中线，且AD=12BC．求证：∠BAC=90°．证明：∵BD=CD，AD=12BC，∴AD=BD=DC，∴∠B=∠BAD，∠C=∠CAD，∵∠B+∠BAD+∠CAD+∠C=180°，∴∠BAD+∠CAD=90°，即∠BAC=90°．（2）此题实际上是直角三角形的另一个判定定理，请你用文字语言叙述出来．（3）直接运用这个结论解答下列题目：一个三角形一边长为2，这边上的中线长为1，另两边之和为13+，求这个三角形的面积．【解析】略【答案】（1）为题目信息，不用解答．（2）根据题意用语言表述为：如果三角形斜边上的中线等于斜边的一半，那么这个三角形是直角三角形．（3）因为一个三角形一边长为2，这边上的中线长为1，所以这个三角形为直角三角形，设一边长为x，则另一边长为：[（13+）-x]，根据勾股定理，[（13+）-x]2+x2=4，解得x=1或3，根据直角三角形的面积可得3．模块二勾股定理与特殊三角形含30o角的直角三角形【例6】如图，△ABC和△DCE都是边长为4的等边三角形，点B、C、E在同一条直线上，连接BD，则BD 的长为（）A、3B、23C、33D、43【解析】∵△ABC和△DCE都是边长为4的等边三角形，∴∠DCE=∠CDE=60°，BC=CD=4．∴∠BDC=∠CBD=30°．∴∠BDE=90°．∴2222BD BE DE=--=8443【答案】D【巩固】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上．另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，如图，则三角板的最大边的长为（）A、3B、6C、32D、62【解析】过点C作CD⊥AD，∴CD=3，在直角三角形ADC中，∵∠CAD=30°，∴AC=2CD=2×3=6，又三角板是有45°角的三角板，∴AB=AC=6，∴BC2=AB2+AC2=62+62=72，∴BC=6 2，【答案】D．【例7】如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是（）A、3.5B、4.2C、5.8D、7【解析】利用垂线段最短分析AP最小不能小于3；利用含30度角的直角三角形的性质得出AB=6，可知AP最大不能大于6．此题可解．根据垂线段最短，可知AP的长不可小于3；∵△ABC中，∠C=90°，AC=3，∠B=30°，∴AB=6，∴AP的长不能大于6．【答案】D．【巩固】在△ABC 中，∠A ：∠B ：∠C=l ：2：3，CD ⊥AB 于点D ．若BC=a ，则AD 等于A 、12aB 、32aC 、32a D 、3a【解析】首先由已知△ABC 中，∠A ：∠B ：∠C=l ：2：3求出∠A=30°，∠B=60°，∠ACB=90°，根据直角三角形中30°角所对的边等于斜边的一半，求出AB=2a ，由CD ⊥AB 得∠BCD=30°，所以得BD=12a ，从而求出AD ．【答案】C【例8】如图所示，已知∠1=∠2，AD=BD=4，CE ⊥AD ，2CE=AC ，那么CD 的长是（）【解析】在Rt △AEC 中，由于12CE AE ，可以得到∠1=∠2=30°，又AD=BD=4，得到∠B=∠2=30°，从而求出∠ACD=90°，然后由直角三角形的性质求出CD ．【答案】2【巩固】如图，在Rt △ABC 中，已知，∠ACB=90°，∠B=15°，AB 边的垂直平分线交AB 于E ，交BC 于D ，且BD=13cm ，则AC 的长是（）【解析】∵AB 边的垂直平分线交AB 于E ，交BC 于D （已知）∴AD=BD （线段垂直平分线的性质）∴∠DAE=∠B=15°且AD=BD=13cm （等腰三角形的性质） ∴∠ADC=30°（外角性质）∴12AC AD ==6.5cm ．【答案】6.5cm【例9】已知∠MAN ，AC 平分∠MAN ．（1）在图1中，若∠MAN=120°，∠ABC=∠ADC=90°，求证：AB+AD=AC ；（2）在图2中，若∠MAN=120°，∠ABC+∠ADC=180°，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；【解析】（1）根据含30°角的直角三角形的性质进行证明；（2）作CE ⊥AM 、CF ⊥AN 于E 、F ．根据角平分线的性质，得CE=CF ，根据等角的补角相等，得∠CDE=∠ABC ，再根据AAS 得到△CDE ≌△CBF ，则DE=BF ．在（1）的基础上，知AE+AF=AC ，进而证明AD+AB=AC 仍成立．【答案】（1）∵AC 平分∠MAN ，∴∠CAD=∠CAB=60°．又∠ABC=∠ADC=90°， ∴11,22AD AC AB AC ==， ∴AB+AD=AC ．（2）结论仍成立．理由如下：作CE ⊥AM 、CF ⊥AN 于E 、F ． ∵AC 平分∠MAN ， ∴CE=CF ．∵∠ABC+∠ADC=180°，∴∠CDE=∠ABC，∴△CDE≌△CBF，∴DE=BF．∵∠MAN=120°，由（1），知AE+AF=AC．∴AD+AB=AC．含45o角的直角三角形【例10】解答下列各题：(1)等腰直角△ABC和等腰直角△CDE的位置如图所示，连接BE，并延长交AD于F，试问AD与BE之间有什么关系？证明你的结论；（2）若保持其他条件不变，等腰直角△CDE绕C点旋转，位置如下图所示，试问AD与BE之间的关系还存在吗？若存在，给予证明，若不存在，则说明理由．【解析】（1）、（2）通过证明△BEC≌△ADC得到AD与BE的数量关系与位置关系．【答案】（1）AD⊥BE，AD=BE，∵等腰直角△ABC和等腰直角△CDE，∴DC=EC，∠DCA=∠ECB，AC=BC，∴△BEC≌△ADC，∴AD=BE，∠DAC=∠EBC，又∠BEC=∠AEF，∠BEC+∠EBC=90°，∴∠AEF+∠DAC=90°，∴∠AFB=90°，∴AD⊥BE．（2）仍存在．如图，∵等腰直角△ABC和等腰直角△CDE，∴DC=EC，AC=BC，∠DCE=∠ACB，∴∠DCA=∠ECB，∴△BEC≌△ADC∴AD=BE，∠DAC=∠EBC，又∠BOC=∠AOE，∠BOC+∠EBC=90°，∴∠AOE+∠DAC=90°，∴AD⊥BE．【例11】如图，以等腰直角三角形ABC的斜边AB与边面内作等边△ABD，连接DC，以DC当边作等边△DCE，B、E在C、D的同侧，若AB=2求BE的长．【解析】∵△ABD是等边三角形∴AC=BC，DC=DC又∵ABC等腰直角三角形∴BD=AD∴△ADC≌△BDC∴∠BCD=（360°-90°）÷2=135°又∵∠CBD=60°-45°=15°∴∠CDB=180°-135°-15°=30°，∠BDE=60°-30°=30°∴CD=ED，∠CDB=∠BDE，BD=BD∴△BCD≌△BED∴根据勾股定理BE=CB=1【答案】1．【例12】已知：如图所示，AC⊥CD，BD⊥CD．线段AB的垂直平分线EF交AB于点E，交CD于点F，且AC=FD，求证：△ABF是等腰直角三角形．【解析】根据线段垂直平分线的性质，得FA=FB，只需证明∠AFB=90°．根据HL可以证明Rt△ACF≌Rt△FDB，则∠CAF=∠DFB，结合∠CAF+∠CFA=90°，即可求证．【答案】∵EF是AB的垂直平分线，∴FA=FB．∵AC⊥CD，BD⊥CD，∴△ACF与△FDB是直角三角形．在Rt△ACF与Rt△FDB中，AC=FD，FA=BF，∴Rt△ACF≌Rt△FDB（HL）．∴∠CAF=∠DFB．∵∠C=90°，∴∠CAF+∠CFA=90°，∴∠CFA+∠BFD=90°，∴∠AFB=90°．∴△ABF是等腰直角三角形．【巩固】如图（1）是某种台灯的示意图，灯柱BC固定垂直于桌面，AB是转轴，可以绕着点B转动，AB=10cm，BC=20cm，圆锥形灯罩的轴截面△APQ是等腰直角三角形，∠PAQ=90°，且PQ∥AB．转动前，点A、B、C在同一直线上．（1）转动AB，如图（2）所示，若灯心A到桌面的距离AM=25cm，求∠ABC的大小；（2）继续转动AB，使AB⊥BC，求此时台灯光线照在桌面上的面积？（假设桌面足够大）【解析】（1）过B作BD⊥AM于D，求出BD的长度为5，因为AB=10，所以∠ABD=30°，再加上90°就是∠ABC的度数；（2）AB⊥BC时，光线照在桌面上的轴截面是等腰直角三角形，斜边上的高等于BC的长度20，所以光线所照部分圆的半径为20，代入面积公式求解即可．【答案】（1）过点B作BD⊥AM于D，∵AM=25，∴AD=5，又∵AB=10，∠ADB=90°，∴∠ABD=30°，∴∠ABC=90°+30°=120°．（2）∵AB⊥BC，∴AM=20，设AP，AQ与桌面交于E，F，△AEF为等腰直角三角形，AM为斜边上的高，∴ME=MF=20，台灯照在桌面上的最大面积为π•202=400π．1. 如图所示，在四边形ABCD中，已知：AB：BC：CD：DA=2：2：3：1，且∠B=90°，求∠DAB的度数．【解析】连接AC．设DA=k，则AB=2k，BC=2k，CD=3k．∵∠B=90°，AB：BC=2：2，∴∠BAC=45°，AC2=AB2+BC2=4k2+4k2=8k2，∵（3k）2-k2=8k 2，∴∠DAC=90°，∴∠DAB=∠BAC+∠DAC=135°．【答案】135o课后作业2. 如图，在△ABC 中，CD ⊥AB 于D ，AC=4，BC=3，DB=95．（1）求CD ，AD 的值；（2）判断△ABC 的形状，并说明理由．解：（1）∵CD ⊥AB 且CB=3，BD=95，故△CDB 为直角三角形， ∴在Rt △CDB 中，22229123()55CD CB BD =-=-=，在Rt △CAD 中，222212164()55AD AC CD =-=-=．（2）△ABC 为直角三角形．理由：∵AD=165，BD=95，∴AB=AD+BD=165+95=5， ∴AC 2+BC 2=42+32=25=52=AB 2，∴根据勾股定理的逆定理，△ABC 为直角三角形．3. 如图，在△ABC 中，已知AB=AC=2a ，∠ABC=15°，CD 是腰AB 上的高，求CD 的长．【解析】过点C 作CD ⊥AB 于D ，根据等腰三角形的性质，三角形的内角与外角的关系得到∠DAC=30°．在直角△ACD 中，根据30°角所对的直角边等于斜边的一半解得CD 的长．【答案】a4. 如图，△ABC 中，AB=AC ，∠BAC=120°，AD ⊥AC 交BC 于点D ，求证：BC=3AD ．【解析】在△ABC 中，AB=AC ，∠BAC=120°，所以∠B=∠C=30°，又AD ⊥AC ，即有CD=2AD ，AD=DB ，所以BC=CD+BD=3BD=3AD ．【答案】如解析．。

勾股定理培优题

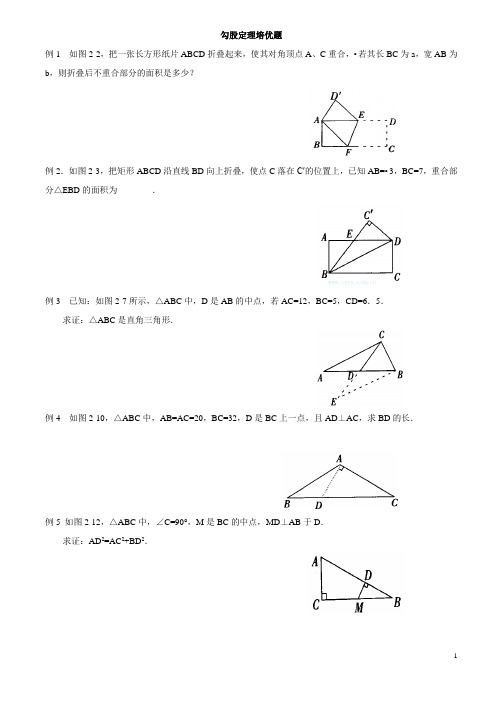
勾股定理培优题例1 如图2-2，把一张长方形纸片ABCD折叠起来，使其对角顶点A、C重合，•若其长BC为a，宽AB为b，则折叠后不重合部分的面积是多少？例2．如图2-3，把矩形ABCD沿直线BD向上折叠，使点C落在C′的位置上，已知AB=•3，BC=7，重合部分△EBD的面积为________．例3 已知：如图2-7所示，△ABC中，D是AB的中点，若AC=12，BC=5，CD=6．5．求证：△ABC是直角三角形．例4 如图2-10，△ABC中，AB=AC=20，BC=32，D是BC上一点，且AD⊥AC，求BD的长．例5 如图2-12，△ABC中，∠C=90°，M是BC的中点，MD⊥AB于D．求证：AD2=AC2+BD2．例6在中，，于D ，求证：（1）（2）例7、如图，已知四边形ABCD 的四边AB 、BC 、CD 和DA 的长分别为3、4、13、12， ∠CBA =90°,求S 四边形ABCD例8、在正方形ABCD 中, F 为DC 的中点, E 为BC 上一点, 且EC = ,求证: ∠EF A = 90︒例9 如图2-21所示．已知：在正方形ABCD 中，∠BAC 的平分线交BC 于E ，作EF ⊥AC 于F ，作FG ⊥AB 于G ．求证：AB 2=2FG 2．例10如图2-22所示．AM 是△ABC 的BC 边上的中线，求证：AB 2+AC 2=2(AM 2+BM 2)．CA D B例11 如图2-23所示．求证：任意四边形四条边的平方和等于对角线的平方和加对角线中点连线平方的4倍．例12 如图2-24所示．已知△ABC 中，∠C=90°，D ，E 分别是BC ，AC 上的任意一点．求证：AD 2+BE 2=AB 2+DE 2．例13 求证：在直角三角形中两条直角边上的中线的平方和的4倍等于斜边平方的5倍．作业：1：已知：如图，△ABC 中，AB =AC ，D 为BC 上任一点，求证：AB 2－AD 2=BD ·DC2 已知：钝角，CD 垂直BA 延长线于D ，求证：3、已知：如图，在正方形ABCD 中，E ，F 分别AB ，AD 上的点，又AB =12，EF =10，△AEF 的面积等于五边形EBCDF 面积的，求AE ，AF 的长。

11.专题勾股定理中的动点问题专练(二)原卷版2020-2021学年八年级数学上册专题培优训练

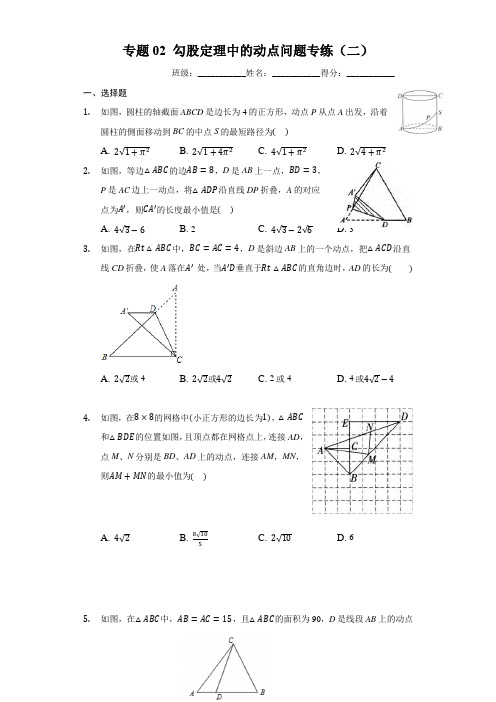
专题02 勾股定理中的动点问题专练（二）班级：___________姓名：___________得分：___________一、选择题1.如图，圆柱的轴截面ABCD是边长为4的正方形，动点P从点A出发，沿着圆柱的侧面移动到BC的中点S的最短路径为()A. 2√1+π2B. 2√1+4π2C. 4√1+π2D. 2√4+π22.如图，等边△ABC的边AB=8，D是AB上一点，BD=3，P是AC边上一动点，将△ADP沿直线DP折叠，A的对应点为A′，则CA′的长度最小值是()A. 4√3−6B. 2C. 4√3−2√6D. 33.如图，在Rt△ABC中，BC=AC=4，D是斜边AB上的一个动点，把△ACD沿直线CD折叠，使A落在A′处，当A′D垂直于Rt△ABC的直角边时，AD的长为()A. 2√2或4B. 2√2或4√2C. 2或4D. 4或4√2−44.如图，在8×8的网格中(小正方形的边长为1)，△ABC和△BDE的位置如图，且顶点都在网格点上，连接AD，点M、N分别是BD、AD上的动点，连接AM，MN，则AM+MN的最小值为()C. 2√10D. 6A. 4√2B. 8√1055.如图，在△ABC中，AB=AC=15，且△ABC的面积为90，D是线段AB上的动点(包含端点)，若线段CD的长为正整数．．．，则点D的个数共有()A. 2个B. 3个C. 4个D. 5个6.如图，在△ABC中，AB=6，BC=8，∠B=90°，若P是AC上的一个动点，则AP+BP+CP的最小值是()A. 14.8B. 15C. 15.2D. 16二、填空题7.如图，在每个小正方形的边长为1的网格中，点O，A，B，M均在格点上，P为线段OM上的一个动点．(I)OM的长等于______；(Ⅱ)当点P在线段OM上运动，且使PA2+PB2取得最小值时，请借助网格和无刻度的直尺，在给定的网格中画出点P的位置，并简要说明你是怎么画的．8.在Rt△ABC中，∠ACB=90°，AB=13cm，AC=5cm，动点P从点B出发沿射线BC以lcm/s的速度移动，设运动的时间为t秒，当△ABP为等腰三角形时，t的值为______．9.如图，长方形ABCD中，∠DAB=∠B=∠C=∠D=90°，AD=BC=8，AB=CD=17.点E为线段DC上的一个动点，△ADE与△△AD′E关于直线AE对称，当△AD′B′为直角三角形时，DE的长为________________10.如图，在△ABC中，AB=AC=4，BC=3，D为BC边的中点，点E、F分别是线段AC、AD上的动点，且AF=CE，则BE+CF的最小值为______．11.如图，在△ABC中，AB=AC=5，BC=8.P是BC上的动点，过点P作PD⊥AB于点D，PE⊥AC于点E，则PD+PE=_________．三、解答题12.如图所示，已知△ABC中，∠B=90°，AB=16cm，AC=20cm，P、Q是△ABC的边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为ts．(1)则BC=____cm；(2)当t为何值时，点P在边AC的垂直平分线上？此时CQ=____；(3)当点Q在边CA上运动时，直接写出使△BCQ成为等腰三角形的运动时间．13.如图，∠ABC=90∘，AB=6cm，AD=24cm，BC+CD=34cm，点C是直线l上一动点，请你探索当点C离点B多远时，▵ACD是一个以CD为斜边的直角三角形？14.如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm，P、Q分别为AB、BC边上的动点，点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B 开始B→C→A方向运动，且速度为每秒2cm，它们同时出发；设出发的时间为t 秒．(1)出发2秒后，求PQ的长；(2)当点Q在边BC上运动时，通过计算说明PQ能否把△ABC的周长平分？(3)当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间(直接写答案)．。

勾股定理培优

<勾股定理 >复习培优1．勾股定理勾股定理：直角三角形两条直角边的平方和等于斜边的 .即：对于任意的直角三角形，如果它的两条直角边分别为a 、b ，斜边为 c ，那么一定有 .勾股定理表达式的常见变形：a 2＝c 2－b 2, b 2＝c 2－a 2，c ＝a 2＋b 2，a ＝c 2－b 2，b ＝c 2－a 2.勾股定理分类计算：如果已知直角三角形的两边是a 、b(且a ＞b)，那么，当第三边c 是斜边时，c ＝；当a 是斜边时，第三边c ＝2．勾股定理的验证据说验证勾股定理的方法有五百多种，其中很多是用平面图形的面积来进行验证的，比如我国古代的数学家赵爽就用了下面的方法：如图14－1，以a 、b 为直角边(b>a)、以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于 .把这四个直角三角形拼成如图14－1所示的正方形ABCD ，它是一个边长为c 的正方形，它的面积等于 .而四边形EFGH 是一个边长为的正方形，它的面积等于 .∵四个直角三角形与中间的小正方形拼成了一个大正方形，∴4×12ab ＋(b －a)2＝c 2， ∴a 2＋b 2＝c 2.3．勾股定理的逆定理如果三角形的三边长a 、b 、c 有关系：a 2＋b 2＝，那么这个三角形是直角三角形．利用此定理判定直角三角形的一般步骤：(1)确定最大边；(2)算出最大边的平方与另两边的；(3)比较最大边的平方与另两边的平方和是否相等，若相等，则说明这个三角形是三角形．到目前为止判定直角三角形的方法有：(1)说明三角形中有一个角是；(2)说明三角形中有两边互相；(3)用勾股定理的逆定理．[注意] 运用勾股定理的逆定理时，要防止出现一开始就写出a2＋b2＝c2之类的错误．4．勾股数能够成为直角三角形三条边长的三个数，称为勾股数，即满足的三个数a、b、c，称为勾股数．[注意] 勾股数都是正整数．5．勾股定理的应用应用勾股定理及其逆定理可解决如下问题：(1)已知三角形的任意两边，求第三边长或图形周长、面积的问题；(2)说明线段的平方关系问题；(3)在上作表示2、3、5等数的点的问题；(4)解决实际问题．一些实际问题，如解决圆柱侧面两点间距离问题、航海问题、折叠问题、梯子下滑问题等，常直接或间接运用勾股定理及其逆定理．6．勾股定理中的思想(1)分类的思想，斜边不确定时，要分类讨论；(2)数形结合的思想，通过边的数量判断三角形的形状，反之也可以；(3)方程的思想，建立方程，求边；(4)转化思想，把实际问题转化为勾股定理的问题来解决．考点攻略考点一勾股定理例1在△ABC中，已知BD是高，∠B＝90°，∠A、∠B、∠C的对边分别是a、b、c，且a＝6，b＝8，求BD的长．考点二勾股定理的逆定理例2已知在△ABC中，∠A、∠B、∠C的对边分别是a、b、c，a＝n2－1，b＝2n，c＝n2＋1(n＞1)，判断△ABC是否为直角三角形．考点三勾股定理在数学中的应用例3已知△ABC是边长为1的等腰直角三角形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，第n个等腰直角三角形的斜边长的平方是________．例4如图14－3所示，一只蚂蚁从实心长方体的顶点A出发，沿长方体的表面爬到对角顶点C1处(三条棱长如图14－3所示)，问怎样走路线最短？最短路线长为多少？考点五方程思想在勾股定理中的应用例6如图14－6，有一张直角三角形纸片，两直角边AC＝6 cm，BC＝8 cm，将△ABC折叠，使点B与点A重合，折痕是DE，求CD的长．例7如图14－11，有一个高为4，底面直径为6的圆锥，现有一只蚂蚁在圆锥的顶部A，它想吃到圆锥底部B的食物，蚂蚁需要爬行的最短路线长是多少？例8如图14－14所示，某住宅社区在相邻两楼之间修建一个上方是一个半圆，下方是长方形的仿古通道，现有一辆卡车装满家具后，高4米，宽2.8米，请问这辆送家具的卡车能否通过这个通道？专项练习：1．一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的证明方法，如图14－16，火柴盒的一个侧面ABCD倒下到AB′C′D′的位置，连结CC′，设AB＝a，BC＝b，AC＝c，请利用四边形BCC′D′的面积证明勾股定理：a2＋b2＝c2.2现有一张矩形纸片ABCD(如图14－12)，其中AB ＝4 cm ，BC ＝6 cm, 点E 是BC 的中点，将纸片沿直线AE 折叠，点B 落在四边形AECD 内，记为点B ′，求线段B ′C 的长．3已知：四边形ABCD 中，BD 、AC 相交于O ，且BD 垂直AC ，求证：AB CD AD BC 2222+=+。

勾股定理经典培优题及答案

勾股定理经典培优题类型之一勾股定理的验证1．小明利用如图17－X－1①所示的图形(三个正方形和一个直角三角形)验证勾股定理，他的方法如下：过点D作直线FG∥AC，过点E作直线GH∥BC，直线FG与直线GH交于点G，与直线BC交于点F，直线GH与直线AC交于点H，如图②所示．请你回答：(1)△ABC与△BDF，△DEG，△EAH有什么关系？为什么？(2)用含a，b的代数式表示正方形CFGH的面积；(3)你能否根据图形面积之间的关系找到a，b，c之间的数量关系？(4)你能得到什么结论？图17－X－12．勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小明灵感，他惊喜地发现，当四个全等的直角三角形如图17－X－2摆放时，可以用“面积法”来证明a2＋b2＝c2.(请你写出证明过程)图17－X－2类型之二勾股定理及其应用3．等腰三角形的底边长为6，底边上的中线长为4，则它的腰长为()A．7 B．6 C．5 D．44．我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”．如图17－X－3是由弦图变化得到的，它由八个全等的直角三角形拼接而成．记图中正方形ABCD、正方形EFGH、正方形MNKT 的面积分别为S1，S2，S3.若正方形EFGH的边长为2，则S1＋S2＋S3＝________.17－X－317－X－45．图17－X－4①是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC＝12，BC＝10，将四个直角三角形中边长为12的直角边分别向外延长一倍，得到图②所示的数学“风车”，则这个数学“风车”的外围周长是________．6．知识回顾：在学习《二次根式》时，我们知道：2＋3≠5；在学习《勾股定理》时，由于2，3，5满足(2)2＋(3)2＝(5)2，因此以2，3，5为三边长能构成直角三角形．探索思考：请通过构造图形来说明：a＋b≠a＋b(a＞0，b＞0)．(画出图形并进行解释)7．在△ABC中，AB＝15，AC＝20，D是直线BC上的一个动点，连接AD，如果线段AD的长度最短是12，请你求△ABC的面积．类型之三勾股定理的逆定理及其应用8．已知三组数据：①2，3，4；②3，4，5；③1，3，2.分别以每组数据中的三个数为三角形的三边长，能构成直角三角形的有()A．②B．①②C．①③D．②③9．如果△ABC的三边长分别是m2－1，m2＋1，2m(m>1)，那么下列说法中正确的是()A．△ABC是直角三角形，且斜边长为m2＋1B．△ABC是直角三角形，且斜边长为2mC．△ABC是直角三角形，且斜边长为m2－1D．△ABC不是直角三角形10．若△ABC的三边长a，b，c满足关系式(a＋2b－60)2＋|b－18|＋c－30＝0，则△ABC是________三角形．类型之四勾股定理及其逆定理的综合应用图17－X－511．如图17－X－5，E是正方形ABCD内的一点，连接AE，BE，CE，将△ABE绕点B顺时针旋转90°到△CBE′的位置．若AE＝1，BE＝2，CE＝3，则∠BE′C＝________°.12．如图17－X－6，在4×3的正方形网格中有从点A出发的四条线段AB，AC，AD，AE，它们的另一个端点B，C，D，E均在格点上(正方形网格的交点)．(1)若每个正方形的边长都是1，分别求出AB，AC，AD，AE的长度(结果可以保留根号)；(2)在AB，AC，AD，AE四条线段中，是否存在三条线段，它们能构成直角三角形？如果存在，请指出是哪三条线段，并说明理由．图17－X－6类型之五勾股定理在实际生活中的应用图17－X－713．如图17－X－7是矗立在高速公路旁水平地面上的交通警示牌，经测量得到如下数据：AM＝4米，AB＝8米，∠MAD＝45°，∠MBC＝30°，则警示牌的高CD为________米(结果精确到0.1米，参考数据：2≈1.41，3≈1.73)．14．如图17－X－8，A，B两地之间有一座山，汽车原来从A地到B地需经过C地沿折线ACB行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC＝10千米，∠A＝30°，∠B＝45°.则隧道开通后，汽车从A地到B地比原来少走多少千米？(结果保留根号)图17－X－8。

勾股定理培优(教案)

3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“勾股定理在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解勾股定理的基本概念。勾股定理指的是直角三角形中，斜边的平方等于两个直角边平方和的数学关系。它是解决直角三角形相关问题的重要工具，广泛应用于建筑、工程等领域。
2.案例分析：接下来，我们来看一个具体的案例。通过测量三角形形的边长，应用勾股定理计算斜边长度，展示其在实际中的应用。
五、教学反思
在上完这节勾股定理培优课后，我对教学过程进行了深入的思考。首先，我发现学生在理解勾股定理的推导和应用过程中存在一定难度。在今后的教学中，我需要更加注重引导学生从具体的实例中抽象出数学规律，帮助他们理解并掌握勾股定理。
在讲授新课的过程中，我尝试通过生动的案例和实际操作，让学生感受勾股定理在实际生活中的应用。这种教学方法得到了学生的积极响应，他们表现出浓厚的兴趣。但同时，我也发现部分学生在将理论知识应用到实际问题解决时仍显得有些吃力。针对这一点，我计划在接下来的教学中，增加一些更具挑战性的实际问题，让学生在解决问题的过程中，提高勾股定理的应用能力。
三、教学难点与重点
1.教学重点
（1）勾股定理的表述及证明：让学生掌握勾股定理的表述，理解其证明过程，并能够运用定理解决相关问题。
举例：a² + b² = c²，其中c为直角三角形的斜边，a、b为两个直角边。

初二-第01讲-勾股定理(培优)-教案

学科教师辅导讲义学员编号：年级：八年级(上) 课时数：3 学员姓名：辅导科目：数学学科教师：授课主题第01讲——勾股定理授课类型 T 同步课堂P 实战演练S 归纳总结教学目标①了解探索勾股定理的各种方法； ②运用勾股定理解决一些实际问题；③掌握直角三角形的判别条件,掌握勾股数的概念。

授课日期及时段T （Textbook-Based ）——同步课堂1、直角三角形：有一个角是直角的三角形叫做直角三角形。

2、直角三角形的两个锐角互余。

3、三角形的三边关系：三角形任意两边之和大于第三边，任意两边之差小于第三边。

4、直角三角形中，30°角所对的直角边是斜边的一半。

一、知识梳理1、我国古代把直角三角形中较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”。

2、勾股定理：直角三角形两直角边的平方和等于斜边的平方。

体系搭建如果用,a b 和c 分别表示直角三角形的两直角边和斜边，那么有222a b c += 。

3、勾股定理的常见证明：4、勾股数：我们把满足勾股定理的这样一组数称为够股数。

常见的够股数有：3、4 、5； 5、12、13 ； 6、8、10 ； 7、24、25；8、15、 17； 9、12、15；5、直角三角形的判定：若三角形的三条边满足两边的平方等于第三边的平方，则这个三角形是直角三角形。

其中第三边所对的角是直角。

考点一：勾股定理例1、在△ABC中，AB=AC=5，BC=6，D为BC中点，则AD的长为（）A．3 B．4 C．5 D．6【解析】∵AB=AC，点D是BC中点，∴AD⊥BC，∴∠ADB=90°，∵点D是BC中点，∴BD=BC=3，在Rt△ADB中，AB=5，∴AD==4，故选B例2、如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x、y表示直角三角形的两直角边（x＞y），下列四个说法：①x2+y2=49，②x﹣y=2，③2xy+4=49，④x+y=9．其中说法正确的是（）A．①② B．①②③C．①②④D．①②③④【解析】由题意，①﹣②得2xy=45 ③，∴2xy+4=49，①+③得x2+2xy+y2=94，∴（x+y）2=，∴①②③正确，④错误．故选B，以AB、AC为边向外作正方例3、如图，Rt△ABC的周长为(553)cm形ABPQ和正方形ACMN．若这两个正方形的面积之和为25 cm2，则△ABC的面积是 cm2．【解析】如图，a2=c2+b2=25，则a=5．又∵Rt△ABC的周长为，∴a+b+c=5+3，∴b+c=3（cm）．∴△ABC的面积=bc=[（c+b）2﹣（c2+b2）]÷2=[（3）2﹣25]÷2=5（cm2）．故答案是：5．考点二：勾股定理的证明例1、2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图，它是由四个全等的直角三角形和中间的小正方形拼成的大正方形，如图所示，如果大正方形的面积是13，小正方形的面积为1，直角三角形的较短直角边长为a，较长直角边长为b，那么（a+b）2的值为（）A．13 B．19 C．25 D．169【解析】根据题意得：c2=a2+b2=13，4×ab=13﹣1=12，即2ab=12，则（a+b）2=a2+2ab+b2=13+12=25，故选C例2、中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽，他为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它是用八个全等的直角三角形拼接而成．将图中正方形MNKT，正方形EFGH，正方形ABCD的面积分别记为S1，S2，S3，若S1+S2+S3=18，则正方形EFGH的面积为（）A．9 B．6 C．5 D．【解析】将四边形MTKN的面积设为x，将其余八个全等的三角形面积一个设为y，∵正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，S1+S2+S3=18，∴得出S1=8y+x，S2=4y+x，S3=x，∴S1+S2+S3=3x+12y=18，故3x+12y=18，x+4y=6，所以S2=x+4y=6，即正方形EFGH的面积为6．故选：B．例3、在直角三角形中，两条直角边的长度分别为a和b，斜边长度为c，则a2+b2=c2．即两条直角边的平方和等于斜边的平方，此结论称为勾股定理．在一张纸上画两个同样大小的直角三角形ABC和A'B'C'，并把它们拼成如图形状（点C和A'重合，且两直角三角形的斜边互相垂直）．请利用拼得的图形证明勾股定理．【解析】证明：在直角三角形ABC中，∵∠1+∠2=90°，∠1=∠3，∴∠2+∠3=90°，又∵∠ACC′=90°，∴∠2+∠3+∠ACC′=180°，∴B、C（A′）、B′在同一条直线上，又∠B=90°，∠B′=90°，∴∠B+∠B′=180°，∴AB∥C′B′，连接AC′，过点C′作C′D⊥AB交AB于点D，则四边形ABB′C′面积等于三个直角三角形面积，∴（a﹣b）（a+b）+（a+b）b=ab+ab+c2，即a2﹣b2+ab+b2=ab+ab+c2，a2+2ab+b2=2ab+c2，∴a2+b2=c2．例4、勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2证明：连接DB，过点D作BC边上的高DF，则DF=EC=b﹣a．∵S四边形ADCB=S△ACD+S△ABC=b2+ab．又∵S四边形ADCB=S△ADB+S△DCB=c2+a（b﹣a）∴b2+ab=c2+a（b﹣a）∴a2+b2=c2请参照上述证法，利用图2完成下面的证明．将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．求证：a2+b2=c2证明：连结，过点B作，则．∵S五边形ACBED=S△ACB+S△ABE+S△ADE= ．又∵S五边形ACBED= =ab+c2+a（b﹣a），∴=ab+c2+a（b﹣a），∴a2+b2=c2．【解析】证明：连结BD，过点B作BF⊥DE于F，则BF=b﹣a，∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab，又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a（b﹣a），∴ab+b2+ab=ab+c2+a（b﹣a），∴a2+b2=c2．故答案为：BD，BF⊥DE于F，BF=b﹣a，ab+b2+ab，S△ACB+S△ABE+S△ADE，ab+b2+ab．考点三：直角三角形的判定例1、满足下列条件的△ABC，不是直角三角形的是（）A．b2=a2﹣c2 B．a：b：c=3：4：5C．∠C=∠A﹣∠B D．∠A：∠B：∠C=3：4：5【解析】A、b2=a2﹣c2，是直角三角形，故此选项不合题意；B、∵32+42=52，∴是直角三角形，故此选项不合题意；C、∵∠C=∠A﹣∠B，∠A+∠B+∠C=180°，∴∠A=90°，∴是直角三角形，故此选项不合题意；D、∠A：∠B：∠C=3：4：5，则∠C=180°×=75°，不是直角三角形，故此选项符合题意，故选：D．例2、甲、乙两艘客轮同时离开港口，航行的速度都是40m/min，甲客轮用15min到达点A，乙客轮用20min 到达点B，若A，B两点的直线距离为1000m，甲客轮沿着北偏东30°的方向航行，则乙客轮的航行方向可能是（）A．北偏西30°B．南偏西30°C．南偏东60°D．南偏西60°【解析】甲的路程：40×15=600m，乙的路程：20×40=800m，∵6002+8002=10002，∴甲和乙两艘轮船的行驶路线呈垂直关系，∵甲客轮沿着北偏东30°，∴乙客轮的航行方向可能是南偏东60°，故选：C．例3、适合下列条件的△ABC中，直角三角形的个数为（）①a=3，b=4，c=5；②a=6，∠A=45°；③a=2，b=2，c=2；④∠A=38°，∠B=52°．A．1个B．2个C．3个D．4个【解析】：①a=3，b=4，c=5，∵32+42=25=52，∴满足①的三角形为直角三角形；②a=6，∠A=45°，只此两个条件不能断定三角形为直角三角形；③a=2，b=2，c=2，∵22+22=8=，∴满足③的三角形为直角三角形；④∵∠A=38°，∠B=52°，∴∠C=180°﹣∠A﹣∠B=90°，∴满足④的三角形为直角三角形．综上可知：满足①③④的三角形均为直角三角形．故选C．例4、三角形的两边长分别为3和5，要使这个三角形是直角三角形，则第三边长是．【解析】当第三边是直角边时，根据勾股定理，第三边的长==4，三角形的边长分别为3，4，5能构成三角形；当第三边是斜边时，根据勾股定理，第三边的长==，三角形的边长分别为3，5，亦能构成三角形；综合以上两种情况，第三边的长应为4或．例5、已知a，b，c是直角三角形的三条边，且a＜b＜c，斜边上的高为h，则下列说法中正确的是．（只填序号）①a2b2+h4=（a2+b2+1）h2；②b4+c2h2=b2c2；③由可以构成三角形；④直角三角形的面积的最大值是．【解析】根据直角三角形的面积的不同算法，有ab=ch，解得h=．①将h=代入a2b2+h4=（a2+b2+1）h2，得a2b2+（）4=（a2+b2+1）（）2，得a2b2+（）4=（c2+1）（）2，得a2b2+（）4=a2b2+，得即（）4=，a2b2=c2，不一定成立，故本选项错误；②将h=代入b4+c2h2=b2c2，得b4+c2（）2=b2c2，b4+b2a2=b2c2，整理得b4+b2a2﹣b2c2=0，b2（b2+a2﹣c2）=0，∵b2+a2﹣c2=0，∴b2（b2+a2﹣c2）=0成立，故本选项正确；③①∵（+）2=a+b+2，（）2=c，又∵a+b＞c，∴（+）2＞（）2，∴+＞，故本选项正确；④直角三角形的面积为ab，随ab的变化而变化，所以无最大值，故本选项错误．故答案为②③．考点四：勾股数例1、下列各组数中不是勾股数的是（）A．3，4，5 B．4，5，6 C．5，12，13 D．6，8，10【解析】A、∵32+42=52，∴以3、4、5为边能组成直角三角形，即3、4、5是勾股数，故本选项错误；B、∵42+52≠62，∴以4、5、6为边不能组成直角三角形，即4、5、6不是勾股数，故本选项正确；C、∵52+122=132，∴以5、12、13为边能组成直角三角形，即5、12、13是勾股数，故本选项错误；D、∵62+82=102，∴以6、8、10为边能组成直角三角形，即6、8、10是勾股数，故本选项错误；故选B．例2、下列几组数中，是勾股数的是（）A．1，，B．15，8，17 C．13，14，15 D．，，1【解析】A、∵1，，不都是整数，∴此选项不符合题意；B、∵152+82=172，且15，8，17都是整数，∴此选项符合题意；C、∵132+142≠152，∴此选项符合题意；D、∵，，1不都是整数，∴此选项不符合题意．故选B．P(Practice-Oriented)——实战演练实战演练➢课堂狙击1、如图，在△ABC 中，AB=AC=5，BC=8，D 是线段BC 上的动点（不含端点B 、C ）．若线段AD 长为正整数，则点D 的个数共有（）A ．5个B ．4个C ．3个D ．2个【解析】过A 作AE ⊥BC ，∵AB=AC ，∴EC=BE=BC=4，∴AE==3，∵D 是线段BC 上的动点（不含端点B 、C ）．∴3≤AD ＜5，∴AD=3或4， ∵线段AD 长为正整数，∴点D 的个数共有3个，故选：C ．2、如图，A 、B 是4×5网格中的格点，网格中的每个小正方形的边长都是1，图中使以A 、B 、C 为顶点的三角形是等腰三角形的格点C 有（）A ．2个B ．3个C ．4个D ．5个【解析】∵A 、B 是4×5网格中的格点， ∴AB==，同理可得，AC=BD=AC=，∴所求三角形有：△ABD ，△ABC ，△ABE ．故选B ．3、如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC=6，BC=5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到如图2所示的“数学风车”，则这个风车的外围周长是（）A ．76B ．72C ．68D ．52【解析】依题意，设“数学风车”中的四个直角三角形的斜边长为x ，则x 2=122+52=169 所以x=13所以“数学风车”的周长是：（13+6）×4=76．故选：A ． 4、下列条件中，不能判断△ABC 为直角三角形的是（）A ．a=1.5，b=2，c=2.5B ．a ：b ：c=3：4：5C ．∠A+∠B=∠CD ．∠A ：∠B ：∠C=3：4：5 【解析】A 、正确，1.52+22=2.52符合勾股定理的逆定理，故成立；B 、正确，因为a ：b ：c=3：4：5，所以设3,4,5a x b x c x ===，则()()()222345x x x +=，为直角三角形；C、正确，因为∠A+∠B=∠C，∠A+∠B+∠C=180°，则∠C=90°，故为直角三角形；D、错误，因为∠A：∠B：∠C=3：4：5，所以设∠A=3x，则∠B=4x，∠C=5x，故3x+4x+5x=180°，解得x=15°，3x=15×3=45°，4x=15×4=60°，5x=15×5=75°，故此三角形是锐角三角形．故选D．5、在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积．某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路完成解答过程．【解析】如图，在△ABC中，AB=15，BC=14，AC=13，设BD=x，则CD=14﹣x，由勾股定理得：AD2=AB2﹣BD2=152﹣x2，AD2=AC2﹣CD2=132﹣（14﹣x）2，故152﹣x2=132﹣（14﹣x）2，解之得：x=9．∴AD=12．∴S△ABC=BC•AD=×14×12=84．6、中国古代的数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位．尤其是三国时期的数学家赵爽，不仅最早对勾股定理进行了证明，而且创制了“勾股圆方图”，开创了“以形证数”的思想方法．在图1中，小正方形ABCD的面积为1，如果把它的各边分别延长一倍得到正方形A1B1C1D1，则正方形A1B1C1D1的面积为；再把正方形A1B1C1D1的各边分别延长一倍得到正方形A2B2C2D2（如图2），如此进行下去，得到的正方形A n B n C n D n的面积为（用含n的式子表示，n为正整数）．【解析】已知小正方形ABCD的面积为1，则把它的各边延长一倍后，△AA1B1的面积是1，新正方形A1B1C1D1的面积是5，从而正方形A2B2C2D2的面积为5×5=25=52，…正方形A n B n C n D n的面积为5n．故答案为：5n．➢课后反击1、如图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中小正方形顶点A，B 在围成的正方体上的距离是（）A．0 B．1 C．D．【解析】将图1折成正方体后点A和点B为同一条棱的两个端点，故此AB=1．故选：B．2、在△ABC中，∠A、∠B、∠C的对边分别是a、b、c，则下列条件中不能判断是直角三角形的是（）A．∠A=∠B﹣∠C B．∠A：∠B：∠C=1：1：2C．a：b：c=4：5：6 D．a2﹣c2=b2【解析】A、由条件可得∠A+∠C=∠B，且∠A+∠B+∠C=180°，可得∠B=90°，故△ABC是直角三角形；B、∵∠A：∠B：∠C=1：1：2，∠A+∠B+∠C=180°，∴∠C=90°，故△ABC是直角三角形；C、不妨设a=4k，b=5k，c=6k，此时a2+b2=41k2，而c2=36k2，即a2+b2≠c2，故△ABC不是直角三角形；D、由条件可得到a2=b2+c2，满足勾股定理的逆定理，故△ABC是直角三角形；故选C．3、三角形的三边长为a，b，c，且满足（a+b）2=c2+2ab，则这个三角形是（）A．等边三角形B．钝角三角形C．直角三角形D．锐角三角形【解析】化简（a+b）2=c2+2ab，得，a2+b2=c2所以三角形是直角三角形，故选：C．4、在四边形ABCD中，AB=AD=8，∠A=60°，∠D=150°，四边形周长为32，求BC和CD的长度．【解析】如图，连接BD，由AB=AD，∠A=60°．则△ABD是等边三角形．即BD=8，∠1=60°．又∠1+∠2=150°，则∠2=90°．设BC=x，CD=16﹣x，由勾股定理得：x2=82+（16﹣x）2，解得x=10，16﹣x=6所以BC=10，CD=6．5、在△ABC中，BC=a，AC=b，AB=c，设c为最长边，当a2+b2=c2时，△ABC是直角三角形；当a2+b2≠c2时，利用代数式a2+b2和c2的大小关系，探究△ABC的形状（按角分类）．（1）当△ABC三边分别为6、8、9时，△ABC为三角形；当△ABC三边分别为6、8、11时，△ABC为三角形．（2）猜想，当a2+b2 c2时，△ABC为锐角三角形；当a2+b2 c2时，△ABC为钝角三角形．（3）判断当a=2，b=4时，△ABC的形状，并求出对应的c的取值范围．【解析】（1）两直角边分别为6、8时，斜边==10，∴△ABC三边分别为6、8、9时，△ABC为锐角三角形；当△ABC三边分别为6、8、11时，△ABC为钝角三角形；故答案为：锐角；钝角；（2）当a2+b2＞c2时，△ABC为锐角三角形；当a2+b2＜c2时，△ABC为钝角三角形；故答案为：＞；＜；（3）∵c为最长边，2+4=6，∴4≤c＜6，a2+b2=22+42=20，①a2+b2＞c2，即c2＜20，0＜c＜2，∴当4≤c＜2时，这个三角形是锐角三角形；②a2+b2=c2，即c2=20，c=2，∴当c=2时，这个三角形是直角三角形；③a2+b2＜c2，即c2＞20，c＞2，∴当2＜c＜6时，这个三角形是钝角三角形直击中考1、【2006•临沂】△ABC中，BC=a，AC=b，AB=c．若∠C=90°，如图1，根据勾股定理，则a2+b2=c2．若△ABC 不是直角三角形，如图2和图3，请你类比勾股定理，试猜想a2+b2与c2的关系，并证明你的结论．【解析】若△ABC是锐角三角形，则有a2+b2＞c2（1分）若△ABC是钝角三角形，∠C为钝角，则有a2+b2＜c2．（2分）当△ABC是锐角三角形时，证明：过点A作AD⊥BC，垂足为D，设CD为x，则有BD=a﹣x（3分）根据勾股定理，得b2﹣x2=AD2=c2﹣（a﹣x）2即b2﹣x2=c2﹣a2+2ax﹣x2．∴a2+b2=c2+2ax（5分）∵a＞0，x＞0，∴2ax＞0．∴a2+b2＞c2．（6分）当△ABC是钝角三角形时，证明：过B作BD⊥AC，交AC的延长线于D．设CD为y，则有BD2=a2﹣y2（7分）,根据勾股定理，得（b+y）2+a2﹣y2=c2．即a2+b2+2by=c2．（9分）∵b＞0，y＞0，∴2by＞0，∴a2+b2＜c2．（10分）2、【2016•东湖区】我们运用图（Ⅰ）中大正方形的面积可表示为（a+b）2，也可表示为c3+4（ab），即（a+b）2=c2+4（ab）由此推导出一个重要的结论a2+b2=c2，这个重要的结论就是著名的“勾股定理”．这种根据图形可以极简单地直观推论或验证数学规律和公式的方法，简称“无字证明”．（1）请你用图（Ⅱ）（2002年国际数学家大会会标）的面积表达式验证勾股定理（其中四个直角三角形的较大的直角边长都为a，较小的直角边长都为b，斜边长都为c）．（2）请你用（Ⅲ）提供的图形进行组合，用组合图形的面积表达式验证：（x+2y）2=x2+4xy+4y2．【解析】（1）S阴影=4×ab，S阴影=c2﹣（a﹣b）2，∴4×ab=c2﹣（a﹣b）2，即2ab=c2﹣a2+2ab﹣b2，则a2+b2=c2；（2）如图所示，大正方形的面积为x2+4y2+4xy，也可以为（x+2y）2，则（x+2y）2=x2+4xy+4y2．S (Summary-Embedded)——归纳总结1、勾股定理：222a b c +=2、勾股定理的证明；3、勾股定理的逆定理：若三角形的三条边满足两边的平方等于第三边的平方，则这个三角形是直角三角形。

勾股定理培优题

勾股定理一、知识要点1、勾股定理勾股定理在西方又被称为毕达哥拉斯定理，它有着悠久的历史，蕴含着丰富的文化价值，勾股定理是数学史上的一个伟大的定理，在现实生活中有着广泛的应用，被人誉为“千古第一定理” .勾股定理反映了直角三角形（三边分别为a 、b 、c ，其中c 为斜边）的三边关系，即a 2+b 2=c 2，它的变形式为c 2-a 2=b 2或c 2-b 2=a 2.勾股定理是平面几何中最重要的几何定理之一，在几何图形的计算和论证方面，有着重要的应用，它沟通了形与数，将几何论证转化为代数计算，是一种重要的数学方法. 2、勾股定理的逆定理如果三角形的三边长a 、b 、c 满足a 2+b 2=c 2，则这个三角形是以c 为斜边的直角三角形.勾股定理的逆定理给出了判定一个三角形是直角三角形的方法，这种方法与前面学过的一些判定方法不同，它是通过代数运算“算”出来的，实际上利用计算证明几何问题在几何里也是很重要的，这是里体现了数学中的重要思想——数形结合思想，突破了利用角与角之间的转化计算直角的方法，建立了通过求边与边的关系来判断直角的新方法，它将数形之间的联系体现得淋漓尽致.因此也有人称勾股定理的逆定理为“数形结合的第一定理”.二、基本知识过关测试1.如果直角三角形的两边为3，4，则第三边a 的值是 .2.如图，图形A 是以直角三角形直角边a 为直径的半圆，阴影S A = .3.如图，有一个圆柱的高等于12cm ，底面半径3cm ，一只蚂蚁要从下底面上B 点处爬至上底与B 点相对的A 点处，所需爬行的最短路程是 .4.如图.在 △ABC 中，CD ⊥AB 于D ，AB =5，CD=BCD =30° ，则AC = . 5.的线段.6.在下列各组数中 ①5，12，13 ；②7，24，25；③32，42，52；④3a ，4a ，5a ；⑤a 2+1，a 2-1，2a (a ＞1)；⑥m 2-n 2，2mn ，m 2+n 2(m ＞n ＞0)可作直角三角形三边长的有组.7.如图，四边形ABCD 中，AB =1，BC =2，CD =2，AD =3，AB ⊥BC ，则四边形ABCD 的面积是 .第2题图第3题图第4题图第7题图8.如图，在正方形ABCD 中，F 为DC 中点，E 为BC 上一点，且EC =14BC ，试判断△ AEF 的形状.三、综合.提高.创新BADCBADCBAFE DCB A【例1】（1）在三角形纸片ABC 中，∠C =90°，∠A =30°，AC =3，折叠该纸片，使点A 与点B 重合，折痕与AB 、AC 分别相交于点D 和点E （如图），折痕DE 的长是多少？（2）如图，在矩形ABCD 中，AB =8，AD =10，按如图所示折叠，使点D 落在BC 上的点E 处，求折痕AF 的长.（3）如图，正三角形ABC 的边长为2，M 是AB 边上的中点，P 是BC 边上任意一点，PA +PM 的最大值和最小值分别记作S 和T ，求S 2-T 2的值.【练】如图，四边形ABCD 是长方形，把△ACD 沿AC 折叠到△ACD ′，AD ′与BC 交于E ，若AD =4，DC =3，求BE .【例2】（1）如图，△ABC 中，∠C =60°，AB =70，AC =30，求BC 的长.EDC BAFEDCBAPMCAD 'EDCB A（2）如图，在四边形ABCD 中，AB =2，CD =1，∠A =60°， ∠B =∠D =90°，求四边形ABCD 的面积.【练】如图，△ABC 中，A =150°，AB =2，BCAC 的长.【例3】（1）如图，△ABC 中，AB =AC =20，BC =32，D 为BC 上一点，AD ⊥AB ，求CD .（2）如图，在Rt △ABC 中，∠C =90°，D 、E 分别是BC 、AC 中点，AD =5，BE=，求AB .【例4】如图，△ABC 中，∠ACB =90°，CD ⊥AB 于D ，设AC =b ，BC =a ，AB =c ，CD =h ，求证：CBADCBACBADCBAEDC BA（1）222111a b h +=；（2）a +b ＜c +h ；（3）以a +b ，h 和c +h 为边的三角形是直角三角形.【例5】（1）如图，ABCD 为矩形，P 为矩形ABCD 所在平面上一点，求证：PA 2-PB 2=PD 2 -PC 2.（2）锐角△ABC 中，AD ⊥BC 于D ，若∠B =2∠C ，求证：AC 2=AB 2+AB ·BC .变式：如图，AM 是△ABC 的BC 边上的中线，求证：AB 2+AC 2=2(AM 2+BM 2).（3）如图，△ABC 中，AB =AC ，P 为线段BC 上一动点，试猜想AB 2，AP 2， PB ，PC 有何关系，并加以证明.D CBAPDCB ADCBAM BA变式：若点P 在BC 的延长线上，如图，（3）中结论是否仍然成立？并证明.（4）在等腰Rt △ABC 的斜边AB 所在的直线上取点P 并设s =AP 2+BP 2，试探求P 点位置变化时，s 与2CP 2的大小关系，并证明.变式：若点P 在BA 的延长线上，如图中，（4）中结论是否仍然成立？并证明.【例6】（1）如图，△ABC 中，D 为BC 边上的中点，以D 为顶点作∠EDF =90°，DE 、DF 分别交AB 、AC 于E 、F ，且BE 2+FC 2=EF 2，求证：∠BAC =90°.P CB APC APCBACBAFED（2）在Rt△ABC中，∠BAC=90°，AB=AC，E，F分别是BC上两点，若∠EAF=45°，试推断BE，CF，EF之间的关系，并证明.AB C变式一:将（2）中△AEF旋转至如图所示，上述结论是否仍然成立？试证明.AE变式二：如图，△AEF中∠EAF=45°，AG⊥EF于G，且GF=2，GE=3，求S△AEF.AG【例7】（1）在△ABC中，∠ACB=90°，AC=BC，P为△ABC内一点，且PA=3，PB=1，PC=2，求∠BPC的度数.（2）如图，在四边形ABCD 中，∠ABC =30°，∠ADC =60°，AD =CD ，求证BD 2=AB 2+BC 2.【例8】在等腰△ABC 中，AB =AC ，边AB 绕点A 逆时针旋转角度m ，得到线段AD . （1）如图1，若∠BAC =30°，30°＜m ＜80°，连接BD ，请用含m 的式子表示∠DBC ;（2）如图2，若∠BAC =90°，0°＜m ＜360°，射线AD 与直线BC 相交于点E ，是否存在旋转角度m，使AEBE若存在，求出所有符合条件的m 的值；若不存在，请说明理由.【例9】（1）已知点P 在一、三象限的角平分线上，且点P 到点A （3，6）的距离为PA =15，求点P 的坐标；PCBADCBADCB AE DCBA（2）已知直角坐标平面内的△ABC三个顶点的坐标分别为A（-1，4），B（-4，-2），C（2，-2），试判断△ABC的形状；（3的最小值；（4）已知a＞0，b＞0.自我归纳：四、课后练习1.如图，一艘货轮向正北方向航行，在点A处测得灯塔M在北偏西30°，货轮以每小时20海里的速度航行，1小时后到达B处，测得灯塔M在北偏西45°，问该货轮到达灯塔正东方向D处时，货轮与灯塔M的距离是多少？2.在△ABC 中，A =30°，B =45°，BC =10cm ，求AB ，AC 及△ABC 的面积.3.（1）如图，把长方形沿ABCD 对角线折叠，重合部分为△EBD . 1）求证和：△EBD 为等腰三角形； 2）若AB =2，BC =8，求AE .（2）如图，折叠长方形ABCD 的一边AD ，使点D 落在BC 边上，已知AB =8cm ，CE =4cm ，求AD .4．如图，△ABC 是等腰三角形，∠BAC =90°，AB =AC ，D .E .是BC 上的两点，且∠DAE =45°，若BD =6，EC =8，求DE 的长.MDB A北C 'EDCB AFED CBA5．如图，在等腰三角形中，AB=AC，D是斜边BC的中点，E、F分别为AB，AC边上的点，且DE⊥DF. （1）求证：BE2+CF2=EF2；（2）若BE=12，CF=5，试求△DEF的面积.6．如图，等腰Rt△ABC中，∠A=90°，P为△ABC内一点，PA=1，PB=3，PC，求∠CPA.7．（1）如图1，已知点P是矩形ABCD内一点，求证：PA2+PC2=PB2+PD2. （2）①如果点P移动到矩形的一边或顶点时，如图2，（1）中结论仍成立；C BAEDFC BAEPCB AAB CDP②如果点P移动到矩形ABCD的外部时，如图3，（1）中结论仍成立.请在以上两个结论中任选一个并给出证明.归纳结论：8．如图，△ABC中，AD是BC边的中点，AE是BC边上的高，求证：AB2-AC2=2BC·DE.9.10．试判断，三边长分别为2n2+2n，2n+1，2n2+2n+1（n>0）的三角形是否为直角三角形？11．已知a，b，x，y.PDCBAPDCBAED C BA12．如图，Rt△ABC的两直角边AB=4，AC=3，△ABC内有一点P，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，且AB PF+AC PE +BCPD=12，求PD、PE、PF的长.PFED CBA欢迎您的下载，资料仅供参考！致力为企业和个人提供合同协议，策划案计划书，学习资料等等打造全网一站式需求。

勾股定理专题培优学案(勾股定理和几何计算、勾股定理和几何证明和勾股弦图)

勾股定理辅助线一、本章概述本章共分为勾股定理与几何计算、勾股定理与几何证明和勾股弦图三部分，都是勾股定理的重难点内容二、知识回顾1.勾股定理（1）直角三角形两直角边的平方和等于斜边c的平方和。

（即：）2.勾股定理的逆定理（2）如果三角形的三边长：。

满足关系，那么这个三角形是直角三角形。

3.勾股定理的证明：（3）勾股定理的证明方法很多，常见的是拼图方法，用拼图的方法验证勾股定理的思路是：①图形进行割补拼接后，只要没有重叠，没有空隙，面积不会改变②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理。

（4）常见方法如下：方法二：四个直角三角形的面积与小正方形面积的和等于大正方形的面积。

方法三：美国第二十任总统伽菲尔德的“总统证法”.1. 勾股定理与几何计算一、本节概述本节主要讲解勾股定理常见的三个辅助线模型，将斜三角形问题，转化为直角三角形问题。

当遇到三角形内的几何计算，特别是长度计算时，可以考虑用勾股定理解决。

在没有直角三角形时，我们就构造直角三角形，方法就是作高。

要尽量作与题中条件有关系的高，总有一条适合你的，比如特殊角所对的高。

二、典例精析知识点：勾股定理与几何计算【例1】如图，已知AC=2,思路分析：标记条件，题目中给出三角形的两个角和一条边，符合“AAS”，故三角形形状固定，可通过作高转化为勾股定理来解决，作高的时候，要充分利用特殊角。

作AB角形问题。

解：，先从右边已知一边和一角的直角三角形入手，这是个（）的特殊直角三角形。

得到CD后，再看左边已知一边和一角的直角三角形，这是个（）的特殊直角三角形。

方法总结这是利用勾股定理时常见的辅助线做法之一：三角形给出的条件满足“AAS”，作高的时候要充分利用特殊角，使分割后得到的直角三角形可求解即可，此例题是垂线在三角形内，并获得特殊直角三角形的例子。

【例2】思路分析：标记条件，给出的三角形符合“SAS”，故形状固定，可通过作高解决，作高时要充分利用特殊三角形，因为给出的特殊角是钝角，故可利用它的补角。

八年级数学勾股定理培优

225400 A225400B256112C144400D勾股定理【知识要点】1、勾股定理是：直角三角形两直角边的平方和等于斜边的平方，即：222c b a =+2、勾股定理逆定理：如果三角形的三边长a 、b 、c 满足222a b c +=那么这个三角形是直角三角形。

【典型习题】例1、如图，有一块直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于（）A. 2cmB. 3cmC. 4cmD. 5cm例2、求下列各图字母中所代表的正方形的面积。

=A S =B S =C S =D S例3、如图，一次“台风”过后，一根旗杆被台风从离地面8.2米处吹断，倒下的旗杆的顶端落在离旗杆底部6.9米处，那么这根旗杆被吹断裂前至少有多高？米米例4、如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为7cm ,则正方形A ，B ，C ，D 的面积之和为___________cm 2。

例5、在平静的湖面上，有一支红莲，高出水面1米，阵风吹来，红莲被吹到一边，花朵齐及水面，已知红莲移动的水平距离为2米，问这里水深是________m 。

例6、为丰富少年儿童的业余文化生活，某社区要在如图所示的AB 所在的直线上建一图书阅览室，该社区有两所学校，所在的位置分别在点C 和点D 处。

CA ⊥AB 于A ，DB ⊥AB 于B ，已知AB=25km ，CA=15km,DB=10km,试问：阅览室E 建在距A 点多远时，才能使它到C 、D 两所学校的距离相等？例 7、如图所示，MN 表示一条铁路，A 、B 是两个城市，它们到铁路的所在直线MN 的垂直距离分别AA1=20km,BB1=40km ，A1B1=80km.现要在铁路A1，B1=80km 。

现要在铁路A1，B1之间设一个中转站P ，使两个城市到中转站的距离之和最短。

勾股定理章末测试卷(培优卷)(学生版)

第1章勾股定理章末测试卷（培优卷）【北师大版】考试时间：60分钟；满分：100分姓名：___________班级：___________考号：___________考卷信息：本卷试题共23题，单选10题，填空6题，解答7题，满分100分，限时60分钟，本卷题型针对性较高，覆盖面广，选题有深度，可衡量学生掌握本章内容的具体情况！一．选择题（共10小题，满分30分，每小题3分）1．（3分）（2021春•平罗县期末）已知一直角三角形，三边的平方和为800cm2，则斜边长为（）A．20cm B．40cm C．400cm D．不能确定2．（3分）（2021•滨州）在Rt△ABC中，若∠C＝90°，AC＝3，BC＝4，则点C到直线AB的距离为（）A．3B．4C．5D．2.43．（3分）（2021春•南川区期中）三个正方形的面积如图所示，则S的值为（）A．3B．12C．9D．44．（3分）（2021春•官渡区期末）勾股定理是历史上第一个把数与形联系起来的定理，其证明是论证几何的发端．下面四幅图中不能证明勾股定理的是（）A．B．C．D．5．（3分）（2021春•宣化区期末）下列各组数中，是勾股数的是（）A ．0.3，0.4，0.5B ．10，15，18C ．13，14，15D ．6，8，106．（3分）（2021春•怀宁县期末）在△ABC 中以下条件不能判定△ABC 是直角三角形的个数有（）个．条件①：∠A ＝∠C ﹣∠B ；条件②：三角形三边a ，b ，c 的比3：4：5；条件③：∠A ：∠B ：∠C ＝3：4：5；条件④：a ＝5、b ＝12、c ＝13．A ．1B ．2C ．3D ．07．（3分）（2021春•天河区期末）小明向东走80m 后，沿方向A 又走了60m ，再沿方向B 走了100m 回到原地，则方向A 是（）A ．南向或北向B ．东向或西向C ．南向D ．北向8．（3分）（2021春•丰宁县期末）如图，一块三角形木板，测得AB ＝13，BC ＝5，AC ＝12，则三角形木板ABC 的面积为（）A ．60B ．30C ．65D ．不能确定9．（3分）（2021春•保山期末）如图，“今有竹高两丈五尺，末折抵地，去本五尺，问折者高几何？”意思是：一根竹子，原来高两丈五尺（一丈为十尺），虫伤有病，一阵风将竹子折断，其竹梢恰好抵地，抵地处离原竹子根部五尺远，则折断处离地面的高度为（）A ．5尺B ．25尺C ．13尺D ．12尺10．（3分）（2021春•咸安区期末）将一根长24cm 的筷子，置于底面直径为5cm ，高为12cm 的圆柱形水杯中，设筷子露出在杯子外面长为hcm ，则h 的取值范围是（）A ．0≤h ≤12B ．12≤h ≤13C ．11≤h ≤12D ．12≤h ≤24二．填空题（共6小题，满分18分，每小题3分）11．（3分）（2021春•绥滨县期末）已知△ABC中，AB＝k，AC＝k﹣1，BC＝3，当k＝时，∠C＝90°．12．（3分）（2021春•黔南州期末）如图所示的正方形是由四个全等的直角三角形拼成的，直角三角形的两条直角边长分别为2，3，则大正方形的面积为．13．（3分）（2021春•北京期末）在没有直角工具之前，聪明的古埃及人用如图的方法画直角：把一根长绳打上等距离的13个结，然后以3个结间距、4个结间距、5个结间距的长度为边长，用木桩钉成一个三角形，其中5这条边所对的角便是直角．依据是．14．（3分）（2021春•宜州区期末）在△ABC中，AB＝15，AC＝20，BC边上的高线为12，则△ABC的面积为．15．（3分）（2021春•长沙期末）勾股定理a2+b2＝c2本身就是一个关于a，b，c的方程，显然这个方程有无数解，满足该方程的正整数（a，b，c）通常叫做勾股数．如果三角形最长边c＝2n2+2n+1，其中一短边a＝2n+1，另一短边为b，如果a，b，c是勾股数，则b＝（用含n的代数式表示，其中n为正整数）16．（3分）（2021春•恩施市期末）如图，圆柱形玻璃怀高为10cm，底面周长为24cm，在杯内壁离杯底3cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm 与蜂蜜相对的点A处，则蚂蚁从外壁A处到内壁B处的最短距离为cm．（杯壁厚度不计）三．解答题（共7小题，满分52分）17．（6分）（2021春•富川县期末）已知：如图，在Rt△ABC中，两直角边AC＝6，BC ＝8．（1）求AB的长；（2）求斜边上的高CD的长．18．（6分）（2021春•科左中旗期末）如图所示，小明制作一个模具，AD＝4cm，CD＝3cm，∠ADC＝90°，AB＝13cm，BC＝12cm，求这个模具的面积．19．（8分）（2021春•滑县期末）如图是用硬纸板做成的四个全等的直角三角形，两直角边的长分别为a和b，斜边长为c．请你开动脑筋，用它们拼出正方形图案，要求拼图时直角三角形纸片不能互相重叠．（1）请你画出拼成的这个图形的示意图；（2）利用（1）中画出的图形证明勾股定理．20．（8分）（2021春•梁山县期末）绿地广场有一块三角形空地将进行绿化，如图，在△ABC中，AB＝AC，E是AC上的一点，CE＝5，BC＝13，BE＝12．（1）判断△ABE的形状，并说明理由；（2）求线段AB的长．21．（8分）（2021春•新抚区期末）如图，一架云梯AB长25m，斜靠在一面墙上，梯子靠墙的一端A距地面24m．（1）这个梯子底端B离墙有多少米？（2）如果梯子的顶端下滑的距离AD＝4m，求梯子的底部B在水平方向滑动的距离BE 的长．22．（8分）（2021春•殷都区期末）在甲村至乙村的公路旁有一块山地需要开发，现有一C处需要爆破，已知点C与公路上的停靠点A的距离为800米，与公路上另一停靠点B 的距离为600米，且CA⊥CB，如图，为了安全起见，爆破点C周围半径450米范围内不得进入，问在进行爆破时，公路AB段是否有危险需要暂时封锁？请通过计算进行说明．23．（8分）（2021春•海珠区月考）如图，（1）一只蚂蚁要从长方体的一个顶点B沿表面爬行到顶点D，怎样爬行路线最短？为什么？（2）若长方体的长为3、宽为1、高为2，蚂蚁要沿长方体的表面，从顶点B1走到顶点D，试画出不重复情况的展开示意图，并通过计算比较求出最短距离．。

人教版初中数学培优-勾股定理(2)

第17章勾股定理一．勾股定理：1.勾股定理内容：如果直角三角形的两直角边长分别为a ，b; 斜边长为c ，那么a 2+b 2=c 2，即直角三角形两直角边的平方和等于斜边的平方。

2.勾股定理的证明：勾股定理的证明方法很多，常见的是拼图的方法用拼图的方法验证勾股定理的思路是：（1）图形进过割补拼接后，只要没有重叠，没有空隙，面积不会改变；（2）根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理。

3. 勾股定理的变式：在△ABC 中，∠C=90，则222a cb -=,222b c a -=,22b a c +=,22b c b -=,22b c a -=4.勾股定理的适用范围：勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征。

二、勾股定理的逆定理1.逆定理的内容：如果三角形三边长a ，b ，c 满足a 2+b 2=c 2，那么这个三角形是直角三角形，其中c 为斜边。

说明：（1）勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状，在运用这一定理时，可用两小边的平方和与较长边的平方作比较，若它们相等时，以a ，b ，c 为三边的三角形是直角三角形；（2）定理中a ，b ，c 及a 2+b 2=c 2只是一种表现形式，不可认为是唯一的，如若三角形三边长a ，b ，c 满足a 2+b 2=c ，那么以 a ，b ，c 为三边的三角形是直角三角形，但此时的斜边是b.2.利用勾股定理的逆定理判断一个三角形是否为直角三角形的一般步骤：（1）确定最大边；（2）算出最大边的平方与另两边的平方和；（3）比较最大边的平方与别两边的平方和是否相等，若相等，则说明是直角三角形。

一、选择题：1．如图1字母B 所代表的正方形的面积是 ( )A ． 12B ． 13C ． 144D ． 1942．小刚准备测量河水的深度，他把一根竹竿插到离岸边1.5m 远的水底，竹竿高出水面0.5m ，把竹竿的顶端拉向岸边，竿顶和岸边的水平刚好相齐，河水的深度为（）A ．2mB ．2.5cmC ．2.25mD ．3m3． △ABC 中，若AB =15，AC =13，高AD =12，则△ABC 的周长是( ) A ．42 B ．32 C ．42或32 D ．37或334．已知x 、y 为正数，且│24x -│+22(3)0y -=，如果以x 、y 的长为直角边作一个直角三角形，那么以这个直角三角形的斜边为边长的正方形的面积为（） A ．5 B ．25 C ．7 D ． 155．直角三角形的两条直角边长为a ，b ，斜边上的高为h ，则下列各式中总能成立的是 ( )A ． ab =h 2B ． a 2+b 2=2h 2C ． a 1+b 1=h 1D ． 21a +21b =21h6．如图2，在矩形ABCD 中，P 是边AD 上的动点，AC PE ⊥于E ，BD PF ⊥于F ，若AB =3，AD = 4，那么（）A ．125PE PF +=B ．121355PE PF <+< C ． 5PE PF += D ． 34PE PF <+<7．直角三角形有一条直角边长为13，另外两条边长都是自然数，则周长为（）A ．182B ．183C ．184D ．1858．三角形的三边长分别为6，8，10，它的最短边上的高为（）A ．6B ．4.5C ．2.4D ．89．下列各组线段中的三个长度①9、12、15； ②1、2、3； ③32、42、52； ④3a 、4a 、5a （a >0）；⑤m 2-n 2、2mn 、m 2+n 2（m 、n 为正整数，且m >n ）其中可以构成直角三角形的有（） A ．5组 B ．4组 C ．3组 D ．2组10．在同一平面上把三边BC =3，AC =4、AB =5的三角形沿最长边AB 翻折后得到△ABC ′，则CC ′的长等于（）A．125 ； B ．135 ； C ．56 ； D ．24511．如图3，在单位正方形组成的网格图中标有AB 、CD 、EF 、GH 四条线段，其中能构成一个直角三角形三边的线段是（） A ． CD 、EF 、GH B ． AB 、EF 、GH C ． AB 、CD 、GH D ． AB 、CD 、EF 12．下列说法中，不正确的是（）A ．三个角的度数之比为1:3:4的三角形是直角三角形B ．三个角的度数之比为3:4:5的三角形是直角三角形C ．三边长度之比为3:4:5的三角形是直角三角形D ．三边长度之比为5:12:13的三角形是直角三角形 13．下列四组数中是勾股数的有（）①1.5，2.5，2 ，2 ③12，16，20 ④5，12，14A ．1组B ．2组C ．3组D ．4组14．若ABC △的三边a 、b 、c 满足a 2＋b 2＋c 2十338＝10a ＋24b ＋26c ，则△ABC 的面积是（）A ．338B ．24C ．26D ．3015．直角三角形三条边的比是3∶4∶5。

培优专题2_勾股定理及应用(含解答)-[1]

第17章勾股定理点击一：勾股定理勾股定理：如果直角三角形两直角边分别为a ，b ，斜边为c ，那么a 2＋b 2= c 2．即直角三角形两直角的平方和等于斜边的平方．因此，在运用勾股定理计算三角形的边长时，要注意如下三点：（1）注意勾股定理的使用条件：只对直角三角形适用，而不适用于锐角三角形和钝角三角形；（2）注意分清斜边和直角边，避免盲目代入公式致错；（3）注意勾股定理公式的变形：在直角三角形中，已知任意两边，可求第三边长．即c 2= a 2＋b 2，a 2= c 2－b 2，b 2= c 2－a 2．点击二：学会用拼图法验证勾股定理拼图法验证勾股定理的基本思想是：借助于图形的面积来验证，依据是对图形经过割补、拼接后面积不变的原理．如，利用四个如图1所示的直角三角形三角形，拼出如图2所示的三个图形．请读者证明．如上图示，在图（1）中，利用图1边长为a ，b ，c 的四个直角三角形拼成的一个以c 为边长的正方形，则图2（1）中的小正方形的边长为（b －a ），面积为（b －a ）2，四个直角三角形的面积为4×21ab = 2ab ．由图（1）可知，大正方形的面积 =四个直角三角形的面积＋小正方形的的面积，即c 2=（b －a ）2＋2ab ，则a 2＋b 2 = c 2问题得证．请同学们自己证明图（2）、（3）．（图1）（2）（3）ABC点击三：在数轴上表示无理数将在数轴上表示无理数的问题转化为化长为无理数的线段长问题．第一步：利用勾股定理拆分出哪两条线段长的平方和等于所画线段（斜边）长的平方，注意一般其中一条线段的长是整数；第二步：以数轴原点为直角三角形斜边的顶点，构造直角三角形；第三步：以数轴原点圆心，以斜边长为半径画弧，即可在数轴上找到表示该无理数的点．点击四：直角三角形边与面积的关系及应用直角三角形有许多属性，除边与边、边与角、角与角的关系外，边与面积也有内的联系.设a 、b 为直角三角形的两条直角边，c 为斜边，S ∆为面积，于是有：222()2a b a ab b +=++，222a b c +=，12442ab ab S ∆=⨯=，所以22()4a b c S ∆+=+.即221[()]4S a b c ∆=+-.也就是说，直角三角形的面积等于两直角边和的平方与斜边平方差的四分之一.利用该公式来计算直角三角形的有关面积、周长、斜边上的高等问题，显得十分简便. 点击五：熟练掌握勾股定理的各种表达形式．如图2，在Rt ABC ∆中,90=∠C 0,∠A 、∠B 、∠C 的对边分别为a 、b 、c,则c 2=a 2+b 2, a 2=c 2-b 2 ,b 2=c 2-a 2,点击六：勾股定理的应用（1）已知直角三角形的两条边，求第三边；（2）已知直角三角形的一边，求另两条边的关系；（3）用于推导线段平方关系的问题等．（4）用勾股定理，在数轴上作出表示2、3、5的点，即作出长为n 的线段．针对练习:1．下列说法正确的是（）A ．若 a 、b 、c 是△ABC 的三边，则a 2＋b 2＝c 2B ．若 a 、b 、c 是Rt △ABC 的三边，则a 2＋b 2＝c 2C ．若 a 、b 、c 是Rt △ABC 的三边， 90=∠A ，则a 2＋b 2＝c 2D ．若 a 、b 、c 是Rt △ABC 的三边， 90=∠C ，则a 2＋b 2＝c 22．一个直角三角形中，两直角边长分别为3和4，下列说法正确的是（） A ．斜边长为25 B ．三角形周长为25C ．斜边长为5D ．三角形面积为203．如图，正方形网格中，每个小正方形的边长为1，则网格上的三角形ABC 中，边长为无理数的边数是（）A ． 0B ． 1C ． 2D ． 34．如图，数轴上的点A 所表示的数为x，则x 2—10的立方根为（）A ．．2 D ．-25．把直角三角形的两条直角边同时扩大到原来的2倍，则斜边扩大到原来的（） A ． 2倍B ． 4倍C ． 6倍D ． 8倍6．小明想知道学校旗杆的高，他发现旗杆上的绳子垂到地面还多1 m ，当它把绳子的下端拉开5 m 后，发现下端刚好接触地面，则旗杆的高为（） A ．8cm B ．10cm C ．12cm D ．14cm7．△ABC 中，AB ＝15，AC ＝13，高AD ＝12，则△ABC 的周长为（） A ．42 B ．32 C ．42 或 32 D ．37 或 33 8．如图，直线l 上有三个正方形a b c ，，，若a c ，的面积分别为5和11，则b的面积为（）（Ａ）4（Ｂ）6（Ｃ）16（Ｄ）559.已知直角三角形的周长为21，求它的面积.10.直角三角形的面积为120，斜边长为26，求它的周长.11.如图，在Rt △ABC 中，∠ACB=90°，CD ⊥AB 于D ，AB=13cm ，AC 于BC 之和等于17cm ，求CD 的长.l类型之一：勾股定理例1：如果直角三角形的斜边与一条直角边的长分别是13cm 和5cm ，那么这个直角三角形的面积是 cm 2．解析：欲求直角三角形的面积，已知一直角三角形的斜边与一条直角边的长，则求得另一直角边的长即可．根据勾股定理公式的变形，可求得．解：由勾股定理，得132－52=144，所以另一条直角边的长为12．所以这个直角三角形的面积是21×12×5 = 30（cm 2）．例2：如图3(1),一只蚂蚁沿棱长为a 的正方体表面从顶点A 爬到顶点B,则它走过的最短路程为( ) A ．a 3 B ．a )21(+C ．3aD ．a 5解析:本题显然与例2属同种类型,思路相同．但正方体的各棱长相等,因此只有一种展开图．解:将正方体侧面展开得,如图3⑵．由图知AC=2a,BC=a ．根据勾股定理得.a 5a5a)a 2(AB 222==+=故选D ．类型之二：在数轴上表示无理数例3解析：根据在数轴上表示无理数的方法，需先把在数轴上作出．解：以3和1，所以需在数轴上找出两段分别长为3和1的线段，如下面的问题是关于数学大会会标设计与勾股定理知识的综合运用∙ ∙ ABC图3⑵∙ A B图3⑴例5：阅读材料，第七届国际数学教育大会的会徽．它的主题图案是由一连串如图所示的直角三角形演化而成的．设其中的第一个直角三角形OA1A2是等腰三角形，且OA1=A1A2=A2A3=A3A4=……=A8A9=1，请你先把图中其它8条线段的长计算出来，填在下面的表格中，然后再计算这8条线段的长的乘积．解：2；3；2；5；6；7；22；3；这8条线段的长的乘积是7072例6：2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图所示）．如果大正方形的面积是13，小正方形的面积是1，直角三角形的较短直角边为a，较长直角边为b，那么()2ba+的值为（）（A）13 （B）19 （C）25 （D）169解析：由勾股定理，结合题意得a2+b2=13 ①.由题意，得 (b-a)2=1 ②.由②，得 a2+b2-2ab =1 ③.把①代入③，得 13-2ab=1∴ 2ab=12.∴ (a+b)2 = a2+b2+2ab =13+12=25.因此，选C.说明：2002年8月20日~28日，我国在首都北京成功举办了第24届国际数学家大会. 这是在发展中国家举行的第一次国际数学家大会，也是多年来在我国举行的最重要的一次国际会议. 它标志着我国数学已度过了六百多年的低谷，进入了数学大国的行列，并向着新世纪成为数学强国迈开了步伐. 这次大会的会标如下图所示：它取材于我国三国时期（公元3世纪）赵爽所著的《勾股圆方图注》.类型之四：勾股定理的应用（一）求边长例1：已知：如图，在△ABC中，∠ACB＝90º，AB＝5cm，BC＝3cm，CD⊥AB于D，求CD的长..（二）求面积例2：（1）观察图形思考并回答问题（图中每个小方格代表一个单位面积）①观察图1－1.正方形A中含有__________个小方格，即A的面积是__________个单位面积；正方形B中含有__________个小方格，即B的面积是__________个单位面积；正方形C中含有__________个小方格，即C的面积是__________个单位面积.②在图1－2中，正方形A，B，C中各含有多少个小方格？它们的面积各是多少？③你能发现图1－1中三个正方形A，B，C的面积之间有什么关系吗？图1－2中的呢？（2）做一做：①观察图1－3、图1－4，并填写下表：②三个正方形A，B，C的面积之间有什么关系？（3）议一议：①你能用三角形的边长表示正方形的面积吗？②你能发现直角三角形三边长度之间存在什么关系吗？③分别以5厘米、12厘米为直角边作出一个直角三角形，并测量斜边的长度，②中的规律对这个三角形仍然成立吗？解析：注意到图中每个小方格代表一个单位面积，通过观察图形不能得到答案：①99 9 9 18 18；②A中含4个，B中含4个，C中含8个，面积分别为4，4，8；③A与B的面积之和等于C，图1－2中也是A与B的面积之和等于C.（2）①答案：②答案：.（3）答案：①设直角三角形三边长分别为a，b，c（如图）；②，.③成立.（三）作线段例3 作长为、、的线段．解析：作法：1．作直角边长为1（单位长）的等腰直角三角形ACB（如图）；2．以斜边AB为一直角边，作另一直角边长为1的直角三角形ABB1；3．顺次这样作下去，最后作到直角三角形AB2B3，这时斜边AB、AB1、AB2、AB3的长度就是、、、．证明：根据勾股定理，在Rt△ACB中，∵AB>0，∴AB=．其他同理可证．点评由勾股定理，直角边长为1的等腰直角三角形，斜边长就等于，直角边长为边长就是．类似地也可作出（四）证明平方关系例4：已知：如图，在ABC∆中，=∠E222BEAEAC-=.解析：根据勾股定理，在ACDRt∆中，2AC在ADERt∆中，222DEAEAD+=，在Rt∆222BEBDDE-=，∴222222BDAECDDEAEAC-+=-+=又∵CDBD=，∴222BEAEAC-=.点评三角形，以便为运用勾股定理创造必要的条件.（五）实际应用例5：台风是一种自然灾害，它以台风中心为圆心在周围数十千米范围内形成气旋风暴，有极强的破坏力，如图，据气象观测，距沿海某城市A 的正南方向220千米B 处有一台风中心，其中心最大风力为12级，每远离台风中心20千米，风力就会减弱一级，该台风中心现正以15千米/时的速度沿北偏东30º方向往C 移动，且台风中心风力不变，若城市所受风力达到或走过四级，则称为受台风影响.（1）该城市是否会受到这交台风的影响？请说明理由.（2）若会受到台风影响，那么台风影响该城市持续时间有多少？（3）该城市受到台风影响的最大风力为几级？解析（1）由点A 作AD⊥BC 于D ，则AD 就为城市A 距台风中心的最短距离在Rt△ABD 中，∠B=30º，AB ＝220，∴AD=21AB=110.由题意知，当A 点距台风（12－4）20＝160（千米）时，将会受到台风影响．故该城市会受到这次台风的影响．（2）由题意知，当A 点距台风中心不超过60千米时，将会受到台风的影响，则AE ＝AF ＝160．当台风中心从E 到F 处时，该城市都会受到这次台风的影响.由勾股定理得∴EF＝2DE ＝6015.因为这次台风中心以15千米/时的速度移动，所以这次台风影响该城市的持续时间为154151560 小时.（3）当台风中心位于D 处时，A 城市所受这次台风的风力最大，其最大风力为12－20110＝6.5级．一、选择题1、有六根细木棒，它们的长度分别是2、4、6、8、10、12（单位：cm ），从中取出三根首尾顺次连结搭成一个直角三角形，则这三根细木棒的长度分别为（）（A ）2、4、8 （B ）4、8、10 （C ）6、8、10 （D ）8、10、122、木工师傅想利用木条制作一个直角三角形的工具，那么他要选择的三根木条的长度应符合下列哪一组数据？（）A.25，48，80 B ．15，17，62 C ．25，59，74 D ．32，60，68 3、如果直角三角形的三条边2，4，a ，那么a 的取值可以有（）（A ）0个（B ）1个（C ）2个（D ）3个4、已知直角三角形中30°角所对的直角边长是2厘米，则斜边的长是（）（A ）2厘米（B ）4厘米（C ）6厘米（D ）8厘米5、如图，直角三角形三边上的半圆的面积依次从小到大记作S 1、S 2、S 3，则S 1、S 2、S 3之间的关系是（）（A ）S 1+S 2>S 3 （B ）S 1+S 2<S 3 （C ）S 1+S 2=S 3 （D ）S 12+S 22=S 32二、填空题1、若直角三角形斜边长为6，则这个三角形斜边上的中线长为______.2、如果直角三角形的两条直角边的长分别是5cm 和12cm ，那么这个直角三角形斜边上的中线长等于 cm ．3、如图，CD 是Rt ⊿ABC 斜边AB 上的中线，若CD=4，则AB= ．4、在△ABC 中，∠A ：∠B ：∠C ＝1：2：3．已知BC ＝3cm ，则AB ＝ cm ．5、如图，是一个外轮廓为矩形的机器零件平面示意图，根据图中标出尺寸（单位：mm ）计算两圆孔中心A 和B 的距离为 .6、如图：有两棵树，一棵高8米，另一棵高2米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了米．7、如图，为了求出湖两岸A 、B 两点之间的距离，观测者从测点A 、B 分别测得∠BAC ＝90°，∠ABC ＝30°，又量得BC ＝160 m ，则A 、B 两点之间的距离为 m （结果保留根号）8、利用四个全等的直角三角形可以拼成如图所示的图形，这个图形被称为弦图．从图中可以看到：大正方形面积＝小正方形面积＋四个直角三角形面积．因而c 2＝＋．化简后即为c 2＝．第6题图第5题图abc9、如图，是2002年8月北京第24届国际数学家大会会标，由4个全等的直角三角形拼合而成，若图中大小正方形的面积分别为52和4，则直角三角形的两条直角边的长分别为．10、2002年8月20～28日在北京召开了第24届国际数学家大会．大会会标如图所示，它是由四个相同的直角三角形拼成的（直角边长分别为2和3），则大正方形的面积是．11、已知第一个等腰直角三角形的面积为1，以第一个等腰直角三角形的斜边为直角边画第二个等腰直角三角形，又以第二个等腰直角三角形的斜边为直角边画第三个等腰直角三角形，以此类推，第13个等腰直角三角形的面积是 . 12、如图，梯子AB 靠在墙上，梯子的底端A 到墙根O 的距离为2米，梯子的顶端B 到地面的距离为7米．现将梯子的底端A 向外移动到A′，使梯子的底端A′ 到墙根O 的距离等于3米，同时梯子的顶端B 下降至B′，那么BB′等于1米；②大于1米；③小于1米.其中正确结论的序号是________________.13、观察下面各组数：（3，4，5）、（5，12，13）、（7，24，25）、（9，40，41）、…，可发现：4＝2132-，12＝2152-，24＝2172-，…，若设某组数的第一个数为k ，则这组数为（k ，，）．三、解答题1、张老师在一次“探究性学习”课中，设计了如下数表：（1）分别观察a 、b 、c 与n 之间的关系，并用含自然数n (n>1)的代数式表示：a = ，b = ，c =（2）猜想：以a 、b 、c 为边的三角形是否为直角三角形？并证明你的猜想.2、若正整数a 、b 、c 满足方程a 2+b 2=c 2 ，则称这一组正整数（a 、b 、c ）为“商高数”，下面列举五组“商高数”：（3，4，5），（5，12，13），（6，8，10），（7，24，25），（12，16，20），注意这五组“商高数”的结构有如下规律：根据以上规律，回答以下问题：（1）商高数的三个数中，有几个偶数，几个奇数？（2）写出各数都大于30的两组商高数．（3）用两个正整数m 、n （m ＞n ）表示一组商高数，并证明你的结论． 3、阅读并填空：寻求某些勾股数的规律：⑴对于任何一组已知的勾股数都扩大相同的正整数倍后，就得到了一组新的勾股数．例如：222543=+，我们把它扩大2倍、3倍，就分别得到2221086=+和22215129=+，……若把它扩大11倍，就得到，若把它扩大倍，就得到．⑵对于任意一个大于1的奇数，存在着下列勾股数：若勾股数为3，4，5，因为222453-=，则有5432+=；若勾股数为5，12，13，则有131252+=；若勾股数为7，24，25，则有；……若勾股数为m (m 为奇数)，n ，，则有=2m ，用m 来表示n ＝；当17=m 时，则n ＝，此时勾股数为． ⑶对于大于4的偶数：若勾股数为6，8，10，因为2228106-=，则有……请找出这些勾股数之间的关系，并用适当的字母表示出它的规律来，并求当偶数为24的勾股数．4、一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的证明方法.如图，火柴盒的一个侧面A B C D 倒下到A B C D '''的位置，连结C C '，设,,AB a BC b AC c ===，请利用四边形B C C D ''的面积证明勾股定理：222a b c +=.aD 'B 'DC ' A BCb c 第4题图5、如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案，其中四边形ABCD 和EF 都是正方形. 证：△ABF ≌△DAE6、仔细观察图形，认真分析各式，然后解答问题.;23,4)3(;22,31)2(;21,21)1(322212==+==+==+S S S（1）请用含有n （n 是正整数）的等式表示上述变化规律；（2）推算出OA 10的长；（3）求出210232221S S S S ++++ 的值．一、选择题1、如图，字母A 所代表的的正方形的面积为（数字表示该正方形的面积）（） A 、13B 、85C 、8D 、都不对2、在Rt△ABC 中，有两边的长分别为3和4，则第三边的长（） A 、5B 、7C 、5或7D 、5或113、等腰三角形底边上的高是8，周长是32，则三角形的面积是（） A 、56B 、48C 、40D 、32214、若线段a 、b 、c 能构成直角三角形，则它们的比为（） A 、2:3:4B 、3:4:6C 、5:12:13D 、4:6:75、一个长方形的长是宽的2倍，其对角线的长是5cm ，则长方形的面积（） A 、25cmB 、225cmC 、210cmD 、275cm6、一个三角形三个内角之比为1：2：1，其相对应三边之比为（） A 、1:2:1B 、1:2:1C 、1:4:1D 、12:1:27、斜边长25，一条直角边长为7的直角三角形面积为（） A 、81B 、82C 、83D 、848、若直角三角形中，有一个锐角为 30，且斜边与较短直角边之和为18，则斜边长为（） A 、4cmB 、6cmC 、8cmD 、12cm9、如图△ABC 中，∠C ＝90°，AD 平分∠BAC ，DE ⊥AB 于E ，下面等式错误的是（） A 、AC 2+DC 2=AD 2B 、AD 2－DE 2＝AE 2C 、AD 2=DE 2+AC 2D 、BD 2－BE 2＝41BC 210.图是2002年8 月北京第24届国际数学家大会会标，由4 个全等的直角三角形拼合而成.若图中大小正方形面积分别是6221和4，则直角三角形的两条直角边长分别为（）A 、6，4B 、6221，4 C 、6221，421 D 、6， 421二、填空：1、在△ABC 中， ∠C ＝90°，a ，b ，c 分别为∠A ∠B ∠C 的对边（1）若a=6，c=10则b= （2）若a=12，b=5 则c= （3）若c=25，b=15则a= （4）若a ＝16，b=34则b=2、三边长分别为1，1，1的三角形是角三角形.3、在△ABC中，AB=10，AC=8，BC=6，则△ABC的面积是4、如图要修一个育苗棚，棚宽a=3m，高b=4m，底d=10m，覆盖顶上的塑料薄膜的面积为2m5、如图点C是以为AB直径的半圆上的一点，4∠BCACACB则图中阴影部分的面积︒=,,390==是6、在Rt△ABC中，3︒=ABC且BC=136则AC=∠AC90=:5:,7、直角三角形的一直角边为8cm，斜边为10cm，则这个直角三角形的面积是斜边上的高为8、△ABC中，︒,C则a:b:c=90a∠30==∠︒9、三角形三个内角之比为1：2：3，它的最长边为a，那么以其余两边为边所作的正方形面积分别为10、有两根木条，长分别为60cm和80cm，现再截一根木条做一个钝角三角形，则第三根木条x长度的取值范围三解答题1、如如图要建一个苗圃，它的宽是a=4.8厘米，高b=3.6米.苗圃总长是10米（1）求苗圃的占地面积（2）覆盖在顶上的塑料薄膜需要多少平方米?2、如图在四边形ABCD中，12=︒∠∠BCABBAD求正方形DCEF的面积CBDAD=,,4,3︒90,==90=3、如图在锐角△ABC中，高AD=12，AC=13，BC=14求AB的长4、八年级学生准备测量校园人工湖的深度，他们把一根竹竿插到离湖边1米的水底，只见竹竿高出水面1尺，把竹竿的顶端拉向湖边（底端不变）竿顶和湖沿的水面刚好平齐，求湖水的深度和竹竿的长．5、如图己知在△ABC中，DE︒∠∠垂直平分AB，E为垂足交BC于D，BD=16cm，求AC长．==90︒C,B15,6、某校要把一块形状是直角三角形的废地开发为生物园，如图80∠ACACB米，BC=60米，若线段CD为一=,︒90=条水渠，且D在边AB上，己知水渠的造价是10元/米，则点D在距A点多远，水渠的造价最低，最低价是多少？勾股定理及应用勾股定理是数学史上一颗璀璨的明珠，在西方数学史上称之为“毕达哥拉斯定理”．例1 已知一直角三角形的斜边长是2，周长是，求这个三角形的面积．分析由斜边长是2，周长是4，列关于两直角边的方程，只需求出两直角边长的积，即可求得三角形的面积．本题中用到数学解题中常用的“设而不求”的技巧，要熟练掌握．解：设直角三角形的两直角边为a 、b ，根据题意列方程得：2222,22a b a b ⎧+=⎪⎨++=+⎪⎩即224,a b a b ⎧+=⎪⎨+=⎪⎩ ②式两边同时平方再减去①式得： 2ab=2， ∴12ab=12．∴S=12．因此，这个三角形的面积为12．练习11．已知：如图2-1，AD=4，CD=3，∠ADC=90°，AB=13，∠ACB=90°，•求图形中阴影部分的面积．2-12．已知：长方形ABCD，AB∥CD，AD∥BC，AB=2，AD≠DC，长方形ABCD的面积为S，沿长方形的对称轴折叠一次得到一个新长方形，求这个新长方形的对角线的长．3．若线段a、b、c能组成直角三角形，则它们的比值可以是（）A．1：2：4 B．1：3：5 C．3：4：7 D．5：12：13例2 如图2-2，把一张长方形纸片ABCD折叠起来，使其对角顶点A、C重合，•若其长BC为a，宽AB为b，则折叠后不重合部分的面积是多少？分析图形沿EF折叠后A、C重合，可知四边形AFED′与四边形CFED全等，则对应边、角相等，∴AF=FC，且FC=AE，则△ABF≌△AD′E，•由三角形面积公式不难求出不重合部分的面积．解：∵图形沿EF折叠后A、C重合，∴四边形AFED′与CFED关于EF对称，则四边形AFED′≌四边形CFED．∴∠AFE=∠CFE．∴AF=FC，∠D′=∠D=∠B=90°AB=CD=AD′．∵AD∥BC，∴∠AEF=∠EFC．∴∠AEF=∠AFE．则AE=AF．∴Rt△ABF≌Rt△AD′E．在Rt△ABF中，∵∠B=90°，∴AB2+BF2=AF2．设BF=x，b2+x2=（a-x）2，∴x=222a ba-．∴S=2S△ABF =2×12bx=2×12·b·222a ba-=22()2b a ba-．练习22-21．如图2-3，把矩形ABCD沿直线BD向上折叠，使点C落在C′的位置上，已知AB=•3，BC=7，重合部分△EBD的面积为________．2．如图2-4，一架长2.5m的梯子，斜放在墙上，梯子的底部B•离墙脚O•的距离是0.7m，当梯子的顶部A向下滑0.4m到A′时，梯子的底部向外移动多少米？2-43．如图2-5，长方形ABCD中，AB=3，BC=4，若将该矩形折叠，使C点与A点重合，•则折叠后痕迹EF的长为（）A．3.74 B．3.75 C．3.76 D．3.772-5例3 试判断，三边长分别为2n2+2n，2n+1，2n2+2n+1（n为正整数）•的三角形是否是直角三角形？分析先确定最大边，•再利用勾股定理的判定定理判断是否为直角三角形．解：∵n为正整数，∴（2n2+2n+1）-（2n2+2n）=2n2+2n+1-2n2-2n=1>0，（2n2+2n+1）-（2n+1）=2n2+2n+1-2n-1=2n2>0．∴2n2+2n+1为三角形中的最大边．又（2n2+2n+1）2=4n4+8n3+8n2+4n+1，（2n2+2n）2+（2n+1）2=4n4+8n3+8n2+4n+1．∴（2n2+2n+1）2=（2n2+2n）2+（2n+1）2．∴这个三角形是直角三角形．练习31．若△ABC的三边a、b、c满足a2+b2+c2+50=6a+8b+10c，则△ABC是（）A．等腰三角形 B．直角三角形 C．锐角三角形 D．钝角三角形2．如图2-6，在正方形ABCD中，F为DC的中点，E为BC上一点，且EC=14BC，猜想AF•与EF的位置关系，并说明理由．2-63．△ABC中的三边分别是m2-1，2m，m2+1（m>1），那么（）A．△ABC是直角三角形，且斜边长为m2+1．B．△ABC是直角三角形，且斜边长为2m．C．△ABC是直角三角形，但斜边长由m的大小而定．D．△ABC不是直角三角形．例4 已知：如图2-7所示，△ABC中，D是AB的中点，若AC=12，BC=5，CD=6．5．求证：△ABC是直角三角形．分析欲证△ABC是直角三角形，在已知两边AC、BC的情况下求边AB的长，比较困难；但注意到CD是边AB的中线，我们延长CD到E，使DE=CD，•从而有△BDE•≌△ADC，这样AC、BC、2CD就作为△BCE的三边，再用勾股定理的逆定理去判定．证明：延长CD到E，使DE=CD，连结BE．∵AD=BD，CD=ED，∠ADC=∠BDE．∴△ADC≌△BDE（SAS）．∴BE=AC=12．∴∠A=∠DBE．∴AC∥BE．在△BCE中，∵BC2+BE2=52+122=169．CE2=（2CD）2=（2×6.5）2=169．∴BC2+BE2=CE2．∴∠EBC=90°．又∵AC∥BE，∴∠ACB=180°-∠EBC=90°．∴△ABC是直角三角形．练习41．已知a、b、c为△ABC的三边，且满足a2c2-b2c2=a2-b2，试判断△ABC的形状．先阅读下列解题过程：解：∵a2c2-b2c2=a4-b4，①∴c2（a2-b2）=（a2+b2）（a2-b2）．②∴c2=a2+b2．③∴△ABC为直角三角形．④问：（1）上述推理过程，出现错误的一步是________；（2）本题的正确结论是________．2．如图2-8，△ABC的三边分别为AC=5，BC=12，AB=13，将△ABC沿AD折叠，使AC落在AB上，求折痕AD的长．3．如图2-9，△ABC中，∠ACB=90°，AC=BC，P是△ABC内一点，满足PA=3，PB=1，•PC=2，求∠BPC的度数．例5 如图2-10，△ABC中，AB=AC=20，BC=32，D是BC上一点，且AD⊥AC，求BD的长．分析若作AE⊥BC于E，如图2-11，利用勾股定理可求出AE=12，AD是Rt•△ADC的直角边．∴AD=CD-AC ，若设DE=x ，借助于AD 这个“桥”可以列出方程．解：作AE ⊥BC 于E ． ∵AB=AC ，AE ⊥BC ， ∴BE=EC=12BC=12×32=16．在Rt △AEC 中，AE 2=AC 2-CE 2=202-162=144， ∴AE=12．设DE=x ，则在Rt △ADE 中，AD 2=AE 2+DE 2=144+x 2，在Rt △ACD 中，AD 2=CD 2-AC 2=（16+x ）2-202． ∴144+x 2=（16+x ）2-202 解得x=9．∴BD=BE-DE=16-9=7．练习51．如图2-12，△ABC 中，∠C=90°，M 是BC 的中点，MD ⊥AB 于D ．求证：AD 2=AC 2+BD 2．2-122．如图2-13，AB ⊥AD ，AB=3，BC=12，CD=13，AD=4，求四边形ABCD 的面积．2-133．如图2-14．长方体的高为3cm ，底面是正方形，边长为2cm ，现有绳子从A 出发，沿长方形表面到达C 处，问绳子最短是多少厘米？2-102-112-14勾股定理及应用答案: 练习11．24（提示：利用勾股定理即可求出） 2．长方形的对称轴有2条，要分别讨论：（1）以A 、B 为对称点（如图） ∵S=AB ×BC ，AB=2， ∴BC=AD=2S ．根据对称性得DF=12AB=1．由于∠D=90°，据勾股定理得：AF==12（2）以A 、D 为对称点（如图） ∴BF=12BC=4S ．由∠B=90°，据勾股定理得：AF==3．D练习2 1．214（提示：利用Rt △ABE 的勾股定理即可求出） 2．0.8m 3．B练习31．B 2．AF ⊥EF （提示：连结AE ，设正方形的边长为a ，则DF=FC=2a ，EC=4a ，在Rt △ADF 中，由勾股定理得：AF 2=AD 2+DF 2=a 2+（2a ）2=54a 2．同理：在Rt△ECF 中，EF 2=（2a ）2+（4a ）2=516a 2，在Rt△ABE 中，BE=34a ，则AE 2=a 2+916a 2=2516a 2．∵54a 2+516a 2=2516a 2，∴AF 2+EF 2=AE 2． ∴∠AFE=90°． ∴AF ⊥EF ．3．A （点拨：利用勾股定理的逆定理来判定）练习41．（1）③、④（2）△ABC 为直角三角形或等腰三角形． 2．∵AC 2+BC 2=52+122=132=AB 2， ∴∠C=90°．将△ABC 沿AD 折叠，使AC 落在AB 上，C 的对称点为E （如图） ∴CD=DE ， AC=AE=5．则△ACD ≌△AED ．又BE=AB-AE=8．设CD 为x ，则x 2+82=（12-x ）2．解之得x=103． ∴AD 2=52+（103）2． ∴3．3．过点C 作CE ⊥CP ，并截CE=CP=2，连结PE ，BE ．（如图） ∵∠ACB=∠PCE=90°， ∴∠ACB-∠PCB=∠PCE-∠PCB ．即∠ACP=∠BCE ．∴△PCA ≌△ECB （SAS ）． ∴BE=AP=3．在Rt △PCE 中， PE 2=PC 2+CE 2=8．又∵BP 2=1，BE 2=9，∴BE 2=BP 2+PE 2．∴△PBE 是直角三角形，其中∠BPE=90° 在Rt △PCE 中，PC=CE ， ∴∠CPE=∠CEP=45°．∴∠BPC=∠CPE+∠BPE=45°+90°=135°．练习5 1．连结AM ． ∵M 为CB 的中点， ∴CM=MB ．又∵AC 2=AM 2-CM 2，BD 2=BM 2-MD 2， ∴AC 2+BD 2=AM 2-MD 2．又∵AD 2=AM 2-DM 2， ∴AD 2=AC 2+BD 2．2．36（提示：连结BD ，利用勾股定理及逆定理即可求出）．3．5cm （提示：将该长方体的右面翻折，使它与前面在同一平面，连结AC （如图），此时线段AC 的长度即为最短距离． ∴（cm ）．勾股定理的逆定理1班级姓名号次一．选择题（本题有10小题，每题3分，共30分）1.在△ABC 中，,,A B C ∠∠∠的对边分别为,,a b c ，且ab c b a 2)(22+=+，则（）A.A ∠为直角B.B ∠为直角C.C ∠为直角D.不能确定 2.如图，下列三角形中是直角三角形的是( )51213 C467 B7 58 A73 53.下列各命题的逆命题不成立的是( )A.两直线平行,内错角相等B.若b a =,则b a =C.对顶角相等D.如果a =b ,那么a 2=b 24.下面四组数中，其中有一组与其他三组规律不同，这一组是（）A. 4，5，6B. 6，8，10C. 8，15，17D. 9，40，415.如图有五根小木棒，其长度分别为7、15、20、24、25，现想把它们摆成两个直角三角形，则摆放正确的是（）715242520715202425157252024257202415(A)(B)(C)(D)A B C D6.放学后，斌斌先去同学小华家玩了一回，再回到家里。

勾股定理经典培优题及答案

勾股定理经典培优题类型之一勾股定理的验证1．小明利用如图17－X －1①所示的图形(三个正方形和一个直角三角形)验证勾股定理验证勾股定理，，他的方法如下：过点D 作直线FG ∥AC ，过点E 作直线GH ∥BC ，直线FG 与直线GH 交于点G ，与直线BC 交于点F ，直线GH 与直线AC 交于点H ，如图②所示．请你回答：(1)△ABC 与△BDF ，△DEG ，△EAH 有什么关系？为什么？(2)用含a ，b 的代数式表示正方形CFGH 的面积；(3)你能否根据图形面积之间的关系找到a ，b ，c 之间的数量关系？(4)你能得到什么结论？图17－X －1 2．勾股定理神秘而美妙勾股定理神秘而美妙，，它的证法多样它的证法多样，，其巧妙各有不同其巧妙各有不同，，其中的“面积法”给了小明灵感其中的“面积法”给了小明灵感，，他惊喜地发现他惊喜地发现，，当四个全等的直角三角形如图17－X －2摆放时摆放时，，可以用“面积法”来证明a 2＋b 2＝c 2.(请你写出证明过程) 图17－X －2 类型之二勾股定理及其应用3．等腰三角形的底边长为6，底边上的中线长为4，则它的腰长为() A ．7 B ．6 C ．5 D ．4 4．我国汉代数学家赵爽为了证明勾股定理我国汉代数学家赵爽为了证明勾股定理，，创制了一幅“弦图”创制了一幅“弦图”，，后人称其为“赵爽弦图”．如图17－X －3是由弦图变化得到的是由弦图变化得到的，，它由八个全等的直角三角形拼接而成．记图中正方形ABCD 、正方形EFGH 、正方形MNKT 的面积分别为S 1，S 2，S 3.若正方形EFGH 的边长为2，则S 1＋S 2＋S 3＝________. 图17－X －3 图17－X －4 5．图17－X －4①是我国古代著名的“赵爽弦图”的示意图①是我国古代著名的“赵爽弦图”的示意图，，它是由四个全等的直角三角形围成的．若AC ＝12，BC ＝10，将四个直角三角形中边长为12的直角边分别向外延长一倍的直角边分别向外延长一倍，，得到图②所示的数学“风车”得到图②所示的数学“风车”，，则这个数学“风车”的外围周长是________．6．知识回顾：在学习《二次根式》时知识回顾：在学习《二次根式》时，，我们知道：2＋3≠5；在学习《勾股定理》时在学习《勾股定理》时，，由于2，3，5满足(2)2＋(3)2＝(5)2，因此以2，3，5为三边长能构成直角三角形．三角形．探索思考：请通过构造图形来说明：a ＋b ≠a ＋b (a ＞0，b ＞0)．(画出图形并进行解释) 7．在△ABC 中，AB ＝15，AC ＝20，D 是直线BC 上的一个动点上的一个动点，，连接AD ，如果线段AD 的长度最短是12，请你求△ABC 的面积．的面积．类型之三勾股定理的逆定理及其应用8．已知三组数据：①2，3，4；②3，4，5；③1，3，2.分别以每组数据中的三个数为三角形的三边长分别以每组数据中的三个数为三角形的三边长，，能构成直角三角形的有( ) A ．②B ．①②．①②C ．①③．①③D ．②③．②③ 9．如果△ABC 的三边长分别是m 2－1，m 2＋1，2m (m >1)，那么下列说法中正确的是( ) A ．△ABC 是直角三角形是直角三角形，，且斜边长为m 2＋1 B ．△ABC 是直角三角形是直角三角形，，且斜边长为2m C ．△ABC 是直角三角形是直角三角形，，且斜边长为m 2－1 D ．△ABC 不是直角三角形不是直角三角形10．若△ABC 的三边长a ，b ，c 满足关系式(a ＋2b －60)2＋|b －18|＋c －30＝0，则△ABC 是________三角形．类型之四勾股定理及其逆定理的综合应用图17－X －5 11．如图17－X －5，E 是正方形ABCD 内的一点内的一点，，连接AE ，BE ，CE ，将△ABE 绕点B 顺时针旋转90°到△CBE ′的位置．若AE ＝1，BE ＝2，CE ＝3，则∠BE ′C ＝________°. 12．如图17－X －6，在4×3的正方形网格中有从点A 出发的四条线段AB ，AC ，AD ，AE ，它们的另一个端点B ，C ，D ，E 均在格点上(正方形网格的交点)．(1)若每个正方形的边长都是1，分别求出AB ，AC ，AD ，AE 的长度(结果可以保留根号)；(2)在AB ，AC ，AD ，AE 四条线段中四条线段中，，是否存在三条线段是否存在三条线段，，它们能构成直角三角形？如果存在它们能构成直角三角形？如果存在，，请指出是哪三条线段条线段，，并说明理由．并说明理由．图17－X －6 类型之五勾股定理在实际生活中的应用图17－X －7 13．如图17－X －7是矗立在高速公路旁水平地面上的交通警示牌是矗立在高速公路旁水平地面上的交通警示牌，，经测量得到如下数据：AM ＝4米，AB ＝8米，∠MAD ＝45°，∠MBC ＝30°，则警示牌的高CD 为________米(结果精确到0.1米，参考数据：2≈1.41，3≈1.73)．14．如图17－X －8，A ，B 两地之间有一座山两地之间有一座山，，汽车原来从A 地到B 地需经过C 地沿折线ACB 行驶行驶，，现开通隧道后隧道后，，汽车直接沿直线AB 行驶．已知AC ＝10千米千米，，∠A ＝30°，∠B ＝45°则隧道开通后则隧道开通后，，汽车从A 地到B 地比原来少走多少千米？(结果保留根号) 图17－X －8 。

人教版八下数学勾股定理专题培优

第十七章勾股定理 7.勾股定理（一）基础题训练01.在Rt △ABC 中，∠C =90°，a ＝3,b ＝4,则c =______. 【解答】：c =502. 在Rt △ABC 中，∠C =90°，a =6, c =10,则b =______. 【解答】：b =803. 在△ABC 中, ∠C =90°, ∠A=30°，则其三边a ：b ：c =__________ 【解答】：a ：b ：c =1:3:204. 在Rt △ABC 中，∠C =90°，∠A ，∠B , ∠C 的对边分别为a ，b ，c ，则下列结论正确的是（） A.222a cb =+ B. 222c b a =- C. 222b c a -= D. 222b c a =- 【解答】：C05.一个直角三角形的三边为三个连续偶数，则它的三边分别为（）A.2、4、6B.4、6、8C.6、8、10D.3、4、5 【解答】：C06.等腰直角三角形的直角边为2，则斜边的长为（） A.2 B. 22 C.1 D.2【解答】：B07.已知等边三角形的边长为2cm,则等边三角形的面积为（）A. 32B.3 C.1 D. 2【解答】：B08.如图，在△ABC 中，∠C =90°，AB =15，则两个正方形面积的和为（）A.150B.200C.225D.350【解答】：C09. 在△ABC 中, ∠C =90°,c =20, a ：b =3:4，则a =_____. 【解答】：12ABC10. 如图，在△ABC 中，AB =AC =10cm ，高AD =8cm ，求BC 的长及S △ABC .【解答】：BC =12，S △ABC =48. 11.（2013·资阳）如图，点E 在正方形内，∠AEB = 90°，AE =6，BE =8，求阴影部分的面积.【解答】：S 阴 = 76.12. 如图，在△ABC 中，AD ⊥BC 于D ，AB =3，BD =2，DC =1，求AC 的长.【解答】：AC=6.中档题训练13．已知直角三角形的两边为2和3，则第三边的长为【解答】（答案13或5）14．如图，已知直角△ABC 中，∠C =90°，3BC =，4AC =，CD ⊥AB 于D ．()1求AB 的长；()2 求CD 的长．DCBAABCDECBDA[解析] （1）5AB =；(2) 由面积法可求 125CD =15．已知直角△ABC 的周长为12cm ，一直角边的长为4cm ，求斜边的长？ [解析] 设另一直角边为x ，则斜边为8-x ，在Rt △ABC 中，2224(8x x +=-） ∴ 3x =， ∴ 斜边为835-= 16．如图在△ABC 中，AB BC =,∠ABC =90°，D 为AC 的中点，DE ⊥DF ,DE 交AB 于E ,DF BC 交于F1（）求证：BE CF =；(2) 若3AE =，1CF =，求EF 的长[解析] 1（）证△BED ≌△CFD (2) 10EF =综合题训练17．如图CA CB =，CD CE = ，∠ACB =∠ECD 90=°，D 为AB 边上一点．若1AD =，3BD =，求CD 的长．[解析] 由△ACE ≌△BCD 可得，∠EAC =∠45B =°，∠90EAD =°，2222210DE AD AE AD BD =+=+=，10DE =5CD =8. 勾股定理（二）基础训练01.在直角坐标系中，点P（－2,3）到原点的距离为【解答】：1302.如图，∠ACB＝∠ABD＝90，AC＝2，BC＝1，AD＝14,则BD＝【解答】303.已知△ABC中，AB＝AC＝10，BD是AC边上的高，CD＝2，则BD为（）A.4B.6C.8D.210【解答】B04.如图，每个小正方形的边长为1，ABC中边长为无理数的边共有（)条A.0B.1C.2D.3【解答】C05.一座建筑物发生了火灾，消防车到达现场后，发现最多只能靠近建筑物底端5米，消防车的云梯最大升长为13米，则云梯可以达到该建筑物的最大高度是（)A.12米B.13米C.14米D.15米【解答】A06.把三角形的两条直角边同时扩大到原来的2倍，则其斜边扩大到原来的（）A.1倍B.2倍C.3倍D.4倍【解答】B07.如图，在水塔的东北方向32m 处有一抽水站A,在水塔的东南方向24m 处有一建筑工地B,在A,B间建一条水管，则水管AB的长为（)A.45mB.40mC.50mD.60m【解答】B08.一直角三角形的斜边长比一直角边的长大2，另一直角边长为6，则斜边长为（)A.4B.8C.10D.12【解答】C09.如图，有两棵树，一棵树高10米，另一棵树高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，则小鸟至少飞行（ )A.8米B.10米C.12米D.14米【解答】B10.如图，将一个有45°角的三角板ABC 的直角顶点C 放在一张宽为3cm 的纸带边沿上，另一顶点B 在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，求三角板最大边AB 的长。