八年级讲义(1)
人教版八年级上新目标第一单元SectionA 讲义

2021秋季八年级英语〔第1讲讲义〕姓名成绩Unit 1 Section A【词汇】【语法知识点】anyone pron.任何人eg: Is anyone here?有人在吗?考向一:辨析anyone与someone这两个复合不定代词作主语时,谓语动词用单数,区别如下:eg: Did anyone call me just now?刚刚有人给我打过吗?Someone is knocking at the door.有人在敲门。
考向二:形容词修饰anyone,someone,anything,something等不定代词时,形容词要后置。
eg: someone new新人anything interesting任何有趣的事情Long time no see,好久不见。
用于口语中,本不符合英语语法习惯。
但它简单明了,已经成为标准英语口语。
此句话用于交际用语中,是老朋友好久不见时的寒喧语。
eg: Hi, Zhang Ming. Long time no see.嗨,张明,好久不见。
anywhere adv.在任何地方eg:I can't see it anywhere.我哪儿也见不到它。
考向一[重点]:辨析anywhere,somewhere:everywhere与nowhere, 三者都是副词,区别如下:eg: Are you going anywhere tonight? 今晚你要去什么地方吗?I think I saw it somewhere. 我想我在某个地方见过它。
-Where did you visit when you were living in that city? 当你在那座城市住的时候,你都参观哪儿了?-Everywhere.哪儿都参观了。
考向二:形容词修饰anywhere,somewhere,nowhere,等不定代词时,形容词要后置。
eg: We went somewhere nice yesterday. 昨天我们去了一个美丽的地方。
上海初二物理讲义(1)长度(1)

嘉定2014暑期八年级物理资料-1序言让我们起航—长度《摆的故事和启示》事情发生在400多年前的意大利比萨,年轻的伽利略当时正在比萨大学学习。
有一天,伽利略在教堂内做弥撒。
教堂穹顶上挂着的吊灯不停地来回摆动,这本是司空见惯的现象却引起了伽利略的注意,他被吊灯摆动的节律性吸引住了。
伽利略看到出了神,尽管吊灯摆动的幅度越来越小,但每摆动一次的时间似乎是相等的。
这个现象令他大为惊奇,于是他决定仔细地观察。
他记得医学老师讲过,脉搏的跳动是有规律的,于是,他一面按住手腕数脉搏跳动的次数,一面注视着灯的摆动。
果然不错,灯每往返一次摆动的时间完全相同。
接着,又一个疑问冒了出来:假如吊灯受到强风吹动,摆得高了些,它每摆动一次的时间还是一样吗?回到宿舍,伽利略模仿吊灯开始了实验,他把铁块固定在绳子的一端后挂起来,将铁块从竖直位置向侧面拉开不同的距离,仍用脉搏测量摆动的时间。
实验结果证明他最初的假设是正确的,即“不论摆动的幅度大些还是小些,完成一次摆动的时间是相同的”。
在物理学中这叫做摆的等时性原理。
直到今天仍在使用的各种机械摆钟,都是根据这个原理制成的。
发现摆的等时性后,伽利略决定继续研究下去。
他换用不同质量的铁块系在绳端作为摆锤,结果发现,只要绳子的长度一样,摆动一次的时间并不受摆锤质量的影响。
随后伽利略又猜测:如果将摆绳缩短,摆是否会摆动得快些?于是他固定摆锤的质量,改变摆绳的长度进行实验,结果也证实了他的猜测:摆绳越短,摆动一次的时间就越短。
多年之后,荷兰物理学家惠更斯找到了摆的周期与摆长之间的定量关系。
又过了100多年,牛顿发现了万有引力定律,摆的等时性终于从理论上得到了圆满的解释。
根据以上的原理,人们制造出了摆钟,之后又制成了各种各样的钟表。
思考:1.研究物体等时性运动现象的著名科学家是2.伽利略在研究单摆的运动中先后提出个假设或猜想,分别是________________________________ 3. 探究物理规律可以有很多方法。
第1讲 等腰三角形八年级数学下册同步讲义(北师大版)

第1讲 等腰三角形 1. 掌握等腰三角形,等边三角形的性质,并能利用它证明两个角相等、两条线段相等以及两条直线垂直.2. 掌握等腰三角形,等边三角形的判定定理.3. 熟练运用等腰三角形,等边三角形的判定定理与性质定理进行推理和计算. 知识点01 等腰三角形1.等腰三角形的定义有两条边相等的三角形,叫做等腰三角形,其中相等的两条边叫做腰,另一边叫做底,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角. 如图所示,在△ABC 中,AB =AC ,则它叫等腰三角形,其中AB 、AC 为腰,BC 为底边,∠A 是顶角,∠B 、∠C 是底角.要点诠释:等腰直角三角形的两个底角相等,且都等于45°.等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角).∠A =180°-2∠B ,∠B =∠C =1802A ︒-∠ . 2.等腰三角形的性质性质1:等腰三角形的两个底角相等(简称“等边对等角”).性质2:等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合(简称“三线合一”).3.等腰三角形的性质的作用性质1证明同一个三角形中的两角相等.是证明角相等的一个重要依据.性质2用来证明线段相等,角相等,垂直关系等.4.等腰三角形是轴对称图形 目标导航知识精讲等腰三角形底边上的高(顶角平分线或底边上的中线)所在直线是它的对称轴,通常情况只有一条对称轴.5.等腰三角形的判定如果一个三角形中有两个角相等,那么这两个角所对的边也相等(简称“等角对等边”).要点诠释:等腰三角形的判定是证明两条线段相等的重要定理,是将三角形中的角的相等关系转化为边的相等关系的重要依据.等腰三角形的性质定理和判定定理是互逆定理.【知识拓展1】根据等边对等角求角度例1.(2021·贵州·思南县张家寨初级中学八年级阶段练习)如图,在等腰三角形ABC中,AB=AC,点D为AC上一点,且AD=BD=BC,则∠A等于多少?例2.(2021·黑龙江省八五一一农场中学八年级期末)如图,△ABC中,AB=AC=CD,BD=AD,求△ABC中∠CAB 的度数例3.(2021·广东·广州市白云区广大附中实验中学九年级阶段练习)已知:如图所示,在Rt△ABC中,∠C =90°,D是BC上一点,且DA=DB,∠B=15°.求∠CAD的度数.例4.(2021·广西三江·八年级期中)如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,求∠C的度数.【即学即练1】如图,已知△ABC中,AB=BD=DC,∠ABC=105°,求∠A,∠C度数.【即学即练2】已知:如图,D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,求∠B的度数.【知识拓展2】利用三线合一求解与证明例1.(2021·湖北武汉·八年级阶段练习)如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证:BD =CE.⊥,垂足为D,E是BC延长线上的一点,例2.(2021·重庆·八年级期中)如图:已知等边ABC中,BD AC=,且CE CD(1)求证:BD DE=;(2)若M为BE中点,求证:DM平分BDE∠.例3.(2021·河南镇平·八年级阶段练习)下面是某数学兴趣小组探究用不同方法作一个角的平分线的讨论片段,请仔细阅读,并完成相应的任务.小明:如图1,(1)分别在射线OA,OB上截取OC=OD,OE=OF(点C,E不重合);(2)分别作线段CE,DF的垂直平分线l1,l2,交点为P,垂足分别为点G,H;(3)作射线OP,射线OP即为∠AOB的平分线.简述理由如下:由作图知,∠PGO=∠PHO=90°,OG=OH,OP=OP,所以Rt△PGO≌Rt△PHO,则∠POG=∠POH,即射线OP是∠AOB的平分线.小军:我认为小明的作图方法很有创意,但是太麻烦了,可以改进如下,如图2,(1)分别在射线OA,OB 上截取OC=OD,OE=OF(点C,E不重合);(2)连接DE,CF,交点为P;(3)作射线OP.射线OP即为∠AOB的平分线.……任务:(1)小明得出Rt△PGO≌Rt△PHO的依据是_______(填序号).①SSS;②SAS;③AAS;④ASA;⑤HL(2)如图2,连接EF.①求证:△CEF ≌△DFE ;②求证:△PEF 是等腰三角形;③小军作图得到的射线OP 是∠AOB 的平分线吗?请判断并说明理由.例4.(2021·广东广州·八年级阶段练习)如图,在ABC 中,AB AC =,AD BC ⊥,垂足为D ,AB :AD :13BD =:12:5,ABC 的周长为36,求ABC 的面积.例5.(2022·黑龙江富裕·八年级期末)已知:在△ABC 中,∠ABC =45°,CD ⊥AB 于点D ,点E 为CD 上一点,且DE =AD ,连接BE 并延长交AC 于点F ,连接DF .(1)求证:BE =AC ;(2)若AB =BC ,且BE =2cm ,则CF = cm .例6.(2021·江苏滨海·八年级期中)如图,厂房屋顶的人字架是等腰三角形,AB=AC,AD⊥BC,若跨度BC =16m,上弦长AB=10m,求中柱AD的长.【即学即练1】(2021·福建·福州三牧中学九年级阶段练习)如图,在△ABC中,∠A=40°,∠ABC=80°,BE 平分∠ABC交AC于点E,ED⊥AB于点D,求证:AD=BD.【即学即练2】(2021·黑龙江五常·八年级阶段练习)已知:以线段AB为边在线段的同侧作△ABC与△BAD,BC与AD交于点E,若AC=BD,BC=AD.(1)如图1,求证:CE=DE;AB的线段.(2)如图2,当∠C=90°,∠AEB=2∠AEC时,作EF⊥AB于F,请直接写出所有等于12【即学即练3】(2021·吉林·八年级期末)如图,在ABC 中,AB AC =,AD 为边BC 的中线,E 是边AB 上一点(点E 不与点A 、B 重合),过点E 作EF BC ⊥于点F ,交CA 的延长线于点G .(1)求证:AD //FG ;(2)求证:AG AE =;(3)若3AE BE =,且4AC =,直接写出CG 的长.【即学即练4】(2021·江苏·扬州市梅岭中学八年级阶段练习)在平面直角坐标系中,三角形△ABC 为等腰直角三角形,AC =BC ,BC 交x 轴于点D .(1)若A (﹣8,0),C (0,6),直接写出点B 的坐标 ;(2)如图2,三角形△OAB 与△ACD 均为等腰直角三角形,连OD ,求∠AOD 的度数;(3)如图3,若AD 平分∠BAC ,A (﹣8,0),D (m ,0),B 的纵坐标为n ,求2n +m 的值.【知识拓展3】等腰三角形中的分类讨论例1.在等腰三角形中,有一个角为40°,求其余各角.例2、已知等腰三角形的周长为13,一边长为3,求其余各边.【即学即练】如图,△ABC 中BD 、CD 平分∠ABC 、∠ACB ,过D 作直线平行于BC ,交AB 、AC 于E 、F ,AB=5,AC=7,BC=8,△AEF 的周长为( )A .13B .12C .15D .20【知识拓展4】等腰三角形性质和判定综合应用例1、已知:如图,ABC △中,45ACB ∠=︒,AD⊥BC 于D ,CF 交AD 于点F ,连接BF 并延长交AC 于点E , BAD FCD ∠=∠.求证:(1)△ABD≌△CFD;(2)BE⊥AC.知识点02 等边三角形1.等边三角形定义:三边都相等的三角形叫等边三角形.要点诠释:由定义可知,等边三角形是一种特殊的等腰三角形.也就是说等腰三角形包括等边三角形.2.等边三角形的性质:等边三角形三个内角都相等,并且每一个内角都等于60°.3.等边三角形的判定:(1)三条边都相等的三角形是等边三角形;(2)三个角都相等的三角形是等边三角形;(3)有一个角是60°的等腰三角形是等边三角形.【知识拓展4】等边三角形例1、如图.在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.(1)试判定△ODE的形状,并说明你的理由;(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.【即学即练】等边△ABC,P为BC上一点,含30°、60°的直角三角板60°角的顶点落在点P上,使三角板绕P点旋转.如图,当P为BC的三等分点,且PE⊥AB时,判断△EPF的形状.【知识拓展5】在直角三角形中,30°角所对的直角边等于斜边的一半。
八年级物理上册知识讲义-1.认识熔化与凝固-北师大版

课标定位一、考点突破1. 知道物质的固态和液态之间是可以转化的,知道熔化和凝固的概念。
2. 能够区分生活、生产中的熔化与凝固现象。
3. 知道晶体和非晶体的区别。
4. 知道物质的状态与熔点(凝固点)的关系。
二、重难点提示重点:能够辨别熔化与凝固现象及伴随着的吸、放热过程。
难点:晶体与非晶体的异同点。
考点精讲一、熔化和凝固(重点)1. 熔化:物质由固态变为液态的过程叫做熔化。
如冰变为水,由固态变为液态属于熔化现象。
2. 凝固:物质由液态变为固态的过程叫做凝固。
如水结成冰,由液态变为固态属于凝固现象。
【归纳·整理】熔化和凝固是发生在固态和液态之间的物态变化过程,判断物态变化是否属于熔化和凝固,关键是看物质是由固态变液体,还是由液态变固态。
熔化和凝固是两个相反的物态变化过程。
【课堂练习】下列自然现象中,属于熔化现象的是()A. 春天,河里的冰化成水B. 夏天清晨,花草叶子上花附着的露水C. 秋天清晨,笼罩大地的雾D. 冬天,空中纷飞的雪花思路分析:要判断物态变化是否属于熔化,关键要看物质是不是从固态变为液态。
选项A冰化成水,由固态变为液态,属于熔化现象;选项B露水不是由固态的冰变成的;选项C 雾也不是由固态的冰变成的;选项D雪是固态,不是液态,所以本题应选A。
答案:A二、晶体和非晶体1. 固体分为晶体和非晶体两大类(1)晶体:通过实验探究固体熔化时温度的变化规律,发现有些固体在熔化过程中尽管不断吸热,温度却保持不变。
这类固体有确定的熔化温度,我们把这类固体叫做晶体。
晶体分子的排列是整齐的、有规则的,冰、食盐、石墨、金属等都是晶体。
(2)非晶体:有些固体在熔化过程中,只要不断地吸热,温度就不断上升,没有固定的熔化温度。
这类固体没有确定的熔化温度,我们把这类固体叫做非晶体。
非晶体分子的排列是杂乱无章的。
石蜡、松香、玻璃、沥青等都是非晶体。
2. 熔点和凝固点(1)定义:晶体熔化时的温度叫做熔点,晶体凝固时也有确定的温度,这个温度叫做凝固点。
牛津译林版英语八年级寒假复习预习讲义01

第一讲Grammar 形容词和副词Part 1形容词的比较级和最高级形容词有三种等级:原级、比较级、最高级。
原级:句中只有一者时用原级,其标志词是very, so, too, quite等。
⏹His handwriting is very good.他的书法很好。
(一个人不作比较。
)★形容词比较级和最高级的构成:一般在原级后加er 构成比较级,加est构成最高级。
①规则变化②. 不规则变化①.⏹My bike is more beautiful than hers.我的自行车比她的漂亮。
⏹He works harder than before. 他工作比以前努力。
②.表示“两者之间较……之一”⏹Which is nearer to the sun, the moon or the earth? 哪个离太阳更近,月球还是地球?⏹He is the thinner of the two. 他是两人中较瘦的那个。
③“more and more 原级”。
⏹The weather is being colder and colder. 天气变得越来越冷了。
⏹She is being more and more beautiful. 她变得越来越美了。
④. 表示“越……越……”时,用“the+比较级,the+比较级”结构。
⏹The more careful you are, the more points you will get. 你越细心,得分越多。
①. 表示三者及以上人或物进行比较时用最高级,结构为⏹The picture is the best of all. 这幅画是所有画中最好的。
⏹She is the most beautiful girl in the class. 她是班上最美的女孩。
②. 表示在三者及以上之间选择,用⏹Who is the tallest, Tom, Kate or Bill? 汤姆、凯特、比尔,谁最高?③. 表示“最……之一”用⏹She is one of the most popular teachers in our school. 她是我们学校最受欢迎的老师之一。
人教版物理八年级上册第一章《机械运动》讲义

物理八年级上册第1章《机械运动》讲义(一)知识点1.长度的测量1. 长度单位及换算常用的长度单位由大到小排列为km 、m 、dm 、cm 、mm 、µm、nm .记忆它们之间的换算关系时,有以下方法: 按单位的大小顺序记忆: 先记住长度单位大小的排列顺序;再记住相邻单位之间的换算关系(如下图所示);需进行单位换算时,根据上图便可算出所需换算的两单位之间换算关系:如要知道km 与cm 之间的换算关系,则可由图得出:3113+1+151km=101010cm=10cm=10cm ⨯⨯;又如要知道nm 与dm 之间的换算关系,则可由图得出:3311331181nm=10101010dm=10dm=10dm ---------⨯⨯⨯知识点2.正确选择、使用刻度尺、认识长度测量长度的工具是刻度尺。
(1)使用刻度尺测量物体长度前,首先要弄清刻度尺的量程、分度值和零刻线的位置。
(2)选择刻度尺时应根据测量的要求来选择。
(例如:要测量一支钢笔的长度,精确到mm ,则可选用分度值是1mm 、量程是150mm 左右的刻度尺;而在体育课上要测量跳远的长度,则可选用分度值是1cm 的皮卷尺。
)(3)使用刻度尺测量物体长度时,刻度线要紧贴被测物体,被测长度的一端要与刻度尺的零刻线对齐(若零刻线已磨损,则选择刻度尺上另一完好的刻度线),读数时视线要与尺面垂直,且正对刻度线读数。
例题:1、下列各物体中接近130厘米的是:( )A .体温表长度; B .乒乓球的直径; C .课桌高; D .写字台长度.2、用塑料皮尺测量物体长度时,若用力拉尺测量时,测量结果比真实值:( )A .偏大B .偏小C .不变D .无法确定练习:一本书的厚度为8 ; 课桌的高度约为80 ;一支粉笔的长度约为8 ; 一位学生的身高为160 ;双人课桌的长度是120 ; 圆珠笔芯塑料管的直径是3 ;乒乓球的直径约是40 ; 教室门的宽度是0.95 。
人教版英语八年级上册暑假班讲义+1动词

新初二暑假班讲义 1实义动词系动词be动词(am,is,are),感官动词(feel,look,smell,sound,taste,seem)+动原/形容词,“变得”词(get,become,turn,grow),“保持”(remain)。
情态动词助动词协助主要动词构成谓语的词叫助动词,也叫辅助动词。
被协助的动词称作主要动词。
助动词用来构成时态和语态。
最常用的助动词有:have/has, do/does/did 等。
考点二.七上到八上所有动词及词组分类(需要死记硬背.硬背.硬背)四个看see see sb doing sthlook look at注视;考察固定搭配,完型或语填watch watch TVread Read newspaper四个说speak speak Chinese;演讲give a speech(n.) say say sthtalk talk about(关于某事)/to(对某人)tell Tell(告诉;讲述) sb(not) to do sth四个花费spend(人)spend on sth spend (in )doing sth cost(物)cost sb some moneytake(物)It takes sb some money to do sthpay pay for(支付) pack back回报pay off付清四个变化turn颜色变化get天变黑.变长.变短become天气变暖.变冷grow形状变大或变小三个穿dress dress sb/dress sb upwear穿着He wears a coat today. put on He is putting on a coat.三个听hear听到sound听起来;n.声音listen listen to三个到达get get toreacharrive arrive in arrive atbe good at doing sth.= do well in doing sth. be good with sb. be good for. be strict with sb. be strict in sth.be afraid to do sth. be afraid of doing sth.+doing+to do+动原thank you for doing sth need sb. to do sth let sb do sth. what/how about doing sth help sb. to do sth make sb do sth practice doing sth want sb. to do sth Why not do. sth.?■■既可以remember/forget to do sth remember/forget doing sth (指动作尚未发生) (指动作已经发生)stop to do sth stop doing sth 停止手中事,去做另一件事停止正在做的事go on to do sth go on doing sth 接着做另外一件事接着做同一件事try to do sth try doing sth 设法,努力去做,尽力试试去做,看有何结果mean to do sth mean doing sth 打算做,企图做意识是,意味着can’t help to do sth can’t help doing sth 不能帮忙做忍不住要做give 短语give away赠送,给予,背弃,泄露,让掉give out 用完,耗尽,发出(声音),宣布,分发give off 释放,发出放出(烟.光.热等) give up 停止,放弃,自首give in 承认,投降,屈服;交上,呈上give back 归还,返还look短语look into 调查look after 照顾,照料,照管;注意,关心look out=be careful=take care留神,当心,注意,警惕,提防look up 查找,查阅, 查字典look through 快速浏览,翻阅,温习look at 朝..看;看待;考虑,研究look for 调查,研究;寻找look forward to sth(doing sth)期望,盼望look over把...看一遍,把...过目;察看,参观look around 环顾四周;转头看look like...看起来像...get 短语get away 移走,拿走,逃脱,逃离get down 下来,降下get in 进入,收获,达到get into... 进入...... get on 上车get off 下车get on / along with..进展,与...相处get out 离开,出去get over 克服,恢复,原谅get up 起床,起身have a good time=have a great time =have fun ( doing sth)ask sb. to do sth ask sb not to do sthenjoy doing sth like/love doing sth tell sb.to do sth.tell sb. (not) to do sth.be interested in doing sth decide to do sth.keep(on) doing sth.seem+(to be)+ adj.feel like doing sth.it’s adj. for sb. to do sth miss doing sth.plan to do sthmind doing sth.hope to do sthstand doing sth.happen to do sthplay a role in doing sth.expect to do sthlook forward to doing sth.try one’s best to do sthbe ready to do sthpromise to do sthagree to do sth.the way to do sth.invite sb. to do sthadvise sb. to do sth.advise sb (not) to do sth.get to 到达,抵达go短语go away 走开,离去go by 走过,经过,(时间)消逝,过去按go off 走开,熄灭,(闹钟)闹响go on 发生,进行,继续go over 复习,审阅,仔细检查go back 回去come 短语come across 偶然相遇come along 出现,随同,进展,加油come in 进来,进入come on 过来,跟我来,加油,来吧,赶快come out 露出,出来,出现,出版,发(芽),(花)开come true 变为现实,成为事实come up with... 提出,想出(主意),找出(答案),赶上turn 短语.turn on 打开(灯,气,水,电器等)turn off 关掉(灯,气,水,电器等) turn up 把音量大,卷起,翻起,发生,出现,到达turn down 关小/调低(音量/热度),拒绝turn over 把......翻过来,翻动,犁翻(土地),细想turn in 上缴,归还turn into 变成turn out 结果是,生产turn right / left 向右/向左拐keep短语keep away from 避开,别靠近keep off sb / sth 不接触或不接近某人/某事物keep...out 把......挡住,把......留在外面keep up with... = catch up with...跟上,赶上keep (on) doing sth 继续不停地做某事keep... from doing 阻止....做,不让....做take短语take away 拿走,拿去,使离开take down 拿下,记下,记录take off (飞机)起飞,脱掉(衣帽/鞋),成名,成功,很快上升,开始流行/畅销take out 拿出,取出take over 继承,接管,接替take up 从事,开始,专注于,占去(时间.空间.地位等)take a message (to sb) (给某人)捎个口信take care of 照顾,照看take part in 参加take place 发生,出现,举行take pride in ...= be proud of...对......感到自豪put短语put on 穿上; put into 使进入;把...放进;在......上种植put up 提供;建造;举起;推举,提名;供给...住宿put together ..放在一起;组合;装配put out 熄灭;伸出;出版;使不方便,打扰put down 镇压;记下;贬低;制止put off 推迟;扔掉;阻止put away把......收起来1.--- Jane’s spoken English is pretty good.---- Yeah, she works hard and practices _________ (speak)it both in and out of class.2.----The weather report says it's going to have a shower this afternoon.-It does?We'd better____(leave)now,just in case.3.We are glad ________ (know)that traditional Chinese medicine can work wonders in preventing some diseases.4.You ______(be) from India. Brian _____(be) from Korea. And I _____ (be)from China.5.Peter____________English very well.(speak.say.tell.talk)6.Don‘t forget___________(bring)your clothes.7.Could you ask her____________(have)dinner with me?8.It‘s6:20.It‘s time___________(get)up now.9.Why not___________(come)to China?Good idea.10.Let me___________(help)you.11. -- How about____________(swim)this Sunday?-- No problem.12.Do you know her? I remember you ______ (tell)about her.13.My brother practices _________ (swim)e very Sunday.14.Jack, are you having a great time (swim)in the pool?15.They _____ a tent and made a fire to keep them warm .A put upB put onC put downD put off16.Food is good _______ our health,and my friend Lily is good ________ cooking(烹饪) nice food. A. at;for B. with;for C. for;at D. at;with 17.The baby is sleeping.Don’t the radio!A turn upB turn onC turn downD turn off 考点三.七上到八上动词时态(没错,就是重点中的重点) 练习:一.用动词的正确形式填空1. Tom always __________(get) up at seven in the morning .2. Lynn seldom ___________ (play) the guitar because she is good at ________ (dance)3. Listen ! Who is ___________ (sing) in the classroom ?4. The pen ____________ (look) nice .5. I usually ____________(play) sports at 4:306. She often _____________(go) shopping on the weekend .7. He is___________ (write) a letter now.8. I'm going to ______________(visit)my grandparents tomorrow.9. Janet ______________ (get) up at 7:30 a.m. every day, so she is always late for school. 10. We_______________ (go) a park last weekend.11.He______________(read) when the teacher comes in. 12.I am reading while he____________(wash) the clothes 13.He ________(visit) his aunt next week.14.There ________(be) more people in the future. 二.单项选择( )1. What _____ you _____ over the weekend? A. will; do B. does; do C. did; do D. were,; doing ( )2. Xiao Li usually _____ to school by bike last year.时态类别一般现在时 现在进行时 一般过去时 一般将来时概 念表示经常发生的或习惯性的动作或目前的状态。
八年级物理下册同步讲义第1讲-运动和力(知识点、例题、答案与解析)

初二春季讲义运动和力学生姓名:上课时间:运动和力知识点睛知识点1:力的概念:1.力是物体对物体的相互作用。
2.力是不能离开物体而单独存在的3.力的作用是相互的,因此,力的出现必须是成对的,即必须有作用力和反作用力。
4.力作用的物体不一定要相互接触,相互接触的物体间不一定有力的作用。
5.影响力作用效果的三要素:力的大小、方向、作用点6.力的作用效果:一是改变物体的运动状态,二是改变物体的形状。
例题精讲【例1】托起两个鸡蛋的力约为()A. 0.1NB. 1NC. 10ND. 100N【例2】(多选)下列关于力的叙述中,正确的是()A.力是物体对物体的作用,总是成对出现B.物体只有相互接触,才有力的作用C.两物体相互作用不一定要直接接触D.直接接触的物体间一定有力的相互作用【例3】(多选)下列关于力的作用效果的叙述中,正确的是()A.物体的运动状态发生改变,则物体必定受到力的作用B.物体运动状态没有发生改变,物体也可能受到力的作用C.力的作用效果不仅取决于力的大小和方向,还与力的作用点有关D.力作用在物体上,必定同时出现形变和运动状态的改变【例4】(多选)下列情况中,物体运动状态发生变化的是()A.运动的汽车减速行驶B.匀速下降的跳伞运动员C.停在车站内的火车D.在空中飞行的足球【例5】用手通过一根绳子提起一重物时,会感到手受到一个向下的力的作用,这个力的施力物体是()A.重物B.地球C.绳子D.绳子和重物【例6】图中甲、乙都表示力的作用效果,其中甲表示________________,乙表示___________________。
【例7】(多选)用脚踢球时,下列说法正确的是A.脚是施力物体,所以它不受力B.脚是施力物体,也是受力物体C.脚受到的力的施力物体是足球D.脚踢足球的力和球对脚的作用力同时发生【例8】小明用桨向后划水,使船前进的力的施力物体是()A.船桨B.船C.小明D.水【例9】下列过程中,有一个力的作用效果与其他三个不同类,它是()A.把橡皮泥捏成不同造型B.进站的火车受阻力缓缓停下C.苹果受重力竖直下落D.用力把铅球推出【例10】不会影响力的作用效果的是()A.力的作用点B.力的方向C.力的大小D.力的单位课堂检测【题1】下列物体间没有发生力的作用的是()A.手提水桶B.相互靠的很近的同名磁极C.马路上的红灯和绿灯D.蚂蚁搬运食物【题2】下列关于力的说法中不正确的是()A.力是物体对物体的作用B.力能脱离物体而独立存在C.不直接接触的物体间也能产生力的作用D.一个物体不能产生力的作用【题3】如图24-2所示,运动员用网球拍击打飞过来的网球时,网球拍击打网球的力应该( ) A.比球撞击球拍的力更早产生。
八年级(上)培优讲义:第1讲-三角形的初步知识(1)

第1讲三角形的初步知识1(认识三角形、定义与命题、证明)一、知识建构1. 三角形按角分类:(1)锐角三角形:三角形的,这样的三角形称之为锐角三角形(2)直角三角形:三角形有,这样的三角形称之为直角三角形(3)钝角三角形:三角形有,这样的三角形称之为钝角三角形2. 三角形的角平分线:在三角形中,,这个角的顶点与交点之间的线段叫做三角形的角平分线。
3.三角形的中线:在三角形中,,叫做这个三角形的中线。
(1)三角形的中线的形状也是一条;(2)三角形的三条角中线.4.三角形高的定义:从三角形的一个顶点线,的线段叫做三角形的高。
5.三角形三边之间的关系为:6.能清楚地规定某一名称或术语的句子叫做该名称或术语的______.7.对某一件事情作出_______判断的句子叫做命题.•每个命题都是由______•和______两部分组成的.8.思考下列命题的条件和结论分别是什么?并判断那些命题正确? 那些命题不正确?(1)相等的角是对顶角。
(2)直角三角形两锐角互余。
(3)同位角相等。
(4)一个角的补角一定大于这个角的余角。
9. 阅读教材内容后请回答:(1)怎样判断一个命题是真命题还是假命题?(1)真命题、公理、定理三者的区别与联系各是什么?10.判断下列命题是真命题还是假命题?如果是假命题,请说明理由;如果是真命题,请用推理的方法来说明.(1)如果ab=0,那么a=b=0;(2)如图,若AC∥DE,∠1=∠2,则AB∥CD.二、经典例题例1.对于同一平面内的三条直线a,b,c,给出下列5个判断:①a∥b②b∥c;•③a⊥b;④a∥c;⑤a⊥c.请以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题(至少写两个命题).例2.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于()A.44°B.60°C.67°D.77°例3. 如图,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连接A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连接A2B2…按此规律下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠A n+1B n B n+1=θn,则(1)θ1= , (2)θn= .例4.如图,在Rt△ABC中,∠ACB=90°,∠A=α,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,则旋转角的大小为.图1图2DC EA B例5. 一个三角形的三条边长分别为1、2、x ,则x 的取值范围是( )A .1≤x ≤3B .1<x ≤3C .1≤x <3D .1<x <3例6. 已知实数x ,y 满足,则以x ,y 的值为两边长的等腰三角形的周长是 .例7. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B C E ,,在同一条直线上,连结DC .(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母); (2)证明:DC BE .例8.如图,已知AB ∥CD ,直线EF 分别截AB 、CD 于 点M 、N ,MG 、NH 分别是∠EMB 与∠END 的平分线.求证:MG ∥NH . 请根据分析思路,写出证明过程.三、基础演练1.在△ABC 中,若∠A +∠B =88°,则∠C =_______,这个三角形是______ 三角形.∠EMG=12∠∠ENH=12∠END可证∠EMG=∠MNH要证MG ∥NH 只需证:∠EMB=∠END已知AB ∥CDABCDE FHMN2.直角三角形的一个锐角为42°,则另一个锐角为_________.3.在△ABC 中,若∠A =35°,∠B =68°,则与∠C 相邻的外角等于_______ °.4.若5条线段长分别为1cm ,2cm ,3cm , 4cm ,5cm ,则以其中3条线段为边长可以构成三角形的个数是___________ .5.一木工师傅有两根70,100长的木条,他要选择第三根木条,将它们钉成三角形木架,则第三根木条取值范围_____________ ,木架周长的取值范围_____________ . 6. 如图所示,下面的推理中正确的是 ( ) A .∵∠1=∠2,∴AB ∥CDB .∵∠ABC +∠BCD =180°,∴AD ∥BC C .∵AD ∥BC ,∴∠3=∠4D .∵∠ABC +∠DAB =180°,∴AD ∥BC 7.命题“若a b >,则1ab>”是真命题还是假命题?请说明理由.8.若等腰三角形腰长为6,则底边x 的取值范围是 ( ) A . 6<x <12 B . 0<x <6 C . 0<x <12 D . 无法确定9. 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A .锐角三角形B .直角三角形C .钝角三角形D .锐角三角形 10.如图所示,在△ABC 中,∠C =90°,BD 平分∠ABC 交AC 于点D ,过点D 作DE ∥BC •交AB 于点E ,过点D 作DF ⊥AB 于点F .求证:BC =DE +EF .四、直击中考1. (2013广西)一个三角形的周长是36cm ,则以这个三角形各边中点为顶点的三角形的周长是( )A .6cmB .12cmC .18cmD .36cm2.(2013衡阳)如图,∠1=100°,∠C =70°,则∠A 的大小是( )A .10°B .20°C .30°D .80°3241D CBA B CE DF A3.(2013鄂州)一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )A .165°B .120°C .150°D .135°4.(2013黔东南州)在△ABC 中,三个内角∠A 、∠B 、∠C 满足∠B ﹣∠A =∠C ﹣∠B ,则∠B = 度.5.(2013温州)如图,直线a ,b 被直线c 所截,若a ∥b ,∠1=40°,∠2=70°,则∠3= 度.6.(2013雅安)若(a ﹣1)2+|b ﹣2|=0,则以a 、b 为边长的等腰三角形的周长为 .7.(2013东城).如图,∠ACD 是△ABC 的外角,ABC ∠的平分线与ACD ∠的平分线交于点1A ,1A BC ∠的平分线与1A CD ∠的平分线交于点2A ,…,1n A BC -∠的平分线与1n A CD -∠的平分线交于点n A . 设A θ∠=,则1A ∠= ;n A ∠= 8.(2014杭州)下列命题中,正确的是( )A .梯形的对角线相等B . 菱形的对角线不相等C . 矩形的对角线不能互相垂直D . 平行四边想的对角线可以互相垂直五、能力拓展1.如图,OB 、OC 是∠AOD 的任意两条射线,OM 平分∠AOB ,ON 平分∠DOC ,若∠MON =α,∠BOC =β,则∠AOD 可表示为( )A . 2α-βB . α-βC . α+βD . 2α2.如图,在锐角△ABC中,CD、BE分别是AB、AC上的高,•且CD、BE交于一点P,若∠A=50°,则∠BPC的度数是()A.150°B.130°C.120°D.1003.已知等腰三角形的周长为14cm,底边与腰的比为3:2,求各边长.4. 已知a,b,c是一个三角形的三条边长,则化简|a+b-c|-|b-a-c|的结果是多少?5.如图所示,已知等腰直角三角形ABC中,∠ACB=90°,直线L经过点C,•AD•⊥L,BE⊥L,垂足分别为D,E.(1)证明:△ACD≌△CBE;(2)求证:DE=AD+BE;(3)当直线L经过△ABC内部时,其他条件不变,(2)中的结论还成立吗?如果成立,请给出证明;如果不成立,猜想这时DE,AD,BE有什么关系?证明你的猜想.六、挑战竞赛1. 在△ABC中,∠A= 50°, 高BE,CF所在的直线相交于点O,求∠BOC.FEC AB2.△ABC 中,已知∠ABC = 74°, ∠A = 56°, BE 是AC 边上的高,CF 是△ ABC 的角平分线,求∠ACF 和∠BFC .4.如图,在△ABC 中,D 、E 分别是BC 、AD 的中点,S △ABC =4cm 2,求S △ABE .5.如图,45AOB ∠=,过OA 上到点O 的距离分别为1,4,7,10,13,16,…的点作OA 的垂线与OB 相交,得到并标出一组黑色梯形,它们的面积分别为,,,321s s s …,观察图中的规律,第4个黑色梯形的面积=4S ,第n (n 为正整数)个黑色梯形的面积=n S .6.在△ABC 中,AC AB =,D 是底边BC 上一点,E 是线段AD 上一点,且∠BAC CED BED ∠=∠=2.(1) 如图1,若∠︒=90BAC ,猜想DB 与DC 的数量关系为 ; (2) 如图2,若∠︒=60BAC ,猜想DB 与DC 的数量关系,并证明你的结论; (3)若∠︒=αBAC ,请直接写出DB 与DC 的数量关系.OA BCDEA EBCD图1 图2。
八年级上全册讲义

第一章走进实验室第一节走进实验室:学习科学探究一、观察奇妙的物理现象物理实验的显著特点是在一定条件下物理现象可以有规律的重复出现。
一切奇妙的现象,其发生都是有原因的,科学探究就是要找出其中的原因和规律。
例1、下列现象解释错误的是()A、一束阳光透过冷静后会出现七色光带,这是光的色散现象。
B、敲击右边的音叉没有被击打的音叉也会震动说明气体可以传声C、只要这个玩具鸟面前有水它就会不断点头饮水利用了鸟附中不断汽化和液化的原理。
D、用两面平面镜和几只小彩灯就能制作一个无尽的长廊利用了平面镜成像二、认识科学探究的工具___________是科学探究的重要工具。
走进实验室的目的,是让同学们认识各种仪器,初步了解仪器的使用规则,为今后设计实验选择器材打下基础,测量是物理实验的基本内容,物理实验的结果要通过测量才能知道,你知道以下测量仪器的名称和用途吗?测量同一物理量的仪器,可能有不同的____________、不同的___________和不同的___________,应根据实验的需要合理选择。
三、像科学家一样探究科学家认识自然就是从每一个奇异的现象出发深入观察和思考,不懈探究,我们也要像科学家一样进行探究。
实验探究的七个重要环节1、 ________________________ 夏天,用电风扇吹风为什么感觉凉快?2、_________________________ 可能是电风扇吹出的风温度较低3、_________________________ 用温度计测量不吹风时空气的温度为t1,用电风扇吹风,在用温度计测量温度为t2。
4、_________________________ 只进行一次实验就得出结论,结论不一定可信应该进行多次实验再得出结论。
5、_________________________按制定计划的计划进行实验,测得t1=26℃,t2=26℃。
6、_________________________ 用电风扇吹风不能降低温度感觉凉快应该另有原因7、_________________________解析实验探究中不一定所有的环节都经历有些探究智能经历三四个环节,这些环节没有固定的顺序,如提出问题后可能进行评估,制定计划后就进行交流合作。
Unit1单词知识点讲义人教版英语八年级上册

2023年人教版初中英语八年级上册Unit 1单词知识点讲解(讲义)1. anyonea.pron. 任何人,某个人 (否定句和疑问句)I won’t tell anyone that I saw you here.我不会告诉任何人我在这儿见着你了。
You needn’t talk to anyone if you don’t want to.如果你不想的话,你不需要跟任何人说话。
Why would anyone want that job?为什么会有人想要做那样的工作?Is there anyone in the classroom?教室里有人么?b.pron. 任何人(肯定句表强调)或者用在“anyone who +句子”的结构中Anyone can do what I am doing now.任何人都可以做我正在做的事情。
This job isn’t for anyone who is slow with numbers.这份工作不适合对数字不感冒的人。
c.anyone同义词anybody2. anywherea. adv.任何地方(否定句和疑问句中)Do you have anywhere to live?Did you try to get help from anywhere?Did you go anywhere interesting?Have you ever been to Beijing, Shanghai or anywhere?b. adv.任何地方(肯定句表强调)I’ll meet you anywhere you want.3. wonderfuladj. 极棒的; 绝妙的;It’s wonderful to see you here.She is a wonderful mother.wonder v.想知道 n. 奇迹4. fewdet./pron./adj. 几个;很少a few +可数名词复数, 译为”几个,一些”a few apples 几个苹果few+可数名词复数, 译为”很好,没有”few houses 很少房子;几乎没有房子a liitle +不可数名词, 译为”一些”little+不可数名词, 译为”没有,很少”I have little time to chat with you.5. quite a few 相当多的Quite a few people are going there.6. mostdet./pron./adj. 大多数的much,many,a lot of的最高级, 译为最多adv.极其,最大程度上的;最Most animals are afraid of fire.Most of my friends are Chinese.I like most vegetables.He thought the whales were the most beautiful animals.The most important thing in life is that you never lost yourself.7. somethingpron. 某事;某物There was something wrong with the car.something like 有点儿像…She made a sound, something like a cat.真不错She’s really something.or something; or something like that诸如此类的…Could you please give some water, milk or something?Many foreigners think all Chinese people can do Gongfu or something like that.8. nothingpron./adj./adv./n. 没什么;没一个;不重要She nodded her head but said nothing.Nothing beats home cooking. 什么也比不上家里做的好吃。
北师大版数学八年级下第一章、一元一次不等式与不等式组培优复习讲义(一)

戴氏西门总校数学资料北师大版八年级下第一章、一元一次不等式与不等式组复习讲义(一)第一部分、要点概况(一)不等关系1、一般地,用符号“<”、“≤”、“>”、“≥”、“≠”连接的式子叫做不等式。
注意:⑴要弄清不等式和等式的区别:等式有等号,而不等式没有。
⑵常用的不等号有:<、≤、>、≥、≠。
⑶列不等式是数学化与符号化的过程,它与列方程类似,列不等式注意找到问题中不等关系的词,如: “正数(>0)”, “负数(<0)”, “非正数(≤0)”, “非负数(≥0)”, “超过(>0)”, “不足(<0)”, “至少(≥0)”, “至多(≤0)”, “不大于(≤0)”, “不小于(≥0)”⑷除了⑶常见不等式所表示的基本语言与含义还有: ①若a -b >0,则a 大于b ; ②若a -b <0,则a 小于b ; ③若a -b ≥0,则a 不小于b ; ④若a -b ≤0,则a 不大于b ;⑤若ab >0或0ab >,则a 、b 同号; ⑥若ab <0或0ab<,则a 、b 异号。
⑸不等号具有方向性,其左右两边不能随意交换:a <b 可转换为b >a ,c ≥d 可转换为d ≤c 。
例1:判断下列哪些式子是不等式,哪些不是不等式。
①32>-; ②21x ≤; ③21x -; ④s vt =; ⑤283m x <-;⑥124x x ->-;⑦38x ≠;⑧5223x x -≈-+;⑨240x +>;⑩230xπ+>。
不等式: 。
变式训练1:已知下列各式:①-1<0,②2+3=5 ③3x>7 ④2x-3y=1 ,其中不等式有不等式: 。
例2:⑴a 是正数: ;⑵x 的平方是非负数: ; ⑶a 不大于b : ;⑷x 的3倍与-2的差是负数: ;⑸长方形的长为x cm ,宽为10cm ,其面积不小于200cm 2: 。
变式训练2:用不等式表示:(1)x 与1的差不大于y 的3倍; (2)a 与b 的平方和是非负数;例3:试判断237a a -+与32a -+的大小变式训练3-1:比较1415-与1314-的大小。
2020浙教版科学八年级上册暑假培优讲义 第1讲:浮力知识的运用(含答案)
浮力知识的运用【复习回顾】1.水的分布:海洋水是地球水的主体,约占地球总水量的96.53%,覆盖了地球大约71%的表面。
陆地淡水尽管只占总水量的2.53%,目前人类利用的淡水资源主要是河流水、湖泊淡水以及浅层地下水。
2.水循环(1)形成水循环的内因:水的物理属性,即水随着温度的不同,会以固态、液态和气态三种形态出现。
(2)导致水循环的外因:太阳辐射和地心引力。
(3)水循环:<1>小循环:①陆上内循环:陆地—大气;②海上内循环:海洋—大气。
<2>大循环:海陆间水循环:海洋—陆地—大气。
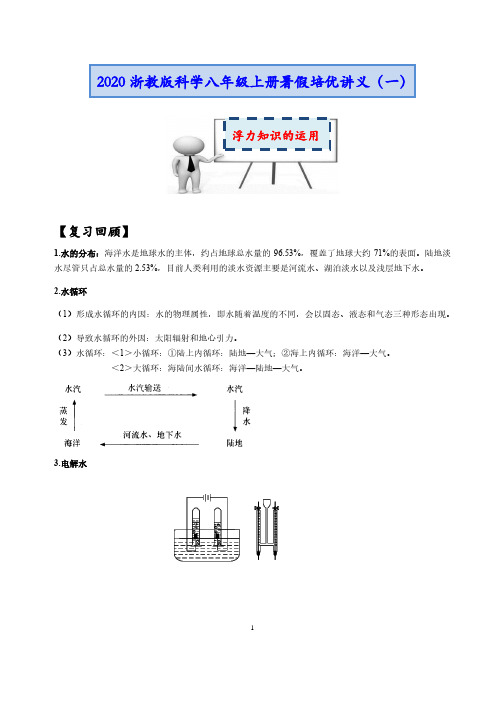
3.电解水12实验结论:氢气中的氢和氧气中的氧是从水中产生的,所以水是由氢和氧组成的。
4.浮力的概念:一切浸入液体(气体)的物体都受到液体(气体)对它竖直向上的力叫浮力。
5.浮力的方向:竖直向上 施力物体:液(气)体6.浮力的计算:(1)浮力产生的原因:液(气)体对物体上下表面都有压力,浮力是上下表面的压力差(F 浮=F 下-F 上)。
(2)示重差法测浮力:物体在空气中的重与物体在液体中的重的差值等于浮力。
即F 浮=G 空-G 液。
(3)阿基米德原理:浸在液体里的物体,受到向上的浮力,浮力的大小等于物体排开的液体受到的重力, 表达式:F 浮 = G 排液= m 排g = ρ液gV 排液(4)沉浮条件法:物体漂浮或悬浮时:F 浮=G 物7.物体的浮沉条件(1)物体在水中的浮沉状态分为“两动”——上浮、下沉;“三静”——漂浮、悬浮、沉底。
根据物体处于受力平衡或非平衡状态,可得出相应的受力分析。
(2)浸没在液体中的物体,受到竖直向下的重力和竖直向上的浮力两个力的作用。
这两个力的相对大小决定了物体是上浮、悬浮还是下沉。
(如图物体为实心物体)上浮 漂浮 悬浮 下沉示意图F 浮与G 物F 浮〉G 物 F 浮=G 物 F 浮=G 物 F 浮<G 物 ρ液与ρ物ρ液〉ρ物 ρ液=ρ物 ρ液=ρ物 ρ液<ρ物 8.怎样判断物体的浮沉及浮沉的应用气体体积 体积比 检验气体 是什么气体 正极 少 负极正极V V =21 能使带火星木条复燃 氧气 负极 多 能燃烧,火焰呈淡蓝色 氢气 特别提醒: ①物体沉底时:G 物 = F 支 + F 浮 (物体与底面之间相互有力的作用,非悬浮)②沉入底部,且底部与水底“紧密接触”“缝合”的柱体,不受浮力,反而受到液体产生的向下的压力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形有关的内角、外角习题课一、填空题1. (1)在△AB C中,若∠A=80°,∠C=20°,则∠B=__________°;(2)若∠A=80°,∠B=∠C,则∠C=__________°;(3)已知△ABC的三个内角的度数之比∠A∶∠B∶∠C=2∶3∶5,则∠B=°.2.(1)在△ABC中,∠A等于和它相邻的外角的四分之一,这个外角等于∠B的两倍,那么∠A=__________,∠B=__________,∠C=__________.(2)如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=__________.3. 已知在△ABC中,∠A=40°,∠B-∠C=40°,则∠B=__________,∠C=__________.4.(1)如图(1),P为△ABC中BC边的延长线上一点,∠A=50°,∠B=70°,则∠ACP=________°.(2)如图(2)所示,已知∠ABE=142°,∠C=72°,则∠A=__________°,∠ABC=__________°.(3)如图(3),∠3=120°,则∠1-∠2=________°.(图4)5.如果三角形的三个外角的比为3∶4∶5,那么这个三角形是三角形.6.如图4,△ABC,∠A=40°,则(1)∠1+∠2+∠B+∠C=______°;(2)∠3+∠4=_______°.(图5)(图6)(图7)7.如图5所示,在△ABC中,∠B的平分线与∠ACB的外角的平分线相交于点E,若∠A=40°,则∠E=_____________.8.如图6所示,∠1+∠2+∠3+∠4+∠5=_____________.9. 如图7,BC⊥ED,垂足为O,∠A=27°,∠D=20°,则∠ACB= ,∠B= .10.在△ABC中,∠A-∠C=25°,∠B-∠A=10°,则∠B=___________.二.选择题:11.下列说法正确的是()A.在一个三角形中最多有两个锐角B.在一个三角形中最多有两个钝角C.在一个三角形中最多有两个直角D.在一个三角形中最少有两个锐角12.三角形的一个外角等于与它相邻内角的4倍,等于与它不相邻的一个内角的2倍,则该三角形的各角的度数是()A.45°,45°,90°B.30°,60°,90°C.36°,72°,72°D.25°,25°,130°13.已知在△ABC中,∠B=∠C=2∠A,则∠C等于()A.45°B.36°C.72°D.144°14.已知在△ABC中,∠A=105°,∠B-∠C=15°,则∠B等于()A.45°B.36°C.72°D.144°15.如图所示,∠A+∠B+∠C+∠D+∠E+∠F等于()A.180°B.360°C.540°D.720°16. 一个三角形三个内角的度数之比为2∶3∶7,这个三角形一定是( ).A .直角三角形B .等腰三角形C .锐角三角形D .钝角三角形17. 锐角三角形的三个内角是∠A ,∠B ,∠C .如果∠α=∠A +∠B ,∠β=∠B +∠C ,∠γ=∠C +∠A ,那么∠α,∠β,∠γ这三个角中( ).A .没有锐角B .有1个锐角C .有2个锐角D .有3个锐角 18.如图,a ∥b ,则下列式子中值为180°的是( ).A .∠α+∠β-∠γB .∠α+∠β+∠γC .∠β+∠γ-∠αD .∠α-∠β+∠γ 三.解答题:19. 在△ABC 中,若∠A =2∠B =3∠C ,试判断这个三角形的形状.20.如图,在△ABC 中,∠1=∠2,∠3=∠4,∠BAC =54°,求∠DAC 的度数。
21.如图所示,将三角形纸片ABC 的一个角折叠,折痕为EF ,若∠A =80°,∠B =68°,∠CFE =78°,求∠CEF 的度数.22.如图AD 是△ABC 的外角∠CAE 的平分线,∠B=30°,∠DAE=55°,求∠ACD 的度数.23.如图,△ABC 中,∠A=50°,点P 是∠ABC 与∠ACB 平分线的交点. (1)求∠P 的度数;(2)∠P 与∠A 有怎样的大小关系?(3)若点P 是∠CBD 与∠BCE 平分线的交点,∠P 与∠A 又有怎样的大小关系? (4)若点P 是∠ABC 与∠ACF 平分线的交点,∠P 与∠A 又有怎样的大小关系?B D CD A B C2 4 31 A多边形1,填表2.下列多边形中是正多边形的是().A.直角三角形B.长方形C.等腰三角形D.正方形3.以线段a=2,b=4,c=6,d=8为边作四边形,则满足条件的四边形有().A.1个B.2个C.3个D.无数个4.从十边形的一个顶点出发,画所有的对角线,则它将十边形分成().A.6个三角形B.7个三角形C.8个三角形D.9个三角形5.六边形的对角线有().A.3条B.6条C.9条D.12条6.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形割成6个三角形,则n的值是()A.6 B.7 C.8 D.97.若n边形恰好有n条对角线,则n为()A.4 B.5 C.6 D.78.过一个多边形的顶点可作5条对角线,则这个多边形是()A.六边形B.七边形C.八边形D.九边形9.下列说法正确的是()A.一个多边形外角的个数与边数相同B.一个多边形外角的个数是边数的二倍C.每个角都相等的多边形是正多边形D.每条边都相等的多边形是正多边形10.从多边形一个顶点出发画对角线将它分成4个三角形,这个多边形是边形.11. 从n边形的一个顶点引出的对角线有条,把这个n边形分成个三角形,它一共有条对角线.12.从五边形的一个顶点引出的对角线有条,把这个五边形分成个三角形,它一共有条对角线.13.过m边形的一个顶点出发对角线把这个多边形割成7个三角形,,n边形没有对角线,k边形有2条对角线,则(m+n-k)=________.14.过m边形的一个顶点有7条对角线,n边形没有对角线,k边形共有k条对角线,则(m-k)n的值是。
15.将一个四边形截去一个角后,会变成几边形?请画图说明.将五边形截去一个角,会变成边形;将一个n边形截去一个角后,会变成边形。
16. n边形中,从一个顶点出发可以引条对角线,n边形一共有条对角线.(1)世界杯足球比赛有32支参赛队伍,若进行单循环赛,一共需要赛几场;(2)六一儿童节同学们互相赠送礼物,小明班上有40人,一共需要准备份礼物。
多边形的内角和一.选择题.1.若n边形每个内角都等于150°,那么这个n边形是()A.九边形B.十边形C.十一边形D.十二边形2.随着多边形的边数n的增加,它的外角和()A.增加B.减小C.不变D.不定3.一个多边形的内角和是1800°,那么这个多边形是()A.五边形B.八边形C.十边形D.十二边形4.一个多边形每个外角都是60°,这个多边形的外角和为()A.180°B.360°C.720°D.1080°5.多边形的内角和为它的外角和的4倍,这个多边形是()A.八边形B.九边形C.十边形D,十一边形6.下列判断中正确的是()A.四边形的外角和大于内角和.B.若多边形边数从3增加到n(n为大于3的自然数),它们外角和的度数不变.C.一个多边形的内角中,锐角的个数可以任意多.D.一个多边形的内角和为1880°7.多边形每一个内角都等于150°,则从此多边形一个顶点发出的对角线有()A.7条B.8条C.9条D.10条8.若从一个多边形的一个顶点最多可以引10条对角线,则它是 ( )A.十三边形B.十二边形C.十一边形D.十边形二.填空题.9.多边形边数每增加一条,它的内角和,外角和.10.四边形的∠A、∠B、∠C、∠D的外角之比为1:2:3:4,那么∠A:∠B:∠C:∠D=.11.四边形的四个内角中,直角最多有个,钝角最多有个,锐角最多有个.12.一个多边形的内角和为720°,那么这个多边形的对角线条数为.13.一个多边形的每个外角都为30°,则这个多边形的边数为;一个多边形的每个内角都为135°,则这个多边形的边数为.14.乘火车从A站出发,沿途经过3个车站方可到达B站,那么A、B两站之间需要安排______种不同的车票.15.将一个正六边形纸片对折,并完全重合,那么得到的图形是________边形,•它的内角和(按一层计算)是_______度.16.内角和等于外角和的多边形是边形.17.一个多边形的内角的度数从小到大排列时,恰好依次增加相同的度数,其中最小角为100°,最大的是140°,那么这个多边形是边形.18. 多边形的一个内角的外角与其余内角的和为600°,则这个多边形的边数是.三、判断题(1)当多边形边数增加时,它的内角和也随着增加.()(2)当多边形边数增加时.它的外角和也随着增加.()(3)三角形的外角和与一多边形的外角和相等.()(4)从n边形一个顶点出发,可以引出(n一2)条对角线,得到(n一2)个三角形.()(5)四边形的四个内角至少有一个角不小于直角.()四、解答题19.一个多边形少一个内角的度数和为2300°(1)求它的边数(2)求少的那个内角的度数.20.某同学在计算多边形的内角和时,得到的答案是1125°,老师指出他少加了一个内角的度数,你知道这个同学计算的是几边形的内角和吗?他少加的那个内角的度数是多少?21.已知五边形内角度数之比为4∶4∶5∶5∶6,求该五边形各外角对应度数之比.22.如果一个多边形除了一个内角外,其余各内角之和为1190°,则这个多边形的边数是多少?这个内角是多少度?23.如图,四边形ABCD中,∠A=50︒,∠ABC=105︒,∠BCD=90︒,∠1、∠2、∠3、∠4中哪个角是四边形ABCD的外角?求出它的度数.ABC D1234 24. .如图,在四边形ABCD中,∠C与∠D的平分线相交于P,且∠A=70°,∠B=80°25.如图,∠B+∠F=55°,求∠A+∠C+∠D+∠E的度数.26.如图,求∠1+∠2+∠3 +∠4+∠5+∠6+∠7的度数.1234567ABCDF第11章三角形单元复习课1.在活动课上,小红有两根长为4cm,8cm的小木棒,现打算拼一个等腰三角形,则小红应取的第三根小木棒的长应为.2.△ABC中,若∠A∶∠B∶∠C=1∶2∶3,则△ABC是三角形.3.三角形中至少有一个角不小于;没有对角线的多边形是;一个多边形中,锐角最多有个;一个四边形截去一个角后可以得到的多边形是.4.一个多边形的每个外角都是30°,则它是边形,其内角和是.5.一个多边形的每个内角都相等,且比它的一个外角大100°,则边数n =.6.如图⑴,在直角△ABD中,∠D=90°,C为BD上一点,则x可能是()A、10B、20C、30D、407.如图⑵有两个正方形和一个等边三角形,则图中度数为30°的角有()A、1个B、2个C、3个D、4个8、等腰三角形一腰上的中线将周长分为6和15两部分,求此三角形的腰长.9、如图⑶一个四边形ABCD模板,设计要求AD与BC的夹角应为30°,CD与BA的夹角应为20°.现在已测得∠A=80°,∠B=70°,∠C=90°,请问:这块模板是否合格?并说明理由.10、△ABC中,⑴如图⑷,∠DBC和∠ECB的角平分线相交于点O;⑵如图⑸,∠ABC的角平分线BD和∠ACE的角平分线相交于点O;如图⑹,∠CBD的角平分线BO和∠BCE的角平分线CO相交于点0,试猜想∠A与∠D的关系,并选择其中一个进行证明.三角形单元自测题一.选择题1.一个正多边形,它的一个外角等于与它相邻的内角的1/5,则这个多边形是()A、五边形B、八边形C、地、九边形D、十二边形2.如图(1),把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A、∠1、∠2之间的关系是()A、∠A=∠1-∠2B、2∠A=∠1-∠2C、3∠A=2∠1-∠2D、3∠A=2(∠2-∠1)二.填空题3.有四条线段,长度分别是12cm,10cm,8cm,4cm,选其中的三条组成三角形,则可组成个不同的三角形.4.如果等腰三角形的两边长为5cm和9cm,则三角形周长为.5.△ABC中,若∠A∶∠B∶∠C=3∶4∶7,则△ABC是三角形.6.一个多边形中,锐角最多有个;三角形中至少有一个角不小于°;7.如图⑺,AB∥CE, ∠C=37°,∠A=114°,则∠F的度数为.8.如图⑻所示,△ABC中AB=AC,请你添加一个条件.使得AD∥BC.9.如图⑼,D、E是边AC的三等分点若△ABC的面积为12㎝2,则△BDC的面积是㎝10.如图⑽,∠1+∠2+∠3+∠4的度数是.11.三角形最长边等于10,另两条边的长分别为x和4,周长为C,则x和C的取值范围分别是.三.解答题12.如图⑿,已知∠1+∠2=180°,DG∥AC,求证:∠A=∠DFE.13.如图⒀, △ABC中,点D在AC上,且∠ABC=∠C=∠BDC, ∠ABD=∠A,求∠A的度数.图(1)E D BA C 14.如图⒁,已知D 为△ABC 边BC 延长线上一点,DF ⊥AB 于F 交AC 于E, ∠A =35°,•∠D =42°,求∠ACD 的度数.15.如图,△ABC 中,∠B =∠C ,∠BAD =40°,且∠ADE =∠AED .求∠CDE 的度数.16.如图⒂,已知△ABC 中,∠ACB =90°,CD 是AB 边上的高,BE 是AC 边上的中线, AB =10cm,BC =8cm,AC =6cm. ⑴求CD 的长;⑵求△ABE 的面积.17.如图,已知∠xoy =90°,点A 、B 分别在射线ox,oy 上移动,BE 是∠ABy 的平分线,BE 的反向延长线与∠OAB 的平分线相交于点C ,试问∠C 的大小是否随点A 、B 的移动而发生变化?如果保持不变,求出∠C 的大小,如果随点A 、B 的移动而发生变化,请求出变化范围.全等三角形一.选择题1.若△ABC与△DEF全等,A和E,B和D分别是对应点,则下列结论错误的是( ) A.BC=EF B.∠B=∠D C.∠C=∠F D.AC=EF2.如图1,△ABC≌△CDA,AB=5,BC=7,AC=6,则AD边的长为( ) A.5 B.6 C.7 D.不确定3.如图2,△ABC≌△AED,AD与AC是对应边,∠B和∠E是对应角,与∠DAC相等的是()A.∠ACB B.∠CAE C.∠BAE D.∠BAC4.下列说法正确的是()A.全等三角形是指形状相同的两个三角形B.全等三角形是指面积相等的两个三角形C.全等三角形的周长和面积分别相等D.所有的等边三角形都是全等三角形5.如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF,②∠FAB=∠EAB, ③EF=BC,④∠FAC=∠EAB,其中正确结论的个数是()A.1个B.2个C.3个D.4个二.填空题6.如图3,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD=_______.7.如图4,△ABC≌△BAD,则A和,C和是对应顶点,如果AB=8cm,BD=6cm,AD=5cm,则BC=________cm.8.如图5,若△ABC≌△EBD,且BD=4cm,∠D=60°,则∠ACE=°,BC=_____cm.三.解答题9.如图6,△ABC与△DFE是全等三角形,其中A和D、B和E是对应点.⑴用符号“≌”表示这两个三角形全等(要求对应顶点写在对应位置上).⑵写出图中相等的线段和相等的角.⑶写出图中互相平行的线段,并说明理由.FECBA图6F D EA C B10.已知ΔABC ≌ΔDEF, ΔABC 的三边分别为3,m,n, ΔDEF 的三边分别为5,p,q,若ΔABC 的三边均为整数,求m+n+p+q 的最大值.11.已知,如图△ABE ≌△ADE ,△ADE ≌△CDE ,AB 与CD 相等吗?为什么?12.如图,已知△ABC ≌△ADE ,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB 和∠DGB 的度数?13.如图,△ABE 和△ADC 是△ABC 分别沿着AB 、AC 边翻折180°形成的,若∠BAC :∠ABC :∠ACB =28:5:3,求∠EFC 的度数.14.如图所示,A ,D ,E 三点在同一直线上,且△BAD ≌△ACE .⑴试说明BD =DE +CE ;⑵△ABD 满足什么条件时,BD ∥CE ?三角形全等的判定 (1)一.选择题1.下列说法正确的是( )A .全等三角形是指形状相同的两个三角形B .全等三角形的周长和面积分别相等C .全等三角形是指面积相等的两个三角形D .所有等边三角形都全等. 2.如图1,在ABC ∆中,AC AB =,D 为BC 的中点,则下列结论中:①ABD ∆≌ACD ∆;②C B ∠=∠;③AD 平分BAC ∠;④BC AD ⊥,其中正确的个数为( ) A .1个 B .2个 C .3个 D .4个图1 图2 图3 图43.如图2,AD AB =,CD CB =,︒=∠30B ,︒=∠46BAD ,则ACD ∠的度数是( ) A .120° B .125° C .127° D .104° 二.填空题4.如图3,若,AB AD BC DC ==,根据 可得ABD ∆≌ACD ∆.5.在ABC ∆和111C B A ∆中,已知11B A AB =,11C B BC =,则补充条件____________,可得到ABC ∆≌111C B A ∆.6.如图4,CD AB =,DE BF =,E 、F 是AC 上两点,且CF AE =.欲证D B ∠=∠,可先运用等式的性质证明AF =________,再用“SSS ”证明________≌_________•得到结论. 三.解答题7.请你以下面提供的a 、b 、c 三条线段画一个三角形.8.如图,点B 、E 、C 、F 在同一直线上,CF BE =,DE AB =,DF AC =. 求证:D EGC ∠=∠9.在ABC ∆中,︒=∠90C ,D 、E 分别为AC 、AB 上的点,且BD AD =,BC AE =,DC DE =.求证:AB DE ⊥.10.如图,点A 、C 、F 、D 在同一直线上,DC AF =,DE AB =,EF BC =求证:DE AB //.11.如图,在四边形ABCD 中,CD AB =,BC AD =. 求证:①CD AB //;②BC AD //.12.如图,已知CD AB =,BD AC =,求证:D A ∠=∠.13.如图,AC 与BD 交于点O ,CB AD =,E 、F 是BD 上两点,且CF AE =,BF DE =. 求证:⑴B D ∠=∠;⑵CF AE //14.如图,AB=AE ,AC=AD ,BD=CE ,求证:△ABC ≌ ADE.15.已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC.三角形全等的判定(2)一.选择题1.如图1,下列条件中能使ABD ∆≌ACD ∆的是( )A .AC AB =,C B ∠=∠ B .AC AB =,ADC ADB ∠=∠ C .AC AB =,CAD BAD ∠=∠ D .CD BD =,CAD BAD ∠=∠2.如图2,线段AB 、CD 互相平分交于点O ,则下列结论错误的是( ) A .BC AD = B .D C ∠=∠ C .BC AD // D .OB OC =3.如图3,BC DE ⊥于点E ,且CE BE =,15=+AC AB ,则ABD ∆的周长为( ) A .15 B .20 C .25 D .30图1图2 图3 图4 图54.已知两边及其中一边的对角,作三角形,下列说法中正确的是( ) A .能作唯一的一个三角形 B .最多能作两个三角形 C .不能作出确定的三角形 D .以上说法都不对5.如图4,已知1∠=∠B ,CF BE =,要使ABC ∆≌DEF ∆,下面所添的条件正确的是( ) A .DF AC = B .EF BC = C .EF AC = D .DE AB =6.如图5,在ABC ∆中,AC AB =,点E 、F 是中线AD 上的两点,则图中可证明为全等的三角形有( )A . 3对B .4对C .5对D .6对 二.解答题7.如图,已知BC AD //,BC AD =. 求证:ADC ∆≌CBA ∆8.点A 、D 、F 、B 在同一直线上,BF AD =,且BC AE //. 求证:⑴AEF ∆≌BCD ∆ ⑵CD EF //9.如图,DE CD ⊥于D ,DB AB ⊥于B ,BE CD =,DE AB =. 求证:AE CE ⊥10.如图,ABC ∆和ECD ∆都是等边三角形,连接BE 、AD 交于O . 求证:⑴BE AD = ⑵︒=∠60AOB11.如图,已知:AD ∥BC ,AD =CB ,AE =CF. 求证:∠D =∠B.12.如图,AD ⊥BC ,D 为BC 的中点,那么结论正确的有A 、△ABD ≌△ACDB 、∠B=∠C C 、AD 平分∠BAC D 、△ABC 是等边三角形13.如图,已知OA=OB,应填什么条件就得到△AOC ≌△BOD (允许添加一个条件)14.如图,已知E 、F 是线段AB 上的两点,且BF AE =,BC AD =,B A ∠=∠. 求证:CE DF =15. 如图,在ABC △中,D 是AB 上一点,DF 交AC 于点E ,DE FE =,AE CE =,AB 与CF 有什么位置关系?证明你的结论.AD BCFEDBCOAED FAB C全等三角形判定(3)一.选择题1.如图1,ABC ∆和DEF ∆中,下列能判定ABC ∆≌DEF ∆的是( ) A .DF AC =,EF BC =,D A ∠=∠ B .E B ∠=∠,F C ∠=∠,DF AC = C .D A ∠=∠,E B ∠=∠,F C ∠=∠ D .E B ∠=∠,F C ∠=∠,DE AC =2.如图2为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )A .带①去B .带②去C .带③去D .带①和②去 3.如图3,BC AD =,BD AC =,则图中全等三角形有( ) A .1对 B .2对 C .3对 D .4对4.如图4,AB CD ⊥于D ,AC BE ⊥于E ,AO 平分BAC ∠,则图中全等三角形有( ) A .1对 B .2对 C .3对 D .4对图1 图2 图3图4 图55.如图5,AD 平分BAC ∠,AC AB =,则图中全等三角形的对数是( ) A .2对 B .3对 C .4对 D .5对6.ABC ∆和DEF ∆中,DE AB =,E B ∠=∠,要使ABC ∆≌DEF ∆ ,则下列补充的条件中错误的是( )A .DF AC =B .EF BC = C .D A ∠=∠ D .F C ∠=∠ 二.解答题7.如图,已知21∠=∠,43∠=∠ 求证:BE BD =8.如图,AE AC =,E C ∠=∠,21∠=∠.求证:ABC ∆≌ADE ∆.9.如图,已知CE BD =,21∠=∠,那么AC AB =,你知道这是为什么吗?10. 如下图,D 在AB 上,E 在AC 上,AB=AC ,∠B=∠C .求证:AD=AE .11. 已知:点D 在AB 上,点E 在AC 上, BE ⊥AC, CD ⊥AB,AB=AC求证:BD=CE12.如图,AE ⊥BE ,AD ⊥DC ,CD =BE ,∠DAB =∠EAC .求证:AB =AC .13.已知如图,AB CE ⊥于点E ,AC BD ⊥于点D ,BD 、CE 交于点O ,且AO 平分BAC ∠. (1)中有多少对全等的三角形?请你一一列举出来(不要求说明理由) ⑵小明说:欲证CD BE =,可先证明AOE ∆≌AOD ∆得到AD AE =,再证明ADB ∆≌AEC ∆得到AC AB =,然后利用等式的性质即可得到CD BE =,请问他的说法正确吗?•如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.⑶要得到CD BE =,你还有其他的思路吗?若有,请仿照小明的说法具体说一说你的想法.D C AB E D EC BA全等三角形判定(4)一.选择题1.下列命题中正确的有( )①两直角边对应相等的两直角三角形全等;②两锐角对应相等的两直角三角形全等; ③斜边和一条直角边对应相等的两直角三角形全等; ④一锐角和斜边对应相等的两直角三角形全等.A .2个B .3个C .4个D .1个2.在下列所给的四组条件中,不能判定ABC Rt ∆≌C B A Rt '''∆ (其中︒='∠=∠90C C )的是( ) A .C A AC ''=,A A '∠=∠ B .C A AC ''=,C B BC ''= C. A A '∠=∠,B B '∠=∠ D. C A AC ''=,B A AB ''= 3.使两个直角三角形全等的条件是( )A .一组锐角对应相等B .两组锐角对应相等C .一条边对应相等D .两条边对应相等4.如图1,ABC ∆和EDF ∆中,︒=∠=∠90D B ,E A ∠=∠,点B 、F 、C 、D 在同一条直线上,在增加一个条件,不能判定ABC ∆≌EDF ∆的是( )A .ED AB = B .EF AC = C .EF AC //D .DC BF =5.如图2,AC AB =,AC BD ⊥于D ,AB CE ⊥于E ,图中全等三角形的组数是( ) A .2 B .3 C .4 D .56.如图3,在ABC ∆中,BC AD ⊥于点D ,AB CE ⊥于点E ,AD 、CE 交于点H , 已知3==EB EH ,4=AE ,则CH 的长为( ) A .1 B .2 C .3 D .4图1 图2 图3 二.解答题7.如图3,BD AE ⊥于E ,BD CF ⊥于F ,CD AB =,CF AE =.求证:CD AB //8.如图,点A 、B 、C 、D 在同一条直线上,CD AB =,AD EB ⊥,AD FC ⊥,且DF AE = 求证:DE AF =9.如图,AC AB =,BC AD ⊥于D .求证:AD 平分BAC ∠,CD BD =10.如图,AC AB =,AF AE =,EC AE ⊥于E ,FB AF ⊥于F . 求证:21∠=∠11. 如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系?12.如图,B 、E 、F 、C 在同一直线上,AF ⊥BC 于F ,DE ⊥BC 于E , AB=DC ,BE=CF ,你认为AB 平行于CD 吗?说说你的理由13.在ABC ∆中,︒=∠90BAC ,AC AB =,AE 是过点A 的一条直线,且AE BD ⊥于D ,AE CE ⊥于E .⑴当直线AE 处于如图1的位置时,猜想BD 、DE 、CE 之间的数量关系,并证明. (2)你在图2选择与⑴不同位置进行操作,并猜想⑴中的结论是否还成立?加以证明; (3)归纳⑴、⑵,请你用简洁的语言表达BD 、DE 、CE 之间的数量关系.图1FABCDE 图2FABCDEOP R图3ABC 全等三角形习题课一.填空题1.如图1,已知AE ⊥BD 于E ,CF ⊥BD 于F ,AB =CD ,AE =FC ,则图中全等三角形 共有 对.2.如图2,已知,∠ABC =∠DEF ,AB =DE ,要说明△AB C ≌△DEF , (1)若以“SAS”为依据,还须添加的一个条件为 ; (2)若以“ASA”为依据,还须添加的一个条件为 ; (2)若以“AAS”为依据,还须添加的一个条件为 ;3.如图3,在∠POR 内有一点A ,若AB ⊥OP 于B ,AC ⊥OR 于C ,且AB =AC ,则点A 在 ,根据是 . 4.已知△ABC ≌△DEF ,∠A =50°,∠E -∠F =40°,则∠B = 度.5.如图4,在△ADC 和△AEB 中,AB =AC ,要说明△ADC ≌△AEB ,需添加的条件不能..是 .图4 图5 6.已知:如图5,△ABC 中,∠C =90°,AC =BC ,CD =8cm ,AD 是∠CAB 的角平分线, 那么点D 到AB 的距离是 二.选择题7.下列说法错误的有( )(1)有两边和一角对应相等的两个三角形全等,(2)有一角为80°,且腰长相等的两个等腰三角形全等,(3)有两边对应相等的两个直角三角形全等,(4)两个等边三角形全等 A .1个 B .2个 C .3个 D .4个8.对于下列各组条件,不能判断△ABC ≌△A /B /C /的一组是( )A .∠A =∠A /,∠B =∠B /,AB =A /B / B .∠A =∠A /,AB =A /B /,AC =A /C / C .∠A =∠A /,AB =A /B /,BC =B /C /D .AB =A /B /,AC =A /C /,BC =B /C /9.如图7,△ABC 中,∠B =∠C =50°,BD =CF ,BE =CD ,则∠EDF 的度数是 ( )A .50°B .80°C .130°D .无法确定 10.如图8,直线a ,b ,c 表示三条相互交叉的公路,现要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A .一处B .两处C .三处D .四处11.如图9所示,在∠AOB 的两边上截取AO =BO ,CO =DO ,连结AD 、BC 的线交于点P ,则:EDBC AAB C DE FABMNOA B C D EF ①△AOD ≌△BOC ;②△APC ≌△BPD ;③P 在∠AOB 的平分线上,以上结论正确的是( ) A .只有① B .只有② C .只有①② D .①②③图7 图8 图9 图1012.如图10,在△ABC 中,AB =AC ,AD 平分∠BAC ,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F ,则下列结论:(1)DE =DF ;(2)BD =CD ;(3)AD 上任意一点到AB 、AC 的距离相等;(4)AD 上任意一点到BC 两端点的距离相等.其中正确的命题有( )A .1个B .2个C .3个D .4个三.解答题13.已知∠AOB 和直线MN ,请你在直线MN 上确定一点,使这点到∠AOB 的两边距离相等(要求:用尺规作图, 保留作图痕迹,写出结论,不写作法)答:..14. 如图,点A 、D 、B 、E 在同一直线上,AC =FD ,AD =BE ,BC =EF . 求证:△ABC ≌△DEFFEDCBAc b aPCAO DB15.如图,已知:点B 、F 、C 、E 在一条直线上,FB =CE ,AC =DF .能否由上面的已知条件证明AB ∥ED ?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件.......,添加到已知条件中,使AB ∥ED 成立,并给出证明. 供选择的三个条件(请从其中选择一个): ①AB =ED ; ②BC =EF ; ③∠ACB =∠DFE .16.八(1)班同学上数学活动课,利用角尺平分一个角(如图),设计了如下方案: (Ⅰ)∠AOB 是一个任意角,将角尺的直角顶点P 介于射线OA 、OB 之间,移动角尺使角尺两边相同的刻度与M 、N 重合,即PM =PN ,过角尺顶点P 的射线OP 就是∠AOB 的平分线. (Ⅱ)∠AOB 是一个任意角,在边OA 、OB 上分别取OM =ON ,将角尺的直角顶点P 介于射线OA 、OB 之间,移动角尺使角尺两边相同的刻度与M 、N 重合,即PM =PN ,过角尺顶点P 的射线OP 就是∠AOB 的平分线. (1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由.(2)在方案(Ⅰ)PM =PN 的情况下,继续移动角尺,同时使PM ⊥OA ,PN ⊥OB .此方案是否可行?请说明理由.DABCDEO ABCDEHA B C DEF 17.已知:如图AB =AC , AD ⊥BC 于D ,BE ⊥AC 于E ,AD 、BE 交于点H . (1)求证:△ABD ≌△ACD . (2)若AH =2BD ,求证:AE =BE .18.已知:如图AB =AC , BD ⊥AC 于D ,CE ⊥AB 于E ,BD 、CE 交于点O . (1)求证:△ABD ≌△ACE . (2)求证:点O 在∠BAC 的平分线上.19.如图,已知:在△ABC 中,AD 是∠BAC 的平分线,E 、F 分别是AB 、AC 上的点,AE >AF ,且∠EDF +∠BAF =180°, (1)求证:DE =DF . (2)如果把最后一个条件改为:AE >AF ,且∠AED +∠AFD =180°,那么(1)中的结论还成立吗?若成立,请说明理由;若不成立,请举例说明.P D C B A E2DB A 35146D C B AE OE D CBA角平分线的性质(1)一.选择题1.下列说法:①角的内部任意一点到角的两边的距离相等;•②到角的两边距离相等的点在这个角的平分线上;③角的平分线上任意一点到角的两边的距离相等;④△ABC 中∠BAC 的平分线上任意一点到三角形的三边的距离相等,其中正确的 ( ) A .1个 B .2个 C .3个 D .4个2. 已知AD 是△ABC 的角平分线,DE ⊥AB 于E ,且DE =3cm,则点D 到AC 的距离是 ( ) A.2cm; B.3cm; C.4cm; D.6cm3.如图,已知点P 到AE 、AD 、BC 的距离相等,则下列说法:①点P 在∠BAC 的平分线上;②点P 在∠CBE 的平分线上;③点P 在∠BCD 的平分线上; ④点P 是∠BAC 、∠CBE 、∠BCD 的平分线的交点,其中正确的是 ( ) A .①②③④ B .①②③ C .④ D .②③4.如图,AB =AD ,∠ABC =∠ADC =90°,则下列结论:①∠3=∠4;•②∠1=∠2; ③∠5=∠6;④AC 垂直且平分BD ,其中正确的有 ( ) A .①②③④ B .①②③ C .①③ D .①③④5.如图,AB ∥CD ,AP 、CP 分别平分∠BAC 和∠ACD ,PE ⊥AC 于E ,且PE =•2cm ,则AB 与CD 之间的距离是___________. 6.如图,已知CD ⊥AB 于D ,BE ⊥AC 于E ,CD 交BE 于点O . ①若OC =OB ,求证:点O 在∠BAC 的平分线上.②若点O 在∠BAC 的平分线上,求证:OC =OB .7.如图:在△ABC 中,∠C =90°,AD 是∠BAC 的平分线,DE ⊥AB 于E ,F 在AC 上,BD =DF ; 求证:CF =EB8.在Rt △ABC 中,BD 平分∠ABC , DE ⊥AB 于E ,则⑴图中相等的线段有哪些?相等的角呢? ⑵哪条线段与DE 相等?为什么?⑶若AB =10,BC =8,AC =6,求BE ,AE 的长和△AED 的周长.DEB CAF D EB AO21DE B CAM DB A9. 如图,在△ABC 中,∠C =90°,AC =4cm, AB =7cm ,AD 平分∠BAC ,DE ⊥AB 于F(1)求证:△ACD ≌△AED ; (2)求EB 的长.10. 如图,∠B =∠C ,D 为BC 的中点,ED ⊥AB , DF ⊥AC ,求证:AD 平分∠BAC11.如图,CD ⊥AB 于D ,BE ⊥AC 于E ,CD ,BE 交于点O ,且∠1=∠2 ,求证:OB =OC12. 如图,∠A =∠B =90°,M 是AB 的中点,DM 平分∠ADC ,求证:CM 平分∠BCD13.如图,BA 平分∠CAD ,BC ⊥AC 于D ,BD ⊥AD 于D ,E 是AB 上一点,EB 平分∠CED 吗?为什么?当E 点在AB 的延长线上或AB 的反向延长线时,上述结论成立吗?请选择一个证明.EB DCA A C DE B A CDE B角平分线的性质(2)1.已知,如图,AB =CD ,△P AB 和△PCD 面积相等,求证:OP 平分∠AOC .2.如图,△ABC 的角平分线BM ,CN 相交于点P ,求证:点P到三边AB ,BC ,CA 的距离相等,且P 点在∠BAC 的角平分线上。
