第一型曲线积分
第一型曲线积分 第一型曲线积分的定义

n
i
f ( ( i), ( i)) 2 ( i) 2 ( i )t i . (4)
令 t max{t1 , t 2 ,
t 0
, t n }, 则当 T 0 时, 必有
t 0. 现在证明 lim 0.
这里 t i 1 i, i ti . 设
f ( ( i), ( i))[ 2 ( i ) 2 ( i ) 2 ( i) 2 ( i)]ti ,
i 1 n
则有
f ( , )s
i 1 i i n i 1
n ||T || 0
, n). 若有极限
i i i
lim
f ( , )s
i 1
J,
且 J 的值与分割 T 与点 ( i , i ) 的取法无关, 则称此 极限为 f ( x , y ) 在 L 上的第一型曲线积分, 记作
L
f ( x , y )ds .
若 L 为空间可求长曲线段 , f ( x , y , z ) 为定义在 L上 的函数, 则可类似地定义 f ( x , y , z )在空间曲线 L 上
, k ) 都存在, 则 L f ( x , y )ds
也存在, 且
L
L
f ( x , y )ds f ( x , y )ds .
i 1 Li
k
3. 若 f ( x , y )ds 与 g ( x , y )ds都存在, 且在 L 上
L
f ( x , y ) g( x , y ), 则
且
L
f ( x , y )ds g ( x , y )ds .
L
第一型曲线积分

L xyds
2 0
a cos t b sin t ( a sin t )2 (b cos t )2 dt
ab02 sin t cos t a 2 sin 2 t b 2 cos2 t dt
ab 02 (a 2 b 2 ) sin 2 t b 2 d (sin 2 t ) 2
( x ) 0.
L ( x y )ds
2 ( x 0 ) 1 0 dx 0
2
0 x dx
2
2.
(2) L: x ( y ) 2, 0 y 3.
( x ) 0.
L ( x y )ds
2 ( 2 y ) 1 0 dy 0
x2 y2
x2 y2
ds. 其中曲线 x 2 y 2 a 2 , 直
线 x 0, y x 在第一象限中所围的图 形边界。
解
Le
ds ds AB e
x2 y2
oA e
x2 y2
ds oB e
x2 y2
ds
oA : x 0, 0 y a .
I xyz ds
0 a 2 cos sin k ( a sin )2 (a cos )2 k 2 d
2 2 2 a k a k 2
2Байду номын сангаас
0 sin 2 d
2
1 ka 2 a 2 k 2 . 2
例5
计算
Le
0
ab(a 2 ab b 2 ) . 3(a b )
y
例2
计算
L ( x y ) ds.
曲线积分

(2) C f ( x, y) ds C 1 f ( x, y) ds C 2 f ( x, y) ds
(3) C ds l ( l 曲线C 的长度)
机动 目录 上页 下页 返回 结束
3. 计算 • 对光滑曲线
2 2 f ( x , y ) d s ( t ) (t ) d t f [ (t ), (t )] C
1.引例: 曲线形物质的质量 假设曲线形细长物质在空间所占 弧段为AB , 其线密度为
B
Mk ( k ,k ) sk M k 1
计算此物质的质量.
n
采用 “大化小, 常代变, 近似求和, 求极限”
可得
M
A
k 1
机动
目录
上页
下页
返回
结束
2.定义 设 二元函数f(x,y)在可求长曲线C(A,B)有定义. 若通过对 曲线C 的任意分割T和局部的任意取点, 下列“乘积和式极限”
2 3 a 2 X 2 a 3
圆C的圆心 在原点, 故
X 0
机动 目录 上页 下页 返回 结束
例5. 计算
2 2 x y 其中C为球面
与平面 x z 1 的交线 . z2 9 2
则
1 2 1 2 1 2 (x 2) 4 y 1 解: C : , 化为参数方程 x z 1 x 2 cos 1 2 C : y 2 sin 0 2 z1 2 cos 2
2
I y C y ds.
2
(5) 曲线C的重心坐标
xds C x , C ds
yds C y . C ds
例1. 计算
第一型曲线积分

Li
L
k
也存在,且 f ( x, y)ds
f ( x, y)ds
L
i 1 Li
3 保号性若L f ( x, y)ds与L g( x, y)ds都存在,
且在 L上 f ( x, y) g( x, y),
则L f ( x, y)ds L g( x, y)ds
4 积分绝对值 若L f ( x, y)ds存在,则 L f ( x, y)ds也存在,且| L f ( x, y)ds | L f ( x, y)ds
2(t) 2(t) 2(t)dt;
例1. 计算L yds. 其中 L 为y2=2x自点(0, 0)到点(2, 2)
的一段弧. 解1:
y 2
y2=2x
ds
1
dy dxyds 2 2x 1 1 dx
L
0
2x
0
2x
2 2x+1dx 1 (5 5 1)
0
3
解2: L : x y2 , 0≤y≤2 2
f ( (t ), (t ))关于t 连续, 则
M>0, 使得 f ( (t ), (t )) M .
又 2(t) 2(t)在[, ]上一致连续
。
即 0, 0,使当t<时有
2( ) 2( ) 2( ) 2( ) ,
从而
n
M ti M (b a) 0. i 1
由定积分的定义
5 平均值公式 若L f ( x, y) d存s在,L的弧长为s,
则存在常数c,使得L f ( x, y)ds cs。
其中inf f ( x, y) c sup f ( x, y)
L
L
二 第一型曲线积分的计算
定理 20.1
第一型曲线积分的定义

第一型曲线积分的定义第一型曲线积分,是微积分中的一种重要概念与计算方法,它涉及曲线和向量场之间的积分。
本文将介绍第一型曲线积分的定义、性质和计算方法。
一、第一型曲线积分的定义第一型曲线积分,也称为曲线的线积分,是指在曲线上某个有向长度元素$\mathrm{d}s$上的函数值与该长度元素的乘积$d\boldsymbol{s}$在整个曲线上的积分。
设$C$是曲线,其参数方程为$\boldsymbol{r}(t)=(x(t), y(t), z(t)), t\in[a,b]$,则$C$的长度由公式:$$ L(C)=\int_{C}\mathrm{d}s=\int_{a}^{b}\left[\ left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\r ight)^{2}+\left(z^{\prime}(t)\right)^{2}\right]^{\f rac{1}{2}} \mathrm{d}t $$计算曲线$C$上的一个标量函数$f(x,y,z)$在曲线上的第一型曲线积分,即为:$$ \int_{C} f(x, y, z) \mathrm{d}s=\int_{a}^{b}f\left(\boldsymbol{r}(t)\right)\left[\left(x^{\prim e}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}+\left(z^{\prime}(t)\right)^{2}\right]^{\frac{1}{2}}\mathrm{d}t $$若积分路径可以看成向量值函数$\boldsymbol{r}(t)$的积分,第一型曲线积分就可以写作:$$ \int_{\boldsymbol{r}}\boldsymbol{F}(\boldsymbol{r}) \cdot \mathrm{d}\boldsymbol{r}=\int_{a}^{b}\boldsymbol{F}\left(\boldsymbol{r}(t)\right) \cdot \boldsymbol{r}^{\prime}(t) \mathrm{d}t=\int_{a}^{b} \boldsymbol{F} \cdot \mathrm{d}\boldsymbol{s} $$其中$\boldsymbol{F}(\boldsymbol{r})$是向量场,$\mathrm{d}\boldsymbol{r}$表示一个有向长度元素,$\cdot$表示向量内积运算,$\mathrm{d}\boldsymbol{s}=\boldsymbol{r}^{\prime}(t ) \mathrm{d} t$表示线元素。
第一类曲线积分的极坐标形式

第一类曲线积分的极坐标形式曲线积分是微积分中的一个重要概念,它描述了沿着一条曲线的积分过程。
在曲线积分中,第一类曲线积分是最基本的一种类型,它描述了沿着曲线的标量场积分。
而在极坐标系下,第一类曲线积分的计算方法也有其独特的形式。
首先,我们来回顾一下第一类曲线积分的定义。
设曲线L为参数方程r(t)=(x(t),y(t)),其中a≤t≤b,f(x,y)为定义在曲线L上的标量场,则曲线L上f(x,y)的第一类曲线积分为:∫L f(x,y)ds = ∫b_a f(x(t),y(t))√[x'(t)²+y'(t)²]dt其中,ds表示曲线L上的弧长元素,x'(t)和y'(t)分别表示x(t)和y(t)对t 的导数。
接下来,我们来看第一类曲线积分在极坐标系下的形式。
在极坐标系下,曲线L可以表示为r(θ)=(r(θ)cosθ,r(θ)sinθ),其中a≤θ≤b,r(θ)为极径函数。
此时,曲线L上f(x,y)的第一类曲线积分可以表示为:∫L f(x,y)ds = ∫b_a f(r(θ)cosθ,r(θ)sinθ)√[r'(θ)²+r(θ)²]dθ其中,ds表示曲线L上的弧长元素,r'(θ)表示r(θ)对θ的导数。
通过上述公式,我们可以看出,在极坐标系下,第一类曲线积分的计算方法与直角坐标系下有所不同。
在直角坐标系下,我们需要计算曲线L上的弧长元素ds,而在极坐标系下,我们需要计算曲线L上的弧度元素dθ。
此外,由于极坐标系下的曲线L是由极径函数r(θ)和极角θ共同确定的,因此在计算曲线积分时,我们需要将f(x,y)表示为f(r(θ)cosθ,r(θ)sinθ)的形式。
总之,第一类曲线积分是微积分中的一个重要概念,它描述了沿着曲线的标量场积分。
在极坐标系下,第一类曲线积分的计算方法也有其独特的形式,需要注意弧度元素dθ的计算和将f(x,y)表示为f(r(θ)cosθ,r(θ)sinθ)的形式。
高数9-1(第一型曲线积分)

(3) L : r r( ),
L f ( x, y)ds
f [r ) cos, r( )sin ]
r2 ( ) r2 ( )d
推广 : x (t), y (t), z (t) ( t )
f ( x, y, z)ds
f [(t), (t),(t)] 2(t) 2(t) 2(t)dt ( )
2 f ( x, y)ds,当f ( x, y) 是L上关于x (或y)的偶函数 L1
L1是曲线L落在y (或x)轴一侧的部分.
运用对称性简化对弧长的曲线积分 计算时, 应同时考虑被积函数 f ( x, y)与积 分曲线L的对称性.
6/19
例 计算 ( x y3 )ds. 其中L是圆周 x2 y2 R2. L
(对路径具有可加性)
4/19
5.性质
(1) [ f ( x, y, z) g( x, y, z)]ds
f ( x, y, z)ds g( x, y, z)ds
(2) kf ( x, y, z)ds k f ( x, y, z)ds (k为常数)
(3) 与积分路径的方向无关, 即
(
⌒ f
f ( x, y)ds
b
f [ x, ( x)]
1 2( x)dx (a b)
L
a
ds 1 2( x)dx
(2) L : x ( y), c y d
f ( x, y)ds
d
f [( y), y]
1 2( y)dy (c d )
L
c
ds 1 2( y)dy
10/19
解 对称性,得
y x2 y2 R2
( x y3 )ds xds y3ds 0
L
曲线曲面积分公式(一)

曲线曲面积分公式(一)曲线曲面积分公式本文将介绍曲线曲面积分的相关公式,并通过举例进行解释说明。
一、曲线积分公式1. 第一型曲线积分第一型曲线积分表示对曲线上的函数在曲线长度方向上的积分,其公式为:(_C f(x, y, z) ds)其中,(C)为曲线,(f(x, y, z))为曲线上的函数,(ds)表示曲线微元的长度。
举例:考虑计算曲线(C: x = t, y = t^2, z = t^3)上函数(f(x, y, z) = x^2 + y + z)的第一型曲线积分。
首先需要计算曲线的参数方程可微分区间([a, b])上的导数:( = 1)( = 2t)( = 3t^2)曲线微元的长度(ds)可以表示为:(ds = dt = dt)因此,对函数(f(x, y, z) = x^2 + y + z)进行第一型曲线积分的结果为:(_C (x^2 + y + z) ds = _a^b (t^2 + t^2 + t^3) dt)2. 第二型曲线积分第二型曲线积分表示对曲线上的矢量场在曲线长度方向上的积分,其公式为:(_C d)其中,(C)为曲线,()为矢量场,(d)表示曲线微元的矢量。
举例:考虑计算曲线(C: x = t, y = t^2, z = t^3)上的矢量场( =(2xy, 3x^2, z))的第二型曲线积分。
首先需要计算曲线的参数方程可微分区间([a, b])上的导数:( = 1)( = 2t)( = 3t^2)曲线微元的矢量(d)可以表示为:(d = (, , ) dt = (1, 2t, 3t^2) dt)因此,对矢量场( = (2xy, 3x^2, z))进行第二型曲线积分的结果为:(_C (2xy, 3x^2, z) (1, 2t, 3t^2) dt = _a^b (2t(t^2),3(t2)2, t^3) (1, 2t, 3t^2) dt)二、曲面积分公式1. 第一型曲面积分第一型曲面积分表示对曲面上的函数在曲面面积方向上的积分,其公式为:(_S f(x, y, z) dS)其中,(S)为曲面,(f(x, y, z))为曲面上的函数,(dS)表示曲面微元的面积。
理学第一型曲线积分的计算
M ( x, y,z) ,取包含点 M 的一体积微元dV ,
则质量微元为 dm f ( x, y,z)dV ,点M 到 x 轴 的距离
为 y2 z2 ,于是点M 处 的质量微元关于 x 轴 的转
动惯量为 dJ x ( y2 z2 ) f ( x, y,z)dV ,从而
J x ( y2 z2 ) f ( x, y,z)dV ,
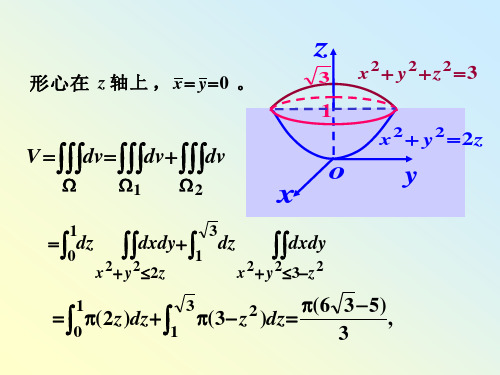
形心在 z 轴上 ,x y0 。
z
3 x2 y2z23
V dvdvdv
1 2
1
o
x
x2 y2 2z
y
1
3
0dz dxdy1 dz dxdy
x2 y22z
x2 y23z2
1
0(2z)dz 1
3(3 z2 )dz (6
3 5), 3
zdv zdv zdv
1
2
1
3
0 zdz dxdy1 zdz dxdy
同理可得 J y (z2 x2 ) f ( x, y,z)dV ,
J z ( x2 y2 ) f ( x, y,z)dV 。
若 是平面区域 D,面密度函数为 f ( x, y) ,则平面 薄片对 x 轴 、 y 轴 的转动惯量为
J x y2 f ( x, y)d , J y x2 f ( x, y)d 。
x2 y22z
x2 y23z2
1
0 z(2z)dz1
3 z(3 z2 )dz 5 3
5
z 1 V
zdv
(6
3 3 5)
5(6
3 5) 83
,
3
∴形心的坐标为(0,0, 5(6 3 5) )。
83
二.物体的转动惯量
设在 R3 上 有 n 个质量为 m1, m2 , , mn 的质点组, 它们的坐标分别为 ( xi , yi , zi ) (i 1, 2, , n) ,这个 质点组绕着某一条直线 l 旋转,设这 n 个质点到直线 l 的距离分别是 d1, d2, , dn ,由力学可知,质点组 对直线l 的转动惯量为
考研数学-第一型曲线曲面积分

3 2 C在xoy面上投影D xy {( x , y ) x y 1} 4
2
2x 2 y z z z 1 1 x y y 2z y 2z
2
2
2
2
4 y 2 z 2 4 yz y 2z
2 2
8 16 8 5 5 R R R 5 15 5 3
例14
练习十二/五
设有一个由曲线y ln x, y 0, x e所围成的 均匀薄片, 其面密度为 1, 若此薄片关于直线 x t的转动惯量为I (t ), 求使I (t )取得最小值的t. y 2 解:I (t ) ( x t ) d
dx 2 2 解 : ds 1 ( ) dy dy 2 dy 4 y
( x y 1)ds
L
2
2
( 4 y y 1)
2
2 4 y
2
dy
8 2
例2 练习十三/二(2)
x2 y 2 设L为椭圆 1,已知其周长为a, 2 3 则 (3x 2 5 xy 2 y 2 )ds _______ .
λ 0
i 1
n
2. 计算:
: z z( x , y ) , ( x , y ) D x y , 则
f ( x , y, z )dS
Dxy
f [ x, y, z( x , y )]
1 zx zy dxdy;
2 2
方法:一投、二代、三换.
3. 对称性
对面积的曲面积分 f ( x , y , z ) d S,
第十节 第一型曲线曲面积分 积分应用
第一类曲线积分的三种计算方式

第一类曲线积分的三种计算方式1.参数方程法参数方程法是最常用的计算第一类曲线积分的方法之一、它利用参数方程将曲线分成若干小段,然后计算每一小段上的积分,最后将所有小段上的积分相加得到整个曲线上的积分值。
具体步骤如下:1.将曲线的参数方程表示为x=f(t),y=g(t),z=h(t),其中t的取值范围为[a,b]。
2.求出曲线的切线向量T(t)和曲率向量K(t)。
3.将向量场F(x,y,z)表示为F(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k。
4. 计算曲线段的长度ds=sqrt(dx^2+dy^2+dz^2),其中dx=f'(t)dt,dy=g'(t)dt,dz=h'(t)dt。
5.将向量场在曲线上的投影F·T计算出来。
6. 将F·T乘以ds,再积分得到曲线上的积分。
参数方程法的优点是适用于任意形状的曲线,缺点是当曲线的参数方程比较复杂时,计算较为繁琐。
2.向量场法向量场法是计算第一类曲线积分的另一种常见方法。
它直接利用向量场在曲线上的投影与曲线段的长度相乘然后积分,而无需转化为参数方程。
具体步骤如下:1.将向量场F(x,y,z)表示为F(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k。
2.将曲线表示为r(t)=x(t)i+y(t)j+z(t)k,其中t的取值范围为[a,b]。
3. 计算向量场在曲线上的投影F·dr,其中dr=dx i+dy j+dz k,dx=x'(t)dt,dy=y'(t)dt,dz=z'(t)dt。
4. 将F·dr积分得到曲线上的积分。
向量场法的优点是计算较为简单直接,而无需转化为参数方程,缺点是不适用于复杂的曲线形状。
3.微积分基本定理法微积分基本定理法是计算第一类曲线积分的另一个重要方法。
它利用微积分基本定理将曲线积分转化为定积分,从而简化计算过程。
高等数学第一型曲线积分

第十章
第一型曲线积分
一、第一型曲线积分的概念与性质 二、第一型曲线积分的计算法
一、第一型曲线积分的概念与性质
1.引例1: 曲线形构件的质量
B
假设曲线形细长构件在空间所占
弧段为AB , 其线密度为 为计算此构件的质量, 采用
(k ,k , k )
Mk Mskk1
“大化小, 常代变, 近似和, 求极限”
0
4 4 a2 cos d 0
例4. 计算曲线积分 线
解: (x2 y2 z2 ) ds
其中为螺旋 的一段弧.
a2 k 2 2 [a2 k 2t 2]d t 0
2 a2 k 2 (3a2 4 2k 2 )
3
例5. 计算
其中为球面
被平面
所截的圆周.
解: 由对称性可知 x2 ds y2 ds z2 ds
x2 ds 1 (x2 y2 z2 ) ds
3
1 a2 ds 1 a22 a
3
3
2 a3
3
思考: 例5中 改为 计算
, 如何
解: 令
YX
x y
1 1,
Z z
则
:
X
2
Y2 Z2 X Y Z
a2 0
(X 1)2 ds
2 X ds
2 a3 2 X 2 a
3
圆的形心 在原点, 故
n
可得 M
A
k 1
2.定义
设 是空间中一条有限长的光滑曲线,
义在 上的一个有界函数, 若通过对 的任意分割 和对
局部的任意取点, 下列“乘积和式极限” (k ,k , k )
n
记作
lim
0
1 第一型曲线积分解析

y
R cos R sin
( )
O
L Rx
R2 sin 2 (R sin )2 (R cos )2d
R3 sin 2
d
2
R3
2
sin 2
4
0
R3( sin cos )
例8. 设均匀螺旋形弹簧L的方程为
解
I y L
x2 y 1 x2
ds
2 1
x2 ln x 1 x2
1 1 x2 dx
2
1
x
ln
xdx
ln
4
3 4
.
例7. 计算半径为R ,中心角为
的圆弧 L 对于它的对
称轴的转动惯量 I (设线密度 = 1).
解: 建立坐标系如图, 则
y
I y2 ds L
L
:
x
2π
cos t d t 0
0
a
a2 k2
2π
sin t d t
0
0
k
a2 k2
2π
tdt
2π2k
0
a2 k2
故质心坐标为 ( 0, 0, k π )
内容小结
1. 定义 f (x, y) ds L
f (x, y, z)ds
2. 性质
(1) f (x, y, z) g(x, y, z) ds g(x, y, z)ds (, 为常数)
2 (
i)
2 (
i
)ti
.
§6.4第一型曲线积分的计算

故 ( x2 y2 z2 )ds 9 ds 2 9 2dt 18 .
L
L2
02
例 4.设 L 为椭圆 x2 y2 1 ,其周长为 a, 43
求 (3x 2 4 y 2 2xy)ds 的值. L
解:∵ x2 y2 1 ,∴ 3 x2 4 y2 12 , 43
∴ (3x 2 4 y 2 2xy)ds (代入L的方程) L
L
x2 y2 z2 9 与平面x z1 的交线. 2
解: L
:x2 y2Biblioteka x z1z29 2
(x 1)2 2
2 z1 x.
y2 4
1,
其参数方程为:
x 1 2cost, 2
y 2sint,
z
1 2
2 cos t .
(0t 2 ) ,
ds ( 2 sint)2 (2cos t)2 ( 2 sint)2 dt 2dt,
ds 1 y2 (x)dx R dx
R2 x2
R xR
xds
dx 0
L
R R2 x2
(法二)
:
L
:
x
y
R R
cos s in
,0
ds R 2 sin 2 R 2 cos2 d
xds R 2 cosd R 2 sin 0
L
0
0
例 2 L (x y)ds, L : 连接三点O(0,0), A(1,0), B(0,1)的折线.
而平面 x y z0 通过原点,
∴ L 为平面 x y z 0 上半径为 R 的圆,其周长为 2R .
∵曲线 L 的 方程对 x,y,z 具有轮换对称性,
∴ zds xds yds 1 ( x y z)ds 0 ,
第一型曲线积分公式

第一型曲线积分公式第一型曲线积分公式是一个在向量函数上定义的积分,用于计算曲线在给定向量场下的功。
这个公式是在微积分学中非常重要的概念之一,在数学、物理学、工程学等领域都有广泛的应用。
在以下的讨论中,我们假设曲线是一个光滑的连续曲线,定义在有限实区间[ a,b ]上。
我们记曲线C = { r ( t ) | t∈ [ a,b ]},其中r(t) = ( x(t), y(t), z(t) )是一个向量值函数。
向量函数r表示了曲线在三维空间中的路径,即在时间t处的曲线点。
我们记向量函数F = ( P(x,y,z), Q(x,y,z), R(x,y,z) )是一个连续向量场,P、Q、R分别是第一、第二、第三坐标上的方程。
在这个设定下,第一型曲线积分I可以表示为:I = ∫C F • dr其中,符号•表示点积,dr表示微小的弧长元素:dr = ( dx, dy, dz ) = ( dx/dt, dy/dt, dz/dt ) dt等价地,我们可以写出以下的积分形式:I = ∫a^b F ( r ( t ) ) . r'( t ) dt这里,r' (t)是r对t的导数,也就是t时刻曲线的切向量。
F是在曲线上的向量场,它根据r的每个点来确定曲线上的向量。
首先,我们可以将C分为多个局部线段。
每个线段都可以近似地看作直线,从而可以使用线性积分的概念。
然后,我们对每个局部线段进行积分,把它们的结果加起来。
因为线性积分的结果只依赖于曲线的起点和终点,所以我们可以把曲线C的长度定义为:L = ∫C || dr || = ∫ a^b || r'(t) || dt这里,|| . || 表示向量的模。
这个长度可以用来换算单位弧长元素。
具体来说,我们可以定义曲线C的弧长参数s,它满足:s' (t) = || r' (t) ||因此,我们可以把积分变换到弧长参数下:I = ∫ L F ( r(s) ) . T(s) ds这里,T(s) = r' (s) / || r'(s) || 是曲线在点s处的单位切向量。
数学分析PPT课件第四版华东师大研制--第20章-曲线积分

[ , ]上一致连续, 即对任给的 0, 必存在 0, 使当 t 时,
2( i) 2( i)
2
(iΒιβλιοθήκη )2(i
)
,
从而
n
| | M ti M (b a), i 1
所以 lim 0. t 0
前页 后页 返回
再由定积分定义
例1 设 L是半圆周
L
:
x y
a a
cos t, sin t,
0
t
π,
试计算第一型曲线积分
( x2 y2 )ds. L
解
( x2 y2 )ds π a2 a2(cos2 t sin2 t )dt a3π.
L
0
前页 后页 返回
例2 设 L 是 y2 4x 从 O(0,0) 到 A(1,2) 一段(图20-2),
轴的 0 z a2 x2 的那部分柱面. 由第一型曲面
积分的几何意义可知它的面积为
A0 a2 x2 ds.
L
前页 后页 返回
L的参数方程为:
x a cos t, y a sin t, 0 t . 2
A0 L
a2 x2 ds= 2 a 0
a2 0
2 sin tdt
a2 .
这里 ti1 i, i ti . 设
n
f (( i), ( i))[ 2( i) 2( i) 2( i) 2( i)]ti , i 1
则有
前页 后页 返回
n
f (i , i )si
i 1 n
f ( ( i), ( i)) 2 ( i) 2 ( i )ti . (4) i 1
n
数学分析 第一型曲线积分

其中
∆si
=
s(ti )
−
s(ti−1).
如果极限 lim π →0
m i =1
f (σ(ξi ))∆si
存在且与
{ξi }
的选取无关,
则称此极限为
f
在 σ 上的第一型曲线积分, 记为
m
f ds = lim f (σ(ξi ))∆si .
σ
π →0 i =1
当 f = 1 时, 第一型曲线积分也就是曲线的长度.
β
(f ) = sup v (f ; π).
α
π
根据定义不难验证, 单调函数, Lipschitz 函数, C1 函数都是有界变差函数.
问题: 你能举一个连续但不是有界变差函数的例子吗?
可求长的充要条件
(Jordan 定理) 曲线 σ(t) 可求长当且仅当其分量均为有界变差函数.
可求长的充要条件
i =1
如果 supπ v (f ; π) 有限, 则称 f 为 [α, β] 上的有界变差函数, 它在 [α, β] 中的全变 差记为
β
(f ) = sup v (f ; π).
α
π
有界变差函数
为了确定曲线可求长的充分必要条件, 我们引入有界变差函数的概念.
设 f 为定义在 [α, β] 中的函数. 任给分割 π : α = t0 < t1 < t2 < · · · < tm = β, 记
若 σ 的弧长参数存在, 第一型曲线积分可化为 Riemann 积分:
L(σ)
f ds =
f (σ(s)) ds.
σ
0
例子
例1
设曲线 σ
是椭圆
x2 a2
第一型曲线积分计算公式

第一型曲线积分计算公式:第一型曲线积分也称为路径积分或弧长积分,用于计算向量场沿着曲线的积分。
其计算公式如下:∫C F · dr其中,C 是曲线,F 是向量场,dr 是曲线上的微元弧长向量。
以下是两个实例:实例1:考虑曲线C,由参数方程r(t) = (cos(t), sin(t)),其中0 ≤ t ≤ π/2。
向量场F(x, y) = (x, y)。
我们可以首先计算曲线的切向量r'(t) = (-sin(t), cos(t))。
然后计算F · dr:F · dr= (x, y) · (dx, dy) = (x, y) · (dx/dt, dy/dt) dt [使用链式法则将dr 转换为dt] = (cos(t), sin(t)) · (-sin(t), cos(t)) dt = -sin(t)cos(t) + sin(t)cos(t) dt = 0由于F · dr = 0,因此该曲线上的第一型曲线积分为0。
实例2:考虑曲线C,由参数方程r(t) = (t, t^2),其中0 ≤ t ≤ 1。
向量场F(x, y) = (y, x)。
首先计算曲线的切向量r'(t) = (1, 2t)。
然后计算F · dr:F · dr = (y, x) · (dx, dy) = (y, x) · (dx/dt, dy/dt) dt = (t^2, t) · (1, 2t) dt = t^2 + 2t^2 dt = 3t^2 dt要计算第一型曲线积分,我们需要将积分限从参数t 转换为实际的曲线长度。
曲线长度由下式给出:s = ∫[a, b] ||r'(t)|| dt计算曲线长度:s = ∫[0, 1] ||r'(t)|| dt = ∫[0, 1] ||(1, 2t)|| dt = ∫[0, 1] sqrt(1^2 + (2t)^2) dt = ∫[0, 1] sqrt(1 + 4t^2) dt = ∫[0, 1] sqrt(4t^2 + 1) dt现在我们可以计算第一型曲线积分:∫C F · dr = ∫[0, 1] 3t^2 dt = 3∫[0, 1] t^2 dt = 3[t^3/3] [0, 1] = 1因此,该曲线上的第一型曲线积分为1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f ( x, y)在闭曲线L上对弧长的曲线积分记为L f ( x, y)ds.
第一型曲线积分的计算
1.设 f ( x, y) 在曲线 L 上连续,L 的参数方程为 x x(t) ,
y y(t) ( t ) ,其中 x(t) , y(t) 在[ , ]上有 连续的一阶导数,且 x2(t) y2(t) 0,则
L
x 2 y 2 1 到 B( 2 , 2 )处的一段劣弧. 22
解法 1 L : x cost , y sint , t ,
42
y
被积函数 xe x 2 y 2 e cos t,
A
ds ( sint)2 (cost)2 dt dt,
o
x
B
xe
L
x2 y2 ds e
y x, ds 1 4x2 dx,
0 x 1
故 L yds OA AB B⌒O
1
0 dx
1
ydy
1
x
1 4x 2 dx
0
0
0
0 2 1 (5 5 1) 1 (5 5 7).
3 12
12
y
B
y x2 x1
o y0 A x
例2. 计算 xe x 2 y 2 ds, 其中L 是从 A( 0, 1 ) 沿圆周
分割 M1 ,M 2 , ,M n1 li ,
近似 ( i ,i )li ,
mi f ( i ,i )si .
求和
n
m f (i ,i )si .
i 1
y
A o
B
L Mn1
(i ,i ) Mi
M2
M1
M i 1
x
n
取极限
令 d max{si },
1in
m lim f ( i ,i )si .
ds 2 ( ) 2 ( )d ,
f ( x, y)ds f [( )cos, ( )sin] 2 ( ) 2 ( )d
L
4. 若空间光滑曲线 L的参数方程为
x x(t) , y y(t) , z z(t) ( t ) ,则
ds x2 (t) y2 (t) z2 (t)dt ,
L[ f ( x, y) g( x, y)]ds L f ( x, y)ds L g( x, y)ds .
性质2 (可加性) 设 L1 与 L2 首尾相接成 L, 则有
L f ( x, y)ds L1 f ( x, y)ds L2 f ( x, y)ds ,
简记为 L f ( x, y)ds L1 L2 .
例 1.计算 yds ,其中 L 为抛物线 y x2 ,直线 L x1 及 x 轴所围成的曲边三角形的整个边界.
解:L
OA
AB
⌒
BO
y
B
OA :
y0 ,
y 0, ds dx,
0 x 1
y x2 x1
AB
y , ds dy,
0 y 1
y0 A x
⌒
BO :
y
x2
,
2
A
被积函数 xe x 2 y 2 e 1 y2 ,
o
x
B
xy
y ,
1 y2
ds
1
x
2 y
dy
dy , 1 y2
xe
x2 y2 ds e
1 2
L
2
1 y2
dy
(1
1 y2
2 )e. 2
例 3. 计 算 ( x 2 y 2 z 2 )ds , 其 中 L 为 球 面
L
x 2 y 2 z 2 9 与 平 面 x z 1 的 交 点. 2
d 0i1
2.第一型曲线积分的定义
设 L 为oxy 面上的一条光滑(或分段光滑)曲线弧,
f ( x, y) 在 L 上有界.任取点列 M1 , M 2 , , M n1 ,把 L 分为 n 小 段 li (i 1, 2, , n) ,并以si 表示 li 的弧
n
长. 任取 (i ,i ) si ,作和式 f ( i ,i )si ,设
1
y2 ( x)dx.
若 L由 方 程 x x( y) (c y d ) 给 出, 则 取 y 为 参 数,
ds 1 x2 ( y)dy,
d
L f ( x, y)ds c
f [x( y), y]
1 x2 ( y)dy.
3.若 L由方程 ( ) ( ) 给出,则取 为参数,
f ( x, y, z)ds f [x(t), y(t), z(t)] x2 (t) y2 (t) z2 (t)dt
L
注意:
(1)第一型曲线积分与曲线的方向无关,化为关于 参数的定积分计算时,上限必须大于下限.
(2)对 f ( x, y)ds 来说, f ( x, y) 是定义在 L 上的, L 被积函数中的 x,y 应满足 L 的方程,故可利 用 L 的方程化简被积函数.
2
cos tdt
(1
4
2 )e. 2
解法 2 L 的极坐标方程为 1 , ,
42
被积函数 xe x 2 y 2 e cos ,
y A
ds 2 2 d d ,
o
x
B
xe
x2 y2 ds e
2
cos d (1
2 )e. 2
L
4
解法 3 L : x 1 y2 , 2 y1 , y
(1)当 f ( x, y) 在光滑曲线 L 上连续时, f ( x, y)ds 存在. L
(2)将上述定义推广,可得空间曲线 L 上的第一型曲线
n
积分:
L
f
( x,
y, z)ds
lim
d 0i1
f
( i
,i
,
i
)si
.
第一型曲线积分的性质
性质1 (线性性质) 设 f , g 可积, 又, 为常数, 则有
解: L :
x 2
y2
z2
9 2
x z 1
( x
1)2 2
y2
2
4
z 1 x.
i 1
d max {si } ,如果当d 0时 ,和式的极限总存在,
1in
则称此极限为 f ( x, y) 在曲线弧 L 上的第一型曲线积分
或对弧长的曲线积分,记作 f ( x, y)ds ,即 L
被积函数
弧长元素
n
L
f (x, y)
ds lim f (i ,i )si
d 0i1
注:
积分弧
ds x2 (t) y2 (t)dt,
L f (x, y)ds
f [x(t), y(t)]
x2(t) y2 (t)dt.
2. 若 L由 方程 y y( x) (a x b) 给 出, 则 取 x 为 参数,
ds 1 y2 ( x)dx,
b
L f ( x, y)ds a f [ x, y( x)]
