华东师大版八年级上册数学 12.1 同底数幂的乘法 课件(17张PPT)
合集下载
华东师大版八年级上册 12.1.1 同底数幂的乘法 课件(共18张PPT)

想一想: Ø 指出 an 中各部分的名称
指数
底数 an =a·a·a···a
n个a
幂
问题1 一种电子计算机 每秒可进行1千万亿(1015 ) 次运算,它工作103 s 可进行 多少次运算? 解:1015×103
怎样计算1015×103呢?
探究新知
请同学们先根据乘方的意义,解答
1015 ×103 =(10×10×…×10)×(10×10×10)
猜想: am ·an= ? (当m、n都是正整数)
猜想: am ·an=am+n (当m、n都是正整数)
am ·an (= aa…a)(aa…a)(乘方的意义)
m个a
n个a
= aa…a (乘法结合律)
(m+n)个a
=am+n (乘方的意义)
你的猜想是正确的!
八年级 数学
同底数幂的乘法公式:
a ·a = a m
(5) (x+y)3 ·(x+y)4 = (x+y)3+4 =(x+y)7
am · an = am+n 公式中的a可以代 表一个数,一个字 母,一个式子
辨一辨:
1、下面的计算对不 对?如果不对,应怎样改正?
⑴ a3a32aa333 a6 ( 2) a2a3a b 6 5 a5
⑶ bb6 bb166 b7 ⑷ b2b2b24b 2
15个10
=(10×10×···×10)
3个10
18个10
= 10( 18 )
探究
根据乘方的意义填空,观察计算结果你能发现 什么规律?
25 ×22 = 2(7 ) a3× a2 = a(5 ) 5m× 5n = 5(m+n )
华东师大版八年级上册 数学 课件 12.1.4同底数幂的乘法(18张PPT)

(3) 5m=5( n 5×5×…)××5( 5×5×…) ×5
(m、n都是正整数)
m个5
n个5
= 5×5×…×5 =5( m )n
(m n)个5 思考:观察上面各题左右两边,底数、指数有什么关系?
猜想: am an ?
(m、n都是正整数)
am ·an等于什么?(m,n都是正整数),为什么?
? 解:104×105=
进入新课
“神州六号”宇宙飞船载人航天飞行是我 国航天事业的伟大壮举。它飞行的速度约为 104米/秒,每天飞行时间约为105秒。它每天 约飞行了多少米?
10 ×10 4
5 = (10×10×10×10) ×(10×10×10 ×10×10)
(根据 乘方的意义 )
= 10×10×10×10 ×10×10×10 ×10×10 (根据 乘法结合律 )
同底数幂的乘法
➢思考:
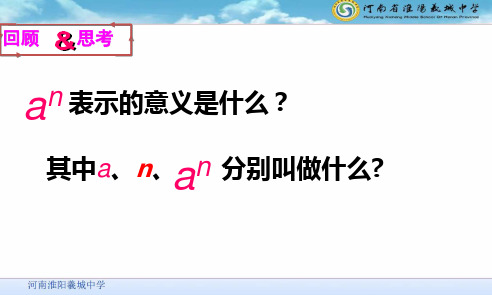
➢ an 表示的意义是什么?其中a、n、an分
别叫做什么?
an
底数
指数幂Βιβλιοθήκη an aaaan个a
试试看,你还记得吗?
1、2×2 ×2=2 (3)
• 2、a·a·a·a·a = a(5) • 3、a•a • ···• a = a( n)
n个
宇宙飞船载人航天飞行是我国航天事业的伟 大壮举。它飞行的速度约为104米/秒,每天飞 行时间约为105秒。它每天约飞行了多少米?
23 (2) 8× 4 = 2x,则 x = ; 5
23× 22 = 25 (3) 3×27×9 = 3x,则 x = . 6
3×33 ×32 = 36
4.已知:am=2, an=3. 求am+n =?
解: am+n = am ·an =2 × 3=6
华东师大版八年级上册12.1.1同底数幂的乘法课件(47张PPT)
思考:
观察上面各题的算式和结果,底数、指数有什么关
系?
猜想: am an __?__ (m、n都是正整数)
(3)a3 · a2=( a×a×a )×( a×a ) =( a×a×a×a×a )=_a_5__
同底数幂的乘法法则:
am an amn (m、n为正整数 )
同底数幂相乘,底数不变,指数相加
巩固练习.
判断(正确的打“√”,错误的打“×”)
(1) x3·x5=x15 (×) (2) x·x3=x3 (×) (3) x3+x5=x8 (×) (4) x2·x2=2x4 (×) (5) a3·b5=(ab)8 (×) 注意:x的指数是“1”而不是“0”.
例1 计算: (1) a·a6 (2) 2×24×23 (3) xm·x3m+1 (4) (x y)2 (x y)
(4) 原式 (x y)21 (x y)3
巩固训练
计算:
(1)b5·b ;
要求:
(2)10×102×103; (3) –a2·a3
(4) y2n·yn
(1)合上课本独立完成在 “巩固训练”上. (2)注意解题格式的规范
巩固训练
计算:
解: (1) b5·b=b5+1=b6 (2) 10×102×103=101+2+3=106 (3) –a2·a3 =–a2+3 =–a5
(4) -x4·x
(5) x2·y2
(6) (-x)3·(-x)5
(7) (x-y)(x+y)3
(8) (x+y)(x+y)3
理解概念
下列式子不能利用“同底数幂的乘法法则”
计算的有(1)(3)(5)(7).
观察上面各题的算式和结果,底数、指数有什么关
系?
猜想: am an __?__ (m、n都是正整数)
(3)a3 · a2=( a×a×a )×( a×a ) =( a×a×a×a×a )=_a_5__
同底数幂的乘法法则:
am an amn (m、n为正整数 )
同底数幂相乘,底数不变,指数相加
巩固练习.
判断(正确的打“√”,错误的打“×”)
(1) x3·x5=x15 (×) (2) x·x3=x3 (×) (3) x3+x5=x8 (×) (4) x2·x2=2x4 (×) (5) a3·b5=(ab)8 (×) 注意:x的指数是“1”而不是“0”.
例1 计算: (1) a·a6 (2) 2×24×23 (3) xm·x3m+1 (4) (x y)2 (x y)
(4) 原式 (x y)21 (x y)3
巩固训练
计算:
(1)b5·b ;
要求:
(2)10×102×103; (3) –a2·a3
(4) y2n·yn
(1)合上课本独立完成在 “巩固训练”上. (2)注意解题格式的规范
巩固训练
计算:
解: (1) b5·b=b5+1=b6 (2) 10×102×103=101+2+3=106 (3) –a2·a3 =–a2+3 =–a5
(4) -x4·x
(5) x2·y2
(6) (-x)3·(-x)5
(7) (x-y)(x+y)3
(8) (x+y)(x+y)3
理解概念
下列式子不能利用“同底数幂的乘法法则”
计算的有(1)(3)(5)(7).
华东师大版八年级上册 12.1 同底数幂的除法 课件(共19张PPT)

12a0
1a0
210a 210a
1 0a2 1 0a2
10a120a10a2 10a 2
2 1 0 ((12))1205721303_____2 ______4________11_;22aa00_442_1;a0 210a10a
25
课堂达标测试
第一关:火眼金睛:判断并说明理由
(1) a6÷ a3 = a2 (×)
a6÷ a3 = a3
(2) a5÷ a = a5 (×)
a5÷ a = a4
(3)(-c)4 ÷ (-c)2 =-c2(×)
(-c)4 ÷ (-c)2 =c2
第二关:大显身手
(1) s7÷s3 =s4
(2) (-t)11÷(-t)2 =-t9 (3)(ab)5÷(ab) =(ab)4 =a4b4
(3)ab4ab2
能力挑战
(1) (-3)5 ÷33 -32=-9
(2) (-x)6 ÷x2 x4 (3) (a-b)6÷(b-a)3 -(a-b)3
(b-a)3 注:若底数不同,先化为同底数,后运用法则.
让我们来抢答
(1)510 58
(2)a6 a2
(3) a2 3 a4
解 : a2m 3na2ma3n
(am)2 (an)3
39 2
23
8
已知:am=3,an=5. 求: (1)am-n的值 (2)a3m-2n的值 解:(1) am-n= am ÷ an= 3 ÷5 = 0.6 (2) a3m-2n= a 3m ÷ a 2n
= (am)3 ÷(an)2 =33 ÷52=27 ÷25 = 27
(4)
b2
华东师大版八年级上册 12.1.2 幂的乘方 课件(共17张PPT)

( a m ) 3amamam a3m =amn (乘法的意义)
看看计算的结果有什么规律?
猜想:(am)n = amn (m、n都是正整数)
幂的乘方法则:
幂的乘方,底数不变 ,指数相乘。
(a ) = a 可以 是字母,也可以是单项式和多项式
( ×)
➢ 计算:( 口答)
(1) 105×106 1011
(3) a7 ·a3 a10
(5) x5 ·x5
x10 (7) x5 ·x ·x3
x9
(2) (105)6 1030
(4) (a7)3 a21
(6) (x5)5
x25
(8)(y3)2·(y2)3
= y 6 ·y 6 = y 12
14.2.2 幂的乘方
例1:计算:
(1) (103)5; (2) (a2m)2;
(3) -(x4)3 ; (4) (y2)3·y. 解: (1) (103)5= 103Χ5 = 1015
(2) (a2m)2= a 2m Χ 2 = a 4m (3) -(x4)3 = - x 4Χ3 = - x12
(4) (y2)3·y= y6·y= y6+1 = y7
想一想:同底数 幂的乘法法则与
幂的乘方法则有 什么相同点和不 同点?
同底数幂相乘
am·an=am+n
指数相加 底数不变 指数相乘
(am)n=amn
幂的乘方
下列各式对吗?请说出你的观点和理由:
(1) (a4)3=a7
( ×)
(2) a4 a3=a12
( ×)
(3) (a2)3+(a3)2=(a6)2
1、2.若 [(x3)m ]2x12,则 m__2___
华师大版八年级数学上册第12章第1节《同底数幂的乘法》优质课件

6、已知: 12
x
=
1 2
1 4
1 8
1 16
1 32
1 64
,
试求x的值 。
7、已知xm-n x2n+1=x11且 ym-1 y4-n =y5,求m-n的值。
b4m1
对前面两个问题如何解?
地球与太阳的距离 = 5 102 3 105 千米 3 5 102 105 15107 千米
比邻星与地球的距离 = 3107 4.22 3105 千米 3 3 4.22107 105 37.981012 3.7981013 千米
判断:
(1) x3 x5 x15 × (2) x x3 x3 × (3) x3 x5 x8 × (4) x2 x2 2x4 ×
根据 路程 = 时间 × 速度 有
地球与太阳的距离 = 5 102 3 105 千米 比邻星与地球的距离 = 3107 4.22 3105 千米
如何计算 102 105 和 107 105 呢?
根据幂的意义:10 2 105 (10 10) (10 10 10 10 10)
2个10
5个10
(5) (x)2 (x)3 (x)5 x5 √ √ (6) a3 a2 a2 a3 0
(7) a3 b5 (a b)8 × × (8) y 7 y 7 y14
这节课我们学习了同底数幂的乘法的运 算性质,你有何新的收获和体会n
(m,n都是正整数)
智力大冲浪
第12章 整式的乘除
12.1幂的运算 1.同底数幂的乘法
指数
an
幂
底数
它的意义呢?
an a a a a
n 个a
问题一 、光的速度为 3×105 千米/秒,太阳光照射到地球
华东师大版八年级数学上册12.1.1同底数幂的乘法 优质课 课件

(1) x2(-x4)(-x)3(-x2)
(2) -b3(-b)2n+1 (3) (x-y)n(x-y)n(y-x)2n(y-x)2n-1
反思 同底数幂的乘法法则: 同底数幂相乘,底数不变,指数相加.
am ·an =am+n (m,n都是正整数) am ·an ·ap=am+n+p (m,n,p都是正整数)
作业
课本P 24 习题12.1 1,
总结:★不能疏忽指数为1的情况;
★运算时可先确定符号结果的底数一般应为正数. ★若底数不同,先化为相同,后运用法则.
演练
1. 判断下列计算是否正确,并简要说明理由:
① a ·a2= a2 (×) ② a+a2 = a3 (×) ③ a3 ·a3= a9 (×) ④ a3+a3 = a6 (×)
2. 计算:
m+n个a
= am+n
(乘方的意义) (乘法结合律) (乘方的意义)
理论
同底数幂的乘法
同底数幂的乘法法则:
即: am·an = am+n (当m、n都是正整数)
同底数幂相乘,底数不变,指数相加 .
思考:am·an·ap =?
例题
例1:计算
(1) 103×104 (2)(-2)2·(-2) 3·(-2) (3) a4n·an+3·a3 (4)(a+b)(a+b)m(a+b)n 解:(1)原式=103+4=107 (2)原式=(-2)2+3+1=(-2)6=26=64 (3)原式=a4n+n+3+3=a5n+6 (4)原式=(a+b)m+n+1
思考
(2) -b3(-b)2n+1 (3) (x-y)n(x-y)n(y-x)2n(y-x)2n-1
反思 同底数幂的乘法法则: 同底数幂相乘,底数不变,指数相加.
am ·an =am+n (m,n都是正整数) am ·an ·ap=am+n+p (m,n,p都是正整数)
作业
课本P 24 习题12.1 1,
总结:★不能疏忽指数为1的情况;
★运算时可先确定符号结果的底数一般应为正数. ★若底数不同,先化为相同,后运用法则.
演练
1. 判断下列计算是否正确,并简要说明理由:
① a ·a2= a2 (×) ② a+a2 = a3 (×) ③ a3 ·a3= a9 (×) ④ a3+a3 = a6 (×)
2. 计算:
m+n个a
= am+n
(乘方的意义) (乘法结合律) (乘方的意义)
理论
同底数幂的乘法
同底数幂的乘法法则:
即: am·an = am+n (当m、n都是正整数)
同底数幂相乘,底数不变,指数相加 .
思考:am·an·ap =?
例题
例1:计算
(1) 103×104 (2)(-2)2·(-2) 3·(-2) (3) a4n·an+3·a3 (4)(a+b)(a+b)m(a+b)n 解:(1)原式=103+4=107 (2)原式=(-2)2+3+1=(-2)6=26=64 (3)原式=a4n+n+3+3=a5n+6 (4)原式=(a+b)m+n+1
思考
华师大版八年级数学上册第12章第1节《同底数幂的乘法》教学课件

(1)102×104×105
(2)
(3) xm •a表示. 求:(1)a3+n (2)am+n+2
( )个5 = 5( )
( )个5
它们的积都是什么形式?积的各个部分与乘数有什 么关系?
一般地,对于任意底数a与正整数m、n, am×an =(a×a×···×a)×(a×a×···×a)
( )个a
= a×a×···×a ( )个a
=a(m+n) (m,n都是正整数)
( )个a
根据幂的意义
根据乘法结合律 根据幂的意义
合作探究 达成目标 探究点一 探究并推导同底数幂的乘法法则
(1) 思考:乘方的意义是什么?(即am表示什么?) (2)根据乘方的意义填空,看看计算结果有什么规律: 23×22=[( )×( ) ×( )]×[( )×( ) ]
=2( ) a3.a2=[( )×( )×( )]×[( )×( )]
= a( ) 5m× 5n=(5×5×……×5 )×(5×5×……×5 )
,不是 .
的形式,
运用同底数幂的乘法的运算性质
练习1 判断下列计算是否正确,并简要说明理由: (1) n3 n7 n10; (2) a2 a5 a8;
(3) y5 y4 y20; (4) x x2 x2; (5) b4 b4 2b4.
运用同底数幂的乘法的运算性质
练习2 计算:
(1)(- 1 )(- 1 )2 (- 1 )3;
2
2
2
(2) a2 a6.
总结梳理 内化目标
1.知识结构图
乘方的意义
推导
同底数幂
类比、归纳、转化 乘法法则
2.在探索同底数幂的乘法运算法则时,进一 步体会幂的意义,从而更好的理解该法则.
华师大八年级数学上册《同底数幂的乘法》课件

12.1.1 同底数幂的乘法
[备选例题] 计算: (1)(b+2)3·(b+2)5·(b+2); (2)(x-2y)2·(2y-x)3. [解析] 把 b+2,x-2y 均看作一个整体,运用同底数幂 的乘法法则计算,第(2)题必须先化为同底数,即将(x-2y)2 转化为(2y-x)2,或者将(2y-x)3 转化为-(x-2y)3. 解:(1)原式=(b+2)3+5+1=(b+2)9. (2)解法 1:原式=(x-2y)2·[-(x-2y)3]=-(x-2y)5; 解法 2:原式=(2y-x)2·(2y-x)3=(2y-x)5.
12.1.1 同底数幂的乘 法
探究问题二 逆用同底数幂的乘法法则 例 2 [拓展创新题] (1)若 3m=5,3n=7,求 3m+n+1 的值; (2)若 2m=A,2n=B,求 2m+n.
[解析] 本题主要考查同底数幂的乘法法则的逆用. 解:(1)3m+n+1=3m·3n·3=5×7×3=105. (2)2m+n=2m·2n=a·b=ab. [归纳总结] 公式的逆用:am+n=am·an(m,n 为正整数). 作用:可以把一个幂分成两个或两个以上同底数幂相乘 的形式.
12.1.1 同底数幂的乘法
新知梳理
► 知识点 同底数幂的乘法法则 法则:同底数幂相乘,_底__数_不变,指数相__加_. 字母表达式:am·an=am+n(m,n 为正整数). 推广:am·an·…·ap=am+n+…+p(m,n,…,p 为正整数).
12.1.1 同底数幂的乘法
重难互动探究
探究问题一 运用同底数幂的乘法法则进行计算 例 1 [课本例 1 变式题] 计算: (1)x2·x5;(2)a·a6;(3)2×24×23; (4)xm·x3m+1.
1、教师的影响是永恒的;无法估计他的影响会有多深远。 2、gladly would learn, and gladly teach.勤于学习的人才能乐意施教。 3、is not the filling of a pail but the lighting of a fire. 4、好的教师是让学生发现真理,而不只是传授知识。 5、与其不受教育,不知不生,因为无知是不幸的根源。
华东师大版八年级上册数学 12.1 同底数幂的乘法 课件(17张PPT)

3xmxm1; 4ab2ba3.
解 1103104 1034 1 0 7
2aa3 a 1 3 a 4
3 xmxm1 xmm1 x 2 m 1
4ab2ba3ab2ab3
a b 23 a b5
例2计算:
1333435;
2aa3 a5.
3xnx2n1x; 4ab2ba3.
解 1333435 3345 3 1 2
4)x3x4____ x_7___; 5 )x 2x x 3 x 3 x 2x _ _ 2_ x_ 6_ _ _ ;
6 )x m y n 2 y n 2 y x m _ _ _ 0_ _ _ _ .
这节课我们学习了同底数幂的乘法的运 算性质,你有何新的收获和体会?
aaa m n
m n (m,n都是正整数)
2m 2n 等于什么?
1 7
m
1 7
n
(m,n都是正整数)
a a m
n (m,n都是正整数)等于什么乘,底数不变,指数相加
例题讲解 计算:
37 36313 313
1 10
3
1 10
1
4
1 0
x3 x5 x8
b2mb2m1 b4m1
解 b 2 b m 2 b b m 1 b 3 b m 5 b 2
b 2 m 2 b 1 m 1 b 3 m 5 2
bmbmbm bm
练习1)5x2xx5__ 5_ x_ 8 _;
2 )2 a 1 22 a 1 3 _ _ 2_ a_ _ _ 1_ 5;
3)a6a4___a_1_ 0 _;
同底数幂的乘法
an •am ?
学习六步曲
学习目标 回顾思考 探究新知 例题讲解 巩固练习 课堂小结
解 1103104 1034 1 0 7
2aa3 a 1 3 a 4
3 xmxm1 xmm1 x 2 m 1
4ab2ba3ab2ab3
a b 23 a b5
例2计算:
1333435;
2aa3 a5.
3xnx2n1x; 4ab2ba3.
解 1333435 3345 3 1 2
4)x3x4____ x_7___; 5 )x 2x x 3 x 3 x 2x _ _ 2_ x_ 6_ _ _ ;
6 )x m y n 2 y n 2 y x m _ _ _ 0_ _ _ _ .
这节课我们学习了同底数幂的乘法的运 算性质,你有何新的收获和体会?
aaa m n
m n (m,n都是正整数)
2m 2n 等于什么?
1 7
m
1 7
n
(m,n都是正整数)
a a m
n (m,n都是正整数)等于什么乘,底数不变,指数相加
例题讲解 计算:
37 36313 313
1 10
3
1 10
1
4
1 0
x3 x5 x8
b2mb2m1 b4m1
解 b 2 b m 2 b b m 1 b 3 b m 5 b 2
b 2 m 2 b 1 m 1 b 3 m 5 2
bmbmbm bm
练习1)5x2xx5__ 5_ x_ 8 _;
2 )2 a 1 22 a 1 3 _ _ 2_ a_ _ _ 1_ 5;
3)a6a4___a_1_ 0 _;
同底数幂的乘法
an •am ?
学习六步曲
学习目标 回顾思考 探究新知 例题讲解 巩固练习 课堂小结
同底数幂的乘法(课件)华东师大版数学八年级上册

课堂总结
法则
同底数幂相乘,底数不变,指数相加.
同底数幂相乘 公 式
am ·an=am+n (m,n 都是正整数).
注意
同底数幂的乘法法则,只有在底数相同时才能 使用,并且底数不变,指数相加。底数可以是 数、单独的字母、也可以是一个多项式。
am·an·ap= am+n+p
(m、n、p都是正整数)
新知讲解
例1 计算 (1)103x104 (2)a·a3 (3)a·a3·a5
新知讲解
解: (1)103x104=103+4=107 (2)a·a3=a1+3=a4 (3)a·a3·a5=a1+3+5=a9
新知讲解
变式 计算: (1)x2·x5; (2)a·a6; (3)2×24×23;
光在真空中的速度大约是3×105 千米/秒,太阳系 以外距离地球最近的恒星是比邻星,它发出的光到达 地球大约需要年。一年以3×107 秒计算,比邻星与地 球的距离约为多少千米?
3×105 ×3×107 ×(105 × 107 )
105 × 107 怎样计算?
复习导入
计算下面各题 4×4×4×4 =____4__4______ 6×6×6-3)×(-3)×(-3) =__(___-_3_)__5___
12.1.1 同底数幂的乘法
学习目标: 1、能说出同底数幂相乘的法则,并会用法则解决简 单的实际问题. 2、通过法则的探究过程,培养学生的归纳概括能力. 3、体会探究过程,激发学生的探索创新的精神. 重点难点; 能说出同底数幂相乘的法则,并会用法则解决简单的 实际问题
回顾 1.什么叫做幂? n中,a和n分别叫做什么?
新知讲解
根据幂的意义填空: (1)23x24=(2x2x2)x(2x2x2X2)
华东师大初中数学八上《12.1.1同底数幂的乘法》(共19张PPT)

= 2×__2_×__2__×__2_×__2_×__2_×2 =2( 7) ;
(2)a3×a2 = ( a×a×a ) ×( a×a )
=_a_×__a_×__a_×__a×__a___= a( 5 ) ;
(3) 5m ·5n
=(
5×···×5)
×(
5×···×5)
=
5(
m+n )
.
m个5
n个5
思考:观察上面各题左右两边,底数、指数有什
么关系?
猜想: am ·an= ?m·an =(a·a··a) (a·a··a)
m个a
n个a
= a·a·…·a
(m+n)个a
即
= am+n
am·an = am+n(m,n都是正整数)。
同底数幂的乘法法则:
am·an =am+n(m,n都是正整数)。
4、已知:am+1 bn+2 a2n-1 b2m
=a 5 b3则m+n=___。
6、已知: 12
x
=
1 2
1 4
1 8
1 16
1 32
1 64
,
试求x的值 。
7、已知xm-n x2n+1=x11且 ym-1 y4-n =y5,求m-n的值。
同底数幂相乘,底数不变,指数相加。
例1 计算:
(1)(-3)7×( -3)6;
(2)(
─1
10
)3 ×( ─1 ); 10
(3) -x3 • x5; (4) b2m • b2m+1.
解:
(1)(-3)7×( -3)6 = (-3)7+6 = (-3)13;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上大约需要 5 × 1 0 2 秒,地球距太阳大约多远?
问题二 、光在真空中的速度为 3×1 0 5 千米/秒,太阳系以
外距地球最近的恒星是比邻星,它发出的光到达地球约4.22 年,一年以3 ×1 0 7 秒计算,比邻星与地球距离约多少千米?
根据 路程 = 时间 × 速度 有
地球与太阳的距离 = 51023105 千米 比邻星与地球的距离 = 3 1 0 7 4 .2 2 3 1 0 5 千米
(5) (x)2(x)3(x)5x5 √ √ (6) a3a2a2a30
(7) a3b5 (ab)8 ×
Are you clear?
× (8) y7 y7 y14
例1.计算:
1103104; 2 a a3;
3xmxm1; 4ab2ba3.
解 1103104 1034 1 0 7
2aa3 a 1 3 a 4
(m,n都是正整数)
a a m
n (m,n都是正整数)等于什么?为什么?
amanamn
同底数幂相乘,底数不变,指数相加
例题讲解 计算:
37 36313 313
1 10
3
1 10
1 1 0
4
x3 x5 x 8
b2mb2m1 b 4m1
对前面两个问题如何解?
地球与太阳的距离 = 51023105 千米 35102105 15107 1.5108 千米
bmbmbm bm
练习1)5x2xx5__ 5_ x_ 8 _;
2 )2 a 1 22 a 1 3 _ _ 2_ a_ _ _ 1_ ;5
3)a6a4___a_1_ 0 _;
4)x3x4___ _ x_7___; 5 )x 2x x 3 x 3 x 2x _ _ 2_ x_ 6_ _ _ ;
同底数幂的乘法
an •am ?
学习六步曲
学习目标 回顾思考 探究新知 例题讲解 巩固练习 课堂小结
学习目标
1、理解同底数幂的乘法性质并会用式子表 示.
2、能主动探索并判断两个幂是否是同底幂,并 能掌an
幂
底数
它的意义呢?
anaaa La
n 个a
问题一 、光的速度为 3× 1 0 5 千米/秒,太阳光照射到地球
探究新知
如何计算 102 105 和 107 105 呢?
根据幂的意义:1 0 2 1 0 5 ( 1 0 1 0 ) ( 1 0 1 0 1 0 1 0 1 0 )
2个10
5个10
= 1 0 1 0 L 1 0 1 0
7个10
=1 0 7
我们观察 102 105 可以 发现, 1 0 2 和 1 0 5
这两个因数底数相同,是同底的幂的形式
所以我们把 102 105 这种运算叫做
你知道了吗?
同底数幂的乘法
探究新知 计算下列各式:
102 103
108 105
10m 10n (m,n都是正整数)
你发现了什么?计算前后底数和指数 有什么变化?用自己的语言描述
2m 2n 等于什么?
1 7
m
1 7
n
3 xnx2n1xxn2n11 x 3 n 2
4ab2ba3ba2ba3
b a 23 b a 5
例3 计算:b 2 b m 2 b b m 1 b 3 b m 5 b 2 .
解 b 2 b m 2 b b m 1 b 3 b m 5 b 2
b 2 m 2 b 1 m 1 b 3 m 5 2
3 xmxm1 xmm1 x 2 m 1
4ab2ba3ab2ab3
a b 23 a b5
例2计算:
1333435; 2aa3 a5.
3xnx2n1x; 4ab2ba3.
解 1333435 3345 3 1 2
2aa3a5 a4 a5 a 9
底数(a-b)与(b-a) 互为相反数,要利 用符号的转化把他 们转化为相同的底 数。
比邻星与地球的距离 = 3 1 0 7 4 .2 2 3 1 0 5 千米 3 3 4 .2 2 1 0 7 1 0 5 37.981012 3.7981013 千米
判断:
(1) x3x5 x15 × (2) x x3 x3 × (3) x3x5 x8 × (4) x2x2 2x4 ×
6 )x m y n 2 y n 2 y x m _ _ _ 0_ _ _ _ .
这节课我们学习了同底数幂的乘法的运 算性质,你有何新的收获和体会?
aaa m n
m n (m,n都是正整数)
问题二 、光在真空中的速度为 3×1 0 5 千米/秒,太阳系以
外距地球最近的恒星是比邻星,它发出的光到达地球约4.22 年,一年以3 ×1 0 7 秒计算,比邻星与地球距离约多少千米?
根据 路程 = 时间 × 速度 有
地球与太阳的距离 = 51023105 千米 比邻星与地球的距离 = 3 1 0 7 4 .2 2 3 1 0 5 千米
(5) (x)2(x)3(x)5x5 √ √ (6) a3a2a2a30
(7) a3b5 (ab)8 ×
Are you clear?
× (8) y7 y7 y14
例1.计算:
1103104; 2 a a3;
3xmxm1; 4ab2ba3.
解 1103104 1034 1 0 7
2aa3 a 1 3 a 4
(m,n都是正整数)
a a m
n (m,n都是正整数)等于什么?为什么?
amanamn
同底数幂相乘,底数不变,指数相加
例题讲解 计算:
37 36313 313
1 10
3
1 10
1 1 0
4
x3 x5 x 8
b2mb2m1 b 4m1
对前面两个问题如何解?
地球与太阳的距离 = 51023105 千米 35102105 15107 1.5108 千米
bmbmbm bm
练习1)5x2xx5__ 5_ x_ 8 _;
2 )2 a 1 22 a 1 3 _ _ 2_ a_ _ _ 1_ ;5
3)a6a4___a_1_ 0 _;
4)x3x4___ _ x_7___; 5 )x 2x x 3 x 3 x 2x _ _ 2_ x_ 6_ _ _ ;
同底数幂的乘法
an •am ?
学习六步曲
学习目标 回顾思考 探究新知 例题讲解 巩固练习 课堂小结
学习目标
1、理解同底数幂的乘法性质并会用式子表 示.
2、能主动探索并判断两个幂是否是同底幂,并 能掌an
幂
底数
它的意义呢?
anaaa La
n 个a
问题一 、光的速度为 3× 1 0 5 千米/秒,太阳光照射到地球
探究新知
如何计算 102 105 和 107 105 呢?
根据幂的意义:1 0 2 1 0 5 ( 1 0 1 0 ) ( 1 0 1 0 1 0 1 0 1 0 )
2个10
5个10
= 1 0 1 0 L 1 0 1 0
7个10
=1 0 7
我们观察 102 105 可以 发现, 1 0 2 和 1 0 5
这两个因数底数相同,是同底的幂的形式
所以我们把 102 105 这种运算叫做
你知道了吗?
同底数幂的乘法
探究新知 计算下列各式:
102 103
108 105
10m 10n (m,n都是正整数)
你发现了什么?计算前后底数和指数 有什么变化?用自己的语言描述
2m 2n 等于什么?
1 7
m
1 7
n
3 xnx2n1xxn2n11 x 3 n 2
4ab2ba3ba2ba3
b a 23 b a 5
例3 计算:b 2 b m 2 b b m 1 b 3 b m 5 b 2 .
解 b 2 b m 2 b b m 1 b 3 b m 5 b 2
b 2 m 2 b 1 m 1 b 3 m 5 2
3 xmxm1 xmm1 x 2 m 1
4ab2ba3ab2ab3
a b 23 a b5
例2计算:
1333435; 2aa3 a5.
3xnx2n1x; 4ab2ba3.
解 1333435 3345 3 1 2
2aa3a5 a4 a5 a 9
底数(a-b)与(b-a) 互为相反数,要利 用符号的转化把他 们转化为相同的底 数。
比邻星与地球的距离 = 3 1 0 7 4 .2 2 3 1 0 5 千米 3 3 4 .2 2 1 0 7 1 0 5 37.981012 3.7981013 千米
判断:
(1) x3x5 x15 × (2) x x3 x3 × (3) x3x5 x8 × (4) x2x2 2x4 ×
6 )x m y n 2 y n 2 y x m _ _ _ 0_ _ _ _ .
这节课我们学习了同底数幂的乘法的运 算性质,你有何新的收获和体会?
aaa m n
m n (m,n都是正整数)
