第7章 放宽条件的回归模型(3)自相关
经济计量学之自相关

经济计量学之自相关引言经济计量学是以数理统计方法为基础,应用于经济现象的研究和分析的一门学科。
自相关是经济计量学中的一个重要概念。
自相关指的是观测序列中不同时刻之间的相关性。
在经济学中,自相关经常应用于时间序列的分析,用于研究经济现象在时间上的相关性与趋势。
自相关的基本概念自相关是指同一时间序列的不同观测值之间的相关性。
一般情况下,时间序列的自相关用自相关系数(autocorrelation coefficient)来衡量。
自相关系数的取值范围为-1到1之间,取决于观测值之间的相关性。
自相关系数的计算公式如下所示:formulaformula其中,Cov表示时间点t和时间点t-k之间的协方差,sigma和sigma分别表示时间点t和时间点t-k的标准差。
当自相关系数接近于1时,表示观测序列在不同时间点上具有很强的相关性,即存在显著的长期相关性。
当自相关系数接近于-1时,表示观测序列在不同时间点上呈现出负相关性。
当自相关系数接近于0时,表示观测序列在不同时间点上呈现出随机性,不存在相关性。
自相关的应用自相关在经济学中有广泛的应用。
下面列举了几个常见的应用场景:1. 时间序列预测自相关分析可用于时间序列预测。
利用过去观测数据之间的自相关性,可以对未来的观测值进行预测。
通过分析自相关系数,可以确定合适的预测模型,如自回归移动平均模型(ARMA模型)或自回归积分滑动平均模型(ARIMA模型)。
2. 经济周期分析自相关分析可用于研究经济周期的波动特征。
经济周期是一种重要的经济现象,对宏观经济政策制定和企业经营决策具有重要意义。
通过对经济数据进行自相关分析,可以发现周期性的波动模式,从而对未来的经济变化进行预测和研究。
3. 时间序列平稳性检验自相关分析可用于检验时间序列的平稳性。
平稳性是时间序列分析的基本假设之一,意味着时间序列的均值和方差在不同时间段上保持不变。
通过计算自相关系数,可以评估时间序列的平稳性,并对序列进行必要的转换以满足平稳性的要求。
计量经济学 第七章答案

练习题7.1参考解答(1)先用第一个模型回归,结果如下:22216.4269 1.008106 t=(-6.619723) (67.0592)R 0.996455 R 0.996233 DW=1.366654 F=4496.936PCE PDI =-+==利用第二个模型进行回归,结果如下:122233.27360.9823820.037158 t=(-5.120436) (6.970817) (0.257997)R 0.996542 R 0.996048 DW=1.570195 F=2017.064t t t PCE PDI PCE -=-++==(2)从模型一得到MPC=1.;从模型二得到,短期MPC=0.,长期MPC= 0.+(0.)=1.01954练习题7.2参考答案(1)在局部调整假定下,先估计如下形式的一阶自回归模型:*1*1*0*tt ttu Y X Y +++=-ββα估计结果如下:122ˆ15.104030.6292730.271676 se=(4.72945) (0.097819) (0.114858)t= (-3.193613) (6.433031) (2.365315)R =0.987125 R =0.985695 F=690.0561 DW=1.518595t t t Y X Y -=-++根据局部调整模型的参数关系,有****11 ttu u αδαβδββδδ===-=将上述估计结果代入得到: *1110.2716760.728324δβ=-=-=*20.738064ααδ==-*0.864001ββδ==故局部调整模型估计结果为: *ˆ20.7380640.864001ttYX =-+ 经济意义解释:该地区销售额每增加1亿元,未来预期最佳新增固定资产投资为0.亿元。
运用德宾h 检验一阶自相关:(121(1 1.34022d h =-=-⨯=在显著性水平05.0=α上,查标准正态分布表得临界值21.96h α=,由于21.3402 1.96h h α=<=,则接收原假设0=ρ,说明自回归模型不存在一阶自相关。
自相关(中级计量经济学总结(四川大学,杨可扬)

自相关(中级计量经济学总结(四川大学,杨可扬)自相关(wooldridge, Gujarati 12章)一,自相关的概念自相关:当误差项协方差不为零。
即,对某些观察值 i 和 m,cov(,)0 i m u u 1 ,i m1 二,自相关的后果自相关不影响无偏性和一致性。
但是自相关使得OLS 不再是BLUE, 且 t,F 检验不再有效。
只要满足平稳性和弱相依性的条件则 R-squared 仍然是一致的。
三,自相关的侦测1,图表法用残差对时间做图,或者用残差对滞后一期的残差作图。
2,直接对r 进行 t 检验假设自变量是严格外生的,且扰动项是 AR(1),即,1 u u e t t tr =+ - 那么我们只需要对 r 进行一个 t 检验就可以了。
备择假设既可以是 0 : 0 H r 1 也可以是, 0: 0 H r > 当然在这里还可以采用异方差稳健的统计量。
我们还可以放松严格外生的假定,并且可以考虑高阶的自回归:01111 ? ? ? t t k tk t k t ku x x u u b b b r r -- =+++++ …… ……+我们只需要对残差的K 个滞后值进行 F 检验就可以了。
注意: tk x 中可以包括因变量的滞后值。
其实利用上面回归所得 R-squared 我们还可以进行 BG 检验:2() u LM n q R =- 2q LM c : 对于 LM 统计量的计算各种书上略有差异。
上面的公式来自 Wooldridge ,其中 q 表示残差滞后的期数。
在 EVIEWS5 中所用的 LM 统计量的计算是 2 ? uLM nR = 。
3,D-W 检验有上面的检验之后,已经不用再搞什么 D-W 检验了。
但是它仍然被广泛使用,所以有必要了解。
重点要注意它的局限性。
(1) 12(1)1 2d d r r ?-? 也即,- r ££££既然-11,那么0d 4。
这样我们就把 d 与上面的知识联系起来了。
第七章自相关计量经济学,南开大学

可以对 Y t* a bX * vt (t 2,3, n)进行OLS估计 t
再计算出β1、β2。
在CLRM中,假定干扰项u不存在自相关,即 Cov(ui,uj) = 0,i <>j 如果这一条件被破坏,即干扰项存在自相关,那么使用OLS估计就可能存 在问题。实际上,在经济计量研究中,自相关士一种常见的现象。如,消 费支出要受到当期和前几期收入的影响;某一年的GDP要受到前期的GDP 水平的影响;某种商品的供给量要受到前一期的其它变量影响,等等。
原假设H 0 : 0 备择假设H1 : 0 定义检验变量d d
2 ˆ ˆ ( u u ) t t 1 t 2 n
d
ˆ t 2 u ˆt u ˆt 1 2 u
2 t 2 t 2 2 ˆ u t t 2 n
n
n
21 t 2n
uˆ uˆ
若 u ˆ t 随时间变化不断变换符号,说明存在负相关;若连续几个为正, 后边几个为负,则可能存在正相关。
ut
ut
t
t
二、杜宾—瓦特森(Durbin-Watson)检验 基本假定: (1)回归式中有截距项 (2)解释变量是非随机的 (3)干扰项的模式为一阶自回归模式:ut
ut 1 v
(4)回归模型中,物质后因变量被当作解释变量。 (5)没有缺落数据。 检验方法如下: ut ut 1 vt
第三节 自相关的探察
一、图示法
ˆt , u ˆt 1 的散点图 1、绘制 u
ˆ1, u ˆ2 ,, u ˆt 1, u ˆt 。 首先利用OLS回归后,求出残差 u
ˆ1, u ˆ2 ), (u ˆ2 , u ˆ3 ),, (u ˆt 1, u ˆt )的散点图。 绘出 (u
回归检验法检验自相关

回归检验法检验自相关自相关是指时间序列中自身过去值与当前值之间的相关关系。
在时间序列分析中,自相关的存在可能会影响建模和预测的准确性。
为了验证时间序列数据中是否存在自相关,常常使用回归检验法进行检验。
回归检验法是一种常用的统计方法,用于检验时间序列数据中的自相关性。
它可以帮助我们判断时间序列数据是否存在自相关,并进一步确定是否需要进行自相关修正。
具体步骤如下:1. 收集并整理时间序列数据。
首先,我们需要收集所需的时间序列数据,并按照时间顺序进行整理。
确保数据的准确性和完整性是非常重要的,因为数据的质量直接影响到后续的分析和检验结果。
2. 统计学描述。
在进行回归检验之前,我们需要对数据进行统计学描述,包括均值、方差、偏度和峰度等指标。
这些指标可以帮助我们对数据的分布情况和特征进行初步了解。
3. 绘制自相关图。
自相关图是判断数据自相关性的一种常用图形方法。
通过绘制自相关图,我们可以观察不同滞后阶数下的自相关系数,并判断是否存在显著的自相关。
4. 设置假设。
在进行回归检验之前,我们需要设置相应的假设。
通常,我们假设时间序列数据不存在自相关(原假设),然后根据样本数据进行统计检验,以判断是否拒绝原假设。
5. 进行回归检验。
在进行回归检验时,我们可以使用多种方法,如Durbin-Watson检验、Ljung-Box检验和皮尔逊相关系数检验等。
这些检验方法基于不同的统计指标和算法,旨在判断自相关是否显著,并对其进行修正。
6. 解读结果。
根据回归检验的结果,我们可以得出结论,判断时间序列数据中的自相关性程度。
如果结果显示存在自相关,我们可以进一步进行自相关修正,以提高建模和预测的准确性。
回归检验法可以帮助我们判断时间序列数据中是否存在自相关,并进一步确定是否需要进行自相关修正。
通过合理使用回归检验方法,我们可以更好地分析和预测时间序列数据,提高决策的准确性和可靠性。
在使用回归检验法进行自相关检验时,我们需要注意数据的质量和准确性,选择合适的检验方法,并根据结果进行解读和处理。
回归模型的要素

回归模型的要素
回归模型是一种统计分析方法,用于建立变量之间的关系模型。
它基于变量之间的线性关系假设,并通过拟合数据来估计模型参数。
回归模型包含以下要素:
1. 因变量(Dependent Variable):也称为被解释变量或目标变量,它是我们想要预测或解释的变量。
2. 自变量(Independent Variables):也称为解释变量或预测变量,它们是用来解释或预测因变量的变量。
回归模型可以包含一个或多个自变量。
3. 线性关系(Linear Relationship):回归模型假设因变量与自变量之间存在线性关系,即自变量的变化对因变量的影响是线性的。
4. 残差(Residuals):在回归模型中,残差是指观测值与模型预测值之间的差异。
回归模型的目标是通过最小化残差的平方和来找到最佳拟合线。
5. 模型参数(Model Parameters):回归模型的参数是用来描述自变量与因变量之间关系的数值。
在线性回归模型中,参数表示自变量对因变量的影响程度。
6. 截距(Intercept):截距是回归模型中的常数项,表示在自变量为零时,因变量的预测值。
它反映了因变量在没有自变量影响时的基准水平。
通过确定回归模型的要素,并进行数据拟合和参数估计,我
们可以使用回归模型来预测或解释因变量的变化。
放宽基本假定的模型--异方差课本试验及练习讲解
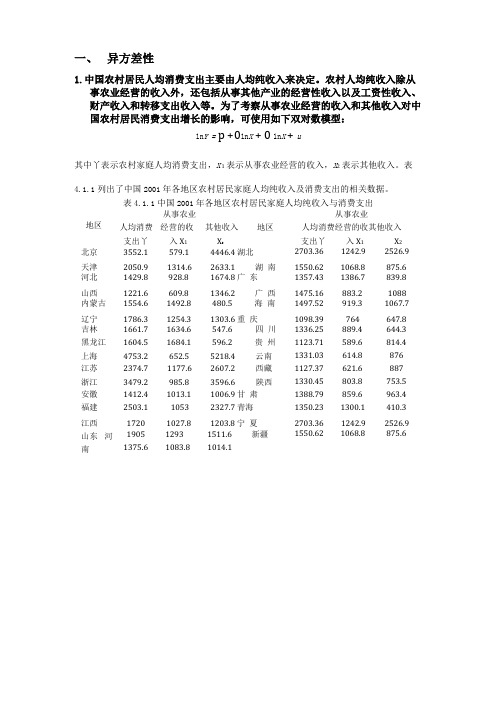
一、异方差性1.中国农村居民人均消费支出主要由人均纯收入来决定。
农村人均纯收入除从事农业经营的收入外,还包括从事其他产业的经营性收入以及工资性收入、财产收入和转移支出收入等。
为了考察从事农业经营的收入和其他收入对中国农村居民消费支出增长的影响,可使用如下双对数模型:ln Y = p +0ln X + 0 ln X + u其中丫表示农村家庭人均消费支出,X 1表示从事农业经营的收入,X2表示其他收入。
表4.1.1列出了中国2001年各地区农村居民家庭人均纯收入及消费支出的相关数据。
表4.1.1中国2001年各地区农村居民家庭人均纯收入与消费支出从事农业从事农业地区人均消费经营的收其他收入地区支出丫入X1 X2人均消费经营的收其他收入支出丫入X1 X2北京3552.1 579.1 4446.4 湖北2703.36 1242.9 2526.9天津2050.9 1314.6 2633.1 湖南1550.62 1068.8 875.6 河北1429.8 928.8 1674.8 广东1357.43 1386.7 839.8山西1221.6 609.8 1346.2 广西1475.16 883.2 1088 内蒙古1554.6 1492.8 480.5 海南1497.52 919.3 1067.7辽宁1786.3 1254.3 1303.6 重庆1098.39 764 647.8 吉林1661.7 1634.6 547.6 四川1336.25 889.4 644.3 黑龙江1604.5 1684.1 596.2 贵州1123.71 589.6 814.4 上海4753.2 652.5 5218.4 云南1331.03 614.8 876 江苏2374.7 1177.6 2607.2 西藏1127.37 621.6 887 浙江3479.2 985.8 3596.6 陕西1330.45 803.8 753.5 安徽1412.4 1013.1 1006.9 甘肃1388.79 859.6 963.4 福建2503.1 1053 2327.7 青海1350.23 1300.1 410.3 江西1720 1027.8 1203.8 宁夏2703.36 1242.9 2526.9山东河南1905 1293 1511.6 新疆1375.6 1083.8 1014.11550.62 1068.8 875.6用OLS 法进行估计,结果如下:Dependent Variable: LOG(Y) Method: Least SquaresDate: 07/03/08 Time: 16:31 Sample: 1 31Included observations: 31VariableCoefficient Std. Error t-Statistic Prob. C 1.602528 0.860978 1.861288 0.0732 LOG(X1) 0.325416 0.103769 3.135955 0.0040 LOG(X2)0.5070780.04859910.43385□ ,□□00R-squared□796506 Mean dependent var 7.448704 Adjusted R-squared □781971 S.D. dependent var 0.364648 S.E. of regression 0.170267 Akaike info criterion -0.611128 Sum squared resid 0.811747 Schwarz criterion -0.472355Log likelihood12,47249 F-statistic54,79806 Durbin-Watson stat1.964720Prob(F-statistic)0.000000对应的表达式为:In Y = 1.603 + 0.325ln X 1 + 0.507ln X 2(1.86) (3.14) (10.43)R 2 = 0.7965, R = 0.78, RSS = 0.8117不同地区农村人均消费支出的差别主要来源于非农经营收入及其他收入的差 别,因此,如果存在异方差性,则可能是X 2引起的。
第七章 自相关

第七章 自相关§1 自相关的含义和类型一、自相关(Autocorrelation): 1、定义在经典线性后果模型,我们假设随机扰动项序列的各项之间不相关,如果这一假定不满足,则称之为自相关。
即用符号表示为,j i u u E u u Cov j i j i ≠∃≠= 0)(),( (7.1.1) 2、简化记号)var(),cov(0t t t u u u r == ),cov(),cov(111+-==t t t t u u u u r ),cov(22-=t t u u r ),cov(s t t s u u r -=3、自相关系数)var()var(),(r r u u u u Cov st s t s t -==ρ 011r r =ρ,022r r=ρ,…, 0r r s s =ρ 4、⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=--------11)var(212111202121110n n n n n n n n r r r r r r r r u ρρρρρρσ二、类型1、一阶自回归AR(1)形式: t t t u u ερ+=-1 11<<-ρ (7.1.2) 其中t ε为白噪声(White Noise),满足:⎪⎩⎪⎨⎧≠===+0s 0),cov()var(0)(2s t t t t E εεσεεε (7.1.3) 2、一阶移动平均MA(1)形式: 1-+=t t t v v u λ 11<<-λ (7.1.4)其中t v 为白噪声。
3、ARMA(1,1)形式: 11--++=t t t t v v u u λρ (7.1.5) 三、一阶自回归AR(1)扰动项的特性u X Y +=β,t t t u u ερ+=-1,11<<-ρ1、∑=∞=-0s s t st u ερ2、0)(=t u E3、2221)var(ut u σρσε=-= 4、su s t t u u ρσ2),cov(=±5、⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=----11)var(2121112n n n n u u ρρρρρρσ6、s s ρρ=§2 自相关的来源 一、惯性大多数经济时间序列都有一个明显的特点,就是它的惯性。
计量经济考试题试卷学习题

《计量经济学》习题1第一部分一、单项选择题1.当存在异方差现象时,估计模型参数的适当方法是()。
A、加权最小二乘法B、工具变量法C、广义差分法D、使用非样本先验信息2.对于恰好识别方程,在简化式方程满足线性模型的基本假定的条件下,间接最小二乘估计量具备()。
A、精确性B、无偏性C、真实性D、一致性3. 对联立方程模型进行参数估计的方法可以分两类,即()。
A、间接最小二乘法和系统估计法B、单方程估计法和系统估计法C、单方程估计法和二阶段最小二乘法D、工具变量法和间接最小二乘法4.如果一个回归模型中不包含截距项,对一个具有m个特征的质的因素要引入虚拟变量数目为()。
A、mB、m-1C、m-2D、m+25. 设某商品需求模型为Yt=β0+β1Xt+Ut,其中Y是商品的需求量,X是商品的价格,为了考虑全年12个月份季节变动的影响,假设模型中引入了12个虚拟变量,则会产生的问题为()。
A、异方差性B、序列相关C、不完全的多重共线性D、完全的多重共线性6.最小二乘准则具有的()特性。
A、有偏B、无偏C、距离最短D、驻点7. 以下说法错误的是()。
A、在总体中随机抽取的一组个体称为样本B、从总体中随机抽取样本的过程称为随机抽样C、任何样本都是有限的D、样本与总体具有不同的概率分布8. 以Y表示实际观测值,表示OLS估计回归值,则用OLS得到的样本回归直线=+满足()。
B、=09. 以下关系错误的有()。
B、D、10.以下选项不属于多元线性回归假设条件的()。
A、D、存在完全的多重共线性二、多项选择题1. 回归模型中引入虚拟变量时需要主要的问题包括以下()。
A、明确虚拟变量的对比基准B、避免出现“虚拟变量陷阱”C、拓展回归模型的功能D、减少滞后项的数目E、以上都正确2.对于经典线性回归模型,各回归系数的普通最小二乘法估计量具有的优良特性有()。
A、无偏性B、最优性C、一致性D、确定性E、线形特性3.DW检验不适用于下列情况的序列相关检验()。
[经济学]第七章自相关
![[经济学]第七章自相关](https://img.taocdn.com/s3/m/894e6ffde109581b6bd97f19227916888486b971.png)
三、序列相关性的后果
计量经济学模型一旦出现序列相关性,如果仍采用 OLS法估计模型参数,会产生下列不良后果:
1. 参数估计量非有效
因为,在有效性证明中利用了
E ( ) 2I 即同方差性和互相独立性条件。
可以利用模型直接得到1的参数估计值ˆ1,并得 到A的估计值Aˆ 。
再利用该估计值得到原模型参数0的估计
值ˆ0 Aˆ 1 ˆ 。
这种克服误差序列相关问题的参数估计,称 “广义差分法”。
广义差分法的缺点
首先是差分变换会减少一个样本容量。这通常可 以通过对第一组数据作变换后保留的方法解决。
(二)广义差分法
设模型为Yt 0 1Xt t ,且已知模型的误 差项有一阶自相关性,即 t t1 t 其中 0 1
同样把滞后一期的观测值代入模型,可得
Yt1 0 1 X t1 t1
(6.3)
把上式减去(6.3)式与的乘积,可得
Yt Yt1 0 0 1X t 1X t1 t t1
i是满足以下标准OLS假定的随机干扰项:
E(i ) 0, var(i ) 2 , cov(i ,is ) 0 s 0
由于序列相关性经常出现在以时间序列为样本 的模型中,因此,本节将用下标t代表i。
二、序列相关性产生的原因
1. 经济变量固有的惯性
大多数经济时间数据都有一个明显的特点:惯性, 表现在时间序列不同时间的前后关联上。
另一个问题是,假设已知的一阶自回归系数实
际上是无法知道的,只能根据原模型的回归残差 序列求其估计值。既然原模型存在误差序列相关, 那么回归残差就会受到影响,从而估计值也有偏 差。
6.1自相关的概念及产生原因

(2)高阶自回归形式
当随机误差项ut 不仅与其前一期值有关,而且与其 前若干期的值都有关时,即
ut f (ut 1,ut 2, ) vt
称ut 具有高阶自回归形式。
计量经济模型中自相关的最常见的形式是一 阶线性自回归形式
ቤተ መጻሕፍቲ ባይዱ
ut ut 1 vt
其中, 是ut 与ut 1的相关系数,vt 是满足基本假定的 随机误差项。的取值范围是[-1, 1]。当 0时,称 ut 存在正自相关,当 0时,称ut 存在负自相关,当
如果不同的随机误差项之间存在着相关关系,即
Cov(ui , u j ) E(ui u j ) 0, i j, i, j 1, 2,, n
则称模型存在自相关性。
二、自相关的分类
自相关按形式可分为两类:
(1)一阶自回归形式
当随机误差项ut 只与其滞后一期值ut 1有关时,即
ut f (ut 1 ) vt
第六章 自相关
• 本章主要内容: 第一节 自相关的概念及产生原因 第二节 自相关的后果 第三节 自相关的检验 第四节 自相关的解决方法 第五节 案例分析
第一节 自相关的概念及产生原因
• 自相关的概念 • 自相关的分类 • 自相关产生的原因
一、自相关的概念 对于k元线性回归模型
Yi 0 1 X1i 2 X 2i k X ki ui
三、自相关产生的原因
1.模型中遗漏了重要的解释变量
例如,以年度资料建立居民消费函数时,居民 消费除了受收入水平影响之外,还受消费习惯、 家庭财产等因素的影响,这些因素的各期值一般 是相关的,如果模型中未包含这些因素,它们对 消费的影响就表现在随机误差项中,从而使随机 误差项的各期值之间呈现出相关关系。
处理自相关问题的两种简单方法

处理自相关问题的两种简单方法
自相关问题是指模型中存在自身数据的问题,可能会导致模型过拟合。
以下是两种处理自相关问题的简单方法:
1. 正则化 (Regularization):正则化是指在模型训练过程中,添加一个惩罚项以限制模型的复杂度,从而避免模型过拟合。
常见的正则化方法包括 L1 正则化、L2 正则化和 dropout。
L1 和 L2 正则化会通过减小模型参数量来减少模型的复杂度,而 dropout 则会随机丢弃一些神经元来提高模型的鲁棒性。
2. 数据增强 (Data Augmentation):数据增强是通过在原始数据上进行操作来生成更多的训练数据,从而增加模型的泛化能力。
常见的数据增强方法包括旋转、缩放、平移、翻转等。
通过增加训练数据量,可以避免模型过度拟合原始数据。
第七章(自相关)

第七章 自相关性一、自相关性及其产生的原因定义:对于模型01122...t t t k kt t y x x x u ββββ=+++++如果随机误差项的各期值之间存在着相关关系,即:(,)()0t t i t t i Cov u u E u u --=≠,1,2,3,....,i s =则称模型存在着自相关性。
原因:模型中遗漏了重要的解释变量,经济惯性,随机因素的影响、模型函数形式的设定误差。
自相关的类型:一阶自相关和高阶自相关。
一阶自相关指随机误差项只与它的前一期相关。
1t t t v ερε-=+,高阶自相关指随机误差项与它的前几期都相关。
1122...t t t p t p t v ερερερε---=++++称之为P 阶自回归形式,或称模型存在P 阶自相关。
二、自相关的影响将产生如下不利影响:(一) 最小二乘估计不再是有效估计OLS 估计仍然是无偏估计,但不再具备有效性。
和异方差对回归的影响相同吗?(二) 一般会低估OLS 估计的标准误差 会低估()i S β。
异方差对OLS 估计的标准误差是什么影响?(三) T 检验的可靠性降低 由于低估()i S β,使T 值偏大。
T 值偏大,会带来什么后果?和异方差带来的后果有何不同?(四) 降低模型的预测精度异方差会对模型的预测精度产生何种影响?三、自相关性的检验1. 残差图的分析如果随着时间的推移,残差分布呈现出周期性的变化,说明很可能存在自相关性。
2. 杜宾——瓦森检验检验范围:一阶自相关的检验。
步骤:(1)提出原假设:H 0:0ρ=,即不存在一阶自相关。
(2)构造检验统计量:21222()nt t nte eDW e--=∑∑可以推导出:2(1)DW ρ≈-(3)检验自相关性:DW=0,则,正自相关, DW=4,则,负自相关,DW=2,则,不存在一阶自相关。
0 d L d u 2 4- d U 4- d L 4(1)0,L DW d ≤≤拒绝原假设,认为存在正自相关性。
6.多元回归模型(2),自相关

多元回归模型(2):多元回归模型的若干问题及处理三、自相关1、自相关的定义:原始序列中的观测值之间的相关。
如:如果对某个序列存在如下关系:t t t u y y +=-1ρ则该序列存在自相关。
如果某个回归模型的残差t u 存在类似如下关系:t t t u u ερ+=-1其中0)(,0)(==j i t E E εεε,则说明残差t u 序列存在(一阶)自相关。
2、自相关的产生A 、惯性。
对大多数经济变量来说,如GDP 、价格指数、就业等时间序列都呈现一种商业循环。
B 、模型设定偏误。
1)模型变量缺失。
如果模型的形式为:t t t t t u x x x y ++++=3322110ββββ而我们采用的回归形式为:t t t t v x x y +++=22110βββ则回归误差项:t t t u x v +=33β,误差表现为一种系统性变化的特征,造成自相关。
2)、忽略了模型的滞后效应。
如在消费模型中,消费不仅仅依赖于当期的收入水平,由于消费者不会轻易改变他们的消费习惯,因此他们的消费支出还依赖于前期的消费支出,既有:t u +消费+收入+=消费-1t 2t 10t βββ如果忽略了滞后项,则模型的误差项由于滞后变量对当前变量的影响而反映出一种系统性变化的特征,具有自相关。
3、自相关的影响。
由于模型假定随机误差项非自相关,0)(=j i u u E ,现0)(≠j i u u E ,则误差向量的方差协方差矩阵为:I u Var TT T T T T 2212222111211)(σσσσσσσσσσ≠⎪⎪⎪⎪⎪⎭⎫⎝⎛=Ω= 非对角线上的元素表示误差向量的协方差,非对角线上的元素不为0,表示误差项自相关。
与异方差的影响一样,如果仍用12)(-'X X σ来估计)ˆ(βVar ,这种估计是有偏的,不一致的。
建立在这样一个)ˆ(βVar 的t 检验与F 检验可能产生严重的误导,得出错误的结论。
计量经济学放宽基本假定的模型总结

异方差性1定义: 对于不同的样本点,随机干扰项的方差不再是常数,而是互不相同。
则认为出现了异方差性。
2影响:① OLS 参数估计量非有效:具有:线性性、无偏性 不具有:有效性(大样本下)具有:一致性 不具有:渐进有效性②变量的显著性检验失去意义关于变量的显著性检验中,构造了t 统计量,他是建立在随机干扰项共同的方差σ2不变,而真确地估计了参数方差jB S ∧的基础之上的。
如果出现了异方差性其估计值会偏大或偏小。
t检验失去意义。
③ 模型的预测失效预测值的置信区间中也包含有参数的方差的估计量jB S ∧。
所以当模型出现异方差性是,任然使用ols 估计量,将导致预测区间篇大或小,预测功能失效。
3判断:假设4:2)|(σμ=xi i Var由于异方差性是相对于不同的解释变量观测值,随机误差项具有不同的方差。
那么检验异方差性,也就是检验随机误差项的方差与解释变量观测值之间的相关性及其相关的“形式”。
随机误差项方差的表示! 一般的处理方法:首先采用OLS 估计,得到残差估计值。
用它的平方近似随机误差项的方差。
残差估计值^~)(OLS Y Y e i -=近似随机误差项的方差 2~)()(i e i E i Var ≈=μμ图示检验法帕克检验与戈里瑟检验 由于f(x)的形式未知,所以要进行各种形式的检验。
iji i X f e ε+=)(~2i ji i X f e ε+=)(|~|选择关于变量X 的不同的函数形式,对方程进行估计并进行显著性检验,如果存在某一种函数形式,使得方程显著成立,则说明原模型存在异方差性。
GQ 检验:适合样本容量大,异方差为单调增或单调减的函数形式。
Step1 将样本观测值按照有可能引起异方差的解释变量观测值排序Step2 除去c=0.25n 观测值,讲剩下的观测值分为两组,每个子样样本容量为0.5(n-c ) Step3 对每个子样做OLS ,计算出两个残差平方和, 自由度为 0.5(n-c )-k-1 Step4 构建F 分布F>F a (v1,v2) 拒绝同方差性假设,表明存在异方差。
吉林大学-回归模型的扩展-自相关性

ˆ t 8.0757 2.9589 ln xt ln y
第二节 自相关性
(3)检验自相关性 操作演示
①残差图分析:残差图表明呈现有规律的波动。
② D-W 检 验 : n=21 , k=1 , α =0.05 时 , 查 表 得 dL=1.22 , dU=1.42 ,而 0<0.7028=DW<dL ,所以存在 (正)自相关性。
而建立模型时,模型设定为: Yt = 1 + 2 X 2t + ut 则 X 3t 对 Y 的影响便归入随机误差项 ut 中,由 t 于 ut 在不同观测点上是相关的,这就造成了 在不同观测点是相关的,呈现出系统模式,此 时 ut 是自相关的。
模型形式设定偏误也会导致自相关现象。如将 形成本曲线设定为线性成本曲线,则必定会导致
第二节 自相关性
注意问题:
(1)D-W检验只能判断是否存在一阶自相关性。 (2)D-W检验有两个无法判定的区域。 ( 3 )如果模型的解释变量中间含有滞后的被解释变 量, 此时D-W检验失效。
第二节 自相关性
3.高阶自相关性检验 布罗斯—戈弗雷(Breusch—Godfrey)检验
对于模型 yt=b0+b1x1t+b2x2t+…+bkxkt+ε
第二节 自相关性
ρ 的常用估计方法有: (1)近似估计法 在大样本(n≥30)情况下,DW≈2(1-ρ ),所以,
ˆ 1 DW / 2
ˆ
第二节 自相关性
3.广义差分法的EViews软件实现 (1)LS Y C X (2)IDENT RESID (3)利用广义差分法估计模型,命令为 LS Y C X AR(1) LS Y C X AR(1) AR(2) …… AR(k) (4)迭代估计过程的控制 EViews 软件按照默认的迭代次数( 100 次)和误 差精度(0.001)来控制迭代估计程序,也可以修改。
计量经济学放宽基本假定的模型回归例子

例4.1.4中国农村居民人均消费支出主要由人均纯收入来决定。
农村人均纯收入除从事农业经营的收入外,还包括从事其他产业的经营性收入以及工资性收入、财产收入和转移支付收入等。
为了考察从事农业经营的收入和其他收入对中国农村居民消费支出增长的影响,可使用如下双对数模型:μβββ+++=22110ln ln ln X X Y其中,Y 表示农村家庭人均消费支出,1X 表示从事农业经营的纯收入,2X 表示其他来源的纯收入。
表4.1.1列出了中国内地2006年各地区农村居民家庭人均纯收入及消费支出的相关数据。
表4.1.1 中国2006年各地区农村居民家庭人均纯收入与消费支出(单位:元)地区人均消费 支出Y从事农业经营的纯收入1X其他来源纯收入2X地区人均消费 支出Y从事农业经营 的纯收入1X其他来源纯收入2X北 京 5724.5 958.3 7317.2 湖 北 2732.5 1934.6 1484.8 天 津 3341.1 1738.9 4489.0 湖 南 3013.3 1342.6 2047.0 河 北 2495.3 1607.1 2194.7 广 东 3886.0 1313.9 3765.9 山 西 2253.3 1188.2 1992.7 广 西 2413.9 1596.9 1173.6 内蒙古 2772.0 2560.8 781.1 海 南 2232.2 2213.2 1042.3 辽 宁 3066.9 2026.1 2064.3 重 庆 2205.2 1234.1 1639.7 吉 林 2700.7 2623.2 1017.9 四 川 2395.0 1405 1597.4 黑龙江 2618.2 2622.9 929.5 贵 州 1627.1 961.4 1023.2 上 海 8006.0 532 8606.7 云 南 2195.6 1570.3 680.2 江 苏 4135.2 1497.9 4315.3 西 藏 2002.2 1399.1 1035.9 浙 江 6057.2 1403.1 5931.7 陕 西 2181.0 1070.4 1189.8 安 徽 2420.9 1472.8 1496.3 甘 肃 1855.5 1167.9 966.2 福 建 3591.4 1691.4 3143.4 青 海 2179.0 1274.3 1084.1 江 西 2676.6 1609.2 1850.3 宁 夏 2247.0 1535.7 1224.4 山 东 3143.8 1948.2 2420.1 新 疆2032.42267.4469.9河 南 2229.3 1844.61416.4注:从事农业经营的纯收入由从事第一产业的经营总收入与从事第一产业的经营支出之差计算,其他来源的纯收入由总纯收入减去从事农业经营的纯收入后得到。
自相关模型估计方法和主要步骤

自相关模型估计方法和主要步骤
自相关模型估计方法是基于时间序列数据进行建模的方法之一,用于分析数据的时间依赖性,即数据在不同时间点上的相关性。
主要步骤如下:
1. 数据准备:收集所需的时间序列数据,并进行预处理,包括去除异常值、平滑以及去除季节性等。
2. 模型选择:根据数据的特点和需求选择合适的自相关模型。
常见的自相关模型包括自回归模型(AR)、移动平均模型(MA)
以及自回归移动平均模型(ARMA)等。
3. 模型拟合:对选定的自相关模型进行参数估计,一般使用最大似然估计法或最小二乘法来估计模型的参数。
4. 模型检验:对拟合好的自相关模型进行检验,检查模型是否能够很好地拟合数据,并对模型的残差进行检验。
5. 模型预测:使用已经拟合好的自相关模型进行未来值的预测。
6. 模型评价:对模型的拟合能力和预测能力进行评价,包括误差指标的计算和比较。
根据具体的需求和问题,可能还需要进行模型优化、模型比较和模型选择等步骤。
总的来说,自相关模型估计方法是一个迭
代的过程,需要不断进行模型的调整和优化,以提高模型的拟合能力和预测能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 出现自相关时的BLUE估计量 继续利用双变量模型并假定AR(1)过程,可以证明β2的BLUE估计量 由下式给出:
ˆ 2GLS
(x
t 2
n
t
xt 1 )( yt yt 1 )
n
( xt xt 1 ) 2
t 2
C
其中C是一个校正因子,在实际中我们常常忽略它。从而方差方差:
自相关(autocorrelation)和
序列相关(serial correlation)
自相关和序列相关看做同义词
已经曾为习惯,不过也有的学 者喜欢把二者区分开来。例如 延特纳(Tintner)认为:自相 关是一个给定的序列同它自身 滞后若干期的序列的滞后相关; 而序列相关则是两个不同序列 的滞后相关。 在本课程里我们不加区分的使 用这两个术语。
n2
xt2
t 1
n
n 1 x1 xn n xt2 t 1
没有自相关情形下的平常公式:
ˆ var( 2 )
x
2
2 t
相比二者,前者是后者加上另一与ρ和诸xt的样本协方差有关的项。
ˆ ˆ 一般的来说,我们无法告知 var( 2 )是否大于var( 2 ) AR(1) 。当然如果ρ 是零,则两个方程自然相等。 ˆ 容易证明,出现自相关时, 2 仍然是线性的和无偏的,但不是最优 ˆ 的。我们在前面的研究中知道,GLS估计量 2 是有效地。那么在自 相关的情形中,我们能够找到一个BLUE的估计量吗?
在剩下的问题中,假定7、8和10是紧密相关的,我们在多重
共线性问题中探讨;假定4在异方差问题中探讨;假定5在自 相关问题中探讨。 我们在探讨这些问题的时候,遵循下列各式:
1. 明确问题的性质;
2. 分析它的影响; 3. 提出侦测它的方法; 4. 考虑补救的措施。
3 自相关
(5)“编造”的数据。在经验分
析中,许多原始数据是经过“编 造”的。例如,我们用季度数据 的回归中,季度数据是用月度数 据平均得到的,这种平均减下了 数据的波动性,季度数据都比月 度数据更平滑一些。这种平滑性 本身能使干扰项中出现系统性式 样,从而导致了自相关。 数据编造的另一种来源是 “内插”或“外推”。例如人口 普查不会每年进行,这样在两个 普查年份之间的年份数据是通过 “内插”的方法生成的。这些数 据的加工技术,往往给数据带来 原始数据没有的系统性样式。
我们用它来进行估计和假设检验和预测问题。但是,这个模 型是建立在一些简化了的假定基础之上的。这些假定包括:
1. 回归模型对于参数而言是线性的。
2. 各回归元X的值在重复抽样中是固定的。
3. 给定的X,干扰ui的均值为零。 4. 对于给定的X,ui的方差不变或称之为同方差性。 5. 对于给定的X,干扰无自相关。 6. 如果X是随机的,则干扰项与各个X是独立的至少是不相关的。 7. 观测的次数大于回归元的个数。 8. 回归元的取值必须有足够的变异性。
改图清晰的表明,所拟合的回归线大大的歪曲了真回归线:它严重
ˆ 地低估了真斜率系数而高估了真截距项。同时,由于OLS, u i 一般 都靠近拟合线,却远离了真PRF,所以ui的真方差被大大的低估。
为了洞察真δ2被低估的程度,我们另外再做一次抽样试验,这一次仍
然保留原表中的X值和ε值,但假定ρ=0,即无自相关。由此产生的Y 的新样本值见下表。
产生自相关的原因 如左图:a中显示了周期性;b 和c中有一个上升和下降的趋势; d中有二次趋势项;e中则不存 在系统模式,符合经典线性模 型的规定。
(1)惯性。大多数经济时间序列都有一个明显的特点,就是它的惯
性或粘性。GDP、价格指数、生产和就业、失业率都呈现出周期性。 因此,在涉及到时间序列的回归中,相继的观测值很有可能是相互 依赖的。 (2)设定无偏:模型中丢掉了重要的解释变量。例如,我们做牛肉 需求量的回归,正确的模型中应该包含牛肉的价格、消费者的收入 和猪肉的价格三个解释变量。如果处于某种原因,模型中忽略了猪 肉的价格,则猪肉价格的影响都被包含在干扰项ui之中,这样干扰项 ui就有可能反映出一种系统性模式,从而造成了错误的自相关。 (3)设定无偏:不正确的函数表达形式。假设边际成本和产出之间 真实的关系是: 但是我们采取了不正确的函数形式: 这样,干扰项vi等于(产出)2+ui,从而包含了(产出)2对边际成本 的系统影响。在这种错误的函数形式中,vi反映出自相关。
自相关问题一般更常出现于时间序列数据中,时间序列是按照观测
的时间次序排列的。出现在横截面数据中的自相关有时候被称为 “空间自相关”。以表示自相关出现在空间而非时间上。
2 自相关出现时的OLS估计量
回到双变量的模型中,现在我们除了引进自相关外,其他都保留经
典模型的全部假定。ui的产生机制如下,这样使得 E(ui , u j ) 0 。
5. 侦测自相关
(1)图解法 非自相关的假设是针对真实的干扰项ui而言的。但是一般ui我们是不 ˆ 知道的,我们所能够获知的是来自OLS的残差 u i 。虽然ui的估计值 不同于ui,但是对ui的估计值做图像检查往往能够对ui中可能存在的 自相关现象提供一些线索。 将残差对时间描点得到残差的时间顺序图。另一种方法是将标准化 的残差对时间描图,标准化的残差是用残差除以标准误,这样做的 好处是得到了一个无量纲(无单位)的纯数。 根据美国1960-1991年的数据,做工资对生产力的回归,把回归的残 差和标准化的残差描绘在下列的时间顺序图中。
现在假如把X的值固定在1,2,3,……,10。那么,给定这些X值就能
够产生10个Y值,连同表12.1中的u值,一起放到下表中。
利用表中的数据做Y对
X的回归,得到结果如 下:
真的回归线由方程
E(Yt | X t ) 1.0 0.8 X t
给出, 我们把两条回归线放 置在一起加以比较。
经典线性回归模型假定:
假定5:对于给定的X,干扰无自相关
1. 问题的性质
自相关可以定义为按时间(时间序列数据)或空间(横截面数据)
排序的观测值序列的成员之间的相关。在经典线性回归模型中假定 干扰项ui之间不存在自相关。用符号来表示为:
E(uiu j ) 0
简单地说,经典模型假设,任意一次观测的干扰项都不受到其他任
ˆ GLS var( 2 )
2
( xt xt 1 ) 2
t 2 n
D
其中D也是一个在实际中可以忽略的校正因子。 上述估计量是由GLS得到的。在自相关情形下,GLS给出的估计量是
BLUE,同时给出了最小方差。 如果我们忽略了自相关,而使用OLS程序,会出现什么样的结果呢?
xt2 则情
ˆ 为了看到δ2和是 如何被低估的,我们做如下的蒙特卡罗实验。 2
假定在一个双变量的模型中,我们知道了β1=1和β2=0.8,那么这个随
机的PRF是:
Yt 1.0 0.8 X t ut
从而,
E(Yt | X t ) 1.0 0.8 X t
现在假定ui由如下的一阶自回归模式产生:
ut 0.7ut 1 t
其中εt满足所有的OLS假定。进一步我们假定εt是满足均值为零,方
差为常数的标准正态分布。现在给定
将上表中产生的ui描点,得到
左图。该图表明,开始时每一 个相继的ui大于它前面的值, 后来,一般地说,小于它前面 的值。这种情形通常表明一种 正的相关。
9. 回归模型被正确的设定。
10. 回归元之间无多重共线性。 11. 随机干扰项ui是正态分布的。
遗憾的是,我们尚无法对所有的问题都给出令人满意的答案。
接下来的工作中,我们对某些假定给予更多的注意,当然有 些假定我们并不过分的深究,特别是假定1、2、3、6和11中 的问题。 威瑟里尔(Wetherill)指出,实际上在应用经典线性回归模 型时,有两类问题需要注意:(1)关于模型设定及对干扰 项ui的假定问题,诸如假定1、2、3、4、5、9和11;(2)关 于对数据的假定问题,诸如6、7、8和10。 关于对来自干扰和模型设定的假定问题主要有三:
经济类核心课程· 计量经济学
第七章 放宽条件的回归模型(3)
自相关
教师:卢时光
PowerPoint Presentation by Lu Shiguang 2012 All Right Reserved,
Hunan Institute of Engineering
在前面的学习中,我们详尽的考察了经典正态线性回归模型,
4 出现自相关时使用OLS的后果
为了便于分析,我们仍然采用双变量模型,当然我们可以将结果推广到更多
解释变量的情形。
(1)考虑到自相关的OLS估计
前面已将指出,OLS估计量不是BLUE,GLS才是。这样根据OLS得到的置信
区间很可能要比GLS得到的更宽一些。这样我们很有可能宣称一个系数是统 计上不显著的,而事实上它是显著的。
例如,上图中的b2,根据(正确的)GLS, b2落入了拒绝域,我们拒绝β2=0
的假设。但根据(错误的)OLS, b2落入了接受域中,我们不能拒绝β2=0的 假设。
(2)忽视了自相关的OLS估计 ˆ ˆ 如果我们不顾自相关的存在而使用了 2和 var( 2 ) 2 / 况就会变得非常严重。错误将出自多种原因:
根据上表中的数据,得到回归结果,并与前面的结果比较如下:
ρ
=0
ρ
=0.7
现在,因为Y基本上是随机的,所以回归结果跟“真实”结果接近的
多。注意回归的方差已经从0.8114( ρ=0.7 )增大到0.9752( ρ=0 ), ˆ ˆ 并且 1和 2 的标准误也都增大。这个结果和先前得到的自相关的存 在使得方差被低估的理论分析是一致的。
