坐标系
三个坐标系

o
x
d y dS x ex dydz
dx
y
体积元
dV dxdydz
直角坐标系的长度元、面积元、体积元
2、圆柱面坐标系
坐标变量
, , z
坐标单位矢量 e , e , ez r e ez z 位置矢量 线元矢量 dl e d e d ez dz
散度的表达式:
Fx Fy Fz 直角坐标系 F x y z ( F ) F Fz 柱面坐标系 F z
C C 0 (C为常矢量) (Cf ) C f 散度的有关公式: (kF ) k F (k为常量) f ( f F ) f F F ( F G ) F G
u 1 u u e ez 圆柱面坐标系 u e z
球面坐标系
u 1 u 1 u u er e e r r r sin
C 0 (Cu ) Cu 梯度运算的基本公式: (u v) u v (uv ) uv vu f (u ) f (u )u
面元矢量
dS e dl dl z e ddz dS e dl dl z e ddz dS z ez dl dl ez dd
体积元
dV dddz
3、球面坐标系 坐标变量
坐标单位矢量 er , e , e
标量场的梯度 的旋度恒为零
C 0 (Cf ) f C ( fF ) f F f F ( F G ) F G ( F G ) G F F G F ) 0 ( (u ) 0
坐标系及其关系描述

图2-7 空间点P在直角坐标系中的坐标
2.空间向量的表示
有向线段可以由起始和终止的坐标来表示。如果一个向量起始于点 A,终止于点 B, 则 Ax , Ay 和 Az 是点 A 在直角坐标系中的三个坐标分量, Bx , By 和 Bz 是点 B 在直角坐 标系中的三个坐标分量,则该向量可以表示为
从正 Z 轴来看,自 X 轴按逆时针方向转到 OM 所转过的角,这里 M 为点 P 在 XOY 面上的
投影。我们称 r, , 这三个数为点 P 的球面坐标。
图2-4 球面坐标系
4.其他形式的坐标系 1)参考坐标系
参考坐标系的位置和方向不随工业机器人各关节的运动而变化,对机器人其他坐标系 起参考定位的作用,通常采用三维空间中的固定坐标系 O-XYZ 来描述,如图 2-5 所示。
图2-1 直角坐标系
图2-2 右手坐标系
2.柱面坐标系 如图 2-3 所示,设 M (x ,y ,z) 为空间内一点,并设点 M 在 XOY 面上的投影 P 的极
坐标为 (r , ) ,则 r, ,z 这三个数便称为点 M 的柱面坐标。
图2-3 柱面坐标系
3.球面坐标系 如图 2-4 所示,假设 P (x ,y ,z) 为空间内一点,则点 P 也可用三个有次序的数 (r , ,) 来确定。其中,r 为原点 O 与点 P 间的距离; 为有向线段 OP 与 Z 轴正向的夹角; 为
Omz
则矩阵 M 可简化为
A M
OmO
0 1
也就是说,方向余弦阵 A 表示两坐标系的姿态关系,位置向量 OmO 表示 运动坐标系{m} 的原点 Om 在固定坐标系{O} 中的位置。
四大常用坐标系及高程坐标系

我国四大常用坐标系及高程坐标系1、北京54坐标系BJZ54北京54坐标系为参心大地坐标系,大地上的一点可用经度L54、纬度M54和大地高H54定位,它是以克拉索夫斯基椭球为基础,经局部平差后产生的坐标系;新中国成立以后,我国大地测量进入了全面发展时期,再全国范围内开展了正规的,全面的大地测量和测图工作,迫切需要建立一个参心大地坐标系;由于当时的“一边倒”政治趋向,故我国采用了前苏联的克拉索夫斯基椭球参数,并与前苏联1942年坐标系进行联测,通过计算建立了我国大地坐标系,定名为1954年北京坐标系;因此,1954年北京坐标系可以认为是前苏联1942年坐标系的延伸;它的原点不在北京而是在前苏联的普尔科沃;北京54坐标系,属三心坐标系,长轴6378245m,短轴6356863,扁率1/;2、西安80坐标系1978年4月在西安召开全国天文大地网平差会议,确定重新定位,建立我国新的坐标系;为此有了1980年国家大地坐标系;1980年国家大地坐标系采用地球椭球基本参数为1975年国际大地测量与地球物理联合会第十六届大会推荐的数据,即IAG75地球椭球体;该坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇,位于西安市西北方向约60公里,故称1980年西安坐标系,又简称西安大地原点;基准面采用青岛大港验潮站1952-1979年确定的黄海平均海水面即1985国家高程基准;西安80坐标系,属三心坐标系,长轴6378140m3、WGS-84坐标系WGS-84坐标系WorldGeodeticSystem是一种国际上采用的地心坐标系;坐标原点为地球质心,其地心空间直角坐标系的Z轴指向国际时间局BIH定义的协议地极CTP方向,X轴指向的协议子午面和CTP赤道的交点,Y轴与Z轴、X轴垂直构成右手坐标系,称为1984年世界大地坐标系;这是一个国际协议地球参考系统ITRS,是目前国际上统一采用的大地坐标系;GPS广播星历是以WGS-84坐标系为根据的;WGS84坐标系,长轴6378137.000m由于采用的椭球基准不一样,并且由于投影的局限性,使的全国各地并不存在一至的转换参数;对于这种转换由于量较大,有条件的话,一般都采用GPS联测已知点,应用GPS软件自动完成坐标的转换;当然若条件不许可,且有足够的重合点,也可以进行人工解算;4、2000国家大地坐标系英文缩写为CGCS2000;2000国家大地坐标系是全球地心坐标系在我国的具体体现,其原点为包括海洋和大气的整个地球的质量中心;2000国家大地坐标系采用的地球椭球参数如下:长半轴a=6378137m,,1014m3s-2自转角速度ω=7.292l15×10-5rads-1我国常用高程系“1956年黄海高程系”,是在1956年确定的;它是根据青岛验潮站1950年到1956年的黄海验潮资料,求出该站验潮井里横按铜丝的高度为3.61米,所以就确定这个钢丝以下3.61米处为黄海平均海水面;从这个平均海水面起,于1956年推算出青岛水准原点的高程为72.289米;国家85高程基准其实也是黄海高程基准,只不过老的叫“1956年黄海高程系统”,新的叫“1985国家高程基准”,新的比旧的低0.029m我国于1956年规定以黄海青岛的多年平均海平面作为统一基面,为中国第一个国家高程系统,从而结束了过去高程系统繁杂的局面;但由于计算这个基面所依据的青岛验潮站的资料系列1950年~1956年较短等原因,中国测绘主管部门决定重新计算黄海平均海面,以青岛验潮站1952年~1979年的潮汐观测资料为计算依据,并用精密水准测量接测位于青岛的中华人民共和国水准原点,得出1985年国家高程基准高程和1956年黄海高程的关系为:1985年国家高程基准高程=1956年黄海高程-0.029m;1985年国家高程基准已于1987年5月开始启用,1956年黄海高程系同时废止;各高程系统之间的关系:56黄海高程基准:+85高程基准最新的黄海高程:56高程基准吴淞高程系统:56高程基准+珠江高程系统:56高程基准我国目前通用的高程基准是:85高程基准1兰勃托投影性质兰勃托Lambert投影,又名"等角正割圆锥投影”兰勃托投影采用双标准纬线相割,与采用单标准纬线相切比较,其投影变形小而均匀,兰勃托投影的变形分布规律是:a角度无变形,即投影前后对应的微分面积保持图形相似,亦称为正形投影;b等变形线和纬线一致,即同一条纬线上的变形处处相等;c两条标准纬线上没有任何变形;d在同一经线上,两标准纬线外侧为正变形长度比大于1,而两标准纬线之间为负变形长度比小于1;因此,变形比较均匀,变形绝对值也比较小;e同一纬线上等经差的线段长度相等,两条纬线间的经纬线长度处处相等;我国1:100万地形图采用了兰勃托投影,其分幅原则与国际地理学会规定的全球统一使用的国际百万分之一地图投影一致;纬度按纬差4°分带,从南到北共分成15个投影带,每个投影带单独计算坐标,每带两条标准纬线,第一标准纬线为图幅南端纬度加30′的纬线,第二标准纬线为图幅北端纬度减30′的纬线,这样处于同一投影带中的各图幅的坐标成果完全相同,不同带的图幅变形值接近相等,因此每投影带只需计算其中一幅图纬差4°,经差6°的投影成果即可;由于是纬差4°分带投影的,所以当沿着纬线方向拼接地图时,不论多少图幅,均不会产生裂隙;但是,当沿着经线方向拼接时,因拼接线分别处于上下不同的投影带,投影后的曲率不同,致使拼接时产生裂隙;。
常用坐标系

一、常用坐标系1、北京坐标系北京54坐标系为参心大地坐标系,大地上的一点可用经度L54、纬度M54和大地高H54定位,它是以克拉索夫斯基椭球为基础,经局部平差后产生的坐标系。
1954年北京坐标系的历史:新中国成立以后,我国大地测量进入了全面发展时期,再全国范围内开展了正规的,全面的大地测量和测图工作,迫切需要建立一个参心大地坐标系。
由于当时的“一边倒”政治趋向,故我国采用了前苏联的克拉索夫斯基椭球参数,并与前苏联1942年坐标系进行联测,通过计算建立了我国大地坐标系,定名为1954年北京坐标系。
因此,1954年北京坐标系可以认为是前苏联1942年坐标系的延伸。
它的原点不在北京而是在前苏联的普尔科沃。
北京54坐标系,属三心坐标系,长轴6378245m,短轴6356863,扁率1/298.3;2、西安80坐标系1978年4月在西安召开全国天文大地网平差会议,确定重新定位,建立我国新的坐标系。
为此有了1980年国家大地坐标系。
1980年国家大地坐标系采用地球椭球基本参数为1975年国际大地测量与地球物理联合会第十六届大会推荐的数据,即IAG75地球椭球体。
该坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇,位于西安市西北方向约60公里,故称1980年西安坐标系,又简称西安大地原点。
基准面采用青岛大港验潮站1952-1979年确定的黄海平均海水面(即1985国家高程基准)。
西安80坐标系,属三心坐标系,长轴6378140m,短轴6356755,扁率1/298.257221013、2000国家大地坐标系的定义国家大地坐标系的定义包括坐标系的原点、三个坐标轴的指向、尺度以及地球椭球的4个基本参数的定义。
2000国家大地坐标系的原点为包括海洋和大气的整个地球的质量中心;2000国家大地坐标系的Z轴由原点指向历元2000.0的地球参考极的方向,该历元的指向由国际时间局给定的历元为1984.0的初始指向推算,定向的时间演化保证相对于地壳不产生残余的全球旋转,X轴由原点指向格林尼治参考子午线与地球赤道面(历元2000.0)的交点,Y轴与Z轴、X轴构成右手正交坐标系。
四个坐标轴的坐标系

四个坐标轴的坐标系
在三维空间中,有两种常见的坐标系,它们分别是直角坐标系和球坐标系。
而在更高维度的空间中,还可以有更多的坐标系。
1.直角坐标系(笛卡尔坐标系):
直角坐标系是我们常见的三维空间坐标系,用三个互相垂直的坐标轴来表示一个点的位置。
通常,这三个坐标轴分别称为x轴、y轴和z轴。
一个点在直角坐标系中的位置由它在x轴、y轴和z轴上的坐标值表示,例如(x,y,z)。
2.球坐标系:
球坐标系是一种三维坐标系,用球坐标来表示一个点的位置。
它由三个参数表示,分别是极径(r)、极角(θ)和方位角(φ)。
在球坐标系中,极径r表示点到原点的距离,极角θ表示点与正z轴的夹角,方位角φ表示点在xy平面上的投影与正x轴的夹角。
除了三维空间中的直角坐标系和球坐标系,还可以有其他维度的坐标系,例如:
3.极坐标系:
极坐标系是二维空间中常见的坐标系,用两个参数(极径和极角)来表示一个点的位置。
它与直角坐标系之间的转换关系是通过极坐标转换公式实现的。
4.高维空间中的坐标系:
在高维空间中,我们可以使用更多的坐标轴来表示一个点的位置。
例如,在四维空间中,可以使用四个坐标轴(x、y、z、w)来表示一个点的位置,这就是四维直角坐标系。
这些坐标系是在数学和物理学中广泛应用的工具,用于描述空间中点的位置和物体的运动等信息。
每种坐标系都有其特定的应用场景和方便之处。
坐标系

在平面内,两条线互垂直且 在平面内, 有公共原点的数轴组成平面直角 有公共原点的数轴组成平面直角 坐标系(又称为笛卡儿坐标系)。 坐标系(又称为笛卡儿坐标系)。
y 5 4 3 2 1 -4 -3 -2 -1O -1 -2 -3 -4
y轴(纵轴)
x轴(横轴)
1 2 3 4 5
原 点
x
对于平面内任意一点P,过点 分别向 分别向x轴 对于平面内任意一点 ,过点P分别向 轴、 垂足在x轴 轴上对应的数a,b分 轴上对应的数 y轴作垂线, 轴作垂线, 轴作垂线 垂足在 轴、 y轴上对应的数 分 有序数对(a,b)叫 有序数对 叫 别叫做点P的横坐标 纵坐标, 的横坐标、 别叫做点 的横坐标、纵坐标, 做点P的坐标 的坐标. 做点 的坐标.
y
b
·P
a
x
O
过该点分别向坐标
平面直角坐标系将平面分成 了几个部分? 了几个部分 y轴上的点 横坐标为0
y 5 4 3 第二象限 Ⅱ 2 (-,+) - + 1 -4 -3 -2 -1O -1 第三象限 -2 Ⅲ -3 (-,-) -4
4 3 2 1 -4 -3 -2 -1O -1 -2 -3 -4
(5,4)
2.5
1 2 3 4 5
(2.5,-2) 2.5,
x
在平面直角坐标中描 出下列各点,并将他 们按顺序依次连接起 来: A(-2,0 ) B (-2,1) C(3,1 ) E(-2,3) G(-3,2) D(3,3 ) F(-2,4) H(-2,0)
数学课的课题: 所涉及的内容: 重点、难点: 理解最好的内容: 不很明白,还要进一步请教老师或同学的地方是: 对所学内容感触最深的有:
在x轴上找横坐标对应的点, 轴上找横坐标对应的点, 然后过该点作x轴的垂线; 然后过该点作x轴的垂线; 在y轴上找纵坐标对应的点, 轴上找纵坐标对应的点, 然后过该点作y 然后过该点作y轴的垂线
三种常用的坐标系

它们相互正交,而且遵 循右手螺旋法则
er e e
第一章 矢量分析
1 – 1 三种常用的坐标系
第一章 矢量分析
在点 M r,,处沿er , e , e
z
方向的长度元分别是: dlr dr dl rd dl r sin d 面积元:
dsr dl dl r2 sin d d
y
sin
z z
o
x
(x, y, z)
M (,, z)
r z (r, ,)
y
y
x2 y2
tg 1
y x
sin 1
z
z
x
y cos1 x2 y2
x x2 y2
1 – 1 三种常用的坐标系
第一章 矢量分析
2 直角坐标系与球坐标系的关系 z
x r sin cos
y
r
sin
sin
解
Ax A ex A e ex A e ex Az ez ex A cos A sin
Ay A ey A e ey A e e y Az ez e y A sin A cos
Az A ez A e ez A e ez Az ez ez Az
r
z r cos
y
o
x
r x2 y2 z2
x
cos1
z
sin1
x2 y2 z2
x2 y2 x2 y2 z2
tg 1
y
sin 1
y
cos1
x
x
x2 y2
x2 y2
(x, y, z)
M (,, z)
z (r, ,)
y
1 – 1 三种常用的坐标系
常用坐标系汇总

常⽤坐标系汇总前⾔随着接触的地图种类越来越多,每种产品对地图服务的坐标系的要求不同,今天遇到了整理的好⽂,整理记录分享。
投影坐标系:墨卡托坐标系地理坐标系:经纬度坐标系常⽤坐标系(⼀)WGS84坐标系WGS-84坐标系(World Geodetic System⼀1984 Coordinate System)⼀种国际上采⽤的地⼼坐标系。
坐标原点为地球质⼼,其地⼼空间直⾓坐标系的Z轴指向BIH (国际时间服务机构)1984.O定义的协议地球极(CTP)⽅向,X轴指向BIH 1984.0的零⼦午⾯和CTP⾚道的交点,Y轴与Z轴、X轴垂直构成右⼿坐标系,称为1984年世界⼤地坐标系统。
(⼆)WGS84 Web墨卡托Web墨卡托是2005年⾕歌在⾕歌地图中⾸次使⽤的,当时或更早的Web墨卡托使⽤者还是称其为世界墨卡托 World Mercator - Spherical Mercator (unofficial deprecated ESRI),代号 WKID 54004 (在 EPSG:54004 或 ESRI:54004 中,⾮官⽅)。
在2006年,OSGeo在提出的 Tile Map Service (TMS) 标准中使⽤代号 OSGEO:41001,WGS84 / Simple Mercator - Spherical Mercator (unofficial deprecated OSGEO / Tile Map Service)。
2007年8⽉6⽇ Christopher Schmidt (OpenLayers的重要贡献者之⼀)在通过⼀次GIS讨论中为了在OpenLayers中使⽤⾕歌投影,提出给⾕歌投影(Web墨卡托)使⽤⼀个统⼀的代号(已有如54004、41001之类的代号)900913(也形似 Google),并与同年9⽉11⽇在OpenLayers的OpenLayers/Layer/SphericalMercator.js中正式使⽤代号 900913。
各种坐标系的定义
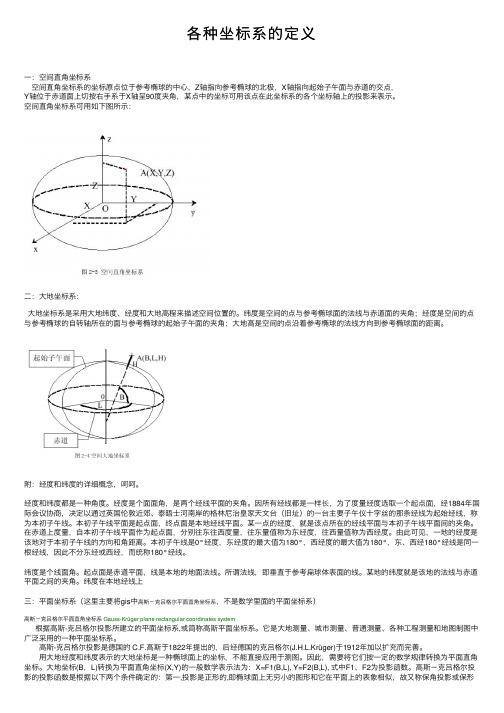
各种坐标系的定义⼀:空间直⾓坐标系空间直⾓坐标系的坐标原点位于参考椭球的中⼼,Z轴指向参考椭球的北极,X轴指向起始⼦午⾯与⾚道的交点,Y轴位于⾚道⾯上切按右⼿系于X轴呈90度夹⾓,某点中的坐标可⽤该点在此坐标系的各个坐标轴上的投影来表⽰。
空间直⾓坐标系可⽤如下图所⽰:⼆:⼤地坐标系:⼤地坐标系是采⽤⼤地纬度、经度和⼤地⾼程来描述空间位置的。
纬度是空间的点与参考椭球⾯的法线与⾚道⾯的夹⾓;经度是空间的点与参考椭球的⾃转轴所在的⾯与参考椭球的起始⼦午⾯的夹⾓;⼤地⾼是空间的点沿着参考椭球的法线⽅向到参考椭球⾯的距离。
附:经度和纬度的详细概念,呵呵。
经度和纬度都是⼀种⾓度。
经度是个⾯⾯⾓,是两个经线平⾯的夹⾓。
因所有经线都是⼀样长,为了度量经度选取⼀个起点⾯,经1884年国际会议协商,决定以通过英国伦敦近郊、泰晤⼠河南岸的格林尼治皇家天⽂台(旧址)的⼀台主要⼦午仪⼗字丝的那条经线为起始经线,称为本初⼦午线。
本初⼦午线平⾯是起点⾯,终点⾯是本地经线平⾯。
某⼀点的经度,就是该点所在的经线平⾯与本初⼦午线平⾯间的夹⾓。
在⾚道上度量,⾃本初⼦午线平⾯作为起点⾯,分别往东往西度量,往东量值称为东经度,往西量值称为西经度。
由此可见,⼀地的经度是该地对于本初⼦午线的⽅向和⾓距离。
本初⼦午线是0°经度,东经度的最⼤值为180°,西经度的最⼤值为180°,东、西经180°经线是同⼀根经线,因此不分东经或西经,⽽统称180°经线。
纬度是个线⾯⾓。
起点⾯是⾚道平⾯,线是本地的地⾯法线。
所谓法线,即垂直于参考扁球体表⾯的线。
某地的纬度就是该地的法线与⾚道平⾯之间的夹⾓。
纬度在本地经线上三:平⾯坐标系(这⾥主要将gis中⾼斯-克吕格尔平⾯直⾓坐标系,不是数学⾥⾯的平⾯坐标系)⾼斯-克吕格尔平⾯直⾓坐标系Gauss-Krüger plane rectangular coordinates system 根据⾼斯-克吕格尔投影所建⽴的平⾯坐标系,或简称⾼斯平⾯坐标系。
三大坐标系

2
e
A
ez A Az 1 1 Az A e e z z z Az
两个矢量点积:A B= Ar Br A B A B ; 两个矢量叉积:
er A B Ar B r
e A B
e A A B A B er A Br Ar B e Ar B A Br e B
位置矢量:r = e ez z ;
其微分为:dr = d e d ez z e d de ez dz e d e d ez dz ;
2
它在 、 和 z 增加方向上的微分分别是: d 、 d 和 dz 。
(圆锥面)
0
z
er e
的投影。 与直角坐标系之间的变换关系:
r x 2 y 2 z 2, arccos z x 2 y 2 z 2 , arctan y x ; x r sin cos ,y r sin sin ,z r cos
位置矢量:r = er r ;其微分为:dr = d (er r ) er dr rder er dr e rd e r sin d ; 它在 er 、 e 和 e 增加方向上的微分分别是: dr 、 rd 和 r sin d 。
球坐标系中的坐标单位矢量 er 、 e 和 e 都不是常矢量,是 和 的函数,且
坐标系的概念

、什么是坐标系?或许很多人心中明白这个概念,却又不甚明白。
什么是坐标系?人们描述空间中的一个点或者一个位置,通常会采用坐标这个概念。
可是这个坐标该怎么计算呢?它的参考是谁呢?如果中国定义中南海坐标是(1921,1949,2012),美国佬也定义他们白宫的坐标是(1921,1949,2012),哪天黑马说咱们打它中南海一炮吧,那就可能把他自己烤熟。
所以必须要建立一个合理的坐标系(⊙﹏⊙b汗~~,这个理由好牵强啊)。
坐标系由原点和坐标轴组成。
坐标系种类很多,我们大家在数学中想必都学过笛卡尔坐标系、极坐标系、球面坐标系和柱面坐标系吧,在地学领域,用到最多的是平面坐标系、空间直角坐标系(前两者属于笛卡尔坐标系)和球面坐标系。
比如说一个点坐标是(-2850017.472,4690744.523,3237959.973)就是指空间直角坐标,而我们经常看到的Google Earth上的点的坐标(37°20′17″N,112°33′20″E)就是指球面坐标。
测量学上,坐标系怎样定义的呢?地球是一个不规则的类椭球,怎样用严格的数学方式表示它,应该是测绘学家们所追求的高峰。
为了表示地球上每一个点的位置,是不是要建立一个统一的世界坐标系呢?建立坐标系是不是要确定坐标原点和坐标轴呢?那怎样建立呢?测量学家们把地球当作一个规则的椭球来处理,这下就好办多了,椭球中心就原点呗,长轴短轴就作为坐标轴,这样一个坐标系就出来了啊。
可是有人会问,那这个椭球怎么表示呢?嘛嘛的,我也想问,原来这是科学家们利用天文观测得到的,而且不同的科学家得到的椭球还不一样,比如,一个叫Krasovsky的人搞了个克拉索夫斯基椭球,还有人搞了什么IUGG-1975、WGS-84、GRS80椭球,他们主要特点是长半轴和扁率不同。
可是又有人会问(Y的,问题好多啊),搞这么多椭球干嘛,有一个不就行啦。
呵呵,我们知道,地球坑坑洼洼的,用严密的椭球来表示肯定有误差,有的国家为了使自己的国家与椭球面吻合(最好大家都站在椭球面上),这样根据各自的情况就定义了不同的参考椭球,比如北京54坐标系就采用了苏联老大哥的克拉索夫斯基椭球。
测量中常用的坐标系统

测量中常用的坐标系一、坐标系类型1、大地坐标系定义:大地测量中以参考椭球面(不准确)为基准面建立起来的坐标系。
一定的参考椭球和一定的大地原点上的大地起算数据,确定了一定的坐标系。
通常用参考椭球参数和大地原点上的起算数据作为一个参心大地坐标系建成的标志。
大地坐标(地理坐标):将某点投影到椭球面上的位置用大地经度L和大地纬度B表示,( B , L)统称为大地坐标。
大地高H:某点沿投影方向到基准面(参考椭球面)的距离。
在大地坐标系中,某点的位置用(B , L,H)来表示。
2、空间直角坐标系定义:以椭球体中心为原点,起始子午面与赤道面交线为X 轴,在赤道面上与X轴正交的方向为Y轴,椭球体的旋转轴为Z轴。
在空间直角坐标系中,某点的位置用(X,Y,Z)来表示。
3、平面直角坐标系在小区域进行测量工作若采用大地坐标来表示地面点位置是不方便的,通常采用平面直角坐标系。
测量工作以x轴为纵轴,以y轴为横轴投影坐标:为了建立各种比例尺地形图的控制及工程测量控制,一般应将椭球面上各点的大地坐标按照一定的规律投影到平面上,并以相应的平面直角坐标表示。
4、地方独立坐标系基于限制变形、方便、实用和科学的目的,在许多城市和工程测量中,常常会建立适合本地区的地方独立坐标系,建立地方独立坐标系,实际上就是通过一些参数来确定地方参考椭球与投影面。
二、国家大地坐标系1.1954年北京坐标系(BJ54旧)坐标原点:前苏联的普尔科沃。
参考椭球:克拉索夫斯基椭球。
平差方法:分区分期局部平差。
存在问题:(1)椭球参数有较大误差。
(2)参考椭球面与我国大地水准面存在着自西向东明显的系统性倾斜。
(3)几何大地测量和物理大地测量应用的参考面不统一。
(4)定向不明确。
2.1980年国家大地坐标系(GDZ80)坐标原点:陕西省泾阳县永乐镇。
参考椭球:1975年国际椭球。
平差方法:天文大地网整体平差。
特点:(1)采用1975年国际椭球。
(2)参心大地坐标系是在1954年北京坐标系基础上建立起来的。
坐标系

1坐标系为了定量地描述物体的位置及位置的变化,需要在参考系上建立适当的坐标系。
有一维坐标系,也有二维和三维坐标系2如果物体沿直线运动,可以以这条直线为x轴,在直线上规定原点、正方向和单位长度,建立直线坐标系。
3一个坐标系有几个要素呢?原点单位长度正方向数字物理量的符号和单位①描述直线运动——建立一维直线坐标系.②描述平面运动——建立二维平面直角坐标系.③描述立体空间内运动——建立三维立体空间坐标系.4坐标系①目的:定量地描述物体的位置及位置的_变化_____.②方法:当物体做直线运动时,可以选取某一点为坐标原点建立坐标轴,坐标轴的方向表示规定的_正方向,坐标轴上的数值表示物体的位置.物体的位置可认为是质点在某时刻所在空间的一点.③原则建立坐标系的原则是确定物体的位置方便、简洁.【特别提醒】(1)建立何种坐标系要针对物体是在直线上、平面内、还是空间中运动而定.5①运动员从距地面4 m高处落下,被蹦床弹到距地面5 m高处,蹦床离地面1 m,坐标原点定在蹦床处,向上为坐标轴的正方向,则开始下落点、地面、弹到的最高点的位置坐标分别是( )A.4 m,0.5 m B.3 m,-1 m,4 mC.0,4 m,-1 m D.4 m,-1 m,5②如图1-1-1所示为三种不同的坐标系,其中:甲中M点位置坐标为x=2 m;乙中N点位置坐标为x=3 m,y=4 m;丙中P点位置坐标为x=2 m,y=3 m,z=0 m.③以灯塔为坐标原点,向东为x轴正方向,向北为y轴正方向建立平面直角坐标系,某时刻一艘海轮的坐标为x=6 km,y=8 km,求该海轮距灯塔的直线距离为多少?④题10 km④一个小球从距地面4 m高处落下,被地面弹回,在距地面1 m高处被接住.坐标原点定在抛出点正下方2 m处,向下方向为坐标轴的正方向.则小球的抛出点、落地点、接住点的位置坐标分别是( )A.2 m,-2 m,-1 mB.-2 m,2 m,1 mC.4 m,0,1 mD.-4 m,0,-1 m解答本题的关键是正确地建立坐标系,并在坐标系中标出各个时刻对应的位置.【自主解答】根据题意建立如图1-1-2所示的坐标系,A点为抛出点,坐标为-2 m,B 点为坐标原点,D点为落地点,坐标为2 m,C点为接住点,坐标为1 m,所以选项B正确⑤李小华所在学校的校门口是朝南的,他进入校门后一直向前走120 m,再向东走40 m就到了他所在的教室,请你画出教室的位置(以校门口为坐标原点).解析:建立直角坐标系,x轴正方向表示东,y轴正方向表示北,则教室位置如图所示.。
常用坐标系

常用坐标系一、常用坐标系1、北京坐标系北京54坐标系为参心大地坐标系,大地上的一点可用经度L54、纬度M54和大地高H54定位,它是以克拉索夫斯基椭球为基础,经局部平差后产生的坐标系。
1954年北京坐标系的历史:新中国成立以后,我国大地测量进入了全面发展时期,再全国范围内开展了正规的,全面的大地测量和测图工作,迫切需要建立一个参心大地坐标系。
由于当时的“一边倒”政治趋向,故我国采用了前苏联的克拉索夫斯基椭球参数,并与前苏联1942年坐标系进行联测,通过计算建立了我国大地坐标系,定名为1954年北京坐标系。
因此,1954年北京坐标系可以认为是前苏联1942年坐标系的延伸。
它的原点不在北京而是在前苏联的普尔科沃。
北京54坐标系,属三心坐标系,长轴6378245m,短轴6356863,扁率1/298.3;2、西安80坐标系1978年4月在西安召开全国天文大地网平差会议,确定重新定位,建立我国新的坐标系。
为此有了1980年国家大地坐标系。
1980年国家大地坐标系采用地球椭球基本参数为1975年国际大地测量与地球物理联合会第十六届大会推荐的数据,即IAG75地球椭球体。
该坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇,位于西安市西北方向约60公里,故称1980年西安坐标系,又简称西安大地原点。
基准面采用青岛大港验潮站1952-1979年确定的黄海平均海水面(即1985国家高程基准)。
西安80坐标系,属三心坐标系,长轴6378140m,短轴6356755,扁率1/298.257221013、2000国家大地坐标系的定义国家大地坐标系的定义包括坐标系的原点、三个坐标轴的指向、尺度以及地球椭球的4个基本参数的定义。
2000国家大地坐标系的原点为包括海洋和大气的整个地球的质量中心;2000国家大地坐标系的Z轴由原点指向历元2000.0的地球参考极的方向,该历元的指向由国际时间局给定的历元为1984.0的初始指向推算,定向的时间演化保证相对于地壳不产生残余的全球旋转,某轴由原点指向格林尼治参考子午线与地球赤道面(历元2000.0)的交点,Y轴与Z轴、某轴构成右手正交坐标系。
我国常用的坐标系

我国常用的坐标系【原创版】目录1.我国常用的坐标系概述2.北京 54 坐标系3.西安 80 坐标系4.WGS84 坐标系5.2000 国家大地坐标系6.1985 国家高程标准正文一、我国常用的坐标系概述在我国,地理数据常用的坐标系有北京 54 坐标系、西安 80 坐标系、WGS84 坐标系和 2000 国家大地坐标系等。
这些坐标系在各个领域有着广泛的应用,例如大地测量、工程测量、地图制图等。
二、北京 54 坐标系北京 54 坐标系是我国常用的一种大地坐标系,其全称为“北京 54 世界大地坐标系”。
它是以克拉索夫斯基椭球为基础,经局部平差后产生的坐标系。
在这个坐标系中,大地上的一点可以用经度 l54、纬度 m54 和大地高 h54 来定位。
三、西安 80 坐标系西安 80 坐标系是我国于 1980 年建立的一种大地坐标系,其全称为“西安 80 世界大地坐标系”。
该坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇,位于西安市西北方向约 60 公里。
西安 80 坐标系采用克拉索夫斯基椭球作为基准椭球,与北京 54 坐标系相比,其采用了更加精确的测量数据。
四、WGS84 坐标系WGS84 坐标系是全球定位系统(GPS)采用的坐标系,全称为“世界大地坐标系 1984”。
它是一种地心坐标系,以地球质心为坐标原点,采用WGS84 椭球作为基准椭球。
WGS84 坐标系在全球范围内得到了广泛应用,是国际上最常用的坐标系之一。
五、2000 国家大地坐标系2000 国家大地坐标系是我国于 2000 年建立的一种新的大地坐标系,全称为“2000 国家大地坐标系”。
该坐标系采用 CGCS2000 椭球作为基准椭球,是我国当前正在推广使用的坐标系。
与北京 54 和西安 80 坐标系相比,2000 国家大地坐标系具有更高的精度和更广泛的应用范围。
六、1985 国家高程标准1985 国家高程标准是我国于 1985 年颁布的一项国家标准,用于规定高程测量的基准面和高程值。
坐标系分类

2、造型坐标系
造型坐标系(MCS:Modeling Coordinate System) 是右手坐标系。它是用来描述世界坐标系中每个具体物体的 形状,每个物体均由其自身的造型坐标系定义。
造型坐标系 局部坐标系 世界坐标系 整体坐标系。
3、观察坐标系
观察坐标系(VCS:View Coordinate System)是为了 将三维物体投影到显示屏幕(观察平面)上而建立起来的, 是左手坐标系。
一、点与字符的裁剪 点的裁剪比较简单,当图形系统的窗口确定之后,
设被裁剪的点的坐标为(x,y),则只有当该点的坐标
满足下式
该点才位于窗口之内,并经过窗口-视图变换后送视 区中显示,否则该点位于窗口之外而被舍去。
16
字符的裁剪,根据裁剪精度不同,可分为三种情况。 如图所示。 (1)字串裁剪
用一个限界矩形来包含整个文本字符串,判断该限界矩 形是否全部位于裁剪窗口的内部,如果是,则字符串全部 保留,如果不是,则字符串全部不可见。这是字符裁剪的 最简单方法,裁剪速度最快,但精度最低。
2、视区(Viewport)
设备坐标系中的一个矩形区域,在图形设备上用来输出图
形的最大区域称之为屏幕域,它是有限的整数域,任何小于
或等于屏幕域的区域都可定义为视区。视区由用户在屏幕
域中用设备坐标定义,一般也由左下角点和右上角
点坐标来表示,同样视区也可以是多层的。而
且,在同一屏幕还可以定义多个视区。
6
视区 窗口
视区
13
3、如果视区的纵横比与窗口的纵横比不一致时,经 变换后的图形在视区中输出时会产生失真现象,因此在定 义窗口和视区时,要保证它们的纵横比一致。
窗口
视区
视区
测量坐标系的种类

测量坐标系的种类
测量坐标系的种类有以下几种:
1. 直角坐标系:也称为笛卡尔坐标系,是最常见的坐标系。
以直角为基础,通过横坐标和纵坐标表示点的位置。
2. 极坐标系:采用径向和角度来表示点的位置。
径向表示点到原点的距离,角度表示点与指定轴的夹角。
3. 背光坐标系:通常用于光学测量,特别是在逆向工程和三维扫描中。
背光坐标系以视觉系统的光学轴作为基础,通过给定的距离和角度来表示点的位置。
4. 地理坐标系:用于地理信息系统(GIS)中,以地球表面的经度和纬度来表示点的位置。
5. 天球坐标系:在天文学中使用,以地球为中心的球面上的点的位置。
它使用赤经(类似于经度)和赤纬(类似于纬度)来表示点的位置。
6. 二维坐标系:主要用于平面几何,通过横坐标和纵坐标表示点的位置。
7. 三维坐标系:用于三维几何,在直角坐标系的基础上增加了第三个坐标轴,通过横坐标、纵坐标和高度/深度来表示点的位置。
各种坐标系的定义

各种坐标系的定义一:空间直角坐标系空间直角坐标系的坐标原点位于参考椭球的中心,Z轴指向参考椭球的北极,X轴指向起始子午面与赤道的交点,Y轴位于赤道面上切按右手系于X轴呈90度夹角,某点中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用如下图所示:二:大地坐标系:大地坐标系是采用大地纬度、经度和大地高程来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角;大地高师空间的点沿着参考椭球的法线方向到参考椭球面的距离。
附:经度和纬度的详细概念,呵呵。
经度和纬度都是一种角度。
经度是个面面角,是两个经线平面的夹角。
因所有经线都是一样长,为了度量经度选取一个起点面,经1884年国际会议协商,决定以通过英国伦敦近郊、泰晤士河南岸的格林尼治皇家天文台(旧址)的一台主要子午仪十字丝的那条经线为起始经线,称为本初子午线。
本初子午线平面是起点面,终点面是本地经线平面。
某一点的经度,就是该点所在的经线平面与本初子午线平面间的夹角。
在赤道上度量,自本初子午线平面作为起点面,分别往东往西度量,往东量值称为东经度,往西量值称为西经度。
由此可见,一地的经度是该地对于本初子午线的方向和角距离。
本初子午线是0°经度,东经度的最大值为180°,西经度的最大值为180°,东、西经180°经线是同一根经线,因此不分东经或西经,而统称180°经线。
纬度是个线面角。
起点面是赤道平面,线是本地的地面法线。
所谓法线,即垂直于参考扁球体表面的线。
某地的纬度就是该地的法线与赤道平面之间的夹角。
纬度在本地经线上三:平面坐标系(这里主要将gis中高斯-克吕格尔平面直角坐标系,不是数学里面的平面坐标系)高斯-克吕格尔平面直角坐标系Gauss-Krüger plane rectangular coordinates system 根据高斯-克吕格尔投影所建立的平面坐标系,或简称高斯平面坐标系。
坐标系的定义

间直角坐标系,大地坐标系,平面坐标系,高斯投影,高斯平面直角坐标系的定义一:空间直角坐标系空间直角坐标系的坐标原点位于参考椭球的中心,Z轴指向参考椭球的北极,X轴指向起始子午面与赤道的交点,Y轴位于赤道面上切按右手系于X轴呈90度夹角,某点中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用如下图所示:二:大地坐标系:大地坐标系是采用大地纬度、经度和大地高程来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角;大地高师空间的点沿着参考椭球的法线方向到参考椭球面的距离。
附:经度和纬度的详细概念,呵呵。
经度和纬度都是一种角度。
经度是个面面角,是两个经线平面的夹角。
因所有经线都是一样长,为了度量经度选取一个起点面,经1884年国际会议协商,决定以通过英国伦敦近郊、泰晤士河南岸的格林尼治皇家天文台(旧址)的一台主要子午仪十字丝的那条经线为起始经线,称为本初子午线。
本初子午线平面是起点面,终点面是本地经线平面。
某一点的经度,就是该点所在的经线平面与本初子午线平面间的夹角。
在赤道上度量,自本初子午线平面作为起点面,分别往东往西度量,往东量值称为东经度,往西量值称为西经度。
由此可见,一地的经度是该地对于本初子午线的方向和角距离。
本初子午线是0°经度,东经度的最大值为180°,西经度的最大值为180°,东、西经180°经线是同一根经线,因此不分东经或西经,而统称180°经线。
纬度是个线面角。
起点面是赤道平面,线是本地的地面法线。
所谓法线,即垂直于参考扁球体表面的线。
某地的纬度就是该地的法线与赤道平面之间的夹角。
纬度在本地经线上三:平面坐标系(这里主要将gis中高斯-克吕格尔平面直角坐标系,不是数学里面的平面坐标系)高斯-克吕格尔平面直角坐标系Gauss-Krüger plane rectangular coordinates system根据高斯-克吕格尔投影所建立的平面坐标系,或简称高斯平面坐标系。
3大常用坐标系

3大常用坐标系
摘要:
1.笛卡尔坐标系
2.极坐标系
3.球坐标系
正文:
一、笛卡尔坐标系
笛卡尔坐标系,也称直角坐标系,是一种平面坐标系统,用来表示平面上点的位置。
它由两条互相垂直的数轴组成,通常分别表示为x 轴和y 轴。
每个点在平面上的位置由其在x 轴和y 轴上的坐标值(通常为实数)来表示。
笛卡尔坐标系广泛应用于数学、物理、工程和计算机科学等领域。
二、极坐标系
极坐标系是一种平面坐标系统,用来表示平面上点的位置。
它由一个半径和一个角度来表示一个点在平面上的位置。
半径表示点到原点(极点)的距离,角度表示从极轴逆时针旋转到连接极点和该点的线段的角度。
极坐标系在数学、物理和工程等领域有广泛应用,特别是在涉及旋转和周期性现象的问题中。
三、球坐标系
球坐标系是一种三维坐标系统,用来表示空间中点的位置。
它由三个坐标值组成,通常表示为r、θ和φ。
其中,r 表示点到原点(球心)的距离,θ表示从赤道面逆时针旋转到连接球心和该点的线段的角度,φ表示从北极向下看,连接球心和该点的线段与x 轴正半轴之间的夹角。
球坐标系在物理、天文
学和地球科学等领域有广泛应用,特别是在涉及球面和球体相关计算的问题中。
总结:
笛卡尔坐标系、极坐标系和球坐标系是三种常用的坐标系,分别用于表示平面和空间的点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大地测量中以参考椭球面为基准面的坐标。
地面点P的位置用大地经度L、大地纬度B和大地高H表示。
当点在参考椭球面上时,仅用大地经度和大地纬度表示。
大地经度是通过该点的大地子午面与起始大地子午面之间的夹角,大地纬度是通过该点的法线与赤道面的夹角,大地高是地面点沿法线到参考椭球面的距离。
高斯坐标即高斯-克吕格坐标系(1)高斯-克吕格投影性质高斯-克吕格(Gauss-Kruger)投影简称“高斯投影”,又名"等角横切椭圆柱投影”,地球椭球面和平面间正形投影的一种。
德国数学家、物理学家、天文学家高斯(Carl FriedrichGauss,1777一1855)于十九世纪二十年代拟定,后经德国大地测量学家克吕格(Johannes Kruger,1857~1928)于1912年对投影公式加以补充,故名。
该投影按照投影带中央子午线投影为直线且长度不变和赤道投影为直线的条件,确定函数的形式,从而得到高斯一克吕格投影公式。
投影后,除中央子午线和赤道为直线外,其他子午线均为对称于中央子午线的曲线。
设想用一个椭圆柱横切于椭球面上投影带的中央子午线,按上述投影条件,将中央子午线两侧一定经差范围内的椭球面正形投影于椭圆柱面。
将椭圆柱面沿过南北极的母线剪开展平,即为高斯投影平面。
取中央子午线与赤道交点的投影为原点,中央子午线的投影为纵坐标x轴,赤道的投影为横坐标y轴,构成高斯克吕格平面直角坐标系。
高斯-克吕格投影在长度和面积上变形很小,中央经线无变形,自中央经线向投影带边缘,变形逐渐增加,变形最大之处在投影带内赤道的两端。
由于其投影精度高,变形小,而且计算简便(各投影带坐标一致,只要算出一个带的数据,其他各带都能应用),因此在大比例尺地形图中应用,可以满足军事上各种需要,能在图上进行精确的量测计算。
(2)高斯-克吕格投影分带按一定经差将地球椭球面划分成若干投影带,这是高斯投影中限制长度变形的最有效方法。
分带时既要控制长度变形使其不大于测图误差,又要使带数不致过多以减少换带计算工作,据此原则将地球椭球面沿子午线划分成经差相等的瓜瓣形地带,以便分带投影。
通常按经差6度或3度分为六度带或三度带。
六度带自0度子午线起每隔经差6度自西向东分带,带号依次编为第1、2…60带。
三度带是在六度带的基础上分成的,它的中央子午线与六度带的中央子午线和分带子午线重合,即自 1.5度子午线起每隔经差3度自西向东分带,带号依次编为三度带第1、2…120带。
我国的经度范围西起73°东至135°,可分成六度带十一个,各带中央经线依次为75°、81°、87°、……、117°、123°、129°、135°,或三度带二十二个。
六度带可用于中小比例尺(如1:250000)测图,三度带可用于大比例尺(如1:10000)测图,城建坐标多采用三度带的高斯投影。
(3)高斯-克吕格投影坐标高斯- 克吕格投影是按分带方法各自进行投影,故各带坐标成独立系统。
以中央经线投影为纵轴(x), 赤道投影为横轴(y),两轴交点即为各带的坐标原点。
纵坐标以赤道为零起算,赤道以北为正,以南为负。
我国位于北半球,纵坐标均为正值。
横坐标如以中央经线为零起算,中央经线以东为正,以西为负,横坐标出现负值,使用不便,故规定将坐标纵轴西移500公里当作起始轴,凡是带内的横坐标值均加500公里。
由于高斯-克吕格投影每一个投影带的坐标都是对本带坐标原点的相对值,所以各带的坐标完全相同,为了区别某一坐标系统属于哪一带,在横轴坐标前加上带号,如(4231898m,21655933m),其中21即为带号。
(4)高斯-克吕格投影与UTM投影某些国外的软件如ARC/INFO或国外仪器的配套软件如多波束的数据处理软件等,往往不支持高斯-克吕格投影,但支持UTM投影,因此常有把UTM投影坐标当作高斯-克吕格投影坐标提交的现象。
UTM投影全称为“通用横轴墨卡托投影”,是等角横轴割圆柱投影(高斯-克吕格为等角横轴切圆柱投影),圆柱割地球于南纬80度、北纬84度两条等高圈,该投影将地球划分为60个投影带,每带经差为6度,已被许多国家作为地形图的数学基础。
UTM 投影与高斯投影的主要区别在南北格网线的比例系数上,高斯-克吕格投影的中央经线投影后保持长度不变,即比例系数为1,而UTM投影的比例系数为0.9996。
UTM 投影沿每一条南北格网线比例系数为常数,在东西方向则为变数,中心格网线的比例系数为0.9996,在南北纵行最宽部分的边缘上距离中心点大约363公里,比例系数为 1.00158。
高斯-克吕格投影与UTM投影可近似采用Xutm=0.9996 * X高斯,Yutm=0.9996 * Y高斯进行坐标转换。
高斯-克吕格尔投影的投影函数是根据以下两个条件确定的:第一,投影是正形的,即椭球面上无穷小的图形和它在平面上的表象相似,故又称保角投影或保形投影;投影面上任一点的长度比(该点在椭球面上的微分距离与其在平面上相应的微分距离之比)同方位无关。
第二,椭球面上某一子午线在投影平面上的表象是一直线,而且长度保持不变,即长度比等于1。
该子午线称为中央子午线,或称轴子午线。
这两个条件体现了高斯-克吕格尔投影的特性。
我国幅员辽阔,含有11个6°带,即从13~23带(中央子午线从75°~135°),21个3°带,从25~45带。
北京位于6°带的第20带,中央子午线经度为117°。
1)子午线收敛角子午线收敛角,又称坐标纵线偏角,系过某点的坐标纵线对真子午线的夹角(r)。
以真子午线为准,坐标纵线东偏为正,西偏为负。
在高斯-克吕格投影带中,除了中央经线外,所有经线都投影成向两极收敛的弧线,因而在高斯平面直角坐标系中,除了该坐标系的纵轴(中央经线)与真子午线重合外,其它坐标纵线由于与真子午线不平行而构成一个夹角,故称之子午线收敛角(图2-58)。
在每个投影带内各点的子午线收敛角不一定相等,在中央经线和赤道线上各点的子午线收敛角为零,离中央经线越远或纬度越高,则子午线收敛的绝对值就越大,到极点处等于经差,在6°投影带的最大偏角为±3虽然各国都可以发展适合本国需要的特殊系统。
但是,有一种系统是通用的,即通用横墨卡托UTM)格网系统。
该种格网系统及其所依据的投影,已经广泛用于地形图,作为卫星影像和自然资源数据库的参考格网以及要求精确定位的其他应用。
在UTM格网系统中,北纬84度和南纬80度之间的地球表面积,按经度6度划分为南北纵带,称为投影带。
从180度经线开始向东将这些投影带编号,从1编至60。
每个带再划分为纬差8度的四边形。
四边形的横行从南纬80度开始。
用字母c至X(去掉I 和O)依次标记(参见图)(第X行含纬度12度,包括北半球从北纬72度至84度全部陆地面积)每个四边形用数字和字母组合标记。
读取参考格网,总是向右向上读取。
每一四边形划分为很多边长为1000 000米的小区,用字母组合系统标记。
在每个投影带中,位于带中心的经线,赋予横坐标值为500 000米。
赤道的标记是:对于北半球的坐标值,赤道为0,对于南半球的坐标值。
赤道为10000000米,往南递减。
UTM系统采用的是横墨卡托投影,结果沿每一条南北格网线(只有带中心的一条格网线为经线),比例系数为常数,在东西方向则为变数。
沿每一UTM格网的中心格网线的比例系数应为0.999 60(比例尺较小),在南北纵行最宽部分(赤道)的边缘上,包括带的重叠部分,距离中心点大约363公里,比例系数为1. 00158。
地图坐标UTM坐标系统UTM(UNIVERSAL TRANSVERSE MERCARTOR GRIDSYSTEM,通用横墨卡托格网系统)坐标是一种平面直角坐标,这种坐标格网系统及其所依据的投影已经广泛用于地形图,作为卫星影像和自然资源数据库的参考格网以及要求精确定位的其他应用。
在UTM系统中,北纬84度和南纬80度之间的地球表面积按经度6度划分为南北纵带(投影带)。
从180度经线开始向东将这些投影带编号,从1编至60(北京处于第50带)。
每个带再划分为纬差8度的四边形。
四边形的横行从南纬80度开始。
用字母C至X(不含I和O)依次标记(第X行包括北半球从北纬72度至84度全部陆地面积,共12度)每个四边形用数字和字母组合标记。
参考格网向右向上读取。
每一四边形划分为很多边长为1000 000米的小区,用字母组合系统标记。
在每个投影带中,位于带中心的经线,赋予横坐标值为500 000米。
对于北半球赤道的标记坐标值为0,对于南半球为10000000米,往南递减。
大比例尺地图UTM方格主线间距离一般为1KM,因此UTM系统有时候也被称作方里格。
因为UTM系统采用的是横墨卡托投影,沿每一条南北格网线(带中心的一条格网线为经线)比例系数为常数,在东西方向则为变数。
沿每一UTM格网的中心格网线的比例系数应为0.99960 (比例尺较小),在南北纵行最宽部分(赤道)的边缘上,包括带的重叠部分,距离中心点大约363公里,比例系数为1.00158。
1、椭球面地图坐标系由大地基准面和地图投影确定,大地基准面是利用特定椭球体对特定地区地球表面的逼近,因此每个国家或地区均有各自的大地基准面,我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。
我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系,1978年采用国际大地测量协会推荐的IAG 75地球椭球体建立了我国新的大地坐标系--西安80坐标系,目前GPS定位所得出的结果都属于WGS84坐标系统,WGS84基准面采用WGS84椭球体,它是一地心坐标系,即以地心作为椭球体中心的坐标系。
因此相对同一地理位置,不同的大地基准面,它们的经纬度坐标是有差异的。
采用的3个椭球体参数如下(源自“全球定位系统测量规范GB/T 18314-2001”):椭球体长半轴短半轴Krassovsky 6378245 6356863.0188IAG 75 6378140 6356755.2882WGS 84 6378137 6356752.3142理解:椭球面是用来逼近地球的,应该是一个立的椭圆旋转而成的。
2、大地基准面椭球体与大地基准面之间的关系是一对多的关系,也就是基准面是在椭球体基础上建立的,但椭球体不能代表基准面,同样的椭球体能定义不同的基准面,如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky椭球体,但它们的大地基准面显然是不同的。
在目前的GIS商用软件中,大地基准面都通过当地基准面向WGS84的转换7参数来定义,即三个平移参数ΔX、ΔY、ΔZ表示两坐标原点的平移值;三个旋转参数εx、εy、εz表示当地坐标系旋转至与地心坐标系平行时,分别绕Xt、Yt、Zt的旋转角;最后是比例校正因子,用于调整椭球大小。
