16届高三理科数学一诊考试双向细目表及打分板

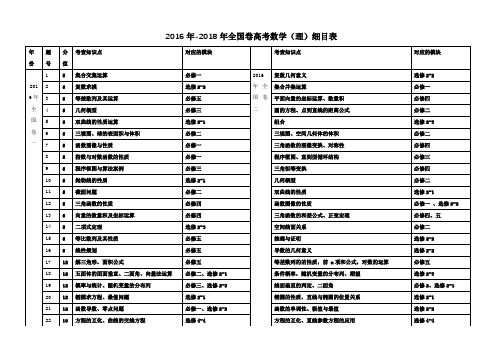
2016年-2018年高考数学(理)细目表(印刷版)

5
圆、折叠、三棱锥体积最值
必修2
抛物线焦点弦弦长
选修2-1
17
12
解三角形、面积公式、和角公式
必修五
解三角形、面积
必修五
18
12
面面垂直、二面角
必修二、选修2-1
直方图、独立性检验、中位数
必修三、选修2-319Leabharlann 12期望、正态分布
选修2-3
线面平行证明、线面角、二面角
必修二、选修2-1
20
12
椭圆方程、定点问题
选修2-2、选修2-3
三棱锥线面垂直、二面角
必修二、选修2-1
21
12
导数单调性、极值不等式
选修2-2
导数不等式、零点个数求参数
选修2-2
22
10
方程互化、曲线交点个数
选修4-4
椭圆参数方程、中点弦
选修4-4
2017年全国卷三
1
5
点集、交集运算
必修一
2018年全国卷三
集合交集
必修一
2
5
复数模
选修2-2
必修五
极值点、极小值
选修2-2
12
5
推理新概念
选修2-3
三角形、向量数量积（坐标法运算）
必修四
13
5
向量夹角、模
必修四
二项分布方差
选修2-3
14
5
线性规划
必修五
非齐次三角函数式最值（换元法、二次函数）
必修四
15
5
双曲线渐近线方程、离心率
选修2-1
等差数列基本计算（求首项、公差）裂项相消法求和
必修五
16
必修二

2007-2016年高考数学新课标1理科双向细目表

2013（卷Ⅱ）2014（卷Ⅰ）2014（卷Ⅱ）2015（卷Ⅰ）2015（卷Ⅱ）2016（卷Ⅰ）2016（卷Ⅱ）选择题选择题选择题选择题选择题选择题选择题抛物线与圆零点求参数范围三棱柱中求异面直线夹角三视图双曲线平面的截面问题双曲线的性质.离心率直线与三角形面积问题三视图极值求参数范围函数不等式求参数范围导数不等式三角函数的性质函数图象的性质填空题填空题填空题填空题填空题填空题填空题向量的数量积二项式二项式定理函数奇偶性求参数平面向量向量的数量积及坐标运算三角函数和差公式，正弦定理概率推理问题三角函数的最大值椭圆与圆线性规划二项式定理空间中的线面关系三角函数向量的夹角函数性质解不等式线性规划二项式等比数列及其应用推理等差数列求最值解三角形圆上点坐标范围解三角形数列求和（递推）线性规划导数的几何意义解答题解答题解答题解答题解答题解答题解答题集合(交集)程序框图，直到型循环结构三角恒等变换几何概型新课标理科双向细目表复数几何意义集合(并集)集合(交集)复数（求模）三视图及球的表面积与体积函数图像与性质指数与对数函数的性质程序框图与算法案例抛物线的性质平面向量的坐标运算、数量积圆的方程、点到直线的距离公式计数原理、组合三视图，空间几何体的体积三角函数的图象变换与对称性平面向量三视图等差数列及其运算几何概型概率（独立重复实验）统计（柱形图）命题的否定双曲线的性质程序框图程序框图程序框图三角函数的定义与图象二项式求参数古典概型概率集合(交集)集合(交集)等比数列函数奇偶性向量的模与数量积复数（除法运算）复数（除法运算）复数（乘法运算）抛物线求面积二项式函数图像球的表面积导数抛物线线性规划求参数线性规划与命题线性规划求最大值程序框图对数比较大小三角恒等变换已知切线求参数三角函数图像单调区间程序框图圆圆锥体积三视图双曲线解三角形等比数列性质三视图（体积比）分段函数求值双曲线（向量）线面关系复数相等求参数三角变换（和差角公式）复数乘除、模集合交集2016（卷Ⅲ）选择题集合(交集)复数（除法运算）向量夹角公式平均数、统计图同角三角函数间的基本关系倍角公式幂函数的图象与性质（比较大小）程序框图余弦定理三视图（面积）三棱柱的内切球及体积椭圆方程与几何性质计数原理的应用填空题线性规划平移及三角变换奇偶性及导数直线与圆的位置关系解答题。

成都市2016届高中毕业班一诊检测数学文理科参考答案及评分标准(含双向细目表及打分板)(20161226171633)

��８分 ��９分
), 使 u( 即 x０－２＝ ʑ 存在 x０ ɪ ( ３, ４ x０) l n x０．＝０, 此时函数 g( ʑ当x ɪ ( １, x０)时 , ᶄ( x )＜０, x )单调递减 ; g
又当 n ＝１时 , 上式也满足．㊀
��１１分 ��１２分 ��２分 ��３分 ��４分 ��６分 ��７分 ��１０分
( ) 解: 在正方形 A １９． I B C D 中 ,øA , øB , øC 为直角． ʑPD ʅ 平面 P E F． ȵ
n＋１ ʑ 当 n ɪ N∗ 时 , Sn ＝２ n ＋２．－４
ʑ 在三棱锥 P －D E F 中, P E, P F, PD 三条线段两两垂直．
D G B R D G P R , , 即 ʑ 在 әPDH 中 , R G ʊ PD ．＝＝ GH RH GH RH
��１１分 ��１２分 ��１分 ��２分

2016届高三诊断性大联考(一)数学(理)试卷(含解析)

绝密★启用前数学 ( 理科）班级姓名注意事项：1. 本试卷分第 I 卷 ( 选择题 ) 和第Ⅱ卷 ( 非选择题 ) 两部分。

考试时间 120 分钟，总合 150分。

2.答卷前，考生务势必自己的姓名、准考据号填写在答题卡上。

3.回答第 I 卷时，选出每题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

回答第Ⅱ卷时，将答案写在答题卡上，答在本试卷上无效。

4.考试结束后 , 将试卷和答题卡一并交回。

第 I 卷( 选择题共 60 分)一、选择题：本大题共12 小题，每题5 分，在每题给出的四个选项中，只有一项为哪一项符合题目要求的 .1. 已知会合 A ={X ∣X-1>0}, 会合 B={X ∣∣ X ∣≤ 2} ，则 A ∩ B= A. (-1,2)B.[-2,2]C. (1,2]D.[-2 ， +)2. 复数 Z 知足（ 1-2i)z =(1+i)2，则 z 对应复平面上的点的坐标为A.（-4 ，2）B.（-2 ，3 ）C.（4，-2）D.（2，3）555 555 553. 已知向量 a 、 b ，此中 a=（-2 ， -6 ），b=， a?b=-10，则 a 与 b 的夹角为0 C.-60 00 A.150 B.-30D.1204. 设 a ， b 表示两条不一样的直线，、、表示三个不一样的平面，则以下命题中正确的是A. 若 a 丄 , 且 a 丄 b, 则 b ∥ aB. 若丄且丄,则∥C.若 a ∥ 且 a ∥ , 则∥D.若∥且∥,则∥5. 函数 f(x)=asin3x+bx 3+4, 此中 a ，b ∈R ，f'(x)为 f(x) 的导函数，则 f( 2014 )+f(-2014 )+f'( 2015 )-f'(-2015) =A. 0B.2014C. 8D. 20156. 已知右侧程序框图（如图） , 若输入 a 、 b 分别为 10、 4, 则输出的 a 的值为A.0B.2C.4D.147.在△ ABC中，角 A、 B、 C 所对应的边长分别为 a、 b、 c，若asinA+bsinB=2sinC, 则 cosC 的最小值为A. B.11 C. D. -228.有以下几种说法：①若 pVq 为真命题，则p、 q 均为真命题；②命题“x0≤ 0”的否认是Xx0∈ R， 2x∈ R,2 > 0；221的充足③直线 l:y=kx+l 与圆 O:x+y =1 订交于 A、 B 两点，则“ k=l ”是△ OAB的面积为2而不用要条件；④随机变量-N(0,1)，已知(-1.96)=0.025，则 P(∣ f ∣< 1.96 )=0.975.此中正确的为A. ①④B. ②③C.②③④D.②④9. 将函数 f(x)=Sin(2x+) 的图象向右平移个单位长度，获得函数y=g(x) 的图象，则32g(x)dxA. 0B.C.2D.110. 任取 k∈[-1 ， 1],直线 L:y=kx+3与圆 C:(x-2)2+(y-3)2 =4 订交于 M、N 两点，则∣ MN ∣≥的概率为A.33C.2D.1 B.32 3211. 已知函数1- ∣ x∣ ,x ≤ 1函数 g(x)=4-f(1-x), f （ x）=,(x-1)2 ,x > 15则函数 y=f(x)-g(x)的零点的个数为A.2B.3C.4D.512. 多面体的三视图以下图，则该多面体表面积为（单位cm2)A.28+B. 30+C. 28+D. 28+第Ⅱ卷 ( 非选择题共90 分）二、填空题 : 本大题共 4小题,每题 5分.13. 二项式 (2x+ 1) 6 的睁开式中的常数项是.x14. 实数 x 、 y 知足条件x-y+5 ≥ 0, ，则 ,z=-2x+y的最小值为.x+y ≥ 0,x ≤ 3,15. 已知 sina= 3，∈ (0,) ， tan= 1，则 tan(+))=.52416. 已知 AB 是圆 C:（ x+2) 2+(y-l)2=2的一条直径，若楠圆 x 2+4y 2=4b 2(b ∈R)经过 A 、B 两5点，则该椭圆的方程是.三、解答题：本大题共6 小题，共 70 分 . 解答应写出文字说明，证明过程或演算步骤.17.( 本小题满分 12 分）已知各项均为正数的等差数列2212{a n } ，且 a +b =20,a +a =64.(I) 求数列 {a n } 的通项公式；an ( Ⅱ ) 设 b n =, 求数列的前 n 项和 .2 X 4n18.( 本小题满分 12 分）如图，在四边形 ABCD 中，△ABC 是边长为 2 的等边三角形，AD 丄 DC ，AD=DC ， E 、 F 是平面 ABCD 同一侧的两点， BE 丄平面 ABCD, DF 丄平面 ABCD ，且 DF=1. (I) 若 AE 丄 CF ，求BE 的值；( Ⅱ ) 求当 BE 为什么值时，二面角 E -AC-F 的大小是 60°.19. ( 本小题满分 12 分）2015 年 10 月 4 日，强台风“彩虹”登岸广东省湛江市，“彩虹”是 1949 年以来登岸中国陆地的最强台风。

2016届高三年级第一次综合诊断考试理数答案

2016届高三年级第一次综合诊断考试理数答案一、选择题 (本大题共12小题，每小题5分,满分60分.) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D C A B D B C A BDAC二、填空题(本大题共4小题，每小题5分,满分20分.)13. 35 14.2211612x y += 15. 1(0,)216. 2015 三、解答题(本大题共6小题，满分70分.) 17、【解】（Ⅰ）.1)6sin(22)cos(12)sin(3)(m x m x x x f +-+=+-⋅-=πωωω依题意函数.32,32,3)(==ωπωππ解得即的最小正周期为x f 所以.1)632sin(2)(m x x f +-+=π分所以依题意的最小值为所以时当6.1)632sin(2)(.0,.)(,1)632sin(21,656326,],0[ -π+==≤π+≤π≤π+≤ππ∈x x f m m x f x x x （Ⅱ）.1)632sin(,11)632sin(2)(=+∴=-+=ππC C C f 22252,..863663622,,2sin cos cos(),2152cos sin sin 0,sin .102510sin 1,sin .122Rt C C C ABC A B B B A C A A A A A A πππππππ<+<+==∆+==+--±∴--==-<<∴= 而所以解得分在中解得分分18、∵EF ⊥平面AEB ，AE ⊂平面AEB ，BE ⊂平面AEB∴EF AE ⊥，EF BE ⊥ 又A E E B ⊥∴,,EB EF EA 两两垂直以点E 为坐标原点，,,EB EF EA 分别为轴建立如图所示的空间直角坐标系由已知得，A （0，0，2），B （2，0，0），C （2，4，0），F （0，3，0），D （0，2，2），G （2，2，0）∴(2,2,0)EG = ，(2,2,2)BD =-,,x y z∴22220BD EG ⋅=-⨯+⨯=∴B D E G ⊥-----------------6分()2由已知得(2,0,0)EB = 是平面DEF 的法向量,设平面DEG 的法向量为(,,)n x y z =∵(0,2,2),(2,2,0)ED EG ==∴00ED n EG n ⎧⋅=⎪⎨⋅=⎪⎩ ，即00y z x y +=⎧⎨+=⎩，令1x =,得(1,1,1)n =- 设平面DEG 与平面DEF 所成锐二面角的大小为θ则||23cos |cos ,|3||||23n EB n EB n EB θ=<>===∴平面DEG 与平面DEF 所成锐二面角的余弦值为33----------------12分 19．(本题满分12分) 解：（1）众数：8.6；中位数：8.75 ；……………2分（2）设i A 表示所取3人中有i 个人是“极幸福”，至多有1人是“极幸福”记为事件A ，则140121)()()(3162121431631210=+=+=C C C C C A P A P A P ； …………6分（3）ξ的可能取值为0，1，2，3.6427)43()0(3===ξP ；6427)43(41)1(213===C P ξ； 64943)41()2(223===C P ξ；641)41()3(3===ξP ………………10分所以ξ的分布列为：ξE 27279101230.7564646464=⨯+⨯+⨯+⨯=. ……………12分另解：ξ的可能取值为0，1，2，3.则1~(3,)4B ξ，3313()()()44k k kP k C ξ-==.所以ξE =75.0413=⨯． 20.(本小题满分12分) 解：（Ⅰ）∵错误！未找到引用源。

2016届成都一诊理科数学答案及评分标准

成都市高2013级高中毕业班第一次诊断性检测数学(理工类)参考答案及评分意见第Ⅰ卷㊀(选择题㊀共50分)一㊁选择题:(本大题共10小题,每小题5分,共50分)1.B ;㊀2.C ;㊀3.C ;㊀4.B ;㊀5.D ;㊀6.A ;㊀7.A ;㊀8.B ;㊀9.D ;㊀10.A.第Ⅱ卷㊀(非选择题,共100分)二.填空题:(本大题共5小题,每小题5分,共25分)11.1+5i ;㊀㊀12.-280;㊀㊀13.25;㊀㊀㊀14.23;㊀㊀15.[2,1+3].三㊁解答题:(本大题共6小题,共75分)16.解:(Ⅰ)ȵ2(a n +a n +2)=5a n +1,㊀ʑ2(a n +a n q 2)=5a n q .由题意,得a n ʂ0,ʑ2q 2-5q +2=0.ʑq =2或12.ȵq >1,ʑq =2.㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ 6分㊀(Ⅱ)ȵa 25=a 10,㊀ʑ(a 1q 4)2=a 1q 9.ʑa 1=2.ʑa n =a 1q n -1=2n .ʑa n 3n =(23)n .ʑS n =23[1-(23)n ]1-23=2-2n +13n .㊀㊀㊀㊀㊀㊀㊀㊀㊀ 12分17.解:(Ⅰ)由题意,X 的所有可能取值为15,20,25,30.ȵP (X =15)=C 34C 39=121,P (X =20)=C 24㊃C 15C 39=514,P (X =25)=C 14㊃C 25C 39=1021,P (X =30)=C 35C 39=542,ʑX 的分布列为:X15202530P 1215141021542㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ 7分(Ⅱ)E (X )=15ˑ121+20ˑ514+25ˑ1021+30ˑ542=703.㊀㊀ 12分18.解:(Ⅰ)f (x )=c o s 2x +(32s i n x -12c o s x )2=c o s 2x +(34s i n 2x +14c o s 2x -32s i n x c o s x ))页4共(页1第案答)理(题试考诊一学数=12-(-34c o s 2x +34s i n 2x )=12-32s i n (2x -π3).㊀㊀㊀㊀㊀㊀㊀ 3分要使f (x )取得最大值,须满足s i n (2x -π3)取得最小值.ʑ2x -π3=2k π-π2,k ɪZ .ʑx =k π-π12,k ɪZ .㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ 5分ʑ当f (x )取得最大值时,x 取值的集合为{x |x =k π-π12,k ɪZ }. 6分(Ⅱ)由题意,得s i n (2C -π3)=32.ȵC ɪ(0,π2),ʑ2C -π3ɪ(-π3,2π3).ʑC =π3.㊀㊀㊀㊀㊀㊀ 9分ȵB ɪ(0,π2),ʑs i n B =45.ʑs i n A =s i n (B +C )=s i n B c o s C +c o s B s i n C =45ˑ12+35ˑ32=4+3310.㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ 12分19.解:(Ⅰ)如图,过点E 作E H ʅB C 于H ,连接HD .ʑE H =3.ȵ平面A B C D ʅ平面B C E ,E H ⊆平面B C E ,平面A B C D ɘ平面B C E =B C ,ʑE H ʅ平面A B C D .又ȵF D ʅ平面A B C D ,F D =3.ʑF D ʏE H .ʑ四边形E HD F 为平行四边形.ʑE F ʊHD .ȵE F ⊄平面A B C D ,HD ⊆平面A B C D ,ʑE F ʊ平面A B C D .㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ 6分(Ⅱ)连接HA .由(Ⅰ),得H 为B C 中点,又øC B A =60ʎ,ΔA B C 为等边三角形,ʑHA ʅB C .分别以H B ,HA ,H E 所在直线为x ,y ,z 轴建立如图所示的空间直角坐标系H -x y z .则B (1,0,0),F (-2,3,3),E (0,03),A (0,3,0).B F ң=(-3,3,3),B A ң=(-1,3,0),B E ң=(-1,0,3).设平面的法向量为n 1=(x 1,y 1,z 1).由n 1㊃B F ң=0n 1㊃B E ң=0{,得-3x 1+3y 1+3z 1=0-x 1+3z 1=0{.令z 1=1,得n 1=(3,2,1).设平面A B F 的法向量为n 2=(x 2,y 2,z 2).由n 2㊃B F ң=0n 2㊃B A ң=0{,得-3x 2+3y 2+3z 2=0-x 2+3y 2=0{.)页4共(页2第案答)理(题试考诊一学数令y 2=1,得n 2=(3,1,2).ʑc o s <n 1,n 2>=n 1㊃n 2|n 1|㊃|n 2|=3+2+28=78.ȵ二面角A -F B -E 为钝角,故二面角A -F B -E 的余弦值是-78.㊀㊀㊀㊀㊀ 12分20.解:(Ⅰ)A (-3,0),B (3,0).设点P (x ,y )(y ʂ0).则有x 23+y 22=1,即y 2=2(1-x 23)=23(3-x 2).ʑk P A ㊃k P B =y x +3㊃y x -3=y 2x 2-3=23(3-x 2)x 2-3=-23.㊀ʑ直线P A 与P B 斜率乘积的值为-23.㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ 4分(Ⅱ)令M (x 1,y 1),N (x 2,y 2).ȵM N 与x 轴不重合,ʑ设l M N :x =m y +t (m ɪR ).由x =m y +t 2x 2+3y 2-6=0{,得(2m 2+3)y 2+4m t y +2t 2-6=0.ʑΔ=16m 2t 2-4(2m 2+3)(2t 2-6)>0y 1+y 2=-4m t 2m 2+3y 1㊃y 2=2t 2-62m 2+3ìîí.㊀㊀㊀㊀㊀㊀ (∗)由题意,得AM ʅA N .即AM ң㊃A N ң=0.ȵx 1=m y 1+t ,x 2=m y 2+t ,ʑAM ң㊃A N ң=[m y 1+(t +3)][m y 2+(t +3)]+y 1y 2=0.ʑ(1+m 2)y 1y 2+m (t +3)(y 1+y 2)+(t +3)2=0.将(∗)式代入上式,得(1+m 2)2t 2-62m 2+3+m (t +3)-4m t 2m 2+3+(t +3)2=0.即2t 2-6+2m 2t 2-6m 2-4m 2t 2-43m 2t +(2m 2+3)(t 2+23t +3)=0.展开,得2t 2-6+2m 2t 2-6m 2-4m 2t 2-43m 2t +2m 2t 2+43m 2t +6m 2+3t 2+63t +9=0.整理,得5t 2+63t +3=0.解得t =-35或t =-3(舍去).经检验,t =-35能使Δ>0成立.故存在t =-35满足题意.㊀㊀㊀㊀㊀㊀㊀㊀ 13分21.解:(Ⅰ)f (x )的定义域为(0,+¥),f ᶄ(x )=-(a x -1)(x -1)x (a >0).①当a ɪ(0,1)时,1a >1.由f ᶄ(x )<0,得x >1a 或x <1.ʑ当x ɪ(0,1),x ɪ(1a ,+¥)时,f (x )单调递减.ʑf (x )的单调递减区间为(0,1),(1a ,+¥).)页4共(页3第案答)理(题试考诊一学数②当a =1时,恒有f ᶄ(x )ɤ0,ʑf (x )单调递减.ʑf (x )的单调递减区间为(0,+¥).③当a ɪ(1,+¥)时,1a <1.由f ᶄ(x )<0,得x >1或x <1a .ʑ当x ɪ(0,1a ),x ɪ(1,+¥)时,f (x )单调递减.ʑf (x )的单调递减区间为(0,1a ),(1,+¥).综上,当a ɪ(0,1)时,f (x )的单调递减区间为(0,1),(1a ,+¥);当a =1时,f (x )的单调递减区间为(0,+¥);当a ɪ(1,+¥)时,f (x )的单调递减区间为(0,1a ),(1,+¥).㊀㊀. 6分(Ⅱ)当a =0时,g (x )=x 2-x l n x ,x ɪ(0,+¥),g ᶄ(x )=2x -l n x -1,[g ᶄ(x )]ᶄ=2-1x .当x ɪ[12,+¥)时,[g ᶄ(x )]ᶄ=2-1x ⩾0,ʑg ᶄ(x )在[12,+¥)上单调递增.又g ᶄ(12)=l n 2>0,ʑg ᶄ(x )⩾g ᶄ(12)>0在[12,+¥)上恒成立.ʑg (x )在[12,+¥)上单调递增.由题意,得m 2-m l n m =k (m +2)-2n 2-n l n n =k (n +2)-2{.原问题转化为关于x 的方程x 2-x l n x =k (x +2)-2在[12,+¥)上有两个不相等的实数根.㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ 9分即方程k =x 2-x l n x +2x +2在[12,+¥)上有两个不相等的实数根.令函数h (x )=x 2-x l n x +2x +2,x ɪ[12,+¥).则h ᶄ(x )=x 2+3x -2l n x -4(x +2)2.令函数p (x )=x 2+3x -2l n x -4,x ɪ[12,+¥).则p ᶄ(x )=(2x -1)(x +2)x 在[12,+¥)上有p ᶄ(x )⩾0.故p (x )在[12,+¥)上单调递增.ȵp (1)=0,ʑ当x ɪ[12,1)时,有p (x )<0即h ᶄ(x )<0.ʑh (x )单调递减;当x ɪ(1,+¥)时,有p (x )>0即h ᶄ(x )>0,ʑh (x )单调递增.ȵh (12)=910+l n 25,h (1)=1,h (10)=102-10l n 212>102-1012=233>h (12),ʑk 的取值范围为(1,910+l n 25].㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ 14分)页4共(页4第案答)理(题试考诊一学数。

宜昌市2016届高三年级第一次调研考试理科数学参考答案及评分标准

宜昌市2016届高三年级第一次调研考试数学（理科）评分标准命题：孟章林（长阳一中）审题：郭和庆（三峡高中）李力（夷陵中学）韩山（宜昌市十三中）一、选择题：DBCCB CDBDA AB二、填空题：13.),1()1,(+∞--∞ 14. 6π 15.49错误！未找到引用源。

16.44+n n 错误！未找到引用源。

三、解答题：17.解：（1）由已知结合正弦定理可得sin sin sin cos C A C C A - ………2分s i n 0,3s i n c o s 2s i n ()6C A A A π≠∴-=- ，即1sin()62A π-= ………4分又5(0,),(,),,666663A A A A πππππππ∈∴-∈-∴-=∴= ………6分（2）11sin 22S bc A bc ==1bc ∴= ① ………7分又22222cos ()22cos 3a b c bc A b c bc bc π=+-=+--，即21()3b c =+-，且b,c 为正数2b c ∴+= ② ………10分由①②两式解得1==c b ………12分18.解：（1）设等差数列}{n b 的公差为d ,由已知得：d b d b q a q a 123,33,3,3134232+=+===即,⎩⎨⎧+=+=d q dq 12333332 …………………2分解得20()31d d q q ==⎧⎧⎨⎨==⎩⎩或舍，所以2=d ……4分所以12,3+==n b a n n n …………………6分(2)由题意得n n n n n n n a b c 3)12()1()1(++⋅-=+-=,所以)12()1()12()1(...)97()53(...121+-+--+++-++-=+++=-n n c c c S n n n n )3333(132-+++++n …………………8分当n 为偶数时,得232331)31(31-+=--+=+n n S n n n …………………10分当n 为奇数时,得272331)31(3)12(11--=--++--=+n n n S n n n ………12分 (另解：用错位相减法求得})1{(n n b -的前n 项和为)1()1(1+-+-n n ， ………9分利用等比数列求和得到}{n a 的前n 项和为2331-+n ， …………11分从而得到=n S )1()1(2531+-+-+n n n ………………12分） 19.（1）证明：设F 为CD 的中点，连接BF ，则DF=AB.AB ⊥AD ，AB=AD ，AB//DC ，∴四边形ABFD 为正方形 ………………2分O 为BD 的中点，∴O 为AF ，BD 的交点，PD=PB=2， ∴PO ⊥BD ………………3分22AD 22=+=AB BD , ∴2P 22=-=BO B PO ,221==BD AO , 在△P AO 中，4222==+PA AO PO ,∴PO ⊥AO ……………4分（2）连接PF , O 为AF 的中点，E 为P A 中点，∴OE //PF ……………5分PDC PF PDC OE 平面平面⊂⊄,OE ∴//平面PDC ……………7分（3）由（1）知PO ⊥AO 且PO ⊥BD ，所以PO ⊥平面ABCD ，又AB ⊥AD ，所以过点O 分别作AD 、AB 的平行线（如图），并以它们分别为x 、y 轴，以OP 为z 轴建立如图所示的空间直角坐标系，由已知得：()0,1,1--A ，)0,1,1(-B ，)0,3,1(C ，()0,1,1-D ，()0,1,1--A ，()2,0,0P)22,21,21(--E )……………………9分设平面PDC 的法向量为),,(111z y x =，直线CB 与平面PDC 所成角θ，则⎪⎩⎪⎨⎧=⋅=⋅,0,0即⎪⎩⎪⎨⎧=--=-+020********z y x z y x 解得⎩⎨⎧==11120z x y令11=z ，则平面PDC 的一个法向量为)1,0,2(=n ………………10分又)0,2,2(--=CB ，则3322322cos sin =⨯=><=，θ ∴直线CB 与平面PDC 所成角的正弦值为33 ………………12分 20.解：（1）设椭圆C 的标准方程为)0(12222>>=+b a by a x ， ………………………1分由题可得⎪⎩⎪⎨⎧=+=-121112222b ab a ………………………2分解得1,222==b a ……………………3分所以椭圆C 的标准方程为1222=+y x 错误！未找到引用源。

四川省绵阳市2016届高三上学期第一次诊断性考试数学理试题 Word版含答案

绵阳市高中2016届高三第一次（11月）诊断性考试数学理试题本试卷分第I 卷（选择题）和第II 卷（非选择题）．第I 卷.1至2页，第II 卷2至4 页．共4页．满分150分．考试时间120分钟．考生作答时，须将答案答在答题卡上，在本试题卷、草稿纸上答题无效．考试结束后，将答题卡交回．第I 卷（选择题，共50分）注意事项：必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑．第I 卷共10小题．一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的．1．集合S={x ｜｜x-4｜<2，x ∈N ＊｝，T ＝｛4，7，8｝，则S U T ＝(A){4} (B){3，5，7，8} (C) {3， 4, 5，7，8} (D) {3，4, 4, 5, 7, 8} 2．命题“2000,23x N x x ∃∈+≥”的否定为(A) 2000,23x N x x ∃∈+≤ (B) 2,23x N x x ∀∈+≤ (C) 2000,23x N x x ∃∈+< (D) 2,23x N x x ∀∈+<3．己知幂函数过点（2，则当x=8时的函数值是（A ）（B ）±（C ）2 （D ）644.若,,a b c ∈R,己知P ：,,a b c 成等比数列；Q: P 是Q 的（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充分也不必要条件5.下列四个函数中，最小正周期为π，且关于直线x ＝一512π对称的函数是（A ）sin()23x y π=+（B ）sin()23x y π=- （C ）sin(2)3y x π=-（D ）sin(2)3y x π=+6．在等差数列｛n a ｝中，若a 4＋a 9＋a l4＝36，则101112a a -＝（A ）3 （B ）6 （C ）12 （D ）247．在△ABC 中，角A ，B ，C 的对边分别是,,a b c ，若22,sin c b A B ==，则cosC ＝（A ）2 （B ）4 （C ）一2 （D ）一48．若实数x ，y 满足不等式组024010x y x y x my +≥⎧⎪+-≤⎨⎪--≤⎩，且x y +的最大值为3，则实数m=（A ）一1 （B ）12（C ）l （D ）2 9．设函数y ＝f （x ），x ∈R 满足f （x ＋l ）＝f （x 一l ），且当x ∈（－1，1］时，f （x ）＝1一x 2，函数g （x ）＝lg ||,01,0x x x ≠⎧⎨=⎩，则h （x ）＝f （x ）一g （x ）在区间［－6，9］内的零点个数是（A ）15 （B ）14 （C ）13．（D ）1210．直角△ABC 的三个顶点都在单位圆221x y +=上，点M （12，12），则｜MA MB MC ++｜的最大值是（Al （B2 （C1 （D2第II 卷（非选择题共100分）注意事项：必须使用0．5毫米黑色墨迹签字笔在答题卡上题目所指的答题区域内作答．作图题可先用铅笔绘出，确认后再用0．5毫米黑色墨迹签字笔描清楚．答在试题卷、草稿纸上无效．第II 卷共11小题．二、填空题：本大题共5小题，每小题5分，共25分， 11、·函数()f x =的定义域为12，式子0000tan 20tan 4020tan 40+的值是．13·已知函数266,2(),2x x x x f x a a x ⎧-+-≤⎪=⎨->⎪⎩其中a ＞0，1a ≠，若对任意的1212,,x x R x x ∈≠，恒有1212[()()]()f x f x x x --＞0，则实数a 的取值范围．14.二次函数2()f x ax =+2bx+c 的导函数为'()f x ，已知'(0)0f >，且对任意实数x ，有()0f x ≥，则(1)'(0)f f 的最小值为． 1 5．设集合M 是实数集R 的一个子集，如果点0x ∈R 满足：对任意ε＞0，都存在x ∈M ，使得0＜0||x x ε-<；，称x 0为集合M 的一个“聚点”．若有集合：①有理数集； ②cos|*1n N n π⎧⎫∈⎨⎬+⎩⎭③sin|*1n N n π⎧⎫∈⎨⎬+⎩⎭ ④|*1n N n π⎧⎫∈⎨⎬+⎩⎭其中以0为“聚点”的集合是．（写出所有符合题意的结论序号）三、解答题：本大题共6小题，共75分．解答应写出文字说明．证明过程或演算步骤． 16．（本小题满分12分）已知向量(cos ,1sin ),(cos ,sin )()m n R ααααα=-=-∈（1)若m n ⊥，求角α的值；（2）若||m n -=cos2α的值．17、（本小题满分12分）已知数列{n a }的首项a 1＝1，且a n+1＝2a n ＋(*,)n N R λλ∈∈（1)试问数列{n a ＋λ}是否为等比数列？若是，请求出数列{n a }的通项公式；若不是，请说，明理由； (2)当λ＝1时，记1n n nb a =+，求数列{n b }的前n 项和Sn18．（本小题满分12分）某民营企业家去年为西部山区80名贫困大学生捐资奖学金共50万元妥该企业家计划从今年起（今年为第一年）10年内每年捐资总金额都比上一年增加10万元，资助的贫困大学生每年净增a 人。

成都市2016届高中毕业班第一次诊断性检测数学(理科)试卷和参考答案

成都市２０１４级高中毕业班第一次诊断性检测
数学参考答案及评分标准 ( 理科 )
( 一㊁选择题 : 每小题５分 , 共６０分) １． B; ２． A; ３． B; ４． C; ５． B; ６． C; ７． B; ８． D; ９． C; １０． A; １１． A; １２． D．第 Ⅱ 卷( 非选择题 , 共９０分) ( 二㊁填空题 : 每小题５分 , 共２０分) ９３ ; １３．㊀１４． ; ㊀１５．㊀１６．３．－２; －２２ ( 三㊁解答题 : 共７０分) ( )ȵ ��１分解: １７． I a１＝－２,ʑ a１＋４＝２． ,ʑ ( )． ��３分 ȵ a ２ a a ２ a ２ a n＋１＝ n ＋４ n＋１＋４＝ n ＋８＝ n ＋４ a n＋１＋４ ��４分 ʑ ＝２． a n ＋４ }是以２为首项 , ��５分 ʑ{ a ２为公比的等比数列． n ＋４ n n ( ) ( ) , ��７分 I I 由 I 可知 a ２．㊀ʑ a ２－４． n ＋４＝ n ＝ , ; ��８分当 n ＝１时 , a１＝－２＜０ ʑS１＝ a１ | | ＝２当 n ȡ２时 , a n ȡ０． ��９分 ʑSn ＝－a１＋a２＋ �� ＋a n ２ n ２ n ( ) �� ( ) �� ( ) ＝２＋２－４＋＋２－４＝２＋２＋＋２－４ n －１ n ( ) ２１－２ n＋１ ( ) ��１ n －１ n ＋２．１分＝－４＝２－４１－２又当 n ＝１时 , 上式也满足． n＋１ ��１ ʑ 当 n ɪ N∗ 时 , Sn ＝２ n ＋２．２分－４ ( ) 解: 由题意 , 可知１１８． I ０ x ＋０．０１２ˑ１０＋０．０５６ˑ１０＋０．０１８ˑ１０＋０．０１０ˑ１０＝１． ��２分 ʑx ＝０．００４． ��３分 ʑ 甲学校的合格率为１－１０ˑ０．００４＝０．９６．２ ��４分而乙学校的合格率为１－９６．＝０．５０ ��５分乙两校的合格率均为９ ʑ 甲㊁６％． ( ) ��６分样本中甲校 C 等级的学生人数为０． I I ０１２ˑ１０ˑ５０＝６．而乙校 C 等级的学生人数为４． ��７分甲校学生人数 X 的可能取值为０, ʑ 随机抽取３人中 , １, ２, ３．３１２ C C １３４６C ４ ) , ) , ʑP ( X ＝０ P( X ＝１＝３＝＝３＝３０１０ C C １０１０２１３ C C C １１６４６ ) ) P( X ＝２ P( X ＝３＝３＝ , ＝３＝．２６ C C １０１０ ʑ X 的分布列为０１２３１３１１ P ３０１０２６３１１９㊀㊀数学期望 EX ＝１ˑ ＋２ˑ ＋３ˑ ＝．１０２６５第 Ⅰ 卷( 选择题 , 共６０分)

青岛市2016年高三一模考试理科数学答案

青岛市高三统一质量检测数学（理科）参考答案及评分标准一、选择题：本大题共10小题．每小题5分，共50分． B B A A C A C C D B二、填空题：本大题共5小题，每小题5分，共25分．11. i 12. 1215 13.1cos 2x π 14．3+ 15．14 三、解答题：本大题共6小题，共75分，解答时应写出必要的文字说明、证明过程或演算步骤．16. （本小题满分12分）解：（Ⅰ）22()sin sin ()6f x x x πωω=--1cos(2)1cos 2322x x πωω---=-111(cos 22)cos 2222x x x ωωω=+-112cos 2)22x x ωω=- 1sin(2)26x πω=- …………………………………………………………………………3分由直线x π=是()y f x =图象的一条对称轴，可得sin(2)16πωπ-=±，所以2(Z)62k k ππωππ-=+∈，即123k ω=+ (Z)k ∈1(,1)2ω∈ ，Z k ∈，所以1k =，56ω= ………………………………………………6分所以15()sin()236f x x π=-则函数()f x 最小正周期26553T ππ==………………………………………………7分（Ⅱ）15()sin()236f x x π=-311()sin()5264f A A π∴=-=,1sin()62A π∴-=0A π<< 5666A πππ∴-<-<,663A A πππ∴-==…………………………………9分 1a = ， ∴222212cos23b c bc b c bc bc bc bc π=+-=+-≥-=，即1bc ≤1sin 2ABC S bc A ∆∴==≤∴ABC ∆面积的最大值为4. …………………………………………………………１2分 17．（本小题满分12分）解：（Ⅰ）两人所付费用相同，相同的费用可能为0,40,80元两人都付0元的概率为11114624P =⨯= …………………………………………………1分两人都付40元的概率为2121233P =⨯= …………………………………………………2分两人都付80元的概率为31112111(1)(1)42634624P =--⨯--=⨯= ………………………………………3分则两人所付费用相同的概率为12311152432412P P P P =++=++= …………………5分（Ⅱ）设甲、乙所付费用之和为ξ，ξ可能取值为0,40,80,120,160111(0)4624P ξ==⨯=12111(40)43264P ξ==⨯+⨯=1112115(80)46234612P ξ==⨯+⨯+⨯=11121(120)26434P ξ==⨯+⨯=111(160)4624P ξ==⨯=ξ的分布列为……………………………………………………………………………………10分11511()040801201608024412424E ξ=⨯+⨯+⨯+⨯+⨯= ………………………12分 18．（本小题满分12分）解：（Ⅰ）在四边形ABCD 中， AC AD ⊥，2AD AC ==，045ACD ∴∠=45BCA ∠= ， 90BCD BCA ACD ∴∠=∠+∠= ，DC BC ⊥又AB BC ⊥ //AB CD ∴………………2分AB ⊂面PAB ，CD ⊄面PAB∴//CD 面PAB ……………………4分CD ⊂ 面PCD ，面PAB 面PCD l =∴//CD l ………………………5分（Ⅱ） PA ⊥平面ABCD ，AC AD ⊥，∴以A 为原点，以AD 所在的直线为x 轴，建系如图，则(0,0,2)P ，(0,0,1)E ，(2,0,0)D ，(0,2,0)C ，(1,1,0)B - ………………6分设面DCE 的法向量为1111(,,)n x y z =(0,2,1)CE =- ，(2,0,1)DE =-由111111020200n CE y z xz n DE ⎧⋅=-+=⎧⎪⇒⎨⎨-+=⋅=⎩⎪⎩令11x =，则11y =，12z =，1(1,1,2)n ∴=…………………………………8分设面BCE 的法向量为2222(,,)n x y z =(1,1,0)BC = ，(0,2,1)CE =-由22222200200n BC x y y z n CE ⎧⋅=+=⎧⎪⇒⎨⎨-+=⋅=⎩⎪⎩令21x =，则21y =-，22z =-，2(1,1,2)n ∴=--………………………………10分设二面角B CE D --的平面角为θ，则1212122cos cos ,3||||n n n n n n θ⋅=<>===-⋅…………………………………12分19．（本小题满分12分）解：（Ⅰ）因为1)22n T =+所以1)122T =+，所以1)1224b =+=，解得：11a =所以1(1)221n a n n =+-⨯=-，所以2(121)2n n n S n ⨯+-==, …………………………………………………………3分所以122n n T +=+,122n n T +=-当2n ≥时，1122(22)2n n n n n n b T T +-=-=---= 因为12b =适合上式所以2nn b = ……………………………………………………………………………6分（Ⅱ）令14(21)214nn n n c a b n =-=--，显然112c =-，22c =-，3n ≥，0n c > ……………………………7分3n ≥，12312312............22n n n W c c c c c c c c c c =--+++=++++--21232.................(21)214+28n n W n n =⨯+⨯++-- ……………………8分令21232.................(21)2n n Q n =⨯+⨯++-；则2 n Q =2311232......(23)2(21)2n n n n +⨯+⨯++-+- 两式做差得：23122222......22(21)2n n n Q n +-=+⨯+⨯++⨯-- 所以231222222......222(21)2 n n n Q n +-=⨯+⨯+⨯++⨯---2312(222......2)2(21)2n n n +=++++---21242(21)2n n n ++=----所以1(23)26n n Q n +=-+ ………………………………………………………11分所以112, (1)14, (2)(23)21434,(3)n n n W n n n n +⎧=⎪==⎨⎪--+≥⎩……………………………………12分20．（本小题满分13分）解：（Ⅰ）设MAB ∆的垂心为H ，AB边上的高所在的直线方程为：x =MAB ∆垂心的纵坐标为-H ∴-……………………………………………………………………………2分∴直线BH的斜率为BH k ==所以直线AM的斜率1AM BHk k =-=则AM的方程为：y x =+ ……………………………………………………4分由222184y x x x y y ⎧⎧=+=⎪⎪⎪⎪⇒⎨⎨⎪⎪+==⎪⎪⎩⎩,所以P点的坐标为(2 ………………6分（Ⅱ）设P 点的坐标为11(,)x y ，Q 点坐标为22(,)x y ，则22111(8)2y x =-，22221(8)2y x =- 直线AP的方程为：y x =+由y x M x ⎧=+⎪⇒⎨⎪=⎩………………………………7分由于,,M B Q 共线，所以BMBQ k k ===22221291(8)(8)x x --=⇒=⇒=化简得：12122)160x x x x -++=……()* ………………………………9分设直线PQ 的方程为：y kx m =+由22222(12)4280184y kx m k x kmx m x y =+⎧⎪⇒+++-=⎨+=⎪⎩所以2121222428,1212km m x x x x k k-+=-=++,代入()*得：2280m k ++=解得：m =，或m =- ………………………………………………11分当m =时，直线PQ的方程为：y kx =，即(y k x =，恒过；当m =-时，直线PQ的方程为：y kx =-，即(4y kx =-，恒过，此种情况不合题意综上可知：直线PQ恒过 …………………………………………………13分21．（本小题满分14分）解：（Ⅰ）由()0f x >得:sin 0x ax ->,因为01x <<，所以sin xa x< 令sin ()x g x x =，2cos sin ()x x xg x x -'= ……………………………………2分再令()cos sin m x x x x =-，()cos sin cos sin 0m x x x x x x x '=--=-< 所以()m x 在)1,0(上单调递减，所以()(0)0m x m <= …………………………………………………………4分所以()0,g x '<则()g x 在)1,0(上单调递减，所以()(1)sin1g x g >=，所以sin1a ≤ ………………………………………6分（Ⅱ）当1a =时，()sin f x x x =-,()ln 1h x x x ∴=-+ 11()1xh x x x-'=-= 由()0h x '=得：1x = ……………………………………………………………8分当(0,1)x ∈时，()0h x '>，()h x 在(0,1)上单调递增；当(1,)x ∈+∞时，()0h x '<，()h x 在(1,)+∞上单调递减；max ()(1)0h x h ∴== ……………………………………………………………………10分（Ⅲ）由（Ⅱ）可知：当(1,)x ∈+∞时，()0h x <,即ln 1x x <- 令1n x n +=，则11ln1n n n n ++<-，即1ln(1)ln n n n+-< …………………………12分分别令1,2,3,,n n = 得：l n 2l n 11-<,1ln 3ln 22-<,1ln 4ln 33-<,………………,1ln(1)ln n n n+-< 将上述n 个式子相加得：1111ln(1)1231n n n +<+++++- （*N n ∈） …………14分。

2018年11月1日绵阳市高中2016级第一次诊断性考试理科数学试题及参考答案及评分标准

数学（理工类）参考答案及评分意见第1页（共6页）绵阳市高中2016级第一次诊断性考试数学（理工类）参考答案及评分意见一、选择题：本大题共12小题，每小题5分，共60分．BBABD CBDAD CC二、填空题：本大题共4小题，每小题5分，共20分．13．7 14．-7 15．216．32-三、解答题：本大题共6小题，共70分．17．解：（Ⅰ）设等差数列{a n }的公差为d (d >0)，由a 4=7，得a 1+3d =7，① ……………………………………………………2分又∵ a 2，a 6-2a 1，a 14是等比数列{b n }的前三项，∴ (a 6-2a 1)2=a 2a 14，即(5d -a 1)2=(a 1+d )(a 1+13d )，化简得d =2a 1，② ……………………………4分联立①②解得a 1=1，d =2．∴ a n =1+2(n -1)=2n -1． ………………………………………………………6分（Ⅱ）∵ b 1=a 2=3，b 2=a 6-2a 1=9，b 3=a 14=27是等比数列{b n }的前三项， ……………………………………………………8分 ∴ 等比数列{b n }的公比为3，首项为3．∴ 等比数列{b n }的前n 项和S n =3(13)13n −−=3(31)2n −． ……………………10分由S n >39，得3(31)2n −>39，化简得3n >27．解得n >3，n ∈N *． …………………………………………………………12分18．解：（Ⅰ）2())4cos 3f x x x π=−+=2cos cos2sin )33x x ππ−+2(1+cos2x ) ………………2分=32cos222x x −+2cos2x +2=12+cos22x x +2数学（理工类）参考答案及评分意见第2页（共6页） =sin(2)26x π++， ……………………………………………4分由题意得()sin[2()]2266g x x ππ=−++−，化简得g (x )=sin(2)6x π−． ……………………………………………………6分（Ⅱ）由6π≤x ≤23π，可得6π≤2x -6π≤76π．当2π≤2x -6π≤76π即3π≤x ≤23π时，函数()g x 单调递减． ∴ ()g x 在2[]63ππ，上的单调递减区间为2[]33ππ，． ………………………9分 ∵ ()g x 在[]63ππ，上单调递增，在2[]33ππ，上单调递减， ∴ ()g x ma x =()3g π=sin 12π=．又2()3g π=7sin 6π=sin (+6ππ)=-1sin 62π=−<()6g π=1sin 62π=， ∴ 12−≤()g x ≤1，即()g x 在2[]63ππ，上的值域为1[1]2−，．……………………………………12分 19．解：（Ⅰ）∵ 2c sin B =3a tan A ，∴ 2c sin B cos A =3a sin A ．由正弦定理得2cb cos A =3a 2， ………………………………………………2分由余弦定理得2cb •222+2b c a bc−=3a 2，化简得b 2+c 2=4a 2， ∴ 2224b c a+=． ………………………………………………………………5分（Ⅱ）∵ a =2，由（Ⅰ）知b 2+c 2=4a 2=16，∴由余弦定理得cos A =222+2b c a bc −=6bc， …………………………………6分根据重要不等式有b 2+c 2≥2bc ，即8≥bc ，当且仅当b =c 时“=”成立，数学（理工类）参考答案及评分意见第3页（共6页）∴ cos A ≥68=34．………………………………………………………………8分由cos A =6bc，得bc =6cos A ，且A ∈(0)2π，， ∴ △ABC 的面积S =12bc sin A =12×6cos A ×sin A =3tan A ． ………………10分 ∵ 1+tan 2A =1+22sin cos A A =222cos sin cos A A A +=21cos A ， ∴ tan A=≤∴ S =3tan A≤∴ △ABC 的面积S的最大值为． ……………………………………12分20．解：（Ⅰ）()x f x e a '=−．当a ≤0时，()0f x '>，()f x 在R 上单调递增； …………………………2分当a >0时，由()0f x '>解得x >ln a ，由()0f x '<解得x <ln a . ……………4分综上所述：当a ≤0时，函数()f x 在R 上单调递增；当a >0时，函数()f x 在(ln )a +∞，上单调递增，函数()f x 在(ln )a −∞，上单调递减． ………………5分（Ⅱ）由（Ⅰ）知，当a ≤0时，函数()f x 在R 上单调递增，∴ 函数()f x 在[1，2]上的最小值为f (1)=e -a +3=4，即1a e =−>0，矛盾. …………………………………………………………6分当a >0时，由（Ⅰ）得x =ln a 是函数()f x 在R 上的极小值点．① 当ln a ≤1即0<a ≤e 时，函数()f x 在[1，2]上单调递增，则函数()f x 的最小值为f (1)=e -a +3=4，即a =e -1，符合条件． …………7分 ②当ln a ≥2即a ≥e 2时，函数()f x 在[1，2]上单调递减，则函数()f x 的最小值为f (2)=e 2-2a +3=4即212e a −=<e 2，矛盾．…………8分 ③当1<ln a <2即e <a <e 2时，函数()f x 在[1，ln a ]上单调递减，函数()f x 在[ln a ，2]上单调递增，则函数()f x 的最小值为f (ln a )=e ln a -a ln a +3=4即a -a ln a -1=0．数学（理工类）参考答案及评分意见第4页（共6页）令h (a )=a -a ln a -1(e <a <e 2)，则()ln h a a '=−<0，∴ h (a )在(e ，e 2)上单调递减，而h (e )=-1，∴ h (a )在(e ，e 2)上没有零点，即当e <a <e 2时，方程a -a ln a -1=0无解．综上，实数a 的值为e -1． …………………………………………………12分21．解：（Ⅰ）)(x f 的定义域为(0，+∞)．当a =e -1时，()f x =ln x -e x +(e -1)x -e +1，则()f x '=1x-e x +e -1，令1()()1x h x f x e e x '==−+−，则21()0x h x e x '=−−<．………………………2分即()f x '在(0+)∞，上单调递减，又(1)0f '=，故(01)x ∈，时，()f x '>0，)(x f 在(0，1)上单调递增，(1+)x ∈∞，时，)(x f '<0，)(x f 在(1+)∞，上单调递减．所以函数()f x 有极大值f (1)=-e ，无极小值． ………………………………4分（Ⅱ）由()f x '=1x -e x +a ，令g (x )=()f x '=1x -e x +a ，则21()x g x e x '=−−<0，所以g (x )在(0+)∞，上单调递减，即)(x f '在(0+)∞，上单调递减．又0x →时，()f x '→+∞；x →+∞时，()f x '→−∞，故存在0x ∈(0+)∞，使得0()f x '=01x 0x e −+a =0． ……………………………6分当x ∈(0，x 0)时，)(x f '>0，f (x )在(0，x 0)上单调递增，x ∈(x 0，+∞)时，)(x f '<0，f (x )在(x 0，+∞)上单调递减．又()f x =0有唯一解，则必有0000()ln 0x f x x e ax a =−+−=．由0000010ln 0x x e a x x e ax a ⎧−+=⎪⎨⎪−+−=⎩，，消去a 得000001ln (1)()0x x x e x e x −+−−=．数学（理工类）参考答案及评分意见第5页（共6页）令1()ln (1)()x x x x e x e x ϕ=−+−−=1ln 2+1x x x e xe x−+−，……………………8分则211()2x x x x e e xe x xϕ'=−++− 21=(1)x x x e x −+− =21(1)()x x e x −+．故当x ∈(0，1)时，)(x ϕ'<0，)(x f 在(0，1)上单调递减，当x ∈(1，+∞)时，)(x ϕ'>0，)(x f 在(1，+∞)上单调递增．…………10分由1(1)0(2)ln 202e ϕϕ=−<=−+>，，得存在0(1,2)x ∈,使得0()0x ϕ=即0()0f x =.又关于x 的方程()f x =0有唯一解x 0，且*0(1)x n n n ∈+∈N ，，，∴ 0(12)x ∈，．故n =1． ………………………………………………………………………12分22．解：（Ⅰ）将t =2y 代入x=3+，整理得30x −= ，所以直线l的普通方程为30x −=． …………………………………2分由4cos ρθ=得24cos ρρθ=，将222x y ρ=+，cos x ρθ=代入24cos ρρθ=，得2240x y x +−=，即曲线C 的直角坐标方程为22(2)4x y −+=． ……………………………5分（Ⅱ）设A ，B 的参数分别为t 1，t 2．将直线l 的参数方程代入曲线C 的直角坐标方程得221(32)()42t −+=，化简得230t −=，由韦达定理得12t t +=于是122P t t t +== ………………………………………………………6分数学（理工类）参考答案及评分意见第6页（共6页）设P (x 0，y 0)，则0093(41(2x y ⎧=+=⎪⎪⎨⎪=⨯=⎪⎩，即P (94，． ……………………………………………………………8分所以点P 到原点O的距离为2=． ……………………10分 23．解：（Ⅰ）当x ≤12−时，)(x f =-2x -1+(x -1)=-x -2，由)(x f ≥2解得x ≤-4，综合得x ≤-4； ……………………………………2分当112x −<<时，)(x f =(2x +1)+(x -1)=3x ，由)(x f ≥2解得x ≥23，综合得23≤x <1； …………………………………3分当x ≥1时，)(x f =(2x +1)-(x -1)=x +2，由)(x f ≥2解得x ≥0，综合得x ≥1． ………………………………………4分所以)(x f ≥2的解集是2(4][+)3−∞−∞，，． ………………………………5分（Ⅱ）∵ )(x f =|2x+1|-|x -m |≥|x -3|的解集包含[3，4]，∴ 当x ∈[3，4]时，|2x+1|-|x -m |≥|x -3|恒成立． …………………………7分原式可变为2x+1-|x -m |≥x -3即|x -m |≤x +4， ……………………………8分 ∴ -x -4≤x -m ≤x +4即-4≤m ≤2x +4在x ∈[3，4]上恒成立，显然当x =3时，2x +4取得最小值10，即m 的取值范围是[-4，10]． ………………………………………………10分。

2016全国卷111细目表

2016年全国Ⅲ卷双向细目表题号考点知识要求能力要求难度要求了解理解（掌握）综合应用接受、吸收、整合化学信息的能力分析问题和解决（解答）化学问题的能力化学实验与探究能力7 元素化合物［物质性质与应用］√√易8 必考有机［有机物的结构与性质］√√易9 化学实验［浓硫酸的稀释、实验室制取气体的操作、萃取操作］√√易10 必考有机［异丙苯的结构与性质］√√√中11 基本概念及理论［电化学（锌-空气燃料电池）］√√√中12 基本概念及理论［元素推断与元素周期律］√√√中13 基本概念及理论［电解质溶液（电离平衡、水解平衡、沉淀溶解平衡）］√√√中难26 化学实验［化学实验基本操作、化学实验方案的设计与评价］√√√中27 基本概念及理论［化学反应原理（化学平衡常数、化学反应速率与化学平衡）］、化学计算［反应热计算］√√√√中难28 元素化合物［化学工艺流程（用废钒催化剂制备五氧化二钒）］√√√中难36 化学与技术［聚合硫酸铁的工业制备流程］√√√中难37 物质结构与性质［电子排布式、晶体类型、杂化轨道、化学键、晶体的空间结构分析］√√√中难38 有机化学基础［有机合成与推断（有机方程式书写，考查结构简式、名称、反应类型、同分异构体、合成路线设计）］√√√中难。

宜宾市2016级高三理科一诊数学试题含答案

宜宾市高2016级高三第一次诊断测试题数学（理工类）注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试时间：120分钟，满分150分，考试结束后，将本试卷和答题卡一并交回。

1、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知全集，集合，则R U ={}24A x x =≤U A =ðA. B. C. D. (,2)-∞2][2+-∞-∞U （，，）22-∞-+∞U （，）（，）[2,2]-2．设，则= 12i1iz -=-z A.B.C. D. 3i 22-3i 22+3i22-+3i 22--3．若命题“，”为真命题，则的取值范围是x ∀∈R 1+()02x m >m A. B. C. D. R (,0]-∞(0,)+∞[0,)+∞4．从甲、乙两种棉花中各抽测了根棉花的25纤维长度(单位：)组成一个样本，得到mm 茎叶图如图：甲、乙两种棉花纤维的平均长度分别用表示，标准差分别用21,x x 表示，则21,s s A. B. 1212x x s s >>1212x x s s ><C. D. 1212x x s s <>1212,x x s s <<5乙3乙乙642 54 6 72 3 5 5 6 7 80 2 3 4 6 81 3 6 863 2 17 5 0 5 4 2 8 7 3 3 1 9 7 0 8 6 5 3 6 5 142728293031323334乙乙6．二项式的展开式中的系数是，则8()ax x -2x 7-a =A. B.C. D. 11212-1-7．已知是边长为的正三角形，分别是ABC ∆2F E ,AC ,的中点，是的中点，则G EF FE AG ⋅=u u u r u u u rA. B. C.D. 1-12-1218．已知程序框图如图，则输出结果是A. B. 9191021C.D.181920219．若，则的大小关系是0.50.21ln ,log 3,log 62a b c ===,,a b c A. B. C. D. a b c <<c a b <<c b a <<b c a<<10．已知函数的一条对称轴为，又的)sin()(ϕω+=x A x f 002π(,||)A ωϕ>><，4πx =-)(x f 一个零点为，且的最小值为，则0x 0|4π|x +2πϕ=A. B.C.D. 4π-38π4π38-π11．若数列的前项和为，，，，且，则k ＝{}n a n n S 11a =0n a ≠131n n n S a a +=+2018k a =A. B. C. D. 134413451346134712．设函数，，其中，若存在唯一的整数使得()2e x f x x a =+()e x g x ax =+1a <0x ，则的取值范围是00()()f x g x <a A. B. C. D. )1,e23[-)1,e23[)43,e 23[-43,e 23[二、填空题：本大题共4个小题，每小题5分，共20分。

成都市2016级高中毕业班第一次诊断性检测数学(文科、理科)参考答案及评分标准(含双向细目表及打分板)

π ʑC ＝ π－A －B ＝．２
π ．６
��６分 ʑP A ʊ 平面 BMD ． ( 如图 , 取线段 B 连结 AH ． Ⅱ) C 的中点 H , ȵA B C D 是菱形 , øA B C＝ ȵP A ʅ 平面 A B C D, ʑAH ʅP A． π , ʑAH ʅAD ．３
２２即ρ ＝２ s i n θ＋２ c o s θ ��ʑx２＋ x �� y ＝２ y＋２ ρ ρ ２２ )＋ ( ) 故曲线 C 的直角坐标方程为 ( x－１＝２ �� y－１
２２ ( ) ) 将直线l 的参数方程代入 ( 得 Ⅱ) x－１＋( ＝２中 , y－１
且tʂʃ１ ʑ tʂʃ１ ��ʑ－３７＜ t＜３７, ��
数学 ( 文科 ) 一诊考试题参考答案㊀第㊀共４页) ２页(
２３６ t ９ t －９ , ʑx１＋x２＝－ x１ x２＝ �� ３７３７
) ( y１－１ y２－１４ x１ x２＋ ( t－１ x１＋x２) , ȵ kHM ＋ kHN ＝＋＝ x１ x２ x１ x２ ) ( ４ x１ x２＋ ( t－１ x１＋x２) ４ t ʑ ＝４－＝１ �� x１ x２ t＋１解得t＝３ �� ʑ t 的值为３ ��
��１１分 ��１２分
{
x＝３ m －３ x �� n＝－３ y－ y
��２分 ��４分 ��５分

凉山州2016届高中毕业班第一次诊断性测试题数学(理科)答案

∴3
………………………………5 分
(Ⅱ)∵ n n•
(错位相减法求和略)
显然成立 ………………………12 分
19.（12 分）解：(Ⅰ)∵f(3) 9 a
15
∴a
-5
∴f( )
a
1=
………………………………5 分
(Ⅱ)
2x
①当 a＞0 时
恒成立∴f(x）在（0，+ ）为增函数
∴f(x） f(0）
∵x ,y 0 ∴f(x） 1 在 x 时不恒成立
(Ⅱ)过 O 作 OP⊥C 于点 P，连接 BP 易得∠BPO 为二面角的平面角 ∵∠A 60º
∴∠PCA 60º在 Rt△OPC 中，OP
在 Rt△BOP 中，BO ，BP
∴
………………………………12 分
（本题也可用坐标运算，略）
18.（12 分）解：(Ⅰ)由题意得：
3
………………2 分
∴ 是首项 3，公比 q 3 的等比数列
(Ⅱ) f(x)在定义域内有两个不同的极值点即是有两个不同零点
∴
0即
的两根为 ,
∴
• =1 ……………………………8 分
∴
（）
…………………………………………10 分
∴要证
即是证
也就是证 -x-1
令 g(x)= -x-1
= 1 -1
x
∴g(x)在（0，1）为增函数，在[1,
)为减函数
∴
=g(1)= ln1-3 显然成立，故得证…………………14 分
（分布列略）…………12 分
17.（12 分）(Ⅰ)证明：
∵ 在平面 ABC 上的射影是 AC 的中点 O
∴ O⊥平面 ABC

高三数学上学期第一次诊断性测验试题理(扫描版)

乌鲁木齐地区2016年高三年级第一次诊断性测验理科数学参考答案及评分标准一、选择题：共12小题，每小题5分，共60分． 1~5 ADDCB 6~10 ACCAA 11~12 DB 1.选A .【解析】∵{}1N x x =≤R ð，∴()(]0,1MN =Rð，故选A .2.选D.【解析】∵()()()2121111i i iz i i i i -===+++-，∴1z i =-，故选D.3.选D ．【解析】∵,n m αα⊥⊥,∴m ∥n ,又n β⊥,∴m β⊥，故选D.4.选C ．【解析】31125656362a a d d a =+=⎧⎪⎨⨯+=⎪⎩，得112a d =⎧⎨=⎩，∴91989812d S a ⨯=+=，故选C . 5.选B ．【解析】∵()2cos2sin 12sin sin f x x a x x a x =+=-+，令sin t x =，由,62x ππ⎛⎫∈⎪⎝⎭得1,12t ⎛⎫∈ ⎪⎝⎭，依题意有()221g t t at =-++在1,12t ⎛⎫∈ ⎪⎝⎭是减函数， ∴142a ≤，即2a ≤，故选B . 6.选A ．【解析】由图可得，故选A.7.选C .【解析】执行第一次循环体运算，得1,i s a ==；执行第二次，2,i s a aq ==+；执行第1n +次，1,ni n s a aq aq =+=++，故选C .8.选C .【解析】∵0OB AC ⋅=，∴OA BC ⊥，∴152OABCS OB AC ==，故选C . 9.选A .【解析】如图，2AF FB =,∴112AA BB =，∴1BB 是1CAA ∆的中位线，∴3CB AB FB ==,4CF FB =, ∴4λ=-,故选A . 10.选A .【解析】依题意()()ln 1fx x =+的图像如图所示，由()()f a f b =，得()()l n 1l n 1a b -+=+，即0a b a b ++=.()204a b ab a b a b +=++<++，即()()40a b a b +++>显然10a -<<，0b >，∴40a b ++>，∴0a b +>，故选A .11.选D .【解析】tan b a α=，∴sin b c α=，cos acα=，∴sin cos ac βα==，211212sin sin sin PF PF F F F PF αβ-=-∠, ∴221a cb ac c=-，∴2a b =，∴5e =，故选D . 12.选B .【解析】令()()212g x fx x =-，则()()212g x f x x -=--，则()()()()20g x g x fx f x x +-=+--=，得()g x 为R 上的奇函数，∵0x >时，()()0g x f x x ''=->，故()g x 在()0,+∞单调递增，再结合()00g =及()g x 为奇函数，知()g x 在(),-∞+∞为增函数，又()()()()()2222222a a g a g a f a f a -⎛⎫--=---- ⎪⎝⎭()()()22222220fa f a a a a =---+≥--+=则()()221g a g a a a a -≥⇔-≥⇔≤，即(],1a ∈-∞.故选B . 二、填空题：本大题共4小题，每小题5分.13.填1．【解析】∵92a x x ⎛⎫+ ⎪⎝⎭的二项式展开式的通项为9319r r rr T C a x -+=，令930r -=，即3r =，常数项为33349=84T C a a =，依题意，有38484a =，∴1a =．14.填1．【解析】由约束条件确定的可行域如图所示，∴z 的最小值为1． 15.填518．【解析】由题意知，所有基本事件有()()1,11,2，，（6,6），共36个，其中满足点数之和小于6的基本事件有()()()()()()()()()1,11,21,31,42,12,22,33,1,3,2，，，，，，， ()4,1，共10个，所以所求概率为105=3618. 16.填31n +．【解析】当1n =时，2111634S a a =+-，即211340a a --=，得14a =或11a =-（舍）.由题意得：2111634n n n S a a +++=+-…① 2634n n n S a a =+-…②①-②得：22111633n n n n n a a a a a +++=-+-，即()()1130n n n n a a a a +++--=，∵0n a >，∴13n n a a +-=，∴{}n a 是以4为首项，3为公差的等差数列，∴()43131n a n n =+-=+.三、解答题：第17~21题，每题12分，解答应在答卷的相应各题中写出文字说明，说明过程或演算步骤． 17.（12分）．易知()sin 23cos 22sin 23fx x x x π⎛⎫=-=- ⎪⎝⎭ …2分（Ⅰ）由222232k x k πππππ-≤-≤+，解得，51212k x k ππππ-≤≤+，其中k ∈Z∴()f x 的单调递增区间为()5,1212k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z ； …6分（Ⅱ）∵()2sin 23f B B π⎛⎫=-⎪⎝⎭,又()3f B =，∴3sin 232B π⎛⎫-= ⎪⎝⎭ ∵02B π<<，∴22333B πππ-<-<，故，233B ππ-=，∴3B π=在ABC ∆中，sin sin sin BC AC AB A B C ==，且23C A B A ππ=--=-，2sin ACB= ∴22sin ,2sin 3BC A AB A π⎛⎫==-⎪⎝⎭， ABC ∆的周长22sin +32sin 3l AB AC BC A A π⎛⎫=++=-+ ⎪⎝⎭3sin 3cos 323sin 36A A A π⎛⎫=++=++ ⎪⎝⎭∵203A π<<，∴5666A πππ<+<，故当62A ππ+=，即3A π=时，ABC ∆的周长最大，最大值为33. …12分18.（12分）（Ⅰ）如图，取1CC 中点M ，连结,EM FM ,∵,E F 分别是111,BB A C 的中点,∴1//,//EM BC FM A C ,∴平面EFM //平面1A BC ，∴//EF 平面1A BC ； …6分（Ⅱ）根据题意，建立如图空间直角坐标系A xyz -：则11(0,0,0),(1,0,0),(0,1,0),(0,0,1),(0,,1)2A B C A F11(1,0,1),(1,1,0),(0,,1)2A B BC FC =-=-=-设平面1A BC 的法向量1111(,,)x y z =n ，∵1(1,0,1),(1,1,0),A B BC =-=-由110AB BC ⎧⋅=⎪⎨⋅=⎪⎩n n ，得00x z x y ì-=ïïíï-+=ïî，令1z =，得1,1x y ==，∴1(1,1,1)n = 同理可得平面FBC 的一个法向量2(2,2,1)n =，∴12121253cos ,9n n ×==×n n n n 所以二面角1A BC F --的余弦值为539． …12分 19.（12分）（Ⅰ）由频率分布直方图可知，月平均用水量的中位数为2.02()t ；根据物价部门对城市居民月平均用水的定价为() 1.6022.72 3.54.0 3.5 4.5t W t t t <<⎧⎪=≤<⎨⎪≤≤⎩，其中()W t 单位是元，t 单位为吨.知平均水价为：()0.080.250.160.750.30 1.250.44 1.75 1.6⨯+⨯+⨯+⨯⨯+⎡⎣()()0.50 2.250.28 2.750.12 3.25 2.70.08 3.750.04 4.2540.5⨯+⨯+⨯⨯+⨯+⨯⨯⨯⎤⎦ 5.05275=（元） …6分（Ⅱ）依题意知这100户中所交水费价格少于9.45元，即每月用水量少于3.5吨.这样的用户占94%，则每月从这100户中随机抽取1户居民获奖的概率为0.94，则连续10个月抽取的获奖户数X 服从二项分布()10,0.94XB ,所以()100.949.4E X=⨯=. …12分20.（12分）（Ⅰ）由题意得，焦点为椭圆的左焦点，即(),0F c -设弦与椭圆的交点为()()1122,,,A x y B x y ，代入椭圆方程得2211221x y a b +=…① 2222221x y a b+=…②①式-②式，得2221222212y y b a x x --=- …③ ∵点M 平分弦AB ，弦经过焦点，∴12223x x +=-，12123y y +=，21211323y y x x c -=--+，代入③式得，2221334233b a c ⨯-=⎛⎫-⨯-+ ⎪⎝⎭，即221263b a c =⎛⎫- ⎪⎝⎭，又∵22c a =，222a b c -=，∴22212c b a ==，∴112263c =⎛⎫- ⎪⎝⎭，即1c =，2a =， ∴椭圆方程为2212x y += …5分（Ⅱ）设点N 坐标为()11,x y ，由对称性，不妨设10y >，由2212x y +=得椭圆上半部分的方程为212x y =-，()2211212122x y x x x -'=⋅⋅-=--，∴11211=2212x x k y x --=-切， ∴N 点处的切线方程为()11112x y y x x y --=- …① 过F 且垂直于FN 的直线方程为()1111x y x y +=-+ …② 由①②两式，消去y 得()()111111112x xy x x x y y +=-++⋅-…③ 其中221112x y +=，代入③式，可得2x =- ∴点P 在定直线2x =-上. …12分21.（12分）（Ⅰ）()()00ln 011fe =++=，()11xf x e x '=++，()010201f e '=+=+ ∴()y fx =在点()()0,0f 处的切线方程为：()120y x -=-，即21yx =+.…5分（Ⅱ）令()()1g x fx ax =--，则()()11x g x f x a e a x ''=-=+-+令()11xh x e x =++，则()()211x h x e x '=-+，当0x ≥时，1xe >，()21011x <≤+，∴()0h x '>，∴函数()()0y h x x =≥为增函数，∴()()02h x h ≥=，∴()2g x a '≥- ī）当2a ≤时，20a -≥，∴当2a ≤时，()0g x '≥ ∴函数()()0y g x x =≥为增函数，∴()()00g x g ≥= 故对0x ∀≥，()1fx ax ≥+成立.īī）当2a >时，11a ->，由0x ≥时1011x <≤+ ()()111x x g x f x a e a e a x ''=-=+-<+-+，当()()0,ln 1x a ∈-知10xe a +-<，即()0g x '<，∴函数()y g x =，()()0,ln 1x a ∈-为减函数， ∴当()0ln 1x a <<-时，()()00g x g <=从而()1fx ax <+这与题意不符，综上，对0x ∀≥，()1fx ax ≥+成立时，实数a 的取值范围为(],2-∞. …12分请考生在第22、23、24题中任选一题作答，并将所选的题号下的“○”涂黑．如果多做，则按所做的第一题记分，满分10分． 22．（10分）（Ⅰ）由切割线定理，得2MA MC MB =⋅，而MA PM =，∴2PM MC MB =⋅∴PM MCMB PM=，PMC BMP ∠=∠，∴P M C ∆∽BMP ∆，∴M P C ∠=∠又MBP PFE ∠=∠，∴MPC PFE ∠=∠，∴EF ∥PA …5分（Ⅱ）∵PM ∥EN ，∴PMC BNE ∠=∠，又∵MPC NBE ∠=∠∴PMC ∆∽BNE ∆，∴PM NB MC NE =，而MA PM =，∴MA NBMC NE=，即MA NE MC NB ⋅=⋅ …10分23．（10分）（Ⅰ）由()20ρθπ=≤≤，得()2240x y y +=≥设()11,P x y ，(),Q x y ，则112,22x yx y +==，即1122,2x x y y =-=，代入()221140x y y +=≥，得()()222224x y -+=，∴()()22110x y y -+=≥； …5分（Ⅱ）轨迹C 是一个以()1,0为圆心，1半径的半圆，如图所示，设()1cos ,sin M ϕϕ+，设点M 处切线l 的倾斜角为α 由l 斜率范围33,3⎡⎤--⎢⎥⎣⎦，可得2536ππα≤≤，而2πϕα=-，∴63ππϕ≤≤，∴3231cos 22ϕ+≤+≤，所以，点M 横坐标的取值范围是323,22⎡⎤+⎢⎥⎣⎦． …10分24．（12分）（Ⅰ）()32,2,32,x a b x bf x x a b b x a x a b x a -+-≤-⎧⎪=++-<<⎨⎪-+≥⎩，其图形如图所示因此，()f x 的最小值是()f b a b -=+，依题意，有1a b +=； …5分（Ⅱ）0,0a b >>，且1a b +=，()121222332322b a b a a b a b a b a b a b ⎛⎫+=++=++≥+⋅=+ ⎪⎝⎭当且仅当2b aa b=时，上式取等号，又1a b +=，故，当且仅当21,22a b =-=-时，12a b+有最小值322+． …10分以上各题的其他解法，限于篇幅，从略，请酌情给分．。

高考专题高考模拟试卷数学卷命题双向细目表.docx

题序考查内容分值难易程度高中数学学习材料唐玲出品2016年高考模拟试卷数学卷命题双向细目表1 常用逻辑用语 5 容易题2 函数的基本性质 5 容易题3 三视图，直观图 5 容易题4 等比数列性质5 中档题5 不等式恒成立 5 中档题6 线性规划与基本不等式 5 中档题7 双曲线的定义与几何性质 5 中等偏难题8 函数与方程、函数的零点及不等式 5 较难题9 集合运算 6 容易题10 数列的通项与求和 6 容易题11 函数值与不等式的解法 6 中档题12 解三角形 6 中档题13 平面向量概念及数量积的几何意义 4 中档题14 直线与圆的位置关系． 4 较难题15 函数的性质（自定义问题） 4 较难题16 三角函数的性质与解三角形14 容易题17 空间中线线、线面垂直的判断及用向量、几何法求面面角15 中档题18 圆锥曲线的方程与函数的最值15 中等偏难题19 绝对值和分段函数及二次函数的最值15 较难题20 数列的通项及非特殊数列利用放缩法求和15 较难题说明：题型及考点分布按照《2016考试说明》参考样卷。

说明1、本试卷的命题方向和命题意图主要从以下几点为出发点：（1）、强化主干知识，强化知识之间的交叉，渗透和综合：基础知识全面考，重点知识重点考，注意信息的重组及知识网络的交叉点。

（2）、淡化特殊技巧，强调数学思想方法。

考查与数学知识联系的基本方法、解决数学问题的科学方法。

（3）、深化能力立意，突出考察能力与素质，对知识的考察侧重于理解和运用。

淡化繁琐、强调能力，提倡学生用简洁方法得出结论。

（4）、控制难度. “易︰中︰难=3︰5︰2” .（5）、新增知识考查力度及所占分数比例可略超课时比例。

基础题象“会考”，压轴题似“竞赛”.2、试卷结构与2015年样卷保持一致⑴题型结构为， 8道选择、7道填空、5道解答的结构；⑵赋分设计为，选择每题5分、填空题单空体每题4分，多空题每题6分，解答题共74分；⑶考查的内容，注重考查高中数学的主干知识：函数，三角函数和解三角形，立体几何，解析几何，数列等。

新疆乌鲁木齐地区2016届高三第一次诊断性测验数学理试题含解析

乌鲁木齐地区2016年高三年级第一次诊断性测试理科数学（问卷）（卷面分值:150分考试时间：120分钟）注意事项：1。

本卷分为问卷（4页)和答卷(4页），答案务必书写在答卷（或答题卡）的指定位置上。

2。

答卷前，先将答卷密封线内（或答题卡中的相关信息）的项目填写清楚.第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.1。

已知集合{}{}|02|1M x x N x x =<<=>，，则()RM C N =A 、(0,1］B 、［0,1）C 、（1，2）ｃ、［1,2） 2。

复数21ii+的共轭复数为 A. 1+i B. -1+iC. -1-iD. 1-i3。

设αβγ，，为平面，,m n 为直线,则m β⊥的一个充分条件是A 。

=,n m n αβαβ⊥⊥，B. =,,m αγαγβγ⊥⊥C 。

m αγβγα⊥⊥⊥，， D. n ,,n m αβα⊥⊥⊥4。

等差数列{}na 中，365,S 36,a==则9S =A. 17B. 19 C 。

81 D 。

1005。

若函数()cos 2sin f x x a x =+在区间62ππ⎛⎫⎪⎝⎭，上是减函数,则a 的取值范围是A 。

()24， B. (],2-∞ C 。

(],4-∞ D. [)4+∞，6.一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是()()111,01,1,0011,0,122⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，，，，，，画该四面体三视图中的正视图时,以yOz 平面为投影面，则得到的正视图可以为7，执行如图的程序框图（n N *∈）,则输出的S=A.1n a aq aq -+++B 。

n (1)1a q q--C. n a aq aq +++D.n +1(1)1a q q--8.凸四边形OABC 中,(24)(21)OB AC ==-，，，则该四边形的面积为 A.5B 。