高中数学随机变量分布列知识点
分布列知识点总结

分布列知识点总结一、概念介绍1.1 分布列的定义分布列是离散随机变量的取值和相应概率的列。
对于离散型随机变量X,其所有可能取值x1,x2,……,xn及其上对应的概率P(X=x1),P(X=x2),……,P(X=xn)就构成了X的分布列。
1.2 分布列的性质(1)分布列的概率和为1对于任意一个随机变量X,其分布列中所有可能取值的概率之和为1,即∑P(X=xi)=1。
(2)随机变量的取值是有限个或可列无限个分布列中的随机变量的取值只能是有限个或可列无限个,不可能是连续的。
二、分布列的应用2.1 用分布列计算期望和方差分布列是计算离散随机变量的期望和方差的有力工具。
根据期望和方差的公式,可以直接利用分布列中的取值和概率来计算期望和方差。
2.2 利用分布列进行概率计算通过分布列,可以计算得到随机变量取某个值的概率,或者计算随机变量在某个范围内取值的概率等。
这对于一些概率问题的求解非常有用。
三、分布列的例子3.1 二项分布二项分布是一种常见的离散型概率分布,用于描述在n次独立重复的伯努利试验中成功的次数。
设X为二项分布随机变量,其分布列为:X 0 1 2 …… nP C(n,0) * p^0 * (1-p)^n C(n,1) * p^1 * (1-p)^(n-1) C(n,2) * p^2 * (1-p)^(n-2) …… C(n,n) * p^n * (1-p)^0其中,p为成功的概率,n为试验的次数。
3.2 泊松分布泊松分布描述了单位时间内随机事件发生的次数。
设X为泊松分布随机变量,其分布列为:X 0 1 2 3 4 ……P e^(-λ) * λ^0 / 0! e^(-λ) * λ^1 / 1! e^(-λ) * λ^2 / 2! e^(-λ) * λ^3 / 3! e^(-λ) * λ^4 / 4! ……其中,λ为单位时间内随机事件发生的平均次数。
四、分布列与其他概率分布的关系4.1 分布列与连续型概率分布分布列适用于离散型随机变量,而连续型随机变量则需要用概率密度函数进行描述。
高考数学总复习考点知识专题讲解11 离散型随机变量及其分布列

高考数学总复习考点知识专题讲解 专题11离散型随机变量及其分布列知识点一 随机变量的概念、表示及特征1.概念:一般地,对于随机试验样本空间Ω中的每个样本点ω都有唯一的实数X (ω)与之对应,我们称X 为随机变量.2.表示:用大写英文字母表示随机变量,如X ,Y ,Z ;用小写英文字母表示随机变量的取值,如x ,y ,z .3.特征:随机试验中,每个样本点都有唯一的一个实数与之对应,随机变量有如下特征:(1)取值依赖于样本点. (2)所有可能取值是明确的. 知识点二 离散型随机变量可能取值为有限个或可以一一列举的随机变量,我们称之为离散型随机变量. 判断离散型随机变量的方法 (1)明确随机试验的所有可能结果; (2)将随机试验的结果数量化;(3)确定试验结果所对应的实数是否可以一一列出,如能一一列出,则该随机变量是离散型随机变量,否则不是.【例1】((2023•丰台区期末)下面给出的四个随机变量中是离散型随机变量的为() ①高速公路上某收费站在半小时内经过的车辆数1X ;②一个沿直线2y x 进行随机运动的质点离坐标原点的距离X;③某同学射击3次,命中的次数3X;④某电子元件的寿2命X;4A.①②B.③④C.①③D.②④【例2】(2023•从化区期中)袋中有大小相同的5个球,分别标有1,2,3,4,5五个号码,现在在有放回抽取的条件下依次取出两个球,设两个球的号码之和为随机变量X,则X所有可能取值的个数是()A.25B.10C.9D.5知识点三离散型随机变量的分布列及其性质1.定义:一般地,设离散型随机变量X的可能取值为x1,x2,…,x n,我们称X取每一个值x i的概率P(X=x i)=p i,i=1,2,3,…,n为X的概率分布列,简称分布列.2.分布列的性质(1)p i≥0,i=1,2,…,n.(2)p1+p2+…+p n=1.分布列的性质及其应用(1)利用分布列中各概率之和为1可求参数的值,此时要注意检验,以保证每个概率值均为非负数.(2)求随机变量在某个范围内的概率时,根据分布列,将所求范围内各随机变量对应的概率相加即可,其依据是互斥事件的概率加法公式.【例3】(2023•辽宁期末)随机变量X的分布列如下表所示,则(2)(…)P XA .0.1B .0.2C .0.3D .0.4【例4】(2022•朝阳区开学)设随机变量X 的分布列为()(1P X k k k λ===,2,3,4),则λ的值为() A .10B .110C .10-D .110-【例5】(2023•珠海期末)已知某离散型随机变量ξ的分布列为:则(q =)A .13和1-B .13C .12D .1-【例6】(2022•多选•天津模拟)设随机变量ξ的分布列为()(15kP ak k ξ===,2,3,4,5),则()A .115a =B .141()255P ξ<<= C .112()10215P ξ<<=D .23()510P ξ=…【例7】(2023•湖北模拟)设随机变量ξ的分布列如表:则下列正确的是()A .当{}n a 为等差数列时,5615a a += B .数列{}n a 的通项公式可以为109(1)n a n n =+C .当数列{}n a 满足1(1,2,9)2n na n ==时,10912a =D .当数列{}n a 满足2()(1k P k k a k ξ==…,2,10)时,1110(1)n a n n =+知识点四 两点分布如果P (A )=p ,则P (A )=1-p ,那么X 的分布列为我们称X 服从两点分布或0-1【例8】(多选)若离散型随机变量X 的分布列如下表所示,则下列说法错误的是()A .常数c 的值为23或13B .常数c 的值为23C .1(0)3P X ==D .2(0)3P X ==【例9】(2023•阜南县期末)从6名男生和4名女生中随机选出3名同学参加一项竞技测试.(1)求选出的3名同学中至少有1名女生的概率;(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.【例10】(2023•崂山区期末)某电视台“挑战主持人”节目的挑战者闯第一关需要回答三个问题,其中前两个问题回答正确各得10分,回答不正确得0分,第三个问题回答正确得20分,回答不正确得10-分.如果一位挑战者回答前两个问题正确的概率都是2 3,回答第三个问题正确的概率为12,且各题回答正确与否相互之间没有影响.若这位挑战者回答这三个问题的总分不低于10分就算闯关成功.(1)求至少回答对一个问题的概率.(2)求这位挑战者回答这三个问题的总得分X的分布列.(3)求这位挑战者闯关成功的概率.同步训练1.(2022•多选•临朐县开学)下列X是离散型随机变量的是()A.某座大桥一天经过的某品牌轿车的辆数XB .一天内的温度为XC .某网页一天内被点击的次数XD .射击运动员对目标进行射击,击中目标得1分,未击中目标得0分,用X 表示该运动员在一次射击中的得分2.(2023•上蔡县校级月考)设随机变量ξ的概率分布列如下表:则(|2|1)(P ξ-==) A .712B .12C .512D .163.(2023•周至县期末)设随机变量X 的分布列为()(1,2,3,4,5,6)2kcP X k k ===,其中c 为常数,则(2)P X …的值为() A .34B .1621C .6364D .64634.(2023•多选•宝安区期中)已知随机变量ξ的分布如下:则实数a 的值为()A .12-B .12C .14D .14-5.(2023•和平区校级期末)设随机变量与的分布列如下:则下列正确的是()A .当{}n a 为等差数列时,5615a a +=B .当数列{}n a 满足1(12n na n ==,2,⋯,9)时,10912a = C .数列{}n a 的通项公式可以为109(1)n a n n =+D .当数列{}n a 满足2()(1k P k k a k ξ==…,2,⋯,10)时,1110(1)n a n n =+6.(2023•郫都区模拟)甲袋中有2个黑球,4个白球,乙袋中有3个黑球,3个白球,从两袋中各取一球.(Ⅰ)求“两球颜色相同”的概率;(Ⅱ)设ξ表示所取白球的个数,求ξ的概率分布列.。
高中理科数学-离散型随机变量和分布列

理科数学复习专题 统计与概率 离散型随机变量及其分布列知识点一1、离散型随机变量:随着实验结果变化而变化的变量称为随机变量,常用字母,X,Y ,x h g g g 表示,所有取值可以一一列出的随机变量,称为离散型随机变量。
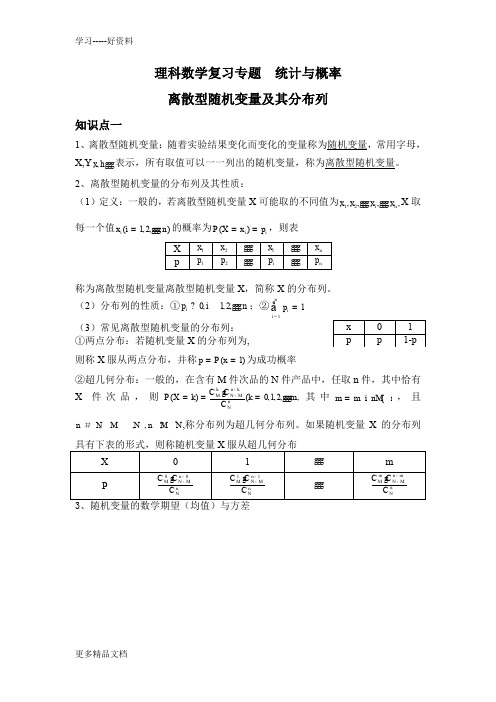
2、离散型随机变量的分布列及其性质:(1)定义:一般的,若离散型随机变量X 可能取的不同值为12,,,,,,i n x x x x g g g g g g X 取每一个值(1,2,,)i x i n =g g g 的概率为()i i P X x p ==,则表称为离散型随机变量离散型随机变量X ,简称X 的分布列。
(2)分布列的性质:①0,1,2,,i p in ?g g g ;②11ni i p ==å(3)常见离散型随机变量的分布列:①两点分布:若随机变量X 的分布列为,则称X 服从两点分布,并称(1)p P x ==为成功概率②超几何分布:一般的,在含有M 件次品的N 件产品中,任取n 件,其中恰有X件次品,则()(0,1,2,,k n k M N MnNC C P X k k m C --===g g g g 其中m i n {,m M n =,且*,,,,)n N M N n MN N #?,称分布列为超几何分布列。
如果随机变量X 的分布列题型一 由统计数据求离散型随机变量的分布列【例1】已知一随机变量的分布列如下,且E (ξ)=6.3,则a 值为( )A. 5 【变式1】 某公司有5万元资金用于投资开发项目,如果成功,一年后可获利12%;一旦失败,一年后将丧失全部资金的50%.下表是过去200例类似项目开发的实施结果:则该公司一年后估计可获收益的期望是________.题型二 由古典概型求离散型随机变量的分布列(超几何分布)【例2】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖.某顾客从此10张奖券中任抽2张,求:(1)该顾客中奖的概率;(2)该顾客获得的奖品总价值X 元的概率分布列.【变式2】某饮料公司招聘了一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A 饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料.若4杯都选对,则月工资定为3 500元;若4杯选对3杯,则月工资定为2 800元;否则月工资定为2 100元.令X表示此人选对A饮料的杯数.假设此人对A和B两种饮料没有鉴别能力.(1)求X的分布列;(2)求此员工月工资的期望.知识点二1.条件概率及其性质对于两个事件A和B,在已知事件B发生的条件下,事件A发生的概率叫做条件概率,用符号P(A|B)来表示,其公式为P(A|B)=P(AB)P(B)(P(B)>0).在古典概型中,若用n(B)表示事件B中基本事件的个数,则P(A|B)=n(AB) n(B).2.相互独立事件(1)对于事件A、B,若事件A的发生与事件B的发生互不影响,称A、B是相互独立事件.(2)若A与B相互独立,则P(AB)=P(A)P(B).(3)若A与B相互独立,则A与B,A与B,A与B也都相互独立.(4)若P(AB)=P(A)P(B),则A与B相互独立.3.二项分布(1)独立重复试验是指在相同条件下可重复进行的,各次之间相互独立的一种试验,在这种试验中每一次试验只有__两__种结果,即要么发生,要么不发生,且任何一次试验中发生的概率都是一样的.(2)在n次独立重复试验中,用X表示事件A发生的次数,设每次试验中事件A发生的概率为p,则P(X=k)=C k n p k(1-p)n-k(k=0,1,2,…,n),此时称随机变量X服从二项分布,记为X~B(n,p),并称p为成功概率.题型三 条件概率例1 (1)从1,2,3,4,5中任取2个不同的数,事件A 为“取到的2个数之和为偶数”,事件B 为“取到的2个数均为偶数”,则P (B |A )= ________.(2)如图所示,EFGH 是以O 为圆心,半径为1的圆的内接正方形,将一粒豆子随机地扔到该圆内,用A 表示事件“豆子落在正方形EFGH 内”,B 表示事件“豆子落在扇形OHE (阴影部分)内”,则P (B |A )=________.练:某地空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是________.题型四 由独立事件同时发生的概率求离散型随机变量的分布列(二项分布)例1 在一场娱乐晚会上,有5位民间歌手(1至5号)登台演唱,由现场数百名观众投票选出最受欢迎歌手.各位观众须彼此独立地在选票上选3名歌手,其中观众甲是1号歌手的歌迷,他必选1号,不选2号,另在3至5号中随机选2名.观众乙和丙对5位歌手的演唱没有偏爱,因此在1至5号中随机选3名歌手.(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;(2)X 表示3号歌手得到观众甲、乙、丙的票数之和,“求X ≥2”的事件概率.例2在一次数学考试中,第21题和第22题为选做题.规定每位考生必须且只须在其中选做一题.设4名学生选做每一道题的概率均为12.(1)求其中甲、乙两名学生选做同一道题的概率;(2)设这4名考生中选做第22题的学生个数为ξ,求ξ的概率分布.练习:一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为12,且各次击鼓出现音乐相互独立.(1)设每盘游戏获得的分数为X ,求X 的概率分布. (2)玩三盘游戏,至少有一盘出现音乐的概率是多少?【误区解密】抽取问题如何区分超几何分布和二项分布?例:某学校10个学生的考试成绩如下:(≥98分为优秀) (1)10人中选3人,求至多1人优秀的概率(2)用10人的数据估计全级,从全级的学生中任选3人,用X 表示优秀人数的个数,求X 的分布列练:18、某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,远离毒品”的电视公益广告,期望让更多的市民知道毒品的危害性.禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段在[)10,20,[)20,30,[)30,40,[)40,50,[)50,60的市民进行问卷调查,由此得到样本频率分布直方图如图所示.(Ⅰ)求随机抽取的市民中年龄在[)30,40的人数; (Ⅱ)从不小于40岁的人中按年龄段分层抽样的方法随机抽取5从,求[)50,60年龄段抽取的人数;(Ⅲ)从(Ⅱ)中方式得到的5人中再抽到2人作为本次活动的获奖者,记X 为年龄在[)50,60年龄段的人数,求X 的分布列及数学期望.2、一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25](25,35],(35,45],由此得到样本的重量频率分布直方图,如图.(Ⅰ)求a 的值; (Ⅱ)根据样本数据,试估计盒子中小球重量的平均值; (Ⅲ)从盒子中随机抽取3个小球,其中重量在(5,15]内的小球个数为ξ,求ξ的分布列和数学期望及方差.。
高中理科数学-离散型随机变量及分布列汇编
理科数学复习专题 统计与概率 离散型随机变量及其分布列知识点一1、离散型随机变量:随着实验结果变化而变化的变量称为随机变量,常用字母,X,Y ,x h g g g 表示,所有取值可以一一列出的随机变量,称为离散型随机变量。
2、离散型随机变量的分布列及其性质:(1)定义:一般的,若离散型随机变量X 可能取的不同值为12,,,,,,i n x x x x g g g g g g X 取每一个值(1,2,,)i x i n =g g g 的概率为()i i P X x p ==,则表称为离散型随机变量离散型随机变量X ,简称X 的分布列。
(2)分布列的性质:①0,1,2,,i p in ?g g g ;②11ni i p ==å(3)常见离散型随机变量的分布列:①两点分布:若随机变量X 的分布列为,则称X 服从两点分布,并称(1)p P x ==为成功概率②超几何分布:一般的,在含有M 件次品的N 件产品中,任取n 件,其中恰有X件次品,则()(0,1,2,,k n k M N MnNC C P X k k m C --===g g g g 其中m i n {,m M n =,且*,,,,)n N M N n MN N #?,称分布列为超几何分布列。
如果随机变量X 的分布列题型一 由统计数据求离散型随机变量的分布列【例1】已知一随机变量的分布列如下,且E (ξ)=6.3,则a 值为( )A. 5 【变式1】 某公司有5万元资金用于投资开发项目,如果成功,一年后可获利12%;一旦失败,一年后将丧失全部资金的50%.下表是过去200例类似项目开发的实施结果:则该公司一年后估计可获收益的期望是________.题型二 由古典概型求离散型随机变量的分布列(超几何分布)【例2】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖.某顾客从此10张奖券中任抽2张,求:(1)该顾客中奖的概率;(2)该顾客获得的奖品总价值X 元的概率分布列.【变式2】某饮料公司招聘了一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A 饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料.若4杯都选对,则月工资定为3 500元;若4杯选对3杯,则月工资定为2 800元;否则月工资定为2 100元.令X表示此人选对A饮料的杯数.假设此人对A和B两种饮料没有鉴别能力.(1)求X的分布列;(2)求此员工月工资的期望.知识点二1.条件概率及其性质对于两个事件A和B,在已知事件B发生的条件下,事件A发生的概率叫做条件概率,用符号P(A|B)来表示,其公式为P(A|B)=P(AB)P(B)(P(B)>0).在古典概型中,若用n(B)表示事件B中基本事件的个数,则P(A|B)=n(AB) n(B).2.相互独立事件(1)对于事件A、B,若事件A的发生与事件B的发生互不影响,称A、B是相互独立事件.(2)若A与B相互独立,则P(AB)=P(A)P(B).(3)若A与B相互独立,则A与B,A与B,A与B也都相互独立.(4)若P(AB)=P(A)P(B),则A与B相互独立.3.二项分布(1)独立重复试验是指在相同条件下可重复进行的,各次之间相互独立的一种试验,在这种试验中每一次试验只有__两__种结果,即要么发生,要么不发生,且任何一次试验中发生的概率都是一样的.(2)在n次独立重复试验中,用X表示事件A发生的次数,设每次试验中事件A发生的概率为p,则P(X=k)=C k n p k(1-p)n-k(k=0,1,2,…,n),此时称随机变量X服从二项分布,记为X~B(n,p),并称p为成功概率.题型三 条件概率例1 (1)从1,2,3,4,5中任取2个不同的数,事件A 为“取到的2个数之和为偶数”,事件B 为“取到的2个数均为偶数”,则P (B |A )= ________.(2)如图所示,EFGH 是以O 为圆心,半径为1的圆的内接正方形,将一粒豆子随机地扔到该圆内,用A 表示事件“豆子落在正方形EFGH 内”,B 表示事件“豆子落在扇形OHE (阴影部分)内”,则P (B |A )=________.练:某地空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是________.题型四 由独立事件同时发生的概率求离散型随机变量的分布列(二项分布)例1 在一场娱乐晚会上,有5位民间歌手(1至5号)登台演唱,由现场数百名观众投票选出最受欢迎歌手.各位观众须彼此独立地在选票上选3名歌手,其中观众甲是1号歌手的歌迷,他必选1号,不选2号,另在3至5号中随机选2名.观众乙和丙对5位歌手的演唱没有偏爱,因此在1至5号中随机选3名歌手.(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;(2)X 表示3号歌手得到观众甲、乙、丙的票数之和,“求X ≥2”的事件概率.例2在一次数学考试中,第21题和第22题为选做题.规定每位考生必须且只须在其中选做一题.设4名学生选做每一道题的概率均为12.(1)求其中甲、乙两名学生选做同一道题的概率;(2)设这4名考生中选做第22题的学生个数为ξ,求ξ的概率分布.练习:一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为12,且各次击鼓出现音乐相互独立.(1)设每盘游戏获得的分数为X ,求X 的概率分布.(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?【误区解密】抽取问题如何区分超几何分布和二项分布?例:某学校10个学生的考试成绩如下:(≥98分为优秀) (1)10人中选3人,求至多1人优秀的概率(2)用10人的数据估计全级,从全级的学生中任选3人,用X 表示优秀人数的个数,求X 的分布列练:18、某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,远离毒品”的电视公益广告,期望让更多的市民知道毒品的危害性.禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段在[)10,20,[)20,30,[)30,40,[)40,50,[)50,60的市民进行问卷调查,由此得到样本频率分布直方图如图所示.(Ⅰ)求随机抽取的市民中年龄在[)30,40的人数; (Ⅱ)从不小于40岁的人中按年龄段分层抽样的方法随机抽取5从,求[)50,60年龄段抽取的人数;(Ⅲ)从(Ⅱ)中方式得到的5人中再抽到2人作为本次活动的获奖者,记X 为年龄在[)50,60年龄段的人数,求X 的分布列及数学期望.2、一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25](25,35],(35,45],由此得到样本的重量频率分布直方图,如图.(Ⅰ)求a 的值;(Ⅱ)根据样本数据,试估计盒子中小球重量的平均值;(Ⅲ)从盒子中随机抽取3个小球,其中重量在(5,15]内的小球个数为ξ,求ξ的分布列和数学期望及方差.。
离散型随机变量及其分布列知识点

离散型随机变量及其分布列知识点离散型随机变量及其分布列知识点离散型随机变量是指在有限个或无限个取值中,只能取其中一个数值的随机变量。
离散型随机变量可以用分布列来描述其概率分布特征。
离散型随机变量的概率分布列概率分布列是描述离散型随机变量的概率分布的表格,通常用符号P 表示。
其一般形式如下:P(X=x1)=p1P(X=x2)=p2P(X=x3)=p3…P(X=xn)=pn其中,Xi表示随机变量X的取值,pi表示随机变量X取值为Xi的概率。
离散型随机变量的特点1. 离散型随机变量只取有限或无限个取值中的一个,变化不连续。
2. 取值之间具有间隔或间距。
3. 每个取值对应一个概率,概率分布可用概率分布列来体现。
4. 概率之和为1。
离散型随机变量的常见分布1. 0-1分布0-1分布是指当进行一次伯努利试验时,事件发生的概率为p,不发生的概率为1-p的离散型随机变量的分布。
其分布列为:P(X=0)=1-pP(X=1)=p2. 二项分布二项分布是进行n次伯努利试验中,事件发生的概率为p,不发生的概率为1-p时,恰好出现k次事件发生的离散型随机变量的分布。
其分布列为:P(X=k)=C(n,k)p^k(1-p)^(n-k)其中,C(n,k)为从n中选出k个的组合数。
3. 泊松分布泊松分布是指在某个时间段内,某一事件发生的次数符合泊松定理的离散型随机变量的分布。
其分布列为:P(X=k)=λ^ke^(-λ)/k!其中,λ为这段时间内事件的平均发生次数。
总结离散型随机变量及其分布列是概率论中的重要基础概念之一,具有广泛的应用。
掌握离散型随机变量及其分布列的知识点对于深入理解概率论及其实际应用有重要意义。
高中数学 概率与统计知识点总结

高中数学概率与统计知识点总结概率与统计一、概率及随机变量的分布列、期望与方差1.概率及其计算概率是指某个事件发生的可能性大小,可以用数值表示。
计算概率时,可以采用几个互斥事件和事件概率的加法公式。
如果事件A与事件B互斥,则P(AB)=P(A)+P(B)。
如果事件A1,A2,…,An两两互斥,则事件A1+A2+…+An发生的概率等于这n个事件分别发生的概率的和,即P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An)。
如果事件B与事件A互为对立事件,则P(A)=1-P(B)。
2.随机变量的分布列、期望与方差随机变量是指在随机试验中可能出现的各种结果所对应的变量。
常用的离散型随机变量的分布列包括二项分布和超几何分布。
二项分布指在n次独立重复试验中,事件A发生k次的概率为C(n,k)p^k(1-p)^(n-k),事件A发生的次数是一个随机变量X,其分布列为X~B(n,p)。
超几何分布指在含有M件次品的N件产品中,任取n件,其中恰有X件次品的概率为C(M,k)C(N-M,n-k)/C(N,n),其中m=min(M,n),且n,N,M,N∈N*,称随机变量X的分布列为超几何分布列,称随机变量X服从超几何分布。
2.条件概率及相互独立事件同时发生的概率条件概率是指在已知事件A发生的条件下,事件B发生的概率。
一般地,设A,B为两个事件,且P(A)>0,则P(B|A)=P(AB)/P(A)。
在古典概型中,若用n(A)表示事件A中基本事件的个数,则P(B|A)=n(AB)/n(A)。
相互独立事件是指两个或多个事件之间互不影响,即其中一个事件的发生不会影响其他事件的发生。
如果A,B相互独立,则P(AB)=P(A)P(B)。
如果A与B相互独立,则A与B,A与B,A与B也都相互独立。
3.独立重复试验与二项分布独立重复试验是指在一系列相互独立的试验中,每个试验的结果只有两种可能,即成功或失败。
在n次独立重复试验中,事件A发生k次的概率为C(n,k)p^k(1-p)^(n-k),事件A发生的次数是一个随机变量X,其分布列为X~B(n,p)。
2022年人教A版高中数学选择性必修第三册第七章随机变量及其分布列 章末知识梳理

返回导航
第七章 随机变量及其分布列
数学(选择性必修·第3册 RJA)
事实上,对于具体问题,若能设出 n 个事件 Ai(i=1,2,…,n),使之 满足AA1iA+j=A2∅+…+An=Ω,(任意两个事件互斥,i,j=1,2,…,n,i≠j).(1) 就可得 B=BΩ=BA1+BA2+…+BAn.(2)这样就便于应用概率的加法公 式和乘法公式.
返回导航
第七章 随机变量及其分布列
数学(选择性必修·第3册 RJA)
③二项分布与超几何分布的区别:有放回抽样,每次抽取时的总体 没有改变,因而每次抽到某物的概率都是相同的,可以看成是独立重复 试验,此种抽样是二项分布模型.而不放回抽样,取出一个则总体中就 少一个,因此每次取到某物的概率是不同的,此种抽样为超几何分布模 型.因此,二项分布模型和超几何分布模型最主要的区别在于是有放回 抽样还是不放回抽样.
i=1
i=1
返回导航
第七章 随机变量及其分布列
数学(选择性必修·第3册 RJA)
P(Ai|B)=PAPiPBB |Ai
=
PAiPB|Ai
k
,i=1,2,…,n
PAkPB|Ak
i=1
3.独立性与条件概率的关系:当 P(B)>0 且 P(AB)=P(A)P(B)时,
有 P(A|B)=PPABB=PAPPBB=P(A)
率公式求解.
返回导航
第七章 随机变量及其分布列
数学(选择性必修·第3册 RJA)
[解析] 解法一:记“至少出现 2 枚正面朝上”为事件 A,“恰好出 现 3 枚正面朝上”为事件 B,所求概率为 P(B|A),事件 A 包含的基本事 件的个数为 n(A)=C52+C53+C54+C55=26,
离散型随机变量、分布列、数学期望、方差

离散型随机变量、分布列、数学期望、方差:一、框架第一方面:离散型随机变量及其分布列1. 离散型随机变量:对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量。
常用大写英文字母X 、Y 等或希腊字母ξ、η等表示。
2.分布列:设离散型随机变量ξ可能取得值为: x 1,x 2,…,x 3,…, ξ取每一个值x i (i =1,2,…)的概率为()i i P x p ξ==,则称表ξx 1x 2…x i…P P 1 P 2 … P i …为随机变量ξ的分布列 3. 分布列的两个性质:⑴P i ≥0,i =1,2,… ⑵P 1+P 2+…=1.常用性质来判断所求随机变量的分布列是否正确!第二方面:条件概率、事件的独立性、独立重复试验、二项分布与超几何分布1. 相互独立事件:如果事件A (或B )是否发生对事件B (或A )发生的概率没有影响,这样的两个事件叫做相互独立事件。
①如果事件A 、B 是相互独立事件,那么,A 与_B 、_A 与B 、_A 与_B 都是相互独立事件②两个相互独立事件同时发生的概率,等于每个事件发生的概率的积。
我们把两个事件A 、B 同时发生记作A·B ,则有P (A·B )= P (A )·P (B )推广:如果事件A 1,A 2,…A n 相互独立,那么这n 个事件同时发生的概率,等于每个事件发生的概率的积。
即:P (A 1·A 2·…·A n )= P (A 1)·P (A 2)·…·P(A n )★相互独立事件A ,B 有关的概率的计算公式如下表:事件A ,B 相互独立 概率计算公式 A ,B 同时发生 P (AB )=P (A )P (B )A ,B 同时不发生 P (A -B -)=P (A -)P (B -)=[1-P (A )][1-P (B )]=1-P (A )-P (B )+P (A )P (B ) A ,B 至少有一个不发生 P =1-P (AB )=1-P (A )P (B )A ,B 至少有一个发生 P =1-P (A -B -)=1-P (A -)P (B -)=P (A )+P (B )-P (A )P (B )A ,B 恰有一个发生P =P (A B -+A -B )=P (A )P (B -)+P (A -)P (B )=P (A )+P (B )-2P (A )P (B )2.条件概率:称)()()|(A P AB P A B P =为在事件A 发生的条件下,事件B 发生的概率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章随机变量及其分布
内容提要:
一、随机变量的定义
设是一个随机试验,其样本空间为,若对每一个样本点,都有唯一确定的实数
与之对应,则称上的实值函数是一个随机变量(简记为)。
二、分布函数的概念和性质
1.分布函数的定义
设是随机变量,称定义在上的实值函数
为随机变量的分布函数。
2.分布函数的性质
(1) ,
(2)单调不减性:,
(3)
(4)右连续性:。
注:上述4个性质是函数是某一随机变量的分布函数的充要条件。
在不同的教科书上,分布函数的定义可能有所不同,例如,其性质也会有所不同。
(5)
注:该性质是分布函数对随机变量的统计规律的描述。
三、离散型随机变量
1.离散型随机变量的定义
若随机变量的全部可能的取值至多有可列个,则称随机变量是离散型随机变量。
2.离散型随机变量的分布律
(1)定义:离散型随机变量的全部可能的取值以及取每个值时的概率值,称为离散型随机变量的分布律,表示为
或用表格表示:
x1 x2 … x n…
p k P1 p2… p n…
或记为
~
(2)性质:,
注:该性质是是某一离散型随机变量的分布律的充要条件。
其中。
注:常用分布律描述离散型随机变量的统计规律。
3.离散型随机变量的分布函数
=,它是右连续的阶梯状函数。
4.常见的离散型分布
(1)两点分布(0—1分布):其分布律为
即
0 1
p 1–p p
(2)二项分布
(ⅰ)二项分布的来源—重伯努利试验:设是一个随机试验,只有两个可能的结果
及,,将独立重复地进行次,则称这一串重复的独立试验
为重伯努利试验。
(ⅱ)二项分布的定义
设表示在重伯努利试验中事件发生的次数,则随机变量的分布律为
,,
称随机变量服从参数为的二项分布,记作。
注:即为两点分布。
(3)泊松分布:若随机变量的分布律为
,,
则称随机变量服从参数为的泊松分布,记作(或。
高中数学系列2—3练习题(2.1)
一、选择题:
1、如果X 是一个离散型随机变量,则假命题是( ) A. X 取每一个可能值的概率都是非负数; B. X 取所有可能值的概率之和为1;
C. X 取某几个值的概率等于分别取其中每个值的概率之和;
D. X 在某一范围内取值的概率大于它取这个范围内各个值的概率之和
2①某寻呼台一小时内收到的寻呼次数X ;②在(0,1)区间内随机的取一个数X ;③某超市一天中的顾客量X 其中的X 是离散型随机变量的是( ) A .①; B .②; C .③; D .①③
3、设离散型随机变量ξ的概率分布如下,则a 的值为( )
X
1 2 3 4
P
1
6 13
16
a
A .12
B .16
C .13
D .1
4
4、设随机变量X 的分布列为()()1,2,3,,,k
P X k k n λ===⋯⋯,则λ的值为( )
A .1
; B .
12; C .13; D .1
4
5、已知随机变量X 的分布列为:()1
2
k p X k ==, ,3,2,1=k ,
则()24p X <≤=( ) A.163 B. 41 C. 161 D. 16
5 6、设随机变量X 等可能取1、2、3...n 值,如果(4)0.4p X ≤=,则n 值为( )
A. 4
B. 6
C. 10
D. 无法确定
7、投掷两枚骰子,所得点数之和记为X ,那么4X =表示的随机实验结果是( ) A. 一枚是3点,一枚是1点 B. 两枚都是2点
C. 两枚都是4点
D. 一枚是3点,一枚是1点或两枚都是2点 8、设随机变量X 的分布列为()()21,2,3,,,k
P X k k n λ
==⋅=⋯⋯,则λ的值为( )
A .1;
B .
12; C .13; D .1
4
二、填空题:
9 、下列表中能成为随机变量X 的分布列的是 (把全部正确的答案序号填上)
X
-1 0 1 p 0.3 0.4 0.4
X 1 2 3 p 0.4 0.7 -0.1 X 5 0 -5 p 0.3 0.6 0.1 ()1
,2,3,4,5,P X k k k
===
④
⑤
()1
2,1,2,3,
,21
k n P X k k n -===-
10、已知2Y X =为离散型随机变量,Y 的取值为1,2,3,,10,则X 的取值为
11、一袋中装有5只同样大小的白球,编号为1,2,3,4,5 现从该袋内随机取出3只球,被取出的球的最大号码数X 可能取值为 三、解答题:
12、某城市出租汽车的起步价为10元,行驶路程不超出4km ,则按10元的标准收租车费若行驶路程超出4km ,则按每超出lkm 加收2元计费(超出不足1km 的部分按lkm 计).从这个城市的民航机场到某宾馆的路程为15km .某司机常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm 路程计费),这个司机一次接送旅客的行车路程ξ是一个随机变量,他收旅客的租车费可也是一个随机变量
(1)求租车费η关于行车路程ξ的关系式;
(2)已知某旅客实付租车费38元,而出租汽车实际行驶了15km ,问出租车在途中因故停车累计最多几分钟?
13、一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球个数是绿球个数的两倍,黄球个数是绿球个数的一半.现从该盒中随机取出一个球,若取出红球得1分,取出黄球
得0分,取出绿球得-1分,试写出从该盒中取出一球所得分数X 的分布列.
分析:欲写出ξ的分布列,要先求出ξ的所有取值,以及ξ取每一值时的概率.
14、一个类似于细胞分裂的物体,一次分裂为二,两次分裂为四,如此继续分裂有限多次,而随机终止.设分裂n 次终止的概率是n 2
1
(n =1,2,3,…).记X 为原物体在分裂终止后所生成的子块数目,求(10)P X ≤.
高中数学系列2—3练习题(2.1)参考答案
一、选择题:
1、D
2、D
3、C
4、B
5、A
6、C
7、D
8、C 二、填空题:
9、 ③④ 10、
13579,1,,2,,3,,4,,522222
11、 3,4,5
三、解答题:
12、解:(1)依题意得η=2(ξ-4)+10,即η=2ξ+2 (2)由38=2ξ+2,得ξ=18,5×(18-15)=15. 所以,出租车在途中因故停车累计最多15分钟.
13、解:设黄球的个数为n ,由题意知
绿球个数为2n ,红球个数为4n ,盒中的总数为7n .
∴ 44(1)77n P X n ===,1(0)77n P X n ===,22(1)77
n P X n =-==. 所以从该盒中随机取出一球所得分数X 的分布列为
X 1
0 -1 P
74 71 7
2
14、解:依题意,原物体在分裂终止后所生成的数目X 的分布列为
X 2
4 8 16 ...
n 2
... P
2
1 41 81 161 ... n
21 ...
∴ (10)(2)(4)(8)P X P X P X P X ≤==+=+==8
842=++.。
