2013年全国高考理科数学试题分类汇编12:程序框图 Word版含答案]
2013年高考理科数学全国新课标卷2试题与答案word解析版

2013年普通高等学校夏季招生全国统一考试数学理工农医类(全国新课标卷II)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2013课标全国Ⅱ,理1)已知集合M ={x |(x -1)2<4,x ∈R },N ={-1,0,1,2,3},则M ∩N =( ).A .{0,1,2}B .{-1,0,1,2}C .{-1,0,2,3}D .{0,1,2,3} 2.(2013课标全国Ⅱ,理2)设复数z 满足(1-i)z =2i ,则z =( ).A .-1+iB .-1-IC .1+iD .1-i3.(2013课标全国Ⅱ,理3)等比数列{a n }的前n 项和为S n .已知S 3=a 2+10a 1,a 5=9,则a 1=( ).A .13B .13-C .19D .19-4.(2013课标全国Ⅱ,理4)已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l ⊥m ,l ⊥n ,lα,lβ,则( ).A .α∥β且l ∥αB .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l5.(2013课标全国Ⅱ,理5)已知(1+ax )(1+x )5的展开式中x 2的系数为5,则a =( ).A .-4B .-3C .-2D .-16.(2013课标全国Ⅱ,理6)执行下面的程序框图,如果输入的N =10,那么输出的S =( ).A .1111+2310+++B .1111+2!3!10!+++C .1111+2311+++D .1111+2!3!11!+++7.(2013课标全国Ⅱ,理7)一个四面体的顶点在空间直角坐标系O -xyz 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到的正视图可以为( ).8.(2013课标全国Ⅱ,理8)设a =log 36,b =log 510,c =log 714,则( ).A .c >b >aB .b >c >aC .a >c >bD .a >b >c9.(2013课标全国Ⅱ,理9)已知a >0,x ,y 满足约束条件1,3,3.x x y y a x ≥⎧⎪+≤⎨⎪≥(-)⎩若z =2x +y 的最小值为1,则a =( ).A .14 B.12 C .1 D .210.(2013课标全国Ⅱ,理10)已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( ).A.∃x0∈R,f(x0)=0B.函数y=f(x)的图像是中心对称图形C.若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)单调递减D.若x0是f(x)的极值点,则f′(x0)=011.(2013课标全国Ⅱ,理11)设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( ).A.y2=4x或y2=8x B.y2=2x或y2=8xC.y2=4x或y2=16x D.y2=2x或y2=16x12.(2013课标全国Ⅱ,理12)已知点A(-1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( ).A.(0,1) B.11,22⎛⎫-⎪⎪⎝⎭ C.1123⎛⎤-⎥⎝⎦ D.11,32⎡⎫⎪⎢⎣⎭第Ⅱ卷本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须做答。
2013年高考数学(全国卷)理科及答案

2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)数学(理科)注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置。
2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号标黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合M={x|(x+1)2 < 4,x∈R},N={-1,0,1,2,3},则M∩N=()(A){0,1,2}(B){-1,0,1,2}(C){-1,0,2,3} (D){0,1,2,3}(2)设复数z满足(1-i)z=2 i,则z= ()(A)-1+i (B)-1-i (C)1+i (D)1-i(3)等比数列{a n}的前n项和为S n,已知S3 = a2 +10a1 ,a5 = 9,则a1= ()(A)(B)-(C)(D)-(4)已知m,n为异面直线,m⊥平面α,n⊥平面β。
直线l满足l ⊥m,l ⊥n,l β,则()(A)α∥β且l ∥α(B)α⊥β且l⊥β(C)α与β相交,且交线垂直于l (D)α与β相交,且交线平行于l(5)已知(1+ɑx)(1+x)5的展开式中x2的系数为5,则ɑ=(A)-4 (B)-3 (C)-2 (D)-1(6)执行右面的程序框图,如果输入的N=10,那么输出的s=(A)1+ + +…+(B )1++ +…+(C )1+ + +…+(D )1++ +…+(7)一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是(1,0,1),(1,1,0),(1,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为搞影面,则得到正视图可以为(A) (B) (C) (D)(8)设ɑ=log 36,b=log 510,c=log 714,则(A )c >b >a (B )b >c >a(C )a >c >b (D)a >b >c(9)已知a >0,x ,y 满足约束条件 ,若z=2x+y 的最小值为1,则a=(A)(B) (C)1 (D)2(10)已知函数f(x)=x2+αx2+bx+,下列结论中错误的是(A )∑x α∈R f(x α)=0(B )函数y=f(x)的图像是中心对称图形(C )若x α是f(x)的极小值点,则f(x)在区间(-∞,x α)单调递减(D )若xn 是f (x )的极值点,则f 1(x α)=0(11)设抛物线y2=3px(p ≥0)的焦点为F ,点M 在C 上,|MF|=5若以MF 为直径的园过点(0,3),则C 的方程为(A )y2=4x 或y2=8x (B )y2=2x 或y2=8x(C )y2=4x 或y2=16x (D )y2=2x 或y2=16x(12)已知点A (-1,0);B (1,0);C (0,1),直线y=ax+b(a>0)将△ABC 分割为面积相等的两部分,则b 的取值范围是x ≥1, x+y ≤3, y ≥a(x-3). {(A)(0,1)(B)(1-,1/2)( C)(1-,1/3)(D)[ 1/3, 1/2)第Ⅱ卷本卷包括必考题和选考题,每个试题考生都必修作答。
2013年普通高等学校招生全国统一考试湖北卷(数学理)word版含答案

2013年普通高等学校招生全国统一考试(湖北卷)数 学(理工类)一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1.在复平面内,复数2i1iz =+(i 为虚数单位)的共轭复数对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限2.已知全集为R ,集合1{()1}2x A x =≤,2{680}B x x x =-+≤,则A B =R ðA .{0}x x ≤B .{24}x x ≤≤C .{024}x x x ≤<>或D .{024}x x x <≤≥或3.在一次跳伞训练中,甲、乙两位学员各跳一次.设命题p 是“甲降落在指定范围”,q 是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为 A .()p ⌝∨()q ⌝ B .p ∨()q ⌝C .()p ⌝∧()q ⌝D .p ∨q4.将函数sin ()y x x x +∈R 的图象向左平移(0)m m >个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是A .π12B .π6C .π3D .5π65.已知π04θ<<,则双曲线1C :22221cos sin x y θθ-=与2C :222221sin sin tan y x θθθ-=的A .实轴长相等B .虚轴长相等C .焦距相等D .离心率相等6.已知点(1,1)A -、(1,2)B 、(2,1)C --、(3,4)D ,则向量AB 在CD方向上的投影为AB C . D .7.一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度25()731v t t t=-++(t 的单位:s ,v 的单位:m/s )行驶至停止. 在此期间汽车继续行驶的距离(单位:m )是A .125ln 5+B .11825ln 3+C .425ln 5+D .450ln 2+第8题图8.一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有A .1243V V V V <<<B .1324V V V V <<<C .2134V V V V <<<D .2314V V V V <<<9.如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体. 经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X ,则X 的均值()E X = A .126125 B .65C .168125D .75 10.已知a 为常数,函数()(ln )f x x x ax =-有两个极值点1x ,212()x x x <,则A .1()0f x >,21()2f x >-B .1()0f x <,21()2f x <-C .1()0f x >,21()2f x <-D .1()0f x <,21()2f x >-二、填空题:本大题共6小题,考生共需作答5小题,每小题5分,共25分. 请将答案填在答题卡对应题......号.的位置上. 答错位置,书写不清,模棱两可均不得分. (一)必考题(11—14题)11.从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示.(Ⅰ)直方图中x 的值为_________;(Ⅱ)在这些用户中,用电量落在区间[100,250)内的户数为_________.第11题图12.阅读如图所示的程序框图,运行相应的程序,输出的结果i =_________.13.设,,x y z ∈R ,且满足:2221x y z ++=,23x y z ++=x y z ++=_________.第9题图14.古希腊毕达哥拉斯学派的数学家研究过各种多边形数. 如三角形数1,3,6,10, ,第n 个三角形数为2(1)11222n n n n +=+. 记第n 个k 边形数为(,)(3)N n k k ≥,以下列出 了部分k 边形数中第n 个数的表达式:三角形数 211(,3)22N n n n =+,正方形数 2(,4)N n n =,五边形数 231(,5)22N n n n =-,六边形数 2(,6)2N n n n =-, ………………………………………可以推测(,)N n k 的表达式,由此计算(10,24)N =_________.(二)选考题(请考生在第15、16两题中任选一题作答,请先在答题卡指定位置将你所选的题目序号后的方框用2B 铅笔涂黑. 如果全选,则按第15题作答结果计分.)15.(选修4-1:几何证明选讲)如图,圆O 上一点C 在直径AB 上的射影为D ,点D 在半径OC 上的射影为E .若3AB AD =,则CEEO的值为_________. 16.(选修4-4:坐标系与参数方程)在直角坐标系xOy 中,椭圆C 的参数方程为cos ,sin x a y b ϕϕ=⎧⎨=⎩(ϕ为参数,0a b >>). 在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴 为极轴)中,直线l 与圆O的极坐标方程分别为πsin()4ρθ+=(m 为非零常数) 与b ρ=. 若直线l 经过椭圆C 的焦点,且与圆O 相切,则椭圆C 的离心率为_________.三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c . 已知cos23cos()1A B C -+=. (Ⅰ)求角A 的大小;(Ⅱ)若△ABC的面积S =5b =,求sin sin B C 的值. 18.(本小题满分12分)已知等比数列{}n a 满足:23||10a a -=,123125a a a =. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)是否存在正整数m ,使得121111ma a a +++≥ ?若存在,求m 的最小值;若不存在,说明理由. 19.(本小题满分12分)D EOBA 第15题图C如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,直线PC ⊥平面ABC ,E ,F 分别是PA ,PC 的中点.(Ⅰ)记平面BEF 与平面ABC 的交线为l ,试判断直线l 与平面PAC 的位置关系,并加以证明;(Ⅱ)设(Ⅰ)中的直线l 与圆O 的另一个交点为D ,且点Q满足12D Q C P =. 记直线PQ 与平面ABC 所成的角为θ,异面直线PQ 与EF 所成的角为α,二面角E l C --的大小为β,求证:s i n s i n s i n θαβ=.20.(本小题满分12分)假设每天从甲地去乙地的旅客人数X 是服从正态分布2(800,50)N 的随机变量. 记一天中从甲地去乙地的旅客人数不超过900的概率为0p . (Ⅰ)求0p 的值;(参考数据:若X ~2(,)N μσ,有()0.6826P X μσμσ-<≤+=,(22)0.9544P X μσμσ-<≤+=,(33)0.9974P X μσμσ-<≤+=.)(Ⅱ)某客运公司用A 、B 两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次. A 、B 两种车辆的载客量分别为36人和60人,从甲地去乙地的营运成本分别为1600元/辆和2400元/辆. 公司拟组建一个不超过21辆车的客运车队,并要求B 型车不多于A 型车7辆. 若每天要以不小于0p 的概率运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A 型车、B 型车各多少辆?第19题图21.(本小题满分13分)如图,已知椭圆1C 与2C 的中心在坐标原点O ,长轴均为MN且在x 轴上,短轴长分别为2m ,2()n m n >,过原点且不与x 轴重合的直线l 与1C ,2C 的四个交点按纵坐标从大到小依次为A ,B ,C ,D .记mnλ=,△B D M 和△ABN 的面积分别为1S 和2S .(Ⅰ)当直线l 与y 轴重合时,若12S S λ=,求λ的值;(Ⅱ)当λ变化时,是否存在与坐标轴不重合的直线l ,使得12S S λ=?并说明理由. 22.(本小题满分14分)设n 是正整数,r 为正有理数.(Ⅰ)求函数1()(1)(1)1(1)r f x x r x x +=+-+->-的最小值;(Ⅱ)证明:1111(1)(1)11r r r r rn n n n n r r ++++--+-<<++; (Ⅲ)设x ∈R ,记x ⎡⎤⎢⎥为不小于...x 的最小整数,例如22=⎡⎤⎢⎥,π4=⎡⎤⎢⎥,312⎡⎤-=-⎢⎥⎢⎥.令S + S ⎡⎤⎢⎥的值.(参考数据:4380344.7≈,43350.5≈,43124618.3≈,43126631.7≈)2013年普通高等学校招生全国统一考试(湖北卷)数学(理工类)试题参考答案一、选择题1.D 2.C 3.A 4.B 5.D 6.A 7.C 8.C 9.B 10.D 二、填空题11.(Ⅰ)0.0044 (Ⅱ)70 12.5 1314.1000 15.8 16三、解答题 17. (Ⅰ)由cos23cos()1A B C -+=,得22cos 3cos 20A A +-=, 即(2cos 1)(cos 2)0A A -+=,解得1cos 2A = 或cos 2A =-(舍去). 因为0πA <<,所以π3A =.第21题图(Ⅱ)由11sin 22S bc A bc ====得20bc =. 又5b =,知4c =. 由余弦定理得2222cos 25162021,a b c bc A =+-=+-=故a =又由正弦定理得222035sin sin sin sin sin 2147b c bc B C A A A a a a =⋅==⨯=.18.(Ⅰ)设等比数列{}n a 的公比为q ,则由已知可得331211125,||10,a q a q a q ⎧=⎪⎨-=⎪⎩ 解得15,33,a q ⎧=⎪⎨⎪=⎩ 或15,1.a q =-⎧⎨=-⎩ 故1533n n a -=⋅,或15(1)n n a -=-⋅-. (Ⅱ)若1533n n a -=⋅,则1131()53n n a -=⋅,故1{}n a 是首项为35,公比为13的等比数列,从而131[1()]191953[1()]111031013m mm n na =⋅-==⋅-<<-∑.若1(5)(1)n n a -=-⋅-,则111(1)5n n a -=--,故1{}n a 是首项为15-,公比为1-的等比数列,从而11,21(),1502().mn n m k k a m k k +=+⎧-=-∈⎪=⎨⎪=∈⎩∑N N , 故111mn n a =<∑.综上,对任何正整数m ,总有111mn na =<∑.故不存在正整数m ,使得121111ma a a +++≥ 成立.19.(Ⅰ)直线l ∥平面PAC ,证明如下:连接EF ,因为E ,F 分别是PA ,PC 的中点,所以EF ∥AC . 又EF ⊄平面ABC ,且AC ⊂平面ABC ,所以EF ∥平面ABC . 而EF ⊂平面BEF ,且平面BEF 平面ABC l =,所以EF ∥l .因为l ⊄平面PAC ,EF ⊂平面PAC ,所以直线l ∥平面PAC .(Ⅱ)(综合法)如图1,连接BD ,由(Ⅰ)可知交线l 即为直线BD ,且l ∥AC .第19题解答图1第19题解答图2因为AB 是O 的直径,所以AC BC ⊥,于是l BC ⊥.已知PC ⊥平面ABC ,而l ⊂平面ABC ,所以PC l ⊥. 而PC BC C = ,所以l ⊥平面PBC .连接BE ,BF ,因为BF ⊂平面PBC ,所以l BF ⊥.故CBF ∠就是二面角E l C --的平面角,即CBF β∠=.由12DQ CP = ,作DQ ∥CP ,且12DQ CP =.连接PQ ,DF ,因为F 是CP 的中点,2CP PF =,所以DQ PF =, 从而四边形DQPF 是平行四边形,PQ ∥FD .连接CD ,因为PC ⊥平面ABC ,所以CD 是FD 在平面ABC 内的射影, 故CDF ∠就是直线PQ 与平面ABC 所成的角,即CDF θ∠=. 又BD ⊥平面PBC ,有BD BF ⊥,知BDF ∠为锐角,故BDF ∠为异面直线PQ 与EF 所成的角,即BDF α∠=, 于是在Rt △DCF ,Rt △FBD ,Rt △BCF 中,分别可得sin CF DF θ=,sin BF DF α=,sin CF BFβ=, 从而sin sin sin CF BF CFBF DF DFαβθ=⋅==,即sin sin sin θαβ=. (Ⅱ)(向量法)如图2,由12DQ CP = ,作DQ ∥CP ,且12DQ CP =.连接PQ ,EF ,BE ,BF ,BD ,由(Ⅰ)可知交线l 即为直线BD . 以点C 为原点,向量,,CA CB CP所在直线分别为,,x y z 轴,建立如图所示的空间直角坐标系,设,,2CA a CB b CP c ===,则有(0,0,0),(,0,0),(0,,0),(0,0,2),(,,)C A a B b P c Q a b c ,1(,0,),(0,0,)2E a cF c .于是1(,0,0)2FE a = ,(,,)QP a b c =-- ,(0,,)BF b c =- ,所以||cos ||||FE QP FE QP α⋅==⋅sin α=.又取平面ABC 的一个法向量为(0,0,1)=m,可得||sin ||||QP QP θ⋅==⋅ m m设平面BEF 的一个法向量为(,,)x y z =n ,所以由0,0,FE BF ⎧⋅=⎪⎨⋅=⎪⎩ n n 可得10,20.ax by cz ⎧=⎪⎨⎪-+=⎩ 取(0,,)c b =n .于是|||cos |||||β⋅==⋅m n m n,从而sin β==.故sin sin sin αβθ===,即sin sin sin θαβ=.20.(Ⅰ)由于随机变量X 服从正态分布2(800,50)N ,故有800μ=,50σ=(700900)0.9544P X <≤=.由正态分布的对称性,可得0(900)(800)(800900)p P X P X P X =≤=≤+<≤11(700900)0.977222P X =+<≤=. (Ⅱ)设A 型、B 型车辆的数量分别为, x y 辆,则相应的营运成本为16002400x y +.依题意, , x y 还需满足:021, 7, (3660)x y y x P X x y p +≤≤+≤+≥.由(Ⅰ)知,0(900)p P X =≤,故0(3660)P X x y p ≤+≥等价于3660900x y +≥. 于是问题等价于求满足约束条件21,7,3660900,, 0, ,x y y x x y x y x y +≤⎧⎪≤+⎪⎨+≥⎪⎪≥∈⎩N ,且使目标函数16002400z x y =+达到最小的,x y . 作可行域如图所示, 可行域的三个顶点坐标分别为(5,12), (7,14), (15,6)P Q R .由图可知,当直线16002400z x y =+经过可行域的点P 时,直线16002400z x y =+在y 轴上截距2400z 最小,即z 取得最小值.故应配备A 型车5辆、B 型车12辆.21. 依题意可设椭圆1C 和2C 的方程分别为1C :22221x y a m +=,2C :22221x y a n+=. 其中0a m n >>>, 1.m n λ=>(Ⅰ)解法1:如图1,若直线l 与y 轴重合,即直线l 的方程为0x =,则 111||||||22S BD OM a BD =⋅=,211||||||22S AB ON a AB =⋅=,所以12||||S BD S AB =. 在C 1和C 2的方程中分别令0x =,可得A y m =,B y n =,D y m =-, 于是||||1||||1B D A B y y BD m n AB y y m n λλ-++===---. 若12S S λ=,则11λλλ+=-,化简得2210λλ--=. 由1λ>,可解得1λ=.第20题解故当直线l 与y 轴重合时,若12S S λ=,则1λ=. 解法2:如图1,若直线l 与y 轴重合,则||||||BD OB OD m n =+=+,||||||AB OA OB m n =-=-;111||||||22S BD OM a BD =⋅=,211||||||22S AB ON a AB =⋅=.所以12||1||1S BD m n S AB m n λλ++===--. 若12S S λ=,则11λλλ+=-,化简得2210λλ--=. 由1λ>,可解得1λ=. 故当直线l 与y 轴重合时,若12S S λ=,则1λ=.(Ⅱ)解法1:如图2,若存在与坐标轴不重合的直线l ,使得12S S λ=. 根据对称性, 不妨设直线l :(0)y kx k =>,点(,0)M a -,(,0)N a 到直线l 的距离分别为1d ,2d ,则因为1d ==,2d ==12d d =.又111||2S BD d =,221||2S AB d =,所以12||||S BD S AB λ==,即||||BD AB λ=. 由对称性可知||||AB CD =,所以||||||(1)||BC BD AB AB λ=-=-, ||||||(1)||AD BD AB AB λ=+=+,于是||1||1AD BC λλ+=-. ① 将l 的方程分别与C 1,C 2的方程联立,可求得A x =B x =.根据对称性可知C B x x =-,D A x x =-,于是2||||2A B x AD BC x == ② 从而由①和②式可得1(1)λλλ+-. ③第21题解答图1第21题解答图2令1(1)t λλλ+=-,则由m n >,可得1t ≠,于是由③可解得222222(1)(1)n t k a t λ-=-.因为0k ≠,所以20k >. 于是③式关于k 有解,当且仅当22222(1)0(1)n t a t λ->-, 等价于2221(1)()0t t λ--<. 由1λ>,可解得11t λ<<,即111(1)λλλλ+<<-,由1λ>,解得1λ>,所以当11λ<≤+l ,使得12S S λ=;当1λ>l 使得12S S λ=. 解法2:如图2,若存在与坐标轴不重合的直线l ,使得12S S λ=. 根据对称性, 不妨设直线l :(0)y kx k =>,点(,0)M a -,(,0)N a 到直线l 的距离分别为1d ,2d ,则因为1d ==,2d ==12d d =.又111||2S BD d =,221||2S AB d =,所以12||||S BD S AB λ==.因为||||A B A Bx x BD AB x x λ+==-,所以11A B x x λλ+=-. 由点(,)A A A x kx ,(,)B B B x kx 分别在C 1,C 2上,可得222221A A x k x a m +=,222221B B x k x a n +=,两式相减可得22222222()0A B A B x x k x x a m λ--+=, 依题意0A B x x >>,所以22AB x x >. 所以由上式解得22222222()()A B B A m x x k a x x λ-=-. 因为20k >,所以由2222222()0()A B B A m x x a x x λ->-,可解得1A B x x λ<<. 从而111λλλ+<<-,解得1λ>当11λ<≤+l ,使得12S S λ=;当1λ>l 使得12S S λ=.22. (Ⅰ)因为()(1)(1)(1)(1)[(1)1]r r f x r x r r x '=++-+=++-,令()0f x '=,解得0x =.当10x -<<时,()0f x '<,所以()f x 在(1,0)-内是减函数; 当0x >时,()0f x '>,所以()f x 在(0,)+∞内是增函数.故函数()f x 在0x =处取得最小值(0)0f =. (Ⅱ)由(Ⅰ),当(1,)x ∈-+∞时,有()(0)0f x f ≥=,即1(1)1(1)r x r x ++≥++,且等号当且仅当0x =时成立,故当1x >-且0x ≠时,有1(1)1(1)r x r x ++>++. ①第11页(共11页) 在①中,令1x n =(这时1x >-且0x ≠),得111(1)1r r n n +++>+. 上式两边同乘1r n +,得11(1)(1)r r r n n n r +++>++,即11(1).1r r rn n n r +++-<+ ② 当1n >时,在①中令1x n =-(这时1x >-且0x ≠),类似可得 11(1).1r r r n n n r ++-->+ ③ 且当1n =时,③也成立. 综合②,③得1111(1)(1).11r r r r r n n n n n r r ++++--+-<<++ ④ (Ⅲ)在④中,令13r =,n 分别取值81,82,83,…,125,得44443333338180(8281)44--(),444433333382(8382)44-<-(,44443333338382(8483)44-<<-(, ………4444333333125124(126125)44-<-(). 将以上各式相加,并整理得444433333312580(12681)44S -<<-(. 代入数据计算,可得4433312580210.24-≈(),4433312681210.94-≈(). 由S ⎡⎤⎢⎥的定义,得211S =⎡⎤⎢⎥.。
2013年全国高考理科数学试题及答案详解

绝密*启用前2013年普通高等学校招生全国统一考试(新课标)理科数学注息事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.问答第Ⅰ卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动.用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效.3.回答第Ⅱ卷时。
将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回。
第一卷一. 选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1)已知集合{1,2,3,4,5}A =,{(,),,}B x y x A y A x y A =∈∈-∈;,则B 中所含元素的个数为( )()A 3 ()B 6 ()C 8 ()D 10【解析】选D5,1,2,3,4x y ==,4,1,2,3x y ==,3,1,2x y ==,2,1x y ==共10个 (2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( )()A 12种 ()B 10种 ()C 9种 ()D 8种【解析】选A甲地由1名教师和2名学生:122412C C =种(3)下面是关于复数21z i=-+的四个命题:其中的真命题为( ) 1:2p z = 22:2p z i = 3:p z 的共轭复数为1i + 4:p z 的虚部为1-()A 23,p p ()B 12,p p ()C ,p p 24 ()D ,p p 34【解析】选C 22(1)11(1)(1)i z i i i i --===---+-+--1:p z =22:2p z i =,3:p z 的共轭复数为1i -+,4:p z 的虚部为1-(4)设12F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,P 为直线32ax =上一点,∆21F PF 是底角为30的等腰三角形,则E 的离心率为( )()A 12 ()B 23 ()C 34()D 45【解析】选C∆21F PF 是底角为30 的等腰三角形221332()224c PF F F a c c e a ⇒==-=⇔==(5)已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=( )()A 7 ()B 5 ()C -5 ()D -7【解析】选D472a a +=,56474784,2a a a a a a ==-⇒==-或472,4a a =-= 471101104,28,17a a a a a a ==-⇒=-=⇔+=- 471011102,48,17a a a a a a =-=⇒=-=⇔+=-(6)如果执行右边的程序框图,输入正整数(2)N N ≥和实数12,,...,n a a a ,输出,A B ,则( )()A A B +为12,,...,n a a a 的和()B 2A B+为12,,...,n a a a 的算术平均数 ()C A 和B 分别是12,,...,n a a a 中最大的数和最小的数 ()D A 和B 分别是12,,...,n a a a 中最小的数和最大的数【解析】选C(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )()A 6 ()B 9 ()C 12 ()D 18【解析】选B该几何体是三棱锥,底面是俯视图,高为3 此几何体的体积为11633932V =⨯⨯⨯⨯= (8)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B两点,AB =;则C 的实轴长为( )()A ()B()C 4 ()D 8【解析】选C设222:(0)C x y a a -=>交x y 162=的准线:4l x =-于(A-(4,B --得:222(4)4224a a a =--=⇔=⇔=(9)已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减。
2013年高考全国Ⅰ理科数学试题及答案(word解析版)

2013年普通高等学校招生全国统一考试(全国Ⅰ)数学(理科)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)【2013年全国Ⅰ,理1,5分】已知集合{}{2|20,|A x x x B x x =->=<,则( ) (A )A B =∅ (B )A B =R (C )B A ⊆ (D )A B ⊆ 【答案】B【解析】∵2()0x x ->,∴0x <或2x >.由图象可以看出A B =R ,故选B . (2)【2013年全国Ⅰ,理2,5分】若复数z 满足(34i)|43i |z -=+,则z 的虚部为( )(A )4- (B )45- (C )4 (D )45【答案】D【解析】∵(34i)|43i |z -=+,∴55(34i)34i 34i (34i)(34i)55z +===+--+.故z 的虚部为45,故选D . (3)【2013年全国Ⅰ,理3,5分】为了解某地区的中小学生视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大,在下面的抽样方法中,最合理的抽样方法是( )(A )简单随机抽样 (B )按性别分层抽样 (C )按学段分层抽样 (D )系统抽样 【答案】C【解析】因为学段层次差异较大,所以在不同学段中抽取宜用分层抽样,故选C .(4)【2013年全国Ⅰ,理4,5分】已知双曲线C :()2222=10,0x y a b a b->>C 的渐近线方程为( )(A )14y x =± (B )13y x =± (C )12y x =± (D )y x =±【答案】C【解析】∵c e a ==,∴22222254c a b e a a +===.∴224a b =,1=2b a ±. ∴渐近线方程为12b y x x a =±±,故选C .(5)【2013年全国Ⅰ,理5,5分】执行下面的程序框图,如果输入的[]1,3t ∈-,则输出的s 属于( ) (A )[3,4]- (B )[5,2]- (C )[4,3]- (D )[2,5]- 【答案】D【解析】若[)1,1t ∈-,则执行3s t =,故[)3,3s ∈-.若[]1,3t ∈,则执行24s t t =-,其对称轴为2t =.故当2t =时,s 取得最大值4.当1t =或3时,s 取得最小值3,则[]3,4s ∈. 综上可知,输出的[]3,4s ∈-,故选D .(6)【2013年全国Ⅰ,理6,5分】如图,有一个水平放置的透明无盖的正方体容器,容器高8cm , 将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚 度,则球的体积为( )(A )35003cm π (B )38663cm π (C )313723cm π(D )320483cm π【答案】B【解析】设球半径为R ,由题可知R ,2R -,正方体棱长一半可构成直角三角形,即OBA ∆为直角三角形,如图,2BC =,4BA =,2OB R =-,OA R =,由()22224R R =-+,得5R =,所以球的体积为34500533ππ=(cm 3),故选B .(7)【2013年全国Ⅰ,理7,5分】设等差数列{}n a 的前n 项和为11,2,0,3n m m m S S S S -+=-==,则m =( )(A )3(B )4 (C )5 (D )6【答案】C 【解析】∵12m S -=-,0m S =,13m S +=,∴()1022m m m a S S -=-=--=,11303m m m a S S ++=-=-=.∴1321m m d a a +=-=-=.∵()11102m m m S ma -=+⨯=,∴112m a -=-. 又∵1113m a a m +=+⨯=,∴132m m --+=.∴5m =,故选C . (8)【2013年全国Ⅰ,理8,5分】某几何体的三视图如图所示,则该几何体的体积为( ) (A )168π+ (B )88π+ (C )1616π+ (D )816π+ 【答案】A【解析】由三视图可知该几何体为半圆柱上放一个长方体,由图中数据可知圆柱底面半径2r =,长为4,在长方体中,长为4,宽为2,高为2,所以几何体的体积为24422816r ππ⨯⨯+⨯⨯=+,故选A .(9)【2013年全国Ⅰ,理9,5分】设m 为正整数,()2m x y +展开式的二项式系数的最大值为a , ()21m x y ++展开式的二项式系数的最大值为b ,若137a b =,则m =( )(A )5 (B )6 (C )7 (D )8 【答案】B【解析】由题意可知,2m m a C =,21mm b C +=,又∵137a b =,∴2!21!13=7!!!1!m m m m m m ()(+)⋅⋅(+),即132171m m +=+.解得6m =,故选B .(10)【2013年全国Ⅰ,理10,5分】已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为(3,0)F ,过点F 的直线交椭圆于,A B 两点.若AB 的中点坐标为(1,1)-,则E 的方程为( ) (A )2214536x y +=(B )2213627x y += (C )2212718x y += (D )221189x y +=【答案】D【解析】设11()A x y ,,22()B x y ,,∵A ,B 在椭圆上,∴2211222222221,1,x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩①②,①-②,得 1212121222=0x x x x y y y y a b (+)(-)(+)(-)+,即2121221212=y y y y b a x x x x (+)(-)-(+)(-), ∵AB 的中点为()1,1-,∴122y y +=-,122x x +=,而1212011=312AB y y k x x --(-)==--, ∴221=2b a .又∵229a b -=,∴218a =,29b =.∴椭圆E 的方程为22=1189x y +,故选D . (11)【2013年全国Ⅰ,理11,5分】已知函数()()220ln 10x x x f x x x ⎧-+≤⎪=⎨+>⎪⎩,若()f x a x ≥|,则a 的取值范围是( ) (A )(],0-∞ (B )(],1-∞ (C )[2,1]- (D )[2,0]-【答案】D【解析】由()y f x =的图象知:①当0x >时,y ax =只有0a ≤时,才能满足()f x ax ≥,可排除B ,C .②当0x ≤时,()2222y f x x x x x ==-+=-.故由()f x ax ≥得 22x x ax -≥.当0x =时,不等式为00≥成立.当0x <时,不等式等价于2x a -≤.∵22x -<-,∴2a ≥-.综上可知:[]2,0a ∈-,故选D .(12)【2013年全国Ⅰ,理12,5分】设n n n A B C ∆的三边长分别为n a ,n b ,n c ,n n n A B C ∆的面积为n S ,1,2,3.n =⋯,若11b c >,1112b c a +=,1n n a a +=,12n n n c a b ++=,12n nn b a c ++=,则( )(A ){}n S 为递减数列 (B ){}n S 为递增数列(C ){}21n S -为递增数列,{}2n S 为递减数列 (D ){}21n S -为递减数列,{}2n S 为递增数列 【答案】B第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题~第(24)题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分(13)【2013年全国Ⅰ,理13,5分】已知两个单位向量a ,b 的夹角为60°,()1t t =+-c a b .若·0=b c ,则t = . 【答案】2【解析】∵()1t t =+-c a b ,∴()2··1t t =+-bc ab b .又∵1==a b ,且a 与b 夹角为60°,⊥b c , ∴()0 601t cos t =︒+-a b ,1012t t =+-.∴2t =.(14)【2013年全国Ⅰ,理14,5分】若数列{}n a 的前n 项和2133n n S a =+,则{}n a 的通项公式是n a = .【答案】()12n --【解析】∵2133n n S a =+,① ∴当2n ≥时,112133n n S a --=+.② ①-②,得12233n n n a a a -=-,即12n n aa -=-.∵1112133a S a ==+,∴11a =.∴{}n a 是以1为首项,-2为公比的等比数列,()12n n a -=-.(15)【2013年全国Ⅰ,理15,5分】设当x θ=时,函数()2f x sinx cosx =-取得最大值,则cos θ= .【答案】 【解析】()s 2x f x sinx cosx x ⎫⎪==⎭-,令cos α=,sin α=,则()()f x x α=+,当22()x k k ππα=+-∈Z 时,()sin x α+有最大值1,()f x,即22()k k πθπα=+-∈Z ,所以cos θ=πcos =cos 2π+cos sin 22k πθααα⎛⎫⎛⎫-=-=== ⎪ ⎪⎝⎭⎝⎭(16)【2013年全国Ⅰ,理16,5分】若函数()()()221f x x x ax b =-++的图像关于直线2x =-对称,则()f x 的最大值为 .【答案】16【解析】∵函数()f x 的图像关于直线2x =-对称,∴()f x 满足()()04f f =-,()()13f f -=-,即151640893b a b a b =-(-+)⎧⎨=-(-+)⎩,得815a b =⎧⎨=⎩∴()432814815f x x x x x =---++.由()324242880f x x x x '=---+=,得12x =-22x =-,32x =-.易知,()f x在(,2-∞-上为增函数,在()22--上为减函数,在(2,2--上为增函数,在()2-+-∞上为减函数.∴(((((222122821588806416f ⎡⎤⎡⎤-=---+-+=---=-=⎢⎥⎢⎥⎣⎦⎣⎦.()()()()()22212282153416915f ⎡⎤⎡-=---+⨯⎤==-⎣⎦⎣⎦-+--+(((((222122821588806416f ⎡⎤⎡⎤-=---++-++=-++=-=⎢⎥⎢⎥⎣⎦⎣⎦.故f (x )的最大值为16.三、解答题:解答应写出文字说明,证明过程或演算步骤.(17)【2013年全国Ⅰ,理17,12分】如图,在ABC ∆中,90ABC ∠=︒,AB =,1BC =,P为ABC ∆内一点,90BPC ∠=︒.(1)若12PB =,求PA ;(2)若150APB ∠=︒,求tan PBA ∠.解:(1)由已知得60PBC ∠=︒,30PBA ∴∠=︒.在PBA ∆中,由余弦定理得211732cos 30424PA =+-︒=.故PA =(2)设PBA α∠=,由已知得sin PB α=.在PBA ∆sin sin(30)αα=︒-,4sin αα=.所以tan α,即tan PBA ∠= (18)【2013年全国Ⅰ,理18,12分】如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=︒. (1)证明:1AB A C ⊥;(2)若平面ABC ⊥平面11AA B B ,AB CB =,求直线1A C 与平面11BB C C 所成角的正弦值.解:(1)取AB 的中点O ,连结OC ,1OA ,1A B .因为CA CB =,所以OC AB ⊥.由于1AB AA =,160BAA ∠=︒,故1AA B ∆为等边三角形,所以1OA AB ⊥.因为1OC OA O = ,所以AB ⊥平面1OA C . 又1A C 平面1OA C ,故1AB A C ⊥.(2)由(1)知OC AB ⊥,1OA AB ⊥.又平面ABC ⊥平面11AA B B ,交线为AB ,所以OC ⊥平面11AA B B ,故OA ,1OA ,OC 两两相互垂直.以O 为坐标原点,OA 的方向为x 轴的正方向,OA为单位长,建立如图所示的空间直角坐标系O xyz -.由题设知()1,0,0A,1()0A ,(0,0C ,()1,0,0B -.则(1,03BC =,11()BB AA =-=,(10,A C = .设()n x y z =,,是平面11BB C C 的法向量,则100BC BB ⎧⋅=⎪⎨⋅=⎪⎩n n即0x x ⎧=⎪⎨-=⎪⎩可取1)n =-.故111cos ,n AC n AC n AC ⋅==⋅ .所以1A C 与平面11BB C C. (19)【2013年全国Ⅰ,理19,12分】一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n .如果n =3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n =4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.假设这批产品的优质品率为50%,即取出的每件产品是优质品的概率都为12,且各件产品是否为优质品相互独立.(1)求这批产品通过检验的概率;(2)已知每件产品的检验费用为100元,且抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X (单位:元),求X 的分布列及数学期望.解:(1)设第一次取出的4件产品中恰有3件优质品为事件1A ,第一次取出的4件产品全是优质品为事件2A ,第二次取出的4件产品都是优质品为事件1B ,第二次取出的1件产品是优质品为事件2B ,这批产品通过检验为事件A ,依题意有()()1122A A B A B = ,且11A B 与22A B 互斥,所以 ()()()()()()()112211122241113||161616264P A P A B P A B P A P B A P A P B A ==⨯++⨯==+.(2)X 可能的取值为400,500,800,并且()41114001161616P X ==--=,()500116P X ==,()80140P X ==. 所以X 的分布列为()111400+500+800506.2516164E X =⨯⨯⨯=. (20)【2013年全国Ⅰ,理20,12分】已知圆()2211M x y ++=:,圆()2219N x y -+=:,动圆P 与圆M 外切并且与圆N 内切,圆心P 的轨迹为曲线C .(1)求C 的方程;(2)l 是与圆P ,圆M 都相切的一条直线,l 与曲线C 交于A ,B 两点,当圆P 的半径最长时,求AB . 解:由已知得圆M 的圆心为()1,0M -,半径11r =;圆N 的圆心为()1,0N ,半径23r =.设圆P 的圆心为(),P xy ,半径为R .(1)因为圆P 与圆M 外切并且与圆N 内切,所以()()12124PM PN R r r R r r +=++-=+=.由椭圆的定义可知,曲线C 是以M ,N 为左、右焦点,长半轴长为2(左顶点除外),其方程为()22=1243x y x +≠-.(2)对于曲线C 上任意一点()P x y ,,由于222PM PN R -=-≤,所以2R ≤,当且仅当圆P 的圆心为()2,0时,2R =.所以当圆P 的半径最长时,其方程为()2224x y -+=.若l 的倾斜角为90︒,则l 与y 轴重 合,可得AB =l 的倾斜角不为90︒,由1r R ≠知l 不平行于x 轴,设l 与x 轴的交点为Q ,则1||||QP R QM r =,可求得()4,0Q -,所以可设()4l y k x =+:.由l 与圆M ,解得k =. 当k =时,将y =+22=13x y +,并整理得27880x x +-=,解得1,2x =. 2118|7AB x x =-=.当k =时,由图形对称性可知187AB =.综上,AB =187AB =. (21)【2013年全国Ⅰ,理21,12分】设函数()2f x x ax b =++,()()x g x e cx d =+.若曲线()y f x =和曲线()y g x =都过点()0,2P ,且在点P 处有相同的切线42y x =+.(1)求a ,b ,c ,d 的值;(2)若2x ≥-时,()()f x kg x ≤,求k 的取值范围.解:(1)由已知得()02f =,()02g =,()04f '=,()04g '=.而()2f x x a '=+,()()x g x e cx d c '=++, 故2b =,2d =,4a =,4d c +=.从而4a =,2b =,2c =,2d =. (2)由(1)知,()242f x x x =++,()()21x g x e x =+.设函数()()()()22142x F x kg x f x ke x x x =-=+---,()()()()2224221x x F x ke x x x ke '=+--=+-.()00F ≥ ,即1k ≥.令()0F x '=得1ln x k =-,22x =-. ①若21k e ≤<,则120x -<≤.从而当12()x x ∈-,时,()0F x '<;当1()x x ∈+∞,时,()0F x '>. 即()F x 在1(2)x -,单调递减,在1()x +∞,单调递增.故()F x 在[)2-+∞,的最小值为()1F x . 而()()11111224220F x x x x x =+---=-+≥.故当2x ≥-时,()0F x ≥,即()()f x kg x ≤恒成立. ②若2k e =,则()()()2222x F x e x e e -'=+-.∴当2x >-时,()0F x '>,即()F x 在()2-+∞,单调递增. 而()20F -=,故当2x ≥-时,()0F x ≥,即()()f x kg x ≤恒成立. ③若2k e >,则()()22222220F k eek e ---=-+=--<.从而当2x ≥-时,()()f x kg x ≤不可能恒成立.综上,k 的取值范围是2[1]e ,. 请考生在(22)、(23)、(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,做答时,请用2B 铅笔在答题卡上将所选题号后的方框涂黑.(22)【2013年全国Ⅰ,理22,10分】(选修4-1:几何证明选讲)如图,直线AB为圆的切线,切点为B ,点C 在圆上,ABC ∠的角平分线BE 交圆于点E ,DB 垂直BE 交圆 于点D . (1)证明:DB DC =;(2)设圆的半径为1,BC =CE 交AB 于点F ,求BCF ∆外接圆的半径. 解:(1)连结DE ,交BC 于点G .由弦切角定理得,ABE BCE ∠=∠.而ABE CBE ∠=∠,故CBE BCE ∠=∠,BE CE =.又因为DB BE ⊥,所以DE 为直径,90DCE ∠=︒,DB DC =.(2)由(1)知,CDE BDE ∠=∠,DB DC =,故DG 是BC的中垂线,所以BG =设DE 的中点为O ,连结BO ,则60BOG ∠=︒.从而30ABE BCE CBE ∠=∠=∠=︒,所以CF BF ⊥,故Rt BCF ∆.(23)【2013年全国Ⅰ,理23,10分】(选修4-4:坐标系与参数方程)已知曲线1C 的参数方程为45cos 55sin x ty t=+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2sin ρθ=. (1)把1C 的参数方程化为极坐标方程;(2)求1C 与2C 交点的极坐标(0ρ≥,02θπ≤<).解:(1)将45cos 55sin x t y t =+⎧⎨=+⎩消去参数t ,化为普通方程()()224525x y -+-=,即221810160C x y x y +--+=:.将cos sin x y ρθρθ=⎧⎨=⎩代入22810160x y x y +--+=得28cos 10sin 160ρρθρθ--+=. 所以1C 的极坐标方程为28cos 10sin 160ρρθρθ--+=.(2)2C 的普通方程为2220x y y +-=.由222281016020x y x y x y y ⎧+--+=⎨+-=⎩,解得11x y =⎧⎨=⎩或02x y =⎧⎨=⎩, 所以1C 与2C交点的极坐标分别为π4⎫⎪⎭,π2,2⎛⎫ ⎪⎝⎭.(24)【2013年全国Ⅰ,理24,10分】(选修4-5:不等式选讲)已知函数()212f x x x a =-++,()3g x x =+.(1)当2a =-时,求不等式()()f x g x <的解集;(2)设1a >-,且当1,22a x ⎡⎫∈-⎪⎢⎣⎭时,()()f x g x ≤,求a 的取值范围.解:(1)当2a =-时,()()f x g x <化为212230x x x -+---<.设函数21223y x x x =-+---,则y =15,212,1236,1x x y x x x x ⎧-<⎪⎪⎪=--≤≤⎨⎪->⎪⎪⎩,其图像如图所示.从图像可知,当且仅当()0,2x ∈时,0y <.所以原不等式的解集是{}2|0x x <<.(2)当1,22x a ⎡⎫-⎪⎢⎣⎭∈时,()1f x a =+.不等式()()f x g x ≤化为13a x +≤+.所以2x a ≥-,对1,22x a ⎡⎫-⎪⎢⎣⎭∈都成立.故22a a -≥-,即43a ≤.从而a 的取值范围是41,3⎛⎤- ⎥⎝⎦.。
专题三:程序框图2013-2016高考数学全国卷(理)

1、(2016全国I 卷9题)执行右面的程序框图,如果输入的011x y n ===,,,则输出x ,y 的值满足(A )2y x = (B )3y x = (C )4y x = (D )5y x = 【答案】C 【解析】试题分析:当0,1,1x y n ===时,110,1112x y -=+=⨯=,不满足2236x y +≥;2112,0,21222n x y -==+==⨯=,不满足2236x y +≥;13133,,236222n x y -==+==⨯=,满足2236x y +≥;输出3,62x y ==,则输出的,x y 的值满足4y x =,故选C. 考点:程序框图与算法案例2、(2015全国I 卷9题)执行右面的程序框图,如果输入的t=0.01,则输出的n=(A )5 (B )6 (C )7 (D )8【答案】C 【解析】试题分析:执行第1次,t=0.01,S=1,n=0,m=12=0.5,S=S-m=0.5,2mm ==0.25,n=1,S=0.5>t=0.01,是,循环,执行第2次,S=S-m=0.25,2mm ==0.125,n=2,S=0.25>t=0.01,是,循环, 执行第3次,S=S-m=0.125,2mm ==0.0625,n=3,S=0.125>t=0.01,是,循环,执行第4次,S=S-m=0.0625,2mm ==0.03125,n=4,S=0.0625>t=0.01,是,循环,执行第5次,S=S-m=0.03125,2mm ==0.015625,n=5,S=0.03125>t=0.01,是,循环,执行第6次,S=S-m=0.015625,2mm ==0.0078125,n=6,S=0.015625>t=0.01,是,循环,执行第7次,S=S-m=0.0078125,2mm ==0.00390625,n=7,S=0.0078125>t=0.01,否,输出n=7,故选C. 考点:程序框图3. (2014全国I 卷7题)执行下图的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M =A .203 B .165 C .72 D .158【答案】:D【解析】:输入1,2,3a b k ===;1n =时:1331,2,222M a b =+===; 2n =时:28382,,3323M a b =+===;3n =时:3315815,,28838M a b =+===;4n =时:输出158M = . 选D.4、(2013全国I 卷5题)运行如下程序框图,如果输入的[1,3]t ∈-,则输出s 属于A .[-3,4]B .[-5,2]C .[-4,3]D .[-2,5]【命题意图】本题主要考查程序框图及分段函数值域求法,是简单题.【解析】有题意知,当[1,1)t ∈-时,3s t =[3,3)∈-,当[1,3]t ∈时,24s t t =-[3,4]∈, ∴输出s 属于[-3,4],故选A .5、(2016全国II 卷8题)中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的2x =,2n =,依次输入的a 为2,2,5,则输出的s =(A )7 (B )12 (C )17 (D )34【解析】C第一次运算:0222s =⨯+=, 第二次运算:2226s =⨯+=, 第三次运算:62517s =⨯+=, 故选C .6、(2015全国II 卷8题)右边程序抗土的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。
2013年普通高等学校招生全国统一考试(全国新课标II卷)数学试题 (理科) word解析版

2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)数学(理科)注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置。
2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号标黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷(选择题 共50分)一、 选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合M ={x |(x -1)2<4,x ∈R },N ={-1,0,1,2,3},则M ∩N 等于( ) A .{0,1,2} B .{-1,0,1,2} C .{-1,0,2,3} D .{0,1,2,3} 答案 A解析 化简集合M 得M ={x |-1<x <3,x ∈R },则M ∩N ={0,1,2}.2.设复数z 满足(1-i)z =2i ,则z =( )A .-1+iB .-1-IC .1+iD .1-i 答案 A解析 由已知得z =2i1-i =2i (1+i )(1-i )(1+i )=-1+i.3.等比数列{a n }的前n 项和为S n ,已知S 3=a 2+10a 1,a 5=9,则a 1等于( )A.13 B .-13 C.19 D .-19 答案 C解析 设等比数列{a n }的公比为q ,由S 3=a 2+10a 1得a 1+a 2+a 3=a 2+10a 1,即a 3=9a 1,q 2=9,又a 5=a 1q 4=9,所以a 1=19.4.已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l ⊥m ,l ⊥n ,l ⊄α,l ⊄β,则( ) A .α∥β且l ∥α B .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l 答案 D解析 假设α∥β,由m ⊥平面α,n ⊥平面β,则m ∥n ,这与已知m ,n 为异面直线矛盾,那么α与β相交,设交线为l 1,则l 1⊥m ,l 1⊥n ,在直线m 上任取一点作n 1平行于n ,那么l 1和l 都垂直于直线m 与n 1所确定的平面,所以l 1∥l .5.已知(1+ax )(1+x )5的展开式中x 2的系数为5,则a 等于( ) A .-4 B .-3 C .-2 D .-1 答案 D解析 (1+ax )(1+x )5中含x 2的项为:(C 25+C 15a )x 2,即C 25+C 15a =5,a =- 1.6.执行右面的程序框图,如果输入的N =10,那么输出的S =( )A .1+12+13+…+110B .1+12!+13!+…+110!C .1+12+13+…+111D .1+12!+13!+…+111!答案 B解析 k =1,T =11,S =1,k =2,T =11×2=12!,S =1+12!,k =3,T =11×2×3=13!,S =1+12!+13!,…由于N =10,即k >10时,结束循环,共执行10次.所以输出S =1+12!+13!+…+110!.7.一个四面体的顶点在空间直角坐标系O -xyz 中的坐标分别是(1,1,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为()答案 A解析 在空间直角坐标系中,先画出四面体O -ABC 的直观图,以zOx 平面为投影面,则得到正视图,所以选A.8.设a =log 36,b =log 510,c =log 714,则( )A .c >b >aB .b >c >aC .a >c >bD .a >b >c 答案 D解析 设a =log 36=1+log 32=1+1log 23,b =log 510=1+log 52=1+1log 25,c =log 714=1+log 72=1+1log 27,显然a >b >c.(9)已知a >0,x ,y 满足约束条件()133x x y y a x ⎧≥⎪+≤⎨⎪≥-⎩,若z=2x+y 的最小值为1,则a=(A) 14 (B) 12(C)1(D)210.已知函数f (x )=x 3+ax 2+bx +c ,下列结论中错误的是( ) A .∃x 0∈R ,f (x 0)=0B .函数y =f (x )的图象是中心对称图形C .若x 0是f (x )的极小值点,则f (x )在区间(-∞,x 0)上单调递减D .若x 0是f (x )的极值点,则f ′(x 0)=0 答案 C解析 若c =0,则有f (0)=0,所以A 正确.由f (x )=x 3+ax 2+bx +c 得f (x )-c =x 3+ax 2+bx ,因为函数f (x )=x 3+ax 2+bx 的对称中心为(0,0),所以f (x )=x 3+ax 2+bx +c 的对称中心为(0,c ),所以B 正确.由三次函数的图象可知,若x 0是f (x )的极小值点,则极大值点在x 0的左侧,所以函数在区间(-∞,x 0 )单调递减是错误的,D 正确.选C.11.设抛物线C :y 2=2px (p ≥0)的焦点为F ,点M 在C 上,|MF |=5,若以MF 为直径的圆过点(0,2),则C 的方程为( ) A .y 2=4x 或y 2=8x B .y 2=2x 或y 2=8x C .y 2=4x 或y 2=16x D .y 2=2x 或y 2=16x 答案 C解析 由题意知:F ⎝⎛⎭⎫p 2,0,抛物线的准线方程为x =-p 2,则由抛物线的定义知,x M =5-p2,设以MF 为直径的圆的圆心为⎝⎛⎭⎫52,y M 2,所以圆的方程为⎝⎛⎭⎫x -522+⎝⎛⎭⎫y -y M 22=254,又因为圆过点(0,2),所以y M =4,又因为点M 在C 上,所以16=2p ⎝⎛⎭⎫5-p2,解得p =2或p =8,所以抛物线C 的方程为y 2=4x 或y 2=16x ,故选C.12.已知点A (-1,0),B (1,0),C (0,1),直线y =ax +b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是( )A .(0,1) B.⎝⎛⎭⎫1-22,12 C.⎝⎛⎭⎫1-22,13 D.⎣⎡⎭⎫13,12 答案 B二、填空题13.已知正方形ABCD 的边长为2,E 为CD 的中点,则AE →·BD →=________. 答案 2解析 由题意知:AE →·BD →=(AD →+DE →)·(AD →-AB →)=(AD →+12AB →)·(AD →-AB →)=AD →2-12AD →·AB →-12AB →2=4-0-2=2.14.从n 个正整数1,2,…,n 中任意取出两个不同的数,若取出的两数之和等于5的概率为114,则n=________. 答案 8解析 由题意,取出的两个数只可能是1与4,2与3这两种情况,∴在n 个数中任意取出两个不同的数的总情况应该是C 2n=n (n -1)2=2÷114=28,∴n =8.15.设θ为第二象限角,若tan ⎝⎛⎭⎫θ+π4=12,则sin θ+cos θ=________. 答案 -105解析 ∵tan ⎝⎛⎭⎫θ+π4=12,∴tan θ=-13,即{ 3sin θ=-cos θ,2θ+cos 2θ=1,解得sin θ=1010,cos θ=-31010. ∴sin θ+cos θ=-105.16.等差数列{a n }的前n 项和为S n ,已知S 10=0,S 15=25,则nS n 的最小值为________. 答案 -49解析 由题意知a 1+a 10=0,a 1+a 15=103.两式相减得a 15-a 10=103=5d ,∴d =23,a 1=-3.∴nS n =n ·⎝⎛⎭⎫na 1+n (n -1)2d =n 3-10n 23=f (n ), f ′(n )=13n (3n -20).由函数的单调性知f (6)=-48,f (7)=-49. ∴nS n 的最小值为-49.三、解答题17.△ABC 中内角A ,B ,C 的对边分别为a ,b ,c ,已知a =bcos C +c sin B . (1)求B ;(2)若b =2,求△ABC 面积的最大值. 解 (1)由已知及正弦定理得sin A =sin B cos C +sin C sin B ,① 又A =π-(B +C ),故sin A =sin(B +C )=sin B cos C +cos B sin C .② 由①,②和C ∈(0,π)得sin B =cos B .又B ∈(0,π),所以B =π4.(2)△ABC 的面积S =12ac sin B =24ac .由已知及余弦定理得4=a 2+c 2-2ac cos π4.又a 2+c 2≥2ac ,故ac ≤42-2,当且仅当a =c 时,等号成立. 因此△ABC 面积的最大值为2+1.18.如图,直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点,AA 1=AC =CB =22AB . (1)证明:BC 1∥平面A 1CD ;(2)求二面角D -A 1C -E 的正弦值.(1)证明 连结AC 1交A 1C 于点F ,则F 为AC 1的中点. 又D 是AB 的中点,连结DF ,则BC 1∥DF . 因为DF ⊂平面A 1CD ,BC 1⊄平面A 1CD , 所以BC 1∥平面A 1CD .(2)解 由AC =CB =22AB 得,AC ⊥BC .以C 为坐标原点,CA →的方向为x 轴正方向,CB →的方向为y 轴正方向,CC 1→的方向为z 轴正方向,建立如图所示的空间直角坐标系C -xyz .设CA =2,则D (1,1,0),E (0,2,1),A 1(2,0,2), CD →=(1,1,0),CE →=(0,2,1),CA 1→=(2,0,2). 设n =(x 1,y 1,z 1)是平面A 1CD 的法向量,则{n ·CD →=0,n ·CA 1→=0,即{ x 1+y 1=0,x 1+2z 1=0.可取n =(1,-1,-1).同理,设m 是平面A 1CE 的法向量,则{m ·CE →=0,m ·CA 1→=0.可取m =(2,1,-2).从而cos 〈n ,m 〉=n ·m |n ||m |=33,故sin 〈n ,m 〉=63.即二面角D -A 1C -E 的正弦值为63.19.经销商经销某种农产品,在一个销售季度内,每售出1 t 该产品获利润500元,未售出的产品,每1 t 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t 该农产品.以X (单位: t,100≤X ≤150)表示下一个销售季度内的市场需求量,T (单位:元)表示下一个销售季度内经销该农产品的利润.(1)将T 表示为X 的函数;(2)根据直方图估计利润T 不少于57 000元的概率; (3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x ∈[100,110),则取X =105,且X =105的概率等于需求量落入[100,110)的T 的数学期望.解 (1)当X ∈[100,130)时,T =500X -300(130-X )=800X -39 000. 当X ∈[130,150]时,T =500×130=65 000.所以T ={ 800X -39 000,100≤X <130,,130≤X ≤150. (2)由(1)知利润T 不少于57 000元当且仅当120≤X ≤150.由直方图知需求量X ∈[120,150]的频率为0.7,所以下一个销售季度内的利润T 不少于57 000元的概率的估计值为0.7.(3)依题意可得T 的分布列为所以E (T )=45 000×20.平面直角坐标系xOy 中,过椭圆M :x 2a 2+y 2b 2=1(a >b >0)右焦点的直线x +y -3=0交M 于A ,B 两点,P 为AB 的中点,且OP 的斜率为12.(1)求M 的方程;(2)C ,D 为M 上的两点,若四边形ACBD 的对角线CD ⊥AB ,求四边形的最大值.解 (1)设A (x 1,y 1),B (x 2,y 2),则 x 21a 2+y 21b 2=1① x 22a 2+y 22b2=1②①-②,得(x 1-x 2)(x 1+x 2)a 2+(y 1-y 2)(y 1+y 2)b 2=0.因为y 1-y 2x 1-x 2=-1,设P (x 0,y 0),因为P 为AB 的中点,且OP 的斜率为12,所以y 0=12x 0,即y 1+y 2=12(x 1+x 2).所以可以解得a 2=2b 2,即a 2=2(a 2-c 2),即a 2=2c 2, 又因为c =3,所以a 2=6,所以M 的方程为x 26+y 23=1.(2)因为CD ⊥AB ,直线AB 方程为x +y -3=0, 所以设直线CD 方程为y =x +m ,将x +y -3=0代入x 26+y 23=1得:3x 2-43x =0,即A (0,3),B ⎝⎛⎭⎫433,-33, 所以可得|AB |=463;将y =x +m 代入x 26+y 23=1得:3x 2+4mx +2m 2-6=0, 设C (x 3,y 3),D (x 4,y 4),则|CD |=2(x 3+x 4)2-4x 3x 4=22318-2m 2,又因为Δ=16m 2-12(2m 2-6)>0,即-3<m <3,所以当m =0时,|CD |取得最大值4,所以四边形ACBD 面积的最大值为12|AB |·|CD |=863.21.已知函数f (x )=e x -ln(x +m ).(1)设x =0是f (x )的极值点,求m ,并讨论f (x )的单调性; (2)当m ≤2时,证明f (x )>0.(1)解 f (x )=e x -ln(x +m )⇒f ′(x )=e x -1x +m ⇒f ′(0)=e 0-10+m=0⇒m =1,定义域为{x |x >-1},f ′(x )=e x-1x +m =e x (x +1)-1x +1,令1)1()(-+=x e x g x ,则0)2()(>+='x e x g x ,又0)0(=g显然f (x )在(-1,0]上单调递减,在[0,+∞)上单调递增.(2)证明 令g (x )=e x -ln(x +2),则g ′(x )=e x -1x +2(x >-2).h (x )=g ′(x )=e x -1x +2(x >-2)⇒h ′(x )=e x +1(x +2)2>0,所以h (x )是增函数,h (x )=0至多只有一个实数根,又g ′(-12)=1e -132<0,g ′(0)=1-12>0,所以h (x )=g ′(x )=0的唯一实根在区间⎝⎛⎭⎫-12,0内, 设g ′(x )=0的根为t ,则有g ′(t )=e t -1t +2=0⎝⎛⎭⎫-12<t <0,所以,e t =1t +2⇒t +2=e -t , 当x ∈(-2,t )时,g ′(x )<g ′(t )=0,g (x )单调递减; 当x ∈(t ,+∞)时,g ′(x )>g ′(t )=0,g (x )单调递增;所以g (x )min =g (t )=e t-ln(t +2)=1t +2+t =(1+t )2t +2>0,当m ≤2时,有ln(x +m )≤ln(x +2),所以f (x )=e x -ln(x +m )≥e x -ln(x +2)=g (x )≥g (x )min >0.22.[选修4-1]几何证明选讲如图,CD 为△ABC 外接圆的切线,AB 的延长线交直线CD 于点D ,E 、F 分别为弦AB 与弦AC 上的点,且BC ·AE =DC ·AF ,B 、E 、F 、C 四点共圆.(1)证明:CA 是△ABC 外接圆的直径;(2)若DB =BE =EA ,求过B 、E 、F 、C 四点的圆的面积与△ABC 外接圆面积的比值.(1)证明 因为CD 为△ABC 外接圆的切线,所以∠DCB =∠A ,由题设知BC F A =DCEA,故△CDB ∽△AEF ,所以∠DBC =∠EF A .因为B ,E ,F ,C 四点共圆,所以∠CFE =∠DBC , 故∠EF A =∠CFE =90°. 所以∠CBA =90°,因此CA 是△ABC 外接圆的直径.(2)解 连结CE ,因为∠CBE =90°,所以过B ,E ,F ,C 四点的圆的直径为CE , 由DB =BE ,有CE =DC , 又BC 2=DB ·BA =2DB 2, 所以CA 2=4DB 2+BC 2=6DB 2. 而DC 2=DB ·DA =3DB 2,故过B ,E ,F ,C 四点的圆的面积与△ABC外接圆面积的比值为12.23.[选修4-4]坐标系与参数方程已知动点P 、Q 都在曲线C :{ x =2cos t ,y =2sin t (t 为参数)上,对应参数分别为t =α与t =2α(0<α<2π),M 为PQ 的中点. (1)求M 的轨迹的参数方程;(2)将M 到坐标原点的距离d 表示为α的函数,并判断M 的轨迹是否过坐标原点. 解 (1)依题意有P (2cos α,2sin α),Q (2cos 2α,2sin 2α), 因此M (cos α+cos 2α,sin α+sin 2α).M 的轨迹的参数方程为{ x =cos α+cos 2α,y =sin α+sin 2α,(α为参数,0<α<2π). (2)M 点到坐标原点的距离d =x 2+y 2=2+2cos α(0<α<2π). 当α=π,d =0,故M 的轨迹过坐标原点.24.[选修4-5]不等式选讲设a 、b 、c 均为正数,且a +b +c =1,证明:(1)ab +bc +ac ≤13;(2)a 2b +b 2c +c 2a ≥1.证明 (1)由a 2+b 2≥2ab ,b 2+c 2≥2bc ,c 2+a 2≥2ac 得 a 2+b 2+c 2≥ab +bc +ca . 由题设得(a +b +c )2=1,即a 2+b 2+c 2+2ab +2bc +2ca =1.所以3(ab +bc +ca )≤1,即ab +bc +ca ≤13.(2)因为a 2b +b ≥2a ,b 2c +c ≥2b ,c2a +a ≥2c ,故a 2b +b 2c +c2a +(a +b +c )≥2(a +b +c ), 即a 2b +b 2c +c 2a ≥a +b +c .所以a 2b +b 2c +c 2a ≥1.。
【解析分类汇编系列二:北京2013(一模)数学理】12.程序与框图 Word版含答案

【解析分类汇编系列二:北京2013(一模)数学理】12程序与框图
1.(2013届北京石景山区一模理科)4.执行右面的框图,输出的结果s的值为()
A.-3 B.2 C.
1
2
-D.
1
3
【答案】A
第1次循环,S=﹣3,i=2;第2次循环,S=﹣,i=3;第3次循环,S=,i=4;
第4次循环,S=2,i=5;第5次循环,S=﹣3,i=6;
…
框图的作用是求周期为4的数列,输出S的值,不满足2014≤2013,退出循环,循环次
数是2013次,即输出的结果为﹣3,故选A.
2.(2013届北京大兴区一模理科)执行如图所示的程序框图.若5
n=,则输出s的值是()A.-21 B.11
C.43 D.86
【答案】A
第一次循环,11(2)1,2s i =+-=-=;第二次循环,21(2)3,3s i =-+-==;
第三次循环,33(2)5,4s i =+-=-=;第四次循环,41(2)11,5s i =-+-==,第五次循环,511(2)21,6s i =+-=-=,此时不满足条件,输出21s =-,所以选A.
3.(2013届北京丰台区一模理科)执行右边的程序框图,输出k 的值是
( ) A .3 B .4 C .5 D .6
【答案】A。
2013年全国高考理科数学试题分类汇编13:排列、组合及二项式定理(S)

2013年高考数学(理)真题分类解析汇编10:排列、组合及二项式定理一、选择题1 .(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))已知5)1)(1(x ax ++的展开式中2x 的系数为5,则=a ( )A .4-B .3-C .2-D .1-【答案】D2 .(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))用0,1,,9十个数字,可以组成有重复数字的三位数的个数( )A .243B .252C .261D .279【答案】B3 .(2013年高考新课标1(理))设m 为正整数,2()m x y +展开式的二项式系数的最大值为a ,21()m x y ++展开式的二项式系数的最大值为b ,若137a b =,则m =( )A .5B .6C .7D .8【答案】B4 .(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))()()8411+x y +的展开式中22x y 的系数是( ) A .56B .84C .112D .168【答案】D5 .(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))满足{},1,0,1,2a b ∈-,且关于x 的方程220ax x b ++=有实数解的有序数对(,)a b 的个数( ) A .14 B .13 C .12 D .10【答案】B6 .(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))使得()3nx n N n+⎛+∈ ⎝的展开式中含有常数项的最小的为( ) A .4 B .5C .6D .7【答案】B7 .(2013年高考四川卷(理))从1,3,5,7,9这五个数中,每次取出两个不同的数分别为,a b ,共可得到lg lg a b -的不同值的个数( ) A .9B .10C .18D .20【答案】C8 .(2013年高考陕西卷(理))设函数61,00.,()x x f x x x ⎧⎛⎫-<⎪ ⎪=⎝≥⎭⎨⎪⎩ , 则当x >0时, [()]f f x 表达式的展开式中常数项为( )A .-20B .20C .-15D .15【答案】A9.(2013年高考江西卷(理))(x 2-32x )5展开式中的常数项为( ) A .80 B .-80C .40D .-40【答案】C二、填空题10.(2013年高考四川卷(理))二项式5()x y +的展开式中,含23xy 的项的系数是_________.(用数字作答【答案】1011.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))将F E D C B A ,,,,,六个字母排成一排,且B A ,均在C 的同侧,则不同的排法共有________种(用数字作答) 【答案】48012.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))从3名骨科.4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科.脑外科和内科医生都至少有1人的选派方法种数是___________(用数字作答) 【答案】59013.(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))6x ⎛⎝的二项展开式中的常数项为______.【答案】1514.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))设二项式53)1(xx -的展开式中常数项为A ,则=A ________.【答案】10-15.(2013年高考上海卷(理))设常数a R ∈,若52a x x ⎛⎫+ ⎪⎝⎭的二项展开式中7x 项的系数为10-,则______a =【答案】2a =-16.(2013年高考北京卷(理))将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是_________.【答案】9617.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))若8x ⎛+ ⎝的展开式中4x 的系数为7,则实数a =______.【答案】2118.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))6个人排成一行,其中甲、乙两人不相邻的不同排法共有____________种.(用数字作答).【答案】48019 .2013年上海市春季高考数学试卷.10(1)x +的二项展开式中的一项是( )A .45xB .290xC .3120xD .4252x【答案】C 二、填空题1.(2013年上海市春季高考数学试卷(含答案))36的所有正约数之和可按如下方法得到:因为2236=23⨯,所以36的所有正约数之和为22222222(133)(22323)(22323)(122)133)91++++⨯+⨯++⨯+⨯=++++=(参照上述方法,可求得2000的所有正约数之和为________________________【答案】48362.(2013年高考四川卷(理))二项式5()x y +的展开式中,含23x y 的项的系数是_________.(用数字作答)【答案】103.(2013年上海市春季高考数学试卷(含答案))从4名男同学和6名女同学中随机选取3人参加某社团活动,选出的3人中男女同学都有的概率为________(结果用数值表示).【答案】454.(2013年高考北京卷(理))将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是_________.【答案】96。
2013年高考理科数学试题(大纲卷,新课标Ⅰ、Ⅱ卷)参考答案

1952013年普通高等学校招生全国统一考试理科数学(大纲卷)参考答案 第Ⅰ卷(选择题 60分)一、选择题(共60分) 1-12 BABBA CDBDA DC第Ⅱ卷(非选择题 90分)二、填空题(共20分)13..480 15.1[,4]216.16π 三、解答题17.(本小题满分10分)解:(Ⅰ)等差数列{}n a 的公差为d . 由232=S a 得21232+=a a a a +,即2223a a =,20a =,或23a =.由124,,S S S 成等比数列得2214S S S =. ∵1122242,2,42S a a d S a d S a d ==-=-=+, ∴()()()2222242a d a d a d -=-+,即222d a d =,0d =或223d a =. 当20a =时,0d =,从而0n S =,不符合题意;当23a =量,0d =或2d =.∴{}n a 的通项式为3n a =或21n a n =-. 18.(本小题满分12分) 解:(Ⅰ)∵()()a b c a b c ac ++-+=,∴222a cb ac +-=-. 由余弦定理得,2221cos 22a c b B ac +-==-,∴0120B =.(Ⅱ)由(Ⅰ)知060A C +=,∴cos()cos cos sin sin A C A C A C -=+ cos cos sin sin 2sin sin A C A C A C =-+cos()2sin sin A C A C=++122=+= ∴030A C -=或030A C -=-, ∴015C =或045C =.19.解:(Ⅰ)证明:取BC 的中点E ,连结DE ,则ABED 为正方形.过P 作OP ⊥平面ABCD ,垂足为O .连接,,,OA OB OD OE .由PAB ∆和PAD ∆都是等边三角形知PA PB PD ==,∴OA OB OD ==,即点O 为正方形ABED 对角线的交点,∴OE BD ⊥,从而PB OE ⊥. ∵O 是BD 的中点,E 是BC 的中点,∴OE //CD .∴PB CD ⊥. (Ⅱ)由(Ⅰ)知,PB CD ⊥,OP CD ⊥,PB OP P = , ∴CD ⊥平面PBD .∵PD ⊂平面PBD ,∴CD PD ⊥. 由知取PD 的中点F ,PC 中点G ,连接GF ,则GF //CD ,GF PD ⊥.连接AF ,由PAD ∆都是等边三角形知AF PD ⊥.∴AFG α∠=是二面角A PD C --的平面图角.连接,AG EG ,则EG //PB . 又PB AE ⊥,∴EG AE ⊥. 设2AB =,则112AE EG PB ===,3AG =.∴在AFG ∆中,12FG CD AF ===3AG =.∴222cos 23FG AF AG FG AF α+-==- ,二面角A PD C --的大小为196π-. 注:(Ⅱ)第小题可以用坐标方法求解. 20.(本小题满分12分) 解:(Ⅰ)记1A 表示事件“第2局结果为甲胜”,2A 表示事件“第3局甲参加比赛时,结果为甲负”,A 表示事件“第4局甲当裁判”.则12=A A A ⋅.12121()=P()()()4P A A A P A P A ⋅==. (Ⅱ)由条件知X 的可能取值为0,1,2. 3A 表示事件“第3局乙和丙比赛时,结果为乙胜”,记1B 表示事件“第1局结果为乙胜”,2B 表示事件“第2局乙和甲比赛时,结果为乙胜”,3B 表示事件“第3局乙参加比赛时,结果为乙负”. 则123(0)()P x P B B A ==⋅⋅1231()()()8P B P B P A =⋅⋅=,13(2)()P X P B B ==⋅131()()4P B P B ==,∴5(1)1(0)(2)8P X P X P X ==-=-==. ∴1519()0128848E X =⨯+⨯+⨯=. 21.(本小题满分12分) 解: (Ⅰ)由题设知3ca=,即 2229a b a+=,∴228b a =, ∴C 的方程为22288x y a -=.将2y =代入上式,求得,x =由题设知,=,解得,21a =.∴1,a b ==(Ⅱ)由(Ⅰ)知,1(3,0)F -,2(3,0)F ,C 的方程为2288x y -=. ①由题意可设l 的方程为(3)y k x =-,||k <,代入①并化简得2222(8)6980k x k x k --++=. ② 设11(,)A x y ,22(,)B x y ,则12,x x 是方程的两个根,且11x ≤-,21x ≥,212268k x x k +=-, 2122988k x x k +∙=-.∴1||AF =1(31)x ==-+,1||BF =231x ==+由11||||AF BF =得,12(31)31x x -+=+,即1223x x +=-. ∴226283k k =--,解得245k =,从而 12199x x ∙=-.由于2||AF =113x ==-,2||BF =231x ==-,∴2212||||||23()4AB AF BF x x =-=-+=,221212||||3()9-116AF BF x x x x ∙=+-=.∴222|||||AB|AF BF ∙=, ∴22AF AB BF ,,成等比数列. 22.(本小题满分12分)197解:(Ⅰ)由已知条件得22(12)(0)0,(),(0)0(1)x x f f x f x λλ--''===+.若12λ<,则当02(12)x λ<<-时,()0f x '>,∴()0f x >.若12λ≥,则当0x >时,()0f x '<,∴当0x >时,()0f x <.综上可得:λ的最小值为12.(Ⅱ)令1x k =12λ=由(Ⅰ)得当0x >时,()0f x <,即 ()()2ln 122x x x x+>++.取1x k =,则()21ln 1ln 2(1)k k k k k +>+-+. ∴214n n a a n -+11111224n n n n ⎛⎫=++⋅⋅⋅++ ⎪++⎝⎭111122(1)2(1)2(2)n n n n ⎛⎫⎛⎫=+++ ⎪ ⎪+++⎝⎭⎝⎭112(21)2(2)n n ⎛⎫+++⎪-⎝⎭21232(1)2(1)(2)n n n n n n ++=++++ 412(21)(2)n n n -++-()()ln(1)ln ln(2)ln(1)n n n n >+-++-+ ()ln(2)ln(21)n n ++--ln(2)ln n n =- ln 2=.∴21ln 24n n a a n-+>.2013年普通高等学校招生全国统一考试 理科数学理科数学(新课标I 卷)参考答案第Ⅰ卷(选择题 60分)一、选择题(共60分)1-12 BDCCA ACABD DB第Ⅱ卷(非选择题 90分)二填空题(共20分) 13.2 14.1(2)n --15. 16.16 三、解答题 17.(本小题满分12分)解:(Ⅰ)由已知得,∠PBC =o60, ∴∠PBA =30o .在△PBA 中,由余弦定理得2PA=o 1132cos3042+-=74, ∴PA(Ⅱ)设∠PBA =α,由已知得, sin PB α=.在△PBA中,由正弦定理得 o o sin sin150sin(30)αα=-,化简得 4sin αα=,即tanα, ∴tan PBA ∠说明:本题主要考查利用正弦定理、余弦定理解三角形及两角和与差公式,是容易题. 18.(本小题满分12分) 解:(Ⅰ)取AB 中点O ,连接OC ,1A B ,1OA .∵AB =1AA ,1BAA ∠=060,198∴1BAA ∆是正三角形,∴1OA ⊥AB . ∵AC BC =, ∴OC ⊥AB ,∵1OC OA O ⋂=,∴AB ⊥面1CEA , ∴AB ⊥1AC .(Ⅱ)由(Ⅰ)知OC ⊥AB ,1OA ⊥AB . 又∵面ABC ABC ⊥面11ABB A ,面ABC ∩面11ABB A =AB , ∴OC ⊥面11ABB A ,∴OC ⊥1OA . ∴OA ,OC ,1OA 两两相互垂直. 以O 为坐标原点,OA 的方向为x 轴正方向,OA 为单位长度,建立如图所示空间直角坐标系O xyz -.由题设知1(1,0,0),A A,C ,(1,0,0)B -,则11(1(1BC BB AA ===-,1(0,AC = . 设n =(,,)x y z 是平面11CBBC 的法向量,则100BC BB ⎧⋅=⎪⎨⋅=⎪⎩n n,即0,0.x x ⎧=⎪⎨-+=⎪⎩,可取,1)=-n ,∴111cos ,|AC AC AC ⋅<>==n n |n ||, ∴直线C A 1 与平面C C BB 11所成角的正弦说明:本题主要考查空间线面、线线垂直的判定与性质及线面角的计算,考查空间想象能力、逻辑推论证能力,是容易题. 19.(本小题满分12分)解:(Ⅰ)设第一次取出的4件产品中恰有3件优质品为事件A ,第一次取出的4件产品中全为优质品为事件B ,第二次取出的4件产品都是优质品为事件C ,第二次取出的1件产品是优质品为事件D ,这批产品通过检验为事件E ,根据题意有()()E AB CD = ,且AB 与CD 互斥,∴()()()P E P AB P CD =+()()()()P A P B A P C P D C =+244341111132222264C ⎛⎫⎛⎫⎛⎫=⨯⨯+⨯= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭. (Ⅱ)X 的可能取值为400,500,800,并且 343411111(400)122216P X C ⎛⎫⎛⎫==-⨯-= ⎪ ⎪⎝⎭⎝⎭,1(500)16P X ==,334111(800)224P X C ⎛⎫==⨯= ⎪⎝⎭,∴X 的分布列为1111()400500800506.2516164E X =⨯+⨯+⨯=. 20.(本小题满分12分)解:由已知得圆M 的圆心为(1,0)M -,半径1r =1,圆N 的圆心为(1,0)N ,半径2r =3. 设动圆P 的圆心为(,)P x y ,半径为R. (Ⅰ)∵圆P 与圆M 外切且与圆N 内切, ∴|PM|+|PN|=12()()R r r R ++-=12r r +=4,由椭圆的定义可知,曲线C 是以M ,N 为左、右焦点,长半轴长为2,的椭圆(左顶点除外),其方程为221(2)43x y x +=≠-. (Ⅱ)对于曲线C 上任意一点(,)P x y ,由于|PM|-|PN|=22R -≤2,∴2R ≤.当且仅当圆P 的圆心为(2,0)时,2R =, ∴当圆P 的半径最长时,其方程为22(2)4x y -+=.当l 的倾斜角为090时,则l 与y 轴重合,可得|AB|=199GF D EB A O 当l 的倾斜角不为090时,由1r R ≠知l 不平行x 轴,设l 与x 轴的交点为Q ,则||||QP QM =1Rr ,可求得(4,0)Q -,∴设l :(4)y k x =+.由l 于圆M1=,解得k =.当k时,将y x =+221(2)43x y x +=≠-并整理得 27880x x +-=,解得1,2x=47-±,∴12|x x -=187.当k =-时,由图形的对称性可知|AB |=187.综上,|AB |=187或|AB|=21.(本小题满分12分) 解:(Ⅰ)由已知得(0)2,(0)2,(0)4,(0)4f g f g ''====,而()2f x x b '=+,()()xg x e cx d c '=++, ∴a =4,b =2,c =2,d =2.(Ⅱ)由(Ⅰ)知,2()42f x x x =++,()2(1)x g x e x =+.设函数()F x =()()kg x f x -=22(1)42xke x x x +---(2x ≥-),则()F x '=2(2)24x ke x x +--=2(2)(1)xx ke +-.由题设可得(0)0F ≥,即1k ≥. 令()F x '=0得,1x =ln k -,22x =-.(1)若21k e ≤<,则120x -<≤, ∴当1(2,)x x ∈-时,()F x '<0, 当1(,)x x ∈+∞时,()F x '>0,即()F x 在1(2,)x -单调递减,在1(,)x +∞单调递增,∴()F x 在x =1x 取最小值1()F x ,而1()F x =21112242x x x +---=11(2)0x x -+≥, ∴当2x ≥-时,()0F x ≥,即 ()()f x kg x ≤恒成立.(2)若2k e =,则()F x '=222(2)()x e x e e -+-. ∴当2x ≥-时,()0F x '≥,∴()F x 在(-2,+∞)单调递增,而(2)F -=0,∴当2x ≥-时,()0F x ≥,即 ()()f x kg x ≤恒成立.(3)若2k e >,则(2)F -=222ke --+=222()e k e ---<0, ∴当2x ≥-时,()f x ≤()kg x 不可能恒成立.综上所述,k 的取值范围为[1,2e ].说明:本题主要考查利用导数的几何意义求曲线的切线、函数单调性与导数的关系、函数最值,考查运算求解能力及应用意识,是中档题. 22.(本小题满分10分) 解:(Ⅰ)连接DE ,交BC 与点G . 由弦切角定理得,ABF BCE ∠=∠, ∵ABE CBE ∠=∠,∴CBE BCE ∠=∠,BE CE =,200又∵BD BE ⊥,∴DE 是直径,90DCE ∠=︒, 由勾股定理可得DB DC =(Ⅱ)由(Ⅰ)知,CDEBDE ∠=∠,DB DC =,∴DG 是BC 的中垂线,∴BG =.设DE 中点为O ,连接OB ,则 60BOG ∠=︒,30ABE BCE CBE ∠=∠=∠=︒, ∴CF BF ⊥,∴Rt △BCF 说明:本题主要考查几何选讲的有关知识,是容易题. 23,(本小题满分10分)解(Ⅰ)将45cos 55sin x ty t =+⎧⎨=+⎩消去参数t ,化为普通方程22(4)(5)25x y -+-=,即1C :22810160x y x y +--+=. 将cos sin x y ρθρθ=⎧⎨=⎩ 代入22810160x y x y +--+=得,28cos 10sin 160ρρθρθ--+=,∴1C 的极坐标方程为28cos 10sin 160ρρθρθ--+=.(Ⅱ)2C 的普通方程为2220x y y +-=,由2222810160,20x y x y x y y ⎧+--+=⎪⎨+-=⎪⎩ 解得11x y =⎧⎨=⎩或02x y =⎧⎨=⎩,∴1C 与2C 的交点的极坐标分别为4π),(2,)2π. 说明:本题主要考查参数方程与普通方程互化、极坐标方程与直角坐标方程互化及两曲线交点求法、极坐标与直角坐标互化,是容易题.24.(本小题满分10分) 解:(Ⅰ)当2a =-时,不等式()f x <()g x 化为|21||22|30x x x -+---<. 设函数y =|21||22|3x x x -+---,则y =15, ,212, 236, 1,x x x x x x ⎧-<⎪⎪⎪--≤⎨⎪->⎪⎪⎩其图像如图所示,从图像可知,当且仅当(0,2)x ∈时,0y <,∴原不等式解集是{|02}x x <<.(Ⅱ)当x ∈1,22a ⎡⎫-⎪⎢⎣⎭时,()f x =1a +,不等式()()f x g x ≤化为13a x +≤+,∴2x a ≥-对x ∈[2a -,12)都成立,故2a-≥2a -,即a ≤43,∴a 的取值范围为41,3⎛⎤- ⎥⎝⎦.说明:本题主要考查含绝对值不等式解法、不等式恒成立求参数范围,是容易题.2012013年普通高等学校招生全国统一考试理科数学(新课标Ⅱ卷)参考答案 第Ⅰ卷(选择题 60分)一、选择题:(共60分) 1-12 AACDD BADBC CB第Ⅱ卷(非选择题 90分)二、填空题:本大题共4小题,每小题5分.13.2 14.8 15.510-16.-49 三.解答题:解答应写出文字说明,证明过程或演算步骤。
(完整word版)2013年全国高考理科数学试题及答案、解析-陕西卷

试题及答案、解析2013年普通高等学校招生全国统一考试理科数学注意事项:1. 本试卷分为两部分,第一部分为选择题,第二部分为非选择题 .。
2. 考生领到试卷后,须按规定在试卷上填写姓名、准考证号,并在答题卡上填涂对应的试卷 类型信息.。
3. 所有解答必须填写在答题卡上指定区域内。
考试结束后,将本试卷和答题卡一并交回。
第一部分(共50分)一、选择题:在每小题给出的四个选项中,只有一项符合题目要求(本大题共 分,共50分) 1.设全集为R,函数f(x)乞1 -x 2的定义域为 M,则C R M 为 (A) [ - 1,1] (B) (- 1,1)(C) ( J :,-1] -•[1, (D) ( -::, -〔)_. (1, ■::)【答案】D2. 根据下列算法语句,当输入x 为60时, 输出y 的值为(A) 25 (B) 30 (C) 31 (D) 61 【答案】C【解析】 x =60,. y =25 0.6 (x-50) =31 ,所以选 C3.设 a, b 为向量,贝U “ab |=|a || b |”是 a // b”的 (A)充分不必要条件 (B)必要不充分条件 (C)充分必要条件(D)既不充分也不必要条件【答案】C10小题,每小题5【解析】1-X 2 _0,. 一1 乞 x 叮.即 M =[-1,1],c M—(—cQ , 一 1)U (1&),所以选D:输入xI:If x < 50 ThenI:y=0.5 * x :Else; y=25+0.6*( x-50) :End If i 输出y【解析】a b a | |b | COST若| a b|=| a | |b| : cos)- -1,则向量a与b的夹角为0或二,即a//b为真;相反,若a//b,则向量0与b的夹角为0或二,即|a 6鬥2| |b|。
所以“ab 旧a || b |”是a // b”的充分必要条件。
另:当向量a 或b 为零向量时,上述结论也成立。
2013年全国高考数学试题分类汇编算法初步与框图
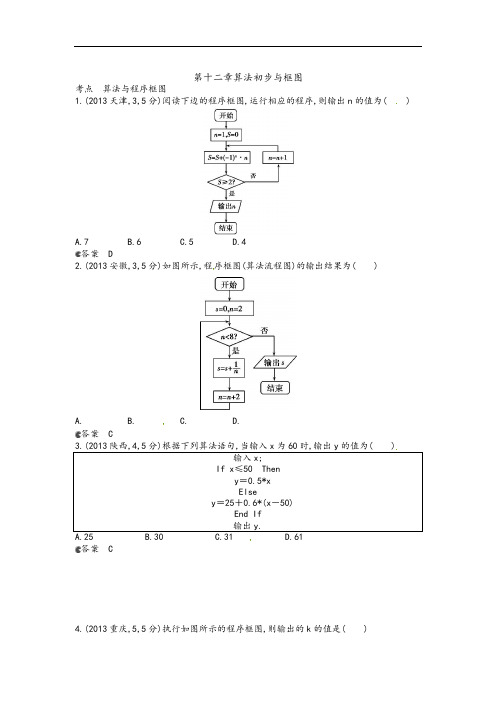
第十二章算法初步与框图考点算法与程序框图1.(2013天津,3,5分)阅读下边的程序框图,运行相应的程序,则输出n的值为( )A.7B.6C.5D.4答案 D2.(2013安徽,3,5分)如图所示,程序框图(算法流程图)的输出结果为( )A. B. C. D.答案 C3.(2013陕西,4,5分)根据下列算法语句,当输入x为60时,输出y的值为( )输入x;If x≤50Theny=0.5*xElsey=25+0.6*(x-50)End If输出y.A.25B.30C.31D.61答案 C4.(2013重庆,5,5分)执行如图所示的程序框图,则输出的k的值是( )A.3B.4C.5D.6答案 C5.(2013北京,6,5分)执行如图所示的程序框图,输出的S值为( )A.1B.C.D.答案 C6.(2013山东,6,5分)执行两次如图所示的程序框图,若第一次输入的a的值为-1.2,第二次输入的a的值为1.2,则第一次、第二次输出的a的值分别为( )A.0.2,0.2B.0.2,0.8C.0.8,0.2D.0.8,0.8答案 C、7.(2013江西,7,5分)阅读如下程序框图,如果输出i=4,那么空白的判断框中应填入的条件是( )A.S<8B.S<9C.S<10D.S<11答案 B8.(2013课标全国Ⅱ,7,5分)执行下面的程序框图,如果输入的N=4,那么输出的S=( )A.1+++B.1+++C.1++++D.1++++答案 B9.(2013辽宁,8,5分)执行如图所示的程序框图,若输入n=8,则输出S=( )A. B. C. D.答案 A10.(2013广东,5,5分)执行如图所示的程序框图,若输入n的值为3,则输出s的值是( )A.1B.2C.4D.7答案 C11.(2013湖北,13,5分)阅读如图所示的程序框图,运行相应的程序.若输入m的值为2,则输出的结果i=.答案 412.(2013浙江,14,4分)若某程序框图如图所示,则该程序运行后输出的值等于.答案13.(2013湖南,12,5分)执行如图所示的程序框图,如果输入a=1,b=2,则输出的a的值为.答案9。
2013年全国高考理科数学试题分类汇编12:程序框图Word版含答案
2013 年全国高考理科数学试题分类汇编 12:程序框图一、选择题1 .( 2013 年高考北京卷(理) )履行以下图的程序框图, 输出的 S 值为开始i0, S 1SS 2 12 S 1i i 1i ≥2 否是输出 S结束()A . 1B .2 C .13D . 610【答案】 C3219872 .( 2013 年一般高等学校招生一致考试浙江数学(理)试题(纯WORD 版)) 某程序框图如图所示 , 若该程序运转后输出的值是9, 则()5D . a 7A . a 4B . a 5C . a 6开始 S=1,k=1是k>a?否1 S=S+k(k+1)k=k+1输出 S结束(第 5 题图)【答案】 A3 .( 2013 年一般高等学校招生一致考试安徽数学(理)试题(纯WORD版))以下图,程序框图( 算法流程图 ) 的输出结果是()A.1B.25C.3D.11 624412【答案】 D4 .( 2013 年一般高等学校招生一致考试重庆数学(理)试题(含答案))履行如题 (8) 图所示的程序框图 , 假如输出s 3 , 那么判断框内应填入的条件是()A.k 6B.k 7C.k 8D.k 9【答案】 B5 .( 2013 年高考江西卷(理))阅读以下程序框图, 假如输出i 5 ,那么在空白矩形框中应填入的语句为()A.S2* i2B.S2* i1C.S2* i D.S2* i4【答案】 C6 .( 2013 年一般高等学校招生一致考试福建数学(理)试题(纯WORD版))阅读以下图的程序框图, 若输入的k10 ,则该算法的功能是()A.计算数列2n1的前 10 项和B.计算数列2n 1的前 9项和C.计算数列2n 1 的前10项和D.计算数列2n 1 的前9项和【答案】 A7 .( 2013 年一般高等学校招生一致考试新课标Ⅱ卷数学(理)(纯WORD版含答案))履行右边的程序框图 , 假如输入的N 10 ,那么输出的S开始输入 Nk 1,S 0,T1T T kS S Tk k 1否k N ?是输出 S结束()111B 111⋯⋯ +1A.13⋯⋯ +!!!210.2310111D 111⋯⋯ +1C.13⋯⋯+!!!211.2311【答案】 B8 .( 2013 年一般高等学校招生一致考试辽宁数学(理)试题(WORD版))履行以下图的程序框图 , 若输入n10, 则输出的 S()A.5B.10C.36D.72 11115555【答案】 A9 .( 2013 年高考新课标1(理))运转以下程序框图, 假如输入的t[ 1,3] ,则输出s属于()A.[ 3,4]B. [ 5,2]C.[4,3]D.[2,5]【答案】 A10.( 2013 年高考陕西卷(理))依据以下算法语句,当输入 x 为60时 ,输出 y 的值为输入 xIf x≤ 50 Theny=0.5 * xElsey=25+0.6*( x-50)End If输出 y()A. 25B. 30C. 31D. 61【答案】 C11.( 2013 年一般高等学校招生一致考试天津数学(理)试题(含答案))阅读右侧的程序框图 ,运转相应的程序 ,若输入 x 的值为1,则输出 S 的值为()A. 64B. 73C. 512D. 585【答案】 B二、填空题12.( 2013 年高考湖南卷(理))履行如图 3 所示的程序框图, 假如输入a1,b 2, 则输出的 a的值为_____9_____.【答案】 913.( 2013 年一般高等学校招生全国一致招生考试江苏卷(数学)(已校正纯WORD版含附带题)), 则输出的n 的值是________.以下图是一个算法的流程图【答案】314.( 2013年一般高等学校招生一致考试广东省数学(理)卷(纯WORD版))履行以下图的程序框图, 若输入n 的值为4,则输出s 的值为______.开始输入 ni1,s1否i n是输出 ss s i 1结束i i1第 11题图7【答案】15.( 2013年高考湖北卷(理))阅读以下图的程序框图, 运转相应的程序, 输出的结果i___________.开始a10, i1a 4?是否是a 是奇数?否a 3a1a a输出i2i i 1结束【答案】516.( 2013 年一般高等学校招生一致考试山东数学(理)试题(含答案))履行右图的程序框图 ,若输入的的值为0.25, 则输出的 n 的值为 _____.【答案】 3。
2013年高考理科数学试卷及答案---全国卷(新课标版)word版

2013年全国卷新课标数学(理)一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知集合}5,4,3,2,1{=A ,},,|),{(A y x A y A x y x B ∈-∈∈=,则B 中所含元素的个数为A. 3B. 6C. 8D. 102. 将2名教师,4名学生分成两个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由一名教师和2名学生组成,不同的安排方案共有 A. 12种 B. 10种 C. 9种 D. 8种3. 下面是关于复数iz +-=12的四个命题: :1P 2||=z:2P i z 22= :3P z 的共轭复数为i +1:4P z 的虚部为1-其中的真命题为A. 2P ,3PB. 1P ,2PC. 2P ,4PD. 3P ,4P4. 设21,F F 是椭圆:E 12222=+by a x )0(>>b a 的左右焦点,P 为直线23a x =上的一点,12PF F △是底角为︒30的等腰三角形,则E 的离心率为A.21B.32 C.43 D.54 5. 已知}{n a 为等比数列,274=+a a ,865-=a a ,则=+101a aA.7B. 5C.5-D. 7-6. 如果执行右边的程序框图,输入正整数N )2(≥N 和 实数N a a a ,,,21 ,输出A ,B ,则A. B A +为N a a a ,,,21 的和B.2BA +为N a a a ,,,21 的算术平均数 C. A 和B 分别是N a a a ,,,21 中最大的数和最小的数D. A 和B 分别是N a a a ,,,21 中最小的数和最大的数7. 如图,网格纸上小正方形的边长为1,粗线画出的 是某几何体的三视图,则此几何体的体积为 A. 6 B. 9 C. 12 D. 188. 等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于A ,B ,两点,34||=AB ,则的实轴长为A.2B. 22C. 4D. 89. 已知0>ω,函数)4sin()(πω+=x x f 在),2(ππ单调递减,则ω的取值范围是A. ]45,21[B. ]43,21[C. ]21,0(D. ]2,0(10. 已知函数xx x f -+=)1ln(1)(,则)(x f y =的图像大致为11. 已知三棱锥ABC S -的所有顶点都在球O 的球面上,ABC △是边长为1的正三角形,SC 为球O 的直径,且2=SC ,则此棱锥的体积为A.62 B.63 C.32 D.22 12. 设点P 在曲线xe y 21=上,点Q 在曲线)2ln(x y =上,则||PQ 的最小值为A. 2ln 1-B.)2ln 1(2- C. 2ln 1+D.)2ln 1(2+二、填空题.本大题共4小题,每小题5分.13.已知向量a ,b 夹角为︒45,且1=||a ,102=-||b a ,则=||b .14. 设y x ,满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤+-≥-0031y x y x y x 则y x Z 2-=的取值范围为 .15. 某一部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)服从正态分布)50,1000(2N ,且各元件能否正常工作互相独立,那么该部件的使用寿命超过1000小时的概率为 .16. 数列}{n a 满足12)1(1-=-++n a a n n n ,则}{n a项和为 . 三、解答题:解答题应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分) 已知a ,b ,c 分别为ABC △三个内角A ,B ,C 的对边,0sin 3cos =--+c b C a C a . (Ⅰ) 求A ;(Ⅱ) 若2=a ,ABC △的面积为3,求b ,c .18. (本小题满分12分) 某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.(Ⅰ) 若花店某天购进16枝玫瑰花,求当天的利润y (单位:元)关于当天需求量n (单位:枝,N n ∈)的函数解析式;(Ⅱ) 花店记录了100以100天记录的各需求量的频率作为各需求量发生的概率. (ⅰ)若花店一天购进16枝玫瑰花,X 表示当天的利润(单位:元),求X 的分布列、数学期望及方差; (ⅱ)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.19. (本小题满分12分)如图,直三棱柱111C B AABC -中,121AA BC AC ==,D 是棱1AA 的中点,BD DC ⊥1 (Ⅰ) 证明:BC DC ⊥1(Ⅱ) 求二面角11C BD A --的大小.20. (本小题满分12分)设抛物线:C py x 22=)0(>p 的焦点为F ,准线为l ,A 为C 上一点,已知以F 为圆心,FA 为半径的圆F 交l 于B 、D 两点(Ⅰ) 若90BFD ∠=︒,ABD △面积为24,求p 的值及圆F 的方程;(Ⅱ)若A 、B 、F 三点在同一直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到m ,n 的距离的比值.21. (本小题满分12分) 已知函数121()(1)(0)2x f x f ef x x -'=-+. (Ⅰ) 求)(x f 的解析式及单调区间;(Ⅱ) 若b ax x x f ++≥221)(,求b a )1(+的最大值请考生在第22、23、24题中任选一题作答,如果多做,则按所做第一题记分,作答时请写清题号. 22. (本小题满分10分)选修4—1:几何证明选讲 如图,D ,E 分别为ABC △边AB ,AC 的中点,直线DE 交ABC △的 外接圆于F ,G 两点.若AB CF //,证明: (Ⅰ) BC CD =;(Ⅱ) GBD BCD ∽△△.23. (本小题满分10分)选修4—4:坐标系与参数方程已知曲线1C 的参数方程是2cos 3sin x y ϕϕ=⎧⎨=⎩(ϕ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程是2=ρ.正方形ABCD 的顶点都在2C 上,且A ,B ,C ,D 依逆时针次序排列,点A 的极坐标为)3,2(π.(Ⅰ)点A ,B ,C ,D 的直角坐标;(Ⅱ) 设P 为1C 上任意一点,求2222||||||||PD PC PB PA +++的取值范围.24. (本小题满分10分)选修4—5:不等式选讲 已知函数|2|||)(-++=x a x x f .(Ⅰ) 当3a =-时,求不等式3)(≥x f 的解集;(Ⅱ) |4|)(-≤x x f 的解集包含]2,1[,求a 的取值范围.参考答案1-12:DACCD CBCAB AB 13、 14、[]3,3-. 15、3816、1830. 17、解:(Ⅰ)由cos sin 0a C C b c --=及正弦定理可得sin cos sin sin sin 0A C A C B C --=,()sin cos sin sin sin 0A C A C A C C +-+-=,sin cos sin sin 0A C A C C --=,sin 0C >,cos 10A A --=,2sin 106A π⎛⎫∴--= ⎪⎝⎭,1sin 62A π⎛⎫-= ⎪⎝⎭,0A π<< ,5666A πππ∴-<-<,66A ππ∴-=3A π∴=(Ⅱ)ABC S = △1sin 2bc A ∴==4bc ∴=, 2,3a A π==,222222cos 4a b c bc A b c bc ∴=+-=+-=, 228b c ∴+=. 解得2b c ==.18、解:(Ⅰ) ()()1080,1580,16 n n y n -≤⎧⎪=⎨≥⎪⎩(n N ∈); (Ⅱ) (ⅰ)若花店一天购进16枝玫瑰花,X 的分布列为X 的数学期望()E X =60×0.1+70×0.2+80×0.7=76,X 的方差()D X =(60-762)×0.1+(70-762)×0.2+(80-762)×0.7=44.(ⅱ)若花店计划一天购进17枝玫瑰花,XX 的数学期望()E X =55×0.1+65×0.2+75×0.16+85×0.54=76.4,因为76.4>76,所以应购进17枝玫瑰花. 19、(Ⅰ) 证明:设112AC BC AA a ===, 直三棱柱111C B A ABC -, 1DC DC ∴==, 12CC a =,22211DC DC CC ∴+=,1DC DC ∴⊥. 又1DC BD ⊥ ,1DC DC D =,1DC ∴⊥平面BDC .BC⊂ 平面BDC ,1DC BC ∴⊥.(Ⅱ)由 (Ⅰ)知,1DC =,1BC =,又已知BD DC ⊥1,BD ∴=. 在Rt ABD △中,,,90BD AD a DAB =∠= , AB ∴=.222AC BC AB ∴+=,AC BC ∴⊥.取11A B 的中点E ,则易证1C E ⊥平面1BDA ,连结DE ,则1C E ⊥BD , 已知BD DC ⊥1,BD ∴⊥平面1DC E ,BD ∴⊥DE ,1C DE ∴∠是二面角11C BD A --平面角.在1Rt C DE △中,1111sin 2C EC DE C D∠===,130C DE ∴∠= .即二面角11C BD A --的大小为30.20、解: (Ⅰ)由对称性可知,BFD △为等腰直角三角形,斜边上的高为p ,斜边长2BD p =.点A 到准线l的距离d FB FD ===.由ABD S =△,11222BD d p ⨯⨯=⨯=2p ∴=.圆F 的方程为()2218x y +-=.(Ⅱ)由对称性,不妨设点(),A A A x y 在第一象限,由已知得线段AB 是圆F 的在直径,90o ADB ∠=,2BD p ∴=,32A y p ∴=,代入抛物线:C py x 22=得A x . 直线m的斜率为3AF k ==.直线m的方程为0x =. 由py x 22= 得22x y p=,x y p '=.由3x y p '==, 3x p =.故直线n 与抛物线C的切点坐标为6p ⎫⎪⎪⎝⎭, 直线n的方程为06x -=. 所以坐标原点到m ,n3=. 21、解: (Ⅰ) 1()(1)(0)x f x f ef x -''=-+,令1x =得,(0)1f =, 再由121()(1)(0)2x f x f e f x x -'=-+,令0x =得()1f e '=. 所以)(x f 的解析式为21()2x f x e x x =-+. ()1x f x e x '=-+,易知()1x f x e x '=-+是R 上的增函数,且(0)0f '=.所以()00,()00,f x x f x x ''>⇔><⇔<所以函数)(x f 的增区间为()0,+∞,减区间为(),0-∞.(Ⅱ) 若b ax x x f ++≥221)(恒成立,即()()21()102x h x f x x ax b e a x b =---=-+-≥恒成立, ()()1x h x e a '=-+ ,(1)当10a +<时,()0h x '>恒成立, ()h x 为R 上的增函数,且当x →-∞时, ()h x →-∞,不合题意;(2)当10a +=时,()0h x >恒成立, 则0b ≤,(1)0a b +=;(3)当10a +>时, ()()1xh x e a '=-+为增函数,由()0h x '=得()ln 1x a =+, 故()()()0ln 1,()0ln 1,f x x a f x x a ''>⇔>+<⇔<+当()ln 1x a =+时, ()h x 取最小值()()()()ln 111ln 1h a a a a b +=+-++-.依题意有()()()()ln 111ln 10h a a a a b +=+-++-≥,即()()11ln 1b a a a ≤+-++, 10a +> ,()()()()22111ln 1a b a a a ∴+≤+-++,令()()22ln 0 u x x x x x =->,则()()22ln 12ln u x x x x x x x '=--=-, ()00()0u x x u x x ''>⇔<<⇔,所以当x =, ()u x取最大值2e u =.故当12a b+==时, ()1a b+取最大值2e.综上, 若baxxxf++≥221)(,则ba)1(+的最大值为2e.22、证明:(Ⅰ) ∵D,E分别为ABC△边AB,AC的中点,∴//DE BC.//CF AB,//DF BC,CF BD∴ 且=CF BD,又∵D为AB的中点,CF AD∴ 且=CF AD,CD AF∴=.//CF AB,BC AF∴=.CD BC∴=.(Ⅱ)由(Ⅰ)知,BC GF,GB CF BD∴==,BGD BDG DBC BDC∠=∠=∠=∠BCD GBD∴△∽△.23、解:(Ⅰ)依题意,点A,B,C,D的极坐标分别为.所以点A,B,C,D的直角坐标分别为、(、(1,-、1)-;(Ⅱ) 设()2cos,3sinPϕϕ,则2222||||||||PDPCPBPA+++())2212cos3sinϕϕ=-+()()222cos13sinϕϕ++-()()2212cos3sinϕϕ+--+)()222cos13sinϕϕ++--2216cos36sin16ϕϕ=++[]23220sin32,52ϕ=+∈.所以2222||||||||PD PC PB PA +++的取值范围为[]32,52.24、解:(Ⅰ) 当3a =-时,不等式3)(≥x f ⇔ |3||2|3x x -+-≥⇔ ()()2323x x x ≤⎧⎪⎨----≥⎪⎩或()()23323x x x <<⎧⎪⎨-++-≥⎪⎩或()()3323x x x ≥⎧⎪⎨-+-≥⎪⎩⇔或4x ≥.所以当3a =-时,不等式3)(≥x f 的解集为{1x x ≤或}4x ≥. (Ⅱ) ()|4|f x x ≤-的解集包含]2,1[,即|||2||4|x a x x ++-≤-对[]1,2x ∈恒成立,即||2x a +≤对[]1,2x ∈恒成立,即22a x a --≤≤-对[]1,2x ∈恒成立, 所以2122a a --≤⎧⎨-≥⎩,即30a -≤≤.所以a 的取值范围为[]3,0-.。
2013年高考理科数学(陕西卷)解析版Word版含答案

2013年普通高等学校招生全国统一考试理科数学注意事项:1. 本试卷分为两部分, 第一部分为选择题,第二部分为非选择题.。
2. 考生领到试卷后,须按规定在试卷上填写姓名、准考证号,并在答题卡上填涂对应的试卷类型信息.。
3. 所有解答必须填写在答题卡上指定区域内。
考试结束后,将本试卷和答题卡一并交回。
第一部分(共50分)一、选择题:在每小题给出的四个选项中,只有一项符合题目要求(本大题共10小题,每小题5分,共50分)1. 设全集为R, 函数的定义域为M, 则为(A) [-1,1] (B) (-1,1)(C)(D)【答案】D【解析】,所以选D输入xIf x≤50 Theny=0.5 * xElsey=25+0.6*(x-50)End If输出y2. 根据下列算法语句, 当输入x为60时,输出y的值为(A) 25(B) 30(C) 31(D) 61【答案】C【解析】,所以选C3. 设a, b为向量, 则“”是“a//b”的(A) 充分不必要条件 (B) 必要不充分条件(C) 充分必要条件 (D) 既不充分也不必要条件【答案】C【解析】若,为真;相反,若,则。
所以“”是“a//b”的充分必要条件。
另:当为零向量时,上述结论也成立。
所以选C4. 某单位有840名职工, 现采用系统抽样方法, 抽取42人做问卷调查, 将840人按1, 2, …, 840随机编号, 则抽取的42人中, 编号落入区间[481, 720]的人数为(A) 11 (B) 12 (C) 13 (D) 14【答案】B【解析】使用系统抽样方法,从840人中抽取42人,即从20人抽取1人。
,所以从编号1~480的人中,恰好抽取24人,接着从编号481~720共240人中抽取12人。
故选B5. 如图, 在矩形区域ABCD的A, C两点处各有一个通信基站, 假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源, 基站工作正常). 若在该矩形区域内随机地选一地点, 则该地点无信号的概率是(A)(B)(C)(D)【答案】A【解析】该地点信号的概率=所以该地点无信号的概率是。
2013年高考试题分类汇编(程序框图)

2013年高考试题分类汇编(程序框图)1.(2013·全国卷Ⅰ·文理科)执行右面的程序框图,如果输入的[1,3]t∈-,则输出的S属于A.[3,4]- B.[5,2]- C.[4,3]- D.[2,5]-2.(2013·全国卷Ⅱ·理科)执行右面的程序框图,如果输入的10N =,那么输出的S=A.11112310++++ B.11112!3!10!++++C.11112311++++ D.11112!3!11!++++3.(2013·全国卷Ⅱ·文科)执行右面的程序框图,如果输入的4N =,那么输出的S =A.1111234+++B.1111232432+++⨯⨯⨯ C.111112345++++111112324325432++++⨯⨯⨯⨯⨯⨯4.(2013·山东卷·理科)执行右面的程序框图,若输入的ε的值为025,则输出的n 的值为 .5.(2013·安徽卷·文理科)如图所示,程序框图(算法流程图)的输出结果是A.16B.25C.3D.11126.(2013·浙江卷·理科)某程序框图如图所示,若该程序运行后输出的值是95,则aA.4 B.5 C.6 D.77.(2013·浙江卷·文科)某程序框图如图所示,则该程序运行后输出的值等于______.8.(2013·北京卷·文理科)执行如图所示的程序框图,输出的S 值为A.1B.23C.1321 D.6109879.(2013·天津卷·文理科)阅读右边的程序框图,运行相应的程序,则输出n的值为A .7B .6C .5D .410.(2013·福建卷·文科)阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的(10,20)S∈那么n的值是A.3 B.4 C.5 D.611.(2013·辽宁卷·理科)执行如图所示的程序框图,若输入10n=,则输出S=A.511B.1011C.3655D.725512.(2013·辽宁卷·文科)执行如图所示的程序框图,若输入8n=,则输出S=A.511B.1011C.3655D.725513.(2013·湖南卷·文理科)执行如图所示的程序框图,如果输入1a =,2b =,则输出a 的值是 .14.(2013·江西卷·文理科)阅读如下程序框图,如果输出5i =,那么在空白矩形框中应填入的语句为A.22s i =-B.21s i =-C.2s i =D.24s i =+S15.(2013·湖北卷·理科)阅读如图所示的程序框图,运行相应的程序,输出的结果i= .入m的值为2,则输出的结果i= .17.(2013·重庆卷·理科)执行如图所示的程序框图,如果输出3s =,那么判断框内应填入的条件是A.6k ≤B.k 8k ≤ D.9k ≤18.(2013·广东卷·文理科)执行如图所示的程序框图,若输入n 的值为4,则输出s 的值为 .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年全国高考理科数学试题分类汇编12:程序框图
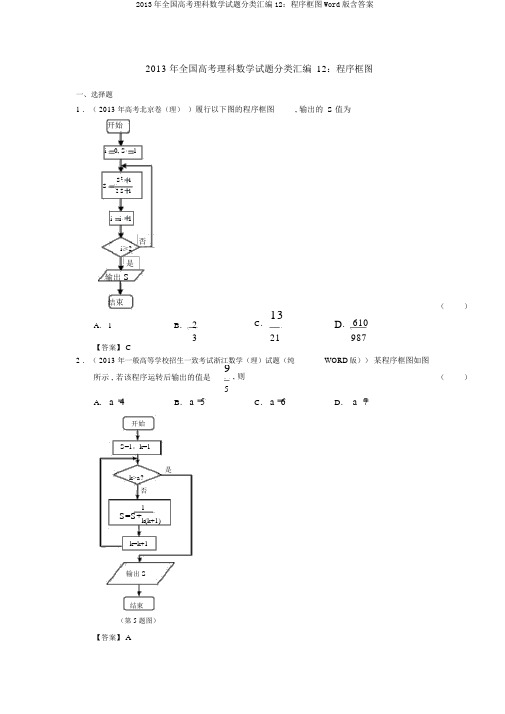
一、选择题
1 .(2013年高考北京卷(理))执行如图所示的程序框图,输出的S 值为
( )
A .1
B .
2
3
C .
1321
D .
610
987
【答案】C
2 .(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))某程序框图如图
所示,若该程序运行后输出的值是5
9,则 ( )
A .4=a
B .5=a
C .6=a
D . 7=a
【答案】A
(第5题图)
3 .(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))如图所示,程序框
图(算法流程图)的输出结果是
( )
A .
1
6
B .
2524 C .
34
D .
1112
【答案】D
4 .(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))执行如题(8)图所示
的程序框图,如果输出3s =,那么判断框内应填入的条件是
( )
A .6k ≤
B .7k ≤
C .8k ≤
D .9k ≤
【答案】B
5 .(2013年高考江西卷(理))阅读如下程序框图,如果输出5i =,那么在空白矩形框中应填
入的语句为
( )
A .2*2S i =-
B .2*1S i =-
C .2*S i =
D .2*4S i =+
【答案】C
6 .(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))阅读如图所示的
程序框图,若输入的10k =,则该算法的功能是
( )
A .计算数列{}
12n -的前10项和 B .计算数列{}12n -的前9项和 C .计算数列{}21n -的前10项和
D .计算数列{
}
21n -的前9项和
【答案】A
7 .(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))执行右面
的程序框图,如果输入的10N =,那么输出的S =
( )
A .1111+2310+
++…… B .
111
1+2310+
++……!!! C .1111+2311+
++……
D .
1
1
1
1+2311+++……!!! 【答案】B
8 .(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))执行如图所示的程序
框图,若输入10,n S ==则输出的 ( )
A .
5
11
B .
1011 C .
3655
D .
7255
【答案】A
9 .(2013年高考新课标1(理))运行如下程序框图,如果输入的[1,3]t ∈-,则输出s 属于
( )
A .[3,4]-
B .[5,2]-
C .[4,3]-
D .[2,5]-
【答案】A
10.(2013年高考陕西卷(理))根据下列算法语句, 当输入x 为60时, 输出y 的值为
( )
A .25
B .30
C .31
D .61
【答案】C
11.(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))阅读右边的程序框图,
运行相应的程序, 若输入x 的值为1, 则输出S 的值为
()
A.64 B.73 C.512 D.585
【答案】B
二、填空题
12.( 2013年高考湖南卷(理))执行如图3所示的程序框图,如果输入
==则输出的的值为_____9_____.
1,2,
a b a
【答案】9
13.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD版含附加题))下图是一个算法的流程图,则输出的n的值是________.
【答案】3
14.(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD版))执行如图所示的程序框图,若输入n的值为4,则输出s的值为______.
【答案】7
15.( 2013年高考湖北卷(理))阅读如图所示的程序框图,运行相应的程序,输出的结果i=___________.
【答案】 5
16.(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))执行右图的程序框图,若输入的ε的值为0.25,则输出的n的值为_____.
【答案】3。
