第三章第一节振动理论基础
振动基础必学知识点

振动基础必学知识点
以下是振动基础必学的知识点:
1. 振动的定义:振动是物体围绕某个平衡位置来回周期性地运动。
2. 振动的周期和频率:振动的周期是振动一个完整循环所需要的时间,单位是秒;频率是单位时间内振动的次数,单位是赫兹。
它们之间有
以下关系:频率 = 1/周期。
3. 振动的幅度:振动的幅度是指物体离开平衡位置的最大距离。
4. 简谐振动:简谐振动是指物体在没有阻力的情况下,围绕平衡位置
做匀速往复运动的振动。
简谐振动的特点是周期恒定、频率固定且幅
度不断变化。
5. 谐振:谐振是指当外力作用频率与物体固有频率相同时,物体容易
发生共振现象,振幅会明显增大的现象。
6. 弹簧振子:弹簧振子是指一个质点通过与弹簧连接,形成一个可以
进行振动的系统。
弹簧振子的运动方程可以用简谐振动的方程表示。
7. 摆钟:摆钟是指一个由质点与一个固定的绳或杆连接,形成可以进
行振动的系统。
摆钟的运动方程可以用简谐振动的方程表示。
8. 声音的传播和振动:声音是由物体的振动引起的机械波。
声音的传
播需要介质的存在,并且介质中的分子通过相互振动来传递能量。
9. 波动的特征:波动的特征包括传播速度、波长、频率和振幅。
10. 波的类型:根据波动传播介质的性质,波可以分为机械波和电磁波两种类型。
以上是振动基础必学的知识点,掌握这些知识可以帮助理解振动和波动以及它们在不同物理现象中的应用。
振动试验理论基础与方法培训

申 奥
2.1.3 电动振动台原理 励磁线圈如图示 2-2 在振动台台体内建立磁场,励磁线圈与直流电源相连,在环行气隙里产生一个高磁
通量。动圈部件,包括台面、骨架和驱动线圈,悬挂在振动台的环行气隙里,当交流电流通过驱动线圈时, 电磁力会在驱动线圈的绕组上产生,使得台面产生向上和向下的往复移动,如图示 2-2 中双向箭头处显示。 台面的移动量取决于振动控制器输出的驱动信号的大小和频率以及扩展台面(如果有的话)的质量、所加的 负载质量和台面悬挂系统的刚度。
根据输出信号不同,分为常规电荷压电和 ICP 压电传感器。
奥 b 压阻式加速度传感器,自发式传感器,其电阻的变化与所承受的机械应力成正比。
c 变电容式加速度传感器,其电容的变化与所承受的机械应力成正比。 (3)按功能分:控制传感器、监测传感器。
测 2.2.3 结构 加速度传感器通常由质量块、阻尼器、弹性元件(弹簧)、敏感元件和适调电路等部分组成,在加速过 程中,通过测量质量块所受的惯性力,利用牛顿第二定律获得加速度。
3.8 响应监测与分析 3.8.1 频率响应分析 系统在外激振作用下发生振动响应,通过采集反馈的振动输出信号,分析各振动参量在频率域的响应信号, 包括加速度频响、速度频响、位移频响。
3.8.2 共振分析 (1)目的:分析在测试振动频率范围,夹具或试样是否发生共振,及固有频率。
(整理)第三章晶体子的热振动

第三章 晶体中原子的热振动第一章、第二章中在讨论晶体的结合、固体中结合力性质以及相关物质性质(例第二章中的压缩系数或体弹性模量、抗张强度等)时曾忽略了晶体中原子热运动的影响(例当时考虑了T=0K 这种最简单的情况),认为固体中原子是处在平衡位置(即()()最小0,00r u rr u rr =∂∂=),这时整个晶体的势能最小,而实际上晶体中原子并非固定不动的,而是在其平衡位置附近或围绕其平衡位置作振动。
这种振动即本章所讨论的所谓热振动,在高于绝于零度以上的任何温度,这种运动都会发生,其振动频率大体在1012-1013次/S ,其振幅的数值决定于温度和晶体本身的性质,其振幅数量便大体为10-9cm 。
在较高温度下,振动原子通过偶然性的统计涨落,可获得高于平均能量的能量,当这种能量的大小足以摆脱周围原子束缚时,原子可离开其平衡位置而到达一个新的平衡位置,即产生扩散现象。
关于这方面的问题将在第四章中讨论。
本章讨论原子的热振动的情况,即在温度不太高时原子作微小振动的情况。
晶体中原子的热振动同晶体的许多重要宏观性质有关,例固体的比热、热膨胀、热传导等热学性质,电阻、超导电性等固体的电学性质,红外吸收与辐射等光学性质等。
所以,对晶体中原子热振动的研究和讨论是认识和了解固体中许多宏观性质、微观过程及其机理的重要基础。
本章只着重讨论其中的有关固体热学性质的部分,其它部分在本章最后的小结及后续章节、后续课程中可能有介绍(例电阻的产生机理、声子、电子运动等),因为热学性质是原子的振动在宏观性质上最直接的表现,对晶体原子振动的研究,最早是从热学性质开始的。
(在“统计热力学”中将讨论有关配分函数的处理及热力学函数的计算,本章中固体比热的计算,同上述内容有联系。
)§3.1晶体中原子的微振动及其量子化1.设晶体由N 个原子组成,它们相对于平衡位置的位移,分别用(x 1,x 2,x 3)、(x 4,x 5,x 6)……、(x 3N-2,x 3N-1,x 3N )来表示,则其动能可表示为:∑=∙=Ni ii x m T 31221 (1)()(212∙===x dt dx v mv T ) 其中m i 是坐标为x 1的原子的质量。
固体物理基础第3章 晶格振动理论

第3章 晶格振动理论
3.1 一维单原子链 3.2 一维双原子链 3.3 三维晶格的振动 3.4 声子 3.5 晶格振动谱的实验测定 3.6 晶格热容的量子理论 3.7 晶体的非简谐效应 热膨胀和热传导
1
第3章 晶格振动理论
2
第3章 晶格振动理论
3
第3章 晶格振动理论
图3.1 一维单原子链模型
6
第3章 晶格振动理论 将μ(x-Δx,t)和μ(x+Δx,t)在x处泰勒展开,并且只保留到二 阶项,这种假设称为简谐近似,于是有
(x-x, t)(x, t)-12dd(xt,t)x-12d2d(t2x,t)x2 (x+x, t)(x, t)+12dd(xt,t)x+12d2d(t2x,t)x2
把这些连续量带入方程(3.1)整理后即可得到:
率。
根据这种长波近似的极限情形,就可以设想,当长波近
似的条件λ>>a不成立时,方程(3.1)的解仍应具有类似的形式,
即只需在式(3.4)的简谐波的解中用na替代x即可,也就是式
(3.2)
8
第3章 晶格振动理论
3.1.3 色散关系 为了进一步研究一维单原子链振动的特点,可以将式
(3.2)所示的格波ห้องสมุดไป่ตู้式的解代入振动方程(3.1),得:
10
第3章 晶格振动理论
-π<qa≤π
即
-π q π
(3.6)
a
a
而
-
π a
,π a
正好是一维单原子链的第一布里渊区。该范围以
外的q并不能提供其他不同的波。晶体中的格波之所以具有
这样的特点,可以用图3.2来说明。为了便于图示,图中把
振动理论基础及激励源分析
(3-13)
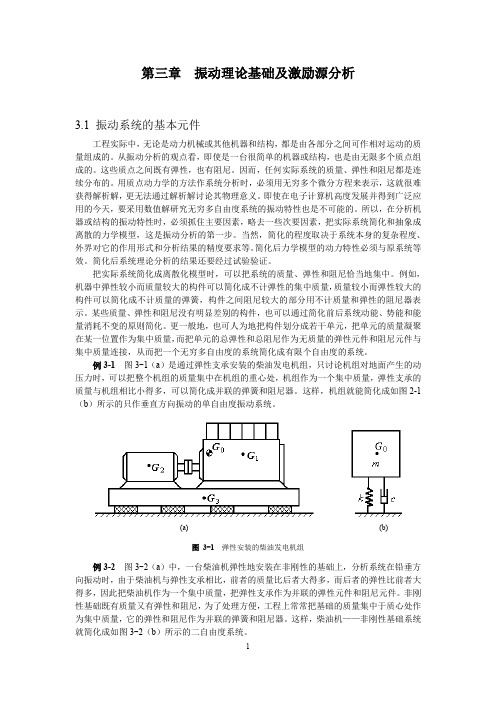
例 3-3 图 3-8 所示凸轮-从动杆机构利用一个轴的旋转运动实现阀的往复运动。从动杆系统 由质量为 m p 的推杆、质量和绕质心转动惯量分别为 mr 、 J r 的摇臂、质量为 mv 的阀门和不 计质量的阀门弹簧组成。求该机构在位置 A 点和 C 点的等效质量。
图 3-8
凸轮-从动杆系统
图 3-7 平动和转动多质量系统
(3-8)
1 1 1 1 m a2 1 1 2m (2a)2 2 2 T m1 x12 m2 x2 3 2 3 2 2 2 3 3 2 3 3
假设 xe x1 ,且 x1 a , x2 2 a ,则
(3-9)
1 1 T m1 xe2 2m2 xe2 m3 xe2 2 2
(1) 如果假设等效质量的位置在 A 点,则其速度为 xeq x p ,动能表达式为
(3-14)
1 2 Teq meq xeq 2
5
(3-15)
令 T 与 Teq 相等,并注意到下列关系:
x p x , xv l2 l1 x , xr l3 l1 x ,
得
r x l1
(3-16)
F F F ( x* ) dF dx (x)
x*
(3-24)
注意到弹簧 F F ( x* ) , F 可以写成如下的形式:
F k x
dF 显然,等效线性弹簧常数为 k dx
(3-25)
x*
为了简单,可以利用式(3-25) ,但有时由于这种近似带来的误差可能比较大。 像梁这样的弹性元件其作用也相当于弹簧。例如,如图 3-4 所示端部有集中质量 m 的 悬臂梁,为了简单,可以假设梁的质量相对于集中质量 m 可以忽略不计。根据材料力学的 结果,梁在自由端的静变形为
机械振动学总结全

机械振动学总结 第一章 机械振动学基础第二节 机械振动的运动学概念第三节机械振动是种特殊形式的运动。
在这运动过程中,机械振动系统将围绕其平衡位置作往复运动。
从运动学的观点看,机械振动式研究机械系统的某些物理量在某一数值近旁随时间t 变化的规律。
用函数关系式来描述其运动。
如果运动的函数值,对于相差常数T 的不同时间有相同的数值,亦即可以用周期函数来表示,则这一个运动时周期运动。
其中T 的最小值叫做振动的周期,Tf 1=定义为振动的频率。
简谐振动式最简单的振动,也是最简单的周期运动。
一、简谐振动物体作简谐振动时,位移x 和时间t 的关系可用三角函数的表示为式中:A 为振幅,T 为周期,ϕ和ψ称为初相角。
如图所示的正弦波形表示了上式所描述的运动,角速度ω称为简谐振动的角频率简谐振动的速度和加速度就是位移表达式关于时间t 的一阶和二阶导数,即可见,若位移为简谐函数,其速度和加速度也是简谐函数,且具有相同的频率。
因此在物体运动前加速度是最早出现的量。
可以看出,简谐振动的加速度,其大小与位移成正比,而方向与位移相反,始终指向平衡位置。
这是简谐振动的重要特征。
在振动分析中,有时我们用旋转矢量来表示简谐振动。
图P6旋转矢量的模为振幅A ,角速度为角频率ω若用复数来表示,则有)sin()cos()(ψωψωψω+++==+t jA t A z Ae z t j用复指数形式描述简谐振动,给计算带来了很多方便。
因为复指数t j e ω对时间求导一次相当于在其前乘以ωj ,而每乘一次j ,相当于有初相角2π。
二.周期振动满足以下条件:1)函数在一个周期内连续或只有有限个间断点,且间断点上函数左右极限存在;2)在一个周期内,只有有限个极大和极小值。
则都可展成Fourier 级数的形式,若周期为T 的周期振动函数,则有式中22n n n b a A += nn n b a =ψt a n 三、简谐振动的合成一、同方向振动的合成1.俩个同频率的简谐振动)sin(222ψω+=t A x ,)sin(2222ψω+=t A x它们的合成运动也是该频率的简谐振动2.俩个不同频率振动的合成若21ωω≤,则合成运动为若21ωω≥ ,对于A A A ==21 ,则有上式可表示为二、两垂直方向振动的合成1.同频率振动的合成如果沿x 方向的运动为沿y 方向的运动为2不同频率振动的合成对于俩个不等的简谐运动它们的合成运动也能在矩形中画出各种曲线。
固体物理基础第3章 晶格振动理论

第3章 晶格振动理论
基于如下的物理考虑:首先,晶体的宏观热性质取决于 组成晶体的绝大多数原子的运动状态;其次,晶体边界(表 面)原子的数目远小于晶体内部原子数目,因此对晶体热性 质的影响很小;第三,按照近邻作用近似,边界原子对内部 原子运动状态的影响很小。于是,玻恩-卡曼提出了这样的 周期性边界条件:假定由数目巨大的N个原子组成的一维单 原子链首尾衔接(间距也为a),构成一个如图3.3所示的半径 很大的圆环,局部范围内原子沿环方向的振动仍然可以看做
2
第3章 晶格振动理论 μn+2,…表示,第n个原子的实际位移为Xn=na+μn,如图 3.1(b)所示。尽管晶格中任一原子都会受到其他(n-1)个原子 的作用,但是这种作用会随着原子间距的增加而快速减小, 这是比较容易理解的,因此,为了使问题进一步简化,可以 进行近邻作用近似,即假定晶格中任一原子只受到其最近邻 原子的作用。这样的话,由于晶格中相邻原子间的相互作用 (化学键)都相同,就可以把一维单原子链想象成N个原子由 完全相同的弹簧连接的情况,如图3.1(c)所示,于是对于第n 个原子,只受到前后两个原子的作用fn-1,fn+1,它们与原子 的相对位移成正比,并且具有相同的弹性系数(或者叫回复 力系数)β。
把这些连续量带入方程(3.1)整理后即可得到:
m 2 ( t2 x ,t) 2 x (x 2 ,t)a 2 2 ( t2 x ,t)0 2 2 x (x 2 ,t)
(3.3)
7
第3章 晶格振动理论
这是数理方程中的波动方程,其中
2 0
程的特解为
a2 m
为波速度,该方
(x,t)Aei(tqx)
这是由2N个方程组成的联立方程组。同样,该方程组 应该具有下列形式的格波解,只是由于P原子和Q原子质量 的不同,其格波解的振幅不同:
机械动力学之振动的基本理论(ppt 37页)

1
返回首页
振动理论与应用
引言
振动问题的研究方法-与分析其他动力学问题 相类似:
• 选择合适的广义坐标; • 分析运动; • 分析受力; • 选择合适的动力学定理; • 建立运动微分方程; • 求解运动微分方程,利用初始条件确定积分常数。
Theory of Vibration with Applications
Theoretical Mechanics
Theory of Vibration with Applications
目录
5
返回首页
• 第1章 振动的基本理论
• 1.1 振动系统
Theory of Vibration with Applications
6
返回首页
• 1.1 振动系统
振动系统一般可分为连续系统或离散系统。
Theory of Vibration with Applications
8
返回首页
• 1.1 振动系统
振动问题的分类
按系统特性或运动微分方程类型划分:
• 线性振动-系统的运动微分方程为线性方程的
振动。
m y ky0
m e q keq= F 0si n t)(
• 非线性振动-系统的刚度呈非线性特性时,将 得到非线性运动微分方程,这种系统的振动称
2
可得到加速度与位移有如下关系
x 2x
重要特征:简谐振动的加速度大小与位移成正比,但方向总是 与位移相反,始终指向平衡位置。
Theory of Vibration with Applications
15
返回首页
• 1.2 简谐振动
1.2.1简谐振动的表示
2. 用旋转矢量表示简谐振动
振动基础知识点总结

振动基础知识点总结一、基础概念1. 振动的定义振动是指物体相对固定位置或平衡位置的周期性运动。
当物体相对于平衡位置发生周期性移动时,我们就称其为振动。
在自然界和日常生活中,我们可以观察到很多不同形式的振动,比如弹簧的拉伸振动、弦的横向振动、机械系统的转子振动等。
2. 振动的分类振动可以根据其运动形式、引起振动的原因、系统的特性等多种方式进行分类。
常见的分类方式包括:- 按运动形式可分为直线振动、旋转振动和复合振动;- 按引起振动的原因可分为自由振动、受迫振动和阻尼振动;- 按系统的特性可分为单自由度振动和多自由度振动等。
3. 振动的基本参数在描述振动时,常用的基本参数包括振幅、周期、频率、角频率、相位等。
这些参数描述了振动的幅度、速度和相位关系,是分析和描述振动运动特性的重要工具。
二、自由振动1. 自由振动概念自由振动是指系统在没有外力作用下的振动运动。
在自由振动的过程中,系统的振幅会随着时间不断变化,最终趋于稳定。
自由振动的运动方程一般为二阶线性微分方程,解析求解需要用到振动的基本理论知识。
2. 自由振动的特性自由振动的特性主要包括振动频率、振幅和相位。
对于简谐振动系统,其振动频率和振幅与系统的质量、刚度和阻尼相关。
而相位描述了系统中各个振动部件之间的相对位置关系。
3. 自由振动的应用自由振动的应用非常广泛,比如桥梁的结构振动、地震的振动运动、建筑物的自由振动等。
通过对自由振动的分析,可以评估结构的稳定性和安全性,为工程设计和地震防护提供重要参考。
三、受迫振动1. 受迫振动概念受迫振动是指系统在外部周期性力作用下的振动运动。
在受迫振动的过程中,系统受到外部力的影响,振动的频率和振幅会受到外部力的调控,产生共振等现象。
2. 受迫振动的特性受迫振动的特性与外部激励力的频率和幅度有关。
当外部激励力的频率接近系统的固有频率时,系统会产生共振现象,振动幅度会急剧增大。
另外,受迫振动也与系统的阻尼特性相关,阻尼会削弱系统的受迫振动响应。
振动原理及应用

振动原理及应用振动原理是指物体围绕其平衡位置做周期性的往复运动或摆动的现象。
振动是存在于自然界和人类生活中的普遍现象,具有重要的理论和实际应用价值。
振动原理的基础是质点受到力的作用而发生的周期性运动。
当质点离开平衡位置后,会受到向平衡位置恢复的力的作用,这个力称为恢复力。
若恢复力与质点的偏离方向相反,大小与偏离位置成正比,那么质点就会做简谐振动。
简谐振动的周期只与质点的质量和恢复力的大小有关,与振幅无关。
振动在物理学中有着广泛的应用。
首先,振动是研究物体结构及其性质的重要手段之一。
很多材料和结构会在受到外力激励时发生振动,通过研究振动特性可以了解物体的结构以及材料的物理性质。
例如,通过物体的固有频率和阻尼特性可以评估材料的刚性、弹性、稳定性等。
振动还可以用于测量物体的质量、密度等物理参数,例如利用共振原理测量空气中的气体浓度、液体中的浓度等。
其次,振动还在机械工程领域有重要应用。
例如,振动在机械传动中可用于实现转速变换,例如摆线传动和椭圆传动。
振动也可以用于筛分和充填设备中,例如在煤矿行业中,振动筛主要通过振动筛将煤炭分级,以便于提高煤炭的利用率。
此外,振动在工程结构的性能评价和优化中也有广泛的应用,例如利用振动测试和分析评估建筑物的结构安全性。
另外,振动还在电子技术和通信领域有重要应用。
例如,振动传感器可以用于测量物体的振动和冲击,用于机械故障诊断和结构健康监测。
同样地,振动也可以用于电子设备中的能量转换和信息传输。
例如,振动发电机可以利用机械振动转化为电能,广泛应用于自动化设备和无线传感器网络中。
此外,振动还可以通过模拟振动信号实现信息传输,例如利用超声波传感技术进行物体定位和通信。
总之,振动原理是物理学中的重要概念,它广泛应用于科学研究、工程技术和生活实践中。
从材料性质评估到结构优化设计,从机械工程到电子技术,振动都发挥着重要的作用。
通过深入研究振动原理,我们可以更好地理解和应用振动现象,推动科学技术的发展和进步。
汽车振动与噪声控制(第二版)

汽车振动与噪声控制(第二版)
第一章振动理论基础
第一节介绍
第二节单自由度系统
第三节多自由度系统
第四节连续系统振动
第五节随机振动分析基础
练习题
第二章声学理论基础
第一节波动方程与声的基本性质
第二节声传播及结构声辐射
第三节声阻抗、声强及声功率
第四节噪声及其控制技术
练习题
第三章汽车发动机的振动分析与控制
第一节发动机的振动激励源分析
第二节发动机隔振技术
第三节发动机气门振动
练习题
第四章汽车动力传动及转向系统振动
第一节振动分析的传递矩阵法
第二节汽车动力传动系统振动
第三节汽车转向系统振动
第四节汽车制动时的振动
练习题
第五章汽车平顺性
第一节平顺性定义
第二节人体反应与平顺性评价
第三节道路路面不平度的统计描述
第四节平顺性分析
第五节影响汽车平顺性的结构因素
练习题
第六章发动机及动力总成噪声
第一节发动机及动力总成噪声分析与控制
第二节传动系噪声
第三节发动机的空气动力噪声
练习题
第七章底盘系统噪声
第一节轮胎噪声
第二节制动噪声
练习题
第八章车身及整车噪声
第一节车身结构噪声及其控制
第二节车内噪声
第三节汽车整车噪声及其控制第四节汽车噪声有源控制
练习题。
振动原理资料

振动原理振动原理是力学中一个重要的概念,它涉及物体在受到外力作用时产生的周期性运动。
振动是许多物理现象的基础,包括声音传播、机械波的传播等,因此对振动原理的深入理解对于理解自然界中许多现象至关重要。
振动基本概念振动的基本概念可以通过一个简单的例子来说明:当一个弹簧悬挂着一个重物,当将这个重物向下拉开一段距离然后释放,重物会因为受到的重力而产生来回运动,这种周期性的来回运动就称为振动。
在这个过程中,弹簧被拉伸和压缩,这种弹簧的变形是振动的结果。
振动的特征振动具有一些特征,包括振幅、频率和周期。
振幅是指振动物体从平衡位置到最大位移的距离,频率是指单位时间内振动的次数,周期是指完成一个完整振动运动所需的时间。
这些特征可以帮助我们描述和分析振动。
振动的分类根据振动的性质和特点,振动可以分为自由振动和受迫振动。
自由振动是指没有外力作用下的振动,比如弹簧振子在没有外力作用下的来回摆动;受迫振动则是指有外力作用下的振动,比如摆钟受到重力的影响进行来回摆动。
此外,振动还可以分为谐振动和非谐振动。
谐振动是指振动物体的加速度与位移成正比的振动,非谐振动则是指振动物体的加速度与位移不成正比的振动。
振动的应用振动原理在生活和工程领域有着广泛的应用。
例如,振动传感器可以用于检测机械设备的振动情况,振动吸收器可以用于减少汽车行驶时产生的震动,振动台可以用于测试产品的耐用性等。
振动原理也被应用于音响设备、振动筛选机等各个领域。
结语振动原理是一门深奥的物理学原理,它在自然界和工程领域都有着广泛的应用。
通过对振动原理的研究和理解,我们可以更好地掌握自然规律,提高生产效率,改善生活质量。
深入学习和探索振动原理将会给我们带来更多的启示和机遇。
振动理论-第3章 单自由度系统的强迫振动

x0 0
、
x0
n
F0 k
1
r r
2
则初始条件为:
x0 0
x0
n
F0 k
r 1 r2
讨论:
x(t
)
C1
cos
nt
C2
sin
nt
F0
m(n2
2
)
cos
t
x(0) x0
C1
x0
F0 k
1
1 r
2
x(0) x0
C2
x0
n
故全解:
x(t)
x0
cos nt
x0
n
sin
nt
F0 k
1
1 r
2
cos nt
a
复数的三角函数表示:Z Z cos i sin
复数的指数函数表示:Z Z ei
对于复数域内复函数 H () a() ib() A() iB()
可表示为 H () H () ei ()
H ()
a2 b2 A2 B2
() arctan Im[H ()] Re[H ()]
二. 激励力引起的强迫振动
n
2
2
2
n
2
激励与响应的相位角
arctan
2
n
1
n
2
或写为:
X st
1
1 r 2 2 2 r 2
arctan
2 r
1 r2
st
F0 k
r n
系统的最大静位移 频率比
所以,强迫振动的稳态解为:
x2
F0 k
1
sin(t )
1 r 2 2 2 r 2
机械振动第1章:振动理论基础

期T. 解:取位移轴ox,m在平 衡位置时,设弹簧伸长量 为l,则
mg kl 0
k
T F2
m
RJ o
m
aT
mg
x
当m有位移x时
mg T ma
T k(l x)R J a
R 联立得
kx
m
J R2
a
d 2 x
k
dt 2 m J
R2
x0
RJ k
T F2
m
aT
o
m
mg
x
物体作简谐振动
m
O
y
光滑斜面上的谐振子 X
k 0
m
简谐振动的速度、加速度
速度 dx dt Asin(t )
Acos( t 2)
(t ) m cos( t )
速度也是简谐振动 比x领先/2
加速度 a d 2 x dt 2 2 Acos( t )
a(t ) am cos( t a ) 也是简谐振动
(3). 描述简谐振动的特征量---周期、振幅、相位
a、周期T----物体完成一次全振动所需时间。
频率 1 T 物体在单位时间内完成振动的次数。
角频率
2 2 对弹簧振子:
T
T 2 m
k
1 2
2 k m
k m
o
T t
b. 振幅 A 谐振动物体离开平衡位置的最大位移的绝对值。
c. 相位 t+ 决定振动物体的运动状态
d2x m kx
dt 2
l0
两端除以质量m,并设
2 n
k m
移项后得:
d2x dt 2
2 n
x
0
st O
第三章 晶格振动Ⅰ—声子

π
<q≤
π
考虑图3.1-4(a)所示的一维复式格子,相邻同种原子间的距离 为2a(2a是这复式格子的晶格常数)。设质量为m的原子位 于…2n-1,2n+1,2n+3…各点;质量为M的原子位于…2n-2, m 2n,2n+2…各点,且设 M > 。类似于方程式(3.1-5)得到 d 2 x 2 n +1 (3.1-13) ) m = β (x + x − 2x
hω
§3.1 一维晶格振动的动力学基础
晶体点阵中的质点(原子、离子)总是围绕着平衡位置作微小振动, 称为晶格振动,由于晶体内原子间存在着相互作用力,因此各个原子的 振动并非是孤立的,而是相互联系着的,这种相互联系着的晶格振动在 晶体中形成了各种振动模式的波 振动模式的波。只有当振动甚为微弱时,原子间的非 振动模式的波 谐的相互作用才可以忽略,即只有在简谐近似下,这些模式才是相互独 立的。由于晶格的周期性,使得振动的模式所取的能量值不是连续的, 而是分立的。对于这些独立而又分立的振动模式,可以用一系列独立的 谐振子来描述,我们把晶格振动的能量量子 称为声子,其中为晶格振 动模式的角频率。这样处理后,我们就可把晶格振动的总体看成是声子 的系综。如可把原子间的非谐相互作用看成微扰项,则声子间发生能量 交换,并且在相互作用过程中,会有某种频率的声子产生,也会有某种 频率的声子湮灭。又如晶格振动破坏了晶格的周期性,使电子在晶格中 的运动受到散射而增加电阻,这可以看成是电子受到声子的碰撞。另外, 光子与声子的相互作用也会对晶体的光学性质有重要影响。晶格振动是 三维的,可以根据空间力系将其分解成三个方向的线性振动。为便于理 解,我们先讨论一维晶格的振动问题,然后给出三维晶格振动的一些结 论。
理论力学经典课件-振动

2 n
x C1er1t C2er2t
本征值与运动微分方程旳通解旳形式与阻尼比有关。
3. 小阻尼情形
当 n< n 时,阻尼系数 c 2 mk ,这时阻尼较小,
称为小阻尼情形。其两个根为共轭复数,即:
r1 n i
2 n
n2
r2 n i
2 n
n2
其方程旳解为
或
x Aent sin(
2 n
F l 3 3EI
Fl 3 3EI
F ky yst
k
3EI l3
k-等效刚度
Wl 3 mgl 3 yst 3EI 3EI
k
3EI l3
my mg F
F ky yst
my ky 0 此即梁-物块旳运动微分方程
y Asin(nt )
串联弹簧与并联弹簧旳等效刚度
1. 串 联
meq-等效质量:使系统在广 义坐标方向产生单位加 速 度,需要在这一坐标方 向施加的力或力矩。
meq q keq q=0
q=C1cosnt C2cosnt
q
2 n
q=0
q=Asinnt
=
n
keq -系统的固有频率;A meq
q02
q0
n
2
振动的振幅;
arctan
n q0
q0
-振动的初位相; q0-初始广义坐标; q0-初始速度。
l
处于平衡,若k、m、a、l 等均
为已知。
ak
m
求:系统微振动旳固有频率
解:取静平衡位置为其坐标原点,
由动量矩定理,得
F
JO
d 2
dt 2
mgl cos
Fa cos
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
外因——激励(振源)
内因——系统振动
• 阻尼:阻碍物体振动的因素,如空气的阻力,材料的内阻, 物体之间的摩擦等。 动力学是研究系统动态行为的学科。包括: • 已知振源和系统振动特性,求系统响应(输出); • 已知系统振动特性和响应,求系统激励(输入); • 已知系统的输入和输出,确定系统动态特性(模态分析, 系统识别)。
k m
得系统固有圆频率为:
k 100000 100 rad / s 10 m
15.92(Hz) 固有频率为: f 2
二、单自由度系统的自由振动
又已知初始条件为: x0 = -0.01m,v0 = 0。得:
A
2 2 2 x0 v0
x0 0.01(m)
2 2
0 令v A cos( ), x0 A sin( )
v0 2 x0
x(t ) A sin(t )
x0 , arctan( ) v0
二、单自由度系统的自由振动
• 无阻尼自由振动的固有频率和固有圆频率
物块振动一次经历的时间Τ称为周期。根据正弦函数的性 质,时间每经历一个周期,正弦函数的相位角增加2π,故:
二、单自由度系统的自由振动
• 当n <ω时,设 j 1 ,故
n j 2 n 2
将上式代入
x et 中得: x e nt e j
x1 e nt cos 2 n 2 t x2 e nt sin 2 n 2 t
2 n2 t
二、单自由度系统的自由振动
• 作用在质量块上的弹性力总是指向平衡位置(恢复力) 。 • 若没有能量损耗,振动时离开平衡位置的最大位移不变, 称之为振幅。 • 自由振动具有周期性。 从某一位置开始运动,总是在一个固定的时间 T 内回到 开始位置,这一时间 T 叫做振动的周期,单位为秒。 为了描述振动的快慢程度,引入振动的频率 f ,它定义为 单位时间内振动的次数,单位为赫兹(Hz)。 频率 f 和周期 T 互为倒数,即:
k 解:系统的固有圆频率为: 2 f m k 100 rad / s 得无阻尼固有圆频率为: m
阻尼系数为: n 100 0.05 5 振动周期为:T
2
1
2
0.063 s
二、单自由度系统的自由振动
又已知初始条件为:x0 =-0.01m,v0 = 0 得 A x02
阻尼对自由振动的影响主要表现在振幅。设相邻两次振动 的振幅分别为 Ai 和 Ai 1 ,则前后两次的振幅比为:
Ai Ae nT1 d n t T e Ai 1 Ae i 1
d 称为减幅系数,由上式得:
nti
Ai A1 A2 A1 …… Ai 1 i A3 2 d d d d 因为d >1 ,所以小阻尼自由振动的振幅按几何级数的规律 迅速衰减。
将它按欧拉公式展开,得到两个特解:
将这两个特解线性组合,即得通解为
x Ae nt sin
2 n2 t
二、单自由度系统的自由振动
由上式可以看出: • 小阻尼n <ω时质量块系统的运动规律为正弦波形; • 因为-1≤ s i n
2
n2t
nt
≤1,所以质量块系统的位移
由于包装缓冲系统都是有阻尼的,所以,分析有阻尼单自由 度系统的自由振动具有十分重要的作用。
• 力学模型
• 建立运动方程
质量块m作自由振动,在任一 瞬时t,作用在质量块上的力有: 重力 弹性力 阻力 mg
F k st x
R cx
根据牛顿第二定律,质量块的运动微分方程为:
F R mg k ( st x) cx mg kx cx mx
k 因为 m
所以,周期为 T
2
2
m k
频率为
f
1 2
k m
二、单自由度系统的自由振动
• 无阻尼单自由度系统自由振动的速度与加速度方程 对位移方程 由振动的速度方程为 求一次导数,得系统自
V t A cost
求二次导数,得系统自
对位移方程 由振动的加速度方程为
一、振动系统
• 按系统自由度分——单自由度系统振动 多自由度系统振动 • 按微分方程分——线性振动 非线性振动 • 按系统输入类型分——自由振动 强迫振动(受迫振动) 自激振动 • 按输出规律分——周期振动 随机振动
二、单自由度系统的自由振动
• 自由振动
• 给弹簧一个初始位移后,如果没有外力干扰, 它按自身的特性进行的有规律的往复运动。
2
at A sin t
二、单自由度系统的自由振动
例:已知一包装件的产品质量m = 10 kg,缓冲垫等效弹 性系数为k = 100000 N/m,将其简化为无阻尼单自由度模 型,给缓冲垫一个初始位移x0 = -0.01m,使之从静止开始 振动,求固有频率和位移方程。 解:由公式
二、单自由度系统的自由振动
二、单自由度系统的自由振动
F R mg kx cx 将方程 mx
简化后得:
x
k c 0 x x m m
k c 2 令上式中 m , 2n ,就得到有阻尼自由振动的 m 运动微分方程的标准形式
2x 0 x 2nx
——是质量块弹簧系统的固有圆频率; 式中:
• 力学模型
设弹簧的原长为L0,弹簧静 变形
弹簧总变形 • 物体所受 弹性力
x st
mg st k
F kx k st F kx mg
• 由牛顿第二定理得:
d 2x F F mg kx, F ma m dt 2 2 k k mx kx x m x 0, 设 m x 0 x
nt
被限制在两条曲线 x Ae
和 x Ae
之间;
• 质量块系统的振动随时间的增加而逐渐衰减,是衰减振 动。
二、单自由度系统的自由振动
设初始条件为:
nt 和 。计算公式为:x Ae sin
,由此可确定常数A
2 n2 t
,得:
衰减振动虽然不是真正地 周期性运动,但它仍具有 等时性,因此质量块来回 往复一次所经历的时间仍 然称为周期,用 T1 表示
-0.0075
x t 0.01e 5t sin 99.87t 1.555 nT 0.3146 1.37 因为 n 5 , T 0.063 s ,所以振幅系数为:d e 1 e A1 1 有 Ai 1 i 0.05 A1 即要求 d i 20 i 9.52 d 0.05
2 n2 t
得位移方程为:
二、单自由度系统的自由振动
n n 2 2
• n >ω,特征方程的两个根全是实数,而且都是负的,假 设方程的两个特解为 x1 e 1t , x2 e 2t 方程的通解为: 根据初始条件: 代入上式得: 由此求得:
x c1e 1t c2 e 2t
第三章 包装动力学的振动理论
第一节 振动理论基础
一、振动系统 二、单自由度系统的自由振动 三刚性物块、线性弹簧和线性阻尼组成的振动系统称为线 性振动系统。 • 振动:是物体在其平衡位置附近所做的来回往复运动,描述 最基本参数是频率和加速度。
一、振动系统
振动是由振源向系统输入信号,系统所作的响应。
二、单自由度系统的自由振动
显然,由于阻尼的作用,振动的周期增大了,但是,当阻 尼很小时,周期的增加是微不足道的,例如,当
n 0.1 0.1, 时,T1 1.005T ,
仅仅增加了百分之五,所以当阻尼很小时,可以不计阻尼 对振动周期的影响,而近似认为 T1 T。
二、单自由度系统的自由振动
nx0 v0
n
2 2
2
0.01
0.01m
0.0075 0.005 0.0025
x0 2 n 2 tan 63.24 2 nx0 v0
0.1 -0.0025 -0.005
0.2
0.3
0.4
0.5
0.6
得 1.555 rad
nt x Ae sin 由公式
nti
因为d >1 ,所以小阻尼自由振动振幅按几何级数的规律迅 速衰减。
二、单自由度系统的自由振动
每振动一次,对振幅影响很大,振幅减少迅速。仍以
n 0.1 0.1, 时为例, 可算得 2 0.1 d exp 2 1 0 . 1 Ai 1.88, Ai 1 0.53 Ai d
可见,每振动一次,振幅就减少47%,只要振动6次,振幅 就小于0.05A1。可见在阻尼很小时,周期的变化虽然不大, 但振幅的衰减却非常迅速。
二、单自由度系统的自由振动
例:已知一包装件产品质量m =10kg,缓冲垫等效弹性系 数为k = 100000N/m,将其简化为有阻尼单自由度模型,设 阻尼比为 0.05 。给缓冲垫一个初始位移x0 =-0.01m ,使 之从静止开始振动,求振动周期、位移方程,并计算振动多 少次后的振幅小于初始振幅的5%。
2
• 位移方程的求解
2 x 0 x t 0时,初始位移和速度 (0) v0 x(0) x0 , x (0) v0 x(0) x0 , x
2x 0 x
x(t )
可得A
v0
sin( t ) x cos( t ) 0
v0 t 0, x x0 , x
