2019年§2 连续函数的性质.doc

合集下载

2019年最新-函数的连续性(2)-精选文档

x 0
x 0
lim f(x )li(m x 1 ) 1
x 0
x 0
在x=0处y是否间断，
yx1
1
o1 x
lim f(x)lim f(x)
x 0
x 0
所以函数在x=0处间断。 x=0是跳跃间断点
例函y数 x21在x点 1没定 ,所义以函数
x 1
x 1
但f (1) 1,所以 2
limf(x)f(1).
x1
1
1
2o 1 x
因此，点x=1是函数 f(x)的间断点.但如果改变
函数f(x)在x=1处的定义：令f(1)=1，则f(x)在 x=1成为连续.所以x=1也称为该函数的可去间断点.
1.6.3.2 第二类间断点函数f(x)在点x0的左右极限中至少有一个不存在的间断点，则称x0为第二类间断点。例1.29 f (x) 2
x2
limf (x)不存在 x2
所以x = 2为函数的跳跃间断点
1.6.4 闭区间上连续函数的性质
定理1.6 如果函数f(x)在闭区间[a,b]上连续，则 f(x)在闭区间[a,b]上有界。
定理1.7 （最值定理）设函数f(x)在闭区间[a,b]上连续，则f(x)在[a,b]上有最大值和最小值
x2
x2
能不连续，而
limf(x) limf (x)
x2
x2
在其它定义区
limf (x)不存在 x2
间上连续。
所以函数在x = 2 处不连续
ax 当x1时
例设f(x)1
当x1时
axb 当x1时
在x = 1处连续，求a、b的值
解 f(1)1

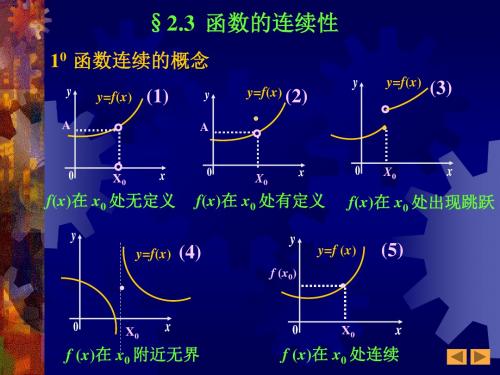
03.函数的连续性

并且, lim sin x = sin x0
x → s x = cos x0
x→x0
所以, 多项式及正, 余弦函数在任何点x0处连续.
一、函数的连续点与间断点
x, 当x ≥ 0时, 在x = 0处连续. 例1. 证明f ( x) =| x |= − x, 当x < 0时,
0
x→ x0
间断点有2类：跳跃间断点：f ( x0 + 0), f ( x0 − 0)存在但不相等；第一类间断点：可去间断点： f ( x)存在但 lim f ( x) ≠ f ( x ).或f ( x )无定义 lim 0 0 x → x0 x → x0 第二类间断点：f ( x0 + 0), f ( x0 − 0)中至少有一不存在.
第二类间断点
0
x0
y
y
x
0
x 振荡型
无穷型
一、函数的连续点与间断点
lim f ( x) ≠ f ( x0 )或f ( x0 )无定义
+ 0 − 0
间断点
可去间断点
x → x0
跳跃间断点 xlim f ( x ) ≠ xlim f ( x ) →x →x 无穷间断点
f ( x ) 在 x 0点左右极限至少有一个为无穷大
x →0
故, f (x)在x=0间断. 图形为
y 1 o –1
y=f (x)
x
一、函数的连续点与间断点
若f (x)在(a, b)内每一点连续, 则称f (x)在开区间(a, b)内连续.
若f (x)在(a, b)内连续, 且f (x)在x=a右连续. 在x=b左连续. 则称f (x)在闭区间[a, b]上连续.

第四章函数的连续性

有下列三种情形之一时，函数 f (x) 在 x0处间断。
（1）在 x x0 近旁有定义，但在 x0处没有定义。
（2）虽在
x0 处有定义，但
lim
x x0
f
(x)
不存在。
（3）虽在
x0 处有定义，且
lim
x x0
f
(x)
存在，但
lim
x x0
f (x)
f (x0 )
❖间断点的类型
通常把间断点分成两类
f (x)
lim (1
x0
x) x
e
lim f (x) lim (x a) a
x0
x0
欲使 f (x)在
x
0
处连续，须有lim x0
f (x) lim x0
f (x)
即 a e ，此时 lim f (x) e
x0
（3）
lim
x0
f
(x)
f
(0)
所以 a e 时，f (x) 在 x 0 处连续。
，lim或f有(x定) 义li但m
x x0
x x0
f
( x),
则称f点(xx00)为函A数,则f称(x)x的0为跳f 跃(x)间的断可点去.间断点.
例如：
（1）函数 f (x) x2 4 在 x 2 处无定义 y
x2 所以 x 2 是该函数的间断点。
2
y f (x)
（2）函数
f
(x)
x1x,1x,
连续函数的图象是一条连续不间断的曲线。
3、函数在区间上的连续性
在区间上每一点都连续的函数叫做在该区间上的连续函数或者说函数在该区间上连续
•连续函数举例

§2 连续函数的性质一连续函数的局部性质 - 山东师范.

f (x0) 0
即方程 f (x) 0 在 (a,b) 内至少有一个根.
若 Aa, f a 与 Bb, f b 分别在 x 轴的两侧, 则连接 A, B
的连续曲线 y f x 与x 轴至少有一个交点.
这个推论的几何解释如图4—3所示：
首页 ×
首页 ×
下面举例说明介值性定理的应用
若函数连续使得对一切连续若函数定理42局部有界性定理43局部保号性在具体应用局部保号性时常取使在其内有定理44四则运算上的连续性在其定义域的每一点都是连续的
§2 连续函数的性质
一、连续函数的局部性质二、闭区间上连续函数的基本性质三、反函数的连续性四、一致连续性——数学分析的一个难点
首页 ×
§2 连续函数的性质
（1）
又由 u0 f (x0)及 u f (x)在点 x0 连续, 故对上述 1 0, 存在
0 使得当 x x0 时，有| u u0 || f (x) f (x0) | 1 .
联系(1)得: 对任给的 0, 存在 0 , 当 | x x0 | 时有
g( f (x)) g( f (x0)) .
这就证明了 g f 在点 x0连续.
注1 根据连续性的定义, 上述定理的结论可表为
lim
x x0
g(
f
( x))

g( lim x x0
f
( x))

g(
f
( x0 )).
首页 ×
二、闭区间上连续函数的基本性质
数学分析课程中主要的研究对象是连续函数,很自然地, 闭区间上的连续函数的整体性质在微积分理论中具有相当的重要性.
右连续与左连续, 所以 f 1 在 f a, f b 上连续.

连续函数的运算性质

§2.2 连续函数的运算与初等函数的连续性【导语】对于一般函数，从定义出发讨论其连续性不仅困难，也没必要。

因为许多函数都是由简单函数经过四则运算和复合运算得到的。

得到了简单函数的连续性结果后，只要再了解连续函数经过运算之后的连续性结论，我们就可以得到一般函数的连续性结果。

本讲将介绍连续函数的和、差、积、商函数，复合函数，以及反函数的连续性结果，并给出初等函数在其定义区间上的连续性。

【正文】一、连续函数的四则运算定理2 如果函数()f x 和()g x 均在0x 处连续，那么它们的和、差、积、商函数()()f x g x +，()()f x g x -，()()f x g x ，0()(()0)()f xg x g x ≠均在0x 处连续．二、复合函数的连续性定理3 如果函数()f u 在0u 处连续，函数()g x 在0x 处连续，且00()u g x =，那么复合函数(())f g x 在0x 处连续．从运算的角度看，有000lim (())(lim ())((lim ))x x x x x x f g x f g x f g x →→→== 成立．即对连续函数来说，极限求值运算与函数求值运算可以交换次序．三、反函数的连续性定理 4 设1()f y -是函数()f x 的反函数，且00()y f x =．如果函数()f x 在0x 处连续，那么函数1()f y -在0y 处连续．例 1 证明：对数函数ln y x =在(0,)+∞内连续．解对任意的0(0,)x ∈+∞，记00ln y x =，因为指数函数e y x =在0y 处连续，所以其反函数ln y x =在0x 处连续。

由0x 的任意性可知：对数函数ln y x =在(0,)+∞内连续．例 2 证明：幂函数y x α=在(0,)+∞内连续．证当(0,)x ∈+∞时，根据指数函数与对数函数的性质，得ln ln e e x x y x ααα===．对任意的0(0,)x ∈+∞，因为函数ln x α在0x 处连续，且指数函数e u 在00ln u x α=处连续，所以ln e x y x αα==在0x 处连续．由0x 的任意性可知：幂函数y x α=在(0,)+∞内连续．例 3 证明：如果函数()f x 和()g x 均在0x 处连续，且0()0f x >，则函数()()g x y f x =在0x 处连续．证根据指数函数与对数函数的性质，得()()ln ()()ln ()()e e g x g x f x g x f x y f x ===．因为0()0f x >，所以对数函数ln u 在0()f x 处连续。

函数的连续性

第四章函数的连续性教学目的：1.使学生深刻掌握函数连续性的概念和连续函数的概念；2.熟练连续函数的性质并能加以应用；3.知道所有初等函数都是在其定义域上的连续函数，并能加以证明；4.理解函数在某区间上一致连续的概念，并能清楚地认识到函数在一区间上连续与这一区间上一致连续的联系与区别。

教学重点、难点：本章重点是函数连续性的概念和闭区间上连续函数的性质；难点是一致连续性的概念与有关证明。

教学时数：14学时§ 1 函数的连续性（4学时）教学目的：使学生深刻掌握函数连续性的概念和连续函数的概念。

教学要求：1. 使学生深刻理解函数在一点连续包括单侧连续的定义，并能熟练写出函数在一点连续的各种等价叙述；2. 应使学生从分析导致函数在一点不连续的所有可能的因素出发，理解函数在一点间断以及函数间断点的概念，从反面加深对函数在一点连续这一概念的理解力并能熟练准确地识别不同类型的间断点；3. 明确函数在一区间上连续是以函数在一点连续的概念为基础的，使学生清楚区分“连续函数”与“函数连续”所表述的不同内涵。

教学重点：函数连续性概念。

教学难点：函数连续性概念。

一、引入新课：通过生活和科学研究中的实例说明学习连续函数的必要性。

二、讲授新课：（一）函数在一点的连续性：1．连续的直观图解：由图解引出解析定义.2.函数在一点连续的定义: 设函数在点某邻域有定义.定义用例如 [1]P87例1和例2, P88 例3.定义用定义用先定义和定义连续的Heine定义.”定义.)定义( “（注：强调函数例1 用“”定义验证函数在点连续.例2 试证明: 若在点连续.则3.单侧连续: 定义单侧连续, 并图解.Th ( 单、双侧连续的关系 )例3讨论函数在点的连续或单侧连续性.（二）间断点及其分类: 图解介绍间断点的分类.跳跃间断点和可去间断点统称为第一类间断点, 其他情况或中至少有一个不存在称为第二类间断点.即例4讨论函数的间断点类型.例5延拓函数使在点连续.例6举出定义在[0,1]上且仅在点三点间断的函数的例.讨论Dirichlet函数和Riemann函数的连续性. （三）区例7开区间上连续，闭区间上连续, 按段连续.§ 2 连续函数的性质（6学时）教学目的：熟悉连续函数的性质并能灵活应用。

函数的连续性(6)

f (x)
f ( x0 )
且 0 f ( x) f ( x0 ) f ( x) f ( x0 )
lim x x0
f (x)
f ( x0 )
lim
x x0
f
2(
x)

lim
x x0
f
(
x
)

lim
x x0
f ( x)
f 2( x0 )
故| f ( x) |、 f 2 ( x) 在x0 都连续.
但反之不成立.
例
f
(
x)

1, 1,
x0 x0
在 x0 0不连续
但 | f ( x) |、 f 2 ( x) 在x0 0 连续
三、连续函数的四则运算
定理1 若函数 f ( x), g( x)在点 x0处连续,
则 f ( x) 断点)
特点：左右极限都存在
例2：f
(x)

2 1,
x,
0 x 1 x 1
1 x, x 1
(可去间断点)
特点：左右极限都存在
y
o
x
y y 1 x
2
y2 x
1
o1
x
情形2：左右极限不同时存在的间断点
M max f (x), m min f (x)
x[ a , b ]
x[ a , b ]
则对任意 (m, M ), (a, b), 使得
f ( )
y
M f(x)
g(x)

m
a

o
x
b

高等数学第4章第2节连续函数的性质

§２连续函数的性质引言函数的连续性是通过极限来定义的，因而有关函数极限的诸多性质，都可以移到连续函数中来．一、连续函数的局部性质性质１（局部有界性）若f 在0x 连续．则f 在某0()U x 有界．性质２（局部保号性）若f 在0x 连续，且0()0(0)f x or ><则对任何正数0(0,())r f x ∈0(((),0))r f x ∈，存在某0()U x 有()0(()0)f x r f x r >><<．注 ①在具体应用局部保号性时，r 取一些特殊值，如当0()0f x >时，可取0()2f x r =，则存在0()U x ，使得当0()x U x ∈有0()()2f x f x >；②与极限相应的性质做比较可见，这里只是把“极限存在”，改为“连续”，把0()U x 改为00()U x 其余一致．性质３．（四则运算）若f 和g 在0x 点连续，则0,,(()0)ff g f g g x g±⋅≠也都在点0x 连续．问题两个不连续函数或者一个连续而另一个不连续的函数的和、积、商是否仍旧连续？性质４（复合函数的连续性）若f 在点0x 连续，记00()f x u =，函数g 在0u 连续，则复合函数g f 在点0x 连续．注 1) 据连续性定义，上述定理可表为：00lim [()][()][lim ()]x x x x g f x g f x g f x →→==.（即函数运算与极限可以交换次序，条件是函数连续利用它可来求一些函数的极限．）例１．求21limsin(1)x x →-.2) 若复合函数g f 的内函数f 当0x x →时极限为a ，又外函数g 在u a =连续，上面的等式仍成立．（因此时若00lim ()()x x f x a f x →==的话是显然的；若00lim ()()x x f x a f x →=≠，或()f x 在0x x =无定义，即0x 是f的可去间断点时，只需对性质４的证明做修改：“0||x x δ-<”为“00||x x δ<-<”即可）．故可用来求一些函数的极限．例２求极限（１）0x →（２）x 性质５（反函数的连续性）若函数f 在[,]a b 上严格单调并连续，则反函数1f -在其定义域[(),()]f a f b 或[(),()]f b f a 上连续．二、初等函数的连续性１．复习（关于初等函数）（１）初等函数：由基本初等函数经过有限次四则运算与复合运算所得到的函数．（２）基本初等函数：常量函数y C =；幂函数y x α=；指数函数(0,1)x y a a a =>≠；对数函数log (0,1)a y x a a =>≠；三角函数sin ,cos ,,y x x tgx ctgx =；反三角函数arcsin ,arccos ,,y x x arctgx arcctgx =．２．初等函数的连续定理１任何初等函数都是在其定义区间上的连续函数．定理２一切基本初等函数都是其定义域上连续函数．３．利用初等函数的连续性可计算极限例３．设0lim ()0x x u x a →=>，0lim ()x x v x b →=，证明：0()lim ()v x b x x u x a →=．例４．求0ln(1)limx x x→+．例５求20ln(1)lim cos x x x→+．三区间上连续函数的基本性质引言闭区间上的连续函数具有一些重要的性质．现将将基本的列举如下．从几何上看，这些性质都是十分明显的．但要严格证明它们，还需其它知识，将在第七章§２给出．先给出下面的关于“最大大值”的定义：定义１设f 为定义在数集Ｄ上的函数，若存在0x D ∈，使得对一切x D ∈都有0()()f x f x ≥（0()()f x f x ≤），则称f 在Ｄ上有最大（小）值，并称0()f x 为f 在Ｄ上的最大（小）值．例如，sin ,[0,]y x π=．max 1y =、min 0y =．一般而言， f 在其定义域上不一定有最大（小）值，即使()f x 在Ｄ上有界．例如：(),(0,1)f x x x =∈无最大（小）值；1,(0,1)()2,0,1x f x xx ⎧∈⎪=⎨⎪=⎩在［０，１］上也无最大（小）值．１．性质性质１（最大、最小值定理）若f 在闭区间[,]a b 上连续，则f 在[,]a b 上有最大值与最小值．性质２（有界性定理）若f 在[,]a b 上连续，则f 在[,]a b 上有界．思考 ①考虑函数(),(0,1)f x x x =∈，1,(0,1)()2,0,1x g x x x ⎧∈⎪=⎨⎪=⎩上述结论成立否？说明理由；②f 要存在最大（小）值或有界是否一定要f 连续？是否一定要闭区间呢？结论上述性质成立的条件是充分的，而非必要的．性质３（介值定理）设f 在[,]a b 上连续，且()()f a f b ≠．若μ是介于()f a 和()f b 之间的任何实数，则至少存在一点0(,)x a b ∈，使得0()f x μ=．注表明若f 在[,]a b 上连续，又()()f a f b <的话，则f 在[,]a b 上可以取得()f a 和()f b 之间的一切值．（如左图）．性质４（根存在定理）若f 在[,]a b 上连续，且()f a 和()f b 异号（()()0f a f b ⋅<），则至少存在一点0[,]x a b ∈，使得0()0f x =．几何意义若点(,())A a f a 和(,())B b f b 分别在x 轴两侧，则连接Ａ、Ｂ的曲线()y f x =与x 轴至少有一个交点．２．闭区间上连续函数性质应用举例关健构造适当的f ；构造适当的闭区间．例６．证明：若0r >，n 为正整数，则存在唯一正数0x ，使得0n x r =．例７．设f 在[,]a b 上连续，满足([,])[,]f a b a b ⊂．证明：存在0[,]x a b ∈，使得00()f x x =．四一致连续性引言在连续函数的讨论和应用中，有一个极为重要的概念，叫做一致连续．我们先叙述何谓一致连续．设()f x 在某一区间Ｉ连续，按照定义，也就是()f x 在区间Ｉ内每一点都连续．即对00,0,(;)x I x U x εδ∀∈∀>∀∈时，就有0|()()|f x f x ε-<．一般说来，对同一个ε，当0x 不同时，δ一般是不同的．例如图左．中1y x=的曲线，对接近于原点的0x ，δ就应取小一些．而当0x 离原点较远时，δ取大一些．（对后者的δ值就不一定可用于前者．但在以后的讨论中，有时要求能取到一个时区间Ｉ内所有的点都适用的η，这就需要引进一个新概念——一致连续．１．一致连续的定义定义（一致连续）设f 为定义在区间Ｉ上的函数．若对任给的0ε>，存在一个()0δδε=>，使得对任何,x x I '''∈，只要||x x δ'''-<，就有()()||f x f x ε'''-<，则称函数f 在区间Ｉ上一致连续．２．函数在区间上连续与一致连续的比较若f 在Ｉ上一致连续，则f 在Ｉ上连续；反之不成立（即若f 在Ｉ上连续，f 不一定在Ｉ上一致连续．３．问题：如何判断一个函数是否一致连续呢？有下面的定理：定理（康托Cantor 定理）若函数f 在闭区间[,]a b 上连续，则f 在[,]a b 上一致连续．４．一致连续的例子例１．证明 ()f x ax b =+(0)a ≠在(,)-∞+∞上一致连续．例２．（１）证明函数1y x=在(0,1)内不一致连续．（２）0c ∀>，证明 1y x=在(,1)c 内是一致连续的．例３．证明 1sinx在(,1)c (0)c >内是一致连续的，而在(0,1)内连续但非一致连续．例４．设区间1I 的右端点为1c I ∈，区间2I 的左端点也为2c I ∈（12,I I 可分别为有限或无限区间）．试按一致连续性定义证明：若f 分别在1I 和2I 上的一致连续，则f 在12I I I =⋃上也一致连续．作业：P81,1， 2， 3， 8， 9, 14。

19连续函数的运算与初等函数的连续性

返回
上页下页返回退出
三、初等函数的连续性 ★ 三角函数及反三角函数在它们的定义域内是连续的.
★ 指数函数 y a x (a 0, a 1)
在(,)内单调且连续;
★ 对数函数 y log x (a 0, a 1) a 在(0,)内单调且连续;
Jlin Institute of Chemical Technology
上页下页返回退出
返回
上页下页返回退出
二、反函数与复合函数的连续性
定理4 如果函数y=f(x),在区间Ix上单调增加(或单调减少) 且连续,那么它的反函数x=φ(y)也在对应的区间
Iy={y|y=f(x),x ∈Ix}上单调增加(或单调减少)且连续
例1 y sin x在[ , ]上单调增加且连续,
22 故 y arcsin x 在[1,1]上也是单调增加且连续. 同理 y arccos x 在[1,1]上单调减少且连续; y arctan x, y arccot x 在[,]上单调且连续.
上页下页返回退出
例6 求 lim a x 1 .
x0
x
解令 ax 1 t,
则 x log (1 t), a
当x 0时, t 0.
原式 lim t y0 log (1 t )
a
1
lim t0
1
log (1 t)tห้องสมุดไป่ตู้
a
lna
Jlin Institute of Chemical Technology
9

1 6 66
定理4 设函数u ( x)在点x x 连续, 且 0
( x ) u , 而函数y f (u)在点u u 连续,

函数的极限函数的连续性(2019年12月整理)

记作 lim f(x)=a或者当x→－∞时，f(x)→a x
(3)如果
lim
x
f(x)=a且
lim
x
f(x)=a，那么就
说当x趋向于无穷大时，函数f(x)的极限
是a，记作：lim f(x)=a或者当x→∞时， x
f(x)→a
常数函数f(x)=c(x∈R)，有lim f(x)=c
函数的极限、函数的连续性
1、函数极限的定义: (1)当自变量x取正值并且无限增大时，如果函数f(x)无限趋近于一个常数a，就说当x趋向于正无穷大时，函数f(x)的极限是a
记作：lim f(x)=a，或者当x→+∞时，f(x)→a x
(2)当自变量x取负值并且绝对值无限增大时，如果函数f(x)无限趋近于一个常数a，就说当x 趋向于负无穷大时，函数f(x)的极限是a
趋向于定值的函数极限概念：
当自变量无限趋近于x0（ x x0）时，如果函数f(x)无限趋近于一个常数a，就说当x趋向x0时，函数y=f(x)的极限是a，记作特别地， lim f (x) a；
xx0
lim C C
x x0
lim
x x0
x

x0
lim f (x) a lim f (x) lim f (x) a
xx0
xx0
xx0
其趋中近于xlxim0x时0 f的(x左) 极 a限表，示当x从左侧
于xxl0im时x0 的f (右x)极 a限表示当x从右侧趋近
对于函数极限有如下的运算法则：
如果，lim f (x) A, lim g(x) B
xxo
xxo
那么,
lim [ f (x) g(x)] A B

连续函数的性质-9页文档资料

§2 连续函数的性质(一) 教学目的：掌握连续函数的局部性质和闭区间上连续函数的整体性质． (二) 教学内容：连续函数的局部保号性，局部有界性，四则运算；闭区间上连续函数的最大最小值定理，有界性定理，介值性定理，反函数的连续性，一致连续性．基本要求：1）掌握函数局部性质概念，可去间断点，跳跃间断点，第二类间断点；了解闭区间上连续函数的性质．2) 理解一致连续于逐点连续的本质区别．(三)教学建议：1) 函数连续性概念是本节的重点．要求学生掌握函数在一点和在区间上连续的定义，间断点的分类，了解连续函数的整体性质．对一致连续性作出几何上的解释． 2）本节的难点是连续函数的整体性质，尤其是一致连续性和非一致连续性的特征．难点：连续函数的保号性；一致连续性一连续函数的局部性质根据函数的在0x 点连续性，即)()(lim 00x f x f x x =→可推断出函数)(x f 在0x 点的某邻域)(0x U 内的性态。

定理4.2（局部连续性）若函数)(x f 在0x 点连续，则)(x f 在0x 点的某邻域内有界。

定理4.3（局部保号性）若函数)(x f 在0x 点连续，且0)(0>>αx f ，则对任意αα<'<0存在0x 某邻域 )(,)(00x U x x U ∈ 时，0)(>'>αx f定理4.4（四则运算性质）若函数则)(,)(x g x f 在区间I 上有定义，且都在I x ∈0 连续，则)(/)(,)()(,)()(x g x f x g x f x g x f ±（0)(0≠x g ）在0x 点连续。

例因x y c y == 和连续，可推出多项式函数n n n n a a xa x a x P ++++=--1)1(10)(Λ 和有理函数Q P, ( )()()(x Q x P x R =为多项式）在定义域的每一点连续。

函数的连续性01604

x x 0
均不存在，所以 x 0 是 f ( x ) 的一个第二类间断点 .
§3.2 连续函数的性质
一、连续函数的局部性质二、闭区间上连续函数的性质三、反函数的连续性四、初等函数的连续性性
一、连续函数性质 1、连续函数的四则运算性
定理若函数 f(x),g(x)均在 x0连点,续则函数 (1 ) f(x ) g (x ), (2 ) f(x ) g (x ),
x 0
x 0x 0
由上面的定义和例题应该可以看出: 函数在点 x0 有极限与在点 x0 连续是有区别的. 首先 f (x) 在点 x0 连续，那么它在点 x0 必须要有极限(这就是说, 极限存在是函数连续的一个必要条件)，而且还要求这个极限值只能是函数在该点的函数值.
3.函数在一点左(右)连续的定义:
定义3 函数 f (x) 在一点 x 0 连续
lim y 0.
(3)
x0
这里我们称 x 是自变量 ( 在 x 0 处 ) 的增量 , y 为相应的函数(在 y0 处)的增量
例1 证明 f ( x ) x D ( x ) 在 x 0 处连续 , 其中 D ( x )
2.函数 f (x) 在一点 x 0 连续的等价定义
定义2 设 f ( x ) 在点 x 0 的某个邻域内有定义 .如果
对任意的 0, 存在 0,当 xx0 ,时
f(x)f(x 0),
则称 f(x )在点 x 0 连续 .
设 xxx 0, y y y 0 f ( x ) f ( x 0 ) f ( x 0 x ) f ( x 0 ).

极限连续性——精选推荐

§2 连续函数的性质1．讨论复合函数g f o 与f g o 的连续性：（1）=)(x f x sgn ，21)(x x g +=；（2）=)(x f x sgn ，x x x g )1()(2−=。

解：（1）由于 =)(x f x sgn ，21)(x x g +=，故 )(g f o 1)1sgn()(2≡+=x x ，可见g f o 是连续函数。

又因为 ⎩⎨⎧=≠=.0,1,0,2))((x x x f g o因此0=x 是f g o 的可去间断点，其余点处处连续。

（2）由于 =)(x f x sgn ，x x x g )1()(2−=，于是0))((≡x f g o ，可见f g o 处处连续。

又因为⎪⎩⎪⎨⎧+∞−∈−−=−−∞∈=U U o ).,1()0,1(,1,1,0,1,0),1,0()1,(,1))((x x x x g f故 1,0,1−=x 是g f o 的跳跃间断点。

2．设g f ,在点0x 连续，证明：（1）若)()(00x g x f >，则存在),(0δx U ，使在其内有)()(x g x f >；（2）若在某)(00x U 内有)()(x g x f >，则)()(00x g x f ≥。

解：（1）由于)()(00x g x f >，从而02)()(000>−=x g x f ε，因f 在0x 连续，于是)()(lim 00x f x f x x =→因此存在正数1δ，使得当10δ<−x x 时，便有00)()(ε<−x f x f ，可得 2)()()(00x g x f x f +>（1）又因g 在0x 连续，从而存在正数2δ，当20δ<−x x 时，有00)()(ε<−x g x g 可见 2)()()(00x g x f x g +< （2）现取},min{21δδδ=，当δ<−0x x 时，（1），（2）同时成立。

连续函数的性质

§2.2 连续函数的性质♦ 连续函数的局部性质若函数f 在点0x 连续，则f 在点0x 有极限，且极限值等于函数值0()f x 。

从而，根据函数极限的性质能推断出函数f 在0()U x 的性态。

定理1（局部有界性）若函数f 在点0x 连续，，则f 在某0()U x 内有界。

定理2（局部保号性）若函数f 在点0x 连续，且0()0f x >（或0<），则对任何正数0()r f x <（或0()r f x <-），存在某0()U x ，使得对一切0()x U x ∈有()f x r >（或()f x r <-）。

注：在具体应用局部保号性时，常取01()2r f x =，则当0()0f x >时，存在某0()U x ，使在其内有01()()2f x f x >。

定理3（四则运算）若函数f 和g 在点0x 连续，则,,f fg f g g±⋅（这里0()0g x ≠）也都在点0x 连续。

关于复合函数的连续性，有如下定理:定理4 若函数f 在点0x 连续，g 在点0u 连续，00()u f x =，则复合函数gf在点0x 连续。

证明：由于g 在点0u 连续，10,0εδ∀>∃>，使得当01||u u δ-<时有0|()()|g u g u ε-<。

（1）又由00()u f x =及()u f x =f 在点0x 连续，故对上述1δ，存在0δ>，使得当0||x x δ-<时有001|||()()|u u f x f x δ-=-<，联系（1）式得:对任给的0ε>，存在0δ>，使得当0||x x δ-<时有 0|(())(())|g f x g f x ε-<。

这就证明了gf在点0x 连续。

注：根据连续必的定义，上述定理的结论可表为0lim (())(lim ())(())x x x x g f x g f x g f x →→==定理 5 ()x f xx 0lim →存在的充要条件是()()0lim 000+=+→x f x f x x 与()()0lim 000-=-→x f x f x x 存在并且相等．证明：必要性显然，仅须证充分性．设()A x f x x =+→00lim ()x f x x 00lim -→=，从而对任给的0>ε，存在01>δ和02>δ，当 100δ<-<x x 时，()ε<-A x f ①当－002<-<x x δ时， ()ε<-A x f ②取{}0,m in 21>=δδδ时，当δ<-<00x x 时，则δ<-<00x x 和00<-<-x x δ二者必居其一，从而满足①或②，所以()ε<-A x f ．定理6 函数()x f 在0x 点连续的充要条件是()x f 左连续且右连续．证明：()x f 在x 点连续即为()()00lim x f x f xx =→．注意左连续即为()()000x f x f =-，右连续即为()()000x f x f =+，用定理5即可证．此外，在讨论函数的极限时往往必须把连续变量离散化，下面我们来讨论这方面的问题．定理7 海涅（Heine ）定理：()x f xx 0lim →存在的充分必要条件是对任给的序列{}n x ，若满足0lim x x n n =∞→（0x x n≠），则有()n n x f ∞→lim 存在．分析：必要性的证明是显然．充分性的证明我们用反证法．证明：必要性。

二元函数连续条件的探讨【】.docx

指导老师：张颖媛摘要：本文研究的是二元函数连续的条件，若二元函数连续，则二元函数按每一个单变量必连续。

反之，二元函数按每一个单变量都连续，但二元函数不一定连续，当增加某些条件后，二元函数就连续了。

关键词：二元函数；连续；单变量连续* * 1刖S二元函数的“全面连续”是指二维连续，相应地，“按单变量连续”可理解为函数f(x,y)分别对x和y连续。

关于二元函数连续条件，有下面结果:全面连续必按各单变量连续；反之，按各单变量连续，不一定全面连续，只有补充某些条件之后，才能保证二元函数的连续性，以下通过两种方法对此证明。

正面证明：因f(x,y)全面连续，不妨设其定义在DuR?上,Pq (Xq> y0)e D是D上的聚点或孤立点，则对于任给的正数总存在相应的正数5,只要P w U (人，5) C D, 就有即|./'(儿刃一/(兀，儿)|<£故有：f(x,y)按各单变量连续。

举出反例证明：心」拦-当八Z时0 ,当x2 + y2 = 0时在原点处显然不连续。

但由于/(O,y) = /(x,O)^O因此，在原点处f(x,y)对x和y对分别都连续。

1二元函数的连续性概念定义1.1 (用“£-3”定义二元函数连续)设函数f(.r,y)为定义在点集DUR?上的二元函数，P o eD (它或者是D 的聚点，或者是D 的孤立点)，若对0£〉0, E J>0, 使得当Peo(^,J)nD 时，都有则称/(-r,v)关于集合D 在人点连续，简称/在人点连续。

若函数/在D 上任何点都连续，则称/■为D 上的连续函数。

由连续定义，若P 。

是D 的孤立点，则厶必定是/■关于集合D 的连续点；若佗是D 的聚点，则/■关于集合D 在人连续等价于limf(P) = /(^)P&D如果是D 的聚点，而上式不成立，则称/•关于集合D 在厶不连续(或间断点)。

特别iimy (p )= A^y (q )时，称p°是/■的可去间断点。

二元函数连续性

一二元函数的连续性概念二有界闭域上连续函数的性质返回返回返回返回返回返回返回返回一二元函数的连续性概念连续性的定义上任何点都关于集合d连续则称f为定义在点集上的二元函数返回返回返回返回的孤立点则必定是pppdfpfp称间断点
§3 二元函数的连续性
无论是单元微积分还是多元微积分, 其中所讨论的函数, 最重要的一类就是连续函数. 二元函数连续性的定义比一元函数更一般化了些; 而它们的局部性质与在有界闭域上的整体性质, 二者完全相同.
本段讨论有界闭域上多元连续函数的整体性质. 这可以看作闭区间上一元连续函数性质的推广.
定理16. 8 ( 有界性定理与最大、小值定理 ) 若二元
函数 f 在有界闭域
D R2 上连续, 则 f 在 D上有界,
且能取得最大值与最小值.
定理16.9 (一致连续性定理) 若函数 f 在有界闭域
D R2上连续, 则 f 在 D 上一致连续. 即
注2 由定理16. 10 又可知道, 若 f 为区域 D 上的连续函数, 则 f (D) 必定是一个区间 (有限或无限).
f (P1 ) f (P2 )
(4)
的实数 , 必存在点
P0 D , 使得 f ( P0 ) .
注1 定理16. 8 与 16. 9 中的有界闭域 D 可以改为有界闭集 (证明过程无原则性变化). 但是介值性定理中所考察的点集 D 只能假设是一区域, 这是为了保证它具有连通性, 而一般的开集或闭集是不一定具有连通性的.
因此 lim f ( x, y) 0 f (0,0), 此时 f 在原点连 ( x, y) (0,0)
续; 而当 2 时, lim f ( x, y) 不存在， ( x, y) (0,0) 在原点间断．

函数的连续性(1-32)

f ( x0 0)
lim
x x0
f (x)
f (x0)
定理函数 f ( x)在 x0 处连续函数 f ( x)在 x0 处既左连续又右连续 , 即有
f ( x0 0) f ( x00) f ( x0 )
f(x) 在 (a , b) 内连续：若 f (x) 在 (a , b) 内每一点处都连续 ( 称 f (x)为 (a , b) 内的连续函数 )
f(x) 在 [a , b] 上连续：若 f (x) 在 (a , b) 内连续 , 在 x = a 处右连续 , 在 x = b 出左连续 , 则称 f(x) 在 [ a , b ] 上连续 (称为[ a , b ]上的连续函数)
20 连续函数的运算性质
定理 ( 连续函数的四则运算性质)
设 f(x) , g(x) 在点 x0 处连续 , 则 (1) f(x)± g(x) 在点 x0 处也连续 ;
tanxcotxsecxcscx在其定义域上连续所以基本三角函数在定义域上连续绿色食品的开发和生产不仅是为了满足人民群众对优质安全食品的需求更重要的是保护我国农业资源改善农业生态环境维持我国农业持续发展基础的生产条件证明对任意的x证明对任意的xlimlnln在其定义域上连续在其定义域上连续绿色食品的开发和生产不仅是为了满足人民群众对优质安全食品的需求更重要的是保护我国农业资源改善农业生态环境维持我国农业持续发展基础的生产条件loglimlnlnlimlnlog在其定义域上连续证明对任意的xlnlimlnlim绿色食品的开发和生产不仅是为了满足人民群众对优质安全食品的需求更重要的是保护我国农业资源改善农业生态环境维持我国农业持续发展基础的生产条件定理反函数的连续性上连续并且严格单调增或严格单调减上连续并且也是严格单调增加或严格单调减少