2016年中考数学模拟试题汇编 专题28 解直角三角形
历年初三数学中考解直角三角形练习题及答案

D
B C
图19-7
⒊ 在Rt∆ABC中,∠C=900. a-b=2. tanA= ,求a、b、c的值。
⒋ 如图 19-7,已知∆ABC中,∠BAC=900.AB=AC. BD是AC边上的中线. 求cot∠DBC的值.
⒌ 在∆ABC中,已知BC=1+ ∠B=600∠C=450.求AB的长.
A
Q
B P C
图19-8
⒍ 身高相同的甲、乙、丙三人放风筝,各人放出的线分别为300m、250m、200m,线与平面所成的角分别为300、450、600(假定风筝线是拉直的)。问三人中谁放的风筝最高?
⒎∆ABC中,∠C=900,BC=8cm,sinB= ,一只蜜蜂从点B开始沿BC向点C以2cm/s的速度移动。另一只蜜蜂从点C开始沿CA边向点A以1cm/s的速度移动。如果两只 蜜蜂分别从B、C点同时出发各自运动到P、Q,如图19-8,第几秒钟时PQ∥AB?
第二课时(勾股定理、解直角三角形及有关知识解决实际问题)
课标要求
1、熟悉勾股定理的探索过程,会用勾股定理解决简单的实际问题。
2、运用三角函数解决与直角三角形有关的简单的实际问题。
3、能综合运用直角三角形的勾股定理与边角关系解决简单的实际问题。
中招考点
1、用勾股定理解决实际问题。
2、直角三角形的基本解法(运用三角函数、勾股定理)。
A. B. C. D.
分析:sinA= , sinA=sinBCD= ;sinA= ,从而判断D不正确。故应选D.。
2、在Rt△ABC中,C=900,A=B,则cosA的值是( )
A. B. C. D.1
分析:先求出A的度数,因为C=900,A=B,故A=B=450,再由特殊角的三角函数值可得:cosA=cos450= 故选B.。
全国各地2016年中考数学试题分类总汇编(第2期)专题28解直角三角形(含解析汇报)

解直角三角形一.选择题1. (2016 •山东省荷泽市3分)如图,△ ABC与△A'B'C '都是等腰三角形,且AB=AC=5A B =A C =3,若Z B+ ZB =90。
,则公BC与从B C '的面积比为()A. 25 : 9B. 5: 3C. :D. 5 : 3【考点】互余两角三角函数的关系.【分析】先根据等腰三角形的性质得到Z B= Z C,Z B = Z C ',根据三角函数的定义得到AD=AB ?sinB , A D =A B ' s?nB ' ,BC=2BD=2AB ?cosB , B C =2B D =2A B ' COsB ',然后根据三角形面积公式即可得到结论.【解答】解:过A作AD丄BC于D,过A '作A 'D ' _B C ' 于)',•••公BC与M B C '都是等腰三角形,/•ZB= ZC,Z B = ZC ' ,BC=2BD , B 'C =2B D ',•••AD=AB ?sinB , A 'D '=A B ' SinB ' ,BC=2BD=2AB ?cosB , B C '=2B 'D '=2A 'B ' COsB ',•/J3+ ZB '=90 ° ,/•sinB=cosB ' ,sinB '=cosB ,•.•S ZBAC= ^AD ?BC= :AB?sinB ?2AB ?cosB=25sinB ?cosB , 丄PS/A B C '= 'D ' B C '= 'B ' cosB ' 2A B ' sinB '=9sinB ' cosB ',...S/BAC : S/A B C =25 : 9 .故选A.【点评】本题考查了互余两角的关系,解直角三角形:在直角三角形中,由已知元素求未知 元素的过程就是解直角三角形•也考查了等腰三角形的性质和三角形面积公式.2. (2016 •重庆市A 卷4分)某数学兴趣小组同学进行测量大树CD 高度的综合实践活动, 如图,在点A 处测得直立于地面的大树顶端 C 的仰角为36。
专题28 解直角三角形(58题)(原卷版)--2024年中考数学真题分类汇编

专题28解直角三角形(58题)一、单选题1.(2024·吉林长春·中考真题)2024年5月29日16时12分,“长春净月一号”卫星搭乘谷神星一号火箭在黄海海域成功发射.当火箭上升到点A 时,位于海平面R 处的雷达测得点R 到点A 的距离为a 千米,仰角为θ,则此时火箭距海平面的高度AL 为()A .sin a θ千米B .sin aθ千米C .cos a θ千米D .cos aθ千米2.(2024·天津·2cos451- 的值等于()A .0B .1C .212-D 213.(2024·甘肃临夏·中考真题)如图,在ABC 中,5AB AC ==,4sin 5B =,则BC 的长是()A .3B .6C .8D .94.(2024·四川自贡·中考真题)如图,等边ABC 钢架的立柱CD AB ⊥于点D ,AB 长12m .现将钢架立柱缩短成DE ,60BED ∠=︒.则新钢架减少用钢()A .(243m-B .(243m-C .(2463m-D .(243m-5.(2024·四川德阳·中考真题)某校学生开展综合实践活动,测量一建筑物CD 的高度,在建筑物旁边有一高度为10米的小楼房AB ,小李同学在小楼房楼底B 处测得C 处的仰角为60︒,在小楼房楼顶A 处测得C 处的仰角为30︒.(AB CD 、在同一平面内,B D 、在同一水平面上),则建筑物CD 的高为()米A .20B .15C .12D .10+6.(2024·广东深圳·中考真题)如图,为了测量某电子厂的高度,小明用高1.8m 的测量仪EF 测得的仰角为45︒,小军在小明的前面5m 处用高1.5m 的测量仪CD 测得的仰角为53︒,则电子厂AB 的高度为()(参考数据:sin 5345︒≈,cos5335︒≈,tan 5343︒≈)A .22.7mB .22.4mC .21.2mD .23.0m7.(2024·内蒙古包头·中考真题)如图,在矩形ABCD 中,,E F 是边BC 上两点,且BE EF FC ==,连接,,DE AF DE 与AF 相交于点G ,连接BG .若4AB =,6BC =,则sin GBF ∠的值为()A .10B .10C .13D .238.(2024·黑龙江大兴安岭地·中考真题)如图,菱形ABCD 中,点O 是BD 的中点,AM BC ⊥,垂足为M ,AM 交BD 于点N ,2OM =,8BD =,则MN 的长为()A 5B 455C 355D 259.(2024·四川乐山·中考真题)如图,在菱形ABCD 中,60ABC ∠=︒,1AB =,点P 是BC 边上一个动点,在BC 延长线上找一点Q ,使得点P 和点Q 关于点C 对称,连接DP AQ 、交于点M .当点P 从B 点运动到C 点时,点M 的运动路径长为()A .36B 33C 32D 310.(2024·山东泰安·中考真题)如图,菱形ABCD 中,=60B ∠︒,点E 是AB 边上的点,4AE =,8BE =,点F 是BC 上的一点,EGF △是以点G 为直角顶点,EFG ∠为30︒角的直角三角形,连结AG .当点F 在直线BC 上运动时,线段AG 的最小值是()A .2B .432-C .23D .411.(2024·四川泸州·512-的美感.如图,把黄金矩形ABCD 沿对角线AC 翻折,点B 落在点B '处,AB '交CD 于点E ,则sin DAE ∠的值为()A 55B .12C .35D 25512.(2024·黑龙江大兴安岭地·中考真题)如图,在正方形ABCD 中,点H 在AD 边上(不与点A 、D 重合),90BHF ∠=︒,HF 交正方形外角的平分线DF 于点F ,连接AC 交BH 于点M ,连接BF 交AC 于点G ,交CD 于点N ,连接BD .则下列结论:①45HBF ∠=︒;②点G 是BF 的中点;③若点H 是AD 的中点,则sinNBC ∠BN =;⑤若12AH D H =,则112BND AHM S S =△△,其中正确的结论是()A .①②③④B .①③⑤C .①②④⑤D .①②③④⑤二、填空题13.(2024·黑龙江绥化·中考真题)如图,用热气球的探测器测一栋楼的高度,从热气球上的点A 测得该楼顶部点C 的仰角为60︒,测得底部点B 的俯角为45︒,点A 与楼BC 的水平距离50m AD =,则这栋楼的高度为m (结果保留根号).14.(2024·内蒙古赤峰·中考真题)综合实践课上,航模小组用无人机测量古树AB 的高度.如图,点C 处与古树底部A 处在同一水平面上,且10AC =米,无人机从C 处竖直上升到达D 处,测得古树顶部B 的俯角为45︒,古树底部A 的俯角为65︒,则古树AB 的高度约为米(结果精确到0.1米;参考数据:sin 650.906︒≈,cos 650.423︒≈,tan 65 2.145︒≈).15.(2024·湖北武汉·中考真题)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼AB 的高度,具体过程如下:如图,将无人机垂直上升至距水平地面102m 的C 处,测得黄鹤楼顶端A 的俯角为45︒,底端B 的俯角为63︒,则测得黄鹤楼的高度是m .(参考数据:tan632︒≈)16.(2024·四川内江·中考真题)如图,在矩形ABCD 中,3AB =,5AD =,点E 在DC 上,将矩形ABCD 沿AE 折叠,点D 恰好落在BC 边上的点F 处,那么tan ∠=EFC .17.(2024·江苏盐城·中考真题)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面30m 的点P 处,测得教学楼底端点A 的俯角为37︒,再将无人机沿教学楼方向水平飞行26.6m 至点Q 处,测得教学楼顶端点B 的俯角为45︒,则教学楼AB 的高度约为m .(精确到1m ,参考数据:sin370.60︒≈,cos370.80︒≈,tan370.75︒≈)18.(2024·北京·中考真题)如图,在正方形ABCD 中,点E 在AB 上,AF D E ⊥于点F ,CG DE ⊥于点G .若5AD =,CG 4=,则AEF △的面积为.19.(2024·甘肃临夏·中考真题)如图,对折边长为2的正方形纸片ABCD ,OM 为折痕,以点O 为圆心,OM 为半径作弧,分别交AD ,BC 于E ,F 两点,则 EF的长度为(结果保留π).20.(2024·黑龙江齐齐哈尔·中考真题)如图,数学活动小组在用几何画板绘制几何图形时,发现了如“花朵”形的美丽图案,他们将等腰三角形OBC 置于平面直角坐标系中,点O 的坐标为(00),,点B 的坐标为(1)0,,点C 在第一象限,120OBC ∠=︒.将OBC △沿x 轴正方向作无滑动滚动,使它的三边依次与x 轴重合,第一次滚动后,点O 的对应点为O ',点C 的对应点为C ',OC 与O C ''的交点为1A ,称点1A 为第一个“花朵”的花心,点2A 为第二个“花朵”的花心;……;按此规律,OBC △滚动2024次后停止滚动,则最后一个“花朵”的花心的坐标为.21.(2024·黑龙江大兴安岭地·中考真题)矩形ABCD 中,3AB =,4BC =,将AB 沿过点A 的一条直线折叠,折痕交直线BC 于点P (点P 不与点B 重合),点B 的对称点落在矩形对角线所在的直线上,则PC 长为.22.(2024·山东泰安·中考真题)在综合实践课上,数学兴趣小组用所学数学知识测量大汶河某河段的宽度,他们在河岸一侧的瞭望台上放飞一只无人机,如图,无人机在河上方距水面高60米的点P 处测得瞭望台正对岸A 处的俯角为50︒,测得瞭望台顶端C 处的俯角为63.6︒,已知瞭望台BC 高12米(图中点A ,B ,C ,P 在同一平面内),那么大汶河此河段的宽AB 为米.(参考数据:3sin 405︒≈,9sin 63.610︒≈,6tan 505︒≈,tan 63.62︒≈)23.(2024·四川达州·中考真题)如图,在Rt ABC △中,90C ∠=︒.点D 在线段BC 上,45BAD ∠=︒.若4AC =,1CD =,则ABC 的面积是.24.(2024·贵州·中考真题)如图,在菱形ABCD 中,点E ,F 分别是BC ,CD 的中点,连接AE ,AF .若4sin 5EAF ∠=,5AE =,则AB 的长为.25.(2024·广东深圳·中考真题)如图,在ABC 中,AB BC =,5tan 12B ∠=,D 为BC 上一点,且满足85BD CD =,过D 作DE AD ⊥交AC 延长线于点E ,则CEAC=.26.(2024·黑龙江绥化·中考真题)在矩形ABCD 中,4cm AB =,8cm BC =,点E 在直线AD 上,且2cm DE =,则点E 到矩形对角线所在直线的距离是cm .三、解答题27.(2024·内蒙古通辽·0322sin60(π)-+︒--.28.(2024·四川甘孜·中考真题)如图,一艘海轮位于灯塔P 的北偏东37︒方向,距离灯塔100海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东45︒方向上的B 处.这时,B 处距离A 处有多远?(参考数据:sin 370.60︒≈,cos370.80︒≈,tan 370.75︒≈)29.(2024·北京·中考真题)计算:()0582sin 302π-︒+-30.(2024·湖南长沙·中考真题)计算:()011(32cos 30π 6.84-+-︒-.31.(2024·广东深圳·中考真题)计算:()112cos 45 3.14124π-⎛⎫-⋅︒+-++ ⎪⎝⎭.32.(2024·黑龙江大兴安岭地·中考真题)先化简,再求值:22222111m m m m m m ⎛⎫-+÷- ⎪-+⎝⎭,其中cos60m =︒.33.(2024·吉林·中考真题)图①中的吉林省广播电视塔,又称“吉塔”.某直升飞机于空中A 处探测到吉塔,此时飞行高度873m AB =,如图②,从直升飞机上看塔尖C 的俯角37EAC ∠=︒,看塔底D 的俯角45EAD ∠=︒,求吉塔的高度CD (结果精确到0.1m ).(参考数据:sin 370.60︒=,cos370.80︒=,tan 370.75︒=)34.(2024·青海·018tan 452π︒+--.35.(2024·内蒙古呼伦贝尔·中考真题)计算:301tan6032(π2024)2-⎛⎫--+︒-+- ⎪⎝⎭.36.(2024·内蒙古呼伦贝尔·中考真题)综合实践活动中,数学兴趣小组利用无人机测量大楼的高度.如图,无人机在离地面40米的D 处,测得操控者A 的俯角为30︒,测得楼BC 楼顶C 处的俯角为45︒,又经过人工测量得到操控者A 和大楼BC 之间的水平距离是80米,则楼BC 的高度是多少米?(点A B C D ,,,都3 1.7≈)37.(2024·内蒙古通辽·中考真题)在“综合与实践”活动课上,活动小组测量一棵杨树的高度.如图,从C 点测得杨树底端B 点的仰角是30︒,BC 长6米,在距离C 点4米处的D 点测得杨树顶端A 点的仰角为45︒,求杨树AB 的高度(精确到0.1米,AB ,BC ,CD 在同一平面内,点C ,D 在同一水平线上.参考数据:3 1.73)≈.38.(2024·湖南·中考真题)某数学研究性学习小组在老师的指导下,利用课余时间进行测量活动.活动主题测算某水池中雕塑底座的底面积测量工具皮尺、测角仪、计算器等活动过程模型抽象某休闲广场的水池中有一雕塑,其底座的底面为矩形ABCD ,其示意图如下:测绘过程与数据信息①在水池外取一点E ,使得点C ,B ,E 在同一条直线上;②过点E 作GH CE ⊥,并沿EH 方向前进到点F ,用皮尺测得EF 的长为4米;③在点F 处用测角仪测得60.3CFG ∠=︒,45BFG ∠=︒,21.8AFG ∠=︒;④用计算器计算得:sin60.30.87︒≈,cos60.30.50︒≈,tan60.3 1.75︒≈.sin21.80.37︒≈,cos21.80.93︒≈,tan21.80.40︒≈.请根据表格中提供的信息,解决下列问题(结果保留整数):(1)求线段CE 和BC 的长度:(2)求底座的底面ABCD 的面积.39.(2024·贵州·中考真题)综合与实践:小星学习解直角三角形知识后,结合光的折射规律进行了如下综合性学习.【实验操作】第一步:将长方体空水槽放置在水平桌面上,一束光线从水槽边沿A 处投射到底部B 处,入射光线与水槽内壁AC 的夹角为A ∠;第二步:向水槽注水,水面上升到AC 的中点E 处时,停止注水.(直线NN '为法线,AO 为入射光线,OD 为折射光线.)【测量数据】如图,点A ,B ,C ,D ,E ,F ,O ,N ,N '在同一平面内,测得20cm AC =,45A ∠=︒,折射角32DON ∠=︒.【问题解决】根据以上实验操作和测量的数据,解答下列问题:(1)求BC 的长;(2)求B ,D 之间的距离(结果精确到0.1cm ).(参考数据:sin 320.52︒≈,cos320.84︒≈,tan 320.62︒≈)40.(2024·河南·中考真题)如图1,塑像AB 在底座BC 上,点D 是人眼所在的位置.当点B 高于人的水平视线DE 时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A ,B 两点的圆与水平视线DE 相切时(如图2),在切点P 处感觉看到的塑像最大,此时APB ∠为最大视角.(1)请仅就图2的情形证明APB ADB ∠>∠.(2)经测量,最大视角APB ∠为30︒,在点P 处看塑像顶部点A 的仰角APE ∠为60︒,点P 到塑像的水平距离PH 为6m .求塑像AB 的高(结果精确到0.1m 3 1.73≈).41.(2024·天津·中考真题)综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔AB 的高度(如图①).某学习小组设计了一个方案:如图②,点,,C D E 依次在同一条水平直线上,36m,DE EC AB =⊥,垂足为C .在D 处测得桥塔顶部B 的仰角(CDB ∠)为45︒,测得桥塔底部A 的俯角(CDA ∠)为6︒,又在E 处测得桥塔顶部B 的仰角(CEB ∠)为31︒.(1)求线段CD 的长(结果取整数);(2)求桥塔AB 的高度(结果取整数).参考数据:tan310.6,tan60.1︒≈︒≈.42.(2024·四川乐山·中考真题)我国明朝数学家程大位写过一本数学著作《直指算法统宗》,其中有一道与荡秋千有关的数学问题是使用《西江月》词牌写的:平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?词写得很优美,翻译成现代汉语的大意是:有一架秋千,当它静止时,踏板离地1尺,将它往前推进10尺(5尺为一步),秋千的踏板就和某人一样高,这个人的身高为5尺.(假设秋千的绳索拉的很直)(1)如图1,请你根据词意计算秋千绳索OA 的长度;(2)如图2,将秋千从与竖直方向夹角为α的位置OA '释放,秋千摆动到另一侧与竖直方向夹角为β的地方OA '',两次位置的高度差PQ h =.根据上述条件能否求出秋千绳索OA 的长度?如果能,请用含α、β和h 的式子表示;如果不能,请说明理由.43.(2024·山东·中考真题)【实践课题】测量湖边观测点A 和湖心岛上鸟类栖息点P 之间的距离【实践工具】皮尺、测角仪等测量工具【实践活动】某班甲小组根据湖岸地形状况,在岸边选取合适的点B .测量A ,B 两点间的距离以及∠PAB 和PBA ∠,测量三次取平均值,得到数据:60AB =米,79PAB ∠=︒,64PBA ∠=︒.画出示意图,如图【问题解决】(1)计算A ,P 两点间的距离.(参考数据:sin640.90︒≈,sin790.98︒≈,cos790.19︒≈,sin370.60︒≈,tan370.75︒≈)【交流研讨】甲小组回班汇报后,乙小组提出了另一种方案:如图2,选择合适的点D ,E ,F ,使得A ,D ,E 在同一条直线上,且AD DE =,DEF DAP ∠=∠,当F ,D ,P 在同一条直线上时,只需测量EF 即可.(2)乙小组的方案用到了________.(填写正确答案的序号)①解直角三角形②三角形全等【教师评价】甲、乙两小组的方案都很好,对于实际测量,要根据现场地形状况选择可实施的方案.44.(2024·北京·中考真题)如图,在四边形ABCD 中,E 是AB 的中点,DB ,CE 交于点F ,DF FB =,AF DC .(1)求证:四边形AFCD 为平行四边形;(2)若90EFB ∠=︒,tan 3FEB ∠=,1EF =,求BC 的长.45.(2024·甘肃临夏·中考真题)乾元塔(图1)位于临夏州临夏市的北山公园内,共九级,为砼框架式结构,造型独特别致,远可眺太子山露骨风月,近可收临夏市城建全貌,巍巍峨峨,傲立苍穹.某校数学兴趣小组在学习了“解直角三角形”之后,开展了测量乾元塔高度AB 的实践活动.A 为乾元塔的顶端,AB BC ⊥,点C ,D 在点B 的正东方向,在C 点用高度为1.6米的测角仪(即 1.6CE =米)测得A 点仰角为37︒,向西平移14.5米至点D ,测得A 点仰角为45︒,请根据测量数据,求乾元塔的高度AB .(结果保留整数,参考数据:sin370.60︒≈,cos370.80︒≈,tan370.75︒≈)46.(2024·安徽·中考真题)科技社团选择学校游泳池进行一次光的折射实验,如图,光线自点B 处发出,经水面点E 折射到池底点A 处.已知BE 与水平线的夹角36.9α=︒,点B 到水面的距离 1.20BC =m ,点A 处水深为1.20m ,到池壁的水平距离 2.50m AD =,点B C D ,,在同一条竖直线上,所有点都在同一竖直平面内.记入射角为β,折射角为γ,求sin sin βγ的值(精确到0.1,参考数据:sin 36.90.60︒≈,cos36.90.80︒≈,tan 36.90.75︒≈).47.(2024·浙江·中考真题)如图,在ABC 中,AD BC ⊥,AE 是BC 边上的中线,10,6,tan 1AB AD ACB ==∠=.(1)求BC 的长;(2)求sin DAE ∠的值.48.(2024·甘肃·中考真题)习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒AH 垂直于地面,测角仪CD ,EF 在AH 两侧, 1.6m CD EF ==,点C 与点E 相距182m (点C ,H ,E 在同一条直线上),在D 处测得简尖顶点A 的仰角为45︒,在F 处测得筒尖顶点A 的仰角为53︒.求风电塔筒AH 的高度.(参考数据:sin 5345︒≈,cos5335︒≈,tan 5343︒≈.)49.(2024·河北·中考真题)中国的探月工程激发了同学们对太空的兴趣.某晚,淇淇在家透过窗户的最高点P 恰好看到一颗星星,此时淇淇距窗户的水平距离4m BQ =,仰角为α;淇淇向前走了3m 后到达点D ,透过点P 恰好看到月亮,仰角为β,如图是示意图.已知,淇淇的眼睛与水平地面BQ 的距离 1.6m ==AB CD ,点P 到BQ 的距离 2.6m PQ =,AC 的延长线交PQ 于点E .(注:图中所有点均在同一平面)(1)求β的大小及tan α的值;(2)求CP 的长及sin APC ∠的值.50.(2024·四川广元·中考真题)计算:()2012024π32tan 602-⎛⎫-++︒- ⎪⎝⎭.51.(2024·四川广元·中考真题)小明从科普读物中了解到,光从真空射入介质发生折射时,入射角α的正弦值与折射角β的正弦值的比值sin sin αβ叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.(1)若光从真空射入某介质,入射角为α,折射角为β,且7cos 4α=30β=︒,求该介质的折射率;(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点A ,B ,C ,D 分别是长方体棱的中点,若光线经真空从矩形2121A D D A 对角线交点O 处射入,其折射光线恰好从点C 处射出.如图②,已知60α=︒,10cm CD =,求截面ABCD 的面积.52.(2024·内蒙古包头·中考真题)如图,学校数学兴趣小组开展“实地测量教学楼AB 的高度”的实践活动.教学楼周围是开阔平整的地面,可供使用的测量工具有皮尺、测角仪(皮尺的功能是直接测量任意可到达的两点间的距离;测角仪的功能是测量角的大小).(1)请你设计测量教学楼AB 的高度的方案,方案包括画出测量平面图,把应测数据标记在所画的图形上(测出的距离用,m n 等表示,测出的角用,αβ等表示),并对设计进行说明;(2)根据你测量的数据,计算教学楼AB 的高度(用字母表示).53.(2024·甘肃·中考真题)马家窑文化以发达的彩陶著称于世,其陶质坚固,器表细腻,红、黑、白彩共用,彩绘线条流畅细致,图案繁缛多变,形成了绚丽典雅的艺术风格,创造了一大批令人惊叹的彩陶艺术精品,体现了古代劳动人民的智慧.如图1的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图2,已知O 和圆上一点M .作法如下:①以点M 为圆心,OM 长为半径,作弧交O 于A ,B 两点;②延长MO 交O 于点C ;即点A ,B ,C 将O 的圆周三等分.(1)请你依据以上步骤,用不带刻度的直尺和圆规在图2中将O 的圆周三等分(保留作图痕迹,不写作法);(2)根据(1)画出的图形,连接AB ,AC ,BC ,若O 的半径为2cm ,则ABC 的周长为______cm .54.(2024·黑龙江牡丹江·中考真题)如图,某数学活动小组用高度为1.5米的测角仪BC ,对垂直于地面CD 的建筑物AD 的高度进行测量,BC CD ⊥于点C .在B 处测得A 的仰角=45ABE ∠︒,然后将测角仪向建筑物方向水平移动6米至FG 处,FG CD ⊥于点G ,测得A 的仰角58AFE ∠=︒,BF 的延长线交AD 于点E ,求建筑物AD 的高度(结果保留小数点后一位).(参考数据:sin580.85,cos580.53,tan58 1.60︒≈︒≈︒≈)55.(2024·广东·中考真题)中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN 充电站的平面示意图,矩形ABCD 是其中一个停车位.经测量,60ABQ ∠=︒, 5.4m AB =, 1.6m CE =,GH CD ⊥,GH 是另一个车位的宽,所有车位的长宽相同,按图示并列划定.根据以上信息回答下列问题:(结果精确到0.1m 3 1.73≈)(1)求PQ 的长;(2)该充电站有20个停车位,求PN 的长.56.(2024·广东广州·中考真题)2024年6月2日,嫦娥六号着陆器和上升器组合体(简称为“着上组合体”)成功着陆在月球背面.某校综合实践小组制作了一个“着上组合体”的模拟装置,在一次试验中,如图,该模拟装置在缓速下降阶段从A 点垂直下降到B 点,再垂直下降到着陆点C ,从B 点测得地面D 点的俯角为36.87︒,17AD =米,10BD =米.(1)求CD 的长;(2)若模拟装置从A 点以每秒2米的速度匀速下降到B 点,求模拟装置从A 点下降到B 点的时间.(参考数据:sin 36.870.60︒≈,cos36.870.80︒≈,tan 36.870.75︒≈)57.(2024·青海·中考真题)如图,某种摄像头识别到最远点A 的俯角α是17︒,识别到最近点B 的俯角β是45︒,该摄像头安装在距地面5m 的点C 处,求最远点与最近点之间的距离AB (结果取整数,参考数据:sin170.29︒≈,cos170.96︒≈,tan170.31︒≈).58.(2024·陕西·中考真题)问题提出(1)如图1,在ABC 中,15AB =,30C ∠=︒,作ABC 的外接圆O .则 ACB 的长为________;(结果保留π)问题解决(2)如图2所示,道路AB 的一侧是湿地.某生态研究所在湿地上建有观测点D ,E ,C ,线段AD AC ,和BC 为观测步道,其中点A 和点B 为观测步道出入口,已知点E 在AC 上,且AE EC =,60DAB ∠=︒,120ABC ∠=︒,1200m AB =,900m AD BC ==,现要在湿地上修建一个新观测点P ,使60DPC ∠=︒.再在线段AB 上选一个新的步道出入口点F ,并修通三条新步道PF PD PC ,,,使新步道PF 经过观测点E ,并将五边形ABCPD 的面积平分.请问:是否存在满足要求的点P 和点F ?若存在,求此时PF 的长;若不存在,请说明理由.(点A ,B ,C ,P ,D 在同一平面内,道路AB 与观测步道的宽、观测点及出入口的大小均忽略不计,结果保留根号)。
中考数学解直角三角形试题汇编

中考数学解直角三角形试题分类汇编含答案一、选择题1、(2007山东淄博)王英同学从A 地沿北偏西60º方向走100m 到B 地,再从B 地向正南方向走200m 到C 地,此时王英同学离A 地 ( )D(A )350m(B )100 m(C )150m (D )3100m解:作出如图所示图形,则∠BAD =90°-60°=30°,AB =100,所以BD =50,cos30°=ADAB,所以,AD =503,CD =200-50=150,在Rt △ADC 中, AC =22AD CD +=22(503)150+=1003,故选(D )。
2、(2007浙江杭州)如图1,在高楼前D 点测得楼顶的仰角为30︒,向高楼前进60米到C 点,又测得仰角为45︒,则该高楼的高度大约为( )AA.82米B.163米C.52米D.70米3、(2007南充)一艘轮船由海平面上A 地出发向南偏西40º的方向行驶40海里到达B 地,再由B 地向北偏西10º的方向行驶40海里到达C 地,则A 、C 两地相距( ).B (A )30海里 (B )40海里 (C )50海里 (D )60海里4、(2007江苏盐城)利用计算器求sin30°时,依次按键则计算器上显示的结果是( )AA .0.5B .0.707C .0.866D .15、(2007山东东营)王英同学从A 地沿北偏西60º方向走100m 到B 地,再从B 地向正南方向走200m 到C 地,此时王英同学离A 地 ( )D(A )150m(B )350m(C )100 m(D )3100m6、(2007浙江台州)一次数学活动中,小迪利用自己制作的测角器测量小山的高度CD .已知她的眼睛与地面的距离为1.6米,小迪在B 处测量时,测角器中的60AOP ∠=°(量角器零度线AC 和铅垂线OP 的夹角,如图);然后她向小山走50米到达点F 处(点B F D ,,在同一直线上),这时测角器中的45EO P ''∠=°,那么小山的高度CD 约为( ) A.68米 B.70米 C.121米 D.123米图145︒30︒BAD C(注:数据3 1.732≈,2 1.414≈供计算时选用)B二、填空题1、(2007山东济宁)计算45tan 30cos 60sin -的值是 。
中考数学真题分类汇编(第三期)专题28 解直角三角形试题(含解析)-人教版初中九年级全册数学试题

解直角三角形一.选择题1.(2018·某某市B卷)5.坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)()【分析】作BM⊥ED交ED的延长线于M,⊥DM于N.首先解直角三角形Rt△CDN,求出,DN,再根据tan24°=,构建方程即可解决问题;【解答】解:作BM⊥ED交ED的延长线于M,⊥DM于N.在Rt△CDN中,∵==,设=4k,DN=3k,∴CD=10,∴(3k)2+(4k)2=100,∴k=2,∴=8,DN=6,∵四边形BMNC是矩形,∴BM==8,BC=MN=20,EM=MN+DN+DE=66,在Rt△AEM中,tan24°=,∴0.45=,∴AB=21.7(米),故选:A.【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.2.(2018·某某某某·3分)如图,某地修建高速公路,要从A地向B地修一条隧道(点A.B在同一水平面上).为了测量A.B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A.B两地之间的距离为()A.800sinα米B.800tanα米C.米D.米【分析】在Rt△ABC中,∠CAB=90°,∠B=α,AC=800米,根据tanα=,即可解决问题;【解答】解:在Rt△ABC中,∵∠CAB=90°,∠B=α,AC=800米,∴tanα=,∴AB==.故选:D.【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是熟练掌握基本知识,属于中考常考题型.3.(2018·某某某某·2分)某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是()A.B.C.D.【分析】如图,连接AD.只要证明∠AOB=∠ADO,可得sin∠AOB=sin∠ADO==;【解答】解:如图,连接AD.∵OD是直径,∴∠OAD=90°,∵∠AOB+∠AOD=90°,∠AOD+∠ADO=90°,∴∠AOB=∠ADO,∴sin∠AOB=sin∠ADO==,故选:D.【点评】本题考查圆周角定理、直径的性质、锐角三角函数等知识,解题的关键是学会用转化的思想思考问题,属于中考创新题目.二.填空题1. (2018·某某江汉·3分)我国海域辽阔,渔业资源丰富.如图,现有渔船B在海岛A,C附近捕鱼作业,已知海岛C位于海岛A的北偏东45°方向上.在渔船B上测得海岛A位于渔船B的北偏西30°的方向上,此时海岛C恰好位于渔船B的正北方向18(1+)n mile 处,则海岛A,C之间的距离为18n mile.【分析】作AD⊥BC于D,根据正弦的定义、正切的定义分别求出BD.CD,根据题意列式计算即可.【解答】解:作AD⊥BC于D,设AC=x海里,在Rt△ACD中,AD=AC×sin∠ACD=x,则CD=x,在Rt△ABD中,BD=x,则x+x=18(1+),解得,x=18,答:A,C之间的距离为18海里.故答案为:182. (2018·某某荆州·3分)荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为米(≈1.73,结果精确到0.1).【解答】解:如图,设CD为塔身的高,延长AB交CD于E,则CD=40,DE=7,∴CE=33,∵∠CBE=45°=∠BCE,∠CAE=30°,∴BE=CE=33,∴AE=a+33,∵tanA=,∴tan30°=,即33=a+33,解得a=33(﹣1)≈24.1,∴a的值约为24.1米,故答案为:24.1.3.(2018·某某省某某市) 如图,某景区的两个景点A.B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C 处时、测得景点A的俯角为45°,景点B的俯角为知30°,此时C到地面的距离CD为100米,则两景点A.B间的距离为100+100米(结果保留根号).【解答】解:∵∠MCA=45°,∠NCB=30°,∴∠ACD=45°,∠DCB=60°,∠B=30°.∵CD=100米,∴AD=CD=100米,D B=米,∴AB=AD+DB=100+100(米).故答案为:100+100.4. (2018·某某某某·3分)如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110m,那么该建筑物的高度BC约为_____m(结果保留整数,≈1.73).【答案】300【解析】【分析】在Rt△ABD中,根据正切函数求得BD=AD•tan∠BAD,在Rt△ACD中,求得CD=AD•tan∠CAD,再根据BC=BD+CD,代入数据计算即可.【详解】如图,∵在Rt△ABD中,AD=110,∠BAD=45°,∴BD= AD•tan45° =110(m),∵在Rt△ACD中,∠CAD=60°,∴CD=AD•tan60°=110×≈190(m),∴BC=BD+CD=110+190=300(m),即该建筑物的高度BC约为300米,故答案为:300.【点睛】本题考查了解直角三角形的应用-仰角俯角问题,熟练应用锐角三角函数关系是解题关键.5.(2018·某某某某·3分)如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6m的位置,在D处测得旗杆顶端A的仰角为53°,若测角仪的高度是1.5m,则旗杆AB的高度约为m.(精确到0.1m.参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)解:过D作DE⊥AB,∵在D处测得旗杆顶端A的仰角为53°,∴∠ADE=53°.∵BC=DE=6m,∴AE=DE•tan53°≈6×1.33≈7.98m,∴AB=AE+BE=AE+CD=7.98+1.5=9.48m≈9.5m.故答案为:9.5.三.解答题1. (2018·某某贺州·8分)如图,一艘游轮在A处测得北偏东45°的方向上有一灯塔B.游轮以20海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:≈1.41,≈1.73)【解答】解:过点C作CM⊥AB,垂足为M,在Rt△ACM中,∠MAC=90°﹣45°=45°,则∠MCA=45°,∴AM=MC,由勾股定理得:AM2+MC2=AC2=(20×2)2,解得:AM=CM=40,∵∠ECB=15°,∴∠BCF=90°﹣15°=75°,∴∠B=∠BCF﹣∠MAC=75°﹣45°=30°,在Rt△BCM中,tanB=tan30°=,即=,∴BM=40,∴AB=AM+BM=40+40≈40+40×1.73≈109(海里),答:A处与灯塔B相距109海里.2. (2018·某某某某·8分)随着人们生活水平的不断提高,旅游已成为人们的一种生活时尚.为开发新的旅游项目,我市对某山区进行调查,发现一瀑布.为测量它的高度,测量人员在瀑布的对面山上D点处测得瀑布顶端A点的仰角是30°,测得瀑布底端B点的俯角是10°,AB与水平面垂直.又在瀑布下的水平面测得CG=27m,GF=17.6m(注:C.G、F三点在同一直线上,CF⊥AB于点F).斜坡CD=20m,坡角∠ECD=40°.求瀑布AB的高度.(参考数据:≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)【分析】过点D作DM⊥CE,交CE于点M,作DN⊥AB,交AB于点N,在Rt△CMD中,通过解直角三角形可求出CM的长度,进而可得出MF、DN的长度,再在Rt△BDN、Rt△ADN中,利用解直角三角形求出BN、AN的长度,结合AB=AN+BN即可求出瀑布AB的高度.【解答】解:过点D作DM⊥CE,交CE于点M,作DN⊥AB,交AB于点N,如图所示.在Rt△CMD中,CD=20m,∠DCM=40°,∠CMD=90°,∴CM=CD•cos40°≈15.4m,DM=CD•sin40°≈12.8m,∴DN=MF=CM+CG+GF=60m.在Rt△BDN中,∠BDN=10°,∠BND=90°,DN=60m,∴BN=DN•tan10°≈10.8m.在Rt△ADN中,∠ADN=30°,∠AND=90°,DN=60m,∴AN=DN•tan30°≈34.6m.∴AB=AN+BN=45.4m.答:瀑布AB的高度约为45.4米.【点评】本题考查了解直角三角形的应用中的仰角俯角问题及坡度坡角问题,通过解直角三角形求出AN、BN的长度是解题的关键.3. (2018·某某某某·7分)如图,一艘海轮位于灯塔C的北偏东45方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处,求此时船距灯塔的距离(参考数据:≈1.414,≈1.732,结果取整数).【分析】过C作CD垂直于AB,根据题意求出AD与BD的长,由AD+DB求出AB的长即可.【解答】解:过C作CD⊥AB,在Rt△ACD中,∠A=45°,∴△ACD为等腰直角三角形,∴AD=CD=AC=50海里,在Rt△BCD中,∠B=30°,∴BC=2CD=100海里,根据勾股定理得:BD=50海里,则AB=AD+BD=50+50≈193海里,则此时船锯灯塔的距离为193海里.【点评】此题考查了解直角三角形﹣方向角问题,熟练掌握各自的性质是解本题的关键.4.(2018·某某省某某·7分)小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,≈1.73)【分析】如图作AE⊥BD于E.分别求出BE.DE,可得BD的长,再根据CD=BD﹣BC计算即可;【解答】解:如图作AE⊥BD于E.在Rt△AEB中,∵∠EAB=30°,AB=10m,∴BE=AB=5(m),AE=5(m),在Rt△ADE中,DE=AE•tan42°=7.79(m),∴BD=DE+BE=12.79(m),∴CD=BD﹣BC=12.79﹣6.5≈6.3(m),答:标语牌CD的长为6.3m.【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是学会添加常用辅助线面构造直角三角形解决问题.5.(2018·某某省某某·8分)图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,X角∠HAC 为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)【分析】作CE⊥BD于F,AF⊥CE于F,如图2,易得四边形AHEF为矩形,则EF=AH=3.4m,∠HAF=90°,再计算出∠CAF=28°,则在Rt△ACF中利用正弦可计算出CF,然后计算CF+EF 即可.【解答】解:作CE⊥BD于F,AF⊥CE于F,如图2,易得四边形AHEF为矩形,∴EF=AH=3.4m,∠HAF=90°,∴∠CAF=∠CAH﹣∠HAF=118°﹣90°=28°,在Rt△ACF中,∵sin∠CAF=,∴CF=9sin28°=9×0.47=4.23,∴CE=CF+EF=4.23+3.4≈7.6(m),答:操作平台C离地面的高度为7.6m.【点评】本题考查了解直角三角形的应用:先将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题),然后利用勾股定理和三角函数的定义进行几何计算.6.(2018·某某省某某市)两栋居民楼之间的距离CD=30米,楼AC和B D均为10层,每层楼高3米.(1)上午某时刻,太阳光线GB与水平面的夹角为30°,此刻B楼的影子落在A楼的第几层?(2)当太阳光线与水平面的夹角为多少度时,B楼的影子刚好落在A楼的底部.【解答】解:(1)延长BG,交AC于点F,过F作FH⊥BD于H,由图可知,FH=CD=30m.∵∠BFH=∠α=30°.在Rt△BFH中,BH=,,答:此刻B楼的影子落在A楼的第5层;(2)连接BC\1BD=3×10=30=CD,∴∠BCD=45°,答:当太阳光线与水平面的夹角为45度时,B楼的影子刚好落在A楼的底部.7.(2018·某某省某某市)(12.00分)如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A.B.C.D.M、N均在同一平面内,CM∥AN).(1)求灯杆CD的高度;(2)求AB的长度(结果精确到0.1米).(参考数据:=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)【分析】(1)延长DC交AN于H.只要证明BC=CD即可;(2)在Rt△BCH中,求出BH、CH,在Rt△ADH中求出AH即可解决问题;【解答】解:(1)延长DC交AN于H.∵∠DBH=60°,∠DHB=90°,∴∠BDH=30°,∵∠CBH=30°,∴∠CBD=∠BDC=30°,∴BC=CD=10(米).(2)在Rt△BCH中,CH=BC=5,BH=5≈8.65,∴DH=15,在Rt△ADH中,AH===20,∴AB=AH﹣BH=20﹣8.65=11.4(米).【点评】本题考查解直角三角形的应用﹣坡度坡角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.8. (2018•呼和浩特•8分)如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:3(沿斜坡从B到D时,其升高的高度与水平前进的距离之比).已知在地面B处测得山顶A的仰角为33°,在斜坡D处测得山顶A的仰角为45°.求山顶A到地面BC的高度AC是多少米?(结果用含非特殊角的三角函数和根式表示即可)解:作DH⊥BC于H.设AE=x.∵DH:BH=1:3,在Rt△BDH中,DH2+(3DH)2=6002,∴DH=60,BH=180,在Rt△ADE中,∵∠ADE=45°,∴DE=AE=x,∵又HC=ED,EC=DH,∴HC=x,EC=60,在Rt△ABC中,tan33°=,∴x=,∴AC=AE+EC=+60=.答:山顶A到地面BC的高度AC是米9. (2018•某某•8分)据调查,超速行驶是引发交通事故的主要原因之一.小强用所学知识对一条笔直公路上的车辆进行测速,如图所示,观测点C到公路的距离CD=200m,检测路段的起点A位于点C的南偏东60°方向上,终点B位于点C的南偏东45°方向上.一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处的时间为10s.问此车是否超过了该路段16m/s的限制速度?(观测点C离地面的距离忽略不计,参考数据:≈1.41,≈1.73)【分析】根据直角三角形的性质和三角函数得出DB,DA,进而解答即可.【解答】解:由题意得:∠DCA=60°,∠DCB=45°,在Rt△CDB中,tan∠DCB=,解得:DB=200,在Rt△CDA中,tan∠DCA=,解得:DA=200,∴AB=DA﹣DB=200﹣200≈146米,轿车速度,答:此车没有超过了该路段16m/s的限制速度.【点评】本题考查了解直角三角形的应用﹣方向角问题,解答本题的关键是利用三角函数求出AD与BD的长度,难度一般.10. (2018•莱芜•9分)在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C.E.D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)【分析】过点B作BF⊥AC于F,BG⊥CD于G,根据三角函数和直角三角形的性质解答即可.【解答】解:过点B作BF⊥AC于F,BG⊥CD于G,在Rt△BAF中,∠BAF=65°,BF=AB•sin∠×0.9=0.72,AF=AB•cos∠×0.4=0.32,∴FC=AF+AC=4.32,∵四边形FCGB是矩形,∴BG=FC=4.32,CG=BF=0.72,∵∠BDG=45°,∴∠BDG=∠GBD,∴GD=GB=4.32,∴CD=CG+GD=5.04,在Rt△ACE中,∠AEC=50°,CE=,∴≈1.7,答:小水池的宽DE为1.7米.【点评】此题考查的知识点是解直角三角形的应用﹣仰角俯角问题,关键是本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.11.(2018·某某某某·6分)如图,校园内有两幢高度相同的教学楼AB,CD,大楼的底部B,D在同一平面上,两幢楼之间的距离BD长为24米,小明在点E(B,E,D在一条直线上)处测得教学楼AB顶部的仰角为45°,然后沿EB方向前进8米到达点G处,测得教学楼CD 顶部的仰角为30°.已知小明的两个观测点F,H距离地面的高度均为1.6米,求教学楼AB 的高度AB长.(精确到0.1米)参考值:≈1.41,≈1.73.【解答】解:延长HF交CD于点N,延长FH交AB于点M,如右图所示,由题意可得,MB=HG=FE=ND=1.6m,HF=GE=8m,MF=BE,HN=GD,MN=BD=24m,设AM=xm,则=xm,在Rt△AFM中,MF=,在Rt△H中,HN=,∴HF=MF+HN﹣MN=x+x﹣24,即8=x+x﹣24,解得,x≈11.7,∴AB=11.7+1.6=13.3m,答:教学楼AB的高度AB长13.3m.12.(2018·某某某某·8分)京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A.B和点C.D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH 的长).【分析】过D作DE⊥AB,可得四边形CHED为矩形,由矩形的对边相等得到两对对边相等,分别在直角三角形ACH与直角三角形BDE中,设CH=DE=xm,利用锐角三角函数定义表示出AH与BE,由AH+HE+EB=AB列出方程,求出方程的解即可得到结果.【解答】解:过D作DE⊥AB,可得四边形CHED为矩形,∴HE=CD=40m,设CH=DE=xm,在Rt△BDE中,∠DBA=60°,∴BE=xm,在Rt△ACH中,∠BAC=30°,∴AH=xm,由AH+HE+EB=AB=160m,得到x+40+x=160,解得:x=30,即CH=30m,则该段运河的河宽为30m.【点评】此题考查了解直角三角形的应用,熟练掌握锐角三角函数定义是解本题的关键.。
2016北京中考数学各区一模分类题-几何图形28题
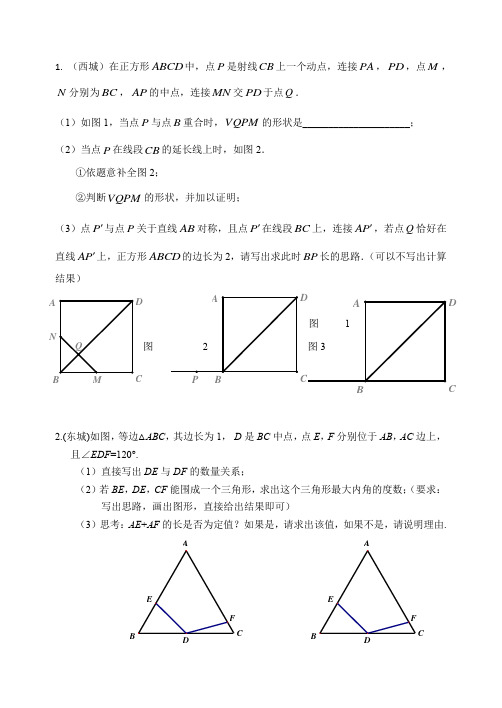
NDA CDCCBCB1.(西城)在正方形ABCD 中,点P 是射线CB 上一个动点,连接PA ,PD ,点M ,N 分别为BC ,AP 的中点,连接MN 交PD 于点Q .(1)如图1,当点P 与点B 重合时,QPM V 的形状是_____________________; (2)当点P 在线段CB 的延长线上时,如图2. ①依题意补全图2;②判断QPM V 的形状,并加以证明;(3)点P '与点P 关于直线AB 对称,且点P '在线段BC 上,连接AP ',若点Q 恰好在直线AP '上,正方形ABCD 的边长为2,请写出求此时BP 长的思路.(可以不写出计算结果)2.(东城)如图,等边△ABC ,其边长为1,D 是BC 中点,点E ,F 分别位于AB ,AC 边上,且∠EDF =120°.(1)直接写出DE 与DF 的数量关系;(2)若BE ,DE ,CF 能围成一个三角形,求出这个三角形最大内角的度数;(要求:写出思路,画出图形,直接给出结果即可)(3)思考:AE +AF 的长是否为定值?如果是,请求出该值,如果不是,请说明理由.3.(海淀)在△ABC 中,AB =AC ,∠BAC =,点D 在射线BC 上(与B 、C 两点不重90︒合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.(1)若点D在线段BC上,如图1.①依题意补全图1;②判断BC与CG的数量关系与位置关系,并加以证明;(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB,则GE的长为_______,并简述求GE长的思路.4.(朝阳)在等腰三角形ABC中,AC=BC,点P为BC边上一点(不与B、C重合),连接P A,以P为旋转中心,将线段P A顺时针旋转,旋转角与∠C相等,得到线段PD,连接DB.(1)当∠C=90º时,请你在图1中补全图形,并直接写出∠DBA的度数;(2)如图2,若∠C=α,求∠DBA的度数(用含α的代数式表示);(3)连接AD,若∠C =30º,AC=2,∠APC=135º,请写出求AD长的思路.(可以不写出计算结果)PCB A图2图1PCB A5.(丰台)在矩形ABCD 中,将对角线CA 绕点C 逆时针旋转得到CE ,连接AE ,取AE的中点F ,连接BF ,DF .(1)若点E 在CB 的延长线上,如图1.①依题意补全图1;②判断BF 与DF 的位置关系并加以证明;(2)若点E 在线段BC 的下方,如果∠ACE =90°,∠ACB =28°,AC =6,请写出求BF长的思路.(可以不写出计算结果.........)6.(房山)如图1,在四边形ABCD 中,BA =BC ,∠ABC =60°,∠ADC =30°,连接对角线BD .(1)将线段CD 绕点C 顺时针旋转60°得到线段CE ,连接AE .①依题意补全图1;②试判断AE 与BD 的数量关系,并证明你的结论;(2)在(1)的条件下,直接写出线段DA 、DB 和DC 之间的数量关系; (3)如图2,F 是对角线BD 上一点,且满足∠AFC =150°,连接FA 和FC ,探究线段FA 、FB 和FC 之间的数量关系,并证明.7.(石景山)在正方形ABCD 中,E 为边CD 上一点,连接BE .(1)请你在图1画出△BEM ,使得△BEM 与△BEC 关于直线BE 对称; (2)若边AD 上存在一点F ,使得AF+CE=EF ,请你在图2中探究∠ABF 与∠CBE 的数量关系并证明;(3)在(2)的条件下,若点E 为边CD 的三等分点,且CE<DE ,请写出求CD 图1备用图ABCDABCDEA CD B cos ∠FED 的思路.(可以不写出计算结果.........).图1 图2 备用图8.(门头沟)在正方形ABCD 中,连接BD .(1)如图1,AE ⊥BD 于E .直接写出∠BAE 的度数.(2)如图1,在(1)的条件下,将△AEB 以A 旋转中心,沿逆时针方向旋转30°后得到△AB'E',AB'与BD 交于M ,AE'的延长线与BD 交于N . ①依题意补全图1;②用等式表示线段BM 、DN 和MN 之间的数量关系,并证明.(3)如图2,E 、F 是边BC 、CD 上的点,△CEF 周长是正方形ABCD 周长的一半,AE 、AF 分别与BD 交于M 、N ,写出判断线段BM 、DN 、MN 之间数量关系的思路.(不必写出完整推理过程)图1 图29.(怀柔)在正方形ABCD 中,点H 在对角线BD 上(与点B 、D 不重合),连接AH ,将HA 绕点H 顺时针旋转 90º与边CD (或CD 延长线)交于点P ,作HQ ⊥BD 交射线DC 于点Q.(1)如图1:①依题意补全图1;②判断DP 与CQ 的数量关系并加以证明;EDACBNMEDAC BF AC DB(2)若正方形ABCD 的边长为3,当 DP=1时,试求∠PHQ 的度数.10.(燕山)在等边△ABC 外侧作直线AP ,点B 关于直线AP 的对称点为D ,连接AD ,BD ,CD ,其中CD 交直线AP 于点E .设∠PAB =α,∠ACE =β,∠AEC =γ.(1) 依题意补全图1;(2) 若α=15°,直接写出β和γ的度数; (3) 如图2,若60°<α<120°,①判断α,β的数量关系并加以证明;②请写出求γ大小的思路.(可以不写出计算结果.........)11.(顺义)已知:在△ABC 中,60BAC ∠=︒.(1)如图1,若AB =AC ,点P 在△ABC 内,且150APC ∠=︒,3PA =,4PC =,把△APC 绕着点A 顺时针旋转,使点C 旋转到点B ,得到△ADB ,连结DP . ①依题意补全图1; ②直接写出PB 的长;图2A BPCAB CP图1(2)如图2,若AB =AC ,点P 在△ABC 外,且3PA =,5PB =,4PC =,求APC∠的度数;(3)如图3,若2AB AC =,点P 在△ABC 内,且PA =5PB =,120APC ∠=︒,直接写出PC 的长.12.(大兴)已知正方形ABCD ,E 为平面内任意一点,连结DE ,将线段DE 绕点D 顺时针旋转90°得到DG ,连结EC ,AG. (1)当点E 在正方形ABCD 内部时,①依题意补全图形;② 判断AG 与CE 的数量关系与位置关系并写出证明思路.(2)当点B, D, G 在一条直线时,若AD=4,求CE 的长.13.(平谷)如图,在△ABC 中,∠ACB =90°,AC =BC=CD ,∠ACD =α,将线段CD 绕点C 顺时针旋转90°得到线段CE ,连接DE ,AE ,BD . (1)依题意补全图1;(2)判断AE 与BD 的数量关系与位置关系并加以证明;CBAP图2图3图1CBAPB AP(3)若0°<α≤64°,AB =4,AE 与BD 相交于点G ,求点G 到直线AB 的距离的最大值.请写出求解的思路(可以不写出计算结果.........).14.(通州)△ABC 中,45ABC ∠=︒,AB BC ≠,BE AC ⊥于点E ,AD BC ⊥于点D .(1)如图1,作A D B ∠的角平分线DF 交BE 于点F ,连接AF . 求证:FAB FBA ∠=∠; (2)如图2,连接DE ,点G 与点D 关于直线AC 对称,连接DG 、EG .①依据题意补全图形;②用等式表示线段AE 、BE 、DG 之间的数量关系,并加以证明.15.(延庆)在平面直角坐标系xOy 中,对于点P (x ,y )和Q (x ,y ′),给出如下定义:如果()()0'0y x y y x ⎧⎪=⎨-⎪⎩≥<,那么称点Q 为点P 的“妫川伴侣”.例如:点(5,6)的“妫川伴侣”为点(5,6),点(-5,6)的“妫川伴侣” 为点(-5,-6).(1)①点(2,1)的“妫川伴侣”为;②如果点A (3,-1),B (-1,3)的“妫川伴侣”中有一个在函数3y x=的图象上,那么这个点是(填“点A ”或“点B ”).图1备用图图2图1(2)①点M *(-1,-2)的“妫川伴侣”点M 的坐标为;②如果点N *(m +1,2)是一次函数y = x + 3图象上点N 的“妫川伴侣”, 求点N 的坐标.(3)如果点P 在函数24y x =-+(-2<x ≤a )的图象上,其“妫川伴侣”Q 的纵坐标y ′的取值范围是-4<y ′≤4,那么实数a 的取值范围是.()。
2016中考解直角三角形试题汇编

解直角三角形一、选择题1.(2016,9,3分)如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是()A.(sinα,sinα) B.(cosα,cosα) C.(cosα,sinα) D.(sinα,cosα)【考点】解直角三角形;坐标与图形性质.【专题】计算题;三角形.【分析】过P作PQ⊥OB,交OB于点Q,在直角三角形OPQ中,利用锐角三角函数定义表示出OQ与PQ,即可确定出P的坐标.【解答】解:过P作PQ⊥OB,交OB于点Q,在Rt△OPQ中,OP=1,∠POQ=α,∴sinα=,cosα=,即PQ=sinα,OQ=cosα,则P的坐标为(cosα,sinα),故选C.【点评】此题考查了解直角三角形,以及坐标与图形性质,熟练掌握锐角三角函数定义是解本题的关键.2.(2016·)一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要()A.米2B.米2C.(4+)米2D.(4+4tanθ)米2【考点】解直角三角形的应用.【分析】由三角函数表示出BC,得出AC+BC的长度,由矩形的面积即可得出结果.【解答】解:在Rt△ABC中,BC=AC•tanθ=4tanθ(米),∴AC+BC=4+4tanθ(米),∴地毯的面积至少需要1×(4+4tanθ)=4+tanθ(米2);故选:D.【点评】本题考查了解直角三角形的应用、矩形面积的计算;由三角函数表示出BC是解决问题的关键.3.(2016·)一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说确的是()A.斜坡AB的坡度是10°B.斜坡AB的坡度是tan10°C.AC=1.2tan10°米D.AB=米【考点】解直角三角形的应用-坡度坡角问题.【分析】根据坡度是坡角的正切值,可得答案.【解答】解:斜坡AB的坡度是tan10°=,故B正确;故选:B.4.(2016省聊城市,3分)聊城“水城之眼”摩天轮是亚洲三大摩天轮之一,也是全球首座建筑与摩天轮相结合的城市地标,如图,点O是摩天轮的圆心,长为110米的AB是其垂直地面的直径,小莹在地面C点处利用测角仪测得摩天轮的最高点A的仰角为33°,测得圆心O的仰角为21°,则小莹所在C点到直径AB所在直线的距离约为(tan33°≈0.65,tan21°≈0.38)()A.169米 B.204米 C.240米 D.407米【考点】解直角三角形的应用-仰角俯角问题.【分析】过C作CD⊥AB于D,在Rt△ACD中,求得AD=CD•tan∠ACD=CD•tan33°,在Rt△BCO 中,求得OD=CD•tan∠BCO=CD•tan21°,列方程即可得到结论.【解答】解:过C作CD⊥AB于D,在Rt△ACD中,AD=CD•tan∠ACD=CD•tan33°,在Rt△BCO中,OD=CD•tan∠BCO=CD•tan21°,∵AB=110m,∴AO=55m,∴A0=AD﹣OD=CD•tan33°﹣CD•tan21°=55m,∴CD==≈204m,答:小莹所在C点到直径AB所在直线的距离约为204m.故选B.【点评】此题主要考查了仰角与俯角的问题,利用两个直角三角形拥有公共直角边,能够合理的运用这条公共边是解答此题的关键.5.(2016.省市,3分)如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到s in68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)()A.22.48 B.41.68 C.43.16 D.55.63【分析】过点P作PA⊥MN于点A,则若该船继续向南航行至离灯塔距离最近的位置为PA的长度,利用锐角三角函数关系进行求解即可【解答】解:如图,过点P作PA⊥MN于点A,MN=30×2=60(海里),∵∠MNC=90°,∠CPN=46°,∴∠MNP=∠MNC+∠CPN=136°,∵∠BMP=68°,∴∠PMN=90°﹣∠BMP=22°,∴∠MPN=180°﹣∠PMN﹣∠PNM=22°,∴∠PMN=∠MPN,∴MN=PN=60(海里),∵∠CNP=46°,∴∠PNA=44°,∴PA=PNsin∠PNA=60×0.6947≈41.68(海里)故选:B.【点评】此题主要考查了方向角问题,熟练应用锐角三角函数关系是解题关键.6.(2016·)如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为()A.2m B.2m C.(2﹣2)m D.(2﹣2)m【考点】解直角三角形的应用-坡度坡角问题.【分析】先在Rt△ABD中利用正弦的定义计算出AD,然后在Rt△ACD中利用正弦的定义计算AC即可.【解答】解:在Rt△ABD中,∵sin∠ABD=,∴AD=4sin60°=2(m),在Rt△ACD中,∵sin∠ACD=,∴AC==2(m).故选B.7.(2016•)如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是()A. B.4 C.8D.4【考点】解直角三角形.【分析】根据cosB=及特殊角的三角函数值解题即可.【解答】解:∵在Rt△ABC中,∠C=90°,∠B=30°,AB=8,cosB=,即cos30°=,∴B C=8×=4;故选:D.【点评】本题考查了三角函数的定义及特殊角的三角函数值,是基础知识,需要熟练掌握.二、填空题1.(2016·)一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为海里/小时.【考点】解直角三角形的应用-方向角问题.【分析】设该船行驶的速度为x海里/时,由已知可得BC=3x,AQ⊥BC,∠BAQ=60°,∠CAQ=45°,AB=80海里,在直角三角形ABQ中求出AQ、BQ,再在直角三角形AQC中求出CQ,得出BC=40+40=3x,解方程即可.【解答】解:如图所示:设该船行驶的速度为x海里/时,3小时后到达小岛的北偏西45°的C处,由题意得:AB=80海里,BC=3x海里,在直角三角形ABQ中,∠BAQ=60°,∴∠B=90°﹣60°=30°,∴AQ=AB=40,BQ=AQ=40,在直角三角形AQC中,∠CAQ=45°,∴CQ=AQ=40,∴BC=40+40=3x,解得:x=.即该船行驶的速度为海里/时;故答案为:.【点评】本题考查了解直角三角形的应用中的方向角问题、等腰直角三角形的性质、含30°角的直角三角形的性质等知识;通过解直角三角形得出方程是解决问题的关键.2.(2016·)在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为(30+10)米.(结果保留根号)【考点】解直角三角形的应用-方向角问题.【分析】如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,设CK=HB=x,根据tan30°=列出方程即可解决问题.【解答】解:如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,设CK=HB=x,∵∠CKA=90°,∠CAK=45°,∴∠CAK=∠ACK=45°,∴AK=CK=x,BK=HC=AK﹣AB=x﹣30,∴HD=x﹣30+10=x﹣20,在RT△BHD中,∵∠BHD=30°,∠HBD=30°,∴tan30°=,∴=,解得x=30+10.∴河的宽度为(30+10)米.【点评】本题考查解直角三角形的应用、方向角、三角函数等知识,解题的关键是添加辅助线构造直角三角形,学会利用三角函数的定义,列出方程解决问题,属于中考常考题型.3.(2016年省市)如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为10+1 m(结果保留根号).【考点】解直角三角形的应用-仰角俯角问题.【分析】首先过点A作AE∥DC,交BC于点E,则AE=CD=10m,CE=AD=1m,然后在Rt△BAE 中,∠BAE=60°,然后由三角形函数的知识求得BE的长,继而求得答案.【解答】解:如图,过点A作AE∥DC,交BC于点E,则AE=CD=10m,CE=AD=1m,∵在Rt△BAE中,∠BAE=60°,∴BE=AE•tan60°=10(m),∴BC=CE+BE=10+1(m).∴旗杆高BC为10+1m.故答案为:10+1.【点评】本题考查仰角的定义.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键.4.(2016,18,4分)如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是.【考点】菱形的性质;解直角三角形.【专题】网格型.【分析】如图,连接EA、EB,先证明∠AEB=90°,根据tan∠ABC=,求出AE、EB即可解决问题.【解答】解:如图,连接EA,EC,设菱形的边长为a,由题意得∠AEF=30°,∠BEF=60°,AE=a,EB=2a∴∠AEB=90°,∴tan∠ABC===.故答案为.【点评】本题考查菱形的性质,三角函数、特殊三角形边角关系等知识,解题的关键是添加辅助线构造直角三角形解决问题,属于中考常考题型.5.(2016·)如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C 的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为208 米.(精确到1米,参考数据:≈1.73)【考点】解直角三角形的应用-仰角俯角问题.【分析】分别利用锐角三角函数关系得出BD,DC的长,进而求出该建筑物的高度.【解答】解:由题意可得:tan30°===,解得:BD=30,tan60°===,解得:DC=90,故该建筑物的高度为:BC=BD+DC=120≈208(m),故答案为:208.【点评】此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.6.(2016,15,3分)如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为海里(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4).【考点】解直角三角形的应用-方向角问题.【分析】作PC⊥AB于C,先解Rt△PAC,得出PC=PA=9,再解Rt△PBC,得出PB=≈11.【解答】解:如图,作PC⊥AB于C,在Rt△PAC中,∵PA=18,∠A=30°,∴PC=PA=×18=9,在Rt△PBC中,∵PC=9,∠B=55°,∴PB=≈≈11,答:此时渔船与灯塔P的距离约为11海里.故答案为11.【点评】本题考查了解直角三角形的应用﹣方向角问题,含30°角的直角三角形的性质,锐角三角函数定义.解一般三角形的问题可以转化为解直角三角形的问题,解决的方法就是作高线.三、解答题1. (2016·)(本题满分9分)为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度。
人教版九年级数学下册 28.2 解直角三角形及其应用 同步测试题(有答案)

28.2 解直角三角形及其应用同步测试题(满分120分;时间:120分钟)一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 在△ABC,∠B=45∘,∠C=30∘,BC边上的高为3,则△ABC的周长是()A.9+3√2B.6+3√2+2√3C.9+3√2+3√3D.3√2+3√32. 如图,点A(1.5, 3)在第一象限,OA与x轴所夹的锐角为α,tanα=()A.1B.1.5C.2D.33. 如图,太阳光线与水平线成70∘角,窗子高AB=2米,要在窗子外面上方0.2米的点D 处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是()A.2tan70∘米 B.2sin70∘米 C. 2.2tan70∘米 D.2.2cos70∘米4. 如图,甲、乙两艘轮船分别在P,M两个港口停靠,港口P在港口M的南偏西22∘方向上.某一天,甲、乙两艘轮船分别从P,M两个港口同时出发,以相同的速度航行,乙轮船向正南方向航行,若干小时后,两轮船在N处相遇,则甲轮船的航行方向是()A.北偏东22∘B.北偏东44∘C.南偏西68∘D.南偏西44∘5. 某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30∘,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60∘,则观光塔AB的高度是()A.50米B.100米C.125米D.150米,则AC是()6. 如图,已知Rt△ABC中,斜边BC上的高AD=4,cos B=45A.5B.4C.3D.45,AC=2√3,则AB=()7. 如图,在△ABC中,∠A=30∘,tan B=√32A.4B.5C.6D.78. 在Rt△ABC中,CD是斜边AB上的高,∠A=30∘,那么下列结论正确的是()A.3AD=7BCB.AB=2ACC.AC=8CDD.16CD2=3AB29. 某落地钟钟摆的摆长为0.5米,来回摆动的最大夹角为60∘,已知在钟摆的摆动过程中,摆锤离地面的最低高度为a米,最大高度为b米,则b−a等于()A.1 2B.12−√32C.12+√34D.12−√3410. 如图,淇淇一家驾车从A地出发,沿着北偏东60∘的方向行驶,到达B地后沿着南偏东50∘的方向行驶来到C地,C地恰好位于A地正东方向上,则()①B地在C地的北偏西50∘方向上;②A地在B地的北偏西30∘方向上;③cos∠BAC=√32;④∠ACB=50∘.其中错误的是()A.①②B.②④C.①③D.③④二、填空题(本题共计10 小题,每题3 分,共计30分,)11. 如图,Rt△ABC中,∠C=90∘,D是BC上一点,AD=BD,tan∠ADC=43,AB=4√5,则CD=________.12. 如图,在Rt△ABC中,∠C=90∘,AM是BC边上的中线,cos∠CAM=45,则tan∠B的值为________.13. 从A处测得B处仰角α=18∘36′,那么从B处测得A处的俯角β=________.14. 如图,河坝横断面迎水坡AB的坡比是1:√3,堤高BC=5米,则坝底AC的长度是________米.15. 如图,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,tan∠CPN为________.16. 如图,在△ABC中,∠A=30∘,∠B=45∘,D在AB上,E在AC上,且使AE=EC=DE,那么AD2:BC2等于________.17. 某处欲建一观景平台,如图所示,原设计平台的楼梯长AB=6m,∠ABC=45∘,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30∘,则调整后楼梯AD的长为________m.(结果保留根号)18. 在边长为1的正方形网格中,△ABC的位置如图所示,则cos A=________.19. 一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60∘,距离为60海里的A处;上午9时到达C处,看到灯塔在它的正北方向.则这艘船航行的速度为________海里/时.三、解答题(本题共计6 小题,共计60分,)20. 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A,B两个基地前去拦截,6分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡逻艇的航向为北偏西40∘.(1)求甲巡逻艇的航行方向;(2)成功拦截后,甲、乙两艘巡逻艇同时沿原方向返回且速度不变,3分钟后甲、乙两艘巡逻艇相距多少海里?21 小强从自己家的阳台上,看一栋楼顶部的仰角为30∘,看这栋楼底部的俯角为60∘,小强家与这栋楼的水平距离为42m,这栋楼有多高?22 如图,某施工单位为测得某河段的宽度,测量员先在河对岸边取一点A,再在河这边沿河边取两点B、C,在点B处测得A在北偏东30∘方向上,在点C处测得点A在西北方向上,量得BC长为400米,请你求出该河段的宽度.(结果保留根号)23. 安装在屋顶的太阳能热水器的横截面示意图如图所示.集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O处,⊙O的半径为0.2m,AO与屋面AB的夹角为32∘,BF⊥AB于B,AB=2m,求支架BF的长(精确到0.1m).参考数据:sin32∘=0.32,cos32∘=0.84,tan32∘=0.62.24 随着社会的发展,人们对防洪的意识越来越强,今年为了提前做好防洪准备工作,某市正在长江边某处常出现险情的河段修建一防洪大坝,其横断面为梯形ABCD,如图所示,根据图中数据计算坝底CD的宽度(结果保留根号).25 北盘江大桥坐落于云南宣威与贵州水城交界处,横跨云贵两省,为目前世界第一高桥.左图是大桥的实物图,右图是从左图中引申出的平面图,测得桥护栏BG=1.8米,拉索AB与护栏的夹角为26∘,拉索ED与护栏的夹角是60∘,两拉索底端距离BD为300m,若两拉索顶端的距离AE为90m,请求出立柱AH的长.(tan26∘≈0.5,sin26∘≈0.4,√3≈1.7)参考答案一、选择题(本题共计10 小题,每题 3 分,共计30分)1.【答案】C【解答】解:作AD⊥BC,∵ AD=3,∠B=45∘,∵ BD=AD=3,AB=√BD2+AD2=3√2,∵ AD=3,∠C=30∘,∵ AC=2AD=6,CD=√AC2−CD2=3√3,∵ △ABC的周长=AB+AC+BC=3√2+6+3√3+3=9+3√2+3√3.故选C.2.【答案】C【解答】解:根据题意得:tanα=31.5=2;故选C.3.【答案】C【解答】解:∵ DA=0.2米,AB=2米,∵ DB=DA+AB=2.2米,∵ 光线与地面成70∘角,∵ ∠BCD=70∘.又∵ tan∠BCD=DBDC,∵ DC=DBtan∠BCD = 2.2tan70m.故选C. 4.【答案】B【解答】解:如图,由题意可知,∠PMN=22∘,PN=MN,所以∠MPN=22∘.所以∠2=∠1=22∘+22∘=44∘.故甲轮船的航行方向是北偏东44∘.故选B.5.【答案】A【解答】解:作EF⊥AC于F,EG⊥DC于G,在Rt△DEG中,EG=12DE=75米,∵ BF=BC−CF=BC−EG=100−75=25米,EF=BFtan∠BEF =BFtan30∘=25√3,∵ ∠AEF=60∘,∵ ∠A=30∘,∵ AF=EFtan A =√3√33=75(米),∵ AB=AF−BF=50(米),故选A.6.【答案】A【解答】解:∵ AD是△ABC的高,∠BAC=90∘,∵ ∠ADB=∠ADC=∠BAC=90∘,∵ ∠B+∠BAD=90∘,∠BAD+∠DAC=90∘,∵ ∠B=∠CAD,∵ cos B=45,AD=4,∵ cos B=cos∠CAD=45=ADAC,即4AC =45,∵ AC=5,故选A.7.【答案】B【解答】解:作CD⊥AB于点D.由题意知,∵ sin A=CDAC,∵ CD=AC sin A=AC sin30∘=2√3×1 =√3,∵ cos A=ADAC,∵ AD=AC cos30∘=2√3×√3 2=3.∵ tan B=CDBD =√32,∵ BD=2.∵ AB=AD+BD=2+3=5.故选B.8.【答案】D【解答】解:∵ 在Rt△ABC中,CD是斜边AB上的高,∠A=30∘,∵ AD=√3CD,CD=√32BC,AC=√32AB,AC=2CD,CD=√32BC,BC=12AB,∵ AD=32BC,AB=2√33AC,CD=√32×12AB=√34AB,∵ 4CD=√3AB,∵ 16CD2=3AB2.故选D.9.【答案】D【解答】解:如上图所示,OA、OB为最大摆幅,OC为摆锤离地最低即和地面垂直时,所以AD=b,CE=a,CF=b−a,∠AOB=60∘,∵ ∠AOC=30∘.作AF⊥OC与F,则在△AOC中,OF=OA cos30∘=√34,∵ CF=b−a=OC−OF=12−√34,∵ 摆长为0.5米,∵ OA=0.5米,∵ OF=√34,∵ b−a=0.5−√34,∵ b−a=(12−√34)米.故选D.10.【答案】B【解答】如图所示,由题意可知,∠1=60∘,∠4=50∘,∵ ∠5=∠4=50∘,即B在C处的北偏西50∘,故①正确;∵ ∠2=60∘,∵ ∠3+∠7=180∘−60∘=120∘,即A在B处的北偏西120∘,故②错误;∵ ∠1=∠2=60∘,∵ ∠BAC=30∘,∵ cos∠BAC=√32,故③正确;∵ ∠6=90∘−∠5=40∘,即公路AC和BC的夹角是40∘,故④错误.二、填空题(本题共计10 小题,每题 3 分,共计30分)11.【答案】3【解答】解:在Rt△ACD中,tan∠ADC=ACCD =43,设AC=4x,CD=3x,∵ AD=√AC2+CD2=5x,∵ BD=AD=5x,∵ BC=BD+CD=8x,在Rt△ABC中,AC=4x,BC=8x,∵ AB=√AC2+BC2=4√5x,而AB=4√5,∵ 4√5x=4√5,解得x=1,∵ CD=3x=3.故答案为3.12.【答案】23【解答】解:在Rt△ACM中,cos∠CAM=ACAM =45,设AC=4x,则AM=5x,则CM=√AM2−AC2=3x,而AM是BC边上的中线,所以BC=2CM=6x,在Rt△ABC中,tan∠B=ACBC =4x6x=23.故答案为23.13.【答案】18∘36′【解答】解:设A、B两点的水平线分别为AM、BN,依题意,得AM // BN,∠BAM=α=18∘36′,由平行线的性质可知,β=∠ABN=∠BAM=18∘36′.故答案为:18∘36′.14.【答案】5√3【解答】解:∵ 河坝横断面迎水坡AB的坡比是1:√3,∵ BC:AC=1:√3,∵ 堤高BC=5米,∵ 坝底AC=5√3米.故答案为:5√3.15.【答案】2【解答】解:连接格点MN,DM,如图所示:则四边形MNCE是平行四边形,△DAM和△MBN都是等腰直角三角形,∵ EC // MN,∠DMA=∠NMB=45∘,DM=√2AD=2√2,MN=√2BM=√2,∵ ∠CPN=∠DNM,∵ tan∠CPN=tan∠DNM,∵ ∠DMN=180∘−∠DMA−∠NMB=180∘−45∘−45∘=90∘,∵ tan∠CPN=tan∠DNM=DMMN =√2√2=2.故答案为:2.16.【答案】3:2【解答】连接CD,∵ 在△ACD中,AE=EC=DE.∵ ∠CDA=90∘,∵ ∠A=30∘,∵ AC=2CD,AD=√3CD,在Rt△BCD中,∠B=45∘,∵ BD=CD,BC=√2CD,∵ AD2:BC2=(√3CD)2:(√2CD)2=3:2 17.【答案】6√2【解答】解:由题意可得,AB=6m,∠ABC=45∘,∠ACB=90∘,∵ AC=AB⋅sin∠ABC=6×√22=3√2m,又∵ ∠ADC=30∘,∠ACD=90∘,∵ AD=2AC=6√2m.故答案为:6√2m.18.【答案】35【解答】如图,过点C作CD⊥AB于D.∵ AC=√32+42=5,在RtACD中,cos A=ADAC =35,19.【答案】30√3【解答】解:易得∠ABC=30∘,AB=60.∵ BC=AB×cos∠ABC=30√3(海里).∵ 这艘船航行的速度为30√3÷(9−8)=30√3(海里/时).三、解答题(本题共计6 小题,每题10 分,共计60分)20.【答案】解:(1)由已知得,AC=120×660=12(海里),BC=50×660=5(海里),∵ AC2+BC2=AB2,∵ △ABC是直角三角形.∵ ∠CBA=50∘,∵ ∠CAB=40∘∵ 甲的航向为北偏东50∘.(2)甲巡逻船航行3分钟的路程为:120×360=6(海里),乙巡逻船航行3分钟的路程为:50×360=2.5(海里),3分钟后,甲、乙两艘巡逻船相距为:√62+2.52=6.5(海里).【解答】解:(1)由已知得,AC=120×660=12(海里),BC=50×660=5(海里),∵ AC2+BC2=AB2,∵ △ABC是直角三角形.∵ ∠CBA=50∘,∵ ∠CAB=40∘∵ 甲的航向为北偏东50∘.(2)甲巡逻船航行3分钟的路程为:120×360=6(海里),乙巡逻船航行3分钟的路程为:50×360=2.5(海里),3分钟后,甲、乙两艘巡逻船相距为:√62+2.52=6.5(海里).21【答案】这栋楼的高度为56√3m【解答】在Rt△ABD中,∵ ∠BDA=90∘,∠BAD=30∘,AD=42m,∵ BD=AD tan30∘=42×√33=14√3(m).在Rt△ACD中,∠ADC=90∘,∠CAD=60∘,∵ CD=AD tan60∘=42×√3=42√3(m).∵ BC=BD+CD=14√3+42√3=56√3(m).22【答案】解:过A作AH⊥BC于点H,设AH=x,由题意得:∠BAH=30∘,∠ACH=45∘,x,∵ HC=AH=x,BH=√33∵ BC=400米,x+x=400,∵ √33解得:x=600−200√3,即河宽为(600−200√3)米.【解答】解:过A作AH⊥BC于点H,设AH=x,由题意得:∠BAH=30∘,∠ACH=45∘,x,∵ HC=AH=x,BH=√33∵ BC=400米,x+x=400,∵ √33解得:x=600−200√3,即河宽为(600−200√3)米.23【答案】支架BF的长为1.0米.【解答】解:∵ BF⊥AB,∵ 在Rt△OAB中,∵ AB=2米,∠OAB=32∘,∵ OB=AB⋅tan∠OAB,=2⋅tan32∘≈2×0.62=1.24米,∵ BF=OB−OF=1.24−0.2=1.04≈1.0米,24【答案】坝底DC的宽为(19+3√3)m.【解答】.解:在Rt△ADF中,∠D=60∘,cot∠D=DFAF∴DF=AF⋅cot∠D=9×cot60∘=3√3.=9×√33在Rt△BEC中∵∠C=45∘.∴△BEC为等腰三角形.∴EC=BE=9.在矩形AFEB中,FE=AB=10.∴DC=DF+FE+EC=3√3+10+9 =(19+3√3).(m)25【答案】解:设CD=x米,∵ ∠CDE=60∘ , ∠ACB=90∘,在Rt△CED中,CE=DC⋅tan60∘=√3x,∴ AC=AE+CE=90+√3x,∵ ∠ABC=26∘,∴ AC=BC⋅tan26∘=0.5(x+300),90+√3x=0.5(x+300),≈48,解得x=240√3+12011∴ AC=90+48√3≈171.6(m),∴ AH=AC+CH≈171.6+1.8=173.4(m).答:立柱AH的长约为173.4m.【解答】解:设CD=x米,∵ ∠CDE=60∘ , ∠ACB=90∘,在Rt△CED中,CE=DC⋅tan60∘=√3x,∴ AC=AE+CE=90+√3x,∵ ∠ABC=26∘,∴ AC=BC⋅tan26∘=0.5(x+300),90+√3x=0.5(x+300),≈48,解得x=240√3+12011∴ AC=90+48√3≈171.6(m),∴ AH=AC+CH≈171.6+1.8=173.4(m).答:立柱AH的长约为173.4m.。
人教版数学九年级下28.2《解直角三角形的应用》测试题(含答案及解析)

人教版数学九年级下28.2《解直角三角形的应用》测试题(含答案及解析) 1 / 14解直角三角形的应用 测试题时间:100分钟 总分: 100一、选择题(本大题共10小题,共30.0分)1. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度 如图,旗杆PA 的高度与拉绳PB 的长度相等 小明将PB 拉到 的位置,测得 为水平线 ,测角仪 的高度为1米,则旗杆PA 的高度为A.B.C. D.2. 如图,长4m 的楼梯AB 的倾斜角 为 ,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角 为 ,则调整后的楼梯AC 的长为 A. B.C. D. 3. 一座楼梯的示意图如图所示,BC 是铅垂线,CA 是水平线,BA 与CA 的夹角为 现要在楼梯上铺一条地毯,已知 米,楼梯宽度1米,则地毯的面积至少需要A. 米B.米 C.米D. 米4. 上午9时,一条船从A 处出发,以每小时40海里的速度向正东方向航行,9时30分到达B 处 如图 从A 、B 两处分别测得小岛M 在北偏东 和北偏东 方向,那么在B 处船与小岛M 的距离为A. 20海里B. 海里C. 海里D. 海里 5. 如图,某游乐场一山顶滑梯的高为h ,滑梯的坡角为a ,那么滑梯长m 为A. B. C. D.6.如图所示,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为,则这个电视塔的高度单位:米为A. B. 61 C. D. 1217.某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西方向航行50千米,第二艘快艇沿南偏西方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是A. 南偏东,千米B. 北偏西,千米C. 南偏东,100千米D. 北偏西,100千米8.如图,一艘海轮位于灯塔P的南偏东方向,距离灯塔60nmile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东方向上的B处,这时,B处与灯塔P的距离为A. nmileB. nmileC. nmileD. nmile9.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度:,则坝底AD的长度为A. 26米B. 28米C. 30米D. 46米10.如图是某水库大坝的横截面示意图,已知,且AD、BC之间的距离为15米,背水坡CD的坡度:,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度:4,则大坝底端增加的长度CF是米.A. 7B. 11C. 13D. 20二、填空题(本大题共10小题,共30.0分)人教版数学九年级下28.2《解直角三角形的应用》测试题(含答案及解析) 3 / 1411. 为加强防汛工作,某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形已知迎水坡面 米,背水坡面 米, ,加固后拦水坝的横断面为梯形ABED ,,则CE 的长为______ 米12. 如图,航拍无人机从A 处测得一幢建筑物顶部B 的仰角为 ,测得底部C 的俯角为 ,此时航拍无人机与该建筑物的水平距离AD 为90米,那么该建筑物的高度BC 约为______ 米 精确到1米,参考数据:13. 小明沿着坡度i 为1: 的直路向上走了50m ,则小明沿垂直方向升高了______ 14. 如图,长4m 的楼梯AB 的倾斜角 为 ,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角 为 ,则调整后楼梯AC 长为______ 米15. 如图,一名滑雪运动员沿着倾斜角为 的斜坡,从A 滑行至B ,已知 米,则这名滑雪运动员的高度下降了______米 参考数据: , ,16. 如图,为测量某栋楼房AB 的高度,在C 点测得A 点的仰角为 ,朝楼房AB 方向前进10米到达点D ,再次测得A 点的仰角为 ,则此楼房的高度为______ 米 结果保留根号 .17. 如图,从热气球C 处测得地面A 、B 两点的俯角分别为 、 ,如果此时热气球C 处的高度为200米,点A 、B 、C 在同一直线上,则AB 两点间的距离是______米 结果保留根号 .18.如图,水库堤坝的横断面是梯形,测得BC长为30m,CD长为,斜坡AB的坡比为1:3,斜坡CD的坡比为1:2,则坝底的宽AD为______19.如图,某堤坝的斜坡AB的斜角是,坡度是:,则______.20.某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为,B处的仰角为已知无人飞机的飞行速度为3米秒,则这架无人飞机的飞行高度为结果保留根号______ 米三、计算题(本大题共4小题,共24.0分)21.如图,某数学兴趣小组要测量一栋五层居民楼CD的高度该楼底层为车库,高米;上面五层居住,每层高度相等测角仪支架离地米,在A处测得五楼顶部点D的仰角为,在B处测得四楼顶部点E的仰角为,米求居民楼的高度精确到米,参考数据:22.某兴趣小组借助无人飞机航拍校园如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为,B处的仰角为已知无人飞机的飞行速度为4米秒,求这架无人飞机的飞行高度结果保留根号人教版数学九年级下28.2《解直角三角形的应用》测试题(含答案及解析)23.如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为,教学楼底部B的俯角为,量得实验楼与教学楼之间的距离.求的度数.求教学楼的高结果精确到,参考数据:,24.如图,在大楼AB的正前方有一斜坡CD,米,坡角,小红在斜坡下的点C处测得楼顶B的仰角为,在斜坡上的点D处测得楼顶B的仰角为,其中点A、C、E在同一直线上.求斜坡CD的高度DE;求大楼AB的高度结果保留根号5 / 14四、解答题(本大题共2小题,共16.0分)25.如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为,测得大楼顶端A的仰角为点B,C,E在同一水平直线上,已知,,求障碍物B,C两点间的距离结果精确到参考数据:,26.如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:米,,请求出小桥PQ的长,结果精确到米人教版数学九年级下28.2《解直角三角形的应用》测试题(含答案及解析)7 / 14答案和解析【答案】 1. A 2. B 3. D 4. B5. A6. C7. B8. B 9. D 10. C11. 8 12. 208 13. 2514. 15. 280 16.17. 18. 130 19.20.21. 解:设每层楼高为x 米,由题意得: 米, , ,在 中, ,,在 中, ,, ,,解得: ,则居民楼高为 米. 22. 解:如图,作 , 水平线,由题意得: , , ,, , ,, , ,则 .23. 解: 过点C 作 ,则有 , ,;由题意得: ,在 中, , 在 中, ,教学楼的高 , 则教学楼的高约为 .24. 解:在 中, 米, , ,米;过D作,交AB于点F,,,,即为等腰直角三角形,设米,四边形DEAF为矩形,米,即米,在中,,米,米,米,,,,在中,根据勾股定理得:,解得:,则米.25. 解:如图,过点D作于点F,过点C作于点H.则,在直角中,,,.在直角中,,,,.答:障碍物B,C两点间的距离约为.26. 解:设米,在直角中,,,在直角中,,,米,,解得:米.答:小桥PQ的长度约是米.【解析】1. 解:设,在中,,,人教版数学九年级下28.2《解直角三角形的应用》测试题(含答案及解析) 9 / 14, ,.故选:A .设 ,在 中,根据,列出方程即可解决问题.本题考查解直角三角形、三角函数等知识,解题的关键是设未知数列方程,属于中考常考题型.2. 解:在 中,,, 在 中,,.故选B .先在 中利用正弦的定义计算出AD ,然后在 中利用正弦的定义计算AC 即可.本题考查了解直角三角形的应用 坡度坡角:坡度是坡面的铅直高度h 和水平宽度l 的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i 表示,常写成 :m 的形式 把坡面与水平面的夹角 叫做坡角,坡度i 与坡角 之间的关系为: . 3. 解:在 中, 米 , 米 ,地毯的面积至少需要 米 ; 故选:D .由三角函数表示出BC ,得出 的长度,由矩形的面积即可得出结果.本题考查了解直角三角形的应用、矩形面积的计算;由三角函数表示出BC 是解决问题的关键.4. 解:如图,过点B 作 于点N .由题意得,海里, .作 于点N .在直角三角形ABN 中, . 在直角 中, ,则 , 所以 海里 . 故选B .过点B 作 于点 根据三角函数求BN 的长,从而求BM 的长.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.5. 解:,. 故选A .根据三角函数的定义即可求解.本题考查了三角函数的定义,理解定义是关键. 6. 【分析】根据题意求出CE 的长,根据三角形的外角的性质和等腰三角形的性质求出AE 的长,根据正弦的定义计算即可.本题考查的是解直角三角形的应用仰角俯角问题,理解仰角的概念、熟记锐角三角函数的定义是解题的关键.【解答】解:由题意得,,,,,,.故选:C.7. 解:第一艘快艇沿北偏西方向,第二艘快艇沿南偏西方向,,,,,第二艘快艇沿南偏西方向,,,第二艘快艇航行的方向和距离分别是:北偏西,千米.故选:B.根据题意得出以及,进而得出第二艘快艇航行的方向和距离.此题主要考查了方向角以及勾股定理,正确把握方向角的定义是解题关键.8. 解:如图作于E.在中,,,,在中,,,故选:B.如图作于在中,求出PE,在中,根据即可解决问题.本题考查方向角、直角三角形、锐角三角函数的有关知识解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.9. 解:坝高12米,斜坡AB的坡度:,米,米,米,故选:D.先根据坡比求得AE的长,已知,即可求得AD.此题考查了解直角三角形的应用中的坡度坡角的问题及等腰梯形的性质的掌握情况,将相关的知识点相结合更利于解题.10. 解:过D作于G,于H,,,背水坡CD的坡度:,背水坡EF的坡度:4,,,米,人教版数学九年级下28.2《解直角三角形的应用》测试题(含答案及解析) 11 / 14 故选C .过D 作 于G , 于H ,解直角三角形即可得到结论.本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度,难度一般.11. 解:分别过A 、D 作 , ,垂点分别为F 、G ,如图所示.在 中, 米, ,,, .在 中, , 米,.在 中, ,,,.即CE 的长为8米.故答案为8.分别过A 、D 作下底的垂线,设垂足为F 、 在 中,已知坡面长和坡角的度数,可求得铅直高度AF 的值,也就得到了DG 的长;在 中,由勾股定理求CG 的长,在 中,根据正切函数定义得到GE 的长;根据 即可求解. 本题考查的是解直角三角形的应用 坡度坡角问题,锐角三角函数的定义,勾股定理 作辅助线构造直角三角形是解答此类题的一般思路.12. 解:由题意可得:, 解得: ,,解得: ,故该建筑物的高度为: ,故答案为:208.分别利用锐角三角函数关系得出BD ,DC 的长,进而求出该建筑物的高度. 此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键. 13. 解:如图,过点B 作 于点E ,坡度: : ,:, ,,.他升高了25m .故答案为:25.首先根据题意画出图形,由坡度为1: ,可求得坡角,又由小明沿着坡度为1:的山坡向上走了50m,根据直角三角形中,所对的直角边是斜边的一半,即可求得答案.此题考查了坡度坡角问题此题比较简单,注意能构造直角三角形并用解直角三角形的知识求解是解此题的关键,注意数形结合思想的应用.14. 解:在中,,,在中,,.故答案是:.先在中利用正弦的定义计算出AD,然后在中利用正弦的定义计算AC即可.本题考查了解直角三角形的实际应用中的坡度坡角问题,难度不大,注意细心运算即可.15. 解:如图在中,,这名滑雪运动员的高度下降了280m.故答案为280如图在中,,可知这名滑雪运动员的高度下降了280m.本题考查解直角三角形、坡度坡角问题、锐角三角函数等知识,解题的关键是熟练掌握锐角三角函数的定义,属于中考常考题型.16. 解:在直角三角形ADB中,,,,在直角三角形ABC中,,,,,解得:.故答案为:.首先根据题意分析图形;本题涉及到两个直角三角形,应利用其公共边AB及构造方程关系式,进而可解,即可求出答案.本题考查解直角三角形的应用仰角俯角问题,要求学生能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形.17. 解:从热气球C处测得地面A、B两点的俯角分别为、,,,,,是等腰直角三角形,,人教版数学九年级下28.2《解直角三角形的应用》测试题(含答案及解析) 13 / 14在 中, , ,,.故答案为: .先根据从热气球C 处测得地面A 、B 两点的俯角分别为 、 可求出 与 的度数,再由直角三角形的性质求出AD 与BD 的长,根据 即可得出结论.本题考查的是解直角三角形的应用 仰角俯角问题,熟知锐角三角函数的定义是解答此题的关键.18. 解:作 于E , 于F ,斜坡CD 的坡比为1:2,即 ,,又 ,, ,由题意得,四边形BEFC 是矩形,, ,斜坡AB 的坡比为1:3,,即 , ,故答案为:130m .作 于E , 于F ,根据坡度的概念分别求出AE 、DF ,结合图形计算即可.本题考查的是解直角三角形的应用 坡度坡角问题,掌握坡度是坡面的铅直高度h 和水平宽度l 的比是解题的关键,掌握矩形的判定和性质的应用.19. 解: : ,则 .故答案是: .根据坡度就是坡角的正切值即可求解.本题主要考查了坡度的定义,理解坡度和坡角的关系是解题的关键.20. 解:如图,作 , 水平线,由题意得: , , ,, ,,, ,,.故答案为: .作 , 水平线,根据题意确定出 与 的度数,利用锐角三角函数定义求出AD 与BD 的长,由 求出BC 的长,即可求出BH 的长.此题考查了解直角三角形的应用 仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.21. 设每层楼高为x 米,由 求出 的长,进而表示出 与 的长,在直角三角形 中,利用锐角三角函数定义表示出 ,同理表示出 ,由 求出AB 的长即可.此题属于解直角三角形的应用 仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.22. 如图,作 , 水平线,根据题意确定出 与 的度数,利用锐角三角函数定义求出AD 与BD 的长,由 求出BC 的长,即可求出BH 的长.此题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.23. 过点C作CE与BD垂直,根据题意确定出所求角度数即可;在直角三角形CBE中,利用锐角三角函数定义求出BE的长,在直角三角形CDE中,利用锐角三角函数定义求出DE的长,由求出BD的长,即为教学楼的高.此题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.24. 在直角三角形DCE中,利用锐角三角函数定义求出DE的长即可;过D作DF垂直于AB,交AB于点F,可得出三角形BDF为等腰直角三角形,设,表示出BC,BD,DC,由题意得到三角形BCD为直角三角形,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出AB的长.此题考查了解直角三角形仰角俯角问题,坡度坡角问题,熟练掌握勾股定理是解本题的关键.25. 如图,过点D作于点F,过点C作于点通过解直角得到DF的长度;通过解直角得到CE的长度,则.本题考查了解直角三角形仰角俯角问题要求学生能借助仰角构造直角三角形并解直角三角形.26. 设米,在直角和直角中分别利用x表示出AQ和BQ的长,根据,即可列方程求得x的值.本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数表示出相关线段的长度,难度一般.。
浙江省衢州市2016年中考数学(浙教版)专题训练:解直角三角形..

浙江省衢州市2016年中考数学(浙教版)专题训练:解直角三角形一、选择题(共5小题)1.如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是()A.20海里B.40海里C.海里D.海里2.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是()A.2海里B.2sin55°海里C.2cos55°海里D.2tan55°海里3.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD是()A.20海里B.40海里C.20海里D.40海里4.如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为()A.4km B.(2+)km C.2km D.(4﹣)km5.有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是()海里.A.10B.10﹣10 C.10 D.10﹣10二、填空题(共4小题)6.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为.7.如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行海里可使渔船到达离灯塔距离最近的位置.8.如图,在小山的东侧A 点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C 处,此时热气球上的人测得小山西侧B 点的俯角为30°,则小山东西两侧A 、B 两点间的距离为 米.9.如图,为了测量河的宽度AB ,测量人员在高21m 的建筑物CD 的顶端D 处测得河岸B 处的俯角为45°,测得河对岸A 处的俯角为30°(A 、B 、C 在同一条直线上),则河的宽度AB 约为 m (精确到0.1m ).(参考数据:≈1.41,,1.73)三、解答题(共21小题)10.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A 处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C 处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D 处成功拦截蓝方,求拦截点D 处到公路的距离(结果不取近似值).11.如图所示,港口B 位于港口O 正西方向120km 处,小岛C 位于港口O 北偏西60°的方向.一艘游船从港口O 出发,沿OA 方向(北偏西30°)以vkm/h 的速度驶离港口O ,同时一艘快艇从港口B 出发,沿北偏东30°的方向以60km/h 的速度驶向小岛C ,在小岛C 用1h 加装补给物资后,立即按原来的速度给游船送去.(1)快艇从港口B到小岛C需要多长时间?(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.12.如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:≈1.732)13.(2015•济宁)阅读材料:在一个三角形中,各边和它所对角的正弦的比相等,==,利用上述结论可以求解如下题目:在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.解:在△ABC中,∵=∴b====3.理解应用:如图,甲船以每小时30海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10海里.(1)判断△A1A2B2的形状,并给出证明;(2)求乙船每小时航行多少海里?14.如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:≈1.414,结果精确到0.1)15.为保护渔民的生命财产安全,我国政府在南海海域新建了一批观测点和避风港.某日在观测点A处发现在其北偏西36.9°的C处有一艘渔船正在作业,同时检测到在渔船的正西B处有一股强台风正以每小时40海里的速度向正东方向移动,于是马上通知渔船到位于其正东方向的避风港D处进行躲避.已知避风港D在观测点A的正北方向,台风中心B在观测点A的北偏西67.5°的方向,渔船C与观测点A相距350海里,台风中心的影响半径为200海里,渔船的速度为每小时18海里,问渔船能否顺利躲避本次台风的影响?(sin36.9°≈0.6,tan36.9≈0.75,sin67.5≈0.92,tan67.5≈2.4)16.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).17.如图,海面上B、C两岛分别位于A岛的正东和正北方向.一艘船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C岛,此时测得B岛在C岛的南偏东43°.求A、B两岛之间的距离.(结果精确到0.1海里)【参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93】18.如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);(2)用方向和距离描述灯塔P相对于B处的位置.(参考数据:sin53°=0.80,cos53°=0.60,tan53°=0.33,=1.41)19.如图,要测量A点到河岸BC的距离,在B点测得A点在B点的北偏东30°方向上,在C点测得A 点在C点的北偏西45°方向上,又测得BC=150m.求A点到河岸BC的距离.(结果保留整数)(参考数据:≈1.41,≈1.73)20.如图,某渔船在小岛O南偏东75°方向的B处遇险,在小岛O南偏西45°方向A处巡航的中国渔政船接到求救信号后立刻前往救援,此时,中国渔政船与小岛O相距8海里,渔船在中国渔政船的正东方向上.(1)求∠BAO与∠ABO的度数(直接写出答案);(2)若中国渔政船以每小时28海里的速度沿AB方向赶往B处救援,能否在1小时内赶到?请说明理由.(参考數据:tan75°≈3.73,tan15°≈0.27,≈1.41,≈2.45)21.如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).22.如图,某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为300(+l)米,求供水站M分别到小区A、B的距离.(结果可保留根号)23.如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60千米的地方有一城市A.(1)问:A市是否会受到此台风的影响,为什么?(2)在点O的北偏东15°方向,距离80千米的地方还有一城市B,问:B市是否会受到此台风的影响?若受到影响,请求出受到影响的时间;若不受到影响,请说明理由.24.如图,一海伦位于灯塔P的西南方向,距离灯塔40海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).25.某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).26.如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北1.5海里D处,渔政船航行到点C处时测得点D在南偏东53°方向上.(1)求CD两点的距离;(2)渔政船决定再次调整航向前去救援,若两船航速不变,并且在点E处相会合,求∠ECD的正弦值.(参考数据:sin53°≈,cos53°≈,tan53°≈)27.我国为了维护队钓鱼岛P的主权,决定对钓鱼岛进行常态化的立体巡航.在一次巡航中,轮船和飞机的航向相同(AP∥BD),当轮船航行到距钓鱼岛20km的A处时,飞机在B处测得轮船的俯角是45°;当轮船航行到C处时,飞机在轮船正上方的E处,此时EC=5km.轮船到达钓鱼岛P时,测得D处的飞机的仰角为30°.试求飞机的飞行距离BD(结果保留根号).28.如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为26.6°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)29.如图,山顶有一铁塔AB的高度为20米,为测量山的高度BC,在山脚点D处测得塔顶A和塔基B 的仰角分别为60°和45°.求山的高度BC.(结果保留根号)30.小亮和小红在公园放风筝,不小心让风筝挂在树梢上,风筝固定在A处(如图),为测量此时风筝的高度,他俩按如下步骤操作:第一步:小亮在测点D处用测角仪测得仰角∠ACE=β.第二步:小红量得测点D处到树底部B的水平距离BD=a.第三步:量出测角仪的高度CD=b.之后,他俩又将每个步骤都测量了三次,把三次测得的数据绘制成如下的条形统计图和折线统计图.请你根据两个统计图提供的信息解答下列问题.(1)把统计图中的相关数据填入相应的表格中:(2)根据表中得到的样本平均值计算出风筝的高度AB(参考数据:,,结果保留3个有效数字).浙江省衢州市2016年中考数学(浙教版)专题训练:解直角三角形参考答案与试题解析一、选择题(共5小题)1.如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是()A.20海里B.40海里C.海里D.海里【考点】解直角三角形的应用-方向角问题.【分析】作AM⊥BC于M.由题意得,∠DBC=20°,∠DBA=50°,BC=60×=40海里,∠NCA=10°,则∠ABC=∠ABD﹣∠CBD=30°.由BD∥CN,得出∠BCN=∠DBC=20°,那么∠ACB=∠ACN+∠BCN=30°=∠ABC,根据等角对等边得出AB=AC,由等腰三角形三线合一的性质得到CM=BC=20海里.然后在直角△ACM中,利用余弦函数的定义得出AC=,代入数据计算即可.【解答】解:如图,作AM⊥BC于M.由题意得,∠DBC=20°,∠DBA=50°,BC=60×=40海里,∠NCA=10°,则∠ABC=∠ABD﹣∠CBD=50°﹣20°=30°.∵BD∥CN,∴∠BCN=∠DBC=20°,∴∠ACB=∠ACN+∠BCN=10°+20°=30°,∴∠ACB=∠ABC=30°,∴AB=AC,∵AM⊥BC于M,∴CM=BC=20海里.在直角△ACM中,∵∠AMC=90°,∠ACM=30°,∴AC===(海里).故选D.【点评】本题考查了解直角三角形的应用﹣方向角问题,平行线的性质,等腰三角形的判定与性质,余弦函数的定义,难度适中.求出CM=BC=20海里是解题的关键.2.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是()A.2海里B.2sin55°海里C.2cos55°海里D.2tan55°海里【考点】解直角三角形的应用-方向角问题.【分析】首先由方向角的定义及已知条件得出∠NPA=55°,AP=2海里,∠ABP=90°,再由AB∥NP,根据平行线的性质得出∠A=∠NPA=55°.然后解Rt△ABP,得出AB=AP•cos∠A=2cos55°海里.【解答】解:如图,由题意可知∠NPA=55°,AP=2海里,∠ABP=90°.∵AB∥NP,∴∠A=∠NPA=55°.在Rt△ABP中,∵∠ABP=90°,∠A=55°,AP=2海里,∴AB=AP•cos∠A=2cos55°海里.故选C.【点评】本题考查了解直角三角形的应用﹣方向角问题,平行线的性质,三角函数的定义,正确理解方向角的定义是解题的关键.3.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD是()A.20海里B.40海里C.20海里D.40海里【考点】解直角三角形的应用-方向角问题.【分析】根据方向角的定义及余角的性质求出∠CAD=30°,∠CBD=60°,再由三角形外角的性质得到∠CAD=30°=∠ACB,根据等角对等边得出AB=BC=20,然后解Rt△BCD,求出CD即可解答.【解答】解:根据题意可知∠CAD=30°,∠CBD=60°,∵∠CBD=∠CAD+∠ACB,∴∠CAD=30°=∠ACB,∴AB=BC=40海里,在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC=,∴sin60°=,∴CD=40×sin60°=40×=20(海里).故选:C.【点评】本题考查了解直角三角形的应用,难度适中.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.4.如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为()A.4km B.(2+)km C.2km D.(4﹣)km【考点】解直角三角形的应用-方向角问题.【专题】压轴题.【分析】根据题意在CD上取一点E,使BD=DE,进而得出EC=BE=2,再利用勾股定理得出DE的长,即可得出答案.【解答】解:在CD上取一点E,使BD=DE,可得:∠EBD=45°,AD=DC,∵从B测得船C在北偏东22.5°的方向,∴∠BCE=∠CBE=22.5°,∴BE=EC,∵AB=2,∴EC=BE=2,∴BD=ED=,∴DC=2+.故选:B.【点评】此题主要考查了解直角三角形的应用,得出BE=EC=2是解题关键.5.有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是()海里.A.10B.10﹣10 C.10 D.10﹣10【考点】解直角三角形的应用-方向角问题.【分析】由题意得:∠CAP=30°,∠CBP=45°,BC=10海里,分别在Rt△BCP中和在Rt△APC中求得BC 和AC后相减即可求得A、B之间的距离.【解答】解:由题意得:∠CAP=30°,∠CBP=45°,BC=10海里,在Rt△BCP中,∵∠CBP=45°,∴CP=BC=10海里,在Rt△APC中,AC===10海里,∴AB=AC﹣BC=(10﹣10)海里,故选D.【点评】本题考查了解直角三角形的应用,解题的关键是能够从实际问题中整理出直角三角形,并选择合适的边角关系求解.二、填空题(共4小题)6.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为2km.【考点】解直角三角形的应用-方向角问题.【专题】压轴题.【分析】过点A作AD⊥OB于D.先解Rt△AOD,得出AD=OA=2km,再由△ABD是等腰直角三角形,得出BD=AD=2km,则AB=AD=2km.【解答】解:如图,过点A作AD⊥OB于D.在Rt△AOD中,∵∠ADO=90°,∠AOD=30°,OA=4km,∴AD=OA=2km.在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB﹣∠AOB=75°﹣30°=45°,∴BD=AD=2km,∴AB=AD=2km.即该船航行的距离(即AB的长)为2km.故答案为2km.【点评】本题考查了解直角三角形的应用﹣方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.7.如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行50海里可使渔船到达离灯塔距离最近的位置.【考点】解直角三角形的应用-方向角问题.【分析】过M作东西方向的垂线,设垂足为N.由题易可得∠MAN=30°,在Rt△MAN中,根据锐角三角函数的定义求出AN的长即可.【解答】解:如图,过M作东西方向的垂线,设垂足为N.易知:∠MAN=90°=30°.在Rt△AMN中,∵∠ANM=90°,∠MAN=30°,AM=100海里,∴AN=AM•cos∠MAN=100×=50海里.故该船继续航行50海里可使渔船到达离灯塔距离最近的位置.故答案为50.【点评】本题主要考查了解直角三角形的应用﹣方向角问题,三角函数的定义,利用垂线段最短的性质作出辅助线是解决本题的关键.8.如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为750米.【考点】解直角三角形的应用-仰角俯角问题.【专题】压轴题.【分析】作AD⊥BC于D,根据速度和时间先求得AC的长,在Rt△ACD中,求得∠ACD的度数,再求得AD的长度,然后根据∠B=30°求出AB的长.【解答】解:如图,过点A作AD⊥BC,垂足为D,在Rt△ACD中,∠ACD=75°﹣30°=45°,AC=30×25=750(米),∴AD=AC•sin45°=375(米).在Rt△ABD中,∵∠B=30°,∴AB=2AD=750(米).故答案为:750.【点评】本题考查了解直角三角形的应用,解答本题的关键是根据仰角和俯角构造直角三角形并解直角三角形,难度适中.9.如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,(参测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约为15.3m(精确到0.1m).考数据:≈1.41,,1.73)【考点】解直角三角形的应用-仰角俯角问题.【专题】压轴题.【分析】在Rt△ACD中求出AC,在Rt△BCD中求出BC,继而可得出AB.【解答】解:在Rt△ACD中,CD=21m,∠DAC=30°,则AC=CD≈36.3m;在Rt△BCD中,∠DBC=45°,则BC=CD=21m,故AB=AC﹣BC=15.3m.故答案为:15.3.【点评】本题考查了解直角三角形的应用,解答本题关键是构造直角三角形,理解俯角的定义,能利用三角函数表示线段的长度.三、解答题(共21小题)10.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).【考点】解直角三角形的应用-方向角问题.【分析】过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.解Rt△BCE,求出BE=BC=×1000=500米;解Rt△CDF,求出CF=CD=500米,则DA=BE+CF=(500+500)米.【解答】解:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D 作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.在Rt△BCE中,∵∠E=90°,∠CBE=60°,∴∠BCE=30°,∴BE=BC=×1000=500米;在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=BC=1000米,∴CF=CD=500米,∴DA=BE+CF=(500+500)米,故拦截点D处到公路的距离是(500+500)米.【点评】本题考查了解直角三角形的应用﹣方向角问题,锐角三角函数的定义,正确理解方向角的定义,进而作出辅助线构造直角三角形是解题的关键.11.如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.(1)快艇从港口B到小岛C需要多长时间?(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.【考点】解直角三角形的应用-方向角问题.【分析】(1)要求B到C的时间,已知其速度,则只要求得BC的路程,再利用路程公式即可求得所需的时间;(2)过C作CD⊥OA,垂足为D,设相会处为点E.求出OC=OB•cos30°=60,CD=OC=30,OD=OC•cos30°=90,则DE=90﹣3v.在直角△CDE中利用勾股定理得出CD2+DE2=CE2,即(30)2+(90﹣3v)2=602,解方程求出v=20或40,进而求出相遇处与港口O的距离.【解答】解:(1)∵∠CBO=60°,∠COB=30°,∴∠BCO=90°.在Rt△BCO中,∵OB=120,∴BC=OB=60,∴快艇从港口B到小岛C的时间为:60÷60=1(小时);(2)过C作CD⊥OA,垂足为D,设相会处为点E.则OC=OB•cos30°=60,CD=OC=30,OD=OC•cos30°=90,∴DE=90﹣3v.∵CE=60,CD2+DE2=CE2,∴(30)2+(90﹣3v)2=602,∴v=20或40,∴当v=20km/h时,OE=3×20=60km,当v=40km/h时,OE=3×40=120km.【点评】此题考查了解直角三角形的应用﹣方向角问题,锐角三角函数的定义,勾股定理等知识,理解方向角的定义,得出∠BCO=90°是解题的关键,本题难易程度适中.12.如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:≈1.732)【考点】解直角三角形的应用-方向角问题.【分析】过点C作CD⊥AB于点D,则若该船继续向西航行至离灯塔距离最近的位置为CD的长度,利用锐角三角函数关系进行求解即可.【解答】解:如图,过点C作CD⊥AB于点D,AB=20×1=20(海里),∵∠CAF=60°,∠CBE=30°,∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°﹣∠CAF=30°,∴∠C=180°﹣∠CBA﹣∠CAB=30°,∴∠C=∠CAB,∴BC=BA=20(海里),∠CBD=90°﹣∠CBE=60°,∴CD=BC•sin∠CBD=≈17(海里).【点评】此题主要考查了方向角问题,熟练应用锐角三角函数关系是解题关键.13.(2015•济宁)阅读材料:在一个三角形中,各边和它所对角的正弦的比相等,==,利用上述结论可以求解如下题目:在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.解:在△ABC中,∵=∴b====3.理解应用:如图,甲船以每小时30海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10海里.(1)判断△A1A2B2的形状,并给出证明;(2)求乙船每小时航行多少海里?【考点】解直角三角形的应用-方向角问题.【专题】压轴题.【分析】(1)先根据路程=速度×时间求出A1A2=30×=10,又A2B2=10,∠A1A2B2=60°,根据有一个角是60°的等腰三角形是等边三角形即可得出△A1A2B2是等边三角形;(2)先由平行线的性质及方向角的定义求出∠A1B1B2=75°﹣15°=60°,由等边三角形的性质得出∠A2A1B2=60°,A1B2=A1A2=10,那么∠B1A1B2=105°﹣60°=45°.然后在△B1A1B2中,根据阅读材料可知,=,求出B1B2的距离,再由时间求出乙船航行的速度.【解答】解:(1)△A1A2B2是等边三角形,理由如下:连结A1B2.∵甲船以每小时30海里的速度向正北方向航行,航行20分钟到达A2,∴A1A2=30×=10,又∵A2B2=10,∠A1A2B2=60°,∴△A1A2B2是等边三角形;(2)如图,∵B1N∥A1A2,∴∠A1B1N=180°﹣∠B1A1A2=180°﹣105°=75°,∴∠A1B1B2=75°﹣15°=60°.∵△A1A2B2是等边三角形,∴∠A2A1B2=60°,A1B2=A1A2=10,∴∠B1A1B2=105°﹣60°=45°.在△B1A1B2中,∵A1B2=10,∠B1A1B2=105°﹣60°=45°,∠A2A1B2=60°,由阅读材料可知,=,解得B1B2==,所以乙船每小时航行:÷=20海里.【点评】本题考查了解直角三角形的应用﹣方向角问题,等边三角形的判定与性质,方向角的定义,锐角三角函数的定义,学生的阅读理解能力以及知识的迁移能力.正确理解阅读材料是解题的关键.14.如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:≈1.414,结果精确到0.1)【考点】解直角三角形的应用-方向角问题.【分析】过B作BD⊥AP于D,由已知条件得:AB=20×2=40,∠P=75°﹣30°=45°,在Rt△ABD中求出BD=AB=20,在R t△BDP中求出PB即可.【解答】解:过B作BD⊥AP于D,由已知条件得:AB=20×2=40,∠P=75°﹣30°=45°,在Rt△ABD中,∵AB=40,∠A=30,∴BD=AB=20,在R t△BDP中,∵∠P=45°,∴PB=BD=20≈28.3(海里).答:此时海监船与黄岩岛P的距离BP的长约为28.3海里.【点评】此题主要考查了方向角问题的应用,根据已知得出△PDB为等腰直角三角形是解题关键.15.为保护渔民的生命财产安全,我国政府在南海海域新建了一批观测点和避风港.某日在观测点A处发现在其北偏西36.9°的C处有一艘渔船正在作业,同时检测到在渔船的正西B处有一股强台风正以每小时40海里的速度向正东方向移动,于是马上通知渔船到位于其正东方向的避风港D处进行躲避.已知避风港D在观测点A的正北方向,台风中心B在观测点A的北偏西67.5°的方向,渔船C与观测点A相距350海里,台风中心的影响半径为200海里,渔船的速度为每小时18海里,问渔船能否顺利躲避本次台风的影响?(sin36.9°≈0.6,tan36.9≈0.75,sin67.5≈0.92,tan67.5≈2.4)【考点】解直角三角形的应用-方向角问题.【分析】先解Rt△ADC,求出CD=AC•sin∠DAC≈350×0.6=210海里,AD==280海里,那么渔船到的避风港D处所用时间:210÷18=11小时.再解Rt△ADB,求出BD=AD•tan∠BAD≈280×2.4=672海里,那么BC=BD﹣CD≈672﹣210=462海里.设强台风移动到渔船C后面200海里时所需时间为x小时,根据追及问题的等量关系列出方程(40﹣18)x=462﹣200,解方程求出x=11,由于11<11,所以渔船能顺利躲避本次台风的影响.【解答】解:由题意可知∠BAD=67.5°,∠CAD=36.9°,AC=350海里.在Rt△ADC中,∵∠ADC=90°,∠DAC=36.9°,AC=350海里,∴CD=AC•sin∠DAC≈350×0.6=210海里,AD==280海里.∴渔船到的避风港D处所用时间:210÷18=11小时.在Rt△ADB中,∵∠ADB=90°,∠BAD=67.5°,∴BD=AD•tan∠BAD≈280×2.4=672海里,∴BC=BD﹣CD≈672﹣210=462海里.设强台风移动到渔船C后面200海里时所需时间为x小时,根据题意得(40﹣18)x=462﹣200,解得x=11,∵11<11,∴渔船能顺利躲避本次台风的影响.【点评】本题考查了解直角三角形的应用﹣方向角问题,难度中等,求出强台风移动到渔船C后面200海里时所需时间是解题的关键.16.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).。
中考数学模拟试卷精选汇编:解直角三角形附答案

解直角三角形一.选择题1. (2015·北京市朝阳区·一模)如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60 m,ST=120 m,QR=80 m,则河的宽度PQ为A.40 m B.60 m C.120 m D.180 m答案:C二.填空题1.(2015·江苏江阴青阳片·期中)如图,小红站在水平面上的点A处,测得旗杆BC顶点C的仰角为60°,点A到旗杆的水平距离为a米.若小红的水平视线与地面的距离为b米,则旗杆BC的长为____▲____米。
(用含有a、b的式子表示)第1题答案:b+3a2. (2015·屯溪五中·3月月考)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为__________答案:2倍根号23.(2015•山东潍坊广文中学、文华国际学校•一模)如图2,菱形ABCD 的周长为20cm ,且tan ∠ABD =34,则菱形ABCD 的面积为 cm 2. 答案:24;4.(2015·邗江区·初三适应性训练)如图,△ABC 的顶点都在正方形网格的格点上,则cosC 的值为 ▲ .答案:552 第2题 5.(2015·重点高中提前招生数学练习)在某海防观测站的正东方向12海里处有A ,B 两艘船相遇,然后A 船以每小时12海里的速度往南航行,B 船以每小时3海里的速度向北漂移.则经过 小时后,观测站及A ,B 两 船恰成一个直角三角形. 【答案】26.(2015·重点高中提前招生数学练习)已知∠A 为锐角,且4sin 2A -4sinAcosA +cos 2A =0,则tanA = . 【答案】12【解析】由题意得(2sinA -cosA )2=0,∴2sinA -cosA =0,∴sinA cosA =12. ∴tanA =sinA cosA =12.7(2015·网上阅卷适应性测试)小聪有一块含有30°角的直角三角板,他想只利用量角器来测量较短直角边的长度,于是他采用如图的方法,小聪发现点A 处的三角板读数为12cm ,点B 处的量角器的读数为74°,由此可知三角板的较短直角边的长度约为 ▲ cm .(参考数据:sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75).答案:98.(2015·山东省东营区实验学校一模)为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出___个这样的停车位.(2≈1.4)答案:17三.解答题1.(2015·江苏江阴长泾片·期中)2015年4月18日潍坊国际风筝节拉开了帷幕,这天小敏同学正在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,试求A、B之间的距离;(2)在(1)的条件下,若在A处背向旗杆又测得风筝的仰角为75°,绳子在空中视为一条线段,求绳子AC为多少米?(结果保留根号)答案:解:(1)在Rt△BPQ中,PQ=10米,∠B=30°,则BQ= tan60°×PQ=103, ……………2分又在Rt△APQ中,∠PAB=45°,则AQ=tan45°×PQ=10,即:AB=(103+10)(米)……………4分(2)过A作AE⊥BC于E,在Rt△ABE中,∠B=30°,AB=103+10,∴AE=sin30°×AB=12(103+10)=53+5,……………6分∵∠CAD=75°,∠B=30°∴∠C=45°,……………7分在Rt△CAE中,sin45°=AEAC,图8∴AC =2(53+5)=(56+52)(米) ……………9分2.(2015·江苏江阴青阳片·期中)如图,某广场一灯柱AB 被一钢缆CD 固定,CD 与地面成40°夹角,且CB =5米.(1)求钢缆CD 的长度;(精确到0.1米)(2)若AD =2米,灯的顶端E 距离A 处1.6米,且∠EAB =120°,则灯的顶端E 距离地面多少米?(参考数据:tan 400=0.84, sin 400=0.64, cos 400=34)答案:(1)在Rt ⊿BCD 中∵cos 40°=CDBC…………1分 ∴CD =40cos BC =5÷43=320…………3分 (2)∵∠EAF =180°-120°=60° 在Rt ⊿AEF 中 cos 60°=AEAF ∴AF =AE ·cos 60°=1.6·21=0.8…………5分 在Rt ⊿BCD 中 tan 40°=BCBDBD =BC ·tan 40°=5·0.84=4.2…………7分 BF =4.2+2+0.8=7…………8分3.(2015·江苏江阴夏港中学·期中)如图,轮船从点A 处出发,先航行至位于点A 的南偏西15°且点A 相距100km 的点B 处,再航行至位于点B 的北偏东75°且与点B 相距200km 的点C 处.(1)求点C 与点A 的距离(精确到1km ) (2)确定点C 相对于点A 的方向 (参考数据:2≈1.414,3≈1.732)答案:解法1:(1)如答图2,过点A 作AD ⊥BC ,垂足为D .············1分由图得,∠ABC =︒=︒−︒601575.·······························2分在Rt △ABD 中,∵∠ABC =60°,AB =100,∴BD =50,AD =350····················3分 ∵BC =200,∴CD=BC -BD =150.·································4分 ∴在Rt △ABD 中,AC =22CD AD +=3100≈173(km ). 答:点C 与点A 的距离约为173km .························5分(2)在△ABC 中,∵2222)3100(100+=+AC AB =40 000,22200=BC =40 000. ∴222BC AC AB =+,∴︒=∠90BAC .···················7分 ∴︒=︒−︒=∠−∠=∠751590BAF BAC CAF 答:点C 位于点A 的南偏东75°方向.················8分 解法2:(1)如答图3,取BC 的中点D ,连接AD.············ 1分由图得,∠ABC =︒=︒−︒601575···················2分 ∵D 为BC 的中点,BC =200,∴CD=BD =100. 在△ABD 中,∵BD =100,AB =100,∠ABC =60°, ∴△ADB 为等边三角形,··························3分 ∴AD=BD=CD ,∠ADB =60°,∴∠DAC =∠DCA =30°. ∴∠BAC =∠BAD +∠DAC =90°,···················4分 ∴AC =)(km 173310022≈=−AB BC 答:点C 与点A 的距离约为173km .·······················5分 (2)由图得,︒=︒−︒=∠−∠=∠751590BAF BAC CAF答:点C 位于点A 的南偏东75°方向.······························8分4.(2015·江苏江阴要塞片·一模)如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E 到地面的距离EF .经测量,支架的立柱BC 与地面垂直,即∠BCA =90°,且BC =1.5m ,点F 、A 、C 在同一条水平线上,斜杆AB 与水平线AC 的夹角∠BAC =30°,支撑杆DE ⊥AB 于点D ,该支架的边BE 与AB 的夹角∠EBD =60°,又测得AD =1m .请你求出该支架的边BE 及顶端E 到地面的距离EF 的长度.答案:解:在Rt △ABC 中,∵∠BAC =30°,BC =1.5m ,∴AB=3m,∵AD=1m,∴BD=2m,·········1分在Rt△EDB中,∵∠EBD=60°,∴∠BED=90°﹣60°=30°,∴EB=2BD=2×2=4m,·········3分过B作BH⊥EF于点H,∴四边形BCFH为矩形,HF=BC= 1.5m,∠HBA=∠BAC=30°,········4分又∵∠HBA=∠BAC=30°,∴∠EBH=∠EBD﹣∠HBD=30°,∴EH=EB=2m,∴EF=EH+HF=2+1.5=3.5(m).········7分答:该支架的边BE为4m,顶端E到地面的距离EF的长度为3.5m.5. (2015·屯溪五中·3月月考)如图,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(结果都保留根号)(1)求点P到海岸线l的距离;(2)小船从点P处沿射线AP的方向航行一段时间后,到达点C处.此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.答案:解:(1)如图,过点P 作PD ⊥AB 于点D .设PD =xkm . 在Rt △PBD 中,∠BDP =90°,∠PBD =90°﹣45°=45°, ∴BD =PD =xkm .在Rt △P AD 中,∠ADP =90°,∠P AD =90°﹣60°=30°, ∴AD =PD =xkm .∵BD +AD =AB , ∴x +x =2, x =﹣1,∴点P 到海岸线l 的距离为(﹣1)km ;(2)如图,过点B 作BF ⊥AC 于点F . 在Rt △ABF 中,∠AFB =90°,∠BAF =30°, ∴BF =AB =1km .在△ABC 中,∠C =180°﹣∠BAC ﹣∠ABC =45°. 在Rt △BCF 中,∠BFC =90°,∠C =45°, ∴BC =BF =km ,∴点C 与点B 之间的距离为km .6. (2015·安徽省蚌埠市经济开发·二摸)合肥新桥国际机场出港大厅有一幅“黄山胜景”的壁画.聪聪站在距壁画水平距离15米的地面,自A 点看壁画上部D 的仰角为045,看壁画下部C的仰角为030,求壁画CD 的高度.3 1.7≈2 1.4≈,精确到十分位)答案:过A 点作AB ⊥DC 于点B ,则AB =15,在Rt ABD ∆中,045DAB ∠=,∴BD =AB =15 ……… 3分 在Rt ABC ∆中,030BAC ∠=, ∴03tan 3015533BC AB ==⨯= ………… 6分 ∴CD =BD -BC =15-53155 1.7 6.5≈−⨯=答:壁画CD 的高度为6.5米 …………… 8分7. (2015·安庆·一摸)为维护南海主权,我海军舰艇加强对南海海域的巡航.2015年4月10日上午9时,我海巡001号舰艇在观察点A 处观测到其正东方向802海里处有一灯塔S ,该舰艇沿南偏东450的方向航行,11时到达观察点B ,测得灯塔S 位于其北偏西150方向,求该舰艇的巡航速度?(结果保留整数)(参考数据:73.13,41.12≈≈)答案:解:过点S 作SC ⊥AB ,C 为垂足.在Rt △ACS 中,∠CAS =450,AS =802,∴SC =AC =80;………3分在Rt △BCS 中,∠CBC =450-150=300,∴BC =803,AB =AC +BC =80+803;………6分∴该舰艇的巡航速度是(80+803)÷(11-9)=40+403≈109(海里/时)…………8分8. (2015·屯溪五中·3月月考)如图,在△ABC 中,AB =AC =5,BC =8.若∠BPC =∠BAC ,求tan ∠BPC 的值。
人教版九年级数学下册 28.2 解直角三角形及其应用 同步测试题(有答案)

28.2 解直角三角形及其应用同步测试题(满分120分;时间:120分钟)一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 在△ABC中,AB=12√2,AC=13,cos∠B=√22,则BC边长为()A.7B.8C.8或17D.7或172. 如图AD⊥CD,AB=13,BC=12,CD=3,AD=4,则sin B=()A.5 13B.1213C.35D.453. 如图,一艘海轮位于灯塔P的北偏东30∘方向,距离灯塔60海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45∘方向上的B处,这时,海轮所在的B处与灯塔P的距离为()A.30√2海里B.30√3海里C.60海里D.30√6海里4. 如图,在高为2m,坡角为30∘的楼梯表面铺地毯,地毯的长度至少需要()A.2(√3+1)mB.4mC.(√3+2)mD.2(√3+3)m5. 在离电视塔am的A处,测得塔顶仰角为β,若测角仪高度为bm,则电视塔高为()A.(a tanβ+b)mB.(a cotβ+b)mC.(a sinβ+b)mD.(a cosβ+b)m6. 如图,沿AC方向开山修路,为加快施工进度,要在小山的另一边同时施工.现在AC 上取一点B,使∠ABD=145∘,BD=500 m,∠D=55∘,要使A,C,E成一直线,那么开挖点E离点D的距离为()mA.500⋅sin55∘ mB.500⋅cos55∘ mC.500⋅tan55∘ mD.50cos55∘,AC=2√3,则AB=()7. 如图,在△ABC中,∠A=30∘,tan B=√32A.4B.5C.6D.78. 如图是一长为50米的游泳池的纵切面,该游泳池的最浅处为1.2米,最深处为2.2米,底面为斜坡,则底面的坡度为()A.50B.1:50C.3:125D.11:2509. 在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60∘方向走了5km到达B 地,然后再沿北偏西30∘方向走了若干千米到达C地,测得A地在C地南偏西30∘方向,则A,C两地的距离为()A.10√33km B.5√33km C.5√2km D.5√3km10. 如图,等腰△ABC的底角为30∘,底边上的高AD=5,则腰AB、AC的值为()A.20B.15C.10D.7.5二、填空题(本题共计10 小题,每题3 分,共计30分,)11. 在Rt△ABC中,∠C=90∘,AB=2√3,BC=√3,那么∠B=________度.12. 小明同学从A地出发沿北偏东30∘的方向到B地,再由B地沿南偏西40∘的方向到C地,则∠ABC=________∘.13.在Rt△ABC中,∠A=90∘,AB=2,若sin C=15,则BC的长度为________.14. 如图,C岛在A岛的北偏东50∘,C岛在B岛的北偏西40∘方向,且BC为5海里,AC为12海里,则sin∠CAB=________.15. 在△ABC中,AB=AC=6cm,BD为AC边上的高,∠DAB=60∘,则线段CD的长为________.16. 如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离出发点的水平距离为________m.17. 如图,A,B之间是一座山,一条高速公路要通过A,B两点,在A地测得公路走向是北偏西111∘32′.如果A,B两地同时开工,那么在B地按________方向施工,才能使公路在山腹中准确接通.18. 如图,设∠AOC=α,∠BOC=β,P为射线OC上一点,PD⊥OA于D,PE⊥OB于E,则PD等于________(用α、β的三角函数表示)PE19. 如图,在点B处测得塔顶A的仰角为30∘,点B到塔底C的水平距离BC是30m,那么塔AC的高度为________m(结果保留根号).20. 如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60∘,沿山坡向上走到B处测得宣传牌顶部C的仰角为45∘.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度为________.(测角器的高度忽略不计,结果精确到0.1米.参考数据:√2≈1.414,√3≈1.732).三、解答题(本题共计6 小题,共计60分,)21. 已知一艘轮船从港口A出发以80km∕ℎ的速度向正东方向航行,30min后到港口B,又从港口B以同样的速度15min后航行到港口C,此时在C处测得港口A位于港口C的南偏西63.4∘方向上,求该艘轮船以80km∕ℎ的速度返回到港口A所需的时间.(精确到0.01ℎ,参考数据:cos63.4∘≈0.45,sin26.6∘≈0.45,cos26.6∘≈0.89,tan26.6∘≈0.50,√2≈1.41,√5≈2.24)22. 如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45∘,小英同学在距A处50米远的B处测得∠CBD=30∘,请你根据这些数据算出河宽.(精确到0.01米,参考数据√2≈1.414,√3≈1.732)23. 如图,一幢居民楼OC临近山坡AP,山坡AP的坡度为i=1:√3,小亮在距山坡坡脚A 处测得楼顶C的仰角为60∘,当从A处沿坡面行走10米到达P处时,测得楼顶C的仰角刚好为45∘,点O,A,B在同一直线上,求该居民楼的高度.(结果保留整数,√3≈1.73)24. 教育部布的《基础教育课程改革纲要》要求每位学生每学年都要参加社会实践活动,某学校组织了一次测量探究活动,如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53∘,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45∘,已知山坡AB的坡度1:√3,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:√2≈1.41,√3≈1.73,,cos53∘≈0.60)tan53∘≈4325. 某课桌生产厂家研究发现,倾斜为12∘−24∘的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1所示,AB可绕点A旋转,在点C处安装一根长度一定且C处固定,可旋转的支撑臂CD,AC=30cm.(1)如图2中,当CD⊥AB于D时,测得∠BAC=24∘,求此时支撑臂CD的长.(2)在图3中,当CD不垂直AB时,测得∠BAC=12∘,求此时AD的长(结果保留根号).[参考数据:sin24∘=0.40, cos24∘=0.91, tan24∘=0.46, sin12∘=0.20]参考答案与试题解析一、选择题(本题共计10 小题,每题 3 分,共计30分)1.【答案】D【解答】解:∵ cos∠B=√22,∵ ∠B=45∘,当△ABC为钝角三角形时,如图1,∵ AB=12√2,∠B=45∘,∵ AD=BD=12,∵ AC=13,∵ 由勾股定理得CD=5,∵ BC=BD−CD=12−5=7;当△ABC为锐角三角形时,如图2,BC=BD+CD=12+5=17,故选D.2.【答案】A【解答】解:由勾股定理知,AC2=CD2+AD2=25,∵ AC=5.∵ AC2+BC2=169=AB2,∵ △CBA是直角三角形.∵ sin B=ACAB =513.故选A.3.【答案】A【解答】解:过点P作PC⊥AB于点C.在Rt△PAC中,∵ PA=60海里,∠PAC=30∘,AP=30海里.∵ CP=12在Rt△PBC中,∵ PC=30海里,∠PBC=∠BPC=45∘,∵ PB=√2PC=30√2海里.即海轮所在的B处与灯塔P的距离为30√2海里.故选:A.4.【答案】A【解答】解:由题意得:地毯的竖直的线段加起来等于BC,水平的线段相加正好等于AC,即地毯的总长度至少为(AC+BC),在Rt△ABC中,∠A=30∘,BC=2m,∠C=90∘.,∵ tan A=BCAC∵ AC=BC÷tan30∘=2√3.∵ AC+BC=2√3+2.故选A.5.【答案】A【解答】解:根据题意画出相应的图形,如图所示:在Rt△BCD中,∠CBD=β,BD=AE=am,则tanβ=CDBD,即CD=BD tanβ=a tanβ(m),又因为DE=AB=bm,则CE=CD+DE=(a tanβ+b)m.故选A.6.【答案】B【解答】解:由题意可得,∠DBC=180∘−∠ABD=180∘−145∘=35∘,BD=500m,∵ 要使A,C,E成一直线,则∠DEB=180∘−∠DBE−∠D=90∘,∵ DE=BD⋅cos50∘=500⋅cos55∘,故选B.7.【答案】B【解答】解:作CD⊥AB于点D.由题意知,∵ sin A=CDAC,∵ CD=AC sin A=AC sin30∘=2√3×1 2=√3,∵ cos A=ADAC,∵ AD=AC cos30∘=2√3×√3 2=3.∵ tan B=CDBD =√32,∵ BD=2.∵ AB=AD+BD=2+3=5.故选B.8.【答案】B【解答】解:因为水平距离为50米,则底面的坡度为2.2−1.250=1:50.故选B.9.【答案】A【解答】解:如图.由题意可知,AB=5km,∠2=30∘,∠EAB=60∘,∠3=30∘.∵ EF // PQ,∵ ∠1=∠EAB=60∘又∵ ∠2=30∘,∵ ∠ABC=180∘−∠1−∠2=180∘−60∘−30∘=90∘.∵ △ABC是直角三角形.又∵ MN // PQ,∵ ∠4=∠2=30∘.∵ ∠ACB=∠4+∠3=30∘+30∘=60∘.∵ AC=ABsin∠ACB =√32=10√33(km).故选A.10.【答案】C【解答】解:∵ 等腰△ABC的底角为30∘,底边上的高AD=5,∵ AB=AC=2AD=2×5=10.故选C.二、填空题(本题共计10 小题,每题 3 分,共计30分)11.【答案】60【解答】解:在Rt△ABC中,∵ ∠C=90∘,AB=2√3,BC=√3,∵ BC=12AB,∵ ∠A=30∘,∵ ∠B=60∘(直角三角形的两个锐角互为余角).故答案是:60∘.12.【答案】10【解答】解:如图:由题意知,∠1=30∘,∠2=40∘,∵ ∠ABC=∠2−∠1=10∘.故答案为:10.13.【答案】10【解答】解:∵ ∠A=90∘,∵ sin C=ABBC =15,∵ AB=2,∵ BC=10;故答案为:10.14.【答案】513【解答】解:过C点作CD // AE,∵ C岛在A岛的北偏东50∘,C岛在B岛的北偏西40∘方向,AC // CD,CD // BC,∵ ∠EAC=∠ACD=50∘,∠FBC=∠DCB=40∘,∵ ∠ACB=90∘,∵ sin∠CAB=BCAB,∵ BC为5海里,AC为12海里,∵ AB=13海里,∵ sin∠CAB=BCAB =513.故答案为:513.15.【答案】3cm或9cm【解答】解:①如图1,△ABC是锐角三角形时,∵ AB=AC,∠DAB=60∘,∵ △ABC是等边三角形,∵ CD=12AC=12×6=3cm,②ABC是钝角三角形时,∵ ∠DAB=60∘,∵ ∠ABD=90∘−60∘=30∘,∵ AB=6cm,∵ AD=12AB=12×6=3cm,∵ CD=AD+AC=3+6=9cm,综上所述,线段CD的长为3或9cm.故答案为:3cm或9cm.16.【答案】4√5【解答】解:∵ AB=10米,tan A=BCAC =12.∵ 设BC=x,AC=2x,由勾股定理得,AB2=AC2+BC2,即100=x2+4x2,解得x=2√5,∵ AC=4√5,BC=2√5米.故答案为4√5.17.【答案】北偏东68∘28′【解答】解:在B地按北偏东68∘28′施工,就能使公路在山腹中准确接通.∵ 指北方向相互平行,A、B两地公路走向形成一条直线,∵ 这样就构成了一对同旁内角,∵ ∠A+∠B=180∘,(两直线平行,同旁内角互补),∵ 可得在B地按北偏东180∘−111∘32′=68∘28′施工.故答案为:北偏东68∘28′.18.【答案】sinαsinβ【解答】解:∵ PD⊥OA于D,PE⊥OB于E,∵ ∠PDO=∠PEO=90∘,∵ sinα=PDPO ,sinβ=PEPO,∵ PDPE =sinαsinβ.故答案为:sinαsinβ.19.【答案】10√3【解答】∵ 在点B处测得塔顶A的仰角为30∘,∵ ∠B=30∘,∵ BC=30m,∵ AC=√33BC=30×√33=10√3m,20.【答案】5.4米【解答】解:过B 作BF ⊥AE ,交EA 的延长线于F ,作BG ⊥DE 于G .Rt △ABF 中,∵ ∠AFB =90∘,∠BAF =180∘−60∘−90∘=30∘, ∵ BF =12AB =10,AF =√3BF =10√3,∵ BG =AF +AE =10√3+30.在Rt △BGC 中,∵ ∠BGC =90∘,∠CBG =45∘,∵ CG =BG =10√3+30.Rt △ADE 中,∵ ∠AED =90∘,∠DAE =60∘,AE =30,∵ DE =√3AE =30√3,∵ CD =CG +GE −DE =10√3+30+10−30√3≈5.4.答:宣传牌CD 高约5.4米. 故答案为5.4米.三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 ) 21.【答案】解:∵ AB =80×12=40km ,BC =80×14=20km . 根据勾股定理可以得出:AD 2+CD 2=AC 2,BD 2+CD 2=BC 2,在以上式子中,设AD 为x ,那么BD =40−x ,设AC 为y ,又因为∠ACD =63.4∘,所以CD =x ⋅tan 26.6∘,根据以上设定可列出如下方程组:{(40−x)2+(x tan 26.6∘)=202x 2+(x ⋅tan 26.6∘)2=y 2, ∵ {x ≈24y ≈26.832. 以轮船80km/ℎ的速度从C 返回A ,所需的时间为:26.832×180=0.3354小时.【解答】解:∵ AB =80×12=40km ,BC =80×14=20km .根据勾股定理可以得出:AD 2+CD 2=AC 2,BD 2+CD 2=BC 2,在以上式子中,设AD 为x ,那么BD =40−x ,设AC 为y ,又因为∠ACD =63.4∘,所以CD =x ⋅tan 26.6∘,根据以上设定可列出如下方程组:{(40−x)2+(x tan 26.6∘)=202x 2+(x ⋅tan 26.6∘)2=y 2,∵ {x ≈24y ≈26.832.以轮船80km/ℎ的速度从C 返回A ,所需的时间为:26.832×180=0.3354小时.22.【答案】河宽为68.30米.【解答】过C 作CE ⊥AB 于E ,设CE =x 米,在Rt△AEC中:∠CAE=45∘,AE=CE=x在Rt△BCE中:∠CBE=30∘,BE=√3CE=√3x,∵ √3x=x+50解之得:x=25√3+25≈68.30.23.【答案】解:如图,过点P作PE⊥OB于点E,PF⊥CO于点F,∵ 山坡AP的坡度为i=1:√3,AP=10,∵ 可设PE=x,则AE=√3x.在Rt△AEP中,x2+(√3x)2=102,解得x=5或x=−5(舍去),∵ PE=5,则AE=5√3.∵ ∠CPF=∠PCF=45∘,∵ CF=PF.设CF=PF=m米,则OC=(m+5)米,OA=(m−5√3)米.在Rt△AOC中,tan60∘=OCOA =m−5√3,即m+5m−5√3=√3,解得m=10(√3+1),∵ OC=10(√3+1)+5≈32(米).【解答】解:如图,过点P作PE⊥OB于点E,PF⊥CO于点F,∵ 山坡AP的坡度为i=1:√3,AP=10,∵ 可设PE=x,则AE=√3x.在Rt△AEP中,x2+(√3x)2=102,解得x=5或x=−5(舍去),∵ PE=5,则AE=5√3.∵ ∠CPF=∠PCF=45∘,∵ CF=PF.设CF=PF=m米,则OC=(m+5)米,OA=(m−5√3)米.在Rt△AOC中,tan60∘=OCOA =m−5√3,即m−5√3=√3,解得m=10(√3+1),∵ OC=10(√3+1)+5≈32(米).24【答案】宣传牌CD高约6.7米.【解答】过B作BG⊥DE于G,BH⊥AE,由(1)得:BH=5,AH=5√3,∵ BG=AH+AE=5√3+21,Rt△BGC中,∠CBG=45∘,∵ CG=BG=5√3+21.Rt△ADE中,∠DAE=53∘,AE=21,∵ DE=43AE=28.∵ CD=CG+GE−DE=26+5√3−28≈6.7m.答:宣传牌CD高约6.7米.25.【答案】解:(1)在Rt△ACD中,∵ ∠DAC=24∘,∠ADC=90∘,∵ sin24∘=CDAC,∵ CD=AC⋅sin24∘=30×0.40=12cm;∵此时支撑臂CD的长为12cm;(2)如图,过点C作CE⊥AB于点E,当∠BAC=12∘时,∵ sin12∘=CEAC =CE30,∵ CE=30×0.20=6cm,∵ CD=12,∵ DE=√CD2−CE2=√122−62=6√3,∵ AE=2−62=12√6cm,∵ AD的长为(12√6+6√3)cm或(12√6−6√3)cm.【解答】解:(1)在Rt△ACD中,∵ ∠DAC=24∘,∠ADC=90∘,∵ sin24∘=CDAC,∵ CD=AC⋅sin24∘=30×0.40=12cm;∵此时支撑臂CD的长为12cm;(2)如图,过点C作CE⊥AB于点E,当∠BAC=12∘时,∵ sin12∘=CEAC =CE30,∵ CE=30×0.20=6cm,∵ CD=12,∵ DE=√CD2−CE2=√122−62=6√3,∵ AE=√302−62=12√6cm,∵ AD的长为(12√6+6√3)cm或(12√6−6√3)cm.21/ 21。
【最新】2016年中考数学专题复习:解直角三角形题及答案

的俯角为45°,求岛屿两端A .B 的距离(结果精确到0.1米,参考数据:)【答案】解:过点A 作AE⊥CD 于点E ,过点B 作BF ⊥CD 于点F ,∵AB ∥CD ,∴∠AEF =∠EFB =∠ABF =90°。
∴四边形ABFE 为矩形。
∴AB =EF ,AE =BF 。
由题意可知:AE =BF =100,CD =500。
在Rt △AEC 中,∠C =60°,AE =100,∴0AE100100CE ==33tan 603。
在Rt △BFD 中,∠BDF =45°,BF =100,∴0BF100DF ==1001tan45。
∴AB =EF =CD +DF ﹣CE =500+100﹣10033≈600﹣1003×1.73≈600﹣57.67≈542.3(米)。
答:岛屿两端A .B 的距离为542.3米。
2.如图,一居民楼底部B 与山脚P 位于同一水平线上,小李在P 处测得居民楼顶A 的仰角为60°,然后他从P 处沿坡角为45°的山坡向上走到C 处,这时,PC =30 m ,点C 与点A 恰好在同一水平线上,点A 、B 、P 、C 在同一平面内.(1)求居民楼AB 的高度;(2)求C 、A 之间的距离.(精确到0.1m ,参考数据:41.12,73.13,45.26)【答案】解:(1)过点C 作CE ⊥BP 于点E ,在Rt △CPE 中,∵PC =30m ,∠CPE =45°,∴CE sin45PC 。
∴CE =PC ?sin 45°=30×2=1522(m)。
∵点C 与点A 在同一水平线上,∴AB =CE =152≈21.2(m )。
的俯角为45°,求岛屿两端A .B 的距离(结果精确到0.1米,参考数据:)【答案】解:过点A 作AE ⊥CD 于点E ,过点B 作BF ⊥CD 于点F ,∵AB ∥CD ,∴∠AEF =∠EFB =∠ABF =90°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解直角三角形选择题 1、(2016 苏州二模)如图,把一张长方形卡片ABCD 放在每格宽度为12 mm 的横格纸中,恰好四个顶点都在横格线上,已知α=36°,求长方形卡片的周长.(精确到 1 mm ,参考数据:sin360.60,cos360.80,tan360.75︒≈︒≈︒≈)答案:解:长方形卡片周长为200mm. 2、(2016齐河三模)在△ABC 中,若+(1-tanB)2=0, 则∠C 的度数是( )A .45°B .60°C .75°D .105° 答案:D3. (2016·山东枣庄·模拟)如图,在半径为6cm 的⊙O 中,点A 是劣弧的中点,点D 是优弧上一点,且∠D=30°,下列四个结论:①OA ⊥BC ;②BC=6;③sin ∠AOB=;④四边形ABOC 是菱形.其中正确结论的序号是( )A .①③B .①②③④C .②③④D .①③④【考点】垂径定理;菱形的判定;圆周角定理;解直角三角形. 【专题】几何图形问题.【分析】分别根据垂径定理、菱形的判定定理、锐角三角函数的定义对各选项进行逐一判断即可.【解答】解:∵点A 是劣弧的中点,OA 过圆心,∴OA ⊥BC ,故①正确; ∵∠D=30°,∴∠ABC=∠D=30°,∴∠AOB=60°,∵点A是劣弧的中点,∴BC=2CE,∵OA=OB,∴OA=OB=AB=6cm,∴BE=AB•cos30°=6×=3cm,∴BC=2BE=6cm,故②正确;∵∠AOB=60°,∴sin∠AOB=sin60°=,故③正确;∵∠AOB=60°,∴AB=OB,∵点A是劣弧的中点,∴A C=AB,∴AB=BO=OC=CA,∴四边形ABOC是菱形,故④正确.故选:B.【点评】本题考查了垂径定理、菱形的判定、圆周角定理、解直角三角形,综合性较强,是一道好题.二、填空题1、(2016齐河三模)如图,上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米,甲身高1.8米,乙身高1.5米,则甲的影长是_____ 米.答案:62、(2016齐河三模)将一副三角尺按如图所示方式放置,使含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,则∠1的度数是_____ .答案:75°3. (2016·广东深圳·一模)如图所示,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为10米.(保留根号)【考点】解直角三角形的应用.【专题】压轴题;探究型.【分析】如图,因为60°的角是△ABC的一个外角,且∠B为30°已知,所以根据三角形外角和可知∠CAB=30°,即AC=BC=10m,从而利用△ABD求出BD的长,即可求出CD,利用30°角的余弦值,进而求出AB.【解答】解:如图,作AD⊥CD于D点.∵∠B=30°,∠ACD=60°,∠ACD=∠B+∠CAB,∴∠CAB=30°.∴BC=AC=10m,在Rt△ACD中,CD=AC•cos60°=10×0.5=5m,∴BD=15.∴在Rt△ABD中,AB=BD÷cos30°=15÷=10m.故答案为:10.【点评】本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.4. (2016·湖南湘潭·一模)如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为cm(参考数据:sin20°≈ 0.342,cos20°≈0.940,sin40°≈ 0.643,cos40°≈ 0.766.精确到0.1cm ,可用科学计算器). 答案:14.15. (2016·黑龙江大庆·一模)如图,等腰△ABC 中,AB =AC ,tan ∠B =43,BC =30,D 为BC 中点,射线DE ⊥AC .将△ABC 绕点C 顺时针旋转(点A 的对应点为A ’,点B 的对应点为B ’),射线A ’ B ’分别交射线DA 、DE 于M 、N .当DM =DN 时,DM 的长为________.B第1题答案: 5+106解答题1.(2016·重庆铜梁巴川·一模)如图,高36米的楼房AB 正对着斜坡CD ,点E 在斜坡CD 的中点处,已知斜坡的坡角(即∠DCG)为30°,AB⊥BC.(1)若点A 、B 、C 、D 、E 、G 在同一个平面内,从点E 处测得楼顶A 的仰角α为37°,楼底B 的俯角β为24°,问点A 、E 之间的距离AE 长多少米?(精确到十分位)(2)现计划在斜坡中点E 处挖去部分斜坡,修建一个平行于水平线BC 的平台EF 和一条新的斜坡DF ,使新斜坡DF 的坡比为:1.某施工队承接这项任务,为尽快完成任务,增加了人手,实际工作效率提高到原计划的1.5倍,结果比原计划提前2天完成任务,施工队原计划平均每天修建多少米?(参考数据:cos37°≈0.80,tan37°≈0.75,tan24°≈0.45,cos24°≈0.91)【分析】(1)延长FE交AB于M,设ME=x,根据直角三角形函数得出AM=tanα•x,BM=tanβ•x,然后根据tanα•x+tanβ•x=36,即可求得EM的长,然后通过余弦函数即可求得AE;(2)根据BM=NG=DN,得到DN的长,然后解直角三角形函数求得EN和FN,进而求得EF和DF的长,然后根据题意列出方程,解方程即可求得.【解答】解:(1)延长FE交AB于M,∵EF∥BC,∴MN⊥AB,MN⊥DG,设ME=x,∴AM=tanα•x,BM=tanβ•x,∵AB=36,∴tanα•x+tanβ•x=36,∴tan37°x+tan24°x=36,0.75x+0.45x=36,解得x=30,∴AE==≈37.5(米);(2)延长EF交DG于N,∵GN=BM=tan24°•30=13.5,DE=CE,EF∥BC,∴DN=GN=13.5(米),∵∠DCG=30°,∴∠DEN=30°,∴EN=DN•cot30°=13.5×,∵=,∴∠DFN=60°,∴∠EDF=30°,FN=DN•cot60°=13.5×,∴DF=EF=EN﹣FN=13.5×,∴EF+DF=27×=18,设施工队原计划平均每天修建y米,根据题意得, =+2,解得x=3(米),经检验,是方程的根,答:施工队原计划平均每天修建3米.2.(2016·山西大同·一模)(1)如图,在△ABC中用直尺和圆规作AB边上的高CD(保留作图痕迹,不写作法).(2)图中的实线表示从A到B需经过C点的公路,且AC=10km,∠CAB=25°,∠CBA=37°. 现因城市改造需要在A、B两地之间改建一条笔直的公路。
问:公路改造后比原来缩短了多少千米?(参考数据:sin25°≈0.41,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75,结果精确到0.01)答案:(1)图略(2)在Rt△ACD中CD=ACsin25°=4.2AD=ACcin25°=9.1在Rt△BCD中BD=CD÷tan37°=5.6AB=AD+DB=4.7BC=CD÷sin37°=7.0∴AC+BC-AB=2.33.(2016·四川峨眉·二模)如图,两座建筑物AB与CD,其地面距离BD为60米,E 为BD的中点,从E点测得A的仰角为30︒,从C处测得E的俯角为60︒,现准备在点A与点C之间拉一条绳子挂上小彩旗(不计绳子弯曲),求绳子AC的长度.(结果保留一位小1.41≈1.73≈)答案:解:连结AC ,∵BD =60,E 为BD 的中点,∴1302BE DE BD ===. 在Rt AEB V 中,30AEB ∠=︒,cos BEAEB AE ∠=,∴3030AE COS ==︒在Rt CED V 中,30ECD ∠=︒,∴60EC =.在Rt AEC V 中,tan AE ACE EC ∠===, ∴30AEC ∠=︒,∴269.2AC AE ==≈(米).答:绳子AC 的长度大约为69.2米。
4.(2016·重庆巴蜀 ·一模)为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD 与通道BC 平行),通道水平宽度BC 为8米,∠BCD=135°,通道斜面CD 的长为6米,通道斜面AB 的坡度i=1:.(1)求通道斜面AB 的长;(2)为增加市民行走的舒适度,拟将设计图中的通道斜面CD 的坡度变缓,修改后的通道斜面DE 的坡角为30°,求此时BE 的长.(答案均精确到0.1米,参考数据:≈1.41,≈2.24,≈2.45)【分析】(1)过点A 作AN⊥CB 于点N ,过点D 作DM⊥BC 于点M ,解Rt△CMD,得出DM=CM=CD=3,则AN=DM=3,再解Rt△ANB,由通道斜面AB 的坡度i=1:,得出BN=AN=6,然后根据勾股定理求出AB ;(2)先解Rt△MED,求出EM=DM=3,那么EC=EM ﹣CM=3﹣3,再根据BE=BC ﹣EC即可求解.【解答】解:(1)过点A 作A N⊥CB 于点N ,过点D 作DM⊥BC 于点M , ∵∠BCD=135°,∴∠DCM=45°.∵在Rt△CMD中,∠CMD=90°,CD=6,∴DM=CM=CD=3,∴AN=DM=3,∵通道斜面AB的坡度i=1:,∴tan∠ABN==,∴BN=AN=6,∴AB==3≈7.4.即通道斜面AB的长约为7.4米;(2)∵在Rt△MED中,∠EMD=90°,∠DEM=30°,DM=3,∴EM=DM=3,∴EC=EM﹣CM=3﹣3,∴BE=B C﹣EC=8﹣(3﹣3)=8+3﹣3≈4.9.即此时BE的长约为4.9米.5.(2016·重庆巴南·一模)如图,某建筑物BC上有一旗杆AB,小刘在与BC相距24m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°,小刘的观测点与地面的距离EF为1.6m.(1)求建筑物BC的高度;(2)求旗杆AB的高度.(结果精确到0.1m.参考数据:≈1.41,sin52°≈0.79,tan52°≈1.28)【分析】(1)先过点E 作ED⊥BC 于D ,由已知底部B 的仰角为45°得BD=ED=FC=24m ,DC=EF=1.6m ,从而求出BC .(2)由已知由E 点观测到旗杆顶部A 的仰角为52°可求出AD ,则AB=AD ﹣BD . 【解答】解:(1)过点E 作ED⊥BC 于D , 根据题意得:EF⊥FC,ED∥FC, ∴四边形CDEF 是矩形,已知底部B 的仰角为45°即∠BED=45°, ∴∠EBD=45°, ∴BD=ED=FC=24m,∴BC=BD+DC=BD+EF=12+1.6=25.6(m ), 答:建筑物BC 的高度为25.6m .(2)已知由E 点观测到旗杆顶部A 的仰角为52°,即∠AED=52°, ∴AD=ED•tan52° ≈24×1.28≈30.8,∴AB=AD﹣BD=30.8﹣24=6.8. 答:旗杆AB 的高度约为6.8m .5.(22)(2016·天津北辰区·一摸) (本小题10分)如图,甲、乙两数学兴趣小组测量山CD 的高度. 甲小组在地面A 处测量,乙小组在上坡B 处测量,AB =200 m. 甲小组测得山顶D 的仰角为45°,山坡B 处的仰角为30°;乙小组测得山顶D 的仰角为58°. 求山CD 的高度(结果保留一位小数).参考数据:tan 58 1.60︒≈1.732≈,供选用.解:过B 作BE ⊥AC ,BF ⊥DC ,E ,F 为垂足根据题意,有∠DAC =45°,∠BAC =30°, ∠DBF =58°,AB=200.∵ BE ⊥AC ,BF ⊥DC ,DC ⊥AC , ∴ 四边形BECF 是矩形.∴ BF EC =,BE FC =. …2分 设BF =x , 则CE =BF =x .在Rt△ABE中,sinBEBAEAB∠=,cosAEBAEAB∠=,∴ sin200sin30100BE AB BAE=∠=⋅︒=,cos200cos30173.2AE AB BAE=∠=⋅︒=. …5分在Rt△DBF中,tanDF DBFBF∠=,∴ tan tan58 1.60DF BF DBF x x=∠=⋅︒≈. …7分在Rt△DAC中,∠DAC=45°,∴ AC=DC. 即AE EC DF FC+=+∴ 173.2100 1.60x x+=+. 解得,122.0x=.∴ 173.2122.0295.2DC AC=≈+=.答:山高约为295.2 m..…10分6.(2016·天津市和平区·一模)在一次军事演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000m的反潜直升机B测得潜艇C的俯角为60°,求潜艇C离开海平面的下潜深度.【考点】解直角三角形的应用-仰角俯角问题.【分析】过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,分别在Rt△ACD中表示出CD和在Rt△BCD中表示出BD,从而利用二者之间的关系列出方程求解.【解答】解:过点C作CD⊥A B,交BA的延长线于点D,则AD即为潜艇C的下潜深度,根据题意得:∠ACD=30°,∠BCD=60°,设AD=x,则BD=BA+AD=1000+x,在Rt△ACD中,CD===x,在Rt△BCD中,BD=CD•tan60°,∴1000+x=x•tan60°解得:x=500,∴潜艇C离开海平面的下潜深度为500米.【点评】本题考查了解直角三角形的应用,解题的关键是从题目中抽象出直角三角形并选择合适的边角关系求解.7.(2016·天津市南开区·一模)如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.【考点】解直角三角形的应用-方向角问题.【专题】几何图形问题.【分析】过A作AD⊥BC于D,先由△ACD是等腰直角三角形,设AD=x,得出CD=AD=x,再解Rt△ABD,得出BD==x,再由BD+CD=4,得出方程x+x=4,解方程求出x的值,即为A到岸边BC的最短距离.【解答】解:过A作AD⊥BC于D,则AD的长度就是A到岸边BC的最短距离.在Rt△ACD中,∠ACD=45°,设AD=x,则CD=AD=x,在Rt△ABD中,∠ABD=60°,由tan∠ABD=,即tan60°=,所以BD==x,又BC=4,即BD+CD=4,所以x+x=4,解得x=6﹣2.答:这个标志性建筑物底部A到岸边BC的最短距离为(6﹣2)公里.【点评】本题考查了解直角三角形的应用﹣方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.(2016·天津五区县·一模)如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,≈1.7,≈1.4 )9、(2016青岛一模)如图,一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头,已知A、B两码头所在的河岸均为东西走向,河宽为16km,求该客轮至少用多长时间才能到达B码头?(结果精确到0.1h,参考数据:sin53°≈,cos53°≈,tan53°≈)【考点】解直角三角形的应用-方向角问题.【分析】首先过点A作AE⊥BD于点E,由题意可得:cos53°=,进而得出AB的长即可得出答案.【解答】解:如图所示:过点A作AE⊥BD于点E,由题意可得:AE=16km,∠EAB=53°,故cos53°===,解得:AB=,∵客轮的速度为30km/h,∴÷30=≈0.9(h),答:该客轮至少用0.9h才能到达B码头.10、(2016齐河三模)一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图23-12,当李明走到点A处时,张龙测得李明直立时身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m).答案:设CD长为x米,∵AM⊥EC,CD⊥EC,BN⊥EC,EA=MA∴MA∥CD∥BN ∴EC=CD=x∴△ABN∽△ACD,∴ ,即,解得:x=6.125≈6.1.经检验,x=6.125是原方程的解,∴路灯高CD约为6.1米11、(2016泰安一模)为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有()A.1组B.2组C.3组D.4组【考点】相似三角形的应用;解直角三角形的应用.【分析】根据三角形相似可知,要求出AB,只需求出EF即可.所以借助于相似三角形的性质,根据=即可解答.【解答】解:此题比较综合,要多方面考虑,①因为知道∠ACB和BC的长,所以可利用∠ACB的正切来求AB的长;②可利用∠ACB和∠ADB的正切求出AB;③,因为△ABD∽△EFD可利用=,求出AB;④无法求出A,B间距离.故共有3组可以求出A,B间距离.故选C.12、(2016枣庄41中一模)我国为了维护队钓鱼岛P的主权,决定对钓鱼岛进行常态化的立体巡航.在一次巡航中,轮船和飞机的航向相同(AP∥BD),当轮船航行到距钓鱼岛20km 的A处时,飞机在B处测得轮船的俯角是45°;当轮船航行到C处时,飞机在轮船正上方的E处,此时EC=5km.轮船到达钓鱼岛P时,测得D处的飞机的仰角为30°.试求飞机的飞行距离BD(结果保留根号).【考点】解直角三角形的应用-仰角俯角问题.【专题】压轴题.【分析】作AF⊥BD,PG⊥BD,在Rt△ABF和△PDG中分别求出BF、GD的值,继而可求得BD=BF+FG+GD的值.【解答】解:作AF⊥BD,PG⊥BD,垂足分别为F、G,由题意得:AF=PG=CE=5km,FG=AP=20km,在Rt△AFB中,∠B=45°,则∠BAF=45°,∴BF=AF=5,∵AP∥BD,∴∠D=∠DPH=30°,在Rt△PGD中,tan∠D=,即tan30°=,∴GD=5,则BD=BF+FG+GD=5+20+5=25+5(km).答:飞机的飞行距离BD为25+5km.【考点】解直角三角形的应用-仰角俯角问题.【分析】利用30°的正切值即可求得AE 长,进而可求得CE 长.CE 减去DE 长即为信号塔CD 的高度.【解答】解:根据题意得:AB=18,DE=18,∠A=30°,∠EBC=60°,在R t △ADE 中,AE===18∴BE=AE﹣AB=18﹣18,在R t △BCE 中,CE=BE•tan60°=(18﹣18)=54﹣18,∴CD=CE﹣DE=54﹣18﹣18≈5米.【点评】本题考查了解直角三角形﹣仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形;难点是充分找到并运用题中相等的线段. 13. (2016·浙江丽水·模拟)(本题6分)如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB 位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动2 m (即BD =2 m )到达CD 位置时,它与地面所成的角∠CDO=45°,求梯子的长.解:解设OB=x,则OD=x+2 ∵∠OBA=60°∴cos∠OBA=21=ABOB∴AB=2x∵∠ODA=45°∴cos∠ODA=22=CDOD∴CD=)(22+x∵AB= CD,即2x=)(22+x ∴x=222+∴梯子的长AB=424+14.(2016·绍兴市浣纱初中等六校·5月联考模拟)(本题8分)如图,某大楼的顶部树有一块广告牌CD ,小李在山坡的坡脚A 处测得广告牌底部D 的仰角为60°.沿坡面AB 向上走到B 处测得广告牌顶部C 的仰角为45°,已知山坡AB 的坡度i =1:,AB =10米,AE =15米.(i =1:是指坡面的铅直高度BH 与水平宽度AH 的比) (1)求点B 距水平面AE 的高度BH ; (2)求广告牌CD 的高度. 解:(1) 过B 作BG⊥DE 于G , Rt△ABF 中,i=tan∠BAH==,∴∠BAH=30°,∴BH=AB=5; (2)由(1)得:BH=5,AH=5, ∴BG=AH+AE=5+15, Rt△BGC 中,∠CBG=45°, ∴CG=BG=5+15.Rt△ADE 中,∠DAE=60°,AE=15, ∴DE=AE=15.∴CD=CG+GE﹣DE=5+15+5﹣15=20﹣10 . 答:宣传牌CD 高20﹣10 米.15.(2016·浙江镇江·模拟)从一幢建筑大楼的两个观察点A ,B 观察地面的花坛(点C ),测得俯角分别为15°和60°,如图,直线AB 与地面垂直,AB=50米,试求出点B 到点C 的距离.(结果保留根号)解:作AD ⊥BC 于点D ,∵∠MBC =60°, ∴∠ABC =30°,∵AB ⊥AN ,∴∠BAN =90°,∴∠BAC =105°, 则∠ACB =45°,在Rt △ADB 中,AB =1000,则AD =500,BD =3500,在Rt △ADC 中,AD =500,CD =500, 则BC =3500500+. ……4分 答:观察点B 到花坛C 的距离为)3500500(+米.16.(2016·新疆乌鲁木齐九十八中·一模)如图,MN路线图.在点M 测得点N 在它的南偏东30°的方向,测得另一点A 向;取MN 上另一点B ,在点B 测得点A 在它的南偏东半径的圆形区域为某居民区,已知MB=400m ,通过计算回答:如果不改变方向,高速公路是否会穿过居民区?【考点】解直角三角形的应用-方向角问题. 【专题】应用题. 【分析】高速公路是否会穿过居民区即是比较点A 到MN 的距离与半径的大小,于是作AC⊥MN 于点C ,求AC 的长.解直角三角形ACM 和ACB . 【解答】解:作AC⊥MN 于点C∵∠AMC=60°﹣30°=30°,∠ABC=75°﹣30°=45° 设AC 为xm ,则AC=BC=x 在Rt△ACM 中,MC=400+x ∴tan∠AMC=,即解之,得x=200+200∵>1.5∴x=200+200>500.∴如果不改变方向,高速公路不会穿过居民区.C【点评】怎么理解是否穿过居民区是关键,与最近距离比较便知应作垂线,构造Rt△求解.17.(2016·云南省·一模)如图,某同学站在旗杆正对的教学楼上点C处观测到旗杆顶端A 的仰角为30°,旗杆底端B的俯角为45°,已知旗杆距离教学楼12米,求旗杆AB的高度.(结果精确到0.1.≈1.732,≈1.414)(参考数据:sin30°=,cos30°=,tan30°=,sin45°=,cos45°=,tan45°=1)【考点】解直角三角形的应用-仰角俯角问题.【分析】根据在Rt△ACD中,tan∠ACD=,求出AD的值,再根据在Rt△BCD中,tan∠BCD=,求出BD的值,最后根据AB=AD+BD,即可求出答案.【解答】解:在Rt△ACD中,∵tan∠ACD=,∴tan30°=,∴=,∴AD=4m,在Rt△BCD中,∵∠BCD=45°,∴BD=CD=12m,∴AB=AD+BD=34+12(m).答:旗杆AB的高度为34+12m.【点评】此题考查了解直角三角形的应用﹣仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形. 18.(2016·郑州·二模)图l 是小明在健身器材上进行仰卧起坐锻炼时的情景,图2是小明锻炼时上半身由EN 位置运动到与地面垂直的EM 位置时的示意图.已知BC =0.64米,AD =0.24米,α=18°(sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)(1)求AB 的长(精确到0.01米)(2)若测得EN =0.8米,计算小明头顶由N 点运动到M 点的路径⌒MN 的长度(结果保留π) 【解答】解:(1)作AF ⊥BC 于点F .∴∠AFB =90°. ∴∠AFB =∠AFC =∠ADC =90°. ∴四边形ADCF 是矩形. ∴FC =AD.∴BF = BC ﹣CF =BC ﹣AD =0.64-0.24=0.4米,∴AB =BF ÷sin18°=0.4÷0.31≈1.29米; (2)∵∠NEM =90°+18°=108°,19. (2016·广东河源·一模)一测量爱好者在海边测量位于其正东方向的小岛高度AC.如图所示,他先在点B 测得小岛的顶点A 的仰角是︒30,然后沿正东方向前行62 m 到达点D ,在点D 测得小岛的顶点A 的仰角为︒60(B ,C ,D 三点在同一水平面上,且测量仪的高度忽略不计).求小岛的高度AC 。
